Ideaalne gaas

Reaalset looduses esineva gaasi lihtsamaks uurimiseks ja mõistmiseks kasutatakse ideaalse gaasi mudelit. Ideaalse gaasi puhul ei arvestata molekulide mõõtmeid ja nendevahelist vastastikmõju. Selle tingimuse ligikaudseks täitmiseks peaks gaas olema piisavalt hõre ja mitte liiga madalal temperatuuril. Ideaalseks gaasiks võib näiteks lugeda kuiva õhku tavalisel temperatuuril ja rõhul.

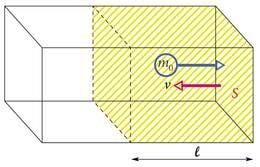
Olgu suletud anumas (joonis 1.25.) ideaalne gaas, mille molekulid liiguvad kaootiliselt ja põrkuvad elastselt anuma seintega. Mõtteliselt eraldatud osas ruumalaga $V$ on $N$ molekuli igaüks massiga $m_{0}$ . Anuma seinale pindalaga $S$ lähenevate molekulide keskmine kiirus on $v$ .

Proovime hinnata molekulide põrgetest tulenevat anuma seinale avaldatavat rõhku. Seinaga jõuavad aja $t$ jooksul põrkuda pooled molekulidest, mis ei asu kaugemal kui

I = v t = \frac{V}{S}

Mehaanikast on teada (M), et impulsi muut elastsel põrkel on $2 m_{0} v$ . Kehale mõjuv jõud (M) on võrdne impulsi muutumise kiirusega.

F = \frac{Δ p}{t}

ja ühe molekuli poolt seinale avaldatav jõud on

\frac{2 m_{0} v^{2}}{t}

Kogu seinale mõjuva jõu saame, korrutades selle põrgete arvuga $N / 2$ . Seinale avaldatav jõud

F = \frac{N}{2} \frac{2 m_{0} v}{t} = \frac{N m_{0} v^{2} S}{V}

Arvestades, et molekulide kontsentratsioon

n = \frac{N}{V}

saame rõhuks

p = \frac{F}{S} = n m_{0} v^{2}

Arutluses eeldasime, nagu liiguksid molekulid ühes sihis. Tegelikult pole kaootilise liikumise korral ükski suund eelistatud ja täpsema tuletuskäigu korral saame:

(1.17.)

p = \frac{1}{3} n m_{0} v^{2}

Valem annab ideaalse gaasi rõhu sõltuvuse mikroparameetritest: kontsentratsioonist, molekuli massist ja kiirusest. Rõhk kui makroparameeter on mõõdetav näiteks baromeetri või manomeetriga.

Kui võtame kasutusele mõiste molekulide keskmine kineetiline energia

¯ E = \frac{m_{0} v^{2}}{2}

saame:

(1.18.)

p = \frac{2}{3} n ¯ E

Ideaalse gaasi rõhk on võrdeline molekulide kaootilise liikumise keskmise kineetilise energiaga.

Eelmises õppetükis saime teada, et gaasi rõhk oli ka võrdeline absoluutse temperatuuriga. Kokkuvõtvalt saab järeldada, et ideaalse gaasi molekulide keskmine kineetiline energia on võrdeline gaasi absoluutse temperatuuriga:

(1.19.)

¯ E = \frac{3}{2} k T

kus suurust $k = 1, 38 \cdot 10^{- 23} J / K$ nimetatakse Boltzmanni konstandiks.

Valemis 4.17 esinev suurus $v^{2}$ on molekulide kiiruste ruutude keskmine väärtus. Ruutjuur sellest on ruutkeskmine kiirus:

(1.20.)

¯ v = \sqrt{v^{2}}