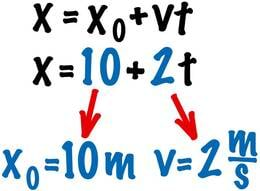Liikumine on nähtus, milles keha asukoht aja jooksul muutub. Erinevatel ajahetkedel on asukoht erinev, st keha koordinaadid sõltuvad ajast. Ajast sõltuvad ka kogu liikumise kestel läbitud teepikkus ning sooritatud nihe. Muutuva liikumise korral võivad ajast sõltuda veel ka kiirus ja kiirendus. Liikumisnähtus on kirjeldatav seda iseloomustavate suuruste ajast sõltuvuste kaudu.

Sõltuvusi saab väljendada analüütiliselt ja graafiliselt. Analüütilise meetodi korral kirjeldatakse sõltuvust matemaatiliste avaldiste abil. Avaldiste kaudu esitatud sõltuvusi on võimalik matemaatiliselt lähemalt uurida ja seeläbi lisainfot saada. Graafiline meetod kasutab liikumise kirjeldamiseks - nagu nimigi ütleb - graafikuid. Graafikud ei võimalda küll liikumist iseloomustavaid suurusi neilt otse välja lugeda, kuid annavad sõltuvustest seevastu ülevaatlikuma pildi.

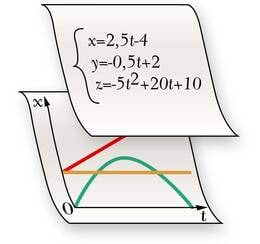
Mehaanika põhiülesanne on määrata keha asukoht mis tahes ajahetkel, st leida keha koordinaatide sõltuvus ajast. Kui paneme selle sõltuvuse kirja matemaatilise avaldise abil, saame liikumisvõrrandi. Liikumisvõrrandiks nimetatakse matemaatilist avaldist, mis näitab keha koordinaatide sõltuvust ajast.

Inimese poolt tajutav ruum on kolmemõõtmeline — ruumil ja igal selles asetseval kehal on pikkus, laius ja kõrgus. Seepärast on keha asukoha määramiseks üldjuhul vaja kolme koordinaati. Juhul, kui keha liigub mööda kindlat pinda, piisab kahest koordinaadist. Merepinnal seilava laeva asukoha saab kirja panna kahe geograafilise koordinaadi — pikkus- ja laiuskraadi abil. Veduri asukoha annab kätte vaid üks arv, näiteks kaugus algjaamast, kuna ilmselt püsib vedur relssidel.

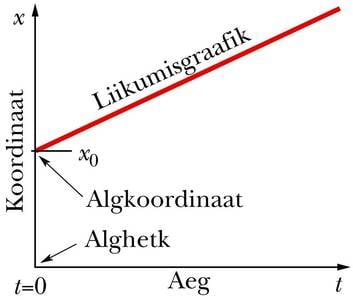
Sirgjoonelise liikumise kirjeldamiseks piisab ühest sirgest koordinaatteljest, mille suund on mõistlik valida piki liikumise trajektoori. Koordinaadi tähiseks võetakse tavaliselt x. Selle punkti koordinaati, kus keha asub ajamõõtmise alghetkel, nimetatakse algkoordinaadiks ja tähistatakse sümboliga x₀.

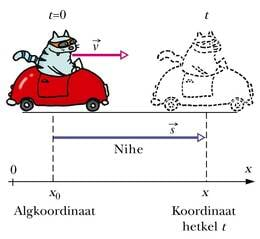
Kirjeldame näiteks auto sõitmist: alghetkel t = 0 on selle koordinaat x₀. Aja t jooksul nihkub auto edasi ning koordinaat muutub nihke pikkuse s võrra suuremaks (vt joonist). Koordinaadi uus väärtus x on seega

Teame, et aja t jooksul sooritatava nihke pikkus sõltub kiirusest. Ühtlase liikumise kiiruse valemist (1.3 ) saame nihke pikkuse avaldada kui s = vt. Paigutades selle nihke avaldise koordinaadi valemisse (1.6 ) tulemuseks seos, mis näitab auto koordinaadi sõltuvust ajast:

See ongi ühtlaselt sirgjooneliselt liikuva keha liikumisvõrrandi üldkuju.

Konkreetsete ülesannete puhul on x₀ ja v kohal võrrandis kindlad arvulised väärtused. Näiteks võrrand x = 10 + 2t väljendab liikumist keha jaoks, mille algkoordinaat on 10 m ning kiirus 2 m/s. Kui soovime teada, kus keha 5 sekundi pärast asub, võtame aja t väärtuseks 5 s ning arvutame, et x = 10 + 2•5 = 20 (m). Liikumisvõrrandi abil saab leida keha asukoha mis tahes ajahetkel. Suurused x₀ ja v võivad omada nii positiivseid kui ka negatiivseid väärtusi. Negatiivne kiirus tähendab seda, et keha liigub koordinaattelje negatiivses suunas. Rõhutamaks seda, et sirgel trajektooril saab liikumine toimuda kahes suunas, kirjutatakse liikumisvõrrand mõnikord kujul

Ühe suuruse teisest sõltuvuse graafiku saamiseks tuleb joonestada kaks ristuvat telge, horisontaalsele teljele märkida muutuv suurus ning vertikaalsele suurus, mis muutujast sõltub. Matemaatikas oleme harjunud, et horisontaaltelje tähiseks võetakse x ja vertikaalse telje tähiseks y. Füüsikas kasutatakse teisi tähiseid.

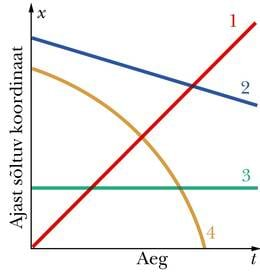
Liikumisgraafikuks nimetatakse graafikut, mis näitab keha asukoha (koordinaadi x) sõltuvust ajast. Liikumisgraafiku horisontaalteljele kantakse aeg t ja püstteljele ajast sõltuv koordinaat x. Erinevat liiki ja erineva suunaga liikumiste graafikud on erineva kujuga.

Ühtlase liikumise korral muutub koordinaat iga sekundiga sama palju ning seepärast on graafikuks sirgjoon. Sirge saab välja joonestada kahe punkti järgi ja seega piisab ühtlase liikumise graafiku saamiseks, kui teame keha asukohta kahel erineval ajahetkel.

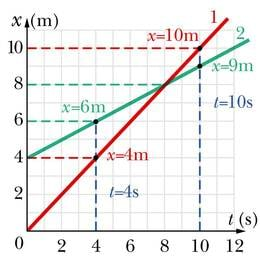
Võrdleme kahe ühtlaselt liikuva keha liikumisgraafikuid. Oletame, et hetkel t₁ = 4 s on nende koordinaadid 4 m ja 6 m ning hetkel t₂ = 10 s vastavalt 10 m ja 9 m. Kui graafikud välja joonestada (vt joonist), siis näeme, et need on erineva tõusuga. Ajavahemik kahe vaatlusaluse hetke vahel oli Δt = 10 – 4 = 6 sekundit. Järsema graafikuga keha koordinaat muutus selle ajaga Δx₁= 10 – 4 = 6 m võrra. Järelikult on kiirus 6 m/ 6 s = 1 m/s. Teise keha koordinaadi muuduks saame Δx₂= 9 – 6 = 3 m ja kiiruseks 3 m/ 6 s = 0,5 m/s.

Jõudsime olulise tulemuseni — liikumisgraafiku tõus näitab liikumise kiirust. Mida suurem kiirus, seda suurem on graafiku tõus. Kui graafik langeb ja tõus on negatiivne, siis on ka kiirus negatiivne, st liikumise suund on koordinaattelje positiivse suunaga vastupidine.

Teiseks saab liikumisgraafikult välja lugeda keha algkoordinaadi. Koordinaati näitav püstine graafikutelg asub just ajatelje nullkohal. Järelikult see punkt, kus graafiku joon püstist koordinaattelge lõikab, vastabki algkoordinaadile. Eespool toodud näites koostatud graafikutelt näeme, et kiiremini liikuva keha algkoordinaat on 0 ja aeglasema oma 4 m.

Liikumisgraafikult saab leida algkoordinaadi	Liikumisgraafik ja nihke graafik

Graafiku võib koostada ka nii, et püstteljele kantakse koordinaadi asemel keha poolt sooritatud nihke pikkus või teepikkus. Selline graafik on kujult liikumisgraafiku sarnane, kuid algab alati nihke või teepikkuse nullist — alghetkel pole ju keha veel jõudnud edasi nihkuda.

Kui liikumisgraafik pole sirge ja selle tõus muutub, siis järelikult muutub ka liikumise kiirus ja tegemist on muutuva liikumisega.