Purunenud majad Mexicos. Madalad ja kõrged hooned on terved, ümber on kukkunud keskmise kõrgusega hooned.	Rippsild, mis 1831.a. ratsaväe ülemarsi ajal kokku varises. Pilt on tehtud pärast silla taastamist.

1985. aastal kukkusid maavärina tõttu Mexicos kokku paljud keskmise kõrgusega hooned. Kõrgemad ja madalamad hooned jäid püsti (vaata pilti). Inglismaal Manchesteri lähedal ületasid ratsaväelased 1831. aastal silda ning marssisid ilmselt samas taktis silla võnkumisega. Sild kukkus kokku pärast seda, kui üks silda toetanud polt purunes. 

Enne kui Apollo 13 avariisse sattus, suunati üks tema kiirendusrakette otsekursile Kuu suunas, nii et see rammis suurel kiirusel Kuu pinda. Miks seda tehti? Kuidas on võimalik kosmoselaevade trajektoore nii täpselt planeerida, et kiiresti tabatakse väga kaugel olevaid ja väga kiiresti liikuvaid objekte?

Kõik me oleme näinud pilte Maa sisemusest. Kuidas on see info saadud, kui puuraugud ulatuvad vaid väga pindmiste kihtideni?

Ringliikumine on kõverjoonelise liikumise erijuht, kus keha punktide trajektooriks on ringjoon või selle osa. Tegemist on lihtsaima kõverjoonelise liikumisega, mille seadusi tundes on võimalik kirjeldada ka keerulisemaid liikumisi. Saab ju erinevate ring- ja sirgjooneliste lõikude kombineerimisel kokku panna mis tahes kujuga trajektoore.

Ringliikumise puhul võime rääkida eraldi ringjoonelisest liikumisest ja pöörlemisest.

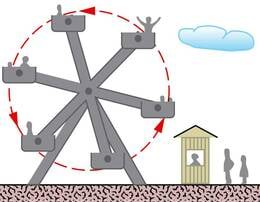
Kui turist sõidab vaaterattal, siis liiguvad kõik tema punktid mööda ühesuguseid ringjoonekujulisi trajektoore ja tegemist on ringjoonelise liikumisega. Ringjooneliseks liikumiseks nimetatakse keha liikumist mööda ringjoonekujulist trajektoori.

Ringjoonelist liikumist nimetatakse tihti ka tiirlemiseks. Ringjoonelisest liikumisest ehk tiirlemisest saame rääkida siis, kui keha mõõtmed ja kuju pole liikumise kirjeldamisel olulised ning me võime kasutada punktmassi mudelit.

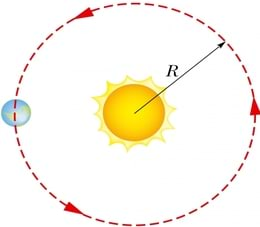
Ringjooneliselt liiguvad näiteks autod kurvis, kellaosuti tipp, karussellil istuv laps ning ümber Maa tiirlev Kuu.

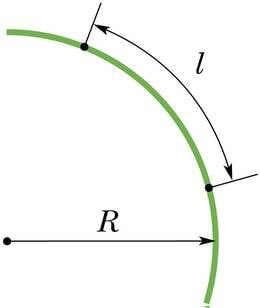
Ringjooneliselt liikuvate kehade trajektoorideks on erineva raadiusega ringjooned. Ringjoone raadius määrab ära trajektoori kõveruse ja on seega ringjoonelist liikumist iseloomustav suurus. Valemites ja joonistel tähistatakse trajektoori kõverusraadiust tähtedega $r$ või $R$ ja selle mõõtühikuks on meeter.

Tihti tuleb ette aga ringliikumist, kus keha punktide trajektoorideks on erinevad ringjooned ning seepärast ei saa keha punktmassiks lugeda. Kui keha erinevad punktid tiirlevad sama keskpunkti ümber mööda erinevate raadiustega ringjooni, on tegemist pöördliikumise ehk pöörlemisega. Pöörlevalt liiguvad näiteks autoratas, grammofoniplaat, avatav uks, saltot sooritav akrobaat ja Maa ümber oma kujuteldava telje.

Liikumisel toimuvat asukohamuutust iseloomustatakse nihke või teepikkuse abil. Ringliikumise kirjeldamiseks nihe ei sobi, kuna samu punkte läbitakse korduvalt. Küll aga saab kasutada läbitud teepikkust l. Ringjoonelisel liikumisel kujutab teepikkus l endast keha poolt läbitud ringjoone kaare pikkust.

Kui tegemist on pöörlemisega, liiguvad keha erinevad punktid mööda erineva raadiusega ringjooni ning nende jaoks on läbitavad teepikkused erinevad.

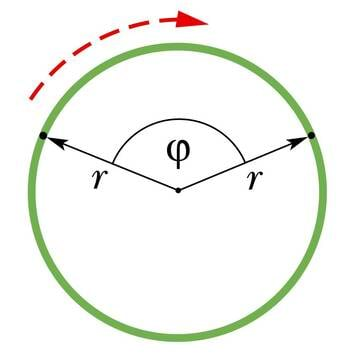
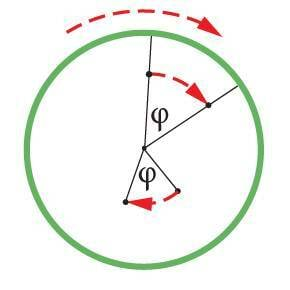
Igale ringjoone kaarele vastab alati kindel kesknurk. Just selle nurga võrra pöördub liikumise käigus raadius, mis ühendab trajektoori keskpunkti keha asukohaga. Nurka, mille võrra pöördub ringliikumisel keha asukohta ja trajektoori kõveruskeskpunkti ühendav raadius, nimetatakse pöördenurgaks. Pöördenurga tähiseks on kreeka täht φ (fii).

Pöörlemist on kõige mugavam iseloomustada pöördenurga abil.	Pöördenurk on kõikidel punktidel sama.

Kuigi pöörlemise korral läbivad pöörlemisteljest eri kaugusel asuvad punktid sama ajaga erinevad teepikkused, siis on pöördenurk nende punktide jaoks ikka ühesugune. Seepärast eelistataksegi ringliikumise kirjeldamisel teepikkusele pöördenurka.

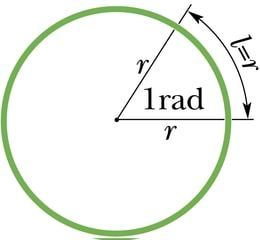
Füüsikas mõõdetakse pöördenurka mitte kraadides, vaid radiaanides. Üks radiaan (lüh rad) on selline kesknurk, mis toetub kaarele, mille pikkus on võrdne selle ringjoone raadiusega. Ühele täisringile vastab pöördenurk $2\pi \text{rad}$, seega 1 rad = 360º/2π ≈ 57º.

Kasutades selliselt defineeritud nurgaühikut, kehtib pöördenurga ja kaarepikkuse vahel lihtne seos:

Kui keha sooritab mis tahes võrdsetes ajavahemikes võrdsed pöördenurgad, on tegemist ühtlase ringliikumisega. Nii nagu ühtlane sirgjooneline liikumine, on ka ühtlane ringliikumine üks liikumise füüsikaline mudel. Looduses ideaalsel kujul sellist liikumist ei esine, kuid paljudel juhtudel saab seda mudelit rakendada suure täpsusega.

Ringliikumine on perioodiline liikumine, kuna keha asukoht kordub võrdsete ajavahemike möödumisel. Perioodilisi liikumisi saab iseloomustada perioodi ja sageduse abil.

Ringliikumise perioodiks nimetatakse ajavahemikku, mille jooksul läbitakse üks täisring. Kella minutiosuti tiirlemisperiood on üks tund, Maa tiirlemisperiood ümber Päikese aga üks aasta. Perioodi mõõdetakse alati ajaühikutes ja SI-s on mõõtühikuks seega 1 sekund. Perioodi tähiseks valime käesolevas kursuses $T$.

Kui tähistame tiirleva keha poolt aja $t$ kestel sooritatud tiirude arvu tähega N, avaldub ühe tiiru sooritamise aeg ehk periood koguaja ja tiirude arvu jagatisena

Sageduseks nimetatakse ajaühikus tehtavate täisringide arvu. Sageduse tähiseks on $f$ (ld frequçns 'sagedane, korduv'). Sageduse leidmiseks tuleb ringide arv $N$ jagada ajaühikute arvuga ehk ajaga $t$:

Võrreldes valemeid (3.2 ) ja (3.3 ), näeme, et ringliikumise sagedus ja periood on teineteise pöördväärtused:

Nii on ka sageduse mõõtühikuks sekundi pöördväärtus, mida nimetatakse hertsiks (Hz). 1 Hz = 1/s.

Liikuval kehal on alati mingi kiirus. Ühtlase liikumise kiirus on võrdne teepikkuse ja selle läbimiseks kuluva aja jagatisega:

Ühtlasel ringjoonelisel liikumisel nimetatakse teepikkuse (läbitud joone pikkuse) ning aja jagatist mitte lihtsalt kiiruseks, vaid joonkiiruseks. Nimetuse täpsustus on tingitud sellest, et ringliikumist saab lisaks joonkiirusele iseloomustada ka ajaühikus sooritatava pöördenurga kaudu.

Joonkiirus on suunatud piki trajektoori puutujat.	Joonkiirus kirjeldab igasugust liikumist.

Valem (3.5 ) võimaldab leida vaid kiiruse arvväärtuse. Joonkiirus on suunatud alati piki ringjoonelise trajektoori puutujat ja on igas punktis trajektoori kõverusraadiusega risti.

Joonkiirusega saab iseloomustada mitte ainult ringjoonelist, vaid ka mis tahes muu kujuga trajektoori mööda toimuvat kõverjoonelist liikumist.

Kuna pöörlemise korral läbivad teljest eri kaugusel asuvad punktid sama ajaga erinevad teepikkused, siis on ka nende punktide joonkiirused erinevad. Mida suurem on punkti tiirlemisraadius, seda suurem on ka kiirus. Kuna aga kõikide punktide jaoks jääb pöördenurk alati samaks, on otstarbekas ringliikumise kirjeldamiseks defineeridagi kiirus just nurga kaudu.

Seepärast kasutataksegi ringliikumise iseloomustamiseks pöördenurga ja selle sooritamiseks kuluva ajavahemiku jagatist. Seda jagatist nimetatakse ringliikumise nurkkiiruseks. Nurkkiirus on võrdne ajaühikus sooritatava pöördenurgaga. Seda suurust tähistatakse kreeka tähega $\omega$ (omega) ja valemiks on

Kui pöördenurka mõõdetakse radiaanides ja aega sekundites, on nurkkiiruse mõõtühikuks radiaan sekundis (1 rad/s).

Nurkkiirus on seotud joonkiirusega $v$. Paneme nurkkiiruse avaldisse (3.6 ) pöördenurga kohale selle väärtuse $\phi =l/r$ ning saame

Et aga $l/t$ kujutab endast joonkiirust $v$, saame

See ongi seos nurkkiiruse ja joonkiiruse vahel.

Peale joonkiiruse on nurkkiirus seotud ka ringliikumise sageduse ja perioodiga. Definitsiooni järgi on sagedus võrdne ajaühikus sooritatavate täisringide arvuga:

Aja $t$ jooksul sooritatud täisringide arv on siis $N=ft$. Et igale täisringile vastab pöördenurk $2\pi$ rad, siis saame, et

millest vastavalt nurkkiiruse definitsioonile $\omega =\phi /t$ saame sagedusega seose valemiks

Näeme, et nurkkiirus on sagedusega võrdeline. Seepärast nimetatakse seda suurust mõnikord ka nurksageduseks või ringsageduseks.

Teades, et periood ja sagedus on teineteise pöördarvud, on lihtne näha, et nurkkiirus sõltub ringliikumise perioodist pöördvõrdeliselt:

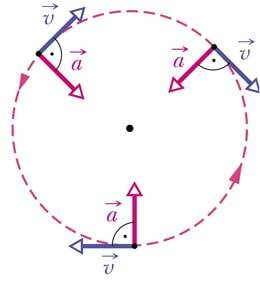
Sirgjoonelisel liikumisel on keha kiirus suunatud piki trajektoori. Seevastu ringliikumisel kiiruse suund muutub pidevalt. Kui trajektoor pole sirge, on kiirus trajektoori erinevates punktides suunatud erinevalt, kuid alati piki trajektoori puutujat (s.o mööda sirget, mis on antud punktis raadiusega risti). Varemalt nimetasime sellist suurust ka joonkiiruseks.

Ringliikumisel muutub liikumise suund pidevalt. Kui kiiruse suund muutub, siis muutub järelikult ka kiirusvektor (kiirus on vektoriaalne suurus). Kui aga kiirusvektor muutub, on olemas ka kiirendus. Kiirendus on ju kiirusvektori muudu ja muutuseks kulunud ajavahemiku jagatis:

Tuleb välja, et ringliikumisel esineb kiirendus ka siis, kui kiiruse arvväärtus ei muutu. Kiirendus on ka ühtlasel ringliikumisel, kuna liikumise suund muutub.

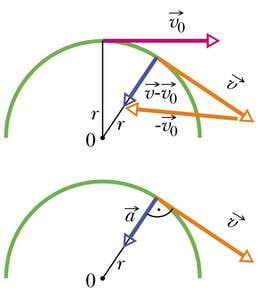
Kuhu on see kiirendus suunatud? Vaatame lühikest ajavahemikku, mille kestel sooritatud pöördenurk on väike. Et ringjoonelise liikumise joonkiirus on suunatud alati raadiusega risti, pöördub ka kiirusvektor sama nurga võrra. Joonisel tähistab kiirust enne pööret vektor $\overrightarrow{v_0}$ ja pärast pöörde sooritamist $\overrightarrow{v}$. Kuna kiiruse arvväärtus ei muutu, on ühtlasel ringliikumisel nende vektorite pikkused võrdsed.

Kiirenduse leidmiseks tuleb leida kiiruse muutus ehk kiirusvektorite vahe $\overrightarrow{v}-\overrightarrow{v_0}$. Vektori $\overrightarrow{v_0}$ lahutamine on samaväärne vastandvektori $-\overrightarrow{v_0}$ liitmisega. Jooniselt on näha, et väikese pöördenurga korral on kiiruse muut $\overrightarrow{v}-\overrightarrow{v_0}$ suunatud piki raadiust trajektoori kõveruskeskpunkti poole. Ringliikumise kiirendus kui kiiruse muutumise kiirus on suunatud samuti kõveruskeskpunkti.

Suunamuutusest tingitud kiirendus on suunatud alati keha trajektoori kõveruskeskpunkti poole ja on seega kiirusvektoriga risti. Seepärast nimetatakse seda kiirendust kesktõmbekiirenduseks.

Kesktõmbekiirenduse väärtus sõltub nii trajektoori kõverusraadiusest $r$ kui ka joonkiirusest $v$. On ju loomulik, et mida kiiremini keha mööda ringjoont liigub, seda kiiremini muutub ka liikumissuund. Samuti muutub suund seda kiiremini, mida kõveram on trajektoor.

Kesktõmbekiirendus sõltub liikumise joonkiirusest ja trajektoori kõverusraadiusest järgmiselt:

Kasutades valemit (3.8 ) seoses nurk- ja joonkiiruse vahel, saame kesktõmbekiirenduse avaldada ka nurkkiiruse kaudu:

Ühtlasel ringliikumisel esineb alati kesktõmbekiirendus. Newtoni II seaduse järgi liigub keha kiirendusega vaid siis, kui sellele mõjub jõud. Ka kesktõmbekiirenduse tekitamiseks on vajalik jõud. See jõud peab mõjuma samas suunas kiirendusega ja on järelikult suunatud trajektoori kõveruskeskpunkti poole.

Kui sellist jõudu kehale ei mõju, ei saa olla ka ringliikumist. Newtoni I seaduse järgi liiguvad ju kõik kehad, millele jõudusid ei mõju, inertsi tõttu ühtlaselt ja sirgjooneliselt. Keha liigub mööda ringjoont vaid siis, kui seda otsesuunast pidevalt kõrvale kallutatakse. Ringliikumine toimub kesktõmbejõu ja inertsi koosmõju tagajärjena. Trajektoori kõveruskeskpunkti suunatud jõudu, mis põhjustab ringliikumist, nimetatakse kesktõmbejõuks ehk tsentripetaaljõuks (ld centrum + petere 'kese + ründama').

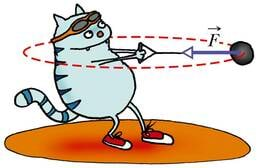
Kesktõmbejõuks võib olla mis tahes liiki jõud. Autot hoiab ringteelt välja libisemast hõõrdejõud, sidesatelliiti hoiab ümber Maa tiirlemas gravitatsioonijõud, vasar liigub heitmiseelse hoovõtu ajal ringjooneliselt trossis tekkiva elastsusjõu mõjul.

Kesktõmbejõudu saab leida Newtoni II seadust kasutades kesktõmbekiirenduse kaudu:

Kõik, kes on sõitnud mööda ringjoont kiiresti pöörleval karussellil või järsult kurvi võtvas autos, on tundnud, et neid surutakse ringi keskmest väljapoole. Ringjooneliselt liikuvale kehale mõjuks nagu mingi keskpunktist eemale suunatud jõud. Sellele jõule on antud ka eraldi nimetus – tsentrifugaaljõud (ld centrum + fugiô 'kese + põgenema'). Tegemist on niinimetatud inertsijõuga, mida vaatleja tajub siis, kui ta liigub kiirendusega.

Kui me istume autos, siis oleme selle suhtes paigal. Sisenedes kurvi, hakkab auto kõrvale pöörama ja sunnib kaasa pöörama ka autosistujaid. Sõitjatele tundub, nagu lükataks neid väljapoole. Maa suhtes vaadeldes seda väljapoole mõjuvat jõudu ei eksisteeri. Inertsi tõttu püüavad auto ja autosistujad liikuda otse ehk ringliikumise keskmest eemale ja ainus jõud, mis neile tegelikult mõjub, on liikumist ringjooneliseks sundiv kesktõmbejõud.

Kõik me teame, et planeedid tiirlevad ümber Päikese ning Kuu tiirleb ümber Maa. Trajektooriks on üsna täpselt ringjoon. Näiteks Maa kaugus Päikesest ei muutu tiirlemise käigus enam kui 3%.

Juba Newton oletas, et planeetide tiirlemine on tingitud gravitatsioonijõust. Tuginedes praegustele teadmistele gravitatsiooni ning ringliikumise kohta, võime väita, et just gravitatsioonijõud kesktõmbekiirenduse tekitajana kallutab planeedid sirgjoonelisest teest kõrvale ja on seega nende tiirlemise põhjuseks.

Oletame, et planeedil massiga $M$ on kaaslane massiga $m$, mis tiirleb selle ümber ringorbiidil raadiusega $r$. Vastavalt gravitatsiooniseadusele tõmbab planeet kaaslast jõuga

See jõud ongi kaaslase tiirlemist põhjustavaks kesktõmbejõuks, mis on valemi (3.15 ) järgi seotud tiirlemise nurkkiirusega järgmiselt:

Siit saame avaldada nurkkiiruse ning sellest omakorda tiirlemisperioodi:

Viimane seos näitab, et tiirlemisel mööda ringorbiiti on perioodi ruut võrdeline tiirlemisraadiuse kuubiga. Selle seaduspärasuse avastas planeetide vaatlusandmeid analüüsides Saksa astronoom Johannes Kepler juba 1619. aastal.

Tiirlemise orbiidiks on ringjoon vaid siis, kui gravitatsioonijõud mõjub kogu aeg liikumisega risti. Paljude taevakehade puhul ei ole see aga alati nii. Kui gravitatsioonijõud pole kiirusega risti, mõjub see liikumisele kiirendavalt või aeglustavalt. Sel juhul on liikumine muutuv ning trajektooriks on ringjoone asemel väljavenitatud ellips või isegi mittekinnine joon nagu parabool või hüperbool.

Lisaks tiirlemisele võivad taevakehad ka pöörelda. Öö ja päev vahelduvad tänu maakera pöörlemisele ja pöörlemistelje kalde muutumatus tingib aastaaegade vaheldumise.

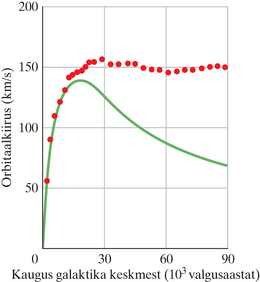
Kui kogu galaktika mass asuks nähtavat valgust kiirgavates allikates, siis peaks kiiruste jaotust kirjeldama joonisel kujutatud pidev kõver, st galaktika keskmest 15–25 kiloparseki kaugusel asuvate galaktikate pöörlemise kiirused peaksid vähenema. Reaalsetest mõõtmistest saadud kõverad on aga teistsugused (tähistatud punktidena joonisel 44-5) ja pöörlemise kiirus on ligikaudu konstantne isegi kaugustel 40 kuni 50 kpc. See erineb ka kiiruste jaotusest meie päikesesüsteemis. Näiteks on Pluto (Päikesest kaugeim planeet) orbitaalkiirus ainult üks kümnendik Merkuuri orbitaalkiirusest (Päikesele lähim planeet).

Nende andmete alusel arvatakse, et galaktikad on tegelikult hoopis suuremad kui nähtub nende visuaalsest pildist. Optiliselt nähtavad galaktikad on ümbritsetud ulatuslikust tumedast halost. Seega on ka meie galaktikas enamus massist nähtamatu, gravitatsioonilist tõmbumist põhjustav tume aine, mida me praegu veel ei tunne.

Seda ainet ei ole õnnestunud näha mitte ühelgi lainepikkusel, raadiokiirgusest kuni gammakiirguseni. Me teame teda vaid tema gravitatsioonilise tõmbe järgi. Tumeda aine olemus ja järeldused sellest evolutsioonile on üks kaasaegse astronoomia olulisemaid küsimusi.

Kuidas saab ainult pöörlemise uurimisest nii põhjapanevaid järeldusi teha? Alljärgnev näiteülesanne illustreerib, kuidas pöörlemise kiirus ja kesktõmbejõud on omavahel seotud – kui on teada üks, siis saab arvutada teise.

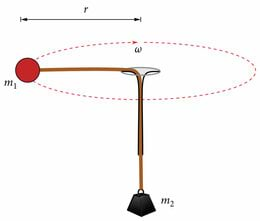
Joonisel kujutatud seadmega keerutatakse massi $m_1$, hoides kinni lehtrikujulisest torust. Olgu kera mass $m_1=1\text{kg}$ ja pöörelgu see mööda ringijoont, mille raadius on $1\text{m}$. Nööri otsa riputatud keha mass on $m_2=4\text{kg}$. Milline peab olema kera nurkkiirus, kui kumbki mass vertikaalselt ei liigu? Lehtri ning nööri vahel hõõrdumist ei ole vaja arvestada. 

Joonisel kujutatud seadmega keerutatakse massi $m_1$, hoides kinni lehtrikujulisest torust. Olgu kera mass $m_1=1\text{kg}$ ja pöörelgu see mööda ringijoont, mille raadius on $1\text{m}$. Nööri otsa riputatud keha mass on $m_2=4\text{kg}$. Milline peab olema kera nurkkiirus, kui kumbki mass vertikaalselt ei liigu? Lehtri ning nööri vahel hõõrdumist ei ole vaja arvestada. 

Lahendus

Nöör muudab koonust läbides massile $m_2$ mõjuva gravitatsioonijõu suuna horisontaalseks. Kera $m_1$ saab liikuda mööda ringjoont, sest talle mõjub kesktõmbejõud. Kui kumbki mass vertikaalselt ei liigu, siis peavad need kaks jõudu olema täpselt võrdsed:

$m_{1}r{\omega }^2=m_{2}g$

Sellest võrrandist saab avaldada nurkkiiruse:

$\omega =\sqrt{\frac{m_{2}g}{m_{1}r}}=\sqrt{\frac{4\text{kg}\cdot 9,81{\text{m/s}}^2}{1\text{kg}\cdot 1\text{m}}}=6,62\text{rad/s}$

See teeb umbes kaks pööret sekundis.

Looduslikku ringliikumist leidub ka maapealsetes mastaapides. Seda küll, et selle märkamiseks tuleb olla tähelepanelik, hammasrattaid või propellereid sealt ei leia. Või siiski?

Sügisel langevad puudelt lisaks lehtedele ka seemned. Näiteks vahtraseemned on kui propellerid – kukkudes nad hakkavad pöörlema. Miks see vajalik on? Sest niimoodi kukkudes takistab õhk langevat seemet rohkem ja see langeb kauem, mis omakorda annab tuulele rohkem aega seemet kaugemale kanda. Tähelepanelikult loodust jälgides on selliseid liikumisi võimalik leida mujaltki – näiteks see, et kass kukub alati jalgadele, tähendab, et ta peab end õhus pöörama.

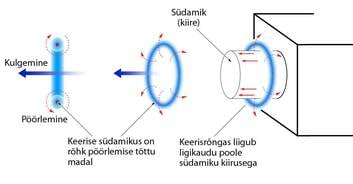
Hea näide on ka suitsurõngad. Kui rõngas tervikuna liigub enam-vähem sirgjooneliselt, siis rõnga osad pöörlevad, nagu näidatud alljärgneval joonisel. Selliseid suitsurõngaid võivad aeg-ajalt tekitada ka vulkaanid.

Õhu liikumine suitsurõngaste tekitamisel ja nende liikumisel.	Islandil asuva Hekla mäe vulkaaniline purse on tekitanud suitsurõnga.

Vooliste (vedelike ja gaaside) liikumisel tekivad tihti keerised. Lauale mahuvad need keerised, mis tekivad vee äravoolul läbi väikeste avade, näiteks kraanikausis. Satelliidipiltidelt võib näha tohutuid maa-alasid katvaid tsükloneid, väiksemas mastaabis tekivad mesotsüklonid ja nendest omakorda tornaadod.

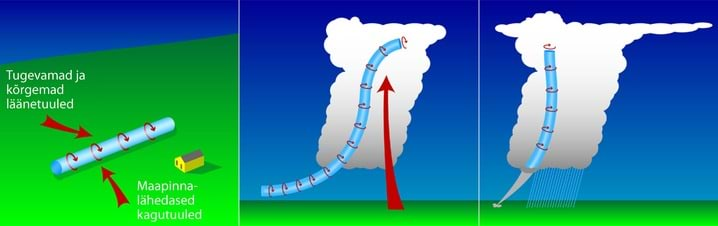
Tornaado ehk tromb on mõne meetri kuni paarikilomeetrise läbimõõduga tugev tuulekeeris rünksajupilve ja maapinna vahel.  Selle tekkimisel on kaks etappi. Esiteks rünksajupilve enese tekkimine, mida illustreerivad alljärgneva pildiseeria kaks esimest pilti. Teiseks tornaado enese moodustumine, kui rünk- või rünksajupilvest alla rippuv koonusekujuline või torujas silmnähtavalt pöörlev keeris ulatub maa või merepinnani (pildiseeria kolmas pilt).

Andres Tarand ja Ain Kallis soovitavad oma raamatus "Eesti tornaadod" keeristormide tekkimisele alljärgneva, mitteasjatundjatele suunatud seletust: "Eilsed tormid tekkisid siis, kui pinnalähedane soe niiske õhk paiknes selle kohal oleva kuivema õhu all, kus temperatuur kõrguse suurenedes kiiresti langes, andes sel moel ebastabiilsuse tekitamise läbi tormile energiat. Suured kõrgusest sõltuvad tuule muutused (tuulenihe) nii madalate (madalaim 1km) kui ka sügavate kihtide (kõige madalam 6 km) kohal – kombinatsioonis õhumassi ebastabiilsuse ja maapinna lähedase suure niiskusega – tekitasid tornaadode moodustumiseks soodsa olukorra."

Tornaado tekkimisel on pöödliikumisel väga suur roll.

Lehterpilv rünksajupilve all. Kui see ulatub maapinnani, siis nimetatakse seda tornaadoks.	F5 klassi tornaado läheneb 22. juunil 2007.a. Elie linnale, Kanadas, Manitoba maakonnas.

Omaette nähtus on ka tuletornaado. Sellised tordnaadod tekivad keerised satuvad tulekoldele, tekitades neile intensiivse hapnikurikka õhu pealevoolu ning leekide äratõmbe läbi keerise keskosa. Tuletornaadosid saab esile kutsuda ka demokatsetes. 

Tuletornaado Austraalia metsapõlengus.	Demokatsetes tekitatakse tuulekeeris kas ventilaatori või pöörleva võrksilindriga. Sellise keerise keskosas on õhurõhk veidi väiksem ning seetõttu hakkab leegiga kokku puutuv õhk kiiresti ülespoole liikuma.

Tehnikas leidub ringliikumise kohta palju näiteid. Autod sõidavad tänu pöörlevatele ratastele, informatsiooni salvestatakse pöörlevatele laserplaatidele ning magnetketastele, sidet peetakse ümber Maa tiirlevate tehiskaaslaste abil.

Ringliikumisega kaasneva kesktõmbekiirenduse abil saab ka kaalu muuta. Näiteks treenivad astronaudid tiirlevatel trenažööridel oma keha vastupidavust, tsentrifuugi saab eraldada erineva tihedusega aineid.

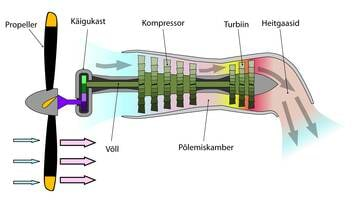
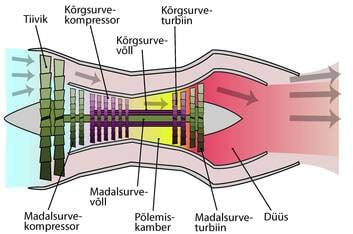
Anname siin uurimiseks ja nuputamiseks kahe näiliselt erineva, ehkki samas funktsioonis kasutatava seadme läbilõike: vaatame lähemalt turbopropellermootorit ja turboventilaatormootorit. Ühed lükkavad edasi propelleritega lennukeid, teised reaktiivlennukeid

Näeme, et oma olemuselt on need kaks üsna sarnased – nende põhiliseks osaks on gaasiturbiin, kus põlemisel tekkivad kuumad gaasid ajavad ühelt poolt ringi tiivikute süsteemi, st mootorit ennast, teisalt lükkavad edasi lennukit. 

Turbopropellerlennuki mootori läbilõige. Põlemiskambris tekkiv kuum gaas paneb pöörlema turbiini, mis on võlli abil ühendatud propelleriga.	Turboventilaatormootori läbilõige. Sellise mootori tõukejõud on reaktiivjõud, mis tekib gaasi väljapaiskumisel mootori tagaosast. Osa sellest energiast kantakse madalsurveturbiini kaudu üle mootori esiosas olevale tiivikule, mis omakorda õhku mootori tagaosast välja surub. Teine osa energiast läheb kõrgsurveturbiini kaudu õhu kokkusurumisele põlemiskambris.

Lõpuks üks lugu, mis räägib pöörlemise kineetilisest energiast ja võimalikest ohtudest seoses pöördliikumisega.

Plahvatus pöörlemisel

Suuri masinaosi, mis peavad pikka aega väga kiiresti pöörlema, testitakse spetsiaalses katseseadmes. Detail pannakse pöörlema silindriliselt paigutatud vooderdatud pliitelliste vahel. Kogu süsteem asub teraskestas, mille peal on klambriga kinnitatud kaas. Kui detail pöörlemise tõttu puruneb, püüavad pehmed pliitellised selle tükid hilisema analüüsi tarbeks kinni.

1985. aasta algul pandi seadmesse puhtast terasest rootor massiga 272 kilogrammi ja raadiusega 38 sentimeetrit. Kui detail oli saavutanud kiiruse 14 000 pööret minutis, kuulsid katset korraldanud insenerid katseruumist tuhmi mütsu. Ruum ise asus korrus allpool kõrvaltoa all. Kui mindi uurima, selgus, et pliitellised olid lennanud katseruumi koridori, uks paiskunud välja parkimisplatsile ning üks tellis lennanud läbi seina naabrite kööki. Ka hoone tugitalad olid saanud kahjustada, katseruumi betoonpõrand oli vajunud aga pool sentimeetrit allapoole ning 900-kilogrammine kaas lennanud läbi lae ja kukkunud tagasi katseseadmete peale. Oli suur õnn, et tuppa, kus olid insenerid, lendavad detailid ei jõudnud.

Enamik looduses aset leidvaid nähtusi toimub perioodiliselt. Teatud aja möödudes kordub kõik jälle uuesti. Nii vahelduvad öö ja päev ning aastaajad, kordub lindude ränne igal kevadel lõunamaalt koju pesitsema ja igal 1. septembril minnakse jälle kooli. Kõikjal igapäevases elus, looduses ja tehnikas võime kohata perioodiliselt korduvat liikumist – merelained loksuvad vastu kaldakive, puuoksad kõiguvad tuules, linnud lehvitavad tiibu, õmblusmasina nõel liigub üles-alla, praam sõidab edasi-tagasi Virtsu ja Kuivastu vahet. Seda tüüpi liikumiste tundmaõppimine ning ühiste joonte väljaselgitamine aitab meil ümbritsevat paremini mõista ja kogutud teadmisi enda kasuks rakendada.

Ühte osa perioodiliselt korduvatest liikumistest me juba õppisime lähemalt tundma. Selleks on ringliikumine. Teiseks suureks grupiks on võnkumine. Erinevalt teistest perioodilistest liikumistest kordub võnkumisel liikumine võrdsete ajavahemike tagant nii, et esialgsesse asendisse läheb keha tagasi sama teed mööda. Võnkumiseks nimetatakse perioodilist edasi-tagasi liikumist teatud tasakaaluasendist kord ühele, kord teisele poole. Nii on võnkumine mootorikolvi üles-alla liikumine, mitte aga väntvõlli pöörlemine. Viimasel juhul jõuab vändaots küll korduvalt esialgsesse seisu tagasi, kuid ikka mööda ringjoont tiireldes.

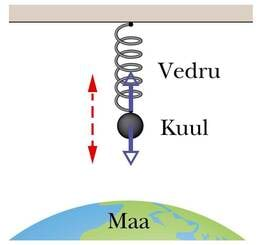
Kuna võnkumine kujutab endast muutuvat liikumist, on selle tekkimiseks vaja vastastikmõju. Kuna vastastikmõjus osaleb alati mitu keha, siis saab ka võnkumine toimuda mitte ühe keha, vaid kehade süsteemi korral. Näiteks ei saaks vedru otsa riputatud raskus võnkuda, kui puuduks maakera oma külgetõmbega. Iga sellist mitmest vastastikmõjus olevast kehast koosnevat süsteemi, milles võib tekkida võnkumine, nimetatakse võnkesüsteemiks.

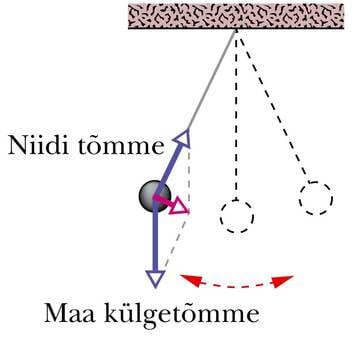
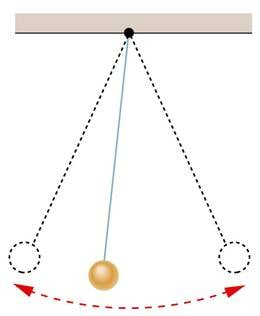
Kui võnkumine toimub vaid süsteemi kuuluvate kehade vaheliste mõjujõudude toimel, on tegemist vabavõnkumisega. Vabavõnkumiseks nimetatakse süsteemi sisejõudude mõjul toimuvat võnkumist. Näiteks võib vabalt võnkuda niidi otsas rippuv kivi, kui miski selle tasakaalust välja viib. Süsteemi moodustavad siin ülalt kinnitatud niit, kivi ja maakera. Süsteemisisesteks jõududeks on gravitatsioonijõud Maa ja kivi vahel ning niidi tõmbejõud. Mõnikord nimetatakse vabavõnkumist ka omavõnkumiseks.

Vabavõnkumine toimub süsteemi sisejõudude mõjul.	Vabavõnkumise tekkimiseks peab olema püsiv tasakaal, inerts ja väline tõuge.

Mehaanilise vabavõnkumise tekkimiseks peab süsteemis olema täidetud kolm tingimust. 

• Kõigepealt peab süsteemil olema püsiv tasakaaluolek. Püsiv tasakaal on selline, millest väljumisel tekkivad jõud viivad süsteemi tasakaaluolekusse tagasi.
• Teiseks peab süsteem omama inertsi. Kui keha liigub tasakaaluasendi poole suunatud jõu mõjul kiirenevalt, ei jää see kohale jõudes mitte silmapilkselt seisma, vaid liigub hooga edasi ning eemaldub tasakaaluasendist teisele poole.
• Kolmandaks peab süsteem saama võnkumise käivitamiseks (tasakaalust väljaviimiseks) välise tõuke.

Kuna igale kehale mõjub liikumist takistav hõõrdejõud, siis ei saa vabavõnkumine kesta ilma välise abita igavesti. Võnkumise kiirus ja ulatus hääbuvad aja jooksul nullini. Sellist võnkumist nimetatakse sumbuvaks. Looduses on vabavõnkumised alati sumbuvad. Sumbumatu võnkumise saamiseks tuleb hõõrdumist millegi välisega kompenseerida. Näiteks pommidega kellas annab spetsiaalse mehhanismi kaudu pendlile igal võnkel hoogu juurde pomme allapoole tõmbav raskusjõud.

Kui võnkumine toimub mingi välise perioodilise jõu mõjul, on tegemist sundvõnkumisega. Nii võngub õmblusmasina nõel üles-alla vaid seepärast, et käsi või mootor vänta ringi ajab. Kuna siin saab süsteem energiat välisest allikast, on sundvõnkumine alati sumbumatu. Sundvõnkumiseks on näiteks lõiketera liikumine höövelpingis, pintsli liikumine värvimisel ja klaasipuhastaja liikumine autoaknal.

Nagu iga perioodilist liikumist, iseloomustab ka võnkumist ajavahemik, mille möödumisel liikumine uuesti kordub. Ühe täisvõnke sooritamiseks kuluvat aega nimetatakse võnkeperioodiks. Võnkeperioodi tähis ja mõõtühik on samasugused kui ringliikumise perioodil, seega $T$ ja üks sekund.

Kui võnkeperiood on täpseks mõõtmiseks liiga lühike, saab täpsust tõsta, mõõtes mitte ühe, vaid suurema arvu võngete sooritamise koguaega $t$. Kui võngete arvu tähiseks võtta $N$, saame perioodi arvutada valemist

Ajaühikus sooritatavate täisvõngete arvu nimetatakse võnkesageduseks. Võnkesageduse tähis on sarnaselt ringliikumisega $f$ ja mõõtühik herts (Hz). Analoogiliselt ringliikumise sagedusega on võnkesagedus võrdne võnkeperioodi pöördväärtusega:

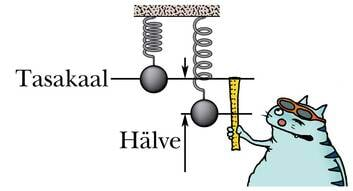
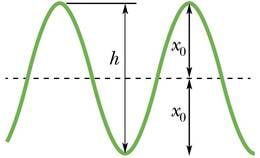
Võnkumisel liigub keha tasakaaluasendist kord ühele, kord teisele poole. Võnkuva keha kaugust tasakaaluasendist nimetatakse keha hälbeks. Hälve on ajas muutuv suurus ja sõltuvalt sellest, kummal pool tasakaaluasendit keha asub, loetakse see kas positiivseks või negatiivseks. Kuna hälve kujutab endast tegelikult keha koordinaati, on selle tähiseks võetud $x$ ja mõõtühikuks on pikkusühik meeter.

Hälve on keha kaugus tasakaaluasendist.	Amplituud on suurim hälve.

Maksimaalset hälvet ehk suurimat kaugust tasakaaluasendist nimetatakse võnkeamplituudiks. Amplituudi tähiseks on $x_0$. Kui sumbumatul võnkumisel amplituud ei muutu, siis sumbuval väheneb see aegamisi nullini.

Võnkuvat liikumist esineb looduses kõikjal meie ümber. Kui soovime loodust uurida ja võimalikult täpselt arvude abil kirjeldada, peame oskama ka võnkumist matemaatiliste meetoditega väljendada. Selleks et jõuda võnkumise võrrandini, vaatleme veel kord ringliikumist.

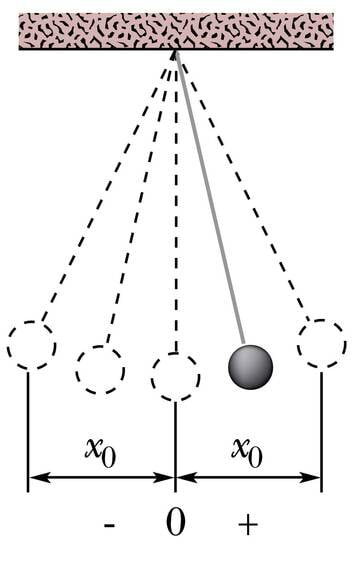
Kujutame ette mingit tiirlevat eset, näiteks vinüülplaadimängija pöörleva ketta servale asetatud tikutoosi (vt joonist). Kui nüüd keha valgustada küljelt, piki tiirlemistasandit, liigub tikutoosi vari seinal mitte ringjooneliselt, vaid edasi-tagasi. Vari võngub, kusjuures selle võnkumise sagedus langeb kokku eseme tiirlemise sagedusega ning võnkeamplituud tiirlemise raadiusega. Niisugust varju edasi-tagasi liikumist pole raske matemaatiliselt kirja panna.

Joonisel on koordinaattelg on suunatud piki varju liikumist nii, et nullpunkt asuks tiirlemiskeskme kohal. Tiirleva eseme asukohta kirjeldab pöördenurk $\phi$ ja varju hälvet (kaugust koordinaadi nullpunktist) $x$. Joonisel tekib täisnurkne kolmnurk, mille hüpotenuusiks on trajektoori kõverusraadius $r$ ning nurga $\phi$ vastaskaatetiks varju hälve $x$. Matemaatikas õpitud siinusfunktsiooni definitsiooni järgi

Tiirlemise pöördenurga saame asendada valemis nurkkiiruse ja aja korrutisega:

Nii kehtib varju võnkumise hälbe jaoks seos

Kuna vari ei saa keskpunktist kaugemale minna, kui tiirlemise raadius $r$, siis on selle väärtus ka võnkeamplituudiks $x_0=r$. Pärast asendust saamegi hälbe arvutamiseks mis tahes ajahetkel valemi:

Saadud valem kirjeldab varju liikumist seinal, näidates selle koordinaadi sõltuvust ajast.

Kõiki selliseid võnkumisi, mida saab kirjeldada siinus- või koosinusfunktsiooni abil, nimetatakse harmoonilisteks võnkumisteks. Seos (3.26 ) on seega harmoonilise võnkumise võrrand.

Siinusfunktsiooni argumendiks olevat suurust

nimetatakse võnkumise faasiks. Faasi mõõtühikuks on radiaan (rad) ning seda saab avaldada võnkesageduse ja perioodi kaudu:

Suurust $\omega$, mis tiirlemise jaoks on nurkkiirus, nimetatakse võnkumise korral ring- ehk nurksageduseks. Ringsageduse mõõtühik on 1 rad/s.

Paljud looduses esinevad võnkumised on harmoonilised või sellele lähedased. Seepärast omab harmoonilise võnkumise võrrand (3.6 ) suurt tähtsust. Võrrand võimaldab kirjeldada peaaegu kõiki võnkumisega seotud nähtusi.

Lisaks võrrandile saab võnkumisi kirjeldada ka graafiku abil. Võnkumise graafik näitab keha koordinaadi sõltuvust ajast. Püstteljele kantakse koordinaat ehk võnkumise hälve ja horisontaalteljele aeg. Reaalselt saab võnkumise graafikut joonistada näiteks vedrupendli raskuse külge kinnitatud viltpliiatsi abil, mis surub vastu ühtlase kiirusega nihutatavat pabeririba.

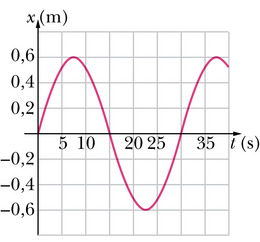
Harmoonilise võnkumise graafiku võib joonestada ka võnkumise võrrandi järgi erinevatele ajahetkedele vastavaid koordinaate välja arvutades ja teljestikku kandes. Nii talitades saame võnkumise graafikuks sujuva lainelise joone, mida nimetatakse sinusoidiks.

Sinusoid läbib kordamööda teljestiku positiivset ja negatiivset ala, jäädes samal ajal amplituudiga määratud horisontaaljoonte vahele. Sinusoid lõikab ajatelge iga poole perioodi tagant. Seda teades on graafikult võnkumise amplituudi ja perioodi lihtne välja lugeda.

Veel annab graafik informatsiooni võnkuva keha kiiruse muutumise kohta. Teatavasti näitab kiirust liikumisgraafiku tõus. Uurides sinusoidi, näeme, et suurima hälbega punktides graafiku puutuja mitte ei tõuse ega lange, vaid on horisontaalne. Seega on neil hetkedel keha paigal ja liikumise suund muutub vastupidiseks. Suurim tõus või langus toimub hetkedel, mil joon lõikub ajateljega. Järelikult liigub keha tasakaaluasendi poole kiirenevalt, maksimumkiirus saavutatakse tasakaaluasendis ja sellest eemaldumisel liikumine jälle aeglustub.

Me teame, et keha muudab vastastikmõju teel teise keha liikumist või kuju, st muudab selle seisundit. Seisundi muutmise protsessi nimetatakse tööks ja töö tegemiseks peab keha omama energiat. Keha omab energiat tänu liikumisele (kineetiline energia) või sellele mõjuvatele jõududele (potentsiaalne energia). Kuna võnkumine on liikumine, mis toimub võnkesüsteemis mõjuvate jõudude toimel, siis omab selline süsteem energiat nii kineetilisel kui ka potentsiaalsel kujul. Seejuures võib kineetiline energia muunduda potentsiaalseks ning vastupidi nii, et nende summa jääb muutumatuks. 

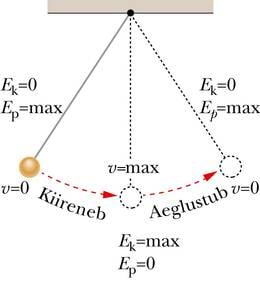
Uurime võnkumise energia muundumist niidi otsa riputatud kivi võnkumise näitel. Kivile mõjub Maa külgetõmbejõud ehk raskusjõud. Kallutades pendlit tasakaaluasendist kõrvale, tehakse tööd ja kivi tõuseb kõrgemale, omandades potentsiaalse energia. Raskusjõust tingitud potentsiaalne energia on seda suurem, mida suurem on kõrgus.

Päästes kivi lahti, algab võnkumine. Kiirus ja sellega koos ka liikumis- ehk kineetiline energia kasvavad ning saavutavad maksimumväärtuse tasakaaluasendisse jõudmisel. Samal ajal kõrgus väheneb ja sellega väheneb ka potentsiaalne energia, jõudes tasakaaluasendis nulli. Kivi jätkab inertsi tõttu liikumist, mida raskusjõud nüüd aeglustab. Kiirus ja kineetiline energia kahanevad ning kõrgus ja potentsiaalne energia kasvavad, kuni pendel peatub teises äärmises asendis. Edasi kordub kõik vastupidises suunas ikka nii, et energia kogusumma jääb samaks. Seda muidugi takistava jõu puudumisel. Takistuse ületamine kulutab energiat ning amplituud ja maksimumkiirus vähenevad – võnkumine sumbub aegamööda.

Nagu nägime, võivad võnkuvad süsteemid olla väga erinevad. Ometigi saab neid sarnaste joonte põhjal grupeerida ning ühise lihtsustatud mudeli alla viia. Võnkuva süsteemi füüsikalist mudelit nimetatakse pendliks. Kõige sagedamini kasutatavateks mudeliteks on matemaatiline pendel, vedrupendel ja füüsikaline pendel. Kõiki pendleid iseloomustab isokroonsus ehk võime võnkeamplituudi muutumisel võnkeperioodi säilitada. See võimaldab pendleid kasutada kellade käigu regulaatorina.

Matemaatiliseks pendliks nimetatakse venimatu kaalutu niidi otsa riputatud punktmassi. Tasakaalust väljaviimisel liigub niidi otsa riputatud keha mööda ringjoone kaart, mille kõverusraadius on võrdne niidi pikkusega.

Sarnaselt matemaatilise pendliga võngub mis tahes raske ese, mis on riputatud sellega võrreldes palju kergema ja pikema niidi või nööri otsa. Matemaatilise pendli võnkumist põhjustab raskusjõud koos niidis tekkiva tõmbejõuga. Väikese võnkeamplituudi korral sõltub periood ainult pendli pikkusest $l$ ning vaba langemise kiirendusest $g$:

Matemaatilise pendli abil on lihtne määrata vaba langemise kiirendust. Asjaolu, et selline pendel säilitab oma võnketasandi, kasutas prantsuse füüsik Jean Foucault 1848. aastal maakera pöörlemise tõestuseks.

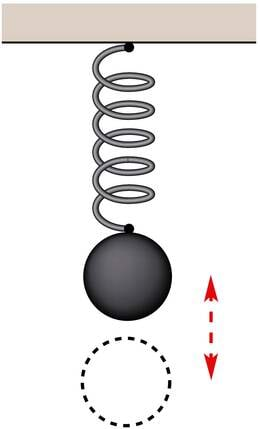
Vedrupendliks nimetatakse absoluutselt elastse vedru otsa riputatud punktmassi. Võnkumist põhjustab siin elastsusjõu ja raskusjõu resultant.

Vedrupendli võnkeperiood on määratud vedru jäikuse k ning keha massiga $m$:

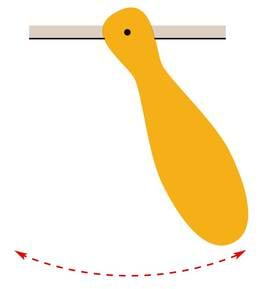
Füüsikaliseks pendliks nimetatakse suvalise kujuga jäika keha, mis saab rippudes võnkuda liikumatu punkti ümber. Füüsikaliseks pendliks võib olla näiteks kiikuv pilt seinal või naela otsa riputatud mutrivõti. Füüsikalise pendli võnkeperiood sõltub keha kujust, massist, kinnituskoha ning raskuskeskme vahekaugusest ja vaba langemise kiirendusest.

Kuna keha kuju ja riputuspunkt võivad olla väga erinevad, pole siinkohal võimalik anda füüsikalise pendli võnkeperioodi üldist valemit. Näiteks ühest otsast üles riputatud ühtlase varda võnkeperiood sõltub varda pikkusest $l$ järgmiselt:

Võnkumisi võib kohata nii looduses kui ka inimese valmistatud objektide juures. Neid on vabu ja sunnituid, sumbuvaid ja sumbumatuid. Tihti me isegi ei teadvusta endale, et tegemist on võnkumisega.

Looduses võib kohata mitmeid vabalt võnkuvaid kehi. Puud kõiguvad tuules, haavalehed värisevad ning vees ujuv puunott õõtsub üles-alla. Enamik sellistest võnkumistest ei täida mingit kindlat eesmärki, kuid mõned võivad siiski ka kasu tuua. Õite kõikumine äratab tolmeldavate putukate tähelepanu, kõikuvatest viljadest levivad seemned kaugemale ning peente ja lapikute rootsude otsas rippuvate haavalehtede värisemine aitab puul paremini valgust püüda ja vee aurumist reguleerida.

Sundvõnkumist kasutavad elusolendid liikumiseks. Näiteks me liigutame kõndimisel käsi ning jalgu edasi-tagasi. Paljud mikroorganismid liiguvad viburi võngutamise abil, linnud ja putukad lehvitavad tiibu, vee-elanikud liigutavad saba, uimi või loibi.

Sundvõnkumist kasutatakse edasiliikumiseks.	Võnkuv pillikeel tekitab heli.

Inimesed on leidnud mitmesugustele võnkumistele rakendust. Kes meist poleks näiteks lapsepõlves kiikunud! Kiikumises korraldatakse isegi võistlusi. Veel üheks näiteks on heliallikad. Kõik kehad, mis võnguvad sagedusvahemikus 16 – 20 000 Hz, tekitavad kuuldavat heli. Heliallikaks võib olla vabalt võnkuv pillikeel, kirikukell või ka trumminahk. Ka akordionis ja saksofonis teeb häält võnkuv keel, kuid see on kitarrikeelega võrreldes hoopis teistsugune. Kõlaris tekitab heli valjuhääldi membraan, mille on võnkuma sundinud muutuv elektrivool.

Sundvõnkumist rakendatakse masinates, mis viivad korduvalt läbi üht ja sama operatsiooni. Sundvõnkumise abil töötavad näiteks õmblusmasin, kolbpump, aurumasin ja pudelikorkija.

Võnkumine võib olla kas vaba või sunnitud. Mis juhtub aga siis, kui vabalt võnkuvale süsteemile mõjub lisaks väline perioodiline jõud? Juhul, kui välise mõju sagedus langeb kokku süsteemi vabavõnkumise sagedusega, hakkab amplituud kasvama ja võib ka väikese jõu korral väga suureks muutuda. Kõik me teame, et kiigele hoo andmiseks ei tule pidevalt ühes suunas lükata, vaid kiike kergelt kindlate ajavahemike tagant tõugata.

Ka mitmetonnise auto saab suhteliselt väikese jõuga poriaugust välja lükata. Selleks kõigutatakse autot edasi-tagasi, kuni võnkliikumise amplituud kasvab sedavõrd, et masin välja pääseb.

Nendes näidetes väljendub resonantsinähtus.

Resonantsiks nimetatakse nähtust, kus välise mõju sageduse kokkulangemisel süsteemi vabavõnkumise sagedusega suureneb võnkeamplituud märgatavalt.

Näiteks võib kõlar mingi ühe kindla madala noodi kõlamisel valjult plärisema hakata. Siis ongi tegemist resonantsiga – mängitava kindla kõrgusega heli sagedus langeb kokku valjuhääldi membraani enda võnkumise sagedusega.

Resonantsi saab kasutada tundmatu võnkesageduse määramisel. Selleks viiakse võnkuva kehaga kokkupuutesse näiteks erineva pikkusega plekiribad. Riba, mille võnkesagedusega mõõdetav sagedus kokku langeb, hakkab suure amplituudiga võnkuma.

Resonantsi kasutatakse paljude muusikariistade juures. Nii võimendab viiuli kõlakast keelte helisemist just tänu resonantsile. On ka selliseid pille, millel saavutatakse eriline kõlapilt põhikeelte kõrvale tõmmatud lisakeelte abil, mis tänu resonantsile iseenesest helisema hakkavad.

Resonantsil töötav sagedusmõõtja. 50 Hz märgi juures on näha, et kaks haamrikest võnguvad, kui kõik teised on paigal. Ilmselt mõõdetakse võrgusagedust.	Ühes vapustavaimas füüsikavideos on näha vana Tacoma Narrowsi silla jõhkrat väändumist 7. novembril 1941.a. Kuigi tol hommikul puhus mõõdukas tuul (umbes 68 kilomeetrit tunnis ehk 19 meetrit sekundis), rebenes toekas sild mõni tund pärast kõverdava võnkumise algust pooleks.

Resonants võib ka ohtlik olla. Võime näiteks ette kujutada, mis juhtuks, kui silla kõikumise ning silla konarlikul kattel sõitva auto õõtsumise sagedused kokku langeksid. Seepärast peavad arhitektid suurte ehitiste projekteerimisel arvestama võimalike perioodiliste välismõjudega, nagu näiteks inimeste kõndimine, tuulekeerised ja maavärinad.

Teadmisi resonantsi olemusest saab kasutada maavärinate kahjude vähendamiseks. Kui maakoores levivad pikilained, siis need kõigutavad sinna ehitatud maju maapinnaga paralleelselt edasi-tagasi. Kahju, mida selline võnkumine majadele teeb, sõltub võnkumise sagedusest. Täpsemalt sellest, kas ja kui sarnane on võnkumise sagedus majade omavõnkesagedusega. Kui on sarnane, siis tekib resonants.  Kui ehitada maju selliselt, et nende omavõnkesagedus erineb tunduvalt maavärina korral maapinna võnkumise sagedusest, siis on maavärina kahjud väiksemad.

Lõpuks seome läbi ühe konkreetse näite omavahel looded, võnkumised ja resonantsi. 

Looded Fundy lahes.

Fundy lahes Nova Scotias Kanadas on märkimisväärsed looded: veetase võib seal teinekord muutuda mõne tunniga kuni 15 meetrit. Miks on tõusu-mõõna erinevused seal nõnda suured?

Tõus Fundy lahes.	Mõõn Fundy lahes.

Vee saab panna vannis lainetama, kui vajutada seda korrapäraselt mõlaga alla, justkui pumbates. Suurim lainetus saavutatakse siis, kui mõlaga vajutatakse sel ajal, kui vesi on vanni ühes otsas kõrgeim. Sellise ajastusega pumbatakse vett resonantselt ja vajutustevaheline ajavahemik ühtib vannivee võnkeperioodiga.

Ka lahevee võib panna võnkuma, kui seda resoneerivalt pumbata. Näiteks põhjustavad Kuu tekitatud loodeefektid lahes vee võnkumist ning panevad vee lainetama. Enamikus lahtedes on võnked siiski väikesed, sest loodete ajastus ei sobitu lahe võnkeperioodiga. Fundy laht on erinev: selle võnkeperiood on umbes 13,3 tundi, mis on kaunis lähedane 12,4-tunnisele loodete vahemikule. Seetõttu tekivad Fundy lahes märkimisväärse amplituudiga looded.

Ajalookirjutised viitavad faktile, et Fundy lahe tõusu-mõõna erinevused on järk-järgult kasvanud, sest lahe võnkeperiood on järjest loodete vaheldumise perioodile lähemale nihkunud. Selle nihke võib olla põhjustanud lahe kuju muutus, mida tekitab merepinna kõrguse tõus.

Lained seostuvad meie mõtetes tavaliselt merega, kus vesi rütmiliselt kaldakive uhub. Samuti oleme kuulnud maavärinate tekitatud hiidlainetest, mis pühivad maapinnalt terveid linnu. Lained ei kuulu aga ainult mere juurde, tegemist on palju mitmekesisema nähtusega. Lained on näiteks heli ja valgus. Teleprogrammid ja mobiilikõnedki jõuavad meieni raadiolainete vahendusel. Lainetest räägitakse isegi poliitikas, majanduses ja muusikas (new wave).

Mehaaniliste lainete puhul on alati tegemist millegi liikumise või muutumisega. See, mis liigub, võib olla aine nii tahkes, vedelas kui ka gaasilises olekus, õhus, vees ja maakoores. Kui mehaanilised lained saavad levida vaid aines, siis valguse ja raadiolainete korral kanduvad elektrilise ja magnetilise vastastikmõju muutused edasi ka läbi tühjuse.

Rahulikul veepinnal tekivad lained siis, kui sinna kivi visata ja helilainete tekitamiseks peab valjuhääldi membraan õhku kord tihendama, kord hõrendama. Laine tekkimiseks on vaja keskkonda häirida, tasakaalust välja viia. 

Lainetada ei saa igasugune keskkond. Kui viskame kivi liiva sisse, siis ei teki selle pinnal mingeid liikuvaid laineid, vaid ainult lohk. Liiv pole elastne ega püüa oma esialgset olekut taastada. Mehaanilised lained tekivad vaid elastses keskkonnas, nagu kivi saab võnkuda elastse vedru otsas.

Elastse keskkonna tasakaalu häirimisel tekivad tasakaalu taastavad jõud, mis panevad keskkonna osakesed võnkuma. Et osakesed on vastastikmõjus naabritega, hakkavad omakorda ka need võnkuma. Võnkumine levib ruumis edasi. Seejuures aine ise edasi ei kandu. Selles võime veenduda, kui jälgime veelainetel hüplevat puutükki. Edasi ei kandu mitte aine (puutükk, vesi), vaid ainult selle häiritus – elastses keskkonnas toimuv võnkumine. Edasi kandub võnkumise energia. Energia edasikandumisele annab kinnitust tumeda pinna soojenemine valguslainete neeldumise tõttu.

Ülaltoodu põhjal võimegi sõnastada laine definitsiooni: laineks nimetatakse võnkumiste edasikandumist ruumis.

Definitsiooni järgi kujutab laine endast võnkumiste edasikandumist ruumis. Võnkumine saab toimuda mingis kindlas sihis. Sõltuvalt sellest, millises sihis võnkumine laine levimissuuna suhtes toimub, eristatakse kahte liiki laineid.

Tiiki visatud kivi poolt tekitatud lained levivad piki veepinda kalda poole, pinnal lebavad vesiroosilehed õõtsuvad samal ajal üles-alla. Võnkumine toimub levimissuunaga risti ja tegemist on ristlainega. Ristlaineks nimetatakse lainet, milles võnkumine toimub levimissuunaga risti.

Ristlained on näiteks lained veepinnal, raadio- ja valguslained, maavärina tekitatud seismilised pinnalained ning võimleja tekitatud liikumine võimlemislindis.

Kui lüüa pika vedru otsa pihta, hakkavad ka selles võnkumised levima. Erinevalt merelainetest toimub võnkumine siin piki levimissuunda. Vedrukeerud kord lähenevad, kord eemalduvad üksteisest. Piki vedru liiguvad edasi kokkusurutud ja hõredaks tõmmatud keerdudega kohad. Tegemist on pikilainega. Pikilaineks nimetatakse lainet, milles võnkumine toimub piki levimissuunda. Pikilainena levib näiteks heli.

Kuna laine on ruumis leviv võnkumine, siis iseloomustavad seda ka kõik võnkumist kirjeldavad suurused. Nii iseloomustavad lainet võnkeamplituud $x_0$ (mõõtühik 1 m), periood $T$ (1 s) ja sagedus $f$ (1 Hz).

Laine võnkeamplituudi ei tohi segi ajada laine kõrgusega. Laine kõrgus $h$ on näiteks lainetava veepinna puhul laineharja (kõrgeima punkti) ning lainenõo (madalaima punkti) kõrguste vahe. Laine amplituud on seevastu üles-alla võnkuvate veeosakeste suurim kaugus tasakaaluasendist ehk tasasest veepinnast lainete puudumisel. Laine kõrgus on võrdne kahekordse amplituudiga:

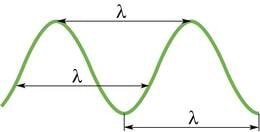
Lisaks loetletutele on veel kaks suurust, mille abil lainete levimist iseloomustatakse. Esimene neist on lainepikkus. Lainepikkuseks nimetatakse kaugust kahe teineteisele lähima samas taktis võnkuva punkti vahel. Laineallikast kaugemate punktide võnkumine on lähemate võnkumistest hilisem ning kui hilinemine on võrdne ühe võnkeperioodiga, võnguvad punktid samas taktis ehk samas faasis. Neis punktides on kogu aeg võnkumise hälve ja kiiruse suurus ning suund ühesugused. Nii on lainepikkus võrdne näiteks kahe naaberlaineharja vahekaugusega, sest kõikides harja punktides on hälve ühtviisi maksimaalne ja osakeste kiirus null. Täpselt samamoodi on lainepikkusega võrdne lainenõgude vaheline kaugus.

Lainepikkust tähistatakse tavaliselt kreeka tähega $\lambda$ (lambda) ning selle mõõtühikuks on meeter.

Teiseks iseloomustab võnkumise edasikandumist laine levimiskiirus. Teame, et kiirus on võrdne nihke pikkuse ja aja jagatisega:

Võttes aja võrdseks võnkeperioodiga $T$, jõuab võnkumine selle ajaga edasi kanduda ühe lainepikkuse võrra. Vastab ju ühele lainepikkusele üks täisvõnge. Nii saame laine levimiskiirust väljendada lainet iseloomustavate suuruste kaudu järgmiselt:

Kui keskkond on ühtlane ning häirivaid tegureid pole, siis levib laine sirgjooneliselt. Keskkonna muutused ja teele jäävad takistused muudavad ka levimist ning kutsuvad esile täiendavaid nähtusi. Et sellised nähtused kaasnevad vaid lainetega ega saa muudel juhtudel aset leida, on nende esinemine tõestuseks sellest, et tegemist on just lainega.

Kõik me oleme kokku puutunud sellise nähtusega nagu kaja. Kui hõigata mägedes või metsaäärsel lagedal, siis kuuleme enda tekitatud heli hetke pärast uuesti. Mõnes suures ruumis võib heli üsna kauaks kõlama jääda. Tegemist on helilainete peegeldumisega.

Peegelduvad kõik lained sõltumata liigist. Laine peegeldub siis, kui jõuab teistsuguse keskkonnani. Näiteks merelaine jõuab kaljuni või valguslained satuvad kuuma ja külma õhu piirile. Peegeldumine toimub kahe erineva keskkonna lahutuspinnalt.

Seejuures pole tähtis, mis ainest ja millises olekus need keskkonnad on. Peaasi, et need on erinevad. Peegeldumise tunnuseks on see, et kohates teist keskkonda, pöördub laine esialgsesse tagasi. Peegeldumiseks nimetatakse laine tagasipöördumist kahe keskkonna lahutuspinnalt lähtekeskkonda.

Lainete peegeldumisel kehtib seaduspärasus, et pinnanormaali (pinna ristsirge) suhtes mõõdetud langemisnurk ja peegeldumisnurk on võrdsed.

Ultrahelilainete peegeldumist kasutavad näiteks nahkhiired pimedas orienteerumisel ning arstid siseorganite uurimisel.

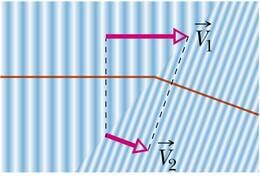
Jõudes teise keskkonda, võib laine selles edasi levida. Seejuures levimissuund sageli muutub. Tegemist on laine murdumisega. Laine murdumiseks nimetatakse laine levimissuuna muutumist ühest keskkonnast teise üleminekul. Murdumine toimub sarnaselt peegeldumisega erinevate keskkondade lahutuspinnal.

Murdumise põhjuseks on laine levimiskiiruse erinevus keskkondades. Laine pöördub selle keskkonna poole, kus levimiskiirus on väiksem. Sarnane suunamuutus võib juhtuda suure kiirusega sõitva auto kaldumisel teeserva. Kui auto parempoolsed rattad satuvad pehmele teepeenrale ning pidurduvad ja vasakpoolsed jätkavad samas endise hooga, pöörab auto paremale kraavi.

Lainete murdumisel kehtib seaduspärasus, et keskkondade lahutuspinna normaali suhtes mõõdetud langemis- ja murdumisnurkade siinuste suhe on võrdne levimiskiiruste suhtega.

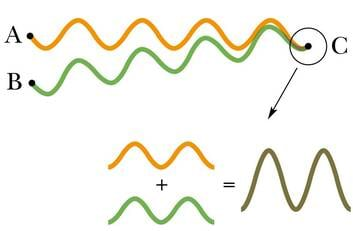
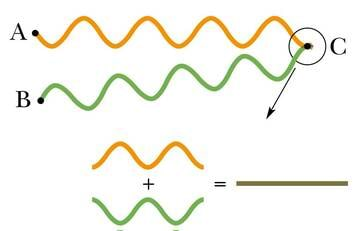
Kui vette visata korraga kaks kivi, hakkavad lained mõlemast kukkumispaigast mööda veepinda ringidena laiali levima. Kohtumisel need erinevatest allikatest lähtunud lained liituvad ja veepinnal tekib uus lainepilt, mis erineb piltidest, mille tekitanuks kumbki kivi eraldi visatult. Siin on tegemist lainete interferentsiga (ld inter + ferîre 'vahel + mõjuma'). Interferentsiks nimetatakse nähtust, kus kahe või enama laine liitumisel tekib uus laine, mille kuju on erinev liituvate lainete kujust. Interferents avaldub selles, et mõnes keskkonna punktis lained liitumisel võimendavad üksteist, teistes aga nõrgendavad. Tulemuseks on see, et mõnes kohas toimub võnkumine suure amplituudiga, teisal jälle väiksema amplituudiga või puudub sootuks. Interferentsi korral tekib ruumis võnkumiste püsiv jaotus amplituudi järgi. Interferents jaotab lainete energia ruumis ringi.

Interferents ei teki siiski igasuguste lainete liitumisel. Kõik teavad, et koori esituses kõlab laul alati valjemini kui solisti suust. Erinevate lauljate tekitatud helilained ei nõrgenda üksteist mitte kunagi. Interferentsi tekkimiseks peavad lained olema sama sagedusega ning võnkumisfaaside erinevus ei tohi muutuda. Teisisõnu – erinevate lainete allikad peavad võnkuma muutumatult ühtmoodi. Sagedused peavad olema võrdsed ja ühe allika võnkumine ei tohi teise suhtes muutuda.

Kui kaks lainet on kohtumisel samas faasis (võnkumine on samas taktis), siis täiendavad need liitumisel teineteist ja amplituud kasvab. Sel juhul on tegemist interferentsimaksimumiga. Vastandfaasis lainete puhul kohtub ühe laine hari teise nõoga ning lained kustutavad teineteist. Amplituud väheneb ning tegemist on interferentsimiinimumiga.

Samas faasis liituvad lained võimenduvad.	Vastandfaasis liituvad lained nõrgenevad.

Lained võivad oma teel kohata suuremaid ja väiksemaid tõkkeid. Näiteks jäävad merelainete ette erineva suurusega kivid ning sadade meetrite pikkused laiud. Väikeste tõkete taha pääsevad lained kergesti, suuremate taga on vesi aga rahulik, seal on vari.

Siin on tegemist nähtusega, mis leiab aset igasuguste lainete korral. Nimelt osutub, et lained on võimelised tõkete taha painduma. Seejuures pääsevad lained vaid nende tõkete taha, mille mõõtmed on lainepikkusest väiksemad või sellega võrreldavad.

Tegemist on difraktsiooniga (ld diffrâctus 'murdunud, paindunud'). Difraktsiooniks nimetatakse nähtust, kus lained painduvad tõkete taha. Tänu difraktsioonile kuuleme tänaval sõitva auto mootorimüra ka majanurga taha. Helilained painduvad tõkkeks oleva majanurga juures otsesihist kõrvale.

Difraktsioon avaldub ilmekalt, kui veepinnal levivaid laineid tõkestada ekraaniga, milles on kitsas pilu. Lained levivad siis läbi pilu rõngastena ekraani taha.

Lained painduvad tõkke taha.	Lained levivad läbi pilu rõngastena ekraani taha.

Eesti on mereriik. Eestlased hoolivad väga oma keskkonnast ja otsivad võimalusi katta oma energiavajadust taastuvenergia arvelt. Kas üks võimalus energiat saada võiks olla kasutada ära laineenergiat?

Füüsika aitab sellistele küsimustele vastata. Sest lisaks täpsetele arvutustele, mida saab kasutada lihtsate füüsikaliste süsteemide kirjeldamiseks ja mida kohtame koolifüüsikas, suudab füüsika anda ka teaduspõhiseid hinnanguid keerukate süsteemide käitumisele.

Laineenergia kasutamisest räägib David J. C. MacKay raamat „Sustainable Energy – without the hot air“ (taastuvenergiast ilma udujututa). Toome siia ära katke tema teosest. Kas sellist käsitlust annaks ka Eesti kontekstis kasutada?

Lained

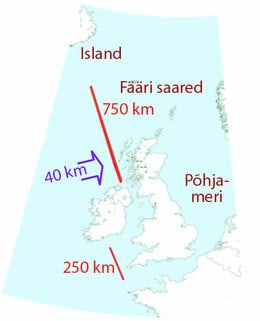
Kui on üldse riike, mis võiksid loota lainete energiale, siis on selleks Suurbritannia ja Põhja-Iiri Ühendkuningriik, mis külgneb ühelt poolt Atlandi ookeaniga ja teiselt poolt Põhjamerega.

Kõigepealt selgitame, kust tulevad lained: päike tekitab tuule ja tuul tekitab lained.

Enamus Maale jõudvast päiksevalgusest soojendab ookeane. Soe vesi soojendab omakorda õhku selle kohal ja tekitab veeauru. Kui soe õhk ülespoole tõuseb, siis see jahtub ning veeaur selle sees kondenseerub, moodustades pilvi ja tekitades vihma. Kõige kõrgemas punktis jahtub õhk veelgi, puutudes kokku kosmose jäise pimedusega. Külm õhk vajub uuesti alla. Selline suur, päikese jõul töötav pump keerutab õhku ringiratast mööda suuri konvektsioonikanaleid. Merepinnal tekib tänu nendele kanalitele tuul. Seega on tuul n-ö teise ringi päikeseenergia. Tuul omakorda tormab mööda veepinda ja tekitab laineid. Järelikult on lained n-ö kolmanda ringi päikseenergia.

Avamerel tekivad lained alati, kui tuul puhub kiiremini kui $0,5m/s$. Laineharjad liiguvad umbes sama suure kiirusega ja samas suunas kui seesama tuul, mis neid tekitas. Lainete lainepikkus (vahemaa laineharjade vahel) ja periood (aeg laineharjade vahel) sõltuvad tuule kiirusest. Mida kauem tuul puhub ja mida suurem on selle vee pindala, üle mille tuul puhub, seda kõrgemaks kerkivad selle tuule poolt tekitatud lained. Seega: kuna Atlandi ookeanil puhuvad tuuled valdavalt läänest itta, on Atlandi ookeanilt Euroopa rannikule jõudvad lained eriti suured. (Briti saarte idarannikule jõudvad lained on tavaliselt palju väiksemad, sellepärast keskendun ma oma laineenergia hinnangutes Atlandi ookeanile.)

Lainetel on pikk mälu ja need jätkavad oma liikumist ühes suunas veel päevi pärast seda, kui tuul on lakanud, kuni põrkavad lõpuks millegi vastu. Meredel, kus tuule suund tihti muutub, moodustavad kattuvad, erinevatel päevadel tekkinud ja erinevates suundades liikuvad lained paraja segaduse.

Kui lained kohtavad oma teel midagi, mis nende energia neelab – näiteks liivarandadega saarte rivi –, siis on meri saarte taga rahulikum. Sellised objektid tekitavad enda taha varju ja edasi liikuvates lainetes on vähem energiat. Seega, kui arvestame päikeselt saadavat energiat ruutmeetri kohta, siis lainte antavat energiat arvestame ranniku pikkuse kohta. Nii nagu ei ole võimalik kooki ühtaegu süüa ja alles hoida, ei ole võimalik laineenergiat koguda kõigepealt kahe miili kaugusel rannikust ja seejärel uuesti ühe miili kaugusel rannikust. Kahe miili kaugusel olev seade neelab sellisel juhul energia, mis oleks muidu jõudnud ühe miili kaugusel olevasse seadmesse, ja seda ei ole võimalik asendada. Tuulel kulub suurte lainete tekitamiseks tuhandeid miile.

Lainetest toodetavale energiale on võimalik seada ülemine piir. Selleks peame hindama ranniku ühikpikkusele jõudvat energiat ja korrutama selle läbi ranniku pikkusega. Me ei uuri, millise seadeldisega võiks kogu seda energiat koguda. Küsime lihtsalt alustuseks, kui palju seda energiat on.

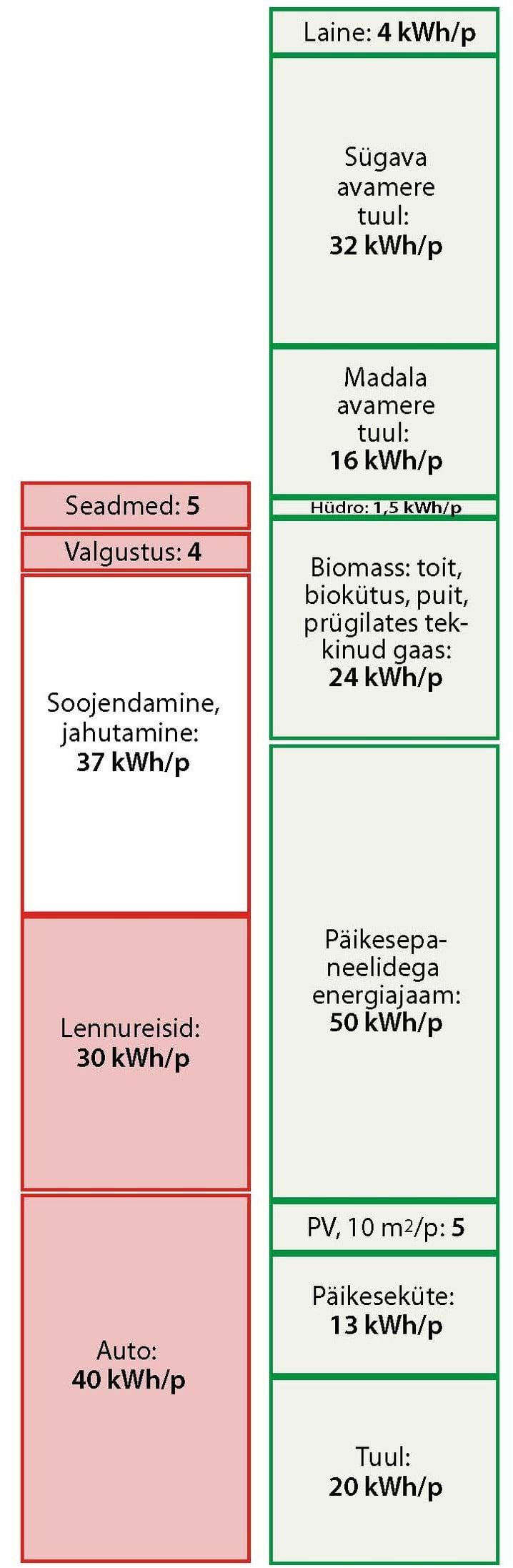
Atlandi ookeani lainete võimsust on mõõdetud: see on ligikaudu $40kW$ avatud ranniku meetri kohta. See kõlab väga suure võimsusena! Kui igal inimesel oleks üks meeter rannikut, saaks me sealt kätte kogu oma $40kW$, mida me tarbimisühiskonna liikmena igapäevaselt vajame. Paraku on meie elanikkond liiga suur. Igaühele ei jätku ühte meetrit Atlandi ookeani suunas vaatavat rannikut.

Kaardilt on näha, et Suurbritannial on umbes $1000km$ Atlandi ookeani rannikut (üks miljon meetrit), mis teeb $1/60m$ elaniku kohta. Seega saame ühe elaniku kohta $16kWh$ energiat päevas. Kui me eraldaksime kogu selle energia, oleks Atlandi ookeani rannik peegelsile. Siiski ei suuda ükski olemasolev süsteem eraldada kogu laineenergiat, midagi läheb mehaanilise energia elektrienergiaks muundamisel paratamatult kaotsi. Oletame, et meil on suurepärane lainemasin, mis muudab $50\%$ laineenergiast elektrienergiaks, ja me suudame selliste masinatega täita $500km$ Atlandi ookeani rannikust. See tähendaks, et me saame teoreetilisest maksimumist kätte $25\%$. See teeks $4kWh$ inimese kohta päevas. Teen siin jällegi tahtlikult üsna ekstreemseid eeldusi, et rohelise energia panust võimendada – ma arvan, et paljudele lugejatele tundub mõte täita pool Atlandi ookeaniga piirnevast rannikust lainete neelajatega üsna utoopilisena.

Kuidas paistavad selles arutluses kasutatud numbrid kui neid võrrelda praegu olemasoleva tehnoloogiaga? Selle raamatu kirjutamise ajal leidub vaid kolm seadet, mis töötavad sügavas vees: kolm laineenergia kogujat Pelamis (joonis 12.1), mis on ehitatud Šotimaal ja paigaldatud Portugali. Nende kohta ei ole reaalseid andmeid avaldatud, aga Pelamise seadmete tootjad ennustavad, et pigem vastupidavust silmas pidades konstrueeritud kahe kilomeetri pikkune lainefarm, mis koosneb $40$ meremaost, võiks anda lainefarmi iga meetri kohta $6kW$. Kasutades oma arvutustes seda numbrit, kahaneb $500km$ lainefarmi tootlikkus ühe inimese kohta $1,2kWh$-ni. Nii et ma kahtlustan, et ehkki laineenergia võib olla kasulik väikeste, kaugetel saartel asuvate kogukondade jaoks, ei mängiks see Suurbritannia energiaprobleemi lahendamisel eriti olulist rolli.

Kui palju kaalub Pelamis ja kui palju sisaldab see terast? Üks madu, mille maksimaalne võimsus on $750kW$, kaalub $700$ tonni, ning selle sisse mahub $350$ tonni ballasti. Seega on selles ligikaudu $350$ tonni terast. Kaalu ja võimsuse suhe on ligikaudu $500kg$ ühe $kW$ kohta (maksimaalselt). Seda saab võrrelda avamere tuuleparkide kohta käivate sarnaste andmetega: avamere tuuleturbiin, mille maksimaalne võimsus on $3MW$, kaalub koos vundamendiga $500$ tonni. Seega on tuuleparkide kaalu ja võimsuse suhe umbes $170kg$ ühe $kW$ kohta. Samas, Pelamis on alles esimene prototüüp ning võib arvata, et tulevikus see suhe paraneb.

Kuidas me teeme vahet puidust ja puidu imitatsioonist tehtud seinal? Me koputame seina, st paneme selle võnkuma ja kuulatame. Et teada saada, kas tegemist on tühja või täis bensiinitünniga, pole vaja korki lahti keerata. Aitab koputusest tünni seinale ja on selge, millega tegu. 

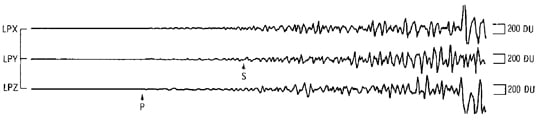
Kuidas saab teada, mis toimub Maa sügavustes? Samamoodi – tuleb koputada ja kuulata, mis vastu kajab.

Maad me tegelikult ei pea ise koputama, piisab maavärinatest tekkinud tõugete kuulamisest. Sest maas levivad lained üsna samamoodi, nagu atmosfääris.

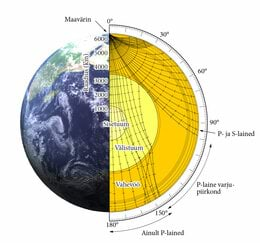
Kõrvaloleval pildil on näha, et maavärina epitsentris moodustuvad lained ei jõua igal pool Maa teisele küljele. Maa tuum tekitab varju, nii et kui on teada maavärina toimumise koht ning seismojaamade võrgustik annab piisavalt tihedalt andmeid maapinna võnkumiste kohta, saab selle järgi teada Maa tuuma suuruse. Enamgi veel – pildil on näha, et lained ei levi läbi Maa otse, vaid nad murduvad. Lainete murdumine on sarnane sellega, mida õppisime põhikooli valgusõpetuses – nii nagu muutub valguskiire suund, kui see levib hõredamast (väikese tihedusega) keskkonnast tihedamasse (suurema tihedusega keskkonda), muutub ka laine suund. Seetõttu saame maavärina lainete levides andmeid ka Maa kihilise sisestruktuuri kohta.

Maa võnkumiste füüsika on keerulisem ja mitmekesisem, kui siin kirjeldasime, aga ehk saite veidi aimu sellest põnevast füüsika ja geograafia puutepunktist.

Aga kuidas saaks teada, mis on Kuu sees? Maavärinaid asendavad seal meteoorid. Seismojaamad toimetati sinna erinevatel kuumissioonidel. 

Kuidas uurida Kuud?

11. aprilil 1970. aastal startis Apollo 13 missioon. Selle kanderakett Saturn V koosnes kolmest astmest. Esimene ja teine aste kukkusid pärast kütuse ärapõlemist tagasi Maale, aga kolmandat astet (S-IVB) kasutati teenindusmooduli, juhtmooduli ja kuumooduli Kuu poole suunduvale trajektoorile tõukamiseks. Kui astme kütus oli ära
kulutatud, eraldus see moodulitest, jätkas iseseisvalt teed Kuu poole
ning lõpuks rammis seda. Mooduli raadiosignaale jälgides oli võimalik kokkupõrke koht ja aeg üsna täpselt kindlaks teha.

S-IVB astmete kokkupõrked andsid asendamatuid kalibratsioonisignaale Apollo seismojaamade võrgustikule, mis töötas Kuu pinnal aastatel 1969–1977. Kuna nende kokkupõrked toimusid kindlatel aegadel ja kohtades, siis oli võimalik heli levimise kiirust Kuu koores otseselt mõõta.

Apollo 13 missiooni ajal asus Kuul vaid üks seismomeeter, mille oli sinna viinud Apollo 12 viis kuud varem. Apollo 13 S-IVB astme kokkupõrge Kuuga toimus sellest 135 kilomeetri kaugusel.

Umbes 30 m läbimõõduga kraater, mis tekkis 14. aprillil 1970. a kokkupõrkel Kuuga. See asub Mare Cognitumist põhjas –2,55° laiuskraadil ja –27,88° pikkuskraadil.	Seismojaam Apollo 12 maandumiskohas Kuul. Seismograaf jälgib pinna liikumisi, registreerides seismilisi laineid. Vasakul paiknev mõõteseade on muutuva temperatuuri ja sellega kaasnevate soojuspingete eest kaitstud metallfooliumiga.

LROC (Lunar Reconnaissance Orbiter Camera) töörühm on praeguseks leidnud ja tuvastanud enamiku selliste kokkupõrgete asukohad. Kasutades LRO täpseid koordinaate ja LROC suuna andmeid, on nende koordinaate ja kauguseid seismojaamadest praegu võimalik palju täpsemalt kindlaks teha kui varem, seda isegi mõnesaja meetri täpsusega. Nii on võimalik veelgi täpsem kalibratsioon, et luua detailsem Kuu sisemuse mudel.

Apollo programmi seismovõrk salvestas üle 13 000 seismilise sündmuse ja see andmestik on kogu programmi üks tähtsamaid saavutusi.

Gravitatsioonilained on massi liikumisega kaasnevad aegruumi võnked, mis levivad tekkeallikast lainetena. Gravitatsioonilainete olemasolu ennustas üldrelatiivsusteooria põhjal Albert Einstein 1916. aastal.

Mida gravitatsioonilaine „teeb“? Ehkki piltidel kujutatakse neid laineid tavaliselt samamoodi nagu veelaineid, siis tegelikult ei kõigu gravitatsioonilaine peal olev objekt üles-alla, vaid objekti pikkus muutub hoopis gravitatsioonilainete levimise suunas risti. See tähendab, et näiteks gravitatsioonilaines olev pall muutub õige pisut loperguseks.

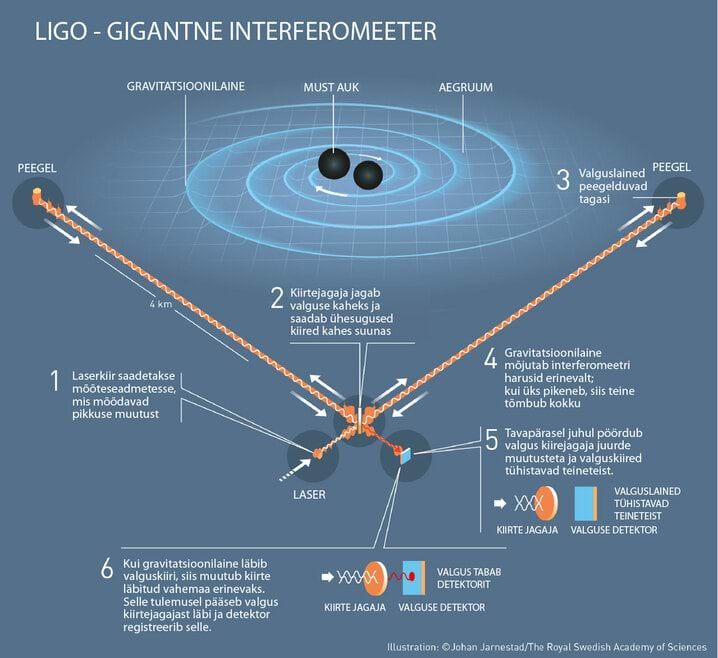
Siit ka idee, et gravitatsioonilainete avastamiseks tuleb võrrelda mingi objekti mõõtmeid kahes ristuvas suunas. Kui objekti kuju muutub, siis on põhjust andmeid uurida. Gravitatsioonilainete mõõtmiseks ehitati USAs laserinterferomeetri-gravitatsioonilainete observatoorium LIGO (Laser Interferometer Gravitational-Wave Observatory), mis moodustub kahest ristuvast 4 km pikkusest õlast.

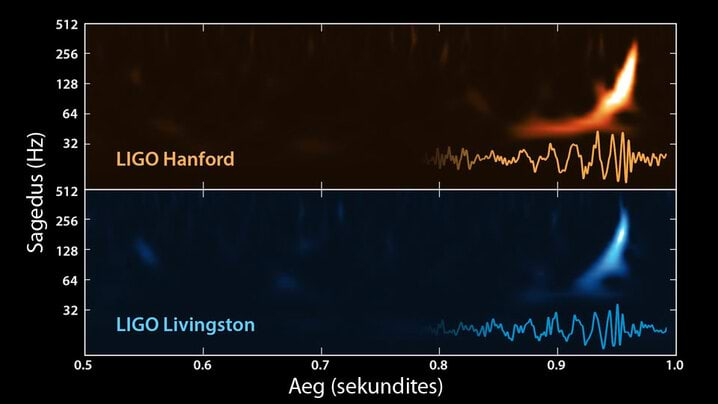
Gravitatsioonilained läbivad pidevalt Maad, kuid isegi kõige tugevamatel neist on imeväike mõju ning nende allikad on üldiselt kaugel. Näiteks 14. septembril 2015. aastal tuvastati signaal, mida hakati nimetama sündmuseks GW150914. Sündmus ise oli see, et Maale jõudsid lained, mis tekkisid kahe musta augu liitumisest üle miljardi valgusaasta tagasi ning muutsid 4 km LIGO õla pikkust prootoni 1/10000 laiuse võrra. See muutus on samaväärne lähima galaktika kauguse muutusega ühe millimeetri võrra. Isegi äärmuslike gravitatsioonilainete toime on väga väike ning neid on võimalik märgata ainult keerukate detektorite abil.

Nüüdseks on sündmuseid registreeritud juba märksa rohkem.

Oskate ehk arvata, mida sellises olukorras kõige põnevam proovida oleks?