BEST Jõud ja liikumine
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
Füüsika üheks suureks ideeks on lained, sest lainete abil saab seletada, kuidas energia kiirguse teel ühelt kehalt teisele üle kandub - seda isegi siis, kui kehad üksteisega kokku ei puutu. Lained kannavad informatsiooni, mida inimesed või spetsiaalsed detektorid tuvastada suudavad. Lainete mõistmine aitab meil suhelda, universumi ehitust uurida ja energiat soovitud paika üle kanda.
Füüsika üheks suureks ideeks on elekter ja magnetism. Elektrilaengute omadused ja mõju mõjutavad meie elukeskkonda suurel määral. Elektrostaatilised jõud hoiavad ainet koos ning mõjutavad keemilisi muutusi. Elekter ja magnetism näivad esmapilgul erinevate nähtustena, kuid selgub, et need on omavahel tihedalt seotud. Elektri ja magnetismi mõistmine aitab erinevaid tehnoloogiaid välja arendada ning leida rakendusi, mis meie igapäevaelu paremaks muudavad.
Et keha hakkaks liikuma, peab miski seda tõukama või tõmbama. Siis võime öelda, et kehale mõjub jõud. Ka liikuva keha aeglustamiseks, peatamiseks või selle liikumissuuna muutmiseks peab sellele mõjuma jõud.
Raskemate ja/või kiiremini liikuvate kehade liikumist on raskem muuta. Kehale mõjuv jõud võib muuta ka selle kuju. Kehale üheaegselt mõjuvad kaks jõudu võivad moonutada selle kuju (nt venitades, surudes või keerates).
Inimene oma silmaga jõudu ei näe, näeme vaid selle mõju. Keha liikumise või kuju muutumine näitab, et sellele mõjub jõud.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
| 1. | Mõista, et raskemate ja/või kiiremini liikuvate kehade liikumist on keerulisem muuta | P | Impulss | Jõud või impulss? |
| 2. | Tunda ära olukorrad, milles (tõmbe- või tõuke) jõud mõjuvad | P | Kas tegu on jõuga | |
| 3. | Kirjeldada erinevates olukordades muutusi, mida jõud põhjustab keha kiirusele, suunale ja/või kujule | Mida see jõud teeb? | ||
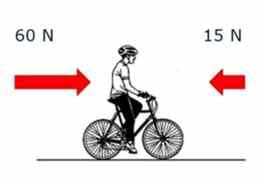
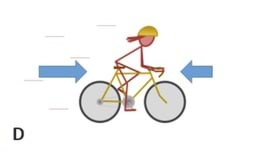
| 4. | Ennustada korrektselt erineva suuruse ja suunaga jõudude mõju kehale | Suur jõud, väike jõud | Jalgratturile mõjuvad jõud | |
| 5. | Selgitada muutusi, mida põhjustavad rohkem kui üks üheaegselt mõjuv jõud | B | Lisajõud |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Õpilaste seas leidub on tõenäoliselt neid, kel esineb jõu teadusliku arusaama osas püsivaid valestimõistmisi. Nad võivad omada jõu kohta kindlaid ettekujutusi, mis tulenevad selle sõna kasutamisest erinevates kontekstides ja/või oma kogemustest. Tunnis tasub kulutada aega selleks, et õpilastel tekiks jõu mõjudest väga selge arusaam. Harjutades selle arusaama kasutamist mitmesugustes igapäevastes olukordades aitame kinnistada strateegiaid, mida edaspidi keerulisemate näidete käsitlemisel vaja läheb.
Impulsi õpetamine (kvalitatiivselt) enne jõu mõistet annab õpilastele nimetuse, millega kutsuda objekti liikumises või paigal hoidvat omadust. See on üsna intuitiivne näiteks õpilastele, kes on kogenud olukorda, kus ostukäru muutub suurema koorma all raskemini manööverdatavaks. Edaspidi saab tutvustada jõudu kui midagi, mis muudab keha liikumist (või kuju). Selline lähenemine aitab õpilastel mõelda jõust kui kahe keha vahelisest vastastikmõjust ning mitte ühe keha sisemisest omadusest.
Selles etapis on oluline rõhutada, et „jõud põhjustab kiiruse, suuna ja/või kuju muutusi."
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon arendab olemasolevatele jõudude toimimise kogemustele tuginedes suurt ideed, et mõista, kuidas ennustatakse erinevates olukordades kehale mõjuvaid jõude.
Mõistmise arendamise esimese sammuna kontrollime arusaama sellest, miks on liikuva keha liikumise muutmine raske. Seejärel uurime, mis juhtub liikuva kehaga, kui sellele mõjub sirgjooneliselt rohkem kui üks jõud.
Gunstone ja Watts (1985) kirjeldavad selgelt, millised on jõudude eduka õpetamise väljakutsed. Nad viitavad paljudele teistele teadlastele, kes väidavad, et sissejuhatavas mehaanikas on õpilaste uskumusi raskem muuta kui mõnes muus loodusteaduslikus valdkonnas. See on teema, millest õpilastel on väga tugevad arusaamad, sageli koos paljude väärarusaamadega. Eksimused põhinevad tavaliselt õpilaste tõlgendustel nende enda kogemustest ja seetõttu on neid väga raske muuta.
Nooremad õpilased seostavad sõna "jõud" sageli elusolenditega, sest kujutatakse ette, et kehadel on „jõud," mis paneb asju liikuma või kutsub aktiivselt mingit tegevust esile. Näiteks võivad õpilased kirjeldada ülespoole visatud palli kui keha, mis osutab gravitatsioonijõule vastupanu (Driver et al, 1994). Sageli seostatakse jõude ka „aktiivsete" kehadega, nagu näiteks autodega, mis võivad ise liikuda või panna teisi asju liikuma.
Uuringud näitavad (Gunstone ja Watts, 1985, Driver et al, 1994), et õpilased arvavad sageli, et liikuv keha omab jõudu, mis hoiab seda liikumises, ning mis lõpeb, kui keha seisma jääb. Osborne (1985) leidis, et vanemaks saades on õpilased üha enam seisukohal, et keha liikumas hoidmiseks on vaja liikumissuunas mõjuvat jõudu. Uuringus, milles osales 200 õpilast, leidis ta, et 46% 13-aastastest õpilastest usub seda; 14-aastaste puhul kasvas antud uskumus 53- protsendini ning 15-aastaste puhul 66-protsendini.
Varasemates õpingutes on õpilased tõenäoliselt kirjeldanud jõude kui tõukeid või tõmbeid. Shevlin (1989) märgib aga, et õpilased ei pruugi mõningaid väga kiireid tegevusi, näiteks „lööke" või „viskeid", üleüldse tõukejõududega seostada.
Tundides õpivad õpilased sageli „füüsiku vaatenurka" ja rakendavad seda ilmselgelt „füüsika tüüpi" probleemidele, ent tegelikku maailma tõlgendatakse jätkuvalt teistmoodi. Jõud on sõna, mida kasutatakse mitmesugustes tuttavates kontekstides, kuid millel on loodusteaduses konkreetne tähendus. Õpilase väärarusaamad võivad olla nii tugevalt kinnistunud, et tulemuste kooskõlastamiseks oma maailmavaatega tehakse valesid vaatlusi. Näiteks kahe väliselt identse palli kukutamisel võivad õpilased end veenda, et nähakse, et raskem pall tabab maad esimesena.
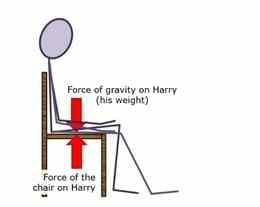
Samuti on keeruline mõista paigalolevatele kehadele mõjuvaid jõude. Paljud õpilased arvavad, et need jõud, mis lükkavad, tõmbavad ja põhjustavad muutusi liikumises, erinevad neist jõududest, mis hoiavad asju paigal. Näiteks Norra uuringus (Sjoberg ja Lie, 1981) ei tundnud 1000st keskkooliõpilasest pooled ära laual seisvale raamatule laua poolt mõjuvat ülespoole suunatud jõudu.
Antud arengutööriistade komplektis tuuakse kõige esimesena sisse esimesena impulsi kvalitatiivne mõiste. Driver jt (1994) viitavad paljudele uuringutele, mille kohaselt võimaldab impulsi õpetamisest alustamine näha jõudu kui midagi, mis põhjustab impulsimuutusi. Nii on võimalik ära hoida olukorda, kus õpilased kasutavad nimetust „jõud" selleks, et kirjeldada "liikuva keha sisemist mõju, mis hoiab keha liikumas". Pärast seda, kui arutletakse selle üle, mis muudab keha liikumise muutmise raskemaks, võib mõnel õpilasel olla vaja jõudude tuvastamist harjutada ning kirjeldada, kuidas üksikud jõud olukorda muudavad. Teised õpilased võivad olla aga võimelised jõudude mõju kohe kirjeldama. Kui õpilastele esitatakse ülesanne ennustada eri suurusega jõudude mõju olukordades, kus need mõjuvad esemele üksikult ja seejärel paarikaupa, tugevdab nende arusaama ning võimaldab neil õpitut ka tundmatutes olukordades rakendada.
Driver, R., Squires, A., Rushworth, P. and Wood-Robinson, V. (1994) Making sense of secondary science, research into children’s ideas, Routledge, London, England.
Gunstone, R. and Watts, M. (1985) ‘Force and Motion’ in Driver, R., Guesne, E. and Tiberghien, A. Children’s Ideas In Science, Open University Press, Milton Keynes, England.
Osborne, R. (1985) ‘Building on children’s intuitive ideas’, in Osborne, R. and Freyberg, P., Learning in Science, Heinemann, Aukland, New Zealand.
Shevlin, J. (1989) ‘Children’s prior conceptions of forces aged 5-11 and their relevance to Attainment target 10 of the National Curriculum of Science’, Unpublished M.Ed. thesis, University of Leeds.
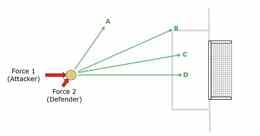
Jõud tekivad, kui kaks keha on vastasmõjus. Kehad võivad vastasmõjusse sattuda otsese kokkupuute teel või ka distantsilt (näiteks kaks magnetit, elektrilaengut või massi). Mida kaugemal kaks keha üksteisest asuvad seda nõrgemad on nende vahel mõjuvad jõud.
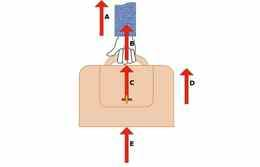
Joonistel esitatakse jõudusid ning jõu suunda noolte abil. Noole ots näitab kehale mõjuva jõu suunda. Noole ots või saba näitab, millises keha punktis antud jõud mõjub (pole oluline, kas kasutatakse noole otsa või saba; tähendus on sama).
Jõu suurust mõõdetakse njuutonites (N). Igapäevastes olukordades saab seda sageli teha vedrukaalu või tavalise köögikaalu abil.
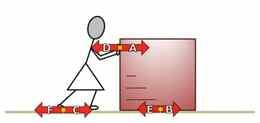
Jõudu avaldab alati miski ning see mõjub alati millelegi. Kõige selgem viis jõu noole sildistamiseks on: keha A poolt kehale B mõjuv jõud.
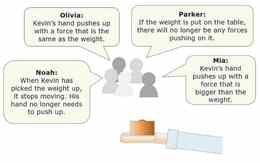
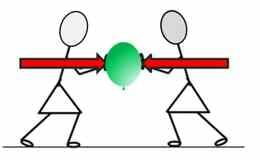
Kui kaks keha on vastasmõjus, avaldub neile mõlemale alati mingi jõud. Keha A avaldab kehale B jõudu ning keha B avaldab kehale A jõudu. Jõud tekivad alati paarikaupa. Vastasmõju olukorras on igal ajahetkel keha A poolt kehale B mõjuv jõud keha B poolt kehale A mõjuva jõuga võrdne ja vastassuunaline.
Õppefookus
Jõud tekivad kahe keha vastasmõjul; ühele kehale mõjuv jõud on teisele kehale mõjuva jõuga alati sama suur ent vastassuunaline; nooltega tähistatakse jõu suurust, suunda ja asukohta.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | P | Diagnostilised küsimused | Töölehed | |
| 1. | Nimetada igapäevaolukordades esinevaid jõude | Nimeta antud jõud | ||
| 2. | Esitada jõude sobiva suuruse ja suunaga noole abil | Kui suur on jõud? | Jõudude mõõtmine | |
| 3. | Asetada nooled kohta, mis esitavad korrektselt jõu rakendumist | Kus jõud asub? | ||
| 4. | Sildistada nooli, et kirjeldada jõu mõju: keha B poolt kehale A mõjuv jõud | Massi lisamine | ||
| 5. | Kirjeldada, et jõud esinevad alati paaridena ning et keha A poolt kehale B mõjuv jõud keha B poolt kehale A mõjuva jõuga suuruselt võrdne ja suunalt vastupidine | B | Massi hoidmine |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon arendab suurt ideed, tuginedes jõudude kujutamisele noolte abil. Seeläbi luuakse alus arusaamale, kuidas täpselt kehadele mõjuvaid jõude kujutatakse ja kirjeldatakse.
Mõistmise arendamise esimese sammuna kontrollime arusaama sellest, kuidas igapäevaseid jõude nimetatakse. Seejärel töötatakse välja jõudude kujutamise ja kirjeldamise täpsem meetod, võimaldades ka keerukamate jõudiagrammide mõistmist.
Mõne õpilase jaoks on jõududest suuruse ja suuna järgi mõtlemine raske (Driver et al, 1994). Terry jt (1985) leidsid, et paljud 11-14 aastased õpilased kasutasid jõude esitavaid nooli üsna vabavoliliselt: neid ei märgitud jõu rakenduspunkti, ei kasutatud jõu suuna ega suuruse tähistamiseks.
Õpilased ei tunnista igale jõule vastavat „reaktsioonijõudu" alati intuitiivselt. Erickson ja Hobbs (1978) soovitavad kasutada tegevusi, milles õpilastel tuleb jõupaarid tuvastada näiteks nii, et „keha A lükkab keha B." Seeläbi paraneb paarisjõudude äratundmine ja mõistmine.
Terry jt (1985) uuringud on näidanud, et Newtoni kolmanda seaduse väljendamine kujul: „Igale mõjule (jõule) vastab võrdne ja vastupidine reaktsioon" on 11-16 aastaste õpilaste jaoks segadusttekitav. Palju selgem on seda kirjeldada täies mahus: kehale A keha B poolt mõjuv jõud on kehale B keha A poolt mõjuva jõuga võrdne ja vastassuunaline.
Jõudude kirjeldamise arengutööriistad tutvustavad õpilastele jõudude üldnimetusi. Mõnel õpilasel võib olla jõunoolte joonistamise oskusi samm-sammult arendada, teised aga suudavad neid kohe algusest korrektselt tõlgendada ja joonistada. Kui õpilastele antakse ülesandeid, milles tuleb kirjeldada keha A poolt kehale B mõjuvaid jõude, arendab see nende võimet analüüsida järk-järgult ka keerulisemaid jõudiagramme. Heaks näitlikustamise viisiks sellest, et jõud tekivad alati paarikaupa ning on võrdsed ja vastassuunalised, on arutleda selle üle, mis juhtub, kui õpilase ühte peopessa asetatakse mingi raskus (Minstrell, 1982).
Driver, R., Squires, A., Rushworth, P. and Wood-Robinson, V. (1994) Making sense of secondary science, research into children’s ideas, Routledge, London, England.
Erickson, G. and Hobbs, E. (1978) ‘The developmental study of student beliefs about force concepts’, Paper presented to the 1978 Annual Convention of the Canadian Society for the Study of Education. 2 June, London, Ontario, Canada.
Minstrell, J. (1982) ‘Explaining the “at rest” condition of an object’, The Physics Teacher 20:10-14.
Terry, C., Jones, G. and Hurford, W. (1985) ‘Children’s conceptual understanding for force and equilibrium’, Physics Education 20(4): 162-5.
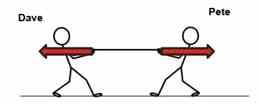
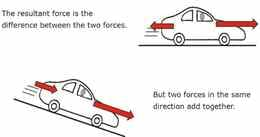
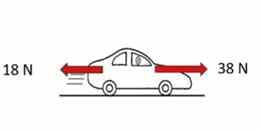
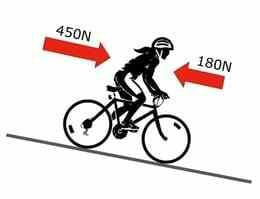
Sageli mõjub kehale korraga rohkem kui üks jõud. Kahe samasihilise (samas suunas või vastassuunas) mõjuva jõu kogumõju leitakse nende liitmisel, võttes arvesse nende suunda. Keha liikumise selgitamiseks on vaja määrata kõik sellele mõjuvad jõud. Nii arvutatakse kehale horisontaalses ja/või vertikaalses suunas mõjuva resultantjõu.
Statsionaarsed kehad: Kui keha ei liigu (seisab paigal) ja sellele mõjuv resultantjõud on null, siis puudub jõud, mis seda liikuma paneks. Keha jääb paigale.
Muutuv liikumine: Kui paigalseisvale kehale mõjub nullist suurem resultantjõud, hakkab keha jõu suunas liikuma ja selle kiirus ühtlaselt suurenema.
Kui liikuvale kehale mõjub liikumissuunaga samassuunaline nullist suurem resultantjõud, suureneb keha kiirus järk-järgult. Kui liikuvale kehale mõjub liikumissuunaga vastassuunaline nullist suurem resultantjõud, siis keha kiirus väheneb.
Igal juhul on (mingi keha) liikumiskiirus seda suurem, mida suurem on resultantjõud. Mida suurem on keha, seda väiksem on selle kiiruse muutus.
Ühtlane liikumine: Kui keha liigub ühtlase kiirusega mööda sirgjoont ja sellele mõjuv resultantjõud on null, siis puudub jõud, mis selle liikumist muudaks. Keha jätkab ühtlase kiirusega liikumist.
Õpifookus
Resultantjõud on kõigi kehale mõjuvate jõudude summa, võttes arvesse nende suunda. Kui resultantjõud puudub, on jõud tasakaalus. Tasakaalustamata jõud muudavad keha kiirust, suunda ja/või kuju.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
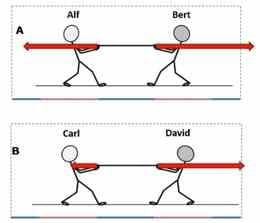
| 1. | Tunda ära tasakaalustatud ja tasakaalustamata jõudude paarid | Tasakaalus või mitte? | ||
| 2. | Hinnata tasakaalustamata jõupaaride võrdlemise teel resultantjõudude suurust | Resultantjõud | ||
| 3. | Arvutada kahe samasihilise jõu resultantjõu suurust ja suunda | Kui palju jääb üle? | Resultantjõu arvutamine | |
| 4. | Kirjeldada mis juhtub, kui kehale mõjub kaks samasihilist tasakaalustamata jõudu | Mis juhtub edasi? | ||
| 5. | Kirjeldada mis juhtub, kui kehale mõjub kaks ühesuurust jõudu, mis on samasihilised ent vastassuunalised | Mis muutub? | Toolil istumine |
Selles tunnis on läbivalt kasutatud samu ühikuid. Mõnele õpilasele võib olla kasulik, kui neid innustatakse kilo-Newtonite ja Newtonite vahel teisendama.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon arendab suurt ideed, tuginedes arusaamisele, et mitme jõu koosmõju korral mõjutab iga jõud tulemust. See aitab arendada õpilaste võimet ühele kehale mõjuva mitme jõu koosmõju tulemit.
Mõistmise arendamise esimese sammuna kontrollime arusaama sellest, kuidas mõistavad õpilased tasakaalustatud ja tasakaalustamata jõude. Seejärel arendatakse resultantjõu arvutamise oskust, et võimaldada mõista, kuidas kaks samasihilist jõudu keha mõjutavad.
Erikson ja Hobbs (1978) leidsid 32 Kanada õpilase (vanuses 6-14 aastat) seas läbi viidud uuringus, et kui õpilased mõtlesid kahest samale kehale mõjuvast jõust, siis näisid nad mõtlevat, et need jõud on omavahelises võitluses, kus suurem jõud domineerib väiksema üle. Osborne (1985) leidis Uus-Meremaa õpilaste seas sarnast mõtlemist. Tema uuringus osalenud 26 õpilasest kümme õpilast nägid tasakaalu kui selle võitluse lõppu, mille järel kõik jõud lakkavad tegutsemast. Tegelikult tegutsevad mõlemad jõud jätkuvalt, st "jõudu, mis paneks asju muutuma, lihtsalt ei jää üle".
Olukorras, kus jõud pole tasakaalus, tuvastasid Driver jt (1994) õpilaste seas mitmeid levinud väärarusaamu, mis võivad olukorra tulemuse osas segadust tekitada:
- Kui keha on liikumises, mõjub sellele resultantjõud
- Ilma liikumiseta jõudu ei eksisteeri
- Kui keha on liikumises, siis mõjub jõud liikumissuunas
- Kui liikumine puudub, siis kehale mingeid jõude ei mõju
- Kui puudub jõud, siis keha ei liigu
- Ühtlane kiirus on ühtlase jõu tulemuseks
Esimene neist väärarusaamadest on väga laialt levinud, sest igapäevaelus (näiteks jalgrattasõidul või autoga sõites) peame ühtlase kiirusega liikumise jaoks rakendama ühtlast jõudu, et hõõrdumist ja õhutakistust ületada. See tähendab, et kui keha on paigal, siis tajutakse ekslikult, et sellele ei mõju ühtegi jõudu - siit jsaavad alguse ka teised väärarusaamad. Driver jt (1994) viitavadki Sjobergi ja Lie (1981) poolt 1000 Norra keskkooliõpilase seas läbi viidud uuringule, mille käigus leiti, et vaid 50% noortest tunnistas "passiivseid" jõude, mis mõjuvad siis, kui liikumist ei toimu.
Osade õpilaste jaoks võib raskusi tekitada resultantjõudude arvutamine. Teoses "The language of mathematics in science" (2016) märgib Boohan, et peamine erinevus matemaatikas ja loodusteadustes tehtavate arvutuste vahel on see, et loodusteadustes on arvudel enamasti nii ühik kui ka number. Seega peavad õpilased pöörama tähelepanu mitte ainult numbrite, vaid ka ühikute kasutamisele. Arvude liitmine ja lahutamine on võimalik vaid siis, kui neid väljendatakse samades ühikutes. Vastassuunaliste jõudude kombineerimisel võib õpilastel võib tekkida kiusatus kasutada positiivsete ja negatiivsete arvude arvjooni. See töötab, kuid kui jõud on vastassuunalised, on lihtsam väiksem jõud suuremast lahutada ja jõudude suundasid eraldi käsitleda. See lähenemine võib aidata selgitada ideed, et jõududel on nii suurus kui ka suund.
Tasakaalustatud ja tasakaalustamata jõudude arengutööriist tuletab õpilastele meelde, et igapäevastes olukordades mõjub kehadele tavaliselt mitu jõudu korraga. Õpilased alustavad sellest, et proovivad ära tunda olukorrad, kus jõupaarid on kas tasakaalus või mitte. Kui jõud on tasakaalustamata, võrdlevad õpilased resultantjõu suuruse hindamiseks kahe mõjuva jõu erinevust. Selle jõu arvutamine annab õpilastele võimaluse mõelda analüütiliselt selle üle, kuidas jõupaarid toimivad, ning resultantjõudude mõju hinnates kinnistub resultantjõu idee õpilaste arusaamaga jõudude toimimisest. Neid ideid käsitleti dokumendis PFM 1.3: Mida jõud teevad.
Boohan, R. (2016) The language of mathematics in science, Association for Science Education, Hatfield, England.
Driver, R., Squires, A., Rushworth, P. and Wood-Robinson, V. (1994) Making sense of secondary science, research into children’s ideas, Routledge, London, England.
Erickson, G. and Hobbs, E. (1978) ‘The developmental study of student beliefs about force concepts’, Paper presented to the 1978 Annual Convention of the Canadian Society for the Study of Education. 2 June, London, Ontario, Canada.
Osborne, R. (1985) ‘Building on children’s intuitive ideas’, in Osborne, R. and Freyberg, P., Learning in Science, Heinemann, Aukland, New Zealand.
Sjoberg, S. and Lie, S. (1981) Ideas about force and movement among Norwegian pupils and students, Institute of Physics Report Series: Report 81-11, University of Oslo.
Kui keha libiseb mööda pinda, mõjub sellele hõõrdejõud liikumisele vastupidises suunas. Kui keha proovitakse mööda pinda lükata või tõmmata, ent see ei hakka liikuma, mõjub sellele hõõrdejõud tõuke- või tõmbejõule vastupidises suunas. Hõõrdejõudu avaldab pind, mille peal keha libiseb, või pind, mille peal keha püüab libiseda.
Kehale mõjuv hõõrdejõud tuleneb kokkupuutuvate pindade ebatasasusest mikroskoopilisel tasandil. Kui mingi jõud paneb keha üle mingi pinna libisema (või püüab seda libisema panna), tekib puutetasapinna suunaline jõud. Hõõrdejõudu saab vähendada, kui kasutada vedelikku (määrdeainet), mis täidab pinna tillukesed ebatasasused.
Pinnal asetseva keha puhul tasakaalustab (tühistab) hõõrdejõud rakendatud jõudu, mis püüab seda keha pinnal liikuma panna, kuni teatud piirini (mis sõltub keha kaalust ja kokkupuutes olevatest pindadest). Kui tõmbe- või tõukejõud ületab selle piiri, hakkab keha liikuma. Kui keha hakkab libisema, jääb sellele mõjuv hõõrdejõud sõltumata kiirusest alati sama suureks.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
| 1. | Määrata olukordi, milles hõõrdejõud esineb | P | Millistes olukordades hõõrdejõud tekib? | |
| 2. | Kirjeldada hõõrdejõu mõju kehale | Hõõrdejõud | ||
| 3. | Kirjeldada kahe keha vahel esineva hõõrdejõu tekkepõhjuseid | Hõõrdejõu tekitamine | Hõõrdumiskatsed | |
| 4. | Selgitada, kuidas määrdeained hõõrdejõudu vähendavad | Pidurdamine vihmas | Kaldpind | |
| 5. | Selgitada, kuidas kahe keha vahel tekkiv hõõrdejõud takistab liikumahakkamist | Hõõrdejõu puudumine |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon arendab suurt ideed, tuginedes mõistmisele, et pinnal asetseva keha lükkamise või tõmbamise korral tekib hõõrdejõud. Arendame arusaamist hõõrdejõust kui jõust, mis töötab liikuvate või paigalseisvate kehade liikumisele vastu.
Mõistmise arendamise esimese sammuna kontrollime arusaama sellest, millistes olukordades hõõrdejõud tekib. Seejärel arutleme hõõrdejõu põhjustest ja olemusest, et võimaldada mõista, kuidas hõõrdejõud paigalseisvaid kehasid mõjutab ning nakkumise annab.
Hõõrdumine on jõud, mis tekib kahe keha vahelisel vastasmõjul. See jõud aga erineb enamikust teistest vastastikmõju olukorras tekkivatest jõududest (Hart, 2002). Võib-olla just seetõttu oli kolmekümne kaheksa 12-16 aastase õpilase seas läbi viidud uuringu tulemuseks, et vähem kui pooled õpilastest mõtlevad hõõrdumisest kui jõust (Stead ja Osborne, 1980). Driver jt (1994) väidavad, et paljud õpilased mõtlevad jõududest vaid kui „asjade liikuma panemisest," mitte kui „asjade peatamisest".
Hilisem Steadi ja Osborne'i (1981) uuring, mis viidi läbi 47 keskkooliõpilase seas, näitas, et õpilased arvavad ka, et:
- hõõrdejõud sõltub liikumisest (17 õpilast)
- hõõrdejõud esineb vaid tahkete kehade vahel (12 õpilast)
- hõõrdejõud on sama mis reaktsioonijõud (9 õpilast)
- hõõrdejõul puudub suund ning see erineb liikumisele vastu töötavast jõust (mõned õpilased)
Steadi ja Osborne'i 1980. aasta uuringus leiti, et pooled 13-aastastest õpilastest pidasid hõõrdejõudu hõõrumiseks. Hõõrdejõud esineb aga ka liikumatute kehade vahel. 11-14- aastastele õpilastele mõeldud õpikutes räägitakse sageli sellest, et jalanõud või rehvid on hea nakkuvusega. See tähendab, et jalanõul või rehvil „on suur hõõrdejõud," mis pole aga tõsi. Pigem tuleks öelda, et need jalanõud või rehvid suudavad hästi hõõrdumist tekitatada, kui neid mööda mingit pinda lükata, ning sageli takistab tekkiv hõõrdejõud nende liikumist.
Hõõrdumise arengutööriistad tuletavad õpilastele meelde, et hõõrdeõud on jõud, mis mõjutab peaaegu kõiki meie füüsikalisi tegevusi. Esmalt tuleb õpilastel määrata olukorrad, milles hõõrdumine esineb, ning kirjeldada hõõrdejõu mõju. Uurides pindade karedust ja määrdeainete mõju hõõrdejõule, antakse õpilastele võimalus töötada välja hõõrdejõu teaduslik mudel. Analüüsides paigalseisva keha mõju kaldpinnale innustatakse õpilasi mõtlema hõõrdumisest kui kahe keha vahelise vastastikmõju tulemusel tekkivast jõust.
Driver, R., Squires, A., Rushworth, P. and Wood-Robinson, V. (1994) Making sense of secondary science, research into children’s ideas, Routledge, London, England.
Hart, C. (2002), Teaching Newton’s laws as though the concepts are difficult, Australian Science Teachers' Journal, v48 n4 p14-23 Dec 2002.
Stead, K. E. and Osborne, R. J. (1980) Friction, LISP Working Paper 19, Science Education Research Unit, University of Waikato, Hamilton, New Zealand.
Stead, K. E. and Osborne, R. J. (1981) ‘What is friction: some children’s ideas’, New Zealand Science Teacher 27: 51-7.
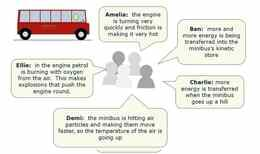
Selleks, et mingit keha üles tõsta või vaatamata vastupanule liigutada, on vaja energiat. Kui kaks või enam keha on vastasmõjus, siis osad kehad kaotavad energiat ning teised saavad energiat juurde. Kõikidesse vastasmõjus olevate kehadesse kätketud energia kogusumma on protsessi lõpus sama mis alguses.
Energiaülekande protsessi lõpus saame energiat juurde saanud või ära andnud kehasid kindlaks määrata, pannes tähele, et nad:
- liiguvad kiiremini (või aeglasemalt) kui varem
- on kuumemad (või külmemad) kui varem
- asuvad gravitatsiooniväljas kõrgemal (või madalamal) kui varem
- on muundunud (venitatud, kokku surutud, painutatud, väänatud) või esialgse oleku taastanud
- on magnetid/elektrilaengud, mille asukoht magnet/elektriväljas on muutunud
Salvestatud energia tüübid on järgmised: kineetiline, soojusenergia, gravitatsiooniline, elastne ja elektromagnetiline.
Kui inimene mingit keha lükkab või tõmbab, väheneb tema keemilise energia varu.
Jõu mõjumise ajal kantakse osa energiavarudest mehaanilise töö abil lõpptarbimisse üle.
Paljud seadmed muudavad energiaülekande meetodit ilma, et nad ise energiat salvestaksid. Näiteks kantakse energiat mootorile sageli üle elektriliselt ning mootorilt edasi mehaaniliselt.
Mitmete protsesside lõpptulemusena kandub osa energiat ümbritsevasse keskkonda, mis muutub seeläbi soojemaks. See on hõõrdumise või takistuse (õhu või vedeliku vastupanu) tagajärg.
Kuigi mistahes protsessi käigus on koguenergia jääv, levib see protsessis hõlmatud kehade ja keskkonna vahel: energia hajub.
Õpifookus
Selleks, et midagi juhtuks, on tarvis potentsiaalset energiat. Igas protsessis toimub energiaülekanne.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
| 1. | Määrata kehad, millel on potentsiaalne energia | Potentsiaalne energia | ||
| 2. | Määrata erinevate kehade potentsiaalne energia | Potentsiaalse energia tüübid | Potentsiaalse energia tsirkus | |
| 3. | Määrata keha potentsiaalne energia mingi sündmuse alguses ja lõpus | Energiaülekanne | ||
| 4. | Kasutada energiaülekannete erinevate vormide kirjeldamisel korrektseid termineid | Energia liigutamine teistesse vormidesse | ||
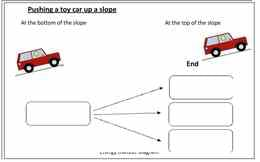
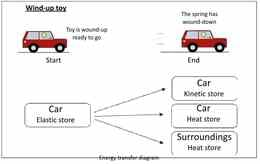
| 5. | Esitada energiaülekandeprotsesse Sankey diagrammi abil | B | Sankey diagramm |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Õpifookus
Jõu mõjul toimub mehaanilise energia muundumine teisteks energia vormideks. Hõõrdejõu abil toimub mehaanilise energia muundamine soojusenergiaks.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | |||
| 1. | Määrata olukorrad, milles toimub energiaülekanne | Kas energiaülekanne toimub? | |||
| 2. | Määrata erinevad energia ülekande viisid | Kuidas energiaülekanne toimub? | Energiaülekande tsirkus | ||
| 3. | Määrata kuhu kantakse energia üle, kui toimub hõõrdumine | Soojenemine tänu hõõrdumisele | |||
| 4. | Kirjeldada, kuidas energiat võib üle kanda erinevatel viisidel | Aeglasem jalgpall | |||
| 5. | Kirjeldada, kuidas energia peaaegu alati kandub lõpuks üle ümbritsevate kehade soojuseks | Kätekõverdus | |||
| Kukkuv õun | Ühtlane kiirus | ||||
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Energiat on peaaegu võimatu seletada ning sageli on õpikutes esitatud definitsioonid valed. Näiteks pole väide „energia paneb asjad liikuma" korrektne. Võib-olla on kõige parem definitsiooni mitte anda, vaid öelda, et "millegi toimumiseks peab olema potentsiaalset energiat".
Õpilaste arusaam energiast areneb aja jooksul. Selles etapis on oluline esitada õpilastele kasulik mudel, mida nad saaksid kasutada oma mõtlemise arendamiseks ning mis ei ole liiga eksitav. BEST-materjalides kasutatav „potentsiaalse energia" ja "energiaahela" mudelid võimaldavad seda saavutada. Selles sissejuhatavas põhiarusaamade materjalis tuvastavad õpilased erinevaid potentsiaalse energia tüüpe ning jälgivad, kas kehade energia erinevate energiaülekannete läbi suureneb või väheneb. Samuti õpivad õpilased kirjeldama mehhanisme ja protsesse, läbi mille energia ühest energia tüübist teise muundub. Edasiste õpingute käigus oskavad õpilased viia läbi ka mõtestatud mõõtmisi ning kasutada võrrandeid, et arvutada igas potentsiaalse energia hulka. Õpilaste kirjeldused energiaülekande mehhanismide ja protsesside kohta muutuvad järk- järgult keerukamaks. Antud õppeetabi energia kvalitatiivse kirjeldamise meetodid on korrelatsioonis sammudega, mis on vajalikud kasuliku kvantitatiivse energiaanalüüsi läbiviimiseks hilisemas õppetöös.
Õpetajana on meil lihtne „libastuda" ning kasutada energiast rääkimisel igapäevaselt, kasutades termineid „energiakasutus," „energiatarve," „energia kasutamine" või „energia tarbimine". See on suures osas vältimatu, mistõttu energia kirjeldamisega seotud probleemide osas on avameelsus suureks abiks. Innustage oma õpilasi enda vigu märkima ning tehke ka mõned tahtlikud vead. Nende vigade parandamine üheskoos on õpilastele hea abivahend, tänu millele areneb nende võime energiast teaduslikult rääkida.
Potentsiaalse energia ja energiaahela väga täpne keelekasutus võib tunduda üsna kohmakas ja tülikas, mistõttu on ebatõenäoline, et see muutuks kunagi energiast rääkimise tavapäraseks viisiks. Energiast mõtlemise varajases etapis toetab selle keele järjepidev kasutamine siiski õpilaste korrektse teadusliku arusaama kujunemist.
Kokkuvõte BESTi lähenemisviisist energia õpetamisele on leitav dokumendist "Best Evidence Science Teaching landing page," mis asub STEM Learning veebilehel (Fairhurst, 2018).
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon arendab suurt ideed, tuginedes mõttele, et millegi toimumiseks on vaja potentsiaalse energia olemasolu. Nii arendame arusaama sellest, et jõudude mõjul toimub energiaülekanne.
Mõistmise arendamise esimese sammuna räägime sellest, et kehad suudavad energiat salvestada mitmel erineval viisil. Seejärel arutleme energiaülekande toimumise üle. Analüüsides, kuidas jõud energiat mehaaniliselt edasi kannab, areneb õpilaste arusaam energiaülekande toimumisest ja sellest, kuidas energia pea alati soojusenergiana hajub.
Energiat on raske õpetada, sest see on abstraktne ja raskesti määratletav mõiste ning sõna energia igapäevase ja teadusliku kasutamise vahel on mitmeid vastuolusid.
Solomon (1983) palus lastel kirjutada kolm või neli lauset, mis näitavad, kuidas nad kasutavad sõna energia. Selgus, et lapsed mõtlevad energiast valdavalt järgmistes mõistetes:
- inimtegevus - „Olen väsinud, sest mul pole rohkem energiat" või "Suudan väga kiiresti joosta, sest mul on palju energiat"
- tervis - „Füüsiline tegevus on hea, sest see suurendab sinu energiavarusid," „Kui energia saab otsa, tuleb tarvitada vitamiine ja ravimeid"
- toit ja kütus - mõned asjad sisaldavad palju energiat, mida saame liikumiseks ja muude tegevuste jaoks kasutada
Õpilaste kõige sagedasem arusaam energiast on see, et nagu toit või kütus, kulub see ära. Seda valearusaama on raske muuta. 12-14 aastaste õpilaste seas läbi viidud uuringus leidis Duit (1981), et isegi pärast õpetamist kasutavad väga vähesed õpilased uute sündmuste kirjeldamiseks energia jäävuse ideed. Tema oletuse kohaselt eelistasid õpilased selle asemel kasutada igapäevaelust tuttavaid ideid. Millar (2011) märkis ka, et õpilased mõtlevad sageli elektrienergiast kui kütusest, mis võib tulla nende kogemusest patareidega, mis „saavad tühjaks".
Energiast rääkides kipuvad õpilased loodusteaduslikke termineid väga vabalt kasutama: Driver jt (1994) kirjeldab mitmetelt teadlastelt kogutud materjalide põhjal, et õpilased ajavad sageli energia mõiste segi jõu, töö või võimsuse mõistetega ning kasutavad neid äravahetatult. Rogers (2018) rõhutab, et on oluline, et õpetajad õpetaksid teaduslike terminite korrektset kasutamist läbi erinevate näidete - nii tekib õpilastel toimuvast korrektne arusaam.
Üldiselt mõeldakse energiast kui ainest, mille voolamine ja jäävus on analoogne ainele. Kuigi see ei ole teaduslikult korrektne, peetakse seda aktsepteeritud analoogiaks (Millar, 2011). Energiaülekande selgitamisel soovitab Tracy (2014) keskenduda protsesside ja mehhanismide kirjeldamisele. Ta väidab, et lihtsalt sildistamise kasutamine energia määratlemiseks protsessi erinevates etappides võib takistada toimuva selget mõistmist.
BESTi materjalides on energia õpetamisel võetud kasutusele raamistik, mis põhineb „potentsiaalsel energial" ja „energiaah[S1]elal;" seda toetavad muuhulgas Boohan (2014), Millar (2014) ja Tracy (2014). Millari (2014) sõnul pole see lähenemisviis „täiuslik - kuid on piisav ja oluliselt parem kui lähenemisviisid, mis põhinevad „energiavormide" loeteludel". Antud lähenemisviisi juhend on leitav Füüsikainstituudi veebilehel.
Millar (2005) soovitab, et energia jäävuse seaduse mõistmiseks peavad õpilased teadma, et peaaegu iga sündmuse puhul esineb mingi soojenemine, olenemata sellest, kas see on soovitud või mitte, ja sellest tulenevalt suureneb ümbritseva keskkonna soojusenergia. Hõõrde- ja takistusjõu ning soojusenergia tekke seostamine tutvustab õpilastele energia hajumise ideed. Energia hajumise kirjeldamine erinevate näidete abil toetab energia jäävuse mõistmist.
Potentsiaalse energia ja energiaülekade esimene arengutööriist tutvustab ideed, mille kohaselt on mingi protsessi toimumiseks vaja potentsiaalset energiat. Järgmise sammuna peaksid õpilased suutma määrata erinevaid potentsiaalse energia liike. Mitmete praktiliste näidete abil õpivad õpilased tuvastama potentsiaalse energia muutusi protsesside alguse ja lõpu vahel. Tänu potentsiaalse energia ja energiaülekannete kirjeldamisele korrektsete terminitega erinevates praktilistes ülesannetes toimub õpitu kinnistumine. Energiülekande kujutamine Sankey diagrammide abil kinnistab samuti õpitut ning tutvustab energia jäävuse seaduse mõistmiseks vajalikku mõtteviisi.
Potentsiaalse energia ja energiaülekade teine arengutööriist paneb õpilasi mõtlema, kuidas energiaülekanne toimub. Energiaülekande protsesside vaatlemine annab õpilastele võimaluse mõningaid sellega seotud protsesse ja mehhanisme kirjeldada. Hõõrde- ja takistusjõude sisaldavate näidete abil tutvustatakse töö tegemise ja soojuse eraldumise vahelist seost. Erinevate näidete ja arutlemise läbi uuritakse soojenemise ja energia hajumise protsesse. Energia hajumise mõistmine on vajalik energia jäävuse seaduse mõistmiseks - seda käsitletakse põhjalikumalt teemas PMA1: Soojenemine ja jahtumine.
Fairhurst, P. (2018). Teaching Energy. [Online]. Available at: https://www.stem.org.uk/best-evidence-science-teaching.
Institute of Physics. Supporting Physics Teaching (SPT): Energy [Online]. Available at: http://supportingphysicsteaching.net/EnHome.html [Accessed July 2018].
Millar, R. (2005). Teaching about energy [Online]. York: White Rose University Press. Available at: http://eprints.whiterose.ac.uk/129328/1/2005_Millar_Teaching_about_energy.pdf.
Millar, R. (2011). Energy. In Sang, D. (ed.) Teaching Secondary Physics. London: Hodder Education.
Millar, R. (2014). Teaching about energy: from everyday to scientific understandings. School Science Review, 96(354), 6.
Rogers, B. (2018). The big ideas in physics and how to teach them, 1 edn Abingdon and New York: Routledge.
Solomon, J. (1983). Messy, contradictory and obstinately persistent: a study of children's out of school ideas about energy. School Science Review, 65(231), 9.
Tracy, C. (2014). Energy in the new curriculum: an opportunity for change. School Science Review, 96(354), 11.
Kui me tahame seletada, miks kehad liiguvad nii, nagu nad liiguvad, peame kõigepealt suutma seda liikumist selgelt ja täpselt kirjeldada.
Üheks kasulikuks mõõdupuuks on vahemaa, mille keha alates mingist algushetkest läbinud on.
Teiseks mõõdupuuks on keha kiirus. Keha kiirus on suurus, mis näitab, millise vahemaa keha mingi ajaperioodi jooksul läbib. Keha kiirus võib antud ajavahemiku jooksul muutuda, mistõttu mõõdame tegelikult selle keskmist kiirust antud ajavahemiku jooksul. Keskmine kiirus on määratletud valemiga: läbitud vahemaa / kulunud aeg.
Et leida keha kiirus mingil ajahetkel (selle hetkkiirus), mõõdame keha keskmist kiirust väga lühikese ajavahemiku jooksul selle hetke ümber.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | |||
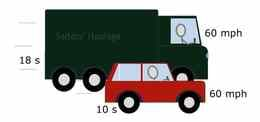
| 1. | Määrata suurima kiirusega keha, sest see läbib etteantud ajavahemikus suurima vahemaa | P | Suur kiirus 1 | ||
| 2. | Määrata erinevaid vahemaid erineva ajaga läbinud kehade hulgast kõige kiireim | Suur kiirus 2 | |||
| 3. | Arvutada keha keskmist kiirust kasutades valemit kiirus = vahemaa/aeg | Asjade liigutamine | Suurima kiiruse mõõtmine | ||
| 4. | Selgitada, miks pole hetkkiirus alati sama mis keskmine kiirus | 100 m jooksu maailmarekord | Probleemid ajavõtuga | ||
| 5. | Määrata, millal kiiruse ja kiirenduse muutus on kõige suurem | Kiirus või kiirendus | B | Kas keha liigub kiirenevalt? | |
| Kiirendus | |||||
| Suurim kiirendus |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Antud materjalides keskendutakse kiiruse ja kiirenduse kvalitatiivsetele kirjeldustele. Liikumise mõistmiseks on oluline, et õpilased suudaksid liikumist ja selle muutusi erinevates olukordades täpselt kirjeldada.
Kiirendust käsitletakse üksikasjalikumalt järgnevates materjalides juba põhjalikumalt.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See põhimõiste aitab arendada suurt ideed, tuginedes olemasolevale arusaamale sellest, mis on kiirus. Seejärel töötatakse liikumise mõistmiseks välja selged ja täpsed kirjeldused, mida on vaja liikumisgraafikute ja dünaamiliste süsteemide kasutamiseks.
Mõistmise arendamise esimese sammuna kontrollime, mida õpilased kiirusest teavad. Seejärel töötame välja kiiruse võrrandi, et võimaldada erinevate kiiruste võrdlemist ja kiirenduse kvalitatiivset mõistmist.
Kiirusest rääkides on korrektne keelekasutus oluline, sest see, mis on meile selge, võib õpilastele kergesti segadust tekitada. Ühtlast kiirust võidakse mõista kui „pidevat liikumist" ning püsivat kiirust kui „mitte liiga kiiret liikumist". Kiiremini liikumist nähakse sageli kui „järelejõudmist" ning kui üks keha möödub teisest, arvatakse sageli, et möödumise hetkel olid kehadel samad kiirused (Driver et al., 1994b). Enne kvantitatiivsete lähenemisviiside tutvustamist on vaja veenduda, et õpilastel on kiirusest selge kvalitatiivne arusaam (Driver et al., 1994a).
Õpilased peavad õppetöös kiiruste võrdlemiseks ja arvutamiseks kasutama graafilisi ja numbrilisi esitusi ning mõnikord pööravad õpetajad ja õpikud sellega seotud matemaatilistele protseduuridele suurt tähelepanu, selle asemel et esmalt kiiruse kontseptuaalset arusaama arendada (Stump, 1999; Lingefjard ja Farahani, 2018). Õpilastel on tugev kalduvus vaadelda liikumisgraafikuid kui pilte ja kohandada enda olemasolevad füüsikalised teadmised joonise kujuga (Clement, 1986). Et jõuda mõistmiseni, et liikumisgraafikud kujutavad väärtustevahelisi seoseid, peaksid õpilased oskama selgitada, kuidas kiirus vahemaa ja ajaga seotud on, olema kiirust mõõtnug ning erinevaid tähelepanekuid tõlgendanud.
„Õpilased vajavad enamat kui lihtsalt rutiinset numbritega manipuleerimist. Nad peavad mõistma, et suurema kiirusega keha jõuab mingisse punkti lühema ajaga ning ühtlasi läbib antud ajavahemikus ka suurema vahemaa. Vaid seeläbi kinnistub kiiruse kui ajaühikus läbitud vahemaa praktiline tähendus. (Driver et al., 1994b)
Praktiline töö võimaldab õpilastel mõõta liikuvate kehade poolt läbitud vahemaad ja selleks kulunud aega ning liikumist üksikasjalikult jälgida(Kibble, 2011; Driver et al., 1994b). Tehtavaid tähelepanekuid kirjeldada võimaldava sõnavara tutvustamine ja harjutamine on oluline esimene samm liikumise mõistmise suunas. Õpilased ei tee tavaliselt kiirusel ja kiirendusel selget vahet. Sageli ei kasuta õpilased sõna „kiirendus" väljaspool loodusteaduste tundi ja räägivad selle asemel kiiremini liikuma hakkamisest või aeglustumisest. Kiirendust võidakse mõista kui „kiiret liikumist" (Driver et al., 1994b).
Arengutööriistade komplektis „Kiiruse kirjeldamine" tuuakse esimesena sisse kiiruse kvalitatiivne mõiste. Kirjeldades põhjusi, mille põhjal teame, et mingi keha liigub suurema kiirusega kui teine, jõuavad õpilased kiiruse ja kiiruse võrrandi selge kirjeldamiseni. Selle mõistmise kinnistamiseks on praktilised tegevused, mille käigus õpilased kiirust mõõdavad. Täiendavate liikumisülesannete uurimine tutvustab õpilastele ka muutuvat kiirust. Mõned õpilased suudavad kehade kiirendamist kergesti ära tunda, teised aga võivad kiirendust kvalitatiivselt määratleda ning arutelu kaudu areneb nende arusaam ka negatiivsest kiirendusest.
Clement, J. (1986). Adolescents' Graphing Skills: A Descriptive Analysis. Cambridge, Mass.: Technical Education Research Center.
Driver, R., et al. (1994a). Making Sense of Secondary Science: Research into Children's Ideas, London, UK: Routledge.
Driver, R., et al. (1994b). Making Sense of Secondary Science: Support Materials for Teachers, London: Routledge.
Kibble, B. (2011). Forces. In Sang, D. (ed.) Teaching secondary physics. London: Hodder Education.
Lingefjard, T. and Farahani, D. (2018). The Elusive Slope. International Journal of Science and Mathematics Education, 16, 1187-1206.
Stump, S. (1999). Secondary Mathematics Teachers' Knowledge of Slope. Mathematics Education Research Journal, 11(2), 124-144.
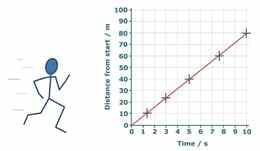
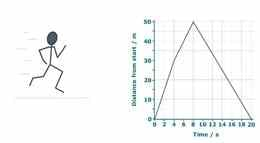
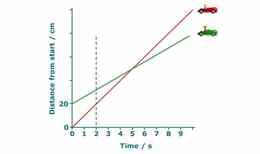
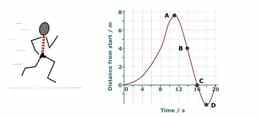
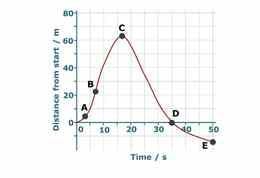
Keha liikumise kohta käivad andmed saab kokku võtta liikumisgraafikus (mis näitab, millise vahemaa on keha mingiks ajahetkeks läbinud). Graafiku tõus mingil ajahetkel näitab keha kiirust.
Õppefookus
Liikuvat keha kirjeldava informatsiooni saab kokkuvõtvalt esitada liikumisgraafiku abil: graafiku punkt näitab läbitud teekonna pikkust alguspunktist ning joone tõus näitab keha kiirust antud ajahetkel
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
| 1. | Lugeda liikumisgraafiku telgedelt aja ja vahemaa väärtusi | P | Joonelt maas | Joonista graafik |
| 2. | Kirjeldada liikumisgraafiku abil keha asukoha muutusi erinevatel ajahetkedel | Graafiku lugu | Kiired graafikud | |
| 3. | Kirjeldada liikumisgraafikul kujutatud sirge abil keha liikumist | Joone lugu | ||
| Kaks kaldpinda | ||||
| 4. | Selgitada, kuidas näitab liikumisgraafik keha muutuvat asukohta | Kus on Sally | ||
| 5. | Selgitada, kuidas näitab liikumisgraafik keha muutuvat kiirust | B | Dwight'i kiirus |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Matemaatikatundides õpitakse skaalasid, graafikute joonestamist ja regressioonisirgete joonestamist. Paljude 11-14 aastaste õpilaste puhul on need oskused hästi arenenud, teistel aga mitte. Loodusteaduste tundides pole tavaliselt piisavalt aega, et neid oskusi nii põhjalikult õpetada kui matemaatikatundides, mistõttu on kasulikum keskenduda graafikute mõistmisele ja nende seostamisele reaalsete olukordadega. See täiendab joonestamis- ja analüüsioskusi, mida õpilased matemaatikatundides arendavad.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See põhimõiste aitab arendada suurt ideed, tuginedes liikumise selgetele ja täpsetele kirjeldustele. Nii areneb arusaam sellest, kuidas neid suurusi liikumisgraafikutel kujutatakse ning muutuvat liikumist üksikasjalikult analüüsitakse.
Mõistmise arendamise esimese sammuna kontrollime, kas õpilased oskavad graafiku telgedelt väärtusi lugeda. Seejärel arendatakse telgedevaheliste lihtsate seoste kirjeldamist, näiteks sirgjoonte abil kujutatud seoste põhjal. Selle tulemusena tekib õpilastel arusaam sellest, kuidas vahemaa ja aja graafikud kujutavad liikumist reaalsetes olukordades.
Enne liikumist kirjeldavate seaduspärasuste, näiteks Newtoni liikumisseaduste, mõistmise arendamist peavad õpilased oskama liikumist kirjeldada ja graafikul kujutada. Nad peavad oskama kasutada sõnalisi kirjeldusi, graafilist kujutamist ja arvulisi sõnastusi, näiteks . Nende oskuste arendamisel on kriitilise tähtsusega arutlemine, mis nõuab aega ja selleks hoolikalt koostatud ülesandeid. (Driver et al., 1994)
Paljud õpilased näevad liikumisgraafikuid kui pilte, mis on mingi olukorra kohta olemasolevate füüsikaliste teadmistega seotud. (Lingefjard ja Farahani, 2018; Stump, 1999; Brasell, 1987; Clement, 1986). Näiteks Clement (1986) leidis, et ülesandes, kus 12-14 aastastel õpilastel (n=25) paluti jalgrattaga läbitud trajektoori kohta joonistada liikumisgraafik, kujutas 28 protsenti jalgratta liikumist üles- ja allamäge sõidetud teekonda kujutavate piltidena. Samamoodi leidsid Lingefjard ja Farahani (2018), et 35 protsenti 18-aastastest (n=17) õpilastest tõlgendas liikumisgraafikuid intuitiivselt, justkui oleks tegu piltidega. Seejuures paljud neist alustasid sellise tõlgendusega, enne kui end korrigeerisid.
Sageli pööravad õpikud (ja õpetajad) suurt tähelepanu graafikute joonistamisele ja tõusu arvutamisele, ent ei proovi arendada arusaamist seostest, mida graafik näitab (Stump, 1999). Konstruktiivsem on keskenduda järgmiste oskuste õpetamisele:
- otse graafikult andmete lugemise oskus ning mõlema telje eraldi tõlgendamise oskus
- lihtsamate telgedevaheliste seoste, näiteks sirgjoone, kirjeldamise oskus
- oskus graafikut tõlgendada ning tegelikkuses toimuvaga seostada (Friel, Curcio ja Bright, 2001; Lingefjard ja Farahani, 2018)
Graafikute tõlgendamisel peavad õpilased suutma määrata, millised graafiku andmed vastavad konkreetsetele füüsikalistele mõistetele. Liikumisgraafikute puhul aetakse sageli segamini graafiku tõus (kiirus) ja kõrgus (vahemaa) (Clement, 1986; McDermott, Rosenquist ja van Zee, 1987). Üks strateegia selle probleemi ületamiseks on kasutada reaalajas liikumisgraafikute joonistamiseks liikumisandureid ja andmelogijaid. Seeläbi saavad õpilased erinevate liikumiste graafiku kuju ennustamist harjutada ning ka etteantud graafiku kuju liikumisanduri ees liikudes reprodutseerida. 17-18 aastaste õpilaste (n=75) seas läbi viidud uuring näitas, et selline lähenemine parandas oluliselt õpilaste võimet liikumisgraafikuid tõlgendada (Brasell, 1987).
Selle kohta, miks liikumisgraafikute reaalajas kujutamine õppimist parandab, on mitmeid võimalikke selgitusi: see võimaldab õpilastel toimuva ja graafiku kohta tulevat teavet samaaegselt töödelda; andmelogi dünaamiline kuvamine koondab tähelepanu ühele andmekogule korraga; graafikute sagedane kordamine toetab ideede kinnistumist. Braselli (1987) edasine uurimine näitab, et isegi lühike, 20-30 sekundiline viivitus liikumise vaatlemise ja graafiku nägemise vahel piirab õpilaste võimet liikumisandmeid graafiku tunnustega seostada.
Antud arengutööriistas keskendutakse pigem liikumisgraafikute mõistmisele kui joonistamisele. Enne, kui asutakse graafikul punktide ja sirgete abil kujutatud liikumiste tõlgendamisele, kontrollitakse õpilaste oskust graafiku telgedelt aja ja vahemaa väärtusi lugeda. Alles seejärel keskendutakse graafikul kujutatud liikumiste tõlgendamisele. Diagnostiliste küsimustega uuritakse graafikute intuitiivsest tõlgendamisest tingitud vääritimõistmisi ning pakutakse vastuseid, mis aitavad õpilastel graafikutelt struktureeritumalt ja tõhusamalt andmeid leida. Praktiline töö aitab õpilastel arendada ja kinnistada arusaamist sellest, kuidas graafikutel liikumise vahemaa ja aja suhet kujutatakse. See võimaldab andekamatel õpilastel ka keerukamatel liikumisgraafikutel asukohta, kiirust ja kiirendust tõlgendada.
The effect of real-time laboratory graphing on learning graphic representations of distance and velocity
Brasell, H. (1987). The effect of real-time laboratory graphing on learning graphic representations of distance and velocity. Journal of Research in Science Teaching, 24(4), 385-395.Making Sense of Secondary Science: Research into Children's Ideas
Driver, R., et al. (1994). Making Sense of Secondary Science: Research into Children's Ideas, London, UK: Routledge.Making Sense of Graphs: Critical Factors Influencing Comprehension and Instructional Implications
Friel, S. N., Curcio, F. R. and Bright, G. W. (2001). Making Sense of Graphs: Critical Factors Influencing Comprehension and Instructional Implications. Journal for Research in Mathematics Education, 32(2), 124-158.
Student difficulties in connecting graphs and physics: Examples from kinematics
McDermott, L. C., Rosenquist, M. L. and van Zee, E. H. (1987). Student difficulties in connecting graphs and physics: Examples from kinematics. American Journal of Physics, 55, 503-513.Keha liikumise selgitamiseks on kõigepealt vaja kindlaks teha kõik sellele mõjuvad jõud. Selle põhjal saame välja arvutada resultantjõu, mis mõjub kehale horisontaalselt ja/või vertikaalselt.
Muutuv liikumine: Kui paigalseisvale kehale mõjub nullist erinev resultantjõud, hakkab keha liikuma jõu suunas ja selle kiirus suureneb ühtlaselt.
Kui liikuvale kehale mõjub liikumissuunas nullist erinev resultantjõud, suureneb keha kiirus ühtlaselt.
Kui liikuvale kehale mõjub liikumisele vastupidises suunas nullist erinev resultantjõud, väheneb selle kiirus ühtlaselt. Kui keha kiirus langeb nullini ning jõud mõjub edasi, hakkab keha liikuma jõu suunas ning selle kiirus suureneb ühtlaselt.
Kõikidel juhtudel on liikumiskiirus (mingi keha puhul) seda suurem, mida suurem on resultantjõud. Mida raskem on keha, seda väiksem on ka liikumiskiiruse muutumise kiirus.
Ühtlane liikumine: Kui keha liigub sirgjooneliselt ühtlase kiirusega, on sellele mõjuv resultantjõud null. Resultantjõud on vajalik selleks, et muuta keha liikumist, kuid mitte selleks, et säilitada ühtlast liikumiskiirust.
Õpifookus
Kehale mõjuv resultantjõud põhjustab olenevalt jõu suunast kas keha kiirenemist või aeglustumist.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | ||
| 1. | Arvutada kahe samal sihil mõjuva jõu resultantjõu suurust ja suunda | P | Kui palju jääb üle? | Resultantjõu arvutamine |
| 2. | Kirjeldada, kui kiiresti muutub keha kiirus erineva suurusega resultantjõudude mõjul | P | Kiirendusvõistlus | Ühtlane jõud |
| 3. | Kirjeldada, kuidas muutub keha kiirus ajavahemikus, mil sellele mõjub mingi resultantjõud | Langevarjuhüpe | ||
| Veerev kivi | ||||
| 4. | Selgitada, kuidas vähendavad hõõrdumine ja teised takistavad jõud mootorita keha kiirust | Õnnetus ostukäruga | Vastujõud | |
| 5. | Selgitada, miks on hõõrdumise ja teiste takistavate jõudude tõttu keha ühtlase liikumise jätkamiseks tarvis rakendada ühtlast jõudu | B | Kiirendusvõistlus toidupoes | Võidusõit ostukärudega |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
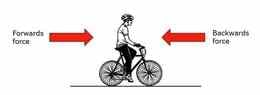
Arengutööriistade abil kontrollitakse sirgjooneliselt mõjuvate resultantjõudude arvutamise oskust ning mõistmist, et mida suurem on resultantjõud seda kiiremini keha kiirus muutub. Diagnostiliste küsimustega uuritakse arusaamist sellest, kuidas raskusjõud kiirendab kehasid kogu mõjuperioodi jooksul. Liikumisandurite abil koostatatakse reaalajas liikumisgraafikuid, et ennetada mistahes väärarusaamu. Praktiline töö aitab õpilastel arendada selgitusi selle kohta, kuidas hõõrdumine kahandab mootorita keha kiirust. Tänu sellele õpivad mõned õpilased selgitama, miks on reaalsetes olukordades (kus mõjub hõõrdejõud) ühtlase liikumise jaoks vaja püsivalt mõjuvat jõudu.
Liikumist kirjeldavad selged ja täpsed väited on vajalikud, et mõista Newtoni liikumisseadustega kirjeldatud dünaamilisi süsteeme. Uuringud näitavad, et reaalajas koostatud liikumisgraafiku kasutamine on vahend, mis aitab õpilastel mõista liikumise muutumist ajas ning kiirenduse olemust. Selleks võib kasutada dokumendis PFM2.2 „Liikumisgraafikud" toodud BEST ülesannet „Kiirgusgraafikud."
Diagnostikaküsimuses „Kiirendusvõistlus toidupoes" nimetatakse takistusjõududeks „hõõrdumist," ent see hõlmab kõiki erinevaid hõõrdumise liike, sealhulgas õhutakistust ja veeremistakistust.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See võtmekontseptsioon aitab arendada suurt ideed, tuginedes olemasolevale arusaamale sellest, kuidas resultantjõud kehade kiirust muudavad. Analüüsides areneb õpilaste arusaam sellest, kuidas pidevalt mõjuvad jõud kehade liikumist reaalsetes olukordades mõjutavad.
Mõistmise arendamise esimese sammuna kontrollime, kuidas arvutada sirgjooneliselt mõjuvat resultantjõudu ning jõu mõju liikumisele. Seejärel proovitakse kirjeldada, kuidas kiirus resultantjõu mõjumise ajal muutub. Nii tekib õpilastel arusaam tõsiasjast, et hõõrdumise olemasolu tõttu on liikumise jätkamiseks tarvis ettepoole suunatud jõudu.
Liikuvale kehale mõjuvale resultantjõule mõeldes kasutavad õpilased sageli väärarusaama, et liikumise korral eksisteerib alati mingi jõud, mis kehale mõjub. See võib aga viia edasiste väärarusaamadeni: konstantse jõu tulemuseks on ühtlane kiirus; liikumise korral mõjub jõud alati liikumissuunas (Driver et al., 1994a). Tegelikult jätkab keha sirgjoonelist liikumist ühtlase kiirusega, kui sellele resultantjõudu ei mõju; liikumissuunas mõjuv resultantjõud muudab keha kiirust.
Õpilased kalduvad kiiremini liikuma hakkamist võrdsustama „järele jõudmisega" ning kui üks keha jõuab teisele järele, siis tavaliselt arvatakse, et hetkel, mil üks keha jõuab teisele järele, liiguvad mõlemad kehad liiguvad sama kiirusega. See võib õpilaste kogemustega kokku sobida: kiirendamisest, kui kedagi taga aetakse; jooksmisest ühtlase kiirusega (kuigi kiiremini kui tagaaetav), kuni jälitatavale järele jõutakse; jälitatavaga samale kiirusele aeglustades. Mida õpilased aga liikumisest mõeldes tihtipeale ei arvesta ning mis sellest kogemusest puudu on, on aja arvesse võtmine (Driver et al., 1994b).
Alla 11-aastased lapsed kalduvad kiiruse muutumisest mõtlema kui lühikesest intensiivsest pingutusest, millele järgneb ühtlane kiirus. Uuringus (Hast ja Howe, 2013) jälgisid lapsed vabalangevat palli, kaldteel kiirenevalt allapoole veerevat palli ning mööda tasapinda veerevat palli. Õpilastel paluti ennustada, kas liikumise teise etapi osas pall kiireb, aeglustub või liigub ühtlase kiirusega. Kiirenevate pallide puhul tegid 36 11-aastast õpilast õigeid ennustusi vaid veidi sagedamini kui nad oleksid seda teinud juhuslikult. Oluliselt halvemini osati ennustada, et mööda horisontaalset pinda veerev pall aeglustub kogu liikumise vältel.
9-13 aastaste Ameerika õpilaste (n=103) seas läbi viidud uuringus (Dykstra ja Sweet, 2009) leiti, et enamik õpilastest (vanuses 11-12) kirjeldas keha liikumist kui hetkepilti selle suunast ja kiirusest (liigub kiiresti nii või aeglaselt nii). Vaid 11% õpilastest andis kiireneva, vabalanguses oleva või kaldpinnal veereva keha kohta kirjelduse, mis sisaldas muutuvat kiirust.
Dykstra ja Sweet (2009) leidsid samuti, et paljudel õpilastel oli kiirenduse modelleerimisega raskusi. Uuringus paluti õpilastel „alustada puhkeasendist ja kõndida kiirenevas tempost üle ruumi." Enamik õpilastest kõndis kas ühtlases tempos või esmalt aeglaselt ning kiirendasid järsku enne lõppu. Seejärel anti õpilastele tunnis võimalus kasutada liikumisandureid, et reaalajas oma liikumise kohta graafikuid koostada. Pärast seda sekkumist selgus, et rohkem kui 50% valimist kirjeldas kiirenevalt liikuvate kehade muutuvat kiirust ilma probleemideta.
Kui keha kiirus suureneb, kipuvad õpilased keskenduma kehale mõjuvale jõule -see näib olevat vajalik, et keha liikuma saada ja liikumises hoida. Sageli arvatakse, et liikuval kehal on jõud, mis hoiab seda liikumas ja mis lõpeb, kui keha jääb seisma (Gunstone, R ja Watts, 1985; Driver et al., 1994a). Osborne (1985) leidis, et vanemaks saades on õpilased üha enam seisukohal, et liikumissuunas mõjuv jõud hoiab keha liikumises. Uuringus, milles osales 200 õpilast, leidis ta, et 46% 13-aastastest õpilastest usub seda. 14-aastaste puhul kasvas antud väärtus 53%-ni ja 15-aastaste puhul 66%-ni.
Selle asemel, et keskenduda kehale mõjuvale jõule, peavad õpilased mõtlema kõigile mõjuvatele jõududele ja sellele, kuidas nende koosmõjul tekib resultantjõud. Tuleb kindlaks teha, millal resultantjõud mõjub, millal muutub ja millal lakkab. See eeldab, et õpilased mõistavad hõõrdumist ja selle suunda ning seda, kuidas hõõrdejõud aitab kaasa resultantjõu tekkimisele (Driver et al., 1994b).
Enamiku õpilaste jaoks on mõte, et suurem jõud annab suurema efekti, intuitiivne, kuid oluline on rõhutada, et jõud ei põhjusta mitte kiirust vaid kiiruse muutust (Driver et al., 1994b). Teisisõnu: mistahes liikuv keha jätkab kiirendamist kui sellele mõjub resultantjõud.
Driver, R., et al. (1994a). Making Sense of Secondary Science: Research into Children's Ideas, London, UK: Routledge.
Driver, R., et al. (1994b). Making Sense of Secondary Science: Support Materials for Teachers, London: Routledge.
Dykstra, D. and Sweet, D. (2009). Conceptual development about motion and force in elementary and middle school students. American Journal of Physics, 77:5, 468-476.
Gunstone, R and Watts, M. (1985). Force and Motion. In Driver, R, Guesne, E. & Tiberghien, A. (eds.) Children's Ideas in Science. Milton Keynes, England: Open University Press.
Hast, M. and Howe, C. (2013). The Development of Children's Understanding of Speed Change: A Contributing Factor Towards Commonsense Theories of Motion. Journal of Science Education and Technology, 22, 337-350.
Osborne, R. (1985). Building on children's intuitive ideas. In Osborne, R & Freyberg, P. (eds.) Learning in Science Aukland, New Zealand: Heinemann.
Vedelikus liikuvale kehale mõjuv takistus kasvab kiiruse suurenemisega. Takistust saab vähendada, kui anda liikuvale kehale voolujoonelisem kuju.
Kui liikuvale kehale mõjub liikumise suunas nullist suurem resultantjõud, suureneb keha kiirus ühtlaselt.
Kui liikuvale kehale mõjub liikumisele vastupidises suunas nullist erinev resultantjõud, väheneb keha kiirus ühtlaselt.
Kui keha liigub sirgjooneliselt ühtlase kiirusega, on sellele mõjuv resultantjõud null. Resultantjõud on vajalik keha liikumise muutmiseks, kuid mitte ühtlase kiirusega liikumise säilitamiseks.
Õpifookus
Vedelikus liikuvale kehale mõjuv takistus kiiruse kasvades suureneb; takistust saab vähendada läbi voolujoonelisema disaini.
| Õpilaste kontseptuaalse mõistmise arengu läbi suudavad nad | Diagnostilised küsimused | Töölehed | |||
| 1. | Määrata, millistes vedelikes on kehale mõjuv takistus suurim | P | Takistusjõud | ||
| 2. | Kirjeldada, kuidas voolujoonelisem disain takistust vähendab | Kiivritele mõjuv takistus | Takistus pallimeres | ||
| 3. | Selgitada, miks kehale mõjuv takistus kiiruse kasvades suureneb | Kiirus suurendab takistust | |||
| 4. | Kirjeldada vedelikus ühtlase kiirusega liikuvale kehale mõjuvaid jõude | Maksimumkiirus | |||
| 5. | Selgitada, miks muudab langevarju kasutamine lennukist alla hüppamise ohutuks | B | Ohutu maandumine | Langevarjud |
P - Varasemalt õpitud teadmised.
B - Tulevaste teemade sildamine.
Õhutakistus on konkreetne näide takistusjõust, mida kogeb läbi õhu liikuv keha.
Füüsika üheks suureks ideeks on jõud, sest see on võti keha liikumise või kuju muutuste selgitamiseks. Keha liikumist saab selgitada või ennustada, kui teame kõigi sellele mõjuvate jõudude suurusi ja suundasid. Jõudude mõistmine aitab meil ennustada ja kontrollida meid ümbritsevat füüsilist maailma.
See põhimõiste aitab arendada suurt ideed, tuginedes õpilaste teadmistele sellest, kuidas takistusjõud mõjutab keha liikumist erinevates vedelikes. Nii õpivad õpilased mõistma, kuidas keha kuju ja kiirus muudavad sellele mõjuva takistuse suurust ning kuidas see mõjutab keha liikumist reaalsetes olukordades.
Mõistmise arendamise esimese sammuna kontrollime õpilaste teadmist, et läbi mõningate vedelike on raskem liikuda kui läbi teiste. Seejärel selgitatakse takistusjõu põhjuseid ja seda, miks kehale mõjuv takistus kiiruse kasvades suureneb. Seeläbi tekib õpilastel arusaamine sellest, miks on reaalses elus ühtlase kiiruse säilitamiseks vajalik ettepoole suunatud jõud.
Takistus (õhu korral nimetatakse õhutakistuseks) on jõud, mis mõjub vedelikus liikuva keha liikumissuunale vastupidiselt. Takistus on vedeliku poolt liikuvale kehale avaldatav jõud. Energia, mis on vajalik vedelikuosakeste eemale lükkamiseks, kannab keha kineetilist energiat vedelikuosakestele üle ja vähendab seeläbi keha kiirust.
Kui keha kiirust suurendatakse, kipuvad õpilased keskenduma jõule, mis näib olevat vajalik, et keha liikuma saada ja liikumises hoida. Sageli arvatakse, et liikuval kehal on jõud, mis hoiab seda liikumises, ja mis lõpeb, kui keha seisma jääb (Gunstone, R ja Watts, 1985; Driver et al., 1994a). Osborne (1985) leidis, et vanemaks saades on õpilased üha enam seisukohal, et keha liikumises hoidmiseks on vaja liikumissuunas mõjuvat jõudu. Uuringus, milles osales 200 õpilast, leidis ta, et 46% 13-aastastest õpilastest usub seda väidet. 14-aastaste seas kasvas antud väärtus 53 protsendini ja 15-aastaste puhul 66 protsendini.
Selle asemel, et keskenduda rakendatud jõule, peavad õpilased mõtlema kõigile kehale mõjuvatele jõududele ja sellele, kuidas nende koosmõjul resultantjõud tekib. Nad peavad kindlaks tegema, millal resultantjõud mõjub, millal muutub ja millal lõpeb. Et mõista, kuidas resultantjõud takistusest sõltub, peavad õpilased mõistma takistust ja selle mõju suunda (Driver et al., 1994b).
Enamik õpilasi mõistab intuitiivselt, et suuremal resultantjõul on suurem efekt, kuid on oluline rõhutada, et resultantjõud ei põhjusta mitte kiirust vaid kiiruse muutust (Driver et al., 1994b). Teisisõnu: mistahes liikuv keha jätkab kiirendamist, kui sellele mõjub resultantjõud.
Takistusjõu mõju kukkuvatele kehadele võib olla väga segadusttekitav, sest kuigi takistusjõud võib langeva keha liikumist oluliselt mõjutada, ei võta õpilased seda sageli arvesse. Uuringus leidsid Lee ja Kwok (2009), et kui 11-12-aastastel õpilastel (n=204) paluti nimetada kukkuvale pallile mõjuvad jõud, suutis 90% neist nimetada gravitatsioonijõudu, kuid mitte ükski ei nimetanud takistusjõudu.
Kui kahel pallil lastakse üheaegselt alla kukkuda, siis Newtoni liikumisseaduste kohaselt kiirenevad mõlemad sama kiiresti ja ning peaksid langema sama aja jooksul võrdse vahemaa. See on vastuolus sellega, mida väikesed lapsed arvavad: raskem keha jõuab esimesena maapinnale (Hise, 1988). Kuid selgub, et kui võtta arvesse ka takistust, siis on väikestel lastel tavaliselt õigus!
Kui kaks palli on täpselt ühesugused ent erineva kaaluga, siis kukkumisel mõjub neile mõlemale võrdse suurusega õhutakistus. Kiirenedes pallidele mõjuv õhutakistus suureneb ning resultantjõud väheneb, sest resultantjõud = kaal (gravitatsioonijõud) miinus takistusjõud. Kui resultantjõud väheneb, siis pallide kiirus väheneb ja kiirendus aeglustub. Kui takistusjõud muutub raskusjõuga võrdseks, siis allapoole suunatud resultantjõud puudub ning pallid langevad ühtlase tippkiirusega. Selles analüüsis unustatakse sageli ära, et selleks, et takistus ja kaal võrdsustuksid, peab raskem pall liikuma kiiremini kui kergem. Teisisõnu: raskem pall peab suurema tippkiiruse saavutamiseks kiirendama kauem (et sellele mõjuv takistus oleks kaaluga võrdne). Keerukam analüüs selle kohta, kuidas takistus palle mõjutab*, näitab ka, et mistahes kiiruse korral on raskema palli kiirendus suurem ning see kiireneb kiiremini kui kergem pall.
Oberle jt (2005) leidsid 17-23-aastaste üliõpilaste (n=50) seas läbi viidud uuringus, et enamik neist pidas järjekindlalt kinni väärarusaamast, mille kohaselt kõik reaalmaailma objektid langevad täpselt sama kiiresti. Selgus, et see uskumus oli füüsikaharidusega inimeste seas tugevaim! See on seisukoht, mis on kooskõlas Newtoni liikumisseadustega olukordades, kus õhutakistus puudub. Tõepoolest: hilisemates õpingutes õpivad füüsikaüliõpilased tihtipeale lihtsuse huvides Newtoni seaduste rakendamist olukordades, kus õhutakistus on tühine.
*Kukkuvale pallile mõjuv resultantjõud = palli kaal miinus takistusjõud. Newtoni teine seadus ütleb meile, et ; . Seega langeva palli puhul: . Jagades mõlemad pooled massiga, saame palli kiirenduse: . Kuna antud näites on pallid peale masside identsed, siis on iga kiiruse korral pallidele mõjuv takistusjõud võrdne. Seega: kui palli mass on suurem, on väiksem, mis tähendab, et takistusjõud vähendab palli kiirendust aeglasemalt kui siis, kui pall kaaluks vähem.
Arengutööriistas „Takistusjõud" kontrollitakse teadmisi sellest, et liikuvatele kehadele mõjub mõnes vedelikus suurem takistusjõud kui teistes. Arutatakse, kuidas voolujooneline kuju takistusjõudu vähendab ning kiirem liikumine seda suurendab. Mudeli abil arendatakse õpilaste arusaamist sellest, miks takistusjõud tekib. Seeläbi oskavad õpilased takistusjõudu selgelt kirjeldada ning mõistavad, miks on päriselus (kus takistusjõudu tuleb arvesse võtta) ühtlase liikumise säilitamiseks vajalik liikumissuunas mõjuv jõud. Praktiline töö kinnistab seda arusaamist ning võimaldab õpilastel õpitut uutes olukordades rakendada.
“Definition of Drag”, Merriam-Webster online dictionary. [Online]. Available at: https://www.merriam-webster.com/dictionary/drag [Accessed February 2019].
Driver, R., et al. (1994a). Making Sense of Secondary Science: Research into Children's Ideas, London, UK: Routledge.
Driver, R., et al. (1994b). Making Sense of Secondary Science: Support Materials for Teachers, London: Routledge.
Gunstone, R and Watts, M. (1985). Force and Motion. In Driver, R, Guesne, E. & Tiberghien, A. (eds.) Children's Ideas in Science. Milton Keynes, England: Open University Press.
Hise, Y. A. V. (1988). Student misconceptions in mechanics: and international problem? The Physics Teacher, 26, 498-502.
Lee, Y. C. and Kwok, P. W. (2009). Can an egg-dropping race enhance students' conceptual understanding of air resistance? Physics Education, 44(2), 151-158.
Oberle, C., et al. (2005). The Galileo Bias: A naive conceptual belief that influences people's percerptions adn performance in a ball-dropping task. Journal of Experimental Psychology: Learning, Memory, and Cognition, 31(4), 643-653.
Osborne, R. (1985). Building on children's intuitive ideas. In Osborne, R & Freyberg, P. (eds.) Learning in Science Aukland, New Zealand: Heinemann.