Mistahes loodusteaduslik uurimistöö algab vaatlusest, edasi tuleb hüpotees, tehakse ennustusi, viiakse läbi katseid või sihipäraseid vaatlusi ning võrreldakse nende tulemusi ennustustega. Kuidas jõutakse teadmiste juurde, mis on usaldusväärsed? Missugused on need absoluutsed mõõdupuud, mis lubavad katseid ja vaatlusi üksteisega võrrelda?
Kui keemilise ja bioloogilise füüsika instituudis tehakse ülimadalatel temperatuuridel tehniliselt väga keerukaid teaduslikke eksperimente, siis mis on nendel ühist tavalise koolieksperimendiga?
Vaatleja poolt looduse tunnetamise protsess on esitatav jadana: sündmus → signaal → retseptor → närviprotsess → aisting → taju → kujutlus → mõtteseoste koostamine → uus mõttekujund (hüpotees) → eksperiment või sihipärane vaatlus (tagasi loodusesse) → otsustus hüpoteesi tõesuse kohta.
Selles skeemis oli pearõhk info saamisel looduse kohta ühe kindla vaatleja poolt.
Tähelepanekute tegemist looduse kohta meeleelundite abil nimetatakse vaatluseks, mis on ka esimene samm loodusteadusliku meetodi rakendamisel. Loodusliku protsessi vaatlemine tähendab protsessi kohta info kogumist ise sellesse sekkumata. Niisugune määratlus on vajalik, kui soovime eristada vaatlust katsest ehk eksperimendist, mille puhul loodusnähtus kutsutakse kunstlikult esile ja uuritavaid objekte võib ise mõjutada. Vaatlus on loodusteadusliku uurimistöö esimene etapp, millele järgneb vaatlustulemuste liigitamine oluliseks peetavate tunnuste järgi. Seejärel toimub vaatluslike faktide kõrvutamine juba tuntutega. Alles nüüd on võimalik formuleerida teaduslikult sõnastatud küsimus ehk probleem ja teha selle lahenduse kohta teaduslikult põhjendatud oletusi, mida nimetatakse hüpoteesideks. Järgnevalt formuleeritakse hüpoteesidest tulenevaid konkreetseid ennustusi ja kontrollitakse nende täitumist eksperimendi abil. Kui hüpotees on osutunud tõeseks, siis sõnastatakse vastav seaduspärasus. Seaduspärasuse sõnastamisel tuleb kindlasti nimetada katse tingimusi, sest teistsugustes tingimustes ei pruugi katse tulemus enam olla selline.
Illustreerime kõike ülaltoodut konkreetse näitega. Olgu meil esmase vaatluse tulemuseks fakt, et puuleht langeb aeglaselt ja lehe langemistee pole isegi täiesti tuuletu ilmaga sirgjoon. Samas aga õun kukub lehest kiiremini ja sirgjooneliselt.
Probleem: miks puuleht kukub aeglaselt, õun aga kiiresti?
Hüpotees: keha langemise kiirus võib sõltuda keha kujust, aga ka keha raskusest. Õun ja puuleht erinevad mõlema omaduse poolest. Tuleb teostada katse kehadega, millel üks neist omadustest on mõlemal kehal sama.
Katse: võtame A4-paberipakist kaks uut paberilehte. Paberi tootja on garanteerinud, et nad on ühesugused (erinevus ei ületa 1%). Kahel katsekehal on ühesugune mass ning raskusjõud, seega erinevus nende käitumises ei saa olla põhjustatud raskusest. Kägardame ühe paberilehe võimalikult väikeseks nutsakaks. Laseme kägardamata jäänud lehe ja nutsaka üheaegselt ning samalt kõrguselt langema.
Ennustus: kui langemise kiirus sõltub keha kujust, siis peavad leht ja nutsakas jõudma põrandani erineva aja jooksul.
Tulemus: kägardamata leht jõudis põrandani oluliselt hiljem kui nutsakas.
Järeldus: keha langemise kiirus sõltub keha kujust.
Katse tingimus: me uurisime kehade langemist õhus.
Seaduspärasus: õhus langemisel sõltub langemise kiirus keha kujust.
Loodusteadusliku meetodi all mõistetakse niisiis meetodit, mis seisneb vaatluste põhjal hüpoteeside püstitamises, nende põhjal ennustuste tegemises ja ennustuste paikapidavuse kontrollimises katsete (eksperimentide) läbiviimise teel. Esimesena rakendas neid juhiseid järjekindlalt mehaanikateaduse alusepanija Galileo Galilei (1564–1642). Galilei töödest lähtudes andis Isaac Newton (1642–1727) tolleaegsel teadmiste tasemel kõikehõlmava seletuse kehade liikumisoleku muutumise põhjuste kohta. Sellega eristus füüsika filosoofiast, ehkki aastal 1687 ilmunud Newtoni peateos kandis veel pealkirja „Loodusfilosoofia matemaatilised printsiibid" (ld Philosophiae naturalis principia mathematica). Füüsika sai teerajajaks teistele loodusteadustele, mis kujunesid välja alles sadakond aastat hiljem.
Kõik eelnev käsitles eksperimentaalset loodusteadust, kus hüpoteese oli võimalik kohe katseliselt kontrollida. Kaasajal tehakse aga palju ka puhtalt teoreetilist teadustööd. Teoreetiline loodusteadus lähtub üldtunnustatud ja kõigis senistes katsetes kinnitust leidnud faktidest looduse kohta ja enamasti püüab antud loodusnähtuse kirjeldamisel rakendada mingit uut matemaatilist mudelit. Päris uus teooria tugineb mingile seni mitte kasutatud lähte-eeldusele ehk postulaadile. Teooria üksikjäreldused tuletatakse antud loodusteaduse üldistest printsiipidest ja arendatava teooria konkreetsetest postulaatidest. Teoreetilise tulemuse usaldusväärsuse tagab esialgu mitte eksperiment, vaid läbiproovitud matemaatiliste võtete korrektne sooritamine ja loogikareeglite täpne järgimine. Teaduslikke teooriaid tunnustab või lükkab tagasi teadlaskonna enamuse seisukohavõtt. Teooriaid vaidlustatakse enamasti nii, et viidatakse looduse olulistele omadustele, mida vastav teooria pole arvestanud. Mingit teooriat tunnustatakse lõplikult alles siis, kui sellest teooriast lähtuvad ennustused on saanud eksperimentaalse kinnituse. Näiteks võeti Albert Einsteini 1916. aastal formuleeritud üldrelatiivsusteooria teadusüldsuse poolt omaks pärast seda, kui kaks sõltumatut vaatlejate rühma tegid 1919. aasta päikesevarjutuse ajal kindlaks, et Päikesest lähedalt mööduv kaugete tähtede valgus kaldub Päikese gravitatsiooniväljas kõrvale just niipalju, kui seda oli ennustanud üldrelatiivsusteooria. Kaasajal on teoreetiline osakestefüüsika ligikaudu 50 aastat eksperimentaalsest ees. Nii palju võtab aega tehniliste võimaluste loomine teoreetikute ühe või teise ennustuse katseliseks kontrollimiseks. Näiteks ennustas Peter Higgsi juhitud teadlasrühm Higgsi bosonite olemasolu 1964. aastal, esimesed katseandmed nende osakeste kohta saadi kevadel 2012, usaldusväärselt avastatuks tunnistati Higgsi bosonid aga alles märtsis 2013. Higgsi bosonid on osakesed, mis lõppkokkuvõttes põhjustavad kehade inertsust ehk kalduvust säilitada oma liikumisolekut.
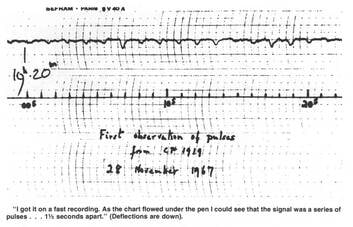
| Selle antennide süsteemiga avastas Jocelyn Bell Burnell 1967. aastal pulsarid. Avastus oli küll juhuslik, ent selleni viinud katse on korratav, sest põhineb loodusteaduslikul meetodil. | Pulsarid on massiivsed pöörlevad tähed, mis kiirgavad perioodiliselt raadiolaineid. Jocelyn Bell Burnelli avastatud pulsari kiirgusperiood on 1,3373 s ning selle üks pulss kestab 0,04 s. Pildil on 1967. aasta katseandmed. |
Uuritavad objektid ja nähtused erinevad alati üksteisest mingite omaduste poolest. Näiteks vääriskivid erinevad suuruse, kuju, värvi, kõvaduse ja kauniduse poolest. Osa neist omadustest on arvuliselt kirjeldatavad, teised mitte. Rubiinikristalli pikkust ja isegi kõvadust saame arvude abil kõigile ühtemoodi mõistetavalt kirjeldada, kuid vääriskivi emotsionaalset mõju inimesele mitte. Füüsikalise objekti mingi omaduse sellist kirjeldust, mida saab väljendada arvuliselt, nimetatakse füüsikaliseks suuruseks. Mõnikord öeldakse lihtsalt, et füüsikaline suurus ongi objekti arvuliselt kirjeldatav omadus. Siiski ei tohi unustada, et füüsikaline suurus on vaid inimlik väljamõeldis, vaatlejate ühine kokkuleppeline kujutlus, loodusobjekti mudel. Füüsikalisteks suurusteks on näiteks keha mass või ruumala, keha liikumise kiirus, keha temperatuur või aine hulk kehas.
Põhjendatud hinnangu andmist füüsikalise suuruse väärtusele nimetatakse selle suuruse mõõtmiseks. Veelgi lihtsam on aga öelda, et mõõtmine on füüsikalise suuruse väärtuse võrdlemine mõõtühikuga. Vajadus mõõtmiste järele tuleneb asjaolust, et vaatleja ei või täielikult usaldada oma meeleelundeid. Üksikisiku meeleline taju on subjektiivne ja vaatlustulemus oleneb isiku eelnevast kogemusest. Eksituste vältimiseks tuleb kasutada mõõtmisi.
Milles seisneb mõõtmine ja kuidas mõõdetava suuruse arvväärtus kindlaks tehakse? Kõik me teame, et näiteks õuna massi saab määrata kaalumise teel. Selleks asetatakse ühele kaalukausile õun ja teisele sellises koguses teadaoleva massiga kaaluvihte, et kaal tasakaalu jääks. Me võrdleme kaalude abil õuna ja vihte. Mõõtmine seisneb alati tundmatu suuruse võrdlemises teadaolevaga. Näiteks pliiatsi pikkuse mõõtmisel võrdleme seda mõõtjoonlauale kantud jaotise (kriipsude vahe) pikkusega ning määrame, kui mitu joonlaua jaotist mahub pliiatsi pikkusesse. Samamoodi võiksime koolilaua pikkust või laiust mõõta, võrreldes laua pikkust õpiku pikkusega.
Mõõtmine on mingi füüsikalise suuruse konkreetse väärtuse võrdlemine sama suuruse teise, mõõtühikuks võetud väärtusega. Võrdlemise tulemusena saadud arvu nimetatakse mõõtarvuks ehk mõõdetava suuruse arvväärtuseks. Eelnenud näidetes oli uuritavaks objektiks pliiats või koolilaud. Füüsikaliseks suuruseks ehk mõõtesuuruseks oli pikkus, suuruse konkreetseks väärtuseks ehk mõõtmistulemuseks oli vaadeldava pliiatsi pikkus. Mõõtühikuks oli pliiatsi mõõtmisel mõõtjoonlaua jaotise pikkus (1 cm), koolilaua pikkuse mõõtmisel aga õpiku pikkus. Mõõtühik on füüsikalise suuruse (nt pikkus) konkreetne väärtus, mida kokkuleppeliselt kasutatakse sama suuruse teiste väärtuste (nt pliiatsi pikkus) arvuliseks iseloomustamiseks.
Mõõtmisi saab jagada otsesteks ja kaudseteks. Otsene on selline mõõtmine, mille korral meid huvitav füüsikalise suuruse väärtus on vahetult loetav mõõteriista skaalalt. Kaudne on mõõtmine, mille korral mõõtetulemus leitakse arvutuste teel otsemõõdetud suuruste kaudu. Näiteks auto kiirust saab otseselt mõõta spidomeetri abil, aga ka leida kaudselt, arvutades kiiruse mõõdetud teepikkuse ning sõiduaja jagatisena.
Seda teadaolevat mõõtesuuruse väärtust, millega mõõtmise käigus mõõdetavat suurust võrreldakse, nimetatakse teatavasti mõõtühikuks. Kuna mistahes füüsikaline suurus kui mõõtesuurus on vaatlejate ühine kujutlus (looduse mudel, mitte loodus ise), siis on seda ka vaadeldava suuruse mõõtühik. Mõõtjad peavad kokku leppima selles, millega nad mõõdetavat suurust võrdlevad. Kui aednik soovib ruudukujulise lillepeenra kontuure maha märkida, võib ta kasutada mistahes pikkusega nöörijuppi. Lillepeenart nööri pikkusega võrreldes saab aednik oma lillepeenra kõik küljed ühepikkuseks mõõta. Kui naaberaednik peab kõnealust peenart sedavõrd kauniks, et otsustab oma aias samasuguse lillepeenra rajada, siis ei piisa tal peenra väljamõõtmiseks teadmisest, kui mitu nöörijupi pikkust peenra külg pikk on. Ta peab kas saama kasutada sedasama nöörijuppi või siis teadma, mitu sentimeetrit pikk oli algsel mõõtmisel kasutatud mõõdunöör. Erinevad mõõtjad peavad kokku leppima ühesugused mõõtühikud.
Niisiis on mõõtühik kokkuleppeline suurus. Mõõtühikut on võimalik kokku leppida vaid siis, kui kõik mõõtjad saavad oma isikliku mõõtevahendi valmistamisel lähtuda ühest ja samast mõõtühiku näidisest. Mõõtühiku kokkuleppimisel kasutatavat näidist nimetatakse mõõtühiku etaloniks (pr étalon 'sugutäkk').
Mõõtühiku aluseks olev etalon tuleb kokku leppida nii, et see tugineks mingile looduses väga püsivale objektile. Etaloniks ei sobi näiteks kivi või metallvarras, kuna nende hävinemise korral ei saaks etaloni täpselt taastada.
Mõtisklused etalonide päritolu üle viivad meid mõõtühikute süsteemi vajalikkuse mõistmiseni. Näiteks omal ajal Inglismaal kehtestatud pikkusühik jalg (ingl foot) olevat kokku lepitud briti meeste keskmisest jalalaba pikkusest lähtudes. Teise legendi kohaselt olevat see olnud Inglise kuninga Henry I (valitses 1100–1135) jalalaba pikkus. Samas me arvatavasti nõustume sellega, et ammu surnud kuninga jalalaba pikkus või ka mingi lõpliku arvu inglaste jalalabade keskmine pikkus pole etaloniks kuigi sobiv suurus. Mõõtühikute etalonideks peavad olema looduses muutumatuna püsivad suurused. Samas pole võimalik ega ka vajalik kõikide suuruste mõõtühikute kokkuleppimiseks looduslikke näidiseid leida. Piisab, kui lepitakse kokku vaid mõned väga stabiilse etaloniga ühikud. Kõik ülejäänud saab tuletada nende kaudu. Seetõttu liigitatakse mõõtühikud põhiühikuteks ja tuletatud ühikuteks.
Põhiühikuteks nimetatakse vähest arvu üksteisest sõltumatuid mõõtühikuid, mida saab etalonide abil võimalikult täpselt määratleda. Ülejäänud suuruste mõõtühikud on tuletatud ühikud, mis defineeritakse põhiühikute kaudu suurustevaheliste seoste abil. Kokkulepitud põhiühikud ning neist tuletatud ülejäänud mõõtühikud moodustavad kogumi, mida nimetatakse mõõtühikute süsteemiks.
Juba siis, kui algelised inimesed kasutasid enda kehaosadega seotud mõõtühikuid, püüdsid nad leida ühikute vahel seoseid. Tuntumad kehaosade mõõtmetest tulenevad ühikud on järgmised:
1 toll – pöidlalüli pikkus;
1 vaks – väljasirutatud pöidla ja väikese sõrme vaheline kaugus;
1 jalg – jalalaba pikkus;
1 küünar – käsivarre pikkus väljasirutatud sõrmeotstest kuni küünarnukini;
1 süld – laialisirutatud käte sõrmeotste vahe.
Minevikus oli kombeks arvata, et üks süld võrdub kolme küünra või kuue jalaga.
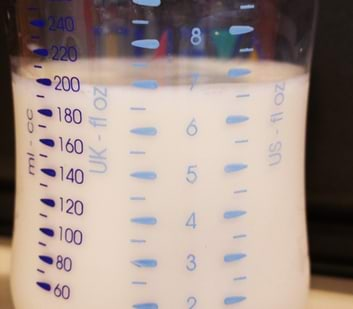
| Kolm mõõtühikute süsteemi ühel pudelil. Lisaks õige vedelikukoguse määramisele saaks seda pudelit kasutada mahuühikute teisendamise vahendina – kaks ühes. | Versta (1,067 km) kasutati Eestimaal vahemaade mõõtmiseks 18. sajandi esimesest poolest kuni 1920. aastateni, mil seda hakkas järk-järgult asendama kilomeeter. Esimesed verstapostid olid 6,6 m kõrged ning näitasid vahemaad postijaamani või kubermangulinnani. |
Üleriigilised mõõtühikute süsteemid kehtestati 17.–19. sajandil. Kuna Eesti kuulus kuni 1917. aastani Vene tsaaririigi koosseisu, siis kehtis ka Eestis nimetatud aastani Vene pikkusmõõtude süsteem, mille peamised seosed olid järgmised:
1 toll = 2,54 cm;
1 küünar = 12 verssokit = 21 tolli = 53,3 cm;
1 arssin = 16 verssokit = 28 tolli = 71,7 cm;
1 süld = 3 arssinat = 2,13 m;
1 verst = 500 sülda = 1,067 km;
1 penikoorem = 7 versta = 7,468 km.
1824. aastal kehtestati kogu Briti impeeriumis ametlik mõõtude süsteem (System of Imperial Units), mille aluseks oli pikkusühik jard (Imperial yard, 1 yd = 0,9144 m). Kolmandik jardi moodustab jala (foot, 1 ft = 30,48 cm) ja üks toll (inch) on 1/12 jalga (1 in = 2,54 cm). Jardi, jala ja tolli süsteemiga puutume kokku näiteks Ameerika filmide kaudu, kuna USA-s, Kanadas, Inglismaal ja Austraalias kehtib imperiaalne mõõtude süsteem väikeste muudatustega argielus veel tänapäevalgi. Pikemaid vahemaid mõõdetakse miilides (1 mi = 1760 yd = 1,609 km), ruumala pintides (0,568 dm3) ja gallonites (8 pinti = 4,55 liitrit), massi naelades (0,454 kg) ja untsides (1/16 naela = 28,4 g).
19.–20. sajandil võeti enamikus mitte-ingliskeelsetes riikides järk-järgult kasutusele meetermõõdustik. Meetermõõdustikust lähtub ka tänapäevane rahvusvaheline mõõtühikute süsteem (SI), mis aastal 1960. aastal ülemaailmseks eelissüsteemiks tunnistati. Rahvusvaheline mõõtühikute süsteem on alates 1982. aastast kohustuslik ka Eestis. Isegi ülalpool loetletud ingliskeelsetes maades kasutavad teadlased süsteemi SI, kuna teadusajakirjade toimetused ei kipu tänapäeval enam vastu võtma artikleid, mis sisaldavad teiste süsteemide ühikuid.
Rahvusvahelise mõõtühikute süsteemi loomine sai alguse revolutsiooniliselt Prantsusmaalt, kus üks aasta peale Bastille’ vallutamist, seega 1790. aastal, tehti algust meetri defineerimisega (kr metron 'mõõt'). Prantsuse keelest pärineb ka selle süsteemi lühend SI (Système International d’unités). Üle maailma kehtivaid otsuseid süsteemi SI kohta võtab vastu Kaalude ja Mõõtude Peakonverents (pr Conférence Générale des Poids et Mesures lühendatult CGPM). SI algseteks (1960) põhiühikuteks olid pikkuse ühik meeter, massi ühik kilogramm, aja ühik sekund, temperatuuri ühik kelvin, elektrivoolu tugevuse ühik amper ja valgustugevuse ühik kandela. 1971. aastal lisati neile ka ainehulga ühik mool. Tegemist on detsimaalse süsteemiga, st suuremate ja väiksemate ühikute saamiseks kasutatakse kümnendeesliiteid (kümne astmetega korrutamist või jagamist), mitte enam arve 3, 12 või 16, mida võisime leida vanadest Vene ja Inglise süsteemidest.
| Suurus | Mõõtühik | Tähis | Kehtiv etalon |
|---|---|---|---|
| Pikkus | meeter | Meeter on määratud vaakumis leviva valguse kiiruse fikseerimisega väärtusel väljendatuna ühiku − abil, kus sekund on määratletud alusel. Sümboliga tähistatakse aatomi kahe häirimata põhiseisundi struktuurinivoo vahelisele üleminekule vastavat sagedust. | |
| Aeg | sekund | Sekund, tähis s, on SI aja ühik. Sekund on määratud tseesiumi sageduse , milleks on tseesiumi aatomi isotoobi 133 häirimata põhiseisundi ülipeenstruktuuri kahe energianivoo vahelisele üleminekule vastav sagedus, fikseerimisega arvväärtusel väljendatuna ühiku abil, mis on võrdne . | |
| Mass | kilogramm | Kilogramm on määratud Plancki konstandi fikseerimisega arvväärtusel väljendatuna ühiku abil, mis on võrdne , kus meeter on määratletud ja sekund alusel. | |
| Temperatuur | kelvin | Kelvin, tähis K, on SI temperatuuri ühik. Kelvin on määratud Boltzmanni konstandi fikseerimisega arvväärtusel väljendatuna ühiku abil, mis on võrdne , kus kilogramm on määratletud , meeter ja sekund alusel. | |
| Voolutugevus | amper | Amper, tähis , on SI elektrivoolu tugevuse ühik. Amper on määratud elementaarlaengu fikseerimisega arvväärtusel väljendatuna ühiku C abil, mis on võrdne , kus sekund on määratletud alusel. | |
| Valgustugevus | kandela | Kandela, tähis cd, on määratud monokromaatse hertsise kiirgussagedusega kiirgusallika valgusviljakuse fikseerimisega väärtusel väljendatuna ühiku abil, mis on võrdne või , kus kilogramm on määratletud , meeter ja sekund alusel. Sümboliga h tähistatakse Plancki konstanti, c tähistatakse valguse kiirust vaakumis ja tähistatakse aatomi kahe häirimata põhiseisundi struktuurinivoo vahelisele üleminekule vastavat sagedust. | |
| Ainehulk | mool | Mool, tähis mol, on SI ainehulga ühik. Üks mool sisaldab täpselt elementaarset koostisosakest. See arv on Avogadro konstandi fikseeritud arvväärtus väljendatuna ühiku abil ja nimetatakse Avogadro arvuks. Ainehulk, tähis n, on teatud koostisosakeste arvu mõõt süsteemis. Koostisosakesteks võivad olla aatomid, molekulid, ioonid, elektronid, mingid teised osakesed või eespool nimetatud osakeste kindlalt määratletud grupid. | |
| Põhiühikutele lisaks on defineeritud veel kaks lisaühikut, millel pole etaloni: | |||
| Suurus | Mõõtühik | Tähis | Definitsioon |
| Tasanurk | radiaan | Tasanurk, mille korral nurga tippu ümbritseva ringjoone kaare pikkus võrdub raadiusega (). | |
| Ruuminurk | steradiaan | Ruuminurk, mille korral nurga tippu ümbritseva sfääri vastava osa pindala võrdub raadiuse ruuduga (). | |
Allikas: Metrosert AS
Mõõtesuurus
Rahvusvaheline mõõtühikute süsteem (SI) on detsimaalne süsteem. Mõõtühikute endiga võrreldes ebamugavalt suurte või väikeste mõõtesuuruste väärtuste väljakirjutamisel kasutatakse kümnendeesliiteid. Mõõtühikute kümnend- ehk detsimaaleesliited on tähised, mille abil lihtsustatakse ühikute üleskirjutamist kümnendsüsteemis. Näiteks eesliidet kilo kasutatakse massiühikutes ja pikkusühikutes .
Eesliite kasutamine tähendab sellele vastava arvuga korrutamist:
Kui mõõtühik sisaldab astendajaid, tuleb vastavasse astmesse võtta ka eesliide:
Nagu ülalpool öeldud, tohib igapäevaelus kasutada ka mõningaid mõõtühikuid, mis ei kuulu rahvusvahelisse süsteemi.
Mittesüsteemsetes ühikutes väljendatud suurusi on kõige lihtsam SI-sse teisendada, asendades kõik neis sisalduvad eesliited ja ühikud vastavate SI väärtustega ja siis arvutada tulemus kokku. Näiteks:
Lõpetuseks märgime, et alates 1968. aastast kehtiva kokkuleppe kohaselt kirjutatakse teadlaste nimedest tuletatud mõõtühikute nimetused väikese algustähega, kuid nende mõõtühikute tähised suure tähega. Näiteks kelvin (1K), amper (), njuuton (), džaul () ja vatt (). Näeme ka, et mõõtühikute nimetusi on lubatud esitada eesti keelele mugandatud kujul (amper, njuuton, džaul ja vatt), ehkki vastavate teadlaste endi nimesid kirjutame originaalkeele reeglite järgi (Ampère, Newton, Joule, Watt).
Mõõtühikute süsteem
Mõõtühikute süsteem on kogum, mille moodustavad kokkulepitud põhiühikud ning neist tuletatud ülejäänud mõõtühikud.
Mõõtmine on teatavasti mingi füüsikalise suuruse konkreetse väärtuse võrdlemine sama suuruse teise, mõõtühikuks võetud väärtusega. Võrdlemise protseduur toimub aga alati olukorras, kus mõjuvad erinevad välised tegurid. Mõned neist välistest mõjuteguritest võivad olla juhusliku iseloomuga ja mõned süstemaatilised ehk mõõteväärtust kindlas suunas mõjutavad. Kui me näiteks soovime mõõta, kui kõrgele üles põrkab tagasi mingilt kindlalt kõrguselt vertikaalselt kukkuma lastud lauatennisepall, siis sõltub mõõtetulemus kindlasti sellest, millise osaga pall vastu horisontaalset jäika aluspinda põrkab. Pingpongipallid valmistatakse enamasti kahe pallipoole kokkusulatamise teel, pallikeste omadused liitekohas ja väljaspool seda on erinevad. Me ei suuda prognoosida palli asendit põrkehetkel, mistõttu see asend on mõõteväärtuse juhuslik mõjur.
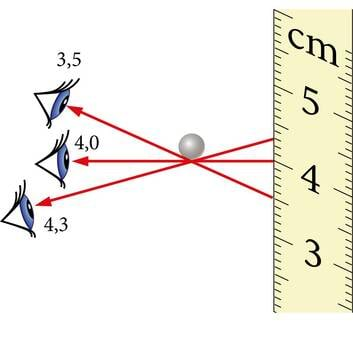
Vertikaalselt mõõtjoonlaualt palli kõige ülemise asendi kõrgust lugev katsetaja peab lugemi fikseerimisel vaatama joonlauda horisontaalselt ehk risti joonlaua endaga. Selleks peab lugemit võttev katsetaja kas kummardudes või mingile täiendavale alusele ronides muutma oma pea asukohta. Kui ta seda ei tee ning vaatab joonlauda kogu aeg näiteks kõrgemalt kui vaja, siis ta fikseerib tõusu kõrguse lugemi, mis on tegelikust väärtusest süstemaatiliselt veidi väiksem. Kasutades veidi etteruttavalt mõõtevea mõistet (vt allpool), olgu märgitud, et mõõteviga, mis tekib juhul, kui mõõtja vaatesuund ei ole risti kasutatava skaalaga, nimetatakse parallaktiliseks mõõteveaks.
Üks mõõtmiste täpsust piirav tegur on mõõtühiku enda pikkus. Kui me kasutame lauatennisepalli tagasipõrke kõrguse määramisel mõõtjoonlauda, millele on kantud kriipsud iga sentimeetri tagant, siis on mõõtühikuks 1 cm. Sentimeetri murdosi me mõõteväärtuses enam usaldusväärselt kajastada ei suuda. Lisaks võivad paljud mõõtmise täpsust piiravad tegurid olla meile ka täiesti tundmatud.
Kõike seda arvestades oleme sunnitud nentima, et absoluutselt täpne mõõtmine pole põhimõtteliselt võimalik. Järelikult on üldjuhul väga oluline lisaks mõõteväärtuse saamisele hinnata ka mõõtmise täpsust.
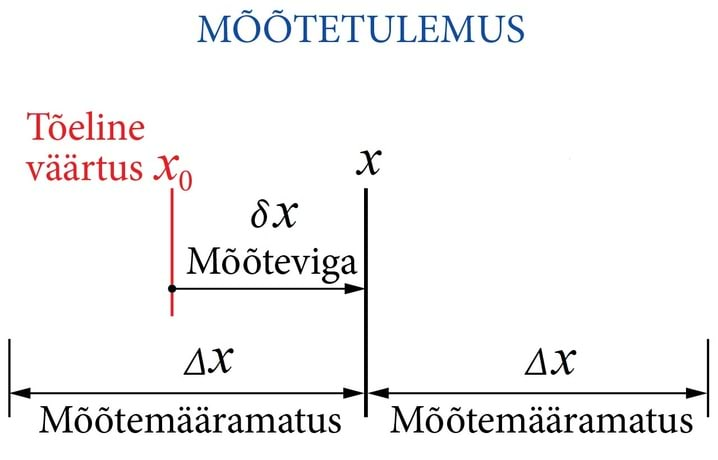
Tähistame mingi konkreetse suuruse (näiteks koolilaua pikkuse) mõõtmisel saadud mõõteväärtuse tähega . Kuna absoluutselt täpne mõõtmine pole põhimõtteliselt võimalik, siis see väärtus üpris kindlasti erineb mõõtesuuruse tõelisest väärtusest . Mõõteväärtuse ja suuruse tõelise väärtuse vahet nimetatakse mõõteveaks. Suuruse mõõteviga tähistatakse enamasti sümboliga (loe: väike delta x):
Mida väiksem on mõõteviga, seda täpsema mõõtmisega on tegemist. Paraku me ei tea ega saagi kunagi teada mõõdetava suuruse tõelist väärtust . Seetõttu ei saa me ka kunagi teada konkreetsel mõõtmisel tehtavat mõõteviga .
Mõõteviga on vähemasti osaliselt juhuslik suurus. Iga järgmise mõõtmise tulemus võib eelmisest veidi erineda. Seega kaasneb mõõtmisega alati teatav teadmatus ehk määramatus. Mõõtesuuruse tõeline väärtus ja konkreetne mõõteviga jäävad meile küll teadmatuks, kuid me saame mingi tõenäosusega hinnata, milline on kõige suurem võimalik mõõteviga. Me saame anda tõenäosusliku hinnangu väärtuste vahemiku kohta, milles mõõtesuuruse tõeline väärtus asub. Seda mõõtesuuruse väärtuste vahemikku, millesse suuruse tõeline väärtus piisavalt suure tõenäosusega jääb, kirjeldab mõõtemääramatus.
Suuruse mõõtemääramatus (ingl uncertainty) on suurus, mis kuulub mõõtetulemuse juurde ja iseloomustab tõenäosuslikult mõõtesuuruse võimalike väärtuste vahemikku. Mõõtemääramatusel on mitmeid tähistusviise. Kui räägitakse mõõtemääramatusest kõige üldisemas tähenduses, siis kasutatakse enamasti tähist (loe: delta x). Niisiis, mõõtemääramatus on mõõtevea suurim lubatav väärtus. Mõõtetulemus x ei tohiks mõõtesuuruse tõelisest väärtusest erineda rohkem kui mõõtemääramatuse võrra. See tähendab, et suuruse tõeline väärtus jääb väärtuste ja vahele. Matemaatiliselt väljendab seda võrratus
Paraku pidime eelmises lõigus kasutama tingivat kõneviisi (ei tohiks). Nimelt ei ole mitte ükski tõenäosuslik väide ju kunagi sajaprotsendiliselt kindel. Tõenäosust selleks, et mitte ükski mõõteviga ei ületa konkreetset mõõtemääramatuse väärtust, nimetatakse mõõtemääramatuse usaldatavuseks või ka usaldusnivooks. Kui me soovime, et mõõtemääramatusega antav suurima mõõtevea hinnang oleks kindlasti tõene (et usaldatavus oleks 100%), siis peame kasutama väga suurt väärtust. Siis aga muutuks mõõtetulemus ise üpris mõttetuks. Näiteks klaasilõikajal on vähe kasu teadmisest, et aknaava kõrgus jääb 50 ja 150 sentimeetri vahele. On ilmne, et mõõtjal tuleb leida mõistlik kompromiss kahe vastandliku soovi vahel: tõsta usaldatavust ja vähendada mõõtemääramatust.
Mõõtemääramatus esitatakse tavaliselt usaldatavusega kas 68% või 95%. Eeldades usaldatavust 95%, pannakse mõõtetulemus tavaliselt kirja koos mõõtemääramatusega kujul
.Näiteks on korrektne pliiatsi pikkuse mõõtmise tulemus esitatav kujul
See tähendab, et konkreetse pliiatsi tõeline pikkus jääb 139 mm ja 143 mm vahele tõenäosusega (usaldatavusega) 95%. Kui tegemist on mingi muu usaldatavusega, siis peab selle mõõtetulemuse taga eraldi ära märkima.
Usaldatav mõõtetulemus tuleb alati esitada koos mõõtemääramatusega. Mõõtemääramatuse hindamiseks on erinevaid meetodeid, kuid üldjoontes eksisteerib kaks põhilist hinnangu tüüpi. Need on A-tüüpi ja B-tüüpi hinnangud, mida sageli nimetatakse ka A-tüüpi ja B-tüüpi mõõtemääramatusteks.
Kui me kordusmõõtmisi tehes saame kogu aeg veidi erinevaid tulemusi, nii et iga konkreetne mõõteväärtus varem saadutega üldjuhul kokku ei lange, siis peame andma mõõtemääramatusele A-tüüpi hinnangu. A-tüüpi mõõtemääramatus on põhjustatud juhuslikest mõjuritest ja see leitakse kordusmõõtmiste tulemustest matemaatilise statistika meetoditega. A-tüüpi määramatust saab mõõtmiste arvu suurendamisega vähendada.
Matemaatilise statistika teooria kinnitab, et juhusliku mõõteveaga suuruse mõõtmisel on tulemuse parimaks hinnanguks paljude mõõtmistulemuste aritmeetiline keskmine. Selle saamiseks liidetakse kõik mõõtmistulemused kokku ja jagatakse mõõtmiste arvuga.
Mõõtemääramatuse hindamiseks sobib tulemuste hajumist keskväärtuse ümber iseloomustav statistiline suurus, mis kannab nimetust standardhälve.
Kui kordusmõõtmised annavad alati sama tulemuse, siis ei saa mõõtemääramatust hinnata kordusmõõtmisi tehes. Sellisel juhul peame andma mõõtemääramatusele B-tüüpi hinnangu. Sageli öeldakse ka, et tegemist on B-tüüpi määramatusega. B-tüüpi hinnang mõõtemääramatusele saadakse mitte enam mõõtja enda poolt rakendatavate statistiliste meetoditega, vaid muudest allikatest pärineva info põhjal. Eelkõige kasutab mõõtja mõõteriista tootja poolt antud infot mõõteriista täpsuse kohta. Kõige suurem erinevus A- ja B-hinnangute vahel ongi see, et B-tüüpi määramatuse korral teeb sisulise töö mõõtemääramatuse hindamisel ära mõõtevahendi või mõõteriista valmistaja. Tootjad märgivad mõõtemääramatuse alase teabe kas otse mõõteriistale või selle passi. Kui aga selline info puudub, siis on üldine tava võtta mõõtemääramatuseks pool väikseimast skaalajaotisest.
Enamasti esinevad nii A- kui B-tüüpi määramatus korraga. Liitmääramatus leitakse kui ruutjuur A- ja B-määramatuste ruutude summast. Tähistades suuruse A-tüüpi määramatuse sümboliga ja B-tüüpi määramatuse sümboliga võime liitmääramatuse avaldada kujul
Mõõtemääramatus
Mõõtemääramatus on suurus, mis kuulub mõõtetulemuse juurde ja iseloomustab tõenäosuslikult mõõtesuuruse võimalike väärtuste vahemikku.
Standardhälve
Standardhälve on suurus, mis kirjeldab üksikute mõõteväärtuste puhtjuhuslikku hajumist keskväärtuse ümber.
Mõõteasjanduses peavad kehtima kindlad kokkulepped, tagamaks mingi mõõtmise korratavust ja vältimaks ülearu pikki mõõtmisprotsessi kirjeldusi. Seda mõisteti juba keskajal, mil iga suurema linna ümbruses kasutati selle linna valitsuse poolt kehtestatud mõõtühikuid. Näiteks olid Vana-Liivimaal mahuühikutena kasutusel Tallinna vakk (44,277 liitrit) ja Riia vakk (66,415 liitrit), Tallinna toop (1,09 liitrit) ja Riia toop (1,32 liitrit). Sõltumatu mõõdusüsteemi omamine oli konkreetse linna kindel eriõigus ehk privileeg, osa tema iseolemisest. See süsteem toimis hästi meie poolt ajaloos õpitud naturaalmajanduse tingimustes, mil suurem osa elanikkonnast üldse rahaga tegemist ei teinud, äritehinguid sooritati lähima linna turul ja naaberlinnas toimuv polnud kuigi oluline. Kui uusajal tekkisid ühtsed rahvusriigid, siis tuli seoses turgude avardumisega mõõteasjandus ehk metroloogia (kr metron 'mõõt') kogu riigis ühtlustada. Oli ju vaja tagada, et kõik mõõtjad saaksid mõõtmisprotsessist vähemasti selle riigi piires ühtemoodi aru. Samuti soodustas ühesuguste mõõtühikute kasutamine kaubanduse arengut, sest nii kadus vajadus pidevalt mõõtühikuid teisendada. Sai selgeks, et mõõteasjandus tuleb vastavate seadustega ära reguleerida.
Tungiva vajaduse omaette seadusandluse järele mõõteasjanduses tingib tõsiste varaliste vaidluste paratamatu jõudmine kohtusse. Kujutlegem segadust, mis tekiks, kui mingi kaubakoguse ostu-müügi lepingus poleks täpsustatud mõõtühikut, mida tuleb selle kauba mõõtmisel kasutada. Loodetavasti mõistame kõik, et sada vakka teravilja keskaegses Tallinna ühikusüsteemis ja Riia süsteemis on sootuks kaks eri asja. Tänapäeval tuleb pea kõigil inimestel maksta kasutatud vee ja elektrienergia eest. Vastavaid korrektseid arveid saab aga esitada ja neid on mõtet tõrkumata tasuda vaid juhul, kui vett või elektrienergiat on mõõdetud kehtivate õigusnormide kohaselt.
Omaette valdkonna moodustavad õigusrikkumised, mida tuvastatakse mõõtmise teel. Tuntuim näide selle kohta on trahv, mille liikluspolitsei määrab autojuhile lubatud kiiruse piirmäära ületamise eest. Kuna seaduses ettenähtud trahvisumma on tugevas sõltuvuses rikkumise ulatusest, siis muutub ülioluliseks politsei poolt teostatud kiirusmõõtmise korrektsus. Me õpime praegu mõõteasjandust mitte niivõrd füüsika vajadustest lähtuvalt, vaid eelkõige põhjusel, et kõik kodanikud peavad hästi mõistma lihtsat tõde – ebakorrektse mõõtmise alusel esitatud pretensioon on õigustühine! Näiteks oli mõõteasjandus taasiseseisvunud Eesti Vabariigis esialgu reguleerimata, mistõttu polnud kuigi raske liikluspolitsei tehtud trahviotsuseid kohtus vaidlustada. Metroloogiat tundvad kodanikud võisid end sellega lausa lõbustada, sest vastavat seadusandlust polnud veel olemas.
Tänapäeval reguleerib Eestis kõike mõõtmistega seonduvat 2004. aastal kehtestatud mõõteseadus. Soovi korral saab igaüks mõõteseadusega täies pikkuses tutvuda elektroonilises Riigi Teatajas. Mõõteseaduse täitmine on kohustuslik kõigile, kelle tegevus on mingilgi viisil mõõtmisega seotud. Piirkiiruse ületamise eest trahvi määrav politseiametnik on kohustatud tutvustama autojuhile dokumente, mis tõendavad, et auto kiiruse mõõtmine on toimunud täies vastavuses mõõteseadusega.
Eesti Vabariigi mõõteseaduse peamised reguleerimisalad on järgmised.
– Rahvusvahelisele mõõtühikute süsteemile (SI) vastavate mõõtühikute (vt p 2.3) kasutamise tagamine Eestis.
– Seaduses on öeldud, et rahvusvahelise mõõtühikute süsteemi kasutamine on Eestis kohustuslik majandustegevuses, rahvatervise ja avaliku ohutuse valdkonnas, haldus- ja õppetegevuses.
– Mõõtetulemuste jälgitavuse tõendamine. Seadus nõuab, et juriidiliselt korrektseid mõõtmisi teostaks vastavat tunnistust omav mõõtja, kes kasutab sobivaks tunnistatud mõõtevahendeid.
– Mõõtevahendite kontroll ja taatlemine.
– Mõõtmistegevuse riikliku järelevalve korraldus.
Mõõteseaduses on defineeritud kõik olulised mõõteasjanduslikud ehk metroloogilised mõisted. Järgmises alapunktis refereerime ja kommenteerime vastavaid määratlusi.
Mistahes mõõtmise läbiviimiseks on kindlasti vaja mõõtevahendit. Mõõtevahend on kindlate omadustega tehniline vahend, mida saab kasutada mõõtmiste sooritamiseks kas üksi või koos lisaseadmetega. Temperatuuri mõõtmise vahendiks võib olla näiteks mingile alusele keritud pikk vasktraat, kuna selle elektritakistus sõltub temperatuurist. Ainult traadi abil me aga temperatuuri väärtust teada ei saa. Me vajame lisaseadmena takistusmõõtjat. Üldiselt on mõõtmiste korral alati tegemist mõõtesignaaliga ehk endas mõõtarvu kandva infoga. Mõõtarv aga ei pruugi olla sellest otsekohe välja loetav. Vasktraadi kui temperatuuri mõõtmise vahendi korral on mõõtesignaaliks takistusmõõtja näit, aga see ei esine mõõtjale kui vaatlejale vahetult tajutaval kujul. Mõõtevahend (traat) on koos abivahendiga (takistusmõõtja) kasutatav temperatuuri mõõtmiseks alles siis, kui takistusmõõtja näit on kõigi kehtivate reeglite kohaselt viidud vastavusse temperatuuri väärtustega. See vastavusse viimine on tuntud kui mõõtevahendi kalibreerimine.
Mõõtevahendit, mis esitab mõõtesignaali juba vaatlejale vahetult tajutaval kujul, nimetatakse mõõteriistaks. See tähendab, et mõõteriista korral me võime mõõtesuuruse väärtust lugeda mõõteriista skaalalt või numbriliselt tabloolt. Mõõteriistadeks on näiteks joonlaud, sekundkell, termomeeter või ampermeeter.
Mõõtevahendite ja mõõteriistade omadused võivad ajas muutuda. Seetõttu tuleb õiguslikku aspekti omavatel mõõtmistel kasutatavaid mõõtevahendeid ja mõõteriistu perioodiliselt taadelda. Mõõteseadus ütleb, et „taatlemine on protseduur, mille käigus pädev taatluslabor või teavitatud asutus kontrollib mõõtevahendi vastavust kehtestatud nõuetele ja märgistab nõuetele vastavaks tunnistatud mõõtevahendi taatlusmärgisega. Taatlusmärgis on taatluskleebis, taatlusplomm või taatlustempli jäljend. Mõõtevahendil või mõõteriistal peab olema ka tüübikinnitus. See on pädev otsustus, mille kohaselt vaadeldavat tüüpi mõõtevahend vastab õigusaktidega kehtestatud nõuetele ning on kasutatav õiguslikult reguleeritud toimingutes, võimaldades teatud ajavahemiku ehk taatluskehtivusaja jooksul saada usaldatavaid mõõtetulemusi.“ Neis määratlustes korduvalt esinenud sõna pädev tähendab, et taatlusprotseduuride läbiviijate teadmisi, oskusi ja nende käsutuses olevaid vahendeid on kontrollitud veelgi kõrgema tasemega ning paremini varustatud taatlejate poolt. Kontrolli tulemustega on jäädud rahule ja konkreetsele taatluslaborile on antud vastav tunnistus.
Füüsikalistest mudelitest oli meil natuke juba eespool juttu. Füüsikaline mudel rõhutab loodusobjekti neid omadusi, mis on antud kontekstis olulised. Siin vaatleme mudeleid lähemalt, alustades mudeli üldisest määratlemisest. Loodusteadustes nimetatakse üldiselt mudeliks (ld modulus 'näidis') loodusobjekti jäljendust, mis asendab originaali selle lihtsamaks mõistmiseks ning uurimiseks. Kuna füüsikalist suurust kui mudelit on esmapilgul raske sobitada selle definitsiooni alla, siis paljud ka ei mõista, et füüsikaline suurus on looduse mudel. Me teame, et füüsikalises uurimistöös on tähtsal kohal vaatlus. Vaatleja loob endale uuritavast objektist või nähtusest kujutluse. Seejuures on tal palju abi mudelitest kui lihtsustustest. Mudeli saab luua mistahes makrokehast, vee molekulist, lihtaine aatomist, elektromagnetlainest või koguni päikesesüsteemist ja tervest meie galaktikast. Modelleerida saab aga ka füüsikalisi nähtusi nagu elektrivool, auto liikumine maanteel või valguse murdumine vihmapiisas.
| Vee molekuli mudel. Hapniku suure elektronegatiivsuse tõttu on kogu molekul polaarne ning moodustab teiste vee molekulidega vesiniksidemeid. Hapniku suur elektronegatiivsus seletab ka ainulaadset aatomitevahelist nurka, 105 kraadi. Elektronegatiivsus on aatomi kalduvus teiste aatomite elektrone osaliselt endaga liita. Punane värv tähistab suurt elektronegatiivsust. | Plastikust DNA-mudel. |
Kõikidele mudelitele on iseloomulik see, et nad ei jäljenda originaali kunagi täpselt. Originaali omaduste täpne edastamine mudelis pole juba sellepärast võimalik, et vaatleja ei pruugi üldse kõiki üksikasju näha. Pealegi puudub ideaalse täpsuse järele ka vajadus. Mudel edastab vaid originaali kõige olulisemaid tunnuseid ja omadusi. Mudel on lihtsustus, kus jäetakse arvestamata kõik antud kontekstis mitteoluline. Kõige üldisemaid loodusteaduslikke mudeleid, mida loob füüsika ja mida kasutavad kõik loodusteadused, nimetatakse füüsikalisteks mudeliteks.
Loodusteaduslikke, sealhulgas ka füüsikalisi mudeleid, liigitatakse tavaliselt ainelisteks ja abstraktseteks mudeliteks. Ainelisi mudeleid kasutatakse siis, kui uuritav objekt on palja silmaga vaatlemiseks kas liiga väike või liiga suur. Üldiselt kujutab aineline mudel mikro- või megamaailma objekti. Sellise objekti aineline mudel aitab meil tekitada kujutlust vahetutele aistingutele kättesaamatust objektist. Vee molekuli suurendav mudel edastab käegakatsutaval viisil keemiliste sidemete vahelist spetsiifilist nurka (105°) selles molekulis koos hapniku ja vesiniku aatomite suuruste suhtega ning elektronpilve jaotusega. See võimaldab paremini mõista vee ja jää kristallstruktuuri moodustumist. Analoogiliselt aitab DNA-molekuli mudel mõista geneetilise informatsiooni talletamist selles aines. Neid mudeleid kasutavad palju keemia ja bioloogia, aga nad on loodud füüsikaliste uurimismeetodite abiga ning teiste füüsikaliste mudelite baasil. Gloobus kui Maa vähendatud mudel võimaldab paremini aru saada öö ja päeva vaheldumisest. Süsteemi Maa-Kuu-Päike mehaaniline mudel aitab paremini mõista aastaaegade vaheldumist Maal ning kuu- ja päikesevarjutuste teket. Ka need mudelid on algselt loonud füüsika, kuid neid kasutab laialdaselt geograafia.
Aineliste mudelite spetsiifilise alaliigina võib vaadelda pildilisi mudeleid. Nende korral pole modelleeritavast objektist tehtud reaalset kolmemõõtmelist vähendatud või suurendatud osalist koopiat. Seda koopiat on vaid kujutatud kahemõõtmelisel joonisel, mis rõhutab originaali neid omadusi, mis on mudeli looja jaoks olulised. Tänapäeval kasutatakse üha rohkem ka arvutimudeleid ehk animatsioone. Need on järjestikuste piltide seeriad ehk videod. Loodusteaduslikud arvutimudelid võimaldavad kas ühte ja sedasama loodusobjekti vaadelda erinevates vaadetes ehk rakurssides või siis jälgida loodusnähtuse ehk protsessi arengut läbi protsessi kirjeldavate järjestikuste kujutiste. Arvutite riist- ja tarkvara areng on võimaldanud kaasajal üha rohkem kasutada ka interaktiivseid arvutimudeleid, mille korral mudeli kasutaja saab ise mudeli tingimusi varieerida ja seeläbi paremini tunnetada looduses valitsevaid põhjuslikke seoseid.
Juhul, kui loodusobjekti uuritakse ja kirjeldatakse mitte ainelise mudeli, vaid mõtteliste kujutluste ning neid väljendavate matemaatiliste avaldiste abil, on tegemist abstraktse mudeliga (ld abstractus 'mõtteline'). Abstraktne mudel on objekti mõtteline visioon, kontseptsioon objektist mõtleva inimese teadvuses. Vaatleja suudab abstraktseid mudeleid luua vaid seetõttu, et tal on olemas mõistus ehk süllogismide moodustamise võime.
Selleks, et ennustada, millal jõuab rong järgmisesse jaama, pole vaja kasutada rongi ainelist mudelit ehk laste mängurongi. Me võime tõelist rongi lihtsalt ette kujutada. Seejuures pole üldse tähtis, mitmest, kui pikast ning millist värvi vagunitest see rong koosneb – lõppjaama jõudmise aja ennustamisel pole oluline, milline rong välja näeb. Tähtis on vaid see, kus rong asub erinevatel ajahetkedel. On vaja teada rongi asukoha sõltuvust ajast. Sellise ülesande puhul piisab, kui kujutame tervet rongi ette vaid punktina, millel mõõtmed puuduvad. Rongi mõõtmed, kuju ja muud omadused pole hetkel olulised. Oluline on vaid see, kus asub rongi tähistav punkt ja kuidas selle punkti asukoht aja jooksul muutub. Ühe punktina kujuteldav rong, auto või lennuk on tuntud füüsika üldmudelina, millel nimeks punktmass. Selle mudeliga tegeleme peagi lähemalt. Praegu nendime vaid, et rongi liikumise modelleerimiseks piisab, kui lihtsalt kujutame selle liikumist ette ja esitame matemaatilise valemi, mis võimaldab leida rongi asukoha mistahes ajahetkel.
Rongi liikumise visiooni ehk mõttekujundi abstraktseks mudeliks on matemaatiline avaldis, mis lubab liikumisoleku omadusi teades välja arvutada rongi kaugust lähtejaamast mistahes võimalikul ajahetkel. Kui rongi kaugust lähtejaamast (avaldatuna meetrites) tähistada tähega ja sekundites avaldatud aega, mis on möödunud liikumahakkamisest, tähistada tähega , siis väljendab selle rongi liikumist näiteks avaldis . See avaldis ongi rongi liikumist kirjeldav matemaatiline mudel.
Matemaatilisele avaldisele tuginevat loodusnähtuse (nt rongi liikumise) kirjeldust nimetatakse analüütiliseks mudeliks. Rongi asukoha sõltuvust ajast saab peale matemaatilise valemi väljendada ka graafiku abil. Sel puhul on tegemist loodusnähtuse graafilise mudeliga.
Analüütilise mudeli loomist alustame rongi liikumise sihipärasest vaatlusest, millega kaasneb mõõtmine. Olgu meil näiteks raudteel iga kilomeetriposti juurde paigutatud ajamõõtja, mis fikseerib rongi jõudmise selle konkreetse postini. Ajamõõtjast lähevad signaalid arvutisse. Moodustub andmefail, mis sisaldab lähtejaamast alates loendatud kilomeetripostide järjekorranumbreid, postide kaugusi lähtejaamast ja rongi jõudmiseks vastava kilomeetripostini kulunud aegu. Arvuti võib olla programmeeritud väljastama neid andmeid otsekohe alljärgneva tabeli kujul, kus füüsikaliste suuruste tähiste järel on sulgudes toodud mõõtühik.
| Kilomeetriposti number | Posti kaugus lähtejaamast x või s (m) | Kulunud aeg t (s) | Läbitud teepikkuse ja kulunud aja suhe ehk kiirus v = s/t (m/s) |
|---|---|---|---|
| 1 | 1000 | 50 | 20 |
| 2 | 2000 | 100 | 20 |
| 3 | 3000 | 150 | 20 |
| 4 | 4000 | 200 | 20 |
| 5 | 5000 | 250 | 20 |
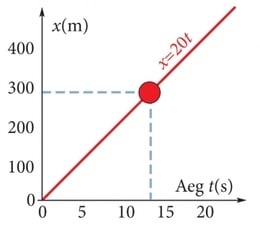
Meie järgmiseks tegevuseks on andmetöötlus. Selleks koostame kõigepealt graafiku, mille horisontaalsele ehk matemaatiliselt väljendudes abstsissteljele märgime aja väärtused (joonis 2.4). Vertikaalsele ehk ordinaatteljele kanname kaugused lähtejaamast (või läbitud teepikkused ). Näeme, et graafik on tõusev sirge, mis läbib koordinaatide alguspunkti. Matemaatikast teame, et sel juhul on tegemist võrdelise sõltuvusega ehk lineaarfunktsiooniga , kus on funktsioon ja on argument. Meie mudelis on argumendiks aeg ja funktsiooniks läbitud teepikkus . Seega meie juhul , kuna põhikooli mehaanikast me juba teame, et
Tabelist näeme ka, et graafiku mistahes punkti järgi arvutades saame muutumatu ehk konstantse kiiruse v = 20 m/s. Konstantse kiirusega toimuvat liikumist nimetatakse füüsikas ühtlaseks liikumiseks. Vaadeldes läbitud teepikkust kaugusena lähtejaamast ehk suurusena, mida mehaanika kursuses nimetatakse koordinaadiks, olemegi saanud rongi liikumise protsessi analüütilise mudeli, mida mehaanika kursuses nimetatakse liikumisvõrrandiks:
Liikumisvõrrand võtab kõige kompaktsemalt ja üldisemalt kokku meie üksikud katsetulemused.
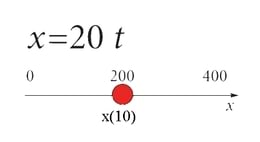
Tekib ka küsimus, mis kasu on meil loodud mudelist? Oletagem, et meid huvitab, kas uuritav rong võib 15 minuti jooksul jõuda järgmisesse jaama, mis on lähtejaamast 20 km kaugusel. Asendame aja liikumisvõrrandisse ja saame:
Seega vastus püstitatud küsimusele on eitav. Rong läbib 15 minuti jooksul 18 km ja ei jõua veel jaama, mis asub 20 km kaugusel lähtejaamast.
Kõik me teame, et kumminöör venib selle tõmbamisel ühest otsast, kui teine ots on paigal. Uurime kumminööri venimise nähtust lähemalt katse abil. Selleks vajame kumminööri, mõõtjoonlauda ning teadaoleva massiga kehi, mille kaalu saaks kasutada teadaoleva jõuna. Katse käigu kohta koostame protokolli.
Töövahendid: traadist kinnituskonksudega uuritav kummipael; mõõtjoonlaud 0...30 cm ±0,5 mm; neli ühesugust rauast koosnevat detaili, igaüks massiga (30 ±3) g
Töö käik: kinnitame kumminööri vertikaalasendisse paigutatud mõõtjoonlaua külge rippuma.
Märgime üles, millise jaotise kohal asub nööri lõpus olev traadist osuti koormiste puudumisel. Nüüd asume uurima, kuidas kumminööri külge riputatud seibid nööri venitavad. Riputame nööri otsa erineval hulgal seibe ning märgime üles nende arvu , summaarse massi ning väljaveninud kumminööri pikkuse . Hindame katse oludest lähtuvalt kumminööri pikkuse mõõtmise määramatust. Kanname kõik mõõteväärtused tabelisse. Kõige lõpuks mõõdame, kui pikaks venitab kumminööri selle otsa riputatud kohuke.
Arvutame iga koormise ehk seibide arvu jaoks kumminööri pikenemise . Selleks lahutame väljavenitatud kumminööri pikkusest ilma koormiseta mõõdetud algpikkuse.
Katsetulemuste tabel. Katse käigus selgus, et kuigi mõõtjoonlaua skaala vähima jaotise pikkus on 1 mm, tuleb kumminööri pikkuse mõõtemääramatuseks võtta 0,5 cm. Mõõtmise ajal koormis võnkus ja osuti näitu polnud võimalik täpsemini fikseerida.
| Nr | Koormiste arv | Mass m (g) | Pikkus l (cm) | Pikenemine Δl (cm) |
|---|---|---|---|---|
| 1 | 0 | 0 | 10,9 ± 0,5 | 0 |
| 2 | 1 | 30 ± 3 | 13,0 ± 0,5 | 2,1 ± 0,5 |
| 3 | 2 | 60 ± 6 | 16,3 ± 0,5 | 5,4 ± 0,5 |
| 4 | 3 | 90 ± 9 | 20,6 ± 0,5 | 9,7 ± 0,5 |
| 5 | 4 | 120 ± 12 | 24,4 ± 0,5 | 13,5 ± 0,5 |
| 6 | Kohuke | pole teada | 15,1 ± 0,5 | 4,2 ± 0,5 |
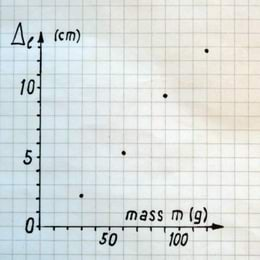
Mõõtmistulemuste analüüs. Andmeid vaadates on näha, et mida suurema massiga on koormis, seda rohkem kumminöör pikeneb. Milline see sõltuvus aga täpsemalt on, saame öelda alles graafiku põhjal. Koostame katsetulemuste graafiku. Selleks joonestame esmalt sobivas mõõtkavas teljestiku, mille horisontaalteljele märgime katse käigus muudetud raskuste massi ja püstteljele kumminööri pikenemise. Seejärel kanname graafikule katsepunktid.
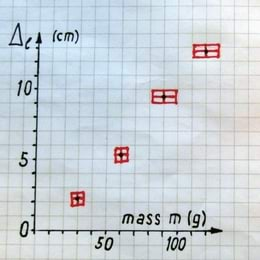
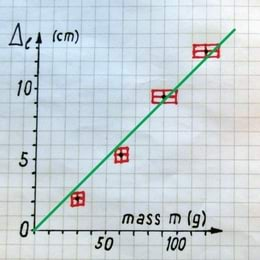
Me ei tohi nüüd katsepunkte otsekohe joonega ühendada. Selline teguviis väljendaks veendumust, et meie mõõtmised olid absoluutselt täpsed. Me peame märkima iga punkti ümber mõõtemääramatuse piirkonna ehk kasti, mille keskel paikneb katsepunkt ja mille laiuseks ning kõrguseks on vastava mõõtesuuruse kahekordsed mõõtemääramatused. Nüüd joonestame uuritavat sõltuvust kirjeldava graafiku, püüdes selleks valida võimalikult lihtsa joone. See joon ei pea läbima kõiki katsepunkte, vaid ainult katsepunkte ümbritsevaid mõõtemääramatuse piirkondi. Näeme, et meie katses saab graafikuks võtta sirgjoone.
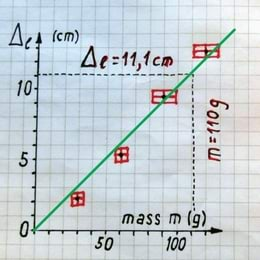
Sirget on võimalik väljendada matemaatilise võrrandi abil. Võrrandi tuletamiseks valime joonestatud sirgel välja ühe punkti ning leiame graafikult sellele punktile vastava massi ja pikenemise. Valime näiteks väärtused ja . Selle arvupaari põhjal leiame, kui palju venib kumminöör ühikulise massiga koormise mõjul. Jagame valitud pikenemise vastava massiga. Tulemuseks saame
Kasutasime seni katses ja tulemuste analüüsis mõõtühikutena sentimeetrit ja grammi, kuna need olid graafiku koostamisel mugavamad kasutada. Lõpptulemuse avaldame siiski ka kujul, mis sisaldab SI ühikuid meeter ja kilogramm.
Kui me soovime ennustada, kui palju venib kumminöör näiteks 50-grammise koormise korral, siis tuleb mass saadud arvuga läbi korrutada. Me saame
Sama protseduur sobib ka mistahes muu koormise korral. Pikenemise leidmiseks tuleb mass korrutada graafikult leitud suurusega 0,10 cm/g. Oleme pikenemise arvutamiseks saanud valemi:
Kumminööri pikenemine on võrdelises sõltuvuses otsariputatud raskuse massist, kuna mass on saadud valemis esimeses astmes. Jällegi on tegemist matemaatikast tuntud lineaarfunktsiooniga , kus on funktsioon ja on argument. Meie praegusel juhul on argumendiks koormise mass m ja funktsiooniks kumminööri pikenemine . Saadud valem on kumminööri venimise analüütiline mudel. Mudeliks on ka meie eespool joonestatud graafik. Kui me katsetaksime mõne teise kumminööri või vedruga, tuleksid arvud küll teised, aga nähtuse olemus jääks samaks – valem ja graafik oleksid meie poolt saadutega sarnased. Seega oleme loonud ühe üpris üldise loodusnähtuse mudeli. Rõhutame veelkord, et sirge, mille me graafikule tõmbasime, ei läbi tegelikult kõiki katsepunkte. Tegemist on lihtsustusega, mis ei kajasta reaalset nähtust absoluutselt täpselt. Füüsikaline mudel on alati lihtsustus. Võimalik, et teostades täpsemaid mõõtmisi ja proovides graafikuna mõnd teist joont ja sellele vastavat matemaatilist avaldist, saaksime kumminööri venimise kirjeldamiseks täpsema mudeli.
Mudeli tingimused. Meenutagem näidet hüpoteesi katselise kontrollimise kohta. Nimelt oli tähtis rõhutada katse tingimusi, sest teistsugustes tingimustes ei oleks katse tulemus pruukinud olla selline. Sama probleem tekib mudeli loomisel. Kui näiteks mõõtjoonlaua asend ülalkirjeldatud praktilises töös erineb oluliselt vertikaalsest ning kumminööri otsa riputatud detailid on mõõtjoonlauaga tugevas kontaktis, siis hakkab koormise raskusjõu mõjul toimuvat kumminööri pikenemist takistama hõõrdejõud. Me eeldasime ülalpool, et ainsaks kumminöörile mõjuvaks jõuks on koormise raskusjõud. Kui see nii ei ole, siis me ei pruugi enam saada võrdelise sõltuvuse mudelile alluvaid katsetulemusi. Mudel kirjeldab loodust kindlates fikseeritud tingimustes. Nende puudumisel ei tarvitse selline mudel enam kehtida. Niisiis, võrdeline sõltuvus koormise massi ja kumminööri pikenemise vahel kui looduse mudel, kehtib eeldusel, et koormisele mõjub ainult kaks jõudu: allapoole suunatud raskusjõud ja kumminööri esialgset pikkust taastada püüdev jõud, mis on suunatud ülespoole. Muud jõud puuduvad. See on uuritava mudeli tingimus.
Mudeli rakendamine. Saime kumminööri venimise mudeli nii graafiliselt kui ka analüütilisel kujul ehk valemina. Mudeli abil võime ennustada, kui palju venib kumminöör siis, kui me riputame tema otsa selliseid kehi, millega me veel katsetanud pole. Lisaks märkame, et uuritav kumminöör on nüüd ise kasutatav mõõtevahendina. Me võime tema abil mõõta erinevate esemete masse, kuna valemis 2.9 sisalduva suuruse 0,10 cm/g leidmisega oleme kumminööri kui mõõtevahendi esimeses lähenduses ära kalibreerinud. Katsetulemuste tabeli viimasest reast loeme, et kumminöör pikenes kohukese raskuse toimel 4,2 cm võrra. Avaldades valemist 2.9 massi, saame et
Järelikult on uuritava kohukese mass 42 grammi. Pole kahtlust, et need, kes on kogu mudeli loomise korralikult kaasa teinud, on selle kohukese ausalt ära teeninud.
Loodusteaduslik mudel
Loodusteaduslik mudel on loodusobjekti jäljendus, mis asendab originaali selle lihtsamaks mõistmiseks ning uurimiseks.
Kui mõõtmistulemused ja teooria omavahel ei klapi, siis on kaks võimalust - kas mõõtmised on halvasti tehtud või on kasutatav mudel ebasobiv. Et kass saaks oma uuri pendli järgi õigeks seada, peab eelnevalt olema piisava täpsusega määratud pendli periood. Pendel on aga füüsikas hästi tuntud mudel. Mudelitest järgmine peatükk räägibki.