Spektrijooned kui redel aatomimaailma

Kuidas on aatomite siseehitus seotud aatomite kiiratava valguse spektriga.
Kuidas on aatomite kiirgus- ja neeldumisspektrid seotud aatomite omadustega.

Aatomite spektrijooned ja energiatasemed

Optikakursuses õppisime, et kui hõrendatud gaasidest elektrivoolu läbi juhtida, kiirgavad need valgust, mille spekter on joonspekter. Teisisõnu, nende helendus ei sisalda igasuguse lainepikkusega valgust, vaid liitub teatavate kindlate lainepikkustega valgusvoogudest. Hõrendatud gaasides (nt elektrilahenduses läbi vesiniku, neooni, naatriumiauru jne) kiirgavad üksteist vähe mõjutavad üksikaatomid. Niisiis, joonspektrid on aatomite spektrid.

Kindlad lainepikkused tähendavad ka kindlaid sagedusi, sest sagedus

f = \frac{c}{λ}

kus $c$ on valguse kiirus vaakumis ja $λ$ lainepikkus. Kui meenutame valguse kaksisust (dualismi), taipame, et joonspekter tähendab ühtlasi seda, et aatomeist kiiratakse kindla energiaga footoneid. On ju footoni energia

E = h f

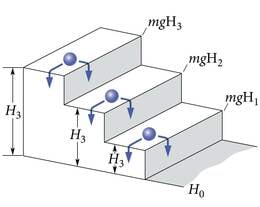
( $h$ on Plancki konstant). Kindla energiaga footonit kiirates peab aatom kaotama footoni energiaga $E$ võrdse energiaportsjoni (energia on jääv!). Samaviisi kaotab trepil astmelt astmele veerev kuulike (joon. 3.1) oma potentsiaalset energiat $m g H$ Maa raskusväljas hüpete $Δ E_{1} = m g (H_{3} - H_{2})$ , $Δ E_{2} = m g (H_{2} - H_{1})$ , $Δ E_{3} = m g (H_{1} - H_{0})$ kaupa. Siin on $m$ – kuulikese mass, $g$ – raskuskiirendus, $H$ – astme kõrgus; $H$ , et seda ei aetaks segi Plancki konstandiga $h$ .

Δ E = m g H_{i} - m g H_{j}

See hüppelisus viib mõttele, et aatomiski on elektronid kindlail energiatasemeil, mis püsivalt omased igale aatomiliigile (elemendile). (Meenutame spektraalanalüüsi – aatomite “sõrmejälgi”.) Nõndasamuti saame meiegi seista vaid redeli pulkadel, mitte nende vahel. Elektroni langedes kõrgemalt (suurema energiaga) tasemelt madalamale, kiiratakse valguskvant energiaga

h f = E_{k} - E_{m}

kus $E_{k}$ ja $E_{m}$ on vastavalt kõrgema ja madalama taseme energia.

Siinkohal tuleks märkida, et aatomifüüsikas mõõdetakse energiat sageli süsteemivälistes ühikutes – elektronvoltides. Neis ühikuis väljenduvad mikromaailma energiakvantumid lühikeste, ülevaatlike arvudena.

$1$ elektronvolt ( $e V$ ) on energia, mille omandab elektron, läbides elektriväljas potentsiaalide vahet $1$ volt. $1 e V = 1, 60 \cdot 10^{- 19} J$ .

Joon. 3.2. Sageduste kombineerumine spektris.

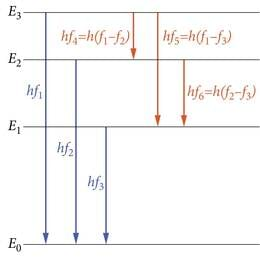
Analüüsides erinevate gaaside spektrijoonte paiknemist sagedusskaalal, leiame veelgi kinnitust kujutlusele energiatasemeist. Nimelt, kui spektris esinevad jooned sagedustel $f_{1}$ , $f_{2}$ , $f_{3}$ jne, siis leiduvad samas spektris arutihti ka jooned, millele vastab sagedus $f_{4} = f_{1} - f_{2}$ , $f_{5} = f_{1} - f_{3}$ , $f_{6} = f_{2} - f_{3}$ . (sageduste kombinatsiooniprintsiip, tihti nimetatud ka tema märkaja, Šveitsi füüsiku Walter Ritzi (1878 - 1909) järgi Ritzi kombinatsiooniprintsiibiks).

Silmitsedes joonist 3.2, leiame, et kõik kombinatsioonid saavad lihtsa seletuse, kui footoneid kiiratakse elektroni “hüpetel” tasemelt $E_{3}$ tasemele $E_{0}$ , $E_{2} \to E_{0}$ jne., nii et $h f_{1} = E_{3} - E_{0}$ , $h f_{2} = E_{2} - E_{0}$ , $h f_{3} = E_{1} - E_{0}$ , $h f_{4} = E_{3} - E_{2}$ jne.

Allakäigutrepilt üles

Joon. 3.3. Vesiniku aatomi kiirgusspekter (A) ja neeldumisspekter (B) nähtavas spektriosas; skaala ühikuis 10^-8m (pügalad 50 nm kaupa).

Et kuulike saaks trepiastmeilt alla veereda, tuleb ta enne üles viia. Aatomi ja elektronide puhul ütleme: aatomit tuleb ergastada, talle energiat sisestada, et tal oleks, mida välja kiirata. Seda võib teha väga mitmel viisil, nt kiiritades aatomeid sobiva spektraalkoostisega valgusega või elektronkimbuga, ainet kuumutades jne. Kas aatomi elektronide energiatasemed avalduvad ka ergastamisel?

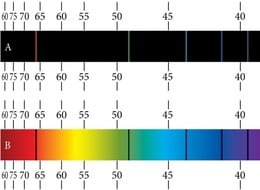
Meenutame optikast neeldumisspektreid, mis saadakse, kui pideva spektriga valgusallika valgus läbib nt. gaasi või auru. Tumedad neeldumisjooned neeldumisspektris langevad täpselt kokku heledate joontega kiirgusspektris (joon. 3.3). See näitabki, et aatomid saavad energiat ka vastu võtta üksnes kindlate portsjonite kaupa. Neelatavad energiakvantumid peavad vastama energiatasemete vahedele.

Franck-Hertzi katse

Aga mis siis, kui energiat ei loovuta footonid, vaid aatomitega põrkuvad elektronid? Sellele küsimusele saab vastust otsida joon. 3.4 visandatud katseriista abil.


Joon. 3.4 Francki ja Hertzi katseseade.	Francki ja Hertzi katse tulemus.

Klaasballooni $B$ on joodetud 3 elektroodi: hõõgkatood $K$ , võre $V$ ja anood $A$ . Toru $T$ kaudu saab ballooni õhust tühjaks pumbata ja täita mitmesuguste gaaside või aurudega. Hõõgkatood kiirgab elektrone, mida kiirendatakse võrele antud positiivse pinge $U_{K V}$ ajel. Pinget $U_{K V}$ saab sujuvalt muuta ( $0...30 V$ ). Elektroodide $V$ ja $A$ vahele on rakendatud nõrk ( $\sim 0, 5 V$ ) vastupinge $U_{V A}$ , mis võret läbinud elektrone pisut aeglustab.

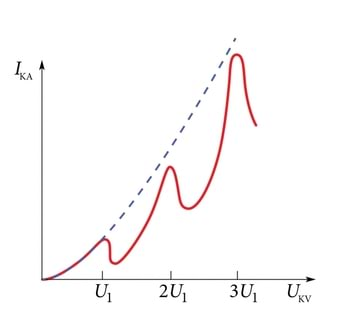
Tõstame pinget $U_{K V}$ ja mõõdame anoodile $A$ jõudvate elektronide voolu $I_{K A}$ pikoampermeetriga $p A$ . Kui balloonis on vaakum, kasvab vool sujuvalt (punktiir graafikul). Laseme ballooni pisut naatriumiauru (rõhuni umb. $1 / 1000$ atmosfäärirõhust) ja kordame katset. Vool kasvab nüüd hoopis keerukamalt, perioodiliselt korduvate hüpetena. Kui esimene langus ilmub pingel $U_{1}$ , siis järgmine pingel $2 U_{1}$ , edasi $3 U_{1}$ jne. Pinge jõudes $U_{1}$ -ni ilmub ballooni $N a$ kollane helendus.

Mis toimub? Kui elektronide energia on väiksem kui $E_{1} = e U_{1}$ , ei kaota nad energiat põrgetel $N a$ -aatomitega, suudavad ületada vastupinget $U_{V A}$ ja jõuavad anoodile. Kuid pingel $U_{1}$ saavutatakse energia, mida $N a$ -aatomid saavad elektronidelt põrgetel omastada. Aatomid ergastuvad ja hakkavad helenduma. Energiat kaotanud elektronid ei suuda enam ületada vastupinge “astangut”, pöörduvad võrele tagasi ja vool langeb järsult. Langused $2 U_{1}$ , $3 U_{1}$ jne juures näitavad, et elektronid on saanud elektriväljalt piisavalt energiat $2$ , $3$ jne aatomi ergastamiseks.

Kriitiliste pingete väärtused sõltuvad ballooni täitvast gaasist/aurust: naatriumi puhul on $U_{1} \sim 2, 1 V$ , elavhõbeda aurus $\sim 4, 9 V$ , vesinikus $\sim 10, 2 V$ , heeliumis $20, 6 V$ . Energiad $E_{1} = e U_{1}$ on võrdsed kiirguvate footonite energiatega.

Neist katseist järeldub, et mitte ainult footonid, vaid ka mikroosakesed saavad loovutada aatomeile energiat ainult kindlate kvantumite viisi.

Seda katset tuntakse esmasooritajate, Saksa füüsikute James Francki (1882-1964) ja Gustav Hertzi (1887-1975) järgi Francki ja Hertzi katsena (1914).

Seaduspära vesiniku aatomi spektris

Joon. 3.5. Vesiniku spektrijoonte seeriad:
A – laias spektriosas ultravalgusest infravalguseni,
B – Balmeri seeria (osalt nähtav) spektrifoto (vrdl ka joon. 3.3)

Meil on nüüd küllaldaselt tõendusmaterjali, et iga elemendi aatom võib asuda ainult talle omastel energiatasemetel. Energiat võtab ja annab aatom üksnes kindlate kvantumitena, mis võrduvad mingi kahe taseme energia vahega. Jääb küsimus, miks need tasemed kujunevad. Vihje vastuse leidmiseks annavad taas spektrid.

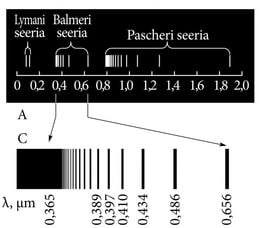
Võtame vaatluse alla lihtsaima, vesiniku aatomi spektri (joon. 3.5). Tundmatusse tungimist tuleb ikka alustada võimalikult lihtsast erijuhust, et vältida hägustavaid keerukusi, mis segavad tabamast peamist, põhilist.

Märkame seaduspära spektrijoonte asendeis: jooned on rühmitunud spektraalseeriatesse, igas seerias moodustavad jooned koonduvaid jadasid. Täppisanalüüs näitab, et kõiki seeriajadasid kirjeldab valem

(3.1)

\frac{1}{λ} = R (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})

kus $λ$ on joone lainepikkus, $R = 1, 0974 \times 10^{7} m^{- 1}$ on Rydbergi konstant, ning $n_{1}$ ja $n_{2}$ on täisarvud: $n_{1}$ on igas seerias konstantne täisarv (vt. tabel) ja $n_{2} = n_{1} + 1, n_{1} + 2, n_{1} + 3 . . .$ .

Valemi (3.1 ) koostas juba 1885 lihtsalt proovimismeetodil Šveitsi gümnaasiumiõpetaja Johann Balmer (1825–1898), siintoodud ülevaatliku ja lihtsa kuju andis Balmeri valemile rootslane Johannes Rydberg (1854–1919), tema nimest ka konstant $R$ .

Vesiniku spektraalseeriad

Seeria nimi avastaja järgi (sulgudes avastamisaasta)	$n_{1}$	$n_{2}$
Lymani seeria (1906)	$1$	$2, 3, 4 . . .$	Ultravalgus ( $91, 2 - 121, 6 n m$ )
Balmeri seeria (1885)	$2$	$3, 4, 5 . . .$	Nähtav valgus ( $364, 7 - 656, 5 n m$ )
Pascheni seeria (1908)	$3$	$4, 5, 6 . . .$	Infravalgus ( $820, 1 - 1875, 6 n m$ )
Bracketti seeria (1922)	$4$	$5, 6, 7 . . .$	Infravalgus ( $1458, 8 - 4052, 2 n m$ )
Pfundi seeria (1924)	$5$	$6, 7, 8 . . .$	Infravalgus ( $2279, 4 - 7459, 9 n m$ )

Rõhutasime sõna täisarvud. Kas kohtame lihtsat täisarvulist, diskreetset muutumist ka kusagil makrofüüsikas, kus üldiselt oleme harjunud kõigi suuruste ühtlase, sujuva varieerumisega?

Helisev pillikeel

Joon. 3.6. Mõned võimalikest seisulaineist otstest kinnitatud pinguli traadil (hele triip – traadi paigalasend).

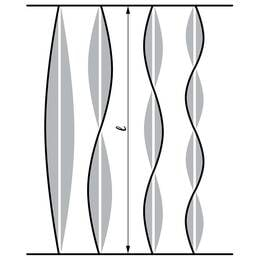
Kui sõrmega või poognaga tõmmates viime pillikeele tasakaaluseisust välja, tekitame keeles laineid. Olenevalt puutekohast ja keele pingsusest, võivad need lained olla väga mitmesuguste pikkustega. Kõik lained on aga sulustatud keele kinnituskohtade vahele. Sulustatud lained teisenevad alati seisulaineteks, milles võnked toimuvad ainult paisudes, paigale jäävate sõlmede vahel. Levides keele kinnitisteni, peegelduvad lained nendelt tagasi. Keelel levivate ja kinnitiselt peegeldunud lainete interferentsist sünnivadki seisulained. Tõusuinterferentsis paisuda saavad ainult kindla pikkusega seisulained, sellised, mille poollaine pikkus mahub täisarv kordi keele pikkusele $L$ (joon. 3.6):

(3.2)

\begin{matrix} 1 \cdot \frac{1}{2} λ_{1} = L 2 \cdot \frac{1}{2} λ_{2} = L 3 \cdot \frac{1}{2} λ_{3} = L \dots n \cdot \frac{1}{2} λ_{n} = L \end{matrix}

Ei saa tekkida seisulained, milles nt. $1, 2 \cdot λ_{1} = L$ : siis peaks ka kinnitatud keeleots võnkuma. Kõik lained, mille pikkus ei rahulda seost (3.2 ), kustuvad kiiresti leviva ja peegeldunud laine mõõnainterferentsil. Pikemalt kestma jäävad üksnes seisulained pikkusega $λ = 2 L / n$ . Nende summa annabki keele helina: pikim, $λ_{1} = 2 L$ tekitab põhitooni, lühemad – ülemtoonid.

Olemegi leidnud täisarvulised suhted ning diskreetse, hüppelise muutumise ka makromaailmast: need ilmuvad seisulainete juures.

Questions and tasks

Miks värvub gaasileek kollaseks, kui veepott tulel üle keeb ja veepiisad leeki satuvad?

Miks ilmuvad neeldumisspektrisse tumedad jooned? Kui aatom neelab footoni energiaga

h f = E_{k} - E_{m}

, peaks ta kohe tagasisiirdel ju samasuguse kvandi ka tagasi kiirgama, nii et ainet läbiv valgusvoog ei tohiks üldse nõrgeneda. Teisipidi: miks ei kahane valguse heledus neeldumisjoontes nulliks? (Vihje: footoneid kiiratakse kõikvõimalikes suundades.)

Lühilainelise ultravalguse spektrite uurimiseks tuleb kogu spektraalaparatuur koos uuritava valguse allikaga paigutada vaakumisse. Miks? (Vihje: miks näeme halvasti läbi tumeda klaasi?)

Mis liiki energiaks muundub lõppeks astmelt astmele veereva kuulikese potentsiaalne energia?

Stopp! Jäta meelde!

Aatomite kiirgus- ja neeldumissepektrid on joonspektrid, seega võib aatom energiat omandada ja loovutada ainult kindlate kvantumite viisi.

Spektrijoonte asetuses on täheldatav korrapära.

Lihtsaima aatomi, vesnikiku aatomi spektrijooned paiknevad koonduvate jadade - spektraalseeriatena. Kõiki seeriaid kirjeldab Balmeri-Rydbergi valem

\frac{1}{λ} = R (\frac{1}{n_{1}^{2}} - \frac{1}{n_{2}^{2}})

Siin $n_{1}$ ja $n_{2}$ on täisarvud. See viitab seosele seisulainetega, mille sõlmede-paisude arv muutu

Testi ennast!

Spektrijooned kui redel aatomimaailma: kas sain aru ja oskan kasutada?

Testi tegemiseks on aega 30 minutit. Tulemused ilmuvad kohe ePortfooliosse.

Open

Here we find out

Elektronvolt

Aatomite energiatasemed

Spektrijoonte asetus

Vesiniku spektrijooned

Spektrijooned kui redel aatomimaailma: kas sain aru ja oskan kasutada?