Peagi (p2.7.2) veendume selles, et induktiivsus kirjeldab kehade süsteemi võimet säilitada endas elektrivoolu ja seeläbi tekitada magnetvälja. Mõistagi on kasutusel ka füüsikaline suurus, mis iseloomustab kehade süsteemi võimet salvestada endasse laengut ja seeläbi tekitada elektrivälja. Kõnealuseks suuruseks on elektrimahtuvus, mida me edaspidi nimetame lihtsalt mahtuvuseks.

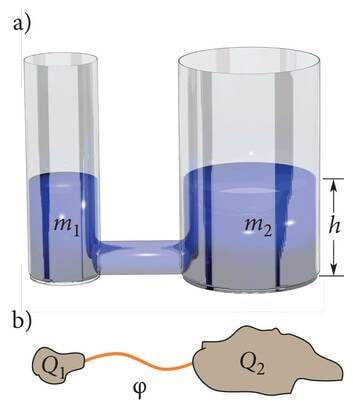
Kallates vedelikku ühekõrgustesse kuid erineva läbimõõduga klaasidesse, näeme otsekohe, et laiemasse klaasi mahub rohkem vedelikku. Suurema läbimõõduga anumal on suurem põhja pindala ja seega ka ruumala (J.2.28). Samamoodi on lood erinevate elektrit juhtivate kehade laadimisel. Ühele kehale "mahub" rohkem laengut kui teisele. Järelikult on mõtet võtta kasutusele keha laadumisvõimet kirjeldav suurus, mida nimetatakse keha mahtuvuseks.

J.2.28 Elektrimahtuvus on erinevatel kehadel erinev analoogiliselt sellele, kuidas me saame erineva läbimõõduga klaase ühe kõrguseni täites valada neisse erineva koguse vedelikku.	J.2.29 Pinge tekkimine kahe keha vahel laengu Q viimisel ühelt kehalt teisele.

Rangelt võttes on mahtuvus alati kahe keha omavaheline mahtuvus. Andes ühele kehale mingi laengu, peame selle mingilt teiselt kehalt ära võtma, kuna kehtib laengu jäävuse seadus.

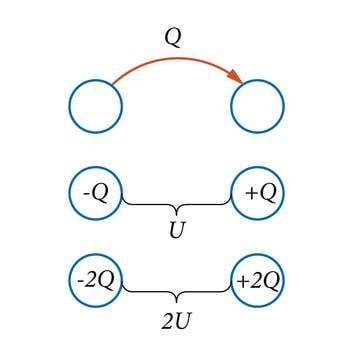
Vaatleme kahte algselt neutraalset keha. Kui me võtame ühelt kehalt ära laengu $Q$ ja anname selle teisele kehale, siis omandab esimene keha laengu $-Q$ ja teine $+Q$. Kehade vahel tekib elektriväli ja seega ka potentsiaalide vahe (pinge) $U$ (J.2.29). Kuna potentsiaal on võrdeline teda tekitava laenguga (valem 1.22), siis teostades sama toimingu laenguga $2Q$, tekitame kehade vahel pinge $2U$. Peagi märkame, et laengu ja pinge jagatis jääb kõigis sellelaadsetes katsetes muutumatuks, antud kehade süsteemi iseloomustavaks suuruseks. See ongi vaadeldavate kehade omavaheline mahtuvus.

Kahe keha omavaheline mahtuvus näitab, kui suure laengu viimisel ühelt kehalt teisele tekib kehade vahel ühikuline pinge. Mahtuvuse $C$ leidmiseks tuleb üle viidud laeng $Q$ jagada tekkiva pingega

Saavutamaks mahtuvuse definitsiooni suuremat sarnasust induktiivsuse määratlusega (2.10) ja rõhutamaks ajalise muutuse tähtsust võib üleviidavat laengut Q vaadelda keha laengu lõppväärtuse $q_2$ ja algväärtuse $q_1$ vahena: $Q=q_2-q_1=\Delta q$. Siis on keha iseloomustav laeng $q$ meile mehaanikast tuntud koordinaadi rollis ja üleviidav laeng $Q$ vastab kahe koordinaadi vahele ehk teepikkusele. Vaadeldes keha laengut ajast sõltuva suurusena $q=q\left(t\right)$, peame ajast sõltuvana käsitlema ka kahe keha vahel tekkivat pinget $u=u\left(t\right)$. Niimoodi võtab kahe keha omavahelise mahtuvuse definitsioon kuju

J.2.29 a Kaitsemaandus. Fotol on näha, kuidas torud on omavahel juhtmega ühendatud, see juhe on omakorda ühendatud maandusvardaga, vt järgmine pilt.	J.2.29 b Kaitsemaandus. Juhe on ühendatud masse löödud vaskvardaga.

Nüüd saab meile selgeks elektriseadmete kaitsemaanduse põhimõte, millest oli juttu juba põhikooli Elektriõpetuses. Maandamisel ühendatakse seadme metallkorpus juhtme abil Maaga. See kaitseb seadme kasutajat elektrilöögi eest juhul, kui seadme korpus satub rikke tagajärjel Maa suhtes pinge alla. Kaitsemaandus juhib seadme korpusele sattunud laengu ära Maasse. Maa on aga niivõrd suure mahtuvusega keha, et talle võib anda kuitahes suure laengu, ilma et tema potentsiaal märgatavalt muutuks. Laeng liigub Maasse läbi maandusjuhtme, mitte aga läbi seadme kasutaja keha. Seega on mingi keha maandamine samaväärne suure augu tegemisega niisuguse anuma põhja, millesse vesi mitte mingil juhul koguneda ei tohi. Kui ka vesi eksikombel satub anumasse, jookseb vesi läbi augu otsekohe maha.

Kehade süsteemi, mis on loodud mingi kindla mahtuvuse saamiseks, nimetatakse kondensaatoriks. Lihtsaim kondensaator koosneb kahest elektrit juhtivast plaadist ehk kattest, mille vahel paikneb dielektrikukiht. Kondensaatori mahtuvus näitab, kui suure laengu $Q$ andmisel ühele plaadile suureneb plaatidevaheline pinge $U$ ühe ühiku võrra. Seega on kondensaatori mahtuvus sisuliselt tema plaatide omavaheline mahtuvus (valem 2.12 või 2.13).

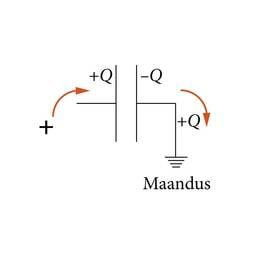
Kondensaatori laadimiseks reeglina ei võeta laengut ühelt plaadilt, et anda seda teisele plaadile. Piisab vaid ühe plaadi laadimisest. Laetud plaadi elektrivälja mõjul hakkavad laengukandjad teisel plaadil ja sellega ühendatud juhtides liikuma. Näiteks laengu $+Q$ andmisel kondensaatori ühele plaadile omandab teine (algselt neutraalne) plaat sama suure laengu $-Q$, sest just siis tasakaalustavad plaatide elektriväljad väljaspool kondensaatorit vastastikku teineteist. Samanimeliste laengute tõukumise tõttu lahkub laeng $+Q$ teiselt plaadilt. Laengu $-Q$ saab kergesti teisele plaadile tuua siis, kui plaat on maandatud (J.2.30) ja laeng $+Q$ võib lahkuda Maasse.

Ka vooluringis paikneva kondensaatori korral saab laeng teiselt plaadilt alati ära minna. Järelikult on ühe plaadi laadimine samaväärne laengu $Q$ üleviimisega ühelt plaadilt teisele.

Mahtuvuse ühik SI-süsteemis kannab M. Faraday auks nime farad. Üks farad ($1\text{F}$) on sellise keha mahtuvus, millele tuleb anda laeng üks kulon, selleks et suurendada tema potentsiaali ühe voldi võrra. Kondensaatori mahtuvus on $1\text{F}$, kui laengu $1\text{C}$ viimine ühelt plaadilt teisele tekitab plaatide vahel pinge $1\text{V}$. Seega

Kuna üks kulon on väga suur laeng, siis ka üks farad on väga suur mahtuvus. Seetõttu kasutatakse praktikas enamasti mikro-, nano- ja pikofaradeid ($1\text{F}={10}^{-6}\text{F}$, $1\text{nF}={10}^{-9}\text{F}$, $1\text{pF}={10}^{-12}\text{F}$).

Kondensaatoreid võib leida kõikvõimalikes elektroonikaseadmetes, alustades mikrofonidest ning lõpetades näiteks satelliitidega. Esimese kondensaatori valmistasid teineteisest sõltumatult sakslane Ewald von Kleist (1700-1748) ja hollandlane Pieter van Musschenbroek (1692-1761). Kondensaatori leiutamist on õigem nimetada avastuseks, sest see toimus täiesti juhuslikult. Uurides vee elektriseerumist, tegi Kleist 1745. aastal järgmise katse. Ta laadis raudnaela, mis ulatus välja veega täidetud klaaspudelist. Hoides pudelit ühes käes, puudutas ta kogemata teise käega naela ja sai er akordselt tugeva elektrilöögi. Kleist mõistis, et pudelisse oli kogunenud väga suur laeng. Pudelkondensaatori üheks katteks oli vesi, teiseks aga katsetaja käsi. Pudeli klaaskest toimis dielektrikuna.

J.2.32 Pudelkondensaator. Tavaline limonaadipudel on täidetud soolveega, pudeli korgist on läbi pandud polt, mille ots ulatub soolvette. Pudeli välisküljele on liimitud fooliumiriba. Sellist kondensaatorit saab laadida näiteks elektrofoormasinaga. Ettevaatust, kondensaatorist saadav "särts" võib olla üsnagi tuntav!	Kui purgi sisemisele ja välimisele küljele kinnitada kaks alumiiniumfooliumi lehte, käitub see seade kondensaatorina. Tuntakse ka Leideni purgi nime all.

Analoogilise katse teostas Musschenbroek 1746. a. hollandi linnas Leidenis. Kuna laiemalt tuntuks sai just nimelt tema tulemus, siis hakati kõiki sellelaadseid laengut koguvaid klaasanumaid nimetama leideni purkideks.

Leideni purgi konstruktsioonis asendati vesi peagi anuma sisepinda katva metallkilega. Ka välimine kate valmistati metallfooliumist. Nii saadi leideni purk, mis on kooli füüsikakabinetis kasutusel tänapäevani.