Elektrijuhtivus tahkistes

Füüsiku pilguga

Tahkisefüüsika ja tahkise-elektroonika on tänapäeva elu radikaalselt muutnud. Näiteks põhinesid arvutid esialgu elektronlampidel ja võtsid enda alla palju ruumi. Tänapäeva võrreldamatult võimsamad arvutid põhinevad kiipides olevatel tillukestel transistoridel ja mahuvad sülle (või on veelgi väiksemad). Tundub, et elektronlambid kuuluvad minevikku; need on tõepoolest elektriinseneride põhiõppekavadest välja jäetud. Siiski – paljud praegusaja rokk-kitarristid nõuavad lampvõimendeid, nagu ka Jimi Hendrix, kes 1960ndate lõpul roki elektriliselt ümber kujundas. Miks eelistavad rokk-kitarristid transistorvõimendite asemel lampvõimendeid?

Selles peatükis tutvume füüsikaprobleemiga, mis on viimasel poolsajandil muutunud erakordselt oluliseks. Otsime vastust küsimusele: millised on need mehhanismid, mis teevad aine elektrijuhiks või isolaatoriks? Vastused on siin keerulised ja seni veel mitte lõpuni selged, seda suuresti seetõttu, et need sisaldavad kvantfüüsika kasutamist mitte üksikutel (eraldiasuvatel) osakestel ja aatomitel, nagu vaatasime eelmistes peatükkides, vaid osakeste ja aatomite hiiglasuurel kogumil, mis on korrastunud omavahel vastastikmõjulistesse rühmadesse. Raskustele vaatamata on insenerid ja teadlased teinud materjalide kvantfüüsikas suuri edusamme, tänu millele on meil nüüd olemas arvutid, kalkulaatorid, mobiiltelefonid ja palju muud tahkisolekul põhinevat elektroonikat.

Alustame seda peatükki kirjeldusega nendest tahkistest, mis saavad elektrit juhtida, ja nendest, mis ei saa.

Tahkiste elektrilised omadused

JOONIS 41-1 (a) Vase ühikrakk on kuup, millel on üks vase aatom (tumedam) igas nurgas ja üks vase aatom (heledam) iga tahu keskel. Niisugust struktuuri nimetatakse tahkkesendatud kuubiliseks. (b) Räni või süsiniku ühikrakk on samuti kuup, milles aatomid on korrastatud teemandivõrena. Siin on üks (tume) aatom kuubi igas nurgas ja üks (hele) aatom iga tahu keskel; lisaks on kuubi sees veel neli (keskmise heledusega) aatomit. Iga aatom on seotud nelja lähima naabriga kaheelektronilise kovalentsidemega (näidatud nelja aatomi jaoks kuubi sees).

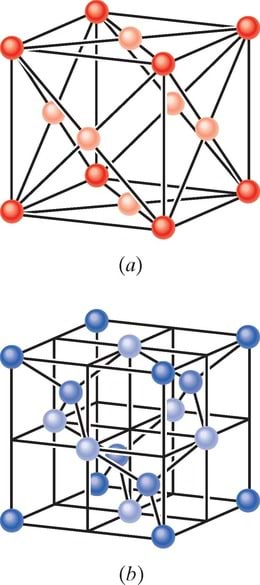
Käsitleme siin vaid kristallilisi tahkiseid, s.t tahkiseid, millede aatomid on korrastatud perioodiliselt korduvasse kolmemõõtmelisse struktuuri, mida nimetatakse võreks. Me ei vaata selliseid tahkiseid nagu puit, plast, klaas või kumm, mille aatomid ei ole korduvatesse mustritesse korrastatud. Joonis 41-1 näitab võrestruktuuride korduvaid põhiühikuid (ühikrakke) tüüpilise metalli vase (joonis 41-1a), tüüpilise pooljuhi räni (joonis 41-1b) ja tüüpilise isolaatori teemandi (süsiniku) (joonis 41-1b) korral.

Elektrijuhtivuse seisukohalt saame tahkiseid liigitada kolme põhiomaduse järgi:

Nende eritakistus $ρ$ toatemperatuuril, SI ühikutes oom-meetrit ( $Ω \cdot m$ ); eritakistus on defineeritud punktis 26-4.
Nende eritakistuse temperatuuritegur $α = (1 / ρ) (d r / d T)$ (valemis 26-17), mille SI ühik on pöördkelvin ( $K^{- 1}$ ). Me saame $α$ välja arvutada mistahes tahkise jaoks, kui mõõdame $ρ$ teatud temperatuurivahemikus.
Nende laengukandjate arvtihedus $n$ . Seda suurust – laengukandjate arvu ühikruumalas – saab leida Halli efekti mõõtes, nagu punktis 28-5, aga ka teistest mõõtmistest. SI ühikuks on pöördkuupmeeter ( $m^{- 3}$ ).

Mõõtes üksnes eritakistust toatemperatuuril, leiame, et on olemas aineid, nn isolaatoreid, mis praktiliselt elektrit üldse ei juhi. Neil ainetel on väga suur eritakistus. Hiilgavaks näiteks on siin teemant, mille eritakistus ületab vase eritakistuse lausa $10^{24}$ kordselt.

Kui mõõta $ρ$ , $α$ ja $n$ , saab mitteisolaatoreid vähemalt madalatel temperatuuridel
jaotada kahte rühma: metallideks ja pooljuhtideks.

Pooljuhtidel on metallidega võrreldes märgatavalt suurem eritakistus $ρ$ .

Pooljuhtide eritakistuse temperatuuritegur $α$ on suur ja negatiivne. See tähendab seda, et pooljuhi eritakistus väheneb temperatuuri tõustes, samal ajal kui metallil see suureneb.

Pooljuhtidel on metallidega võrreldes tunduvalt väiksem laengukandjate arvtihedus $n$ .

Tabel 41-1 näitab neid suurusi tüüpilise metalli vase ja tüüpilise pooljuhi räni jaoks.

Nüüd, kus meil on käepärast $ρ$ , $α$ ja $n$ mõõtetulemused, on meil olemas eksperimentaalne baas, et pöörduda uuel tasemel tagasi keskse küsimuse juurde tahkiste elektrijuhtivusest: mis on see eripära, mis teeb teemandist isolaatori, vasest metalli ja ränist pooljuhi? Vastused saame jällegi kvantfüüsikast.

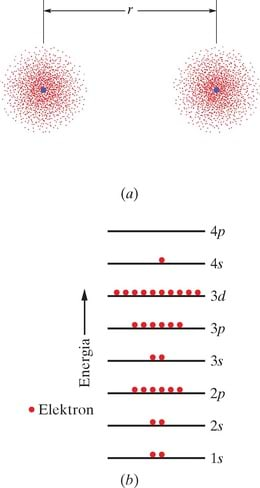
Energianivood kristallilistes tahkistes

JOONIS 41-2 (a) Kaks vaseaatomit on teineteisest kaugel, nende elektronjaotused on joonistatud täpp-kujutisena. (b) Kummalgi vaseaatomil on $29$ elektroni, mis on jaotunud alamkihtideks. Neutraalse aatomi põhiseisundis on kõik alamkihid kuni $3 d$ tasemeni täidetud, $4 s$ alamkihis on vaid $1$ elektron (võiks olla kaks) ning kõrgemad kihid on tühjad. Lihtsuse mõttes on kihid kujutatud võrdsete energiavahedega.

Tahkes vases on vahemaa külgnevate vaseaatomite vahel $260 p m$ . Joonis 41-2a kujutab kaht eraldiasuvat vaseaatomit vahekaugusega $r$ , mis on palju suurem kui $260 p m$ . Nagu näidatud joonisel 41-2b, korrastab iga selline isoleeritud neutraalne vase aatom oma $29$ elektroni alamkihtideks

1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{1}

Siin oleme energianivoode (energiatasemete) jaoks kasutanud punkti 40-9 lühitähistusi. Tuletame meelde, et näiteks nivood, mille peakvantarv $n = 3$ ja orbitaalkvantarv $ℓ = 1$ , nimetatakse $3 p$ nivooks; see võib hõivata kuni $2 (2 ℓ + 1) = 6$ elektroni; elektronide arv, mida see tegelikult sisaldab, on näidatud ülaindeksis. Nagu ülal näeme, on vases esimesed kuus nivood täidetud, aga (kõige välimisel) $4 s$ nivool, millel saaks olla kaks elektroni, on vaid üks.

Kui toome aatomid joonisel 41-2 teineteisele lähemale, hakkavad nende lainefunktsioonid kattuma, alates väliskihi elektronide omadega. Kui kahe aatomi lainefunktsioonid kattuvad, ei räägi me mitte enam kahest eraldi aatomist vaid ühest kahe-aatomilisest süsteemist; antud süsteem sisaldab $2 \times 29 = 58$ elektroni. Pauli keeluprintsiip kehtib ka taolise suure süsteemi korral, nii et igaüks sellest $58$ elektronist peab olema erinevas kvantseisundis. Vajalikud $58$ kvantseisundit on tõepoolest olemas, sest isoleeritud aatomi iga energianivoo lõheneb kaheaatomilises süsteemis kaheks.

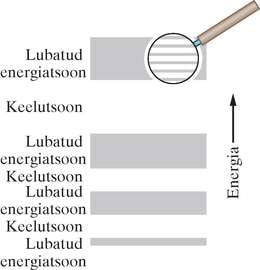
JOONIS 41-3 Energianivoode lubatud energiatsoonide-keelutsoonide skeem ideaalse kristallilise tahkise korral. Nagu näitab suurendatud vaade, koosneb iga lubatud tsoon väga suurest arvust väga lähestikku asuvatest energianivoodest. (Paljudes tahkistes võivad naabertsoonid osaliselt kattuda; selguse mõttes pole sellist võimalust siin näidatud.)

Kui toome kokku rohkem aatomeid, siis moodustame me järk-järgult tahke vase võre. Kui meie võre sisaldab näiteks $N$ aatomit, siis üksiku vaseaatomi iga nivoo peab tahkises lõhenema $N$ nivooks. Niisiis, tahkise üksikud energianivood moodustavad lubatud energiatsoonid ja naabertsoonid on üksteisest eraldatud keelutsooniga, viimane esindab seda energiavahemikku, mida elektronidel olla ei saa. Tsoonide tüüpiline ulatus on mõne elektronvoldi piires. Kuna $N$ võib olla suurusjärgus $10^{24}$ , siis näeme, et üksiknivood tsoonis on üksteisele tõepoolest väga lähedal ning et neid on seal hiigelsuur arv.

Joonisel 41-3 on skemaatiliselt kujutatud energianivoode lubatud energiatsoonidekeelutsoonide struktuur üldises kristallilises tahkises. Pange tähele, et madalama energiaga tsoonid on kitsamad kui kõrgema energia omad. Seda seetõttu, et madalamates energiatsoonides olevad elektronid veedavad suurema osa ajast aatomi elektronpilve sügavamas osas. Selliste nn südamikuelektronide lainefunktsioonid ei kattu nii suures ulatuses kui väliselektronide omad. Järelikult on (südamikuelektronide) madalamate energianivoode lõhenemine väiksem kui (väliselektronide) kõrgematel energianivoodel.

Isolaatorid

JOONIS 41-4 Lubatud energiatsoonide-keelutsoonide skeem isolaatori korral; täidetud nivood on punased ja tühjad sinised.

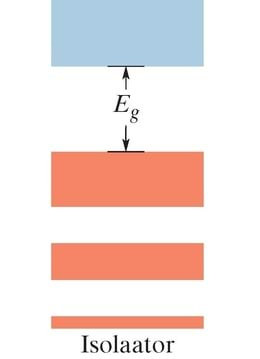
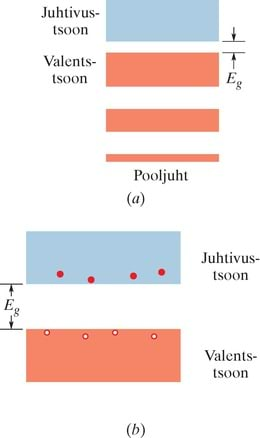
Tahkist nimetatakse isolaatoriks, kui selles puudub vool, olgugi et sellele on rakendatud pinge. Voolu tekkeks on vaja, et elektroni kineetiline energia suureneks. Teisisõnu, osa elektrone tahkises peab liikuma kõrgematele energianivoodele. Nagu näha jooniselt 41-4, on isolaatoris kõrgeim elektrone sisaldav tsoon täielikult täidetud. Kuna Pauli keeluprintsiip ei lase elektronidel minna juba täidetud nivoodele, ei saa need sellises tahkises liikuda.

Seega pole elektronidel isolaatorite täidetud tsoonides kohta, kuhu minna; need on võresse lukustatud. Just nagu laps püüaks ronida mööda redelit, mille igal pulgal seisab juba üks laps; kuna pole vaba pulka, ei saa keegi liikuda.

Küll aga on palju hõivamata nivoosid (ehk vakantseid nivoosid) tsoonis, mis on täidetud tsooni kohal (joonis 41-4). Kuid selleks, et elektron saaks hõivata üht neist nivoodest, peab sel olema piisavalt energiat, et hüpata üle laiast keelutsoonist laiusega $E_{g}$ , mis kahte tsooni eraldab. Teemandis on see keelutsoon nii lai (tuleb ületada energia $5, 5 e V$ , mis on ligikaudu $140$ korda suurem vaba osakese keskmisest soojusenergiast toatemperatuuril), et peaaegu ükski elektron ei suuda sellest üle hüpata. Teemant on niisiis isolaator ja seejuures veel väga hea.

Milline on ligikaudne tõenäosus, et toatemperatuuril (

300 K

) oleva teemandi elektron kõrgemast täidetud tsoonist hüppaks üle keelutsooni laiusega

E_{g}

(joonis 41-4)? Teemandis

E_{g} = 5, 5 e V

.

Lahendus

JUHTMÕTE 40. peatükis kasutasime valemit (40-29)

\frac{N_{x}}{N_{0}} = e^{- (E_{x} - E_{0}) / k T}

et seostada aatomite arvu $N_{x}$ energianivool $E_{x}$ vastava arvuga $N_{0}$ energianivool $E_{0}$ , kus aatomid on osa süsteemist temperatuuril $T$ (mõõdetuna kelvinites); $k$ on Boltzmanni konstant ( $8, 62 \times 10^{- 5} e V / K$ ). Siin peatükis võime kasutada valemit 41-1, et leida ligikaudset tõenäosust $P$ , et elektron isolaatoris võiks hüpata üle keelutsooni laiusega $E_{g}$ joonisel 41-4.

Arvutused: alustame energiate vahest, asendades $E_{x} - E_{0} = E_{g}$ . Siis on hüppe tõenäosus $P$ ligikaudu võrdne keelutsooni kohal olevate elektronide arvu ja keelutsooni all olevate elektronide arvu suhtega, $N_{x} / N_{0}$ . Teemandi korral on eksponendi aste valemis 41-1

- \frac{E_{g}}{k T} = \frac{5, 5 e V}{(8, 62 \times 10^{- 5} e V / K) (300 K)} = - 213

Küsitud tõenäosus on siis

P = \frac{N_{x}}{N_{0}} = e^{- (E_{x} - E_{0}) / k T} = e^{213} \approx 3 \times 10^{- 93} - -------- - - -------- -

See tulemus tähendab seda, et kui elektronide arv oleks $10^{93}$ , siis umbes $3$ elektroni hüppaks üle keelutsooni. Kuna mistahes teemanditükis on vähem kui $10^{23}$ elektroni, siis näeme, et hüppe tõenäosus on kaduvväike. Pole ime, et teemant on nii hea isolaator.

Metallid

JOONIS 41-5 Lubatud energiatsoonide-keelutsoonide skeem metalli korral. Kõrgeim täidetud nivoo, nn Fermi nivoo, asub ligikaudu tsooni keskel. Kuna tühjad nivood on tsooni sees kättesaadavad, siis võivad elektronid kergesti nivoosid vahetada, tingides elektrijuhtivuse.

Metalle iseloomustab asjaolu, et kõrgemad täidetud energianivood ulatuvad energiatsooni keskpaigani, nagu näidatud joonisel 41-5. Kui nüüd rakendada metalli otstele potentsiaalide vahe, tekib vool, sest sealsamas tsoonis kõrgematel energiatel on olemas hulk vakantseid nivoosid, kuhu elektronid (ehk laengukandjad metallis) saavad hüpata. Seega saab metall juhtida elektrit tänu asjaolule, et kõrgeimas täidetud tsoonis asuvatel elektronidel on soodne võimalus kõrgematele energianivoodele liikuda.

Punktis 26-6 käsitlesime metalli vabade elektronide mudelit, milles juhtivuselektronid on vabad liikuma objekti kogu ulatuses, nii nagu gaasi molekulid kinnises anumas. Seda mudelit kasutasime metallide eritakistuse valemi tuletamiseks eeldusel, et elektronid järgivad Newtoni mehaanika seadusi. Siin kasutame sama mudelit seletamaks juhtivuselektronide käitumist osaliselt täidetud tsoonis (joonis 41-5). Kuid nüüd järgime kvantfüüsika seadusi – eeldame elektronide kvanditud
energiaid ja Pauli printsiibi kehtivust.

Samuti eeldame, et juhtivuselektroni elektrilisel potentsiaalsel energial $U$ on ühesugune konstantne väärtus võre kogu ulatuses. Võtame $U = 0$ . Siis on juhtivuselektronide mehaaniline energia $E$ tervenisti kineetiline.

Osaliselt täidetud tsooni põhjas asub nivoo $E = 0$ (joonis 41-5). Selles tsoonis null-temperatuuril ( $T = 0 K$ ) hõivatud kõrgeimat nivood nimetatakse Fermi nivooks ja vastavat energiat Fermi energiaks $E_{F}$ ; vase korral $E_{F} = 7, 0 e V$ .

Fermi energiale vastavat elektroni kiirust nimetatakse Fermi kiiruseks $v_{F}$ . Vase jaoks on Fermi kiirus $1, 6 \times 10^{6} m / s$ . Seega ei lakka null-temperatuuril mitte kogu liikumine,
vaid Pauli keeluprintsiibi tõttu peavad juhtivuselektronid osaliselt täidetud tsoonis hõivama kõik nivood energiatega nullist kuni Fermi energiani (joonis 41-5).

Kui palju on juhtivuselektrone?

Kui hakkaksime metalli kokku panema üksikutest aatomitest, siis leiaksime, et juhtivuselektronid metallis on aatomite valentselektronid (elektronid aatomite hõivatud väliskihtides). Ühevalentse metalli aatom loovutab ühe sellise elektroni juhtivuselektroniks; kahevalentne aatom annab kaheelektronilise panuse. Niisiis, juhtivuselektronide koguarv on

(41-2)

(juhtivuselektronide koguarv objektis) = (aatomite koguarv objektis) (valentselektronide arv aatomis)

(Käesolevas peatükis kirjeldame mitmeid võrrandeid sõnades, sest sümbolid, mis varem tähistasid neis esinevaid suurusi, esindavad nüüd teisi suurusi.)

Juhtivuselektronide arvtihedus $n$ objektis on juhtivuselektronide arv ühikruumalas:

(41-3)

n = \frac{juhtivuselektronide arv objektis}{objekti ruumala}

Näidise aatomite arvu saame seostada selle mitmete teiste omadustega ja materjaliga, millest see koosneb:

(41-4)

(aatomite arv objektis) = \frac{objekti mass M_{o b j e k t}}{aatommass} = \frac{objekti mass M_{o b j e k t}}{(molaarmass M) / N_{A}} = \frac{(materjali tihedus) (objekti ruumala V)}{(molaarmass M) / N_{A}}

kus molaarmass $M$ on aine ühe mooli mass ja $N_{A}$ on Avogadro arv ( $6, 02 \times 10^{23} m o l^{- 1}$ ).

Kui palju on juhtivuselektrone magneesiumist kuubikujulises objektis ruumalaga

2, 00 \times 10^{- 6} m^{3}

? Magneesiumiaatomid on kahevalentsed.

Lahendus

JUHTMÕTTED (1) Kuna magneesiumi aatomid on kahevalentsed, siis annab iga magneesiumi aatom kaks juhtivuselektroni. (2) Juhtivuselektronide arv objektis on seotud magneesiumi aatomite arvuga vastavalt valemile 41-2. (3) Aatomite arvu saame leida valemi 41-4 järgi, kasutades teadaolevaid andmeid kuubi ruumala ja magneesiumi omaduste kohta.

Arvutused: kirjutame valemi 41-4 kujul

(aatomite arv objektis) = \frac{(tihedus) (objekti ruumala V) N_{A}}{molaarmass M}

Magneesiumi tihedus on $1, 738 g / c m^{3}$ ( $= 1, 738 \times 10^{3} k g / m^{3}$ ) ja molaarmass on $24, 312 g / m o l$ ( $= 24, 312 \times 10^{- 3} k g / m o l$ ) (vt Lisa F). Murru lugeja annab meile

(1, 738 \times 10^{3} k g / m^{3}) (2, 00 \times 10^{- 6} m^{3}) (6, 02 \times 10^{23} m o l^{- 1}) = 2, 0926 \times 10^{21} k g / m o l

Seega

(aatomite arv objektis) = \frac{2, 0926 \times 10^{21} k g / m o l}{24, 312 \times 10^{- 3} k g / m o l} = 8, 61 \times 10^{22}

Kasutades seda tulemust ja asjaolu, et magneesiumi aatomid on kahevalentsed, leiame valemist 41-2

(juhtivuselektronide arv objektis) = (8, 61 \times 10^{22} a a t o m i t) (2 \frac{elektroni}{aatomi kohta}) = 1, 72 \times 10^{23} e l e k t r o n i - --------------------- - - --------------------- -

Juhtivus ülalpool absoluutset nulli

Metallide elektrijuhtivus pakub meile praktilist huvi kõrgematel temperatuuridel kui absoluutne null. Mis toimub elektronide joonisel 41-5 kujutatud jaotusega kõrgematel temperatuuridel? Nagu kohe näeme: suurt ei midagi.

Osaliselt täidetud tsoonis on üksnes Fermi nivoo lähedal olevatel elektronidel lähedase energiaga, kuid hõivamata nivood (joonis 41-5) ning üksnes neid elektrone saab soojuslikult ergastada kõrgematele nivoodele. Isegi temperatuuril $T = 3000 K$ , mille juures vask hakkab eredalt hõõguma (pimedas ruumis), ei erine elektronide jaotus nivoode järgi oluliselt jaotusest null-temperatuuril.

Vaatame, miks see nii on. Sobivaks mõõduks energiale, mida võre juhuslik soojusliikumine võib juhtivuselektronile anda, on suurus $k T$ , kus $k$ on Boltzmanni konstant. Temperatuuri $T = 3000 K$ korral $k T = 0, 086 e V$ . Soojuslik ergastus üksi ei lase ühelgi elektronil oma energiat muuta rohkem kui selle suhteliselt väikese suuruse mõnekordselt; parimal juhul saavad ainult need vähesed juhtivuselektronid, millede energia on Fermi energiale ligilähedane, võimaluse tänu soojuslikule ergastusele kõrgematele nivoodele hüpata. Poeetiliselt väljendades: soojuslik ergastus kutsub tavaliselt esile vaid säbrulainetuse elektronide Fermi mere pinnal; see meri jääb sügavuti häirimata.

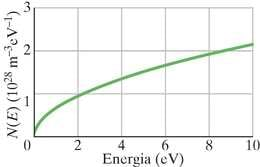
Kui palju kvantseisundeid on olemas?

Metalli elektrijuhtivusvõime sõltub sellest, kui palju kvantseisundeid on elektronidele kättesaadavad ja millised on nende energiad. Seega kerkib küsimus: millised on üksikute seisundite energiad osaliselt täidetud tsoonis joonisel 41-5? See küsimus on vastamiseks liiga keeruline, sest arvatavasti ei saa me loetleda nii paljude seisundite energiaid eraldi. Selle asemel küsime: kui paljudel olekutel objekti ühikruumalas on energiad vahemikus $E$ , $E + d E$ ? Tähistame selle arvu $N (E) d E$ , kus $N (E)$ on energiaga $E$ seisundite tihedus. Tavapärane ühik $N (E) d E$ jaoks on seisundit kuupmeetri kohta ( $seisundite arv / m^{3}$ ehk lihtsalt $m^{- 3}$ ) ning $N (E)$ jaoks seisundit kuupmeetri ja elektronvoldi kohta ( $m^{- 3} e V^{- 1}$ ).

JOONIS 41-6 Seisundite tihedus $N (E)$ , s.t elektronide energianivoode arv ühikulise energiamuudu kohta ühikruumalas, kujutatud graafiliselt elektroni energia funktsioonina. Seisundite tiheduse funktsioon lihtsalt loendab võimalike seisundite arvu; see ei ütle midagi selle kohta, kas need seisundid on elektronide poolt hõivatud või mitte.

Avaldise seisundite tiheduse jaoks võime leida, kui loendame elektroni selliste seisvate ainelainete arvu, mis mahuvad meie objekti suurusesse kasti. See on analoogiline selliste seisvate helilainete loendamisega, mis saavad olla kinnises oreliviles. Erinevus on selles, et meie ülesanne on kolmemõõtmeline (orelivile on ühemõõtmeline) ja lained on ainelained (oreliviles helilained). Saab näidata, et loendamise tulemus peab olema

(seisundite tihedus, 41-5)

N (E) = \frac{8 \sqrt{2} π m^{3 / 2}}{h^{3}} E^{1 / 2}

kus $m$ ( $= 9, 109 \times 10^{- 31} k g$ ) on elektroni mass, $h$ ( $= 6, 626 \times 10^{- 34} J \cdot s$ ) on Plancki konstant, $E$ on energia džaulides ning $N (E)$ on seisundid kuupmeetri ja džauli kohta ( $m^{- 3} J^{- 1}$ ). Kui teisendada seda võrrandit nii, et $E$ on antud elektronvoltides ja $N (E)$ seisundites kuupmeetri ja elektronvoldi kohta ( $m^{- 3} e V^{- 1}$ ), tuleb võrrandi paremat poolt korrutada konstandiga $e^{3 / 2}$ , kus $e$ on elementaarlaeng, $1, 602 \times 10^{- 19} C$ . Joonisel 41-6 on toodud võrrandi 41-5 selle versiooni graafik. Pange tähele, et võrrand 41-5 ja joonis 41-6 ei sõltu objekti kujust, temperatuurist ega koostisest.

(a) Kas vahemaa naabernivoode vahel vases

E = 4 e V

juures on suurem, niisama suur või väiksem kui

E = 6 e V

juures? (b) Kas vahemaa naabernivoode vahel vases

E = 4 e V

juures on suurem, niisama suur või väiksem kui sama ruumalaga alumiiniumi korral sama energia juures?

Näidisülesanne 41-3

Kasutades andmeid jooniselt 41-6, määrake seisundite arv elektronvoldi kohta

7 e V

juures metallobjektis ruumalaga

V = 2 \times 10^{- 9} m^{3}

.

Lahendus

JUHTMÕTE Antud energiaga seisundite arvu elektronvoldi kohta saame seisundite tihedusest $N (E)$ selle energia juures ja objekti ruumalast $V$ .

Arvutused: energia $7 e V$ juures

(seisundite arv ¨ u he e V kohta 7 e V juures) = (seisundite tihedus N (E) 7 e V juures) (objekti ruumala V)

Jooniselt 41-6 näeme, et $E = 7 e V$ kohal on seisundite tihedus umbes $1, 8 \times 10^{28} m^{- 3} e V^{- 1}$ . Seega,

(seisundite arv ¨ u he e V kohta 7 e V juures) = (1, 8 \times 10^{28} m^{- 3} e V^{- 1}) (2 \times 10^{- 9} m^{3}) =< b r > 3, 6 \times 10^{19} e V^{- 1} \approx 4 \times 10^{19} e V^{- 1} - ------------ - - ------------ -

Määrake seisundite arv

N

objektis väikeses energiavahemikus

Δ E = 0, 003 e V

energia

E = 7 e V

ümbruses.

Lahendus

Arvutused: valemi 41-5 ja joonise 41-6 põhjal teame, et seisundite tihedus on energia $E$ funktsioon. Kuid energiavahemiku $Δ E$ jaoks, mis on energiaga $E$ võrreldes väike, võime seisundite tiheduse (ja seega ka seisundite arvu elektronvoldi kohta) lugeda konstantseks. Niisiis, leiame seisundite arvu $N$ energiavahemikus $Δ E = 0, 003 e V$ $7 e V$ ümbruses valemiga

(seisundite arv N energiavahemikus Δ E 7 e V juures) = (seisundite arv ¨ u he e V kohta 7 e V juures) (energiavahemik Δ E)

ehk

N = (3, 6 \times 10^{19} e V^{- 1}) (0, 003 e V) = 1, 1 \times 10^{7} \approx 1 \times 10^{7} - ------ - - ------ -

(Kui teilt küsitakse seisundite arvu kindlas energiavahemikus, siis veenduge esmalt, kas see vahemik on küllalt väike, et lubada seda tüüpi lähendust.)

Nivoo hõive tõenäosus

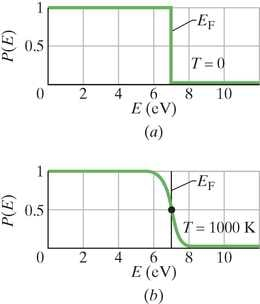
Metalli võime juhtida elektrit sõltub tõenäosusest, millega kättesaadavad vakantsed nivood tegelikult hõivatakse. Siin kerkib küsimus: kui energianivoo on kättesaadav energia $E$ korral, siis milline on tõenäosus $P (E)$ , et see on tegelikult elektroni poolt hõivatud? Kui $T = 0$ , siis teame, et kõikide nivoode jaoks allpool Fermi energiat on $P (E) = 1$ , mis tähendab, et nivoo on kindlasti hõivatud. Samuti teame, et $T = 0$ korral on kõikide nivoode jaoks Fermi nivoo kohal $P (E) = 0$ – need nivood ei ole hõivatud. Joonis 41-7a illustreerib seda situatsiooni.

JOONIS 41-7 Hõive tõenäosus $P (E)$ on tõenäosus, et seisund on elektroni poolt hõivatud. (a) $T = 0 K$ korral $P (E) = 1$ kõigi nivoode jaoks energiaga $E$ alates nullenergiast kuni Fermi energiani $E_{F}$ , ja $P (E) = 0$ kõrgemate energiatega nivoode jaoks. (b) Kui temperatuur $T = 1000 K$ , siis liiguvad mõned Fermi energiast pisut väiksema energiaga elektronid nivoodele, millede energia on pisut suurem Fermi energiast. Punkt kõveral näitab, et $E = E_{F}$ jaoks $P (E) = 0, 5$ .

Et leida P(E) temperatuuride jaoks ülalpool absoluutset nulli, peame kasutama kvantfüüsika teatud reegleid, mida nimetatakse Fermi-Diraci statistikaks nende füüsikute järgi, kes selle välja töötasid. Kasutades neid reegleid, on võimalik näidata, et hõive tõenäosus $P (E)$ on

(hõive tõenäosus, 41-6)

P (E) = \frac{1}{e^{(E - E_{F}) / k T} + 1}

kus $E_{F}$ on Fermi energia. Pange tähele, et $P (E)$ sõltub mitte nivoo energiast $E$ , vaid üksnes vahest $E - E_{F}$ , mis võib olla nii positiivne kui ka negatiivne.

Et näha, kas valem 41-6 kirjeldab joonist 41-7a, võtame selles $T = 0 K$ .

Kui $E < E_{F}$ , siis on eksponentsiaalne liige $e^{- \infty}$ ehk $0$ ; seega $P (E) = 1$ , mis on kooskõlas joonisega 41-7a.

Kui $E > E_{F}$ , siis on eksponentsiaalne liige $e^{+ \infty}$ ; seega $P (E) = 0$ , mis on jällegi kooskõlas joonisega 41-7a.

Joonis 41-7b on $P (E)$ graafik $T = 1000 K$ korral. See näitab, nagu juba eespool kinnitatud, et muutused elektronide jaotuses kättesaadavate seisundite vahel hõlmavad ainult neid seisundeid, mis on Fermi energia $E_{F}$ lähedal. Pange tähele, et kui $E = E_{F}$ (pole oluline, milline on temperatuur), siis on valemis 41-6 $e^{0} = 1$ ning $P (E) = 0, 5$ . Siit järeldub Fermi energia kasulikum definitsioon:

antud aine Fermi energia on kvantseisundi energia, mille elektronhõive tõenäosus on $0, 5$ .

Joonistel 41-7a ja b on graafikud vase jaoks, mille Fermi energia on $7, 0 e V$ . Niisiis, vase korral nii $T = 0 K$ kui ka $T = 1000 K$ puhul on seisund energiaga $E = 7, 0 e V$ hõivatud tõenäosusega $0, 5$ .

Näidisülesanne 41-4

Missugune on hõive tõenäosus, kui kvantseisundi energia on

0, 10 e V

ülalpool Fermi nivood? Objekti temperatuur on

800 K

.

Lahendus

JUHTMÕTE Mistahes seisundi hõive tõenäosuse metalli korral saab leida Fermi-Diraci statistikat kasutades vastavalt valemile 41-6.

Arvutused: leiame esmalt dimensioonita eksponendi

\frac{E - E_{F}}{k T} = \frac{0, 10 e V}{(8, 62 \times 10^{- 5} e V) (800 K)} = 1, 45

Pannes selle astendaja valemisse 41-6, saame

P (E) = \frac{1}{e^{1, 45} + 1} = 0, 19 = 19 %

Missugune on hõive tõenäosus, kui kvantseisundi energia on

0, 10 e V

allpool Fermi nivood?

Lahendus

Arvutus: siin on kasutatav eelmise osa (a) lahenduskäik, kuid nüüd on energia allpool Fermi energiat. Seega on astendajal sama arvväärtus, aga vastasmärgiga:

P (E) = \frac{1}{e^{- 1, 45} + 1} = 0, 81 = 81 %

Seisundite korral allpool Fermi energiat oleme sageli rohkem huvitatud tõenäosusest, et seisund ei ole hõivatud. See tõenäosus on $1 - P (E)$ ehk $19 %$ . Pange tähele, et see on sama mis hõive tõenäosus osas (a).

Kui palju on hõivatud seisundeid?

JOONIS 41-8 (a) Hõivatud seisundite tihedus $N_{0} (E)$ vase jaoks absoluutse nulli korral. Kõvera alune pindala on elektronide arvtiheduse väärtus $n$ . Pange tähele, et kõik seisundid kuni Fermi energiani $E_{F} = 7 e V$ on hõivatud ja et seisundid ülalpool Fermi energiat on tühjad. (b) Sama vase jaoks $T = 1000 K$ korral. Pange tähele, et üksnes Fermi energia lähedase energiaga elektronid on mõjutatud ja nende jaotus on muutunud.

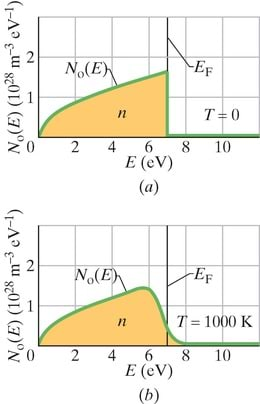
41-6 ja joonis 41-7 näitavad meile, kuidas kättesaadavad seisundid on energiate järgi jaotunud. Hõive tõenäosus (valem 41-6) annab mistahes seisundi jaoks tõenäosuse, et see on tegelikult elektroni poolt hõivatud. Et leida $N_{0} (E)$ – hõivatud seisundite tihedust – peame iga seisundit korrutama vastava hõive tõenäosuse väärtusega

(h ˜ o ivatud seisundite tihedus N_{0} (E) energia E juures) = (seisundite tihedus N (E) energia E juures) (h ˜ o ive t ˜ o en ¨ a osus P (E) energia E juures)

ehk

(hõivatud seisundite tihedus, 41-7)

N_{0} (E) = N (E) P (E)

Joonis 41-8a on valemi 41-7 graafiline esitus vase puhul $T = 0 K$ korral. See leitakse korrutades seisundite tiheduse väärtuse (joonis 41-6) iga energia korral hõive tõenäosuse väärtusega absoluutse nulli juures (joonis 41-7a). Joonisel 41-8b on näidatud vase hõivatud seisundite tihedus $T = 1000 K$ korral.

Kui metall näidisülesandes 41-3 on vask, mille Fermi energia on

7, 0 e V

, siis kui palju hõivatud seisundeid elektronvoldi kohta mahub kitsasse energiavahemikku

7, 0 e V

ümber?

Lahendus

JUHTMÕTTED (1) Näidisülesande 41-3 arutluskäiku saab ka siin kasutada, kui tuleb silmas pidada, et nüüd on meil hõivatud seisundite tihedus $N_{0} (E)$ , mis on antud valemiga 41-7 ( $N_{0} (E) = N (E) P (E)$ ). (2) Kuna meil on vaja arvutada suurusi kitsa energiavahemiku jaoks (vase Fermi energia) $7, 0 e V$ juures, siis hõive tõenäosus $P (E) = 0, 5$ .

Arvutused: joonisel 41-6 näeme, et seisundite tihedus $7, 0 e V$ juures on ligikaudu $1, 8 \times 10^{28} m^{- 3} e V^{- 1}$ . Seega annab valem 41-7 meile hõivatud seisundite tiheduseks

N_{0} (E) = N (E) P (E) = (1, 8 \times 10^{28} m^{- 3} e V^{- 1}) (0, 50) = 0, 9 \times 10^{28} m^{- 3} e V^{- 1}

Valemit näidisülesandest 41-3a saab ümber kirjutada hõivatud seisundite jaoks kujul

(h ˜ o ivatud seisundite arv ¨ u he e V kohta 7 e V juures) = (h ˜ o ivatud seisundite tihedus N_{0} (E) 7 e V juures) (objekti ruumala V)

Asendame siin $N_{0} (E)$ ja $V$ nende arvväärtustega, saame

(h ˜ o ivatud seisundite arv ¨ u he e V kohta 7 e V juures) = (0, 9 \times 10^{28} m^{- 3} e V^{- 1}) (2 \times 10^{- 9} m^{3}) = 1, 8 \times 10^{19} e V^{- 1} \approx 2 \times 10^{19} e V^{- 1} - ------------ - - ------------ -

Fermi energia arvutamine

Oletame, et liidame kokku (integreerimise teel) hõivatud seisundite arvud ühikruumalas (joonis 41-8a, $T = 0 K$ ) üle kõikide energiate alates $E = 0$ kuni $E = E_{F}$ . Tulemus peab võrduma juhtivuselektronide arvuga n metalli ühikruumalas. Võrrandi kujul on see

(41-8)

n = \int_{0}^{E_{F}} N_{0} (E) d E

(Graafiliselt vastab integraal jaotuskõvera all olevale pindalale joonisel 41-8a.) Kuna $T = 0 K$ korral ja kõiki energiaid allpool Fermi energiat arvesse võttes peab $P (E) = 1$ , saame valemi 41-7 põhjal valemis 41-8 asendada tiheduse $N_{0} (E)$ tihedusega $N (E)$ ning seejärel kasutada valemit 41-8, et leida Fermi energia $E_{F}$ . Asetades valemi 41-5 avaldisse 41-8, leiame

n = \frac{8 \sqrt{2} π m^{3 / 2}}{h^{3}} \int_{0}^{E_{F}} E^{1 / 2} d E = \frac{8 \sqrt{2} π m^{3 / 2}}{h^{3}} \frac{2 E_{F}^{3 / 2}}{3}

kus $m$ on elektroni mass. Lahendame selle võrrandi $E_{F}$ jaoks, saame

(41-9)

E_{F} = {(\frac{3}{16 \sqrt{2} π})}^{2 / 3} \frac{h^{2}}{m} n^{2 / 3} = \frac{0, 121 h^{2}}{m} n^{2 / 3}

Niisiis, kui meil on teada juhtivuselektronide arv metalli ühikruumalas, saame selle metalli jaoks leida Fermi energia.

Pooljuhid

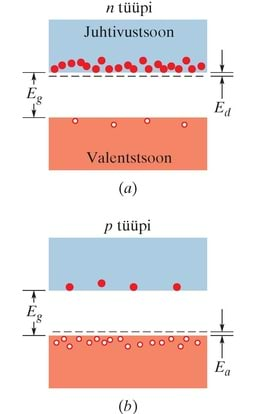
Kui võrdlete joonist 41-9a joonisega 41-4, siis näete, et pooljuhi tsoonistruktuur on sarnane isolaatori omaga. Peamine erinevus on selles, et pooljuhil on kõrgeima täidetud tsooni (nimetatud valentstsooniks) lae ja selle kohal oleva vakantse tsooni põhja vahel (nimetatud juhtivustsooniks) palju väiksem keelutsooni laius $E_{g}$ . Seega pole kahtlust, et räni ( $E_{g} = 1, 1 e V$ ) on pooljuht ja teemant ( $E_{g} = 5, 5 e V$ ) on isolaator. Ränis – aga mitte teemandis – on reaalne võimalus, et soojusliikumine toatemperatuuril kutsub esile elektronide hüppe valentstsoonist juhtivustsooni.

Tabelis 41-1 võrdlesime kolme põhilist elektrilist omadust tüüpilise metalljuhi vase ja tüüpilise pooljuhi räni korral. Vaatame seda tabelit uuesti, üks rida korraga, et näha, kuidas pooljuht erineb metallist.

Laengukandjate arvtihedus n

Tabeli 41-1 alumine rida näitab, et vasel on laengukandjaid ühikruumalas oluliselt rohkem kui ränil, tervelt $10^{13}$ korda rohkem. Vase puhul annab iga aatom ühe elektroni – oma ainsa valentselektroni – juhtivusprotsessi. Laengukandjad ränis tekivad ainult seetõttu, et soojuslikus tasakaalus toimuv soojusliikumine ergastab teatud (väga väikese) arvu valentstsooni elektrone hüppama üle keelutsooni juhtivustsooni, jättes endast valentstsooni järele sama arvu hõivamata energiaseisundeid, mida nimetatakse aukudeks (joonis 41-9b).

JOONIS 41-9 Lubatud energiatsoonide-keelutsoonide skeem pooljuhi korral. See meenutab isolaatori oma (vt joonis 41-4), välja arvatud see, et siin on energia keelutsoon $E_{g}$ palju kitsam; seega on elektronidel soojusliikumise tõttu arvestatav tõenäosus keelutsoon ületada. (b) Soojusliikumise mõjul on mõned elektronid hüpanud valentstsoonist juhtivustsooni, jättes valentstsooni endast sama arvu auke maha.

Mõlemad, nii elektronid juhtivustsoonis kui ka augud valentstsoonis, on laengukandjateks. Augud juhivad seeläbi, et need annavad teatud liikumisvabaduse valentstsooni jäänud elektronidele, mis muidu oleksid võresse lukustatud. Kui pooljuht asetada elektrivälja $\to E$ , siis püüavad valentstsooni negatiivselt laetud elektronid triivida elektriväljale $\to E$ vastassuunas. See aga tingib aukude asukohtade triivi elektriväljaga $\to E$ samas suunas. Nii et augud käituvad nagu liikuvad osakesed laenguga $+ e$ .

Piltlikult võib ette kujutada tihedalt pargitud autode rida, kusjuures rea esimese auto ja tõkke vahel on ühe auto pikkune tühimik. Kui nüüd esimene auto liigub tõkkeni, avaneb selle taga vaba parkimisruum. Seejärel täidab selle teine, järgmine auto, lubades ka kolmandal autol edasi liikuda ja nii edasi. Paljude autode liikumist tõkke suunas on lihtne analüüsida, kui esitada seda ainsa „augu” (parkimiskoha) triivina tõkkest eemale.

Pooljuhtides on aukude poolt tekitatud juhtivus sama tähtis kui elektronide liikumisega tekitatud juhtivus. Kui räägitakse aukjuhtivusest, siis mõeldakse selle all seda, et kõik hõivamata seisundid valentstsoonis on hõivatud osakeste poolt laenguga $+ e$ ja et elektrone valentstsoonis pole, nii et nood positiivse laenguga osakesed saavad tsoonis vabalt liikuda.

Eritakistus

ρ

Tuletame meelde (26. ptk), et aine eritakistus $ρ = m / e^{2} n τ$ , kus $m$ on elektroni mass, $e$ elementaarlaeng, $n$ laengukandjate arv ühikruumalas ja $τ$ keskmine ajavahemik laengukandjate põrgete vahel. Tabelist 41-1 on näha, et toatemperatuuril on räni eritakistus vase omast $10^{11}$ korda suurem. Seda hiigelsuurt erinevust võib selgitada hiigelsuure erinevusega laengukandjate arvus $n$ . Teiste tegurite mõju eritakistusele jääb viimase varju.

Eritakistuse temperatuuritegur

α

Tuletame meelde, et $α$ (vt võrrand (26-17)) on eritakistuse suhteline muutus temperatuuri ühikmuutuse korral

(41-40)

α = \frac{1}{ρ} \frac{d ρ}{d T}

Vase eritakistus kasvab koos temperatuuriga (s.t $d ρ / d T > 0$ ), sest vase laengukandjate põrked sagenevad kõrgemal temperatuuril. Seega on vase korral $α$ positiivne.

Põrkesagedus suureneb temperatuuri tõustes ka räni puhul. Kuid räni eritakistus tegelikult väheneb temperatuuriga ( $d ρ / d T < 0$ ), sest laengukandjate arv (elektronid juhtivustsoonis ja augud valentstsoonis) suureneb kiiresti temperatuuri tõustes (rohkem elektrone hüppab üle keelutsooni valentstsoonist juhtivustsooni.) Seega on suhteline muutus $α$ räni korral negatiivne.

Dopeeritud pooljuhid

Pooljuhtide kasulikkust tehnoloogias saab oluliselt parandada, kui sisestada pooljuhi võresse teatud hulk sobivaid asendusaatomeid (nn lisandeid) – protsess, mida nimetatakse legeerimiseks ehk dopeerimiseks. Tavaliselt on dopeeritud pooljuhis lisandiaatomiga asendatud vaid $1$ räni aatom $10^{7}$ aatomi kohta. Peaaegu kõik tänapäeva pooljuhtseadised baseeruvad dopeeritud materjalidel. Neid materjale on kaht tüüpi, mida nimetatakse $n$ -tüübiks ja $p$ -tüübiks; käsitleme neid eraldi.

n

-tüüpi pooljuhid

Isoleeritud räniaatomis on elektronid paigutatud alamkihtidesse vastavalt skeemile

1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2}, 3 p^{2}

milles, nagu tavaliselt, ülaindeksid (millede summa on $14$ – räni aatomnumber) näitavad elektronide arvu antud alamkihis.

JOONIS 41-10 (a) Puhta räni võrestruktuuri tasapinnaline esitus. Iga räni aatom on seotud nelja lähinaabriga kaheelektronilise kovalentsidemega (kujutatud punaste punktide paarina mustade joonte vahel). Elektronid kuuluvad sidemete, mitte üksikute aatomite juurde, moodustades objekti valentstsooni. (b) Üks räni aatomeist on asendatud fosfori aatomiga (valents $= 5$ ). „Ekstra” elektron on vaid lõdvalt seotud ioonjäägiga, niisiis kergesti tõstetav juhtivustsooni, kus see saab vabalt liikuda kogu võre ulatuses. (c) Üks räni aatomeist on asendatud alumiiniumi aatomiga (valents $= 3$ ). Ühes kovalentsidemeist – ning seega valentstsoonis – on nüüd auk. Auk saab kergesti liikuda läbi võre, kuna elektronid naabersidemeist ruttavad seda täitma. Pildil näeme augu liikumist paremale.

Joonis 41-10a on tasapinnaline esitus puhta räni võre osast (tükk võrest, mis on projekteeritud tasandile); võrdle seda joonisega 41-1b, kus on toodud võre ühikrakk kolmes mõõtmes. Iga räniaatom annab panusena oma kaks $3 s$ elektroni ja kaks $3 p$ elektroni, et moodustada jäik kaheelektroniline kovalentside igaühega oma neljast naabrist. (Kovalentside on selline seos kahe aatomi vahel, milles aatomid jagavad elektronpaari.) Joonisel 41-1b kujutatud ühikraku igal aatomil on oma naabritega neli kovalentsidet.

Elektronid räni-räni sidemetes moodustavad räni valentstsooni. Kui elektron on tõmmatud sidemest välja nii, et see on vaba rändama läbi võre, siis ütleme, et elektron on tõstetud valentstsoonist juhtivustsooni. Selleks vajalik minimaalne energia on keelutsooni energia $E_{g}$ .

Kuna elektronidest neli on haaratud sidemetesse, siis on räni iga „aatom” tegelikult ioon inertse, neoonile omase elektronpilvega (see sisaldab $10$ elektroni), mis ümbritseb tuuma laenguga $+ 14 e$ , kus $14$ on räni aatomnumber. Iga sellise iooni kogulaeng on $+ 4 e$ ning öeldakse, et ioonide valentsarv on $4$ .

Joonisel 41-10b on keskmine räniioon asendatud fosforiaatomiga ( $valents = 5$ ). Fosfori valentselektronidest neli moodustavad sidemeid nelja ümbritseva räniaatomiga. Viies („ekstra”) elektron on fosfori iooni ülejäänud osaga vaid lõdvalt seotud. Energiatsooni diagrammis hõivab selline elektron lokaliseeritud energiaseisundi, mis asub keelutsoonis kaugusel $E_{d}$ allpool juhtivustsooni põhja; see on näidatud joonisel 41-11a. Kuna $E_{d} ≫ E_{g}$ , siis on vajalik energia elektronide ergastamiseks juhtivustsooni nendelt nivoodelt palju väiksem kui räni valentstsooni nivoodelt.

Fosfori aatomit nimetatakse doonoriks, sest see on varmas annetama (ingl donate – annetama) oma elektroni juhtivustsooni. Tegelikult on toatemperatuuril juhtivustsoonis kõik doonorite panustatud elektronid. Lisades ainesse doonori aatomeid, on võimalik elektronide arvu juhtivustsoonis oluliselt suurendada – palju suuremal määral kui joonisel 41-11a kujutatud.

Doonori aatomitega legeeritud pooljuhte nimetatakse $n$ -tüüpi pooljuhtideks; $n$ tähistab negatiivset, siin ületavad juhtivustsooni viidud negatiivsed laengukandjad arvuliselt positiivseid laengukandjaid, milledeks on augud valentstsoonis. Elektrone nimetatakse $n$ -tüüpi pooljuhtides enamuslaengukandjaiks ja auke vähemuslaengukandjaiks.

p

-tüüpi pooljuhid

JOONIS 41-11 (a) Dopeeritud $n$ -tüüpi pooljuhis on doonori elektroni nivood väikesel kaugusel $E_{d}$ allpool juhtivustsooni põhja. Et doonori elektrone saab kergesti juhtivustsooni ergastada, siis on seal nüüd palju rohkem elektrone. Valentstsoon sisaldab sama arvu auke, nagu seal oli enne dopeerimist. (b) Dopeeritud $p$ -tüüpi pooljuhis asuvad aktseptori nivood väikesel kaugusel $E_{a}$ ülalpool valentstsooni lage. Nüüd on valentstsoonis palju rohkem auke. Juhtivustsoon sisaldab sama arvu elektrone, nagu seal oli enne dopeerimist. Enamuslaengukandjate suhe vähemuskandjatesse on tegelikult palju kordi suurem kui diagrammidel (a) ja (b) kujutatud.

Nüüd vaadake joonist 41-10c, kus üks räniaatomeist ( $valents = 4$ ) on asendatud alumiiniumiaatomiga ( $valents = 3$ ). Alumiiniumiaatom saab olla kovalentselt seotud üksnes kolme räniaatomiga, seega tuleb ühe alumiiniumi-räni sideme kohta üks „puuduv” elektron (auk). Väikese energiakuluga saab räni-räni naabersidemest rebida elektroni selle augu täiteks, tekitades augu omakorda tolles sidemes. Siis aga liigub elektron mõnest teisest sidemest seda uut auku täitma. Niiviisi saab auk läbi võre rännata.

Alumiiniumiaatomit nimetatakse aktseptoriks, sest see on varmas vastu võtma (ingl accept – vastu võtma) elektroni naabersidemest, s.t räni valentstsoonist. Nagu kujutatud joonisel 41-11b, hõivab see elektron lokaliseeritud energiaseisundi, mis asub keelutsoonis, keskmiselt energia $E_{a}$ võrra ülalpool valentstsooni lage. Kuna energia $E_{a}$ on väike, saab valentselektrone hõlpsasti aktseptori nivoole üles pumbata, jättes augud valentstsooni. Niisiis, lisades aktseptori aatomeid, on võimalik
oluliselt suurendada aukude arvu valentstsoonis – palju suuremal määral kui joonisel 41-11b kujutatud. Toatemperatuuril on ränis praktiliselt kõik aktseptori nivood elektronidega asustatud.

Aktseptori aatomitega legeeritud pooljuhte nimetatakse $p$ -tüüpi pooljuhtideks; $p$ tähistab positiivset, siin ületavad valentstsooni viidud augud, mis käituvad nagu positiivsed laengukandjad, arvuliselt elektrone juhtivustsoonis. Augud on ptüüpi pooljuhtides enamuslaengukandjateks ja elektronid on vähemuslaengukandjateks.

Tabel 41-2 võtab kokku tüüpilise $n$ -tüüpi ja tüüpilise $p$ -tüüpi pooljuhi omadused. Pöörake erilist tähelepanu asjaolule, et doonori ja aktseptori ioonjäägid, ehkki laetud, ei ole laengu kandjad, sest normaaltemperatuuril on need võresõlmedes paigal.

Toatemperatuuril on juhtivuselektronide tihedus

n_{0}

puhtas ränis

10^{16} m^{- 3}

. Oletame, et dopeerides räni võret fosforiga, tahame suurendada seda arvu miljon (

10^{6}

) korda. Kui palju räni aatomeid peame asendama fosfori aatomitega? (Meenutage, et toatemperatuuril on soojusliikumine nii efektiivne, et praktiliselt iga fosforiaatom annetab ühe „ekstra” elektroni juhtivustsooni.)

Lahendus

Väävli aatomite arv: kuna iga fosfori aatom annab ühe juhtivuselektroni ja kuna me tahame juhtivuselektronide kogutiheduseks $10^{6} n_{0}$ , siis peab fosforiaatomite tihedus $n_{P}$ olema

10^{6} n_{0} = n_{0} + n_{P}

Siis

n_{P} = 10^{6} n_{0} - n_{0} \approx 10^{6} n_{0} = (10^{6}) (10^{16} m^{- 3}) = 10^{22} m^{- 3}

Saime teada, et meil on vaja lisada $10^{22}$ fosfori aatomit ühe kuupmeetri räni kohta.

Räni aatomite osakaal: võime leida räni aatomite tiheduse $n_{S i}$ puhtas ränis (enne dopeerimist) valemi 41-1 järgi, mille võime kirjutada kujul

(aatomite arv objektis) = \frac{(r ¨ a ni tihedus) (objekti ruumala V)}{(r ¨ a ni molaarmass M_{S i}) / N_{A}}

Jagades võrrandi mõlemad pooled läbi objekti ruumalaga $V$ , et saada vasakul poolel räniaatomite tihedust, on meil

n_{S i} = \frac{(r ¨ a ni tihedus) N_{A}}{M_{S i}}

Lisas F on antud räni tihedus $2, 33 g / c m^{3}$ ( $= 2330 k g / m^{3}$ ) ja molaarmass $28, 1 g / m o l$ ( $= 0, 0281 k g / m o l$ ). Seega

n_{S i} = \frac{(2330 k g / m^{3}) (6, 02 \times 10^{23} a a t o m i t / m o l)}{0, 0281 k g / m o l} = 5, \times 10^{28} a a t o m i t / m^{3} = 5 x 10^{29} m^{3}

Otsitav suhe on ligikaudu

\frac{n_{P}}{n_{S i}} = \frac{1}{5 \times 10^{6}} - ---- - - ---- -

Kui asendaksime fosfori aatomiga ainult ühe räni aatomi viiest miljonist, siis suureneks elektronide arv juhtivustsoonis miljon korda.

Kuidas saab selline imeväike fosforilisand anda nii suure efekti? Vastus: ehkki efekt on märgatav, ei ole see siiski „suur”. Juhtivuselektronide tihedus oli enne dopeerimist $10^{16} m^{- 3}$ ja pärast seda $10^{22} m^{- 3}$ . Vase korral aga on juhtivuselektronide tihedus ligikaudu $10^{29} m^{- 3}$ (vt tabel 41-1). Niisiis, isegi pärast dopeerimist jääb juhtivuselektronide tihedus ränis palju – tervelt $10^{7}$ korda väiksemaks kui tüüpilises metallis nagu vask.

Tabel 4-2 Kahe dopeeritud pooljuhi omadused

	Pooljuhi tüüp
Omadus	$n$	$p$
Maatriksi materjal	Räni	Räni
Maatriksi tuumalaeng	$+ 14 e$	$+ 14 e$
Maatriksi keelutsooni laius	$1, 2 e V$	$1, 2 e V$
Dopant	Fosfor	Alumiinium
Dopandi tüüp	Doonor	Aktseptor
Enamuslaengukandjad	Elektronid	Augud
Vähemuslaengukandjad	Augud	Elektronid
Dopandi keelutsooni laius	$E_{d} = 0, 045 e V$	$E_{d} = 0, 067 e V$
Dopandi valents	$5$	$3$
Dopandi tuumalaeng	$+ 15 e$	$+ 13 e$
Dopandiiooni laeng	$+ e$	$- e$

p n

-siire

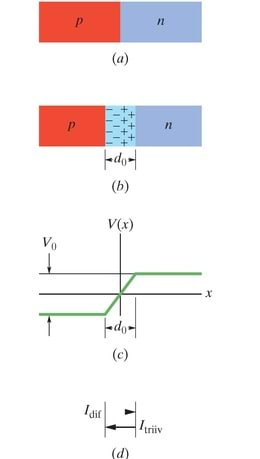
Joonisel 41-12a on kujutatud $p n$ -siire – kiht monokristalses pooljuhis, mis on valikuliselt dopeeritud nii, et üks piirkond on $n$ -tüüpi materjal ja sellega külgnev kiht on $p$ -tüüpi materjal. Niisugused siirded on pea kõikide pooljuhtseadmete sees.

Lihtsustavalt oletame, et see siire on tekitatud mehaaniliselt, lükates kokku $n$ -tüüpi pooljuhtkristalli ja $p$ -tüüpi pooljuhtkristalli. Siis on üleminek ühest piirkonnast teise ideaalselt järsk, toimudes ühelainsal siirdepinnal.

Vaatame elektronide ja aukude liikumist kohe pärast $n$ -tüüpi kristalli ja ptüüpi kristalli (mõlemad elektriliselt neutraalsed) kokkuviimist. Käsitleme esmalt enamuslaengukandjaid, milleks $n$ -tüüpi materjalis on elektronid ja $p$ -tüüpi materjalis augud.

Enamuslaengukandjate liikumine

Kui lasete lõhki heeliumiga täidetud õhupalli, siis heeliumiaatomid difundeeruvad (levivad) väljapoole ümbritsevasse õhku. See leiab aset seetõttu, et normaalses õhus on väga vähe heeliumi aatomeid. Täpsemalt öeldes, õhupalli ja õhu piirpinnal on heeliumi tiheduse gradient (piirpinna läbimisel heeliumiaatomite arvtihedus muutub); heeliumi aatomid liiguvad nii, et gradient väheneks.

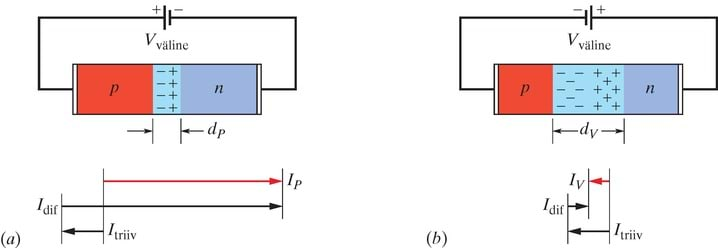
Samamoodi püüavad elektronid (joonise 41-12a $n$ -poolel), mis paiknevad siirdepinna lähedal, difundeeruda sellest läbi (joonisel paremalt vasakule) $p$ -poolele, kus on väga vähe vabu elektrone. Analoogiliselt, augud $p$ -poolel siirdepinna lähedal püüavad difundeeruda läbi selle pinna (vasakult paremale) $n$ -poolele, kus on väga vähe auke. Nii elektronide kui aukude liikumine moodustab difusioonvoolu $I_{d i f}$ , mis loetakse kokkuleppeliselt vasakult paremale suunatuks nagu näidatud joonisel 41-12d.

Kuid $n$ -kiht on tihedalt täis pikitud positiivselt laetud doonoriioonidega, mis on kindlalt oma võresõlmedes paigal. Tavaliselt on iga sellise iooni liigne positiivne laeng elektriliselt kompenseeritud ühega juhtivustsooni elektronidest. Kui aga $n$ -poole elektron difundeerub läbi siirdepinna, jätab see „katteta” mõne doonorioonidest, tekitades siirdepinna lähedal $n$ -poolel paigaloleva positiivse laengu. Kui difundeeruv elektron jõuab $p$ -poolele, ühineb see kiiresti aktseptoriooniga (millel puudub üks elektron), seega tekib paigalolev negatiivne laeng siirdepinna lähedal $p$ -poolel.

Sel moel moodustavad läbi siirdepinna paremalt vasakule difundeeruvad elektronid ruumlaengu mõlemal pool siirdepinda (joonis 41-12b). Augud, difundeerudes läbi siirdepinna vasakult paremale, tekitavad täpselt samasuguse efekti. (Võtke endale aega selles veendumiseks.) Nii tekitavad elektronid ja augud kaks ruumlaengu piirkonda – ühe positiivse ja teise negatiivse. Need kaks piirkonda moodustavad tõkkekihi paksusega $d_{0}$ (joonis 41-12b).

Laengute tõttu tekib p- ja n-poole vahel kontaktpotentsiaalide vahe $V_{0}$ läbi tõkkekihi (joonis 41-12c). See piirab elektronide ja aukude edasist difusiooni läbi siirdepinna. Negatiivsed laengud püüavad vältida madala potentsiaaliga piirkonda. Seega elektron, mis jõuab siirdepinda paremalt (joonis 41-12b), liigub madala potentsiaali piirkonna suunas ja püüab pöörduda tagasi $n$ -poolele. Analoogiliselt, siirdepinnale vasakult lähenev positiivne laeng (auk) liigub kõrgema potentsiaali piirkonna suunas ja kaldub minema tagasi $p$ -poolele.

Vähemuslaengukandjate liikumine

Nagu on näha jooniselt 41-11a, ehkki $n$ -tüüpi materjalides on enamuslaengukandjad elektronid, ei puudu seal ka mõningad augud. Samamoodi ka $p$ -tüüpi materjalis (joonis 41-11b), leidub lisaks enamuslaengukandjatele aukudele seal ka mõningaid elektrone. Need vähesed elektronid ja augud on vastavates materjalides vähemuslaengukandjateks.

Kui potentsiaalide vahe $V_{0}$ (joonis 41-12c) toimib enamuslaengukandjate jaoks nagu tõke, siis vähemuslaengukandjatele on see liumägi. Positiivsed laengud (augud $n$ -poolel) püüavad leida madala potentsiaaliga piirkondi ja negatiivsed laengud (elektronid $p$ -poolel) kõrge potentsiaaliga piirkondi. Niisiis, mõlemat tüüpi vähemuslaengud lükatakse läbi siirdepinna potentsiaalide vahe poolt ning koos moodustavad need triivvoolu $I_{t r i i v}$ läbi siirdepinna vasakult paremale (joonis 41-12d).

Seega on isoleeritud $p n$ -siire tasakaaluolekus, kus kahe otsa vahel on potentsiaalide vahe $V_{0}$ . Sel juhul on keskmine difusioonivool $I_{d i f}$ $p$ -poolelt $n$ -poolele tasakaalustatud keskmise triivvooluga $I_{t r i i v}$ vastassuunas. Need kaks voolu kustutavad teineteist, sest koguvool läbi siirdepinna peab olema null; muidu võiks laeng kanduda piiramatult siirde ühest otsast teise.

Milline alljärgnevast viiest voolust läbi siirdepinna (joonis 41-12a) peab olema null?
(a) Aukude koguvool, arvestades nii enamus- kui vähemuslaenguid.
(b) Elektronide koguvool, arvestades nii enamus- kui ka vähemuslaenguid.
(c) Mõlemate, nii elektronide kui ka aukude koguvool, arvestades mõlemate enamusja vähemuslaenguid.
(d) Enamuslaengute koguvool, arvestades nii elektrone kui auke.
(e) Vähemuslaengute koguvool, arvestades nii elektrone kui auke.

Alaldusdiood

JOONIS 41-13 Pinge-voolu graafik $p n$ -siirde korral näitab, et siire on hästi juhtiv päripinge korral ja peaaegu mittejuhtiv vastupinge korral.

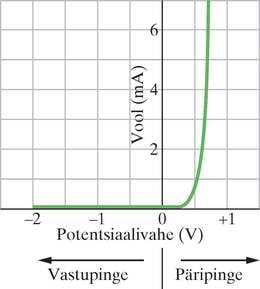
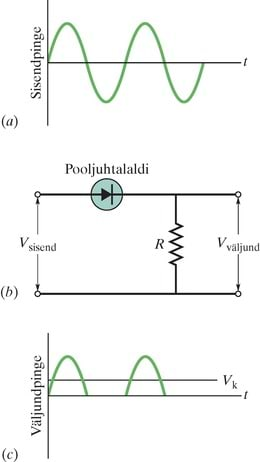
Vaadake nüüd joonist 41-13. See näitab, et kui tekitame potentsiaalide vahe siirde pärisuunas, s.t rakendame siirdele päripinge, siis tekib vool läbi siirde. Kui aga muudame potentsiaalide vahe suuna vastupidiseks – rakendame vastupinge, siis vool läbi siirde praktiliselt kaob.

JOONIS 41-14 Alaldusdioodiga vooluring (b) toimib nii, et laseb läbi positiivse poole sisendlainest (a) ja surub maha negatiivse poole. Antud kujuga sisendlaine pinge keskväärtus on null; väljundlaine (c) keskmine pinge aga positiivse väärtusega $V_{k}$ .

Selle omaduse üks rakendusi on pooljuht-alaldusdiood, mille tingmärk on toodud joonisel 41-14b; noole tipp vastab seadise $p$ -tüüpi otsale ja osutab ühtlasi kokkuleppelisele voolusuunale. Siinuslaine kujuline sisendpinge (joonis 41-4a) transformeerub alaldi toimel poollaine kujuliseks väljundpingeks (joonis 41-14c); s.t alaldi nagu töötaks suletud lülitina (lõpmata takistus) sisendpinge ühe polaarsuse jaoks ning avatud lülitina (nulltakistus) teise jaoks.

Sisendpinge keskväärtus on joonise 41-14a järgi null, seda pole aga väljundpinge keskväärtus (joonis 41-14c). Seega saab pooljuhtalaldit kasutada alaldusseadmes, mis muundab vahelduvpinget alalispingeks.

Joonis 41-15 näitab, miks $p n$ -siire toimib alaldina. Joonisel 41-15a on patarei pluss-klemm ühendatud $p$ -kihiga. Sellise pärilülituse korral kasvab $p$ -kihi positiivne ja $n$ -kihi negatiivne laeng, vähendades potentsiaalibarjääri kõrgust $V_{0}$ (joonis 41-12c). Madalama barjääri saab läbida rohkem enamuslaengukandjaid; järelikult difusioonvool $I_{d i f}$ suureneb märgatavalt.

Barjäär puudub aga vähemuslaengukandjate jaoks, mis moodustavad triivvoolu, teisisõnu, triivvoolu Itriiv väline patarei ei mõjuta. Voolude tasakaal, mis eksisteeris potentsiaalide vahe puudumise korral (joonis 41-12d), on seega rikutud ning nagu näidatud joonisel 41-15a, tekib vooluringis tugev pärivool $I_{P}$ .

Teiseks päripinge mõjuks on tõkkekihi kitsamaks muutmine, nagu näitab jooniste 41-12b ja 41-15a võrdlus. Tõkkekiht kitseneb, sest päripinge tekitatud barjääri alanemine on ühtlasi seotud väiksema ruumlaenguga. Kuna ruumlaengut tekitavad ioonid on kinnistatud võresõlmedesse, saab ruumlaeng väheneda ainult tänu ruumala vähenemisele tõkkekihi kitsenemisel.

Et tõkkekiht sisaldab tavaliselt väga vähe laengukandjaid, siis on see suure eritakistusega ala. Kuid kui selle laius on päripinge tõttu oluliselt kahanenud, siis on ka eritakistus oluliselt vähenenud, mis on kooskõlas tugeva pärivooluga.

JOONIS 41-15 (a) Päripingestatud $p n$ -siirdele on iseloomulik kitsas tõkkekiht ja tugev pärivool $I_{P}$ . (b) Vastupingestatud siirdel on kitsas tõkkekiht ja seda läbib nõrk vool $I_{V}$ .

Joonis 41-15b näitab vastulülitust, milles patarei miinusklemm on ühendatud $p n$ -siirde $p$ -kihiga. Nüüd suurendab rakendatud elektromotoorjõud potentsiaalide vahet, difusioonvool väheneb oluliselt, samal ajal kui triivvool jääb muutumatuks; tulemuseks on suhteliselt nõrk tagasivool $I_{T}$ . Tõkkekiht laieneb, selle suur eritakistus on kooskõlas nõrga tagasivooluga $I_{T}$ .

Valgusdiood (LED)

Tänapäeval meil vaevalt õnnestub vältida eredavärvilisi „elektroonilisi” numbreid, mis helendavad meile vastu küll kassadelt ja bensiinijaamadelt, küll mikrolaineahjudelt ja äratuskelladelt, ning me ei tuleks enam toime ilma nähtamatute infrapunakiirteta, mis kontrollivad liftiuksi ja opereerivad televiisoritega juhtimispultide kaudu. Paljudel juhtudel kiirgab seda valgust $p n$ -siire valgusdioodis (LED, ingl light-emitting diode). Kuidas saab $p n$ -siire valgust kiirata?

Vaatame kõigepealt lihtsat pooljuhti. Kui elektron langeb juhtivustsooni põhjast valentstsooni auku, vabaneb energia $E_{g}$ , mis on võrdne keelutsooni laiusega. Ränis, germaaniumis ja paljudes teistes pooljuhtides muundub see energia võnkuva võre soojusenergiaks ning mingit valgust ei kiirgu.

JOONIS 41-16 Päripingestatud $p n$ -siirdes on elektronid viidud $n$ -tüüpi materjali ja augud $p$ -tüüpi materjali. (Augud liiguvad voolu $I$ suunas, mis on ekvivalentne elektronide liikumisele vastassuunas.) Valgus kiirgab kitsast tõkkekihist iga kord, kui toimub augu ja elektroni rekombinatsioon.

Kuid mõnes pooljuhis, näiteks galliumarseniidis, võib see energia kiirguda footonina energiaga $h f$ lainepikkusel

(41-11)

λ = \frac{c}{f} = \frac{c}{E_{g} / h} = \frac{h c}{E_{g}}

Kiirgamaks küllaldaselt valgust, et olla valgusdioodina kasutatav, peab materjalis toimuma piisavalt palju elektron-auk-üleminekuid. See tingimus ei ole täidetud puhaste pooljuhtide korral, sest toatemperatuuril seal lihtsalt pole küllalt palju elektron-auk-paare. Nagu järeldub jooniselt 41-11, siis dopeering siin ei aita. Dopeeritud $n$ -tüüpi aines suureneb kõvasti küll juhtivuselektronide hulk, kuid jääb vajaka aukudest, millega ühineda; dopeeritud $p$ -materjalis on palju auke, aga mitte piisavalt elektrone. Seega ei sobi LEDiks praktiliselt ei puhas ega ka lisanditega pooljuht.

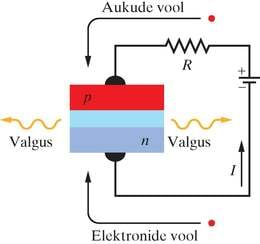
JOONIS 41-17 Valgusdioodi läbilõige (seade on telgsümmeetriline). $p$ -tüüpi materjalist ketas peab olema küllalt õhuke, et valgus seda läbiks. Ühendus $p$ -tüüpi materjaliga on tehtud metallist rõnga kaudu. Tõkkekihti $n$ - ja $p$ -tüüpi materjalide vahel ei ole näidatud.

Mida meil vaja läheb, on pooljuhtmaterjal väga suure elektronide arvuga juhtivustsoonis ja vastava arvu aukudega valentstsoonis. Niisuguse omadusega seadist saab valmistada, kui rakendada tugevalt dopeeritud $p n$ -siirdele suurt päripinget, nagu näidatud joonisel 41-16. Siis toimib vool $I$ läbi seadme $n$ -tüüpi aines elektrone lisavalt ja $p$ -tüüpi aines auke lisavalt. Kui dopeering on küllalt tugev ja ka vool küllalt suur, siis võib tõkkekiht muutuda väga õhukeseks, võib-olla vaid mõne mikromeetri paksuseks. Tulemuseks on väga suur elektronide tihedus $n$ -tüüpi materjalis vastakuti samuti väga suure aukude tihedusega $p$ -tüüpi materjalis, vahel üksnes kitsas tõkkekiht. Nüüd saab toimuda palju elektron-auk-rekombinatsioone, mis tekitab valguskiirguse sellest piirkonnast. Joonisel 41-17 on näidatud tegeliku LEDi ehitus.

Tööstuslikud LED-lambid, mis kiirgavad nähtava valguse piirkonnas, baseeruvad tavaliselt arseeni ja fosfori aatomitega dopeeritud galliumil. Kui $60 %$ neist võresõlmedest, kus pole galliumi, on hõivatud arseeni ioonide poolt ja $40 %$ fosfori ioonide poolt, siis on keelutsooni laius $E_{g}$ umbes $1, 8 e V$ , mis vastab punasele valgusele. Teistsugune dopeering ja üleminekunivoode korraldus võimaldavad konstrueerida LED-lampe, mis kiirgavad valgust nähtava ja lähinähtava spektri mistahes soovitud piirkonnas.

Fotodiood

Vool, mis läbib sobivalt korraldatud $p n$ -siiret, võib genereerida valgust. Võimalik on ka pöördprotsess – valgustades sobivalt konstrueeritud $p n$ -siiret, saab tekitada voolu vooluringis, mis seda siiret sisaldab. See on fotodioodi tööpõhimõte.

Kui te klõpsutate televiisori juhtimispulti, siis LED-seade saadab välja infrapunase valguse kodeeritud impulsside jada. Selle võtab vastu fotodiood teleri vastavas lülituses, milles võimendatud ja dekodeeritud signaalid võivad korraldada kanalivahetust või reguleerida hääle valjust.

Pooljuhtlaser

Joonisel 41-16 toodud skeemis on palju elektrone $n$ -tüüpi materjali juhtivustsoonis ja palju auke $p$ -tüüpi materjali valentstsoonis. Seega eksisteerib siin elektronide asustusinversioon ehk pöördhõive, mis tähendab, et kõrgematel energianivoodel on rohkem elektrone kui madalamatel. Nagu käsitletud punktis 40-12, on see laseri tööks tavaliselt tarvilik, kuid mitte piisav tingimus.

Kui üksik elektron liigub juhtivustsoonist valentstsooni, võib see vabastada oma energiat footoni kujul. See footon võib stimuleerida teist elektroni langema valentstsooni, mis omakorda annab stimuleeritud kiirgusena teise footoni. Sel moel, kui vool läbi siirde on küllalt suur, saab toimuda stimuleeritud kiirgusaktide ahelreaktsioon ning genereeritakse laserkiirgus. Viimase tekkeks on vaja, et $p n$ -siirde kristalli otspinnad oleksid tasased ja paralleelsed, nii et valgus saaks kristalli sees edasi-tagasi peegelduda. (Meenutame, et heelium-neoonlaseris (joonis 40-21) oli peeglite paar, mis täitis sama ülesannet.) Seega saab pn-siire funktsioneerida kui pooljuhtlaser, mille valgusväljund on väga koherentne ja palju kitsamas lainepikkuste vahemikus kui LEDi kiirgus.

Pooljuhtlaserid on kasutusel CD-mängijates, kus need registreerivad peegeldusi pöörlevalt CD-plaadilt ja on osa seadmest, mis tõlgib plaadi mikroskoopilised täkked kuuldavaks heliks. Samuti kasutatakse neid laialdaselt kiudoptikal põhinevates kommunikatsioonisüsteemides. Joonis 41-18 demonstreerib selliste laserite miniatuursust. Pooljuhtlasereid kavandatakse tavaliselt elektromagnetkiirguse spektri infrapunase osa jaoks, kuna valguskiududel on selles piirkonnas kaks „akent” ( $λ = 1, 31$ ja $1, 55 m m$ ), millede korral energia neeldumine fiibri ühikpikkuse kohta on minimaalne.

Valgusdiood on konstrueeritud pn-siirdest, mis põhineb

G a - A s - P

pooljuhtmaterjalil keelutsooni laiusega

1, 9 e V

. Milline on kiiratud valguse lainepikkus?

Lahendus

Arvutus: eeldame, et üleminekud leiavad aset juhtivustsooni põhjast kuni valentstsooni laeni; siis kehtib valem 41-11

λ = \frac{h f}{E_{g}} = \frac{(6, 63 \times 10^{- 34} J \cdot s) (3, 00 \times 10^{8} m / s)}{(1, 9 e V) (1, 60 \times 10^{- 19} J / e V)} = 6, 5 \times 10^{- 7} m = 650 n m - ------ - - ------ -

Sellise lainepikkusega valgus on punane.

Transistor

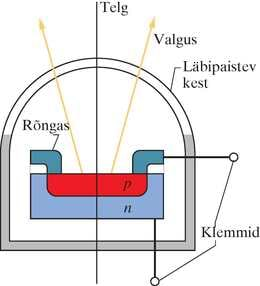
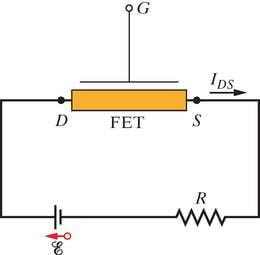
Transistor on kolme elektroodiga pooljuhtseadis, mida saab kasutada elektrisignaalide võimendamiseks. Joonis 41-19 näitab skemaatiliselt väljatransistorit (FET, ingl field-effect transistor); siin saab elektronide voogu otsast $S$ (läte) vasakule läbi värvitud piirkonna otsani $D$ (neel) juhtida elektriväljaga (seega väljaefekt), milleks rakendatakse vastav elektripotentsiaal paisuelektroodile $G$ (pais). Paljudest transistoritüüpidest käsitleme siin vaid üht konkreetset väljatransistorit, nimelt MOSFETi (ingl metal-oxide-semiconductor-field-effect transistor – metalloksiidpooljuht-väljatransistor) kui tänapäeva elektroonikatööstuse tõelist tööhobust.

Enamikus rakendustes opereerib MOSFET vaid kahes olekus: neelu-lätte vool $I_{N A}$ kas on olemas või puudub. Neist esimesele võib seada vastavusse arvu $1$ ja teisele arvu $0$ kahendsüsteemis. Kuna kahendsüsteem on digitaalse loogika alus, saab MOSFETe kasutada digitaalloogika vooluringides. Ümberlülitus sees-väljas seisundite vahel toimub peaaegu hetkeliselt, nii et kahendsüsteemi arve saab liigutada läbi MOSFETi vooluringi väga kiiresti. $500 n m$ (aastal 2009 juba $32 n m$ , toim.) kanalipikkusega MOSFETe – umbes sama lainepikkus on kollasel valgusel – toodetakse massiliselt kõikvõimalike elektroonikaseadmete jaoks.

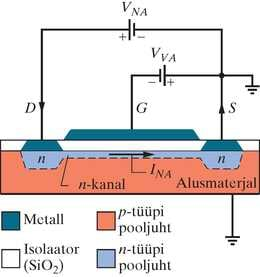
Joonisel 41-20 on toodud MOSFETi ehituse põhimõtteline skeem. Räni või mõne muu pooljuhi monokristalli dopeeritakse veidi, et saada $p$ -tüüpi materjal, mis oleks põhimikuks. Alusesse lükitakse sisse (tugevalt „üledopeerides” $n$ -tüüpi lisanditega) kaks $n$ -tüüpi materjali „saart”, moodustades nii neelu $D$ ja allika $S$ . Neel ja allikas on ühendatud kitsa kanaliga $n$ -tüüpi materjalist, seda nimetatakse $n$ -kanaliks. Ränidioksiidi kitsas isoleerkiht on paigutatud kristalli peale ja seda läbivad $D$ ja $S$ väljaviigud. Värav $G$ on $n$ -kanalile paigutatud kitsas metallkiht. Pange tähele, et väraval puudub otsene elektriline kontakt transistoriga kitsamas mõttes, see on isoleeriva oksiidkihiga eraldatud.

JOONIS 41-20 MOS-väljatransistor, nn MOSFET. Neelu-lätte-voolu $I_{N A}$ tugevust läbi $n$ -kanali tüüritakse pingega $V_{V A}$ , mis on rakendatud lätte $S$ ja neelu $D$ vahele. Tõkkekihti $n$ -tüüpi materjali ja $p$ -tüüpi alusmaterjali vahel ei ole näidatud.

Olgu algul allikas ja $p$ -tüüpi alusaine maandatud (nullpotentsiaal), nii et värav „hõljub“, s.t värav ei ole ühendatud välise elektromotoorjõu allikaga. Tekitame potentsiaali $V_{N A}$ neelu ja allika vahel, nii et neel on positiivne. Siis sööstavad elektronid läbi $n$ -kanali allikalt neelu suunas ning kokkuleppeline vool $I_{N A}$ , nagu näidatud joonisel 41-20, on neelult allikale.

Rakendame nüüd potentsiaali $V_{V A}$ väravale, tehes selle allika suhtes negatiivseks. Negatiivne värav tekitab seadmes elektrivälja (siit ka nimi – väljatransistor), mis püüab elektrone tõrjuda $n$ -kanalist alla alusainesse. Elektronide selline liikumine laiendab (iseeneslikult tekkivat) tõkkekihti $n$ -kanali ja aluse vahel ja seda $n$ -kanali arvel. Koos laengukandjate arvu vähenemisega kanalis suurendab $n$ -kanali kokkutõmbunud laius kanali takistust ning seega vähendab voolu $I_{N A}$ . Sobiva $V_{V A}$ väärtuse korral saab selle voolu täielikult ära lõigata; järelikult, kontrollides potentsiaali $V_{V A}$ , saab MOSFETis teha sees-väljas (ON-OFF) ümberlülitusi.

JOONIS 41-21 Sülearvutite protsessori Intel® Core™ 2 Duo integraallülitus. (Foto avaldatud Inteli loal)

Laengukandjad ei lenda läbi alusmaterjali, sest see (1) on nõrgalt dopeeritud, (2) ei ole hea juht ja (3) on eraldatud $n$ -kanalist ja kahest $n$ -tüüpi saarest isoleeriva tõkkekihiga, mida joonisel 41-20 eraldi näidatud pole. Selline tõkkekiht on $n$ -tüüpi ja $p$ -tüüpi materjalide piiril alati olemas, nagu näidatud joonisel 41-12b.

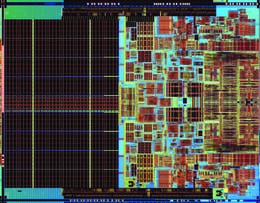
Arvutites ja teistes elektroonikaseadmetes on tuhandeid (kui mitte miljoneid) transistoreid ja teisi elektroonikakomponente, näiteks kondensaatoreid ja takisteid. Need ei ole seal eraldi detailidena, vaid ühendatud ühte pooljuhtkiipi, mis moodustab miljonitest transistoridest ja teistest komponentidest koosneva integraallülituse (joonis 41-21).

Rokikitarride võimendid

Mehaanilised võnked, mida mängija elektrikitarri keelel tekitab, muudetakse keele alla paigutatud poolis elektrilisteks võngeteks. Neid elektrivõnkeid tuleb võimendada ja kõlaritega kuuldavaks teha.
1960ndatel, mil elektrikitarr populaarseks muutus, kasutati lampvõimendeid, sest transistorvõimendid ei olnud veel töökindlad. Kui rokk liikus psühhodeelia ja hevi suunas, keerasid kitarristid oma võimendid põhja, et publikut raputada. Lampvõimendite selline põhjakeeramine kutsus esile heli märgatava moonutuse, mida aga varsti hakatigi pidama rokile omaseks tämbriks.

Transistorvõimendid ei anna põhja keerates sama tüüpi helimoonutust, vaid annavad „puhta” heli. Seepärast ei kasuta paljud kitarristid neid tänapäevalgi, sest nad ei anna seda „õiget” roki saundi. Jimi Hendrix, kes esimesena mõistis, et ühtse muusikainstrumendi moodustab elektrikitarr koos võimendiga, on ütelnud „Mulle tõesti meeldivad vanad Marshalli lampvõimendid, sest kui ... nende heli on põhja keeratud, siis pole midagi sellega võrreldavat....”

Kokkuvõte

Kristalliliste tahkiste liigitamisel on aluseks kolm elektrilist põhiomadust: eritakistus $ρ$ , eritakistuse temperatuuritegur $α$ ja laengukandjate arvtihedus $n$ . Laias laastus saab tahkiseid jagada kolme kategooriasse: isolaatorid (väga suur $ρ$ ), metallid (väike $ρ$ , positiivne ja väike $α$ , suur $n$ ) ning pooljuhid (suur $ρ$ , negatiivne ja suur $α$ , väike $n$ ).

Isoleeritud aatom saab olla ainult teatud kindlate energiatega seisundites. Kui aatomid koonduvad tahkiseks, liituvad üksikaatomite energianivood energiatsoonideks. Need lubatud energiatsoonid on eraldatud keelutsoonidega – energiavahemikega, kus elektronid ei saa asuda.

Iga energiatsoon koosneb hiigelarvust väga lähestikku asuvatest nivoodest. Pauli keeluprintsiibi järgi saab igal nivool olla vaid üks elektron.

Isolaatoris on elektrone sisaldav kõrgeim tsoon täielikult hõivatud ja vakantsest tsoonist nii laia keelutsooniga eraldatud, et elektronide soojusergastusest üksi ei piisa sellest ülehüppamiseks.

Metallis on elektrone sisaldav kõrgeim tsoon vaid osaliselt täidetud. Kõrgeima täidetud nivoo energiat temperatuuril $0 K$ nimetatakse metalli Fermi energiaks $E_{F}$ ; vase korral $E_{F} = 7, 0 eV$ .

Elektronid osaliselt täidetud tsoonis on juhtivuselektronid ja nende arv on

aatomite arv objektis = \frac{objekti mass M_{objekt}}{aatommass} = = \frac{objekti mass M_{objekt}}{(molaarmass M) N_{A}} = = \frac{(materjali tihedus)(objekti ruumala) V}{(molaarmass M) N_{A}}

Juhtivuselektronide tihedus on

n = \frac{juhtivuselektronide arv objektis}{objekti ruumala V}

$N (E)$ on võimalike energianivoode arv objekti ühikruumalas energia ühikintervallis ja see antakse valemiga

N (E) = \frac{8 \sqrt{2} π m^{3 / 2}}{h^{3}} E^{1 / 2}

kus $m (= 9, 109 \times 10^{- 31} kg)$ on elektroni mass, TeX parse error: '\cdot' is only supported in math mode Plancki konstant ning $E$ energia (džaulides), mille juures $N (E)$ arvutatakse. Kui teisendada võrrandit nii, et $E$ on elektronvoltides ja $N (E)$ ühikutes $m^{- 3} {eV}^{- 1}$ , tuleb paremat poolt korrutada konstandiga $e^{3 / 2}$ (kus $e = 1, 602 \times 10^{- 19} C$ ).

$P (E)$ on tõenäosus, et antud seisund on elektroni poolt hõivatud, ja see avaldub valemiga

P (E) = \frac{1}{e^{(E - E_{p}) / k T} + 1}

$N_{0} (E)$ on määratud kahe valemites 41-5 ja 41-6 esineva suuruse korrutisega:

N_{0} (E) = N (E) P (E)

Metalli Fermi energia leitakse integreerides $N_{0} (E) T = 0$ jaoks rajades $E = 0$ kuni $E = E_{F}$ . Vastuseks saame

E_{F} = (\frac{3}{16 \sqrt{2} π})^{2 / 3} \frac{h^{2}}{m} n^{2 / 3} = \frac{0, 121 h^{3}}{m} n^{2 / 3}

Pooljuhi tsoonistruktuur on sarnane isolaatori omaga, välja arvatud asjaolu, et keelutsooni laius $E_{g}$ on pooljuhis palju väiksem. Näiteks ränis tõstab soojusliikumine toatemperatuuril osa elektrone juhtivustsooni, jättes sama arvu auke valentstsooni. Nii elektronid kui ka augud toimivad laengukandjatena.

Elektronide arvu räni juhtivustsoonis saab oluliselt suurendada, kui tuua sisse (dopeerida) väike hulk fosforit ja sel viisil tekitada n-tüüpi materjal. Aukude arvu valentstsoonis saab märgatavalt suurendada alumiiniumi lisamisega, mis tekitab p-tüüpi materjali.

pn-siirdeks nimetatakse pooljuht-monokristalli, mille üks pool on dopeeritud p-tüüpi materjaliks ja teine n-tüüpi materjaliks; kaks poolt on ühendatud siirdepinnaga. Soojustasakaalu korral toimuvad siin järgmised protsessid:

Enamuslaengukandjad (elektronid n-poolel ja augud ppoolel) difundeeruvad läbi siirdepinna, tekitades difusioonvoolu $I_{dif}$ .

Vähemuslaengukandjad (augud n-poolel ja elektronid p-poolel) lükatakse läbi siirdepinna, tekitades triivvoolu Itriiv. Need kaks voolu on tugevuselt võrdsed ja suunalt vastupidised, nii et summaarne vool on null.

Tõkkekiht tekib siirdetasandi lähikonnas, see koosneb doonori ja aktseptori laetud ioonidest.

Kontaktpotentsiaalide vahe $V_{0}$ tekib läbi tõkkekihi.

Kui pn-siirdele rakendatakse pinge, juhib seade ühes suunas elektrit paremini kui vastassuunas. Nii võib pn-siire olla pooljuhtalaldiks.

Kui pn-siire on päripidi pingestatud, võib see kiirata valgust, töötades kui LED (ingl light-emitting diode). Kiiratud valguse lainepikkus $λ$

λ = \frac{c}{f} = \frac{h c}{E_{g}}

Tugevalt päripingestatud paralleelsete otspindadega pnsiire võib toimida pooljuhtlaserina, kiirates väga kitsas lainepikkuste vahemikus.

Küsimused

Hõive tõenäosus antud energia

E_{1}

juures metalli valentstsoonis temperatuuril

300 K

on

0, 6

. Kas

E_{1}

on ülal- või allpool Fermi energiat?

Joonisel 41-22 on kolm nummerdatud nivood tsoonis, kus asub ka aine Fermi nivoo. Temperatuur on

0 K

. Järjestage nivood vastavalt hõive tõenäosusele, suurim esimesena, kui temperatuur on (a)

0 K

ja (b)

1000 K

. (c) Viimase temperatuuri korral järjestage nivood vastavalt seisundite tihedusele

N (E)

, suurim esimesena.

Kui metallitüki temperatuuri tõsta, kas siis hõive tõenäosus

0, 1 eV

ülalpool Fermi nivood suureneb, väheneb või jääb samaks?

Joonisel 41-1a on kujutatud 14 aatomit, mis moodustavad vase ühikraku. Kuid kuna igaühte neist aatomeist jagatakse ühe või enama naaberrakuga, siis ainult murdosa igast aatomist kuulub näidatud ühikrakule. Milline on aatomite arv ühikraku kohta vases? (Vastuse saate kui loendate kokku aatomite need murdosad, mis kuuluvad üksikule ühikrakule.)

Joonisel 41-1b on näidatud 18 aatomit, mis moodustavad räni ühikraku. Neljateist neist jagatakse naaberühikrakkudega. Milline on aatomite arv räni ühikrakus? (Vt küsimus 4.)

Kust tuleb räni võre korral otsida (a) juhtivuselektroni, (b) valentselektroni ning (c) elektroni, mis on seotud isoleeritud räniaatomi

2 p

alamkihiga?

Kas juhtivuselektroni triivikiirus

v_{t}

vooluga vasktraadis on võrdne, palju suurem või palju väiksem kui Fermi kiirus

v_{F}

vase jaoks?

Isoleeritud germaaniumiaatomil on 32 elektroni, mis on alamkihtidesse korrastatud vastavalt skeemile

1 s^{2} 2 s^{2} 2 p^{6} 3 s^{2} 3 p^{6} 3 d^{10} 4 s^{2} 4 p^{2}

. Sel elemendil on sama kristallstruktuur nagu ränil ja see on samuti pooljuht. Millised neist elektronidest moodustavad kristallilise germaaniumi valentstsooni?

Millistest järgmistest asjaoludest sõltub naabernivoode energiate vahe metalli kõrgeimas energiatsoonis: (a) objekti materjalist, (b) objekti suurusest, (c) nivoo asukohast tsoonis, (d) objekti temperatuurist, (e) metalli Fermi energiast?

Pingestatud pn-siirete korral joonistel 41-15 mõjub elektriväli

\to E

mõlemale tõkkekihile tänu rakendatud potentsiaalide vahele. (a) Kas

\to E

on suunatud vasakult paremale või paremalt vasakule? (b) Kas selle suurus on suurem päri- või vastupinge korral?

Keelutsooni laius

E_{g}

pooljuhtide räni ja germaaniumi korral on vastavalt

1, 12

ja

0, 67 eV

. Millised järgmistest väidetest on tõesed? (a) Mõlemal ainel on sama laengukandjate tihedus toatemperatuuril. (b) Toatemperatuuril on germaaniumil suurem laengukandjate tihedus kui ränil. (c) Mõlemal ainel on juhtivuselektronide tihedus suurem aukude omast. (d) Mõlemal ainel on elektronide tihedus võrdne aukude omaga.

Ülesanded

Näidisülesanne 41-1

Näidisülesanne 41-2

KONTROLLKÜSIMUS 1

(a)

(b)

(a)

(b)

Näidisülesanne 41-5

Näidisülesanne 41-6

KONTROLLKÜSIMUS 2

Näidisülesanne 41-7

Metallid, pooljuhid ja isolaatorid

Energianivood ja keelutsoonid kristallides

Isolaatorid

Metallid

Seisundite tihedus

Seisundi hõive tõenäosus

Hõivatud seisundite tihedus

Pooljuhid

pn-siire

pn-siirde rakendusi