1. Vihmapiisk
Lahendus
Tähistused: , , , - vihmapiisa mass, ruumala, raadius ja tihedus; - vihmapiisa ristlõikepindala; - vaba langemise kiirendus; - vihmapiisa langemise kiirus; - konstant; - vihmapiisale mõjuv raskusjõud; - vihmapiisale mõjuv takistusjõud õhu poolt.
Teame, et
Vabal langemisel oleks tilgale mõjub jõud null. Järelikult õhutakistuse mõjudes võrdub takistav jõud tilgale mõjuva raskusjõuga:
Avaldades sellest valemist kiiruse saame:
3. Matk
Lahendus
Selle ülesande lahendust on mugav illustreerida tabelina, kuhu on kantud matka erinevate etappide kohta käivad andmed.
Matka etapidIIIIIIIV
KokkuKestus, t0,5 h4,5 h1 h5 h11 hLäbitud tee, s?18 km0 km??Kiirus, v40 km/h?0 km/h5 km/h?
Kiirused ja läbitud teepikkused leiame keskmise kiiruse valemi järgi: . Kogu läbitud tee arvutame valemist . Kaido
Matka etapidIIIIIIIVKokkuKestus, t0,5 h4,5 h1 h5 h11 hLäbitud tee, s20 km18 km0 km25 km63 kmKiirus, v40 km/h4 km/h0 km/h5 km/h5,7 km/h
Vastus: Kogu matka jooksul läbis turist , keskmise kiirusega .
4. Teekond
Lahendus
Teekonna esimese poole läbis auto aja , teise poole aja jooksul. Kuna , siis . Definitsiooni kohaselt on keskmise kiirus
ning järelikult .
5. Buss
Lahendus
Keskmine kiirus võrdub läbitud teepikkus jagatud läbimiseks kulutatud ajaga. Tähistame kogu tee pikkuse . Esimese poole teest läbis buss ajaga , teise poole aga ajaga . Kuna tee pooled on võrdsed, siis vastavalt ülesande tingimustele tuleneb ehk . Kogu tee läbimiseks kulus ning keskmine kiirus on , millist kiirus esimesel poolel teel ning kiirus teisel poolel teel
6. Paat
7. Vihm
Lahendus
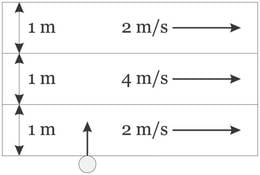
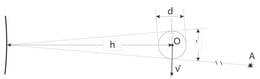
Paigalseisvale pallile langevad ajaühikus vihmapiisad silindrilisest õhu piirkonnast, mille ristlõikepindala on võrdne palli vertikaalse ristlõikepindalaga ning pikkus on arvuliselt võrdne vihmapiiskade langemise kiirusega .
Liikumise suhtelisuse pärast võib liikuvat palli pidada paigalseisvaks, millele vihm langeb nurga all kiirusega . Seetõttu langevad liikuvale pallile piisad silindrilisest õhu piirkonnast pikkusega .
Lugedes vihmapiiskade jaotust õhus ühtlaseks, saame, et paigalseisvale pallile langev piiskade arv on ning liikuvale pallile langev piiskade arv on , kus on palli ristlõikepindala resultantkiiruse suunas. Järelikult on piiskade arvu suhe
Kui pall on kerakujuline, siis on tema ristlõige kõikides suundades ühesugune, järelikult ning
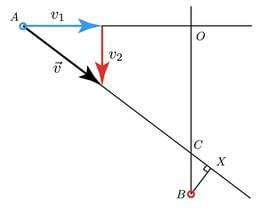
8. Jõgi
Lahendus
Selleks, et liikuda risti kaldaga, peab paadi kiiruse kaldasuunaline komponent olema võrdne jõevoolu kiirusega: . Paadi kiiruse kaldaga risti oleva komponendi leiame valemist . Pythagorase teoreemist leiame paadi kogu kiiruse, teades kiiruse vektori mõlemaid komponente:
9. Kärbes
Lahendus
Inimesed lähenevad üksteisele kiirusega . Vahemaa läbivad nad ajaga . Sama palju aega lendab ka kärbes inimeste vahel. Selle aja jooksul läbib kärbes vahemaa .
10. Bussid
Bussid sõidavad tänava ühest otsast teise ja tagasi. Tänav on pikk. Bussid väljuvad tänava kummastki otsast iga järel ja sõidavad keskmise kiirusega . Reisija läheb bussi peale tänava ühes otsas ja sõidab tänava teise otsa. Mitu bussi tuleb talle teel vastu?
Lahendus
Buss reisijaga sõidab keskmise kiirusega . Vastusõitvate busside vahelised kaugused on , järelikult sõidab tänaval ühes suunas bussi. Reisija kohtab oma teekonnal kõik need bussis ning lisaks veel bussid, mis väljuvad tänava teisest otsast reisija bussisõidu ajal. Kuna iga buss läbib tänavapikkuse aja jooksul, siis nende lisabusside arv on . Järelikult näeb reisija oma sõidu ajal busse. Asendades kõik suurused nende arvväärtustega, saame , mis tähendab, et reisija kohtas 7 bussi.
11. Rong
Rong läbis esimese poole teest korda suurema kiirusega kui teise poole teest. Keskmine kiirus teel oli . Millise kiirusega läbis rong kummagi poole teest?
Lahendus
Olgu rongi kiirus esimesel poolel teest ja selle kiirus teisel poolel teest. Kogu läbitud tee pikkus olgu . Selle tee läbimiseks kulub ajavahemik . Teiselt poolt, vastavalt keskmise kiiruse definitsioonile . Võttes arvesse, et , saame
taandub välja ja saame ning .
12. Film
Filmis näidatakse, kuidas poiss sõidab jalgrattaga. Kui poiss hakkab sõitma, veerevad rattad õiget pidi. Kiiruse kasvades paistavad rattad pöörlevat tagurpidi. Veel suurema kiiruse puhul näib, nagu ei pöörleks rattad üldse. Leidke kiirus , kui on teada, et ratta ümbermõõt on ning rattal on . Filmis vahetuvad kaadrid sagedusega (kaadrit sekundis).
Lahendus
Ratas näib seisvat, kui järgmise kaadri ajaks on järgmine kodar jõudnud sama koha peale, kus eelmise kaadri ajal oli eelmine kodar. Kahe kaadri vahelise ajavahemiku jooksul pöördub ratas ühe kodara võrra edasi ning korda pikema aja jooksul teeb ta täispöörde. Täispöördega liigub ratas edasi vahemaa , seega on ratta kiirus , numbriliselt . Pilt kordub kui jalgratta kiirus on , kus on täisarv.
13. Laevad
Kaks laeva liiguvad samas suunas. Esimese laeva kiirus on ja tagumisel . Laevade vaheline kaugus on . Esimeselt laevalt tõuseb õhku kajakas ja lendab tagumisele laevale. Kui kaua lind lendab, kui tema kiirus on ?
Lahendus
Tagumise laeva kiirus on . Kajakas ja tagumine laev lähenevad teineteisele kiirusega . Järelikult jõuab kajakas tagumise laevani aja jooksul.
14. Buss
Lahendus
Olgu teepikkus Tallinnast kohtumispaigani ja Tartust kohtumispaigani ning
Tartust väljunud bussi kiirus . Saame võrrandisüsteemi
Selle lahendamisel leiame kiiruse . Kogu sõiduks kulunud aeg on siis
15. Põhupallid
Punase ja sinise autoga veetakse põhupalle põllult lauta. Punane auto sõidab sinisest iga järel mööda (``teeb ringiga pähe'') ning iga järel sõidab sinine auto punasele vastu. Kui kaua kulub kummalgi autol ühe täisringi tegemiseks? Maha- ja pealelaadimise aeg lugeda tühiselt väikseks (autosse mahub ainult üks põhupall).
Lahendus
Olgu edasi-tagasi tee pikkus , punase auto kiirus ja sinise auto kiirus . Siis punane auto läheneb sinisele autole tagantpoolt kiirusega ning ``süüakse ära'' täisringine edumaa , st . Eestpoolt läheneb punane auto sinisele autole kiirusega , peale kohtumist hakkab sellise kiirusega kahanema täisring, mis tuleb punase auto ninast ühte teeotsa, sealt teise teeotsa ning lõpuks sinise auto ninani: , kus . Otsime suurusi ja . Paneme tähele, et eespooltoodud võrrandid võib ümber kirjutada kujul
Liites need võrrandid omavahel leiame
ja lahutades:
16. Liikuv rada
Kiirusega liikuva raja ühele otsale astuvad Henn ja Kalev. Henn jääb rajale seisma, Kalev aga liigub raja suhtes kiirusega . Samal hetkel hakkab liikuva raja teisest otsast lendama vastupidises suunas sääsk. Sääsk lendab Hennuni ja pöörab tagasi. Millise minimaalse kiirusega peab lendama sääsk, et jõuda Kalevini enne kui Kalev raja lõppu jõuab?
Lahendus
Olgu liikuva raja pikkus , selle kiirus , sääse kiirus ning Kalevi kiirus . Sääsk liigub Hennu suhtes kiirusega , seega jõuab sääsk Hennuni ajaga . Tagasi jõuab sääsk ajaga . Kalev jõuab liikuva raja lõppu ajaga . Et sääsk jõuaks Kalevini enne seda, peab kehtima . Piirjuhul saame võrrandi:
18. Eskalaator
Mikk ja Mann astuvad üheskoos eskalaatorile, mis sõidab ühes suunas kiirusega . Kui nad on jõudnud eskalaatori keskele, pöördub Mann ümber ja hakkab tagasi kõndima kiirusega . Mikk aga seisab eskalaatoril rahulikult lõpuni, pöördub siis ümber ja hakkab mööda eskalaatorit tagasi kõndima kiirusega . Kui Mann on kõndinud eskalaatori algusesse, pöördub ta ümber ja jääb eskalaatorile seisma. Kui kaugel eskalaatori algusest kohtuvad Mikk ja Mann, kui eskalaatori pikkus on ?
Lahendus
Tähistame Miku ja Manni kohtumispaiga kauguse eskalaatori algusest tähisega . Alates hetkest, mil Mann hakkab eskalaatori keskelt algusesse kõndima, läbib Mikk kohtumispaigani jõudmiseks teepikkuse
milleks kulub aeg
Mann läbib kohtumispaigani jõudmiseks teepikkuse , milleks kulub aeg
Kuna , siis saame:
millest . Järelikult kohtuvad Mikk ja Mann uuesti eskalaatori keskel ehk kaugusel eskalaatori algusest.
Alternatiivne lahendus:
Eskalaatori keskelt lõpuni kulub Mikul aeg
Mannil eskalaatori alguseni aga aeg
Lõpust keskele tagasi kulub Mikul aeg
ja Mannil aeg
Paneme tähele, et , seega kohtuvad nad uuesti eskalaatori keskel.
19. Laev
Lahendus
Kui traadijupid on laeva tekil, on traadijuppide poolt väljatõrjutud vee ruumala
aga kui traadijupid on kausi põhjas, siis nende poolt väljatõrjutud vee ruumala on
Võrdleme ruumalasid ja :
Sellest järeldub, et veetase kausis langeb.
20. Laev kanalis
Laev, mille kiirus seisva vee suhtes läbib pikkuse kanali pärivoolu. Kanali alguses on vee voolamise kiirus . Kanali teine pool on esimesest kaks korda kitsam. Vee sügavus kanalis on kõikjal ühesugune. Kui palju aega kulub laeval kanali läbimiseks?
Lahendus
Oluline on aru saada, et kanali teises pooles on vee voolamise kiirus kaks korda suurem (vooluhulga jäävusest), seega
Asendades suurused võrrandisse saame, et laeval kulub kanali läbimiseks .
21. Buss
Lahendus
Olgu aeg (minutites), mis kulub bussil poole vahemaa läbimiseks peatuste vahel. Peale Jukust möödasõitmist pidi buss läbima poole teed lõpp-peatuseni (selleks kulus minutit aega), seisma ühe minuti lõpp-peatuses ja veel läbima terve vahemaa kahe peatuse vahel (selleks kulus aeg ). Selle ajaga (kokku minutit) jõudis Juku joosta poole teekonnast peatuste vahel. Et esimese poole tuli ta kaks korda väiksema kiirusega, siis selleks kulus tal aega minutit ning kogu teekonna läbimine võttis tal seega minuitit aega. Järgmine buss alustas lõpp-peatusest sõitu peale eelmise bussi lahkumist, lisaks oli ta teel järgmisesse peatusesse minutit. Et Juku ja buss jõudsid peatusesse üheaegselt, siis saame , kust . Seega esimese poole läbimiseks kulus Jukul aega , tema kiirus oli . Selle ajaga kõndis ta , seega kogu teepikkus oli .
22. Ringrada
Lahendus
Olgu ringraja pikkus . Esikohal oleval autol kulub ringi läbimiseks aega ja viimasel autol - . Jõudku esimene auto
viimasele järgi siis, kui esimene on sõitnud ringi. Viimane auto on siis sõitnud ringi. Mõlemad autod on sõitnud ühekaua.
Esikohal olev auto peab sõitma ringi, et viimasele autole järele jõuda.
23. Sprinter
Lahendus
Kogu distantsi läbis jooksja ajaga , kus on kiirenduseks kulunud aeg ja on püsiva kiirusega jooksmiseks kulunud aeg.
Distantsi pikkus , kus on kiirendades joostud distantsi osa ja - püsiva kiirusega joostud distantsi osa. Leiame keskmise kiiruse, millega jooksja läbis esimese osa distantsist: . Teades, et kiirendamine toimus ühtlaselt, võime kirjutada
Kiirendades joostud distantsiosa pikkus
ja ühtlaselt joostud distantsi osa pikkus
mille läbimise aeg on
Sprinteri saja meetri aeg on
24. Rongid
Lahendus
Seome taustsüsteemi ühe rongiga ehk loeme ühe rongidest paigalseisvaks. Teineteisest möödumisel on rongide pikkus kokku
Liikuva rongi kiirus uues taustsüsteemis on seega
Teineteisest möödasõiduks kulub seega
25. Autod
Auto väljus linnast linna suunas kell , sõites keskmise kiirusega . Linnast väljus 10 minutit hiljem auto linna suunas, mis sõitis keskmise kiirusega . Autod kohtusid kell . Kell väljus linnast auto, mis sõitis terve tee keskmise kiirusega . Kui kaugel linnast jõuab kolmas auto esimesele autole järele?
Lahendus
Määrame autode kohtumise järgi linnadevahelise kauguse, .
Linnas väljunud auto oli teel , linnast väljunud auto , seega
Teine auto, mis alustab sõitu hiljem, jõuab esimesele järele siis, kui on täidetud tingimus , kust . Kohtumine toimub 2 tundi pärast esimese auto väljasõitu. Kohtumiskoht on seega kaugusel linnast . Linnast on kohtumiskoht . Tehes arvutused saame, et ja kaugus linnast on .
26. Autod
Kaks autot, mis lähenevad täisnurksele teeristile mööda erinevaid teid, asuvad alghetkel teeristist kaugustel ja . Autod liiguvad jäävate kiirustega ja . Leida autodevaheline minimaalne kaugus.
Lahendus
Seome paigalseisva taustsüsteemi autoga , siis auto kiirus auto suhtes on . Minimaalne kaugus autode vahel avaldub järgmiselt:
27. Rattasõit
Miku sõitis jalgrattaga. Maksimaalse kiiruse saavutas ta paigalseisust ühtlaselt kiirendades jooksul. Edasi sõitis Miku teatud aja muutumatu kiirusega. Ühtlaseks pidurdamiseks täieliku seismajäämiseni kulus tal . Kui pika tee läbis Miku, kui ta keskmine kiirus sõidu ajal oli ?
Lahendus
Miku sõit jaguneb kolmeks etapiks: esimene - ühtlane kiirenemine, teine - liikumine muutumatu kiirusega ja kolmas - ühtlane pidurdamine. Tähistame nende kohta käivaid suurusi vastavalt indeksitega 1, 2 ja 3. Ühtlase kiirenemise ja ühtlase pidurdamise puhul kehtib valem keskmise kiiruse leidmiseks:
Esimese ja kolmanda etapi keskmised kiirused olid võrdsed:
Veel teame me suurusi: ja . Kogu teekonna pikkus oli:
Siit leiame teise etapi kestuse:
Järelikult: .
28. Buss ja jalakäija
Rohelise tule süttides alustas ristmikult kõndimist inimene ja sõitmist liinibuss. Inimese keskmine kiirus oli . Järgmise ristmiku juurde jõudsid buss ja inimene korraga, kuid buss oli vahepeal teinud peatuse. Bussi keskmine kiirus väljaspool peatust oli . Kui kaua buss peatus, kui ristmike vahemaa oli ?
Lahendus
Kuna inimene ja buss alustasid ja lõpetasid liikumise koos, siis kulub neil sama maa läbimiseks võrdne aeg. Kestku bussi peatus ajavahemiku . Inimesel kulus teise ristmikuni jõudmiseks .
Buss läbis sama vahemaa ajaga .
Võrdsustame omavahel ja : . Avaldame võrrandist aja :
29. Putukad
Lahendus
Kuna sipelgas on kergem kui lepatriinu, aga nad asuvad varda keskpunkist sama kaugel, peab põrnikas tasakaalu saavutamiseks paiknema sipelgale lähemal.
Olgu põrnika kaugus varda keskpunktist. Kirjutame välja putukate jõumomendid varda keskpunkti suhtes:
Lepatriinu jõumoment on võetud miinusmärgiga, kuna tema asub tasakaalu keskpunktist teisel pool. Tasakaalu korral on jõumomentide summa . Seda võrdust kasutades leiame, et . Seega lepatriinu asub kaugusel sipelgast.
Paneme tähele, et roomamise käigus sipelga ja lepatriinu summaarne jõumoment keskpunkti suhtes jääb samaks: aja jooksul muutub siplega jõumoment võrra, lepatriinu jõumoment aga võrra. Kuna aga , siis saamegi, et nende summaarne jõumoment ei muutu.Järelikult tasakaalu hoidmiseks ei pea põrnikas midagi ette võtma. Kuna sipelgas asub algselt põrnikale lähemal ja ta liigub lepatriinust kiiremini, saab sipelgas esimesena põrnikaga kokku. See juhtub pärast roomamise algust.
30. Laserpointer
Vaatleme hüpoteetilist olukorda, kus valguse kiirus on väike, . Juku asetseb raadiusega silindrilise ekraani teljel. Tal on käes lasepointer, mida ta keerutab ümber silindri telje (pointeri telg on risti silindri teljega). Millise vähima sagedusega peaks Juku keerutama laserpointerit, et täpp ekraanil paistaks talle asuvat täpselt pointeri sihil?
Lahendus
Sagedus on vähim siis, kui valguse leviaaeg edasi-tagasi võrdub ühe täispööre ajaga. Seega
31. Parvetaja
Aurik läbib linnade vahelise veetee mööda jõge pärivoolu 3 tunniga ja vastuvoolu 5 tunniga. Mitme tunniga jõuaks parvega allavoolu kulgedes ühest linnast teise?
Lahendus
Olgu teepikkus , jõevoolu kiirus ja auriku enda kiirus . Saame, et
Teisendades, saame
Lahutades esimesest võrrandist teise, leiame et . Aeg, mis kulub parvega allavoolu liikumiseks on seega
32. Ralli
Le Mans'i 24 tunni rallit sõidetakse ringrajal. Sõit kestab ühe ööpäeva ja ralli võidab enim ringe läbinud osaleja. Ühe ringi pikkus on . Kui palju erinesid esimese ja teise koha saanute keskmised kiirused, kui teise koha omanik sõitis võitjast kümme ringi vähem?
Lahendus
Läbigu võitja ringi. Siis sõidab teise koha omanik ringi. Võitja keskmine kiirus on , kus . Teise koha saanu keskmine kiirus on: . Keskmiste kiiruste vahe on:
Teadmiseks: 2007. aastal läbis Le Mans’i ralli võitja 369 ringi, teise koha omanik kümme ringi vähem ja kolmanda koha saaja teiseks tulnust ühe ringi vähem. Võitja läbis ja tema keskmine kiirus oli .
33. Pagas
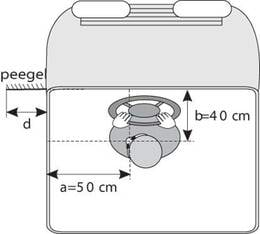
Lennujaama ruudukujulise pagasilindi ühe nurga juures seisab Janno. Ühel hetkel märkab ta lindi naabernurgas oma eemalduvat kohvrit. Kuidas jõuaks Janno oma kohvrini kiiremini: kas minnes talle järele või vastu? Pagasilindi kiirus , Janno liikumise kiirus .
Lahendus
Kilomeetrites tunnis on pagasilindi kiirus . Olgu ruudu küljepikkus. Minnes kohvrile järele on Janno ja kohvri esialgne vahekaugus ja lähenemise kiirus . Minnes kohvrile vastu on Janno ja kohvri esialgne vahekaugus ja lähenemise kiirus . Teisel juhul on lähenemise kiirus korda suurem kui esimesel juhul, samas vahemaa on suurem ainult 3 korda. Järelikult minnes kohvrile vastu saab Janno ta varem kätte.
34. Möödasõit
Mööda teed sõidavad teineteisele vastu veoauto ja buss. Veoauto kiirus on , bussi kiirus . Veoauto taga sõidab sõiduauto. Kui suure minimaalse keskmise kiirusega peab sõitma sõiduauto, et mööduda ohutult veoautost, kui möödasõidu algul on veoauto ja bussi kaugus ninast ninani , sõiduauto on veoautost kaugusel ja veoauto pikkus on ? Ohutu on möödasõit, mille sõiduauto lõpetab kaugusel veoautost ja kaugusel vastutulevast bussist.
Lahendus
Möödasõidu lõpul on veoauto ja bussi vaheline kaugus . Möödasõit kestab seega
Möödasõidul sõidab sõiduauto rohkem kui veoauto. Sõiduauto kiirus peab veoauto suhtes olema .
Sõiduauto minimaalne kiirus maantee suhtes on seega .
35. Sillad
Mööda teed sõidavad vastassuundades ühtlase kiirusega auto ja jalgrattur. Auto liigub kiirusega , jalgrattur kiirusega . Mingil hetkel sõidab auto üle silla, üks minut hiljem sõidab üle teise silla jalgrattur. Auto kohtub jalgratturiga kaugusel jalgratturi poolt ületatud sillast. Kui kaugel asuvad teineteisest sillad?
Lahendus
Pärast oma silla ületamist sõidab jalgrattur kohtumispaika
Auto sõidab kohtumispaika
kus . Sildade vaheline kaugus on seega
Saame sildade vaheliseks kauguseks .
37. Jalgratturid
Lahendus
Arvutame kummagi jalgratta ülekandearvu:
Jalgratturid teevad distantsi läbimiseks pedaalipöördeid vastavalt
kus tähistab tagumise ratta ümbermõõtu.
Kuivõrd mõlemad jalgratturid väntavad sama sagedusega, siis jõuab enne kohale see, kes teeb vähem vändapöördeid, seega teine jalgrattur. Esimene rattur teeb
korda rohkem pöördeid, järelikult kulutab ta ka aega korda rohkem.
Teisel ratturil kulub distantsi läbimiseks . Esimesel kulub distantsi läbimiseks , seega sekundit rohkem kui teisel ratturil.
38. Lennukid
Kaks hävituslennukit, lennates samal kõrgusel vastas- suundades, mööduvad teineteisest, lennates kiirustega vastavalt ja . Esimesest lennukist tulistatakse teist risti liikumissuunaga. Kui pika vahemaa tagant tekivad teise lennuki keresse kuuliaugud, kui kuulipilduja tulistab minutis? Kas ja kuidas sõltub kuuliaukude vaheline kaugus lennukite kaugusest teineteisest?
Lahendus
Teisendame kiirused: ja .
Lennukite kiirus teineteise suhtes on .
Kuulipilduja teeb sekundis 70 lasku ja kahe lasu vaheline aeg on .
Teine lennuk liigub esimese lennuki suhtes kahe kuuli vahelisel ajal .
Kuuliaukude vahe lennuki keres on seega .
Vastus ei sõltu lennukite kaugusest teineteisest.
39. Koer
Tarmo ja Taivo sõitsid jalgratastega kodust poodi (). Nad alustasid kodust samal ajal, kusjuures Tarmo sõitis ühtlase kiirusega ja Taivo kiirusega . Poe juures jäi Taivo Tarmot järgi ootama. Nende koer jooksis algusest peale nende vahel kiirusega , kuni mõlemad olid kohale jõudnud. Koer jooksis muudkui otse ühe juurest teiseni ja tagasi esimese juurde, ja nii kogu aeg. Mis oli koera poolt läbitud teepikkus ? Võib eeldada, et koeral kulus ümberpööramiseks väga vähe aega.
Lahendus
Paneme tähele, et koer jookseb kiirusega täpselt nii kaua kui Tarmol kulub kohale jõudmiseks aega. Tarmol kulub aega . Seega .
40. Auto
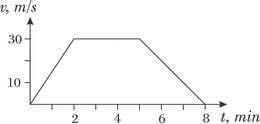
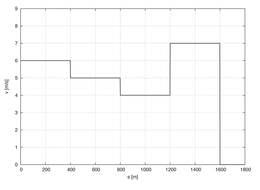
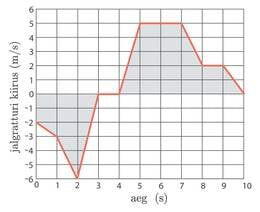
On antud auto kiiruse graafik (vt. joonis). Leida läbitud tee pikkus.
Lahendus
Teepikkus on leitav valemist , kuna graafik on antud teljestikus ja , siis otsitav teepikkus on graafiku joonealune pindala. Seetõttu on hea jagada läbitud teepikkus kolmeks osaks: , kus on kiireneva liikumise käigus läbitud tee, ühtlase kiirusega läbitud tee ja aeglustuva liikumise käigus läbitud tee.
41. Kauboid
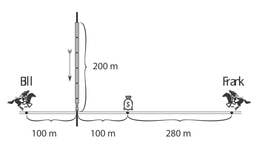
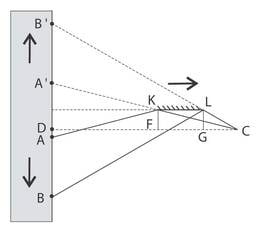
Kauboid Bill ja Frank ratsutasid mööda teed teineteisele vastu, kui märkasid ühtäkki postitõllalt mahakukkunud kullakotti ning hakkasid selle poole kappama. Kullani jõudmiseks peab Bill ületama teega ristuva raudtee, mida mööda sõitev rong on joonisel kujutatud hetkel jõudnud ristteeni. Rongi kiirus on . Täpselt sama kiiresti suudavad liikuda ka mõlema kauboi hobused. Billil on kaks võimalust: 1) jääda teele ja oodata rongi möödumist, 2) üritada rongist ringiga mööda ratsutada. Vaadelge mõlemat juhtu ja leidke nii Billil kui Frankil kullani jõudmiseni kulunud aeg, alates joonisel kujutatud hetkest. Kumb kauboi saab kulla endale? Kiirendamise ja pidurdamisega arvestama ei pea, ehk võib eeldada, et hobune hakkab kohe liikuma tippkiirusega.
Lahendus
Rongi ja kauboide kiirus on . Frankil kullani
jõudmiseks kulunud aeg on leitav valemi järgi:
Esimesel juhul peab Bill ootama kuni rong läbib oma pikkuse jagu maad ning seejärel ratsutama ristteest kullani. Kokku kulub seega
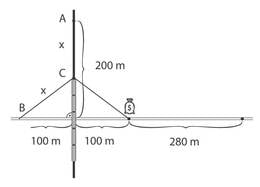
Aega, mis kulub Billil raudteeni jõudmiseks siin eraldi arvestama ei pea, sest see on ilmselgelt väiksem alghetkest rongi möödumiseni kuluvast ajast. Teisel juhul ei saa Bill rongi eest mööda ratsutada, sest võrdsete kiiruste tõttu ei jõuaks ta kunagi rongist ette. Jääb üle rongist tagantpoolt mööda sõita. Vähim aeg kulub juhul, kui tühjal maal liikuda sirgjooneliselt ja tagumisest vagunist mööduda võimalikult lähedalt ehk Bill ja rongi tagumine ots jõuavad punkti täpselt samal ajal (vaata joonist). Võrdsete kiiruste tõttu on võrdsed ka lõigud ja , mille pikkust tähistame -ga. Tekib täisnurkne kolmnurk, mille külgede pikkused meetrites on: hüpotenuus , üks kaatet ja teine kaatet . Täisnurkses kolmnurgas kehtib Pythagorase teoreem: , kus ja on kaatetite ning hüpotenuusi pikkus. Seega saame kirjutada võrrandi Pärast sulgude avamist koonduvad -i ruutliikmed välja ja saame lihtsa lineaarvõrrandi, mille lahendiks on . Kullani jõudmiseks peab Bill läbima vahemaa ja selleks kulub
Eraldi võib vaadelda vahepealset juhtu, kus Bill jõuab raudteeni punktis , mis jääb punkti ja risttee vahele. Seal ootab ta rongi möödumist ja kappab siis otsejoones kullani. Ajaliselt on see võrdväärne juhuga, kus Bill punktis ootamise asemel ratsutaks raudteega paralleelselt rongi otsale vastu ja selleni jõudes koos rongiga tagasi punkti , pärast mida ta eemalduks raudteest ja sööstaks otse kulla poole. See võtaks aga kauem aega, kui pärast rongi lõpuni jõudmist kohe kulla poole liikumisel, mis tähendab, et igasugune ootamine ei ole mõistlik ja on vähim võimalikest.
42. Keskmine kiirus
Graafikul on kujutatud auto kiiruse sõltuvus ajast. Arvutage auto keskmine kiirus.
Lahendus
Keskmine kiirus on läbitud vahemaa ja selle läbimiseks kulunud aja suhe. Leiame jooniselt, kui suure vahemaa läbis auto 20s jooksul läbitud. Selleks tuleb leida graafikualune pindala. Jaotame graafiku kolmnurkadeks ja trapetsiteks. Leiame üksikute kujundite pindalad ja liidame kokku. Kolmnurga ja trapetsi pindala saame leida valemitest
ja
| Ajavahemik | Kiiruse vahemik | Kujund | Pindala |
| 0s-2s | 0m/s-10m/s | Kolmnurk | (10m/s⋅2s)/2=10m |
| 2s-8s | 10m/s-25m/s | Trapets | (10m/s+25m/s)/2⋅6s=10m |
| 8s-10s | 25m/s-0m/s | Kolmnurk | (25m/s⋅2s)/2=25m |
| 10s-12s | 0m/s | Kolmnurk | 0m |
| 12s-17s | 0m/s-15m/s | Kolmnurk | (15m/s⋅5s)/2=37,5m |
| 17s-20s | 25m/s-0m/s | Kolmnurk | (15m/s⋅3s)/2=22,5m |
Kokku läbis auto teepikkuse s=200m. Selleks kulus autol t=20s. Auto keskmine kiirus on v=st=10m/s
43. Koer
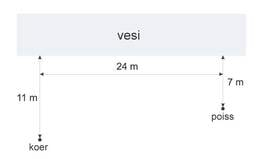
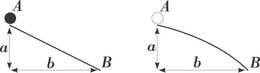
Poiss on koos oma koeraga rannas. Joonisel kujutatud hetkel kutsub ta koera enda juurde, kuid koer soovib teel poisi juurde korraks ka veest läbi hüpata. Millise minimaalse ajaga jõuab ta sel juhul poisini? Koer jookseb kiirusega .
Lahendus
Oletame, et koer hüppab veest läbi punktis (vt joonis). Peegeldame poisi veepiiri suhtes, saame punkti . Paneme tähele, et , seega on teekond koera juurest punkti läbi punkti sama pikk, kui teekond punkti läbi punkti . Lühim on see teekond juhul, kui tegemist on sirgega, mille korral koer hüppab veest läbi punktis . Täisnurkses kolmnurgas on ning . Niisiis . Selle teekonna läbimiseks kulub aeg . Märkus: Sama tulemuseni oleksime jõudnud siis, kui kasutaksime Fermat’ printsiipi, mille kohaselt valguskiir ühest punktist teise läbib mööda teed, mille läbimiseks kulunud aeg on minimaalne, ja peegeldumisseadust, mille kohaselt langemis-ja peegeldumisnurgad on võrdsed.
44. Konn
Kolm paralleelset linttransportööri laiusega liiguvad kiirustega nagu kujutatud joonisel. Risti üle nende hüppab konn. Konna hüppe pikkus (lähtepunkti suhtes) on ja hüppeks kuluv aeg . Millise vahemaa võrra lintide liikumise sihis on konn edasi liikunud maandumisel maapinnale pärast lintide ületamist? Eeldage, et konn alustab hüppamist vahetult esimese transportöörilindi servast, hüpete vahel aega ei kuluta ja maandumisel lindile ei libise.
Lahendus
Teades hüppe pikkust ja lintide laiusi, näeme, et konn ületab lindid hüppega. Neist esimesel stardib ta maapinnalt (lindisuunaline kiiruse komponent ), teisel - esimeselt lindilt (lindisuunaline kiiruse komponent ), kahel järgmisel - keskmiselt lindilt (lindisuunaline kiiruse komponent ) ja viimasel hüppel - viimaselt lindilt (lindisuunaline kiiruse komponent ). Tähistades hüppe kestvust , saame kõrvalekaldeks
45. Kuulid
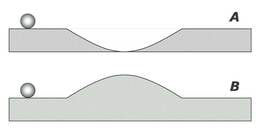
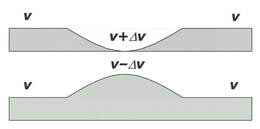
Horisontaalses lauas on lohk ja samasuguse suurusega ning kujuga muhk. Üle laua veerevad kuulid. Kuul läheb läbi lohust, kuul läheb üle muhu. Kuulid on vaatluse alghetkel laua vasakpoolsest servast ühekaugusel (vt. joonis) ja liiguvad ühesuguse kiirusega. Kumb kuulidest jõuab laua teise ääreni kiiremini? Põhjendage vastust. Hõõrdumist ei arvestata.
Lahendus
Kuul jõuab laua teise servani väiksema ajaga kui kuul . Kuna kuulide kiirus on ühesugune, siis need jõuavad samaaegselt laua ebatasasuseni. Kuul laskub lohku ja kiirus suureneb võrra. Kuul tõuseb muhule ja kiirus väheneb võrra. Kuuli kiirus lohu põhjas on .
Kuuli kiirus muhu harjal on . Kuul jõuab lohu põhja väiksema ajaga kui kuul muhu harjale. Et kuul läbis sama teepikkuse väiksema ajaga kui kuul , siis on kuuli keskmine kiirus lohku laskumisel suurem kuuli keskmisest kiirusest muhu harjale tõusmisel.
Ka tõusmisel lohu põhjast laua horisontaalsele osale on kuuli keskmine kiirus suurem muhu harjalt laskuva kuuli keskmisest iirusest. Seega, kuul läbib lohu väiksema ajaga kui kuul muhu.
Ülejäänud tee liiguvad kuulid jälle võrdse kiirusega. Kuul jõuab laua servani lühema ajaga kui kuul . Öeldud on hea llustreerida joonisega, kuhu on kantud kuulide kiirused kolmes erinevas punktis. Alguses ja lõpus on kuulide kiirused võrdsed, lohu läbimisel aga kuuli kiirus on kogu aeg suurem, kui , muhu läbimisel kuuli kiirus on kogu aeg väiksem, kui .
Järelikult kuuli keskmine kiirus kogu tee jooksul on väiksem, kui kuulil .
46. Lennukid
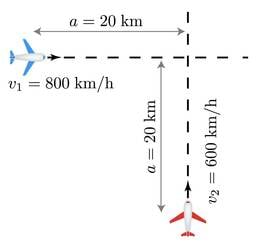
Kaks lennukit lendavad samal kõrgusel kiirustega ja . Vaadeldaval hetkel on lennukite liikumise sihid omavahel risti ning kumbki lennuk paikeb sihtide ristumispunktist kaugusel . Leidke, milline on lennukite vähim vahekaugus järgneva liikumise jooksul, kui eeldada, et kumbki lennuk kurssi ei muuda.
Lahendus
Lahendus muutub lihtsaks, kui vaatleme ühe lennuki
suhtelist liikumist teise suhtes.
Nimelt, lähme mõtteliselt punase lennukiga kaasaliikuvasse taustsüsteemi. Sel juhul paistab lennuk paigal püsivat, kuid lennuk näib liikuvat kiirusega , mille komponendid on joonisel välja toodud. Kiiruse mooduli leiame Pythagorase teoreemist
. Vähim kaugus kahe lennuki vahel kogu liikumise jooksul on mõistagi trajektoorini tõmmatud ristlõik , mille pikkuse järgnevalt leiamegi. Punkti jõudes oli lennuk ida-lääne sihis liikunud vahemaa ning põhja-lõuna sihis järelikult . Järelikult .Kolmnurga ning
kiirusvektorite kolmikust moodustatud kolmnurga küljepikkuste võrdelisusest leiame meid huvitava pikkuse
47. Liikumine
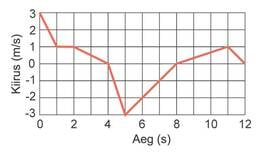
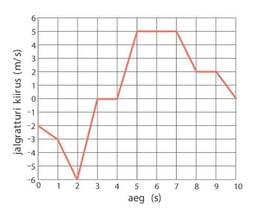
Graafikul on kujutatud liikuva keha kiiruse sõltuvust ajast. Kui suur oli vaadeldava aja jooksul keha suurim kaugus algasendist? Kui kaugel oli keha algasendist vaadeldava ajavahemiku lõpus?
Lahendus
Ülevalpool ajatelge olev graafiku joon kirjeldab liikumist positiivses suunas, allpool ajatelge olev joon negatiivses suunas. Kuna liikumise iseloom igal etapil on erinev, tuleb arvutada iga etapi jooksul läbitud teepikkus arvestades ka liikumise suunda. Teepikkust võib arvutada graafiku joone ja ajatelje vahelise pindala kaudu. Kuna enamjaolt on tegemist ühtlaselt muutuva liikumisega, võib teepikkuse leida ka seosest
Keha on algpunktist kõige kaugemal neljanda sekundi lõpus, s.o. kaugusel. Keha lõpetab liikumise samas punktis, kus alustas.48. Liikuv latt
Miku konstrueeris seadme, mis koosneb kahest teineteise suhtes liikuvast latist. Alumises latis on iga tagant avaused, ülemise lati küljes ripuvad ühtlase vahemaa tagant elektromagnetite pooluste küljes raudkuulikesed, mille läbimõõt on veidi väiksem avause läbimõõdust. Latid asuvad vertikaalsuunas teineteisest kaugusel (vt. joonis). Miku pani latid samas suunas liikuma ja vabastas kuulid järgemööda sobivatel hetkel, et need kukuksid läbi avauste alumise lati all olevasse kaussi. On teada, et alumine latt liigub ühtlaselt kiirusega ja ülemine latt ühtlaselt kiirusega . Kukkumisel on kuulikese keskmine kiirus vertikaalsuunas . Kui kaugel horisontaalsuunas peaks asuma kuulikese keskpunkt avause keskpunktist hetkel, kui kuulike vabastatakse elektromagneti küljest? Millise ajavahemiku tagant tuleks vabastada kuulikesed ja kui kaugel üksteisest peaksid ülemise lati küljes asuma kuulikesed, et seade töötaks?
Lahendus
Kuulikese kukkumise aeg
Alumine latt liigub kiiremini kui ülemine latt. Kujutades ülemist latti seisvana, saame kauguse, mille ulatuses peab kuul kukkumise hetkel eespool avaust olema Kuulikeste vabastamine sõltub sellest, millal alumise lati auk jõuab kausi kohale. Kuna alumise lati kiirus on ja avauste vahemik latis on , siis tuleb kuulikesi vabastada iga möödudes. Ülemine latt liigub jooksul . Järelikult, kuulikesed peavad ülemisele latile olema kinnitatud kaugusele.49. Litter
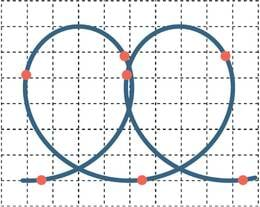
Joonisel on kujutis, mille jättis pealtvaates pika säriajaga tehtud fotole lambike, mis oli kinnitatud jääl hõõrdevabalt libisevale ja pöörlevale kettakujulisele litrile. Lambi kinnituskoht asub kaugusel litri püstteljest. Lamp põleb tuhmilt siniselt, kuid vilgatab iga järel heledamalt punaselt. Fotole on lisatud tundmatu sammuvahega ruudustik. Leidke litri edasiliikumiskiirus.
Lahendus
Esmalt paneme tähele, et trajektoori madalaima ja kõrgeima punkti vahe vertikaalsuunas peab olema , joonisel loeme selleks kuus ruutu, seega on ruudustiku sammuvahe .
Teiseks paneme tähele, et iga pöörlemisperioodi järel kordub küll trajektoori kuju, kuid see nihkub horisontaalsuunas nelja ruudu võrra. Seega läbib litter pöörlemisperioodi jooksul vahemaa .
Kolmandaks märkame, et pöörlemisperioodi sisse mahub täpselt kolm punaste vilgatuste vahelist intervalli, seega on pöörlemisperioodi kestus .
50. Paadid
Laial jõel sõidavad kaks paati, mõlema kiirused ja kiiruste suunad on konstantsed. Veevoolu kiirus on jões samuti kõikjal üks ja sama ning paralleelne kallastega. Juuresolev foto on tehtud õhust, otse ülevalt alla; paatide asukohad on tähistatud ruudu ja kolmnurgaga, paatidelt vette kukkunud praht aga tähekestega. üks paat alustas teekonda punktist ; on teada, et paadid kohtusid. Milisest jõekalda punktist alustas teekonda teine paat? Lahendus leidke geomeetrilise konstrueerimise teel.
Lahendus
Leiame paatide trajektoorid veega seotud taustsüsteemis - need on sinised jooned joonisel (kolmnurkne paat on kahe prügiga ühel joonel, seetõttu pidid need sellest paadist olema kukkunud).
Paadid kohtusid siniste joonte lõikepunktis. Kolmnurkse paadi trajektoor maaga seotud taustsüsteemis läheb läbi punkti (punane joon). Paatide kohtumispunkt maaga seotud taustsüsteemis peab olema samuti punasel joonel ning siniste joonte lõikepunktiga samal kõrgusel (lillal joonel).
Ühendades lilla ja punase joone lõikepunkti teise paadi asukohaga, leiame teise paadi trajektoori maaga seotud taustsüsteemis ning selle lähtepunkti .
51. Auto ja jalgrattur
Mööda teed sõidavad samas suunas jääva kiirusega auto ja jalgrattur. Auto liigub kiirusega , jalgrattur kiirusega . Mingil hetkel ületab auto esimese ristmiku, hiljem ületab jalgrattur teise ristmiku. Auto möödub jalgratturist kaugusel teisest ristmikust. Kui suur on ristmike vaheline kaugus?
Lahendus
Auto ja jalgratta kiirused on vastavalt ja . Ajahetkel ületab auto esimese ristmiku. Ajahetkel ületab jalgratas teise ristmiku. Auto on ajahetkeks läbinud vahemaa
. Ajahetkel on nii auto kui ka jalgratas kaugusel teisest ristmikust. Jalgratas läbis vahemaa ajavahemiku jooksul. Auto oli sama ajavahemiku jooksul läbinud vahemaa .Ristmike vahelise kauguse saab leida nii: kõigepealt leida vahemaa , mille auto läbis ajavahemiku jooksul, ja siis lahutada sellest vahemaa , mille jalgratas läbis ajavahemiku jooksul:
52. Pall
Avatud akna kaudu lendas tuppa väike pall. Palli ja lae vaheline kaugus vähenes kiirusega , palli ja vastasseina vaheline kaugus - kiirusega , palli ja kõrvalseina vaheline kaugus - kiirusega . Pärast lendu sattus pall lae ja kõrvalseina vahelisse nurka. Toa kõrgus on , laius ja pikkus . Aken on mõõtmetega ruut, mis asub seina keskel. Põrkumine toimub peegeldumisseaduse järgi ning põrkel kiiruse arvväärtus ei muutu. Palli liikumist lugeda sirgjooneliseks. Leida a) punkt akna tasapinnas, mida läbis pall tuppa sisenedes; b) punkt akna tasapinnas, mida läbib pall toast väljudes pärast mitme põrke sooritamist seintega.
Lahendus
a) Aja jooksul läbis pall vahemaa laeni ja vahemaa kõrvalseinani . Järelikult punkt akna tasapinnas, mida läbis pall tuppa sisenedes, asus kaugusel laest ja kõrvalseinast ehk akna ülemisest servast ja akna kõrvalservast (vt. joonis).
b) Pall saab väljuda toast kui ta jõuab tagasi akna tasapinnani, milleks ta peab läbima kauguse aknaga risti olevas sihis. Selleks kulub tal aeg . Selle aja jooksul läbib ta kõrvalseinaga risti olevas sihis kauguse ning laega risti olevas sihis kauguse .
Joonisel on näidatud palli põhimõtteline liikumisskeem seinte vahel (see ei vasta palli reaalsele trajektoorile, kuid õigesti näitab põrkumiste arvu ja trajektoori lõpp-punkti ). Järelikult punkt akna tasapinnas, mida läbis pall toast väljudes, asus kaugusel põrandast ja kõrvalseinast ehk akna alumisest servast ja akna kõrvalservast (vt. joonis).
53. Rong
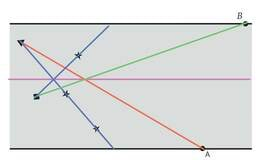
Lahendus
Vaatleme situatsiooni liikuva auto suhtes. Asugu autojuht punktis . Peeglile vastab lõik KL. Jooniselt on tähistatud , , , , . Autojuht näeb igal ajahetkel peegli vasakpoolses servas liikuva rongi punkti kujutist ja peegli parempoolses servas liikuva rongi punkti kujutist .
Kuna autojuht näeb peeglis rongi kujutise liikumist vasakult paremale, siis see vastab joonisel rongi punkti kujutise liikumisele joonisel üles ehk autoga samas suunas. Iga rongi punkti kujutis läbib lõigu aja jooksul. Sarnastest kolmnurkadest ja leiame, et , sarnastest kolmnurkadest ja leiame, et , millest nüüd . Seega leiame, et rongi peegelduse kiirus on auto suhtes . Et rongi peegeldus liigub joonisel üles ehk autoga samas suunas, siis rong liigub auto suhtes kiirusega vastupidises suunas.
See tähendab, et rongi kogukiirus maapinna suhtes on ning rong sõidab autoga samas suunas.
54. Satelliit
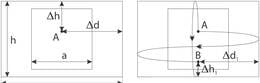
Kerakujuline satelliit läbimõõduga tiirleb orbiidil ümber Maa kõrgusel kiirusega . Kui suur on satelliidi nurkläbimõõt (nurk, mille all satelliit paistab mapinnal asuvale vaatlejale)? Mingil ajahetkel fikseeriti Maa pealt tähe varjutuse algus satelliidi poolt (vt. joonis). Jooniselt on näha, et sellel hetkel on satelliidi keskpunkti näiva asukoha ja tähe vaheline nurkkaugus (nurk vaatesuundade vahel tähele ja satelliidi keskpunktile). Kui suur on sellel hetkel satelliidi keskpunkti tegeliku asendi ja tähe vaheline nurkkaugus? Valguse kiirus on .
Lahendus
Tähe ja satelliidi tsentri vaheline nurkkaugus vastavalt joonisele on
Seega asub satelliidi tsenter tegelikult juba tähest paremal ning tähe ja satelliidi tsentri vaheline nurkkaugus on:
Ülaltoodud valemitest avalduvad nurgad ja radiaanides. Kui me tahaksime avaldada need nurgad kraadides, siis peaksime korrutama tulemused avaldisega .
55. Sprint
Poistest ja tüdrukutest moodustatud kooli võistkond jookseb teatejooksu. Võistlejate kiiruse sõltuvus võistkonna poolt läbitud teepikkusest on toodud graafikul. Leidke võistkonna keskmine kiirus kogu distantsi läbimisel.
Lahendus
Keskmise kiiruse arvutame kogu teepikkuse ning selle läbimiseks kujunud aja kaudu. Tähistame ringi pikkuse . Jooksjate ringide ajad on vastavalt: , , ja . Summaarne aeg on mõistagi nende summa. Kogu distantsi pikkus on . Siit saame keskmiseks kiiruseks
56. Valguse kiirus
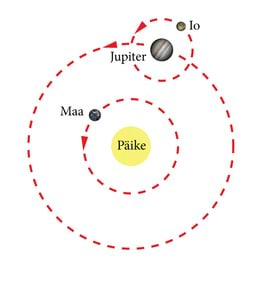
Esimese hinnangu valguse kiirusele andis Rømer 1675. a., uurides Jupiteri kaaslase Io liikumist. Io orbiit asetseb ligikaudu Maa orbiidi tasapinnas, nii et kaaslane kaob periooditi Jupiteri varju. Mõõtmised näitavad, et intervall kahe järjestikuse hetke vahel, kui Io ilmub nähtavale Jupiteri varjust, kõigub maksimaalselt ulatuses teatava keskväärtuse () ümber sõltuvalt Päikese, Maa ja Jupiteri vastastikusest asendist (vt. joonis). Teades, et Maa kaugus Päikesest on 1,5⋅108km, hinda valguse kiirust. Eeldada, et Jupiteri orbitaalkiirus ümber Päikese on palju väiksem kui Maal.
Lahendus
Io tiirlemisperioodi jooksul muutub Maa ja Jupiteri vahekaugus. Kaugus muutub kõige kiiremini, kui Maad ja Jupiteri ühendav sirge on Maa orbiidile puutujaks. Aja jooksul, mis Iol kulub ühe tiiru tegemiseks, muutub Maa ja Jupiteri vahekaugus
võrra. Selle täiendava vahemaa läbib valgus 15s jooksul, seega valguse kiirus avaldub:
57. Veevool
Jaak otsustas katseliselt määrata veevoolu kiiruse jões. Selleks pani ta vette puutüki ja sõudis ise paadiga pärivoolu minutiga meetri kaugusel oleva märgi juurde ning pöördus sealt tagasi. Jõudnud puutükini pööras ta paadi uuesti ja minutit pärast puutükiga kohtumist jõudis ta jälle sama märgi juurde. Kui suur oli veevoolu kiirus jões ja paadi kiirus vee suhtes, kui eeldada, et puutükk liikus muutumatu kiirusega ja Jaak sõudis kogu aeg ühesuguselt? Paadi pööramiseks kulunud aega mitte arvestada.
Lahendus
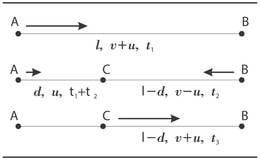
Olgu - paadi kiirus ja - veevoolu kiirus. Pärivoolu sõites oli paadi kiirus kalda suhtes Kuna puutüki suhtes liigub paat nii päri- kui vastuvoolu sama kiirusega, siis pärast pööret kulus Jaagul puutükini jõudmiseks samuti minutit. Seega liikus puutükk kohtumiseni paadiga . Kuna pärast puutükiga kohtumist sõitis paat märgini veel minutit, siis asus kohtumispaik märgist kaugusel. Paadi ja puutüki kohtumiskoht oli seega allpool stardipaigast. Seega on veevoolu kiirus jões
Paadi kiirus vee suhtes aga .
Teine lahendus: Seda ülesannet võib ka teistmoodi lahendada (vt. joonis). Olgu - kaugus stardipunkti ja märgi vahel. Poiss ja puutükk stardivad üheaegselt punktist , kuid liiguvad erinevate kiirustega. Puutükk liigub kiirusega , poiss aga kiirusega . Aja möödumisel jõuab poiss punkti , läbides vahemaa . Puutükk selleks ajaks läbis vahemaa . Poiss pöörab tagasi ja nüüd liigub ta kiirusega . Kohtumishetkel puutükiga läbib ta veel vahemaa , puutükk aga . Nüüd pöörab poiss teist korda ja läbib veel kauguse aja jooksul kiirusega . Võime panna kirja järgmise võrrandisüsteemi:
Selles võrrandisüsteemis tuntud on ja , tundmatud on , ja . Järelikult on see süsteem täielikult lahenduv. Avaldame teisest võrrandist ja asendame teises võrrandis selle avaldisega esimesest võrrandist:
Nüüd lihtsustub meie võrrandisüsteem kahe võrrandini:
Avaldades esimesest võrrandist ja asendades see teises võrrandis, saame
58. Autod
Maanteel paiknevad valgusfoorid iga tagant. Iga valgusfoori punane tuli põleb sekundit, siis süttib kohe roheline tuli ja põleb samuti sekundit; seejärel tsükkel kordub. Kõik kiirusega liikuvad autod, mis mööduvad ühest valgusfoorist rohelise tulega, mööduvad ka kõigist teistest valgusfooridest rohelise tulega. Milliste teiste kiirustega võiksid autod liikuda, et möödudes ühest valgusfoorist rohelise tulega mööduksid nad ka kõikidest teistest fooridest rohelise tulega?
Lahendus
Joonistame auto liikumise graafiku. Tähistame graafikul fooride punase tule põlemise perioode pideva joonega ja rohelise tule perioode lüngaga. Kuna kiirusega liikuv auto läbib ühe kilomeetri jooksul, siis võivad fooride punased ja rohelised tuled jaotuda ainult nii, nagu joonisel näidatud.
Graafikult on näha, et autod suudavad läbida kõiki foore peatuseta, kui nad suudavad läbida ühe kilomeetri , , , sekundi jooksul, kus on täisarv. Seega sobiv kiirus võib omada väärtusi , ehk , , jne.
59. Autod
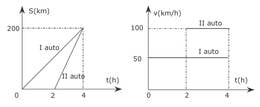
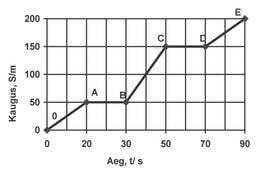
Punktist sõitis välja auto konstantse kiirusega . tunni pärast väljus punktist samas suunas teine auto ka konstantse kiirusega. Teine auto jõudis esimesele järele punktis , mis asub punktist kaugusel. Milline oli teise auto kiirus? Esitada a) teepikkuste graafikud; b) kiiruste graafikud.
Lahendus
Tähistused: - esimese auto kiirus; - teise auto kiirus; - aeg, mille pärast punktist väljus teine auto; - punktide ja vaheline kaugus.
Esimene auto sõitis aja . Teine auto sõitis aja . Teise auto kiirus on .
60. Bussiliin
Tartu-Tallinn bussiliini pikkus on . Buss sõidab läbi Põltsamaa ja Mäo. Tallinnast Mäoni on , Tartust Põltsamaani (vt. joonis). Tallinnast väljub Tartu poole buss kell ja sõidab Mäoni keskmise kiirusega . Mäos teeb buss pikkuse peatuse ja sõidab edasi Tartu poole keskmise kiirusega . Tartust väljub teine buss Tallinna poole kell . Buss sõidab Põltsamaale keskmise kiirusega . Seal teeb buss pikkuse peatuse ja jätkab sõitu sama keskmise kiirusega Tallinna poole. Mis kell kohtuvad bussid ja kui kaugel on nende kohtumiskoht Tartust?
Lahendus
Mäost Põltsamaale on . Tallinna buss jõuab Mäosse pärast (kell ) ja väljub sealt kell . Tartu buss jõuab Põltsamaale pärast (kell ) ja väljub sealt kell . Selleks hetkeks on Tallinna buss jõudnud Mäost juba kaugusele ja busside vahemaa on . Bussid sõidavad teineteisele vastu suhtelise kiirusega . Nad kohtuvad
pärast ehk kell . Kohtumispunkt asub Tartust kaugusel.
61. Golfilöök
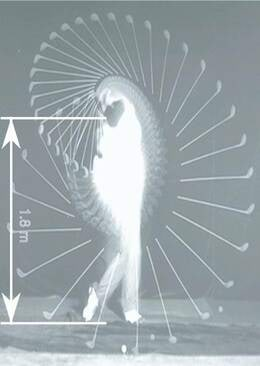
Sarivõttega pildistati golfimängijat nii, et iga kahe pildi vahel oli ajavahemik . Hinnake golfipalli algkiirust joonise abil. Pall liigub risti vaatesuunaga.
Lahendus
Lendu läinud golfipall on pildile jäädvustunud kolmes punktis. Paneme tähele, et heledaim valge täpp meile aga infot ei anna, sest see näitab vaid golfipalli algasendit enne seda, kui kepp teda lõi! Kahele järjestikkusele pildile on jäädvustunud heledast pallist paremale jäävad kaks tuhmimat valget palli kujutist. Nende ajaline vahe on . Mõõdame pallide vahekauguse joonlauaga. Samuti mõõdame golfimängija pikkust märkivat skaalat või golfimängija pikkust . Teades, et skaalajoone pikkusele vastab saame, et golfipalli nihke pikkus kahe pildi vahel on
Selleks nihkeks kulunud aeg oli . Kuna golfipalli kiirus on suur, siis raskuskiirendusega me ei arvesta, loeme, et tegu on kulgliikumisega. Kiiruseks saame .62. Jalgratas
Graafikul (vt. joonis) on kujutatud jalgratturi kiiruse sõltuvus ajast. Millistel ajavahemikel liikus jalgrattur kiirenevalt? Milline oli jalgratturi poolt läbitud teepikkus graafikul kujutatud ajavahemiku jooksul?
Lahendus
Jalgratas liigub kiirenevalt seal, kus kiirus ei ole konstantne ja parasjagu ei vähene. Ehk ajavahemikel ja (vt. joonis). Kuna teepikkus , siis jalgratturi poolt läbitud teepikkus meetrites on arvuliselt võrdne graafikul värvitud ruutude arvuga: .
63. Jalgrattur
Joonisel on kujutatud jalgratturi liikumise graafik. Millisel teelõigul oli jalgratturi kiirus suurim? Leida selle kiiruse väärtus. Mitu peatust tegi jalgrattur? Kui kaua kestsid peatused? Kui suur oli jalgratturi keskmine kiirus tee läbimisel?
Lahendus
Jalgratturi kiirus oli suurim lõigul . Kiirus oli siis .
Jalgrattur tegi kaks peatust. Üks kestis ja teine sekundit.
Jalgratturi keskmine kiirus oli .
64. Kaks kuuli
Kaks kuuli (must ja valge) alustavad võrdsete kiirustega liikumist punktist mööda joonisel näidatud pindu (vt. joonis). Kummal kuulil on punkti B jõudes kiirus suurem, kas mustal või valgel? Kummal kulub kohalejõudmiseks rohkem aega? Hõõrdejõudu mitte arvestada.
Lahendus
Energia jäävuse seadusest tuleneb, et mõlema kuuli kiirused punktis on ühesugused ().
Liikumisaja arvutamiseks paneme tähele, et kui valge ja must kuul on sooritanud võrdse kaldpinna suunalise nihke, siis valge kuul on mustast kõrgemal (kaldpinna normaali mööda ülespoole) ja energia jäävuses johtuvalt väiksema kiirusega. Valge kuuli kaldpinna-sihilise kiiruse leidmiseks tuleb niigi väiksem kiirusmoodul korrutada teatava nurga koosinusega, samal ajal kui must kuul liigub koguaeg kaldpinna sihis.
Niisiis on võrdsete kaldpinna-sihiliste nihete juures musta kuuli kiiruse kaldpinna-sihiline komponent alati suurem ning seepärast jõuab ta ka esimesena kohale.
65. Jõe ületamine
Paat sõitis üle jõe, mille laius oli , nii, et paadi siht oli kogu aeg risti jõega. Kui suur pidi olema paadi keskmine kiirus jõevoolu suhtes, kui on teada, et paadi maabumiskoht teisel kaldal asetses lähtekohast allavoolu? Vee voolukiirus jões oli ?
Lahendus
Paat võtab osa kahest liikumisest: sõidab risti jõge ning liigub allavoolu. Jõe laius
; allavoolu liikumine .
Sõidu aeg .
Pannes arvandmed asemele, saame
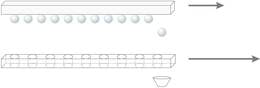
66. Püstolkuulipilduja
Korraldati katse, milles mõõdeti püstolkuulipilduja kuulide keskmist kiirust ja laskude arvu minutis. Selleks sõitsid kahel paralleelsel raudteel vastassuunas rongid. Rong, millest tulistati, sõitis katse ajal muutumatu kiirusega ja rong, mis oli märklauaks, muutumatu kiirusega . Rongide kaugus teineteisest oli . Esimene lask tehti hetkel, kui rongiga risti oleva püstolkuulipilduja toru ots oli täpselt vastakuti teisele rongile joonistatud märgiga. Kuuliaukude asukohtade mõõtmisel täheldati, et esimene kuul oli tabanud rongi märgist eemal ja kõikide teiste kuuliaukude kaugus üksteisest oli . Kui suur on püstolkuulipilduja kuuli lennukiirus ja mitu lasku teeb püstolkuulipilduja minutis?
Lahendus
Kuuli lennuaeg võrdub kõrvalekalle märgist jagatud rongide suhtelise kiirusega.
Kahe järgneva lasu vaheline aeg
Laskude sagedus .
67. Ringrada
Juhan, Kalle ning Lauri sõidavad ringrajal jalgratastega võidu. Kõik kolm stardivad korraga ühest kohast ning iga rattur sõidab muutumatu kiirusega. On teada, et Kalle teeb Juhanile ringi sisse siis, kui Kalle on just lõpetanud viienda ringi. Lauri teeb Kallele ringi sisse siis, kui Lauri on just lõpetanud kuuenda ringi. Mitu ringi oli Juhan sõitnud, kui Lauri temast esimest korda ringiga möödus?
Lahendus
Kui Lauri lõpetas kuuenda ringi, pidi Kalle lõpetama viienda ringi ning seega Juhan neljanda. Näeme, et Lauri läbib kolm ringi selle ajaga, mis Juhanil kulub kahe läbimiseks, järelikult mööduti Juhanist esimest korda ringiga siis, kui ta oli lõpetanud oma teise ringi.
68. Liiklusummik
Autod seisavad punase fooritule taga tiheda kolonnina, kus kahe järjestikuse auto esiotste vaheline kaugus on keskmiselt ning autode rivi pikkus . Peale rohelise tule süttimist hakkavad autod järjest liikuma ning saavutavad kiiruse . Kiiruse saavutanud autode esiotste vaheline kaugus . Lihtsuse mõttes jätke arvestamata autode kiirendamisele kuluv aeg. Kui kaua alates rohelise tule süttimisest peab viimane auto ootama, enne kui saab liikuma hakata? Kas ta jõuab üle ristmiku juba esimese rohelise tulega või peab uuesti punase tule taha ootama jääma? Rohelise tule kestus on .
Lahendus
Selleks hetkeks, kui liikuma hakkab viimane auto, on autoderivi pikkuseks kujunenud ligikaudu . Järelikult esimene auto pidi läbima selleks hetkeks vahemaa , milleks kulub aega
Viimane auto peab läbima vahemaa , et jõuda ristmikuni, milleks kulub tal aega ts˜oit=L0/v=10,8s
Kogu aeg ristmikuni jõudmiseks on seega Δt+ts˜oit=54s. Seega jõuab ka viimane auto rohelise tulega üle ristmiku.
69. Rong
Kaubarong läbis kahe jaama vahelise teelõigu keskmise kiirusega . Kogu sõiduajast esimese vältel liikus rong ühtlaselt kiirenevalt ja saavutanud maksimaalse kiiruse, hakkas kohe pidurdama liikudes pidurdamise ajal ühtlaselt aeglustuvalt. Kui suur oli rongi maksimaalne kiirus kahe jaama vahelisel teel?
Lahendus
Idee asendada muutuvate kiirustega liikumine keskmiste kiirustega liikumistega. Kiireneva või aeglustuva liikumise korral alg- ja lõppkiiruse asendamine keskmise kiirusega .
Mõlemal juhul üks kiirustest on võrdne nulliga . Jaamadevahelise teepikkuse avaldamine lõikude ja kogu keskmiste kiiruste kaudu seosega . Maksimaalse kiiruse avaldamine ehk .
70. Jõgi
Jõel vastuvoolu sõitev mootorpaat möödub kaldal olevast suurest kivist ja kohtab kivi juures allavoolu liikuvat parve. minutit pärast kohtumist hakkab mootorpaat sõitma pärivoolu ja jõuab parvele järele siis, kui see on kivist kaugusel. Kui suur on voolukiirus jões? Mootorpaat liigub üles- ja allavoolu vee suhtes sama kiirusega.
Lahendus
Lähme üle taustsüsteemi, kus vesi ei voola. Sel juhul kuluks mootorpaadil tagasisõiduks minutit ning kogu süiduaeg oleks . Seega ujub parv kivi juurest allajõge minutit ning siis möödub parvest mootorpaat. Jõevoolukiirus avaldub
71. Bussid
Jalgrattur Rein tegi maantee ääres trenni. Mööda teed tulid talle vastu bussid, mis lahkusid algpeatusest iga minuti tagant. Vähemalt mitu bussi tuli Reinule treeningu jooksul vastu, kui ta sõitis ja läbis ? Busside sõidukiirus oli .
Lahendus
Kahe järjestikuse bussi vahekaugus on . Jalgratturi taustsüsteemis sõitsid bussid talle vastu kiirusega , ehk Rein nägi bussi iga tunni järel. Trenn kestis , seega treeningu jooksul tuli Reinule vastu vähemalt bussi.
72. Kolksatused
Raudteerööbas on pikk. Kui pika aja vältel tuleks lugeda vaguni ühe telje rataste kolksatusi, et nende arv võrduks vaguni kiirusega kilomeetrites tunnis?
Lahendus
Vaguniratta kolksatus toimub ratta üleminekul ühelt rööpalt järgmisele rööpale. Teatud arvu kolksatuste jooksul läbib vagun vahemaa , kus on kolksatuste arv ja rööpa pikkus.
Kuna , saab panna kirja seose . Teisendades kiiruse , saab seose avaldada kujul , millest .
73. Võidusõiduautod
Võidusõiduauto keskmine kiirus ringrajal peetud treeningu jooksul oli . Kui arvutati peale esimese ja teise kõikide ülejäänud sõidetud ringide keskmine kiirus, leiti, et see oli täpselt sama, . Esimese ringi läbimiseks kulus aega . Kui palju aega kulus teise ringi läbimiseks? Ühe ringi pikkus oli .
Lahendus
Paneme tähele, et võidusõiduauto keskmine kiirus esimese kahe ringi jooksul peab samuti olema , ehk siis . Sellest saame, et , .
74. Orav
Orav kasutab liikumiseks reisirongide katuseid. Istudes jaamas peatunud rongi katusel, märkab orav, et kõrvalteel liigub rong kiirusega . Kui rongid on kohakuti, hüppab orav mööduva rongi katusele, püüdes maanduda vaguni lähemast servast võimalikult kaugele. Teisest rongist üle hüpata ta siiski ei suuda. õhus on orav . Uues asukohas talle aga ei meeldi ja pärast hüppab ta maandumiskohast samamoodi tagasi. Kui suur on orava endise ja uue asukoha vahekaugus esimese rongi katusel? Maandumisel orav ei libise.
Lahendus
Vaatleme orava liikumist seisva rongiga seotud taustsüsteemis piki raudteed suunatud koordinaattelje sihis (-telg).
Jõudmaks maksimaalsele kaugusele vaguni servast, peab orav esimene hüpe toimuma risti valitud koordinaattelje sihiga, tema kiirus piki -telge on null ja -koordinaadi väärtus ei muutu. Teise rongi vaguni katusel liigub orav valitud (seisva rongiga seotud) taustsüsteemis kiirusega ja läbib vahemaa .
Tagasihüppel, mis toimub nüüd risti -teljega aga teise rongiga seotud taustsüsteemis (see tagab jälle maandumiskoha maksimaalse kauguse vaguni servast) on orava kiirus seisva vaguniga seotud taustsüsteemis (teise rongi kiirus) ja ta läbib selles tausüsteemis piki -telge vahemaa .
Seega on orava endise ja uue asukoha vahe seisva vaguni katusel .
75. Mootorpaat
Hetkel, mil sadamast möödus parv, alustas sealt pärivoolu mööda jõge liikumist mootorpaat, mis suundus allavoolu kaugusel olevasse asulasse. Paat jõudis asulani minutiga ning pöördus kohe tagasiteele. Asulast ülesvoolu kohtas paat parve. Kui suur on voolu kiirus jões ja paadi kiirus seisvas vees?
Lahendus
Vaatleme paadi liikumist parvega seotud taustsüsteemis. Allavoolu sõites viib jõe vool mõlemat kaasa ning paat eemaldub parvest kauguse võrra. Kuivõrd ka paadi ülesvoolu sõites viib vool mõlemat võrdselt allavoolu, tuleb sama vahemaa paadil parvega seotud taustsüsteemis läbida ka tagasisõites. Seega kulub tagasisõidule parvega kohtumiseni samuti 45 minutit.
Parv läbib selle ajaga vahemaa , mis on . Vee voolukiirus jões on seega
Paadi kiiruse saame arvutada seosest , millest .
76. Trepp
Juku kõndis vanaema Juulaga trepist üles. Juku kõndis trepist üles kiirusega (korrust/minutis). Kui ta jõudis viiendale korrusele, siis hakkas ta alla tulema kiirusega . Juku ja vanaema kohtusid teisel korrusel. Mitmendale korrusele jõuaks Juku ajaga, mis vanaemal kulub viiendale korrusele minekuks? Juku liigub trepist alla kaks korda kiiremini kui üles. Maja esimene korrus asus maapinnal.
Lahendus
Kui esimene korrus asub maapinnal, siis teisele korrusle jõudmiseks tuleb tõusta ühe korruse võrra ja viiendale korrusele jõudmiseks on vaja tõusta korrust. Olgu Juula kiirus . Juulal ja Jukul kulus teise korruseni jõudmiseks sama aeg:
kust leiame .
Kui Juula jõuab viiendale korrusele, siis oleks Juku tõusnud korrust, seega jõuaks ta korrusele.
77. Liiklushuligaan
Liiklushuligaan sõidab Tartust Tallinnasse ja tagasi. Tavaliselt sõidab ta teel kiirusega , kuid enne kiiruskaamerat sõidab ta kiirusega . Teel Tallinnast Tartusse on kaks kiiruskaamerat rohkem kui vastassuunas. Mitu minutit sõidab liiklushuligaan Tallinnast Tartusse kauem kui vastassuunas? Eeldage, et kiiruskaamerate vahemaad linnadest ja omavahel on suuremad kui .
Lahendus
Liiklushuligaan sõidab Tallinnast Tartusse kauem, sest sel sõidusuunal on kaks kiiruskaamerat rohkem kui vastassuunas.
Teel Tallinnast Tartusse sõitis liiklushuligaan kiirusega kaks kilomeetrit rohkem kui vastassuunas.
Vastassuunas sõites läbis liiklushuligaan need kaks kilomeetrit kiirusega . Leiame, kui palju erinevad vahemaa läbimiseks kulunud ajad, sõites kiirusega ja sõites kiirusega :
kust .
Seega sõitis liiklushuligaan Tallinnast Tartusse minutit kauem kui Tartust Tallinnasse.