Keha mehaaniliseks liikumiseks nimetatakse selle asukoha muutumist teiste kehade suhtes. Keha liikumist iseloomustab liikumise kiirus. Kuidas nii?
Kiiruse arvutamisega oled juba kokku puutunud. Kiiruseks nimetatakse füüsikalist suurust, mis näitab, kui pika tee läbib keha mingi ajavahemiku jooksul:
ehk
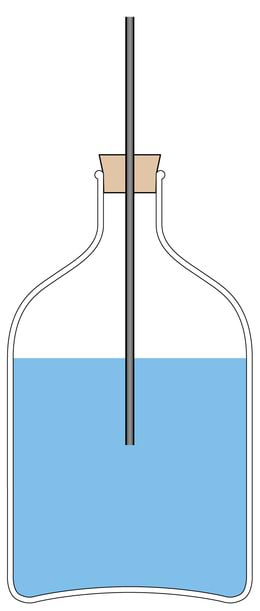
Vaatleme nüüd inimese liikumist sõitvas rongis. Milline on inimese kiirus, kui ta liigub vaguni ühest otsast teise?
Sellele küsimusele saame anda kaks vastust. Me saame leida inimese kiiruse vaguni suhtes, kui teame vaguni pikkust ja aega, mis kulub selle läbimiseks. Me saame leida ka inimese kiiruse maapinna suhtes. Kui inimene liigub rongis sõidusuunas, on tema kiirus maapinna suhtes suurem rongi liikumise kiirusest, kuna lisaks enda kõndimisele liigub inimene ka koos rongiga edasi.
Pildil liigub inimene rongi suhtes kiirusega vi=3m/s ning rong liigub maapinna suhtes kiirusega vr=20m/s. Inimese kiiruse leidmiseks maapinna suhtes peame need kiirused liitma:
Kui inimene liigub kiirusega 3m/s rongi liikumisele vastassuunas, siis tuleb inimese kiiruse leidmiseks maapinna suhtes rongi kiirusest lahutada inimese liikumise kiirus rongi suhtes, kuna inimene ja rong liiguvad vastassuundades. Inimene liigub seega maapinna suhtes kiirusega
Keha kiirus on alati suhteline, kuna keha kiirust väljendatakse alati mingi teise keha suhtes. Kui pole mainitud, mis keha suhtes me kiiruse peame leidma, mõeldakse enamasti kiirust maapinna suhtes.
Mehaanilisi liikumisi võib liigitada kaheks: ühtlane sirgjooneline liikumine ja muutuv liikumine. Ühtlase sirgjoonelise liikumise korral keha kiirus ei muutu. Selliste liikumiste erijuht on paigalseis. Muutuva liikumise korral muutub keha kiirus või suund.
Vaatleme liikumist kodust kooli. Kool asub kodust 2km kaugusel ning meil kulus kooli jõudmiseks pool tundi. Kogu teekonna vältel ei olnud meie kiirus ühtlane, kuna vahepeal tuli peatuda, et üle tee minna. Meie liikumine kodust kooli oli mitteühtlane.
Mitteühtlase liikumise korral saame arvutada keskmise kiiruse, kui jagame läbitud teepikkuse liikumiseks kulunud ajaga. Keskmise kiiruse arvutamiseks tuleb arvestada liikumise aja hulga sisse ka peatusteks kulunud aeg. Selle näite puhul on kodust kooli liikumise keskmine kiirus
Näiteülesanne
Kiirusega v1=99km/h sõitva auto juht märkab temale lähenevat autot ning käivitab stopperi. sekundi pärast autod kohtuvad. Kui kaugel oli lähenev auto, eeldades, et ta sõitis kiirusega v2=90km/h?
Lahendus
Vaatleme liikumisi kiirusega sõitva auto suhtes. Sellisel juhul läheneb sõitvale autole auto kiirusega
Teades, mis aja pärast autod kohtusid, saame leida, kui kaugel nad teineteisest olid.
Andmed
v1=90km/h=25m/s
v2=99km/h=27,5m/s
t=40s––––––––
s−?
Arvutused
Vastus. Lähenev auto oli alguses 2,1km kaugusel.
Mechanical movement, medium speed
Mechanical motions can be classified into two categories: uniform rectilinear motion and variable motion. In case of uniform straight line movement, the speed of the body does not change. In variable motion, the speed or direction of the body changes.
For non-uniform motion, we can calculate the average speed by dividing the distance traveled by the time taken to move.
Mõnikord on mõistlik ja ülevaatlik kujutada liikumisi graafiliselt, näidates ära, kuidas läbitud teepikkus sõltub ajast. Sellist graafikut me nimetame teepikkuse graafikuks.
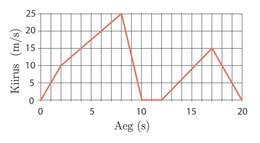
Mõnikord ei näidata liikumise graafilisel kujutamisel teepikkuse muutumist ajas, vaid kiiruse muutumist ajas – selliseid graafikuid me nimetame kiiruse graafikuks.
Vaatleme I lõiku. Kiirus muutub seal ühtlaselt (graafik on sirgjoon) 0 m/min kuni 100 m/min. Kuna tegemist on ühtlaselt muutuva kiirusega liikumisega, saame keskmine kiiruse sellel lõigul arvutada aritmeetilise keskmisena: (0 + 100)/2 = 50 m/min.
Näiteülesanne
Matkaja liikumist esimese kümne minuti jooksul kajastab üleval toodud teepikkuse graafik. Vasta järgmistele matkajat puudutavatele küsimustele.
- Millise ajavahemiku jooksul liikus matkaja kõige kiiremini?
- Mitu minutit matkaja vahepeal järjest puhkas?
- Milline oli matkaja keskmine kiirus kogu teekonna vältel?
- Kui palju oli matkaja keskmine kiirus pärast puhkust väiksem/suurem kui enne puhkust?
- Miks keskmised kiirused enne ja pärast puhkust on suuremad kui kogu matka keskmine kiirus?
Lahendus
- Kõige kiiremini liigub matkaja sellel lõigul, kus graafiku tõus on kõige suurem. Graafikut lugedes saame teada, et esimese ja teise minuti jooksul läbis matkaja minutis meetrit, mis on ka kõige kiirem lõik kogu matka jooksul. Ülejäänud matka vältel matkaja nii kiiresti enam ei liikunud. Ajavahemikul 6-8 minutit läbis matkaja ühes minutis meetrit.
- Matkaja puhkas selles ajavahemikus, kus graafiku tõus on (graafik on horisontaalne). Graafikult näeme, et matkaja puhkas minutit ajavahemikus 4-6 minutit.
- Keskmise kiiruse saame leida, kui jagame kogu läbitud teepikkuse selleks kulunud ajaga.
Andmed
s=720m
t=10min=600s––––––––––––––––––––
v−?
Arvutused
Vastus. Matkaja keskmine kiirus kogu matka vältel oli 1,2m/s. - Matkaja puhkas ajavahemikus 4-6 minutit. Leiame matkaja keskmise kiiruse ajavahemikus 0-4 minutit ning keskmise kiiruse ajavahemikus 6-10 minutit.
Andmed
s1=420m
s2=720m–420m=300m
t2=4min=240s–––––––––––––––––––
v1−?
v2−?
Arvutused
Vastus. Matkaja keskmine kiirus oli pärast puhkust väiksem kui enne puhkust. - Kogu matka keskmise kiiruse arvutamise hulka arvestati ka puhkuseks kulunud aeg, mistõttu on kogu matka keskmine kiirus väiksem kui matkaja kiirused enne ja pärast puhkust.
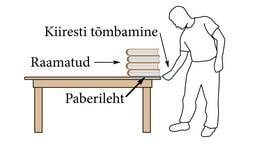
Asetame raamatute kuhja (või ka näiteks veeklaasi) paberilehe peale. Tõmmates paberit järsult ja kiiresti, jäävad raamatud paigale ning paber libiseb nende alt ära. Kui aga liigutada paberit aeglaselt ja ettevaatlikult, siis liiguvad raamatud paberiga kaasa. Miks jäävad raamatud siis paigale, kui paberit järsult tõmmata?
Kui raamatud hakkavad paberiga kaasa liikuma, siis sellepärast, et me mõjutame neid paberi kaudu.
Aga kirjeldatud katses ilmneb ka raamatute inertsus – nad püüavad säilitada oma liikumisolekut, st jääda paigale.
Nii keha kiiruse suurendamiseks kui ka vähendamiseks tuleb rakendada jõudu, kusjuures jõud peab olema seda suurem, mida järsemalt me tahame kiirust muuta. Raamatute kuhja kiiruse järsuks suurendamiseks peaksime rakendama väga suurt jõudu ja seda ei ole võimalik teha paberilehte sikutades – pigem tuleb paber raamatute alt välja või rebeneb, kui et raamatud nihkuvad.
Niisiis, kehade omaduse tõttu, mida kutsutakse inertsuseks, ei saa nende kiirust muuta hetkeliselt, selleks kulub alati aega. Keha inertsust iseloomustab tema mass – mida suurem on keha mass, seda inertsem on keha ja seda raskem on selle kiirust muuta.
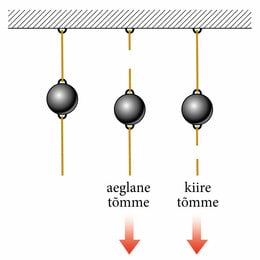
Teeme veel ühe katse. Kinnitame kuuli niidiga lae külge. Kuuli alla on kinnitatud teine täpselt samasugune niit. Kumb niit katkeb, kui alumist niiti allapoole tõmmata?
Selgub, et see, kas katkeb ülemine või alumine niit, sõltub sellest, kui järsult niiti tõmmata.
Olukorra analüüsimiseks peaksime aru saama, kummale niidile, kas alumisele või ülemisele, mõjub suurem jõud. Seda teades saame ka otsustada, kumb niit katkeb.
Tõmmates alumist niiti aeglaselt ja rahulikult, katkeb ülemine niit. Sellisel juhul mõjub alumisele niidile ainult tõmbejõud, seevastu ülemisele niidile mõjub lisaks tõmbejõule veel ka kuuli raskus. Järelikult mõjub ülemisele niidile suurem jõud kui alumisele ja ülemine niit puruneb. Kuuli inertsus siin suurt rolli ei mängi, sest talle antakse oma liikumisoleku muutmiseks piisavalt aega.
Tõmmates niiti järsult, katkeb alumine niit. See juhtub nii sellepärast, et kuul nagu ka iga teine keha püüab säilitada oma liikumisolekut ja jääda liikumatult rippuma. Järsult niiti tõmmates üritame järsult kuuli kiirust muuta. Aga järsuks kiiruse muutmiseks on vaja rakendada väga suurt jõudu. Alumine niit ei pea sellele vastu ja katkeb. Kui suur on jõud, mis mõjub ülemisele niidile? Kuna järsult alumist niiti tõmmates katkeb see enne, kui kuul liikuma jõuab hakata, siis ülemisele niidile mõjuv jõud jääb peaaegu muutumatuks, igal juhul on see jõud väiksem kui see, mis mõjub alumisele niidile.
Kehade inertsus on kehade omadus säilitada oma liikumisolekut – kas jääda paigale või liikuda ühtlaselt ja sirgjooneliselt.
Kehade inertsus avaldub eriti ilmekalt, kui üritame ääreni täidetud laia veeanumat ühest kohast teise kanda. Vesi loksub siis üle serva vähimagi kiiruse muutuse korral – kui kiirendame veidi, üritab vesi kausist „maha jääda“, kui aeglustame, üritab vesi jätkata liikumist endise kiirusega.
Kehade inertsus mängib meie igapäevaelus väga suurt rolli ja me oskame sellega arvestada ka siis, kui me vastavat füüsikaseadust sõnastada ei oska. Me teame, et suurema massiga palli on raskem kaugele visata, uisutaja liugleb jääl ka siis, kui ta parajasti hoogu ei anna, jalgrattaga sõites tuleb õigel ajal pidurdama hakata, muidu on kokkupõrge vältimatu, jne.
| Kui kehad ei oleks inertsed, ei oleks liiklusõnnetused probleemiks – põrkuvad autod muudaksid hetkega oma liikumisolekut ja jääksid seisma ilma, et üksteisele kahju teeksid. Reaalses kokkupõrkes ei ole niisugune asi võimalik – laupkokkupõrkes jätkavad autode tagumised otsad liikumist ka siis, kui esimesed otsad juba seisavad. | Võidusõiduautode edu võistlustel sõltub paljuski sellest, kui kiiresti nad suudavad oma liikumisolekut muuta. Sellepärast püütakse nende mass võimalikult väike hoida – mida väiksem mass, seda väledam auto. |
Kehade inertsus
Kehade inertsuseks nimetatakse nähtust, kus kehad püüavad säilitada oma liikumisolekut. Keha inertsust iseloomustab tema mass – mida suurem on keha mass, seda inertsem on keha ja seda raskem on selle kiirust muuta. Kehade inertsuse omaduse tõttu ei saa nende kiirust muuta hetkeliselt, selleks kulub alati aega.
Põrandale asetatud pall seisab paigal, kui miski teda ei mõjuta. Pall hakkab liikuma alles siis, kui me seda tõukame, nagu seda juba oleme näinud kehade inertsuse omadusega tutvudes. Teame ka, et liikuma lükatud pall ei veere kuigi kaua, vaid jääb mõne aja pärast seisma. Kuidas neid nähtusi seletada?
Sellele küsimusele vastamiseks peame uurima kehade vastastikmõju seaduspärasusi. Varasemast teame, et
- keha püsib paigal või liigub ühtlaselt ja sirgjooneliselt, kui seda ei mõjuta teised kehad;
- keha kiirus võib muutuda ainult siis, kui seda mõjutavad teised kehad.
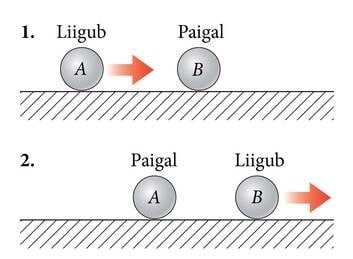
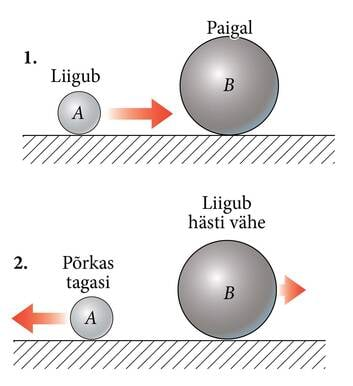
Veeretame nüüd paigalseisva palli pihta teise täpselt samasuguse palli. Paigalseisev pall hakkab siis liikuma ning see pall, mida tema pihta veeretati, jääb praktiliselt seisma (või hakkab aeglasemalt liikuma) – pallid mõjutavad teineteist ning mõlema palli kiirus muutub.
Kui korrata eelnevat katset nii, et paigalseisev pall on suure massiga ning tema vastu veeretatakse palju väiksema massiga pall, siis hakkab suurem pall hästi aeglaselt liikuma, kuid väike pall põrkab tagasi ja liigub praktiliselt sama kiirusega, mis tal enne põrget oli. Katsest võib järeldada, et kehade vastastikmõju tõttu muutub suurema massiga keha kiirus palju vähem ning väiksema massiga keha kiirus rohkem.
Kehadevahelise vastastikmõju kohta tasub meelde jätta järgmist.
- Kehade mõju on alati vastastikune – üks keha mõjutab teist ning teine esimest.
- Kehade vastastikmõju korral muutub suure massiga keha kiirus vähem kui väiksema massiga keha kiirus.
Siit järeldub ka, et kui põrand pidurdab palli hoogu, siis pall omakorda kiirendab põrandat. Aga kuna põranda ja selle külge kinnitatud maja mass on palli massist palju suurem, siis me märkame vaid palli kiiruse muutumist.
Füüsikalist suurust, mis iseloomustab ühe keha mõju teisele kehale, nimetatakse jõuks.
Jõudu tähistatakse tähega F ning jõu ühikuks on njuuton (lühend N). Jõu ühik on saanud oma nime Inglise teadlase Isaac Newtoni järgi, kes tegeles paljude loodusteadusi puudutavate teemadega ning sõnastas mehaanika põhiseadused, mis on tänapäeva füüsika nurgakiviks. Täpsemalt õpite Newtoni seadusi gümnaasiumis.
Jõud mõjub alati ühes kindlas suunas. Joonistel näidatakse jõu mõjumise suunda noolega. Noole algus tehakse alati sinna punkti, kuhu jõud mõjub. Jõu mõjumise punkti nimetatakse jõu rakenduspunktiks.
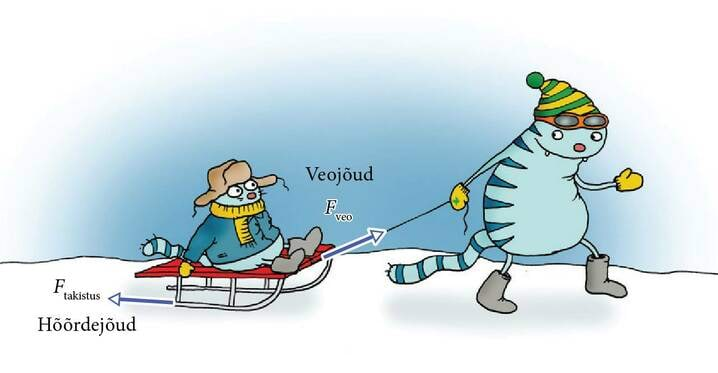
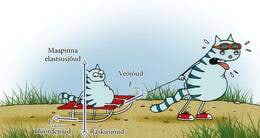
Enamasti mõjub kehale samal ajal mitu jõudu. Näiteks kelgu vedamisel mõjub kelgule veojõud, mis on kelgu tõmbamise suunaline. Samal ajal mõjub talle tee ja kelgu põhja vaheline hõõrdejõud, mis on sõidusuunale vastupidine.
Kui me tahame vaadelda seda, kuidas kehale mõjuvad jõud mõjutavad keha liikumist, on meil vaja leida kehale mõjuv summaarne jõud ehk resultantjõud. Kõrvalolevas näites saame leida resultantjõu, kui me lahutame veojõust hõõrdejõu. Me peame jõudusid lahutama, kuna need jõud on vastassuunalised:
Kelgu liikumissuunalise resultantjõu leidmisel pole vaja arvestada raskusjõu ning maapinna elastsusjõuga, kuna need jõud on veo- ja takistusjõuga risti.
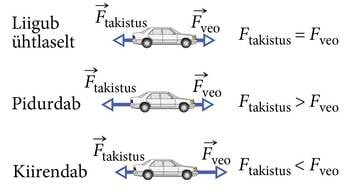
Uurime joonisel kujutatud autole mõjuvaid jõudusid. Kui veojõud on takistusjõust suurem, liigub auto kiirenevalt. Kui aga takistusjõud on suurem veojõust, liigub auto aeglustavalt.
Millal liigub joonisel kujutatud auto ühtlaselt? Me juba teame, et kui kehale ei mõju ühtegi jõudu, siis on keha paigal või liigub ühtlaselt ja sirgjooneliselt. Selgub, et sama kehtib ka siis, kui kehale mõjuvate jõudude summa on 0 (resultantjõud on 0 N).
Keha on paigal või liigub ühtlaselt ja sirgjooneliselt, kui sellele mõjuvad jõud tasakaalustavad üksteist.
Seega liigub joonisel kujutatud auto ühtlaselt siis, kui veojõud ja takistusjõud on võrdsed.
Change in body movement
A body's speed or direction can only change if it is acted upon by other bodies.
Interaction of bodies
The effect of bodies is always mutual - one body affects the other and the other affects the first. When bodies interact, the velocity of the body with a large mass changes less than the velocity of the body with a smaller mass.
Summaarne jõud ehk resultantjõud
Kui tahame teada, kuidas kehale mõjuvad jõud muudavad keha liikumist, peame leidma kehale mõjuva summaarse jõu ehk resultantjõu. Kui kehale mõjuvad jõud on vastassuunalised, tuleb need resultantjõu leidmisel üksteisest lahutada. Keha on paigal või liigub ühtlaselt ja sirgjooneliselt, kui sellele mõjuvad jõud tasakaalustavad üksteist.
Ilma kehadevahelise vastastikmõjuta liiguks kõik kehad ühtlaselt ja sirgjooneliselt või seisaks paigal. Miks siis kukub üles visatud pall tagasi maapinnale, ehkki ei ole mingit nähtavat takistust, miks see ei võiks jäädagi ülespoole liikuma? Miks Kuu tiirleb ümber Maa, kui hõlpsam oleks liikuda otse nagu nööri otsa seotud kivi, mida on keerutatud ja siis lahti lastud?
Looduses esineb kehadevaheline vastastikmõju, mida nimetatakse gravitatsiooniks ehk gravitatsiooniliseks vastastikmõjuks. Gravitatsioonilises vastastikmõjus olevate kehade vahel mõjub tõmbejõud, mida nimetatakse gravitatsioonijõuks.
Gravitatsioonijõud mõjub kõikidele vastastikmõjus olevatele kehadele ühtemoodi ja see on suunatud kehade keskpunktide poole.
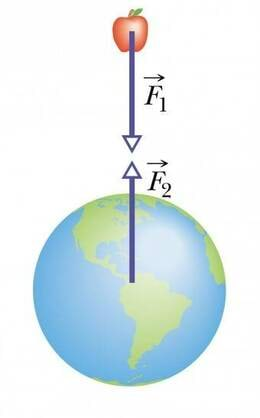
Miks siis üles visatud pall tagasi maapinnale kukub?
Maa ja palli vahel mõjub gravitatsioonijõud. Kui pall kaalub 100 grammi, siis on gravitatsioonijõu suuruseks ligikaudu 1 N. Selline jõud mõjub nii pallile kui ka Maale, nii et rangelt võttes peaksid pall ja Maa hakkama teineteisele vastu liikuma. Kuna aga Maa mass on palli massist väga palju suurem, nihkub ta sellises vastastikmõjus väga vähe. See-eest palli mõjutab gravitatsioonijõud märgatavalt – see „kukub alla“.
Gravitatsioon esineb kõigi kehade vahel, isegi kahe pinginaabri vahel ning pinalis olevate pliiatsite vahel. Kui me seda ei tunne, siis sellepärast, et näiteks kahe pinginaabri vaheline gravitatsioonijõud on kõigest 0,0000001 N. Millest sõltub gravitatsioonijõu suurus?
Gravitatsioonijõu suurus sõltub kehade massist – mida suurem on kehade mass, seda suurem on gravitatsioonijõud.
Kui üks pinginaabritest kaaluks miljon tonni, siis oleks täpsete mõõteriistadega võimalik pinginaabrite vahel tekkiv gravitatsioonijõud ka ära mõõta. Lisaks kehade massile sõltub gravitatsioonijõu suurus ka kehade omavahelisest kaugusest. Mida kaugemal on kehad üksteisest, seda väiksem on gravitatsioonijõud. Näiteks kui inimesele mõjub maapinnal gravitatsioonijõud 800 N, siis 10 000 km kaugusel maapinnast on gravitatsioonijõud kõigest 120 N (vt tabel).
Maa või mõne teise taevakeha lähedal asuvatele kehadele mõjuvat gravitatsioonijõudu nimetatakse ka raskusjõuks. Maapinna lähedal olevatele kehadele mõjuvat raskusjõudu saab arvutada valemiga:
Selles valemis tegur g näitab, millise jõuga mõjutab Maa (või mõni muu taevakeha) tema pinnal asetsevat 1 kg keha. Tegurit g nimetatakse raskuskiirenduseks, selle ligikaudne väärtus maapinnal on g = 9,8 N/kg.Raskusjõu valem Fr = mg on igapäevaelus väga oluline, kuna annab mõtte sõnadele kaal ja kaalumine. Kaal mõõdab temale asetatud keha poolt talle avaldatavat raskusjõudu. Keha mass m on selle raskusjõuga võrdeline ja selle saab arvutada valemist m = Fr/g, kui me teame raskusjõudu Fr ja raskuskiirendust g.
Keha mass on konstantne suurus, aga keha kaal võib väga suurtes piirides muutuda, sest raskuskiirenduse g väärtus ei ole alati ja igal pool ühesugune.
Näiteks on raskuskiirenduse väärtus ekvaatoril natuke väiksem kui poolustel ning ühte ja sama keha ekvaatoril ja poolusel kaaludes saame erineva tulemuse. See erinevus on suhteliselt väike, aga kaubanduses peab sellega arvestama – banaanilasti kaal põhja poole sõites pisut kasvab.
Kuna gravitatsioonijõud sõltub kehadevahelisest kaugusest, siis sõltub raskuskiirenduse g väärtus ka kaugusest maapinnast.
Kuna raskuskiirenduse väärtus sõltub taevakehade massist, siis on erinevate planeetide läheduses raskuskiirenduse väärtus erinev ja järelikult on seal teistsugune ka kehade kaal. Näiteks Kuu pinnal on g väärtuseks 1,6 N/kg, mistõttu on Kuul mõjuv gravitatsioonijõud ja kehade kaal umbes kuus korda väiksem kui Maal. Tõstes Maal keha, mille mass on 50 kg, mõjub talle gravitatsioonijõud 500 N. Kuul tuleb aga rakendada sama palju jõudu, et tõsta keha, mille mass on suurem kui 300 kg.
Gravitational force and gravity
Between bodies in gravitational interaction there is an attractive force called the gravitational force. The greater the mass of the bodies, the greater the gravitational force. The farther the bodies are from each other, the smaller the gravitational force. We call the force of gravity acting near the earth the force of gravity.
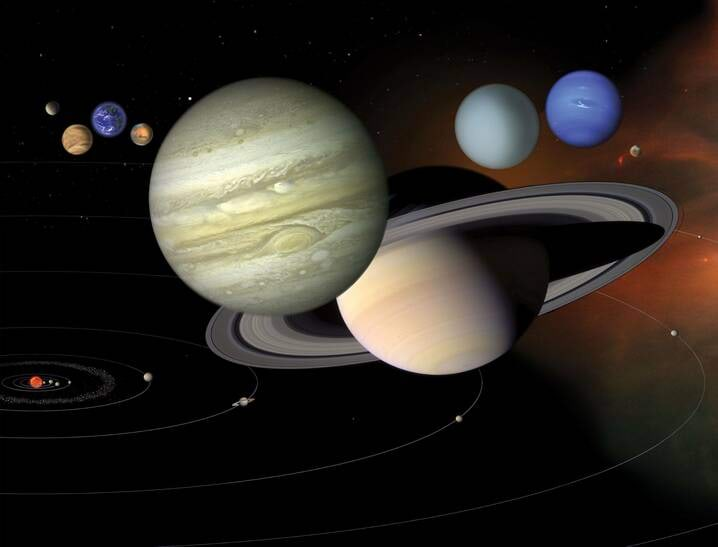
Päikesesüsteem tekkis ligikaudu 4,6 miljardit aastat tagasi.
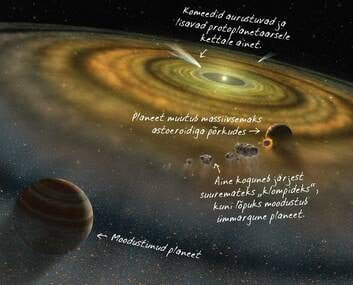
Algselt oli Päikesesüsteem suur gaasipilv, mis gravitatsiooni mõjul järjest kokku tõmbus. Umbes 50 miljoni aasta jooksul muutusid rõhk ja temperatuur gaasipilve keskele tekkinud prototähe keskmes piisavalt suureks termotuumareaktsioonide käivitumiseks ning tekkis Päike.
Esialgses gaasipilves polnud aine ühtlaselt jaotunud. Kokkutõmbuv gaasipilv hakkas järjest kiiremini pöörlema ning umbes kümnendik esialgse pilve ainest paiskus väljapoole. Väljapaiskunud aine venis pöörlemise tõttu lapikuks ning moodustas lapiku protoplanetaarse pilve – ketta, milles hakkasid tekkima Päikesesüsteemi planeedid ja muud taevakehad. Teadlased arvavad, et praegu Marsi ja Jupiteri vahel asuv asteroidide vöö on nende Päikesesüsteemi algaegade jäänus, mis valdavalt Jupiteri gravitatsioonilise mõju tõttu ei ole saanud suuremaks objektiks kokku koonduda.
Algselt tekkisid kõikidel planeetidel kivimitest koosnevad tuumad, mille ümber oli ulatuslik vesiniku ja heeliumi kiht. Päikese kiirguse tugevnedes Päikesele lähemal olevate nn Maa tüüpi planeetide ümbert (Merkuur, Veenus, Maa, Marss) gaasipilv hajus. Päikesest kaugel olevad hiidplaneedid (Jupiter, Saturn, Uraan ja Neptuun) on säilitanud oma tiheda atmosfääri praeguseni.
| Protoplanetaarne ketas raadioteleskoobis. HL Tauri on noor täht Sõnni tähtkujus ja asub Maast 450 valgusaasta kaugusel. Palja silmaga vaatlemiseks on see objekt liiga nõrk, valguse nähtavas piirkonnas näeb see ala ka hoopis teistsugune välja. | Planeedid tekivad universumis ka praegu. Selle pildil on kunstnik kujutanud planeetide teket väga noore tähe Beta Pictoris ümber. Pilt on joonistatud vaatlusandmete põhjal. Arvatakse, et selle tähe ümber tekkivatel planeetidel on palju süsinikku ja need võiks olla sobilikud elu tekkeks. |
Päikesesüsteemi planeetide ümber tiirleb teadaolevalt 219 kaaslast. Suurem osa neist paikneb hiidplaneetide ümber – praeguseks on Jupiteril leitud 79 ja Saturnil 82 kaaslast. Maa-tüüpi planeetide ümber tiirleb vaid kolm kuud (Maa kaaslane Kuu ning kaks Marsi kaaslast – Phobos ja Deimos).
Päikesesüsteemi äärealadele jäävad veel kääbusplaneedid. Tuntuim neist on Pluuto – kuni 2006. aastani loeti see veel planeediks. Kuid kääbusplaneet on ka Marsi ja Jupiteri vahel tiirlev suurim asteroid Ceres.
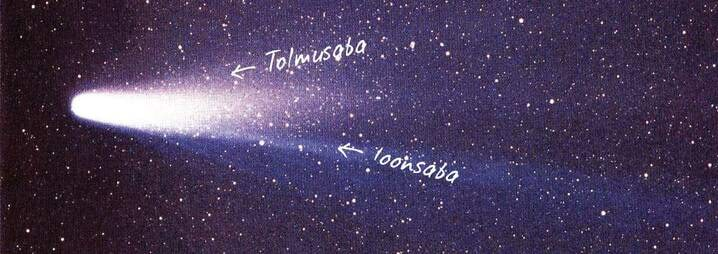
Mõnikord on taevas näha ka komeete ehk sabatähti. Komeedid koosnevad peamiselt jääst ning külmunud gaasidest ja vähemal hulgal tolmuosakestest ning väikestest kivikestest. Päikesest kaugel on suurimate komeetide tuumade läbimõõt mõnikümmend kilomeetrit, enamiku komeetide tuuma läbimõõt on mõni kilomeeter. Päikesele lähenedes hakkab komeet soojenema. Komeedi pinnas olevad gaasid aurustuvad ning eemalduvad komeedi tuumast, moodustades kuni 200 000 km läbimõõduga komeedi pea.
Päikesetuul puhub gaasid komeedi juurest minema ning moodustub komeedi gaasiline ioonsaba (Halley komeedi pildil sinine). Saba pikkus võib olla kuni 100 miljonit kilomeetrit. Komeedi ioonsaba on alati suunatud Päikesest eemale – Päikesele läheneb komeet pea ees ning eemaldub saba ees. Komeetidel on alati ka teine saba, mida nimetatakse tolmusabaks. See tekib komeedi aurustumisel vabanenud tolmuosakestest ja jääb komeedist maha piki komeedi orbiiti. Kuna orbiidid on alati ümber Päikese, siis võivad komeedi tolmu- ja ioonsaba osutada väga erinevatesse suundadesse.
Mõned komeedid liiguvad Päikese ümber väljavenitatud ovaalset orbiiti mööda. Sellised komeedid satuvad Maa lähedale mõne või mõnesaja aasta tagant. Näiteks Halley komeet möödub maast iga 70 aasta järel. Enamik komeete on aga tähtedevahelised hulkurid, mis on pärit Päikesesüsteemi kaugetest äärealadest ja peale esimest lähenemist Päikesele lahkuvad Päikesesüsteemist igaveseks. Heledamaid komeete on võimalik jälgida ka palja silmaga, kuid neid satub Päikese lähedale harva – umbes iga 10 aasta tagant üks komeet.
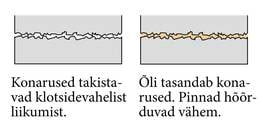
Hõõrdumine on kehade kokkupuutepindade vahel esinev vastastikmõju, mis takistab kehade liikumist üksteise suhtes. Hõõrdumine esineb kõigi kehade vahel, mis kokku puutuvad. Hõõrdejõu mõjumise suund on keha liikumissuunaga alati vastupidine.
Mõnikord on hõõrdumine kasulik, näiteks siis, kui tahame jalgadega tee pealt hoogu tõugata ning liikuda. Mõningates kohtades on vaja jälle hõõrdumist vähendada – jalgrattaga on palju lihtsam sõita siis, kui rattalaagrid on õlitatud ning hõõrdumine on väga väike, kelk aga libiseb palju paremini siis, kui lumi on maas ja tee jäine.
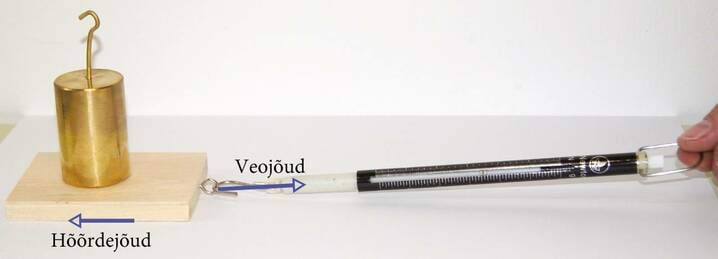
Hõõrdumist iseloomustab hõõrdejõud – jõud, mis takistab kokkupuutes olevate kehade liikumist teineteise suhtes.
Hõõrdejõudu saab mõõta dünamomeetriga. Selleks tuleb keha külge kinnitada dünamomeeter ning vedada seda dünamomeetrist tõmmates ühtlaselt ning paralleelselt laua pinnaga. Dünamomeeter näitab siis jõudu, millega keha veetakse (veojõudu) – see on ühtlase liikumise korral võrdne hõõrdejõuga keha ja pinna vahel.
Hõõrdumise tekkimiseks on erinevaid põhjuseid, üheks peamiseks on see, et kehade pinnad ei ole siledad. Kui vaadelda luubiga raamatu pinda, võib seal märgata väikeseid konarusi. Raamatu kaane konarused jäävad laua konaruste taha kinni – see takistabki raamatu liikumist ning põhjustab hõõrdumist. Nii et üldiselt on hõõrdumine seda väiksem, mida siledamad on pinnad, ja hõõrdumine väheneb, kui panna libisevate pindade vahele õli või muud vedelikku, kuna õli täidab suuremad konarused.
Hõõrdejõud sõltub materjalidest, mis omavahel kokku puutuvad, samuti rõhumisjõust – mida suurema jõuga on hõõrduvad pinnad kokku surutud, seda suurem on hõõrdejõud. Hõõrdejõud sõltub ka sellest, kuidas kehad üksteise suhtes liiguvad. Paigalseisvat kappi on palju raskem liikuma lükata kui juba liikuvat kappi liikumas hoida.
Hõõrdejõudu, mis takistab kehade liikuma hakkamist, nimetatakse seisuhõõrdejõuks. Hõõrdejõudu, mis tekib keha libisemisel teise keha pinnal, nimetatakse liugehõõrdejõuks.
Kehade vahel tekkiv hõõrdejõud on vahel hea, vahel ebasoovitav. Näiteks autode pidurisüsteemides on hõõrdejõud kindlasti soovitav.
| Hõõrdudes kehad soojenevad, äärmuslikes oludes võivad nad lausa hõõguma hakata. Vasakpoolsel pildil hõõguvadki võidusõiduauto esimeste rataste pidurikettad punaselt. | Auto pidurisüsteem. Ratta külge on kinnitatud ketas (piduriketas), mis on servapidi pilus. Pidurdades surutakse vastu piduriketast piduriklotsid, tekib tugev hõõrdumine. |
Paljudel juhtudel üritatakse hõõrdumist igati vähendada. Õli ja teiste määrdeainete kasutamist me juba mainisime – ilma õlita automootor kuumeneb hõõrdumise tõttu väga kiiresti ning kuumade detailide paisumise pärast n-ö jookseb kokku. Aga meenutada tasub ka näiteks suuskade määrimise keerukat tööd.
Lisaks libisemisele võivad kehad ka veereda. Ehkki kehade veeremist takistav jõud on mitu korda väiksem kui liugehõõrdejõud, on see siiski olemas ja seda nimetatakse veerehõõrdejõuks.
Friction and friction force
Friction is the interaction between the contacting surfaces of bodies, which prevents the bodies from moving relative to each other. Friction is characterized by the force of friction - the force that prevents the movement of bodies in contact with each other.
Static friction force and sliding friction force
The force of friction that prevents bodies from moving is called static friction. The frictional force that occurs when a body slides on the surface of another body is called sliding frictional force.
Although the force preventing the bodies from rolling is several times smaller than the sliding friction force, it still exists and is called the rolling friction force.
Kõik kehad muudavad vähemal või suuremal määral oma kuju, kui neid jõuga mõjutada. Sellist keha kuju muutumist nimetatakse deformatsiooniks. Näiteks kui istud toolile, siis tool deformeerub, samuti deformeerub laud, kui asetad sellele raamatu, ning raamat deformeerub ükskõik, kuhu sa selle toetad. Me lihtsalt ei märka neid deformatsioone, kuna need on väga väikesed. Samas paljudel juhtudel on kehade deformatsioon vägagi märgatav. Kuidas deformatsiooni kirjeldada?
Kehasid, mis taastavad oma kuju pärast deformeeriva jõu lõppemist, nimetatakse elastseteks. Kummist ja terasest valmistatud kehad on enamasti elastsed. Kehasid, mis säilitavad oma kuju pärast deformeeriva jõu lõppemist, nimetatakse plastseteks ehk plastilisteks kehadeks. Näiteks plastiliinist valmistatud kehad on plastsed, sama võib öelda leivale määritava või kohta.
Sarnaselt öeldakse, et deformatsioon on elastne, kui deformeeriva jõu lõppemisel keha taastab oma esialgse kuju. Deformatsioon on plastiline, kui deformeeriva jõu lõppemisel keha oma esialgset kuju ei taasta.
Kuju muutmiseks on vaja rakendada jõudu. Keha ise aga takistab oma kuju muutumist. Kehas selle deformeerimisel tekkivat jõudu nimetatakse elastsusjõuks. Elastsusjõud on vastassuunaline keha deformeeriva jõuga.
Elastsete kehade korral kirjeldab kehas tekkivat elastsusjõudu Hooke’i seadus: kehas tekkiv elastsusjõud on võrdeline keha pikenemisega.
Üks ja sama keha võib olla nii elastne kui ka plastiline. Venitades dünamomeetri vedru väikese jõuga, st natuke, taastab ta pärast deformatsiooni oma kuju ja me saame seda uuesti kasutada. Venitades aga vedru suure jõuga – tõmmates vedru sirgeks –, ei taasta vedru endist kuju, vaid jääbki väljavenitatuks. Midagi sarnast toimub ka näiteks joonlauaga, mida saab natuke painutada, aga rohkem painutades läheb see lõpuks katki.
Näidisülesanne
Määra katseliselt tundmatu keha mass. Kasutada on järgmised katsevahendid: tundmatu keha, 100grammine keha, mõõtejoonlaud, kumminiit.
Lahendus
Kumminiiti saame kasutada dünamomeetrina. Kinnitame 100grammise keha kumminiidi külge. Mõõdame kumminiidi pikkuse enne kummi välja venitamist.Mõõdame kumminiidi pikkuse , kui 100grammine keha ripub kumminiidi küljes. Lahutades viimasest kumminiidi esialgse pikkuse , saame teada, kuipalju kumminiit pikenes
Kui keha ripub kumminiidi küljes, siis on elastsusjõud kumminiidis võrdnekeha raskusjõuga. Kumminiidi pikenemine on võrdeline kumminiidis tekkiva elastsusjõuga ning kumminiidi külge kinnitatud keha raskusjõuga.
Teades, et 100grammisele kehale mõjuv raskusjõud on
saame leida ka kumminiiti iseloomustava jäikusteguri väärtuse:
Riputame nüüd sama pika kumminiidi külge tundmatu keha ning mõõdame kumminiidi pikkuse . Tundmatu keha korral venis kumminiit seega
Teades kumminiidi jäikustegurit , saame leida tundmatule kehale mõjuva raskusjõu .
Sellele valemile saab anda ka üldise kuju, kui asendame tuntud keha massi -ga
Vastus: Katses tuleks mõõta kumminiidi pikenemine, kui selle külge on riputatud tuntud ja tundmatu keha. Pärast seda tuleks kasutada arvutuskäigus leitud valemit.
Deformation
The phenomenon where the shape of bodies changes under the influence of force is called deformation. Deformation is elastic when the body recovers its original shape when the deforming force is removed. Deformation is plastic if the body does not return to its original shape when the deforming force is removed
Pehmet saia on kõige parem lõigata hästi terava noaga. Lõigates saia nüri noaga, vajub sai lihtsalt kokku ning lõikamisest ei tule midagi välja. Mida füüsika selle kohta ütleb?
Terava ja nüri noaga lõikamise erinevus seisneb selles, et nugade kokkupuutepindala saiaga on erinev ning lõikekohas avaldatakse saiale küll sarnast jõudu, aga väga erinevat rõhku.
Rõhk iseloomustab rõhumisjõu mõju pinnale. Rõhk arvutatakse jagades rõhumisjõu pindalaga, millele jõud mõjub.
Rõhku tähistatakse tähega p, jõudu tähega F ning kokkupuutepindala tähega S. Seega saame avaldada rõhu valemina
Rõhu ühik on paskal (lühend Pa). Rõhk üks paskal näitab seda, et ühele ruutmeetrisele pinnale rõhub jõud üks njuuton:
Terava noaga lõigates on noa ja saia kokkupuutepindala hästi väike ning lõikekohas saiale avaldatav rõhk on seega palju suurem kui nüri noaga lõigates.
Samamoodi tuleb rõhuga arvestada ka põllutöömasinate ehitamisel. Traktoritel on enamasti suured ja laiad rehvid just seetõttu, et traktori rõhk maapinnale oleks võimalikult väike. Mida väiksema rõhuga traktor maapinda mõjutab, seda vähem vajub traktor pehmesse pinnasesse ning vajutab seda vähem kokku.
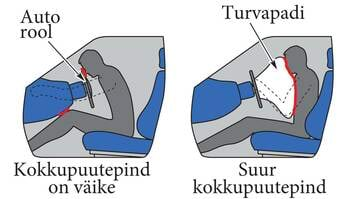
Kui autos ei ole turvapatja, lendab autojuht autode kokkupõrkel vastu rooli (nüüd me juba teame, et selles avaldub keha inertsus). Kuna inimese ja rooli vaheline kokkupuutepindala on väike, mõjub seal inimesele suur rõhk – seetõttu võivad näiteks roided murduda.
Kui autos on turvapadi, siis lendab inimene avarii korral vastu turvapatja. Kuna turvapadja ja inimese vaheline kokkupuutepindala on palju suurem, siis mõjub inimesele palju väiksem rõhk ning vigastused, mis võivad tekkida, on samuti palju väiksemad.
Näiteid rõhu hindamise kasulikkusest on lõputult. Terav või nüri naaskel, lumeräätsad, tikk-kontsad ...
Näidisülesanne
Mitu korda suuremat rõhku avaldab kaaluv õpilane põrandale, kui ta tooliga kiigub võrreldes sellega, kui ta toolil istub? Neljal jalal seistes on tooli ühe jala ja põranda kokkupuutepindala . Kiikudes on tooli ühe jala ja põranda kokkupuute pindala umbes . Tooli massi võib antud ülesandes jätta arvestamata.
Lahendus
Kui õpilane istub toolil, mõjutab tool põrandat nelja jalaga, seega kogu kokkupuutepindala on S1=4⋅3cm2=12cm2. Kiikudes toetab tool põrandat kahe jalaga, seega kokkupuutepindala on S2=2⋅0,1cm2=0,2cm2.
Andmed
m=50kg
S1=4⋅3cm2=12cm2=0,0012m2
S2=2⋅0,1cm2=0,2cm2=0,00002m2––––––––––––––––––––––––––––––––––––––––––––
p1−?
p2−?
Arvutused:
p1=FS1=4900,0012=408333Pa=408kPa
p2=FS2=4900,00002=24500000Pa=24500kPa
k=p2p1=24500408=60korda––––––––––––––––––
Vastus. Tooliga kiikudes avaldab õpilane põrandale korda suuremat rõhku kui rahulikult toolil istudes.
Tahketes kehades mõjub rõhk ainult ühes kindlas suunas. Nuga mõjutab saia peamiselt vajutamise suunas. Kui toolil istuda, mõjutab tool põrandat raskusjõu mõju suunas. Vedelikes ja gaasides mõjub rõhk teistmoodi. Kuidas?
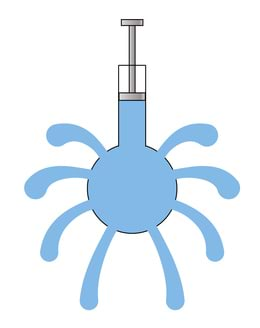
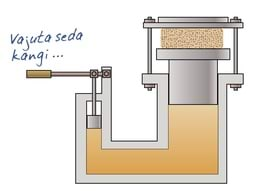
Võtame õõnsa kera, milles on palju väikseid avasid, ja avaldame keraga ühendatud silindri kaudu keras olevale vedelikule rõhku. Rõhu mõjul purskab vedelik välja ka rõhu mõju suunaga vastupidistes suundades, joonisel otse üles. Sarnaseid katseid võib välja mõelda veelgi:
Selliste katsete põhjal saab sõnastada üldise seaduse, mida tuntakse Pascali seaduse nime all.
Vedelikule või gaasile avaldatud rõhk levib vedelikes ja gaasides igas suunas ühtemoodi.
Rõhu levimist vedelikes ja gaasides uuris Blaise Pascal (1623–1662), kes oli Prantsuse matemaatik, füüsik ja filosoof. Teda peetakse üheks hüdrostaatika (teadusharu, mis uurib tasakaalus olevat vedelikku) rajajaks. Oma eksperimentide tulemusena sõnastas ta seaduse, mida tuntakse kui Pascali seadust, mille kohaselt kandub rõhk vedelikes ja gaasides edasi igas suunas ühtlaselt. Pascal oli ka üks esimesi, kes arvutas välja atmosfääri ligikaudse massi.
Pascal ei piirdunud ainult teoreetiliste uurimistega. Selleks, et abistada oma matemaatikust isa arvutuste juures, leiutas ta mehaanilise arvutusmasina, milles oli kaheksa liikuvat ketast. Selle abil oli võimalik arvutada kuni 8kohalisi summasid.
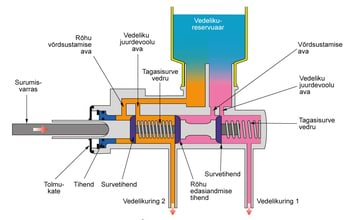
Pascali seaduse rakendusi me kohtame igapäevaelus väga tihti. See on ju tegelikult väga mugav – kui avaldad vooliku ühes otsas selle sees olevale vedelikule rõhku, siis vooliku teises otsas mõjub seesama rõhk millelegi, mida on vaja liigutada. Ja seda jõudu on võimalik lihtsalt jagada, kui lisada voolikule üks või mitu haru. Kastmissüsteemid, autode pidurisüsteemid, linnade ja majade veevärk ... seda nimekirja võiks jätkata pikalt.
| Sõiduauto piduripumba ehitus. Õli surutakse kahte voolikusse, üks läheb esimeste, teine tagumiste rataste juurde. Autodes kasutatavad hüdraulikaseadmed on tihti ootamatult nutikad. See pump näiteks surub õli vedelikuringi 1 ka siis, kui vedelikuringi 2 voolik läbi lõigata. Ja vastupidi. Kas oskad näha, kuidas see võimalik on? | Väliselt näeb piduripump välja niisugune. |
Olgu meil kolm ühesugust klaasi, üks on täidetud liiva, teine vee ja kolmas vatiga. Milline neist klaasidest on kõige raskem?
Oma kogemuse põhjal oskame kohe öelda, et kõige raskem on liivaga täidetud klaas ning kõige kergem vatiga täidetud klaas. Oleme sellega tihti kokku puutunud, et ühesuguse ruumalaga kehade massid on erinevad. Ütleme selle kohta, et liiv on kõige suurema tihedusega ning vatt kõige väiksema tihedusega.
Aine tihedus on füüsikaline suurus, mis näitab, kui suur on ühe ruumalaühiku aine mass.
Teame ka, et aine tiheduse definitsiooni saab kirja panna kujul:
Tiheduse ühik on massiühik jagatud ruumalaühikuga. Sagedamini kasutatavad ühikud on g/cm3, kg/dm3 ja kg/m3.
Meile kõige olulisem aine on vesi ning selle tihedust võikski peast teada. Vee ligikaudne tihedus väljendatuna erinevates ühikutes on
ρvesi = 1 g/cm3 = 1 kg/dm3 = 1000 kg/m3
Nende kehade puhul, mis koosnevad mitmest ainest, saame leida keha keskmise tiheduse. Keha keskmise tiheduse leidmiseks jagame keha kogu massi keha kogu ruumalaga. Suured laevad seisavad samuti vee peal, sest laevas on palju ruumi, mida täidab ainult õhk, ning laeva keskmine tihedus on vee tihedusest palju väiksem.
Aine tiheduse teadmine on oluline erinevate masinate ehitamisel. Näiteks peavad olema lennukid tehtud väikese tihedusega kergest materjalist, et lennuki mass oleks võimalikult väike. Enamasti kasutatakse lennukite ehitamisel alumiiniumi sulameid, kuna need on tugevad, kuid võrreldes rauaga kolm korda väiksema tihedusega.
Tihti on meil vaja teisendada tiheduse ühikuid ühest mõõtühikust teise. Teades vee tihedust erinevates ühikutes, on kerge teisendada ka kõigi teiste ainete tihedusi. Näiteks alumiiniumi tihedus on 2700 kg/m3. Meil on vaja seda väljendada ühikutes g/cm3. Teades, et vee tihedus on 1000 kg/m3 = 1 g/cm3, saab öelda, et alumiiniumi tihedus on 2700 kg/m3 = 2,7 kg/dm3 = 2,7 g/cm3. Vee tiheduse ühikutest näeme, et ühikud kg/m3 ning g/cm3 erinevad teineteisest 1000 korda, seega erinevad ka alumiiniumi tiheduse ühikud 1000 korda.
Kui meil on aga vaja väljendada alumiiniumi tihedus mõnes teises ühikus, näiteks g/dm3, peame teisendama eraldi massiühiku ja ruumalaühiku.
1 kg = 1000 g
1 m3 = 1000 dm3
Teisendades saame
Tuletame ka meelde, et ainete tihedus sõltub temperatuurist. Kõige rohkem mõjutab temperatuur gaaside tihedust. Vedelike ja tahkete ainete tihedus muutub temperatuuri tõustes või langedes vähe. Vee täpne tihedus 4 ˚C juures on 0,997 g/cm3, kuid tabelis on antud ümardatud tihedus (1,0 g/cm3).
Tahkete ainete tihedused 20°juuresVedelike tihedused 25°juuresGaaside tihedused 0°juuresAine tihedus
Aine tihedus on füüsikaline suurus, mis näitab, kui suur on ühe ruumalaühiku aine mass. Selle definitsiooni saab kirja panna kujul
Tiheduse ühikuks on kg/m3. Nende kehade puhul, mis koosnevad mitmest ainest, saame leida keha keskmise tiheduse.
Kui suurt rõhku peaksime taluma sügaval vee all? Et seda teada saada, lahendame lihtsama ülesande ja uurime, millist rõhku avaldab vesi anuma põhjale. Teeme seda nii, nagu füüsikas kombeks – kasutame olemasolevaid üldiseid teadmisi uute teadmiste tuletamiseks.
Let the bottom area of the cylindrical container be S and the height of the liquid column in it be h . The volume of water in the container is therefore:
We can find the mass of water through the density of water:
Knowing the mass of the water, we can find the force of gravity that the water exerts on the bottom of the container:
Using the pressure definition formula, we calculate the water pressure at the bottom of the container:
perhaps
Kokkuvõttes võime öelda, et vedelikusamba rõhk on võrdne vedelikusamba kõrguse, vedeliku tiheduse ja raskuskiirenduse g korrutisega. Tulemusest näeme ka, et rõhk anuma põhjale ei sõltu vedelikusamba mõõtmetest (anuma põhja pindalast) – ehkki me ülesande lahendamist alustades arvestasime põhja pindalaga, siis lahenduse käigus see taandus valemitest välja.
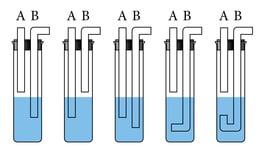
Detailsemad arvutused näitavad, et rõhk anuma põhjale ei sõltu ka anuma kujust. Veendume selles katseliselt, vaadeldes vedelikku erineva kujuga ühendatud torudes (vt pilt allpool). Katses näeme, et vedeliku tase kõigis torudes on ühesugune, ehkki torude kuju, seega ka vedeliku kogus torudes on erinev. Selline olukord on võimalik vaid juhul, kui rõhk on ühesugune kõikide torude ühenduskohtades alumise horisontaalse toru külge. Tõepoolest, kui rõhud oleksid erinevad, hakkaks vedelik voolama väiksema rõhuga torusse.
Näidisülesanne
Kui suurt rõhku avaldab silindrilises klaasis olev vesi klaasi põhjale, kui klaas on ääreni vett täis? Klaasi põhjapindala on .
Lahendus
Vedeliku poolt avaldatud rõhu leidmiseks peame teadma vedeliku tihedust ning vedelikusamba kõrgust. Kuna me teame, et klaasi ruumala on ning põhjapindala , saame leida, kui kõrgele vedelik klaasi põhjast ulatub.
Andmed
V=200cm3
S=25cm2
ρ=1,0g/cm3=1000kg/m3–––––––––––––––––––––––––––––––
p−?
Arvutused:
p=1000kg/m3⋅9,8N/kg⋅0,08m≈780Pa––––––––––––––
Vastus. Vedelik avaldab klaasi põhjale rõhku 780Pa.
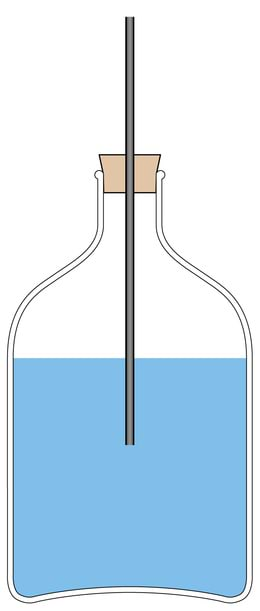
Manomeeter on seade, millega saab mõõta vedeliku või gaasi poolt anuma seintele avaldatavat rõhku. Pascali seaduse järgi on see ühtlasi rõhk vedeliku või gaasi sees. Üheks lihtsamaks manomeetriks, mida saab ise ehitada, on U-toru manomeeter. Kuidas see töötab?
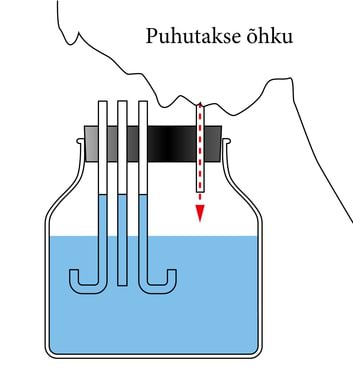
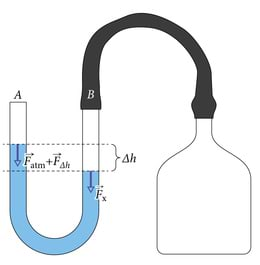
Uurime veega täidetud U-kujulist toru (U-toru), mis on osaliselt täidetud veega ja mille üks ots on kummivoolikuga ühendatud kinnise anumaga, kus oleva gaasi rõhku me mõõta tahame. Vedeliku sambad U-toru haarades on erinevatel kõrgustel, järelikult erineb rõhk anumas atmosfäärirõhust. Aga kui palju?
Rõhk ühendatud anumates on igal kõrgusel ühesugune, sest muidu hakkaks vedelik anumas voolama kõrgema rõhuga piirkonnast madalama rõhuga piirkonda. Seega on rõhk õhu ja vee piiril haaras B samasugune kui rõhk vees sellel kõrgusel haaras A. Järelikult on uuritavas anumas rõhk parajasti sama palju atmosfäärirõhust suurem, kui palju avaldab rõhku Δh kõrgune vedelikusammas. Nii et saame kirjutada:
ja
Tulemusest näeme, et kui mõõdame selliselt ühendatud U-torus ära Δh ja teame atmosfäärirõhku patm, siis saame leitud valemi abil arvutada rõhu anumas px. Näeme ka, et U-toruga saab mõõta rõhu erinevust atmosfäärirõhust, st tulemuse saamiseks peame teadma atmosfäärirõhku patm.
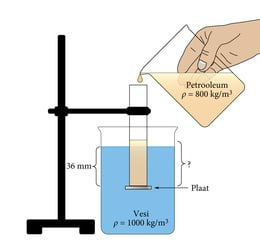
U-toru on osaliselt täidetud veega. U-toru ühte harusse kallatakse kõrgune toiduõli kiht. Kui palju muutub veetase teises toru harus võrreldes veetasemega enne toiduõli lisamist? Vee tihedus on ning toiduõli tihedus .
Lahendus
Joonistame kujutletava sirge õli ja vee piirpinnalt horisontaalselt U-toru teisele haarale. Selliselt eraldame ainult veega täidetud U-toru harus osa vedelikusambast. Rõhk samal sügavusel vees on ühendatud anumates igal pool sama. Seega on rõhk kujutletava sirgega määratud kõrgusel mõlemas U-toru harus ühesugune. Ja rõhk, mida avaldab toiduõli sellel kõrgusel, on sama suur kui rõhk, mida avaldab vesi U-toru teises harus samal kõrgusel.
Andmed
ρvesi=1,0g/cm3=1000kg/m3
ρ˜oli=0,9g/cm3=900kg/m3
h˜oli=2cm=0,02m–––––––––––––––––––––––
hvesi=?
Arvutused
p˜oli=ρ˜oligh˜oli=900kg/m3⋅9,8N/kg⋅0,02m=176,4Pa
Avaldades rõhu arvutamise valemist vedelikusamba kõrguse ja kasutades seda seost, saame:
hvesi=pvesiρvesig=176,4Pa1000kg/m3⋅9,8N/kg=0,018m=1,8cm
Niisiis, veetase ühes torus on 1,8cm kõrgemal kui veetase (vee ja toiduõli piirpind) teises harus. Ilma toiduõlita oleksid veetasemed samal kõrgusel ehk siis 0,9cm allpool.
Vastus. Veetase tõuseb toiduõli lisades 0,9cm võrra.
Tehnoloogias ja teaduses on vaja vedelikus või gaasis olevat rõhku päris tihti mõõta – autoga sõites me kontrollime pidevalt rõhku mootori õlisüsteemis, lennukis kontrollitakse rõhku salongis, edaspidi räägime ka õhurõhu mõõtmisest. Nii on olemas ka väga erinevaid manomeetreid.
Üheks lihtsamaks metallmanomeetriks on suletud otsaga poolkaarekujuline toru. Kui sellises torus rõhk kasvab, siis hakkab toru sirgemaks painduma samamoodi, nagu tühja piklikku õhupalli õhku puhudes ajab see ennast sirgu. Elastsusjõud aga takistab toru paindumist. Mida suurem on torus olev rõhk, seda rohkem toru paindub, toru külge on kinnitatud osuti ja skaalalt on võimalik rõhk välja lugeda.
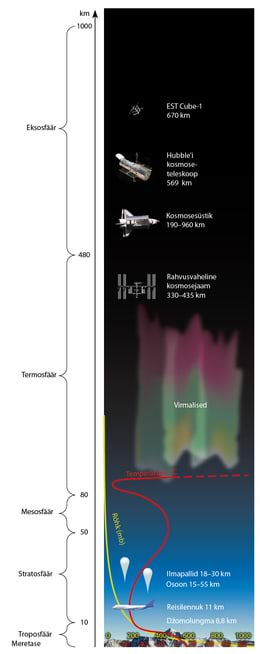
Maa atmosfääri poolt avaldatavat rõhku nimetatakse õhurõhuks. Õhurõhku me ise ei taju, kuna see mõjutab meid kogu aeg ning me oleme sellega harjunud. Aga me tajume õhurõhu kiiret muutumist – lennuki maandumisel ja õhkutõusmisel, autoga mäest üles või alla sõites, isegi kiires liftis lähevad meie kõrvad lukku. Kuidas õhurõhk tekib ja miks on ta erinevatel kõrgustel erinev?
Atmosfääris tekkivast õhurõhust saab mõelda sarnaselt sellega, nagu tegime vedelikusamba poolt anuma põhjale avaldatavat rõhku arvutades. Kujutagem lihtsalt ette, et atmosfäär on kui üks tohutu õhuookean, mida gravitatsioonijõud õhukese kihina Maa ümber hoiab. Oma igapäevaelus jalutame selle õhuookeani põhjas. Sellisest kujutluspildist peaks meile kohe selge olema, et õhurõhk on see, kui ülemised atmosfäärikihid suruvad alumisi. Ja kuna kõrgel mägedes on õhu kiht meie kohal õhem, peab seal ka õhurõhk väiksem olema.
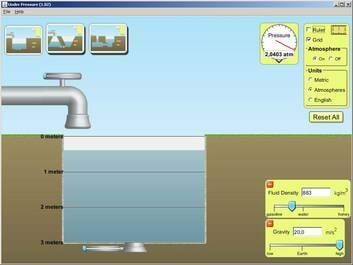
Siiski õhurõhku ei ole võimalik arvutada valemiga p = ρhg. Põhjuseks on see, et erinevalt vedelikest saab gaase kokku suruda ja nii on kõrgemal õhu tihedus väiksem (õhk on hõredam). Õhurõhu väärtust erinevatel kõrgustel saame teada tabelitest ja joonistelt, üks selline on ka juuresoleval pildil. Aga kuidas õhurõhku mõõta?
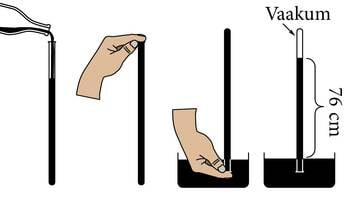
Õhurõhku on võimalik mõõta kaudsel teel. 1643. aastal tegi Itaalia füüsik Torricelli katse, kus ta täitis ühest otsast suletud toru elavhõbedaga ning asetas selle tagurpidi elavhõbeda anumasse. Osa elavhõbedast voolas torust välja ning torusse jäänud elavhõbeda kõrgus oli 760 mm. Torricelli kordas katset erineva kuju ning pikkusega elavhõbeda toruga, kuid torusse jäänud elavhõbeda kõrgus oli ikka 760 mm. Järelikult ei mõjuta tulemust mitte toru kuju, vaid välised tegurid – ehk siis õhurõhk. Seega saab sellist katseseadet kasutada õhurõhu mõõtmiseks.
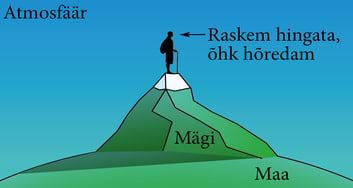
| Nii tegi Torricelli oma katset. Elavhõbeda samba kõrgus torus sõltub vaid õhurõhust. | Kõrgel mägedes on raskem hingata. Selle põhjuseks on väiksem õhurõhk – kopsudes asuvad alveoolid, milles on respiratoorne membraan, kust kaudu toimub hapniku omastamine. Aga need membraanid ei toimi enam, kui hapniku rõhk kopsudes ei ole piisavalt suur. |
Sellest katsest pärineb ka laialdaselt kasutatav kokkuleppeline normaalrõhu suurus 760 mmHg (loe 760 millimeetrit elavhõbeda sammast). Paskalites teeb see ligikaudu 100 000 Pa (p = ρgh = 13600 · 9,8 · 0,76 = 101 292,3 Pa).
Torricelli kasutatud seadet nimetatakse elavhõbebaromeetriks – elavhõbedaga täidetud toru saab varustada skaalaga ja rõhu ühikuks on siis mmHg. Tänapäeval on elavhõbe kui tervisele kahjulik aine tavakasutuses keelatud ja õhurõhku mõõdetakse teistsugustel põhimõtetel töötavate baromeetritega.
Õhurõhu muutused põhjustavad ilma muutusi. Seetõttu on baromeetreid kasutatud ka ilma ennustamiseks. Tõepoolest, kui õhurõhk on mingis piirkonnas kõrgem kui normaalrõhk, siis on selle piirkonna kohal kõrgrõhkkond. Suvel kaasneb sellega enamasti ilus selge ilm ning võib esineda kuumalaineid. Talvel aga võib kõrgrõhkkonnaga kaasneda käre pakane. Kui õhurõhk on mingis piirkonnas normaalrõhust väiksem, siis valitseb selles piirkonnas madalrõhkkond, mis toob endaga kaasa enamasti pilvise ilma ning sademed. Suvel kaasneb sellega ilma jahenemine, kuid talvel seevastu ilma soojenemine.
Ka meie kõrv mõõdab omal moel rõhku. Et sisekõrv ei ole atmosfääriga ühenduses, siis õhurõhu muutudes tekib kahel pool trummikilet rõhkude erinevus. Sellise rõhkude erinevuse tõttu surutakse trummikilet kas sissepoole (õhurõhk suureneb) või tõmmatakse seda väljapoole (õhurõhk väheneb). Neelatamisel see tunne enamasti kaob, kuna neelamise ajal ühendatakse sisekõrv välisõhuga ning rõhud kõrvas võrdsustuvad.
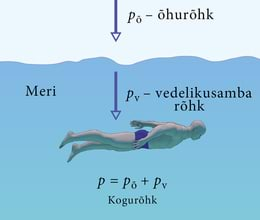
Paneme tähele, et ka vee all mõjutab meid lisaks vedelikusamba rõhule ka õhurõhk – see mõjub vedeliku pinnale ning kandub siis Pascali seaduse kohaselt ka vee alla. Seega võime öelda, et rõhk vedelikes võrdub õhurõhu ja vedelikusamba rõhu summaga.
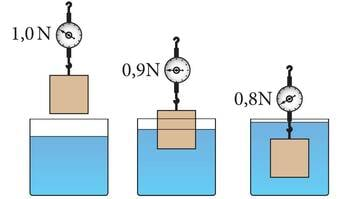
Vesi mõjutab vette asetatud keha ka sel moel, et „lükkab“ seda ülespoole. Oleme seda nähtust kindlasti tähele pannud, kui kergeid esemeid vee alla surume. Jõudu, mis lükkab vedeliku või gaasi sisse asetatud keha ülespoole, nimetatakse üleslükkejõuks. Miks see jõud tekib ja kui suur see on?
Üleslükkejõu uurimiseks riputame dünamomeetri külge metallkeha ning sukeldame selle järk-järgult vette, samal ajal dünamomeetri näitu jälgides. Katses näeme, et dünamomeeter näitab kõige suuremat jõudu siis, kui keha on õhus. Kõige väiksem jõud mõjub dünamomeetrile siis, kui keha on täielikult vee all.
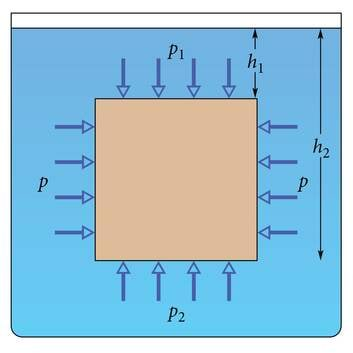
Üleslükkejõu tekkimise põhjuste mõistmiseks vaatleme vette asetatud metallist kuupi küljepindalaga ning uurime, millised jõud sellele kuubile mõjuvad.
Teame, et rõhk vedelikus sõltub vaid vedelikusamba kõrgusest. Seega on paremalt ja vasakult ning eest ja tagant klotsi külgedele avalduvad rõhumisjõud võrdsed ja need jõud klotsi liigutada ei saa. Samas klotsi ülemisele ja alumisele tahule mõjuvad rõhumisjõud on erinevad – kuna alumine tahk on sügavamal vees, avaldab vesi sellele suuremat rõhku. Et ülespoole suunatud jõud on suurem kui allapoole suunatud jõud, siis on ka summaarne jõud suunatud üles. See ongi üleslükkejõud.
Kuidas üleslükkejõudu arvutada? Teame, et ülemisele tahule avaldab vesi rõhku p1=ρgh1 ning alumisele tahule rõhku p2=ρgh2. Ülemisele ja alumisele tahule mõjuva jõu saame arvutada rõhu valemist , kus on klotsi ülemise ja alumise tahu pindala:
ning
Summaarne jõud, mida vesi klotsile avaldab, on nende jõudude vahe ning see on suunatud alt üles.
Kõrguste ja vahe on klotsi kõrgus, järelikult on korrutis S(h2−h1) klotsi ruumala . Seega saame kuubile mõjuva üleslükkejõu kirja panna valemina
Seda valemit saab kasutada igasuguse kujuga kehadele mõjuva üleslükkejõu arvutamiseks. Vedelikes kehale mõjuv üleslükkejõud on arvuliselt võrdne selle vedeliku tiheduse, raskuskiirenduse ja vedelikus oleva keha ruumala korrutisega.
Tuleme nüüd tagasi katse juurde, kus osaliselt vette sukeldatud keha korral näitas dünamomeeter suuremat jõudu (ja väiksemat üleslükkejõudu) kui täielikult vette sukeldatud keha korral.
Ilmselt saab vedelik üleslükkejõudu avaldada vaid sellele osale kehast, mis on reaalselt vette sukeldatud. Kui keha on vaid osaliselt sukeldatud, siis peaks vähenema ka üleslükkejõud, ja seda kinnitab ka katse.
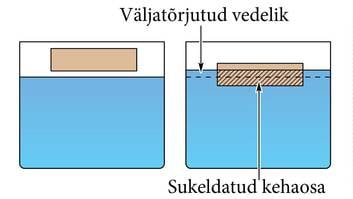
Kui uurime üleslükkejõu valemit, siis näeme, et selle parema poole võib kirja panna kui , kus on sellise vedeliku koguse mass, mille ruumala võrdub vedelikku sukeldatud keha ruumalaga. Sellise veekoguse kohta võime öelda, et see on keha poolt välja tõrjutud vedelik. Seega võib kehale mõjuvat üleslükkejõudu defineerida ka välja tõrjutud vedeliku hulga kaudu. Vedelikku sukeldatud kehale mõjuv üleslükkejõud on võrdne keha poolt välja tõrjutud vedelikule mõjuva raskusjõuga.
Üleslükkejõud mõjub ka gaaside korral, kuid enamasti me seda tähele ei pane, kuna gaasi tihedus on väga väike. Gaasides mõjuvat üleslükkejõudu märkame näiteks heeliumiga täidetud õhupalli korral.
Näidisülesanne
Kui suurt jõudu tuleb rakendada, et tõsta vee all olevat 104kg raskust graniidist kivi? Graniidi tihedus on 2,6g/cm3.
Lahendus
Vee all mõjub kivile raskusjõud ning vee üleslükkejõud. Üleslükkejõud on raskussuunale vastupidine, seega aitab üleslükkejõud kivi tõsta. Kivile rakendatav jõud on nende jõudude vahe.
Andmed
m=104kg
ρvesi=1000kg/m3
ρkivi=2,6g/cm3=2600kg/m3––––––––––––––––––––––––––––––––––
Ft˜oste−?
Arvutused
Vkivi=mρkivi=104kg2600kg/m3=0,04m3
Ft˜oste=Fr−F¨u=1019N−392N=627N≈630N––––––––––––
Vastus Kivi tõstmiseks vees tuleb rakendada jõudu 630N.
Buoyant force on the body in liquid
The buoyant force acting on a body in liquids is numerically equal to the product of the density of the liquid, the acceleration of gravity and the volume of the body in the liquid:
This also means that the buoyant force acting on a body immersed in a liquid is equal to the force of gravity acting on the liquid displaced by the body.
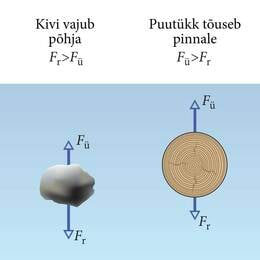
Vette asetatud kivi vajub põhja. Vette asetatud puutükk tõuseb pinnale isegi siis, kui seda vee alla vajutada. Kui suure puidust parve peaks ehitama, et see kivi raskuse all põhja ei vajuks?
Me juba teame, et vees olevatele kehadele mõjub kaks jõudu – keha raskusjõud, mis on suunatud alla, ning vedeliku üleslükkejõud, mis on suunatud üles. Kivi raskusjõud on vee üleslükkejõust suurem, mistõttu keha vajub põhja. Puutüki puhul on aga vee üleslükkejõud suurem kui puutükile mõjuv raskusjõud, mistõttu tõuseb puutükk pinnale.
Pöörame nüüd tähelepanu ka sellele, et pinnale tõustes jääb osa puidust veest välja. Tõepoolest, et veest välja kerkides puutükile mõjuv üleslükkejõud väheneb, siis mingil hetkel üleslükkejõud ja raskusjõud võrdsustuvad. Puutükk jääb veepinnale ujuma.
Raskusjõudu ja üleslükkejõudu võrreldes võime niisiis öelda, et keha ujub, kui kehale mõjuv üleslükkejõud on arvuliselt võrdne keha raskusjõuga ning osa kehast on veest väljas. Kui keha asub täielikult vedelikus ning üleslükkejõud ja raskusjõud on arvuliselt võrdsed, siis ütleme, keha heljub. Kui keha raskusjõud on suurem kui kehale mõjuv üleslükkejõud, siis keha upub.
Seostame nüüd ujumise ja uppumise tingimuse keha omadustega. Vaatleme massiga m ning tihedusega ρk klotsi, mis heljub vees. Klotsile mõjuv raskusjõud on . Avaldades klotsi massi tiheduse kaudu, saame:
kus V on klotsi ruumala. Klotsile mõjuv üleslükkejõud on
kus on vee tihedus. Kuna me teame, et heljumise korral on Fr=F¨u, siis saame kirjutada
Lihtsustades avaldist, saame heljumise tingimuseks
Seega sõltub keha heljumine vees keha ja vedeliku tihedusest, mitte keha mõõtmetest. Keha heljub, kui keha ja vedeliku tihedused on võrdsed. Raskusjõu ja üleslükkejõu võrdlusest saame ka järeldada, et keha ujub, kui keha tihedus on vedeliku tihedusest väiksem, ning keha upub, kui keha tihedus on vedeliku tihedusest suurem.
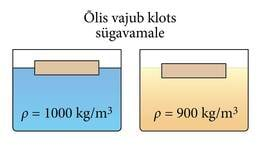
Kui uurime puidust klotsi ujumist vees ja õlis, siis näeme, et õlis vajub see natuke sügavamale kui vees. See on ka oodatav tulemus – õli tihedus (900 kg/m3) on vee tihedusest (1000 kg/m3) väiksem, seega mõjub õlis klotsile väiksem üleslükkejõud.
Sellest saab järeldada, et mida suurem on vedeliku tihedus võrreldes keha tihedusega, seda väiksem osa ujuvast kehast asub vedelikus. Seda asjaolu kasutatakse vedelike tiheduste mõõtmiseks areomeetriga. Areomeetri alaosas paikneb koormis ning ülaosas peenike skaalaga toru. Areomeeter asetatakse vedelikku ning selle järgi, kui sügavale areomeeter sukeldub, saab teada vedeliku tiheduse.
Näidisülesanne
Kolmeliitrise metallist kausi mass on 200 grammi. Kauss koos puuviljadega pannakse vee peale ujuma. Mitu kilogrammi puuvilju võib kausis olla, et kauss ujuks vee peal?
Lahendus
Kauss jääb vee peale ujuma, kui kausi ja puuviljade keskmine tihedus on väiksem (piirjuhul võrdne) vee tihedusega.
Andmed
mkauss=200g=0,2kg
Vkauss=3dm3=0,003m3
ρvesi=1000kg/m3––––––––––––––––––––
mpuuviljad−?
Arvutused
mkaussjapuuviljad=ρkaussjapuuviljad⋅Vkauss=1000kg/m3⋅0,003m3=3kg
mpuuviljad=mkaussjapuuviljad−mkauss=3kg−0,2kg=2,8kg––––––––––––––
Vastus. Kauss jääb vee peale ujuma, kui seal on vähem kui 2,8kg puuvilju.
Keha ujumine, ujumise ja uppumise tingimus
Raskusjõudu ja vees kehale mõjuvat üleslükkejõudu võrreldes võime öelda, et keha ujub, kui kehale mõjuv üleslükkejõud on arvuliselt võrdne keha raskusjõuga ning osa kehast on veest väljas. Kui keha asub täielikult vedelikus ning üleslükkejõud ja raskusjõud on arvuliselt võrdsed, siis ütleme, keha heljub. Kui keha raskusjõud on suurem kui kehale mõjuv üleslükkejõud, siis keha upub. Heljumise korral:
Igapäevaelus kasutame sõnu töö ja energia väga erinevates tähendustes. Räägime näiteks, et käimiseks, jooksmiseks ja mõtlemiseks kulub energiat. Töö võib olla näiteks kraavi kaevamine, rääkimine, laulmine või auto juhtimine. Aga kuidas tööd ja energiat mõõta?
Käesolevas peatükis uurime mehaanilist tööd. Mehaanilist tööd tehakse siis, kui keha liigub mingi jõu mõjul. Lükates kappi ühest kohast teise, kulutame energiat ja teeme mehaanilist tööd. Üritades lükata seina või näiteks veoautot, me küll väsime, kuid mehaanilist tööd samal ajal ei tee, kuna sein või veoauto ei liigu.
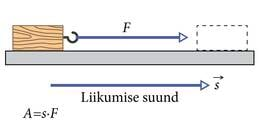
Mehaaniline töö võrdub kehale rakendatud jõu ning selle jõu mõjul läbitud teepikkuse korrutisega.
Kapi nihutamisel kolme meetri võrra teeme kolm korda rohkem tööd kui kapi nihutamisel ühe meetri võrra. Kelgu vedamiseks jäisel lumel kulutame palju vähem energiat (teeme vähem tööd) kui kelgu vedamiseks liivatatud lumel, kuna hõõrdejõud jääl on palju väiksem ja seega peame rakendama palju väiksemat jõudu. Füüsikas tähistatakse tehtud tööd tavaliselt tähega A, jõudu tähega F ning teepikkust tähega s. Vastavalt saame töö definitsiooni kirja panna valemiga:
Töö ühikuks on džaul (lühend J). Tehtud töö suuruseks on 1 džaul siis, kui kehale rakendatakse jõudu 1 njuuton ning keha liigub selle mõjul 1 meetri: 1 J = 1N · m.
Näidisülesanne
Kui palju tööd peab tegema koer, et vedada kelku 100 meetri kaugusele? Kelk koos koormaga kaalub 150kg ning hõõrdejõud kelgu ja lume vahel moodustab 3% kelgule mõjuvast raskusjõust.
Lahendus
Kelgu ühtlase vedamise korral on koera veojõud võrdne kelgule mõjuva hõõrdejõuga.
Andmed
mkelk=150kg
s=100m
p=3%––––––––
A−?
Arvutused
Vastus. Koer peab tegema tööd 4,4kJ.
Aga kuidas jääb energiaga? Mis see on, kust seda saab ja kui palju seda kulub?
Füüsikas nimetatakse energiaks keha (või kehade süsteemi) võimet teha tööd. Näiteks omab Maa gravitatsiooniväljas üles tõstetud pall energiat – lastes palli lahti, hakkab see raskusjõu mõjul allapoole liikuma ja sealjuures tehakse mehaanilist tööd. Kuna tööd tehakse energia arvelt, siis on ka energia ühikuks džaul.
Alljärgnevast kahest pildist vasakpoolsel toodetakse inimestele füüsika poolt käsitletavat energiat. Ka laulukaare alt saavad inimesed energiat, aga see on üks hoopis teistmoodi energia, mida füüsika seni veel ei käsitle.
Kui palju energiat kulub ühe või teise töö tegemiseks? Mehaanilise tööga on lihtne – kui me teeme kapi nihutamiseks mehaanilist tööd 10 džauli, siis me kulutame selleks ka energiat 10 džauli.
Aga kui palju vajab rakett või lennuk energiat, et sihtkohta jõuda? Kui kaugele saab elektriautoga ühe laadimisega sõita? Kui palju peaks sööma pärast väsitavat füüsilist trenni? Aga pärast malemängu? Reaalse elu probleemid on reeglina palju keerulisemad kui need, millega me siin õpikus tegeleme. Aga selles osas ei erine teadus palju viiulimängust – võib ju üritada kohe Paganini esimest viiulikontserti mängima hakata, aga pigem tasuks alustada poogna õigest hoidmisest ja mõnest lihtsamast muusikapalast.
Mechanical work
Mechanical work is done when a body moves under the influence of a force. Mechanical work is equal to the product of the force applied to the body and the distance covered under the influence of this force:
The unit of work is the joule (abbreviation ). The amount of work done is 1 joule when a force of newton is applied to the body and the body moves meter under its influence: .
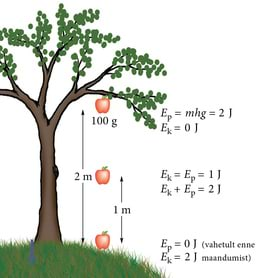
Energiaks me nimetasime keha võimet teha tööd. Aga kumb õun on võimeline rohkem tööd tegema, kas see, mille endale pealaele asetame, või see, mis meile puu otsast pähe kukub? Kas liikumisel on ka energia? Aga puu otsas rippumisel?
Puu otsas rippuvale õunale mõjub raskusjõud. Kui õun tuleb oksa küljest lahti, kukub see maha. Me oskame arvutada ka kukkudes tehtava töö – kui õun massiga m kukub kõrguselt h alla, siis saame kirjutada:
kus F = mg on õunale mõjuv raskusjõud. Kuna läbitud teeks on kõrguste vahe, siis oleme selle tähistanud tähega h. Kus on selles pildis energia?
Me teame, et puu otsas rippuva õuna ja Maa vahel toimib gravitatsiooniline vastastikmõju ja õuna alla kukkumisel teeb tööd gravitatsioonijõud. Järelikult on otsitav energia „salvestunud“ gravitatsioonilises vastastikmõjus. See energia on õunal puu otsas rippudes kogu aeg olemas, aga see vabaneb, st hakkab tööd tegema alles hetkel, kui õuna vars puu küljest lahti tuleb ja õunal tekib võimalus alla kukkuda.
Energiat, mida kehad omavad vastastikmõju tõttu, nimetatakse potentsiaalseks energiaks.
Maapinnast kõrgusel h olev õun omab niisiis potentsiaalset energiat:
Kui õun hakkab puu otsast kukkuma, siis õuna potentsiaalne energia väheneb, sest õun läheneb maapinnale. Aga energia ei saa lihtsalt ära kaduda. Kukkuva õuna kiirus kasvab ning selle potentsiaalne energia muutub liikumise energiaks ehk kineetiliseks energiaks.
Kineetiliseks energiaks nimetatakse energiat, mida keha omab liikumise tõttu.
Kehade kineetilise ja potentsiaalse energia summat me nimetame keha mehaaniliseks koguenergiaks. Oletame hetkeks, et keha liikumist ei takista kõrvalised jõud – näiteks kukkuva õuna korral puudub õhutakistus, veereva palli korral puudub hõõrdumine. Sel korral kehtib mehaanilise energia jäävuse seadus, mis ütleb, et keha või kehade süsteemi mehaaniline koguenergia ei muutu, see on jääv suurus:
Selgub, et keha kineetiline energia sõltub keha massist ja keha kiirusest kujul
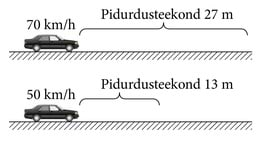
Pange tähele – valemis on kiiruse ruut. See tähendab muuhulgas seda, et sõites autoga kaks korda kiiremini, on auto kineetiline energia neli (22 = 4) korda suurem. Järelikult on ka auto pidurdusteekond kaks korda suurema kiiruse korral umbes neli korda suurem.
Näidisülesanne
Millise kiirusega põrkab 100grammine pall vastu maad, kui ta lasta nelja meetri kõrguselt alla kukkuda?
Lahendus
Algselt on pallil ainult potentsiaalne energia. Kineetiline energia on null, kuna pall ei liigu. Maapinnale jõudes muutub palli kogu potentsiaalne energia kineetiliseks energiaks.
Andmed
h=4m
m=100g=0,1kg–––––––––––––––––––––
v−?
Arvutused
Vastus. Nelja meetri kõrguselt lahti lastud pall põrkab vastu maad kiirusega .
Ühe ja sama massiga õpilased teevad 400 meetri läbimisel sama palju mehaanilist tööd, kuid ometi kulub ühel õpilasel selle distantsi läbimiseks 60, teisel 70 sekundit. Töö tegemise kiirust iseloomustab võimsus. See õpilane, kes jooksis kiiremini, tegi ühes sekundis rohkem tööd, tema võimsus oli suurem.
Võimsus on füüsikaline suurus, mis väljendab ühe ajaühiku jooksul tehtud töö hulka (ehk kulutatud energiat). Võimsust tähistatakse tähega N ning seda saab arvutada valemiga:
Võimsuse ühikuks on vatt (lühend W): 1 W = 1 J / 1 s. Võimsus 1 vatt on väga väike võimsus. Rahulikult kõndides on inimese võimsus umbes 50 W. Paljude sõiduautode võimsus jääb vahemikku 70–120 kW, mis tähendab, et ühes sekundis teevad need autod tööd 70–120 kJ.
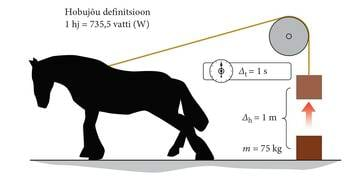
| Hubble'i kosmoseteleskoobi orbiidile saatmine (STS-31). 30 000 kN jõud tõstab 2000 tonni kaaluva kosmosesüstiku Discovery. Süstiku kaubaruumis on Hubble'i kosmoseteleskoop. | Võimsuse mõõtmiseks kasutatakse tihti ka mõõtühikut hobujõud (tähis hj). Selle mõõtühiku võttis kasutusele Šoti insener James Watt 18. sajandil, et võrrelda veohobuste ja aurumootorite võimsusi. Hobujõu suurus on 735,499 vatti. Inglismaal ja USAs on hobujõu suurus 745,7 vatti. |
Näidisülesanne
Kui suurt keskmist võimsust arendab inimene, kes tõstab 2 sekundiga 0,4m kõrgusele 50kg kaaluva kivi?
Lahendus
Võimsuse arvutamiseks on meil vaja teada seda, kui palju tehakse tööd. Kivi tõstmiseks peame ületama raskusjõu, seega on kivi tõstmiseks kõrgusele tehtav töö kivile mõjuva raskusjõu ja läbitud teepikkuse () korrutis.
Andmed
t=2s
h=0,4m
m=50kg–––––––––––
N−?
Arvutused:
Vastus. Kivi tõstmisel arendab inimene keskmiselt võimsust 100W.
| See on RT-flex96C, väidetavalt maailma kõige võimsam diiselmootor, mille on loonud ja mida toodab Soome firma Wärtsilä. Mootor on 13,5 m kõrge ja 26,59 m pikk ning kaalub 2300 tonni. Võimsust suudab see arendada kuni 80 000 kW. | Gordoni jõe tamm Tasmaanias on 140 m kõrge ning selle kaar on 190 m pikk. Kaare paksus on kõige jämedamas kohas (all) 17,7 m ning kõige õhemas kohas (üleval) 2,75 m. Kolmele 450 MW koguvõimsusega generaatorile annab hoogu 11,3 km3 vett mahutav Gordoni veehoidla. Võrdluseks: näiteks Peipsi järve maht on 25 km3. |
Power
Power is a physical quantity that expresses the amount of work done in one unit of time (or energy expended). The power is denoted by the letter and can be calculated using the formula:
The unit of power is the watt (abbreviation ): 1W=1J/1s.
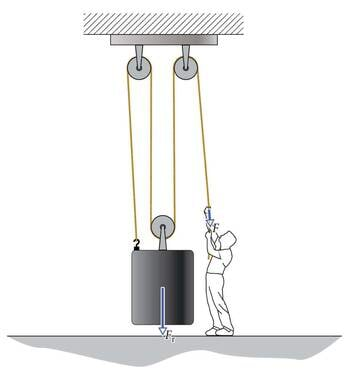
Jalgrattaga sõites väntame pedaale, kuid ratast ajab ringi kettülekanne. Kivi saame kergemini august kätte kangi abil. Auto ratta vahetamiseks tõstetakse auto üles tungrauaga. Koormiste tõstmiseks kasutatakse plokke ja talisid. Salvkaevust saame vee kätte pööra käepidet keerates. Miks nii?
Kõik mainitud abivahendid koosnevad ühest või mitmest lihtmehhanismist.
Lihtmehhanismid on lihtsa ehitusega (ilma mootorita) seadmed, millega muudetakse ülekantava jõu suurust või suunda.
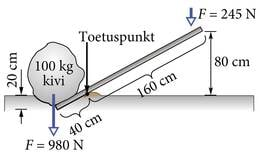
Kui asetame toetuspunktile pika jäiga ridva, siis oleme saanud lihtmehhanismi, mida nimetatakse kangiks. Uurime, kui palju tööd me peame tegema, et tõsta kivi kangiga august välja.
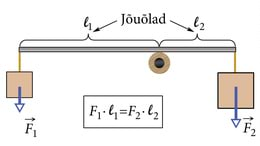
Kivi tõstmiseks 20 cm kõrgusele peame tõstma kivi jõuga
Seega töö, mida peame tegema, on
Me kasutame kahemeetrist kangi. Kivi on kangi toetuspunktist 40 cm kaugusel ning meie käsi on toetuspunktist 160 cm kaugusel. Et kangi kiviga ots tõuseks 20 cm võrra, peab kangi teist otsa alla vajutama 80 cm võrra – meie käsi on kangi toetuspunktist neli korda kaugemal, seega peab meie käsi läbima ka neli korda pikema tee. Töö, mida peame kivi tõstmiseks tegema, on 196 J. Seega teades, kui pika tee meie käsi läbib, saame leida jõu, millega peame kangi vajutama.
Ilma kangita oli vaja kivile rakendada jõudu 980 N, mis on neli korda rohkem kui kangi kasutades.
Kõikide lihtmehhanismide kohta saame kirja panna seaduspärasuse.
Lihtmehhanismid ei muuda töö hulka, mida tuleb teha. Lihtmehhanism muudab vajaminevat jõudu ja läbitud teepikkust. Nii mitu korda, kui lihtmehhanismi kasutamisel võidetakse jõus, kaotatakse läbitud tee pikkuses, ja vastupidi.
Seda seaduspärasust tuntakse kui mehaanika kuldreeglit.
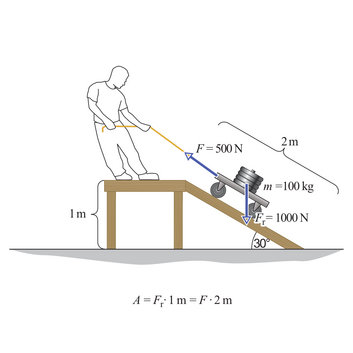
Mehaanika kuldreegel väidab, et töö, mida peame tegema, on alati sama suur ega sõltu sellest, kas me kasutame lihtmehhanisme või mitte. Tegelikult peame lihtmehhanisme kasutades tegema alati rohkem tööd kui ilma nendeta, sest osa energiat kulub hõõrdejõudude ületamiseks lihtmehhanismide sees. Näiteks veeretades keha mööda kaldpinda üles, peame rakendama jõudu nii keha ülespoole liigutamiseks kui ka hõõrdejõu ületamiseks. Ilma kaldpinnata on meil vaja ainult rakendada jõudu keha tõstmiseks.
Seda, kui suure osa tehtud tööst moodustab kasulik töö, näitab kasutegur. Raskuse tõstmisel on kasulik töö see, mis kulub gravitatsioonijõu ületamiseks. Kogutöö, mis tehakse, on alati kasulikust tööst suurem, kuna lisaks töö tegemisele peame kulutama energiat hõõrdejõu (või mõne teise takistusjõu) ületamiseks. Kasuteguriks nimetatakse kasuliku töö suhet kogutööga:
Enamasti antakse kasutegur protsentides:
Simple mechanisms, lever
Simple mechanisms are devices with a simple construction (without a motor) that change the size or direction of the transmitted force. If we place a long rigid rod on the fulcrum, we have obtained a simple mechanism called a lever.
The Golden Rule of Mechanics
Simple mechanisms do not change the amount of work that needs to be done. A simple mechanism changes the required force and the distance traveled. As many times as you gain in strength when using a simple mechanism, you lose in the length of the path traveled, and vice versa.
Useful work, total work, efficiency
How much of the work done is useful work is shown by the efficiency factor. Total work is always greater than useful work, because in addition to doing work, we have to spend to overcome various hindering forces. The ratio of useful work to total work is called the efficiency factor:
In most cases, the efficiency is given as a percentage:
Asetades joonlaua pliiatsi peale, saame kõige lihtsama kangi. Joonlaud on tasakaalus, kui pliiats on täpselt joonlaua keskel. Asetades joonlaua otstele erineva massiga koormised, tuleb pliiatsi asukohta (joonlaua toetuspunkti) muuta, et ta oleks jätkuvalt tasakaalus. Mida kaugemal on koormis toetuspunktist, seda suurem on selle pöörav toime, nii et samasuguse toime saavutamiseks tuleb kergem koormis kangi toetuspunktist kaugemale asetada.
Jõu pöörava toime iseloomustamiseks on vaja kasutusele võtta jõu õla mõiste. Jõu õlg on kaugus kangi keskpunktist jõu rakenduspunktini. Jõu õlga tähistatakse tavaliselt tähega l. Kasutades jõu õlga, saame kirja panna kangi reegli ehk kangi tasakaalu tingimuse:
Kui kangi üks jõu õlg on teisest mingi arv kordi pikem, siis võib sinna rakendada sama arv kordi väiksemat jõudu, et kang püsiks tasakaalus.
Näidisülesanne 1
Ühe meetri pikkuse puitvarda ühe otsa külge on riputatud 100grammine raskus ning teise otsa külge 300grammine raskus. Kui kaugel peab olema toetuspunkt varda otsast, kui tahame, et varras oleks tasakaalus? Puitvarda massiga ei ole vaja arvestada.
Lahendus
Kang on tasakaalus, kui mõlemal pool olevate raskuste raskusjõudude ja jõu õlgade korrutised on võrdsed. Tähistame vasakul pool oleva jõu õla -ga ning paremal pool -ga. Kuna kogu kangi pikkus on meeter, siis l2=1m−l1.
Andmed
m1=100g
m2=300g
l=1m––––––––
l1−?
l2−?
Arvutused
Kuna
siis saame
Vastus. Toetuspunkt peab olema raskusest 25cm kaugusel.
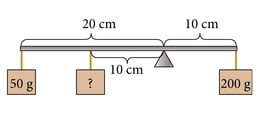
Näidisülesanne 2
Milline peab olema tundmatu massiga keha mass, et kang oleks tasakaalus?
Lahendus
Paremal pool mõjutab kangi ainult üks koormis. Vasakul pool mõjutab kangi kaks koormist. Kang on tasakaalus, kui vasakul pool olevate koormiste raskusjõudude ja jõu õlgade korrutiste summa on võrdne paremal pool oleva koormise raskusjõu ja jõu õla korrutisega.
Andmed
m1=200g
m2=50g
l1=10cm
l2=20cm
l3=10cm–––––––––––
m3−?
Arvutused
Avaldades viimasest võrrandist , saame
m3=200g⋅10cm−50g⋅10cm10cm=100g––––––––––––
Vastus. Tundmatu massiga keha peab kaaluma 100g, et kang oleks tasakaalus.
The shoulder of power. The condition of equilibrium of the lever
The shoulder of the force is the distance from the center of the lever to the point of application of the force. The lever rule, or the lever balance condition, can be written with a formula
The balance condition of a lever says that if one force arm of the lever is a certain number of times longer than the other, then the same number of times less force can be applied to it, so that the lever remains in balance.
Looduses on võnkumine loomulik nähtus. Puuoksad kõiguvad tuules, puulehed värisevad oksa küljes, lind liigutab oma tiibu lendamise ajal üles-alla. Võnkliikumiseks ehk võnkumiseks nimetatakse liikumist, mis kordub kindla ajavahemiku järel.
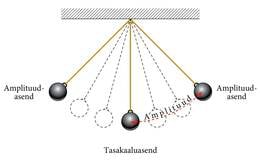
Uurime niidi abil toe külge kinnitatud kuuli liikumist. Füüsikas nimetatakse sellist võnkuvat keha pendliks.
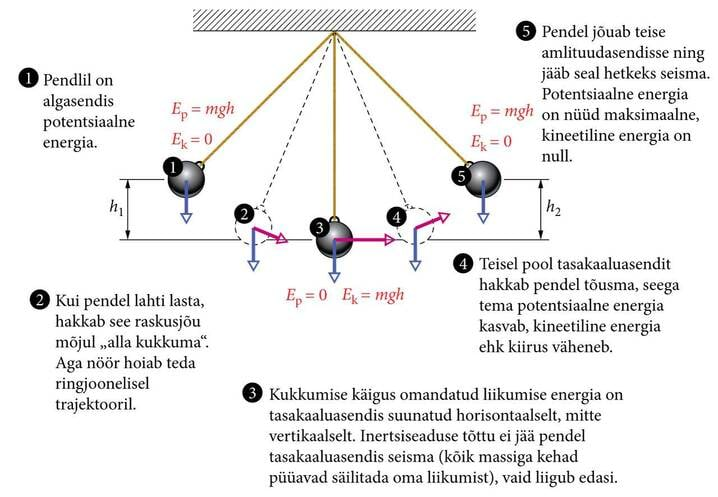
Kui pendlit lükata, siis hakkab see edasi-tagasi liikuma. Asendit, kus kuul algul paigal püsis, nimetatakse tasakaaluasendiks. Kõige kaugemat punkti tasakaaluasendist, kuhu pendel liigub, nimetatakse amplituudasendiks. Selles asendis jääb pendel hetkeks seisma ning hakkab tagasi liikuma. Kaugust tasakaaluasendist amplituudasendini nimetatakse amplituudiks. Täisvõnkeks nimetatakse pendli liikumist ühest amplituudasendist teise ning tagasi esimesse.
Korraldasime katse, kus mõõtsime, kui palju aega kulub pendlil 5, 10, 15 ja 20 täisvõnke tegemiseks. Katse tulemused kandsime tabelisse.
Andmetest saame teada, et 10 täisvõnke tegemiseks kulus pendlil 20 sekundit. Sellest saame järeldada, et ühe täisvõnke tegemiseks kulub pendlil 2 sekundit. Sama tulemuseni jõuame kõikide katsete korral.
Ajavahemikku, mis kulub võnkuval kehal ühe täisvõnke tegemiseks, nimetatakse selle keha võnkeperioodiks. Lisaks võnkeperioodile saab pendlit iseloomustada võnkesagedusega. Võnkesagedus näitab, mitu täisvõnget teeb võnkuv keha ühes ajaühikus.
On lihtne näha, et võnkesagedus ja võnkeperiood on omavahel seotud. Kui pendli võnkeperiood on kaks sekundit, siis kahe sekundi jooksul teeb selline pendel ühe täisvõnke. Seega ühe sekundi jooksul teeb pendel pool täisvõnget ja pendli võnkesagedus on pool võnget sekundis.
Matemaatiliselt saame võnkesageduse ja võnkeperioodi omavahelise seose kirja panna valemiga
See valem saab füüsikas tavapäraste tähistustega kirja pannes kuju
Sageduse ühik on herts (lühend Hz). 1 Hz on selline sagedus, mille korral võnkuv keha teeb ühe täisvõnke sekundis, st
Pendli liikumine on hea näide sellest, kuidas mehaanilisel liikumisel kineetiline ja potentsiaalne energia teineteiseks muunduvad. Seda protsessi kirjeldab alljärgnev joonis.
Miks jääb võnkuma pandud pendel mõne aja pärast siiski seisma? Pendli liikumist takistab õhk, nii et osa selle kineetilisest energiast kulub õhutakistuse ületamisele. Mehaanilise energia jäävuse seaduses tähendab see mehaanilise koguenergia vähenemist, väheneb ka pendli maksimaalne potentsiaalne energia. Järelikult väheneb ka võnkumise amplituud ja mõne aja pärast jääb pendel seisma.
| Veel üsna hiljuti olid pendelkellad hinnatud ajamõõtjad. Uuri seda joonist. Kas saad aru, miks pendel seisma ei jää, ehkki selle liikumist takistab nii hõõrdumine kui ka õhk? | F. L. Löbneri Saksamaal valmistatud pendelkell. Eesti õige aja teenistuse peakell 1920-1940, mida kontrolliti Naueni või Eiffeli torni raadiojaama ajasignaalide järgi. Üle Eesti saadeti tähetornist signaal |
Näidisülesanne
Vaatleme pendlit, mis võngub sagedusega 2Hz. Milline on pendli võnkeperiood?
Lahendus
Andmed
Arvutused
Võnkeperiood ja sagedus on omavahel seotud valemiga . Teades sagedust, saame arvutada pendli võnkeperioodi:
Helid ümbritsevad meid kõikjal. Looduses kuuleme puude sahinat, linnulaulu, kaugel maanteel sõitva auto mürinat jne. Helide kaudu saame ka märkimisväärse osa infost meid ümbritseva maailma kohta – me teame, et puud sahisevad, lind laulab ja autod sõidavad ka ilma, et me kõike seda näeksime.
Teame oma kogemuse põhjal, et heli tekitamiseks on tarvis midagi kiiresti võnkuma panna. Parim viis selleks on elastne ese tasakaaluasendist välja viia ning siis lahti lasta. Võime näiteks üle laua serva ulatuva joonlaua põrisema panna. Kitarri keeled hakkavad helisema, kui neid tasakaaluasendist eemale tõmmata ja siis lahti lasta. Trumm teeb häält siis, kui seda lüüa. Kõik need kehad võnguvad kiiresti. Võnkuvat keha nimetatakse heliallikaks.
Miks me kuuleme heli? Heli levimist ruumis võib võrrelda laine liikumisega veekogus, millesse on visatud kivi. Kivi vette kukkumise kohta tekib laine, see kandub üle veekogu edasi ja paneb võnkuma ka seal hulpivad puupilpad.
Võnkuv joonlaud paneb koos endaga võnkuma joonlauda ümbritseva õhu osakesed. Need osakesed mõjutavad sellest kaugemal olevaid õhu osakesi, need omakorda järgmisi jne. Lõpuks jõuab võnkumine kõrvas oleva trummikileni ning seda me tajume helina.
Laineks nimetatakse võnkumise levimist keskkonnas.
Kuna heli levimisel puudub otsene vastasmõju heli allika ja vastuvõtja vahel, võnkumised levivad osakeselt osakesele, siis võtab heli levimine paratamatult aega. Katseliselt on kindlaks tehtud, et õhus on heli levimise kiirus umbes 340 m/s.
Teades heli levimise kiirust, võime hinnata, kui kaugel välku lööb. Selleks tuleb lugeda sekundeid välgulöögist kuni müristamiseni. Tõepoolest, kuna valgus levib võrreldes heliga väga kiiresti, u 300 000 km/s, ja jõuab vaatlejani peaaegu hetkeliselt, siis saame niimoodi teada aja, mis kulus helilainel meieni jõudmiseks. Sellest omakorda saab heli kiirust teades arvutada teepikkuse. Kuuldes müristamist kolm sekundit pärast välgulööki, tead, et välgu sähvatus toimus sinust umbes ühe kilomeetri kaugusel.
Heli saab levida ka tahkistes ja vedelikes. Kuna sellistes keskkondades on aineosakesed üksteisele palju lähemal, kandub võnkumine edasi palju kiiremini. Heli levimise kiirus erinevates keskkondades on toodud kõrvalolevas tabelis.
Kindlasti oled kuulnud suures ruumis rääkides oma hääle kaja. Kaja tekib sellepärast, et hääl, mida sina tekitad, levib ruumi seinteni, peegeldub nendelt ning jõuab sinuni tagasi. Kaja tekib alati, kui heli teel on takistus, aga vaid suures ruumis (piisavalt kaugete takistuste korral) võtab seinani ja tagasi levimine nii palju aega, et kaja oleks võimalik otse allikast tulevast helist eristada. Eriti kaua tuleb kaja oodata, kui hüüda kauge metsa või mäe poole. Tasub proovida, sest niimoodi saab ka ligikaudu teada metsa või mäe kauguse. Mõnikord võib kuulda ka kahte kaja, kui heli peegeldub kahelt eri kaugusel olevalt takistuselt.
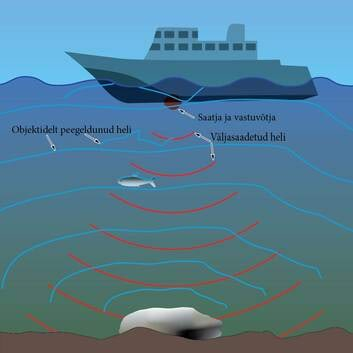
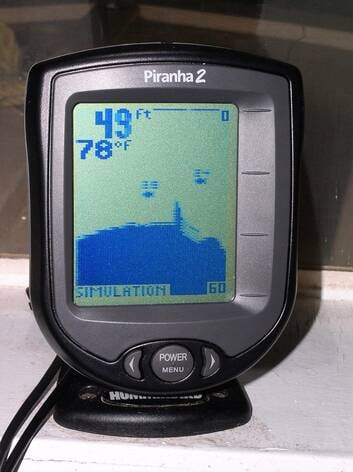
Heli peegeldumist (kaja) kasutatakse näiteks kajaloodi töös, kui on vaja merepõhja sügavust määrata või vee alt kalaparvi otsida. Kajalood saadab merepõhja ultrahelisignaali ning registreerib aja, millal signaal tagasi laeva peegeldub. Teades heli levimise kiirust vees, saame arvutada merepõhja sügavuse.
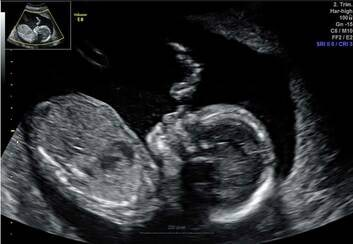
Sama põhimõtet kasutades on võimalik ultraheliga naise kõhus olevat loodet vaadata. Ultrahelilained suunatakse lootele ning registreeritakse aeg, millal peegeldunud heli tagasi jõuab. Kuna erinevatelt loote osadelt võtab peegeldumine erineva aja, on võimalik erinevatest suundadest ultraheli peegeldumise registreerimisega saada lootest pilt.
Looduses kasutavad kajalokatsiooni näiteks nahkhiired ja delfiinid.
Heli tekkimine ja levimine
Heli tekitamiseks on tarvis midagi kiiresti võnkuma panna. Võnkuv keha paneb koos endaga võnkuma joonlauda ümbritseva õhu osakesed. Need osakesed mõjutavad sellest kaugemal olevaid õhu osakesi, need omakorda järgmisi jne. Seda nähtust me nimetamegi heliks ja selle levimiseks. Võnkuvat keha nimetatakse heliallikaks. Heli levimise kiirus õhus on ca 340m/s.
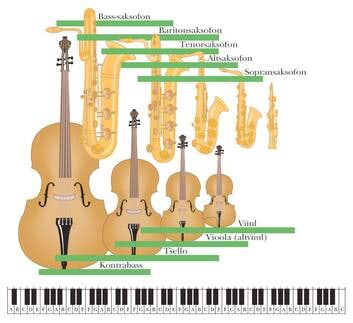
Me räägime kõrgest ja madalast helist. Näiteks lauljatest sopranid suudavad tekitada kõrgeid helisid ning bassid madalaid helisid. Aga miks on helid erineva kõrgusega?
Kordame joonlaua katset, muutes üle laua serva ulatuva joonlaua osa pikkust. Kindlasti märkate, et kui joonlaud on vaid veidi üle laua serva, kuuleme joonlaua võnkudes kõrget heli. Mida rohkem aga nihutame joonlauda üle laua serva, seda madalamat heli selle võnkudes kuuleme. Ühtlasi näeme, et mida lühem osa on laua servast üle, seda „kiiremini“ joonlaud võngub. Sellest joonlaua võnkumise „kiirusest“ heli kõrgus sõltubki. Kui joonlaud võngub kiiremini, on selle võnkesagedus suurem ning heli, mida kuuleme, kõrgem. Mida suurem on heliallika võnkesagedus, seda kõrgemat heli see tekitab.
Kõik võnkuvad kehad tekitavad heli, kuid inimene ei ole võimeline kõiki neid helisid kuulma. Madalaimaks helisageduseks, mida inimene kuuleb, loetakse 16 Hz ning kõrgeimaks sageduseks 20 000 Hz. Heli sagedusega alla 16 Hz nimetatakse infraheliks. Suurema kui 20 000 Hz sagedusega heli nimetatakse ultraheliks. Ultraheli täiskasvanud inimesed ei kuule, kuid on tõestatud, et imikud kuulevad ka ultraheli.
| Koeravile – inimesed seda ei kuule, kuna see tekitab ultraheli. | Saksofonide ja viiulite pered. Pildil on näidatud muusikariista pikkuse seos temast tuleva heliga. Iga muusikariista sagedusvahemik on tähistatud horisontaalse ribaga sageduste skaalal, milleks on kõige all asuv klaviatuur. Sagedus suureneb paremale poole. |
Lüües käega rahulikult trummi, tekib vaikne heli, kuid lüües trummi pihta kõvasti, tekib vali heli. Sagedus, millega trumm võnkuma hakkab, on mõlemal juhul sama, kuid see, millise amplituudiga trumm võnkuma hakkab, on erinev. Heli valjus ehk heliintensiivsus sõltub sellest, millise amplituudiga heliallikas võngub.
| Suurema amplituudiga võnkumine tekitab valjema heli. | Heli valjuse mõõtmiseks on igaühel võimalik oma nutitelefoni leida soblik rakendus (nt otsisõnaga soundmeter). Tuleb siiski tähele panna, et tihti ei näita need rakendused päris õiget väärtust ja usaldusväärsete tulemuste saamiseks tuleks rakendus kalibreerida. |
Heliintensiivsuse ühikuna kasutatakse kõige sagedamini detsibelli (dB). Keskmiselt hakkab inimene kuulma heli, mille valjus on 0 dB (see vastab rõhule 2 · 10-5 Pa). Vaikse häälega rääkides on heliintensiivsus umbes 20–30 dB. Kui heliintensiivus on suurem kui 130 dB, siis tekitab see inimese kõrvas valuaistingu – kõrvas asuv trummikile hakkab liiga suure amplituudiga võnkuma. Heli, mille valjus on 180 dB, loetakse inimese jaoks surmavaks.
Inimese kõrv on kaugelt tundlikum ja täiuslikum, samas ka keerukam seade kui mistahes mikrofon. Selles veendumiseks piisab, kui uurida alljärgnevat joonist. Siinkohal saame anda vaid väga ligikaudse kirjelduse sellest, mismoodi me helisid kuuleme. Hoidke ja säästke oma kuulmist – liiga vali heli, üldse igasugused kiired rõhu muutused võivad seda kahjustada. Ja kord juba tekkinud kahju on väga keeruline parandada.
Heli kõrgus
Mida suurem on heliallika võnkesagedus, seda kõrgemat heli see tekitab. Madalaimaks helisageduseks, mida inimene kuuleb, loetakse 16 Hz ning kõrgeimaks sageduseks 20 000 Hz. Heli sagedusega alla 16 Hz nimetatakse infraheliks. Suurema kui 20 000 Hz sagedusega heli nimetatakse ultraheliks.
Heli tekitamiseks on vaja võnkuvat keha, olgu selleks siis helihark või viiuli kõlakoja seinad. Aga mitte kõik helid ei ole meile ühtviisi meeldivad.
Kui viiul juhtub häälest ära olema või ei ole mängijal piisavalt oskusi, kostub sealt kägin, mida vaid mööndustega saab heliks nimetada. Haamriga plekitükki kolkides me tekitame müra. Müra kuuleme ka siis, kui paljude heliallikate tekitatud helid liituvad korrapäratult.
Kodus tekitavad müra näiteks kodumasinad – külmkapp, pesumasin, arvuti, tolmuimeja jne. Koolis tekitavad müra peamiselt lapsed. Müra tekitamiseks ei pea lapsed kõvasti rääkima ega jooksma, piisab sellest, et nad räägivad korraga. Sellisel juhul helilained liituvad ning tulemuseks on korrapäratu õhuosakeste võnkumine – see ongi müra.
Müra on inimese tervisele kahjulik. Pidev müras viibimine väsitab ning tekitab peavalu. Inimene võib küll müraga harjuda ega pane seda enam tähelegi, kuid sellele vaatamata kahjustab müra tervist.
Samas ei pruugi igasugune müra olla alati kahjulik. Looduses tekkiv müra, nagu puude kahin või mere kohin, mõjub enamasti pigem rahustavalt.
Kahjuliku müra eest on vaja ennast kaitsta. Töötades müra tekitavate masinatega, tuleb kanda müra summutavaid kõrvaklappe.
Lisaks kuuldavale helile levib meie ümber ka madalasageduslik infraheli. Infraheli me ei kuule ja me ei tea, kas asume selle mõjualas või mitte. Infraheli tekib looduses tugeva tuulega, maavärinates ja laviinides. Mitmed loomad, nagu näiteks elevandid ja vaalad, kasutavad infraheli suhtlemiseks. Tehislikku infraheli tekitavad ka näiteks tuulikud.
31. mail 2003. aastal viis rühm Ühendkuningriikide uurijaid läbi eksperimendi, kus nad lasid umbes 700 inimesel kuulata muusikat, millele oli lisatud vaevu kuuldav 17 Hz infraheli toon. Infraheli tekitamiseks kasutasid nad spetsiaalset, eriti suure võnkeamplituudiga kõlarit, mis oli kinnitatud seitsme meetri pikkuse plastiktoru külge. Peaaegu veerand eksperimendis osalenutest kaebas rahutust, ebamugavustunnet, äärmist kurbust, närvilisust, hirmupuhanguid, külmavärinaid või surutusetunnet rinnus. Oma kõnes ütles professor Richard Wiseman: „Need tulemused viitavad, et madalsageduslik heli võib inimestes esile kutsuda ebaharilikke kogemusi, isegi kui nad ei suuda infraheli kuulda. Teadlased on oletanud, et selliseid helisid võidakse kasutada mõnes väidetavalt nõiutud kohas veidrate aistingute esile kutsumiseks, mida inimesed vaimudega seostavad. Meie tulemused igatahes kinnitavad seda oletust.“
Millised on maailma kõige vaiksemad kohad? Täieliku vaikuse saavutamiseks ehitatakse spetsiaalseid ruume, kus on hoolitsetud nii selle eest, et väljastpoolt ükski heli sisse ei pääseks, kui ka selle eest, et ruumis sees tekitatud helid ruumi seintelt tagasi ei peegelduks.
| Väga vaikne ruum Fraunhofferi instituudis Saksamaal. Siin on hoolitsetud ka selle eest, et puuduks igasugune kaja. Ruumi kasutatakse akustilisteks täppismõõtmisteks. | Spetsiaalsed kõrvatropid muusikutele. Sellised kõrvatropid vähendavad kõrva jõudva heli valjust ilma seda moonutamata. Paljudel teenekatel muusikutel esineb akuutne kuulmisvaegus, kuna nad on pikka aega viibinud väga valju heliga keskkonnas. Sellised kõrvatropid aitavad kuulmisvaeguseid ära hoida. |
Muidugi, võib minna ka kosmosesse – kui ei ole õhku, siis ei ole ka heli, on täielik rahu ja vaikus.