Esimene katse inimese Veenusele saatmiseks teostati Marylandis Baltimoris 1928. aastal. Robert Condit ja tema kaks abilist ehitasid raketi nurkraudadest ja purjeriidest. Kütuseks kasutati aurustatud bensiini, mis suunati terastorudesse ja süüdati seejärel elektrisädemega. Condit pidi reisi sooritama üksi, ta oli varunud veidi toitu, vett, kaks taskulampi ja esmaabipauna. Testlennu päeval ronis piloot sõidukisse ja käivitas mootori, et lennata veerand miili kõrgusele lihtsalt selleks, et seadet kontrollida. Terastorudest paiskus välja suitsu ja tuld, aga mingit õhkutõusu ei toimunud. Condit suurendas bensiini pealevoolu, mistõttu leegid muutusid nii pilkupüüdvaks, et liiklus tänaval seiskus. Seade ei liikunud aga endiselt paigast. Condit jätkas üritamist, kuni kütus lõppes.

Kui Craig Breedlove purustas 1964. aasta oktoobris Bonneville soolajärvel maapealse kiirusrekordi oma rakettidel töötaval sõidukil Spirit of America'ga, avas ta kiirusel 846km/h aeglustamiseks langevarju, kuid selle nöör purunes, samuti ei avanenud teine langevari. Nüüd surus ta piduripedaali põhja, temast jäid maha ligi 10 kilomeetri pikkused pidurdusjäljed, enne kui pidurid läbi põlesid. Lõpuks auto peatus, kui ta plartsatas kaldapealselt viie meetri sügavusse soolvee basseini kiirusega umbes 300km/h.

Nähtusi ja objekte kirjeldavad füüsikalised suurused jagunevad kaheks. Ühed saavad muutuda ja omada erinevaid väärtusi. Sellisteks on näiteks koordinaat, kiirus, jõud ja temperatuur. Teised säilitavad oma väärtuse kõikides protsessides. Jäävateks suurusteks on näiteks mass, impulss, energia ja elektrilaeng. 

Kui füüsikud on leidnud, et mingi suurus jääb kõikide senituntud nähtuste toimumisel muutumatuks ehk konstantseks, võib suure kindlusega arvata, et see ei muutu ka muudel juhtudel. Selline eeldus lihtsustab looduse uurimist. Suuruste jäävusele tuginemine võimaldab üles ehitada uusi füüsikateooriaid. 

Mehaanika põhiülesanne on leida keha asukoht mis tahes ajahetkel. Teades algtingimusi ja kõiki kehale mõjuvaid jõude, on Newtoni seaduste abil see ülesanne lahendatav. Paljude ülesannete lahendamisel ei saa aga neid seadusi rakendada, kuna jõud on teadmata. Nii on näiteks kehade põrgete korral, mil jõude ning nende mõjumise aega on raske määrata.

Taolistel juhtudel võetakse jõu ja kiirenduse asemel kasutusele impulss ja energia. Impulss ja energia on erilised suurused, kuna nende puhul kehtib jäävus.

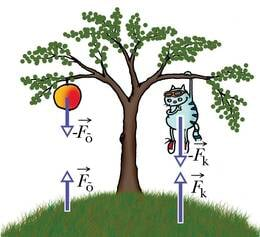
Dünaamikas defineeritakse impulss keha massi ja kiiruse korrutisena. Newtoni seaduste analüüs näitab, et impulsi muutumise kiirus on võrdne muutust põhjustava jõuga ning väliste mõjude puudumisel jääb süsteemi impulss muutumatuks. Kahest kehast koosneva süsteemi impulsi jäävust väljendab valem:

Suletud süsteemi impulsi jäävus kehtib mitte ainult kahe, vaid mis tahes arvu kehade korral:

Konkreetsete ülesannete lahendamisel on tihti lihtsam kehade koguimpulss enne ja pärast vastastikmõju toimumist eraldi välja kirjutada ning seejärel jäävust arvestades omavahel võrduma panna:

Nüüd saab leida, milline on liikumine pärast vastastikmõju toimumist. Seejuures pole vaja teada, kui tugev ja millise kestusega see vastastikmõju oli.

Põrkeks nimetatakse üksteise suhtes liikuvate kehade kokkupuutel toimuvat lühiajalist vastastikust mõjumist. Põrgetele on iseloomulik vastastikmõju lühike kestus ning jõudude ja kiirenduste suured väärtused, mida on sageli raske mõõta. Kõikide põrgete puhul kehtib impulsi jäävuse seadus.

Põrked jaotatakse elastseteks ja mitteelastseteks. Elastse põrke tagajärjel kehad eemalduvad üksteisest ning nende liikumise koguenergia selle käigus ei muutu. Mitteelastsel ehk plastsel põrkel jäävad kehad kokku, moodustades liitkeha ning liikumisenergia muundub osaliselt või täielikult mingit muud liiki energiaks, tavaliselt soojuseks.

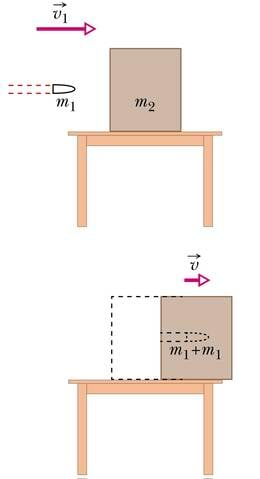
Leiame impulsi jäävuse seadust kasutades, kui suure kiirusega hakkab libisema paigalseisev klots, millesse jääb kinni teadaoleva massi ja kiirusega lendav püssikuul.

Uuritav süsteem, milles kehtib impulsi jäävuse seadus, koosneb antud juhul kahest kehast — kuulist ja klotsist. Tegemist on mitteelastse põrkega, kuna pärast tabamust moodustub klotsist ja kuulist liitkeha. Kui kasutame tähiseid, kus kuuli mass on m₁ ja lennukiirus v₁, siis kuuli impulsiks on m₁v₁. Kuna klots algul ei liigu ja sel impulss puudub, on meie süsteemi koguimpulss enne põrget võrdne kuuli impulsiga:

Et liikumishulk ei saa väliste mõjude puudumisel muutuda (eeldame, et hõõrdumine klotsi ja aluse vahel puudub), peab liikumine ka pärast tabamust edasi toimuma. Tähistades selle tabamusjärgse liikumise kiiruse tähega v ning klotsi massi sümboliga m₂, saame liitkeha massiks m₁ + m₂ ning süsteemi impulsiks

Impulsi jäävuse tõttu

ja lihtsad teisendused annavad, et klots saab kuulitabamuse tagajärjel kiiruse

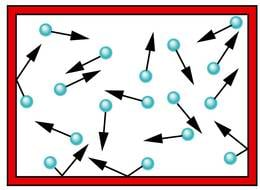
Impulsi jäävuse seaduse abil saab kirjeldada ka gaasides toimuvaid protsesse. Hõredat gaasi võib ette kujutada süsteemina, mis koosneb paljudest korrapäratult liikuvatest mõõtmeteta molekulidest, mis mõjutavad anumat ning muid kehi vaid elastsete põrgete kaudu. Niisugust gaasi mudelit nimetatakse ideaalseks gaasiks.

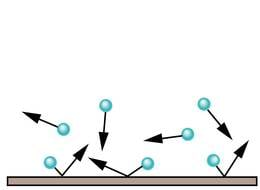
Kui sellise gaasi iga molekuli mass on m₀ ja kiirus v, omavad need kõik impulssi p₀ = m₀v. Absoluutsellt elastsel põrkel vastu mingit pinda muutub liikumine vastassuunaliseks ja uus impulss on –m₀v. Molekuli impulsi muut on siis Δp₀ = m₀v – (–m₀v) = 2 m₀v.

Lühikese ajavahemiku Δt jooksul saavad mingi pinna poole liikuvatest osakestest sellega põrkuda vaid need, mis ei asu kaugemal kui vahemaa s = v Δt. Kui pinna suurus on S, asuvad need molekulid kõik piirkonnas, mille ruumala V = S•s = SvΔt.

Gaaside iseloomustamiseks kasutatakse molekulide kontsentratsiooni (tähis n). See suurus näitab osakeste arvu ruumalaühikus. Molekulide koguarvu N saab leida, kui korrutada kontsentratsioon ruumalaga: N = nV.

Eelnevalt leidsime ruumala, milles asuvad molekulid võiksid aja Δt jooksul pinnani jõuda. Nende molekulide arv on N = nV = nSvΔt. Tegelikult on põrkuvate molekulide arv väiksem. Range tuletuskäik näitab, et kolmemõõtmelises ruumis on molekulide kaootiline liikumine oma mõju poolest samaväärne sellega, kui nad liiguksid vaid kolmes sõltumatus ristsihis. Konkreetse pinnaga ristuvas sihis liikuvaid osakesi on kolmandik koguarvust. Pinnale lähenevad neist vaid pooled, ülejäänud eemalduvad. Põrkuda saavaid molekule on seega vaid kuuendik koguarvust. Kui igal põrkel muutub molekuli impulss Δp₀ võrra, siis kõikide põrkuvate molekulide impulsside muut kokku on

Sellest seosest saame avaldada impulsi muutumise kiiruse, mis on teatavasti võrdne jõuga:

Jagades selle jõu pindalaga S, saamegi rõhu, mida ideaalne gaas avaldab selles asuvatele kehadele:

(P ei tähista siin impulssi vaid rõhku)

Mehaanika kursuses me sellel valemil pikemalt ei peatu. Tulemus on leidnud katselist kinnitust ning see näitab, et impulsi jäävuse seadust saab füüsikas rakendada ka väljaspool mehaanikat.

Impulsi jäävuse seaduse üheks huvitavaks ning oluliseks rakenduseks on reaktiivliikumine (re- + activus — ladina k vastu + tegutsev), mida kasutatakse nii tehnikas kui ka mõne looma poolt looduses. Selleks et paigalt liikuma pääseda, on vaja vastastikmõju — teist keha, millest end eemale tõugata, nii et see vastavalt Newtoni III seadusele sama suure jõuga vastu mõjuks. Just tänu sellele saavadki kehad liikuma hakata. Jalad tõukavad teekatet, aerud vett, lennukipropeller õhku.

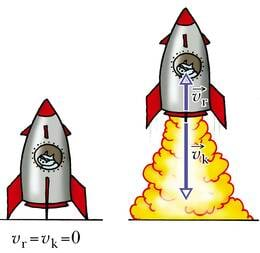
Kuidas lendavad aga kosmoseraketid õhutühjas maailmaruumis, kus pole midagi, millest end eemale tõugata? Kui läheduses sobiv keha puudub, tuleb see endaga kaasa võtta. Just niiviisi toimitakse rakettide lennutamisel. Rakett hakkab liikuma tänu sellele, et selle ühest otsast paisatakse läbi spetsiaalse ava (düüsi) suure kiirusega välja kütuse põlemisel tekkivad gaasid. Enne starti on paigalseisva raketi ja selles sisalduva kütuse impulss null. Kui nüüd kütuse põlemisel tekkivad gaasid ühes suunas välja lendavad, hakkab rakett ise vastassuunas liikuma. Muidu ei jääks raketist ja gaasidest koosneva süsteemi koguimpulss ju nulliks.

Nii tekibki raketi reaktiivliikumine. Reaktiivliikumiseks nimetatakse liikumist, mille tekitab kehast eemale paiskuv keha osa.

Hindame, millise kiiruse võib rakett kütuse ärapõlemisel saada. Oletame lihtsuse mõttes, et põlemisgaasid ei välju raketist tasapisi, vaid ühekorraga.

Olgu raketikesta ja selles asuva aparatuuri ning meeskonna mass m_r, kütuse ja sellest tekkivate gaaside mass m_k ning gaaside väljapaiskumise kiirus v_k. Et algul on rakett paigal ja impulss null, saame impulsi jäävuse seaduse välja kirjutada järgmiselt:

Avaldame siit raketi kiiruse

Sellest valemist näeme, et rakett liigub gaaside väljapaiskumisele vastassuunaliselt (miinusmärk!) ja kiirus on seda suurem, mida suurem on kütuse ning raketi masside suhe ja mida suurema kiirusega gaasid välja pääsevad. Et kosmoselaev saavutaks Maalt lahkumiseks piisavalt suure kiiruse, peab kütuse mass ületama ülesviidava kasuliku massi hulka sadu kordi ning valida tuleb võimalikult kiiresti põlev kütus.

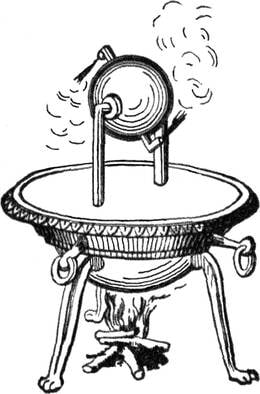
Esimese reaktiivliikumise põhimõttel töötava seadme ehitust on esimesel sajandil kirjeldanud antiikkreeka matemaatik ja insener Heron. Tegemist oli kahe düüsiga varustatud õõnsa metallkeraga, millesse suunati vee keemisel tekkiv aur. Düüsidest suure kiirusega väljuva auru reaktiivjõud pani selle nn Heroni kera pöörlema.

Tore näide reaktiivliikumise rakenduste kohta on muidugi ka hiinlaste poolt 13. sajandil leiutatud püssirohuraketid, mida kasutatakse ilutulestikes siiamaani.

Tänapäeval on reaktiivmootorid väga levinud, kuna need võimaldavad saavutada suuri kiirusi. Nendeta ei saa läbi ükski kosmoselennuaparaat ning enamik kiireid lennukeid liigub samuti reaktiivjõul. Reaktiivmootoreid ei kasutata aga mitte ainult lennumasinatel. Neid on monteeritud ka autodele, millega maapealseid kiirusrekordeid püstitatakse. Kui reaktiivautod on üsna haruldased, siis veejoa reaktiivjõul Tallinna ja Helsingi vahet kihutavad Jeti kiirlaevad (Jet — inglise k juga) on üsna igapäevased.

Reaktiivliikumist võib kohata ka mitme veelooma juures. Näiteks kasutavad kalmaarid, meduusid ja rannakarbid edasiliikumiseks endasse imetud vee kiiret väljasurumist.

Kulgevat liikumist iseloomustab liikumishulk ehk impulss ja kehtib impulsi jäävuse seadus. Impulsiga analoogilise suuruse saab defineerida ka pöörlemise jaoks. Kui kulgliikumise hulka nimetatakse lihtsalt impulsiks, siis pöördliikumise hulka nimetatakse pöördimpulsiks ehk impulsimomendiks.

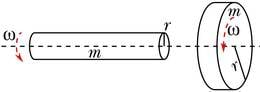
On loomulik, et massiivsema keha ja kiirema pöörlemise korral on pöörlemise energia suurem. Seepärast sõltubki impulsimoment keha massist ja pöörlemise nurkkiirusest. Kuid erinevalt kulgliikumisest, kus keha võib lugeda punktmassiks, on impulsimomendi määramisel keha kuju, mõõtmed ja massi jaotumine väga olulised. Mida kaugemal paikneb mass pöörlemisteljest, seda suurem on pöörlemishulk, kuna raadiuse suurenemisel joonkiirus kasvab. Lihtsama kujuga pöördkehade impulsimoment L on võrdeline keha massi, raadiuse ruudu ja pöörlemise nurkkiirusega:

Võrdetegur b sõltub keha kujust. Mõne lihtsama keha jaoks on selle väärtused esitatud tabelis.

Sarnaselt impulsiga on ka impulsimoment jääv. Kehtib pöörlemishulga ehk impulsimomendi jäävuse seadus. Välismõjude puudumisel säilitab süsteem oma pöörlemishulga ja sellega koos ka pöörlemistelje asendi. Sellepärast ei kukugi pöörlev vurr ja veerev rõngas ümber ning Maa telje kalde muutumatus paneb aastaajad vahelduma. Kiiresti pöörleva keha telje orientatsiooni muutumatust kasutatakse güroskoopides (γυρος + σκοπος — kreeka k pöörlemine + vaatleja), mille abil kontrollitakse näiteks lennukite kallet.

Impulssmomendi jäävuse tõttu peab helikopteril olema kaks tiivikut. Kui panna pöörlema vaid üks tiivik, hakkaks helikopter ise vastassuunas pöörlema. Viimast efekti kasutavad näiteks libedal teel tasakaalu kaotanud inimesed, kes kukkumise vältimiseks hakkavad instinktiivselt keha pöördumisega vastassuunas käteringe tegema.

Impulsimomendi jäävuse seadust kasutavad ka tantsijad ja iluuisutajad. Vastavalt seosele (4.10 ) peab raadiuse r muutumisel muutuma ka nurkkiirus. Kui iluuisutaja käed keha ligi tõmbab ja nii nende ringliikumise raadiust vähendab, kasvab tema pöörlemiskiirus järsult, sest korrutis $r^2\omega$ peab endiseks jääma.

Põhinähtus, mida mehaanika kirjeldab ja uurib, on liikumine. Liikumist võib muuta vastastikmõju abil. Vastastikmõju võib esile kutsuda ka kehade kuju muutumist ehk deformeerumist, mis oma olemuselt on samuti liikumine. Deformeerunud kehad võivad omakorda jälle liikumist esile kutsuda või muuta. Näeme, et liikumine ja vastastikmõju on tihedalt seotud ning määravad ära kehade erinevad seisundid ehk olekud. Sellised olekud võivad muutuda või olla püsivad. Kehade mehaanilist olekut saab muuta nende asukoha, liikumise või kuju muutmise teel. Oleku muutmise protsess on töö. Tööks nimetatakse keha või kehade süsteemi mehaanilise oleku muutmise protsessi kirjeldavat suurust.

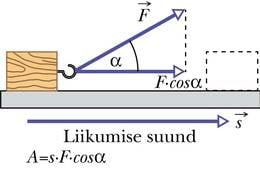
Kuna oleku muutust põhjustab vastastikmõju, siis sõltub ka tehtava töö hulk vastastikmõju tugevusest ehk kehale mõjuvast jõust. Seejuures läheb arvesse vaid jõu liikumise sihiline komponent. Veel oleneb tehtav töö läbitud teepikkusest s. Kui töö tähiseks võtta A (arbeit — saksa k töö), saame ülaltoodut arvestades töö definitsioonivalemiks

kus α on nurk keha liikumissuuna ja jõu mõjusuuna vahel ning F·cos α seega jõu liikumissihiline komponent.

Kui töö abil kirjeldatakse mehaanilise oleku muutumise protsessi, siis olekut ennast iseloomustatakse energia abil. Energiaks nimetatakse keha või kehade süsteemi mehaanilist olekut kirjeldavat suurust, mis näitab võimet teha tööd.

Nii töö kui ka energia mõõtühikuks on töö, mida teeb 1 N suurune jõud keha nihutamisel 1 m võrra. Seda ühikut nimetatakse džauliks (J). 1 J = 1 N·1 m = 1 N·m.

Tööd saab teha väga erinevatel viisidel. Näiteks võivad tööd teha liikuv haamer, väljavenitatud vedru, kuum aur, elektrivool ja plahvatusreaktsioon. Järelikult on ka energialiike mitmeid erinevaid. Liikumise ja kehade vahel mõjuvate jõududega kaasnev energia on mehaaniline energia.

Mehaanikas eristatakse liikumisenergiat ja vastastikmõju energiat. Keha liikumisolekust tingitud energiat nimetatakse kineetiliseks energiaks (κινημα — kreeka k liikumine).

Leiame, kui suurt kineetilist energiat omab keha massiga m, mis liigub kiirusega v. See energia on võrdne tööga, mis tehakse paigalseisvale kehale sellise kiiruse andmisel. Lugedes liikumist ühtlaselt muutuvaks, võib kiirendamise kestel läbitud teepikkuse leida avaldisest (1.18 ):

Kuna kiirendus on vastavalt Newtoni II seadusele võrdeline jõuga F ja pöördvõrdeline massiga m, saame teepikkuse avaldiseks

Tehtav töö on võrdne jõu ja teepikkuse korrutisega. Just nii suure energia keha kiirendamise käigus omandaski. Võttes kineetilise energia tähiseks E_k, saame kineetilise energia valemiks

Näeme, et kineetiline energia on võrdeline keha kiiruse ruudu ja massiga.

Kui liikuvatel kehadel on kineetiline energia, siis mitmest omavahel vastastikmõjus olevast kehast koosnevad süsteemid omavad potentsiaalset energiat. Potentsiaalseks energiaks nimetatakse kehade vahel mõjuvatest jõududest tingitud energiat. Nimetus on tulnud ladinakeelsest sõnast potentia, mis tähendab võimet või väge.

Väljavenitatud vedru ja mäetippu veeretatud kivi võivad tööd teha, kui need lahti pääsevad, aga ei pruugi pääseda ja tööd teha. Erinevalt liikumisenergiast, mis on loomu poolest aktiivne (toimub asukoha muutumine) on potentsiaalne energia passiivne ja varjatud.

Vedru energia sõltub sellest, kui pikaks me selle venitame, ülestõstetud kivi energia aga tõstmise kõrgusest. Potentsiaalne energia sõltub alati kas keha enda osade või selle ja teiste kehade vastastikusest asendist.

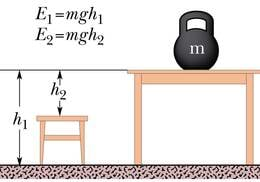
Leiame ülestõstetud keha potentsiaalse energia. Kui kõrgusele h tõstetud keha, mille mass on m, lahti pääseb, läbib see kukkudes teepikkuse s = h ja raskusjõu F = mg poolt tehtav töö A = Fs = mgh. Et kogu see töö tehakse potentsiaalse energia arvel, saamegi energia jaoks avaldise:

Ülestõstetud keha potentsiaalne energia on võrdeline massi ja kõrgusega. Et kõrgust h tuleb mõõta alati mingi taustkeha (näiteks maapinna) suhtes, sõltub potentsiaalne energia nullnivoo valikust. 

Mõnel juhul võib kõrgus tulla negatiivne, näiteks mõõtes kivi asukohta augus. Nii saab potentsiaalne energia olla erinevalt kineetilisest ka negatiivne.

Ühel kehal võib samaaegselt olla nii kineetiline kui ka potentsiaalne energia. Näiteks on langeval vihmapiisal nii kukkumise kineetiline kui ka Maa külgetõmbe potentsiaalne energia. Keha või kehade süsteemi kineetilise ja potentsiaalse energia summat nimetatakse mehaaniliseks koguenergiaks:

Kõik me oleme kogenud, et lenduvisatud kivi kõrgus ja kiirus muutuvad. Sellega koos muutuvad ka kivi kõrgusest sõltuv potentsiaalne ja kiirusest sõltuv kineetiline energia. Analüüsime vabalt langeva keha mehaanilise energia muutumist lähemalt.

Kuna kukkumisel mõjub kehale raskusjõud ning toimub liikumine, tehakse potentsiaalse energia kahanemise arvel tööd. Maapinnale jõudmise hetkeks on kogu potentsiaalne energia ära kulutatud. Järelikult on kukkumise käigus tehtud töö võrdne kulunud potentsiaalse energiaga:

Töö on keha mehaanilise oleku muutumise protsess. Raskusjõud teeb tööd ning selle käigus muutub keha kiirus. Mehaanilise energia mõiste avamise juures selgus, et kui jõud paneb keha liikuma, on tehtav töö võrdne kehale antava kineetilise energiaga:

Näeme, et tehtud töö käigus on keha potentsiaalne energia muundunud keha liikumis- ehk kineetiliseks energiaks. Seega ei lähe energia kukkumise käigus mitte kaduma, vaid mehaaniline energia muundub ühest liigist teise. Kukkuva keha potentsiaalne energia muundub kineetiliseks energiaks. Ülesvisatud keha tõusmisel toimub vastupidine protsess — kineetiline energia muundub potentsiaalseks. Võnkumise käigus kordub selline ühest liigist teise ja tagasi muundumine perioodiliselt.

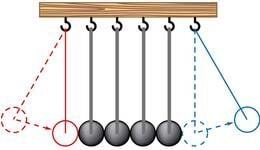
Esineb ka selliseid protsesse, mille käigus mehaanilise energia liik ei muutu, kuid milles toimub energia ülekandumine mõnele teisele kehale. Nii antakse elastsel põrkel ühelt metallkuulilt teisele edasi kineetiline energia. Vedru otsa riputatud koormis annab allapoole vajudes oma potentsiaalse energia venivale vedrule üle.

Mehaanilise energia ülekandumine ja muundumine võivad toimuda ka samal ajal. Nii läheb vinnastatud vibu potentsiaalne energia üle noolele ning muundub samal ajal kineetiliseks.

Äsja nägime, et mehaaniline energia võib muunduda potentsiaalsest kineetiliseks ja vastupidi ning kanduda ühelt kehalt teistele. Kui muundumise ja ülekandumise käigus pole vaja näiteks hõõrdumise ületamiseks täiendavat tööd teha, jääb potentsiaalse ja kineetilise energia summa alati muutumatuks. Potentsiaalse energia vähenemisel kasvab kineetiline energia täpselt sama hulga võrra. Kui keha annab oma energiat teisele kehale ära, saab see täpselt sama palju juurde.

See kehtib muidugi vaid suletud süsteemis, kuhu kuuluvad kehad pole süsteemivälistega vastastikmõjus ega saa nendega energiat vahetada.

Arvukad vaatlus- ja katsetulemused kinnitavad, et mehaaniline koguenergia on jääv. Pole täheldatud ühtegi protsessi, mis oleks selle tulemusega vastuolus. Seega võime sõnastada ühe olulisema loodusseaduse — mehaanilise energia jäävuse seaduse: suletud süsteemi kuuluvate kehade mehaaniline koguenergia on jääv. Süsteemi kehade energia võib muunduda ühest liigist teise või kanduda ühelt kehalt teisele, kuid kineetilise ja potentsiaalse energia summa ei muutu, st see jääb konstantseks (cônstâns — ladina k muutumatu).

Mehaanilise energia jäävuse seadust väljendab avaldis

Tuleb silmas pidada, et see jäävusseadus kehtib vaid süsteemides, milles mehhaaniline energia ei muundu mittemehaanilisteks energialiikideks, näiteks hõõrdumisel ja mitteelastsel põrkel soojuseks või tuulegeneraatoris elektrienergiaks.

Eespool nägime, et ühe ja sama töö tulemusena väheneb potentsiaalne energia ning niisama palju suureneb kineetiline energia. Sellest järeldub, et töö on võrdne ühest liigist teise muundunud energia hulgaga.

Kui süsteem pole suletud, võib tehtava töö tulemusena mehaaniline energia muunduda mittemehaaniliseks. Võimalik on ka vastupidine protsess, kus välise energia arvel tehtav töö suurendab süsteemi mehaanilist energiat. Mõlemal juhul mehaaniline koguenergia muutub, kusjuures muut ΔE_meh on võrdne süsteemiväliste jõudude tööga:

Pidurdamisel muutub kihutava auto kineetiline energia hõõrdejõu töö tagajärjel soojuseks, mis paneb kummid lausa suitsema. Seevastu mootoris bensiini põlemisel eralduva soojuse arvel tehtav töö annab autole kineetilise energia.

Seos (4.20 ) võimaldab mehaanilise energia jäävuse seaduse rakendamist laiendada. Näiteks saame seda kasutades hõõrdeteguri kaudu välja arvutada auto pidurdusteekonna pikkuse. Selleks tuleb sõiduki kineetiline energia võrdsustada hõõrdejõu pidurdava tööga, mis on võrdne jõu ja teepikkuse korrutisega. Saadud seosest on pidurdustee pikkuse avaldamine lihtne:

Suurt osa meie ümber toimuvatest nähtustest ei saa selgitada ainult mehaanikaseaduste abil. Mehaanika kirjeldab ja uurib liikumist. Lisaks liikumisele kirjeldab füüsika veel näiteks soojust ja valgust, elektri ja magnetismi nähtuseid, aatomites ja tuumades toimuvat...

Need nähtused on väga erinevad, kuid siiski omavahel seotud. Kõiki nähtusi ühendavaks lüliks on energia. Erinevate nähtuste juures avalduvad erinevat liiki energiad. Lisaks mehaanilisele energiale tuntakse veel keemilist, elektromagnetilist, tuuma- ja soojusenergiat.

Kui vaadata kõiki energialiike tervikuna, kehtib üldine energia jäävuse seadus: suletud süsteemi koguenergia on ajas muutumatu. Energialiik pole oluline. Peaasi, et puudub energiavahetus süsteemist väljapoole. Energia ei saa tekkida eimillestki ega kaduda olematuks.

Tänapäeval peavad füüsikud meie universumit suletud süsteemiks. Kui see tõsi on, peab selles leiduva energia koguhulk olema jääv. Energia saab vaid kehalt kehale üle kanduda või mis tahes liigist mis tahes teiseks liigiks muunduda.

Põhjalikumalt tutvustatakse energiaga seonduvat füüsika neljanda kursuse käigus.

Energia jäävus on üldine loodusseadus ning puudutab suuremal või vähemal määral kõiki nähtusi. Sellegipoolest saab nii looduses kui ka tehnikas välja tuua valdkonnad, mis on energia ning selle muundumise ja jäävusega otseselt seotud. Nendeks on energia kasutamine, saamine, transport ja salvestamine. Tutvume mõne näitega lähemalt.

Energia kasutamine on seotud eelkõige tööga, mida selle arvel teha saab. Kuna energia ei teki eimillestki, saab tööd teha vaid mingi energiaallika olemasolul. Kõik loomad — inimesed nende hulgas — vajavad ringi liikumiseks ning toimetamiseks energiat, mida nad saavad toidust. Inimesed on oma elu lihtsamaks muutmiseks leiutanud masinaid, mis töö nende eest ära teevad. Masinaid, mis välise energia arvel tööd teevad, nimetatakse jõumasinateks ehk mootoriteks.

Jõumasinate käimapanekuks kasutatakse erinevaid energialiike. Tuule kineetiline energia paneb tööle tuuleturbiinid ning kõrgele kogutud vee potentsiaalne energia käivitab hüdroturbiine. Sõidukite liikumapanekuks kasutatakse enamasti mootoreid, milles tehakse tööd kütuse põlemisel eralduva soojusenergia arvel. Järjest enam rakendatakse tööstuses ja majapidamises elektrienergiat tarbivaid masinaid.

Jõumasinate tarbeks energia hankimine on alati seotud kulutustega. Seepärast on juba ammustest aegadest saati üritatud ehitada masinaid, mis töötaksid lõputult ilma välise energiaallikata. Igavese jõumasina ehk perpetuum mobile (ladina k igavesti liikuv) loomine pole energia jäävuse seaduse kohaselt võimalik. Energia jäävuse seaduse järgi ei saa ükski masin teha rohkem tööd, kui see selleks kulutab. Veel enam: hõõrdumise tõttu pole võimalik ehitada isegi igiliikurit, mis ei teeks küll tööd, kuid säilitaks liikumise. Nii ei võtagi patendibürood enam läbivaatamiseks igaveste jõumasinate projekte, mis leiutajate arvates peaksid töötama lõputult eimillegi arvel.

Jäävusseadus ütleb, et energia ei saa kaduda. Miks siis räägitakse, et kui me energiat kokku ei hoia, lõpeb see varsti otsa? Asi on selles, et töö tegemisel muutub energia mingist ühest liigist teise. Vastupidine muundumine aga sama lihtsasti toimuda ei saa.

Kui põletatakse naftat, siis selles leiduv süsinik ja vesinik reageerivad hapnikuga, tekib süsihappegaas ja veeaur ning selle käigus vabaneb soojus- ja valgusenergia, mida siis inimene kasutab. Ka vastupidine protsess on võimalik. Taimed võtavad juurtega maast vett ja lehtedega õhust süsihappegaasi ning sünteesivad Päikeselt tulevat valgusenergiat kasutades need biomassiks. Just selle nn fotosünteesi teel toodetud biomass ladestus miljonite aastate kestel kivimikihtide vahele. Biomassist tekkis päikeseenergiat salvestanud kivisüsi, nafta ja maagaas, mida me tänapäeval fossiilsete kütustena kaevandame ja põletame.

Fossiilne energia pole jääv	Taastuv energia tuleb kõik Päikeselt

Energiat saab kerge vaevaga muundada vaid ühes suunas. Vastupidine protsess on keerukas ja aeglane. Seepärast tuleb eelistada energiaallikaid, mille taastumine toimub kiiresti. Maised energiaallikad taastuvad Päikeselt tuleva kiirguse arvel. Päike paneb kineetilist energiat andes õhu tuulena liikuma ja tõstab potentsiaalset energiat andes vee meredest jõgedesse. Taimed talletavad Päikeselt tulevat energiat, tootes tselluloosi, tärklist, õli ja suhkrut.

Päike kiirgab Maale tohutul hulgal energiat veel mitme miljardi aasta kestel. Inimese ülesanne on seda paremini kasutama õppida.

Üks huvitav ja mitmeid rakendusi leidnud nähtus, mida saab selgitada mehaanilise energia jäävuse seaduse kaudu, puudutab gaaside ja vedelike voolamist. Tutvume sellega lihtsustatud käsitluse kaudu.

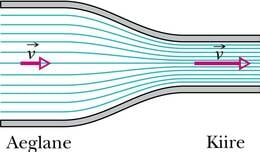
Oletame, et ideaalne (so kokkusurumatu ja mitteviskoosne) vedelik voolab torus, mille läbimõõt pole kõikjal ühesugune. Siis toru erinevaid ristlõikepindu läbib sama ajaga alati sama ruumalaga vedelikukogus. On selge, et sellisel juhul peab voolukiirus toru peenemates osades olema suurem kui jämedamates.

Kui toru peenemas osas on vedeliku kiirus suurem, siis on seal suurem ka selle kineetiline energia. Hõõrdumise puudumisel on vedeliku mehaaniline energia jääv. Kui kineetiline energia suureneb, peab potentsiaalne samavõrra vähenema. Potentsiaalne energia on aga teatavasti tingitud süsteemi sees mõjuvatest jõududest. Antud juhul on tegemist vedeliku rõhumisjõududega. Näeme, et mida suurem on voolukiirus, seda väiksem on selles kohas vedeliku rõhk. Sama kehtib ka gaaside voolamisel.

Kirjeldatud seaduspärasuse avastas 1738. aastal šveitsi matemaatik ja füüsik Daniel Bernoulli. Tänapäeval tuntakse seda Bernoulli printsiibi nime all: voolava gaasi või vedeliku rõhk on suurem nendes piirkondades, kus kiirus on väiksem, ja väiksem seal, kus kiirus on suurem.

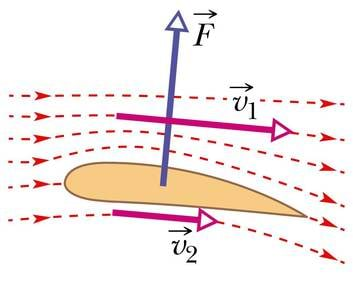
Bernoulli printsiipi kasutatakse mitmesuguste füüsikaliste nähtuste selgitamiseks. Näiteks võib öelda, et tormituul tõstab majalt katuse lendu sellepärast, et maja sees, kus õhk on paigal, on rõhk suurem kui katuse kohal tuule käes ja katus surutaksegi alt üles. Või siis pallimängudes, kus saab väita, et pöörlevana lendu löödud pall kaldub otsesihist kõrvale kuna õhu liikumise kiirus selle eri külgedel erinev ja tekib rõhkude vahe. Analoogiliselt seletatakse ka lennuki tiiva tõstejõudu —  tiiva asendi ja erilise kuju tõttu voolab õhk selle kohal kiiremini kui all, nii on tiiva all rõhk suurem ja see hoiabki lennukit õhus. Peab siiski ütlema, et kuigi nende nähtuste seletustes Bernoulli võrrandi alusel on tera tõtt, ei ole need paljudes põhiküsimustes täielikud. Sest Bernoulli printsiip kehtib vaid voolutorus, aga seda ei saa rakendada seeläbi, et me võrdleme üksteisest eraldatud vedelike (või gaaside) voolusid (nagu ühel ja teisel pool katust, palli või lennuki tiiba). Teiseks, Bernoulli printsiip kehtib vaid ideaalsete vedelike (ja gaaside) korral. Samas reaalsete vedelike liikumine on väga keerukas nähtus, mida ka tänapäeval täielikult ei mõisteta.

Daniel Bernoulli	Bernoulli printsiip leiab rakendust lennunduses