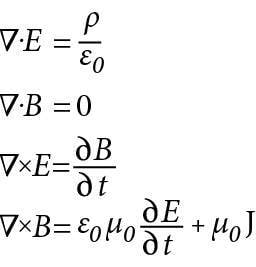3D kinoga me oleme ära harjunud, paneme spetsiaalsed prillid ette ning ühtäkki omandab muidu lame kinolina sügavuse.
Tegelikult meile muidugi meeldiks nautida sellist elamust ilma, et peaksime end selleks prillidega ehtima. Niisamuti ei oleks meil midagi selle vastu, kui meie arvutiprojektorid suudaksid kuvada ruumilisi pilte. Ja arvatavasti ei oleks meil midagi selle vastu, kui meie telefonid saaksid hakkama sellega, mis näha parempoolsel pildil?
Küllap teavad seda ka need, kes filme, projektoreid ja telefone toodavad. Milles siis asi?
Elektromagnetvälja ühtse teooria lõi Faraday katsetulemuste põhjal šoti füüsik James Clerk Maxwell. Faraday oli veenvalt näidanud, et magnetvälja muutumisel tekib pööris-elektriväli sõltumatult muutuse päritolust. Maxwell oletas, et elektrivälja muutumine põhjustab samamoodi muutuva magnetvälja tekkimise, sõltumatult muutuva elektrivälja päritolust. Maxwelli käsitluse kohaselt jõuab elektrivälja muutus ühest ruumi punktist teise magnetvälja vahendusel. Elektrivälja muutumine ühes punktis põhjustab kõigepealt muutuva magnetvälja ja selle magnetvälja muutus kutsub elektromagnetilise induktsiooni teel esile elektrivälja muutumise naaberpunktis. See tähendab, et igasugune elektri- või magnetvälja muutus levib ruumis lainena. Just lainele on ju omane kindlate hälbeseisundite järjestikune esinemine laine levikusuunal paiknevates punktides. Tekkivat lainet nimetas Maxwell elektromagnetlaineks.
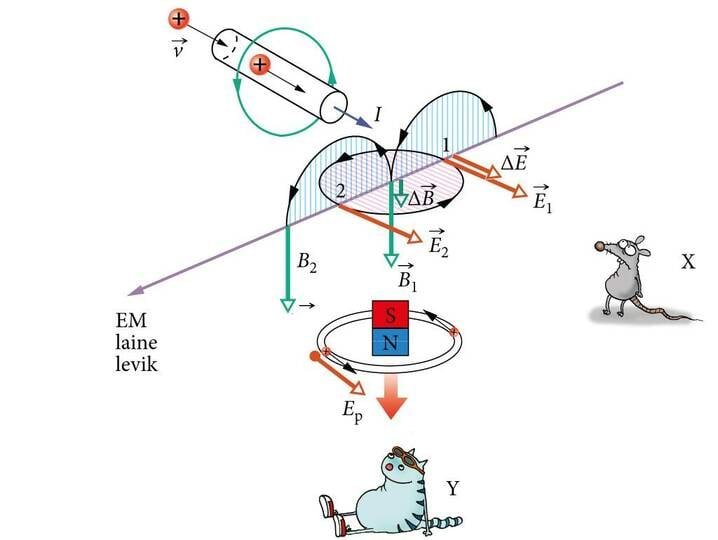
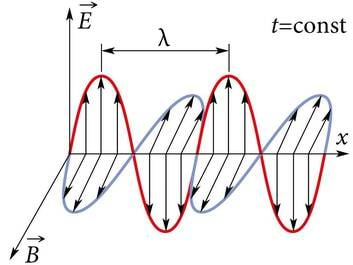
Püüame nüüd joonise 3.1 abil mõista elektromagnetlainete tekkemehhanismi. Lähenegu joonise ülemise vasaku nurga poolt vaatlejale X kiirusega liikuv positiivselt laetud keha. Täheldame, et selline liikumine on samaväärne vaatleja X poole kulgeva vooluga joonisel kujutatud juhtmes. Vaatleja X registreerib tema poole suunatud elektrivälja , sest tegemist on positiivse laenguga. See väli tugevneb, kuna välja tekitav keha läheneb vaatlejale, väljatugevus aga on teatavasti pöördvõrdeline kauguse ruuduga. Järelikult on ka väljatugevuse muut vektorina suunatud vaatleja X poole, seega paremale alla. Tugevnev elektriväli tekitab tugevneva magnetvälja, mille jõujooned ümbritsevad parempoolsete pööristena elektrivälja tugevuse muudu vektorit . Nad ümbritsevad punktis 1 vektorit samamoodi, nagu nad joonise vasakpoolses ülemises osas ümbritsevad vooluga juhet, olles suunatud juhtme taga üles ja ees vasakul alla.
Seega tekib punktist 1 vasakul alla suunatud ja tugevnev magnetväli magnetinduktsiooniga . Kuna see väli on tugevnev, siis on alla suunatud ka magnetinduktsiooni muut . Vektoritega ja samal sihil allpool paiknev vaatleja Y registreerib tugevnevat magnetvälja samamoodi nagu siis, kui tema poole liiguks ülalt alla püsimagnet, põhjapoolus ees. Kui see magnet läbiks liikudes juhtmerõngast, siis tekiks selle rõnga parempoolses tagumises ääres tahapoole (vasakule üles) ning rõnga vasakpoolses esiääres ettepoole (paremale alla) suunatud induktsioonivool, mida võib vaadelda põhjustatuna samamoodi suunatud pööriselektriväljast tugevusega . Pööriselektrivälja jõujooned ümbritsevad vasakpoolsete pööristena magnetvälja kasvu suunda. Nende pööriste vasakpoolsus tuleneb elektromagnetilise induktsiooni seaduses (valem 2.7 ) sisalduvast miinusmärgist.
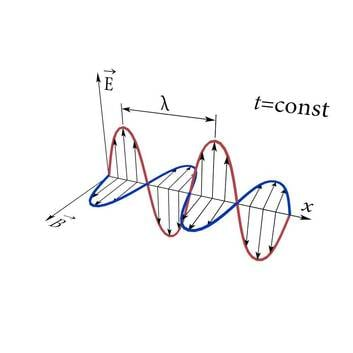
Samamoodi tekib paremale alla suunatud pööriselektriväli tugevusega , ka punktis 2, mis ju samuti jääb horisontaaltasandis paikneva ning suunda ümbritseva pöörise vasakule esiäärele. Võime teha kokkuvõtte: muutuv elektriväli tugevusega on magnetvälja vahendusel ruumis vasakule ettepoole liikunud. Temast on saanud väli . Punktis 2 aga kordub seesama protsess, mis leidis aset punktis 1. Horisontaaltasandis paiknev, paremale ette suunatud elektriväli tekitab endast vasakul eespool vertikaaltasandis paikneva ja alla suunatud magnetvälja . Võime nentida: magnetväljast on elektrivälja vahendusel saanud magnetväli . Ehk teisisõnu, magnetväli on elektrivälja vahendusel liikunud vasakule ettepoole. Seega elektromagnetväli liigub ruumis lainena algse elektrivälja muutusega ristuvas suunas. Elektriväli ja magnetväli on laines omavahel risti ja nad mõlemad on ka risti laine levimissuunaga. Elektromagnetlaine on ristlaine.
Olgu öeldud, et täpselt samamoodi kiirgaks elektromagnetlaineid raadio saateantenn, mille juhtme tükk paikneb joonise 3.1vasakpoolses ülemises osas ja mille juhtmes kulgeks ajas muutuv vool. Elektromagnetlained kiirguvad juhtmega ristuvas suunas, joonisel 3.1 vasakule alla.
| Heinrich Rudolf Hertz (1857 - 1894). 1887. aastal tegi ta rea eksperimente, kus suutis esmakordselt tekitada ja ka detekteerida elektromagnetlaineid, samuti demonstreerida nende polarisatsiooni ja interferentsi. Maxwelli võrrandite formuleerimisest oli selleks ajaks möödas juba kakskümmend aastat. | Hertz suutis oma katseseadmes tekitada piisavalt suure sagedusega elektrivõnkumisi (sagedusega ca 500MHz). Tagumisel laual on näha kõrgepinget tekitanud pool. Antenniks oli esiplaanil kahe suure sfääri vahel paiknev varraste süsteem. |
Kogu meid ümbritsev ruum on täidetud elektromagnetlainetega. Õnneks me lõviosa nendest ei taju, muidu oleks võimatu aru saada, mis meie ümber toimub.
Elektromagnetlainetel võivad olla väga erinevad omadused ja seepärast on neil ka erinevad nimed. Suurt osa elektromagnetlaineid kutsutakse kiirgusteks.
Ühe osa neist lainetest on inimene tekitanud ja pannud need ennast teenima. Näiteks raadiolained kannavad edasi infot, lambivalgus lubab inimestel pimeda ajal näha, infrapunakiirgus ehk infravalgus aitab teleri puldi abil mängima panna. Aga ka tavaline vahelduvvool juhtmes tekitab elektromagnetlaineid.
Teine osa lainetest aga tekib niisama, ilma inimese osaluseta. Näiteks Päikeselt tulev ultraviolettkiirgus ehk ultravalgus päevitab meid kenasti pruuniks, radioaktiivne kiirgus, mis tekib radioaktiivsete ainete lagunemisel, ohustab meie tervist, jaaniusside salapärane kuma rõõmustab meid suveööl.
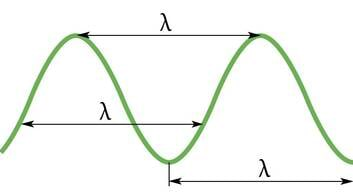
Elektromagnetlainete toime sõltub lainete sagedusest ehk ajaühikus toimuvate võngete arvust. Samas sõltub see ka lainepikkusest ehk naaber-laineharjade vahekaugusest. Nende kahe suuruse seos tuleneb ühtlase liikumise kiiruse valemist . Teepikkuseks s on laine korral lainepikkus , mille läbimiseks kuluv aeg on võnkeperiood . Perioodi pöördväärtus on aga sagedus . Seega
laine levimiskiirus on lainepikkuse ja sageduse korrutis. Kui tegemist on elektromagnetlainetega vaakumis, siis asendub valguse kiirusega vaakumis ning lainepikkuse all tuleb mõista lainepikkust vaakumis, niisiis
Sageduse mõõtühikuks on . Elektromagnetlainete korral peetakse silmas E- või B-vektori võnkumisi. Lainepikkuse mõõtühikuks on .
Valem 3.1 põhjal on lainepikkus vaakumis ja sagedus omavahel pöördvõrdelised:
Näide 3.1.
Tühjuses (vaakumis) levib elektromagnetlaine suurima võimaliku kiirusega maailmas, mis on kõigi vaatlejate jaoks ühesugune. Füüsikalise looduskäsitluse aluste kursuses nimetati seda kiirust absoluutkiiruseks ja tähistati tähega (kr celeritas – kiirus). Teatavasti absoluutkiirus c = 299 792 458 m/s ≈ 3·108 m/s.
Elektromagnetlaine üleminekul ühest keskkonnast teise võib laine kiirus muutuda. See kutsub esile ka lainepikkuse muutumise, kuid laine sagedus sealjuures ei muutu kunagi.
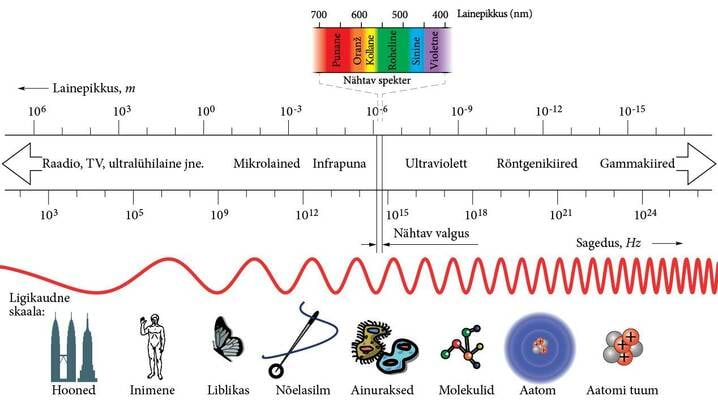
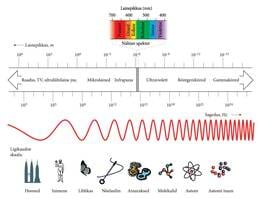
Ülevaate saamiseks kõikvõimalikest elektromagnetlainetest on kombeks paigutada nad sageduse või lainepikkuse järgi astmikule ehk skaalale, mille ühes otsas paiknevad madalsageduslikud ja pikad, teises (parempoolses) otsas aga kõrgsageduslikud ja lühikesed lained. Saame nn elektromagnetlainete skaala. Järgnevalt loetletud elektromagnetlainete põhiliigid erinevad lisaks sagedusele või lainepikkusele veel tekkimise viisi, levimise seaduspärasuste ning ainest läbitungimise võime poolest.
Madalsageduslained (, ja enam) on sisuliselt vahelduvvool, millega lähem tutvumine seisab meil ees Energia kursuses. Need lained levivad elektrijuhtides. Vaakumis või dielektrikus (näiteks õhus) on vastava elektromagnetvälja energia ja seega ka lainete intensiivsus tühiselt väikesed. Nimetatud põhjusel kantaksegi vahelduvvooluga kaasneva elektromagnetvälja energiat (ehk kõnekeeles lihtsalt elektrienergiat) üle juhtmete abil.
Raadiolained (, ) kaasnevad vahelduvvooluga, mida me uurime lähemalt Energia kursuses. Võnkumisi tekitab elektrooniline generaator ja vastavaid laineid kiirgab raadioantenn. Ajaloolise tava kohaselt jagatakse raadiolainete piirkonda omakorda millimeeter- ja sentimeeterlainealaks lainepikkustega vastavalt 1...10 mm ja 1...10 cm (satelliittelevisiooni ning radarite tööpiirkond), televisiooni detsimeeter- ja meeterlainealaks (lainepikkustega 1...10 dm ja 1...10 m), raadio ultralühilainealaks (levinuim lainepikkus 3 m) ning raadio lühilaine (λ = 10...100 m), kesklaine (λ = 100...1000 m) ja pikklaine alaks (lainepikkus üle 1000 m).
Optiline kiirgus (, ) on peaosatäitjaks valgusnähtustel. Pikalaineline optiline kiirgus tekib molekulide võnkumistel, aga peamiselt tekitavad optilist kiirgust siiski aatomite väliskihtide elektronid. Optiline kiirgus jaguneb omakorda ultravalguseks (λ = 10…380 nm, 1 nm = 10-9 m), nähtavaks valguseks (λ = 380...760 nm) ja infravalguseks (λ = 760 nm...1 mm).
Röntgenikiirgus (, )
tekib kas kiirete elektronide järsul pidurdumisel või siis protsessidel, milles osalevad aatomite sisekihtide elektronid. Röntgenikiirguse lainepikkuse suurusjärk ühtib aatomite vahekaugusega tahkistes. Meditsiinis leiab laialdast kasutamist röntgenikiirguse võime tungida läbi inimkeha.
Gammakiirgust (, ) väljastavad radioaktiivsel lagunemisel aatomite tuumad. Gammakiirguse laineomadusi on raske uurida, sest lainepikkus on väiksem aatomi mõõtmetest. Gammalainet pole enam millegagi võrrelda. Gammakiirgus tungib raskusteta läbi peaaegu igast ainest.
Nagu näeme, kaasneb kiirgaja mõõtmete vähenemisega ülaltoodud reas (antenn → molekul → aatomi väliskiht → aatomi sisekiht → tuum) lainepikkuse vähenemine ja sageduse suurenemine. Koos sagedusega suureneb ka kiirguse energia ning läbitungimisvõime.
Peab lisama, et erinevate lainepiirkondade vahel puuduvad täpsed piirid. Jaotuse aluseks on eelkõige laineallikad, kusjuures erinevate laineallikate poolt tekitatud lainete sagedused kattuvad. Kõikidest elektromagnetlainetest näeb inimese silm ainult seda osa, kus laine sagedus jääb vahemikku 1014...1015 Hz. Sellise sagedusega elektromagnetlaineid nimetatakse nähtavaks valguseks. Teistel elusolendeil võivad tekitada nägemisaistingu aga teistsuguste sagedustega elektromagnetlained. Näiteks maod tajuvad hästi infravalgust, aga mesilased ultravalgust.
Elektromagnetlaineid tajub inimene lisaks nägemisele ka soojusena. Pole ju vaja käega katsuda, kas ahi või radiaator on soe, juba eemalt tunneme, kuidas see "sooja õhkab". Seda tunnet tekitavad elektromagnetlained, mille sagedus jääb vahemikku 1012...1014 Hz.
Elektromagnetlaineid kasutab inimene väga paljudes eluvaldkondades. Paljudega neist saame me põgusalt tuttavaks järgnevates alajaotustes.
Tänapäeval osatakse käsitseda pea kõikvõimalike lainepikkuste ja sagedustega elektromagnetlained. Peatüki lõpetuseks esitame joonisel 7-10 elektromagnetlainete spektri skeemi, ühtlasi täpsustades mõningaid nendega seotud mõisteid.
Nähtava valguse pikalainelisest punasest servast edasi tuleb nähtamatu infrapunavalgus ehk lihtsalt infravalgus. Seda tajume tema soojusliku toime kaudu. Infravalgus läheb järkjärgult üle raadiolaineteks, millest lühimad on ultralühilained ehk mikrolained Teravat piiri nende piirkondade vahel ei ole. Tanapaeval kasutatakse raadiosides ja teabelevis kõiki lainepikkusi alates umbes ühest mikromeetrist lähi-infravalguses kuni ühpdckade raadiolaineteni, mille pikkus küünib tuhandete kilomeetntem. on viirutatud. Esimesi rakendatakse kiudoptilistes sidesüsteemides, viimaseid sidepidamiseks sukeldunud allveelaevadega. Lühilainelisel poolel läheb ultraviolett- e. ultravalgus üle röntgenikiirteks, mille lainepikkused on lähedased aatomi mõõtmetega, edasi gammakiirteks, millest lühimate lainepikkused ei ulatu isegi aatomituuma mõõtmeteni.
Välja arvatud nähtav valgus, on kõik need kiirgused avastatud pärast Maxwelli eluaega. Tema loodud elektri, magnetismi ja valguse ühendteooria viis otseteed neist mõnede avastamisele, aidates mõista ka ülejäänuid. Vaevalt võib tuua paremat näidet puhta teaduse tulemustest, mis oleksid andnud nii tohutu tähtsusega praktilisi rakendusi. Kui nüüdsed teadlased püüavad õigustada maksumaksjate raha kulutamist asjadele, millel ei ole veel ilmset või kohest praktilist rakendust, on nad tänu võlgu James Clerk Maxwelli varjule.
Optika ehk valgusõpetus kirjeldab valguse tekkimist, levimist ja kadumist. Optikas nimetatakse valguse tekkimist kiirgumiseks ja valguse kadumist neeldumiseks. Kiirgumine seisneb selles, et aineline objekt tekitab oma energia arvel täiendava väljaportsjoni ehk kvandi. Neeldumisel annab kvant oma energia ja impulsi mingile ainelisele objektile ära ning haihtub ise olematusse. Ehk siis selleks, et valgus tekiks, peab olema keha, mis sel moel muudab teisi energialiike valguseks. Sellist keha nimetatakse valgusallikaks.
Näiteks nii hõõglambis kui valgusdioodlambis muudetakse valgusenergiaks elektrienergiat. Seejuures kiiratakse hõõglambis suurem osa (üle 80 %) muundunud elektrienergiast infravalgusena (soojuskiirgusena), aga valgusdioodlambis nähtava valgusena. Valgusdioodlampi tuntakse ka LED-lambina (ingl.k. light emitting diode).
Valguse levimine toimub erinevalt vaakumis või mingis keskkonnas ehk aines.
Vaakumis levib valgus nagu iga elektromagnetlaine: muutuv elektriväli tekitab muutuva magnetvälja ja see omakorda uuesti muutuva elektrivälja ning kõik kordub. Nii kandub valgus ruumis edasi kiirusega c.
Valgus levib ühtlases ehk homogeenses keskkonnas sirgjooneliselt. Mitteühtlases keskkonnas levib valgus kõverat teed pidi.
Valguse levimise teed saab leida looduses kehtiva printsiibi järgi, mis väidab, et valgus levib teed mööda, mille läbimiseks kulunud aeg on minimaalne. Seda printsiipi tuntakse Fermat' printsiibina, sest selle sõnastas 1662. aastal prantsuse matemaatik Pierre de Fermat. Kui keskkond on ühtlane, siis kõige kiiremaks levimisteeks on sirge, aga kui keskkond ei ole ühtlane, siis pole kiireim tee sugugi sirge. Seda väidet saab illustreerida järgmise näitega.
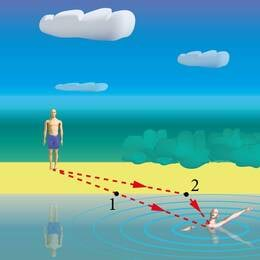
Oletame, et me oleme järve kaldal ja äkki hakkab järves keegi uppuma (J.3.2). Uppujale tuleks appi jõuda nii kiiresti kui võimalik. Kas joosta punkti 1 ja ujuda otsejoones uppujani või on mõni teine variant otstarbekam?
Tuleb arvestada, et inimene jookseb kiiremini kui ujub ja sellepärast tuleks ujumismaad lühendada ja jooksmismaad pikendada. Sellepärast tulekski joosta punkti 2 ja sealt uppujani ujuda. Punkti 2 täpse asukoha saab välja arvutada, aga uppuja päästmisel pole selleks aega ning valik tuleb teha oma sisetunde järgi.
Kui valgus langeb mingile kehale, siis võib valgus kas kehalt peegelduda, kehast läbi minna või kehas neelduda. Ükski nendest protsessidest ei toimu täielikult. Ka kõige parem peegel ei peegelda valgusest 100 %, mingi osa valgusest siiski neeldub peeglis. Samuti ei lase ka kõige puhtam aknaklaas läbi kogu valgust, ikka neeldub mingi osa valgusest klaasis.
Kui valgus langeb ainele, mis valgust läbi ei lase ja ei peegelda ka, siis öeldakse, et valgus neeldus selles aines. Lihtsamalt öeldes: valgus kadus ära. Aga me teame, et kehtib energia jäävuse seadus, järelikult pidi neeldumisel valgusenergia muutuma mõneks teiseks energialiigiks. Tavaliselt muutub neeldunud valgusenergia soojuseks, kuid see võib muutuda ka näiteks elektrienergiaks, nagu see juhtub päikesepatareides.
Valgus ei neeldu aines kunagi täielikult, sest ka kõige mustem pind peegeldab natuke valgust tagasi. See hulk võib olla küll tühine, aga nulliks ei saa see kunagi. Näiteks tahma korral peegeldub sellele langenud valgusest tagasi vähem kui 0,1 %.
Elektromagnetväli
Elektromagnetvälja levimine
Elektromagnetväli levib ruumis elektromagnetlainena, milles elektriväli ja magnetväli perioodiliselt muutuvad.
Väljavektorite suund elektromagnetlaines
Elektromagnetlainete põhiliigid
Elektromagnetlainete põhiliikideks on madalsageduslained, raadiolained, optiline kiirgus (infravalgus, nähtav valgus ja ultravalgus), röntgenikiirgus ja gammakiirgus.
Elektromagnetlainete tekkimine
Elektromagnetlaineid võib tekitada nii inimtegevus kui looduslikud protsessid.
Scale of electromagnetic waves
Elektromagnetlainete skaala on diagramm, kus kõik elektromagnetlainete liigid on reastatud sageduse või lainepikkuse järgi.
Elektromagnetlainet kirjeldakse samade suurustega, mis on meile tuttavad Mehaanika kursuses mehaaniliste lainete õppimisest: amplituud, hälve, lainepikkus, periood, sagedus, ringsagedus, faas ja levimiskiirus. Käesolevas kursuses kirjeldame me nende suuruste abil E-vektori ja B-vektori ajalist käitumist. Elektrivektori kohta kirjutame harmoonilise võnkumise võrrandi kujul
kus on E-vektori hetkväärtus ehk hälve, selle vektori amplituudväärtus, on aeg, on ringsagedus ja siinusfunktsiooni argument on laine faas. B-vektori kohta kirjutame vastavalt , kus on B-vektor ja selle amplituudväärtus. Selliseid laineid saab esitada kahesuguste graafikutega. Ühel juhul näidatakse, kuidas ühes kindlas ruumipunktis muutub aja jooksul E-vektori väärtus. Teisel juhul näidatakse, millised on E-vektori väärtused ühel ajahetkel mingis ruumipunktis.
Valgus on üks elektromagnetlainete liik. Kuid käesolevas kursuses ei kasuta me valguslaine kirjeldamisel magnetvälja, räägime ainult E-vektorist. Sellisel lihtsustusel on vähemalt kaks põhjust. Esiteks on elektromagnetlaine moodustavad E-vektor ja B-vektor risti ning nad võnguvad samas faasis (vaata J.3.3). Järelikult ei ole meil tarvidust neid mõlemaid välja joonistada, kui me teame üht siis teame automaatselt ka teist. Ja kuna vaid kahemõõtmelist lainet on võimalik korralikult paberil või arvutiekraanil kujutada, siis jäetaksegi B-vektor tihti vaatluse alt välja. Teine põhjus seisneb selles, et valgusaistingu silmas või signaali mõnes tajuris tekitab just valguslaine elektriväli, mõjudes neis olevatele elektronidele.
Valguslained eristuvad teistest elektromagnetlainete liikidest selle poolest, et nad tekitavad inimesel valgusaistingu. Selliste lainete sagedus jääb vahemikku 3,95·1014... 7,9·1014 Hz ja lainepikkus vahemikku 760...380 nm.
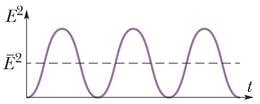
Kõiki füüsikalisi suurusi peab olema võimalik mõõta. Aga E-vektori muutumissagedus on ca 1014 Hz ja nii kiiresti muutuvat suurust pole võimalik ühegi riistaga mõõta. Sellepärast kasutatakse E-vektori keskmist väärtust. Täpsemalt öeldes, kasutatakse E-vektori ruudu keskväärtust E2kesk. See on ühe laine korral muutumatu suurus ja seda on võimalik mõõta.
Suurust, mis on võrdeline E2kesk-ga, nimetatakse valguslaine tugevuseks ehk valguse intensiivsuseks:
kus on võrdetegur. Intensiivsus näitab valgusenergia hulka, mis ajaühikus langeb pinnaühikule. Selle mõõtühikuks on
Mida suurem on E-vektori amplituud, seda suurem on ka E2kesk ja seega ka suurem valguse intensiivsus. Selline seos kehtib kõigi elektromagnetlainete korral.
Olukord on sarnane teiste lainetega. Näiteks madalad, väikese amplituudiga veelained ei lõhu merekallast, küll aga kõrged lained, millel on rohkem energiat.
Valguslaine ei ole mingisuguse keskkonna võnkumine nagu veelaine on vee võnkumine. Valguse korral muutub ainult E-vektori väärtus. Järelikult pole valguslaines ka mingeid laineharjasid ega -nõgusid. On ainult E-vektori maksimaalsed ja minimaalsed väärtused.
Valguse intensiivsuse asemel kasutatakse valgustehnikas mõistet kiiritustihedus, mida mõõdetakse ka ühikutes W/m2. Et saada ettekujutus sellise ühiku suurusest, võib aluseks võtta fakti, et südasuve keskpäeval, selge ilmaga on Eestis päikesevalguse intensiivsus ehk kiiritustihedus maapinnal veidi vähem kui 700 W/m2.
Valguse kiirus on erinevates keskkondades erinev. Kehtib seaduspärasus, et mida suurem on keskkonna tihedus, seda väiksem on seal valguse kiirus. Näiteks õhus normaaltingimustel on valguse kiirus v = 2,9970·108 m/s, mis on praktiliselt võrdne valguse kiirusega vaakumis. Seevastu ühes suurema tihedusega läbipaistvas aines, teemandis, on valguse kiirus punase valguse jaoks ca 1,24·108 m/s.
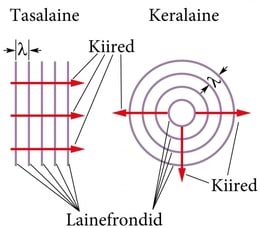
Valguslainete ja mistahes elektromagnetlainete levimist kirjeldatakse samamoodi nagu lainete levimist mehaanikas. Laine levimist ruumis kirjeldab lainefront (J.3.5). Lainefront on pind ruumis, kus kõik laine punktid võnguvad ühes faasis. Näiteks, kui veelaineid ülevalt vaadata, siis lainefrontideks võivad olla kõik laineharjad.
Joonistel esitatakse lainepinnad iga perioodi järel, lainepindade vahekaugus on võrdne ühe lainepikkusega.
Lainefrontide kuju järgi nimetatakse ka lainete tüüpe. Elektromagnetlainete uurimisel on kõige olulisemad neist keralained ja tasalained. Esimesel juhul on lainefrondiks kerapind ehk sfäär, mida joonisel kujutatakse ringjoonena. Lainefrondid moodustavad sel juhul kontsentriliste sfääride (joonisel ringide) süsteemi. Teisel juhul on lainefrondiks tasand, mida joonisel kujutatakse sirge joonena. Lainefrondid moodustavad sel juhul paralleelsete tasapindade (joonisel sirgete) süsteemi (J.3.5).
Lainefrontide ristsirgeid nimetatakse kiirteks.
Punkvalgusallikast hakkab ühtlases keskkonnas levima keralaine. Kui laine on allikast juba väga kaugele jõudnud, siis muutuvad lainefrondid väiksemas ruumipiirkonnas paralleelseteks ja seal võib rääkida tasalainest (J.3.6).
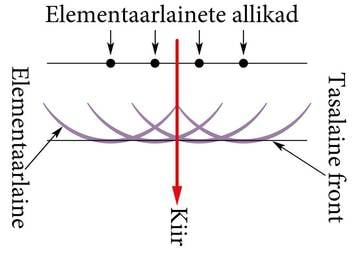
Kui on teada üks lainepind, siis järgmise saab leida, kasutades Huygensi printsiipi: lainefrondi iga punkt on uue laine allikaks. Neid uusi laineid nimetatakse elementaar- või sekundaarlaineteks, mis on keralained. Järgmise lainefrondi leidmiseks tuleb leida sekundaarlainete puute- ehk mähispind (J.3.7).
Tõkestamata laine levib ainult frondi esialgse levimise suunas. Teistes suundades lained kustutavad üksteist, st alati leidub mingi sekundaarne allikas, kus võnkumised on vastandfaasis sinna jõudva lainega ja lained kustuvad.
Valgeks valguseks nimetatakse Päikeselt tulevat valgust ehk päikesevalgust, mis sisaldab kõikvõimalikke värvilisi valgusi. Sageli öeldakse päikesevalguse asemel päevavalgus, mille all mõistame valgust, mis tuleb päevasel ajal nii selgest taevast kui läbi pilvede. Tinglikult võib valgeks pidada ka hõõglambi valgust, kuigi selles on punast ja kollast valgust rohkem kui päevavalguses. Paremini sarnaneb päevavalgusele säästulambi valgus.
Valguse lainepikkus on meie jaoks imeväike. Kui kasutada piltlikku võrdlust, siis on valguse lainepikkus žiletitera paksusest keskeltläbi samapalju väiksem kui inimese pikkus on väiksem teletorni kõrgusest.
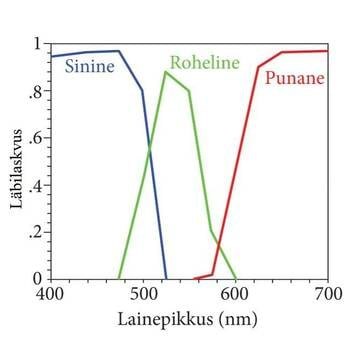
Sellele vaatamata on erineva lainepikkusega valguslaineid üksteisest eristada küllalt lihtne. Seda saab teha ka silma järgi, kuna erineva lainepikkusega valguslained põhjustavad erinevaid värvusaistinguid. Näiteks, kui meie silma satub valgus, mille lainepikkus , tekib meil mingi värvusaisting. On kokku lepitud, et seda värvust nimetatakse roheliseks. Kui aga lainepikkus on 650 nm, siis tekib punase värvuse aisting. Inimsilm on nii tundlik, et see võib tajuda erinevaid värvitoone, kui lainepikkus erineb ainult 5 nm võrra.
|
Värvus |
Lainepikkus, nm |
|
Punane |
760…630 |
|
Oranž |
630…600 |
|
Kollane |
600…570 |
|
Roheline |
570…520 |
|
Helesinine |
520…470 |
|
Sinine |
470…420 |
|
Violetne |
420…380 |
Kõiki värvusi on võimalik saada, kui liita erinevas vahekorras kahte või kolme põhivärvust. Põhivärvused on punane (R), roheline (G) ja sinine (B). Neid värvusi kasutatakse ka televiisori või arvuti ekraanil pildi tekitamiseks.
Värvuste liitmiseks tuleb erinevat värvi valgused näiteks juhtida valgel ekraanil ühte kohta. Televiisori või arvuti kuvaril on erivärvilised täpikesed ekraanil üksteisele aga nii lähedal, et meie silm ei suuda neid eristada ja nad liituvad meie silmas iseenesest.
Värvuste liitmist ei tohi segi ajada värvide liitmise ehk segamisega. Kui segada punast, rohelist ja sinist värvi, saame tulemuseks mingi tumeda värvi, pruunikasmusta.
Värviliste valguste korral kasutatakse nn RGB süsteemi (red, green, blue), kus aluseks on värvused, mis vastavad kindlatele lainepikkustele: R = 700,0 nm; G = 546,1 nm; B = 435,8 nm. Neist kaks viimast vastavad elavhõbeda kiirgusspektris esinevatele joontele.
Põhivärvuste liitmisel võib saada ka valget valgust. Retsept on järgmine: tuleb liita punast, rohelist ja sinist valgust nii, et nende intensiivsused suhtuksid kui
1 : 4,6 : 0,06.
Kuidas aga värvusi liita? Selleks tuleb valgele ekraanile juhtida üheaegselt erinevate lainepikkustega valgusvihud. Nende saamiseks võib kasutada värvilisi klaase, nn. valgusfiltreid, mis pannakse valge valguse allika (näiteks hõõglambi) ette. Punane klaas laseb läbi punast valgust, roheline rohelist ja sinine sinist. Ekraanil värvused liituvad.
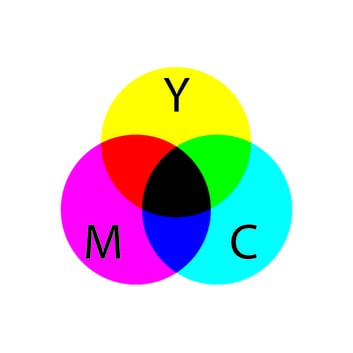
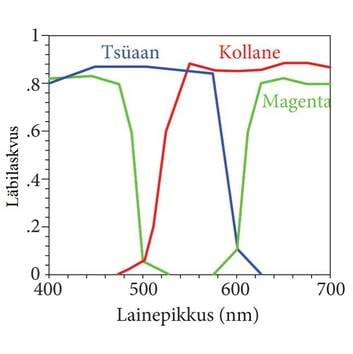
Erinevaid värvitoone võib saada ka erinevate värvainete või värvide segamisel. Näiteks on meil midagi vaja värvida roheliseks, aga rohelist värvi ei ole, küll on aga sinist ja kollast värvi. Mida teha? Tuleb segada kokku sinist ja kollast värvi ning saamegi rohelise värvi. Selline värvide liitmine on nn CMYK süsteemi aluseks, mida kasutatakse värvitrüki korral. Tähed lühendis tähistavad: C – tsüaan (sinine); M – magenta (roosa); Y – kollane; K – must (K on viimane täht sõnast black). Kui RGB süsteemi põhivärvuste segamisel saame valge valguse, siis CMYK süsteemi põhivärvide segamisel saame musta värvi.
Enamik inimesi tajub värvusi ühtviisi, kuid leidub inimesi, kellel esineb kõrvalekaldumisi normaalsest värvusnägemisest. Neid inimesi nimetatakse värvipimedateks. Täieliku värvipimeduse puhul näib kogu maailm must-valgena, kus kõik on kas must, valge või hall. Niisugust värvipimedust esineb väga harva. Rohkem esineb osalist värvipimedust. Peamiselt ei suudeta eristada punast ja rohelist värvust. Selle häda all kannatajad näevad kõiki värvusi kahes värvitoonis: kollakas ja sinakas. Niisugust värvipimedust nimetatakse ka daltonismiks. See on tuletatud inglise keemiku ja füüsiku John Daltoni nimest, kes 1794. aastal avastas nähtuse iseenda juures.
Õppisime Füüsikalise looduskäsitluse aluste kursuses, et kogu meile teadaolev universum koosneb ainest ja väljast. Ainel ja väljal on väga erinevad omadused. Näiteks mingi osakene asub ruumis kindlas kohas ja tal on kindlad mõõtmed. Aga väljal, mida see osake tekitab, ei ole mõõtmeid, see levib lainetena üle kogu ruumi.
Oleme ka rääkinud, et atomistlik printsiip kehtib ka väljade kohta. Makromaailmas pidevana tunduv väli osutub mikrotasemel samuti koosnevaks jagamatutest osakestest, mida nimetatakse välja kvantideks.
Käesolevas peatükis me uurime elektromagnetlaineid ning sellega seoses tutvume veel ühe looduse fundamentaalse printsiibiga. Selgub nimelt, et ühelt poolt saab loodust kirjeldada ainena (osakestega), mida võib põhimõtteliselt "näha ja katsuda". Teisalt saab neidsamu nähtuseid kirjeldada ka väljadega, mida pole näha, kuid mis vahendavad osakeste vahel mõjuvaid jõude. Sellist omaduste kahesust nimetatakse dualismiks (lad duo – kaks). Looduses vastab igale lainele osake ja iga osakesega kaasneb laine. Näiteks elektrone, mida me oleme joonistel harjunud nägema ümber aatomi tuuma tiirlevate pallikestena, saab kirjeldada ka lainete abil (selliseid laineid nimetatakse ka De Broglie laineteks).
Ka valgust saab kirjeldada kaheti. Siiani oleme rääkinud valgusest kui elektromagnetväljast, mis levib ruumis lainena. Selgub aga, et valgust saab kirjeldada ka osakeste abil, nimelt on olemas valguse osakesed ehk kvandid. Valguse kvanti nimetatakse footoniks (kr phos – valgus).
Footonitest oleme juba rääkinud kursuses Füüsikalise looduskäsitluse alused. Sealt saime teada, et footon on osake, millel seisumass on võrdne nulliga, see tähendab, et paigalolekus footon olla ei saa. Teisiti öelduna: kui footon peatatakse, siis muutub ta millekski muuks, tema energia muutub mõneks teiseks energialiigiks.
Valguse kvantiseloom ilmneb selgemalt valguse kiirgumisel (tekkimisel) ja neeldumisel (kadumisel). Laineline olemus tuleb esile peamiselt valguse levimisel.
| Kahe pilu interferentsi eksperiment, mida saab läbi viia igasuguste lainetega, olgu selleks siis valgus või vee lainetus. | Kui valgus on nii nõrk, et tundlik detektor näeb iga footoni neeldumist, siis interferentsipilt tekib sellegipoolest - vaadake video lõpuni. See katse on üks ilusamaid valguse dualistlikku iseloomu demonstreeriv katse. |
Valguse lainelised ja korpuskulaarsed (osakesetaolised) omadused ühendas omavahel M. Planck 1900. aastal, kui ta võttis kasutusele valemi
kus on footoni energia, vastava valguslaine sagedus ja võrdetegur, mida tuntakse Plancki konstandina: TeX parse error: '\cdot' is only supported in math mode. Toodud valem kehtib kõigi elektromagnetlainete korral, mitte ainult valguse puhul.
Ühe footoni energia on nii väike, et seda otseselt mõõta on võimatu. Näiteks sääse ühe tiivalöögi energia on keskmiselt 1012 (miljon miljonit) korda suurem footoni energiast.
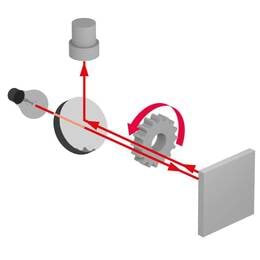
Footonite olemasolu tõestati fotoefekti katsetega. Fotoefektiks, täpsemalt välisfotoefektiks nimetatakse elektronide väljalöömist ainest (J.3.8, a). On olemas ka sisefotoefekt, mille korral valgus lööb elektrone välja keemilistest sidemetest aatomite vahel, aga elektronid ainest ei välju. Sisefotoefekt on näiteks päikesepatareide töö aluseks.
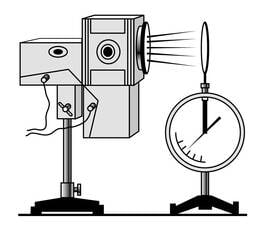
Välisfotoefekti uurimiseks kasutame katseseadet, mille skeem on toodud joonisel. 3.8 b.
Katsete tulemused võib kokku võtta järgnevalt:
- Kui elektroskoobiga ühendatud metallplaat laadida negatiivselt, siis selle valgustamisel kaob laeng mõne aja jooksul
- Kui plaat laadida positiivselt, siis laeng valguse toimel ei kao
- Kui me plaati üldse ei lae, siis valguse toimel plaat ei laadu
- Kui asetada valguse teele klaasplaat, siis ei kao ka negatiivselt laetud plaadi laeng
Teeme katsetest järeldused.
Esimene katse näitas, et valguse toimel kadus plaadilt elektrilaeng. Kuna negatiivse laengu kandjad on elektronid, siis võib järeldada, et valgus lõi plaadist välja elektrone.
Viimane katse aga näitas, et kui valguse teel oli klaasplaat, siis ei löödud plaadist elektrone välja. Põhjus on selles, et klaas laseb läbi ainult nähtavat valgust, aga mitte ultravalgust. Järelikult mitte igasugune valgus ei vabasta elektrone, vaid ainult suurema kvandienergiaga valgus ehk ultravalgus. On ju ultravalguse sagedus suurem kui nähtaval valgusel ja seega on ultravalgusel ka suurem kvandienergia. Tuleb märkida, et välisfotoefekt võib esineda üksikute ainete korral ka nähtava valguse toimel.
Kui plaat polnud laetud, siis valguse toimel ei laadunud sellepärast, et väljalöödud elektronid tõmmati plaati tagasi. Põhjus on selles, et enne oli plaadis elektronide negatiivsete laengute ja prootonite positiivsete laengute summa null. Aga elektronide lahkudes jäi ülekaalu prootonite positiivsete laengute summa ja plaat omandas positiivse laengu.
Kui plaat juba on positiivselt laetud, siis tõmmatakse väljalöödud elektrone plaati tagasi veel tugevamini kui laadimata plaadi korral.
Välisfotoefekti avastas 1887. aastal H. Hertz, kui ta uuris elektroodide vahel tekkivat sädelahendust. Ta märkas, et säde tema elektromagnetlainete tekitamiseks loodud katseseadmes tekkis paremini, kui elektroode valgustada. Põhjalikumalt uuris efekti A. Stoletov 1888. aastal. Kuid nemad ei osanud nähtust seletada. Seda tegi A. Einstein footonite abil 1905. aastal ja talle anti selle eest 1921. aastal Nobeli füüsikapreemia. Einsteini teooria sisu võtab kokku valem, mida tuntakse kui Einsteini valemit fotoefekti kohta.
kus on Plancki konstant, – valguse sagedus, – väljumistöö (töö, mida peab valguskvant tegema, et vabastada elektron positiivsete ioonide tõmbejõududest), – elektroni mass ja – vabanenud elektroni kiirus.
Nägime, et valgusnähtusi seletatakse nii lainete kui kvantide abil. Sageli öeldaksegi, et valgus on olemuselt dualistlik ehk kahene. Täpsem oleks öelda, et mitte valguse olemus ei ole dualistlik, vaid dualistlik on meie käsitlus valgusest: mõnede nähtuse juures avaldub valguse laineline olemus, teiste korral kvantolemus.
Valguse laine- ja kvantteooriad ei ole vastandlikud, nad täiendavad teineteist. Mida see tähendab? Aga seda, et kui me käsitleksime valgust kui ainult elektromagnetilist lainet, siis jääks meile mõistetamatuks mitmed valgusega seotud nähtused nagu juba eespool mainitud fotoefekt või valguse rõhk. Siis oleks leiutamata ka laserid ja kõik nendega seotu alates laserite kasutamisest meditsiinis ja lõpetades CD- ja DVD-mängijatega. Ja kui me käsitleksime valgust kui ainult footonite voogu, siis oleks meil keerulisem seletada valguse difraktsiooni ja interferentsiga seotud nähtuseid.
Mida väiksem on elektromagnetlaine sagedus , seda väiksem on ka kvandi energia , sest . Ja ühe kvandi energia võib olla nii väike, et meil ei ole võimalik seda avastada. Näiteks raadiolainetel, sagedusega 100 MHz, on ühe kvandi energia nii väike, et raadios registreeritava signaali tekitamiseks peab antennini jõudma vähemalt 1010 kvanti sekundis. Sellise osakeste arvu puhul on võimatu neid üksteisest eristada ja neid võib käsitleda lainena.
Ka veelaine koosneb ülipaljudest veemolekulidest, aga keegi ei räägi veeosakeste liikumisest, vaid ikka veelainest.
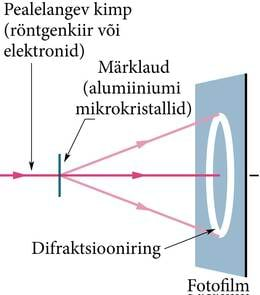
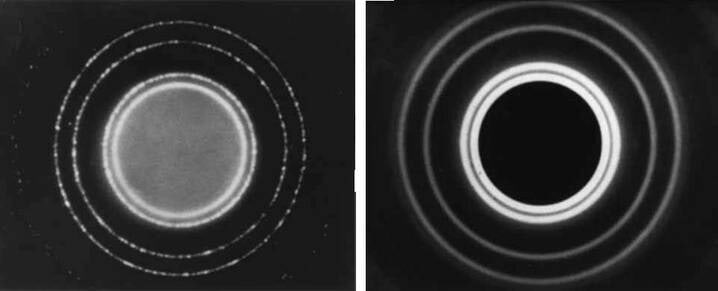
Kimp suunatakse alumiiniumi mikrokristallide õhukesele kihile. Röntgenkiirte lainepikkus on λ. elektronid kiirendatakse energiani, kus nende de Broglie’ lainepikkus on samuti λ. Fotofilmil tekib nii röntgenkiirtest
Kuid suure sagedusega elektromagnetlainete, näiteks γ-kiirguse korral on nende lainelisi omadusi raske märgata. Sel juhul käitub kiirgus pigem osakese kui lainena. Näiteks juba ühest γ-kvandist piisab, et esile kutsuda tuumareaktsiooni nagu seda võib teha ka mingi osakene, näiteks neutron.
Valgusel, mis on sageduste poolest raadiolainete ja γ-kiirguse vahepealne, avalduvad nii lainete kui osakeste omadused. See on aga ebatavaline ja harjumatu, sest me ei oska endale midagi taolist ette kujutada. Midagi muud sarnast pole me looduses märganud. Oleme harjunud, et osakene asub ikka mingis kindlas kohas, aga laine täidab mingi osa ruumist. Valguse korral on aga osake ka samal ajal laine ja laine osake. Sellise ebatavalise olukorra põhjuseks on fakt, et inimene ei saa vahetult tajuda valguse olemust.
Valguslaine E-vektori kaudu
Valguslainet kirjeldatakse E-vektori kaudu, B-vektor jäetakse tavaliselt vaatluse alt välja.
Kera- ja tasalained
Valguslaineid kirjeldatakse kera- või tasalainete abil. Esimestel on lainefrondiks kera pind, teisel juhul tasand.
Põhivärvused
On olemas kolm põhivärvust: punane, roheline ja sinine (RGB), millest koosnevad kõik teised värvused.
Elektromagnetlainete difraktsioon ja interferents on põhimõtteliselt sarnased mehaaniliste lainete difraktsiooni ja interferentsiga. Mehaaniliste lainete difraktsiooni ja interferentsi käsitlesime Mehaanika kursuses. Tuletame kõigepealt lühidalt seal õpitu meelde.
Difraktsiooniks nimetatakse lainete kandumist teele jäävate tõkete taha. Näiteks veelained jõuavad vees oleva kivi taha ja kanduvad avade läbimisel varju piirkonda (vt J.3.9).
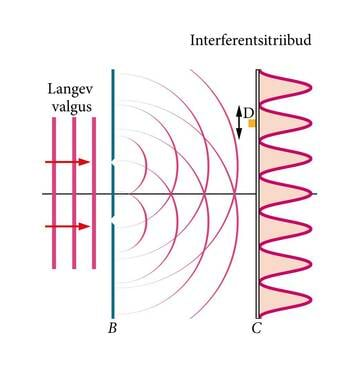
Interferentsiks nimetatakse lainete liitumist, mille tulemusena mõnes kohas lained muutuvad suuremaks (amplituud saab suuremaks kui ühe liituva laine amplituud), teises kohas väiksemaks (amplituud väheneb). Näiteks kui visata tiiki samaaegselt kaks kivi, siis kohtudes muutuvad tekkivad lained mõnes kohas suuremaks, teises kohas väiksemaks (vt J.3.10).
Veelainete abil saame endale ette kujutada ka elektromagnetiliste tasalainete ja keralainete difraktsiooni ja interferentsi – joonisel 3.9 kujutatud situatsioon on ühtlasi ristlõige tasalainete difraktsioonist pilult (pilu on suunatud risti joonisega) ning (joonisel 3.10) on ristlõige kahe keralaine interferentsist. Seda analoogiat saab kasutada elektromagnetlainete difraktsiooni ja interferentsi uurimiseks lainevannis.
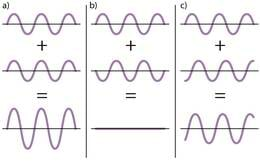
Katses nähtud veelainete amplituudi suurenemist või vähenemist mõnes kohas aitab mõista (joonis 3.11). Seal on kujutatud kaks liituvat lainet mingis veepinna punktis. Liitlaine saamiseks tuleb liita lainete hälbed igal ajahetkel. Joonisel on toodud kolm juhtu. Joonise osas a on lained täpselt samas faasis, st lainete miinimumid ja maksimumid esinevad täpselt ühel hetkel mõlemas laines. Sellises olukorras tugevdavad lained teineteist maksimaalselt, liitlaine amplituud on võrdne liituvate lainete amplituudide summaga. Joonise osas b on lained täpselt vastandfaasis, st ühe laine maksimum esineb täpselt samal ajal, kui teisel lainel on miinimum. Sellises olukorras nõrgendavad lained teineteist maksimaalselt, liitlaine amplituud on võrdne liituvate lainete amplituudide vahega.
Loomulikult esineb rohkem selliseid kohti veepinnal, kus lained pole täpselt samas või vastandfaasis. Neis on liitlaine amplituud maksimaalse ja minimaalse vahepealne nagu on see joonise osas c.
Selleks et tekiks interferents, peavad liituvad lained olema koherentsed – see tähendab, et lainetel peab olema ühesugune lainepikkus ja nende faaside vahe ei tohi aja jooksul muutuda.
Kui me ütleme, et difraktsioon ja interferents esinevad ka elektromagnetlainete korral, siis tekivad kohe küsimused, millele polegi nii lihtne vastata.
Kui esineb valguse difraktsioon, siis valgus levib ka tõkete taha. Kas siis peaks olema võimalik näha "nurga taha"?
Kui esineb valguse interferents, siis peaks kahe valgusallika korral kuskil valguslained üksteist tugevdama ja kuskil nõrgendama. Kas kahe lambi põlemisel tekivad tühja toa põrandal heledamad ja tumedamad piirkonnad?
Mõlemale küsimusele peaksime vastama eitavalt, sest midagi sellist tavaelus ei juhtu. Aga miks?
Sellepärast, et me pole arvestanud kaht asjaolu, mida tuleb lainete difraktsiooni ja interferentsi uurimisel arvestada.
Esiteks, lained difrageeruvad (kalduvad sirgjoonelisest levimissuunast kõrvale) märgatavalt ainult siis, kui nende teele jäävad tõkete või avade mõõtmed on võrreldavad nende lainepikkusega.
Valguse lainepikkus on väga väike ja tavaelus nii väikesi objekte pole või me ei märka neid. Küll aga saab valguse difraktsiooni vaadelda selleks korraldatud katsetes.
Lepime kokku, et edaspidi räägime ainult avadest, kuigi kogu jutt kehtib ka tõkete korral.
Ava väiksuse nõude põhjendamine pole lihtne ja sellele annab vastuse ülikooli optikakursus. Meie piirdume ainult eksperimentaalse fakti konstateerimisega.
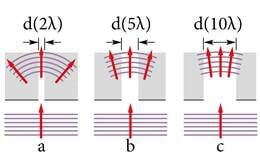
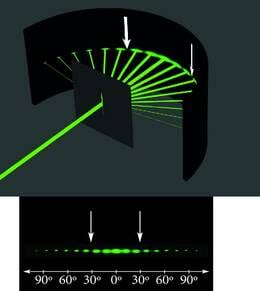
Ühe pilu difraktsiooni katses näeme, et pilust läheb osa laserivalgust otse läbi ja see tekitab difraktsioonipildi keskele nn tsentraalse täpi, mis on kõige heledam (J.3.12). Sellest kahele poole jäävad valgustäppide read, kus tsentraalsest täpist kaugenedes täppide heledus järjest väheneb. Need täpid on laserikiire kujutised ekraanil ja see tähendab, et osa valgust ei lähe läbi pilu otse edasi, vaid kaldub erinevatesse suundadesse pärast pilu läbimist.
Kui vähendada pilu laiust, siis vahekaugused täppide vahel suurenevad. Kui pilu laiust suurendada, siis täpid tõmbuvad kokku tsentraalse täpi ümber. Pilu suure laiuse (paarist millimeetrist suurem) korral ei ole difraktsioon jälgitav.
Teiseks esineb interferents ainult siis, kui valguslained on koherentsed. Tavalised laelambid aga ei kiirga koherentseid laineid, st neil pole ühesugune lainepikkus ja muutumatu faaside vahe. Selles, et lampidel pole ühesuguse lainepikkusega valgus, saame veenduda palja silmaga. Kui valgusallikas kiirgab mingi kindla lainepikkusega valgust, siis on see valgus ühevärviline. Kui valgus on "valge", siis on tegemist liitvalgusega, mis koosneb mitmete värvuste segust.
Lainete faaside kindlakstegemine pole silma järgi võimalik, see nõuab juba täpsemat uurimist.
Koherentseid valguslaineid kiirgab laser. Sellepärast kasutataksegi interferentsi ja difraktsioonikatsetes peamiselt laserivalgust.
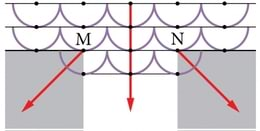
Valguse difraktsiooni saab seletada Huygensi printsiibi alusel. Joonisel 3.13. on näidatud tasalainete läbiminek kitsast pilust. Varju piirkonda ("nurga taha", mis on joonisel hall) satub valgus pilu servades olevaist sekundaarlaine allikaist M ja N. Tegelikkuses on neid sekundaarallikaid muidugi palju rohkem, kust valgus varju piirkonda satub, aga neid kõiki pole joonisel kujutatud.
Nii saab seletada valguse levimist "nurga taha", aga siis peaks valgus täitma varju piirkonna ühtlaselt. Meie aga nägime valgustäppide rida, kus täppide vahel olid tumedad kohad. Sinna ilmselt valgus ei sattunud.
Püüame olukorda seletada joonisel 3.14.
Lainefrondi punktidest A ja B lähtuvad sekundaarlained. Need kohtuvad omavahel ja juhul kui lained on samas faasis nagu on punktis C, siis nad tugevdavad teineteist ning tekib valgustäpp. Kui aga kohtuvad lained on vastandfaasides, siis nad kustutavad teineteise ja tekib tume koht. See, milline on liituvate lainete faaside vahe, oleneb teepikkuste erinevusest, mis laineil tuleb liitumispunkti jõudmiseks läbida, antud juhul AC – BC või AD – BD. Seda teepikkuste erinevust nimetatakse käiguvaheks. Järelikult tekivad valgustäpid seal, kus kohtuvad sekundaarlained on samas faasis ja tumedad kohad seal, kus need lained on vastandfaasides. Sarnane olukord tekib ka pilu teises servas, sellepärast ongi täppide rida mõlemal pool tsentraalset täppi.
Kokkuvõtvalt võib öelda, et valguse difraktsioon ja interferents on otsesed tõendid selle kohta, et valgus on laine. Selle tõestamine, et valgus on just elektromagnetiline laine, on juba palju keerulisem.
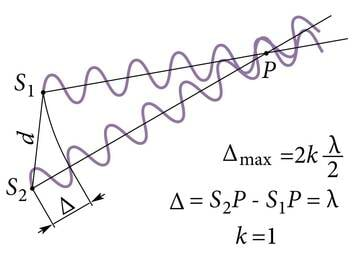
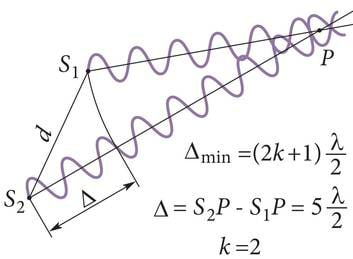
Interferentsi maksimumide ja miinimumide tekkimise tingimused on toodud allpool.
Valguse interferentsimaksimumid tekivad kohtades, kus käiguvahe jaoks on täidetud tingimus
(J.3.15). Kohtades, kus valgust ei ole, on interferentsimiinimumid. Seal on täidetud tingimus
(J.3.16). Tuleb välja, et difraktsioon saab nähtavaks tänu sellele, et pärast pilu läbimist valguslained liituvad ja tugevdavad või kustutavad üksteist. Mitmest avast tulevad valguslained saavad liituda ainult sellepärast, et pärast ava läbimist kanduvad lained varju piirkonda. Kõik see näitab, et ei saa rääkida difraktsioonist ilma interferentsita ja vastupidi. Nimetusi difraktsioon ja interferents kasutatakse suuresti ajaloolistel põhjustel, mis sai alguse ajast, kui neid nähtusi ei osatud omavahel siduda.
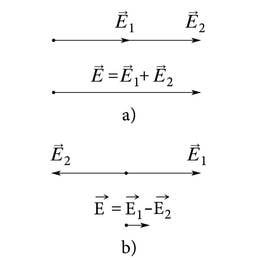
Kui uurida valguslainete liitumist lähemalt, siis selgub, et lainete kohtumispunktis liituvad lainete E-vektorid, olenemata sellest, kui palju laineid on. Sellist nähtust nimetatakse elektriväljade superpositsiooniks ja seda kirjeldab kursusest Füüsikalise looduskäsitluse alused tuntud superpositsiooniprintsiip: summaarne elektrivälja tugevus antud punktis on võrdne kõikide E-vektorite summaga selles punktis. Superpositsiooniprintsiibi kehtivus on eksperimentaalne fakt, mis iseloomustab looduse omapära, ja seda ei ole võimalik põhjendada.
Joonisel 3.17 on toodud näiteid E-vektorite liitumisest valguslainete kohtumisel.
Esimesel juhul on liituvad lained samas faasis ja tulemuseks on valguse intensiivsuse suurenemine: ehk . Kui , siis ja .
Teisel juhul on liituvad lained vastandfaasides ja tulemuseks on valguse intensiivsuse vähenemine: ehk . Kui , siis ja .
Kindlasti oleme nautinud ilusaid värvilisi seebimulle või uudistanud mitmevärvilisi õlilaike veeloigu pinnal. Ka kiilide ja teiste putukate tiivad sillerdavad päikesevalguses mitmevärviliselt. Kogu see värvidemäng looduses on tingitud valguse interferentsist.
Järgnevalt vaatleme mõningaid interferentsi ja difraktsiooni tehnilisi rakendusi, kus inimene kasutab neid nähtusi oma huvides.
Difraktsioonivõre
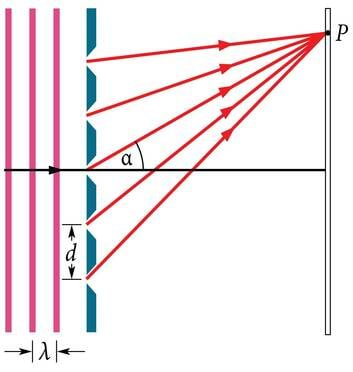
Üheks väga kasulikuks tööriistaks valguse ja valgust kiirgavate objektide uurimisel on difraktsioonivõre, mis kujutab endast paljude paralleelsete pilude süsteemi (J.3.18, a). Pilud on kitsad ja tihti on nende tihedus kuni mõni tuhat pilu millimeetri kohta. Kõige tähtsamaks difraktsioonivõre iseloomustavaks parameetriks on võrekonstant, mis näitab pilude omavahelist kaugust (J.3.18, b).
Kui monokromaatne valgus läbib võre, siis tekivad kitsad interferentsiribad, millede analüüs lubab määrata valguse lainepikkuse.
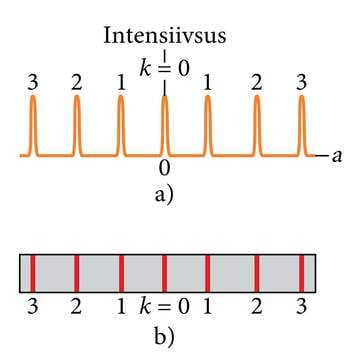
Kui difraktsioonivõrele langeb monokromaatne valgus, siis kujuneb välja joonisel 3.19 a olev intensiivsuse jaotus. Joonisel 3.19 b on pilt, mida võib näha vaateekraanil, kui võrele langeb laserivalgus. Maksimumid on kitsad (seepärast kutsutakse neid ka difraktsioonipildi joonteks) ja neid eraldavad suhteliselt laiad tumedad piirkonnad.
J.3.18 b Difraktsioonivõre tekitamas interferentsipilti punktis P. J.3.19 a) Suure pilude arvuga
difraktsioonivõre abil saadud
intensiivsuse jaotus koosneb kitsastest maksimumidest, mis on tähistatud nende järguga m, b) Ekraanil on näha vastavad heledad ribad, nn jooned, mis siin on samuti tähistatud järguga m.
Heledate joonte asukoha leidmiseks kasutame joonistelt 3.15 ja 3.16 tuttavat protseduuri ning arvutame igalt pilult punkti P jõudnud valguste käiguvahed. Selgub, et interferentsi maksimumid tekivad suundades, kus on täidetud tingimus:
(J.3.19). Valemis 3.1 on võrekonstant, on nurk, mille võrra valgus muudab oma levimissuunda, on difraktsioonimaksimumi järk ja valguse lainepikkus. Asendades valemis 3.1 erinevad k väärgused saame teada, millistes suundades on jälgitavad k-ndat järku difraktsioonimaksimumid. Nende suundade vahele jäävad alad, kus valguslained nõrgendavad üksteist.
Kirjutades selle valemi kujul
näeme, et antud võre puhul mingit joont (näiteks 3. järku joont, kus ) iseloomustav nurk a sõltub kasutatud valguse lainepikkusest. Seega, kui suuname tundmatu lainepikkusega valguse difraktsioonivõrele ja mõõdame nurki, siis on valemi 3.1 abil võimalik määrata valguse lainepikkus.
Seega erineva värvusega valgused kalduvad difraktsioonivõrest läbi minnes erinevatesse suundadesse ja neid on võimalik üksteisest eristada. Me saame teada, millistest komponentidest liitvalgus koosneb.
Teeme mõttelise katse, mis võimaldab kindlaks teha, millist värvi valgusi mingi liitvalgus sisaldab. Olgu meil näiteks valgusallikas, mis kiirgab ainult kahte värvi valgust: sinist ja kollast. Koondame valguse läätse abil ekraanile ja näeme seal valgusallika rohelist värvi kujutist (J.3.20, a). Kujutis on roheline sellepärast, et seal kohtuvad nii sinine kui kollane valguses. Sinise ja kollase värvuse liitumisel saame rohelise värvuse.
Asetame nüüd valguse teele difraktsioonivõre (joon. 3.20, b). Sümmeetriateljele jääb ikkagi allika roheline kujutis. Kuid sellest kahele poole tekib rida siniseid ja kollaseid valgusallika kujutisi. Need on tingitud sellest, et sinise valguse lainepikkus on väiksem kui kollasel valgusel. Sellepärast tekivad kollase valguse difraktsioonimaksimumid sümmeetriateljest kaugemale, sinine valgus kaldub vähem kõrvale kui kollane.
Ülalkirjeldatud metoodikat nimetatakse spektraalanalüüsiks ning selle rakendamise näidetega tutvume jaotises 4.3.3
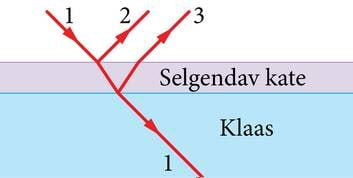
Selgendav kate
Kõik me oleme kindlasti märganud, et prilliklaasid või fotoaparaadi objektiivid paistavad mõne nurga alt vaadates natuke kollakad, rohekad või sinakad.Ilmselt on need pinnad millegagi kaetud, sest puhast klaasi võid vaadata kuidas tahes, mingit värvivarjundit peegeldunud valgusel pole. Milleks on vaja aga prilliklaase ja objektiive millegagi katta? Aga selleks, et need laseks rohkem valgust läbi.Neid katteid nimetatakse selgendavateks kateteks, sest need vähendavad peegeldunud valguse hulka ja sellega suurendavad klaasi läbinud valguse hulka. See muudab tekkiva kujutise selgemaks. Siit ka katte nimi. Selgendavaid katteid kasutatakse ka päikesepatareide katteklaasides, et suurendada valguse hulka, mis jõuab energia muundurini.
Sellest, et peegeldumise vähendamine suurendab läbinud valguse hulka, on suhteliselt lihtne aru saada. Kui läbipaistvalt materjalilt, milles valgus ei neeldu, vähem valgust peegeldub, siis peab suurenema sellest materjalist läbi läinud valguse hulk, sest valgusenergia ei saa ju lihtsalt ära kaduda.
Kuidas aga peegelduse vähendamine aitab kujutist selgemaks teha? Alustame sellest, et täpsustame, mida tähendab selge kujutis. Kujutis on siis selge ehk hästi nähtav, kui tal on teravad piirjooned ja kujutis on piisavalt hele. Kujutame ette, et me tahame ekraanile projektoriga tekitada mingi pildi. Siis on mõistetav, et kujutis on seda heledam, mida vähem valgust objektiivi läätsede pindadelt tagasi peegeldub. Kuidas aga peegeldunud valgus muudab kujutise kontuurid ebateravaiks? See juhtub sellepärast, et peegeldumisel jaotub valgus ümber laiemaks kimbuks, mis ei anna enam teravat kujutist. Olukord on sarnane joonestamisega: kui tahetakse hästi täpset joonist teha, siis kasutatakse väga teravat pliiatsit. Siis on täpselt näha, kust jooned kulgevad.
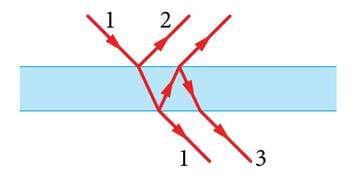
Valguse hajumist klaasitükist läbiminekul on kujutatud joonisel 3.21. Lihtsuse mõttes pole seal kujutatud läätse, vaid siledat klaasitükki.
Kui mõlemad klaasi pinnad on kaetud selgendavate katetega, siis kaovad ära peegeldunud lained 2 ja 3, mis lähevad mujale kui laine 1 (J.3.22).
Muidugi peab ütlema, et peegeldunud valguse osa pole just suur ja seetõttu pole suured ka segavad efektid. Puhtalt klaasi pinnalt peegeldub tagasi sellele risti langevast valgusest umbes 4%. Kui langemisnurk suureneb, siis suureneb ka peegeldunud valguse hulk.
Selgendava katte töö põhineb katte ülemiselt ja alumiselt pinnalt peegeldunud lainete vastandfaasi viimisel. Seda on võimalik teha, kui valida sobivalt katte aine murdumisnäitaja ja kihi paksus.
Kui lained 2 ja 3 on vastandfaasis, siis nad kustutavad teineteise ja selle võrra suureneb kattest läbi läinud valguse hulk (J.3.23). Sobiv katte paksus on samas suurusjärgus valguse lainepikkusega, seega väga väike. Varem olid selgendavad katted väga õrnad ja riknesid kergesti igasugusel mehaanilisel töötlemisel (näiteks lapiga pühkimisel), kuid nüüdisaegne tehnoloogia võimaldab teha väga vastupidavaid katteid.
Märgime, et õhukeste kilede erinevatelt pindadelt peegeldunud valguslainete interferentsiga seletatakse ka seebimullide või putukatiibade värvusi.
Holograafia leiutas 1947. aastal Ungari päritolu füüsik Dennis Gabor, kes sai selle eest 1971. aastal Nobeli füüsikapreemia. Hologrammile nime andes lähtus D. Gabor kreeka keelest, kus "holos" tähendab täielik ja "gramma" – üleskirjutus. Seega tähendab "hologramm" täielikku üleskirjutust.
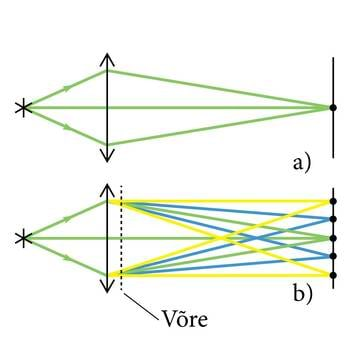
Mis aga on hologramm ja kuidas teda tehakse? Hologramm on holograafilisel meetodil saadud kolmemõõtmeline ehk ruumiline kujutis. Holograafia on esemete ruumilise kujutise fotograafiline jäädvustamine. Selle tulemusena saadakse esemest ruumiline pilt, mida nimetatakse hologrammiks ja mis põhimõtteliselt erineb nii tavalisest fotost kui ka 3D-kinos esitatavast ruumilisest elamusest.
Fotol jäädvustatakse esemete tasapinnaline, mitteruumiline kujutis. Tähtis on tähele panna, et fotografeerimisel me salvestame valguse E-vektori ruudu keskväärtuse, aga kogu info valguslainete faasi kohta läheb paratamatult kaduma. Fotot vaadates tekib küll mingi ruumilisuse mulje, sest harilikult on fotol meile tuttavad asjad ja neid me oskame omale ette kujutada. Ruumilisuse muljet aitavad tekitada perspektiiv, samuti varjud fotol. Põhiline erinevus foto ja hologrammi vahel seisneb selles, et fotol pole võimalik näha mingi eseme taga olevat teist eset, aga hologrammil on. Selleks tuleb ainult pead liigutada, et vaadata hologrammi teisest suunast.
3D-filmis ruumilise elamuse tekkimise põhimõtet tutvustame punktis 3.4.2 .
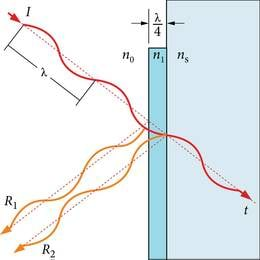
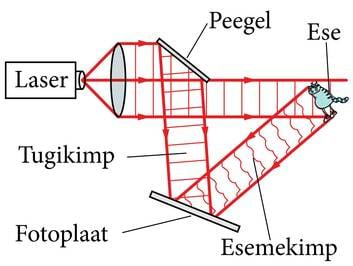
Vaatame lähemalt hologrammi valmistamist fotograafilisel meetodil ehk holografeerimist. Mingi eseme holografeerimiseks kasutatakse kahe koherentse kiirtekimbu interferentsi. Nende kimpude saamiseks kasutatakse kõigepealt kaht kumerläätse, mille abil muudetakse kitsas laserikiir laiaks paralleelsete lainete kimbuks. Üks osa sellest kimbust, nn tugikimp, suunatakse peegliga enne holografeeritava esemeni jõudmist fotoplaadile või -filmile (J.3.24)
Teine osa suunatakse sinna pärast holografeeritavalt esemelt peegeldumist. See on esemekimp.
Tugikimbus olevad lained jõuavad kõik fotoplaadini samas faasis, sest tegemist on tasalainega (paralleelne kimp). Esemekimp ei ole aga enam tasalaine – esemelt peegeldudes sisaldab selle lainefront kogu informatsiooni eseme väliskujust. Fotoplaadil kimbud kohtuvad ja interfereeruvad, sest laserivalgus on koherentne. Tulemuseks on keerulise kujuga interferentspilt, milles kajastub eseme ruumiline kujutis. Selgub, et sellises interferentsipildis on olemas ka info valguse E-vektori faasi kohta.
See pilt salvestatakse fotograafiliselt ja hologramm ongi valmis.
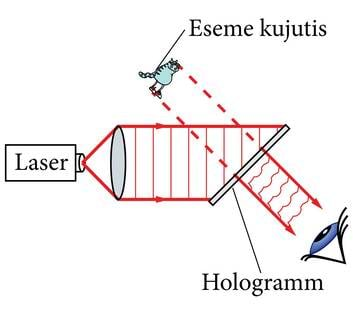
Hologrammi vaatamiseks kasutatakse ainult tugikimpu, st laiaks muudetud laserikiirte kimpu. See kimp suunatakse hologrammile, kus toimub valguse difraktsioon. Et hologrammis on salvestatud ka informatsioon valguse ajalise käitumise kohta, siis tekib täpselt samasugune lainekimp, nagu oli esemekimp. Kui seda kimpu vaadata, siis näeme esemega sarnast kujutist (J.3.25). Tekkinud kujutis on ruumiline.
Hologrammil on fotoga võrreldes mitmeid erinevaid omadusi:
- lihtne on koopiate tegemine, sest pole erinevust positiivi ja negatiivi vahel;
- purunemisel säilib igal tükil tervikpilt, sest valmistamisel pole kasutatud koondavat optikat ja kõik hologrammi osad sisaldavad infot kõigi originaali osade kohta;
- ühele fotoplaadile saab jäädvustada palju hologramme, piisab, kui näiteks iga kord enne holografeerimist fotoplaati pisut pöörata;
- kujutise suurust saab muuta, kui muuta vaatamisel kasutatava laseri lainepikkust: mida suurem lainepikkus, seda suurem kujutis.
| Hologramm hiirest. Seda hologrammi on pildistatud kahest suunast. Nagu näeme, erinevatest suundadest paistab pilt erinev, ruumiline info on hologrammi salvestatud. | Holograafia on väga võimas meetod ka teistsugustes kehade ruumilist kuju uurivates ülesannetes. Sellel pildil on näeme interferentsimustris kohti, kus kitarr rohkem võngub. |
Oleme seni rääkinud objektide ruumilise kuju üleskirjutamisest, aga valguslainete abil saab teha veel palju rohkem. Nii on interferentsinähtuse abil võimalik üles kirjutadada ka esemete liikumist, st põhimõtteliselt on võimalik hologrammi salvestada liikuvat ruumilist pilti sisaldav film. Selliste teemadega tegeleb nn. aegruumiline ehk 4D holograafia. Aegruumilise holograafia võimalikkuse tõestasid 1983. aastal Eesti TA Füüsika Instituudi (tänane TÜ Füüsika Instituut) teadlased akadeemik Peeter Saari juhtimisel.
Aga kui see kõik nii hea ja võimas on, miks me siis endiselt kasutame fotograafiat ja 2D videosid, selle asemel, et salvestada elu kogu oma täiuses? Põhjused on ühtaegu tehnilised ja põhimõttelised. Näiteks on üsna lihtne aru saada, et esemete ruumilise kuju üleskirjutamine tähendab rohkem informatsiooni ning holografeerimisel tuleb see ka kusagile üles kirjutada ja see tähendab suurema pikslite arvuga salvestus- ja esitlusseadmete kasutamist. Kui suure lahutusega fotoaparaatide tegemine ei ole täna põhimõtteliselt probleem, siis kättesaamatuks jääb holografeerimiseks tarvilik piksli suurus - ca poole mikromeetrilise serva pikkusega piksleid ei ole täna võimalik valmistada. Nii et ainus võimalus on kasutada vanamoodsaid fotoplaate. Vist isegi põhimõttelisem probleem on see, et igapäevaste olukordade holografeerimiseks on vaja kasutada üsnagi spetsiifilist laserivalgust.
Viimastel aastatel on aga tekkinud tehnika arengus uued suunad, mis annavad lootust, et vahepeal unustusehõlma vajunud tõeliselt ruumilise kino idee uuesti ellu ärkab. Nimelt on võimalik hologramme ka arvutada, kui on teada holografeeritavate objektide täpne kuju. 3D-animatsioonides on see info olemas, ainsaks põhimõtteliseks probleemiks jääb videoprojektorite lahutusvõime, mis peaks olema tuhandeid kordi suurem.
Aga kuidas jääb reaalse elu holografeerimisega? Ka siin võib läbimurre tulla tänu järjest kasvavale arvutusvõimsusele - põhimõtteliselt on võimalik esemete täpne kuju välja arvutada, kui on olemas piisav hulk erinevatest rakurssidest tehtud fotosid. Tulevik näitab, kas ja millises suunas see seni realiseerumata võimalus edasi areneb.
| Hologramm ühest optika õppevahendite komplektist. Annab aimu, mis moodi sellised hologrammid reaalselt välja näevad ja kuidas neid vaadatakse - ülemises vasakus nurgas on laser, millest väljub hajuv kiirtekimp ja satub hologrammile. Võrdle joonisega 3.25. | Hologrammi valmistamise komplekti LitiHalo Kit tutvustav video. Vaata, kas tunned seal ära protsessi etapoid, mis ülalpool tekstis juba räägitud. |
Interferents
Interferentsiks nimetatakse lainete liitumist, mille tulemusena liitlaine amplituud võib suureneda või väheneda võrreldes liituvate lainete amplituudidega.
Koherentsed lained
Koherentsed on lained, millel on ühesugune lainepikkus ja mille faaside vahe ei muutu aja jooksul.
Difraktsioon, interferents ja valguse laineline iseloom
Difraktsioon ja interferents on otsesteks tõenditeks selle kohta, et valgus on laine.
Difraktsioonivõre
Difraktsioonivõre on seade, mis kujutab endast paljude paralleelsete pilude süsteemi. Difraktsioonivõret kasutatakse valguse lainepikkuse määramiseks ja liitvalguse koostise uurimiseks (spektraalanalüüsiks).
Olgu meil valgusvoog, kus kõikide lainete levimissuunad on omavahel paralleelsed. Vaatame otse sellele kimbule vastu ja kujutame ette, et me suudame näha iga laine E-vektori võnkumist. Siis me näeksime umbes sellist pilti, mis on toodud joonisel 3.26. Valguslaine E-vektor võib võnkuda igas sihis, sest üksikute lainete kiirgumine pole mitte mingil viisil kooskõlastatud. Selline on nn loomulik valgus.
Kui asetaksime sellise valguse teele seadme, mis laseb läbi ainult mingis kindlas sihis, näiteks vertikaalsihis võnkuvate E-vektoritega laineid, siis näeksime joonisel 3.27 kujutatud pilti. Sellist valgust nimetatakse polariseeritud valguseks.
Valgust polariseerivat seadet nimetatakse polaroidiks. Loomulik valgus polariseerub läbi polaroidi minnes sellepärast, et see laseb läbi ainult valguslaineid, mille E-vektor võngub mingis kindlas sihis või tasandis. Seda tasandit nimetatakse polaroidi läbilasketasandiks ehk polarisatsioonitasandiks. Kui mingi laine E-vektor ei võngu läbilasketasandis, siis see laine neeldub polaroidis kas osaliselt või täielikult. Kõik valguslained, mille E-vektor võngub risti läbilasketasandiga, neelduvad täielikult ja nende energia muutub polaroidi siseenergiaks. Olukord on mõneti sarnane sellega, kui tahate suuski toast õue viia. Siis tuleb uksest läbi minnes suuski püsti hoida, muidu jäävad need ukse piitade taha kinni ja ei saa toast välja.
Seda, kas valgus on polariseeritud või mitte, tehakse kindlaks ka polaroidi abil. Kui vaadata loomulikku valgust läbi polaroidi, siis polaroidi pööramine ümber vaatesuuna ei põhjusta valguse intensiivsuse muutust. Kui aga vaadata polariseeritud valgust, siis polaroidi pööramisel valguse intensiivsus muutub.
On kokku lepitud, et seda polaroidi, mis valgust polariseerib, nimetatakse polarisaatoriks, ja seda, mille abil tehakse kindlaks valguse polarisatsioon – analüsaatoriks.
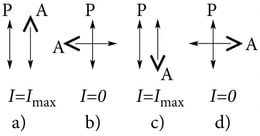
Uurime lähemalt, kuidas muutub polariseeritud valguse intensiivsus, kui seda valgust vaadata läbi analüsaatori, mida pööratakse ümber vaatesihi. Selleks hoiame polaroidi ühes kindlas asendis ja vaatame sealt tulnud valgust läbi analüsaatori. Pöörame analüsaatorit ümber vaatesihi, näiteks vastupäeva, ühe täisringi. Olukorda aitab mõista joonis 3.28, kus on näidatud polarisaatori P ja analüsaatori A neli asendit.
Kui polarisaatori läbilasketasand on vertikaalne ja analüsaatori läbilasketasand on ka vertikaalne, siis on analüsaatorist väljunud valguse intensiivsus maksimaalne (olukorrad a ja c). Kui läbilasketasandid on omavahel risti, siis ei pääse valgus üldse analüsaatorist läbi (olukorrad b ja d). Seega ühe täisringi jooksul esineb kaks intensiivsuse I maksimumi ja kaks miinimumi.
Valguse intensiivsuse sõltuvust valguse polarisatsioonitasandi ja analüsaatori läbilasketasandi vahelisest nurgast seletatakse järgmiselt.
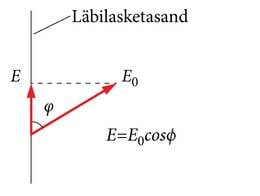
Langegu polariseeritud valgus analüsaatorile, mille läbilasketasand on vertikaalne ja mille E-vektor moodustab läbilasketasandiga nurga . Sel juhul saab analüsaatorit läbida ainult komponent (vt J.3.29.)
Kuna valguse intensiivsus , saame intensiivsuse avaldiseks
Selle seaduse avastas Prantsuse füüsik E. Malus 1808. aastal.
Valgus polariseerub mitmetes protsessides, näiteks peegeldumisel või valikulisel neeldumisel, nagu see toimub polaroidides.
Peegeldunud valguse polariseerumises saame veenduda, kui vaatame näiteks lauapinnalt või kilekaantelt peegeldunud valgust läbi analüsaatori. Kui seda pöörata ümber vaatlussuuna, siis mingis analüsaatori asendis kaob peegeldunud valgus. Kui aga vaadata mõnelt metallesemelt peegeldunud valgust, siis see ei kao analüsaatori pööramisel. Kuna laualakk ja kilekaaned on dielektrilisest materjalist, siis meie katse näitab, et peegeldumisel polariseerub ainult dielektrikutelt peegeldunud valgus.
Eriti ilmekalt tuleb erinev polarisatsioon esile autodelt peegeldunud valguse korral: aknaklaasid muutuvad polaroidi mõne asendi korral täiesti mustaks, aga metallosad säravad kogu aeg.
Polaroidprillid. Nagu eespool räägitud, polariseerub valgus dielektrikutelt peegeldumisel. Järelikult mere- või järveveelt peegeldunud päikesevalgus on polariseeritud. Sellepärast kasutataksegi mõnedes päikeseprillides silmade kaitseks klaasidele kantud polaroidkilesid. Need vähendavad oluliselt veepinnalt, lumelt või märjalt asfaldilt peegeldunud valguse tugevust (J.3.30). Sellepärast kasutavad polaroid-päikeseprille peamiselt kalamehed, mäesuusatajad või autojuhid. Teistel on nad rohkem edevuse asjad.
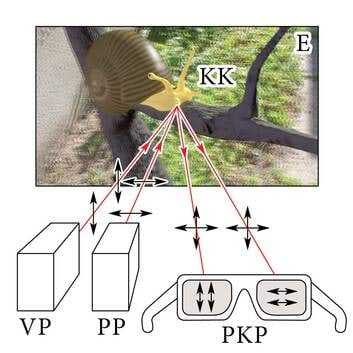
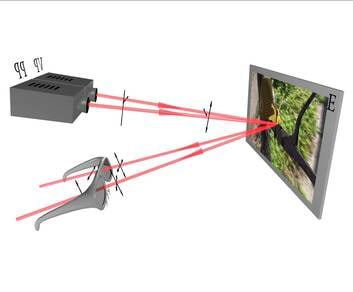
Polaroidprille kasutatakse ka 3D-filmide vaatamiseks.(J.3.31) 3D-filmi tegemisel kasutatakse filmimiseks kaht kaamerat üheaegselt. Kaamerad asuvad kõrvuti nagu meie silmadki. Filmi näitamisel kasutatakse kaht projektorit, millest üks näitab vasakpoolse kaameraga tehtud filmi ja teine parempoolse kaameraga tehtud filmi. Mõlemad projektorid on suunatud ekraani ühte kohta. Ruumilise kujutise tekkimiseks peab vaataja nägema vasaku silmaga vasakpoolse kaamera filmitut ja parema silmaga parempoolse kaameraga filmitut. Selle saavutamiseks kasutatakse projektorite ees ristiolevate läbilasketasanditega polaroide. Ka vaatajal on ees polaroidklaasidega prillid, mille vasaku klaasi läbilasketasand on sama mis vasakpoolsel projektoril ning parempoolsel sama mis parempoolsel projektoril.
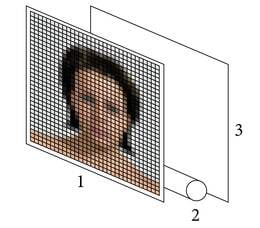
Vedelkristall-kuvar. Vedelkristall-kuvareid (VK-kuvareid, inglise keeles LCD ehk Liquid Crystal Display) kasutatakse televiisorites ja arvutites pildi nähtavaks tegemiseks ehk kuvamiseks. Vedelkristall-kuvari põhiosad on ekraan pikslitega, valge taustvalguse allikas ja valguse hajutaja. Sellelt tulev valgus juhitakse ekraanile läbi pikslite, mis tekitavad soovitud pildi (J.3.32).Pikslid on on paigutatud kindlatesse ridadesse ja veergudesse ning igaüks neist laseb läbi kas punast, rohelist või sinist valgust. Neid värvusi kombineerides on võimalik saada igasuguseid värvitoone.
Piksli nimi tuleb ingliskeelsetest sõnadest picture ja element, seega eesti keeles oleks nimi pildielement.
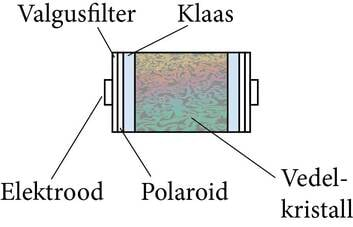
Pikslid on imeväikesed, palja silmaga eristamatud. Iga piksel koosneb klaasplaatide vahele pandud vedelkristallist (J.3.33). Plaatide pinnad on kaetud polaroidkile ja kas punase, rohelise või sinise valgusfiltriga (ainega, mis laseb läbi ainult vastavat värvi valgust). Kummalgi pinnal on ka läbipaistvast materjalist elektrood, mis lubab tekitada pikslis elektrivälja. Piksli pindadel olevate polaroidide läbilasketasandid on omavahel risti ja pingestamata elektroodide korral valgus pikslit ei läbi. Selline piksel paistab ekraanil musta täpina.
Pikslis olev vedelkristall on aine, mis on vedel, aga millel on kristallidele omane struktuur. Elektriväljas muutub vedelkristall optiliselt aktiivseks – teda läbiva polariseeritud valguse võnketasand pöördub. Pingestatud pikslis ei ole polaroidide läbilasketasandid enam omavahel risti ja pikslist hakkab valgus läbi minema. Polarisatsioonitasandi pöördenurk oleneb kasutatud pinge suurusest. See võimaldab muuta pikslit läbinud valguse hulka. Nii saame tekitada ekraanile erineva heleduse ja värvusega punkte, mis kokku annavad soovitava värvilise kujutise.
Loomuliku valguse polarisatsioon
Loomulikus valguses võivad valguslainete E-vektorid võnkuda suvalises sihis.
Polariseeritud valgus
Polariseeritud valguses on kõikide lainete E-vektorite võnketasandid paralleelsed.
Polaroid töötab
Kui polariseeritud valgust vaadata läbi polaroidi, siis polaroidi keeramisel umber vaatesuuna muutub valguse intensiivsus.
Niisiis, kui salvestada objektist erinevate nurkade alt piisav hulk fotosid, siis peaks arvuti olema põhimõtteliselt võimeline sellest kokku panema hologrammi, ehk selle objekti täieliku ruumilise üleskirjutuse. Teisalt... meil on ju vaid kaks silma, kas on mõtet luua salvestust, mille täielikuks nautimiseks peaks meil olema tuhat silma?