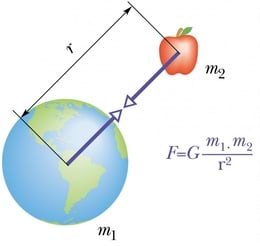
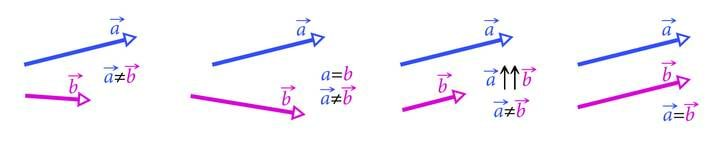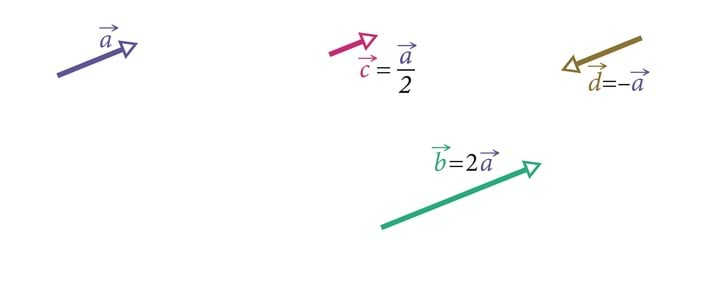Füüsikast on aastasadade jooksul kirjutatud tohutu hulk raamatuid. Iga päev avaldatakse sadu uusi teadusartikleid. Seda kõike ei ole võimalik läbi lugeda. Samuti ei suuda üks inimene ära õppida kogu füüsikat. Õnneks kehtivad looduses mõned vääramatud põhimõtted ehk üldprintsiibid, mis aitavad senitundmatuid nähtusi või olukordi mõtestada. Allpool nähtava panoraamvõtte saatis meile marsikulgur Curiosity. Selle pildi tegemise muutis võimalikuks meie veendumus, et planeet Marsil kehtivad needsamad füüsika üldprintsiibid, mis Maalgi.

Füüsikas kasutatakse looduse kirjeldamisel mitmesuguseid mudeleid. Kumminööri venimise nähtuse uurimisel õnnestus meil luua selle nähtuse abstraktne mudel, mille võis esitada graafiku või valemina. See mudel kirjeldab ühe konkreetse kumminööri venimist otsariputatud koormise mõjul. Mudel on ka laiemalt kasutatav, kuna saadud valem kehtib tõenäoliselt kõigi kumminööride puhul. Iga kumminööri jaoks tuleb eraldi määrata vaid võrdeteguri väärtus. Sellegipoolest jääb saadud mudel kirjeldama üpris kitsast nähtuste ringi. 

Saab aga luua ka selliseid mudeleid, mis sõltumata konkreetsest nähtusest või isegi füüsikaharust on kasutatavad kogu füüsikas. Selliseid mudeleid, mis on kasutatavad kogu füüsikas, nimetatakse füüsika üldmudeliteks. Füüsika üldmudeliks on näiteks keha. Rääkides füüsikalistest kehadest, peame silmas ükskõik mida, millel on kindlad piirjooned, mõõtmed ja mass. Füüsikaline keha võib olla õun, auto, inimkeha või terve planeet Maa. Füüsikaliste kehadega toimuvate nähtuste kirjeldamisel pole sageli olulised nende kuju ja mõõtmed. Vaja on teada vaid nende asukohta ja massi. Kui me kujutame keha ette punktikujulisena, saame omakorda keha mudeli, mida nimetatakse punktmassiks. Niisiis on punktmass selline keha mudel, mille korral keha massi vaadeldakse koondununa ühte punkti. Iga mudeli kasutamisel peaksime iseendalt küsima, mis on need reaalse loodusobjekti omadused, mis konkreetse mudeli poolt arvestamata jäetakse. Punktmassi korral on selleks keha kuju ja mõõtmed. 

Põrkava palli liikumine.	Kurika massi võib vaadelda koondununa ühte punkti, mis liigub viskamisel mööda parabooli – nii nagu pall parempoolsel pildil.

Juba korduvalt on juttu olnud ka sellest, et füüsika üldmudeliteks on füüsikalised suurused. Kõik suurused kirjeldavad mingite loodusobjektide ühte kindlat omadust. Kui see on väga üldine omadus, siis oleme vastavat suurust käsitlenud käesoleva kursuse 2. osas. Nii näiteks kirjeldab keha liikumisolekut kiirus, liikumisoleku muutumist kiirendus, keha võimet vastu panna liikumisoleku muutumisele – mass. 

Füüsikaline objekt on mõiste, mida kasutatakse kahes tähenduses. Üks võimalus on nimetada füüsikalisteks objektideks ainult kehi ja väljasid (kitsam tähendus). Teine variant hõlmab füüsikalise objekti mõiste alla ka loodus­nähtused ehk protsessid (lai tähendus). Lai tähendus on eelistatavam, sest inimene kui looduse vaatleja on subjekt, kes uurib nii kehi, väljasid kui nende osalusel toimuvaid protsesse. Need kõik on tema vaatlusobjektid. Laias tähenduses on ka liikumine, liikumisoleku muutumine ja vastastikmõju füüsikalised objektid, mida kirjeldatakse vastavate füüsikaliste suuruste abil. Me usume, et kõik füüsikalised objektid on olemas objektiivselt, see tähendab – sõltumatult mistahes vaatlejast või koguni inimkonnast tervikuna. Füüsikalised suurused on aga vaatlejate ühised kujutlused, ühised väljamõeldised. Nad on füüsika üldmudelid, mille abil on mugav füüsikalisi objekte kirjeldada. 

Väljad on mitteainelised objektid. Väljade tunnuseks on see, et nad mõjutavad kehi ja omavad energiat. Näiteks Maa gravitatsiooniväli kutsub esile kõigile kehadele mõjuva raskusjõu, elektriväli mõjutab aga jõuga elektrilaengut omavaid osakesi ja kutsub seeläbi esile elektrivoolu. Väljaliste objektide korral ei ole rakendatavad ruumi ja aja mõisted. Lähemalt tuleb selle põhjustest juttu allpool. 

Kehad on ainelised objektid. Kehadeks on näiteks vee molekul kui mikrokeha, inimkeha kui makromaailma keha või Päike kui megamaailma kuuluv keha. Kehade juures saab uurida nende kuju, värvust, mõõtmeid, koostist, aga ka nende omavahelist liikumist ja vastastikmõjusid. Kehade puhul saab kasutada ruumi ja aja mõisteid. Ruumi mõiste kujundab vaatleja kehade omavahelisel mõõtmelisel võrdlemisel (pikem-lühem, laiem-kitsam, kõrgem-madalam jne). Aja mõiste kujundab vaatleja kehade omavahelise liikumise võrdlemisel. Lähemalt sellest allpool. 

Nähtused on aineliste ja väljaliste objektidega toimuvad muutused. Füüsikaliseks nähtuseks on näiteks kehade omavaheline liikumine, ahju soojenemine, valguse peegeldumine või neeldumine. Füüsikalist nähtust kirjeldab nähtuse mudel, mida saab teatavasti esitada kas a) tabeli abil, b) graafiku abil või c) valemi abil. Seejuures suureneb selles reas kirjelduse üldisus. Tabelis näeme vastavust füüsikaliste suuruste üksikute väärtuste vahel. Meie tähelepanu keskendub üksikule väärtuste paarile. Graafikul näeme juba korraga kõiki mõõteväärtusi. Meie tähelepanu keskendub joonele, mis kirjeldab füüsikaliste suuruste omavahelist sõltuvust tervikuna. Valem aga võib kirjeldada vaadeldavat sõltuvust mitte ainult konkreetse uurimisobjekti korral, vaid mistahes samalaadse objekti uurimisel. Kahe füüsikalise suuruse omavahelise sõltuvuse kui põhjusliku seose korral esineb üks suurus põhjusena ja teine tagajärjena. Matemaatikas nimetatakse esimest argumendiks $x$ ja teist funktsiooniks $y=f\left(x\right)$. Graafiku joonistamisel kantakse põhjusena toimiva suuruse (argumendi) $x$ väärtused reeglina rõhtteljele (abstsissteljele) ning tagajärjeks osutuva suuruse (funktsiooni) $y$ väärtused püstteljele (ordinaatteljele). Nii toimisime ka meie kumminööri venimise mudeli loomisel.

Füüsikalist suurust, mis on esitatav vaid ühe mõõtarvu ja mõõtühikuga, nimetatakse skalaarseks suuruseks ehk skalaariks (ld scala 'redel, astmestik'). Skalaarsetel suurustel on arvuline väärtus, kuid neil pole suunda. Skalaarsed suurused on näiteks aeg, pikkus, mass, rõhk, ruumala, energia, temperatuur. Mõnikord võib jääda ekslik mulje, et mõnel skalaaril on siiski suund olemas. Näiteks aeg näib kulgevat ühes suunas ja soojendatava vee temperatuur muutub suurenemise suunas. Nende näidete puhul on tegemist vaid nähtustega, kus toimub suuruse arvulise väärtuse muutumine. Siin pole otseselt tegemist suunaga ruumis. Siiski kujutleme me skalaarse suuruse väärtusi reeglina paiknevatena arvteljel. Sellel teljel on sageli olemas kokkuleppeline nullpunkt, millest ühele poole jäävad skalaarse suuruse positiivsed ja teisele poole negatiivsed väärtused. Miinusmärk skalaarse suuruse arvväärtuse ees väljendab mõttelist liikumist arvteljel negatiivses suunas ehk siis vastupidiselt kokkuleppelisele positiivsele suunale. Näiteks keha negatiivne kõrgus maapinnast tähendab seda, et keha asub tegelikult maapinnast allpool. Negatiivne aeg tähendab seda, et sündmus leidis aset enne kokkulepitud nullhetke. Negatiivne temperatuuri­muutus tähendab seda, et temperatuur mitte ei tõusnud, vaid langes. 

Skalaarne suurus omab arvulist väärtust ja mõõtühikut. Selline suurus pannakse alati kirja kui arvu ja mõõtühiku korrutis, kusjuures korrutusmärki tavaliselt välja ei kirjutata. Näiteid selle kohta sai toodud juba eespool. Skalaarsete suurustega saab sooritada erinevaid matemaatilisi tehteid. Seejuures ei tohi muidugi unustada mõõtühikuid. Tehe sooritatakse eraldi nii arvväärtustega kui ka mõõtühikutega. Mõned näited.

Skalaarse suuruse korrutamine arvuga: kolme 100-grammise vihi mass on kokku 3 × 100 g = 300 g.

Skalaarsete suuruste omavaheline liitmine või lahutamine: kui tõstame 1 m kõrguse kasti otsa 75 cm kõrguse kasti, on tekkiva kastivirna kogukõrgus 1 m + 0,75 m = (1 + 0,75) m = 1,75 m. Meenutagem, et omavahel liita ja lahutada saab vaid sama tüüpi suurusi, millel on ühesugune mõõtühik.

Skalaarsete suuruste omavaheline korrutamine või jagamine: 1,5 m kõrguse ja 3 m² põhja pindalaga veepaagi ruumala on 1,5 m × 3 m² = (1,5 × 3) × (m × m²) = 4,5 m³. Kui inimene tõuseb mööda treppi 5 sekundi jooksul maja esimeselt korruselt teisele, tehes raskusjõu vastu 2000 džauli tööd, siis on selle inimese lihaste keskmine võimsus (2000 J)/(5 s) = (2000/5) (J/s) = 400 W. 

Kui me teame palli koordinaati, aga ei tea selle liikumise suunda, siis ei saa me kuidagi teada, kas kass just viskas palli või hakkab seda kohe püüdma.	Elusolend saab vaid vananeda, mitte nooreneda. Tema aeg „kulgeb” ainult ühes suunas.

Me kohtame füüsikas palju ka selliseid suurusi, mida iseloomustab lisaks arvulisele väärtusele suund. Näiteks ei saa me ennustada, kuhu teadaoleva kiirusega sammuv matkaja kolme tunni pärast kohale jõuab, kui me ei tea, millises suunas ta liigub. Matemaatikas nimetatakse suunatud sirglõiku vektoriks (ld vector 'kandja, edasiviija'). See nimetus on üle võetud ka füüsikasse. Ruumilist suunda omavaid füüsikalisi suurusi nimetatakse vektoriaalseteks suurusteks. Vektoriaalseteks suurusteks on näiteks kiirus, kiirendus ja jõud. Joonistel ja valemites tähistatakse vektoriaalseid suurusi nii, et suuruse tähise kohale märgitakse väike nooleke. Näiteks kiirusvektori tähis on $\overrightarrow{v}$ ja jõuvektori tähis $\overrightarrow{F}$. 

Vektori pikkust nimetatakse vektori mooduliks. Kii­rus­vektori pikkus on võrdne kiiruse arvväärtusega ja jõuvektori pikkus on võrdne jõu arvväärtusega. Vektoreid ehk suunaga lõike iseloomustab korraga nii lõigu pikkus kui ka suund. Kaks vektorit on võrdsed, kui nende pikkused on võrdsed ja nad on samal ajal ka ühesuguse suunaga. Pikkuste või suundade võrdsusest veel vektorite võrdsuseks ei piisa. Pikkused ja suunad peavad võrdsetel vektorsuurustel korraga ühesugused olema (joonis 3.1)

Vaatleme nüüd tehteid vektoritega. Vektori korrutamisel või jagamisel arvuga jääb suund samaks, tehe mõjutab vektori pikkust (joonis 3.2). Miinus ühega korrutamisel ehk vektoriaalse suuruse märgi vastupidiseks muutmisel jääb vektori pikkus samaks, aga suund muutub vastupidiseks.

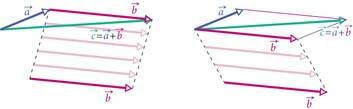
Vektorite liitmiseks on kaks võimalust: kolmnurga reegel ja rööpküliku reegel.

Kolmnurga reegli järgi liitmisel tuleb teist vektorit iseendaga paralleelselt nihutada nii, et teise vektori algus ühtiks esimese vektori lõpuga. Vektorite summaks on esimese vektori algusest teise lõppu suunatud vektor (joonis 3.3 a).

Rööpküliku reegli järgi liitmisel tuleb teist vektorit nihutada nii, et mõlema vektori alguspunktid langeksid kokku. Vektorite summaks on liidetavatest vektoritest moodustuva rööpküliku diagonaali suunaline ja pikkune vektor (joonis 3.3 b).

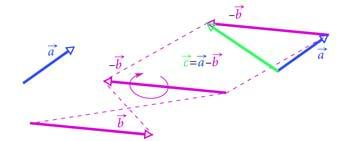
Kui vektorite liitmine on selge, ei tohiks ka lahutamine raskusi valmistada. Vektori lahutamine teisest pole ju midagi muud kui vastupidise suunaga vektori liitmine (joonis 3.4).

Joonis 3.3 Vektorite liitmise a) kolmnurga reegel, b) rööpküliku reegel.	Joonis 3.4 Vektorite lahutamine.

Füüsika uurib looduses leiduvaid kehi ja teeb seda kõigepealt vaatluse teel. Vaadeldes erinevaid kehi, võime nende juures leida sarnasusi ja erinevusi. Me saame vaadeldavaid kehi omavahel võrrelda. Võrdleme näiteks harja ja prügikühvlit. Eriti sarnased nad ei tundu olevat. Materjal on tõenäoliselt küll sama, kuid värv ja eriti kuju on täiesti erinevad. Raskuse kohta ei oska eemalt vaadeldes midagi öelda. Ometi võib leida ühe omaduse, mis on mõlemal enam-vähem ühesugune. Nimelt, hari ja kühvel tunduvad olevat ühepikkused.

Kühvel ja hari, kumb on pikem?	Kaks erineva pikkusega pliiatsit.

Pikkus on füüsikas väga oluline ja samas väga üldine suurus. Pikkuse abil saab iseloomustada kõiki kehi ja nende paiknemist üksteise suhtes. Kui ütleksime, et pikkus on füüsikaline suurus, mis kirjeldab kehade ruumilist ulatuvust, siis ei tekiks meil veendumust, et oleme selle suuruse nüüd defineerinud. Ausam oleks öelda, et pikkus on vaatleja kujutlus, mis tekib kehade omavahelisel võrdlemisel piki ühte sihti ehk mõõdet. Pikkuse kui füüsikalise suuruse üldlevinud tähis on l (ld longitudo 'pikkus') ja tema mõõtühik meeter (1 m).

Pliiatseid on lihtne omavahel võrrelda. Fotolt on selgesti näha, et ülemine pliiats on alumisest lühem. Soovi korral võime pikkused ära mõõta ning arvutada, mitu korda pikkused erinevad.

Paberilehtede võrdlemine pole aga nii lihtne. Kui need on sarnase kujuga, probleemi ei teki. Võime kindlalt väita, et teisel fotol kujutatutest on punane paberileht rohelisest väiksem, sest tema pikkus on väiksem. Kuidas aga omavahel võrrelda punast ja sinist paberilehte? Kumb neist suurem on? Siin ei piisa enam kummagi lehe pikkuse võrdlemisest. Lisaks tuleb võrrelda ka laiuseid. Kui pikkuste ja laiuste kaudu pindalad välja arvutada, osutub, et punane ja sinine paberileht on tegelikult ühesuurused. Näeme, et kehi võib iseloomustada korraga mitu pikkusmõõtu. Laius on ju tegelikult ka pikkus. Seda mõõdetakse lihtsalt teises sihis. 

Pikkuse abil ei saa võrrelda mitte ainult kehi, vaid kirjeldada ka nende asetsemist üksteise suhtes. Näiteks võime pikkusi mõõtes leida, kui kaugel puust istub viinamarju kätte saada ihkav rebane ning kui kõrgel maast viinamarjad puuoksal asuvad. Me ütleme selle kohta, et rebane ja viinamarjad paiknevad ruumis erinevates kohtades. Seda ruumi, kus kehad asuvad, saab kirjeldada erinevate pikkusmõõtude abil. Ruum pole vajalik mitte ainult kehade asukoha kirjeldamiseks. Ka kehad ise võtavad enda alla mingi ruumi. Kehad on ruumilised. Seda kinnitavad suurepäraselt vene käsitöökunstnike poolt treitud ja maalitud matrjoškad, mida saab üksteise sisse mahutada.

Samas on raske täpselt öelda, mis see ruum tegelikult on. Me saame seda vaid ette kujutada. Järelikult on ruum füüsikaline mudel. Ilma ruumi ette kujutamata ei saa me kirjeldada mitte ühtegi füüsikalist objekti ega nähtust. Ruum on füüsika üldmudel, mida saab kirjeldada pikkuste võrdlemise teel. Ruum on samas ka geomeetria kui ühe matemaatika haru põhimõiste. Matemaatika tegeleb ruumiga enamasti ilma liikumist käsitlemata.

Kui me võrdlesime pliiatseid, siis piisas vaid ühest pikkusmõõdust. Samuti piisab vaid ühest mõõtarvust, kui tahame kirjeldada liiklusõnnetuse toimumise paika. Selleks peab teadma vaid lähimale kilomeetripostile kantud numbrit. Olukorra kirjeldamiseks ei pea me ruumi ette kujutama keerulisemana kui ühemõõtmelisena. Märkame ka, et toodud näites pole üldse oluline, kas maantee on sirge või kõver. Kirjeldamiseks piisab ikkagi vaid ühest mõõtmest. Paberilehti võrreldes nägime, et siin oli vaja juba kahte mõõdet – pikkust ja laiust. Kui soovime kirjeldada paberil sibava sipelga asukohta, siis on ka selleks vaja kahte mõõtarvu. Seejuures pole tähtis, kas paber on sirge või näiteks rulli keeratud. Mingil kindlal pinnal paiknevate kehade ja nähtuste kirjeldamiseks saab kasutada ruumi kahemõõtmelist mudelit. Kõige keerulisem ruum, mida inimesed enda ümber tajuvad, on kolmemõõtmeline. Pikkusele ja laiusele lisandub veel kõrguse mõõde. Igapäevaselt tajutavate nähtuste kirjeldamisel rohkem mõõtmeid tarvis ei lähe. 

Kolmemõõtmeline ruum võib sisaldada vähemamõõtmelisi ruume. Vaatame näiteks ühte traadijuppi, mida mööda sammub sipelgas. Kuna sipelgas lennata ei oska ja traadilt maha hüpata ei julge, on tema traadi poolt määratud maailm ühemõõtmeline. Kui sipelgas tahab ühest otsast teise jõuda, tuleb tal läbi sammuda kogu traadi pikkus, sõltumatult sellest, kas traat on sirge või kõver. Kui sipelgas suudaks kasvõi natukeseks ajaks ühemõõtmeliselt traadilt väljuda ja kasutada kõrgemat mõõdet, väheneks tema jalavaev märgatavalt. 

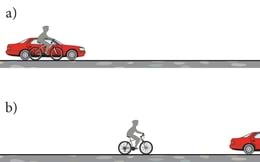
Üheks esmaseks tähelepanekuks, mille me loodust uurides teeme, on see, et kehad ei ole mitte alati üksteise suhtes paigal – nad liiguvad. Liikumine on alati suhteline, ühe keha liikumist saab vaadelda vaid mingi teise keha suhtes. Kuna selle teise keha olemasolu loob tingimused või tausta esimese keha liikumise käsitlemiseks, siis me nimetame teist keha taustkehaks. Kirjeldades maantee ääres seistes autode liikumist, on väga mugav kasutada taustkehana iseenda keha. Kui aga vaatleme liikuvas autos istudes teist, möödasõitu sooritavat autot, siis hindame möödasõitja liikumist kõigepealt omaenda auto kui taustkeha suhtes. 

Nüüd nendime, et mistahes liikumise uurimiseks peab vaatlejal olema mälu. Vaatlejal peab olema võimalik korraga töödelda liikuva keha erinevaid asukohti käsitlevat infot. Vaatleja ütleb: „Mulle lähenev keha oli kõigepealt minust kaugel, seejärel lähemal ja lõpuks päris minu juures.” Vaatleja järjestab oma mälupilte, ta järjestab erinevaid sündmusi skaalal varem-hiljem. Seega asub vaatleja vältimatult kujundama aja mõistet. Samas võime ka väita, et kui liikumist ei esineks või mingeid sündmusi ei toimuks, siis poleks vaatlejal ka mitte mingit alust aja mõiste tekitamiseks. Liikumine ja aeg on lahutamatult seotud mõisted. 

Järgnevalt märkame, et kehad võivad liikuda väga erinevalt. Piki maanteed jalutades paneme tähele, et kui meist möödunud jalgrattur on alles ligikaudu saja meetri kaugusel, on jalgratturiga samal hetkel möödunud sõiduauto juba nägemisulatusest väljumas. Nendime, et jalgrattur liigub kiiremini kui jalakäija, aga auto omakorda kiiremini kui jalgrattur. Keha liikumisolekut (või „liikumise ägedust”) kirjeldab füüsikaline suurus, mida me nimetame kiiruseks v (lad velocitas 'kiirus'). Juba põhikoolis õppisime, et kiirus näitab ajaühiku jooksul läbitavat teepikkust. Kuid mis on aeg? On ilmne, et aja mõiste kujundamine liikumist käsitlevate mälupiltide alusel sõltub selle keha kiirusest, mille liikumisest me lähtume. Me oleme siin selgelt nii-öelda muna-kana probleemi ees: aja mõiste kujundamine sõltub kiirusest, kiiruse määratlemiseks aga oleks vaja juba kasutada aja mõistet.

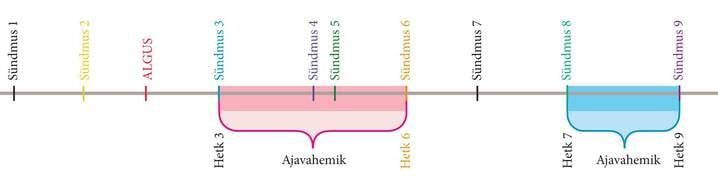
Isaac Newton lahendas ülaltoodud probleemi, järjestades sündmused mõtteliselt mingile joonele, mis meenutas ühemõõtmelise ruumi mudelit (joonis 3.5). Kui sündmused on järjestatud, siis saab neid võrdlema hakata. Enne tuleb muidugi veel kokku leppida, millise sündmusega me kõiki teisi võrdlema hakkame. Näiteks on ajaloo­sündmuste järjestamisel nullpunktiks võetud päev, mil keskaegsete arusaamade kohaselt sündis Jeesus Kristus. Hiljem on küll leitud, et tegelikult sündis Kristus tõenäoliselt veidi varem. Probleemid Jeesuse sünniaasta määramisel tulenevad esimesel sajandil valitsenud segadusest kalendriasjanduses. Aja mõiste kujundamisel asus Newton eeldama, et sündmuste toimumishetkede järjestus ajateljel ning kahe sündmuse vahele jäävate ajavahemike pikkused on kõigi vaatlejate jaoks ühesugused. Nii määratletud aega nimetatakse absoluutseks ajaks. 

Lühidalt, Newton asus seisukohale, et kiirust $v$, teepikkust $s$ ja aega $t$ omavahel siduvas üldtuntud valemis 

tuleb aega vaadelda mitte­defineeritava suurusena. Valem 3.1 osutub siis mõistagi kiiruse definitsiooniks. Jääb aga probleem: mille alusel otsustada, kui palju on üks ajavahemik absoluutse aja teljel teisest pikem? 

Siin viitas Newton teadagi võimalusele kasutada perioodilisi protsesse ehk nähtusi, millele on omane korduvus. Nendeks on näiteks päikese näiv liikumine taevas (öö ja päeva vaheldumine) või kuu faaside vaheldumine (kuu loomine, noorkuu, täiskuu, vanakuu), samuti mitmesuguste pendlite võnkumine. Ajavahemikku võib võrrelda vastava võnkeperioodiga. Aja mõõtmisel võib võtta võrdluse aluseks ka muutumatu kiirusega kulgevad protsessid, näiteks küünla lühenemise põlemise käigus või liiva voolamise läbi liivakella väikese ava. Kuid mille põhjal me teame, et kasutatava korduva protsessi periood on konstantne või et liiva voolamine liivakellas toimub alati ühesuguse kiirusega? Kuidas saab vaatleja usaldusväärset infot absoluutse aja kohta?

Läheme nüüd aja mõiste uurimisel tagasi Vana-Kreekasse, kus liikumise ja aja probleemid erutasid väga eleaate ehk Elea filosoofilisse koolkonda kuuluvaid mõtlejaid. Vana-Kreekas oli filosoofiaga tegelemine vabade kodanike privileeg, mistõttu katseline loodusteadus seal veel tekkida ei saanudki. Looduse muutmise ehk raske füüsilise tööga tegelesid orjad. Vabad kodanikud pidid suutma mistahes probleemi lahendada mõtlemise ja arutlemise teel. Korrastatud mõtlemise reeglite õpetamisel kasutati Vana-Kreeka koolides vastuoluga lõppevaid mõtteskeeme ehk apooriaid. Tuntuim eleaat Zenon konstrueeris terve rea apooriaid, mis tõestasid, et liikumist ei saa vaadelda järjestikuste paigalseisude summana. 

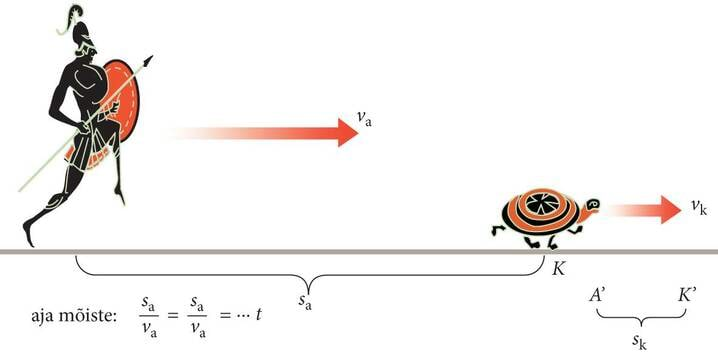
Üks Zenoni apooria kannab nime "Achilleus ja kilpkonn". Kuulsaim kreeka sõjamees, Trooja sõja kangelane Achilleus otsustab kilpkonnaga võidu joosta ning oma võidus ette kindel olles annab kilpkonnale edumaa, mis on allpool toodud joonisel tähistatud s_a -ga. Võidujooksu alguses paikneb Achilleus punktis A ja kilpkonn punktis K. Kui Achilleus on jõudnud sinna, kus kilpkonn oli liikumise alguses (K), siis kilpkonn on juba jõudnud punkti K’, olles läbinud pikkuse s_k. Kui ka Achilleus on jõudnud punkti K’, olles täiendavalt läbinud pikkuse s_k, siis on kilpkonn juba punktis K’’, mis paikneb punktist K’ pikkuse s_k’ võrra eespool. Ja nii edasi. 

Zenon väidab, et Achilleus ei saa kunagi kilpkonna kätte, sest Achilleuse ja kilpkonna vahekaugus ei saa kunagi nulliks. Kilpkonna algse edumaa s_a ja tema poolt hiljem läbitud teepikkuste summa s_a + s_k + s_k’+ s_k’’+… osutub Achilleuse poolt läbitud teepikkusest suuremaks, seda nimelt kilpkonna poolt kõige viimati läbitud teepikkuse võrra. Seega kilpkonn on alati natuke Achilleusest eespool. Pole raske taibata, et Zenon eeldab vaikimisi nii Achilleuse kui ka kilp­konna kiiruste sujuvat ühtlustumist. See tähendab, et mida lähemale kilpkonnale Achilleus jõuab, seda väiksemaks muutub nende kiiruste erinevus. Õigupoolest saabki Zenoni arutlus võimalikuks ainult tänu sellele, et Zenon ei kasuta kiiruse mõistet ning ei tegele ka aja mõiste päritoluga. 

Teades Achilleuse kiirust v_a ja kilpkonna kiirust v_k ning eeldades nende kiiruste konstantsust, pole kuigi raske leida aega, mis tegelikult kulub Achilleusel kilpkonna kinnipüüdmiseks. Jäägu selle ülesande lahendamine asjast huvitatutele. Meie jaoks on hetkel oluline, et Achilleuse ja kilpkonna liikumiste võrdlemine kujundab tegelikult meie jaoks aja mõiste. Üldisemal juhul me vaatleme näiteks tervet hulka samast punktist liikumist alustavaid kehi, millest esimene liigub kiirusega v₁, teine kiirusega v₂, kolmas kiirusega v₃ jne. Kui esimene keha läbib pikkuse s₁, teine pikkuse s₂, kolmas pikkuse s₃ jne, siis jääb suhe 

vaatleja jaoks konstantseks. Seda suhet me nimetamegi ajaks. Niisiis me vajame aja mõiste kujundamiseks vähemasti kolme keha: taustkeha ning veel kahte liikuvat keha, mille liikumisi me omavahel võrdleme. Ülalpool oli taustkehaks Maa ning kaheks liikuvaks kehaks Achilleus ja kilpkonn. Tavaelus me võrdleme ühe keha liikumist mingi etalonkeha sees toimuva liikumisega. Seda erilist keha me nimetame kellaks. 

Rõhutame veel kord, et aeg kui füüsikaline suurus on selline vaatleja kujutlus, mis tekitatakse liikumiste omavahelisel võrdlemisel. Aeg järjestab sündmused omavahel varem või hiljem toimunuteks.

Füüsika uurib loodusobjektidega toimuvaid nähtusi. Nähtus ehk protsess tähendab millegi muutumist. Igal muutumisel on aga mingi põhjus ja iga muutus kutsub omakorda esile uue muutumise. Nähtuste vahel esineb põhjuslik seos – üks sündmus põhjustab teise sündmuse toimumise. Füüsika uuribki looduse kõige üldisemaid põhjuslikke seoseid. Looduses toimuva mõistmine, looduse tunnetamine saab võimalikuks nähtustevaheliste põhjuslike seoste avastamisel.

Toome mõned näited füüsikalise põhjuslikkuse teel seotud nähtuste ahelatest. 

õun tuleb oksa küljest lahti → õun langeb allapoole → õun jõuab maapinnale

püssikuul tabab palkseina → kuul peatub seinas → seina sisse tekib auk

valgus neeldub kehas → see keha soojeneb → see keha paisub

elektrivool läbib metallkeha → see keha soojeneb → selle keha takistus suureneb 

Füüsika üks olulisi väärtusi avaldub võimes ennustada loodusnähtusi. Vaadeldes konkreetsete objektidega asetleidvaid nähtusi ja avastades nendevahelisi põhjuslikke seoseid, saame ka uutes, veel läbi proovimata olukordades ennustada, mida üks või teine tegevus esile kutsub. Näiteks kui laseme kristallvaasi kivipõranda kohal käest lahti, siis on üpris lihtne ennustada, et vaas kukub peagi maha ja läheb katki. Kui inimesele, kes oskab sellist asjade käiku ennustada, esitada küsimus tema teadmiste päritolu kohta, siis viitab ta tõenäoliselt oma elukogemusele. Tegelikult aga seisneb see kogemus teadmistes füüsikalise põhjuslikkuse kohta. Gravitatsioon põhjustab vaasi järjest kiirema kukkumise ning kohtumisel kivipõrandaga mõjub viimane vaasile lühiajalise ning suure jõuga, mis tekitab omakorda suuri jõude vaasi osade vahel. Tulemusena habras kristallvaas puruneb. Selle ennustamiseks ei pea me olema varem täpselt samasuguse vaasiga samades tingimustes mahakukutamise katset läbi teinud. Me oskame füüsikaliselt üldistada teiste sarnaste nähtuste vaatlemisel avastatud põhjuslikke seoseid. 

Enamasti nimetatakse kaht sündmust põhjuslikult seotuks, kui ühe sündmuse ehk põhjuse toimumine toob teatava vältimatusega kaasa teise sündmuse ehk tagajärje.

Põhjuslikud seosed eksisteerivad kogu looduses ja osadega neist tegelevad teised loodusteadused, kuna nende uurimismeetodid sobivad selleks füüsika meetoditest paremini. Näiteks bioloogias kehtivad tuntuimad põhjuslikud seosed on pärilikkuse seadused või siis toitumisahelates kehtivad seadused, mille kohaselt saakloomade arvukus määrab vastavate kiskjate arvukuse. Inimese sekkumine ökoloogilistesse protsessidesse võib tõsiselt rikkuda ökoloogilist tasakaalu. Näiteks on rebaste massiline vaktsineerimine marutaudi vastu põhjustanud Eestis viimastel aastatel rebaste arvukuse järsu kasvu. Rebased ei sure enam massiliselt marutaudi, metsas ei jätku neile kõigile enam toitu ja nad hulguvad linnatänavatel nagu koerad. 

Keemias kehtiva spetsiifilise põhjusliku seose näiteks võib tuua aine lahustuvuse sõltuvuse temperatuurist või rõhust. Kui mingi vedeliku jahutamisel tekib vedelikus sade, siis võime üpris kindlasti öelda, et see vedelik osutus lahuseks ja sisaldas mingit ainet, mille lahustuvus temperatuuri langetamisel vähenes ja see aine sadenes põhja. Heaks biokeemilise põhjusliku seose näiteks on vingumürgitus. Kui inimene hingab sisse vingugaasi (CO), mille molekulid seostuvad hemoglobiiniga hapniku molekulidest tugevamini, siis hemoglobiin enam hapnikku siduda ei saa. Selle tulemusena veri enam vajalikul määral hapnikku edasi ei toimeta ning organismis tekib hapnikupuudus. 

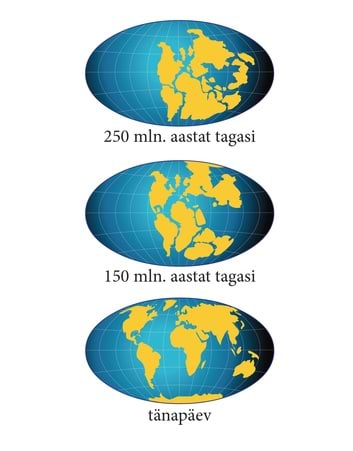
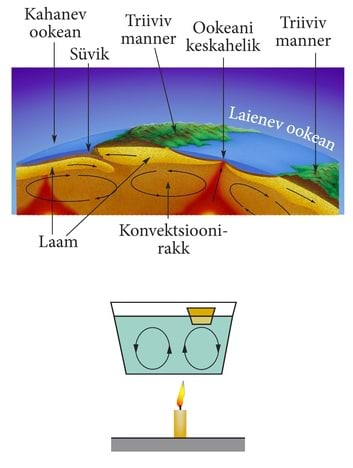
Geograafias nenditi juba ammu Aafrika lääneranniku ja Lõuna-Ameerika idaranniku rannajoone kuju sarnasust. Hüpotees, et kunagi on need mandrid moodustanud ühtse terviku, viis geograafid kõnealuse sarnasuse põhjuse avastamiseni. Selleks on mandrite triiv kui kaasaegses geograafias üldtunnustatud teaduslik fakt. Maakoore suured tahked osad ehk laamad libisevad väga aeglaselt maakoore-alusel tulisel ja poolvedelal ainel. Seal, kus üks mandrilaam libiseb teise alla, kerkib teise laama äär ülespoole ja tekivad noored mäed. Samas on just seal palju tegevaid vulkaane ja esineb oluliselt rohkem maavärinaid. 

Geograafia vaid kirjeldab mandrite triivi, geofüüsika aga seletab seda nähtust, kasutades füüsikas loodud üldist konvektsiooni mudelit.	Mandrite triivi lihtsustatud füüsikaline mudel. Kas leiad geofüüsikalise pildi (üleval) ja küünlaga anuma kuumutamisel tekkivas konvektsioonis liikuma hakkava laevukese liikumise vahel analoogia?

Füüsika uuritavad põhjuslikud seosed on reeglina üldisemad põhjuslikest seostest teistes loodusteadustes. Näiteks keemias oli tagajärjeks sademe teke ja selle põhjusena tuuakse esile temperatuuri langemine. Füüsika aga seletab, mis asi on üldse suurus nimega temperatuur, mille muutumine oli keemia jaoks põhjuseks. Füüsika loob temperatuuri mõiste põhjusliku mudeli, mille kohaselt aine molekulid on kaootilises soojusliikumises. Selle liikumise keskmine kineetiline energia ühe osakese kohta määrabki temperatuuriks nimetatava füüsikalise suuruse. Kõrgemal temperatuuril on osakeste keskmine kineetiline energia suurem, osakesed liiguvad kiiremini ja seetõttu on ka lahustuvus suurem. Geograafia vaid nendib, et laamade libisemine põhjustab mandrite triivi, mis omakorda miljonite aastate jooksul muudab Maa geograafilist kaarti. Füüsika aga seletab, millisest ning kui kõrgel rõhul ja temperatuuril olevast ainest Maa sel või teisel sügavusel tõenäoliselt koosneb. Füüsika näitab, et erinevatel temperatuuridel paiknevate vedelate ainekihtide vahel esineb vältimatult konvektsioon. See tähendab, et Maa sisemuse mingis piir­konnas kerkib kuum aine ülespoole ja selle kõrval toimub jahedama aine laskumine alla. Maakoore all liigub vedel aine tõusu tsoonist laskumise piirkonna suunas ning veab maakoore osi endaga kaasa. Nii tekibki laamade liikumine. Füüsika kasutab geograafias olulise loodusnähtuse seletamisel juba põhikoolis õpitud konvektsiooni mudelit, mis kirjeldab nii aine liikumist maakoore all, merevee liikumist ookeanides, õhumasside liikumist atmosfääris kui ka õhu ringkäiku meie tubades. Füüsikaline põhjuslik seos on kõige üldisem. 

Põhjuslikkust võib füüsikas liigitada mitmeti. Üks võimalus on seda teha, rakendades ruumi ja aja mõisteid.

Ruumiliseks võib nimetada sellist põhjuslikkust, mille korral omavahel põhjuslikult seotud sünd­mused on korraga vaadeldavad. Võib ka öelda, et ruumilise põhjuslikkuse korral puudub alus nende sündmuste järjestamiseks. Nende kirjeldamisel võib alus­tada ükskõik millisest sündmusest. Ruumiline põhjuslikkus avaldub ühe füüsikalise objekti koosne­mises teistest objektidest. Näiteks liivahunnik koosneb liivateradest. Liivaterade olemasolu on liiva­hunniku olemasolu põhjus. Või siis, aatomi tuum koosneb prootonitest ja neutronitest. Prootonite ja neutronite olemasolu on tuuma olemasolu põhjus.

Ajaliseks võib nimetada sellist põhjuslikkust, mille korral omavahel põhjuslikult seotud sünd­mused ei ole korraga vaadeldavad. Sündmuste vahel on olemas kindel järjestus. Ajaline põhjuslikkus avaldub teise sündmuse järgnevuses esimesele. Siin sobib hästi juba uuritud näide: vaas paikneb kivipõranda kohal õhus ja talle mõjub ainult raskusjõud (sündmus 1, põhjus); vaas on jõudnud põrandale (sündmus 2, tagajärg).

Põhjuslikkust saab ka liigitada võimalike tagajärgede arvu järgi. Kui mingi sündmus saab põhjustada vaid ühe kindla tagajärje, on tegemist fatalistliku põhjuslikkusega (ld fatalis 'ette määratud'). Põhikooli füüsika mudelid on reeglina fatalistlikud. Näiteks me võisime sajaprotsendiliselt kindlad olla, et kiirusega 20 m/s ühtlaselt ja sirgjooneliselt liikuv rong jõuab 5 sekundiga oma esialgsest asukohast 100 meetri kaugusele (näide ptk 2.5.1). Muud võimalust lihtsalt pole. Niisugune füüsika sisendab meisse jõuliselt arvamust, et kõik protsessid looduses ongi fatalistlikud. 

Fatalistliku põhjusliku seose korral on võimalik täpne füüsikaline ennustamine. Mitme võimaliku tagajärje korral aga kindlat tagajärge täpselt ennustada ei saa ja mängu tuleb juhuslikkus. Juhuslikuks nimetame põhjuslikkust, mille korral võimalikke tagajärgi on lõplik ja kindel arv ning me saame hinnata ühe või teise tagajärje esinemise tõenäosust. Näiteks ei saa me täringuviske tulemust täpselt ennustada, kuid me teame, et tagajärgedeks on kuus erinevat võimalust ja nende esinemise tõenäosused on võrdsed. Realiseerub üks variant kuuest, tõenäosusega ¹/₆ ^. 100 ehk 16,7%. Kaasaegne füüsika erineb klassikalisest tõenäosusliku mõtteviisi laialdase rakendamise poolest. 

Kui võimalike tagajärgede arv pole mitte mingil moel eelnevalt määratav ja mitte ükski realiseerunud tagajärg pole täpselt korratav, siis on tegemist kaootilise põhjuslikkusega. Kaootilise põhjuslikkuse näiteks võib tuua õnnevalamise tulemuse või mullide tekkimise vee väljavoolamisel pudelist. Kui põhjaga taeva poole keeratud pudelist vesi välja voolab, siis siseneb õhk pudelisse kaootiliselt. Me ei suuda ennustada, millist pudeli serva mööda õhumull ülespoole kerkib. Kui aga pudelit enne keerutada, siis saab ennustada keerise teket ja vee kiiremat voolamist. Kaootilise põhjuslikkuse uurimisega tegeleb kaasaegse füüsika ja matemaatika piiriteadus sünergeetika. 

Loodusteadustes esineb alati oht, et põhjuslike seoste otsimisel avastatakse tõelise põhjuslikkuse asemel näiv põhjuslikkus. Näiva põhjuslikkuse korral on tagajärje rollis esinev sündmus tegelikult põhjustatud mitte põhjuseks peetavast sündmusest, vaid mingist muust, esmapilgul märkamata jäänud sündmusest. Kõige tuntumaks näiteks selle kohta on astroloogilised seaduspärasused, näiteks inimese iseloomu sõltuvus tema sünnikuupäevast. Kui see sõltuvus üldse esineb, siis kindlasti ei ole ta põhjustatud Maast väga erineval kaugusel paiknevate tähtede omavahelisest asendist maapealse vaatleja jaoks. Kuid Päikese ja Kuu võimalikku mõju maapealsetele protsessidele ei saa eitada, mistõttu see võib olla nimetet sõltuvuse tõeline põhjus. 

Elektrinähtuste uurimise algaastatel arvati, et kuna säde on sinaka värvusega, siis elekter armastab sinist ja kardab punast värvi. Seepärast kasutati isoleeriva materjalina just punast siidniiti ja katsed kinnitasid sellise valiku õigsust. Punase siidniidi otsa riputatud metallkuulile jäi elektrilaeng püsima, aga hõbedane traat juhtis laengu minema. Tollal arvati, et siidniidi käitumine mittejuhina on põhjustatud tema punasest värvusest. Hiljem selgus, et tegelik põhjus peitub hoopis niidi või juhtme materjalis. Siidis puuduvad vabad laetud osakesed ja sellepärast siid ei juhigi elektrit. 

Lähtudes vaatleja definitsioonist (ptk 1.2.1) peame aga kõigile teistele looduses esinevatele põhjuslikkuse liikidele lisama veel ühe. See on tahteline põhjuslikkus, mis realiseerub inimese vaba tahte ilminguna. Püüdkem vastata küsimustele, miks ma just praegu püsti tõusin? Miks ma just praegu kätt liigutasin? Milline ka poleks vastus neile küsimustele, see vastus ei kipu mahtuma mitte ühegi ülalpool loetletud põhjuslikkuse liigi alla. Me loodetavasti ei kahtle selles, et ka inimkeha on osa loodusest, koosnedes eelkõige kindlaviisiliselt paigutunud ja vastastikmõjustuvatest süsiniku, vesiniku ja hapniku aatomitest. Seetõttu peaksid ka inimkehas toimuvad protsessid alluma samadele põhjuslikele seostele, mis kehtivad kogu ülejäänud looduses. Kuna me ei oska seletada, millisel looduse struktuuritasemel toimivad need põhjuslikud seosed, mis määravad meie otsuse midagi teha või mitte teha, siis oleme sunnitud võtma kasutusele erilise põhjuslikkuse liigi – tahtelise põhjuslikkuse. Selle uurimisega peaksid aga käsikäes tegelema loodusteadused, arstiteadus ja psühholoogia. Kindlasti ei ole see ainult füüsika uurimisobjekt. 

Loodusnähtuse ennustamine on väide selle nähtuse toimumise kohta tulevikus ja/või mingis teises kohas. Juba korduvalt on juttu olnud sellest, et võimes pädevalt ennustada loodusnähtusi avaldub füüsika prognostiline ehk ennustuslik väärtus.

Ennustamise aluseks on põhjuslike seoste tunnetamine. Näiteid selle kohta on kahes eelmises alapunktis juba toodud üksjagu. Rõhutame vaid veel kord, et uurides põhjuslikkuse kõige üldisemaid avaldumise vorme, annab füüsika teistele loodus­teadustele üldise meetodi looduses esineva põhjuslikkuse käsitlemiseks. Füüsika näitab, kuivõrd saab selle või teise loodusnähtuse lõpptulemus olla ette määratud. Ettemääratus on mingi sündmuse kindel esinemine tulevikus, sõltumata sünd­mus­test, mis esmapilgul võiksid antud sündmuse kui tagajärje võimatuks muuta. Füüsikalise ettemääratuse tingib loodusseaduste vältimatu, mistahes inimese tahtest sõltumatu kehtivus, aga need seadused ei pruugi olla ranged. Nad võivad olla ka statistilised ehk juhuslikust põhjuslikkusest tulenevad. 

Füüsikal kui peamisel tehnilist progressi käivitaval ja toetaval loodusteadusel on kindlasti ka rakenduslik väärtus. Mehaanika välja­arendamine 18. sajandil võimaldas ehitada masinaid, mis oluliselt kergendasid inimtööd. Ehkki masinate kasutuselevõtuga vabrikutes kaasnes küll varem käsitsitöös hõivatud inimeste töötuks jäämine, lõid ketrus- ja kudumismasinad, trei- ja frees­pingid ning stantsid siiski aluse enneolematuks tööviljakuse tõusuks, millega kaasnes arenenud riikide elanikkonna keskmise elujärje tunduv paranemine. Soojusfüüsika saavutused võimaldasid 18. sajandi lõpul luua aurumasina ning 19. sajandi lõpul sisepõlemismootori. Elektro­magnetismi põhiseaduste avastamine 19. sajandil tegi võimalikuks telegraafi, telefoni ja raadioside kasutuselevõtu, elektrienergia jõudmine kodudesse suurendas enneolematul viisil olmemugavusi. Füüsika rakenduslikust väärtusest võiksime rääkida veel pikalt, aga selle kohta leidub hulgaliselt infot ka mujal, mitte ainult füüsikaõpikutes. 

Kuni teise maailmasõjani oli füüsikal ühiskonnas selgelt positiivne kuvand. Füüsika aitas elu paremaks muuta ja temast ei lähtunud veel tõsiseid ohte. Kui 1945. aastal võeti aatomi- ja tuumafüüsika tulemustest lähtudes kasutusele tuumarelv, siis pidi inimkond vist esmakordselt selgesti tõdema, et füüsika arenguga kaasnevad ohud. Loomulikult pole neis ohtudes süüdi füüsika ise, vaid mõnede vastutustundetute poliitikute võimuahnus ja relvatootjate rikastumissoov. Paraku ei muuda selle fakti mõistmine ohtu olematuks. Kahe tohutu tuumaarsenaliga üliriigi Nõukogude Liidu ja Ameerika Ühendriikide vastasseisu tulemusena elas maailm aastail 1950–1990 pidevas globaalse tuumasõja ohus. Vastasseisu ajastu lõpul oli kõigi loodud tuuma­relvade summaarne purustusjõud paljukordselt piisav kogu inimkonna hävitamiseks. Samas on ilmselt just tuuma­katastroofi tagajärgede füüsikalised prognoosid seni ära hoidnud kolmanda maailma­sõja puhkemise. Kõik asjatundjad teavad, et globaalses tuumasõjas ei jää lõpuks ellu mitte keegi. Ka neil, kes suudaksid esialgu varjenditesse peituda, tuleks sealt millalgi välja tulla. 

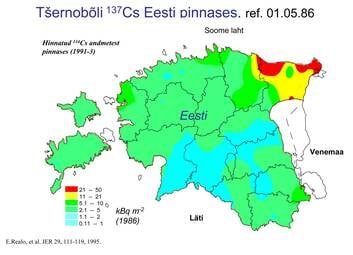
Plahvatus lõhkus Tšernobõli tuumajaama neljanda reaktori pea täielikult.	1986. aasta 26. aprillil Tšernobõli tuumajaamas toimunud avarii oli tuumaenergeetika ajaloo rängim. Avariis atmosfääri paiskunud radioaktiivsete ainete levikut uuriti põhjalikult ka Eestis. Leiti, et Eestini kandunud ainest sadestus kuni 60% Ida- Virumaal.

Nõukogude Liidu lagunemise tulemusena on kahe üliriigi vahelise tuumasõja oht tänapäeval jäänud tagaplaanile, kuid jätkuvalt ohtlikud on kohalikud tuumakonfliktid, sest tuumarelva omanikeks on saamas või juba saanud mitu avalikku arvamust eiravat ja agressiivsest ideoloogiast juhinduvat riiki (näiteks Iraan ja Põhja-Korea). Seoses tuumaenergia üha laialdasema kasutuselevõtuga on tänapäeval muutunud aktuaalseks mingis tuumaelektrijaamas toimuva avariiga kaasnev võimalik oht. Esimene tõsine märk sellest ohust oli Tšernobõli katastroof aprillis 1986. Tšernobõli avarii põhjused on heaks näiteks füüsikalise põhjuslikkuse ja füüsikaliste ennustuste piiride kohta. Nimelt toimus Tšernobõli tuumaelektrijaama reaktorite töö reguleerimine grafiitvarraste abil, mis neelavad tuumareaktsiooni käigus tekkivaid ja uusi tuumareaktsioone vallandavaid vabu neutroneid. Kui reaktsioon muutub liiga intensiivseks, lükatakse seda tüüpi reaktoris grafiitvardaid rohkem reaktorisse sisse, vähendamaks vabade neutronite arvu. Piltlikult öeldes „valatakse tuumatulele pisut vett peale”, hoidmaks seda kontrolli all. Paraku ei arvestatud Tšernobõlis aga sellega, et kui temperatuur reaktoris on juba ohtlikult kõrge, siis materjalide omadused muutuvad ja grafiitvarraste nihutamise mehhanismid võivad kinni kiiluda. Nii paraku juhtuski. Ohtlik loodusnähtus (tuumareaktsioon) on ise füüsikaline nähtus, tema ohjamisel kasutatav mehhanism (grafiitvardad) rajanes põhjusliku seose füüsikalisel tunnetamisel, mehhanismi ootamatul ülesütlemisel olid aga samuti füüsikalised põhjused. Katastroof sai teoks füüsikaliste põhjuslike seoste ignoreerimise tulemusena. 

Tänapäevaste tuumaelektrijaamade turvasüsteemid on piisavalt kõrgel tasemel, muutmaks Tšernobõli tragöödia kordumise tõenäosust tühiselt väikeseks. Kuid siiski jääb alles prognoosimatust loodusõnnetusest tulenev tuumaavarii oht. Seda näitas meile selgesti hiljutine avarii Fukushima tuumaelektrijaamas Jaapanis. Avarii põhjustas teatavasti maavärin. Kümned Jaapani tuumaelektrijaamad paiknevad alal, kus maavärinate esinemise tõenäosus on väga kõrge. See on ohtlik, kuid valikut pole, sest energiat on vaja. Paraku on inimkond jõudnud selleni, et ohtlikku tegevust jätkatakse, ehkki kõik on ohust teadlikud. Millele me saame sellises olukorras oma lootuse panna? Ainult füüsika arengule. Tuleb loota, et geofüüsika jõuab peagi nii kaugele, et suudab maavärinaid piisava tõenäosusega ette ennustada. Kui maavärinat on oodata, tasub tuumalelektrijaamade võimsust vastavas piirkonnas vähendada ja viia nad üle avariivalmiduse seisundisse. 

Kõigi vaatleja kujutluste hulgas looduse kohta on erilisel kohal printsiibid. Füüsikaline printsiip (ld principium 'algus, alus') on looduse vaatlemisel tehtud kõige laiema kehtivusalaga üldistus. Printsiipide paikapidavust tõestab see, et loodust vaadeldes me veendume ikka ja jälle printsiipide kehtivuses ning ei näe mitte kusagil erandeid printsiipidest. Füüsika koosneb vaatluste ja katsete põhjal tehtud üldistustest. Vaatlusi ja katseid ning neist tulenevaid järeldusi saab olla palju erinevaid. Millised neist siis väärivad kõige muu alguse või aluse nimetust?

Kui tahame seletada mingit nähtust, peame ridamisi vastama paljudele üksteisega seotud miks-küsimustele. Iga vastus kutsub reeglina esile uue küsimuse. Siiski me saame neile miks-küsimustele vastata vaid teatud piirini. Varem või hiljem jõuame olukorrani, kus me enam miks-küsimusele vastata ei oska ja peame piirduma tõdemusega, et nii lihtsalt on. Kui me paneme kokku kuuma ja külma keha, siis ilma välismõjuta läheb soojus alati kuumemalt kehalt külmemale, mitte vastupidi. Loodus on selline ja me ei oska öelda, miks. Füüsikalised printsiibid on miks-küsimuste ahelate lõpud. Nad on looduse kohta käivad kõige üldisemad tõdemused, mis vastavad absoluutselt kõikide eksperimentide tulemustele. 

On väga oluline mõista, et see, mida pidada printsiibiks ja mida mitte, on iga vaatleja vaba otsus. Loodus on terviklik ja seetõttu tundub meile ühe või teise printsiibi käsitlemisel korduvalt, et samalaadsest asjast on juba juttu olnud. Leidub inimesi, kes on valmis kõiki printsiipe taandama ühele ainsale ning kogu oma maailmapilti sellele üles ehitama. Siin peame jälle meeles pidama, et füüsika pole matemaatika, kus on olemas ainult üks õige vastus. Füüsikas peab arvamuste paljusus olema lubatud – seni, kuni arvamused pole vastuolus katsefaktidega. 

Juba eespool oli juttu matemaatika ja füüsika seostest. Matemaatika on rangelt defineeritud tähendusega sümbolite keel. Matemaatika ja füüsika peamine erinevus seisneb selles, et kui esimene neist uurib loogilisi seoseid ettekujutatavate objektide ja nende omaduste vahel, siis füüsika kirjeldab reaalselt olemasolevat loodust. Tõsi küll, füüsika kasutab väga sageli selleks matemaatika keelt. Matemaatikas ei tehta vaatlusi ega katseid. Tulemused saadakse vaid rangete loogiliste arutluste teel. 

Kuna matemaatika ei kirjelda otseselt loodust, siis võib selle teooriate aluseks võtta väiteid, mis ei nõua katselist tõestust, kuid on täielikus vastavuses meie igapäevase kogemusega. Matemaatiliste teooriate aluseks olevaid ilmselgeid ja tõestust mittevajavaid väiteid nimetatakse aksioomideks (kr aksioma 'kindel, vaieldamatu'). Toome mõned näited matemaatika aksioomidest.

• Arv null on väikseim võimalik naturaalarv. 
• Läbi kahe erineva punkti saab tõmmata ainult ühe sirge. 
• Läbi sirgel mitte asuva punkti saab tõmmata ühe ja ainult ühe antud sirgega paralleelse sirge. 
• Paralleelsed sirged ei lõiku.

Kolm viimast aksioomi on näiteks Eukleidese geomeetria alusväideteks. Pole kuigi raske veenduda selles, et nad kehtivad ainult tasandil. Sfäärilisel pinnal, milleks on näiteks gloobuse pind, on kaks erinevat meridiaani ekvaatoril paralleelsed, kuid ometi lõikuvad poolusel. 

Aksioomidest tegime siin juttu põhjusel, et füüsikaline printsiip sarnaneb aksioomiga matemaatikas. Mõlemad on alusväited, mida eraldi ei tõestata ja mille tõesust kinnitab kõige neist tuletatu kehtivus. Samas ei maksa unustada, et füüsika kirjeldab tegelikke loodusobjekte: kehi, välju ja nendega toimuvaid nähtusi. Füüsikateooriate aluseks võib võtta vaid selliseid tõdemusi, mida vaatlused ja katsed alati kinnitavad. 

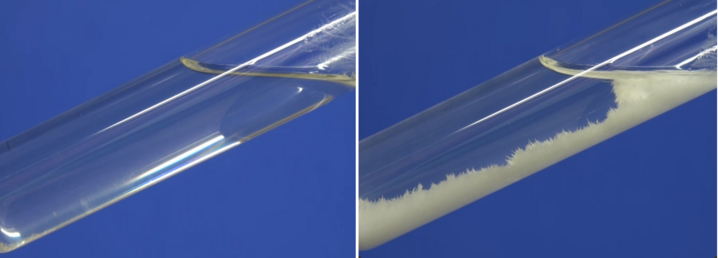
Võtame tüki juustu, asetame lõikelauale ning lõikame pooleks. Tulemuseks on kaks poole väiksemat juustutükki. Kõik oskavad sellise tegevuse tulemust ennustada. Kui jätkame sellist juustupoolitamist, siis saame järjest väiksemaid juustutükke. Isegi siis, kui juustu tükeldamine on kaotanud igasuguse kulinaarse mõtte, poolitame neid juustutükke aina edasi. Kas võime juustu lõputult järjest pisemateks paladeks lõikuda, nii et saadud tükid ikka sama maitsega juustuks jäävad? Juustumeistrite kinnitusel pole see võimalik. Juust pole ühtlane mass, vaid koosneb suurest hulgast mitmete omaduste poolest erinevatest osakestest. Meile toiduainena tuttav juust on segu erinevatest vee, rasvade, valkude, hapete ja soolade osakestest. Juustu tükeldamisel jõuame varem või hiljem piirini, mille ületamisel ei või saadud tükikesi enam juustuks nimetada. Rasvade, valkude, soolade ja vee molekulidel on oma kindlad omadused, aga need pole enam juustu omadused. Kehi ei saa lõputult väiksemateks osadeks jagada nii, et saadud osadel säiliksid kõik jagatava terviku omadused. 

Jagatavuse piiri olemasolu idee esitas juba aastatuhandeid tagasi Vana-Kreeka filosoof Demokritos. Ta väitis, et ainet ei saa lõputult jagada üha väiksemateks osadeks. Demokritose ettepanekul hakati selliseid vähimaid jagamatuid aineosakesi nimetama aatomiteks (kr atomos 'jagamatu'). Demokritose väide oli õigupoolest hüpotees, mille katseliseks kontrollimiseks puudusid tema eluajal võimalused täielikult. Kaasaegses füüsikas on see aga leidnud korduvalt katselist kinnitust. Kehtib atomistlik printsiip, mis väidab, et loodusobjekte pole võimalik lõputult samal viisil jagada endiste omadustega osadeks. 

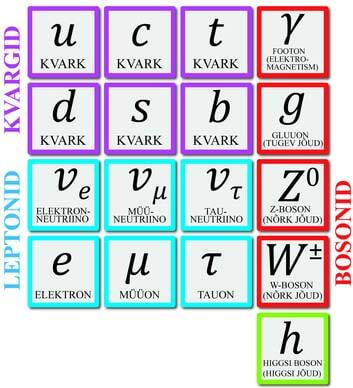
Mida väiksemad on osakesed, seda rohkem energiat peab nende lõhkumiseks rakendama. LHC (Large Hadron Collider) ehk Suur Hadronite Põrguti on inimajaloo suurim ja kahtlemata võimsaim teadusinstrument.	Standardmudel sisaldab kõiki hetkeseisuga teada olevaid vähimaid osakesi. Nendest koosnebki aine ja väli. Aineosakesed on kvargid ning leptonid. Väljaosakesi nimetatakse bosoniteks. Nende hulgas on ka äsja avastatud Higgsi boson.

Atomistliku printsiibi kehtivus aine kohta tõestati katseliselt juba 19. sajandil. Nimelt avastati siis lihtainete aatomid kui vähimad kindlate keemiliste omaduste kandjad. 20. sajandi alguses õnnestus Ernest Rutherfordil aatomit siiski osadeks jagada. Ta näitas katseliselt, et aatom koosneb tuumast ja elektronidest. Peagi selgus, et tuum koosneb omakorda prootonitest ja neutronitest. Elektroni, prootonit ja neutronit peeti ligi 50 aasta jooksul füüsika jaoks vähimateks aine jagamatuteks osakesteks. Seetõttu hakati neid nimetama elementaarosakesteks. Samas avastati aga veel kümneid erinevaid elementaarosakesi, mis sundis kahtlema prootoni ja neutroni elementaarsuses. 20. sajandi lõpul tõestatigi katseliselt, et prootonid ja neutronid koosnevad omakorda kolmest veel väiksemast osakesest – kvargist. Kogu kaasaegne katseliselt kontrollitud osakestefüüsika lähtub osakeste standardmudelist, mille kohaselt aine koosneb kaheteistkümnest fundamentaal- ehk alusosakesest: kuuest leptonist ja kuuest kvargist. Tavalise aine ehituskivideks on vaid kaks kõige väiksema massiga kvarki ning elektron kui levimuim lepton. Ülejäänud alusosakesi saab tekitada vaid laboris ja nende eluiga on väga lühike. Niisiis saab rääkida vaid antud teadmiste tasemel jagamatutest aineosakestest. Jagatavuse piiri ehk inimkonna sisemist nähtavushorisonti on viimase 150 aasta jooksul kogu aeg edasi nihutatud. Muuseas on ka osakestefüüsikas jäänud kehtima juustulõikamisel ning aatomite lõhkumisel ilmnenud seaduspärasus, mille kohaselt jagatavuse piiri ületamisel ei säili enam jagatava objekti endised omadused. Alusosakesed õigupoolest enam ei jagune väiksemateks samalaadseteks osakesteks, vaid nad muunduvad üksteiseks, kui selleks vajalikud tingimused on täidetud. 

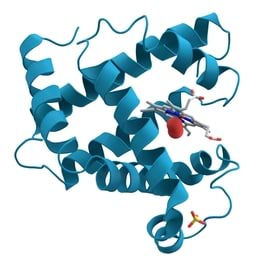
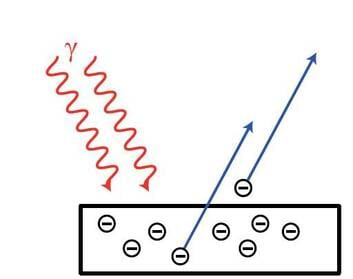
Esimesena jõudis kvantide reaalse olemasolu mõistmiseni Albert Einstein, kui ta otsis seletust fotoelektrilisele efektile. Joonisel punase lainetusena kujutatud valguskvandid löövad metallist välja negatiivse laenguga elektrone, mis joonisel esinevad miinusmärgiga kuulikestena.	Välja kvante vahetavad osakesed on omavahel seotud.

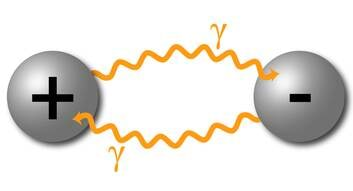
Eelmise sajandi teisel poolel tõestati atomistliku printsiibi kehtivus ka välja kohta. Tehti kindlaks, et makromaailmas pidevana tunduv väli osutub mikrotasemel samuti koosnevaks jagamatutest osakestest, mida nimetatakse välja kvantideks (lad quantum 'portsjon'). Joonisel 3.2 (p 3.4.3) kujutatud vastastikmõju mehhanism toimib tegelikult ka atomistlikul tasandil. Üks aine alusosake „viskab teise suunas“ kvandi ehk väljaosakese nagu palli. See kvant tekitatakse energia jäävuse seadust lühiajaliselt rikkudes. Kuna energia jäävuse seadus ei saa jäädagi rikutuks, siis on teine vastastik­mõjus osalev alusosake „sunnitud palli püüdma“. Seni, kuni „pall on õhus“, on mõjus osalevad aineosakesed omavahel seotud. Mõlemad aine alusosakesed aga on „nii pallide viskajateks kui ka püüdjateks“. Selles avaldubki mõju vastastikusus mikromaailmas.

Atomistlik printsiip toimib mitte ainult füüsikas ja keemias. Me märkame tema ilminguid ka tavaelus. Näiteks koosnevad kõik mingis keeles kirjutatud sõnad ju tähtedest, mida võib vaadelda kirja jagamatute algühikutena. Samas rollis on suulise kõne korral häälikud. Atomistikast võime rääkida kõikjal, kus on tegemist mingite osadega, mis moodustavad terviku. Osadel reeglina ei ole enam neid omadusi, mis on tervikul. Osa ja terviku probleemi matemaatiline esitus on hulgateooria. Hulk koosneb elementidest samamoodi, nagu mingi muu tervik koosneb osadest. Elementidel, mis moodustavad ühe kindla hulga, on kõigil mingi tunnus, mis määrab nende kuuluvuse just sellesse hulka. 

Kordame veel atomistlikku printsiipi täiesti kaasaegses ning detailses sõnastuses: Ei ainet ega välja pole võimalik lõputult jagada samade omadustega osadeks. Mõlemal on olemas antud teadmiste tasemel vähimad osakesed, mida aine korral nimetatakse fundamentaal- või alusosakesteks, välja korral aga kvantideks. 

Kui me peaksime ebatasasel maastikul kaotama palli, siis asume seda ilmselt otsima kõige madalamatest paikadest, mitte künkatippudest. Miks me nii toimime? Me teame, et kõik veerevad kehad jäävad lõpuks pidama paika, mille asukoht on kõigist võimalikest madalaim. Nad jäävad pidama sinna, kus nende energia Maa raskusväljas on kõige väiksem.

Toodud näide väljendab kogu looduses kehtivat energia miinimumi printsiipi. See printsiip väidab, et kõik iseeneslikud ehk mitte välismõjust tingitud protsessid kulgevad looduses alati energia kahanemise suunas. Nii üksikul kehal kui kehade süsteemil on kalduvus energiat loovutada või töö tagavara ära kulutada, suundudes minimaalse energiaga olekusse. Võib ka öelda, et kõik loodusobjektid tahavad energiat ära anda, kuid miski peab seda energiat ju ka vastu võtma. Seetõttu toimub loodusobjektide vahel pidev vastastikune „energia kaela määrimine“. Omavahelise vastastikmõju tulemusena lähevad mistahes süsteemi osad lõpuks omavahel energia andmise ja vastuvõtmise tasakaalu, mille määravad konkreetsed tingimused.

Energia miinimumi printsiibi kehtivuse kohta võib tuua järgmisi näiteid.

• Vihmapiisad langevad maale, ojad voolavad jõkke, jõed omakorda merre. Kehade liikumine allapoole (lähemale Maa keskpunktile) on liikumine energia miinimumi poole. 
• Kui me paneme kokku kuuma ja külma keha, siis ilma välismõjuta läheb soojus alati kuumemalt kehalt külmemale, mitte vastupidi. Kuum keha jahtub, liikudes energia miinimumi poole. 
• Kompassi magnetnõel võtab ruumis kindla asendi põhja-lõuna-sihis ja tuleb sellesse asendisse jälle tagasi, kui me oleme ta sealt välja viinud. Maa magnetvälja suunaline asend on magnetnõelale energia miinimumi asendiks. 
• Ained hakkavad kuumutamisel ning elektrivoolu läbiminekul helenduma, sest aatomid kiirgavad teistelt osakestelt põrgetel saadud lisaenergia valgusena välja. 
• Mingi aine põlemisel eraldub soojust. Põleva aine aatomid ühinevad hapniku aatomitega, tekib oksiid. Iga oksiidi molekuli moodustumisel vabaneb mingi kindel energia, mida nimetatakse selle molekuli seoseenergiaks. Aatomid loovutavad selle energia, liikudes summaarse energia miinimumi poole. 

Me teame hästi, et kehi ei saa paigutada teineteise sisse. Kus üks keha on juba ees, sinna me teist panna ei saa. Me saame panna ühe raamatu teise peale või kõrvale, aga mitte teise sisse. Kui pista vett sisaldavasse anumasse mingi keha, siis veetase tõuseb. Vesi ja keha ei saa üheskoos samas ruumiosas paikneda, seepärast tõrjub keha oma asukohast vee välja. Nii jääbki vette asetatud kivi anuma põhja. Veest väiksema tihedusega keha, näiteks korgi või vahtplasti tükike aga tõuseb pinnale – vesi tõrjub ta endast välja. Ka kaks veejuga ei saa teineteist segamatult läbida. Kokkupuute­kohas veejoad põrkuvad ja tõrjuvad teineteist – vesi pritsib laiali. Kõigis sellistes nähtustes avaldub seaduspärasus, mida on eesti keeles hakatud nimetama tõrjutusprintsiibiks. Makromaailmas tähendab tõrjutusprintsiip seda, et kaks ainelist objekti ei saa korraga paikneda samas ruumiosas. 

Mikromaailmas on asi veidi keerulisem, sest aatomid ning nende koostisosad käituvad makrokehadest üksjagu erinevalt. Sellegipoolest kehtib tõrjutusprintsiip ka nende kohta. Mikromaailma jaoks sõnastas tõrjutusprintsiibi 1925. aastal austria füüsik Wolfgang Pauli (1900–1958), mistõttu nimetatakse seda sageli ka Pauli printsiibiks. Oma lihtsaimal kujul väidab Pauli printsiip, et kaks samas aatomis paiknevat elektroni ei saa olla täpselt samas kvantolekus.

Kaks elektroni ei saa aatomis käituda täpselt ühtemoodi, omades täpselt ühepalju energiat. Nende seisundid peavad millegi poolest erinema. Elektroni jaoks on aatomis lõplik arv „kortereid“ ja kus üks elektron juba on, sinna teist enam panna ei saa. 

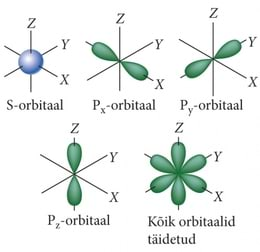
Energia miinimumi printsiip ja tõrjutusprintsiip määravad kahekesi kogu aine ehituse looduses. Võib ka öelda, et nad on kogu keemia füüsikaliseks aluseks. Keemiliste elementide perioodilisuse süsteem sisaldab kaheksat perioodi põhjusel, et aatomi välimises elektronkihis võib olla kuni kaheksa elektroni. Elektronid võivad aatomis perioodiliselt liikuda sümmeetriliselt mingi ruumisuuna suhtes. Seda liikumisviisi nimetavad keemikud p-orbitaaliks. Samas võivad elektronid täita ruumi ka ilma eelissuunata, sfäärilise kujuga „pilvena“. Seda nimetavad keemikud s-orbitaaliks. Kuna meie ruum on kolmemõõtmeline, siis on elektronidel kokku neli sellist ruumilise käitumise võimalust – kolm „teljelist“ ja üks „ilma teljeta“ variant. Elektronidel on aga lisaks veel sisemine liikumine, mida nimetatakse spinniks. Esmatähenduses võib seda kujutleda elektroni kui osakese pöörlemisena ümber oma telje. Kaks elektroni võivad täita sama ruumiosa, kui nende sisemine pöörlemine toimub samal teljel vastandlikes suundades, nii et üks elektron pöörleb päripäeva ja teine vastupäeva. Kolmandat võimalust ei ole. Seega võib samal orbitaalil viibida kuni kaks elektroni, aga kolmas tõrjutakse juba välja. Olemegi saanud kokku 4 × 2 = 8 erinevat võimalust elektroni paiknemiseks aatomi väliskihis. Kuna sisemistele elektronkihtidele vastavad elektroni energia väärtused on väiksemad, siis energia miinimumi printsiibi kohaselt täituvad kõigepealt sisemised elektronkihid. Need elektronid, millel tõrjutusprintsiip ei luba enam viibida mingis sisemises kihis, peavad paigutuma väliskihti. Just aatomite väliskihtide elektronid ehk valents­elektronid aga tekitavad keemilise sideme aatomite vahel. Sellest kõigest tuleb lähemalt juttu mikro- ja megamaailma füüsika kursuses. 

Mitteaineliste ehk väljaliste objektide puhul tõrjutusprintsiip ei kehti. Kõik katsed näitavad, et erinevad väljad võivad üksteist segamata samas paigas asuda. Välja mõju kehale ei sõltu teiste väljade olemasolust või puudumisest. Näiteks püsimagnet tõmbab raudmutrit magnetjõuga ühtemoodi nii Maa pinnal kui ka kosmoses teostatud katses. Maa pinnal alati katse tulemust mõjutav Maa gravitatsioonijõud orbitaaljaamas ei avaldu, kuna kõik kehad viibivad kaaluta olekus. Samas tõmbab Maa sedasama raudmutrit maa­pinnal teostatud katses sama gravitatsioonijõuga enda poole sõltumata sellest, kas mutrile magnetjõud mõjub või mitte. Antud näites vaatlesime kahte erineva päritoluga välja, kuid täpselt sama tulemuse saaksime ka samaliigiliste väljade koostoimel. Kaks ühesugust püsimagnetit tõmbavad neist ühesugusel kaugusel paiknevat, niidi otsas rippuvat raudmutrit ühesuuruste jõududega. Ühe magneti tõmbejõud ei sõltu teise magneti olemasolust või puudumisest. Mutrile mõjub kahe teineteisest sõltumatu tõmbejõu vektorsumma. 

Kui keha asub korraga mitme välja mõjupiirkonnas, siis väljade mõjud liituvad, sõltumata väljade arvust või nende päritolust. Iga väli mõjub kehale sõltumata teiste väljade juuresolekust mingi jõuga. Jõuvektorite liitmisel punktis 3.1.3 toodud vektoriaalse liitmise reeglite kohaselt saame leida summaarse jõu.

Väljaliste objektide puhul tõrjutusprintsiip ei kehti. Seetõttu võib ühe masti otsast vastu võtta ning edastada väga erinevate sagedusalade raadiosignaale.	Ei maksa lasta end segadusse viia – värvide liitumisel teeb kogupildi valgeks meie taju, mitte eri värvi valguslainete omavaheline vastastikmõju.

Printsiipi, mille kohaselt väljad üksteist ei sega ja nende mõjud vektoriaalselt liituvad, nimetatakse superpositsiooniprintsiibiks (ld super 'peal'; positio 'asetsemine'). Superpositsiooniprintsiibi kehtivust kinnitab näiteks tõik, et erinevalt ainelistest veejugadest saavad kaks valguskiirt kui väljalist objekti teineteisest segamatult läbi minna. Seda on suhteliselt lihtne katses kontrollida. Kui üks valguskiir kohtub teisega, siis võime näha, et kummagi poolt tekitatud valguslaik selle tagajärjel ei muutu. Mitte mingit vastastikust tõrjumist ei esine. 

Kõik me oleme äikese ajal tähele pannud, et müristamist kuuleme tavaliselt mitmeid sekundeid hiljem, kui näeme välgusähvatust. Põhjust teame samuti – pikselöögi tagajärjel tekkinud heli kohalejõudmine võtab aega. Heli levimiskiirus õhus on ligikaudu 1/3 kilomeetrit sekundis ning seda teades on lihtne äikesepilve kaugust määrata. Loeme sekundeid välgusähvatuse ja kõuekärgatuse vahel ning iga kolm järgnevat loendatud sekundit tähendavad lisakaugust üks kilomeeter.

Niiviisi arutledes eeldame, et valguse levimine aega ei võta. Kuidas aga tegelikult on? Kas valgus jõuab tõesti igale poole silmapilkselt, kas valguse kiirus on lõpmatult suur? Looduse uurimise algusaegadel just niimoodi arvatigi. Toonased vaatlusoskused muudeks järeldusteks võimalust ei andnud. Vana-Kreeka mõttetark Aristoteles oli veendunud, et valgus jõuab kaugetelt tähtedelt meieni silmapilkselt. Alles sajandeid hiljem hakkas lõpmatu kiiruse võimalikkuses kahtlema Galileo Galilei. Itaalia teadlane pani kirja isegi plaani, kuidas valguse kiirust eksperimentaalselt määrata võiks. 

Selle kohaselt peaksid kaks laternatega varustatud meest seisma täielikus pimeduses mingil kaugusel teineteisest ning esialgu oma laternat naabri eest millegagi varjama, näiteks kübaraga. Esimese mehe kõrval seisab kellaga varustatud abiline, kes käivitab oma kella, kui esimene mees eemaldab oma lambilt katte. Kui teine mees näeb esimese katsetaja lambi valgust, siis eemaldab ta katte ka oma lambilt. Kui aega mõõtev abiline näeb teise katsetaja lambi valgust, siis ta fikseerib kella näidu. Lampidega meeste kahekordse vahemaa ja kulunud aja suhe ongi valguse kiirus. Kahjuks polnud tollal veel piisavalt täpseid kelli ning plaan jäi esialgu vaid plaaniks. Tänapäevase tarkusega võiksime öelda, et sellisel viisil saab mõõta vaid teise katsetaja reaktsiooniaega. Kuigi valguse kiirus jäi mõõtmata, uskus Galilei selle lõplikusse. 

Juba põhikooli valgusõpetuses saime teada, et valguse kiiruse lõpliku väärtuse arvutas esimesena oma vaatlustulemuste põhjal välja Taani astronoom Olaf (Ole) Rømer [röömer] (1644–1710). Ta jälgis planeet Jupiteri kaaslasi ning pani tähele, et nende tiirlemisega seonduvad nähtused ei toimunud alati täpselt nendel hetkedel, mil arvutuste järgi pidanuks. Eriti suur oli erinevus pooleaastase vahega sooritatud vaatluste korral. Rømer taipas, et poole aastaga oli Maa Jupiterist ligi 300 miljonit kilomeetrit kaugemale liikunud. Vaadeldav nähtus hilines, kuna valgusel kulus vaatlejani jõudmiseks nüüd rohkem aega. 1675. aastal sai Rømer nende vaatluste alusel valguse kiiruse väärtuseks 220 000 km/s. Olgu veel ka rõhutatud, et Rømer teostas mitte eksperimenti, vaid sihipärast vaatlust, aga ta sai siiski teha arvuliselt väljendatava järelduse. 

Füüsika arenedes on valguse kiiruse mõõtmise täpsus järjest kasvanud. Tänapäevaks on selle väärtus teada juba sedavõrd täpselt, et pikkusühik 1 meeter on defineeritud valguse levimise kaudu. Valguse kiirust tähistatakse valemites tähega c (kr celeritas 'kiirus') ja selle väärtus on tänapäeval teada üheksa kümnendkoha täpsusega:
c = 299 792 458 m/s = 299,792458 Mm/s ≈ 300 Mm/s = 3 ^. 10⁸ m/s.

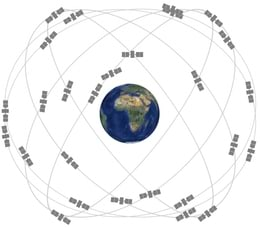
1877. aastal sooritasid Ameerika füüsikud Albert Michelson ja Edward Morley keerulise eksperimendi, mille üheks eesmärgiks oli näidata, et Maa liikumine mõjutab valguse vaatlemise tulemusi. Michelson ja Morley oletasid, et kui Maa tiirleb suure kiirusega (30 km/s) ümber Päikese, siis peaksid täpsed katseriistad suutma eristada olukordi, mil Maal asuv vaatleja liigub valguslainega samas sihis või sellega risti. Samas sihis liikumisel peaks katse tulemus viitama valguse ja Maa kiiruste omavahelisele liitmisele või lahutamisele, sarnaselt maanteel liikuvate autode omavahelise kiiruse leidmisega. Michelson ja Morley ei suutnud aga avastada mitte mingeid jälgi valguse ja Maa kiiruste liitumisest. Nende katse negatiivne tulemus oli senise füüsikaga suures vastuolus. Newtoni mehaanika aluseks on teadmine, et kiirusi saab alati ülalkirjeldatud viisil liita või lahutada. Michelson ja Morley näitasid aga, et valguse kiiruse katseline väärtus ei sõltu valgusallika ega vaatleja liikumisest. Valguse kiirus on kõigi vaatlejate jaoks ühesugune. Tegemist on füüsika üldprintsiibiga, mida nimetatakse absoluutkiiruse printsiibiks. 

Makromaailma kirjeldavat füüsikat, mille aluseks on Newtoni sõnastatud mehaanika seadused (ptk 3.5. eespool), nimetatakse klassikaliseks füüsikaks (ld classicus 'kõrgeimate hulka kuuluv'). Klassikalises füüsikas on liikumine suhteline ja mingi objekti kiirus on erinevate vaatlejate jaoks erinev. Samas aja kulgemine, kaugused ja kehade mõõtmed ning mass on kõikide vaatlejate jaoks ühesugused ega sõltu liikumisest. Aeg, ruum ja mass on klassikalises füüsikas absoluutsed. Aeg on nagu kõigi vaatlejate jaoks ühesugune rong, mille vaguniteks on päevad ja mis ühtemoodi (igavalt?) möödub kõigist vaatlejatest. See vagun, mis parajasti möödub, on tänane päev või olevik, „äsja möödunud vagun“ on eilne päev või minevik, „järgmine vagun“ või homne päev aga tulevik. Me teame, et rong on olemas ja liigub sõltumatult sellest, kas keegi seda raudtee kõrvalt parajasti vaatleb või mitte. Selle põhjal tekib pettekujutlus, et ka aeg on olemas vaatlejatest sõltumatult. 

Samalaadne lugu on ruumiga. Klassikaline kujutlus käsitleb ruumi kui mingit kinga­karpi, mis on olemas ka kingade puudumisel. Eesti keel soodustab kujutlusi ruumist kui kingakarbist ja füüsikalistest kehadest kui kingadest selles karbis. Kui näiteks inglise keeles tähistab ruumi mingis hoones sõna room ning maailmaruumi (füüsikalist ruumi) sõna space, siis eesti keeles on mõlema kohta kasutusel üks ja seesama sõna ruum. Me tajume klassiruumi kui karpi. Tajume kui midagi, millel on servad kui koordinaatteljed ja nurgad kui telgede lõikepunktid. See asjaolu sisendab meisse jõuliselt analoogilisi kujutlusi füüsikalise ruumi kohta. 

Absoluutkiiruse printsiip aga väidab, et valguse kui väljalise objekti jaoks pole liikumine suhteline, vaid vastupidi – absoluutne. Suhtelisteks osutuvad hoopis pikkus, aeg ja mass. Aega kui lõputut ja kõigile ühesugust rongi pole olemas. Samuti pole olemas ruumi kui kõigile võimalikele kingadele ühesugust kingakarpi. Aeg ja ruum on vaid vaatleja kujutlused. Iga vaatleja tekitab need omaenda aistingute põhjal ja kannab neid endaga kaasas. Kui kaks vaatlejat saavad erinevaid aistinguid, siis nende vaatlejate kujutlused ajast ja ruumist peavadki olema erinevad. Ruum on olemas vaid sedavõrd, kui temas on kehi. Aeg on olemas vaid sedavõrd, kui temas toimuvad sündmused. 

Inimkond on universumi protsesse ning ulatust arvestades pea tühine nähtus. Siiski usume, et meie avastatud füüsikaseadused kehtivad kogu universumis, selle algusest veel ebaselge tulevikuni välja. Ent avastada on veel palju. Maailm meie ümber on täis maagilisi asju, mis kannatlikult ootavad meie mõistuse teravamaks muutumist.