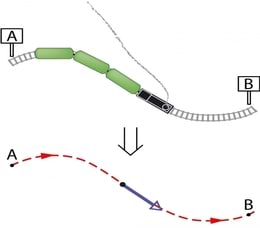
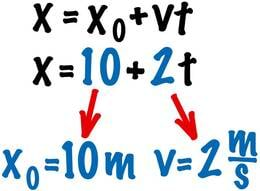Moodsates lõbustusparkides võib leiduda küll palju põnevat, kuid see kõik kahvatub jalgrattatrikkide kõrval, mida sooritati tsirkustes aastatel 1900–1912. Üks kõigi aegade hulljulgemaid rattatrikke sooritati ilmselt Barnumi ja Bailey tsirkuses Madison Square Gardenis 1905. aastal. Etteaste alguses seisis Ugo Ancillotti oma jalgrattaga ühe ja tema vend Ferdinand teise, vastas asuva kaldtee tipus. Märguande peale alustasid vennad laskumist. Kui Ugo jõudis oma kaldtee järsult ülespoole painutatud osale, visati ta sealt 14 meetri kaugusele järgmisele kaldteele, mis lõppes jällegi kõverdatud osaga. Sealt sooritas Ugo teise, 9 meetri pikkuse õhulennu. Samal ajal kihutas Ferdinand läbi oma kaldtee nõgusa alaosa, sooritas pea alaspidi õhulennu ja maandus teisele painutatud kaldteele. Triki muutis eriti närvekõditavaks asjaolu, et tagurpidi pööratud Ferdinand lendas kõigest meetri või paari kauguselt oma esimest õhulendu sooritava Ugo alt läbi.

Kes meist poleks näinud taevas sõudvaid pilvi, lillelt lillele lendlevat liblikat, mööda teed kihutavat autot, paberile tähti kirjutavat pliiatsiotsa... Kõigi nimetatud kehade ühine tunnus on see, et need liiguvad. Kui eemal lööb välku, jõuab valgussähvatus meieni pea kohe ning mürin veidi hiljem. Meie soontes voolab veri ja sarnane on elektrivool, mis kujutab endast elektronide suunatud liikumist juhtmes. Meie sees liiguvad aatomid ja aatomite sees liiguvad elektronid. Liikumine on kõikjal. Liikumine on looduse kõige üldisem nähtus.

Füüsika uurib loodust ja sealhulgas ka liikumist. Füüsika see haru, mis uurib liikumist ja selle muutumise põhjusi, kannab nime mehaanika. Mehaanika tekkis antiikajal, mil hakati rasket käsitsitööd kergemaks muutvaid masinaid ehitama. Et masinaid täiustada, tuli lähemalt tundma õppida eelkõige neid nähtusi, mis masinates aset leidsid. Tuli uurida liikumist ning liikumist mõjutavaid tegureid. Sõna „mehaanika“ ongi tulnud kreeka keelest (kr μηχανικη 'masinatesse puutuv').

Tänapäeval ei piirdu mehaanika ainult masinate ehitamisega, vaid uurib liikumist üldisemalt. Vist igaüks meist on planeerinud mõnda retke ja arvutanud, millal kuhugi pärale jõuab. Sarnane, kuid märgatavalt keerulisem ülesanne on välja arvutada, kuhu jõuab planeetide mõju all olev kosmoseaparaat paari aasta pärast. See ongi mehaanika põhiülesanne – leida keha asukoht mis tahes ajahetkel.

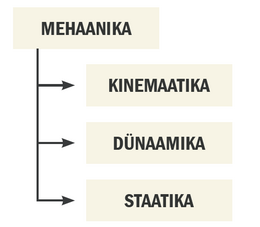
Mehaanika saab jaotada kolmeks haruks:

Kinemaatika (kr κινημα 'liigutus, liikumine') uurib ja kirjeldab kehade liikumist ruumis. Seejuures pole oluline, mis on liikumise põhjuseks. Näiteks saab kinemaatikaseaduste abil arvutada, kui kõrgele lendab otse üles visatud kivi.

Dünaamika (kr δυναμη 'jõud, vägi') uurib, kuidas liikumine tekib ning erinevate mõjude tagajärjel muutub. Näiteks saab arvutada, millise kiiruse saavutab vihmapiisk, mida kiirendab Maa külgetõmme ja pidurdab õhutakistus.

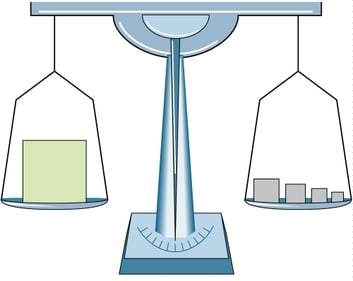
Staatika (kr στατικη 'püsiv, muutumatu') uurib, mis tingimustel liikumine ei muutu, st keha on tasakaalus. Staatika võimaldab näiteks välja arvutada, mitu inimest võib vaatetorni ronida, ilma et see ümber kukuks.

Staatika on teadus tasakaalust. Kui järele mõelda, siis on meie ümber väga palju esemeid, millest me eeldame, et nad ei kuku ümber, alustades näiteks hommikukohvi tassist ja lõpetades majadega. Staatika oskab tasakaalulist maailma kirjeldada ja ennustada, millal tasakaal kaob.	Staatika uurib tasakaalu.

Mille järgi tunneme ära, et keha liigub? Algul käes olnud vaas asub pärast mahapillamist põrandal. Sadamast väljunud laev on tunni aja pärast mitu miili eemal. Kui kellaosuti on number kahe kohal, siis mõni aeg hiljem on see juba viie peal. Vaas, laev ja osuti on liikunud – nad on oma asukohta muutnud.

Kõikide liikumiste ühine tunnus on see, et keha asukoht muutub. Seejuures on vaja liikumise kindlakstegemiseks ja uurimiseks mõnda teist keha, mille suhtes me asukohta määrame. Liikumine toimub alati millegi suhtes, st liikumine on suhteline. Asukoha muutumine võtab aega. Pole võimalik, et puult kukkuv õun on mingil hetkel oksa küljes ja siis kohe juba mujal. Sel juhul oleks õun ju mitmes kohas korraga! Liikumine on alati seotud ajaga. Seega võime öelda, et liikumine on keha asukoha muutumine teiste kehade suhtes mingi aja jooksul.

Liikumise suhtelisus tähendab seda, et erinevate kehade suhtes võib liikumine olla väga erinev. Näiteks meile tundub, nagu Maa oleks paigal ja Päike tiirleks ümber meie. Samas teame, et Maa tegelikult pöörleb ümber oma telje ja tiirleb samas suure kiirusega (30 km/s) ümber Päikese.

Kuna liikumine on asukoha muutumine, siis tuleb liikumise kirjeldamist alustada keha asukoha määramisest. Mida aga lugeda näiteks 20 meetri pikkuse veoauto asukohaks? Kas eesmise numbrimärgi, juhi ninaotsa, koorma keskpunkti või hoopis haagisekonksu asukohta? Tegelikult polegi ühest linnast teise liikumise kirjeldamisel auto mõõtmed ja kuju olulised. Suurt veokit võime kahe linna vahemaaga võrreldes ette kujutada lihtsalt ühe punktina. Seda punkti nimetatakse punktmassiks.

Kui me edaspidi räägime keha liikumisest, siis mõtleme selle all enamasti punktmassi liikumist. Sellist keha, mille mõõtmed võib antud liikumistingimustes arvestamata jätta, nimetatakse punktmassiks. Kehaks võetakse punkt, mille mass on sama suur kui keha mass. Kuju ja mõõtmed jäetakse lihtsuse mõttes arvestamata. Tegemist on reaalse keha lihtsustuse ehk füüsikalise mudeliga.

Keha ei või siiski igas olukorras punktmassiks lugeda. Näiteks praamile sõitmisel on auto mõõtmed vägagi olulised.

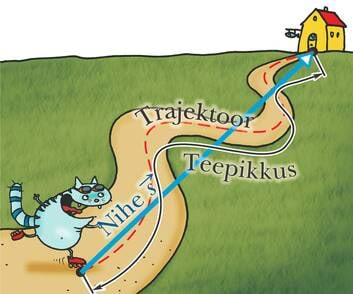
Need punktid, mida liikuv keha (punktmass) läbib, moodustavad alati mingi pideva joone. Kujutletavat kontuuri, mida mööda keha liigub, nimetatakse trajektooriks. Liikumistrajektoori ei tohi samastada teega! Auto trajektoor on kujuteldav joon, maantee aga teetammist ja teekattest koosnev keha.

Liikumisi saab liigitada trajektoori kuju järgi. Sirge trajektoori korral on liikumine sirgjooneline. Kui trajektoor pole sirge, siis on liikumine kõverjooneline.

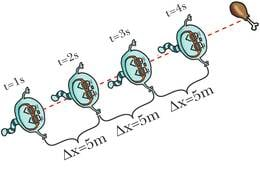
Teiseks saab eristada ühtlast ja mitteühtlast liikumist. Ühtlane on selline liikumine, mille korral mistahes võrdsetes ajavahemikes muutub keha asukoht sama palju. Muul juhul on liikumine mitteühtlane. Näiteks laskub avatud langevarjuga parašütist enne maandumist ühtlaselt ja maapinnale jõudmisel pidurdudes mitteühtlaselt.

Sirgjooneline ja kõverjooneline liikumine.	Kulgev ja pöörlev liikumine.

Veel eristatakse kulgevat ja pöörlevat liikumist. Kulgev on näiteks õmblusmasina nõela üles-alla liikumine. Kogu liikumise kestel jääb nõel oma esialgsete asenditega paralleelseks. Kulgevalt liikuva keha kõikide punktide trajektoorid on sama kujuga. Kulgeva liikumise korral võib kehasid käsitleda punktmassidena. Pöörleva liikumise korral liiguvad keha erinevad punktid mööda erineva raadiusega ringjooni. Näiteks kellaosuti üks ots liigub mööda suurt ringjoont ja teine ots on hoopis paigal. Pöörlemise korral ei tohi keha punktmassiks lugeda, sest siin on kuju ja mõõtmed olulised.

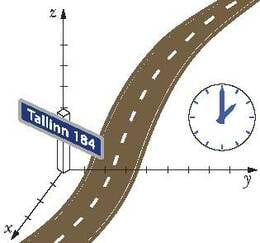
Kuna liikumine on suhteline, tuleb välja valida mingi keha, mille suhtes me liikumist jälgime. Keha, mille suhtes liikumist vaadeldakse, nimetatakse taustkehaks. Taustkehaks võib valida mistahes sobiva objekti: kilomeetriposti, mäetipu, raudteevaguni, Päikese jne. Tingimuseks on see, et liikumine taustkeha suhtes ikka toimuks ja poleks samas liiga keeruline.

Füüsika on täppisteadus, mis kirjeldab objekte ja nähtusi arvude abil. Arvude abil saab kirjeldada ka liikuva keha asukohta. Keha asukoha kirjeldamiseks kasutatavaid arve nimetatakse koordinaatideks. Koordinaatide määramiseks valitakse mingid kindlad suunad, milles asukohta taustkeha suhtes mõõdetakse. Samuti lepitakse kokku mõõtühikud. Kokkulepitud mõõtmissuunad, mõõtühikud ja asukoha mõõtmise eeskirjad moodustavad koordinaadistiku ehk koordinaatsüsteemi.

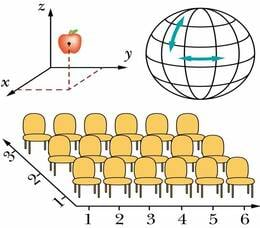
Matemaatikas ja füüsikas kasutatakse enamasti ristkoordinaadistikku. Samuti on kõigile tuttav maakaartidel kasutatav geograafiline koordinaadistik. Teatrisaalis istekoha leidmiseks loodud istmeridade ja kohanumbrite süsteem on samuti koordinaatsüsteem.

Peale asukoha määramise tuleb liikumise kirjeldamisel arvestada ka aega. Selleks tuleb kokku leppida aja mõõtmise alghetk ja mõõtühik. Taustkeha, sellega seotud koordinaadistik ja ajamõõtmise süsteem moodustavad taustsüsteemi.

Kui tahame liikumist kirjeldada, on vaja mõõta keha asukoha muutu. Selleks on erinevaid võimalusi.

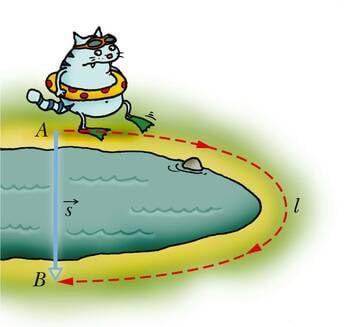
Kui mõõdame alg- ja lõppasukoha vahekauguse täpselt piki trajektoori, saame teepikkuse. Teepikkust tähistatakse valemites tähega $l$ (ld longitudo 'pikkus').

Mõõtes kaugust aga mööda sirgjoont ehk linnulennul, saadakse nihe. Nihkeks nimetatakse keha algasukohast lõppasukohta suunatud sirglõiku.

Teepikkust mõõdetakse piki trajektoori.	Teepikkus ja nihkepikkus pole tavaliselt võrdsed.

Erinevalt teepikkusest, mida iseloomustab vaid arv, on nihkel peale pikkuse ka suund. Seega on nihe vektoriaalne suurus. Nihkevektori tähiseks valemites ja joonistel on $\overrightarrow{s}$  (ingl shift 'nihe'). Nihkevektor on suunatud algasukohast lõppasukohta.

Teepikkus $l$ ja nihke pikkus $s$ pole tavaliselt võrdsed. Näiteks kui õpilane jõuab pärast kooli koju, on vaatamata päeva kestel läbitud suurele teepikkusele tema nihe null. Teepikkus ja nihe on võrdsed vaid sirgoonelisel muutumatu suunaga liikumisel.

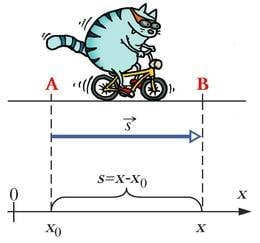
Nihet saab avaldada keha alg- ja lõppasukoha koordinaatide kaudu. Kui liikumine toimub piki x-telge ning keha alg- ja lõppasukoha koordinaatide tähisteks on vastavalt $x_0$ ja $x$, saame nihke pikkuseks

Sümboliga $\Delta$ (loe: delta) tähistatakse suuruse lõpp- ja algväärtuse vahet ehk muutu.

Teepikkuse ja nihke mõõtühikuks on rahvusvahelises mõõtühikute süsteemis 1 meeter. Pikkade või lühikeste teepikkuste ja nihete korral kasutatakse kümnendeesliideseid. Näiteks 1000 m = 1 km, 1/100 m = 1 cm.

Mehaanika põhiülesanne on keha asukoha määramine mis tahes ajahetkel.

Kõige lihtsam on asukohta arvutada lihtsaima liikumise korral, milleks on ühtlane sirgjooneline liikumine.

Ühtlaseks sirgjooneliseks liikumiseks nimetatakse sirgjoonelist liikumist, mille korral mis tahes võrdsetes ajavahemikes läbitakse võrdsed teepikkused.

Niisuguse liikumise suund ei muutu ja võrdsete teepikkuste läbimisel sooritatud nihked on võrdsed. Nihke kaudu defineerimisel nimetatakse ühtlaseks sirgjooneliseks liikumiseks sellist liikumist, mille korral mis tahes võrdsetes ajavahemikes sooritatakse võrdsed nihked. Trajektoori kuju pole sel juhul vaja eraldi mainida.

Millised on sellise liikumise näited? Ideaalselt ühtlast sirgjoonelist liikumist me looduses tegelikult ei leiagi. Enam-vähem saame selliseks lugeda näiteks rongisõidu sirgel teel, kuigi raudtee pole Maa kumeruse tõttu päris sirge ja ükski rong ei saa sõita igavesti peatumata.

Sellegipoolest võib paljudel juhtudel väikesed kõrvalekalded ideaalist arvestamata jätta ning liikumist siiski ühtlaseks sirgjooneliseks pidada. Lihtsustuste tegemine tähendab füüsikas mudeli kasutamist. Ühtlane sirgjooneline liikumine on lihtsaima liikumise mudel.

Nii võib sirgjoonelise liikumise mudeli abil kirjeldada sirgel maanteel kihutava auto, ujuva sportlase ja laskuva langevarjuri liikumist.

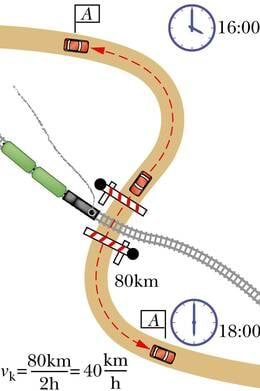
Liikumine on keha asukoha muutumine mingi aja jooksul. Muutumise aeg võib seejuures olla erinev. Näiteks jõuab jalgrattur ühest asulast teise varem kui samal ajal liikumist alustanud jalakäija. Sel puhul öeldakse, et jalgratturi kiirus on jalakäija omast suurem.

Kiirus näitab, kui suure teepikkuse läbib keha ajaühiku jooksul. Valemites tähistatakse kiiruse arvväärtust tähega $v$ (ld velocitas 'kiirus'). Ühtlasel sirgjoonelisel liikumisel on teepikkus võrdne nihke pikkusega ning sel juhul võime öelda, et kiirus on võrdne ajaühikus sooritatud nihkega. Kiiruse leidmiseks tuleb sooritatud nihe jagada liikumisajaga $t$:

Tähis $\overrightarrow{v}$ viitab sellele, et kiirus on suunaga ehk vektoriaalne suurus.

Kui suund pole liikumise kirjeldamisel oluline, võime sama valemit kasutada skalaarkujul:

Kiiruse mõõtühik SI-s on 1 m/s ehk 1 meeter sekundis.

Tuleb tähele panna, et valemites 4.2 ja 4.3 ei tähista $t$ mitte ühte ajahetke, vaid liikumise kestust. Tegemist on lõpp- ja algpunktis paiknemise hetkede vahega, mida väljendatakse kreeka tähe delta ($\Delta$) abil:

Siin tähistab $t_0$ alghetke ja $t$ lõpphetke. Enamasti võetakse alghetk nulliks ja siis on liikumisaeg $\Delta t=t$. Seda aega $t$ ongi kiiruse valemites 4.2 ja 4.3 silmas peetud.

Võttes nüüd ajavahemiku tähiseks $\Delta t$ ja vastavalt valemile 4.1 nihke tähiseks $\Delta x$, saame kiiruse valemile veel ühe kuju:

Valguse kiiruse väärtus õnnestus esmakordselt välja arvutada taevakehade vaatlusandmete järgi kuulsas Michelson-Morley katses, mille järeldusena avastati absoluutkiiruse printsiip. Nendele ja mitmetele teistele megamaailma uurimise tulemustele tuginedes õnnestus Albert Einsteinil 1905. aastaks välja töötada aega ja ruumi uut moodi käsitlev relatiivsusteooria. Relatiivsusteooria aluseks on absoluutkiiruse printsiip, mis väidab, et

1. kõik vaatlusandmed on suhtelised (relatiivsusprintsiip). Füüsikaliste suuruste väärtused on üksteise suhtes liikuvate vaatlejate jaoks erinevad ning ükski vaatleja pole eelistatud. Igal vaatlejal on oma tõde;
2. on olemas suurim võimalik kiirus – kiirus ehk absoluutkiirus, millega alati levib väli ainelise objekti suhtes (valguse kiirus vaakumis c = 299 792 458 m/s). See kiirus on kõigi vaatlejate jaoks üks ja sama (absoluutkiiruse konstantsuse  printsiip). Aine ei saa liikuda sama kiiresti kui väli.

Relatiivsusteooria leiab tänapäeval rakendust mitte ainult megamaailmas, vaid see kehtib ka mikromaailma nähtuste puhul.

Tutvume mõne efektiga, mis järelduvad relativistliku füüsika aluseks olevast relatiivsusteooriast.

Relatiivsusprintsiibi järeldustest aimu saamiseks jälgime üht mõttekäiku Peter Marchi raamatust "Füüsika võlu".

Relatiivsusprintsiip nõuab, et valguse kiiruse mõõtmine peab alati andma sama tulemuse, vaatamata sellele, millises taustsüsteemis ta on sooritatud või mis suunas valgus levib. Et mõista, mis sellest postulaadist järeldub aja mõõtmise kohta, vaatame aja mõõtmist liikuvas rongis.

Tulemus peab näitama, et valgus liigub ettearvatud kiirusel rongi suhtes. Ühtaegu peab rongi kõrval seisev vaatleja saama kasutada sedasama mõõtmistulemust näitamaks, et valgus levib täpselt samal kiirusel ka Maa suhtes.

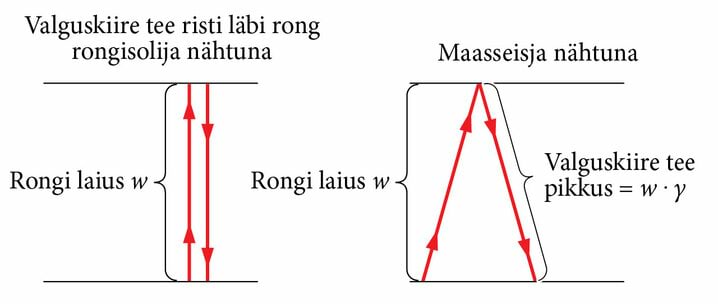
Teeme mõõtmise ainsa kellaga, mis asub rongis, võttes rongi sõidusuunaga risti leviva valguse edasi-tagasi teekonna aega. Ühe kella kasutamine kõrvaldab eri kohas olevate kellade sünkroniseerimise raskuse. Edasi, ristsuunas leviva valguse puhul pole muret rongi laiusega, sest selles suunas puudub liikumiskomponent Maa suhtes.

Maas seisev vaatleja peab nõustuma kõigi rongis tehtud mõõtmiste õigsusega, kuid ta võib neid tõlgendada mistahes viisil, näitamaks, et valgus levib nii rongi kui ka Maa suhtes ühesuguse kiirusega.

Jooniselt on näha, et kummagi vaatleja arvamused lähevad lahku valguse poolt läbitud teepikkuse suhtes. Kui sõitjale tundub, et kiir jõuab lähtepunkti tagasi, siis kõrvalseisja meelest jõuab ta hoopis edasi nihkunud punkti. Seepärast ei tehtudki mõõtmist Maa taustsüsteemis: siis oleks läinud vaja kahte kella. Geomeetriliselt on olukord täpipealt sama kui ujujaga (ptk 8). Kui rongi laius on $w$, siis kaasasõitva vaatleja meelest läbib kiir vahemiku $2w$, maas seisva vaataja arvates aga vahemiku $2\gamma w$, kus

Laseme nüüd kummalgi vaatlejal arvutada valguse kiiruse. Vastavalt relatiivsuspostulaadile peavad mõlemad saama vastuseks $c$, mis on 300000 km/s. Sõitja jagab läbitud vahemikuajaga $t$, mida tema stopper-kell näitab:

Seisja rehkenduses peab lugejas olema $2\gamma w$. Kuidas siis saada vastuseks seesama $c$? Kuna vaatlejatel pole lahkarvamusi rongi laiuse $w$ suhtes, siis katsumegi sellest lähtuda. Õige vastuse saamiseks on vaid üks tee: korrutame ka lugejat $\gamma$-ga. Siis gammad taanduvad ja vastus tulebki sama,

Mis on $\gamma t$ tähendus nimetajas? Kuna lugejas on valguse teepikkus Maa taustsüsteemis, siis peab nimetajas seisma aeg, mis möödus sama taustsüsteemi kella järgi. Ainult siis annab jagatis valguse kiiruse Maa süsteemis. Kuna $\gamma$-ga korrutamine suurendab $t$-d, on seisvas taustsüsteemis kulunud rohkem aega, kui liikuv kell näitab. Seda tähendabki väide, et liikuv kell käib aeglasemalt, s.o jääb maha.

Kuid sõitja suhtes liiguvad kõik maas olevad kellad, siis peavad just need maha jääma. Kummagi vaatleja meelest kasutab teine mahajäävat kella.

Kui te tõrgute omaks võtmast väidet, et kaks vaatlejat üheaegselt peavad teise kella mahajäävaks, siis pidage silmas seda olulist tõika, et üksteise suhtes liikuvail vaatlejail on ainult üks võimalus oma kelli vastakuti võrrelda, nimelt möödumishetkel. Seejärel kaugenevad nad kiiresti teineteisest. Siis võivad nad teateid vahetada üksnes valguse või raadiosignaalide kaudu. Nende levik aga võtab aega, seda enam, mida kaugemale nad üksteisest jõuavad. Kumbki arvutab teise kella lugemi, tehes paranduse sellele viivisele, eeldades, et nimelt teine liigub. Nende paranduste vahe aiva kasvab. Edaspidi toome selle kohta ka arvulise näite.

Tulles tagasi eelmise peatüki ronginäite juurde, laseme sõitjail kohtuda keset rongi ja seada seal oma kellad ühte. Seisev raudteevaht väidaks, et rongis vastassuunas liikudes muudavad sõitjad oma kiirust Maa suhtes. Rongi peasse suunduja liigub kiiremini, seepärast peab tema kella käik olema aeglasem kui rongis paigal oleval kellal. Rongi sappa mineja kellal aga peab olema kiirem käik, sest tema liigub aeglasemalt. Jõudes rongi otstesse, pole nende kellad enam sünkroonis. Jällegi tuleb välja, et rongi sabaga rinnastuvat posti täheldatakse varem kui rongi peaga kohakuti jõudvat.

Relatiivsusteooria ütleb, et suurel kiirusel lühenevad paigalseisja jaoks kiiresti liikuva keha pikkused sama palju kui aeg aeglustub. On ka teada, et liikuva keha mass sõltub liikumiskiirusest.

Jätame need teemad siin pikemalt lahti rääkimata. Huviline võib kätte võtta näiteks juba viidatud Robert Marchi raamatus.

Kinnitame ka, et relatiivsusteooriat ei ole lihtne mõista, samas on seda on lihtne vääriti mõista. Hea meeles pidada!

Kursuse alguses saime teada, et objektide mõõtmete järgi jaotatakse füüsika uuritav maailm mikro-, makro- ja megamaailmaks. Makromaailma, mis koosneb inimesega samas suurusjärgus mõõtmetega objektidest, tajub vaatleja ilma eriliste abivahenditeta.

Makromaailm on see, mida me ümberringi näeme ning milles toimuvaid nähtusi tähele paneme. Selle  maailma kirjeldamisest saigi alguse kogu loodusteadus, sealhulgas ka füüsika. Päris süsteemseks teaduseks muutus füüsika seoses Galilei ja Newtoni silmapaistva uurimistööga 17. sajandil. Seda makromaailma kirjeldavat füüsikat, mille aluseks said Newtoni sõnastatud mehaanikaseadused, nimetatakse klassikaliseks füüsikaks (ld classicus 'kõrgeimate hulka kuuluv').

19. sajandi lõpus hakkas teadlastele tunduma, et kõik on selgeks saanud ja midagi uut enam välja uurida pole. Füüsika arenes järjest kiirenevas tempos, kuni 20. sajandi alguses võimaldasid uued vaatlusmeetodid avastada objekte ja nähtusi, mida klassikaline füüsika enam seletada ei suutnud. Näiteks ei osatud põhjendada hõõguvate kehade poolt kiiratava valguse värvust, elektronide käitumist aatomites, valguse mõju laetud osakestele, vastavastatud valguse kiiruse absoluutsust ning mitmeid muid vaatlustulemusi. Just siis, kui tekkis arvamus, et füüsika on valmis saanud, tehti ridamisi uusi avastusi, mis senise füüsika raamidesse ei mahtunud. Alguse sai nn füüsika kriis, mis leidis lahenduse 20. sajandi esimesel veerandil uute füüsikateooriate väljatöötamisega.

Valdkonnad, mida klassikaline füüsika seletada ei suutnud kuulusid mikro- ja megamaailma. Uus, kaasaegne füüsika, asus uurima aatomeid (mikromaailm) ning mõõtmatut ruumi (megamaailm). Kaasaegne füüsika koosnebki kahest suurest teooriast – mikromaailma kirjeldavast kvantmehaanikast ning aega ja ruumi käsitlevast relatiivsusteooriast (ld relātīvus 'suhteline').

Klassikaline füüsika kirjeldab makromaailma sellisena nagu me seda tavaelus tajume. Liikumine on suhteline, sest on erinevate vaatlejate suhtes erinev. Samas aja kulgemine, kaugused ja kehade mõõtmed ning mass on kõikide vaatlejate jaoks ühesugused ega sõltu liikumisest. Aeg, ruum ja mass on klassikalises füüsikas absoluutsed.

19. sajandi lõpus avastatud absoluutkiiruse printsiip väitis aga midagi hoopis teistsugust – laineliste objektide jaoks pole liikumine suhteline, vaid vastupidi, absoluutne! Albert Einsteini 1905. aastal avaldatud relatiivsusteooria näitas veel teisigi erinevusi kaasaegse ja klassikalise füüsika vahel. Relativistliku füüsika järgi pole megamaailmas suurte kauguste ja ülisuurte (valguse kiirusele lähedaste) kiiruste korral aeg, ruum ja mass enam absoluutsed!

Klassikalise ja kaasaegse füüsika erinevuse saame kokku võtta sellise tabelina:

Füüsika uurib ainelisi ja väljalisi objekte ning nende osalusel toimuvaid protsesse ehk nähtusi. Aineliste ja väljaliste objektide kõige üldisem ühine omadus on nende olemasolu. Tutvumisel aine ja välja üldiste omadustega saime ka juba teada, et ainet ja välja võib vastastikku teineteiseks muundada. See viib meid mõttele, et aine ja välja olemasolu kirjeldavad või siis kummagi konkreetset kogust määravad füüsikalised suurused peaksid olema omavahel seotud. „Kui ühte valuutat on võimalik teise vastu vahetada, siis peab ju eksisteerima vahetuskurss,“ ütleks rahandusspetsialist. Millise suuruse ühikutes toimub aga arveldamine aine ja välja vastastikustel muundumistel?

Aine tunnuseks on see, ainelistel kehadel on kindlad mõõtmed ja nad koosnevad osakestest. Ainelisi kehi iseloomustavateks suurusteks on näiteks mass ja ruumala. Mida suurem on keha, seda rohkem on temas kindla massiga aineosakesi ning seda suurem on keha kui terviku mass. Mass on aineliste objektide üldkoguse loomulikuks mõõduks, kõige üldisemaks olemasolu väljendavaks suuruseks. Rangelt peaksime siiski ütlema, et aineliste objektide olemasolu, aine mingi kindel kogus avaldub vaatleja aistingutes kõigepealt läbi massiks nimetatava füüsikalise suuruse. 

Väljaliste objektide olemasolu ning mingi kindel kogus välja avaldub vaatleja aistingutes aga kõigepealt läbi energiaks nimetatava füüsikalise suuruse. Me teame, et valgus kui kõige tuntum väljaline objekt kannab endas energiat. Valgus neeldub kehades, mis selle tagajärjel soojenevad. Me ütleme selle kohta, et valguse energia muutus soojuseks. Valguse energiat saab aga päikesepatareide abil muuta ka elektrienergiaks. Kuna nii aineliste kui ka väljaliste objektide kohta kehtib atomistlik printsiip, siis võib neelduva valguse kogust mõõta valguse osakeste ehk footonite arvuga. Igal footonil on aga kindel energia, mis on määratud vastavat liiki valguse võnkesagedusega. Mida rohkem on footoneid, seda rohkem on ka valguse energiat. 

Meenutame eelmises punktis arendatud mõttekäiku, mis selgitas keha kiirendamisega kaasnevat massi kasvamist. Kuna keha kiirendamisel mõjub jõud ja toimub liikumine, siis tehakse tööd. Keha kiirendamisel tehtav töö suurendab keha energiat. Liikuva keha energia on kineetiline ja selle hulk on määratud keha massi ja kiirusega. Mida suuremaks saab keha kiirus, seda suurem on ka keha kineetiline energia. Kui aga keha kiirus hakkab lähenema absoluutkiirusele, siis kasvab kiirus vaatamata pidevalt lisatavale energiale järjest vähem. Lõpuks jõuame olukorrani, kus vaatamata energia juurdeandmisele jääb kiirus praktiliselt muutumatuks. Kuhu see energia siis koguneb, kui kiirus enam kasvada ei saa? Vastus on lihtne: kuna suurel kiirusel hakkab kasvama keha mass, siis järelikult salvestub energia lisamassina. 

Sama järelduseni jõudis relativistliku füüsika loomise käigus Albert Einstein. Kui energia kasvuga kaasneb massi suurenemine, siis järelikult mass ja energia on samaväärsed ehk võõrsõnaga väljendudes – ekvivalentsed. Nad on füüsikalised suurused, mis väljendavad vastavalt aine ja välja tähtsaimat omadust – olemasolu. Nende taga on looduse üks ja seesama omadus, mis avaldub vaatlejale erinevalt. See erinevus on üks tunnustest, mille alusel me teeme vahet aine ja välja vahel. Massi ja energia sama­väärsust väljendab kõigi aegade kuulsaim füüsikavalem

mida me oleme arvatavasti ammu harjunud nägema kõrvuti selle valemi tuletaja Einsteini pildiga. Valemi 4.9 range tuletamine nõuab kõrgema matemaatika kasutamist, aga esmatähenduses võiks meid valemi 4.9 kehtivuses veenda võrdlus kineetilise energia valemiga

Kineetilise energia valemisse tekib arv 2 ju põhjusel, et kehale kineetilise energia andmiseks peame keha kiirendama paigalseisust ($v=0$) kuni kiiruse lõppväärtuseni v. Keha keskmine kiirus selles protsessis on pool algväärtuse ja lõppväärtuse summast $(0+v)/2=v/2$. Valgus aga liigub aineliste objektide suhtes alati absoluutkiirusega, teda kiirendada ei saa. Seetõttu võrdub valguse keskmine kiirus alati absoluut­kiirusega, kahega jagamist kineetilise energia valemis ei teki ning valgusosakese ehk footoni kineetilise energia valem võtab kuju 4.9, kus $m$ on footoni mass. Kuna valguse olemasolu avaldub vaatlejale ainult läbi liikumise, siis on footoni koguenergia ja kineetiline energia üks ja seesama asi. Ainelise objekti olemasolu aga avaldub vaatlejale eelkõige läbi vastava ainekoguse massi. Seetõttu tuleb ainelise objekti ehk keha summaarne energia leida massi $m$ kaudu sama kujuga valemist 4.9. 

Kui keha on vaatleja suhtes paigal, siis esineb samaväärsusseoses 4.9 keha seisumass $m_0$ ja vastavat puhast olemasolu-energiat nimetatakse keha seisuenergiaks $E_r$. Tähistusviis tuleneb ingliskeelsest sõnast rest – paigalseis. Niisiis,

Kui me uurime mitterelativistlikult ehk absoluutkiirusest palju väiksema kiirusega liikuvat keha, siis võime keha koguenergia $E$ esitada kas seisuenergia $E_r$, kineetilise energia $E_k$ ja potentsiaalse energia $E_p$ summana või siis väljendada kõiki energiaid korraga läbi keha massi, mis on kineetilise ja potentsiaalse energia olemasolu tõttu suurem seisumassist. Kui tegemist on näiteks raskusjõu potentsiaalse energiaga, siis konkreetselt

Kuna massi ja energia samaväärsusseoses 4.9 sisalduv absoluutkiiruse ruut on tohutult suur arv, siis on aines talletuv olemasolu-energia hiiglasuur. Kui ainekogus massiga üks gramm õnnestuks täielikult muuta väljaks, siis vabaneks sama palju energiat, kui me saaksime 3000 tonni ehk 50 vagunitäie kivisöe täielikul ärapõletamisel. Tegelikkuses muutub väljaks vaid väike osa reaktsioonis osalevast ainest. 

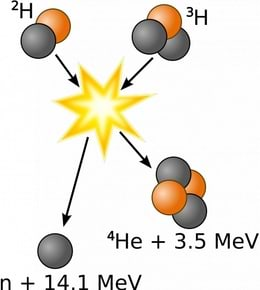
Aine osalisel muutmisel väljaks vabanevat energiat nimetatakse tuumaenergiaks. Tuumaelektrijaamade reaktorites vabaneb see energia uraanituumade pooldumisel. Osa laguneva uraanituuma massist muutub väljade energiaks. Veel rohkem energiat vabaneb reaktsioonides, mille käigus liituvad vesiniku aatomite tuumad, moodustades heeliumi tuumasid. Selline reaktsioon toimub meie Päikese ja kõigi teiste tähtede sisemuses ja on kogu maapealse elu olemasolu tagavaks energiaallikaks. Lähemalt uurime tuumareaktsioone "Mikro- ja megamaailma füüsika kursuses". 

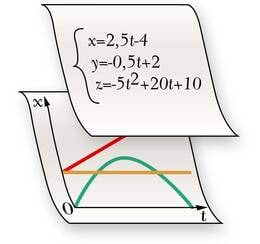
Liikumine on nähtus, milles keha asukoht aja jooksul muutub. Erinevatel ajahetkedel on asukoht erinev, st keha koordinaadid sõltuvad ajast. Ajast sõltuvad ka kogu liikumise kestel läbitud teepikkus ning sooritatud nihe. Muutuva liikumise korral võivad ajast sõltuda veel ka kiirus ja kiirendus. Liikumisnähtus on kirjeldatav seda iseloomustavate suuruste ajast sõltuvuste kaudu.

Sõltuvusi saab väljendada analüütiliselt ja graafiliselt. Analüütilise meetodi korral kirjeldatakse sõltuvust matemaatiliste avaldiste abil. Avaldiste kaudu esitatud sõltuvusi on võimalik matemaatiliselt lähemalt uurida ja seeläbi lisainfot saada. Graafiline meetod kasutab liikumise kirjeldamiseks – nagu nimigi ütleb – graafikuid. Graafikud ei võimalda küll liikumist iseloomustavaid suurusi neilt otse välja lugeda, kuid annavad sõltuvustest seevastu ülevaatlikuma pildi.

Mehaanika põhiülesanne on määrata keha asukoht mis tahes ajahetkel, st leida keha koordinaatide sõltuvus ajast. Kui paneme selle sõltuvuse kirja matemaatilise avaldise abil, saame liikumisvõrrandi. Liikumisvõrrandiks nimetatakse matemaatilist avaldist, mis näitab keha koordinaatide sõltuvust ajast.

Inimese tajutav ruum on kolmemõõtmeline – ruumil ja igal selles asetseval kehal on pikkus, laius ja kõrgus. Seepärast on keha asukoha määramiseks üldjuhul vaja kolme koordinaati. Juhul, kui keha liigub mööda kindlat pinda, piisab kahest koordinaadist. Merepinnal seilava laeva asukoha saab kirja panna kahe geograafilise koordinaadi – pikkus- ja laiuskraadi abil. Veduri asukoha annab kätte vaid üks arv, näiteks kaugus algjaamast, kuna ilmselt püsib vedur relssidel.

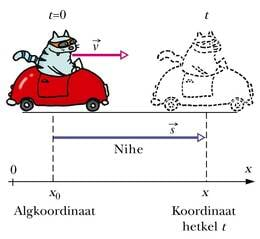
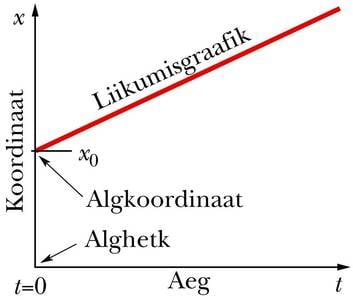
Sirgjoonelise liikumise kirjeldamiseks piisab ühest sirgest koordinaatteljest, mille suund on mõistlik valida piki liikumise trajektoori. Koordinaadi tähiseks võetakse tavaliselt $x$. Selle punkti koordinaati, kus keha asub ajamõõtmise alghetkel, nimetatakse algkoordinaadiks ja tähistatakse sümboliga $x_0$.

Kirjeldame näiteks auto sõitmist: alghetkel $t=0$ on selle koordinaat $x_0$. Aja $t$ jooksul nihkub auto edasi ning koordinaat muutub nihke pikkuse $s$ võrra suuremaks (vt joonist). Koordinaadi uus väärtus $x$ on seega

Teame, et aja $t$ jooksul sooritatava nihke pikkus sõltub kiirusest. Ühtlase liikumise kiiruse valemist 4.2 saame nihke pikkuse avaldada, kui $s=vt$. Paigutades selle nihke avaldise koordinaadi valemisse 4.11 , on tulemuseks seos, mis näitab auto koordinaadi sõltuvust ajast:

See ongi ühtlaselt sirgjooneliselt liikuva keha liikumisvõrrandi üldkuju.

Konkreetsete ülesannete puhul on $x_0$ ja $v$ kohal võrrandis kindlad arvulised väärtused. Näiteks võrrand $x=10+2t$ väljendab liikumist keha jaoks, mille algkoordinaat on 10 m ning kiirus 2 m/s. Kui soovime teada, kus keha 5 sekundi pärast asub, võtame aja $t$ väärtuseks 5 s ning arvutame, et $x=10+2\cdot 5=20\left(\text{m}\right)$. Liikumisvõrrandi abil saab leida keha asukoha mis tahes ajahetkel. Suurused $x_0$ ja $v$ võivad omada nii positiivseid kui ka negatiivseid väärtusi. Negatiivne kiirus tähendab seda, et keha liigub koordinaattelje negatiivses suunas. Rõhutamaks seda, et sirgel trajektooril saab liikumine toimuda kahes suunas, kirjutatakse liikumisvõrrand mõnikord kujul

Ühe suuruse teisest sõltuvuse graafiku saamiseks tuleb joonestada kaks ristuvat telge, horisontaalsele teljele märkida muutuv suurus ning vertikaalsele suurus, mis muutujast sõltub. Matemaatikas oleme harjunud, et horisontaaltelje tähiseks võetakse $x$ ja vertikaalse telje tähiseks $y$. Füüsikas kasutatakse teisi tähiseid.

Liikumisgraafikuks nimetatakse graafikut, mis näitab keha asukoha (koordinaadi x) sõltuvust ajast. Liikumisgraafiku horisontaalteljele kantakse aeg $t$ ja püstteljele ajast sõltuv koordinaat $x$. Erinevat liiki ja erineva suunaga liikumiste graafikud on erineva kujuga.

Ühtlase liikumise korral muutub koordinaat iga sekundiga sama palju ning seepärast on graafikuks sirgjoon. Sirge saab välja joonestada kahe punkti järgi ja seega piisab ühtlase liikumise graafiku saamiseks, kui teame keha asukohta kahel erineval ajahetkel.

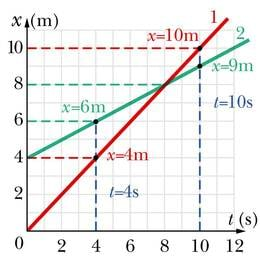
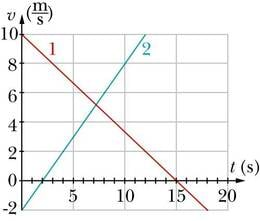
Võrdleme kahe ühtlaselt liikuva keha liikumisgraafikuid. Oletame, et hetkel $t_1=4\text{s}$ on nende koordinaadid 4 m ja 6 m ning hetkel $t_2=10\text{s}$ vastavalt 10 m ja 9 m. Kui graafikud välja joonestada (vt joonist), siis näeme, et need on erineva tõusuga. Ajavahemik kahe vaatlusaluse hetke vahel oli $\Delta t=10-4=6$ sekundit. Järsema graafikuga keha koordinaat muutus selle ajaga $\Delta x_1=10-4=6\text{m}$ võrra. Järelikult on kiirus $6\text{m}/6\text{s}=1\text{m/s}$. Teise keha koordinaadi muuduks saame $\Delta x_2=9-6=3\text{m}$ ja kiiruseks $3\text{m}/6\text{s}=0,5\text{m/s}$.

Jõudsime olulise tulemuseni – liikumisgraafiku tõus näitab liikumise kiirust. Mida suurem kiirus, seda suurem on graafiku tõus. Kui graafik langeb ja tõus on negatiivne, siis on ka kiirus negatiivne, st liikumise suund on koordinaattelje positiivse suunaga vastupidine.

Teiseks saab liikumisgraafikult välja lugeda keha algkoordinaadi. Koordinaati näitav püstine graafikutelg asub just ajatelje nullkohal. Järelikult see punkt, kus graafiku joon püstist koordinaattelge lõikab, vastabki algkoordinaadile. Eespool toodud näites koostatud graafikutelt näeme, et kiiremini liikuva keha algkoordinaat on 0 ja aeglasema oma 4 m.

Liikumisgraafikult saab leida algkoordinaadi.	Sama liikumise liikumisgraafik ja nihke graafik.

Graafiku võib koostada ka nii, et püstteljele kantakse koordinaadi asemel keha sooritatud nihke pikkus või teepikkus. Selline nihkegraafik on kujult liikumisgraafikuga sarnane, kuid algab alati nihke või teepikkuse nullist – alghetkel pole ju keha veel jõudnud edasi nihkuda.

Kui liikumisgraafik pole sirge ja selle tõus muutub, siis järelikult muutub ka liikumise kiirus ja tegemist on muutuva liikumisega.

Nagu juba teame, saab liikumine olla kas ühtlane või mitteühtlane. Ühtlase liikumise korral sooritab keha mis tahes võrdsete ajavahemike kestel võrdsed nihked.

Sel juhul annab valem $v=s/t$ kiiruse jaoks kogu aeg sama tulemuse ja kiirus on järelikult muutumatu. Pole oluline, kas kiiruse arvutamiseks mõõdetakse kogu tee või ainult mingi selle osa nihke pikkus ja läbimise aeg.

Mitteühtlasel liikumisel ei pruugi võrdsete ajavahemike kestel sooritatud nihked trajektoori erinevates paikades ühesugused olla ja järelikult kiirus muutub. Sellise muutuva liikumise iseloomustamiseks ei saa leida kiirust ühtlase liikumise valemi järgi, kuna tulemus sõltub nüüd mõõtmiseks valitud ajavahemikust ning teelõigust.

Seepärast kasutatakse muutuva liikumise iseloomustamiseks teistmoodi defineeritud kiirust. Selleks on kaks võimalust: keskmine kiirus ja hetkkiirus.

Kõik me oleme sõitnud liinibussiga ja teame, et suurema osa ajast liigub see üsna nobedasti, kuid auklikel teelõikudel aeglustab sõitu ning peatustes ja punase fooritule taga seisab hoopis paigal. Mõõtes kogu läbitud teepikkuse ja jagades selle kulunud ajaga, saame mingi kiiruse. Arvutatu pole aga kiirus, millega buss liinil tegelikult sõitis. Kiirus muutus suures vahemikus ega pruukinud nimetatud väärtust üldse omadagi. Ometi iseloomustab kogu teepikkuse ja liikumisaja kaudu arvutatud kiirus bussi sõitu ja lubab ligikaudselt välja arvutada, millal kuhugi peatusesse välja jõutakse.

Selliselt arvutatud kiirust nimetatakse keskmiseks kiiruseks. Keskmine kiirus on võrdne kogu läbitud teepikkuse ja selleks kulunud koguaja jagatisega. Keskmise kiiruse tähiseks on $v_k$ ja mõõtühikuks 1 m/s.

Igasuguste sõidugraafikute ja matkaplaanide koostamisel, liiklusteede läbilaskevõime hindamisel ja muudel sarnastel juhtudel võetakse aluseks just liikumise keskmine kiirus.

Märkused

• Keskmise kiiruse leidmisel ei tohi lasta end eksitada mõiste kõlalisest sarnasusest sagedasti kasutatava aritmeetilise keskmisega. Keskmist kiirust ei saa leida aritmeetilise keskmisena, vaid seda tuleb teha ikka kogu teepikkuse ja koguaja kaudu!
• Keskmise kiiruse arvutamiseks ei kasutata mitte nihke pikkust, vaid ikka teepikkust. Kui alg- ja lõppasukohad langevad kokku ja nihe on seetõttu null, ei saa ju ometi väita, et terve päeva ringi sõitnud ja garaaži naasnud bussi keskmine kiirus oli null.
• Kasutusel on ka kiiruste statistilise keskmise mõiste. Sel juhul on uuritakse palju erinevate kiirustega liikuvaid kehi ja keskmist väärtust hinnatakse statistikaseadustele tuginedes. Nii leitakse näiteks elutoas ringisebivate õhumolekulide keskmine kiirus.

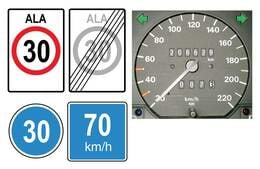
Kõik me oleme näinud sõidukite liikumiskiirust reguleerivaid teemärke ja teame, et politseinikud mõõdavad teedel sagedasti kiirust. Ohtlikematele teelõikudele on isegi automaatselt töötavaid kiiruskaameraid üles seatud. Autojuhtidel aitab kiiruspiiranguid järgida armatuurlaual paiknev spidomeeter (ingl speed 'kiirus') ja sarnase kiirusemõõtja saab monteerida isegi jalgrattale.

Mis liiki kiirusega siin tegemist on? Vaevalt, et keskmisega, sest kuidas saaks liiklusmärgi ülespanija või politseinik arvestada sõidukijuhi juba asetleidnud ja veel vähem alles eel olevaid kihutamisi ja seisakuid! Pealegi ei oma juba toimunud ja tulevane liikumine konkreetse hetke liiklusolukorras mingit tähtsust. Oluline on ju see, kuidas liigutakse selles paigas just sellel ajahetkel. Siin kirjeldatud juhtudel kasutatav kiirus on hetkkiirus.

Hetkkiiruse nimetus viitab sellele, et mõeldud on kiirust mingil konkreetsel ajahetkel. Samas on hetke kestus null ja selle kestel läbitav teepikkus samuti null. Püüdes nüüd kiirust arvutada, jõuame välja võimatu tehteni, mida matemaatikud tunnevad kui 0/0 määramatust. Mis ikkagi hetkkiirus on ja kuidas seda mõõdetakse?

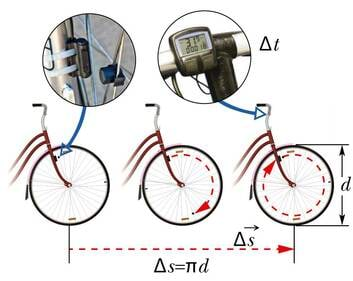
Jalgratta kiirusemõõtja kujutab endast pisikest kellaga arvutit, mille külge on ühendatud väike magnetvälja muutusi tajuv andur. Andur paikneb esiratta kõrval nii, et kodara külge kinnitatud magnet annab ratta iga täisringi järel andurile oma möödumisest teada. Arvuti kell mõõdab ratta täisringi tegemiseks kulunud aja ja lähtudes mälusse sisestatud ratta läbimõõdu väärtusest, leiab ühe rattaringi jooksul sooritatud nihke pikkuse ning arvutab välja selle lühikese teejupikese läbimise keskmise kiiruse.

Jalgratta kiirusemõõtja tööpõhimõte.	Kõverjoonelise liikumise hetkkiiruse leidmine. Ka siin peab  t olema võimalikult väike.

Hetkkiiruse all mõistetakse küll keha liikumiskiirust kindlal ajahetkel, aga selle väärtust saab hinnata siiski mitte hetke, vaid lühikese ajavahemiku kestel leitava keskmise kiirusena.

Hetkkiiruse tähistamiseks kasutatakse sarnaselt ühtlase liikumise kiirusega sümbolit $v$. Kui võtame lühikese ajavahemiku, mille kestel kiirus ei jõua oluliselt muutuda, tähiseks $\Delta t$, ja selle aja jooksul sooritatud nihke pikkuse tähiseks $\Delta s$, saame hetkkiiruse arvutusvalemiks

Mida lühem on uuritav ajavahemik $\Delta t$, seda täpsemini saab hetkkiiruse teada, sest seda vähem jõuab kiirus selle ajaga muutuda. Mitteühtlase liikumise hetkkiirus on sarnaselt ühtlase liikumise kiirusega vektoriaalne ehk suunaga suurus. Kui liikumise kirjeldamisel on ka suund oluline, tuleb hetkkiiruse valemit kasutada vektorkujul.

Muutuv liikumine võib olla väga erinev, sest kiirus saab muutuda mitmesugustel viisidel – pidevalt kasvada, olla vahepeal muutumatu, jälle kasvada, kuid aeglasemalt, ja siis hoopis kahaneda... Tihti kohtame aga sellist liikumist, mille kiirus kasvab või kahaneb mis tahes võrdsetes ajavahemikes ühepalju.

Sellist liikumist, mille kiirus muutub mistahes võrdsete ajavahemike jooksul ühesuguse väärtuse võrra, nimetatakse ühtlaselt muutuvaks liikumiseks. Näiteks kasvab õhutakistuseta kukkuva kivi kiirus iga sekundiga ligikaudu 10 m/s võrra. Käest lahti lastud kivi saavutab ühe sekundiga kiiruse 10 m/s, teise sekundi lõpuks 20 m/s, kolmanda lõpuks 30 m/s jne. Samas on vabalt kukkuva kivi trajektooriks sirgjoon ja seega on tegemist ühtlaselt muutuva sirgjoonelise liikumisega.

Kukkuva kivi kiirus ei kasva muutumatuna siiski lõputult, kuna langemise käigus ei jää endiseks ei liikumist mõjutav kaugus Maast ega ka õhutakistus. Tegelikult looduses me ideaalset ühtlaselt muutuvat sirgjoonelist liikumist ei kohtagi. Sellist liikumist saab vaid ette kujutada ja matemaatika meetoditega kirjeldada. Tegemist on teatud liikumise füüsikalise mudeliga. Kuigi puhast sellist liikumist olemas pole, saab nimetatud mudeli juures väljaselgitatud lihtsaid seaduspärasusi siiski suurepäraselt sarnaste reaalsete liikumiste uurimisel kasutada.

Näiteks võib teatud piirides ühtlaselt muutuvaks sirgjooneliseks liikumiseks pidada suusahüppaja laskumist hüppemäel, hokilitri libisemist jääl, kaubarongi liikumahakkamist ning otse üles visatud palli lendu.

Kui jälgida foori taga ootavaid sõidukeid, siis võib tähele panna, et rohelise tule süttimisel ei hakka need kõik liikuma ühtemoodi. Sõiduautod võtavad paigalt ja saavutavad lubatud maksimumkiiruse üsna kärmesti, kuid pungil täis liinibussil kulub sellise kiiruse saavutamiseks märgatavalt rohkem aega. Ka aeglustumine võib olla erinev. Kui turvavarustuse katsetamisel peatub suurel kiirusel vastu müüri paiskuv auto peaaegu silmapilkselt, siis palju väiksema kiirusega sõitva kaubarongi peatamine kestab mitu minutit. Liikumise muutumine võib toimuda erineva kiirusega.

Ülaltoodud näited viitavad sellele, et muutuvat liikumist kirjeldab peale keskmise ja hetkkiiruse ka hetkkiiruse muutumise kiirus. Tegemist on liikumist iseloomustava omadusega, mida saab mõõta ja arvuliselt väljendada, seega on tegemist füüsikalise suurusega. Füüsikud on kokku leppinud, et seda kiiruse muutumise kiirust väljendavat suurust nimetatakse kiirenduseks.

Mis tahes suuruse muutumiskiirust saab määrata nii, et leitakse, kui palju see suurus ühe ajaühiku jooksul muutuda jõuab. Selleks tuleb muutuse suurus jagada muutumiseks kulunud ajaühikute arvuga ehk muutumise ajaga. Samamoodi tuleb toimida ka kiiruse muutumise kiiruse iseloomustamisel. Seega võime kiirenduseks nimetada liikumist iseloomustavat suurust, mis on võrdne kiiruse muudu ja selle muutumise aja jagatisega. See definitsioon on matemaatiline, kuna kasutab sõnastuses matemaatilisi tehteid. Samaväärselt võime kasutada ka füüsikalist definitsiooni: kiirenduseks nimetatakse füüsikalist suurust, mis on võrdne kiiruse muuduga ajaühikus.

Kiirenduse valemi kirjapanekuks peame kokku leppima sobivad tähistused. Tähistame alghetke (hetke, mil kiiruse muutumine algab) sümboliga $t_0=0$. Kui võtame muutumise lõpphetke tähiseks $t$, siis on muutumise kestus võrdne ajavahemikuga $\Delta t=t-t_0=t$ (sest $t_0=0$). Nimetame kiiruse, mida keha omas muutumise alguses, algkiiruseks ja tähistame selle vektoriaalse suuruse sümboliga ${\overrightarrow{v}}_0$. Kiirus muutumise lõpus olgu lõppkiirus $\overrightarrow{v}$. Liikumiskiiruse muut on selliste tähistuste puhul $\Delta v=v-v_0$. Kiirenduse tähisena kasutatakse sümbolit $\overrightarrow{a}$ (ingl acceleration 'kiirendus'). Nooleke tähe kohal näitab mäletatavasti seda, et tegu on suunaga suuruse ehk vektoriga. Kuna definitsiooni järgi on kiirendus võrdne kiiruse muudu ja kiiruse muutumise aja jagatisega, saame kiirenduse valemiks

Kiirenduse valemi saab esitada ka skalaarkujul:

Et kiiruse muudu mõõtühik on sarnaselt kiiruse ühikuga 1 m/s ja ajavahemiku ühik 1 s, saame kiirenduse mõõtühikuks nende jagatise $\frac{1m/s}{1s}=1\frac{m}{s^2}$, mida loetakse kui 1 meeter sekundi ruudu kohta.

Kui on teada algkiirus ja kiirendus, on ühtlaselt muutuva liikumise korral lihtne leida keha kiirust mis tahes ajahetkel. Selleks tuleb kiirus avaldada kiirenduse definitsioonivalemitest 4.17 või  4.18 :

või

Alghetkel, mil $t=0$, annab valem kiiruseks $v=v_0$ ehk algkiiruse. Muudel momentidel on liidetav $at$ sõltuvalt kiirenduse väärtusest kas positiivne või negatiivne ja kiirus võib kas kasvada või kahaneda. Kui kiirendus on algkiirusega võrreldes vastupidiselt suunatud, siis $a<0$ ja võib juhtuda olukord, et ka kiirus muutub negatiivseks. See tähendab seda, et kiiruse suund on algkiirusega võrreldes vastupidine ja keha on hakanud kiirenevalt tagasi liikuma.

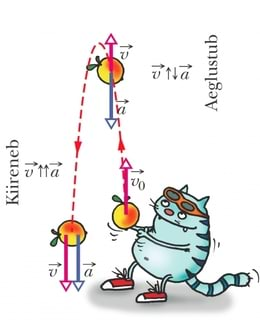
Nii juhtub näiteks ülesvisatud õunaga. Tõusul on liikumine aeglustuv, kuid langemisel muutub kiirenevaks. Langemisel on liikumise suund esialgsega vastupidine ja kiirendusega samasuunaline. Kui kiirendus on kiirusega samasuunaline, on liikumine kiirenev ning vastassuunalise kiirenduse korral aeglustuv:

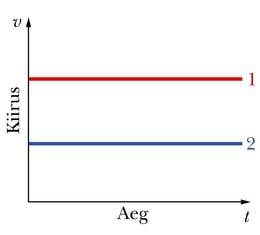
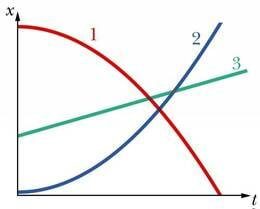
Kui liikumisgraafik näitab keha koordinaadi sõltuvust ajast, siis kiiruse graafik kiiruse sõltuvust ajast. Kiiruse graafiku püstteljele kantakse kiiruse väärtused ja horisontaalteljele sarnaselt liikumisgraafikuga aeg. Kõige lihtsam kiiruse graafik on ühtlasel liikumisel. Kuna ühtlasel liikumisel kiirus ei muutu, on selle väärtus igal ajahetkel sama ja graafikuks on horisontaalne sirgjoon (vt joonist). Kiirema liikumise korral asub graafik teljestikus kõrgemal ja aeglasema korral madalamal positsioonil.

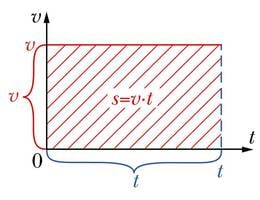
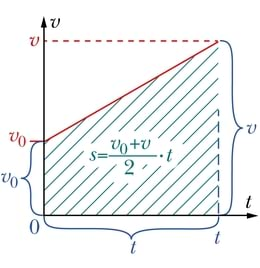
Kuigi kiiruse graafikul on näidatud vaid kiiruse sõltuvus ajast, saab selle abil ka sooritatud nihke pikkuse leida. Vaatame ühtlase liikumise graafikut. Kui märgime sellel ära ajavahemiku 0 kuni $t$, saame ristküliku, mille külgede pikkusteks püstsihis on kiirus $v$ ja horisontaalsihis aeg $t$. Selle ristküliku pindala on võrdne külgede pikkuste korrutisega ehk $vt$. Kiiruse ja liikumiseks kulunud aja korrutis on aga võrdne sooritatud nihke pikkusega: $s=vt$. Jõudsime olulise tulemuseni: kiiruse graafiku alla jääv pindala on võrdne keha poolt sooritatud nihke pikkusega. See kehtib mitte ainult ühtlase, vaid ka muutuva liikumise korral.

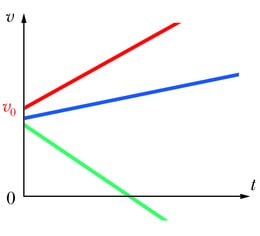
Ühtlaselt muutuva liikumise korral muutub kiirus võrdsetes ajavahemikes sama palju ja kiiruse graafikuks on tõusev või langev sirge. Graafiku tõus või langus on seda suurem, mida kiiremini kiirus muutub ehk mida suurem on kiirendus. Tõusva graafiku korral liikumine kiireneb, langeva korral aeglustub. Kui graafik on ajateljest allpool, on kiirus negatiivne, liikumine toimub koordinaattelje negatiivses suunas ning langev graafik tähistab sel juhul kiiruse kasvamist. Graafiku lõikepunkt püstise kiiruse teljega annab kiiruse hetkel $t=0$ ehk algkiiruse $v_0$. Kui graafik pole sirge, on tegemist mitteühtlaselt muutuva liikumisega.

Selleks, et tuletada valem, mis näitaks ühtlaselt muutuva liikumise korral nihke sõltuvust ajast, saame kasutada teadmist, et nihke pikkus on võrdne kiiruse graafiku alla jääva pindalaga. Olgu keha kiirus alghetkel $v_0$ ja saavutagu aja $t$ möödumisel väärtuse $v$. Kiiruse graafikuks on tõusev sirge, mille alla jääv kujund on trapets, mille alusteks on kiirused $v_0$ ja $v$ ning kõrguseks aeg $t$.

Aja $t$ jooksul keha poolt sooritatava nihke pikkus on võrdne selle trapetsi pindalaga, mille leidmiseks tuleb aluste poolsumma korrutada kõrgusega:

Teades seosest 4.20 , et kiirus avaldub kiirenduse kaudu kujul $v=v_0+at$, saame pärast asendamist

Selle lihtsustamisel jõuamegi avaldiseni, mis näitab nihke sõltuvust ajast ühtlaselt muutuval liikumisel:

Näeme, et nihe sõltub ajast ruutfunktsiooni järgi. Mõne probleemi lahendamisel pole liikumise aeg teada, küll aga on teada lõppkiirus. Sel juhul leitakse aeg kiiruse valemist 4.20

Selle  ajaga asendamisel omandab seos 4.21 kuju

ehk

Pärast lihtsustamist ruutude vahe valemi abil saame nihke arvutamiseks valemi:

Teades nihke sõltuvust ajast, on liikumisvõrrandit lihtne koostada. Näitab ju see võrrand keha koordinaadi sõltuvust ajast, ja nagu ütleb seos 4.11 , saame keha koordinaadi arvutada mis tahes ajahetke jaoks, liites algkoordinaadile selleks hetkeks sooritatud nihke pikkuse: $x=x_0+s$. Lähtudes nihke avaldisest 4.23 , näeme, et ühtlaselt muutuva liikumise liikumisvõrrandiks on

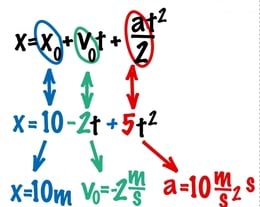
Tegemist on ruutfunktsiooniga, mille liikmed võivad olla sõltuvalt algkoordinaadi, algkiiruse ja kiirenduse märgist nii positiivsed kui ka negatiivsed. Liikme märk sõltub vastava suuruse suunast koordinaattelje suhtes. Märgi olulisuse rõhutamiseks kasutatakse võrrandi üldkujus + asemel mõnikord sümbolit ±. Sel juhul näeb liikumisvõrrand välja veidi teistsugune:

Iga konkreetse liikumise korral on võrrandis $x_0$, $v_0$ ja $a$ kohal vastavate suuruste arvväärtused.

Nüüd, mil teame, et ühtlaselt muutuva liikumise liikumisvõrrand 4.28 kujutab endast aja ruutfunktsiooni, mis on sarnane matemaatikast tuntud funktsiooniga $y=a{x}^2+bx+c$, pole raske konstrueerida ka selle liikumise graafikut.

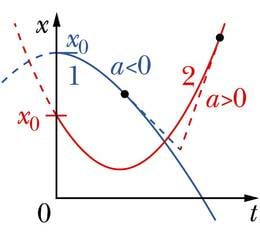
Koordinaat $x$ sõltub ajast $t$ kui ruutfunktsioon. Ruutfunktsiooni graafik on teatavasti parabool ja nii ongi ühtlaselt muutuva liikumise graafik parabooli kujuga. Sõltuvalt ruutliikme kordaja (kiirenduse) märgist on parabooli harud suunatud kas üles ($a>0$) või alla ($a<0$).

Gravitatsioon (ld gravitas 'raskus') on vastastikmõju, millele alluvad kõik kehad, nii kosmilised kui ka maapealsed. Meie tajutav gravitatsioon on Maa külgetõmme. Kõik kehad tõmbuvad Maa keskpunkti poole ja omavad seepärast raskust. Kui keha lahti pääseb, kukub see alla.

Selle üle, kuidas kehad Maa külgetõmbe tõttu kukuvad, juureldi juba tuhandeid aastaid tagasi. Kui Kreeka mõttetark Aristoteles oli veendunud, et rasked kehad kukuvad kergematest kiiremini, siis 2000 aastat hiljem näitas Itaalia teadlane Galileo Galilei, et kõik kehad liiguvad Maa külgetõmbe mõjul ühtmoodi.

Tegelikult oli õigus ka Aristotelesel. Kõik me oleme kogenud, et korraga käest lahti lastud metallraha ja paberileht ei maandu samal ajal. Paber kukub aeglasemalt, kuna langemist segab õhutakistus. Suhteliselt raskete esemete korral (metallkuulid, kivid) jääb õhutakistus raskusjõu kõrval aga väikeseks ja kehad maanduvad siis korraga.

Õhutakistuse puudumisel kukkumine on vaba langemine.	Kuuli ja udusule katse maailma kõige suuremas vaakumkambris.

Sellist kehade kukkumist, kus õhutakistus puudub või on väike, nimetatakse vabaks langemiseks. Katsed näitavad, et vabalt langevatel kehadel kasvab kiirus ühtemoodi – see ei sõltu raskusest ja kujust. Torus, millest on õhk välja pumbatud, kukuvad tinahaavel ja udusulg kõrvuti.

Vaba langemine on ühtlaselt muutuv liikumine. Kõik kehad saavad sõltumata massist ja juba olemasoleva kiiruse suurusest ning suunast Maa külgetõmbe toimel ühesuguse kiirenduse. Seda nn vaba langemise kiirendust on mõõdetud Maa eri paigus ja erinevatel meetoditel ning tulemuseks on saadud alati ligikaudu 9,8 m/s². Vaba langemise kiirenduse tähis on $g$ ja see on suunatud alati alla, Maa keskpunkti poole.

Vaba langemine on ühtlaselt muutuv liikumine ja selle käigus keha kõrgus muutub. Sellise liikumise korral on püstsuunaliseks koordinaadiks mõistlik võtta keha kõrgus. Telg on sel juhul suunatud alt üles ning koordinaadi ehk kõrguse tähiseks on tavaliselt $h$ (ingl height 'kõrgus'). Sageli kasutatakse püstkoordinaadina ka $y$.

Keha liikumist Maa külgetõmbe mõjul saab kirjeldada ühtlaselt muutuva liikumise mudeli abil. Lähtume kiiruse ajast sõltuvuse valemist 4.20 ja liikumisvõrrandist 4.28 :

Neis avaldistes tuleb kiirenduseks võtta vaba langemise kiirendus ning koordinaadiks kõrgus $h$.

Et kõrgus on suunatud alt üles ja vaba langemise kiirendus ülalt alla, on sellises koordinaatsüsteemis vaba langemise kiirendus negatiivne ja valemites tuleb võtta $a=-g$. Selliselt toimides saame vabalt langeva keha kiiruse ja kõrguse ajast sõltuvuse jaoks järgmised seosed:

Kui näiteks kivi üles visata, on valemites algkiirus $v_0$ positiivne, allaviskamisel negatiivne ja lihtsalt käest pillamisel null. Sümbol $h_0$ tähistab kõrgust aja alghetkel ehk algkõrgust. Kõrguse nullpunkt valitakse vastavalt olukorrale. Enamasti on selleks maapind. Vaba langemise kiirenduse väärtuseks võetakse 9,8 m/s², ent kui pole öeldud teisiti, võib kooliülesannete lahendamisel kasutada väärtust 10 m/s².

Kui kõrgushüppaja võitleb gravitatsiooniga, et tõusta kõrgele, siis kuulitõukaja peab kuuli lennutama võimalikult kaugele. Mismoodi toimida? Algkiirus peab olema võimalikult suur, kuid ka tõukesuund on oluline. Mida kõrgemale kuul tõuseb, seda kauem see õhus püsib. Samas ei saa kogu energiat kõrguse saavutamiseks kulutada, osa tuleb panustada edasiliikumisse.

Kaldu visatud keha liikumist saab vaadata kui kahte korraga toimuvat sõltumatut liikumist. Üks on suunatud üles-alla ja allub vaba langemise seadustele ning teine horisontaalsuunas ja on kõrvaliste mõjude puudumisel ühtlane sirgjooneline. Kaks erisihilist korraga toimuvat liikumist on teineteisest täiesti sõltumatud ja neid saab kirjeldada eraldi võrrandite abil.

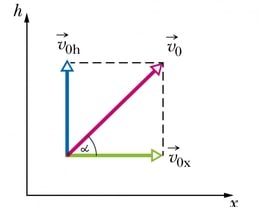
Kaldu visatud keha liikumise kirjeldamiseks on vaja kahte koordinaattelge. Üles-alla toimuva muutuva liikumise jaoks kasutame püstist kõrguse telge $h$ ja horisontaalsuunas ühtlaselt edasi liikumise jaoks telge $x$. Selleks et nende kahe koordinaattelje jaoks saaks liikumisvõrrandid kirja panna, on vaja ka algkiirus $v_0$ jagada kaheks komponendiks – püstsuunaliseks $v_{\text{0h}}$ ja horisontaalsuunaliseks $v_{\text{0x}}$.

Jooniselt on näha, et kiiruse komponentide suurused saab täisnurksetest kolmnurkadest siinus- ja koosinusfunktsiooni abil (α on viskenurk horisontaalsihi suhtes):

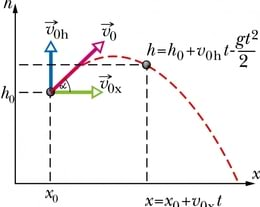
Nende avaldistega tuleb vastavad suurused asendada liikumisvõrrandites 4.13 ja 4.31 . Kuna nüüd on meil ühe liikumise asemel korraga kaks, siis peame selle kirjeldamiseks kasutama ühe liikumisvõrrandi asemel kahest võrrandist koosnevat süsteemi:

Sagedamini tulevad ette ülesanded, kus keha alustab liikumist maapinnalt. Sel juhul võetakse mõlemad algkoordinaadid $h_0$ ja $x_0$ nulliks. Liikumisvõrrandite süsteemi (4.34 ) abil saame leida horisondiga nurga $\alpha$ all visatud keha koordinaadid $h$ ja $x$ mis tahes ajahetkel $t$. Kui soovime leida lennukaugust ja -kõrgust, tuleb esmalt leida lennuaeg. Lennu lõpus kukub keha maha ning kõrgus $h=0$. Seda väärtust kasutades saame esimesest võrrandist avaldada lennuaja. Teades lennuaega, leiame teisest võrrandist sellele vastava kauguse $x$. Lennukõrguse leidmiseks kasutame jälle esimest võrrandit, võttes ajaks seekord poole kogu lennuajast, kuna just lennu keskmomendil on keha oma trajektoori kõrgeimas punktis.

Trampliinilt õhku lendav jalgrattur on kui horisondiga kaldu visatud keha ja kui kirjeldame jalgratturit punktmassina, siis saame tema liikumist kirjeldada äsja õpitud liikumisvõõranditega. Iseasi, kas jalgratturit saab siin punktmassina kirjeldada. Kas saab?