Dr John Stapp, New Mexicos asuva Hollomani õhujõudude baasi kolonel, kinnitati 1954. aasta detsembris rihmadega üheksa raketiga rakettkelgu istmele. Kui raketid süüdati, kiirendas see teda viie sekundi jooksul kiiruseni 632 miili ehk 1018 kilomeetrit tunnis. Tõsisem katsumus kolonel Stappi jaoks oli siiski pidurdamine vesipiduritega, milleks kulus vaid 1,4 sekundit. 1958. aasta mais saavutas Eli L. Beeding jr sarnase kelguga kiiruse 72,5 miili (117 kilomeetrit) tunnis. Tema kiirus polnud küll märkimisväärne – see on maanteedel suhteliselt tavaline –, kuid märkimist väärib peatumiseks kulunud aeg, 0,04 sekundit, mis on sõna otseses mõttes vähem kui silmapilk.
|
|
|---|---|
| Kolonel J. P. Stapp rakettkelgul, kui see saavutab suure kiiruse ... | ... mida siis väga järsult pidurdatakse. (USA Õhujõudude foto). |
|
|
|---|---|
Kui päästerõngas vee alla suruda, tõukab vesi selle pinnale tagasi. Tuul puhub purje pingule ning paneb jahi mööda veepinda liikuma. Riputatud koormise toimel venib vedru pikemaks. Tõstja sikutab raske kangi maast lahti. Udusulg hõljub õhus ega kuku maha. Pärast kammimist hakkab kamm juukseid ligi tõmbama. Sepavasara löök painutab kuuma raudlati kõveraks.
|
|
|---|---|
| Vastastikmõjud on väga erinevad. | Vastastikmõjud ahelmasinas. |
Selliseid näiteid võib tuua väga palju. Need on küll kõik väga erinevad, kuid ühes siiski sarnased – ühe kehaga juhtub midagi teise keha mõjul. Neid näiteid ühendab nähtus, mida nimetatakse vastastikmõjuks.
Mille järgi tunneme ära, et vastastikmõju on aset leidnud? Kui üks keha mõjutab teist, siis selle tagajärjel toimub mingi muutus. Siin on mitu võimalust – vastastikmõju tagajärjel võib muutuda keha kuju, ruumala või liikumise iseloom.
|
|
|---|---|
| Vastastikmõju tagajärjel võib muutuda keha liikumise iseloom. | Vastastikmõju tagajärjel muutub keha kuju. |
Näiteks muutub õhupalli kuju, kui me selle täis puhume, ja muutub ka kristallvaasi kuju, mis maha pillatakse. Alati ei pruugi me kujumuutust märgatagi. Kui me trepile astume, ei näi midagi erilist juhtuvat.
Liikumise juures saab vastastikmõju muuta kiiruse arvväärtust ja suunda. Kui tahame auto kiirust vähendada, kasutame kummide ja teekatte vahelist pidurdavat mõju. Kiiruse väärtus muutub Maa külgetõmbe tõttu näiteks ülesvisatud pallil. Algul see väheneb, siis pall peatub hetkeks ning allakukkumisel hakkab kiirus jälle kasvama. Viimases näites muutub ka palli liikumise suund.
Kui auto suure kiirusega kurvi siseneb, siis libeda korral ei pruugi ta teel püsida. Kurvis püsimiseks peab rataste ja teekatte vahel olema piisava tugevusega vastastikmõju, et liikumise suund selle tagajärjel vajalikul määral muutuks.
Vastastikmõju tagajärjel muutub keha liikumise iseloom. Et liikumise muutumise põhjusi uurib mehaanika haru dünaamika, siis ongi vastastikmõju dünaamika jaoks üks olulisemaid nähtusi.
Ühegi keha liikumist ei saa muuta ilma teise keha mõjuta. Näiteks ei saa paati seisvas vees liikuma panna, kui pole tuult ega aere. Ka auto ei saaks paigalt sõita, kui puuduks teine keha, millelt end liikuma tõugata (teekate). Vastastikmõjus osaleb alati vähemalt kaks keha.
Vastastikmõjud võivad olla erineva tugevusega. Seda näeme tagajärje suuruse järgi. Erinevad raskused venitavad sama vedru erineva pikkuse võrra ja tugevam mängija suudab pallile anda suurema hoo.
Et vastastikmõjusid omavahel võrrelda ja uurida, mil määral sõltuvad tagajärjed vastastikmõju tugevusest, on kasutusele võetud füüsikaline suurus jõud.
Jõud on vastastikmõju mõõduks ja selle arvväärtus iseloomustab vastastikmõju tugevust. Vastastikmõju põhjustab kas keha kuju või kiiruse muutuse. Kuna nii kujumuutusel kui ka kiiruse muutumisel (kiirendusel) on kindel suund, siis peab ka jõud olema suunaga. Järelikult on jõud vektoriaalne suurus.
Jõu tähiseks valemites ja joonistel on (ld fortis 'tugev, võimas'). Jõu arvulise väärtuse väljendamisel, kui suund pole oluline, kasutatakse ilma vektorimärgita tähist .
Jõu mõõtmiseks on kaks põhimõtteliselt erinevat võimalust. Võib mõõta vastastikmõju poolt tingitud kujumuutuse ehk deformatsiooni suurust. Näiteks meile tuttav dünamomeeter näitab jõu suurust vedru pikenemise kaudu.
|
|
|---|---|
| Jõudu saab mõõta selle poolt tekitatud deformatsiooni ja kiirenduse kaudu. | Jõud 1 N annab 1 kg massiga kehale kiirenduse 1 m/s2, kui hõõrdumist ei arvestata. |
Teiseks saab jõu suurust arvutada selle kaudu, kui palju vastastikmõju tuntud massiga keha kiirust muudab ehk siis mõju poolt antava kiirenduse kaudu.
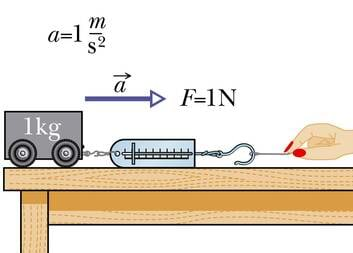
Klassikalise mehaanika rajaja Isaac Newtoni auks on SI jõu mõõtühiku nimeks võetud njuuton (N). Üks njuuton on sellise suurusega jõud, mis annab kehale massiga kiirenduse .
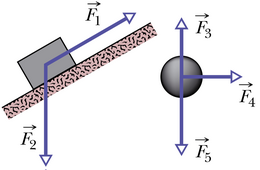
See, et vastastikmõjus osaleb vähemalt kaks keha, ei tähenda, et kehasid ei võiks rohkem olla. Tihti ongi just nii, et korraga mõjub mitu jõudu. Korraga kehale mõjuval mitmel jõul ei ole aga siiski mitut erinevat tagajärge. Näiteks kui vees ujuvale õngekorgile mõjuv raskusjõud on suunatud alla ja samal ajal vee üleslükkejõud üles, ei hakka kork ju korraga mõlemas suunas liikuma. Jõud liituvad ning nende mõjul on üks ühine tagajärg – kork püsib paigal. Samale kehale mõjuvate jõudude summat nimetatakse resultantjõuks.
Kuna jõud on suunaga suurused, ei saa neid liita niisama lihtsalt kui arve. Jõudude liitmisel tuleb järgida vektorite liitmise reegleid. Et jutt on samale kehale mõjuvate jõudude liitmisest, siis joonisele kandmisel peavad need algama kõik samast punktist. Kulgeva liikumise korral, mil pöörlemist ei toimu, kujutame keha ette punktmassina.
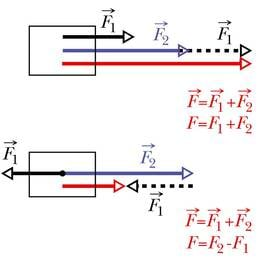
Kõige lihtsam on leida kahe samasuunalise jõu summat. Samasuunaliste jõudude arvväärtused liituvad ning resultantjõud on liidetavate jõududega samas suunas.
Vastassuunaliste jõudude liitmisel lahutatakse suurema väärtusest väiksem ning resultantjõud jääb suurema jõu suunaliseks.
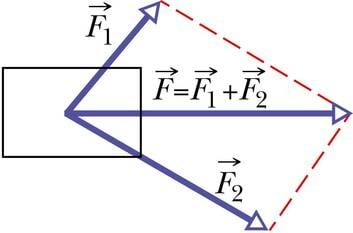
Erisuunaliste jõudude liitmise lihtsaim viis on kasutada rööpküliku reeglit. Selle järgi tuleb liidetavatele jõuvektoritele üles ehitada rööpkülik ning viimase diagonaal ongi resultantjõuks.
|
|
|---|---|
| Erisuunaliste jõudude liitmimine rööpküliku reegli järgi. | Kui kehale mõjuvad jõud on üksteisega tasakaalus, siis öeldakse, et need jõud kompenseerivad üksteist. Sel korral keha liikumisolek ei muutu. |
Kui kehale mõjub suurem arv jõude, tuleb esmalt summeerida kaks jõudu ning tulemusele liita samm-sammult ülejäänud.
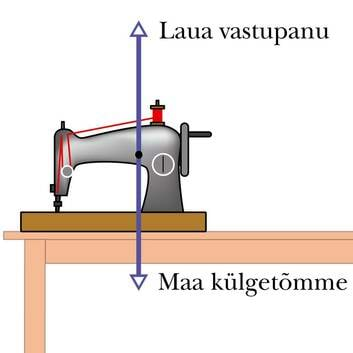
Sageli tuleb ette, et kehale mõjuvate jõudude resultant on null. Siis öeldakse, et jõud on tasakaalus ehk kompenseerivad üksteist. Näiteks laual seisvale õmblusmasinale mõjuvat Maa külgetõmmet tasakaalustab laua vastumõju, mis ei luba masinal sellest läbi kukkuda. Need kompenseerunud jõud liikumist ei mõjuta ja õmblusmasin püsib paigal.
Kõik meist on kogenud, et tool nihkub põrandal edasi vaid siis, kui seda lükata. Pärast lükkamise lõppu lakkab liikumine jalgade ja põranda vahelise hõõrdumise tõttu.
Kuidas liiguvad aga kehad siis, kui ümbritsev neid ei sega, kui puudub vastastikmõju teiste kehadega?
Teame, et vastastikmõju üheks tagajärjeks on liikumise muutumine. Kui vastastikmõju pole, siis ei saa muutuda ei liikumise kiirus ega ka suund. Sel juhul on tegemist ühtlase sirgjoonelise liikumisega. Kui aga keha juhtub seisma, siis jääbki see muutumatult paigale.
Vastastikmõjude puudumisega on samaväärne olukord, kus jõud on kompenseerunud ja resultantjõud null.
Need tähelepanekud võtabki kokku Newtoni esimene seadus, mis kirjeldab keha liikumist jõudude puudumisel: kehale mõjuvate jõudude puudumisel või nende kompenseerumisel on keha kas paigal või liigub ühtlaselt ja sirgjooneliselt.
Nähtust, kus keha püüab oma liikumisseisundit säilitada, nimetatakse inertsiks. Seepärast nimetatakse Newtoni esimest seadust ka inertsiseaduseks.
Matemaatiliselt saab inertsiseadust väljendada nii:
Kui kehale jõude ei mõju, jääb liikumine vastavalt inertsiseadusele muutumatuks. Kuidas muutub aga liikumine siis, kui kehale mõjub jõud?
On kindlaks tehtud, et kui kehale mõjub jõud, siis keha kiirus muutub ehk keha liigub kiirendusega. Järelikult põhjustab jõud kiirenduse. Millest ja kuidas kiirendus sõltub, on kindlaks tehtud katsete abil.
Kui mõjutada erinevaid kehi sama suure jõuga, võivad saadud kiirendused olla erinevad. Mõne keha kiirus muutub aeglasemalt ja kiirendus on väiksem. Need kehad säilitavad oma liikumisseisundit teistega võrreldes paremini ja öeldakse, et nende inertsus on suurem. Inertsus on keha omadus, mis iseloomustab selle võimet liikumisolekut säilitada.
Suurema inertsusega keha kiirust on raskem muuta. Näiteks on rasket veoautot määratult raskem liikuma lükata kui mänguautot. Selles pole midagi kummalist – päris autol on mänguasjaga võrreldes ju palju suurem mass.
Mass on keha inertsuse mõõt. Selle tähiseks on ja mõõtühikuks .
Katsed näitavad, et jõu toimel tekkiv kiirendus on pöördvõrdeline keha massiga. Mida suurem mass, seda väiksema kiirenduse see jõud tekitab.
Veel näitavad katsed, et kiirendus on seda suurem, mida suurem jõud kehale mõjub. See on ka mõistetav – kui liikumise muutuse tingib vastastikmõju, siis mida tugevam on mõju, seda suurem peab olema ka selle põhjustatud muutus. Kiirendus on võrdeline jõuga.
Ülaltoodud tulemused võimaldasidki Newtonil jõuda oma mehaanika teise põhiseaduse sõnastamiseni.
Newtoni teine seadus ütleb: kui kehale mõjub jõud, siis liigub see kiirendusega, mis on võrdeline mõjuva jõuga ning pöördvõrdeline selle keha massiga. Matemaatiliselt väljendab Newtoni II seadust valem
Kuna sel seadusel on suur tähtsus mehaanika põhiülesande lahendamisel, nimetatakse Newtoni II seadust ka dünaamika põhiseaduseks.
Kui me teame keha algkoordinaati, algkiirust, massi ja mõjuvat jõudu, saame Newtoni II seadusest arvutada kiirenduse ning välja kirjutada keha liikumisvõrrandi. Liikumisvõrrand lubab keha asukoha välja arvutada mis tahes ajahetkel ning sellega ongi põhiülesanne lahendatud.
Kui Newtoni I ja II seadus kirjeldavad, kuidas keha liigub välise mõju puudumisel või olemasolul, siis kolmas seadus käib vastastikmõju enda kohta. Newton ise nimetas seda seadust mõju ja vastumõju seaduseks.
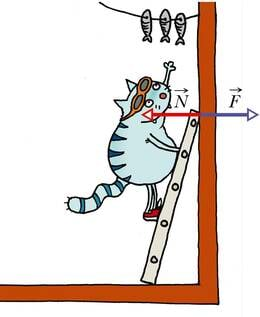
Kogemused näitavad, et kehad mõjutavad teineteist alati vastastikku. Kui toetame redeli seinale, siis mõjub sein redelile vastu ja seda nii, et redel püsib paigal.
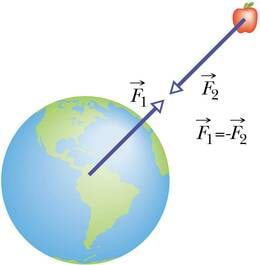
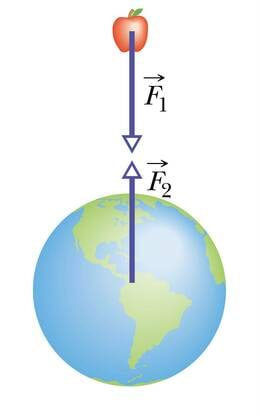
Kehad osalevad vastastikmõjus alati paarikaupa. Seejuures mõjuvad jõud mitte ainult ühele, vaid mõlemale kehale. Need kehadele mõjuvad jõud on suuruselt võrdsed ja suunalt vastupidised. Kui Maa tõmbab kukkuvat õuna jõuga , siis õun tõmbab maakera vastu täpselt sama suure jõuga.
Selles väljendubki mõju ja vastumõju ehk Newtoni kolmas seadus: kaks keha mõjutavad teineteist suuruselt võrdsete vastassuunaliste jõududega.
Kui eristada kahele vastastikmõjus osalevale kehale mõjuvaid jõude indeksitega 1 ja 2, saab Newtoni III seadust väljendada valemiga
Tuleb meeles pidada, et Newtoni III seaduse jõud mõjuvad eri kehadele ja seepärast ei saa need teineteist tasakaalustada, kuigi on võrdsed ja vastupidised.
Newtoni teine seadus näitab keha kiiruse muutumise sõltuvust keha massist ja sellele mõjuvast jõust. Kiiruse sama suure muutuse jaoks on suurema massi korral vaja kas suuremat jõudu või pikemat aega. Samas on mõju vastastikune – keha, mille kiirus muutub, mõjub teisele kehale sama aja jooksul sama jõuga vastu ja võib muuta selle liikumist või kuju. Näeme, et liikuval kehal on võime muuta teiste kehade liikumist.
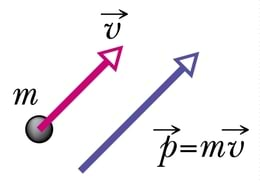
Keha võime vastastikmõju korral teist keha mõjutada sõltub kehade kiirusest ja massist. Sellele teadmisele tuginedes on liikumise iseloomustamiseks võetud kasutusele suurus, mida nimetatakse keha liikumishulgaks ehk impulsiks. Impulsi tähiseks on (pulsus – ld 'löök, impulss') ning see on defineeritud keha massi ja kiirusvektori korrutisena:
Impulsi mõõtühikuks on 1 kg·m/s. Tegemist on vektoriaalse suurusega, mille suund ühtib kiirusvektori suunaga.
Impulsi füüsikalist tähendust võib mõista näiteks põrgete vaatlemisel. Põrke mõju on seda suurem, mida suurem on keha impulss. Seepärast tuleb sadamakai ehitada väga tugev, muidu purustaks selle ka väga aeglaselt liikuv, kuid suure massiga laev. Samamoodi võib väike püssikuul tekitada suuri purustusi oma suure kiiruse tõttu. Nii laeval kui ka kuulil on suur impulss, ühel oma suure massi ja teisel suure kiiruse tõttu, ning need võivad teisi kehi suure jõuga mõjutada.
Osutub, et impulss on jõuga otseselt seotud. Võtame Newtoni II seaduse (1.2) ja asendame selles kiirenduse selle definitsiooni avaldisega
saame
Kui korrutame saadud võrduse mõlemad pooled keha massiga läbi, saame
Et massi ja kiiruse korrutis kujutab endast keha impulssi, siis avaldis
pole midagi muud kui impulsi muut. Seega võime kirjutada, et
Saime Newtoni II seadusele uue kuju, mis näitab, et impulsi muutumise kiirus on võrdne seda muutust põhjustava jõuga. Tegemist on väga olulise tulemusega, mida kasutatakse peale klassikalise dünaamika ka elementaarosakesi uurivas kvantmehhaanikas.
Liikumishulgal ehk impulsil on füüsika jaoks väga oluline omadus – jäävus.
Uurime kahe keha vastastikmõju. Newtoni III seaduse järgi mõjutavad need kehad teineteist võrdsete ja vastassuunaliste jõududega:
Kehale mõjuv jõud on vastavalt seosele (1.7 ) võrdne keha impulsi muutumise kiirusega. Nii saame Newtoni III seadusele kuju:
Et kehad mõjutavad teineteist sama kaua, võime ajavahemikud taandada ning avaldis lihtsustub:
ehk
Avaldis
kujutab endast mõlema keha impulsside muutude summat. Sisuliselt on tegemist kehade koguimpulsi
muuduga, mida võib tähistada kui
Seda tähistust kasutades saame seosele (1.9 ) kuju, mis väljendabki impulsi jäävuse seadust:
ehk
Näeme, et kui kaks keha teineteist mõjutavad, siis selle käigus nende koguimpulss ei muutu (muut = 0). Saab näidata, et impulsi jäävus kehtib ka kui tahes paljudest kehadest koosneva süsteemi jaoks. Ainsaks tingimuseks on see, et süsteemi mittekuuluvate kehade mõjud puuduvad.
Nii võimegi sõnastada impulsi jäävuse seaduse: väliste mõjude puudumisel on süsteemi koguimpulss sinna kuuluvate kehade igasugusel vastastikmõjul jääv.
Seaduse rakendamisel ei tohi unustada, et impulss on vektoriaalne ehk suunaga suurus.
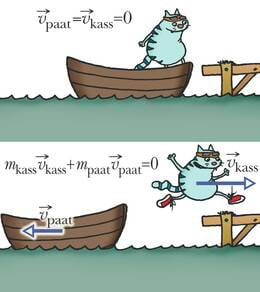
Impulsi jäävuses võib igaüks ise veenduda, kui astub kinniköitmata paadist kaldale. Enne väljaastumist on paat koos inimesega paigal ja nende koguimpulss null. Astumisel hakkab inimene kalda poole liikuma ja omab teatud impulssi. Et koguimpulss ei muutu ja jääb nulliks, saab paat vastassuunalise impulsi ning eemaldub kaldast.
Kogu teaduse ajaloo vältel pole avastatud ühtegi nähtust, mis oleks impulsi jäävusega vastuolus. See seadus on universaalne ning kehtib ka väljaspool mehaanika uurimisvaldkondi.
Impulsi jäävuse seaduse üheks huvitavaks ning oluliseks rakenduseks on reaktiivliikumine (re- + activus – ld 'vastu + tegutsev'), mida kasutatakse nii tehnikas kui ka mõne looma poolt looduses. Selleks et paigalt liikuma pääseda, on vaja vastastikmõju – teist keha, millest end eemale tõugata, nii et see vastavalt Newtoni III seadusele sama suure jõuga vastu mõjuks. Just tänu sellele saavadki kehad liikuma hakata. Jalad tõukavad teekatet, aerud vett, lennukipropeller õhku.
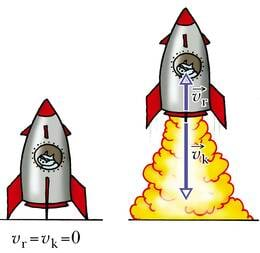
Kuidas lendavad aga kosmoseraketid õhutühjas maailmaruumis, kus pole midagi, millest end eemale tõugata? Kui läheduses sobiv keha puudub, tuleb see endaga kaasa võtta. Just niiviisi toimitakse rakettide lennutamisel. Rakett hakkab liikuma tänu sellele, et selle ühest otsast paisatakse läbi spetsiaalse ava (düüsi) suure kiirusega välja kütuse põlemisel tekkivad gaasid. Enne starti on paigalseisva raketi ja selles sisalduva kütuse impulss null. Kui nüüd kütuse põlemisel tekkivad gaasid ühes suunas välja lendavad, hakkab rakett ise vastassuunas liikuma. Muidu ei jääks raketist ja gaasidest koosneva süsteemi koguimpulss ju nulliks.
Nii tekibki raketi reaktiivliikumine. Reaktiivliikumiseks nimetatakse liikumist, mille tekitab kehast eemale paiskuv keha osa.
Hindame, millise kiiruse võib rakett kütuse ärapõlemisel saada. Oletame lihtsuse mõttes, et põlemisgaasid ei välju raketist tasapisi, vaid ühekorraga.
Olgu raketikesta ja selles asuva aparatuuri ning meeskonna mass , kütuse ja sellest tekkivate gaaside mass ning gaaside väljapaiskumise kiirus . Et algul on rakett paigal ja impulss null, saame impulsi jäävuse seaduse välja kirjutada järgmiselt:
Avaldame siit raketi kiiruse
Sellest valemist näeme, et rakett liigub gaaside väljapaiskumisele vastassuunaliselt (miinusmärk!) ja kiirus on seda suurem, mida suurem on kütuse ning raketi masside suhe ja mida suurema kiirusega gaasid välja pääsevad. Et kosmoselaev saavutaks Maalt lahkumiseks piisavalt suure kiiruse, peab kütuse mass ületama ülesviidava kasuliku massi hulka sadu kordi ning valida tuleb võimalikult kiiresti põlev kütus.
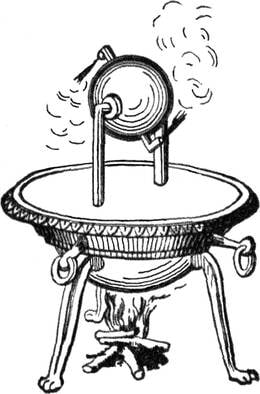
Esimese reaktiivliikumise põhimõttel töötava seadme ehitust on esimesel sajandil kirjeldanud antiikkreeka matemaatik ja insener Heron. Tegemist oli kahe düüsiga varustatud õõnsa metallkeraga, millesse suunati vee keemisel tekkiv aur. Düüsidest suure kiirusega väljuva auru reaktiivjõud pani selle nn Heroni kera pöörlema.
Tore näide reaktiivliikumise rakenduste kohta on muidugi ka hiinlaste 13. sajandil leiutatud püssirohuraketid, mida kasutatakse ilutulestikes siiamaani.
Tänapäeval on reaktiivmootorid väga levinud, kuna need võimaldavad saavutada suuri kiirusi. Nendeta ei saa läbi ükski kosmoselennuaparaat ning enamik kiireid lennukeid liigub samuti reaktiivjõul. Reaktiivmootoreid ei kasutata aga mitte ainult lennumasinatel. Neid on monteeritud ka autodele, millega maapealseid kiirusrekordeid püstitatakse. Kui reaktiivautod on üsna haruldased, siis veejoa reaktiivjõul Tallinna ja Helsingi vahet kihutavad Jeti kiirlaevad (jet – ingl 'juga') on üsna igapäevased.
Reaktiivmootoritega kohtume selles õpikus veel üks kord, kui räägime pöördliikumise kasutamisest tehnikas.
Reaktiivliikumist võib kohata ka mitme veelooma juures. Näiteks kasutavad kalmaarid, meduusid ja rannakarbid edasiliikumiseks endasse imetud vee kiiret väljasurumist.
See, kuidas keha liigub, sõltub sellele mõjuvatest jõududest. Millised need jõud aga olla võivad ning millest ja kuidas sõltuvad? Järgnevalt tutvumegi suurema osaga peamistest jõududest, mida looduses kohata võime. Elektri-, magnet- ja tuumajõud leiavad käsitlemist järgmistes füüsikakursustes.
1638. aastal avaldas Galilei oma raamatus „Discorsi“ uurimistulemused, mille järgi kukuvad kõik kehad Maa külgetõmbe tõttu ühesuguse kiirendusega. Kust aga pärineb see jõud, mis kõiki kukkuvaid kehi kiirendab? Selle ja muude liikumisega seotud küsimuste kallal juurdles üsna pikalt tolleks ajaks juba mitmete optikanähtuste selgitamisega tuntuks saanud Newton.
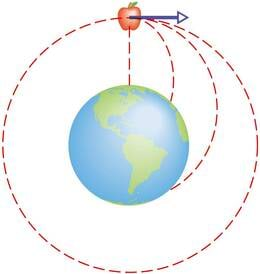
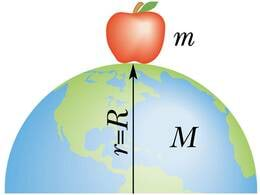
Legendi järgi kukkunud kord murul istunud Newtonile pähe õun. See pannud mehe juurdlema, miks õun alati maha kukub ja miks see üldse kukub. Kas tõmbab ainult Maa õuna või on ka õunal selline külgetõmbejõud?
Otse üles visatud õun kukub samasse kohta tagasi. Eemale visatud õun maandub seda kaugemal, mida kiiremini seda visatakse. Kas õun võiks teha terve tiiru ümber Maa, kui kiirus oleks piisavalt suur? Kas Kuu tiirlemine ümber Maa polegi just selline kukkumine?
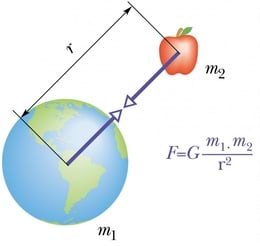
Kas õun toona 23-aastasele Newtonile ka tegelikult pähe kukkus, pole teada. Igal juhul on ta ise mitu korda jutustanud, et just kukkuv õun viis mõtted külgetõmbeprobleemidele. Lisaks oma uurimustele üldistas teadlane ka Galilei avastatud vaba langemise seadust ning Koperniku ja Kepleri astronoomiliste vaatluste andmeid. Pingsa mõttetöö ja omaleiutatud matemaatilise analüüsi meetodi rakendamise tulemusena avastaski Newton seaduse, millele kehadevaheline külgetõmbejõud allub: kaks punktmassi tõmbuvad teineteise poole jõuga, mis on võrdeline nende masside korrutisega ning pöördvõrdeline nendevahelise kauguse ruuduga.
Matemaatiliselt avaldub gravitatsiooniseadus valemina:
Valemis tähistab mõlemale kehale (punktmassile) võrdselt mõjuvat gravitatsioonijõudu, ja kummagi keha massi ning nendevahelist kaugust. Tähega tähistatud kordajat nimetatakse gravitatsioonikonstandiks.
Tegemist on universaalse seadusega. Gravitatsioonijõud mõjub kõikidele kehadele ning ulatub valgusaastate kaugusele.
Kui valemis võtta mõlema keha massiks ja vahekauguseks , saame valemist (1.13 )
Järelikult on gravitatsioonikonstant arvuliselt võrdne jõuga, millega tõmbuvad kaks teineteisest kaugusel asuvat massiga keha. Selle arvuline väärtus sõltub mõõtühikute valikust ning on määratav vaid eksperimentaalselt.
Maapealsete suhteliselt väikese massiga kehade vaheline tõmbumine on äärmiselt nõrk. See muudab gravitatsioonikonstandi mõõtmise keeruliseks. Esimest korda määras gravitatsioonikonstandi väärtuse täpsete väändkaalude abil 1798. aastal inglise füüsik Henry Cavendish. Ta sai tulemuseks 6,754·10−11 N·m2/kg2, mis on üsna lähedane tänapäeval tuntud väärtusele 6,67428·10−11 N·m2/kg2.
|
|
|---|---|
| Cavendishi katses tõmbusid kuulid massiga 0,7 kg kuulide poole, mille mass oli 158 kg. | Cavendishi gravitatsioonikonstandi määramiseks kasutatud väändkaalude rekonstruktsioon. Muide, selle seadme konstrueeris John Michell, mees, keda mainime siin raamatus ka kui mustade aukude väljamõtlejat. |
Meie jaoks on eriline muidugi see gravitatsioonijõud, millega Maa tõmbab kõiki seda ümbritsevaid kehi. Tänu sellele jõule kukuvad kõik kehad alla Maa keskpunkti poole ja on tõstmisel rasked. Tegemist on meile tuttava raskusjõuga. Raskusjõud pole iseloomulik mitte ainult Maale, vaid ilmneb tugevamalt või nõrgemalt kõikidel taevakehadel. Raskusjõuks nimetatakse gravitatsioonijõudu, millega Maa või mis tahes muu taevakeha tõmbab enda poole selle lähedal asuvaid kehi.
Raskusjõu saame leida gravitatsiooniseadusest (1.13 ). Võttes ühe keha massiks Maa massi ning vahekauguseks Maa raadiuse , tuleb maapinnal asuvale kehale massiga mõjuvaks raskusjõuks
Kui suure kiirenduse see jõud kehale annab? Kasutame Newtoni II seadust (1.2 ):
ehk
Et Maa mass on 5,98·1024 kg ja raadius 6370 km = 6,37·106 m, annavad arvutused
See kiirenduse väärtus on meile tuttav kui vaba langemise kiirendus. Vaba langemise kiirendust nimetatakse veel raskus- ehk gravitatsioonikiirenduseks. Viimasest ongi tulnud tähis .
Teades nüüd, et vabalt langeva keha kiirendus on , saame Newtoni II seadusest seda kiirendust tekitava jõu ehk raskusjõu arvutamiseks lihtsa valemi:
See raskusjõud on suunatud Maa keskpunkti ega ole seepärast Maa kõigis punktides samasuunaline.
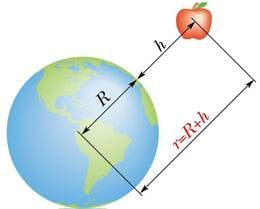
Kõrguse kasvades raskuskiirendus väheneb, sest valemis (1.21 ) tuleb Maa raadiusele liita ka kõrgus maapinnast h:
Kuna raskuskiirenduse vähenemine muutub märgatavaks alles 100 km kõrgusel, mida loetakse kokkuleppeliselt kosmose piiriks, siis on tavaelus mugavam kasutada nn lapiku Maa mudelit (midagi antiikaegse ettekujutuse sarnast). Selle mudeli puhul mõjub kõikidele Maa-lähedastele kehadele vertikaalselt alla suunatud raskusjõud, mis kõrgusest ei sõltu.
Tänu gravitatsioonile mõjutab keha oma alust või riputusvahendit, mis takistab keha liikumist Maa keskpunkti poole. Seda jõudu, millega keha Maa külgetõmbe tõttu mõjub alusele, keskkonnale või riputusvahendile, nimetatakse keha kaaluks. Kaalu tähis käesolevas kursuses on ning mõõtühik 1 N (mitte igapäevasele kõnepruugile vastavalt 1 kg, kuna tegemist pole massiga!).
Kui alus või riputusvahend on paigal või liigub ühtlaselt ja sirgjooneliselt, on keha kaal võrdne raskusjõuga. Kui alus liigub vertikaalsuunalise kiirendusega, siis kaal enam raskusjõuga võrdne pole. Kaal sõltub kiirendusest.
Kui alus liigub kiirendusega üles, peab see kehale kiirenduse andmiseks rakendama lisajõudu. Kaal on sel juhul raskusjõust suurem ja öeldakse, et tegemist on ülekoormusega:
Kiirendusega alla liikumisel on vastupidi. Tegemist on alakoormusega:
Kaalu sõltuvust kiirendusest võime tajuda liftis. Tõusu alguses tunneme ülekoormust ja lõpus alakoormust.
Ülaltoodut arvestades saab kaalu seost kiirendusega väljendada ühe kokkuvõtva valemiga:
Kui aga alus või riputusvahend üldse eemaldada, siis kaob ka keha mõju sellele. Kui pole mõju alusele või riputusvahendile, ei saa olla ka kaalu ning tegemist on kaalutuse ehk kaaluta olekuga. Kõik vabalt langevad kehad on kaaluta olekus.
Kaalu ja raskusjõudu ei tohi samastada, sest need jõud mõjuvad eri kehadele. Keha kaal mõjub alusele või riputusvahendile ja on olemuselt elastsusjõud. Raskusjõud on olemuselt gravitatsioonijõud, mis mõjub kehale endale. Need on täiesti erinevad jõud.
Raskusjõud
Raskusjõuks nimetatakse gravitatsioonijõudu, millega Maa või mis tahes muu taevakeha tõmbab enda poole selle lähedal asuvaid kehi.
Raskuskiirendus
Gravitatsioonijõu mõjul vabalt langemise kiirendust nimetatakse raskus- ehk gravitatsioonikiirenduseks.
Igapäevaelus me ei pane gravitatsiooni tähele. Aga kui järele mõelda, siis on selle mõju kõikjal. Anname siin vaid ühe lihtsa näite, räägime põlemisest - kui ei oleks gravitatsiooni, siis ei tekiks ka konvektsiooni ja leek lämbuks omaenda tekitatud süsinikdioksiidi "mullis".
|
|
|---|---|
| Küünla põlemine koos gravitatsiooniga (vasakul) ja ilma selleta (paremal). | Kui tõmmata kaaluta olekus tikku, siis ... |
Veel maapealsetest asjadest.
Kuu ja Päikese gravitatsiooniline tõmbumine põhjustab maailmamere loodeid ehk tõuse ja mõõne. Eriti tugevad looded esinevad siis, kui Päike ja Kuu paiknevad samal pool Maad viimasega ühel sirgel, st kuu loomise ajal. Korraga on Maal tõus nii sellel poolel, mis asub Kuu suunas, kui ka vastasküljel. Kuna vesi saab voolata, siis koguneb see rohkem Maa Kuu-poolsele küljele ja tõstab meretaset. Pöörlemisel tekivad inertsijõud, mis püüavad kõike pöörlemisteljest eemale paisata. Kuust kaugeimas punktis avaldub see kõige märgatavamalt, kuna seal on Maa kaaslase külgetõmme kõige nõrgem.
Pöördume loodete juurde veel üks kord tagasi, kui käsitleme võnkumisi ja resonantsi.
Refereerime järgnevalt Piret Kuuse artiklit, mis ilmus ajakirjas Horisont.
Vaatlused ja kogemused kinnitavad, et taevakehad on meile nähtavad, sest kiirgavad või peegeldavad valgust, ja tuntavad, kui satume nende lähedusse, sest need rakendavad meile külgetõmbavat raskus- ehk gravitatsioonijõudu. Kuulus inglane Isaac Newton (1642/3–1727) formuleeris kaks teooriat – optika ja mehaanika –, mis neid kahte mõju – valgust ja raskusjõudu – kirjeldavad teineteisest täiesti sõltumatult. Kuid 1783. aastal küsis teine Inglise loodusteadlane John Michell (1724–1793): aga mis siis, kui ka valguskorpusklile (Newtoni optikas käsitati valgust korpusklite voona) mõjub raskusjõud? Newtoni mehaanikast on teada, et paokiirus ümmarguselt kehalt massiga raadiusega on
kus on Newtoni gravitatsioonikonstant. Kui ükskõik milline objekt visata sellise keha pinnalt üles suurema kiirusega kui , siis selle kineetiline energia ületab gravitatsiooni potentsiaalse energia ning see ei kuku enam tagasi. Jupiteri kuude liikumise vaatluste põhjal oli juba 1676. aastal järeldatud, et valguse kiirus on lõplik. Niisiis kui taevakeha paokiirus on suurem kui valguse kiirus, ei saa valguskorpusklid enam selle juurest eemalduda lõpmata kaugele: „üles visatud" valguskorpusklid langevad taevakeha pinnale tagasi ja viimane muutub küllalt kaugel olevale vaatlejale nähtamatuks.
Selliseid taevakehasid nimetas Michell tumetähtedeks. Michelli arvutuste kohaselt muutuks näiteks Päikese massiga täht tumetäheks, kui selle raadius oleks 18,5 kilomeetrit. Kuna oli teada, et Päikese raadius on määratult palju suurem, ligi 700 000 kilomeetrit, olid Michelli tumetähed vaid võimalikud teoreetilised konstruktsioonid korpuskulaaroptika raames. Huvi nende vastu kustus täielikult, kui Inglise teadlane Thomas Young (1773–1829) avastas valguse interferentsi ja korpuskulaaroptika asendus laineoptikaga.
Tänapäeval ei kirjeldata gravitatsiooni ja valgust enam Newtoni teooriatega, vaid Einsteini-Maxwelli võrranditega.
Einstein formuleeris oma gravitatsioonivõrrandid 1915. aasta novembris ning avaldas need lühiteatena Preisi Teaduste Akadeemia toimetiste 25. novembril ilmunud numbris. Seda luges Esimese maailmasõja idarindel Saksa astrofüüsik Karl Schwarzschild (1873–1916), kes sõja puhkedes 1914. aastal oli astunud sõjaväkke ning jõudnud kahe aastaga suurtükiväe leitnandi auastmeni. Sealsamas sõjaväljal õnnestus tal leida Einsteini võrrandite üks väga lihtne lahend, nimelt selline, mis kirjeldab aegruumi geomeetriat väljaspool täpselt kerasümmeetrilist staatilist keha massiga M. Seda lahendit nimetatakse praegu Schwarzschildi välimiseks lahendiks ehk lihtsalt Schwarzschildi lahendiks.
Schwarzschild telegrafeeris leitud lahendi Einsteinile, kes esitas selle Preisi TA koosolekul 13. jaanuaril 1916. Mõned nädalad hiljem saatis Schwarzschild Einsteinile veel teisegi lahendi, mis kirjeldab aegruumi geomeetriat staatilise kerasümmeetrilisena ainelise keha sees. Seda nimetatakse praegu Schwarzschildi sisemiseks lahendiks. Kuigi see ei ole nii kuulus kui too eelmine, on mõlemal lahendil võrdselt oluline roll relativistlikus astrofüüsikas: kerasümmeetrilise tähe lihtsaima mudeli konstrueerimist tuleb alustada tähe pinnast seespool kehtivast Schwarzschildi sisemisest lahendist, mis tähe pinnal tuleb sujuvalt (siledalt, nagu ütlevad matemaatikud) ühendada Schwarzschildi välimise lahendiga.
Schwarzschildi valemid sisaldavad matemaatilist võimalust, mis on mõneti analoogne Michelli tumetähega: kui massiga M kerasümmeetrilise tähe raadiust vähendada seni, kuni see on jõudnud väärtuseni
(seda nimetatakse ka selle tähe Schwarzschildi raadiuseks), siis ei saa tähe pinnalt mitte miski eemalduda, isegi mitte valgus. Pind raadiusega Rg osutub läbimatuks kõigele, mis tahaks liikuda keskelt läbi selle pinna väljapoole.
Vaid mõni kuu hiljem, 19. juunil 1916, pidi Einstein Preisi Teaduste Akadeemias teatavaks tegema kurva sõnumi: Karl Schwarzschild on Vene rindel haigestunud ja 11. mail jäädavalt lahkunud.
Kuna Einsteini võrrandid kirjeldavad gravitatsiooninähtusi, mis oletatavasti on taevakehade ehituse ja liikumiste alus, siis on üsna loomulik küsida, kas taevas on olemas ka midagi sellist, mida matemaatiliselt võiks kirjeldada Schwarzschildi välimine lahend. Kas üldse ja kui, siis kuidas võiksime ära tunda kosmilise objekti, mis tegelikult ei olegi ju objekt, vaid ainult tühja kõvera aegruumi teatud konfiguratsioon?
Seda võimalikku konfiguratsiooni on hakatud kutsuma mustaks auguks.
Ajalooliselt kõige esimesena väljaarvutatud protsess, mis universumis võiks toimuda ja kus mustad augud võiksid mängu tulla, on gravitatsiooniline kollaps. Oma arengu hilistes staadiumides, kui tähed on ära põletanud kogu oma tuumkütuse ja hakkavad jahtuma, ei ole enam väljapoole suunatud kiirgusrõhku, mis võiks vastu seista täheainet kokku suruvale raskusjõule. Suurte tihedusteni jõudmise järel võib kiirgusrõhu asemel raskusjõudu tasakaalustada elektrongaasi või neutrongaasi rõhk, kuid juba 1939. aastal avaldati arvutused, mis andsid stabiilse lõppseisundiga tähe massi ülempiiriks umbes kolm Päikese massi (nn Tolmani-Oppenheimeri-Volkoffi piir). Sõna "umbes" tähistab siin asjaolu, et arvutused on tehtud teooria raames, mis ei pruugi nii äärmuslikes tingimustes olla päris täpne. Siiski annab see alust väita, et juhul kui tähe mass on nimetatud piirmassist suurem, surutakse täht kokku pöördumatult ja kogu täheaine kaob lõkspinna taha, mis ühtlasi tähendab musta augu teket.
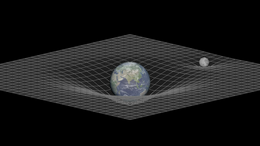
Omalt poolt mainime siin veel aegruumi ja selle kõverdumist gravitatsiooniväljas. Seda eelkõige põhjusel, et internetist ja raamatutest leiab tihti illustratsioone, kus Maa või mõni täht on justkui kummikelme sisse vajunud (vt joonist). Mida raskem objekt, seda "sügavamale" see vajuks, nii et musta augu keskel olev kustunud täht moodustaks väga kitsa ja väga sügava augu. Kui panna sellisele pinnale veerev kuul, siis ta veereks massiivsele objektile lähemale, sarnaselt, kui seda tõmbaks gravitatsiooniväli. Siiski on tähtis meeles pidada, et ilmaruumis ei ole selliseid auke, on vaid objektid, millel on tugev gravitatsiooniväli. Lihtsalt aegruum on neljamõõtmeline ja meie kolmemõõtmelises ruumis on seda keeruline päris õigesti kujutada.
Tähed tekivad tähtedevahelisest keskkonnast ja selle protsessi algpõhjus on gravitatsioon.
Tähtedevahelise keskkonna moodustavad küllalt heas lähenduses gaas ja tolm. Keskmiselt on tolmu osakaal massi järgi vaid 1% ja gaasi osakaal 99%. Tolmuosakeste keskmine arvtihedus on 10−6 – 10−7 m−3, gaasiaatomitel 106 m−3 (gaasi tihedus on seega 1 osake kuupsentimeetris). Aga gravitatsioonijõud mõjub ka sellises keskkonnas.
Tähtede teke algab, kui osa tähtedevahelisest keskkonnast − mõni eespool kirjeldatud tumedatest pilvedest − hakkab oma raskuse mõjul kokku tõmbuma. Seda nimetatakse gravitatsiooniliseks ebastabiilsuseks. Kokku tõmbudes pilve osad kuumenevad. Teatud ajal on temperatuur pilve tsentris tõusnud nii kõrgele, et algavad termotuuma reaktsioonid. Siis kokkutõmbumine peatub ja on sündinud täht.
Paneme siiski tähele, et selline on äärmuseni lihtsustatud skeem ning täheteadlased peavad vaatamata üha kasvavatele arvutusvõimsustele tähtede tekke numbrilistes mudelites mitmeid lihtsustusi tegema.
Mis määrab selle, milline tähtedevahelise gaasi pilv kokku tõmbuma hakkab? Pilves toimivad kaks vastandlikku protsessi: gravitatsioon mõjub tõmbavalt ja soojusliikumise kiirused mõjuvad hajutavalt. Tasakaalu gaasipilvedes uuris James Jeans ning vastavat stabiilsuse kriteeriumit nimetatakse Jeansi kriteeriumiks.
Keha võib teisi kehi mõjutada lisaks kaalule veel muudki liiki jõududega. Arvuti taga istuv õpilane toetub seljatoele, õhupalli puhutav õhk paneb selle paisuma, press surub korgitüki õhemaks, magnet hoiab nõela ... Mõjutatava keha jaoks pole seejuures oluline, mis liiki need jõud on. Tähtis on vaid jõu ja sageli ka mõjupinna suurus.
Et kõiki selliseid mõjusid saaks kirjeldada ühtse mudeli abil, on võetud kasutusele rõhumisjõu mõiste. Rõhumisjõuks nimetatakse jõudu, millega üks keha mõjutab teist risti kokkupuutepinnaga. Rõhumisjõu tähisena kasutatakse jõu üldtähist . Rõhumisjõud mõjub alati pinnaga risti.
Vastavalt Newtoni III seadusele tekib keha mõjutamisel alati vastumõju ehk reaktsioon. Tegemist on jõuga, mida nimetatakse toereaktsiooniks. Rõhumisjõu toimel keha kuju muutub (keha deformeerub) ja see põhjustab vastassuunas mõjuva elastsusjõu, mis ongi toereaktsioon. Toereaktsiooniks nimetatakse rõhuvale kehale toetuspinnaga risti mõjuvat vastujõudu.
Kuna toereaktsioon on alati suunatud piki pinna ristsirget ehk normaali, on selle tähiseks käesolevas kursuses valitud . Rõhumisjõud ja toereaktsioon on alati võrdsed ja vastassuunalised:
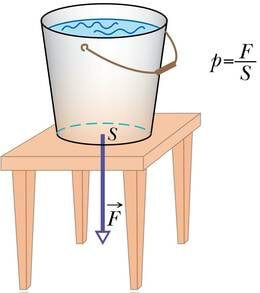
Kui teineteist mõjutavaid kehi ei või ette kujutada punktmassidena, kuna nende kuju on oluline, mõjub rõhumisjõud mingile konkreetse suurusega pinnale. Rõhumisjõu tagajärg sõltub selle pinna suurusest. Kui pind on suur, hajub jõud üle selle laiali ning mõju kindla suurusega pinnatükile jääb väiksemaks. Arvestamaks rõhumisjõu jaotumist mõjupinnale kasutatakse mõistet rõhk. Rõhuks nimetatakse füüsikalist suurust, mis on võrdne rõhumisjõu F ja pindala S jagatisega. Rõhu tähiseks on (ld pressûra 'rõhk')
Rõhu mõõtühik on 1 paskal – 1 Pa = 1 N/m2. Ühik on nime saanud prantsuse füüsiku Blaise Pascali järgi.
Erinevalt jõust ei ole rõhk vektoriaalne suurus. Põhjus on selles, et rõhu leidmisel arvestatakse vaid pinnaga risti olevat jõudu. Näiteks gaasides ja vedelikes ei saagi me suunast üldse rääkida, kuna rõhk antakse edasi kõikides suundades ühtemoodi.
Oletame, et inimene suudab lükata jõuga 500 N, ja oletame, et ta lükkab veoautot massiga 5000 kg. Selline jõud peaks veokile andma kiirenduse 0,1 m/s2 ning 10 sekundiga läbiks see 5 m ja saavutaks kiiruse 5 m/s. Ometi ei jaksa ükski inimene viietonnist autot paigalt lükata. Miks?
Siin tuleb mängu uus jõuliik hõõrdejõud. Hõõrdejõud on väga oluline, kuna mõjub maapealsetes tingimustes kõikidele liikuvatele kehadele. Iga liikuv keha jääb hõõrdejõu tõttu lõpuks seisma, kui mingi muu jõud hõõrdejõude ei kompenseeri. Hõõrdejõu vähendamise vajadusega on kokku puutunud kõik suusatajad, seevastu teemeistrid näevad vaeva, et talvistel teedel hõõrdumist suurendada. Hõõrdejõuga seonduva tundmine on eluliselt tähtis.
Hõõrdejõud mõjub mitte ainult liikuvatele, vaid ka paigalseisvatele kehadele. Näiteks püsib veeklaas käes ja nael seinas just tänu hõõrdejõule.
Hõõrdejõuks nimetatakse jõudu, mis takistab keha liikumist või liikumahakkamist. Et jõud takistab liikumist, nimetatakse seda vahel ka takistusjõuks. Hõõrdejõud tekib alati kehade vahetul kokkupuutel, mõjub piki kokkupuutepinda ja on suunatud vastassuunas liikumisele. Seejuures on olemas mitmesuguseid võimalusi.
Näiteks on olemas võimalus, et mingi jõud püüab keha liikuma panna, kuid hõõrdumise tõttu jääb keha paigale. Nähtust, kus hõõrdejõu tõttu püsib keha paigal, nimetatakse seisuhõõrdumiseks. Seisuhõõrdejõud on alati suuruselt võrdne ja vastassuunaline jõuga, mis püüab keha liikuma panna.
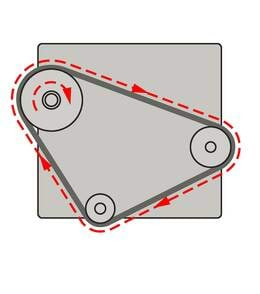
Kui inimene kõnnib, siis on edasiviivaks jõuks hõõrdejõud. Et tald teekatte suhtes ei liigu, on siin tegemist just seisuhõõrdumisega. Ka see jõud, mis annab rihmülekande korral liikumise ühelt rattalt teisele üle, on seisuhõõrdejõud rihmarataste ja rihma vahel.
On ka võimalik olukord, kus keha liigub ning libiseb mööda teise keha pinda. Nähtust, kus hõõrdumine takistab mööda teise keha pinda libiseva keha liikumist, nimetatakse liugehõõrdumiseks. Liugehõõrdumise korral on hõõrdejõud suunatud alati liikumisele vastassuunas.
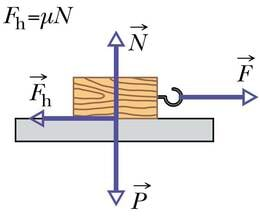
Jõu suurus sõltub kokkupuutuvate pindade omadustest ning pindu kokku suruva jõu suurusest. Vastu mingit pinda surumisel mõjub kehale rõhumisjõuga võrdne vastassuunaline toereaktsioon N. Katsed näitavad, et liugehõõrdejõud on võrdeline kehale mõjuva toereaktsiooniga:
Võrdetegurit μ (kreeka täht müü) selles valemis nimetatakse hõõrdeteguriks. Sageli, kui keha libiseb mööda horisontaalset pinda, on toereaktsioon arvuliselt võrdne kehale mõjuva raskusjõuga ja sel juhul
Avaldame hõõrdejõu valemist (1.25 ) hõõrdeteguri:
Näeme, et hõõrdetegur on võrdne hõõrdejõu ja toereaktsiooni jagatisega.
Hõõrdetegur ei iseloomusta mitte keha, millele hõõrdejõud mõjub, vaid libisevaid pindu. See sõltub kokkupuutuvate kehade materjalist, pindade töötlusest ja puhtusest. Samas ei sõltu hõõrdetegur kokkupuutepinna suurusest ega libisemise kiirusest, kui surve ja kiirus pole väga suured.
Hõõrdeteguri suurust saab määrata katseliselt. Siledate pindade vahelised hõõrdetegurid mõnede materjalide jaoks on esitatud järgnevas tabelis.
Hõõrdejõud võib olla nii kasulik kui ka kahjulik. Kui on vaja keha paigal hoida või pidurdada, peab hõõrdejõud olema võimalikult suur. Liikumist segavat hõõrdumist tuleb aga vähendada.
Et osata hõõrdumist muuta, on vaja teada, miks hõõrdumine üldse tekib. Hõõrdumisel on kaks peamist põhjust.
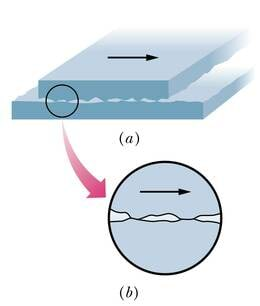
Esiteks põhjustab hõõrdumist pindade ebatasasus. Pinnakonarused jäävad üksteise taha kinni ja takistavad libisemist.
Teiseks põhjuseks on aineosakeste vahelised tõmbejõud. Väga siledad pinnad pääsevad teineteisele sedavõrd lähedale, et molekulidevahelised jõud kasvavad märgatavaks. Nii kleepuvad kokku kaks siledat plii- või klaasplaati.
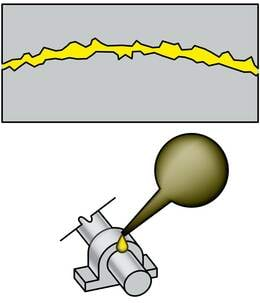
Hõõrdejõu vähendamiseks kasutatakse määrimist. Määre tungib kokkupuutuvate pindade vahele ja surub need teineteisest eemale. Pinnakonarused ja molekulide tõmbejõud siis enam nii tugevasti mõjule ei pääse. Määrdena kasutatakse tavaliselt õlisid. Õlikihtide omavaheline liikumine tekitab küll teatavat takistust, kuid see on tavalisest hõõrdumisest tunduvalt väiksem.
Hõõrdumist saab suurendada pindade karestamise abil. Et tagada ohutu liiklemine, pinnatakse maanteed peene killustikuga ja liikluseeskiri nõuab piisavalt sügava mustriga autokummide kasutamist.
Suurema hõõrdumise saavutamiseks kasutatakse ka spetsiaalseid materjale, mis tagavad suurema hõõrdeteguri. Nii valmistatakse autode piduriklotsid vähekuluvast kuumakindlast ainest, mille hõõrdetegur kokkupuutel terasega ulatub väärtuseni 0,7.
Hõõrdetegur
Liugehõõrdejõud on võrdeline kehale mõjuva toereaktsiooniga, vastavat võrdetegurit nimetatakse hõõrdeteguriks.
Teame, et vastastikmõju üheks võimalikuks tagajärjeks on kuju muutumine. Keha kuju muutumist nimetatakse deformeerumiseks ning selle tagajärjel tekkivat kujumuutust deformatsiooniks (ld de- + fôrma 'ära, vastupidi + kuju').
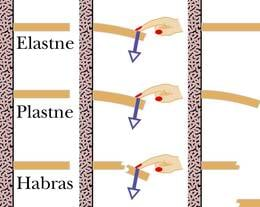
Deformeerumine võib olla kas pöörduv või pöördumatu protsess. Kui keha pärast deformeeriva mõju lõppemist taastab oma esialgse kuju kas täielikult või osaliselt, on tegemist elastse deformatsiooniga. Absoluutselt elastse deformatsiooni korral taastub endine kuju täielikult. Kui pärast surve lõppu säilub deformeerimisel saadud kuju, on tegemist plastse deformatsiooniga.
Keha elastsus või plastsus sõltub selle materjalist ja kujust. Väga elastsed on näiteks terasvedru ja kumminöör ning plastsed pehme savi ja plastiliin. Paljude kehade korral on väikene deformatsioon elastne, kuid suure kujumuutuse järel nende kuju enam ei taastu. Niimoodi käitub näiteks alumiinium- või vasktraat.
Kui keha aga juba väga väikese deformatsiooni tagajärjel puruneb, siis öeldakse, et see on habras.
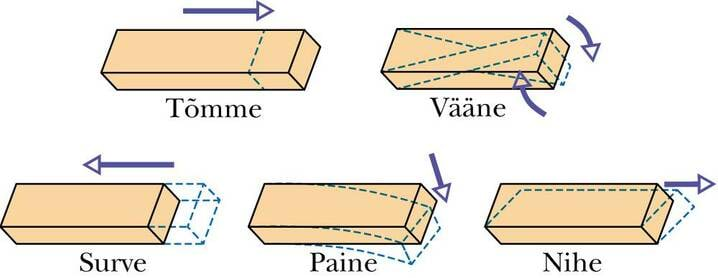
Keha kuju võib muutuda mitmel viisil. Näiteks saame kummipaela venitada, puuoksa painutada ja svammi kokku suruda. Selle põhjal, kuidas kuju muutub, eristatakse viit liiki deformatsioone: tõmme, surve, paine, vääne ja nihe.
Sageli ei pane me kehade kuju muutumist tähele, sest deformatsioon on väike. Kui keegi ronib näiteks suure kivirahnu otsa, siis ei suuda selle lamedamaks vajumist keegi ka luubiga vaadates märgata.
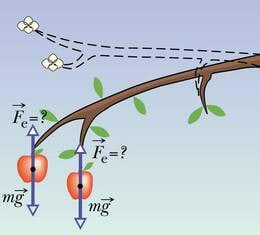
Kevadel on õunapuuoks täis õhkkergeid õisi. Siis hakkavad õitest õunad arenema ja viljad paisuvad ning muutuvad aina raskemaks. Kuidas need oksa küljes püsivad? Koos raskusjõu kasvamisega peab suurenema ka jõud, mis tasakaalustab raskusjõu. Kust on see jõud pärit ja milline on selle olemus?
Jälgides oksa juures toimunud muutusi, võib näha, et oks on paindunud. Oksa deformatsioon ongi uue jõu tekkimise põhjuseks. Jõudu, mis tekib keha kuju muutmisel ehk deformeerimisel, nimetatakse elastsusjõuks.
Elastsusjõud on deformatsiooniga alati vastassuunaline. Elastsusjõud püüab keha esialgset kuju taastada. Absoluutselt plastse deformatsiooni korral mingit kuju taastumist ei toimu ja järelikult puudub seda põhjustav jõud, st elastsusjõud on null.
Elastsusjõudude tekkepõhjuseks on aineosakeste vaheline vastastikmõju. Osakeste vahel esineb nii tõmbumine kui ka tõukumine, kusjuures mõlema tugevus sõltub vahekaugusest. Tavalises deformeerimata olekus on need jõud tasakaalus.
Kokkusurumisel osakeste vahekaugused vähenevad ning ülekaalu saavutavad tõukejõud, mis takistavad deformeerimist. Tõmbedeformatsioonil seevastu vahekaugused kasvavad ja ülekaalu jäävad venitamist takistavad tõmbejõud.
Elastsusjõudu võib kohata kõikjal ümberringi. Seda kasutatakse näiteks vibunoole lendulaskmisel, kellamehhanismis, soengute tegemisel (juuksekumm), ukse sulguris, dokumentide kooshoidmisel (kirjaklamber) jm. Elastsusjõuga on seotud kõik põrked. Elastsel põrkel taastab elastsusjõud põrandaga kokkupuutel deformeerunud palli kuju ja tõukab sellega palli vastassuunas liikuma. Plastse põrke korral jäävad kehad kokku ja liikumine muutub vähem.
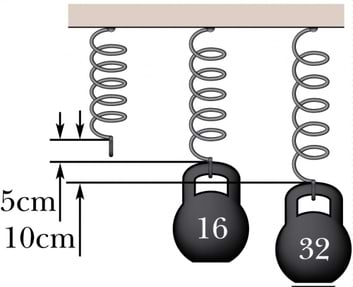
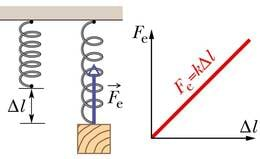
Mõõtmised näitavad, et suhteliselt väikeste deformatsioonide korral tekkiv elastsusjõud on võrdeline kujumuutuse ehk deformatsiooni suurusega. Kujumuutust on kõige lihtsam mõõta tõmbe ja surve korral. Siis iseloomustab deformatsiooni alg- ja lõpp-pikkuse vahe ehk pikenemine, mida järgnevas tähistame sümboliga . Elastsusjõu sõltuvust pikenemisest kirjeldab valem:
Selle seaduspärasuse avastas 1660. aastal inglise füüsik ja loodusteadlane Robert Hooke. Tänapäeval tuntakse seda seost Hooke’i seaduse nime all. Miinusmärk viitab asjaolule, et elastsusjõud on suunatud alati deformatsiooni suunale vastupidiselt. Võrdetegurit nimetatakse deformeeritud keha jäikusteguriks ehk lihtsalt jäikuseks. Jäikustegur sõltub keha materjalist, mõõtmetest ja kujust ning selle mõõtühik on 1 N/m.
Hooke’i seadus kehtib vaid keha mõõtmetega võrreldes väikeste kujumuutuste korral, mil deformatsioon jääb absoluutselt elastseks. Suuremad deformatsioonid põhjustavad keha sisemises ehituses pöördumatuid muutusi ja seetõttu muutub ka esialgset kuju taastav elastsusjõud.
Deformeerumine ja deformatsioon
Keha kuju muutumist nimetatakse deformeerumiseks ning selle tagajärjel tekkivat kujumuutust deformatsiooniks.
Elastne deformatsioon
Plastne deformatsioon
Kui pärast surve lõppu säilub deformeerimisel saadud kuju, on tegemist plastse deformatsiooniga.
Dünaamika on teadus kehade liikumisest, kui neile mõjuvad jõud. Kes tahab Kuule lennata, peab dünaamikat hästi teadma ja ei roni lennukiiruse saavutamiseks kahurisse.
