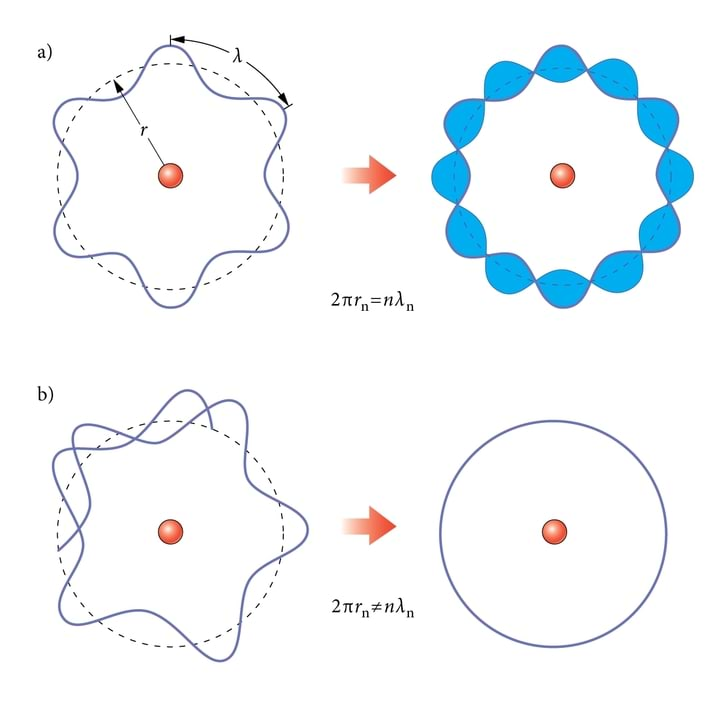
Elektronlained orbiidil. Bohri aatom

Elektroni leiulaineid ei sulusta aatomisse muidugi mitte kujuteldava karbi seinad, vaid elektrilised tõmbejõud tuuma ja elektroni(de) vahel. Astume sammu karbimudelilt tegelikkusele lähemale ja üritame sobitada elektroni laineloomust aatomi planetaarmudeliga. Vaatame lihtsaimat, vesiniku aatomit ainsa elektroniga ringorbiidil raadiusega $r$ (joon. 7.4). Kui elektron tiirleb orbiidil, peavad tema leiulained olema orbitaallained, s.o. tiirutama orbiiti pidi ümber tuuma. Elektroni statsionaarsetele, püsiseisunditele vastavad seisulained.

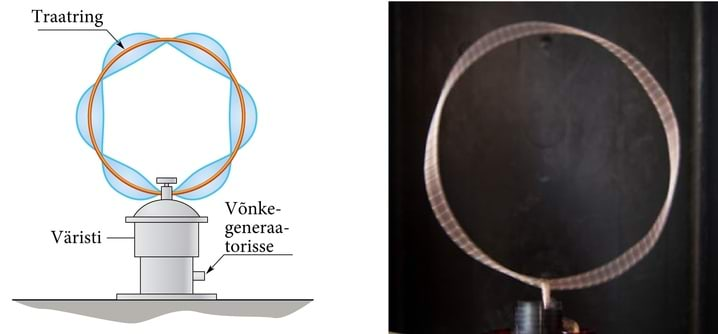
Joon. 7.4. Elektronlaine ringorbiidil. Juhul A üksteisele järgnevad lained ühtuvad, lainete tõusuinterferents tekitab püsiva seisulaine. Juhul B kustutab mõõnainterferents laine, elektroni leiutõenäosus kahaneb nulliks, püsiolekut ei teki.

Otsteta ringil saavad orbitaallaineist tekkida seisulained ainult siis, kui laine ringeldes end lakkamatult kordab (joon. 7.4). Selleks peab ringile sobituma parajasti täisarv laineid:

(7.5)

2 π r = n λ, n = 1, 2, 3 . . .

Asendades $λ$ de Broglie’ valemist (4.1 ), saame

2 π r = n \cdot \frac{h}{m v}

ehk

(7.6)

m v r = n \cdot \frac{h}{2 π} = n \cdot ℏ

kus tähistasime, nagu kvantfüüsikas tavaks,

ℏ = \frac{h}{2 π}

$m$ on elektroni mass, $v$ – tema kiirus. (Meenutame mehaanikakursusest, et $m v r$ on tiirleva elektroni pöördimpulss e. impulssmoment.) Seega on orbiidi raadius $r$ ja elektroni orbitaalkiirus $v$ , siis ka energia, vastastikuses sõltuvuses. Avaldades $r$ valemist (7.6 ), näeme et püsiseisundeile sobivad üksnes

(7.7)

\begin{matrix} r_{1} = 1 \cdot \frac{ℏ}{m v_{1}} r_{2} = 2 \cdot \frac{ℏ}{m v_{2}} r_{3} = 3 \cdot \frac{ℏ}{m v_{3}} \dots r_{n} = n \cdot \frac{ℏ}{m v_{n}} \end{matrix}

kus kvantarvuks on $n = 1, 2, 3...$ .

Seega järeldub elektroni laineloomusest, et ta võib tuuma ümber tiirelda vaid teatud kindlatel orbiitidel raadiusega $r_{n}$ .

Joon. 7.5. De Broglie laine mehaaniliseks analoogiks võiks olla kahest otsast kinnitatud keele võnkumine, aga veel parem on vaadata võnkuvat rõngast. Rõngal saab püsiv seisulaine tekkida siis, kui sinna sobitub täisarv lainepikkusi. Bohri mudeli orbiite peeti ringikujulisteks ja oli loogiline arvata, et lubatud orbiidid on need, kuhu mahub täisarv elektroni seisulaine lainepikkusi. Kuigi selle laine iseloomu kohta ei olnud veel midagi teada, sobis de Broglie elektronlaine mudelisse väga hästi.

Niels Bohr (1885-1962) oli väljapaistev taani füüsikateoreetik, üks kaasaegse kvantfüüsika loojaid. Bohr on sündinud, õppinud ja veetnud suurema osa oma elust Kopenhaagenis. Tema isa Christian Bohr oli sealse ülikooli f&uu

Valemi (7.6 ) avaldas 1913. a. esimesena üks maailma tippfüüsikuid, taanlane Niels Bohr (l. nils boor). Tollal ei teadnud ta midagi elektroni laineomadustest. Toetudes vaid intuitsioonile ning soovides seletada aatomi püsivust ja spektraalseeriaid, ta lihtsalt postuleeris (ld. k. postulare - nõudma), et lubatud orbiitidel, mille raadius rahuldab seost (7.6 ), elektronid ei kiirga, kuigi tiirlevad (Bohri I postulaat). See oli muidugi järsus vastuolus makrofüüsika seadustega ja kohtas füüsikkonnas laialdast umbusku. Kuid nõnda õnnestus Bohril “päästa” planetaarmudel kiirgusvaringust (vt. alajaotus 1.2). Sündis uus, Bohri aatomimudel (joon.7.7 c), mis on mänginud mikrofüüsika arengus väga tähtsat osa. Lainesisu (vastavalt valemeile (7.5 ) ja (7.7 )) andis sellele postulaadile 10 aastat hiljem L. de Broglie.

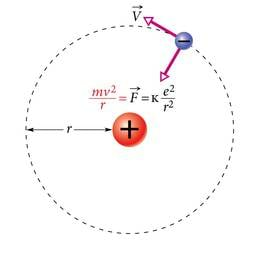
Kesktõmbe- e. tsentripetaaljõuksjõuks $F$ , mis hoiab elektroni tuuma ümber tiirlemas, on elektrijõud tuuma ja elektroni vahel (joon. 7.6). Coulombi seaduse järgi

F = \frac{κ e^{2}}{r_{n}^{2}}

kus $e$ on elementaarlaeng, $κ = \frac{1}{4 π ε_{0}}$ ja $ε_{0}$ elektriline konstant. Teatavasti kesktõmbekiirendus

a = \frac{v_{n}^{2}}{r_{n}}

Rakendades Newtoni II seadust $F = m a$ , saame

F = \frac{m v_{n}^{2}}{r_{n}}

Seega

(7.8)

\frac{κ e^{2}}{r_{n}^{2}} = \frac{m v_{n}^{2}}{r_{n}}

kust saab arvutada orbiitidele raadiusega $r_{n}$ vastavad energiatasemed $E_{n}$ . Tulemuseks on

(7.9)

E_{n} = - \frac{2, 17 \cdot 10^{- 18}}{n^{2}} J = - \frac{13, 6}{n^{2}} e V

Miinusmärk johtub sellest, et nullnivooks loetakse elektroni potentsiaalne energia, kui ta on tuumast eemaldatud lõpmata kaugele. Joonisel 7.7 on valemi (7.9 ) järgi arvutatud energiatasemete skeem.

Bohri II postulaadi järgi kiirgab või neelab aatom valgust ainult elektroni hüpetel lubatud orbiitide vahel (joon.7.7), kusjuures tekivad või kaovad footonid energiaga

(7.10)

h f = E_{k} - E_{m}

kus $E_{k}$ on mingi kõrgema ja $E_{m}$ madalama taseme energia.

Joon. 7.7. Atomaarse vesiniku spektrijooned (a) ja neid tekitavad siirded (b) vesinikuaatomi energiatasemete vahel. Punktiiris – seeriate serv. (c) Bohri – de Borgile´mudeli mõned "lubatud" orbiidid ja siirded nende vahel.

Vastaku kõrgemale tasemele kvantarvu $n$ väärtus $n_{2}$ , madalamale $n = n_{1}$ . Siis, asendades $E_{k}$ ja $E_{m}$ (7.9 )-st, saame

(7.11)

\begin{matrix} h f & = & 2, 17 \cdot 10^{- 18} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) J & = & 13, 6 \cdot (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) e V \end{matrix}

ehk, kuna $λ f = c$ ,

(7.12)

\frac{1}{λ} = 1, 097 \cdot 10^{7} (\frac{1}{n_{1}^{2}} - \frac{1}{n_{1}^{2}}) m^{- 1}

Võrreldes äsja leitud valemit (7.12 ) p. 3 toodud Balmeri-Rydbergi valemiga (3.1 ), mis saadud katses mõõdetud spektrite töötlemisel, näeme oivalist kokkulangevust. Järelikult kirjeldab Bohri - de Broglie’ aatomimudel vesiniku aatomit päris hästi. Ta selgitab mitte üksnes vesiniku joonspektrite tekkepõhjust ja struktuuri, vaid näitab õigesti kätte ka joonte lainepikkused.

Valemi 7.9 tuletamine

Huvilistele, kes väikest rehkendust paljuks ei pane, toome ära ka valemi (7.9 ) tuletuskäigu. Lähtume avaldistest (7.7 ) ja (7.8 ). Avaldame neist $r_{n}$ . Mugavamaks teisendamiseks viime (7.8 ) kujusse

\frac{m^{2} v_{n}^{2}}{m} = \frac{κ e^{2}}{r_{n}}

Siit, avaldades $m_{2} v_{n}^{2}$ (7.7 )-st,

\frac{n^{2} ℏ^{2}}{r_{m}^{2}} = \frac{κ e^{2}}{r_{n}}

millest

(7.13)

r_{n} = \frac{ℏ^{2}}{κ m e^{2}} \cdot n^{2}

Elektroni koguenergia $E_{n}$ $n$ -dal statsionaarsel orbiidil $r_{n}$ liitub tema kineetilisest energiast $E_{k i n} = m v_{n}^{2} / 2$ ja potentsiaalsest energiast tuuma elektriväljas, mis avaldub kuju $E_{p o t} = - k e^{2} / r_{n}$ :

E_{n} = \frac{m v_{n}^{2}}{2} - \frac{κ e^{2}}{r_{n}}

Võrrandist (7.8 ) leiame

\frac{m v_{n}^{2}}{2} = \frac{κ e^{2}}{2 r_{n}}

seega

E_{n} = - \frac{κ e^{2}}{2 r_{n}}

Teisendades avaldist (7.7 ), saame

v_{n} = \frac{n ℏ}{m r_{n}}

Asetades $v_{n}$ sel kujul valemisse (7.8 ), osutub, et

(7.13)

r_{n} = \frac{ℏ^{2}}{κ m e^{2}} \cdot n^{2}

Asendades $r_{n}$ (7.13 )-st leitu koguenergia valemisse, tuleb välja

E_{n} = - \frac{κ^{2} m e^{4}}{2 ℏ^{2}} \cdot \frac{1}{n^{2}}

ehk

(7.14)

E_{n} = - \frac{m e^{4}}{8 ε_{0}^{2} h^{2}} \cdot \frac{1}{n^{2}}

Asendades konstandid $m$ , $e$ , $ε_{0}$ ja $h$ nende arvväärtustega, saamegi valemi (7.9 ).