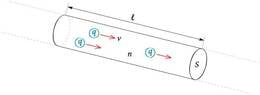
Elektrivooluks nimetatakse laengukandjate suunatud liikumist. Elektrivoolu iseloomustavaks suuruseks on voolutugevus, mis näitab, kui suur elektrilaeng läbib juhtme ristlõiget ajaühikus. Voolutugevuse SI -ühik on $1$ amper ($1A$). Juhi ristlõiget läbib sel juhul $1$ sekundi jooksul laeng $1$ kulon. Voolu suunaks on kokku lepitud positiivsete laengute suunatud liikumise suund. Joonisel 1.1. on kujutatud ühte vooluringi lõiku pikkusega $l$, milles liiguvad elektrivälja sihis ühesugused osakesed laenguga $q$ keskmise kiirusega $v$.

Olgu vabade laetud osakeste arv juhtme ruumalaühikus ehk kontsentratsioon $n$ ja aja $t$ jooksul jõuavad kõik osakesed läbida juhtmelõigu parempoolse otsa pindalaga $S$. Laetud osakeste arv

milles

ja juhtme ristlõiget läbinud kogulaeng

Voolutugevuse leidmiseks tuleb kogulaeng jagada ajaga, seega

Saadud valemist on näha, millised suurused määravad voolutugevuse juhis. Kolm nendest, $q$, $n$ ja $v$, on mikroosakesi iseloomustavad suurused. Metallide puhul on laengukandjateks tuuma mõjupiirkonnast vabanenud juhtivuselektronid, mis liiguvad positiivsete laengukandjate liikumise vastassuunas ning nendel on elementaarlaeng $q=-e=-1,60\cdot {10}^{-19}C$. Vabade elektronide kontsentratsioon $n$ välistingimustest oluliselt ei sõltu, küll aga elektronide triivimise kiirus v metalli kristallvõre aatomite vahel. Vabade elektronide puhul tuleb eristada kahte arvväärtuse poolest oluliselt erinevat kiirust, kaootilise soojusliikumise kiirus ja elektrivälja poolt tekitatud triivikiirus. Esimene nendest on palju suurem, aga kaootilisuse tõttu triivliikumisse mingit panust ei anna. Elektrivoolu tugevuse määrab elektrivälja poolt tekitatud aeglane triivikiirus. Kui $1mm$ diameetriga vaskjuhtmes triivivad elektronid kiirusega $0,1mm/s$, on voolutugevus umbes $1A$. Elektronide kaootilise liikumise kiirus on toatemperatuuril ligi miljard korda suurem.

Võib jääda mulje, et taskulambi sisselülitamisel võtaks süttimine kaua aega, kuni elektronid patareist lambini triivivad. Nii see ei ole, sest vabu elektrone on kogu vooluringi ulatuses ning elektriväli levib väga kiiresti, valguse kiirusega.

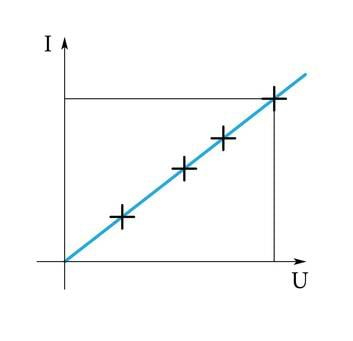
Kui mõõta metallist juhti läbiva voolutugevuse sõltuvust tema otstele rakendatud pingest (joonis 1.2. a), siis on näha, et voolutugevus juhis on võrdeline pingega juhi otstel (joonis 1.2. b).

Joonis 1.2. a	Joonis 1.2. b

Seega on antud juhi jaoks pinge ja voolutugevuse suhe sama ning seda suhet, takistust $R$, võib kasutada metallist keha iseloomustamiseks voolu takistamise seisukohalt. Seos ongi valemi kujul esitatud Ohmi seadus.

Kui sama kehaga korrata katset kõrgemal temperatuuril, jääb sõltuvus võrdeliseks, kuid graafiku tõus on väiksem. Temperatuuri tõus suurendab metallist keha takistust. Saksa füüsiku Georg Simon Ohmi poolt korraldatud katsed näitasid, et metalli takistus sõltub juhi pikkusest, ristlõikepindalast ja materjalist, ning hilisemate mõõtmistega leiti seos, kus $\rho$ on materjali eritakistus, mis määratakse katseliselt.

Võrdeline sõltuvus pinge ja voolutugevuse vahel pole üldkehtiv. Näiteks ioone sisaldavas lahuses, pooljuhis ja elektrivoolu juhtivas gaasis on sõltuvus keerulisem.

Eritakistuse järgi võib aineid ja materjale jaotada juhtideks, isolaatoriteks ja pooljuhtideks. Juhtidel on eritakistus suhteliselt väike ja isolaatoritel (dielektrikutel) suur. Pooljuhtide eritakistus on vahepealne, kusjuures see sõltub olulisel määral temperatuurist, valgustatusest ja lisanditest.

Elektrimõõteriistu võib jaotada osutmõõteriistadeks ja numbrilisteks mõõteriistadeks. Vastavad sünonüümid on analoog- ja digitaalmõõteriist.

Joonis 1.3. a Osutmõõteriist	Joonis 1.3. b Osutmõõteriista tööpõhimõte

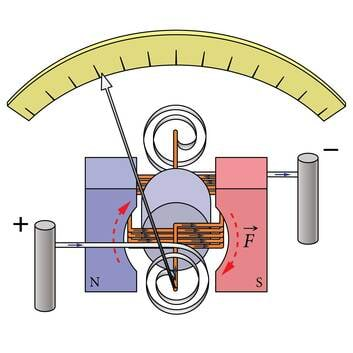
Vooluga raamile mõjub magnetväljas jõud ja voolutugevust saab mõõta magnetväljas vooluga raamile mõjuva jõu kaudu (joonis 1.3.). Raami vastaskülgedele mõjuvad jõud pööravad seda päripäeva. Raami külge pannakse osuti ja jõu tasakaalustamiseks spiraalvedrud.

Osuti kaldenurga järgi saab määrata voolutugevuse. Kui laseme voolu läbi takistuse, saame määrata ka pinget, mis on võrdeline voolutugevusega. Digi­taalses mõõteriistas muudetakse pinge muunduriga kahendkoodiks ja see omakorda ekraanil numbriliseks näiduks (joonis 1.4.).

Joonis 1.4. a Digitaalmõõteriista põhimõtteline skeem	Joonis 1.4. b Multimeeter

Elektriliste suuruste mõõtmisel esinevad erineva päritoluga vead FLA. Elektrimõõtmistel on tegemist B-tüüpi mõõtemääramatusega, mis saadakse mõõteriista tootja poolt antud mõõteriista täpsuse hinnangust. Ebatäpsust iseloomustatakse absoluutse ja relatiivse piirveaga. Üleskirjutus katse protokollis $I=(1,26\pm 0,05)A$ tähendab seda, et voolutugevuse mõõdetud väärtus on $1,26A$, absoluutne piirviga $\Delta I=0,05A$ ja voolutugevuse tegelik väärtus asub vahemikus $1,21A$ kuni $1,31A$. Relatiivne piirviga on absoluutse piirvea ja mõõtetulemuse suhe, mis antud juhul on umbes $4\%$ ning iseloomustab ka mõõtmise täpsust.

Osutmõõteriistale on kirjutatud täpsusklass (joonis 1.3. a). See on arv, mis näitab mõõteriista suhtelist piirviga protsentides maksimaalse näidu korral. Täpsusklassid võivad olla $4$; $2,5$; $2,0$; $1,5$; $1$; $0,5$; $0,2$; $0,1$; $0,05$ ja $0,02$. Mida väiksem arv, seda täpsem mõõteriist. Kui laboratoorses töös kasutataval amper- meetril on täpsusklass $2,5$ ja mõõtepiirkond $2A$, siis ampermeetri mõõtemääramatus (absoluutne piirviga) $\Delta I=\pm 0,05A$. Numbrilise mõõteriista passis on esitatud mõõtemääramatus näiteks kujul $\pm 0,5\%\pm 2D$. See tähendab, et piirviga on $0,5\%$ näidust pluss näidu viimase numbri $2$ ühikut.

Elektrimõõtmistel tuleb arvestada, et mõõteriistad on samuti elektrivoolu tarbijad (tarvitid). Mõõteriistade ühendamisel vooluringi peaks riistade põhjustatud muutused olema võimalikult väiksed. Voolutugevust mõõdetakse ampermeetriga, mis ühendatakse tarvitiga jadamisi. Ampermeetril endal on samuti takistus ja see muudab voolutugevust vooluringis. Selleks, et muutus oleks väike, peaks ampermeetri takistus olema tarviti omast oluliselt väiksem. Voltmeeter seevastu ühendatakse rööbiti ja tema takistus peaks olema võimalikult suur.

Elektrimõõtmisi kasutatakse ka mitteelektriliste suuruste kaudseks mõõtmiseks. Selleks tuleb mõõdetav suurus muuta pingeks või vooluks. Termopaar koosneb kahest erinevast metallist vardast, mille ühed otsad on kokku joodetud. Kui jootekohta kuumutada, tekib vabade otste vahel pinge, mille väärtus oleneb jootekoha temperatuurist. Teades pinge ja temperatuuri seost, saame määrata temperatuuri kaudselt pinge mõõtmise abil. Lisaks toodud näitele on palju füüsikalisi nähtusi, kus mehaaniline, soojuslik või kiirguse energia muudetakse elektrienergiaks.

Elektrimõõtmiste eeliseks on asjaolu, et mõõtetulemusi on hea üle kanda, salvestada, töödelda ja kasutada protsesside automaatseks juhtimiseks.

Vigade arvutamise ja katsetulemuste esitamise näide

Mõõdame osutmõõteriistaga, mille mõõtepiirkond on $250V$ ja täpsus­klass $2,5$, võrgupinget ja saame tulemuseks $232V$. Arvutame absoluutse piirvea $\Delta U=250\cdot 2,5/100=6,25V$. Mõõdetud pinge viimaseks numbriks on ühelised. Ka vea ümardame ühelisteks, aga alati ülespoole $\Delta U=6,25V\approx 7V$. Seega võrgupinge on $U=(232\pm 7)V$.

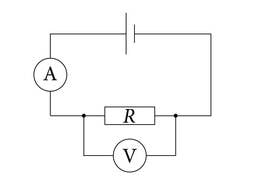
Kaudse mõõtmise korral võib viga arvutada erinevate meetoditega. Vaatame ülem- ja alamtõkke meetodit, mida kutsutakse ka halvima võimaluse meetodiks. Oletame, et määrame järgneval joonisel toodud vooluringiga takisti takistust pinge ja voolutugevuse kaudu. Mõõtes voltmeetriga pinge takisti otstel ja ampermeetriga voolutugevuse, saame Ohmi seadusest arvutada takistuse valemiga

$R=\frac{U}{I}$

Kui tahame hinnata takistuse mõõtemääramatust, siis tuleb arvestada mõlema mõõteriista viga. Lahendame ülesande konkreetse näite põhjal.

Voltmeeter mõõtepiirkonnaga $6V$ ja täpsusklassiga $4$ näitas pinget $4,3V$ ning ampermeeter mõõtepiirkonnaga $2,5A$ ja täpsusklassiga $2,5$ näitas voolutugevust $2,25A$. Arvutades voltmeetri ja ampermeetri absoluutse piirvead, saame $\Delta U=0,24V$ ja $\Delta I=0,0625A$. Suurima takistuse väärtuse ehk ülemtõkke saame siis, kui pinge on kõige suurem ja voolutugevus kõige väiksem. 

$R_{\ddot{\text{u}}}=\frac{U_{\ddot{\text{u}}}}{I_{\ddot{\text{u}}}}=\frac{4,3+0,24}{2,25-0,0625}=2,075\Omega$

Vähima takistuse ehk alamtõkke saame siis, kui pinge on vähim ja voolutugevus suurim.

$R_a=\frac{U_a}{I_a}=\frac{4,3-0,24}{2,25+0,0625}=1,756\Omega$

Takistuseks oleks mõistlik võtta nende aritmeetiline keskmine $R=1,916\Omega$ ja absoluutseks piirveaks pool nende erinevusest.

$\Delta R=\frac{R_{\ddot{\text{u}}}-U_a}{2}=0,160\Omega$

Absoluutne piirviga ümardatakse ülespoole ühe tüvenumbrini ($0,160\approx 0,2$). Määratud suuruse väärtus ümardatakse nii, et viga parandab selle viimast numbrit. Lõpuks kirjutame takistuse koos absoluutse piir­veaga $R=(1,9\pm 0,2)\Omega$.

Takistuse arvutamiseks tuleb pinge jagada voolutugevusega. Saab näidata, et jagatise ja korrutise relatiivne piirviga avaldub suuruste relatiivsete piirvigade summaga. 

$\frac{\Delta R}{R}=\frac{\Delta U}{U}+\frac{\Delta I}{I}$

Kui asetada ülaltoodud andmed valemisse, avaldada takistuse absoluutne piirviga ja esitada takistus koos veaga parajasti ümardatult, saab veenduda, et erinevus halvima võimaluse meetodiga saadud tulemusest on tühine.

Temperatuuri tõustes väheneb metallis vabade elektronide triivikiirus, kuna intensiivistub kristallvõre aatomite võnkumine. See takistabki elektronide liikuvust ja metalli takistus kasvab. Katsed näitavad, et metalli takistuse sõltuvus temperatuurist on ligikaudu lineaarne (joonis 1.5. a).

Selle sõltuvuse võib kirja panna valemiga, kus $R_0$ on takistus $0^{\circ }C$ juures, $a$ (${}^{\circ }{C}^{-1}$ või $K^{-1}$) takistuse temperatuuritegur ja $t$ temperatuur Celsiuse kraadides.

Takistuse temperatuuritegur on puhastel metallidel suurusjärgus ${10}^{-3}{}^{\circ }{C}^{-1}$, näiteks volframil $0,0045{}^{\circ }{C}^{-1}$.

Lülitades toas põlema algul toatemperatuuril oleva hõõglambi, tõuseb volframist hõõgniidi temperatuur kiiresti rohkem kui kaks tuhat kraadi ja hõõgniidi takistus ligi kümme korda. Hõõglamp kipubki läbi põlema sisselülitamisel, mil tema takistus on veel väike ja lambis eralduv võimsus umbes $10$ korda suurem kui stabiliseerunud tööolukorras. Elektrilistes küttekehades kasutatakse tavaliselt sulameid, mille takistuse temperatuuritegur on väike. Näiteks nikeliinil on see umbes ${10}^{-4}{}^{\circ }{C}^{-1}$ ja elektripliidi takistus on külmalt ja kuumutatult praktiliselt ühesugune. On aineid, mille takistuse temperatuuritegur on negatiivne, st takistus temperatuuri tõustes väheneb. Elektrolüütide, grafiidi ja pooljuhtide takistus väheneb mittelineaarselt.

Teades keha takistuse sõltuvust temperatuurist, saame seda keha kasutada näiteks takistustermomeetri andurina: vooluallikaga ühendatud anduri temperatuuri muutus põhjustab takistuse ja voolutugevuse muudu. Voolu muutust on aga mugav mõõta, salvestada, töödelda ning protsesside automatiseeritud juhtimisel rakendada.

20. sajandi alguses avastati nähtus, kus metalli takistus muutus väga madalal temperatuuril hüppeliselt nulliks. Tahke elavhõbedaga toimus see temperatuuril $–269{}^{\circ }C$ (joonis 1.5. b). Sellises olukorras voolu soojuslik toime kaob ja kord liikuma pandud vool ei lakkagi. Hiljem avastati ülijuhtivus veel paljudel ainetel ja ka kõrgematel temperatuuridel. Kui saaksime ülijuhtivuse tekitada looduses esinevatel temperatuuridel, saaksime elektrienergia edastamisel esinevaid soojuslikke kadusid vältida. On valmistatud aineid, milles ülijuhtivusele üleminek toimub kõrgemal temperatuuril, näiteks $HgBaCuO–138{}^{\circ }C$ juures.

Joonis 1.5. b

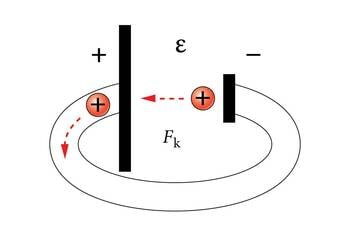
Vooluring koosneb vooluallikast, tarbijatest ja ühendusjuhtmetest. Et tekiks püsiv vool, peab vooluring olema suletud. Kui positiivne laeng on jõudnud vooluallika plussklemmilt läbi vooluringi miinusklemmile, peab voolu säilitamiseks mingi kõrvaljõud $F_k$ (joonis 1.6. a) elektriväljale vastu töötades selle laengu uuesti plussklemmile viima.

Joonis 1.6. a	Joonis 1.6. b

Selle kõrvaljõu töö arvelt saabki vooluringis eralduda soojushulk. Kõrvaljõud teevad tööd vooluallikas, kus toimub mingi teise energialiigi (mehaanilise, keemilise vms) muutmine elektrienergiaks positiivsete ja negatiivsete laengute lahutamise teel. Vooluallika elektromotoorjõud on võrdne kõrvaliste jõudude tööga ühikulise laengu ümberpaigutamisel kogu suletud voolu­ringi ulatuses.

Elektromotoorjõu ühik on sarnaselt pinge ühikuga volt, sest

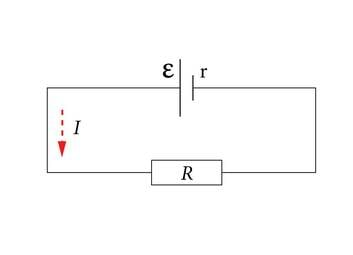
Kõrvaljõudude töö muutub vooluringis soojushulgaks, mis eraldub nii voolu- ringi välisosas kui ka vooluallikas (joonis 1.6. b). $A_k=\epsilon q=\epsilon It=I^{2}Rt+I^{2}rt$, kus $R$ on vooluringi välisosa takistus ja $r$ vooluallika sisetakistus. Avaldades viimasest võrdusest voolutugevuse, saame:

Saadud seos väljendab Ohmi seadust kogu suletud vooluringi kohta. Voolutugevus suletud vooluringis on võrdne vooluallika elektromotoorjõu ja vooluringi kogutakistuse suhtega.

Vooluringi kogutakistus koosneb vooluallika sisetakistusest $r$ ja vooluringi välisosa takistusest $R$. Üldjuhul tuleb viimase hulka arvestada ka ühendusjuhtmete takistus.

Vooluallika elektromotoorjõudu ja sisetakistust võib vaadelda kui vooluallikat iseloomustavaid suurusi, mis lühikese aja jooksul ei muutu. Kui aga keemiline vooluallikas vananeb, väheneb pisut tema elektromotoorjõud ja suureneb oluliselt sisetakistus.

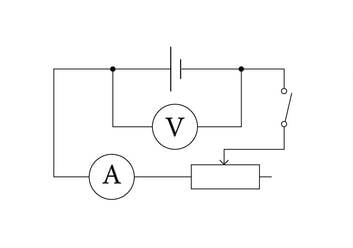
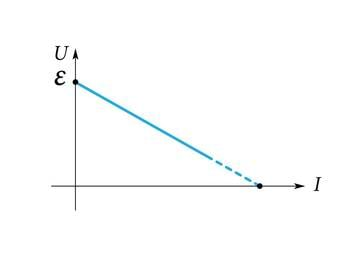
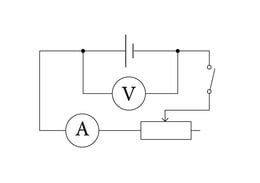
Avaldades valemist 1.6. elektromotoorjõu, saame $\epsilon =IR+Ir$, milles suurus $IR=U$ on vooluallika klemmipinge $U=\epsilon –Ir$. Viimasest valemist on näha, et elektromotoorjõud on vooluallika maksimaalne klemmipinge ja voolu kasvades vooluallika klemmipinge väheneb. Joonisel 1.7. a on klemmipinge mõõtmise vooluringi skeem ja katsetulemuste graafik 1.7. b.

Joonis 1.7. a	Joonis 1.7. b

Kui vooluringi välisosa takistus muutub nulliks, tekib lühis. Lühisvoolu tugevus on määratud vooluallika elektromotoorjõu ja sisetakistuse suhtega