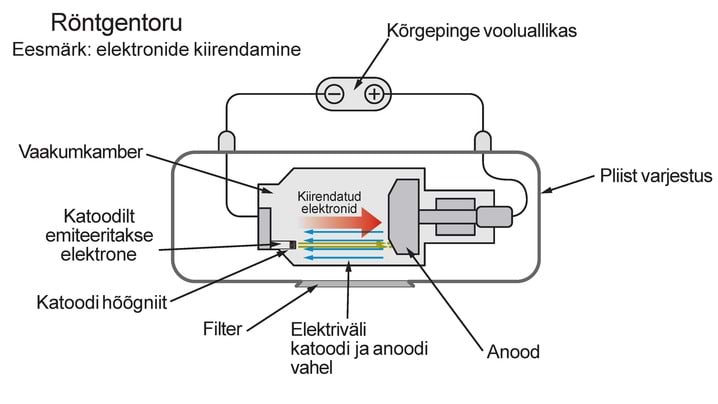
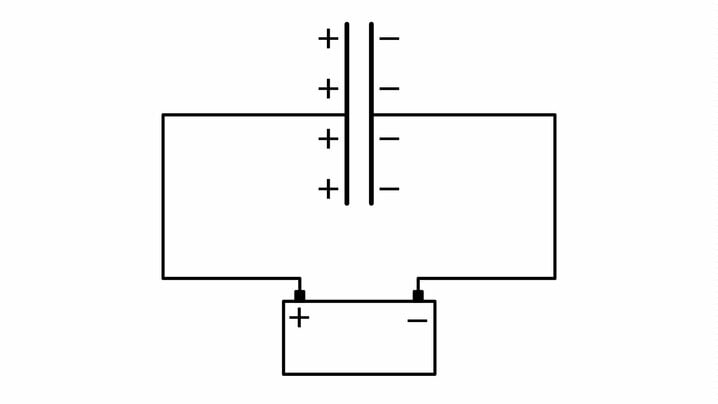
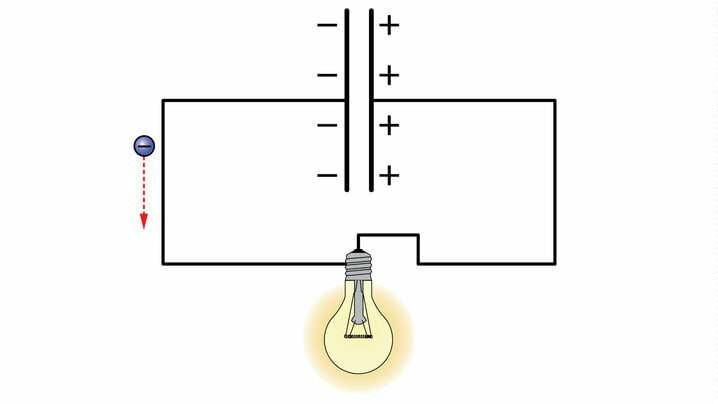
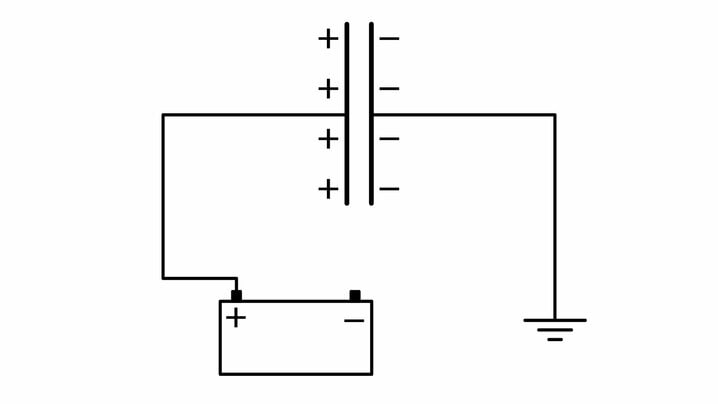
Elektrivälja kasutatakse laetud osakeste kiirendamiseks. Üks tuntumaid elektronide kiirendeid on röntgentoru ehk röntgenlamp. Röntgenlambis kiirendatakse väga tugeva elektrivälja abil elektrone, mida emiteerib katood. Suure kineetilise energia saanud elektronid põrkavad vastu anoodi. Elektronide kineetiline energia muutub väga tugeval pidurdusel röntgenkiirguse energiaks. Spetsiaalse filtri abil filtreeritakse välja madalama energiaga röntgenkiirgus, mis neelduks kudedes neid kahjustades. Vabaneb röntgenkiirgus, mis sobib röntgenpildi tegemiseks.
Positiivse ja negatiivse (laengu) ristiisaks võib lugeda Benjamin Franklinit (1706–1790), kes oli ühtlasi ka piksevarda leiutaja ja Ameerika Ühendriikide iseseisvusdeklaratsiooni üks autoreid. Franklin tähistas mõistega „positiivne elekter“ siidiriidega hõõrutud klaasist pulgale tekkinud elektrilaengut, ja mõistega „negatiivne elekter“ karusnahaga hõõrutud eboniitpulga laengut.
Kehade laadumine on seotud vabade elektronide ümberpaiknemisega kehades. Kui muidu neutraalsel kehal on elektrone liiga palju, on keha laetud negatiivselt, ja kui neutraalne keha on elektrone ära andnud, on see laetud positiivselt.
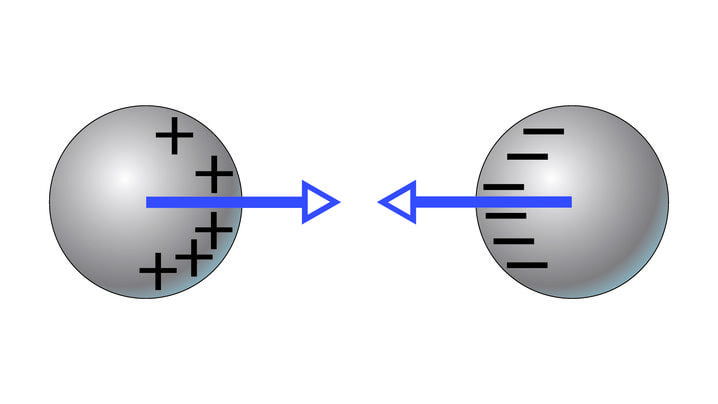
Olgu meil tegemist kahe metallkeraga. Laeme ühe neist positiivselt, teise negatiivselt. Laenguid võib saada, kui kasutada Franklini ülal kirjeldatud elektriseerimise viise. Kuna metallkerad on erinimeliselt laetud, esineb nende vahel tõmbejõud. Metallis saavad aatomi väliskihi elektronid liikuda kogu uuritava ainetüki piires ja nii paiknevad elektrijõudude tõttu laengud keradel ümber (joonis 1.2). Elektrijõud mõjuvad nii laetud kehade kui ka metallis olevate elektronide vahel. Mõlemal juhul vahendab jõudusid elektriväli.
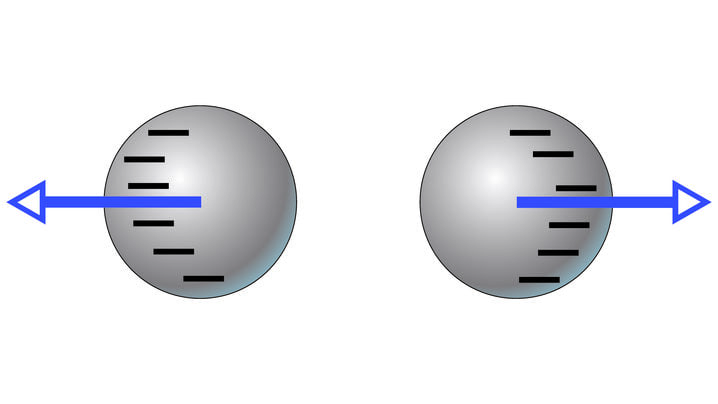
Kui laadida neutraalsed kerad uuesti, seekord mõlemad samanimeliselt, näiteks negatiivse laenguga, siis tekib kehade vahel tõukejõud (joonis 1.3). Ka laengud metallkera pinnal vahetavad asukohta.
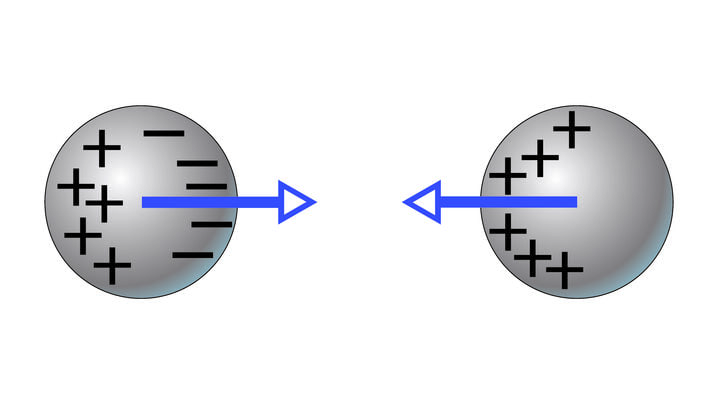
Kolmandal juhul jätame ühe metallkera neutraalseks, aga teise laeme positiivselt. Kuigi üks on neutraalne, võib täheldada kehadevahelist tõmbejõudu. Põhjuseks on vabade laengute ümberasetumine elektrit juhtivas kehas väliste elektrijõudude tõttu, mistõttu keha pind laadub teise kehaga võrreldes vastasmärgiliselt (joonis 1.4). Sellist nähtust nimetatakse elektriliseks või elektrostaatiliseks induktsiooniks (ld inducere ’esile kutsuma, põhjustama’).
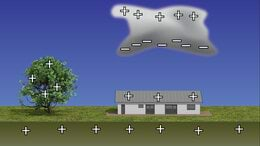
Äikesepilvede laadumisprotsess on seotud õhumasside liikumisega üksteise suhtes, mille käigus toimub õhumassiivides asuvate pilveosakeste – lumekristallide, raheterade – vastastikune hõõrdumine ja selle tulemusena nende laadumine. Positiivselt laetud lumekristallide ja negatiivselt laetud raheterade pilvesisesel liikumisel ja raskuse järgi kuhjumisel laaduvad ka pilve osad. Negatiivselt laetud ja raskemad raheterad on pigem pilve alaosas ja kergemad positiivselt laetud lumekristallid ülaosas (joonis 1.5). Äike tekib, kui elektriväli muutub küllalt tugevaks. Äikesepilvedes mõõdetud elektrivälja tugevusest ei piisa siiski välgu tekkimiseks, vaja läheks veelgi tugevamaid elektriväljasid ja seetõttu on atmosfääriteadlaste arvates vaja lisafaktorina päikesetuuli (suure energiaga laetud osakeste voog) või atmosfääri enda jääklaengut ja polariseeritust. Äikeselöögi kestvus on u sekundit ja selle ajaga liigub välgus kuni impulssi.
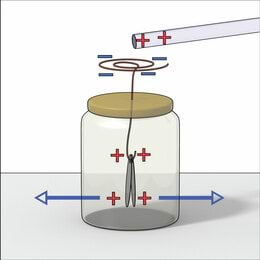
Elektroskoop on katseseade, millega saab uurida kehade laenguid ja elektrilist induktsiooni. Lihtsa elektroskoobi saab valmistada järgmistest vahenditest: umbes klaasanum (keeduklaas või klaaspurk), õhuke foolium, plastikkaas või muu plastikust kate, jämedam () vasktraat ja teipi. Fooliumist lõigatakse umbes – pikkused ovaalid, mille ühte otsa tehakse avad. Vasktraat keritakse ühest otsast spiraaliks ja teine ots surutakse läbi plastikkaane ning tehakse otsa väike konks. Konksu külge riputatakse fooliumovaalid. Seejärel suletakse purk kaanega ja fikseeritakse teibiga katseseadme osad. Seade ongi valmis. Elektrilise induktsiooni uurimiseks tuleb vaskspiraalile lähendada elektriliselt laetud keha, nt õhupall, klaaspulk või joonlaud, ja uurida fooliumlehekeste käitumist. Elektroskoopi saab laadida ka laengut jagades. Selleks tuleb laetud kehaga puudutada vaskspiraali.
Mõistel „elektrilaeng“ on mitu tähendust. Siiani käsitlesime elektrilaengut kas keha omaduse või portsu laetud osakeste tähenduses. Elektrostaatikas on olulisel kohal elektrilaengu kui füüsikalise suuruse mõiste.
Elektrilaeng füüsikalise suurusena iseloomustab, kui tugevasti osaleb laetud keha elektromagnetilises vastastikmõjus.
Elektrilaengu tähis on või ja ühik on kulon, lühendina C.
kulon on väga suur laeng. Äikesepilve laengud võivad olla suurusjärgus . Kui meie juuksed on „elektrit täis“, siis on juuksekarvade laengu väärtused vahemikus .
45∘45∘45∘45∘ kulon on väga suur laeng. Äikesepilve laengud võivad olla suurusjärgus F1,res=√F21,res,x+F21,res,y=1,78×10−24N––––––––––––––––––––––––––––––––F1,res=√F21,res,x+F21,res,y=1,78×10−24N––––––––––––––––––––––––––––––––F1,res=√F21,res,x+F21,res,y=1,78×10−24N––––––––––––––––––––––––––––––––F1,res=√F21,res,x+F21,res,y=1,78×10−24N––––––––––––––––––––––––––––––––. Kui meie juuksed on „elektrit täis“, siis on juuksekarvade laengu väärtused vahemikus F1,res,y=F12,y+F14,y=0+F14sin60∘=(2,05×10–24N)(sin60circ)=1,78×10–24NF1,res,y=F12,y+F14,y=0+F14sin60∘=(2,05×10–24N)(sin60circ)=1,78×10–24NF1,res,y=F12,y+F14,y=0+F14sin60∘=(2,05×10–24N)(sin60circ)=1,78×10–24NF1,res,y=F12,y+F14,y=0+F14sin60∘=(2,05×10–24N)(sin60circ)=1,78×10–24N – θ=tan−1F1,res,yF1,res,x=−86,0∘θ=tan−1F1,res,yF1,res,x=−86,0∘θ=tan−1F1,res,yF1,res,x=−86,0∘θ=tan−1F1,res,yF1,res,x=−86,0∘.
Kõige väiksemat vabalt eksisteerivat elektrilaengut looduses nimetatakse elementaarlaenguks .
on elektroni laeng ja on prootoni laeng.
Keemias kasutatakse ioonide tähistamisel suhtelisi laenguid, mis näitavad, mitu korda on iooni laeng suurem elementaarlaengust. Näiteks naatriumi katioon on ja sulfiidi anioon . Kui suhteliste laengute asemel kasutada elektrilaengu väärtusi, on naatriumi katiooni laenguks , sest naatriumi aatom on ühe elektroni loovutanud. Sulfiidioonil on laenguks , sest väävli aatom on liitnud kaks elektroni.
–86,0∘+180∘=94,0∘–––––––––––––86,0∘+180∘=94,0∘–––––––––––––86,0∘+180∘=94,0∘–––––––––––––86,0∘+180∘=94,0∘–––––––––––– on elektroni laeng ja F1,res,x=F12,x+F14,x=F12+F14cos60∘=–1,15×10–24N+(2,05×10–24N)(cos60∘)=–1,25×10–25NF1,res,x=F12,x+F14,x=F12+F14cos60∘=–1,15×10–24N+(2,05×10–24N)(cos60∘)=–1,25×10–25NF1,res,x=F12,x+F14,x=F12+F14cos60∘=–1,15×10–24N+(2,05×10–24N)(cos60∘)=–1,25×10–25NF1,res,x=F12,x+F14,x=F12+F14cos60∘=–1,15×10–24N+(2,05×10–24N)(cos60∘)=–1,25×10–25N on prootoni laeng.
Keemias kasutatakse ioonide tähistamisel suhtelisi laenguid, mis näitavad, mitu korda on iooni laeng suurem elementaarlaengust. Näiteks naatriumi katioon on →F1,res=→F12+→F14→F1,res=→F12+→F14→F1,res=→F12+→F14→F1,res=→F12+→F14 ja sulfiidi anioon F14=14πε0|q1||q2|(34R)2=(8,99×109N⋅m2/C2)×(1,60×10−19C)(3,20×10−19C)(34)2(0,0200m)2=2,05×10−24N. Kui suhteliste laengute asemel kasutada elektrilaengu väärtusi, on naatriumi katiooni laenguks →F14=(1,025×10–24N)^i+(1,775×10–24N)^j→F14=(1,025×10–24N)^i+(1,775×10–24N)^j→F14=(1,025×10–24N)^i+(1,775×10–24N)^j→F14=(1,025×10–24N)^i+(1,775×10–24N)^j, sest naatriumi aatom on ühe elektroni loovutanud. Sulfiidioonil on laenguks →F1,res=→F12+→F14=–(1,15×10–24N)^i+(1,025×10–24N)^i+(1,775×10–24N)^j≈(–1,25×10–25N)^i+(1,78×10–24N)^j––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––→F1,res=→F12+→F14=–(1,15×10–24N)^i+(1,025×10–24N)^i+(1,775×10–24N)^j≈(–1,25×10–25N)^i+(1,78×10–24N)^j––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––→F1,res=→F12+→F14=–(1,15×10–24N)^i+(1,025×10–24N)^i+(1,775×10–24N)^j≈(–1,25×10–25N)^i+(1,78×10–24N)^j––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––→F1,res=→F12+→F14=–(1,15×10–24N)^i+(1,025×10–24N)^i+(1,775×10–24N)^j≈(–1,25×10–25N)^i+(1,78×10–24N)^j––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––, sest väävli aatom on liitnud kaks elektroni.
a) Selgita, miks fooliumist lehed üksteisest eemalduvad.
b) Kas fooliumlehed saavad töötada elektroskoobina ka ilma klaaspurgi ja plastikkaaneta, kui riputame need nailonniidiga statiivi külge? Põhjenda vastust. Kui oled elektroskoobi ise ehitanud, tee katse!
a) kui kuulid viia üksteisele lähemale, aga mitte kokku;
b) kui panna kuulid üksteise vastu.
Joonisel 1.7 on kujutatud tundlikku kaalu, millele on asetatud alus, mis on vähemalt 15 cm kõrge, ja aluse peal seisvat laetud kuuli. Kui laetud kuulile lähendada teine kuul, mis on laetud vastasnimeliselt, siis kaalu näit väheneb. Kaalu esialgset näitu saab muuta mitut moodi. Üks võimalus on anda kehadele rohkem laengut või seda vähendada. Teine võimalus on viia kuuli lähemale kaalul asuvale kuulile või eemaldada kuulid üksteisest. Kolmas võimalus on panna vastastikmõjusse samanimeliselt laetud kuulid. Sellest eksperimendist saab järeldada, et a) laetud kuulide vahel mõjub elektriline jõud, b) see jõud sõltub nii kehade laengust kui ka nendevahelisest kaugusest ja c) me saame mõjuvat jõudu kaudselt mõõta.
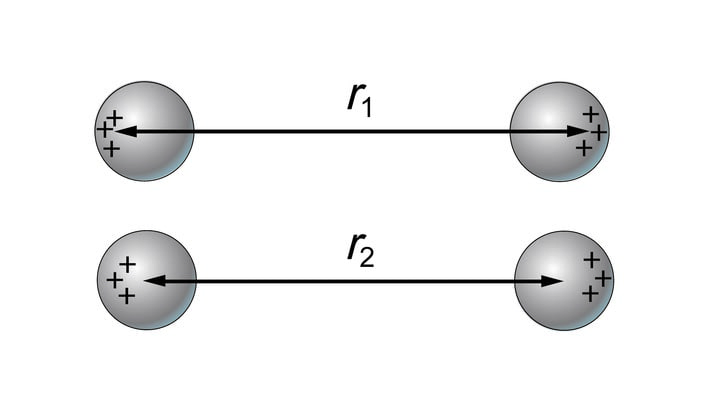
18. sajandil uuris elektrilisi jõudusid Charles-Augustin de Coulomb (1736–1806), kes silmapaistva insenerina konstrueeris oluliselt tundlikuma seadme, kui on kujutatud joonisel 1.7. Coulomb’i mõõtmistulemustest selgus, et lisaks laengute väärtusele muutub laetud kehade vaheline jõud pöördvõrdeliselt kauguse ruuduga. Seda nimetataksegi Coulomb’i seaduseks.
Coulomb’i seadus matemaatilisel kujul:
Kui tahame arvutada kahe laetud keha vahel mõjuvat jõudu, saame kasutada valemit:
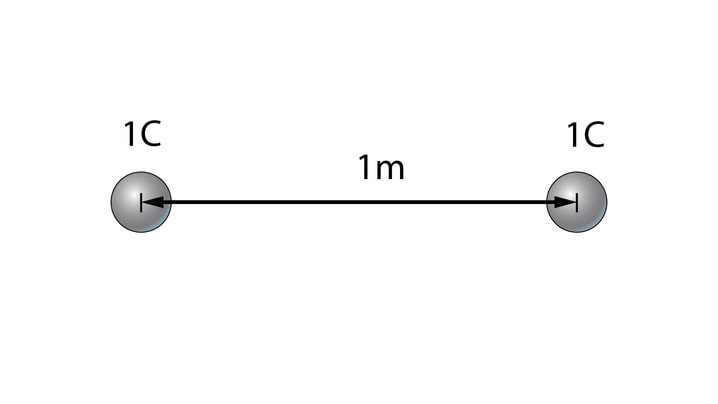
kus on Coulomb’i konstant, mille väärtus on . Et paremini mõista Coulomb’i konstandi tähendust, uurime järgmist skeemi (joonis 1.8).
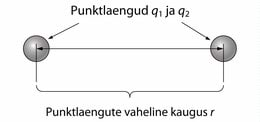
Skeemil on kujutatud kaks keha laengutega ja kehad on asetatud üksteisest ühe meetri kaugusele. Kuna tegu on samanimeliste laengutega, esineb kehade vahel tõukejõud ja selle jõu väärtuseks on . See on väga suur jõud ja nii lähedale üksteisele on ühekulonilisi laenguga kehi võimatu asetada. Seega, ühekuloniline laeng on väga suur laeng.
Eelmises peatükis uurisime elektrilise induktsiooni nähtust ja sellega seoses peame täpsustama, mida kaugus täpsemalt tähendab. Uurime joonist 1.9.
Elektrilise induktsiooni tõttu nihkuvad laengud ka keha sees. Seega laengutevaheline kaugus on suurem kehade vahelisest kaugusest . Seetõttu saame Coulomb’i seadust rakendada vaid vaid siis, kui kehade mõõtmed on võrreldes kehadevahelise kaugusega tühiselt väikesed. Seetõttu kasutatakse elektrostaatikas tihti punktlaengu mõistet.
Punktlaenguteks nimetatakse laetud kehi, mille mõõtmed on tühiselt väikesed võrreldes nende vahekaugusega. Teisiti, punktlaeng on keha, mille elektrilaengut võib vaadelda koondununa ühte punkti.
Coulomb’i seadust kirjeldav valem kehtib vaakumis. Kui laetud kehad asuvad keskkonnas, on nendevaheline jõud väiksem. Näiteks vees on laengutevaheline jõud ligikaudu korda nõrgem, kui see oleks vaakumis.
Füüsikas nimetatakse suurust, mis näitab, mitu korda on antud keskkonnas elektrijõud nõrgemad võrreldes vaakumiga, selle keskkonna dielektriliseks läbitavuseks, tähis (kreeka tähestiku lühike e – epsilon).
Toatemperatuuril on vee dielektriline läbitavus ligikaudu . Õhu dielektriline läbitavus erineb vaakumi läbitavusest väga vähe ja seega . Tabelist 1.1 on näha, et on materjale, mille dielektriline läbitavus on sadu, isegi tuhandeid kordi suurem vaakumi dielektrilisest läbitavusest.
Elektrilaengute liikumise ja ülekandega seotud olukordade mõtestamisel on vaja silmas pidada ka elektrilaengu jäävuse seadust, mis väidab, et elektriliselt isoleeritud süsteemi kogulaeng on jääv suurus. Laeng võib tekkida ja kaduda vaid paarikaupa ( ja üheskoos).
1. näidisülesanne
Olgu ühel elektroskoobil laeng ja teisel . Elektroskoopide metallkerad on ühesuurused ja võrdse massiga. Metallkerad viidi kontakti ja eemaldati siis uuesti üksteisest.
a) Kui suure laengu sai kumbki metallkera?b) Kuidas muutus kehade vastastikmõju?
Lahendus
a) Kuna tegu on samasuguste parameetritega metallist seadmetega, toimub kokkupuutel laengu ülekanne, mille tulemusena laengud võrdsustuvad. Looduses kehtiva laengu jäävuse seaduse järgi on kehade kogulaeng enne ja pärast laenguülekannet võrdne. Antud juhul enne ja ka pärast kokkupuudet. Seega saavad mõlemad metallkerad pärast üksteisest eemaldamist laengu .
b) Kui katse alguses olid elektroskoobid laetud erinimeliselt, siis pärast kokkupuudet on nad laetud samanimeliselt. Seega muutus elektroskoopide-vaheline tõmbejõud tõukejõuks.
Coulomb’i seadust ütleb, et kuna ülesandes jääb kehadevaheline kaugus samaks, siis sõltub vastastikmõju ainult laengute korrutisest. Saame, et vastastikmõju muutus korda nõrgemaks.
2. näidisülesanne
Lahendus
Arvutame jõu, kasutades Coulomb’i seadust.
Negatiivne vastus näitab, et tegu on tõmbejõududega positiivsete ja negatiivsete laengute vahel.
Kuna lähteandmed on antud ühe tüvenumbri täpsusega, on ka vastuses ainult üks tüvenumber. Samuti on tegu väga ligikaudsete andmetega, sest saame hinnata vaid pilvede laetud piirkondade ligikaudset vahekaugust, samuti on ka laengud hinnangulised.
Vastuseks saime üsna suure väärtuse . Küsimus on, mida see jõud teeb pilvedega. Vastuse saamiseks kasutame Newtoni teist seadust ja leiame kiirenduse a. Selleks peaksime omakorda hindama pilve massi, mis võib ulatuda tuhandete tonnideni.
Kui pilve mass on , siis kiirendus, mis tekib meie poolt arvutatud jõu mõjul, on . See on võrreldes pilvede loomuliku liikumisega tühine, järelikult nimetatud elektrijõud pilvede liikumist ei mõjuta. Kindlasti on pilvedevaheline elektriline tõmbejõud veelgi väiksem, sest kõik äikesepilved sisaldavad nii positiivselt kui ka negatiivselt laetud piirkondi ja seetõttu on kogulaeng oluliselt väiksem.
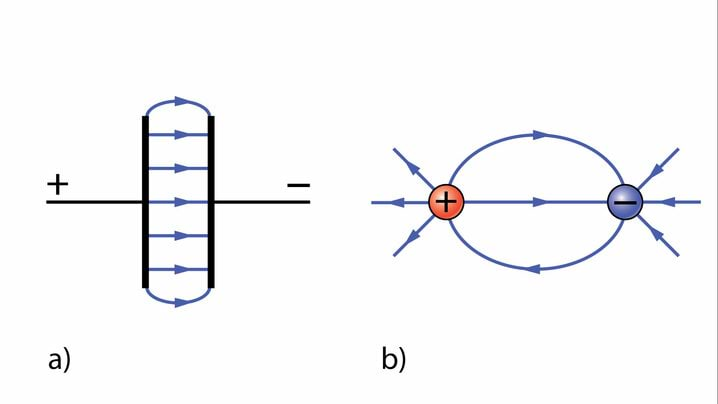
Elektrijõud ei vaja mõjumiseks kontakti nagu ka gravitatsiooni- ja magnetjõud. Mõju avaldub elektriliselt laetud kehade ümber oleva elektrivälja kaudu. Elektriväli ümbritseb iga laetud keha. Elektrivälja aitavad paremini ette kujutada elektrivälja jõujooned.
Elektrivälja jõujoone puutuja suund mingis punktis näitab elektriväljas selles punktis positiivsetele laengutele mõjuva elektrijõu suunda.
9. klassis käsitlesime magnetvälja jõujooni. Neid on suhteliselt lihtne näidata rauapuru ja magnetite abil – rauapuru orienteerub jõujoonte-sihiliselt ja tekitab nähtava joonestiku. Elektrivälja jõujooni on keerulisem näidata, kuna vajalikud katsevahendid on tehnilisemad ja eeldavad suure pingeväärtusega vooluallika kasutamist.
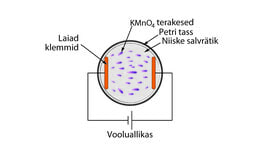
Katse jaoks on vaja Petri tassi, viskoosset vedelikku (näiteks kastoorõli), võimalikult pisikesi taimeseemneid, mis võiksid olla tumeda värvusega (näiteks puneseemned), vasktraati ja elektrofoormasinat. Vasest valmistatakse elektroodid ja asetatakse viskoossesse vedelikku, kuhu on puistatud seemneid (vt joonis 1.10). Kui ühendada elektroodid elektrofoormasina klemmidega, orienteeruvad seemned piki elektrivälja jõujooni.
Miks see nii on? Elektriväljas tekivad seemnete otstesse indutseeritud laengud. Laengutele mõjub elektrivälja suunas jõud, positiivsetele ühes, negatiivsetele teises suunas, mistõttu seemned orienteeruvad elektriväljasuunaliselt. Üksteise lähedal asetsevate seemnete positiivne ja negatiivne pool tõmbuvad samuti, mistõttu tekivad miniahelad. Et sellised miniahelad tekivad elektrijõu mõjumise suunas, siis näitavad need meile elektrivälja jõujooni.
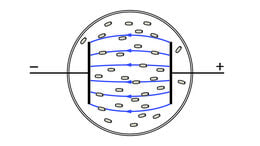
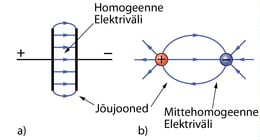
Elektriväli on homogeenne, kui selle jõujooned on paralleelsed. Joonisel 1.11 a on elektrivälja jõujooned kahe sirge paralleelse traadi vahel. Näeme, et ka elektrivälja jõujooned on paralleelsed, kaardudes ainult traadi otstel. Seega on sirgete traatide, samuti ka tasaste plaatide vahel elektriväli heas lähenduses homogeenne.
Kahe kera vahel on elektriväli ebaühtlane ehk mittehomogeenne – elektriväli ja jõujooned on tihedamalt laetud kehade ümber (joonis 1.11 b). Teame, et laetud kehade lähedal on elektrijõud tugevamad (Coulomb’i seadus). Seega võime väita, et mida tugevam on elektrijõud, seda tugevam on elektriväli ja seda tihedamalt paiknevad elektrivälja jõujooned.
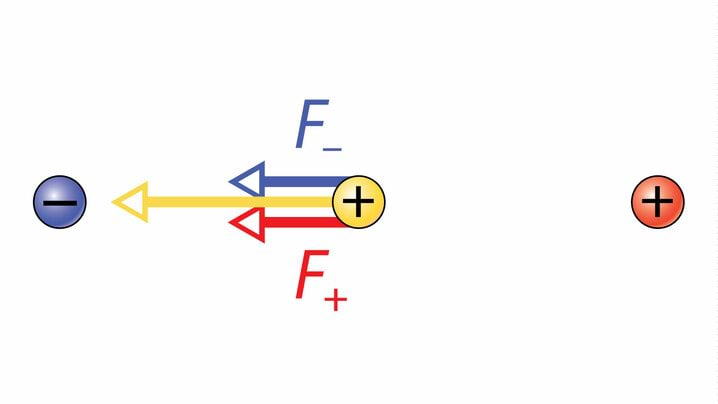
Vaatame joonist 1.12. Olgu kahe vastasmärgiliselt laetud keha vahele asetatud positiivselt laetud proovilaeng, st elektrilaeng, mille enda tekitatud elektriväli uuritavat elektrivälja oluliselt ei mõjuta.
Kui kehade laengud on absoluutväärtuselt võrdsed, mõjutavad nad proovilaengut võrdsete ja samasuunaliste jõududega ja . Kui me need jõud kokku liidame, saame proovilaengule mõjuva kogujõu, mis on kaks korda suurem, kui proovilaeng oleks ainult ühe laetud keha elektriväljas.
Elektrivälja omadust mõjutada laetud kehi kirjeldab elektrivälja tugevus. Elektrivälja tugevus näitab, millises suunas mõjuks elektrijõud elektrivälja asetatud positiivsele laengule. Elektrivälja tugevus on seega vektoriaalne suurus ja elektrivälja tugevuse suund ühtib mistahes punktis elektrivälja jõujoonte puutuja suunaga. Nimetame edaspidi elektrivälja tugevuse vektorit lühidalt E-vektoriks. Joonisel 1.12 on jõuvektorite suunad ühtlasi ka E-vektori suunaks.
Elektrivälja tugevust saab defineerida valemiga
kus tähistab kehale mõjuvat elektrijõudu ja on selle keha laeng. Seega elektrivälja tugevus näitab positiivsele ühiklaengule mõjuvat jõudu.
Elektrivälja tugevuse tähis on ja ühik .
1. näidisülesanne
Lahendus
Elektrivälja tugevust defineerivast valemist
saame avaldada elektrijõu
Ülesande tekstis on elektrivälja tugevus määratud vahemikuna. Valime elektrivälja tugevuseks näiteks . Elektroni laeng on . Nii et
.Miinusmärk vastuses näitab, et elektronile mõjuv jõud on vastupidine E-vektori suunale. Edaspidi me kasutame elektrijõu arvutamiseks pigem jõu absoluutväärtuseid. Seega saime tulemuseks, et elektronile mõjub jõud .
Kas elektron hakkab selle mõjul liikuma? Küllap hakkab, sest elektroni mass on suurusjärgus ja seega kiirendus on tohutu, jäädes suurusjärku .
On teada, et sellisest elektriväljast välgu tekitamiseks siiski ei piisa. Äikesepilves on elektronid seotud vee molekulidega ning nende vabastamiseks on vaja elektrivälja, mille tugevus on umbes .
2. näidisülesanne
Lahendus
Kasutame Coulomb’i seadust ja elektrivälja tugevuse definitsioonvalemit:
Tähistame elektrivälja tekitava laengu -ga:
ja asendame esimese valemi teise valemisse:
Arvutades saame
Vastuse ümardame ühe tüvenumbrini, sest ka lähteandmed on ühe tüvenumbriga ja tegu on hinnangulise suurusega.
Saadud elektrivälja tugevuse väärtus ei ole eriti suur võrreldes äikesepilve elektrivälja tugevusega. Samas on see piisav, et panna induktsioonilaenguga paberitükikesi selles kauguses liikuma.
Väli erineb ainest selle poolest, et kui näiteks mitme erineva laengu tekitatud väljad saavad koos eksisteerida ühes ruumipunktis, siis näiteks kaks prootonit samaaegselt ühes kohas olla ei saa. Lisaks saab väljasid liita. Nii näiteks on tõusud ja mõõnad ookeanis tugevamad siis, kui Kuu ja Päike asuvad Maa suhtes ühel pool. Nõrgemad on nad siis, kui Kuu ja Päike on Maa suhtes vastaspooltel. Võime väita, et Kuu ja Päikese gravitatsiooniväljad liituvad.
Kui ruumis on mitu laetud keha, siis nende elektriväljad liituvad. Sellises elektriväljade liitumises ehk superpositsioonis tekkiv elektrivälja tugevus leitakse, kui omavahel liidetakse laetud kehade elektrivälja tugevuste vektorid. Vektorite liitmisel tekkiva vektori suund määrab ka summaarses elektriväljas proovilaengule mõjuva jõu suuna.
3. näidisülesanne
Lahendus
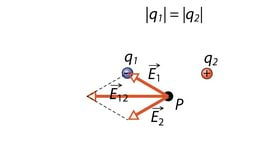
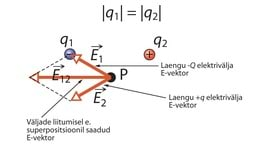
Konstrueerime punktis mõlema laengu tekitatud E-vektorid ja tähistame need ja .
Kuna punkt asub mõlemast laengust samal kaugusel, on laengute tekitatud elektrivälja tugevuse väärtused, seega ka E-vektorite pikkused ühesugused. E-vektori suund mingis punktis on määratud sellesse punkti asetatud positiivsele proovilaengule mõjuva jõu suunaga. Seega on suunatud laengu suunas ja on suunatud laengust eemale.
Summaarse elektrivälja E-vektori suuna saame, kui liidame laengute E-vektorid. Kasutame selleks vektorite liitmise rööpküliku reeglit.
E-vektori suund määraks ka sellesse punkti asetatud prootonile mõjuva jõu suuna. Elektronile mõjuv jõud oleks vastassuunaline.
Paljud meist on külastanud Energia Avastuskeskust Tallinnas, kus demonstreeritakse Faraday puuri, et varjestada külastajaid Tesla transformaator tekitatud tugeva elektrivälja eest. Miks on elektrivälja vaja karta? Sest tugev elektriväli võib tekitada ohtliku elektrivoolu.
Lennukikere käitub Faraday puurina, kaitstes meid pikselöögi eest. Ka metallkerega autos on äikese ajal turvaline. Kuidas töötab puur, mis kannab inglise füüsiku Michael Faraday (1791–1867) nime?
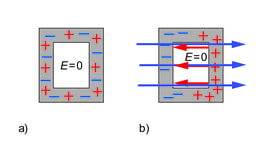
Faraday puuriks on metallist korpus või metallvõrgust puur. Faraday puur töötab elektrilise induktsiooni põhimõttel. Joonisel 1.15a näeme olukorda, kus väline elektriväli puudub. Metallkorpuse laengud paiknevad sel juhul ühtlaselt kogu korpuse ulatuses ning korpus tervikuna on neutraalne.
Välise elektrivälja tekkides paiknevad laengud ümber ja korpuse sees tekib sisemine elektriväli (joonisel 1.15b tähistatud punaste nooltega). Elektriväljad ja on absoluutväärtuselt võrdsed ja vastassuunalised, nii et liitudes on summaarse elektrivälja tugevuseks jällegi .
Kui väline väli tugevneb, siis teeb seda ka sisemine väli, sest indutseeritud laeng muutub suuremaks ja summaarse elektrivälja tugevus on ikka võrdne nulliga. Seega metallkorpuses elektriväli puudub.
Faraday puuri kasutatakse mikrolaineahju tekitatud mikrolainete varjestamiseks, et kiirgus ei pääseks väliskeskkonda. Samuti telekommunikatsioonikaablite signaali kaitsmiseks väliste signaalide ehk müra eest.
Niisiis saab elektrivälja kasutada laengute kiirendamiseks. Just elektrivälja põhjustatud elektrijõud paiskab röntgenlambis elektronid vastu sihtmärki. Genfis asuvas CERNi hiidlaboris kiirendatakse prootoneid ja plii-ioone ning uuritakse nende põrkeid. Elektriväli paneb laengud liikuma päevavalguslampides. Looduses kiirendab elektriväli laenguid äikesepilvedes. Ka elektrivoolu tekkeks ükskõik millises juhtmes või metallesemes on vaja elektrivälja.
Kui enamasti kiirendatakse CERNis elektrivälja abil prootoneid, et LHCs (suures hadronite põrgutis) nende põrkeid uurida, siis korra aastas juhitakse kiirendisse plii-ioonid. Plii-iooni mass on palju suurem prootonite omast [] ja seetõttu on nende ioonide kokkupõrke energia väga suur. Kokkupõrke tulemusena tekib tohutu kogus osakesi, mis kosmoloogilise Suure Paugu mudeli järgi täitsid meie kõige varajasemat universumi.
Täpsemalt on tegu kvark-gluuon plasmaga, millest hilisemas faasis hakkavad moodustuma prootonid. Kvargid on osakesed, millest koosnevad nii prootonid kui ka neutronid. Gluuonid (ingl in glue ’liimis’) on osakesed, mis vahendavad kvarkide-vahelist vastastikmõju, seega hoiavad koos ka prootoneid ja neutroneid. Kvark-gluuon plasma uurimine loob selgust meie varasema universumi arengule.
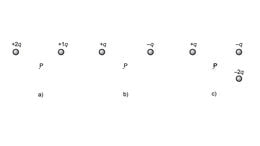
a) Kui suur on kummagi laengu tekitatud elektrivälja tugevus punktis , mis asub täpselt kahe laengu vahel?
b) Kui suur on laengute tekitatud elektrivälja tugevus punktis ?
c) Visanda joonis koos vastavate väljavektoritega.
d*) Lisaülesanne. Kui kaugel esimesest laengust asub punkt, kus väljatugevus on võrdne nulliga?
Elektriväli paneb vabad laengukandjad liikuma ka erinevates keskkondades – metallides liiguvad suunatult vabad väliskihi elektronid (juhtivuselektronid), elektrolüütide lahuses või sulatatud soolades liiguvad ioonid. Õhu elektrijuhtivus on palju väiksem kui metallides või elektrolüütide lahustes, sest vabu laengukandjaid (ioone) on seal vähe. Ioonide arv õhus suureneb tugeva kiirguse või elektrivälja toimel ning siis kasvab ka õhu elektrijuhtivus.
Elektriväli levib keskkondades ligikaudu valguse kiirusega ja nii hakkavad selle toimel kõik vabad laetud osakesed suunatult liikuma ühekorraga ja tekib elektrivool. Uurime, kuidas tekib elektrivool vaskjuhtmes.
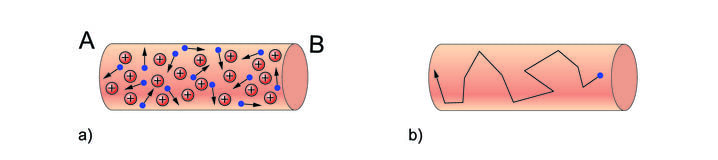
Joonisel 1.17a on skemaatiliselt kujutatud vaskjuhtme lõik. Kui juhtmes puudub elektriväli, liiguvad siniselt tähistatud elektronid kaootiliselt. Kui ühendame juhtme vooluallikaga, mõjub elektronidele elektrijõud ja nad hakkavad suunatult liikuma.
Elektroni kujuteldav trajektoor on esitatud joonisel 17b. Kuigi elektroni hetkkiirus on väga suur – suurusjärgus –, siis osakestevaheliste vastastikmõjude tõttu on triivimise kiirus liikumisel punktist A punkti B väga väike – suurusjärgus üks millimeeter sekundis.
Elektrilaengu suunatud liikumist iseloomustab voolutugevus. Voolutugevuse tähis on ja ühikuks amper, mida tähistame .
-amprine elektrivool on keskmise tugevusega. Elektrirongi jaoks on see väike väärtus, elusorganismidele aga tappev. Töötavas elektriseadmes, näiteks elektrirongi mootoris on voolutugevus mitusada amprit, veekeetja küttekehas suurusjärgus ja väikestes elektripirnides – . Inimesele on eluohtlikud juba voolutugevused alates . Ka väiksemad voolutugevused võivad olla ohtlikud, eriti kui vool läbib inimest pikema aja vältel.
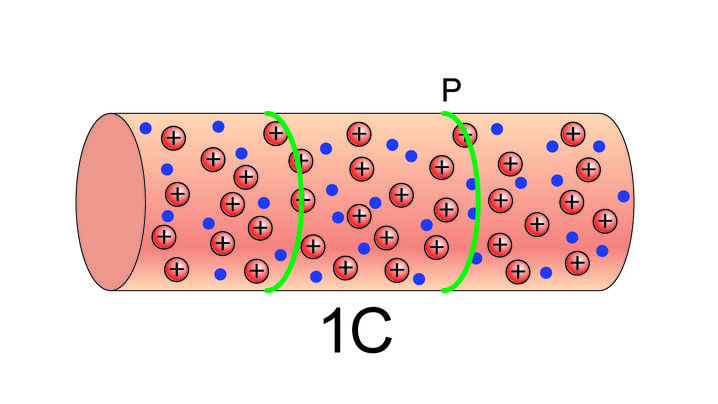
Anname voolutugevuse ühikule füüsikalise tähenduse. Kujutleme juhtme lõiku, kuhu mahub parasjagu nii palju juhtivuselektrone, et nende laeng on võrdne kuloniga (roheliste joontega tähistatud lõik joonisel 1.18).
Kui laeng läbib sekundi jooksul tähega tähistatud juhtme ristlõiget, on voolutugevus võrdne ampriga. Kui laeng läbib nimetatud ristlõiget sekundi jooksul, on voolutugevus korda väiksem ehk .
Valemina
Voolutugevus näitab, kui suur laeng läbib juhi ristlõiget ajaühikus.
Kokkuleppeline voolu suund on vastupidine juhtivuselektronide triivimissuunale ja ühtib elektrivälja vektori suunaga ehk selle suunaga, kuhu liigub positiivne laeng.
Näidisülesanne
Lahendus
Kui uurida voolutugevust mikrotasandil, siis voolutugevuse määravad a) vabade laengukandjate arv ruumalaühiku kohta ehk kontsentratsioon n, b) laetud osakese laeng , c) laetud osakeste triivkiirus ja d) juhi ristlõike pindala .
Kuna voolutugevus sõltub kõigist neist suurustest võrdeliselt, saame kokku valemi
Valemist
avaldub laengukandjate liikumise kiirus kujul
Arvutades saame
Leitud kiirus on üsna väike, sest LED-lampi läbib üldiselt üsna väike vool.
Kui me suudaks ära märkida elektroni, mis lahkub negatiivselt klemmilt ja triivib LED-lambi klemmi suunas, ja kui juhe oleks u pikk, peaksime ootama minutit, enne kui märgitud elektron LEDi klemmile jõuab.
Kuidas oleks võimalik laetud osakeste liikumist kaudselt jälgida? Selleks peame laengukandjatena kasutama ainet, mis on intensiivse värvusega ja ka väikese kontsentratsiooni korral hästi nähtav.
Kasutame katses kaaliumpermanganaati (). Katseks läheb vaja ka Petri tassi või klaasplaati, filterpaberit, krokodillidega juhtmeid, kõrgema pingega alalisvooluallikat ja ammoniaagi vesilahust. Kaaliumpermanganaadi lahustumisel tekkivate – ioonide liikumise jälgimiseks piisab ligikaudu pingest. Võimalusel ühendage juhtmed vasest klemmidega, mille kuju on võimalik muuta.
Kõigepealt tehakse paber ammoniaagi lahusega märjaks, paberiga kaetud plaat ühendatakse krokodillide abil vooluallikaga, nagu on näha joonisel 1.19. Seejärel asetatakse paberile pintsettidega üks kaaliumpermanganaadi kristall.
Kui vooluring on ühendatud, hakkavad ioonid liikuma. Kui kiiresti värvilaik liigub ja mis suunas? Kuna värvust põhjustab permanganaadi anioon, siis liikumine toimub pluss-klemmi suunas. Milline on pilt siis, kui lisada kaaliumpermanganaadi kristalle mitmesse kohta või suurendada pinget?
Oleme õppinud, kuidas gravitatsiooniväljas mõjub kehadele gravitatsioonijõud ning see teeb tööd veemasside liikuma panemiseks looduses, olgu see siis vihma, jõgede või koskede näol. Elektriväljas mõjub laetud osakestele elektrijõud ja vabad laengukandjad hakkavad jõu tõttu liikuma. Nii teeb elektriväli tööd laengukandjate liigutamiseks näiteks röntgenlambis, elektrivooluringis, äikesepilvedes või osakeste kiirendis.
Mehaanikast on tuttav mehaanilise töö mõiste – keha liikumisel jõu mõjul on tehtud töö võrdne jõu ja sooritatud nihke korrutisega
Kui elektrijõud mõjub laetud osakeste liikumise suunas, siis ja . Saame
Kuidas elektrivälja tööd arvutada? Elektrivälja tugevust defineerivast valemist
saame avaldada elektrijõu
Asendades selle mehaanilist tööd defineerivasse valemisse, saame elektrivälja töö valemiks
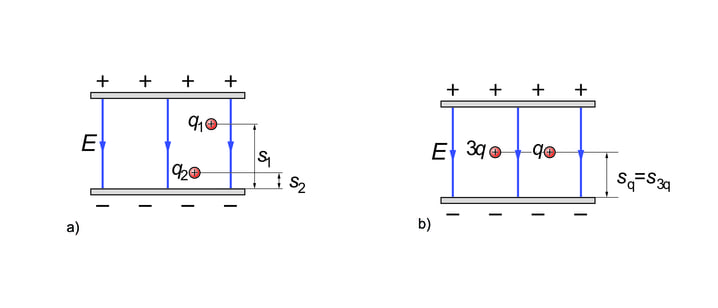
Joonisel 1.20a on laengud ja homogeenses elektriväljas tugevusega . Positiivne plaat tõukab ja negatiivne plaat tõmbab positiivset laengut. Et laengud paiknevad laetud plaatidest erinevatel kaugustel, on nende nihked negatiivselt laetud plaadini erinevad, kusjuures . Mida suurem nihe, seda suurem töö. Seega teeb elektriväli rohkem tööd laengu liigutamisel.
Joonisel 1.20b paiknevad kaks laengut ja laetud plaatidest võrdsel kaugusel. Laengu nihutamisel teeb elektriväli kolm korda rohkem tööd kui laengu nihutamisel, sest laeng on kolm korda suurem.
Paneme tähele, et laengute liigutamisel tuleb teha suuremat tööd ka siis, kui elektrivälja tugevus on suurem, st kui plaatidel joonisel 1.20 on suurem laeng.
Mida suurem on elektrivälja tugevus, seda suurem jõud mõjub laetud osakesele ja seda suurem on elektrivälja töö.
Näidisülesanne
Lahendus
Teame, et
Asendame valemis elektrivälja tugevuse, laengu ja nihke väärtused, saame
See on väga suur töö. Gravitatsioonijõud teeks sama suure töö, kui kukutaksime -tonnise raskuse meetri kõrguselt maapinnale.
Selleks, et teha tööd, on vaja energiat. Gravitatsioonijõud teeb tööd potentsiaalse energia arvelt, mida mehaanikas arvutame kujul
kus on keha mass, on raskuskiirendus ja on keha kõrgus potentsiaalse energia kokkuleppelise nullnivoo, antud juhul siis maapinna suhtes. Suurt potentsiaalset energiat omab maapinna suhtes kõrgel paiknev suure massiga keha. Kui keha paikneb potentsiaalse energia nullnivool, st maapinnal, siis on keha potentsiaalne energia võrdne nulliga ja gravitatsioonijõud keha liigutada ei saa.
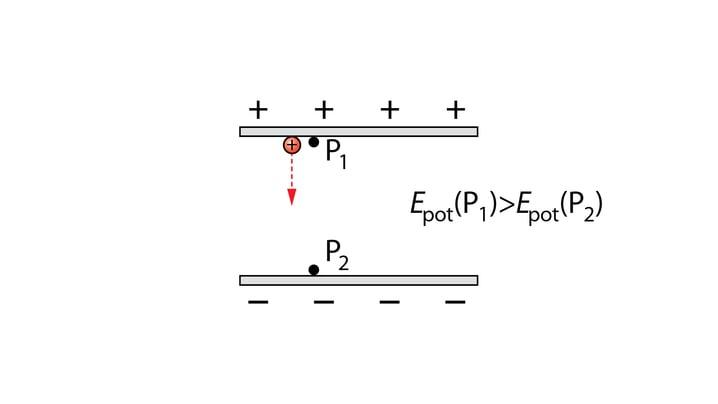
Sarnased seaduspärasused kehtivad ka elektriväljas paiknevate laengute potentsiaalse energia kohta. Kui võimalik elektrijõu-suunaline liikumisulatus on suur, on ka laengu potentsiaalne energia suur. Kui laeng elektrijõu suunas enam liikuda ei saa, on laengu potentsiaalne energia võrdne nulliga. Joonisel 1.21 on punktis laengu potentsiaalne energia maksimaalne. Kui laeng liigub elektrivälja mõjul punkti , on tema potentsiaalne energia null, st . Sealjuures on elektriväli teinud tööd laengu viimisel punktist punkti .
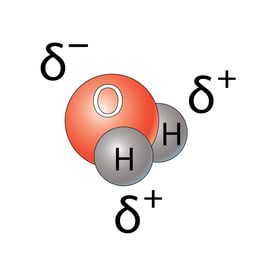
Elektriväli paneb laetud osakesed liikuma, aga samas võib ka liikumist pidurdada. Tugeva elektrivälja abil on võimalik vett jahutada. Kuidas see toimub? Vihjeks vaata vee molekuli dipoolset kuju joonisel, seal on deltadega tähistatud hapniku ja vesiniku aatomite osalaengud.
Eelmises osas kirjeldasime tööd, mida teeb elektriväli laengute liigutamisel. 9. klassist tuttav mõiste pinge on otseselt seotud elektrivälja poolt tehtud tööga.
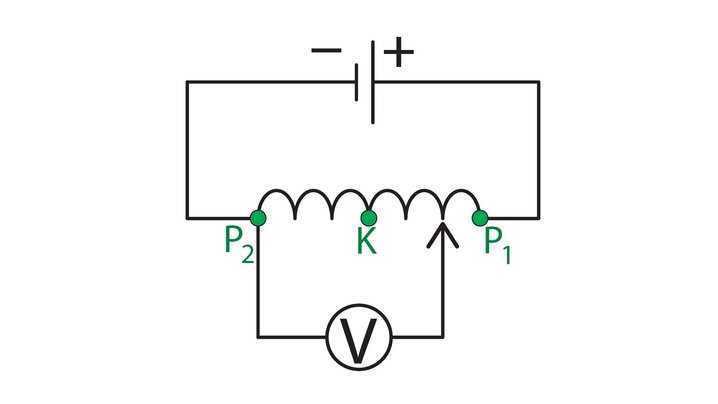
Joonisel 1.22 on kujutatud vooluringi ühendatud reostaadi mähist. Pinget reostaadil saab mõõta voltmeetriga, mille üks klemm on ühendatud püsivalt reostaadi mähise ühe otsaga ja mille teist klemmi saame nihutada reostaadi mähise keerdudel.
Kõige suurem on pinge väärtus reostaadi mähise otstel, st punktide ja vahel. Kui nihutame liugkontakti punktist punkti K suunas, siis pinge väärtus väheneb.
Kui mõtleme tööst, mida elektriväli teeb laengute liigutamisel, siis ilmselt on see suurim, kui laengud liiguvad läbi terve reostaadi. Seda mõttekäiku saab üldistada ja öelda, et suurema pingega töötavad seadmed teevad rohkem tööd – nii on vaja röntgenlambis elektronide kiirendamiseks vähemalt , et toota suure energiaga röntgenkiirgust, aga LED-lambi põlemiseks piisab pingest .
Pinge mistahes kahe punkti vahel on arvuliselt võrdne tööga, mida tehakse ühekulonilise laengu nihutamisel ühest punktist teise. Pinge definitsioonvalem on
Vooluringis mõõdetakse pinget mistahes kahe punkti vahel voltmeetriga.
Võrgupinged maailma riikides jäävad vahemikku –230V. Kõige madalam on pinge Jaapanis: , Eestis ja Euroopas on pinge vooluvõrgu klemmidel keskmiselt 230V, Ameerika Ühendriikides . Kui osta seadmeid välismaalt, tuleb uurida seadme tehnilisi andmeid, sealhulgas ka nimipinget.
Elektrivälja kirjeldamiseks kasutatakse ka elektrivälja potentsiaali mõistet.
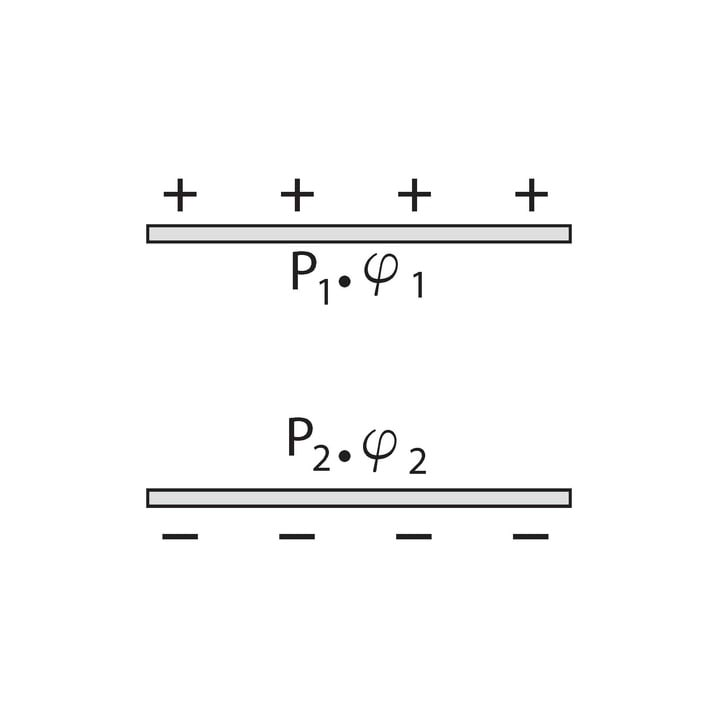
Joonisel 1.23 oleme laetud plaatide tekitatud elektriväljas märkinud punktid ja . Neid punkte iseloomustab ka elektrivälja potentsiaal, mille tähistame kreeka tähega (fii). Elektrivälja potentsiaal on seotud elektrivälja asetatud laengu potentsiaalse energiaga antud punktides. Kuna punktis on laengu potentsiaalne energia suurem kui punktis , saame sama öelda ka elektrivälja potentsiaali kohta: .
Elektrivälja potentsiaal näitab, kui suur on elektrivälja potentsiaalne energia mingis punktis positiivse ühiklaengu kohta.
Miks just ühiklaengu kohta? Aga sellepärast, et elektrivälja potentsiaal on välja omadus, see ei sõltu sellest, kui suur laeng seal väljas paikneb. Nii mitu korda, kui erinevad kehade laengud, erinevad ka laetud kehade potentsiaalsed energiad antud elektrivälja punktis.
Elektrivälja potentsiaal on väljendatav valemiga:
Rõhutame, et elektrivälja potentsiaal iseloomustab elektrivälja sõltumata sellest, kas seal on laetud keha või mitte.
Füüsikas on suurema tähendusega elektrivälja kahe punkti potentsiaalide erinevus, sest see määrab ära, kui palju teeb elektriväli tööd laengu nihutamisel elektrivälja ühest punktist teise.
Kui mõõdame pinget elektriseadme kahe punkti vahel, siis mõõdame nende punktide potentsiaalide erinevust . Pinge ja elektrivälja potentsiaali vahelist seost väljendab valem
Näiteks kui mõõdame vooluringis vooluallika klemmipingeks , saame öelda, et klemmide potentsiaalide erinevus on 9V.
Nii pinge kui ka elektrivälja potentsiaali ühikuks on 1V.
Pinget ja potentsiaali ei tohi omavahel segamini ajada. Erinevus nende kahe füüsikalise suuruse vahel:
- pinge võrdleb kahe punkti potentsiaali ja annab võimaluse arvutada näiteks elektrivälja poolt tehtavat tööd laengute nihutamisel ühest punktist teise, potentsiaal aga kirjeldab olukorda ühes punktis;
- pinget mõõdetakse voltmeetriga otseselt, potentsiaali kaudselt. Kasutusele on võetud ka erinevad tähised: pinge tähis on ja elektrivälja potentsiaali tähis on (fii).
Enamik traditsioonilisi tähiseid on eesti keelde tulnud saksa kultuuriruumist ja sageli vene keele kaudu, mistõttu eestikeelsed füüsikaliste suuruste tähistused erinevad ingliskeelses erialakirjanduses kasutatavatest tähistustest. Inglise keeles on võetud tähiseks vastava sõna esimene täht. Näiteks tiheduse tähis on meil , aga inglise keeles (density), meil on töö tähis , inglise keeles (work), meil on pinge tähis , inglise keeles (voltage). Samuti tähistatakse inglise keeles -tähega elektrilist potentsiaali. Nii võime leida ingliskeelsetes õpikutes üleskirjutuse , mis näitab, et pinge on võrdne potentsiaalide vahega klemmide otstel ja selle väärtus on volti.
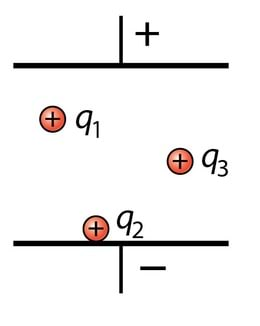
Uurime elektrivälja potentsiaali kahe sirge traatelektroodi vahel, mis on asetatud ammoniaagi vesilahusega immutatud paberile ja ühendatud alalisvooluallikaga pingeväärtusega . (Vt joonis 1.24.)
Potentsiaalide mõõtmiseks kasutame voltmeetrit, mille üks klemm on ühendatud negatiivse elektroodiga. Sellel elektroodil on potentsiaal vähima väärtusega ja potentsiaali nullnivoo on kokkuleppeline, loeme selle võrdseks nulliga . Voltmeetri teise klemmi saame ühendada mistahes välja punktiga. Kasutame valemit . Kui
asendame , saame öelda, et voltmeetri näit on ühtlasi ka antud punkti potentsiaali väärtus:
Katses uurime elektrivälja potentsiaale kuues erinevas punktis. Kui ühendada liikuv klemm punktiga (joonis 1.24a), näitab voltmeeter . Sama potentsiaali väärtuse saame ka siis, kui ühendame liikuva klemmi punktiga . Nende kahe punkti potentsiaalide erinevus on seega . Meie mõõtmised ja arvutused näitavad, et pinge elektroodi ja punkti vahel on , aga pinge punkti ja vahel on .
| Elektrivälja punkt | Elektrivälja punkti potentsiaal |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Kui mõõta sarnaselt kõikide teiste punktide potentsiaalid (vt tabel 1.2) ja arvutada potentsiaalide erinevused, märkame, et
a) punktide ja vahel ning ka punktide ja vahel on pinge ;
b) pinge punktide ja vahel on , samuti punktide ja ning ja vahel;
c) punktide ja ning ja vahel on pinge ;
d) suurim on pinge kahe elektroodi vahel, kus .
Elektriväli teeb tööd ainult siis, kui on olemas potentsiaalide erinevus (pinge). Mida suurem on elektrivälja punktide potentsiaalide erinevus, seda suurem on pinge ja elektrivälja töö. Kui ehk potentsiaalide erinevus puudub, siis ei tehta ka tööd.
Valemina saab selle kirja panna kas
või
Potentsiaali mõiste on kesksel kohal näiteks närvirakkude toimemehhanismi seletamisel
bioloogias ja vooluallika parameetrite väljaarvutamisel elektrokeemias.
Mikromaailma füüsikas kasutatakse energiaühikut elektronvolt (). Kuidas on see seotud energia põhiühikuga 1J? Loogiline oleks arvata, et kui on tegu üliväikeste osakestega, näiteks elektronide, prootonite või footonitega, siis on ka nende energia võrreldes makromaailma objektidega väga väike. Nii ta ongi, sest . Milline osake omab energiat ? Sellises suurusjärgus on nähtava valguse footoni energia. Tuumaosakeste energiat mõõdame megaelektronvoltides (). Näiteks et eraldada raua aatomi tuumast üks tuumaosake, tuleb kulutada energiat u .
Ühik on tuletatud meile tuttavast valemist . Kui kasutame elektrilaengu ühikut ja pinge ühikut 1V, on nii töö kui ka energia ühik 1J. Kui kasutame ühe kuloni asemel elementaarlaengut , ongi töö ja energia ühikuks , mis on väga sobilik mikromaailma energia ja töö ühikuks.
on võrdne tööga, mida teeb elektriväli elektroni viimisel ühest väljapunktist teise, kui nende punktide potentsiaalide erinevus on 1V. Makromaailmas on see suurus üliväike.
Uurime nüüd elektrivälja tugevuse ja pinge omavahelist seost.
Oskame juba arvutada homogeense elektrivälja poolt laengu liigutamisel tehtavat tööd:
ja teame pinge definitsioonivalemit:
mille annab kirja panna ka kujul
Kõigis neis valemites tähistame -ga ühte ja sama füüsikalist suurust. Kui on võrdsed võrrandi vasakud pooled, siis on võrdsed ka paremad pooled ja saame võrrandi
Lihtsustamisel saame uueks seoseks
Asendame nihke sümboli sümboliga , mis väljendab erineva potentsiaaliga alade vahekaugust. Saame homogeense elektrivälja tugevuse ja pinge seoseks
Pinge kahe punkti vahel on seda suurem, mida suurem on elektrivälja tugevus ja mida suurem on nende punktide vahekaugus , mõõdetuna piki elektrivälja jõujooni.
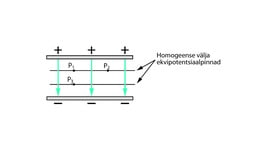
Elektriväljade kirjeldamisel kasutatakse ka ekvipotentsiaalpindade mõistet.
Ekvipotentsiaalpind on pind elektriväljas, kus naaberpunktide potentsiaalide väärtused on võrdsed. Seega, ekvipotentsiaalpinna punktide vaheline pinge V (lad ekvi – aequus ’võrdne, sama’).
Joonisel 1.27 kujutatud situatsioonis on elektrivälja punktid ja ekvipotentsiaalpinnal, seega . Elektriväljas asuvad punktid ja erinevatel ekvipotentsiaalpindadel, nii et .
1. näidisülesanne
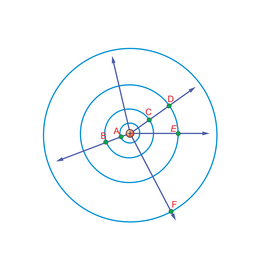
Joonisel 1.27 on kujutatud punktlaeng ja seda ümbritsev elektriväli. Elektrivälja kirjeldavad joonisel välja jõujooned. Siniste joontega tähistatud punktid asuvad punktlaengust samal kaugusel, järelikult on seal elektrivälja potentsiaal sama väärtusega ja tegemist on ekvipotentsiaalpindadega. Kõigi kõrvuti asuvate pindade vahel on ühesugune potentsiaalide vahe. Kahe sellise pinna vahekaugus on punklaengust kaugemal suurem ja lähemal väiksem.
Vasta küsimustele.a) Kas laengut ümbritseb homogeenne või mittehomogeenne väli?b) Milliste joonisel toodud elektrivälja punktide vahel on suurim pinge?c) Milliste punktide vahel on pinge vähima väärtusega, aga siiski nullist erinev?d) Milliste punktide vaheline pinge on ?
Lahendus
a) Visuaalselt näeme, et punktlaengust kaugemal jõujoonte vahekaugus suureneb. Järelikult on tegu mittehomogeense väljaga. Mittehomogeensuse füüsikaliseks põhjuseks on asjaolu, et punktlaengu elektriväli on laengust kaugemal nõrgem:
b) Pinge on suurim punktide ja vahel, sest nende kahe punkti potentsiaalide
erinevus on suurim.
c) Laengust kaugemal on siniste joonte vaheline kaugus d järjest suurem, aga samas kahaneb väärtus. Vastamiseks oleks vaja täpsemaid andmeid.
d) Punktide ja vaheline pinge on võrdne nulliga, sest need asuvad ekvipotentsiaalpindadel, st samasuguse potentsiaaliga pindadel.
2. näidisülesanne
Olgu röntgenlambi elektroodidele rakendatud pinge (joonis 1.28).
a) Kui suure kineetilise energia omandab elektron sellises röntgenlambis?b) Kui suur on elektrivälja tugevus, kui anoodi ja katoodi vaheline kaugus on ?c) Kas tegu on homogeense või mittehomogeense elektriväljaga? Visanda elektroodide elektrivälja jõujooned.
Lahendus
a) Elektriväli teeb tööd elektroni kiirendamiseks. Eeldame, et energiakaod on tühised ja kogu töö muundub elektroni kineetiliseks energiaks ja elektroni algkiirus . Siis
Kasutame pinge definitsioonivalemit ja avaldame sealt töö . Saame kineetilise energia valemiks
nii et
Esmapilgul tundub see olevat tühine energia. Aga kui kasutame mehaanikast tuntud kineetilise energia avaldist
ja hindame sellise kineetilise energiaga elektroni kiirust, saame
Leitud kiirus on valguse kiiruse suurusjärgus.
Reaalselt elektronid siiski selliseid kiiruseid ei saavuta, sest lambis ei ole absoluutne vaakum, vaid suur hõrendus, ja tegu ei ole ka üksiku isoleeritud elektroniga, vaid osaga suuremast laengust.
b) Elektrivälja tugevuse hindamiseks kasutame valemit
Arvutades saame
c) Kindlalt saame öelda vaid seda, et elektrivälja jõujooned on suunaga n-ö plussilt miinusele, st positiivselt laetud elektroodilt negatiivselt laetud elektroodile. Aga et elektroodid ei ole üksteisega paralleelsed, siis ei ole elektriväli nende vahel homogeenne ka siis, kui elektroodid on suured. Siiski on kahe paralleelse plaadi vahelise elektrivälja mudel parim, mis me oma teadmiste põhjal oskame välja pakkuda (vt joonisel 1.1 kujutatud elektrivälja jõujooni). Paneme tähele, et elektrivälja töö laengute liigutamisel, st elektronide saavutatud maksimaalne kineetiline energia sõltub ainult pingest.
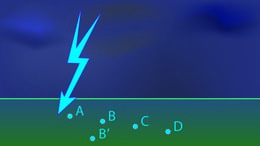
Joonisel 1.29. on skemaatiliselt kujutatud välgu löök maasse. Me teame, et välk tähendab tohutu suurt laengu ülekannet. Järelikult on laeng väga suur ka kohas, kus välgukanal maapinnani jõuab.
Punktid joonisel 1.29 asetsevad sellest kohast eri kaugustel, aga punktid
ja sama kaugusel. Situatsioon on sarnane joonistel 1.24 ja 1.27 kujutatuga. Nii võime väita, et pinge punktide ja vahel on suurim, samas pinge punktide ja vahel on võrdne nulliga.
Kuidas me peaksime äikese ajal käituma, kas paigal seisma, äikesepilvest pika sammuga eemalduma või hoopis jooksma? Kuni maad puudutab ainult üks jalg, ei ole meie keha pingestatud – pingeks on vaja kahte punkti. Kui seisame sarnaselt, nagu paiknevad punktid ja , on pinge väärtus meie keha mistahes punkti vahel võrdne nulliga. Samas pika sammuga eemaldumisel (punktid ja ) on potentsiaal kahe jalalaba vahel suur. Järelikult on suur ka pinge ning elektrivälja töö meie kehas laengute liigutamisel võib saatuslikuks saada.
Sarnaselt võib olukord ohtlikuks kujuneda ka katkiste, maapinnale kukkunud või puudesse takerdunud kõrgepingeliinide läheduses – maapinnalähedaste punktide potentsiaalid võivad olla väga erinevad ning seal kõndides või ka jalad harki seistes võime saada elektrilöögi. Õnneks hoitakse Eestis liinialused puhtad ja tormide ajal tegutsetakse väga kiiresti, et kõrgepingeliinid korras püsiksid.
Mass-spektromeetris kasutatakse ioonide kiirendamiseks pinget . Elektroodi plaatide vaheline kaugus on . Vasta küsimustele.
a) Kui suur on elektrivälja tugevus kiirendis?
b) Millise energia saab metalli katioon, mille suhteline laeng on ? Anna vastus ka -des.
c) Kas sama aparaadiga saab uurida ka negatiivseid ioone? Selgita vastust.
d) Kumb ioon saab mass-spektromeetris suurema kiiruse, kas arseeni- või pliikatioon, kui mõlema laengud on võrdsed? Põhjenda.
a) Kui pika ajaga tühjeneb patarei?
b) Kui suur on mootoris elektrivälja töö?
c) Milline on elektrijalgratta mootori võimsus?
Mõni aeg tagasi ilmus Äripäevas artikkel „Eesti superkondensaatorid lähevad Briti bussidesse“. Artiklis teatati, et Eesti superkondensaatoreid tootev firma Skeleton sõlmis mitme miljoni euroni ulatava lepingu. Selle järgi varustatakse ühe- ja kahekorruselised hübriidmootoriga bussid superkondensaatoritel põhinevate kineetilise energia taaskasutamise süsteemidega, mille tulemusena muutuvad bussid energiasäästlikumaks, samas ka mahukamaks, sest see süsteem on suhteliselt väike ega võta palju ruumi.
Selleks, et aru saada artiklis esitatud infost, tuleb kõigepealt selgitada, mis on kondensaator ja milleks seda kasutada saab. Sõna „kondenseeruma“ on meile tuttav seoses veeauru veeldumisega. Kondenseerumisel koonduvad veemolekulid suuremateks kogumiteks. Eriti hea on seda jälgida niiskes toas piisavalt jahedate aknaklaaside juures, sest vesi kondenseerub külmale pinnale. Kondensaatoris „kondenseeruvad“ kondensaatori plaatidele laengud.
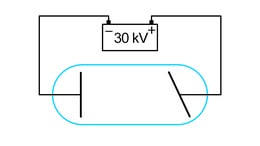
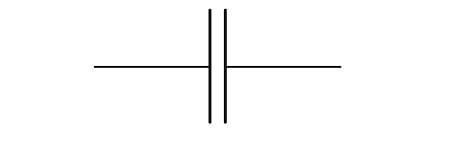
Joonisel 1.31 on esitatud lihtsa, kahest õhuvahega eraldatud metallplaadist koosneva kondensaatori mudel.
Kui ühendada plaadid elektrijuhtmete abil vooluallika poolustega, siis plaadid laaduvad. Alguses toimub laadumine väga kiirelt, aga plaatidele kogunenud laengu tõukejõud hakkab seda järjest tugevamalt takistama.
Laadimine lõpeb, kui kondensaatori plaatide vaheline pinge saab võrdseks pingega vooluallika klemmidel (joonis 1.32).
Võime ka öelda, et vooluallika negatiivse klemmi potentsiaal saab võrdseks kondensaatori negatiivse plaadi potentsiaaliga. Seega kondensaatori plaatide potentsiaalide erinevus ja elektriväli enam laengu nihutamiseks tööd teha ei saa. Sama olukord on ka vooluallika positiivse klemmi ja kondensaatori positiivse plaadi vahel.
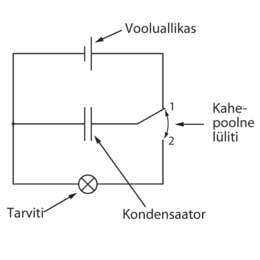
Kui eemaldada vooluallikas ja ühendada kondensaator tarvitiga, hakkab kondensaator tühjenema, tekitades vooluringis elektrivoolu (vt joonis 1.33). Seega võime öelda, et kondensaator salvestab energiat ja kondensaatorit saab kasutada vooluallikana.
Kondensaatorisse saab energiat salvestada kahel viisil. Üks võimalus on ühendada kondensaatori plaadid vooluallikaga, nagu on kirjeldatud eelmises lõigus. Teine võimalus on laadida vooluallikaga ainult üks kondensaatori plaat, nagu näidatud joonisel 1.34.
Kui nüüd kondensaatori teine plaat maandada, siis laetud kondensaatori plaat tekitab sellele sama suure vastasmärgilise induktsioonilaengu. Nii on meil sama olukord nagu joonisel 1.32 ja saame kondensaatori tühjendada läbi mõne tarviti.
Kondensaatori peamist füüsikalist omadust salvestada laengut nimetatakse mahtuvuseks. Mahtuvuse tähis on ja ühik farad ().
Mahtuvuse definitsioonvalem on
mis ütleb, et mahtuvus on arvuliselt võrdne laenguga, mis koguneb plaatidele ühikulise pinge rakendamisel.
Seega
Kuna kulon on väga suur laeng, siis on ka mahtuvus väga suur. Elektroonikas kasutavate kondensaatorite mahtuvused jäävad millifaradi () ja pikofaradi () vahele. Peatüki alguses mainitud superkondensaatorite mahtuvus on vahemikus , st neisse saab salvestada väga suure energia. Siit ka nende nimetus – superkondensaator.
Kõigil tehnikas kasutatavatel kondensaatoritel on ühesugune tööpõhimõte. Kuidas on siis võimalik, et kondensaatorite mahtuvused erinevad tuhandeid kordi?
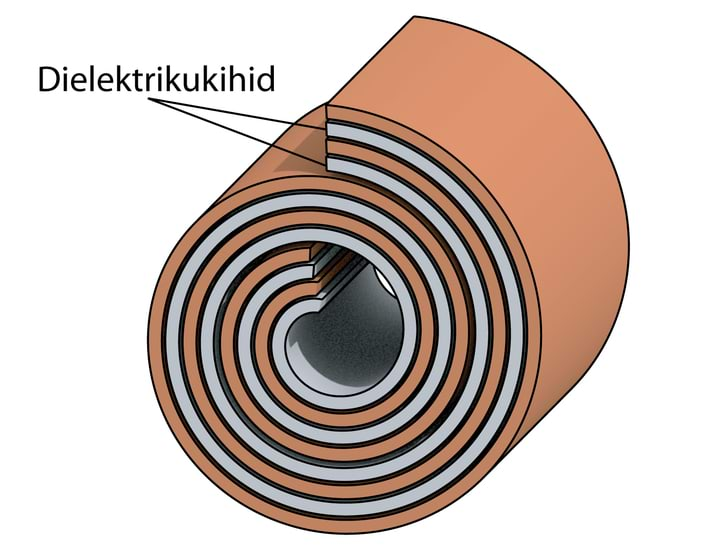
Et mahutada kondensaatorite plaatidele suuremat laengut, on vaja nende pindala suurendada. Lihtsaim võimalus saada suure pindalaga kondensaatoreid on nende plaadid rulli keerata (joonis 1.35). Nii võivad üsna suurte kondensaatorite mõõtmed olla päris väikesed.
Superkondensaatorite plaatide pindalad on hiigelsuured, sest nende pind on poorne. Joonisel 1.36 kujutatud sile plaat ja poorne plaat on väliselt sama suured, aga nende pindalad võivad erineda sadu tuhandeid kordi.
Kondensaatori mahtuvust saab suurendada ka siis, kui asetada plaadid võimalikult lähestikku ja plaatide vahel on dielektriku kiht. Joonisel 1.35 kujutatud kondensaatoris ongi kondensaatori plaadid toodud üksteisele lähedale, dielektriku kiht on tähistatud halli värviga. Dielektriku kihil on ka praktiline funktsioon – isoleerida üksteisele lähedal asuvaid plaate ja vältida lühise tekkimist.
Kuna kondensaator saab tühjenemisel tööd teha, võime väita, et laetud kondensaatorisse on võimalik salvestada energiat. Kondensaatorisse salvestatava energia arvutamiseks kasutame valemit
Nagu füüsikas tavaks, tuletame valemeid varem teadaolevatest seostest. Kui tahame arvutada, kui suurt energia hulka kondensaator mahutab, kasutame teadaolevaid valemeid. Esiteks, täislaetud kondensaatori energia on võrdne maksimaalse tööga ehk
Teiseks, kondensaatori mahtuvus
nii et
Laadudes pinge kondensaatori plaatide vahel kasvab algväärtusest kuni maksimaalse väärtuseni . Sarnaselt ei saa me elektrivälja poolt tehtud töö valemis
kasutada pinge maksimumväärtust, vaid pinge keskmist väärtust:
Et enne laadimist kondensaatori pinge , siis
Kondensaatori laenguks saame siis
ja sellise laengu korral on kondensaatorisse salvestatav energia
mis annabki energia valemiks
Sellise seose kehtivust on võimalik tõestada ka katseliselt.
Pange tähele, et kasutame nii elektrivälja tugevuse kui ka kondensaatorisse salvestatud energia tähisena -d. Valemite lugemisel tuleb segaduse vältimiseks arvestada kontekstiga.
Näidisülesanne
Skeletoni toodetud superkondensaatorite moodulile on märgitud ja . Arvutame, a) kui suur on sellesse kondensaatorisse salvestatud energia, b) kui suurt laengut superkondensaator mahutab ja c) kui suur on voolutugevus kondensaatori tühjenemisel minuti jooksul.
Lahendus
a) Salvestatud energia on võimalik arvutada otse vastavast valemist:
See energia on väiksem, kui mahub näiteks ühte AA-patareisse. Aga et kondensaatorit saab laadida ja tühjendada miljoneid kordi ilma, et selle omadused muutuksid, on saadud energia siiski märkimisväärne.
b) Ka laengu arvutamiseks on meil valem olemas. Et
siis
ja
Tegu on väga suure laenguga. Superkondensaatori mahtuvus on väga suur.
c) Voolutugevuse arvutame, kasutades voolutugevuse definitsioonvalemit
Kondensaatori tühjenemise aeg ja seega ka voolutugevus sõltuvad vooluringist, kus kondensaatorit kasutatakse. Praeguses näites on tegu küllalt suure voolutugevusega võrreldes näiteks töötava veekeetja küttekeha voolutugevusega (umbes ).
Kondensaatoreid kasutatakse raadiosaatjate võnkeringis, nutiseadmete laadijates, alaldites, elektrisõidukite energiasalvestussüsteemides ja kosmosetehnoloogias. Osade klaviatuuride töö põhineb mahtuvuse muutmisel; raadiokanali häälestamisel ehk kanali otsimisel muudetakse raadiolainete vastuvõtusüsteemi mahtuvust; CCD-sensor, millel põhineb digikaamerate, skannerite ja teleskoopide töö, koosneb arvukatest minikondensaatoritest.
Kehade laadumine on seotud vabade elektronide ümberpaiknemisega kehades. Kui kehas on elektronide liig, on keha laetud negatiivselt, ja kui keha on elektrone ära andnud, laadub keha positiivselt.
Elektriline või elektrostaatiline induktsioon on vabade laengute ümberasetumine elektrit juhtivas kehas väliste elektrijõudude tõttu, mistõttu keha pind laadub teise kehaga võrreldes vastasmärgiliselt.
Elektrilaeng füüsikalise suurusena iseloomustab, kui tugevasti osaleb laetud keha elektromagnetilises vastastikmõjus.
Elektrilaengu tähis on ja ühik .
kulon on väga suur laeng. Äikesepilve laengud võivad olla suurusjärgus . Kui juuksed on elektrit täis, siis on juuksekarvade laengu väärtused vahemikus .
Elementaarlaeng () on looduses kõige väiksem vabalt eksisteeriv laeng.
Coulomb’i seadus – laetud kehade vahel mõjuv elektrijõud sõltub võrdeliselt laengute suurusest ja pöördvõrdeliselt laengutevahelise kauguse ruudust.
– punktlaengute vaheline kaugus
ja – laengud
– Coulomb’i konstant,
Kui kaks keha laengutega on üksteisest meetri kaugusel, esineb kehade vahel tõukejõud väärtusega .
Keskkonna dielektriliseks läbitavuseks nimetatakse suurust, mis näitab, mitu korda on antud keskkonnas elektrijõud nõrgemad võrreldes vaakumiga. Näiteks , mis näitab, et vees on laengutevahelised jõud korda nõrgemad
kui vaakumis.
Elektriväli eksisteerib kõikide laetud kehade ümber.
Elektrivälja jõujooned näitavad elektriväljas positiivsetele laengutele mõjuva elektrijõu suunda.
Joonisel on elektrivälja jõujooned a) homogeenses elektriväljas, b) mittehomogeenses elektriväljas.
Elektrivälja tugevus on vektoriaalne suurus, mis näitab elektrivälja asetatud positiivsele laengule mõjuva jõu suurust ja suunda ning on arvuliselt võrdne positiivsele ühiklaengule mõjuva jõuga.
– elektrivälja tugevus
– kehale mõjuv elektrijõud
– keha laeng
Elektrivälja tugevuse ühik on väga väike suurus. Laetud joonlaua läheduses oleva elektrivälja tugevus .
Elektrivälja tugevuse suund ühtib mistahes punktis elektrivälja jõujoonte suunaga.
E-vektor – elektrivälja tugevuse vektor
Superpositsioon ehk elektriväljade liitumine. Mitme laetud keha poolt tekkinud elektrivälja tugevus leitakse laetud kehade elektriväljade -vektorite liitmisel.
Elektriväli levib keskkondades ligikaudu valguse kiirusega ja nii hakkavad selle toimel kõik vabad laetud osakesed ühekorraga suunatult liikuma ning tekib elektrivool.
– voolutugevus
– elektrilaeng
– aeg
Voolutugevus näitab, kui suur laeng läbib juhi ristlõiget ajaühikus.
– elektrivälja tugevus
– elektrilaeng
– laengu poolt sooritatud nihe
Elektrivälja töö seisneb laengute liikuma panemises, liikumas hoidmises või pidurdamises.
Kui on teada plaatidevaheline pinge , saab elektrivälja tööd arvutada valemiga .
Elektrivälja asetatud positiivse laengu potentsiaalne energia .
– elektrivälja tugevus
– laeng
– kaugus negatiivsest plaadist
(elektronvolt) on võrdne tööga, mida teeb elektriväli elektroni viimisel ühest väljapunktist teise, kui nende punktide potentsiaalide erinevus on 1V.
Pinge kahe punkti vahel on seda suurem, mida suurem on elektrivälja tugevus ja mida suurem on nende punktide vaheline kaugus mõõdetuna piki elektrivälja jõujooni.
– pinge
– elektrivälja tugevus
– elektrivälja kahe punkti vaheline kaugus
Ekvipotentsiaalpind on pind elektriväljas, kus naaberpunktide potentsiaalide
väärtused on võrdsed. Seega ekvipotentsiaalpinna punktide vaheline pinge .
Elektrivälja punktid ja asuvad ekvipotentsiaalpinnal: .
Elektrivälja punktid ja asuvad erinevatel ekvipotentsiaalpindadel: .
Kondensaator on seade, mis salvestab energiat. Kondensaatorit saab
kasutada vooluallikana. Kondensaatori põhikomponendid: a) elektrit juhtivad plaadid, b) plaatide vahel paiknev dielektriku kiht.
Kondensaatorit saab laadida, kui lüliti on asendis 1. Kondensaator tühjeneb, kui lüliti on asendis 2.
Kondensaatori mahtuvus on arvuliselt võrdne laenguga, mis koguneb plaatidele ühikulise pinge rakendamisel.
on väga suur mahtuvus. Elektroonikas kasutatavate kondensaatorite mahtuvused on vahemikus .