Molekulide soojusliikumine

Temperatuur

Tihti kasutatakse vestluses sõnu soe ja külm. Kumb on soojem, kas soe talv või külm suvi? Ütlus „kraanivesi on kuum” tähendab, et vesi on soojem kui seda katsuv käsi. Täpsemate väidete korral kasutatakse mõistet temperatuur, mille määramiseks on juba väga ammu valmistatud mõõteriistu – mitmesuguseid termomeetreid. Termomeeter mõõdab soojuspaisumist, termoelektromotoorjõu tekkimist, infrapunakiirgust või muud temperatuurist sõltuvat suurust. Arusaam temperatuuri olemusest tekkis aga hiljem, 19. sajandil koos teadmiste avardumisega ainete siseehitusest.


Joonis 1.23.

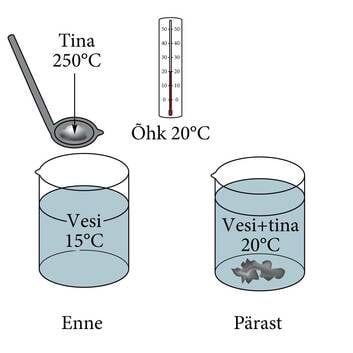
Oletame, et õnnevalamisel kallasime külma vette teatava koguse sulatina (joonis 1.23.). Vee temperatuur tõusis kiiresti ja sai võrdseks toatemperatuuriga ning edasi mingeid muutusi enam ei toimunud. Kuum keha (tina) andis teatud hulga soojust külmale kehale (veele). Tina temperatuur alanes ja vee temperatuur tõusis seni, kuni nende temperatuurid võrdsustusid. Kuna nende ühine temperatuur osutus võrdseks toatemperatuuriga, siis edasisi muutusi ei toimunud ja süsteem jäi tasakaalu. Soojus läheb iseenesest üle soojemalt kehalt külmemale, kuni nende temperatuurid võrdsustuvad. Selline olek vastab soojuslikule tasakaalule. Keha temperatuur iseloomustab soojusliku tasakaalu olekut. Tal on ühesugune väärtus soojuslikus tasakaalus oleva süsteemi kõikides osades.

Temperatuur oleneb keha koostisosakeste energiast – siseenergiast.

Euroopas kasutatakse temperatuuri mõõtmisel ühikuna Celsiuse kraadi. Temperatuurile $0^{\circ} C$ vastab jää sulamine ja $100^{\circ} C$ -le vee keemine normaalrõhul.


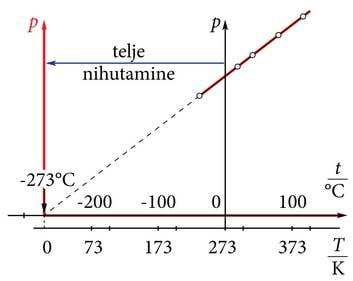
Joonis 1.24. a) Piirtemperatuur - absoluutne null	Joonis 1.24. b) Celciuse ja Kelvini võrdlus

17. ja 18. sajandi vahetusel uuris prantsuse füüsik Guillaume Amonton gaasi rõhu sõltuvust temperatuurist jääval ruumalal (joonis 1.24. a). Ta leidis, et temperatuuri vähenedes kahanes rõhk lineaarselt. Mingil temperatuuril, $- 273, 15^{\circ} C$ , peaks gaasi rõhk muutuma nulliks. Seda temperatuuri alumist piiri nimetatakse absoluutseks nulliks. Inglise füüsik lord Kelvin võttis kasutusele nn absoluutse temperatuuriskaala FLA. Selle skaala nullpunktiks on absoluutne null ja ühik $1 K$ (üks kelvin) on võrdne Celsiuse skaala ühikuga. Temperatuur $T$ Kelvini skaalas on alati positiivne ja Celsiuse temperatuurist $273$ võrra suurem.

(1.16)

T = t + 273

Rõhu telje nihutamisel absoluutsesse nulli saame lineaarsest sõltuvusest võrdelise. Jääval ruumalal on gaasi rõhk võrdeline absoluutse temperatuuriga.

Küsimused

Missugune on kõige madalam ja kõige kõrgem temperatuur?

Missugustel füüsikalistel nähtustel lisaks eelpool nimetatutele võiks põhineda termomeetri töö?

Summary

Soojus levib iseenesest soojemalt kehalt külmemale, kuni temperatuurid võrdsustuvad.

Soojusliku tasakaalu korral on temperatuur keha kõikides osades ühesugune.

On olemas kõige madalam piirtemperatuur absoluutne null, millest keha temperatuur on alati suurem.

Rahvusvahelise mõõtühikute süsteemi temperatuuri põhiühik on $1 K$ (kelvin). Kelvini absoluutses temperatuuriskaalas on temperatuurid umbes $273$ võrra suuremad võrreldes Celsiuse skaalaga $T = t + 273$ .

Ülesanded

Teisenda toatemperatuur

20^{\circ} C

ja kehatemperatuur

36^{\circ} C

kelviniteks.

Termotuumareaktsioon toimub temperatuuril

10^{8} K

. Mitu kraadi Celsiust see on?

Additional materials Additional tasks

Ideaalne gaas

Reaalset looduses esineva gaasi lihtsamaks uurimiseks ja mõistmiseks kasutatakse ideaalse gaasi mudelit. Ideaalse gaasi puhul ei arvestata molekulide mõõtmeid ja nendevahelist vastastikmõju. Selle tingimuse ligikaudseks täitmiseks peaks gaas olema piisavalt hõre ja mitte liiga madalal temperatuuril. Ideaalseks gaasiks võib näiteks lugeda kuiva õhku tavalisel temperatuuril ja rõhul.

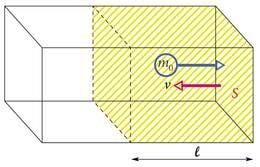
Olgu suletud anumas (joonis 1.25.) ideaalne gaas, mille molekulid liiguvad kaootiliselt ja põrkuvad elastselt anuma seintega. Mõtteliselt eraldatud osas ruumalaga $V$ on $N$ molekuli igaüks massiga $m_{0}$ . Anuma seinale pindalaga $S$ lähenevate molekulide keskmine kiirus on $v$ .

Proovime hinnata molekulide põrgetest tulenevat anuma seinale avaldatavat rõhku. Seinaga jõuavad aja $t$ jooksul põrkuda pooled molekulidest, mis ei asu kaugemal kui

I = v t = \frac{V}{S}

Mehaanikast on teada (M), et impulsi muut elastsel põrkel on $2 m_{0} v$ . Kehale mõjuv jõud (M) on võrdne impulsi muutumise kiirusega.

F = \frac{Δ p}{t}

ja ühe molekuli poolt seinale avaldatav jõud on

\frac{2 m_{0} v^{2}}{t}

Kogu seinale mõjuva jõu saame, korrutades selle põrgete arvuga $N / 2$ . Seinale avaldatav jõud

F = \frac{N}{2} \frac{2 m_{0} v}{t} = \frac{N m_{0} v^{2} S}{V}

Arvestades, et molekulide kontsentratsioon

n = \frac{N}{V}

saame rõhuks

p = \frac{F}{S} = n m_{0} v^{2}

Arutluses eeldasime, nagu liiguksid molekulid ühes sihis. Tegelikult pole kaootilise liikumise korral ükski suund eelistatud ja täpsema tuletuskäigu korral saame:

(1.17.)

p = \frac{1}{3} n m_{0} v^{2}

Valem annab ideaalse gaasi rõhu sõltuvuse mikroparameetritest: kontsentratsioonist, molekuli massist ja kiirusest. Rõhk kui makroparameeter on mõõdetav näiteks baromeetri või manomeetriga.

Kui võtame kasutusele mõiste molekulide keskmine kineetiline energia

¯ E = \frac{m_{0} v^{2}}{2}

saame:

(1.18.)

p = \frac{2}{3} n ¯ E

Ideaalse gaasi rõhk on võrdeline molekulide kaootilise liikumise keskmise kineetilise energiaga.

Eelmises õppetükis saime teada, et gaasi rõhk oli ka võrdeline absoluutse temperatuuriga. Kokkuvõtvalt saab järeldada, et ideaalse gaasi molekulide keskmine kineetiline energia on võrdeline gaasi absoluutse temperatuuriga:

(1.19.)

¯ E = \frac{3}{2} k T

kus suurust $k = 1, 38 \cdot 10^{- 23} J / K$ nimetatakse Boltzmanni konstandiks.

Valemis 4.17 esinev suurus $v^{2}$ on molekulide kiiruste ruutude keskmine väärtus. Ruutjuur sellest on ruutkeskmine kiirus:

(1.20.)

¯ v = \sqrt{v^{2}}

Küsimused

Loetlege mikroparameetreid, mis määravad gaasi rõhu.

Klassi õhus esineb nii lämmastiku kui ka hapniku molekule. Missuguse aine molekulid liiguvad kiiremini? Põhjendage.

Summary

Ideaalne gaas on selline gaas, mille molekulide mõõtmeid pole vaja arvestada ja mille molekulide vastastikmõju on tühine.

Gaasi rõhk on tingitud kaootiliselt liikuvate molekulide põrgetest vastu anuma seina. Rõhk sõltub molekulide kontsentratsioonist, massist ja kiirusest

p = \frac{1}{3} n m_{0} v^{2}

Molekulide keskmine kineetiline energia on võrdeline absoluutse temperatuuriga

¯ E = \frac{3}{2} k T

Ülesanded

Gaasi temperatuur muutus

20^{\circ} C

kuni temperatuurini

200^{\circ} C

. Mitu korda muutus temperatuur Celsiuse ja Kelvini skaala põhjal? Mitu korda suurenes rõhk ja gaasimolekulide keskmine kineetiline energia?

Balloonis on hapnik normaaltingimustel (

0^{\circ} C

10^{5} P a

). Arvuta molekulide keskmine kineetiline energia, ühe molekuli mass, kiiruste ruutude keskmine väärtus ja ruutkeskmine kiirus.

Additional materials Additional tasks

Ideaalse gaasi olekuvõrrand

Gaasiga toimuvate protsesside käigus võivad muutuda selle rõhk, ruumala ja temperatuur – olekuparameetrid. Näitame, et ideaalse gaasi olekuparameetrid on omavahel seotud nn ideaalse gaasi olekuvõrrandiga.

Valemitest 1.17, 1.18 ja 1.19 saame rõhu jaoks:

\begin{matrix} p = \frac{1}{3} n m_{0} v^{2} = \frac{2}{3} n ¯ E = = n k T = \frac{N}{V} k T \end{matrix}

Molekulide arvu saame avaldada ainehulga ja Avogadro arvu järgi:

N = \frac{m}{M} N_{A}

kus $m$ on gaasi mass ja $M$ molaarmass. Asendades ja avaldades, saame rõhu ja ruumala korrutiseks:

p V = \frac{m}{M} N_{A} k T

Suurust $R = N_{A} k = 8, 31 J / (m o l \cdot K)$ nimetatakse gaasikonstandiks ja seega:

(1.21.)

p V = \frac{m}{M} R T

Ideaalse gaasi rõhu ja ruumala korrutis on võrdeline tema absoluutse temperatuuriga. Kui me vaatleme antud gaasikogust kahes erinevas olekus, saame olekuvõrrandi teise kuju:

(1.22.)

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}

Antud gaasikoguse rõhu ja ruumala korrutis jagatud absoluutse temperatuuriga on jääv suurus. Viimase valemi kontrolliks on vaja määrata gaasi ruumala, mõõta manomeetriga rõhk ning termomeetriga temperatuur (joonis 1.26.). Valemi 1.21. kontrollimiseks peab määrama gaasi massi ja teadma molaarmassi (piisab ka ainehulgast).


Joonis. 1.26. Katseseade gaasi seaduste uurimiseks.	Kass ja kamin

Gaaside omadused sõltuvad temperatuurist ja õhurõhust. Seetõttu on võetud kasutusele mõiste normaaltingimused: temperatuur $0^{\circ} C \approx 273 K$ ja rõhk $760 m m H g \approx 1, 01 \cdot 10^{5} P a$ . Ühe mooli gaasi ruumala normaaltingimustel on $22, 4$ liitrit.

Küsimused

Kahes sama suures anumas on ideaalne gaas samal temperatuuril. Ühes on

32 g

hapnikku ja teises

28 g

lämmastikku. Kumma gaasi rõhk on suurem?

Selgel suvepäeval unustati murule kaks ühesugust tühja plastpudelit. Hilisõhtuks oli üks neist tõmbunud kortsu, teine oli aga endise kujuga. Põhjendage nähtust, kasutades olekuparameetreid.

Summary

Ideaalse gaasi olekuvõrrand ühendab omavahel makroskoopilised olekuparameetrid rõhu, ruumala ja absoluutse temperatuuri. Ideaalse gaasi rõhu ja ruumala korrutis on võrdeline tema absoluutse temperatuuriga

p V = \frac{m}{M} R T

kus $m$ on gaasi mass, $M$ molaarmass ja $R = 8, 31 J / m o l \cdot K$ gaasikonstant.

Antud ideaalse gaasikoguse rõhu ja ruumala korrutis jagatud absoluutse temperatuuriga on jääv suurus

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}} = c o n s t

Ülesanded

Balloonis ruumalaga

200

liitrit on

0, 4 k g

argooni temperatuuril

295 K

. Arvutage argooni rõhk, kui tema molaarmass on

0, 04 k g / m o l

Kindla hulga ideaalse gaasi olekuparameetrid muutusid. Rõhk vähenes kaks korda ja absoluutne temperatuur suurenes kaks korda. Mitu korda muutus gaasi ruumala? Kas see suurenes või vähenes?

Additional materials Additional tasks

Isoprotsessid

Isoprotsessi käigus ei muutu üks olekuparameetritest ja vastav parameeter taandub gaasi olekuvõrrandist välja.

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}

Isotermilise protsessi käigus ei muutu temperatuur. Saame ideaalse gaasi jaoks võrrandi:

p_{1} V_{1} = p_{2} V_{2}

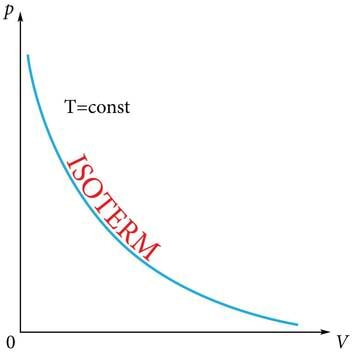
millest järgnev valem annab pöördvõrdelise sõltuvuse rõhu ja ruumala vahel (joonis 1.27. a).

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}


1.27a Isoterm	1.27b Isobaar

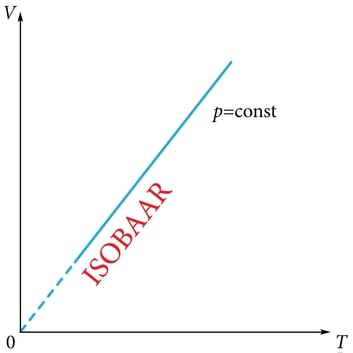
Isobaarilise protsessi käigus ei muutu rõhk. Saame gaasi jaoks võrrandi:

\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}

millest järgnev valem väljendab ruumala võrdelist sõltuvust absoluutsest temperatuurist (joonis 1.27. b).

\frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}}

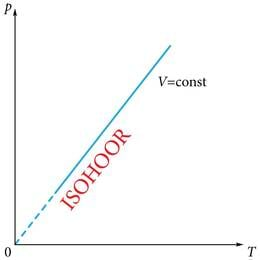
Isohoorilise protsessi käigus ei muutu ruumala. Saame võrrandi:

\frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}}

millest järgnev valem väljendab ideaalse gaasi rõhu võrdelist sõltuvust absoluutsest temperatuurist (joonis 1.27. c).

\frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}}

Isoprotsessidest koosnev ringprotsess

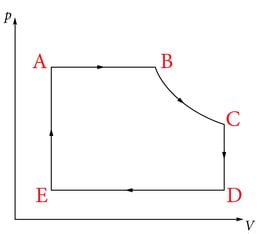
Joonisel on kujutatud erinevatest isoprotsessidest koosnev lõpuks samasse olekusse tagasi jõudev ringprotsess $p V$ -teljestikus. $A B$ on isobaariline paisumine, $B C$ isotermiline paisumine, $D E$ isobaariline kokkusurumine ning isohooriline protsess $E A$ lõpetab ringprotsessi ühe tsükli.

Küsimused

Tooge näide protsessist, milles gaasi rõhk ja temperatuur muutuvad, aga ruumala ei muutu.

Gaasi võib kokku suruda aeglaselt või kiiresti. Kuidas peaks seda tegema, et protsess oleks isotermiline? Põhjendage.

Summary

Isoprotsessi käigus ei muutu keha üks olekuparameetritest.

Isotermilise protsessi käigus ei muutu temperatuur ja ideaalse gaasi rõhk on pöördvõrdeline ruumalaga:

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}

Isobaarilise protsessi käigus ei muutu rõhk ja ideaalse gaasi ruumala on võrdeline absoluutse temperatuuriga:

\frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}}

Isohoorilise protsessi käigus ei muutu ruumala ja ideaalse gaasi rõhk on võrdeline absoluutse temperatuuriga:

\frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}}

Ülesanded

Isotermilises protsessis suureneb ideaalse gaasi ruumala

2

korda. Mitu korda suureneb või väheneb gaasi rõhk?

Suletud silindris on hõre gaas ning hõõrdevabalt liikuv kolb. Mitu korda suureneb silindris oleva gaasi ruumala, kui temperatuur muutub miinus kahekümnelt pluss kahekümnele kraadile Celsiusele?

Additional materials Additional tasks

Siseenergia ja selle muutumise viisid

Kõik ained koosnevad osakestest, mis liiguvad kaootiliselt ja mõjutavad üksteist. Järelikult omavad kehade koostisosad nii kineetilist kui ka potentsiaalset energiat. Keha siseenergiaks nimetatakse tema kõikide koostisosakeste kineetiliste ja potentsiaalsete energiate summat. Seda energiat vaadeldakse kehaga seotud taustsüsteemi suhtes.

Vastastikmõju potentsiaalset energiat on raske arvutada. Seepärast toome näite ideaalsest gaasist, mis koosneb ühesugustest üksikuna esinevatest aatomitest, ehk üheaatomilisest ideaalsest gaasist. Ideaalse gaasi molekulid ei mõjuta üksteist (potentsiaalne energia on $0$ ) ja sellise gaasi siseenergia on kõikide molekulide kineetiliste energiate summa. Siseenergia leidmiseks tuleb molekuli keskmine kineetiline energia korrutada molekulide (antud juhul aatomite) arvuga.

U = N ¯ E = \frac{m}{M} N_{A} \frac{3}{2} k T = \frac{3}{2} \frac{m}{M} R T

Üheaatomilise ideaalse gaasi siseenergia on võrdeline absoluutse temperatuuriga. Kui ideaalse gaasi molekulis on rohkem aatomeid, siis võrdelisus absoluutse temperatuuriga jääb kehtima, aga võrdetegur on erinev. Näiteks kaheaatomilise gaasi korral on see $3 / 2$ asemel $5 / 2$ . Siseenergia on suurem seetõttu, et kaheaatomilise gaasi puhul lisanduvad võnkumise ja pöörlemise energiad.

Siseenergia sõltub ainult keha või kehade süsteemi siseolekust. Siseenergia hõlmab kõigi süsteemi osakeste, näiteks molekulide, aatomite, ioonide ja vabade elektronide liikumise, kineetilise ning vastastikmõju potentsiaalse energia, samuti nende sisestruktuuriga seoses oleva elektronkatte, tuuma jne energia. Rakenduste korral on oluline siseenergia muut, seetõttu jäetakse tavaliselt arvestamata need komponendid, mis uuritavas protsessis ei muutu. Soojusliku tasakaalu olekus on siseenergial kindel väärtus, siseenergia on olekufunktsioon. Siseenergia seob omavahel makro- ja mikrosuurused ning soojusõpetuse mehaanikaga.

Kui keha on soojusvahetuses teiste kehadega soojusjuhtivuse, konvektsiooni ja soojuskiirguse kaudu, nimetatakse saadud või ära antud siseenergiat soojushulgaks.

Soojushulk on siseenergia hulk, mille keha saab või annab ära soojusülekandel.

Jalgrattakummi pumpamisel kokkusurutud õhk ja pump soojenevad. Kuum gaas teeb mootoris paisudes tööd siseenergia vähenemise arvelt ja jahtub. Keha siseenergia muutmiseks on kaks võimalust – soojushulga saamine või äraandmine ja mehaaniline töö. Järgnevatel fotodel on raudlati temperatuuri ja siseenergia suurendamine soojushulga saamisega koldes ning lati töötlemisel ketaslõikuriga.


Metall hõõgub punaselt	Ketassaag lõikab

Küsimused

Miks reaalse gaasi siseenergia sõltub peale temperatuuri ka ruumalast?

Kas prootonite ja neutronite vastastikmõju energia aatomituumas on ka siseenergia?

Summary

Keha siseenergia on tema kõikide koostisosakeste kineetiliste ja potentsiaalsete energiate summa.

Ideaalse gaasi siseenergia on võrdeline tema absoluutse temperatuuriga.

Soojushulk on siseenergia, mille keha saab või annab ära soojusvahetuses teiste kehadega.

Ülesanded

Arvutage

80 g

argooni siseenergia temperatuuril

127^{\circ} C

. Argooni massiarv on

40

Hermeetiliselt suletud kilekotis tõusis õhu temperatuur päikse käes

10^{\circ} C

-lt kuni

30^{\circ} C

-ni. Mitu korda suurenes/vähenes õhu siseenergia?

Additional materials Additional tasks

Soojus levib

Warm balance

Madalaim võimalik temperatuur

Temperatuuri ühik SI süsteemis

Ideaalne gaas

Ideaalse gaasi rõhk

Molekulide keskmine kineetiline energia

Ideaalse gaasi olekuvõrrand

Ideaalse gaasi rõhk, ruumala ja tempratuur

Isoprotsess

Isotermiline protsess

Isobaariline protsess

Isohooriline protsess

Internal energy of the body

Ideaalse gaasi siseenergia

Soojushulk