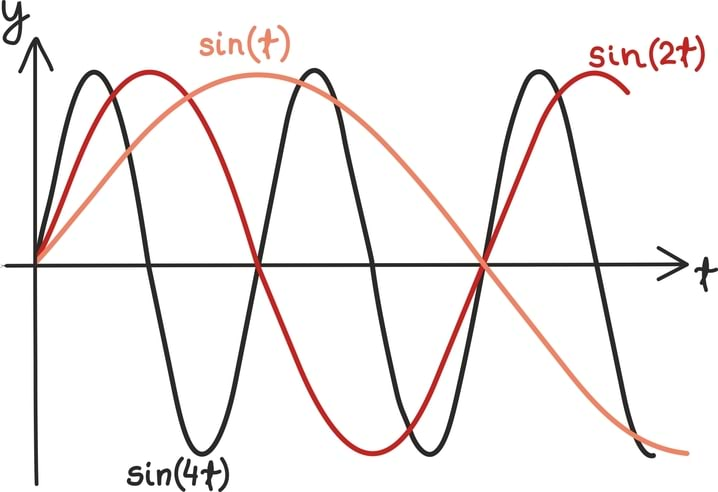
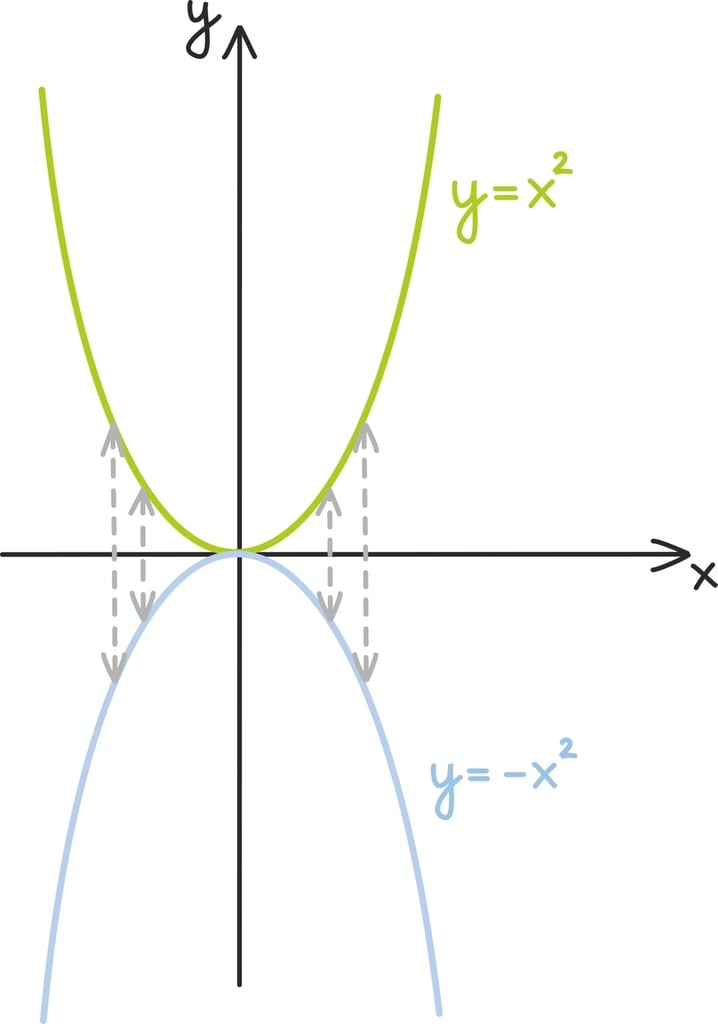
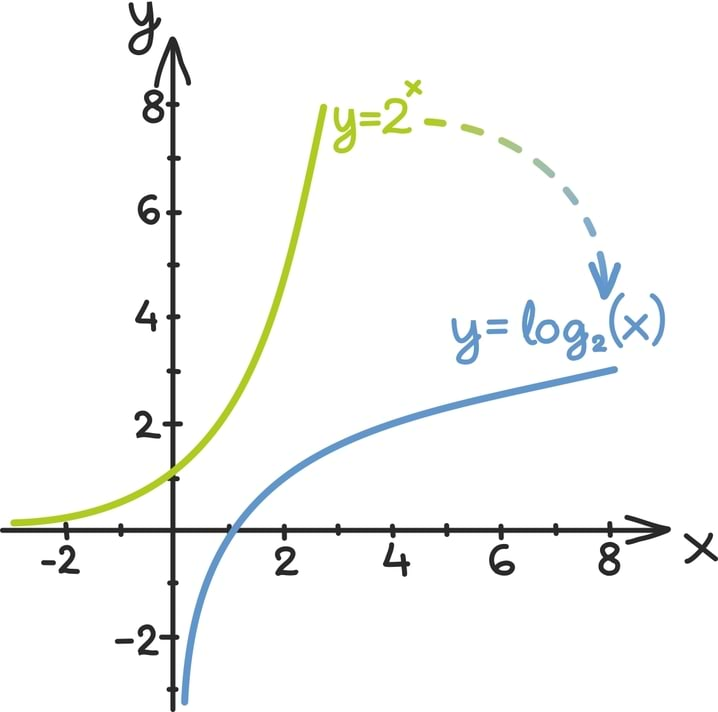
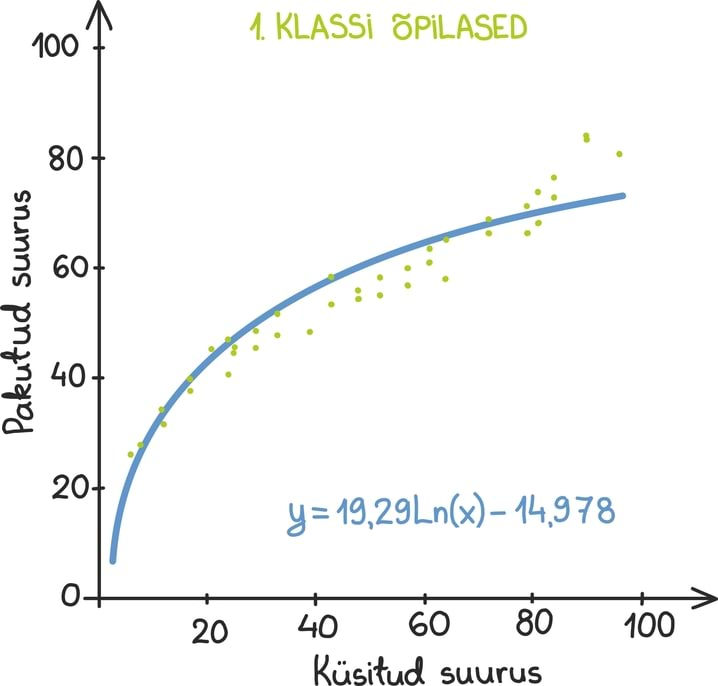
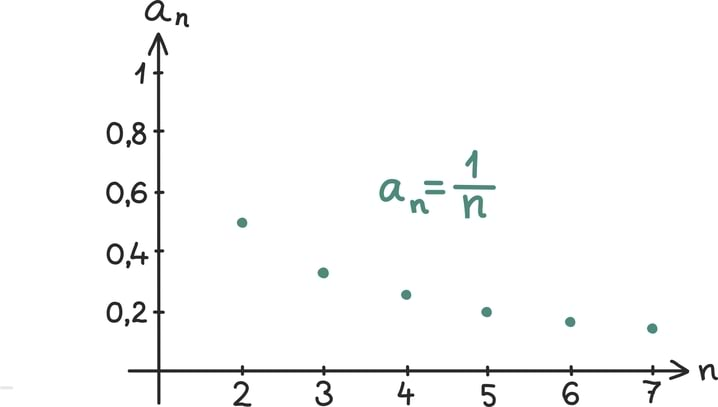
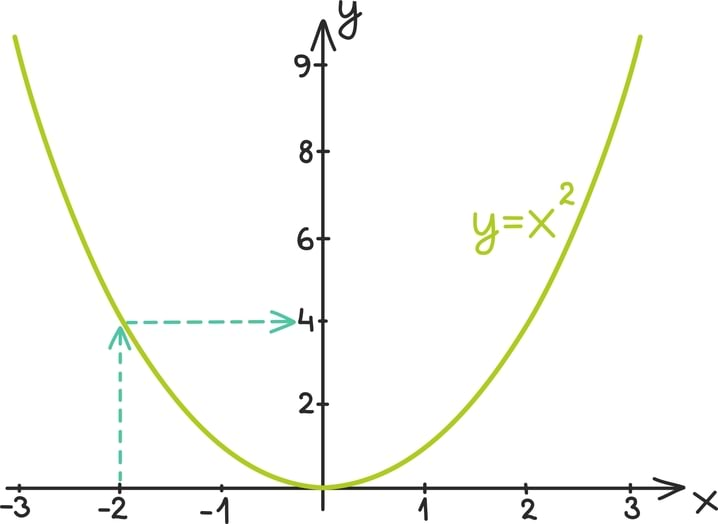
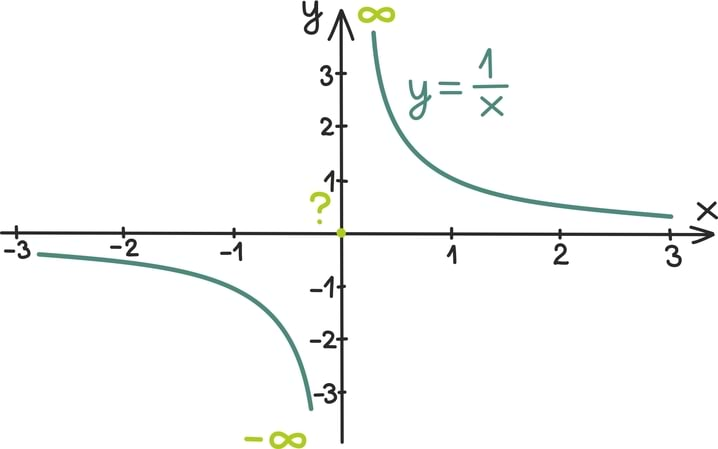
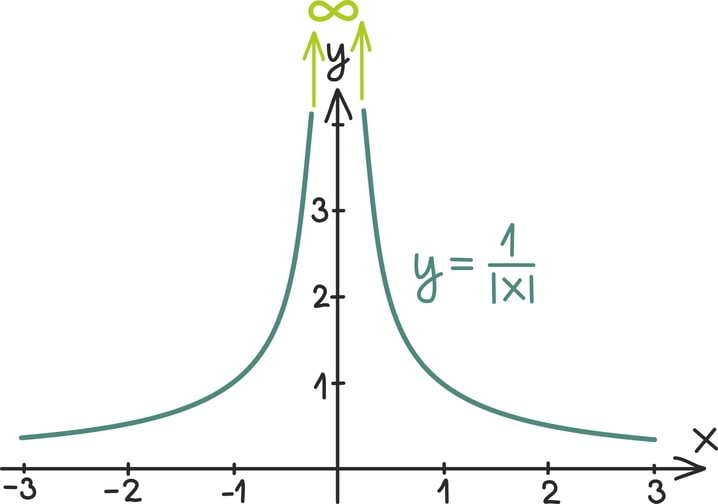
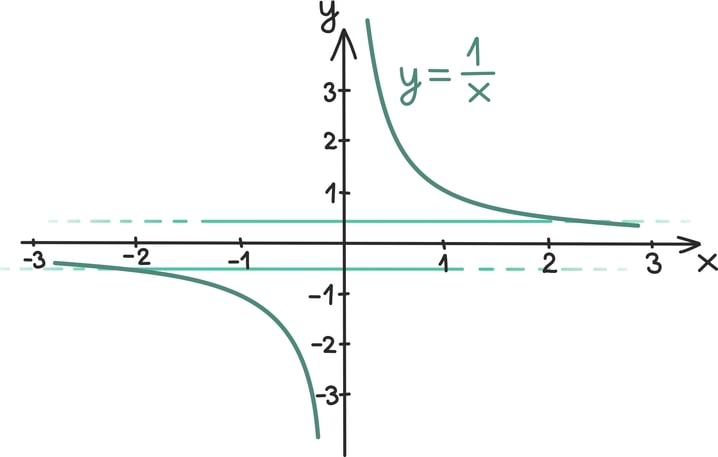
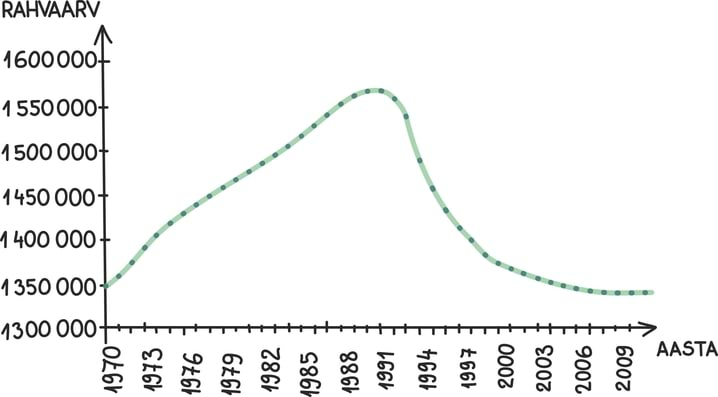
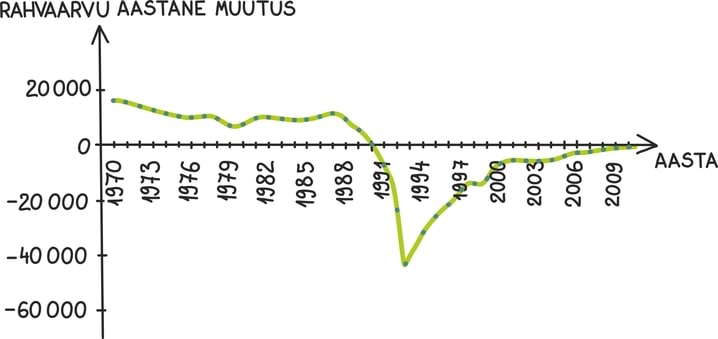
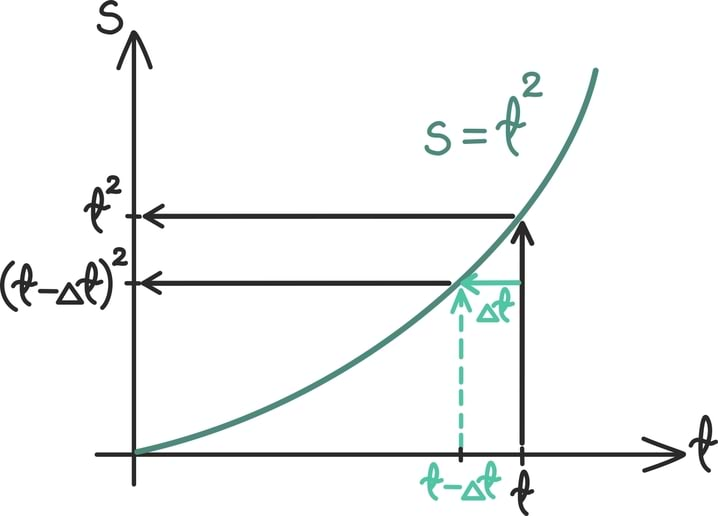
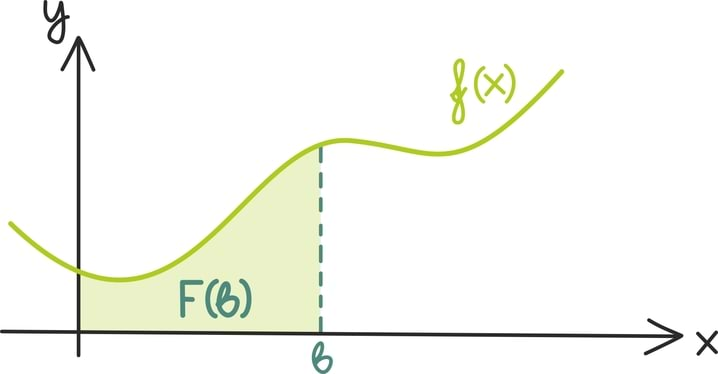
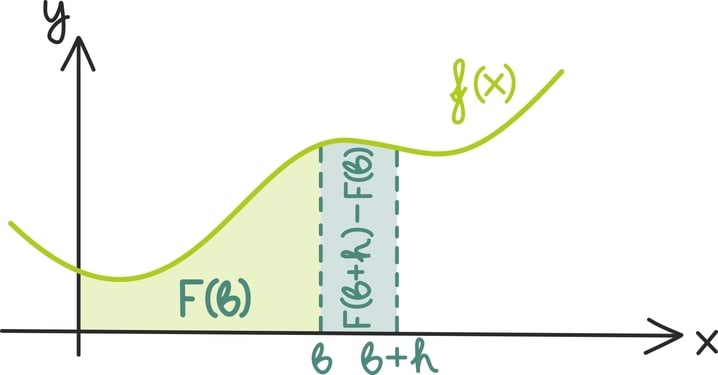
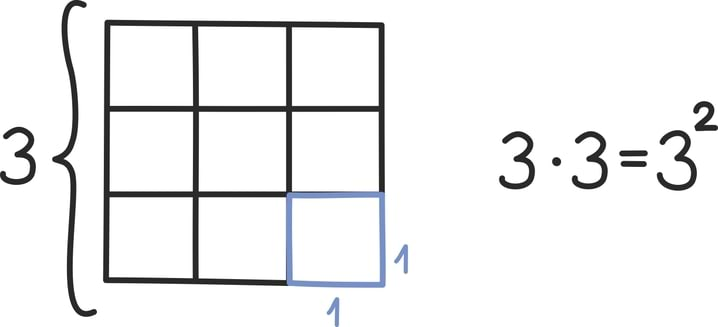
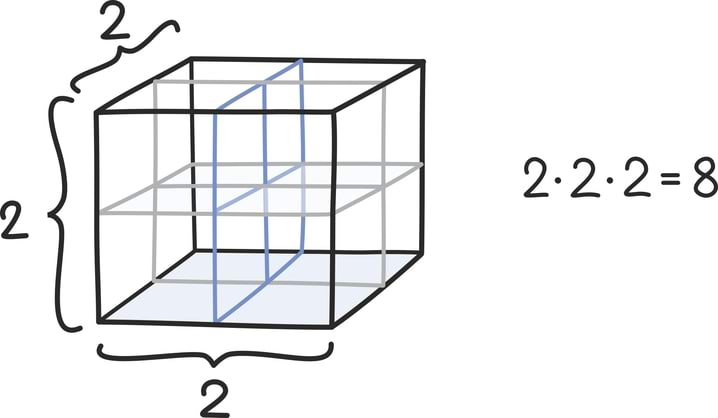
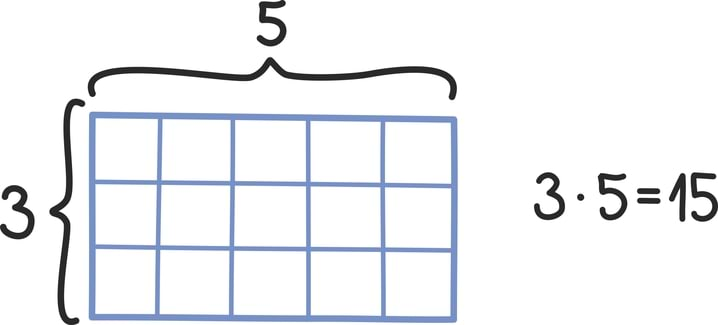
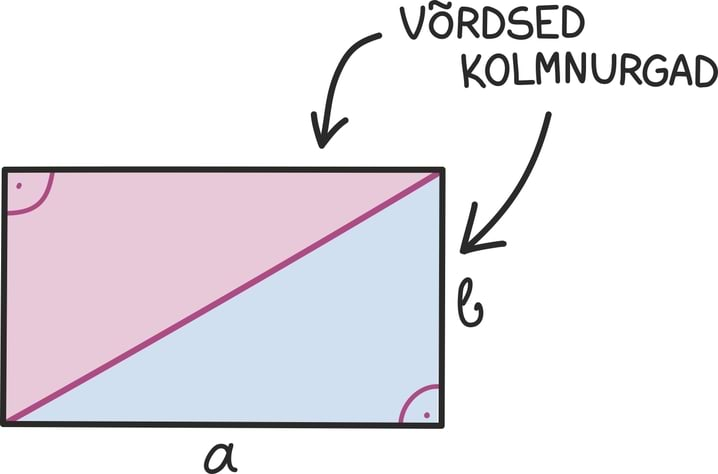
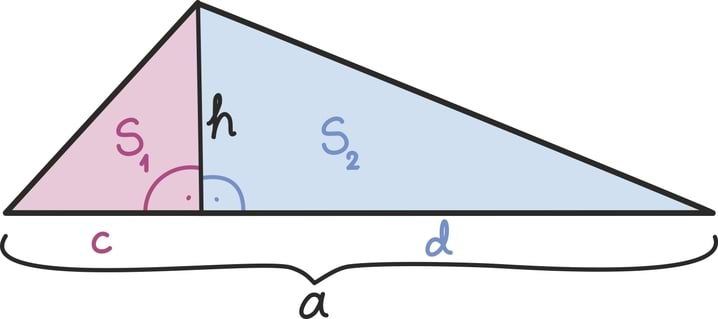
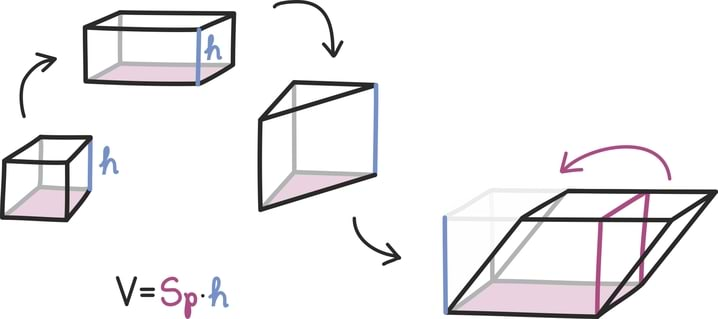
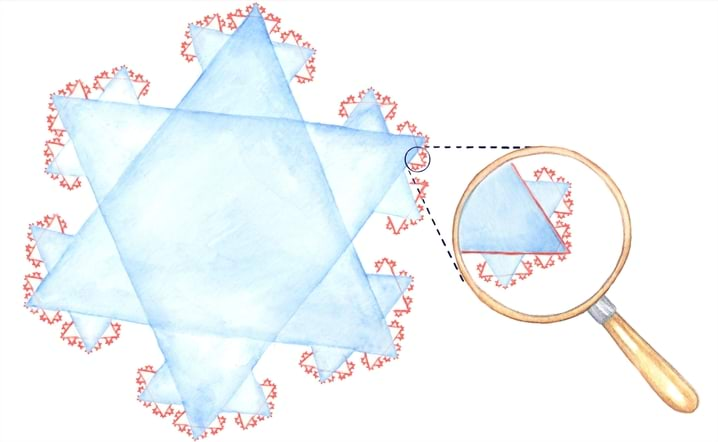
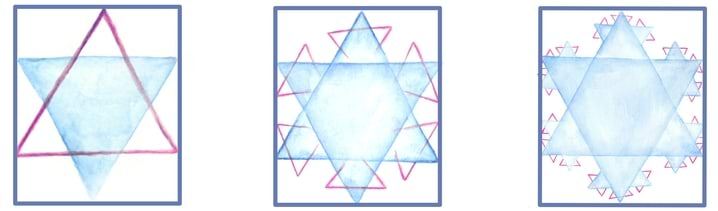
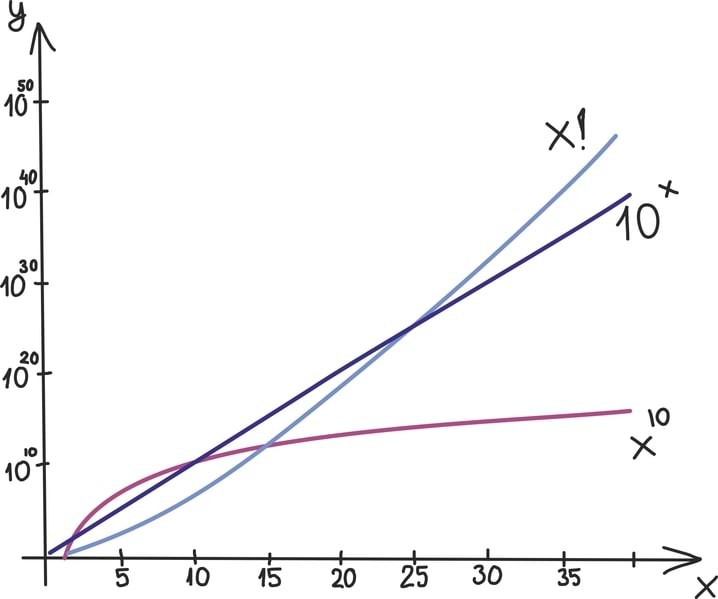
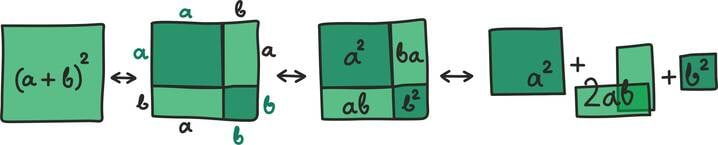
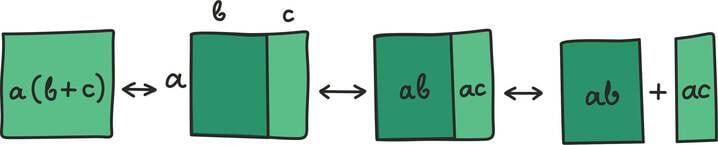
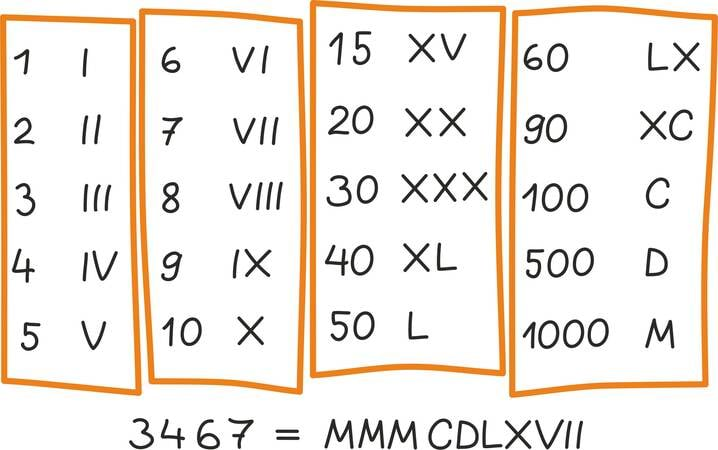
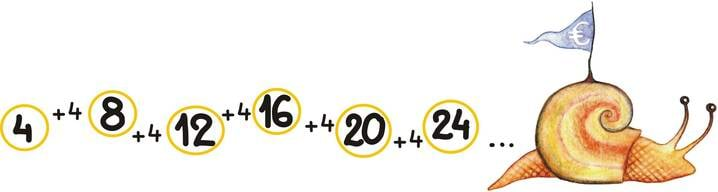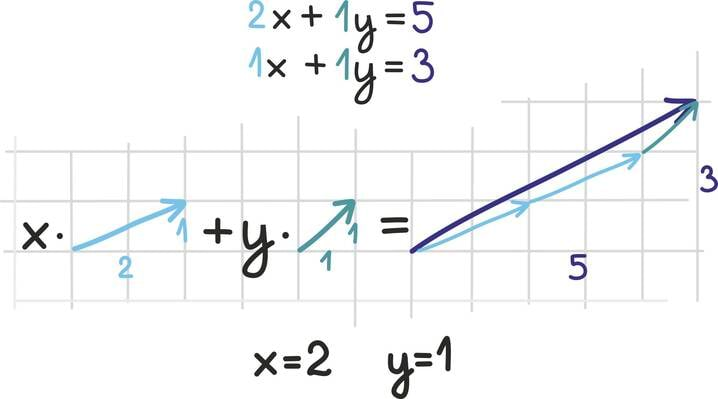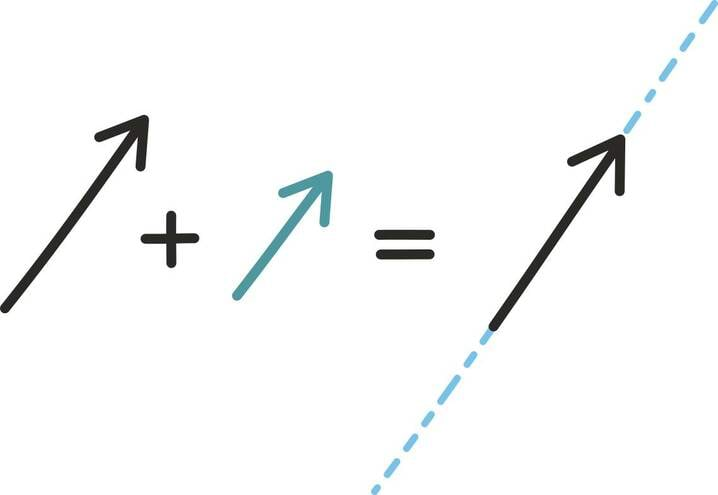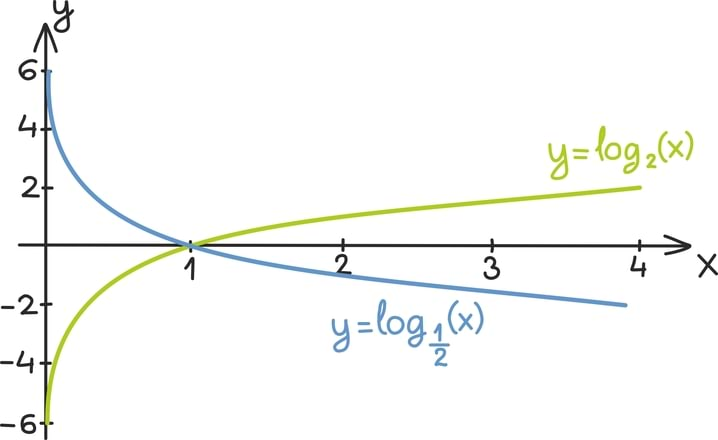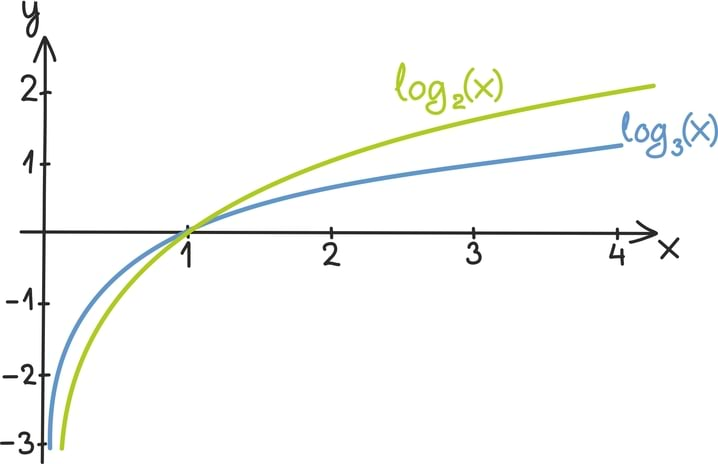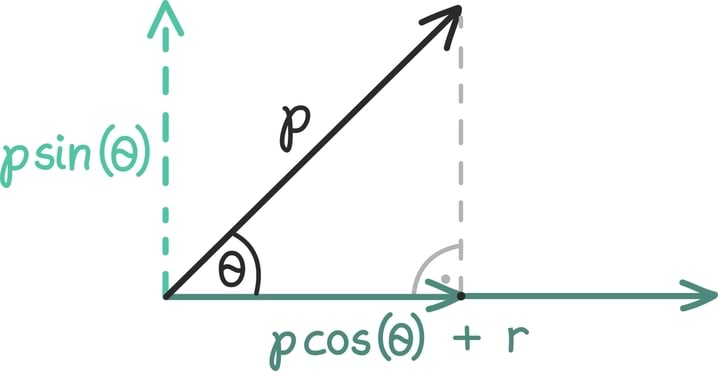Matemaatika õhtuõpik
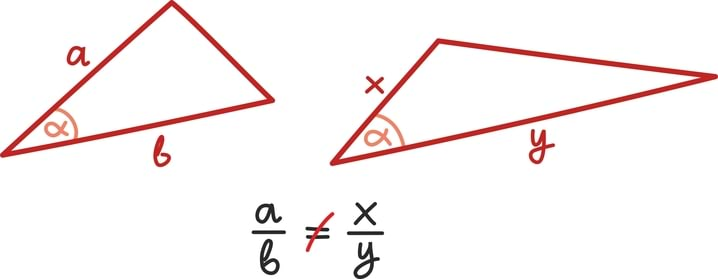
Arvujada mõistet võib selgitada pikkade sõnadega, aga alustame parem näidetega.
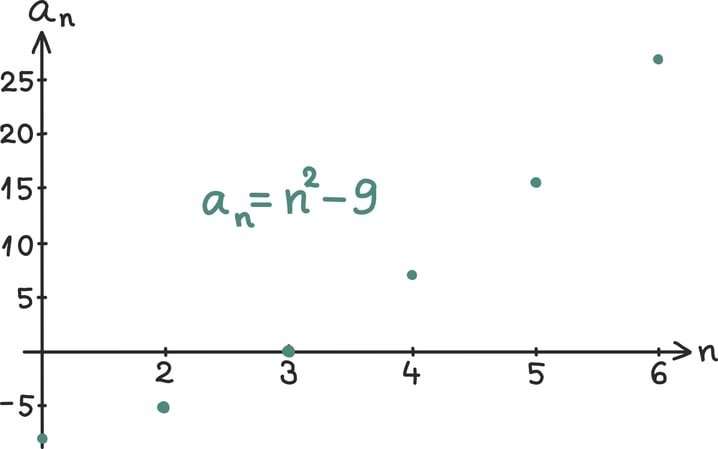
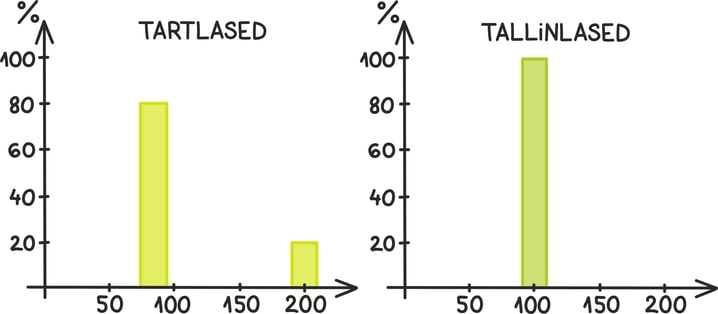
paarisarvude jada ehk aritmeetiline jada vahega kaks
suvaline lõplik üheksaliikmeline täisarvude jada
lõpmatu konstantne jada
arvule π lähenev ratsionaalarvude jada
geomeetriline jada teguriga kolm
Fibonacci arvude jada
Jada ongi tavaline arvude järjend, mis võib koosneda kas lõplikust hulgast arvudest või lausa lõpmatult paljudest. Kui hakkad lihtsalt arve ritta seadma, ongi tulemuseks arvujada. Igaüks võib muidugi kirja panna oma lemmikjada ja kinkida selle südamekaaslasele sünnipäevaks ning kui ka seda juhtub harva, on jadad siiski nii päriselus kui matemaatikas levinud ja olulised objektid.
Näiteks võib õppelaenu igakuistest tagasimaksetest mõelda kui arvujadast ja ka vihmaste päevade arv igas aastas tekitab arvujada.
Jadade kohta võib esitada erinevaid matemaatilisi küsimusi ning selgub, et neil küsimustel on ka täiesti elulised tähendused. Mis on jada kümnes liige ehk mis on mu kümnes laenu tagasimakse? Mis on jada kuuekümne esimese liikme summa või kui palju päevi sadas esimese kuuekümne aasta jooksul? Kas on võimalik öelda, mis on kõikide jada liikmete summa?
Üldjuhul võivad need küsimused osutuda üsna keerulisteks. Nii huvitavadki matemaatikuid algul lihtsamad juhud, mille korral nad kõikidele küsimustele vastata oskavad. Ka see on põnev, sest
- esiteks võib nii leida ideid ka keerulisemate olukordade jaoks
- ning teiseks selgub, et tihti ongi kõk elus ettetulevad jadad tegelikult matemaatiliselt üsna lihtsad.
Need lihtsamad jadad tulevad ette kooliprogrammis ja järgnevalt tutvustamegi neid lühidalt.
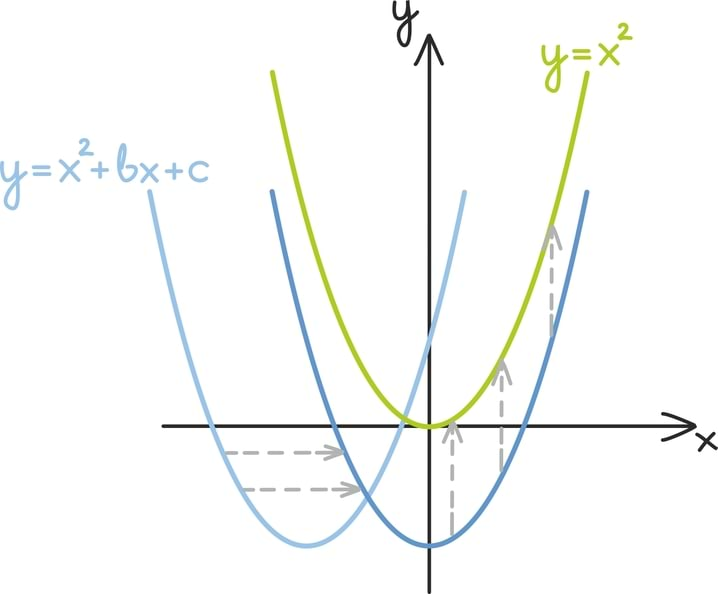
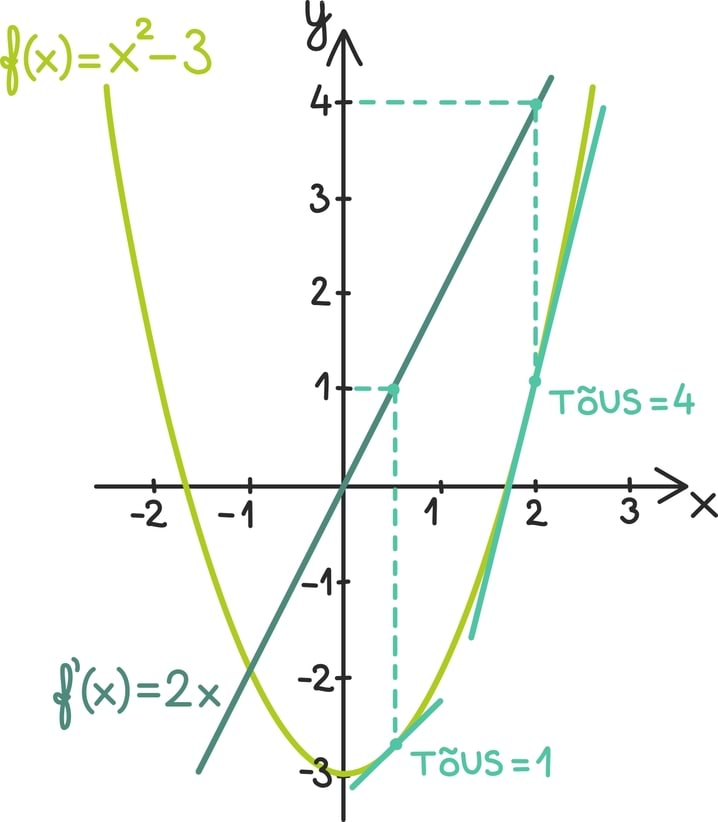
Kõige lihtsamad jadad on konstantsed ja lõplikud jadad. Lihtsuselt järgnevad aritmeetilised jadad. Nendel jadadel on iga kahe järjestikuse liikme vahe võrdne. Järgnevas näites on see vahe –3. Seda vahet kutsumegi jada vaheks ja tähistame tihti d-ga.
Aritmeetilise jadaga teevad ihnuskoid algust algkoolis – pannes iga nädal kõrvale kogu antud taskuraha. Nii moodustavad nende iganädalased rahakogused aritmeetilise jada ja koolis õpivad nad ennustama, millal võiksid miljonäriks saada. Peab kahjuks tunnistama, et aritmeetiline jada kasvab sellise eesmärgi tarvis pisut liiga aeglaselt.
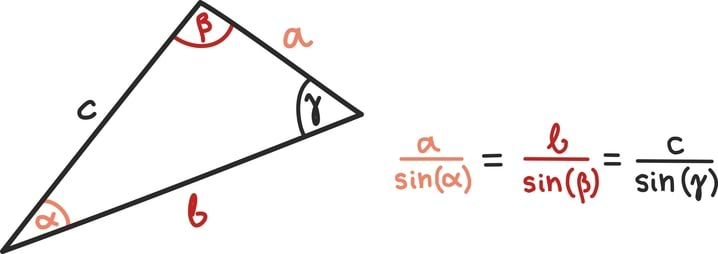
Aritmeetilise jada jaoks on eeltoodud küsimustele lihtne vastuseid leida.
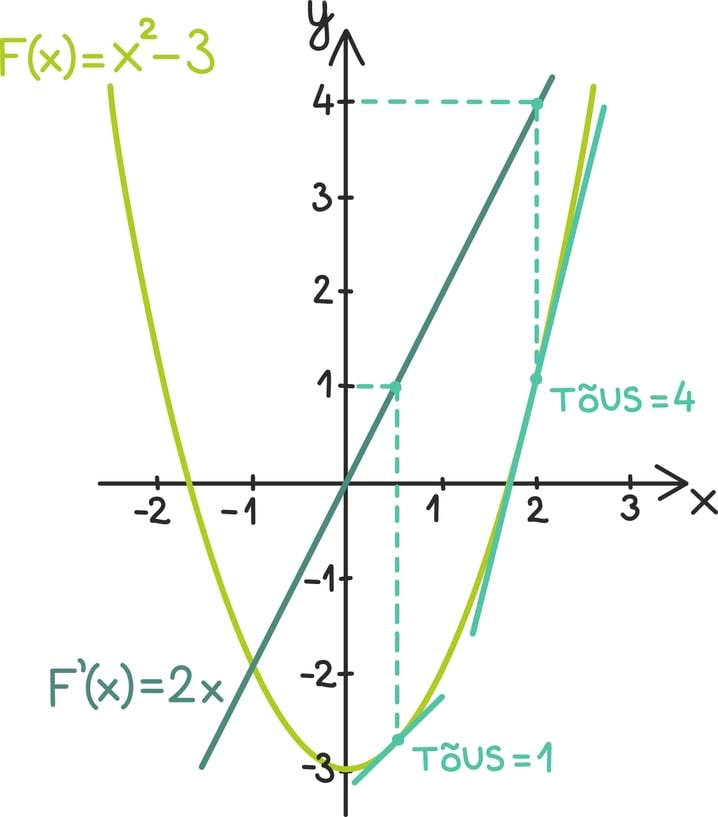
Näiteks teades jada esimest liiget oskame lihtsalt kirja panna ka teise liikme: liidame esimesele liikmele vahe juurde. Nii saamegi, et näiteks jada sajanda liikme võime leida esimese liikme põhjal talle lihtsalt 99 korda vahet juurde liites ehk matemaatiliselt: a100 = a1 + 99 · d. Siin tuleb märgata, et võtsime salamahti kasutusele uue tähistuse: a100 all mõtleme jada sajandat liiget.
Üldkujus võime jada n-nda liikme an kirjutada kujul
Jada summa valemi leidmiseks tuleb märgata, et kahte jada, millest üks suureneb ja teine väheneb sama arvu võrra, on kerge kokku liita. Näiteks kui tahame leida jada summat, mille liikmed on ühest sajani, võime jada lihtsalt kokku liita tema ümberpööratud versiooniga, mille liikmed on sajast üheni.
Tulemiks on konstante jada, milles on täpselt sada liiget, iga neist väärtuseks 101. Kuna ümberpööratud jada liikmete summa on võrdne algse jada liikmete summaga, järeldub tehtud tähelepanekust ka esimese 100 arvu summa:
Leidmaks üldkujus aritmeetilise jada
esimese n liikme summavalemit, peame talle lihtsalt juurde liitma jada
Kasutades seejärel eelnevat arutelu, saame tulemuseks:
Kui soovid, et valem oleks lühem, siis ei pea viimast liiget välja kirjutama:
Nimetus
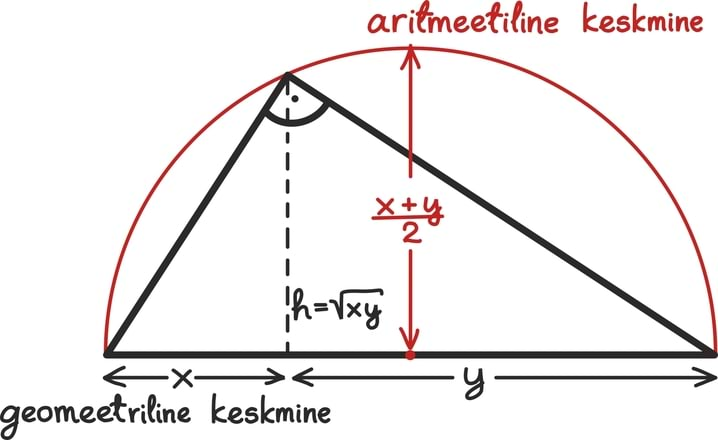
Viimaks on õigustatud ka uudishimu: kust õige pärineb nimi „aritmeetiline jada“? Täpset vastust meil lugejale pole. Üks võimalus on öelda, et aritmeetiline jada on seotud aritmeetilise keskmisega: kolmest järjestikusest aritmeetilise jada liikmest on keskmine liige äärmiste aritmeetiliseks keskmiseks [lk 198].
Teine võimalus on mõelda aritmeetikast laiemalt. Nimelt võib mõelda, et kõige lihtsamas vormis tegeleb aritmeetika naturaalarvude liitmise, korrutamise ja võimaluse korral ka lahutamise, jagamisega. Kui nüüd vaatame lõpmatult pikka aritmeetilist jada, mille esimene liige on null ning vahe d, siis saame arvud kujus 0; d; 2d; 3d; 4d; …. Lihtne on näha, et sellise aritmeetilise jada arve omavahel liites ja korrutades saame alati tulemuseks jälle sama aritmeetilise jada liikme. Seega mingis mõttes võime teha aritmeetilise jada liikmetega aritmeetikat! See pole muidugi suur ime, kui mõelda, et toodud aritmeetiline jada on peaaegu naturaalarvude koopia, ainult arvuga d läbikorrutatult.
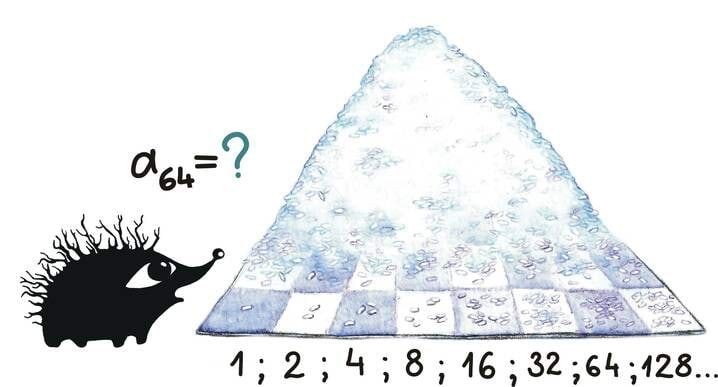
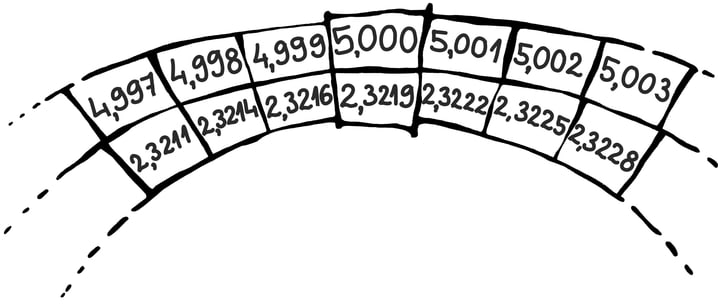
Kui võtta malelaud (8 × 8 ruutu) ning asetada esimesele ruudule üks riisitera, teisele juba kaks riisitera ja igale järgnevale ruudule kaks korda rohkem riisiterasid kui eelnevale, siis mitu tera on lõpuks malelaual kokku?
Legendi kohaselt tutvustas male leiutaja oma uut mängu kohalikule valitsejale. Valitseja oli uue mänguga väga rahul ning lubas leiutajal endale valida ka väärilise tasu. Mees, kellel tarkust puudu ei tulnud, sõnas kuningale: „Auväärt kuningas, ma paluksin endale niipalju riisiterasid, kui on kokku malelaual asetades esimesele maleruudule ühe, teisele kaks, kolmandale neli ning igale järgnevale veel kaks korda enam riisiteri.” Valitseja, kes polnud matemaatika ega matemaatiliste veidrustega sina peal, nõustus kiirelt ettepanekuga, pidades seda vahest isegi solvavalt vähenõudlikuks. Niisiis käskiski ta varahoidjal riisiterade hulga välja arvutada ning leiutajale üle anda. Varahoidjal läks aga terve nädal lubatud riisikoguse leidmiseks. Kui valitseja päris viivituse põhjust, siis varahoidja näitas talle arvutuse lõpptulemust ning selgitas, et sellist tasu ei suudaks kuningas ka oma elu jooksul välja käia. Nüüd oli valitsejale selge, mis leiutajaga pihta hakata: ta lasi nutika mehe nutika pea maha lüüa, et seeläbi igasugustele ülekavaldajatele koht kätte näidata.
Terade arv malelaua ruutudel on järgnev:
Mis on selle jada 64. liige?
Mis on jada 64 esimese liikme summa?
Kui aritmeetilises jadas leitakse iga järgmine liige, liites eelnevale teatud kindla arvu, siis praegu leiame iga järgmise jadaliikme, korrutades eelmist liiget mõne kindla arvuga – meie konkreetsel juhul on selleks arvuks kaks. Selliseid jadasid nimetatakse geomeetrilisteks jadadeks ning arvu, millega iga järgnevat läbi korrutatakse, jada teguriks.
Kui tähistame jada kordajat q-ga ning jada liikmeid nagu ikka tähistusega an, saame analoogiliselt aritmeetilise jada juhuga a2 = a1 · q, seejärel a3 = a2 · q = a1 · q · q, … ning üldisel kujul
Nii võime ka välja arvutada, et malelaua viimasel ruudul peab olema a64 = 1 · 263 = 9 223 372 036 854 775 808 riisitera, mis on umbes 200 miljardit tonni riisi.
Geomeetrilise jada summa valem
Geomeetrilise jada summa valemi leidmiseks on taas kord vaja vaid ühte tähelepanekut ja head kannatust sümbolitemölluga.
Meenutame, et korrutades suvalise jada liikme ai arvuga q, saame jada järgmise liikme ai+1. Seega on jada esimese liikme n summa a1 + a2 + … + an ainult q korda erinev summast a2 + … + an+1, mis on sama jada n liikme summa alates teisest liikmest.
Kuna need jadad erinevad aga ainult kahes liikmes – esimeses neist esineb a1 ja ei esine an+1 ning teises esineb an+1, aga ei esine a1 –, siis on nende jadade summade vahe täpselt võrdne a1 – an+1-ga.
Seega tähistades geomeetrilise jada esimese n liikme summat jällegi Sn abil, võime eelneva arutluse kirja panna kompaktsemalt nii:
Jagades mõlemad pooled läbi q–1-ga, jõuame valemini
mis kasutades jada üldliikme valemit annab tulemuseks
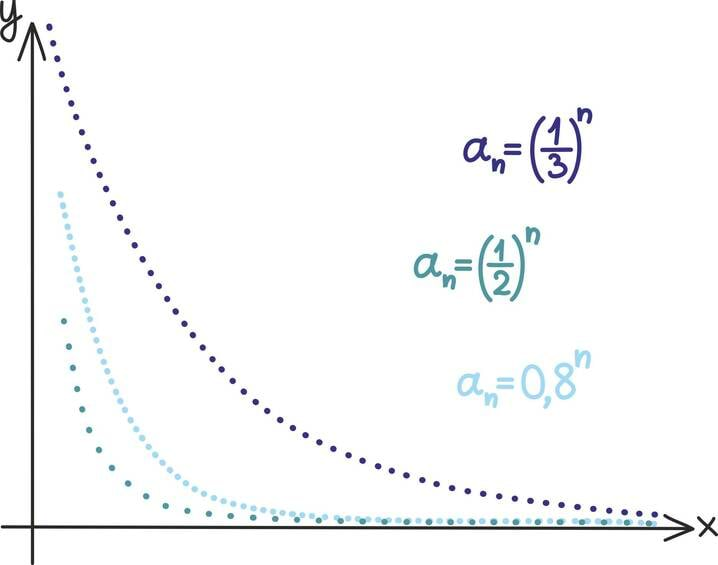
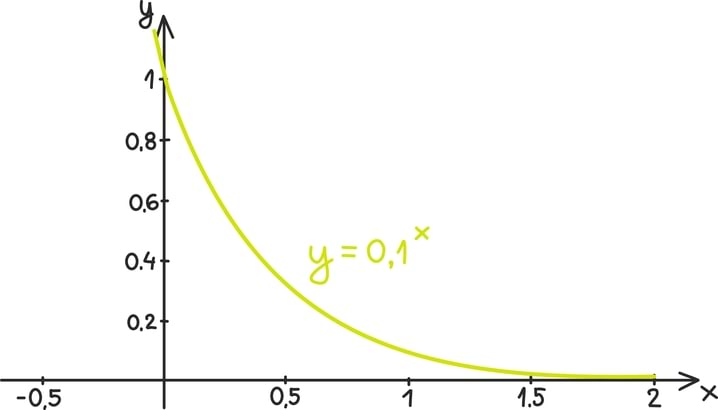
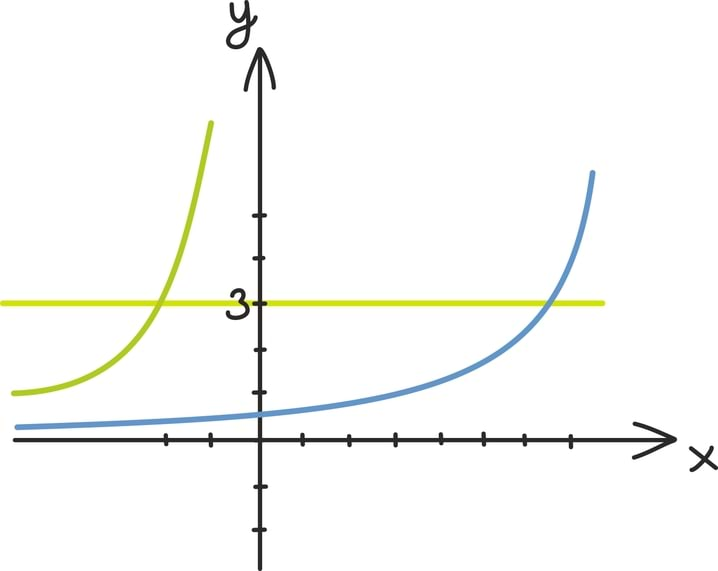
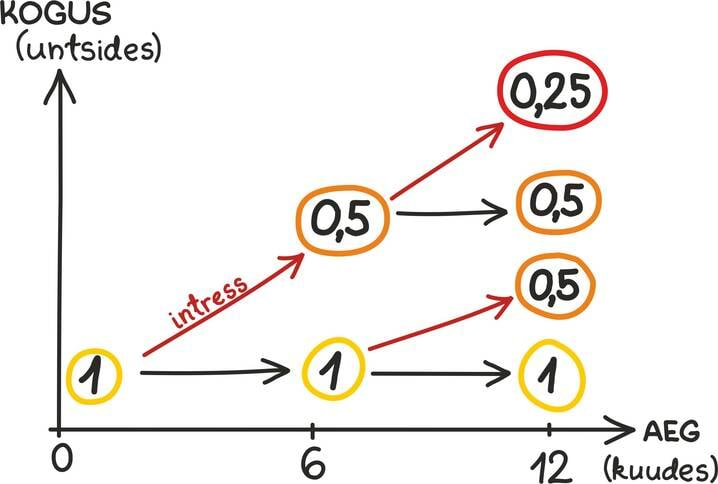
Hääbuv geomeetriline jada
Kui geomeetrilise jada tegur on absoluutväärtuselt väiksem kui üks, nimetatakse saadud jada hääbuvaks geomeetriliseks jadaks.
Näiteks jada 1⁄2; 1⁄4; 1⁄8; 1⁄16 … on hääbuv jada teguriga 1⁄2. Mis on sellise jada kõikide liikmete summa?
Kuna kokku on sellises jadas liikmeid lõpmata palju, võiks ju arvata, et seda summat ei annagi hästi arvutada – ta võiks ju ka olla lõpmatult suur, nii suur, et teda ühe arvuga väljendada ei saagi. Selgub siiski, et tegemist on alati lõpliku ning tihti isegi mitte väga suure arvuga.
Selle probleemiga on tihedalt seotud ka vanakreeka filosoofi Zenoni paradoks, mis väidab järgmist: kui aeglasemale startijale on antud võidujooksus edumaa, siis ei saa kiirem jooksja kunagi aeglasemast jooksjast ette jõuda. Nimelt enne, kui kiirem jooksja aeglasest möödub, peab ta esiteks jõudma punkti, kust aeglasem alustas. Selleks hetkeks on aga aeglasem jooksja juba edasi, järgmisesse punkti jõudnud. Nüüd peab kiirem jooksja enne möödumist hoopis sellesse punkti jõudma. Ja jälle on aeglasem edasi jõudnud. Nii võime lõpmatult jätkata, kuna iga kord, kui kiirem jooksja jõuab aeglasema eelmisesse punkti, on too sealt juba lahkunud.
Ometigi teame, et kiiremad jooksjad mööduvad aeglastest – sellest siis ka põhjus, miks seda arutlust paradoksiks kutsutakse. Võib-olla suudate pärast selle peatüki läbitöötamist näha, miks see „intuitiivne” argument siiski päris hästi paika ei pea.
Pirukad ja hääbuva geomeetrilise jada summa
Vaatleme nüüd enne toodud jada 1⁄2; 1⁄4; 1⁄8; 1⁄16; … pisut lähemalt.
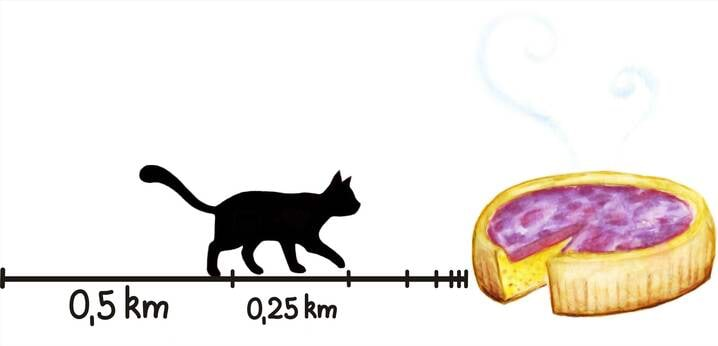
Võime sellest jadast ka muinasjutuliselt mõelda. Oletame, et täpselt kilomeetri kaugusel asub pirukaputka, mille poole hiilib saabasteta kass. Jõudnud poolele teele, on tal läbitud pool kilomeetrit ja läbida jäänud samuti veel pool kilomeetrit. Tähistagu jada esimene liige selle esimese jalutuse pikkust:a1 = 1⁄2 km.
Luuranud hetke, otsustab ta hiilida veel poole jäänud maast – see tähendab pool poolest kilomeetrist ehk veerand kilomeetrit. Tähistame selle jalutuse a2 = 1⁄4 km.
Piilunud veel kord ümberringi ja hinganud sügavalt sisse, otsustab kass kõndida veel poole järele jäänud maast – veel poole veerandist kilomeetrist ehk kaheksandiku kilomeetrit. Tähistame selle jalutuse a3 = 1⁄8 km.
Nii ongi iga edasiliikumine vastavuses ühe jada liikmega ja jada summa on vastavuses kokku läbitud distantsiga. Aga pirukaputkani oli alguses täpselt üks kilomeeter ja seega, kuna kass putkast kaugemale kindlasti ei jõua, ei saa ka jada summa olla suurem kui üks. Tegelikult on see summa täpselt üks, sest pirukaputkani jääv maa muutub nii olematuks, et saabasteta kass paneb tingimata mõne piruka ka nahka.
Seda, et jada summa on lõplik, võib muidugi selgitada ka kasutades eelnevas tärniga osas leitud jada liikmete summa valemit:
Nüüd kui q < 1, siis on see valem igati lõpliku väärtusega ning lisaks kahaneb qn astendaja n kasvades järjest väiksemaks ning läheneb kiiresti nullile.
Nii võime tegelikult näha, et kõikide liikmete summa läheneb arvule
Täpsemalt on S jada Sn piirväärtus [lk 310].
Jada 1⁄2; 1⁄4; 1⁄8; 1⁄16 jaoks on a1 = 1⁄2 ja q = 1⁄2 ning seega on tõesti selle jada summa täpselt 1.
Nimetus
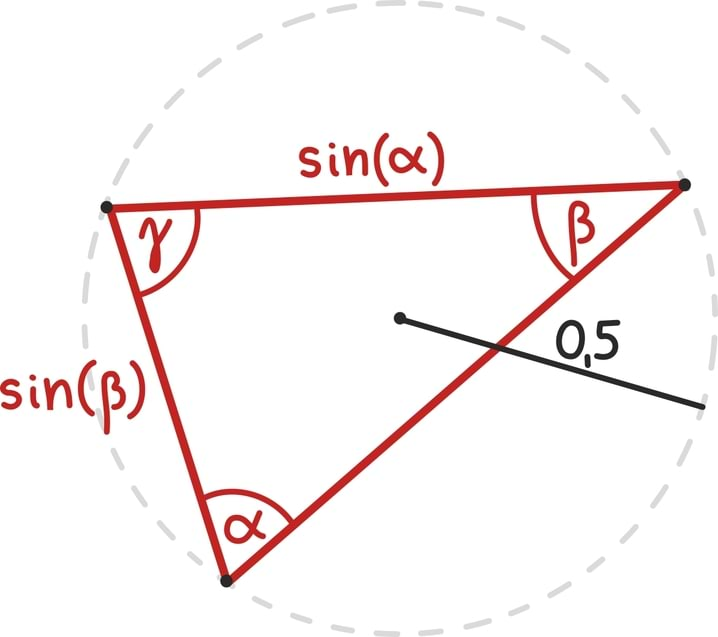
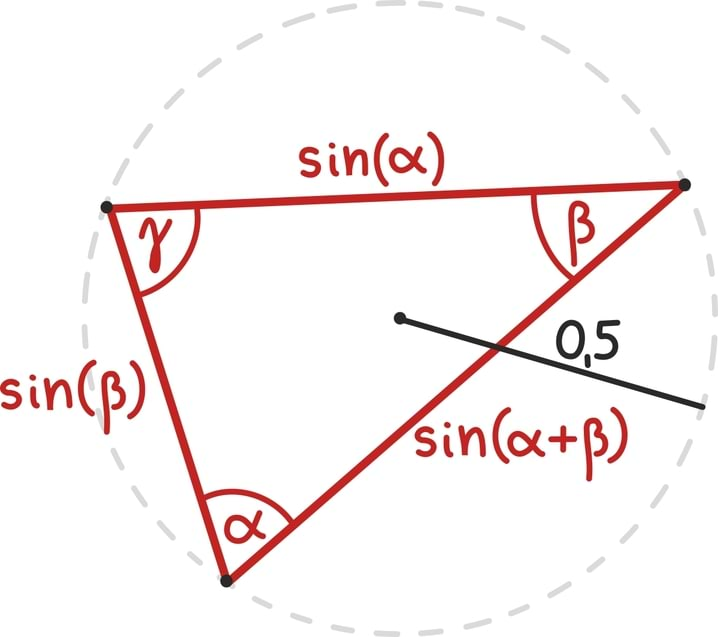
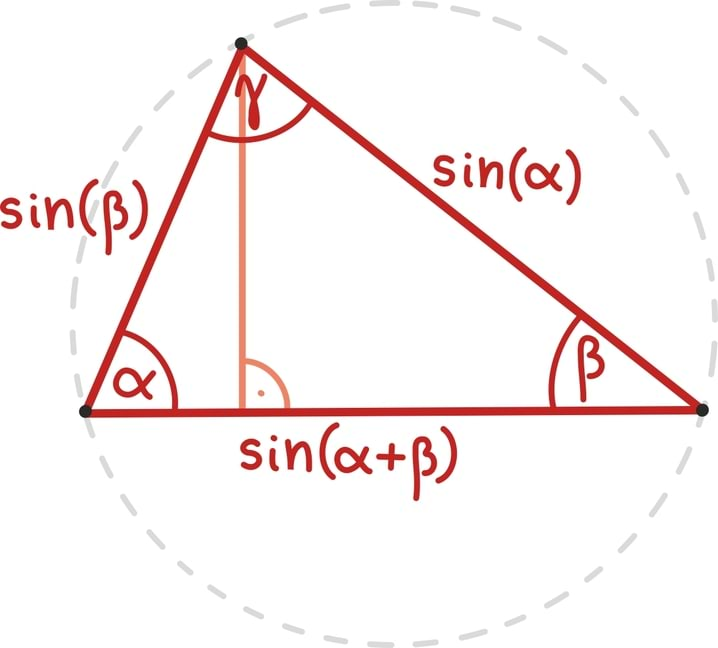
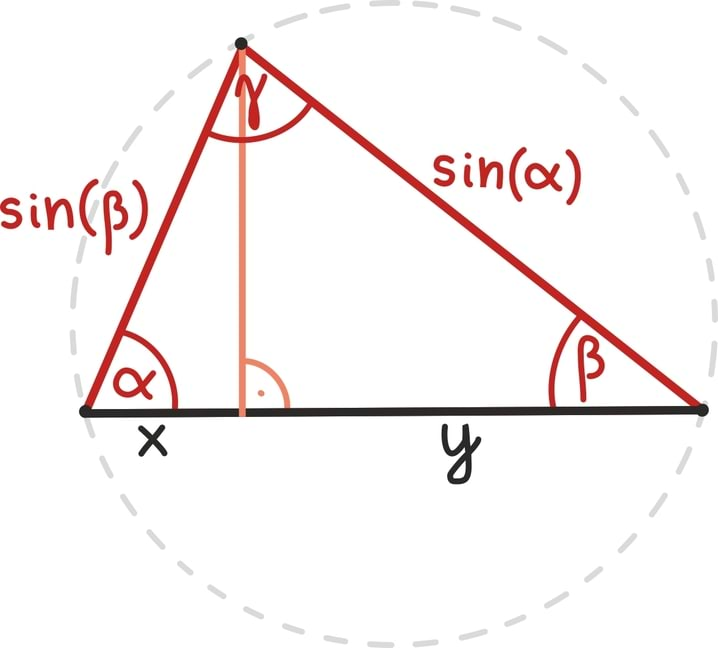
Aritmeetilise jada nime põhjendasime osati hüüdlausega „Aritmeetilise jadaga saab teha aritmeetikat!“. Oleks ju väga tore, kui geomeetrilise jadaga saaks teha geomeetriat... ja mingis mõttes saabki! Nimelt võib mõelda, et alustame ühest teatava pikkusega lõigust ja kõik edasised liikmed lihtsalt suurendavad seda teataval määral. Seega on geomeetriline jada seotud ühe lihtsaima geomeetrilise teisenduse – skaleerimise ehk suurendamise ja vähendamisega.
Kuigi lihtne mõte, võib see vaateviis siiski osutuda kasulikuks. Näiteks pirukapoe külastuse juures illustreerisimegi jada an = 1⁄2n summa lõplikkust ka geomeetriliselt.
Muidugi on lisaks sellele ka geomeetriline jada seotud geomeetrilise keskmisega – jällegi on kolmest järjestikusest liikmest keskmine äärmiste geomeetriliseks keskmiseks [lk 198].
Nagu juba sissejuhatusest näha, leidub ka teisi põnevaid jadasid, mille omaduste kallal on matemaatikud palju pead murdnud. Toome neist mõned matemaatikutele meelepärased näited.
Algarvude jada
Meenutame, et algarvudeks kutsutakse arve, mis jaguvad ainult iseenda ja ühega. Esimeses osas näitasime, et algarvusid on lõpmatult palju [lk 46]. Algarvude jada algab nii:
Algarvudega on endiselt seotud palju veel lahendamata küsimusi. Näiteks ei ole teada, kas leidub lõpmatult palju kaksikalgarve – algarvude paare, mis erinevad teineteisest kahe võrra. Sellisteks paarideks oleks näiteks (3; 5) või (197; 199). Suurimal leitud paaril on tänaseks kümnendesituses 200700 numbrit!
Huvitav hiljuti tõestamist leidnud teoreem väidab, et algarvude jadade sees võib leida soovitud pikkusega aritmeetilisi jadasid. Teisisõnu, on võimalik leida nii 10, 1000 kui 20 350 liikmega aritmeetiline jada, mille kõik liikmed on algarvud. Proovige kasvõi leida 4 liikmega aritmeetiline jada, mille liikmed on algarvud!
Algarvude pöördarvude jada
Huvitavaks osutub ka algarvude pöördarvude jada
Selle jada muudab huvitavaks tema liikmete summa ääretult aeglane, kuid visa suurenemine. Ükskõik mis arvu jaoks võime alati leida teise arvu n, nii et algarvude pöördarvude jada n esimese jada liikme summa oleks mõeldud arvust suurem.
Samas aga suureneb see jada nii aeglaselt, et näiteks kui soovime, et esimese n liikme summa oleks kokku 7, peab selleks summeerima ligikaudu 1010 000 000 jada liiget!
See jada on ka ilus näide sellest, kuidas arvutitega tehtavad katsed võiksid meid eksiteele viia. Algarvude pöördarvude jada kasvab nii aeglaselt ning iga arvutiga tehtud eksperiment veenaks meid, et jada summa ei saa kuidagi olla lõpmatult suur.
Ometigi on matemaatiliselt võimalik näidata, et jada summa on lõpmatult suur.
Naturaalarvude pöördarvude ruutude jada
Selle jada kõikide liikmete kokkuliitmine annab jälle ühe üsnagi üllatava seose:
Kas oskate leida mõne põhjuse, miks naturaalarvude pöördarvude ruutude summa peaks olema seotud ringi pindalast tuntud arvuga π?
Selle huvitava seose leidis üks läbi aegade suurimaid matemaatikuid Leonhard Euler 1735. aastal.
Huvitaval kombel ei rahuldanud tema tõestus teisi tolleaegseid matemaatikuid ning läks veel kuus aastat pärast avastust, enne kui ta suutis ka teisi selle seose tõesuses veenda.
Fibonacci jada
Fibonacci jada iga järgnev liige tekib kahe eelneva liikme liitmisel. Jada alustamiseks tuleb meil seega lihtsalt määrata kaks esimest liiget
Kõik järgnevad liikmed saame seejärel lihtsalt välja arvutada.
Näiteks
ja nii edasi. Üldkujus võiksime kirjutada Fibonacci jada liikmeid siduva võrrandi
Fibonacci arvud tulevad esile erinevates ja üllatavates kohtades. Üks lihtsam ülesanne, mille lahendavad Fibonacci arvud, on järgmine:
Kui mitu erinevat võimalust on n astmega trepist ülesronimiseks, hüpates korraga alati kas ühe või kaks astet edasi? Näiteks kolmeastmelisest trepist on võimalik üles minna kolme moodi: 1 + 1 + 1, 1 + 2 või 2 + 1, neljaastmiselisest viit moodi jne.
Üllatavalt palju rakendatakse Fibonacci arve viimasel ajal informaatikas: nende abil üritatakse tekitada juhuslikke arve, leida uusi otsingualgoritme ning luua isegi andmestruktuure. Kahtlustatakse, et Fibonacci jada on kasutatud ka muusika komponeerimiseks ning hoolikas loodusvaatleja leiab Fibonacci jadaga seotud spiraale ja mustreid ka kosutaval matkal.
Lisaks selgub, et Fibonacci järjestikuste liikmete suhe läheneb ühele kindlale arvule. Veelgi enam, see arv pole mingi suvaline arv, vaid niinimetatud kuldlõike suhtarv
Kuldlõike suhtarv on leidnud läbi ajaloo palju austust ja lugupidamist. Tema nimetus tuleb sellest, et ta peaks olema aluseks ilusaimatele proportsioonidele. Näiteks arvatakse, et just kuldlõige annab ristküliku jaoks kõige ilusama pikkuse ja laiuse proportsiooni. Seetõttu on nii mõnigi autor otsustanud ka oma raamatu välja anda just nendes proprotsioonides.
Siinkohal lõpetame veel tänaseks lahendamata matemaatilise küsimusega. Kas eksisteerib lõpmata palju Fibonacci arve, mis on algarvud (esimesed sellised arvud: 2, 3, 5, 13, 89, 233, 1597)? Arvatakse, et vastuseks on jah, aga seda tõestada ei osata. Huvitav, mis selles nii rasket on?
Väike mõistatus neile, kellel on aega ja agarust ülearu:
Antud on ühe jada algus:
Mis on jada järgmine liige?
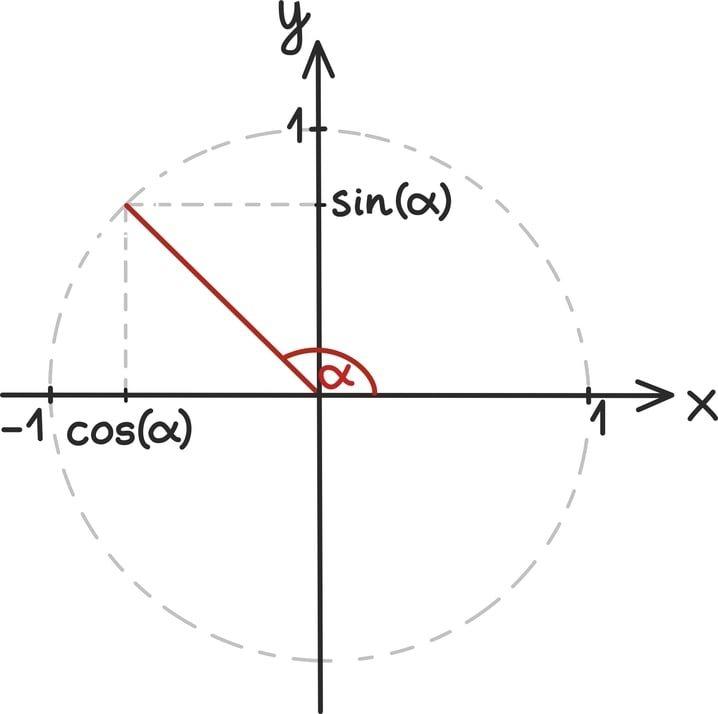
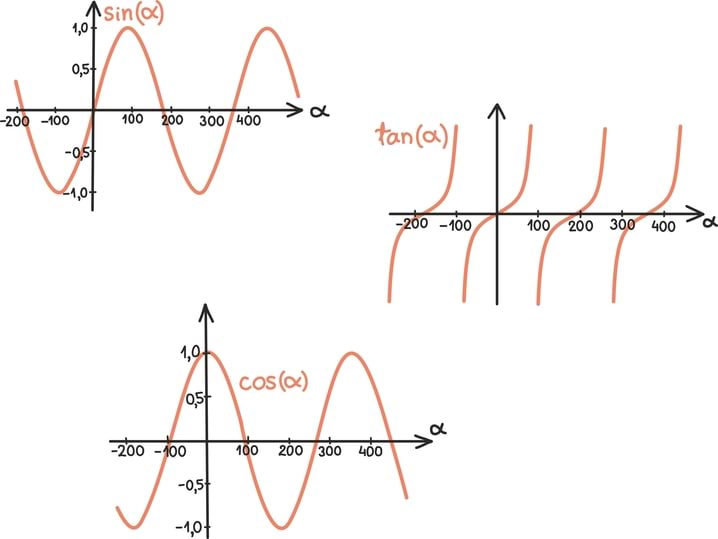
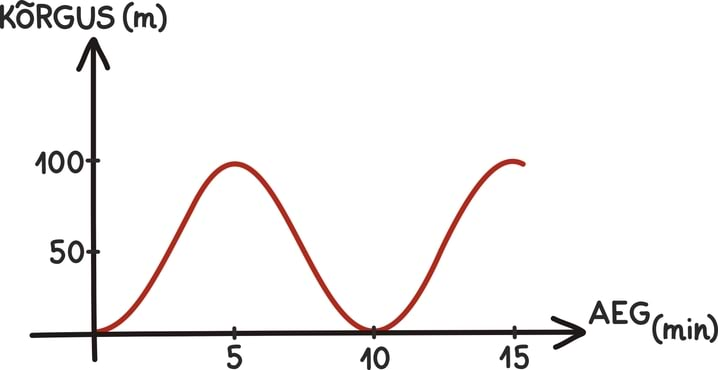
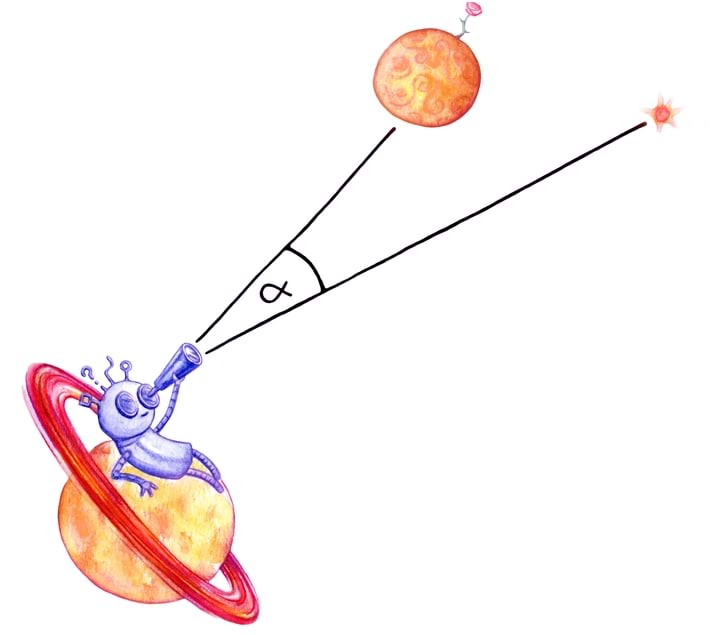
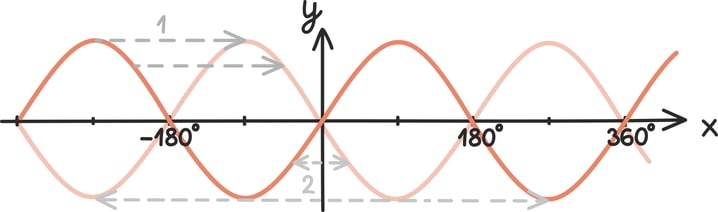
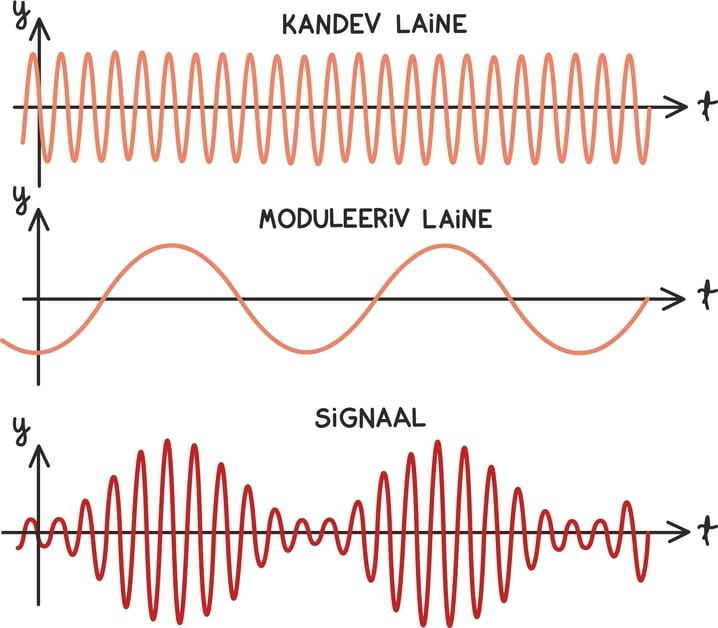
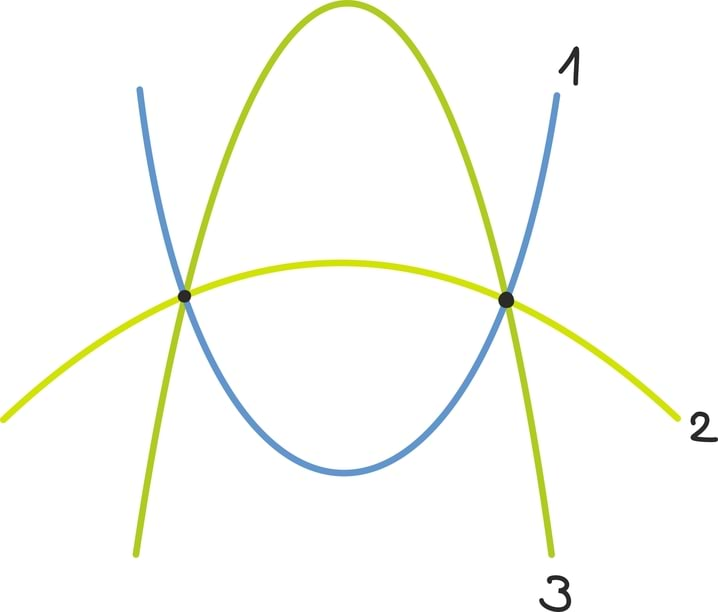
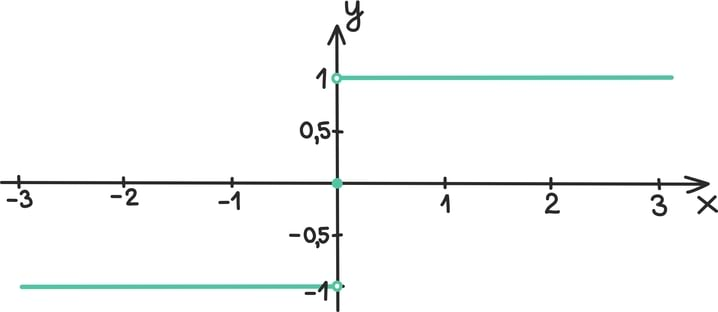
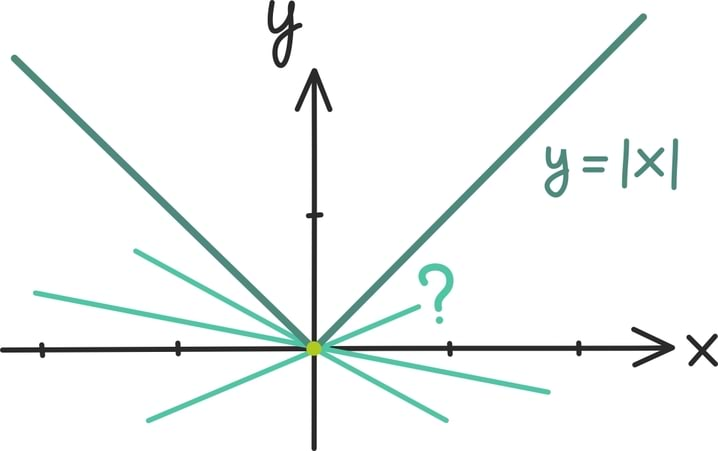
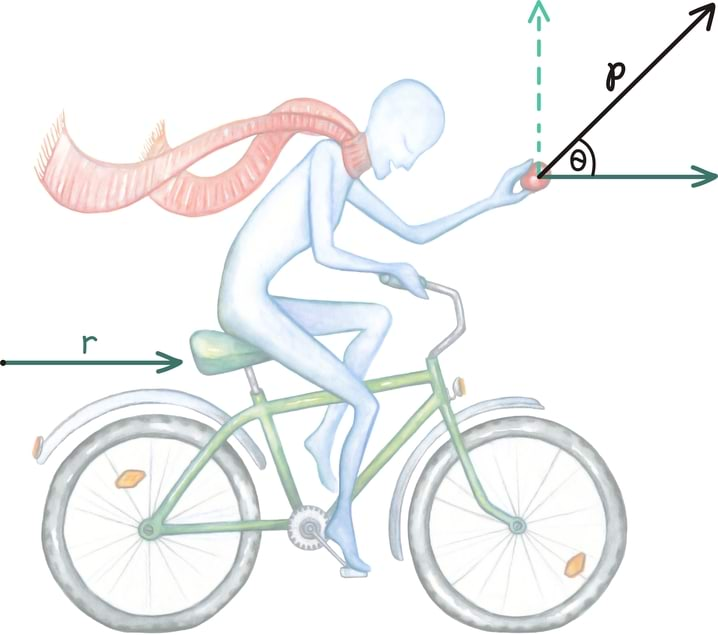
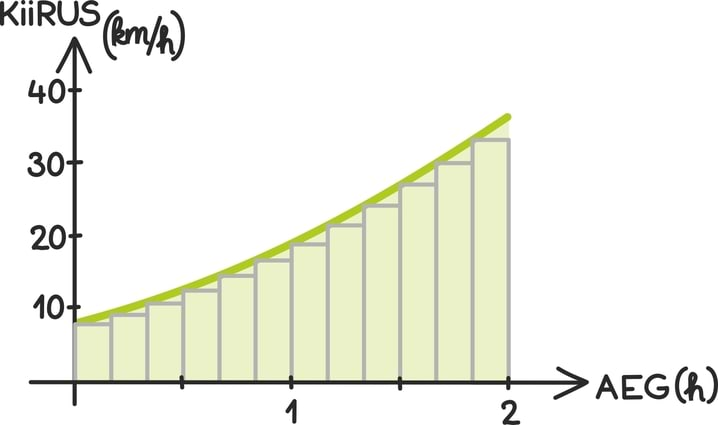
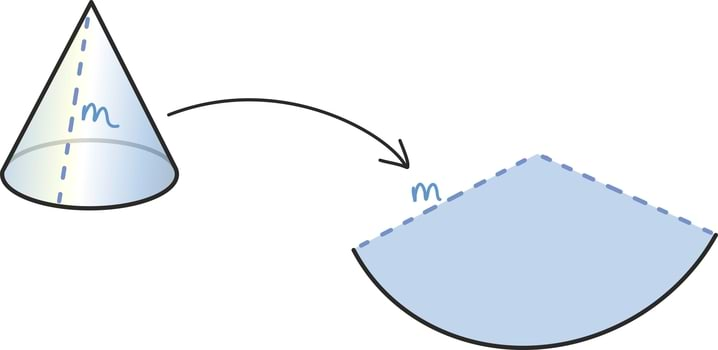
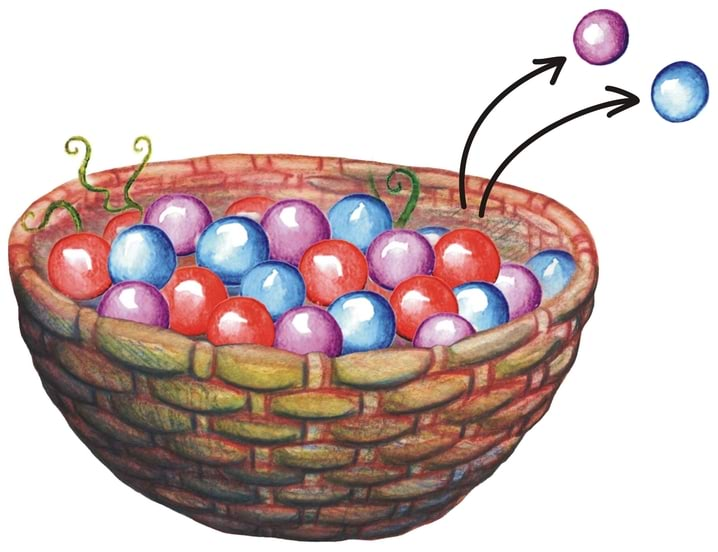
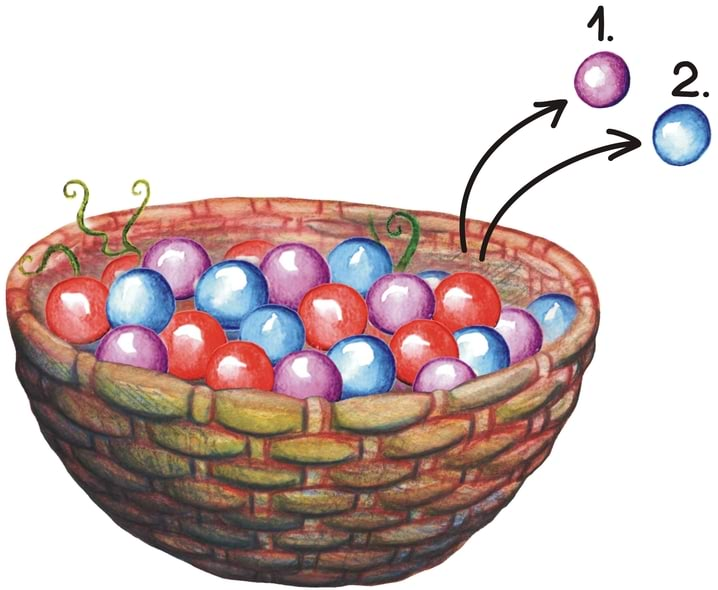
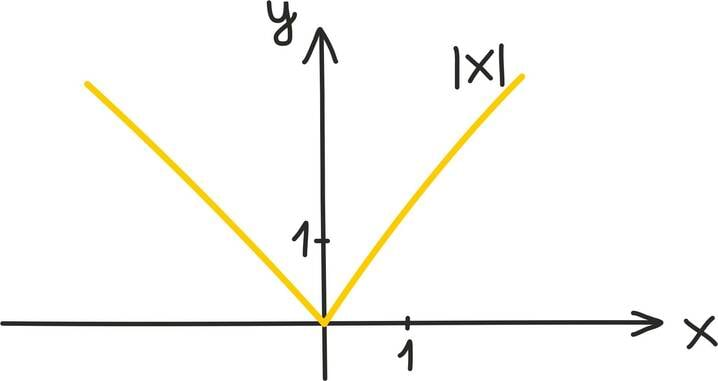
Kui eelmise peatüki lõpetasime väikese mõistatusega, siis seekord alustame väikese mõistatusega: mis on pildil?
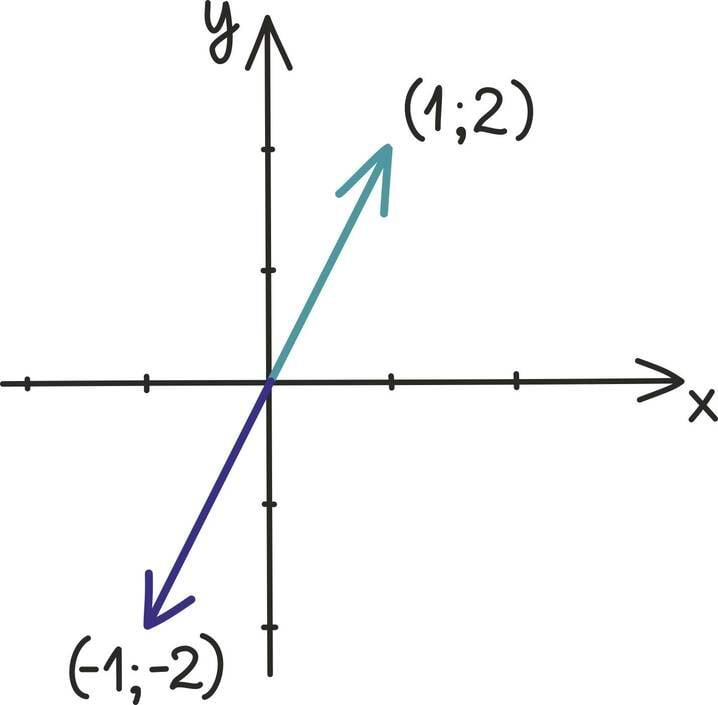
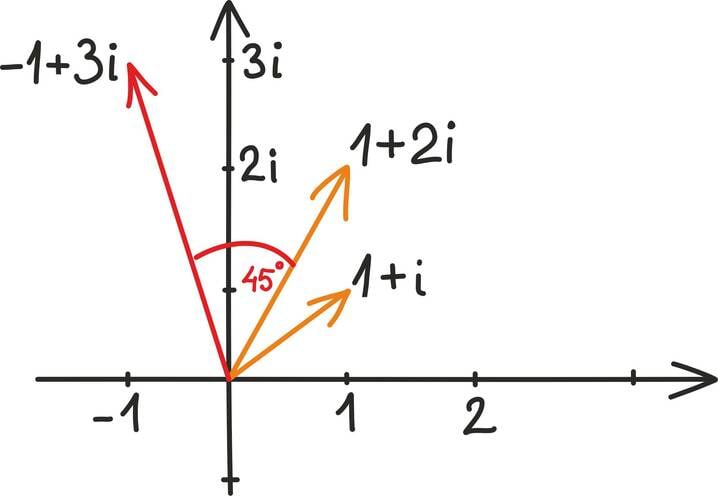
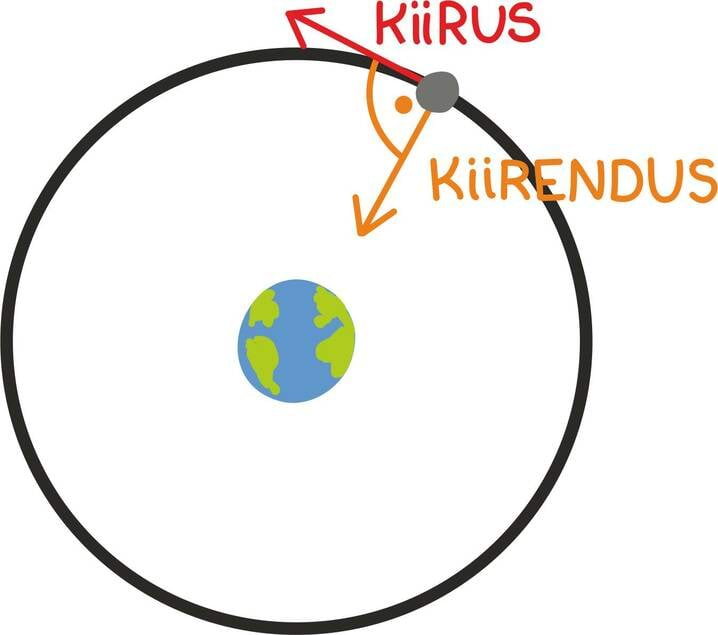
Tahtsite vastata nooled? Ei, matemaatiku, füüsiku ning hoolsa koolijütsi jaoks on need hoopis vektorid!
Vektoritest võibki lihtsalt mõelda kui nooltest. Nagu iga noolt, iseloomustab vektoreidki teatav suund ja teatav pikkus. Vektorid osutuvad oluliseks, kuna nende abil võib kirjeldada objekte, mille puhul on olulised nii nende suund kui tugevus.
Näiteks professionaalsed tuulelohetajad (või purjetajad) on kindlasti uurinud kohaliku piirkonna tuulte kaarti – sealsed paljud nooled, mis kirjeldavad tuulte suunda ja tugevust, on tuulevektorid.
Samuti on füüsikutel kombeks rääkida jõuvektoritest: kui ikkagi kellegagi kätt surute, tuleb jõudu avaldada nii teatud tugevusega kui ka õiges suunas.
Iga liikujat võib aga iseloomustada kiirusvektoriga: igas punktis liigub ta mingis suunas mingi kiirusega.
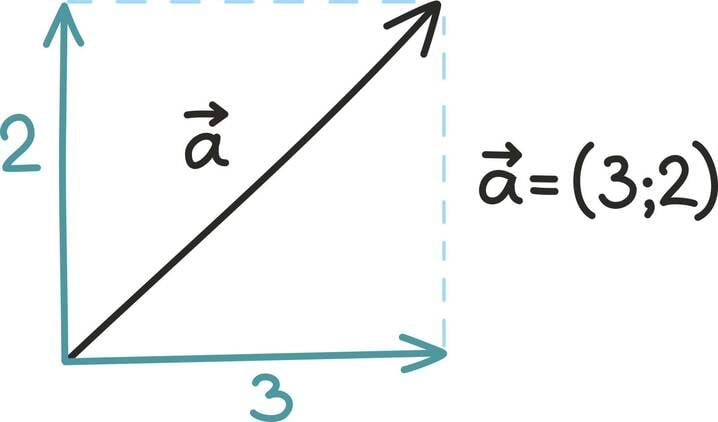
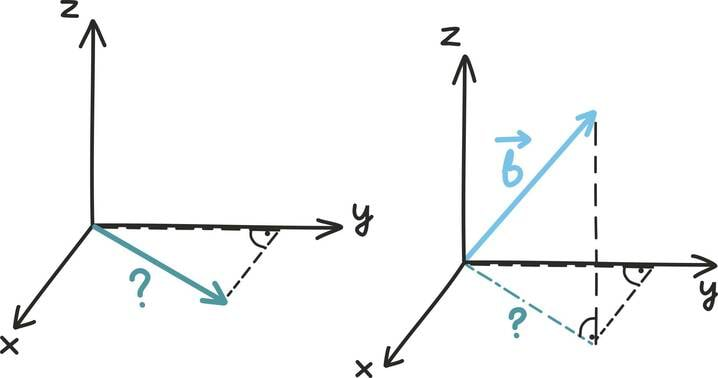
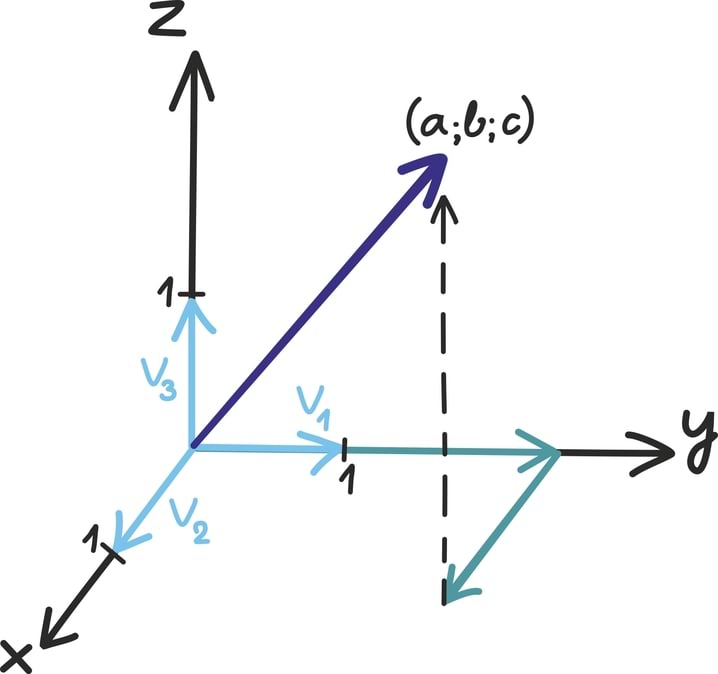
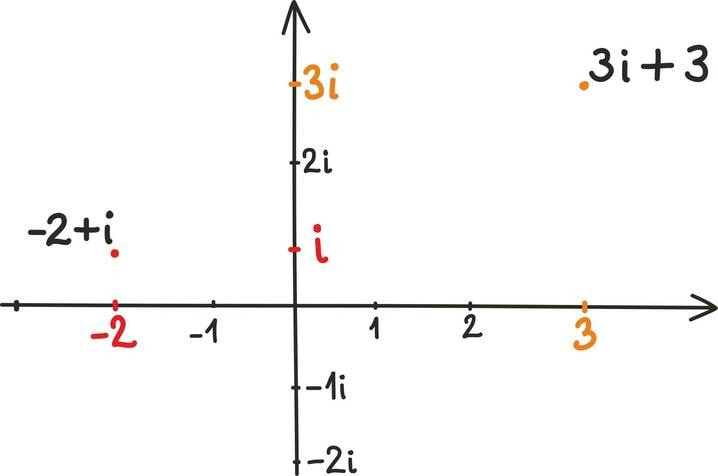
Kahemõõtmeline vektor ei ole midagi muud kui lihtsalt reaalarvude paar – näiteks (1; 3). Kolmemõõtmeline vektor on tavaline reaalarvude kolmik – näiteks .
Kena näide kümnemõõtmelisest vektorist on igal juhul (0; 1; 2; 3; 4; 5; 6; 7; 8; 9) ja mis on kahe tuhande üheteistkümne mõõtmeline vektor, pole vist ka keeruline välja nuputada... kuigi võib olla keerulisem kirja panna.
Et seost nooltega meelde tuletada, tähistatakse vektoreid ka tavaliselt tähe ja noolekesega, nagu näiteks
Muidugi ei keela keegi näiteks liikumisvektorile nimeks panna
ainult kirjavaeva oleks nii rohkem.
Arvulise kirjapaneku ja visuaalse mõtte vahelist seost illustreerib järgmine joonis. Kahemõõtmelist vektorit kirjeldavad kaks arvu (mida kutsutakse koordinaatideks) näitavad, kui kaugele ulatub nool kahes ristuvas suunas. Kolmemõõtmelise vektori korral oleks meil juba vaja kolme ristuvat suunda, neljamõõtmelise joonistamine läheks juba raskeks...
Vektorile on väga lihtne intuitiivne selgitus – nooleke pikkuse ja suunaga. Ometi on vektoril kui matemaatilisel objektil palju erinevaid omadusi, teda võib mitmel moel teisendada ning temaga teha erinevaid tehteidki.
Sellest lähtuvalt on kogu see alapeatükk täis uusi mõisteid ja trikikesi, millest ühe korraga läbinärimine võib olla üsna väsitav. Nii soovitamegi vaadata kõiki järgnevaid kirjutusi ühe- või kahekaupa ja iga omaduse, teisenduse ja tehte juures võtta kõrvale mõni konkreetne näide, nägemaks, et midagi keerulist kogu peatükis siiski pole.
Võrdsed vektorid
Kui oleme defineerinud mõne uue matemaatilise objekti, siis on esimene loomulik küsimus: millal on kaks sellist objekti võrdsed? Ehk millal on kaks vektorit võrdsed?
Õnneks on vektorite puhul vastus üsna ilmne ja lihtne. Kui mõelda vektorist kui mitmest ritta seatud arvust, on üsna kärmelt selge, mida peaksid tähendama võrdsed vektorid: kõik vektori koordinaadid peavad olema võrdsed.
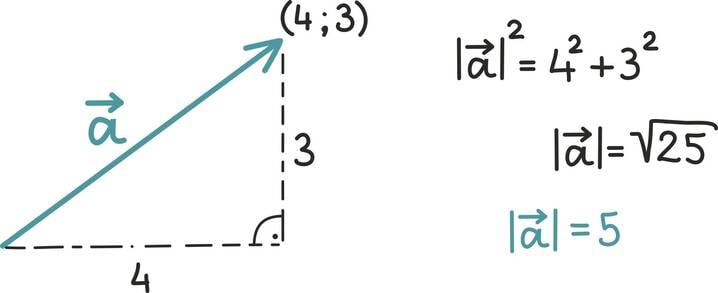
Vektori pikkus
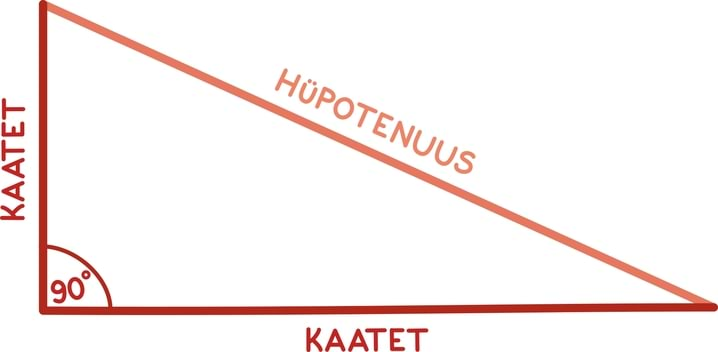
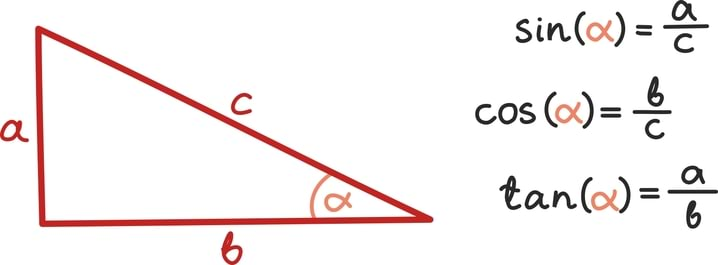
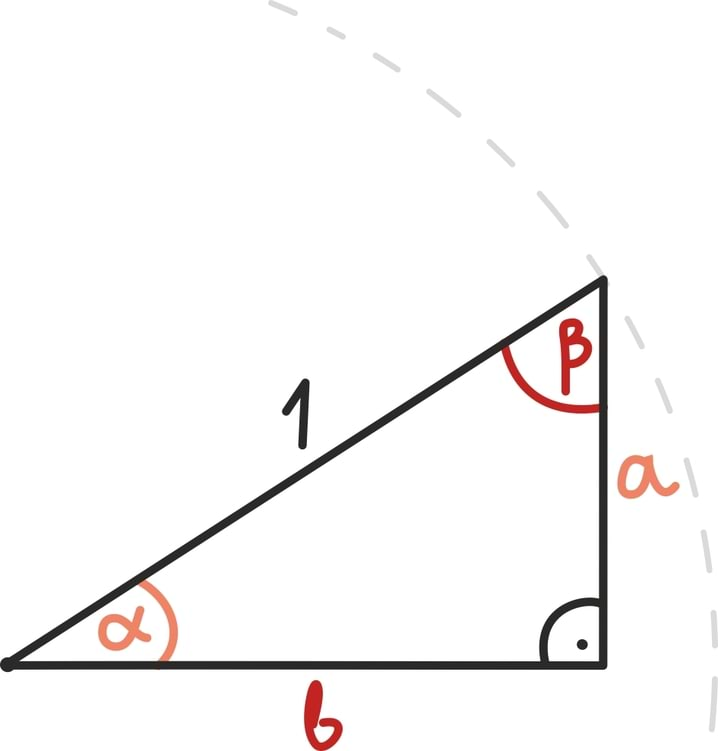
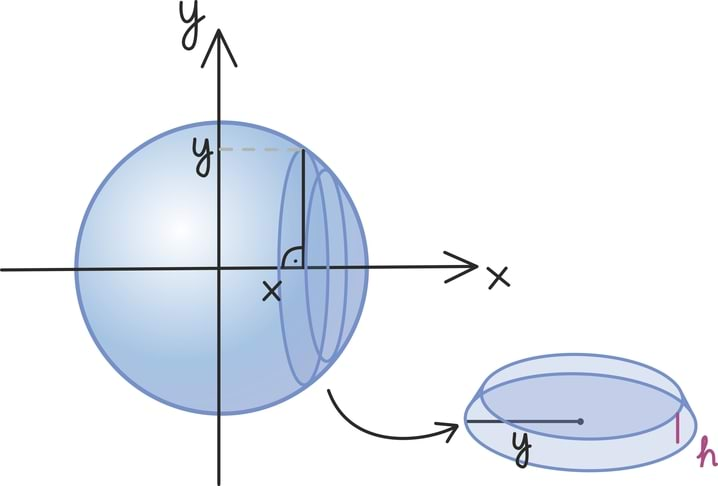
Vektori pikkust ||arvutame täpselt nagu punkti kaugust nullpunktist. Seega kahemõõtmelise vektori pikkuse võime välja arvutada nii nagu ikka täisnurkse kolmnurga hüpotenuusi.
Juhul kui vektor on kolmemõõtmeline, peame seda arutluskäiku rakendama lihtsalt kaks korda. Siin on näide vektoriga
Vektorite liitmine
Vektorite liitmisest saame mõelda mitmel viisil. Vektoreid on vaja liita näiteks siis, kui tahame kokku liita mitu erinevat ühele objektile mõjuvat jõudu.
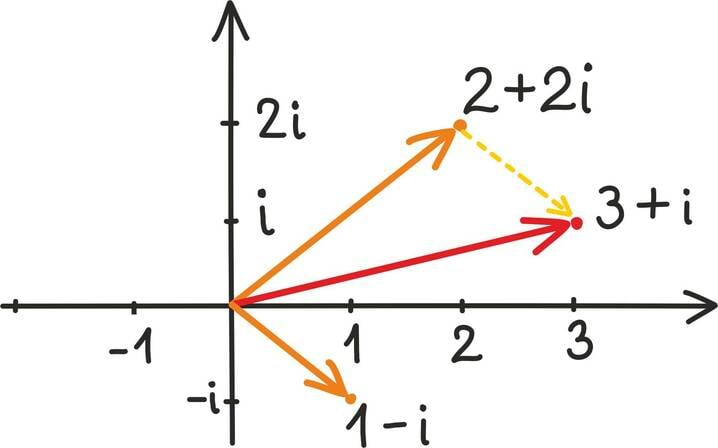
Esmalt võime liitmisest mõelda arvulise esituse abil. Sel juhul teeme seda koordinaatide kaupa: näiteks
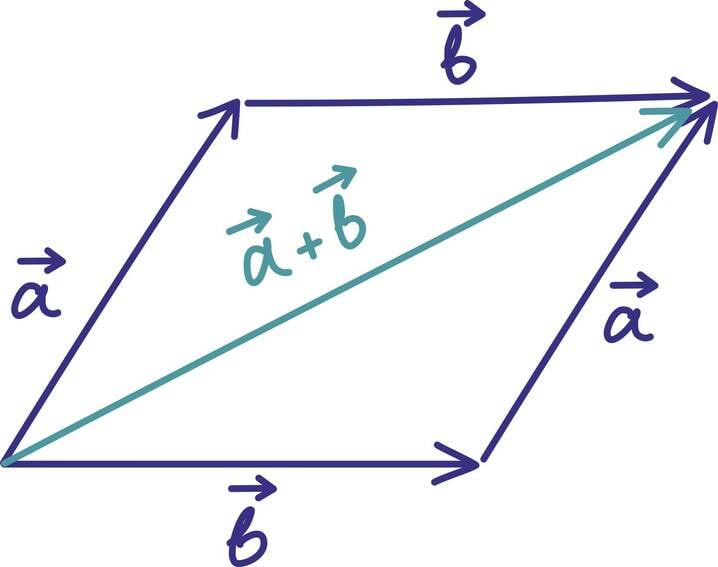
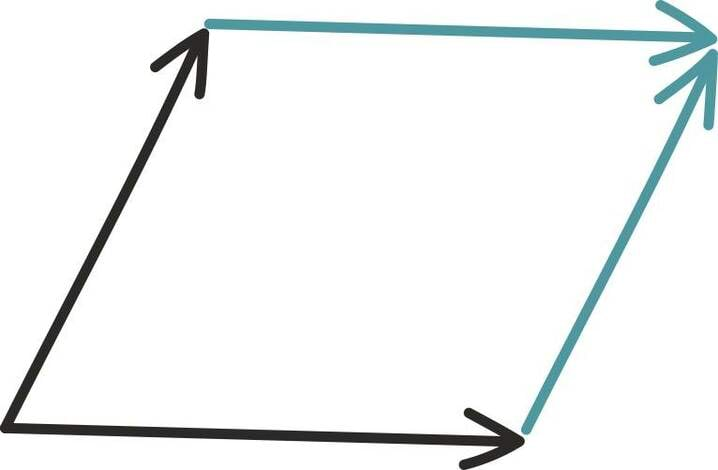
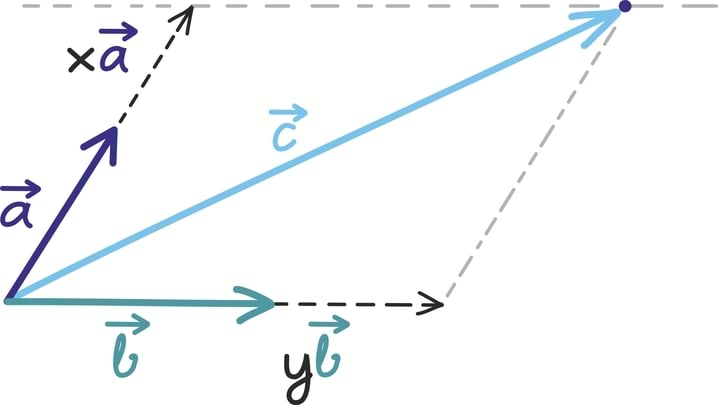
Samas võime vektorite liitmisest mõelda ka geomeetriliselt. Summavektori leidmiseks peame lihtsalt liidetavad vektorid teineteise järele seadma.
Summavektor viib niisiis esimese vektori alguspunktist teise lõpp-punkti. Toodud jooniselt on hästi näha, miks geomeetrilist liitmist kutsutakse ka „rööpküliku reegliks”.
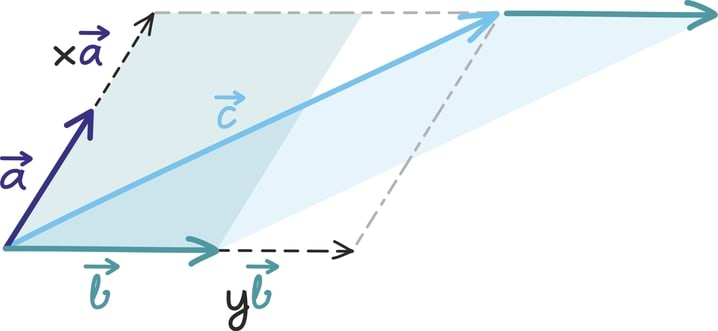
Toodud geomeetriline mõtteviis annab hea tõlgenduse juhule, kui näiteks kolme või nelja või kuue vektori summa on null.
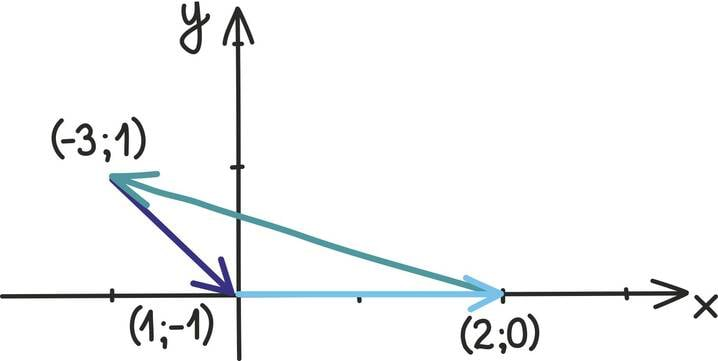
Tõepoolest, kui kolme vektori summa on null, siis peab kolmanda vektori lõpp-punkt olema esimese vektori alguspunktiks ning joonisele tekib kolmnurk. Näiteks kui meil on vektorid (–3; 1), (1; –1) ja (2; 0), siis kokku liites saame tõesti nullvektori
Samamoodi kui näiteks nelja vektori summa on null, defineerime selle abil nelinurga, ja kui kuue vektori summa on null, siis kuusnurga.
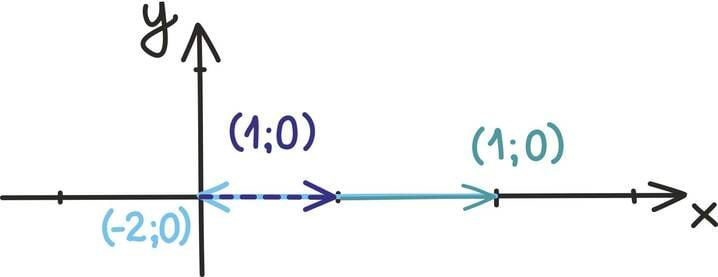
Hoolikas lugeja muidugi märkab, et oleme siin natuke luisanud. Kui võtame vektorid (1; 0), (1; 0) ja (–2; 0) siis ei teki ju siiski kolmnurka, sest kõik vektorid on samal sirgel.
Õnneks ongi see pisiasi ainus, mis saab muidu nii ilusa seose untsu ajada.
Nullvektor, vastandvektor
Arvude liitmisel on ühel arvul eriline roll: arv null. Mõnda arvu temaga kokku liites saame tulemuseks selle arvu enda. Analoogne objekt vektorite hulgas on nullvektor: vektor, millega liitmisel on tulemuseks vektor ise. Kolmemõõtmeline nullvektor on siis muidugi (0; 0; 0). Sarnaselt arvudega võib siis defineerida ka vastandvektori: vektori, millega liitmisel saame tulemuseks nullvektori. Näiteks vektori (1; 2) vastandvektor on (–1; –2).
Vektorid ja korrutamine
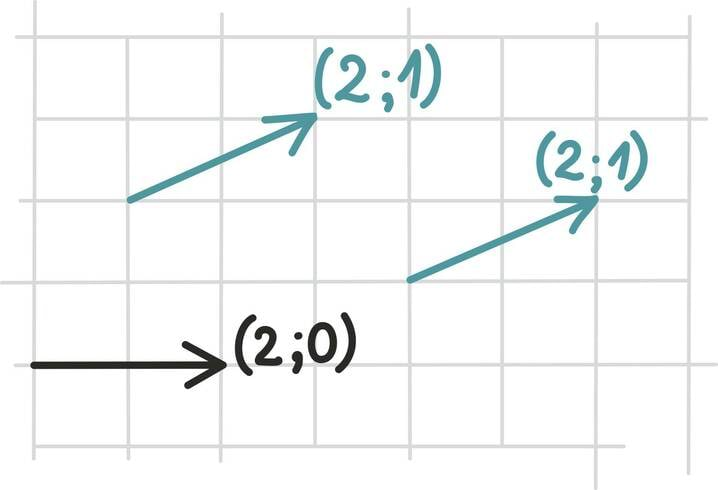
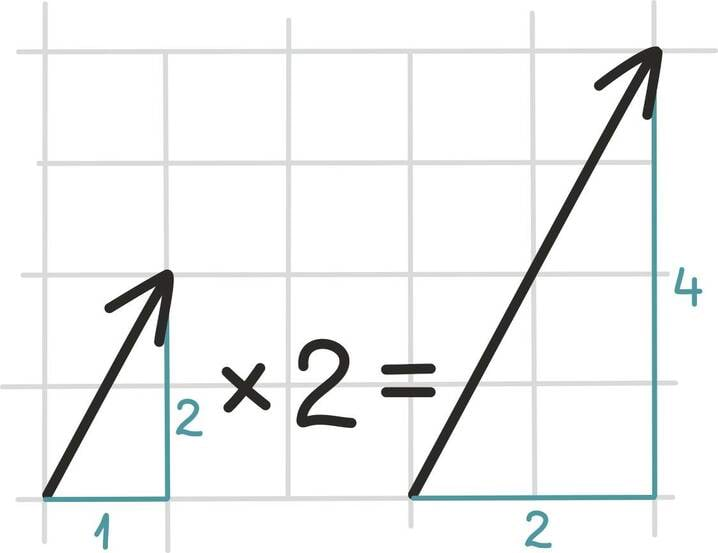
Vektoreid võime reaalarvudega korrutada. Sellest võib jällegi mõelda vektori koordinaatide abil: korrutame lihtsalt iga koordinaati reaalarvuga.
Samas on olemas ka geomeetriline mõtteviis: vektorit reaalarvuga korrutades pikendame või lühendame vektoreid. Kui reaalarv, millega vektorit korrutame, on negatiivne, siis muudame lisaks veel vektori suuna vastupidiseks.
Seega ei ole väga raske korrutada vektoreid reaalarvudega. Aga kas vektoreid saab ka omavahel korrutada?
Vastus on jällegi jah, aga selle jaoks peame natuke loobuma oma senisest arusaamast korrutamise kohta. Õigem oleks siis võib-olla öelda, et neid saab omavahel „korrutada“.
Õigupoolest saab vektoreid omavahel korrutada mitmel moel, aga kuna ükski neist ei ole päris analoogne arvude korrutamisega, on neile antud ka eraldi nimetused: 1) skalaarkorrutis ja 2) vektorkorrutis. Kahe vektori skalaarkorrutis annab tulemuseks lihtsalt reaalarvu, vektorkorrutis aga jälle ühe uue vektori.
Omaette küsimus on muidugi, miks peaksime tahtma vektoreid üldse omavahel „korrutada”. Matemaatiliselt on see soov üsna loomulik, kuna kõik hästi valitud teisendused ja tehted kannavad endas lootust luua rohkem seoseid erinevate matemaatika harude vahel ning seega võivad viia parema arusaamani kogu matemaatikast.
Õnneks leidub praktilisele lugejale siiski ka eluline vastus: nimelt nagu varsti näeme, on füüsikutel nii skalaarkorrutise kui vektorkorrutise jaoks olemas igati intuitiivne ja looduslik tõlgendus: skalaarkorrutis näitab, mil määral füüsikalised suurused töötavad ühe eesmärgi nimel. Näiteks kui üht keha liigutatakse teatavas suunas ühe jõu abil, siis skalaarkorrutis annab meile teada, kui palju tehti keha liigutamisel kasulikku tööd. Vektorkorrutis omakorda aitab kirjeldada, mil määral üks või teine jõud suudab kehasid pöörlema panna.
Lisaks selgub, et skalaar- ja vektorkorrutis osutuvad oluliseks arvutigraafikas. Nimelt võib nende abil taandada kõiksugu geomeetrilised teisendused nagu pöörded, peegeldused puhtalt koordinaatidega arvutustele, millega arvutid kenasti toime tulevad.
Lõpetuseks võib õhku jääda muidugi küsimus: kas vektoreid kuidagi omavahel „jagada" ka saab?
Seekord saame lõpuks vastata „ei“, vähemalt skalaarkorrutise ja vektorkorrutise jaoks jagamistehet ei leidu. Põhjus on üsna proosaline – kui me fikseerime ühe vektori, siis leidub terve hulk teisi vektoreid, mis temaga „korrutades” annavad täpselt sama skalaar- või vektorkorrutise. Näiteks vektoriga (1; 0; 0) annavad skalaarkorrutise null kõik vektorid kujus (0; a; b) . Need moodustavad aga kogu y–z tasandi ja me ei suuda nende hulgast jagamistehte vastust välja valida!
Skalaarkorrutis
Kui intuitiivselt kannab skalaarkorrutis samasuunalisuse mõtet, siis matemaatiliselt võib skalaarkorrutisest mõelda ja teda defineerida [lk 44] kahel viisil. Need kaks viisi on ka igati samaväärsed. Seda samaväärsust tuleks matemaatiliselt tõestada, aga siinkohal piirdume siiski ainult nende kahe viisi tutvustamisega.
Skalaarkorrutis läbi koordinaatide
Üks viis skalaarkorrutise defineerimiseks on koordinaatide põhine: kahe vektori skalaarkorrutise saame, kui esmalt korrutame kahe vektori vastavad koordinaadid ning seejärel liidame kõik saadud korrutised omavahel kokku.
Tähistades skalaarkorrutist silmapaistva punktiga, võime kirjutada näiteks:
Huvitav on märgata, et nii defineeritud korrutustehte tulemuseks on reaalarv.
Ei ole sugugi lihtne kohe aru saada, miks selline üsna lihtne definitsioon võiks samaaegselt ka huvitav või kasulik olla. Teatavat lootust annab juba teadmine, et võime teda samahästi defineerida ka hoopis teisel viisil.
Skalaarkorrutis läbi vektorite vahelise nurga
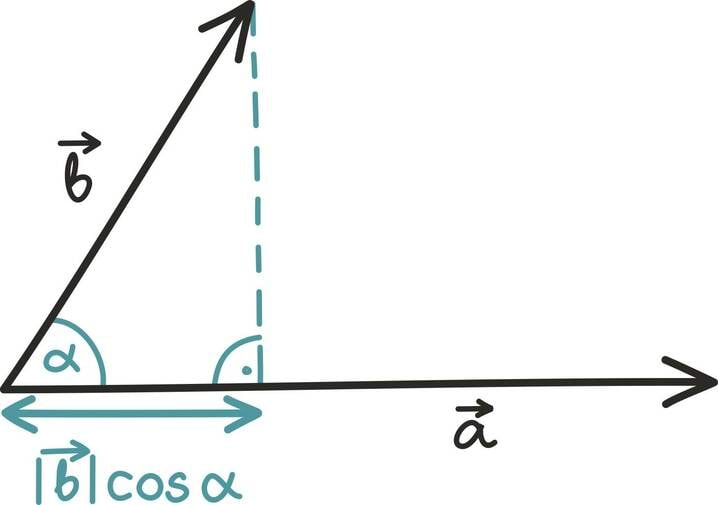
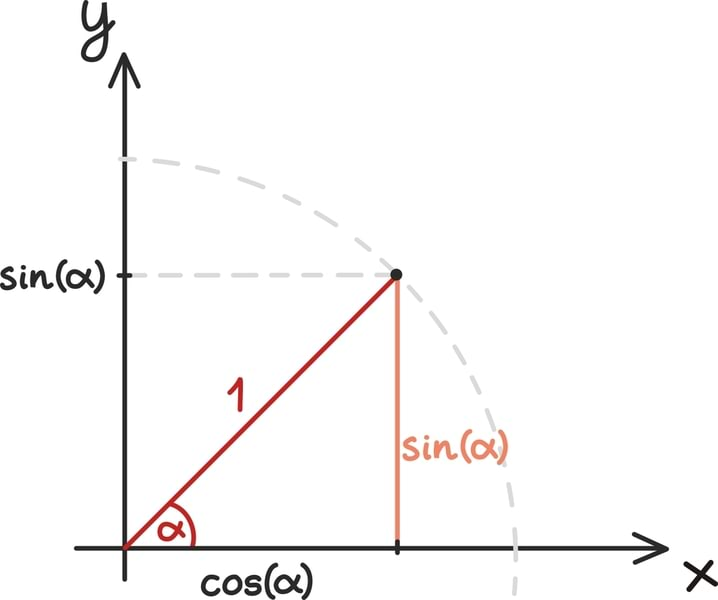
Skalaarkorrutis seob ka kavalalt vektorite vahelise nurga ja nende pikkused. Ta on võrdne vektorite pikkuse ning nendevahelise nurga koosinuse korrutisega:
Kuigi sel moel on koordinaatidega antud vektorite vahelist skalaarkorrutist raskem leida, pakub see definitsioon hea viisi, kuidas skalaarkorrutisest näidete abil pisut aimu saada.
Märkame, et sellest definitsioonist lähtuvalt võime skalaarkorrutist vaadelda kui vektori pikkuse korrutist selle osaga vektorist , mis näitab vektoriga samas suunas.
Seega
- kui üks vektoritest on nullvektor, siis skalaarkorrutis on 0, sest nullvektori pikkus on null,
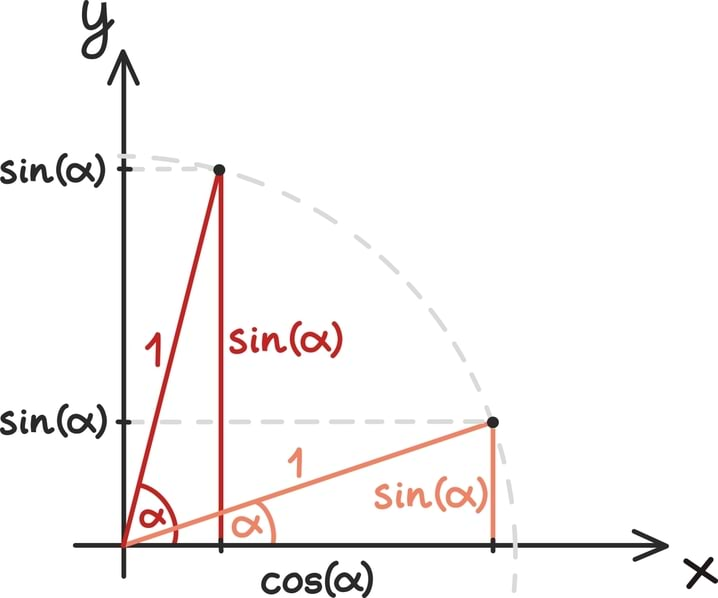
- ühe vektori korrutis iseendaga annab täpselt vektori pikkuse ruudu, sest nurk vektorite vahel on 0° ja cos0° = 1 – vektorid näitavad täiesti samas suunas,
- kui kaks vektorit on omavahel risti, siis on nende skalaarkorrutis null, sest cos90° = 0.
Üldisemalt näemegi, et kahe vektori skalaarkorrutis on maksimaalne, kui vektorid on samasuunalised. Hakates vektorite vahelist nurka suurendama, skalaarkorrutis väheneb ning tema väärtus on minimaalne siis, kui vektorid on vastassuunalised.
Fakt, et skalaarkorrutist saab defineerida kahel moel, muudab tema omaduste tõestamise üsna mugavaks – vähemalt ühes kujus on iga omadust lihtne tõestada.
Samuti on erinevad kujud kasulikud erinevates probleemides: pikkuste ja nurga abil antud kuju on füüsikute lemmik, samal ajal kui arvutigraafikas on lihtsam kasutada skalaarkorrutise leidmist koordinaatide abil.
Skalaarkorrutis ja füüsika
Suur osa füüsikalistest suurustest on samuti suuruse ning suunaga – näiteks liikumine toimub ju teatud suuna ja kiirusega ning jõud mõjuvad mingis suunas ja mingi tugevusega. Skalaarkorrutis tuleb mängu füüsikaliste suuruste kombineerimisel.
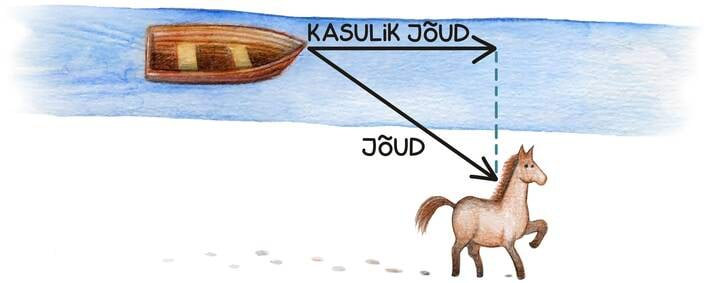
Näiteks kui vanasti kasutati hobuseid, et paati mööda jõge edasi viia, siis oli kõige targem hobust paralleelselt mööda jõeäärt talutada võimalikult kalda lähedalt.
Sellest võib mõelda skalaarkorrutise abil. Kui paat piki jõge liigub, võime tema liikumist kirjeldada kiirusvektoriga. Hobune avaldab talle tõmbamisega jõudu, mida kirjeldame jõuvektoriga. Nende vektorite omavaheline skalaarkorrutis annab nüüd ajaühikus tehtava kasuliku töö ehk võimsuse. Intuitiivselt kannab skalaarkorrutis endas teadmist, et paadi edasiliikumisele aitab kaasa ainult jõu kiirusvektori suunaline komponent. Seda võiks kutsuda kasulikuks jõuks. Tõepoolest, kui hobune tõmbaks paati risti jõega, oleksid jõuvektor ja kiirusvektor risti, skalaarkorrutis oleks null ja hobune paadi edasiliikumises rolli ei mängiks. Mida lähemal hobune jõele jalutab, seda paralleelsem on kiirusvektoriga ka jõuvektor, seda suurem skalaarkorrutis, seda suurem kasulik jõud.
Mõned skalaarkorrutise omadused ja Pythagorase teoreem*
Skalaarkorrutisel on tavalise korrutamisega mitmeid sarnaseid omadusi.
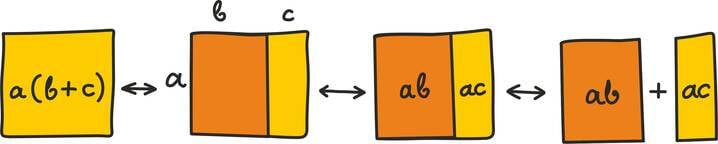
Esiteks võime koordinaatkuju abil kergesti näidata, et ka skalaarkorrutis on distributiivne: teisisõnu, iga kolme vektori
jaoks kehtib
Näiteks kahemõõtmeliste vektorite = (a1; a2) korral võime kirjutada koordinaatkuju definitsiooni abil:
Samamoodi näeme emmast-kummast definitsioonist, et skalaarkorrutis on kommutatiivne, ehk vektorite järjekord skalaarkorrutise võtmisel ei loe:
Samas meenutame, et nurga abil antud definitsioonist järeldasime, et ristiolevate vektorite skalaarkorrutis on null ning vektori skalaarkorrutis tema endaga on võrdne vektori pikkuse ruuduga.
Kasutades nüüd neid kahte omadust, võime näiteks tuletada Pythagorase teoreemi.
Olgu antud täisnurkne kolmnurk, mille küljevektorid ja on risti – ehk siis
Samas nägime ennist, et kolmnurga küljevektorite jaoks kehtib ka
ehk
[lk 142]Võtame nüüd mõlema poole skalaarkorrutise iseendaga ja saame:
Kasutades peatüki alguses toodud esimest skalaarkorrutise omadust näeme, et vasema poole väärtus on
Kuid
ning
Seega tõepoolest jääb järele samasus,
mis ongi Pythagorase teoreem.
Vektorkorrutis*
Nägime, et kui keha liigub mööda sirgjoonelist trajektoori ning talle mõjub teatav jõud, võime keha liikumiskiirust mõjutava kasuliku, samasuunalise jõu leida jõu- ning kiirusvektori skalaarkorrutise abil.
Kui aga näiteks fikseerime keha kauguse teatavast keskmest (ehk pöörlemisteljest) mingi hoova abil ning piirame seeläbi sirgjoonelise liikumise, võib keha veel ainult pöörelda ümber selle telje.
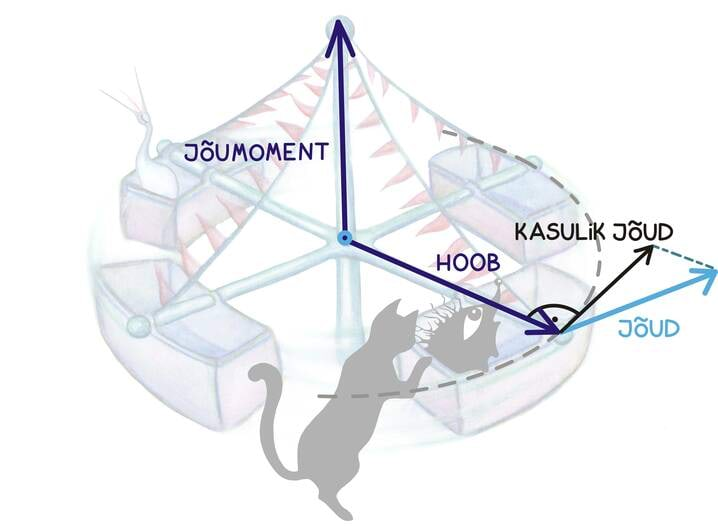
Keha pöörlemiskiirust mõjutab sel juhul hoopis hoovaga ristsuunaline jõukomponent, mida võib siis seekord kasulikuks jõuks nimetada. Kõige mugavam on pöörlema panevat mõju kirjeldada niinimetatud jõumomendi abil, milleks ongi täpselt hoova defineeriva vektori (füüsikute keeles: jõu mõjumispunkti tõmmatud kohavektori) ja kehale mõjuva jõuvektori vektorkorrutis.
Nagu jooniselt näeme, on jõumomendi näol tegemist mingi üsna kummalise vektoriga. Järgnevalt üritamegi selgitada, kuidas on vektorkorrutis ja seega ka jõumoment defineeritud ning miks just nii.
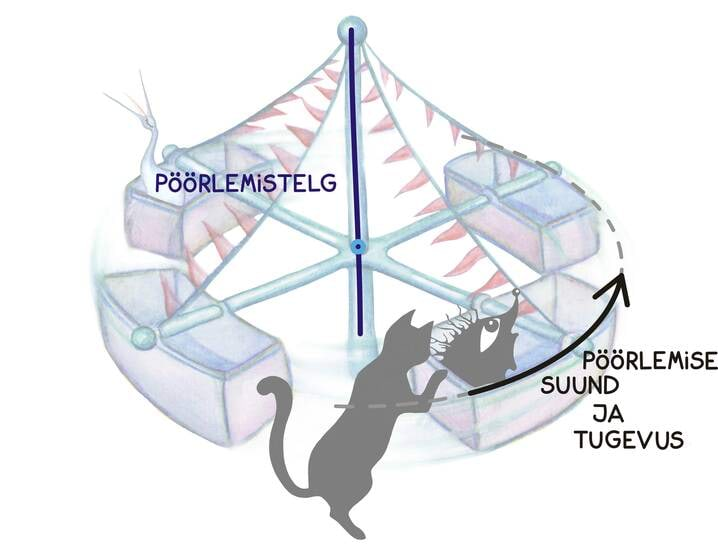
Alustame pöörlemise kirjeldamisest. Määratud sihis, näiteks sirgjoonelisel liikumisel mõjuva jõu kirjeldamiseks on vaja ainult ühte arvu – mõju suund on ju teada. Samas, pöörlemisse panustava mõju kirjeldamine on juba keerulisem, sest pöörlemine ise on pisut keerulisem liikumine. Kõige loomulikum on pöörlemist kirjeldada: 1)pöörlemistelje, 2) pöörlemissuuna ja 3) pöörlemiskiiruse või -tugevuse abil.
Need kõik kolm peavad olema seega peidetud ka jõumomendi kirjeldusse ehk jõu ning hoova vektorite vektorkorrutisse.
Seetõttu ongi vektorkorrutise tulemuseks uus vektor, mille suund annab meile pöörlemistelje, mille siht annab meile pöörlemise suuna ning mille pikkus määrab pöörlemise kiiruse.
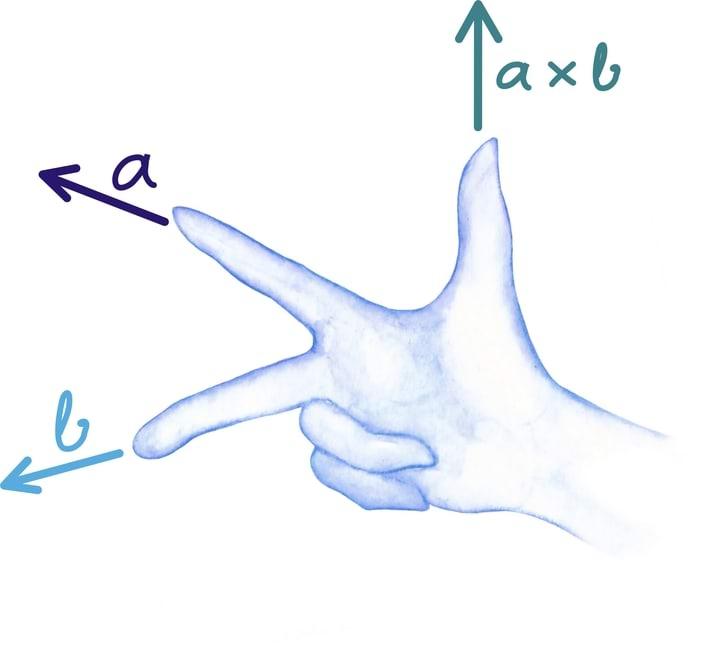
Sihi valikuks on meil kaks võimalust – kokkuleppeliselt toimub pöörlemine vastupäeva ümber pöörlemistelje sihi. Sellest kokkuleppest tuleneb ka nii-öelda parema käe reegel.
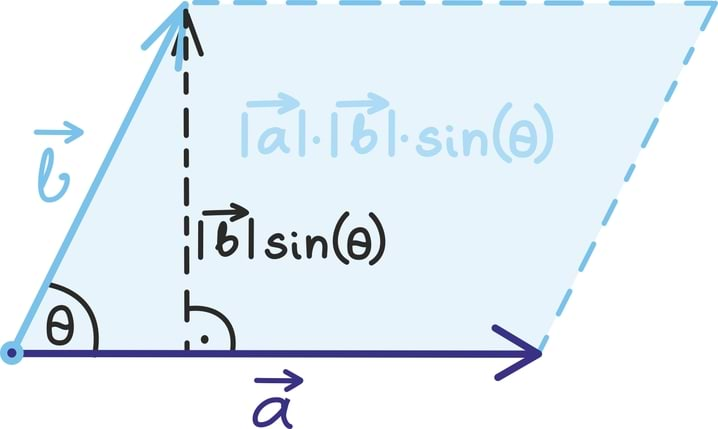
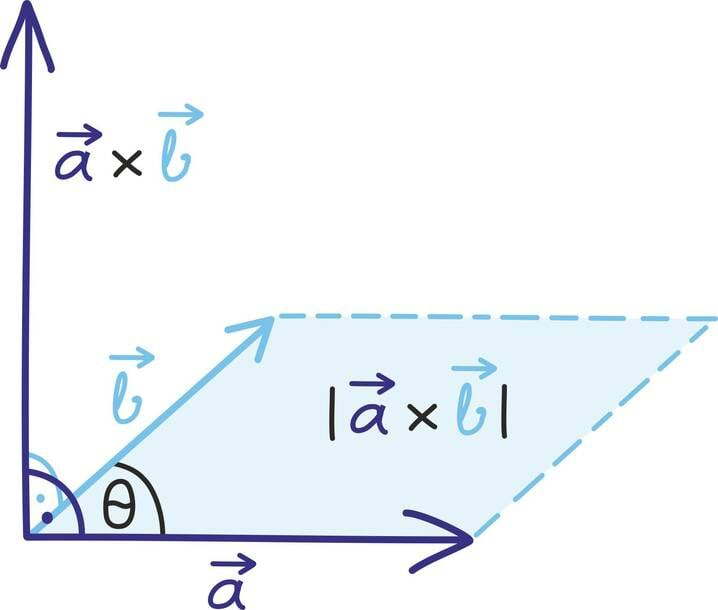
Kui skalaarkorrutise korral leidsime tema suuruse vektorite samasuunaliste komponentide korrutisest, siis vektorkorrutise suuruse leiame ristkomponentide abil. Vektorkorrutise suuruseks on
Seega, mida enam „risti” on kaks vektorit, seda suurem on ka nende vektorkorrutis. Nagu jooniselt näeme, on sellele suurusele ka kena tõlgendus: ta on võrdne kahe vektori poolt määratud rööpküliku pindalaga. Tõepoolest, võime mõelda, et annab meile rööpküliku aluse,
rööpküliku kõrguse ja pindala leiame nende korrutisest [lk 366]. Selle pindalade põhise tõlgenduse tõttu on vektorkorrutis seotud ka determinantidega, millest räägime maatriksite peatükis [lk 152].
Kokkuvõtlikult on vektorkorrutise tulemina saadud vektor risti mõlema vektoriga ning tema pikkus on võrdne esialgsete vektorite poolt moodustatud rööpküliku pindalaga. Kõike seda võib meelde jätmiseks ette kujutada järgmisel joonisel.
Lisaks jõumomendile aitab vektorkorrutis kirjeldada ka muud pöörlemisega seotut – näiteks pöörlemisimpulssi –, aga ka elektromagnetväljas toimuvat: näiteks magnetväljas liikuvale laengule mõjuv jõud on võrdeline tema kiirusvektori ning magnetväljavektori vektorkorrutisega.
Nägime, et kui ühe arvu asemel seada ritta mitu arvu, saame vektori. Aga miks peaks meil ainult üks rida arve olema? Meil võiks ju olla terve arvutabel!
Tõepoolest, ka arvutabelid osutuvad matemaatiliselt väga põnevaks ning neid nimetatakse maatriksiteks.
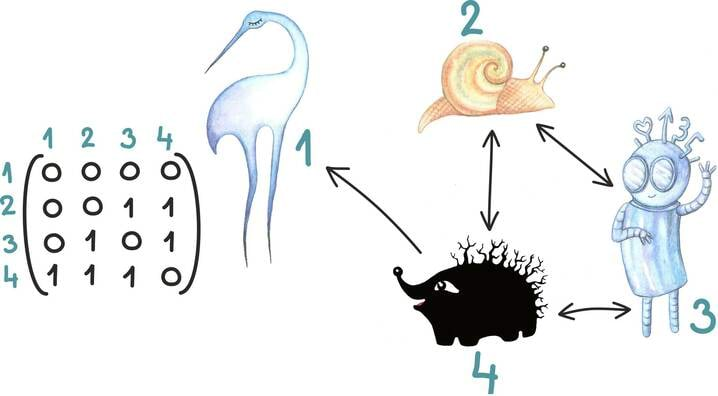
Maatriksite abil annab väga mõnusalt esitada toredaid andmeid ja seoseid. Näiteks võib tabelis kirjeldada neljase seltskonna sõprusvõrgustikku järgmiselt.
- Nummerdame olendid arvudega 1; 2; 3; 4.
- Seame lahtritesse (i; j) arvu 1, kui isikule i meeldib j, ning 0, kui ei meeldi.
Nagu näeme, on see, et isendile 1 ei meeldi ükski teine kolmest isendist, lihtsalt väljaloetav nii maatriksist kui jooniselt.
Esitus maatriksina võimaldab uurida ka palju suuremaid ja keerulisemaid võrgustikke kui meie raamatu tegelaste sõpruskond. Näiteks võime maatrikskujul esitada närvirakkude võrgustikke või rakus toimuvate protsesside vaheliste seoste võrgustikke. Närvirakkude võrgustikud võivad olla kuni 10 miljardi neuroniga ja nii on neid päris raske geomeetriliselt ette kujutada või kirja panna, maatrikskirjeldus aitab neid siiski arvutite abil uurida.
Meid huvitab aga siin raamatus pisut teistmoodi, geomeetriline mõtteviis maatriksitest.
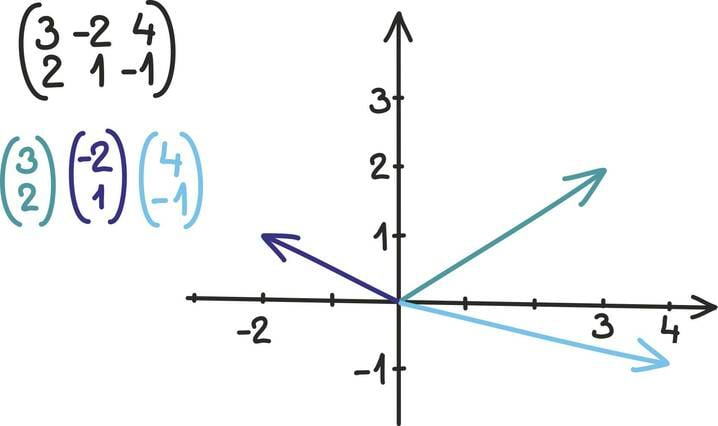
Idee on vaadata iga arvutabeli veergu kui ühte vektorit. Nii annab näiteks 3 × 3 maatriks kolm kolmemõõtmelist vektorit, 3 × 2 kaks kolmemõõtmelist vektorit ja 2 × 2 maatriks kaks kahemõõtmelist vektorit.
Märkame, et nüüd ja edaspidi selles peatükis ei kirjuta me vektoreid enam arve ritta seades, vaid neid tulpa ladudes. See vahetus teeb edasise kirjutamise lihtsalt mugavamaks.
Selline vaatevinkel aitab meil varsti siduda maatriksid ka lineaarvõrrandite süsteemiga.
Determinant ja lineaarvõrrandisüsteem
Kuigi väga põnevaks osutuvad nii 4 × 10, 10 × 10, 30 × 2 kui muu suurusega maatriksid, keskendume edasises 2 × 2 ning 3 × 3 maatriksitele.
Esiteks tutvustame ühte ruutmaatriksite (ruutmaatriksis on sama palju tulpasid ja veerge) karakteristikut, mida kutsutakse determinandiks. Seejärel üritame selgitada, kuidas determinandid on seotud lineaarvõrrandisüsteemide lahenditega ning kust ikkagi pärinevad kooliõpikute mõned müstilised võrrandisüsteemide lahendamisviisid.
Käesolev peatükk ulatub kindlasti kooliprogrammist välja, aga ühtlasi aitab ehk paremini mõista teisi teemasid. Võibolla on kasulik enne lugemist lähemalt tutvuda võrrandite lahendamisega osas 4 [lk 176].
Determinant
Determinandiga tutvumist võime alustada ühest üsna ehituslikust küsimusest.
Mida saame konstrueerida kahe kahemõõtmelise vektoriga
ning mida kolme kolmemõõtmelise vektoriga
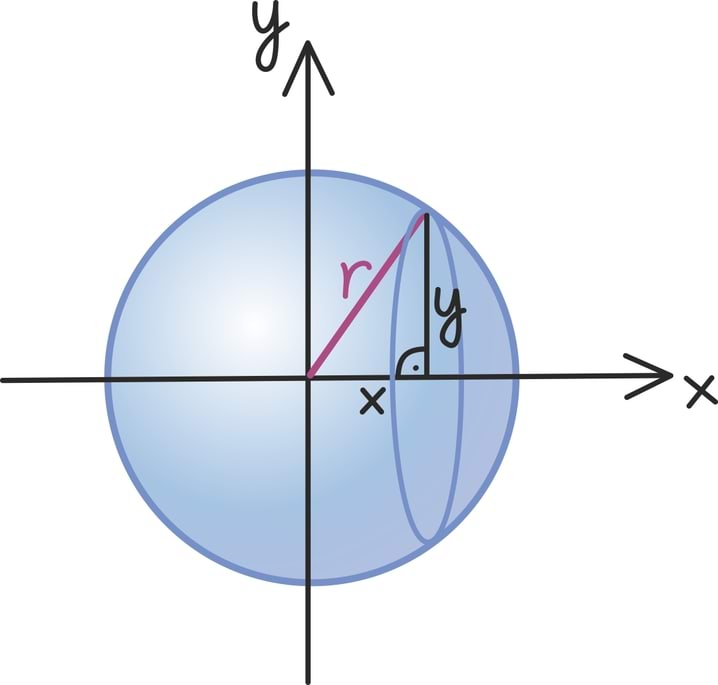
Kui kaks kahemõõtmelist vektorit pole juhuslikult samasihilised ehk kui neid ei saa asetada piki sama sirget, võime nende abil moodustada rööpküliku.
Sarnaselt saame, juhul kui kolm kolmemõõtmelist vektorit ei asu ühel tasandil, ehitada nende abil kena rööptahuka.
Mõlemal juhul on neil geomeetrilistel kujunditel üks kena parameeter – nende maht. Ruutmaatriksi determinant kirjeldabki seda mahtu.
2 × 2 maatriksi puhul on tema determinandi absoluutväärtus võrdne kahe tulpvektori poolt moodustatud rööpküliku pindalaga.
Näiteks maatriksi
determinandi absoluutväärtus on võrdne kahega, kuna maatriksi tulbad kirjeldavad ristkülikut küljepikkustega 2 ja 1. Tuletame meelde, et rööpküliku pindala andis meile ka vektorkorrutise pikkuse. Tõepoolest, 2 × 2 maatriksi determinant annabki tema tulpvektorite vektorkorrutise pikkuse.
3 × 3 maatriksi puhul on determinandi absoluutväärtus võrdne kolme tulpvektori poolt moodustatud rööptahuka ruumalaga.
Determinantide abil võib otsustada, millal lineaarvõrrandisüsteemidel lahendid leiduvad ning kuidas neid lahendeid ka leida. Järjepanu need küsimused nüüd ette võtamegi.
Millal leidub kahe muutujaga lineaarvõrrandisüsteemil lahend?
Tuletame meelde, et kahe muutujaga lineaarvõrrandisüsteemi võib üldkujus kirja panna järgnevalt:
Kõigil kümnel tähistusel on siin oma roll ja see pole sugugi segaduse tekitamine. Arve a1, a2, b1, b2, c1 ja c2 vaatleme kui juba teadaolevaid arve. Tähistame neid tähtedega, lihtsalt et käsitleda paljusid võrrandeid korraga [lk 48]. Seega palub käesolev võrrandisüsteem lihtsalt leida väärtused kahele tundmatule x ja y, nii et võrdusmärgid kehtiksid. Näiteks võiksime anda teadaolevatele arvudele kindlad väärtused ning saada konkreetsema näite:
Neid kahte lineaarvõrrandit võib ka vaadata eraldi ning kirjeldada näiteks sirgega nagu võrrandite peatükis [lk 184].
Võrrandisüsteemi lahendamiseks tuleb kaks võrrandit omavahel kuidagi siduda. Üks võimalus seda teha on seada mõlemad võrrandeid kirjeldavad sirged ühele koordinaattasandile [lk 184]. Veel kavalam on aga kasutada maatriksit:
Nagu enne kirjeldasime, võime mõelda tulpadest
ja
kui kahemõõtmelistest vektoritest, ja kuna tulpasid on tüütu pidevalt välja kirjutada, tähistame neid vastavalt
gaLineaarvõrrandisüsteemi lahendamisest võime nüüd mõelda järgnevalt: eesmärk on leida reaalarvud x ja y, nii et saame vektori
kirjutada vektorite
summana:
Esialgu on lihtsam seda ette kujutada joonise ja konkreetse näite abil: joonistame vektorid
ja
ning üritame neid kokku liita, nii et saaksime vektori
Milal on see võimalik? Kui meile on antud kaks vektorit, siis millal saame neid pikendades/lühendades ja liites esitada mingi kolmanda vektori?
Kui kaks antud vektorit oleksid
ja
x ning y-telje ühikuid kirjeldavad vektorid, siis saaksime muidugi selle protsessi käigus kätte iga teise vektori. Vektor
on võrdne lihtsalt
ga:See on ilmne ka võrrandisüsteemist endast. Sel juhul oleks süsteem väga lihtsas kujus
Põnev on – ja selles võib hea usu korral usina joonistamise abil veenduda –, et olukord on sarnane peaaegu iga algvektorite valiku korral! Peaaegu alati saame iga kolmanda vektori esitada antud kahe vektori summana ja seda ühel ja ainsal viisil.
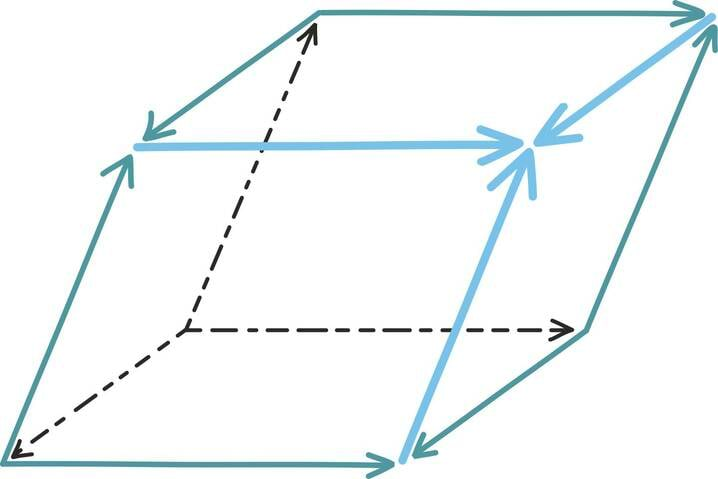
Ainult juhul kui vektorite poolt moodustatud rööpküliku pindala on 0 ehk ainult siis, kui vektorid on samasihilised, pole see võimalik. Sel juhul saab nende summana esitada ainult teisi samasihilisi vektoreid.
Nüüd aga tuletame meelde, et vektorite
ja
poolt moodustatud rööpküliku pindala oli võrdne maatriksi
determinandiga.
Sellest järeldubki õpikutest leitav tingimus:
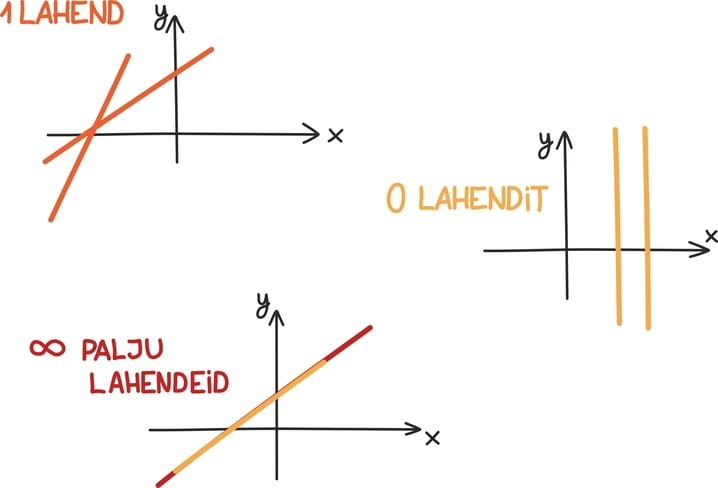
- kui determinant pole võrdne nulliga ja seega vektorid pole samasihilised, leidub võrrandisüsteemile alati täpselt üks lahend,
- kui aga determinant on võrdne nulliga ja seega vektorid on samasihilised, leidub null või lõpmatult palju lahendeid:
- kui vektor on vektoritega samasihiline, leidub lõpmatult palju lahendeid ja
- muul juhul ei leidu ühtegi lahendit.
Järgnevalt lähme sammu edasi ja näitame, kuidas determinantide abil ka kahe muutujaga lineaarvõrrandi süsteemi täpsed lahendid üles leida.
Kahe muutujaga lineaarvõrrandisüsteemi lahendamine determinandiga
Nagu nägime, võime lineaarvõrrandisüsteemi
vektorite abil kirja panna järgnevalt:
Mugavuse ja tindi kokkuhoiu eesmärgil tähistame tulpvektorid jälle järgmiselt:
Seega saame võrrandi:
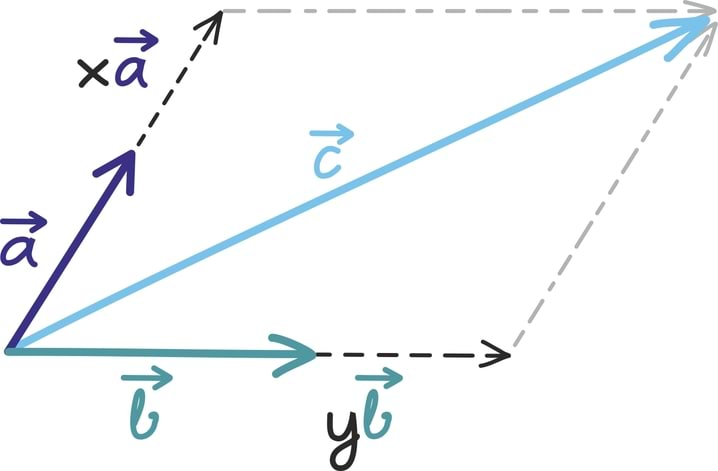
Teisisõnu, tahame vektoreid
parasjagu lühendada ja pikendada, just niipalju, et nende kokkuliitmisel saaksime kolmanda vektori
Oletame, et
ei ole samasihilised ning nendest võib moodustada ilusasti rööpküliku. Just selle rööpküliku abil võime siis visualiseerida ka oma ülesannet:
Lühendamise ja pikendamise mahtu kannavad endas reaalarvud x ja y. Kuidas nende suurust leida?
Joonise abil märkame, et meie otsitav arv x peab vektori otspunkti viima „sama kaugele” vektorist
kui on vektori
otspunkt.
Nüüd tuletame meelde, et rööpküliku pindala võime kirjutada tema aluse ja kõrguse korrutisena [lk 366]. Nii saame omavahel võrduma panna kaks võrdse pindalaga rööpkülikut:
- esiteks rööpkülik, mis tekib vektorite vahele,
- teiseks rööpkülik, mis tekib vektori vahele.
Tõepoolest, mõlema alus on ning nende kõrgused on samad.
Puhtalt sellest tähelepanekust võimegi tuletada muutujale x sobiva väärtuse. Nimelt rööpkülik, mis on tekkinud vektoritest
on x korda „kõrgem” kui rööpkülik, mis tekib vektoritest
Samas teame, et vektorite
vahele tekkiva rööpküliku pindala kirjeldab just determinant
Seega on intuitiivselt üsna selge, et vektoritele
ehitatud rööpküliku pindala leidmiseks peame determinandi
lihtsalt arvuga x läbi korrutama.
Samas on vektoritele
ehitatud rööpküliku pindala antud determinandiga
Seega saamegi võrrandi kordaja x suhtes:
Siit saame juba kergesti leida x-i enda väärtuse:
Kui sooviksime leida y-i väärtust, siis peaksime lihtsalt sama protseduuri läbi tegema, kasutades vektoreid vektoritest
Tulemuseks on:
Sarnane meetod toimib ka kolmes, neljas, kaheksas mõõtmes, kuigi selle geomeetriline ettekujutamine läheb muidugi järjest keerulisemaks. Teisisõnu saab determinantide abil lahendada ükskõik kui paljude muutujatega lineaarvõrrandisüsteeme. Saadud valemid on eriti väärtuslikud arvutitega töötamisel – nad annavad väga kiire ja vähemalt arvutite jaoks lihtsa viisi ka väga suurte lineaarvõrrandisüsteemide lahendamiseks.
Millal leidub kolme muutujaga lineaarvõrrandisüsteemil lahend?
Et kindlaks teha, kas kõik sai kenasti selgeks, arutame lühidalt läbi ka kolme muutujaga juhu. Kõik on tegelikult analoogne. Kui vaatame võrrandisüsteemi
võime moodustada maatriksi
ja mõelda vektoritest
kui kolmest kolmemõõtmelisest vektorist.
Seegi kord tahame kirjutada vektori
vektorite
lineaarse summanaJällegi on küsimus, millal saame kolme antud vektori abil ühte antud vektorit nõnda kirjeldada, ja on ilmne, et vektorite
korral on see alati võimalik.
Näiteks vektori
saaksime, kui korrutaksime vektorid
vastavalt reaalarvudega a, b ja c ning liidaksime kokku:
Sellest on võibolla lihtsam mõelda hoopiski graafiliselt:
Selgub, et ka ainus takistus on väga sarnane kahemõõtmelisele juhule – iga vektori
saame vektorite
lineaarse summana ühel moel kirjutada just siis, kui vektorid
ei asu kõik ühel tasandil, ehk teisisõnu kui nende poolt moodustatud rööptahuka ruumala pole null. Kui vektorid asuvad aga ühel tasandil, saab nende summana esitada ainult sel samal tasandil esitatavaid vektoreid.
Nüüd, kuna toodud maatriksi determinant oli vastavuses rööptahuka
ruumalaga, leidubki kolme muutujaga lineaarvõrrandisüsteemil ühene lahend parajasti siis, kui see determinant pole nulliga võrdne.
Kui determinant on võrdne nulliga, siis tuleb uurida, kas
asub vektoritega
samal tasandil või mitte – kui asub, on lahendeid lõpmatult palju, ja kui ei asu, siis lahendeid polegi.
Ka seekord saab determinandi abil lahendidki kirja panna, selle jätame aga huvilistele nuputada.
Võrrand aitab täpselt ja matemaatiliselt kirja panna teatavaid tingimusi. See on looduse ja ümbritseva kirjeldamise esimene etapp – maailma matemaatilistesse seostesse surumine.
Oletame näiteks, et tahame ehitada uut lauluväljakut. Kõige olulisem on ehituse juures muidugi, et laulukaare alla mahuks piisavalt huvilisi. Teades, kuivõrd lauljatele meeldib ligistikku ümiseda, võib näiteks optimistlikult arvestada, et ühele trepiruutmeetrile mahub kolm lauljat.
Selle tingimuse võime matemaatiliselt kirja panna järgmiselt:
Kui meid pikk kirjutamine ära tüütab, võime võimalikku lauljate arvu tähistada A-ga, vabade ruutmeetrite arvu B-ga ning kirjutada sama võrrandi järgmiselt:
Kuigi nüüd peame hoolega meeles pidama, mida ikkagi A ja B tähistavad, on kirjutamisvaeva vähem.
Võrrandid aitavadki tingimusi ökonoomselt kirja panna ja elulisi küsimusi ümber sõnastada, nii et järele jääb ainult küsimuse jaoks oluline. Näiteks oleme ju täiesti unustanud, milline on laulupeo ajal ilm või kuidas keegi riides on, ja seda õigustatult.
Võrrandi moodustavad
- mõned muutujad ehk meile veel tundmata väärtusega suurused [lk 48];
- mõned arvud, mida kutsutakse kordajateks, kui nad korrutavad läbi mõnda muutujat, ning vabaliikmeteks, kui nad on omapäi;
- võrdusmärk „=”, mis neid muutujaid ja arve omavahel seosesse seab.
Näiteks meie võrrandis on kaks muutujat: A ja B, arv 3 on meie võrrandis kordajaks ja ühtegi vabaliiget nagu polegi.
Kui tahaksime juurde lisada tingimuse, et 100 ruutmeetrit peab siiski ka orkestri tarvis jääma, peaksime lauljatele mõeldud ruutmeetrite arvu 100 võrra vähendama ja saaksime koos vabaliikmega võrrandi:
Muidugi tuleks lõpetuseks võrrand ka veel ära lahendada ehk leida kõik arvupaarid, mis kirjapandud võrrandit lahendavad.
Siin pole see eriti raske: seos A = 3 · B seab ju ainult piirangu, et üks arv on teisest kolm korda suurem. Nii on lahendiks näiteks A = 3, B = 1, kui A = 1200, B = 3600, kui A = –1, B = –1⁄3.
Nagu varsti näeme, kogunevad kõik need lahendid ühele sirgele. On kerge märgata, et mitte sugugi iga lahend ei ole enam tõlgendatav meie algülesande raames. Tõepoolest, lahendite tagasitõlkimisel elu konteksti peame jälle olema hoolikad – üks viis järgimaks, et kõik läheb sobivalt, on uurida algses ülesandes peituvaid ühikuid.
Võrrand ja ühikud
Elulise alusega võrranditel on tavaliselt kaasas ka ühikud. Näiteks rääkisime meie võrrandis ruutmeetritest ja inimestest.
Esiteks on oluline neil järge ajada, sest kui sassi lähevad 10 m/s ja 10 km/h võib ikka üsna hiljaks jääda.
Teiseks aitavad nad aru saada, kas kirja on saanud mõistlik võrrand. Nimelt võime näiteks vaadata, kas võrrandi mõlemal poolel olevad arvud kirjeldavad võrreldavaid suuruseid ehk kas neid saab loendada samades ühikutes – võrduse mõlemal poolel peavad olema ju samad ühikud.
Näiteks meie võrrandi vasakul poolel on lauljate arv ehk teatud inimeste arv. Mis on aga võrrandi paremal poolel?
Esmapilgul oleks seal justkui ainult ruutmeetrite arv – pindala ühik. Siiski, tuletades meelde, et kordaja 3 tähistab inimeste arvu iga ruutmeetri kohta, saame ikkagi ühikuks inimeste arvu:
Võrrandite matemaatilise lahendamise ajaks võib aga ühikud unustada – peaasi, et nad alguses ja lõpus õigesti ritta saavad.
Võrrandid võivad välja näha väga erinevad, näiteks kõik järgnevad on võrrandid:
Esimene erinevus on muidugi selles, et oleme muutujatele valinud erinevaid tähiseid. Mõned oleme tähistanud tähtedega, mõned sõnadega.
Erinevusi on aga teisigi: mõnes võrrandis on üks muutuja, mõnes mitu. Mõnes võrrandis on muutuja esimeses astmes, mõnes on ta kõrgemasse astmesse tõstetud. Mõnes võrrandis tolkneb ka mõni nullist erinev arv, mida nimetasime vabaliikmeks, teises on ainult muutujad.
Erinevat tüüpi võrrandid aitavad kirjeldada erinevaid tingimusi, kuid küsivad ka erinevate lahendusmeetodite järele.
Ühe muutujaga võrrand
Võrrandites VANUS – 4 = 12 ning x3 – 4x = 4 on mõlemas ainult üks muutuja ehk otsitav suurus. Kuna matemaatiliselt pole mingit vahet, kuidas muutujaid tähistada, eristab neid võrrandeid eelkõige aste, millel muutuja ette tuleb.
Esimest nimetataks lineaarvõrrandiks, kuna muutuja x kõige kõrgem aste on 1, teist kuupvõrrandiks, kuna muutuja kõige kõrgem aste on 3.
Kooliprogrammi kõige ohtlikum on muidugi ruutvõrrand, mille lahendivalemit nõutakse une- ja mängupealt. Seetõttu näitame ka, et see lahend ei ole sugugi müstilise päritoluga, vaid üsna selge matemaatilise arutluse tagajärg [lk 275].
Muidugi ei ütle keegi, et astmed peaksid ainult ühest suuremad olema. Nii räägitakse ka juurvõrranditest, kui mängu tuleb ka ruutjuur muutujast. Näiteks √x + 2 = 4.
Üldiselt on nii, et mida keerulisemad muutuja astmed on mängus, seda keerulisem on võrrandit ka lahendada.
Mitme muutujaga võrrand
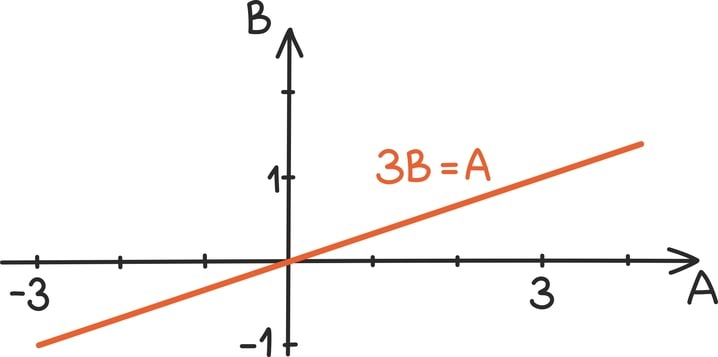
Võrrandis võib muidugi ka olla mitu muutujat. Näiteks peatüki alguses toodud lauljate ja laululava pindalaga võrrand oli kahe muutujaga võrrand. Võrrand xn + yn = zn on aga näiteks kolme muutujaga võrrand, kus n on teadaolev arv.
Ühed lihtsamad mitme muutujaga võrrandid on kahe muutujaga lineaarvõrrandid, kus mõlemate muutujate aste peab olema üks. Näiteks x + 3y = 4 või 0,5x + y = 2 on kahe muutujaga lineaarvõrrandid.
Kuna siin on kaks muutujat, võime nende suhte kirja panna ka koordinaattasandil. Nendest võrranditest võib visuaalselt mõelda kui sirgetest: kõik arvupaarid, mis kahe muutujaga lineaarvõrrandit rahuldavad, moodustavad sirge tasandil.
Ka meie algne võrrand A = 3 · B on tegelikult sirge võrrand.
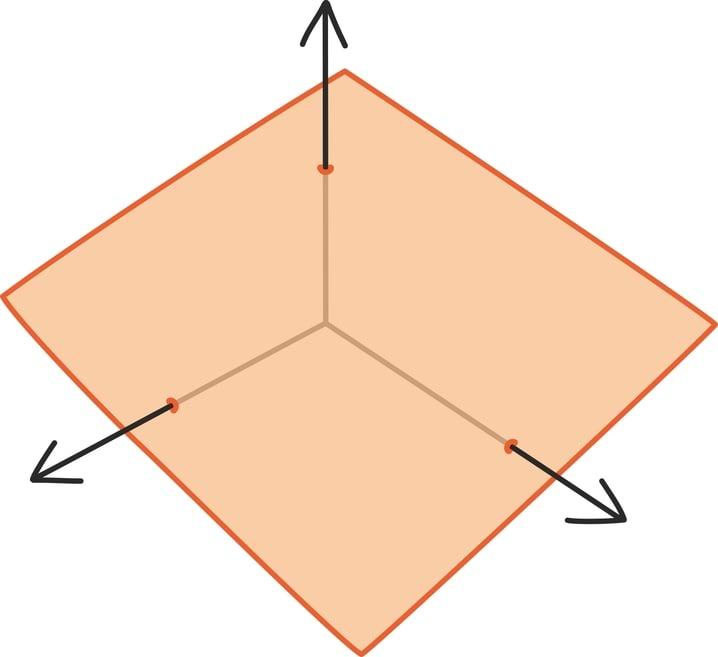
Sarnaselt moodustavad kõik arvukolmikud, mis rahuldavad kolme muutujaga lineaarvõrrandit, ühe ilusa tasandi.
Sirge ja tasandi võrrandist räägime muidugi varsti ka pikemalt [lk 184].
Keegi ei keela moodustada ka nelja, kuue või kahesaja liikmega võrrandeid. Näiteks on tore võrrand
Kas seda võrrandit oleks võimalik kuidagi ka tõlgendada? Üks pisut hullumeelne võimalus oleks öelda, et võrrandi lahendite hulk moodustab 27-mõõtmelises ruumis 26-mõõtmelise tasandi. Seda on aga pigem raske ette kujutada! Lihtsam on sellest võrrandist mõelda kui 27 sahkerdajast, kes jagavad omavahel ära kokku näpatud miljon eurot.
Mõnikord ei õnnestu kõiki soovitavaid tingimusi ühe võrrandiga kirja panna. Otsitavad suurused rahuldavad mitut tingimust samaaegselt. Nii saamegi mitmest võrrandist koosneva võrrandisüsteemi. Võrrandisüsteemi lahendamine tähendab, et otsime suurusi, mis rahuldavad kõiki võrrandeid korraga.
Näiteks võib meil olla teada, et ristküliku kujuga toa pindala on kümme ruutmeetrikest ja ümbermõõt neliteist meetrit, ning meid huvitaks, mis kujuga see tuba on. Mis on toa pikkus ja mis tema laius?
Ümbermõõtu kirja pannes saame võrrandi:
Pindala kirjeldades aga võrrandi:
Et leida sobivat pikkust-laiust, peame nüüd üheaegselt lahendama mõlemad võrrandid.
Proovimise teel näeme, et näiteks PIKKUS = 1 ja LAIUS = 6 rahuldab esimest võrrandit, ent ei rahulda teist võrrandit. Samas PIKKUS = 10 ja LAIUS = 1 rahuldab esimest, kuid mitte teist võrrandit.
Üheaegselt lahendavad mõlemat võrrandit ainult:
- PIKKUS = 2 ja LAIUS = 5
- LAIUS = 2 ja PIKKUS = 5
Muidugi ei olnud võrrandil endal aimugi, kumba meie nimetasime toa „pikkuseks” ja kumba tema „laiuseks“, ning nii saamegi sisuliselt sama toa kuju kaks korda.
Kuna meil on kaks erinevat muutujat, võime jällegi seda võrrandisüsteemi ka geomeetriliselt ette kujutada. Nagu ennist, võime esimest võrrandit kirjeldada sirgega
teist võrrandit kirjeldab aga joon kujus
Nende kahe joone lõikepunktid annavadki meile lahendid:
Sellest räägime aga pikemalt juba võrrandite ja geomeetria peatükis [lk 184].
Võrrand ei ole mitte ainult üks tähtsamaid matemaatilisi seoseid, vaid on lisaks üks tihedamaid seoseid matemaatika ja meid ümbritseva vahel.
Nagu mainisime, aitavad võrrandid tingimusi ja olukordi täpselt ning matemaatiliselt kirja panna. Kui võrrandite lahendamisega tulevad suurepäraselt toime ka arvutid, siis nende kirjapanemine jääb siiski veel inimeste hooleks.
Võrrandite koostamiseks on väga hästi vaja lahti mõtestada olukord ning otsustada, millisel täpsusel seda kirjeldada. Milliseid nähtuseid, omadusi ja komponente peaksime arvesse võtma? Kuidas nad täpselt omavahel seotud on? Võrrandi kirjapanek on tähtis ja huvitav etapp, kus ebatäpsest elulisest probleemist saab täpne matemaatiline ülesanne.
Seetõttu kutsume lugejat veel kord kogu seda protsessi läbi tegema.
Oletame, et valid endale uut mobiilioperaatorit, kelle paketid on järgnevad.
- Operaator A: 5 eurot kuumaks pluss 0,01 eurot kõneminut.
- Operaator B: 1 euro kuumaks pluss 0,02 eurot kõneminut.
On üsna intuitiivne, et kui satume hoogu ja räägime ülemäära palju, siis peaks operaator A hinnapakett odavam tulema, sest kõneminuti hind on poole väiksem. Samas kui räägime väga vähe, on jällegi operaatori B pakett kasulikum.
Seega on üsna mõistlik ja oluline küsida: vähemalt kui mitu minutit peaks kuu jooksul rääkima, et tasuks valida operaator A?
Sellele küsimusele vastamiseks on üks võimalus koostada võrrand ja leida, millise kõneaja korral on operaatorite tasud võrdsed. Intuitiivselt on siis selge, et rohkem rääkides oleks kasulik valida operaator A ja vähem rääkides operaator B. Selle „rohkem kui” idee saaksime veel täpsemalt kirja panna võrratuste abil [lk 190].
Võrrandi koostamine
Rolli mängivad siin olukorras räägitud kõneminutite arv, kõneminuti hind ja kuumaks. Viimased kaks neist on lihtsalt arvud, kõneminutite arvu me alles otsime – tema on muutujaks ning võime tema väärust tähistada k-ga.
Kogutasu saamiseks peame kuutasule liitma kõneminutite ja minutihinna korru- tise. Kokku maksaksime siis kuus:
- operaator A juures: 5 + 0,01k eurot,
- operaator B juures: 1 + 0,02k eurot.
Tingimuse, et mõlema operaatori juures oleks kogumakse võrdne, võime siis kirja panna järgmiselt:
Võrrandi lahendamine
Nüüd võime kogu konteksti ära unustada ja võrrandi
muutuja k suhtes juba tunnis õpitud teisenduste varal ära lahendada:
Tegelikult oleme siin juba tunginud järgneva peatüki, võrrandite teisendamise ja lahendamise territooriumile, millest räägime kohe palju pikemalt ja põhjalikumalt.
Enne jääb vaid üle veel saadud lahendust tõlgendada.
Võrrandi tõlgendamine
Tuleb välja, et kuutasud on võrdsed, kui räägiksime täpselt 400 minutit. See teeb üle 10 minuti päevas, mis tundub ikka päris palju. Seega tasub ilmselt ikka valida operaator B.
Enamasti on võrrandi kirjapanek alles esimene samm. Järgneb võrrandi lahendamine: see tähendab, et tahame leida kõik arvud, mis kõiki võrrandiga ette kirjutatud tingimusi rahuldavad.
Võrrandi lahendamise ajaks võib kõikide võrrandi liikmete ühikud ja konteksti ära unustada – võrrandi lahendamise ajal ei loe, kust see võrrand tuli, loeb vaid matemaatika.
Võrrandi tõlgendamisel tuleb muidugi lisada jälle juurde ka kontekst ja ühikud. Siis seome taas elu matemaatikaga ja see vajab palju tähelepanu, sest tihti tekivad vead just selles etapis.
Praegu asume aga lahendamise juurde. Alustame võrrandi teisendamise matemaatilisest küljest ja seejärel teeme kogu protsessi läbi veel ühe konkreetse luguloo taustal.
Niipea kui võrrand on kirja saanud, on eesmärk seda lahendada. See toimub tihti võrrandi teisendamise abil. Võrrandi teisendamine tähendab võrrandi viimist teise, ent siiski samaväärsesse kujusse. Ideaalselt jõuame võrrandiga kujusse, kust on vastust juba kerge välja lugeda.
Kõik teisendused, mis pähe tulevad, ei säilita muidugi võrrandi samaväärsust: näiteks kui korrutame mõlemad pooled arvuga null, siis saame mõlemale poole võrdusmärki nulli. Null on aga nulliga võrdne, ükskõik millise väärtuse me algsele muutujale ka annaksime.
Kõige lihtsam viis võrrandi erinevate kujude samaväärsuse näitamiseks on veenduda, et võime võrrandi uuest kujust mõne teise sammu abil jälle võrrandi algsesse kujusse tagasi jõuda.
Näiteks võime võrrandile alati arve liita, sest vastandarvude liitmine teisendaks uue võrrandi jälle tema algkujusse. Nii on näiteks samaväärsed võrrandid
ja
Esimesest saame teise kahte lahutades, teisest esimese kahte juurde liites.
Samamoodi võime võrrandeid nullist erineva arvuga korrutada, kuna sama arvuga jagamine (sellest siis ka nullist erinevus!) viiks võrrandi taas algkujusse tagasi. Nii on samaväärsed ka võrrandid
ja
Esimesest saame teise pooli neljaga jagades ning teisest esimese, kui mõlemat poolt neljaga korrutame.
Neid kahte teisendust järjepanu tehes näeme, et võrrand 4 · x + 2 = 10 on samaväärne võrrandiga x = 2. Ehk teisisõnu selle esimese võrrandi lahendiks on x = 2.
Vaatame igaks juhul veel teistki näidet – sisu ja soustita võrrandit 4x + 1 = 17. Tema lahenduskäigu saame kompaktselt kirja panna nii:
Siin oleme püstkriipsu taha lihtsalt märkinud, mida täpselt teeme ühelt realt järgnevale üleminekuks, kõik need on samaväärsed teisendused.
Tihti on võrrandi teisendamisel samaväärsust säilitavatel sammudel ka hea intuitiivne selgitus:
- näiteks võime võrrandi mõlemale poole juurde liita arve. Intuitiivselt on see selge: kui meil on täna sõbraga sama vanus, siis on meil ka täpselt kahe aasta pärast sama vanus;
- samuti võime võrrandi mõlemaid pooli korrutada suvalise nullist erineva arvuga – kui oleme praegu võrdses kaalus, oleksime ka siis, kui meie mõlema kaalud kolmekordistuksid. (Loodame siiski, et seda ei juhtu.)
Kõik teisendused aga samaväärsust ei säilita.
Võrrandi teisendamine nii, et samaväärsus ei säili
Võrrandit saab muidugi teisendada ka nii, et uus võrrand ei ole päris samaväärne. Sel juhul võib võrrandile uusi lahendeid juurde tekkida või ära kaduda – mõne teisenduse korral muudame lihtsalt võrrandi algset tingimust väetimaks ja mõnikord lisame hoopis juurde väärinformatsiooni.
Näiteks kui korrutame võrrandi mõlemat poolt 0-ga, kaotame ju kohe kogu tingimusega antud informatsiooni, sest pärast seda on mõlemad võrrandi pooled võrdsed 0-ga ning see võrdus kehtib iga muutuja väärtuse jaoks.
Samamoodi võime ruutu võttes lahendeid juurde tekitada: öelda, et x = 3, annab täpselt ühe vastuse, aga x2 = 9 juba kaks vastust, kuna teist võrrandit rahuldab ka x = –3.
Üldiselt ei tasu sellepärast aga väga muretseda – teisendage võrrandit mõnuga, kuni oskate temast midagi välja lugeda. Pärast tuleb lihtsalt üle kontrollida, kas saadud lahendid ka algseid tingimusi rahuldavad või on kaasa tulnud teisendustega kaasnenud informatsiooni kao käigus. Ettevaatlik ja hoolas tasub siiski olla.
Tõestus, et 0 = 1, ehk miks võrrandi teisendamisel tuleb ette vaadata.
Kirjutame välja üsna sisutühja võrrandi x = 0 ja hakkame teda põnevuse tekitamiseks teisendama.
korrutame mõlemaid võrrandi pooli
avame sulud
liidame mõlemale poole liikme x
jagame x-iga läbi
saame uue vastuse
Aga kui me nüüd vaatame ühes algset võrrandit x = 0 ning viimast võrrandit x = 1, siis saame, et sama arv x on võrdne nii nulli kui ühega, ja peame järeldama, et 1 = 0!
Ometigi teame, et see on jaburus ning algne võrrand x = 0 ei ole samaväärne viimase võrrandiga x = 1.
Seega peame tee peal olema kasutanud mõnda algtingimusi väänavat teisendust. Tõepoolest, vaadates üleminekut sammult 4 sammule 5, oleme võrrandi mõlemat poolt läbi jaganud x-iga. Ent x on ju võrdne nulliga ning nulliga jagamine toobki alati ainult jama kaasa!
Nüüd aga aitab hetkeks puhtast matemaatikast, lähme pimekohtingule ja vaatame, kas kõik sai selgeks.
Juba joomegi meile üsna mokkamööda seltsilisega koos kohvi, sööme kooki, naeratame ja tutvume. Küsime kaaslaselt ka piinlikkust tundmata vanust. Ent mis juhtub? Kaaslane hakkab vastu õhtut kiusama ja vigurdama!
Ta sõnab muiates, et kui võtta tema vanusest kaks kolmandikku ja lahutada sealt kaks, saate sama tulemuse, kui võtta tema vanusest pool ja liita sinna üks. Milline õudus, kaaslane tahab teada, kas oskame võrrandeid koostada ja neid lahendada!
Võtame väljakutse vastu! Taskust välja salvrätt, ja kaaslase avaldused lähevad sinise tindiga hoolikalt kirja. Teisisõnu, koostame elulise loo põhjal võrrandi.
Võrrandi koostamine
Ainsaks tundmatuks on kaaslase vanus, mida alguses kirjeldamegi muutujaga VANUS. Tema sõnades järge ajades võime kirjutada:
Nüüdseks on meil kõik tingimused kirjas ning edasi on meie töö võrrand ka ära lahendada.
Võrrandi lahendamine
Kaaslase vanuse väljalugemiseks võime oma võrrandit näiteks teisendada järgmiselt:
(kellele meeldiksid murrud, saagem neist lahti!)
(tahame leida vanust, lahutame mõlemalt poolt 3 · VANUS viies kõik tema kordsed ühele poolele)
(liidame, lahutame)
Hurrraa, matemaatiline osa on läbi!
Ja siinkohal vist suurt midagi ka jäänud pole. Võrrandi lahendi tõlgendamine pole eriti raske – isegi muutuja nime jätsime selliseks, mis päriselulist mõtet kenasti kaasas kannab.
Siin alapeatükis ründame kahte küsimust: mida ikkagi peame silmas võrrandi lahendamise all ning miks seda üldse õppima peaks.
Võrrandi lahendamine erinevates arvuhulkades
Seni oleme rääkinud, et võrrandi lahendamine tähendab teatud tingimusi täitvate arvude leidmist. Matemaatiliselt pole see mitmel põhjusel päris täpne kirjeldus.
Näiteks oleme jätnud mainimata, milliseid arve silmas peame. Ometigi nägime arvuhulkade peatükis [lk 78], et leidub mitu erinevat arvude hulka. Seega kui räägime arvude leidmisest, kas mõtleme naturaalarve, täisarve, reaalarve, kompleks-arve?
Kui kirjeldame võrrandi abil mõnda elulist olukorda, määrab seesama olukord lahenditele antavad tingimused.
Näiteks kui meil on otsitavaks muutujaks inimeste arv, oleks tore, kui tegemist oleks naturaalarvuga. Samuti oleks meid üllatanud, kui kaaslase vanus oleks osutunud nullist väiksemaks. Samas kui otsitavaks on sõbra sõidukiirus, võiks see vabalt olla mistahes positiivne reaalarv.
Kui lahendame võrrandeid oma lõbuks, võime täiesti ise otsustada, milliste arvudega ennast piirame. Näiteks kahe muutujaga lineaarvõrrandi korral on mõistlik end piirata reaalarvudega – nii saame ilusa vastavuse sirgetega tasandil [lk 184].
Ka ruutvõrrandi korral piirame end reaalarvudega [lk 87], kui tahame joonistada ilusat graafikut, ja samas võtame arvesse ka kompleksarvud [lk 89], kui soovime lahendit leida igale võimalikule ruutvõrrandile.
Üldiselt kehtibki, et mida rohkem arve endale lubame, seda rohkem lahendeid võime ka leida. Näiteks võrrandil x2 = 2 puuduvad lahendid ratsionaalarvudes, ent ometi eksisteerivad nad juba irratsionaalarvude hulgas. Võrrandil x4 = –1 ei leidu lahendeid reaalarvude hulgas, aga neid on täpselt neli, kasutades kompleksarve.
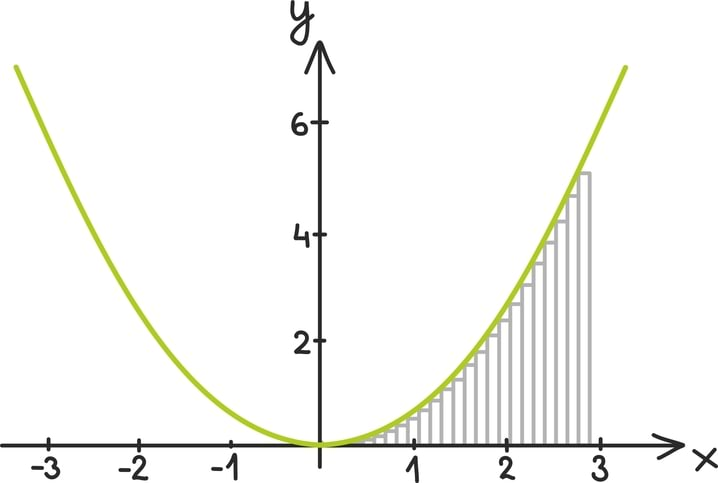
Võrrandite lahendamine erinevates arvuhulkades on väga erineva raskusega. Näiteks ei ole mingit raskust lahendada kolme muutujaga võrrandit X10 + Y10 = Z10 kompleksarvudes – nimelt igale X-i ja Y-i kompleksarvulisele väärtusele saame leida kompleksarvulisi Z-i väärtusi täpselt 10.
Täisarvudes suudeti seesama võrrand aga lahendada alles pärast kolmesaja-aastast pingutust – positiivsetes täisarvudes ühtegi lahendit ei leidugi!
Teoreemi, mis väidab, et kui n on kahest suurem täisarv, siis ühelgi võrrandil kujus
positiivsetes täisarvudes lahendit ei leidu, kutsutakse Fermat’ suureks teoreemiks.
Teoreemi nimi on antud 17. sajandi prantsuse matemaatiku Pierre de Fermat’ järgi. Ta oli küll ametilt jurist, aga vabal ajal tegeles kõige meelsamini just matemaatikaga. Ta mõtles põhjalikult küsimusele, millal ikkagi ülaltoodud võrrandi lahendid leiduvad, ning ühe paberilehe äärel väitis ka, et tal on lihtne tõestus, mis näitab, et juhul kui on kahest suurem täisarv, täisarvulisi lahendeid ei leidugi. Seda tõestust aga keegi tema paberitest leidnud pole ning pole keegi suutnud lihtsat tõestust ka välja mõelda.
Tänaseks on küll Fermat’ suur teoreem tõestatud, kuid lahendus laiutab üle paarisaja lehekülje ning on matemaatiliselt ikka parajalt keeruline.
Miks võrrandeid lahendada?
Isegi kui arvutid ei oska elu võrranditesse panna, on nad tingimata head võrrandite lahendamisel. Neile tuleb lihtsalt võrrand ja mõned lahendusnipid ette sööta ning jääda vastuseid ootama.
Näiteks kasutades maatriksesitlust [lk 152], võib arvutitele anda täpse algoritmi, mille abil võivad nad iga lineaarvõrrandisüsteemi täpselt ja kiiresti lahendada. Sadade muutujate ja lineaarvõrranditega võrrandisüsteem võtab arvutil aega ainult hetke.
Võib tekkida küsimus: miks siis üldse ise õppida nende lahendamist?
Esiteks, kuna meid ei huvita mitte ainult võrrand ise, vaid ka tema eluline kontekst, siis võib ka võrrandi lahendamine anda ideid sellesama konteksti kohta. Nii mõnigi kord saame lahendussamme ka eluliselt tõlgendada ja sellest kasugi saada.
Teiseks annab võrrandite lahendamine oskused matemaatiliste tehetega möllamiseks, mida tuleb ette mujalgi, kus elu matemaatikasse lööme.
Viimaks, paljude kõrgema astme võrrandite lahendamise jaoks ei leidu (veel) täpseid retsepte, mida arvutile ette sööta – nende lahendamine vajab tõepoolest nupukust. Näiteks on teada, et võrrandil x2 – 2y3 = 58 leidub lahendeid, neid kõiki leida aga arvuti ei oska. Ja ka kõik praegused retseptid, mida arvutid kasutavad, tulenevad just varasemate matemaatikute mõttetööst – ka sellele tahab ehk mõni lugeja ükspäev kaasa aidata.
Mõni muutujarägastikuga võrrand võib alguses üsna eemaletõukav tunduda. Kuid ühte ilusti tõmmatud kõverat, mis väljendab sedasama võrrandit, on alati kaunis vaadata.
Õnneks tuli 16. sajandil prantsuse matemaatik ja filosoof Descartes selle peale, kuidas omavahel võrrandeid ja geomeetriat siduda.
Kõige lihtsam seos on kahe muutujaga lineaarvõrrandite ja sirgete ning kolme muutujaga lineaarvõrrandite ja tasandite vahel. Nendest seostest pajatame ka käesolevas peatükis.
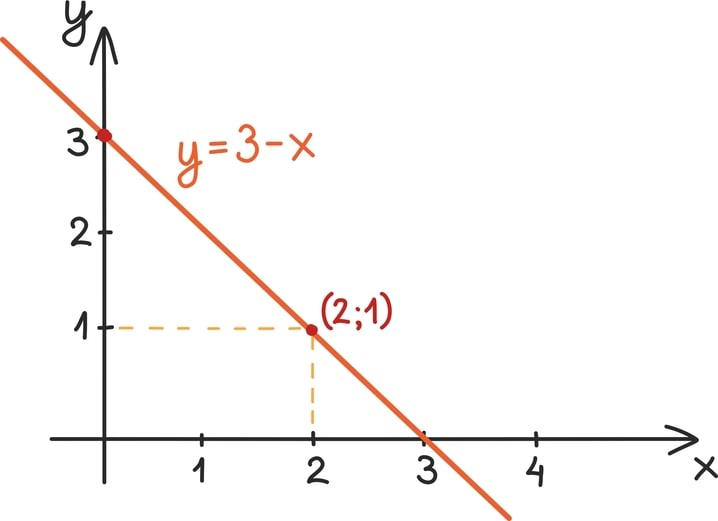
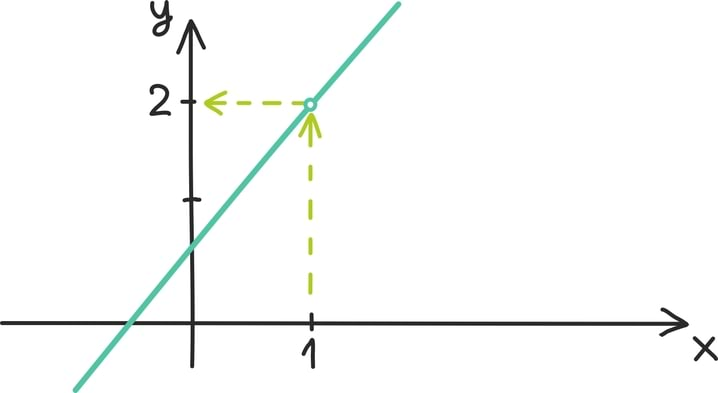
Võrrandil x + 2 = 3 on muutujale antud väga karmid tingimused ning võimalik on täpselt üks lahend: x peab olema võrdne ühega. Geomeetriliselt võime sellest võrrandist mõelda kui sellise arvtelje punkti leidmisest, mis on arvust 3 kahe ühiku võrra vasemal.
Üks viis tingimusi väetimaks muuta ja võrrandile rohkem lahendeid tekitada, on mängu tuua rohkem muutujaid. Näiteks võrrandil x + y = 3 on lahendeid maa ja ilm: iga y-i väärtuse jaoks leidub sobiv väärtus ka x-ile. Kui y on võrdne 2-ga, peab x olema võrdne ühega. Kui y on võrdne 3-ga, peab x võrduma nulliga ja nii edasi.
Kõik võrrandi x + y = 3 lahendid on antud arvupaaridena - üks neist ütleb võimaliku muutuja y väärtuse ja teine muutuja x väärtuse. Iga selline arvupaar tähistab aga täpselt ühte punkti arvutasandil: x-i väärtus annab punkti x-koordinaadi ning y-i väärtus punkti y-koordinaadi.
Kui hakkame kõiki neid punkte joonistama, näeme, et nad otsustavad kõik ennast kenasti ühele sirgele ritta seada.
Selgub, et iga kahe muutujaga lineaarne võrrand (mõlema muutuja aste on üks) kirjeldabki täpselt ühte sirget tasandil ja vastupidi ka: kui meile on antud üks sirge tasandil, võime kirjeldada teda kahe muutujaga lineaarse võrrandi abil.
Kõikvõimalikud sirged tasandil oskame kergesti joonistada, kõikvõimalikud kahe muutujaga lineaarvõrrandid on aga antud järgmise kujuga:
Siin on a, b lihtsalt suvalised reaalarvulised kordajad ning c reaalarvuline vabaliige.
See seos on päris kihvt! Meil on ühelt poolt midagi geomeetrilist, joon, mida võime pliiatsi või pastakaga paberile vedada, ning teiselt poolt kuivana näiv võrrand ja ometigi kirjeldavad mõlemad sama matemaatilist objekti!
Ka praktilisema poole pealt on see seos vägagi kasulik, kuna võimaldab tingimusi ja seoseid kirjeldada nii geomeetria kui võrrandite keeles. Seega kui sirgel on mõni omadus, siis peab see vastav omadus olema kirjeldatav ka võrrandite keeles ja vastupidi.
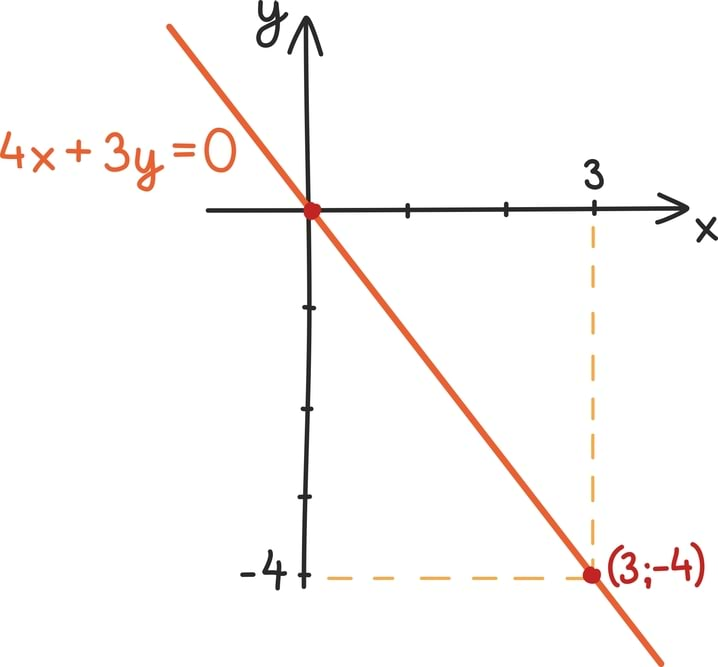
Oletame näiteks, et meie geomeetriliseks omaduseks on teadmine, et sirge läbib punkti null. Milline oleks see omadus võrrandite keeles?
Kui sirge läbib punkti null, siis rahuldab arvupaar (0; 0) võrrandi tingimusi. Sisestades x = 0 ja y = 0 võrrandi üldkujusse, saame, et 0 = c. Seega kui sirge läbib punkti null, puudub vastaval võrrandil vabaliige ning sellise võrrandi võib kirja panna kujul ax + by = 0. Näiteks joonistatud sirge võrrand on 4x + 3y = 0
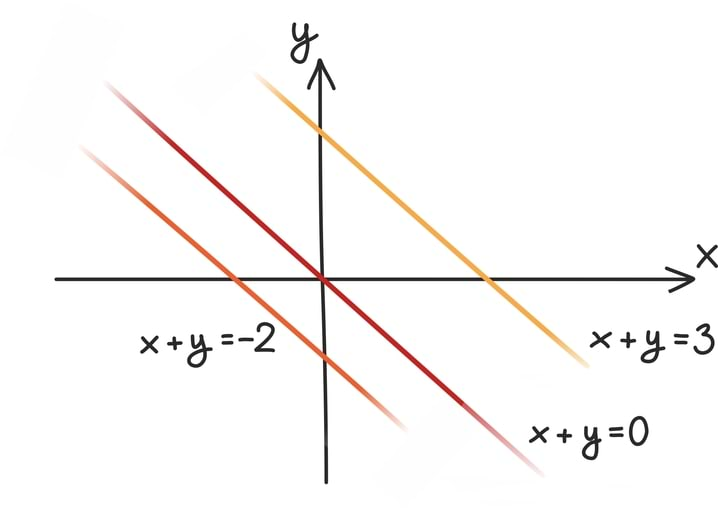
Lähtudes võrrandite keelest võiksime aga küsida: millised sirged vastavad võrranditele kujus x + y = c mingi suvalise arvu c jaoks?
Joonistades võib veenduda, et kõik need sirged on kenasti paralleelsed.
Nii nagu iga kahe muutujaga lineaarne võrrand on täpselt vastavuses mõne tasandi sirgega, on iga kolme muutujaga lineaarne võrrand ilusas vastavuses mõne tasandiga kolmemõõtmelises ruumis.
Ka siin võime geomeetrilisi omadusi kirjeldada võrrandite keeles ja vastupidi. Näiteks võrrandid kujus ax + by + cz = 0 kirjeldavad kõik tasandeid, mis läbivad koordinaatteljestiku nullpunkti. Kõike seda on muidugi juba palju keerulisem joonistada
Nagu nägime, on iga sirge tasandil vastavuses ühe lineaarvõrrandiga kujus ax + by = c. Seeläbi on sirgete omaduste kirjeldamine võrdväärne lineaarvõrrandi kirjeldamisega.
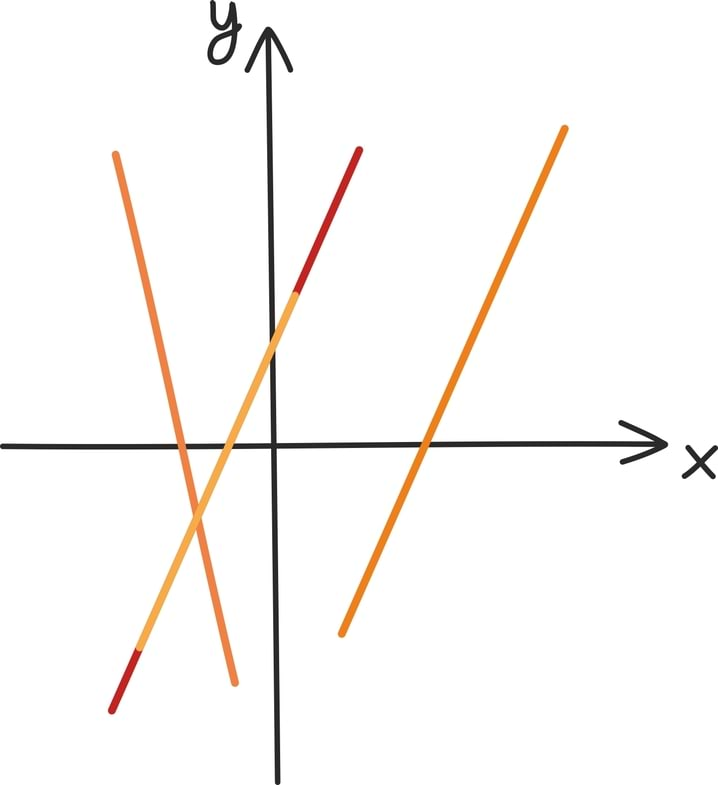
Olukord muutub veelgi põnevamaks, kui tasandile asetada neid mitu. Kui meil on kaks sirget, tekib ju mitmeid geomeetrilisi võimalusi nende kahe sirge suhestumiseks. Kaks sirget võivad kas
- lõikuda ühes punktis,
- olla paralleelsed,
- või kattuda.
Samaaegselt võime mõlemat sirget aga kirjeldada ka kahe muutujaga lineaarse võrrandiga. Mis kirjeldab nende võrrandite omavahelist suhestumist?
Selleks on muidugi neist kahest võrrandist koosnev võrrandisüsteem!
Tõepoolest, võrrandisüsteem otsib ju kõiki punkte, mis rahuldavad mõlemat sirge võrrandit ühtaegu, ehk teisisõnu kõiki punkte, mis asuvad korraga nii ühel kui teisel sirgel.
Neid punkte on
- täpselt üks, kui sirged lõikuvad,
- null, kui sirged on paralleelsed,
- lõpmatult palju, kui mõlemad sirged on üks ja sama sirge.
Nii saamegi võrrandisüsteemi lahendamisega täpselt teada, kuidas nende võrranditega kirjeldatud sirged omavahel asetsevad.
Sirgete ja tasandite võrrandid, nende koostamine ja nendega mängimine kuuluvad väheste lemmikhobide kilda. Siiski tasub nendega hästi läbi saada juba näiteks sellepärast, et nad mängivad täiesti arvestatavat rolli arvutigraafikas.
Näiteks võivad sirge ja tasandi võrrandid ette tulla arvutimängude loomisel.
Kujutame ette, et arvutimängus on kolmemõõtmeline tuba. Ühes seinas on aken, millest paistab sisse ilus päevane valgus. Mõni päikesekiir levib kenasti sirgjooneliselt ning muidugi otse vastu põrandat, millest võime mõelda kui tasandist. Valguskiire levikut kirjeldab seega sirge võrrand ja põrandat tasandi võrrand.
Kuid päris elus ei jää valgus lihtsalt põrandale, vaid peegeldub sealt edasi. Sellepärast tulebki iga sellise valguskiire ehk sirge jaoks välja arvutada tema peegelduse järgne suund ning seega jälle uus sirge. Muidugi ei piirdu valguskiir ainult ühe peegeldusega, vaid levib ja peegeldub järjest edasi seintelt, laelt, mööblilt. Nii tuleb korduvalt välja arvutada sirgete ja tasandite võrrandeid.
Õnneks ei pea me seda ise tegema – tuleb lihtsalt arvutile õpetada, kuidas arvutamine käib, ja edasi teeb ta kõiki neid tehteid meeletu kiiruse ja täpsusega.
Päris lõpmatult valguskiiri siiski põrgatama ei pea. Pärast sadat põrget on toas juba kenasti eri toonides seinad, pehmete servadega varjud ja kõik muu, mis tekitab meile hea koduse tunde. Oleme arvutile päriselu selgeks teinud ja meie mäng näeb realistlik välja.
Nagu nägime, võimaldab võrrand [lk 168] üsna täpselt ja arvuliselt tingimusi ja seoseid kirja panna. Mõnikord ei ole aga tingimused nii põhjalikud, et neid saaks võrrandiga kirja panna, ning mõnikord ei huvitagi meid see, millised on suuruste täpsed väärtused. Meid huvitab ainult nende suuruste vaheline seos – mis on suurem, mis väiksem.
Näiteks valides kahe rahapauna vahel, ei huvita rahalembelist, kui palju on täpselt ühes või teises paunas raha, vaid huvitab pigem, kummas paunas on rohkem raha. Samuti ei huvita meid näiteks kahe marsruudi vahel valides, kui pikad teekonnad täpselt on, vaid kumb on lühem, kumb pikem.
Ka võrrandi peatükis toodud näited oleksid loomulikumad võrratuste keeles. Küsime ju tegelikult, mitu inimest maksimaalselt mahuks nii või nii suurele laululavale. Nii saaksime ka toodud võrrandi asemele hoopis võrratuse.
Märk ≤ asetataksegi kahe suuruse vahele, kui vasem on paremast väiksem või sellega võrdne. Märk < isepäini tähendab, et vasem suurus on paremast rangelt väiksem ehk võrdus pole sel juhul lubatud. Näiteks π < 3,5 tähendab, et arv π on arvust 3,5 väiksem. Mõlemat märki võib muidugi kasutada ka teisipidi, näiteks 3,5 > π.
Nagu võrrandi korralgi, koostame ka võrratusi tihti mõne elulise situatsiooni kirjeldamiseks või mõne elulise küsimuse lahendamiseks. Võrratuste ja võrrandite koostamine on väga sarnane – seame elulistele suurustele vastavusse muutujad ja määrame nendevahelised suhted.
Meenutame näiteks mobiilioperaatorite näidet. Meil oli kaks operaatorit järgmiste pakettidega:
- operaator A: 5 eurot kuumakse pluss 0,01 eurot kõneminut,
- operaator B: 1 eurot kuumakse pluss 0,02 eurot kõneminut
Võrrandi peatükis küsisime, kui palju peaksime telefoniga rääkima, et operaatorite juures oleksid kuutasud võrdsed. Kuna on aga selge, et operaator A muutub soodsamaks, kui räägime palju, oleks loomulikum küsida: kui palju peaksime telefoniga rääkima, et operaator A muutuks soodsamaks?
Kuna kuutasu sõltub mõlemal juhul otseselt räägitud kõneminutite arvust, tuleb ta kindlasti mängu tuua ning võime ta tähistada näiteks muutujaga k. Seega võime kuutasud välja kirjutada järgmiselt:
- Operaator A juures: 5 + 0,01k eurot
- Operaator B juures: 1 + 0,02k eurot
Meie küsimust, millal on operaator A kuutasu odavam, esitab siis täpselt võrratus:
Nagu võrranditegi korral, on võrratuses endas nüüd kontekst kadunud: küsime lihtsalt, milliste k-de korral on vasem pool väiksem paremast. Pärast võime vastuse tõlkida jälle elukeelde ja vastatagi, milliste kuuminutite arvu korral on operaator A pakett odavam.
Nüüd räägimegi võrratuste lahendamisest lähemalt.
Võrratuse lahendamine tähendab täpselt sama, mida võrrandi lahendaminegi – tuleb leida antud tingimustega sobivad muutuja väärtused [lk 176].
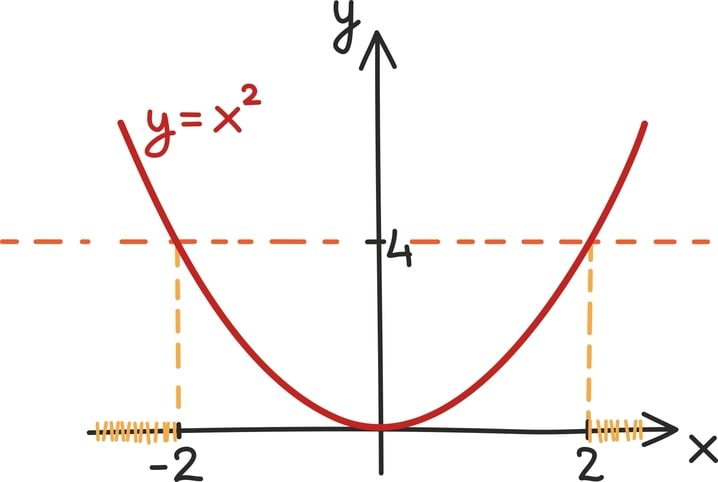
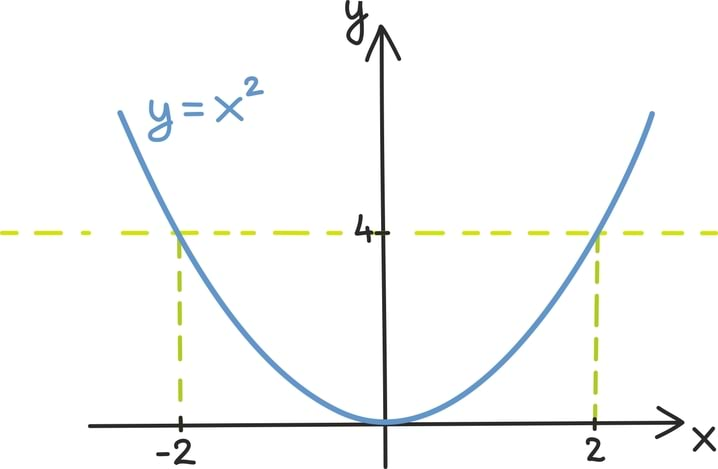
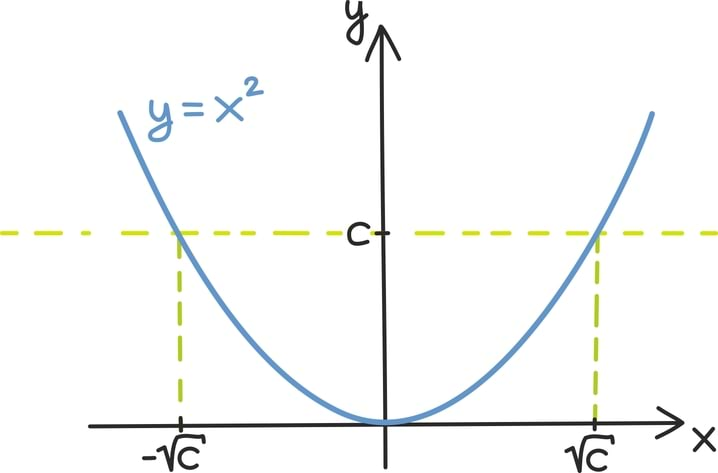
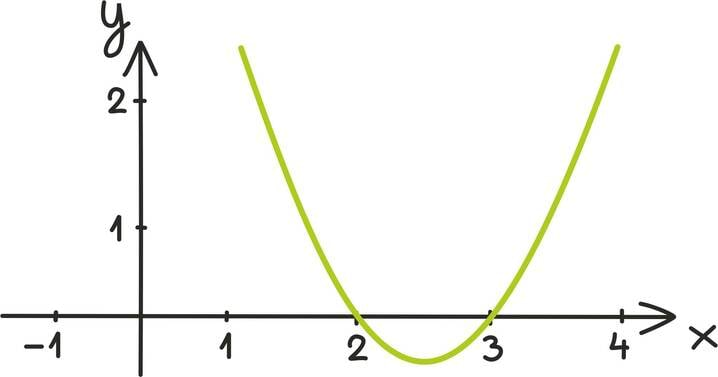
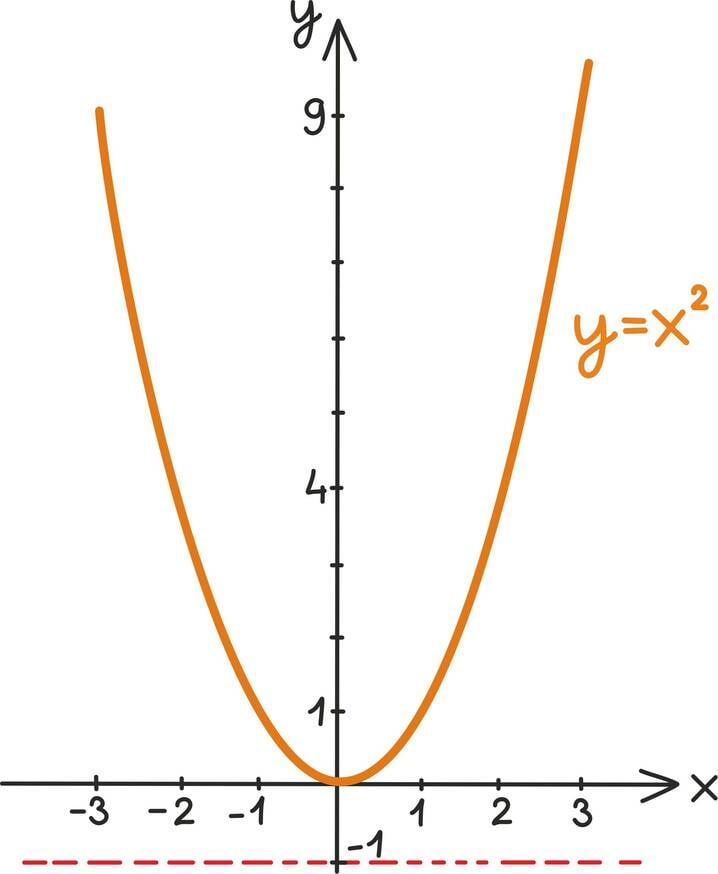
Näiteks kui tahtsime leida arve, mille ruut oli võrdne 4-ga, saime võrrandi: x2 = 4. Samamoodi võime otsida arve, mille arvuruut on 4-st suurem. Seda kirjeldab võrratus: x2 > 4.
Võrratuste lahendamisel on tihti kasulik mõelda geomeetriliselt – üritame kogu võrratuse taandada mõne funktsiooni graafiku uurimisele.
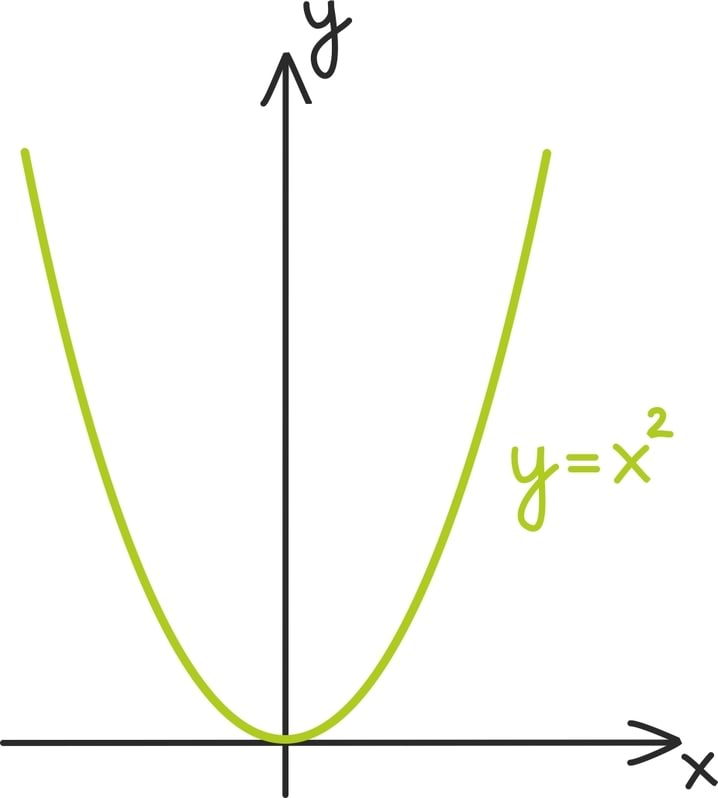
Ülaltoodud võrratuse korral näeme, et kõik otsitavad arvud peavad olema kas kahest suuremad või miinus kahest väiksemad, sest muudel juhtudel on ruutfunktsiooni y = x2 graafik 4-st madalamal.
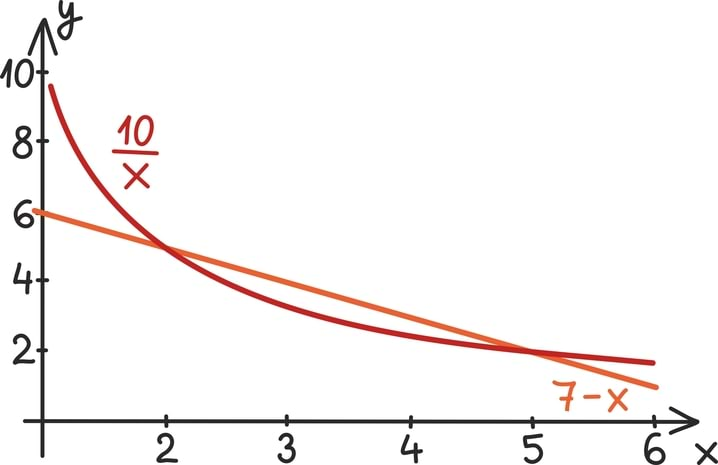
Sama strateegia toimib ka keerulisemate võrratuste puhul. Näiteks oletame, et küsitakse, milliste reaalarvude x jaoks on
Kasutades võrratuse omadusi võime selle võrratuse ümber viia kujusse
Sellises kujus vastab võrratus küsimusele: millal asub kuupfunktsioon x-teljest üleval pool?
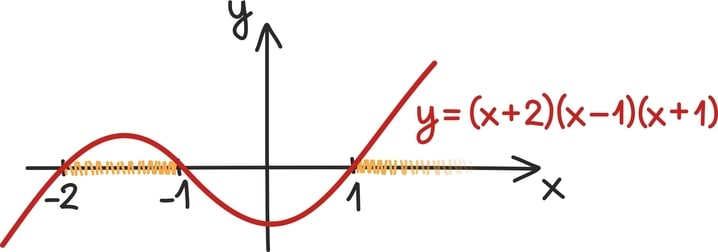
Kuupfunktsiooni graafik teeb kokku maksimaalselt kaks pööret, aga sellest räägime pikemalt osa 6 juures [lk 266].
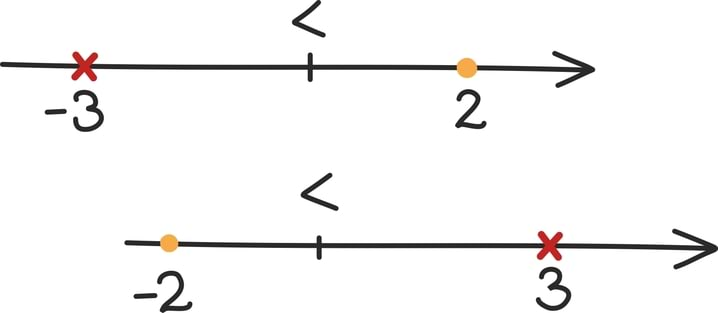
Kuupfunktsiooni oskame umbkaudu joonistada niipea, kui teame ta nullkohti [lk 269]. Seega tegurdame vasemat poolt ja saame samaväärse võrratuse (x + 2) (x – 1) (x + 1) > 0. Nüüd võime vastuse välja lugeda joonistades umbkaudselt kuupfunktsiooni y = (x + 2) (x - 1) (x + 1) graafiku.
Meile sobivad kõik arvud vahemikus (–2, –1) ning kõik ühest suuremad arvud:
Graafiline meetod põhineb sisuliselt funktsioonide graafikute võrdlemisel. Oleksime võinud eelnevalt ka lihtsalt võrrelda funktsioonide x3 + 2x2 ja x + 2 graafikuid, aga lihtsam oli teisendada võrratust nii, et üks funktsioon oli kuuppolünoom ja teine lihtne nullfunktsiooni, mille graafikuks on siis x-telg ise.
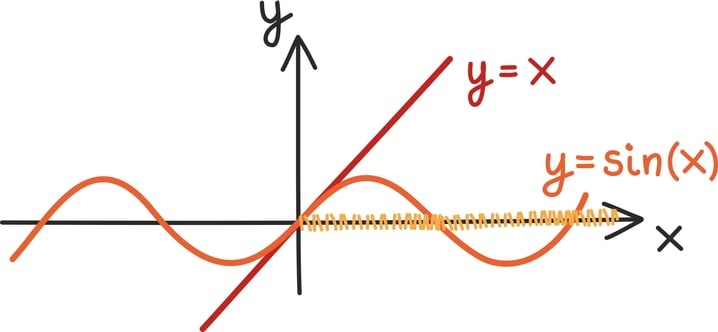
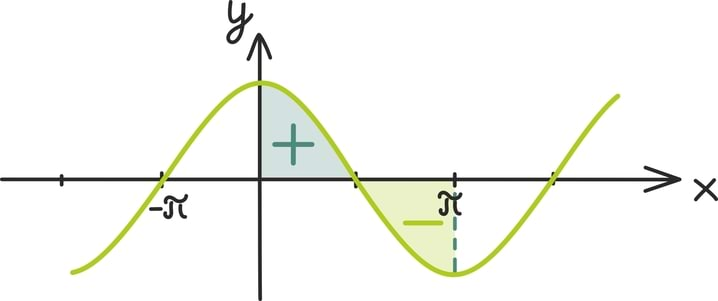
Mõnikord peame aga tõesti joonistama välja kaks erinevat funktsiooni. Näiteks näeme graafikult, et x ≥ sin(x) iga mittenegatiivse x-i jaoks.
Selle fakti range tõestus kasutab tuletist [lk 320] ja põhineb täpselt graafikult saadud intuitsioonil: kohal 0 on mõlemad funktsioonid võrdsed ning edasi kasvab funktsioon y = x kiiremini kui funktsioon y = sin(x).
Kuna võrdusjuht on mingis mõttes võrratuse piirjuhuks, võime võrratuste lahendamise taandada tihti võrrandite lahendamisele. Mingis mõttes tegime seda ka kogu eelnenud arutelus: leidsime geomeetriliselt, kus on mingid lõikepunktid, ning otsustasime, kummale poole jäävad siis võrratuse lahendid. Lõikepunktid ise aga tähistasidki võrrandite lahendeid ja piirasid võrratuse lahendite ala. Just selle seose tõttu saime ka tegelikult mobiilioperaatorite küsimusele ainult võrrandite raames vastuse leida.
Võrratustega võib teha peaaegu kõike, mis võrranditegagi. Samaväärsed võrratused saame näiteks, kui
- liidame mõlemale võrratuse poolele sama arvu juurde. See on ju igati intuitiivne – kui Sul on rohkem raamatuid kui vennal, on Sul neid rohkem ka pärast seda, kui kirjandushuviline tädi mõlemale teile uue raamatu kingib;
- korrutame võrratuse mõlemat poolt sama positiivse arvuga. Ka see on loomulik: perepitsa on suurem kui tavaline pitsa ning ka pool või neljandik perepitsat on suurem kui pool või neljandik tavalisest pitsast.
Siinkohal on oluline märgata, et mõlemaid pooli võib ainult positiivse arvuga läbi korrutada ja mitte negatiivse arvuga. Negatiivse arvu korral tuleb võrratuse märk muuta vastupidiseks. Miks see nii on?
Alustame ühest näitest, võrratusest –3 < 2. Kui mõlemad pooled korrutada läbi –1-ga, saame arvudeks vastavalt 3 ja –2. Kuid enam ei ole 3 väiksem kui 2. Selle välistamiseks pöörame märgi vastupidiseks ning saame, et 3 > –2.
Tähendab ju mõlema võrratuse poole miinus ühega läbi korrutamine tegelikult arvtelje peegeldust 0 punkti suhtes ja nii muutubki võrratuse märk – suurus, mis enne oli arvteljel kõige paremal ning seega suurim, asub pärast peegeldust kõige vasemal ning on seega väikseim.
Kui korrutame võrratuse pooled läbi mõne miinus ühest erineva negatiivse arvuga, nagu näiteks arvuga –4,5, siis võime sellest mõelda kahes sammus: 1) esmalt korrutame mõlemat poolt arvuga –1 ja seega vahetame võrratuse märgi ning 2) seejärel korrutame pooli arvuga 4,5.
Muidugi võib ka võrratusega teha teisendusi, mis samaväärsust tingimata ei säilita. Siin tuleb hoolikas olla just sellepärast, et iga kord negatiivse arvuga korrutades võib märk muutuda. Näiteks kui võrratuse mõlemad pooled ruutu võtame, siis saadud võrratus on algsega samaväärne ainult juhul, kui mõlemad võrratuse pooled on positiivsed.
Tõepoolest, kui 3 > 2, siis ka 32 > 22. Samas aga –3 < –2, kuid (–3)2 > (–2)2.
Matemaatiline planeerimine tegeleb teatud mõttes elulistele probleemidele parimate lahenduste leidmisega. Seejuures on võrratustel matemaatilises planeerimises oluline osa. Toome mõned näited.
- Kuidas peaks bussifirma korraldama bussiliiklust, nii et teenida võimalikult palju kasumit? Ühelt poolt tahab bussifirma teha võimalikult vähe kulutusi bussijuhtidele, bussidele ja kütusele. Teiselt poolt peab ta pakkuma võimalikult head teenust, et reisijad ei läheks konkurentide juurde või ei hakkaks sõitma autoga.
- Milline on parim istekohtade jaotus klassiruumis, et õpilased oleksid võimalikult õnnelikud? Arvesse tuleb võtta nii õpilaste istekoha- kui ka pinginaabrite eelistusi.
- Mida peaks vaene üliõpilane sööma nii, et ta kulutused toidule oleksid võimalikult väiksed, kuid päevased toitainete normid oleksid täidetud?
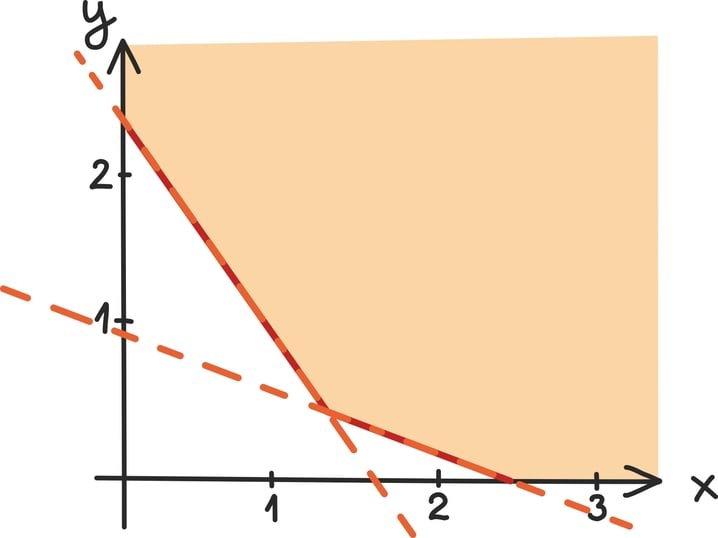
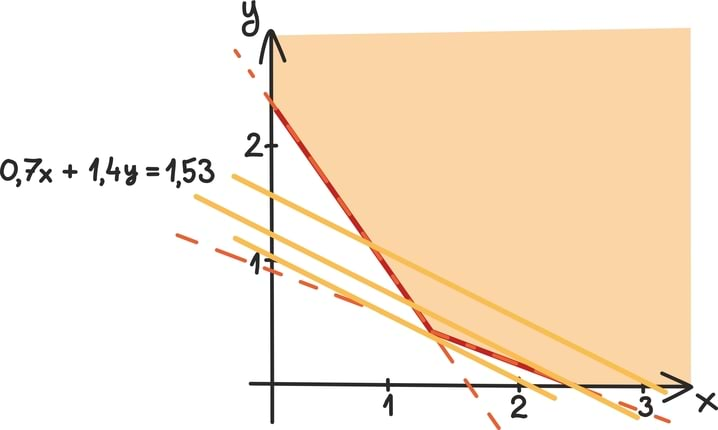
Järgnevalt vaatame viimast probleemi lähemalt üsna lihtsustatud näite varal, kus tudengi ostukorvi saavad kuuluda vaid kartulid ja oad. Peab tõdema, et päriselt ei taha küll vist keegi ainult kartulitest ja ubadest toituda, aga realistlikumad probleemid on liiga keerulised, et neid paberil ilma arvutite abita lahendada.
Igal juhul alustame oma teadmiste ülesloetlemisega.
- Kilo kartuleid maksab 0,7 eurot, sisaldab 20g valke ning 170g süsivesikuid.
- Kilo ubasid tomatikastmes maksab 1,4 eurot, sisaldab 60g valke ja 120g süsivesikuid.
- Täiskasvanud inimene vajab 50g valke ja 300g süsivesikuid.
Meie küsimus on, millise toidurahaga saab vaene tudeng päevas hakkama ainult kartuleid ja ubasid süües, nii et päeva valkude ja süsivesikute norm oleks täidetud?
Kõigepealt peame selle ülesande tõlkima matemaatika keelde ehk koostama matemaatilise mudeli.
Esmalt leiame koguhinna. Selle jaoks tähistame kartulite kogust kilodes x-iga ning ubade kogust kilodes y-iga. Nii lähevad kartulid maksma 0,7x eurot, oad 1,4y eurot ning mõlemad kokku 0,7x + 1,4y eurot. Tahaksime seda maksumust minimeerida, kusjuures kogustele x ning y on seatud teatud piirangud, mis tulevad päevastest toitainete normidest – peame sööma vähemalt teatud arvu valke ja süsivesikuid.
Üritame nüüd need piirangud võrratuste keeles kirja panna.
Valke on kartulites 20x grammi ja ubades 60y grammi. Kuna täiskasvanud inimene peaks päevas sööma vähemalt 50 grammi valke, siis saame võrratuse 20x + 60y ≥ 50.
Sarnaselt saame süsivesikute jaoks tingimuse 170x + 120y ≥ 300.
Lisaks ei saa ei kartulite ega ubade kogused olla negatiivsed arvud. Seetõttu on meil veel võrratused x ≥ 0 ja y ≥ 0
Oleme saanud järgneva matemaatilise mudeli. „min” tähendab siin, et otsime võrrandi väikseimat ehk minimaalset väärtust ning muidugi peavad lisaks olema rahuldatud kõik toodud võrratused:
Seda ülesannet on kõige lihtsam lahendada graafiliselt. Selleks kanname koordinaatteljestikku kõik neli võrratust ning märgime ära piirkonna, mis kõiki võrratusi rahuldab.
Viimaks leiame märgistatud piirkonnas punkti, kus funktsiooni 0,7x + 1,4y väärtus on minimaalne. Kuidas seda teha?
Meenutame, et sirged kujus 0,7x + 1,4y = c on kõik omavahel paralleelsed ning vähendades c väärtust, liigutame seda sirget lihtsalt allapoole. Nüüd asub 0,7x + 1,4y minimaalne väärtus kindlasti ühel sellistest sirgetest ning lahendiks on paar (x, y) täpselt siis, kui ta ka omakorda lahendipiirkonda jääb. Seega on meie ülesanne leida minimaalne c väärtus, mille korral sirge 0,7x + 1,4y = c lõikab veel endiselt lahendipiirkonda.
Nagu jooniselt näeme, juhtub see täpselt sirgete 20x + 60y = 50 ja 170x + 120y = 130 lõikumispunktis, mida oskame juba lihtsalt leida: 1,54 kg kartuleid ja 0,32 kg ubasid lähevad maksma 1,53 eurot.
Nii nagu koolist on hästi teada, et õpetaja on alati targem kui õpilane, kehtivad ka teatud võrratused väga paljude erinevate arvude või elementide jaoks. Näiteks kehtivad mõned võrratused absoluutselt kõikide positiivsete reaalarvude jaoks või kõikide ühest suuremate reaalarvude jaoks või kõikvõimalike kolmnurkade jaoks. Loetleme ja selgitame neist siinkohal mõnda.
Reaalarvu ruut
Kõige tuntum võrratus on ilmselt järgmine: iga reaalarvu ruut on mittenegatiivne ehk a2 ≥ 0. Võrdus kehtib muidugi parajasti juhul, kui a on võrdne nulliga. Miks see ikkagi on nii?
Nulli puhul on muidugi asi selge, on ju nulli ruut jällegi null.
Ka positiivsete arvude puhul pole asi palju keerulisem: a2 on ju täpselt küljega a ruudu pindala ning ruudu pindala peabki positiivne olema.
Iga negatiivse arvu võime aga kirjutada kujul –a = (–1) · a, kus a on ise positiivne. Sel juhul võime kirjutada
ning tulemus on jällegi positiivne.
Kumb on suurem, arv või tema ruut?
Võibolla kõlab see alguses natuke mitteintuitiivselt, aga arvu ruut ei ole mitte sugugi alati suurem kui arv ise. Negatiivse arvu ruut on muidugi alati temast suurem, sest eelneva põhjal on arvuruut ise alati positiivne.
Samuti, kui positiivne reaalarv on ühest suurem, siis on ta ruut arvust suurem. Kui aga positiivne reaalarv on ühest väiksem, siis on ta ruut arvust väiksem:
Ka seda pole väga raske tõestada – teame ju, et võime iga võrratust positiivse täisarvuga läbi korrutada:
- korrutades võrratuses a >1 mõlemad pooled a-ga, saame võrratuse a2 > a,
- korrutades võrratuses a < 1 mõlemad pooled a-ga, saame võrratuse a2 < a.
Aritmeetiline ja geomeetriline keskmine
Arvude aritmeetiline keskmine tuleb esile üsna tihti: näiteks arvutatakse välja keskmist hinnet, eksamitulemuste keskmist või rahva keskmist vanust. Selle jaoks liidetakse lihtsalt kõik uuritavad tulemused kokku ja jagatakse summa tulemuste arvuga:
Keskmistada võib aga teisiti: võib kõik tulemused kokku korrutada ning siis võtta nendest nii mitmes juur, kui palju tulemusi oli.
Geomeetriline keskmine tuleb esile näiteks televiisorite kuvasuhete määramises. Vana kinostandard oli kuvasuhe 2,39:1 (pilt on 2,39 korda laiem) ning vana televiisor näitas filme suhtes 4:3. Nende kahe standardi vahel kompromissi leidmiseks kasutati geomeetrilist keskmist ning saadi tulemuseks 16:9 standard. Geomeetrilise keskmise kasutamine võimaldas saavutada olukorra, kus mõlemaid proportsioone „muudeti” ühepalju.
Nii aritmeetiline kui geomeetriline keskmine on ka seotud vastavanimeliste jadadega [lk 128]. Nimelt on aritmeetilise jada kolmest järjestikusest liikmest keskmine äärmiste aritmeetiliseks keskmiseks ning täpselt sama juhtub ka geomeetrilises jadas, kasutades geomeetrilist keskmist.
Üks tuntud võrratus väidab, et kahe mittenegatiivse reaalarvu aritmeetiline keskmine on vähemalt sama suur kui kahe arvu geomeetriline keskmine. Ehk:
Kuidas seda tõestada?
Vaatame arvu
Kuna tegemist on arvuruuduga, siis on ta mittenegatiivne. Avades sulud, saame
ehk tõesti
Graafiliselt võib aritmeetilisest ja geomeetrilisest keskmisest ning nendevahelisest võrratusest mõelda järgnevalt:
Tõestus vajaks natuke kolmnurkade ja trigonomeetriaga mängimist. Huvitunud lugeja võib seda proovida näiteks peale trigonomeetria peatüki läbimist [lk 205].
Kuigi meie tõestasime siin ainult, et kahe arvu aritmeetiline keskmine on suurem geomeetrilisest keskmisest, siis tegelikult kehtib väide mistahes paljude arvude kohta. Suvalise mittenegatiivse arvu aritmeetiline keskmine on suurem kui geomeetriline keskmine. Seda on siiski juba pisut keerulisem tõestada.
Lühim murdjoon
Lõpetame peatüki ühe väga lihtsa geomeetrilise võrratusega. See väidab, et kahe punkti vahelistest murdjoontest on vähima pikkusega neid punkte ühendav sirglõik.
Sellest võrratusest järeldub kohe näiteks tuntud kolmnurga võrratus: kolmnurga iga kahe küljepikkuse summa on pikem kui kolmas külg. See lihtne väide osutub järelikult üsna sisukaks.
Meie eesmärk siin raamatus ei ole alati õpetada – õpetada oskavad palju paremini õpetajad ise – vaid pigem anda ideid, kuidas koolimatemaatikast mõelda. Seega üritame ka siin pisikeses peatükis ainuüksi selgitada, kuidas absoluutväärtusega võrrandit tõlgendada. Meenutame, et arvu absoluutväärtusest kirjutasime juba ka arvude peatükis [lk 120].
Oletame, et teid on vastamisi seatud võrrandiga:
Tundub päris hirmuäratav? Põhjuseta!
On mitu viisi, kuidas ennast veenda, et tegemist on üsna ohutu olukorraga.
Esmalt võib üritada võrrandi lahti sõnastada „kauguste” abil.
Oletame näiteks, et meil on lihtsam võrrand |x –1| = 2. Võrrandi vasak pool kirjeldab siis punkti x kaugust arvust 1 ja võrrandi lahendamine tähendab kõikide selliste punktide x leidmist arvteljel, mis on arvust 1 kahe ühiku kaugusel:
Jooniselt on lihtne näha, et võimalikud on täpselt kaks punkti: x = 3 või x = –1. Kui meile on aga antud keerulisem võrrand nagu lehekülje alguses, on joonise abil lahendamine juba päris raske. Näiteks võrrandi
võime küll lahti sõnastada kauguste abil:
- võrrandi vasak pool kirjeldab arvu x kauguste summat arvudest 2 ja 0,
- võrrandi parem pool kirjeldab arvu x kaugust arvust 1 ja lisab selle kaugusele veel 2 juurde.
Ent siiski läheb joonise abil lahendamine keeruliseks. Niisiis mõtleme korra, kuidas veel lihtsama võrrandi |x –1| = 2 lahendamisest mõelda.
Joonisel hakkame automaatselt proovima kahte erinevat juhtu:
- punkt x asub arvust 1 paremal pool
- punkt x asub arvust 1 vasemal pool
Sümbolites tähendab see aga, et me vaatasime läbi kaks juhtu:
- x – 1 on positiivne
- x – 1 on negatiivne
Kasutades absoluutväärtuse definitsiooni, annavad need kaks juhtu meile kaks erinevat võrrandit:
- x – 1 = 2
- –(x –1) = 2
On lihtne näha, et esimene annab täpselt meile vastuse 3 ja teine vastuse .
Täpselt sama strateegia aitab ka keerulisemate võrrandite puhul. Peame iga võrrandis asuva absoluutväärtuse jaoks vaatama läbi kaks juhtu – juhu, kus absoluutväärtuste vahel olev avaldis on positiivne, ja juhu, kus ta on negatiivne.
Nii ei erine absoluutväärtusega võrrandi lahendamine sugugi tavalise võrrandi lahendamisest – absoluutväärtusega võrrandi puhul tuleb lihtsalt läbi vaadata mitu tavalist võrrandit.
Siin peatükis läheneme trigonomeetriale eelajaloolisest vaatevinklist, vaadeldes trigonomeetriat kitsamalt kui õpetust seostest kolmnurkades ning laiemalt kui õpetust suhetest ja proportsioonidest.
Trigonomeetria motivatsiooniks tuuakse tihti õigustatult majaehitust: hea ehitise projekteerimine nõuab täpset nurkade ja pikkuste seadmist.
Meie aga läheme esimese looga Maa pealt veidi kaugemale ja vaatame, kuidas trigonomeetria avakosmoses kasuks võib tulla.
Oletame, et pärast keskkooli pääsed tööle kosmosejaama. Milline rõõm, kosmosejaam!
Kosmosejaam on aga katki ja vajab paikamist ühe antenni otsa juurest. Seega tuleb välja saata astronaut ja ta õigesse kohta toimetada. Kuidas kosmonauti avakosmoses liigutada?
Tänases kosmosejaamas on astronautide liigutamine lahendatud mitmeosalise robotkäe abil, mille moodustavad pööratavad liigesed ja sirged jupid – just nagu inimkäegi.
Kuidas seda robotkätt kontrollida? Kuidas välja arvutada, kui palju ja kuidas erinevaid liigeseid pöörata, et astronaut õigesse paika viia ja jaam ära paigata?
Selgub, et siin tuleb appi kolmnurga elementide ühendamine trigonomeetria abil. Tõepoolest, lihtsamale juhule leiad lahenduse käesoleva peatüki lõpust.
Rännakut trigonomeetriasse alustame aga väikese sissejuhatusega kolmnurkadesse.
Nagu juba raamatu esimeses osas mainisime, on kaks kolmnurka võrdsed või uhkemalt öeldes kongruentsed siis, kui neid võib täpselt üksteise peale asetada, kusjuures seejuures on lubatud kolmnurk ka tasandilt välja tõsta ja teistpidi pöörata.
Kahe kolmnurga kongruentsuse garanteerib näiteks kõigi kolme külje võrdsus. See kõlab esialgu üsna lihtlabaselt, aga tegelikult vajab tõestamist.
Tõepoolest, näiteks sellest, kui kõik kolm nurka on võrdsed, kolmnurkade endi võrdsus ju ei järeldu, sest kolmnurgad võivad olla erineva suurusega.
Samuti ei järeldu nelinurkade puhul kõige nelja külje võrdsusest nelinurkade kongruentsus.
Selle tõestamine, et kolme külje võrdsusest järeldub kolmnurkade kongruentsus, siiski väga raske ei ole. Tuleb lihtsalt märgata, et sirkli ja joonlaua abil võib kolme külge teades konstrueerida täpselt ühe kindla kolmnurga.
Esmalt võtame suvaliselt ühe kolmest küljest ja paigutame selle joonisele. Järgnevalt tahaksime selle külje otspunktidesse paigutada teised kaks nii külge, et nad lõikuksid. Selle jaoks kirjeldame mõlema külje jaoks sirkliga kõik tema võimalikud otspunktid: saame kaks ringjoont. Need ringjooned lõikuvad kahes punktis ja seega saame kaks võimalikku kolmnurka. Õnneks on aga ülemine ja alumine pool sümmeetrilised ning mõlemad võimalused annavad sama tulemuse: üheainsa võimaliku kolmnurga.
Tegelikult jagub kolmnurkade kongruentsuse garanteerimiseks veel teisigi tingimusi: piisab sellest, kui näiteks kaks külge ja nendevaheline nurk on võrdsed, või isegi sellest, kui kolmnurga kõik kõrgused on võrdsed. Kõik need tingimused põhinevad trigonomeetrilistel seostel.
Sarnased kolmnurgad
Käesolevas peatükis huvitab meid aga eelkõige see, millal on kolmnurgad „sama kujuga” ehk millal võib neid suurendamise ja vähendamise teel kongruentseteks muuta. Selliseid kolmnurki nimetatakse sarnasteks kolmnurkadeks.
Esimese joonise hoolikam silmitsemine vihjab, et ilmselt piisab „sama kuju” garanteerimiseks juba ainuüksi nurkade võrdsusest. Tõepoolest, järgnev joonis peaks seda tõest fakti veelgi veenvamalt esitama:
Kasulik on märgata, et kuna kolmnurga nurkade summa on 180 kraadi, piisab kolmnurga kõikide nurkade kindlaks määramiseks tegelikult ainult kahe nurga teadmisest.
Kuidas on omavahel seotud sarnaste kolmnurkade küljed?
Nagu mainisime, võib sarnaseid kolmnurki suurendamise ja vähendamise teel võrdseteks muuta ning võrdsetel kolmnurkadel on muidugi võrdsed küljed.
Geomeetriliste kujundite suurendamisest ja vähendamisest võib aga mõelda lihtsalt kui kõikide pikkuste läbikorrutamisest positiivse reaalarvuga, jättes nende paiknemise samaks. Näiteks kui suurendame kolmnurka kaks korda, korrutame kõik küljepikkused läbi kahega.
Seega teame, et kui kolmnurgad on sarnased, siis ühe kolmnurga külgede pikkustest a1, b1, c1 saab teise kolmnurga küljepikkused a2, b2, c2, kui korrutada neid sama reaalarvuga. Teisisõnu küljepikkused on proportsionaalsed ehk võrdelised:
Sellest aga lähtub, et sarnastes kolmnurkades on võrdsed ka vastavate külgede vahelised suhted. Tõepoolest, mõlemaid külgi suurendame sama palju kordi ning see kordaja taandub külgede suhtes välja. Võime seda näha ka toodud seose esimest võrdust pisut teisendades – võime selle ümber kirjutada kujus
Sarnaselt ka
ning
Kokkuvõttes näeme, et nii nurgad kui külgedevahelised suhted on suurusteks, mis kolmnurga suurendamisel ja vähendamisel ei muutu. Võime nii ainult nurkade kui ka ainult külgedevaheliste suhete abil kirjeldada tervet sarnaste kolmnurkade peret. See vihjab, et nurgad ja külgedevahelised suhted võiksid ka omavahel kuidagi seotud olla. Selle seose annavadki just nimelt trigonomeetrilised põhiseosed, mis on algupäraselt defineeritud täisnurksete kolmnurkade jaoks.
Tuletame meelde, et täisnurkseks kolmnurgaks nimetatakse kolmnurka, mille üks nurk on 90 kraadi. Täisnurkse kolmnurga külgedel on erilised nimetused: 90-kraadilise nurga lähiskülgi nimetatakse kaatetiteks ning vastaskülge hüpotenuusiks.
Nagu mainisime on „sama kujuga” kolmnurkades võrdsed kõik nurgad ning ka üksteisele vastavate nurkade lähiskülgede suhted.
Kui teame lisaks, et kolmnurk on täisnurkne, siis piisab kõikide nurkade määramiseks veel ainult ühe nurga teadmisest – on ju sel juhul üks nurk 90 kraadi, teist nurka teame ja kolmanda nurga võime välja arvutada, kuna kõige kolme nurga summa on 180 kraadi.
Ehk teisisõnu, kui meile on antud üks kindel teravnurk (miks just teravnurk?), mille tähistame kokkuleppeliselt kreeka tähestiku esimese tähega α, siis teame, millise kujuga on meie kolmnurk ning saame kindlaks määrata ka külgedevahelised suhted:
- nurga α vastaskaateti pikkus jagatud hüpotenuusi pikkusega
- nurga α lähiskaateti pikkus jagatud hüpotenuusi pikkusega
- nurga α vastaskaateti pikkus jagatud lähiskaateti pikkusega
Kõik kolm suhet annavad vastuseks ühe arvu. Kuna need arvud sõltuvad üheselt ainult valitud nurgast α, on tegemist funktsioonidega [lk 64] nurgaväärtusest.
Näiteks kui α = 45º, siis on ka teine teravnurk 45º ning seega kolmnurk võrdhaarne. Kaatetitevaheline suhe on seega täpselt 1.
Leitud funktsioonid on käibel nii tihedasti, et neile on mõistlik anda lühemad nimetused:
- vastaskaateti ja hüpotenuusi suhet kutsutakse siinuseks nurgast α,
- lähiskaateti ja hüpotenuusi suhet kutsutakse koosinuseks nurgast α,
- vastaskaateti ja lähiskaateti suhet nimetatakse tangensiks nurgast α.
Neid kolme funktsiooni kokku kutsutakse trigonomeetrilisteks funktsioonideks ning otse definitsioonist võib märgata seost nende vahel: tangens on võrdne siinuse ja koosinuse jagatisega.
Nende vanamoodsate nimetuste jaoks on matemaatiliselt kasutusel veel järgnevad lühendid:
Eelneva tulemuse, kus 45-kraadise nurga puhul on kaatetitevaheline suhe täpselt 1, saaksime nüüd kirja panna järgnevalt:
Olgugi et nende funktsioonide väärtused ise on leitud külgedevaheliste suhete kaudu ühes nurga poolt kindlaks määratud täisnurkses kolmnurgas, siis ei pea funktsiooni ennast sugugi rakendama ainult täisnurkse kolmnurga nurkadele. Trigonomeetrilisi funktsioone võib vabalt rakendada ka nurgaväärtustele, mis pärinevad viisnurgast, lihtsalt kahe haara vahelt või mujaltki.
Tõsi küll, praegu nõuame endiselt, et kasutatav nurgaväärtus oleks teravnurkne ehk väiksem kui 90 kraadi, sest oskame ainult sel juhul külgedevahelisi suhteid leida ja seega trigonomeetrilisi funktsioone defineerida. Kohe vabaneme aga sellestki ettekirjutusest, alustades üsna loomulikust küsimusest.
Kuidas trigonomeetrilised funktsioonid välja näevad?
Sellele küsimusele vastamiseks peame lihtsalt joonistama kolmnurki erinevate nurga α väärtustega.
Kolmnurga suuruse võime muidugi ise valida. Kaval on valida kolmnurga suurus nii, et hüpotenuusi pikkuseks on üks. Sel juhul on nurga siinus võrdne täpselt vastaskaateti pikkusega ning nurga koosinus võrdne lähiskaateti pikkusega.
Seame nüüd ühe kolmnurga tipu koordinaatteljestiku nullpunkti ning joonistame sinna hüpotenuusi pikkusega üks. Kaatetiteks jäävad hüpotenuusi otsast x-teljele viiv lõik ja ka lõik, mis sealt tagasi nullpunkti jõuab.
Nüüd, siinus mingist nurgast on vastaskaateti ja hüpotenuusi pikkuste suhe. Kuna hüpotenuus on üks, siis siinus ongi siin võrdne vastaskaateti pikkusega. Joonisel on näha, kuidas siinuse väärtus kasvab koos nurga väärtusega.
Vastaskaateti pikkuse annab aga täpselt haara ja ringjoone lõikepunkti y-koordinaat. Koosinuse annab samas raamistikus selle lõikepunkti x-koordinaat ning tangensi y- ja x-koordinaadi suhe. Seda viimast võime tõlgendada veel lihtsamaltki: tangens näitab haara poolt määratud sirge tõusu. Kui jagame y-koordinaadi x-koordinaadiga, siis saame teada, kui palju haara määratud sirge iga ühiku kohta tõuseb.
Edasi on lihtne panna arvuti, mõni sõber või sõbranna siinuse, koosinuse ja tangensi graafikuid joonistama:
Märkame aga, et meie nüüdses konstruktsioonis ei ole küll midagi teravnurkade jaoks spetsiifilist. Leidsime nurga siinuse, koosinuse ja tangensi lihtsalt kui nurgahaara ja ühikringjoone lõikepunkti koordinaadid. See nurga haar võib ju aga x-teljega jätta ükskõik millise nurga, mitte ainult teravnurga. Nii saamegi defineerida trigonomeetrilised funktsioonid suvalise nurgaväärtuse, näiteks 2013 kraadi jaoks.
Trigonomeetrilised funktsioonid näevad oma täies pikkuses välja järgmised:
Esiteks võib märgata, et trigonomeetrilised funktsioonid on ilusasti perioodilised ehk teisisõnu nende kuju on mööda x-telge edasi liikudes korduv. See tuleneb muidugi otseselt definitsioonist – nurgad, mis erinevad täispöörde võrra, paiknevad ju x-telje suhtes täpselt ühte moodi ning seega annavad ka täpselt sama siinuse, koosinuse, tangensi. Trigonomeetrilistest funktsioonidest ja perioodilisusest räägime aga pikemalt juba teises alapeatükis [lk 230].
Teise asjana ehmatab muidugi ära tangensi katkevus iga poolringi ehk iga 180 kraadi järel. Seejuures esimene katkemine on juba 90 kraadi juures. Selles ei ole siiski midagi ehmatavat – see juhtub ju lihtsalt sellepärast, et neis kohtades on koosinus võrdne nulliga ning kuna nulliga jagada ei saa, ei saa ka tangensile väärtust leida.
Sellest murest võib mõelda ka sirge tõusu raames: sirgele, mis on vertikaalne ehk y-teljega paralleelne, ei oskagi ju tõusu vastavusse seada. Tõuseb ta lõpmatult kiiresti ülespoole või allapoole?
Trigonomeetriliste funktsioonide pöördfunktsioonid
Mitmel pool õpikus tulevad esile pöördfunktsioonid. Lühidalt rääkisime neist juba funktsioonide peatükis [lk 68], kus täheldasime, et pöördfunktsioonid rahuldavad järgmist seost:
Teisisõnu, ühe funktsiooni pöördfunktsioon nullistab täpselt tema efekti ning annab tagasi algse väärtuse.
Näiteks võiks öelda, et kolme liitmise pöördfunktsioon on kolme lahutamine. Hiljem näeme, et eksponentsiaalfunktsiooni pöördfunktsioon on logaritmfunktsioon [lk 290], ning et tuletis ja integraalgi on teineteise pöördoperatsioonid [lk 352].
Trigonomeetria kontekstis mõtleme pöördfunktsiooni all üsna lihtsat küsimust: kui enne leidsime nurga abil tema siinuse või koosinuse või tangensi, siis nüüd tahaksime ette antud väärtuse abil leida, mis nurga siinus, koosinus või tangens ta parasjagu on.
Graafiliselt tähendab see järgmist: joonistame oma trigonomeetrilise funktsiooni graafiku, valime mingi väärtuse c ning siis küsime, kus kohas funktsiooni graafik lõikab sirget y = c .
Näiteks kui teaksime, et siinus annab väärtuseks nulli, läheksime tema graafiku juurde ja vaataksime, kus ta lõikab x-telge. Vastuseks saaksime, et nurk võiks olla 0 kraadi või 180 kraadi või mõni teine 180 kraadi kordne.
Arkussiinus ja arkuskoosinus
Nagu graafikult näeme, siis siinus- ning koosinusfunktsiooni jaoks neid lõikepunkte alati ei leidugi. Nimelt kui |c| > 1, on sirge y = c funktsiooni graafikust täienisti ülal- või allpool. Kõikidel teistel juhtudel on aga lõikepunkte lõpmatult palju.
See tähendab, et pöördfunktsiooni defineerimisel peame olema üsna ettevaatlikud. Esiteks saame pöördfunktsioonile väärtuse anda ainult vahemikus [–1; 1], mis siis on tema nii-öelda määramispiirkonnaks. Teiseks tuletame meelde, et funktsioon saab võtta täpselt ühe väärtuse – seega peame iga sirge jaoks kuidagi välja valima just ühe lõikepunkti.
Üks võimalus selle tegemiseks on lihtsalt nõuda, et vastus oleks mingis kindlas vahemikus – jooniselt näeme, et siinusfunktsioon võtab kõik oma võimalikud väärtused vahemikus [–90º; 90º] ning koosinusfunktsioon näiteks vahemikus [0; 180º]. Nendes piirkondades on funktsioonid üksühesed [lk 68] ning võime kohe defineerida ka pöördfunktsioonid.
Nii ongi enamasti defineeritud arkussiinus, mida tähistatakse tihti arcsin(x), kui funktsioon, mis on siinuse pöördfunktsioon vahemikus [–90º; 90º] ehk siis rahuldab selles vahemikus seost arcsin(sin(x)) = x.
Sarnaselt on siis defineeritud ka arkuskoosinus ehk arccos(x), ainult vahemikuna on kasutuses [0; 180º].
Olenevalt eesmärgist võib mõnikord kasutada muidugi ka mõnda muud vahemikku. Veelgi enam, vahepeal tahaksime kõiki vastuseid korraga esitada. Siis kirjutame umbes nii:
Sel juhul ei ole meil küll rangelt enam funktsioon, vaid loetleme lihtsalt kõik sirge y = 0 ning siinusfunktsiooni lõikepunktid ja neid on palju!
Arkustangens
Tangensiga on selles suhtes lihtsam lugu, et ta võib võtta kõiki reaalarvulisi väärtusi. Seega on tangensi pöördfunktsiooni ehk arkustangensi määramispiirkonnaks kogu reaaltelg.
Probleem, et tangensfunktsioon on mitmes kohas sama väärtusega, muidugi säilib. Seega tuleb ka arkustangensi kui funktsiooni määramiseks välja valida üks kindel piirkond. Mõistlik valik on näiteks (–90º; 90º), aga sobiks ka mõni teine.
Arkustangensit tähistatakse arctan(x).
Tähistustest
Nobeli auhinna võitjale füüsik Richard Feynmanile ei meeldinud trigonomeetriliste funktsioonide tähistused sugugi. Talle tundus, et sin tähendab kolme arvu s, i ja n kokkukorrutamist. Veel vähem meeldis talle siinuse pöördfunktsioon, mida mõnel pool mujal tähistatakse kui sin–1(α). Õigusega tekitas see segadust, sest seda võiks tõlgendada kui
mida sellega enamasti silmas ei peeta. Igal juhul kasutas ta kooliajal siinuse ja siinuse pöördfunktsiooni järgmisi tähistusi:
Üsna varsti märkas ta siiski, et selliseid tähistusi kasutades ei saanud keegi teine tema mõtetest ja selgitustest suurt midagi aru. Seega soovitame siiski jääda tähiste sin ja arcsin juurde.
Miks just täisnurksed kolmnurgad?*
Natuke järele mõeldes võib kummitama jääma üks küsimus. Miks me seome nurki ja külgedevahelisi suhteid ikkagi just kolmnurkade kaudu ning miks just täisnurksete kolmnurkade kaudu? Kas see on lihtsalt ajalooline relikt või võib sellele ka selgitust leida?
Esimese vastusena võiks kohe öelda, et kolmnurkadest ei saa üle ega ümber. Niipea kui meil on defineeritud kaks lõigupikkust ja nendevaheline nurk, ongi meil juba kolm punkti – nurgatipp ja lõikude teised otspunktid – ja seega ka kolmnurk. Lisaks võib ju iga teise hulknurga alati kolmnurkadeks jagada.
Eelkõige on aga põhjus järgmine: kolmnurgad on ainsad hulknurgad, kus
- küljepikkuste vahelised suhted määravad üheselt ära kõik nurgad
- ning ka vastupidi, teades kõiki kolmnurga nurkasid, on määratud kõik külgedevahelised seosed.
Kumbki neist seostest näiteks nelinurkade puhul enam ei kehti. Nimelt kui nelinurga neli külge on võrdsed, võivad nurgad olla endiselt erinevad: meil võib olla nii kena ruut või ka üsna lapergune romb.
Teistpidi, teadmine, et kõik neli nurka on täisnurgad, ütleb meile vaid, et tegemist on ristkülikuga, ning muidugi leidub väga erineva külgede suhtega ristkülikuid.
Aga isegi kui lepime, et just kolmnurgad on mõeldud nurkade ja külgedevaheliste suhete sidumiseks, siis miks on kasutusel just täisnurksed kolmnurgad?
Nagu mainisime, on kolmnurga „kuju” määramiseks vaja teada vähemalt kahte nurka. Ainult ühest nurgast lähiskülgede suhte määramiseks ei piisa, sest sama nurga lähiskülgede suhe võib olla väga erinev:
Kuna teame, et iga kahe nurga teadmisest piisab kolmnurga „kuju” määramiseks, on kaval nipp üks nurk alatiseks fikseerida. Nagu eespool ka nägime, on sel juhul kolmnurga „kuju” leidmiseks vaja veel teada ainult ühte nurka ning on täiesti mõistlik rääkida selle nurga lähiskülgede vahelisest suhtest.
Fikseeritava nurga suuruse võiksime muidugi vabalt valida. Siiski, kõige paremini käsitletava, loomulikuma ja ilusama teooria saame kasutades täisnurkseid kolmnurki – ehk siis fikseerime ühe nurga täisnurgaks.
Põhjuseid selle valiku eelistamiseks on mitmeid, mõned üksikud neist on näiteks järgnevad.
- Nurk 90º on kõige sõmmeetrilisem valik – ta on täpselt poolel teel 0 kraadist 180 kraadini.
- Nagu nägime,võime sel juhul trigonomeetrilisi funktsioone defineerida lihtsalt ühikringjoone x- ning y-koordinaatide abil.
- Skalaarkorrutisel on tänu sellele valikule ilus valem vektorite pikkuste ja nendevahelise nurga koosinuse abil [lk 144].
- Iga muu kolmnurga saame jagada täisnurkseteks kolmurkadesks ja seeläbi leida ka nurkade ja külgede vahelisi seoseid – ühte neist nimetatakse siinusteoreemiks.
Kasutades täisnurkse kolmnurga jaoks defineeritud trigonomeetrilisi põhiseoseid, võime omavahel siduda nurkasid ja külgi ka mittetäisnurksetes kolmnurkades.
Tuntuim selline seos on ilmselt siinusteoreem, mis väidab, et iga nurga vastaskülje ja selle nurga siinuse suhe on võrdse väärtusega. Kuigi intuitiivselt on selge, et nurgad ja külgede suhted peavad olema omavahel seotud, siis siinusteoreemi täpne sõnastus on siiski üllatavalt leidlik ja lihtne:
Enne kui siinusteoreemi tõestama asume, räägime mõnest tema matemaatilisest rakendusest.
Mõned siinusteoreemi rakendused
Esimese rakendusena aitab siinusteoreem leida puuduvaid elemente kolmnurgas – tema abil võime teadmised nurkadest pöörata teadmisteks küljepikkuste kohta ja vastupidi.
Samuti võime siinusteoreemist vähemalt teravnurkse kolmnurga jaoks üsna kergesti järeldada midagi päris ilusat: kolmnurga pikemate külgede vastas on suuremad nurgad.
Tõepoolest, siinusteoreemist teame, et
Nüüd kui küljepikkuste vahel kehtib a > b, siis peab kehtima ka sin(α) > sin(β). Samas aga nägime ennist, et teravnurksete nurkade jaoks on siinus kasvav funktsioon. Seega järeldame, et nurk α peab nurgast β suurem olema. Ehk suurema nurga vastas on ka suurem külg.
Siinusteoreemi tõestus teravnurkse kolmnurga jaoks
Lugeja võib paberi, pastaka ja natukese kritseldamisega veenduda, et siinusteoreem ei ütle täisnurkse kolmnurga jaoks midagi uut – kogu seos järeldub siinuste definitsioonist.
Mittetäisnurkse kolmnurga jaoks on siiski tegemist millegi uue ja põnevaga, mida on vaja ka tõestada, teisisõnu selgitada meile juba varasemate teadmiste abil. Miks muidu peaksime seda uskuma?
Kuidas siis argumenteerida? Tuletame meelde, et siinus on defineeritud täisnurkse kolmnurga kaudu. Seega tuleks kuidagi konstrueerida täisnurkne kolmnurk, milles neid definitsioone kasutada võiksime.
Üks võimalus on lihtsalt tõmmata kõrgus. Nii jagame algse kolmnurga kaheks täisnurkseks kolmnurgaks. See tundub juba päris hea algusena, sest nende täisnurksete kolmnurkade üks külg on ju lisaks veel võrdne – just seesama külg, mille abil saame nurga siinust välja kirjutada.
Seega kirjutamegi lihtsalt välja mõlemast kolmnurgast siinuse definitsiooni:
Avaldades mõlemast avaldisest kõrguse h, näeme, et h = b sin(α) ja samuti h = a sin(β)
Seega kehtib ka b sin(α) = a sin(β) ehk
Samamoodi võiksime muidugi ka tõmmata mõne teise kõrguse ja nii näidata kõikide suhete võrdsust.
Nürinurkse kolmnurga puhul satub kõrgus küll kolmnurgast välja, aga see ei põhjusta probleeme. Nimelt kui vaadata hoolikalt siinusfunktsiooni definitsiooni suvalise nurga jaoks, näeme, et sin(α) = sin(180º – α). Tõepoolest, mõlemad haara otspunktid lõikavad ju ühikringjoont samal kõrgusel.
Siinusteoreemi laiendus
Tuleb välja, et tegelikult võib siinusteoreemi veel laiendada.
Nimelt on teada ka selle iga vastaskülje ja nurga siinuse suhte täpne väärtus – see on alati võrdne kolmnurga ümberringjoone diameetri pikkusega. Seega võime, kasutades ikka samu vanu tähiseid nurkade külgede jaoks ning tähistades kolmnurga ümberringjoone raadiuse R-iga, kirjutada siinusteoreemi täiskujul välja järgnevalt:
Sellel korral on tõestus pisut kavalam ja jätame ta huvitunutele nuputamiseks või järele pärimiseks.
Teine tuntud trigonomeetriline seos iga kolmnurga jaoks on koosinusteoreem.
Koosinusteoreem võimaldab leida kahe küljepikkuse ning nende külgede vahelise nurga abil kolmanda külje pikkust:
Koosinusteoreemist järeldub näiteks kohe ka see, et iga kolmnurga määravad üheselt ära kaks küljepikkust ning nende külgede vaheline nurk. Tõepoolest, lähtudes neist teadmistest võime leida kolmanda külje pikkuse ja seda me juba teame, et kolme küljepikkusega on kolmnurk üheselt määratud.
Koosinusteoreem näeb juba peaaegu välja nagu Pythagorase teoreem. See visuaalne seos pole sugugi petlik. Tuletades meelde, et cos(90°) = 0 näeme, et täisnurkse kolmnurga korral väidabki koosinusteoreem täpselt sedasama, mida Pythagorase teoreemgi.
Oleks tore ka teada, kuidas koosinusteoreemi eelnevatest teadmistest järeldada. Teisisõnu on küsimus: kuidas kahe külje ja nendevahelise nurga abil leida kolmanda külje pikkus?
Konkreetsemalt seame siis eesmärgiks leida külje a pikkus külgede b, c ja nendevahelise nurga α abil.
Üks võimalus on alustada siinusteoreemi puhul kirjeldatud viisil ning tekitada kõrguse abil täisnurkne kolmnurk. Nii seame end toredasse olukorda, kus saame kasutada koosinuse definitsiooni täisnurkses kolmnurgas ning lisaks veel koosinusteoreemi sugulast Pythagorase teoreemi.
Seega saame Pythagorase teoreemi abil kirjutada külje a pikkuse kolmnurga kõrguse h ning abilõigu x toel:
Edasi tahaksime kuidagi kirjutada lahti ka need abiliikmed. Kõrguse võime omakorda avaldada Pythagorase teoreemist, kasutades teist, vasemale tekkinud täisnurkset kolmnurka:
Abilõigu x pikkuse saame aga kirjutada külje c ning sama abilõigu y abil: x = c – y ja seega x2 = (c – y)2.
Võib küsida, mis sellest ikkagi kasu on, kui kirjutame abilõigu x asemele hoopis abilõigu y. Õnneks on meil ka vastus: uurides veel kord vasemal asuvat täisnurkset kolmnurka, võime välja kirjutada koosinuse definitsiooni:
Seega abilõigu y pikkuse võime esitada meile sobivate elementide abil.
Pannes kõik kokku, saame
Lihtsustame
Asendades nüüd leitud abilõigu y pikkuse y = b cos(α), saamegi koosinusteoreemi nime all välja kuulutatud seose:
Nürinurkse nurga puhul on jällegi olukord pisut segasem, aga hoolikalt näpuga jälge ajades võime siiski kasutada peaaegu samasugust arutlust.
Alternatiivne viis oleks kasutada vektoreid ja skalaarkorrutise omadusi. Et midagi sellist võiks toimida, vihjab muidugi juba kahe vektori skalaarkorrutise definitsioon [lk 144]:
Siin on ju olemas täpselt seesama liige, mis koosinusteoreemi Pythagorase teoreemist eristab! Pärast vektoritega seose loomist järeldubki kogu koosinusteoreem tegelikult ainult skalaarkorrutise omadustest.
Sisuliselt on tõestus sama kui see, mille pakkusime lisaloona Pythagorase teoreemi jaoks vektorite peatükis [lk 147], – huvitunud lugejal soovitame detailid siiski ise kokku panna.
Naaseme nüüd probleemi juurde peatüki algusest: kuidas kontrollida kahe liigesega robotkätt, et ta jõuaks katkise antenni otsani?
Meenutame, et olukord oli täpselt nii hea või halb nagu pildil.
Olukorrast matemaatiliseks mõtlemiseks peame üleliigsetest detailidest lahti saama ning kõike veidi lihtsustama. Näiteks oletame, et robotkäsi liigub ainult ühel tasandil ning et see ongi just jooniseks valitud tasand. Võib ju näiteks optimistlikult mõelda, et kolmandas mõõtmes võime robotkätt niisama nihutamise teel liigutada.
Edasi peame meile olulised elemendid kuidagi tähistama. Meile on teada robotkäe kahe hoova pikkused l1 ja l2 ning oletame, et võime mootorite abil kontrollida liigeste pöördenurkasid α ja β. Nimetame neist alumist õla- ja teist küünarliigeseks. Meie eesmärk on viia robotkäe ots (ja astronaut) etteantud punkti A, kusjuures muuta võime nurkade α ja β väärtuseid.
Ülesande lahendamiseks on muidugi vaja ka veel täpsustada, mida me punkti A kohta juba teame. Tundub üsna mõistlik eeldada, et teame esiteks punkti A kohta tema kaugust õlaliigesest – näiteks laserite peegeldust uurides. Teisalt võime eeldada, et teame nurka, mille jätab see kiir õlaliigesest punkti A horisontaalse tasandiga. Tähistame saadud kaugust näiteks l-iga ning nurka ennast γ-iga. Nii on meil lõplik joonis järgmine:
Siin võime anda oma ülesande juba üsna matemaatiliselt: eesmärk on seega leida pikkuste l, l1 ja l2 ning nurga γ abil nurgad α ja β. Lahendusviisiks on meil trigonomeetria.
Tuletame meelde, et kolmnurga kolm küljepikkust määravad täpselt ära kolmnurga kuju ja suuruse. Kuna lisaks on veel teada kaks kolmnurga tippudest – õlaliiges ja punkt A –, jääb meil saadava kolmnurga jaoks täpselt kaks võimalust, olenevalt sellest, kuidas punktile A läheneme.
Oletame, et valime joonisel näidatud viisi. Järgmine küsimus on siis, kuidas küljepikkustest nurgad leida. Selle jaoks leiame abi juba läbitud peatükist: koosinusteoreem seob omavahel kõik kolmnurga küljed ning ühe nurga koosinuse. Nii võime leida nurga β koosinuse:
Nagu nägime pöördfunktsioonide juures, võime nurga koosinuse põhjal kergesti leida ka nurga enda väärtuse. Kõige lihtsam on küsida nurga väärtust taskuarvutilt – igal uhkemal taskuarvutil on nurga koosinuse väärtuse põhjal nurga leidmine tähistatud funktsiooniga arccos(x) või cos–1(x).Täpselt samamoodi võime leida ka nurga δ koosinuse:
ja seejärel arkuskoosinuse abil nurga δ väärtuse.
Viimaks saame nüüd ka nurga α lihtsalt välja arvutada. Olenevalt sellest, kummalt poolt läheneme, on α = γ + β või α = γ – β.
Oleme nüüd täpselt kirjeldanud arvutusi, mis tuleks teha robotkäe antennini juhtimiseks. Edasi tuleks need tehted ja kõikide andmete täpsed väärtused arvutile edasi anda ning kosmosejaam saabki korda!
Eelmises peatükis jõudsime trigonomeetriliste funktsioonideni, uurides küljepikkuste suhteid täisnurkses kolmnurgas. Saadud funktsioone kasutasime edasi seoste leidmiseks suvalise kolmnurga küljepikkuste ning nurkade vahel.Tänu neile seostele muutus kolmnurga puuduvate elementide kindlaks tegemine hoobilt üsna lihtsaks.
Siinus ja koosinus tulevad funktsioonidena aga esile veel teiseski kontekstis – looduse perioodiliste ehk korduvate protsesside kirjeldamisel.
Seda võib igaüks (juhul kui koristamine vastumeelt ei ole) ka kodus proovida. Seo pika nööri otsa üks korralik pang, kalla värvi täis ning tee põhja sisse auk. Lisaks varu suur rull paberit.
Nüüd pane see pang pendlina võnkuma ning tõmba paberit ühtlase kiirusega pange alt läbi. Paberile tekkiv värvijoon ongi ilus siinuse või koosinuse graafik.
Skeptiline lugeja võib muidugi kahelda, miks peaks paberile joonistuma täpselt siinus või koosinusfunktsioon ja mitte mõni teine sarnase kujuga perioodiline funktsioon.
See kahtlus on igati õigustatud – on ju nii palju erinevaid perioodilisi funktsioone, miks peaks loodus just trigonomeetriliste funktsioonide otsa komistama? Ometigi komistab. Selle põhjendamine on aga juba pisut keerulisem ning nõuab ka parasjagu füüsikat – huvitunu ja skeptik saab sellest lugeda lisapeatükist [lk 236].
Järgnevalt üritame aga intuitiivselt aru saada, kuidas perioodilised liikumised trigonomeetriaga seotud on, ja teeme seda kõige kaunima perioodilise liikumise, ringliikumise näitel.
Lähed sõitma 100-meetrise diameetriga vaaterattaga. Kas oled mõelnud, kuidas muutub vaaterattaga sõidu ajal Sinu kõrgus maapinnast? Võibolla Su kaaslane kardab kõrgust, võibolla armastab. Oskad talle öelda, kui palju aega veedate äärmustes – hästi kõrgel või hästi madalal – ning kui palju ülesminekul ja allatulekul?
Neile küsimustele saab matemaatiliselt kenasti vastata. Matemaatiliseks lähenemiseks peame kõigepealt nii mõnedki detailid ära unustama: näiteks selle, kui ilus on vaade, kui kaunis kaaslane või kui logu on vaateratas ise. Järele jääb pöörlev ringjoon koos punktikesega, millele võime mõõtmiseks taustale lüüa ka koordinaattasandi nii, et x-teljeks on maapind.
On üsna mõistlik oletada, et vaateratas liigub ühtlase kiirusega – muidu saaks ju mõnes kabiinis istujad ägedamat sõitu kui teised.
Kõrgus on nüüd vastavuses teljestiku y-koordinaadiga. Kui oletame lisaks, et täispöörde läbime 10 minuti jooksul, võime joonistada ka oma kõrguse profiili. Peale ronid vaaterattale muidugi päris alt.
See näeb ju aga välja täpselt nagu siinusfunktsioon, ainult pisut ülespoole nihutatult ning pisut suurendatult. Ja tõepoolest, tuletades meelde, kuidas me eelmises peatükis siinusfunktsiooni defineerisime, ei tohiks see üllatada.
Defineerisime ju nurga siinuse täpselt kui nurga haara ja ühikringjoone lõikepunkti y-koordinaadi. Seega kui nüüd nurka ühtlaselt suurendada, saamegi ringliikumise ja seega kõrguskoordinaat joonistab siinusfunktsiooni. Muidugi, see funktsioon ei pruugi olla täpselt kujus sin(t), vaid võib olla kujus
kus T on aeg, mis kulub ühe täispöörde jaoks.
Nüüd võime ka vastata tekkinud küsimustele. Kui palju aega veedad vaaterattaga päris üleval, kõrguse ülemises neljandikus?
Graafikul huvitab siis meid, kui palju aega asub kõrgusfunktsioon oma maksimumi suhtes ülemises neljandikus:
Kuna liikumine on ühtlane ja veedame ringjoone igas punktis sama kaua aega, võime oma küsimuse ümber tõlgendada üsna lihtsaks geomeetriliseks küsimuseks: kui suur osa ühikringjoonest asub kõrgemal kui ½?
Seega on vaja lihtsalt leida, milliste x-i väärtuse korral on sin(α) ≥ ½. Õnneks näitab järgnev ilus geomeetriline konstruktsioon täpselt, et
Joonistame 60º-30º kraadi kolmnurgale juurde teise samasuguse. Kuna tekkinud kolmnurk on võrdkülgne, siis tema servad on võrdsed. Järelikult sin(30º) on pool külge jagatud terve küljega ehk 0,5.
Kuna 150 – 30 = 120 kraadile vastav ringjoone osa on täpselt kolmandik kogu ringjoonest, võimegi öelda, et ülemises neljandikus veedate kolmandiku koguajast. Päris hea tehing!
Meelde jätta võiks sellest peatükist aga hoopis seda, et trigonomeetrilistele funktsioonidele võibki läheneda ka hoopis ringliikumise vaatevinklist!
Seni oleme hoidunud arutelust, kuidas nurka peaks mõõtma – kas seda oleks targem teha kraadides või radiaanides? Õigupoolest oleme seda seni teinud ainult kraadides. Ometigi on nii mõnigi kord kasulikum kasutada hoopis radiaane.
Juba kraadidest ja radiaanidest mõtlemine on üsna erinev.
Kraadid
Kraadides mõõtmine on nurga tipus istujale. Kraadide leidmiseks vaatame lihtsalt, kui suure osa täispöördest moodustab nurk kahe nurgahaara vahel.
Kraadides arvestatakse näiteks tihti kaugete objektide mõõte ja vahemaid.
Kraadide juurde käib ka üks huvitav kokkulepe. Nimelt tundub, et kuskil ajaloohämaras on mingi hetk üsna vägivaldselt otsustatud, et täispööre olgu täpselt 360 kraadi. Muud nurgad arvestatakse siis vastavalt sellele, kui suure osa täispöördest nurk moodustab – näiteks pool pöördest on siis täpselt 180 kraadi.
Aga miks peaks täispööre olema just 360 kraadi ja mitte näiteks 100 või 222 kraadi?
Paistab, et see võib seotud olla päevade arvuga aastas – vanasti tundus, et taevased objektid teevad ringi peale umbes 360 ööpäeva jooksul.
Lisaks on arvul 360 kena omadus, nimelt jagub ta väga paljude erinevate arvudega. Kõik järgnevad arvud on tema jagajad, neid on kokku tervelt 24:
Nii saab aastat jagada väga paljudeks erinevateks ühepikkusteks täistsükliteks. Näiteks senini on ju kasutusel 12 kuud, mille pikkused on küll meie teadmiste varal ebaühtlaseks muutunud.
Radiaanid
Nurga radiaanmõõdu arvestamiseks on vaja minna ja ringjoone kaare pikkus korralike sammudega ära mõõta – seega on siinkohal tegemist matkamehe nurgamõõduga.
Kui kraadide leidmiseks arvutasime, kui suure osa moodustab nurk täispöördest, siis radiaanide puhul lööme kokku selle ringjoone osa pikkuse, mille moodustab nurga haarade vahele jääv ühikringjoone kaar.
Tuletame meelde, et ühikringjoone pikkus on 2π ning seega on täispöörde suuruseks 2π radiaani. Poole pöörde suuruseks jääb aga näiteks π radiaani.
Ka radiaanide juures on tegelikult mängus teatud meelevaldne valik – miks me pidime just valima ühikringjoone? Kui oleksime oma nurgamõõduks valinud näiteks raadiusega 0,5 ringjoone, osutuks täispöörde suuruseks π radiaani. Kas see poleks kenam? Või oleks hoopis kenam, kui π ise oleks teisiti defineeritud [lk 101]?
Kumba neist ikkagi kasutada?
Tuleme nüüd tagasi peatüki alguses püstitatud küsimuse juurde: kas kasutada kraade või radiaane? Selgub, et see oleneb kontekstist. Nii kaua kui kasutame trigonomeetriat ainult kolmnurkadega tegelemiseks, suurt vahet ei olegi – kraadid ja radiaanid on mõlemad ühtmoodi head ning kasutame neid siin raamatuski läbisegi.
Nii pea kui aga hakkame trigonomeetriliste funktsioonidega tegelema, tuleks eelistada radiaane.
Näiteks radiaane kasutades on siinusfunktsiooni graafiku tõus nullpunkti juures täpselt üks ehk matemaatiliselt:
Kraade kasutades see valem enam ei kehti. Intuitsiooni selle valemi tagamaadest annab järgnev graafik: nimelt on siinus täpselt võrdne haara otspunkti kõrgusega. Kui aga nurk on väga väike, siis on see peaaegu sama pikk kui tema kõrvale jääv kaare pikkus. Seda kaare pikkust mõõdab aga täpselt nurga radiaan!
Tänu sellele ilusale omadusele on näiteks siinusfunktsiooni sin(α) tuletis [lk 320] radiaanide korral cos(α), kraadide korral aga hoopis
Miks see nii peaks olema, näeme juba varsti [lk 251].
Lõpuks ei ole ka väga hullu, kui sõbraga erinevat mõõtu kasutate, radiaanidest kraadidesse ja tagasi viivad lihtsad teisendused. Radiaanidest kraadide saamiseks peame nurga korrutama lihtsalt
ga ning vastupidi kraadidest radiaanide saamiseks korrutama
ga.
Meie oleme seni töötanud kraadidega, aga nüüd lähemegi vahelduseks hoopis radiaanidele üle ja edasi kasutame neid täpselt nii, kuidas tuju on.
See alapeatükk on skeptilisele ja huvitunud lugejale, kes ei taha uskuda, et pendel on seotud just täpselt siinuse ja koosinusega, mitte mõne muu perioodilise funktsiooniga.
See on igati õigustatud kahtlus!
Õnneks annavad füüsika ja matemaatika käsikäes siiski hea põhjendatud vastuse. Lihtsuse mõttes käsitleme küll siin peatükis hoopis elastset vedru, aga situatsioon ja ideestik on täpselt sama:
- meil on üks keha
- mida liigutab üksainus jõud,
- mis surub objekti tagasi tasakaaluasendisse,
- aga kahjuks liiga tugevasti ning keha jääb võnkuma tasakaaluasendi ümber.
Elastse vedru korral on mõjuvaks jõuks elastsusjõud. Inglise füüsik Hooke tegi 17. sajandil hoolega katseid ja veendus, et mida pikemalt on vedru välja venitatud, seda suurem jõud tõmbab teda kokku ning vastupidi, mida rohkem vedru on kokku surutud, seda suurem jõud lükkab teda jälle lahti.
Hooke oli hoolikas sell ja ta mõõtis ka täpselt välja, kuidas see jõud täpselt vedru väljavenitusest või kokkusurutusest sõltub. Ta tegi kaks järeldust:
- jõud on erinevatest materjalidest vedrude jaoks erinev,
- jõud sõltub täpselt ühtemoodi vedru pikkuse muudust – alati võrdeliselt.
Tähistame nüüd vedru suurusemuutu tasakaaluasendi suhtes x-ga (positiivse x-i korral on vedru välja veninud, negatiivse korral kokku surutud) ning keha materjali jäikust iseloomustavat tegurit k-ga. Sel juhul väidab Hooke’i seadus, et vedru algkujusse kiskuvat elastsusjõudu Fe võib igal ajahetkel t kirjeldada valemiga
Samaaegselt oli Hooke’i kaasaegne ja rahvuskaaslane Newton leidnud veelgi üldisemaid printsiipe meid ümbritseva maailma kirjeldamiseks.
Ta märkas, et kui kehale mõjub mingi jõud, siis keha kiirendus – see, kuidas keha liikumiskiirus muutuma hakkab, – sõltub täpselt võrdeliselt mõjuvast jõust.
Veelgi enam, ta avastas, et mõõtes ka keha massi, võib ta täpselt kirjeldada, kuidas jõud keha kiiruse muutuma paneb: tähistades keha kiirendust a-ga, tema massi m-iga ning kehale ajahetkel t mõjuvat kogujõudu F(t)-ga, võib Newtoni teise seaduse välja kirjutada kujus:
Meie olukorras on ainus vedrule mõjuv jõud igal hetkel antud täpselt eeltoodud elastsusjõuga, mis tema kuju taastada üritab. Gravitatsiooni võime näiteks lihtsalt eirata, kuna horisontaalset liikumist ta ei mõjuta.
Seega võime kirjutada, et vedrule mõjub kogujõud F = Fe, ning valemitest asendades saame
Nii on liikumine igal ajahetkel t kirjeldatud võrrandiga
Selles võrrandis on peidus kaks arvkonstanti m ja k, mis sõltuvad keha omadustest; a(t) ja x(t) kirjeldavad aga igal ajahetkel vastavalt vedru venituse kiirendust ja väljavenituse suurust.
Ometigi on intuitiivselt üsna selge, et ühe objekti kiirendus – tema kiiruse muutumine – on juba olemuslikult ka seotud tema asupaigaga.
Seda seost toob täpsemalt esile tuletise peatükk [lk 320]. Nimelt kiirenduse näol on tegemist läbitud teepikkust või teisisõnu vaadeldava keha asukohta kirjeldava funktsiooni teise tuletisega. Isegi kui tuletis tundub ohtliku sõnana, ei ole selles suurt midagi keerulist – funktsiooni esimene tuletis näitab lihtsalt, kui kiiresti funktsiooni väärtus muutub, ning funktsiooni teine tuletis näitab, kui kiiresti see muutumine ise muutub. Nii ongi näiteks kiirus teepikkuse esimene tuletis ning kiirendus tema teine tuletis.
Seega ütleb meie võrrand, et igal hetkel t on vedru venituse muutumise kiirendus võrdeline tema kogumuutusega:
Võime neid iga ajahetke kohta antud võrrandeid vaadata ka ühe seosena üle kogu aja korraga – seosena ajast sõltuva funktsiooni ning tema teise tuletise vahel.
Sellist võrrandit, mis seostab funktsiooni ja tema tuletisi nimetatakse uhkelt diferentsiaalvõrrandiks – diferentseerimine tähendab ju lihtsalt tuletise võtmist. Nende lahendamine päris käkitegu pole, aga sel korral võib sellega siiski hakkama saada, kui meenutame trigonomeetriliste funktsioonide tuletisi.
Siinusfunktsiooni sin(t) tuletiseks on cos(t) ning sarnasel on koosinusfunktsiooni cos(t) tuletiseks – sin(t).
Need kaks teadmist kokku pannes näeme, et siinusfunktsiooni teine tuletis on – sin(t). Seega rahuldab ta etteantud diferentsiaalvõrrandit, juhul kui
Saamegi ilusa siinuskujulise liikumise, mille periood on täpselt 2π.
Kui aga
on mõne teise väärtusega, peame vastuse leidmiseks muutma oma siinuslaine sagedust kas aeglasemaks või kiiremaks.
Tuleb välja, et üldjuhul on sobivaks lahendiks
Siingi võiks veel nuriseda – sarnaselt sobib ju lahendiks ka koosinusfunktsioon ning veelgi enam, ka koosinus ja siinusfunktsiooni summa! Vedru võngub ju aga ometigi täpselt ühtemoodi, mitte mitut moodi korraga. Tõepoolest, selgub, et puhta siinus- või koosinusfunktsiooni määramiseks tuleb teha veel üks tähelepanek. Nimelt on vedru kiirus kõige suurema väljavenimise ja kokkusurutuse hetkel võrdne nulliga. See tuleneb energia jäävuse seadusest – neil hetkedel on kogu energia muundunud potentsiaalseks energiaks. Seda teadmist arvesse võttes on meie siinusfunktsioon juba üheselt määratud.
Loodame, et nüüd on ka skeptilisem lugeja veendunud, et vedru või ka pendli perioodilise liikumise kirjeldamiseks ei sobi sugugi mitte mingi suvaline siksak või muu perioodiline funktsioon. Sobib just meile juba teada ja tuntud siinusfunktsioon.
Üks koolimatemaatikas enim tuska põhjustavaid teemasid on ilmselt trigonomeetriliste valemite teisendamine ja lihtsustamine.
Antakse ette mingi järjestus sümboleid ja kästakse sellest teha natuke lühem järjestus sümboleid. Selle jaoks, et teisendusi läbi viia, tuleb kasutada käputäit valemeid, mis näevad kõik välja täpselt ühesugused, aga mille hulgast iga kord vaid üks viib kiirelt sihile!
Nii jääbki tunne, et teha tuleb mingit maagiat ja on üsna selgusetu, mis kogu selle vaeva ja maagia mõte on.
Kui tegevus tundub raske ja ebameeldiv, tekivad muidugi automaatselt kaitsva hoiakuga küsimused: kas see trigonomeetriliste valemite teisendamine on ikka oluline tegevus? Kus seda vaja võiks minna? Kas lihtsamalt kuidagi ei saaks?
Tuleb välja, et neid läheb tõesti tarvis. Juba sellessamas raamatus läheb meil neid tarvis mitmel korral. Esiteks, matemaatilise rakendusena saame tänu siinusfunktsiooni summavalemile leida siinusfunktsiooni tuletise [lk 251]. Teiseks peame trigonomeetriliste funktsioonide teisendusi kasutama, et leida kõige paremat viskenurka veepommi lennutamisel [lk 333].
Lisaks on trigonomeetriliste funktsioonide teisendamine olulisel kohal ka signaalianalüüsis. Näiteks aitab ta aru saada, kuidas ikkagi toimub raadiosignaalide edastamine näiteks AM-raadios.
Käesolevas osas tahamegi selgitada, kuidas trigonomeetriliste valemite ning nende teisendamisega hästi läbi saada. Peatüki algus on üsna visuaalne, kuid mingist hetkest võtavad koha üle valemid. Valemirohketele alapeatükkidele viskasime juurde ka tärnid, meenutamaks, et võibolla esimesel lugemisel see kõik väga meeldiv ei tundu. Midagi väga rasket siiski pole, lihtsalt palju sümboleid.
Trigonomeetriliste funktsioonidega on seotud väga mitmeid erinevaid valemeid ja teisendusi. Võibolla kõige tuntumad ja lihtsamad neist pärinevad juba siinuse ja koosinuse definitsioonist täisnurkse kolmnurga kaudu. Nendest alustamegi. Seejärel käsitleme valemeid, mis on seotud trigonomeetriliste funktsioonide graafikute ilusate omadustega. Viimaks leiame valemeid, mis aitavad leida erinevaid summa- ja vahevalemeid.
Seosed täisnurksest kolmnurgast
Vaatleme täisnurkset kolmnurka, mille hüpotenuusi pikkus on 1 ning mille teravnurgad on α ja β = 90º – α, täpselt sellist, millega on ka trigonomeetrilised funktsioonid defineeritud.
Esimese seose trigonomeetriliste funktsioonide vahel leiamegi juba, kui esitame kaateti a pikkuse kahel viisil.
Esiteks võime seda teha nurga α ja vastaskaateti abil, saades tulemuseks sin(α). Teiseks võime kaateti α pikkuse leida ka nurga β ja lähiskaateti abil, saades cos(β). Kuna β = 90º – α, saamegi
Teise tuntuima seose saame Pythagorase teoreemist. Teame, et täisnurkses kolmnurgas on kaatetite pikkuste ruutude summa võrdne hüpotenuusi pikkuse ruuduga
Samas võime kirjutada
Asendades need väärtused Pythagorase teoreemi, saamegi, et
Graafikute ilusatest omadustest pärit seosed
Järgnevalt vaatame aga valemeid, mis on seotud trigonomeetriliste funktsioonide graafikute ilusate omadustega.
Tuletame meelde, et funktsiooni graafiku teisendamine on aidanud meil ennegi funktsioonist aimu saada – näiteks näeme varsti, kuidas ruutfunktsiooni lahendivalemi taga on mingis mõttes tegelikult peidus lihtsad geomeetrilised teisendused [lk 278].
Trigonomeetriliste funktsioonide korral tuleb jällegi funktsiooni graafiku teisendamine suuresti abiks – nimelt on siinus- ja koosinusfunktsiooni graafikud mitmete geomeetriliste teisenduste suhtes invariantsed ehk teisisõnu neid parajal määral nihutades ja peegeldades saame jälle uuesti samad funktsioonid. Nii aitab teisenduste raames mõtlemine hästi meeles hoida siinus- ning koosinusfunktsiooniga seotud valemeid.
Nimelt, joonise abil on end kerge veenda, et siinusfunktsioon on perioodiline – nihutades tema graafikut täispöörde ehk 360º võrra emmas-kummas suunas, saame taas tagasi siinusfunktsiooni graafiku
Sellest järeldub, et
Lisaks on siinusfunktsioonil teatav sümmeetria x-telje suhtes – graafikut poole täispöörde ehk 180º võrra emmas-kummas suunas nihutades ning siis x-teljest peegeldades saame jälle siinusfunktsiooni graafiku.
Sellest järeldub, et
Veel on seal teatav sümmeetria ka y-telje suhtes – graafikut 180º võrra emmas- kummas suunas nihutades ja siis y-teljest peegeldades saame tagasi siinusfunktsiooni graafiku.
Meenutame, et peegeldamine y-telje suhtes juhtub, kui argument läbi korrutada arvuga –1, ning paremale poole liikumine toimub, kui argumendist lahutada (mitte liita) mingi suurus. Näiteks kui liigutame graafikut paremale, siis sellest järeldub, et
Siinusfunktsiooni graafikut järjepanu vertikaal- ning horisontaaltelgedest peegeldades saame jälle tagasi siinusfunktsiooni graafiku.
Järelikult
Kõigele lisaks on siinus- ning koosinusfunktsiooni graafikud samasugused: nihutades siinusfunktsiooni graafikut veerandpöörde ehk võrra vasemale, saame koosinusfunktsiooni graafiku.
Sellest järeldub, et
Kasutades lisaks ka eelnevat omadust, mis ütleb, et sin(180º – α) = sin(α), leiame taas kord ka peatüki alguses leitud teada-tuntud seose:
Samuti näeme nüüd, et see valem ei kehti sugugi ainult teravnurksete nurkade, vaid kõikvõimalike nurkade korral. Süda on rahulik, kui kõik klapib!
Kõik need omadused vajaksid tegelikult tõestuseid ning neid tõestuseid pole sugugi väga keeruline kokku keevitada: tuleb vaid tõlkida funktsiooni graafikute teisendused ühikringjoone teisendusteks ning kasutada siinus- ja koosinusfunktsioonide omadusi.
Valemite meeldejätmiseks piisab aga sellest, kui neid omadusi usute, ja ega oma silm ju ei peta!
Täpselt analoogiliselt võime mängida ka koosinusfunktsiooniga ning tuletada jällegi terve ämbritäie valemeid. Kõik nad võiks muidugi välja lugeda ka kasutades lihtsalt viimasena kirjeldatud omadusest saadud seost siinus- ja koosinusfunktsioonide abil. Mõned neist valemitest:
Viimaks, kui peaks tekkima suur huvi lisaks teada ka tangensfunktsiooni valemeid, tuleb meil eelnevaga kombineerida tangensfunktsiooni kirjutus kujus
Näiteks
Seosed nurkade liitmise ja lahutamise kaudu*
Eelmises alapeatükis nägime, kuidas siinusfunktsiooni graafikut hoolikalt nihutades ja peegeldades saame tulemuseks jällegi siinusfunktsiooni või mõnikord ka koosinusfunktsiooni graafiku. Kas meil õnnestuks aga kuidagi kirjeldada ka funktsiooni, mille graafikuks on suvalisel määral nihutatud siinusfunktsiooni graafik?
Näiteks kui nihutame funktsiooni sin(α) vasemale β kraadi võrra, saame funktsiooni sin(α + β). Kas seda õnnestub kuidagi kirjutada baasfunktsioonide sin(α), sin(β), cos(α) ja cos(β) abil?
Tuleb välja, et see on igati võimalik. Meenutame, et siinus- ja koosinusfunktsioon andsid meile võimaluse seostada kolmnurga nurgad külgede suhetega. Veelgi enam, näiteks täisnurkses kolmnurgas hüpotenuusiga 1 ongi kaks kaatetit pikkustega sin(α) ja cos(α).
Kui tahaksime samasse kolmnurka paigutada nii nurgad α ja β, kui ka küljepikkused sin(α), sin(β) peame olema ainult veidi kavalamad. Esmalt oletame lihtsustuseks, et nurgad α ja β on teravnurksed – siis võime kindlasti konstrueerida kolmnurga, millel on täpselt kaks nurka α ja β. Nende vastasküljed a ja b võime seejärel leida laiendatud siinusteoreemist [lk 222]:
kus R on kolmnurga ümberringjoone raadius. Seega, kui valiksime kolmnurga, mille ümberringjoone diameeter on pikkusega üks, olekski nurkade α ja β vastas küljed pikkustega sin(α) ning sin(β).
See on juba üsna hea algus. Päris rõõmsaks teeb aga tähelepanek, et kolmnurga kolmas nurk on ju
ning eespool leitud valemite põhjal kehtib võrdus
Seega, kasutades veel kord laiendatud siinusteoreemi, näeme, et kolmas, puuduv külg on täpselt pikkusega (α + β). Nüüd on üsna selge, et siit jooniselt saame ilusaid valemeid.
Nagu siinus- ning koosinusteoreemi tõestuste juureski, on trigonomeetriliste funktsioonidega mängides alati hea mõte tõmmata üks kõrgus, seekord siis küljele pikkusega sin(α + β).
Meie kolmnurk jaguneb nüüd kaheks täisnurkseks kolmnurgaks, millest ühe hüpotenuus on sin(α) ning alusnurk β, ning teise hüpotenuus on sin(β) ning alusnurk α.
Kasutades trigonomeetrilisi seoseid neis mõlemas täisnurkses kolmnurgas, võime leida, kui pikkadeks tükkideks kõrgus vaadeldava külje jagab:
Pikkuse x saame leida järgnevalt:
järelikult
Sarnaselt saame leida ka pikkuse y.
Kuna nende tükkide pikkuste summa annab külje enda pikkuse, olemegi tuletanud valemi
Praegu tõesti tegime seda küll ainult teravnurksete nurkade α ja β jaoks, ent kasutades eelmise alapeatüki valemeid, võib lugeja end veenda, et valem kehtib suvaliste nurkade α ja β jaoks.
Siit edasi on üsna kerge tuletada ka nurkade vahe valem, kirjutades α – β = α + (–β):
kus teises võrduses kasutasime jällegi eelmise alapeatüki valemeid.
Topeltnurga 2α lihtsustava valemi leidmine on seejärel veelgi lihtsam – asendame summa valemisse β = α:
Poolnurga valemiga vajame veel veidi kannatust!
Nimelt üritame enne leida ka koosinuse summavalemi ehk kirjutada cos(α + β) lahti sin(α), sin(β), cos(α) ja cos(β) abil.
Seda võime teha, kombineerides mitmeid meile juba teadaolevaid võtteid
Asendades β = α, leiame siit ka koosinuse topeltnurga valemi:
Seades aga β = –α, leiame, et
ehk teisisõnu oleme taas tuletanud Pythagorase teoreemist tuleneva seose siinus- ja koosinusfunktsiooni vahel.
Koosinuse topeltnurga valemist on lihtne omakorda tuletada poolnurgavalemid: seades α = ½γ, leiame, et
Kasutades nüüd Pythagorase teoreemist pärinevat seost, võime selle kirjutada kahes erinevas kujus:
Neid valemeid läheb meil hiljem vaja siinusfunktsiooni tuletise leidmiseks. Lisaks saame nende abil välja kirjutada ka niinimetatud poolnurga valemid:
kusjuures märgi ruutjuurele peame valima olenevalt sellest, kui suur nurk
parasjagu on.
Viimaks heidame lühikese pilgu ka tangensile. Nagu ikka, pole meil siin muud taktikat, kui lihtsalt siinuse ja koosinuse valemeid ära kasutada. Kirjutame
Nüüd tahaksime hädasti siit segadusest üles leida funktsioonid tan(α) ja tan(β). Selle jaoks jagame lihtsalt nii murru nimetaja kui lugeja läbi korrutisega cos(α) cos(β)
Saamegi kohe
Ehk teisisõnu
Analoogselt võiksime leida ka nurkade vahe, topeltnurga ja muud kooliõpikuis figureerivad valemid. Siinkohal sai meil aga jaks otsa.
Trigonomeetriliste funktsioonide liitmine ja lahutamine*
Seni rääkisime, mis juhtub, kui teeme tehteid trigonomeetriliste funktsioonide argumendiga. Teisisõnu tuletasime lihtsustavaid valemeid näiteks nurkade summa siinuse sin(α + β) või poolnurga siinuse
jaoks.
Samas võiks aga ka küsida, kas õnnestub kuidagi teisiti kirjutada ka tehteid funktsioonide endaga.
Näiteks kõrvutades valemeid
näeme, et neid kokku liites kaob üks liige hoopis ära ja saame:
Selle võime kirjutada kujus:
või asendades α + β = γ, α – β = μ ka kujus
See on väga kena! Oleme näidanud, et koosinusfunktsioonide korrutise võib lahti kirjutada nende summana ning vastupidi. Sama kehtib muidugi ka siinusfunktsiooni kohta ja suurema vaeva korral leiame valemeid ka tangensfunktsiooni tarvis.
Kui selle kõige tarvilikkus tundub esmapilgul ka küsitav, siis aitab see näiteks paremini mõista, kuidas ikkagi toimib AM-raadio [lk 259].
Siinusfunktsiooni tuletis*
Kuna trigonomeetrilised funktsioonid on peidus pea iga perioodilise liikumise kirjeldamisel, siis osutub oluliseks ka nende funktsioonide muutumise kiirus ehk tuletis. Näiteks on meil endalgi tarvis see tuletis välja arvutada, kui asume leidma, kuidas ikka veepommi kõige kaugemale visata [lk 333]. Nagu juba mainisime, on trigonomeetriliste funktsioonide tuletiste leidmisel kasulikum kasutada radiaane [lk 234], niisiis seda teemegi.
Eelteadmised
Siinusfunktsiooni tuletise võtmiseks on (lisaks tuletisest arusaamisele [lk 320]) vaja kasutada kahte juba tuletatud trigonomeetrilist valemit:
Lisaks peame kasutama teadmist, et kui x on mõõdetud radiaanides, siis väga väikeste argumendi x väärtuste korral on sin(x) umbes võrdne x-iga. Täpsemalt, kehtib järgmine piirväärtuste [lk 313] abil kirjapandud seos:
Miks see nii on, selgitasime intuitiivselt juba ühes eelnevas peatükis [lk 99].
Tuletuskäik
Asume nüüd julgelt sin(x) tuletist leidma, lähtudes täpselt tuletise definitsioonist [lk 321]:
Kasutades siinuste summavalemit, võime selle omakorda kirjutada kui
Edasi on kaval murru nimetaja ümber kirjutada kahte ossa ning kuna summa piirväärtus on igal mõistlikul juhul võrdne piirväärtuste summaga, saame
Järgmisena võime ainult liikmega x seotud olevad väärtused piirväärtusest välja tõsta – nad ei sõltu ju sellest, mis me parajasti muutujaga d pihta hakkame:
Nüüd kasutame esimese liikme jaoks valemit 2) ning teise jaoks seost 3) ja saame:
Viimaks võime esimeses liikmes veel korra kasutada seost 3), seekord funktsiooni
jaoks:
Asendades selle juba leitud valemisse, näeme, et esimene liige on piirprotsessis võrdne
ga:
Kuid me teame, et siinusfunktsioon on pidev ning võrdne nulliga kohal null. Seega on ka piirprotsessis, kus d ise muutub nulliks, esimese liikme väärtus null.
Nii jääb piirprotsessis alles ainult teine liige ning saamegi
Huh, tehtud! Siinusfunktsiooni tuletis on koosinusfunktsioon. Tuletus on sisuliselt ainult viis rida pikk, aga nõudis siiski kahte trigonomeetrilist avaldist.
Harva on asjad tasakaalus, ikka kipuvad nad minema veidi paremaks ja siis jälle veidi halvemaks ja nii edasi. Füüsikud kirjeldavad sellist korduvat tasakaaluasendi ümber toimuvat pendeldamist sõnaga võnkumine. Meie ümber võib märgata palju ilusaid võnkumisi: kiiged, pendlid, vedrud, helikeeled ja nii edasi. Võnkumise matemaatiliseks kirjelduseks kasutame perioodilisi funktsioone. Siinus- ja koosinusfunktsioon on ilmselt kõige ilusamad näited perioodilistest funktsioonidest. Nagu elastse vedru näite juures nägime [lk 236], kirjeldavad nad mingis mõttes kõige lihtsamaid ja loomulikumaid võnkumisi. Kuna need võnkumised on kõige levinumad ja üpris ilusad, kutsutakse neid ka harmoonilisteks võnkumisteks.
Kuigi trigonomeetriliste funktsioonide sin(t) ja cos(t) periood on alati sama – täpselt 2π –, võime otsustada nurka ka kiiremini või aeglasemalt muuta ning seega kirjeldada kiiremaid ja aeglasemaid harmoonilisi võnkumisi. Nägime seda juba ka vedru juures [lk 236], kus olenevalt vedru omadustest olid lahendiks kiiremad või aeglasemad harmoonilised võnkumised.
Funktsiooni sin(t) asemel võime nii vaadata ka funktsioone sin(2t) või sin(4t) , mille perioodid on vastavalt kaks ja neli korda väiksemad.
Funktsioonid kujus sin(nt) ning cos(nt), kus n on positiivne täisarv, kirjeldavad kõiki siinus- ja koosinusfunktsioone, mis läbivad vahemikus [0,2π] täpselt täisarvu täisperioode.
Sellised funktsioonid kirjeldavad ühe otstest kinnitatud pillikeele kõiki erinevaid põhivõnkumisi ehk osahelisid. Nende võnkumiste sagedused (ehk kui mitu täisperioodi nad läbivad) annavad kõik põhivõnkesagedused.
Nagu muusikast teame, võime iga liitheli või akordi lahti kirjutada osahelidena. Samamoodi selgub, et tegelikult võime iga piisavalt ilusa perioodilise funktsiooni esitada põhivõnkumiste summana. Eri põhivõnkumisi tuleb erinevate funktsioonide esitamiseks muidugi kasutusele võtta erineval määral.
Sellist perioodiliste funktsioonide esitamist põhivõngete abil nimetatakse nende Fourier’ esituseks. Vaatame näiteks niinimetatud saehamba funktsiooni:
Ettevaatlikuks peaks muidugi tegema asjaolu, et funktsiooni graafikul asuvad vertikaalsed jooned. Nii jääb mulje, nagu kohtadel π ja 3π ja nii edasi oleks funktsioonil lõpmatult palju väärtuseid, aga ometigi on definitsiooni järgi funktsioonil igale kohale lubatud vaid üks väärtus [lk 64]. Ja kõik on õige, teemegi siin natuke haltuurat, õigupoolest on saehamba funktsioon nendes kohtades võrdne täpselt poolega, aga see näeks hoopis koledam välja.
Saehamba Fourier’ esitus ehk lahtikirjutus võnkumiste summana on järgmine keeruline moodustis:
Nagu näeme, peab aeglaseid võnkumisi võtma suuremal määral kui kiiremaid – kordaja siinusfunktsioonide ees ju aina kahaneb. Järgmisel joonisel näitame kõigepealt viit esimest siinusfunktsiooni oma kordajatega. Seejärel liidame nad kokku, paneme veel juurde pool ning saamegi midagi üsna saehamba sarnast:
Mida rohkem siinusfunktsioone kokku liidame, seda sarnasem on tulemus ka saehambaga. Nagu näeme, ei tea ka meie lihtne lähendus saehambale, kas olla π juures väärtusega üks või null.
Fourier’ esitus ja spekter
Fourier’ esitus pakub hea vaatevinkli signaalide ja protsesside uurimiseks. Fourier’ esitus paneb teatud mõttes tööle analoograadiod, võimaldab leida kosmilisi objekte ning teha automaatset pilditöötlust.
Kogu asja võlu seisneb lihtsustatult selles, et teatud signaalidest on palju lihtsam aru saada, kui mitte vaadata nende arengut ajas, vaid uurida, kui palju üht või teist põhivõnkumist signaali kirjeldamiseks kasutama peab. Tihti on see ka ainus loomulik vaateviis. Funktsiooni Fourier’ esitust saab näidata graafiliselt nii-öelda spektri abil: spekter näitab täpselt, kui suure osa signaalist moodustab üks või teine põhivõnkumine.
Näiteks järgnevalt võtame kaks võnkumist, ühe madalamal ja teise kõrgemal sagedusel. Seejärel leiame signaali, milles esimese võnkumise amplituud on kaks, teise amplituud aga üks. Kogu see informatsioon ongi kompaktselt kirjas joonisel paremal all nurgas olevas spektris.
Tavaliselt on muidugi sagedused ka täpsete arvuliste väärtustega ning sageduskomponendid näitavad iga osavõnkumise amplituudi. Need on aga juba detailid.
Toome järgnevalt ka näite, kus signaali esitamisest võnkumiste summana võiks ka otseselt kasu olla.
Oletame, et otsustad sõbrale sünnipäevaks ühe omamoodi sünnipäevalaulu lindistada. Mikrofon on olemas, arvuti ka ja lindistamine ise ei valmista mingeid muresid.
Ometigi jääb salvestisele tugev sahin. Kas sellest on võimalik kuidagi lahti saada?
Võtmetähelepanek on järgmine: sahin on tihti seotud eelkõige üleliigsete kiirete võnkumistega. Ehk teisisõnu, kui vaatame oma salvestist tema Fourier’ esituses ehk võngete summana, siis on sahin sinna suurel määral salvestunud väga kõrge sagedusega komponentidesse.
Kuna laul ise koosneb põhiliselt hoopis väiksema sagedusega võngetest, on Fourier’ esituses sahin ja hääl teatud mõttes eraldatud. Seda näeme spektrist, kust häälele vastavad eelkõige need kõrged tipud spektri vasemal ja sahin on paremale jääv madal osa.
Nüüd võime sahina komponendi Fourier’ esituses ära kustutada ja ülejäänu jälle kokku liita. Saame uue signaali, mis kannab peaaegu kõiki häälega kaasas käivaid võnkumisi, kuid ei sisalda enam sahinat ja kõlab seega puhtamalt. Uus signaal ja tema spekter näevad välja järgmised:
Umbes nii töötavadki digitaalsed filtrid näiteks muusikaloomeprogrammides. Kas pole kaval?
Võnkumise levimisprotsessi ruumis kutsutakse laineks. Helilised võnkumised levivad helilainetena. Oma vestluse ja muusika kaugele sõbrale saatmine oli vanasti päris keeruline – lihtsalt suuga teele saadetud helilained eriti kaugele ei ulatu.
Kaval viis helilainete edastamiseks on teisendada nad elektromagnetlaineteks ning hoopis neid edasi saata. Aga sealgi on omad raskused. Näiteks on kohe probleemiks see, et meie hääl ja muusika on madalal sagedusel ning madalsageduslike elektromagnetlainete saatmiseks peab olema kilomeetrite pikkune antenn! Teine probleem tuleb sellest, et samal ajal tahaksime võibolla ringi saata väga erinevat sisu ja kui need oleksid kõik salvestatud sama sagedusega elektromagnetlainetesse, seguneksid sisud omavahel ja välja tuleks mingi tohuvabohu. Seega on hea raadiosüsteemi väljatöötamine parajalt keeruline.
Õnneks on alati leidunud nupukaid selle, kes keerulistele olukordadele lahenduse leiavad. Toodud muredest lahti saamiseks hakati raadiosignaale edastama niiöelda moduleerimise teel – madalsageduslik sisu salvestati väga kõrgsageduslikele lainetele. Esiteks saab selliseid laineid saata ja vastu võtta täitsa mõistliku antenniga. Teiseks tuleb välja, et nii võime paralleelselt saata ka väga palju erinevaid signaale.
Kõige lihtsam neist moduleerimise tehnoloogiatest, AM ehk amplituudi modulatsioon on lähedalt seotud tähelepanekuga, et trigonomeetriliste funktsioonide korrutise võib lahti kirjutada nende summana ning vastupidi. Amplituudi modulatsioon ei tähenda seejuures midagi muud kui seda, et ühe laine amplituudi muudetakse teise laine abil. Seeläbi salvestatakse algsesse lainesse informatsiooni.
Lihtsustatult võib mõelda, et saatjast teelepandav raadiosignaal y(t) koosneb ühest kandvast lainest kõrgel sagedusel ωk. Kui tahame talle informatsiooni külge pookida, muudame kandva laine amplituudi mingi madalama sagedusega laine abil.
Näiteks kui sagedusega ωk liigub kandev laine, mille amplituudi muudetakse koosinuselainega sagedusel ωm, siis võiks kogu signaal olla kujus:
Kuna trigonomeetriliste funktsioonide korrutise võime lahti kirjutada ka nende summana [lk 250], võime signaali samas näha ka kui eraldiseisvate lainete kooslust:
Teisisõnu, meie signaal koosneb kolme laine summast: kandvast lainest ja kahest lisalainest. Nende lainete taga peidus olevate võnkumiste sagedusesitus ehk spekter oleks siis järgmine:
Need lisalained või lisavõnkumised saab nüüd vastuvõtjas Fourier’ teisenduse [lk 257] abil eraldada, just nii nagu sahina eraldamiselgi. Seeläbi õnnestub meil kandvale lainele lisatud signaal vastuvõtjas välja lugeda!
Veelgi enam, kui meie kandev laine on näiteks sagedusel 1000 kHz ja sisuks on signaal alla 5 kHz, siis mahub ju kogu signaal ehk kõik kasutatavad lainekomponendid 995 kHz ja 1005 kHz vahele. Seega juba sagedusega 1020 kHz kandelainel võiksime julgelt paralleelselt teise sisuga signaali edastada – kasutatavad lained ei kattuks ja neid saaks ilusasti vastuvõtjas eraldatult välja lugeda.
Muidugi on kandelainele lisatav sisu enamasti palju keerulisem kui üks pisike laine ning lisaks muutub ta veel ajas, ent põhimõte jääb samaks: saatjas lisatakse informatsioon kandjalaine amplituudi muutmise teel ning vastuvõtjas saadakse see signaali komponentideks jagamise abil taas kätte.
Siinkohal sai küll kirjeldus kiire ning ebatäpne, aga huvi korral uurige, see on päris põnev! Tõtt-öelda on muidugi AM-raadio juba üsna iganenud tehnoloogia. Tänaseks on pigem kasutusel niinimetatud FM-raadio, kus muudetakse hoopis kandva laine sagedust, mitte amplituudi. Ja juba varsti minnakse ilmselt kõikjal üle digitaalsete signaalide edastamisele. See jääb aga kahjuks siit raamatust väljapoole.
Polünoom on üks keeruline võõrsõna, aga sellel ei maksa end heidutada lasta – hullemategi sõnade taga peitub vahel täiesti toredaid selle: näiteks trubaduur või seismoloog. Polünoomide korral on tegemist vaid teatud lihtsate ja hästi uuritud funktsioonidega.
Üks polünoom oskab sisendarvudega teha ainult väga tavalisi tehteid: ta võib neid võtta erinevatesse naturaalarvulistesse astmetesse, neid mingi arvuga (kordajaga) läbi korrutada ning siis saadud tulemusi liita ja lahutada. Seega vägagi sõbralik sell.
Kui räägitakse reaalarvulistest polünoomidest, siis on nii sisendarvud, kordajad kui ka saadav väljund reaalarvud. Näiteks kõik järgmised funktsioonid on reaalarvulised polünoomid:
Nagu majaga katus, nii käib polünoomiga alati kaasas tema aste. Siin peetakse lihtsalt silmas kõige kõrgema astmega liikme astet. Näiteks esimene toodud polünoomidest on teise astme polünoom ehk ruutfunktsioon, teine on esimese astme polünoom ehk lineaarne funktsioon ning kolmas viienda astme polünoom.
Polünoomi aste on oluline, sest ta määrab, kui palju jõnkse võib maksimaalselt olla polünoomi graafikul – lineaarfunktsioonil neid polegi, ruutfunktsioonil on üks, kuupfunktsioonil kuni kaks ja nii edasi.
Kas Sa usud, et kui liidad või korrutad omavahel kaks polünoomi, siis on tulemuseks jällegi üks polünoom?
See omadus on hea ja kasulik sellepärast, et nüüd võime alati julgelt polünoome kokku liita, lahutada ja korrutada, ilma et peaksime kartma, et meid ootab ees mingisugune hirmus funktsioon, mille arvutamine võiks meil üle jõu käia.
Katsetame neid omadusi järgnevate polünoomide peal: 3x2 + 3 ja x4 – 2x. Tähistame esimest polünoomi p(x)-ga ja teist q(x)-ga. Neid kokku liites, lahutades ja korrutades saame kolm uut polünoomi:
Teiseks heaks omaduseks on polünoomide sile ja mõnus graafik – nende graafiku saab tõmmata joonisele ühe joonega ehk nad on pidevad. Pidevuse kirjeldusest ja tähtsusest loe pidevuse peatükist [lk 317].
Kolmandaks on polünoomid sõbralikud ka kahe reaalfunktsioonidega ette võetava teisenduse suhtes. Esimest teisendust nimetatakse tuletiseks – sisuliselt näitab tuletis funktsiooni muutumise kiirust [lk 320]. Teist nimetatakse integraaliks ning see iseloomustab näiteks funktsiooni graafiku ja -telje vahele jäävat pindala [lk 340]. Tuleb välja, et polünoomidega neidsamu teisendusi tehes saame vastu jälle polünoomid.
- Polünoomi tuletis on ühe võrra väiksema astmega polünoom.
- Polünoomi määramata integraal on ühe võrra kõrgema astmega polünoom.
Polünoomide pere on üsna kinnine – pea kõik tähtis, mis nendega teha võib, annab tulemuseks taas polünoomi.
Polünoomid on tänu piiratud operatsioonidele üsna lihtsad – neid on lihtne kirjeldada, nendega on lihtne ringi käia, nende väärtusi on lihtne leida nii inimesel kui ka arvutil.
Samas on nad kõigest sellest lihtsusest hoolimata uskumatult laia haardega tegelased: ükskõik millise teise vähegi mõistliku (näiteks pideva) funktsiooni jaoks leidub alati polünoom, mis näeb temaga nii sarnane välja, et isegi luubiga vaadates võiks nad omavahel sassi ajada.
Näiteks polünoom
näeb piirkonnas –π kuni π välja täpselt nagu siinusfunktsioon [lk 214]:
ning polünoom
kirjeldab nulli lähedal hästi eksponentsiaalfunktsiooni y = ex.
See, et võime teisi funktsioone nii kergelt polünoomidega segamini ajada, tähendab, et nii mõnigi kord võimegi reaalses elus ning arvutustes käsitleda ainult polünoomfunktsioone – oskame nendega hästi ringi käia ning samas annavad nad meile piisavalt head informatsiooni päriselt toimuva kohta.
Võime lugeja meelehärmiks avaldada lausa ühe saladuse: isegi kui käsite oma taskuarvutil logaritmi võtta, arvutab too kaabakas ainult polünoome – ta jäljendab õiget funktsiooni aga nii kavalalt ja tublilt, et sellest ei olegi võimalik taskuarvuti täpsuse juures aru saada. Arvutid kasutavadki kõikide enda arvutuste jaoks ainult polünoome.
Oluliseks märksõnaks on polünoomide puhul nende nullkohad: sisendarvud, mille korral polünoomi väärtus on null.
Selgub, et nende abil on võimalik esitada polünoomi väga mugaval kujul: kui teame, et polünoomi P(x) nullkohad on r1, r2, …, rn, võime P kirjutada kujul
kus c on lihtsalt üks reaalarv.
Näiteks ruutfunktsiooni korral saame
mis ongi kogu see tegurdamise (ja igasuguse teisendamise) lõbu, mida koolipingis hoolega õpitakse: funktsioonide esitamine mugavamas kujus.
Võib tekkida küsimus, miks peaksid meid huvitama just nullkohad ja mitte näiteks „kolmkohad” – kohad, kus polünoomi väärtus on kolm. Õigupoolest on vastus õige lihtne: nulli korral on tekkiv kuju lihtsalt kõige kompaktsem ning nullkohad jäävad paika ka funktsiooni läbikorrutamisel mõne reaalarvuga.
Lisaks kui oskame leida nullkohti, siis kolmkohtade leidmiseks tuleb polünoomist lahutada kolm ning leida saadud tulemuse nullkohad.
Saame näidata, et kui polünoomi aste on n, siis tal ei saa olla rohkem kui n nullkohta (või „kolmkohta”). Sellest tulemusest võib intuitiivselt aru saada, kui mõelda, et lineaarfunktsioon ei tee ühtegi jõnksu, ruutfunktsioon teeb maksimaalselt ühe jõnksu, kuupfunktsioon kaks jõnksu ja analoogselt teeb n astme polünoom n – 1 jõnksu. Et pärast teatud nullkohta polünoomiga jälle nulli tagasi jõuda, on meil alati tarvis ühte jõnksu ja n – 1 jõnksu abil võime nõnda nulli jõuda täpselt n korda.
Kõigest sellest võib kavalam järeldada, et kui kaks n -astme polünoomi on võrdsed n + 1 punktis, siis on nad võrdsed absoluutselt igal pool (tõestuseks tuleb lihtsalt uurida nende kahe polünoomi lahutamisel saadavat polünoomi). Sellel üllataval teadmisel on rakendused ka päriselus.
Oletame, et leiate sõpradega seiklusmatkalt kena koguse briljante ja otsustate peita kogu saagi viieks aastaks seifi. Eks ikka selleks, et enne hästi järele mõelda, mis kogu varaga pihta hakata.
Teil on olemas ka 9-märgilise salakoodiga ultramodernne seif, kuhu briljandid varjule panna. Kuidas aga kindlaks teha, et te ainult kolmekesi üheskoos saaksite seifi avada? Toredaks abimeheks osutub siin polünoomide tundmine, eriti üks märkus lisateadmistest – iga n-kohalise polünoomi määravad üheselt ära temal asetsevat n + 1 punkti.
Seega, kui näiteks on antud ruutpolünoom x2 + ax + b, siis niipea kui teame kolme temal asetsevat punkti, teame tegelikult kõiki polünoomil asetsevaid punkte. Kuid suvalise kahe punkti teadmine ei ütle polünoomi kohta just väga palju.
Idee on nüüd selge: lasete arvutil välja mõelda mõne suvalise polünoomi ning igaühele väljastada täpselt ühe punkti sealt polünoomilt. Salakoodiks saab olema kokkukirjutatult selle polünoomi väärtus kohtadel –1, 0 ja 2.
Näiteks kui salajaseks polünoomiks osutub
siis osutub salakoodiks 345308240, sest näiteks funktsiooni väärtus kohal –1 on –12 – 36 · (–1) + 308 = 345 jne.
Kui sõber Mart saab punkti (1; 273), sõber Ants punkti (20; –12) ning ise saad punkti (9; 65), siis nagu graafikult näete, pole Mardil ja Antsul kahekesi õigeks vastuseks suurt lootust: neil ei olekski õigupoolest põhjust ühtegi kombinatsiooni väga eelistada, sest kaks punkti ei ütle võimaliku polünoomi kohta peaaegu mitte midagi.
Tähelepanelik lugeja võiks vaielda, et miks ei võiks seda olukorda lahendada tunduvalt lihtsamalt: andes igale sõbrale lihtsalt kolm salakoodi numbrit. See on tõesti võimalik, kuid siis peaks kood olema tunduvalt pikem, sest vastasel korral võivad kaks sõpra kokku tulla ning kolmanda sõbra puuduvad numbrid lihtsalt läbi proovida, mis eelneva lahenduse puhul poleks võimalik.
Ruutfunktsioon või teisisõnu ruutpolünoom on ilmselt koolitunni populaarseim ning käsitletuim funktsioon.
Seda populaarsust saab ka natuke selgitada: ta on väga levinud (mäletate ehk füüsikast läbitud distantsi avaldamist kiirenduse kaudu?), teda on piisavalt lihtne joonistada ning kirja panna ja samas on ruutfunktsiooni nullkohtadel esmapilgul keerulisena näiv lahendivalem, millega õpilasi hirmutada. Või siiski?
Alustame ruutfunktsiooniga tutvumist tema graafiku juurest ja näitame, kuidas kõik erinevad ruutfunktsioonid on lihtsate geomeetriliste teisenduste kaudu omavahel seotud. Seejärel leiame ruutfunktsiooni lahendivalemi ja anname sellelegi geomeetrilise intuitsiooni.
Ruutfunktsiooni graafik
Niipea kui oleme joonistanud ühe funktsiooni graafiku, saame hakata sellega mängima. Näiteks võime seda graafikut nihutada ja erinevatest sirgetest peegeldada.
Kuigi lõbus on see alati, saab sellest protseduurist ka mõnikord kasu lõigata. Näiteks saame nende teisenduste abil meeles pidada trigonomeetriliste teisenduste valemeid [lk 242]. Ruutfunktsiooni korral võime selliste geomeetriliste teisenduste teel luua ühest algfunktsioonist pea kõik teised ruutfunktsioonid ning, nagu hiljem näeme, leida isegi ruutvõrrandi lahendivalemi.
Alustame ruutfunktsioonist
Teda üles-alla nihutades saame funktsioonide kujus
graafikud.
Nihutades algset funktsiooni aga horisontaalselt – või teisisõnu nihutades x-telge tema suhtes –, saame kõik funktsioonid kujus
Nüüd, kui peegeldame esialgset funktsiooni x-telje suhtes, saame funktsiooni
graafiku.
Algse funktsiooni peegeldus y-telje suhtes ei tee aga midagi huvitavat – meie funktsioon on y-telje suhtes sümmeetriline ja jääb peegelduse tõttu samaks.
Kõiki neid teisendusi võib muidugi teha ka järjepanu ning nii neid kombineerides leiaksime kõikide funktsioonide kujus
graafikud. Kui tahaksime päris üldkujusse jõuda, peaksime lisaks veel lubama ka y-telje skaleerimist.
Varsti näeme, et selline geomeetriline mõtlemine annab aimu ka ruutfunktsiooni lahendivalemi tagamaadest. Enne seda lahendame aga ruutvõrrandi puhtalt algebraliselt.
Ruutfunktsiooni lahendivalem
Ruutfunktsiooni lahendivalem võib jääda pisut müstiliseks, kuna tihti ei ole aega seda korralikult tuletada. Tegelikult ei ole selles lahendivalemis midagi hirmsat, kui on viitsimist pisut kaasa mõtelda. Lubame, et ei lähe kauem, kui korraliku suure koorejäätise söömine aega võtaks, ning lubame jäätise ka seltsi võtta. Üritame siis valemi samm-sammult tuletada.
Kõige lihtsam võrrand, mis võib ette tulla, on muidugi x2 + c = 0 ehk x2 = –c. Sel juhul – kuna ruutjuurt [lk 111] oskame ju hästi võtta – teame, et vastuseks on ±√–c. Oluline on märgata, et miinusmärk c ees ei tähenda sugugi, et meil peaks kohe tegemist olema negatiivse arvuga. Näiteks kui c = –4 saame võrrandi x2 – 4 = 0 ning lahenditeks oleksid
ehk 2 ja –2.
Raskusi ei valmista ka võrrand a · x2 + c = 0, kuna sel juhul võime lihtsalt kogu võrrandi jagada a-ga läbi ning jõuame sarnaselt eelnevaga vastuseni
Mis aga juhtub, kui juurde tuleb liige b · x ehk kui ruutvõrrand on kujus x2 + bx + c = 0? Tuletame meelde, et võrrandi lahendamine tähendab endiselt, et leiame vastuse kujul
Üldkujus on aga sees ka x-i ruut. Eelnevalt saime temast lahti, rakendades ruutjuurt, ja ausalt öelda, ega mingit muud müstilist trikki ruudust lahti saamiseks pole. Seega tahame ka seekord võtta ruutjuurt. Aga millest?
Ruutjuurt oskame võtta hästi ainult ruutavaldistest. Esimesel juhul oli meil lihtne ruutavaldis x2, seekord jõlgub kaasa aga ka libe bx-liige. Kuidas temast lahti saada?
Tuleb lihtsalt märgata, et tegelikult oskame me võtta ruutjuurt mitte ainult x2-st, vaid ka näiteks (x + 4)2-st või (x –1)2-st.
See on abiks, kuna (x + 4)2 = x2 + 8x + 16 annab meile ka x-iga liikme! Nii saame avaldisest x2 + 8x + 16 võtta ilusti ruutjuurt
Seega tuleb juurimise jaoks leida x-ile sulgudesse õige kaaslane, mis lahtikorrutades annaks liikme bx.
Tuletame meelde, et ruutliikme tegurdamine käib järgnevalt:
Kui nüüd valime
ongi liikme x ees soovitud kordaja b
See näeb välja juba peaaegu nagu meie algne võrrand x2 + b · x + c = 0.
Ainsa vahena on ülemises valemis lihtsalt üks üleliigne liige
ning liige c on hoopis puudu.
Seega peame algse ruutfunktsiooni kirjeldamiseks lihtsalt ruudust
maha lahutama üleliigse osa
ja tagasi liitma c:
Nii saab meie võrrand x2 + b · x + c = 0 kuju
Viies osa liikmeid teisele poole, oleme juba väga heas positsioonis juurimiseks:
Siin saame võtta ruutjuure ning vastuseks tuleb
ehk
Taandatud ruutvõrrandi lahendivalem ongi käes!
Kui x2 ees on veel kordaja a, peame lihtsalt b ja c läbi jagama a-ga ning jõuame just läbi arutatud olukorrani. Nii on ruutvõrrandi üldkuju ax + bx + x = 0 lahendivalemiks
mida tihti kirjutatakse ka kujus
Kontrolli, et ka viimane teisendus kehtib!
Selle valemi abil võib lahendada ükskõik millist ruutvõrrandit. Näiteks kui õpetaja lööb lauale ruutvõrrandi x2 – 3x – 10 = 0, võime välja võtta oma valemi, sinna sisse pookida a = 1, b = –3 ning c = –10 ning saamegi vastuseks lahendid –2 ja 5.
Lahendivalem geomeetriliselt
Lubasime, et lahendivalemi leidmisest saab ka geomeetriliselt mõelda. Kuna meil on tegelikult juba ruutvõrrandi lahendivalem leitud, siis mingis mõttes on see muidugi tühi töö. Siiski aitab järgnev mõttekäik anda ruutvõrrandi lahendivalemi leidmise erinevatele etappidele ja seega ka lahendivalemile endale geomeetrilist intuitsiooni ning seeläbi ehk aitab valemit ja selle tuletust meeles pidada.
Aluspunktiks on tähelepanek, et ruutvõrrandi x2 = c lahendamine tähendab geomeetriliselt täpselt funktsioonide y = x2 ning y = c graafikute lõikepunktide x-koordinaatide leidmist. Seda muidugi oskame teha ruutjuurt võttes ja vastuseks on
Peaaegu üldkujus ruutvõrrandi x2 + bx + c = 0 lahendamine tähendab omakorda muidugi ruutfunktsiooni y = x2 + bx + c ning x-telje lõikepunktide leidmist.
Kogu ruutfunktsiooni lahendivalemi leidmiseks vaja läinud teisendusterea eesmärk oli taandada teine olukord esimesele, taandada keerulisemate lõikepunktide leidmine lihtsamate lõikepunktide leidmisele. Mingis mõttes tähendab see, et tahame oma suvalise ruutfunktsiooni graafiku teisendada ruutfunktsiooni y = x2 graafikuks.
Selle jaoks nihutame esmalt funktsiooni graafikut
võrra horisontaalselt (positiivne suund on paremale), et funktsiooni graafik oleks sümmeetriline y-telje suhtes.
Seejärel liigutame graafikut
võrra vertikaalselt (positiivne suund on üles), et viia graafiku kõige alumine punkt täpselt koordinaatteljestiku nullpunkti.
Nii oleme kahe teisenduse abil jõudnud funktsiooni y = x2 graafikuni.
Kuidas on teisenenud algse ruutvõrrandi nullkohad? Kui enne olid nad sirge y = 0 ning algse ruutfunktsiooni lõikepunktid, siis teisenduste käigus esiteks nihutasime neid lõikepunkte
võrra horisontaalselt ning seejärel tõstsime
võrra.
Nende teisenduste järel said nullkohtadest funktsiooni y = x2 ning sirge
lõikepunktid.
Nende lõikepunktide x-koordinaadid on aga täpselt antud valemiga
Kuna vertikaalsed, üles-alla teisendused x-koordinaate ei muuda, peame ainult arvesse võtma veel horisontaalse nihke. Uued lõikepunktid on algsete suhtes
võrra nihutatud, seega peame algsete lõikepunktide x-koordinaatide leidmiseks lahutama veel
Saamegi taas kord loodetud vastuse.
Seekord on aga mõlemal liikmel ka taust: esimene tuleb funktsiooni sellisest üles-alla nihutamisest, et ta istuks täpselt horisontaalteljel. Teine pärineb horisontaalsest nihutamisest, mis viib funktsiooni graafiku sümmeetriliseks vertikaaltelje suhtes.
Kui mõni pahaloomuline bakter on organismi jõudnud, ei pruugi sellest algul aimugi saada, sest iga bakteripere ei hakka kohe tramburaid korraldama, vaid ootab vahel veel päris mitmeid tunde. Miks nii?
Nimelt ei ole ühel või kahel või isegi tuhandel bakteril mõtet hakata vallatusi tegema ja mürkaineid eritama, sest immuunsüsteem saadaks selle peale kohe välja oma ustava armee ja teeks neile tuule alla.
Seega paljunevad bakterid vaikselt, kuni neid on piisavalt palju, ja hakkavad alles seejärel kurja tegema. Sel juhul on immuunsüsteem juba raskustes. Bakteritel ei lähe paljunemiseks eriti palju aega, sest iga bakter pooldub ideaalsetes tingimustes umbes iga poole tunni järel.
Selle tagajärjeks on väga kiire kasv! Näiteks kui 1000 bakteril lasta ideaalsetes tingimustes seltsida, kasvab nende arv järgmise 12 tunni jooksul järgnevalt:
Juba poole päevaga on tuhandest saanud rohkem kui sada tuhat! Tuleb välja, et saadud graafikut kirjeldab täpselt üks ilus ja tähtis funktsioon: eksponentsiaalfunktsioon. Ja kuigi maos ei ole bakteritele ideaalsed kasvutingimused, aitab see ikkagi ehk piisavalt hirmutada – ka pisike pahaloomuline bakteripere on juba ohtlik!
Eksponentsiaalfunktsioonideks on näiteks funktsioonid y = 2x või y = ex, kus x võib olla ükskõik mis reaalarv.
Samuti võib eksponentsiaalfunktsiooni alus olla ühest väiksem, näiteks y = 0,1x.
Üldkujul on eksponentsiaalfunktsioon kujus ax, kus a on positiivne reaalarv. Õpikutes otsustatakse tihti ka lisada tingimus, et a ≠ 1. Seda lihtsalt selle jaoks, et välistada konstantne funktsioon y = 1. Mõnikord arvatakse juurde veel ka kordaja: loetakse eksponentsiaalfunktsiooniks ka funktsioone b · ax, kus b on suvaline reaalarv.
Seda, miks a peab olema positiivne, selgitab kõige paremini üks võimalik eksponentsiaalfunktsiooni definitsioon: eksponentsiaalfunktsiooni näol ei ole tegemist millegi enama kui astendamise laiendamisega irratsionaalarvulistele astmetele ja astme aluselt nõudsime ju ka positiivsust [lk 110].
See laiendus on täpselt analoogne ratsionaalarvude reaalarvudele laiendamisega: tuleb lihtsalt graafikule jäävad imepisikesed augud täis toppida. Rangelt tähendab see ratsionaalarvulistele astmetele nende piirväärtuste lisamist [lk 313]. Negatiivsete aluste korral on graafik aga hüplik ja mingist aukude täitmisest seal väga juttu olla ei saagi.
Õigupoolest, nagu astme peatükist mäletame, tekib negatiivsete aluste korral häda juba täisarvulistelt astmetelt ratsionaalarvulistele üle minnes – et anda tähendus arvule
pidime ju sisse tooma hoopis kompleksarvud [lk 89]. Ühesõnaga negatiivsed alused jätame mängust välja.
Eksponentsiaalfunktsiooni võib defineerida ka teisiti. Näiteks alusel e võib eksponentsiaalfunktsiooni defineerida järgmise polünoomi meenutava avaldise abil:
Selle valemi tagamaid selgitasime natuke ilusate arvude peatükis [lk 106].
Eksponentsiaalfunktsioon ax on määratud kõikide reaalarvude korral ehk tema määramispiirkonnaks on reaalarvude hulk. Tema graafik on ilus ja pidev ehk teda võib joonistada pliiatsit paberilt tõstmata.
Eksponentsiaalfunktsiooni kuju sõltub tema alusest.
- Kui alus a on suurem kui üks, on ax kasvav funktsioon.
- Kui alus a asub nulli ja ühe vahel, siis on tegemist kahaneva funktsiooniga.
- Alusel üks on tegemist konstantse funktsiooniga, mida nii mõnigi kord eksponentsiaalfunktsioonide hulka ei loeta, kuna ta ei kasva ega kahane.
- Viimaks, nagu mainisime, negatiivsete aluste korral eksponentsiaalfunktsiooni defineerida ei saagi.
Selgub, et see, kas alus on ühest suurem või väiksem, ei muuda teatud mõttes eksponentsiaalfunktsiooni olemust, vaid lihtsalt tema suunda.
Nimelt on pöördarvulistel alustel (näiteks alustel 2 ja ½) eksponentsiaalfunktsioonid teineteise peegeldused y-telje suhtes. Ühel juhul rändab eksponentsiaalfunktsioon x-telje kohal nullist lõpmatusse ja teisel juhul vastupidi.
Miks see nii peaks olema, pole just raske näha: teame ju, et
ja seega
ax loetuna negatiivses suunas.
Eksponentsiaalfunktsiooni ax muutumispiirkonna moodustavad kõik positiivsed reaalarvud. Teisisõnu leidub iga positiivse reaalarvu b jaoks x, nii et ax = b. Selles võib ilmselt veenduda puhtalt graafikut vaadates – graafik on pidev, ühel pool läheneb nullile, teisel pool tormab lõpmatusse. Tegemist on olulise omadusega, mis võimaldab meil hiljem defineerida eksponentsiaalfunktsiooni pöördfunktsiooni – logaritmfunktsiooni [lk 290].
Eksponentsiaalfunktsiooni graafikut uurides näeme, et ühest suurema aluse korral kasvab ta aina kiiremini. Selgub, et asi on veelgi hullem – ka eksponentsiaalfunktsiooni kasvamise kiirus ehk tuletis [lk 320] kasvab järjest kiiremini, ja ka tema kiirendus ja nii edasi.
Funktsiooni kasvamise kiirust näitab tema tuletis. Selgub, et eksponentsiaalfunktsiooni ax tuletise võtmiseks tuleb funktsiooni ainult mingi reaalarvulise konstandiga läbi korrutada: ehk siis ax tuletiseks on b · ax, kus konstandi b väärtus sõltub a väärtusest. Seda fakti võib tõlgendada järgmiselt: eksponentsiaalfunktsiooni hetkeline kasv on alati võrdeline funktsiooni väärtuse endaga. See osutub oluliseks just kasvuprotsesside tõlgendamisel.
Eksponentsiaalfunktsioon kasvab igas kindlas vahemikus sama arv kordi. Tõepoolest, näiteks vahemikus pikkusega üks kehtib
iga reaalarvu x jaoks.
Üldisemalt võibki mõelda, et eksponentsiaalfunktsioon teeb liitmisest korrutamise. See on tegelikult juba astendamisest tuntud omadus: ax+y = ax · ay. Ka selle omaduse kaudu saab tegelikult eksponentsiaalfunktsiooni defineerida: tegemist ongi ainsa pideva reaalarvulise funktsiooniga, mis teeb liitmisest korrutamise ehk mille korral kehtib võrrand ƒ(x + y) = ƒ(x) · ƒ(y).
Eksponentsiaalfunktsioon erinevatel alustel
Nägime juba, et eksponentsiaalfunktsiooni ax käitumine sõltub tema alusest a. Huvitaval kombel võime aga tegelikult kõiki eksponentsiaalfunktsioone kirjutada ka ühel ja samal alusel – peame selle jaoks lihtsalt astendajat muutma.
Näiteks funktsiooni 4x võime kirjutada alusel 2 funktsioonina 22x ning alusel 16 funktsioonina 160,5x, sest ühtepidi 4 = 22 ja teisalt 4 = √16 = 160,5. Üldisemalt, kui tahame kirjeldada funktsiooni ax alusel b, peame lihtsalt otsima välja arvu c nii et bc = a. See on iga positiivse reaalarvu a korral ka võimalik, kuna eksponentsiaalfunktsiooni muutumispiirkonnaks on kõik positiivsed reaalarvud.
Seega võime kirjutada
Funktsioonide ühel astmel kirjutamine on lihtsustav, sest nii on neid kergem omavahel võrrelda – näiteks oleks ju päris raske öelda, kas kiiremini kasvab protsess 50,5x või 30,8x. Jääb küsimus, milline ühine alus valida.
Mõnikord kasutatakse kümnendsüsteemist pärit alust 10, mis räägib kümnekordistamisest, mõnikord alust 2, mis räägib kahekordistamisest. Kõige enam kirjutatakse aga eksponentsiaalfunktsioon ilusa-arvulisele alusele e [lk 102]. Funktsioon ex annab teatud mõttes kõige loomulikuma kasvuprotsessi: sellel juhul on kasvu hetkekiirus alati täpselt võrdne hetkesuurusega ehk funktsioonide keeles: ex tuletis on igas punktis täpselt ex [lk 320].
Kõikide teiste eksponentsiaalfunktsioonide korral peame juba tuletise leidmiseks funktsiooni ise veel niinimetatud naturaallogaritmiga [lk 295] läbi korrutama. Näiteks 2x tuletis on loge 2 · 2x. Lisaks, nagu nägime kuulsate arvude peatükis [lk 102], on protsessile ex ka ilus tõlgendus – see on protsess, mille saame, kui ajaühiku peale lubatud 100% intressi makstakse hetkeliselt, pausideta.
Kuna alus e teeb mugavaks nii arvutused kui tõlgendused, on tavaks, et kõiki eksponentsiaalselt kasvavaid protsesse esitataksegi kujus beax ning eksponentsiaalselt kahanevaid protsesse kujus be–ax, kus a on mõlemal juhul positiivne reaalarv. Siin tähistab b siis algkogust ning a iseloomustab kasvukiirust.
Eksponentsiaalfunktsioonist on kõige õigem mõelda kui teatavat tüüpi väga kiirest kasvamisest või kahanemisest ajas. Nagu nägime, on eksponentsiaalse kasvamise korral kasvamise kiirus igal hetkel proportsionaalne ehk võrdeline koguse või suuruse endaga. Nii nimetatakse eksponentsiaalset kasvamist ka proportsionaalseks kasvamiseks. Just seetõttu kirjeldas ta ka bakterite koloonia laienemist – koloonia kasvu kiirus igal hetkel sõltub ju täpselt sellest, palju baktereid parasjagu pooldumas on, ehk tegelikult koloonia enda suurusest.
Eksponentsiaalne kasvamine on palju kiirem kui polünomiaalne ehk polünoomiga antud kasvamine.
Arvutite kiiruse kasv on eksponentsiaalne
Transistor on hirmutav sõna ja tõepoolest, selle taga peidab end võimas seade. Transistoreid kasutatakse elektrisignaalide tekitamiseks, võimendamiseks, muundamiseks ja lülitamiseks. Transistoritel põhineb kogu elektroonika ning nad on ka arvutite protsessorite arvutuskomponentideks.
Transistorite arv arvutis väljendab tema kiirust – seda, kui palju operatsioone ta suudab ajahetkes teha. Arvutite võimsus kasvab kiiresti, umbes iga kahe aasta järel kahekordistub transistorite arv protsessoris.
Teisisõnu umbes iga kahe aasta järel saab arvuti kaks korda võimsamaks:
Seda seaduspära märkas esimest korda juba 1965. aastal arvutiprotsessorite tootja Inteli kaasasutaja Gordon E. Moore. Nii kutsutakse seaduspära vahel ka Moore’i seaduseks. Kasvu kiiruse illustreerimiseks kasutas Moore ise järgnevat analoogiat: kui autotööstus areneks sama kiiresti kui elektroonikatööstus, siis tänaseks sõidaks auto liitri bensiiniga miljon kilomeetrit ning odavam oleks auto maha kanda kui teda kesklinnas tunniks ajakski parkida.
Graafikut on natukene keeruline lugeda, sest esimesed punktid tunduvad kõik olevat praktiliselt nullis. See tuleneb just nimelt väga kiirest, eksponentsiaalsest kasvust. Tuleb välja, et sellisel juhul on mõttekas y-telge kujutada nii-öelda logaritmiliselt, kus ühikud ei muutu liitmise vaid korrutamise teel. Selle võtte kasulikkust näitame järgmises peatükis [lk 299].
Mõni arvutiprogramm jääb aga ikka aeglaseks
Kuna arvuti kiirus kahekordistub iga kahe aastaga, võiks arvata, et ükskõik kui keerulist tööd me ka arvutile ei annaks, varem või hiljem on see vaid minutite küsimus.
Siiski nii lihtne olukord ei ole. Nimelt on paljud ülesanded, mida arvutiga lahendada võiks, lahendatavad ainult eksponentsiaalse ajaga: see tähendab, et iga kord kui arvutiprogrammi sisendit suurendada ühe ühiku võrra, kasvab programmi aeg kindla arvu kordi. Näiteks võiks programmi aeg iga sisendi jaoks pikeneda kaks korda – sel juhul kirjeldaks aja kulumist funktsioon 2sisendi pikkus ning isegi kui sisend pikkusega 10 võtaks 10 sekundit arvutusaega, siis sisend pikkusega 40 võtaks juba 340 aastat. Eluliste probleemide lahendamiseks on vahel aga vaja sisendeid suurusjärgus tuhat või isegi miljon.
Kuigi Moore’i seadus protsessorite kiirenemisest on üsna hämmastav, siis praeguse murega ta toime ei tule. Nimelt, oletame, et arvutustele kuluva aja kulumist kirjeldab tõesti eksponentsiaalfunktsioon 2sisendi pikkus. Sel juhul, isegi kui kaks korda rohkem transistoreid tähendaks tõesti ka kaks korda rohkem arvutusi ajaühikus, saaksime ühel arvutil arvutades iga kahe aasta järel sisendit vaid ühe ühiku võrra pikendada!
Sellest lähtuvalt ei või endiselt arvutiprogrammidega hooletu olla – tuleb leida häid ja efektiivseid viise arvutite tegemiseks ning selliste heade programmide kirjutamine on üks tänapäevase arvutiteaduse põhilisi eesmärke.
Temperatuuri ühtlustumine
Oled äsja valanud endale tassi kohvi ja kohe jooma hakates põletaksid kindlasti oma keelt ja huuli. Õnneks pole sellest hullu. Selgub, et kohvi jahtumine toimub eksponentsiaalse kiirusega ehk nagu juba nägime – väga kiiresti.
Nimelt märkas juba Newton oma vaatlustest, et kui asetada üks väiksem keha suurde väliskeskkonda, siis sõltub selle väiksema keha temperatuuri muutumise kiirus proportsionaalselt väliskeskkonna ja keha temperatuuride erinevusest. Nagu juba teame, tähendab see aga täpselt, et temperatuuri ühtlustumine on antud eksponentsiaalse funktsiooniga. Seega kui väiksem objekt on alguses väliskeskkonnast soojem, kirjeldab temperatuuride vahe vähenemist hästi eksponentsiaalselt kahanev protsess kujus
kus t tähistab aega ning ΔT0 on lihtsalt algne vahe temperatuurides.
Kui tahate täpselt ennustama hakata, kui kiiresti kohv ikkagi jahtub, oleks esmalt vaja teha mõned katsed, mille abil määrate konstandi a, mis sõltub kohvi enda omadustest ja näiteks ka tassist.
Edaspidi on – vähemalt sama kohvi ning sama tassi korral – igal hommikul vaja ainult mõõta kohvi ja toa temperatuuri. Seejärel saad täpselt ennustada, kaua aega läheb, kuni kohv joodavaks muutub. Loomulik on küsida: mil määral need ennustused kehtivad ja mil määral nad erinevad rohelise tee, kuumade pirukate ja teistsuguste, näiteks suuremate ja väiksemate tasside jaoks? Aus vastus on, et ega me täpselt ei tea – rohelise tee jaoks ei tohiks suurt midagi muutuda, aga pirukatega on lugu juba kahtlasem.
Edasi võib veel nuputada, kuidas käituda, kui lisad kohvile ka piima. Mis Sa arvad, kas 15 minuti möödudes on külmem kohv, millele on lisatud kohe veidi piima, või kohv, millele lisad piima alles 15 minuti lõppedes? Newtoni seaduse ja mõne lisaeelduse abil saab vastuse välja nuputada, või lihtsalt katsetades.
Muidugi pole ennustused alati sajandiku pealt täpsed – tegelikult on soojusülekande protsess palju keerulisem ning Newtoni seadus on nagu ikka lihtsustatud kirjeldus ja kehtib ainult osaliselt. Siiski on see väga tore, et klassikaline füüsika ja veidi lihtsat matemaatikat aitavad selgitada ja ennustada igapäevaseid olukordi.
Logaritm on eksponentsiaalfunktsiooni pöördfunktsioon [lk 69] ehk teisisõnu, kui järjest rakendada arvule 1000 kõigepealt eksponentsiaalfunktsiooni mingil alusel ning siis logaritmfunktsiooni samal alusel, saame jälle tulemuseks sama arvu: 1000.
Intuitiivselt tähendab see järgmist. Meenutame, et eksponentsiaalfunktsiooniga kirjeldame kasvavaid suuruseid. Söötes talle ette teatava ajahetke, saame vastuseks kasvava suuruse väärtuse selleks hetkeks. Logaritm vastab aga vastupidisele küsimusele: kui kaua võtaks aega, et eksponentsiaalne kasvuprotsess jõuaks ühe või teise suuruseni?
Näiteks oletame, et panete oma vaevaga kogutud 1000 eurot panka kasvama ning pangas makstakse intressi 5% aastas.
Kuna iga aasta möödudes suureneb summa täpselt 1,05 korda, võime summa kasvamist kirjeldada eksponentsiaalfunktsiooni abil:
Logaritm vastab aga küsimusele, mitu aastat läheb aega, et sellest algsummast kasvaks 10 000 eurot ehk summa kümnekordistuks. Teisisõnu küsib logaritm sellist x-i väärtust, mille jaoks
ehk
Matemaatiliselt kirjutatakse see välja nii:
Vastus on muuseas 47,2 aastat...
Oletame, et meile on antud mingi alus a > 0, a ≠1 nagu eksponentsiaalfunktsiooni korralgi. Kui ay = x, siis kirjutame loga(x) = y ja loeme, et logaritm arvust x alusel a on y. Kolm sümbolit järjest! Näiteks kuna 25 = 32, siis log2(32) = 5 ehk logaritm arvust 32 alusel 2 on 5.
Logaritmfunktsiooni alusel a saame nüüd, kui vaatamegi arvu x funktsiooni sisendina. Ei ole muidugi kohe päris selge, mis loom see logaritmfunktsioon ikka on ning mis väärtuste jaoks ta on üldsegi defineeritud.
Ilusam on võibolla mõelda geomeetriliselt. Nimelt kuna logaritmfunktsioon on eksponentsiaalfunktsiooni pöördfunktsioon, võib teda kirjeldada eksponentsiaalfunktsiooni enda graafiku abil.
Kui joonistame koordinaattasandile eksponentsiaalfunktsiooni y = ax graafiku, siis saame logaritmfunktsiooni alusel a lihtsalt siis, kui x- ja y-teljed ära vahetame. Nagu juba nägime, võib sellest mõelda ka kui eksponentsiaalfunktsiooni graafiku peegeldamisest sirgest y = x.
Graafikult näeme, et logaritmfunktsioon on kenasti defineeritud kõikide positiivsete reaalarvude jaoks – põhjuseks on muidugi see, et eksponentsiaalfunktsiooni väärtused saavad olla ainult positiivsed arvud.
Võib tekkida ka teine küsimus: miks me nõudsime, et alus a peab olema positiivne? Vastus tuleneb eelmisest peatükist: eksponentsiaalfunktsioon ise on defineeritud ainult positiivsete aluste korral. Negatiivsete alustega tekkis ju teadupärast probleeme: näiteks ei oska me reaalarvude raames võtta arvu –4 ruutjuurt ehk tõsta teda astmele 0,5. See on küll võimalik, tuues sisse kompleksarvud [lk 89], aga praegu tahaksime, et meie funktsioonid võtaksid nii sisendina kui annaksid ka väljundiks ainult reaalarve.
Logaritm: tehe või funktsioon?
Logaritm tuleb mõnikord lisaks funktsioonile esile ka tehete kontekstis, kui temast räägitakse kui logaritmimisest. See võib alguses üllatav tunduda, aga tihti võib mõnest matemaatilisest objektist või teisendusest mõelda mitut moodi.
Näiteks ka astendamisest võisime mõelda kui tehtest või kui funktsioonist. Tehtest rääkisime peatükis arvu aste – valisime arvu a ja arvu b ning andsime tähenduse arvu astmele ab – kahest arvust meisterdasime kokku ühe kolmanda. Eelmises peatükis aga fikseerisime astendamise aluse a ja rääkisime hoopis eksponentsiaalfunktsioonist ax – masinast, mis võttis sisendiks reaalarve ja andis vastu positiivseid reaalarve.
Samamoodi võime logaritmimisest mõelda kui tehtest: kui valime positiivse reaalarvu a logaritmi aluseks ning mingi arvu b, siis võime võtta logaritmi loga(b). Niipea, kui aga oleme otsustanud fikseerida mõne aluse, näiteks kahe, võime vaadelda funktsiooni y = log2(x).
Muidugi ei piirdu näited ainult astendamise ja logaritmimisega, lugeja võib veenduda, et ka näiteks liitmisest võime mõelda nii tehete kui funktsioonide raames. Selline paindlikkus on matemaatikale üsna omane – mida rohkem vaatevinkleid, seda rohkem võimalusi.
Ka selles peatükis käsitleme logaritmi nii ühes kui teises võtmes.
Logaritmfunktsiooni omadused
Kõige olulisem on vahest logaritmfunktsiooni juures see, et tegemist on eksponentsiaalfunktsiooni pöördfunktsiooniga. Oleme seda juba mitu korda öelnud, aga sõnastame selle veel korra ümber ka skemaatilis-matemaatiliselt!
Logaritmfunktsiooni võime võtta kõikidest positiivsetest reaalarvudest. Väärtustena annab ta lahkelt vastu kõikvõimalikke reaalarve. Ka logaritmfunktsiooni käitumine sõltub tema alusest. Näiteks logaritmfunktsioonid alusel 2 ja alusel ½ on teineteise peegeldused x-telje suhtes:
Põnev on ka meenutada, et eksponentsiaalfunktsiooni korral tuli aluse pöördarvuks muutmisel funktsiooni peegeldada hoopis y-teljest. Oskad seda mustrit selgitada?
Ka logaritmfunktsioon on kenasti pidev. Vaadeldes natuke tema graafikut näiteks ühest suurema aluse korral, näeme, et logaritmfunktsioon küll kasvab piiramatult, aga järjest aeglasemalt.
Tõepoolest, logaritmfunktsiooni kasvu kiirust näitav tuletis on antud funktsiooniga kujus
ning see on suurte x väärtuste korral nullist juba üsna eristamatu.
Konstandi b väärtus sõltub logaritmfunktsiooni alusest, näiteks kui aluseks on e, on b võrdne ühega nagu eelneval joonisel.
Muudel juhtudel on selleks konstandiks
kus a on logaritmi aluseks. Miks see nii on, selgitame juba varsti logaritmi erinevate aluste peatükis.
Korrutamisest liitmine
Kui eksponentsiaalfunktsioon tegi liitmisest korrutamise, siis logaritmfunktsioon teeb korrutamisest liitmise. Kuna tegemist on eksponentsiaalfunktsiooni pöördfunktsiooniga, pole seda muidugi raske uskuda. Enda täielikuks veenmiseks võib aga näiteks läbi teha järgneva arutelu.
- Kuna logaritmfunktsioon ja eksponentsiaalfunktsioon on pöördfunktsioonid, siis
- Samamoodi aga ka ja
- Eksponentsiaalfunktsioon teeb aga korrutamisest liitmise: seega
Kokkuvõttes saame, et
Kas sellest järeldub ka kohe, et loga(xy) = loga(x) + loga(y)? Päris automaatselt ei järeldu, peame oleme ettevaatlikud. Näiteks teame ju, et ruutu võtmisel annavad 3 ja –3 sama tulemuse, ja seega kui teaksime, et a2 = b2, ei saaks me järeldada, et a = b.
Õnneks on eksponentsiaalfunktsiooni korral olukord lihtsam. Nägime eksponentsiaalfunktsiooni graafikult, et tegemist on kas rangelt kasvava või rangelt kahaneva funktsiooniga ja seega ei võta ta ühtegi väärtust mitu korda. Seega kui teame, et ax = ay, võime järeldada, et x = y. Nii võime sellest, kui
tõesti ka järeldada, et
Logaritmi erinevad alused
Nagu eksponentsiaalfunktsiooni korral, on ka logaritmfunktsiooni iseloom alusest sõltuvalt natuke erinev. Samas on ka logaritmfunktsiooni aluse vahetamine päris lihtne ja analoogne eksponentsiaalfunktsiooni puhul toimunuga.
Nimelt oletame, et meile on antud mingi arvu y logaritm alusel 3. Tähistame seda x = log3(y) ning võime võrdväärselt ka kirjutada 3x = y. Kuidas nüüd üle minna alusele 2?
Eksponentsiaalfunktsiooni peatükis nägime, et võime arvu 3 kirjutada arvu 2 astmena, ehk 2w = 3. Edasi saame kirjutada
See tähendab täpselt, et log2(y) = wx. Aga me teame juba, et x = log3(y) ning samas puhtalt definitsioonist w = log2(3).
Seega saame log2(y) = log3(y) · log2(3) ehk logaritmfunktsiooni alusel 2 saame lihtsalt, kui korrutame logaritmfunktsiooni alusel 3 ühe kindla arvuga. Selle arvu võime leida: log2(3) ≈ 1,58 ning log2(x) ≈ 1,58 · log3(x).
Üldkujus astme vahetamist, üleminekut aluselt a alusele b iseloomustab valem:
Jällegi tähendab see ainult, et astme vahetamiseks korrutame logaritmfunktsiooni lihtsalt läbi ühe teatava arvuga – arvuga logb(a). Seetõttu jõuame pisut ehk üllatavale järeldusele: erinevatel alustel logaritmfunktsioonid on äärmiselt sarnased, võime alustada logaritmfunktsioonist alusel 2 ja saada kõik teised logaritmfunktsioonid seda funktsiooni lihtsalt nullist erineva arvuga läbi korrutades.
Millist alust valida?
Ka seekord on teatud olukordades mõne alusega kergem ja mugavam ringi käia, eriti kui sõna saavad ka loodusteadlased ja arvutimehed. Logaritm mingil alusel a muutub oluliseks, kui vaadeldav „suurusjärk” ehk olulised erinevused suurustes on määratud arvu a kordsetega.
Päriselus ja füüsikas teeme arvutusi kümnendsüsteemis. Loomulikud suurusjärgud on ühelised, kümnelised, sajalised ehk siis kümnekordsed. Seega on mugav kasutada ka logaritme alusel 10.
Kui aga näiteks töötame kahendsüsteemis, on kõik arvud antud kahe astmete summana ehk oluline muutus toimub arvude kahega korrutamisel. Nii on ka loomulik suurusjärk kaks ning loomulik logaritmimine käibki alusel kaks. Kuna arvutid teevad kõike kahendsüsteemis, tuleb ka logaritm alusel kaks ehk log2x esile just arvutitega tegelemisel.
Logaritmi alusel e nimetatakse naturaallogaritmiks ning teda tähistatakse vahel ka loge(x) asemel lihtsalt ln(x)-ga. Nagu nimest võib aimata, on temaski midagi loomulikku ja ilusat.
Näiteks nägime juba, et sel juhul on tuletis kõige lihtsamas kujus:
Arvust e oleme juba rääkinud nii ilusate arvude peatükis [lk 102] kui äsja eksponentsiaalfunktsiooni juures. Temaga on tore koostööd teha.
Logaritmid on ajalooliselt panustanud tublisti ka loodusteaduste ja eriti just astronoomia arengusse: nad võimaldasid juba enne arvutite leiutamist inimestel korrutada suuri ja keerulisi arve.
Logaritmide abi oli nii määrav, et uhke astronoom ja matemaatik Laplace oli omal ajal logaritmidest lausa joovastuses: „Imetlusväärne nõks, mis taandab mitme kuu töö vaid mõnele päevale, kahekordistades nõnda astronoomi elu ja hoides teda pikkade arvutustega kaasnevatest vigadest ja tülgastusest.” Kust see kõik tuleb?
Kõige motiveerivam on ilmselt veidi peast arvutada: 7323118 · 919222!
Õudus! Mida küll teha sellise tehtega? Tänapäeval on muidugi väga lihtne: võtad pinginaabri kotist taskuarvuti või nutitelefoni ja arvutus saab pärast mitut ebaõnnestunud katset siiski tehtud. Võib ka pikalt ja kirjalikult korrutama hakata, aga see võtab mõistuspäratult aega ja pole ei põnev ega lõbus.
17. sajandil ei olnud astronoomidel veel taskuarvuteid, kuid nende arusaam lõbust polnud sugugi nii palju erinev: neilegi ei meeldinud pikki ja igavaid arvutusi teha. Ometigi oli taevakehade liikumises tihti vaja korrutada suuri ja kosmiliselt suuri arve. Appi tuli logaritm.
Kuidas logaritm siis arvutusi lihtsustas?
Logaritmi idee arvutuste lihtsustamisel peitub tema kuulsas omaduses teha korrutamisest liitmine: log(ab) = log(a) + log(b).
Nii taandame korrutamise liitmisele ja liita on ju määratult lihtsam.
Kuidas siis näiteks korrutada omavahel 7323118 ja 919222?
Võtame kõigepealt mõlemast arvust logaritmid alusel 10, seejärel liidame need logaritmid kokku ning kasutame tulemust 10 astendamisel:
Kaks esimest tehet on muidugi võimalikud, kuna logaritmfunktsioon on igal alusel määratud kõikide positiivsete reaalarvude korral.
Tulemuse saamiseks piisaks nüüd ühest suurest tabelist. Esiteks peaks sealt saama piisava täpsusega järele vaadata arvude logaritme ehk kuidas neid esitada kümne astmena – näiteks 7323118 juures oleks kirjas 6,864 ning 919222 juures 5,963. Teiseks peaks sealt leidma ka vastupidist teavet: iga arvu x jaoks astme 10x väärtuse – näiteks 5,001 koha peal oleks kirjas 10023. Muidugi ei saaks tabelis olla lõpmatult palju arve ja seega peaksid kõik arvud tabelis olema antud mingi teatava täpsusega, näiteks kolme või nelja komakohaga.
Nii võiksime oma arvutuse teha väga kiirelt. Alustuseks leiaksime tabelist arvud 6,864 ja 5,963, siis liidaksime nad, et saada 12,827, ning viimaks vaataksime tabelist järele arvu 1012,827 väärtuse: 6 714 000 000 000. Kuna päris vastus on 6 731 571 174 196, näeme, et meie täpsus on nõnda üsna talutav.
Muidugi pidid logaritmitabelid olema kavalalt kokku pandud, et sinna mahutada võimalikult palju arve. Võid ise näha, kui pikaks läheks tabel, kui lihtsalt laduda ühte ritta arvud ja teise nende logaritmid:
Ülemisel real oleme edasi liikunud seitsme lahtriga ainult 0,006 võrra! Joonisel asuv tabel on küll tõesti avatud hoopis teiselt kohalt ja on ka hoopis teisel alusel, aga see suurt ei muuda. Muuseas, võibolla nuputad välja, mis aluse jaoks see tabel on?
Siiski on ka suurtest arvutabelitest vaatlemine ja ise kokku liitmine tüütu ning peatselt peale logaritmi leiutamist tuldi lagedale veel kavalama idee ja riistapuuga. Selle nimeks on lükati ja teda kasutati veel 20. sajandi keskpaigaski, niikaua kui taskuarvutid ta välja puksisid.
Korrutamist lihtsustaval lükatil on arvud paigutatud kavalalt, logaritmskaalalisel kaugusel ja nii võib korrutamistehtega ühele poole saada lihtsalt lükati ülemist hooba alumise suhtes liigutades. Näiteks antud joonisel on omavahel korrutatud 2 ja 3. Suure täpsuse jaoks joonistati skaaladki ülitäpsed. Räägitakse, et observatooriumites kasutati tähtsamateks arvutusteks mitmemeetriseid lükateid ning skaalasid uuriti samal ajal mikroskoobiga.
Kui soovime mingeid andmeid graafiliselt kujutada, ei olegi arvtelgedel tavalise skaala kasutamine alati parim valik. Tavalise ehk lineaarse skaala all peame siis silmas seda, et ühikud vertikaalteljel muutuvad ühtlaselt, nagu näiteks eelmises peatükis transistorite arvu tutvustaval graafikul:
Kuigi kõik nägi väga kena välja, on suurem osa protsessoritest tegelikult üsna eristamatult nulljoone külje all. Probleem on selles, et ettetulevad suurused erinevad mitu suurusjärku ja lineaarne skaala jääb lihtsalt liiga kitsaks. Mingis mõttes toimus transistorite arvu areng mitte liitmise, vaid korrutamise teel. Seda saab ka graafiliselt kujutada, võttes appi arvude kujutamise logaritmilisel skaalal. Sel juhul tähendab iga ühikuline samm vertikaalteljel tervet suurusjärgu muutumist – jällegi liitmise asemel korrutame.
Näiteks kasutades transistorite arvu esitamiseks logaritmilist skaalat, on pilt palju ilusam ja ülevaatlikum:
Logaritmiliseks nimetatakse seda skaalat seetõttu, et logaritmimise suhtes muutuvad vertikaaltelje ühikud jällegi ühtlaselt, nagu kombeks. Tõepoolest, meenutades kümnendlogaritmi tähistust, võime vertikaaltelje skaala ümber tõlkida järgmise tabeli abil:
Maavärinad
Logaritmilised skaalad on kasutusel ka paljude nähtuste hindamiseks, mis võivad esineda väga erinevates suurusjärkudes.
Ka maavärinate tugevust mõõdetakse logaritmilisel skaalal. Seda skaalat kutsutakse pidulikult tema kasutusele võtja järgi Richteri skaalaks. Lihtsustatult näitab maavärina tugevus Richteri skaalal, kui mitu suurusjärku võimsam on värinaga kaasnenud maakoore võnkumine maakoore tavapärasest võnkumisest.
Kuna Richteri skaala kasutab kümnendlogaritmi, tähendab iga lisapall tegelikult 10 korda suuremat maavärinat.
Väikseid maavärinaid on päris palju: maavärinaid, mille suurus on 3 kuni 4 palli, juhtub üle 10 000 korra aastas. Neid maavärinaid on nõrgalt tunda, aga õnneks need tavaliselt purustusi ei tekita. Maavärinad, mis on 1000 korda suuremad ehk 6 kuni 7 palli, on nõrgematele majadele hävitava jõuga sadade kilomeetrite raadiuses ja neid juhtub maakeral keskmiselt iga kolme päeva tagant. Üle 9 palli maavärinaid juhtub paar korda sajandis ning nende läheduses ei jää enam püsti ükski maja.
Suurim maavärin, mille tugevust on mõõdetud, juhtus Tšiilis 1960. aastal. Tema võimsuseks oli lausa 9,5 palli – seega oli ta isegi purustavatest 6- kuni 7-pallistest maavärinatest veel 1000 korda võimsam. Selle asemel, et õudustele mõelda, mõtle hoopis, kui seda kõike peaks kirjeldama lineaarse skaalaga – 9 palli asemel peaksime näiteks kasutama arvu 1 000 000 000.
Kuidas paigutada punkte arvteljele
Joonista endale arvtelg. Pane kuskile kirja nullpunkt ja kuskile punkt 100. Kuhu paigutaksid arvu 20?
Koolitunnis kasutame arvteljel peaaegu alati lineaarset skaalat: kui arvude vahed on võrdsed, on võrdsed ka nendevahelised kaugused arvteljel. Seda mõttelaadi järgides peaksid arvu 20 paigutama viiendikule 0 ja 100 vahelisest kaugusest.
Selgub siiski, et see ei olegi võibolla meile kõige loomuomasem valik. Näiteks on leitud, et esimese klassi juntsud paigutavad arvu 20 arvteljel palju kaugemale kui meie. Umbes siia:
Leidmaks selle paigutuse tagant mingit loogikat, paluti lastel arvteljele seada ka paljusid teisi arve. Selgus, et üldine komme on jätta väiksematele arvudele rohkem ruumi kui suurematele. Täpsem uurimine näitas, et arvteljel kasutatud kaugus sõltub arvu enda suurusest logaritmiliselt ehk teisisõnu lapsed kasutasid arvteljel hoopis logaritmilist skaalat!
Seda valikut saab võibolla ka natuke intuitiivselt selgitada. Nimelt tundub ju, et arvude 87 ja 88 erinevus on vähem tähtis kui arvude 2 ja 3 erinevus. Mõõtes arvude vahet mitte absoluutselt, vaid suhteliselt, on see tunne ka igati täpne: 87 on 88-st umbes 1,01 korda suurem, aga 3 arvust 2 tervelt 1,5 korda suurem. Selline suhtelise erinevuse kasutamine tookski näiteks endaga kaasa logaritmilise skaala.
Kuidas joonistada logaritmilist skaalat?
Oleme üritanud selgitada, et logaritmiline skaala on kasulik, laialt kasutatav ja tore. Aga kuidas seda ise joonistada? Kõige lihtsam on muidugi anda ülesanne mõnele andmetöötlusprogrammile – ütled neile logaritmiline skaala ja ongi valmis.
Järgnevalt mõtiskleme, kuidas seda käsitsi teha, ja selle jaoks vaatleme näiteks võrdlevalt Eesti linnade suurust.
Kas saaksime kuidagi ühele graafikule kanda nii Eesti kõige rohkem kui kõige vähem rahvastatud linnad? Nende linnade rahvaarv varieerub tuhandest inimesest kuni peaaegu poole miljonini: Tallinn 400292, Tartu 103740, Kallaste 1106 ning Mõisaküla 1002.
Tavaline, lineaarne skaala meid jällegi väga ei aita. Kuna vertikaalteljel on ühtlane samm, siis mahuvad pildile kas ainult väikesed linnad või mahub Tallinn ja väiksemaid linnu polegi näha. Tuhandese sammu korral peaksime ju liikuma 400 ühikut ülespoole, et ka Tallinna leida!
Nagu ennist juba rääkisime, peaks logaritmiline skaala seda olukorda parandama, sest seal tähendab iga samm ülespoole hoopis korrutamist.
Logaritmilise skaala joonistamiseks peame esmalt fikseerima sammu suuruse ehk mis arvuga me ülespoole liikudes korrutame. Populaarsed valikud on 10 ja 2, aga täpne valik sõltub eelkõige kontekstist – mis suurusjärkudes tegelikult suuruseid võrrelda tahame. Praegu võtamegi selleks suhtarvuks kümne.
Nüüd hakkame vertikaaltelje samme nimetama 10 astmete abil, iga edasine samm tähendab kümnega korrutamist. Kuskilt tuleb alustada ja linna rahvastiku kokkulöömisel võime alustada näiteks arvust 1 = 100. Järgmine samm vertikaalteljel viiks rahvaarvu 10 korda suuremaks, seega järgmise joone juurde kirjutame juba 10. Veel üks ühik edasi tähendaks juba arvu 100 ja nii edasi, iga sammuga ikka kümme korda suuremaks. Kõnealusel juhul, kuna üheski linnas pole rohkem kui miljon elanikku, jätkame veel neli sammu, kuni miljonini välja. Saame järgneva graafiku:
Kui nüüd lisame suurimate ja väikseimate linnade rahvaarvu kujutavad tulbad, siis näeme hoopis ilusamat pilti. Samale graafikule mahuvad nii suurimad kui väikseimad linnad:
Niisiis, logaritmiline graafik ei ole sugugi keerulisem kui tavaline graafik, ent mõnikord palju ülevaatlikum. Vertikaalsel teljel tuleb siis liitmise asemel lihtsalt korrutada.
Piirväärtustest räägitakse kooliprogrammis eelkõige jadade ja funktsioonide puhul.
Näiteks jada
liikmed muutuvad järjest väiksemaks ja lähenevad hoogsalt nullile. Tõepoolest:
Sellisel juhul tundub mõistlik rääkida ka sellest, mis juhtub siis, kui jada liikmed otsa lõpevad. Mingis mõttes tahame rääkida jada „lõpmatult kaugest” liikmest. Tema väärtus konkreetsel juhul peakski olema null.
Jada piirväärtuse mõiste annab sellisele „lõpmatu kaugele” liikmele täpse tähenduse, aitab kindlaks teha, millal ta eksisteerib, ning leida tema väärtuse.
Ka funktsioonide korral võime rääkida väärtustest, mis jäävad lõpmatult kaugele – näiteks funktsiooni
piirväärtus, minnes lõpmatult kaugele, on analoogselt jada näitega null.
Funktsioonide korral on piirväärtustel siiski ka teine, ilustav roll.
Vaatame näiteks funktsiooni
Kui x on ühest erinev, võime nimetaja ja lugeja x – 1-ga läbi jagada. Saame, et iga ühest erineva arvu korral on meie funktsioon võrdne sirgega ƒ(x) = x + 1. Kohal 1 me funktsiooni väärtust aga välja arvutada ei tohi – nulliga ju jagada ei saa.
Ometigi, joonistades funktsiooni
graafiku kõikide ühest erinevate argumendi x väärtuste jaoks, näeme, et valides argumendi väärtuseid järjest lähemal ühele, läheneb ƒ(x) väärtus ühtlaselt kahele.
Näiteks
Seda demonstreerib ka kenasti funktsiooni graafik:
Nii tundub, et funktsiooni
loomulik väärtus kohal üks peaks olema täpselt kaks.
Piirväärtus annabki funktsioonide korral sellisele loomulikule augutäitmisele täpse tähenduse.
Kokkuvõttes võib öelda, et piirprotsessid aitavad meil aru saada ja kindlaks määrata, mis juhtub seal, kuhu meil pole lubatud vaadata või kuhu me ei ulatu vaatama.
Tuletame meelde, et märgiga ∞ tähistavad matemaatikud lõpmatust – midagi, mis on suurem kui ükski teine reaalarv. Nii on mõistlik jada piirväärtust ehk tema lõpmatu kauget liiget tähistada:
Kirjutame igaks juhuks veel kord välja ka tõlgenduse:
tähendab, et jada liikmete väärtused hakkavad mingist hetkest alates järjest enam lähenema väärtusele A, kusjuures jada väga kaugetel liikmetel ja arvul A on pea võimatu vahet teha. Matemaatikutele meeldib seda sõnastada öeldes, et jada an koondub väärtusesse A või et jada an piirväärtus on A.
Näiteks on jadade
või
piirväärtuseks null: mõlema jada liikmed muutuvad järjest väiksemaks ja nullile lähemale.
Räägitakse ka sellest, et jada koondub lõpmatusse – sel juhul mõeldakse, et jada liikmed muutuvad mingist hetkest järjest suuremaks ja nende suurusel pole ühtegi tõket ning tähistatakse
Näiteks on jada an = n või ka jada an = n2 – 9 piirväärtuseks lõpmatus.
Tegelikult ei ole sugugi selge, millal me üldse piirväärtusest täpselt rääkida tohime. Millised on tingimused selleks, et jada piirväärtus eksisteeriks?
Millal piirväärtus eksisteerib?
Seni oleme rääkinud, mida piirväärtus vaistlikult tähendab ning kuidas temast mõtelda, kuid oleme hoidunud rangest matemaatilisest definitsioonist.
Matemaatiliselt range definitsiooni kirjapanek ei ole küll hirmraske, kuid vajab teatavat täpsust ja tähelepanu – selleni jõuti alles 19. sajandil, just siis, kui romantism nõudis tundetäpsust.
Järgnevalt üritamegi jada näitel vastata küsimusele: millal oleks mõistlik öelda, et piirväärtus eksisteerib, ning kuidas seda täpselt matemaatiliselt defineerida? Siinkohal vaatame ainult juhtu, kus piirväärtus on lõplik.
Mõtleme korra veel sissejuhatuses toodud jadale
mille piirväärtus oli 0. Tundub, et esimene mõistlik nõue piirväärtuse leidumiseks on see, kui võime jõuda teatud väärtusele nii lähedale, kui süda lustib.
Ainult sellest siiski ei piisa, sest näiteks jada
korral jõuame argumendi n suurenemisel lähedale nii väärtustele 1 kui ka –1.
Kuna pendeldame nende kahe arvu lähedal, ei tundu mõistlik defineerida piirväärtust. Tahaksime piirprotsessides näha ikka teatavat eelistust!
Seega nõuame lisaks sellele, et jada väärtused jõuaksid mõnele arvule väga lähedale, ka seda, et nad jääksid sinna lähedale püsima. Selgub, et nendest kahest tingimusest juba täiesti piisab.
Jada an piirväärtuseks saame lugeda arvu A parasjagu siis, kui võime alati leida mõne jadaliikme an
- mis on arvule A nii lähedal, kui vähegi soovime,
- ja millele järgnevad jadaliikmed on A-le vähemalt sama lähedal.
Graafiliselt võime mõelda sellest nii.
Tõmbame väärtuse A ümber kaks horisontaalset sirget. Jada koondub väärtusesse A parajasti siis, kui olenemata sellest, kui lähedale A-le need sirged tõmbasime, on kõik jada liikmed mingist hetkest alates ikkagi nende kahe sirge vahel. Näiteks meie esimesel jadal on see omadus kindlasti olemas.
Kui tõmbaksime jooned nullile palju lähemale, näiteks kaugusele 0,001, siis peaksime ootama 1000 liiget, enne kui jõuaksime jadaga kahe joone vahele. Kui aga 0,000001 siis 1 000 000 liiget. Igal juhul jõuame alati kahe joone vahele ja selle pärast ütlemegi, et jada piirväärtus on 0.
Fanaatikutele anname ka matemaatilise kirjelduse, aga ärge peljake – esimest korda nähes peab igaüks seda lauset mitu korda lugema:
parajasti siis, kui iga positiivse arvu R jaoks saame leida mõne naturaalarvu N nii, et iga N-ist suurema naturaalarvu n korral kehtib |an – A| < R.
Tegelikult oleme muidugi lihtsalt ümber sõnastanud geomeetrilise mõtte – R tähendab siin seda, kui kaugele arvust sirged tõmbasime, ning N tähistab seda hetke, millest alates kõik jada väärtused nende sirgete vahele jäävad.
Võib tekkida küsimus: miks sellist keerulist matemaatilist kirjeldust üldse vaja on? Esiteks on punktides üks ja kaks toodud intuitiivsetel kirjeldustel endiselt veel palju tõlgendamisvabadust ning seega ei sobi need hästi matemaatika tegemiseks. Teiseks teeb esialgne keeruline definitsioon pärast elu lihtsamaks. Selline lühike kirjeldus aitab kiiresti, graafikuid joonistamata, otsustada, kas jadal leidub piirväärtus ja mis ta parasjagu on.
Funktsiooni ƒ(x) piirväärtust kohal x0 tähistatakse väga sarnaselt jadadega:
Piirväärtuse tõlgenduski on analoogne. Toodud kirjeldus tähendab, et kui funktsiooni argumendi x väärtus läheneb väärtusele x0, siis funktsiooni ƒ(x) väärtus läheneb järjest väärtusele a. Vahel öeldakse ka, et funktsioon ƒ(x) koondub kohal x0 väärtusesse a või et funktsiooni ƒ(x) piirväärtus kohal x0 on a.
Mõnikord on funktsioni piirväärtuse leidmine päris lihtne. Näiteks ruutfunktsiooni y = x2 korral on igas punktis piirväärtus võrdne funktsiooni enda väärtusega. Näiteks kohal –2 on tema piirväärtus seega 4. See tuleneb lihtsalt sellest, et ruutfunkt- sioon on kena pidev funktsioon – tema graafikut võib joonistada pastakat paberilt tõstmata.
Ent funktsiooni
piirväärtus kohal 0 puudub, sest nulli lähedal võtab funktsioon nii väga suuri positiivseid kui negatiivseid väärtusi ning jällegi ei suuda me otsustada, mida täpselt siis ikkagi piirväärtuseks valima peaks.
Samas funktsiooni
piirväärtus kohal 0 on lõpmatus.
Siin oleme otsustusvaevast pääsenud, mõlemal pool nulli muutub funktsiooni väärtus aina suuremaks. Matemaatika keeles võiks kirjutada:
Muidugi võib ka funktsioonide piirväärtuse olemasolu üle mõtiskleda veel pikemaltki.
Millal leidub funktsioonil piirväärtus?
Nagu nägime, pole seekordki sugugi selge, millistel funktsioonidel ja millistel kohtadel leidub piirväärtus. Tuleb välja, et ranged tingimused piirväärtuse leidumiseks on umbes sarnased kui jadade korral. Erinevus on vaid selles, et seekord ei vaata me järjest suuremaid jada liikmeid, vaid järjest sarnasemaid funktsiooni argumente.
Sellest on kõige lihtsam ilmselt mõelda jällegi geomeetriliselt.
Oletame, et tahame teada, kas funktsiooni ƒ(x) piirväärtus kohal x0 on a. Tõmbame nagu jadadegi puhul väärtuse a ümber alt ja ülevalt tõkestavate sirgjoonte paari. Kui nüüd olenemata valitud sirgjoontest võime alati leida argumendi x0 ümber vahemiku, mille jaoks ƒ(x) graafik jääb nende sirgjoonte vahele, siis ongi ƒ(x) piirväärtus kohal x0 võrdne a-ga.
Näiteks eelmise funktsiooni
piirväärtus kohal lõpmatus on null ehk
sest me saame nulli ümber tõmmata kaks horisontaalset sirget ning võime kindlad olla, et piisavalt suure sisendi korral jääb funktsiooni väärtus kindlasti nende joonte vahele.
Muuseas, on võibolla natuke üllatav, aga see tingimus jätab vabaks ka järgmise võimaluse: funktsioonil leidub küll mingil kohal kindel väärtus, aga piirväärtust seal pole. Näiteks võib vaadata funktsiooni, mis võtab väärtuseks miinus ühe, kui sisendarv on negatiivne; pluss ühe, kui sisendarv on positiivne, ning nulli, kui sisendarv on null. Mis peaks olema selle funktsiooni piirväärtus kohal null?
Piirväärtuse tähtsus matemaatikas
Funktsiooni piirväärtus võib esmapilgul tunduda ehk tühi-tähi, justkui ainult mingi augutäide. Üllatavalt on tema roll funktsioonide uurimisel väga märkimisväärne. Miks?
Esiteks aitab piirväärtus rangelt kirja panna matemaatilisi mõisteid, mis räägivad „lõpmatult väikesest“. Näiteks on piirväärtuste abil defineeritud tuletis – funktsiooni muutumise hetkekiirus. Võime mõelda, et tegemist on keskmise kiirusega lõpmatult väikese ajavahemiku jooksul.
Samamoodi on piirväärtuste abil defineeritud integraal [lk 340], millest võime mõelda kui kõverkujundi pindalast ja mille võime arvutada lõpmatult väikeste ristkülikute pindalade kokkuliitmisel.
Põnevust lisab ka see, et saame piirväärtuse abil defineerida ka näiteks arvud e ja π ning veel teisigi põnevaid arve [lk 96]. Muuseas, π defineerimisel on seejuures piirprotsess oma olemuselt geomeetriline: vaatame, kuidas korrapärased hulknurgad järjest enam ringjoonega sarnanema hakkavad. Tegelikult osutuvadki oluliseks mitte ainult arvulised, vaid ka geomeetrilised piirprotsessid.
Õigupoolest võib ka reaalarvude hulga kokku panna ratsionaalarvudest ja hästi valitud piirväärtustest: näiteks arvu π koondub jada 3; 3,1; 3,14; 3,141; 3,1415 …, kus võtame lihtsalt appi järjest rohkem π komakohti.
Piirväärtusi kasutades saame lisaks irratsionaalarvude leidmisele nendega ka tehteid tegema hakata. Nimelt selgub, et kui piirväärtused eksisteerivad ja on lõpliku suurusega, saab neid väga kenasti liita ja korrutada.
Näiteks kui soovime leida funktsioonide x2 ja x summa x2 piirväärtust kohal 2, siis võime
- esmalt leida piirväärtuse funktsioonile x2 kohal 2 – vastuseks 4,
- seejärel piirväärtuse funktsioonile x kohal 2 – vastuseks 2,
- viimaks saadud piirväärtused kokku liita – lõppvastuseks 6.
Matemaatiliselt kirjutaksime:
Selle reegli kasutamisel peab siiski ettevaatlik olema: tuleb alati kontrollida, et mõlema liidetava piirväärtused üksipäini eksisteerivad. Samasugune reegel kehtib ka korrutamise jaoks, kusjuures peab olema samavõrra ettevaatlik.
Piirväärtuse kõige suurem sõber on aga pidevuse mõiste.
Intuitiivselt on funktsioon pidev siis, kui võime tema graafiku joonistada pliiatsit paberilt tõstmata. Aga kas saaksime ka kuidagi graafikut joonistamata teada, kas funktsioon on pidev?
Selle jaoks peame üritame aru saada, mida ikkagi tähendab, et me ei pea pliiatsit paberilt tõstma.
Oletame, et oleme joonistanud juba funktsiooni piirkonnas näiteks nullist peaaegu kolmeni ja tahame nüüd graafikut edasi päris argumendi kolm väärtuseni välja tõmmata. Selle jaoks, et saaksime kolmele vastava punkti joonistatud pliiatsit paberilt tõstmata, peame tema väärtusele olema pliiatsi otsaga jõudnud juba väga lähedale, võiks isegi öelda „lõpmatult lähedale”.
Vahele ei või jääda kõige miniatuursematki auku – muidu peaksime pliiatsiga ju teatava hüppe tegema:
Toodud kirjelduses võib ära tunda jälle idee koondumisest – uurime, kuidas funktsiooni väärtused muutuvad, kui jõuame argumendile 3 järjest lähemale. Ja tõepoolest, funktsiooni pidevust saab rangelt kirja panna just piirväärtuste abil.
Funktsiooni pidevusest räägitakse alguses lokaalselt, ühe valitud punkti ümbruses. Funktsiooni nimetatakse mingil kohal pidevaks, kui selles punktis eksisteerib funktsioonil piirväärtus ning see piirväärtus on sama, mis funktsiooni enda väärtus.
Mõned sõnad võime matemaatilisemaks ja kompaktsemaks esitamiseks asendada ka sümbolitega.
Funktsioon ƒ(x) on pidev kohal a, kui leidub piirväärtus
ning ta on võrdne funktsiooni väärtusega kohal ƒ(a).
Näiteks ƒ(x) = x2 on pidev kohal 2, sest
ning samas
Muidugi ei ole see kellelegi uudiseks, sest teame, et ruutfunktsiooni graafikut võib joonistada ühe kiire pliiatsitõmbega, isegi märkamata, kuidas kohast 2 möödume.
Ruutfunktsioon on pidev kogu reaalteljel ning üldisemalt nimetatakse selliseid funktsioone, mis on pidevad kõikides oma määramispiirkonna punktides, pidevateks funktsioonideks.
Kõik eelmises peatükis nähtud funktsioonid – eksponentsiaalfunktsioon, logaritm ja polünoomid – on pidevad. Samuti on pidevad trigonomeetrilised funktsioonid. Võib küll mõelda, et tangensfunktsioon teeb ju kummalise hüppe, aga see hüpe ei kuulu tema määramispiirkonda.
Võib mõelda, et pidevus lisab funktsioonidele teataval määral regulaarsust, korrapära ja muudab neid seega lihtsamaks: nimelt ei saa pidev funktsioon hüppeid teha, funktsiooni väärtust igal kohal on võimalik ennustada teda ümbritsevate väärtuste abil.
Siiski võib ka pidev funktsioon välja näha väga hüplik ja näiteks leidub pidevaid funktsioone, millel ei leidu üheski kohas tuletist [lk 320] – neile ei saa üheski punktis tõmmata puutujajoont! See avastati alles 19. sajandi lõpus ning nii mõnigi tähtis matemaatik nimetas selliseid funktsioone peletisteks.
Pidevuse trikk: funktsioonist ratsionaalarvude funktsioonini reaalarvudel*
Pidevast funktsioonist võime rääkida ka ratsionaalarvuliste funktsioonide korral: sel juhul on lihtsalt kõik piirprotsessid defineeritud ainult ratsionaalarvude hulgal.
Näiteks arvude puhul defineerisime arvu astme ainult ratsionaalarvuliste astendajate korral ja tulemuseks oli pidev funktsioon ratsionaalarvudel [lk 110].
Üldiselt on pideva ratsionaalarvulise funktsiooni laiendamiseks reaalarvudele väga palju võimalusi. Võime ju iga lubatud irratsionaalarvu jaoks valida mingi suvalise funktsiooni väärtuse.
Näiteks oleks täiesti lubatud funktsioon, mis igale ratsionaalarvule seab vastuseks iseenda ning igale irratsionaalarvule hoopis nulli. See poleks küll eriti kena masin, aga igati lubatud.
Samas kui nõuame, et ka saadud reaalfunktsioonil säiliks pidevus, on laienduseks täpselt üks võimalus: kõik augud tuleb täita funktsiooni piirväärtuste abil.
See trikk võimaldabki meil tihti alustada ühe funktsiooni defineerimist ratsionaalarvudel ning alles lõpus pidevuse abil reaalarvudele üle minna. Näiteks saime täpselt selle triki abil laiendada astendamise ilusaks pidevaks eksponentsiaalfunktsiooniks [lk 280]. Täpselt sama meetod aitab meid veel ka näiteks ristküliku pindalade defineerimisel tükeldamise meetodil [lk 362].
Rahvaarv on riigi seisukohalt tähtis näitaja – ta mõõdab mõne rahva suurust ja vägevust, meie puhul küll vist pigem väiksust ja haavatavust. Siin on viimase poole sajandi Eesti rahvaarvu graafik:
Rahvaarvu suurus määrab selle, kui palju riik makse koguda saab ja kui paljude kodanike eest on vaja hoolt kanda. Nii ei piisa meile lihtsalt rahvaarvu teadmisest, vaid tuleb ka aru saada, kuidas rahvaarv muutub.
Kas pole põnev, kuidas rahvastiku kasvamise üleminek kahanemiseks langeb kokku Eesti riigi taastekkimisega? Või see, et kuigi nüüdseks on rahvastiku kahanemine aeglustunud, pole kasv siiski veel taastunud? Veel näeme, et 1970-ndate alguses paistab kasv olevat olnud kõige kiirem. Miks just siis?
Rahvastiku muutumisest parema ülevaate saamiseks oleks kaval joonistada rahvaarvu muutumise graafik. Kui soovime näha, kui mitme inimese võrra rahvaarv aasta jooksul muutus, siis võiksime iga aasta rahvaarvust lahutada eelneva aasta rahvaarvu.
Kui teeme seda iga aasta kohta ja tõmbame saadud punktidest läbi ilusa joone, saame sellise graafiku:
See graafik ongi juba peaaegu rahvaarvu kirjeldava funktsiooni tuletise graafik! Tuletis annab meile ühe funktsiooni muutumise kiiruse igas punktis, täpsem definitsioon on küll pisut keerukam.
Lisakeerukus tuleneb sellest, et rahvaarvu puhul peame muutumise kiiruse leidma mingite ajavahemike abil, nagu aasta või kuu või nädal – liiga lühikeses ajavahemikus (näiteks üks nanosekund) ei juhtu ju tihti midagi. Lisaks peame valima, kas vaatame muutust lähitulevikus või lähiminevikus. Matemaatikas juhtub aga kogu aeg midagi ja nii kirjeldab tuletis funktsiooni väärtuse hetkelist muutumise kiirust – muutumist, mis toimub kiiremini kui mistahes nano- või pikosekund ja seda nii mineviku kui tuleviku suunal.
Käesolevas peatükis uurimegi, kuidas sellest hetkekiirusest siis ikkagi mõtelda ja kuidas teda etteantud funktsioonide jaoks ka leida.
Tuletis on ajast sõltuva funktsiooni jaoks justkui spidomeeter – iga ajahetke kohta näitab ta funktsiooni muutumise hetkekiirust. Aga kuidas leida spidomeetri näitu, kui teada on ainult läbitud tee pikkus?
Vastates sellele küsimusele jõuame ka tuletise range definitsioonini, kõike seda ühe talvise loo saatel.
Talvine lugu
Kujutle, et oled metsa vahel suusatades jõudnud kõrgele mäe otsa ning võid nüüd hakata vabakäigul alla kihutama. Sind huvitab väga, kui suur on Su kiirus näiteks kümnendaks sekundiks. Kuidas võiksid seda hinnata?
Üks võimalus oleks lihtsalt mõõta, kui kaugele oled kümnendaks sekundiks jõudnud ning kaua see aega on võtnud. Jagades tee pikkuse ajaga, võiksid leida esimese kümne sekundi keskmise kiiruse ning selle abil oma kiirust ka kümnendal sekundil hinnata. Kogemuse põhjal aga teame, et kiirus kasvab päris hoogsalt ning ilmselt see poleks eriti hea hinnang.
Täpsema hinnangu saaksid aga näiteks siis, kui teaksid, kui kaugele oled jõudnud ka viiendaks sekundiks. Võiksid oma kümnenda sekundi kiirust hinnata vahemikus viiendast kümnenda sekundini toimunud laskumise keskmise kiirusena. Kui aga teaksid, kaugele oled jõudnud üheksandaks sekundiks, võiksid vaadata, palju läbisid veel viimasel sekundil, ning vastus oleks veelgi täpsem. Ja nii edasi – kui teaksid oma läbitud tee pikkust 9,99-ndal sekundil, oleks Su vastus juba peaaegu sama täpne nagu GPS-il. GPS-gi peab ju kiiruse kuidagi arvutama!
Leitud kiirus läheb järjest lühemat ajavahemikku kasutades aina täpsemaks, ent mis on see täpne vastus? Täpse vastuse nimi ongi tuletis ehk hetkekiirus. Kui tahame teda leida, peame keskmise kiiruse leidma järjest väiksemate vahemike jaoks ning lootma, et lõpuks koorub välja üks kindel vastus.
Sellist järjest väiksemate vahemike uurimist nägime eelmises peatükis piirprotsesside all. Tuletis ongi määratud piirprotsessiga [lk 313]: tuletis teatud hetkel on võrdne keskmise kiiruse piirväärtusega, kui uuritava ajavahemiku pikkus muutub olematult väikeseks. Matemaatilistes sümbolites tähendab see järgmist:
Konkreetne näide
Praktikas on küll hetkekiiruse leidmine võimalik ainult juhul, kui oma liikumist juba kuidagi matemaatiliselt kirjeldame – on ju võimatu, et leiame tee pikkuse iga nanosekundi tagant. Ise mõõtes jääme alati lähendusteni.
Täpsuseni aitab meid aga näiteks füüsika. Mäest alla sõitu võime füüsikatunni tarkuse abil lihtsalt matemaatiliselt kirjeldada. Nimelt kui kallak on ühtlase nurga all, kui hõõrdejõu, liikumisele vastu võitleva tuulejõu ja muu tühja-tähja ära unustame ning kui alustad mäe otsast nullkiirusega, siis on laskumisel läbitud tee pikkus antud ruutfunktsiooniga ajast: kujus ct2.
Konstant c peaks olema konkreetne reaalarv, mis sõltub gravitatsioonikonstandist ja kaldenurgast, aga lihtsuse huvides ütleme, et valisid kõige ilusama mäe siin maailmas ning c = 1. Sel juhul saame läbitud tee pikkuse funktsiooniks s = t2 ehk näiteks 10 sekundit pärast laskumise algust oled jõudnud 100 meetri kaugusele.
Selle valemi põhjal võime nüüd kergesti leida ka oma hetkekiiruse. Kusjuures enam ei ole vahet, kas teeme seda ainult 10 sekundi või iga üldise ajahetke t jaoks. Lühikese ajavahemiku pikkust kirjeldame sümboliga Δt, aga nagu ikka on see kokkuleppeline.
Teame, et suvalisel ajahetkel t oleme jõudnud t2 meetri kaugusele.
Ajahetkeks t – Δt oleme samas jõudnud (t – Δt)2 kaugusele:
Nüüd on meil olemas kõik keskmise kiiruse leidmiseks ajavahemikus t – Δt kuni t:
Edasi võime saadud valemit pisut lihtsustada. Korrutades ruudus oleva liikme lahti, koondades sarnased liikmed ning taandades murru, saame järgmise hinnangu:
Märkame, et ajavahemiku pikkus Δt mõjutab üsna selgelt meie kiiruse hinnangut. Samas, kui muudame selle ajavahemiku järjest väikesemaks, kahaneb tema mõju järjepanu. Viimaks on ta nullist päris eristamatu ning alles jääbki ainult 2t. Järelikult funktsiooni t2 muutumise hetkekiirus ehk tuletis suvalisel hetkel t on v = 2t.
Seega meie füüsikalise kirjelduse põhjal suureneb sellest ideaalsest mäest alla lastes laskumiskiirus iga sekundi kohta 2 m/s võrra. Seega näiteks viiendal sekundil on kiiruseks 10 m/s ning kümnendal sekundil juba 20 m/s ehk üle 70 km/h – kui kiirust kardad, ära pikka laskumist ette võta.
Matemaatiline definitsioon
Matemaatikud ei viitsi muidugi iga kord nii pikalt sõnu seada ning seega on tuletise leidmine võimalik ka lihtsalt mõne rea sümbolitega. Visates tee pikkuse ja aja asemele ka tavapärasema funktsiooni nime ƒ ning argumendi x, saame funktsiooni y = ƒ(x). Võime esmalt uhkelt välja kuulutada järgmist.
Funktsiooni ƒ(x) tuletis kohal x on defineeritud kui:
@{918}@
Märkame, et kui lugulaulus defineerisime tuletise ühel kohal argumendist vasakule jäävate vahemike abil, siis nüüd nõuame muutumise vahemikult Δx ainult seda, et ta koonduks nulli. Ta võib olla nii positiivsete (tulevikku vaatav), negatiivsete (minevikku vaatav) kui vaheldumisi väärtustega. Nagu hiljem näeme, on selline üldisus oluline, et võiksime tuletisest üheselt rääkida.
Eelneva arutluskäigu funktsiooni y = x2 tuletise leidmiseks võiks seetõttu kompaktselt kirja panna ka tulevikku vaatavalt:
@{919}@
Tore, et vastus on sama!
Igaks juhuks mainime, et tähistused ƒ'(x) ja y' tähendavad täpselt sama asja. Tihti tähistatakse reaalarvulisi funktsioone y abil, sest meile meeldib ju funktsiooni graafikuid joonistada x- ja y-telje abil. Sel juhul unustatakse tihti üldse märkida, et argumendiks on x – seda loetakse vaikimisi teadmiseks. Vahel nimetatakse funktsioone ƒ(x)-ks, kuna ƒ on ju sõna funktsioon esimene täht. Siis märgitakse segaduse vältimiseks ka ära, et funktsiooni argumendiks on ikkagi just nimelt x. Märgi ' võttis tuletise tähistamiseks alles 18. sajandi lõpus kasutusele itaallane J.L. de Lagrange.
Funktsiooni tuletisest saab mõelda ka funktsiooni graafikule tõmmatud puutujasirgete abil. Nimelt on funktsiooni tuletis igas punktis võrdne seal punktis funktsiooni graafikut puudutava sirge tõusuga.
Miks see peaks nii olema? Keskmise kiiruse idee ise on juba seotud sirge tõmbamisega: selle asemel, et uurida, kuidas tee pikkus detailselt muutub, võtame ajavahemiku otspunktid ning ühendame need sirgega. Selle sirge tõus on siis ka selle vahemiku keskmine kiirus.
Tuletise leidmiseks teeme aga ajavahemiku lõpmatult väikeseks ehk teisisõnu muudame ajavahemiku ots- ja alguspunkti samaks: nii saab sirgest puutujasirge.
Vaatame näitena veel siinusfunktsiooni graafikut, mille abil saab kirjeldada paljusid perioodilisi protsesse, sealhulgas näiteks ka pendli liikumist [lk 236]. Tõmbame siinusfunktsiooni graafikule lahkesti erinevaid puutujasirgeid:
Nende puutujasirgete tõusudest uut joonist tehes näeme, et see ei paista eelmisest sugugi väga palju erinevat – ainult nihutamise võrra. Natukene mälus sobrades leiame, et saadud joonis sarnaneb väga koosinusfunktsiooni graafikule:
Tõepoolest, tulebki välja [lk 251], et siinusfunktsiooni tuletis on koosinusfunktsioon ning koosinusfunktsiooni tuletis omakorda horisontaalteljest peegeldatud siinusfunktsioon. Seega on trigonomeetrilised funktsioonid üsna eraldihoidev pere.
Ekstreemumid
Graafiline mõtteviis aitab ka aru saada sellest, miks tuletise nullkohad on nõnda olulised. Nimelt näeme, et tuletis on võrdne nulliga täpselt kohtades, kus puutujasirge on paralleelne x-teljega – ehk teisisõnu kohtades, kus funktsioonil on kogu oma ümbrusest suurem või väiksem väärtus. Selliseid kohti nimetatakse ekstreemumiteks. Ekstreemumit, mis on mingil väiksel alal kõige suurema väärtusega, nimetatakse maksimumpunktiks ning madalamat punkti miinimumpunktiks.
Ekstreemumite uurimine on päris oluline, kuna tänapäeval on ikka kombeks kõike kas maksimeerida või minimeerida: majandusteadlased tahavad maksimeerida kasumit, vormeli-insenerid tippkiiruseid ja õpilased uneaega.
Kuidas see täpsemalt käib, räägime lahendades vägagi olulist probleemi näiteks tutipäevaks: mis nurga alt visata ratta seljast veepomme [lk 333]? Enne aga veel midagi pisut matemaatilisemat.
Sissejuhatuses rääkisime rahvaarvu muutumisest – see oli tuletise kontekstis pisut eksitav, kuna rahvaarvu täpselt kirjeldavale funktsioonile ei saagi igal pool tuletist leida.
Nimelt, tegelikult ei ole ju rahvaarvu muutumine sugugi pidev protsess, vaid toimub konkreetsete juhtumite kaupa, keegi sünnib, keegi sureb. Nii meenutab rahvaarvu graafik sissesuumitult treppi:
Seega on piisavalt väikesel ajavahemikul rahvaarvu muutus alati kas null või absoluutväärtuselt vähemalt üks – just on keegi sündinud või surnud. Esimesel juhul on tuletis null ning teisel juhul hoopis defineerimata. Tõepoolest, kui muutu ei ole üheski suunas, on tuletis definitsiooni järgi null. Teisalt, kui muut on aga ükskõik kui väikese ajavahemiku jaoks fikseeritud, siis ju keskmine kiirus vahemiku vähenedes aina kasvab või kahaneb ning jõuabki lõpmatusse. Kui see jäi segaseks, võib mõelda näiteks puutujasirgetele – hüppepunktis muutub ta ühe suunas hoopis vertikaalseks ehk tõus saab lõpmata suureks või väikeseks:
Seega ei kanna tuletis rahvaarvu muutuse kohta tegelikkuses eriti mingit teavet. Teda ei saa isegi igal pool ilusasti defineerida ning peame rahvaarvu uurimisel kasutama ebatäpsemaid hinnanguid, nagu tegime seda sissejuhatuses – peame uurima muutust ühe aasta, ühe kuu või muu lõpliku ajavahemiku vältel.
Nii mõnelgi teisel funktsioonil ei saa osades kohtades tuletist leida ja tuleb välja, et leidub lausa funktsioone, mis on küll pidevad, aga kus ei saa üheski kohas tuletist leida! Need on parajad monstrumid ning mõned neist meenutavad mõningal määral fraktaalset lumehelvest, mille kohta saab lugeda juba järgmisest osast [lk 377].
Ja isegi kui füüsikud tegelevad peaaegu alati funktsioonidega, millel tuletis leidub – nagu näiteks juba nähtud ruutfunktsioon või siinusfunktsioon – on oluline küsida, millal üldse on tuletisest mõistlik rääkida. Seda järgnevalt arutamegi.
Meenutame, et defineerisime funktsiooni tuletise mingil kohal piirprotsessi kaudu. Seega leidubki funktsiooni tuletis sellel kohal täpselt siis, kui sellel piirprotsessil tõepoolest leidub piirväärtus.
Seda tingimust veidi lähemalt uurides selgub näiteks, et iga funktsioon, millel leidub mingis punktis tuletis, peaks olema tingimata sealsamas punktis ka pidev. See oli täpselt probleem, mida kohtasime mõni lehekülg tagasi rahvaarvu kirjeldavat funktsiooni uurides – hüppekohale ei saa tuletist joonistada.
Tuleb välja, et tuletise olemasoluks ei piisa ka lihtsalt pidevusest – näiteks ei leidu absoluutväärtuse funktsioonil y = |x| tuletist punktist 0. Ka sellest on lihtne aru saada just geomeetriliselt. Teravikule on jällegi väga raske joonistada puutujasirget. Paremalt poolt lähenedes tundub, et puutujasirge peaks olema võrdne sirgega y = x, vasemalt poolt lähenedes sirgega y = –x. Kumma peaksime valima?
Või hoopis mõne keskmise? Ükski sirge ei kirjelda funktsiooni muutumist üheaegselt nii negatiivses kui positiivses suunas.
Üldiselt kehtib, et kui ühel funktsioonil leidub igas punktis tuletis, on ta konaruste ja teraviketa. Proovi ise – ainult siis saad igasse punkti joonistada üheselt puutujasirge. Puutujasirge olemasolu aga tähendab, et funktsioon muutub vähemalt imepisikeses piirkonnas üsna lineaarselt ehk sirgjooneliselt mõlemas suunas, umbes nii nagu kerajas Maa pind tundub koduümbruses igati lame.
Tuletis on põnev, kuna oleme teatud mõttes asunud teisendama keerulisemaid objekte kui arve.
Kui ühel funktsioonil leidub igas punktis tuletis, siis võime tuletise võtmisest mõelda kui ühe funktsiooni teisendamisest uueks funktsiooniks: funktsioonist y = ƒ(x) saab tuletise võtmisel uus funktsioon, mida tavaliselt tähistatakse y' = ƒ'(x) ning mille väärtus igas punktis annabki algse funktsiooni tuletise väärtuse selles punktis.
Nüüd ka y' on funktsioon ning seega võime ju samamoodi uurida tema muutumist. Kui ta muutub piisavalt kenasti, võime võtta temastki tuletise ning saada funktsiooni y''. Kui nüüd omakorda funktsioon y'' on kena ning sile, võime leida veel kolmandagi tuletise ja nii edasi.
Funktsioonid, millest saame palju tuletisi võtta, on eriti sujuvad ja siledad. Heaks näiteks on jälle polünoomid või trigonomeetrilised funktsioonid siinus ja koosinus. Nagu mainisime, muutub siinusfunktsioon tuletist võttes koosinusfunktsiooniks ning koosinusfunktsioon x-teljest peegeldatud siinusfunktsiooniks. Nii võime tuletise võtmist lõputult jätkata:
Füüsikas esineb teine tuletis väga sagedasti ning tähistab kiirendust ehk kiiruse muutumise kiirust. Newtoni teine seadus on ju kirja pandud just kiirenduse abil: F = ma ehk keha kiirenduse ja massi korrutis on võrdne talle mõjuva jõuga! Teades, et kiirendus on kiiruse esimene tuletis, võiksime kirjutada F = mv' ja nüüd, lisades, et kiiruse enda leiame tee pikkuse tuletisena, võiks ka kirjutada F = ms''.
Füüsikas kasutatakse küll tihti ülakoma tähistuse asemel hoopis punkte: näiteks
ning
Nii saame näiteks pendli liikumist üsna täpselt kirjeldada kolme funktsiooniga: esiteks pendli kaugus nullpunktist, seejärel tuletis sellest funktsioonist ehk pendli liikumise kiirus ning viimaks tuletis kiirust kirjeldavast funktsioonist ehk pendli liikumise kiirendus.
Oled gangsterifilmidest saanud natukene halba inspiratsiooni ja otsustad jalgrattalt veepomme pilduda. Mis nurga all peaksid viskeid sooritama, et veepommid võimalikult kaugele lendaksid?
Tänaseks on vist üsna levinud tarkus, et seisult on kõige kasulikum palli või ka veepommi visata täpselt 45-kraadise nurga alt. Aga kuidas muutub see nurk siis, kui sõidad samal ajal ratta või autoga või hoopis jooksed?
Järgnevalt üritamegi üheaegselt leida põhjendust rahvatarkusele ning arvutada ka välja parima nurga hoo pealt viskamiseks. Selle jaoks peame esiteks leidma olukorrale sobiva füüsikalise kirjelduse, seda veidi matemaatiliselt analüüsima ning siis järeldustesse ruttama. Seejuures tähendab analüüsimine siinkohal mingi optimaalse väärtuse leidmist ja mängu tulebki tuletis, mis võrdub nulliga just funktsiooni maksimumpunktis.
Füüsikaline kirjeldus
Hea füüsikalise kirjelduse aluseks on otsus, milliseid faktoreid veepommi viskel arvesse võtta ning mida eirata.
Veepommi langemist põhjustab gravitatsioonijõud, nii et sellest me loobuda ei saa. Tähistame gravitatsioonijõust tulenevat kiirendust tähega g. Samuti mängivad kindlasti rolli jalgratta kiirus ning veepommile meie poolt antav algkiirus. Kuna nende täpseid väärtuseid me ei tea, tähistame ratta kiirust tähega r ning palliviske kiirust tähega p. Viimaks on oluline muidugi otsitav viskenurk ise – tähistame teda θ-ga.
Selline üldkujus lahendamine võimaldab meil ka hiljem proovida, kuidas vastus sõltub näiteks sõidu- või viskekiirusest.
Kõike muud aga otsustame esmajoones eirata – kui veepomm on piisavalt kompaktne, siis tuuletakistus ei tohiks liialt suurt rolli mängida. Samuti näiteks eirame fakti, et vise ei toimu päris maapinnalt, vaid veidi kõrgemalt.
Newtoni teise seaduse põhjal võime keha liikumist kirjeldada temale mõjuvate jõudude abil – ainult jõudude mõjumisel muutub ka keha liikumise kiirus. Kõnealuses olukorras on meil ainult üks jõud, gravitatsioonijõud, mis mõjub vertikaalselt allapoole. Horisontaalselt ei mõju ühtegi jõudu ning seega jääb horisontaalkiirus ka terve lennu ajal samaks.
Võime need kiirused ka trigonomeetriliste funktsioonide abil kirja panna:
Horisontaalkiirus on konstantselt
Vertikaalkiirus on algselt antud
hakkab seejärel tänu gravitatsioonijõule vähenema, kuni jõuab nulli (kõrgeim punkt!), ning seejärel jälle suurenema, kuni veepomm prantsatab maapinnale.
Just selle vertikaalkiiruse kirjelduse abil saame leida ka lennuaja.
Leiame esmalt lennuaja, mis kulub veepommi tõusmiseks kuni kõrgeima punktini. Teame, et vertikaalkiiruse tuletis ehk kiirendus on ülesviskel võrdne g-ga. Seega võime kiiruse ajahetkel t kirjutada kujus:
Kõrgeimas punktis on vertikaalkiirus täpselt null ning saame võrrandi tõusmiseks kulunud aja T suhtes:
Siit võime avaldada üleslennule kulunud aja:
Natuke mõeldes selgub, et ka allalennule kulub täpselt sama aeg. Üks viis selles veendumiseks on kasutada energia jäävuse seadust. Nii viske kui maandumise hetkel peab palli koguenergia olema sama. Kuna potentsiaalne energia on neil hetkedel võrdne ning samuti ka horisontaalne kiirus, peavad suuruselt võrdsed olema ka vertikaalsed kiirused – ainult vastupidises suunas. Seega langemisel muutub vertikaalkiirus sama palju nagu tõusmisel. Kuna kiiruse muudu määrab endiselt ainult raskuskiirendus, kulub ka kiiruse muutumiseks täpselt sama aeg.
Seega peame kogu lennuaja leidmiseks korrutama tõusule kulunud aja kahega. Tähistades kogu lennuaega lihtsalt t-ga, saamegi:
Nüüd võime horisontaalkiiruse abil leida ka viske pikkuse. Kuna horisontaalses suunas on kiirus konstantne, peame selle jaoks lihtsalt korrutama kiiruse ning ajapikkuse.
Saame:
Kasutades siinusfunktsiooni topeltnurga valemit [lk 245]
saame seda veel veidi lihtsustada:
Ikkagi päris õudne valem! Vähemalt näeme, millest viskepikkus sõltub: viskekiirusest p, jalgratta kiirusest r, viskenurgast θ ning gravitatsioonilisest g kiirendusest. Just nagu ootasime. Nüüd asume seda viskepikkust analüüsima!
Matemaatiline analüüs
Eesmärk on viskepikkust nurgast θ sõltuvalt maksimeerida. Võime esmalt vaadata, mis juhtub mingil konkreetsel juhul. Teame, et gravitatsiooniline kiirendus on
Eeldame näiteks, et veepommi viskekiirus on
ning rattasõidu kiirus näiteks
Sel juhul võime viskekauguse sõltuvust viskenurgast kirjeldada järgmisel graafikul:
Näeme, et veepomm lendab kõige kaugemale, kui viskenurk on veidi suurem kui 55º ja veidi väiksem kui 60º.
Kui tahame aga optimaalse viskenurga leida üldjuhul sõltuvuses viskekiirusest ning sõidukiirusest, peame lahendama ekstreemumülesande: maksimaalse kauguse korral on kauguse tuletis viskenurga suhtes võrdne nulliga. Tõepoolest, nagu nägime, on funktsiooni maksimumis ja miinimumis puutujasirge paralleelne x-teljega ja seega on tuletis null [lk 328].
Samas, sellest, et punktis on tuletis null, ei selgu küll kohe, et tegemist on maksimumiga, sama hästi võiks tegemist olla ka miinimumiga. Siiski, vaadeldes eelnevat joonist või usaldades füüsikalist intuitsiooni, võime selle mure kõrvale jätta – konkreetsel juhul annab ekstreemum meile just nimelt maksimumi.
Leiame siis selle tuletise. Teame, et siinusfunktsiooni tuletis on koosinusfunktsioon [lk 251] ning analoogiliselt saab näidata, et funktsiooni sin(2θ) tuletis on 2cos(2θ).
Seega saame:
@{934}@
Ekstreemumi ning sel juhul just nimelt maksimumi leidmiseks peame tuletise nulliks seadma ehk lahendama võrrandi:
Võime seda võrrandit lihtsustada, korrutades mõlemad pooled läbi liikmega
Nüüd on meil trigonomeetriline võrrand optimaalse viskenurga suhtes ning oleme juba heas seisus – parameetritena on mängus ainult viskekiirused ja viskenurk. Kas pole pisut huvitav, et gravitatsioonilise kiirenduse väärtus ei mängigi mingit rolli ehk et Kuu peal on optimaalne täpselt sama viskenurk, mis Maa peal!
Edasi peame veidi kavaldama, et leida lahend nurga θ suhtes.
Kasutame topeltnurga valemit [lk 245]
ja saame sarnaseid liikmeid koondades:
Nüüd jääb veel vaid lahendada ruutvõrrand cos(θ) suhtes, mille lahendame ruutvõrrandi lahendivalemi abil [lk 275]:
Mõistliku vastuse annab ilmselt ainult üks kahest lahendist. Näiteks võime eeldada, et vise ja liikumine on samas suunas ning et liikumine on positiivses suunas. Seega peaks viskenurk olema 0 ja 90 kraadi vahel. Kuna selles piirkonnas on koosinusfunktsioon positiivne, peame valima ka positiivse lahendi:
See ongi üldkujul lahend. Iga konkreetse juhu jaoks võiksime nüüd siia arvud sisse visata ning järeldusi teha.
Mida järeldada?
Järeldusi saame aga kaardistada ka üldisemalt.
Nimelt kuna teame, et 0 ja 90 kraadi vahel on koosinusfunktsioon rangelt kahanev, võime graafikult iga koosinusfunktsiooni väärtuse kohta leida ka nurgaväärtuse. Seost, mis selle annab, nimetatakse ka arkuskoosinuseks ning tähistatakse arccos θ. Nii võiks lahendi lausa välja kirjutada:
Nüüd võime selle lahendi abil koostada pildi, mis näitab, kuidas optimaalne viskenurk sõltub viskekiirusest ning liikumiskiirusest.
Nagu näeme, tuleb suurte kiiruste korral tõesti oma strateegiat muuta. Näiteks kui ratta kiirus on 20 m/s ja viske kiirus on 5 m/s, siis pikima viske saavutaks umbes 77° puhul, mis on juba päris erinev 45 kraadist. Samas väikeste kiiruste puhul suurt vahet pole.
Pärast pikka talve on käes kevad, viskad suusad nurka ja asud rattaga ärkavat loodust avastama. Sõidad hoogsalt kodust eemale, kuid sooviksid siiski teada, kui kaugele oled jõudnud – jõudu peab ju jätkuma ka naasmiseks. Sul on võimalik igal hetkel näha ratta spidomeetri näitu ehk hetkekiirust. Kuidas saaksid leida kogu läbitud tee pikkuse?
Kui sõidaksid esimesed kaks tundi muutumatu kiirusega 30 km/h, siis selle ajaga jõuaksid läbida 2 · 30 = 60 kilomeetrit. Seda võib ka graafiliselt kujutada, joonistades kiiruse sõltuvuse ajast. Sellel graafikul on esimese kahe tunniga läbitud tee pikkus antud täpselt kiiruse ning ajatelje vahele jääva ristküliku pindalaga:
Täpselt ühtlase kiirusega sõidetakse väga harva. Tegelikult muutub Su kiirus ilmselt peaaegu kogu aeg. Kuidas sellisel juhul leida läbitud tee pikkus?
Ka seda olukorda võime kirjeldada graafiliselt, just nii nagu enne. Tuleb ka välja, et jällegi on läbitud tee pikkus antud kiiruse ning ajatelje vahele jääva piirkonna pindalaga. Läbitud tee pikkuse ehk funktsiooni graafiku alla jääva ala pindala aga annabki integraal.
Kui tuletis oli ajast sõltuva funktsiooni spidomeetriks ning näitas funktsiooni hetkelist muutumise kiirust, siis integraali tähendus on vastupidine: integraal leiab funktsiooni spidomeetri põhjal tema kogumuudu. Järgnevalt alustame integraali idee selgitamisest ja loodame jõuda lõpuks siiski ka integraali matemaatilise definitsioonini [lk 44].
Lugulaul
Kuna integraal ja tuletis on tihedalt seotud, alustame ka sarnase lugulauluga – kihutad mäest alla. Muidugi, nagu sissejuhatuses juba mainisime, on nüüd käes kevad ning suuskade asemel oleme andnud Sulle hoopis ratta. Lisaks on meil seekord käepärast spidomeeter ja tahame arvutada hoopis läbitud tee pikkust.
Kuidas seda teha? Oskame tee pikkust kiiruse ja aja abil leida siis, kui kiirus on konstantne. Sellisel juhul on ka kiiruse graafiku alla jääv kujund kenasti ristkülik ning pindala valem ühtib täpselt tee pikkuse leidmise valemiga: s = vt
Probleem on aga selles, et mäest alla veeredes kiirus aina suureneb. Seega kümnendaks sekundiks läbitud tee pikkuse leidmiseks ei piisa enam sellest, kui vaataksime spidomeetrit näiteks alles viimasel sekundil ning kasutaksime seda kiirust oma läbitud tee pikkuse leidmiseks. Probleemi lahendus on siiski üsna lihtne: jagame aja lühikesteks vahemikeks ehk vaatame spidomeetrit üsna tihedalt.
Idee peitub selles, et väga lühikese ajavahemiku jooksul kiirus väga ei muutu. Seega võime igas lühikeses ajavahemikus läbitud tee pikkuse leida üsna täpselt, kui korrutame lihtsalt ajavahemiku pikkuse ning spidomeetrilt saadud kiiruse. Liites seejärel kokku igas lühikeses ajavahemikus läbitud tee pikkused, saamegi päris täpse vastuse.
Nagu tuletisegi peatükis – mida väiksemad ajavahemikud võtame ehk mida tihedamalt spidomeetrit vaatame, seda täpsem on ka meie vastus. Seekord annab integraal selle täpse vastuse, mida otsime – täpse tee pikkuse – ja taas kord tulevad matemaatiliselt mängu ka piirprotsessid [lk 308]. Nagu hiljem näeme, on nad seekord ainult veidi keerulisemad kirja panna.
Kõike seda võib ette kujutada ka geomeetriliselt.
Esiteks, aja lühikesteks vahemikeks jagamine tähendab geomeetriliselt lihtsalt kiiruse graafiku alla jääva kujundi jagamist väikesteks tükkideks.
Teiseks, igas vahemikus tavalise teepikkuse valemi kasutamine tähendab, et iga väikese tüki pindala lähendame ristkülikukujulise tüki pindalaga.
Lõpuks liidame kõik need pindalad kokku.
Joonist lähemalt vaadates on üsna selge, et mida väiksemad ajavahemikud, seda täpsem vastus. Kasutades ristkülikutega lähendamist, teeme iga väikese pindala arvutamisel teatava vea, aga mida väiksem vahemik, seda vähem oma hinnangus eksime.
Seega kokkuvõttes, täpne läbitud tee pikkus ongi kiirusfunktsiooni integraal ning omakorda on see antud kiirusfunktsiooni alla jääva kõvertrapetsi (nii nad seda kutsuvad...) pindalaga.
Taas kord on praktikas, spidomeetri abil täpse tee pikkuse ehk integraali leidmine võimatu – lõpmatult tihedalt ei ole võimalik spidomeetrit vaadata. Niipea kui meil on käest võtta matemaatiline kirjeldus, saame aga kohe asuda integreerima.
Konkreetne näide
Täpsustame nüüd, et tuiskad rattaga jällegi alla meile juba tuntud ideaalsest mäest. Tuletame meelde ka tuletise peatükist, et sel juhul on Su kiirus ajas antud valemiga v = 2t. Kuna laskumised pole väga pikad, mõõdame jälle aega sekundites.
Nagu juba märkasime, võime kiiruse ja aja suhet kirjeldada graafiliselt:
Nii on kahe sekundi möödudes juba saavutatud kiirus 4 m/s. Kui tahame nüüd leida nende kahe sekundiga läbitud tee pikkust, peame lihtsalt leidma joone alla jääva kujundi pindala.
Kavalpead võivad kohe näha, et võime seda teha näiteks kolmnurga pindala valemist ning saada vastuseks
Teine ning levinuim viis selle integraali leidmiseks on kasutada seost tuletise ja integraali vahel – kuna integraal ja tuletis on teatud mõttes pöördoperatsioonid, võime integraali leidmise taandada tuletise teadmisele ning vastupidi. Sellest pikemalt integraali ja tuletise peatükis [lk 352].
Viimaks näitame aga, kuidas integraali leida näppudel, kiiruse graafiku alla jäävat kujundit väikesteks tükkideks jagades ning nende pindalasid kokku liites, ehk lühemalt – kuidas käsitsi integreerida:
Jagame oma lühikese ajavahemiku 2 sekundit n väikeseks vahemikuks, millest iga pikkus on täpselt
Vahemik i ulatub siis ajahetkest
kuni ajahetkeni
Igas selles vahemikus hindame kiirust vahemiku lõppkiiruse abil.
Kasutades valemit v = 2t, on meie hinnang vahemiku i lõppkiiruse jaoks
Selles vahemikus läbitakse seega hinnanguliselt tee pikkus
Liites need väikesed tee pikkused kokku, saame
See kõverik on juba varem kirjeldatud [lk 50] summa märk, aga meeldetuletuseks kirjutame summa ka pikalt välja:
Me juba teame (näiteks aritmeetilise jada summavalemist), et
seega
Meie hinnang sõltub selgelt ajavahemike arvust n liikme
kaudu.
Samas kui n viia lõpmatult suureks, muutub see liige imepisikeseks ning piirprotsessis kaob hoopis. Seega saame kogu tee pikkuseks ehk integraaliks vastuse 4. Ühikud tuleks muidugi eraldi juurde sobitada, et saada nagu enne vastus 4 meetrit.
Integraali tähis ja matemaatiline kirjapanek
Matemaatilisemaks kirjelduseks on kunstilembesed matemaatikud integraalile andnud ka tähise, mis on lihtsalt üks välja venitatud s.
S on ta just sellepärast, et integraal ise on lõputult paljude asjade kokkuliitmisel justkui üks välja venitatud summa.
Sellises kõverikus endas on aga veel üsna vähe informatsiooni. Et teda mõistlikult kasutada, on veel vaja ära märkida, mida me integreerime, mille suhtes ja kui pikas vahemikus.
Kui meil on antud mingi muutumist kirjeldav funktsioon ƒ(x), siis tema integraali või kogumuutust x-i suhtes vahemikus [a, b] tähistame:
Graafiliselt on see integraal vastavuses siis x-telje, joonte x = a ning x = b ja funktsiooni ƒ(x) graafiku vahele jääva piirkonna pindalaga:
Ülaltoodud näites integreerime kiirust v(t) aja t suhtes, vahemikus ajahetkest 0 kuni ajahetkeni 2, sel juhul võime integraali kirja panna kujus:
Meie konkreetse näite korral leidsime siis järgmise integraali:
Kuhu jääb definitsioon?
Aga kuhu jääb integraali matemaatiline definitsioon?
Lihtne vastus: suur osa täpsest definitsioonist jääb ülikooli. Integraali mõistlikuks defineerimiseks tuleb olla päris hoolas.
Tuletame meelde, et integraal mõõtis spidomeetri põhjal tee pikkuse kogumuutu mingis vahemikus. Tema leidmiseks jagasime ahemiku väikesteks tükkideks ning leidsime muudu neis vahemikes. Liites need muudud kokku, saime hinnangu integraalile. Piirprotsessis, kus vahemikke oli aina rohkem ning nad olid aina lühemad, saimegi integraali enda.
Konkreetses näites kasutasime tee pikkuse leidmiseks ühepikkuseid ajavahemikke ning mõõtsime igas vahemikus kiirust ajavahemiku otspunkti põhjal.
Võttes sellest kõigest malli, võiksime matemaatiliselt defineerida, et integraal tähendab just seda, et jagame ajavahemiku järjest rohkemateks osadeks, valime alati pisikeste ajavahemike otspunktid ning arvestame neid tee pikkuse leidmiseks. Integraali saame piirprotsessis, kus n tormab lõpmatusse.
Sümbolite keelde tõlkides tähendaks see, et defineeriksime:
Ent stopp! Siin teeme kaks üsna suvalist valikut. Esiteks on suvaline see, et jagame kogu vahemiku võrdseteks tükkideks. Teiseks, miks peaksime muutu hindama just vahemiku parema otspunkti põhjal?
Ühtegi väga head põhjust kummakski ei ole ja see peaks juba valvsaks tegema – kas me tegime õiged valikud? Kas teised valikud annaksid ikka sama integraali? Kas leidub mõni „õige” valik? Kas saab kuidagi üldisemalt integraali defineerida, nii et ei täpsustagi täpselt, kuidas vahemikke võtame ning millise punkti neis valime?
Kõik need on põnevad küsimused, kahjuks jäävad aga sellest raamatust juba kaugemale. Integraali rangeks defineerimiseks leidubki tegelikult mitu erinevat viisi intuitsiooni jääb aga alati samaks, selleks, mille ülalpool ka esile tõime. Kusjuures võibolla on ka oluline lisada, et konkreetsed siin tehtud valikud pole just parimad – neid kasutades võime integreerida ainult üsna ilusaid funktsioone, kõik keerulisem toob juba kaasa probleeme.
Viimaks, kui siiski definitsiooni puudumine teeb tõesti tuska, võib integraali defineerida tuletise ja integraali vahelise seose toel. Nii teeme seda juba tuletise ja integraali peatükis [lk 352].
Arutlesime, et integraalist võib mõelda ka kui mingi kindla joone ja x-telje vahele jääva ala pindalast. Tegelikult võime pisut kavaldades leida integreerimise abil ka paljude teiste kujundite pindalad.
Üks viis kavaldada polegi nii väga keeruline. Vaatame näiteks üht kena väljavenitatud ringjoont ehk ellipsit.
Kuidas integraali abil selle ellipsi pindala leida? Esiteks peame ta muidugi asetama koordinaatteljestikule. Nagu näeme, tekib siis tegelikult kaks kaart – ülemine ja alumine –, mida mõlemat võiksime vaadata funktsioonina x-st:
Leides ülemise kaare integraali, saame vastuseks ellipsi ülemise osa pindala. Aga ellips on ju kenasti sümmeetriline ja nii võime saadu lihtsalt kahega korrutada ning saadagi kogupindala!
Üldisemalt, isegi kui kena sümmeetriat abiks pole, võime mõne kõvera kujundi pindala leidmiseks jagada kujundi horisontaalteljega kaheks, leida ülemise ja alumise kaare integraalid ning lõpuks lahutada ülemise kaare integraalist alumise kaare integraali. Lahutama peame seetõttu, et alumise kaare integraal annab meile negatiivse vastuse – allpool x-telge asuv osa tähendab ju negatiivset muutu.
See pole aga kõik! Tegelikult ei ole alati loomulik jagada kujundit just ristkülikute abil tükkideks. Näiteks ringi pindala leidmiseks võiksime ta ju jagada hoopis väikesteks rõngasteks ning seeläbi leida ringi pindala. Sellest aga pikemalt juba pindalade peatükis [lk 367].
Viimaks ei ole muidugi mingit põhjust piirduda ainult pindalade ehk kahemõõtmeliste mahtudega. Integreerimist võime kasutada ka näiteks ruumalade leidmiseks. Osas 8 leiamegi sel viisil näiteks kera ruumala valemi [lk 375].
Eluliste ülesannetega maadeldes kohtame vahel ka funktsioone, mille integreerimine on paras piin. Ei saa nende integraali leida mõne kavala pindala valemiga ega ole abi ka seosest tuletisega – me lihtsalt ei tea, millise funktsiooni tuletiseks nad on. Nii peame määramata integraali leidma käsitsi integreerimisega.
Päris käsitsi oleks see muidugi paras õudus, ent õnneks on meil tänapäeval olemas arvutid, kes oskavad teha miljoneid väikseid tehteid sekundis. Nii võime eeltoodud mooduse integraali leidmiseks – jagada piirkond paljudeks vahemikeks, leida muut igas vahemikus ning need muudud kokku liita – arvutile selgeks teha.
Näiteks võime lasta arvutil jagada integreerimisvahemiku miljoniks võrdseks osaks, leida nende osade pikkused ning kogumuudud ja arvutadagi lähenduse integraalile.
Muidugi saame seeläbi alati natuke ebatäpse väärtuse, ent samas võime selle ebatäpsuse teha nii väikseks kui vähegi soovime.
See viis ei ole aga integraalide arvutamiseks kõige efektiivsem ning praeguseks on välja arendatud kümneid algoritme, mis on täpsemad, usaldusväärsemad ja efektiivsemad.
Näiteks väga mitmemõõtmeliste ja keeruliste funktsioonide puhul osutub vahel kõige paremaks algoritmiks niinimetatud Monte Carlo meetod. Tutvustame seda lihtsa näitega: oletame, et soovime leida väärtuse integraalile
Monte Carlo meetodi idee on kasutada niinimetatud geomeetrilist tõenäosust: [lk 402] kui me võtaksime mõne juhusliku arvu ruudust [0; 2] × [0; 2], siis tõenäosus, et ta jääb funktsiooni √x graafiku alla, on täpselt võrdne graafiku alla jääva pindala ning kogupindala suhtega.
Edasi on meil vaja lihtsalt juhuslikke arve genereerida ning seda tõenäosust hinnata. Sobivate juhuslike arvude genereerimine on aga üsna vähenõudev ning samuti on kiire ka kontrollimine, kas arv jääb funktsiooni graafiku alla. Nii saamegi ühe üsna efektiivse meetodi integraalide ligikaudseks arvutamiseks. Seekord on meie vastus seda täpsem, mida rohkem juhuslikke arve kasutame.
Pöördoperatsioonid on matemaatikas üsna levinud. Kõige lihtsam näide tulebki võibolla pööretest endast: kui pöörame oma joonist tasandil 90 kraadi päripäeva, siis teda seejärel 90 kraadi vastupäeva keerates on ta jälle algseisus tagasi. Samuti võime liitmisest ja lahutamisest mõelda kui pöördoperatsioonidest: kui liidame mõnele arvule kolm ja siis jälle lahutame, jõuame algpunkti tagasi.
Teineteisele vastupidiselt käituvad ka integraal ja tuletis. Näiteks võib mõelda, et tuletis arvutab funktsiooni muutumise kiirust, integraal aga liidab funktsiooni muute kokku.
Liikumise kirjeldamise korral on lugu näiteks järgmine:
- tuletis annab meile etteantud tee pikkuse abil liikumise kiiruse
- ning integraal arvutab liikumise kiiruse põhjal omakorda läbitud tee pikkuse
Seega on tõesti tegemist justkui teineteise pöördoperatsioonidega. Täpne seos integraali ja tuletise vahel on ainult veidi segasem, veidi tähelepanu vajab näiteks määratud ja määramata integraali eristus.
Tuletise ja integraali seos on ka praktiliselt kasulik. Ühelt poolt on kasu puhtalt arvutuslik: võime integraalide leidmise taandada tuletise teadmisele ja vastupidi. Teisalt annab see seos teatava mõttelise aluse üsna suurele osale looduse kirjeldamisest: selle jaoks, et kirjeldada mingi suuruse kogumuutu ehk integraali ajas, piisab sellest, kui kirjeldame tema hetkelist muutumise kiirust ehk tuletist. Selle lihtsa mõtte rakenduseks on diferentsiaalvõrrandid, mis panevad aluse suurele osale klassikalisest füüsikast. Neil me siiski pikemalt ei peatu.
Meenutame, et kui meile on antud piisavalt sile funktsioon, millele saame igas punktis tuletise leida, võime tuletisest mõelda kui teisendusest, mis seab ühe funktsiooniga F(x) vastavusse tema tuletise funktsiooni F'(x).
Nagu mäletame, tähendab see geomeetriliselt, et sinine graafik on kokku pandud helerohelise graafiku puutujasirgete tõusudest:
Nüüd võib mõelda ka selle teisenduse pöördteisendusele – ehk küsida, mis juhtub siis, kui tahaksime hoopis alustada sinisest joonisest ja leida funktsiooni, mille graafiku puutujatõusudest moodustuks see sinine joon?
Teisisõnu tahaksime leida funktsiooni, mille jaoks igas punktis kehtib F'(x) = ƒ(x).
Iga võimalikku vastust sellele nimetatakse funktsiooni ƒ(x) algfunktsiooniks ning mitmust kasutame siin üsna asjakohaselt – võimalikke vastuseid on palju!
Tõepoolest, kui F(x) on mõne funktsiooni ƒ(x) algfunktsioon, siis on seda ka F(x) + C iga konstandi C jaoks. Konstandi C lisamine ju ainult nihutab funktsiooni F(x) üles-alla, ent ei muuda tema muutumise kiirust – puutujad jäävad paralleelseks. Õigupoolest tuleb välja, et midagi muud teha ei võigi – kõikvõimalikud algfunktsioonid saamegi ühteainsat üles-alla nihutades.
Nüüd funktsiooni ƒ(x) määramata integraal kogubki kõikvõimalikud vastused ehk teisisõnu algfunktsioonid ühte ja samasse avaldisse F(x) + C. Siin F(x) tähistab ühte võimalikest algfunktsioonidest ning C suvalist konstanti. Määramata integraali tähiseks on integraali kõverik ilma ülemise ja alumise rajata. Seega kirjutaksime:
Algfunktsioonide abil võiksime tegelikult defineerida ka määratud integraali.
Nimelt võiksime öelda, et funktsiooni ƒ(x) määratud integraal vahemikus [a; b] on võrdne mõne tema algfunktsiooni muuduga selles vahemikus. Ehk siis:
kus jällegi F(x) on üks ƒ(x) suvaliselt valitud algfunktsioon.
Oluline on märgata, et sellest, millise algfunktsiooni me valime, väärtus ei muutu. Tõepoolest, konstant taandub ju lahutamistehtes välja. Geomeetriliselt mõeldes: kui nihutame funktsiooni F(x) graafikut, nihutame võrdselt nii tema väärtust vahemiku alg- kui lõpppunktis, nende vahe jääb samaks.
Integreerimine tuletise abil
Leitud seosest saame ka üsna lihtsa viisi integreerimiseks – meil on vaja lihtsalt ära arvata vastav algfunktsioon ehk tunda tuletisi!
Tõepoolest, näiteks integraali peatükis käsitletud integraali
leidmiseks piisab teadmisest, et lineaarfunktsiooni 2t üheks algfunktsiooniks on t2.
Seejärel võime kirjutada
Või näiteks, kuna siinusfunktsiooni tuletiseks on koosinusfunktsioon, võiksime kirjutada:
Seda on muidugi võimalik näha ka graafikult, teades koosinusfunktsiooni sümmeetrilisust ja meenutades, et x-telje alla jääv pindala näitab negatiivset kogumuutu:
Newtoni-Leibnizi seoseks nimetatakse juba toodud seost funktsiooni ƒ(x), tema määratud integraali ning algfunktsiooni muudu vahel:
See ongi kõige täpsem ja kasulikum sõnastus integraali ja tuletise vahelisele seosele. Selle seose alusepanijad Isaac Newton ja Gottfried Leibniz ei suutnud omavahel kuidagi kokku leppida, kumb on ikkagi rohkem tunnustust ära teeninud. Mõlemad pidasid just oma panust olulisemaks ja nii nad jäidki Leibnizi surmani tülli. Üsna tühine tüli ilusa matemaatika ümber.
Kui määratud integraal ise selle kurikuulsa seose kaudu defineerida, ei ole seda seost muidugi vaja tõestada, tegemist oleks pigem siis seaduse või aksioomiga.
Samas ei ole ju sugugi selge, miks peaks selle seose kaudu defineeritud määratud integraal ikkagi olema seotud pindalade ning nende jupitamisega.
Seose olemasolus on kõige lihtsam ennast veenda geomeetriliselt. Vaatame näiteks ühte ilusat pidevat funktsiooni ƒ(x) vahemikus [0; b] ja alustame teadmisest, et määratud integraal
annab meile ƒ(x) graafiku ning x-telje vahele jääva pinnatüki pindalaga kuni punktini b. Tähistame seda pindala F(b)-ga.
Funktsiooni F(x) tuletis punktis b tähendab nüüd pindala hetkemuutu. Tuletame meelde definitsiooni:
@{969}@
Geomeetriliselt võime murru lugejast seega mõelda kui funktsiooni ƒ(x) graafiku alla jäävate pindalade vahest vastavalt punktideni b + h ja b:
Ehk siis parempoolse osa pindala on F(b + h) – F(b). Väga väikese h väärtuse jaoks on aga see pindalade vahe peaaegu nagu ristkülik. Seega kuna ristküliku laiuseks on h ise, siis annab jagatis
meile ristküliku kõrguse.
Mis aga on see kõrgus? Jooniselt näeme, et kõrguseks on funktsiooni ƒ väärtus b ja b + h vahel. Kui h väärtus muuta lõpmatult väikeseks, siis saab sellest muidugi ƒ-i väärtus kohal b ise. Nii näemegi, et
@{971}@
Ehk teisisõnu annab pindade põhine integraal meile kenasti ühe algfunktsiooni ja kõik klapib.
Alustame väikese mõtisklusega teemal, mida üldse tähendab mõõtmine. Mida me täpselt teeme, kui igapäevaelus asju mõõdame?
Üks võimalus on mõõtmisest mõelda kui teatavast võrdlusest mingite kokkulepitud suurustega. Joonlauale või mõõdulindile on täpselt kirja pandud, mida võime lugeda üheks sentimeetriks ja mida üheks meetriks, ning nende kokkulepitud näidissuurustega võrreldes leiamegi oma jala- või ninapikkuse. Sarnaselt võime kasutada mõõtmiseks ka mõnda nööri, mille pikkuseks teame üht meetrit, keraamikaplaati pindalaga sada ruutsentimeetrit või miks mitte ka poolt liitrit vett: idee on ikka ja jälle sama, leiame, kui palju kordi meile juba teatud suurus mingit pikkust, pinda või ruumala katab.
Seega on meil vaja mõõtmiseks mõnda mõistlikku „etaloni”, mille suurust tema lihtsuse tõttu teame, ja seejärel vilumust temaga hästi katta erinevaid pikkuseid või pindu. Järgnevalt näitame, millised on matemaatilised „etalonid” ja kuidas neid kavalalt kasutada.
Päriselus käib iga mõõtmisega kaasas ka teatav mõõteviga – oleme ise mõõtmisel ebatäpsed ja ka kehad ise pole päris ideaalse kujuga. Siin peatükis tegeleme aga matemaatikaga, kus saame kõik mõõtmised absoluutse täpsuseni viia.
Ümbermõõdu või joonepikkuse mõõtmiseks on meil varnast võtta suur hulk häid mõõdutükke: pisikesed sirglõigud erinevate pikkustega. Ilmselgelt piisab neist, et mõõta iga sirglõikudest koosneva murdjoone pikkust:
Aga tegelikult ei valmista muret ka kõverjooned, kui oleme nõus väikest viga sallima: nimelt jagades kõverjoone väga pisikesteks tükkideks on iga tükk peaaegu sirgjoon:
Sellisele lähendamisele annab matemaatilise tähenduse integreerimine [lk 340] ja tuleme selle juurde veel hiljem tagasi.
Pindalade leidmisel valime samuti kõige lihtsama võimalikest etalonikomplektidest: erineva küljepikkusega ruudud. Esmalt peaksime end aga veenma, et teame iga etaloni enda pindala.
Õnneks pole see väga keeruline: niipea kui teame, et näiteks ühikruudu pindala on 1, võime teisi ruute võrrelda ühikruuduga ja joonis aitab meil veenduda, et küljepikkus a annab pindalaks a2:
Matemaatilise tõestuse tarvis peaks muidugi olema pisut hoolikam.
- Naturaalarvuliste küljepikkustega ruutude jaoks võime kasutada joonisel toodud strateegiat.
- Naturaalarvude pöördarvude jaoks kasutame joonisel toodud strateegiat vastupidi: täidame ühikruudu ruudukestega küljepikkusega .
- Kasutades nüüd seda teadmist, võime jällegi joonist järgides leida pindala kõikide ratsionaalarvuliste küljepikkuste jaoks.
- Viimaks peame midagi tegema ka irratsionaalarvuliste küljepikkustega. Siin on tarvilik pisut teistmoodi, kuid üsna levinud strateegia, millest kirjutame üldisemalt funktsioonide pidevuse all [lk319] –idee on selles, et kui mõni reaalarvuline suurus muutub pidevalt, siis tema määramiseks piisab ainult ratsionaalarvuliste väärtuste teadmisest.
Selle argumendi võib aga siinjuhul kergesti ka üksipulgi kirja panna.
Idee on selles, et iga irratsionaalarvu a jaoks võime leida ratsionaalarvude jada qn, mille piirväärtuseks on meie valitud irratsionaalarv. Kuid iga ratsionaalarvulise küljepikkusega qn ruudu pindala me juba teame – see on qn2. Lõpuks, kui arvud qn koonduvad arvu a, siis nende arvude ruudud koonduvad arvu, a2 mis annabki soovitud tulemuse.
Võib ka küsida: miks peaks ühikruudu pindala olema 1? Pragmaatiline lugeja võib siinkohal otsustada, et see tundub mõistliku valikuna, ja las filosoofilisem lugeja mõtleb, mis ta mõtleb.
Ruumalade tarvis kasutame kuupe ning näeme sarnaselt eelnevaga, et kuubi küljepikkusega a ruumalaks on a3.
Ruut ja ristkülik
Mõtleme nüüd, kuidas oma ruudukujulise jupi abil välja nuputada ristküliku pindala. Kui küljepikkused on piisavalt sõbralikud, on see lihtne: näiteks jooniselt näeme, et külgedega 3 ja 5 ristküliku pindala on 3 · 5 = 15 ning külgedega 3⁄7 ja 1⁄2 ristküliku pindala on 3⁄14.
Ilmselt pole raske märgata, et näiteks kõik ratsionaalarvuliste küljepikkustega ristkülikud on sõbralikud: saame alati leida mingi imepisikese ruudu, mille abil ristkülik ruudukestega täielikult katta. Iga kord saame tulemuseks, et a · b ristküliku pindala on täpselt S = a · b.
Edasi peame taas kasutama ruudu küljepikkuse leidmisel mainitud „pidevuse printsiipi” – kui meil on mingi pidevalt muutuv reaalarvuline suurus, siis piisab sellest, kui me teame tema väärtusi ainult ratsionaalarvulistes kohtades. Nii võimegi väita, et iga a · b ristküliku pindala on
Kolmnurk
Kolmnurkadest on kõige lihtsam alustada täisnurksete kolmnurkadega – neid kaks tükki kokku pannes saame täpselt ristküliku:
Siit pole muidugi raske järeldada, et täisnurkse kolmnurga pindala on pool moodustunud ristküliku pindalast ehk
kus a ja b on tema kaatetite pikkus.
Aga nüüd võime ju etalonina juba kasutada ka täisnurkseid kolmnurki ja see teeb iga teise kolmnurga pindala leidmise väga lihtsaks: tõmbame lihtsalt kolmnurka mõne kõrguse ja jagame ta kaheks täisnurkseks kolmnurgaks!
Isegi kui joonised on erinevad, näeme, et järeldus on nii kolmnurga sisse kui kolmnurgast välja jääva kõrguse puhul sama – iga kolmnurga pindala on
kus a on mõni kolmnurga küljepikkus ja h tema vastastipust tõmmatud kõrguse pikkus.
Rööpkülik ja trapets
Rööpküliku võime jagada lihtsalt kaheks kolmnurgaks. Nii näeme, et rööpküliku pindala on S = a · h, kus a on tema vaadeldav küljepikkus ning h nende külgede vaheline kaugus. See tuleneb muidugi sellest, et mõlema kolmnurga pindala on eelmise osa põhjal
Nagu jooniselt näeme, võime rööpküliku pindala tuletada veel vähemalt kahel erineval moel:
Ja trapets? Sama lugu, kasutame seniseid etalone, täisnurkseid kolmnurki ja ristkülikut, ning saamegi väikese kavaluse abil õpetaja väljakuulutatud tulemuse.
Tegelikult saame ju nüüd leida ka iga viisnurga, kuusnurga või ka kakssadanurga pindala, kui ainult kannatust jagub: võime nad ju alati jagada ühel või teisel viisil kolmnurkadeks (nii kuidas mugavam on) ja kolmnurkade pindalad kokku liita.
Ring on oma olemuselt üks lihtsamaid ja ilusamaid kujundeid. Nagu nägime kuulsate arvude peatükis, võib teda ka mitmel moel defineerida ning temast mitmel moel mõelda [lk 96]. Siiski, hoolimata sellest, et ring on peale vaadates ilus ja lihtne kujund, peab temaga matemaatiliselt ümber käima teistmoodi ja isegi pisut keerulisemalt kui hulknurkadega.
Ringi ümbermõõduga pole asi siiski liiga hull. Kuna π on juba defineeritud kui ümbermõõdu ja diameetri suhe
siis ümbermõõdu P saabki sealt lihtsalt avaldada:
Traditsiooniliselt kirjutatakse see välja ringi raadiuse abil:
Kuidas aga leida ringi pindala?
Meie seniseid pindalade etalone on siin raskem ära kasutada – kõik nad olid nurgelised, samas kui ringjoon on ju kenasti kaardus. Seega peame olema kavalamad.
Üks võimalus on siiski kasutada juba teadaolevaid etalone, kuid seda koos integraaliga. Tuletame meelde, et integraali abil saame lähendada kujundite pindalasid, jagades kujundi õhukesteks ristkülikukujulisteks juppideks ning liites nad kokku. Piirprotsessis, kus õhukesi tükke on järjest enam, saamegi vastuseks täpse pindala. Sellest on meil natuke pikemalt juttu integraali peatükis [lk 347].
Siin kasutame vägagi sarnast ideed, ainult loobume kujundi ristkülikuteks jagamisest ning jagame ta hoopis väga paljudeks peenikesteks rõngasteks paksusega h, mis on õige sarnased juba ringidele. Nende raadiused muutuvad siis 0-ist kuni r-ini sammuga h.
Iga väike rõngas panustab algringi pindalasse umbkaudu 2πxh, kus x on näiteks rõnga välimise ringi raadius.Tõepoolest, kui paksus h on väga väike, siis ei pea rõnga sise- ja välisraadiust eristama. Pindala leidmiseks peame seejärel liitma kokku kõik need lõpmata paljud ümbermõõdud ja saame
Siin x1, … xn moodustavad aritmeetilise jada vahega h ja seega lähendavad lineaarfunktsiooni. Nüüd peaks meenuma, et see on juba väga sarnane meie määratud integraali kirjeldusele. Tõepoolest, piirprotsessis, kus ketaste paksus h→0, võimegi pindala kirja panna määratud integraali abil [lk 340]:
Edasi jääb vaid integreerida ja leiamegi kuulsa ringi valemi:
Kui tahame lugu veel enam integraali ja tuletise raamistikus näha, võib mõelda, et ringi pindala muutumise kiiruse annab just tema ümbermõõt. See on üsna loomulik, kuna ringi raadiust õige pisut, h võrra suurendades, muutub ringi pindala umbes hP võrra. h oleks selles kontekstis seega „aja parameetriks” ning kiiruse annakski ümbermõõt P.
Võib korraks ka mõtiskleda, kas see valem meile üldse usutav näib. Järgnev joonis, kus on antud neli ruutu küljega 1 ning ring raadiusega 1, võib veenda, et ringi pindala võiks tõesti olla umbes 3 kuni 4 korda (ja seega umbes π korda) suurem ühe ruudu pindalast.
Lisaks kahemõõtmelistele kujunditele võib meid muidugi huvitada ka mõne kolmemõõtmelise kujundi välispinna suurus.
Hulktahukate ehk igasugu erinevate risttahukate ja püramiididega, mille tahud on hulknurksed, käib asi üsna lihtsalt: lõikame kujundi mööda servasid lahti ning arvutame iga tahu pindala eraldi välja. Liites need kõik kokku, saamegi kogu pindala.
Näiteks kolmnurkse põhjaga püramiidi külgpindala leidmiseks peame kokku liitma nelja kolmnurga pindala.
Koonuse pindala
Üldiselt läheb kumeramate kehadega olukord keerulisemaks, aga koonuse korral aitab siiski üsna sarnane strateegia. Alustuseks võime koonuse pinna jagada kaheks – saame ringikujulise põhja ning teatava kujuga külgpinna.
Kuna ringi pindala juba oskame leida, on põhja pindala arvutamine kerge. Aga kuidas leida selle allesjäänud koonuselise tüki pindala?
Seegi kord aitab meid veel lõikamine ning tasandile asetamine. Nimelt kui lõikame koonuse külgpinna mööda moodustajat – ehk mööda suvalist koonuse tippu ja põhja äärt ühendavat sirglõiku – lahti ja laotame tasandile, saame ilusa ringi sektori.
See sektor moodustab teatava osa suurest ringist raadiusega m, kus m on siis niinimetatud koonuse moodustaja. Selle algse ringi pindala oskame jälle lihtsalt leida:
Seega oleks vaja lihtsalt aru saada, kui suure osa moodustab laiali laotatud sektor kogu ringist. Ringjoone sektori pindala suhe kogu ringi pindalasse on aga täpselt sama kui sektori kaarepikkuse suhe kogu ringjoone ümbermõõtu. Kuna kogu ringi ümbermõõt on meile teada (2mπ), siis piisab lihtsalt sektori kaare pikkusest. Sektori kaare pikkus on aga täpselt koonuse põhja ümbermõõt! Seega, kui põhja raadiuseks on näiteks r, siis saame põhja ümbermõõduks ja ka kaare pikkuseks 2rπ.
Kui jagame saadud tulemused, näeme, et sektori pindala moodustab kogu pindalast
Nüüd võime külgpindala leida, korrutades saadud suhte läbi suure ringi pindalaga:
Liites põhja pindala:
Võime leida ka koonuse täispindala
Kera pindala
Kera pindala leidmiseks aga mõnest lõikamisest enam tõesti ei piisa.Võite proovida apelsinikoort mõistlikult laua peale laiali laotada, nii et ükski koht õhus ei oleks – lihtne see ei ole. Tuleb kasutada juba ringi pindalast tuttavat integreerimise strateegiat.
Intuitiivselt tahaksime ka seekord pinna rõngasteks jagada ning seejärel nende rõngaste pindalad osavalt kokku liita.
Ringi pindala leidmisest on olukord pisut keerulisem, kuna rõngaste pindalad ise ei muutu enam ilusalt ühtlaselt.
Seega piirdume siinkohal lihtsalt kera pindala valemiga:
Kera ruumala juures anname siiski ka ühe viisi selle pindala leidmiseks.
Laias plaanis võime ruumalade leidmisel käituda üsna analoogiliselt pindalade juhule: alustame kuubi ruumalast, siis leiame risttahuka ruumala, seejärel rööptahuka ruumala ja nii edasi.
Natuke keerulisemaks läheb püramiidide korral, aga siiski aitab natukene kavalust meid hädast välja.
Näiteks toodud jooniselt näeme, kust tuleb vähemalt ruutpüramiidi korral kurikuulus üks kolmandik: nimelt saame täita ühikkuubi kuue võrdse ruumalaga püramiidiga, mille kõrgus on täpselt pool kuubi küljest.
Kõikide võimalike eripüramiidide jaoks samasuguste konstruktsioonide väljanuputamine osutub juba aeganõudvaks, kuigi on ilmselt võimalik nii kaua, kuni aluspinnaks on mõni hulknurk. Jällegi on idee alustada lihtsamatest püramiiditüüpidest ning samm-sammult minna üldise kuju poole – see osutub üsna pikaldaseks, kuna peame sisuliselt iga püramiidi külge ükshaaval lihtsamast keerulisemaks muutma.
Võib siiski kinnitada, et püramiidi ruumala valem jääb samaks:
kus Spõhi on seekord püramiidi aluse pindala ning h tema vastastipust tõmmatud kõrgus. Seesama valem jääb kehtima ka siis, kui aluseks on hoopis ring.
Toodud valemi sarnasus kolmnurga pindala valemiga võib mõtlema panna, kas neil kahel on mingi seos – räägime mõlemal korral ju alusest ja kõrgusest ning eesolev kordaja paistab täpselt seoses olevat ruumimõõtmete arvuga. See seos põhineb tegelikult väga lihtsal mõttel, mida juba ka mainisime.
Nimelt nägime ringi pindala juures, et ringi raadiust suurendades võime mõelda, et ringi pindala kirjeldava funktsiooni tuletiseks on tema ümbermõõt.
Samamoodi võime mõelda, et mõõtes kolmnurga kõrgust, on kolmnurga pindala muutumise kiiruseks tema alumise külje pikkus. Kui aga leiame püramiidi ruumala kõrgusest sõltuvalt, on muutumise kiiruseks hoopis tema põhja pindala:
Nüüd on lihtne veenduda, et kolmnurga aluse pikkus sõltub tema kõrgusest lineaarselt – ehk seda võib kirjeldada funktsiooni abil. Püramiidi pindala aga muutub kõrguse suhtes nagu ruutfunktsioon ax. Esimese integreerimisel saame ette kordaja 1⁄2, sest kui seame integreerimisega kaasaskäiva konstandi nulliks, saame
ning teise integreerimisel leiamegi kordaja 1⁄3?:
Täpsemat näidet esimesest viisist nägime ringi pindala leidmisel, teise näite teeme läbi nüüd kera ruumala arvutamiseks.
Kera ruumala
Kera ruumala on jällegi raske leida lihtsalt nurklike etalonide abil. Peame kasutama ringi pindala puhul abiks olnud strateegiat – integreerimist. Teisisõnu lähendame kera paljude õhukeste ketastega, leiame nende ruumalad ning liidame nad kokku. Piirprotsessis saame integraali, mis annabki meile koguruumala [lk 347].
Tähistame tähega x horisontaalset kaugust kera keskpunktist ning tähega y kera pinnal asuva ringjoone raadiust tollel kaugusel. Ketta, mille välimine äär on kaugusel x ning mille paksus on h, ruumala on umbkaudu h · πy2 ehk πhy2.
Selle ringjoone raadiuse y, mis sõltub x-ist ja kera raadiusest r, saame avaldada Pythagorase teoreemi kaudu: y2 = r2 – x2.
Neid kettaid aina väiksema paksuse korral kokku liites saame nagu kera pindala leidmiselgi integraali [lk 340], seejuures vasemalt äärelt paremale välja jõudmiseks muutub horisontaalne kaugus x vahemikus [–r, r]. Seega võime ruumala kirjutada järgmise integraalina:
Seda oskame kooliõpiku abil juba arvutada:
Tulemuseks saamegi kera ruumala valemi
Huvitav on see, et sellest kera ruumala valemist saame tegelikult nüüd tuletada ka kera pindala valemi. Nimelt võiksime ju ka mõelda, et kera koosneb mitte ketastest, vaid hoopis sfäärilistest kihtidest:
Seega saaksime kera ruumala, kui liidaksime kokku nende sfääriliste kihtide ruumalad. Keskpunktist kaugusel x asuva peenikese sfäärilise kihi ruumala oleks nüüd umbes Sxh, kus Sx on raadiusega x kera pindala ning h siis õhukese sfääri paksus. Seega võiksime analoogiliselt eelnevaga kirjutada ruumala integraalina üle nende sfääriliste kihtide:
See aga tähendab täpselt, et kui vaatame kera ruumala kui funktsiooni raadiusest, siis on kera pindala selle funktsiooni tuletis! Seega kui teame juba kera ruumala, võime leida tema pindala, kasutades integraali ja tuletise vahelist seost.
Tõepoolest, nägime ju tuletise ja integraali vahelise seose peatükis [lk 352], et ühe funktsiooni ƒ(x) integraal annab meile vastuseks ühe niinimetatud algfunktsiooni: funktsiooni, mille tuletis on igas punktis võrdne funktsiooniga ƒ(x).
Nüüd aga, vaadates kera pindala funktsioonina raadiusest, annabki ruumala ühe võimaliku algfunktsiooni. Seega peame pindala leidmiseks ühes punktis lihtsalt leidma ruumala tuletise samas kohas. Valemites:
@{997}@
Muidugi tahaksime, et matemaatikas oleks kõik nii, nagu meie vaist seda õigeks peab. Siiski selgub, et niipea kui mõne definitsiooni rangelt matemaatiliselt kirja paneme, alustab ta justkui oma elu, libiseb meie käe alt välja ja korraldab midagi üllatavat.Tihti peame seejärel matemaatikaga paremaks läbisaamiseks oma intuitsiooni ümber kujundama.
Kirjeldame järgnevalt ühte kujundit, mis näibki algul pigem mõistusevastane: tal on lõplik pindala, aga lõputu ümbermõõt. Seda kujundit kutsutakse Kochi lumehelbeks.
Kochi lumehelbe saamiseks peame läbima järgmise protsessi:
- alustame võrdkülgsest kolmnurgast,
- esimesel sammul jaotame iga külje kolmeks võrdseks osaks ja ehitame iga külje keskmisele kolmandikule väljapoole võrdkülgse kolmnurga, nagu jooniselt näha, võib nüüd eristada kuut väiksemat kolmnurka, millest igal on kaks väljapoole avatud külge,
- edasi konstrueerime analoogselt eelnevaga iga väljapoole avatud külje keskele uuekolmnurga,
- Aina jätkame ja jätkame protsessi uute, väiksemate külgedega...
Nagu jooniselt näeme, tekib nii midagi lumehelbe sarnast. Kui protsessi kangekaelselt jätkata, näeb tekkiva kujundi piirjoon iga suurusega luubi all välja umbes ühesugune (alati paistab, et on üks külg, mille keskele on konstrueeritud kolmnurk, ja siis veel natukene väikest müra):
Mis võiks olla tekkiva kujundi ümbermõõt? Kui alguses on kolmnurga ühe külje pikkus 1, siis pärast esimest etappi oleme külje asendanud 4 lõiguga, millest igaühe pikkus on 1⁄3 ehk kokku on tema pikkus 4⁄3. Igal järgmisel etapil on 4 korda rohkem lõike, kuid iga lõik on 3 korda lühem ehk lõikude kogupikkus suureneb 4⁄3 korda.
Seega pärast sajandat konstruktsiooni on lõikude kogupikkus juba
ning protsessi lõpmatult jätkates muutub ka kujundi ümbermõõt lõpmata suureks:
Lähemalt vaadeldes selgub samas, et pindala ei saa sellel kujundil väga suur olla ja kindlasti peab ta olema lõplik. Nimelt mahub Kochi lumehelves näiteks alati joonisel toodud sinisesse ristkülikusse:
Pärast mõningat arvutustööd selguks, et tema pindala on täpselt
Kui nüüd järele mõtleme, miks meile toodud olukord paradoksaalne tundub, siis ilmselt on põhjus väga lihtne: igapäevaelus me ilmselt sellist kujundit kohanud pole, kus ümbermõõt oleks lõpmatu ning pindala lõplik. Meie masinavärk ei luba lihtsalt selliseid pikkuseid mõõta: päriselus ei ole meil tegelikult ju kasutada lõpmatu suurendusega luupe ning iga lõpliku suurusega luubi korral tunduks ka Kochi lumehelbe ümbermõõt lõplik. Samuti paistab, et tänane füüsika ei tahaks hästi selliseid kujundeid lubada.
Siiski, matemaatikat need kaalutlused ja kitsendused ei sega – võime sama vabalt leida ka näiteks lõpmatu pindala ja lõpliku ruumalaga kujundeid (näiteks niinimetatud Gabrieli pasun) ning teisi sarnaseid veidrikke.
Permutatsioon on lihtsalt mingite fikseeritud objektide kindel ülesrivistus. Näiteks on jalgpallimeeskonna täpne reastus hümni laulmise aegu üks võimalik põhikoosseisu permutatsioon. Samuti on permutatsioon nelja tinasõduri ülesrivistus aknalaual ning kõikvõimalikud laused, mida võib moodustada kolme sõnaga – mulle, meeldib, matemaatika.
Põhiliselt huvitab meid siin peatükis permutatsioonide arv, mida n objekti korral tähistatakse Pn. Muidugi ei ole siin objektide enda täpne olemus oluline – meil on sama palju reastusi 10-st tinasõdurist kui 10-st tõsisest kaitseväelasest.
Permutatsioonide arv
Kui palju lauseid võib moodustada kolme sõnaga mulle, meeldib, matemaatika? Rõõmuks ja motivatsiooniks paneme nad esiteks muidugi kirja:
Mulle meeldib matemaatika.
Mulle matemaatika meeldib.
Meeldib mulle matemaatika.
Meeldib matemaatika mulle.
Matemaatika mulle meeldib.
Matemaatika meeldib mulle.
Neid lauseid on seega täpselt kuus. Eesti keel on vahva, kuna paljudes teistes keeltes ei oleks kõik toodud kuus lausest grammatiliselt võimalikud, meil aga teatud mööndustega on.
Siiski oleks olnud ilmselt meeldivam, kui ei oleks pidanud kõiki lauseid loetlema ning oleksime võinud kohe mõne valemi abil öelda, palju erinevaid lauseid leidub.
Kuidas sellist valemit leida?
- Märkame, et esimese sõna valikuks on meil kolm võimalust: mulle, meeldib või matemaatika.
- Kui oleme esimese sõna valinud, jääb täpselt kaks võimalust teise sõna valikuks.
- Kui aga teinegi sõna on valitud, võime kolmanda sinna vaid lõppu visata.
Esimesel sammul oli meil 3 võimalust, teisel 2 ja kolmandal ainult 1 võimalus. Kuna kõik valikud on üksteisest sõltumatud, on võimalusi kokku täpselt 3 · 2 · 1 = 6.
Oleks meil neli sõna, ei oleks kõik moodustatavad laused ilmselt enam grammatiliselt korrektsed, ent sarnase arutelu kaudu näeksime siiski, et moodustada on võimalik 4 · 3 · 2 · 1 = 24 erinevat lauset.
Sama mõttemustrit edasi viies näeme, et sõna n jaoks oleks lausete arv n · (n – 1) · … 3 · 2 · 1 ehk teisisõnu
Selgub, et järjestikuste arvude korrutamine on nii mõnus ja nii tihti ettetulev tegevus, et sellele tasub ka päris oma tähistus anda.
Nii tähistabki 10-faktoriaal esimese kümne positiivse täisarvu korrutist 1 · 2 · … · 10 ning n-faktoriaal seega korrutist 1 · 2 · … ·(n – 1) · n. Kuni 19. sajandini tähistati n-faktoriaali sümboliga
Varsti leidis õnneks esteetilise tunnetusega prantsuse matemaatik Christian Kramp, et tegemist ei ole teab mis kena sümboliga, ning tõi kasutusele tänapäevase tähistuse: n!.
Nagu äsja lugesime, ongi n objekti permutatsioonide arv täpselt võrdne n-faktoriaaliga ehk, kuna matemaatikud sümbolitega ei priiska:
Faktoriaali kasv*
Faktoriaali juures on muljet avaldav tema kasvukiirus. Kui hakkame järjest faktoriaali välja arvutama, oleme varsti pigis – taskuarvuti ütleb üles!
Juba 20! annab meile arvu 2 432 902 008176 640 000. Kui faktoriaali meile juba tuntud funktsioonidega võrrelda, siis faktoriaal kasvab kiiremini kui ükskõik milline polünoom [lk 266] ja isegi kiiremini kui ükskõik milline eksponentsiaalfunktsioon [lk 280].
Eks lihtsaim viis ülevaate saamiseks on ikka oma silmaga mõnd näidet uurida. Jälgi, kuidas kolm erinevat funktsiooni (lilla on polünoom, tumesinine eksponentsiaalfunktsioon ning helesinine faktoriaal) kasvavad:
Faktoriaal kihutab juba üsna varakult polünoomist mööda ja veidi hiljem möödub ka eksponentsiaalfunktsioonist. Kui ainult pilt pole veel piisavalt veenev, siis võib lugeda ka järgnevat selgitust, mis küll rangele matemaatilisele täpsusele ei pretendeeri.
Märkame, et ...
- Polünoomi y = x10 kasvust võime mõelda järgmiselt: kui tema argumenti (muutuja x väärtust) 2 korda suurendame, siis funktsioon kasvab 210 korda.
- Eksponentsiaalfunktsiooni y = 10x kasvust võime mõelda järgmiselt: kui tema argumenti ehk x-i suurendada 2 korda, siis on see võrdväärne funktsiooni ruutu tõstmisega.
Kumb neist kasvab kiiremini? Mõtleme juhule, kui meil on argumendiks väga suur arv, näiteks 350.
Selle argumendi väärtuse kahekordistamisel suureneb polünoomfunktsioon ainult 210 korda, eksponentsiaalfunktsioon aga tervelt 350 korda – seega kasvab eksponentsiaalfunktsioon vähemalt selles vahemikus palju kiiremini. Kiire mõtisklus näitab, et küllap ta siis rebib varem või hiljem ette.
Aga mida tähendab faktoriaali jaoks argumendi kahekordistamine?
Arvust m! saab (2m)! ja seega argumendi 350 jaoks saame argumendi kahekordistamisel algse faktoriaali 350! asemele faktoriaali (2 · 350). See tähendab, et korrutame kokku 2 · 350 esimest naturaalarvu.
Seega faktoriaal kasvab täpselt
korda. See arv on aga palju suurem kui 350 – meil on kokku 350 tegurit, millest iga on suurem kui 350!. Teisisõnu, argumendi kahekordistamisel suureneb faktoriaal veel mitu korda rohkem kui ruutuvõtmise korral. Jällegi, varem või hiljem rebib ta ka eksponentsiaalfunktsioonist ette.
Niisiis peaks olema täiesti usutav, et faktoriaal kasvab kiiremini kui eksponentsiaalfunktsioon ja seega ka kiiremini kui polünomiaalfunktsioon.
Järelikult kui keegi räägib oma varade eksponentsiaalsest kasvust, tuleb muidugi üle kelkida ja vastata: see pole veel midagi, minu varandus kasvab faktoriaalselt!
Kui permutatsioonid olid seotud teatud objektide järjekorraga, siis kombinatsioonid ja variatsioonid on seotud objektide valikuga.
Üks kombinatsioon on näiteks kodupeenralt südamekaaslasele valitud kolm lillenuppu või pokkerimängus jagatud viis kindlat kaarti või kolm õpilast, kes tahvli ees vastama peavad.
Ehk teisisõnu on üks kombinatsioon kindla arvu objektide valik mingi kindla arvu objektide hulgast. Kombinatsioonide puhul valime objektid välja ilma kindla järjestuseta.
Variatsioonide puhul on samuti tegemist samasuguse objektide valikuga, aga sel juhul huvitab meid ka nende järjekord – me valime kolm õpilast, kes tahvli ees vastama peavad, ning anname neile lisaks ka vastamisjärjekorra.
Variatsioonid ja kombinatsioonid on omavahel tihedalt seotud.
Variatsioonist saame kombinatsiooni siis, kui võtame variatsiooni ning seejärel unustame elementide järjekorra. Näiteks õpetaja võib tunni jaoks välja valida kolm järjestikust vastajat, seejärel ümber mõelda ja lasta neil korraga kirjalikult vastata, nii et järjekorral ei ole enam tähtsust.
Kombinatsioonist saame aga variatsiooni, kui võtame ühe kombinatsiooni ning siis anname valitud elementidele ka järjekorra. Näiteks õpetaja võib valida kolm vastajat ja siis anda neile vastamisjärjekorra.
Pokkerihaisid (kui nad tahavad olla ohtlikud haid) huvitab muidugi, kui palju leidub erinevaid pokkerikäsi ühest pakist – see võimaldab näiteks arvutada, kui suur on tõenäosus, et mõnel teisel sõbral lauas on paremad kaardid.
Kui mängid pokkerit, kus igale mängijale jagatakse viis kaarti, huvitab meid 5-kaardiste kombinatsioonide arv 52 kaardi hulgast. Seda arvu tähistatakse
Üldisemalt tähendabki
või
võimaluste arvu valida n objekti hulgast k erinevat.
Näiteks leidub
erinevat pokkerikätt.
Variatsioonide arvu tähistatakse omakorda
Näiteks kui tahaksime mingil põhjusel leida kõikvõimalike järjestatud pokkerikäte arvu, siis võib arvutada:
Väikeste arvude korral võime kõik kombinatsioonid ja variatsioonid muidugi üles lugeda, aga nagu nägime, on juba pokkerikäte korral tegemist päris suurte arvudega ning neid järjest lauale seades võime märkamatult päris vanaks saada.
Seega üritame järgnevalt mõelda, kuidas leida kombinatsioonide ja variatsioonide arvu kõiki võimalusi läbi vaatamata.
Variatsioonide arv
Leiame kõigepealt variatsioonide arvu. Arutelu on analoogne permutatsioonide arvu leidmisega – järjestuse esimese kolme elemendi kindlaks määramine ongi ju täpselt kolme järjestatud elemendi väljavalimine.
Ehk siis kui meil on näiteks vaja valida 5 järjestatud kaarti 52-st, siis valime nad ükshaaval, järgemööda. Esimese valik on täpselt 52 võimalust, teise valikuks jääb siis 51 võimalust, kolmanda valikuks 50, neljanda valikuks 49 ja viienda valikuks 48 võimalust. Kuna kõik valikud on sõltumatud, näeme, et
mis annab tõesti arvu 311 875 200.
Üldjuhul saame siis samasuguse arutelu abil, et
Selle korrutise võime ka faktoriaalide abil kirja panna: murru lugejasse seame kogu korrutise ning murru nimetaja abil taandame ära korrutise lõpuosa:
Tegelikult oleksime võinud variatsioonide arvu leidmiseks kasutada ka teistsugust arutelu ja lähtuda otse permutatsioonide arvust. Nimelt n-elemendi reastamisest (ehk ühest permutatsioonist) võime mõelda järgmiselt:
- Kõigepealt seame ritta mingid k esimest elementi ehk valime n elemendist k elementi, arvestades ka järjekorda, milleks ongi variatsioon:
- Seejärel reastame sinna järele kõik ülejäänud n – k elementi ehk valime permutatsiooni: Pn–k
Kuna need sammud on sõltumatud, on n-permutatsioonide arv kokku
ehk
See annabki aga täpselt eelmise valemi, seekord koos intuitiivse selgitusega.
Kombinatsioonide arv
Leidmaks lõpetuseks kombinatsioonide arvu, tuletame meelde enne mainitud seose kombinatsioonide ja variatsioonide vahel: igast k-variatsioonist võime teha k-kombinatsiooni, kui elementide järjekorra ära unustame.
k-elemendi järjekordade arv on aga täpselt võrdne permutatsioonide arvuga k!. Seega on iga kombinatsiooniga seotud täpselt k! erinevat variatsiooni. Nii peame kombinatsioonide arvu saamiseks jagama variatsioonide arvuga k! ehk
Eelmises alapeatükis leidsime, et 5 kaardi võtmiseks (kui järjekord on oluline) on meil
võimalust.
Kui meil on 5 kaarti, siis kaartide permutatsioon näitab erinevaid võimalusi nende kaartide järjestamiseks, milleks on 5! = 120.
Kui järjekord ei ole tähtis, siis kokku on kaardipakist 5 kaardi võtmiseks
võimalust.
Kujutage ette, et istute hubases kohvikus ja vaatate linnatänavale. Kohv on ostetud, rehkendused kassa juures tehtud ja tundub, et matemaatika ongi tänaseks läbi.
Siis aga märkate, et tänaval puhub lõbus tütarlaps seebimulle ja kuigi need on küll peaaegu alati erineva suurusega, on need alati ühtmoodi ümmargused. Miks on seebimullid ümmargused? On see tüdruku või seebimullide süü?
Tegemist ongi juba füüsikalise maiguga lõbusa matemaatilise küsimusega. Tema vastuski on segu füüsikalistest teadmistest ja matemaatikast: füüsikast teame, et seebikile sulgeb endasse võimalikult suure ruumala; matemaatika aga näitab, et sellise printsiibi korral peab mull olema täpselt kerakujuline. Raamatus puudutame ringi sarnast omadust – sama ümbermõõduga kujunditest piirab ta suurima pindala [lk 97].
Matemaatikat võime näha ka kohviku teleekraanil, kus ülekantav jalgpallimäng on jõudnud penaltiseeriani. Kas mängijad valivad väravanurga, kuhu nad palli löövad, mingi mustri järgi? Kas peaks valiku korral alustama penaltiseeriat lööjana või kaitsjana? Uurides möödunud penaltiseeriate tulemusi ja videokordusi, võime leida seaduspärasusi – sellega tegeleb matemaatiline statistika. Seaduspärasused kirjas, võime nende abil ehitada parima strateegia – sellele aitavad kaasa tõenäosuslikud kirjeldused [lk 392].
Kui lõpuks õnnestub ka kohvikust matemaatika juurest põgeneda, jääte tema küüsi jälle esimese lillepeenra kõrval. Matemaatiline kirjeldus aitab kirjeldada ja selgitada erinevate mustrite teket ja seeläbi lillenuppude ilusaid kujusid.
Näiteks teatud päevalillesortide õie paigutuses on 21 sinist ja 13 ookeanisinist spiraali. Need pole sugugi suvalised arvud – 21 ja 13 on Fibonacci arvud [lk 135], mis tulevad looduses tihti esile ning mille esinemist oskame ka selgitada.
Viimaks, kui hakkate lille nime ja peret oma nutitelefoni või arvuti abil kindlaks tegema, küsite jälle abi matemaatikalt: otsingumootorite tööprintsiibid on olnud esmalt kirjas matemaatilises keeles ning arvutite sise-elu põhinebki ainult ühtedel, nullidel ning nendega arvutamisel.
Mõni ütlebki hoopis, et matemaatika ise on keel. Ja tõepoolest, matemaatika aitab ju kirjeldada maailma nagu iga teine keel ning lubab seeläbi omavahel suhelda ning informatsiooni vahetada.
Siiski erineb matemaatika keel tavapärastest keeltest. Tavapärases keeles on meil peaaegu iga ettejuhtuva objekti tarvis üks sõna või sõnapaar. Tavapärased keeled hoomavad ja kirjeldavad peaaegu kõike, millega kokku puutume, ent teevad seda tihti mitmetähenduslikult. Näiteks pall võib tähendada põhimõtteliselt nii ümmargust jalgpalli kui ka ovaalset Ameerika jalgpalli. Matemaatika otsustab kirjeldada vähem, aga see-eest täpsemalt – tihti vaid mõnda väikest detaili ühest või teisest objektist. Samas on need kirjeldused ise täpsed ja üheselt mõistetavad: palli kirjeldaksime kera või ellipsoidina, olenevalt tema kujust, ning mõlemail neist mõistetest on täpne ja ühene matemaatiline definitsioon [lk 44].
Kuna matemaatikud kasutavad eraldiseisvat sõnavara, tundub vahel, et matemaatikud ei hooli üldse elust ning nende mõistetel ja käsitlusel kaob argipäevaga igasugune side. See on ka üks põhjuseid, miks matemaatikat on raske õppida [lk 30].
Siiski ei tähenda matemaatiliste mõistete abstraktsus, et neist ükskord kasu ei võiks tulla. Mõnikord me ei oska lihtsalt seoseid ümbritsevaga näha ning nad võivad alles aastasadade pärast välja tulla. Näiteks kompleksarvud [lk 89], mida peeti pikalt matemaatikute kummaliseks hulluseks, mängivad täna olulist rolli maailma kõige väiksemal skaalal kirjeldamisel – nende abil on hea kirja panna kõige väiksemate osakeste käitumist. Viimaks, kuigi tänagi peetakse üht ja teist osa abstraktsest matemaatikast üsna kasutuks, võime kinnitada, et kogu siin raamatus toodud koolimatemaatika on siiski igati eluline ning maailma kirjeldamisel ja mõistmisel asendamatu tööriist!
Matemaatikas ei ole aga ainult keel – matemaatika uurib, muudab ja arendab ise sedasama keelt, milles ta end väljendab. Matemaatilised mõisted muutuvad ja nende muutumises peitub ka suur osa matemaatikast. Isegi see, kuidas mõeldakse matemaatiliselt arvudest, on muutunud – kunagi ammu tunti ainult arve 1, 2, 3, ..., siis leiti, et ½ on samuti üsna mõistlik arv, ja alles hiljuti lepiti, et ka –1 on arv või et lausa √–1 , mis reaalteljele ei mahu, sobib sama hästi üldmõiste arv alla [lk 78].
Võib tekkida küsimus, et kuidas saab muutuda see, mida tähendab arv. See on vajalik selleks, et tagada matemaatilise keele ühene mõistetavus ja selgus. Või teiselt poolt vaadatuna on matemaatikud aru saanud, et arvutada – liita ja lahutada, korrutada ja jagada – saab mitte ainult arvudega 1, 2, 3, 4, 5 ..., vaid ka palju keerulisemate objektidega. See näitab, kuivõrd on arvude mõiste tegelikult suhteline – kas arvuks nimetame kõike, millega oskame arvutada, või peaksime arvudeks nimetama ainult objekte, mis koosnevad numbritest? Arvude arengust saab pikemalt lugeda aga arvuhulkade peatükist [lk 78].
Matemaatika on tore kombinatsioon rangusest ja vabadusest. On küll üheselt öeldud, mida ühe või teise objekti all mõeldakse, ning on antud ranged reeglid nendega mängimiseks, kuid samas võib neidsamu objektide tähendusi ning reegleid alati väänata. Seda on eriti paslik teha siis, kui see toob kaasa rohkem seoseid, rohkem lihtsust, rohkem ilu ja rohkem mõistmist.
Siiski võib lugejat kummitama jääda õigustatud küsimus: kas oleme ikka vastanud, mis on matemaatika? Ei ole.
Nagu on raske öelda, mis ikkagi on õnn või mis tarkus, on raske ka öelda, mis on matemaatika. Tegemist on lihtsalt nii mitmetahulise ja laia mõistega. Naljakal kombel iseloomustab matemaatikat ennast veel just see, et ta ise tegeleb objektidega, mille korral saab küsimusele „mis?” väga täpselt vastata.
Lõppude lõpuks õpetab matemaatika meile, et meil on millegi defineerimisel ka parasjagu vabadust. Küllap pole sellest suurt kurja, kui igaühel on veidi omamoodi arusaam matemaatikast. Loodame, et see raamatuke aitab oma isiklikku arusaama leida ka lugejal.
Head mängu iseloomustavad kolm omadust: ta on mitmekülgne, ta arendab ja ta võimaldab midagi õppida. Mõnikord räägitakse ka matemaatikast kui mängust. Ja kuigi sellega päris nõus olla ei tahaks – matemaatikast on palju enam kasu kui mõnest mängust –, siis on tal vähemalt kõik need kolm omadust igati olemas.
Matemaatika peidab endas erinevaid ja tihti lausa vastandlikke külgi.
Matemaatikast võib leida täpsust, rangust ja kindlust. Niipea kui ühe matemaatiliselt korrektse selgituse või seose leiad, jääbki see õigeks – mitte nii nagu tuba, mida koristad ja koristad, aga mis ikka jälle mustaks saab. Nii ehitab iga matemaatika õppija oma teadmistele kindlat vundamenti.
Üksluine vundamendi ladumine tüütaks aga kindlasti ära. Vaja on ka ootamatusi ja üllatusi. Matemaatikas selle koha pealt kokku ei hoita – näiteks selgub, et lisaks meile juba tuntud kujunditele, nagu ruudud, ringid, kolmnurgad, leidub ka kujundeid, mille ümbermõõt on lõpmatu, aga pindala lõplik [lk 377]. Või näiteks tuleb välja, et kui ruumis on rohkem kui 23 inimest, siis on rohkem kui 50% tõenäosus, et kahel on täpselt samal päeval sünnipäev [lk 407]. Või et naturaalarve 1, 2, 3, ... on täpselt sama palju kui ratsionaalarve ehk arve kujus 3⁄4 või 39⁄2 ja nii edasi.
Paljudele meeldib aga hoopis loomingulisus, meeldib vabadus. Seda on alguses ehk matemaatikas kõige raskem märgata – kus kogu selle korra ja täpsuse vahel jääb ruumi vabadusele? Aga samamoodi nagu kindel vorm soneti või haiku korral, ei piira ka matemaatilise mõtte kindel vorm loomingulisust. Oluline osa matemaatikast on uute seoste, uute mõtteviiside, uute objektide loomine. Kas pole vahva arusaam, et võime geomeetriast – kehade kujust ja kumerusest – mõelda sugugi mitte ainult kolmemõõtmeliselt, vaid kahekümnes, kolmekümnes või lausa tuhandes mõõtmes? Kuidas üks kolmekümnemõõtmeline kera välja võiks näha? Proovi ette kujutada! Meie näiteks ei oska...
Kui tahad saada juristiks, on matemaatika abiks. Kõige selgemalt oma argumente üles ehitama – olgu nad kui pikad tahes – ning kõige kärmemalt teiste argumentidest vigu leidma – olgu nad kui kavalad tahes – õpetab ilmselt matemaatika. Matemaatilise arutelu jaoks on alati tarvilik välja käia täpsed eeldused, täpne arutluskäik ning täpsed järeldused – hajusad argumendid läbi ei lähe. Oletame, et prokurör leiab, et süüdistatava sissetulek pangakontol ja teatavad linnas toime pandud vargused satuvad samale ajale. Kas seda võib kasutada tõendina tema kahjuks? Näiteks on ju selge, et kui jäätiste läbimüük ja päikesepaiste korreleeruvad, ei järeldu sellest, et jäätise ostmine toob kaasa päikesepaiste. Mida me lisaks peaksime teadma?
Kui tahad saada arstiks, on matemaatika kohustuslik. Statistika aitab aru saada, millal ravimifirmade reklaamloosungitel on ka tegelikku sisu [lk 398] ning mida ikkagi tähendab, kui üks või teine DNA-s olev geen suurendab haigestumise riski.
Kui tahad saada arhitektiks, ei saa samuti ümber matemaatikast. Matemaatika õpetab rangelt kirja panema proportsioone ja seoseid. Samasuguse rangusega töötavad ka kõik arhitektuuriliste mudelite ehitamise programmid, mis tahavad vahel, et arhitekt oskaks kirjeldada oma jooni ka matemaatiliselt, võrranditega. Arhitekt peab oskama arvutada ruumide ja pindade suuruseid, peab teadma, kuidas leida ühe või teise tala kandevõimet.
Kui tahad saada luuletajaks, ei tule matemaatika jällegi kahjuks. Prantsuse luuletaja Paul Valéry näiteks armastas matemaatikat – tema päevikud on täis matemaatilisi ja eriti geomeetrilisi mõttekäike. Matemaatika olevat ta enda sõnul avaldanud suurt mõju ka ta luulele. Samuti on matemaatikuharidusega nii „Alice Imedemaal” kui „Karupoeg Puhhi” loojad.
Kindlasti pole loetletud elukutsed ainsad, kus matemaatikat vaja läheb või kus ta kasuks võiks tulla – väike maadlus matemaatikaga on hea treening kogu eluks.
Kõige enam tuleb matemaatika ehk siiski kasuks kõigile, kes tahavad mõista või kontrollida end ümbritsevat elus ja eluta loodust. Ühe kahekümnenda sajandi suurima füüsiku Richard Feynman’i sõnul on matemaatika valdamine looduse kirjeldamiseks lausa möödapääsmatu.
Matemaatika kirjeldab
Matemaatilise vedelikefüüsika abil saame selgitust jõgede müsteeriumile: miks nii sinikaelpardi, vanaema kui kiirkaatri taha tekivad lained täpselt sama nurga alt?
Matemaatilise bioloogia abil leiame seoseid geenide ja haiguste vahel ning suudame mõista südame ja veresoonkonna tööd. Näiteks matemaatilised kirjeldused südamerakkude kaltsiumiradadest annavad lootust, et suudame paremini kontrollida südame rütmihäireid.
Meil on igas keharakus paarkümmend tuhat geeni, mille avaldumine või mitteavaldumine peaks määrama kogu meie olemise ja tervise.Tahaksime kindlate geenide avaldumist või mitteavaldumist siduda teatud haigustega – nii võiksime leida viise nende haiguste ravimiseks. Selliste seoste leidmine on juba oma olemuselt matemaatiline töö. Töö tulemusi saab esitada aga ka kenade graafikutega, millelt on võimalik näha, mis geenide avaldumiskombinatsioonid võiksid peituda ühe või teise haiguse põhjustajatena. Selliseid graafikuid kutsutakse „kuumuse graafikuteks“:
Sarnast graafikut kasutame ka tuletise peatüki lõpus [lk 338].
Matemaatikaga saame kirjeldada ning seeläbi mõista sotsiaalvõrgustike olemust ja omadusi. Tihti kirjeldatakse selliseid võrgustikke maatriksite abil [lk 152]. Näiteks tuleb välja, et inimtutvuste võrgustik on väga spetsiifilise struktuuriga – nimelt on ta üsna tihedalt seotud, iga inimene siin maailmas on igast teisest maksimaalselt 6 sõprussuhte kaugusel. Mis on Sinu seos Tonga kuningaga?
Matemaatika ehitab
Matemaatiline õpetus dünaamilistest protsessidest ja võnkumistest annab head nõu, kuidas ehitada sildu ning milliseid sildu ehitada ei tohi. Ehitada ei tohi näiteks sildu, mis võiksid tugeva tuule tagajärjel sattuda resonantsi ning hakata järjest vägevamalt võnkuma. Kuigi seda oleks saanud matemaatiliselt ennustada, saime vastava õppetunni hoopis katselisel meetodil – 1940. aastal purunes Tacoma sild Ameerikas just nimelt tuule tekitatud resonantsvõnkumise tõttu.
Ka arvuti on leiutis, mille võimalikkust taipasid ning mille kirjeldusteni jõudsid esmalt just matemaatikud. Nagu juba mainisime, mõistavad arvutid ainult matemaatikal põhinevat algoritmilist keelt ning kui tahame, et arvuti midagi meie eest ära teeks, peab talle seda ütlema täpselt ja konkreetselt – matemaatiliselt. Võibolla tasub ka märkimist, et üks internetiprotokollide leiutajatest – Ameerika arvutiteadlane Vint Cerf – sai oma bakalaureusekraadi samuti matemaatikast.
Matemaatika ennustab
Katseliselt võime küll järele uurida, mis kunagi juhtus või mis juhtub hetkel, aga me ei saa kunagi katseliselt leida, mis juhtub tulevikus – tulevikku ju katsetada ei saa. Ent tihti peame just ennustama, mis tulevikus juhtuda võiks.
Matemaatika abil ennustati, et leidub elektroni antiosake positron, ja nüüdseks oleme seda katseliselt näinud. Matemaatiliselt pakuti, et suurtel kiirustel enam Newtoni klassikaline mehaanika ei kehti, ning ega tõesti ei kehtigi. Ilma selle teadmiseta ei töötaks meie GPS-navigeerimine.
Majandusteoreetikud üritavad aru saada, kuidas üks või teine inim- või inimväline faktor võiks tulevikus mõjutada majandusnäitajaid; hasartmängurid peavad vähemalt üritama ennustada, mis kaardid on teistel peos või jagajal pakis; insenerid peavad suutma ette kujutada ettekujutamatuid tegureid, mis nende uhket konstruktsiooni ohustada või mõjutada saaksid – kõike seda saab teha ainult matemaatiliselt. Nii ongi matemaatika ka meie silm tulevikku.
Muidugi ei ole kõik meie ennustused alati õiged, aga matemaatika südametunnistus jääb puhtaks – eksimused on meie oma eeldustes ja mudelites ja neid eksimusi lubab matemaatika ise ka hinnata.
Tänapäeval on populaarseks saanud ka tõenäosuslikud mudelid, kus me tunnistame, et täpselt ennustada ei olegi võimalik – oskame ainult ennustada, kui tihti üks või teine sündmus võiks juhtuda. Näiteks kui aus sõber viskab ausat münti, võiksime ennustada, et umbes pooltel juhtudel jääb ülespoole kiri [lk 392].
Matemaatika ei ole valmis
Nagu nägime, võimaldab matemaatika päris paljut kirjeldada, kontrollida, ennustada. Siiski on ka üsna palju seda, mida me veel ei mõista ning mida matemaatika ei hooma.
Näiteks on tänapäeva matemaatika endiselt hädas keeruliste ja paljuosaliste süsteemide ning protsesside – nagu näiteks ühe keharaku töö või meie aju töö või maailmamajanduse – kirjeldamisega. Neist arusaamine eeldab suurt katselist tööd, aga küllap ka uut ja põnevat matemaatilist raamistikku.
Ka matemaatikas endas on veel palju lahendamata küsimusi ja mõistatusi. Paljusid neist on keeruline sõnastada, aga nii mõnedki näivad esmapilgul väga lihtsad. Näiteks ei tea me isegi, kui palju leidub algarve (arvud, mis jaguvad ainult iseenda ja ühega), mille vahe on kaks. Arvupaarid 3 ja 5, 5 ja 7, 29 ja 31 sobiksid ja usutakse, et sellised paarid ei saa kunagi otsa, ent tõestada seda 2013. aastaks keegi veel ei oska. Või siis ei oska me öelda, kas meie praegune kirjeldus vedelike liikumisest – niinimetatud Navier Stokes’i võrrand, on üldsegi matemaatiliselt sobilik. Me ei tea, kas võrrandile leidub alati sobilik lahend.
Paljudele tundub, et matemaatika on raske – isegi ületamatult raske – ja et see raskus on midagi muud kui raskus endale pähe õppida keerulisi kunstnikunimesid, aastaarve, rodude viisi riikide pealinnu või hoopiski kirjeldada elusat rakku bioloogiatunnis.
Matemaatikat teeb ilmselt juba keeruliseks levinud kujutlus, et ühed oskavad matemaatikat ja teised ei oska. Pigem on õige, et ühtedele meeldib matemaatika rohkem ja teistele vähem, just nii nagu on ka kirjanduse, lauatennise või koorilauluga. Ja muidugi, kellele meeldib matemaatika rohkem, tegeleb sellega samuti rohkem ning on lõpuks selles ka edukam.
Aga see, mis meile meeldib, võib muutuda üleöö (või pigem üle aastate) ja kui ükskord hommikuvalguses leiate, et matemaatika teile siiski mokkamööda võiks olla, pole mõtet karta – tegelikult on matemaatika samamoodi õpitav nagu kõik muu.
Siiski on matemaatikas ka mõned isemoodi raskused ning neist raskustest on kasulik aru saada.
Üks matemaatika eripära ja raskus peitubki ehk selles, et pähe õppida õnnestub vähe ja sellest ei ole tihti otsest kasu. Kui õpite pähe ühe võrrandi lahendi, ei aita see lahendada mõnda teist võrrandit; kui õpite pähe ringi pindala valemi, ei aita see leida kolmnurga pindala. Ja ometigi on matemaatikas erinevaid küsimusi, mida esitada saab, teiste ainetega võrreldes vahest kõige rohkemgi.
Nii on matemaatika õppimiseks tarvis mingit muud strateegiat. Alustuseks on vaja aru saada matemaatiliste objektide ning arutelude vahelistest seostest ja selgeks õppida teatud üldiseid meetodeid, mis ütlevad, kuidas leida pindala või lahendada võrrandeid. Need meetodid on vahel täitsa kokaraamatu moodi, kuid mida põnevamaks lähevad ülesanded, seda enam tuleb hakata retsepte kasutamise käigus muutma – lisada juurde soola, pipart või tihedamini uusi matemaatilisi mõtteid.
Sellist improviseerimist saab aga õppida ainult katsetamisega ja sellest pole sugugi hullu, kui mõni lahendus alguses vale rada mööda otsustab minna, olulisem on julgus neid proovida.
Teisest matemaatika raskusest oleme juba juttu teinud ja teeme järgmises osas veel [lk 42]. See peitub matemaatikute kirjasõnas, asjaolus, et matemaatiline tähistus ja keel erineb teatud määral igapäeva keelest. See lihtsustatud keel teeb matemaatikat lihtsamaks ja võimaldab matemaatikale tema täpsust ja üheselt mõistetavust.
Lisaks on osa matemaatika enda ilust peidus just selles, et tema tõestused ja tähistused on võimalik kirja panna ümbritsevast sõltumatult, lakooniliselt ja puhtalt. Ainult nii saavutavad matemaatilised argumendid oma võime kirjeldada ühtaegu nii erinevaid ja mitmekoelisi olukordi: x-dest ja y-test koosnev võrrand räägib teile tegelikult kuussada muinaslugu, need peab aga igaüks ise juurde mõtlema.
Aju vajab aga matemaatilise stiili, matemaatiliste sümbolite ja keelega pisut harjumist.
Nii kaua kui tuleb kogu aeg järele vaadata, mida ikkagi tähendab võrrandis istuv x, sümbol > või mis täpselt on tuletis, toimib matemaatika justkui sõnaraamatu abil. Kes sõnaraamatu abil välisriigis vestelda on proovinud, teab, kui vaevaliseks see osutub – tervikliku teksti loomiseks tuleb sõnu juba unepealt vallata, muidu on lause algus lause lõpuks ununenud ja mõtet väljendada ei suudagi.
Kolmas matemaatika raskus peitub ilmselt selles, et teda on keeruline õpetada. Ühelt poolt tahaksid õpetajad alati tundi kindlasti põnevaks teha – näidata ilusaid pilte ja seostuvaid katseid. Sellega riskib ta aga, et lihtsad ja selged matemaatilised argumendid jäävad ilusate juttude ning kaunistuste varju. Nii alustatakse tihti rangelt matemaatilisest sisust ja varju jäävad hoopis seosed eluga.
Muidugi, ideaalis toimuks õppetöö risti-rästi, vahele elulisi lugusid, vahele matemaatilist selgust, ent see vajab väga palju aega. Kooliprogrammis on aga matemaatika jaoks aega aina vähem, samas teadmisi, mida edasi tahetakse anda, aina enam.
Nii antaksegi tihti edasi matemaatilised teadmised nende kõige kompaktsemas vormis – objektide nimed, definitsioonid, arvutusvõtted, ilma pikemalt selgitamata, kust ikka tulevad need nimed, definitsioonid, meetodid. Võrrandite, teoreemide tagamaad jäävad tumedaks ning nad ei seostu muu kui tahvliga. Mõnele ei ole see probleem ning piisabki ainult matemaatilisest sisust, mõnele teisele on aga eluline kontekst ja mõttelugu hädavajalik. Ilmselt tuleb siis selle jaoks aega leida ka väljaspool kooli ning ehk on abiks ka käesolev raamat.
Kuidas neist raskustest üle saada? Tuleb julge olla ja tuleb endale ning matemaatikale aega anda. Matemaatika tahab, et temaga tegeletaks iga päev natukene. Tuleb mängida matemaatikaga ja seeläbi harjuda tema stiili ning keelega. Tuleb lahendada õpetaja antud ülesandeid ja endale ise ülesandeid juurde mõtelda. Tuleb lahendada ülesandeid, mida oskate, ja proovida neid, mida ei oska. Tuleb otsida seoseid ja seoste vahelisi seoseid. Tuleb pabereid sodida ja tindiga mitte kokku hoida. Ja usu või mitte – seda kõike on võimalik teha lõbuga!
Üks on kindel, kui Sulle endale meeldib matemaatika ning temaga tegeled, meeldid varsti ka ise matemaatikale. Igal juhul ei pea matemaatika nautimiseks kindlasti saama kohe matemaatikuks. Nii nagu juba lihtsad, aga tunnetatud kitarriakordid teevad lõkke ääres kõrvale head, võiks mõttemustritele head teha ka natuke lihtsat, aga ilusat matemaatikat.
Õhtuõpiku väljaandmist toetasid 451 lahket hooandjat. Neist kõige innukamatel palusime ka selgitada, miks nad ikka meid nii lahkelt toetasid. Nii kogusime mõned isiklikud mõtisklused matemaatikast ja loodame, et nad mõjuvad omakorda innustavalt ka lugejale.
Matemaatika aitab ajust aru saada
Ajuprotsessid on aluseks kõigele, mis me tahame, mõtleme, tunneme. Aju määrab selle, kes ja millised me oleme. Aga praeguseni on üsna mõistatuslik, kuidas kõik need vaimsed protsessid ajus tekivad. Seega on aju tähtis uurimisobjekt, kui tahame mõista iseennast. Ajust arusaamiseks on tarvis matemaatikat. Ajuandmete uurimiseks kasutatakse matemaatilisi meetodeid ja nende andmete statistiline analüüs põhineb matemaatilistel alustõdedel. Kuid mis peamine, ajust arusaamiseks on tarvis teooriat aju tööprintsiipide kohta, mis suudaks selgitada ja ennustada meie vaimseid protsesse. Sellised teooriad põhinevad matemaatikal. Seega pole käesolev raamat, „Matemaatika õhtuõpik”, sugugi mitte ainult investeering kõrgemasse eksamihindesse või paremasse arusaamisesse matemaatikast, vaid loob aluse ka paljude teiste esialgu näiliselt matemaatikast kaugete nähtuste paremaks mõistmiseks.
Jaan Aru
Frankfurdi Max Plancki Aju-uuringute Instituudi doktorant
Universum on kirjutatud matemaatika keeles
Füüsikuna on mul äärmiselt hea meel sellise raamatu nagu „Matemaatika õhtuõpik” ilmumisest. Kahtlemata on ka „puhtal matemaatikal” omad võlud ja neistki võib raamatu huviline lugeja aimu saada, aga matemaatika tähtsus on palju laiem. See on keel, milles on kirja pandud kaasaegne loodusteadus, füüsika sealhulgas ja eriti. Pole imestada, et üks moodsa füüsika alusepanijatest – Sir Isaac Newton – oli ühtlasi ka diferentsiaal- ja integraalarvutuse looja, viimaseta muutuksid Newtoni kuulsad seadused rakendusväärtuseta metafoorideks. Matemaatilised mudelid ja meetodid leiavad edukat rakendamist eluteadustes, nende kasutamisel omandavad aga ka sotsiaal- ja humanitaarteadused uue üldistus- ja ennustusjõu.
Galileo Galilei on ligi nelisada aastat tagasi kirjutanud: „Filosoofia on kirja pandud suurde raamatusse, mis pidevalt seisab avatuna me silme ees (ma pean silmas Universumit), aga me ei saa seda mõista enne, kui oleme selgeks õppinud keele ja tunneme tähestikku, mille abil see kirjutatud on. See on kirjutatud matemaatika keeles, mille tähtedeks on kolmnurgad, ringid ja teised geomeetrilised kujundid, ilma milleta on inimlikult võimatu mõista kirjapandust ainustki sõna, ilma milleta ekseldakse pimedas labürindis.” (Il Saggiatore, 1623) Head lugema õppimist! Head lugemist! Ja ei pea üks õpik olema ju igav, tüütu ja raskesti mõistetav – „Matemaatika õhtuõpik” pole seda kindlasti mitte.
Jaak Kikas
Tartu Ülikooli Füüsika Instituudi direktor
Matemaatika on teadmistepõhise ühiskonna alus
Matemaatika on mind võlunud alates lapsepõlvest. Ehkki kooliajal oli tegemist ühe minu lemmikõppeainega, on matemaatika saatnud mind läbi elu, olles olnud kaaslaseks nii ülikooliõpingutes kui igapäevases tööelus.
Matemaatika on fundamentaalne ja väga põnev, mille olulisust hariduses ning teadmistes on raske üle hinnata. Võimaldades kirjeldada nähtusi universaalses ja kõigile üheselt mõistetavas keeles, kuulub matemaatiline kirjaoskus hea hariduse juurde ning on targa inimese repertuaari lahutamatu osa.
Matemaatika on aluseks ühiskonnale tervikuna, nii kasutavad seda igapäevaselt insenerid, õpetajad, ärimehed, arstid jne. Ilma matemaatikaalaste oskusteta ei ole võimalik oma teadmisi süstematiseerida ega neid reeglipäraselt edendada.
Numbrimaailmas orienteerumine on sedavõrd oluline, et vead matemaatilises mõtlemises võivad põhjustada korvamatut kahju. Selle väite illustreerimiseks võib tuua hiljutised sündmused seoses meie suusasangarile esitatud väidetava dopingusüüdistusega. Ehkki dopingutesti viga on sisuliselt biokeemiline, oli selle kirjeldamine ja üheselt arusaadavaks tegemine võimalik vaid läbi matemaatilise kirjaoskuse. Inimkonna ajaloos on teisigi selliseid näiteid, kus puudulikud teadmised matemaatikast põhjustavad kas arusaamatusi, eksimusi või otsest kahju. Samas, head matemaatilised oskused annavad informatsiooni, mida saab kasutada konkurentsieelise tekitamiseks.
Võib väita, et teadmistepõhise ühiskonna vundamendiks on matemaatikat hästi tundvad liikmed. Seega, eeskujulik matemaatiline kirjaoskus on väravaks arenenud ühiskonda.
On tervitatav, et traditsiooniliste matemaatikaõpikute kõrvale on tulnud selgelt eristuva lähenemisega raamat, tuues numbrite ilu- ja võlumaailma huvilistele senisest uudsema nurga all lähemale.
Sulev Kõks
Tartu Ülikooli arstiteaduskonna füsioloogilise genoomika professor ja füsioloogia vanemteadur
Matemaatika ei ole ainult krõnksud
Paljude jaoks paistab matemaatika olevat sünonüümne nende krõnksude ja imelike tähtedega, mida põhikooli ja keskkooli matemaatikatundides pähe õppima sunniti. Sellest on aga tohutult kahju, sest tegeliku matemaatikaga on sel umbes sama vähe pistmist kui hiina hieroglüüfidel neis kirjutatud teoste sisuga.
On selge, et kirjatüki täiel määral nautimiseks on vaja tunda selle kirjutamise keelt kõigis selle nüanssides. Sama selge on aga ka see, et suurem osa teose sisulisest ja kirjanduslikust väärtusest on võimalik edasi anda läbi selle osava tõlkimise.
Koolimatemaatika keskendub paraku aga just selle keele õpetamisele ja nii jääbki sisuline tähendus õpilaste jaoks tihti vormi poolt varjatuks. Erinevalt tavalistest õpikutest, mis sarnanevad sisult tihti just klassikaliste keeleõpikutega, on selle raamatu eesmärgiks olla pigem „tõlge”, tutvustades matemaatilise mõtteloo arengut ja selle põhiideid, näidates keelt selle juurde üksnes möödaminnes.
Loodan, et selle tõlke kaudu avaneb ka lugejale pilt sellesse lummavasse ideede maailma, mida mina ning raamatu autorid „päris” matemaatika nime all armastavad. Kui veab, annab see teos ehk mõnele motivatsiooni ka keeleõpinguid jätkata ning lõpuks neid teoseid ka originaalis lugema õppida.
Margus Niitsoo
Tartu Ülikooli arvutiteaduse õppejõud
Matemaatiline intuitsioon aitab rakendajat
Mind on vist alati matemaatikast endast enam paelunud, kuidas see on tegelikult kasulik hoopis teistele valdkondadele. Oma eriala valides tahtsin aru saada, kuidas ikkagi arvuteid õpetatakse midagi sellist tegema, mida inimene soovib saavutada arvuti abil. Selle juures oli vaja aru saada ka arvuti enda töö põhimõtetest ehk näiteks lihtsast matemaatilisest loogikast. Õnneks ma ei kartnud matemaatikat ja mõtlesin, et kui teised on hakkama saanud, siis pean ka mina saama.
Hiljem, otsides omakorda IT-le rakendusi, jäi ette bioloogia, kus oli hakatud tootma tolle aja mõttes suuri andmestikke. Siis sai matemaatikast uuesti sõber, mis aitas lahendada uusi probleeme. Ja mälusoppidest tuli vahel võtta välja oskusi, mida kunagi gümnaasiumis või ülikoolis omandasime.
Ma arvan, et matemaatikal ongi kaks selget suunda – üks, mis kompab matemaatika enda piire ja teine, mis rakenduste kaudu võtab matemaatikat kasutusse. Õppides võib tunduda, et võetakse arvesse vaid matemaatika enda huve. Kuid tegelikult aitab matemaatiline intuitsioon kõige rohkem just rakendajaid, kõikide teiste erialade esindajaid. Loodan, et õpik aitab just neid teisi leidma oma sinasõprust matemaatika õppimisega ning olukordade jaoks, kus matemaatika nõuab tavalisest veidi rohkem tähelepanu.
Jaak Vilo
Tartu Ülikooli Arvutiteaduse Instituudi juhataja
Tõenäosus tundub lihtne ja intuitiivne mõiste. Ühe kindla sündmuse tõenäosus võiks tähendada täpselt seda, kui tihti see konkreetne sündmus juhtub võrreldes teiste, temaga konkureerivate sündmustega.
Teisisõnu tahaksime sümbolite keeles lihtsalt defineerida:
See definitsioon on siiski üsna hägus, sest ta jätab vastamata päris paljudele küsimustele.
- Milliseid teisi sündmuseid me sageduse arvutamiseks arvesse peaksime võtma? Koduõues täringuga kuue viskamine ei ole ju kuidagi seotud näiteks kaardipaki segamisega Austraalias, aga on seotud sama täringuga kahe või kolme viskamisega.
- Kui palju vaatlusi on vaja teha, et võiksime sündmuse sageduse mõistlikult välja arvutada? Ilmselt ühest vaatlusest ei piisa – sel juhul võiks ju tõenäosus olla ainult null või üks. Aga kas näiteks kolmesajast on küll?
- Mida teha sündmustega, mis võivadki juhtuda ainult maksimaalselt üks kord? Tahaksime ju võrrelda tõenäosuseid, et üks või teine meie sõber saab presidendiks, või isegi rääkida tõenäosusest, et maaväline elu eksisteerib. Sageduse abil tõenäosusest mõtlemine on sel juhul üsna selgelt raskendatud.
Selgub, et hoolimata nendest küsimustest on tõenäosus igati mõistlik idee väga paljudes erinevates olukordades. Tema käsitlus nõuab küll tõesti natuke rohkem täpsust, kui alguses välja pakutud idee. Järgnevalt selgitame mõne loo abil, kuidas tõenäosusest võiks mõelda, kuidas teda võib elu kirjeldamisel rakendada ning milliseid ohte mõlemal juhul silmas tuleks pidada.
Hans ja Grete istuvad keset metsa pimedavõitu onnis. Hans, keda pimeduses istumine järsku ära tüütab, süütab salaja kaasa võetud küünla, võtab taskust välja särava mündi ning hakkab Gretet tõenäosusteooriaga kiusama.
Hans: Grete, mis on tõenäosus, et ma nüüd viskan oma mündiga kulli ja mitte kirja? Grete: Kallis Hans, kindlasti hakkad mind nüüd kavaldama, aga praegu arvan küll, et kull ja kiri on täiesti võrdväärsed ning seega on tõenäosus täpselt pool.
Hans viskab sõnagi lausumata münti, aga kohe, kui münt käeseljale maandub, katab ta teise käega, nii et tulemust ei näe ei Grete ega Hans isegi.
Hans: Aga nüüd, Grete, mis on tõenäosus, et siin käe all varjus olev münt varjab kulli?
Grete: Ma ei ole harjunud niimoodi tõenäosusest mõtlema – münt on ju juba visatud, nüüd tal kas on kull pealpool või ei ole. Kuidas ma nii tõenäosusest üldse rääkida saan?
Hans: Aga kas sa oleksid nõus näiteks kihlveoga, kus ma annan sulle kaks šokolaadi, kui tegemist on kulliga, ning sina mulle ühe, kui tegemist on kirjaga?
Grete: See tundub sinust palju lahkem kui tavaliselt. Ma oleksin nõus küll. Sa tead sama vähe kui mina, meie mõlema meelest võiks praegu mündi peal olla sama hästi nii kull kui kiri... Seda sa vist mõtlesidki tõenäosuse all? Minu meelest on tõenäosus, et münt on kull, endiselt pool.
Hans: Väga hea, Grete, väga hea.
Hans piilub nüüd ise münti ja ütleb Gretele, et tegemist on kulliga, ent ei näita seda veel Gretele.
Hans: Mis on Sinu meelest nüüd tõenäosus, et münt on kull?
Grete: Münt ise on ammu juba visatud ja nüüd sa ju just ütlesid, et see on kull, kuidas ma siis saan veel tõenäosusest rääkida?
Hans: Aga Grete, enne ütlesin ma ka sulle, et mul ühtegi küünalt ei ole, sest tahtsin natuke aega sinuga pimedas olla.
Grete: Seega sa võiksid jälle valetada nagu enne?
Hans: Võiksin.
Grete: Münt on visatud, ta on kas kull või kiri, sina juba tead tulemust, ütled mulle, et tegemist on kulliga, ja nüüd peaksin mina ütlema, mis on tõenäosus, et tegemist on kulliga. Ma ei saa enam midagi aru.
Hans: Mõtle, Grete, muidu kustutan küünla jälle ära!
Grete: Ma proovin ju. Kui sa mulle kunagi ei valetaks, siis oleks tegemist kindlasti kulliga ja tõenäosus oleks seega üks. Kui sa kogu aeg valetaksid, oleks tegelikult kiri ülalpool ning kulli tõenäosus oleks null. Kui sa ajaksid kogu aeg täiesti suvalist juttu, siis võiksin sinu ütlust ignoreerida ja tõenäosus oleks jälle pool. Aga...
Hans: Aga vahepeal ma ikka räägin tõtt ka. Näiteks siis, kui ütlesin, et oleme kadunud.
Grete: Jah, kahjuks või õnneks küll. Seega tõenäosus, kas münt on kull või mitte, on nüüdseks hoopis tõenäosus, kas sa räägid tõtt või mitte.
Hans: Väga tubli, Grete. Kas sa seda tõenäosust tead? Grete: Ei tea.
Hans: Aga kas sa saaksid seda kuidagi leida?
Grete: Kui ma oleksin kõik meie jutuajamised lindistanud ning seejärel loeksin pärast kokku, kui palju kordi sa oled valetanud ning kui palju tõtt rääkinud, siis võiksin seda tõenäosust vähemalt hinnata.
Hans: Grete, lindistamine ei ole ilus, Edgar korra juba proovis.
Grete: Tõsi, Hans, aga mis on see tõenäosus, et ka mina vahele jääksin?
Järelnoodid
Tõenäosustest rääkides peab olema väga hoolikas, mis sündmuse tõenäosusest just parasjagu räägime. Iga tõenäosuslik kirjeldus on tegelikult lihtsustus maailmast – me ei tea täpselt, mis juhtub, aga tahame seda ennustada või kirjeldada. Tõenäosusliku kirjelduse jaoks loetleme sündmused, mis juhtuda võiksid, ning anname neile hinnangud, kui tihti üks või teine neist juhtub. Need hinnangud ongi sisuliselt niinimetatud tõenäosused.
Nagu nägime, sõltub nende hinnangute või tõenäosuste määramine meie enda teadmistest. Kui teame, et münt on sümmeetriline, võiksime hinnata, et kulli või kirja viskamine on täpselt pool.
Kui aga teaksime, et ta on natukene vildakas, on selle hinnangu andmine palju raskem – peaksime ilmselt tegema enne sadu viskeid ning selle põhjal tõenäosust hindama. See hinnang jääks aga alati ligikaudseks ja peegeldaks lihtsalt meie tolle hetke teadmist.
Tõenäosusteooria algusloo kohta on liikvel huvitav legend. Selle legendi kohaselt ei ole tõenäosusteooria aluskiviks sugugi intellektuaalne huvi, vaid hoopis kirglik hasartmäng. Nimelt hakkas paadunud ja tunnustatud hasartmängur ning amatöörmatemaatik Chevalier de Méré (1607–1684) enda loodud reeglitega järsku täringumängus pidevalt kaotama.
Probleemile lahenduse leidmiseks otsustas ta kirjutada ühele oma heale sõbrale, kuulsale prantsuse matemaatikule ja filosoofile Blaise Pascalile (1623–1662). See 17. sajandil kirjutatud murekiri panigi praeguse arusaama kohaselt aluse tõenäosusteooria arengule.
Oma kirjas kurtis Chevalier de Méré Blaise Pascalile, et täringutepaar, mis oli talle sisse toonud hulgaliselt raha, on nüüd järsku hakanud alt vedama.
Algupäraselt oli kihlvedu järgmine: Chevalier de Méré väitis, et ta suudab nelja viskega raudselt vähemalt korra kuue visata. Kirja autorile tundus loogiline, et sellise kihlveoga peaks rohkem võitma kui kaotama, ning aja jooksul saadud võidud aina süvendasid seda uskumust. Kui alguses leidus tublisti huvitunud mängijaid, kes olid oma kuueviskamisandes kindlad, ei jätkunud kihlvedusid siiski kuigi kauaks – Chevalier de Méré pidevad võidud kahandasid kiiresti nende inimeste arvu, kes mänguga soostusid.
Nii otsustas Chevalier de Méré mängureegleid muuta. Nüüd väitis ta, et suudab täringupaari viskega saada vähemalt korra topeltkuued. Ta oli veendunud, et siingi peaks kihlvedu tema kasuks olema. Ometigi hakkas aga vaene Chevalier de Méré aina kaotama...
Kuna temagi argumendid olid ta enda meelest üsna matemaatilised, läks ta oma tusatujus nii kaugele, et kuulutas matemaatika ja päriselu vahelise suhte olematuks. Nagu kohe näeme, matemaatika temaga siiski päris nõus ei ole.
Mida arvab Chevalier de Mere kihlvedudest matemaatika
Chevalier de Méré väitis, et ta suudab:
- visata nelja täringuga vähemalt ühe kuue,
- visata kahekümne nelja täringupaariga vähemalt korra topeltkuued.
Esimese kihlveoga oli ta rikkaks saamas, ent teisega mängis oma varanduse kärmelt maha. Chevalier de Méré oleks nende kihlvedudega raha kokku ajanud parajasti siis, kui ta oleks rohkem kui pooltel kordadel suutnud oma lubatut täita.
Kuidas oleks ta võinud ette juba aimata, kui tihti ta võidab või kaotab?
Üks võimalus oleks olnud leida täringuviskele tõenäosuslik kirjeldus. Nimelt, üks tõenäosuse tõlgendus on ju just nimelt sageduslik – tõenäosus näitab, kui tihti üks või teine sündmus meie kirjelduse kohaselt pikas perspektiivis juhtub. Rohkem kui pooltel kordadel tähendab seega, et selle sündmuse tõenäosus on suurem kui pool.
Näeme, et armas hasartmängur pidanuks rikkaks saama parajasti siis, kui tal oleks olnud täringuviskest täpne kirjeldus ning mõlema tema lubaduse tõenäosus selles kirjelduses oleks olnud poolest suurem.
Täringuviske tõenäosuslik kirjeldamine on üsna lihtne. Nii kaua kui mäng on aus (ja vaevalt et petturiga keegi täringuid viskaks!) on mõistlik eeldada, mõelda või postuleerida, et kõik täringu küljed on võrdväärsed – on võrdne võimalus, et viskel tuleb ükskõik milline külgedest. Seega on kõikide nende tõenäosus täpselt 1⁄6.
Esimese kihlveo korral on soodsaks sündmuseks see, et visatakse nelja viske jooksul vähemalt korra üks kuus. Selgub, et lihtsam on aga arvutada selle sündmuse vastandsündmuse tõenäosust – ehk siis sündmuse, et igal viskel visatakse üks kuni viis silma, tõenäosust. Nimelt piisab sel juhul iga viske eraldi uurimisest ja nende sidumisest sõltumatute sündmuste reegli abil.
Tõenäosus, et ühel viskel viskame üks kuni viis silma, on 5⁄6. Kõik visked on aga omavahel sõltumatud ning võime nende tõenäosused kokku korrutada, leidmaks tõenäosus, et me ei viska ühtegi kuut. See on parasjagu
Kuna vastandsündmuste tõenäosuste summa on üks, siis järeldame, et vähemalt ühe kuue viskamise tõenäosus on umbes 0,518 ehk rohkem kui pool. Siit tulevad võidud!
Ka teise kihlveo korral on lihtsam välja arvutada vastandsündmuse tõenäosust – tõenäosust, et igal täringupaari viskel ei saada topeltkuut. Iga sellise viske tõenäosus on täpselt 35⁄36, kuna kokku on 36 võimalikku paari. Seega leiame, kasutades jällegi sõltumatute sündmuste reeglit, et mitte ühegi kuute paari viskamise tõenäosus on
See on aga rohkem kui pool! Seega on ühe 12 silmaga täringupaari viskamise tõenäosus omakorda vähem kui pool ning selge see, et härra de Méré oma rahast ilma jäi.
Matemaatika igal juhul süüdi pole!
Mille vastu Chevlier de Méré siis eksis? Selle asemel, et hoolsalt arvutada (peab tunnistama, et tol ajal ei olnud muidugi arvude 24. astme leidmine nii väga lihtne), uskus ta oma intuitsioonil põhinevat mõtteviisi. Ta arutles, et kahe kuue viskamine kahel viskel on 6 korda vähem tõenäoline kui ühe kuue viskamine ühel viskel ja et seega tuleb 6 korda rohkem viskeid teha, et seda kompenseerida. Kõlab isegi päris usutavalt?
Tore oleks vahel Toompeal teed juua. Üks võimalus selle unistuse realiseerumiseks on see, kui parimast sõbrannast saab Riigikogu liige. See ei ole sugugi kindel, aga päris võimatu ilmselt ka mitte. Kas sellele on võimalik mingi mõistlik tõenäosuslik hinnang anda?
Selle jaoks oleks meil vaja jällegi mingit tõenäosuslikku kirjeldust. Kõige lihtsam võimalik kirjeldus tegelebki ainult lõpptulemusega: meie sõber kas saab või ei saa Riigikogu liikmeks, seega on meil täpselt kaks elementi, millele tahaksime tõenäosused külge pookida. Lisaks peaks nende tõenäosuste summa olema veel üks – seega sisuliselt jääb hinnata ainult üks arv.
Kogu raskus on aga neile võimalustele tõenäosuste määramises. See ongi ju täpselt meie küsimuse ümbersõnastus! Kuidas neid tõenäosuseid määrata?
Võrdväärsuse eeldus siin kehtivat ei paista – tundub siiski tõenäolisem, et sõbrannast ei saa Riigikogu liige. Seega pool ja pool peame ilmselt välja jätma.
Ka statistika ei paista kohe kaasa aitavat: meil on ju üks konkreetne sõbranna ja temaga saame katset teha täpselt ühe korra ja see katse saab läbi alles mitmekümne aasta pärast!
Seega selgub, et meie matemaatiline mudel on liiga täpne – peame seda hajusamaks muutma, et üldse midagi öelda või ennustada.
Üks viis selle tegemiseks on sõbra unikaalsusest loobuda. Võiksime küsida hoopis: mis on tõenäosus, et mõni neiu saab Riigikogu liikmeks? Siin võiksime küll kõik Eesti naiskodanikud kokku arvata ja vaadata, paljud neist on saanud Riigikogu liikmeteks, ning hinnang olekski käes!
Aga ometi, meie sõbranna ei ole ju lihtsalt üks tavaline eestlanna. Tal on näiteks punane pea. Ehk mängib see olulist rolli, ehk peaksime ka seda arvesse võtma? Või seda, et ta on väga tark? Kuidas seda otsustada?
Ideaalis tuleks teha statistikat! Otsustada, millised omadused (juuksevärv, haridus, jalanumber jpt) mängivad rolli Riigikogusse valimisel ja millised ei mängi. Liiga palju omadusi arvesse võtta ei saa – muidu jõuaksime jälle olukorda, kus ainult meie sõbrannal ongi kõik need omadused. Samas, liiga vähe omadusi arvesse võttes oleksime liiga ebatäpsed.
Hea tõenäosusliku kirjelduse ning sinna sobivate tõenäosuste leidmine on väga raske. Mõnikord üritatakse sellest üle hüpata ja mitte täpsustada, mille kohta täpselt tõenäosuslik kirjeldus käib, või jätta teatamata, kust on tõenäosused ise võetud – on nad pärit eeldustest, on nad pärit mingitest andmetest, millistest andmetest nad pärit on.
Näiteks kui reklaam ütleb, et hambapasta tapab 99% bakteritest, siis mida see tähendab? Mis on see tõenäosuslik kirjeldus seal taustal?
Kas see tähendab, et bakterikultuuridele pandi mitmeid kordi peale hambapastat ning 99% juhtudest tapeti kõik bakterid? Milliseid baktereid sel juhul üldse kasutati, kas neid, mis on suus, või suvalisi, mis ehk kannatavad vähem fluori? Millises keskkonnas neid kasvatati? Miks see peaks üldistuma suukeskkonnale?
Või äkki mõõdeti tõesti bakterite arvu suus enne hambapesu ja pärast hambapesu ning iga kord oli pärast pesu alles 1% baktereid? Kas alati just täpselt 1% või keskmiselt 1%?
Arv 99% on ilus, aga mida ta ikkagi tähendab?
Kuigi kõigesse maksab suhtuda optimistlikult – üks korralik inimene ju niisama petuaktsiooni ei korralda –, tuleb siiski olla ettevaatlik. Niipea kui õhku tõusevad protsendid ja tõenäosused, tasub mõelda, mis on ikkagi peidus olev kirjeldus.
Ja kui tahad ikka Toompeal teed juua, on Sul ilmselt vaja rohkem kui ühte sõbrannat.
Oletame, et mingil kummalisel põhjusel tahaksime omavahel võrrelda mehi ja naisi või noori ja vanu. Üldiste järelduste tegemiseks ei piisa sel juhul mõne konkreetse paari tulemuste või mõõtude võrdlemisest. Näiteks selle jaoks, et öelda, kas mehed või naised on pikemad, ei saa ju võtta lühimat meest ja pikimat naist. Tuleb ikka ühte patta panna andmeid paljude meeste kohta, teise andmeid paljude naiste kohta ning võrrelda nende padade sisusid.
Kõiki andmeid ühes pajas koondabki endas tõenäosus- või sagedusjaotus. Tihti esitatakse neid jaotuseid graafiliselt, histogrammi abil, mis näitabki, kui sagedasti üks või teine sündmus juhtus. Näiteks siin on hirmutamiseks toodud matemaatika eksamitulemuste jaotus eraldi poiste ning tüdrukute jaoks:
Kuna jaotuste kõrvutamisel ei võrdle me enam kahte arvu, vaid kahte pajatäit arve, pole see kõrvutamine ega selle põhjal järelduste tegemine enam sugugi nii lihtne ja ühene.
Näiteks oletame, et meil on kaks hõimu „tartlased” ja „tallinlased” ning meil on teada mõlema hõimu kõikide liikmete IQ-testi tulemus. Hõimus „tartlased” on 20% inimestest IQ 200 ning 80% IQ 80. Hõimus „tallinlased” on kõikidel võrdselt IQ 100.
Kumb hõimudest on kõrgema IQ-tasemega?
Ühelt poolt on hõimus „tartlased” keskmine IQ-tase: 0,2 · 200 + 0,8 · 80 = 104 ning hõimus „tallinlased” vaid 100. Teiselt poolt on kõik hõimu „tallinlased” liikmed kõrgema IQ-tasemega kui tervelt 80% hõimu „tartlased” liikmetest.
Selgub, et meie küsimus on liiga ebatäpne: mida me ühe hõimu kõrgema IQ-taseme all silmas pidasime? Seda, et tema keskmine IQ-tase on kõrgem? Et suurema osa tema liikmete IQ-tase on kõrgem? Et hõimu minimaalne või maksimaalne IQ-tase on kõrgem? Või et kõik need parameetrid on kõrgemad? Need on kõik erinevad küsimused ning vastused võivad olla vastukäivad.
Nii ei olegi alati võimalik kõike üheselt omavahel võrrelda ja ega vist ei maksagi seda tingimata üritada. Tallinn on tore ja Tartu ainult natuke toredam.
Konkreetsel juhul oleksime ka jaotuste graafikutelt võinud näha, et lihtne keskmiste võrdlus ilmselt palju ei tähenda:
Tihti ongi kõige lihtsam jaotuseid võrrelda nende graafikute põhjal. Nii on lihtne märgata, kummas jaotuses on suuremad maksimumtulemused, kuhu umbes jääb keskmine tulemus ja nii edasi. Kohe võib ka silma jääda, et mingit mõistlikku võrdlust ei saagi teha.
Koolipingis räägitakse ka millestki, mille nimi on geomeetriline tõenäosus. Geomeetriline tõenäosus ei ole matemaatilise tõenäosuse alternatiiv, tegemist on lihtsalt veel ühe viisiga, kuidas tõenäosust tõlgendada ning mille raames ka küsimusi esitada. Ka siin üritame teatud sündmusi kirjeldada ja nende mahtu mõõta, teeme seda lihtsalt geomeetria abil.
Kahemõõtmelises maailmas põhineb geomeetriline tõenäosus pindaladel. Tõlgendame kõike võimalikku, mis juhtuda võiks, mingi piiratud tasanditükiga ning meid huvitavat sündmust mingi kujundiga selle tüki piires. Selle sündmuse tõenäosuse saaksime siis täpselt, leides meid huvitava kujundi ning kogu tasanditüki pindalade suhte.
Seda meetodit või tõlgendust ümber pöörates võiksime näiteks leida hea lähenduse π [lk 99] väärtusele. Nimelt joonistame ruudukujulisele põrandajupile mõõtmetega 1 m korda 1 m siseringjoone nii nagu joonisel näidatud.
Sel juhul on ringjoone sisse jääv pindala
ning ruudu pindala täpselt 1.
Oletame nüüd, et meil õnnestub lae alt kukutada paberitükikesi, nii et nad kukuvad selle ruudu raames enam-vähem ühtlaselt juhuslikult. Kui ruut on piisavalt väike ning lagi piisavalt kõrge, peaks see üsnagi võimalik olema.
Nüüd, ühelt poolt teame, et ringi ja ruudu pindalade suhe on
ning seega on ringjoone sisse kukkumise tõenäosus täpselt
Teisalt võime seda tõenäosust hinnata, niipea kui oleme kukutanud mõned paberilipakad. Neid piisavalt palju kukutades saame tegelikult väga hea hinnangu ka π väärtusele!
Joonisel võib seda kõike kujutada umbes nii:
Seesama protseduur ja idee on ka aluseks Monte Carlo integreerimisele [lk 349]. Sel juhul ei visata lihtsalt enam paberilipakaid, vaid juhuslikud punktid genereeritakse arvuti abil
Eelmises peatükis nägime, et tõenäosusteooriast mõtlemine ning tõenäosuslike kirjelduste ja vahendite kasutamine praktikas ei olegi alati nii lihtne, kui ainult täringute ja müntide baasil mõelda võiks. Saame lugejat rõõmustada – tegelikult on asi veel hullem! Tõenäosusteooria üllatab juba enne matemaatilistesse ja filosoofilistesse sügavustesse piilumist.
Oletame, et oled telemängus ning pead valima kolme ukse vahel. Ühe ukse taga on soliidne sportauto, ülejäänud kahe ukse taga seisab aga kurvameelne kits. Kuna kõik uksed on täpselt ühesugused, valid ilmselt alustuseks ühe neist ustest üsna suvaliselt. Enne veel, kui kõike teadev mängujuht Monty Hall selle ukse lahti teeb, avab ta kahest allesjäänud uksest veel ühe ukse. Kusjuures ta avab just sellise, mille taga peidab end kurvameelne kits. Nüüd pakub mängujuht Sulle valiku: kas Sa sooviksid muuta oma ukse valikut?
Loomulik küsimus on: kas oleks kasulik see vahetus teha?
Esimene reaktsioon võiks olla, et kui pärast on kaks ust alles, siis ei ole vahet, kas vahetada või mitte – on ju ühe avamata ukse taga kits ja teise taga auto ning seega auto võitmise tõenäosus täpselt pool. Sellist esmast intuitsiooni jagavad paljud, sealjuures ka uhkete doktorikraadidega matemaatikud ja teadlased.
Siiski tuleb välja, et see intuitsioon on ekslik – tegelikult tuleb alati ust vahetada, sel juhul on auto võitmise tõenäosus tervelt kaks kolmandikku.
Tõepoolest, oletame, et valisid alguses suvalise ukse. Kolmandikul juhtudel valisid Sa kohe ukse, kus oli auto. Sellisel juhul on ukse vahetamine kahjulik – teise avamata ukse taga peidab ennast kits.
Kahel kolmandikul (66,7%) juhtudest valid aga alguses ukse, mille taga seisab kits. Kuna mängujuht avab iseseisvalt veel teisegi ukse, mille taga on kits, jääb viimase avamata ukse taha auto. Sel juhul on vahetamine kasulik.
Seega, kui Sa mitte kunagi ust ei vahetaks, siis võidaksid alati esimesel juhul ehk kolmandikul kordadest. Kui Sa aga alati vahetaksid ust, siis võidaksid kahel kolmandikul kordadest.
Segaduse vältimiseks on ilmselt kõige targem kohe alguses välja kirjutada, mis on kogu olukorra tõenäosuslik kirjeldus. Seejärel järge ajades ei saa intuitsioon meie kulul nalja teha.
Edasiseks mõtlemiseks jätame järgmise küsimuse: kuidas muutuksid tõenäosused, kui telejuht ise ei teaks, mis uste taga on, ning avaks kogemata ukse, mille taga on kits?
Järgnevalt toome tõesti sündinud loo neerukivide vastaste ravimite katsetamisest. 1980-ndatel katsetati kahte erinevat ravimit, mõlemat eraldi väikeste neerukividega ja suurte neerukividega patsientidel.
Saadud tulemused võib koondada järgmisesse tabelisse, kus on toodud igas rühmas paranenud juhtumite protsent, sulgudes on veel lisaks kirjas täpselt, kui palju katsealuseid ühte või teise rühma kuulus.
Nagu näeme, näitavad esmapilgul tulemused, et nii väikeste kui suurte neerukivide korral toimib ravim A paremini. Kui jätta aga suurte ja väikeste kivide eristamine ära, näeksid kokku liidetud tulemused välja järgnevad:
Nüüd osutub paremaks hoopis ravim B! Seda on ehk raske uskuda, kontrolli parem arvutused hoolega üle ja veendu, et me Sulle vingerpussi ei mängi.
Selles veendunud, on muidugi mõistlik küsida, kumba ravimit Sa ise eelistaksid. Kas see, kui Sa teaksid, et sul on väikesed neerukivid, peaks Su otsust muutma? Päris raske otsustada!
Sellise paradoksaalse olukorra tagamaa ise ei ole väga keeruline. Nimelt ravimi B jaoks oli meil lihtsalt tunduvalt rohkem katseisikuid väikeste neerukividega, kellel on paremad raviväljavaated ning seega ka parem paranemisprotsent. Need paljud õnnelikud patsiendid viivad ka ravimi B üldise paranemistõenäosuse üles. Ravimi A korral oli küll väikeste neerukividega patsientidel veelgi suurem paranemise tõenäosus, kuid neid patsiente oli ise õige vähe ning seega kogu paranemisprotsenti mõjutasid eelkõige suurte neerukividega patsiendid.
See tagamaa selgitus ei anna muidugi veel head vastust sellele, milline peaks olema õige otsus. Otsus oleneb sellest, kumba tõenäosuslikku kirjeldust peame täpsemaks ja tahame rakendada. Esimeses tabelis toodud tulemused vastavad täpsemale kirjeldusele: siin on eraldatud väikesed ja suured neerukivid. Teine tabel vastab üldisemale kirjeldusele: kõiki neerukivisid käsitletakse ühtlaselt.
Uurides neid tabeleid lähemalt, tundub, et neerukivide suurus siiski mängib ravis ja paranemises teatavat rolli. Seega tundub loomulik, et kui oma neerukivide suurust teame (ja seda teadmist pole keeruline hankida), peaksime kasutama spetsiifilisemat kirjeldust ning valima ravimi A.
Ainus probleem võiks olla selles, et võibolla on liialt vähe katseisikuid näiteks väikeste neerukividega. Võibolla on saadud protsent seeläbi liiga ebatäpne? Kui kardame seda, peaksime valima ravimi B. Nagu juba varemgi, oleme valiku ees: kas spetsiifilisem kirjeldus ja vähem andmeid või vähem spetsiifiline ja rohkem andmeid. Tegelikult on võimalik igati ka välja arvutada, kas ebatäpsus kaalub spetsiifilisuse üles või mitte, siit raamatust jääb see aga väljapoole.
Kui klassis on 36 õpilast, siis kui suur on tõenäosus, et kahel neist on sünnipäev samal päeval? Enne kui arvutusteni läheme, tee oma pakkumine!
Ja nüüd mõtle, mida see tõenäosus täpselt tähendab. Nagu oleme terves osas rõhutanud, viitab sõna tõenäosuse kasutamine kohe, et meil on mõttes mingi lihtsustatud kirjeldus. Lihtsustatud tähendab seda, et peame tegema ja teemegi mõned eeldused.
Näiteks seekord eeldame, et igal aasta päeval on sündimise tõenäosus võrdne. Kuigi tegelikult sünnib nädala sees rohkem lapsi kui nädalavahetusel ning kõik kuud ei ole aasta jooksul päris ühtlased, näeme ühe internetist leitud valimi graafikust, et tegemist on päris mõistliku eeldusega.
Teiseks, kui õpilaste hulgas pole just kaksikvendasid, võime eeldada julgelt, et kõikide õpilaste tõenäosus sündida ühel või teisel päeval on sõltumatu.
Seega võime mõelda, et veeretame lihtsalt 36 täringut, millel igal on 365 võrdväärset külge. Meie küsimus, mis tõenäosusega on kahel õpilasel samal päeval sünnipäev, on siis tõlgendatav kui küsimus, mis tõenäosusega jääb kahel täringul peale sama külg 365-st küljest.
Lihtsam on leida selle sündmuse vastandsündmuse tõenäosus: tõenäosus, et kõik täringud annavad erineva tulemuse.
Selle tarvis hakkame järjepanu arvutama. Kui meil on ainult täring, siis ta annab kindlasti eelnevatest erineva tulemuse. Kui nüüd veeretada järgmine täring, siis tõenäosus, et tulemus tuleb erinev, on
Kui võtta ette kolmas täring, siis juhul, kui esimeste täringute tulemused on erinevad, on tõenäosus, et tema silmade arv erineb mõlemast
Nii võime jätkata kuni 36 täringuni välja ning leida tõenäosuse, et kõik täringud andsid erineva tulemuse
Seega on vastandsündmuse tõenäosus, selle, et vähemalt kaks täringut 36-st andsid sama tulemuse, tervelt 1 – 0,168 = 0,832. Teisisõnu, selle kirjelduse ning nende eelduste põhjal on tõenäosus, et ühes 36 õpilasega klassis on kahel inimesel samal päeval sünnipäev, rohkem kui 0,8 ehk rohkem kui 80%! See on ikka päris kõrge!
Sama kirjeldust kasutades võib ka näidata, et juba 23 õpilasega klassis on tõenäosus, et kahel õpilasel juhtub sünnipäev täpselt samale päevale, rohkem kui pool. Kuidas on lugu Sinu klassis? Kui see tulemus üllatav tundub, siis ürita välja mõelda, miks see ikkagi üllatav tundub!
Avades mõne matemaatikuõpiku, on esmane vaatepilt üsna segane: vähe sõnu, palju sümboleid, jooni ja skeeme ning mis kõige hullem, nad kõik on omavahel puseriti.
Näiteks võib matemaatika õpikus kenasti ette tulla lause: „Võrrandi x2 – 5x + 6 = 0 lahendid on x = 2 ning x = 3” ning selle otsa on joonistatud veel ka järgmine kõverik:
Kui nüüd ei tea, mida tähendab võrrand, mis asjaloom on see x, mida peetakse silmas lahendi all ning mida paganat on sellel imelikul joonel kõige sellega pistmist, võibki kõik jätta üsna maavälise mulje ning südamerahuks tuleb õpik hoopis kinni panna juba enne, kui sisu kallale on jõutud.
Nii hull lugu matemaatikaga siiski pole. Tõesti, matemaatikal on oma oskussõnad nagu näiteks võrrand, lahend, funktsioon või muutuja, mis tähistavad teatud matemaatilisi objekte või teisendusi. Need objektid ei eksisteeri küll alati reaalsel füüsikalisel kujul, aga siiski saab neist tihti üsna loomulikult mõelda.
Näiteks kui õpetaja räägib tasandist, võime mõelda lihtsalt paberilehele, lauapinnale või tasasele maastikule, olgugi et matemaatikas on tasandil täpsem tähendus. Samuti on ju raske öelda, mis on arv kolm füüsikalises maailmas, aga temast mõtelda pole raske – kutsu oma kolm sõpra külla!
Tundub, et oluline ongi tunda nii matemaatiliste mõistete rangeid kirjeldusi kui lihtsaid viise ning intuitsiooni nendest mõtlemiseks. Käesolevas osas tutvustame matemaatika alusmõisteid – muutujat, võrdust, hulka ja funktsiooni. Nendest arusaamine ning nendega harjumine on edaspidi suureks abiks.
Lisaks oskussõnadele leiab matemaatikast palju tähti nagu a, x, y või n ning palju sümboleid nagu näiteks =, <, +, – ja ∞.
Sümbolid tuleb lihtsalt ära õppida, tähtede tähendus oleneb aga situatsioonist. Üldiselt kasutatakse tähti muutujate tähistamiseks [lk 48]. Muutujaid võiks muidugi tähistada ka sõnadega, aga tähtede kasutamine hoiab aega kokku. Lisaks aitavad tähed eraldada matemaatilist arutelu algsest elulisest kontekstist, muutes seeläbi tihti mõtlemist lihtsamaks ning laiemalt rakenduvaks.
Näiteks kui meile on öeldud, et klassis on poisse kolme võrra rohkem kui tüdrukuid, siis matemaatikud kirjutaksid selle järgmiselt:
Miks nii? Võime öeldu ümber sõnastada nii: kui tüdrukute arvule veel kolm juurde liita, siis oleks neid sama palju kui poisse. Fraasi „sama palju” tähistatakse matemaatiliselt sümboliga = ja liitmist muidugi sümboliga +. Seega saame:
Ent see on ju ometigi suurem kirjavaev kui ?
Pealegi on lühemas kujus selge, et sarnaselt saaks kirjeldada ka olukorda, kus poiste ja tüdrukute asemel on hoopis prussakad ja tarakanid.
Üksikute tähtedega võrrandid ei ole niisiis ainult kirjavaeva, vaid ka mõttevaeva kokkuhoidmiseks – võrrandiga ei pea enam siduma mingit konkreetset elulist situatsiooni ja võib tegeleda ainult tema matemaatilise sisu ja tõdedega.
Matemaatilist teksti liigendavad ja ilmestavad pisikesed matemaatilised žanrid: räägitakse näiteks definitsioonist, väitest, tõestusest, teoreemist. Vahel satuvad veel seltsi ka sõnad nagu lemma või hüpotees. Järgnevalt kirjeldame, mida ühelt või teiselt neist žanritest oodata võiks.
Definitsioon
Definitsiooni all peetakse silmas mingi objekti matemaatiliselt täpset kirjeldust. See täpne kirjeldus võib aga olla antud mitmel erineval viisil, erinedes nii lihtsalt lauseehituselt kui ka sisulisemalt.
Näiteks võib positiivseid paarisarve defineerida järgmiselt (ei maksa end hirmutada lasta sõnade „definitsioon” või „defineerima” kalgist kõlast!).
Definitsioon 1: Positiivsed paarisarvud on arvud 2, 4, 6, 8, …
Definitsioon 2: Positiivne paarisarv on naturaalarv, mis jagub kahega.
Definitsioon 3: Iga positiivse paarisarvu saame, kui liidame arvule 0 juurde lõpliku arvu kordi arvu 2.
Need kõik kolm definitsiooni on samaväärsed – ehk iga arv, mis on näiteks definitsiooni 2 järgi paarisarv, on ka definitsioonide 1 ja 3 järgi paarisarv.
Võib tekkida küsimus, miks me peaksime defineerima sama asja mitut moodi? Esimese põhjusena võib esile tuua, et erinevad definitsioonid aitavad meil samast objektist mitut moodi mõelda ja nii saame selle olemusest paremini aimu. Näiteks arvude peatükis defineerime ringjoone lausa viiel erineval moel ning iga erinev viis kannab endas ka pisut erinevat tähendust [lk 96]. Lisaks võivad erinevad definitsioonid viia ka erinevate matemaatiliste arutelude ehk tõestusteni – mõnest definitsioonist lähtudes on tõestused lihtsamad kui mõnest teisest lähtudes. Lõpuks võivad erinevad definitsioonid viia lausa erinevate väideteni. Näiteks võib integraali [lk 340] defineerida mitmel matemaatilisel moel ja olenevalt definitsioonist võivad erinevate funktsioonide integraalid ka erineda! Hästi valitud definitsioonid lihtsustavad matemaatilist arutelu tublisti ja on ilusa matemaatilise maailma aluseks.
Väide
Väide tähendab matemaatikas sama, mida tavakeeleski. Väide võiks olla näiteks: „4 on paarisarv” või „5 on paarisarv”. Vastupidiselt tavaelu väidetele ei saa aga matemaatiliste väidete õigsuse üle lõputult vaielda – iga matemaatiline väide on kokkuvõttes kas tõene või väär.
Väidetega seoses võiks tähelepanu pöörata ka sellele, kui mitmekülgselt käivad matemaatikud ringi sõnaga „siis“. Kasutusel on väljendid „siis” ja „siis ja ainult siis” ehk „parajasti siis”. Nad tähistavad seda, kuidas teatud väited omavahel seoses on.
Näiteks vaatame kolme väidet.
- Abu on klassi kõige pikem poiss.
- Abu on poiss.
- Kõik Abu poistest klassikaaslased on temast lühemad.
Kui kehtib esimene väide, SIIS kehtib ka teine väide – kui Abu on klassi kõige pikem poiss, siis kindlasti on Abu ka poiss. Samas kui kehtib teine väide, siis esimene väide ei pruugi kehtida: kui Abu on poiss, siis see ei tähenda, et ta oleks tingimata kõige pikem poiss. Seega SIIS lubab ühesuunalist järeldamist.
Kui aga lisame teisele väitele veel kolmanda, siis üheskoos on nad esimesega võrdväärsed. Selle kohta ütleme, et esimene väide kehtib PARAJASTI SIIS või samamoodi SIIS JA AINULT SIIS, kui samaaegselt kehtivad teine ja kolmas väide. Seega „parajasti siis” lubab kahesuunalist järeldamist ja näitab, et väited on samaväärsed.
Tõestus
Nagu mainisime, on matemaatilised väited kas tõesed või väärad. Matemaatiliselt veenvat argumenti, mis väite tõesust või väärust põhjendab, nimetataksegi tõestuseks. Tõestust kasutatakse samas tähenduses ka igapäevaselt, aga matemaatikute rangustasemele teised valdkonnad siiski vastu ei saa. Siiski on ka matemaatikute endi rangusstandardid aja jooksul muutunud.
Näiteks argumentide eest, mida üks 18. sajandi matemaatik pidas rangeks matemaatiliseks tõestuseks, ei antaks praegu kindlasti matemaatikaeksamitel maksimumpunkte.
Tõestust peaks olema põhimõtteliselt võimalik kirja panna ka matemaatilise loogika täpses ja lakoonilises keeles, pika sümbolitemölluna. Natuke pikemalt räägime sellest hulkade peatükis [lk 61]. Õnneks päris nii rangeks enamasti aga ei minda ning peamiselt on ka matemaatilised tõestused siiski sõnalised arutelud, mis lähtuvad teatud aksioomidest, definitsioonidest ja tõestest väidetest ning teevad siis mitmeid järeldussamme.
Hoolimata sellest, et sõnal tõestus on ranguse maitse, on tõestuste leidmine vägagi loominguline protsess. Vahel viib tõestuse teekond algsetest väidetest ja eeldustest väga kaugele, enne kui ringiga taas lõppväiteni tagasi jõuab. Erinevad tõestused aitavad paremini mõista matemaatilist maailma, aga ka seal, kus matemaatika on eluga tihedalt seotud, aitavad tõestused mõtlemisele kaasa. Tõestusi saab omavahel võrrelda ja hinnata; neid saab luua, parandada ja kritiseerida nagu ikka ühele kenale loomingule kombeks.
Ka siit raamatust leiab mitmeid tõestusi, vahel on nad matemaatiliselt rangemad, vahel vähem ranged. Näiteks arutleme, miks arvu √2 ei saa väljendada kahe täisarvu suhtena kujus a⁄b [lk 87] või miks kehtivad teatavad matemaatilised suurväited ehk teoreemid: trigonomeetria peatükis jõuame nii siinus- [lk 222] kui ka koosinusteoreemini [lk 224]. Esimene tõestus tuleb aga esile juba järgmises alapeatükis.
Teoreem
Teoreem on ehk matemaatika kõige austusväärsem žanr. Teoreemiks nimetatakse väidet koos matemaatiliselt täpse tõestusega. Õigupoolest julgetakse enamasti teoreemiks nimetada ainult piisavalt ägedaid väiteid koos oma ägedate tõestustega. Teoreemile antakse tihti ka tema avastaja nimi – kuigi peab tunnistama, et paljudel nimelistel teoreemidel pole nimeandjaga siiski suurt pistmist.
Üks kuulus teoreem on järgmine.
Teoreem: Leidub lõpmatult palju algarve. (Eukleides)
Sulgudes seisev „Eukleides” tähistab tõestuse autorit ja tihti nimetataksegi seda teoreemi Eukleidese teoreemiks.
Meenutame, et algarvud on naturaalarvud, mis jaguvad ainult enda ja ühega – nagu näiteks 2, 3 ja 5. Arvud 4 ja 6 aga pole algarvud, sest 4 = 2 · 2 ja 6 = 2 · 3. Algarvud on mingis mõttes kõikide teiste arvude baasiks. Neid ennast ei saa tegurdada, aga kõik teised arvud võime esitada algarvude korrutisena. Näiteks võime algarvude korrutisena kirjutada 8 = 2 · 2 · 2 ja 21 = 7 · 3.
Üritame lugejat selles teoreemis järgnevalt ka veenda. Meenutame, et arutlust, mis veenaks ka kõige skeptilisemat matemaatikut, nimetatakse tõestuseks ning sisuliselt annamegi siin tõestuse.
Tõestus:
Alustuseks märgime, et algarve kindlasti leidub – näiteks 2, 3 ja 5 on algarvud ja nii mõnigi veel. Oletame, et oleme leidnud juba n erinevat algarvu p1, p2, ..., pn. Kas leidub mõni veel? Kuidas teda leida?
Uus algarv ei tohiks kindlasti jaguda ühegagi juba teadaolevatest arvudest. Kõige lihtsam oleks siis vaadata arvu A, mis on ühe võrra suurem kui kõikide seni leitud algarvude korrutis:
Nii ei saa see arv kindlasti jaguda ühegagi juba leitud algarvudest, sest nendega jagamisel jätab ta jäägi 1.
Kui see arv ei jagu enam ühegi teise arvuga peale ühe ja iseenda, ongi tegemist ühe uue algarvuga. Nüüd, kui tegemist ei ole algarvuga, siis nagu meenutasime, saab ta kirjutada erinevate algarvude korrutisena. Ükski neist algarvudest ei ole meile veel aga teada!
Nii olemegi leidnud vähemalt ühe uue algarvu. Veelgi enam, ükskõik kui palju algarve me juba ei teaks, võime iga kord kasutada sama argumenti ja leida vähemalt ühe veel. Seega ongi algarve lõpmatult palju.
Selle väite ja tõestuse peale olevat tulnud Eukleides, kuulus Vana-Kreeka matemaatik, kes armastas geomeetriat ja arve. Tänaseks on sellele teoreemile juba kümneid tõestusi ja õigupoolest teame algarvude kohta nüüd palju rohkem. Teame näiteks üsna täpselt, kui palju leidub mingist kindlast arvust, näiteks tuhandest väiksemaid algarve. Palju küsimusi on aga endiselt ka vastamata.
Kuidas teile meeldiks, kui teil oleks rahatäht, millele kirjutatud väärtust saate kogu aeg muuta? Meeldiks? Siis meeldib teile ka muutuja mõiste matemaatikas.
Muutuja ongi lihtsalt üks matemaatiline objekt, mille väärtus võib muutuda ja mille väärtust võime muuta. Tihti esineb ta mingi kummalise lühikese nimega nagu x, y, z või n – matemaatikud juba niisama tinti ei raiska.
Muutujaid kasutatakse väga erinevates rollides. Tegemist on üsna üldise ja tihti lihtsustamise eesmärgil sisse toodud mõistega. Kuidas ja mis suhtes muutuja täpselt muutub, sõltub konkreetsest kontekstist ning mõnikord kutsutakse teda hoopis mõne teise nimega.
Muutuja, võrdused ja võrrandid
Muutujaid võib kohata võrduste ja võrranditega tegeledes. Kusjuures võrrandis on lihtsalt meile veel tundmatu suurus seotud teiste, meile hästi teadaolevate suurustega. Näiteks
kohta võib sõbrale öelda, et tegemist on võrrandiga muutuja x suhtes või võrdusega juhul, kui muutuja x väärtuseks on 3.
Muutuja on võrrandite kontekstis meie otsitav objekt – selline arv, millele kahte liites saame viie. Tema väärtus on meile alguses teadmata ja nii võikski teda nimetada ka „tundmatuks”.
Keerulisemate, nii-öelda üldkujus võrrandite korral aitab muutuja kui objekti sissetoomine vältida segadust.
Üldkujus võrrand on näiteks
Kui keegi ütleb, et x on selle võrrandi muutuja, siis teame, et otsime just x-ile sobivaid väärtuseid ning teised tähed tähistavad ainult teatavaid kordajaid. Konkreetsel juhul võime tundmatu x leidmiseks võrrandi mõlemalt poolt lahutada arvu a ning leida,
See on üldkujus võrrandi lahend.
Milleks meile üldse üldkujus võrrandid? Nad teevad elu lihtsamaks, aidates lahendada korraga palju erinevaid võrrandeid.
Näiteks ülaltoodud üldkujus võrrandi abil lahendasime ühekorraga ära kõik kolm järgnevat võrrandit:
Esimesel juhul peame valima lihtsalt a = 2, b = 4 ja saame lahendiks x = 2. Teisel juhul valime a = 3, b = 6 ja vastus on x = 3 ning kolmandal juhul annab a = 9, b = 14 valik lahendi x = 5.
Loomulikult võiksime tundmatu võrrandis tähistada ka tähega a ning kordajaid hoopis tähtedega x ja y. Sel juhul peaksime aga iga kord võrrandi juures hoolikalt täpsustama, mis on tundmatuks. Kokkulepe, et just x peaks enamasti olema tundmatu rollis, teeb matemaatika lugemise lihtsalt kergemaks ja kiiremaks. Kui meeldiv on näiteks lugeda järgmises kujus ruutvõrrandit ja tema lahendivalemit?
Kuna selline tähistus hirmutab ja tekitab parasjagu segadust, üritame raamatus kõike tähistada võimalikult levinud sümbolitega.
Muutuja ja funktsioonid
Muutujad tulevad esile ka funktsioonidest rääkides.
Funktsiooni peatükis kirjeldame, et funktsioonist võib mõelda kui teatud masinast, mis võtab muutuja ning teeb temaga mingi operatsiooni või teisenduse. Vahel kutsutakse teda ka funktsiooni argumendiks [lk 64].
Näiteks öeldakse, et ruutfunktsioon on ühe muutujaga funktsioon ehk masin, mis võtab muutuja ja korrutab teda iseendaga. Kui anname muutujale väärtuse 3, saame vastuseks 9, andes muutujale väärtuse 5, saame vastuseks 25.
Ristküliku pindala valem
on aga juba kahe muutujaga funktsioon: võime ju muuta mõlemat ristküliku külge ja pindala aina aga muutub.
Muutuja ja summad
Muutuja võib esile tulla ka pikkades keerulistes summades või integraali nimelises monstrumis [lk 340], aidates matemaatikul end kompaktsemalt ja täpsemalt väljendada.
Kui matemaatik tahab kokku liita arvud ühest kümneni, väljendab ta ennast aga nii:
mida loeme järgnevalt: summeerime üle kõikide arvude i, alates arvust 1 kuni arvuni 10 välja:
Seda hirmsat kõverikku ei maksa sugugi karta. Tegemist on suure kreeka sigma ehk meie S-iga, mis näeb välja nagu ohutu liblikas. Meie jaoks on ta aga lihtsalt kokkuleppeline tähistus summeerimise jaoks.
Näiteks
või
Neile, kes on veidi programmeerinud, on see muidugi vägagi selge – ka arvutitele meeldivad muutujad. Selle asemel, et kirjutada välja summa 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10, ütlete arvutile, et liida kokku kõik arvud i, mis on vahemikus 1, ..., 10, ning kasuta liitmisel abimuutujat n, mille algväärtus on 0. Näiteks kirjutaks informaatik programmeerimiskeeles Python nii:
n = 0
for i in range(0,11) :
n = n + i
print(n)
Muutujateks oleks siin jupis nii „i” kui „n”. Esimesel real antakse muutujale väärtuseks 0. Järgmine rida ütleb, et muutujat tuleb muuta 1-st 10-ni (arve 0 ja 11 ei arvestata). Kolmas rida ütleb, et muutujale n tuleb iga kord juurde liita i väärtus. Nii ongi n-i väärtus algul 0, siis liidetakse n-ile juurde 1 ning n-i väärtuseks saabki 1. Järgmine kord on i väärtus 2 ja see liidetakse n-ile juurde ning uueks väärtuseks on 1 + 2 = 3. Lõpuks on n-i väärtus 55 ning see kuvatakse ekraanil.
Võrdsus on igapäevane mõiste. Räägitakse võrdsetest valikutest, võrdsetest võimalustest, võrdsetest vahetustest. Seega ei ole üllatav, et võrdsus kuulub ka matemaatiliste põhimõistete alla. Matemaatika tahab aga täpsust. Mida me võrdsuse all täpsemalt silmas peame?
Teisisõnu, kui ütleme, et kaks puud on võrdse jämedusega või et kahel meeskonnal on tabelis võrdne seis või et kahte õpetajat kuulati võrdse huviga, siis mis ühendab sõna võrdne kõigis neis fraasides?
Natuke järele mõeldes tundub, et pea igas kontekstis käsitleme teatud omadusi või objekte võrdsetena, kui neid võiks omavahel ära vahetada, nii et keegi vahetusele jälile ei saaks.
Muidugi sõltub äravahetatavus päriselus detailide rohkusest, mida arvestame: kaks head õpetajat on äravahetatavad, kui meid huvitab ainult see, kui palju õpilasi neid põnevil kuulab. Kui aga arvesse võtta ka jutu sisu või nende juuksevärv, siis on neid ilmselt igati võimalik eristada.
Matemaatiline võrdsus on väga sarnane. Tahame võrdseks pidada objekte, mille äravahetamine ei muudaks mitte kübetki. Jällegi peame aga hoolsad olema ja kindlaks määrama, milliseid omadusi silmas peame. Matemaatiliselt pannakse säärane arvude võrdsus kirja matemaatilise võrduse abil.
Näiteks kahte arvu tahame lugeda võrdseteks, kui kõikides seostes teiste arvudega ning kõikide tehete suhtes käituvad nad täpselt ühtemoodi.
Näiteks on võrdsed arvud 2⁄3 ja 6⁄9, kuigi nad näevad välja erinevad. Samuti on matemaatikas arv 1 ja lõpmatu perioodilise esitusega arv 0,999 ... võrdsed, ent nende kümnendesitused on ju erinevad! Seda võib endale selgitada mitmel moel. Kui arvud 1 ja 0,999 ... oleksid erinevad, siis peaksid need arvud erinema mingi nullist erineva arvu võrra. Aga ükskõik kui väiksele arvule 0,999 ... juurde liidame, saame ikkagi ühest suurema aru. Samuti võib tunduda mõistlik, et
Ka paljude teiste objektide jaoks on nende võrdsus saanud eraldi nimetuse. Näiteks kahte kolmnurka, mida võime teineteise peale kattuvalt asetada ja mis seega on iga geomeetrilise teisenduse suhtes võrdsed, nimetatakse kongruentseteks kolmnurkadeks. Neil on täpselt võrdsed küljed ja nurgad.
Mõnikord huvitab meid aga ainult kolmnurkade kuju ja mitte nende täpne suurus. Kolmnurki, mida võime suurendamise ja vähendamise teel teineteiseks muuta, nimetatakse sarnasteks kolmnurkadeks.
Üks matemaatika eesmärke on leida lihtsaid tingimusi, mille korral kaks objekti on võrdsed. Nagu nägime, ei ole arvude puhul nende kümnendesitus ega ka murdesitus sobivaks kriteeriumiks. Näiteks kolmnurkade puhul selgub aga, et kahe kolmnurga võrdsuseks piisab kõigi kolme külje võrdsusest ning nende sarnasuseks kolme nurga võrdsusest.
Nagu mainisime, võime arvude võrdsuse kirja panna matemaatilise võrduse abil. Matemaatilise võrduse tähistamiseks kasutatakse lühikeste rööbaste moodi märki „=”. Näiteks võime eelnevalt väidetud arvvõrduse kirja panna kujus
Matemaatilise võrduse kasutus on muidugi laiem kui ainult arvud: arvude asemel võivad olla ka näiteks arvavaldised. Arvavaldis ei ole midagi keerulist – seal võivad arvude kõrval olla ka mõned tähed, mis võivad tähistada erinevaid arve, ja tehtemärgid.
Näiteks on arvavaldis 1 + 1 ja seega sobib ka võrduseks 1 + 1 = 2.
Keerulisem arvavaldis on näiteks a + 3b, kus a ja b võivad tähistada suvalisi arve. Nad on seega muutujate rollis [lk 48] – nende väärtus võib meie suva järgi muutuda. Kui a tähistab arvu 1 ja b arvu 2, võime kirjutada võrduse a + 3b = 7. Seejuures peame meeles hoidma, mis ikkagi arvude ja väärtused parasjagu on. Nende väärtuseid muutes ei pruugi võrdus ju enam kehtida!
Tõese võrdusega seotud arvud või arvavaldised on iga arvutuse suhtes äravahetatavad: ükskõik mida me kahe võrdusmärgiga seotud arvu või avaldisega ei teeks, siis niikaua kui kohtleme neid täpselt samal viisil, jäävad tulemid alati võrdseks.
Näiteks võime tõsta eeltoodud võrduse märgi mõlemad pooled ruutu: (1 + 1)2 = 22 või lisada mõlemale poolele arvu 5 : 1 + 1 + 5 = 2 + 5. Võrdus jääb nii esimesel kui teisel juhul endiselt kehtima.
Võrdusmärgi tänapäevase tähise võttis kasutusele Walesi matemaatik Robert Recorde 16. sajandil – ta oli lihtsalt tüdinenud välja kirjutamast sõnapaari „on võrdne”. Sedasama võrdusmärki kasutatakse ka paljude teiste matemaatiliste objektide võrdsuse tähistamiseks, näiteks kohtame teda juba järgmises peatükis, kus ta tähistab hulkade võrdsust.
Nagu nägime, on võrdus matemaatiline mõiste, mis aitab meil mõttekäiku täpsustada.
Võrdused teevad üldiselt elu lihtsamaks.Võrdusmärgiga seotud avaldised või arvud või muud matemaatilised objektid on täpselt samad. Seega võime kasutada igas olukorras meile sobivat, lihtsamat esitust.
Näiteks kui teame, et a2 – b2 = (a – b) · (a + b), annab see meile hea kavala mooduse teatud arvude korrutamiseks: Kui palju on 8 · 12? Muidu vajab see omajagu pearaginat, aga kui kirjutame 8 = 10 – 2 ning 12 = 10 + 2 , näeme, et 8 · 12 = (10 – 2) · (10 + 2). Eeltoodud võrduse põhjal on see aga võrdne arvuga 102 – 22. Kuid 10 · 10 = 100 ja 2 · 2 = 4, seega 8 · 12 = 96!
Seega nagu kirjandustunnis tahetakse, et otsiksite ühele sõnale sünonüüme, et end ilusamini väljendada, tasub alati otsida ka matemaatilisele objektile võrdseid objekte ja samaväärseid kirjeldusi. See teeb tihti matemaatika tegemise lihtsamaks: näiteks vahel soovime sama arvu näha kujus 823543, vahel aga kujus 77 – kumb esitus meeldib Sulle rohkem?
Võrdused on kasulikud ka kitsamate matemaatiliste tarkuste edasiandmisel.
Arvutustarkused ja samasus
Võrduse abil võib lühidalt esitada igasugu erinevaid arvutustarkusi, mida vahel kutsutakse ka samasusteks, et rõhutada nende igavest ja ajatut kehtimist.
Näiteks a + b = b + a väljendab, et ükskõik millise kahe arvu summa ei olene liidetavate järjekorrast. Seda nimetatakse matemaatikas kommutatiivsuseks. Tõepoolest, kui a = 2, b = 4, kordame juba eeltoodud tarkust: 2 + 4 = 4 + 2.
Kuulus teisendamisnipp
näitab, et ükskõik millise kahe arvu summa ruudu võime leida, kui liidame kokku nende arvude ruudud ja lisame sellele veel arvude kahekordse korrutise. Kas valem pole mitte lühem kui eelmine lause? Või on toredam hoopis järgmine geomeetriline kirjeldus?
Viimase pildi keskmine liige näitab, et ab ja ba on võrdsed ning nende kokkuliitmisel tekibki 2ab.
Kuna eelmine joonis on väga tore, siis tõestame ka korrutamise jaotumise ehk distributiivsuse
sarnase graafilise meetodiga:
Nagu igapäevakeeleski, tähendab ka matemaatikute jaoks hulk mingite objektide kogumit. Näiteks moodustavad hulga kõik kartulid kastrulis, kõik õpilased klassis või kõik kassid vanaema keldris.
Hulgale kehtib ainult üks tingimus – ühedki kaks hulga elementi ei tohi olla võrdsed.
Matemaatikuid huvitavateks hulkadeks on näiteks kõikide naturaalarvude, negatiivsete reaalarvude, mingit võrrandit rahuldavate arvude või ka täisnurksete kolmnurkade hulk.
Hulkasid keskkoolis põhjalikumalt ei käsitleta – tegemist on ju nii lihtsate objektidega! Otsustasime siinkohal neist siiski rääkida, sest olgugi et lihtsad, on nad kogu matemaatika aluseks.
Hulka kirjeldatakse tihti tema elemente loogeliste sulgude vahele üles loetledes. Näiteks kõik numbrid moodustavad hulga
Kuna igas lõigus ei ole mõtet kogu hulka välja kirjutada, antakse hulkadele tihti nimed. Enamasti tähistatakse hulkasid suurte tähtedega: näiteks võime öelda, et
Hulga elementidel puudub igasugune ambitsioon või kohustus end järjestada – nad on kõik võrdväärsed hulga liikmed. Seega oleksime võinud A elemendid loetleda ka mõnes muus suvalises järjekorras nagu näiteks
Hulka võib kirjeldada ka mõne tingimuse abil. Eeltoodud hulka oleksime näiteks võinud kirjeldada järgmiselt:
või lihtsalt
Paarisarvude hulka võime aga kirjeldada nii:
Lühendatult võib kirjeldus võtta ka järgmise kuju:
või kogenud matemaatikafänni kätetöös muutuda hoopis minimalistlikuks:
Seda avaldist peaks lugema järgnevalt: P on hulk, mis koosneb täisarvudest n nii, et n jagub kahega.
Andes hulgale A erinevaid kirjeldusi, kasutasime juba ühte lihtsat, aga tähtsat hulkade omadust: kaks hulka on võrdsed parajasti siis, kui neis on täpselt samad elemendid. Ehk teisisõnu hulgad on võrdsed parajasti siis, kui kõik elemendid, mis asuvad ühes hulgas, asuvad ka teises ning vastupidi.
Üritame järgnevalt vastata selle peatüki eksistentsiküsimusele: mis kasu on aga sellisest lihtsast objektide kogumist nagu hulk ja miks ta siia põhimõistete alla on sattunud? Veelgi enam, miks me räägime temast nii pikalt?
Tükkide sidumine
Esiteks koosneb peaaegu kõik väiksematest osadest. Nii võib peaaegu kõike juppideks lahti võtta ning nende juppide abil kirjeldada. Näiteks pallivõistkond koosneb tema mängijatest, lause sõnadest, õhk erinevatest molekulidest, aatomituum prootonitest ja neutronitest ja nii edasi. Selliste kirjelduste taga võib juba näha hulkasid.
Sarnaselt tulevad hulgad mängu ka matemaatiliste objektide kirjeldamisel: näiteks ringjoont võib kirjeldada kui kõikide punktide hulka, mis asuvad ühest kindlast punktist – ringjoone keskpunktist – võrdsel kaugusel.
Just see alternatiivne kirjeldus selgitab, miks saame sirkliga ilusaid ringjooni joonistada. Kui asetame sirkli ühe haara ringjoone keskpunkti, siis liigutades teist haara joonistame järjest tollest keskpunktist võrdsel kaugusel olevaid punkte.
Korraga käitlemine
Teiseks tahame tihti midagi ette võtta paljude objektidega korraga.
Näiteks tahab õpetaja hinde panna kõikidele klassi õpilastele või mesilane tolmeldada kõiki ümbruskonna õienuppe. Nii võime rääkida hindamisest või tolmeldamisest kui operatsioonist, mida võib ette võtta kõikide õpilastega või kõikide õienuppudega.
Matemaatikas on hea, kui oskame iga kolmnurgaga seada vastavusse tema pindala või kõikide reaalarvude jaoks leida nende ruutude väärtuseid. Selliseid mõtteid saame täpselt ja matemaatiliselt kirja panna just hulkade abil, defineerides mingi tegevuse – või täpsemalt funktsiooni – kõikidel hulga elementidel.
Näiteks arvu ruutu võtmine on operatsioon, mis valib kõikide reaalarvude hulgast mõne arvu ning seab temaga vastavusse selle arvu korrutise iseendaga. See kõik on tihedalt seotud funktsioonidega ning nende niinimetatud määramis- ja muutumispiirkondadega [lk 67].
Hulgad on matemaatika aluseks
Kolmandaks – ja võibolla kõige üllatavamalt – osutuvad hulgad teatud mõttes kogu matemaatika aluseks.
Kui on rohkesti järjekindlust ja parasjagu kavalust, võib hulkade toel kirjeldada kõiki matemaatilisi objekte ja operatsioone. Nii ongi matemaatika seni kõige levinum vundament ehitatud just hulkadele. Kõik matemaatilised tulemused peaks teoreetiliselt saama ümber tõlkida keelde, kus ainsad objektid on hulgad ning nendega ümberkäimiseks on kümmekond karmi reeglit. See on oluline, kuna sellises keeles kirjutatud argumentide õigsust suudab kontrollida lisaks õpetajale juba ka arvuti – nii on igasugusel vaidlusel ots ja lõpp, arvuti teab täpselt! Tegelikult suudab arvuti juba isegi teatud lihtsamaid argumente sellises väga täpses ja formaalses keeles ka välja mõelda. Siiski on vähegi keerulisemate arutelude hulkade keelde ümber tõlkimine paras vaev ning matemaatikud on esialgu veel leidlikumad uute tulemuste tõestajad kui arvutid. Järgnevalt näitame, kuidas mõnda matemaatilist objekti hulkade abil kirjeldada. Meie raamatu piires neil kirjeldustel küll suurt olulisust pole, kuid võibolla on lihtsalt põnev lugeda.
Näiteks võib hulkade abil kirjeldada kõiki funktsioone [lk 64]. Ruutfunktsiooni – masinat, mis seab igale reaalarvule vastavusse tema ruudu – võime kirjeldada järjestatud arvupaaride hulgana:
Idee on siin mõelda, et iga arvupaari esimese liikmega seatakse vastavusse teine liige.
Kui vaatleksime funktsiooni y = x2 ainult täisarvude nullist seitsmeni, võksime kirjeldava hulga ka elementhaaval välja kirjutada:
Naljakal kombel on mõne lihtsama matemaatilise objekti kirjeldamiseks aga tarvis kauem mõelda. Näiteks kuidas kirjeldada arvu 4 ainult hulkade abil, arvudest rääkimata? Selleks on mitu viisi. Kirjeldame siin ühte võimalikku viisi.
Arv 1 seatakse vastavusse ilma ühegi elemendita tühja hulgaga: Ø. Tühjast hulgast võib mõelda kui tühjast kilekotist.
Arv 2 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 1 vastav hulk ehk tühihulk. Seega võime seda hulka kirjeldada sümbolites kui {Ø}. Oleme oma tühjale kilekotile ümber pannud veel ühe kilekoti – kokku kaks kilekotti.
Arv 3 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 2 vastav eelmises punktis leitud hulk. Tema kirjelduseks on {{Ø}}. Kilekott, mille sees on kilekott, mille sees on kilekott – kokku kolm kilekotti.
Arv 4 seatakse vastavusse hulgaga, mille ainsaks elemendiks on arvule 3 vastav hulk matemaatilise tähistusega {{{Ø}}} ehk neli kilekotti.
Nii võib muidugi jätkata ja kirjeldada kõiki naturaalarve 1, 2, 3, 4... hulkade või tõepoolest... kilekottide abil. Iga kilekoti lisamine ehk uue hulga tekitamine kandis endas arvu üks juurdeliitmise ideed.
Need on ainult kaks väljavalitud näidet, aga ka keerulisemaid objekte saab hulkadega esitleda. Selliselt mõeldes on hulgad ikka üsna ägedad: peaksid võimaldama kirjeldada kõike, mida matemaatikas teame.
Võibolla on tore ka teada, et tänaseks ei ole hulgad enam ainus kasutusel olev matemaatikale vundamendi ladumise viis. Kasutada võib ka teist tüüpi, pisut võimsamaid objektide kogumeid – kategooriaid. Kategooria ei koosne enam üksnes erinevatest objektidest, vaid sisaldab ka seoseid nende objektide vahel.
Hulgad on matemaatikutele ka paradokside näol palju peavalu toonud.
20. sajandi algupoolel tekitas pahandust inglise filosoof ja matemaatik Bertrand Russell järgmise lihtsa küsimusega: kas mõni hulk võiks olla ka iseenda element?
Võibolla arutles ta umbes nii.
Kui mul on hulga koostamiseks vabad käed, võin ju nõuda, et minu hullumeelse hulga iga element oleks selline hulk, mis ei ole iseenda element.
Kas sel juhul mu hullumeelne hulk ise on enda elemendiks?
Kui ta oleks enda element, siis ta peaks olema selline hulk, mis ei ole iseenda element – huhuu, päris vastuoluline!
Kui ta aga on selline hulk, mis ei ole iseenda element, siis ta peaks vastupidi just kuuluma hullumeelsesse hulka ehk olema iseenda element! Ka vastuoluline!
Ma ei saagi sellele küsimusele vastata, katastroof!
Katastroof või mitte, mõtteainet pakkus see paradoks paljudele. Lõpuks leiti ka lahendus – igasugu kummaliste paradokside vältimiseks ei tohi lihtsalt lubada täielikult vabu käsi hulkade koostamisel.
Üldiselt selle üle aga muretsema ei pea – kõik hulgad, millest koolimatemaatikas räägitakse, on tõepoolest ka kõige karmimate nõuete järgi matemaatilised hulgad. Võib vahest lihtsalt meelde jätta, et ka alguses väga lihtsad ja selged mõisted võivad enda varjus peita igasuguseid riukaid.
Mida teha, kui on kakskümmend seitse sõpra ja kõigi nende sünnipäev on tarvis meeles pidada? Ei olegi eriti midagi vaja teha – tuleb lihtsalt lahti võtta arvuti või mõne suhtlusvõrgustiku kalender ja sinna sünnipäevad sisestada. Nii on kuskil sügaval arvuti sisimas iga inimesega vastavusse seatud tema sünnipäeva kuupäev.
Sisuliselt rakendasime äsja ühte funktsiooni! Nimelt üks funktsioon seab iga objektiga vastavusse mingi muu objekti ja täpselt ühe objekti – mitte rohkem ega vähem – ning meie seadsime iga sõbraga vastavusse tema sünnipäeva.
Samamoodi võiksime mõelda, et kalender ise on funktsioon – seab iga kuupäevaga vastavusse õige nädalapäeva!
Muidugi on palju olukordi, kus sellist reeglit kohe järgida ei saa – näiteks ei saaks me iga kuupäevaga vastavusse seada ainult ühte inimest, kellel sel kuupäeval sünnipäev on, sest samal kuupäeval on ju sünnipäev väga mitmel erineval inimesel. Sel juhul ei ole lahti midagi hullu, aga funktsioon matemaatilise kirjeldusena siia lihtsalt kohe ei sobi. Hiljem näeme, et pisut kavaldades võime ka selles olukorras funktsioone kasutada.
Funktsioonist saab mõelda väga mitut moodi. Kirjeldasime juba, kuidas funktsiooni näha teatud kindlat tüüpi nimekirjana. Võibolla lihtsamgi veel on ette kujutada, et funktsioon on teatud tüüpi masin, mis haarab endasse ükshaaval erinevaid objekte, teeb nendega abrakadabra ning seejärel väljastab nad jällegi ükshaaval, mõnikord hoopis tundmatul kujul.
Tore näide elulisest funktsioonist on õiglaselt tiksuv taksomeeter. Kui alustamistasu on 2,5 eurot ja iga kilomeeter maksab 0,5 eurot, siis taksomeeter on masin, mis korrutab kulunud kilomeetrite arvu 0,5-ga ning liidab pärast 2,5 eurot juurde.
Matemaatikakesksem funktsioon on näiteks ruutfunktsioon: sisestate masinasse ühe arvu, seal korrutatakse see arv hookuspookuse abil iseendaga ja väljastatakse tulemus. Sellele masinale võiks peale kirjutada „ruutfunktsioon”, et ta teiste masinatega segamini ei läheks.
Mõni geomeetriline masin võiks näiteks võtta sisendiks kolmnurki ning väljastada nende pindala või ümbermõõdu. Masinale, mis võtab sisendina kolmemõõtmelisi kujundeid, litsub neid suure vasaraga tasandile kokku ning väljastab algse kujundi kahemõõtmelise kujutise, võime anda uhke nime „projektsioon”. See on masin, mis näiteks teeb maakaarte, surudes meie kena ümara maakera kahemõõtmelisele paberile.
Analoogia funktsiooni ja masina vahel on hea ja intuitiivne, kuid matemaatika tarvis on vaja mõte ka täpsesse vormi seada.
Selle jaoks on meil tarvis lihtsalt täpsustada, milliseid objekte meie masin sisendina võtta saab ning milliseid ta väljastab. Kui nüüd meenub, et üldine objektide kogum matemaatikas on hulk, võibki anda funktsiooni range definitsiooni.
Funktsioon hulgast A hulka B on eeskiri, millega hulga A iga elemendiga seatakse vastavusse täpselt üks hulga B element.
Tihti tähistatakse funktsioone näiteks tähega ƒ.
Näiteks arvu ruutu võtmine on funktsioon, sest ta seab igale reaalarvude hulga elemendiga r vastavusse ühe teise reaalarvude hulga elemendi r2. Matemaatiliselt kirjutaksime
Määramispiirkond ja muutumispiirkond
Hulka A nimetatakse ka määramispiirkonnaks, ehk siis funktsioon on määratud kõikide hulga A elementide jaoks. Ta koondab endasse kõikvõimalikud masina sisendobjektid.
Meie definitsioonis ei pea iga hulga B element olema tegelikult masina väljundobjektiks – hulk B moodustab potentsiaalsete väljundobjektide hulga. Näiteks arvuruudud on ju alati mittenegatiivsed, kuid meie definitsioonis täitis ka hulga B rolli reaalarvude hulk. Tihti on lihtsalt raske otsustada, mida täpselt masin ikka väljastada otsustab, isegi kui teame, mis tüüpi need objektid umbkaudu on. Näiteks kui meie funktsioon seab iga maailma majaga vastavusse tema aastase soojakulu, siis on kõik vastused kindlasti mittenegatiivsed reaalarvud, aga raske on ette öelda, milliseid arvväärtusi me tulemustena näha saame.
Siiski suudame vahel täpselt kindlaks määrata kõikvõimalikud objektid, mida masin tõepoolest väljastada oskab. Sellist hulga B alamhulka nimetatakse muutumispiirkonnaks.
Näiteks kolmnurga pindala funktsiooni määramispiirkonna moodustavad kõikvõimalikud kolmnurgad ja muutumispiirkonna positiivsed reaalarvud.
Sissejuhatuses toodud sünnipäevade funktsiooni määramispiirkonnaks olid kõik sõbrad ning muutumispiirkonnaks kõikvõimalikud kuupäevad.
Samuti mainisime sissejuhatuses, et kuupäevadega inimesi vastavusse seades me funktsiooni ei saaks. See on tõsi, aga seda ainult eeldusel, et tahame oma muutumispiirkonnaks just inimeste hulka – sel juhul tõesti pole funktsioon hästi defineeritud, samal kuupäeval on sünnipäev väga paljudel.
Samas aga, kui meil on tõesti suur kihk funktsiooni kirjeldusena kasutada, siis võiksime iga kuupäevaga vastavusse seada hoopis kõik inimesed, kellel on sel päeval sünnipäev. Teisisõnu muudaksime funktsiooni muutumispiirkonda: enam ei oleks muutumispiirkonna elementideks inimesed, vaid hoopis kõikvõimalikud inimeste alamhulgad. Nii saaksime igati toreda funktsiooni ning süda võib rahul olla.
See kehtib ka üldisemalt: tihti võime muutumispiirkonda laiendades saada mittefunktsioonist igati viisaka funktsiooni.
Nii nagu on eri tüüpi, hoopis isesuguste omadustega masinaid, nii on ka erinevate omadustega funktsioone. Kokku on funktsioone väga palju ning nende kõigiga ei saa ühtmoodi ringi käia. Teatud omaduste põhjal õnnestub funktsioone aga natukene liigitada ja klassidesse seada – nii nagu näiteks soo või vanuse põhjal liigitatakse ka inimesi, et teada, mida neile reklaamida tasuks või milliseid riideid neile müüa sobiks. Ei maksa ehmuda, kui mõnikord on eri tüüpi funktsioonidele antud päris keerulised nimed.
Üksühene vastavus ja pöördfunktsioon
Näiteks osutuvad oluliseks funktsioonid, mis seavad iga määramispiirkonna objektiga vastavusse täpselt ühe muutumispiirkonna objekti. Selliseid funktsioone kutsutakse ka üksühesteks vastavusteks.
Toredaks teeb need funktsioonid asjaolu, et sel juhul võime funktsiooni ka ümber pöörata ja muutumispiirkonna iga objektiga vastavusse seada ka täpselt ühe määramispiirkonna objekti.
Selline vastupidine vastavusse seadmine kannabki pöördfunktsiooni nime. Võime mõelda, et sümboolselt tähendab see järgmist:
Lihtne näide on funktsioon, ƒ(r) = 2r mis korrutab iga reaalarvu kahega. Tema pöördfunktsioon peab iga reaalarvu kahega jagama.
Näiteks sobiks ka meie taksomeetri funktsioon, sest juhul, kui ajatasu juures pole, saame makstud summa järgi täpselt arvutada ka läbitud kilomeetrite arvu. Peab muidugi olema hoolikas, et see makstud summa oleks alustustasust suurem ehk asuks taksomeetri funktsiooni muutumispiirkonnas.
Suur osa funktsioone siiski üksühesed vastavused pole. Näiteks funktsioon, mis annab inimese sisestamisel välja tema sünnipäeva, ei ole üksühene vastavus, sest samal kuupäeval on paljudel inimestel sünnipäev. Enamasti ongi üksühesuste takistuseks see, et nad seavad määramispiirkonna eri objektidega vastavusse muutumispiirkonna ühe ja sama objekti.
Nii ei ole ruutfunktsioon üksühene vastavus, kuna ta seab sama arvu vastavusse nii pluss kui ka miinus ühega. Samuti ei ole üksühene vastavus kolmnurga pindala, kuna mitmel erineval kolmnurgal võib ju olla täpselt sama pindala.
Pöördfunktsioone saame siiski tihti defineerida, kui kitsendame oma vahemikku või teisisõnu teeme mõned valikud.
Näiteks võiksime ruutfunktsiooni pöördfunktsiooni defineerida nii, et valime alati positiivse ruutjuure. Sel juhul vaataksime ruutfunktsiooni justkui ainult positiivsetel reaalarvudel defineeritult. Tema pöördfunktsiooni leidmiseks peaksime justkui x- ja y-telje rollid ära vahetama. Nüüd jookseb funktsiooni argument mööda y-telge ning funktsiooni väärtus mööda x-telje posiitivset osa.
Kaval viis sellest mõtlemiseks on järgmine: pöördfunktsiooni leiame täpselt siis, kui peegeldame graafikut sirgest x = y:
Pöördfunktsioone kohtame pikemalt näiteks trigonomeetriliste funktsioonide juures, kus just seesama üksühesuse mure välja tuleb [lk 205].
Funktsioonide esitamiseks on väga palju erinevaid viise ning olenevalt olukorrast on mugavam kasutada ühte või teist või kolmandat, mõnikord mitut korraga.
Tabeli või nimekirjana
Üks lihtsamaid võimalusi on funktsioone esitada nimekirja või tabelina: anname lihtsalt igale sisendile vastava väljundi. See on üsna kompaktne viis, kui funktsiooni määramispiirkond on tilluke ja samas pole väärtustel suurt struktuuri. Näitena sobib sissejuhatuses toodud joonis või näiteks ka sagedustabel, kuhu kirjutame, kui mitu päeva selle aasta ilusas juunis olid päikselised, vihmased või vahepealsed.
Valemina
Teine levinud viis on funktsiooni esitamine valemina. Näiteks on seeläbi defineeritud enamik reaalarvulisi funktsioone. Lihtne näide on ruutfunktsioon:
Algoritmina
Funktsioone võib esitada ka algoritmiliselt ning eriti osutub see oluliseks just asjaajamisel arvutitega. Järgmisel lehel näitame, kuidas algoritmina kirja panna faktoriaal ehk esimese n arvu korrutis [lk 382].
Sõnaliselt
Vahel on kõige lihtsam funktsioone esitada hoopis verbaalselt. Näiteks võiksime võtta funktsiooni, mis seab iga kolmnurgaga vastavusse tema pindala, või funktsiooni, mis seab iga inimesega vastavusse tema pikkuse.
Graafiliselt
Tihti on kasulik funktsioone esitada graafiliselt. Eelkõige on see seotud reaalarvuliste funktsioonidega, mille määramis- ning muutumispiirkond on reaalarvud.
Sageli võib reaalarvuliste funktsioonide uurimise taandadagi graafiku uurimisele. Ja kuigi malli ja joonlauaga täpseid vastuseid ei saa, siis geomeetrilistest argumentidest ja intuitsioonist on võimalik päris palju kasu lõigata.
Selles raamatus näeme, kuidas geomeetriliselt on võimalik leida ruutvõrrandi lahendivalem [lk 275] või meelde jätta trigonomeetrilisi teisendusi [lk 242] või hoopis lahendada lineaarvõrrandisüsteeme [lk 187]. Ka sellistel keerulistel operatsioonidel nagu tuletise ja integraali võtmine on olemas ilusad geomeetrilised tõlgendused [lk 326].
Siinkohal toome näiteks funktsioonide
ning
graafikud ja näeme, et nad lõikuvad täpselt kahes reaalarvulises punktis. Proovige seda algebraliselt näidata!
Mitmest sisendist olenevaid funktsioone on juba keerulisem graafiliselt kujutada. Osas 7 kasutame aga näiteks joonist, mis näitab, kuidas hoo pealt veepommi viskamisel sõltub optimaalne viskenurk korraga viske- ja hookiirusest [lk 338].
Programmeerijatele on funktsioonid igapäevased tööriistad. Arvutiprogrammid ongi tegelikult erinevate väikeste funktsioonide kogumid, mis teevad täpselt määratud sisenditega täpselt määratud protseduure.
Kõige lihtsamad funktsioonid on vahest tabelarvutuse programmides, millest kuulsaim on Microsoft Excel. Seal võib mõnda kasti kirjutada „=A1+B1", mis ütleb arvutile, et selle kasti väärtuseks näidatakse kastide A1 ja B1 summat. Tegemist on funktsiooniga, mille sisendiks on kaks arvu ja väljundiks üks.
Toome ka ühe näite funktsioonist, mis arvutab faktoriaali n! [lk 382]. Tuletame meelde, et faktoriaal on lihtsalt järgnev korrutis
Arvuti võiks seda programmeerimiskeele Python abil leidma panna umbes nii:
def factorial(n) :
f = 1
while (n > 0) :
f = f * n
n = n – 1
return f
Jooksutades seda funktsiooni käsuga factorial(5), saaksime vastuseks järgmise tulemuse: 120.
Arvutite keelest arusaamiseks ning neile käskluste jagamiseks peab teadma-tundma sealset sõnavara.
Antud juhul defineerime, mida teeb funktsioon nimega factorial ning seejärel anname talle käsu jooksutada seda funktsiooni sisendiga 5. Ideeliselt peaks see funktsioon seejärel siis lihtsalt korrutama kokku arvud 5, 4, 3, 2, 1.
Selle funktsiooni kirjapanek on järgmine.
Funktsiooni esimesel real antakse muutujale ƒ väärtus 1. Siia hakkamegi salvestama faktoriaali väärtust. Järgmise käsuga palume arvutil jooksutada järgmist kahte rida nii kaua, kuni muutuja n väärtus on suurem 0-st.
Esmalt korrutatakse ƒ läbi muutuja n väärtusega.
Teisalt vähendatakse muutuja n väärtust ühe võrra.
See tähendab, et korrutame ƒ-i läbi alguses n enda väärtusega, siis n – 1-ga, siis n – 2-ga täpselt nii kaua, kuni oleme läbi korrutanud ka ühega – väiksemaks me muutujal n tänu kolmandale koodireale enam minna ei lase.
Lõpuks ütleb viimane rida lihtsalt, et funktsioon peaks leitud väärtuse küsijale ka väljastama.
Nii mõnigi kord tulevad programmeerimiskeeltes esile ka funktsioonid, mis ei annagi väljundit, vaid lihtsalt teevad mõned kerged muudatused. Neist oleks võibolla segaduse vältimiseks siis lihtsam mõelda kui „protseduuridest“.
Naturaalarvud on arvud, millega loendame õhtul lambaid: 1, 2, 3, 4, 5, 6, ... Neid kõiki korraga ehk nende hulka tähistatakse N-iga.
Naturaalarvud on ilmselt kõige loomulikumad matemaatilised objektid, lihtsad, aga tähtsad. Kuna nad tulevad esile kohe, kui loendama hakkame, ei saa nendest maailma kirjeldamisel üle ega ümber.
Oma loomulikkuse tõttu on nad ka matemaatikas üheks keskseks objektiks ja nende uurimine pole veel sugugi päris lõppenud!
Naturaalarvude matemaatiline kirjeldamine
Naturaalarvud võib üles ehitada ühe arvu – arvu 1 – ning ühe tehte – arvu 1 liitmise baasil. Iga naturaalarvu võime leida, kui ühte piisava arvu kordi iseendaga kokku liidame. Arvu 10 saamiseks peame näiteks arvule 1 veel 9 arvu 1 juurde liitma.
Nii leidub igast naturaalarvust veel ühe võrra suurem naturaalarv. Näiteks isegi kui meil on juba 1000 sõpra, võiksime leida veel ühe sõbraliku selli Tiibeti mägedest ning meil olekski juba 1001 sõpra – ka teda peame oskama arvestada!
Seega kõige suuremat naturaalarvu ei leidugi. See arusaam võib alguses tunduda natuke üllatav, aga teiselt poolt: kas on mingi põhjus, miks peaks leiduma kõige suurem arv? Nii kohtame ka esimest korda lõpmatust – naturaalarve peab kokku olema lõpmatult palju.
Naturaalarve võib kirjeldada ja defineerida ka mitmel muul moel. Näiteks võite hulkade peatükist lugeda, kuidas naturaalarve kirjeldada ainuüksi hulkade abil [lk 61].
Tasub ilmselt veel ära märkida, et mõnikord loetakse ka 0 naturaalarvude hulka, tähistamaks olukorda, kus veel midagi loendatud pole. See on aga rohkem maitse küsimus, nii et lugeja võib täiesti vabalt ise otsustada, kas 0 on naturaalarv või pole. Meie positsioon on aga selge: alustasime ju raamatus esinevate osade loendamist just nullist.
Naturaalarvude tähistamine
Naturaalarvud on väga loomulikud, nad on erinevates kultuuriruumides sõltumatult kasutusele võetud ja välja on arenenud erinevad tähistused. Järgnevalt tutvustame nendest ka mõnda levinumat.
Kümnendsüsteem
Meile on kombeks naturaalarve tähistada kümne numbri abil 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9.
Kuna kasutame täpselt kümmet erinevat sümbolit, siis sellist tähistust nimetataksegi kümnendsüsteemiks. Kümnendsüsteemis ehitame kõik arvud üles ühelistest, kümnelistest, sajalistest (kümme korda kümme), tuhandelistest (kümme korda kümme korda kümme) ja nii edasi – kümnete meri.
Näiteks arv 128 tähendab lahtikirjutatult 1 · 10 · 10 + 2 · 10 + 8
ning arv 9301 tähendab 9 · 10 · 10 · 10 + 3 · 10 · 10 + 0 · 10 + 1.
Arvu astme peatükis [lk 110] näeme, et võime ühelised, kümnelised, sajalised ja nii edasi kõik kirjutada arvu kümme astmete abil – lisame 10 ülemisse paremasse nurka tema astendaja, mis ütleb, mitu korda arvu 10 kokku korrutame:
Nii võime arvu 9301 kirjutada veelgi kompaktsemalt:
Kahendsüsteem
Arvutitekogus toimub arvutamine aga kahendsüsteemis – kõik arvud kirjutatakse kahe numbri 0 ja 1 abil ja arve loendatakse mitte kümneliste, vaid kaheliste kaupa. Näiteks arvu 3 kuju kahendsüsteemis on 11, kuna 3 = 1 · 2 + 1, arv 5 on kujus 101 kuna 5 = 1 · 2 · 2 + 0 · 2 + 1 ning arv 8 on kujus 1000, kuna 8 = 1 · 2 · 2 · 2. Sarnaselt kümnendsüsteemiga võime seega iga naturaalarvu kirjutada üldkujus arvu 2 astmete abil.
Enne juba käsitletud arvu 9301 võime seega kahendsüsteemis kirja panna pisut pikemalt:
Teisisõnu on kahendsüsteemis arvu 9301 kujuks 10010001010101.
Kindlasti tuleks küsida: miks ikkagi arvutites kõik kahendsüsteemis toimub? Põhjus on väga proosaline – kahendsüsteemis on meil vähim erinevaid sümboleid, mida kuidagi masinavärgis tähistama peaks. Kõige lihtsam ongi arvutit üles ehitada „lülititest”, millel on täpselt kaks olekut – kas sees või väljas. Need vastavad siis väärtustele 1 ja 0. Nii on kahendsüsteemis lihtsam arve salvestada ja lihtsam ka tehteid teha. Mõelge ise, on ju endalgi kahte ühte ja nulli omavahel lihtsam kokku liita kui näiteks seitset ja viit.
Ainus raskus võrreldes kümnendsüsteemiga on arvude lugemine – arvud lähevad kiiresti maru pikaks. Meil igapäevaelus oleks see probleem, aga arvuti võib ju ekraanile meie jaoks midagi mugavamat kuvada.
Rooma numbrid
Roomlased vedasid aga naturaalarvude tähistamiseks hoopis kummalisi kriipse: näiteks meie ühte tähistati kriipsuga I, meie 12 kriipsudega XII ja meie 49 kriipsudega IL.
Proovige leida reegleid Rooma numbrite liitmiseks või veel hullem, korrutamiseks. Näiteks liidaksid roomlased arve 69 ja 145 kokku järgnevalt.
LXIX + CXLV
1. Tuleb asendada kõik „lahutavad liikmed”:
LXVIIII + CXXXXV
2. Kokku panna:
LXVIIIICXXXXV
3. Sorteerida:
CLXXXXXVVIIII
4. Kombineerida gruppidesse:
CCXIIII
5. Asendada lahutavad liikmed tagasi:
CCXIV
Veendute ilmselt üsna kiiresti, et sellise arvusüsteemiga on peaaegu võimatu aritmeetikat teha. Ning tõepoolest, roomlased oma matemaatilistelt teadmistelt või tegudelt ajaloos just silma ei paista.
Teisendamine
Oletame, et teie mitte eriti hea sõber on otsustanud põikpäiselt kasutada kahendsüsteemi ja väidab teile, et olete talle võlgu täpselt 101010 eurot. Loetuna kümnendsüsteemis oleks see päris märkimisväärne summa, nii et ilmselt tasub üritada arv kahendsüsteemist kümnendsüsteemi üle viia. Kuidas seda teha?
Kõik on tegelikult juba eelnevalt välja toodud. Kirjutame kõigepealt välja, mida 101010 kahendsüsteemis tähendab: 101010 = 25 + 23 + 2. Edasi kirjutame lihtsalt kõik toodud kahe astmed kümnendesitluses: 25 = 32, 23 = 8, 2 = 2. Lõpetuseks peame saadud arvud (nüüd kümnendesitluses) oma tavaliste liitmisnippidega kokku liitma: saame vastuseks 42.
Naturaalarvud on juba väga toredad, aga nendega tuleb esile ka mõningaid probleeme.
Naturaalarve saame omavahel liita ja summaks on alati naturaalarv: näiteks 3 + 4 = 7 või 2 + 10 = 12. Liitmisest võib siin väga vabalt mõelda lihtsalt loendamise raames: keegi annab teie kolmele õunale neli lisaks või näiteks lisaks teile ja kassapidajale siseneb äkiliselt poodi veel 10 tantsulist.
Tore oleks, kui saaksime ka kuidagi kirjeldada olukorda, kus neli õuna jälle tagasi küsitakse või kus 10 tantsulist jälle poest välja kepslevad. Ütlete kohe, et selleks on muidugi lahutamine: 7 – 4 = 3 või 12 – 10 = 2.
Tekib aga probleem: kui mul on ainult 3 õuna, ei saa mult nelja õuna ära võtta ja kui poes on ainult 2 inimest, ei saa sealt 10 ära minna. Seega osasid arve justkui ei saakski omavahel lahutada.
Veider! Mis on need arvud, mis võiksid tähistada midagi, mis on vähem kui mitte midagi?
Ja kuigi pakuti juba varakult välja, et tegelikult võiksid eksisteerida ka arvud 3 – 4 ning 2 – 10, ei tahetud nendega pikka aega leppida. Neid peeti ebaloomulikeks. Mida peaks tähendama see –1, mida mõni pakkus 3 – 4 vastuseks, või –8, mida pakuti 2 – 10 vastuseks? Kui miski eksisteerib, on teda ju vähemalt üks? Kuidas saab olemas olla mitte millestki veel väiksem kogus?
Tänapäeval kahjuks teab mõni seda liigagi hästi, mida negatiivsed arvud tähistada võivad – näiteks võlga! Katsetage internetis oma pangakontoga, ta võib kergesti sattuda ka miinusesse, kui raha liiga agarasti kulutada. Arvust –1 võibki näiteks mõelda kui õunavõlast vanemale vennale...
Sellega, et negatiivsed arvud on täiesti mõistlikud ja isegi loomulikud, lepiti aga alles 19. sajandil. Enne seda kutsuti neid küll absurdseteks, küll räpasteks ja tihti keelduti nendega igasugusest läbikäimisest. Tegelikult on ju negatiivsete arvudega siiski toredam ja ilusamgi – nende abil ei jää arvsirge poolikuks, vaid on kenasti alguse ja lõputa.
Arvude liitmisest ja lahutamisest võimegi mõelda kui arvsirgel paremale või vasemale poole liikumisest – liites neli, liigume neli sammu paremale; lahutades seitse, seitse sammu vasemale. Kõiki täisarve võime omavahel liita ja lahutada ning alati jälle vastuseks täisarvu saada.
Täisarvude hulka tähistatakse Z-iga.
Ometigi ei paku ka täisarvud veel täit rahulolu! Tõepoolest, lihtne on võrdselt jagada kuus õuna kolme sõbra vahel – annad kõigile kaks. Ent kuidas võrdselt jagada üht suurt arbuusi kolme sõbra vahel?
Meil on muidugi vastus olemas, igale sõbrale tuleb anda kolmandik arbuusist. Probleem on aga, et kolmandik ei ole täisarv – peame jagamise jaoks arve veel mängu juurde tooma. Piisab sellest, kui võtame appi kõik arvud, mis saame täisarvude jagamisel nullist erinevate täisarvudega.
Selliseid arve nimetatakse ratsionaalarvudeks – nad on kujus p⁄q, kus p ja q on täisarvud. Ratsionaalarvud on näiteks 2⁄3, -1⁄2, 231⁄100, aga ka kõik täisarvud, sest näiteks 2 = 2⁄1.
Murrujoone peal olevat arvu nimetatakse murru lugejaks ja murrujoone all asuvat arvu murru nimetajaks. Ratsionaalarvude hulka tähistatakse tähega Q.
Hakates arvjoonele usinalt ratsionaalarve kirja panema, märkame, et neid on väga palju ja nad asuvad arvteljel ütlemata tihedalt. Tegelikult asub iga kahe ratsionaalarvu vahel alati veel üks ratsionaalarv: näiteks arvude –2 ja –1 vahel asub arv –1,7, arvude 2 ja 2,4 vahel 2,31. Üldisemalt, iga kahe suvalise ratsionaalarvu a ja b vahel asub ju nende aritmeetiline keskmine
Taandatud murrud ja tehted
Ütlesime, et kõik ratsionaalarvud saame, kui jagame täisarve nullist erinevate täisarvudega. Nii saame tegelikult liiga palju arve – paljud neist on omavahel võrdsed. See on küll väga lihtne, aga oluline tähelepanek.
Tõepoolest, kuna kahe arbuusi jagamisel kuueks võrdseks tükiks on tükid sama suured kui ühe arbuusi jagamisel kolmeks võrdseks osaks, ei ole mitte kõik täisarvude omavahelisel jagamisel saadud arvud erinevad, näiteks 2⁄6 = 1⁄3.
Kuna mitmed murrud on omavahel võrdsed, oleks tore leida neile kõigile üks parim esindaja. Selleks on murru taandatud esitus. Murru taandatud esituse saamiseks jagame murru nimetaja ja lugeja kõikide nende ühiste teguritega läbi: nii ongi näiteks ratsionaalarvude 1⁄3 , 2⁄6 ja 4⁄12 kõikide ühiseks taandatud kujuks 1⁄3 .
Ratsionaalarvudega on veelgi ohutum ja sujuvam ringi käia kui täisarvudega. Nimelt võime kõiki ratsionaalarve omavahel lisaks liitmisele-lahutamisele ka korrutada ja jagada (siiski mitte nulliga!) ning saame alati jällegi tulemuseks ratsionaalarvu.
Kümnendesitus
Ratsionaalarvudel leidub ka esitus kümnendsüsteemis, kasutusele tuleb lihtsalt võtta komakohad.
Näiteks ½ = 0,5, 13⁄8 = 1,625 ning 1⁄3 = 0,(3), kus sulgudes olev kolm tähistab, et number 3 jääb lõpmatult korduma.
Selgub, et iga ratsionaalarvu saabki esitada kümnendsüsteemis kas lõpliku arvu komakohtadega nagu 1⁄8 = 0,125 või lõpmatult korduma jäävate komakohtadega: näiteks 1⁄7 = 0,(142857) ja 1⁄12 = 0,08(3). Teisel juhul esile tulevaid kümnendesitusi nimetatakse perioodilisteks.
Järgnevalt selgitame natuke lähemalt, miks ratsionaalarvud on just nimelt kas lõpliku või perioodilise kümnendesitusega. Näitame esmalt, et iga lõpliku või perioodilise kümnendesitusega arv on ratsionaalarv:
Oletame, et meil on lõpliku kümnendesitusega arv.
Sel juhul võime arvu korduvalt 10-ga korrutades komakohtadest lahti saada. Näiteks kui arvul on kaks komakohta nagu arvul 0,25, peame seda täisarvu saamiseks korrutama 10-ga täpselt kaks korda – konkreetsel juhul on saadavaks täisarvuks 25. Ja edasi võime juba lihtsalt avaldada arvu 0,25 kahe täisarvu jagatisena, kui jagame võrrandi mõlemad pooled 100-ga läbi.
Oletame, et meie arv on perioodiline kümnendesitus.
Nüüd võime korduvalt kümnega korrutades komakohta liigutada nii palju, et pärast koma jääks alles ainult perioodiline osa. Kui näiteks periood algab üks koht pärast koma, peame korrutama kümnega. Näiteks arvu 0,8(32) korral saame arvu 8,(32).
Edasi võime aga jätkata kümnega korrutamist nii kaua, kuni algab perioodilise osa teine tsükkel. Kui perioodi pikkus on kaks, peame juba saadud arvu veel 100-ga korrutama. Konkreetsel juhul saaksime siis arvu 832,(32).
Lahutades nüüd teisest arvust esimese, jääb alles täisarv – perioodiline osa pärast komakohta taandub ju täpselt välja. Edasi saame juba lihtsalt avaldada arvu 0,8(32) ratsionaalarvuna.
Miks vastupidi igal ratsionaalarvul peaks just kirjeldatud kümnendesitus leiduma, on juba pisut kavalam ja jääb siinkohal tõestamata.
Oluline on ka ära märkida, et kümnendesitus ei ole alati ühene. Näiteks matemaatilise võrduse peatükis [lk 52] näitame, et 1 = 0,(9).
Ratsionaalarvudega saame loendada, liita ja lahutada, korrutada ning jagada. Tundub, et seda on juba päris palju. Üllatuslikult võime aga endiselt välja tulla geomeetrilise konstruktsiooniga, mille kirjeldamiseks ratsionaalarvudest ei piisa.
Ühikruudu diagonaali pikkus ei ole ratsionaalarv!
Joonistame ilusa ühikruudu ja leiame selle ühikruudu diagonaali pikkuse.
Tähistades seda diagonaali d-ga, teame näiteks Pythagorase teoreemist, et d2 = 2. Loomulik küsimus on: kas d on ikka ratsionaalarv?
Oletame, et d on tõesti ratsionaalarv: sel juhul võime d kirjutada taandatud kujus p⁄q , kus p ja q on täisarvud ning neil ei ole ühiseid tegureid. Saame, et p2 = 2q2.
Aga nüüd on ju võrdusmärgist paremal pool paarisarv, seega peab ka vasemal olema paarisarv. Kui p2 on paarisarv, siis ei saa p paaritu olla, sest paaritu arv ruudus annab paaritu arvu. Järelikult ka p on paarisarv ja võime p kirjutada kujul p = 2a.
Seega võime p2 kirjutada kui (2a)2 = 4a2. Asendades selle esialgsesse valemisse saame 4a2 = 2q2. Jagades kahega läbi, jääb alles 2a2 = q2.
Nüüd on aga vasem pool paaris ning seega peab ka q jaguma kahega. See on aga vastuolus meie eeldusega, et p⁄q oli taandatud murd. Seega ei saa d kuidagi olla ratsionaalarv, sest muidu jõuame loogilise vastuoluni. Seega on ta hoopis niinimetatud irratsionaalarv!
Irratsionaalarvud
Oh seda häda, kui Antiik-Kreekas sellele riukale jälile saadi. Nende jaoks olid proportsioonid ehk täisarvude suhted looduse üheks aluseks ning nii ei tahtnud nad sugugi leppida sellega, et leidub geomeetrilisi objekte, mille pikkust ei õnnestugi proportsioonide ehk täisarvude suhete abil kirjeldada. Räägitakse, et mõni matemaatik pidi selle avastuse tõttu lausa elust ilma jääma. Siiski jäädi matemaatikale truuks ja tänaseks ei nähta sellistes irratsionaalarvudes enam suurt ohtu ei tervisele ega ühiskonnale. Tegelikult lepiti nendega hoopis enne kui negatiivsete arvudega – nad tundusid küll kummalised, aga neile oli ometi võimalik looduses ja geomeetrilises ettekujutuses vastet leida.
Irratsionaalarvudeks nimetataksegi kõiki arve arvteljel, millel ei ole esitust kujus p⁄q. Paljud neist on esitatavad täis- või ratsionaalarvude juurtena [lk 111], näiteks
ja ka
on irratsionaalarvud. Irratsionaalarvudeks on aga veel näiteks π ja e. Nende faktide tõestamine on aga päris keeruline ja senini on näiteks teadmata, kas πe on ratsionaalarv või irratsionaalarv.
Ka irratsionaalarvudel leidub kümnendsüsteemis esitus. Ainus mure on, et neid ei saa selles kujus kunagi täpselt esitada – irratsionaalarvude kümnendesitus on lõpmatult pikk. Näiteks arvu π esimesed 20 kohta on 3,14159265358979323846…, aga edasi tulevad jälle täiesti ennustamatud numbrid ning veelgi hullem – neid tuleb lõpmatult palju.
Pannes arvteljele kirja kõik ratsionaalarvud ja irratsionaalarvud, saame lõpuks kokku terve arvtelje – ükski punkt ei jää puudu ega vahele. Kõik arvtelje arvud kokku moodustavad reaalarvude hulga, mida tähistatakse arvuga R.
Kui ratsionaalarvud saime üles ehitada täisarvudest, siis kõikide irratsionaalarvude täpne matemaatiline konstrueerimine on juba veidi keerulisem. Võime küll irratsionaalarvudest mõelda kui arvudest, mida saame kirjutada lõpmatu ja mitteperioodilise kümnendesituse abil, aga kuidas neid liita või korrutada? Õigupoolest jõudsid matemaatikuid rahuldava range kirjelduseni alles 19. sajandil ning selle jaoks võib kasutada piirväärtuseid [lk 319].
Praeguseks on aga tore irratsionaalarvude sissetoomisest mõeldagi geomeetriliselt: irratsionaalarvud täidavad ratsionaalarvudest arvteljele jäänud auke, nende liitmine tähendab – nagu ratsionaalarvude liitminegi – lihtsalt arvtelje nihutamist.
Reaalarvudega saab kõik igapäevatoimetused korda aetud... kui just ei taha igal õhtul leida ruutvõrrandile x2 = –1 lahendit.
Tõepoolest, ükski reaalarvu ruut ei ole ju negatiivne. Näiteks 1 · 1 = 1 ning ka (–1) · (–1) = 1 ehk meie ruutvõrrandi lahendiks ei kõlba 1 ega ka –1. Lihtsam on seda vahest näha isegi ruutfunktsiooni graafikult:
Seega, kui tahame tõesti, et saaksime välja kirjutada lahendit ka ruutvõrrandile x2 = –1 või ruutvõrrandile x2 + x + 1 = 0 või näiteks ka neljanda astme võrrandile x4 + x2 = –3, peame tingimata oma arvusüsteemi veel kord laiendama ja veel rohkem arve kasutusele võtma.
Eelnevat võib ümber sõnastada ka järgmiselt: nägime, et reaalarvude abil saame leida kõik arvud x nii, et x2 = a iga mittenegatiivse a jaoks. Kui nüüd tahame aga lahti saada tingimusest „mittenegatiivne“, siis peamegi sisse tooma kompleksarvud.
Kui lubada natukene mõttel lennata, siis võiksime õigustatult võrrandi
lahendiks pakkuda
Tõepoolest, kuna ruutjuure võtmine ning ruutu võtmine taandavad teineteise välja, võime kirjutada
Seega, lubades ruutvõrrandi lahendiks ka uut leiutist √–1, oleme laiendanud arvusüsteemi. Üllataval kombel piisab sellest laiendusest mitte ainult peatüki alguses toodud võrranditele, vaid tegelikult absoluutselt kõikidele polünoomvõrranditele [lk 266] lahendite leidmiseks!
Imaginaararv i ja komplekstasand
Irratsionaalarvude lisamisel toppisime reaaltelje kõik augud täis. Kuhu need kompleksarvud siis mahtuda võiksid?
Märkame, et isegi kui tõmbame paberile ühe aukudeta sirge, jääb paberile veel ruumi kui palju – sirgest üles ja alla jääb mõlemale poole tühjus. Kompleksarvud täidavad kogu selle tühjuse, nad täidavad arvudega terve paberilehe.
Nii on kompleksarvud mingis mõttes kahemõõtmelised arvud: võib öelda, et neil on reaalmõõde ja imaginaar- ehk kompleksmõõde, mille toob kaasa uus sissetoodud arv √–1. Kohe selgitame!
Seda arvu nimetataksegi imaginaararvuks ja kuna teda on tüütu kogu aeg välja kirjutada, anname talle tähiseks i. Nimi imaginaararv tuleneb just sellest, et i tundus vähemalt esialgu eksisteerivat ainult matemaatikute endi ettekujutuses ja mitte välises maailmas.
Meenutame, et arvu 1 võib pidada reaalmõõtme ühikuks – seda kokku liites või suurendades-vähendades liigume mööda horisontaaltelge. Sarnaselt on i kompleksmõõtme ühikuks, teda liites või suurendades liigume mööda vertikaaltelge. Ta asub nullpunktist sama kaugel kui reaaltelje ühik.
Nii on teised komplekstelje punktid antavad kujus 2i; 0,3i; 14i ja nii edasi.
Kõikvõimalikud kompleksarvud saame, kui vaatame arve kujus c = a + bi, kus a ja b on reaalarvud. Reaalarvu a kutsutakse kompleksarvu c reaalosaks ja b-d tema imaginaarosaks.
Joonistame komplekstasandile näiteks punktid 3, 3i, 3 + 3i, –2 + i.
Iga reaalarvu korral võime rääkida tema suurusest ehk absoluutväärtusest – peame silmas talle vastava punkti kaugust arvtelje nullpunktist [lk 120]. Samamoodi võime ka iga kompleksarvu korral rääkida tema suurusest – talle komplekstasandil vastava punkti kaugusest nullpunktist. Seda kaugust võib muidugi leida Pythagorase teoreemi abil.
Aga kompleksarve pole ju olemas!
Nagu ennist rääkisime, oli matemaatikutel ja kogu inimkonnal suuri raskusi negatiivsete arvudega – alles paarsada aastat tagasi lepiti, et tegemist on ikkagi täiesti mõistlike ja loomulike arvudega, millega tegelemine ei ole sugugi jumalateotus.
Selles valguses on kompleksarvude mõistlikkuse ja loomupärasuse kahtlustamine igati mõistetav. Järgnev tabel, kus võrdleme negatiivseid arve ja imaginaararve, võiks siiski veenda, et ka kompleksarve pole mõtet karta.
Küsimusele, kas arv 4 + 5i eksisteerib, on muidugi raske vastata, kuid sama raske on öelda, kas arv 4 või 5 eksisteerib. Siiski on kompleksarvud leidnud reaalarvude kõrval tänapäevases maailma ja looduse kirjelduses oma kindla koha.
tabelis
Tehted kompleksarvudega
Selgub, et kompleksarvud on väga toredad ja nendega saab teha kõike, mida reaalarvudega, ja veel rohkematki.
Liitmine ja lahutamine
Kompleksarve saab liita ja lahutada, tuleb lihtsalt liita ja lahutada eraldi reaal- ja imaginaarosa: näiteks (1 – i) + (2 + 2i) = 3 + i. Nagu reaalarvude liitmisest võib mõelda kui liikumisest ühes või teises suunas reaalteljel, võib ka kompleksarvude liitmisest mõelda geomeetriliselt. Seekord liigume lihtsalt komplekstasandil, vastava arvu samme reaaltelge mööda, vastava arvu imaginaartelge mööda.
Korrutamine ja jagamine
Kompleksarve saab edukalt ka korrutada ja isegi jagada. Tulemuseks on endiselt alati kompleksarv. Näiteks
ning
Kompleksarvudega korrutamisel on ka ilus geomeetriline tõlgendus – tasandil pööramine.
Näiteks oletame, et meile on antud kompleksarv 1 + 2i ning tahame leida uut kompleksarvu, mis on selle arvu suhtes 45-kraadise nurga all vastupäeva.
Tuleb välja, et sellise kompleksarvu leidmiseks võime lihtsalt algset arvu korrutada mistahes kompleksarvuga, mis on 45-kraadise nurga all reaaltelje suhtes: näiteks arvuga 1 + i.
Seda kõike ei pea muidugi joonise põhjal uskuma. (Ei tohigi uskuda!) Õnneks kinnitab aga algebra kenasti meie väiteid. Tõepoolest, korrutamise võime välja kirjutada järgmiselt:
Ning nagu jooniselt näeme, asub –1 + 3i täpselt 45-kraadise nurga all 1 + 2i suhtes, küll tõesti parasjagu nullpunktist kaugemal. See tuleneb lihtsalt sellest, et korrutamisel ei piisa ainult nurkade liitmisest, vaid tuleb omavahel korrutada ka kaugused.
Imaginaararvuga korrutamisel on järelikult tegemist ainult pöördega 90° – tema kaugus nullist on ju täpselt 1 ühik. Nii liigub arv 1 arvuga i korrutamisel täpselt i-ks, arv 1 + i aga i-ga korrutamisel täpselt –1 + i-ks. See pakub ka arvuga –1 korrutamisele uue tõlgenduse: arvteljel oli –1 arvuga korrutamise tõlgenduseks peegeldus nullpunktist, nüüd aga teades, et –1 = i2, võime komplekstasandil arvuga –1 korrutamisest mõelda ka kui 180 kraadisest pöördest.
Mõnel arvul on matemaatikas päris omamoodi roll. Esimese näitena tulevad pähe näiteks arvud null ja üks.
Null torkab silma, sest käitub korrutamisel ja liitmisel teistest erinevalt: korrutades mistahes arvu nulliga, saame vastuseks nulli, ning liites mistahes arvule nulli, saame sama arvu, mis enne. Samamoodi on üks isemoodi, sest korrutades ükskõik mis arvu ühega jääb see arv samaks ning ühe kõik astmed on tema endaga võrdsed.
Ajalooliselt on mainimist väärt arvuks kindlasti ka √2, mis näitas, et ratsionaalarvudest pole maailma kirjeldamiseks sugugi küllalt [lk 87].
Miks mitte välja tuua ka imaginaararvu, mille abil laiendasime reaalarve kompleksarvudele [lk 89] või iluideaaliks loetud kuldlõike arvu
[lk 135].Käesolevas peatükis räägime aga pikemalt kahest teisest põnevast ja kuulsast arvust, millest ei saa üle ega ümber ka koolimatemaatikas. Tutvustame tegelasi: π ja e.
Arv seostub kõigile meile ilmselt ringjoonega. Nii alustamegi arvuga tutvumist väikese mõtisklusega ringjoonest.
Kuidas mõelda ringjoonest?
Ringjoon on ilus matemaatiline objekt, millele ei ole muidugi raske leida ka pärismaailmas vastet. Nii nagu igapäevaelus kohtame ringikujulisi objekte väga erinevates olukordades, saab ringjoonest ka matemaatiliselt mitut moodi mõelda.
Sirkli abil
Hulkade juures [lk 60] mainisime juba ühte viisi ringjoone kirjeldamiseks: ringjoont võib kirjeldada kui kõikide tasandipunktide (x;y) hulka, mis asuvad ühest välja valitud punktist (ringi keskpunktist) võrdsel kaugusel. See selgitab, miks saame ringjoont joonistada just nimelt sirkli abil.
Kõige ümmargusem
Eelnev ei ole siiski ilmselt esimene kirjeldus, mille peale mittematemaatik tuleks. Eelkõige jääb ju ringjoone juures meelde tema ümarus ja sümmeetria. Näiteks õhku tõstetud jalgratta ratast võib lõpmatult ümber tema telje pöörata ja me märkame ainult kodarate liikumist – ratas ise oleks justkui paigal.
Tuleb välja, et ka sellest vaatlusest lähtudes on võimalik ringjoon rangelt ja matemaatiliselt korrektselt defineerida: ringjoon on ainus kahemõõtmeline suletud joon, mida võime ükskõik kui palju pöörata, ilma et tema kuju muudaksime. Matemaatilisemalt: ringjoon on kõige rohkemate (pöörd)sümmeetriatega kujund.
Pindala ja ümbermõõdu suhe
Kui lambakarjusel oleks vaja lammastele ehitada tara, nii et sama materjalihulga ehk ümbermõõdu korral saaks kasutada võimalikult suurt rohumaad ehk pindala, siis saab ta jällegi täiesti ausa ringi.
Füüsikute kombel
Füüsikud seevastu ütleksid ilmselt, et ringjoon on ainus trajektoor tasandil, mida mööda liikudes on alati kiirendus ja kiirus risti. Sel juhul muudab kiirendus ainult kiiruse suunda ja mitte tema suurust. Tekib ilus ühtlane ringliikumine.
Näiteks on enamik satelliite Maa ümber ringliikumises. Täpselt ringikujulise orbiidi tekitamiseks tuleb siiski kiirus hoolega valida. Füüsikud tulevad sellega hästi toime. Näiteks komeedid seda aga ei oska ja tiirlevad ümber Päikese väga väljaveninud ellipsit mööda.
Parameetrilise võrrandi kaudu
Ülikoolis matemaatikaga kokku puutudes võib aga kohtuda veel hoopis uutmoodi ringjoone definitsiooniga. Nimelt saab iga kõverjoont tasandil vaadelda kui ühe funktsiooni väärtuseid. Õigesti valitud funktsioon kirjeldab täpselt ringjoone kuju ning funktsiooni argument tähistab siis intuitiivselt lihtsalt meie asupaika ringjoonel. Ringjoone kirjeldamiseks peame kasutama funktsioone siinus ja koosinus, millest on juttu ka trigonomeetria peatükis [lk 230].
Ringjoone kõiki punkte (x;y) kirjeldava parameetrilise võrrandi saame, kui muudame funktsiooni sisendit t nullist kuni -ni ning arvutame x-i ja y-i järgnevalt:
Nõnda saadud kirjeldust nimetatakse parameetriliseks võrrandiks.
Kõik ülaltoodud viis ringjoone definitsiooni on matemaatiliselt võrdväärsed. Seega pole vist sugugi liig öelda, et ringjoon on üks mitmekülgne ja ilus matemaatiline objekt. Ringjoon loob seoseid matemaatikas ja on kesksel kohal kogu looduse kirjeldamisel. Ringliikumine oli ideaaliks juba vanadel kreeklastel ja selle valguses on muidugi päris tore, et isegi liikluse planeerijad on otsustanud, et kõige ohutumad ristmikud on just ringristmikud.
Ringjoon ja π
Teame, et kui näiteks ruudu külge kümme korda suurendada, suureneb sama palju kordi ka tema ümbermõõt. Teisisõnu on tema ümbermõõdu ning küljepikkuse suhe alati sama arv – neli. Sama kehtib ka kõikide teiste korrapäraste hulknurkade korral. Tegemist on üldisema reegliga – lihtsad joonelemendid suurenevad või vähenevad suumides täpselt sama palju. Tuleb välja, et ka ringjoone ümbermõõdu ja diameetri suhe on alati üks ja seesama arv. Just seda arvu kutsumegi π-ks.
Nagu irratsionaalarvude juures juba mainisime, on π irratsionaalarv ehk teisisõnu tema kümnendkohti ei saa kunagi välja kirjutada, sest neid on lõpmata palju ja nad ei hakka kunagi perioodiliselt korduma. Komakohti natuke lähemalt uurides tundub, et π komakohtades ei ole ka ühtegi mustrit ega seaduspära – kõiki numbreid paistab esinevat ühe palju ja täiesti juhuslikult läbisegi.
π väärtuse leidmine
Arvu π täpset väärtust ei ole sugugi lihtne arvutada. Babüloonlased kasutasid juba 19. sajandil eKr π-d, mille väärus oli 25⁄8, mis on kõigest 0,5% vale õigest väärtusest. Sarnaseid π ligikaudseid väärtusi on olnud kõikidel iidsetel tsivilisatsioonidel.
Kõik need ümardused on päris lähedal π tegelikule väärtusele ja sellisest täpsusest piisas näiteks igati ehituskonstruktsioonide tarvis. Praktiliste rakenduste jaoks ümardame meie koolis π väärtuseks umbes 3,14 ning Ameerika Ühendriikides kasutatakse näiteks ümardust 22⁄7. Võib tekkida kohe küsimus: kumb ümardus on täpsem?
Siiski jääb õhku üks veelgi huvitavam küsimus: kuidas aga arvutada π täpne arvuline väärtus? Või õigemini, kuidas leida järjest rohkem π komakohti?
Kuna π on võrdne iga ringjoone ümbermõõdu ja diameetri suhtega, võime vabalt valida ringjoone, mille diameeter on võrdne ühega. Sel juhul on meil π arvutamiseks vaja teada veel vaid ümbermõõtu. Koolis õpetatakse muidugi, kuidas ümbermõõtu leida π abil, aga sellest ei ole meile sugugi abi, kui me π väärtustki veel ei tea.
Archimedes oli teadaolevalt esimene, kes leidis 250. a eKr hea viisi ringi ümbermõõdu ja seega π arvulise väärtuse leidmiseks. Auväärt mõtleja hakkas lihtsalt ringjoone ümber ja sisse joonistama järjest rohkemate nurkadega korrapäraseid hulknurki. Nagu jooniselt näha, muutuvad need hulknurgad järjest sarnasemaks ringjoone endaga. Korrapäraste hulknurkade ümbermõõtu on aga lihtne leida ja nii ongi võimalik järjest täpsemalt ka π väärtust välja arvutada.
Archimedes ise viitsis kindlaks määrata ainult, et π asub arvude 3,14084 ja 3,142857 vahel. Siiski teoreetiliselt saaksime tema meetodil π välja arvutada soovitud täpsuseni.
India matemaatik Madhava Sangamagrama leidis 600 aastat tagasi toredalt lihtsa valemi, millega võiks π defineerida hoopis erineval viisil:
Kuna liidetavad selles summas muutuvad järjest väiksemaks, võime ka selle valemiga järjest täpsemalt π väärtust leida.
Arvu π väärtust võime samuti hinnata geomeetrilise tõenäosuse abil, sellest aga pikemalt tõenäosuse osas [lk 402].
Tänapäeval kasutatakse π komakohtade väljaarvutamiseks loomulikult arvuteid ning hetkel on teada rohkem kui 10 000 000 000 000 π komakohta. Selleks kasutatakse John Machini poolt 1706. aastal avastatud valemi analooge:
π komakohtade päheõppimine
Arv π on paljudele tundunud maagilise arvuna ja nii on läbi ajaloo pähe õpitud ka π komakohti. Legendi järgi õppis isegi näiteks Isaac Newton16 π komakohta pähe. Siiski vabandas ta hiljem rahva ees, et sellise lollusega oma aega raiskas. Praeguseks teavad mõned (nii paberiteta kui paberitega) hullud peast juba üle 100 000 π komakoha.
Kas π on õigesti defineeritud?
Kogu selle maania puhul on irooniline, et äkki oleks võinud π defineerida natukene teistmoodi. Selle asemel, et ringi ümbermõõt jagada läbi diameetriga, võinuks ju ringi ümbermõõdu läbi jagada hoopis näiteks raadiusega.
Nii defineeritud arvu π1 väärtus oleks võrdne kahekordse π väärtusega. See oleks mitmes mõttes isegi ilusam: näiteks oleks siis veerand ringjoone kaarest tõesti pikkusega ¼π1 ja mitte kummaline ½π ning siinuse ja koosinuse [lk 214] perioodi pikkuseks oleks kenasti π1 ja mitte 2π. Veelgi enam, siis meenutaks ka ringi pindala uus valem: ½π1r2 füüsikast tuntud valemeid näiteks kineetilise energia või konstantse kiirendusega läbitud teepikkuse leidmiseks.
Muidugi, vaesed π peastlugejad peaksid siis jälle nullist alustama...
Sarnaselt arvuga π tähistab e ühte kindlat arvu –
Täies uhkuses teda siia kahjuks kirja panna ei saa, kuna tegemist on irratsionaalarvuga [lk 87].
Õigupoolest pole see ka täpne arvude järjestus, milles matemaatikud suurt ilu näeksid. Arvu e tähtsus ja ilu seisneb pigem tema mitmenäolisuses. Ta vaatab välja mitmest erinevast matemaatika harust ja loob nende vahel üllatavaid seoseid.
Kus e esile tuleb?
Arv e tuleb kõige tihedamalt esile eksponentsiaalfunktsiooni ja logaritmi raames. Nimelt on just astmel e kõige parem mõelda eksponentsiaalfunktsioonist [lk 284] ja alusel e kõige loomulikum logaritmida [lk 295].
Ta on tuntud ka selle poolest, et peidab ennast paljudes valemites. Juba selles peatükis näeme neist nii mõndagi, näiteks kuidas e-d defineerida lihtsalt korrutamise ja liitmise abil.
Väljaspool raamatut patseerib e veel mujalgi. Näiteks tuleb välja, et kompleksarve võib esitada e abil hoopis mugavamas kujus ning et ka trigonomeetrilisi funktsioone on signaalide analüüsimisel kasulik esitada just e toel. Lisaks astub e üllatuslikult esile veel näiteks tõenäosusteoorias. Võib vist öelda küll, et e on üsna laia ampluaaga sell ja matemaatikas seetõttu tähtsal kohal.
Mitu moodi e kirjeldamiseks ja defineerimiseks
Arvu π peatükki alustasime mitme erineva ringjoone matemaatilise kirjeldusega. Tuleb välja, et ka arvul e on arvukalt erinevaid kirjeldusi. Järgnevalt toome neist esile kaks ja üritame neid ka intuitiivselt siduda.
Arv e läbi liigprotsendi
Oletame, et tekib võimalus vara hoiule panna õige lahkete inimeste panka, mis võimaldab aastasele hoiusele küsida kas
100% intressi aastas
50% intressi pooles aastas
25% intressi kvartalis
Milline neist valikutest kõige kasulikum oleks? Või oleks hoopis kasulik küsida igaks päevaks 1⁄365· 100% intressi ja lahke inimese lahkust veel kuritarvitada?
Et olukorrast täpsemalt mõelda, on mugav oletada, et alushoiuseks on näiteks unts kulda.
100% intressi aasta kohta tähendab, et aasta lõpuks on täpselt 2 untsi kulda.
50% intressi poolaastas tähendab, et poole aasta möödudes on hoius juba 1,5 untsi kulda. Järgneva poolaastaga lisandub sellele veel 50% juba olemasolevast kogusest ja kokku on aasta lõpus juba 2,25 untsi kulda.
25% intressi kvartalis tähendab, et veerandaasta lõpuks on hoius 1,25 untsi kulda. Poolaasta lõpuks lisandub veel 25% ehk kokku oleks tolleks hetkeks 1,5625 untsi kulda. Kolme kvartali lõpuks koguneb juba 1,953125 untsi kulda ning aasta lõpus võib rõõmustada 2,44140625 untsi kulla üle.
Tundub, et kuigi kõigil kolmel juhul on intresside summa kogu perioodil sama, on palju tulusam intresse tihedamalt saada.
Kas sellel tulususel on ka mingi piir või võib üle aasta saada miljonäriks?
Aastas on umbes 3,154 · 107 sekundit. Jagades aasta sekundilisteks perioodideks ning saades intressi iga sekundi järel, koguneb aasta lõpuks
untsi kulda.
Hoolikas lugeja märkab, et saadud kogus on juba väga lähedal sissejuhatuses toodud arvu e väärtusele – esimesed kuus komakohta kattuvad.
Selgubki, et ükskõik kui tihedalt me intresse maksame, leidub aasta koguintressil ülempiir, mis rakendub, kui intressi makstakse pidevalt [lk 317] ehk veelgi kiiremini kui iga nanosekund. Seesama ülempiir ongi võrdne e-ga! Just eelnevast arutelust lähtub ka matemaatika tunnis kohatav kompaktne valem:
Tõepoolest, oletame, et aasta on jagatud n perioodiks. Iga perioodi lõpuks suureneb kullahunnik
korda. Seega esimese perioodi lõpuks on kulda
untsi, teise perioodi lõpuks
untsi ning aasta lõpuks
untsi.
Piirprotsessis, kus n-i väärtus muutub lõpmatult suureks, saabki
väärtusest täpselt arv e.
Arv e läbi funktsioonide
Selgub, et seda pideva intressiga kasvuprotsessi kirjeldab eksponentsiaalfunktsioon kujus ex [lk 280], kus x-ga tähistame siin harjumatult aega. See funktsioon on väga eriline teiste funktsioonide seas, sest igal hetkel on tema kasvukiirus ehk tuletis võrdne funktsiooni enda väärtusega. Teiste sõnadega jääb funktsiooni ex tuletiseks sama funktsioon ehk ex.
Tuleb välja, et kõik toodud tingimust rahuldavad funktsioonid ongi kujus Aex, kus A on mõni suvaline reaalarv. Kui A just null pole, on iga sellise funktsiooni jaoks tema suhteline kasv ühes ühikus ehk suhe
võrdne täpselt e-ga. Tõepoolest, võime kirjutada
Selle tähelepaneku abil võime ka e defineerida: valime ühe funktsiooni ƒ(x), mille tuletis on jälle ƒ(x) ise, ning seejärel defineerime e kui selle funktsiooni suhtelise kasvu ühes ühikus
Faktoriaal ja e*
Eelmise kirjeldusega on seotud ka arvu e defineerimine ainult liitmise ja korrutamise kaudu kujus:
Kui kasutame faktoriaali [lk 382] ja kirjutame näiteks 3! = 1 · 2 · 3 ning lisaks veel summavahemiku kõverikku [lk 50], näeb see valem päris ilus ja kompaktne välja:
Kas pole päris üllatav? Kuidas seda selgitada?
Täpne selgitus on üsna tehniline ja eeldab arusaama nii tuletise [lk 320] kui polünoomi [lk 266] mõistest.
Tuletame alustuseks meelde polünoomide ilusa omaduse [lk 268]. Nägime, et iga funktsiooni saab teatud mõttes väga täpselt kirjeldada hästi valitud polünoomiga.
Kas on ehk isegi võimalik leida polünoomi, mille tuletis on igas punktis peaaegu võrdne tema endaga?
Teame, et iga astmefunktsiooni xn tuletis on nxn–1. Seega kui polünoomis on liige axn, peab seal olema ka liige naxn–1, sest muidu poleks algne polünoom ja tuletise võtmisel saadud polünoomi võrdsed. Vastupidi, kui polünoomis on liige axn–1, peab olema ka liige
Oletame nüüd, et polünoomis on konstantne liige 1. Siis peab kindlasti leiduma ka liige x, edasi liige
ja nii edasi.
Näeme, et me ei saa kunagi lõpetada, sest muidu ei oleks tuletis võrdne funktsiooni endaga. Siiski võime välja kirjutada kõikide nende liikmete summa
See summa ei ole küll enam polünoom ja ei ole selge, kas ta üldse on mõistlik objekt (näiteks võiks ju iga x-i korral väärtus olla lõpmatult suur). Igal juhul puhtalt formaalselt saame tuletise operatsiooni rakendades tulemiks täpselt sama summa.
Õnneks on matemaatika ilus ja tuleb välja, et see summa on igati mõistlik. Tal on tõepoolest iga reaalarvulise x-i korral kindel väärtus ning see on võrdne täpselt funktsiooni ex väärtusega, mida enne juba mainisime. Nii võimegi kirjutada
Rahvasuu
Eesti keeles on kõige sagedasem täht a, aga nii inglise, saksa kui ka prantsuse keeles on selleks täheks e. Ja kuigi vaevalt et seda võiks pidada märgiks nende rahvaste suuremast matemaatika armust, on e just matemaatikutele armsaim täht.
Ka meie armastame teda nõnda palju, et ei suutnud loomata jätta väikest rahvalaulu:
Sa kõnnid nurmel
ja kajab vastu
linnurahva hüüd
lee-lo-lee,
uhkeim matemaatikas on e!
Sa istud klassis
õpetaja kriit
loomas võrrandeid
lee-lo-lee
tahvlilt vastu laulab e!
Sa oled pangas
ja Sulle vaikselt sosistatakse
lee-lo-lee
Su raha kasvab, täna e-d!
Sa kõnnid linnas
ja kajab vastu
linnarahva hüüd
lee-lo-lee,
miks kurat õppima pean e-d?
Käesolevas peatükis oleme maininud korrutamise ühikut – arvu üks, liitmise ühikut – arvu null, eksponentsiaalse kasvamisega seotud arvu e, ringi ja geomeetriaga seotud π-d ning reaalarvudest kompleksarvudesse viivat imaginaararvu i.
Kas need arvud on omavahel kuidagi seotud? Esialgu tundub, et ei tohiks küll olla. Siiski näitab järgnev valem matemaatika võimet pakkuda ilu ja üllatusi:
Seda valemit peavad paljud (üsna õigustatult!) matemaatika kõige ilusamaks valemiks. Näiteks on 20. sajandi suurim füüsik, Nobeli auhinna laureaat Richard Feynman kutsunud seda „meie juveeliks” ning „üheks tähelepanuväärseimaks valemiks kogu matemaatikas”.
Arvu astmele on hea hiilides läheneda läbi analoogia korrutamisega. Mida tähendab korrutamine? Kirjutame välja kaks näidet:
Seega vähemalt neil lihtsatel juhtudel pole korrutamine küll mitte midagi uhkemat kui üksluine korduv liitmine.
Mis aga juhtuks, kui vahetame „+” märgi „ ·” märgi vastu? Saame tehted
ning seega... üksluise korduva korrutamise.
Seda üksluist korduvat korrutamist nimetataksegi astendamiseks. Et lahti saada ka kirjutamisvaevast, tähistame
ja ütleme, et võtame arvu 3 astmesse 4 ning arvu 5 astmesse 6. Nelja ja kuut kutsutakse sellises olukorras astendajateks ning kolme ja viit astendatavaks ehk astme aluseks.
Kas see ongi kõik?
Muidugi mitte, võib tekkida mitmeid küsimusi.
1. Kas astendamisel on vastupidine tehe, nagu näiteks liitmisel on lahutamine?
2. Mis juhtuks, kui astendada komakohti sisaldavate arvudega nagu 0,5 või 1⁄3?
3. Kas saame astendada ka negatiivse arvu või nulliga?
Neile küsimustele üritamegi järgemööda läheneda. Kuna küsimusi on palju ning nende peale mõtlemine näitab päris hästi matemaatika arengut, siis jagub seletusi mitmetele lehtedele: head lugemist!
Nagu korrutamise vastandtehteks on jagamine, on astendamise vastandtehteks juurimine.
Tõepoolest, arvu 12 jagamisest kolmega võime mõelda kui küsimusest: millist arvu on vaja kokku liita täpselt kolm tükki, et saada vastuseks 12?
Muidugi on vastuseks 4, sest .
Kui võtame arvust 81 neljanda juure, on analoogseks küsimuseks: millist arvu on vaja kokku korrutada täpselt neli tükki, et saada vastuseks 81?
Juurimist tähistatakse mitmes erinevas kujus. Näiteks neljandat juurt 81-st võib tähistada kahel viisil järgmiselt:
81 ning 81¼
Kuigi puhtalt peale vaadates võivad need kaks tähistust tekitada väga erinevaid emotsioone, on vastuseks mõlemal juhul muidugi 3.
Teine tähistus on ehk informatiivsem, sest ta vihjab ka järgnevale analoogiale korrutamisega: nii nagu jagamisest kolmega saame mõelda kui korrutamisest arvuga 1⁄3, samuti võime ka neljanda juure võtmisest mõelda kui astendamisest astendajaga 1⁄4.
Juurimise korral tuleb olla ka ettevaatlik: nagu juba arvude peatükis nägime, ei leidu ühtegi reaalarvu, mis annaks endaga korrutades tulemuseks mõne negatiivse reaalarvu nagu –1 või –4 või –100. Seega ei ole võimalik negatiivsetest arvudest reaalarvulist ruutjuurt ega ühtegi teist paarisarvulist juurt võtta.
Kui kasutusele võtta kompleksarvud [lk 89], siis enam sellist muret ei ole – võib kõike rahu ja rõõmuga juurida.
Natukene ajalugu
Matemaatilises mõttes juurimisega tegeleti juba 3700 aastat tagasi Babüloonias. Vana-Kreekas muutus aga olukord matemaatikute jaoks eluohtlikuks.
Nimelt nagu juba irratsionaalarvude juures [lk 87] mainisime, avastasid Pythagorase järeltulijad, et ühikruudu diagonaali pole võimalik kirja panna täisarvude suhtena, ehk teisisõnu √2 ei ole ratsionaalarv, vaid irratsionaalarv.
Ega keegi päris täpselt ei tea, kuidas kõik just juhtus, aga räägitakse, et esimesena märkas ruudu diagonaali irratsionaalsust keegi härra Hippasus Metapontu. Ühe legendi järgi olevat see leid olnud lausa Kreeka riiklik saladus ning kui vaese Hippasuse arutelu enam teisiti ümber lükata ei osatud, uputati ta merre.
Meie tänapäevase sümboli √ leiutas 1525. aastal Christoph Rudolff, kes on ka + ja – märkide autor. Kas oskad näha mõnd head põhjust, miks kasutusele on võetud just sellised märgid ja mitte teistsugused?
Ratsionaalarvulise astendajaga tutvumiseks on hea alustada jälle analoogiast korrutamisega ja mõelda, mida tähendab ratsionaalarvudega korrutamine. Oluline on meelde tuletada, et korrutamisel pole tehete järjekord oluline.
Näiteks korrutades arvu 12 arvuga ¾, teame, et võime seda teha mitmel viisil. Võime esmalt jagada 12 arvuga 4 ning seejärel korrutada arvuga 3:
või korrutada 12 arvuga 3 ja seejärel alles jagada arvuga 4:
Seega võimegi ratsionaalarvudega korrutamisest mõelda kui lihtsalt järjestikusest täisarvudega korrutamisest ja jagamisest.
Täpselt samamoodi võime lahti mõtestada ka ratsionaalarvuga astendamise – tegemist on järjestikuse täisarvuga astendamise ja juurimisega. Ka sel korral pole astendamise ja juurimise järjekord oluline.
Näiteks tehtest 81¾ võime mõelda järgmiselt.
Esiteks pärime arvu 81 neljanda juure ning seejärel võtame saadava arvu kolmandasse astmesse:
või võtame kõigepealt arvu 81 astmesse kolm ning seejärel alles küsime, mis on selle suure arvu neljas juur:
Vastus tuleb muidugi sama, aga esimesel juhul on tema leidmine (vähemalt peast arvutades) palju lihtsam – eks katsuge võtta arvu 81 astmesse 3.
Muidugi on parem, kui sellist pikka ja tüütut mõttekäiku iga kord pikalt läbi ei pea tegema, aga see muutub automaatseks päris kiiresti – vaja on ainult pisut arvutada ja harjutada.
Üritame järgmiseks mõelda, kas ka negatiivne astendaja annab midagi mõistlikku. Ehk teisisõnu, mida võiks tähendada näiteks 4–3? Kuidas sellest mõelda?
Tegelikult ei ole siingi midagi keerulist: kui positiivne astendaja tähendas korduvat korrutamist, siis negatiivne astendaja tähendab mingis mõttes korduvat jagamist.
Näiteks
Ehk teisisõnu võtame kolmandasse astmesse arvu 4 pöördarvu, milleks on ¼.
Märgates nüüd, et pöördarvust võime mõelda kui arvust astmel –1, ning tuletades meelde, et asendamisel tehete järjekord ei loe, võime lihtsalt ka mõelda, et 4–3 ei ole midagi muud kui lihtsalt arvu 43 pöördarv.
Nullist erinevast astmest mõtleme kui korduvast korrutamisest või korduvast jagamisest. Mida tähendab aga astendaja null? Astendaja null võiks siis tähendada, et me ei võtagi ühtegi arvu, mida omavahel kokku korrutada või jagada. Mis võiks olla sellise tühja tehte väärtus?
Üks viis on mõelda, et astmesse null võtmine peaks olema väga sarnane mingi väga väikese astendaja kasutamisega: näiteks arvu
kasutamisega. Ratsionaalarvuliste astendajatega aga oskame juba ringi käia ning võime leida, et näiteks
Kahtlaselt lähedal arvule 1, kas pole?
Tuleb välja, et ükskõik, mis arvu me võtame astmesse 0, saame vastuseks 1. Selle taga on muidugi ka kena matemaatiline põhjendus, millest võite lugeda lisapeatükist [lk 117].
Irratsionaalarvuliste astendajate jaoks ei ole senisest intuitsioonist suurt kasu – näiteks on päris raske vastata küsimusele, mitu korda ma pean korrutama arvu 2, et saada arv 2π või arv ee.
Siiski on neistki võimalik rangelt ja täpselt mõtelda, tuleb lihtsalt muuta oma vaatenurka. Sellest võib täpsemalt juba lugeda eksponentsiaalfunktsiooni peatükist [lk 280]. Teatud mõttes on tegemist täpselt samasuguse aukude täitmisega nagu ratsionaalarvudelt reaalarvudele üle minnes – seekord ei ole augud ainult arvteljel, vaid on eksponentsiaalfunktsiooni graafikul. Oluline on märgata, et seda saab teha ainult positiivsete aluste korral – negatiivsete aluste korral jäime juba ratsionaalarvuliste astmetega hätta, rääkimata siis irratsionaalarvulistest astmetest.
Praktikas võime irratsionaalarvuliste astmetega käituda samamoodi nagu astme null korral – otsime lihtsalt mõne ratsionaalarvulise astendaja, mis on meie irratsionaalarvule piisavalt lähedal. Täpselt nii käituvad ka arvutid – irratsionaalarve nad nagunii salvestada ei oska.
Efektiivne astendamine
Naturaalarvuliste astmete võtmine on üpriski igapäevane tegevus (kui mitte isiklikult Sulle, siis kindlasti mõningatele teadlastele ja ka arvutitele).
Näiteks 33 arvutamiseks on vaja 2 korrutamistehet 3 · 3 = 9 ning 9 · 3 = 27.
Mitme tehtega saaks aga arvutada 3100? Kas tõesti läheb selleks 99 tehet või on võimalik leida mõni kiirem viis?
Selgub, et on olemas ka kiirem viis. Selle kiirema viisi tabamiseks tuleb märgata, et järjest arve ruutu tõstes jõuame päris kiiresti kõrgete astmeteni:
Nüüd on idee kirjutada 100 selliste astmete summadena, mida võime ruutuvõtmise abil leida: 100 = 64 + 32 + 4 ja seega saamegi välja arvutada 3100:
Kokku lugedes näeme, et vajasime ainult 8 korrutustehet 99 asemel.
Hoolas lugeja märkab, et astendajad, mille astmeid oskame kiiresti välja arvutada, on kõik kujus 2m. Teisisõnu peame kiire astendamise jaoks kirjutama lihtsalt astendaja tema kahendesituses: näiteks 100 = 26 + 25 + 22. Kahendesitusest rääkisime pisut pikemalt arvuhulkade juures [lk 80].
Päikese mass on umbes 1989000000000000000000000000000000 kg ning elektroni mass on umbes 0,0000000000000000000000000000009109 kg.
Neid arve on suhteliselt keeruline lugeda ning veel hullem, kui peaks näiteks arvutama, mitu korda on Päikese mass suurem kui elektroni mass. Kuna peame tihti tegelema väga suurte ja väga väikeste arvudega, siis on lihtsam väga suuri ja väga väikseid arve esitada standardkujus: a · 10n, kus a on mingi arv ühe ja kümne vahel. Kümne astendaja n näitab selles kujus arvu suurusjärku.
Näiteks Päikese mass on standardkujus 1,989 · 1030 kg ning elektroni mass on 9,109 · 10–31 kg. Nüüd on ka tunduvalt kergem leida, mitu korda on Päike raskem kui elektron:
ehk ligi 60 suurusjärku!
Üritame järgnevalt ka natuke matemaatiliselt motiveerida, miks kõikide arvude nullis aste peaks ikkagi olema ühega võrdne.
Mõtleme korra uuesti korrutamisest – tuletame meelde, et mistahes arvu nulliga korrutamine annab vastuseks nulli. Sellest, miks nulliga korrutamine peaks nulli andma, võib mõelda mitmel moel.
Üks viis on öelda, et meile meeldiks, kui korrutamine ja liitmine saaksid omavahel hästi läbi. Tahaksime, et võiksime näiteks kenasti sulge avada ja kirjutada:
Seda korrutamise ja liitmise kokkusobimist nimetatakse ka uhkelt korrutamise ja jagamise distributiivsuseks. Tegelikult kasutate seda igapäevaselt, näiteks 7 · 5 + 3 · 5 = 10 · 5 = 50.
Kui nüüd võtaksime aga arvu x võrdseks nulliga ja arvu y näiteks kahega, saaksime, et
Nüüd on mõlemal poolel liige 2 · z ja seega peab parema poole üleliigne liige 0 · z olema võrdne nulliga. Arvu kaks valisime aga täiesti suvaliselt, seega tõesti nulliga korrutamisel peaks iga arv andma tulemuseks nulli.
Millist ilusat omadust tahaksime astendamiselt? Me tahaksime, et ta saaks korrutamisega hästi läbi. Kui korrutame sama arvu läbi esmalt n korda ja seejärel m korda, peab tulemus olema võrdne arvuga, mille saame siis, kui korrutame arve kohe kokku m + n korda ehk teisisõnu tahame, et zm · zn = zm+n. Aga kui nüüd võtame m-i võrdseks nulliga ja z-i võrdseks 2-ga, saame 20 · 2n = 20+n = 2n.
Seega kuna ainult ühega korrutades saame täpselt sama arvu, peab 20 olema võrdne ühega! Ja muidugi jällegi oleksime võinud ju arvu kaks asemel võtta (peaaegu) ükskõik mida muud – seega astendades suvalist arvu nulliga saame vastuseks ühe.
Null astmel null
Eelnev arutelu pole siiski päris korrektne – end eelmises lõigus sulgudes peitev „peaaegu” käib arvu 0 kohta. Nimelt kui võtaksime eelnevas arutelus arvu z võrdseks nulliga, saaksime tehte 00 · 0n = 0n. Kuna aga 0n on võrdne nulliga vähemalt iga n > 0 jaoks (korrutame ju lihtsalt positiivse koguse nulle kokku), ei saa me sellest tehtest midagi öelda 00 väärtuse kohta.
Selgub, et ajalooliselt ongi 00 matemaatikutele suurt peavalu valmistanud, ühel nõul pole olnud ka päris suured matemaatikud. Ka täna leidub veel kaks vastasleeri: ühed ütlevad, et 00 ei olegi defineeritud, ja teised on veendunud, et see peab olema võrdne ühega. Milles on probleem?
Ühelt poolt peaks 00 olema võrdne arvuga, mille saame, kui avaldises 0x muudame positiivset arvu x järjest väiksemaks. Kuna 0n on iga positiivse n-i jaoks võrdne nulliga, siis peaks ka 00 olema võrdne nulliga.
Teiselt poolt peaks aga 00 olema võrdne ka arvuga, mille saame, kui avaldises x0 muudame positiivset arvu x järjest väiksemaks. Eelneva põhjal teame, et x0 on võrdne ühega iga nullist erineva x jaoks. Seega peab ka 00 olema võrdne ühega.
Kuna meil on matemaatiliselt 00 defineerimiseks kaks erinevat võimalust, mis omavahel sugugi kokku ei sobi, ei tundu sugugi ülekohtune teda mittedefineeritavaks pidada. Siiski leidub neid, kes arvavad, et meil on piisavalt põhjuseid arvamaks, et 00 = 1.
Kusjuures kõik on vähemalt selles päri, et kui üldse 00 arvuna defineerida, siis peaks tema väärtuseks saama justnimelt 1 ja mitte näiteks 0 või hoopis mõni muu arv.
Esiteks, nagu juba mainisime, tahaksime kinni hoida juba meile tuntud tehetest ja valemitest. Kui valiksime ükskõik millise teise väärtuse, siis võiksime leida mõne valemi – nagu näiteks ennist kasutatud a(m+n) = am · an –, mis enam selle valiku korral kahjuks ei kehtiks. Kui võtame juba selles samas valemis a = 0, m = 0, n = 0, näeme, et 00 · 00 = 00 . Seega, kui otsustame defineerida arvu 00, peab selle arvu ruut olema tema endaga võrdne. Ehk ta ei tohiks olla ükski teine arv peale arvude 1 ja 0, mida kohtasime võimalike variantidena juba eelnevas arutelus.
Valides aga järgnevalt valemiks
mis kehtib alati kui a > 0, näeme, et 00 väärtuseks ei tahaks hästi sobida isegi arv 0. Muidu oleks ju üks valemi pool 0, ent teisel pool üritaksime jagada nulliga, ja see meile muidugi ei meeldi. Seega, kui 00 on arv, siis olgu ta arv 1.
Lisaks toetab kokkulepet 00 = 1 pisut ka tõlgenduslik pool. Näiteks meiegi mõtlesime astendajast 0 kui tühjast tehtest ja sel juhul ei tohiks ju vahet olla, mis astme aluseks on – tühi tehe jääb alati tühjaks tehteks ning peaks olema ka sama väärtusega. Kõik teised arvud astmel 0 on aga võrdsed ju täpselt 1-ga.
Kokkuvõttes, ega ei teagi, kuidas on parem – kas jätta segaduse vältimiseks 00 defineerimata või talle siiski anda mugavuse tõttu väärtus 1?
Joonistame arvtelje, lööme sinna naelaga keskele nulli, võtame nöörijupi ning tähistame kaks arvu a ja –a. Need arvud on nullpunktist samal kaugusel. Seda kaugust nullpunktist nimetatakse arvu absoluutväärtuseks.
Seega arvude 1 ja –1 absoluutväärtus on 1, kuna nad asuvad mõlemad nullpunktist täpselt ühiku kaugusel, ning samamoodi on arvude π ja –π mõlema absoluutväärtus π.
Kuna arvu absoluutväärtus tähistab kaugust, ei saa ta muidugi olla negatiivne.
Arvu absoluutväärtust tähistatakse, asetades arv püstkriipsude vahele. Näiteks |1| = 1 ja |– 1| = 1. Võibki mõelda, et kriipsud suruvad miinuse kokku.
Matemaatiliselt võib arvu absoluutväärtuse defineerida nii:
kui x on positiivne, siis |x| = x,
kui x on negatiivne, siis |x| = –x,
kui x on võrdne nulliga, siis |0| = 0.
Kui leiame iga reaalarvu jaoks tema absoluutväärtuse, saame järgmise graafiku – funktsiooni |x| graafiku.
Oluline on võibolla ka märgata, et kuigi defineerisime arvu absoluutväärtuse kui tema kauguse nullist, võime absoluutväärtuse abil kirjeldada tõesti kõikide arvude vahelisi kauguseid. On ju arvude x ning y vahelise kauguse leidmine täpselt võrdne nende vahe x – y (või miks ka mitte y – x) kaugusega nullpunktist.
Selgub, et nii mõnigi kord oleneb arvude käitumine rohkem nende absoluutväärtusest kui nende täpsest asetusest arvteljel.
Oletame näiteks, et hakkame ühte arvu iseendaga korrutama. Kui selle arvu absoluutväärtus on suurem kui 1, satume nullist järjest kaugemale, kui aga arvu absoluutväärtus on 1-st väiksem, läheneme järjest nullile. Järgnevatel graafikutel oleme võtnud neli arvu x0, õ0,y0 ja z0 ja hakanud neid iseendaga korrutama. Kahe esimese absoluutväärtus on ühest suurem ning nii suunduvad iseendaga korrutamisel saadud arvud nullist järjest kaugemale. Kahe viimase absoluutväärtus on ühest väiksem ning nende korrutised koonduvad nulli suunas.
Saadud arvude järjendeid kutsutakse geomeetriliseks jadaks ja nendega kohtume veel lähemalt [lk 131]!
Arvu absoluutväärtus tuleb esile ka füüsikas, kus tihti huvitab meid mitte ühe või teise objekti positsioon, vaid hoopis objektide vaheline kaugus. Samamoodi võime mõelda ka kiirustest. Kui oleme ise näiteks keset pikka sirget teed ja lööme enda kõrvale nullpunkti, on meie poole liikuvatel objektidel negatiivne kiirus. Selle kiiruse suurust näitab siis tema absoluutväärtus.
Arvu absoluutväärtusega saab kirja panna ka võrrandeid [lk 168].
Näiteks võrrand kujus
tähendab, et otsitakse väärtusi x, mis on arvust 1 kaugusel 2. Absoluutväärtustega võrrandit käsitleme veidi pikemalt juba raamatu neljandas osas [lk 202].