Elektromagnetväli

Kass küsib, kas elektriautole on vaja rattaid?

Jaapanis, Tokyo ja Nagoya vahel on kõigil huvilistel võimalik sõita rongiga, mis hõljub oma "rööbaste" kohal ja sõidab sealjuures kiirusega kuni 600 km/h, ehk vahemaa Tartu ja Tallinna vahel läbiks selline rong vähem kui poole tunniga. Öeldakse, et sellised rongid kasutavad "magnetilist levitatsiooni". Tõepoolest, teame hästi, et kaks magnetit võivad tõukuda, aga see ei saa olla kogu tõde - üks magnet ei jää teise kohale hõljuma, ükskõik kui hoolikalt me neid üksteise suhtes ka ei asetaks.

Selgub, et elektri- ja magnetnähtuste ampluaa muutub tohutult rikkalikumaks, kui me paneme laengud ja magnetid liikuma. Sest tekivad elektromagetväljad.


Leviteeriv maakera	MAGLEV - maailma kiireim rong

Ühele osakesele mõjuv magnetjõud

Elektromagnetilise induktsiooni nähtus

Tagasiside on nähtus, mille korral ühe füüsikalise suuruse muutumine põhjustab teiste suuruste selliseid muutusi, mis omakorda mõjutavad esimest suurust.

Käesolevas peatükis asume käsitlema elektri- ja magnetvälja muutumist ajas. Vaatleme ka kahe välja sügavamaid omavahelisi seoseid ning vastastikuseid muundumisi.

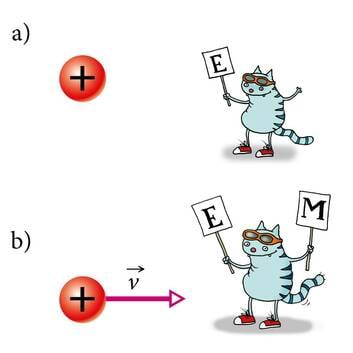
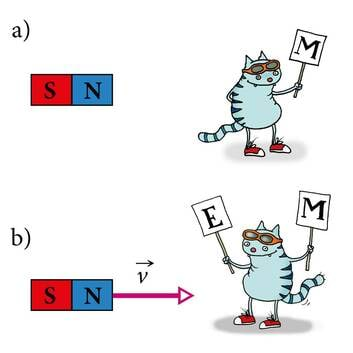
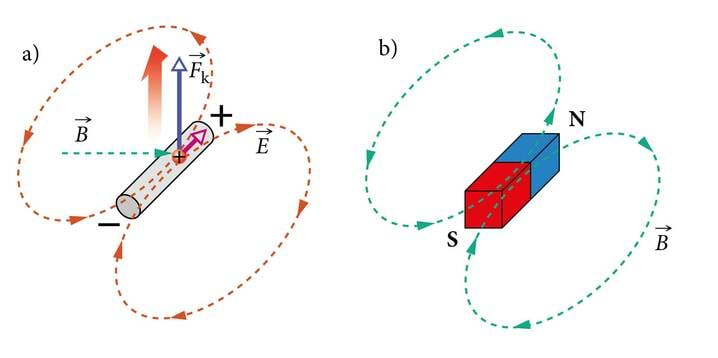
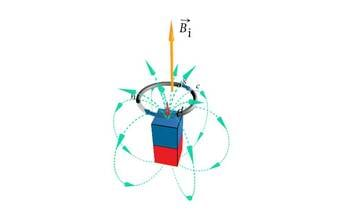
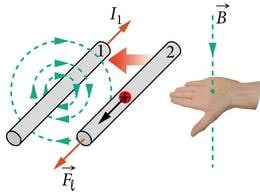
Seejuures tuleb enamasti eeldada laetud osakeste mitteühtlast (kiirenevat või aeglustuvat) liikumist. Samuti pole elektri- ja magnetvälja enam võimalik vaadelda teineteisest lahus. Tegemist on elektromagnetilist vastastikmõju vahendava ühtse elektromagnetväljaga. Selle välja uurimise muudab keeruliseks protsesside tagasisidestatus. Tagasiside on nähtus, mille korral ühe füüsikalise suuruse muutumine põhjustab teiste suuruste selliseid muutusi, mis omakorda mõjutavad esimest suurust. Näiteks põhjustab pendli hälbe suurenemine tasakaaluasendi poole suunatud jõu kasvamist. See jõud aga pidurdab hälbe kasvu ja pendli liikumine aeglustub. Antud juhul pidurdab teise suuruse (jõu) muutus esimese suuruse (hälbe) muutumist. Selle kohta öeldakse, et hälbe muutus on negatiivselt tagasisidestatud. Elektromagnetvälja korral on igasugune elektrivälja muutus tagasisidestatud temaga kaasneva magnetvälja muutuse kaudu. Kui laetud keha vaatleja suhtes liigub, siis muutub keha elektriväli vaatleja asukohas ning vaatleja registreerib ka magnetvälja (J.2.1). Peagi veendume, et see kõik kehtib ka ümberpöördult. Kui magnetvälja tekitaja (püsimagnet) vaatleja suhtes liigub, siis muutub magnetväli vaatleja asukohas ning vaatleja täheldab ka elektrivälja olemasolu (J.2.2). Magnetvälja muutumine tekitab elektrivälja. Seda nimetatakse elektromagnetilise induktsiooni nähtuseks. Märkigem veel, et võõrsõna indutseerima eestikeelseks vasteks ongi tekitama või esile kutsuma.


J.2.1 a) vaatleja registreerib paigalseisva laengu elektrivälja, b) liikuv laeng tekitab vaatleja jaoks ka magnetvälja.	J.2.2 a) vaatleja registreerib paigalseisva püsimagneti magnetvälja, b) liikuv püsimagnet tekitab vaatleja jaoks ka elektrivälja.

Juba põhikooli Elektriõpetuses saime teada, et elektromagnetilisel induktsioonil põhineb generaatori töö. Teatavasti muundab generaator mehaanilist energiat elektrienergiaks, olles nii keskses rollis elektrienergia tootmisel. Elektromagnetnähtuste tundmaõppimine võimaldab meil mõista seda inimkonnale üliolulist protsessi.

Käesolevas peatükis vaatleme siis lähemalt, kuidas muutuv magnetväli saab tekitada elektrivälja. Loomulikult teeme ka kindlaks, millest sõltub vastav väljatugevus või pinge. Lõpuks uurime, mismoodi võib elektromagnetväljas salvestuda energia.

Lorentzi jõud

Selleks, et kirjeldada laengukandjate liikumist elektriväljas, mis tekib magnetvälja muutumisel, peame kõigepealt tutvuma magnetväljas liikuvale laetud osakesele mõjuva jõuga. Seda jõudu nimetatakse hollandi füüsiku Hendrik Antoon Lorentz'i (1853 – 1928) auks Lorentzi jõuks.

Juhtmelõigule, mille pikkus on $l$ ja milles kulgeb vool tugevusega $I$ , mõjub teatavasti magnetväljas induktsiooniga $B$ magnetjõud $F_{m}$ . Selle jõu suurus on leitav Ampère'i seadusest (valem 1.12)

F_{m} = I l B sin α

kus $α$ on nurk voolu suuna ja magnetvälja suuna vahel. Voolu olemasolu tähendab laengukandjate suunatud liikumist keskmise kiirusega $v$ . Mõistagi osalevad laengukandjad ka kaootilises (kindla suunata) liikumises, aga see meid praegu ei huvita. Jõud Ampère'i seaduses summeerub üksikutele liikuvatele laengukandjatele mõjuvatest Lorentzi jõududest. Seega tuleb Lorentzi jõu $F_{L}$ leidmiseks jagada juhtmele kui tervikule mõjuv magnetjõud $F_{m}$ liikuvate laengukandjate arvuga $N$ :

F_{L} = \frac{F_{m}}{N}

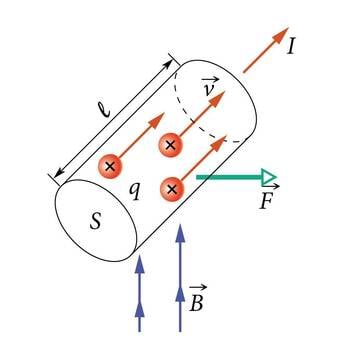
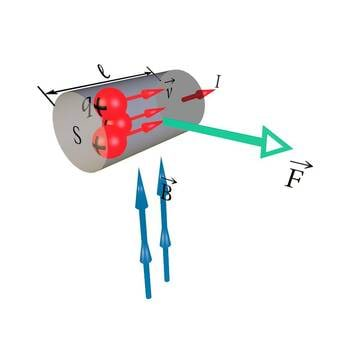
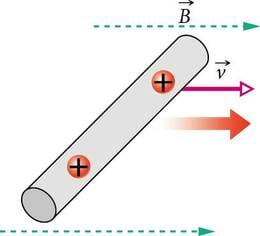
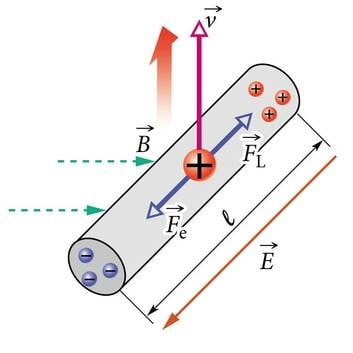
Vaatleme laengukandjaid, mis liiguvad keskmise kiirusega $v$ läbi silindrikujulise juhtmelõigu (J.2.3).


J.2.3 Laengukandjate suunatud liikumine vooluga juhtmelõigus. Laengukandjatele mõjub paremale suunatud magnentjõud.	Laengukandjate suunatud liikumine vooluga juhtmelõigus. Laengukandjatele mõjub paremale suunatud magnentjõud. 3D mudel.

Kui juhtmelõigu pikkus $l$ on parajasti võrdne korrutisega $v t$ (Mehaanika kursuse valem $s = v t$ ), siis jõuavad kõik silindris sisalduvad laengukandjad aja $t$ jooksul juhtmelõigust läbi tagumise otsapinna väljuda. Laengukandjatel, mis on tagumisele otsale lähemal kui $l$ , kulub selleks mõistagi seda vähem aega, mida väiksem pikkus neil läbida tuleb, aga aja $t$ jooksul väljuvad kõik $N$ laengukandjat. Nende kogulaeng on $N q$ , kus $q$ on ühe laengukandja laeng.

Voolutugevuse definitsiooni (valem 1.1) põhjal saame, et:

I = \frac{N q}{t}

Järelikult on Lorentzi jõu vektori pikkus esitatav kujul

F_{L} = \frac{I l B s i n α}{N} = \frac{N q l}{t N} B s i n α = q v B s i n α

kuna juhtmelõigu pikkuse $l$ ja laengukandjal selle läbimiseks kulunud aja $t$ suhe võrdub laengukandja suunatud liikumise kiirusega $v$ . Niisiis mõjub laengut $q$ omavale ja kiirusega $v$ liikuvale osakesele magnetväljas induktsiooniga $B$ Lorentzi jõud

(2.1)

F_{L} = q v B sin α

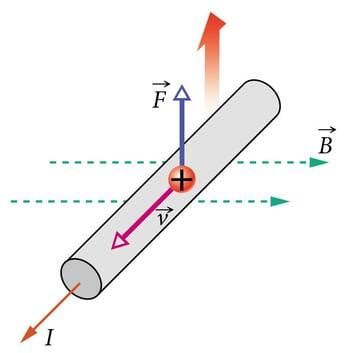
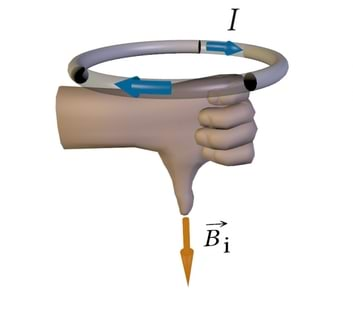
kus $α$ on nurk osakese liikumissuuna (kiirusvektori) ja magnetvälja suuna (B-vektori) vahel (J.2.3). Kuna positiivse laenguga osakesed liiguvad voolu kokkuleppelises suunas, siis võib neile mõjuva Lorentzi jõu suuna määrata vasaku käe reegli abil, mis antud juhul kõlab järgmiselt. Kui vasaku käe väljasirutatud sõrmed näitavad positiivselt laetud osakese liikumise suunda ja magnetvälja jõujooned tulevad peopessa, siis väljasirutatud pöial näitab osakesele mõjuva Lorentzi jõu suunda (J.2.4).

Elektroni kui negatiivselt laetud osakese korral on Lorentzi jõu suund eelnevale vastupidine, sest valemisse 2.1 ilmub miinusmärk. Elektronile mõjuva Lorentzi jõu suunda näitab analoogiliselt paikneva parema käe pöial.

Tasub rõhutada, et Lorentzi jõud mõjub laetud osakestele alati risti nii liikumissuuna kui ka magnetvälja suunaga. Seetõttu ei saa Lorentzi jõud liikumisel tööd teha. Ta võib vaid muuta liikumise suunda. Kõige tugevam on Lorentzi jõud liikumissuunaga ristuvas magnetväljas. Sel juhul $sin α = 1$ ja järelikult

F_{L} = q v B

Kui laengukandja kiirusvektor on risti magnetvälja suunaga (B-vektoriga), siis paneb Lorentzi jõud vaakumis asetseva laengukandja liikuma piki ringjoont ümber magnetvälja suuna, toimides kesktõmbekiirendust andva jõuna. Kui laengukandja liigub piki magnetvälja suunda (v- ja B-vektorid on samasihilised), siis Lorentzi jõudu ei teki, sest on $sin α = 0$ ja seega ka $F_{L} = 0$ .

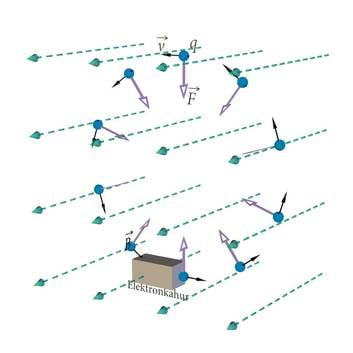
Lorentzi jõu mõju kohta on ka palju demoeksperimente, kus elektronkiir magnetvälja mõjul oma suunda muudab.

Selgitavad joonised selle katse kohta:


Madala rõhu all oleva gaasiga täidetud kambris tiirlevad elektronid (nende orbiit on nähtav helenduva rõngana). Kambrit täidab ühtlane magnetväli, mis on suunatud otse lehekülje tasandist välja. Paneme tähele, et elektronide ringliikumise saavutamiseks peab magnetjõud Fm olema suunatud radiaalselt ringi keskmesse. Ja tõepoolest, valem 2.1 ja parema käe reegel negatiivselt laetud osakeste jaoks ennustavad selle eksperimendi tulemust õigesti.	3D mudel seletab Lorentzi jõudude mõju homogeenses magnetväljas liikuvale elektrilaengule.

Madala rõhu all oleva gaasiga täidetud kambris tiirlevad elektronid (nende orbiit on nähtav helenduva rõngana). Kambrit täidab ühtlane magnetväli, mis on suunatud otse lehekülje tasandist välja. Paneme tähele, et elektronide ringliikumise saavutamiseks peab magnetjõud Fm olema suunatud radiaalselt ringi keskmesse. Ja tõepoolest, valem 2.1 ja parema käe reegel negatiivselt laetud osakeste jaoks ennustavad selle eksperimendi tulemust õigesti.

3D mudel seletab Lorentzi jõudude mõju homogeenses magnetväljas liikuvale elektrilaengule.

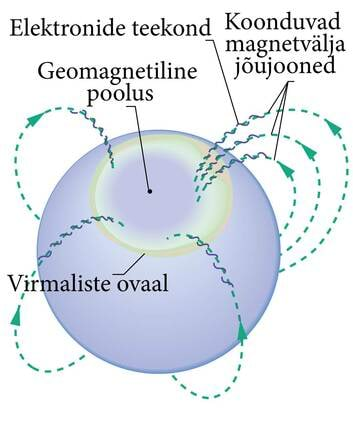
Kui v- ja B-vektorite vahel on suvaline nurk, siis võime laengukandja kiiruse lahutada kaheks komponendiks: B-vektoriga ristuvaks $v_{r}$ ja B-vektoriga paralleelseks $v_{p}$ . Ristuva komponendi olemasolu põhjustab laengukandja täiendava ringjoonelise liikumise ümber magnetvälja suuna. Sellega kaasneb laengukandja liikumine kiirusega $v_{p}$ piki magnetvälja suunda. Tulemusena liigub laengukandja mööda kruvijoont (ruumilist spiraali). Nii liiguvad näiteks kosmilise kiirguse laetud osakesed Maa ionosfääris piki spiraale, mille telgedeks on Maa magnetvälja jõujooned. Pannes kosmilise kiirguse osakesed ümber Maa spiraalima, kaitseb Maa magnetväli otsese kosmilise kiirguse eest kõike elusat Maa peal.


Virmaliste ovaal, mis ümbritseb maakera geomagnetilist poolust (see asetseb praegu Gröönimaa kirdeosas). Magnetvälja jõujooned koonduvad pooluse suunas. Maa poole liikuvad elektronid püütakse kinni ja need liiguvad spiraalselt ümber magnetvälja jõujoonte, sisenedes Maa atmosfääri suurematel laiuskraadidel ja tekitades ovaalis virmalisi.	Virmalisi on aeg-ajalt näha ka Eestis. Sellistena paistavad nad rahvusvahelise kosmosejaama pardalt.

Summary

Elektromagnetväljaks nimetatakse elektromagnetilist vastastikmõju vahendavat välja, mille piirjuhtudeks on elektriväli ja magnetväli.

Elektromagnetilise induktsiooni nähtuseks nimetatakse elektrivälja tekkimist magnetvälja muutumisel.

Laengut $q$ omavale ja kiirusega $v$ liikuvale osakesele mõjub magnetväljas induktsiooniga $B$ Lorentzi jõud $F_{L} = q v B sin α$ , kus $α$ on nurk osakese liikumissuuna ja magnetvälja suuna vahel.

Lorentzi jõud on suunatud alati risti nii liikumise suunaga kui ka magnetvälja suunaga.

Control questions

Kas Lorentzi jõuga saab laetud osakesi kiirendada?

Tehke joonis, mis selgitaks Lorentzi jõu toimimist laengukandjale kesktõmbekiirendust andva jõuna.

Kas kaks ühesuguse kiirusega paralleelselt liikuvat elektroni mõjutavad teineteist magnetjõuga?

Lähtudes Newtoni II seadusest, tuletage valem, mis seoks magnetväljas ringjooneliselt liikuva laetud osakese nurkkiirust w = 2p f = v/r magnetinduktsiooniga B.

Elektron liigub magnetväljas ringorbiidil ja teeb miljard pööret sekundis. Elektroni mass on 9,1 . 10^–31kg ja laeng 1,6 . 10^–19 C. Kui suur on magnetinduktsioon?

Control questions Additional materials

Pööriselektriväli ja induktsiooni elektromotoorjõud

Induktsioonivool ja pööriselektriväli

J.2.5 Vooluga juhtmelõik U-magneti magnetväljas.

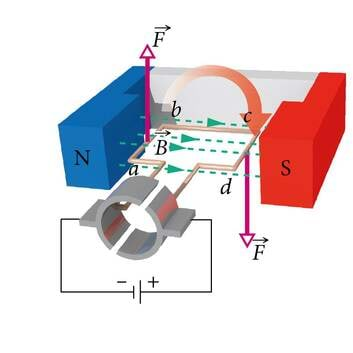
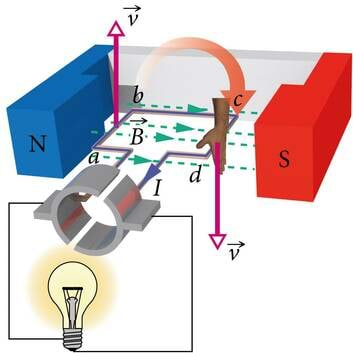
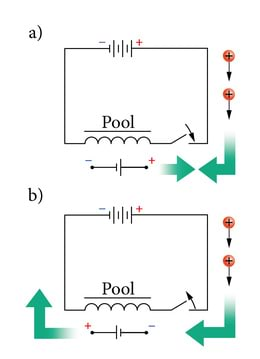
Esimeses peatükis vaatlesime vooluga juhtmele mõjuvat magnetjõudu. Asume nüüd uurima mootori mähisekeeru lõiku ab, mis generaatorina toimivas mootoris liigub ülespoole mitte enam magnetjõu vaid masina võlli päripäeva pöörava välisjõu toimel (J.2.7). Laengukandjad juhtmelõigus ab liiguvad koos juhtmega. Magnetväljas liikuvatele laetud osakestele mõjub aga teatavasti Lorentzi jõud, mis positiivsetele laengukandjatele rakendub vasaku käe reegli kohaselt "meist eemale" ehk suunas a→b. Analoogiliselt mõjub juhtmelõigus cd positiivse laengu kandjatele jõud suunas c→d ehk "meie poole". Järelikult hakkavad positiivsed laengukandjad vaadeldavas juhtmekeerus Lorentzi jõu mõjul liikuma suunas a→b→c→d. Juhtmekeeru otste a ja d ühendamisel moodustub vooluring, milles keeru pööramise tulemusena kulgeb elektrivool. Juhtme liikumine magnetväljas tekitab juhtmes induktsioonivoolu, mille suund on vastupidine mootori korral toiteallika poolt tekitatud voolule. Nende kahe voolu vastassuunalisuses juhtmelõigu sama liikumissuuna korral avaldub Lenzi reegel, millega me hiljem (p.2.5.1) tegeleme pikemalt. Samas ei tohi unustada, et mootori korral on uuritav mähisekeerd tarviti, generaatoris aga vooluallika rollis.


J.2.6 Elektrimootori mähise ühele keerule mõjub magnetväljas magnetjõud.	J.2.7 Magnetväljas liikuvas juhtmes tekib induktsioonivool.

Olgu öeldud, et nii sellel kui ka kõigil järgnevatel joonistel on jämeda noolega tähistatud juhtmelõigu liikumise suund. Samuti uurime nii siin kui ka edaspidi positiivsete laengukandjate liikumist, ehkki tegelikult on metalljuhtmes laengukandjateks negatiivsed juhtivuselektronid. Niisugune lihtsustus on põhjendatud, sest voolu suund ühtib voolu tekitava elektrivälja suunaga ega sõltu laengukandjate märgist (p.1.2.6).

Elektrimootorit saab kasutada ka generaatorina.

Voolu uuritavas mähisekeerus võib vaadelda tingituna elektriväljast, mille jõujooned on kontuuri abcd suunalised kinnised jooned. Meenutagem siinkohal FLA (Füüsikalise looduskäsitluse aluste) kursust, mida alustasime tõdemusest, et iga vaatleja loob füüsikalise maailmapildi omaenda aistingute või mõõtmistulemuste põhjal. Kui vaatleja täheldab elektrivoolu olemasolu ning teab, et vool on tingitud samas suunas toimivast elektriväljast, siis on vaatleja registreerinud ka elektrivälja. Selle elektrivälja tekkepõhjuseid võib vaatleja edaspidi uurida, kuid tal pole põhjust kahelda välja olemasolus. Magnetvälja muutumisel tekkiva elektrivälja suhtes pole enam rakendatav potentsiaali mõiste. Meil ei ole ju mingit alust eelistada suletud kontuuri mingit kindlat punkti teistele ja väita, et just selle punkti potentsiaal on kõrgem kui mõnel teisel punktil. Tekkiv elektriväli ei ole potentsiaalne, tema jõujooned on alguse ja lõputa kinnised jooned ehk pöörised. Seetõttu nimetatakse niisugust elektrivälja pööriselektriväljaks.

J.2.8 Koos juhtmega magnetvälja suunas liikuvatele laengutele jõudu ei mõju.

On märkimisväärne, et kirjeldatud juhul liigub juhtmelõik homogeenses magnetväljas. B-vektor on liikumistee eri punktides ühesugune nii suuruselt kui suunalt. Miks me siis ikkagi võime rääkida magnetvälja muutumisest juhtmelõigu asukohas? Me teeme seda põhjusel, et juhe liigub magnetvälja tekitaja suhtes risti välja suunaga ning lõikab magnetvälja jõujooni. Näiteks liikumisel magnetvälja suunas juhe jõujooni ei lõika (J.2.8). Sellisel liikumisel laengukandjatele magnetjõudu ei mõju, kuna Lorentzi jõu valemis

F_{L} = q v B sin α

on nurk $α$ võrdne nulliga. Järelikult ei teki sel juhul ka induktsioonivoolu.

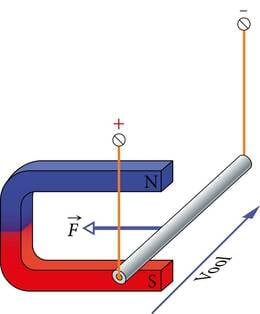
Magnetväljas liikuva juhtmelõigu otstel tekkiv pinge

Juba põhikooli Elektriõpetuses liiguti magnetjõu tekkimise juurest elektromagnetilise induktsioonini (p.2.2.1). Seega tasub meil neid kahte nähtust omavahel võrrelda ka siin. Vaatleme veelkord paremale suunatud magnetväljas asetsevat horisontaalset juhtmelõiku (elektrimootori mähise osa ab).

Kui me tekitame selles juhtmes meie poole suunatud voolu I, siis hakkab juhtmele Ampere’i seaduse ja vasaku käe reegli kohaselt mõjuma ülespoole suunatud magnetjõud (J.2.9). Võimaluse korral hakkab juhe selles suunas liikuma. Kirjeldame nähtust kokkuvõtlikult kujul:

elektrivool + magnetväli → liikumine.


J.2.9 Magnetväljas asuvale vooluga juhtmele mõjuv jõud. Kui me tekitame selles juhtmes meie poole suunatud voolu I, siis hakkab juhtmele Ampère'i seaduse ja vasaku käe reegli kohaselt mõjuma ülespoole suunatud magnetjõud. Võimaluse korral hakkab juhe selles suunas liikuma.	J.2.10 Juhtmes, mis liigub magnetväljas, tekib vool. Laengukandjad juhtmes liiguvad koos juhtmega üles ja neile hakkab mõjuma meist eemale suunatud Lorentzi jõud F_L. Juhtmes tekib induktsioonivool I_ind.

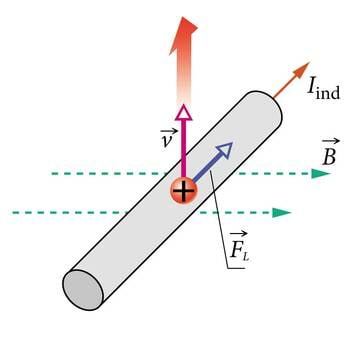
Joonisel 2.10 on aga näha, mis juhtub siis, kui me niisugust magnetväljas asetsevat juhet ise ülespoole liigutame. Laengukandjad juhtmes liiguvad koos juhtmega üles ja neile hakkab mõjuma meist eemale suunatud Lorentzi jõud $F_{L}$ . Juhtmes tekib induktsioonivool $I_{ind}$ . Nähtust võib kokkuvõtlikult kirjeldada kujul:

magnetväli + liikumine → elektrivool.

Niisiis on elektromagnetilise induktsiooni näol tegemist omalaadse pöördprotsessiga magnetjõu tekkimisele.

Pööriselektrivälja jõujooned on kinnised, alguse ja lõputa jooned, nii nagu magnetvälja jõujoonedki. Jõu $F_{k}$ mõjul liikuvat juhtmelõiku ümbritseb ja läbib pööriselektriväli $E$ samamoodi nagu magnetväli $B$ ümbritseb ja läbib püsimagnetit (J.2.11).

J.2.11 a) Liikuva juhtme pööriselektriväli E_p, b) püsimagneti magnetväli B.

Vaatleme nüüd isoleeritud juhtmelõiku, mis liigub kiirusega $v$ magnetväljaga ristuvas suunas ning on ka ise risti selle suunaga (J.2.12). Koos juhtmega üles liikuvatele positiivsetele laengukandjatele (laenguga $q$ ) mõjub Lorentzi jõud $F_{L} = q v B$ . Laengukandjad liiguvad selle magnetjõu mõjul piki juhet tahapoole, aga juhtmest välja nad ei pääse. Juhtme otsad laaduvad erimärgiliselt ja juhtmes tekib ettepoole suunatud elektriväli. Laengukandjate liikumine kestab seni, kuni neile mõjuv elektrijõud $F_{e} = q E$ (valem 1.11) magnetjõu tasakaalustab. Vastav elektrivälja tugevus $E$ on väljendatav pinge kaudu (valem 1.26)

E = \frac{U}{l}

kus $l$ on juhtmelõigu pikkus ( algkujus tähis $d$ ). Tasakaalu tingimuse $F_{L} = F_{e}$ võib siis esitada kujul

q v B = q \frac{U}{l}

millest tulenevalt võime juhtmelõigu otstele indutseeritava pinge avaldada kujul

(2.2)

U = v l B


J.2.12 Elektrijõu F_e ja magnetjõu F_L tasakaal liikuvas juhtmelõigus.	J.2.13 Pinge tekkimine juhtmes, mille liikumissuund moodustab magnetväljaga nurga α.

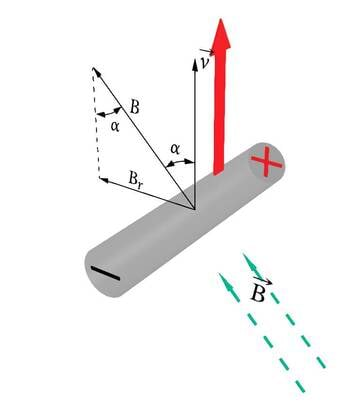
Juhul kui juhtme liikumissuund moodustab magnetväljaga mingi nurga $α$ , mis ei ole täisnurk, siis põhjustab Lorentzi jõudu vaid liikumissuunaga ristuv B-vektori komponent $B_{r} = B sin α$ (J.2.13). Liikumisel magnetvälja sihis ju teatavasti magnetjõudu ei teki (p.2.1.3). Indutseeritud pinge avaldis võtab kuju

(2.3)

U = v l B_{r} = v l B sin α

Tartu-Tallinna kiirrong sõidab kiirusega 108 km/h maa magnetvälja horisontaalkomponendi suunas. Kui suur pinge tekib elektromagnetilise induktsiooni tõttu vaguniratta telje otstele? Rööbaste vahekaugus on 1524 mm ja Maa magnetinduktsiooni vertikaalkomponent Eestis 48 μT.

Lahendus

Andmed

$v = 108 km/h = 30 m/s$
$l = 1524 mm = 1, 524 m$
$B_{v} = 48 μ T = 4, 8 \cdot 10^{- 5} T$

$U = ?$

Arvutused

Rattatelg on vaadeldav kui juhtmelõik, mis on risti nii oma liikumissuuna kui ka magnetinduktsiooni vertikaalkomponendiga $B_{v}$ , seejuures $B_{v} = B_{r}$ .

Kasutades valemit

$U = v l B_{r}$

saame kirjutada:

$U = 30 m/s \cdot 1, 524 m \cdot 4, 8 \cdot 10^{- 5} T = 2, 2 \cdot 10^{- 3} V = 2, 2 mV$ .

Vastus: Telje otste vahel tekib pinge $2, 2 mV$ . Praktikas jäetakse see pinge tema väiksuse tõttu arvestamata.

Induktsiooni elektromotoorjõud

Ilma tööd tegemata ei liigu siin maailmas midagi.

Eelmises punktis jõudsime magnetvälja suhtes liikuvas isoleeritud juhtmelõigus indutseeritud pinge avaldiseni. Seejuures tuginesime oma teadmistele Lorentzi jõu kohta. Elektromagnetilise induktsiooni avastajal Michael Faraday'l neid teadmisi ei olnud. Faraday uuris kinnisi vooluringe, määrates voolutugevust magnetnõela kõrvalekaldumise järgi tasakaaluasendist (Oerstedi katse, p.1.4.2). Kuid Faraday mõistis, et laengukandjate liikumapanemiseks tuleb teha tööd. Kirjeldamaks laengukandjate liikumapanemisel kinnises kontuuris tehtavat tööd hakkas Faraday kasutama elektromotoorjõu mõistet (electromotive force – EMF, vastav eestikeelne lühend EMJ).

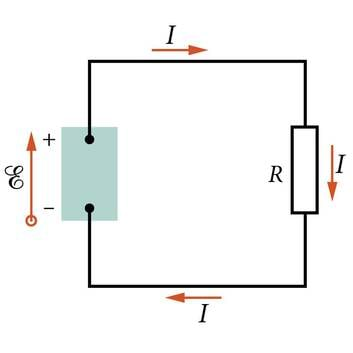
Elektromotoorjõud (tähis $E$ ehk suur ümmargune E) iseloomustab üldjuhul vooluallikas toimivaid mitteelektrilisi jõude ehk kõrvaljõude. Elektrivoolu püsimiseks keemilist vooluallikat (patareid või akut) sisaldavas vooluringis tuleb vooluallika positiivselt pooluselt ehk plussklemmilt läbi vooluringi miinusklemmile jõudnud positiivsed laengukandjad viia läbi vooluallika uuesti plussklemmile. Järelikult tuleb neid nihutada vastupidiselt elektrijõu suunale. Seda suudavad teha ainult kõrvaljõud. Elektromotoorjõud on võrdne kõrvaljõudude tööga A_k ühikulise suurusega laengu ühekordsel läbiviimisel kogu vooluringist:

(2.4)

E = \frac{A_{k}}{q}


J.2.14 Lihtne elektriline vooluring, milles EMJ tekitav seade teeb tööd laengukandjate nihutamisel ja säilitab takistis takistusega R ajas muutumatu voolu I.	Maailma suurim energiat salvestav akupatarei (lammutatud aastal 1996) ühendas rohkem kui 8000 suurt pliiakut 8 ahelaks, igaüks võimega anda 10 MW elektrilist võimsust 4 tunni jooksul. Seda laeti öösel ja pandi elektrisüsteemis tööle päeval elektrienergia tippnõudluse tundidel.

Keemilise vooluallika korral teeb kõrvaljõud selle töö ära vooluallika sees, tekitades vooluallika pooluste vahel elektrivälja, mistõttu laengukandjad saavad väljaspool vooluallikat ehk vooluringi välisosas liikuda juba elektrijõu mõjul. See energia, mille arvel laengukandjad suunatud liikumist takistavate jõudude kiuste kogu vooluringi läbivad, tuleb lõppkokkuvõttes kõrvaljõult. Keemilise vooluallika korral on laengukandjate liikumine vahetult kõrvaljõu toimel vooluallika sees ja elektrijõust põhjustatud laengukandjate liikumine vooluringi välisosas ruumiliselt lahutatud. Seepärast võime EMJ käsitleda kui suurimat pinget, mida keemiline vooluallikas on suuteline oma klemmidele tekitama. Elektromagnetilise induktsiooni korral võib aga üksainus kinnine juhtmerõngas olla üheaegselt nii vooluallika kui vooluringi välisosa rollis. Kõrvaljõu ja elektrijõu toimete ruumilist lahutatust ei ole ning potentsiaali ja pinge mõistetel puudub sisu, kui tõlgendada pinget vaid elektrijõudude tööna ühikulise laengu viimisel ühest punktist teise (p.1.7.4). See ongi peapõhjuseks, miks jätkuvalt kasutatakse kõlaliselt mõnevõrra eksitavat mõistet elektromotoorjõud. EMJ pole ju jõud ja tema ühikuks pole njuuton. EMJ on töö ja laengu suhe ehk pinge ja tema ühikuks on volt. Kuid nii öeldes peame mõistma pinge all kõigi liikumapanevate jõudude (ka kõrvaljõudude) tööd ühikulise laengu nihutamisel. Olles selles kokku leppinud, võime EMJ käsitleda kui kõikide pingete summat kinnises vooluringis.


Selles katses paneb induktsiooni elektromotoorjõud põlema elektripirni.	Ka selles katses paneb induktsiooni elektromotoorjõud põlema elektripirni.

Seni vaadeldud näidetes on kõrvaljõuks just seesama jõud, mis liigutab juhet või pöörab generaatori võlli magnetväljas.

Mingi juhtmelõigu liigutamisel magnetväljas tuleb teha tööd mitte ainult mehaanilise hõõrdejõu ületamiseks, vaid ka laengukandjate liikumapanemiseks juhtmega ühendatud vooluringis, juhul kui see vooluring on olemas. Elektromagnetilist induktsiooni võib vaadelda kui omalaadset ,,lisahõõrdumist" magnetväljas. Kui induktsioonivool viib positiivse ühikulise laengu üks kord läbi tekkiva vooluringi, siis kõrvaljõu poolt selleks tehtavat tööd nimetatakse induktsiooni elektromotoorjõuks. Ülaltoodu põhjal võib induktsiooni elektromotoorjõudu tõlgendada ka kui pinget, mis tekib katkestuskohas, kui me kasutame elektromagnetilisel induktsioonil põhinevat vooluallikat ja katkestame kuskil vooluringi. Lihtsaimaks selliseks vooluallikaks ongi liikumisel magnetvälja jõujooni lõikav juhtmetükk (p.2.2.2).

Summary

Jõud, mis nihutab juhet magnetväljas, paneb elektromagnetilise induktsiooni teel laengukandjad juhtmes liikuma. Kui liikuv juhe on osa vooluahelast, siis esineb selles ahelas induktsioonivool.

Pööriselektriväljaks nimetatakse elektrivälja, mille jõujooned on kinnised jooned ehk pöörisjooned. Selline elektriväli tekib magnetvälja muutumisel.

Magnetväljas liikuva juhtmelõigu otstel tekkiv pinge avaldub kujul $U = v l B sin α$ , kus $v$ on juhtmelõigu liikumise kiirus magnetvälja tekitaja suhtes, $B$ – magnetinduktsioon, $l$ – juhtmelõigu pikkus ja $α$ – nurk liikumise suuna ning

Induktsiooni elektromotoorjõuks nimetatakse tööd, mida juhet liigutav kõrvaljõud teeb ühikulise positiivse laengu ühekordseks läbiviimiseks vooluringist.

Control questions

Töötava elektrimootori korral liiguvad mähise juhtmekeerud magnetväljas. Järelikult peaks neis indutseeritama pinge, mis mõjub mähist läbivale voolule. Kas vool mähises muutub, kui rootor hakkab pöörlema?

Kui vastus eelmisele küsimusele on jaatav, kas siis induktsiooni elektromotoorjõud soodustab või takistab mootori toiteallika tööd?

Pooluste läheduses on Maa magnetväli peaaegu vertikaalne. Seetõttu lõikab polaarpiirkonnas lendava lennuki metallkere Maa magnetvälja jõujooni. Lennukikeret võiks vaadelda magnetväljas liikuva juhtmelõiguna, mille otstel tekib elektromagnetilise induktsiooni teel pinge. Kas suurem pinge indutseeritakse lennuki tiivaotste vahel või lennuki nina ja saba vahel?

Kas piki ekvaatorit lendava lennuki kere mingite osade vahel võib elektromagnetilise induktsiooni vahendusel samuti tekkida pinge? Kui jah, siis millised need kere osad on?

Control questions Additional materials

Faraday katsed

Suure avastuse sünnihetk on teaduse ajaloos harva teada kuupäevalise täpsusega. Elektromagnetilise induktsiooni avastamine kuulub aga nende harvade erandite hulka. See on nii tänu avastuse autori Michael Faraday täpsetele ülestähendustele. 29. augustil 1831 kirjutas Faraday laboripäevikusse, et raudsüdamikule mähitud juhtmepooli ühendamine vooluallikaga kutsub esile lühiajalise voolu ka teises, samale südamikule keritud poolis. Sama aasta 17. oktoobril tehtud sissekanne kõneleb aga voolu registreerimisest poolis, millele mõjuvat magnetvälja püsimagneti nihutamise teel muudeti.

Juba aastal 1822, kaks aastat pärast elektrivoolu magnetilise toime avastamist Oerstedi ja Ampere'i poolt, tuli Faraday mõttele, et see nähtus peaks esinema ka ,,tagurpidi". Kui elektrivool tekitab magnetvälja, kas ei võiks siis magnetvälja abil tekitada elektrivoolu? Aastal 1825 asus Faraday seda oletust katseliselt kontrollima, kuid ei suutnud induktsioonivoolu avastada. Faraday ei mõistnud siis veel, et elektrivälja tekitab mitte magnetväli ise, vaid magnetvälja muutumine. Pealegi ei olnud Faraday käsutuses piisavalt tundlikku mõõteriista. Voolu mõõtis Faraday magnetnõela pöördumise järgi vooluga juhtme läheduses (Oerstedi katse).


Algelised induktiivelemendid, millega katsetades Michael Faraday induktsiooniseaduse avastas. Tol ajal ei olnud veel saadaval isoleeritud juhtmeid. Räägitakse, et Faraday isoleeris juhtmeid riideribadega, mis olid lõigatud tema naise ühest alusseelikust.	Huvitav on ehk teada, teadusteater oli populaarne juba 19. sajandil. Faraday eksperimente tegemas oma 1856. aasta jõuluetendusel.

1831. aasta suvel asus Faraday taas korraldama samalaadseid uuringuid. Nüüd aga tugevdas ta pooli magnetvälja raudsüdamiku abil. Magnetvälja järsk muutmine tekitas samal südamikul paiknevas teises poolis vooluimpulsi. Elektromagnetiline induktsioon oli avastatud.

Faraday tegi elektromagnetilise induktsiooni uurimisel väga palju katseid. Kui kasutada on tester või mõni muu voolutundlik mõõteriist, siis võib neid katseid vastava huvi olemasolu korral teostada ka kodustes tingimustes. Faraday katsed võiks jagada kolme gruppi, mida järgnevalt ka eraldi vaatleme.

Püsimagneti liikumine juhtme suhtes

J.2.15 Meie katsetes kasutatavate poolide valmistamine.

Põhiliseks katsevahendiks elektromagnetilise induktsiooni uurimisel on torukujulisele isoleerivale südamikule keritud juhtmepool. Kõigis allpool kirjeldatud katsetes on vaja koguni kahte niisugust pooli. Pooli võib valmistada ka ise sobiliku jämedusega (0,3-0,5 mm) vasktraadist. Sellist traati võib osta enam-vähem suvalisest elektridetailide poest.Traat tuleb tihedalt kerida silindrilisele papist või plastikust torukesele. Mähis võiks olla 2-3 cm pikkune ja sisaldada ülestikku vähemalt 5 kihti kõrvutiasetsevaid juhtmekeerde. Et mähis traadi elastsuse tõttu laiali ei laguneks, on soovitatav iga kiht pärast kerimise lõpetamist kleepribaga fikseerida.

Sellise katseseadmega on lihtne veenduda, et muutuv magnetväli kutsub poolis esile induktsioonivoolu. Tekkinud voolu võib registreerida tundliku ampermeetrina töötava testri abil. Magnetvälja on kõige lihtsam muuta, torgates pikergust püsimagnetit pooli sisse.

Kirjeldatud katse on põhimõtteliselt teostatav ka üheainsa juhtmekeeruga. Niisugusel juhul on tekkiv induktsioonivool aga niivõrd nõrk, et seda on raske mõõta. Pooli korral liituvad üksikutes keerdudes tekkinud elektromotoorjõud, sest keerud toimivad jadamisi ühendatud vooluallikatena. Seetõttu saame ka mõõtmiseks piisavalt tugeva induktsioonivoolu. Voolu indutseerimist üksikus juhtmekeerus selgitab joonis 2.16. Näiteks liigub juhtmelõik dc täpselt samamoodi paremale suunatud magnetväljas allapoole nagu lõik dc joonisel 2.6. Lõigus dc indutseeritakse selle tagajärjel meie poole (c→d) suunatud vool. Seevastu lõigus gh kulgeb induktsioonivool meist eemale (g→h) ja juhtmekeerus tervikuna (ülalt vaadates) päripäeva.


J.2.16 Püsimagneti lähendamisel juhtmekeerule tekib selles keerus vool.	J.2.17 Induktsioonivoolu magnetvälja suuna määramine.

Parema käe rusikareegli (J.2.17) abil võib veenduda selles, et induktsioonivoolu magnetväli on joonisel suunatud ülalt alla, niisiis vastupidiselt juhtmekeerus tugevnevale püsimagneti väljale. Induktsioonivool takistab sellesama magnetvälja kasvu, mis voolu esile kutsus. Tasub ka rõhutada, et induktsioonivool on olemas vaid seni, kuni juhtmekeerd püsimagneti jõujoonte suhtes liigub. Kui lõpeb liikumine, siis saab laengukandjatele mõjuv Lorentzi jõud nulliks, sest $v = 0$ .

Vooluga juhtme liikumine teise juhtme suhtes

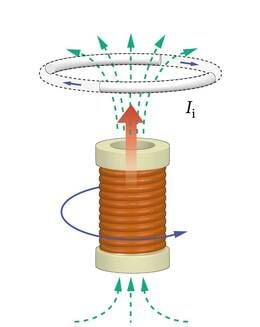
Magnetvälja põhjustajana võib püsimagneti asemel kasutada ka vooluga pooli.

J.2.18 Vooluga pooli nihutamisel juhtmekeeru suhtes tekib keerus induktsioonivool.

Kui me asendame joonisel 2.16 kujutatud katses püsimagneti pooliga (J.2.18), siis tekib ülemises juhtmekeerus induktsioonivool täpselt samamoodi nagu püsimagneti korral. Nii on see muidugi eeldusel, et juhtmekeerdu lähendatakse poolile ja pooli magnetväli on suunatud alt üles. Pooli magnetväljal on selline suund juhul, kui vool pooli keerdudes kulgeb ülalt vaadates vastupäeva (meie silme ees vasakult paremale). Induktsioonivool ise on kirjeldatavas katses teatavasti suunatud päripäeva (külgvaates paremalt vasakule). Seega on induktsioonivoolu suund vastupidine voolu suunale indutseerivat magnetvälja tekitavas poolis. Püüdkem iseseisvalt veenduda selles, et juhtmekeeru kaugenemisel poolist on ka induktsioonivool suunatud vastupäeva. Mõlemad vaadeldavad voolud on sel juhul samasuunalised.

J.2.19 Vooluga juhtme (1) lähendamisel teisele juhtmele (2) tekib selles juhtmes induktsioonivool.

Katsetamisel südamikuta poolidega võib induktsioonivool osutuda liiga nõrgaks. Sel juhul võib voolu tugevdada, paigutades eelnevalt poolide sisse raudsüdamikud (näiteks suured raudpoldid). Rauas on magnetinduktsioon palju suurem kui õhus. Seetõttu on suuremad ka magnetinduktsiooni muutused, millest omakorda sõltub induktsioonivoolu tugevus.

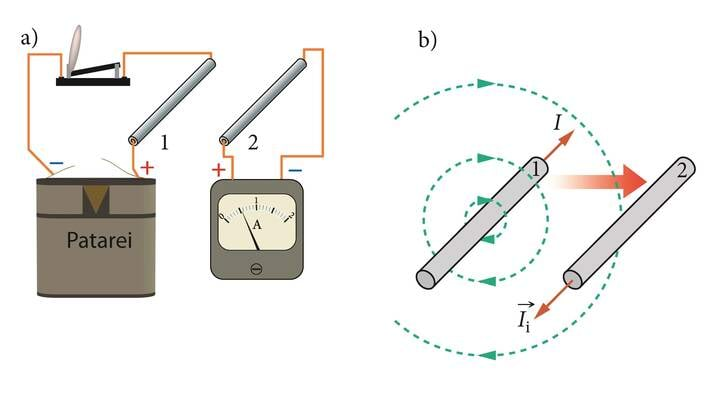
Analoogilised nähtused leiavad aset ka kahe paralleelse sirgjuhtme korral, millest ühes voolab alalisvool (J.2.19). Kui me nihutame üht juhet teisele lähemale, siis lõikavad vooluga juhtme 1 magnetvälja jõujooned vooluta juhet 2. Vasaku käe reegli kohaselt mõjub positiivsetele laengukandjatele juhtmes 2 meie poole suunatud Lorentzi jõud. Juhtmes 2 tekib seeläbi induktsioonivool, mille suund on vastupidine juhtmes 1 kulgeva voolu suhtes. See arutlus jääb kahjuks vaid teoreetiliseks, sest üksiku voolujuhtme magnetväli on väga nõrk ja tekkivat induktsioonivoolu on väga raske mõõta.

Voolu muutumine juhtmes

Kõigil seni vaadeldud juhtudel põhjustab elektromagnetilist induktsiooni puhtmehaaniline liikumine. Uuritav juhe liigub magnetvälja tekitaja suhtes. See aga ei pea alati nii olema. Magnetvälja võib muuta ka seda välja tekitava voolu muutmise teel juhtmes, nii et juhtmed jäävad paigale. Teatavasti toimis just nii ka Faraday oma esimeses katses.

J.2.20 Voolu sisselülitamine ühes juhtmes indutseerib vastupidise suunaga voolu naaberjuhtmes: a) katseseade, b) juhtme 1 magnetväli levib juhtme 2 poole.

Vaatleme näitena jällegi kahte paralleelset sirgjuhet, millest üks on läbi lüliti ühendatud vooluallikaga (J.2.20, a). Lüliti sulgemisel suureneb voolutugevus juhtmes nullist kuni mingi lõppväärtuseni $I$ . Vastavalt kasvab ka selle voolu magnetväli. Magnetvälja tugevnemine on aga samaväärne lähenemisega välja tekitavale juhtmele. Me teame ju (, p.1.5.3), et vooluga sirgjuhtme magnetinduktsioon on pöördvõrdeline kaugusega sellest juhtmest.

Niisiis mõjub juhtmest 1 tingitud magnetvälja levik juhtme 2 suunas (J.2.20, b) laengukandjatele samamoodi nagu juhtme 2 liikumine juhtme 1 poole. Eelmisest alapunktist teame, et seda laadi liikumine indutseerib juhtmes 2 meie poole suunatud voolu (J.2.19). Voolu sisselülitamine juhtmes tekitab vastupidise suunaga voolu naaberjuhtmes. Lõpetuseks märkigem, et kõik senised järeldused oleme me teinud, lähtudes teadmistest Lorentzi jõu kohta. Faraday jõudis samade järeldusteni katsetulemusi üldistades.

Summary

Liikuv püsimagnet tekitab voolu lähedalasuvas juhtmes.

Vooluga juhtme liikumine tekitab magnetvälja vahendusel voolu naaberjuhtmes.

Voolu muutus juhtmes tekitab vastava magnetvälja muutuse kaudu voolu naaberjuhtmes.

Control questions Additional materials

Faraday induktsiooniseadus

Induktsiooni elektromotoorjõudu mõjutavad suurused

Kuidas tekiks võimalikult suur induktsioonivool?

Oleme nüüd päris palju tegelenud pööriselektrivälja tekkimisega magnetvälja muutumisel. Aga mis tähendus on üleüldse sõnadel magnetväli muutub? Millise füüsikalise suuruse muutumisest on jutt? Elektromagnetilise induktsiooni nähtus esineb teatavasti ka homogeenses magnetväljas (p.2.2.1). Seega ei saa otsitavaks muutuvaks suuruseks olla magnetinduktsioon $B$ . Vajalik suurus tuleb meil alles määratleda. Järgnevas katseseerias uurime, millest sõltub induktsiooni elektromotoorjõud.


Ühendame juhtmepooli külge voolutundliku mõõteriista. Kinnitame pooli sisse mahtuva raudpoldi otsa tugeva püsimagneti, muutes niiviisi ka poldi magnetiks. Pistame nüüd poldi pooli sisse, tehes seda ligikaudu ühe sekundi jooksul ja fikseerime poolis tekkiva induktsioonivoolu väärtuse.	Esimesest katsest võime järeldada, et suurem elektromotoorjõud tekib poolis siis, kui magnetinduktsioon pooli asukohas rohkem muutub. Täpsemad mõõtmised näitavad, et induktsiooni elektromotoorjõud on võrdeline suuruse B muutusega. Järelikult on elektromagnetilise induktsiooni nähtuse kirjeldamiseks vajalik suurus võrdeline magnetinduktsiooniga B.


Teisest katsest võime järeldada, et füüsikaline suurus, mille muutumine on vajalik elektromagnetilise induktsiooni tekkimiseks, peab olema (vähemasti ligikaudu) võrdeline pindalaga S, mida läbivad muutuva magnetvälja jõujooned.	Nagu näeme, sõltub induktsioonivool ja järelikult ka induktsiooni elektromotoorjõud nurgast β pooli telje ja muutuva magnetvälja suuna vahel. Seda sõltuvust kirjeldav nurgafunktsioon peab olema maksimaalne juhul, kui nurk on null. Ise peab see funktsioon aga nullistuma täisnurga korral

Faraday seadus phet

Elektrivoolu tekkimine poolis, kui pooli läbiv magnetvälja voog muutub. Simulatsioonis saab liigutada püsimagnetit poolis ning jälgida tekkiva elektrivoolu tugevust ja suunda. PHET

View

Kõiki neid katseid võib läbi viia ka simulatsioonides. Viitame siin ühte sellist. Vaadake ja kontrollige, elu või simulatsiooni, teie valik.

Magnetvoo mõiste

J.2.24 Magnetvoo sõltuvus nurgast β magnetvälja suuna (B) ja juhtmekeeru pinna normaali (n) vahel: a) β = 0, b) 0 < β < π/2, c) β = π/2.

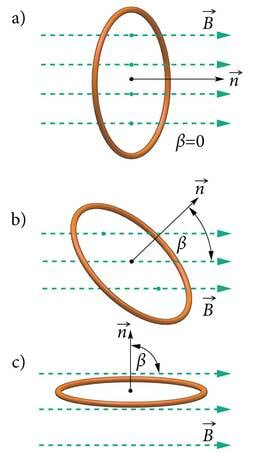
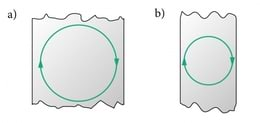
Ülalkirjeldatud katsete tulemuste kokkuvõtlikuks esitamiseks on võetud kasutusele füüsikaline suurus nimega magnetvoog. Magnetvoog $Φ$ näitab, millisel määral läbivad magnetvälja jõujooned vaadeldavat pinda selle pinna suuruse ja asendi tõttu magnetväljas. Piltlikult öeldes näitab magnetvoog pinda läbivate jõujoonte arvu. Loomulikult on see arv eelkõige määratud jõujoonte tihedusega, mida teatavasti iseloomustab magnetinduktsioon. Mingit kindlat pinda läbib joonte suurema tiheduse korral rohkem jõujooni. Magnetvoog läbi vaadeldava pinna on võrdeline magnetinduktsiooniga $B$ . Samas läheb pinnast rohkem jõujooni läbi ka siis, kui pind ise on suurem ning jääb seetõttu jõujoontele rohkem "ette". Magnetvoog on võrdeline pinna pindalaga $S$ . Jõujoonte kindla tiheduse ( $B$ ) ja pinna pindala ( $S$ ) korral sõltub pinda läbiv magnetvoog B-vektori suunast pinna suhtes. Kui pind on $B$ -vektoriga risti ( $β = 0$ ), siis läbib pinda suurim arv jõujooni (J.2.24, a). Sel korral on tegemist suurima magnetvooga. Kui nurk $β$ B-vektori ja pinna normaali vahel erineb nullist, siis on pinda läbivate jõujoonte arv väiksem (J.2.24, b). Seega on väiksem ka magnetvoog. Kui aga nurk $β$ on täisnurk ( $β = π / 2$ ), siis on magnetvälja jõujooned pinnaga paralleelsed. Mitte ükski jõujoon ei läbi pinda. Magnetvoog on null (J.2.24, c). Magnetvoog on maksimaalne nulliga võrduva nurga $β$ korral ning saab ise nulliks, kui see nurk on täisnurk. Seega on magnetvoog võrdeline koosinusega nurgast $β$ magnetvälja suuna ja pinna normaali

Kõik ülaltoodu võib kokku võtta magnetvoo definitsioonivalemisse

(2.5)

Φ = B S cos β

Magnetvoog on skalaarne (suunata), kuid algebraline suurus. Magnetvoo algebralisus tähendab seda, et sõltuvalt magnetvälja suunast võib voog olla nii positiivne kui ka negatiivne suurus. Magnetvoo mõõtühikuks SI-süsteemis on üks veeber ( $1 Wb$ ). Üks veeber on magnetvoog, mis läbib 1 m² suurust magnetvälja suunaga ristuvat pinda, kui välja magnetinduktsioon on $1 T$ . Ühe veebri defineerimisel kasutatakse niisiis valemi 2.5 erijuhtu, mil $β = 0$ , seega $cos β = 1$ ja järelikult $Φ = B S$ , millest

1 Wb = 1 T \cdot 1 m^{2}

Faraday induktsiooniseadus

Induktsioonivool ja ka vastav elektromotoorjõud %i on seda suuremad, mida kiiremini (s.t mida lühema ajavahemiku $Δ t$ jooksul) magnetvälja muutus toimub. Kasutades magnetvoo mõistet, võib kõigi Faraday katsete tulemuse üldistada kujul

(2.6)

E_{i} = - k \frac{Δ Φ}{Δ t}

mis näitab, et induktsiooni elektromotoorjõud on võrdeline magnetvoo muutumise kiirusega. See ongi elektromagnetilise induktsiooni põhiseadus ehk lihtsalt Faraday induktsiooniseadus. Mõistagi on jutt magnetvoost läbi pinna, mis on piiratud vaadeldava juhtmekeeruga. Pooli korral liituvad üksikutes keerdudes tekkivad elektromotoorjõud. Siis tuleb magnetvoo all mõista voogu läbi summaarse keerdudest piiratud pinna ning arvestada ka keerdude magnetväljade vastastikust mõju. Miinusmärk näitab toimuva muutuse suunda.


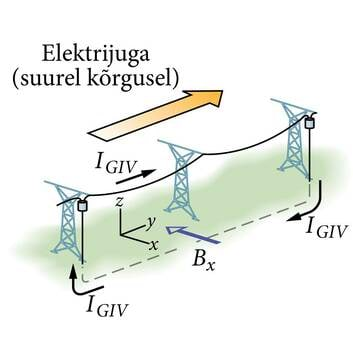
Induktsioonivoolud ei teki ainult laboritingimustes. Kui Päikeselt lähtuv, virmalisi tekitav elektrijuga (vool) ionosfääris tekitab muutuva magnetvoo läbi vertikaalse kontuuri, mille moodustavad elektriliinid, Maa pind ja transformaatorite maandusjuhtmed, indutseeritakse selles juhtivas kontuuris vool I_GIV . Tugevad päikesetormid on sel kombel rivist välja löönud terveid elektrijaotussüsteeme.	Kui suur päikesetorm läheb maast napilt mööda.

Induktsioonivoolud ei teki ainult laboritingimustes. Kui Päikeselt lähtuv, virmalisi tekitav elektrijuga (vool) ionosfääris tekitab muutuva magnetvoo läbi vertikaalse kontuuri, mille moodustavad elektriliinid, Maa pind ja transformaatorite maandusjuhtmed, indutseeritakse selles juhtivas kontuuris vool I_GIV . Tugevad päikesetormid on sel kombel rivist välja löönud terveid elektrijaotussüsteeme.

Kui suur päikesetorm läheb maast napilt mööda.

Võrdetegur $k$ sõltub mõõtühikute süsteemi valikust. SI-s $k = 1$ ja järelikult

(2.7)

E_{i} = - \frac{Δ Φ}{Δ t}

SI korral ei ole induktsiooni elektromotoorjõud mitte ainult võrdeline vaid lausa arvuliselt võrdne magnetvoo muutumise kiirusega. Ühikusüsteem SI ongi loodud nõnda, et elektromagnetilise induktsiooni seaduses võrdetegur puuduks. Just seetõttu ilmub selles süsteemis Coulomb'i seadusesse ühikut omav võrdetegur.

Kasutades Faraday induktsiooniseadust kujul 2.7 , võime magnetvoo ühiku $1 Wb$ defineerida seosest

Δ Φ = - E_{i} Δ t

Vastavalt on üks veeber selline magnetvoo muut, mis ühe sekundi jooksul toimudes tekitab induktsiooni elektromotoorjõu üks volt ( $1 Wb = 1 V \cdot 1 s$ ).

Papptorukesele keriti 400 keerust koosnev juhtmepool. Pooli otste külge ühendati voltmeetrina toimiv multimeeter ehk tester, mille takistuse võib lugeda pooli takistusega võrreldes lõpmata suureks. Seega toimis pool vooluallikana, mille EMJ oli praktiliselt võrdne testril tekkiva pingega. Kui pooli sisse pisteti 1 sekundi jooksul püsimagnet ristlõikepindalaga $0, 5 {cm}^{2}$ , siis hälbis testri osuti väärtuseni $10 mV$ . Kui palju muutus magnetvoog ühes keerus? Kui suur on magnetinduktsioon selle püsimagneti sees?

Lahendus

Andmed

$U_{i} = 10 mV$
$N = 400$
$Δ t = 1 s$
$S = 0, 5 {cm}^{2} = 5 \cdot 10^{- 5} m^{2}$

$Δ Φ = ?$
$B = ?$

Arvutused:
Pooli keerud toimivad jadamisi ühendatud vooluallikatena, mille põhjal induktsiooni EMJ kogu poolis

$E_{i} = N E_{1}$ ,

kus $E_{1}$ – elektromotoorjõud ühes keerus ja $N$ – keerdude arv.

Faraday induktsiooniseadust

$E_{i} = - \frac{Δ Φ}{Δ t}$

võime siin kasutada ilma miinusmärgita, sest meid huvitab vaid muutuse suurus, mitte suund.

Magnetvoo muut:

$Δ Φ = E_{1} \cdot Δ t = 25 μ V \cdot 1 s = 25 μ Wb$ .

Kuna magnetvoo algväärtus on null, siis võrdub lõppväärtus $Φ$ muuduga $Δ Φ$ . Püsimagneti magnetväli on paralleelne pooli teljega ning on seega suunatud piki keerdude ühist normaali. Järelikult $β = 0$ , $cos β = 1$ ja $Φ = B S$ . Sellest

$B = \frac{Φ}{S} = \frac{25 \cdot 10^{- 6} Wb}{5 \cdot 10^{- 5} m^{2}} = 0, 5 T$

Vastus: Magnetvoog ühes keerus muutus 25 mikroveebri võrra. Püsimagneti magnetinduktsioon oli 0,5 teslat.

Summary

Magnetvoog $Φ$ näitab, millisel määral läbivad magnetvälja jõujooned vaadeldavat pinda. Magnetvoog avaldub kujul

Φ = B S cos β

kus $B$ on magnetinduktsioon, $S$ – pinna pindala ning $β$ – nurk pinna normaali ja magnetvälja su

Üks veeber ( $1 Wb$ ) on magnetvoog, mis läbib $1 m^{2}$ suurust magnetvälja suunaga ristuvat pinda, kui välja magnetinduktsioon on $1 T$ . Seega

1 Wb = 1 T \cdot 1 m^{2}

Kehtib Faraday induktsiooniseadus, mille kohaselt juhtmekontuuris tekkiv induktsiooni elektromotoorjõud on võrdeline magnetvoo muutumise kiirusega. Ühikusüsteemis SI:

E_{i} = - \frac{Δ Φ}{Δ t}

kus $Δ Φ$ on magnetvoo muutus kontuuris ja $Δ t$ – ajavah

Control questions

Millised on kolm peamist viisi elektrienergia saamiseks elektromagnetilise induktsiooni teel? Uurigem valemeid 2.5 ja 2.7.

Kas magnetvoo definitsioonivalemis võiks koosinuse asemel esineda ka siinus? Millist nurka tuleks siis kasutada?

Maanteel liikuvate autode loendamiseks paigutatakse teekatte alla keskmise auto mõõtmetega juhtmekontuur, mille otstel paikneb vooluimpulsse registreeriv seade. Selgitage niisuguse loenduri tööpõhimõtet. Arvestagem, et autokered on valmistatud terasest, mis on ferromagneetik.

Kuidas võiks liikluspolitsei eelmises probleemis kirjeldatud loendureid kasutada autode kiiruse mõõtmiseks?

Elektromagneti südamik soojeneb, kui voolu magneti mähises korduvalt sisse ja välja lülitada. Miks on see nii?

Sisestusmehhanism veab magnetkaarti pangaautomaadi sisse kindla kiirusega. Milleks see vajalik on?

Jalgratta spidomeetri (kiirusemõõtja) andur kinnitatakse esikahvli külge nii, et ühe kodara küljes paiknev väike püsimagnet mööduks ratta igal tiirul andurist väga lähedalt (vt joonist). Selgitage spidomeetri tööpõhimõtet.

Control questions Additional materials

Lenzi reegel. Induktsiooniseaduse rakendused

Lenzi reegel

Lugedes veel kord Faraday katsete kirjeldusi punktis 2.3, märkame, et magnetvälja kasvu korral sisaldavad need hulgaliselt sõna vastupidine. Näiteks püsimagneti lähendamisel juhtmepoolile on induktsioonivoolu magnetväli vastassuunaline püsimagneti väljale, mis voolu esile kutsus. Induktsioonivoolu väli takistab magnetvälja kasvu. Poolis tekkiva induktsioonivoolu suund on vastupidine voolu suunale teises poolis, mida esimesele lähendatakse. Voolu sisselülitamine ühes juhtmes indutseerib vastupidise suunaga voolu naaberjuhtmes.

Heinrich Friedrich Emil Lenz (1804 – 1865)

Magnetvälja kahanemise korral on aga kõik teisiti. Püsimagneti eemaldamisel poolist on induktsioonivoolu magnetväli samasuunaline püsimagneti väljaga ning takistab magnetvälja kahanemist. Juhtmepoolide eemaldamisel teineteisest on ühes poolis indutseeritav vool samasuunaline vooluga teises poolis. Voolu väljalülitamine ühes juhtmes indutseerib samasuunalise voolu naaberjuhtmes. Seega soodustab induktsioonivool alati olemasoleva olukorra säilimist.

Elektromagnetiline induktsioon on alalhoidlik ehk konservatiivne nähtus. Seda asjaolu märkas esimesena Emil Lenz (1804-1865), Tartust pärit Vene füüsik, rahvuselt baltisakslane. Kogu maailm tunnustab Emil Lenzi teeneid induktsioonivoolu suunda määrava reegli või seaduse formuleerijana. Seetõttu esinebki nimetatud seadus füüsikaõpikutes Lenzi reegli või Lenzi seaduse nime all.

Järgnevalt toome ära Lenzi reegli mõned sõnastused:

induktsioonivoolu suund on selline, et tema magnetväli kompenseeriks muutust, mis voolu põhjustab;
induktsioonivool toimib alati vastupidiselt seda voolu esile kutsuvale põhjusele;
kui välismõju tingib magnetvoo kasvu kontuuris, siis on induktsioonivoolu magnetväli välise magnetvälja suhtes vastassuunaline (takistab kasvu). Kui aga välismõju põhjustab magnetvoo kahanemist, siis on induktsioonivoolu magnetväli välise magnetväljaga samasuunaline (takistab kahanemist).

Lenzi reegli levinuim sõnastus on (a), lühimaks võib pidada varianti (b), kõige üksikasjalikumaks aga võimalust (c).


Lenzi reeglit demostreeriv katse. Demokatse.	Kiiresti muutuv magnetväli tekitab alumiiniumrõngas tugevad induktsioonivoolud ning induktsioonivoolude tekitatud magnetväli viskab rõnga õhku. Läbi saetud alumiiniumrõngaga me sarnast nähtust ei tähelda. Demokatse.

Lenzi reegli analoogiks mehaanikas on väide, et stabiilsele süsteemile mõjuv jõud on suunatud tasakaaluasendi poole. Kui me viime näiteks pendli tasakaaluasendist välja, siis tekib otsekohe jõud $F$ , mis takistab niisugust muutust. See jõud püüab viia pendlit tagasi tasakaaluasendisse. Samamoodi on lood kuulikesega, mis asetseb nõgusa põhjaga kausis. Kuulikese väljaviimisel kausi madalaimast punktist tekib jõud, mis lükkab kuulikest tagasi tasakaaluasendisse, see tähendab, kausi põhja.

Mõnikord öeldakse ka, et Lenzi reegel väljendab energia jäävuse seadust. Kujutlegem, mis juhtuks siis, kui Lenzi reegel ei kehtiks ja mingist muutusest tingitud induktsioonivool soodustaks muutuse jätkumist. Näiteks püsimagneti lähendamisel juhtmepoolile tekiks poolis sel juhul vool, mille magnetväli oleks püsimagneti väljaga samasuunaline. Poolile mõjuv magnetväli tugevneks ja "tagurpidise" Lenzi reegli kohaselt kasvaks vool seeläbi veelgi. Voolu suurenemine põhjustaks selle kasvu üha kiiremat jätkumist. Tegemist oleks eimillegi arvelt töötava vooluallikaga, niisiis perpetuum mobile'ga. Niisugust masinat ei saa aga energia jäävuse seaduse kohaselt olemas olla.

Lenzi reeglit väljendab induktsiooniseaduses (valemis 2.9) sisalduv miinusmärk. Kui näiteks juhtmekeerdu läbiv magnetvoog kasvab ( $Δ Φ > 0$ valemis 2.9), siis loetakse induktsiooni elektromotoorjõudu ja vastavat voolutugevust kokkuleppeliselt negatiivseteks, kuna induktsioonivoolu magnetväli on keerus mõjuvale väljale vastassuunaline (takistab magnetvoo kasvu). Kui aga magnetvoog juhtmekeerus kahaneb ja tema muut on negatiivne ( $Δ Φ < 0$ ), siis on need kaks välja samasuunalised.

Induktsioonivool püüab kahanevat magnetvoogu alal hoida. Seetõttu loetakse induktsiooni elektromotoorjõudu ja voolutugevust positiivseteks.


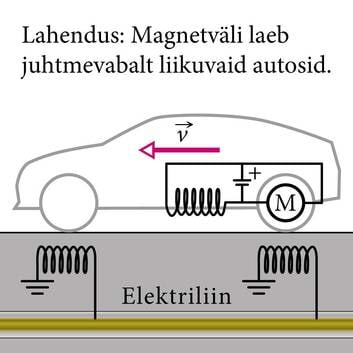
Selles kuulsas 2006.a. Massachusetsi Tehnoloogiainstituudis tehtud eksperimendis pandi elektromagnetväljade tekitatud induktsioonivooludega tööle 60W elektripirn. Täna on sellised seadmed reaalselt saadaval, näiteks oma mobiiltelefoni saame me laadida ilma, et sellele ühtki juhet kinnitama peaks.	Elektriautod ei suuda ilma laadimata sõita Tartust Tallinnasse. Ühe lahendusena võib välja pakkuda akude laadimist induktsioonivoolude abil. Teekattesse monteeritud poolide magnetväli kutsub esile induktsioonivoolud neist üle sõitvate autode analoogilistes poolides, mida siis kasutatakse elektriauto akude laadimiseks. Nende küsimustega tegeleme täpsemalt Energia kursuses.

Katse 2.4.

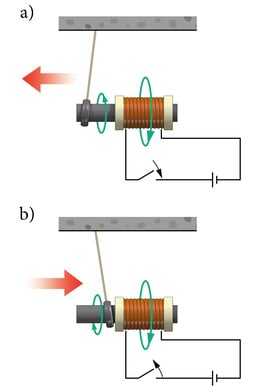
Kui me oleme eespool (p.2.3.1) kirjeldatud viisil valmistanud raudsüdamikuga juhtmepooli, siis saame Lenzi reegli kehtivust üpris lihtsalt kontrollida. Selleks püüame leida vasest, hõbedast või alumiiniumist rõnga, millest kasutatava pooli südamik (raudpolt) takerdumata läbi mahub. Hästi sobib näiteks kerge hõbesõrmus. Paigutame raudsüdamikuga juhtmepooli laual mingile alusele, nii et südamik ulatuks poolist paari sentimeetri pikkuselt välja. Paneme metallrõnga kahe niidiga laualambi või mingi muu raami külge rippuma. Seejuures peab raudsüdamik ulatuma rõnga sisse. Kui me nüüd tekitame südamikuga poolis taskulambipatarei abil voolu, siis nihkub rõngas poolist eemale, kuna rõngas tekkiv induktsioonivool takistab Lenzi reegli kohaselt poolist pärineva magnetvoo kasvu. Seetõttu on induktsioonivool rõngas pooli voolule vastassuunaline (J.2.25, a), vastandlike suundadega voolud aga tõukuvad (p.1.4.2). Loomulikult ei jää rõngas ,,eemaletõukunud“ asendisse. Kui pooli magnetväli enam ei kasva, siis langeb induktsioonivoolu tugevus nullini ja rõngas naaseb raskusjõu mõjul tasakaaluasendisse. Kui me nüüd poolis voolu katkestame (eemaldame patarei), siis poolist pärinev magnetvoog kahaneb. Induktsioonivoolu magnetväli üritab seda aga Lenzi reegli kohaselt alal hoida (takistab kahanemist). Nüüd on voolude magnetväljad ja seega ka voolud ise samasuunalised (J.2.25, b). Samasuunalised voolud aga tõmbuvad. Seetõttu nihkub rõngas pooli poole. Kui poolist pärinev magnetvoog on saanud nulliks (enam ei kahane), siis induktsioonivool katkeb ja rõngas naaseb jällegi raskusjõu mõjul tasakaaluasendisse.

Induktsiooniseaduse rakendusi

J.2.26 Pöörisvooluringid paksus ja õhukeses metallplaadis.

Ülalkirjeldatud viisil tekivad induktsioonivoolud mitte ainult rippuvas rõngas, vaid ka suvalise kujuga metallkehas, millele mõjuv magnetväli piisavalt kiiresti muutub. Selliseid voolusid nimetatakse pöörisvooludeks, kuna neid tekitab elektromagnetilisel induktsioonil esinev pööriselektriväli. Kui mingi metallkeha magnetväljas liigub, siis pöörisvoolude olemasolu pidurdab seda liikumist. Keha kui terviku liikumise kineetiline energia läheb üle laengukandjate liikumise energiaks selles kehas.

Võib ka öelda, et laengukandjad liiguvad pööriselektrivälja energia arvel. Elektritakistuse olemasolu tõttu eraldub see energia aga soojusena. Kineetiline energia muundub soojuseks nii nagu tavalisel hõõrdumisel.


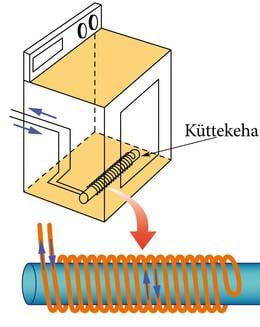
Pöörisvooludel põhineb ka induktsiooniahju töö. See seade võimaldab kiiresti kuumutada elektrit juhtivat ainet. Suure sagedusega perioodiliselt muutuva magnetvälja abil tekitatakse aines pöörisvoolud, mille energia vabaneb soojusena. Induktsiooniahju korral ei toimu soojusülekannet ühelt kehalt teisele. Soojus eraldub sellessamas aines, mida kuumutatakse. Seetõttu on induktsiooniahjul väga kõrge kasutegur.	Siin pildil kujutatud eksperimendis pöörlevad kaks vasest silindrit kiiresti vastassuundades. Silindrite peale asetati tugev magnet, nii et silindrite pööreldes indutseeritakse seal tugevad induktsioonivoolud. Need pöörisvoolud püüavad Lenzi reegli kohaselt elimineerida kiiresti muutuvat magnetvälja, tekitades vastassuunalise magnetvälja. Tulemus on pildil näha - magnet jääb silindrite kohale õhku "rippuma".

Pöörisvooludel põhineb ka induktsiooniahju töö. See seade võimaldab kiiresti kuumutada elektrit juhtivat ainet. Suure sagedusega perioodiliselt muutuva magnetvälja abil tekitatakse aines pöörisvoolud, mille energia vabaneb soojusena. Induktsiooniahju korral ei toimu soojusülekannet ühelt kehalt teisele. Soojus eraldub sellessamas aines, mida kuumutatakse. Seetõttu on induktsiooniahjul väga kõrge kasutegur.

Siin pildil kujutatud eksperimendis pöörlevad kaks vasest silindrit kiiresti vastassuundades. Silindrite peale asetati tugev magnet, nii et silindrite pööreldes indutseeritakse seal tugevad induktsioonivoolud. Need pöörisvoolud püüavad Lenzi reegli kohaselt elimineerida kiiresti muutuvat magnetvälja, tekitades vastassuunalise magnetvälja. Tulemus on pildil näha - magnet jääb silindrite kohale õhku "rippuma".

Summary

Induktsioonivool soodustab alati olemasoleva olukorra säilimist. Kehtib Lenzi reegel, mille kohaselt induktsioonivool toimib alati vastupidiselt voolu esile kutsuvale põhjusele.

Lenzi reeglit väljendab miinusmärk Faraday induktsiooniseaduses.

Control questions

Vanemate autode spidomeeter sisaldab rattateljega mehaaniliselt ühendatud püsimagnetit ja selle vastas paiknevat metallketast. Ketas on omakorda ühendatud spidomeetri osutiga. Mida kiiremini pöörleb püsimagnet, seda suurema nurga võrra pöördub samas suunas ketas ja vastavalt ka spidomeetri osuti. Ketta küljes paikneb tagastusvedru, mis ketta pöördumisel pinguldub. Püsimagneti peatumisel toob see vedru ketta algasendisse tagasi. Miks püüab püsimagnet ketast "kaasa vedada"?

Tugevat püsimagnetit on raske liigutada piki alumiiniumplaati, aga magnet plaadi külge kinni ei jää. Miks on see nii?

Control questions Additional materials

Induktiivsus ja mahtuvus

Endainduktsiooni elektromotoorjõud

Öeldakse, et gaasilekke korral ei tohi ühelgi juhul ... teha mida? Missuguseid ohuallikaid näete selles toas?

Oleme juba korduvalt täheldanud induktsiooni elektromotoorjõu tekkimist poolis, mille keerde läbivat magnetvoogu väljastpoolt muudetakse. Näiteks katsetes kahe pooliga (p.2.4.1) toimub see teises poolis voolu sisse- või väljalülitamise teel. Kuid ka magnetvälja tekitavas poolis esineb voolu kasvul või kahanemisel magnetvoo muutus. See muutus tekitab induktsiooni elektromotoorjõu, mis Lenzi reegli kohaselt takistab muutust ning järelikult pidurdab voolu kasvu või kahanemist. Niisiis võib juhtmes induktsiooni elektromotoorjõu tekkimiseks vajalik magnetvoo muutus olla põhjustatud ka voolu muutumisest juhtmes endas. Elektromagnetilise induktsiooni nähtuse sellist alaliiki nimetatakse endainduktsiooniks.

Katse 2.5.

Endainduktsiooni olemasolu kindlakstegemiseks võib kasutada Faraday katsete (p.2.3) korraldamiseks valmistatud pooli. Ühendame südamikuta pooli otste külge uue lapiku taskulambipatarei. Kui me voolu ahelas katkestame, siis kuuleme praksatust ja märkame katkestuskohas nõrka elektrisädet. Säde on paremini jälgitav, kui teeme katset hämaras või koguni pimedas toas.

Järelikult tekib ahelas voolu katkestamisel täiendav pinge, mis püüab voolu säilitada.

Tekkiv pinge rakendub katkestuskohas, sest just seda kohta on liikuvatel laengukandjatel kõige raskem läbida. Seal tuleb teha kõige rohkem tööd. Paigutame nüüd pooli sisse raudpoldi ja kordame katset. Näeme, et tekkiv säde on oluliselt tugevam. Vahemik, milles õhk hakkab elektrit juhtima, on tunduvalt laiem.

Arvestame, et sädelahendus tekib õhus ühe kindla elektrivälja tugevuse juures ( $E = 3 \cdot 10^{6} V/m$ ).

Konstantsel väljatugevusel E on kahe punkti vaheline pinge $U$ aga seda kõrgem, mida suurem on nende punktide vahekaugus $d$ (valem $U = E d$ ). Seega tekib raudsüdamikuga pooli korral suurem pinge.

Kuna just raudsüdamikuga poolis tekib suurem magnet-induktsioon, siis võib väita, et see pinge sõltub magnetinduktsioonist poolis või pooli keerde läbivast magnetvoost. Pool hakkab voolu muutumisel toimima vooluallikana, mille elektromotoorjõudu nimetatakse endainduktsiooni elektromotoorjõuks. Vooluringi sulgemisel on pooli kui vooluallika polaarsus patarei omale vastupidine (J.2.27, pool takistab voolu kasvu). Vooluringi katkestamisel aga on pool ja patarei ühesuguse polaarsusega (pool püüab voolu alal hoida).

Endainduktsioon võib esineda ka meie igapäevases kasutuses olevates elektriseadmetes, näiteks küttekehades on küttetraat tavaliselt spiraaliks keritud. Seega on nende väljalülitumisel võimalik ka sädeme tekkimine, nagu nägime katses 2.5. Selle ärahoidmiseks keritakse traat joonisel kujutatud viisil - vastandsuunaliste vooludega poolides on magnetväli ja seega ka endainduktsioon minimaalsed.

Katsest 2.5 näeme, et endainduktsiooni nähtus avaldub inertsina laetud osakeste suunatud liikumisele. Endainduktsiooni esinemise korral võtab elektrivoolu tekitamine ja ka peatamine oluliselt rohkem aega võrreldes juhuga, mil endainduktsioon puudub. Tulemus näitab, et sädet tekitav pinge on (vähemasti osaliselt) põhjustatud voolu katkestamisest poolis. Vool raudsüdamikuga pooli sisaldavas ahelas käitub nagu raske raudteerong. Sellist rongi ei saa hetkeliselt liikuma panna ega ka järsult peatada. Palju kuuldud kurvad lood õnnetustest raudteeületuskohtadel ongi ju õigupoolest selle tagajärg, et rasket rongi pole võimalik hetkeliselt seisma jätta. Kuid miks vool mõnes ahelas käitub raske rongina, mõnes aga mitte? Millal esineb endainduktsioon? Ka nendele küsimustele annab vastuse äsja korraldatud katse. Endainduktsiooni tekkimiseks peab vooluga kaasnema tugev magnetväli, mis suudab samas mõjutada ka voolu ennast. Täpsemalt öeldes peab vool vaadeldavas juhtmesüsteemis tekitama suure magnetvoo, sest just magnetvoo muutumine kutsub esile induktsiooni elektromotoorjõu. Raudsüdamikuga juhtmepooli korral on magnetvoog oluliselt suurem kui tühjas poolis.

Seega on endainduktsiooni esinemine määratud voolu suutlikkusega tekitada antud juhtmesüsteemis magnetvoogu. Juhtmesüsteemi vastavate omaduste kirjeldamiseks on kasutusel füüsikaline suurus, mida nimetatakse juhi induktiivsuseks.

Induktiivsuse mõiste

Ülalpool kirjeldatud katse käigus tekkis raudsüdamikuga pooli sisaldavas vooluringis suur endainduktsiooni elektromotoorjõud. Raudsüdamiku puudumisel oli see aga väiksem. Näeme, et juhi (või vooluringi osa) induktiivsust võib määratleda mingil kindlal voolu muutusel tekkiva endainduktsiooni elektromotoorjõu kaudu. Juhi induktiivsus $L$ näitab, kui suur endainduktsiooni elektromotoorjõud $E_{e}$ tekib selles juhis voolutugevuse ühikulisel muutumisel ajaühiku jooksul

(2.8)

L = ∣ ∣ ∣ \frac{E_{e}}{\frac{Δ i}{Δ t}} ∣ ∣ ∣

Poole kasutatakse tehnikas väga laialdaselt ning nende välisilmeid võib olla väga erinevaid. Aga põhiparameeter suvalise pooli iseloomustamiseks on ikka ja alati induktiivsus.

Absoluutväärtuse märk selles valemis näitab, et induktiivsust vaadeldakse kokkuleppeliselt vaid positiivse suurusena. Voolutugevuse muut ja endainduktsiooni elektromotoorjõud võivad aga olla ka negatiivsed. Siin ja allpool asume kasutama elektromagnetismi füüsikas üldlevinud kokkulepet, mille kohaselt mingit kindlat või konstantset laengut, pinget, voolutugevust vms elektrilist suurust tähistatakse suurtähtedega ( $Q$ , $U$ , $I$ ), vastavaid ajas muutuvaid suurusi aga väiketähtedega ( $q$ , $u$ , $i$ ). Kuna induktiivsuse mõiste eeldab olemuslikult voolu muutumist ajas, siis on korrektne tähistada voolutugevust väiketähega ( $i$ ). Voolutugevuse muudu $Δ i$ ja sellele vastava ajavahemiku $Δ t$ suhet valemis 2.8 võib nimetada voolu muutumise kiiruseks. Seega näitab juhi induktiivsus meile, kui suur endainduktsiooni elektromotoorjõud tekib selles juhis, kui voolutugevus temas muutub ühikulise kiirusega.

Avaldades valemist 2.8 endainduktsiooni elektromotoorjõu ning kasutades Lenzi reeglit väljendavat miinusmärki, saame

(2.9)

E_{e} = - L \frac{Δ i}{Δ t}

Võrdleme nüüd valemit 2.9 Faraday induktsiooniseadusega (valem 2.7). Seejuures arvestame, et endainduktsioon on elektromagnetilise induktsiooni erijuht, mistõttu ja 2.9 esinevate murdude väärtused ja seega ka nende murdude lugejad on võrdsed:

Δ Φ = L Δ i

ehk

(2.10)

L = \frac{Δ Φ}{Δ i}

Juhi induktiivsus näitab meile, kui suure magnetvoo muutuse tekitab selle juhi korral ühikuline voolu muutus. Veelgi lihtsamalt öeldes näitab induktiivsus vaadeldava juhtmesüsteemi inertsust temas toimuvate voolu muutuste suhtes.


Induktiivsus on väga oluline mõiste elektrivõrkude projekteerimisel. Fotol on kujutatud transformaator, mis muudab madalpinge elektrienergia suurtele kaugustele ülekandmiseks sobilikuks kõrgepingeks. Transformaatoritest räägime lähemalt Energia kursuses.	Joseph Henry (1797 – 1878).

Endainduktsiooni elektromotoorjõu sõltuvuse voolu muutumise kiirusest avastas aastal 1832 Ameerika füüsik Joseph Henry (1797 – 1878). Seetõttu on valem 2.9 ka tuntud Henry seaduse nime all. Kuna Henry jõudis induktsiooniseaduseni Faraday'st sõltumatult, siis nimetatakse elektromagnetilise induktsiooni seadust mõnikord ka Faraday-Henry seaduseks. J. Henry järgi on oma nime saanud induktiivsuse SI-ühik henri ( $1 H$ ). Valemite 2.8 ja 2.10 põhjal

1 H = \frac{1 V}{\frac{1 A}{1 s}} = \frac{1 V \cdot 1 s}{1 A} = \frac{1 Wb}{1 A}

Induktiivsuse definitsioonina võib vaadelda nii valemit 2.8 kui ka valemit 2.10. Paraku peitub valemis 2.10 tema välisele lihtsusele vaatamata väärtõlgenduse oht. Nimelt on seal sisalduv magnetvoog valemi 2.6 abil leitav vaid ühe juhtmekeeru korral. Juhtmepooli keerud aga tugevdavad vastastikku üksteise magnetvälja. Resultantvälja jõujooned läbivad pooli kõiki keerde. Magnetinduktsioon poolis ja seega ka magnetvoog läbi keerdude on seda suuremad, mida rohkem keerde on poolil pikkusühiku kohta. Vastavalt on sel juhul suurem ka pooli induktiivsus. Valemis 2.10 esinevat magnetvoogu nimetatakse siis pooli kogumagnetvooks ehk aheldusvooks ja selle suuruse väljaarvutamine on üldjuhul keeruline protseduur.

Elektrimahtuvus. Kondensaatorid

Peagi (p2.7.2) veendume selles, et induktiivsus kirjeldab kehade süsteemi võimet säilitada endas elektrivoolu ja seeläbi tekitada magnetvälja. Mõistagi on kasutusel ka füüsikaline suurus, mis iseloomustab kehade süsteemi võimet salvestada endasse laengut ja seeläbi tekitada elektrivälja. Kõnealuseks suuruseks on elektrimahtuvus, mida me edaspidi nimetame lihtsalt mahtuvuseks.

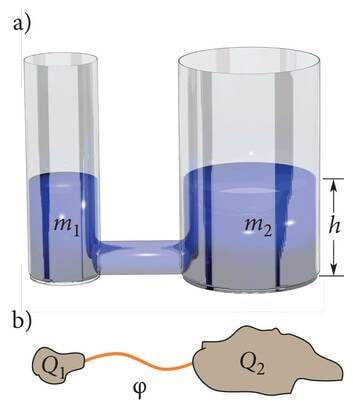
Kallates vedelikku ühekõrgustesse kuid erineva läbimõõduga klaasidesse, näeme otsekohe, et laiemasse klaasi mahub rohkem vedelikku. Suurema läbimõõduga anumal on suurem põhja pindala ja seega ka ruumala (J.2.28). Samamoodi on lood erinevate elektrit juhtivate kehade laadimisel. Ühele kehale "mahub" rohkem laengut kui teisele. Järelikult on mõtet võtta kasutusele keha laadumisvõimet kirjeldav suurus, mida nimetatakse keha mahtuvuseks.


J.2.28 Elektrimahtuvus on erinevatel kehadel erinev analoogiliselt sellele, kuidas me saame erineva läbimõõduga klaase ühe kõrguseni täites valada neisse erineva koguse vedelikku.	J.2.29 Pinge tekkimine kahe keha vahel laengu Q viimisel ühelt kehalt teisele.

Rangelt võttes on mahtuvus alati kahe keha omavaheline mahtuvus. Andes ühele kehale mingi laengu, peame selle mingilt teiselt kehalt ära võtma, kuna kehtib laengu jäävuse seadus.

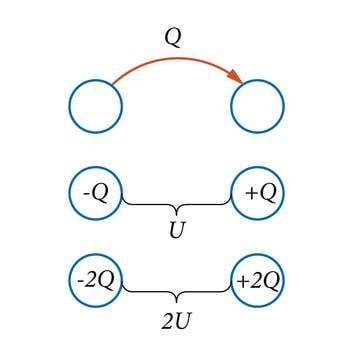
Vaatleme kahte algselt neutraalset keha. Kui me võtame ühelt kehalt ära laengu $Q$ ja anname selle teisele kehale, siis omandab esimene keha laengu $- Q$ ja teine $+ Q$ . Kehade vahel tekib elektriväli ja seega ka potentsiaalide vahe (pinge) $U$ (J.2.29). Kuna potentsiaal on võrdeline teda tekitava laenguga (valem 1.22), siis teostades sama toimingu laenguga $2 Q$ , tekitame kehade vahel pinge $2 U$ . Peagi märkame, et laengu ja pinge jagatis jääb kõigis sellelaadsetes katsetes muutumatuks, antud kehade süsteemi iseloomustavaks suuruseks. See ongi vaadeldavate kehade omavaheline mahtuvus.

Kahe keha omavaheline mahtuvus näitab, kui suure laengu viimisel ühelt kehalt teisele tekib kehade vahel ühikuline pinge. Mahtuvuse $C$ leidmiseks tuleb üle viidud laeng $Q$ jagada tekkiva pingega

(2.12)

C = \frac{Q}{U}

Saavutamaks mahtuvuse definitsiooni suuremat sarnasust induktiivsuse määratlusega (2.10) ja rõhutamaks ajalise muutuse tähtsust võib üleviidavat laengut Q vaadelda keha laengu lõppväärtuse $q_{2}$ ja algväärtuse $q_{1}$ vahena: $Q = q_{2} - q_{1} = Δ q$ . Siis on keha iseloomustav laeng $q$ meile mehaanikast tuntud koordinaadi rollis ja üleviidav laeng $Q$ vastab kahe koordinaadi vahele ehk teepikkusele. Vaadeldes keha laengut ajast sõltuva suurusena $q = q (t)$ , peame ajast sõltuvana käsitlema ka kahe keha vahel tekkivat pinget $u = u (t)$ . Niimoodi võtab kahe keha omavahelise mahtuvuse definitsioon kuju

(2.13)

C = \frac{Δ q}{Δ u}


J.2.29 a Kaitsemaandus. Fotol on näha, kuidas torud on omavahel juhtmega ühendatud, see juhe on omakorda ühendatud maandusvardaga, vt järgmine pilt.	J.2.29 b Kaitsemaandus. Juhe on ühendatud masse löödud vaskvardaga.

J.2.30 Laengu -Q indutseerimine kondensaatori maandatud plaadile.

Nüüd saab meile selgeks elektriseadmete kaitsemaanduse põhimõte, millest oli juttu juba põhikooli Elektriõpetuses. Maandamisel ühendatakse seadme metallkorpus juhtme abil Maaga. See kaitseb seadme kasutajat elektrilöögi eest juhul, kui seadme korpus satub rikke tagajärjel Maa suhtes pinge alla. Kaitsemaandus juhib seadme korpusele sattunud laengu ära Maasse. Maa on aga niivõrd suure mahtuvusega keha, et talle võib anda kuitahes suure laengu, ilma et tema potentsiaal märgatavalt muutuks. Laeng liigub Maasse läbi maandusjuhtme, mitte aga läbi seadme kasutaja keha. Seega on mingi keha maandamine samaväärne suure augu tegemisega niisuguse anuma põhja, millesse vesi mitte mingil juhul koguneda ei tohi. Kui ka vesi eksikombel satub anumasse, jookseb vesi läbi augu otsekohe maha.

Kehade süsteemi, mis on loodud mingi kindla mahtuvuse saamiseks, nimetatakse kondensaatoriks. Lihtsaim kondensaator koosneb kahest elektrit juhtivast plaadist ehk kattest, mille vahel paikneb dielektrikukiht. Kondensaatori mahtuvus näitab, kui suure laengu $Q$ andmisel ühele plaadile suureneb plaatidevaheline pinge $U$ ühe ühiku võrra. Seega on kondensaatori mahtuvus sisuliselt tema plaatide omavaheline mahtuvus (valem 2.12 või 2.13).

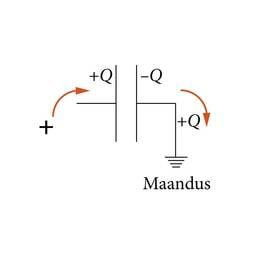
Ka kondensaatoreid on välimuse poolest väga erinevaid.

Kondensaatori laadimiseks reeglina ei võeta laengut ühelt plaadilt, et anda seda teisele plaadile. Piisab vaid ühe plaadi laadimisest. Laetud plaadi elektrivälja mõjul hakkavad laengukandjad teisel plaadil ja sellega ühendatud juhtides liikuma. Näiteks laengu $+ Q$ andmisel kondensaatori ühele plaadile omandab teine (algselt neutraalne) plaat sama suure laengu $- Q$ , sest just siis tasakaalustavad plaatide elektriväljad väljaspool kondensaatorit vastastikku teineteist. Samanimeliste laengute tõukumise tõttu lahkub laeng $+ Q$ teiselt plaadilt. Laengu $- Q$ saab kergesti teisele plaadile tuua siis, kui plaat on maandatud (J.2.30) ja laeng $+ Q$ võib lahkuda Maasse.

Ka vooluringis paikneva kondensaatori korral saab laeng teiselt plaadilt alati ära minna. Järelikult on ühe plaadi laadimine samaväärne laengu $Q$ üleviimisega ühelt plaadilt teisele.

Mahtuvuse ühik SI-süsteemis kannab M. Faraday auks nime farad. Üks farad ( $1 F$ ) on sellise keha mahtuvus, millele tuleb anda laeng üks kulon, selleks et suurendada tema potentsiaali ühe voldi võrra. Kondensaatori mahtuvus on $1 F$ , kui laengu $1 C$ viimine ühelt plaadilt teisele tekitab plaatide vahel pinge $1 V$ . Seega

1 F = \frac{1 C}{1 V}

Kuna üks kulon on väga suur laeng, siis ka üks farad on väga suur mahtuvus. Seetõttu kasutatakse praktikas enamasti mikro-, nano- ja pikofaradeid ( $1 F = 10^{- 6} F$ , $1 nF = 10^{- 9} F$ , $1 pF = 10^{- 12} F$ ).

Kondensaatoreid võib leida kõikvõimalikes elektroonikaseadmetes, alustades mikrofonidest ning lõpetades näiteks satelliitidega. Esimese kondensaatori valmistasid teineteisest sõltumatult sakslane Ewald von Kleist (1700-1748) ja hollandlane Pieter van Musschenbroek (1692-1761). Kondensaatori leiutamist on õigem nimetada avastuseks, sest see toimus täiesti juhuslikult. Uurides vee elektriseerumist, tegi Kleist 1745. aastal järgmise katse. Ta laadis raudnaela, mis ulatus välja veega täidetud klaaspudelist. Hoides pudelit ühes käes, puudutas ta kogemata teise käega naela ja sai er akordselt tugeva elektrilöögi. Kleist mõistis, et pudelisse oli kogunenud väga suur laeng. Pudelkondensaatori üheks katteks oli vesi, teiseks aga katsetaja käsi. Pudeli klaaskest toimis dielektrikuna.


J.2.32 Pudelkondensaator. Tavaline limonaadipudel on täidetud soolveega, pudeli korgist on läbi pandud polt, mille ots ulatub soolvette. Pudeli välisküljele on liimitud fooliumiriba. Sellist kondensaatorit saab laadida näiteks elektrofoormasinaga. Ettevaatust, kondensaatorist saadav "särts" võib olla üsnagi tuntav!	Kui purgi sisemisele ja välimisele küljele kinnitada kaks alumiiniumfooliumi lehte, käitub see seade kondensaatorina. Tuntakse ka Leideni purgi nime all.

Analoogilise katse teostas Musschenbroek 1746. a. hollandi linnas Leidenis. Kuna laiemalt tuntuks sai just nimelt tema tulemus, siis hakati kõiki sellelaadseid laengut koguvaid klaasanumaid nimetama leideni purkideks.

Leideni purgi konstruktsioonis asendati vesi peagi anuma sisepinda katva metallkilega. Ka välimine kate valmistati metallfooliumist. Nii saadi leideni purk, mis on kooli füüsikakabinetis kasutusel tänapäevani.

Summary

Endainduktsiooni nähtuseks nimetatakse elektromagnetilise induktsiooni alaliiki, mille korral magnetvoo muutus on põhjustatud voolu muutusest vaadeldavas juhtmes endas.

Juhi induktiivsus näitab, kui suur endainduktsiooni elektromotoorjõud tekib selles juhis voolutugevuse ühikulisel muutumisel ajaühiku jooksul. Induktiivsus näitab ühtlasi kogumagnetvoo muutust juhis juhti läbiva voolu tugevuse ühikulisel muutumisel.

Kahe keha omavaheline mahtuvus näitab, kui suure laengu viimine ühelt kehalt teisele tekitab kehade vahel ühikulise pinge.

Keha mahtuvus näitab, kui suure laengu andmisel kehale tekib keha potentsiaali ühikuline muutus.

Üks farad (1 F) on sellise keha mahtuvus, millele tuleb anda laeng üks kulon, selleks et muuta tema potentsiaali ühe voldi võrra.

Kondensaatoriks nimetatakse kehade süsteemi, mis on loodud mingi kindla mahtuvuse saamiseks.

Control questions

Lennujaama turvavärav on oma olemuselt juhtmepool, mille otstel paikneb voolu muutusi registreeriv seade. Kuidas teeb turvavärav kindlaks metalleseme olemasolu reisija taskus? Miks ei suuda turvavärav avastada plastikpommi?

Kuidas muutub algselt sirge juhtme induktiivsus selle juhtme kerimisel pooliks? Miks on muutus just selline?

Milline suurus mängib veeanuma täitmisel sama rolli mis mahtuvus keha laadimisel? Pinge osas on veetaseme kõrgus.

Control questions Additional materials

Elektromagnetvälja energia

Elektrivälja energia

Elektrivälja olemasolu tähendab teatavasti jõu tekkimise võimalikkust. Analoogiliselt väljendab termin elektrivälja energia seda, et laetud keha võib elektriväljas omada energiat. Asume uurima, kuidas sõltub elektrivälja energia väljatugevusest või potentsiaalist. Kõige lihtsam on seda teha homogeense välja korral, mis täidab kondensaatori plaatide vahelist ruumi.


Suure mahtuvusega kondensaator lühistamine metallvardaga. Tugev valgussähvatus (säde) ja sellega kaasnev pauk näitavad suure energia eraldumist. See on kondensaatoris salvestatud elektrivälja energia. Kondensaaatori mahtuvus on 300 mF ja see laeti pingeni 700 V.	Suure mahtuvusega kondensaatori lühistamine läbi arbuusi. Arbuusil ei lähe hästi.

Energia olemasolu laetud kondensaatoril pole raske näidata. Kondensaatori lühistamisel tekkiv säde võib olla välguna ere ning kostev pauk kõrvulukustav. Suure mahtuvusega kondensaatori tühjendamist läbi oma keha ei tasu südamehaigetel ja nõrganärvilistel üldse proovida.

Laetud kondensaatori energia on aga tegelikult tema plaatide vahelist ruumi täitva elektrivälja energia. Paremini mõistame seda siis, kui arvestame, et laetud kondensaator sarnaneb kõrge täidetud veenõuga. Avades nõu põhjas oleva kraani, tekitame veejoa. Juga suudab teha tööd, näiteks panna liikuma vesiratta. Seda tööd tehakse mitte veenõu, vaid vee raskusjõu potentsiaalse energia arvelt. Viimane on aga oma sügavamalt olemuselt Maa gravitatsioonivälja energia. Täpselt niisamuti ei tee tööd mitte kondensaator, vaid temas sisalduv elektriväli.

Laetud kondensaator suudab teha tööd tänu sellele, et tööd on tehtud ka tema laadimisel. Kuna katetevaheline pinge muutub laadimise käigus, siis ei saa me tehtavat tööd $A$ otsekohe leida valemist 1.23

A = Q U

sest me ei tea, missugust pinget kasutada. Mida suurem on kondensaatori katetele juba kogunenud laeng, seda suurem on pinge plaatide vahel ja seda rohkem tuleb kondensaatori täiendaval laadimisel tööd teha.

Selleks et leida kogu tööd, mis tehakse kondensaatori laadimisel, tuleb katetele antud laengut $Q$ korrutada mitte pinge lõppväärtusega $U$ , vaid laadimisel esineva keskmise pingega. Pinge kondensaatoril kasvab võrdeliselt laenguga alates nullist kuni lõppväärtuseni $U$ . Keskmine pinge kui pool algväärtuse ja lõppväärtuse summast on seega $U / 2$ . Laadimisel tehtud töö või kondensaatoris tekitatud elektrivälja energia avaldub kujul

(2.18)

E_{e} = \frac{C U^{2}}{2}

kus kogulaeng $Q$ on mahtuvuse definitsiooni põhjal asendatud korrutisega $C U$ ning pinge rollis esineb laadimisprotsessi keskmine pinge $U / 2$ .

Oleme leidnud kondensaatori elektrivälja energia sõltuvuse plaatidevahelisest pingest ehk ühe plaadi potentsiaalist teise suhtes. Selle energia võib avaldada ka väljatugevuse kaudu. Kuna

U = E d

siis plaatide kindla vahekauguse $d$ korral on pinge $U$ ja väljatugevus $E$ omavahel võrdelised. Seega on elektrivälja energia võrdeline ka väljatugevuse ruuduga.

Magnetvälja energia

Oleme juba märkinud, et induktiivsuse osa magnetvälja füüsikas sarnaneb mahtuvuse rolliga elektrivälja käsitlemisel. Mõlemad suurused kirjeldavad mingi keha omadusi. Mahtuvus näitab, kui suur on kondensaatori laengu muutus katetevahelise pinge ühikulisel muutumisel, induktiivsus aga näitab, kui suur on magnetvoo muutus juhtmepoolis, kui seda pooli läbiva voolu tugevust ühiku võrra muudetakse.

Kondensaatori ja pooli rollide sarnasuse põhjal on alust arvata, et energiat ei oma mitte ainult laetud kondensaator vaid ka vooluga pool. Samale järeldusele viib meid katse 2.5 punktis 2.6.1. Voolu katkestamine poolis muudab pooli vooluallikaks, mis muundab voolu magnetvälja energiat elektrienergiaks. Just nimelt magnetvälja nõrgenemisel tekib ju voolu (ja seega ka magnetvälja) säilitada püüdev induktsiooni elektromotoorjõud.

Pildil on näha suure induktiivsusega pool, millega tehakse katsega 2.5 analoogiline katse.

Kondensaatoris salvestunud energia sõltub mahtuvusest. Seega võib oodata poolis salvestunud energia samalaadset sõltuvust pooli induktiivsusest. Kuna selle sõltuvuse kuju korrektne tuletamine nõuaks kõrgema matemaatika rakendamist, siis rajame lihtsama käsitluse uuritava elektrinähtuse sarnasusele mingi tuntud mehaanikanähtusega. Teades, et energia on vaid vooluga poolil, võime seostada pooli energiat liikuvate laengukandjate kineetilise energiaga. Mehaanikast hästi tuntud kineetilise energia avaldis

E_{k} = \frac{m v^{2}}{2}

sisaldab keha kiiruse ruutu. Pooli energia valemis peaks sama rolli mängima suurus, mis on võrdeline laengukandjate suunatud liikumise keskmise kiirusega ning määrab ka otseselt pooli poolt tekitatava magnetvoo. Selliseks suuruseks on voolutugevus. Vooluga pooli energia peaks olema võrdeline voolutugevuse ruuduga.

Kineetilise energia avaldises sisaldub aga ka keha mass. Mass kirjeldab keha inertsust kiiruse muutuste suhtes. Mida suurem on mass, seda rohkem aega kulub keha kiiruse muutmiseks. Näiteks võib kiirusega 5 m/s liikuva lapsevankri peatada hetkeliselt. Raske rongi pidurdusteekond on sama kiiruse korral aga juba kümmekond meetrit pikk ja pidurdamine kestab vastavalt kauem.

Juhtmesüsteemi inertsust voolu muutuste suhtes kirjeldab induktiivsus. Seega täidab induktiivsus elektrilaengu liikumisel sama rolli, mida mass mehaanilise liikumise juures. Juhtmepooli energia avaldise koostamisel tuleb kineetilise energia valemis sisalduv mass asendada induktiivsusega. Ühtekokku saame vooluga juhtmepooli energia jaoks valemi

(2.19)

E_{m} = \frac{L I^{2}}{2}

Vooluga pooli energiat võib nimetada magnetvälja energiaks (sellest ka tähis E_m). Pooli energia on ju olemas tänu sellele, et pooli juhtmes liikuvatele laengukandjatele mõjub pooli enda magnetväli. Magnetvälja energia all mõtleme me energiat, mida selles väljas omaks magnetiliselt aktiivne keha.

Kuidas aga sõltub magnetvälja energia magnetinduktsioonist? Teatavasti (valem 1.15 p.1.5.3) on voolutugevus juhtmes ning juhtme poolt tekitatav magnetinduktsioon võrdelised. Kui vooluga pooli magnetvälja energia on võrdeline voolutugevuse ruuduga, siis on ta järelikult võrdeline ka magnetinduktsiooni ruuduga. Võime järeldada, et nii elektri- kui ka magnetnähtustes on välja energia võrdeline välja jõuparameetri (E või B) ruuduga. See väide kehtib elektromagnetvälja kohta tervikuna.

Energeetilises aspektis võime elektromagnetvälja elektri- ja magnetkomponenti kokkuvõtteks võrrelda järgmiselt.

Tabel 2.1

Elektriväli	Magnetväli
Kehade süsteemi võimet tekitada elektrivälja (salvestada laengut) kirjeldab mahtuvus $C = \frac{Δ q}{Δ u}$ selle SI-ühik on farad $1 F = \frac{1 C}{1 V}$	Juhtmesüsteemi võimet tekitada magnetvälja (salvestada voolu) kirjeldab induktiivus $L = - \frac{E_{e}}{\frac{Δ i}{Δ t}} = \frac{Δ Φ}{Δ i}$ selle SI-ühik on henri $1 H = \frac{1 V \cdot 1 s}{1 A}$
Kondensaator on kehade süsteem, mis on loodud kindla mahtuvuse saamiseks	Induktiivpool on juhtmesüsteem, mis on loodud kindla induktiivsuse saamiseks
Elektrivälja energia kondensaatoris $E_{e} = \frac{C U^{2}}{2}$	Magnetvälja energia induktiivpoolis $E_{m} = \frac{L I^{2}}{2}$

Summary

Elektrivälja energia kondensaatoris on leitav valemist

E_{e} = \frac{C U^{2}}{2}

kus $C$ on kondensaatori mahtuvus ja $U$ pinge tema plaatide vahel.

Magnetvälja energia juhtmepoolis on leitav valemist

E_{m} = \frac{L I^{2}}{2}

kus $L$ on juhtmepooli induktiivsus ja $I$ voolutugevus poolis.

Elektromagnetvälja energia on võrdeline välja jõuparameetri (väljatugevuse $E$ või magnetinduktsiooni $B$ ) ruuduga.

Control questions

Kuidas avaldub laetud kondensaatori energia kondensaatori laengu ja mahtuvuse kaudu?

Tooge näiteid füüsikalistest suurustest $y$ , mis avalduvadsuuruste $a$ ja $x$ kaudu kujul

$y = \frac{a x^{2}}{2}$

Alalispinge allikaga ühendatud kondensaatori katete vahekaugust vähendati kaks korda. Kuidas ja kui mitu korda muutusid kondensaatori laeng, väljatugevus ja elektrivälja energia kondensaatoris?

Fotovälklambi kondensaatoril on laeng 0,12 C ja energia 12 J. Kui suur on selle kondensaatori mahtuvus?

Control questions Additional materials

Elektromagnetiline levitatsioon

J.2.34 Pildil on näha suure induktiivsusega pool, millega tehakse katsega 2.4 analoogiline katse. Metallrõngas ei kuku alla, aga vertikaalvarda puudumisel kukuks see "kõrvale" nagu seda teevad ka kaks püsimagnetit, mis on üksteise peale asetatud.

Juba avapildis näidatud MagLev rongi olemasolu tõestab, et elektromagnetiline levitatsioon on võimalik. Siin on aga suuri probleeme.

Esiteks, magnetid tõepoolest ei saa üksteise peal õhus hõljuda, kui palju me nendega ka ei katsetaks (vt ka J.2.34). Nii et tuleb olla kavalam. Võimalusi on mitmeid:

On võimalik ehitada selline magnetite süsteem, mille kohal magnet vurrina pööreldes stabiilselt hõljuma jääb (J.2.35). Aga kõik, kes on üritanud sellist vurri hõljuma saada võivad kinnitada, et see ei ole lihtne.

Esemeid on võimalik märksa stabiilsemalt leviteerima panna, kui asendame püsimagnetid elektromagnetitega ning muudame neid läbivat voolu suuremaks või väiksemaks vastavalt sellele, kas ese on oma soovitud asendist ühele või teisele poole kaldunud. Niimoodi töötab peatüki avalehe fotol olev maakera.

Teeme nüüd ühe mõttelise eksperimendi. Asetame mittemagneetuva elektrijuhi (so elektrijuhi, mis ei tõmbu magneti külge) magneti kohale. Mis juhtub, kui me hakkame seda elektrijuhti magnetitele lähemale nihutama? Lenzi reegel ütleb, et juhis tekivad voolud, mis üritavad magnetvälja muutumise mõju kompenseerida. Juhi ümber tekib püsimagnetile iseloomulik magnetväli, mis üritab juhti tagasi ülespoole lükata. Mida suurem muutus seda suuremad on induktsioonivoolud ja vastav tõukejõud. Elektrijuht peaks siis magneti kohale hõljuma jääma? Miks tavaelus näiteks vasest rõngas neist vooludest välja ei tee ja alla kukub? Põhjus on lihtne – elektrilise takistuse tõttu kustuvad tekkinud induktsioonivoolud väga kiiresti. Aga kui sellist elektrilist takistust ei esineks?

Selgub, et paljud ained muutuvad väga madalatel temperatuuridel ülijuhtideks, elekter liigub neis siis ilma igasuguse takistuseta. Sel juhul kirjeldatud mõtteline eksperiment töötab ka reaalselt – magnetite kohal ülijuhtivasse olekusse viidud juht jääb sinna hõljuma (vt J.2.36).

Nii et Tallinnast Tartu hõljuva rongi ehitamine on põhimõtteliselt lihtne – tuleb võtta diiselrong, eemaldada sellelt rattad, asendada mootor väga suure ülijuhiga, panna ülijuhid ka vagunitesse, asendada siis rööpad tugevate magnetite reaga (vt J.2.36), tõsta rong uuesti rööbaste kohale, jahutada need vedela lämmastiku temperatuurini (-195 kraadi), eemaldada toed ... ja kui me oleme kõige õigesti teinud, siis jääb rong oma magnetrööbaste kohale hõljuma. Aga kuidas selline rong edasi liikuda võiks? Ja pidurdada? Üks variant on paluda reisijatel korraks maha minna ja rongile hoog sisse lükata? Täiesti võimalik, sest selline rong liiguks ilma takistuseta ... aga mägisel maastikul ei pruugi see olla kõige parem mõte. Paneme vedurisse diiselmootori tagasi, rattad ka uuesti alla ning magnetite kõrvale rööpad ning kasutame seda vanamoodsat süsteemi rongi kiirendamiseks ja aeglustamiseks? Palistada magnetrada elektromagnetitega, mis lülitatakse sisse, kui rong läheneb ja välja, kui rong möödunud on ning mis tõmbavad rongi edasi?


J.2.36. Madala temperatuurini jahutatud ülijuht hõljub magnetrelsi koha.	Sama katse demoeksperimendina.

Additional materials

Lõpetuseks - elektromagnetväli

Tulevik näitab, kas elektromagnetiline levitatsioon ka laiemat rakendust leiab. See on küll üsna kindel, et elektriautod tulevikus ikka ratastel sõidavad - magnetrööbaste ehitamine on ikka väga kallis lõbu. Pealegi on tänapäevased rongid võimelised ka rööbastel väga kiiresti sõitma.

Ja kas meil üldse on vaja mööda maad selliste kolossaalsete kiirustega sõita?