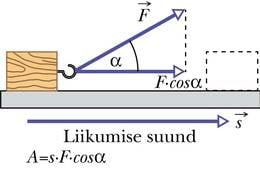
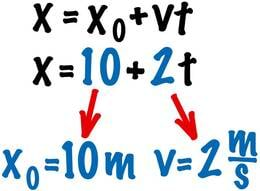Mehaanika
- Saatesõna
- 1 Kinemaatika
- Sissejuhatus
- 1.1 Millega tegeleb mehaanika
- 1.2 Liikumist kirjeldavad suurused
- 1.3 Ühtlase sirgjoonelise liikumise liikumisvõrrand ja -graafik
- 1.4 Muutuv liikumine ja selle kiirus
- 1.5 Ühtlaselt muutuv sirgjooneline liikumine
- 1.6 Ühtlaselt muutuva liikumise liikumisvõrrand ja liikumisgraafik
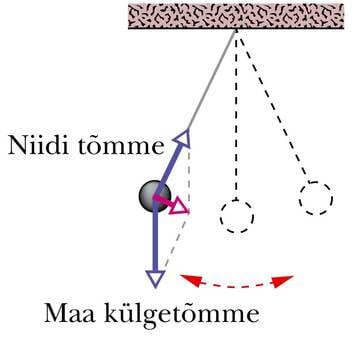
- 1.7 Liikumine Maa külgetõmbe mõjul
- Kokkuvõte
- 2 Dünaamika
- 3 Võnkumised ja lained
- 4 Jäävusseadused mehaanikas
See õpik on koostatud 2010.a. jõustunud riikliku õppekava alusel. Tänaseks on õppekava muutunud ning mehaanika materjal on jagunenud kahe gümnaasiumi kursuse vahel. Uuele õppekavale vastav õpik on siit keskkonnast ka leitav ning me soovitame edaspidi kasutada seda. Uuem õpik on käesoleval hetkel ka tehniliselt paremas seisus – tekstid on üle vaadatud, lisamaterjalid põhimaterjalist eraldatud, kontrollküsimused üle vaadatud jne jms.
Impressum
Autor: Indrek Peil
Toimetaja: Kaido Reivelt
Arvutigraafika: Nils Austa
Kasse joonistab Urmas Nemvalts
Moodsates lõbustusparkides võib leiduda küll palju põnevat, kuid see kõik kahvatub jalgrattatrikkide kõrval, mida sooritati tsirkustes aastatel 1900-1912. Üks kõigi aegade hulljulgemaid rattatrikke sooritati ilmselt Barnumi ja Bailey Tsirkuses Madison Square Gardenis 1905. aastal. Etteaste alguses seisis Ugo Ancillotti oma jalgrattaga ühe ja tema vend Ferdinand teise, vastas asuva kaldtee tipus. Märguande peale alustasid vennad laskumist. Kui Ugo jõudis oma kaldtee järsult ülespoole painutatud osale, visati ta sealt 14 meetri kaugusele järgmisele kaldteele, mis lõppes jällegi kõverdatud osaga. Sealt sooritas Ugo teise, 9 meetri pikkuse õhulennu. Samal ajal kihutas Ferdinand läbi oma kaldtee nõgusa alaosa, sooritas pea alaspidi õhulennu ja maandus teisele painutatud kaldteele. Triki muutis eriti närvekõditavaks asjaolu, et tagurpidi pööratud Ferdinand lendas kõigest meetri või paari kauguselt oma esimest õhulendu sooritava Ugo alt läbi.
Kes meist poleks näinud taevas sõudvaid pilvi, lillelt lillele lendlevat liblikat, mööda teed kihutavat autot, paberile tähti kirjutavat pliiatsiotsa... Kõigi nimetatud kehade ühine tunnus on see, et need liiguvad. Kui eemal lööb välku, jõuab valgussähvatus meieni pea kohe ning mürin veidi hiljem. Meie soontes voolab veri ja sarnane on elektrivool, mis kujutab endast elektronide suunatud liikumist juhtmes. Meie sees liiguvad aatomid ja aatomite sees liiguvad elektronid. Liikumine on kõikjal. Liikumine on looduse kõige üldisem nähtus.
Füüsika uurib loodust ja sealhulgas ka liikumist. Füüsika see haru, mis uurib liikumist ja selle muutumise põhjusi, kannab nime mehaanika. Mehaanika tekkis antiikajal, mil hakati rasket käsitsitööd kergemaks muutvaid masinaid ehitama. Et masinaid täiustada, tuli lähemalt tundma õppida eelkõige neid nähtusi, mis masinates aset leidsid. Tuli uurida liikumist ning liikumist mõjutavaid tegureid. Sõna „mehaanika“ ongi tulnud kreeka keelest (μηχανικη — masinatesse puutuv).
Tänapäeval ei piirdu mehaanika ainult masinate ehitamisega, vaid uurib liikumist üldisemalt. Vist igaüks meist on planeerinud mõnda retke ja arvutanud, millal kuhugi pärale jõuab. Sarnane, kuid märgatavalt keerulisem ülesanne on välja arvutada, kuhu jõuab planeetide mõju all olev kosmoseaparaat paari aasta pärast. See ongi mehaanika põhiülesanne — leida keha asukoht mis tahes ajahetkel.
Mehaanika saab jaotada kolmeks haruks:
Kinemaatika (κινημα — kreeka k liigutus, liikumine) uurib ja kirjeldab kehade liikumist ruumis. Seejuures pole oluline, mis on liikumise põhjuseks. Näiteks saab kinemaatikaseaduste abil arvutada, kui kõrgele lendab otse üles visatud kivi.
Dünaamika (δυναμη — kreeka k jõud, vägi) uurib, kuidas liikumine tekib ning erinevate mõjude tagajärjel muutub. Näiteks saab arvutada, millise kiiruse saavutab vihmapiisk, mida kiirendab Maa külgetõmme ja pidurdab õhutakistus.
Staatika (στατικη — kreeka k püsiv, muutumatu)uurib, mis tingimustel liikumine ei muutu, st keha on tasakaalus. Staatika võimaldab näiteks välja arvutada, mitu inimest võib vaatetorni ronida, ilma et see ümber kukuks.
Mille järgi tunneme ära, et keha liigub? Algul käes olnud vaas asub pärast mahapillamist põrandal. Sadamast väljunud laev on tunni aja pärast mitu miili eemal. Kui kellaosuti on number kahe kohal, siis mõni aeg hiljem on see juba viie peal. Vaas, laev ja osuti on liikunud – nad on oma asukohta muutnud.
Kõikide liikumiste ühine tunnus on see, et keha asukoht muutub. Seejuures on vaja liikumise kindlakstegemiseks ja uurimiseks mõnda teist keha, mille suhtes me asukohta määrame. Liikumine toimub alati millegi suhtes, st liikumine on suhteline. Asukoha muutumine võtab aega. Pole võimalik, et puult kukkuv õun on mingil hetkel oksa küljes ja siis kohe juba mujal. Sel juhul oleks õun ju mitmes kohas korraga! Liikumine on alati seotud ajaga. Seega võime öelda, et liikumine on keha asukoha muutumine teiste kehade suhtes mingi aja jooksul.
Liikumise suhtelisus tähendab seda, et erinevate kehade suhtes võib liikumine väga erinev olla. Näiteks meile tundub, nagu Maa oleks paigal ja Päike tiirleks ümber meie. Samas teame, et Maa tegelikult pöörleb ümber oma telje ja tiirleb samas suure kiirusega (30 km/s) ümber Päikese.
Kuna liikumine on asukoha muutumine, siis tuleb liikumise kirjeldamist alustada keha asukoha määramisest. Mida aga lugeda näiteks 20 meetri pikkuse veoauto asukohaks? Kas eesmise numbrimärgi, juhi ninaotsa, koorma keskpunkti või hoopis haagisekonksu asukohta? Tegelikult polegi ühest linnast teise liikumise kirjeldamisel auto mõõtmed ja kuju olulised. Suurt veokit võime kahe linna vahemaaga võrreldes ette kujutada lihtsalt ühe punktina. Seda punkti nimetatakse punktmassiks.
Kui me edaspidi räägime keha liikumisest, siis mõtleme selle all enamasti punktmassi liikumist. Sellist keha, mille mõõtmed võib antud liikumistingimustes arvestamata jätta nimetatakse punktmassiks. Kehaks võetakse punkt, mille mass on sama suur kui keha mass. Kuju ja mõõtmed jäetakse lihtsuse mõttes arvestamata. Tegemist on reaalse keha lihtsustuse ehk füüsikalise mudeliga.
Keha ei või siiski igas olukorras punktmassiks lugeda. Näiteks praamile sõitmisel on auto mõõtmed vägagi olulised.
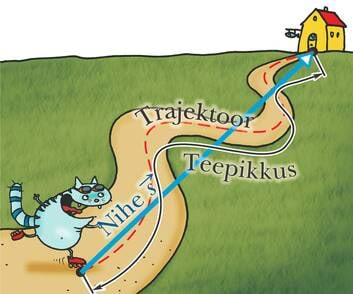
Need punktid, mida liikuv keha (punktmass) läbib, moodustavad alati mingi pideva joone.Kujutletavat kontuuri, mida mööda keha liigub, nimetatakse trajektooriks. Liikumistrajektoori ei tohi samastada teega! Auto trajektoor on kujuteldav joon, maantee aga teetammist ja teekattest koosnev keha.
Liikumisi saab liigitada trajektoori kuju järgi. Sirge trajektoori korral on liikumine sirgjooneline. Kui trajektoor pole sirge, siis on liikumine kõverjooneline.
Teiseks saab eristada ühtlast ja mitteühtlast liikumist. Ühtlane on selline liikumine, mille korral mistahes võrdsetes ajavahemikes muutub keha asukoht sama palju. Muul juhul on liikumine mitteühtlane. Näiteks laskub avatud langevarjuga parašütist enne maandumist ühtlaselt ja maapinnale jõudmisel pidurdudes mitteühtlaselt.
Veel eristatakse kulgevat ja pöörlevat liikumist. Kulgev on näiteks õmblusmasinanõela üles-alla liikumine. Kogu liikumise kestel jääb nõel oma esialgsete asenditega paralleelseks. Kulgevalt liikuva keha kõikide punktide trajektoorid on sama kujuga. Kulgeva liikumise korral võib kehasid käsitleda punktmassidena. Pöörleva liikumise korral liiguvad keha erinevad punktid mööda erineva raadiusega ringjooni. Näiteks kellaosuti üks ots liigub mööda suurt ringjoont ja teine ots on hoopis paigal. Pöörlemise korral ei tohi keha punktmassiks lugeda, sest siin on kuju ja mõõtmed olulised.
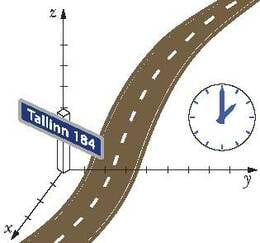
Kuna liikumine on suhteline, tuleb välja valida mingi keha, mille suhtes me liikumist jälgime. Keha, mille suhtes liikumist vaadeldakse, nimetatakse taustkehaks. Taustkehaks võib valida mistahes sobiva objekti: kilomeetriposti, mäetipu, raudteevaguni, Päikese jne. Tingimuseks on see, et liikumine taustkeha suhtes ikka toimuks ja poleks samas liiga keeruline.
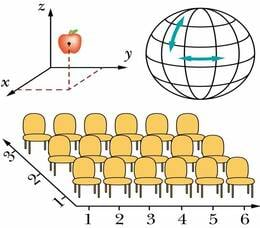
Füüsika on täppisteadus, mis kirjeldab objekte ja nähtusi arvude abil. Arvude abil saab kirjeldada ka liikuva keha asukohta. Keha asukoha kirjeldamiseks kasutatavaid arve nimetatakse koordinaatideks. Koordinaatide määramiseks valitakse mingid kindlad suunad, milles asukohta taustkeha suhtes mõõdetakse. Samuti lepitakse kokku mõõtühikud. Kokkulepitud mõõtmissuunad, mõõtühikud ja asukoha mõõtmise eeskirjad moodustavad koordinaadistiku ehk koordinaatsüsteemi.
Matemaatikas ja füüsikas kasutatakse enamasti ristkoordinaadistikku. Samuti on kõigile tuttav maakaartidel kasutatav geograafiline koordinaadistik. Teatrisaalis istekoha leidmiseks loodud istmeridade ja kohanumbrite süsteem on samuti koordinaatsüsteem.
Peale asukoha määramise tuleb liikumise kirjeldamisel arvestada ka aega. Selleks tuleb kokku leppida aja mõõtmise alghetk ja mõõtühik. Taustkeha, sellega seotud koordinaadistik ja ajamõõtmise süsteem moodustavad taustsüsteemi.
Kui tahame liikumist kirjeldada, on vaja mõõta keha asukoha muutu. Selleks on erinevaid võimalusi.
Kui mõõdame alg- ja lõppasukoha vahekauguse täpselt piki trajektoori, saame teepikkuse. Teepikkust tähistatakse valemites tähega l (longitudo — ladina k pikkus).
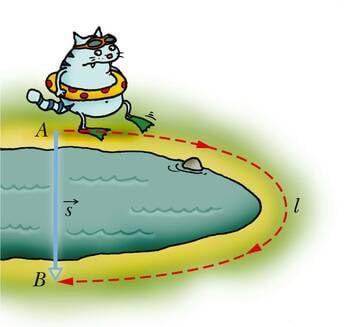
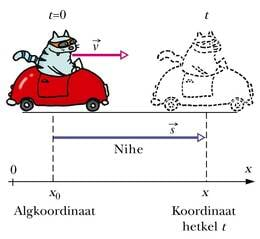
Mõõtes kaugust aga mööda sirgjoont ehk linnulennul, saadakse nihe. Nihkeks nimetatakse keha algasukohast lõppasukohta suunatud sirglõiku.
Erinevalt teepikkusest, mida iseloomustab vaid arv, on nihkel peale pikkuse ka suund. Seega on nihe vektoriaalne suurus. Nihkevektori tähiseks valemites ja joonistel on (shift — inglise k nihe).
Teepikkus l ja nihke pikkus s pole tavaliselt võrdsed. Näiteks kui õpilane jõuab pärast kooli koju, on vaatamata päeva kestel läbitud suurele teepikkusele tema nihe null. Teepikkus ja nihe on võrdsed vaid sirgoonelisel muutumatu suunaga liikumisel.
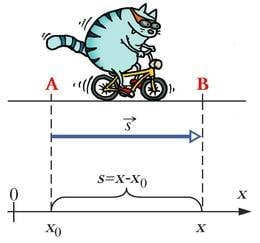
Nihet saab avaldada keha alg- ja lõppasukoha koordinaatide kaudu. Kui liikumine toimub piki x-telge ning keha alg- ja lõppasukoha koordinaatide tähisteks on vastavalt x0 ja x, saame nihke pikkuseks
Sümboliga Δ (loe: delta) tähistatakse suuruse lõpp- ja algväärtuse vahet ehk muutu.
Teepikkuse ja nihke mõõtühikuks on rahvusvahelises mõõtühikute süsteemis 1 meeter. Pikkade või lühikeste teepikkuste ja nihete korral kasutatakse kümnendeesliideseid. Näiteks 1000 m = 1 km, 1/100 m = 1 cm.
Mehaanika põhiülesanne on keha asukoha määramine mis tahes ajahetkel.
Kõige lihtsam on asukohta arvutada lihtsaima liikumise korral, milleks on ühtlane sirgjooneline liikumine.
Ühtlaseks sirgjooneliseks liikumiseks nimetatakse sirgjoonelist liikumist, mille korral mis tahes võrdsetes ajavahemikes läbitakse võrdsed teepikkused.
Niisuguse liikumise suund ei muutu ja võrdsete teepikkuste läbimisel sooritatud nihked on võrdsed. Nihke kaudu defineerimisel nimetatakse ühtlaseks sirgjooneliseks liikumiseks sellist liikumist, mille korral mis tahes võrdsetes ajavahemikes sooritatakse võrdsed nihked. Trajektoori kuju pole sel juhul vaja eraldi mainida.
Millised on sellise liikumise näited? Ideaalselt ühtlast sirgjoonelist liikumist me looduses tegelikult ei leiagi. Enam-vähem saame selliseks lugeda näiteks rongisõidu sirgel teel, kuigi raudtee pole Maa kumeruse tõttu päris sirge ja ükski rong ei saa sõita igavesti peatumata.
Sellegipoolest võib paljudel juhtudel väikesed kõrvalekalded ideaalist arvestamata jätta ning liikumist siiski ühtlaseks sirgjooneliseks pidada. Lihtsustuste tegemine tähendab füüsikas mudeli kasutamist. Ühtlane sirgjooneline liikumine on lihtsaima liikumise mudel.
Nii võib sirgjoonelise liikumise mudeli abil kirjeldada sirgel maanteel kihutava auto, ujuva sportlase ja laskuva langevarjuri liikumist.
Liikumine on keha asukoha muutumine mingi aja jooksul. Muutumise aeg võib seejuures olla erinev. Näiteks jalgrattur jõuab ühest asulast teise varem kui samal ajal liikumist alustanud jalakäija. Sel puhul öeldakse, et jalgratturi kiirus on jalakäija omast suurem. Kiirus näitab, kui suure teepikkuse läbib keha ajaühiku jooksul. Valemites tähistatakse kiiruse arvväärtust tähega v (velocitas — ladina k kiirus). Ühtlasel sirgjoonelisel liikumisel on teepikkus võrdne nihke pikkusega ning sel juhul võime öelda, et kiirus on võrdne ajaühikus sooritatud nihkega. Kiiruse leidmiseks tuleb sooritatud nihe jagada liikumisajaga t:
Tähis viitab sellele, et kiirus on suunaga ehk vektoriaalne suurus.
Kui suund pole liikumise kirjeldamisel oluline, võime sama valemit kasutada skalaarkujul:
Kiiruse mõõtühik SI-s on 1 m/s ehk 1 meeter sekundis.
Tuleb tähele panna, et valemites (1.2 ) ja (1.3 ) ei tähista t mitte ühte ajahetke, vaid liikumise kestust. Tegemist on lõpp- ja algpunktis paiknemise hetkede vahega, mida väljendatakse kreeka tähe delta (Δ) abil:
Siin tähistab t0 alghetke ja t lõpphetke. Enamasti võetakse alghetk nulliks ja siis on liikumisaeg Δt = t. Seda aega t ongi kiiruse valemites (1.2 ) ja (1.3 ) silmas peetud.
Võttes nüüd ajavahemiku tähiseks Δt ja vastavalt valemile (1.1 ) nihke tähiseks Δx, saame kiiruse valemile veel ühe kuju:
Liikumine on nähtus, milles keha asukoht aja jooksul muutub. Erinevatel ajahetkedel on asukoht erinev, st keha koordinaadid sõltuvad ajast. Ajast sõltuvad ka kogu liikumise kestel läbitud teepikkus ning sooritatud nihe. Muutuva liikumise korral võivad ajast sõltuda veel ka kiirus ja kiirendus. Liikumisnähtus on kirjeldatav seda iseloomustavate suuruste ajast sõltuvuste kaudu.
Sõltuvusi saab väljendada analüütiliselt ja graafiliselt. Analüütilise meetodi korral kirjeldatakse sõltuvust matemaatiliste avaldiste abil. Avaldiste kaudu esitatud sõltuvusi on võimalik matemaatiliselt lähemalt uurida ja seeläbi lisainfot saada. Graafiline meetod kasutab liikumise kirjeldamiseks - nagu nimigi ütleb - graafikuid. Graafikud ei võimalda küll liikumist iseloomustavaid suurusi neilt otse välja lugeda, kuid annavad sõltuvustest seevastu ülevaatlikuma pildi.
Mehaanika põhiülesanne on määrata keha asukoht mis tahes ajahetkel, st leida keha koordinaatide sõltuvus ajast. Kui paneme selle sõltuvuse kirja matemaatilise avaldise abil, saame liikumisvõrrandi. Liikumisvõrrandiks nimetatakse matemaatilist avaldist, mis näitab keha koordinaatide sõltuvust ajast.
Inimese poolt tajutav ruum on kolmemõõtmeline — ruumil ja igal selles asetseval kehal on pikkus, laius ja kõrgus. Seepärast on keha asukoha määramiseks üldjuhul vaja kolme koordinaati. Juhul, kui keha liigub mööda kindlat pinda, piisab kahest koordinaadist. Merepinnal seilava laeva asukoha saab kirja panna kahe geograafilise koordinaadi — pikkus- ja laiuskraadi abil. Veduri asukoha annab kätte vaid üks arv, näiteks kaugus algjaamast, kuna ilmselt püsib vedur relssidel.
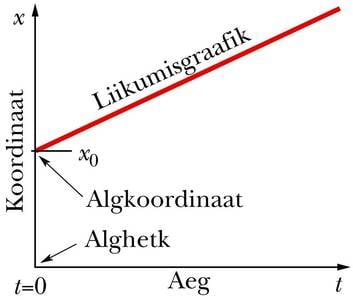
Sirgjoonelise liikumise kirjeldamiseks piisab ühest sirgest koordinaatteljest, mille suund on mõistlik valida piki liikumise trajektoori. Koordinaadi tähiseks võetakse tavaliselt x. Selle punkti koordinaati, kus keha asub ajamõõtmise alghetkel, nimetatakse algkoordinaadiks ja tähistatakse sümboliga x0.
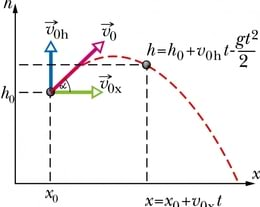
Kirjeldame näiteks auto sõitmist: alghetkel t = 0 on selle koordinaat x0. Aja t jooksul nihkub auto edasi ning koordinaat muutub nihke pikkuse s võrra suuremaks (vt joonist). Koordinaadi uus väärtus x on seega
Teame, et aja t jooksul sooritatava nihke pikkus sõltub kiirusest. Ühtlase liikumise kiiruse valemist (1.3 ) saame nihke pikkuse avaldada kui s = vt. Paigutades selle nihke avaldise koordinaadi valemisse (1.6 ) tulemuseks seos, mis näitab auto koordinaadi sõltuvust ajast:
See ongi ühtlaselt sirgjooneliselt liikuva keha liikumisvõrrandi üldkuju.
Konkreetsete ülesannete puhul on x0 ja v kohal võrrandis kindlad arvulised väärtused. Näiteks võrrand x = 10 + 2t väljendab liikumist keha jaoks, mille algkoordinaat on 10 m ning kiirus 2 m/s. Kui soovime teada, kus keha 5 sekundi pärast asub, võtame aja t väärtuseks 5 s ning arvutame, et x = 10 + 2•5 = 20 (m). Liikumisvõrrandi abil saab leida keha asukoha mis tahes ajahetkel. Suurused x0 ja v võivad omada nii positiivseid kui ka negatiivseid väärtusi. Negatiivne kiirus tähendab seda, et keha liigub koordinaattelje negatiivses suunas. Rõhutamaks seda, et sirgel trajektooril saab liikumine toimuda kahes suunas, kirjutatakse liikumisvõrrand mõnikord kujul
Ühe suuruse teisest sõltuvuse graafiku saamiseks tuleb joonestada kaks ristuvat telge, horisontaalsele teljele märkida muutuv suurus ning vertikaalsele suurus, mis muutujast sõltub. Matemaatikas oleme harjunud, et horisontaaltelje tähiseks võetakse x ja vertikaalse telje tähiseks y. Füüsikas kasutatakse teisi tähiseid.
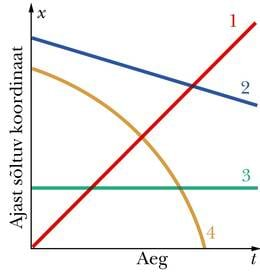
Liikumisgraafikuks nimetatakse graafikut, mis näitab keha asukoha (koordinaadi x) sõltuvust ajast. Liikumisgraafiku horisontaalteljele kantakse aeg t ja püstteljele ajast sõltuv koordinaat x. Erinevat liiki ja erineva suunaga liikumiste graafikud on erineva kujuga.
Ühtlase liikumise korral muutub koordinaat iga sekundiga sama palju ning seepärast on graafikuks sirgjoon. Sirge saab välja joonestada kahe punkti järgi ja seega piisab ühtlase liikumise graafiku saamiseks, kui teame keha asukohta kahel erineval ajahetkel.
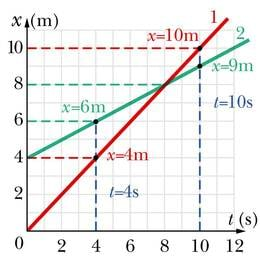
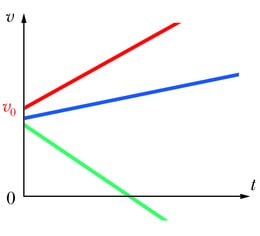
Võrdleme kahe ühtlaselt liikuva keha liikumisgraafikuid. Oletame, et hetkel t1 = 4 s on nende koordinaadid 4 m ja 6 m ning hetkel t2 = 10 s vastavalt 10 m ja 9 m. Kui graafikud välja joonestada (vt joonist), siis näeme, et need on erineva tõusuga. Ajavahemik kahe vaatlusaluse hetke vahel oli Δt = 10 – 4 = 6 sekundit. Järsema graafikuga keha koordinaat muutus selle ajaga Δx1= 10 – 4 = 6 m võrra. Järelikult on kiirus 6 m/ 6 s = 1 m/s. Teise keha koordinaadi muuduks saame Δx2= 9 – 6 = 3 m ja kiiruseks 3 m/ 6 s = 0,5 m/s.
Jõudsime olulise tulemuseni — liikumisgraafiku tõus näitab liikumise kiirust. Mida suurem kiirus, seda suurem on graafiku tõus. Kui graafik langeb ja tõus on negatiivne, siis on ka kiirus negatiivne, st liikumise suund on koordinaattelje positiivse suunaga vastupidine.
Teiseks saab liikumisgraafikult välja lugeda keha algkoordinaadi. Koordinaati näitav püstine graafikutelg asub just ajatelje nullkohal. Järelikult see punkt, kus graafiku joon püstist koordinaattelge lõikab, vastabki algkoordinaadile. Eespool toodud näites koostatud graafikutelt näeme, et kiiremini liikuva keha algkoordinaat on 0 ja aeglasema oma 4 m.
Graafiku võib koostada ka nii, et püstteljele kantakse koordinaadi asemel keha poolt sooritatud nihke pikkus või teepikkus. Selline graafik on kujult liikumisgraafiku sarnane, kuid algab alati nihke või teepikkuse nullist — alghetkel pole ju keha veel jõudnud edasi nihkuda.
Kui liikumisgraafik pole sirge ja selle tõus muutub, siis järelikult muutub ka liikumise kiirus ja tegemist on muutuva liikumisega.
Nagu juba teame, saab liikumine olla kas ühtlane või mitteühtlane. Ühtlase liikumise korral sooritab keha mis tahes võrdsete ajavahemike kestel võrdsed nihked.
Sel juhul annab valem
kiiruse jaoks kogu aeg sama tulemuse ja kiirus on järelikult muutumatu. Pole oluline, kas kiiruse arvutamiseks mõõdetakse kogu tee või ainult mingi selle osa nihke pikkus ja läbimise aeg.
Mitteühtlasel liikumisel ei pruugi võrdsete ajavahemike kestel sooritatud nihked trajektoori erinevates paikades ühesugused olla ja järelikult kiirus muutub. Sellise muutuva liikumise iseloomustamiseks ei saa leida kiirust ühtlase liikumise valemi järgi, kuna tulemus sõltub nüüd mõõtmiseks valitud ajavahemikust ning teelõigust.
Seepärast kasutatakse muutuva liikumise iseloomustamiseks teistmoodi defineeritud kiirust. Selleks on kaks võimalust: keskmine kiirus ja hetkkiirus.
Kõik me oleme sõitnud liinibussiga ja teame, et suurema osa ajast liigub see üsna nobedasti, kuid auklikel teelõikudel aeglustab sõitu ning peatustes ja punase fooritule taga seisab hoopis paigal. Mõõtes kogu läbitud teepikkuse ja jagades selle kulunud ajaga, saame mingi kiiruse. Arvutatu pole aga kiirus, millega buss liinil tegelikult sõitis. Kiirus muutus suures vahemikus ega pruukinud nimetatud väärtust üldse omadagi. Ometi iseloomustab kogu teepikkuse ja liikumisaja kaudu arvutatud kiirus bussi sõitu ja lubab ligikaudselt välja arvutada, millal kuhugi peatusesse välja jõutakse.
Selliselt arvutatud kiirust nimetatakse keskmiseks kiiruseks. Keskmine kiirus on võrdne kogu läbitud teepikkuse ja selleks kulunud koguaja jagatisega. Keskmise kiiruse tähiseks on vk ja mõõtühikuks 1 m/s.
Igasuguste sõidugraafikute ja matkaplaanide koostamisel, liiklusteede läbilaskevõime hindamisel ja muudel sarnastel juhtudel võetakse aluseks just liikumise keskmine kiirus.
Märkused
- Keskmise kiiruse leidmisel ei tohi lasta end eksitada mõiste kõlalisest sarnasusest sagedasti kasutatava aritmeetilise keskmisega. Keskmist kiirust ei saa leida aritmeetilise keskmisena, vaid seda tuleb teha ikka kogu teepikkuse ja koguaja kaudu!
- Keskmise kiiruse arvutamiseks ei kasutata mitte nihke pikkust vaid ikka teepikkust. Kui alg- ja lõppasukohad langevad kokku ja nihe on seetõttu null, ei saa ju ometi väita, et terve päeva ringi sõitnud ja garaaži naasnud bussi keskmine kiirus oli null.
- Kasutusel on ka kiiruste statistilise keskmise mõiste. Sel juhul on uurimise all palju erinevate kiirustega liikuvaid kehi ja keskmist väärtust hinnatakse statistikaseadustele tuginedes. Nii leitakse näiteks elutoas ringisebivate õhumolekulide keskmine kiirus.
Kõik me oleme näinud sõidukite liikumiskiirust reguleerivaid teemärke ja teame, et politseinikud mõõdavad teedel sagedasti kiirust. Ohtlikematele teelõikudele on isegi automaatselt töötavaid kiiruskaameraid üles seatud. Autojuhtidel aitab kiiruspiiranguid järgida armatuurlaual paiknev spidomeeter (speed [spi:d] — inglise k kiirus) ja sarnase kiirusemõõtja saab monteerida isegi jalgrattale.
Mis liiki kiirusega siin tegemist on? Vaevalt, et keskmisega, sest kuidas saaks liiklusmärgi ülespanija või politseinik arvestada sõidukijuhi juba asetleidnud ja veel vähem alles eel olevaid kihutamisi ja seisakuid! Pealegi ei oma juba toimunud ja tulevane liikumine konkreetse hetke liiklusolukorras mingit tähtsust. Oluline on ju see, kuidas liigutakse selles paigas just sellel ajahetkel. Siin kirjeldatud juhtudel kasutatav kiirus on hetkkiirus.
Hetkkiiruse nimetus viitab sellele, et mõeldud on kiirust mingil konkreetsel ajahetkel. Samas on hetke kestus null ja selle kestel läbitav teepikkus samuti null. Püüdes nüüd kiirust arvutada, jõuame välja võimatu tehteni, mida matemaatikud tunnevad kui 0/0 määramatust. Mis ikkagi hetkkiirus on ja kuidas seda mõõdetakse?
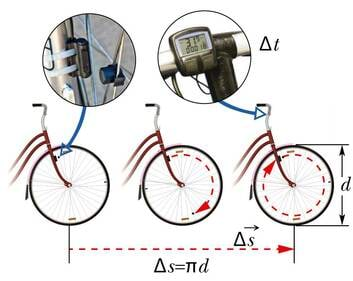
Jalgratta kiirusemõõtja kujutab endast pisikest kellaga arvutit, mille külge on ühendatud väike magnetvälja muutusi tajuv andur. Andur paikneb esiratta kõrval nii, et kodara külge kinnitatud magnet ratta iga täisringi järel andurile oma möödumisest teada annab. Arvuti kell mõõdab ratta täisringi tegemiseks kulunud aja ja lähtudes mälusse sisestatud ratta läbimõõdu väärtusest, leiab ühe rattaringi jooksul sooritatud nihke pikkuse ning arvutab välja selle lühikese teejupikese läbimise keskmise kiiruse.
Hetkkiiruse all mõistetakse küll keha liikumiskiirust kindlal ajahetkel, aga selle väärtust saab hinnata siiski mitte hetke, vaid lühikese ajavahemiku kestel leitava keskmise kiirusena.
Hetkkiiruse tähistamiseks kasutatakse sarnaselt ühtlase liikumise kiirusega sümbolit v. Kui võtame lühikese ajavahemiku, mille kestel kiirus ei jõua oluliselt muutuda, tähiseks Δt ja selle aja jooksul sooritatud nihke pikkuse tähiseks Δs, saame hetkkiiruse arvutusvalemiks
Mida lühem on uuritav ajavahemik Δt, seda täpsemini saab hetkkiiruse teada, sest seda vähem jõuab kiirus selle ajaga muutuda. Mitteühtlase liikumise hetkkiirus on sarnaselt ühtlase liikumise kiirusega vektoriaalne ehk suunaga suurus. Kui liikumise kirjeldamisel on ka suund oluline, tuleb hetkkiiruse valemit kasutada vektorkujul.
Muutuv liikumine võib olla väga erinev, sest kiirus saab muutuda mitmesugustel viisidel — pidevalt kasvada, olla vahepeal muutumatu, jälle kasvada, kuid aeglasemalt, ja siis hoopis kahaneda... Tihti kohtame aga sellist liikumist, mille kiirus kasvab või kahaneb mis tahes võrdsetes ajavahemikes ühepalju.
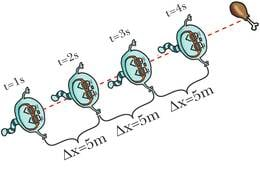
Sellist liikumist, mille kiirus muutub mistahes võrdsete ajavahemike jooksul ühesuguse väärtuse võrra, nimetatakse ühtlaselt muutuvaks liikumiseks. Näiteks kasvab õhutakistuseta kukkuva kivi kiirus iga sekundiga ligikaudu 10 m/s võrra. Käest lahti lastud kivi saavutab ühe sekundiga kiiruse 10 m/s, teise sekundi lõpuks 20 m/s, kolmanda lõpuks 30 m/s jne. Samas on vabalt kukkuva kivi trajektooriks sirgjoon ja seega on tegemist ühtlaselt muutuva sirgjoonelise liikumisega.
Kukkuva kivi kiirus ei kasva muutumatuna siiski lõputult, kuna langemise käigus ei jää endiseks ei liikumist mõjutav kaugus Maast ega ka õhutakistus. Tegelikult looduses me ideaalset ühtlaselt muutuvat sirgjoonelist liikumist ei kohtagi. Sellist liikumist saab vaid ette kujutada ja matemaatika meetoditega kirjeldada. Tegemist on teatud liikumise füüsikalise mudeliga. Kuigi puhast sellist liikumist olemas pole, saab nimetatud mudeli juures väljaselgitatud lihtsaid seaduspärasusi siiski suurepäraselt sarnaste reaalsete liikumiste uurimisel kasutada.
Näiteks võib teatud piirides ühtlaselt muutuvaks sirgjooneliseks liikumiseks pidada suusahüppaja laskumist hüppemäel, hokilitri libisemist jääl, kaubarongi liikumahakkamist ning otse üles visatud palli lendu.
Kui jälgida foori taga ootavaid sõidukeid, siis võib tähele panna, et rohelise tule süttimisel ei hakka need kõik liikuma ühtmoodi. Sõiduautod võtavad paigalt ja saavutavad lubatud maksimumkiiruse üsna kärmesti, kuid pungil täis liinibussil kulub sellise kiiruse saavutamiseks märgatavalt rohkem aega. Ka aeglustumine võib olla erinev. Kui turvavarustuse katsetamisel peatub suurel kiirusel vastu müüri paiskuv auto peaaegu silmapilkselt, siis palju väiksema kiirusega sõitva kaubarongi peatamine kestab mitu minutit. Liikumise muutumine võib toimuda erineva kiirusega.
Ülaltoodud näited viitavad sellele, et muutuvat liikumist kirjeldab peale keskmise ja hetkkiiruse ka hetkkiiruse muutumise kiirus. Tegemist on liikumist iseloomustava omadusega, mida saab mõõta ja arvuliselt väljendada, seega on tegemist füüsikalise suurusega. Füüsikud on kokku leppinud, et seda kiiruse muutumise kiirust väljendavat suurust nimetatakse kiirenduseks.
Mis tahes suuruse muutumiskiirust saab määrata nii, et leitakse, kui palju see suurus ühe ajaühiku jooksul muutuda jõuab. Selleks tuleb muutuse suurus jagada muutumiseks kulunud ajaühikute arvuga ehk muutumise ajaga. Samamoodi tuleb toimida ka kiiruse muutumise kiiruse iseloomustamisel. Seega võime kiirenduseks nimetada liikumist iseloomustavat suurust, mis on võrdne kiiruse muudu ja selle muutumise aja jagatisega. See definitsioon on matemaatiline, kuna kasutab sõnastuses matemaatilisi tehteid. Samaväärselt võime kasutada ka füüsikalist definitsiooni: kiirenduseks nimetatakse füüsikalist suurust, mis on võrdne kiiruse muuduga ajaühikus.
Kiirenduse valemi kirjapanekuks peame kokku leppima sobivad tähistused. Tähistame alghetke (hetke, mil kiiruse muutumine algab) sümboliga t0 = 0. Kui võtame muutumise lõpphetke tähiseks t, siis on muutumise kestus võrdne ajavahemikuga Δt = t - t0 = t (sest t0 =0). Nimetame kiiruse, mida keha omas muutumise alguses, algkiiruseks ja tähistame selle vektoriaalse suuruse sümboliga . Kiirus muutumise lõpus olgu lõppkiirus . Liikumiskiiruse muut on selliste tähistuste puhul . Kiirenduse tähisena kasutatakse sümbolit (acceleration — ingl k kiirendus). Nooleke tähe kohal näitab mäletatavasti seda, et tegu on suunaga suuruse ehk vektoriga. Kuna definitsiooni järgi on kiirendus võrdne kiiruse muudu ja kiiruse muutumise aja jagatisega, saame kiirenduse valemiks
Kiirenduse valemi saab esitada ka skalaarkujul:
Et kiiruse muudu mõõtühik on sarnaselt kiiruse ühikuga 1 m/s ja ajavahemiku ühik 1 s, saame kiirenduse mõõtühikuks nende jagatise , mida loetakse kui 1 meeter sekundi ruudu kohta.
Kui on teada algkiirus ja kiirendus, on ühtlaselt muutuva liikumise korral lihtne leida keha kiirust mis tahes ajahetkel. Selleks tuleb kiirus avaldada kiirenduse definitsioonivalemitest (1.11 ) või (1.11' ):
või
Alghetkel, mil t = 0, annab valem kiiruseks v = v0 ehk algkiiruse. Muudel momentidel on liidetav at sõltuvalt kiirenduse väärtusest kas positiivne või negatiivne ja kiirus võib kas kasvada või kahaneda. Kui kiirendus on algkiirusega võrreldes vastupidiselt suunatud, siis a < 0 ja võib juhtuda olukord, et ka kiirus muutub negatiivseks. See tähendab seda, et kiiruse suund on algkiirusega võrreldes vastupidine ja keha on hakanud kiirenevalt tagasi liikuma.
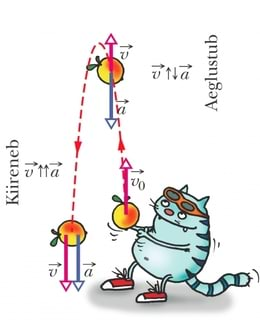
Nii juhtub näiteks ülesvisatud õunaga. Tõusul on liikumine aeglustuv, kuid langemisel muutub kiirenevaks. Langemisel on liikumise suund esialgsega vastupidine ja kiirendusega samasuunaline. Kui kiirendus on kiirusega samasuunaline, on liikumine kiirenev ning vastassuunalise kiirenduse korral aeglustuv:
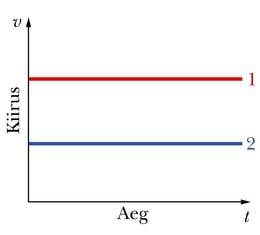
Kui liikumisgraafik näitab keha koordinaadi sõltuvust ajast, siis kiiruse graafik kiiruse sõltuvust ajast. Kiiruse graafiku püstteljele kantakse kiiruse väärtused ja horisontaalteljele sarnaselt liikumisgraafikuga aeg. Kõige lihtsam kiiruse graafik on ühtlasel liikumisel. Kuna ühtlasel liikumisel kiirus ei muutu, on selle väärtus igal ajahetkel sama ja graafikuks on horisontaalne sirgjoon (vt joonist). Kiirema liikumise korral asub graafik teljestikus kõrgemal ja aeglasema korral madalamal positsioonil.
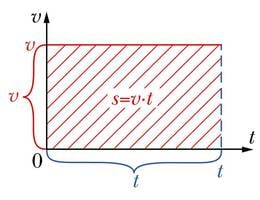
Kuigi kiiruse graafikul on näidatud vaid kiiruse sõltuvus ajast, saab selle abil ka sooritatud nihke pikkuse leida. Vaatame ühtlase liikumise graafikut. Kui märgime sellel ära ajavahemiku 0 kuni t, saame ristküliku, mille külgede pikkusteks püstsihis on kiirus v ja horisontaalsihis aeg t. Selle ristküliku pindala on võrdne külgede pikkuste korrutisega ehk v•t. Kiiruse ja liikumiskorrutise korrutis on aga võrdne sooritatud nihke pikkusega: s = vt. Jõudsime olulise tulemuseni: kiiruse graafiku alla jääv pindala on võrdne keha poolt sooritatud nihke pikkusega. See kehtib mitte ainult ühtlase, vaid ka muutuva liikumise korral.
Ühtlaselt muutuva liikumise korral muutub kiirus võrdsetes ajavahemikes sama palju ja kiiruse graafikuks on tõusev või langev sirge. Graafiku tõus või langus on seda suurem, mida kiiremini kiirus muutub ehk mida suurem on kiirendus. Tõusva graafiku korral liikumine kiireneb, langeva korral aeglustub. Kui graafik on ajateljest allpool, on kiirus negatiivne, liikumine toimub koordinaattelje negatiivses suunas ning langev graafik tähistab sel juhul kiiruse kasvamist. Graafiku lõikepunkt püstise kiiruse teljega annab kiiruse hetkel t = 0 ehk algkiiruse v0. Kui graafik pole sirge, on tegemist mitteühtlaselt muutuva liikumisega.
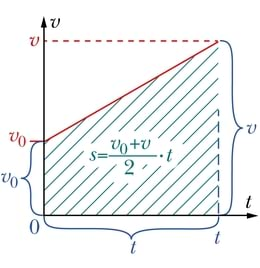
Selleks, et tuletada valem, mis näitaks ühtlaselt muutuva liikumise korral nihke sõltuvust ajast, saame kasutada teadmist, et nihke pikkus on võrdne kiiruse graafiku alla jääva pindalaga. Olgu keha kiirus alghetkel v0 ja saavutagu aja t möödumisel väärtuse v. Kiiruse graafikuks on tõusev sirge, mille alla jääv kujund on trapets, mille alusteks on kiirused v0 ja v ning kõrguseks aeg t.
Aja t jooksul keha poolt sooritatava nihke pikkus on võrdne selle trapetsi pindalaga, mille leidmiseks tuleb aluste poolsumma korrutada kõrgusega:
Teades seosest (1.12 ), et kiirus avaldub kiirenduse kaudu kujul v = v0 + at, saame pärast asendamist
mille lihtsustamisel jõuamegi avaldiseni, mis näitab nihke sõltuvust ajast ühtlaselt muutuval liikumisel:
Näeme, et nihe sõltub ajast ruutfunktsiooni järgi. Mõne probleemi lahendamisel pole liikumise aeg teada, küll aga on teada lõppkiirus. Sel juhul leitakse aeg kiiruse valemist (1.12’ )
Selle ajaga asendamisel omandab seos (1.13 ) kuju
ehk
Pärast lihtsustamist ruutude vahe valemi abil saame nihke arvutamiseks valemi:
Teades nihke sõltuvust ajast, on liikumisvõrrandit lihtne koostada. Näitab ju see võrrand keha koordinaadi sõltuvust ajast ja nagu ütleb seos (1.6 ), saame keha koordinaadi arvutada mis tahes ajahetke jaoks, liites algkoordinaadile selleks hetkeks sooritatud nihke pikkuse: x = x0 + s. Lähtudes nihke avaldisest (1.15 ), näeme, et ühtlaselt muutuva liikumise liikumisvõrrandiks on
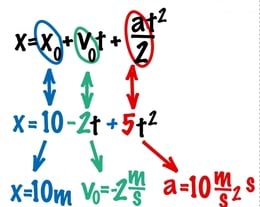
Tegemist on ruutfunktsiooniga, mille liikmed võivad olla sõltuvalt algkoordinaadi, algkiiruse ja kiirenduse märgist nii positiivsed kui ka negatiivsed. Liikme märk sõltub vastava suuruse suunast koordinaattelje suhtes. Märgi olulisuse rõhutamiseks kasutatakse võrrandi üldkujus + asemel mõnikord sümbolit ±. Sel juhul näeb liikumisvõrrand välja veidi teistsugusena:
Iga konkreetse liikumise korral on võrrandis x0, v0 ja a kohal vastavate suuruste arvväärtused.
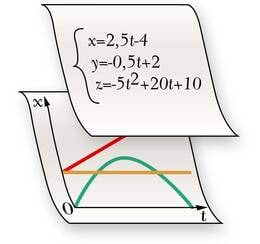
Nüüd, mil teame, et ühtlaselt muutuva liikumise liikumisvõrrand (1.19 ) kujutab endast aja ruutfunktsiooni, mis on sarnane matemaatikast tuntud funktsiooniga y = ax2+ bx + c, pole raske konstrueerida ka selle liikumise graafikut.
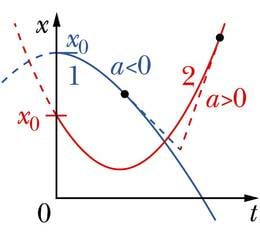
Koordinaat x sõltub ajast t kui ruutfunktsioon. Ruutfunktsiooni graafik on teatavasti parabool ja nii ongi ühtlaselt muutuva liikumise graafik parabooli kujuga. Sõltuvalt ruutliikme kordaja (kiirenduse) märgist on parabooli harud suunatud kas üles (a > 0) või alla (a < 0).
Gravitatsioon (gravitas — ladina k raskus) on vastastikmõju, millele alluvad kõik kehad, nii kosmilised kui ka maapealsed. Meie poolt tajutav gravitatsioon on Maa külgetõmme. Kõik kehad tõmbuvad Maa keskpunkti poole ja omavad seepärast raskust. Kui keha lahti pääseb, kukub see alla. Selle üle, kuidas kehad Maa külgetõmbe tõttu kukuvad, juureldi juba tuhandeid aastaid tagasi. Kui kreeka mõttetark Aristoteles oli veendunud, et rasked kehad kukuvad kergematest kiiremini, siis 2000 aastat hiljem näitas itaalia teadlane Galileo Galilei, et kõik kehad liiguvad Maa külgetõmbe mõjul ühtmoodi.
Tegelikult oli õigus ka Aristotelesel. Kõik me oleme kogenud, et korraga käest lahti lastud metallraha ja paberileht ei maandu korraga. Paber kukub aeglasemalt, kuna langemist segab õhutakistus. Suhteliselt raskete esemete korral (metallkuulid, kivid) jääb õhutakistus raskusjõu kõrval aga väikeseks ja kehad maanduvad siis korraga.
Sellist kehade kukkumist, kus õhutakistus puudub või on väike, nimetatakse vabaks langemiseks. Katsed näitavad, et vabalt langevatel kehadel kasvab kiirus ühtmoodi – see ei sõltu raskusest ja kujust. Torus, millest on õhk välja pumbatud, kukuvad tinahaavel ja udusulg kõrvuti.
Vaba langemine on ühtlaselt muutuv liikumine. Kõik kehad saavad sõltumata massist ja juba olemasoleva kiiruse suurusest ning suunast Maa külgetõmbe toimel ühesuguse kiirenduse. Seda nn vaba langemise kiirendust on mõõdetud Maa eri paigus ja erinevatel meetoditel ning tulemuseks on saadud alati ligikaudu 9,8 m/s2. Vaba langemise kiirenduse tähis on g ja see on suunatud alati alla, Maa keskpunkti poole.
Vaba langemine on ühtlaselt muutuv liikumine ja selle käigus keha kõrgus muutub. Sellise liikumise korral on püstsuunaliseks koordinaadiks mõistlik võtta keha kõrgus. Telg on sel juhul suunatud alt üles ning koordinaadi ehk kõrguse tähiseks on tavaliselt h (height — inglise k kõrgus). Sageli kasutatakse püstkoordinaadina ka y.
Keha liikumist Maa külgetõmbe mõjul saab kirjeldada ühtlaselt muutuva liikumise mudeli abil. Lähtume kiiruse ajast sõltuvuse valemist (1.12’ ) ja liikumisvõrrandist (1.19 ):
Neis avaldistes tuleb kiirenduseks võtta vaba langemise kiirendus ning koordinaadiks kõrgus h.
Et kõrgus on suunatud alt üles ja vaba langemise kiirendus ülalt alla, on sellises koordinaatsüsteemis vaba langemise kiirendus negatiivne ja valemites tuleb võtta a = – g. Selliselt toimides saame vabalt langeva keha kiiruse ja kõrguse ajast sõltuvuse jaoks järgmised seosed:
Kui näiteks kivi üles visata, on valemites algkiirus v0 positiivne, allaviskamisel negatiivne ja lihtsalt käest pillamisel null. Sümbol h0 tähistab kõrgust aja alghetkel ehk algkõrgust. Kõrguse nullpunkt valitakse vastavalt olukorrale. Enamasti on selleks maapind. Vaba langemise kiirenduse väärtuseks võetakse 9,8 m/s2, ent kui pole öeldud teisiti, võib kooliülesannete lahendamisel kasutada väärtust 10 m/s2.
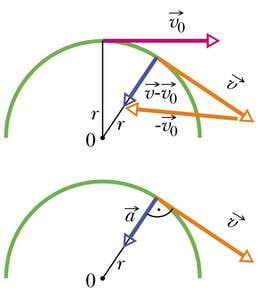
Kui kõrgushüppaja võitleb gravitatsiooniga, et tõusta kõrgele, siis kuulitõukaja peab kuuli lennutama võimalikult kaugele. Mismoodi toimida? Algkiirus peab olema võimalikult suur, kuid ka tõukesuund on oluline. Mida kõrgemale kuul tõuseb, seda kauem see õhus püsib. Samas ei saa kogu energiat kõrguse saavutamiseks kulutada, osa tuleb panustada edasiliikumisse.
Kaldu visatud keha liikumist saab vaadata kui kahte korraga toimuvat sõltumatut liikumist. Üks on suunatud üles-alla ja allub vaba langemise seadustele ning teine horisontaalsuunas ja on kõrvaliste mõjude puudumisel ühtlane sirgjooneline. Kaks erisihilist korraga toimuvat liikumist on teineteisest täiesti sõltumatud ja neid saab kirjeldada eraldi võrrandite abil.
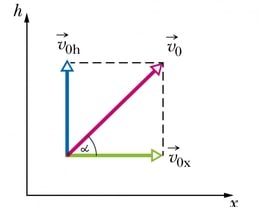
Kaldu visatud keha liikumise kirjeldamiseks on vaja kahte koordinaattelge. Üles-alla toimuva muutuva liikumise jaoks kasutame püstist kõrguse telge h ja horisontaalsuunas ühtlaselt edasi liikumise jaoks telge x. Selleks et nende kahe koordinaattelje jaoks saaks liikumisvõrrandid kirja panna, on vaja ka algkiirus v0 jagada kaheks komponendiks — püstsuunaliseks v0h ja horisontaalsuunaliseks v0x.
Jooniselt on näha, et kiiruse komponentide suurused saab täisnurksetest kolmnurkadest siinus- ja koosinusfunktsiooni abil (α on viskenurk horisontaalsihi suhtes):
Nende avaldistega tuleb vastavad suurused asendada liikumisvõrrandites (1.8 ) ja (1.21 ). Kuna nüüd on meil ühe liikumise asemel korraga kaks, siis peame selle kirjeldamiseks kasutama ühe liikumisvõrrandi asemel kahest võrrandist koosnevat süsteemi:
Sagedamini tulevad ette ülesanded, kus keha alustab liikumist maapinnalt. Sel juhul võetakse mõlemad algkoordinaadid h0 ja x0 nulliks. Liikumisvõrrandite süsteemi (1.24 ) abil saame leida horisondiga nurga α all visatud keha koordinaadid h ja x mis tahes ajahetkel t. Kui soovime leida lennukaugust ja –kõrgust, tuleb esmalt leida lennuaeg. Lennu lõpus kukub keha maha ning kõrgus h = 0. Seda väärtust kasutades saame esimesest võrrandist avaldada lennuaja. Teades lennuaega, leiame teisest võrrandist sellele vastava kauguse x. Lennukõrguse leidmiseks kasutame jälle esimest võrrandit, võttes ajaks seekord poole kogu lennuajast, kuna just lennu keskmomendil on keha oma trajektoori kõrgeimas punktis.
Dr John Stapp, New Mexicos asuva Hollomani Õhujõudude Baasi kolonel, kinnitati 1954. aasta detsembris rihmadega üheksa raketiga rakettkelgu istmele. Kui raketid süüdati, kiirendas see teda viie sekundi jooksul kiiruseni 632 miili ehk 1018 kilomeetrit tunnis. Tõsisem katsumus kolonel Stappi jaoks oli siiski pidurdamine vesipiduritega, milleks kulus vaid 1,4 sekundit. 1958. aasta mais saavutas Eli L. Beeding Jr sarnase kelguga kiiruse 72,5 miili (117 kilomeetrit) tunnis. Tema kiirus polnud küll märkimisväärne — see on maanteedel suhteliselt tavaline —, kuid märkimist väärib peatumiseks kulunud aeg, 0,04 sekundit, mis on sõna otseses mõttes vähem kui silmapilk.
Kui päästerõngas vee alla suruda, tõukab vesi selle pinnale tagasi. Tuul puhub purje pingule ning paneb jahi mööda veepinda liikuma. Riputatud koormise toimel venib vedru pikemaks. Tõstja sikutab raske kangi maast lahti. Udusulg hõljub õhus ega kuku maha. Pärast kammimist hakkab kamm juukseid ligi tõmbama. Sepavasara löök painutab kuuma raudlati kõveraks.
Selliseid näiteid võib tuua väga palju. Need on küll kõik väga erinevad, kuid ühes siiski sarnased — ühe kehaga juhtub midagi teise keha mõjul. Neid näiteid ühendab nähtus, mida nimetatakse vastastikmõjuks.
Mille järgi tunneme ära, et vastastikmõju on aset leidnud? Kui üks keha mõjutab teist, siis selle tagajärjel toimub mingi muutus. Siin on mitu võimalust — vastastikmõju tagajärjel võib muutuda keha kuju, ruumala või liikumise iseloom.
Kuju muutub näiteks õhupallil, kui me seda täis puhume, ja kristallvaasil, mis maha pillatakse. Alati ei pruugi me kujumuutust märgatagi. Kui me trepile astume, ei näi midagi erilist juhtuvat.
Liikumise juures saab vastastikmõju muuta kiiruse arvväärtust ja suunda. Kui tahame auto kiirust vähendada, kasutame kummide ja teekatte vahelist pidurdavat mõju. Kiiruse väärtus muutub Maa külgetõmbe tõttu näiteks ülesvisatud pallil. Algul see väheneb, siis pall peatub hetkeks ning allakukkumisel hakkab kiirus jälle kasvama. Viimases näites muutub ka palli liikumise suund.
Kui auto suure kiirusega kurvi siseneb, siis libeda korral ei pruugi ta teel püsida. Kurvis püsimiseks peab rataste ja teekatte vahel olema piisava tugevusega vastastikmõju, et liikumise suund selle tagajärjel vajalikul hulgal muutuks.
Vastastikmõju tagajärjel muutub keha liikumise iseloom. Et liikumise muutumise põhjusi uurib mehaanika haru dünaamika, siis ongi vastastikmõju dünaamika jaoks üks olulisemaid nähtusi.
Ühegi keha liikumist ei saa muuta ilma teise keha mõjuta. Näiteks ei saa paati seisvas vees liikuma panna, kui pole tuult ega aere. Ka auto ei saaks paigalt sõita, kui puuduks teine keha, millelt end liikuma tõugata (teekate). Vastastikmõjus osaleb alati vähemalt kaks keha.
Vastastikmõjud võivad olla erineva tugevusega. Seda näeme tagajärje suuruse järgi. Erinevad raskused venitavad sama vedru erineva pikkuse võrra ja tugevam mängija suudab pallile anda suurema hoo.
Et vastastikmõjusid omavahel võrrelda ja uurida, mil määral sõltuvad tagajärjed vastastikmõju tugevusest, on kasutusele võetud füüsikaline suurus jõud.
Jõud on vastastikmõju mõõduks ja selle arvväärtus iseloomustab vastastikmõju tugevust. Vastastikmõju põhjustab kas keha kuju või kiiruse muutuse. Kuna nii kujumuutusel kui ka kiiruse muutumisel (kiirendusel) on kindel suund, siis peab ka jõud olema suunaga. Järelikult on jõud vektoriaalne suurus.
Jõu tähiseks valemites ja joonistel on (fortis — ladina k tugev, võimas). Jõu arvulise väärtuse väljendamisel, kui suund pole oluline, kasutatakse ilma vektorimärgita tähist F.
Jõu mõõtmiseks on kaks põhimõtteliselt erinevat võimalust. Võib mõõta vastastikmõju poolt tingitud kujumuutuse ehk deformatsiooni suurust. Näiteks meile tuttav dünamomeeter näitab jõu suurust vedru pikenemise kaudu.
Teiseks saab jõu suurust arvutada selle kaudu, kui palju vastastikmõju tuntud massiga keha kiirust muudab ehk siis mõju poolt antava kiirenduse kaudu.
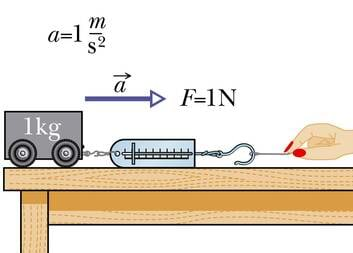
Klassikalise mehaanika rajaja I. Newtoni auks on SI jõu mõõtühiku nimeks võetud njuuton (N). Üks njuuton on sellise suurusega jõud, mis annab kehale massiga 1 kg kiirenduse 1 m/s2.
See, et vastastikmõjus osaleb vähemalt kaks keha, ei tähenda, et kehasid ei võiks rohkem olla. Tihti ongi just nii, et korraga mõjub mitu jõudu. Korraga kehale mõjuval mitmel jõul ei ole aga siiski mitut erinevat tagajärge. Näiteks kui vees ujuvale õngekorgile mõjuv raskusjõud on suunatud alla ja samal ajal vee üleslükkejõud üles, ei hakka kork ju korraga mõlemas suunas liikuma. Jõud liituvad ning nende mõjul on üks ühine tagajärg — kork püsib paigal. Samale kehale mõjuvate jõudude summat nimetatakse resultantjõuks.
Kuna jõud on suunaga suurused, ei saa neid liita niisama lihtsalt kui arve. Jõudude liitmisel tuleb järgida vektorite liitmise reegleid. Et jutt on samale kehale mõjuvate jõudude liitmisest, siis joonisele kandmisel peavad need algama kõik samast punktist. Kulgeva liikumise korral, mil pöörlemist ei toimu, kujutame keha ette punktmassina.
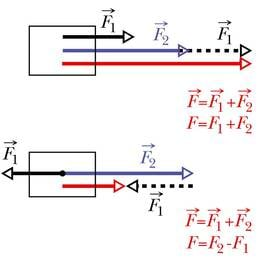
Kõige lihtsam on leida kahe samasuunalise jõu summat. Samasuunaliste jõudude arvväärtused liituvad ning resultantjõud on liidetavate jõududega samas suunas.
Vastassuunaliste jõudude liitmisel lahutatakse suurema väärtusest väiksem ning resultantjõud jääb suurema jõu suunaliseks.
Erisuunaliste jõudude liitmise lihtsaim viis on kasutada rööpküliku reeglit. Selle järgi tuleb liidetavatele jõuvektoritele üles ehitada rööpkülik ning viimase diagonaal ongi resultantjõuks.
Kui kehale mõjub suurem arv jõude, tuleb esmalt summeerida kaks jõudu ning tulemusele liita samm-sammult ülejäänud.
Sageli tuleb ette, et kehale mõjuvate jõudude resultant on null. Siis öeldakse, et jõud on tasakaalus ehk kompenseerivad üksteist. Näiteks laual seisvale õmblusmasinale mõjuvat Maa külgetõmmet tasakaalustab laua vastumõju, mis ei luba masinal sellest läbi kukkuda. Need kompenseerunud jõud liikumist ei mõjuta ja õmblusmasin püsib paigal.
Käru liigub vaid siis, kui seda lükata või vedada. Hakklihamasin ilma väntamiseta ringi ei käi. Miks aga jalgpall pärast löögi mõju lõppu ima kõrvalise abita ise edasi lendab? Mis põhjustel liikumine üldse toimub? Neile küsimustele otsib vastust dünaamika. Suure panuse dünaamika arengusse on andnud inglise füüsik Isaac Newton, kes oma uuringutele tuginedes sõnastas mehaanika kolm põhiseadust. Neid seadusi tuntakse tänapäeval Newtoni seaduste nime all.
Kõik meist on kogenud, et tool nihkub põrandal edasi vaid siis, kui seda lükata. Pärast lükkamise lõppu lakkab liikumine jalgade ja põranda vahelise hõõrdumise tõttu.
Kuidas liiguvad aga kehad siis, kui neid ümbritseva poolt ei segata, kui puudub vastastikmõju teiste kehadega?
Teame, et vastastikmõju üheks tagajärjeks on liikumise muutumine. Kui vastastikmõju pole, siis ei saa muutuda ei liikumise kiirus ega ka suund. Sel juhul on tegemist ühtlase sirgjoonelise liikumisega. Kui aga keha juhtub seisma, siis jääbki see muutumatult paigale.
Vastastikmõjude puudumisega on samaväärne olukord, kus jõud on kompenseerunud ja resultantjõud null.
Need tähelepanekud võtabki kokku Newtoni esimene seadus, mis kirjeldab keha liikumist jõudude puudumisel: kehale mõjuvate jõudude puudumisel või nende kompenseerumisel on keha kas paigal või liigub ühtlaselt ja sirgjooneliselt.
Nähtust, kus keha püüab oma liikumisseisundit säilitada, nimetatakse inertsiks. Seepärast nimetatakse Newtoni esimest seadust ka inertsiseaduseks.
Matemaatiliselt saab inertsiseadust väljendada järgmiselt:
Kui kehale jõude ei mõju, jääb liikumine vastavalt inertsiseadusele muutumatuks. Kuidas muutub aga liikumine siis, kui kehale mõjub jõud?
On kindlaks tehtud, et kui kehale mõjub jõud siis keha kiirus muutub ehk keha liigub kiirendusega. Järelikult põhjustab jõud kiirenduse. Millest ja kuidas kiirendus sõltub, on kindlaks tehtud katsete abil.
Kui mõjutada erinevaid kehi sama suure jõuga, võivad saadud kiirendused olla erinevad. Mõne keha kiirus muutub aeglasemalt ja kiirendus on väiksem. Need kehad säilitavad oma liikumisseisundit teistega võrreldes paremini ja öeldakse, et nende inertsus on suurem. Inertsus on keha omadus, mis iseloomustab selle võimet liikumisolekut säilitada.
Suurema inertsusega keha kiirust on raskem muuta. Näiteks on rasket veoautot määratult raskem liikuma lükata kui mänguautot. Selles pole midagi kummalist – päris autol on mänguasjaga võrreldes ju palju suurem mass.
Mass on keha inertsuse mõõt. Selle tähiseks on m ja mõõtühikuks 1 kg.
Katsed näitavad, et jõu toimel tekkiv kiirendus on pöördvõrdeline keha massiga. Mida suurem mass, seda väiksema kiirenduse see jõud tekitab.
Veel näitavad katsed, et kiirendus on seda suurem, mida suurem jõud kehale mõjub. See on ka mõistetav — kui liikumise muutuse tingib vastastikmõju, siis mida tugevam on mõju, seda suurem peab olema ka selle põhjustatud muutus. Kiirendus on võrdeline jõuga.
Ülaltoodud tulemused võimaldasidki Newtonil jõuda oma mehaanika teise põhiseaduse sõnastamiseni.
Newtoni teine seadus ütleb: kui kehale mõjub jõud, siis liigub see kiirendusega, mis on võrdeline mõjuva jõuga ning pöördvõrdeline selle keha massiga. Matemaatiliselt väljendab Newtoni II seadust valem
Kuna sel seadusel on suur tähtsus mehaanika põhiülesande lahendamisel, nimetatakse Newtoni II seadust ka dünaamika põhiseaduseks.
Kui me teame keha algkoordinaati, algkiirust, massi ja mõjuvat jõudu, saame Newtoni II seadusest arvutada kiirenduse ning välja kirjutada keha liikumisvõrrandi. Liikumisvõrrand lubab keha asukoha välja arvutada mis tahes ajahetkel ning sellega ongi põhiülesanne lahendatud.
Kui Newtoni I ja II seadus kirjeldavad, kuidas keha liigub välise mõju puudumisel või olemasolul, siis kolmas seadus käib vastastikmõju enda kohta. Newton ise nimetas seda seadust mõju ja vastumõju seaduseks.
Kogemused näitavad, et kehad mõjutavad teineteist alati vastastikku. Kui toetame redeli seinale, siis mõjub sein redelile vastu ja seda nii, et redel püsib paigal.
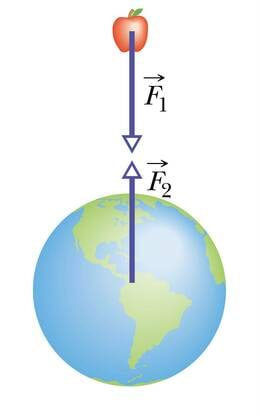
Kehad osalevad vastastikmõjus alati paarikaupa. Seejuures mõjuvad jõud mitte ainult ühele, vaid mõlemale kehale. Need kehadele mõjuvad jõud on suuruselt võrdsed ja suunalt vastupidised. Kui Maa tõmbab kukkuvat õuna jõuga 1 N, siis õun tõmbab maakera vastu täpselt sama suure jõuga.
Selles väljendubki mõju ja vastumõju ehk Newtoni kolmas seadus: kaks keha mõjutavad teineteist suuruselt võrdsete vastassuunaliste jõududega.
Kui eristada kahele vastastikmõjus osalevale kehale mõjuvaid jõude indeksitega 1 ja 2, saab Newtoni III seadust väljendada valemiga
Tuleb meeles pidada, et Newtoni III seaduse jõud mõjuvad eri kehadele ja seepärast ei saa need teineteist tasakaalustada, kuigi on võrdsed ja vastupidised.
Newtoni teine seadus näitab keha kiiruse muutumise sõltuvust keha massist ja sellele mõjuvast jõust. Kiiruse sama suure muutuse jaoks on suurema massi korral vaja kas suuremat jõudu või pikemat aega. Samas on mõju vastastikune — keha, mille kiirus muutub, mõjub teisele kehale sama aja jooksul sama jõuga vastu ja võib muuta selle liikumist või kuju. Näeme, et liikuval kehal on võime muuta teiste kehade liikumist.
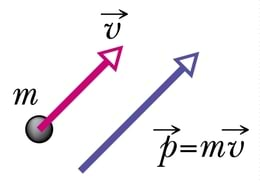
Keha võime vastastikmõju korral teist keha mõjutada sõltub kehade kiirusest ja massist. Sellele teadmisele tuginedes on liikumise iseloomustamiseks võetud kasutusele suurus, mida nimetatakse keha liikumishulgaks ehk impulsiks. Impulsi tähiseks on (pulsus — ladina k löök, impulss) ning see on defineeritud keha massi ja kiirusvektori korrutisena:
Impulsi mõõtühikuks on 1 kg•m/s. Tegemist on vektoriaalse suurusega, mille suund ühtib kiirusvektori suunaga.
Impulsi füüsikalist tähendust võib mõista näiteks põrgete vaatlemisel. Põrke mõju on seda suurem, mida suurem on keha impulss. Seepärast tuleb sadamakai ehitada väga tugev, muidu purustaks selle ka väga aeglaselt liikuv, kuid suure massiga laev. Samamoodi võib väike püssikuul tekitada suuri purustusi oma suure kiiruse tõttu. Nii laeval kui ka kuulil on suur impulss, ühel oma suure massi ja teisel suure kiiruse tõttu, ning need võivad teisi kehi suure jõuga mõjutada.
Osutub, et impulss on jõuga otseselt seotud. Võtame Newtoni II seaduse (2.2) ja asendame selles kiirenduse selle definitsiooni avaldisega (1.11):
ehk
Kui korrutame saadud võrduse mõlemad pooled keha massiga läbi, saame
Et massi ja kiiruse korrutis kujutab endast keha impulssi, siis avaldis
pole midagi muud kui impulsi muut. Seega võime kirjutada, et
Saime Newtoni II seadusele uue kuju, mis näitab, et impulsi muutumise kiirus on võrdne seda muutust põhjustava jõuga. Tegemist on väga olulise tulemusega, mida kasutatakse peale klassikalise dünaamika ka elementaarosakesi uurivas kvantmehhaanikas.
Liikumishulgal ehk impulsil on füüsika jaoks väga oluline omadus — jäävus.
Uurime kahe keha vastastikmõju. Newtoni III seaduse järgi mõjutavad need kehad teineteist võrdsete ja vastassuunaliste jõududega:
Kehale mõjuv jõud on vastavalt seosele (2.7 ) võrdne keha impulsi muutumise kiirusega. Nii saame Newtoni III seadusele kuju:
Et kehad mõjutavad teineteist sama kaua, võime ajavahemikud Δt taandada ning avaldis lihtsustub:
ehk
Avaldis
kujutab endast mõlema keha impulsside muutude summat. Sisuliselt on tegemist kehade koguimpulsi
muuduga, mida võib tähistada kui
Seda tähistust kasutades saame seosele (2.9 ) kuju, mis väljendabki impulsi jäävuse seadust:
ehk
Näeme, et kui kaks keha teineteist mõjutavad, siis selle käigus nende koguimpulss ei muutu (muut = 0). Saab näidata, et impulsi jäävus kehtib ka kui tahes paljudest kehadest koosneva süsteemi jaoks. Ainsaks tingimuseks on see, et süsteemi mittekuuluvate kehade mõjud puuduvad.
Nii võimegi sõnastada impulsi jäävuse seaduse: väliste mõjude puudumisel on süsteemi koguimpulss sinna kuuluvate kehade igasugusel vastastikmõjul jääv.
Seaduse rakendamisel ei tohi unustada, et impulss on vektoriaalne ehk suunaga suurus.
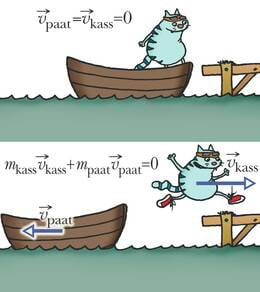
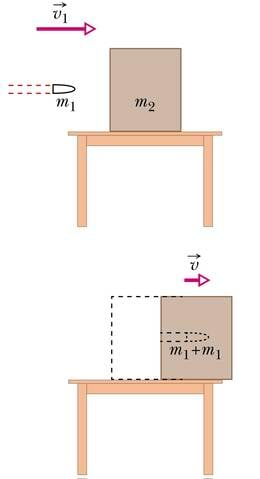
Impulsi jäävuses võib igaüks ise veenduda, kui astub kinniköitmata paadist kaldale. Enne väljaastumist on paat koos inimesega paigal ja nende koguimpulss null. Astumisel hakkab inimene kalda poole liikuma ja omab teatud impulssi. Et koguimpulss ei muutu ja jääb nulliks, saab paat vastassuunalise impulsi ning eemaldub kaldast.
Kogu teaduse ajaloo vältel pole avastatud ühtegi nähtust, mis oleks impulsi jäävusega vastuolus. See seadus on universaalne ning kehtib ka väljaspool mehaanika uurimisvaldkondi.
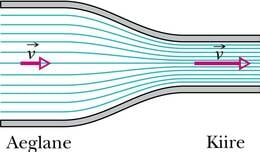
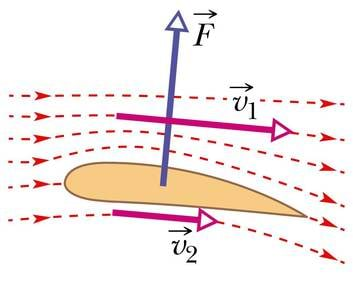
Kindlasti on kõik proovinud vees olles kõndida ja tähele pannud, et see nõuab üsna suurt pingutust. Vesi takistab liikumist tunduvalt rohkem kui õhk. Kuid ka õhk avaldab selles liikuvatele kehadele takistust. Ega muidu pöörata võidusõiduautode voolujoonelisemaks muutmisele nii suurt tähelepanu. Kui mõni suurem auto meist lähedalt möödub, tajume selle poolt liikuma pandud õhku tuulena.
Gaasilise ja vedela keskkonna liikumahakkamine on otseselt seotud neis liikuvatele kehadele avaldatava takistusjõuga. Erinevalt tahketest kehadest on gaasid ja vedelikud voolavad, sest nende aineosakesed pääsevad liikuma. Kui näiteks vees mingi keha liigub, siis sellega kokkupuutuvad veeosakesed liiguvad kehaga kaasa ja panevad kaasa liikuma ka oma kaugemal asuvad naaberosakesed. Keha liikumine kandub veele üle. Osa keha liikumishulgast ehk impulsist antakse mingi aja jooksul keskkonnale. Vastavalt jäävusseadusele peab selle võrra keha liikumishulk vähenema.
Kui keha impulss väheneb, siis vastavalt seosele (2.7 ) on selle vähenemise kiirus võrdne kehale mõjuva jõuga. Antud juhul on tegemist keskkonna takistusjõuga.
Keskkonna poolt selles liikuvale kehale mõjuv takistusjõud on võrdne liikumishulga ehk impulsi ülekandumise kiirusega.
Aastal 1638 avaldas Galilei oma raamatus Discorsi uurimistulemused, mille järgi kukuvad kõik kehad Maa külgetõmbe tõttu ühesuguse kiirendusega. Kust aga pärineb see jõud, mis kõiki kukkuvaid kehi kiirendab? Selle ja muude liikumisega seotud küsimuste kallal juurdles üsna pikalt tolleks ajaks juba mitmete optikanähtuste selgitamisega tuntuks saanud Newton.
Legendi järgi kukkunud kord murul istunud Newtonile pähe õun. See pannud mehe juurdlema, miks õun alati maha kukub ja miks see üldse kukub. Kas tõmbab ainult Maa õuna või on ka õunal selline külgetõmbejõud?
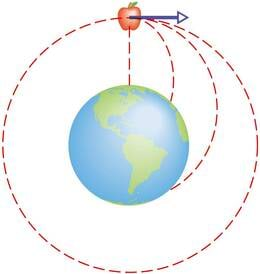
Otse üles visatud õun kukub samasse kohta tagasi. Eemale visatud õun maandub seda kaugemal, mida kiiremini seda visatakse. Kas õun võiks teha terve tiiru ümber Maa, kui kiirus oleks piisavalt suur? Kas Kuu tiirlemine ümber Maa polegi just selline kukkumine?
Kas õun toona 23aastasele Newtonile ka tegelikult pähe kukkus, pole teada. Igal juhul on ta ise mitu korda jutustanud, et just kukkuv õun viis mõtted külgetõmbeprobleemidele. Lisaks oma uurimustele üldistas teadlane ka Galilei avastatud vaba langemise seadust ning Koperniku ja Kepleri astronoomiliste vaatluste andmeid. Pingsa mõttetöö ja omaleiutatud matemaatilise analüüsi meetodi rakendamise tulemusena avastaski Newton seaduse, millele kehadevaheline külgetõmbejõud allub: kaks punktmassi tõmbuvad teineteise poole jõuga, mis on võrdeline nende masside korrutisega ning pöördvõrdeline nendevahelise kauguse ruuduga.
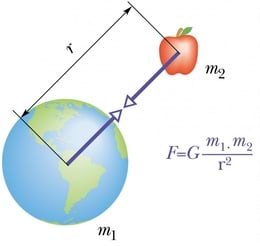
Matemaatiliselt avaldub gravitatsiooniseadus valemina:
Valemis tähistab F mõlemale kehale (punktmassile) võrdselt mõjuvat gravitatsioonijõudu, m1 ja m2 kummagi keha massi ning r nendevahelist kaugust. Tähega G tähistatud kordajat nimetatakse gravitatsioonikonstandiks.
Tegemist on universaalse seadusega. Gravitatsioonijõud mõjub kõikidele kehadele ning ulatub valgusaastate kaugusele.
Kui valemis võtta mõlema keha massiks 1 kg ja vahekauguseks 1 m, saame valemist (2.11 )
Järelikult on gravitatsioonikonstant G arvuliselt võrdne jõuga, millega tõmbuvad kaks teineteisest 1 m kaugusel asuvat 1 kg massiga keha. Selle arvuline väärtus sõltub mõõtühikute valikust ning on määratav vaid eksperimentaalselt.
Maapealsete suhteliselt väikese massiga kehade vaheline tõmbumine on äärmiselt nõrk. See muudab gravitatsioonikonstandi mõõtmise keeruliseks. Esimest korda määras gravitatsioonikonstandi väärtuse täpsete väändkaalude abil 1798. aastal inglise füüsik Henry Cavendish. Ta sai tulemuseks 6,754•10−11 N•m2/kg2, mis on üsna lähedane tänapäeval tuntud väärtusele 6,67428•10−11 N•m2/kg2.
Kooliülesannete lahendamisel võetakse G väärtuseks tavaliselt
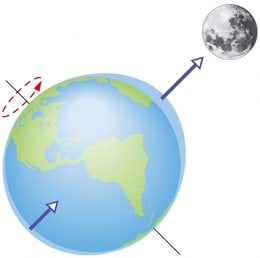
Kõik me tajume Maa külgetõmmet. Gravitatsiooniline tõmbumine ulatub meieni aga ka Kuult ja Päikeselt, põhjustades maailmamere loodeid ehk tõuse ja mõõne.
Eriti tugevad looded esinevad siis, kui Päike ja Kuu paiknevad samal pool Maad viimasega ühel sirgel, st kuu loomise ajal. Korraga on Maal tõus nii sellel poolel, mis asub Kuu suunas, kui ka vastasküljel. Kuna vesi saab voolata, siis koguneb see rohkem Maa Kuu-poolsele küljele ja tõstab meretaset. Pöörlemisel tekivad inertsijõud, mis püüavad kõike pöörlemisteljest eemale paisata. Kuust kaugeimas punktis avaldub see kõige märgatavamalt, kuna seal on Maa kaaslase külgetõmme kõige nõrgem.
Gravitatsioon reguleerib taevakehade liikumist, hoiab koos väikeseid ja suuri tähesüsteeme ning on osaline tähtede arengus sünnist kustumiseni. See mõjub isegi valgusele ning moonutab kaugete objektide kujutisi teleskoobis. Ilma gravitatsioonijõuta poleks galaktikaid, musti auke, Päikest, Maad ega ka meid.
Gravitatsioonijõud sõltub seaduse (2.11 ) põhjal keha massist. Massist sõltub Newtoni II seaduse (2.2 ) järgi ka kiirendus, mille keha vastastikmõju tagajärjel saab. Newton defineeris massi kui keha inertsuse mõõdu ja sellele tuginedes saab massi määrata jõu poolt kehale antava kiirenduse kaudu. Tavaliselt leitakse mass aga hoopis kaalumise ehk kehale mõjuva gravitatsioonijõu mõõtmise teel. Kas niiviisi kahel erineval viisil leitud massid on ikka samad? Kehadel on raskus ja seega mass ka siis, kui nende liikumine ei muutu. Gravitatsioon ja inerts pole omavahel ühelgi viisil seotud. Kas see tähendab, et kehadel ongi kaks põhimõtteliselt erinevat massi — raske ja inertne?
Raskuse ja inertsuse küsimuste kallal töötas omal ajal juba Galileo Galilei ning püüdis vastuseni jõuda mõtteliste eksperimentide teel. Ka Newton pidas kahe massi samaväärsuse küsimust väga oluliseks ning tegi mitmeid praktilisi mõõtmisi.
Tänapäevaks on füüsikud paljude katsete abil jõudnud arusaamisele, et inertse massi ja raske massi samaväärsus on klassikalises mehhaanikas mõõtmistele tuginev kogemuslik tõsiasi, millel puudub teoreetiline põhjendus. Oletus nende masside võrdsusest on Einsteini üldrelatiivsusteooria aluseks.
Meie jaoks on eriline muidugi see gravitatsioonijõud, millega Maa tõmbab kõiki seda ümbritsevaid kehi. Tänu sellele jõule kukuvad kõik kehad alla Maa keskpunkti poole ja on tõstmisel rasked. Tegemist on meile tuttava raskusjõuga. Raskusjõud pole iseloomulik mitte ainult Maale, vaid ilmneb tugevamalt või nõrgemalt kõikidel taevakehadel. Raskusjõuks nimetatakse gravitatsioonijõudu, millega Maa või mis tahes muu taevakeha tõmbab enda poole selle lähedal asuvaid kehi.
Raskusjõu saame leida gravitatsiooniseadusest (2.11 ). Võttes ühe keha massiks Maa massi M ning vahekauguseks Maa raadiuse R, tuleb maapinnal asuvale kehale massiga m mõjuvaks raskusjõuks
Kui suure kiirenduse see jõud kehale annab? Kasutame Newtoni II seadust (2.2 ):
ehk
Et Maa mass on 5,98•1024 kg ja raadius 6370 km = 6,37•106 m, annavad arvutused
See kiirenduse väärtus on meile tuttav kui vaba langemise kiirendus. Vaba langemise kiirendust nimetatakse veel raskus- ehk gravitatsiooni-kiirenduseks. Viimasest ongi tulnud tähis g.
Teades nüüd, et vabalt langeva keha kiirendus on , saame Newtoni II seadusest seda kiirendust tekitava jõu ehk raskusjõu arvutamiseks lihtsa valemi:
See raskusjõud on suunatud Maa keskpunkti ega ole seepärast Maakera kõigis punktides samasuunaline.
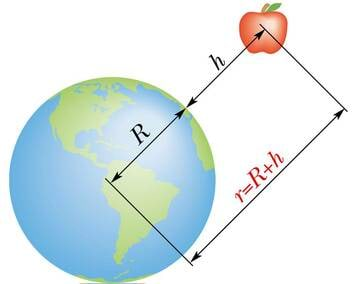
Kõrguse kasvades raskuskiirendus väheneb, sest valemis (2.15 ) tuleb Maa raadiusele liita ka kõrgus maapinnast h:
Kuna raskuskiirenduse vähenemine muutub märgatavaks alles 100 km kõrgusel, mida loetakse kokkuleppeliselt kosmose piiriks, siis on tavaelus mugavam kasutada nn lapiku Maa mudelit (midagi antiikaegse ettekujutuse sarnast). Selle mudeli puhul mõjub kõikidele Maa-lähedastele kehadele vertikaalselt alla suunatud raskusjõud, mis kõrgusest ei sõltu.
Tänu gravitatsioonile mõjutab keha oma alust või riputusvahendit, mis takistab keha liikumist Maa keskpunkti poole. Seda jõudu, millega keha Maa külgetõmbe tõttu mõjub alusele, keskkonnale või riputusvahendile, nimetatakse keha kaaluks. Kaalu tähis käesolevas kursuses on ning mõõtühik 1 N (mitte igapäevasele kõnepruugile vastavalt 1 kg, kuna tegemist pole massiga!).
Kui alus või riputusvahend on paigal või liigub ühtlaselt ja sirgjooneliselt, on keha kaal võrdne raskusjõuga. Kui alus liigub vertikaalsuunalise kiirendusega, siis kaal enam raskusjõuga võrdne pole.
Kui alus liigub kiirendusega üles, peab see kehale kiirenduse andmiseks rakendama lisajõudu. Kaal on sel juhul raskusjõust suurem ja öeldakse, et tegemist on ülekoormusega:
Kiirendusega alla liikumisel on vastupidi. Tegemist on alakoormusega:
Kaalu sõltuvust kiirendusest võime tajuda liftis. Tõusu alguses tunneme ülekoormust ja lõpus alakoormust.
Ülaltoodut arvestades saab kaalu seost kiirendusega väljendada ühe kokkuvõtva valemiga:
Kui aga alus või riputusvahend üldse eemaldada, siis kaob ka keha mõju sellele. Kui pole mõju alusele või riputusvahendile, ei saa olla ka kaalu ning tegemist on kaalutuse ehk kaaluta olekuga. Kõik vabalt langevad kehad on kaaluta olekus.
Kaalu ja raskusjõudu ei tohi samastada, sest need jõud mõjuvad eri kehadele. Keha kaal mõjub alusele või riputusvahendile ja on olemuselt elastsusjõud. Raskusjõud on olemuselt gravitatsioonijõud, mis mõjub kehale endale. Need on täiesti erinevad jõud.
Keha võib teisi kehi mõjutada lisaks kaalule veel muudki liiki jõududega. Arvuti taga istuv õpilane toetub seljatoele, õhupalli puhutav õhk paneb selle paisuma, press surub korgitüki õhemaks, magnet hoiab nõela ... Mõjutatava keha jaoks pole seejuures oluline, mis liiki need jõud on. Tähtis on vaid jõu ja sageli ka mõjupinna suurus.
Et kõiki selliseid mõjusid saaks kirjeldada ühtse mudeli abil, on võetud kasutusele rõhumisjõu mõiste. Rõhumisjõuks nimetatakse jõudu, millega üks keha mõjutab teist risti kokkupuutepinnaga. Rõhumisjõu tähisena kasutatakse jõu üldtähist . Rõhumisjõud mõjub alati pinnaga risti.
Vastavalt Newtoni III seadusele tekib keha mõjutamisel alati vastumõju ehk reaktsioon. Tegemist on jõuga, mida nimetatakse toereaktsiooniks. Rõhumisjõu toimel keha kuju muutub (keha deformeerub) ja see põhjustab vastassuunas mõjuva elastsusjõu, mis ongi toereaktsioon. Toereaktsiooniks nimetatakse rõhuvale kehale toetuspinnaga risti mõjuvat vastujõudu.
Kuna toereaktsioon on alati suunatud piki pinna ristsirget ehk normaali, on selle tähiseks käesolevas kursuses valitud . Rõhumisjõud ja toereaktsioon on alati võrdsed ja vastassuunalised:
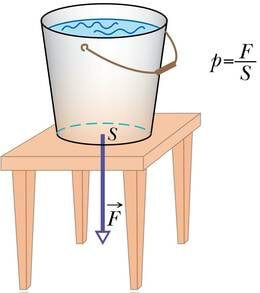
Kui teineteist mõjutavaid kehi ei või ette kujutada punktmassidena, kuna nende kuju on oluline, mõjub rõhumisjõud mingile konkreetse suurusega pinnale. Rõhumisjõu tagajärg sõltub selle pinna suurusest. Kui pind on suur, hajub jõud üle selle laiali ning mõju kindla suurusega pinnatükile jääb väiksemaks. Arvestamaks rõhumisjõu jaotumist mõjupinnale kasutatakse rõhu mõistet. Rõhuks nimetatakse füüsikalist suurust, mis on võrdne rõhumisjõu F ja pindala S jagatisega. Rõhu tähiseks on p (pressûra — ladina k rõhk)
Rõhu mõõtühik on 1 paskal — 1 Pa = 1 N/m2. Ühik on nime saanud prantsuse füüsiku Blaise Pascali järgi.
Erinevalt jõust ei ole rõhk vektoriaalne suurus. Põhjus on selles, et rõhu leidmisel arvestatakse vaid pinnaga risti olevat jõudu. Näiteks gaasides ja vedelikes ei saagi me suunast üldse rääkida, kuna rõhk antakse edasi kõikides suundades ühtemoodi.
Oletame, et inimene suudab lükata jõuga 500 N ja Oletame et ta lükkab veoautot massiga 5000 kg. Selline jõud peaks veokile andma kiirenduse 0,1 m/s2 ning 10 sekundiga läbiks see 5 m ja saavutaks kiiruse 5 m/s. Ometi ei jaksa ükski inimene viietonnist autot paigalt lükata. Miks?
Siin tuleb mängu uus jõuliik — hõõrdejõud. Hõõrdejõud on väga oluline, kuna mõjub maapealsetes tingimustes kõikidele liikuvatele kehadele. Iga liikuv keha jääb hõõrdejõu tõttu lõpuks seisma, kui mingi muu jõud hõõrdejõude ei kompenseeri. Hõõrdejõu vähendamise vajadusega on kokku puutunud kõik suusatajad, seevastu teemeistrid näevad vaeva, et talvistel teedel hõõrdumist suurendada. Hõõrdejõuga seonduva tundmine on eluliselt tähtis.
Hõõrdejõud mõjub mitte ainult liikuvatele vaid ka paigalseisvatele kehadele. Näiteks püsib veeklaas käes ja nael seinas just tänu hõõrdejõule.
Hõõrdejõuks nimetatakse jõudu, mis takistab keha liikumist või liikumahakkamist. Et jõud takistab liikumist, nimetatakse seda vahel ka takistusjõuks. Hõõrdejõud tekib alati kehade vahetul kokkupuutel, mõjub piki kokkupuutepinda ja on suunatud vastassuunas liikumisele. Seejuures on olemas mitmesuguseid võimalusi.
Näiteks on olemas võimalus, et mingi jõud püüab keha liikuma panna, kuid hõõrdumise tõttu jääb keha paigale. Nähtust, kus hõõrdejõu tõttu püsib keha paigal, nimetatakse seisuhõõrdumiseks. Seisuhõõrdejõud on alati suuruselt võrdne ja vastassuunaline jõuga, mis püüab keha liikuma panna.
Kui inimene kõnnib, siis on edasiviivaks jõuks hõõrdejõud. Et tald teekatte suhtes ei liigu, on siin tegemist just seisuhõõrdumisega. Ka see jõud, mis annab rihmülekande korral liikumise ühelt rattalt teisele üle, on seisuhõõrdejõud rihmarataste ja rihma vahel.
On ka võimalik olukord, kus keha liigub ning libiseb mööda teise keha pinda. Nähtust, kus hõõrdumine takistab mööda teise keha pinda libiseva keha liikumist, nimetatakse liugehõõrdumiseks. Liugehõõrdumise korral on hõõrdejõud suunatud alati liikumisele vastassuunas.
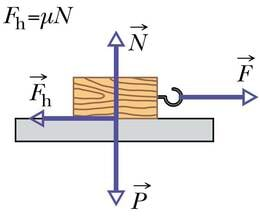
Jõu suurus sõltub kokkupuutuvate pindade omadustest ning pindu kokku suruva jõu suurusest. Vastu mingit pinda surumisel mõjub kehale rõhumisjõuga võrdne vastassuunaline toereaktsioon N. Katsed näitavad, et liugehõõrdejõud on võrdeline kehale mõjuva toereaktsiooniga:
Võrdetegurit μ (kreeka täht müü) selles valemis nimetatakse hõõrdeteguriks. Sageli, kui keha libiseb mööda horisontaalset pinda, on toereaktsioon arvuliselt võrdne kehale mõjuva raskusjõuga ja sel juhul
Avaldame hõõrdejõu valemist (2.22 ) hõõrdeteguri:
Näeme, et hõõrdetegur on võrdne hõõrdejõu ja toereaktsiooni jagatisega.
Hõõrdetegur ei iseloomusta mitte keha, millele hõõrdejõud mõjub, vaid libisevaid pindu. See sõltub kokkupuutuvate kehade materjalist, pindade töötlusest ja puhtusest. Samas ei sõltu hõõrdetegur kokkupuutepinna suurusest ega libisemise kiirusest, kui surve ja kiirus pole väga suured.
Hõõrdeteguri suurust saab määrata katseliselt. Siledate pindade vahelised hõõrdetegurid mõne materjalide jaoks on esitatud järgnevas tabelis.
Hõõrdejõud võib olla nii kasulik kui ka kahjulik. Kui on vaja keha paigal hoida või pidurdada, peab hõõrdejõud olema võimalikult suur. Liikumist segavat hõõrdumist tuleb aga vähendada.
Et osata hõõrdumist muuta, on vaja teada, miks hõõrdumine üldse tekib. Hõõrdumisel on kaks peamist põhjust.
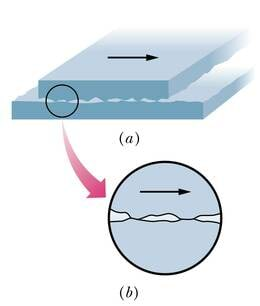
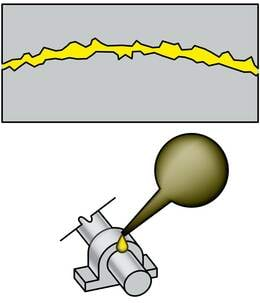
Esiteks põhjustab hõõrdumist pindade ebatasasus. Pinnakonarused jäävad üksteise taha kinni ja takistavad libisemist.
Teiseks põhjuseks on aineosakeste vahelised tõmbejõud. Väga siledad pinnad pääsevad teineteisele sedavõrd lähedale, et molekulidevahelised jõud kasvavad märgatavaks. Nii kleepuvad kokku kaks siledat plii- või klaasplaati.
Hõõrdejõu vähendamiseks kasutatakse määrimist. Määre tungib kokkupuutuvate pindade vahele ja surub need teineteisest eemale. Pinnakonarused ja molekulide tõmbejõud siis enam nii tugevasti mõjule ei pääse. Määrdena kasutatakse tavalisilt õlisid. Õlikihtide omavaheline liikumine tekitab küll teatavat takistust, kuid see on tavalisest hõõrdumisest tunduvalt väiksem.
Hõõrdumist saab suurendada pindade karestamise abil. Et tagada ohutut liiklemist, pinnatakse maanteed peene killustikuga ja liikluseeskiri nõuab piisavalt sügava mustriga autokummide kasutamist.
Suurema hõõrdumise saavutamiseks kasutatakse ka spetsiaalseid materjale, mis tagavad suurema hõõrdeteguri. Nii valmistatakse autode piduriklotsid vähekuluvast kuumakindlast ainest, mille hõõrdetegur kokkupuutel terasega ulatub väärtuseni 0,7.
Teame, et vastastikmõju üheks võimalikuks tagajärjeks on kuju muutumine. Keha kuju muutumist nimetatakse deformeerumiseks ning selle tagajärjel tekkivat kujumuutust deformatsiooniks (de- + fôrma — ladina k ära, vastupidi + kuju).
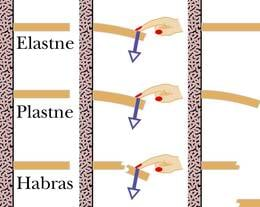
Deformeerumine võib olla kas pöörduv või pöördumatu protsess. Kui keha pärast deformeeriva mõju lõppemist taastab oma esialgse kuju kas täielikult või osaliselt, on tegemist elastse deformatsiooniga. Absoluutselt elastse deformatsiooni korral taastab endine kuju täielikult. Kui pärast surve lõppu säilub deformeerimisel saadud kuju, on tegemist plastse deformatsiooniga.
Keha elastsus või plastsus sõltub selle materjalist ja kujust. Väga elastsed on näiteks terasvedru ja kumminöör ning plastsed pehme savi ja plastiliin. Paljude kehade korral on väikene deformatsioon elastne, kuid suure kujumuutuse järel nende kuju enam ei taastu. Niimoodi käitub näiteks alumiinium- või vasktraat.
Kui keha aga juba väga väikese deformatsiooni tagajärjel puruneb, siis öeldakse, et see on habras.
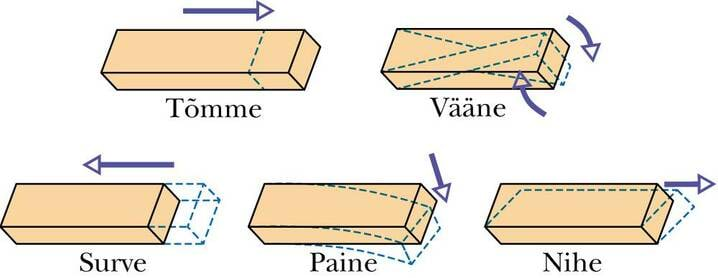
Keha kuju võib muutuda mitmel viisil. Näiteks saame kummipaela venitada, puuoksa painutada ja švammi kokku suruda. Selle põhjal, kuidas kuju muutub, eristatakse viit liiki deformatsioone: tõmme, surve, paine, vääne ja nihe.
Sageli ei pane me kehade kuju muutumist tähele, sest deformatsioon on väike. Kui keegi ronib näiteks suure kivirahnu otsa, siis ei suuda selle lamedamaks vajumist keegi ka luubiga vaadates märgata.
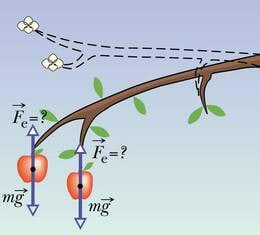
Kevadel on õunapuuoks täis õhkkergeid õisi. Siis hakkavad õitest õunad arenema ja viljad paisuvad ning muutuvad aina raskemaks. Kuidas need oksa küljes püsivad? Koos raskusjõu kasvamisega peab suurenema ka jõud, mis tasakaalustab raskusjõu. Kust on see jõud pärit ja milline on selle olemus?
Jälgides oksa juures toimunud muutusi, võib näha, et oks on paindunud. Oksa deformatsioon ongi uue jõu tekkimise põhjuseks. Jõudu, mis tekib keha kuju muutmisel ehk deformeerimisel, nimetatakse elastsusjõuks.
Elastsusjõud on deformatsiooniga alati vastassuunaline. Elastsusjõud püüab keha esialgset kuju taastada. Absoluutselt plastse deformatsiooni korral mingit kuju taastumist ei toimu ja järelikult puudub seda põhjustav jõud, st elastsusjõud on null.
Elastsusjõudude tekkepõhjuseks on aineosakeste vaheline vastastikmõju. Osakeste vahel esineb nii tõmbumine kui ka tõukumine, kusjuures mõlema tugevus sõltub vahekaugusest. Tavalises deformeerimata olekus on need jõud tasakaalus.
Kokkusurumisel osakeste vahekaugused vähenevad ning ülekaalu saavutavad tõukejõud, mis takistavad deformeerimist. Tõmbedeformatsioonil seevastu vahekaugused kasvavad ja ülekaalu jäävad venitamist takistavad tõmbejõud.
Elastsusjõudu võib kohata kõikjal ümberringi. Seda kasutatakse näiteks vibunoole lendulaskmisel, kellamehhanismis, juuste korrastamisel (juuksekumm), ukse sulguris, dokumentide kooshoidmisel (kirjaklamber) jm. Elastsusjõuga on seotud kõik põrked. Elastsel põrkel taastab elastsusjõud põrandaga kokkupuutel deformeerunud palli kuju ja tõukab sellega palli vastassuunas liikuma. Plastse põrke korral jäävad kehad kokku ja liikumine muutub vähem.
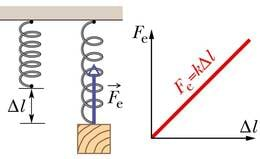
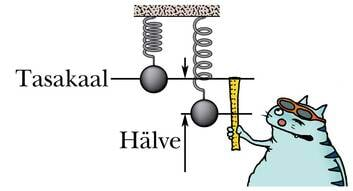
Mõõtmised näitavad, et suhteliselt väikeste deformatsioonide korral tekkiv elastsusjõud on võrdeline kujumuutuse ehk deformatsiooni suurusega. Kujumuutust on kõige lihtsam mõõta tõmbe ja surve korral. Siis iseloomustab deformatsiooni alg- ja lõpp-pikkuse vahe ehk pikenemine, mida järgnevas tähistame sümboliga Δl. Elastsusjõu sõltuvust pikenemisest kirjeldab valem:
Selle seaduspärasuse avastas 1660. aastal inglise füüsik ja loodusteadlane Robert Hooke. Tänapäeval tuntakse seda seost Hooke’i seaduse nime all. Miinusmärk viitab asjaolule, et elastsusjõud on suunatud alati deformatsiooni suunale vastupidiselt. Võrdetegurit k nimetatakse deformeeritud keha jäikusteguriks ehk lihtsalt jäikuseks. Jäikustegur sõltub keha materjalist, mõõtmetest ja kujust ning selle mõõtühik on 1 N/m.
Hooke’i seadus kehtib vaid keha mõõtmetega võrreldes väikeste kujumuutuste korral, mil deformatsioon jääb absoluutselt elastseks. Suuremad deformatsioonid põhjustavad keha sisemises ehituses pöördumatuid muutusi ja seetõttu muutub ka esialgset kuju taastav elastsusjõud.
Ringliikumine on kõverjoonelise liikumise erijuht, kus keha punktide trajektooriks on ringjoon või selle osa. Tegemist on lihtsaima kõverjoonelise liikumisega, mille seadusi tundes on võimalik kirjeldada ka keerulisemaid liikumisi. Saab ju erinevate ring- ja sirgjooneliste lõikude kombineerimisel kokku panna mis tahes kujuga trajektoore.
Ringliikumise puhul võime rääkida eraldi ringjoonelisest liikumisest ja pöörlemisest.
Kui turist sõidab vaaterattal, siis liiguvad kõik tema punktid mööda ühesuguseid ringjoonekujulisi trajektoore ja tegemist on ringjoonelise liikumisega. Ringjooneliseks liikumiseks nimetatakse keha liikumist mööda ringjoonekujulist trajektoori.
Ringjoonelist liikumist nimetatakse tihti ka tiirlemiseks. Ringjoonelisest liikumisest ehk tiirlemisest saame rääkida siis, kui keha mõõtmed ja kuju pole liikumise kirjeldamisel olulised ning me võime kasutada punktmassi mudelit.
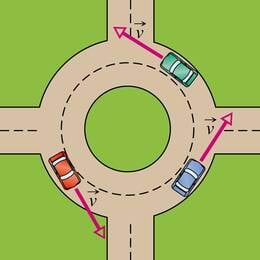
Ringjooneliselt liiguvad näiteks autod kurvis, kellaosuti tipp, karussellil istuv laps ning ümber Maa tiirlev Kuu.
Ringjooneliselt liikuvate kehade trajektoorideks on erineva raadiusega ringjooned. Ringjoone raadius määrab ära trajektoori kõveruse ja on seega ringjoonelist liikumist iseloomustav suurus. Valemites ja joonistel tähistatakse trajektoori kõverusraadiust tähtedega r või R ja selle mõõtühikuks on 1 meeter.
Tihti tuleb ette aga ringliikumist, kus keha punktide trajektoorideks on erinevad ringjooned ning seepärast ei saa keha punktmassiks lugeda. Kui keha erinevad punktid tiirlevad sama keskpunkti ümber mööda erinevate raadiustega ringjooni, on tegemist pöördliikumise ehk pöörlemisega. Pöörlevalt liiguvad näiteks autoratas, grammofoniplaat, avatav uks, saltot sooritav akrobaat ja Maa ümber oma kujuteldava telje.
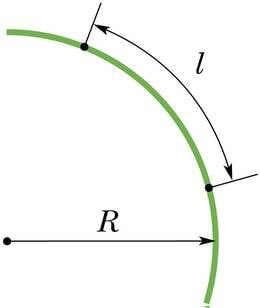
Liikumisel toimuvat asukohamuutust iseloomustatakse nihke või teepikkuse abil. Ringliikumise kirjeldamiseks nihe ei sobi, kuna samu punkte läbitakse korduvalt. Küll aga saab kasutada läbitud teepikkust l. Ringjoonelisel liikumisel kujutab teepikkus l endast keha poolt läbitud ringjoone kaare pikkust.
Kui tegemist on pöörlemisega, liiguvad keha erinevad punktid mööda erineva raadiusega ringjooni ning nende jaoks on läbitavad teepikkused erinevad.
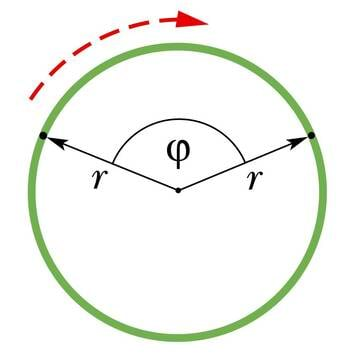
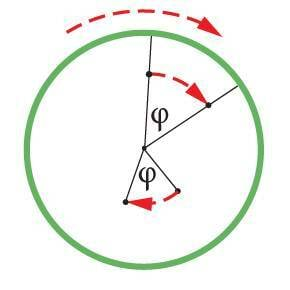
Igale ringjoone kaarele vastab alati kindel kesknurk. Just selle nurga võrra pöördub liikumise käigus raadius, mis ühendab trajektoori keskpunkti keha asukohaga. Nurka, mille võrra pöördub ringliikumisel keha asukohta ja trajektoori kõveruskeskpunkti ühendav raadius, nimetatakse pöördenurgaks. Pöördenurga tähiseks on kreeka täht φ (fii).
Kuigi pöörlemise korral läbivad pöörlemisteljest eri kaugusel asuvad punktid sama ajaga erinevad teepikkused, siis on pöördenurk nende punktide jaoks ikka ühesugune. Seepärast eelistataksegi ringliikumise kirjeldamisel teepikkusele pöördenurka.
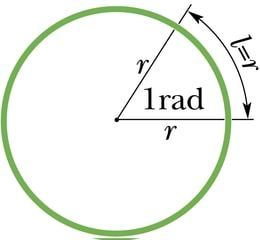
Füüsikas mõõdetakse pöördenurka mitte kraadides vaid radiaanides. Üks radiaan (lüh. rad) on selline kesknurk, mis toetub kaarele, mille pikkus on võrdne selle ringjoone raadiusega. Ühele täisringile vastab pöördenurk 2π rad, seega 1 rad = 360º/2π ≈ 57º.
Kasutades selliselt defineeritud nurgaühikut, kehtib pöördenurga ja kaarepikkuse vahel lihtne seos:
Kui keha sooritab mis tahes võrdsetes ajavahemikes võrdsed pöördenurgad, on tegemist ühtlase ringliikumisega. Nii nagu ühtlane sirgjooneline liikumine, on ka ühtlane ringliikumine üks liikumise füüsikaline mudel. Looduses ideaalsel kujul sellist liikumist ei esine, kuid paljudel juhtudel saab seda mudelit rakendada suure täpsusega.
Ringliikumine on perioodiline liikumine, kuna keha asukoht kordub võrdsete ajavahemike möödumisel. Perioodilisi liikumisi saab iseloomustada perioodi ja sageduse abil.
Ringliikumise perioodiks nimetatakse ajavahemikku, mille jooksul läbitakse üks täisring. Kella minutiosuti tiirlemisperiood on üks tund, Maa tiirlemisperiood ümber Päikese aga üks aasta. Perioodi mõõdetakse alati ajaühikutes ja SI-s on mõõtühikuks seega 1 sekund. Perioodi tähiseks valime käesolevas kursuses T.
Kui tähistame tiirleva keha poolt aja t kestel sooritatud tiirude arvu tähega N, avaldub ühe tiiru sooritamise aeg ehk periood koguaja ja tiirude arvu jagatisena
Sageduseks nimetatakse ajaühikus tehtavate täisringide arvu. Sageduse tähiseks on f (frequçns — lad k sagedane, korduv). Sageduse leidmiseks tuleb ringide arv N jagada ajaühikute arvuga ehk ajaga t:
Võrreldes valemeid (2.26 ) ja (2.27 ), näeme, et ringliikumise sagedus ja periood on teineteise pöördväärtused:
Nii on ka sageduse mõõtühikuks sekundi pöördväärtus, mida nimetatakse hertsiks (Hz). 1Hz = 1/s.
Liikuval kehal on alati mingi kiirus. Ühtlase liikumise kiirus on võrdne teepikkuse ja selle läbimiseks kuluva aja jagatisega:
Ühtlasel ringjoonelisel liikumisel nimetatakse teepikkuse (läbitud joone pikkuse) ning aja jagatist mitte lihtsalt kiiruseks vaid joonkiiruseks. Nimetuse täpsustus on tingitud sellest, et ringliikumist saab lisaks joonkiirusele iseloomustada ka ajaühikus sooritatava pöördenurga kaudu.
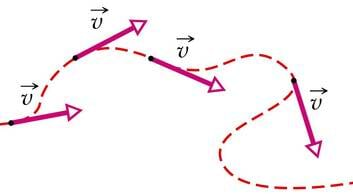
Valem (2.29 ) võimaldab leida vaid kiiruse arvväärtuse. Joonkiirus on suunatud alati piki ringjoonelise trajektoori puutujat ja on igas punktis trajektoori kõverusraadiusega risti.
Joonkiirusega saab iseloomustada mitte ainult ringjoonelist, vaid ka mis tahes muu kujuga trajektoori mööda toimuvat kõverjoonelist liikumist.
Kuna pöörlemise korral läbivad teljest eri kaugusel asuvad punktid sama ajaga erinevad teepikkused, siis on ka nende punktide joonkiirused erinevad. Mida suurem on punkti tiirlemisraadius, seda suurem on ka kiirus. Kuna aga kõikide punktide jaoks jääb pöördenurk alati samaks, on otstarbekas ringliikumise kirjeldamiseks defineeridagi kiirus just nurga kaudu.
Seepärast kasutataksegi ringliikumise iseloomustamiseks pöördenurga ja selle sooritamiseks kuluva ajavahemiku jagatist. Seda jagatist nimetatakse ringliikumise nurkkiiruseks. Nurkkiirus on võrdne ajaühikus sooritatava pöördenurgaga. Seda suurust tähistatakse kreeka tähega ω (omega) ja valemiks on:
Kui pöördenurka mõõdetakse radiaanides ja aega sekundites, on nurkkiiruse mõõtühikuks radiaan sekundis (1 rad/s).
Nurkkiirus on seotud joonkiirusega v. Paneme nurkkiiruse avaldisse (2.30 ) pöördenurga kohale selle väärtuse φ = l/r ning saame
Et aga l/t kujutab endast joonkiirust v, saame
See ongi seos nurkkiiruse ja joonkiiruse vahel.
Peale joonkiiruse on nurkkiirus seotud ka ringliikumise sageduse ja perioodiga. Definitsiooni järgi on sagedus võrdne ajaühikus sooritatavate täisringide arvuga:
Aja t jooksul sooritatud täisringide arv on siis N = ft. Et igale täisringile vastab pöördenurk 2π rad, siis saame, et
millest vastavalt nurkkiiruse definitsioonile ω = φ/t saame sagedusega seose valemiks
Näeme, et nurkkiirus on võrdeline sagedusega. Seepärast nimetatakse seda suurust mõnikord ka nurksageduseks või ringsageduseks.
Teades, et periood ja sagedus on teineteise pöördarvud, on lihtne näha, et nurkkiirus sõltub ringliikumise perioodist pöördvõrdeliselt:
Sirgjoonelisel liikumisel on keha kiirus suunatud piki trajektoori. Seevastu ringliikumisel kiiruse suund muutub pidevalt. Kui trajektoor pole sirge, on kiirus trajektoori erinevates punktides suunatud erinevalt, kuid alati piki trajektoori puutujat (so. mööda sirget, mis on antud punktis raadiusega risti).
Ringliikumisel muutub liikumise suund pidevalt. Kui kiiruse suund muutub, siis muutub järelikult ka kiirusvektor (kiirus on vektoriaalne suurus). Kui aga kiirusvektor muutub, on olemas ka kiirendus. Kiirendus on ju kiirusvektori muudu ja muutuseks kulunud ajavahemiku jagatis:
Tuleb välja, et ringliikumisel esineb kiirendus ka siis, kui kiiruse arvväärtus ei muutu. Kiirendus on ka ühtlasel ringliikumisel, kuna liikumise suund muutub.
Kuhu on see kiirendus suunatud? Vaatame lühikest ajavahemikku, mille kestel sooritatud pöördenurk on väike. Et ringjoonelise liikumise joonkiirus on suunatud alati raadiusega risti, pöördub ka kiirusvektor sama nurga võrra. Joonisel tähistab kiirust enne pööret vektor ja pärast pöörde sooritamist . Kuna kiiruse arvväärtus ei muutu, on ühtlasel ringliikumisel nende vektorite pikkused võrdsed.
Kiirenduse leidmiseks tuleb leida kiiruse muutus ehk kiirusvektorite vahe . Vektori lahutamine on samaväärne vastandvektori liitmisega. Jooniselt on näha, et väikese pöördenurga korral on kiiruse muut suunatud piki raadiust trajektoori kõveruskeskpunkti poole. Ringliikumise kiirendus kui kiiruse muutumise kiirus on suunatud samuti kõveruskeskpunkti.
Suunamuutusest tingitud kiirendus on suunatud alati keha trajektoori kõveruskeskpunkti poole ja on seega kiirusvektoriga risti. Seepärast nimetatakse seda kiirendust kesktõmbekiirenduseks.
Kesktõmbekiirenduse väärtus sõltub nii trajektoori kõverusraadiusest r kui ka joonkiirusest v. On ju loomulik, et mida kiiremini keha mööda ringjoont liigub, seda kiiremini muutub ka liikumissuund. Samuti muutub suund seda kiiremini, mida kõveram on trajektoor.
Kesktõmbekiirendus sõltub liikumise joonkiirusest ja trajektoori kõverusraadiusest järgmiselt:
Kasutades valemit (2.32 ) seoses nurk- ja joonkiiruse vahel, saame kesktõmbekiirenduse avaldada ka nurkkiiruse kaudu:
Ühtlasel ringliikumisel esineb alati kesktõmbekiirendus. Newtoni II seaduse järgi liigub keha kiirendusega vaid siis, kui sellele mõjub jõud. Ka kesktõmbekiirenduse tekitamiseks on vajalik jõud. See jõud peab mõjuma samas suunas kiirendusega ja on järelikult suunatud trajektoori kõveruskeskpunkti poole.
Kui sellist jõudu kehale ei mõju, ei saa olla ka ringliikumist. Newtoni I seaduse järgi liiguvad ju kõik kehad, millele jõudusid ei mõju, inertsi tõttu ühtlaselt ja sirgjooneliselt. Keha liigub mööda ringjoont vaid siis, kui seda otsesuunast pidevalt kõrvale kallutatakse. Ringliikumine toimub kesktõmbejõu ja inertsi koosmõju tagajärjena. Trajektoori kõveruskeskpunkti suunatud jõudu, mis põhjustab ringliikumist, nimetatakse kesktõmbejõuks ehk tsentripetaaljõuks (centrum + petere — ladina k kese + ründama).
Kesktõmbejõuks võib olla mis tahes liiki jõud. Autot hoiab ringteelt välja libisemast hõõrdejõud, sidesatelliiti hoiab ümber Maa tiirlemas gravitatsioonijõud, vasar liigub heitmiseelse hoovõtu ajal ringjooneliselt trossis tekkiva elastsusjõu mõjul.
Kesktõmbejõudu saab leida Newtoni II seadust kasutades kesktõmbekiirenduse kaudu:
Kõik, kes on sõitnud mööda ringjoont kiiresti pöörleval karussellil või järsult kurvi võtvas autos, on tundnud, et neid surutakse ringi keskmest väljapoole. Ringjooneliselt liikuvale kehale mõjuks nagu mingi keskpunktist eemale suunatud jõud. Sellele jõule on antud ka eraldi nimetus — tsentrifugaaljõud (centrum + fugiô — ladina k kese + põgenema). Tegemist on niinimetatud inertsijõuga, mida vaatleja tajub siis, kui ta liigub kiirendusega.
Kui me istume autos, siis oleme selle suhtes paigal. Sisenedes kurvi, hakkab auto kõrvale pöörama ja sunnib kaasa pöörama ka autosistujaid. Sõitjatele tundub, nagu lükataks neid väljapoole. Maa suhtes vaadeldes seda väljapoole mõjuvat jõudu ei eksisteeri. Inertsi tõttu püüavad auto ja autosistujad liikuda otse ehk ringliikumise keskmest eemale ja ainus jõud, mis neile tegelikult mõjub, on liikumist ringjooneliseks sundiv kesktõmbejõud.
Kõik me teame, et planeedid tiirlevad ümber Päikese ning Kuu tiirleb ümber Maa. Trajektooriks on üsna täpselt ringjoon. Näiteks Maa kaugus Päikesest ei muutu tiirlemise käigus enam kui 3%.
Juba Newton oletas, et planeetide tiirlemine on tingitud gravitatsioonijõust. Tuginedes tänastele teadmistele gravitatsiooni ning ringliikumise kohta, võime väita, et just gravitatsioonijõud kesktõmbekiirenduse tekitajana kallutab planeedid sirgjoonelisest teest kõrvale ja on seega nende tiirlemise põhjuseks.
Oletame, et planeedil massiga M on kaaslane massiga m, mis tiirleb selle ümber ringorbiidil raadiusega r. Vastavalt gravitatsiooniseadusele tõmbab planeet kaaslast jõuga
See jõud ongi kaaslase tiirlemist põhjustavaks kesktõmbejõuks, mis on valemi (2.38 ) järgi seotud tiirlemise nurkkiirusega järgmiselt:
Siit saame avaldada nurkkiiruse ning sellest omakorda tiirlemisperioodi:
Viimane seos näitab, et tiirlemisel mööda ringorbiiti on perioodi ruut võrdeline tiirlemisraadiuse kuubiga. Selle seaduspärasuse avastas planeetide vaatlusandmeid analüüsides Saksa astronoom Johannes Kepler juba 1619. aastal.
Tiirlemise orbiidiks on ringjoon vaid siis, kui gravitatsioonijõud mõjub kogu aeg liikumisega risti. Paljude taevakehade puhul ei ole see aga alati nii. Kui gravitatsioonijõud pole kiirusega risti, mõjub see liikumisele kiirendavalt või aeglustavalt. Sel juhul on liikumine muutuv ning trajektooriks on ringjoone asemel väljavenitatud ellips või isegi mittekinnine joon nagu parabool või hüperbool.
Looduses võime ringliikumist kohata eelkõige taevakehade juures. Gravitatsiooni tõttu kõik maailmaruumi kehad tõmbuvad. Vaid tänu tiirlemisele ei kuku Kuu Maale ning planeedid Päikesele. Ka mitmesajast miljardist massiivsest tähest koosnev Linnutee galaktika ei tõmbu kokku, vaid säilitab oma 100 000 valgusaasta suuruse läbimõõdu tänu tähtede tiirlemisele.
Lisaks tiirlemisele võivad taevakehad ka pöörelda. Öö ja päev vahelduvad tänu maakera pöörlemisele ja pöörlemistelje kalde muutumatus tingib aastaaegade vaheldumise.
Looduslikku ringliikumist leidub ka maapealsetes mastaapides. Näiteks saaki otsiva kotka tiirlemine õhus või keeristormid. Looduslik ringliikumine on enamasti ühtlane. Tiirleva taevakeha kiirus muutub, kui trajektoor erineb ringjoonest. Pöörlemiskiirus võib muutuda mõne teise keha mõjul. Näiteks pole Maa pöörlemine absoluutselt ühtlane, kuna Kuu põhjustab maailmamere loodeid.
Tehnikas on ringliikumise kohta palju näiteid. Autod sõidavad tänu pöörlevatele ratastele, informatsiooni salvestatakse pöörlevatele laserplaatidele ning magnetketastele, sidet peetakse ümber Maa tiirlevate tehiskaaslaste abil.
Ringliikumisega kaasnevat kesktõmbekiirendust võib kasutada kaalu muutmiseks. Astronaudid treenivad tiirlevatel trenažööridel vastupidavust ülekoormusele ning tsentrifuugi abil eraldatakse segust erineva tihedusega aineid.
Aastal 1985 kukkusid maavärina tõttu Mexicos kokku paljud keskmise kõrgusega hooned. Kõrgemad ja madalamad hooned jäid püsti (vaata pilti). Inglismaal Manchesteri lähedal ületasid ratsaväelased 1831. aastal silda ning marssisid ilmselt samas taktis silla võnkumisega. Sild kukkus kokku pärast seda, kui üks silda toetanud polt purunes.
Londonis avati 2001.aastal uus üle Thamesi jõe ulatuv sild, mis ühendab Tate’i Moodsa Kunsti Galeriid St. Pauli kiriku ümbrusega ja mis pidi tähistama uue aastatuhande saabumist. Kui esimene jalakäijate voog hakkas Milleeniumisilla nime kandvat ehitist ületama, hakkas see nii tugevasti kõikuma, et mõned jalakäijad jäid vaid käsipuude abil püsti. Kas sarnased võnkumised võivad ilmneda tantsupõrandal või rokk-kontserdil? Kas hea laulja suudaks veiniklaasi või mõne muu klaasanuma lihtsalt lauldes purustada?
Enamik looduses aset leiduvaid nähtusi toimub perioodiliselt. Teatud aja möödudes kordub kõik jälle uuesti. Nii vahelduvad öö ja päev ning aastaajad, kordub lindude ränne igal kevadel lõunamaalt koju pesitsema ja igal 1. septembril minnakse jälle kooli. Kõikjal igapäevases elus, looduses ja tehnikas võime kohata perioodiliselt korduvat liikumist — merelained loksuvad vastu kaldakive, puuoksad kõiguvad tuules, linnud lehvitavad tiibu, õmblusmasina nõel liigub üles-alla, praam sõidab edasi-tagasi Virtsu ja Kuivastu vahet. Seda tüüpi liikumiste tundmaõppimine ning ühiste joonte väljaselgitamine aitab meil ümbritsevat paremini mõista ja kogutud teadmisi enda kasuks rakendada.
Ühte osa perioodiliselt korduvatest liikumistest me juba õppisime lähemalt tundma. Selleks on ringliikumine. Teiseks suureks grupiks on võnkumine. Erinevalt teistest perioodilistest liikumistest kordub võnkumisel liikumine võrdsete ajavahemike tagant nii, et esialgsesse asendisse läheb keha tagasi sama teed mööda. Võnkumiseks nimetatakse perioodilist edasi-tagasi liikumist teatud tasakaaluasendist kord ühele, kord teisele poole. Nii on võnkumine mootorikolvi üles-alla liikumine, mitte aga väntvõlli pöörlemine. Viimasel juhul jõuab vändaots küll korduvalt esialgsesse seisu tagasi, kuid ikka mööda ringjoont tiireldes.
Kuna võnkumine kujutab endast muutuvat liikumist, on selle tekkimiseks vaja vastastikmõju. Kuna vastastikmõjus osaleb alati mitu keha, siis saab ka võnkumine toimuda mitte ühe keha, vaid kehade süsteemi korral. Näiteks ei saaks vedru otsa riputatud raskus võnkuda, kui puuduks maakera oma külgetõmbega. Iga sellist mitmest vastastikmõjus olevast kehast koosnevat süsteemi, milles võib tekkida võnkumine, nimetatakse võnkesüsteemiks.
Kui võnkumine toimub vaid süsteemi kuuluvate kehade vaheliste mõjujõudude toimel, on tegemist vabavõnkumisega. Vabavõnkumiseks nimetatakse süsteemi sisejõudude mõjul toimuvat võnkumist. Näiteks võib vabalt võnkuda niidi otsas rippuv kivi, kui miski selle tasakaalust välja viib. Süsteemi moodustavad siin ülalt kinnitatud niit, kivi ja maakera. Süsteemisisesteks jõududeks on gravitatsioonijõud Maa ja kivi vahel ning niidi tõmbejõud. Mõnikord nimetatakse vabavõnkumist ka omavõnkumiseks.
Mehaanilise vabavõnkumise tekkimiseks peab süsteemis olema täidetud kolm tingimust.
- Kõigepealt peab süsteemil olema püsiv tasakaaluolek. Püsiv tasakaal on selline, millest väljumisel tekkivad jõud viivad süsteemi tasakaaluolekusse tagasi.
- Teiseks peab süsteem omama inertsi. Kui keha liigub tasakaaluasendi poole suunatud jõu mõjul kiirenevalt, ei jää see kohale jõudes mitte silmapilkselt seisma, vaid liigub hooga edasi ning eemaldub tasakaaluasendist teisele poole.
- Kolmandaks peab süsteem saama võnkumise käivitamiseks (tasakaalust väljaviimiseks) välise tõuke.
Kuna igale kehale mõjub liikumist takistav hõõrdejõud, siis ei saa vabavõnkumine kesta ilma välise abita igavesti. Võnkumise kiirus ja ulatus hääbuvad aja jooksul nullini. Sellist võnkumist nimetatakse sumbuvaks. Looduses on vabavõnkumised alati sumbuvad. Sumbumatu võnkumise saamiseks tuleb hõõrdumist millegi välisega kompenseerida. Näiteks pommidega kellas annab spetsiaalse mehhanismi kaudu pendlile igal võnkel hoogu juurde pomme allapoole tõmbav raskusjõud.
Kui võnkumine toimub mingi välise perioodilise jõu mõjul, on tegemist sundvõnkumisega. Nii võngub õmblusmasina nõel üles-alla vaid seepärast, et käsi või mootor vänta ringi ajab. Kuna siin saab süsteem energiat välisest allikast, on sundvõnkumine alati sumbumatu. Sundvõnkumiseks on näiteks lõiketera liikumine höövelpingis, pintsli liikumine värvimisel ja klaasipuhastaja liikumine autoaknal.
Nagu igat perioodilist liikumist, iseloomustab ka võnkumist ajavahemik, mille möödumisel liikumine uuesti kordub. Ühe täisvõnke sooritamiseks kuluvat aega nimetatakse võnkeperioodiks. Võnkeperioodi tähis ja mõõtühik on samasugused kui ringliikumise perioodil, seega T ja üks sekund.
Kui võnkeperiood on täpseks mõõtmiseks liiga lühike, saab täpsust tõsta, mõõtes mitte ühe, vaid suurema arvu võngete sooritamise koguaega t. Kui võngete arvu tähiseks võtta N, saame perioodi arvutada valemist
Ajaühikus sooritatavate täisvõngete arvu nimetatakse võnkesageduseks. Võnkesageduse tähis on sarnaselt ringliikumisega f ja mõõtühik herts (Hz). Analoogiliselt ringliikumise sagedusega on võnkesagedus võrdne võnkeperioodi pöördväärtusega:
Võnkumisel liigub keha tasakaaluasendist kord ühele, kord teisele poole. Võnkuva keha kaugust tasakaaluasendist nimetatakse keha hälbeks. Hälve on ajas muutuv suurus ja sõltuvalt sellest, kummal pool tasakaaluasendit keha asub, loetakse see kas positiivseks või negatiivseks. Kuna hälve kujutab endast tegelikult keha koordinaati, on selle tähiseks võetud x ja mõõtühikuks on pikkusühik meeter.
Maksimaalset hälvet ehk suurimat kaugust tasakaaluasendist nimetatakse võnkeamplituudiks. Amplituudi tähiseks on x0. Kui sumbumatul võnkumisel amplituud ei muutu, siis sumbuval väheneb see aegamisi nullini.
Võnkuvat liikumist esineb looduses kõikjal meie ümber. Kui soovime loodust uurida ja võimalikult täpselt arvude abil kirjeldada, peame oskama ka võnkumist matemaatiliste meetoditega väljendada. Selleks et jõuda võnkumise võrrandini, vaatleme veel kord ringliikumist.
Kujutame ette mingit tiirlevat eset, näiteks vinüülplaadimängija pöörleva ketta servale asetatud tikutoosi. Kui nüüd keha valgustada küljelt, piki tiirlemistasandit, liigub tikutoosi vari seinal mitte ringjooneliselt, vaid edasi-tagasi. Vari võngub, kusjuures selle võnkumise sagedus langeb kokku eseme tiirlemise sagedusega ning võnkeamplituud tiirlemise raadiusega. Niisugust varju edasi-tagasi liikumist pole raske matemaatiliselt kirja panna.
Vaatame kõrvalolevat joonist, millel on näidatud ese, selle tiirlemise trajektoor ning vari seinal. Koordinaattelg on suunatud piki varju liikumist nii, et nullpunkt asuks tiirlemiskeskme kohal. Tiirleva eseme asukohta kirjeldab pöördenurk φ ja varju hälvet (kaugust koordinaadi nullpunktist) x. Joonisel tekib täisnurkne kolmnurk, mille hüpotenuusiks on trajektoori kõverusraadius r ning nurga φ vastaskaatetiks varju hälve x. Matemaatikas õpitud siinusfunktsiooni definitsiooni järgi
Tiirlemise pöördenurga saame asendada valemis nurkkiiruse ja aja korrutisega:
Nii kehtib varju võnkumise hälbe jaoks seos
Kuna vari ei saa keskpunktist kaugemale minna kui tiirlemise raadius r, siis on selle väärtus ka võnkeamplituudiks x0 = r. Pärast asendust saamegi hälbe arvutamiseks mis tahes ajahetkel valemi:
Saadud valem kirjeldab varju liikumist seinal, näidates selle koordinaadi sõltuvust ajast.
Kõiki selliseid võnkumisi, mida saab kirjeldada siinus- või koosinusfunktsiooni abil, nimetatakse harmoonilisteks võnkumisteks. Seos (3.6 ) on seega harmoonilise võnkumise võrrand.
Siinusfunktsiooni argumendiks olevat suurust
nimetatakse võnkumise faasiks. Faasi mõõtühikuks on radiaan (rad) ning seda saab avaldada võnkesageduse ja perioodi kaudu:
Suurust ω, mis tiirlemise jaoks on nurkkiirus, nimetatakse võnkumise korral ring- ehk nurksageduseks. Ringsageduse mõõtühik on 1 rad/s.
Paljud looduses esinevad võnkumised on harmoonilised või sellele lähedased. Seepärast omab harmoonilise võnkumise võrrand (3.6 ) suurt tähtsust. Võrrand võimaldab kirjeldada peaaegu kõiki võnkumisega seotud nähtusi.
Lisaks võrrandile saab võnkumisi kirjeldada ka graafiku abil. Võnkumise graafik näitab keha koordinaadi sõltuvust ajast. Püstteljele kantakse koordinaat ehk võnkumise hälve ja horisontaalteljele aeg. Reaalselt saab võnkumise graafikut joonistada näiteks vedrupendli raskuse külge kinnitatud viltpliiatsi abil, mis surub vastu ühtlase kiirusega nihutatavat pabeririba.
Harmoonilise võnkumise graafiku võib joonestada ka võnkumise võrrandi järgi erinevatele ajahetkedele vastavaid koordinaate välja arvutades ja teljestikku kandes. Nii talitades saame võnkumise graafikuks sujuva lainelise joone, mida nimetatakse sinusoidiks.
Sinusoid läbib kordamööda teljestiku positiivset ja negatiivset ala, jäädes samal ajal amplituudiga määratud horisontaaljoonte vahele. Sinusoid lõikab ajatelge iga poole perioodi tagant. Seda teades on graafikult võnkumise amplituudi ja perioodi lihtne välja lugeda.
Veel annab graafik informatsiooni võnkuva keha kiiruse muutumise kohta. Teatavasti näitab kiirust liikumisgraafiku tõus. Uurides sinusoidi, näeme, et suurima hälbega punktides graafiku puutuja mitte ei tõuse ega lange, vaid on horisontaalne. Seega on neil hetkedel keha paigal ja liikumise suund muutub vastupidiseks. Suurim tõus või langus toimub hetkedel, mil joon lõikub ajateljega. Järelikult liigub keha tasakaaluasendi poole kiirenevalt, maksimumkiirus saavutatakse tasakaaluasendis ja sellest eemaldumisel liikumine jälle aeglustub.
Me teame, et keha muudab vastastikmõju teel teise keha liikumist või kuju, st muudab selle seisundit. Seisundi muutmise protsessi nimetatakse tööks ja töö tegemiseks peab keha omama energiat. Energiat omab keha tänu liikumisele (kineetiline energia) või sellele mõjuvatele jõududele (potentsiaalne energia). Kuna võnkumine on liikumine, mis toimub võnkesüsteemis mõjuvate jõudude toimel, siis omab selline süsteem energiat nii kineetilisel kui ka potentsiaalsel kujul. Seejuures võib kineetiline energia muunduda potentsiaalseks ning vastupidi nii, et nende summa jääb muutumatuks.
Uurime võnkumise energia muundumist niidi otsa riputatud kivi võnkumise näitel. Kivile mõjub Maa külgetõmbejõud ehk raskusjõud. Kallutades pendlit tasakaaluasendist kõrvale, tehakse tööd ja kivi tõuseb kõrgemale, omandades potentsiaalse energia. Raskusjõust tingitud potentsiaalne energia on seda suurem, mida suurem on kõrgus.
Päästes kivi lahti, algab võnkumine. Kiirus ja sellega koos ka liikumis- ehk kineetiline energia kasvavad ning saavutavad maksimumväärtuse tasakaaluasendisse jõudmisel. Samal ajal kõrgus väheneb ja sellega väheneb ka potentsiaalne energia, jõudes tasakaaluasendis nulli. Kivi jätkab inertsi tõttu liikumist, mida raskusjõud nüüd aeglustab. Kiirus ja kineetiline energia kahanevad ning kõrgus ja potentsiaalne energia kasvavad, kuni pendel peatub teises äärmises asendis. Edasi kordub kõik vastupidises suunas ikka nii, et energia kogusumma jääb samaks. Seda muidugi takistava jõu puudumisel. Takistuse ületamine kulutab energiat ning amplituud ja maksimumkiirus vähenevad — võnkumine sumbub aegamööda.
Võnkumisi võib kohata nii elus ja eluta looduses kui ka inimese valmistatud objektide juures. Neid on vabu ja sunnitud, sumbuvaid ja sumbumatuid. Paljude puhul me isegi ei teadvusta endale, et tegemist on võnkumisega.
Looduses võib kohata mitmeid vabalt võnkuvaid kehi. Puud kõiguvad tuules, haavalehed värisevad ning vees ujuv puunott õõtsub üles-alla. Enamik sellistest võnkumistest ei täida mingit kindlat eesmärki, kuid mõned võivad siiski ka kasu tuua. Õite kõikumine äratab tolmeldavate putukate tähelepanu, kõikuvatest viljadest levivad seemned kaugemale ning peente ja lapikute rootsude otsas rippuvate haavalehtede värisemine aitab puul paremini valgust püüda ja vee aurumist reguleerida.
Sundvõnkumist kasutavad elusolendid liikumiseks. Me ise liigutame kõndimisel käsi ning jalgu edasi-tagasi. Paljud mikroorganismid liiguvad viburi võngutamise abil, linnud ja putukad lehvitavad tiibu, vee-elanikud liigutavad saba, uimi või loibi.
Mitmesugused võnkumised on inimeste poolt rakendust leidnud. Kes meist poleks näiteks lapsepõlves kiikunud! Kiikumises korraldatakse isegi võistlusi. Veel üheks näiteks on heliallikad. Kõik kehad, mis võnguvad sagedusvahemikus 16 - 20 000 Hz, tekitavad kuuldavat heli. Heliallikaks võivad olla vabalt võnkuv pillikeel, kirikukell ja trumminahk. Ka akordionis ja saksofonis teeb häält võnkuv keel, kuid see on kitarrikeelega võrreldes hoopis teistsugune. Kõlaris tekitab heli muutuva elektrivoolu poolt võnkuma sunnitud valjuhääldi membraan.
Sundvõnkumist rakendatakse masinates, mis viivad korduvalt läbi üht ja sama operatsiooni. Siin võib näiteks tuua õmblusmasina, kolbpumba, aurumasina ja pudelikorkija.
Nagu nägime, võivad võnkuvad süsteemid olla väga erinevad. Ometigi saab neid sarnaste joonte põhjal grupeerida ning ühise lihtsustatud mudeli alla viia. Võnkuva süsteemi füüsikalist mudelit nimetatakse pendliks. Kõige sagedamini kasutatavateks mudeliteks on matemaatiline pendel, vedrupendel ja füüsikaline pendel. Kõiki pendleid iseloomustab isokroonsus ehk võime võnkeamplituudi muutumisel võnkeperioodi säilitada. See võimaldab pendleid kasutada kellade käigu regulaatorina.
Matemaatiliseks pendliks nimetatakse venimatu kaalutu niidi otsa riputatud punktmassi. Tasakaalust väljaviimisel liigub niidi otsa riputatud keha mööda ringjoone kaart, mille kõverusraadius on võrdne niidi pikkusega.
Matemaatilise pendli sarnaselt võngub mis tahes raske ese, mis on riputatud sellega võrreldes palju kergema ja pikema niidi või nööri otsa. Matemaatilise pendli võnkumist põhjustab raskusjõud koos niidis tekkiva tõmbejõuga. Väikese võnkeamplituudi korral sõltub periood ainult pendli pikkusest l ning vaba langemise kiirendusest g:
Matemaatilise pendli abil on lihtne määrata vaba langemise kiirendust. Asjaolu, et selline pendel säilitab oma võnketasandi, kasutas prantsuse füüsik Jean Foucault 1848. aastal maakera pöörlemise tõestuseks.
Vedrupendliks nimetatakse absoluutselt elastse vedru otsa riputatud punktmassi. Võnkumist põhjustab siin elastsusjõu ja raskusjõu resultant.
Vedrupendli võnkeperiood on määratud vedru jäikuse k ning keha massiga m:
Füüsikaliseks pendliks nimetatakse suvalise kujuga jäika keha, mis saab rippudes võnkuda liikumatu punkti ümber. Füüsikaliseks pendliks võib olla näiteks kiikuv pilt seinal või naela otsa riputatud mutrivõti. Füüsikalise pendli võnkeperiood sõltub keha kujust, massist, kinnituskoha ning raskuskeskme vahekaugusest ja vaba langemise kiirendusest.
Kuna keha kuju ja riputuspunkt võivad olla väga erinevad, pole siinkohal võimalik anda füüsikalise pendli võnkeperioodi üldist valemit. Näiteks ühest otsast üles riputatud ühtlase varda võnkeperiood sõltub varda pikkusest l järgmiselt:
Uurima süsteeme, milles saavad toimuda elektrivälja ja magnetvälja energia perioodilised vastastikused muundumised. Selliseid süsteeme nimetatakse võnkeringideks.
Võnkering sisaldab alati induktiivpooli ja kondensaatorit nii nagu vedrupendel koosneb alati mingist olulise massiga kehast (koormisest) ja elastsest vedrust, mille otsa see keha on kinnitatud. Võnkeringi talitlust ongi kõige lihtsam mõista vedrupendliga võrdlemise teel.
Võnkumise tekitamiseks tuleb vedrupendel kõigepealt tasakaaluasendist välja viia. Seda võib teha vedru täiendava väljavenitamisega (J. 2.38, J. 2.39, a). Deformeeritud vedru omandab potentsiaalse energia Ep = kx2/2. Selle määravad vedru jäikustegur k ja vedru pikkuse muut Dl, mida sageli nimetatakse ka vedru deformatsiooniks x. Pendli lahtilaskmisel paneb vedru elastsusjõud koormise kiirenevalt liikuma oma tasakaaluasendi poole. Tasakaaluasendi läbimise hetkel saab vedru deformatsioon nulliks (J. 2.39, b), seevastu koormise kiirus v on parajasti maksimaalne. Potentsiaalne energia on läinud üle koormise liikumise kineetiliseks energiaks Ek = mv2/2, kus m on koormise mass ja v – selle kiirus.
Inertsi tõttu koormis ei peatu tasakaaluasendis ja vedru surutakse jälle kokku. Koormise kiirus hakkab nüüd vähenema, sest vedru elastsusjõud takistab kokkusurumist ja pidurdab koormise liikumist. Lõpuks peatub koormis asendis, mille korral tema kineetiline energia on täielikult muundunud vedru deformatsiooni potentsiaalseks energiaks (joon. 2.39, c). Kokkusurutud vedru hakkab nüüd elastsusjõu toimel taas pikenema ning koormis liigub kasvava kiirusega eelnevale vastupidises suunas (alla).
Tasakaaluasendis on kiirus jällegi maksimaalne ja pendli energia puhtalt kineetiline (joon. 2.39, d). Pärast tasakaaluasendi läbimist hakkab kiirus uuesti vähenema ning vedru venib välja. Koormise peatumisel on pendli algasend taastunud (J. 2.39, e) ja kogu protsess võib korduda.
Ülalkirjeldatule analoogilise elektromagnetvõnkumise tekitamiseks tuleb võnkering tasakaalust välja viia. Seda võib teha näiteks kondensaatori laadimisel mingi alalisvooluallika abil (J. 2.40). Laetud kondensaator omandab potentsiaalse energia, mille määravad kondensaatori mahtuvus C ja tema pinge U. Oma sügavamalt olemuselt on tegemist plaatide vahele koondunud elektrivälja energiaga Ee = CU2/2.
Lahutamisel vooluallikast ja ühendamisel pooliga hakkab kondensaator läbi pooli tühjenema. Lenzi reegli kohaselt toimib poolis tekkiv endainduktsiooni EMJ kondensaatori pingele vastupidises suunas ja piirab voolu kasvu. Alles siis, kui pinge kondensaatoril on saanud nulliks, saavutab voolutugevus oma maksimaalse väärtuse (J. 2.39, b). Kondensaatori elektrivälja energia on muundunud pooli magnetvälja energiaks Em = LI2/2, mis on vaadeldav laengukandjate liikumise kineetilise energiana.
Laengukandjad jätkavad induktiivsuse (inertsi) olemasolu tõttu liikumist. Voolu kasv asendub küll kahanemisega, sest esialgsele vastupidiselt laaduv kondensaator pidurdab laengukandjate liikumist. Alles siis, kui vool peatub, on kondensaator omandanud absoluutväärtuselt suurima, kuid esialgsele vastupidise märgiga laengu ja pinge (joon. 2.39, e). Pooli magnetvälja energia on muundunud kondensaatori elektrivälja energiaks. Kondensaatori pinge paneb nüüd laengukandjad liikuma esialgsele vastupidises suunas (päripäeva), kuid pooli induktiivsus pidurdab jällegi voolu kasvu. Vool poolis omandab suurima väärtuse alles siis, kui kondensaator on täielikult tühjenenud ja tema elektrivälja energia on pooli magnetväljale üle läinud (joon. 2.39, d). Päripäeva kulgevas voolus liigub positiivne laeng uuesti kondensaatori ülemisele plaadile. Laaduv kondensaator aga pidurdab voolu. Kui vool peatub, on taastunud võnkeringi algolek (joon. 2.39, e). Nüüd võib kogu võnkeprotsess korduda.
Vedrupendli ja võnkeringi sarnasuse põhjal võib oletada, et elektromagnetvõnkumiste periood sõltub võnkeringi pooli induktiivsusest L ning kondensaatori mahtuvusest C viisil, mis meenutab Mehaanika kursuses käsitletud vedrupendli võnkeperioodi valemit
 (2.22)
(2.22)
Massi m elektromagnetiliseks analoogiks on induktiivsus L. Vedru jäikusteguri k analoogiks pole aga mitte mahtuvus C vaid selle pöördväärtus. Vedrupendli koormise kiirust muudab vedru elastsusjõud. Voolutugevust võnkeringis muudab kondensaatori pinge, mis on seega elastsusjõu elektromagnetiliseks analoogiks. Elastsusjõud – k x on võrdeline vedru jäikusteguriga, kondensaatori pinge on aga mahtuvuse definitsiooni (valem 2.14) kohaselt mahtuvusega pöördvõrdeline (U = Q/C). Asendades valemis 2.22 koormise massi m induktiivsusega L ning jäikusteguri k mahtuvuse pöördväärtusega (1/C), saamegi elektromagnetvõnkumiste perioodi avaldise
 (2.23)
(2.23)
mida nimetatakse Thomsoni valemiks inglise füüsiku William Thomsoni ehk lord Kelvini (1824-1907) järgi.
Reaalse võnkeringi juhtmetel ja poolil on olemas takistus, mistõttu mingi osa võnkumise energiast eraldub igal võnkel soojusena. Selle tulemusena võnkumine sumbub. Sumbumise vältimiseks tuleb võnkeringile pidevalt energiat juurde anda.

Energia lisandumist võib aga juhtida ka võnkering ise. Võnkumist mille korral võnkuv süsteem täiendab ise välisest allikast oma energiavarusid, nimetatakse isevõnkumiseks. Elektromagnetilise isevõnkumisega on tegemist elektrongeneraatoris.
Elektrongeneraator on seade mis tekitab sumbumatuid elektromagnetvõnkumisi kasutades selleks kas alalisvooluallikast või mingi teise sagedusega vahelduvvooluallikast saadavat energiat. Elektrongeneraator sisaldab enamasti võnkeringi mille omavõnkesagedus määrab tekitatava võnkumise sageduse. Lisaenergia andmiseks võnkeringile kasutatakse positiivset tagasisidet. Võnkering ise avab ventiili, läbi mille ta vooluallikalt energiat juurde saab (J. 2.41).
See toimub hetkel, mil välise allika poolt tekitatav vool on võnkeringis endas kulgeva vooluga samasuunaline ja tugevdab võnkumist.
Juhul kui võnkeringis rakendub perioodiliselt muutuv väline pinge, on tegemist sundvõnkumisega. See toimub välispinge sagedusel. Sundvõnkumise amplituud sõltub välise pinge sagedusest. Kui sagedus saab võrdseks võnkeringi omavõnkesagedusega, tekib resonants. See on nähtus mille korral võnkumise amplituud (pinge või voolutugevus) kasvab järsult (J. 2.42). Väline pinge toimib omavõnkumisega samas taktis (lükkab laengukandjaid suunas, milles nad juba niigi liiguvad).
Resonants elektromagnetvõnkumistel leiab laialdast kasutamist mingi kindla sagedusega võnkumise väljavalimiseks paljude hulgast. Seda tuleb teha näiteks raadio häälestamisel mingi saatejaama sagedusele.
Raadio häälestamisel muudetakse antenni (p. 2.8.1) ahelas paikneva võnkeringi kondensaatori mahtuvust ja seega ka võnkeringi omavõnkesagedust. Nii tekitatakse resonants vajaliku saatejaama sagedusel. Tulemuseks on just selle jaama poolt lähetatavate võnkumiste võimendamine raadiovastuvõtjas.
Näide 2.5.
Raadio häälestusvõnkeringi pooli induktiivsus on 0,l μH. Milline peab olema võnkeringi kondensaatori mahtuvus, selleks et võtta vastu sagedusel 100 MHz edastatavaid saateid?
Antud:
f = 100 MHz = 108 Hz 
L = 0,1 μH = 10-7 H 

_______________
C = ?
Vastus: Võnkeringi kondensaatori mahtuvus peab olema 25,3 pF.
Võnkumine võib olla kas vaba või sunnitud. Mis juhtub aga siis, kui vabalt võnkuvale süsteemile mõjub lisaks väline perioodiline jõud? Juhul, kui välise mõju sagedus langeb kokku süsteemi vabavõnkumise sagedusega, hakkab amplituud kasvama ja võib ka väikese jõu korral väga suureks muutuda. Kõik me teame, et kiigele hoo andmiseks ei tule pidevalt ühes suunas lükata, vaid kiike kergelt kindlate ajavahemike tagant tõugata.
Ka mitmetonnise raske auto saab suhteliselt väikese jõuga poriaugust välja lükata. Selleks kõigutatakse autot edasi-tagasi, kuni võnkliikumise amplituud kasvab sedavõrd, et masin välja pääseb.
Toodud näidetes väljendub resonantsinähtus.
Resonantsiks nimetatakse nähtust, kus välise mõju sageduse kokkulangemisel süsteemi vabavõnkumise sagedusega suureneb võnkeamplituud märgatavalt.
Näiteks võib kõlar mingi ühe kindla madala noodi kõlamisel valjult plärisema hakata. Siis ongi tegemist resonantsiga — mängitava kindla kõrgusega heli sagedus langeb kokku valjuhääldi membraani enda võnkumise sagedusega.
Resonantsi saab kasutada tundmatu võnkesageduse määramisel. Selleks viiakse võnkuva kehaga kokkupuutesse näiteks erineva pikkusega plekiribad. Riba, mille võnkesagedusega mõõdetav sagedus kokku langeb, hakkab suure amplituudiga võnkuma.
| Resonantsil töötav sagedusmõõtja | Ühes vapustavaimas füüsikavideos on näha vana Tacoma Narrowsi silla jõhkrat väändumist 7. novembril 1941. aastal. Tol hommikul puhus mõõdukas (umbes 68 kilomeetrit tunnis ehk 19 meetrit sekundis) tuul, siiski rebenes toekas sild mõni tund pärast kõverdava võnkumise algust pooleks. |
Resonantsi kasutatakse paljude muusikariistade juures. Nii võimendab viiuli kõlakast keelte helisemist just tänu resonantsile. On ka selliseid pille, millel saavutatakse eriline kõlapilt põhikeelte kõrvale tõmmatud lisakeeltele abil, mis tänu resonantsile iseenesest helisema hakkavad.
Resonants võib ka ohtlik olla. Võime näiteks ette kujutada, mis juhtuks, kui silla kõikumise ning silla konarlikul kattel sõitva auto õõtsumise sagedused kokku langeksid. Seepärast peavad arhitektid suurte ehitiste projekteerimisel arvestama võimalike perioodiliste välismõjudega, nagu näiteks inimeste kõndimine, tuulekeerised ja maavärinad.
Lained seostuvad meie mõtetes tavaliselt merega, kus vesi rütmiliselt kaldakive uhub. Samuti oleme kuulnud maavärinate tekitatud hiidlainetest, mis pühivad maapinnalt terveid linnu. Lained ei kuulu aga ainult mere juurde, tegemist on palju mitmekesisema nähtusega. Lained on näiteks heli ja valgus. Teleprogrammid ja mobiilikõnedki jõuavad meieni raadiolainete vahendusel. Lainetest räägitakse isegi poliitikas, majanduses ja muusikas (new wave).
Mehaaniliste lainete puhul on alati tegemist millegi liikumise või muutumisega. See, mis liigub, võib olla aine nii tahkes, vedelas kui ka gaasilises olekus, õhus, vees ja maakoores. Kui mehaanilised lained saavad levida vaid aines, siis valguse ja raadiolainete korral kanduvad elektrilise ja magnetilise vastastikmõju muutused edasi ka läbi tühjuse.
Rahulikul veepinnal tekivad lained siis, kui sinna kivi visata ja helilainete tekitamiseks peab valjuhääldi membraan õhku kord tihendama, kord hõrendama. Laine tekkimiseks on vaja keskkonda häirida, tasakaalust välja viia.
Lainetada ei saa igasugune keskkond. Kui viskame kivi liiva sisse, siis ei teki selle pinnal mingeid liikuvaid laineid, vaid ainult lohk. Liiv pole elastne ega püüa oma esialgset olekut taastada. Mehaanilised lained tekivad vaid elastses keskkonnas, nagu kivi saab võnkuda elastse vedru otsas.
Elastse keskkonna tasakaalu häirimisel tekivad tasakaalu taastavad jõud, mis panevad keskkonna osakesed võnkuma. Et osakesed on vastastikmõjus naabritega, hakkavad omakorda ka need võnkuma. Võnkumine levib ruumis edasi. Seejuures aine ise edasi ei kandu. Selles võime veenduda, kui jälgime veelainetel hüplevat puutükki. Edasi ei kandu mitte aine (puutükk, vesi), vaid ainult selle häiritus - elastses keskkonnas toimuv võnkumine. Edasi kandub võnkumise energia. Energia edasikandumisele annab kinnitust tumeda pinna soojenemine valguslainete neeldumise tõttu.
Ülaltoodu põhjal võimegi sõnastada laine definitsiooni: laineks nimetatakse võnkumiste edasikandumist ruumis.
Definitsiooni järgi kujutab laine endast võnkumiste edasikandumist ruumis. Võnkumine saab toimuda mingis kindlas sihis. Sõltuvalt sellest, millises sihis võnkumine laine levimissuuna suhtes toimub, eristatakse kahte liiki laineid.
Tiiki visatud kivi poolt tekitatud lained levivad piki veepinda kalda poole, pinnal lebavad vesiroosilehed õõtsuvad samal ajal üles-alla. Võnkumine toimub levimissuunaga risti ja tegemist on ristlainega. Ristlaineks nimetatakse lainet, milles võnkumine toimub levimissuunaga risti.
Ristlained on näiteks lained veepinnal, raadio- ja valguslained, maavärina tekitatud seismilised pinnalained ning võimleja tekitatud liikumine võimlemislindis.
Kui lüüa pika vedru otsa pihta, hakkavad ka selles võnkumised levima. Erinevalt merelainetest toimub võnkumine siin piki levimissuunda. Vedrukeerud kord lähenevad, kord eemalduvad üksteisest. Piki vedru liiguvad edasi kokkusurutud ja hõredaks tõmmatud keerdudega kohad. Tegemist on pikilainega. Pikilaineks nimetatakse lainet, milles võnkumine toimub piki levimissuunda. Pikilainena levib näiteks heli.
Kuna laine on ruumis leviv võnkumine, siis iseloomustavad seda ka kõik võnkumist kirjeldavad suurused. Nii iseloomustavad lainet võnkeamplituud x0 (mõõtühik 1 m), periood T (1 s) ja sagedus f (1 Hz).
Laine võnkeamplituudi ei tohi segi ajada laine kõrgusega. Laine kõrgus h on näiteks lainetava veepinna puhul laineharja (kõrgeima punkti) ning lainenõo (madalaima punkti) kõrguste vahe. Laine amplituud seevastu üles-alla võnkuvate veeosakeste suurim kaugus tasakaaluasendist ehk tasasest veepinnast lainete puudumisel. Laine kõrgus on võrdne kahekordse amplituudiga:
Lisaks loetletutele on veel kaks suurust, mille abil lainete levimist iseloomustatakse. Esimene neist on lainepikkus. Lainepikkuseks nimetatakse kaugust kahe teineteisele lähima samas taktis võnkuva punkti vahel. Laineallikast kaugemate punktide võnkumine on lähemate võnkumistest hilisem ning kui hilinemine on võrdne ühe võnkeperioodiga, võnguvad punktid samas taktis ehk samas faasis. Neis punktides on kogu aeg võnkumise hälve ja kiiruse suurus ning suund ühesugused. Nii on lainepikkus võrdne näiteks kahe naaberlaineharja vahekaugusega, sest kõikides harja punktides on hälve ühtviisi maksimaalne ja osakeste kiirus null. Täpselt samamoodi on lainepikkusega võrdne lainenõgude vaheline kaugus.
Lainepikkust tähistatakse tavaliselt kreeka tähega λ (lambda) ning selle mõõtühikuks on meeter.
Teiseks iseloomustab võnkumise edasikandumist laine levimiskiirus. Teame, et kiirus on võrdne nihke pikkuse ja aja jagatisega:
Võttes aja võrdseks võnkeperioodiga T, jõuab võnkumine selle ajaga edasi kanduda ühe lainepikkuse võrra. Vastab ju ühele lainepikkusele üks täisvõnge. Nii saame laine levimiskiirust väljendada lainet iseloomustavate suuruste kaudu järgmiselt:
Kõik me oleme kokku puutunud sellise nähtusega nagu kaja. Kui hõigata mägedes või metsaäärsel lagedal, siis kuuleme enda tekitatud heli hetke pärast uuesti. Mõnes suures ruumis võib heli üsna kauaks kõlama jääda. Tegemist on helilainete peegeldumisega.
Peegelduvad kõik lained sõltumata liigist. Laine peegeldub siis, kui jõuab teistsuguse keskkonnani. Näiteks merelaine jõuab kaljuni või valguslained satuvad kuuma ja külma õhu piirile. Peegeldumine toimub kahe erineva keskkonna lahutuspinnalt.
Seejuures pole tähtis, mis ainest ja millises olekus need keskkonnad on. Peaasi, et need on erinevad. Peegeldumise tunnuseks on see, et kohates teist keskkonda, pöördub laine esialgsesse tagasi. Peegeldumiseks nimetatakse laine tagasipöördumist kahe keskkonna lahutuspinnalt lähtekeskkonda.
Lainete peegeldumisel kehtib seaduspärasus, et pinnanormaali (pinna ristsirge) suhtes mõõdetud langemisnurk ja peegeldumisnurk on võrdsed.
Ultrahelilainete peegeldumist kasutavad näiteks nahkhiired pimedas orienteerumisel ning arstid siseorganite uurimisel.
Jõudes teise keskkonda, võib laine selles edasi levida. Seejuures levimissuund sageli muutub. Tegemist on laine murdumisega. Laine murdumiseks nimetatakse laine levimissuuna muutumist ühest keskkonnast teise üleminekul. Murdumine toimub sarnaselt peegeldumisega erinevate keskkondade lahutuspinnal.
Murdumise põhjuseks on laine levimiskiiruse erinevus keskkondades. Laine pöördub selle keskkonna poole, kus levimiskiirus on väiksem. Sarnane suunamuutus võib juhtuda suure kiirusega sõitva auto kaldumisel teeserva. Kui auto parempoolsed rattad satuvad pehmele teepeenrale ning pidurduvad ja vasakpoolsed jätkavad samas endise hooga, pöörab auto paremale kraavi.
Lainete murdumisel kehtib seaduspärasus, et keskkondade lahutuspinna normaali suhtes mõõdetud langemis- ja murdumisnurkade siinuste suhe on võrdne levimiskiiruste suhtega.
Kui vette visata korraga kaks kivi, hakkavad lained mõlemast kukkumispaigast mööda veepinda ringidena laiali levima. Kohtumisel need erinevatest allikatest lähtunud lained liituvad ja veepinnal tekib uus lainepilt, mis erineb piltidest, mille tekitanuks kumbki kivi eraldi visatult. Siin on tegemist lainete interferentsiga (inter + ferîre — ladina k vahel + mõjuma). Interferentsiks nimetatakse nähtust, kus kahe või enama laine liitumisel tekib uus laine, mille kuju on erinev liituvate lainete kujust. Interferents avaldub selles, et mõnes keskkonna punktis lained liitumisel võimendavad üksteist, teistes aga nõrgendavad. Tulemuseks on see, et mõnes kohas toimub võnkumine suure amplituudiga, teisal jälle väiksema amplituudiga või puudub sootuks. Interferentsi korral tekib ruumis võnkumiste püsiv jaotus amplituudi järgi. Interferents jaotab lainete energia ruumis ringi.
Interferents ei teki siiski igasuguste lainete liitumisel. Kõik teavad, et koori esituses kõlab laul alati valjemini kui solisti suust. Erinevate lauljate tekitatud helilained ei nõrgenda üksteist mitte kunagi. Interferentsi tekkimiseks peavad lained olema sama sagedusega ning võnkumisfaaside erinevus ei tohi muutuda. Teisitiöeldult — erinevate lainete allikad peavad võnkuma muutumatult ühtmoodi. Sagedused peavad olema võrdsed ja ühe allika võnkumine ei tohi teise suhtes muutuda.
Kui kaks lainet on kohtumisel samas faasis (võnkumine on samas taktis), siis täiendavad need liitumisel teineteist ja amplituud kasvab. Sel juhul on tegemist interferentsimaksimumiga. Vastandfaasis lainete puhul kohtub ühe laine hari teise nõoga ning lained kustutavad teineteist. Amplituud väheneb ning tegemist on interferentsimiinimumiga.
Lained võivad oma teel kohata suuremaid ja väiksemaid tõkkeid. Näiteks jäävad merelainete ette erineva suurusega kivid ning sadade meetrite pikkused laiud. Väikeste tõkete taha pääsevad lained kergesti, suuremate taga on vesi aga rahulik , seal on vari.
Siin on tegemist nähtusega, mis leiab aset igasuguste lainete korral. Nimelt osutub, et lained on võimelised tõkete taha painduma. Seejuures pääsevad lained vaid nende tõkete taha, mille mõõtmed on lainepikkusest väiksemad või sellega võrreldavad.
Tegemist on difraktsiooniga (diffrâctus — ladina k murdunud, paindunud). Difraktsiooniks nimetatakse nähtust, kus lained painduvad tõkete taha. Tänu difraktsioonile kuuleme tänaval sõitva auto mootorimüra ka majanurga taha. Helilained painduvad tõkkeks oleva majanurga juures otsesihist kõrvale.
Difraktsioon avaldub ilmekalt, kui veepinnal levivaid laineid tõkestada ekraaniga, milles on kitsas pilu. Lained levivad siis läbi pilu rõngastena ekraani taha.
Esimene katse inimese Veenusele saatmiseks teostati Marylandis Baltimoris 1928. aastal. Robert Condit ja tema kaks abilist ehitasid raketi nurkraudadest ja purjeriidest. Kütuseks kasutati aurustatud bensiini, mis suunati terastorudesse ja süüdati seejärel elektrisädemega. Condit pidi reisi sooritama üksi, ta oli varunud veidi toitu, vett, kaks taskulampi ja esmaabipauna. Testlennu päeval ronis piloot sõidukisse ja käivitas mootori, et lennata veerand miili kõrgusele lihtsalt selleks, et seadet kontrollida. Terastorudest paiskus välja suitsu ja tuld, aga mingit õhkutõusu ei toimunud. Condit suurendas bensiini pealevoolu, mistõttu leegid muutusid nii pilkupüüdvaks, et liiklus tänaval seiskus. Seade ei liikunud aga endiselt paigast. Condit jätkas üritamist, kuni kütus lõppes.
Kui Craig Breedlove purustas 1964. aasta oktoobris Bonneville soolajärvel maapealse kiirusrekordi oma rakettidel töötaval sõidukil Spirit of America'ga, avas ta kiirusel 846km/h aeglustamiseks langevarju, kuid selle nöör purunes, samuti ei avanenud teine langevari. Nüüd surus ta piduripedaali põhja, temast jäid maha ligi 10 kilomeetri pikkused pidurdusjäljed, enne kui pidurid läbi põlesid. Lõpuks auto peatus, kui ta plartsatas kaldapealselt viie meetri sügavusse soolvee basseini kiirusega umbes 300km/h.
Nähtusi ja objekte kirjeldavad füüsikalised suurused jagunevad kaheks. Ühed saavad muutuda ja omada erinevaid väärtusi. Sellisteks on näiteks koordinaat, kiirus, jõud ja temperatuur. Teised säilitavad oma väärtuse kõikides protsessides. Jäävateks suurusteks on näiteks mass, impulss, energia ja elektrilaeng.
Kui füüsikud on leidnud, et mingi suurus jääb kõikide senituntud nähtuste toimumisel muutumatuks ehk konstantseks, võib suure kindlusega arvata, et see ei muutu ka muudel juhtudel. Selline eeldus lihtsustab looduse uurimist. Suuruste jäävusele tuginemine võimaldab üles ehitada uusi füüsikateooriaid.
Mehaanika põhiülesanne on leida keha asukoht mis tahes ajahetkel. Teades algtingimusi ja kõiki kehale mõjuvaid jõude, on Newtoni seaduste abil see ülesanne lahendatav. Paljude ülesannete lahendamisel ei saa aga neid seadusi rakendada, kuna jõud on teadmata. Nii on näiteks kehade põrgete korral, mil jõude ning nende mõjumise aega on raske määrata.
Taolistel juhtudel võetakse jõu ja kiirenduse asemel kasutusele impulss ja energia. Impulss ja energia on erilised suurused, kuna nende puhul kehtib jäävus.
Dünaamikas defineeritakse impulss keha massi ja kiiruse korrutisena. Newtoni seaduste analüüs näitab, et impulsi muutumise kiirus on võrdne muutust põhjustava jõuga ning väliste mõjude puudumisel jääb süsteemi impulss muutumatuks. Kahest kehast koosneva süsteemi impulsi jäävust väljendab valem:
Suletud süsteemi impulsi jäävus kehtib mitte ainult kahe, vaid mis tahes arvu kehade korral:
Konkreetsete ülesannete lahendamisel on tihti lihtsam kehade koguimpulss enne ja pärast vastastikmõju toimumist eraldi välja kirjutada ning seejärel jäävust arvestades omavahel võrduma panna:
Nüüd saab leida, milline on liikumine pärast vastastikmõju toimumist. Seejuures pole vaja teada, kui tugev ja millise kestusega see vastastikmõju oli.
Põrkeks nimetatakse üksteise suhtes liikuvate kehade kokkupuutel toimuvat lühiajalist vastastikust mõjumist. Põrgetele on iseloomulik vastastikmõju lühike kestus ning jõudude ja kiirenduste suured väärtused, mida on sageli raske mõõta. Kõikide põrgete puhul kehtib impulsi jäävuse seadus.
Põrked jaotatakse elastseteks ja mitteelastseteks. Elastse põrke tagajärjel kehad eemalduvad üksteisest ning nende liikumise koguenergia selle käigus ei muutu. Mitteelastsel ehk plastsel põrkel jäävad kehad kokku, moodustades liitkeha ning liikumisenergia muundub osaliselt või täielikult mingit muud liiki energiaks, tavaliselt soojuseks.
Leiame impulsi jäävuse seadust kasutades, kui suure kiirusega hakkab libisema paigalseisev klots, millesse jääb kinni teadaoleva massi ja kiirusega lendav püssikuul.
Uuritav süsteem, milles kehtib impulsi jäävuse seadus, koosneb antud juhul kahest kehast — kuulist ja klotsist. Tegemist on mitteelastse põrkega, kuna pärast tabamust moodustub klotsist ja kuulist liitkeha. Kui kasutame tähiseid, kus kuuli mass on m1 ja lennukiirus v1, siis kuuli impulsiks on m1v1. Kuna klots algul ei liigu ja sel impulss puudub, on meie süsteemi koguimpulss enne põrget võrdne kuuli impulsiga:
Et liikumishulk ei saa väliste mõjude puudumisel muutuda (eeldame, et hõõrdumine klotsi ja aluse vahel puudub), peab liikumine ka pärast tabamust edasi toimuma. Tähistades selle tabamusjärgse liikumise kiiruse tähega v ning klotsi massi sümboliga m2, saame liitkeha massiks m1 + m2 ning süsteemi impulsiks
Impulsi jäävuse tõttu
ja lihtsad teisendused annavad, et klots saab kuulitabamuse tagajärjel kiiruse
Impulsi jäävuse seaduse abil saab kirjeldada ka gaasides toimuvaid protsesse. Hõredat gaasi võib ette kujutada süsteemina, mis koosneb paljudest korrapäratult liikuvatest mõõtmeteta molekulidest, mis mõjutavad anumat ning muid kehi vaid elastsete põrgete kaudu. Niisugust gaasi mudelit nimetatakse ideaalseks gaasiks.
Kui sellise gaasi iga molekuli mass on m0 ja kiirus v, omavad need kõik impulssi p0 = m0v. Absoluutsellt elastsel põrkel vastu mingit pinda muutub liikumine vastassuunaliseks ja uus impulss on –m0v. Molekuli impulsi muut on siis Δp0 = m0v – (–m0v) = 2 m0v.
Lühikese ajavahemiku Δt jooksul saavad mingi pinna poole liikuvatest osakestest sellega põrkuda vaid need, mis ei asu kaugemal kui vahemaa s = v Δt. Kui pinna suurus on S, asuvad need molekulid kõik piirkonnas, mille ruumala V = S•s = SvΔt.
Gaaside iseloomustamiseks kasutatakse molekulide kontsentratsiooni (tähis n). See suurus näitab osakeste arvu ruumalaühikus. Molekulide koguarvu N saab leida, kui korrutada kontsentratsioon ruumalaga: N = nV.
Eelnevalt leidsime ruumala, milles asuvad molekulid võiksid aja Δt jooksul pinnani jõuda. Nende molekulide arv on N = nV = nSvΔt. Tegelikult on põrkuvate molekulide arv väiksem. Range tuletuskäik näitab, et kolmemõõtmelises ruumis on molekulide kaootiline liikumine oma mõju poolest samaväärne sellega, kui nad liiguksid vaid kolmes sõltumatus ristsihis. Konkreetse pinnaga ristuvas sihis liikuvaid osakesi on kolmandik koguarvust. Pinnale lähenevad neist vaid pooled, ülejäänud eemalduvad. Põrkuda saavaid molekule on seega vaid kuuendik koguarvust. Kui igal põrkel muutub molekuli impulss Δp0 võrra, siis kõikide põrkuvate molekulide impulsside muut kokku on
Sellest seosest saame avaldada impulsi muutumise kiiruse, mis on teatavasti võrdne jõuga:
Jagades selle jõu pindalaga S, saamegi rõhu, mida ideaalne gaas avaldab selles asuvatele kehadele:
(P ei tähista siin impulssi vaid rõhku)
Mehaanika kursuses me sellel valemil pikemalt ei peatu. Tulemus on leidnud katselist kinnitust ning see näitab, et impulsi jäävuse seadust saab füüsikas rakendada ka väljaspool mehaanikat.
Impulsi jäävuse seaduse üheks huvitavaks ning oluliseks rakenduseks on reaktiivliikumine (re- + activus — ladina k vastu + tegutsev), mida kasutatakse nii tehnikas kui ka mõne looma poolt looduses. Selleks et paigalt liikuma pääseda, on vaja vastastikmõju — teist keha, millest end eemale tõugata, nii et see vastavalt Newtoni III seadusele sama suure jõuga vastu mõjuks. Just tänu sellele saavadki kehad liikuma hakata. Jalad tõukavad teekatet, aerud vett, lennukipropeller õhku.
Kuidas lendavad aga kosmoseraketid õhutühjas maailmaruumis, kus pole midagi, millest end eemale tõugata? Kui läheduses sobiv keha puudub, tuleb see endaga kaasa võtta. Just niiviisi toimitakse rakettide lennutamisel. Rakett hakkab liikuma tänu sellele, et selle ühest otsast paisatakse läbi spetsiaalse ava (düüsi) suure kiirusega välja kütuse põlemisel tekkivad gaasid. Enne starti on paigalseisva raketi ja selles sisalduva kütuse impulss null. Kui nüüd kütuse põlemisel tekkivad gaasid ühes suunas välja lendavad, hakkab rakett ise vastassuunas liikuma. Muidu ei jääks raketist ja gaasidest koosneva süsteemi koguimpulss ju nulliks.
Nii tekibki raketi reaktiivliikumine. Reaktiivliikumiseks nimetatakse liikumist, mille tekitab kehast eemale paiskuv keha osa.
Hindame, millise kiiruse võib rakett kütuse ärapõlemisel saada. Oletame lihtsuse mõttes, et põlemisgaasid ei välju raketist tasapisi, vaid ühekorraga.
Olgu raketikesta ja selles asuva aparatuuri ning meeskonna mass mr, kütuse ja sellest tekkivate gaaside mass mk ning gaaside väljapaiskumise kiirus vk. Et algul on rakett paigal ja impulss null, saame impulsi jäävuse seaduse välja kirjutada järgmiselt:
Avaldame siit raketi kiiruse
Sellest valemist näeme, et rakett liigub gaaside väljapaiskumisele vastassuunaliselt (miinusmärk!) ja kiirus on seda suurem, mida suurem on kütuse ning raketi masside suhe ja mida suurema kiirusega gaasid välja pääsevad. Et kosmoselaev saavutaks Maalt lahkumiseks piisavalt suure kiiruse, peab kütuse mass ületama ülesviidava kasuliku massi hulka sadu kordi ning valida tuleb võimalikult kiiresti põlev kütus.
Esimese reaktiivliikumise põhimõttel töötava seadme ehitust on esimesel sajandil kirjeldanud antiikkreeka matemaatik ja insener Heron. Tegemist oli kahe düüsiga varustatud õõnsa metallkeraga, millesse suunati vee keemisel tekkiv aur. Düüsidest suure kiirusega väljuva auru reaktiivjõud pani selle nn Heroni kera pöörlema.
Tore näide reaktiivliikumise rakenduste kohta on muidugi ka hiinlaste poolt 13. sajandil leiutatud püssirohuraketid, mida kasutatakse ilutulestikes siiamaani.
Tänapäeval on reaktiivmootorid väga levinud, kuna need võimaldavad saavutada suuri kiirusi. Nendeta ei saa läbi ükski kosmoselennuaparaat ning enamik kiireid lennukeid liigub samuti reaktiivjõul. Reaktiivmootoreid ei kasutata aga mitte ainult lennumasinatel. Neid on monteeritud ka autodele, millega maapealseid kiirusrekordeid püstitatakse. Kui reaktiivautod on üsna haruldased, siis veejoa reaktiivjõul Tallinna ja Helsingi vahet kihutavad Jeti kiirlaevad (Jet — inglise k juga) on üsna igapäevased.
Reaktiivliikumist võib kohata ka mitme veelooma juures. Näiteks kasutavad kalmaarid, meduusid ja rannakarbid edasiliikumiseks endasse imetud vee kiiret väljasurumist.
Kulgevat liikumist iseloomustab liikumishulk ehk impulss ja kehtib impulsi jäävuse seadus. Impulsiga analoogilise suuruse saab defineerida ka pöörlemise jaoks. Kui kulgliikumise hulka nimetatakse lihtsalt impulsiks, siis pöördliikumise hulka nimetatakse pöördimpulsiks ehk impulsimomendiks.
On loomulik, et massiivsema keha ja kiirema pöörlemise korral on pöörlemise energia suurem. Seepärast sõltubki impulsimoment keha massist ja pöörlemise nurkkiirusest. Kuid erinevalt kulgliikumisest, kus keha võib lugeda punktmassiks, on impulsimomendi määramisel keha kuju, mõõtmed ja massi jaotumine väga olulised. Mida kaugemal paikneb mass pöörlemisteljest, seda suurem on pöörlemishulk, kuna raadiuse suurenemisel joonkiirus kasvab. Lihtsama kujuga pöördkehade impulsimoment L on võrdeline keha massi, raadiuse ruudu ja pöörlemise nurkkiirusega:
Võrdetegur b sõltub keha kujust. Mõne lihtsama keha jaoks on selle väärtused esitatud tabelis.
Sarnaselt impulsiga on ka impulsimoment jääv. Kehtib pöörlemishulga ehk impulsimomendi jäävuse seadus. Välismõjude puudumisel säilitab süsteem oma pöörlemishulga ja sellega koos ka pöörlemistelje asendi. Sellepärast ei kukugi pöörlev vurr ja veerev rõngas ümber ning Maa telje kalde muutumatus paneb aastaajad vahelduma. Kiiresti pöörleva keha telje orientatsiooni muutumatust kasutatakse güroskoopides (γυρος + σκοπος — kreeka k pöörlemine + vaatleja), mille abil kontrollitakse näiteks lennukite kallet.
Impulssmomendi jäävuse tõttu peab helikopteril olema kaks tiivikut. Kui panna pöörlema vaid üks tiivik, hakkaks helikopter ise vastassuunas pöörlema. Viimast efekti kasutavad näiteks libedal teel tasakaalu kaotanud inimesed, kes kukkumise vältimiseks hakkavad instinktiivselt keha pöördumisega vastassuunas käteringe tegema.
Impulsimomendi jäävuse seadust kasutavad ka tantsijad ja iluuisutajad. Vastavalt seosele (4.10 ) peab raadiuse r muutumisel muutuma ka nurkkiirus. Kui iluuisutaja käed keha ligi tõmbab ja nii nende ringliikumise raadiust vähendab, kasvab tema pöörlemiskiirus järsult, sest korrutis peab endiseks jääma.
Põhinähtus, mida mehaanika kirjeldab ja uurib, on liikumine. Liikumist võib muuta vastastikmõju abil. Vastastikmõju võib esile kutsuda ka kehade kuju muutumist ehk deformeerumist, mis oma olemuselt on samuti liikumine. Deformeerunud kehad võivad omakorda jälle liikumist esile kutsuda või muuta. Näeme, et liikumine ja vastastikmõju on tihedalt seotud ning määravad ära kehade erinevad seisundid ehk olekud. Sellised olekud võivad muutuda või olla püsivad. Kehade mehaanilist olekut saab muuta nende asukoha, liikumise või kuju muutmise teel. Oleku muutmise protsess on töö. Tööks nimetatakse keha või kehade süsteemi mehaanilise oleku muutmise protsessi kirjeldavat suurust.
Kuna oleku muutust põhjustab vastastikmõju, siis sõltub ka tehtava töö hulk vastastikmõju tugevusest ehk kehale mõjuvast jõust. Seejuures läheb arvesse vaid jõu liikumise sihiline komponent. Veel oleneb tehtav töö läbitud teepikkusest s. Kui töö tähiseks võtta A (arbeit — saksa k töö), saame ülaltoodut arvestades töö definitsioonivalemiks
kus α on nurk keha liikumissuuna ja jõu mõjusuuna vahel ning F·cos α seega jõu liikumissihiline komponent.
Kui töö abil kirjeldatakse mehaanilise oleku muutumise protsessi, siis olekut ennast iseloomustatakse energia abil. Energiaks nimetatakse keha või kehade süsteemi mehaanilist olekut kirjeldavat suurust, mis näitab võimet teha tööd.
Nii töö kui ka energia mõõtühikuks on töö, mida teeb 1 N suurune jõud keha nihutamisel 1 m võrra. Seda ühikut nimetatakse džauliks (J). 1 J = 1 N·1 m = 1 N·m.
Tööd saab teha väga erinevatel viisidel. Näiteks võivad tööd teha liikuv haamer, väljavenitatud vedru, kuum aur, elektrivool ja plahvatusreaktsioon. Järelikult on ka energialiike mitmeid erinevaid. Liikumise ja kehade vahel mõjuvate jõududega kaasnev energia on mehaaniline energia.
Mehaanikas eristatakse liikumisenergiat ja vastastikmõju energiat. Keha liikumisolekust tingitud energiat nimetatakse kineetiliseks energiaks (κινημα — kreeka k liikumine).
Leiame, kui suurt kineetilist energiat omab keha massiga m, mis liigub kiirusega v. See energia on võrdne tööga, mis tehakse paigalseisvale kehale sellise kiiruse andmisel. Lugedes liikumist ühtlaselt muutuvaks, võib kiirendamise kestel läbitud teepikkuse leida avaldisest (1.18 ):
Kuna kiirendus on vastavalt Newtoni II seadusele võrdeline jõuga F ja pöördvõrdeline massiga m, saame teepikkuse avaldiseks
Tehtav töö on võrdne jõu ja teepikkuse korrutisega. Just nii suure energia keha kiirendamise käigus omandaski. Võttes kineetilise energia tähiseks Ek, saame kineetilise energia valemiks
Näeme, et kineetiline energia on võrdeline keha kiiruse ruudu ja massiga.
Kui liikuvatel kehadel on kineetiline energia, siis mitmest omavahel vastastikmõjus olevast kehast koosnevad süsteemid omavad potentsiaalset energiat. Potentsiaalseks energiaks nimetatakse kehade vahel mõjuvatest jõududest tingitud energiat. Nimetus on tulnud ladinakeelsest sõnast potentia, mis tähendab võimet või väge.
Väljavenitatud vedru ja mäetippu veeretatud kivi võivad tööd teha, kui need lahti pääsevad, aga ei pruugi pääseda ja tööd teha. Erinevalt liikumisenergiast, mis on loomu poolest aktiivne (toimub asukoha muutumine) on potentsiaalne energia passiivne ja varjatud.
Vedru energia sõltub sellest, kui pikaks me selle venitame, ülestõstetud kivi energia aga tõstmise kõrgusest. Potentsiaalne energia sõltub alati kas keha enda osade või selle ja teiste kehade vastastikusest asendist.
Leiame ülestõstetud keha potentsiaalse energia. Kui kõrgusele h tõstetud keha, mille mass on m, lahti pääseb, läbib see kukkudes teepikkuse s = h ja raskusjõu F = mg poolt tehtav töö A = Fs = mgh. Et kogu see töö tehakse potentsiaalse energia arvel, saamegi energia jaoks avaldise:
Ülestõstetud keha potentsiaalne energia on võrdeline massi ja kõrgusega. Et kõrgust h tuleb mõõta alati mingi taustkeha (näiteks maapinna) suhtes, sõltub potentsiaalne energia nullnivoo valikust.
Mõnel juhul võib kõrgus tulla negatiivne, näiteks mõõtes kivi asukohta augus. Nii saab potentsiaalne energia olla erinevalt kineetilisest ka negatiivne.
Ühel kehal võib samaaegselt olla nii kineetiline kui ka potentsiaalne energia. Näiteks on langeval vihmapiisal nii kukkumise kineetiline kui ka Maa külgetõmbe potentsiaalne energia. Keha või kehade süsteemi kineetilise ja potentsiaalse energia summat nimetatakse mehaaniliseks koguenergiaks:
Kõik me oleme kogenud, et lenduvisatud kivi kõrgus ja kiirus muutuvad. Sellega koos muutuvad ka kivi kõrgusest sõltuv potentsiaalne ja kiirusest sõltuv kineetiline energia. Analüüsime vabalt langeva keha mehaanilise energia muutumist lähemalt.
Kuna kukkumisel mõjub kehale raskusjõud ning toimub liikumine, tehakse potentsiaalse energia kahanemise arvel tööd. Maapinnale jõudmise hetkeks on kogu potentsiaalne energia ära kulutatud. Järelikult on kukkumise käigus tehtud töö võrdne kulunud potentsiaalse energiaga:
Töö on keha mehaanilise oleku muutumise protsess. Raskusjõud teeb tööd ning selle käigus muutub keha kiirus. Mehaanilise energia mõiste avamise juures selgus, et kui jõud paneb keha liikuma, on tehtav töö võrdne kehale antava kineetilise energiaga:
Näeme, et tehtud töö käigus on keha potentsiaalne energia muundunud keha liikumis- ehk kineetiliseks energiaks. Seega ei lähe energia kukkumise käigus mitte kaduma, vaid mehaaniline energia muundub ühest liigist teise. Kukkuva keha potentsiaalne energia muundub kineetiliseks energiaks. Ülesvisatud keha tõusmisel toimub vastupidine protsess — kineetiline energia muundub potentsiaalseks. Võnkumise käigus kordub selline ühest liigist teise ja tagasi muundumine perioodiliselt.
Esineb ka selliseid protsesse, mille käigus mehaanilise energia liik ei muutu, kuid milles toimub energia ülekandumine mõnele teisele kehale. Nii antakse elastsel põrkel ühelt metallkuulilt teisele edasi kineetiline energia. Vedru otsa riputatud koormis annab allapoole vajudes oma potentsiaalse energia venivale vedrule üle.
Mehaanilise energia ülekandumine ja muundumine võivad toimuda ka samal ajal. Nii läheb vinnastatud vibu potentsiaalne energia üle noolele ning muundub samal ajal kineetiliseks.
Äsja nägime, et mehaaniline energia võib muunduda potentsiaalsest kineetiliseks ja vastupidi ning kanduda ühelt kehalt teistele. Kui muundumise ja ülekandumise käigus pole vaja näiteks hõõrdumise ületamiseks täiendavat tööd teha, jääb potentsiaalse ja kineetilise energia summa alati muutumatuks. Potentsiaalse energia vähenemisel kasvab kineetiline energia täpselt sama hulga võrra. Kui keha annab oma energiat teisele kehale ära, saab see täpselt sama palju juurde.
See kehtib muidugi vaid suletud süsteemis, kuhu kuuluvad kehad pole süsteemivälistega vastastikmõjus ega saa nendega energiat vahetada.
Arvukad vaatlus- ja katsetulemused kinnitavad, et mehaaniline koguenergia on jääv. Pole täheldatud ühtegi protsessi, mis oleks selle tulemusega vastuolus. Seega võime sõnastada ühe olulisema loodusseaduse — mehaanilise energia jäävuse seaduse: suletud süsteemi kuuluvate kehade mehaaniline koguenergia on jääv. Süsteemi kehade energia võib muunduda ühest liigist teise või kanduda ühelt kehalt teisele, kuid kineetilise ja potentsiaalse energia summa ei muutu, st see jääb konstantseks (cônstâns — ladina k muutumatu).
Mehaanilise energia jäävuse seadust väljendab avaldis
Tuleb silmas pidada, et see jäävusseadus kehtib vaid süsteemides, milles mehhaaniline energia ei muundu mittemehaanilisteks energialiikideks, näiteks hõõrdumisel ja mitteelastsel põrkel soojuseks või tuulegeneraatoris elektrienergiaks.
Eespool nägime, et ühe ja sama töö tulemusena väheneb potentsiaalne energia ning niisama palju suureneb kineetiline energia. Sellest järeldub, et töö on võrdne ühest liigist teise muundunud energia hulgaga.
Kui süsteem pole suletud, võib tehtava töö tulemusena mehaaniline energia muunduda mittemehaaniliseks. Võimalik on ka vastupidine protsess, kus välise energia arvel tehtav töö suurendab süsteemi mehaanilist energiat. Mõlemal juhul mehaaniline koguenergia muutub, kusjuures muut ΔEmeh on võrdne süsteemiväliste jõudude tööga:
Pidurdamisel muutub kihutava auto kineetiline energia hõõrdejõu töö tagajärjel soojuseks, mis paneb kummid lausa suitsema. Seevastu mootoris bensiini põlemisel eralduva soojuse arvel tehtav töö annab autole kineetilise energia.
Seos (4.20 ) võimaldab mehaanilise energia jäävuse seaduse rakendamist laiendada. Näiteks saame seda kasutades hõõrdeteguri kaudu välja arvutada auto pidurdusteekonna pikkuse. Selleks tuleb sõiduki kineetiline energia võrdsustada hõõrdejõu pidurdava tööga, mis on võrdne jõu ja teepikkuse korrutisega. Saadud seosest on pidurdustee pikkuse avaldamine lihtne:
Suurt osa meie ümber toimuvatest nähtustest ei saa selgitada ainult mehaanikaseaduste abil. Mehaanika kirjeldab ja uurib liikumist. Lisaks liikumisele kirjeldab füüsika veel näiteks soojust ja valgust, elektri ja magnetismi nähtuseid, aatomites ja tuumades toimuvat...
Need nähtused on väga erinevad, kuid siiski omavahel seotud. Kõiki nähtusi ühendavaks lüliks on energia. Erinevate nähtuste juures avalduvad erinevat liiki energiad. Lisaks mehaanilisele energiale tuntakse veel keemilist, elektromagnetilist, tuuma- ja soojusenergiat.
Kui vaadata kõiki energialiike tervikuna, kehtib üldine energia jäävuse seadus: suletud süsteemi koguenergia on ajas muutumatu. Energialiik pole oluline. Peaasi, et puudub energiavahetus süsteemist väljapoole. Energia ei saa tekkida eimillestki ega kaduda olematuks.
Tänapäeval peavad füüsikud meie universumit suletud süsteemiks. Kui see tõsi on, peab selles leiduva energia koguhulk olema jääv. Energia saab vaid kehalt kehale üle kanduda või mis tahes liigist mis tahes teiseks liigiks muunduda.
Põhjalikumalt tutvustatakse energiaga seonduvat füüsika neljanda kursuse käigus.
Energia jäävus on üldine loodusseadus ning puudutab suuremal või vähemal määral kõiki nähtusi. Sellegipoolest saab nii looduses kui ka tehnikas välja tuua valdkonnad, mis on energia ning selle muundumise ja jäävusega otseselt seotud. Nendeks on energia kasutamine, saamine, transport ja salvestamine. Tutvume mõne näitega lähemalt.
Energia kasutamine on seotud eelkõige tööga, mida selle arvel teha saab. Kuna energia ei teki eimillestki, saab tööd teha vaid mingi energiaallika olemasolul. Kõik loomad — inimesed nende hulgas — vajavad ringi liikumiseks ning toimetamiseks energiat, mida nad saavad toidust. Inimesed on oma elu lihtsamaks muutmiseks leiutanud masinaid, mis töö nende eest ära teevad. Masinaid, mis välise energia arvel tööd teevad, nimetatakse jõumasinateks ehk mootoriteks.
Jõumasinate käimapanekuks kasutatakse erinevaid energialiike. Tuule kineetiline energia paneb tööle tuuleturbiinid ning kõrgele kogutud vee potentsiaalne energia käivitab hüdroturbiine. Sõidukite liikumapanekuks kasutatakse enamasti mootoreid, milles tehakse tööd kütuse põlemisel eralduva soojusenergia arvel. Järjest enam rakendatakse tööstuses ja majapidamises elektrienergiat tarbivaid masinaid.
Jõumasinate tarbeks energia hankimine on alati seotud kulutustega. Seepärast on juba ammustest aegadest saati üritatud ehitada masinaid, mis töötaksid lõputult ilma välise energiaallikata. Igavese jõumasina ehk perpetuum mobile (ladina k igavesti liikuv) loomine pole energia jäävuse seaduse kohaselt võimalik. Energia jäävuse seaduse järgi ei saa ükski masin teha rohkem tööd, kui see selleks kulutab. Veel enam: hõõrdumise tõttu pole võimalik ehitada isegi igiliikurit, mis ei teeks küll tööd, kuid säilitaks liikumise. Nii ei võtagi patendibürood enam läbivaatamiseks igaveste jõumasinate projekte, mis leiutajate arvates peaksid töötama lõputult eimillegi arvel.
Jäävusseadus ütleb, et energia ei saa kaduda. Miks siis räägitakse, et kui me energiat kokku ei hoia, lõpeb see varsti otsa? Asi on selles, et töö tegemisel muutub energia mingist ühest liigist teise. Vastupidine muundumine aga sama lihtsasti toimuda ei saa.
Kui põletatakse naftat, siis selles leiduv süsinik ja vesinik reageerivad hapnikuga, tekib süsihappegaas ja veeaur ning selle käigus vabaneb soojus- ja valgusenergia, mida siis inimene kasutab. Ka vastupidine protsess on võimalik. Taimed võtavad juurtega maast vett ja lehtedega õhust süsihappegaasi ning sünteesivad Päikeselt tulevat valgusenergiat kasutades need biomassiks. Just selle nn fotosünteesi teel toodetud biomass ladestus miljonite aastate kestel kivimikihtide vahele. Biomassist tekkis päikeseenergiat salvestanud kivisüsi, nafta ja maagaas, mida me tänapäeval fossiilsete kütustena kaevandame ja põletame.
Energiat saab kerge vaevaga muundada vaid ühes suunas. Vastupidine protsess on keerukas ja aeglane. Seepärast tuleb eelistada energiaallikaid, mille taastumine toimub kiiresti. Maised energiaallikad taastuvad Päikeselt tuleva kiirguse arvel. Päike paneb kineetilist energiat andes õhu tuulena liikuma ja tõstab potentsiaalset energiat andes vee meredest jõgedesse. Taimed talletavad Päikeselt tulevat energiat, tootes tselluloosi, tärklist, õli ja suhkrut.
Päike kiirgab Maale tohutul hulgal energiat veel mitme miljardi aasta kestel. Inimese ülesanne on seda paremini kasutama õppida.
Üks huvitav ja mitmeid rakendusi leidnud nähtus, mida saab selgitada mehaanilise energia jäävuse seaduse kaudu, puudutab gaaside ja vedelike voolamist. Tutvume sellega lihtsustatud käsitluse kaudu.
Oletame, et ideaalne (so kokkusurumatu ja mitteviskoosne) vedelik voolab torus, mille läbimõõt pole kõikjal ühesugune. Siis toru erinevaid ristlõikepindu läbib sama ajaga alati sama ruumalaga vedelikukogus. On selge, et sellisel juhul peab voolukiirus toru peenemates osades olema suurem kui jämedamates.
Kui toru peenemas osas on vedeliku kiirus suurem, siis on seal suurem ka selle kineetiline energia. Hõõrdumise puudumisel on vedeliku mehaaniline energia jääv. Kui kineetiline energia suureneb, peab potentsiaalne samavõrra vähenema. Potentsiaalne energia on aga teatavasti tingitud süsteemi sees mõjuvatest jõududest. Antud juhul on tegemist vedeliku rõhumisjõududega. Näeme, et mida suurem on voolukiirus, seda väiksem on selles kohas vedeliku rõhk. Sama kehtib ka gaaside voolamisel.
Kirjeldatud seaduspärasuse avastas 1738. aastal šveitsi matemaatik ja füüsik Daniel Bernoulli. Tänapäeval tuntakse seda Bernoulli printsiibi nime all: voolava gaasi või vedeliku rõhk on suurem nendes piirkondades, kus kiirus on väiksem, ja väiksem seal, kus kiirus on suurem.
Bernoulli printsiipi kasutatakse mitmesuguste füüsikaliste nähtuste selgitamiseks. Näiteks võib öelda, et tormituul tõstab majalt katuse lendu sellepärast, et maja sees, kus õhk on paigal, on rõhk suurem kui katuse kohal tuule käes ja katus surutaksegi alt üles. Või siis pallimängudes, kus saab väita, et pöörlevana lendu löödud pall kaldub otsesihist kõrvale kuna õhu liikumise kiirus selle eri külgedel erinev ja tekib rõhkude vahe. Analoogiliselt seletatakse ka lennuki tiiva tõstejõudu — tiiva asendi ja erilise kuju tõttu voolab õhk selle kohal kiiremini kui all, nii on tiiva all rõhk suurem ja see hoiabki lennukit õhus. Peab siiski ütlema, et kuigi nende nähtuste seletustes Bernoulli võrrandi alusel on tera tõtt, ei ole need paljudes põhiküsimustes täielikud. Sest Bernoulli printsiip kehtib vaid voolutorus, aga seda ei saa rakendada seeläbi, et me võrdleme üksteisest eraldatud vedelike (või gaaside) voolusid (nagu ühel ja teisel pool katust, palli või lennuki tiiba). Teiseks, Bernoulli printsiip kehtib vaid ideaalsete vedelike (ja gaaside) korral. Samas reaalsete vedelike liikumine on väga keerukas nähtus, mida ka tänapäeval täielikult ei mõisteta.