Huvitav füüsika II
- Teine köide
- Mehaanika põhiseadused
- Jõud. Töö. Hõõrdumine
- Ringliikumine
- Ülemaailmne gravitatsioon
- Reis kahurikuulis
- Vedelike ja gaaside omadused
- Soojusnähtused
- Magnetism. Elekter
- Valguse peegeldumine ja murdumine. Nägemine
- Heli. Laineliikumine
- Sada küsimust Huvitav füüsika teise raamatu kohta
- Venekeelse raamatu toimetaja täiendused ja märkused
- Kas tunnete füüsikat?
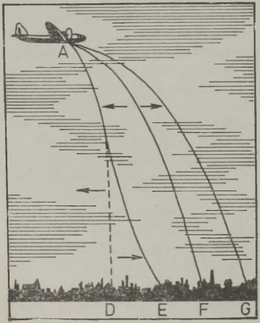
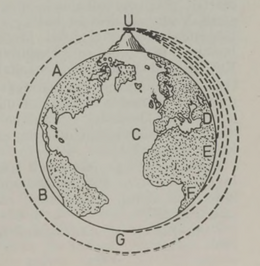
17. sajandi teravmeelne prantsuse kirjanik Cyrano de Bergerac jutustab oma satiirilises teoses «Teine maailm ehk Kuu riigid ja impeeriumid» (1657) muu hulgas imepärase loo, mis olevat temaga juhtunud. Füüsikakatsetega tegeldes kerkinud ta kord täiesti arusaamatul viisil koos kõigi oma katseklaasidega kõrgele õhku. Kui tal mõni tund hiljem läks korda taas maapinnale laskuda, polnud ta enam oma üllatuseks kodusel Prantsusmaal, isegi mitte Euroopas, vaid Põhja-Ameerika mandril Kanadas. Oma ootamatut lendu üle Atlandi ookeani peab kirjanik aga täiesti loomulikuks. Ta seletab asja järgmiselt: sel ajal kui meie sundreisija Maa pinnal ei viibinud, jätkas maakera endist viisi itta pöördumist ja seepärast leidis reisija maha laskudes jalge alt Prantsusmaa asemel hoopis Ameerika mandri.
Odav ja lihtne reisimise viis, eks ole? Tarvitseb vaid maapinnalt üles tõusta ja kas või minutki õhus püsida, kui juba laskute alla täiesti teises, kohas, kaugel lääne pool. Selle asemel, et ette võtta kurnavaid reise läbi mandrite ja üle ookeanide, võiks lihtsalt liikumatult Maa kohal rippuda ja oodata, kuni Maa ise toob soovitud paiga reisija jalge alla.
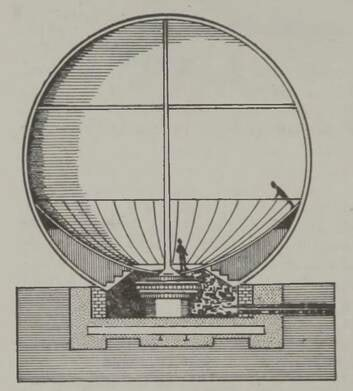
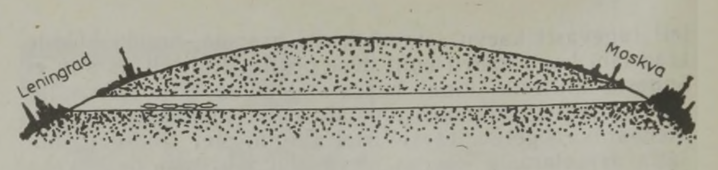
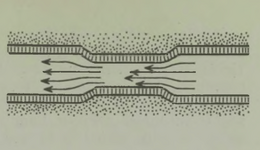
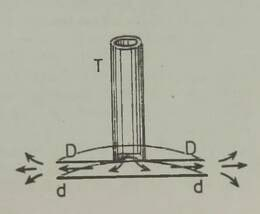
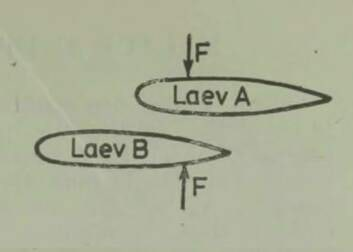
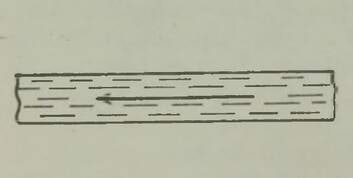
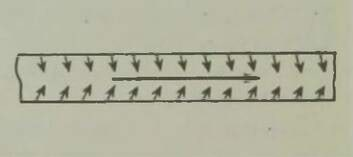
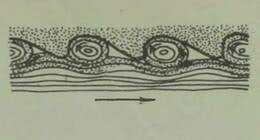
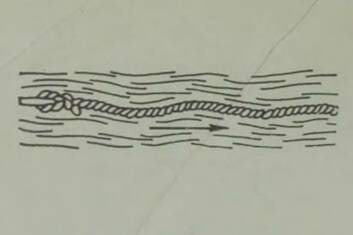
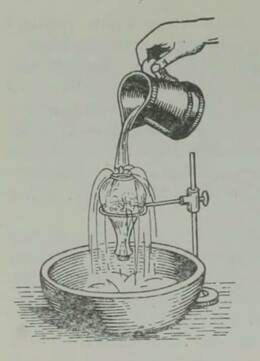
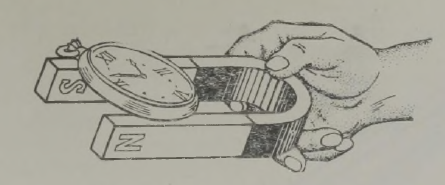
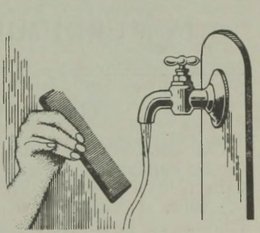
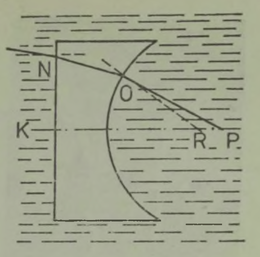
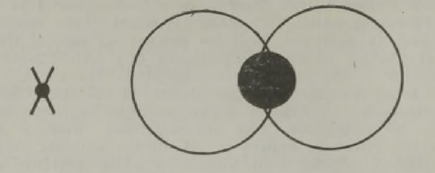
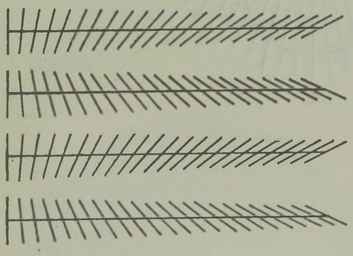
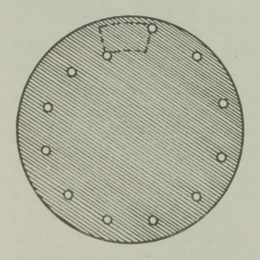
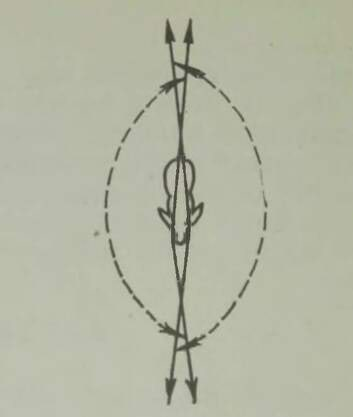
Kahjuks on niisugune imepärane reisimisviis ainult fantaasia. Esiteks, õhku tõusnuna ei eraldu me veel tegelikult maakerast; me jääme seotuks tema õhkkestaga, ripume atmosfääris, mis võtab ju samuti osa meie planeedi pöörlemisest ümber telje (joon. 1). Õhk (õigemini selle tihedamad madalad kihid) pöörleb koos Maaga, tõmmates endaga kaasa kõik, mis temas leidub: pilved, lennukid, lendavad linnud, putukad jne. Kui õhk ei osaleks maakera pöörlemises, tunneksime pidevalt ülitugevat tuult, millega võrreldes kohutavaimgi orkaan näiks õrna tuulepuhanguna (* Orkaani kiirus on 40 m/s= 144 km/h. Näiteks Leningradi laiuskraadil kannaks Maa meid läbi õhu kiirusega 230 m/s= 828 km/h.). On ju täiesti ükskõik, kas seisame paigal ja liigub õhk meie ümber või vastupidi, paigal seisab õhk, aga meie liigume selles; mõlemal juhul tunneme ühetugevust tuult. Sajakilomeetrise tunnikiirusega kihutavale mootorratturile puhub vastu tugev tuul ka täiesti tuulevaikse ilmaga.
Seda esiteks. Teiseks, isegi kui õnnestuks tõusta kõrgematesse õhukihtidesse või kui atmosfäär üldse puuduks, ka siis ei läheks meil korda kasutada niisugust odavat reisimisviisi, millest unistas prantsuse satiirik. Tõepoolest, eraldunud pöörleva Maa pinnast, jätkame inertsi mõjul liikumist endise kiirusega, s. t. sama kiirusega, millega liigub Maa meie all. Kui me uuesti maapinnale laskume, oleme täpselt samas kohas, kust me õhku tõusime, just niisamuti nagu liikuva rongi vagunis langeme pärast üleshüppamist tagasi endisele kohale. Tõsi küll, inertsi mõjul liigume meie sirget (puutujat) mööda, maapind meie all aga kõverjooneliselt, kuid väikeste ajavahemike korral see asja ei muuda.
Tuntud inglise kirjanik Herbert Wells on kirjutanud fantastilise loo sellest, kuidas keegi kontoriametnik saatis korda imesid. Vaimselt üpris piiratud noormees omandas saatuse tahtel tähelepanuväärse võime: tarvitses tal vaid kuuldavale tuua mingi soov, kui see läks otsemaid täide. Kuid selgus, et ahvatlev anne ei toonud selle omajale ega teistelegi inimestele midagi peale ebameeldivuste. Meie jaoks on õpetlik loo lõpp.
Pärast pikaleveninud öist joomapidu otsustas kontoriametnik, kes kartis aovalges koju ilmuda, kasutada oma imetegemisvõimet öö pikendamiseks. Kuidas seda aga teha? On vaja taevatähtedel käskida seisma jääda. Ametnikul tuli sellise ebatavalise vägitüki sooritamiseks algul julgusest puudu ja kui sõber andis talle nõu peatada Kuu, silmitses ta seda tähelepanelikult ning sõnas kõheldes:
««Mulle näib, et Kuu on selleks liiga kaugel ... Kuidas Teie arvate?»
«Miks mitte proovida?» käis Maydig [nii oli sõbra nimi. – J. P.] peale. «Muidugi ta ei peatu, kuid te katkestate Maa pöörlemise. Arvan, et see ei tule kellelegi kahjuks.»
«Hm,» ütles Fotheringay [kontoriametnik. – J. Р.]. «Hüva, ma proovin. Noh ... »
Ta võttis sisse käskija poosi, sirutas käed välja ja lausus pidulikult:
«Peatu, Maa! Lakka pöörlemast!»
Ta ei jõudnud neid sõnu veel lõpetada, kui sõbrad juba lendasid õhus kiirusega mõni tosin miili minutis.
Vaatamata kõigele jätkas Fotheringay mõtlemist. Vähem kui sekundi jooksul jõudis ta otsusele ja sõnastas endamisi järgmise soovi:
«Mis ka ei juhtuks, mina jään ellu ja terveks!»
Peab tunnistama, et soov oli väljendatud õigel ajal. Veel mõni sekund, ja ta kukkus mingile värskelt kaevatud maalapile, tema ümber aga lendasid talle vähimatki häda tegemata kivid, hoonete tükid, mitmesugused metallesemed; lendas ka üks õnnetu lehm, kes vastu maad end surnuks kukkus. Tuul puhus kohutava jõuga, ta ei saanud isegi pead tõsta, et ümber vaadata.
«Mõistmatu lugu,» hüüdis Fotheringay katkeva häälega. «Mis on juhtunud? Torm või? Vististi tegin midagi valesti.»
Vaadanud ringi, niipalju kui lubas tuul ja lehvivad pintsakuhõlmad, jätkas ta: «Näib, et taevas on kõik korras. Ka Kuu on olemas. Noh, aga kõik muu ... Kus on siis linn? Kus majad ja tänavad? Kust tuli see tuul? Ma ei käskinud ju tuulel puhuda!»
Fotheringay katsus püsti tõusta, kuid see osutus täiesti võimatuks ja seepärast hakkas ta neljakäpuli edasi liikuma, hoides kinni kividest ja maapinna konarustest. Minna polnud, muide, mitte kuhugi, sest niipalju kui roomav imetegija tuulega üle pea paisatud pintsakusabade vahelt nägi, pakkus kõik ümberringi pilti täielikust hävingust.
«Miski on maailmas tõsiselt rikki läinud,» mõtles ta, «aga mis nimelt, ei tea.»
Tõepoolest oli miski rikki läinud. Polnud näha ei maju, puid ega ] mitte mingeid elavaid olendeid – mitte midagi. Läbi tolmutormi 7 paistsid ähmaselt ta ümber ainult vormitud varemed ja mitmesugused rusud.
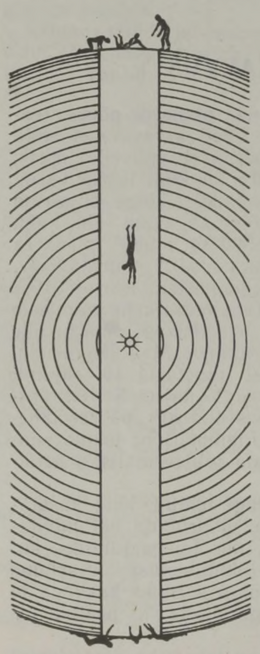
Kogu selle kaose süüdlane ei saanud muidugi aru, milles asi. Ometi oli seletus väga lihtne. Peatanud äkitselt Maa pöörlemise, ei mõelnud Fotheringay üldse inertsist, aga just inerts pidi pöörlemise järsul lakkamisel pühkima Maa pinnalt vältimatult minema kõik, mis seal leidus. Seepärast lendaski kõik, mis polnud vahetult seotud Maaga – majad, inimesed, puud, loomad – maapinna puutujat mööda püssikuuli kiirusel minema. Pärast aga kukkusid nad jälle maha ja purunesid.
Fotheringay taipas, et tema ime polnud kuigi hästi õnnestunud. Seepärast valdaski teda sügav tülgastus igasugus te imede vastu ja ta andis endale sõna, et ei tee edaspidi enam ühtegi imet. Kõigepealt oli vaja korda ajada juba tehtud pahandused, need polnud aga sugugi väikesed. Torm märatses, tolmupilved katsid Kuu ja eemalt oli kuulda läheneva vee kohinat; Fotheringay nägi välgu valgel tervet veeseina, mis kohutava kiirusega lähenes kohale, kus ta lamas. Fotheringay muutus otsustavaks.
«Jää seisma!» hüüdis ta vee poole pöördudes. «Mitte sammugi edasi!»
Seejärel kordas ta sama käsklust kõuele, välgule ja tuulele. Kõik jäi vaikseks. Fotheringay kükitas ja vajus mõttesse.
«Et ma ainult jälle mingit segadus t ei tekitaks!» mõtles ta ja sõnas seejärel: «Esiteks, kui läheb täide kõik, mida ma praegu käsin, siis kadugu mu võime teha imesid ja saagu minust samasugune harilik inimene nagu on teised. Imesid ei ole vaja. See on liiga ohtlik mäng. Teiseks, olgu kõik nii nagu enne: sama linn, samad inimesed, samad majad ja ka ma ise samasugune, nagu olin varem.»»
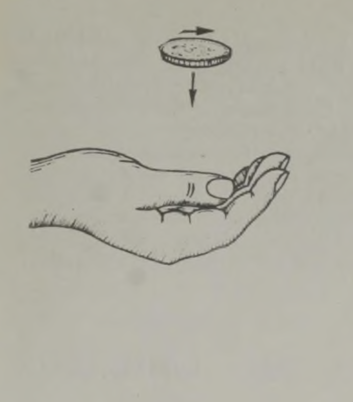
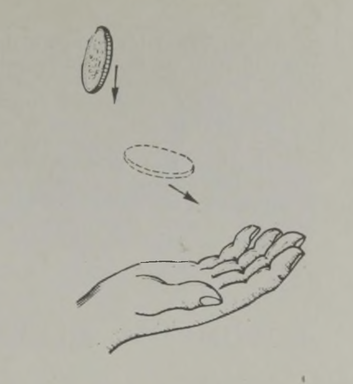
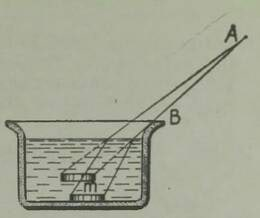
Kujutlege, et istute lennukis. All libisevad mööda tut tavad paigad. Kohe lendate üle maja, kus elab teie sõber. «Tore oleks talle tervisi saata,» välgatab teil peas mõte. Ruttu kirjutate mõne sõna märkmikulehele, seote kirja mingi raske eseme külge, ja tabanud hetke, mil maja on täpselt teie all, lasete pakikese käest lahti. Te olete täiesti kindel, et pakk kukub maja aeda. Kuid ometi ei kuku ta sugugi sinna, ehkki aed ja maja on otse teie all!
Jälgides paki langemist lennukist, täheldate kummalist pilti: pakk küll langeb, kuid jääb samal ajal ikka lennuki alla umbes nii, nagu libiseks ta piki nähtamatut niiti allapoole. Ja kui pakk lõpuks maapinnale jõuab, on ta kaugel eespool sellest kohast, kuhu me kavatsesime ta visata. Siin avaldub seesama inertsiseadus, mis takistab meid rändamast Bergeraci soovitatud ahvatleval viisil. Niikaua kuni pakk oli lennukis, liikus ta sellega kaasa. Te lasksite tal alla kukkuda, kuid langedes ei kaota ta oma esialgset kiirust, vaid liigub langemise vältel õhus esialgses suunas edasi. Mõlemad liikumised, nii püst- kui rõhtsuunaline, liituvad ja tulemusena liigub pakike mööda kõverjoont, jäädes kogu aja lennuki alla (kui lennuk ise muidugi suunda või kiirust ei muuda). Pakk lendab tõepoolest nii nagu rõhtsuunas visatud keha, näiteks horisontaalselt hoitud püssist väljatulistatud kuul; keha liigub mööda kaart, mis lõpeb maapinnal.
Märkigem, et kõik öeldu oleks täiesti õige, kui puuduks õhutakistus. Tegelikult pidurdab õhk nii paki rõht- kui ka püstliikumist, mille tulemusena pakk ei püsi kogu aja lennuki all, vaid jääb sellest veidi maha.
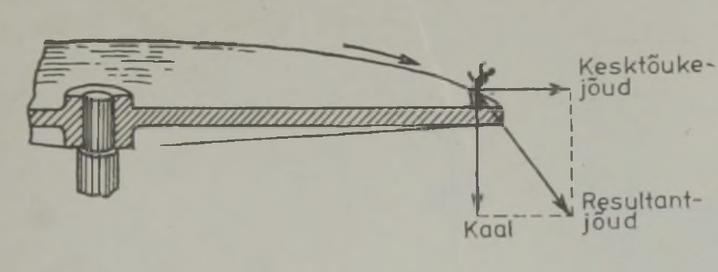
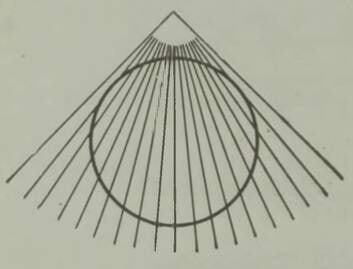
Kõrvalekaldumine püstsihist võib olla väga suur, kui lennuk lendab kõrgel ja kiiresti. Tuulevaikse ilmaga kukub 1000 meetri kõrgusel ja 180-kilomeetrise tunnikiirusega liikuvalt lennukilt visatud pakk ligi 700 meetrit ettepoole viskehetkel otse lennuki all asunud paigast (joon. 2).
Arvutuskäik on lihtne (kui jätta õhutakistus arvestamata ). Ühtlaselt kiireneva liikumise teepikkuse valemist
saame
Järelikult kulub kivil 1000 meetri kõrguselt langemiseks
Selle ajaga jõuab ta rõhtsuunas liikuda
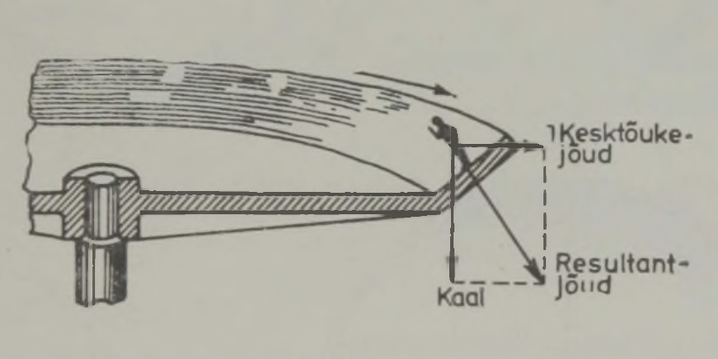
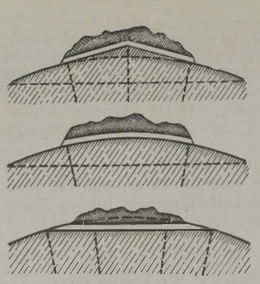
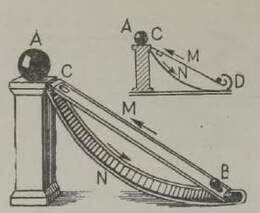
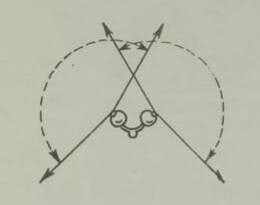
meetri võrra.Eelmise jaotise põhjal peaks olema selge, kui raske on sõjaväelenduril visata pomm täpselt määratud kohta: tal on vaja arvestada nii lennuki kiirust, langevale kehale mõjuvat õhutakistust kui tuule kiirust. Joonisel 3 on skemaatiliselt kujutatud pommi langemisteed erinevatel tin gimustel. Kui tuult ei ole, lendab pomm mööda kõverat AF; miks, seda me juba selgitasime. Pärituulega kandub pomm ettepoole ja langeb mööda kõverat AG. Mõõdukas vastutuul sunnib pommi langema mööda kõverat AD, juhul kui tuul puhub ülal ja maapinna lähedal samas suunas sageli aga juhtub, et maapinna kohal on tuule suund vastupidine ülemistes õhukihtides puhuva tuule suunaga (all näiteks vastu-, üleval pärituul), siis omandab pommi langemiskõver kuju AE.
Kui seisate liikumatul perroonil ja teist kihutab mööda kiirrong, siis on liikuvasse vagunisse hüpata õige suur kunsttükk. Aga kujutlege, et ka perroon liigub sama kiirusega ja samas suunas nagu rong. Kas teil oleks siis raske vagunisse astuda?
Mitte sugugi: te lähete rongi peale niisama rahulikult nagu siis, kui vagun seisaks paigal. Kui teie liigute rongiga samas suunas ja sama kiirusega, siis on rong teie suhtes täiesti paigal. Rattad, tõsi küll, pöörlevad, kuid teile näib, et nad pöörlevad koha peal. Rangelt võttes, kõik need esemed, mida peame harilikult paigalseisvateks — näiteks jaamas seisev rong —, liiguvad koos meiega ümber maakera telje ja tiirlevad ümber Päikese; praktiliselt pole aga seda liikumist vaja arvestada, sest see ei sega meid mitte põrmugi.
Järelikult on täiesti mõeldav korraldada nii, et jaamast mööduv rong võtab reisijaid peale ja laseb välja täiel käigul, peatumata.
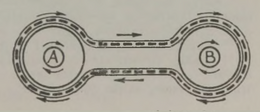
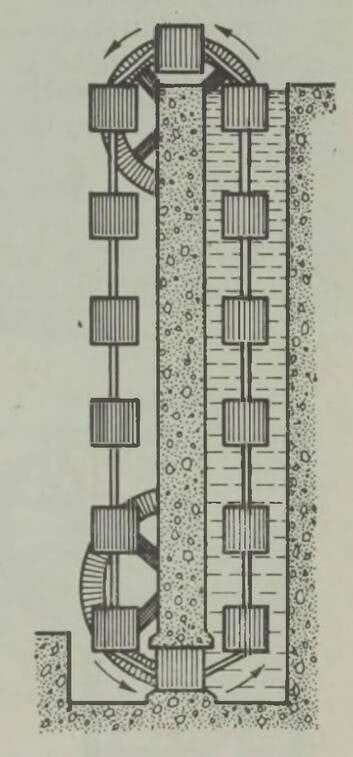
Seda laadi transpordivahendid seatakse sageli üles näitustel, et võimaldada külastajail kiiresti ja mugavalt näha suurel territooriumil kõike, mis on vaatamist väärt. Näituseväljaku äärmisi punkte ühendab justkui lõputu lindina raudtee; reisijad võivad igal hetkel ja igas kohas vagunisse astuda ja sellest väljuda, kuigi rong sõidab täie kiirusega.
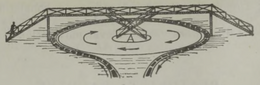
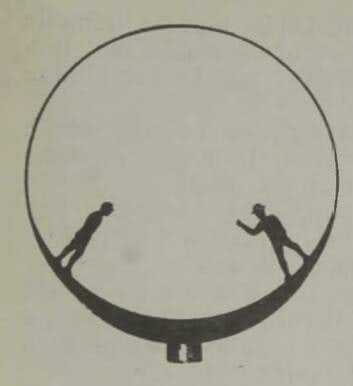
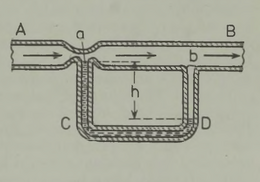
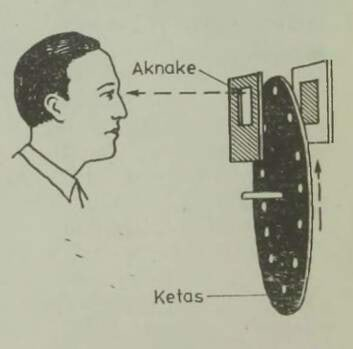
See huvitav seade on näha joonisel 4. Igas jaamas on ümmargune liikumatu platvorm, mida ümbritseb suur pöörlev rõngakujuline ketas. Mõlema jaama pöörleva ketta ümber on tõmmatud köis, mille külge on kinnitatud vagunid. Jälgige nüüd, mis toimub ketta pöörlemisel.
Vagunid liiguvad ümber ketta sama kiirusega nagu ketta välisserv, järelikult võivad reisijad vähimagi ohuta minna ketastelt vagunitesse või väljuda neist. Vagunist väljunud reisija sammub mööda pöörlevat ketast ringi keskpunkti poole, kuni jõuab liikumatu platvormini; liikuva ketta siseäärelt on liikumatule platvormile astuda juba kerge, sest ketta siseääre väikese raadiuse tõttu on väike ka ringkiirus.* Jõudnud liikumatu siseplatvormini, tarvit seb reisijal üksnes laskuda silda mööda väljaspool raudteed maapinnale (joon. 5).
Sagedate peatuste puudumine annab hiiglasuure aja- ja energiasäästu. Linnatrammidel näiteks kulub suurem osa sõiduajast ja peaaegu 2/3 energiast järk-järguliseks kiirenemiseks peatustest väljumisel ja aeglustumiseks peatustesse sõitmisel.**
Raudteejaamades saaksid reisijad minna sõitva rongi peale ja sealt maha tulla ka ilma eriliste liikuvate platvormideta. Kujutlege, et tavalisest liikumatust jaamast kihutab mööda kiirrong. Me tahame, et ta peatust tegemata võtaks siin peale uusi reisijaid. Siirdugu need reisijad esialgu teise rongi, mis seisab rööpsel varuteel, ja hakaku see rong siis liikuma samas suunas ning sama kiirusega mis kiirrong. Kui mõlemad rongid on kohakuti, on nad teineteise suhtes paigal. Tarvitseb ainult mõlema rongi vagunid ühendada sillakestega – ja abirongi reisijad võivad rahulikult siirduda kiirrongi. Kiirrongi peatumine jaamades muutub seega liigseks.
* Kerge on näha, et ketta siseääre punktid liiguvad märksa aeglasemalt, võrreldes välisääre punktidega, sest nad läbivad sama aja jooksul märksa lühema kaare.
** Energiakadu pidurdamisel saab vältida, kui panna elektrimootorid tööle dünamomasinatena, mis annavad voolu võrku tagasi. Berliini eeslinnas Charlottenburgis õnnestus sel kombel vähendada trammide energiakulu 30% võrra.2
Huvitav näide liikumise suhtelisuse kasutamisest on Läänes patenditud seade, mille abil leidur lootis ära hoida autode ja rongide kokkupõrkeid maantee ja raudtee ristumiskohtades. Ülesõidukoha ette ehitatakse eriline platvorm, mille kate hakkab rongi lähenemisel lõputu lindi kombel rullikutel automaatselt tagasi liikuma. Katte liikumiskiirus on suurem auto maksimaalsest kiirusest; seepärast niisugusel liikuval platvormil asuv auto kandub tagasi, ükskõik kui suur ta kiirus ka poleks. Pärast rongi möödumist kate peatub – ja auto kihutab takis tamatult üle platvormi.
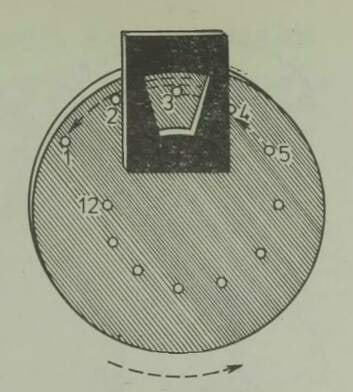
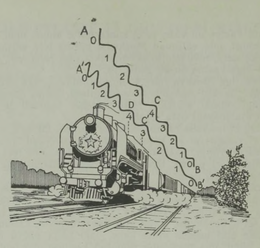
Liikumise suhtelisusel põhineb ka teine seadeldis, mida seni on kasutatud vaid näitustel, nn. liikuvad kõnniteed. Esmakordselt võeti need tarvitusele Chicago näitusel 1893. a., seejärel Pariisi maailmanäitusel 1900. a. Joonisel 6 näete selle seadme skeemi. See koosneb viiest lõputust lindist – kõnniteest, mida eriline mehhanism paneb üksteise sees erineva kiirusega liikuma.
Kõige välimine lint liigub õige aeglaselt – kiirusega kõigest 5 km/h; see on tavaline jalakäija kiirus ja nii aeglaselt roomavale lindile on lihtne peale astuda. Seespool selle kõrval liigub teine lint liirusega 10 km/h. Liikumatult tänavalt otse sellele hüpata oleks ohtlik, kuid üleminek esimeselt lindilt teisele ei tee raskusi, Tõepoolest, esimese lindi suhtes, mis liigub kiirusega 5 km/h, on teise lindi kiirus samuti kõigest 5 km/h (10 km/h – 5 km/h); järelikult on esimeselt lindilt teisele minna niisama hõlbus nagu maapinnalt esimesele lindile. Kolmanda lindi kiirus on juba 15 km/h, kuid teiselt lindilt sellele siirduda pole muidugi mingi kunst. Niisama kerge on astuda kolmandalt lindilt neljandale (selle kiirus on 20 km/h) ja lõpuks neljandalt viiendale, mis liigub kiirusega 25 km/h. Viimane lint viibki reisija soovitud punkti; siit, minnes vastupidises järjekorras üle lindilt lindile, jõuab ta lõpuks liikumatule tänavale.
Tõenäoliselt ei tekita ükski mehaanika kolmest põhiseadusest nii palju arusaamatusi kui Newtoni kolmas seadus – mõju ja vastumõju seadus. Kõik teavad seda, oskavad mõnel juhul isegi õigesti rakendada, kuid peaaegu kellelgi pole asi lõpuni selge. Võib-olla teil, lugeja, on õnnestunud sellest kohe aru saada, kuid tunnistan, et mina mõistsin seda alles kümmekond aastat pärast esmatutvust.
Vestlustes olen rohkem kui kord võinud veenduda, et enamik inimesi on valmis seda seadust õigeks tunnis tama vaid mõningate reservatsioonidega. Ollakse meeleldi nõus, et seadus kehtib liikumatute kehade korral, aga ei mõisteta, mil viisil saab seda rakendada liikuvate kehade vastastikuse mõju puhul ... Seadus väidab, et mõju on alati võrdne ja vastupidine vastumõjuga. See tähendab, et kui hobune tõmbab vankrit, siis vanker tõmbab hobust samasuguse jõuga tagasi. Kuid sel juhul peaks vanker ju paigale jääma: miks ta ikkagi liigub? Miks need jõud ei tasakaalustu vastastikku, kui nad on võrdsed?
Need on tavalised selle seadusega seotud arusaamatused. Kas see tähendab, et seadus pole õige? Ei, see on kindlasti õige, ainult -meie ei saa kõigest õigesti aru. Jõud ei tasakaalusta teineteist lihtsalt sellepärast, et nad on rakendatud erinevatele kehadele: üks vankrile ja teine hobusele. Jõud on muidugi võrdsed, aga kas võrdsete jõudude mõju on siis alati ühesugune? Kas võrdsed jõud annavad kõikidele kehadele ühesuguse kiirenduse? Kas jõu mõju kehale ei olene ka kehast enesest, sellest «vastupanu » suurusest, mida keha avaldab jõule?
Kui sellele mõelda, saab selgeks, miks ikkagi hobune suudab vedada vankrit, ehkki vanker tõmbab teda just niisama suure jõuga tagasi. Vankrile mõjuv jõud ja hobusele mõjuv jõud on igal ajahetkel võrdsed; kuid et vanker saab vabalt ratastel veereda, hobune aga toetub vastu maapinda, siis on selge, miks vanker hakkab liikuma hobuse suunas. Mõelge ka sellele, et kui vanker ei avaldaks hobuse vedavale jõule vastupanu, siis ... saaks ju hobusetagi läbi: ka kõige nõrgemast jõust piisaks vankri liikumapanemiseks. Hobust selleks vaja ongi, et ületada vankri vastumõju.3
Kõike öeldut mõistetaks paremini ja kahtlusigi oleks vähem, kui seadust ei sõnastataks tavalises lühivormis: mõju on võrdne vastumõjuga, vaid näiteks nii: vastumõjuv jõud on võrdne mõjuva jõuga. Võrdsed on ju ainult jõud – nende mõjud aga (kui mõista jõu mõju all nagu tavaliselt keha nihutamist) on erinevad, sest jõud on rakendatud erinevatele kehadele.
Täpselt niisama tugevasti nagu polaarjää surus kokku «Tšeljuskini» kere, surusid laeva pardad omalt poolt jääd. õnnetus tuli sellest, et võimas jäämassiiv suutis niisugusele survele purunemist kartmata vastu seista, laeva kere aga, olgugi terasest, polnud massiivne, andis survele järele, sai muljuda ja litsuti puruks. (Üksikasjalikumalt tuleb «Tšeljuskini» huku füüsikalistest põhjustest juttu hiljem.)
Isegi kehade langemine allub mõju ja vastumõju seadusele. Oun kukub maha sellepärast, et maakera tõmbab teda enda poole, kuid täpselt samasuguse jõuga tõmbab ka õun enda poole meie planeeti. Öieti langevad õun ja Maa teineteise poole, kuid langemise kiirus on õuna ja Maa jaoks erinev. Võrdsed vastastikuse külgetõmbe jõud annavad õunale kiirenduse 10 m/s2, maakerale aga niimitu korda väiksema kiirenduse, kuimitu korda on Maa mass suurem õuna massist. Et maakera mass on muidugi õuna massist kujutletamatult palju kordi suurem, siis nihkub maakera õuna poole nii tühiselt vähe, et praktiliselt võib lugeda selle nulliks. Seepärast ütlemegi, et õun kukub maha, aga mitte, et õun ja Maa liiguvad teineteise poole.
Kas mäletate bõliinat vägilasest Svjatogorist, kes tahtis maakera üles tõsta? Kui uskuda legendi, oli ka Archimedes valmis samasugust vägitükki sooritama ja nõudis oma kangile toetuspunkti. Ent Svjatogor oli tugev ilma kangitagi. Ta otsis vaid midagi, millest kinni haarata, mille külge panna oma vägilaskäed. «Kui ma nüüd õige pideme leiaksin, terve maa ma siis üles tõstaksin.» Juhus tuligi: vägilane leidis maast «sadulapauniku, kuid paun ei liigugi, see ei nihkugi, ei see tõuse veel».
«Hüppab Svjatogor healt hobuselt,
haaras paunast ta kahe käega,
tõstis paunakese kõrgemale põlvedest, –
kuid põlvist saadik maasse vajus Svjatogor –
algelt valgub verd, mitte silmavett.
Kuhu vajus Svjatogor, ei suutnud ta tõusta sealt,
ja seal siis lõpp talle tuligi*.»
Kui Svjatogor oleks tundnud mõju ja vastumõju seadust, oleks ta taibanud, et kui toetada jalgadega vastu maad, siis kutsub hiiglaslik välisjõud, mille ta rakendab Maale, esile võrdse, järelikult niisama vägeva vastupidise jõu, mis võib ta enda maa sisse suruda.
Igatahes on bõliinast näha, et rahva terav silm oli ammu märganud vastumõju, mida avaldab Maa tema pinnale toetumisel. Inimesed kasutasid seda seadust alateadlikult juba aastatuhandeid, enne kui Newton selle esmakordselt sõnastas oma surematus teoses «Loodusteaduse matemaatilised printsiibid».
Käies me tõukame end jalgadega lahti maapinnalt või põrandat, väga siledat põrandat või jääd mööda, millelt jalg ei saa tõukuda, pole võimalik käia. Vedur tõukab end liikumisel rööbastel edasi veorataste abil: kui rööpad õliga kokku määrida, jääb vedur paigale. Mõnikord (kiilasjää ajal) tuleb rongi liikumapanemiseks puistata veoratastele erilisest seadeldisest isegi liiva. Kui rattad ja rööpad tehti raudteeliikluse algusaastail hambulised, siis lähtuti just sellest, et rattad peavad end rööbastelt ära tõukama. Aurik tõukab end edasi sõukruvi labadega. Lennuk tõukab end õhus samuti edasi kruvi – propelleri abil. Ühesõnaga, suvalises keskkonnas liigub ese selle keskkonna enda abil. Kuid kas keha saab liikuma hakata, kui niisugust keskkonda ei ole?
Paistab, et püüda sel viisil liikuda on sama, mis katsuda end juukseid pidi üles tõsta. Nagu teada, on säärane katse õnnestunud vaid parun Münchhausenil. Muide, just niisugune esmapilgul võimatuna näiv liikumine leiab tihti aset meie oma silme all. Tõsi, ainuüksi sisejõudude mõjul ei suuda keha end tervikuna liikuma panna, küll aga saab ta mingi osa endast liikuma panna ühes, ülejäänu aga vastupidises suunas. Kui palju kordi olete näinud lendavat raketti, kuid kas olete järele mõelnud, miks ta liigub? Rakett on õpetlik näide just seda sorti liikumise kohta, mis meid praegu huvitab.
Isegi füüsikat õppinud inimestelt tuleb tihtilugu kuulda raketi lennu täiesti väära selgitust: ta lendavat sellepärast, et püssirohu põlemisel tekkivad gaasid tõukavad teda õhust eemale. Nii mõeldi ka vanasti (rakett on vana leiutis)4. Ent õhuta ruumis üles lastud rakett lendab täpselt niisama hästi. Kui isegi mitte paremini. Raketi liikumise tõeline põhjus on hoopis muus. Väga arusaadavalt ja lihtsalt esitas selle revolutsionäär Kibaltšitš oma surmaeelses töös, kus ta kirjeldas uut lennumasinat. Selgitades lahingurakettide ehitust, kirjutas ta:
«Plekist silindrisse, mille üks ots on lahtine ja teine suletud, surutakse kokkupressitud püssirohust silinder, milles piki telge on tühi kanal. Püssirohu põlemine algab selle kanali pinnalt ja levib teatava aja jooksul kokkupressitud püssirohu välispinnani. Põlemisel tekkivad gaasid avaldavad rõhumist igas suunas; gaaside rõhumine silindri külgpindadele tasakaalustub vastastikku, seevastu plekk-kesta põhjale mõjuvat rõhumist ei tasakaalusta vasturõhumine (sest selles suunas on gaasidel vaba väljapääs) ja need gaasid tõukavad raketti edasi.»
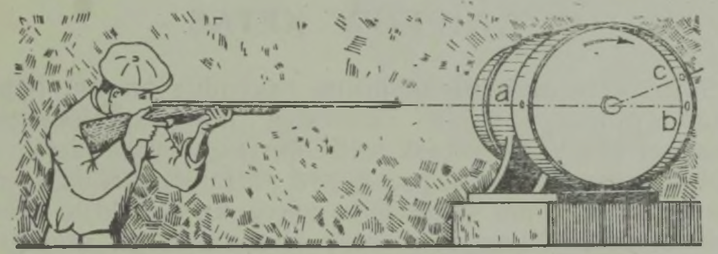
Siin juhtub sama mis kahurist tulistamisel: mürsk lendab ettepoole, kahur ise tõukub aga tagasi. Tuletage meelde püssi ja üldse igasuguse tulirelva tagasilööki. Kui kahur ripuks millelegi toetumata õhus, siis liiguks ta pärast lasku tagasi kiirusega, mis oleks nii mitu korda väiksem mürsu kiirusest, kuimitu korda kahur on raskem mürsust. Jules Verne’i ulmeloos «Pahupidi» kavatsesi ameeriklased hiiglasliku kahuri tagasilööki kasutada grandioosse idee teostamiseks – «Maa telje õgvendamiseks. »
Rakett on seesama kahur, ainult mürskude asemel purskab ta välja püssirohu põlemisgaase. Samal põhjusel tiirleb ka nn. hiina ratas, mida teil arvatavasti on juhust olnud imetleda ilutulestike ajal: ratta külge kinnitatud tõrukestes põleb püssirohi, põlemisgaasid voolavad välja ühes suunas, torukesed ise (ja koos nendega ratas) aga liiguvad vastassuunas. Tegelikult on see ratas üldtuntud füüsikariista – Segneri ratta – erikuju.
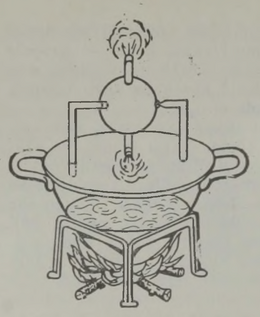
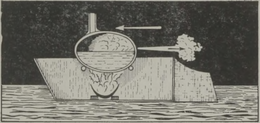
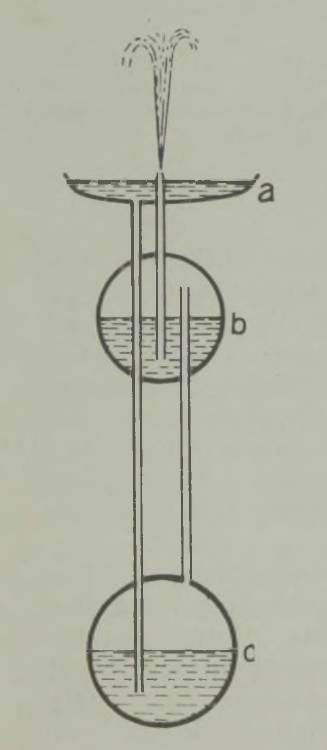
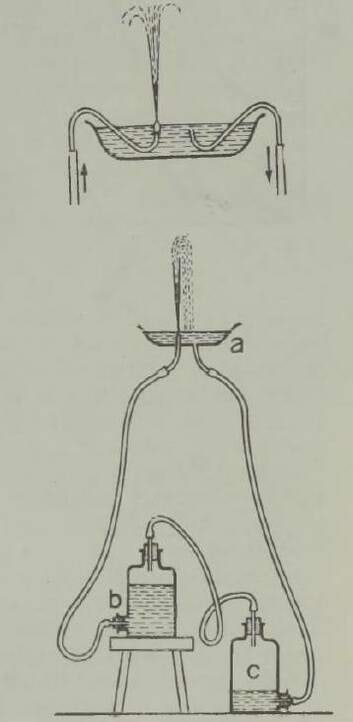
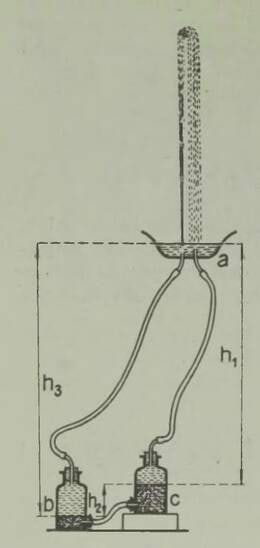
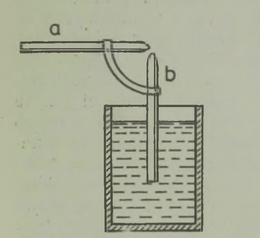
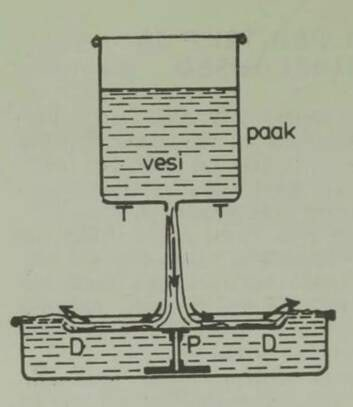
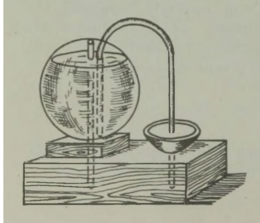
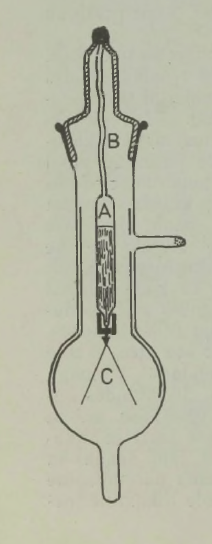
Huvitav on märkida, et enne auriku leiutamist oli olemas mehaanilise laeva projekt, mis põhines samal printsiibil. Laeva veevaru kavatseti ahtris paikneva pumba abil välja paisata; selle tagajärjel pidi laev liikuma ettepoole. Projekti, mille autor oli Ramsay, ellu ei viidud,5 kuid see mängis teatavat osa auriku leiutamises, sest andis Fultonile idee. Me teame ka, et kõige vanem aurumasin, mille ehitas Aleksandria Heron juba II sajandil e. m. a., töötas samal põhimõttel: aur liikus katlast toru mööda horisontaalsele teljele kinnitatud kerasse; pärast seda voolas ta põlvekujuliselt painutatud torusid pidi välja ja pani need vastassuunas liikuma, nii et kera hakkas pöörlema (joon. 7). Kahjuks jäi Heroni auruturbiin vanal ajal huvitavaks mängukanniks, sest orjatöö odavus ei ärgitanud kedagi masinaid praktiliselt kasutusele võtma. Kuid põhimõte pole tehnikas unustusse jäänud: praegu ehitatakse sel printsiibil reaktiivturbiine.
Newtonile, mõju ja vastumõju seaduse autorile, omistatakse üks kõige varasemaid samal põhimõttel töötava auruauto projekte: ratastele paigutatud katlast paiskub aur ühes suunas, katel ise veereb aga tagasilöögi mõjul vastassuunas (joon. 8).
Rakettautod, mille katsetamisest 1928. aastal ajalehtedes ja ajakirjades ohtrasti juttu oli, kujutasid endast Nevvtoni sõiduki teisendit.
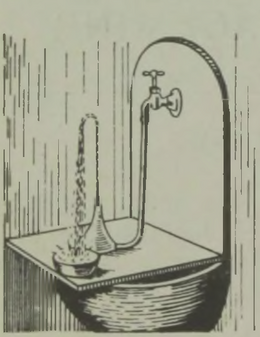
Neile, kes meisterdada armastavad, on siin joonis paberlaevukesest6, mis samuti sarnaneb väga Kewtoni sõidukiga: piirituses niisutatud vatitükk pistetakse sõrmkübarasse ja süüdatakse; tühjakspuhutud munas, mis kujutab endast aurukatelt, tekib aur, mis, paiskudes joana ühes suunas, sunnib laevukest liikuma vasta ssuunas (joon. 9). Selle õpetliku mänguasja ehitamiseks on vaja aga väga osavaid käsi.
Teil on kindlasti imelik kuulda, et leidub hulganisti elusolendeid, kelle jaoks kujutletav «iseenese juukseid pidi ülestõstmine» on tavaline vees liikumise viis.
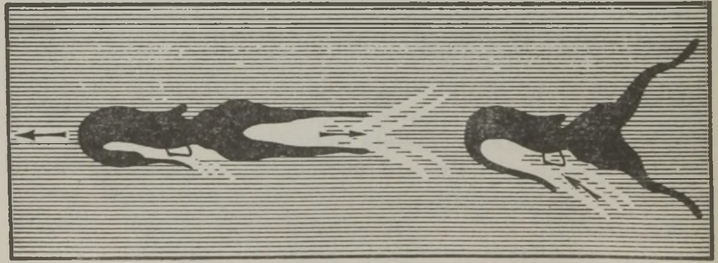
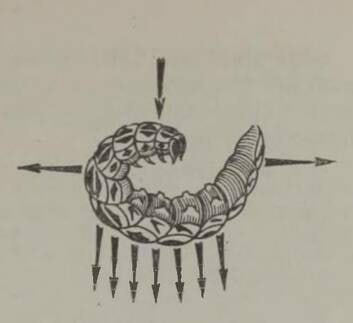
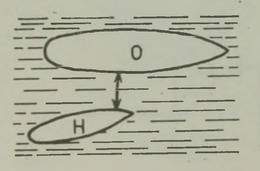
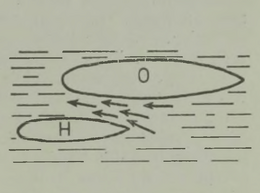
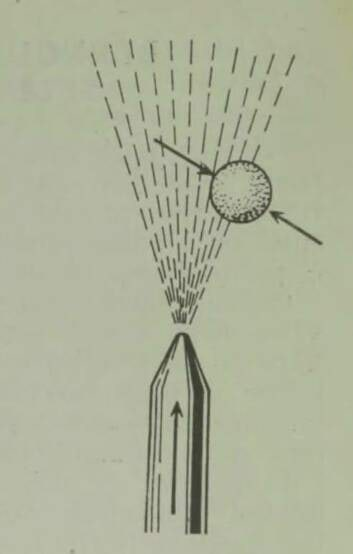
Seepia (joon. 10) ja üldse enamik peajalgseid liigub vees järgmisel viisil: nad tõmbavad vett külgedel olevatesse lõpuspiludesse ja keha esiosas paiknevasse erilisse lehtrisse, seejärel aga purskavad veejoa läbi mainitud lehtri jõuliselt välja; vastumõju seaduse põhjal saavad nad seejuures küllaldase tõuke tahapoole, et liikuda üsna kiiresti, keha tagumine pool ees. Seepia võib muide oma lehtri toru suunata kas külje peale või tahapoole ja sellest hooga vett välja pursates liikuda mistahes suunas.
Samale põhimõttele on rajatud meduusi liikumine: lihaste kokkutõmbega surub ta vee oma kellukakujulise keha alumisest osast välja, saades seejuures tõuke vastassuunas. Sellist liikumisviisi kasutavad ka salbid, kiilide vastsed ja teised veeloomad. Meie aga kahtlesime, kas niiviisi saab liikuda!7
Mis võib olla ahvatlevam, kui lahkuda maakeralt ja rännata lõputus maailmaruumis, lennata Maalt Kuule, ühelt planeedilt teisele? Kui palju ulmeromaane on sel teemal kirjutatud! Kes meid küll kõik pole viinud kujutletavale retkele tähtede juurde! Voltaire oma «Mikromegases », Jules Verne oma «Reisis Kuule» ja «Hector Servadacis», Wells «Esimestes inimestes Kuul» ja paljud nende jäljendajad sooritasid ülihuvitavaid reise teistele taevakehadele – muidugi unistustes.
Kas tõesti pole võimalik seda ammust unistust ellu viia? Kas tõesti on teostamatud kõik need teravmeelsed projektid, mida niisuguse ahvatleva tõepärasusega kirjeldatakse romaanides? Edaspidi teeme veelgi juttu fantastilistest planeedireiside projektidest, nüüd aga tutvume taoliste lendude reaalse projektiga, mille esimesena esitas meie kaasmaalane K. E. Tsiolkovski.
Kas lennukiga saab lennata Kuule? Muidugi mitte, lennukid ja õhulaevad liiguvad ainult seetõttu, et toetuvad õhule, tõukavad end selles edasi, Maa ja Kuu vahel aga õhku pole. Maailmaruumis pole üldse piisavalt tihedat keskkonda, millele meie «planeetidevaheline õhulaev» saaks toetuda. Järelikult on vaja välja mõelda selline aparaat, mis millelegi toetumata suudaks liikuda ja oleks juhitav.
Niisugune mürsk on meile juba tuttav mänguasi rakett. Miks mitte ehitada hiiglasuur rakett, milles oleks eri ruum inimeste, toidu, õhuballoonide jms. tarvis? Kujutlege, et raketis lendavad inimesed veavad kaasa suurt kütusevaru ja võivad põlemisel tekkivaid gaase juhtida igas suunas. Te saate tõelise juhitava taevalaeva, millega võib «ujuda» maailmaruumis, lennata Kuule ja planeetidele ... Reisijad võivad plahvatusi juhtides suurendada järk-järgult selle planeetidevahelise laeva kiirust, ilma et kiiruse kasv mõjuks neile halvasti. Soovides mingile planeedile laskuda, võivad nad oma laeva pöörates vähendada tasapisi selle kiirust ja pehmendada langemist. Lõpuks võivad reisijad samal viisil tagasi pöörduda Maale.
Kõigile on teada lugu sellest,
kuidas kord Luigel, Vähil, Havil tekkis mõte,
mis koos nad ühistööle viis,
et koormat vedada ja selleks siis
nad kohe kolmekesi rakendusid ette.
(vt Krõlоv, /. Valitud valmid. — Tallinn, 1952, lk. 97. Tlk. J. Kärner.)
Aga vaevalt on keegi püüdnud käsitleda seda valmi mehaanika vaatevinklist. Tulemus ei sarnane mitte põrmugi valmikirjutaja Krõlovi järeldusega.
Meie ees on mehaanikaülesanne: liita mitu üksteise suhtes nurga all mõjuvat jõudu. Jõudude suunad on valmi järgi niisugused:
Luik tahab pilvi lennata,
Vähk ronib tagurpidi, Havi kisub vette
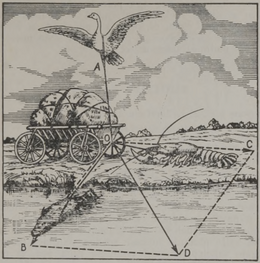
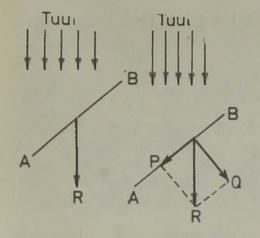
See tähendab (joon. 11), et üks jõud, luige tõmme AO, on suunatud üles; teine, havi tõmme OB — kõrvale; kolmas, vähi tõmme ОС — tahapoole. Ärgem unustagem, et on veel neljaski jõud — koorma raskus, mis on suunatud otse ülalt alla.1 Valm väidab, et «...koorem praegugi on koha peal», teiste sõnadega, kõikide koormale rakendatud jõudude resultant võrdub nulliga.
Kas see ikka on nii? Vaatame. Pilvedesse pürgiv luik ei takista vähi ja havi tööd, vaid isegi soodustab seda: raskusjõuga vastassuunas mõjuv tõmme vähendab rataste hõõrdumist pinna ja telgede vastu, muutes koorma sel moel kergemaks, ja võib-olla isegi tasakaalustab selle raskuse täies ulatuses, sest koorem pole ju suur. Lugedes lihtsuse mõttes kehtivaks viimase juhu, näeme, et jääb vaid kaks jõudu: vähi ja havi tõmme. Nende jõudude suundade kohta on öeldud, et «Vähk ronib tagurpidi, Havi kisub vette». Muidugi polnud vesi otse koorma ees, vaid kusagil kõrval (Krõlovi töömehed ei kavatsenud ju koormat uputada). Järelikult mõjuvad vähi ja havi tõmme teineteise suhtes nurgi; kui aga asi nii on, siis ei saa tõmmete resultant olla null. Ehitame rööpküliku, võttes jõud OB ja ОС külgedeks. Rööpküliku diagonaal OD annabki mehaanika reeglite kohaselt suuna ja suuruse poolest resultandi. Arusaadavalt peab resultant koorma kohalt nihutama, liiati kui koorma raskus on luige tõmbe tõttu vähenenud. Iseküsimus on see, kuhupoole koorem liigub: edasi, tagasi või kõrvale. See sõltub jõudude suhtest ja nurgast nende vahel.
Lugejad, kellel on jõudude liitmises ja lahutamises juba mõningane kogemus, tulevad ülesandega kerge vaevaga toime ka siis, kui luige tõmme ei tasakaalusta koorma raskust; nad veenduvad, et selgi juhul ei saa koorem jääda paigale. Ainult ühel tingimusel ei hakka koorem nende kolme jõu mõjul liikuma: kui hõõrdumine vankri telgedel ja teepinnal on suurem rakendatud jõudude resultandist. See aga pole kooskõlas väitega1 et koorem ei olnud raske. Igal juhul ei saanud Krolov täie kindlusega väita, et «kuis ka püüaksid, ei koormat paigast saa» ja et «koorem praegugi on koha peal». See ei muuda muidugi valmi mõtet.
Nägime just, et Krõlovi elutarkus
Kui puudub üksmeel seltsimeeste seas,
siis nendel kuidagi ei vea
ja rist ning viletsus on nende ettevõte
pole mehaanikas alati rakendatav. Jõud võivad olla suunatud erinevalt, kuid anda sellegipoolest teatava resultandi.
Vähe on neid, kes teavad, et usinad töörügajad sipelgad, keda seesama Krõlov kiidab kui eeskujulikke töötegijaid, töötavad koos just viisil, mida valmikirjanik välja naeris. Siiski läheb asi neil üldiselt korda. Jällegi aitab hädast välja jõudude liitmise seadus. Jälgides töötavaid sipelgaid tähelepanelikult, veendute üsna pea, et nende koostöö on arukas ainult näiliselt: tegelikult töötab iga sipelgas iseendale ega mõtlegi teisi abistada.
Keegi zooloog kirjeldab sipelgate tööd nii:
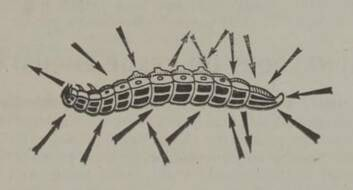
«Kui kümmekond sipelgat tirib suurt saaki mööda tasast maad, siis tegutsevad kõik ühtmoodi ja tekib mulje koostööst. Oletame aga, et saak, näiteks röövik, jääb mingi takistuse, kas kivikese või rohuvarre taha kinni. Otse edasi teda vedada ei saa, tuleb ringi minna. Ja siin ilmnebki selgesti see, et iga sipelgas püüab takistust ületada omamoodi, teistega arvestamata (joon. 12, 13). Üks sikutab paremale, teine va sa kule; üks tõukab edasi, teine tirib tagasi. Sagitakse siia-sinna, haaratakse röövikut kuskilt teisest kohast ja igaüks tõmbab-tõukab teda omamoodi. Kui siis juhuse läbi liituvad töötegijate jõud nii, et ühes suunas veab röövikut näiteks neli ja teises kuus sipelgat, hakkabki röövik liikuma nende kuue sipelga poole, hoolimata «nelja «vastutegutsemisest ».»
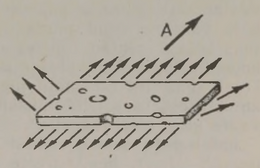
Esitame veel ühe õpetliku näite selle kohta, kui näiline on sipelgate koostöö. Joonisel 14 on kujutatud neljakandiline juustutükk, millest oli kinni haaranud 25 sipelgat. Juust liikus aeglaselt edasi noolega näidatud suunas ja võis tekkida arvamus, et kogu eesmine sipelgate viirg tõmbab saaki, tagumine lükkab seda tagant, külgmised sipelgad aitavad kaasa. Kuid on kerge veenduda, et asi pole sugugi nii: eraldage noaga kogu tagumine sipelgate viirg — ja saak hakkab liikuma märksa kiiremini. On selge, et need 11 sipelgat ei lükanud juustutükki edasi, vaid tõmbasid seda tagasi: igaüks neist püüdis saaki pöörata nii, et seda saaks enda järel pessa lohistada. Järelikult, tagumise viiru sipelgad mitte ei aidanud eesmisi, vaid hoopis segasid neid püüdlikult, muutes suurema osa nende jõupingutustest tühjaks. Juustutüki vedamiseks oleks piisanud kõigest neljast sipelgast, kuid tegevuse kooskõlastamatuse tõttu tiris saaki 25 sipelgat. Seda sipelgate ühistöö iseärasust oli juba ammu tähele pannud Mark Twain. Jutustades kahe sipelga kohtumisest, kellest üks oli leidnud rohutirtsu koiva, kirjutab humorist:
«Nad haaravad teine teisest koiva otsast ja tirivad seda kogu jõust vastassuundades. Mõlemad näevad, et midagi on korrast ära, aga ei saa aru, mis nimelt. Algab sõnelus; vaidlus läheb üle kakluseks ... Toimub leppimine, ja algab taas mõttetu ühistöö, kusjuures kakluses haavata saanud sipelgas on ainult tüliks. Terve seltsimees rabeleb koormat vedades kogu jõust ja tirib koos sellega ka haavatud sopra, kes saagi loovutamise asemel hoopis selle küljes ripub.»
Twain teeb naljatamisi täiesti õige märkuse, et «sipelgas töötab hästi ainult siis, kui teda jälgib kogenematu loodusevaatleja, kes teeb valesid järeldusi».
Filosoofiliste küsimuste seas, mille kallal murdis pead sügavamõtteline Kifa Mokijevitš Gogoli «Surnud hingedest », oli selline probleem: «Noh, aga kui elevant sünniks munast, siis peaks selle muna koor vist õige paks olema, suurtükigagi ei laseks seda katki; tuleb mingi uus laskeriist välja mõtelda.»*
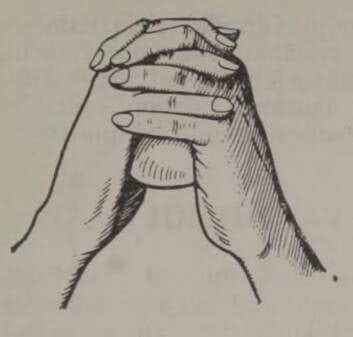
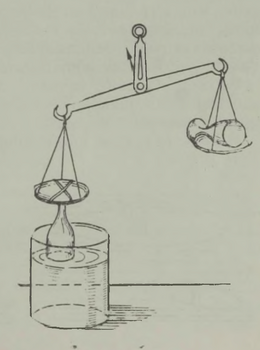
Gogoli filosoof olnuks tõenäoliselt väga imestunud, kui ta oleks teada saanud, et hariliku kanamuna koorgi pole vaatamata väikesele paksusele mingi õrn asi. Surudes käte vahele võetud muna otstele, pole kaugeltki kerge teda kokku vajutada; on vaja õige suurt jõudu, et munakoort niisugusel juhul purustada (joon. 15). (Katse on mõneti ohtlik (munakoor võib vigastada kätt) ja selle tegemisel peab ettevaatlik olema.) Munakoore sedavõrd ootamatu tugevus on tingitud just koore kumerusest ja seletub niisamuti nagu igasuguse muu kaare ning võlvi tugevus.2
Joonisel 16 näeme väikest aknapealset kivivõlvi. Koormus 5 (s. t. peallasuvate müüriosade raskus) surub võlvi keskmisele, kiilukujulisele kivile ülalt alla jõuga, mida joonisel märgib nool A. Allapoole ei saa kivi vajuda oma kiilutaolise kuju tõttu, ta rõhub ainult naaberkividele. Seejuures jaguneb jõud A rööpküliku reegli põhjal kaheks komponendiks С ja B\ need tasakaalustab külgmiste kivide vastusurve, sest viimased on omakorda naaberkivide vahel. Seepärast ei suudagi ülalt alla mõjuv jõud võlvi purustada. Seda on aga võrdlemisi kerge teha alt üles mõjuva jõuga, mis on ka arusaadav, sest kivide langemist takistav kiilu kuju ei sega sugugi neid tõusmast.
Munakoor on seesama võiv, ainult ühes tükis. Väljastpoolt surudes ei lähe ta sugugi nii kergesti katki, nagu selliselt hapralt materjalilt võiks oodata. Võib panna üsna raske laua jalgadega neljale toorele kanamunale — ja munad ei lähe katki (et munad paigal püsiksid ja rõhumispind suureneks, on munade otstesse vaja teha kipsist alused; kips kinnitub lubjast koore külge kergesti).
Nüüd taipate isegi, miks hauduval kanal pole tarvis karta munade purunemist kana raskuse mõjul. Ja samal ajal lööb nõrguke kanapoeg, kes tahab oma looduslikust vanglast vabaks pääseda, koore seestpoolt nokaga kerge vaevaga katki.
Lüües teelusikaga vastu muna külge ja purustades koore õige kergesti, ei aimagi me, kui vastupidav see koor on looduslikes tingimustes ja millise tugeva soomusega kaitseb loodus selles arenevat elusolendit.
Õrnade ja habrastena näivate elektrilampide mõistatusliku tugevuse põhjus on sama mis munakoorelgi. Nende vastupidavus tundub veelgi rabavam, kui meenutame, et paljud neist (vaakum-, mitte gaastäitega lambid) on peaaegu absoluutselt tühjad ja välisõhu survele ei ole seestpoolt mitte mingit vastumõju, õhurõhk elektrilambile pole aga sugugi väike: 10-cm läbimõõdu korral surub välisõhk lambi vastaskülgi rohkem kui 75-kgf jõuga (inimese kaal). Katse näitab, et õhutühi lamp on suuteline välja kannatama isegi 2,5 korda suuremat rõhumist.
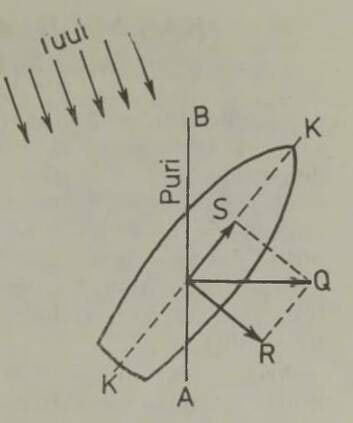
Raske on mõista, kuidas purjekad liiguvad vastutuult. Tõsi, meremees ütleb, et otse vastutuult purjede abil sõita ei saa, küll aga on võimalik liikuda tuule suuna suhtes teravnurga all.3 See teravnurk on üsna väike — umbes veerand täisnurgast — ning jääb arusaamatuks, mis vahet seal siis on, kas purjetada otse vastu tuult või temaga 22-kraadise nurga all.
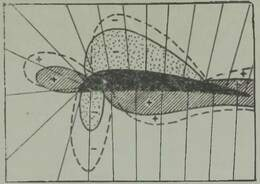
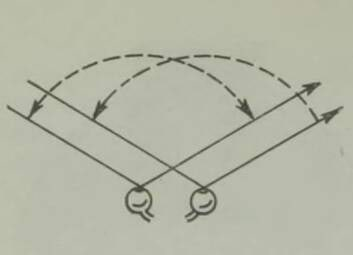
Tegelikult pole see sugugi ükskõik ja kohe selgitame, kuidas saab purjetada vastutuult, kui nurk liikumise suuna ja tuule suuna vahel on väike. Kõigepealt vaatame, kuidas tuul üldse purjele mõjub, s. t. kuhu ta purje tõukab, kui ta sellele puhub. Tõenäoliselt arvate, et tuul tõukab purje alati selles suunas, kuhu ta puhub. Asi pole aga nii: sõltumata puhumise suunast tõukab tuul purje risti selle pinnaga. Tõepoolest, puhugu tuul joonisel 17 noolega näidatud suunas; ristlõik AB kujutagu purje. Et tuul mõjub ühtviisi kogu purjepinnale, siis võime seda rõhumist kujutada noolega R, mis on rakendatud purje keskpunktis. Lahutame selle jõu kaheks komponendiks: purje pinnaga risti olevaks jõuks Q ja piki purje pinda mõjuvaks jõuks P. Viimane jõud ei tõuka purje kuhugi, sest tuule hõõrdumine vastu purjelõuendit on tühine. Jääb jõud Q, mis mõjub purjele täisnurga all.
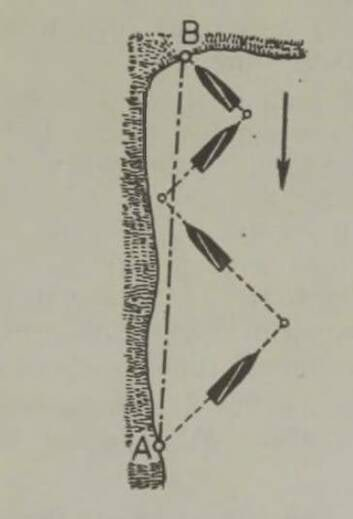
Seda teades taipame kergesti, kuidas purjekas saab liikuda vastutuult teravnurga all. Kujutagu joon KK (joon. 18) laeva kiilujoont. Tuul puhub selle joone suhtes teravnurga all, suunas, mida näitavad kõrval olevad nooled. Sirglõik AB kujutab purje; see paigutatakse nõnda, et tema pind jagaks nurga kiilujoone ja tuule suuna vahel pooleks. Jälgige jõudude paigutust joonisel 18. Tuule rõhumist purjele kujutab jõud Q, mis teadupärast peab olema purjepinnaga risti. Lahutame selle jõu kaheks komponendiks: jõuks R, mis on risti kiiluga, ja jõuks S, mis on suunatud piki kiilujoont ettepoole. Et jgeva liikumist suunas R takistab tugevasti vesi (purjelaevade kiil ulatub väga sügavale), siis vee takistus tasakaalustab peaaegu täiesti jõu R. Jääb ainult jõud S, mis, nagu näete, on suunatud ettepoole ja viib laeva järelikult peaaegu vastutuult edasi. (* Saab tõestada, et jõu S väärtus on kõige suurem siis, kui purje pind jagab nurga kiilu ja tuule suundade vahel pooleks.) Tavaliselt liigub laev siksakilist teed mööda, nagu näidatud joonisel 19. Meremeeste keeli nimetatakse niisugust sõitu loovimiseks.4
«Andke mulle toetuspunkt ja ma tõstan Maa üles.» Legend omistab selle hüüatuse Archimedesele, antiikaja geniaalsele mehaanikule, kangi seaduse avastajale. Plutarchose teosest loeme: «Kord kirjutas Archimedes oma sugulasele ja sõbrale Sürakuusa valitsejale Hieronile, et antud jõuga võib paigast nihutada kuitahes suure koorma. Tõestustest kaasakistuna lisab ta, et leiduks veel teinegi Maa, siis võiks ta sellel asudes nihutada paigast meie oma.»
Archimedes teadis, et pole olemas sellist koormat, mida ei saaks üles tõsta kas või kõige nõrgema jõuga, kui kasutada kangi: on-tarvis ainult rakendada see jõud väga pikale kangi õlale, kuna koorem mõjuks sama kangi lühikesele õlale. Seepärast ta arvas, et rõhudes ülipikale kangiõlale, suudab ta käte jõul üles tõsta koorma, mis võrdub massilt maakera omaga.*
Kui aga vanaaja suur mehaanik oleks teadnud, missugune on meie maakera mass, siis ta tõenäoliselt poleks nii suurustavat mõtet kuuldavale toonud. Kujutlegem hetkeks, et Archimedesele on antud too «teine Maa», too toetuspunkt, mida ta otsis; kujutlegem veel, et ta valmistas ka vajaliku pikkusega kangi. Kas teate, kui palju aega tal kuluks, et kergitada kas või ühe sentimeetri võrra keha, mille mass on võrdne Maa massiga?
Vähemalt kolmkümmend tuhat miljardit aastat!
Tõepoolest, Maa mass on astronoomidel teada.** Sellise massiga keha kaaluks Maa pinnal ümmarguselt 6·1024 kgf. Kui inimene suudab vahetult tõsta ainult 60 kg, siis «Maa tõstmiseks» peab ta hakkama kinni kangi õlast, mis on teisest pikem 1023 korda! Lihtne arvutus veenab meid, et kui kangi lühema õla ots tõuseb 1 cm võrra, siis peab pikema õla ots läbima maailmaruumis tohutu kaare, nimelt
1018 km!
Sellise kujutletamatult pika tee peaks läbima Archimedese käsi, et «tõsta Maad» kõigest ühe sentimeetri võrra. Kui palju aega selleks kulub? Isegi kui Archimedes suudaks 60-kilogrammise raskuse tõsta 1 meetri kõrgusele 1 sekundi jooksul, ka siis kuluks «Maa tõstmiseks» 1 cm võrra
1021 s = 30 000 miljardit aastat!
Kogu oma pika elu jooksul poleks kangile rõhuv Archimedes suutnud «tõsta Maad» isegi mitte kõige õhema juuksekarva võrra ...
Ühegi võttega poleks geniaalne leiutaja suutnud seda ajavahemikku märkimisväärselt lühendada. ‘Mehaanika kuldreegel väidab, et võiduga jõus kaasneb iga masina puhul paratamatult kaotus teepikkuses, s. t. ajas. Kui Archimedes olekski oma kätt liigutanud looduses esineva võimaliku suurima kiirusega 300 000 km/s (valguse kiirus), suutnuks ta «tõsta Maad» 1 cm võrra alles 10 miljoni aasta jooksul.
Kas mäletate Jules Verne’i jõumeest Matifoud? «Imekena pea, mis on proportsioonis vägilaskasvuga; sepalõõtsaga sarnanev rinnakorv; jalad nagu tugevad palgid; käed kui tõelised tõstekraanad; vasaratega sarnanevad rusikad...» Tõenäoliselt on teil meeles selle jõumehe vägitegusid kirjeldavast romaanist «Mathias Sandorff» imepärane juhtum laevaga «Trabocolo», kus meie hiiglane oma vägevate käte jõuga takistas laeva vettelaskmist.
Kirjanik jutustab sellest järgmist:
«Laev oli juba vabastatud tugedest, mis teda külgedelt hoidsid, ja valmis vettelaskmiseks. Vaja oli ainult kõrvaldada kinnitustrossid, et laev oleks hakanud ellingult alla libisema. Juba tegutseski pool tosinat puuseppa laeva kiilu all. Pealtvaatajad jälgisid toimuvat elava huviga. Sel hetkel ilmus lähedase neeme tagant nähtavale lõbusõidujaht. Sadamasse sisenemiseks pidi jaht mööduma kohast, kus valmistuti «Trabocolot» vette laskma, ja niipea kui väike laev märku andis, tulnuks igasugus te juhuslikkuste vältimiseks vettelaskmine seisma panna, et pärast jahi kanalisse jõudmist seda taas jätkata. Kui laevad – üks risti tee peal ees, teine suure kiirusega ellingult alla liikumas – kokku põrganuksid, oleks jaht hukkunud.
Töölised lakkasid vasaratega tagumast. Kõigi pilgud jälgisid graatsilist laeva, mille valged purjed paistsid päikese viltustes kiirtes ülekullatuna. Peagi jõudis jaht otse laevatehase kohale, kus tuhanded uudishimulikud tardunult seisid. Äkitselt kostis õuduskarje: «Trabocolo » värahtas ja hakkas liikuma just sel hetkel, kui jaht pööras tema poole tüürpoordi! Laevad olid kokku põrkamas, polnud ei aega ega võimalust seda kokkupõrget takistada. «Trabocolo» libises kiiresti piki kaldteed allapoole... Hõõrdumisest tekkinud valge suitsuvine keerles veel laeva nina iümber, sellal kui ahter oli juba vette jõudnud [laev lasti vette, ahter ees. – J. Р.].
Äkki ilmus keegi mees, haaras kinni trossist «Trabocolo» esiosas ja püüdis peaaegu vastu maad paindudes laeva kinni hoida. Ainsa hetkega mässis ta trossi maasse löödud raudposti ümber ja, olles ise muljumisohus, hoidis trossi otsa ebainimliku pingutusega 10 sekundi jooksul kinni. Lõpuks tross katkes. Kuid neist kümnest sekundist piisas: vette jõudev «Trabocolo» ainult riivas purjekat ja libises edasi. Jaht oli päästetud. Mis puutub inimesesse, kellele keegi ei jõudnud isegi appi tulla, sest kõik toimus nii kähku ja ootamatult, siis see inimene oli Matifou.»
Kuidas oleks küll romaani autor hämmeldunud, kui keegi oleks talle öelnud, et sellise kangelasteo sooritamiseks pole üldsegi vaja olla mingi vägilane ega omada Matifou kombel «tiigri jõudu». Iga leidlik inimene võinuks teha just sedasama! Mehaanika õpetab, et posti ümber mässitud köie libisemisel suureneb hõõrdumine maksimumini. Mida rohkem keerde on posti ümber mässitud, seda suurem on hõõrdumine, kusjuures keerdude arvu kasvamisel aritmeetilise jada seaduste järgi suureneb hõõrdumine geomeetrilise jada seaduse järgi. Seepärast võib isegi nõrk laps, kelle käes on 3 – 4 korda ümber liikumatu posti keeratud köie ots, tasakaalustada väga suurt jõudu.
Jõesadamates peatavad noorukid sel kombel randuvaid laevu sadade reisijatega pardal. Neid ei aita mitte fenomenaalne kätejõud, vaid köie ja posti vaheline hõõrdumine.
Kuulus 18. sajandi matemaatik L. Euler tegi kindlaks hõõrdejõu sõltuvuse posti ümber mässitud köie keerdude arvust. Nende jaoks, keda ei kohuta algebraliste avaldiste kokkusurutud keel, esitame Euleri valemi:
on siin jõud, mille vastu meie pingutus on suunatud. Täht märgib naturaallogaritmide alust (), on köie ja posti vaheline hõõrdetegur. Täht märgib «pealekerimisnurka», s. t. suhet pealekeeratud köieosa pikkuse ja selle poolt moodustatud kaare raadiuse vahel.
Rakendame seda valemit Jules Verne’i kirjeldatud juhtumi kohta. Tulemus on rabav. Antud juhul on jõud ellingult allalibiseva laeva tõmme. Laeva kaal on romaani järgi 50 tonni. Võtame ellingu kaldeks 1/10. Sel juhul mõjus köiele mitte kogu laeva kaal, vaid ainult 1/10 sellest, s. t. 5 tf 6hk 5000 kgf.
Edasi, köie ja raudposti hõõrdeteguri k võtame võrdseks 73. Nurka a on kerge leida, kui arvestada, et Matifou keeras köie vaid 3 korda ümber posti. Siis
Asetades kõik need väärtused Euleri valemisse, saame võrrandi:
Otsitava , s. t. vajaliku jõu saame sellest võrrandist leida logaritmide abil:
kust
Niisiis oli kangelasteo sooritamiseks vägilasel vaja köit tõmmata kõigest 10-kilogrammise jõuga.
Ärge arvake, et see arv – 10 kgf – on üksnes teoreetiline ja et tegelikult on vaja palju suuremat jõudu. Otse vastupidi, meie tulemus on isegi liiaga võetud: kanepiköie ja puuposti korral on hõõrdetegur suurem ja vajalik jõud naeruväärselt väike. Kui ainult köis on küllalt tugev, et tõmbele vastu pidada, siis võib nõrk lapski, keerutanud köie 3 – 4 korda ümber posti, korrata Jules Verne’i vägimehe tegu ja isegi efektsemalt.
Igapäevaelus kasutame endale aru andmata sageli võimalusi, mida näitab meile Euleri valem. Sõlmgi pole muud kui nöör, mis on mähitud silindrikesele, milleks antud juhul on sellesama nööri teine ots. Iga liiki sõlmede tugevus, olgu need siis tavalised või meremehesõlmed, sidemed, lehvid vms., oleneb ainult hõõrdumisest, mis muutub siin mitu korda suuremaks seetõttu, et nöör on mähitud iseenda ümber nagu köis ümber posti. Selles on kerge veenduda, jälgides nööri lookeid sõlmes. Mida rohkem lookeid, seda rohkem kordi keerdub nöör ümber iseenda, seda suurem on «pealekerimisnurk» ja järelikult seda tugevam sõlm.
Alateadlikult kasutab sedasama asjaolu ka rätsep nööpi ette õmmeldes. Ta mähib niidi pistekohal palju kordi ümber riide koelõngade ja tõmbab ta seejärel katki. Kui niit on tugev, ei tule nööp eest ära. Siingi rakendatakse meile juba tuttavat reeglit: niidi keerdude arvu kasvades aritmeetilise jada seaduste järgi suureneb õmbluse tugevus geomeetrilise jada seaduste järgi.
Kui poleks hõõrdumist, ei saaks me nööpe kasutada: niit keerduks iseenese raskuse tõttu lahti ja nööbid kukuksid eest.
Näete nüüd, kui mitmekesiselt ja vahel isegi ootamatult tuleb meie ümber ilmsiks hõõrdumine. Hõõrdumine etendab üsna olulist osa ka seal, kus me tema olemasolu isegi ei kahtlusta. Kui hõõrdumine maailmast äkki kaoks, kulgeks suur hulk tavalisi nähtusi hoopis teisiti.5
Väga värvikalt kirjeldab hõõrdumise osa prantsuse füüsik Ch. Guillaume:
«Meil kõigil on tulnud kõndida kiilasjääl. Kui palju pingutusi nõuab püstipüsimine, kui palju naljakaid liigutusi tuleb teha, et jalule jääda! See sunnib meid tunnistama, et tavaline maapind, millel käime, on varustatud väärtusliku omadusega, mistõttu tasakaalu hoidmine ei tee meile erilisi raskusi. Sama mõte tekib siis, kui sõidame jalgrattaga mööda libedat sillutist või kui hobune libiseb asfaldil ja kukub. Taolisi nähtusi uurides avastame enda jaoks hõõrdumise mõju. Insenerid püüavad võimaluste piires vabaneda sellest oma masinatesm – ja õigusega. Rakendusmehaanikas räägitakse hõõrdumisest kui äärmiselt ebasoovitavast nähtusest – ja ka see on õige, kuid ainult kitsas valdkonnas. Kõigil ülejäänud juhtudel peame olema hõõrdumisele tänulikud: see annab meile võimaluse käia, istuda ja töötada, ilma et meil oleks vaja karta raamatu või tindipleki põrandale kukkumist, laua nurka libisemist või sulepea käest pudenemist.
Hõõrdumine on nii tavaline nähtus, et, harvad erandid välja arvatud, pole meil kunagi vaja teda appi kutsuda: ta on ise kohal.
Hõõrdumine võimaldab suurendada püsivust. Puusepad teevad põranda parasjagu tasaseks, et lauad ja toolid püsiksid seal, kuhu me nad paneme. Lauale asetatud taldrikud, kausid ja klaasid seisavad paigal ilma meie abitagi, kui tegemist ei ole just tormisel merel viibiva laevaga.
Kujutlegem, et hõõrdumine kaoks täiesti. Siis ei saaks ühtki keha, olgu see kivilahmakas või liivatera, kunagi teisele peale panna: iga asi libiseb ja veereb seni, kuni jõuab teistega samale tasandile. Kui puuduks hõõrdumine, oleks maakera täiesti sile nagu vedelikust kera.»
Siia võib veel lisada, et hõõrdumise puudumisel libiseksid naelad ja kruvid seintest välja, ühtki asja ei saaks käes hoida, ükski keeris ei kaoks, ükski heli ei vaikiks, vaid kõlaks lõputu kajana, peegeldudes nõrgenemata näiteks toa seintelt.
Näitliku õppetunni, mis veenab meid hõõrdumise hiiglasuures tähtsuses, saame iga kord kiilasjää varal. Kiilasjääga kaetud tänaval oleme abitud ja pidevas kukkumisohus. Toome õpetliku väljavõtte ajalehest (1927. a. detsember) :
«London, 21. dets. Tugeva kiilasjää tõttu on tänavaja trammiliiklus märgatavalt häiritud. Umbes 1400 inimest paigutati käe- ja jalaluumurdudega jms. haiglasse.»
«Hyde Parki lähedal toimunud kolme auto ja kahe trammi kokkupõrkes hävisid autod bensiini plahvatamise tagajärjel täielikult.»
«Pariis, 21. dets. Kiilasjää Pariisis ja selle eeslinnades põhjustas arvukalt õnnetusjuhtumeid .. .»
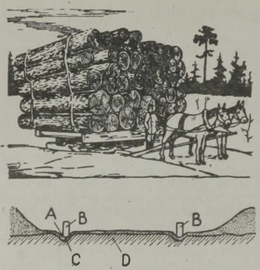
Kuid jääpinnal esinevat tühist hõõrdumist saab edukalt ära kasutada tehnikas. Näiteks võib tuua kas või tavalise kelgu. Veel selgemat keelt räägivad nn. jääteed mida ehitatakse metsamaterjali väljavedamiseks raie lankidelt raudteede juurde või parvetuskohtadesse. Sellisel siledate rööbastega teel (joon. 21) suudavad kaks hobust vedada rege, millel on 10 tonni palke.
Eelöeldust ei maksa teha ennatlikku järeldust, et hõõrdumine vastu jääd on tühine igas olukorras. Isegi nullile lähedastel temperatuuridel võib see hõõrdumine olla märgatav. Seoses jäälõhkujate ehitamisega on viimastel aastatel põhjalikult uuritud polaarjääde ja laeva terassoomuse vahelist hõõret. Tuli välja, et hõõrdumine on ootamatult suur, niisama suur kui raua hõõrdumisel vastu rauda: laeva terassoomuse ja jää vaheline hõõrdetegur on .
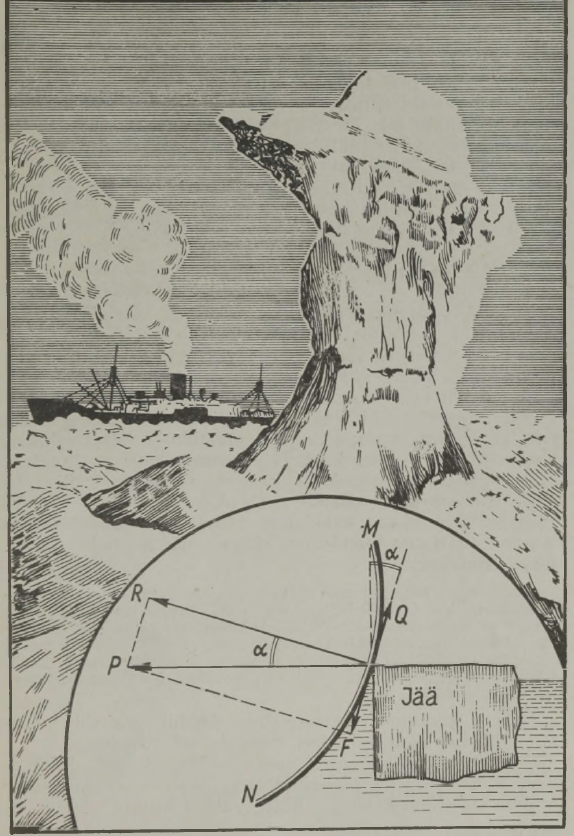
Et mõista selle arvu tähendust jääs liikuvate laevade jaoks, vaatleme joonist 22. See kujutab laevakerele MN jää surumisel mõjuvate jõudude suunda. Jää surve lahutatakse kaheks komponendiks: jõuks , mis on laeva pardaga risti, ja jõuks , mis on suunatud parda puutujat mööda. ja vaheline nurk on võrdne nurgaga , mis kujutab endast laevaparda kaldenurka vertikaali suhtes. Hõõrdejõud jää ja laeva parda vahel on võrdne jõu ja hõõrdeteguri, s. t. korrutisega; saame . Kui hõõrdejõud on väiksem -st, viib viimane laeva parrastele suruva jää vee alla;6 jää libiseb laevale häda tegemata piki kere. Kui jõud on suurem -st, takistab hõõrdumine jäätüki libisemist ja jää võib kestval surumisel laevakere katki muljuda.
Millal on ? Kerge on näha, et ; järelikult peab kehtima võrratus . Et aga , siis omandab võrratus kuju
ehk
Tabelitest leiame nurga, mille tangens võrdub 0,2; see nurk on . Tähendab, et , kui . Sellega on määratud ka nurk laeva parda ja vertikaali vahel, mis tagab laeva ohutu liikumise jääs; kaldenurk ei tohi olla väiksem kui .
Pöördugem nüüd tagasi «Tšeljuskini» huku juurde. See aurik, mis polnud sugugi jäälõhkuja, läbis edukalt kogu Põhja-meretee, kuid jäi Beringi väinas jäävangi.
Jää kandis «Tšeljuskini» kaugele põhja ja muljus ta 1934. a. veebruaris puruks. Paljud mäletavad tšeljuskinlaste kangelaslikku kahekuust talvitumist jääpangal ja nende päästmist lendurite abiga. Katastroofi ennast kirjeldatatakse nii:
«Kere tugev metall ei andnud kohe järele,» teatas raadio teel ekspeditsiooni ülem O. J. Schmidt. «Oli näha, kuidas jää end pardasse pressis ja kuidas vooderdus väljapoole kummudes punni läks. Jää jätkas oma aeglast, kuid vääramatut pealetungi. Kere vooderduse punnis terasplaadid kärisesid õmblustest. Raginaga lendasid minema needid. Üheainsa hetkega oli laeva vasak parras rebitud ära trümmidest saati käilast kuni ahtrini ... »
Pärast käesolevas paragrahvis öeldut peaksid laevahuku füüsikalised põhjused lugejale selged olema. Siit tulenevad ka praktilised järeldused: jääs liikumiseks määratud laevade ehitamisel peab laeva külgedele andma vajaliku kalde — mitte vähem kui vertikaali suhtes,
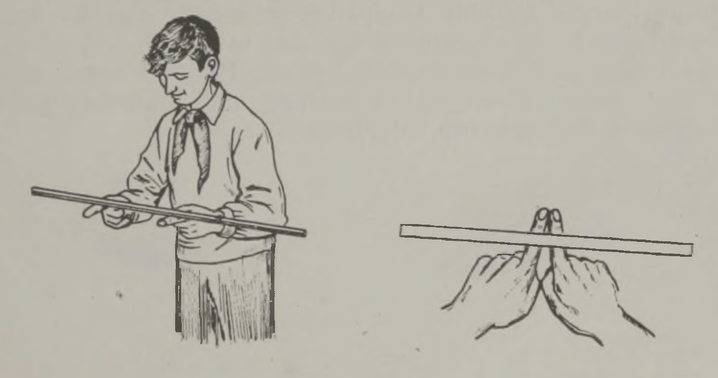
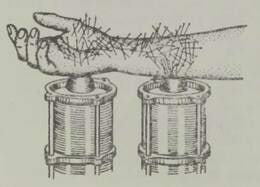
Toetage sile kepp laialiasetatud käte nimetissõrmedele, nagu näha joonisel 23. Nüüd hakake sõrmi teineteisele lähendama, kuni nad on kõrvuti ja puutuvad kokku. Kummaline lugu. Tuleb välja, et kepp ei kukugi maha, vaid säilitab tasakaalu. Tehke katset mitu korda, muutes iga kord sõrmede esialgset asendit – tulemus jääb samaks: kepp on tasakaalus. Asendanud kepi joonlauaga, piljardikiiga, nupuga jalutuskepiga, põrandaharjaga – ikka täheldate sama.
Milles on selle ootamatu nähtuse saladus?
Kõigepealt on selge, et kui kepp on kooshoitavatel sõrmedel tasakaalus, siis peavad sõrmed asetsema kepi massikeskme all (keha jääb tasakaalu, kui massikeskmest tõmmatud püstjoon läbib keha toetuspinda).
Kui sõrmed on teineteisest eemal, langeb suurem koormus sellele sõrmele, mis on kepi massikeskmele lähemal. Koos koormuse suurenemisega kasvab ka hõõrdumine: massikeskmele ligemal olevale sõrmele mõjub suurem hõõrdumine kui sellele, mis on massikeskmest kaugemal. Seepärast ei libisegi massikeskmele lähemal asetsev sõrm piki keppi: alati liigub ainult see sõrm, mis on massikeskmest kaugemal. Niipea kui liikuv sõrm jõuab massikeskmele lähemale seni paigalseisnud sõrmest, nende osad vahetuvad. Niisugune osade vahetumine leiab aset korduvalt seni, kuni sõrmed jõuavad kõrvuti. Ja et iga kord liigub vaid see sõrm, mis on massikeskmest kaugemal, siis kohtuvad mõlemad loomulikult kepi massikeskme all.
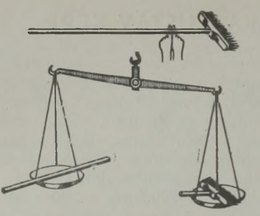
Enne kui lõpetada jutt sellest katsest, korrake kõike põrandaharjaga (joon. 24 ülal) ja esitage endale niisugune küsimus: kui hari sellest kohast pooleks lõigata, kus ta sõrmedele toetub, ja mõlemad tükid kaalule panna (joon. 24 all), siis kumb kaalukauss vajub alla — varrega või harjaga?
Paistab nii, et kui mõlemad osad on sõrme peal tasakaalus, siis peavad nad tasakaalustuma ka kaalukaussidel. Tegelikult vajub alla harjaga kaalukauss. Põhjust on kerge mõista, kui võtta arvesse asjaolu, et harja tasakaalustamisel sõrmedel olid harjapoolte raskused rakendatud mittevõrdsetele õlgadele, kaalumisel on aga samad jõud rakendatud võrdsetele õlgadele.
Tellisin Huvitava Teaduse Paviljoni7 jaoks Leningradi Kultuuripargis keppide komplekti erinevate massikeskme asenditega; kepid jagunesid kaheks, tavaliselt eri pikkusega osaks just massikeskme kohalt. Pannud need osad kaalule, võisid paviljoni külastajad oma hämmastuseks veenduda, et lühem osa oli pikemast raskem.
Tuhandest inimesest, kes end lapsepõlves vurriga lõbustasid, suudavad sellele küsimusele vastat a vähesed. Tõepoolest, kuidas seletada, et püsti või isegi kaldu asetatud pöörlev vurr ei kuku ümber? Milline jõud hoiab teda sellises, näivalt ebapüsivas asendis? Kas raskusjõud talle ei mõju?
Siin on tegemist õige huvitava jõudude vastastikuse mõjuga. Vurriteooria pole just lihtne ja me ei hakka sellesse süvenema. Märgime ära vaid peamise põhjuse, mis takistab pöörlevat vurri ümber kukkumast.
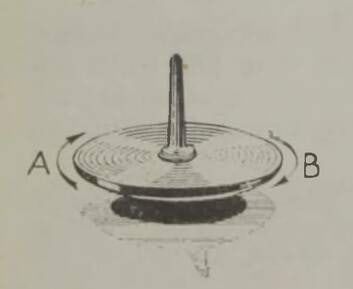
Joonisel 25 on kujutatud vurr, mis pöörleb noolega näidatud suunas. Pöörake tähelepanu serva osale A ja selle vastasserva osale B. Osa A püüab liikuda teist eemale, osa В teie poole. Jälgige nüüd, kuidas need osad liikuma hakkavad, kui te vurri telge enda poole kallutate (joon. 26). Sellise tõukega sunnite osa A liikuma üles-, osa В aga allapoole; mõlemad osad saavad tõuke ristsuunas nende omaliikumise suunaga. Et aga vurri kiirel pöörlemisel on tema ketta osade ringkiirus väga suur, siis teie poolt antud tühine kiirus, liitudes suure ringkiirusega, annab resultantkiiruseks ringkiirusele usna lähedase kiiruse – ja vurri liikumine peaaegu ei muutu. Siit saab selgeks, miks vurr paneb nagu vastu katsetele teda ümber lükata. Mida suurem on vurri mass ja mida kiirem tema pöörlemine, seda visamalt torgub ta vastu kukutamiskatsetele.
Nähtuse seletus on vahetult seotud inertsiseadusega. Vurri iga osa liigub mööda ringjoont pöörlemisteljega ristuvas tasandis. Inertsiseaduse põhjal püüab vurri iga osa lennata ringjoonelt minema mööda sirget, mis on vaadeldavas punktis selle ringjoone puutujaks. Kuid iga puutuja asub samas tasandis, milles ringjoongi, ja seepärast püüab iga vurri osa liikuda nii, et liikumistasand jääks pöörlemisteljega ristuvasse tasandisse. Siit järeldub, et kõik vurri tasandid, mis on risti pöörlemisteljega, püüavad säilitada oma asendit ruumis ja seepärast ka nende ühine ristsirge – vurri telg – püüab säilitada oma suunda.
Me ei käsitle kõiki liikumisi, mida tekitavad vurris kõrvalised jõud. See nõuaks liiga üksikasjalikke seletusi. Ma tahtsin ainult selgitada põhjust, miks iga pöörlev keha katsub säilitada oma pöörlemistelje suunda. Seda omadust kasutab laialt moodne tehnika. Laevadele ja lennukitele paigutatakse mitmesuguseid güroskoopilisi (vurri mainitud omadusel põhinevaid) seadmeid – kompasse, stabilisaatoreid jm.1
Niisugune on selle näiliselt lihtsa mänguasja kasulik rakendus.
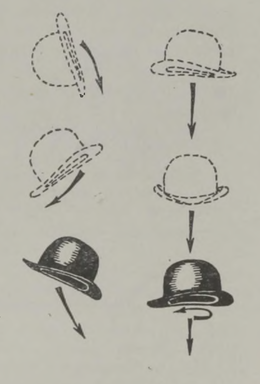
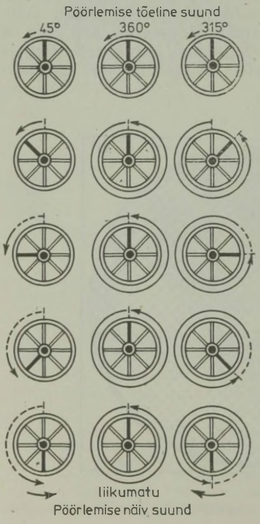
Paljud žonglööride imepärased trikid põhinevad samuti pöörlevate kehade omadusel säilitada oma pöörlemistelje suunda (joon. 27, 28, 29). Luban endale siinkohal esitada katkendi inglise füüsiku John Perry köitvast raamatust «Pöörlev vurr».2
«Kord demonstreerisin mõningaid oma katseid publikule, kes jõi kohvi ja suitsetas Londonis «Victoria» suurepärases saalis. Püüdsin äratada kuulajates niipalju huvi kui vähegi oskasin; ma rääkisin neile sellest, et lame rõngas tuleb panna pöörlema, kui seda tahetakse visata nii, et oleks võimalik määrata ette koht, kuhu ta peab kukkuma. Täpselt samuti talitatakse siis, kui soovitakse kellelegi visata kaabut, nii et ta saaks selle kepi otsa püüda. Alati võib loota vastupanule, mida osutab pöörlev keha katsetele muuta tema pöörlemistelje suunda. Edasi seletasin kuulajatele, et kui kahuritoru seest siledaks poleerida, ei saa kunagi kindel olla tabamistäpsuses, seepärast tehaksegi praegu kahuritorud keermikuga, s. t. toru siseseina lõigatakse spiraalsed sooned, millesse sobituvad kuuli või mürsu väljaulatuvad osad; seepärast hakkabki mürsk pöörlema, kui püssirohuplahvatuse jõud paneb ta mööda kahuritoru liikuma. Tänu sellele lendab mürsk torust välja täpselt kindla pöörlemisega.
See oli kõik, mida loengu ajal teha suutsin, sest ise pole ma küllalt osav rõngaid või kaabusid lennutama. Kuid pärast minu loengu lõppu astus lavale kaks žonglööri ja paremat illustratsiooni mainitud seadustele poleks ma osanud soovidagi. Žonglöörid heitsid teineteisele pöörlevaid kaabusid, rõngaid, taldrikuid, vihma varje ... Üks neist viskas õhku terve hulga nuge, püüdis need kinni, viskas taas väga täpselt üles; minu kuulajaskond, kes just oli kuulnud nende nähtuste seletust, hõiskas heameelest; ta märkas pöörlemist, mille žonglöör andis igale ülesvisatud noale, nii et oli võimalik ette määrata, missuguses asendis nuga tagasi kukub. Olin rabatud, et peaaegu iga tol õhtul esitatud trikk kujutas endast eeltoodud põhimõtte illustratsiooni. »
Oma kuulsa ülesande muna otsale püsti panemisest lahendas Kolumbus üleliia lihtsalt: ta tegi muna katki.
(Tuleb muide märkida, et populaarsel legendil Kolumbuse munast puudub ajalooline alus. Rahvasuu pani kuulsa meresõitja arvele selle, mis oli juhtunud märksa varem teise isikuga ja hoopis teisel põhjusel — nimelt itaalia arhitekti Brunelleschiga (1377— 1466), Firenze katedraali kupli ehitajaga. («Minu kuppel seisab niisama kindlalt nagu see muna oma teraval otsal!»))
Niisugune lahendus on sisuliselt vale: lõhkudes munakoore, muutis Kolumbus muna kuju ja pani seega püsti mitte muna, vaid hoopis teise keha; kuid kogu ülesande mõte ongi just muna kujus: seda muutes asendame muna teise kehaga.3 Kolumbus ei andnud lahendust selle keha tarvis, mille jaoks seda otsiti.
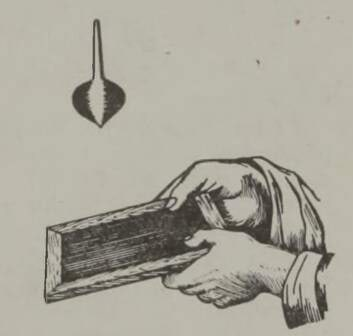
Kasutades vurri omadust, voib selle ülesande lahendada, ilma et oleks vaja muuta muna kuju. Selleks tuleb muna pöörlema panna ümber oma pikema telje, ja muna ei kuku ümber, vaid püsib mõne aja oma tömbil või isegi teraval otsal. Jooniselt 30 näete, kuidas seda teha: muna pannakse sõrmede abil pöörlema. Eemaldanud käed, näete, et muna jätkab veel veidi aega pöörlemist, jäädes seejuures püsti. Seega on ülesanne lahendatud.
Katse jaoks on tingimata vaja keedetud muna. Selline piirang pole vastuolus ülesande tingimustega, sest küllap Kolumbuski võttis muna otse laualt, lauale aga arvatavasti tooreid mune ei toodud. Vaevalt küll õnnestuks kellelgi püsti pöörlema panna toorest muna, sest vedel sisu on antud juhul piduriks. Selles seisneb ka lihtne võte, kuidas eristada tooreid mune keedetuist, mis on tuttav paljudele perenaistele.
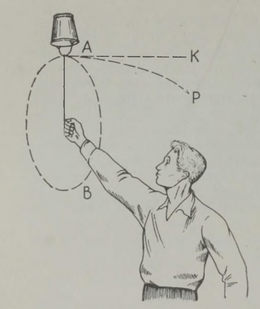
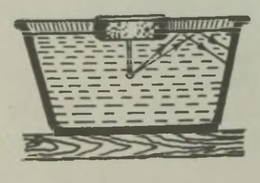
«Vesi ei voola tiirlevast anumast välja isegi mitte siis, kui anumal põhi ülespidi pöörata, sest tiirlemine takistab väljavoolamist,» kirjutas 2000 aastat tagasi Aristoteles. Joonisel 31 on kujutatud see efektne katse, mida paljud kindlasti tunnevad: keerutades veeämbrit küllalt kiiresti, ei voola vesi isegi siis ämbrist välja, kui ämbri põhi on ülespidi.
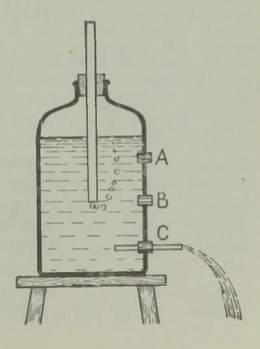
Tavaliselt seletatakse seda nähtust kesktõukejõuga, mõeldes selle all toda kujutletavat jõudu, mis on nagu rakendatud kehale ja püüab teda tiirlemiskeskmest eemale viia. Seda jõudu pole olemas: kirjeldatud püüd pole midagi muud kui inertsi avaldusvorm, igasugune inertsiaalne liikumine toimub aga ilma jõu kaasabita. Füüsikas mõistetakse kesktõukejõu all midagi muud — reaalset jõudu, millega pöörlev keha pingutab teda hoidvat nööri, või siis jõudu, millega pöörlev keha mõjub oma kõverjoonelisele teele. See jõud pole rakendatud liikuvale kehale, vaid takistusele, mis segab keha sirgjooneliselt liikumast: nöörile, rööbastele kõveral teelõigul jne.
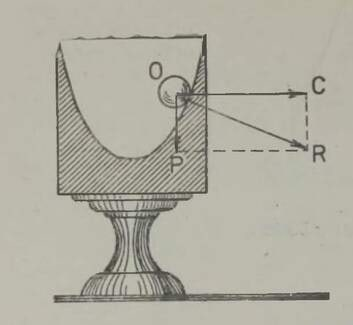
Pöördume tagasi tiirleva ämbri juurde ja püüame nähtusest aru saada ilma kaksipidi mõistetava kesktõukejõu abita. Küsime endalt: kuhupoole suundub veejuga, kui ämbri seina teha auk? Kui raskusjõudu poleks, liiguks veejuga inertsi mõjul ringjoone AB puutujat AK mööda (joon. 31). Raskusjõud sunnib juga madalamale laskuma ja mööda kõverat (parabooli AP) liikuma. Kui ringliikumise kiirus on küllalt suur, paikneb see kõver väljapoole ringjoont AB. Veejuga näitab meile teed, mida mööda (joon. 31). Raskusjõud sunnib juga madalamale selge, et vesi ei püüagi liikuda ülalt alla ja seepärast ei voola ta ämbrist välja. Vesi voolaks ainult sel juhul sealt välja, kui ämbri ava paikneks tiirlemise suunas.
Arvutage nüüd, missuguse kiirusega peame ämbrit keerutama, et vesi välja ei voolaks. Kiirus peab olema niisugune, et tiirleva ämbri kesktõukekiirendus poleks väiksem vaba langemise kiirendusest: siis asetseb tee, mida mööda vesi püüab liikuda, väljaspool ämbri liikumise teed ja vesi ei jää kuskil ämbrist maha. Kesktõukekijrenduse arvutame valemist
,kus on ringkiirus ja ringtee raadius. Et Maa pinnal on vaba langemise kiirendus , siis saame võrratuse
. .Kerge on arvutada, et niisuguse ringkiiruse saavutamiseks peab käsi tegema umbes poolteist tiiru sekundis. Selline keerutamiskiirus on täiesti saavutatav ja katse õnnestub ilma erilise vaevata.
Vedeliku omadust paiskuda vastu anuma seinu, kui anum pöörleb ümber horisontaaltelje, kasutatakse tehnikas nn. tsentrifugaalvalu puhul. Seejuures on olulise tähtsusega asjaolu, et ebaühtlase koostisega vedelik ja guneb tiheduse järgi kihtideks: raskemad koostisosakesed paiknevad pöörlemisteljest kaugemal, kergemad kogunevad teljele lähemale. Tulemusena kõik sulametallis sisalduvad gaasid, nn. valukarbid, eralduvad metallist valu õõnest sisepinda mööda. Sel viisil valmistatud detailid on tihedad ja gaasimullideta. Tsentrifugaalvalu on odavam kui survevalu ega vaja keerulist seadmestikku.
Tugevate elamuste armastajaile korraldatakse mõnikord üsna omapärane atraktsioon, nn. kuradikiik. Selline kiik oli vanasti ka Leningradis. Mulle endalegi meeldis sellel kiikuda ja seepärast esitan siinkohal kiige kirjelduse tea' duslikele lõbustustele pühendatud kogumikust (joon. 32):
«Kiik on kinnitatud tugeva horisontaalse palgi külge, mis ulatub üle toa kindlal kõrgusel põrandast. Kui kõik on istet võtnud, lukustab selleks määratud valvur ukse, võtab sisenemiseks kasutatud laua ära ja teatab, et annab vaatajatele võimaluse sooritada väike õhureis. Seejuures hakkab ta kiike kergelt õõtsutama. Siis astub ta ka ise kiigele nagu kutsar tagapukki või lahkub üldse ruumist.
Samal ajal muutub kiige hoog üha suuremaks ja suuremaks. Ilmselt tõuseb kiik ristpalgi kõrgusele, siis kõrgemale ja kõrgemale üle selle ning teeb lõpuks täistiiru. Liikumine muutub silmanähtavalt kiiremaks ja kiikujad, ehkki eelnevalt hoiatatud, tajuvad kahtlemata kiikumise ja kiire liikumise tunnet; neile näib, et nad tormavad ruumis, pea alaspidi, nii et nad haaravad kukkumist kartes tahtmatult istmete seljatugedest kinni.
Kuid nüüd hakkab hoog raugema; kiik ei tõuse enam ristpalgi kõrguseni ja mõni sekund hiljem jääb ta täiesti seisma.
Tegelikult oli kiik kogu katse ajal paigal, tuba aga pandi lihtsa mehhanismi abil ümber rõhttelje pöörlema. Mööbel oli kinnitatud põranda ja seinte külge; elektrilamp – suure kupliga hõõglamp – oli joodetud laua külge, nii et ta ei saaks ümber paiskuda. Valvur üksnes teeskles kiigutamist, õõtsutades end toa võngete taktis. Kogu õhkkond aitas kaasa pettuse täielikule õnnestumisele.»
Nagu näete, on illusiooni saladus naeruväärselt lihtne. Ja kui te nüüd asjast täit ülevaadet omades kiigele istuksite, laseksite end ikka paratamatult petta. Selline on kord juba illusiooni jõud.
Kas mäletate Puškini luuletust «Liikumine»?
«Ei ole liikumist!» Tark habemik* nii väitis.
Teine** vaikis, võttis nõuks ta ees siis käia.
Oli kaalukamat argumenti raske leida.
Ta vastust igaüks seepeale kiitis.
Kuid, härrased, see lugu meil
toob keele peale teise näite:
eks iga päev me kohal liigu Päike,
kuid õigus oli siiski Galileil!
(* Kreeka filosoof Zenon Eleast (5. saj. e. m. a.) õpetas, et kõik maailmas seisab paigal, ainult meelepette tõttu näib meile, nagu
mingi, keha liiguks. ** Diogenes.)
Asjassepühendamatute kiikujate seas oleksite omamoodi Galilei, ainult ümberpõõrdud mõttes: Galilei tõestas, et Päike ja tähed seisavad paigal, silmanähtavuse kiuste pöörleme aga meie ise; teie tõestate, et seisate paigal, aga kogu tuba pöörleb ümber teie. Võimalik, et teil tuleks seejuures jagada Galilei kurba saatust.
Ega teil polegi nii kerge tõestada oma õigust. Kujutlege, et olete tõepoolest «kuradikiigel» ja tahate oma naabreid veenda, et nood eksivad. Teen teile ettepaneku vaielda minuga. Istugem mõlemad «kuradikiigele» ja oodakem hetke, mil see kiikudes hakkab ilmselt tegema täisringe, siis alustagem vaidlust selle üle, mis nimelt liigub: kas kiik või kogu tuba. Palun ainult meeles pidada, et vaidluse ajal ei tohi me kiigelt lahkuda, kõik vajaliku votame eelnevalt endaga kaasa.
Teie: Kuidas võib kahelda selles, et meie oleme paigal ja pöörleb tuba! Kui meie kiik tõepoolest üle võlli lendaks, siis ei jääks me ju, pead alaspidi, rippu, vaid kukuksime kiigest välja. Seda aga ei juhtu. Järelikult ei pöörle mitte kiik, vaid tuba.
Mina: Tuletage meelde, et vesi ei voola ka kiiresti tiirlevast ämbrist välja, ehkki ämbril on põhi ülespidi (lk. 45). Jalgrattur ei kuku samuti surmasõlmest (lk. 55) välja, ehkki sõidab, pea alaspidi.
Teie: Kui nii, siis arvutame välja kesktõukekiirenduse ja vaatame, kas sellest piisab, et kiigest mitte välja kukkuda. Teades meie kaugust pöörlemisteljest ja tiirude arvu sekundis, võime valemi põhjal hõlpsasti leida ...
Mina: Ärge nähke vaeva arvutamisega. «Kuradikiige» ehitajad, aimates ette meie vaidlust, hoiatasid mind, et tiirude arv lubab nähtust seletada nii, nagu mina seda teen. Järelikult arvutamine meie vaidlust ei lahenda.
Teie: Kuid mina pole kaotanud lootust teid ümber veenda. Näete, vesi sellest klaasist ei voola põrandale ... Nojah, aga te viitaksite praegugi katsele tiirleva ämbriga. Hüva, ma hoian käes loodi, mis on kogu aeg suunatud teie jalgade poole, s. t. alla. Kui pöörleksime meie ja tuba seisaks paigal, oleks lood kogu aeg suunatud põranda poole, s. t. meist küll pea, küll külje poole.
Mina: Eksite: kui me pöörleme küllalt kiiresti, siis püüab loodi suund langeda ühte pöörlemisraadiuse suunaga, s.t. ta on suunatud teljest piki pöörlemisraadiust eemale, meie jalgade poole, nagu võimegi näha.
Lubage nüüd endale nõu anda, kuidas selles vaidluses peale jääda. «Kuradikiigele» tuleb kaasa võtta vedrukaal, panna kaalukausile näiteks kilogrammine viht ja jälgida osuti näitu: see püsib muutumatuna, näidates vihil märgitud raskust, nimelt ühte kilogrammi. See tõendabki, et kiik on paigal.
Tõepoolest, kui me koos vedrukaaluga pöörleksime ümber telje, siis mõjuks kaaluvihile peale raskusjõu veel kesktõukejõud, mis alumistel teeosadel suurendaks vihi raskust, ülemistel aga vähendaks seda; me peaksime mär kama, et viht muutub kord raskemaks, kord kaotab peaaegu kogu oma raskuse. Et me aga niisugust nähtust ei tähelda, siis järelikult pöörleb tuba ja mitte meie.
Üks ameerika ettevõtja ehitas publiku lõbustamiseks väga lustaka ja õpetliku karusselli – kerakujulise pöörleva toa. Selles keras viibivad inimesed tunnevad midagi niisama ebatavalist, nagu muidu peame võimalikuks ainult unenägudes või muinasjutus.
Tuletagem esmalt meelde, mida tunneb kiiresti pöörleval ümmargusel platvormil seisev inimene.
Pöörlev liikumine püüab lükata inimest väljapoole; mida kaugemal pöörlemisteljest te seisate, seda tugevamini teid sellest eemale surutakse. Kui te silmad kinni panete, tundub teile, et te ei seisa horisontaalsel põrandal, vaid kaldpinnal, kus üksnes suuri vaevu õnnestub säilitada tasakaalu. See tunne muutub arusaadavaks, kui vaatame, missugused jõud mõjuvad meie kehale (joon. 33). Pöörlemine püüab suruda meid väljapoole tsentrifugaaljõuga C, raskusjõud G mõjub ülalt alla; need jõud liituvad rööpkülikureegli kohaselt ja annavad resultandi R, mis on kallutatud allapoole.4 Mida kiiremini pöörleb platvorm, seda suurem on resultantjõud ja seda enam on ta kaldu.
Kujutlege nüüd, et platvormi äär on painutatud ülespoole ja te seisate selle kaldsel osal (joon. 34). Kui platvorm on paigal, ei suuda te selles asendis püsida, vaid libisete alla või kukute isegi pikali. Teisiti on asi siis, kui platvorm pöörleb: sel juhul muutub see kaldpind teataval kiirusel teie jaoks nagu rõhtsaks, sest ülaltoodu põhjal on resultantjõud ka kaldu ja moodustab platvormi ülespainutatud osaga täisnurga.* (* See selgitab muuseas ka seda, miks raudteekurvides on välimine rööbas kõrgemal sisemisest, miks jalgratta - ning mootorratta võistlusrajad on sissepoole kaldu ning miks elukutselised võidusõitjad võivad sõita järsult kaldu oleval ringteel.)
Kui anda pöörlevale platvormile niisugune kõverus, et teataval kiirusel oleks tema pind igas punktis risti mainitud resultandiga, siis tunneks inimene end selle pinna igas punktis nagu rõhtsal pinnal. Arvutuste teel on leitud,et selliseks pinnaks on geomeetriline keha, mida nimetatakse paraboloidiks. See pind saadakse näiteks nii, et pooleldi vett täis klaas pannakse kiiresti püsttelje ümber pöörlema: klaasi äärte juures tõuseb vesi siis üles ja vee pind omandab paraboloidi kuju.
Kui vee asemel valada klaasi sulavaha ja lasta klaasil pöörelda seni, kuni vaha hangub, annab hangunud pind meile paraboloidi täpse kuju. Kindla pöörlemiskiiruse korral on see pind sellel asuvate kehade jaoks nagu rõhtpind: pinna suvalisse punkti asetatud kuulike ei veere allapoole, vaid jääb püsima sinna, kuhu ta pandi (joon. 35).
Nüüd on juba kerge mõista «nõiutud» kera ehitust. Kera põhjaks on suur pöörlev platvorm (joon. 36), millele on antud paraboloidi kuju. Ehkki pöörlemine toimub tänu platvormi alla paigutatud mehhanismile äärmiselt sujuvalt, hakkaks platvormil viibijatel siiski pea ringi käima, kui ümbritsevad esemed nendega kaasa ei liiguks; et vaatlejal poleks võimalik liikumist kindlaks teha, ümbritsetakse platvorm suure läbipaistmatu kerakujulise seinaga, mis pöörleb samasuguse kiirusega nagu platvorm ise.
Niisugune on «nõiutud» karusselli ehitus. Mida te tunnete, kui asute sfääri sees oleval platvormil? Kui platvorm pöörleb, on põrand teie all rõhtne, ükskõik millises platvormi punktis te ka ei seisaks – kas telje läheduses, kus põrand on toesti rohtne, või äärel, kus see on 45° all kaldu. Silmad näevad nõgusust selgesti, lihased aga ütlevad, et teie jalge all on rõhtne pind.
Mõlema meele andmed räägivad üliteravalt teineteisele vastu. Minnes ühelt platvormi äärelt teisele, näib teile, et kogu hiiglaslik kera kaldub teie ra skuse all teisele kül jele; igas punktis tunnete end ju viibivat rõhtsal pinnal (joon. 37). Teiste, platvormil kaldu olevate inimeste asend pais tab teile aga äärmiselt ebaloomulik, nad tunduvad sõna otseses mõttes kõndivat mööda seina nagu kärbsed (joon. 38).
«Nõiutud» kera põrandale valatud vesi valguks mööda kõverat pinda ühtlase kihina laiali. Inimestel paistaks, et vesi seisab kaldseinana nende ees püsti. Näib, et har jumuspärased kujutlused ra skusjõu seadustest on tolles imepärases keras kaotanud kehtivuse ja me kandume muinasjutulisse imedemaailma . . .
Samasugused tunded on lenduril, kes sooritab pöördeid suurtel kiirustel. Kui ta lendab kiirusega 200 km/h mööda kaart, mille raadius on 500 m, siis peab maapind paistma talle tõstetuna ja 16° võrr a kallutatuna.*
Saksamaal Göttingenis ehitati selline pöörlev labor teadusuur ingute tarvis. See kujutab endast silindrikujulist kolmemeetrise läbimõõduga tuba (joon. 39). Et toa põrand on tasane, siis paistab seina juures seisvale pöörlevale vaatlejale , nagu oleks tuba kaldu ja ta ise pooleldi lebaks sellel kallakil seinal (joon. 40).
Parim kuju peegelteleskoobi peegli jaoks on parabool, s. t. just see kuju, mille iseenesest võtab vedeliku pind pöörlevas anumas. Teleskoobiehitajad näevad palj u vaeva, et anda peeglile sellist kuju. Peegli valmistamiseks kulub aastaid. Ameerika füüsik Robert Wood hiilis kõigist neist raskustest mööda, ehitades vedela peegli: ta pani elavhõbeda laias anumas pöörlema ja sai ideaal se paraboolse pinna, mis võib etendada peegli osa, sest elavhõbe peegeldab valguskiiri hästi. Woodi teleskoop seati üles madalasse kaevu.
Teleskoobi puuduseks on aga see, et vähimgi tõuge säbrutab vedela peegli pinda ja moonutab kujutist, pealegi võimaldab rõhtne peegel vaadelda ainult neid taevakehi, mis asuvad otse seniidis.
Võib-olla on teile tuttav peadpööritav jalgratta trikk, mida mõnikord esitatakse tsirkuses: jalgrattur sõidab silmuses alt üles ja teeb täisringi, kuigi ringi ülaosas peab ta sõitma, pea alaspidi. Areenile ehitatakse ühe või mitme silmusega laudtee, nagu kujutatud joonisel 41. Artist laskub jalgrat tal alla silmuse kaldset osa mööda, tõuseb seejärel kiiresti oma terasratsul ringikujulist osa mööda üles, teeb täistiiru, ripub korraks sõna otseses mõttes, pea alaspidi, ja lahkub siis õnnelikult silmusest.* (* Surmasõlme leiutasid 1902. a. samaaegselt kaks tsirkuseartisti – Diabolo (Johnson) ja Mefisto (Noisette).)
See kaelamurdev jalgrattatrikk näib pealtvaatajaile akrobaatika tippsaavutusena. Rabatud publik küsib nõutult: milline salapärane jõud hoiab uljaspead õhus, pea alaspidi? Umbusklikumad on valmis kõiges nägema osavat pettust, kuigi trikis pole midagi üleloomulikku, vaid see seletub täielikult mehaanikaseadustega. Seda teed mööda veerema lastud piljardikuul teeks kõike niisama edukalt.
Selle triki kuulus leiutaja ja esitaja Mefisto kasutas surmasõlme kindluse proovimiseks kera, mille raskus oli võrdne jalgratturi ja ratta koguraskusega. Ta laskis kera kaldpinnalt veerema ja kui see läbis silmuse edukalt, siis söandas ka artist selle sõidu ette võtta.
Lugeja taipab muidugi, et kummal ise nähtuse põhjus on sama mis tuntud katsel ämbriga (lk. 45). Trikk ei õnnestu aga alati, vaja on täpselt välja arvutada kõrgus, millelt jalgrattur peab alustama liikumist, muidu lõpeb sõit õnnetusega.
Ma tean, et «hingetute» valemite rida peletab mõnikord eemale nii mõnegi füüsikahuvilise. Kuid loobudes tutvumast nähtuste matemaatilise küljega, võtavad sellised matemaatika vaenlased endalt lõbu ennustada nähtuse kulgu ja määrata tema tekketingimused. Näiteks antud juhul ai tavad 2 – 3 valemit meil täpselt kindlaks teha, millistel tingimustel saab sooritada sellise imepärase triki nagu surmasõlm.
Asugem arvutama. Tähistame need suurused, millega meil tuleb arvutada, järgmiselt:
– kõrgus, millelt algab sõitu jalgrat tur ;
– see kõrguse h osa, mis jääb silmuse kõrgemast punktist ülespoole; jooniselt 41 näeme, et ;
– silmuse raadius;
– artisti ja ratta kogumass; nende raskus on siis võrdne , kus on vaba langemise kiirendus ma apinnal, teatavasti on see ;
– ratta kiirus ringjoone kõige kõrgemas punktis.
Kõik need suurused võime omavahel siduda kahe võrrandiga. Esimene kiirus väljendub valemiga
ehk
.(Seejuures jätame vaatluse alt välja jalgratta pöörlevate pöidade energia, selle mõju arvutus tulemustee on tühine)
Järelikult ka jalgratturi kiirus punktis CHTML - Unknown character: U+412 in MathJax_Main,MathJax_Size1,MathJax_AMS on
ehk
.Edasi, selleks et tee kõrgeimasse punkti jõudnud jalgrattur alla ei kukuks, peab kesktõukekiirendus (vt. lk. 46) olema suurem vaba langemise kiirendusest, s.t .
ehk
Me teame aga juba, et , järelikult ehk
Niisiis saime teada, et tolle kaelamurdva triki edukaks sooritamiseks on vaja ehitada surmasõlm nii, et tee kaldse osa tipp asuks silmuse kõrgeimast punktist kõrgemal kui pool ringjoone raadiust. Kaldpinna kallakusel pole tähtsust, küll aga peab punkt, kus jalgrattur alustab sõitu, olema silmuse kõrgeimast punktist rohkem kui 1/4 silmuse läbimõõdu võrra kõrgemal. Kui näiteks silmuse läbimõõt on 16 m, siis peab artist alus tama laskumist vähemalt 20 m kõrguselt; kui ta seda ei tee, ei aita ükski nipp tal surmasõlme sooritada; silmuse kõrgeimast punktist kukub ta vältimatult alla. Arvutustes ei arvestata hõõrdejõu mõju: eeldatakse, et kiirused punktis С ja punktis В on ühesugused. Seepärast ei tohi teed olla liiga pikad ega kaldpinnad liiga lauged, muidu võib jalgratturi kiirus osutuda punktis В hõõrdumise mõjul väiksemaks kui punktis C. Tuleb märkida, et trikki sooritav jalgrattur sõidab ketita, s. t. ratas liigub ainult raskusjõu mõjul: tema liikumist ei saa kiirendada ega aeglustada ning ega seda tohigi teha. Kogu kunst seisneb laudtee keskel püsimises; kui artist veidigi hälbib, võib ta teelt välja sõita ja alla kukkuda. Ringis liikumise kiirus on õige suur: 16-meetrise läbimõõduga ringi puhul teeb sõitja ühe tiiru 3 sekundiga. See vastab kiirusele 60 km/h. Sellisel kiirusel on ratast muidugi raske juhtida, kuid seda polegi vaja, võib julgesti usaldada mehaanikaseadusi. Bostonsi raamatust «Jalgrattatrikid» loeme: «See jalgrattatrikk pole iseenesest ohtlik, kui arvutused on õiged ja seade vastupidav. Triki ohtlikkus peitub jalgratturis endas. Kui tema käsi vääratab, kui ta on erutatud, kaotab enesevalitsemise või kui tal äkitselt hakkab halb, siis võib kõike oodata.» Samal mehaanikaseadusel põhineb ka kõigile tuntud lendurite surmasõlm ja teised kõrgema pilotaaživigurid. Surmasõlme puhul on esmajärgul ise tähtsusega piloodi õige hoovõtt kõveral teeosal ja lennuki oskuslik juhtimine.
Üks naljahammas kuulutas kord, et oskab ilma pettuseta ostjatele vähem kaaluda. Saladus olevat selles, et kaupa tuleb osta ekvaatori lähedalt ja müüa pooluste ligidal. Ammugi on teada, et ekvaatori lähedal kaaluvad kõik kehad vähem kui pooluse ligiduses; kui kilogrammine raskus viia ekvaatorilt poolusele, muutub ta 5 gf võrra kergemaks. Kaaluda tohib aga ainult vedrukaaluga ja seejuures veel niisugusega, mis on gradueeritud ekvaatoril, muidu pole mingit kasu loota: kaup muutub raskemaks, ja niisama palju lähevad raskemaks ka vihid. Kui osta tonn kulda kusagil Peruus ja müüa see maha näiteks Islandil, siis võib ehk sellega veidi teenida, muidugi eeldusel, et vedu on tasuta.
Ma ei arva, et keegi võiks ni isuguse tehinguga rikastuda, kuid põhimõtteliselt on naljahambal õigus: raskus jõud tõepoolest suureneb ekvaatorist kaugenemisel. Kõik sellepärast, et ekvaatoril asetsevad kehad liiguvad Maa pöörlemisel ümber telje kõige suuremaid ringjooni mööda, aga ka sellepärast, et maakera on ekvaatori kohalt nagu kummis .6
Põhiosa kaalu puudujäägist on tingitud Maa pöörlemisest: see vähendab keha kaalu ekvaatori lähedal 1/290 võrra, võrreldes sama keha kaaluga poolustel.
Kaaluvahe keha viimisel ühelt laiuselt teisele on kergete kehade puhul tühine, kuid raskete korral võib see saavutada üsna soliidse väärtuse. Te näiteks ei oska kahtlustadagi, et Moskvas 60 tf kaaluv vedur muutub Arhangelskisse saabudes 60 kgf võrr a raskemaks, Odessasse jõudes aga niisama palju kergemaks. Omal ajal veeti Teravmägedelt igal aastal lõunapoolsetesse sadamatesse 300 000 tf sütt. Kui see söehulk oleks saadetud mingisse ekvaatori lähedal asuvasse sadamasse, kus seda oleks kaalutud samasuguste vedrukaaludega nagu Teravmägedel, oleks avastatud puudujääk 1200 tf. Arhangelskis 20 000 tf kaaluv liinilaev muutub ekvatoriaalvetes ligi 80 tf kergemaks, ent seda ei ole võimalik märgata, sest vastavalt muutuvad kergemaks ka kõik teised kehad, kaasa arvatud muidugi ookeanivesi. (Seepärast muide on laeva süvis ekvatoriaalvetes samasugune nagu polaarvetes; ehkki laev muutub kergemaks, muutub niisama palju kergemaks ka tema poolt väljatõrjutud vesi.)
Kui maakera pöörleks oma telje ümber praegusest kiiremini, näiteks kui ööpäev kestaks 24 tunni asemel ainult 4 tundi, siis oleks kehade kaaluvahe poolusel ja ekvaatoril märksa suurem. Neljatunnise ööpäeva korral näiteks kaaluks viht, mis poolusel kaalus 1 kgf, ekvaatoril kõigest 875 gf. Umbes sellised on raskusjõu t ingimused Saturnil: selle planeedi pooluste läheduses kaaluvad kehad 1/6 võrra rohkem kui ekvaatoril.
Et kesktõmbekiirendus kasvab võrdeliselt kiiruse ruuduga, siis on kerge arvutada, kui suure pöörlemiskiiruse puhul kasvaks see kiirendus Maa ekvaatoril 290 korda, s.t. muutuks võrdseks raskuskiirendusega. See toimuks kiirusel, mis on 17 korda suurem praegusest ( ) . Niisuguses olukorras lakkavad kehad rõhumast toetuspindadele. Teiste sõnadega, kui Maa pöörleks 17 korda kiiremini, kaotaksid ekvaatoril asetsevad kehad igasuguse kaalu. Saturnil toimuks see juba siis, kui kiirus oleks ainult 2,5 korda suurem praegusest.
«Kui me ei näeks iga hetk kehade langemist, tunduks see meile kõige imepärasema nähtusena,» kirju tas kuulus prantsuse astronoom Arago. Me oleme harjunud kõigi maapealsete kehade tõmbumisega Maa poole ning see paistab meile loomuliku ja tavalise nähtusena. Kui meile aga öeldakse, et kehade vahel valitseb vastastikune tõmbejõud, siis ei taha me seda hästi uskuda, sest igapäevaelus me midagi taolist ei tähelda.
Tõepoolest, miks ei avaldu ülemaailmne gravitatsioon pidevalt meie ümber? Miks me ei näe laevade, arbuuside või inimeste tõmbumist? Sellepärast et väikeste kehade korral on tõmbejõud äärmiselt väike. Toon teile kujuka näite. Kaks teineteisest kahe meetri kaugusel seisvat inimest tõmbuvad teineteise poole, kuid täiesti tühise jõuga: keskmise raskusega inimeste puhul on see jõud väiksem kui 1/100 milligrammi. See tähendab, et need inimesed tõmbavad teineteist külge niisama suure jõuga, millega rõhub kaalukausile 1/100 000 grammi raskune viht. Ainult ülitundlikud laboratooriumikaalud suudavad märgata nii kaduvväikest raskust!
Arusaadavalt pole selline jõud suuteline meid paigast nihutama: seda takistab jalataldade ja põranda vaheline hõõrdumine. Et meid liigutada näiteks mööda puitpõrandat (taldade hõõrdumine põranda vastu on võrdne 30% keha raskusest, s. t. hõõrdetegur on 0,3), on vaja vähemasti 20-kilogrammist jõudu. On naeruväärne võrrelda seda jõudu tühise, sajandikmilligrammise tõmbejõuga. Milligramm on 1/1000 grammi, gramm on 1/1000 kilogrammi, järelikult on 0,01 mgf pool ühest miljardikust sellest jõust, mida oleks vaja meie paigast nihutamiseks. Mis siis imestada, et tavalistes tingimustes ei märka me üldse maapealsete kehade külgetõmmet.
Teisiti oleks asi, kui hõõrdumist poleks; siis ei segaks miski isegi kõige nõrgemal tõmbejõul kehi lähendamast . Kuid jõu 0,01 mgf korral oleks inimeste vastastikuse lähenemise kiirus küll täiesti tühine. Võib arvutada, et hõõrde puudumis el läheneksid kaks teineteisest 2 m kaugusel seisvat inimest esimese tunni jooksul 3 cm, järgmise tunni kestel veel 9 cm, kolmanda tunniga veel 15 cm võrra. Liikumine küll kiireneks, kuid teineteisega ei puutuks need inimesed kokku varem kui 5 tunni pärast. Maapealsete kehade vastastikust külgetõmmet võib täheldada neil juhtudel, kui hõõrdejõud ei ole takistuseks. Niidi otsa riputatud keha allub Maa tõmbejõu mõjule ja seepärast on niidil püstsuund; kui aga selle keha läheduses on mingi massiivne keha, mis esimest keha enda poole tõmbab, siis kaldub esimese keha niit püstsuunast veidi kõrvale ja asetub Maa külgetõmbe ning selle teise keha suhteliselt väga nõrga külgetõmbe resultandi sihis. Sellist külgetõmmet jälgis 1775. a. suure mäe lähedal Sotimaal esmakordselt Maskelyne. Ta võrdles loodi suunda taevapooluse suunaga ühel ja teisel pool mäge. Hiljem lubasid täiuslikumad katsed erilise ehitusega kaalude abil mõõta täpselt Maa tõmbejõu suurust.
Väikeste masside vaheline tõmbumine on tühine. Masside kasvamisel suureneb tõmbejõd võrdeliselt nende masside korrutisega. Kuid paljud kalduvad seda jõudu üle hindama. Keegi teadlane, kes polnud küll füüsik, vaid zooloog, püüdis mind veenda selles, et merel sõitvate laevade vahel sageli täheldatav külgetõmme on tingitud ülemaailmsest gravitatsioonist. Arvutuste najal on kerge näidata, et siin pole midagi tegemist gravitatsioonilise tõmbejõuga: kaks liinilaeva, kumbki massiga 25 000 tonni, tõmbuvad 100 m kauguselt kõigest 400-gf jõuga. Muidugi ei piisa sellisest jõust, et laeva vees kas või tühiselt määral paigast nihutada. Laevade salapärase tõmbumise tõelist põhjust selgitame 6. peatükis. Väikeste masside korral tühiseks jääv külgetõmme muutub õige tugevaks, kui tegemist on taevakehade hiiglamassidega. Nii näiteks meist väga kaugel asetsev planeet Neptuun, mis tiirleb aeglaselt peaaegu Päikesesüs teemi piiril, «tervitab» Maad külgetõmbejõuga 18 miljonit tonni. Vaatamata meid ja Päikest eraldavale tohutule vahemaale püsib Maa oma orbiidil ainult tänu tõmbejõule. Kui Päikese külgetõmme millegipärast lakkaks mõjumast, lendaks Maa mööda oma orbiidi puutujat minema ja kaoks igaveseks maailmaruumi põhjatusse sügavusse (joon. 42).
Kujutlege, et Päikese võimas külgetõmme on tõepoolest millegipära st kadunud ja Maad ootab kurb saatus – eemalduda alatiseks universumi külma ja sünges se lõpmatusse. Kujutlege nüüd – siin on teil vaja fantaasiat –, et insenerid otsustasid asendada nähtama tud külgetõmbeahelad materiaalsete sidemetega, s. t. otsustasid lihtsalt Maa ja Päikese ühendada tugevate terastrosside abil, mis peavad hoidma maakera tiirlemast ümber Päikese. Mis võikski olla tugevam terasest – talub see ju tõmmet kuni 100 kgf /mm2. Kujutlege võimsat terassammast läbimõõduga 5 m. Selle ristlõikepindala on ligikaudu 20 000 000 mm2, järelikult puruneb see sammas alles 200 000-tonnisest tõmbest.
Kujutlege edasi, et see sammas ulatub Maalt Päikeseni, ühendades mõlemat taevakeha. Kas teate, mitu niisugust sammast oleks vaja maakera orbiidil hoidmiseks? Miljon miljonit. Et sellest kõiki meresid ja mandreid täitvast teras sammas te metsast näitlikumat pilti luua, lisan, et sammas te ühtlasel jaotumisel üle kogu Päikese poole pööratud maakera poole oleks naabersammaste vahekaugus vaid veidi suurem sammaste endi läbimõõdust. Kujutlege siis jõudu, mida on vaj a selle hiiglasliku terassammaste metsa puruks rebimiseks ning te saate ettekujutuse Maa ja Päikese vastastikuse tõmbejõu suurusest.
Ja kogu see hiiglajõud avaldub vaid selles, et Maa tee kõverdub — igas sekundis hälbib Maa 3 mm võrra puutuja suunast. Just see jõud muudabki meie planeedi tee kinniseks kõveraks, ellipsiks. Kas pole veider: et nihutada Maad igas sekundis 3 mm võrra, on vaja niisugust vägilasjõudu. See näitab ainult, kui suur on tegelikult Maa mass: isegi nii määratu suur jõud suudab teda ainult nii imevähe liigutada.
Eelnevas fantaseerisime selle üle, mis juhtuks, kui Päikese ja Maa vastas t ikune tõmbejõud kaoks: külgetõmbe nähtamatuist kütkeist vabanenud Maa lendaks universumi lõputusse avarusse. Nüüd mõtisklegem veidi teisel teemal: mis juhtuks kõige maapealsega, kui raskusjõud kaoks? Mitte miski ei seoks midagi meie planeediga ja vähimagi tõuke mõjul kanduks iga asi planeetidevahelisse ruumi. Muide, seda tõuget poleks vaja oodatagi: meie planeedi pöörlemine paiskaks maailmaruumi kõik, mis pole tugevasti kinnitatud tema külge.
Inglise kirjanik Wells kasutas seda laadi ideed, kirjeldades fantastilist reisi Kuule. Oma romaanis «Esimesed inimesed Kuul» esitab ta väga originaalse viisi ühelt planeedilt teisele lendamiseks. Nimelt leiutas tema romaani õpetatud kangelane erilise aine, millel on tähelepanuväärne omadus: sellele ei mõju raskusjõud. Kui katta mingi keha altpoolt selle ainega, vabaneb ta Maa raskusvälja mõjust ja talle jääb mõjuma ainult teiste taevakehade külgetõmme. Selle fantastilise aine nimetas Wells leiutaja Cavori järgi keivoriidiks.
«Me teame,» kirjutab Wells, «et ülemaailmne tõmbejõud, s.t. raskusjõud, tungib läbi kõigi kehade. Te võite püstitada tõkked, mis takistavad valguskiirtel pääsemast kehade juurde; metallplaatide abil võite kaitsta eset raadiotelegraafi elektromagnetlainete eest, kuid mitte mingil viisil ei saa te keha kaitsta Päikese külgetõmbe või Maa raskusjõu eest. Mispärast ei leidu looduses kaitset külgetõmbejõu eest, on raske öelda. Kuid Cavor ei näinud põhjust, miks ei võiks leiduda raskusjõule läbipaistmatut ainet, ja ta pidas end võimeliseks seda kunstlikult looma.
Igaüks, kel on kas või kübeke kujutlusvõimet, suudab kergesti kujutleda neid erakordseid võimalusi, mida toob endaga kaasa niisuguse aine leiutamine. Kui näiteks on vaja koormat tõsta, siis ükskõik kui suur ta ka poleks, aitab õhukesest keivoriitlehekesest, ja koorma võib kas või õlekõrre abil üles tõsta.»
Selle imepärase aine valdajad ehitavad taevalaeva, millega sooritavadki julge lennu Kuule. Sõiduki ehitus on väga lihtne: selles pole mingit mootorit, sest ta liigub taevakehade külgetõmbe mõjul. Siin selle fantastilise mürsu kirjeldus: «Kujutlege kerakujulist mürsku, mis on küllalt avar mahutamaks kaht inimest ja nende pagasit. Mürsul on kaks kesta – sisemine ja välimine. Sisekest on paksust klaasist, väliskest terasest. Kaasa saab võtta suruõhku, toidukontsentraate, vee destilleerimise aparaadi jms. Teraskera katab väljastpoolt üleni keivoriidikiht. Klaasist sisekest on üks tervik, välja arvatud luuk; teraskest koosneb üksikutest osadest ja iga niisuguse osa võib kokku rullida nagu kardina. Seda on lihtne korraldada eriliste vedrude abil; kardinaid võib alla lasta ja kokku rullida elektrivooluga, mis liigub klaaskestas olevaid plaatinajuhtmeid mööda. Need on aga juba tehnilised üksikasjad. Peamine on see, et mürsu väliskest koosneb üleni nagu akendest ja keivoriitkardinatest. Kui kõik kardinad on alla lastud, ei tungi kerasse ei valgust ega üldse mitte mingisugust kiirgusenergiat, ka mitte raskusjõudu. Kujutlege nüüd, et üks kardin on üles tõstetud; siistõmbab iga massiivne keha, mis asub kauguses selle akna vastas, meid enda poole. Praktiliselt on meil võimalus reisida maailmaruumis just selles suunas, milles soovime, lastes mõjuda kord ühel, kord teisel taevakehal.»
Huvi tavalt on kirjeldatud planeetidevahelise laeva stardihetke. Mürsu väliskesta kattev õhuke keivoriidikiht teeb ta nagu täiesti kaalutuks. Mõistagi ei saa kaalutu keha rahulikult lebada õhuookeani põhjas, temaga peab toimuma midagi sellist, nagu juhtub järve põhja pandud korgiga: see tõuseb kiiresti veepinnale. Sama lugu on kaalutu mürsuga, mida pealegi lükkab eemale veel maakera pöörlemisest tingitud inertsijõud: mürsk peab kiiresti kerkima ja jõudnud atmosfääri ülapiirile, jätkama vabalt lendu maailmaruumis . Just nii romaani kangela sed lendasidki. Maailmaruumis talitasid nad järgmiselt: avasid ja sulgesid kardinaid, al lutades oma lennuriista kord Päikese, kord Maa, kord Kuu külgetõmbele, kuni jõudsid lõpuks meie loodusliku kaas lase pinnale. Hiljem pöördus üks reisijaist samas mürsus Maa peale tagasi .
Me ei peatu siin Wellsi ideede analüüsil, seda olen teinud juba mujal*, kus ma näitasin nende kehtetust. Uskugem aga hetkeks teravmeelset kirjanikku ja suundugem koos tema kangelastega Kuu peale.
Vaadelgem, kuidas Wellsi kangelased end Kuu peal tundsid. Olid nad ju sat tunud maai lma, kus ra skusjõud on nõrgem kui Maal.
Esitame siinkohal need huvi tavad leheküljed romaanist «Esimesed inimesed kuul». Jutustab üks äsja Kuule jõudnud Maa elanik:
«Ma hakkasin mürsu kaant lahti kruvima. Põlvili olles pistsin pea luugist välja: kolme jala kaugusel oma peast nägin Kuu neitsilikku lund.
Mässinud end tekisse, istus Cavor luugi servale ja laskis jalad ettevaatlikult rippu. Kui need olid umbes pooie jala kaugusel Kuu pinnast, libistas ta end pärast minutilist kõhklemist maha.
Jälgisin teda läbi kera klaaskesta. Astunud paar sammu, seisatus ta hetkeks, vaatas ümber, võttis siis julguse kokku ja – hüppas ettepoole.
Klaas moonutas tema liigutusi, kuid mulle näis, et hüpe oli tõepoolest ülemäära suur. Cavor oli otsekohe minust 6 – 10 m kaugusel. Kaljul seistes tegi ta mulle mingeid märke, võib-olla ta ka hüüdis midagi, kuid minuni ei jõudnud ainsatki heli ... Kuidas ta aga niiviisi hüpata sai?
Imestunult ronisin luugist välja ja laskusin samuti Kuu pinnale just lumise lohu servale. Astusin sammu edasi ja hüppasin. Ma tundsin, et lendan, ja jõudsin peagi selle kalju lähedale, kus seisis mind ootav Cavor; haarasin kaljust kinni ja jäin kohutavas hämmelduses rippuma.
Cavor kummardus ja hüüdis mulle kiunuva häälega, et oleksin ettevaatlikum. Olin unustanud, et Kuu peal on raskusjõud kuus korda nõrgem kui Maal. Tegelikkus tuletas mulle ise seda meelde.
Ettevaatlikult, oma liigutusi talitsedes, ronisin kalju tippu, ja kõndides nagu reumahaige, astusin Cavori kõrvale päikese kätte. Meie mürsk lebas sulaval lumehangel umbes 30 jalga eemal.
«Vaadake,» ütlesin Cavori poole pöördudes.
Kuid Cavor oli kadunud.
Seisin ootamatusest rabatuna hetke, siis, soovides piiluda üle kaljuserva, astusin kiiresti ettepoole, olles unustanud, et viibin Kuul. Tehtud pingutus oleks Maa peal viinud mu meetri jagu edasi, Kuu peal aga liikusin edasi 6 meetrit ja sattusin 5 meetri kaugusele kalju servast.
Tundsin seda ruumis hõljumise tunnet, nagu võib läbi elada unes, kui näed, et kukud kuristikku. Maa peal langeb kukkuv inimene esimese sekundi vältel 5 meetrit, Kuu peal läbib ta langemisel sekundis 80 sentimeetrit. Seepärast hõljusingi sujuvalt umbes 9 meetri sügavusele. Kukkumine võttis aega: see kestis oma kolm sekundit. Ujusin õhus ja maandusin pehmelt nagu udusulg põlvini kaljuoru põhjas olevasse lumehange.
«Cavor!» hüüdsin ma ümber vaadates, kuid kuskil polnud temast jälgegi.
«Cavor!» hüüdsin ma valjemini.
Ja äkki ma nägin teda: ta naeris ja tegi mulle mingeid märke. Ta seisis paljal kaljunukil paarikümne meetri kaugusel minust. Ma ei kuulnud küll ta sõnu, kuid mõistsin žeste: ta palus mind enda juurde hüpata.
Kõhklesin, sest vahemaa näis liiga suur. Varsti aga. taipasin, et kui juba Cavoril õnnestus selline hüpe teha, siis tõenäoliselt saan minagi sellega hakkama.
Taganesin sammu ja hüppasin kõigest jõust. Kerkisin noolena õhku ja mulle tundus, et ma ei lasku enam kunagi maha. See oli fantastiline lend – kohutav, nagu unenäos, ent samal ajal vaimustavalt meeldiv.
Hüpe osutus liiga tugevaks: ma lendasin üle Cavori pea.»
Järgmine episood, mis pärineb kuulsa vene leiduri K. E. Tsiolkovski raamatust «Kuu peal», aitab meil selgi tada raskusjõu mõjul toimuva liikumise tingimused. Maa õhkkond taktetab selles liikuvaid kehi ja var jab meie eest lihtsaid langemisseadusi, muutes need kõrvalnähtudega keerukamaks. Kuul pole üldse õhku. Kuu oleks suurepärane labor vaba langemise seaduste uurimiseks, kui meil ainult oleks võimalus sinna pääseda ja teadusuuringutega tegelda.
Asume nüüd jutustuse juurde. Loo kaks tegelast on Kuul ja tahavad uurida, kuidas liiguvad seal püssist tulistatud kuulid.
««Kas püssirohi hakkab siin tööle?»
«Lõhkeained peaksid tühjuses veel suurema jõuga mõjuma kui õhus, sest õhk takistab nende paisumist; mis puutub õhuhapnikusse, siis lõhkeained ei vaja seda, sest hapnikku sisaldub vajalikus koguses neis endis.»
«Hoiame püssi vertikaalselt, et kuuli saaks pärast lasku siitsamast ligidalt otsida . . . »
Tulesähvatus, nõrk heli*, pinnase kerge vabin.
«Kus siis tropp on? Ta peaks olema kuskil siin läheduses.»
«Tropp lendas kuuliga kaasa ja vaevalt et ta sellest maha jääb, Maa peal takistab teda kuulile järele jõudmast ainult õhk. Kuul tõuseb ja langeb udusulg aga niisama kiiresti nagu kivi. Võta sina padjast paistev udusulg, mina aga võtan malmkuulikese. Sina võid visata oma udusulge ja tabada sellega isegi kauget märki niisama täpselt nagu mina oma kuulikesega. Mina suudan väikese raskusjõu tõttu visata kuulikest umbes 400 m, sina võid udusule niisama kaugele paisata. Tõsi küll, sa ei tapa sellega kedagi ja viskel sa isegi ei tunne, et oled midagi visanud. Heidame mõlemad oma viskerelvi täiest jõust – jõu poolest ei erine me kuigivõrd teineteisest – ja ühe ning sama märklaua, näe, selle punase graniitkalju pihta ...»
Udusulg jõudis kuulikesest nagu tugevast keerisest kantuna veidi ette.
«Mis see siis tähendab? Lasu hetkest on möödas juba kolm minutit, kuuli aga pole ikka veel?»
«Oota veel kaks minutit ja siis ta tõenäoliselt ongi tagasi.» Tõepoolest, mainitud aja möödumisel tündsime pinnase kerget võbinat ja nägime üsna lähedal hüplevat troppi.
«Kui kaua küll kuul lendas! Kui kõrgele võis ta tõusta?»
«Oma 70 kilomeetrit. Sellist kõrgust on võimalik saavutada raskusjõu väiksuse ja õhutakistuse puudumise tõttu.»»
(* Heli kandus edasi pinnase ja inimeste kehade kaudu, mitte aga
mööda õhku, mida Kuul ei ole.)
Kontrollime öeldut. Kui kuuli püssirauast välja lennukiiruseks võtta suhteliselt tagasihoidlik väärtus 500 m/s (moodsatel püssidel on see ligi 1,5 korda suurem), siis tõuseks kuul Maa peal õhu puudumise korral kõrguseni
s. t. 12,5 km. Kuu peal aga, kus raskusjõud on 6 korda nõrgem, on väärtus ; seega jõuab kuul kõrguseni
.Sellest, mis toimub sügaval meie planeedi põues, teatakse praegu veel väga vähe.1 Ühed arvavad, et sadu kilomeetreid paksu kõva koore all asub tulivedel mass; teised oletavad, et kogu maakera on kuni keskpunktini tahke. Küsimust on raske lahendada: kõige sügavam puurauk ulatub vaid 7,5 km-ni, kõige sügavam šaht, kuhu on tunginud inimene, on vaid 3300 m sügav2, maakera raadius on aga 6400 km. Kui oleks võimalik puurida kaev, mis läbiks meie planeeti mööda diameetrit, leiaksid kõik taolised probleemid lahenduse. Tänapäeva tehnikale pole niisugune ettevõtmine jõukohane, ehkki kõigi puuraukude sügavuste summa ületab pikkuselt meie Maa läbimõõdu. Maad läbiva tunneli kaevamisest unistasid 18. sajandi matemaatik Maupertuis ja filosoof Voltaire. Sellele projektile, tõsi küll, tagasihoidl ikumas ulatuses, pööras tähe lepanu ka prantsuse astronoom Flammarion; toome siinkohal veidi muudetud joonise tema selleteemalisest artiklist (joon. 43).
Midagi taolist pole seni muidugi tehtud, kuid kasutagem kujutletavat põhjatut kaevu, et arutada üht huvi tavat ülesannet. Kuidas te arvate, mis teiega juhtuks, kui te sellisesse kaevu kukuksite (õhutakistuse unustame selle katse puhul ära)? Vastu põhja surnuks kukkuda te ei saa, sest põhja pole olemas, aga kus te siis peatuksite? Kas Maa keskpunktis? Ei.
Kui te jõuate keskpunkti, siis on teie keha omandanud nii kolossaalse kiiruse (umbes 8 km/s), et peatumisest selles punktis ei saa juttugi olla. Te tormate üha aeglustuvalt edasi, kuni jõuate kaevu teise otsani. Siin tuleb teil tugevasti kaevu servast kinni haarata, muidu kukute taas läbi kogu kaevu kuni teise otsani. Kui teil ka siin ei õnnestu millestki kinni haarata, lendate jälle kaevu tagasi ja jäätegi niimoodi lõpmatuseni võnkuma (joon. 44). Mehaanika õpetab, et sellistel tingimustel (kordan, kui jätta arvestamata kaevus oleva õhu takistus) peab keha jäämagi edasi- tagasi võnkuma. (õhutakistuse olemasolul võnkumised kustuvad vähehaaval ja asi lõpeb sellega, et inimene peatub Maa keskpunktis.)
Kui kaua üks võnge kestaks? Kogu tee ühest otsast teise ja tagasi läbitakse 84 minuti ja 24 sekundiga, s .t . ümmarguselt poolteise tunniga.
«Nii oleks juhul,» jätkab Flammarion, «kui kaev oleks kaevatud piki maakera telge pooluselt pooluseni. Tarvitseb aga ainult tunneli lähtekoht üle viia mõnele teisele laiusele, – Euroopasse, Aasiasse või Aafrikasse –, ja kohe on vaja arvestada Maa pöörlemise mõju. On teada, et maapinna iga punkt läbib ekvaatorit 465, Pariisi laiusel aga 300 meetrit sekundis. Et ringliikumise kiirus kasvab koos kaugenemisega pöörlemisteljest, siis kaevu visatud pliikuul näiteks ei lange püstjoont mööda, vaid kaldub veidi ida poole. Kui kaevata põhjatu kaev ekvaatorile, siis peab see olema kas üsna lai või tugevasti kaldu, sest Maa pinnalt langema hakkav keha mööduks Maa keskpunktist kaugelt ida poolt.
Kui kaevu üks ots asuks mõnel Lõuna-Ameerika kiltmaal, oletame, et 2 km kõrgusel, teine ots aga merepinna kõrgusel, siis inimene, kes kogemata kukuks Ameerika-poolsest avast sisse, lendaks teiselt poolt välja nii kiiresti, et tõuseks kahe kilomeetri kõrgusele.
Kui aga kaevu mõlemad avad oleksid merepinna kõrgusel, võiks kaevus lendavale inimesele tema ava juurde ilmumise hetkel, mil tema kiirus võrdub nulliga, käe ulatada. Eelmisel juhul, vastupidi, tuleks liiga hoogsasti liikuvast rändurist hirmuga eemale hoida.»
Omal ajal ilmus Peterburis brošüür kummalise pealkirjaga «Isesõidutav allmaaraudtee St. Peterburi- ja Moskva vahel. Fantastiline romaan esialgu kolmes osas ja needki lõpetamata.» Brošüüri autor A. A. Rodnohh esitas teravmeelse projekti, millega füüsikaliste paradokside armas tajatel on huvitav tutvuda.
Projekt nägi ette «600-kilomeetrise tunneli ehitamise meie maa mõlema pealinna vahele täiesti sirget ma a alust joont mööda. Sel viisil tekiks inimsool esmakordselt võimalus reisida mööda sirget, aga mitte käia kõverteid pidi, nagu see on toimunud tänini.» (Autor tahab sellega öelda, et kõik meie teed, mis jälgivad maapinna kõverust, on kaarjad, kuna projekteeritud tunnel läheks sirget –kõõlu mööda.)
Niisugusel tunnelil, kui seda oleks võimalik ehitada, oleks imeväärne omadus, mida pole ühelgi teisel teel maailmas. Nimelt peab iga sõiduk sellises tunnelis liikuma iseenesest. Meenutagem kogu maakera läbivat kaevu. Leningradi – Moskva tunnel oleks seesama kaev, ainult kaevatuna mitte mööda diameetrit, vaid mööda kõõlu. Tõsi küll, heites pilgu joonisele 45, paistab, et tunnel on rõhtne ja rongil pole järelikult mingit põhjust liikuda mööda seda raskusjõu abil. Kuid see on lihtsalt silmapete: tõmmake mõttes raadiused tunneli otstesse (raadiuste suunad ühtivad ripploodi suunaga ), siis näete, et tunnel pole kaevatud täisnurgi püstsihiga, s. t. pole rõhtne, vaid kaldu.
Niisuguses kaldses kaevus peab iga keha raskusjõu mõjul edasi- tagasi pendeldama, olles kogu aeg surutud vastu kaevu põhja. Kui tunnelisse ehitada rööpad, hakkab vagun iseenesest neid mööda edasi veerema, sest veduri tõmmet asendab vaguni raskus. Algul liigub rong väga aeglaselt. Iga sekundiga iseliikuva rongi kiirus aga suureneb, ja kasvab peagi kujutletamatult suureks, nii et tunnelis olev õhk hakkab juba märgatavalt liikumist takistama. Unustagem aga mõneks ajaks see tülikas takistus, mis segab paljude ahvatlevate projektide elluviimist, ja vaatame, mis juhtub rongiga edasi. Tunneli keskkohta jõudnud rongil on nii fantastiline kiirus – palju kordi suurem kahurimürsu kiirusest –, et ta kihutab hoo arvel peaaegu tunneli teise otsani. Kui puuduks hõõrdumine, poleks ka seda sõna «peaaegu», ja rong sõidaks ise, ilma vedurita Leningradist Moskvasse. Arvutus näitab, et ühe otsa läbimine võtaks niisama palju aega nagu kehade langemisel mööda diameetrit kaevatud tunnelis, s. t. 42 minutit 12 sekundit. Kummalisel kombel ei olene sõidu kestus tunneli pikkusest: reisid Moskva – Leningrad, Moskva – Vladivostok või Moskva – Melbourne võtaksid kõik ühepalju aega. (Võib tõestada veel teisegi, niisama huvitava põhjatu kaevuga seotud väite: võnkumise kestus ei olene planeedi suurusest, vaid tema tihedusest.)
Sama juhtuks ka iga teise sõidukiga – dresiiniga, tõllaga, autoga jm. Tõeline muinasjututee, mis ise jääb liikumatuks, kuid laseb sõidukeil iseenesest liikuda ühest otsast teise ja seejuures veel kujuteldamatu kiirusega.
Silmitsege joonist 46, mis kujutab kolme tunneli kaevamise viisi, ja öelge, milline tunnel on kaevatud rõhtsalt.
Ei ülemine ega alumine, vaid keskmine, mis läheb kaart mööda. See kaar moodustab igas punktis püstjoontega (ehk Maa raadius tega) täisnurgad. See ongi rõhtne tunnel – tema kumerus vastab täielikult maapinna kõverusele.
Pikad tunnelid kaevatakse tavaliselt nii, nagu näidatud ülemisel joonisel: tunneli otspunktidest maapinnale tõmmatud puutujaid mööda. Selline tunnel algul veidi tõuseb, seejärel langeb. Tal on see hea omadus, et vesi ei kogune tunnelisse, vaid valgub otstest välja.
Kui tunneleid kaevataks rangelt rõhtsalt, siis oleks pikk tunnel kaarekujuline. Vesi ei püüaks temast välja voolata, sest oleks igas punktis tasakaalus. Kui niisugune tunnel on üle 15 km pikk (Simploni tunneli pikkus on näiteks 20 km), siis ühe otsa juures seistes ei oleks võimalik näha teist otsa: valguskiir põrkaks vastu lage, sest tunneli keskkoht oleks rohkem kui 4 m kõrgusel tema otstest.
Lõpuks, kui kaevata tunnel mööda tunneli otspunkte ühendavat sirget, on tal otstest keskkohani kerge kalle allapoole. Vähe sellest, et vesi ei voola välja, see hoopis koguneb keskmisse, kõige madalamasse ossa. See-eest, seistes niisuguse tunneli ühe otsa juures, võib nähateist. Joonis 46 selgitab öeldut.*
Lõpetame oma vestluse liikumisseadustest ja tõmbejõust sellega, et analüüsime seda fantastilist Kuu-reisi, mida nii köitvalt on kirjeldanud Jules Verne romaanides «Kahurist Kuule» ja «Ümber Kuu». Te muidugi mäletate, et Baltimore’i kahuriklubi liikmed, kes olid jäänud pärast Põhja-Ameerika Iseseisvussõja lõppemist tegevuseta, otsustasid valada hiiglasliku kahuri, laadida see tohutu suure õõnsa mürsuga, paigutada sellesse reisijad ja tulistada siis vagunmürsk Kuule.
On selline mõte puhas fantastika? Ja kõigepealt: kas kehale saab anda nii suure kiiruse, et ta jäädavalt lahkub Maa pinnalt?
Anname sõna geniaalsele Newtonile, kes avastas ülemaailmse gravitatsiooniseaduse. Oma raamatus «Loodusteaduse matemaatilised printsiibid» kirjutab ta (parema arusaamise huvides esitame selle katkendi vabas tõlkes):
«Visatud kivi hälbib raskusjõu mõjul sirgjooneliselt teelt ja langeb kõverjoont mööda Maa peale. Kui visata kivi suurema kiirusega, lendab ta kaugemale, seepärast võib juhtuda, et ta lendab mööda 10, 100, 1000 miili pikkust kaart, lahkub lõpuks Maa piiridest ega pöördu enam tagasi. Kujutagu AFB (joon. 47) Maa pinda, С Maa keskpunkti ja UD, UE, UF, UG kõverjooni, mida mööda liigub väga kõrgelt mäelt aina suurema ja suurema kiirusega rõhtsuunas visatud keha. Me ei võta arvesse õhutakistust, s. t. eeldame, et see puudub täiesti. Väiksema algkiiruse korral liigub keha mööda kõverat UD, suurema kiiruse puhul mööda kõverat UE, veel suurematel kiirustel on liikumiskõverateks UF, UG. Teatava kiiruse korral lendab keha ümber kogu Maa ja jõuab tagasi sinna mäetippu, kust ta visati. Et lähtepunkti tagasijõudmisel pole keha kiirus algkiirusega võrreldes vähenenud, siis jätkab ta liikumist sama kõverat mööda.»
Kui sellel kujutletaval mäel oleks kahur, siis ei kukuks teatava algkiirusega väljatulistatud mürsk enam kunagi Maale tagasi, vaid hakkaks peatumatult tiirlema ümber maakera. Üsna lihtsate arvutuste varal* on kerge näidata, et niisugune olukord peaks saabuma kiirusel umbes 8 km/s. Teiste sõnadega, kahuri poolt kiirusega 8 km/s väl japaisatud mürsk lahkub igaveseks Maa pinnalt ja temast saab meie planeedi kaaslane. Ta kihutab 17 korda kiiremini kui ekvaatori punktid ja teeb täis tiiru ümber Maa 1 tunni 24 minutiga.
Andes mürsule suurema kiiruse, ei tiirle ta ümber Maa enam ringjoont mööda, vaid piki vähem või rohkem välja venitatud ellipsit, eemaldudes Maast hiiglasuurele kaugusele. Veel suurema algkiiruse korral eemaldub mürsk igaveseks meie planeedi juurest maailmaruumi . Niisugune olukord peab saabuma algkiirusel umbes 11 km/s. (Kõigis arutlustes eeldatakse, et mürsk liigub tühjas ruumis, mitte õhus).
Nüüd vaatame, kas on võimalik lennata Kuu peale nende vahenditega, mida pakkus välja Jules Verne. Tän a päeva kahurid annavad mürskudele maksimaalseks algkiiruseks 2 km/s. See on viis korda väiksem kiirusest, millega keha võib Kuule jõuda. Romaani kangelased arvasid, et kui nad ehitavad hiiglakahuri ja laevad selle tohutu lõhkeainekogusega, siis õnnestub neil saavutada mürsu Kuule lähetamiseks küllaldane kiirus.
Ja ennäe, kahuriklubi liikmed valavadki veerand kilomeetrit pika gigantkahuri, mis kaevatakse püsti Maa sisse. Valmistatakse ka vastav mürsk, mille siseosa kujutab endast reisijatekabiini. Mürsk kaalub 8 tonni. Kahur laetakse 160 tonni püroksüliiniga (nitrotselluloosiga) . Kui kirjanikku uskuda, omandab mürsk plahvatusel kiiruse 16 km/s, ent õhutakistus vähendab selle 11 kilomeetrini sekundis. Seega on Jules Verne’i mürsul õhkkonnast välja jõudes küllaldane kiirus Kuule jõudmiseks. Nii kirjeldatakse kõike romaani s. Mida ütleb selle kohta füüsika?
Jules Verne’i projekti nõrk koht pole sugugi seal, kuhu lugeja kahtlused tavaliselt suunduvad. Esiteks saab tõestada (ma olengi seda teinud raamatus «Planeetidevahelised lennud»), et püssirohuga laetavad kahurid ei saa kunagi anda mürsule suuremat kiirust kui 3 km/s.1
Peale selle ei arvestanud Jules Verne õhutakistust, mis nii suurel kiirusel peab olema õige tugev ja muutma täielikult lennupilti. Ent peale mainitute on veel teisigi tõsiseid vastuväiteid kavatsusele lennata kahurimürsus Kuule.
Kõige suuremat kartust tekitab reisijate eneste saatus. Ärge arvake, et oht ähvardab neid Maalt Kuule lendamise ajal. Kui neil õnnestuks selle hetkeni ellu jääda, mil nad kahuritorust välja lendavad, siis edasise reisi ajal pole neil enam midagi karta. Tohutu kiirus, millega reisijad maailmaruumis edasi tormavad, on neile niisama kahjutu kui meile, Maa elanikele see veelgi suurem kiirus, millega Maa kihutab ümber Päikese.
Kõige ohtlikumad on meie reisijate jaoks need sekundi sajandikosad, mille vältel mürsk liigub kahuritorus. Selle tühiselt väikese ajavahemiku jooksul peab reisijate kiirus kasvama nullist kuni 16 km/s. Egas ilmaasjata oodanud romaanikangelased lasu hetke niisuguse südamevärinaga. Ja Barbicane’il oli täielik õigus kinnitada, et see hetk, mil mürsk lendama hakkab, on reisijatele mürsu sees niisama ohtlik nagu siis, kui nad seisaksid selle ees. Tõepoolest, lasu hetkel lööb kabiini põrand reisijaid altpoolt niisama tugevasti, kui teeks mürsk iga kehaga, mis satub tema teele. Romaani tegelased suhtusid sellesse ohtu ülemäära kergemeelselt, arvates, et halvimal juhul pääsevad nad vaid vere valgumisega pähe ...
Asi on hoopis tõsisem. Kahuritorus liigub mürsk kiirenevalt: tema kiirus kasvab plahvatusel tekkivate gaaside rõhu mõjul pidevalt. Sekundi tühise murdosa jooksul suureneb kiirus nullist kuni 16 km/s. Lihtsuse mõttes oletame, et kiiruse kasv on ühtlane; siis kiirendus, mis on vajalik selleks, et nii tühise aja jooksul suurendada mürsu kiirust kuni 16 km/s, peab olema ligikaudu 600 km/s2 (arvutused on esitatud lk. 78).
Selle arvu saatuslikust tähendusest saame hästi aru, kui tuletame meelde, et tavaline raskuskiirendus Maa pinnal on kõigest 10 m/s2. Siit järeldub, et iga mürsus olev ese rõhuks lasu hetkel mürsu põrandale jõuga, mis oleks 60 000 korda suurem selle eseme raskusest. Niisugune kolossaalne raskus suruks nad hetkeliselt laiaks. Ainuüksi härra Barbicane’i torukübar kaaluks lasu hetkel üle 15 tonni (täis kaubavaguni kaal) ; selliset mütsist piisab omaniku surnuks litsumiseks.*
Tõsi küll, romaanis on kirjeldatud abinõusid, mida löögi pehmendamiseks kasutati: mürsk oli varustatud vedrupuhvritega ja kahekordse põhjaga, kusjuures põhjade vahel oli vesi. Löögi mõju kestus pikeneb veidi ja kiirus kasvab järelikult aeglasemalt. Arvesse võttes aga neid hiiglaslikke jõudusid, millega siin on tegemist, osutub kasu täiesti tühiseks. Jõud, millega reisijad vastu põrandat surutakse, väheneb tühise osa võrra, aga on ju ükskõik, kas meid surnuks muljuva kübara raskus on 14 või 15 tonni.
Mehaanika näitab meile tee, kuidas oleks võimalik vähendada saatuslikku kiiruse kasvamise kiirust. Seda saab teha, kui ehitada palju kordi pikem kahuritoru.
Pikendamine peab olema aga õige tunduv, kui tahame, et lasu hetkel oleks «kunstlik» raskusjõud mürsu sees võrdne tavalise maapealse raskusjõuga. Ligikaudne arvutus näitab, et selleks oleks vaja valmistada kahuritoru pikkusega ... 6000 km. Teiste sõnadega, Jules Verne’i «kolumbiaad» peaks ulatuma Maa keskpunkti välja ... Siis pääseksid reisijad kõigist ebameeldivuste st: nende tavalisele kaalule l isanduks kiirenduse tõttu ainult niisamasugune näiv kaal, ja nad tunneksid end vaid kaks korda raskematena.
Muide, inimorganism on lühikese aja jooksul suuteline ilma kahjuta taluma mitmekordset raskuse suurenemist. Kui me liugleme jäämäest alla ja poole mäe peal järsult liikumise suunda muudame, siis sel lühikesel hetkel meie kaal suureneb, s. t. keha surutakse vastu kelku tugevamini kui muidu. Raskuse kolmekordset suurenemist talume üsna hästi. Kui oletada, et inimene suudab lühikese ajavahemiku vältel välja kanna tada isegi kümnekordset kaalu kasvu, siis peaks valama «kõigest» 600 km pikkuse kahuritoru. Kuid see lohutab meid vähe, sest ka niisugune ehitis ületab tehnika võimaluste piirid.2
Näete nüüd, missugustel tingimustel on mõeldav Jules Verne’i kahurikuulis Kuule lendamise ahvatleva projekti teostamine.*
(* Kirjeldades lendavas mürsus valitsevaid tingimusi, tegi Jules Verne olulise vea, millest on üksikasjalikult juttu «Huvitava füüsika» esimeses raamatus. Kirjanik ei võtnud arvesse seda, et pärast tulistamist on kõik esemed mürsu sees kogu lennu vältel täiesti kaalutud, sest raskusjõud annab nii mürsule kui ka kõigile kehadele temas ühesuguse kiirenduse (vt. ka paragrahvi «Puuduv peatükk Jules Verne’i romaanis»).)
Kindlasti leidub selle ra amatu lugejate seas ka selliseid, kes soovivad ise kontrollida eespool mainitud arvutusi. Need on õiged vaid ligikaudselt, sest põhinevad eeldusel, et mürsk liigub kahuritorus ühtlaselt kiirenevalt (tegelikult kiirus ei kasva ühtlaselt).
Arvutamisel tuleb kasutada kahte järgmist ühtlaselt kiireneva liikumise valemit:
kiirus on -nda sekundi lõpul võrdne , kus on kiirendus:
sekundi jooksul läbitud teepikkuse arvutame valemist
Nende kahe valemi abil leiame kõigepealt mürsu kiirenduse, kui ta liikus veel kahuritorus.
Romaanist on teada, et see osa kahuritorust, mis oli laengust vaba, oli pikk, see ongi mürsu poolt läbitud tee . Me teame mürsu lõppkiirust: . ja võimaldavad leida – aja, mille jooksul mürsk liigub kahuritorus (liikumist vaadeldakse ühtlaselt kiirenevana). Tõepoolest, ;
millest
Tuleb välja, et mürsk liigub kahur itorus kõigest 1/40 sekundit. Asendades valemisse , saame , millest .
Järelikult on mürsu kiirendus kahuritoru 640 000 m/s2, s.t. 64 000 korda suurem vaba langemise kiirendusest.
Kui pikk aga peaks olema kahur, et mürsu kiirendus oleks kõigest 10 korda suurem langeva keha kiirendusest, s. t. oleks 100 m/s2?
See on eelmise ülesande pöördülesanne. Andmed: , (õhutakistuse puudumisel on niisugusest kiirusest küllalt).
Kahuritoru pikkus peab olema
s. t. ligikaudu 600 km.
Niisugused arvutused annavadki tulemuseks arvud, mis nurjavad Jules Verne’i ahvatlevad plaanid.
Niisugust merd tunneb inimkond juba iidsetest aegadest. See on kuulus Surnumeri Palestiinas. Mere vesi on erakordselt soolane, nii soolane, et selles ei saa elada ükski olend. Palestiina lämmatavalt kuumas ja kuivas kliimas aurab vesi mere pinnalt tugevasti. Aurustub aga ainult puhas vesi, selles lahustunud soolad jäävad vette ja suurendavad mere soolsust. Seepärast sisaldabki Surnumere vesi mitte 2-3 kaaluprotsenti soola, nagu enamik meresid ja ookeane, vaid 27 ja enamgi protsenti; soolsus suureneb sügavusega. Niisiis nel jandiku Surnumerest moodustavad vees lahustunud soolad. Soolade üldhulka temas hinnatakse 40 miljonile tonnile.
Surnumere suurest soolsusest on tingitud üks tema iseärasusi: vesi on seal märksa raskem tavalisest mereveest. Uppuda nii raskes vedelikus ei saa: inimese keha on veest kergem.
Meie keha kaalub tublisti vähem kui niisama suurt ruumala täitev väga soolane vesi ja järelikult ei saa inimene ujumisseaduse põhjal Surnumeres uppuda: ta kerkib pinnale nagu kanamuna soolases vees (magedas vees vajub muna põhja).
Humorist Mark Twain, käinud selle järv-mere ääres, kirjeldab koomilise põhjalikkusega tundeid, mis valdasid teda ja tema kaaslasi, kui nad ujusid Surnumere raskes vees:
«Suplus oli väga lõbus. Uppuda polnud siin kuidagi võimalik. Võid siin täies pikkuses, käed rinnal risti, seljali heita, ja ikkagi jäävad su rind, kõht ia lõug vee peale. Soovi korral võib isegi pea veest välja tõsta ... Kui kätega tasakaalu hoida, võid väga mugavasti seljal lebada, nii et pea ja jalad on põlvist saadik veest väljas. Võid vee peal istuda, kui jalad vastu lõuga surud ja neist kätega kinni hoiad, ent samas vajud tingimata kummuli, kuna pole võimalik tasakaalu hoida. Võid sirgelt vees püsti tõusta ja rinnuni kuivaks jääda, ehkki vesi ulatub siin üle pea. Kuid võimatu on sellesse asendisse püsima jääda – peagi paiskab vesi su jalad pinnale. Võimatu on siin selili ujuda ja seejuures mingil määral edasi jõuda, sest et jalad pinnale kerkivad, nii et edasi saab end lükata üksnes kandade abil. Kui ujuda rinnuli, peksad vett nagu rataslaev ega liigu paigastki. Hobune kaotab siin igasuguse tasakaalu, nii et tema ei saa Surnumeres ei ujuda ega seista, vaid paiskub kohe küljeli. »
Joonisel 48 näete inimest, kes on end Surnumere pinnal üsna mugavasti sisse seadnud; vee suure tiheduse tõttu võib ta selles asendis lugeda raamatut, kaitstes end vihmavarjuga põletavate päikesekiirte eest.
Samasugused ebatavalised omadused on Kara-Bogazi lahe veel (Kaspia meri) ja niisama soolasel Eltoni järve veel, mis sisaldab 27% sooli.
Midagi seesugust kogevad haiged, kes võtavad soolavanne. Kui vee soolsus on väga suur nagu näiteks Staraja Russa mineraalvetel, siis tuleb haigel vanni põhjas püsimiseks vaeva näha. Kuulsin kord, kuidas keegi Staraja Russas ravil olnud naine kaebas pahaselt selle üle, et vesi tahtis teda täielikult vannist välja tõugata. Näis, et ta kaldus selles süüdistama mitte Archimedese seadust, vaid kuurordi juhtkonda ...
Vee soolsuse aste on eri meredes mõnevõrra erinev ja vastavalt sellele pole ka laevade süvis alati ühesugune. Võib-olla on mõni lugeja juhtunud nägema laeva küljel veeliini lähedal nn. LLoydi märki, mis näi tab veeliini kõrgust erineva tihedusega vees. Näiteks joonisel 49 kuju tatud laadjoonemärk näitab veeliini äärmist kõrgust:
magedas vees (Fresh Water) – FW
India ookeanis suvel (Indian Summer) – IS
soolases vees suvel ( Summer ) – S
soolases vees talvel (Winter ) – W
Atlandi ookeani põhjaosas talvel (Winter North Atlantic ) – WNA
Venemaal on nende märkide kasutamine kohustuslik alates aasta st 1909.2
Märgime lõpetuseks, et veel on erim, mis ka puhtal kujul, ilma igasuguste lisanditeta, on märksa raskem harilikust veest: selle tihedus on 1,1, s. t. 10% suurem kui harilikul veel. Järelikult ei saaks sellise veega täidetud basseinis kuidagi uppuda ka inimene, kes ei oska ujuda. Niisugune vesi nimetati raskeks veeks, selle keemiline valem on D20 (selle vee koostisse kuuluva vesiniku aatomid on kaks korda raskemad tavalise vesiniku aatomitest ja nende tähis on D). Rasket vett on tähtsusetul määral lahustunud harilikus vees: ühes panges joogivees sisaldub umbes 8 g rasket vett.
Rasket vett D20 (raske vee erimeid võib olla 17)3 toodetakse nüüdisajal peaaegu puhtal kujul: tavali st vett on selles alla 0,005%.
Vannis kümmeldes ärge laske mööda juhust teha järgmine katse. Enne väljaronimist tõmmake kork väljavooluava eest ära ning ise jääge põhja lamama. Sedamööda kuidas suureneb teie keha veest väl jaulatuv osa, tunnete end muutuvat üha raskemaks. Nii veendute kõige näitlikumal viisil, et see osa keha kaalust, mis vees kaduma läks (meenutage, kui kergena tundsite end vannis), tuleb otsekohe tagasi, niipea kui keha on veest välja saanud.
Kui sellise katse teeks tahtmatult vaal – jääks näiteks mõõna ajal kuivale –, osutuksid tagajärjed loomale saatuslikeks: tema enda keha hiiglaslik raskus lömastaks ta. Egas vaalad ilmaas jata vees ela: vedeliku üleslükkejõud pääs tab neid raskusjõu hukatuslikust mõjust.
Öeldul on kõige tihedani seos käesoleva paragrahvi pealkirjaga. Jäälõhkuja töö põhineb sel samal füüsikanähtusel: vee üleslükkejõud ei tasaka alusta enam veest väljaulatuva laevaosa kaalu ja laev omandab «kuivamaakaalu ». Ei maksa arvata, et jäälõhkuja lõikab jä äd pidevalt oma ninaosa – esitäävi – survega. Nii ei tööta mitte jäälõhkuja, vaid jäämurdja. Sedasi võib tegutseda üksnes suhteliselt õhukese jää puhul.
Tõelised jäälõhkujad nagu «Krassin» või «Jermak» töötavad teisiti. Oma võimsate masinate jõul ronib laev ninaga jää peale. Selle hõlbustamiseks on ninaosa vee all laugjas lame. Veest välja kerkinud käil omandab täie raskuse ja see tohutu koorem («Jermakil» näiteks 800 tf) rõhub jää puruks. Mõju tugevdamiseks pumbatakse jää lõhkuja ninaosas paiknevatesse paakidesse veel vett – vedelat ballasti.
Nõnda tegutseb jäälõhkuja seni, kuni jää paksus ei ületa poolt meetrit. Võimsamast jääst murrab laev end läbi löökidega. Jäälõhkuja taganeb ja sööstab siis kogu oma massiga jääle peale. Seejuures ei tööta enam raskus, vaid liikuva laeva kineetiline energia. Laev muutub nagu aeglaseks, kuid suure massiga kahurimürsuks – taraaniks.
Mitme meetri kõrgused jääpangad lõhutakse tükkideks jäälõhkuja tugeva käila korduvate löökide abil.
«Sibirjakovi» 1932. a. toimunud kuulsast retkest osavõtja madrus N. Markov kirjeldab jäälõhkuja tööd nõnda: «Sadade jääkaljude ja paakjää keskel alustas «Sibirjakov» võitlust. Viiskümmend kaks tundi järjest hüppas masinaruumi telegraafinool näidult «Täiskäik edasi» näidule «Täiskäik tagasi». Kolmteist neljatunnilist vahti tungis «Sibirjakov» hooga jäässe, purustas seda käilaga, ronis jää peale, murdis seda ja taganes taas. Kolmveerandi meetri paksune jää andis visalt teed. Iga löögiga tungis laev edasi kolmandiku kerepikkuse võrra.»
Kõige võimsamad ja suuremad jäälõhkujad maailmas on Nõukogude Liidul.4
On levinud arvamus, isegi meremeeste seas, et uppunud laevad ei lange mitte põhja, vaid ripuvad liikumatult teatavas sügavuses, kus vesi on «pealmiste kihtide rõhumise tõttu vastavalt tihenenud».
Ilmselt mõtles nii ka raamatu «20 000 ljööd vee all» autor J. Verne, sest romaani ühes peatükis kirjeldab ta liikumatult vees rippuvat laeva, teisal räägib aga laevadest, mis «kõdunevad, ise vabalt vees rippudes».
Kas selline väide on õige?
Mõningane alus selleks nagu on, sest vee rõhk ookeanisügavuses on tõepoolest hiiglasuur: 10 m sügavuses rõhub vesi sukeldunud keha igale ruutsentimeetri le jõuga 1 kgf; 20 m sügavusel on rõhk juba 2 kgf/cm2, 100 m sügavusel 10 kgf/cm2, 1000 m sügavuses 100 kgf/cm2. Ookeani sügavus on aga paljudes kohtades mitu kilomeetrit, Vaikse ookeani kõige sügavamas osas isegi üle 11 km (Mariaani nõgu) . Kerge on arvutada, milline kohutav rõhk mõjub veele ja selles asetsevatele kehadele neis tohututes sügavustes.
Kui lasta tühi kinnikorgitud pudel sügavasse vette ja seejärel üles tõsta, näeme, et vee rõhumine on surunud korgi pudelisse ja pudel on vett täis. Kuulus okeanoloog John Murray jutustab oma raamatus «Ookean» järgmi sest katsest: kolm mõlemast otsast kinnijoodetud erineva suurusega klaastoru mässiti lõuendisse ja paigutati vasksilindrisse, mis vett vabalt läbi laskis. Silinder sukeldati 5 km sügavusse. Kui ta jälle üles tõsteti, selgus, et lõuenditükki täidab lumetaoline mass – see oli pihustunud klaas. Samale sügavusele sukeldatud puutükid uppusid hiljem vees nagu tellised – sedavõrd olid nad kokku surutud.
Näib olevat loomulik oodata, et selline koletu rõhumine tihendab vett suurtes sügavustes niisuguse määrani, et isegi rasked kehad ei upu, nagu näiteks raudpomm ei upu elavhõbedas.
Kuid taoline arvamus on täiesti põhjendamatu. Katse näitab, et vett nagu teisigi vedelikke saab kokku suruda väga vähe. Mõjudes veele jõuga 1 kgf 1 cm2 kohta, on võimalik vähendada tema ruumala kõigest 1/22 000 võrra ja umbes sama palju väheneb ruumala ka rõhu edasisel suurenemisel (1/22 000 võrra jõu suurenemisel 1 kgf võrra). Kui meil tekiks soov suruda vesi nii tihedaks, et raud jääks temas ujuma, peaksime teda tihendama 8 korda. Samal ajal on vee tiheduse kahekordistamiseks, s . t . tema ruumala kahekordseks vähendamiseks vaja rõhku 11 000 kgf /cm2 (kui vaid mainitud kokkusurumismäär kehtib sellistel suurtel rõhkudel). Niisugune rõhk vastab sügavusele 110 km.
Nüüd on selge, miks vee tihedus ei saa ookeanisügavustes märkimisväärselt suureneda. Kõige sügavamas osas on vee tihedus ainult 1100/22 000, s. t. 1/20 ehk 5% võrra suurem normaalsest tihedusest.* (* Inglise füüsik Tait on välja arvutanud, et kui Maa külgetõmbejõud järsku kaoks ja vesi muutuks kaalutuks, siis tõuseks veetase ookeanis keskmiselt 35 m võrra (sest kokkusurutud vesi omandaks normaalse ruumala). «Ookean ujutaks üle 5 000 000 km2 maismaad, mis võlgneb tänu oma olemasolu eest ainult teda ümbritseva ookeanivee kokkusurutavusele.») See peaaegu ei mõjutagi kehade ujuvust, seda enam, et niisugusesse vette sukeldatud tahketele kehadele mõjub samasugune rõhk ja järelikult ka nende tihedus kasvab.
Seepärast pole vähimatki kahtlust, et uppunud laevad lamavad merepõhjas. «Kõik, mis upub veeklaasis,» väidab Murray, «peab vajuma põhja ka kõige sügavamas ookeanis.»
Mul on tulnud kuulda järgmist vastuväidet. Kui klaas ettevaatlikult, põhi ülespidi, vette lasta, siis võib ta jääda sellesse asendisse püsima, sest tema poolt väl jasurutud vee kaal on võrdne ta enda kaaluga. Raskem metallist anum võib sellises asendis püsima jääda vee sees, vajumata põhja. Täpselt samuti võivat poolel teel jääda püsima ka kiiluga ülespöördunud ristleja või mõni teine laev. Kui mõni laeva ruum on hermeetiliselt suletud, siis vajub laev teatava sügavuseni ja peatub seal.
Eks upu ju õige palju laevu tõesti sellises asendis. Miks ei võiks mõned neist põhja jõudmata jäädagi hõljuma ookeanisügavustesse? Piisaks küll kergest tõukest, et niisugune laev tasakaalust välja viia, ümber pöörata, veega täita ja sundida teda põhja laskuma, aga kust võib ookeanis see tõuge tulla? Valitseb seal ju igavene vaikus ja rahu ning sinna ei ulatu isegi tormide kaja.
Kõik need arutelud põhinevad füüsikaveal. Kummuli klaas ei sukeldu iseenesest – ta tuleb välisjõuga suruda vette, nii nagu puutükki või tühja kinnikorgitud pudelit. Täpselt niisamuti ei hakka ülespoole pööratud kiiluga laev üldse vajuma, vaid jääb veepinnale. Mitte kuidagi ei saa ta jääda hõljuma poolele teele ookeani pinna ja põhja vahele.
Tänapäeva tõelised allveelaevad on mitmeski suhtes järele jõudnud Jules Verne’i fantastilisele «Nautilusele» ja selle isegi ületanud. Tõsi, nende kiirus on kaks korda väiksem «Nautiluse» omast: 24 sõlme Jules Verne’i 50 asemel (sõlm on umbes 1,8 km/h) .5 Moodsa allveelaeva kõige pikem teekond on ümbermaailmareis, kapten Nemo läbis kaks korda pikema vahemaa. See-eest oli «Nautiluse » veeväljasurve kõigest 1500 tf, ta pardal oli ainult 20–30 inimest ja ta võis vahetpidamata jääda vee alla kõige rohkem 48 tunniks. Ühe 1929. a. ehitatud Prantsuse allveelaeva veeväljasurve oli 3200 tf, meeskond koosnes 150 inimesest ja ta võis viibida vee all järjepanu 120 tundi.
Prantsusmaa sadamatest võis see laev sõita Madagaskarini, ilma et tal oleks tarvis olnud sisse keerata ühtegi sadamasse. Eluruumide mugavuselt ei jäänud ta tõenäoliselt alla «Nautilusele». Prantsuse laeval oli kapten Nemo laeva ees ka see ilmne eelis, et tema ülemisel tekil oli veekindel angaar luure-vesilennuki tarvis. Ka ei varustanud Jules Verne «Nautilust» periskoobiga. mis oleks võimaldanud laeval jä lgida silmapiiri vee alt.
Ainult ühes suhtes jäävad tõelised allveelaevad veel kauaks ajaks maha prantsuse romaanikirjaniku fantaasiasünnitisest: sukeldumissügavuse poolest.6 Tuleb aga märkida, et selles osas ületas Jules Verne’i fantaasialend usutavuse piirid. Romaanist loeme: «Kapten Nemo jõudis 3000, 4000, 5000, 7000, 9000 ja 10 000 meetri sügavusele.» Ükskord laskus «Nautilus» isegi kujuteldamatusse sügavusse – 16 000 meetrini. «Ma tundsin, kuidas teraspoltide needitud liitekohad värisesid, sõrestik kõverdus, vaheseinad naksusid ja illuminaatorite klaasid näisid veesurve all kaarduvat . Tugev allveelaev oleks kahtlemata purunenud, kui ta oma ehituse tõttu poleks olnud, nagu ütles tema kapten, niisama vastupidav kui seest täis metallkeha. »
Kartus oli täiesti põhjendatud, sest 16 km sügavusel (kui ainult ookeanis nii sügavaid kohti leiduks) oleks vee rõhk
ehk 1600 atmosfääri; selline rõhk ei purusta küll rauda, kuid litsub kindlasti laevakere kokku. Ent niisugused sügavused on okeanograafias tundmatud. Liialdatud kujutlused ookeani sügavusest, mis valitsesid Jules Verne’i ajal (romaan valmis 1869. a.), seletuvad sügavuse mõõtmise meetodi ebatäiuslikkusega. Sel ajal kasutati loodiliinina mitte traati, vaid kanepist köit; sellist köit pidurdas vee takistus sügavuse kasvades õige tugevasti. Teatavas sügavuses muutus hõõrdumine juba nii suureks, et lood peatus, ja köis, ükskõik kui palju seda järele ka ei lastud, läks lihtsalt sassi, tekitades mulje hiiglasuurest sügavusest.
Moodsad allveelaevad ei suuda taluda 25 atmosfäärist suuremat rõhku. See määrabki suurima sukeldumissügavuse – 250 m. Märksa sügavamale on jõutud erilises aparaadis, nn. batüsfääris (joon. 50), mis on nähtud ette ookeanisügavuste fauna uurimiseks.* Ent see aparaat ei meenuta Jules Verne’i «Nautilust», vaid teise kirjaniku – Wellsi – fantaasiavilja, süvaveekuuli, mida ta kirjeldab jutustuses «Meresügavuses». Selle loo kangelane laskus paksuseinalises teraskeras 9 km sügavusse merepõhja. Aparaat sukeldus trossita, kuid eemaldatava koormuse abil; põhja jõudnult vabanes ta lisakoormusest ja tõusis kiiresti veepinnale. Batüsfääriga on teadlased jõudnud rohkem kui 900 m sügavusse. Batüsfäär lastakse trossi küljes vette laevalt, millega keras istujad sidet peavad.7
Ookeaniavarustes hukkub igal aastal tuhandeid suuri ja väikesi laevu. Kõige hinnalisemaid ja ligipääsetavamaid hukkunud laevu on viimastel aastatel hakatud merepõhjast üles tõstma. Nõukogude insenerid ja tuukrid, kes kuuluvad Eriülesannetega Veealuste Tööde Ekspeditsiooni, said kogu maailmas kuulsaks rohkem kui 150 suure aluse eduka pinnaletõstmisega. Laevade seas oli üks suuremaid jäälõhkuja «Sadko», mis uppus Valges meres 1916. a. kapteni lohakuse tõttu. 17 aastat merepõhjas lebanud laev tõsteti pinnale ja see astus jälle teenistusse.
Tõstmise tehnika rajanes täielikult Archimedese seadusel. Uppunud laeva kere alla merepõhja kaevasid tuukrid 12 tunnelit ja tõmbasid igaühest läbi tugeva terastrossi. Trosside otsad kinnitati hukkunud jäälõhkuja kõrval alla lastud pontoonide külge. Kõik tööd tehti 25 m sügavuses.
Pontoonideks (joon. 51) olid õõnsad 11 m pikkused ja 5,5-m läbimõõduga veekindlad raudsilindrid. Tühi pontoon kaalus 50 tf. Lihtne on välja arvutada ühe pontooni ruumala: umbes 250 m3. Arusaadavalt peab niisugune silinder tühjalt ujuma veepinnal: ta surub vett välja 250 tonni, ise aga kaalub kõigest 50 tonni. Seega on tema tõstejõud 250 tf – 50 tf = 200 tf. Selleks, et sundida pontooni põhja laskuma, täidetakse ta veega.
Kui terastrosside otsad olid tugevasti kinnitatud vee alla lastud pontoonide külge, hakati voolikute kaudu suruma silindritesse õhku. 25 m sügavuses on vee rõhk (25/10+1) kgf/cm2 ≈ 3 ,5 atm. Õhku suruti silindritesse aga umbes 4-atm rõhu all ja järelikult pidi õhk vee pontoonidest välja suruma. Kergeks muutunud silindrid tõukas vesi hiiglasuure jõuga merepinnale. Nad tõusid nagu õhupallid õhku. Nende kogutõstejõud oleks vee täielikul eemaldamisel olnud . Et aga uppunud «Sadko» kaalus vähem, siis tõstmise sujuvuse huvides olid pontoonid ainult osaliselt veest tühjendatud.
Ometi õnnestus kavandatu alles pärast mitut nurjumist. Töid juhtinud peainsener Т. I. Bobritski kirjeldas kõike järgmiselt :
«Päästemeeskond elas üle neli ebaõnnestumist, enne kui töö korda läks. Kolm korda nägime erutatult jäälõhkujat oodates selle asemel lainete ja vahu kaosest ülespaiskuvaid pontoone ning purunenud, madudena vonklevaid* voolikuid. Kaks korda tuli jäälõhkuja nähtavale ja kadus taas meresügavusse, enne kui ta lõplikult pinnale tõusis ja siin püsima jäi.»8
Paljude igiliikuri projektide seas leidub ohtrasti ka niisuguseid, mille aluseks on kehade kerkimine veepinnale (joon. 52, 53). 20 m kõrgune torn on täidetud veega. Torni ülemisse ja alumisse otsa on paigaldatud plokid, mille ümber on lõputu lindina tõmmatud tugev köis. Köie külge on kinnitatud 14 õõnsat kuubikujulist kasti, küsega igaüks 1 m. Kuubid on kokku joodetud raudlehtedest, nii et vesi neisse sisse tungida ei saa.
Kuidas seade töötab? Igaüks, kes tunneb Archimedese seadust, taipab, et vees olevad kastid püüavad pinnale tõusta. Neid surub ülespoole jõud, mis on võrdne kastide poolt väljatõrjutud vee raskusega, s. t. 1 m3 vee raskusega, korrutatud vees olevate kastide arvuga. Jooniselt 53 on näha, et vees asub korraga ainult 6 kasti. Tähendab, jõud, mis tõstab sukeldatud kaste ülespoole, on võrdne 6 m3 vee kaaluga, s. t. 6 tonniga. Allapoole tirib kaste nende endi raskus, mida aga tasakaalus tab torni välisküljel vabalt rippuva kuue kasti raskus.
Niisiis, kirjeldatud köiele mõjub alati tõmbejõud 6 tf, mis on suunatud alt üles. On selge, et see jõud paneb plokkidel liikuva köie pidevalt pöörlema ja teeb igal pöördel tööd 6000 kgf • 20 m = 120 000 kgf/m.
Järelikult, külvanud riigi üle selliste tornidega, võime neilt saada piiramatul hulgal tööd, millest jätkub kõigi rahvamajandusharude vajadus te rahuldamiseks. Tornid käivitavad dünamomas inaid ja annavad soovitavas koguses elektrienergiat.
Kui aga projekti tähelepanelikult uurida, on kerge veenduda selles, et köis ei saa üldse oodatud moel liikuma hakata.
Et lõputu köis pöörleks, peavad kastid sukelduma basseini alt ja väljuma ülalt. Kuid basseini sisenedes peab kast ületama 20 m kõrguse veesamba rõhumise. See aga rõhub kasti pinna ruutmeetrile jõuga 20 tf (20 m3 veeraskus) . Üleslüke on kõigest 6 tf, sellest jääb kasti basseini tõmbamiseks ilmselt väheks.
Arvukate vesi-igiliikurite projektide seas, millest sadu mõtlesid välja hädaleidurid, on ka väga lihtsaid ja teravmeelseid.
Silmitsege joonist 54. Teljele kinnitatud puust trumlist on osa kogu aeg vees. Kui Archimedese seadus on õige, siis peab vette sukeldatud osa pinnale tõusma, ja et üleslükkejõud on tavaliselt suurem hõõrdejõust trumli teljel, siis ei lakka pöörlemine kunagi ...
Ärge aga kiirustage sellist igiliikurit ehitama. Teid seirab kindlasti ebaõnn: trummel ei liigu paigastki. Milles on asi? Kus me arutluses eksisime? Tuleb välja, et me ei arvestanud mõjuvate jõudude suunda, need on aga alati risti trumli pinnaga, s. t. mõjuvad raadiust mööda telje suunas. Igapäevakogemus tes t on kõigile teada, et ra ta st ei saa panna pöörlema raadiuse sihis mõjuva jõuga. Pöörlemise tekitamiseks peab jõud mõjuma risti raadiusega, s. t. ratta puutuja sihis. Nüüd on juba kerge taibata, miks äpardub ka see katse kutsuda esile igavest liikumist.
Archimedese seadus on pakkunud igiliikurite ehitajate fantaasia le ahvatlevat toitu ja ärgi tanud neid välja mõt lema teravmeelseid seadmeid, et kasutada ära näivat kaalukaotust eesmärgiga saada igavest mehaanilis e energia allikat.
Sõna «gaas» kuulub nende sõnade hulka, mida teadlased on välja mõelnud, nii nagu ka sõnad «termomeeter», «elekter», «galvanomeeter», «telefon» ja eelkõige sõna «atmosfäär». Hollandi keemik ja arst Helmont (1577— 1644), Galilei kaasaegne, tuletas sõna «gaas» kreekakeelsest sõnast «kaos». Avastanud, et õhk koosneb kahest osast, millest üks soodustab põlemist ja põleb ära, ülejäänud osal aga see omadus puudub, Helmont kirjutas: «Sellist auru ma nimetasin gaasiks, sest et ta peaaegu ei erinegi antiikrahvaste kaosest. (Sõna «kaos» tähendas algselt «säravat ruumi».)
Kuid veel kaua ei võetud uut sõna tarvitusele. Alles Lavoisier ära tas ta 1789. a. taas ellu. Sõna levis laialdaselt siis, kui kõikjal hakati rääkima vendade Montgolfier’de esimestest õhupallilendudest. Lomonossov kasutas oma teostes gaasiliste kehade jaoks teist nimetust – elastsed vedelikud. Märkigem muide Lomonossovi teenena, et ta võttis tarvitusele hulga sõnu, mis praeguseks on saanud vene teaduskeele igapäevasteks: atmosfäär, baromeeter, õhupump, püdelus, kristallisatsioon, mateeria, manomeeter, optika, optiline, elekter, eeter jt.
Vene loodusteaduse geniaalne rajaja kirjutas sel puhul: «Olin sunnitud otsima sõnu mõnede füüsikariistade, mõjude ja looduslikkude asjade tarvis, mis (s. t. sõnad) paistavad esialgu küll natuke veidratena, aga loodan, et aja jooksul muutuvad nad tarvi tamise läbi tut tavamaks. » Nagu teada, on Lomonossovi lootused täiel määral täid e läinud.
30 klaasi mahutav samovar on vett täis. Pange selle kraani alla klaas ja jälgige kellalt, kui palju aega kulub klaasi täitmiseks. Oletame, et pool minutit. Nüüd küsime: kui ruttu tühjeneb terve samovar, kui kraan lahti jätta?
Näib, nagu oleks tegemist lapsikult lihtsa ülesandega: üks klaas täitub poole minutiga, 30 klaasi saavad täis 15 minutiga.
Aga tehke katset. Selgub, et samovar ei tühjene mitte veerand tunniga, nagu ootasite, vaid kaks korda kauem.
Milles on siis asi? Arvutus oli ju nii lihtne?
Lihtne küll, kuid vale. Pole alust eeldada, et väljavoolukiirus jääb algusest lõpuni samaks. Kui esimene klaasi täis vett on samovarist välja voolanud, on veejuga juba väiksema rõhu all, sest vee tase samovaris on alanenud; arusaadavalt kulub teise klaasi täitumiseks rohkem aega kui pool minutit, kolmas klaas voolab välja veel aeglasemalt jne.
Iga vedeliku väljavoolamiskiirus läbi lahtises nõus oleva ava sõltub otseselt ava kohal oleva vedelikusamba kõrgusest. Galilei õpilane geniaalne Torricelli viitas esimesena sellele seosele ja väljendas seda lihtsa valemiga
kus on väljavoolukiirus, – vaba langemise kiirendus ja – vedelikupinna kõrgus ava kohal. Sellest valemist järeldub, et vedeliku väljavoolukiiru ei olene üldse vedeliku tihedusest: kerge piiritus ja raske elavhõbe voolavad ühekõrguste tasemete puhul välj a ühesuguse kiirusega (joon. 55). Valemist on näha, et Kuul, kus raskusjõud on 6 korda väiksem kui Maal, kuluks klaasi täitmiseks umbes 2,5 korda rohkem aega kui Maal.
Tuleme aga oma ülesande juurde tagasi . Kui pärast 20 klaasi täitumist on vee pind (arvestades kraani avast) langenud neli korda, siis täitub kahekümne esimene klaas juba kaks korda aeglasemalt kui esimene. Ja kui edaspidi veetase alaneb üheksa korda, siis viimaste klaaside täit miseks kulub juba kolm korda rohkem aega kui esimese tarvis. Kõik teavad, kui loiult voolab vesi samovarist, mis on peaaegu tühi. Lahendades selle ülesande kõrgema ma temaatika abil, saab näidata, et anuma täielikuks tühjendamiseks kulub aega kaks korda rohkem, võrreldes selle juhuga, kus vee pind oleks samovar is jäänud esialgsele kõrgusele.9
Öeldust on ainult üks samm kurikuulsa basseiniülesandeni, milleta ei saa läbi ükski aritmeetika- ega algebraülesannete kogu. Kõik mäletavad seda klassikaliselt igavat, skolastilist ülesannet. Toome ühe sellise näiteks:
«Basseinis on kaks toru. Esimese kaudu täitub tühi bassein 5 tunniga, teise kaudu tühjeneb täis bassein 10 tunniga (joon. 56). Mitme tunni jooksul täitub tühi bassein, kui mõlemad torud korraga avada?:»
Seda laadi ülesannetel on auväärt iga – ligi 20 sajandit – ja need pärinevad Aleksandria Heronilt. Esitame siinkohal ühe Heroni ülesande, tõsi küll, mitte nii keerulise kui selle hilisemad variandid:
Purskkaeve on neli. On tohutu veenõu.
Fontäänidest üks ta ööpäevaga täidab.
Kaks päeva ja ööd kulub teisel seks tööks.
Päev kauem kui teisel läeb kolmandal.
Nelja päeva ja ööga neljas järel neil jõuab.
Mul vasta, kui kiiresti täis saab bassein,
Kui avataks korraga koos kõik fontäänid?
Kaks tuhat aastat lahendatakse basseiniülesannet ja – selline on harjumuse jõud, – kaks tuhat aastat tehakse seda valesti. Mispärast valesti, saate isegi aru, kui olete läbi lugenud selle, mis oli öeldud väljavoolamise kohta.
Kuidas õpetatakse lahendama basseiniülesandeid? Esimest lahendatakse näiteks nii: ühe tunni jooksul täidab esimene toru 1/5 basseinist, teine tühjendab 1/10 sellest, järelikult mõlema toru kaudu täitub basseinist igas tunnis 1/5 - 1/10 = 1/10, nii et bassein saab täis 10 tunniga.
Arutluskäik on aga vale: kui vee sissevoolu võime vaadelda jääva rõhu all toimuvana ja seega ühtasena, siis väljavoolamisel veetase muutub ja voolamine on järelikult ebaühtlane. Sellest, et teise toru kaudu tühjeneb bassein 10 tunniga, ei järeldu sugugi, et iga tund voolab välja 1/10 basseini mahust; ülesande koolilahendus on, nagu näeme, vale. Elementaarmatemaatika ei võimalda seda ülesannet õigesti lahendada, seepärast pole väljavoolava veega basseiniülesannete koht üldse aritmeetikaülesannete kogudes.
Kas saab ehitada anumat, millest vedelik voolaks välja ühtlase joana, ilma et voolamine aeglustuks vedelikutaseme alanemise tõttu? Pärast seda, mida saite teada eelmistest paragrahvidest, olete tõenäoliselt valmis vastama eitavalt.
Ometi on see ülesanne teostatav. Joonisel 57 ongi kujutatud just niisugune imetlusväärne anum. See on tavaline kitsa suuga pudel, mille korgist on läbi torgatud klaastoru. Kui avate kraani C, mis paikneb toru alumisest otsast madalamal , hakkab vedelik ühtlase joana välja voolama ja teeb seda seni, kuni vedeliku pind anumas langeb toru alumise otsani (korgi В tasemele ). Nihutades toru peaaegu kraani С kõrgusele, võite sundida kogu avast kõrgemale jäävat vett välja voolama ühtlase, ehkki väga nõrga joana.
Millest see tuleb? Jälgige mõttes seda, mis toimub anumas kraani С avamisel. Kõigepealt voolab välja klaastorus olev vesi, veetase langeb toru alumise servani. Edasisel voolamisel hakkab langema juba veetase anumas ja klaastoru kaudu tungib sisse välisõhk; see imbub mullikestena läbi vee ja koguneb vee kohale anuma ülaossa. Nüüd võrdub rõhk korgi В kõrgusel atmosfääri omaga ning järelikult voolab vesi kraanist С välja ainult vedelikusamba BC rõhumise mõjul. Et aga kihi BC paksus ei muutu, pole ka midagi imestada, kui väl javoolava veejoa kiirus jääb kogu aeg samaks.
Püüdke nüüd vastata küsimusele: kui ruttu voolab vesi välja siis, kui võtta ära kork avalt B, mis on toru otsaga ühel kõrgusel?
Osutub, et vesi ei hakka üldse välja voolama (muidugi kui ava on nii väike, et selle laiuse võib jätta arvestamata; vastasel korral voolaks vesi välja ava läbimõõduga võrdse õhukese veekihi rõhu mõjul) . Tõepoolest, siin on rõhk nii seest- kui väljastpoolt võrdne atmosfäärirõhuga ja miski ei sunni vett välja voolama. Kui te aga avaksite kraani A, mis asub toru alumisest otsast kõrgemal, siis ei hakka vesi samuti anumast välja voolama: anumasse tungib hoopis välisõhk. Mispärast? Väga lihtsal põhjusel: selles anumaosas on rõhk väiksem välisrõhust.
Niisuguste ebatavaliste omadus tega anuma leiutas kuulus füüsik Mariot te ja seda nimetatakse tema järgi Mariotte’i anumaks.
17. sajandi keskel said Regensburgi linna elanikud ja sinna kokku sõitnud keisrikoja liikmed eesotsas keiser Ferdinand III-ga rabava vaatemängu tunnistajaiks: 16 hobust püüdis kogu jõust lahti tõmmata kahte teineteise vastu pandud vaskpoolkera. Mis hoidis neid poolkerasid koos? «Eimiski» – õhk. Ja ometi ei suutnud kaheksa hobust ühelt ja kaheksa teiselt poolt neid lahutada. Nii näitas linnapea Otto von Guericke kõigile, et õhk pole sugugi «eimiski», vaid et tal on raskus ja ta avaldab märkimisväärset rõhumist kõigile maapealsetele esemetele.
Katse korraldati 8. mail 1654. a. väga pidulikus õhkkonnas. Kuigi parasjagu oli laas tavate sõdade ja poliitiliste rahutuste «hooaeg», oskas õpetatud linnapea kõigis ära tada huvi oma teaduslike katsete vastu.
Olen kindel, et lugeja kuulab huviga jutustust kuulsast katsest magdeburgi poolkeradega Guericke enda, ehk nagu kuulsat füüsikut vahel nimetatakse, selle saksa Galilei esituses. Mahukas raamat , kus kirjeldatakse paljusid tema katseid, ilmus ladina keeles Amsterdamis 1672. a. ja nagu kõik tolle aja raamatud kandis pikka pealkirja. Siin see on:
Otto von Guericke
Nõndanimetatud uued Magdeburgi katsed
õhuta ruumi kohta
esialgselt kirjeldatud Würzburgi ülikooli
matemaatikaprofessori Caspar Schotti poolt
Autori enda väljaanne
põhjalikum ja mitmete uute katsetega
täiendatud
Meid huvitavale katsele on pühendatud raamatu XXIII peatükk. Esitame selle sõnasõnalises tõlkes:
«Katse, mis tõestab, et õhurõhumine ühendab kaht poolkera nii tugevasti, et neid ei saa teineteisest eraldada 16 hobuse jõul.
Ma tellisin kaks vasest poolkera, kumbki läbimõõduga kolm neljandikku magdeburgi küünart. (Magdeburgi küünar on võrdne 550 cm.) Ent tegelikult oli nende diameeter kõigest 67/100, sest nagu tavaliselt ei osanud meistrid valmistada täpselt seda, mis nõuti. Mõlemad poolkerad olid täpselt ühesugused. Ühe poolkera küljes oli kraan; selle abil sai kera seest kõrvaldada õhku ja takistada õhu sissetungimist kerasse väljastpoolt. Peale selle oli poolkerade külge kinnitatud neli rõngast, millest tõmmati läbi hobuste rakmete külge seotud köied. Käskisin õmmelda ka nahast rõnga; see oli immutatud vaha ja tärpentini seguga; poolkerade vahele pressituna takistas ta õhu sissetungimist kerasse. Kraaniga ühendati õhupumba toru ja kerast eemaldati õhk. Siis oli näha, missuguse jõuga olid mõlemad poolkerad nahkrõnga kaudu teineteise vastu surutud. Välisõhu rõhumine surus neid vastamisi nii tugevasti, et 16 hobust järsu tõmbega ei suutnud neid lahutada või tulid sellega ainult vaevu toime. Kui poolkerad lõpuks hobuste jõule järele andsid ja eraldusid teineteisest, kostis pauk nagu püssi laskmisel.
Tarvitses aga kraani pöördega avada õhule vaba sissepääs kerasse – ja poolkerasid võis vaevata kätega teineteisest eemaldada. »
Lihtne arvutus võib meile selgeks teha, miks on vaja nii suurt jõudu (8 hobust kummaltki poolt), et lahti tõmmata õhutühje poolkerasid. Öhk rõhub igale ruutsentimeetrile jõuga umbes 1 kgf; 0,67-küünrase (37-cm) läbimõõduga ringi pindala on 1060 cm2. (Arvesse võetakse ringi, mitte aga poolkera pindala, sest õhu
rõhumine võrdub niisuguse arvuga vaid siis, kui see rõhumine on
risti pinnaga; kaldpindade korral on rõhumine väiksem. Antud juhul
vaatleme kerapinna ristprojektsiooni tasandil, s. t. suurringi pindala.) Tähendab, õhu rõhumine kummalegi poolkerale peab ületama 1000 kgf = 1 tf. Kaheksa hobust pidid järelikult tõmbama jõuga 1 tf, et ületada välisõhu rõhumist.
Näib, et see koorem pole kaheksale hobusele (mõlemalt poolt) kuigi suur. Ärge aga unustage, et liigutades näiteks ühetonnist koormat, ületavad hobused mitte ühetonnist, vaid märksa väiksemat jõudu – nimelt rataste hõõrdumist vastu telge ja sillutist. See jõud on aga näiteks maanteel kõigest 5% koorma raskusest, s. t. ühetonnise koorma korral 50 kgf. (Rääkimata sellest, et praktikast on teada: 8 hobuse ühistel jõupingutustel läheb kaotsi 55% tõmbest.) Järelikult tõmbele 1 tf vastab 8 hobuse puhul vankrikoorem 20 tf. See ongi too õhukoorem, mida pidid vedama Magdeburgi linnapea hobused. Nad pidid paigast nihutama otsekui väikese veduri, mis pealegi polnud rööbastel.
On mõõdetud, et tugev hobune suudab tõmmata koormat kõigest jõuga 80 kgf. (Kiiruse puhul 4 km/h arvestatakse, et hobuse tõmme on keskmiselt 15% tema raskusest; kerge hobune kaalub 400 kgf, raske 750 kgf. Lühikese aja (algtõmbe) jooksul võib tõmbejõud olla paar korda suurem.) Järelikult magdeburgi poolkerade lahtitõmbamiseks oleks ühtlase tõmbe korral vaja olnud 1000 kgf/80 kgf, s. t. 13 hobust kummaltki poolt.*** Lugeja on toenäoliselt hämmastunud, teadasaades , et mõned meie luustiku osad seisavad koos samal põhjusel kui magdeburgi poolkerad. Puusaliigese ümbert võib eemaldada lihas- ja kõhrkoed, ometi ei kuku reieluu välja: teda surub puusaluu vastu õhurõhk, sest liigeseõõnes õhku ei ole.10
Tavalist purskkaevu, mille leiutajaks peetakse Aleksandr ia Heronit, teavad tõenäoliselt kõik. Enne kui asume kirjeldama selle huvitava seadme uusi teisendeid, meenutame tema ehitust. Heroni purskkaev (joon. 59) koosneb kolmest anumast; ülemisest, mis on lahtine (a), ja kahest hermeetiliselt suletud kerakujulisest anumast (b ja с). Anumad on ühendatud kolme toru abil. Kui anumas a on ainult veidi vett, kera b on vett täis, kera с on aga täidetud õhuga, siis hakkab purskkaev töötama: vesi voolab toru mööda anumast a anumasse c, tõrjudes sellest õhu kerasse b; sissetungiva õhu rõhumise mõjul tõuseb vesi anumast b toru mööda üles ja purskab joana välja anuma a kohal. Kui kera b saab tühjaks, lakkab purskkaev töötamast.
Niisugune oli Heroni purskkaevu kuju vanasti . Üks itaalia kooliõpetaja, keda ergutas leidlikkusele tema füüsikakabineti kesine varustus, lihtsustas Heroni purskkaevu ehitust ja mõtles sellele välja teisendeid, mida võib ehitada igaüks kõige lihtsamate vahenditega (joon. 60). Kerade asemel kasutas ta apteeginõusid, klaas- või metalltorude asemel kummivoolikuid. Ülemist anumat ei pea läbi puurima: kummitorude otsad võib lihtsalt anumasse pista, nagu näha joonisel 60 vasakul.
Niisugusel kujul on riista märksa hõlpsam kasutada: kui kogu vesi on purgist b purgi a kaudu voolanud purki c, võib purgid b ja с lihtsalt ümber vahetada ja purskkaev hakkab jälle tööle. Muidugi ei tohi unustada otsatükki kinni tamast teisele torule.
Muudetud purskkaev on mugav veel teiseski mõttes: ta võimaldab suvaliselt muuta purkide asendit ja uurida, kuidas mõjub veetasemete vahe joa kõrgusele.
Kui soovite joa kõrgust mitu korda suurendada, siis saate seda teha, asendades vee purkides elavhõbedaga ja õhu veega (joon. 61). Seadme tööpõhimõte on arusaadav: purgist с purki b voolav elavhõbe tõrjub sellest vee joana välja.
Teades, et elavhõbe on ligi 13,5 korda raskem veest, saame välja arvutada kõrguse, millele tõuseb veejuga purskkaevus. Tähistame tasemete vahed vastavalt , , . Nüüd leiame, milliste jõudude mõjul voolab elavhõbe purgist с purki b. Ühendustorus mõjub elavhõbedale rõhk mõlemast suunast. Paremalt mõjub talle elavhõbedasammaste kõrguste vahe (see rõhumine on 13,5 korda suurem vastava veesamba rõhumisest, s. t. pluss veesamba rõhumine. Vasakult rõhub veesammas . Kokkuvõttes liigub elavhõbe jõu mõjul. Kuid , asendades sellega võrdse suurusega , saame s.t. .
Seega jõuab elavhõbe purki rõhu all, mis võrdub niisuguse veesamba rõhuga, mille kõrgus on . Seepärast peabki joa kõrgus teoreetiliselt võrduma elavhõbedatasemete vahega, korrutatud . Hõõrdumine vähendab mõnevõrra seda teoreetiliselt saadud kõrgust. Ometi võimaldab kirjeldatud riist hõlpsasti saada kõrgele purskuvat juga. Et sundida fontääni purskama näi teks 10 m kõrgusele, piisab ühe anuma tõstmisest teisest umbes 1 m võrra kõrgemale. Nagu meie arvutustest näha, ei mõjuta anuma a kõrgus elavhõbedat sisaldavate anumate kohal huvitaval kombel joa kõrgust mitte mingil määral .
17.— 18. sajandil lõbustasid varakad inimesed end järgmise õpetliku mänguasjaga . Nad muretsesid endale kruusi (või kannu) , mille ülaosas oli suur mustriline väljalõige (joon. 62). Kruusi valati veini ja pakuti mõnele vähem tähtsale külalisele, kelle kulul võis karistamatult nalja heita. Kuidas sellest juua? Kallutada ei saa: vein voolab paljude mustriavade kaudu välja, suhu ei jõua aga tilkagi. Tuleb nii välja nagu muinasjutus:
Sõin ja jõin seal minagi,
kuid suhu ei saand midagi.
Kes aga tundis niisuguste kruuside ehituse saladust – see on näidatud joonisel 63 –, sulges sõrmega ava B, võttis suhu kannunoka A ja hakkas ennast kallutamata vedelikku imema: ava E kaudu voolas vein käepidemesse peidetud kanalist üles ja jõudis sealt kannu nokka selle toru pikendust С mööda, mis oli peidetud kannu ülemisse serva.
Meie pottsepad valmistasid selliseid kruuse veel üsna hiljuti. Mul oli ühes perekonnas juhust näha nende töö näidist. Nõu ehituse saladus oli õige osavalt varjatud.
«Muidugi mitte midagi: sellises asendis ei püsi vesi klaasis, vaid voolab välja,» vas tate teie.
«Kui aga ei voola, mis siis?» küsin vastu.
Tõepoolest, on ju võimalik hoida vett kummulipööratud klaasis nii, et ta sellest välja ei voolaks. Selline juhtum on kujutatud joonisel 64. Kummulipööratud pokaal on põhja pidi seotud ühe kaalukausi külge ja täidetud veega, vesi aga ei voola pokaalist välja, sest pokaali serv on sukeldatud veega täidetud anumasse. Teisel kaalukausil on täpselt samasugune tühi pokaal.
Kumb kaalukauss on raskem?
Raskem on see kaalukauss, mille külge on seotud kummulipööratud pokaal veega. Ülevalt mõjub sellele pokaalile kogu õhurõhk, alt aga õhurõhk, mis on vähenenud pokaalis oleva vee raskuse võrra. Kaalude tasakaalustamiseks tuleb ka teisele kaalukausile paigutatud pokaal täita veega.11
Järelikult mainitud tingimustel kaalub vesi kummuli pööratud pokaalis niisama palju kui püstiseisvas.
1912. a. sügisel juhtus maailma ühe tolleaegse suurima laevaga, ookeaniaurikuga «Olympic» järgmine lugu. «Olympic» sõitis merel. Temaga rööbiti, umbes saja meetri kaugusel liikus suure kiirusega teine, märksa väiksem laev – soomusristle ja «Hawk». Kui laevade vastastikune asend oli selline, nagu kujutatud joonisel 65, juhtus midagi ootamatut: väiksem laev muutis järsult kurssi, nagu oleks teda tõmmanud mingi salapärane jõud, pööras käila suurema laeva poole ja liikus tüüri kuulamata peaaegu otse viimase peale. Toimus kokkupõrge. «Hawk» rammis «Olympicut»; löök oli nii tugev, et viimase pardasse tekkis suur auk.
Kui seda kummalist juhtumit arutati merekohtus, tunnistati süüdlaseks hiiglalaeva «Olympic» kapten, sest et ta – nii kõlas kohtuotsus – ei andnud korraldust vabastada teeristsuunas sõitnud «Hawkile».
Järelikult ei leidnud kohus toimunus midagi ebatavalist: asi oli lihtsalt kapteni oskamatuses. Ometi oli juhtunud siin midagi täiesti ettenägematut: laevade vastastikune tõmbumine merel.
Tõenäoliselt oli selliseid juhtumeid varemgi esinenud kahe rööbitisel kursil liikuva laeva korral. Aga seni, kuni laevad polnud väga suured, ei tulnud nähtus sellise jõuga esile. Kui aga ookeanivett hakkasid kündma «ujuvad linnad », muutus laevade vastastikune külgetõmme tublisti märgatavamaks ; seda asjaolu arvestavad ka manööverdavate sõjalaevade komandörid.
Väikeste laevade arvukad mereõnnetused möödumisel suurtest reisi- ja sõja laevadest on olnud tõenäoliselt tingitud samadest põhjustest.
Millega niisugust külgetõmmet selgitada? Muidugi pole sel nähtusel midagi tegemist Newtoni ülemaailmsegravitatsiooniseadusega; 4. peatükis nägime juba, et see külgetõmme oli liiga väike. Nähtuse põhjus peitub hoopis milleski muus ja seletub nende seadustega, mis kehtivad vedelike voolamise kohta torudes ja kanalites. Saab tõestada, et kui vedelik voolab piki kanalit, millel on kitsamaid ja laiemaid kohti, siis kanali ahenevas osas on voolamine kiirem ja rõhumine kanali seintele väiksem kui laiemas osas (joon. 66), kus vool on rahulikum (nn. Bernoulli printsiip) .
Sama kehtib ka gaaside kohta. See nähtus kannab gaaside teoorias Clement ’i – Desorme’i efekti ehk aerostaatilise paradoksi nime selle efekti avastanud füüsikute järgi. Räägitakse, et esmakordselt täheldatud kõnealust nähtust järgmistel asjaoludel. Ühes prantsuse kaevanduses kästud töölisel kilbiga sulgeda välisesse kaevanduskäiku viiv ava, mida mööda juhiti šahti suruõhku. Tööline mässas kaua šahti tungiva õhujoaga, kuni äkki sulges kilp ava iseenesest ja veel niisuguse jõuga, et kui plaat oleks väiksem olnud, oleks õhujuga selle koos ehmunud töölisega ventilatsiooniluugist sisse imenud.
Muide, sama gaaside voolamise iseärasusega seletub ka pihusti töö. Puhudes otsast kitsenevasse torusse a (joon. 67), vähendame selle kitsasse ossa siseneva õhu rõhumist. Seega väheneb toru b kohal oleva õhu rõhumine ja seepärast tõusebki vedelik välisõhu rõhumise mõjul anumast toru b kaudu üles; toru b otsa juures satub vedelik torust a tulnud õhujoasse ja pihustub.
Nüüd mõistame, milles peitub laevade tõmbumise põhjus. Kui kaks laeva sõidavad paralleelsetel kurssidel, tekib nende vahel otsekui veekanal. Tavalise kanali seinad on paigal ja liigub vesi; siin on vastupidi: vesi seisab, liiguvad aga kanali seinad. Jõudude mõju ei muutu sellest põrmugi: liikuva kanali kitsamates osades rõhub vesi nõrgemini seintele kui ülejäänud osades. Teiste sõnadega, laevade vastakuti olevad küljed on väiksema rõhu all kui laevade välimised osad (joon. 68). Mis sel juhul peaks juhtuma? Laevad peavad välisvee surve mõjul teineteisele lähenema ja loomulikult peab väiksem laev seejuures nihkuma rohkem, kuna massiivsem laev jääb peaaegu paigale. Seepärast avaldubki tõmbumine eriti tugevasti siis, kui suur laev möödub väikese lähedalt.
Niisiis on laevade vastastikune külgetõmme tingitud voolava vee imevast mõjust. Sellega seletatakse ka kärestike ohtlikkust suplejaile ja veekeeriste tõmmet. Arvutused näitavad, et kiiru sega 1 m/s liikuv vesi tõmbab inimkeha jõuga 30 kgf. Niisugusele jõule vastu seista pole kerge, eriti vees, kus meie keha enda kaal ei aita tasakaalu säilitada. Lõpuks seletub ka kiiresti kihutava rongi tõmme sellesama Bernoulli printsiibiga: kiirusega 50 km/h liikuv rong tõmbab lähedal seisvat inimest külge umbes jõuga 8 kgf.
Bernoulli printsiibiga seotud nähtused pole küll kuigi haruldased, kuid neid tuntakse üldiselt vähe. Seepärast peatume neil üksikasjalikumalt. Hiljem esitame katkendi ühes populaarteaduslikus ajakirjas ilmunud vas tavateemalisest artiklist.
Printsiip, mille esimesena sõnastas 1726. a. Daniel Bernoulli, kõlab nii: vee- või õhujoas on rõhk suur, kui kiirus on väike, ja rõhk väike, kui kiirus on suur. Sel printsiibil on kindlad kitsendused, kuid siinkohal me nendel ei peatu. Joonis 69 illustreerib seda printsiipi.
Õhku puhutakse läbi toru AВ. Kui toru ristlõige on väike, nagu osas a, siis on õhu kiirus seal suur; kui ristlõige on suur, nagu osas b, muutub rõhk väikeseks; kus kiirus on väike, kasvab rõhk suureks. Väikese õhurõhu tõttu osas a tõuseb vedelik osas C; samal ajal tugev õhurõhk osas b sunnib torus D vedelikku laskuma.
Joonisel 70 on toru T, mille läbi puhutakse õhku, kinnitatud vaskkettale DD. Toru alumisest otsast väljuv õhk liigub ketta DD ja vaba ketta dd vahele.* Õhk ketaste vahel liigub väga kiiresti, aga kiirus kahaneb ruttu ketaste äärtele lähenedes, sest õhujoa ristlõige kasvab ja lisaks tuleb ületada ka ketaste vahel oleva õhu inertsi. Ketast dd ümbritseva õhu rõhk on suur, sest kiirus on väike, õhurõhk ketaste vahel on aga väike, sest joa kiirus on suur. Seepärast avaldabki väljaspool kettaid olev õhk suuremat rõhumist kui ketaste vahel olev õhk. Tulemusena imetakse ketast dd seda tugevamini ketta DD külge, mida tugevam on Õhuvool torus T.12
Joonisel 71 kujutatud katse on analoogiline katsega joonisel 70, kuid toimub veega. Ketta DD kohal kiiresti liikuva vee tase on madalam, kuid ületanud serva, tõuseb veetase sama kõrgele kui seisval veel. Seepärast on ketta all seisva vee rõhk suurem kui ketta peal liikuva vee oma ning järelikult ketas tõuseb üles. Varras P ei luba kettal kõrvale nihkuda.
Joonisel 72 on kujutatud kerge õhujoas hõljuv kuulike. Õhujuga põrkab vastu kuulikest ega lase sel maha kukkuda. Kui kuulike kaldub väljuma õhujoast, surub ümbritsev õhk ta otsekohe sinna tagasi , sest ümbri tseva õhu rõhumine on väiksema kiiruse tõttu suurem, kuna õhujoas on suure kiiruse tõttu rõhumine väike.
Joonis 73 kujutab kahte laeva liikumas kõrvuti vaikses vees või, mis on sisuliselt sama, kaht kõrvutist laeva neist möödavoolavas vees. Laevade vahel on veevool kokku surutud ja seepärast on vee kiirus siin suurem kui väl jaspool laevu. Seega on vee rõhk laevade vahel väiksem kui väljaspool neid; laevu ümbritseva vee suurem rõhk lükkab neid teineteisele lähemale. Meremehed teavad väga hästi, et kaks kõrvuti sõitvat laeva tõmbuvad tugevasti.
Tõsisem olukord võib tekkida siis, kui üks laev sõidab teise sabas, nagu kujutatud joonisel 74. Kaks jõudu F ja F, mis lähendavad laevu teineteisele, püüavad neid pöörata, kusjuures laev В pöördub A poole märkimisväärse jõuga. Kokkupõrge on niisugusel juhul peaaegu vältimatu, sest rool ei jõua muuta laeva liikumise suunda.
Nähtust, mida on kirjeldatud ühenduses joonisega 73, võib demonstreerida ka nõnda: kaks kerget kummipalli on üles riputatud nii, nagu näha joonisel 75. Kui nende vahele õhku puhuda, lähenevad need pallid teineteisele ja põrkavad kokku.
Sellest, millist osa etendab kalade ujupõis, ki rjutatakse ja räägi takse tavaliselt – ja näib, et täiesti õigustatult – järgmist . Kui kala soovib sügavusest pinnakihtidesse tõusta, paisutab ta oma ujupõit, tema keha ruumala suureneb, väljatõrjutava vee kaal muutub suuremaks kala enda kaalust ja ujumise seaduse põhjal tõusebki kala pinnale. Et tõusu katkestada või allapoole laskuda, surub kala, vastupidi, oma ujupõie kokku. Keha ruumala ja koos sellega ka väl jatõr jutava vee kaal vähenevad ja Archimedese seaduse järgi laskub kala põhja.
Niisugune lihtsustatud kujutlus kalade ujupõie talitlusest pärineb Firenze Akadeemia teadlaste ajast 17. sajandil ja selle esitas professor G. A. Borelli 1685. a. Rohkem kui 200 aas ta jooksul loeti seda vaieldamatult õigeks, see juurdus ja alles uurijate Moreau’ ning Charbonneli tööd näitasid tema täielikku paikapidamatust .
Ujupõiel on kahtlemata väga tihe seos kala ujumisega, sest kalad, kellel katsetel kõrvaldati ujupõis, pidid uimedega kõvasti töötama, et vees mitte põhja vajuda. Milline on ujupõie tõeline ülesanne? See on üsna piiratud:, ujupõis aitab kalal püsida kindlas sügavuses – just seal, kus kala poolt väljatõrjutud vesi kaalub niisama palju kui kala ise. Kui kala aga uimedega töötades laskub sellest tasemest sügavamale, kasvab välisrõhumine tema kehale ning see surub kokku ka ujupõit; väljatõrjutava vee kaal väheneb, muutub väiksemaks kala kaalust ja kala langeb pidurdamatult allapoole. Mida sügavamale ta jõuab, seda suuremaks muutub vee rõhumine (iga 10 langetud meetri kohta kasvab see 1 atm võrra) , seda tugevamini surutakse kala keha kokku ja seda hoogsamalt ta langeb.
Seesama, ainult vastupidises suunas, toimub siis, kui kala tõuseb uimede abil kõrgemale sügavuselt, kus ta oli tasakaalus. Ta keha, vabanenud osaliselt välisrõhust ja tundes nagu seespoolset rõhumist ujupõie poolt (kuni selle momendini oli gaasi rõhk ujupõies tasaka alus ümbritseva veerõhuga), paisub ja selle tagajärjel tõuseb kala veel kõrgemale. Mida kõrgemale kerkib kala, seda enam paisub ta keha ja seda hoogsam on järelikult edasine tõus. Kala ei saa seda takistada «ujupõie kokkusurumise teel», sest ujupõie seintes puuduvad lihased, mille abil ta võiks selle ruumala oma tahtmist mööda muuta.
Et kalade keha ruumala niiviisi passiivselt tõesti muutub, on näha järgmisest katsest (joon. 76). Kloroformitud olekus kala paigutatakse kinnisesse veeanumasse, kus on tekitatud rõhk, mis valitseb looduslikus veekogus teatud sügavuses. Veepinnal lebab kala liikumatult, kõht ülespoole. Kui ta veidi vette suruda, tõuseb ta taas pinnale. Viies kala aga põhja lähedale, vajub ta põhja. Mainitud sügavuste vahel on olemas veekiht, milles kala jääb tasakaalu – ei upu ega tõuse ka pinnale. Kõik see seletub ujupõie passiivsest paisumise ja kokkutõmbumisega.
Niisiis, vastupidi levinud arvamusele ei saa kala sugugi tahtlikult täis puhuda või kokku suruda oma ujupõit. Selle ruumala muutused toimuvad passiivselt välisrõhu kasvamise või kahanemise tagajär jel vastavalt Boyle’i – Mariotte’i seadusele. Need ruumala muutused pole kalale sugugi kasulikud, otse vastupidi, teevad talle hoopis kahju, sest kutsuvad esile kas pidurdamatu, üha kiireneva langemise veekogu põhja poole või niisama pidurdamatu ja kiireneva pinnale tõusmise. Teiste sõnadega, ujupõis aitab kalal hoida liikumatus asendis tasakaalu, kuid see tasakaal pole püsiv.
Selline on ujupõie talitlus, kui rääkida kala ujumisest; kas tal on täita muidki funktsioone ja missuguseid nimelt, pole teada, sest see organ on praegu veel üsna salapärane ja ainult tema hüdrostaatilist funktsiooni võib pidada täielikult väljaselgitatuks. Kalurite tähelepanekud kinnitavad öeldut. Kalapüügil suurtest sügavustest juhtub, et mõni kala pääseb poolel teel vabadusse; kuid vastu ootusi ei lasku ta uuesti algsügavusse, kust ta püüti, vaid kerkib kiiresti pinnale. Niisuguste kalade puhul võib mõnikord täheldada, et ujupõis tungib suust välja.
Paljusid igapäevaseid füüsikanähtusi ei saa seletada elementaarsete füüsikaseadustega. Isegi nii sageli jälgitavat nähtust nagu mere lainetamist tuulise ilmaga pole võimalik ammendavalt seletada füüsika koolikursuse alusel. Millest on aga tingitud liikuva auriku nina ees vaikses vees tekkivad hajuvad lained? Miks lehvivad lipud tuulise ilmaga lainjalt? Miks asetub liiv mere rannikul laineliselt? Miks tuprub vabrikukorstnatest väljuv suits?
Et seletada neid ja teisi taolisi nähtusi, on vaja tunda vedelike ja gaaside nn. keeriselise liikumise iseärasusi. Püüame siin rääkida veidi keeristest ja esile tuua nende põhiomadused.
Kujutleme torus voolavat vedelikku. Kui kõik vedeliku osad liiguvad piki toru mööda rööpseid sirgeid, siis on tegemist vedeliku liikumise lihtsaima juhuga – rahuliku, ehk nagu füüsikud ütlevad, laminaarse voolamisega (joon. 77). Selline voolamine ei esine aga sugugi kõige sagedamini. Vastupidi, märksa sagedam on vedelike mitterahulik voolamine torudes: toru seintelt liiguvad toru telje poole keerised. See on keeriseline ehk turbulentne voolamine (joon. 78). Nii voolab näiteks vesi veevärgitorudes (kui jätta vaatluse alt välja peenikesed torud, kus voolamine on laminaarne) . Keerised tekivad alati, kui vedeliku kiirus kindla läbimõõduga torus saavutab teatava kindla väärtuse, nn. kriitilise kiiruse.
Torus voolava vedeliku keeriseid saab jälgida, segades klaastorus voolavasse läbipaistvasse vedelikku veidi kerget pulbrit, näiteks õietolmu. Siis on toru seinte juurest telje poole suunduvad keerised selgesti näha. Seda keeriselise voolamise iseärasust kasutatakse tehnikas külmkappide ja jahutite valmistamisel. Jahutatavate seintega torus turbulentselt voolava vedeliku osad satuvad märksa kiiremini kokkupuutesse toru jahutatud seintega kui laminaarselt voolava vedeliku omad; tuleb meeles pidada, et vedelikud on iseenesest halvad soojusjuhid ja kui neid ei segata , siis jahtuvad ja soojenevad nad väga aeglaselt. Vere ja kudede kiire soojus- ja ainevahetus on võimalik ainult sellepärast, et veri voolab soontes keeriseliselt, mitte laminaarselt .14
Peale torude kehtib öeldu ka jõgede ja kraavide korral: neiski voolab vesi turbulentselt. Jõevoolu kiirust mõõtev täppisriist registreerib pulsatsioone, eriti põhja lähedal: pulsatsioonid vihjavad voolu suuna pidevale muutumisele, s. t. keeristele. Jõevee osad ei liigu mitte ainult piki jõesängi, nagu tavaliselt arvatakse, vaid ka kallaste poolt keskele. Seepärast polegi õige väita, et jõe põhjas valitseb aasta ringi ühesugune temperatuur, nimelt + 4°C: segunemise tagajärjel on voolava vee temperatuur jõe (kuid mitte järve) põhja lähedal niisama kõrge kui vee pinnal.
Jõe põhjas tekkivad keerised haaravad kaasa kerget liiva ja vormivad neist liivalaineid. Sedasama võib täheldada ka liivasel rannikul, mida uhuvad merelained (joon. 79). Kui vesi voolaks põhja lähedal rahulikult, siis oleks liiva pind põhjas sile.
Niisiis tekivad vee poolt uhutavate kehade läheduses keerised. Nende olemasolust annab meile märku näiteks piki veevoolu tõmmatud nööri vonklemine (nööri üks ots on kinni seotud, teine vaba) . Mis siin juhtub? See nööriosa, mille juures tekkis keeris, liigub koos sellega. Järgmisel hetkel liigub seesama osa juba uue keerise mõjul vastassuunas – nii tekibki madujas vingerdamine (joon. 80). Arvestades seda on kerge mõista, miks lipp lehvib tuules lainjalt (joon. 81): temaga toimub sama mis nööriga voolavas vees.
Vedelikelt siirdume gaaside, veest õhu juurde. Kõik on näinud, kuidas õhukeerised tõstavad maapinnalt üles tolmu, õlgi jm. Siingi avaldub õhu keeriseline liikumine maapinna lähedal. Kui aga õhk voolab piki veepinda, siis kohtades, kus tekivad keerised, tõuseb vesi õhurõhu a la nemise tagajärjel kühmuna üles – tekib lainetus. Samal põhjusel tekivad liivalained kõrbes ja luidete nõlvadel (joon. 82). Samal põhjusel lainetab küpse vilja põld. Tuulelipp ei näita tuulega kogu aeg kindlat suunda, vaid võngub keeriste mõjul pidevalt edasi-tagasi. Samasuguse keeriselise päritoluga on vabrikukorstnast tupruvad suitsupilved: põlemisel tekkivad gaasid voolavad korstnas turbulentselt ja säilitavad inertsi mõjul sellise liikumise ka mõnda aega pärast korstnast väljumist (joon. 83).
Õhu turbulentsel liikumisel on väga tähtis osa lennunduses. Lennuki tiivad tehakse alt kujuga, mille korral nad täidavad ruumala, kus õhk hõrenduks, kuna tiiva peal, vastupidi, suurendatakse keeriste mõju. Tulemusena saab tiib altpoolt lisatuge, pealtpoolt imetakse seda aga üles (joon. 84). Analoogiline nähtus esineb lindude liuglemisel laialisirutatud tiibadega.
Kuidas mõjub katusele tuul? Katuse kohal tekitavad keerised õhuhõrenduse. Õhk, püüdes rõhumist võrdsustada, tungib katuse alt üles ja surub katusele. Tulemusena juhtub midagi niisugust, mida me kahjuks üsna sageli näeme: kerge ja halvasti kinnitatud katus lendab tuulega minema. Samal põhjusel surutakse suured aknaruudud tugeva tuulega seest välja (need ei purune väli surve mõjul). Kuid lihtsam on neid nähtusi selgitada rõhu vähenemisega liikuvas õhus (vt. paragrahvi «Bernoulli printsiip ja selle järeldused»).
Kui kohakuti liiguvad kaks erineva temperatuuri ja niiskusega õhuvoolu, tekivad kummaski keerised. Pilvede kuju mitmekesisus ongi suurel määral just sellest tingitud.
Siit näeme, kui lai nähtuste ring on seotud keeriselise voolamisega.
Ükski inimene pole jõudnud maa sees sügavamale kui mõni kilomeeter, ometi on maakera raadius 6400 km. Maa keskpunktini jääb veel väga pikk tee. Kuid leidlik Jules Verne laskis sügavasse maapõue oma kangelased – veidrikust õpetlase Liedenbrocki ja tema vennapoja Axeli. Romaanis «Reis maakera südamesse» jutustab Verne nende allmaarändurite imelistest seiklustest. Üks ootamatusi, millega nad Maa all kokku põrkasid, oli muide õhu tiheduse suurenemine. Ülespoole tõusmisel hõreneb õhk väga kiiresti: tõusu kõrguse suurenedes aritmeetilise jada seaduste järgi väheneb õhu tihedus geomeetrilise jada seaduste järgi. Vastupidi, laskudes allapoole merepinda, peab õhk pealasuvate kihtide rõhumise mõjul muutuma aina tihedamaks. Allmaarändurid pidid seda muidugi märkama.
Teadlasest onu ja tema vennapoja vahel toimus 12 ljöö (48 km) sügavuses järgmine vestlus.
««Vaatame, kui palju näitab manomeeter,» sõnas onu.
«Väga tugevat rõhku.»
«Nüüd näed, et vähehaaval laskudes harjume järk-järgult tihedama õhuga ega kannata seetõttu sugugi.»
«Kui jätta arvestamata valu kõrvades.»
«Tühiasi.»
«Hästi,» vastasin, tahtmata onule vastu vaielda. «Tihendatud õhus olla on isegi meeldiv. Kas panite tähele, kui valjusti kostavad selles hääled?»
«Muidugi. Niisuguses õhus kuuleks isegi kurt.»
«Õhk muutub üha tihedamaks. Kas ta ei lähe lõpuks nii tihedaks nagu vesi?»
«Muidugi: rõhul 770 atmosfääri.»
«Aga veel sügavamal?»
«Tihedus suureneb veelgi.»
«Kuidas me siis laskuma hakkame?»
«Topime taskud kive täis.»
«Noh, onu, teil on küll igale küsimusele vastus valmis.»
Ma ei hakanud rohkem oletuste valda süvenema, sest küllap oleksin jälle välja mõelnud mõne takistuse, mis oleks onu vihale ajanud. Oli aga päevaselge, et mõnetuhandeatmosfäärisel rõhul võib õhk üle minna tahkesse olekusse ja siis, oletades, et suudame välja kannatada isegi sellist rõhku, peame ikkagi peatuma. Siin ei aita enam mitte mingisugune vaidlemine.»
Nii jutustab romaanikirjanik, aga asi näeb veidi teisiti välja, kui kontrollime fakte, millest katkendis juttu oli. Selleks pole meil vaja laskuda Maa sisemusse: väikeseks õppekäiguks füüsika valdkonda piisab täiesti pliiatsist ja paberist.
Kõigepealt püüame kindlaks teha, kui sügavale peame laskuma, et õhurõhk kasvaks 1/1000 võrra, õhu normaalrõhk võrdub 760-millimeetrise elavhõbedasamba rõhuga. Kui me ei oleks mitte õhus, vaid elavhõbedas, siis peaksime laskuma kõigest 760/1000 = 0,76 mm võrra, et rõhk kasvaks 1/1000 võrra. Õhus peame muidugi märksa sügavamale laskuma, ja nimelt niimitu korda sügavamale, kuimitu korda on õhk kergem elavhõbedast – 10 500 korda. Tähendab, selleks et rõhk kasvaks 1/1000 võrra, tuleb meil laskuda mitte 0,76 mm võrra nagu elavhõbedas, vaid 0,76-10 500 mm, s. t. ligi 8 m võrra. Laskudes veel 8 m sügavamale, kasvab õhurõhk veel 1/1000 võrra oma suurusest jne.* Ükskõik millisel kõrgusel me ka ei asuks – kas «maailma lae» juures (22 km), Everesti tipus (9 km) või merepinna lähedal – ikka peame laskuma 8 m võrra, selleks et õhurõhk kasvaks 1/1000 võrra esialgsest väärtusest. Järelikult saame õhurõhu kasvamise kohta sügavuse suurenemisel niisuguse tabeli:
Maapinnal on rõhk normaalne, s. t. 760 mm Hg
| 8 m | sügavusel on rõhk | 1,001 | normaalsest |
| 2 · 8 m | sügavusel on rõhk | (1,001)2 | normaalsest |
| 3 · 8 m | sügavusel on rõhk | (1,001)3 | normaalsest |
| 4 · 8 m | sügavusel on rõhk | (1,001)4 | normaalsest |
jne
Kuni rõhk pole väga suur, kasvab niisama palju kordi ka õhutihedus (Boyle’i - Mariotte’i seadus ) .15
Et romaanis oli juttu kõigest 48-km sügavusest , siis võime raskusjõu vähenemise ja sellega seotud õhu kaalu vähenemise arvestamata jätta. Nüüd võib arvutada, kui suur oli näiteks see rõhk, mis mõjus Jules Verne’i maa-alustele rännumeestele 48 km (48 000 m) sügavusel. Meie valemis n = 48 000/8 = 6000. Arvutame (1,001 )6000. Et korrutada 1,001 iseendaga 6000 korda on üsna igav ja aeganõudev toiming, siis kasutame logaritmide abi, mille kohta Laplace on õigusega öelnud, et need lühendavad arvutaja tööd ja kahekordistavad ta eluiga. Logaritmime ja leiame tundmatu logaritmi:
Logaritmi 2,6 põhjal leiame otsitava arvu. see on 400. Seega 48 km sügavusel on õhurõhk 400 korda suurem normaalrõhust : katsed näitavad, et õhu tihedus on niisugusel rõhul 315 korda suurem. Seepärast on kahtlane, et meie allmaarändurid ei tundnud tõesti midagi muud peale kõrvavalu ... Jules Verne’i romaanis räägi takse veel suuremastki sügavusest , nimelt 120 ja isegi 325 km-st, milleni inimene olevat laskunud. Õhurõhk peaks seal olema koletu; inimene võib tervist kahjustamata taluda kuni 3 atm. Kui me sel lesama valemi põhjal hakkaksime arvutama, kus on õhul niisamasugune tihedus nagu veel, s. t. kus ta on tihenenud 770 korda, siis saaksime 53 km. Tulemus on aga vale, sest suurtel rõhkudel pole gaasi tihedus enam võrdeline rõhuga. Boyle’i-Mariotte’i seadus on täiesti õige ainult rõhkudel, mis ei ületa sadakonda atmosfääri. Toome siin katsetest saadud andmed õhu tiheduse kohta:
| rõhk, atm | 200 | 400 | 600 | 1500 | 1800 | 21000 |
| tihedus, suhtel, ühik | 190 | 315 | 387 | 513 | 540 | 564 |
Nagu näeme, suureneb tihedus märksa aeglasemalt kui rõhk. Asjatult lootis Jules Verne’i teadlane, et ta jõuab sügavuseni, kus õhk on tihedam kui vesi. Seda poleks tal õnnestunud saavutada, sest õhk muutub niisama tihedaks kui vesi alles rõhul 3000 atm, sealtpeale pole teda võimalik enam praktiliselt kokku suruda. Sellest aga, et viia õhk tahkesse olekusse ilma tugeva jahutamiseta (kuni -146 °C), ei saa juttugi olla. Tõele au andes peab märkima, et Jules Verne’i romaan ilmus kaua enne seda, kui esitatud faktid teatavaks said. See küll õigustab autorit, ehkki ei paranda romaanis esinevaid vigu. Kasutades eespool toodud valemit veel üks kord, arvutame suurima sügavuse, millel inimene võib tervist kahjus tamata viibida. Suurim õhurõhk, mida meie organism suudab taluda, on 3 atm. Tähistades šahti otsitava sügavuse , saame võrrandi: , millest logaritmides leiame . Seega võib inimene suurema hädata jõuda ligi 9 km sügavusele. Kui Vaikne ookean järsku ära kuivaks, võiksid inimesed elada peaaegu kõikjal selle põhjas.
Kes on Maa keskpunktile kõige ligemale jõudnud, mitte kirjaniku fantaasias, vaid tegelikkuses? Muidugi kaevurid. Me teame juba (vt. 4. ptk.), et üks sügavamaid šahte maai lmas asub Lõuna-Aafrikas. See ulatub üle 3 km Maa sügavusse. Siin pole juttu sügavusest, milleni ulatub puurimispeitel, vaid inimeste viibimise sügavusest.
Luc Durtain jutustab oma külaskäigust Morro velho kaevanduse ühte šahti (asub Brasiilias, sügavus ligi 2300 m) järgmist :
«Morro velho kuulsad kullakaevandused asuvad 400 km kaugusel Rio de Janeirost. Pärast 16-tunnilist rongisõitu mööda kaljust maastikku laskute sügavas se džunglist ümbritsetud orgu. Siin kaevandab inglise kompanii kulda sellisel sügavusel, kuhu inimene pole kunagi enne tunginud.
Kullasoon suundub sügavus se kaldu. Saht järgib seda kuue astanguna. Püstšahte nimetatakse kaevudeks, rõhtšahte tunneleiks. Tänapäeva ühiskonnale on äärmiselt iseloomulik see, et sügavaim maakoorde rajatud šaht, inimese kõige julgem katse tungida planeedi põue, on tehtud kullaotsinguil.
Tõmmake selga purjeriidest töörõivas ja nahkkuub. Olge ettevaatlikud: vähimgi kaevu kukkuv kivike võib teid haavata. Meid tuleb saatma üks šahti «kapteneist». Te sisenete esimesse, hästi valgustatud tunnelisse. Teid paneb värisema neljakraadine jäine tuul – see on šahti sügavamaid osi jahutav ventilatsioon.
Läbinud kitsas metallpuuris esimese 700 m sügavuse kaevu, jõuate teise tunnelisse. Laskute teise kaevu: õhk muutub soojemaks. Te olete juba allpool merepinda.
Järgmisest kaevust peale põletab õhk juba nägu. Higist märg ja madala lae tõttu kummargil, liigute puurimismasinate möirgamise suunas. Tihedas tolmus töötavad peaaegu alasti mehed; neilt voolab higi, veepudelit antakse vahepidamata käest kätte. Ärge puudutage äsja lahti raiutud maagitükke: nende temperatuur on 57 °C! Missugune on selle kohutava, vastiku tegevuse tulemus? Ligi 10 kilogrammi kulda päevas...*
Kirjeldades tingimusi šahti põhjas ja tööliste äärmusllikku ekspluateerimist, märgib prantsuse kirjanik kõrget temperatuuri, kuid ei maini suurt õhurõhku. Arvutame, milline on rõhk 2300 m sügavusel. Kui temperatuur jääks samasuguseks nagu maapinnal, siis kasvaks õhu tihedus meile juba tuntud valemi järgi
Tegelikult temperatuur aga kasvab. Seepärast ei suurene õhu tihedus nii jõudsalt. Lõpptulemusena ei erine õhu tihedus šahti põhjas ja Maa pinnal palju rohkem kui õhu tihedus lämmataval suvepäeval ja pakaselisel talvepäeval. Nüüd on selge, miks õhurõhu muutumine ei äratanud šahti külastaja tähelepanu.
See-eest on suur tähtsus märgataval õhuniiskusel sellistes sügavates šahtides. Suur niiskus kõrge temperatuuri puhul teeb viibimise neis kaevandus tes väljakanna tamatuks. Ühes Lõuna-Aafrika kaevanduses (Johannesburgis) , mille sügavus on 2553 m, tõuseb niiskus 50 °C temperatuuri puhul 100%-ni. Siin kasutatakse kliimaseadet, mille jahutav toime on samaväärne 2000 tonni jää omaga.
Eelmistes paragrahvides rändas ime mõttes maapõue, kusjuures meid aitas valem, mis väljendab seost õhurõhu ja sügavuse vahel. Olgem nüüd julged ja tõuskem kõrgustesse ning, kasutades sama valemit, vaatame, kuidas muutub õhurõhk kõrguse kasvades. Sel juhul omandab v a lem kuju:
kus on rõhk atmosfäärides, – kõrgus meetrites. Murd 0,999 asendas siin arvu 1,001, sest 8 m võrra ülespoole tõusmisel rõhk mitte ei kasva, vaid väheneb 0,001 võrra.
Lahendame algul ülesande: kui kõrgele tuleb tõusta, et õhurõhk väheneks kaks korda.
Selleks võrdsus tame oma valemis rõhu atmosfäär iga ja hakkame otsima kõrgust . Saame võrrandi
mille lahendamine ei tee logaritme oskavale lugejale raskusi. Vastus määrab kõrguse, kus õhurõhk on kaks korda väiksem rõhust maapinnal.
Siirdume nüüd veel kõrgemale, vaprate nõukogude aeronautide jälgedes, kes tõusid 19 ja 22 km kõrgusele. Need kõrged õhukihid asuvad juba nn. stratosfääris. Seepärast nimetataksegi neid õhupalle, mis tõusevad nii kõrgele, mitte aerostaatideks, vaid stratostaatideks. Ei usu, et vanemate inimeste seas poleks keegi kuulnud midagi nõukogude stratostaatidest «СССР» ja «ОАХ-1», mis püstitasid aastail 1933-34 kõrguse maailmarekordid: esimene tõusis 19 km, teine 22 km kõrgusele. Leiame õhurõhu neil kõrgustel:
19 km kõrguse kohta leiame, et õhurohk peab olema
22 km kõrgusel on rõhk
Ent stratonautide märkmetes olid mainitud kõrgustel valitseva rõhu kohta andmed:
kõrgusel 19 km – 50 mm Hg,
kõrgusel 22 km – 45 mm Hg.
Miks me arvutu sed ei leia kinnitust? Milles on viga?
Boyle’i-Mariotte’i seadus kehtib nii madalatel rõhkudel olevate gaaside korral täiesti, kuid seekord jätsime kahe silma vahele teise asjaolu: me oletasime, et tõustes ei muutu õhutemperatuur kogu 20-km õhuliini ulatuses, kuid tegelikult langeb see kõrguse kasvades tublisti. Keskmiselt võetakse temperatuuri languseks iga kilomeetri kohta 6,5 °C; nii on see kõrguseni 11 km, kus temperatuur on -5 6 °C; veel kõrgemal jääb temperatuur üsna suure kõrguste vahe ulatuses muutumatuks. Seda asjaolu arvestades (siin ei piisa enam elementaarmatemaatikast ) saame arvutused märksa paremasse kooskõlla tegelikkusega. Samal põhjusel tuleb vaadelda ligikaudsetena ka neid tulemusi, mis saadi õhurõhu kohta erinevas sügavuses.
Kui naised tarvitavad lehvikuid, hakkab neil muidugi jahedam. Paistab, et tegevus on täiesti kahjutu teistele ruumisviibijatele, kes võivad naistele üksnes tänulikud olla saali õhu jahutamise eest.
Vaatame, kas asi on nii. Miks meil lehvikut tarvitades jahe hakkab? Vahetult meie näo vastas olev õhk soojeneb ja see soe õhumask, mis nähtamatult ümbritseb meie nägu, «soojendabki» seda, aeglus tades edasist soojakadu. Kui õhk ei liigu, siis tõrjub raskem ja jahedam õhk näo lähedal soojenenud õhku õige aeglaselt ülespoole. Kui me lehviku abil kõrvaldame näolt sooja õhu maski, siis puutub nägu kokku üha uute soojenemata õhu annustega ja annab neile vahetpidamata oma soojust ära; keha jahtub ja meile tundub õhk jahedamana.
Järeldus: lehvikutega eemaldavad naised pidevalt oma näo juurest sooja õhku ja asendavad selle jahedamaga. Soojenenult eemaldatakse ka see õhk ja asendatakse uue jahedama õhu portsjoniga.
Lehvikud kiirendavad õhu segunemist ja ai tavad üht lustada temperatuuri saalis, s.t. toovad omanikele kergendust naabreid ümbritseva jahedama õhu arvel. Lehviku puhul on tähtis veel üks asjaolu, millest kohe juttu teeme.
Kõik muidugi teavad, et vaikse ilmaga on pakast kergem taluda kui tuulisega. Kuid kaugeltki kõik ei saa aru selle nähtuse põhjustest. Külm tundub tuulega tugevam olevat ainult elusolenditele, termomeetri näit ei vähene tuule käes sugugi. Lõikava külma tunne tuulise pakaselise ilmaga seletub eelkõige asjaoluga, et näolt (ja üldse kehalt) võetakse sel juhul rohkem soojust ära kui vaikse ilmaga, mil keha poolt soojendatud õhk ei asendu nii ruttu külma õhuga. Mida tugevam tuul, seda suurem õhukogus puutub ajaühikus kokku meie nahaga ning seda rohkem võetakse kehalt ära soojust. Juba üksnes sellest piisaks, et tekitada külmatunnet.
On veel teinegi põhjus. Meie nahalt toimub pidevalt aurustumine, isegi külmas õhus. Aurustumiseks aga on vaja soojust ja see võetakse meie kehalt ja kehaga kokkupuutuvalt õhukihilt. Kui õhk seisab paigal, on aurustumine aeglane, sest nahalähedane õhukiht küllastub peagi veeauruga (niiskusest kül lastunud õhus aurustumine aeglustub). Kui aga õhk liigub ja nahaga puutuvad kokku üha uued ja uued õhukogused, siis on aurustumine kogu aeg õige ohter, see aga nõuab palju soojust, mis võetakse meie kehalt.
Kui tugev on tuule jahutav toime? See sõltub tuule kiirusest ja õhu temperatuurist; üldiselt on see märksa tugevam kui harilikult arvatakse. Toon näite, mis annab ettekujutuse temperatuuri alanemisest. Olgu õhu temperatuur 4°C, tuult aga ei mingisugust. Sellistel tingimustel on meie naha temperatuur 31 °C, Kui puhub kerge tuul, mis paneb lipud vaevalt liikuma ja jätab puude lehed paigale (kiirus 2 m/s), jahtub nahk 7°C võrra. Kui tuul sunnib lippe laperdama (kiirus 6 m/s) , jahtub nahk 22 °C võrra, s. t. tema temperatuur langeb kuni 9°C! Need andmed pärinevad N. N. Kalitini raamatust «Atmosfääri füüsika alused ja nende rakendamine meditsiinis»; teadmishimuline lugeja leiab sealt palju huvitavaid üksikasju.
Niisiis ei saa selle üle, kui külm meil on, otsustada ainult temperatuuri põhjal, vaid arvesse tuleb võtta ka tuule kiirust. Ühesugust pakast on Leningradis keskmiselt raskem taluda kui Moskvas, sest tuule keskmine kiirus on Läänemere rannikul 5-6 m/s, Moskvas kõigest 4-5 m/s. Veel kergem on pakast väl j a kanna tada Bai kali ääres, kus keskmine tuule kiirus on kõigest 1,3 m/s. Kuul sad Ida-Siberi pakased pole kaugeltki nii karmid, nagu kujutleme meie, kes me oleme har junud Euroopa suhteliselt tugevate tuultega; Ida-Siberis on peaaegu alati tuulevaikus, eriti talvisel ajal.
«Järelikult peab tuul tooma värskendust ka lämmatava kuumaga,» ütleb võib-olla lugeja, kes on tutvunud eelmise paragrahviga. «Miks aga rändurid räägivad siis kõrbe kuumast hingusest?»
Vastuolu leiab seletuse tõsiasjas, et troopikas on õhk soojem kui meie keha. Pole midagi imestada, et seal ori inimestel tuulega palavam, mitte jahedam. Soojust ei anta seal mitte kehalt õhule, vaid vastupidi, õhk soojendab keha. Seepärast ongi nii, et mida suurem õhumass jõuab ajaühikus puutuda kokku kehaga, seda palavam on. Tõsi, siingi suureneb aurustumine tuule käes, kuid esimene põhjus kaalub teise üle. Just sellepärast kannavadki kõrbeelanikud, näiteks turkmeenid, sooje mantleid ja karvamütse.
Veel üks ülesanne igapäevafüüsikast . Naised kinni tavad, et loor soojendab, et ilma selleta hakkab nägu kül metama. Silmitsedes õhukest, tihti väga hõreda koega loori, ei suuda mehed kuidagi uskuda seda väidet, pidades loori antavat sooja lihtsalt kujutluse viljaks.
Meenutades aga eespool öeldut, hakkate sellesse väitesse suhtuma suurema usaldusega. Kui hõre loor ka poleks, aeglustub teda läbiv õhk ikkagi. Vahetult näo vastu jäävat õhukihti, mis moodustab soojenedes midagi õhumaski taolist, ei puhuta loori korral nii kiiresti minema kui muidu. Seepärast võib uskuda naiste juttu, et kerge külma ja nõrga tuulega külmetab käimisel nägu loori taga vähem kui ilma selleta.
Kui te ise pole selliseid kannusid näinud, siis tõenäoliselt olete neist kuulnud või lugenud. Neil põletamata savist kannudel on see huvitav omadus, et neisse valatud vesi muutub külmemaks kui ümbritsevad esemed. Jahutavad kannud on väga levinud lõunamaal (muu hulgas ka meil Krimmis) ja neid nimetatakse erinevalt: Hispaanias alcarazza, Egiptuses goula jne.
Kannude jahutava toime saladus on lihtne: vedelik imbub läbi savist seinte välja ja aurustub aeglaselt, võttes seejuures soojust (latentset auramissoojust ) anumalt ning selles olevalt vedelikult.
Reisikirjadest võib lugeda, et vedelik jahtub nendes anumates väga tugevasti. Niisugune väide pole õige. Jahtumine ei saa olla suur. See oleneb paljudest asjaoludest. Mida kuumem on õhk, seda rutem ja suuremas koguses aurustub anuma välispinnale imbunud vedelik ning seda rohkem jahtub vedelik kannus. Jahtumine sõltub ka ümbritseva õhu niiskusest: kui õhus on palju auru, toimub aurustumine aeglaselt ja vesi ei jahtu kuigivõrd; kuivas õhus, vastupidi, on aurustumine väga intensiivne ja kutsub esile märgatava jahenemise. Ka tuul kiirendab aurustumist ning soodustab jahtumist; seda teavad kõik külmatunde põhjal, mis tekib, kui viibida sooja, ent tuulise ilmaga märgades rõivastes. Jahutavates kannudes ei ületa temperatuuri langus 5°C. Kuuma lõunamaa ilmaga, kui termomeeter näitab mõnikord 33 °C, on veel jahutavaskannus vannivee temperatuur, 28 °C. Nagu näeme, on jahtumine praktiliselt tühine. See-eest säilib vesi kannudes kaua külm.
Püüame arvutada vee jahtumise määra alcarazza's. Olgu meil kann, mis mahutab 5 l vett. Oletame, et 1/10 l on aurustunud. 1 l (1 kg) vee aurustumiseks temperatuuri 33 °C on vaja umbes 580 kcal (2430 J) energiat: Meil aurustus 1/10 l, järelikult kulus energiat 58 kcal. Kui kogu see soojus oleks võetud ainult veelt kannus, langenuks selle temperatuur 58/5, s. t. 12 °C võrra. Ent suurem osa aurustumiseks vaja likust soojusest võetakse kannu seintelt ja ümbritsevalt õhult; teiselt poolt, peale vee jahtumise toimub ka tema soojenemine ümbritseva sooja õhu mõjul. Seepärast küünib vee jahtumine vastavalt pooleni eespool mainitud arvust.
Raske öelda, kus kann jahtub rohkem – päikese käes või varjus. Päikese käes kiireneb auramine, kuid samal ajal on ka soojuse juurdevool tugevam. Tõenäoliselt on jahutavaid kanne kõige parem hoida varjulises, nõrga tuuletõmbega kohas.
Aurustumisega kaasneval jahtumisel põhineb toiduainete säilitamiseks määratud külmkapi, omamoodi jääta «jääkapi» ehitus. See on õige lihtne: puust (või veel parem – tsingitud rauast) kastis on riiulid, millele pannakse jahutatavad toiduained. Kasti ülemises osas on lame, piklik anum koos puhta külma veega; kasti tagaseinas ripub tükk lõuendit, mille üks ots ulatub vette, teine on aga alumise riiuli alla pandud anumas. Kangas imbub vett täis; vesi liigub selles nagu tahti mööda pidevalt allapoole ja jahutab aeglaselt aurustudes kõiki jääta «jääkapi» osi.
Selline «jääkapp» on vaja paigutada jahedasse kohta ja igal õhtul peab vahetama vett, et see säiliks öö läbi külm ja jahutaks hästi. Nii veenõud kui ka kangatükk peavad loomulikult olema täiesti puhtad.
Inimene on kuumale palju vastupidavam kui harilikult arvatakse: ta suudab taluda lõunamaal temperatuure, mis on märksa kõrgemad neist, mida peame parasvöötmes vaevu talutavaks. Kesk-Austra alias on suviti temperatuur sageli 46 °C var jus; seal on registreeritud isegi tempe ra tuuri 55 °C. Punasest merest Pärsia lahte sõitva laeva ruumides tõuseb temperatuur tihti 50°C-ni ja üle selle, vaatamata pidevale ventileerimisele.
Kõige kõrgemad looduses registreeritud temperatuurid Maal ei ületa 57 °C. See on mõõdetud Surmaorus Kalifornias. Nõukogude Liidu kõige kuumemas osas Kesk- Aasias ei ületa palavus 50 °C.
Mainitud temperatuurid on mõõdetud varjus. Seletan ühtlasi, miks meteoroloogi huvitab just temperatuur varjus, mitte päikese käes. Asi on selles, et õhu temperatuuri näitab ainult varju pandud termomeeter. Päikese käes võib termomeeter soojeneda märksa rohkem kui ümbritsev õhk ja tema näit ei iseloomusta enam sugugi õhu soojusolekut. Seepärast polegi mõtet palavast ilmast rääkides viidata päikese kätte asetatud termomeetri näidule.
On tehtud ka katseid määramaks kõrgeimat temperatuuri, mida talub inimese organism. Selgus, et väga aeglasel soojendamisel on meie organism võimeline kuivas õhus taluma nii vee keemistemperatuuri (100 °C) kui veel kõrgematki temperatuuri , kuni 160 °C. Seda tõestasid kaks inglise füüsikut, kes viibisid tunde köetud pagari - ahjus. Sel puhul märkis Tyndall: «Selle ruumi õhus, kus inimesed viibisid häda saamata, võib keeta mune või praadida biifsteeki.»
Millega niisugust talumisvõimet seletada? Asjaoluga, et meie organismi temperatuur nii kõrgele ei tõusegi, vaid jääb lähedaseks normaalsele. Organism võitleb ülekuumenemise vastu ohtra higieritamisega; aurustuv higi neelab tunduva osa sellest soojusest, mida sisaldab nahaga vahetult kokku puutuv õhukiht ja alandab seega tema temperatuuri küllaldasel määral . Ainus vältimatu tingimus on, et keha ei tohi vahetult kokku puutuda soojusallikaga ja õhk peab olema kuiv. Kes on käinud Kesk-Aasias, on pannud kindlasti tähele, kui kerge on taluda kuumust 37 °C ja üle selle. 24-kraadist temperatuuri Leningradis on märksa raskem välja kannatada. Põhjus peitub muidugi Leningradi õhu niiskuses ja Kesk-Aasia õhu kuivuses – vihm on seal äärmiselt harv nähtus.
Kõik teavad anekdooti lihtsameelsest inimesest, kes ei julenud minna vanni järgmisel ebatavalisel põhjusel:
«Torkasin baromeetri vanni ja see näitas tormi... Kümmelda on ohtlik!»
Ärge arvake, et alati on kerge eraldada baromeetrit termomeetrist! On termomeetreid, õigemini termoskoope, mida niisama põhjendatult võiksime nimetada baromeetriteks ja ümberpöördult. Näiteks võiks olla Aleksandria Heroni konstrueeritud termoskoop (joon. 85). Kui päikesekiired soojendavad kera, surub paisuv õhk kera ülaosas veepinnale ja pressib vett mööda kõverat toru välja; vesi hakkab tilkuma toru otsa juures olevasse lehtrisse, millest ta edasi jookseb alumisse kasti. Külma ilmaga, vastupidi, keras oleva õhu elastsus väheneb ja välisõhu rõhk surub vee alumisest kastist sirget toru mööda kerasse.
See riist on tundlik ka õhurõhu muutuste suhtes: kui välisrõhk alaneb, paisub keras olev õhk oma suurema rõhu tõttu ja surub osa vett kõverat toru mööda lehtrisse; välisrõhu suurenedes aga surutakse osa vett kastist kerasse. Ühekraadine temperatuurivahe muudab keras oleva õhu ruumala sama palju kui atmosfäärirõhu muutus 760/273, s.t . umbes 2,5-mm Hg võrra. Moskvas ulatuvad baromeetri võnkumised 20 ja enama millimeetrini, mis vastab 8 °C-le Heroni termoskoobis, tähendab, sellist õhurõhu muutumist on kerge pidada temperatuuri tõusuks 8 °C võrra!
Nüüd näete, et vanaaegset termoskoopi võib õigusega pidada baroskoobiks. Kunagi olid meil müügil vesibaromeetrid, mis samal ajal kujutasid endast termomeetreid; seda ei aimanud, muide, ei ostjad ega vist leiutaja isegi.
Vähesed teavad, kui pikk arengutee on seljataga lambiklaasil. Tuhandeid aastaid kasutasid inimesed valgustamiseks leeki, ümbritsemata seda klaasiga. Läks tarvis Leonardo da Vinci (1452-1519) geniaalsust, et teha lambile see tähtis täiendus. Kuid Leonardo ümbritses lambi mitte klaas-, vaid metalltoruga. Möödus veel 3 sajandit, enne kui tuldi mõttele asendada metallsilinder läbipaistva klaassilindriga. Nagu näete, on lambiklaas leiutis, mille kallal on töötanud kümned inimpõlved.
Miks ta vajalik on?
Vaevalt küll oskavad kõik anda nii loomulikule küsimusele õiget vastust. Kaitsta leeki tuule eest on klaasi teisejärguline ülesanne. Põhiliselt suurendab klaas leegi heledust, kiirendab põlemisprotsessi. Klaas teeb sama mis ahju- või vabrikukorsten: suurendab õhu juurdevoolu leeki, tugevdab «tõmmet».
Vaatleme küsimust lähemalt. Klaasis olev õhusammas soojeneb leegi mõjul palju kiiremini kui lampi ümbritsev õhk. Soojem ja seetõttu kergem õhk surutakse läbi lambipea sissetungiva raskema ja külmema õhu poolt üles (Archimedese seadus!). Sel kombel tekib pidev õhuvool alt üles, vool, mis kannab põlemisel tekkivaid gaase ära ja toob juurde värsket õhku. Mida pikem on klaas, seda rohkem erinevad soojenenud ja jahedama õhu tihedus, seda hoogsam on värske õhu juurdevool ja järelikult seda kiirem on ka põlemine. Siin toimub sama mis kõrgetes vabrikukorstnates. Seepärast tehaksegi need korstnad nii kõrged.1
On huvitav, et juba Leonardo da Vincil oli selge et te kujutus neist nähtustest. Tema käsikirjades leiame järgmise märkuse: «Kus on tuli, seal tekib selle ümber õhuvool: see vool hoiab tuld alal ja tugevdab seda.»
Kui põlemisprotsessi üle mõtiskleda, tekib tahtmatult küsimus: miks leek ei kustu iseenesest? Tekivad ju põlemisel süsihappegaas ning veeaur – ained, mis ei põle ise ega soodusta ka põlemist. Järelikult koguneb leegi ümber selle süttimise hetkest peale mittepõlevaid aineid, mis takistavad värske õhu juurdevoolu; ilma õhuta ei saa põlemine jätkuda ning leek peaks kustuma.
Miks aga nii ei juhtu? Miks kestab põlemine, kuni jätkub põletisainet? Ainult sellepärast, et gaasid paisuvad soojenemisel ja muutuvad järelikult kergemaks. Vaid tänu sellele ei jää soojenenud põlemissaadused tekkekohta, leegi vahetusse lähedusse, vaid värske õhk surub nad aegaviitmata üles. Kui Archimedese seadus gaaside korral ei kehtiks (või kui puuduks ra skusjõud) , kustuks iga leek pärast lühiajalist põlemist iseenesest.
Õige kerge on veenduda, kui hukatuslikult mõjuvad leegile põlemissaadused. Ise endale teadvustama ta kasutate seda asjaolu tule kustutamisel lambis. Kuidas te kustutate petrooleumilampi? Te puhute leegile ülalt, s.t. ajate mittepõlevad põlemissaadused leegi juurde ja see kustub, sest värsket õhku ei tule enam juurde.
Jules Verne kirjeldab põhjalikult, kuidas kolm uljurit viitsid aega mürsus, mis kihutas Kuu poole. Ta ei räägi aga sellest, kuidas Michel Ardan sai hakkama koka ülesannetega sellel ebatavalisel reisil. Kirjanik arvas vist, et söögitegemine lendavas mürsus ei vääri kirjeldamist. Kui nii, siis ta eksis. Asi on selles, et lendavas mürsus kaotavad kõik esemed kaalu. Selle tõiga jättis Jules Verne kahe silma vahele. Aga nõustuge, et keetmine kaalutus köögis on teema, mis täiesti väärib romaani kirjaniku sulge ja jääb üle üksnes kahetseda, et raamatu «Kahurist Kuule» andekas autor ei pööranud sellele tähelepanu. Püüan siinkohal täiendada romaani puuduva peatükiga, et anda lugejaile teatav ettekujutus sellest, kui efektselt võinuks seda kirjeldada Jules Verne’i enese sulg.
Pala lugemisel on vaja kogu aeg meeles pidada fakti, et mürsu sees ei ole raskusjõudu, kõik kehad selles on kaalutud.
«Mu sõbrad, aga me ei ole ju veel hommikust söönud,» kuulutas Michel Ardan oma planeetidevahelise lennu kaaslastele. «Sellest, et oleme kaotanud kaalu, ei järeldu sugugi, et oleme kaotanud ka isu. Ma võtan enda peale, kallid sõbrad, kaalutu hommikueine valmistamise, mis koosneb kahtlemata kõige kergematest roogadest, mida kunagi maailmas on valmistatud.»
Ja kaaslaste vastust ootamata asus prantslane tegutsema. «Meie veepudel teeskleb, et ta on tühi,» pomises Ardan omaette, katsudes suurt pudelit lahti korkida. «Ega sa mind alt vea, ma ju tean, miks sa nii kerge oled ... Noh nii, kork on pealt ära. Suvatse valada kastrulisse oma kaalutu sisu!»
Aga kuidas ta ka pudelit kallutas, ei voolanud vesi sellest välja. «Ara näe vaeva, armas Ardan,» tuli talle appi Nicholl. «Saa aru, et meie inürsus, kus pole raskust, ei saa vesi voolata. Sa pead ta pudelist välja raputama, nii nagu oleks vesi paks siirup.» Pikemalt mõtlemata põrutas Ardan peopesaga vastu kummulipööratud pudeli põhja. Uus ootamatus: pudelikaela juurde tekkis äkitselt rusikasuurune veemull.
«Mis on meie veega juhtunud?» imestas Ardan. «Ausalt öeldes on see üllatus täiesti liigne. Seletage mulle, mu õpetatud sõbrad, mis on siin juhtunud?»
«See on tilk, kallis Ardan, lihtne veetilk. Raskuseta maailmas võivad tilgad olla kui tahes suured ... Tuleta meelde, et vedelikud võtavad raskuse mõjul anuma kuju, voolavad joana jne. Siin raskust ju pole, vedelik on jäetud oma sisemiste molekulaarjõudude hooleks ja nende mõjul võtab ta kera kuju nagu õli kuulsas Plateau katses.»
«Mul pole mingit pistmist ei selle Plateau ega tema katsetega. Ma pean puljongi tarvis vett keetma ja vannun, et mingid molekulaarjõud ei suuda mind takistada,» teatas prantslane ägedalt.
Ta hakkas raevukalt vett õhus hõljuva kastruli kohal pudelist välja raputama, kuid ilmselt oli kõik vandenõus tema vastu. Suured veekuulid, mis kastrulini jõudsid, roomasid kiiresti selle pinda mööda iaiali. Sellega asi ei lõppenud: kastruli sisepinnalt valgus vesi välis pinnale, voolas seda mööda laiali, ja peagi oli keedunõu kattunud paksu veekihiga. Sel kujul vett keeta polnud mingit võimalust.
«Vaat kus huvitav katse, mis näitab kohesioonijõudude tugevust,» sõnas häirimatu Nicholl märatsevale Ardanile. «Sa ära erutu: siin on tegemist tavalise märgamisnähtusega, ainult raskusjõud ei takista praegu sellel nähtusel täie jõuga avaldumast.»
«Ja väga kahju, et ei takista!» vaidles Ardan vastu. «Ükskõik, on siin tegu märgamise või millegi muuga, kuid mina pean saama vee kastruli sisse, aga mitte selle ümber. Mis see siis olgu! Ukski kokk maailmas pole nõus puljongit keetma säärastes tingimustes!»
«Märgamisest saad kergesti jagu, kui see sind nii segab,» sekkus rahustavalt härra Barbicane. «Tuleta meelde, et vesi ei märga kehi, mida katab isegi väga õhuke õlikiht. Määri oma kastrul väljaspoolt õliga kokku ja sa suudad vett selle sees hoida.»
«Braavo! Vaat seda nimetan ma tõeliseks õpetatuseks,» rõõmustas Ardan nõuannet ellu viies. Seejärel asus ta gaasipoleti leegil vett soojendama.
Ent Ardani ebaõnnestumised polnud sellega veel lõppenud. Gaasipõletigi hakkas tujutsema: põlenud pool minutit kahvatu leegiga, kustus ta seletamatul põhjusel. Ardan sekeldas põleti ümber, jändas kannatlikult leegiga, aga kogu vaev oli asjatu: leek keeldus põlemast.
«Barbicane! Nicholl! Kas tõesti pole siis vahendit, et sundida seda kangekaelset leeki põlema nõnda, nagu ta peaks teie füüsika seaduste ja gaasikompaniide eeskirjade järgi seda tegema?» kutsus julguse kaotanud prantslane sõpru appi.
«Kuid siin pole ju midagi erakordset ega ootamatut,» seletas Nicholl. «Leek põleb täpselt nii, nagu nõuavad füüsikaseadused. Mis aga puutub gaasikompaniidesse, siis arvan, et need jääksid kõik pankrotti, kui poleks raskusjõudu. Sa tead ju, et põlemisel tekivad süsihappegaas ja veeaur, s.t. ained, mis ei põle; tavaliselt ei jää need põlemissaadused leegi lähedusse: soojade ja järelikult kergematena surub juurdevoolav värske õhk neid ülespoole. Siin meil aga raskust pole, seepärast jäävad põlemissaadused tekkekohale, ümbritsevad leeki mittepõlevate gaaside kihiga ja takistavad värske õhu juurdepääsu. Seetõttu põleb leek tuhmilt ja kustub ruttu. Tulekustutite toime ju sellel põhinebki, et ümbritseda leek mittepõleva gaasiga. »
«Tähendab, sinu järgi tuleb välja, et kui Maal puuduks raskusjõud, siis poleks vaja ka tuletõrjekomandosid: tulekahju kustuks iseenesest, lämbuks omaenese hinguses,» katkestas prantslane teda.
«Täiesti õige. Aga et asjale kaasa aidata, süüta veel kord leek ja hakkame sellele peale puhuma. Loodan, et meil õnnestub tekitada kunstlikku tõmmet ja sundida leeki põlema nagu Maalgi.»
Nii tehtigi. Ardan süütas põleti ja hakkas süüa tegema, jälgides teatava kahjurõõmuga, kuidas Nicholl ja Barbicane vaheldumisi tulle puhusid ja tuult lehvitasid, et leegile pidevalt värsket õhku anda. Südamepõhjas pidas prantslane oma sõpru ja nende teadust süüdlasteks «kogu selles jamas».
«Te täidate tõmmet alal hoides mingil moel vabrikukorstna osa,» vadistas Ardan. «Mul on teist väga kahju, mu õpetatud sõbrad, aga kui me tahame saada kuuma hommikueinet, tuleb alistuda teie füüsika käskudele.»
Möödus veerand, pool tundi, tund, vesi kastrulis ei mõelnudki keema hakata.
«Sul peab kannatust olema, kallis Ardan. Tavaline kaalu omav vesi läheb ruttu soojaks – miks? Ainult sellepärast, et temas toimub kihtide segunemine: pealt langevad külmad kihid suruvad soojenenud ja kergemad alumised kihid üles ja tulemusena omandab kogu vedelik kiiresti kõrge temperatuuri. Kas sul on kunagi olnud juhust soojendada vett mitte alt, vaid ülevalt? Siis kihid ei segune, sest ülemised, soojenenud kihid jäävad paigale. Vee soojusjuhtivus on ju tühine; ülemised kihid võib keema ajada, sel ajal kui alumises kihis jäävad jäätükid sulamata. Meie kaalutus maailmas on aga ükskõik, kust küljest vett soojendada: ringvoolu kastrulis tekkida ei saa ja vesi peab soojenema väga aeglaselt. Kui soovid soojenemist kiirendada, pead kogu aeg vett segama.»
Nicholl hoiatas Ardani, et see ei laseks vee temperatuuril tõusta 100°-ni, vaid piirduks veidi madalama temperatuuriga. Temperatuuril 100°C tekib palju auru ja et selle erikaal on niisama suur kui veel (mõlemal null), siis seguneb vesi auruga ühtlaseks vahuks.
Pahandav ootamatus tekkis hernestega. Kui koti lahti sõlminud Ardan seda kergelt raputas, paiskusid herned õhku ja hakkasid kabijnjs peatumatult ringi lendlema, põrgates vastu seinu ja sealt tagasi. Need hõljuvad herneterad oleksid põhjustanud peaaegu suure õnnetuse: Nicholl tõmbas ühe neist kurku ja hakkas nii tugevasti köhima, et pidi äärepealt lämbuma. Et pääseda ohust ja puhastada õhk, hakkasid sõbrad lendavaid herneid innukalt püüdma võrguga, mille Ardan oli ettenägelikult kaasa haaranud «kuuliblikate kollektsiooni koostamise eesmärgil».
Polnud kerge süüa teha sellistes tingimustes. Ardanil oli õigus, kui ta kinnitas, et siin oleks loobumisvõidu andnud kogenuimgi kokk. Tublisti tuli vaeva näha ka biifsteegi praadimisel: liha oli vaja kogu aeg kahvliga kinni hoida, muidu oleks lihatüki all tekkinud tihe aur selle pannilt üles tõstnud ja pooleldi praetud liha oleks lennanud «üles», kui on lubatud seda sõna tarvitada seal, kus pole ei «ülemist» ega «alumist» poolt.
Kummalist vaatepilti pakkus ka söömine ise selles raskusvabas maailmas. Sõbrad rippusid õhus õige mitmekesistes poosides, mis muide olid küllalt maalilised, ja põrkasid aeg-ajalt peadpidi üksteise vastu. Istuda muidugi polnud võimalik. Niisugused esemed nagu toolid, diivanid, pingid on täiesti kasutud maailmas, kus puudub raskus. Tegelikult poleks ka lauda vaja olnud, kui mitte Ardan poleks tungivalt soovinud lõunatada laua taga.
Vaevaline oli keeta puljongit, veel vaevalisemaks osutus selle söömine. Kuidagi ei õnnestunud kaalutut puljongit valada tassidesse. Ardan oleks niisuguse katse eest maksnud peaaegu kogu hommikuse töövaeva kaotamisega: unustanud, et puljong ei kaalu midagi, koputas ta pahaselt kummulikeeratud kastruli põhja vastu, et kangekaelset puljongit sealt välja ajada. Tulemusena lendas kastrulist välja hiiglasuur kerajas tilk – kera kuju omandanud puljong. Ardan pidi ilmutama žonglööri osavust, et suure vaevaga keedetud puljong taas kinni püüda ja kastrulisse ajada.
Katse lusikaid kasutada jäi tulutuks: puljong tegi kogu lusika kuni sõrmedeni märjaks ja kattis selle ühtlase kihina. Et takistada märgamist, määriti lusikad võiga kokku, kuid see ei parandanud asja: lusikal tekkis puljongist kera ja polnud mingit võimalust seda kaalutut palli suhu saada.
Lõpuks leidis Nicholl lahenduse: vahapaberist keerati torukesed ja nende abil imeti puljong suhu. Samal meetodil tuli meie sõpradel kogu reisi vältel juua vett, veini ja üldse kõiki vedelikke.
Nii lihtsale küsimusele ei osata sageli õigesti vas tata ja loodame, et lugeja ei pane pahaks, kui selgi tame lühidalt, mismoodi vesi mõjub tulele.
Esiteks, põleva kehaga kokku puutuv vesi muutub auruks, võttes seejuures põlevalt kehalt ohtrasti soojust. Et keeva vett auruks muuta, on vaja üle viie korra rohkem soojust kui sama hulga külma vee soojendamiseks 100 °C-ni.
Teiseks hõivab aur sadu kordi suurema ruumala kui vesi, millest ta tekkis; põlevat keha ümbritsev aur tõrjub õhu kõrvale, ilma õhuta pole põlemine aga võimalik.
Et suurendada vee tulekustutusvõimet, segatakse mõni kord vette ... püssirohtu! Teguviis võib pais ta imelikuna, kuid on ometi täiesti mõistlik: püssirohi põleb kiiresti ja eraldab hulganist i mittepõlevaid gaase, mis põlevaid kehi ümbritsedes takistavad põlemist.
Tõenäoliselt olete kuulnud, et parim, mõnikord isegi ainus metsa- või roht latulekahjuga võitlemise viis on metsa või rohtla süütamine vastasküljest. Uus leek liigub möllavale tulemerele vastu ja põlevat mater ja li hävitades jätab tule toiduta. Kohtudes kustuvad mõlemad tuleseinad silmapilkselt, nagu oleks üks neist teise ära õginud (joon. 86).
Paljud on muidugi lugenud Fenimore Cooperi romaanis «Preeria» kirjeldust sellest, kuidas kasutatakse seda tulekustutamisvõtet Ameerika preeriates. Kas saab unustada seda dramaatilist hetke, kui vana trapper päästis tulesurmast reisijad, kes olid jäänud tulekahju teele? Esitame siin selle kirjelduse.
«Vanamehe ilme muutus äkki otsustavaks.
«On aeg tegude juurde asuda,» lausus ta.
«Liiga hilja ärkate, armetu vanamees,» hüüdis Middleton. «Leegid on vaevalt veerand miili kaugusel ja tuul toob neid kohutava kiirusega edasi.»
«Või nii! Leegid! Mulle teevad need vähe muret. Pange köied selle lühikese närbunud rohu külge, mille peal me seisame, ja kiskuge see üles, nii et maa oleks täiesti paljas.»
...Mõne silmapilguga oli umbes kahekümnejalase läbimõõduga plats rohust puhtaks kistud. Selle väikese platsi ühte serva juhtis trapper naisterahvad ning andis Middletonile ja Paulile korralduse katta nende kerged ning tuldvõtvad riided kõigi kaasasolevate vaipadega. Kui need ettevaatusabinõud olid tarvitusele võetud, läks vanamees ise vastasserva, kus kasvas pikk ning kergestisüttiv rohi, ja valinud peotäie kõige kuivemaid kõrsi, asetas need oma püssirohupannile. Kerge põletis võttis heleda sähvatusega tuld. Seejärel heitis ta leegitseva tuusti tihedasse rohupuhmikusse, tõmbus tagasi ringi keskkohta ning jäi kannatlikult tulemusi ootama.
Salakaval loodusjõud haaras ahnelt uue toidu järele ja hetke pärast nilpsasid haralised leegid rohtu.
«Noh, nüüd te näete,» sõnas vanamees, «kuidas tuli tulega lahingut lööb!»
«Aga kas ei või see meile saatuslikuks saada?» hüüdis jahmunud Middleton. «Kas ei too te meile vaenlast lähemale, selle asemel, et teda eemale ajada?»
Tuli sai hoogu, hakkas levima kolme külge ning kustus iseenesest neljandal küljel toidu puudumise tõttu. Järjest suurenedes ja vihase vuhinaga oma vägevust kuulutades hävitas ning laastas ta kõik enda ees, jättes musta, suitseva pinnase hoopis paljamana maha, kui seda vikat iialgi teha oleks suutnud. Põgenike olukord oleks ikka endiselt ohtlikuks jäänud, kui mitte leegid ise poleks puhastatud kohta suurendanud... Juba mõne hetke pärast hakkasid leegid igast küljest kaugemale nihkuma. Põgenikke ümbritses nüüd tihe suitsupilv, kuid nad olid täiesti kaitstud tuleoja eest, mis üha raevunult edasi tormas.
Pealtvaatajad jälgisid trappen lihtsa abinõu mõju samasuguse imestusega, nagu Ferdinandi õukondlased olevat vahtinud seda, kuidas Kolumbus asetas muna seisma ühe otsa peale.»
See metsa- ja roht latulekahjude kustutamise viis pole siiski nii lihtne, kui esimesel pilgul paistab. Ainult väga kogenud inimene võib kasutada tulekahju kustutamiseks vastutuld, muidu võib õnnetus paisuda isegi suuremaks.
Te saate aru, millist oskust läheb tarvis, kui küsite endalt: miks liikus trapperi süüdatud tuli tulekahjule vastu, aga mitte sellest eemale? Puhus ju tuul tulekahju poolt ja ajas tuld reisijatele peale. Näib, et trapperi süüdatud tuli ei oleks pidanud liikuma tulemerele vastu, vaid tagasi, preeria poole. Kui nii oleks juhtunud, jäänuksid reisijad tulerõngasse ja oleksid vältimatult hukkunud.
Milles oli trapperi saladus?
Lihtsa füüsikaseaduse tundmises. Ehkki tuul puhus põleva preeria poolt reisijate poole, oli tule ees vas tupidine õhuvool – tule poole. Tõepoolest: tulemere kohal soojenev õhk muutub kergemaks ja igast küljest tulest veel puutumata preeriast pealevoolav värske õhk surub teda ülespoole. Tule piiril tekib seetõttu õhutõmme vastu tuld. Vastutuli on vaja süüdata sel hetkel, kui tuli on nii lähedale jõudnud, et on tunda õhutõmmet. Seepärast ei hakanudki trapper tegutsema enne, kui oli käes õige hetk. Tarvitsenuks rohi süüdata vaid veidi varem – enne kui õhutõmmet oli tunda, – ja tuli oleks levinud vastupidi ses suunas, muutes inimeste olukorra väl japääsmatuks . Kuid viivitaminegi võinuks niisama saatuslikuks saada: tuli oleks liiga lähedale jõudnud.
Võtke väike klaaspurk või -kolb, valage sellesse vett ja pange pliidil olevasse puhta veega potti nii, et klaas ei puutuks vastu poti põhja; kolb tuleb muidugi riputada traatsi lmusesse. Näib, et kui vesi läheb potis keema, peaks hakkama keema ka kolvis olev vesi. Kuid võite oodata nii kaua kui soovite, vee keemahakkamist kolvis ei jõuate ära oodata: vesi läheb tuliseks, väga tuliseks, kuid keema ei hakka. Keev vesi pole küllalt kuum, et ajada vett kolvis keema.
Tulemus on veidi ootamatu, kuid ometi oleks võinud seda ette näha. Vee keemaajamiseks ei piisa tema kuumutamisest 100°C-ni, talle tuleb anda veel üsna tublisti soojust, et viia teda uude agregaatolekusse – auruks. Puhas vesi keeb temperatuuril 100 °C ning ükskõik kui palju me seda ka ei soojendaks, sellest kõrgemale tema temperatuur harilikes tingimustes ei tõuse. Tähendab, soojusallikas, mille abil soojendatakse kolvis olevat vett, omab temper atuuri 100 °C ning suudab tõsta kolvis oleva vee temperatuuri samuti 100°C-ni. Niipea kui temperatuurid võrdsustuvad, soojust enam kastrulilt kolvile üle ei lähe.
Niisiis, soojendades kirjeldatud viisil vett kolvis, ei saa me anda talle seda soojuse kogust, mis on vaja tema aurustamiseks (iga 100°C-ni soojendatud veegramm vajab auruks muutumiseks veel üle 500 cal soojust). Just seepärast vesi kolvis küll soojeneb, aga keema ei hakka.
Võib tekkida küsimus, mille poolest vesi kolvis erineb kastrulis olevast veest. On ju kolvis seesama vesi, ainult ülejäänud veest eraldavad teda klaasseinad. Miks temaga ei juhtu sama mis kastrulis oleva veega?
Sellepärast et klaas takistab kolvi veel osalemast neis vooludes, mille tagajärjel seguneb kastruli vesi. Iga kastrulivee osake võib vahetult kokku puutuda anuma kuuma põhjaga, kolvivesi aga puutub kokku ainult keeva veega. Järelikult ei saa puhta keeva veega ajada vett keema. Tarvitseb aga lisada kastrulisse peotäis soola, kui asi muutub otsekohe. Soolane vesi ei kee mitte tempratuuril 100°C, vaid veidi kõrgemal temperatuuril ja järelikult võib ta omakorda ajada keema klaaskolvis oleva puhta vee.
«Kui juba keev vesi selleks ei kõlvanud, mis siis veel lumest rääkida!» võib vastata mõni lugeja. Kuid ärge kiirustage vastusega, vaid tehke parem katse sellesama klaaskolviga, mida te just kasutasite.
Täitke kolb poolest saadik veega ja sukeldage ta keevasse soolvette. Kui vesi hakkab kolvis keema, tõstke kolb kastrulist välja ja sulgege ta varem valmis pandud korgiga. Nüüd pöörake kolb ümber ja oodake, kuni keemine lakkab. Seejärel valage kolb üle keeva veega – vesi ei hakka keema. Kuid pange kolvi põhjale veidi lund või valage see lihtsalt külma veega üle, nagu näidatud joonisel 87, – ja te näete, et vesi hakkab keema ... Lumi sai hakkama sellega, millega ei tulnud toime keev vesi!
Asi on seda mõistatuslikum, et käega katsudes ei tundu kolb olevat eriti kuum. Samal ajal näete oma silmaga, kuidas vesi kolvis keeb!
Tegelikult on seletus järgmine: lumi jahutas kolvi seinu; selle tulemusena tihenes aur kolvi sees veetilkadeks. Et õhk oli kolvist välja surutud juba keemise ajal, siis on vesi nüüd märksa madalama rõhu all. On aga teada, et rõhu vähenemisel keeb vedelik madalamal temperatuuril. Seega on meil kolvis küll keev vesi, kuid mitte kuum keev vesi.
Kui kolvi seinad on väga õhukesed, võib auru äkiline tihenemine kutsuda kolvis esile midagi plahvatusetaolist; välisrõhk, tasakaalustama ta kolvi seest piisava vasturõhuga, võib selle katki suruda (te näete, muide, et sõna «plahvatus» pole siin omal kohal). Seepärast on parem võtta katse jaoks ümmargune kolb, et õhk rõhuks võlvikujulisele pinnale.
Kõige ohutum on taolist katset teha plekist petrooleumi- või õlinõuga. Ajanud niisuguses nõus veidi vett keema, keerake kork kõvasti peale ja valage nõu üle külma veega. Otsekohe muljub välisõhu rõhk plekkpurgi lömmi, sest aur anumas tiheneb veeks. Plekkanum läheb välisõhu rõhumise tõttu mõlki, just nagu raske vasara löögist (joon. 88).
Raamatus «Reisid võõrsil» jutustab ameerika humorist Mark Twain ühest juhtumist oma reisil Alpides (see on muidugi väljamõeldud juhtum; joon. 89).
«Meie ebameeldivused olid lõppenud; seepärast võisid inimesed puhata, aga minul avanes lõpuks võimalus pöörata tähelepanu ekspeditsiooni teaduslikule küljele. Kõigepealt tahtsin ma baromeetri abil määrata meie asukoha kõrgust, kuid see ei andnud kahjuks mitte mingeid tulemusi. Teaduslike raamatute lugemisest oli mulle meelde jäänud, et koha kõrguse leidmiseks tuleb keeta kas termomeetrit või baromeetrit. Kumba, seda ma kindla peale öelda ei osanud, seepärast otsustasin keeta mõlemat.
Ja ikkagi ei saanud ma mingeid resultaate. Mõõteriistu vaadates nägin, et need olid lõplikult rikutud: baromeetrist oli alles ainult vaskosuti, aga termomeetri kuulis tolgendas üksnes tükike elavhõbedat...
Otsisin välja teise baromeetri; see oli täiesti uus ja väga hea riist. Keetsin teda pool tundi oasupis, mida valmistas kokk. Tulemus oli ootamatu: riist lakkas täiesti töötamast, kuid supp omandas nii tugeva baromeetri maitse, et peakokk – väga tark mees – muutis supi nimetust menüüs. Uus roog pälvis üldise heakskiidu, nii et andsin käsu valmistada iga päev baromeetrisuppi. Baromeeter oli loomulikult mokas, kuid mul polnud sellest üldse kahju. Et ta ei aidanud mul koha kõrgust määrata, siis polnud mul teda enam vaja.»
Jätame naljad kõrvale ja püüame vastata küsimusele, mida siis tegelikult tulnuks keeta, kas termomeetrit või baromeetrit.
Termomeetrit, ja vaat mille pärast .
Eelmisel katsel nägime, et mida väiksem on rõhk vee kohal, seda madalam on tema keemistemperatuur. Et mäkketõusmisel õhurõhk väheneb, siis peab samal ajal alanema ka vee keemistemper atuur. Ja tõepoolest, vaatlused näitavad, et erinevatel õhurõhkudel on puhta vee keemistemperatuurid järgmised:
| keemistemp., °C | 101 | 100 | 98 | 96 | 94 | 92 | 90 | 88 | 86 |
| rõhk, mm Hg | 787,7 | 760 | 707 | 657,5 | 611 | 567 | 525,5 | 487 | 450 |
Bernis (Sveits), kus keskmine õhurõhk on 713 mm Hg, keeb vesi lahtistes anumates juba temperatuuril 97,5 °C, Mont Blancil aga, kus baromeeter näi tab 424 mm Hg, on keeva vee temperatuur kõigest 84,5 °C. Tõusmisel langeb keemistemperatuur 3 °C iga kilomeetri kohta. Järelikult, mõõtnud vee keemistemperatuuri (Twaini väljendust mööda: «Kui keedame termomeetrit» ), võime vastavatest tabelitest teada saada koha kõrguse. Selleks peab muidugi omama neid tabeleid, mille Mark Twain «lihtsalt» unustas.
Mainitud otstarbeks kasutatavaid riistu, nn. hüpsotermomeetreid3 on niisama mugav kaasa võtta kui metallbaromeetreid ja nad annavad hoopis täpsemaid väärtusi. Muidugi võib koha kõrgust määrata ka baromeetriga, sest ta näitab õhurõhku otse, ilma igasuguse «keetmiseta »: mida kõrgemale tõuseme, seda väiksemaks muutub rõhk. Kuid selgi korral on tingimata vajalikud kas tabelid, mis näitavad, kuidas muutub õhurõhk kõrguse muutudes, või peame teadma vas tavat valemit. Kõik see oleks humoristi peas nagu segi läinud ja ärgi tas teda keetma «baromeetrisuppi».
Vahva käskjalg Ben Zouf, kellega lugeja on tuttav Jules Verne’i romaanist «Hector Servadac», oli kindlalt veendunud, et keev vesi on alati ja igal pool ühtemoodi kuum. Ilmselt oleks ta sellele arvamusele jäänud kogu eluajaks, kui mitte juhus poleks ta koos komandör Servadaciga heitnud... komeedile. See kapriisne taevakeha põrkas kokku Maaga ja rebis meie planeedi küljest ära tüki, millel juhtusid viibima meie kangelased, ja viis nad endaga kaasa oma kaugele teekonnale mööda elliptilist orbiiti. Ja siis veenduski tentsik iseenese kogemuste põhjal, et keev vesi pole sugugi igal pool ühtviisi kuum. Selle avastuse tegi ta ootamatult hommikueine valmistamise ajal.
«Ben Zouf valas vee kastrulisse, pani selle pliidile ja jäi ootama, millal vesi hakkab keema, et lasta siis vette munad, mis näisid talle olevat tühjad, sest kaalusid nii vähe.
Vähem kui kahe minuti pärast vesi juba kees.
«Pagana pihta! Kuidas küll tuli soojendab!» hüüdis Ben Zouf.
«Mitte tuli ei soojenda paremini,» vastas Servadac mõtlikult, «vaid vesi hakkab kiiremini keema.»
Võtnud seinalt Celsiuse termomeetri, pistis ta selle keevasse vette. Kraadiklaas näitas ainult 66 kraadi.
«Ohoo,» hüüdis ohvitser, «vesi keeb temperatuuril 66 kraadi 100 kraadi asemel!»
«Niisiis, kapten?»
«Niisiis, Ben Zouf, soovitan sul hoida mune keevas vees veerand tundi.»
«Kuid nad keevad ju kõvaks!»
«Ei, sõbrake, nad saavad vaevalt keenuks!»
Mainitud nähtuse põhjuseks oli ilmselt atmosfääri kõrguse vähenemine. õhukiht oli umbes 1/3 võrra madalam ja seepärast keeski väiksema rõhu all olev vesi temperatuuril 66 kraadi 100 kraadi asemel. Samasugune nähtus oleks aset leidnud mäel, mille kõrgus on 11000 m. Ja olnuks kaptenil baromeeter, oleks see näidanud õhurõhu vähenemist.»
Me ei hakka oma kangelaste tähelepanekutes kahtlema: nad kinnitavad, et vesi kees temper atuuril 66 °C, ja meie võtame seda kui fakti. On aga õige küsitav, kas nad oleksid end nii hõredas õhus hästi tundnud.
«Hector Servadaci» autor märgib täie õigusega, et s ama sugune nähtus esineks 11 000 m kõrgusel: nagu arvutustest näha, peab vesi seal keema tõepoolest temperatuuril 66 °C. (* Tõepoolest, nii nagu eelmises paragrahvis öeldud, langeb vee keemistemperatuur 3°C võrra tõusmisel 1 km võrra, seega peab keemistemperatuuri langemiseks 66 °C-ni tõusma 34 : 3 ≈ 11 km kõrgusele.) Aga õhurõhk peab seejuures olema 190 mm Hg, täpselt veerand normaalset õhurõhust. Nii hõredas õhus on hingata praktiliselt võimatu! Jutt on ju kõrgustest, mis asuvad stratosfääris. Me teame, et lendurid, kes tõusid hapnikumaski ta nii kõrgele, kaotasid õhupuudusest teadvuse, sel ajal kui Servadac ja tema tentsik tundsid end rahuldavalt. Oli hea, et Šervadacil polnud käepärast baromeetrit, muidu oleks kirjanik pidanud sundima seda riista näitama teistsugust arvu, kui nõuavad füüsikaseadused.
Kui meie kangelased oleksid kujutletava komeedi asemel sat tunud näiteks Marsile, kus atmosfäärirõhk ei ületa 60–70 mm Hg, siis oleks vesi keenud veel madalamal temperatuuril – temperatuur iga ainult 45 °C.4 Vastupidi, väga kuuma keeva vett võib saada sügavate šahtide põhjas, kus õhurõhk on märksa suurem kui maapinnal. Šahtis sügavusega 300 m keeb vesi temperatuuril 101°, 600-m šahti põhjas temperatuuril 102°C. Tublisti suurema rõhu all keeb vesi ka aurumasina katlas. Näiteks rõhul 14 atm keeb vesi temperatuuril 200 °C. Vastupidi, õhupumba kupli all saab vett sundida tormiliselt keema tavalisel toatemperatuuril, nii et keev vesi on kõigest 20 kraadi soe.5
Rääkisime just jahedast keevast veest. On aga veelgi imepärasem asi – kuum jää. Oleme harjunud mõtlema, et vesi ei saa tahkes olekus eksisteerida kõrgemal tem peratuuril kui 0°C. Inglise füüsiku P.W. Bridgmani uurimised aga näitasid, et asi pole nii: väga suure rõhu all vesi tahkestub ka temperatuuril, mis on tublisti kõrgem kui 0°C. B ridgman näitas, et võib esineda mitut sorti jääd. See jää, mida ta nim etas jääks 5, tekib kohutaval rõhul 20 600 atm ja jääb tahkeks kuni temperatuurini 76 °C. Niisugune jää põletaks käsi, kui me saaksime teda puudutada. Kuid just seda on võimatu teha: jää 5 tekib võimsa pressi survel parimast terasest tehtud paksusei- nalises nõus. Näha või kätte võtta seda ei saa ja kuuma jää omadusi õpitakse tundma kaudsel teel.
Huvitav, et kuum jää on tihedam tavalisest, tihedam isegi veest: tema tihedus on 1,05 g/cm3. Kuum jää upuks vees, kuna harilik jää tõuseks pinnale.
Saada söest sooja asemel külma pole midagi teostamatut: seda tehakse iga päev nn. kuiva jää vabrikutes. Sütt põletatakse kateldes, tekkiv suits puhastatakse, kusjuures süsihappegaas kõrvaldatakse leeliselahusega, soojendamise teel lahusest saadud puhas süsihappegaas viiakse järgneva jahutamise ja 70 atm rõhu abil vedelasse olekusse. See on toosama vedel süsihape, mida paksuseinalistes silindrites veetakse karastusjookide tehastesse ja kasutatakse tööstuse vajadusteks. Süsihape on küllalt külm, et külmutada pinnast, nagu tehti Moskva metroo ehitamisel; kuid paljudel juhtudel on vaja tahket süsihapet, nn. kuiva jääd.
Kuiv jää, s.t. tahke süsihape, tekib vedelast süsihappest selle kiirel aurustumisel alandatud rõhul. Välimuselt meenutavad kuiva jää tükid pigem kokkupressitud lund kui jääd ja üldse erineb ta tahkest veest õige palju. Süsihappejää on raskem tavalisest jääst ja vajub vees põhja. Vaatamata erakordselt madalale temperatuurile (-78°C) ei tunne sõrmed külma, kui tükk kuiva jääd võtta ettevaatlikult pihku: kokkupuutel käega tekkiv süsihappegaas kaitseb nahka külma mõju eest. Ainult siis, kui kuiva jää tükki kõvasti pigistame, riskime oma sõrmed ära külmetada.
Nimetus «kuiv jää» iseloomustab erakordselt õnnestunult selle jää peamist füüsikalist iseärasust: ta ei ole tõepoolest kunagi märg ega tee midagi märjaks. Soojendamisel läheb ta otse üle gaasiks, jättes vedela oleku vahele. Vedelas olekus süsihape rõhul 1 atm eksistee rida ei saa.
Kuiva jää kirjeldatud iseärasus koos tema madala temperatuuriga teeb ta asendamatuks jahutusaineks. Süsihapp- eääga säilitatavad toiduained ei niisku ja on kaitstud riknemise eest: tekkiv süsihappegaas takistab mikroorganismide arengut ning toiduainetele ei teki ei baktereid ega hallitust. Ka putukad ja närilised ei saa elada selles keskkonnas. Lõpuks on süsihape kindel tulekaitsevahend: mõni tükk põlevasse bensiini visatud kuiva jääd kustutab kohe tule. Kõik see on kindlustanud kuivale jääle laialdase rakenduse olmes ja tehnikas.
Niisuguse poeetilise nime andsid hiinlased looduslikule magnetile. Nad räägivad, et armastav kivi (chu shi) tõmbab külge rauda nii nagu hell ema oma lapsi. On tähe epanuväärne, et prantslastel, rahval, kes elab mandri teisel äärel, leiame magneti jaoks analoogilise nimetuse: prantsuskeelne sõna aimant märgib nii magnetit kui ka armastavat.1
Selle armastuse jõud on looduslikel magnetitel tühine ja seepärast kõlab magneti kreekakeelne nimetus Herkulese kivi üsna naiivselt. Kui vana Hellase elanikud olid nii vaimustatud juba loodusliku magneti õige tagasihoidlikust külgetõmbejõust, mida nad küll ütleksid, kui näeksid moodsa metallurgiatehase magneteid, mis suudavad tõsta mitmetonniseid metallikamakaid. Tõsi, need poie looduslikud, vaid elektromagnetid, s.t. rauatükid, mis on magneeditud neid ümbritsevat mähist läbiva elektrivoolu toimel, kuid mõlemal juhul mõjub oma olemuselt üks ja seesama jõud – magnetism.
Ei maksa arvata, et magnet mõjub ainult rauale. On terve hulk teisi aineid, mis samuti alluvad tugeva magneti mõjule, ehkki mitte sel määral nagu raud. Niklit, koobaltit, mangaani, plaatina, kulda, hõbedat, alumiiniumi tõmbab magnet külge nõrgalt. Veel tähelepanuväärsemad on nn. diamagnetiliste ainete, nagu tsingi, plii ja vismuti, omadused: neid aineid tõukab tugev magnet eemale!
Vedelikud ja gaasidki alluvad magneti tõukavale või tõmbavale mõjule, tõsi, õige nõrgalt; magnet peab olema väga tugev, et oleks märgatav tema mõju neile ainetele. Puhast hapnikku tõmbab magnet näiteks enda poole; kui täita seebimull hapnikuga ja viia ta tugeva elektromagneti pooluste vahele, siis venib mull piklikuks, sest teda tõmbavad nähtamatud magnet jõud. Ka küünlaleek muudab oma taval ist kuju tugeva elektromagneti pooluste vahel, olles ilmselt aldis magnetiõudude mõjule (joon. 90).
Oleme harjunud mõtlema, et kompassinõel on alati ühe otsaga pöördunud põhja, teisega lõunasse. Seepärast tundub meile täiesti mõttetuna küsimus: kus maakeral näitavad kompassinõela mõlemad otsad põhjasuunda?
Ja veel mõtte tum küsimus: kus maakeral näitavad mõlemad magnetnõela otsad lõunasuunda?
Te olete valmis kinnitama, et selliseid paiku meie planeedil ei ole ega saagi olla. Ometi on nad olemas.
Tuletage meelde, et Maa magnetpoolused ei lange kokku geograafilistega, ning tõenäoliselt te mõistate, millistest planeedi punktidest on käesolevas ülesandes juttu. Kuhupoole näitab geograafilisele lõunapoolusele paigutatud kompassinõel? Selle üks ots on suunatud lähema magnetpooluse poole, teine vastas suunas. Ent ükskõik millises suunas me geograafiliselt lõunapooluselt ka teele asuksime, läheme alati põhja poole; teist suunda geograafiliselt lõunapooluselt olla ei saa, ümberringi on kõikjal põhi. Tähendab, sinna paigutatud magnetnõela mõlemad otsad on suunatud põhja poole.
Täpselt samuti peab geograafilisele põhjapoolusele paigutatud magnetnõel näitama mõlema otsaga lõuna poole.
Huvitavat pilti on kujutatud joonisel 91, mis on kopeeritud fotolt: elektromagneti peale pandud käel turritavad karmide karvade taoliselt nööpnõelte kimbud. Käsi ise ei tunne midagi sellest magnetjõust: nähtamatud niidid läbivad käe, ilmutamata kuskil oma olemasolu. Aga terasnõelad alistuvad kuulekalt jõu mõjule ja asetuvad kindla korra kohaselt, demonstreerides meile magnetjõujoonte suunda.
Inimesel pole magnetimeelt, seepärast võime magnetit ümbritsevate magnetjõudude olemasolu ainult aimata.* Kuid kaudsel teel pole raske näidata nende jõudude jaotust. Kõige parem on seda teha rauapuru abil. Katke sile papitükk või klaasplaat õhukese rauapurukihiga; pange papi või klaasi alla tavaline magnet ja raputage rauapuru kergelt. Magnet jõud «läbivad» kergesti pappi ja klaasi; järelikult rauapuru magneetub magneti mõjul; raputamisel eralduvad rauapuruosakesed hetkeks papitükilt ja võivad magnet jõu mõjul võtta samasuguse asendi, nagu oleks võtnud antud juhul magnetnõel, s.t. nad asetuvad piki magnetjõujooni. Tulemuseks on raua puru korrastumine kõveratesse ridadesse, mis toovad ilmekalt esile nähtamatute magnet jõujoonte jaotuse.
(* Huvitav on kujutleda meie elamusi, kui meil oleks vahetu
magnetimeel. Cradle’il õnnestus õpetada vähke magneti mõju tajuma. Ta märkas, et vähid topivad endale pärast kestumist kõrvadesse väikesi kivikesi (vaagkivikesi e. statoliite); need mõjuvad oma raskusega tundlikule karvakesele, mis on vähi tasakaaluelundi osaks. Samasugused kivikesed, nn. otoloiidid, on inimese kõrvas põhilise kuulmiselundi lähedal. Mõjudes püstsihis, näitavad need kivikesed raskusjõu suunda. Kivikeste asemel pani Cradle vähkidele alla rauapuru. Magneti lähendamisel vähile asetus see tasandisse, mis oli risti magnet- ja raskusjõu resultandiga.
«Viimasel ajal on samalaadseid katseid muudetud kujul õnnestunud korraldada isegi inimesega. Köler kleepis väikesed rauatükid korva trumminaha külge; seetõttu tajus kõrv magnetjõu võnkumisi helina.» (0 . Wiener.))
Paigutame magneti kohale plaadi rauapuruga ja raputame seda. Saame joonisel 92 näidatud pildi.
Magnetjõujooned moodustavad keerulise kõverjoonte süsteemi. On näha, kuidas nad kiirtetaoliselt lähtuvad magnetpooluste juurest, kuidas rauapuru osakesed ühinevad ja moodustavad lühemaid või pikemaid kaari pooluste vahel. Rauapuru teeb silmaga nähtavaks selle, mida mõttes kujutab ette iga füüsik ja mis nähtamatul kujul ümbritseb iga magnetit. Mida lähemal poolusele, seda tihedamad ja selgemad on magnet jõujooned; poolustest eemaldumisel nad, vastupidi, hõrenevad ja kaotavad selguse, demonstreerides näitlikult magnet jõudude nõrgenemist kauguse kasvades.
Sellele sageli esitatavale küsimusele vastamiseks tuleb kõigepealt endale selgeks teha, mille poolest erineb magnet magneetumata terasetükist. Iga raua aatom, millest koosneb magneeditud või magneetimata teras, kujutab endast väikest magnetit.2 Magneetimata terases paiknevad need väikesed aatommagnetid korrapäratult, nii et tihe mõju hävitab vastupidiselt paikneva magnetikese mõju (joon. 93a). Magnetis, vastupidi, paiknevad kõik aatommagnetikesed korrastatult, ühenimelised poolused ühel pool (joon. 93b).
Mis toimub teraspulgas, kui hõõruda seda magnetiga? Oma külgetõmbejõuga pöörab magnet terasetüki aatom- magnetikeste ühenimelised poolused ühele poole. Joonisel 93c on näidatud, kuidas aatommagnetikesed pöörduvad algul lõunapoolustega magneti põhjapooluse poole, seejärel aga, kui magnetit nihutatakse, asetuvad nad piki tema liikumise suunda, lõunapoolustega terasetüki keskjoone poole.
Nüüd on kerge mõista, kuidas talitada terase magneetimisel. Terasetüki ühele otsale tuleb panna magneti mingi poolus ja seda tihedalt terase vastu surudes liigutada piki terasetüki pinda. See on küll lihtne ja iidne magneetimise viis, kuid kõlbab ainult nõrkade ja väikeste magnetite valmistamiseks. Tugevaid magneteid saab siis, kui magneetimisel kasutatakse elektrivoolu toimet.
Metallurgiatehastes võib näha elektromagnetilisi tõstekraanasid, mis toimetavad tohutuid raskusi ühest kohast teise. Niisugused kraanad osutavad hindamatuid teeneid raudesemete tõstmisel ja nihutamisel terasevalamis- ning muudes taolistes tehastes. Elektromagnetkraanad kannavad massiivseid rauakobakaid või kümneid tonne kaaluvaid masinaosi kerge vaevaga ja ilma eriliste kinnitu steta ühest kohast teise. Täpselt niisamutit ranspordivad nad kastideta ja pakendita lehtterast, traati, naelu, metal limurdu ning muud materjali, mille vedu muul viisil nõuaks küllalt palju vaeva.
Kui tülikas oleks raudplaat ide kokkupakkimine ja hunnikussevedamine – töö, mille ühel hoobil tegi võimas elekt romagnetkraana (joon. 94). Hoiti kokku tööjõudu ja ka töö ise muutus lihtsamaks. Joonisel 95 näete, kuidas elektromagnetkraana veab isegi tünnidesse pakitud naelu, tõstes kuni viis tünni korraga. Ühes metal lurgiatehases on neli elekt romagnetkraanat , millest igaüks võib korraga tõsta 10 relssi; kraanad asendavad kahtsada töölist. Pole vaja hoolitseda raskuste kinnitamise eest kraanade külge: seni, kuni on voolu elektromagneti mähistes, ei kuku ükski koorem maha. Kui aga vool mähises millegipärast katkeb, on avarii vältimatu. Selliseid juhtumeid on varem esinenud.
Ühes ajakirjas näiteks kirjutati järgmist: «Ühes Ameerika tehases tõstis elektromagnet rauavalu vagunitest ja laskis seda ahju. Ootamatult juhtus midagi Niagara elektrijaamas, mis varustas tehast vooluga, ja vool katkes. Metall vabanes elektromagneti küljest ja kukkus kogu oma raskusega tööliseie pähe. Et ära hoida selliste õnnetusjuhtumite kordumist ning säästa elektrienergiat, varustatakse elektromagnetid eriliste seadistega. Kui magnet on transporditavad esemed õhku tõstnud, ümbritsetakse need tugevate teraskäppadega, mis seejärel ise hoiavad koormat ülal, nii et tõstmise ajaks lülitatakse vool välja.»
Joonistel 94 ja 95 kujutatud elektromagnet ite läbimõõt on kuni 1,5 m; iga magnet suudab tõsta kuni 16 tf (kaubavaguni raskus) . Üks selline magnet tõstab ööpäeva jooksul ümber rohkem kui 600 tonni. On olemas elektromagneteid, mille tõstevõime on 75. tonni, s.t. terve veduri raskus!
Va adates sellist elektromagnetit töötamas, võib mõnelgi lugejal tekkida mõte: kui mugav oleks magnetite abil tõsta hõõguvaid raudplokke! Kahjuks on see võimalik
Vahel kasutavad elektromagneteid ka mustkunstnikud. Kerge on kujutleda, milliseid efektseid trikke saavad nad teha selle nähtamatu jõu abil. Dari, kuulsa raamatu Elekter oma rakendustes autor, esitab järgmise loo ühe prantsuse mustkunstniku Alžiiris antud etenduselt:
«Laval on väike rautatud kast, millel on kaanel käepide. Kutsusin vaatajate hulgast mõnd tugevamat meest. Vastuseks tõusis kesk- mist kasvu tugeva kehaehitusega araablane, tõeline araabia Herak- les. Ta astus lavale julge ja enesekindla moega ning peatus veidi üleolevalt naeratades minu lähedal.
«Kas te olete väga tugev?» küsisin, silmitsedes teda pealaest jalatallani.
«Jah,» vastas ta hooletult
«Kas olete kindel, et jääte alati tugevaks?»
«Täiesti kindel.»
«Te eksite: ühe hetkega võin teilt võtta teie jõu ja te muutute nõrgaks nagu väike laps.»
Araablane naeratas põlglikult märgiks, et ei usu mu juttu.
«Tulge siia,» kutsusin mina, «ja tõstke see kast üles.»
Araablane kummardus, tõstis kasti üles ja küsis kõrgilt:
«Ja muud ei midagi?»
«Oodake natuke,» kostsin. Manasin näole tõsise ilme, tegin käega käskiva liigutuse ja sõnasin pidulikult:
«Nüüd olete nõrgem kui naine. Proovige uuesti kasti tõsta!»
Jõumees ei peljanud sugugi mu nõiavõimet ja asis taas kastist kinni, kuid seekord pani kast vastu ja vaatamata araablase meele- heitlikele pingutustele jäi liikumatuks, otsekui oleks ta maa külge kinni kasvanud. Araablane püüdis kasti tõsta sellise jõuga, millest jätkunuks hiiglasliku raskuse tõstmiseks, kuid kõik oli asjatu. Väsi- nult, hingeldades ja häbist põledes jättis ta lõpuks tulutud katsed. Nüüd hakkab ta uskuma nõiakunsti jõusse.»
Tsivilisaatorite esindaja nõiakunsti saladus oli lihtne. Kasti raudpõhi oli alusel, mis kujutas endast tugeva elektromagneti poolust. Kuni voolu polnud, oli kasti kerge üles tõsta. Tarvitses aga vaid vool läbi elektromagneti mähise lasta, kui kasti kergitamiseks poleks piisanud enam isegi 2 – 3 mehe ühistest jõupingutustest.
Ootamatu rakenduse leidis tugev elektromagnet raskejõustiklaste treenimiseks. Tõstekraanades kasutatav elektromagnet riputatakse teatavale kõrgusele lakke, veidi kõrgemale inimese pikkusest. Triikrauda käes hoidev atleet püüab aga ületada elektromagneti külgetõmbejõudu. Sõltuvalt voolust, mida reguleerib treener, on tõmme erinev ja võib saavutada sellise väärtuse, et atleet, kes ei taha triikrauda käest lasta, riskib magneti külge rippu jääda, kui tema seltsimehed ei aita tal ühiste jõupingutustega maa peal püsida.
Veel huvitavam on ülesanne, mida magnet täidab põllumajanduses: ta aitab põllumehel eraldada kultuurtaimede seemneid umbrohuseemnetest. Umbrohuseemned on karvased, nad haakuvad mööduvate loomade karvade külge ja levivad seetõttu kaugele emataimest. Seda umbrohuseemnete iseärasust, mis on kujunenud neil olelus võitluses miljonite aastate jooksul, kasutab põllumajandustehnika selleks, et magnetite abil kõrvaldada umbrohu karvased seemned kasulike taimede nagu lina, ristiku, lutserni siledate seemnete seast.
Kui segada kultuurtaimede ja umbrohtude seemnete segu peenikese rauapuruga, siis jäävad rauakübemed karvaste umbrohuseemnete, mitte aga kultuurtaimede siledate seemnete külge. Sattudes seejärel küllalt tugeva elektromagneti mõjuvälja, jaguneb seemnete segu automaatselt puhasteks seemneteks ja umbrohust lisandiks: magnet püüab segust kinni kõik need seemned, mida ümbritseb rauapuru.4
Selle raamatu alguses mainisin prantsuse kirjaniku Cyrano de Bergeraci huvitavat teost Teine maailm ehk Kuu riigid ja impeeriumid. Muu hulgas kirjeldatakse seal huvitavat lennumasinat, mille ehitus rajanes magneti külgetõmbejõul ja millel lendas üks loo kangelasi. Tsiteerime seda sõna-sõnalt:
«Minu käsul ehitati kerge raudsõiduk. Sisenesin sellesse ja võtsin mugavalt istet. Seejärel hakkasin enda kohal üles viskama magnetkera. Otsemaid tõusis raudsõiduk õhku. Iga kord kui hakkasin lähenema punktile, kuhu mind tõmbas kera, viskasin ta uuesti üles. Isegi siis, kui tõstsin kera lihtsalt kätel üles, kerkis ka sõiduk, püüdes läheneda kerale. Pärast mitmekordseid kera ülesviskamisi ja sõiduki tõusmisi lähenesin punktile, kust algas minu kukkumine Kuule. Ja et ma sel hetkel hoidsin magnetkera kõvasti käes, siis tõmbus sõiduk minu vastu ega eemaldunud enam. Et kukkumisel end mitte surnuks lüüa, viskasin kera õhku niimoodi, et selle külgetõmme aeglustas sõiduki langemist. Kui olin veel ainult kahesaja- kolmesaja sülla kõrgusel Kuu pinnast, hakkasin heitma kera risti kukkumise suunaga, kuni sõiduk jõudis üsna pinna lähedale. Siis hüppasin sõidukist ja laskusin pehmelt liivale.»
Muidugi ei kahelnud keegi, ei romaani autor ega selle lugejad, et kirjeldatud lennumasin on täiesti kasutamiskõlbmatu. Arvan aga, et paljud ei oska õigesti seletada, milles seisneb selle projekti teostamatus: kas selles, et on võimatu heita magnetit, olles ise raudses sõidukis, või selles, et sõiduk ei tõmbu magneti poole, või milleski muus.
Ei, visata magnetit saab ja ta tõmbaks ka sõidukit enda poole, kui ta on ainult küllalt tugev – aga ikkagi ei tõuseks lennumasin karvavõrdki. Kas teil on olnud juhust visata mõnda rasket eset paadist kaldale? Kahtlemata olete seejuures märganud, et paat ise nihkus kaldast eemale. Teie lihased, mis andsid visatavale kehale tõuke ühes suunas, tõukavad samal ajal teie keha (koos paadiga) vastassuunas. Siin avaldub see mõju ja vastumõju seadus, millest meil juba korduvalt juttu on olnud. Magneti heitmisel toimub sama: sõitja, visates magnetkera üles (suure jõupingutusega, sest kera tõmbub raudsõiduki poole), tõukab paratamatult kogu sõidukit allapoole. Kui siis kera ja sõiduk vastastikuse külgetõmbe mõjul taas lähenevad, tulevad nad ainult tagasi esialgsele kohale, järelikult on selge, et isegi kui sõiduk midagi ei kaaluks, pandaks ta magnetkera heitmisega üksnes võnkuma mingi punkti ümber. Edasi liikuma panna pole teda sel viisil võimalik.
Cyrano de Bergeraci ajal (17. sajandi keskel) polnud mõju ja vastumõju seadus veel tuntud; seepärast on kahtlane, kas prantsuse satiirik oleks ise suutnud selgitada oma humoorika projekti alusetust.
Huvitavat juhust oli kord võimalik jälgida töötamisel elektromagnetkraanaga. Üks töölistest märkas, et elektromagnet oli külge tõmmanud raske raudkuuli, mis oli ketiga kinnitatud põranda külge. See kett oli lühike ega lasknud kuulil magnetiga kokku puutuda: kuuli ja magneti vahele jäi umbes käelaiune õhuvahe. Tekkis ebatavaline pilt: vertikaalselt ülespoole tolknev kett! Magneti jõud oli nii suur, et kett jäi püstasendisse isegi siis, kui tööline ronis seda mööda üles, ja püsis õhus nagu tõeline Muhamedi sark (joon. 96). (* See näitab elektromagneti hiiglaslikku jõudu, sest magnetite tõmme nõrgeneb tunduvalt, kui kaugus magneti pooiuste ja külge- tõmmatava keha vahel suureneb. Hoburaudmagnetil, mis vahetul kokkupuutel suudab ülal hoida sajagrammist raskust, väheneb tõste- jõud kaks korda, kui külgetõmmatava eseme ja magneti vahele panna paberileht. Seepärast ei kaetagi magneti pooluste otsi tavaliselt värviga, ehkki see kaitseks neid roostetamise eest.)
Muuseas, Muhamedi sargast. Muhameedlased on veendunud, et kirst prohveti jäänustega asetseb õhus, rippudes ilma igasuguse toeta surnukambri põranda ja lae vahel. On see võimalik?
«Räägitakse,» kijutas Euler oma «Kirjades mitmesugustest füüsikalistest mateeriatest», «nagu hoiaks Muhamedi sarka õhus mingi magneti jõud. See ei tundugi võimatu, sest on olemas kunstlikult tehtud magnetid, mis tõstavad õhku kuni sada naela.» (Kirjutatud 1774. a., kui elektromagneteid veel ei tuntud.)
Niisugune seletus ei pea paika; kui mainitud viisil (s.t. kasutades magneti külgetõmmet) olekski saavutatud tasakaal, oleks see vaid hetkeline olnud: piisanuks pisimastki tõukest, nõrgimastki tuulepuhangust, et seda tasakaalu rikkuda ja siis oleks kirst kas kukkunud maha või tõusnud lae alla. Sarka liikumatult paigal hoida on praktiliselt niisama võimatu kui panna koonust seisma oma tipule (mis samuti on teoreetiliselt võimalik). Muide, Muhamedi sarka võib täiesti magnetite abil järele teha, kuid selleks ei tule kasutada mitte nende vastastikust tõmbumist, vaid hoopis tõukumist. (Selle, et magnetid võivad peale tõmbumise ka tõukuda, unustavad sageli isegi inimesed, kes on füüsikat äsja õppinud.)
Teadupärast magnetite samanimelised poolused tõukuvad. Kaks magneeditud raudtala, mis asetsevad samanimeliste poolustega teineteise vastas, tõukuvad teineteisest eemale. Valmistades ülemise tala sobiva raskusega, võib selle kergesti panna hõljuma alumise kohal püsivas tasakaalus. Selleks tuleb ülemist magnetit mingite mittemagnetilisest materjalist, näiteks klaasist tugedega takistada pöördumast horisontaaltasandis. Nõnda võiks õhus hõljuda ka legendaarne Muhamedi sark.5
Lõpuks on seda sorti nähtust võimalik tekitada ka magnetilise külgetõmbejõu mõjul, kui teha seda liikuva keha puhul. Sellel ideel põhineb hõõrdevabalt liikuva elektromagnetilise raudtee tähelepanuväärne projekt (joon. 97), mille esitas nõukogude füüsik В. P. Veinberg. Projekt on sedavõrd põnev, et igal füüsikast huvitatud inimesel on sellega kasulik tutvuda.
Raudteel, mida soovitab ehitada В. P. Veinberg, on vagunid täiesti kaalutud; nende kaal on tasakaalus tatud elektromagnetilise külgetõmbega. Seepärast ärge imestage, kui saate teada, et projekti järgi ei liigu vagunid rööbastel, ei uju vees ega planeeri õhus, vaid lendavad ilma igasuguse toeta, mitte millegi vastu puutudes, rippudes magneti nähtamatutes vägevates jõujoontes. Neile ei mõju vähimatki hõõrdumist ja järelikult kord liikuma pandult jätkavad nad inertsi mõjul seda liikumist, vajamata vedurit.
Kirjeldatud mõte teosta takse järgmisel viisil. Vagunid liiguvad vasktorus, millest on õhk välja pumbatud, et selle takistus ei segaks vaguni liikumist. Hõõrdumist põhja vastu ei ole, sest vagunid ei puutu toru seintega kokku. Nad ripuvad õhutühjas ruumis, kusjuures neid hoiab üleval elektromagnetite jõud. Selle sihiga on torule kogu tee ulatuses kinnitatud kindlatele kaugustele üksteisest väga tugevaid elektromagnetid. Need tõmbavad torus liikuvaid raudvaguneid enda poole ega lase neil kukkuda. Magnetite jõud on arvestatud nõnda, et torus tormav vagun jääb kogu aeg tema lae ja põranda vahele, puutumata kokku ei ühe ega teisega. Elektromagnetid tõmbavad nende all liikuvat vagunit ülespoole. Vagun ei saa aga vastu lage põrgata , sest raskusjõud veab teda allapoole; vaevalt on vagun valmis põrandat puudutama, kui järg* mise elektromagneti tõmbejõud ta taas ülespoole tõstab... Nii tormab vagun elektromagnetite hõlmas lainelist joont mööda hõõrdumise ja tõugeteta nagu planeet maailmaruumis.
Mida kujutavad endast vagunid? Need on sigarikujulised silindrid läbimõõduga 90 cm ja pikkusega 2,5 m. Muidugi on vagun hermeetiliselt suletud – liigub ta ju õhuta ruumis – ja varus tatud õhu automaatse puhastamise seadmetega nagu allveelaev.
Ka vagunite teelesaatmise viis on täiesti erinev kõigest sellest, mida on kasutatud seni: seda võib võrrelda vahest ainult kahuripauguga. Tõepoolest, vagunid sõna otseses mõttes tulistatakse välja nagu mürsud, ainult kahur on siin elektromagneti line.6 Saate jaama ehitus põhineb spiraalselt mähitud pooli (solenoidi) omadusel tõmmata endasse raudvarrast , kui teda läbib vool. Sissetõmbamine on nii äkiline, et varras võib pooli küllaldase pikkuse ja küllalt tugeva voolu korral omandada hiiglasliku kiiruse. See jõud paiskabki vagunid paigalt uuel, elektromagnetilisel raudteel. Et hõõrdumine torus puudub, siis v ag u nite kiirus ei vähene, vaid nad tormavad inertsi mõjul suure kiirusega seni, kuni nad püüab kinni sihtjaama solenoid.
Esitame siin projekti autori mõned täpsustused:
«Tomski Tehnoloogiainstituudi füüsikalaboris aastail 1911–13 korraldatud katsetel kasutasin 32-cm läbimõõduga vasktoru, mille ülemises osas asetsesid elektromagnetid, nende all alusel aga väike vagun – tükk raudtoru, millel rattad ees ja taga ning eriliselt ehitatud «nina», millega ta seismajäämisel põrkas vastu liivaga täidetud koti külge kinnitatud lauda. Vagun kaalus 10 kgf. Talle võis anda kiiruse kuni 6 km/h; seda kiirust ei lubanud ületada toa piiratud mõõtmed ja ringtoru läbimõõt (6,5 m). Kuid minu projekti järgi on kolmeverstalise saatesolenoidi korral kerge saavutada kiirusi kuni 800–1000 km/h. Et torus puudub õhk, samuti hõõrdumine vastu lage ja põrandat, siis pole tarvis kulutada energiat selle kiiruse säilitamiseks.
Sellise raudtee, eriti vasktoru ehitamine on küll kulukas, kuid see tasub end ära liikluse odavusega (mõni tuhandik kuni 1-2 sajandikku kopikat kilomeetri kohta). Odavus on tingitud sellest, et pole kulusid kiiruse säilitamisele ega mingite masinistide või konduktorite palkadele. Kahetoruline tee suudab ühes suunas läbi lasta 15 000 reisijat ehk 10 000 tonni kaupa ööpäevas.»7
В. P. Veinbergi idee leidis muudetud kujul rakendust Moskva postkontoris kergete pakkide edasitoimetamiseks. Katseseadme pikkus oli 120 m, paki liikumiskiirus 30 m/s. Samasugune elektromagnetiline transpordiseade ehitati Leningradi Riiklikus Raamatukogus lugejate tellitud raamatute kohaletoimetamiseks.
Vanarooma looduseuurija Plinius esitab tollal väga levinud legendi magnetmäest mere kaldal kusagil Indias, mis ebatavalie jõuga tõmbavat külge igasuguseid raudesemeid. Häda meremehele, kes julges oma laevaga läheneda sellele kaljule. Kalju tõmbab laevast välja kõik naelad, kruvid, raudkinni tused – ja laev laguneb puitdetailideks, millest ta koosneb.
Hiljem läks see legend «Tuhande ja ühe öö muinasjuttudesse ».
Loomulikult on see üksnes legend. Me teame, et magnetmäed, s.t. magnet rauast rikkad mäed, on tõepoolest olemas – meenutagem kuulsat Magnetmäge, mille läheduses kõrguvad Magnitogorski kõrgahjud. Kuid selliste mägede külgetõmme on äärmiselt väike, peaaegu märkamatu. Niisuguseid mägesid ja kaljusid, millest kirjutas Plinius, pole Maal kunagi olnud.
Kui praegu ehitataksegi laevu ilma raud- ja terasosadeta, siis ei tehta seda mitte hirmust magnetmägede ees, vaid selleks, et paremini uurida Maa magnetismi.8 Teaduslike romaanide autor Kurd Lasswitz kasutas Pliniuse legendi ideed ära selleks, et välja mõelda ähva r dav relv, mida tema romaanis «Kahel planeedil» kasutavad marslased sõjas Maa elanikega. Varustatuna sellise magnet - (õigemini, elektromagnet-) relvaga, muutsid marslased maalased relvituks enne, kui need jõudsid lahingut alata.
Seda marslaste ja maalaste lahinguepisoodi on kirjeldatud järgmiselt :
«Ratsanike hiilgavad read tormasid pidurdamatult edasi. Ja näis, nagu oleks vägede ennastohverdav otsustavus sundinud võimsat vaenlast [marslasi — J. P.] taganema, sest nende õhulaevade seas tekkis uuesti liikumine. Laevad tõusid õhku, nagu kavatsedes anda pealetungijatele teed.
Samal ajal laskus ülevalt aga mingi suur tume mass, mis alles nüüd ilmus lahinguvälja kohale. See mass, mida igast küljest ümbritsesid õhulaevad, laotus lehviva linana sõdurite kohale. Esimene ratsanike viirg sattus «lina» mõjupiirkonda, ja otsekohe laotus kummaline seade üle kogu rügemendi. Selle mõju oli ootamatu ja koletislik. Lahinguväljalt kostis läbilõikav õudusekarje. Hobused ja ratsanikud lamasid hunnikus maas ning õhk oli tihedalt täis odasid, mõõku ja karabiine, mis kirina ja kärinaga lendasid üles seadme poole, kuhu nad lõpuks kinni jäid.
See seade oli marslaste uus leiutis. Vastupandamatu jõuga tõmbas ta külge kõike, mis oli rauast ja terasest. Selle õhus hõljuva magneti abil rebisid marslased oma vastas te käest relvad, tegemata neile vähimatki häda.
Lendav magnet kandus edasi ja ligines jalaväele. Asjata püüdsid sõdurid mõlema käega oma püsse kinni hoida – vastupandamatu jõud rebis need neil käest; paljud, kes relvi ikkagi lahti ei lasknud, kisti ise õhku. Mõne minutiga oli esimene rügement relvituks tehtud. Siis asus seadeldis linnas marssivate rügementide kannule ja tegi nendega sama töö.
Taoline saatus tabas ka kahurväge.»
Eelmise paragrahvi lugemisel tekkis loomulikult küsimus, kas magnetjõudude eest poleks saanud varjuda mingi tõkke taha, mis neid läbi ei lase.
See on täiesti võimalik ja marslaste fantastiline leiutis poleks mingit kahju teinud, kui õigel ajal oleks tarvitusele võetud vastavad abinõud.
Nii imelik kui see ka on, aga magnetjõudude suhtes läbipaistmatuks aineks on seesama raud, mida nii kerge magneetida! Raudrõnga sees ei kaldu kompassinõel väljapoole rõngast paigutatud magneti mõjul kõrvale.
Rauast kapsliga võib kaitsta taskukella terasmehhanismi magnetjõudude mõju eest (joon. 98). Kui paneksite kuldkella tugeva hoburaudmagneti poolustele, siis kõik kellamehhanismi terasosad, eelkõige aga balanssiiri jõhvvedru (Kui see vedru pole ainult tehtud erilisest sulamist invarist, metallist, mis ei magneetu, ehkki selle koostisse kuuluvad raud ja nikkel.), magneetuksid ja kell jääks seisma. Magneti eemaldamisel ei hakka kell enam käima, sest mehhanismi terasosad jäävad magneedituks ja kell nõuab põhjalikku remonti ning paljude osade asendamist. Seepärast ei tohi säärast katset teha kuldkellaga, see läheks liiga kulukaks.9
Seevastu kelladega, mille mehhanism on tihedalt suletud raud- või teraskapslisse, võite seda julgesti teha läbi raua ja terase magnetjõud ei tungi. Viige niisugune kell tugeva dünamo mähise lähedusse, ja kella käik ei muutu mitte põrmugi. Elektrotehnikute jaoks on niisugused raudkellad otse ideaalsed, kuna hõbe ja kuldkellad lähevad neil magnetite mõjul kiiresti rivist välja.
Igiliikurite leiutamise ajaloos pole magnetil olnud sugugi väike osa. Hädaleidurid on püüdnud magnetit igati ära kasutada, et ehitada mehhanismi, mis liiguks iseenesest igavesti. Toome siinkohal ühe niisuguse projekti, mida on kirjeldanud 17. sajandil Chesteri piiskop John Wilkens.
Tugev magnet A on paigutatud samba otsa (joon. 99). Sambale toetub üksteise all kaks kaldrenni M ja N, kusjuures ülemisel rennil MF on ülemises otsas väike ava С ning alumine renn N on painutatud. Leiutaja arutles järgmiselt. Kui ülemisse renni panna punktis В väike raudkuul, siis veereb see magneti A külgetõmbe mõjul ülespoole; avani С jõudes kukub ta alumisse renni N, veereb seda mööda alla, tõuseb kõveruse D kaudu veidi üles ja satub ülemisse renni M. Siit veereb ta magneti külgetõmbe mõjul taas üles, kukub jälle läbi ava, veereb uuesti alla ja satub järjekordselt ülemisse renni, et oma liikumist otsast peale hakata. Sel viisil jookseb kuulike peatumatult edasi ja tagasi, olles igaveses liikumises.
Mille poolest see leiutis absurdne on?
Seda pole raske näidata. Miks leiutaja arvas, et renni N mööda alumisse otsa jõudnud kuulil on veel küllalt kiirust, tõusmaks üles mööda kõverust D? Asi oleks tõesti nii, kui kuulike veereks ainult raskusjõu mõjul: siis oleks ta liikunud kiirenevalt. Ent meie kuulike on kahe jõu – raskusjõu ja magneti külgetõmbe – mõju all. Viimane on eelduse kohaselt nii tugev, et võib sundida kuulikest tõusma punktist В punkti C. Seepärast ei veeregi kuulike renni N mööda alla mitte kiirenevalt, vaid aeglustuvalt ja kui ta jõuabki renni alumisse otsa, siis igal juhul pole tal niipalju energiat, et tõusta üles mööda kõverust D.
Kirjeldatud projekti on korduvalt esitatud kõikvõimalikes teisendites. Üks selline, nii kummaline kui see ka pole, isegi patenditi Saksamaal 1878. a., s.t. 30 aastat pärast energia jäävuse seaduse avastamist! Leiutaja oskas oma magnetilise igiliikuri põhiideed nii osavasti maskeerida, et viis eksitusse isegi patente välja andva tehnilise komisjoni. Leiutis patenditi, ehkki patendinduse põhikirja järgi ei tohi väljaanda patenti leiutisele, mille idee on vastuolus loodusseadustega. Tõenäoliselt pettus selle ainulaadse patendi õnnelik omanik oma lapses õige pea, sest juba kahe aasta pärast lakkas ta tulumaksu maksmast ja kurioosne patent kaotas kehtivuse: leiutis sai üldiseks omandiks.
Muuseumiasjanduse praktikas tekib tihti vajadus lugeda vanaaegseid paberirulle, mis on niivõrd pehkinud, et murduvad ja rebenevad kõige ettevaat likumalgi katsel eraldada üksteisest käsikirjakihte.
Kuidas selliseid paberirulle siiski lugeda?
NSV Liidu TA juures asub dokumentide taastamise labor, mis lahendab just seda laadi ülesandeid. Kõnesoleval juhul saab labor ülesandega hakkama elektri abil: paberirull elektriseeritakse; paki naaberkihid, mis on saanud ühenimelise laengu, tõukuvad üksteisest eemale ja eralduvad, ilma viga saamata. Sellist kohevat paberipakki on osavate kätega juba suhteliselt lihtne lahti rullida ja paksule paberile kleepida.
Igiliikuri väljamõtleja te seas muutus väga populaar seks idee dünamomas ina ühendamisest elektrimootoriga. Kõik niisugused projektid taanduvad järgmisele. Elektri mootor ja dünamomasin tuleb ühendada ülekanderihmaga ning voolujuhtmed viia dünamolt elektrimootorile. Kui dünamole anda algimpulss, paneb selle tekitatud vool käima elektrimootori, mootor omakorda käitab dünamo, sest nad on ühendatud ülekanderihmaga. Seega arvavad leiutajad, et masinad panevad vastastikku teineteist käima ja see liikumine ei lakka seni, kuni masinad ära kuluvad.
Idee tundus leiutajatele erakordselt ahvatlevana; kuid need, kes on seda praktiliselt püüdnud teostada, pidid oma suureks imestuseks nentima, et kirjeldatud tingimustel ei tööta kumbki masin. Midagi muud sellelt projektilt oodata polnudki. Isegi siis, kui mõlema mas ina ka sutegur oleks 100%, võiksime neid sundida näidatud viisil pidevalt liikuma ainult hõõrde täielikul puudumisel. Mainitud masinate ühendus, nn. agregaat, kujutab endast tegelikult ühteainust masinat , mis peab end ise käima panema. Hõõrdumise puudumisel liiguks selline agregaat igavesti, sellest poleks aga mingisugust kasu: niipea kui agregaadilt nõuda tööd, jääb ta kohe seisma. Meie ees oleks igiliikumine, aga mitte igiliikur. Hõõrdumise olemasolul ei hakkaks agregaat aga üldse liikuma.
Kummaline, et inimestel, keda meelitab see idee, ei tule pähe sama mõtte lihtsam variant: ühendada rihmaga kaks seibi ja panna üks neist pöörlema. Juhindudes samast loogikast, mis eelmise masinate ühenduse puhul, peaks esimene seib panema pöörlema teise ja teise liikumisest hakkab pöörlema esimene. Võib läbi saada ka üheainsa seibiga: paneme ta pöörlema, tema parempoolne osa tõmbab pöörlema vasaku, vasaku poole liikumine toetab parema pöörlemist. Kahel viimasel juhul on seadme mõttetus silmanähtav ja seepärast sellised projektid ei innusta kedagi. Kuid tegelikult on kõigi kolm projekti aluseks üks ja seesama eksiarvamus.
Matemaatiku jaoks pole väljend «peaaegu igavene» mitte midagi ahvatlevat. Liikumine võib olla kas igavene või mitteigavene; «peaaegu igavene» tähendab tegelikult mitteigavest.
Praktika seisukohalt pole aga asi nii. Tõenäoliselt oleksid paljud täiesti rahul, kui saaksid oma käsutusse mitte täiesti igavese, vaid peaaegu igavese jõumasina, mis suudab liikuda kas või näiteks 1000 aastat . Inimese elu on üürike, 1000 aastat on talle sama mis igavik. Praktilise meelelaadiga inimesed peaksid ligiliikuri probleemi lahendatuks ja neil kaoks põhjus edaspidi selle kallal pead murda.
Niisuguseid inimesi võib rõõmustada teatega, et tuhandeaastane jõumasin on juba leiutatud; igaüks võib teatava rahakuluga muretseda endale sellise jõumasina analoogi. Sellele leiutisele pole keegi patenti võtnud ja see ei kujut a endast mingit saladust . Strutti poolt 1903. a. väl jamõeldud seadme, nn. raadiumkella ehitus on lihtne (joon. 100).
Õhutühja klaasballooni on kvartsniidi В (kvarts ei juhi elektrit) külge riputatud väike klaastoru A, milles on mõni tuhandik grammi raadiumisoola. Toru otsa on kinnita tud kaks kuldlehekest nagu elektroskoobiski. Teatavasti kiirgab raadium kolme liiki kiiri – alfa-, beeta- ja gammakiiri. Antud juhul mängivad peaosa klaasi läbivad beetakiired, mis kujutavad endast negatiivselt laetud osakeste (elektronide) voogu. Raadiumi poolt igas suunas väljapaisatavad osakesed viivad kaasa negatiivset laengut ja seepärast laadub toru ise vähehaaval positiivselt. See positiivne laeng läheb üle kuldlehekestele С ja sunnib neid tõukuma teineteisest eemale.
Laiali läinud lehekesed puutuvad vastu ballooni seinu, kaotavad laengu (vastavatele seinaosadele on kleebitud fooliumiribad, mida mööda elekter ära voolab) ja langevad algasendisse tagasi . Peagi koguneb uus laeng, lehekesed tõukuvad taas, annavad jälle oma laengu ära ballooni seintele ning langevad kokku, et uuesti elektriseeruda. Seade töötab täpselt nagu kellavärk, tehes iga 2–3 minuti jooksul ühe võnke. Siit ka nimetus «raadiumkell». Kell töötab aastaid, aastakümneid, sajandeid, seni kuni kestab raadiumi kiirgamine.
Lugeja taipab, et see pole sugugi igavene, vaid ainult tasuta jõumasin.
Kas seda tasuta jõumasinat saab ka praktikas kasutada? Kahjuks mitte. Jõumasina võimsus, s.t. ajaühikus tehtav töö on niivõrd tühine, et selle arvel ei saa tööle panna ühtki mehhanismi. Et saavutada veidigi arvestatavaid tulemusi, on vaja märksa suuremat raadiumikogust. Kui aga meelde tuletada, et raadium on äärmiselt kallis ja haruldane element, siis olete ju nõus, et seda laadi tasuta jõumasin läheb liiga kulukaks.
Kõik teavad, kui ohtlik on puudutada pinge all olevaid trammi- või kõrgepingejuhtmeid. Niisugune puudutus on surmav nii inimeste kui ka suurte loomade jaoks. On teada palju juhtumeid, kus vool on tapnud hobuse või lehma, kes riivasid katkenud juhet.
Millega aga seletada seda, et linnud istuvad juhtmetele täiesti rahulikult ja karistamatult? Võib ju näha neid seda alatihti tegemas (joon. 101). Et seda vastuolulist nähtust mõista, tuleb silmas pidada järgmist : elektritraadil istuva linnu keha kujutab endast nagu vooluahela haru, mille takistus on hiiglasuur, võrreldes teise haru (lühike juhtmelõik linnu jalgade vahel) takistusega. Seepärast on voolutugevus selles harus (linnu kehas) tühine ja kahjutu. Kui aga juhtmel istuv lind puudutaks posti tiiva, saba või nokaga, s.t. viiks oma keha mingil moel ühendusse maapinnaga, siis tapaks tema keha läbiv vool ta silmapilkselt. Seda täheldataksegi vahetevahel.
Lindudel on kombeks kõrgepingeliini tõendil istudes hakata oma nokka puhas tama vastu juhet. Et toend pole isoleeritud, siis lõpeb maandatud linnu kokkupuutumine voolu all oleva juhtmega vältimatult linnu surmaga. Kui arvukalt niisuguseid juhtumeid esineb, on näha kas või juba sellest, et mõnes riigis on võetud erimeetmed, päästmaks linde hukust. Selleks seati kõrgepingeliinidele isoleeritud õrred, millel lind võis istuda ja oma nokka karistamatult vastu juhet puhastada (joon. 102). Teistel juhtudel muudetakse ohtlikud kohad eriliste seadmete abil lindudele juurdepääsmatuteks.
Nõukogude Liidu kõrgepingeliinide suure pikkuse tõttu on metsa- ja põllumajanduse huvides vaja hoolitseda selle eest, et elektrivool ei hävitaks meie sulissõpru.
Kas olete äikese ajal juhtunud nägema elava liiklusega linnatänavat? Te olete muidugi täheldanud seejuures üht kummalist iseärasust: alles äsja liikumist tulvil tänav paistab välgulöögi valgel olevat tardunud. Hobused on seisma jäänud pinguldatud poosides, hoides jalgu õhus; ka sõidukid on liikumatud: iga rattakodar on selgesti näha ...
Näiva liikumatuse põhjuseks on välgu lühiajalisus. Välk nagu iga elektrisäde kestab äärmiselt lühikest aega, niivõrd lühikest, et seda ajavahemikku ei saa tavaliste vahenditega mõõta. Kaudsete võtetega õnnestus kindlaks teha, et mõnikord vältab välk kõigest sekundituhandikke.10 Nii lühikese ajavahemiku vältel võib vaevalt miski silmaga nähtavalt edasi liikuda. Seepärast ei tule imestada, kui elava liiklusega tänav paistab välgusähvatuse valgel tardununa: me märkame ju ainult neid muudatusi, mis kestavad mõne tuhandiku sekundit. Kiiresti veereva vankri iga rattakodar jõuab nihkuda ainult millimeetri kaduv väikese osa võrra; silma jaoks on see sama mis täielik liikumatus.
Tol kaugel ajal, mil välke seostati üleloomulike jõududega, kõlanuks niisugune küsimus jumalateotusena. Ent meie päevil, kui elektrienergia on muutunud kaubaks, mida mõõdetakse ja hinnatakse nagu iga teistki kaupa, ei tohiks küsimus välgu maksumusest paista sugugi mõttetuna. Ülesanne seisneb selles, et välja arvutada välgulahenduseks vajalik elektrienergia hulk ja määrata selle maksumus, kas või näiteks elektrivalgustuse hindade järgi.
Esitame siinkohal arvutused. Äikesepilve pinge on umbes 50 miljonit volti. Maksimaalseks voolutugevuseks hinnatakse sel juhul 200 000 amprit. (Märgime möödaminnes, et voolutugevust määratakse terasvarda magneetumuse järgi, mis tekib, kui varda mähist läbib vool, mis on tekitatud välgulöögist piksevardasse.) Võimsuse vattides saame, korrutades voltide ja amprite arvu; seejuures on vaja aga arvesse võtta seda, et välgu ajal langeb pinge nullini, järelikult on vaja kasutada keskmist pinget, teiste sõnadega, poolt esialgsest pingest. Seega saame:
s.t. 5 miljardit kilovatti.
Saanud võimsuse jaoks nii aukartust äratava väärtuse, on loomulik oodata, et ka välgu hind rahas tuleb hiiglasuur. Et saada energiat kilovatt-tundides (seda, mille eest maksame elektrivalguse puhul), on vaja teada välgu kestust. Niisugune energia antakse ära umbes sekundituhandiku jooksul. Selle ajaga kulub
1 kWh maksab tariifi järgi voolutarbijale 4 kopikat. Siit on kerge välja arvutada välgu hinda:
.Tulemus on üllatav: välk, mille energia on umbes sada korda suurem raskekahuri mürsu energiast, maksab elektrijaamade tariifi järgi kõigest 56 rubla!
Huvitav, et moodne elektrotehnika pole jõudnud tehisvälgu tekitamisel eriti kaugele: laboris on saadud pinget kuni 10 miljonit volti ja sädemeid pikkusega 15 m. Pole just kuigi pikk ...
Väga kerge on tekitada kodus väikest purskkaevu kummitoru abil, mille üks ots pistetakse kõrgemal asuvasse ämbrisse või ühendatakse veekraaniga. Et veejuga jaguneks peenteks jugadeks, peab toru väl jalaskeava olema väga väike; kõige lihtsam on seda teha, pannes toru vabasse otsa pliiatsijupi, millest on kõrvaldatud grafiit. Purskkaevu hõlpsamaks käsitsemiseks kinnitatakse toru vaba ots kummuli lehtrisse (joon. 103)11.
Tekitanud sel viisil poole meetri kõrguse otse üles paiskuva joa, lähendage sellele villase riidega hõõrutud kirjalakitükk või eboniitkamm. Otsekohe märkate midagi õige ootamatut: langeva fontääniosa üksikud nired ühinevad üheks pidevaks joaks, mis kuuldava kohinaga lööb vastu joa alla pandud taldrikut. Heli meenutab äikesevihma iseloomustavat kohinat. «Pole kahtlust,» märgib sel puhul füüsik Boyce, «et just sel põhjusel muutuvad vihmapiisa d äikese ajal nii suureks.» Eemaldage kirjalakk – ja otsekohe pihustub juga taas peenteks niredeks ning iseloomulik heli asendub peenikeste jugade pehme sahinaga.
Võhikute ees võite kirjalakipulgaga tegutseda nagu mustkunstnik võlukepikesega.
Elektrilaengu niisugune ootamatu mõju veejoale seletub sellega, et tilgad elektriseeruvad induktsiooni tõttu, kusjuures tilkade need osad, mis on pööratud laengu poole, laaduvad positiivselt, kaugemale jäävad osad aga negatiivselt. Seega on isenimeliselt laetud tilkade osad väga lähestikku ja tõmbavad üksteist külge. Tilgad ühinevad.
Elektrilaengu mõju veejoale võite demonstreerida ka lihtsamalt: tarvitseb ainult lähendada läbi juuste tõmmatud eboniitkammi kraanist voolavale peenikesele veejoale, kui juga tiheneb ja kaldub kammist märgatavalt eemale (joon. 104). Nähtuse seletus on keerul isem kui eelmisel juhul; see on seotud pindpinevuse muutumisega elektrilaengu mõjul.
Märgime muu hulgas, et kergusega, millega tekib elektrilaeng hõõrdumisel, seletub ka ülekanderihmade elektriseerumine hõõrdumisel vastu seibe. Suured elektrisädemed kujutavad endast mõnes ettevõttes tõsist tulekahjuohtu. Et õnnetusi ära hoida, kaetakse ülekanderihmad õhukese hõbedakihiga, mis muudab rihma elektrijuhiks ning takistab laengu kogunemist .12
Üks fotokunsti kurioosumeid on pildid, millel pildistatav on kujutatud viies erinevas vaates. Joonisel 105 võib näha neid viit asendit. Sellistel fotodel on tavaliste ees see eelis, et nad annavad täielikumalt edasi originaali eripära: on ju teada, et fotograafid püüavad pildistada nägu asendis, milles see paistab kõige kenam; kõnesoleval fotol saadakse nägu korraga mitmes vaates, mille hulgast on rohkem võimalusi leida kõige iseloomulikum.
Kuidas saadakse niisuguseid fotosid? Muidugi peeglite abil (joon. 106). Pildistatav istub seljaga aparaadi A ja näoga püsti asetatud nurkpeegli С poole; nurk peeglite vahel on 1/5 360°-st, s. t. 72°. Niisugune peeglipaar annab neli kujutist, millest igaüks paikneb aparaadi suhtes eri viisil. Aparaat jäädvustabki need kujutised koos pildistatava objektiga, kusjuures peeglid ise (ilma raamideta) muidugi pildile ei jää. Et fotoaparaat ei jääks peeglites näha, varjatakse ta kahe ekraaniga (BB), mille vahel on pilu objektiivi jaoks.
Kujutiste arv oleneb peeglitevahelisest nurgast : mida väiksem see on, seda suurem on tekkivate kujutiste arv. Kui nurk on 360°/4 = 90°, saame neli kujutist, nurga 360°/6=60° puhul kuus kujutist, nurga 360°/8 = 45° korral kaheksa jne. Kui kujutisi on liiga palju, siis on nad ähmased ja nõrgad; seepärast piirdutakse tavaliselt viie võttega.1
Väga ahvatlev on mõte kasutada päikesekiirte energiat vee soojendamiseks aurumasina katlas. Teeme väikese arvutuse. Täpselt on määratud see päikeseenergia hulk, mida saab meie planeedi pinna iga ruutsentimeeter ühe minuti jooksul, kui pind asetseb väljaspool atmosfääri ja on risti päikesekiirtega. See soojushulk on nähtavasti muutumatu, seepärast nimetataksegi teda solaarkonstandiks. Tema väär tus on ligikaudu 1,4 kW/m2. See Päikeselt regulaarselt saabuv soojusvoog ei jõua Maa pinnale tervenisti: umbes 25% temast neeldub atmosfääris . Võib arvutada, et päikesekiirtega risti oleva maapinna ruutmeeter saab igas sekundis ligi 1 J energiat .
Niipalju tööd võib teha päikeseenergia kõige soodsamates tingimustes , s.t. siis, kui kiired langevad pinnaga risti ja energia muundumine on sajaprotsendiline. Kuid seni tehtud katsed kasutada päikeseenergiat otsese liikumapaneva jõuna on veel kaugel ideaalsetest: nende kasutegur ei ületa 5–6%. Realiseeritud seadmetest oli kõige suurem kasutegur tuntud füüsiku S. W. Abbotti päikesemootoril – 15%.2
Hõlpsam on päikeseenergiat kasutada mitte mehaanilise töö saamiseks, vaid soojendamiseks. Kolmekümnendate aastate algul avati Taškendis päikesesaun, mis teenindas 70 inimest ööpäevas. Taškendis ehitati ühe maja katusele ka helioseade (joon. 107). Siia seati üles 20 päikesekatelt, mis mahutasid 200 l vett ja varustasid kogu maja sooja veega. Heliotehnikute sõnade järgi soojendas Päike katlaid lakkamatult 7– 8 kuud aastas; ülejäänud aja võisid katlad soojendada vett ainult selge ilmaga.3 Veesoojendite keskmine kasutegur oli suhteliselt suur – 47% (maksimaalne väärtus oli 61%) .
Turkmeenias katsetati päikesejahutit (joon. 108). Jahutuspatare ide temperatuur külmuti kambrites oli –3°C, sellal kui ümbritseva õhu temperatuur oli 42°C varjus. See oli esimene tööstuslik päikesejahuti.
Suurepäraseid tulemusi andsid katsed sulatada väävlit päikesekiirtega (väävli sulamistemperatuur on 120°C).4 Mainigem veel päikese jõul töötavaid veemagesteid Kaspia ja Araali mere kaldal, veetõsteseadmeid, puuvilja- ja kalakuivateid, kööki, kus kõik road valmivad «päikesekiirtes » jne. Loetelu ei ammenda neid mitmekesiseid rakendusi, mida võimaldavad kunstlikult kinnipüütud päikesekiired. Tulevikus etendab Päike tähtsat osa Kesk- Aasia, Kaukaasia , Krimmi, Alam-Volga ja Lõuna-Ukraina majanduses.
Hall muinasaeg pärandas meile legendi imemütsist, mis teeb nähtamatuks igaühe, kes selle pähe paneb. Puškin, kes elustas «Ruslanis ja Ludmillas» muistsed pärimused, andis võlumütsi omaduste klassikalise kirjelduse:
«Üht isemeelset soovi ta
siis järsku tundis: proovida ta Tšernomori mütsi tahtis ...
Ludmilla peegli eest ei lähe.
Ta mütsi otse, viltu seab
ning paneb tagurpidi pähe ...
Mis juhtus? Oo, kus imeloöd!
Ludmilla peeglist kaob kui vette.
Ta keerab mütsi – peegel toob
näojooned vastselt silma ette.
Taas tagurpidi paneb – kaob!
Peast võtab – ilmub! Tulvil lohtu,
tal süda rõõmsalt põues taob:
«Nüüd pole enam mingit ohtu!»»
Võime nähtama tuks muutuda oli vangistatud Ludmillale ainus kaitsevahend. Nii pääses ta oma valvurite terava pilgu alt. Nähtamatu vangi olemasolu üle sai otsustada ainult tema tegude järgi:
«Kord nähti, kuidas tasahilju
taas kõikuma lõi sahinal
oks puul ning otse silma all
sealt äkki kadus küpseid vilju.
Kord piserdades rohumaad
veejuga lättelt kerkis õhku ...
Nii teati, kust ta juua saab
ja millega ka täidab kõhtu . . .
Kui hõrenes ööudu maas,
Ludmilla ärkvel oli taas
ja küima kose all end pesi:
nõid ise nägi, kuidas vesi
seal nähtamatu pihu all
kord varajasel koidu ajal
teeliiva voolas pladinal.»
Ammugi on teostatud paljud mineviku ahvatlevad unelmad; ohtrasti muinasjutulisi nõidusi on saanud teaduse pärisosaks. Puuritakse läbi mägesid, püütakse kinni välgud, lennatakse võluvaipadel – lennukitel. Kas poleks võimalik leiutada ka nõiamütsi, s. t. vahendit, mis teeb inimese täielikult nähtamatuks? Sellest nüüd juttu tulebki.
Romaanis «Nähtamatu» püüab inglise kirjanik Wells veenda lugejaid, et nähtamatuks muutumine on täiesti teostatav. Tema kangelane (romaani autor kujutab teda geniaalseima füüsikuna, keda maailm kunagi on näinud) avastas inimese keha nähtamatuks tegeva vahendi. Oma tuttavale arstile räägib leiutaja avastuse alustest järgmist:
«Nähtavus oleneb nähtavate kehade reageerimisest valgusele ... Te teate ju hästi, et iga keha kas neelab valguskiiri, peegeldab neid, need murduvad temas või leiavad aset kõik need protsessid. Kui keha ei peegelda ega neela valguskiiri ning need ei murdu temas, siis on ese nähtamatu. Nii näiteks näete te läbipaistmatut punast karpi seetõttu, et mõnigad valguskiired neelduvad värvis, ülejäänud, täpsemalt öeldes, spektri punane osa aga peegeldub ja jõuab teieni. Kui ese ei neela ühtki kindlat spektriosa, vaid peegeldab enam-vähem võrdselt kõiki valguskiiri, siis näete te säravvalget karpi, mis näib hõbedasena. Teemantkarbi puhul ei neelaks ega peegeldaks kuigivõrd valguskiiri mitte kogu tema pind, vaid pinna need lihvitud osad, mille kaldenurk on selleks sobiv. See tekitab mulje poolläbipaistvast, pimestavalt helkivast, säravast esemest. See oleks midagi valguse skeleti taolist. Klaaskarp ei oleks nii särav ega nii selgesti nähtav kui teemantkarp, sest ta peegeldab ja murrab valguskiiri vähem. Kas on selge? Teatavast punktist võite te sellest vabalt läbi vaadata. Mõningad klaasisordid on teistest nähtavamad: flintklaasist karp oleks näiteks säravam kui tavalisest aknaklaasist tehtu. Äärmiselt õhukesest tavalisest klaasist karpi oleks nõrga valguse juures raske näha, sest säärane pind peaaegu ei neela valgust ning ka peegeldab ja murrab seda väga vähe. Kui panna tavaline värvitu klaasitahvel vette, veel parem aga mõnda veest tihedamasse vedelikku, siis muutub ta sootuks nähtamatuks, sest veest klaasisse suunduvad valguskiired murduksid ja peegelduksid äärmiselt nõrgalt, praktiliselt ei muudaks nad üldse oma suunda. Säärane klaas oleks peaaegu niisama nähtamatu kui õhku paisatud süsihappegaasivõi vesinikujuga. Ja täpselt samal põhjusel!»
«Jah,» lausus Kemp [arst — /. P.]. «See kõik on lihtne. Tänapäeval teab seda iga koolipoiss.»
«Toon teile veel ühe fakti, mis on tuttav igale koolipoisile. Kui klaas purustada ja pulbriks tampida, siis muutub ta hoopis paremini nähtavaks kui tavaliselt. Ta muutub lõpuks valgeks läbipaistmatuks tolmuks. Põhjuseks on see, et pulbristatult suureneb klaasi pind, mis on seotud valguskiirte peegeldumise ja murdumisega. Klaasitahvlil on ainult kaks pinda, seevastu aga pulbris murdub ja peegeldub valguskiir igas terakeses, mille tulemusena ainult väike osa valguskiiri suudab seda läbida. Kui aga pulbristatud klaas puistata vette, kaob ta kohe. Pulbristatud klaasil ja veel on peaaegu ühesugused murdumisnäitajad, see tähendab, et valguskiir murdub ja peegeldub üleminekul ühest teise minimaalselt.
Me muutsime klaasi nähtamatuks, asetades ta vedelikku, millel on umbes sama murdumisnäitaja. Iga läbipaistev ese muutub nähtamatuks, kui me paigutame ta keskkonda, millel on temaga enamvähem ühesugune murdumisnäitaja. Kui te vähegi järele mõtlete, siis saate aru, et pulbristatud klaasi võib muuta nähtamatuks ka õhus, kui tema murdumisnäitajat vähendada õhu omani. Sest sel juhul ei alluks valguskiir klaasist õhku tungides mingile murdumisele ega peegeldumisele.»*
(* Täiesti läbipaistva keha täieliku nähtamatuse võime saavutada, kui ümbritseme ta valgust ühtlaselt hajutavate seintega. Silm, mis vaatab läbi väikese külgava sisse, saab keha igast punktist just niisama palju valgust nagu siis, kui keha üldse poleks: mitte mingid helgid või varjud ei reeda tema olemasolu. Seda võib kontrollida järgmise katsega. Valgest papist poolemeetrise diameetriga lehter pannakse teatavale kaugusele 25-küünlasest elektrilambist (joon. 109). Lehtrisse on altpoolt pistetud klaaspulk, võimalust mõõda rangelt püstsihis. Vähimalgi hälbel püstasendist paistab pulk teljelt tumedana ja äärtelt heledana või vastupidi, teljelt heledana ja äärtelt tumedana. Need valguspildid vahelduvad pulga asendi vähimalgi muutusel. Pärast mõningaid proove võib saavutada pulga täiesti ühtlase valgustatuse ja siis kaob ta silmist, kui vaadata teda läbi kitsa (alla 1 cm) laiuse külgpilu. Sellise katsekorralduse puhul saavutatakse klaaseseme täielikult nähtamatuks muutumine, kuigi eseme aine murdumisnäitaja erineb tugevasti õhu murdumisnäitajast. Teine võte, mille abil saab nähtamatuks muuta keha, näiteks lihvitud klaasi, seisneb selles, et keha pannakse kasti, mis on seestpoolt kaetud läikiva värviga. – J. P.)
«Seda küll,» lausus Kemp. «Kuid inimene pole klaasipulber!»
«Ei,» vastas Griffin. «Та on hoopis läbipaistvam.»
«Jama!»
«Ja seda ma kuulen arsti käest! Kuidas kõik unustatakse! Kas te olete kümne aasta jooksul tõesti kogu füüsika unustanud? Mõelge kõigile asjadele, mis on läbipaistvad, kuid ei näi sellistena! Paber näiteks on valmistatud läbipaistvatest kiududest. Kuid samal põhjusel, miks klaasipulber on valge ja läbipaistmatu, on seda ka paber. Valage valgele paberile õli ja täitke sel kombel tema osakeste vahel olevad tühikud, nii et valguskiiri murraks ja peegeldaks ainult üks suur pind, ja paber muutub klaasina läbipaistvaks. Ja mitte ainult paber, vaid ka puuvilla-, lina-, villa- ja tselluloosikiud, aga ka luud, kuulake Kemp: luud, samuti liha, juuksed, küüned, närvid. Tegelikult koosneb kogu inimese koestik peale vere punase värvi ja juuste tumeda pigmendi läbipaistvatest värvitutest kudedest. Selleks et muutuda vastastikku nähtavaks, on vaja väga vähe. Sest oma suuremas osas pole kiud, millest elav olend koosneb, läbipaistmatumad kui vesi.»
Nende kaalutluste kinnituseks võib olla see fakt, et karvkatteta albiinod (loomad, kelle koed ei sisalda vä rvainet) on suurel määral läbipaistvad. 1934. a. leidis üks zooloog Detskoje Seloost albiinokonna ja kirjeldas teda nii: «õhukesed naha- ja lihaskoed kumavad läbi: on näha siseelundid, toes... Albiinokonnal on läbi kõhuseina näha hästi südame ja soolestiku kokkutõmbed.»
Wellsi romaani kangelane leiutas võtte, mis võimaldas teha läbipaistvaks inimese organismi koed ja isegi vä rvained (pigmendid). Ta kasutas oma avastu st edukalt enda peal. Katse õnnestus oivaliselt: leiutaja muutus täiesti nähtamatuks. Kohe saame teada selle nähtama tu inimese edasisest saatusest.
Romaani «Nähtamatu» autor tõestab erakordse teravmeelsuse ja järjekindlusega, et läbipaistvaks ja nähtamatuks muutunud inimene omandab seeläbi peaaegu piiramatu võimu. Ta võib märkamatult tungida igasse majja ja karistamatult võtta kõike. Tänu oma nähtamatusele on ta tabamatu, ta võitleb edukalt terve hulga relvas tatud inimestega. Ähvardades kõiki nähtavaid inimesi möödapääsmatu raske karistusega, hoiab nähtamatu terve linna elanikkonda täielikus alluvuses. Tabamatu ja haavamatuna on tal samal ajal täielik võimalus teha kahju kõigile teistele inimestele; kuidas nad ka ei püüaks end kaitsta, varem või hiljem tabab nähtamatunad ja hävitab. Selline erakordne seisund teiste inimeste seas annab romaani kangelasele võimaluse pöörduda linna ärahirmutatud elanike poole käsuga, mille sisu võib näiteks olla järgmine:
«Port Burdockit ei valitse mitte enam kuninganna, vaid mina, Terror! Täna on uue ajastu, Nähtamatu Mehe ajastu esimese aasta esimene päev. Minu nimi on Nähtamatu Esimene. Oma valitsemise esimesel päeval olen ma armuline. Kõigile õpetuseks leiab sel päeval aset ainult üks hukkamine. Selle mehe nimi on Kemp. Surm tabab teda täna. Ta võib panna end luku taha, peita end ära, hankida valvurid või tõmmata selga raudrüü, kui talle meeldib – surm, nähtamatu surm tuleb siiski. Laskem tal võtta tarvitusele ettevaatusabinõud, see avaldab mu rahvale mõju... Surm alustab teekonda. Mu rahvas, ärge osutage Kempile abi, sest vastasel korral külastab surm ka teid. Kemp sureb täna.»
Ja esialgu nähtama tu võidutsebki. Ainult suurima vaevaga õnnestub ärahirmutatud elanikkonnal jagu saada nähtamatust vaenlasest, kes ihkab valitsejaks saada.
Kas on õiged need füüsikalised arutelud, mis on selle fantastilise loo aluseks? Kahtlemata. Iga läbipaistev keha muutub läbipaistvas keskkonnas nähtama tuks juba siis, kui erinevus murdumi snäi tajates on alla 0,05. Kümme aastat pärast seda, kui Wells kirjutas oma «Nähtamatu», õnnestus saksa anatoomil W. Spalteholzil teostada romaani idee tegelikkuses, tõsi küll, mitte elusorganismidel, vaid surnud preparaatidel. Praegu võib neid erinevate kehaosade, isegi tervete loomade läbipaistvaid preparaate näha paljudes muuseumides.
Spalteholzi poolt 1911. a. leiutatud läbipaistvate preparaatide valmistamise viis seisneb lühidalt järgnevas. Pärast teatavat töötlust – pleegitamist ja pesemist – immutatakse preparaati salitsüülhappemetüüleetriga (see on suure murdumisnäitajaga värvitu vedelik). Sel viisil ettevalmistatud preparaat sukeldatakse sel lesama vedelikuga täidetud anumasse. Seejuures ei püüta muidugi saavutada preparaatide täielikku läbipaistvust, sest sel juhul muutuksid nad täiesti nähtamatuks ja oleksid anatoomi jaoks kasutud. Soovi korral võiks aga ka seda saavutada.
Muidugi on siit veel pikk tee Wellsi utoopilise looni elavast inimesest, kes on sedavõrd läbipaistev, et osutub täiesti nähtamatuks. Pikk tee sellepärast, et esiteks on vaja leida viis immutada elusa organismi kudesid läbipai stvaks muutva vedelikuga nõnda, et seejuures ei kannataks organism.
Teiseks, Spalteholzi preparaadid on küll läbipaistvad, aga mitte nähtamatud; nende preparaatide koed jäävad nähtamatuks vaid seni, kuni nad asetsevad vastavalt valgust murdvates vedelikes, õhus muutuvad nad nähtamatuks ainult siis, kui nende murdumisnäitaja saab võrdseks õhu murdumisnäitajaga, kuidas aga seda sa avutada, me veel ei tea.
Oletame aga, et aja jooksul õnnestub meil teostada nii üks kui teine, järelikult ka kirjaniku unistus.
Romaanis on autor kõik nii hoolikalt läbi mõelnud ja ette näinud, et tahes-tahtmata hakkad uskuma kirjeldatavatesse sündmustesse. Näib, et nähtamatu muutub tõepoolest vägevaimaks surelike seas. Kuid asi pole sugugi nii.
On üks väike asjaolu, mille «Nähtamatu» teravmeelne autor unust as. See on küsimus, kas nähtamatu saab näha.
Kui Wells oleks esitanud endale selle küsimuse enne romaani kirjutamist, poleks seda imepärast lugu kunagi kirjutatud...
Tõepoolest, selle küsimusega puruneb kogu nähtamatu võimsuse oreool. Nähtamatu peab olema pime! Miks me romaani kangelast ei näe? Sellepärast, et kõik tema keha osad – sealhulgas ka silmad – muutusid läbipaistvaks ja organismi murdumisnäitaja sai võrdseks õhu omaga.
Tuletame meelde, mis on silma ülesanne: silmalääts, klaaskeha ja teised osad murravad kiiri nii, et võrkkestal tekib esemete kujutis. Kui aga kiirte murdumine silmas ja õhus on ühesugune, siis kaob ka ainus murdumist esilekutsuv põhjus: üleminekul ühest keskkonnast teise, kus juures keskkondade murdumisnäitajad on võrdsed, kiired oma suunda ei muuda ega saa seepärast ka koonduda ühte punkti. Kiired läbivad nähtamatu silma täiesti takistamatult, murdumata ja peatumata , sest puudub pigment*, järelikult ei saa nad tema ajus esile kutsuda mitte mingisugust nägemisaistingut .
Niisiis ei näe nähtamatu midagi. Kõik tema eelised osutuvad kasutuks. Ähvardav võimupretendent huiguks ringi kobamisi, paludes armuande, mida aga keegi talle anda ei saaks, sest paluja on nähtamatu. Ülivõimsa sureliku asemel on meie ees abitu invaliid, kes on määratud armetult virelema ...**
Seega on nõiamütsi ot singuile kasutu minna mööda Wellsi näidatud teed – see tee, isegi kui otsingud on õige edukad, ei saa viia sihile.5
* Et loomal tekitada mingit aistingut, peavad valguskiired tema silmas esile kutsuma mingisuguse, olgu või kõige tühisema muutuse, s. t. tegema teatavat tööd. Selleks aga peab silma mingi osa kiiri kinni pidama. Kuid täiesti läbipaistev silm kiiri peatada muidugi ei saa: muidu poleks ta läbipaistev. Kõik loomad, kes kaitsevad end läbipaistvusega, omavad aga läbipaistmatuid silmi. «Vahetult merepinna lähedal,» kirjutab kuulus okeanoloog Murray, «on suurem osa loomi läbipaistvad ja värvitud; kui nad võrguga välja püütakse, võib neid näha ainult tillukeste mustade silmade järgi, sest veres neil hemoglobiini (värvainet) pole ja veri on täiesti läbipaistev.»
** Võimalik, et romaanikirjanik tegi selle olulise vea täiesti teadlikult. On ju teada, millist kirjanduslikku võtet kasutab oma ulmelugudes harilikult Wells: ta varjutab fantastilise koe põhipuuduse lugeja eest realistlike üksikasjade küllusega. Eessõnas oma fantastikalugude ameerika väljaandele kirjutab ta otsesõnu: «Niipea kui maagiline trikk on tehtud, peab kõik muu näima tõepärase ja argisena. Tuleb loota mitte loogiliste järelduste jõule, vaid kunsti poolt loodud illusioonile.»
Kuid nõiamütsi ülesande lahendamiseks on veel teinegi tee: värvida kehad värviga, mis muudab nad silmale märkamatuks. Niisugust võtet kasutab pidevalt loodus: varustades oma loomingu varjevärvusega, kaitseb ta seda vaenlase eest ning kergendab tema rasket olelusvõitlust.
See, mida sõjaväelased nimetavad kaitsevärvuseks, on zooloogid juba Darwini aegadest peale samuti nimetanud kaitse- või varjevärvuseks. Niisuguse kaitse näiteid võib loomariigist tuua tuhandeid: me kohtame neid sõna otseses mõttes igal sammul. Kõrbes elutsevad loomad on suuremalt jaolt iseloomulikku «kõrbevärvi»; seda värvi on lõvid, linnud, sisalikud, ämblikud, maod, ühesõnaga, kogu kõrbefauna. Põhjamaa lumelagendike asukad, vastupidi, olgu see ohtlik jääkaru või vagur jääkaur, on saanud looduselt valge värvuse, mis muudab nad valge lume taustal nähtamatuks. Puu koorel elutsevad liblikad ja nende röövikud on niisuguse värvusega, mis hämmastavalt täpselt jäljendab puukoore värvust (okkaliblikas jt.).
Iga putukakoguja teab, kui raske on putukaid leida varjevärvuse tõttu, millega loodus on neid varustanud. Eks proovige tabada heinaritsikat, kes siristab niidul teie jalgade ees – te ei näe teda rohelisel taustal, see neelab ta jäägitult.
Sama on õige ka vee-elanike kohta. Pruunvetikate keskel elutsevad mereloomad on kõik punakaspruunid, mis muudab nad silmale tabamatuks. Punavetikate levikualal on valitsevaks varjevärvuseks punane. Kalasoomuste hõbe on samuti varjevärvus. See kaitseb kalu neid ülalt varitsevate lindude ja alt ähvardavate vee-röövloomade eest; veepind paistab peeglina nii vee kohalt kui ka alt, sügavalt veest vaadatuna (täielik peegeldus), ja selle läikiv-metalse taus taga sulabki kalasoomuse hõbe hästi kokku. Meduusid ja teised läbipaistvad vee-elanikud – ussid, vähid, molluskid, salbid – «valisid» oma varjevärvuseks täieliku värvusetuse ja läbipaistvuse, mis muudab neid nähtamatuks ümbritsevas värvitus ja läbipaistvas keskkonnas.
Looduse «nipid» ületavad selles valdkonnas kaugelt inimese leidlikkuse. Paljudel loomadel on võime muuta oma varjevärvust kooskõlas keskkonna muutumisega. Hõbevalge kärp, kes lume foonil on nähtamatu, kaotaks kõik oma eelised, kui ta karv ei muudaks lume sulades värvi: igal kevadel saab loomake uue, ruske kasuka, mis sulab ühte lumevaba pinnase värvusega, talve tulekul muutub aga jälle vähehaaval hallimaks ja omandab lõpuks lumivalge talverüü.6
Kujutlege, et teile on antud võimalus viibida vee all ükskõik kui kaua ja et te seejuures hoiate silmi lahti. Kas võiksite seal näha?
Et vesi on läbipaistev, ei näi miski segavat vee all nägemast niisama hästi kui õhus. Tuletame aga meelde, et nähtamatu oli pime, ta ei olnud võimeline nägema sellepärast, et ta silma ja õhu murdumisnäitajad olid ühesugused. Vee all oleme umbes samas olukorras nagu Wellsi nähtamatu õhus. Asi muutub selgemaks, kui võtame appi arvud. Vee murdumisnäitaja on 1,34. Inimese silma läbipaistvate osade murdumisnäitajad on järgmised:
sarvkest ja klaaskeha 1,34
silmalääts 1,43
vesivedelik 1,34
Nagu näete, on silmaläätse murdumisnäitaja kõigest 1/10 võrra suurem vee omast, teistel silma läbipaistvatel osadel on see võrdne vee murdumisnäitajaga. Seepärast koonduvad kiired vee all kaugel silma võrkkesta taga; järelikult peab võrkkestal tekkima ähmane kujutis, millest vaid suure vaevaga võib midagi aru saada. Ainult väga lühinägelikud inimesed näevad vee all enam-vähem normaal selt.
Kui tahate endale pilti luua, kuidas näete vee all, pange ette tugevasti hajutavate (kaksiknõgusate) klaasidega prillid; siis nihkub silmas murdunud kiirte fookus kaugele võrkkesta taha ja kõik ümbritsev paistab teile ähmase ning udusena.
Kas inimene ei saaks vee all parandada oma nägemist tugevasti murdvate klaaside abil?
Tavalistes prillides kasutatavad klaasisordid selleks ei sobi: hariliku klaasi murdumisnäi taja on 1,5, s.t. ainult veidi suurem kui veel (1,34); niisugused klaasid murravad vee all kiiri väga nõrgalt. On vaja erilisi, erakordselt tugeva murdmisvõimega klaasisorte (nn. raske flintklaasi murdumisnäitaja on lähedane kahele). Selliste prillidega võiksime näha vee all enam-vähem selgesti (sukeldujate eriprillidest teeme juttu hiljem).
Nüüd on arusaadav, miks kala silmalääts on hästi pungis; see on kerakujuline ja tema murdumisnäitaja on loomadel teadaolevaist suurim. Silma kohanemisel ei muutu läätse kuju, vaid asend (joon. 110 näidatud viisil). Kui nii ei oleks, siis kaladel, kes peavad elama väga suure murdmisvõimega keskkonnas, oleksid silmad täiesti kasutud.
Tõenäoliselt küsivad paljud, kuidas näevad siis tuukrid, kes töötavad oma tuukriülikondades vee all, kui nende silmad vees peaaegu kiiri ei murra. Tuukrikiivrid on ju varus tatud alati tasa-, mitte kumerklaasidega. Edasi. Kas Jules Verne’i «Nautiluse» reisijad said imetleda veealust maast ikku läbi oma allveelaeva illuminaatori?
Meie ees on uus küsimus, millele muide pole raske vastata. Kui viibime vee all ilma tuukriülikonnata, puutub vesi vahetult kokku meie silmaga; tuukrikiivris (või «Nautiluse» kajutis ) eraldab silma veest õhukiht (ja klaas). See muudab asja oluliselt. Veest tulevad valgus kiired läbivad klaasi ja satuvad kõigepealt õhku, alles seejärel silma. Selles peitubki meid hämmastanud vastuolu lahendus. Parim illustratsioon öeldule on see, kui selgesti me näeme akvaariumis ujuvaid kalu.
Kas olete proovinud teha järgmist lihtsat katset: sukeldada kaksikkumer lääts (suurendusklaas) vette ja vaadelda läbi selle vee all olevaid kehi? Proovige, ja teid tabab üllatus: vees suurendusklaas peaaegu ei suurenda. Sukeldage vette vähendusklaas (kaksiknõgus lääts) – ja selgub, et seegi kaotab peaaegu kogu oma vähendamis - võime! Kui teha see katse mitte vee, vaid taimeõliga (näiteks seedriõliga), mille murdumisnäita ja on suurem kui klaasil, siis selgub, et kaksikkumer lääts vähendab, kaksiknõgus aga suurendab kujutisi.
Tuletage meelde valguse murdumis seadust , ja need imed ei üllata teid enam oma ebatavalisusega. Kaksikkumer lääts suurendab õhus sellepärast , et klaas murrab valgust tugevamini kui teda ümbritsev õhk. Kuid vee ja klaasi murdmisvõime erineb vähe; seepärast , pannes klaasläätse vette, ei murdu veest klaasi siirduvad kiired kuigi tugevasti. Siin ongi põhjus, miks vees suurendusklaas ei suurenda ja vähendusklaas ei vähenda sel määral kui õhus.
Taimeõli murrab kiiri tugevamini kui klaas ja seepärast selles vedelikus suurendusklaasid vähendavad ning vähendusklaasid suurendavad. Samamoodi toimivad vee all ka õõnsad (õigemini, õhk-) läätsed: nõgusad suurendavad, kumerad vähendavad. Sukelduja te prillid ongi just sellised õõnsad läätsed (joon. 111). Kiir MN liigub murdudes mööda teed MNOP, eemaldudes läätse sees langemispinna ristsirgest ja lähenedes sellele (s.t. OR-le) väljaspool läätse. Seepärast toimib õõnes lääts suurendus klaasina.
Vilumatuid suplejaid varitseb tihti suur oht ainult seetõttu, et nad unustavad valguse murdumisseaduse ühe huvitava järelduse: nad ei tea, et murdumine tõstab kõik vette sukeldatud kehad näiliselt nende tõelisest asukohast kõrgemale. Tiigi, jõe – iga veekogu põhi paistab olevat tegelikust peaaegu kolmandiku võrra kõrgemal; arvestades seda petlikku madalust, satuvad inimesed tihti ohtlikku olukorda. Eriti tähtis on seda teada lastel ja üldse kõigil lühikasvulistel inimestel, kelle jaoks viga sügavuse määramisel võib osutuda saatuslikuks.
Põhjuseks on valguskiirte murdumine. Seesama optikaseadus, mis annab pooleldi vettesukeldatud lusikale murtud kuju (joon. 112), tingib ka põhja näiva kerkimise.
Te võite seda kontrollida.
Pange oma seltsimees niimoodi laua taha istuma, et ta ei näeks enda ees oleva tassi põhja. Asetage tassi põhja münt, mida tassi serv varjab teie seltsimehe silme eest. Nüüd paluge, et ta pead ei pööraks, ja valage tassi vett. Juhtub midagi ootamatut (joon. 113): münt muutub teie külalisele nähtavaks! Imege vesi ta ssist voolikuga välja, ja tassi põhi koos mündiga laskub taas allapoole.
Joonis 114 selgitab, kuidas kõik toimub.
Põhja osa m paistab vaatlejale (kelle silm on vee kohal punktis A) olevat kerkinud; kiired murduvad veest õhku ja jõuavad silma, mis näeb nende kiirte pikendusele jäävat, s.t. m kohal olevat ala. Mida rohkem längu kiired langevad, seda kõrgemale tõuseb m. Seepärast paistabki, vaadates paadist tasase põhjaga tiiki, et veekogu kõige sügavam koht on otse meie all ning kaugemal muutub vesi üha madalamaks.
Niisiis näib tiigi põhi meile nõgusana. Vastupidi, kui me saaksime tiigi põhjast vaadata üle tiigi viivat silda, näiks see meile kumerana (nagu joonisel 115; sellise foto saamisviisist räägime hiljem). Antud juhul siirduvad kiired nõrgalt murdvast keskkonnast (õhust) tugevasti murdvasse keskkonda (vette), seepärast tekibki vastupidine efekt võrreldes sellega, mida näeme kiirte üleminekul veest õhku. Samal põhjusel paistab ka näiteks kalale tasaste seintega akvaariumi ees seisev inimeste viirg mitte sirgena, vaid kaarena, mille kumer osa on pööratud kalade poole. Sellest, kuidas näevad kalad, õigemini, kuidas nad peaksid nägema, kui neil oleksid inimeste silmad, räägime hiljem üksikasjalikumalt.
Torgake nööpnõel tasasesse siledasse korkkettasse ja pange see kork, nõel allapoole, vette ujuma. Kui kork pole liiga väike, siis võite pead pöörata, kuidas soovite, nööpnõela te ikka ei näe, kuigi paistab, et nööpnõel on küllalt pikk ja kork ei tohiks teda teie eest varjata (joon. 116). Miks siis valguskiired ei jõua nööpnõelalt teie silma? Sest nad alluvad nähtusele, mida füüsikas nimetatakse täielikuks peegelduseks.
Tuletame meelde, milles see seisneb.
Joonisel 117 võite jälgida õhust vette tungivate kiirte käiku (üldiselt peavad kiired liikuma vähem murdvast keskkonnast tugevamini murdvasse keskkonda) ja samuti veest õhku siirduvate kiirte teed. Kui kiired suunduvad õhust vette, lähenevad nad langemistasandi ristsirgele, näiteks kiir, mis langeb keskkondade lahutuspinnale nurga all, siseneb vette nurga all, mis on väiksem kui (joon. 117a).
Mis aga juhtub, kui kiir, libisedes mööda veepinda, langeb veepinnale püstsihi suhtes peaaegu täisnurga all? Siis murdub kiir nurga all, mis on väiksem täisnurgast, nimelt nurga 48,5° all. Suurem kui 48,5° ei saa vette tunginud kiire ja püstsihi vaheline nurk olla; see on piirnurk vee puhul (joon. 1176).
Need lihtsad seosed tuleb kindlasti selgeks teha, et mõista hilisemaid järeldusi murdumisseadustest .
Saime teada, et kõikvõimalike nurkade all vette langevad kiired koonduvad vee all üsna kitsaks koonuseks tipunurgaga 48,5°+48,5° = 97° (joon. 117c).
Jälgime nüüd veest (punktist P) õhku tungivaid kiiri (joon. 118). Optikaseaduste järgi on kiirte teed samad ja kõik mainitud 97-kraadise tipunurgaga koonuses olevad kiired väljuvad õhku erinevate nurkade all, jagunedes kogu 180-kraadisesse ruumi vee kohal.
Ent mis saab väljapoole mainitud koonust jäävast veealusest kiirest? Selgub, et see ei väljugi vee alt, vaid peegeldub tema pinnalt nagu peeglilt täielikult tagasi. Üldiselt, iga veealune kiir7, mis langeb veest vee ja õhu lahutuspinnale piirnurgast (48,5°) suurema nurga all, ei murdu, vaid peegeldub; nagu ütlevad füüsikud, allub ta täielikule peegeldusele.*
(* Peegeldust nimetatakse täielikuks sellepärast, et peegelduvad kõik langevad kiired, kuna isegi parim peegel (poleeritud mangaanist või hõbedast) peegeldab ainult osa talle langevatest kiirtest, ülejäänu a ga neeldub. Nimetatud tingimustel on vesi ideaalne peegel.)
Kui kalad uuriksid füüsikat, siis oleks nende füüsika olulisim osa õpetus täielikust peegeldusest, sest sellel on nende veealuses nägemises esmajärguline tähtsus.8
Üsnagi usutav, et veealuse nägemise iseärasustega on seotud ka kalade hõbedane värvus. Zooloogide arvates näitab see kalade kohastumist nende kohal oleva veepinna värvusega: altpoolt vaadates näib veepind teatavasti täieliku peegelduse tõttu peegelpinnana, sellel taustal jäävad hõbedased kalad neid küttivatele veekiskjatele märkamatuks .
Paljud ei aimagi, kui ebatavaline näiks maailm vaadatuna vee alt: ta peaks paistma vaatlejale peaaegu tundmatuseni muutununa ja moondununa.
Kujutlege, et olete vees ja silmitsete läbi veeliniku veepealset maailma. Otse teie pea kohal rippuva pilve kuju ei muutu vähimalgi määral , sest püstkiir ei murdu. Kuid kõik muud esemed, millest kiired langevad veepinnale teravnurkade all, paistavad moonutatuna: nad oleksid nagu ülespoole kokku surutud, ja seda tugevamini, mida teravama nurga moodustab kiir veepinnaga (joon. 119). See on ka arusaadav: kogu veepealne maailm peab mahtuma kitsasse veealusesse koonusesse; 180° peab kahanema peaaegu kaks korda – 97 kraadini, ja kujutised moonduvad paratamatult. Esemed, millest lähtuvad kiired langevad veepinnale 10-kraadise nurga all, koonduvad vee all sedavõrd, et neid on peaaegu võimatu eraldada. Kuid kõige enam rabaks teid veepinna enese kuju: vee alt ei paista see sugugi olevat tasane, vaid koonusjas. Teile näib, et asute hiigellehtri põhjas, selle lehtri tipunurk on veidi suurem täisnurgast (97°). Koonuse ülaserva ääristavad vikerkaarevärvides rõngad – punane, kollane, roheline ja sinine. Miks? Valge päikesevalgus koosneb eri värvi kiirte segust; iga värvi kiirel on oma murdumisnäitaja ja seepärast ka oma piirnurk. Selle tulemusena paistab kõikide veepealsete kehade ümber vikerkaarevärvi oreool.
Mis on siis näha väljaspool koonust, kuhu mahub kogu veepealne maailm? Seal laiub helkiv veepind, milles nagu peeglis peegelduvad veealused objektid.
Täiesti ebahariliku kuju omandaksid veealuse vaatleja jaoks need esemed, mis osalt on vees, osalt väljas. Olgu jõkke asetatud veemõõdulatt (joon. 120). Mida näeb vaatleja, kes seisab vee all punktis A? Jagame vertikaaltasandi punkti A ümber (360°) osadeks ja vaatleme neid eraldi. Nurga 1 ulatuses näeb ta jõe põhja, muidugi kui see on piisavalt valgustatud. Nurgas 2 näeb ta mõõdulati veealust osa moonutamata kujul. Ligikaudu nurgas 3 näeb ta mõõdulati vetteasetatud osa ümberpööratud kujutist (tuletage meelde seda, mida rääkisime täielikust peegeldusest ). Veel kõrgemal näeb vaatleja mõõdulati veest väljaulatuvat osa, kuid see pole veealuse osa pikendus, vaid paikneb märksa kõrgemal, oma alumisest osast täiesti eraldi. Vaatlejale ei tule loomulikult pähegi, et see hõljuv latt on eelmise lati pikendus! Pealegi näib latt tugevasti kokkusurutuna, eriti alumises osas – seal on jaotised üksteisele märksa lähemale nihkunud. Nurgas 4 peegeldub jõe põhi. Nurgas 5 on näha kogu veepealne maailm koonusja toruna. Nurgas 6 on näha põhja peegeldus veepinna alumiselt küljelt. Üleujutatud puu- paistab vee alt sellisena, nagu kujutatud joonisel 121.
Kui aga mõõdulati asemel oleksid suplejad, siis veealuse vaatleja (näiteks kalade) seisukohast oleks igaüks neist nagu kahestunud, muutunud kaheks olendiks (joon. 122): ülemine on jalgadeta, alumine aga peata ja nelja jalaga! Veealusest vaatlejast kaugenemisel tõmbub supleja keha veepealse osa alumine pool üha rohkem kokku; teataval kaugusel kaob keha veepealne osa peaaegu täiesti, järele jääb vaid vabalt hõljuv pea...
Kas oleks võimalik vahetult katses kontrollida neid ebaharilikke järeldusi? Sukeldunult näeksime väga vähe, isegi siis, kui õpiksime hoidma silmi lahti. Esiteks ei jõua veepind rahuneda nende lühikeste sekundite vältel, mis me suudame vee all viibida, aga läbi lainetava veepinna on raske midagi näha. Teiseks, nagu juba varem selgitasime, erineb vee murdumisnäitaja vähe meie silma läbipaistvate osade murdumisnäitajatest, ja seetõttu tekib võrkkestal väga ähmane kujutis; kõik ümbritsev näib uduse ja laialivalguvana (vt. lk. 181). Vaatlemine tuukrikellast, -kiivrist või allveelaeva klaasaknast ei annaks samuti soovitavaid tulemusi. Nagu me juba selgitasime, asub vaatleja neil juhtudel küll vee all, kuid sugugi mitte veealuse nägemise tingimustes : enne silma jõudmist satuvad kiired pärast klaasi läbimist uuesti õhku ning toimub uus murdumine; seejuures kas taastub kiirte esialgne käik või saab kiir uue suuna, ent vaevalt sellise, nagu tal oli vees. Seepärast ei saagi vaatlused läbi veealuste ehitiste akende anda õiget ettekujutust veealusest nägemisest.
Muide, pole vaja sugugi minna vee alla, et näha, kuidas paistab maailm vee alt vaadatuna. Veealuse nägemise tingimusi võib uurida erilise veega täidetud fotoaparaadi abil. Objektiivi asemel kasutatakse metallplaati, millesse on puuritud auk. Kerge on mõista, et kui kogu ruum kaameras ava ja valgustundliku plaadi vahel on täidetud veega, siis jäädvustub välismaailm plaadile samal kujul, nagu ta paistab veealusele vaatlejale. Seda võtet kasutas ameerika füüsik Robert Wood; ta sai erakordselt huvi tavaid fotosid, millest üks on esitatud joonisel 115. Seda, miks veepealsed esemed paistavad veealusele vaatleja le moondunuina (raudteesilla sirged lõigud jäädvustusid Woodi fotol kaartena), oleme põhjendanud juba seal, kus selgitasime, miks tiigi tasane põhi näib nõgusana (vt. lk. 184).
On veel teinegi viis tutvuda vahetult sellega, milline paistab maailm vee alt: vaiksesse tiigivette asetatakse peegel, ja kallutades teda sobivalt, jälgi takse veepealsete esemete peegeldumist selles. Niisugused vaatlused kinnitavad kõigis üksikasjades neid teoreetilisi kaalutlusi, millest oli juttu eespool.
Niisiis, läbipaistev veekiht silma ja väljaspool seda kihti asetsevate kehade vahel moonutab nende kehade välimust ja annab neile fantastilise kuju. Olend, kes pärast kuivamaaelu satuks vette, ei tunneks äragi oma kodust maailma – nii palju muutuks see vaatamisel läbipaistva vee sügavusest .
Piltlikult kirjeldab valguse varjundite vaheldumist vee all ameerika bioloog W. Beebe:
«Hommikul sulpsatasime veepinna alla ja nagu ma seda tihti olen kogenud, tuli äkiline siirdumine kuldkollasest maailmast rohelisse jälle ootamatu üllatusena. Pärast seda, kui vaht ja veemullid olid eemaldunud klaasist, ujusime rohelises; meie näod, anumad, riistad ja isegi mustad seinad värvusid. Kuid tekilt vaadatuna laskusime selgesse sügavasse ultramariini...
...Nagu olen öelnud, kustutab juba laskum ise esimene järk kõik spektrumi mugavad soojad värvid. Punane ja oranž paistavad sellistena, nagu neid ei oleks iialgi olemas olnud, ja peagi neelab roheline kollase. Maapinnal oleme hellitatud kõigi nende varjunditega, ja kui nad siis 30. või enam meetril kaovad, olgugi moodustades ainult ühe kuuendiku nähtavast spektrumist, muutub meie meeltele kogu ümbrus külma, ööd ja surma meenutavaks. Roheline kadus märkamatult, kui me sukeldusime sügavamale, ja 60. meetril oli võimatu öelda, kas vesi on rohekassinine või sinakas roheline...
180. meetril näis valgus tumeda, helendava sinisena ja see vastu rääkivus mõistetes näitab kirjeldamise raskust. Nagu eelmistel sukeldumistel näis ta säravana, kuid tal puudus sel määral tõeline jõud, et teda ei saanud kasutada lugemiseks ega kirjutamiseks...
300. meetril... ma katsusin iseloomustada vee värvi – mustjas sinine, tumehallikassinine. On kummaline, et kui sinine kaob, siis ei asenda seda violett nähtava spektrumi lõppvärv, nagu seda arvata võiks. See on nähtavasti juba absorbeerunud. Viimane märk sinisest kahvatub nimetuks halliks ja see lõpuks mustaks, kuid praegusest tasapinnast allpool silm tõrgub ja vaim keeldub eraldamast igasuguseid selgeid värvivahesid. Päike on võidetud ja värv on kadunud igaveseks, kuni viimaks inimene sisse tungib ja saadab kollase elektrikiire sellesse keskkonda, mis oli kaks biljonit aastat olnud igipime.»
Suures sügavuses valitsevast pimedusest kirjutab sama uurija teisal järgmist:
«... Mõni päev tagasi oli vesi 760. meetril tundunud mustemana, kui on võimalik kujutella, kuid nüüd näis ta samale kujutlusele mustemana kui must. Näis, nagu peaks kõiki tulevasi öid ülal maailmas võtma ainult kui hämaruse suhtelisi astmeid. Ma ei saa enam kunagi tarvitada sõna must kindla veendumusega.»*9
Kui teile öeldakse, et teie vaateväljas on piirkond, mida te üldse ei näe, ehkki see asub otse teie ees, siis te seda muidugi ei usu. Kas on võimalik, et me kogu elu ei märka niisugust suurt nägemise puudust? Ometi veenab teid selles lihtne katse.
Hoidke joonist 123 umbes 20 cm kaugusel parem ast silmast (vasak pange kinni) ja vaadake vasakul olevat ristikest; lähendage nüüd joonist aeglaselt silmale ilmtingimata saabub hetk, mil suur must täpp ringide lõiku- miskohal kaob jäljetult! Te ei näe seda, ehkki see jääb endiselt teie vaatevälja, kuid mõlemad ringjooned vasakul ja paremal on selgesti näha!
Esimesena tegi selle katse (tõsi, veidi teistsugusel kujul) 1668.a . kuulus füüsik Mariotte ja see lõbustas kuningas Louis XIV õukondlasi väga. Mariotte korraldas katse nii: ta pani kaks ülikut teineteisest 2 m kaugusele ja palus neid ühe silmaga vaadata teatud punkti, mis asetses kõrval; siis paistis kummalegi neist, et tema partneril pole pead.
Võib tunduda kummaline, kuid alles 17. sajandil said inimesed teada, et nende silma võrkkestal on pimetähn, mille olemasolu keegi varem ei kahtlustanudki. Pimetähn on võrkkesta osa, kus nägemisnärv suubub silma ja pole veel hargnenud väikesteks närvilõpmeteks, mis on varustatud valgustundlike elementidega.
Me ei märka seda "musta auku" oma nägemisväljas pikaajalise harjumuse tõttu. Kujutlusvõime täidab automaatselt selle tühiku ümbritseva tausta detailidega; näiteks joonisel 123 pikendame täppi nägemata ringjooni ja oleme veendunud, et näeme selgelt seda kohta, kus nad lõikuvad.
Kui kannate prille, võite teha sellise katse: kleepige prilliklaasile tükike paberit (mitte päris keskele, vaid ääre poole). Esimestel päevadel paberitükk segab, kuid möödub nädal, teinegi, ja te olete sellega nii harjunud, et enam ei märka seda üldse. Muide, seda teab hästi igaüks, kes on juhtunud kandma mõranenud klaasidega prille: pragu märkate ainult esimestel päevadel. Täpselt samuti ei märka me pikaajalise harjumise tõttu silma pimetähni. Peale selle on kummagi silma pimetähnid vaatevälja eri kohtades, nii et kahe silmaga nägemisel üldises vaateväljas tühikut ei teki.
Ärge arvake, et pimetähn on väga väike; kui te vaatate ühe silmaga 10 m kauguselt maja, ei näe te pimetähni tõttu üsna suurt osa läbimõõduga üle 1 m tema fassaadist; sellesse ossa mahub terve aken. Taevas jääb aga nähtamatuks pindala, mis on võrdne 120 täiskuuketta pindalaga!
Mõni sõna Kuu näivatest mõõtmetest. Küsides tuttavatelt, kui suurena paistab neile Kuu, saate kõige mitmekesisemaid vastuseid. Enamik ütleb, et Kuu on taldrikusuurune, aga on ka neid, kellele ta näib moositaldriku, kirsi või õunasuurusena. Ühele koolipoisile näis Kuu alati nii suur kui ümmargune laud 12 inimese jaoks. Keegi belletrist väitis, et taevas oli arssinane Kuu.
Millest niisugune vahe kujutlustes ühe ja sellesama eseme suurusest?
See vahe oleneb erinevustest kauguse hindamisel. Need hinnangud on alati alateadlikud. Inimene, kes tajub Kuud õunasuurusena, kujutleb teda palju lähemal olevat, kui need inimesed, kellele ta näib taldriku või ümara laua suurusena.
Enamik inimesi kujutab Kuud muide taldrikusuurusena. Siit võib teha huvitava järelduse. Kui arvutada (arvuta misviis selgub hiljem) kaugus, millele tuleks paigutada Kuu, et tal oleks selline näiv suurus, siis osutub, et see kaugus ei ületa 30 m.10 Niisugusele tagasihoidlikule kaugusele nihutamegi alateadlikult oma öise valgusallika!
Kauguste väärast hindamisest tuleneb palju nägemisillusioone. Mäletan hästi üht silmapetet varasest lapse- põlvest, kui kõik olemise muljed olid mulle veel uued. Linnalapsena nägin ükskord kevadel maal jalutades aasal söövaid lehmi: et ma hindasin kaugust valesti, paistsid lehmad mulle kääbustena! Selliseid kääbuslehmi pole ma pärast seda enam kunagi näinud ega saagi nägema!
(* Siiski, ka täiskasvanuil esineb mõnikord selliseid illusioone. Seda tõendab järgmine katkend Grigorovitši novellist Kündja: Ümbruskond oli nagu peopesal. Küla näis asuvat otse silla juures; maja, küngas ja kasesalu paistsid liituvat külaga. Kõik see maja, aed ja küla omandas sääraste mänguasjade välimuse, kus garnrnal kujutab puid, peeglikillud aga jõge.)
Taevakehade näivat suurust mõõdavad astronoomid selle nurga järgi, mille all neid nähakse. Nurkmõõtmeks, vaatenurgaks nimetatakse nurka, mille moodustavad kaks sirget, mis on tõmmatud vaadeldava keha äärepunktidest kuni silmani (joon. 125). Nagu teada, mõõdetakse nurki kraadides, minutites ja sekundites. Vastates küsimusele kuuketta näiva suuruse kohta ei ütle astronoom, et ketas on võrdne õuna või taldrikuga, vaid vastab, et ta on võrdne 0,5°, s. t. kuuketta äärepunktidest meie silmani tõmmatud sirgete vaheline nurk on 0,5°. Niisugune näivate mõõtmete määramise viis on ainuõige ega tekita arusaamatusi.
Geomeetria õpetab, et keha, mis asub silmast kaugemal kui 57 oma läbimõõtu, peab vaatlejale paistma umbes nurga 1° all. Näiteks õun diameetriga 5 cm omab nurkläbimõõtu 1° silmast 5 x 5 7 cm kaugusel. Kaks korda suuremal kaugusel paistab ta nurga 0,5° all, s.t. niisama suurena, nagu näeme Kuud.
Kui soovite, võite öelda, et Kuu näib teile õunasuurusena aga tingimusel, et see õun on teie silmast 570 cm (ligi 6 m) kaugusel. Soovides võrrelda kuuketta näivat suurust taldrikuga, tuleb taldrik paigutada ligi 30 m kaugusele. Enamik inimesi ei taha uskuda, et Kuu paistab nii väiksena; aga eks pange kümnekopikaline silmast sellisele kaugusele, mis ületab 114 korda tema diameetri: ta katab täpselt Kuu, ehkki on silmast 2 m kaugusel.
Kui teile tehtaks ettepanek joonistada paberile palja silmaga nähtavat kuuketast kujutav ring, tunduks ülesanne teile õige ebamäärasena: ring võib olla suurem või väiksem sõltuvalt sellest, kui kaugel ta asetseb silmast. Täpsuse huvides võtame selleks kauguse, millel me tavaliselt hoiame raamatuid, jooniseid jne., s.t. parima nägemise kauguse. Normaalse silma puhul on see 25 cm.
Arvutame niisiis, kui suur peab olema ring näiteks selle raamatu lehel, et ta võrduks Kuu näiva kettaga. Arvutus on lihtne: kaugus 25 cm on vaja jagada 114 ga. Saame õige tühise suuruse veidi üle 2 mm. Umbes nii lai on selles raamatustrükitäht o. Lausa võimatu uskuda, et Kuu ja temaga nurksuuruse poolest võrdne Päike paistavad meile nii tillukese nurga all.
Tõenäoliselt olete märganud, et pärast Päikese vaatamist tekivad teie nägemisväljale pikaks ajaks värvilised ringikesed. Need nn. optilised jäljed on sama nurksuurusega mis Päikegi. Ent nende näiv suurus muutub: kui te vaatate taevasse, on nad päikeseketta suurused; kui aga heidate pilgu enda ees olevale raamatule, on Päikese jälg umbes 2-mm läbimõõduga; see kinnitab ilmekalt teie arvutuste õigsust.
Kui me sooviksime nurkmõõtmeid säilitades kujutada paberil Suurt Vankrit, saaksime joonisel 126 esitatud pildi. Vaadates seda parima nägemise kauguselt, näeme tähtkuju samasugusena nagu tähistaevas. See on nn. Suure Vankri kaart loomulikus nurkmastaabis. Kui teile on selle tähtkuju nägemismulje hästi tuttav – mitte ainult kuju, vaid just vahetu nägemismulje –, siis elate joonise 126 vaatamisel nagu uuesti läbi sama mulje. Teades nurkkaugusi üksikute tähtkujude peamiste tähtede vahel (need esitatakse astronoomiakalendrites ja vastavates teatmikes), võite koostada «loomulikus mastaabis » terve taevaatlase. Selleks on tarvis varuda millimeetripaberit ja lugeda iga 4,5 mm sellel võrdseks 1 kraadiga (tähti kujutavate ringide pindalad peavad olema võrdelised nende heledusega).
Läheme nüüd planeetide juurde. Nende näivad mõõtmed on nagu tähtedelgi nii väikesed, et paljale silmale paistavad nad helendavate punktidena. See on ka arusaadav, sest ükski planeet (peale Veenuse selle suurima heleduse ajal) ei paista paljale silmale nurga all, mis oleks suurem ühest kaareminutist , s.t. sellest piirväärtusest, mille puhul me võime eristada eset kui mõõtmetega keha (väiksema nurga korral näib iga keha meile punktina).
Toome siinkohal mõne planeedi suurused (nurgasekundites); iga planeedi kohta on antud kaks arvu – üks vastab taevakeha vähimale, teine suurimale kaugusele Maast:
Merkuur 13-5
Veenus 64-10
Mar ss 25-3,5
Jupiter 50-31
Saturn 20-15
Saturni rõngad 48-35
Neid suurusi loomulikus nurkmastaabis paberile joonistada pole võimalik: ühele nurgaminutile, s.t. 60 nurgasekundile vastab parima nägemise kaugusel kõigest 0,04 mm, suurus, mida me palja silmaga ei näe. Seepärast kujutame planeedikettaid sellistena, nagu nad meile paistavad 100 korda suurendavas teleskoobis. Joonisel 127 on planeetide näivate suuruste skeem sellisel suurendusel. Alumine kaar kujutab kuu- (või päikese-) ketta äärt sajakordse suurendusega teleskoobis. Selle kohal on Merkuur Maale kõige lähemal ja Maalt kõige kaugemal. Edasi tuleb Veenus erinevates faasides; meile koige lähemal asudes pole see planeet üldse nähtav, sest ta on pöördunud Maa poole oma nähtamatu küljega (Teda võib näha sellises asendis ainult neil harvadel juhtudel, kui ta projitseerub musta ringikesena Päikese kettale (nn. Veenuse üleminek Päikese kettast).); seejärel muutub nähtavaks tema kitsas sirp – see on suurim kõigist «planeediketastest»; järgmistes faasides Veenus kahaneb ja täisketta läbimõõt on 6 korda väiksem kui sirbil. Kõrgemal Veenuse kohal on kujutatud Marss. Vasakul näete teda Maale kõige lähemal; sellisena näitab teda meile sajakordse suurendusega teleskoop. Mida sellel väikesel kettal eristada saab? Kujutlege seda sama ringi suurendatuna 10 korda, ja te saate et tekujutuse sellest, mida näeb astronoom, kes uurib Mar ssi 1000 korda suurendava teleskoobi abil. Kas nii väikesel pinnal on võimalik kindlalt märga ta selliseid peeni detaile nagu kuulsad «kanalid » või kindlaks teha värvuse nõrka muutumis t selle ma a ilma «ookeanide» põhjas? Mis siis imestada, et uurijate vaatlused lähevad oluliselt lahku ja et ühed peavad optiliseks illusiooniks seda, mida teised oleksid nagu selgesti näinud...11
Hiiglasel Jupiteril koos oma kuudega on meie skeemis väga silmapaistev koht; tema ketas on märksa suurem teiste planeetide ketastest (välja arvatud Veenuse sirp), neli peamist kuud paiknevad aga joonel, mis on võrdne peaaegu poole kuuketta läbimõõduga. Siin on Jupiter kujutatud Maale kõige lähemas asendis. Lõpuks Saturn oma rõngaste ja kõige suurema kuuga (Titanusega) kujutab endast samuti üsnagi silmatorkavat objekti ajal, mil ta on meile kõige lähemal.
Pärast öeldut on lugejale selge, et iga nähtav ese paistab meile seda väiksem, mida lähemale me end temale kujutleme. Ja ümberpöördult: kui me miskipärast suurendame kaugust esemeni, siis ka see ese ise näib meile vastavalt suuremana.
Järgnevalt esitame Edgar Allan Poe õpetliku loo, mis kirjeldab just niisugust nägemisillusiooni. Näilisest ebatõepärasusest hoolimata pole see jutustus sugugi fantastiline. Langesin kord ise peaaegu sama suguse illusiooni ohvriks, ja küllap ka paljudele minu lugejaist meenuvad taolised juhtumid oma elust.
Koleera kohutava valitsuse ajal New Yorgis olin võtnud vastu ühe sugulase kutse veeta paar nädalat temaga ta mõisa üksinduses Hudsoni kaldal. Sääl oli meil kasutada harilikke vahendeid suvelõbustusteks; seepärast metsas luusimise, joonistamise, lootsikusõidu, kalastamise, suplemise, musitseerimise ja raamatute lugemisega oleksime vahest üsna mõnusasti mööda saatnud aja, poleks mitte igal hommikul saabund meile koledaid uudiseid tollest rahvarikkast linnast. Ei möödund päevagi, mis meile ei toond teadet mõne tuttava surmast. Vähehaaval, kuna taud ägenes, olime iga päev valmis tääsma mõne sõbra kaotusest. Lõppeks värisesime iga sõnumitooja lähenemisel. Kogu lõunast tulev õhk näis meile läbi imbund surmast. See kohutav mõte võttis tõepoolest täielise halduse mu hinge üle. Ma ei võind ei rääkida, mõtelda ega unistada millestki muust. Mu vaut oli vähem erutuva temperamendiga ja kuigi ka ise suuresti masendet meeleolus, pingutus ta ülal hoidma minu oma. Ta rikkalt filosoofiline intdlekt ei lasknud end kunagi mõjutada ebakujutelmadest. Oõva reaalsustele oli ta reesvalt tundeline, kuid selle varikujude ees ei tundnud ta hirmu. Ta püüded mind kiskuda mu ebatavalise sünguse seisundist, millesse olin langenud, nurjusid suurel määral teatavate raamatute mõjul, milled olin leidnud ta raamatukogust. Need olid omased võrsuma panema kõiki neid pärimusliku ebausu idusid, mis varjat kujul peitusid mu põues. Olin neid raamatuid lugend ilma tema teadmata ja nõnda oli ta sageli ümmal endale seletama võimsaid muljeid, mis olid tehtud mu meelekujutusse.
Mu lemmikteemiks oli rahvaomane usk ennustesse, usk, mida ma tol elu järgul peagu tõsiselt kalduv olin kaitsma. Selle aine üle oli meil pikki ja elavaid vaidlusi – tema toonitades äärmist alusettust sellaseis asjus, mina väites, et rahva vaade, tekkind täiesti spontaanselt, see tähendab ilma vähimagi nähtava mõjutuseta väljaspoolt –, evis iseendas ümberlükkamatu tõe elemente ja vääris suuresti tõsiseltvõtmist.
Tõik on, et varsti pärast mu saabumist mõisa oli mulle esinend üks juhtum nii seletamatu ja endas eviv nii palju endelist laadi, et mind küll peaks vabandetama sirnamast seda mingiks ennuseks. See kohutas ja ühtlasi hämmastas ning ärevustas mind seevõrd, et möödus mõni päev, enne kui söandasin kõnelda sellest seigast oma sõbrale.
Ühe ebamääraselt sooja päeva õhtupoolikul istusin, raamat käes, lahtise akna ees, evides läbi pika jõekallaste-rea vaate kaugelolevale künkale, mille külg, mis oli lähim minu seisukohale, oli niinimet maaluhistumise tõttu paljandund suuremast osast oma puudest. Mu mõtted olid juba tüki aega rännand raamatust mu ees naaberlinna õudusele ja nüürusele. Kui tõstsin silmad leheküljelt, langes nende pilk künka alasti küljele ja nimelt esemele — mingile elusale, koletusliku kujuga elukale, kes nobedasti liikus künka harjast selle jalale ja kadus viimaks alla tihedasse metsa. Kui see olend esiteks tuli nähtavale, kahtlesin omaenese terves mõistuses – vähimalt mu omade silmade tunnistuses, ja mitu minutit möödus, enne kui iindsin end veenda, et ma polnd ei hull ega näind und. Ometi kui kirjeldada elukat (keda ma selgesti nägin ja keda rahulikult jälgisin kogu ta edasiliikumise aja kestel), kardan, et mu lugejad leiavad veelgi raskemaks veenduda selles suhtes kui ma ise.
Hinnates eluka suurust võrreldes seda suurte puude läbimõõduga, millede lähedalt ta möödus – need vähesed metshiiglased, mis olid pääsnud maaluhistuse katastroofist –, järeldasin ta olevat kaugelt suurema kui ükski olemasolev liinilaev. Ütlen liinilaev, sest monstri kuju sisendas selle mõtte, – jah, ühe liinilaeva kere meie seitsmekümne nelja hulgast võiks anda üsna ligilähedase kujutelma ta üldisest hahmust. Looma suu asetses londi otsas, mille pikkus võis olla kuus-seitsekümmend jalga ja mis oli paksuselt kui hariliku elevandi keha. Selle londi pääl kere lähedal oli määratu hulk musti lopsakaid ning sasis karvu, rohkem kui neid oleksid võind tarnida paarikümne pühvli nahad; ja neist karvust lähtudes ning külgepidi allapoole sirutudes sööstis kaks läikivat kihva otsegu metssea omad, aga määratumalt suuremate mõõdetega. Ettepoole ulatudes, paralleelselt londiga ja mõlemal pool seda oli hiigla ritv, kolm-nelikümmend jalga pikk, moodustet näilikult puhtast kristallist ja oma kujult täieline prisma; – see heiastas kõige toredamal kombel loojuva päikese kiiri. Rümp oli kiilu kujuline, mis oma terava äärega pöördud maa poole. Sellest sirutus välja kaks paari tiibu, iga tiib peagu sada jardi pikk, kusjuures üks paar oli paigutet teise üle ja kõik paksult kaetud metallsoomustega, iga soomus nähtavasti umbes kümme või kaksteist jalga läbimõõdult. Panin tähele, et tiibade ülemine ja alumine kolmandik oli ühendet tugeva ketiga. Kuid selle koleda eluka päämine iseärasus oli surnupää kujutus, mis kattis peagu kogu ta rinda ja esines oma ereda valgega selgesti märgituna keha tumedal pinnal, nagu oleks see sinna hoolikalt kellegin kunstnikun joonistet. Kuna vaatlesin seda looma ja eriti tähelepanelikult ta rinda hirmuja õõvatundel — läheneva õnnetuse aimusel, mida ma ei saand alla suruda mingil mõistuse ponnistusel, hoomasin hiigla lõuad londi otsas äkki sirutuvat ja neist tuli nii vali ja südantlõhestav kaebehäälitsus, et see mõjus mu närvidele kui surmakell, ja kui koletis kadus künka jalale, langesin ühekorraga minestanult põrandale.
Meelemärkusele tulekul oli mu esimeseks mõtteks oma sõpra informeerida nähtust ja kuuldust, – ja ma võin vaevalt seletada, mis vastumeelne tunne lõppude lõpuks mõjutas mind sellest loobuma.
Viimaks ühel õhtul päeva kolm või neli pärast seda juhtumit viibisime üheskoos toas, kus olin näinud seda ilmungit – mina istudes samal toolil akna ees ja tema lebades lähedal sohval. Mõtteühendus koha ja ajaga pani mind andma temale reite sellest nähtusest. Ta kuulas mind lõpuni, seepääle alguses naeris südamlikult, siis aga sattus äärmiselt tõsisesse olekusse, nagu oleks mu hullumeelsus väljaspool igat kahtlust. Samal ajal silmasin jälle selgesti koletist, millele ma nüüd juhtisin sõbra tähelepanu. Ta vaatas teravalt, kuid väitis mitte midagi nägevat, ehk küll ma osutasin täpselt eluka kulgu allapoole ta liikumisel mööda künka paljast pinda.
Nüüd valdas mind ärarääkimatu ärevus, sest sirnasin seda nägemust oma surma endeks või, mis veel pahem, hullumeelsuse-söösti eel-oireks. Ma tõmbusin ägedasti tagasi toolile ja mõneks hetkeks peitsin näo käte vahele. Kui avasin silmad, poinud ilmung enam nähtav.
Mu vaut oli teataval määral tagasi saanud ema rahulikkuse ja küsiteli mind üsna üksikasjaliselt viirastusliku looma välimusliku kuju üle. Kui olin teda selles suhtes täielikult rahuldand, hingas ta sügavalt, nagu kergendet mingist talumatust koormast, ja peemas jutlema teatava minu meelest julma rahulikkusega mimesuguseist spekulatiivse filosoofia küsimusist, mis enne seda olid moodustand vaidluse aine meie vahel. Mäletan teda muu seas üsna eritiselt toonitand mõtet, et päämine eksitus kõigis inimlikes uurimistes seisneb mõistuse altiduses ala- või ülehinnata ühe eseme tähtsust pelgast selle kauguse valestiarvestamisest. «öieti hindamaks, näiteks, » ütles ta, «inimkonnasse ta üldsuses avaldetavat mõju demokraatia põhjalikust levimisest, ajastu eebe, mil sellane leving võiks olla teostatav, ei mängiks moodustamast teatavat tegurit selle hinnangus. Ometi kas võid mulle nimetada üht autorit valitsusvormi üle, kes kunagi oleks seda oma aine erilist haru pidand üldse käsitlemist väärivaks?»
Siin ta peatus hetkeks, astus raamatukapi juure ja tõi säält ühe harilikest loodusteaduse käsiraamatuist. Paludes mind siis vahetada istekohad temaga, et ta võiks paremini lugeda raamatu peent trükki, nihutas ta mu leentooli akna juure ja, avades raamatu, jatkas oma kõnelemist peagu samal toonil kui enne.
«Poleks sa olnd nii äärmiselt täpne,» ütles ta, «koleeluka kirjeldamises, ei oleks ma vahest kunagi olnud võimeline sulle selgeks tegema, mis see oli. Kõigepäält luba, et loen sulle ühe koolipärase kirjelduse sugukonnast Sphinx, perekonnast Crepuscularia, liigist Lepidoptera, klassist Insecta — putukad. Kirjeldus on järgmine:
«Neli membraanset tiiba, kergelt värvitud ja metalselt läikivate soomustega; suu moodustab rullit londi, mis on kujunend lõualuude pikendusest, millede külgedel leiduvad raulade ja udemeste tundlate jädemed; alumisi tiibu hoiavad jäigad karvad ülemiste ligi; antennid pikerguse nuia kujul, prismaatilised; kõht terkjas. Surnupääga sfinks on mõnikord põhjustand palju õõva lihtrahva seas kaeblikku laadi kisaga, mida ta uldab, ja surma embleemiga, mida kannab oma rinnal.»»* (*Nüüd liigitatakse see liblikas perekonda Acherontia. See on üks väheseid liblikaid, kes suudab teha häält — hiirepiiksumist meenutavat vilet, ja ainus, kes seda häält suiste abil teeb. Heli on üsna vali ja kuuldav mitme meetri taha. Antud juhul võis hääl tunduda vaatlejale eriti tugevana, sest hääle allikas kanti mõttes õige suurele kaugusele (vt. peatükki «Kuulmise kurioosumid» käesoleva raamatu lõpus).)
Siin ta sulges raamatu ja nõjas toolis ettepoole, asudes täpselt samasse asendisse, kus mina olin istunud «koletise» nägemise hetkel. «Aa, sääl ta on!» hüüdis ta –, «praegu ta ronib jälle üles mööda künka pinda, tõesti väga kummaliselt laikiv loom, möönan seda. Ometi pole ta kuidagi mitte nii suur ja nii kaugel kui sina seda kujutelid; sest tõik on, et kui ta ronis üles mööda seda niiti, mis üks ämblik on tõmmand piki seda aknaraami, leidsin ta pikkuse olevat kõige rohkem ühe kuueteistkümnendiku tolli ja samuti ta kauguse ühe kuueteistkümnendiku tolli mu silmaterast.»»
«Sest ta muudab kindlal viisil kiirte käiku,» võib kõige sagedamini sellele küsimusele vastuseks saada. Ent selles vastuses on toodud põhjus, asja olemus jääb aga selgi tamata. Milles siis seisneb mikroskoobi ja teleskoobi suurendava toime peamine põhjus?
Sain seda teada mitte õpikust, vaid juhuslikult, kui märkasin kord koolipoisina erakordselt huvitavat ja mõtlemapanevat nähtust. Seisin suletud akna juures ja silmitsesin kitsa põiktänava vastaspoolel oleva maja tellisseina. Äkki põrkusin õudusega tagasi: teilisseinalt – ma nägin seda selgesti! – vaatas mulle otsa hiiglasuur, mitme meetri laiune inimsilm... Sel ajal polnud ma veel lugenud Edgar Allan Poe ülaltoodud jutustust ega taibanud kohe, et hiigelsilm oli minu enda silma peegeldus, peegeldus, mille ma projitseerisin kaugele seinale ja mis seepärast näis vastavalt suurendatuna.
Sellest kord aru saanud, hakkasin järele mõtlema, kas pole võimalik ehitada niisugusel silmapettel põhinevat mikroskoopi. Ja alles siis, kui katse ebaõnnestus, sain aru, milles on mikroskoobi suurendava toime olemus: üldse mitte selles, et saada eseme suurt kujutist, vaid selles, et vaadata teda suurema vaatenurga all ja järelikult, mis kõige tähtsam, et tema kujutis hõlmaks meie silma võrkkestal suurema pindala (joon. 128).
Selleks et mõista vaatenurga tähtsust kõnesolevas küsimuses, peame pöörama tähelepanu meie silma olulisele iseärasusele: iga ese või selle osa, mis paistab meile ühest nurgaminutist väiksema nurga all, sulab normaalse silma jaoks kokku punktiks, millel me ei erista ei kuju ega osi. Kui ese on silmast nii kaugel või nii väike, et ta tervikuna pais tab meile ühest kaareminutist väiksema nurga all, ei suuda me enam eristada tema ehituse üksikasju ja seda sellepärast, et niisuguse vaatenurga korral eseme (või mingi tema osa) kujutis silma võrkkestal ei haara korraga kaht närvilõpet, vaid mahub üheleainsale tundlikule elemendile: kuju ja ehituse üksikasjad kaovad ja me näeme punkti.
Mikroskoop ja teleskoop, mis muudavad vaadeldavalt esemelt lähtuvate kiirte käiku, peavad näi tama teda meile suurema vaatenurga all; kujutis venib võrkkestal suure maks, hõlmab rohkem närvilõpmeid ja me eristame esemes juba niisuguseid üksikasju, mis varem sulasid kokku üheks punktiks. «Mikroskoop või teleskoop suurendab sada korda» tähendab seda, et riist näitab meile esemeid sada korda suurema vaatenurga all, võrreldes sellega, mille all me näeme eset palja silmaga. Kui optikariist vaatenurka ei suurenda, ei anna ta ka mingit suurendust, ehkki meile võiks näida, et näeme eset suurendatult. Silm paistis tellisseinal mulle hiiglasuur, kuid ma ei näinud selles sugugi rohkem üksikasju, võrreldes sellega, mida näen peeglisse vaadates. Madalal horisondi kohal olev Kuu tundub meile märksa suuremana kui kõrgel taevas – kuid kas näeme sel suuremal kettal olgu või ainustki laiku, mida me ei näeks kõrgel pea kohal oleval Kuul?
Pöördudes E. A. Poe ju tustu ses «Sfinks» kirjeldatud juhu juurde, veendume, et siingi ei märganud jutusta ja suurendatud objektis mitte mingeid uusi detaile. Vaatenurk jäi samaks, liblikas oli näha sama nurga all sõltumata sellest, kas ta projitseerus kaugele metsale või lähedasele aknale. Kui aga vaatenurk ei muutu, siis eseme suurendus, ükskõik kuidas see kujutlusvõimet hämmastaks, ei anna vaatlejale ühtki uut üksikasja. Tõelise kunstnikuna jääb Poe oma jutustuse selles punktis tõetruuks. Kas märkasite , kuidas ta kirjeldab «metsakoletist »: putuka lülide loetelus ei ole ühtki uut lüli, mida ei näe liblikat silmitsev varustama ta silm. Võrrelge mõlemat kirjeldust – ja te veendute, et nad erinevad ainult sõnastuse poolest (10-jalalised plaadid – soomused, hiiglaslikud ridvad – tundlad, metssea kihvad – kobijad jne.), kuid mitte mingeid uusi üksikasju, mida poleks näha palja silmaga, esimeses kirjelduses ei leidu.
Kui mikroskoop suurendaks nõnda, oleks ta teadusele kasutu, ei midagi rohkemat kui huvitav mänguasi . Me teame, et asi pole nii ja et mikroskoop, laiendades meie loomulikku nägemispiiri, avas inimese ees uue maailma.
Küll pilgu terava me saanud looduselt,
ent siiski piir on meie silme selgusel.
Kui palju olevusi siin ja sääl
meil väikse kasvu tõttu nägemata jääb
– kirjutas esimene vene loodusteadlane Lomonossov oma «Kirjas klaasi kasulikkusest». Kuid nüüdisajal avab mikroskoop meile kõige pisemate, nähtama tute olendite ehituse:
Kui väiksed elundid neis, sooned, süda,
ja närvid, elujõud kus pulbitsemas.
Ei vähem, kui on peidus hiiglavaalas.
Võib ussikese ehitus meid üllatada.
Kui palju saladusi mikroskoop
me silmadele nähtavale toob.
Nüüd mõistame selgesti, miks mikroskoop avab meile «saladusi», mida ei märganud oma «koletisliblikas» vaatleja E. A. Poe jutustusest: sel lepärast – võtame öeldu kokku –, et mikroskoop ei näita esemeid üksnes suurematena, vaid näitab neid suurema vaatenurga all; selle tulemusena tekib silma võrkkestal esemest suurendatud kujutis, mis katab suurema hulga närvilõpmeid ja loob seega meie teadvuses rohkem üksikuid nägemisaistinguid. Lühidalt: mikroskoop ei suurenda esemeid, vaid nende kujutisi silma võrkkestal.12
Sageli räägime küll nägemis- ja kuulmispetetest, kuid need väljendid pole õiged. Meelepetteid ei ole olemas. Selle kohta on tabavalt öelnud filosoof I. Kant: «Meeled ei peta meid – mitte sellepärast, et nad arutleksid alati õigesti, vaid sellepärast, et nad ei arutle üldse.»
Mis meid siis viib eksitusse nn. meelepette puhul? Loomulikult see, mis antud juhul arutleb, s. t. meie enese aju. Tõepoolest, suurem osa silmapetteid tuleneb eranditult sellest, et me mitte ainult ei vaata, vaid alateadlikult ka arutleme ja viime end tahtmatult eksiteele. Need on arutluse, mitte meelte petted.
Juba 2000 aastat tagasi kirjutas rooma poeet Lucretius:
Meie silmad ei mõista ju asjade loomust,
neile süüks ära pane, et arutlus väär.
Vaat leme üldtuntud näidet optilisest illusioonist: vasakpoolne kujund joonisel 129 näib kitsam kui parempoolne, ehkki mõlemad on täpselt ühesuurused. Põhjus on selles, et vasakpoolse kujundi kõrguse hindamisel liidame üksikud vahemikud alateadlikult ja seepärast näib ta meile suurem temaga võrdsest laiusest. Vastupidi, samasuguse alateadliku arutamise tulemusena näib parempoolse kujundi laius suurem kõrgusest. Samal põhjusel paistab joonisel 130 kujundi kõrgus suurem tema laiusest.13
Kui te proovite äsjakirjeldatud silmapetet rakendada ka suuremate kujundite korral, mida silm ei suuda haarata korraga, siis see ei õnnestu. On ju teada, et lühike ja täidlane inimene ei näi põikitriipu ülikonnas mitte peenem, vaid hoopis paksem. Vastupidi, pannes selga pikitriipu ning voltidega ülikonna, võivad paksud inimesed mõnevõrra varjata oma paksust.
Millega seletada seda vastuolu? Ülikonda vaadates ei suuda meie silmad haarata teda korraga, vaid liiguvad tahtmatult mööda detaile, antud juhul pikitriipe. Silmalihaste pingutus sunnib meid alateadlikult suurendama keha suurust triipude suunas; me oleme harjunud siduma silmalihaste pingutust ettekujutusega suurematest esemetest, mis ei mahu meie vaatevälja. Seevastu, vaadates väikest triibulist joonist, jäävad silmad liikumatuks ja silmalihased ei pingutu.14
Kumb ellips joonisel 131 on suurem: alumine või ülemine sisemine? Raske on vabaneda mõttest, et alumine. Samal ajal on mõlemad ühesuurused. Muljet tugevdab asjaolu, et kogu kujund näib meile ruumilisena – ämbrina: me muudame ellipsid tahtmatult kokkusurutud ringjoonteks, külgsirged aga ämbri seinteks.
Joonisel 132 paistab kaugus punktide a ja b vahel suuremana kui punktide m ja n vahel. Kolmas samast tipust lähtuv kiir süvendab illusiooni.
Nagu juba öeldud, on enamik nägemispetteid tingitud sellest, et me ainult ei vaata, vaid ka arutleme seejuures alateadlikult. Füsioloogid ütlevad: «Me ei vaata silmade, vaid ajuga.» Te nõustute sellega meelsasti, kui tutvute illusioonidega, mille puhul vaatleja kujutlus võtab nägemisest teadlikult osa.
Vaadake joonist 133. Kui te näi ta te seda teistele, saate küsimusele, mida see kujutab, kolm eri vastust. Ühed väidavad, et see on trepp; teised, et see on trepialune nišš; kolmandad näevad selles pabeririba, mis on kokku volditud ja asetatud viltu ruudukujulisele paberitükile.
Kummaline, aga kõik kolm vastust on õiged! Te võite ise näha kõiki mainitud asju, kui suunate oma pilgu joonist vaadates erinevalt. Ja nimelt: vaadates püüdke kõigepealt suunata pilk joonise vasakpoolsele osale ja te näete treppi. Kui pilk libiseb paremalt vasakule, näete nišši. Kui pilk liigub mööda diagonaali alumisest paremast nurgast ülemisse vasakpoolsesse, näete kokkuvolditud pabeririba.15
Muide, pikemal vaatamisel tähelepanu väsib ja te näete vaheldumisi kord üht, teist ja kolmandat, sõltumata teie soovist. Joonisel 134 on sama iseärasus.
Huvitav on illusioon joonisel 135: tahtmatult tekib mulje, nagu oleks kaugus AB lühem AС-st. Ometi on nad võrdsed.
Kõiki nägemispetteid ei oska me veel seletada. Mõnikord pole võimalik isegi aimata, mis laadi arutlused toimuvad alateadlikult meie ajus ja tingivad ühe või teise nägemispette. Joonisel 136 on selgesti näha kaks kaart, mille kumerad osad on pööratud teineteise poole. Ei teki isegi kahtlust, et asi on just nii. Ent tarvitseb vaid panna nende näivate kaarte peale joonlaud või vaadata neid silmade kõrgusel piki jooni, et veenduda nende sirgjoonelisuses. Seda petet seletada pole lihtne.16 Illusioon kaob, kui 1) tõsta joonis silmade kõrgusele ja hoida seda nii, et pilk libiseb piki jooni; 2) panna pliiatsiteravik mingisse kujundi punkti ja koondada pilk sellele punktile.
Esitame veel mõned seda laadi illusioonid. Joonisel 137 näib sirglõik olevat jagatud ebavõrdseteks osadeks; mõõtmine veenab meid, et lõigud on võrdsed. Joonistel 138 ja 139 paistavad paralleelsed sirged mitteparalleelsetena. Joonisel 140 jätab ringjoon ovaali mulje. Huvitav, et joonistel 137–139 esitatud nägemispetted kaovad, kui vaadata neid elektrisädeme valgel. Ilmselt on need illusioonid seotud silmade liikumisega; sädeme lühiajalisuse tõttu ei jõua silmad veel liikuda.
Veel üks niisama huvitav illusioon. Silmitsege joonist 141 ja öelge, millised kriipsud on pikemad, kas vasak- või parempoolsed. Esimesed näivad pikematena, ehkki mõlemad on täpselt võrdsed. Seda silmapetet nimetatakse piibuillusiooniks.
Neile illusioonidele on pakutud palju seletusi, kuid kõik need on väheveenvad ja me ei hakka neid siinkohal vaatlema. Üks on aga kindel: nende nägemispetete põhjus peitub alateadlikus arutelus, mõistuse tahtmatus «kavaldamises», mis takistab meid nägemast tegelikku olukorda.
Silmitsedes joonist 142, te vaevalt küll kohe taipate, mida sellel on kujutatud. «Lihtsalt must võre, muud midagi, » sõnate. Kuid pange raamat püsti lauale, astuge 3–4 sammu eemale ja vaadake uuesti. Näete inimese silma. Tulge lähemale, ja jälle ilmub teie ette mittemidagiütlev võre ...
Arvate muidugi, et tegemist on osava graveerija «trikiga». Ei, see on lihtsalt näide nägemispettest , mille ohvriks me langeme, vaadates nn. toonpilte ehk autotüüpiaid. Raamatutes ja ajakirjades paistab pildi põhi meile ühtlasena; aga vaadake samu pilte läbi luubi – ja teie ette tekib samasugune võre, nagu kujutatud joonisel 142. See teid hämmastanud pilt ei kujuta midagi muud kui umbes kümme korda suurendatud osa taval isest toonpildist. Erinevus on vaid selles, et peene võre korral sulab ta üht laseks taustaks juba väikeseltki kauguselt, nimelt selliselt, millelt me vaatame raamatut lugemisel. Kui võre on jäme, toimub ühtesulamine, suuremalt kauguselt. Lugeja mõistab öeldut hõlpsasti, kui ta tuletab meelde vaatenurgaga seotud arutlusi.
Kas teil on juhust olnud jälgida läbi plangupragude, või veel parem, kinoekraanil kiiresti liikuva vankri või auto rattakodaraid? Tõenäoliselt täheldasite seejuures kummalist nähtust: auto kihutab peadpööritava kiirusega, aga rattad vaevu pöörlevad või ei pöörle üldse. Vähe sellest: mõnikord pöörlevad nad isegi vastassuunas! Kirjeldatud silmapete on niivõrd ebatavaline, et viib segadusse kõik, kes näevad seda esmakordselt. Seletus on järgmine. Jälgides ratta pöörlemist läbi plangupragude (nihutades pilku piki planku), ei näe me kodaraid pidevalt, vaid võrdsete ajavahemike tagant, mil nad ilmuvad plangulaudade vahelt nähtavale . Täpselt niisamuti jäädvus tab filmikaamera rataste kujutisi vaheaegadega, ainult üksikutel hetkedel (24 kaadrit sekundis). Siin on võimalikud kolm juhtu.
- Kaadritevahelise aja jooksul jõuab ratas teha täisarvu pöördeid – ükskõik kui palju, 2 või 20, peaasi, et täisarv. Siis on kodarad uuel kaadril samas asendis mis eelmiselgi. Järgmise ajavahemiku jooksul teeb ratas jälle täisarvu pöördeid (ajavahemiku pikkus ning auto kiirus ei muutu), ja kodarate asend on taas endine. Nähes kodaraid kogu aeg samas asendis, järeldame siit, et ratas ei pöörlegi (keskmine tulp joonisel 143).
- Igas ajavahemikus jõuab ratas teha täisarvu pöördeid ja veel üsna väikese osa pöördest, näiteks 45°, nagu joonisel 143 vasakpoolses tulbas näidatud. Jälgides nii suguste kujutiste vahetumist, ei oska me täispöörete olemasolu aimatagi ja näeme vaid rata ste aegla st pöörlemist (iga kord väikese nurga võrra) . Tulemusena paistab meile, et vaatamata auto kiirele liikumisele pöörlevad rattad aeglaselt.
- Kaadritevahelise aja jooksul teeb ratas mittetäieliku pöörde, mis erineb täispöördest väikese osa võrra (näiteks pöördub ratas 315°, nagu näha joonise 143 parempoolses osas). Siis paistab mingi kindel kodar pöörlevat vastassuunas. See petlik mulje kestab seni, kuni ratta pöörlemiskiirus ei muutu.
Jääb teha veel väikesed täiendused meie seletustele. Esimesel juhul rääkisime lihtsuse mõttes ratta täispöörete arvust; et aga kodarad on kõik ühesugused, siis piisab sellest, kui kodarate vahemike arv on täisarv.
Sama kehtib ka teiste juhtude kohta.
On võimalikud veel muudki kurioosumid. Kui ratta pöial on märk, kodarad aga ikka kõik ühesugused, siis võib juhtuda, et pöid ja kodarad pöörlevad eri suundades! Kui kodaral on märk, võivad kodarad liikuda märgiga vastas suunas – märk hüppaks nagu ühelt kodaralt teisele.
Kui näidatakse filmi igapäevasest elust, ei kahjusta see illusioon mulje loomutruudust. Kui aga ekraanil tahe takse selgi tada mingi mehhanismi tööd, võib see nägemispete sünni tada tõsiseid arusaamatusi ja isegi täielikult moonutada ettekujutust masina tööst.
Tähelepanelik vaatleja, nähes ekraanil kiiresti kihutava auto näiliselt liikumatut ratast, võib kodaraid kokku lugedes umbkaudu tuvastada, mitu pööret teeb ratas ajaühikus. Tavaline filmi demonstreerimise kiirus on 24 kaadrit sekundis. Kui rattal on 12 kodarat, siis tehakse sekundis 24 :12 = 2 pööret ehk 1 täispööre 0,5 sekundi jooksul. See on kõige väiksem pöörete arv; pöördeid võib olla ka täisarv (2, 3. jne.) korda rohkem.
Hinnanud ratta diameetrit, saab teha järeldusi auto kiiruse kohta. Näiteks 80-cm läbimõõduga ratta kiirus on vaadeldaval juhul 18 km/h (36 km/h, 54 km/h jne.).
Kirjeldatud nägemisillusiooni kasutatakse tehnikas kiiresti pöörlevate võllide pöörete arvu määramiseks. Selgitame, millel see võte põhineb. Vahelduvvooluga toidetava lambi valgustugevus ei ole püsiv: iga sajandiku sekundi järel valgus nõrgeneb, ehkki tavalistelt ingimustel me mingit vilkumist ei märka. Kujutlegem aga, et valgustame sellise valgusega joonisel 144 kujutatud pöörlevat ketast. Kui ketas pöörleb nii, et teeb veerand pööret sajandiku sekundi jooksul, juhtub midagi ootamatut: tavali se halli ketta asemel näeb silm musti ja valgeid sektoreid, nii nagu ketas oleks peatunud.
Loodan, et nähtuse põhjus on autorataste illusiooni mõistnud lugejale selge. Kerge on taibata ka seda, kuidas niisugust nähtust kasutada mootori pöörete arvu kindlakstegemiseks.
«Huvitava füüsika» esimeses raamatus kirjeldatakse «ajaluupi», mis põhineb filmiaparaadi kasutamisel. Siin räägime ühest teisest samasugust efekti andvast võimalusest, mis põhineb eelmises paragrahvis vaadeldud nähtusel.
Me teame juba, et kui mustaks tehtud sektoritega ketast (joon. 144), mis teeb 25 p/s, valgus tada igas sekundis 100 sähvatusega, näib ta silmale liikumatuna. Kujutlege aga, et sähvatusi on sekundis 101. Kahe niisuguse sähvatuse vahelise aja jooksul ei jõua ketas pöörduda nagu enne täieliku veerandpöörde võrra, ja tähendab, vastav sektor ei jõua esialgsesse asendisse.
Silmale paistab, et sektor on maha jäänud ühe sajandiku täispöörde võrra jne. Meile näib, et ketas pöörleb vastassuunas, tehes ühe pöörde sekundis. Pöörlemine on aeglu stunud 25 korda.
Kerge on taibata, mis tuleks teha, et sedasama aeglus tatud pöörlemist näha mitte vastas-, vaid pärisuunas. Selleks on vaja sähvatuste sagedust mitte suurendada, vaid vähendada. Näiteks kui sekundis toimub 99 sähvatust, näib ketas pöörlevat õiges suunas kiirusega 1 p/s. Siin on meil tegemist 25-kordse aeglus tusega «ajamikroskoobiga ». Ent täiesti võimalik on saavutada veel suuremat aeglustust . Kui näiteks sähvatuste arv on 999 kümne sekundi jooksul, s.t. sagedus 99,9 sähvatust sekundis, siis näib ketas tegevat 1 pöörde 10 sekundiga, tähendab, aeglu stus on 250-kordne.
Eelkirjeldatud võttega võib igasugust kiiret perioodilist liikumist aeglustada silmale soovitaval määral . See annab mugava võimaluse uurida väga kiirete mehhanismide liikumise iseärasusi, aeglustades nende liikumist meie «ajamikroskoobiga» 100, 1000 jne. korda.17
Lõpetuseks kirjeldame veel kuuli lennukiiruse mõõtmise viisi, mis põhineb võimalusel määrata teadaoleva kiirusega pöörleva ketta pöörete arvu. Kiiresti pöörlevale võllile on kinnitatud lahtise silindrilise karbi kujuline pappketas (joon. 145). Laskja tulistab kuuli piki selle karbi diameetrit ning karbi seintesse tekib kaks auku.
Kui karp oleks liikumatu, asetseksid mõlemad augud ühe ja sama diameetri otstes. Karp aga pöörleb ja selle aja jooksul, mil kuul lendab ühest seinast teiseni, ta pöördub, nii et punkti b asemel satub kuul punkti c. Teades karbi pöörlemissagedust ja diameetrit, võib kaare bc pikkuse põhjal arvutada kuuli lennukiiruse. See on lihtne geomeetriaülesanne, mille lahendamisega saab kerge vaevaga hakkama iga veidigi matemaat ikat tundev lugeja.18
Silmapette oivaline tehniline rakendus on nn. Nipkow’ ketas, mida kasutati esimestes televisiooniseadmetes. Joonisel 146 näete ketast, mille äärtes on tosin 2-mm läbimõõduga auke; augud paiknevad ühtlaselt mööda spiraali, iga järgmine oma läbimõõdu võrra keskpunktile lähemal kui eelmine. Niisugune ketas ei tõota nagu midagi erilist. Kinnitage see aga telje külge, tehke ta ette aknake, taha paigutage aknasuurune pilt (joon. 147). Kui panna ketas nüüd kiiresti pöörlema, toimub midagi ootamatut: liikumatu ketta poolt varjatud pilt muutub ketta pöörlemisel aknakeses selgesti nähtavaks. Aeglustage pöörlemist – ja pilt ähmastub ning kaob ketta peatumisel täiesti; nüüd jääb pildist nähtavaks vaid see osa, mida võib näha läbi tibatillukese 2-mm augu.
Milles on ketta poolt, esile kutsutud mõistatusliku efekti saladus? Pöörame ketast aeglaselt ja jälgime iga üksiku augu möödumist aknakesest. Keskpunktist kõige kaugemal asetsev ava läheb akna eest läbi ülemist äärt mööda; kui liikumine on kiire, muudab see nähtavaks kitsa riba pildi ülaääres. Järgmine, eelmisest madalamal asetsev ava teeb ketta kiirel liikumisel nähtavaks järgmise riba (joon. 148); kolmas ava muudab nähtavaks kolmanda riba jne. Küllalt kiirel ketta pöörlemisel muutub niiviisi nähtavaks kogu pilt; akna vas tas lõikub kettast välja nagu vastav avaus .19
Nipkow’ ketast on kerge ise teha; selle kiire pöörlemise saavutamiseks võib kasutada ketta võllile mähitud nööri, aga muidugi on parem kasutada elektrimootorit.
Inimene on üks väheseid olendeid, kes näeb binokulaarselt: parema silma vaateväli erineb vasaku omast ainult õige vähe. Enamik loomi vaatab kummagi silmaga eraldi. Nende jaoks ei paista esemed nii reljeefsed nagu meile, inimestele, ent see-eest on nende vaateväli märksa laiem meie omast.
Joonisel 149 on kujutatud inimese vaatevälja: kummagi silma vaateväli on rõhtsuunas umbes 120° ja mõlemad nurgad peaaegu kattuvad (eeldatakse, et silmad ei liigu).
Võrrelge seda joonisega 150, kus on kujutatud jänese silmade vaateväli; pead pööramata näeb jänes oma teineteisest eemal asetsevate silmadega nii seda, mis on ees, kui ka seda, mis jääb taha. Mõlema silma vaateväljad ühinevad nii ees kui ka taga! Nüüd mõistate, miks on nii raske hiilida märkamatult jänese poole. See-eest ei näe jänes, nagu jooniseltki näha, vahetult oma nina ette; õige lähedale vaatamiseks tuleb tal pöörata pead. Peaaegu kõikidel kabjalistel ja mäletsejatel on niisugune «360°-ne vaateväli».
Joonisel 151 on esitatud hobuse silmade vaateväljad: tagant need ei kattu, kuid loomal tarvitseb vaid veidi pead pöörata, kui ta näebki selja taha. Tõsi küll, hobune ei näe eriti selgesti, kuid see-eest märkab ta vähimatki liikumist ümbruskonnas. Kiskjatel, kes on tavaliselt ründavaks pooleks, nii laia vaatevälja pole, kuid see-eest näevad nad binokulaarselt, mis lubab neil täpselt hinnata vajaliku hüppe pikkust.
Füüsik ütleks: «Pimedas on kõik kassid mustad», sest valguse puudumisel pole kehi üldse näha. Ent kõnekäänd ei pea silmas täielikku pimedust, vaid pimedust igapäevamottes, s.t. õige nõrka valgustatust . Täiesti täpselt kõlab kõnekäänd nii: öösel on kõik kassid hallid. Kõnekäänu aluseks on fakt, et vähese valgustatuse korral lakkab meie silm eristamast värvusi – iga pind paistab hallina.20
On see õige? Kas tõesti paistavad nii punane lipp kui ka roheline lehestik hämaras ühtviisi hallidena? Kerge on veenduda selle väite paikapidavuses. Kes on videvikus tähelepanelikult esemete värvust vaadelnud, see on mui dugi märganud, et värvuste vahed kaovad ja kõik asjad paistavad enam-vähem tumehal lidena: nii punane tekk, sinine tapeet, lillad lilled kui ka rohelised lehed.
Tšehhovi novellist «Kiri» loeme: «Läbi allalastud kardinate ei tunginud siia päikesekiired; oli hämar, nii et kõik roosid suures kimbus näisid olevat ühte värvi.»
Täpsed füüsikakatsed kinnitavad täiesti seda tähelepanekut. Kui värvitud pinda valgus tada nõrga valgusega (või valget pinda nõrga värvilise valgusega) , suurendades valgus tugevust järk-järgult, siis näeb silm algul lihtsalt halli, ilma mingi värvusvarjundita eset. Ja alles siis, kui valgustus kasvab teatava kindla piirini, märkab silm, et pind on värvitud. Seda valgustuse astet nimetatakse värvusaistingu alumiseks läveks.
Niisiis on paljudes keeltes esineva kõnekäänu sõnasõnaline ja täiesti õige mõte see, et allpool värvusaistingu läve näivad kõik esemed hallidena.
On kindlaks tehtud, et eksisteerib ka värvusaistingu ülemine lävi. Erakordselt ereda valgustuse korral lakkab silm taas eristamast värvusvarjundeid: kõik värvitud pinnad paistavad ühtmoodi valgetena.
On levinud arvamus, et kõrvuti soojendavate kiirtega on olemas ka jahutavad ehk külmakiired. Mõttele nende eksisteerimisest viib näiteks fakt, et jäätükk levitab enda ümber külma täpselt samuti nagu ahi sooja. Kas ei tähenda see, et jääst väljuvad külmakiired just niisamuti nagu ahjust soojakiired?
Ei, selline tõlgendus on väär. Külmakiiri pole olemas. Jää läheduses ei jahtu kehad mitte külmakiirte mõjul, vaid sellepärast, et nad kaotavad kiirgamise teel rohkem soojust, kui seda jäält juurde saavad. Nii soe keha kui ka külm jää kaotavad soojust kiirgamise teel: keha, mis on jääst soojem, annab rohkem soojust ära, kui juurde saab. Soojuse juurdevool on väiksem selle kulust – ja keha jaheneb.
On üks efektne katse, mis samuti võib viia mõttele külmakiirte olemasolust. Pika saali vastassein tele seatakse üles suured nõguspeeglid. Kui ühe peegli lähedale, tema fookusesse, paigutada tugev soojusallikas, siis selle kiirgus peegeldub peeglilt, langeb teisele peeglile, peegeldub taas ja koondub fookusesse; sellesse punkti pandud must paber süttib. See katse annab tunnistust soojendavate kiirte olemasolust. Kui aga soojusallika asemel panna esimese peegli fookusse tükk jääd, siis selgub, et teise peegli fookusesse pandud termomeeter näitab temperatuuri langust. Kas see ei tähenda, et jää kiirgab külmakiiri, mis peegelduvad peeglitelt ja koonduvad termomeetri kuulikesele?
Ei, ka sel korral võib nähtust seletada saladuslike külmakiirteta. Termomeetri kuulike annab jääle kiirguse teel rohkem soojust, kui ta ise jäält saab; seepärast elavhõbe temas jaheneb. Niisiis pole siingi põhjust oletada külmakiirte olemasolu. Mingeid külmakiiri looduses ei leidu: kõik kiirte liigid annavad energiat juurde, mitte ei võta seda ära.
Heli liigub umbkaudu miljon korda aeglasemalt valgusest; et aga raadiolainete kiirus langeb ühte valgusvõngete levimise kiirusega, siis on heli miljon korda aeglasem raadiosignaalist. Siit tuleneb huvitav järeldus, mille olemus selgub järgmisest ülesandest: kes kuuleb varem pianisti esimesi akorde, kas 10 m kaugusel klaverist istuv kontserdisaali külastaja või raadiokuulaja, kes võtab signaali vastu saalist 100 km kaugusel raadioaparaadi taga?
Nii kummaline kui see ka pole, kuuleb raadioomanik akorde enne kontserdisaali külastajat, ehkki esimene istub muusikariista st 10 000 korda kaugemal. Tõepoolest, raadiolained läbivad 100-km vahemaa
Heli katab 10-m vahemaa
Siit on näha, et heli edas tamine raadio teel nõuab peaaegu sada korda vähem aega kui heli edastamine õhu kaudu.
Kui heli ei leviks õhus kiirusega 340 m/s, vaid tublisti aeglasemalt, tekiksid kuulmispetted märksa sagedamini.
Kujutlege näiteks, et heli läbib 340 meetri asemel sekundis 340 millimeetrit, s.t. ta liigub aegla semalt kui jalakäija. Te istute tugitoolis ja kuulate oma tuttavat, kes on harjunud jutustades toas edasi-tagasi kõndima. Tavalistes tingimustes ei segaks niisugune kõndimine sugugi kuulamist; ent kui heli kiirus oleks väiksem, ei saaks te oma külalise jutust mitte midagi aru: enne lausutud sõnad jõuavad järele hilisematele ja segunevad nendega; helid ühinevad mõttetuks segapudruks.
Muide, neil hetkedel, kui külaline teile läheneb, jõuavad tema sõnad teie kõrva ümberpöördud järjestuses: algul jõuavad need helid, mis alles öeldi, seejärel helid, mis tekitati varem, siis veel varasemad jne., sest kõneleja ruttab pidevalt oma häälest mööda. Kõigist fraasidest mõista te vahest ainult neid, mis tagurpidi tähendavad sama mis õiget pidigi.
Kui te siiski arvate, et heli tõeline kiirus õhus – kolmandik kilomeetrit sekundis – on küllalt suur, siis varsti muudate oma arvamust.
Kujutlege, et Moskva ja Leningradi vahel on elektritelefoni asemel üles seatud tavaline kõnetoru, nagu neid varem tarvitati ühendusepidamiseks kaupluse üksikute ruumide vahel või laevadel sideks masinaruumiga. Te seisate selle 650-km pikkuse toru Leningradi-poolses ja teie sõber Moskva-poolses otsas. Te esitate küsimuse ja ootate vastust. Möödub viis, kümme, viisteist minutit, vastust aga pole. Te hakkate muretsema ja arvate, et kaasvestlejaga on juhtunud õnnetus. Kuid kartus on asjatu: küsimus pole veel Moskvasse jõudnud, vaid on alles poolel teel. Möödub veel veerand tundi, enne kui teie Moskva-sõber kuuleb küsimust ja saab vastata. Ent temagi repliik kulgeb Moskvast Leningradi vähemalt pool tundi, nii et vastuse oma küsimusele saate alles tunni aja pärast.
Võite ise kontrollida arvutusi. Leningradist Moskvasse on 650 km. Heli läbib sekundis 1/3 km, tähendab, linnadevahelise maa läbimiseks kulub veidi üle 2160 sekundi ehk natuke rohkem kui 35 minutit. Niisugustes tingimustes jõuate kogu päeva jooksul vahetada vaid kümmekond lauset.2
Kunagi oli muide aeg, mil isegi niisugust teadete edastamise viisi oleks loetud väga kiireks. Sada aastat tagasi ei unistanud veel keegi elektritelegraafist või -telefonist ja uudis te üleandmine 650 km taha mõne tunni jooksul oleks tunnistatud kiiruse ideaaliks.
Räägitakse, et tsaar Paul I kroonimisel Moskvas teatati tseremoonia algusest põhjapealinna järgmisel viisil. Piki kogu teed ühest pealinnast teise seisid soldatid, kõik 200-meetriste vahedega; katedraali kella esimesel löögil tulistas esimene soldat õhku; tema signaali kuulnud naaber tulistas samuti aegaviitmata, seejärel tulistas kolmas tunnimees – ja nii anti signaal Peterburi kõigest kolme tunni jooksul. Kolm tundi pärast esimest kellalööki Moskvas kajasid juba kahuripaugud 650 km kaugusel asuvas Peeter-Pauli kindluses.
Kui Moskva tornikellade helinat oleks võimalik olnud vahetult Peterburis kuulda, siis oleks heli teadupärast . jõudnud põhjapoolsesse pealinna kõigest pooletunnise hilinemisega. Tähendab, kolmest tunnist, mis signaali edastamiseks kulus, läks 2,5 tundi selle peale, et soldatid võtsid helisignaali vastu ja tegid lasuks vajaliku liigutuse. Kui tühine see viivitus iga sõduri puhul ka polnud, ikkagi kogunes tuhandetest väikestest ajavahemikest 2,5 tundi.
Samal kombel töötas vanal ajal optiline telegraaf, mis andis valgussignaali lähimasse jaama, see omakorda lähetas neid edasi. Valgussignaalide süsteemi kasutasid sageli revolutsionäärid põrandaalus e koosolekute kaitseks: revolutsionääride ahel ulatus koosolekukohast politseimajani ja esimeste ärevust tekitavate tundemärkide ilmnemisel andis see ahel koosolekule teate taskulampide sähvatuste abil.
Teadete edasiandmine helisignaalide abil on praegugi levinud mõnede Aafrika, Kesk-Ameerika ja Polüneesia suguharude seas. Selleks kasutatakse erilisi trumme, millega antakse helisignaale hiiglasuurtele kaugustele: ühes kohas vastuvõetud leppesignaali korratakse teises kohas ja antakse samal moel edasi – ning lühikese aja jooksul on mingi tähtis sündmus teatavaks saanud laialdasel maa-alal (joon. 153).
Esimese Itaalia–Abessiinia sõja ajal said kõik Itaalia vägede liikumised kähku teatavaks neegus Menelikule; see viis segadus se ita al laste staabi, kes ei osanud arvatagi, et vaenlast el on olemas t rummte legraaf.
Teise Itaalia–Abessiinia sõja algul tehti Addis Abebas samal moel teatavaks üldmobilisatsiooni käsk: mõni tund hiljem teati seda juba riigi kõige kaugemates osades.
Sama võtet kasutati ka Inglise–sõja teated harukordse kiirusega Kapimaa elanike seas ja ennetasid ametlikke, kulleritega saadetud teateid mitme ööpäeva võrra.
Rändurite (Leo Forbeniuse) tunnistust mööda on mõned aafrika suguharud töötanud välja nii hea helisignaalide süsteemi, et seda võib pidada täiuslikumaks eurooplaste elektrilise telegraafi eelkäijast optilisest telegraafist. Sellest kirjutati ühes ajakirjas järgmist. Üks Briti muuseumi arheoloog viibis Nigeeria südames asuvas Ibada linnas. ÖÖd ja päevad kostis pidevat tuhmi trummipõrinat. Kord hommikul kuulis teadlane, kuidas neegrid arutasid midagi elavalt. Tema järelepärimise peale vastas üks seersant: «Suur valgete inimeste laev on uppunud, palju valgeid otsa saanud.» Niisugune oli teade, mis saadi trummikeeles. Õpetlane ei omistanud sellele teatele mingit tähtsust. Kuid kolme päeva pärast sai ta hilinenud (ühenduse katkemise tõttu) telegrammi «Lousitania » hukkumise kohta. Siis ta mõistis, et neegrite teade oli õige ja et see oli trummide keeles porisenud läbi kogu mandri Kairost kuni Ibadani. See oli seda imekspandavam, et teadet üksteisele edasi andnud suguharud rääkisid täiesti erinevaid dialekte ja mõned neist olid sel ajal omavahel sõjajalal.
Peale kõvade takistuste võib heli peegelduda ka niisugustelt moodustistelt nagu pilved. Veel enam, isegi täiesti läbipaistev õhk võib teatavatel tingimustel peegeldada helilaineid, nimelt siis, kui tema helijuhtivuse võime erineb ülejäänud õhumassi omast. Siin on tegu nähtusega, mille analoogi nimetatakse optikas täielikuks peegelduseks. Heli peegeldub nähtamatult tõkkelt ja me kuuleme mõistatuslikku kaja, mis tuleb teadmata kust.
Tyndall avastas selle huvitava nähtuse juhuslikult, kui ta katsetas mere kaldal helisignaalidega. «Täiesti läbipaistvast õhust tekkis kaja,» kirjutab Tyndall. «Kaja jõudis meieni nagu võluväel nähtamatutelt helipilvedelt.»3
Helipilvedeks nimetas kuulus füüsik neid kohti läbipaistvas õhus, mis takistavad heli levimist ja sunnivad teda peegelduma, tekitades «õhukaja». Ta kirjutab selle kohta järgmist : «Helipilvi on õhus alati. Neil pole vähimatki seost tavaliste pilvede, udu või sombuga . Neid võib täis olla kõige läbipaistvam atmosfäär. Sel moel võib tekkida õhukaja; vastupidi valitsevale arvamusele võib õhukaja tekkida kõige selgema ilmagagi. Nii suguse õhukaja olemasolu on kindlaks tehtud vaatluste ja katsetega . See võib tekkida erinevalt soojenenud või erinevat auruhulka sisaldavate õhuvoolude mõjul.»
Meile läbipaistmatute helipilvede olemasolu seletab mõningaid salapäraseid nähtusi, mida on täheldatud lahingute ajal. Tyndall esitab järgmise väljavõtte 1871. a. Prantsuse–Preisi sõjast osavõtja mälestustest:
«Kuuenda kuupäeva hommik oli täielik vastand eelmise päeva hommikule. Eile valitses üdini tungiv külm ja udu, mis ei lubanud midagi näha kaugemale kui poole meetri peale. Kuues oli aga selge, hele ja soe. Eile oli õhk olnud täis helisid, aga täna valitses Arkaadias vaikus, millele sõda oli tundmatu. Vaatasime imestunult üksteisele otsa. Kas tõesti on jäljetult kadunud Pariis, tema fordid, suurtükid, tulistamine? .. . Sõitsin Montmorencysse, kust mu pilgule avanes Pariisi põhjaosa panoraam. Kuid siingi valitses surmavaikus ... Kohtasin kolme sõdurit ja hakkain nendega asjade seisu arutama. Nood sõdurid olid valmis arvama, et on alanud rahuläbirääkimised, sest hommikust saadik polnud kuuldud ühtki lasku ...
Läksin edasi Gonesse’i. Hämmeldusega sain teada, et sakslaste patareid olid ägedasti tulistanud hommikul kella kaheksast peale. Pariisi lõunaküljel oli tulistamine alanud umbes samal ajal. Montmoreneys ei kuulnud me ainsatki heli! ... Kõik olenes õhust: täna juhtis ta heli niisama halvasti, kui hästi oli ta teinud seda eile.»
Analoogilist nähtust täheldati korduvalt ka aastatel 1914–1918 peetud suurte lahingute ajal.
On inimesi, kes ei kuule niisugusei d teravaid helisid nagu kilgi siristamine või nahkhiire piiksumine. Nad pole kurdid: nende kõrvad on korras, ja ikkagi ei kuule nad väga kõrgeid toone. Kuulus inglise füüsik Tyndall kinnitas, et mõned inimesed ei kuule isegi varblase sirtsumist!
Üldiselt ei võta meie kõrv vastu kaugeltki kõiki ümbruskonnas toimuvaid õhuvõnkumisi. Kui keha teeb sekundis alla 16 võnke, ei kuule me midagi. Kui võnkeid on üle 15 000-22 000 sekundis, ei kuule me neid samuti. Vastuvõtu ülempiir on erinevatel inimestel erinev; eakatel langeb see kuni 6000 võnkeni sekundis. Seepärast võibki esineda niisugune veider nähtus, et läbitungiv kõrge toon on ühele inimesele selgesti kuulda, teise jaoks aga pole seda olemas.
Paljud putukad (näiteks sääsk, kilk) tekitavad helisid kõrgusega 20 000 võnget sekundis; mõne kõrva jaoks on need helid olemas, teiste jaoks mitte. Sellised kõrgete toonide suhtes tundetud inimesed naudivad täielikku vaikust seal, kus teised kuulevad tervet läbilõikavate helide kakofooniat. Tyndall jutustab, et temaga juhtunud selline asi kord jalutuskäigul oma sõbra seltsis Šveitsis: «Niidud mõlemal pool teed kihasid putukatest, kes minu jaoks täitsid õhku oma terava pininaga, minu sõber aga ei kuulnud midagi: putukate muusika jäi väljapoole tema kuulmisläve.»
Nahkhiire piiksumine on putukate pininast terve oktavi võrra madalam, s.t. õhu võnkumise sagedus on kaks korda väiksem. Ent leidub inimesi, kelle kuuldelävi on veel madalam ja nende jaoks on nahkhiired hääletud olevused. Koerad aga, nagu tuvastati Pavlovi laboris, kuulevad võnkumisi sagedusega kuni 38 000 võnget sekundis.
Meie päevade füüsika ja tehnika käsutuses on vahendid, millega saab tekitada märksa suurema sagedusega «helituid helisid», kui olid need, millest äsja rääkisime: võngete sagedus võib ulatuda neis «ülihelides» (ultrahelides) kuni 700 000 võnkeni sekundis. Selline toon on ligi 18 oktavi võrra kõrgem klaveri kõige kõrgemast la-st sagedusega 3480 võnget sekundis.4
Üks ultrahelivõnkumiste saamisviise põhineb kvartsikristallist kindlal viisil väljalõigatud plaatide pindade omadusel surve toimel elektriseeruda (piesoelektrilised kristallid); kui niisuguse plaadikese pinda perioodiliselt laadida, siis hakkab ta elektrilaengu mõjul vahelduvalt kokku tõmbuma ja paisuma, s.t. võnkuma: tekib ultraheli. Plaati laetakse lampgeneraatorist, mille sagedus valitakse kooskõlas plaadi kese omavõnkesagedusega5.
Ehkki me ultrahelisid ei kuule, avalduvad nad teisiti, üsna tuntaval moel. Kui näiteks pista võnkuv plaat õlinõusse, siis ultrahelivõnkumise all olev vedeliku pind puhetub 10 cm kõrguselt ja õlipiisku pritsib kuni 40 cm kõrgusele. Sukeldades sellisesse õlivanni 1 m pikkuse klaastoru, tunneme käes, mis hoiab toru teist otsa, tugevat, nahalegi jälge jätvat põletust. Kokkupuutel puiduga põletab võnkuv toruots sellesse augu; ultraheli energia muundub soojuseks.
Ultrahelivõnkumised avaldavad tugevat mõju elusorganismidele: vetikaniidid katkevad; loomsed rakud lõhkevad; verelibled lagunevad; väikesed konnad ja kalad surevad 1–2 minuti jooksul; katseloomade kehatemperatuur tõuseb – hiirel näiteks kuni 45 °C. Ultrahelivõnkumisi rakendatakse meditsiinis, kus neil kuuldamatutel helidel on sama ülesanne mis nähtamatutel ultraviolettkiirtelgi: nad aitavad ravida.
Eriti edukalt kasutatakse ultraheli metallurgias ebaühtluste, mõrade, õhumullide ja teiste defektide avastamiseks massiivses metallitükis. Metalli «läbivalgustamiseks» ultraheliga niisuta takse teda algul õliga ja allutatakse siis ultraheli mõjule. Ebaühtlused metallis hajutavad heli, tekitades nagu helivarju; defektide kuju tuleb õlikihti katva ühtlase virvenduse taustal esile nii täpselt, et tekkivat pilti võib isegi fotografeerida6.
Ultraheliga võib «läbi valgustada» kuni rneetripaksust või paksematki metallitükki, mis neelab röntgenikiired täielikult; seejuures avastatakse ka õige väikesi, kuni ühemillimeetrisi defekte. Kahtlemata on ultrahelil ees suur tulevik.7
Filmis «Uus Gulliver» räägivad liliputlased peenikese häälega, mis vastab nende väikesele kõrile, aga hiiglane Petja räägib madalal häälel. Võtetel mängisid liliputlaste osi täiskasvanud ja 'Petjat laps. Kuidas saavutati nõutav muutus häältes? Olin õige imestunud, kui režissöör Ptuško ütles mulle, et näitlejad rääkinud võtetel oma häälega; tooni muudeti võtete ajal originaalsel viisil, mis põhineb heli füüsikalistel iseärasustel.
Et teha liliputlaste hääli kõrgeks, Gulliveri oma aga madalaks, kirjutas režissöör liliputlasi mängivate näitlejate jutu aeglustatult liikuvale lindile, Petja hääle aga, vastupidi, kiirendatult liikuvale lindile. Ekraanile projitseeritakse film normaalse kiirusega. Kerge on taibata, mis siis juhtub. Liliputlaste kõne jõuab kuulajani normaalsega võrreldes suurenenud võnkesagedusega ja tooni kõrgus peab seetõttu tõusma. Petja häält võetakse vastu aeglustatud võnkesagedusega ja järelikult peab toon muutuma madalamaks. Tulemusena räägivad liliputlased «Uues Gulliveris» häälega, mis on kvindi võrra kõrgem normaalsest täiskasvanu häälest, Gulliver ise – Petja – häälega, mis on kvindi võrra madalam normaalsest.
Nii omapäraselt kasutati «ajaluupi» hääle korral. Sellist nähtust võib sageli täheldada, kui mängida grammofoniplaat plaadistamiskiirusest väiksema või suurema kiirusega (33 p/min või 78 p/min) .
Hakkame nüüd tegelema ülesandega, mis esmapilgul paistab kaugel olevat nii helist kui üldse kogu füüsikast. Ometi palun teid sellele tähelepanu pöörata: see aitab teil aru saada edaspidisest.
Tõenäoliselt olete juba kokku puutunud ühega selle ülesande paljudest teisenditest. Moskvast väljub igal keskpäeval rong Vladivostokki. Ja igal keskpäeval väljub rong ka Vladivostokist Moskvasse. Oletame, et sõit kestab 10 päeva. Küsitakse: mitu pikamaarongi tuleb teile vastu, kui sõidate Vladivostokist Moskvasse.
Kõige sagedamini vastatakse: 10 rongi.
Kuid vastus on vale: te ei kohta mitte ainult neid kümmet rongi, mis väljuvad Moskvast pärast teie väljasõitu, vaid ka neid, mis teie ärasõiduhetkel olid juba teel. Järelikult õige vastus on 20, mitte 10.
Edasi, iga Moskva rong toob pealinnast kaasa värskeid ajalehti. Ja kui teid huvitavad uudised, ostate jaamades muidugi õhinal ajalehti. Mitu värsket numbrit te teeloleku aja jooksul osta saate?
Nüüd ei tee teile raskusi vastata õigesti: 20. Igal vastutuleval rongil on ju kaasas värsked ajalehed ja et te kohtate 20 rongi, siis saate ka 20 ajalehte. Ent teel olete ju kõigest 10 päeva, tähendab, te loete päevas ühe päevalehe kaht eri numbrit!
Järeldus on veidi ootamatu .ja tõenäoäliselt ei usukski te seda, kui teil poleks olnud võimalust selle paikapidavuses praktiliselt veenduda. Tuletage meelde kas või seda, et kahepäevase sõidu ajal Sevastoopolist Leningradi jõudsite läbi lugeda mitte kahe, vaid nelja päeva lehed: need lehed, mis olid juba ilmunud Leningradis teie ärasõiduhetkeks, ja veel need, mis ilmusid kahe sõidupäeva jooksul.
Nüüd siis teate, kelle jaoks päevalehed ilmuvad kaks korda päevas: kõigi pealinna sõitvate rongide reisijate jaoks.
Kui teil on arenenud muusikaline kuulmine, olete tõenäoliselt märganud, kuidas muutub vedurivile toon (mitte valjus, vaid just toon, kõrgus), kui vastutulev rong teie rongist mööda kihutab. Kuni rongid lähenevad teineteisele, on toon märksa kõrgem sellest, mida kuuleme rongide kaugenemisel teineteisest. Kui rongide kiiirused on 50 km/h, siis on helikõrguste vahe peaaegu terve toon.
Millest see tuleb?
Teil pole raske põhjust taibata, kui tuletate meelde, et tooni kõrgus oleneb võngete arvust sekundis; kõrvutage seda sellega, mida saite teada eelmisest ülesandest. Vastutulev vedur tekitab kogu aeg kindla sagedusega heli. Teie kõrv aga võtab vastu erineval arvul võnkumisi sõltuvalt sellest, kas liigute teisele rongile vastu, seisate paigal või kaugenete võnkumisallikast.
Ja nii nagu te loete teel Moskvasse värsket Moskvas ilmuvat ajalehte rohkem kui kord päevas, nii ka siin, lähenedes heliallikale, püüate võnkumisi kinni sagedamalt, kui nad lähtuvad vedurivilest. Aga siin te enam ei arutle: teie kõrv püüab kinni suurema sagedusega võnked – ja te kuulete vahetult kõrgemat tooni. Eemaldudes jõuab teieni vähem võnkeid – ja te kuulete madalamat tooni.
Kui see seletus pole teid lõplikult veennud, proovige kujutleda, kuidas vedurivilest lähtuvad helilained levivad (joon. 154). Olgu algul vedur paigal (ülemine lainejoon). Vile tekitab helilaineid. Lihtsuse mõttes vaatame ainult nelja lainet: liikumatust vedurist jõuavad nad mingi ajavahemiku jooksul igas suunas levida ühekaugusele. Laine О jõuab vaatlejani A samal ajal kui vaatlejani B; seejärel jõuavad mõlema vaatlejani üheaegselt lained 1,2,3 jne. Kummagi vaatleja kõrvad saavad sekundis ühepalju võnkeid ja seepärast kuulevad mõlemad üht ja sedasama tooni.
Olukord on teine siis, kui vilistav vedur liigub punktist B’ punkti A ’ (alumine lainejoon). Asugu vile mingil hetkel punktis C selle aja jooksul aga, millal ta kiirgas neli lainet, jõudis ta juba punkti D.
Nüüd võrrelge helilainete levimist. Punktis C’ tekkiv laine О jõuab üheaegselt mõlema vaatlejani A ’ ja B’. Ent nel jas laine, mis tekib punktis D, ei jõua enam nende juurde üheaegselt: teelõik DA’ on lühem kui DB’ ja järelikult jouab hääle laine punkti A ’ varem kui punkti B’. Vahepealse d lained 1 ja 2 jõuavad samuti punkti B’ varem kui punkti A ’, kuid hilinemine on väiksem. Mis siis välja tuleb? Vaatle ja punktis A ’ võtab helilaineid vastu sagedammi kui vaatleja punktis B’: esimene kuuleb kõrgemat tooni kui teine. Nagu jooniselt kerge näha, on punkti A ’ suunas liikuvate helilainete pikkus vastaval t lühem B' poole liikuvate lainete pikkusest*.
(Tuleb silmas pidada, et lainejooned ei kujuta joonisel sugugi helilainete kuju: õhuosakesed võnguvad piki heli levimise suunda, mitte sellega risti. Lainetust kujutatakse siin ristlainetusena ainuüksi piltlikkuse mõttes: ni isuguse laine hari vastab maksimaalsele tihedusele pikilaines)
Äsjakirjeldatud nähtuse avastas füüsik Doppler ja tema järgi on see nimetuse saanudki. Doppleri efekti võib täheldada peale heli ka valguse puhul, mis samuti levib lainetena. Valguslainete sagenemist (mida heli puhul tajutakse tooni kõrgenemisena) võtab silm vastu värvuse muutumisena.
Doppleri efekt annab astronoomidele oivalise võimaluse selgitada, kas täht ligineb meile või kaugeneb meist, ning mõõta ka selle nihkumise kiirust. Astronoomi aitab seejuures spektris esinevate tumedate joonte külgsuunaline nihkumine. Uurides tähelepanelikult, kuhupoole ja kui palju on nihkunud tumedad jooned taevakeha spektris, said astronoomid teha terve hulga avastusi. Näiteks teame tänu Doppleri efektile, et hele täht Siirius eemaldub meist igas sekundis 75 km võrra. See täht asub meist nii uskumatult kaugelt, et kauguse suurenemine isegi miljardite kilomeetrite võrra ei muuda märgatavalt tema näivat heledust. Tõenäoliselt poleks me kunagi teada saanud selle taevakeha liikumisest, kui meid poleks aidanud Doppleri efekt.
See näide tõestab rabava ilmekusega, kuivõrd kõikehõlmav teadus on füüsika. Teinud kindlaks mitme meetri pikkuste helilainete levimise seaduse, kasutab ta seda kaduvväikeste, kõigest mõne tuhandiku millimeetri pikkuste valguslainete puhul ning seejärel saadud teadmisi universumis kujutletamatult kaugele jäävate hiiglaslike päikeste kiirete liikumiste mõõtmiseks.
Kui Doppler 1842. a. esmakordselt tuli mõttele, et vaatleja ja valgus- või heliallika vastastikuse lähenemisega või kaugenemisega peab kaasnema tajutavate valgus- või helilainete pikkuse muutumine, tegi ta julge oletuse, et just see määrabki tähtede värvuse. Ta arvas, et kõik tähed on valged; nad paistavad meile värvilistena sellepärast, et liiguvad meie suhtes kiiresti. Suure kiirusega lähenevad valged tähed saadavad maapealsele vaatlejale lühemalainelist kiirgust, mis loob mulje rohelisest, sinisest või lillast värvusest; kiiresti eemalduvad valged tähed näivad meile, vastupidi, kollaste või punastena.
Idee oli küll originaalne, kuid vale. Selleks et silm võiks märgata värvuse muutumist, mis on tingitud tähtede liikumisest, oleks tähtedele tulnud kõigepealt omistada hiiglasuured kiirused – kümned tuhanded kilomeetrid sekundis. Kuid sellestki poleks piisanud. Asi on selles, et näiteks ühel ajal läheneva valge tähe siniste kiirte muutumisega violetseteks toimub roheliste muutumine sinisteks, ultraviolettkiirte kohale asuvad violetsed, punaste asemele infrapunased; ühesõnaga, kõik valge valguse koostisosad jäävad alles, nii et vaatama ta kõigi spektrivärvuste nihkumisele ei peaks silm märkama mingit vahet üldises värvuses.
Teine asi on liikuvate tähtede spektrite tumedate joonte nihkumisega vaatleja suhtes: neid liikumisi püüavad täppisriistad edukalt kinni ja see lubab määrata tähtede kiirust vaatekiire sihis. Hea spektroskoobiga võib tuvastada isegi tähe kiiruse 1 km/s.8
Doppleri eksitus tuli meelde kuulsale füüsikule Robert Woodile, kui politseinik kavatses teda kord trahvida selle eest, et ta ei peatanud oma kihutavat autot punase tule all. Jutustatakse, et Wood hakanud korravalvurit veenma, et kiirel sõidul signaali suunas paistab punane tuli rohelisena. Oleks politseinik tundnud füüsikat, võinuks ta välja arvutada, et nende sõnade õigustuseks pidanuks auto kihutama lausa uskumatu kiirusega – 135 miljonit km/h.
Siin on arvutus. Kui märgib allikast (antud juhul valgusfoorist) kiirgava valguslaine pikkust, – autos oleva vaatleja poolt tajutava valguslaine pikkust, – auto kiirust, – valguse kiirust, siis on teooria teinud kindlaks nende järgmise sõltuvuse:
Teades, et kõige lühem, punasele valgusele vastav laine on pikkusega 630 nm, kõige pikem, rohelisele valgusele vastav laine aga 560 nm, paneme need väärtused valemisse; valguse kiirus on ka teada: 300 000 km/s. Saame:
kust leiame auto kiiruseks
ehk 135 miljonit km/h. Niisuguse kiirusega sõites oleks Wood veidi rohkem kui tunni ajaga jõudnud politseinikust kaugemale, kui asub Päike. Räägitakse, et politseinik oligi trahvinud teda «lubatud kiiruse ületamise eest».
Mida kuuleksite, kui eemalduksite mängivast orkestrist heli kiirusega?
Inimene, kes postirongiga Leningradist välja sõidab, näeb kõigis jaamades ajalehemüüjatel samu lehenumbreid, nimelt neid, mis ilmusid tema lahkumispäeval. See on ka arusaadav, sest need ajalehed sõidavad samas rongis koos reisijaga, värskemad tulevad aga teistes rongides järele. Sel alusel võiks nagu väita, et eemaldudes orkestrist helikiirusel kuuleme kogu aja üht ja sedasama nooti, mida orkester võttis just meie liikumahakkamise hetkel.
Ent niisugune järeldus pole õige; kui te eemaldute helikiirusega, siis helilained, mis teie suhtes paigale jäävad, ei mõju teie kõrva trumminahale ja järelikult ei kuule te ainsatki heli. Teile näib, et orkester on lakanud mängimast.
Ent miks andis võrdlus ajalehtedega teise tulemuse? Lihtsalt sellepärast, et me kasutasime antud juhul arutlust analoogia põhjal valesti. Reisija, kes igas jaamas näeb samu ajalehti, kujutab ette (s.t. võiks ette kujutada, kui ta unustaks iseenese liikumise), et tema ärasõidupäevast peale on uute lehenumbrite ilmumine üldse lakanud. Tema jaoks on ajalehetoimetused lõpetanud oma töö nagu orkester oma mängu kuulaja jaoks, kes eemaldub orkestrist helikiirusel. Huvitav, et selles küsimuses võivad mõnikord vassida isegi õpetlased, ehkki asi ei ole tegelikult ju üldse keeruline. Vaidluses minuga (olin tookord veel koolipoiss) ei nõustunud üks astronoom pakutud lahendusega ja väitis, et eemaldudes orkestrist helikiirusega peaksime kogu aeg kuulma üht ja sedasama tooni (esitan katkendi tema kirjast ):
«Kõlagu kindla kõrgusega noot. Ta kõlas juba kaua ja jääb ikka kõlama, määramata pikaks ajaks. Ruumis laialipaigutatud kuulajad kuulevad seda üksteise järel ja oletame, et nõrgenemata. Miks siis teie ei kuule seda nooti, kui te heli või isegi mõtte kiirusga kanduksite ükskõik millise kuulaja kohale?»
Täpselt samuti tõestas ta, et välgust valguse kiirusel eemalduv vaatleja peab kogu aeg nägema seda välku: «Kujutlege pidevat silmade rida ruumis. Nad kõik saavad üksteise järel valgusaistinguid. Oletame, et te saate mõttes viibidajärjestikku iga silma asukohas – ilmselt näete siis kogu aja välku.» Loomulikult on mõlemad seletused valed: mainitud tingimustel ei kuule me heli ega näe välku. See selgub muide eelmises paragrahvis tuletatud valemist: kui asendada seal v = -c, muutub vastuvõetava laine pikkus l’ lõpmata suureks, mis on võrdväärne laine puudumisega.
Närides kuivikut, kuuleme kõrvulukustavat raksumist, kuna naabrid söövad samasugust kuivikut ilma märkimisväärse kärata. Kuidas neil see õnnestub?
Asi on selles, et müra ja raksumine kostavad ainult meie kõrvus ja häirivad naabreid vähe. Koljuluud nagu kõik kõvad elastsed kehad juhivad heli väga hästi, aga tihedas keskkonnas tugevneb heli vahel uskumatul määral. Õhu kaudu kõrvani jõudev kuiviku raksumine näib kerge mürana, kuid sama heli muutub lausa kõrvulukustavaks, kui jõuab kuuldenärvini läbi kõvade koljuluude. Veel üks samalaadne katse: suruge taskukella rõngas hammas te vahele ja toppige sõrmed kõrva: te kuulete raskeid lööke – kella tiksumine on sedavõrd võimendunud.
Räägitakse, et kurdiks jäänud Beethoven kuulanud klaverimängu sel teel, et toetanud oma jalutuskepi ühe otsa klaveri vastu, teist hoidnud hammas te vahel.9 Täpselt samuti võivad need kurdid, kelle keskkõrv terve on, muusika saatel tantsida: heli jõuab nende kuulmisnärvini põranda ja luude kaudu.
«Huvitav füüsika» on lõpetatud. Kui ta äratas lugejas soovi lähemalt tutvuda selle mõõtmatult avara teadusega, kust on ammutatud too kirev peotäis kõige lihtsamaid teadmisi, siis on autori eesmärk saavutatud, ja rahuldustundega paneb ta oma tööle punkti.
Esimene peatükk
Kõige tu g ev ama te s troopilistes tsüklonites tõuseb tuule kiirus kuni 110 m/s. Suur im tuule kiirus regis tre er iti 1934. a. USA-s: see oli 115,6 m/s (416 km/h). See fakt on e s i ta tud ra ama tu s : Oksanovitš, L. V. Nä h tama tu konflikt. — M.: Stroiizda t, 1981, lk. 27 (vene keeles). 2 Pra e g u k a su ta tak s e kirje ldatud võtet mõnikord e lektriraudteedel. See an n ab m ä rg a ta v a t e lektrienergia kokkuhoidu teelõikudel, kus rongid s ag ed a s t i peatuvad. 3 Vankri ühtlasel liikumisel tuleb te a ta v a t jõudu r a k en d a d a (see on hobuse ülesandeks) selleks, et ületada hõõrdejõudu, mis mõjub va s ta s su u n a s vankr i liikumisega. «Hobuse ja vankr i paradoksi» seletus J. Pe re lmani e s i ta tud kujul on vaieldav. Muidugi on jõud rak en d a tu d eri kehadele: vankr ile ja hobusele, kuid nende vahel on jäik side — rakmed. See tõttu võib hobust ja vankr it v a ad e ld a tervikkehana. Vankri ette ra k en d a tu d hobuse liikumist on kerge seletada, kui pöörame tähe lepanu sellele, kuidas mõjub ma apind, s. t. toereaktsioon, neile kahele kehale. Kui hobuse jalge all poleks toe tuspinda ja ta tõukuks hoopis vankrilt, siis ükskõik kuidas ta ka p in g u ta k s ja kuidas teda pi it saga t a g a n t s u n nitaks, ei liiguks see kumma line ekipaaž p a ig a s t (vt. p a rag ra h v i «Kas sa ab edasi liikuda toeta?», lk. 16). 4 On teada, et ida rahva s te l olid juba 10.— 12. saj. püss irohuraketid, mis kinnita ti noolte külge ja mida ka suta t i lahinguis (vt. Varvarov, N. A. P o p u la a rn e kosmonautika. — M.: Ma šinostrojenije, 1981, lk. 16; vene keeles). • 5 Hüdrore aktiivmootoreid k a su ta tak s e t än a p ä e v a l mõnikord nn. hüdrokä itur iga laevadel. Niisuguseid laevu ei kohuta vesikasvud ega madalikud; neid k a su ta tak s e väikestel jõgedel nä iteks amfiibtraktoritena pa lgipa rve tuse l. 6 Laevukese ehitamisel on mu g a v k a su tad a hõbepaberit. Kütuseks võib olla kölni vesi. 7 Üks ika s ja likuma l t võib looduslikest re akt iivmootor ites t lugeda pa ljude s t b io o n ik a ra ama tu te s t (vt. näiteks Litinetski, 1. B. Bioonika. — M.: Prosve š tš eni je , 1976, lk. 194; vene keeles). 8 Tänapä eva l, mil k o smose apa ra adid lendavad lähemate plane etideni, toime tavad Ma a peale kuupinna s e proove, mil tehiskaas las i len n u ta ta k se üles pe a a egu iga päev ja inimene on juba a s tunudKuu pinnale, võib planeetidevahelis te lendude propage e r imine näida noorele lugeja le na iivsena, sest kogu tema teadlik elu (võib-olla aga üldse kogu elu) on möödunud 1957. a. a lanud komsose a ja s tul . Kuid pe atükk on r a ama tu s s e sisse jä e tu d a ja loolis t huvi pakkuva osana — J. L. Pe re lman oli üks esimesi v ä s ima tu id kosmose lendude propagee r ija id.
Teine peatükk
1 Range l t võtte s mõjub vankr ile peale kõige muu veel teekatte toereaktsioon. 2 Üks ika s ja likuma l t soovitame ehitiste tu g ev u s e k ü s imus tega tu t vuda r a ama tu s t : Gordon, G. Kons trukts ioonid, ehk miks a s jad katki ei lähe. — M.: Mir, 1980; vene keeles. 3 Ainult tuule jõul on otse v a s tu tu u lt võimalik liikuda siis, kui a s e n d ad a puri tuuleveski tüüpi tuulemootor iga , mida paneb liikuma laeva sõukruvi. On olemas isegi P. L. Kapi ts a l t pä r inev ülesanne niisuguse, esmapilgul eba tava lise laeva kohta (vt. ka a jakirja Katera i jahtõ, 1981, nr. 1, lk. 25; vene keeles). 4 P u r je spordi s on mitmeid füüsika se isukoha lt õige huvitavaid probleeme. Üks ika s ja likult võib selle spordia la ja mõnede p u r je ta mise tehnilis te küs imus te kohta lugeda näiteks ra ama tu te s t : Glovacki, W. Köitev pur jede maailm: Lugus id pur jespordi ajaloost. — M.: Progre s s , 1979; Proktor, ]. Pur je amine . Tuul, la ine tus ja hoovus. — L.: Gidrometeoizdat, 1981; (mõlemad r a ama tu d on venekeelsed). 5 On olemas terve hõõrdumisõpetus. Soovitame lugeja le põhja likumaks tutvumiseks probleemidega r a ama tu t : Silin, A. A. Hõõrdumine ja selle osa tehnika a rengus . — M.: Nauka, 1976; (vene keeles). 6 Seni oli ju t tu jõududes t, mis mõjus id laeva pa rd a le jä ä poolt. Et a n a lüüs ida jä ä liikumist, on v a ja tege likult v a a d a ta jõudusid, mis mõjuvad laeva poolt jääle, k a su tad e s see juure s Newtoni kolmanda t seadust. 7 J. I. Pe re lman oli üks Hu v i tav a Teaduse Paviljoni aktiivseid organisee r ija id. Paviljon anti Leningradi noorsoo k ä su tu s s e Suure I sama a sõ ja eel.
Kolmas peatükk
1 Pöör lemine ta g a b mü r sk u d e ja kuulide lennu püsivuse. Güroskoopilisi se admeid k a su ta ta k s e len n u a p a ra a tid e , rake t tide ja laevade liikumise automa a t s e k s juhtimiseks . On olemas ka mitme suguseid güroskoopilis i naviga t s ioonis e adme id, näiteks gürokompas s, gürove rtikaa l, g ü ro k u r s in ä i tu r jne. Terve rida güroskoopilis i mõõteriistu on ette nä h tu d keha liikumise k a rak te r i s t ik u te — nurkkiiruse, nurkkiirenduse jms. mää ramiseks . Kõigi loetletud r iis tade põhiosaks on güroskoop, kiiresti pöörlev tahke keha, mille pöörlemistelje suund ruumis võib muutuda . 2 Vt. Perry, J. Pöör lev vurr. — Vologda: Severnõi Petša tnik, 1926 (vene keeles). 3 Kehade püs iva s t ta s a k a a lu s t alus tel ja Kolumbuse ülesande s t võib lugeda a jaki r jade s t: Nauka i 2izn, 1968, nr. 10, lk. 77; Kvant, 1977, nr. 7, lk. 10; mõlemad on vene keeles). . Kehale mõjub peale ra skuse veei toereaktsioon — pöörleva p l a t vormi^ poolt mõjuv jõud. Nende jõudude vektor summa annab kehale kesktõukekiirenduse ja keha hakkab pöörlema ümber telje j ä ä v a nurkkiirusega. Kui me ise viibime pöörlevas koordinaa tsüs teemis , n ä i teks pöörleval platvormil, siis sa ab pöörlemist arves se võtta sel teel, et toome sisse fiktiivse kesktõukejõu, n a g u on tehtud joonisel 33. Kuid ka siis ei tohi kõigi kehale mõjuva te jõudude käsitlemisel u n u s tada toereaktsiooni, mille üheks komponendiks võib olla hõõrdejõud. Liikumatu va a t le ja ( iner ts iaa lse s koordina a tsüs te emis ) ei va ja fiktiivset kesktoukejõudu, et se letada inimese pöörlemist platvormil. 5 Joonis 41 on tegelikult ligikaudne. Pu n k t id e s В ja С ei ole ra tta ja ra ttu r i ühine mas sikese samal kõrgusel. 6 Vt. 1. pe atükk «Huvitava füüsika» esimeses r a ama tu s . — T a l linn: Valgus, 1983.
Neljas peatükk
1 Selles, mis toimub meie planeedi põues, a itavad peale süvapuurimise se lgus t s a a d a teisedki füüsikalised uur imismeetodid, eelkõige seismiliste lainete leviku uurimine, ül isuur te rõhkude all olevate kivimite omadus te labora toorsed uur ingud, gravimee tr iamee todid. Üks ikasjalikult võib neist u u r in g u te s t ja u u te s t a n dme te s t Ma a ehituse kohta lugeda pop u la a r te a d u s l ik u s t brošüür is t: Zarkov, V. N. Maa, Kuu ja planeetide siseehitus. — М.: Znanije. (Kosmonavtika i astronomija, 1973; vene keeles). 2 Kul laka evandus Boxburgis (Transva a l, LAV), kus juure s šahti suue asub 1,6 m me re p in n a s t kõrgema l nin g š a h t ula tub 1,7 km s ü gavusele allapoole merepinda. P r a e g u on k orduva lt te a ta tu d süvapuurimistest; meie maal, näiteks Koola poolsaarel on s a a v u ta tu d sü g a v u s üle 10 km. Sellised tööd teenivad peale p u ht te adus l iku huvi ka praktilisi eesmärke: need kuuluvad ühe osana m a a v a r a d e geoloogilise luure p ro g rammide s s e (vt. ajakiri: Horisont, 1983, nr. 10, lk. 13— 15). _____ 3 Keha täisvõnke periood Т= 2 п л / Rtg. Siin R on ma ake ra r a a dius, g — vaba langemis e kiirendus Ma a pinnal: M 4 n R 3Q 4 я g = G — = G ----------- ь R2 3R2 = G --3- --Rqv. G = 6 ,6 7 - 1 0 - u N-m2/k g 2 on g r a v ita t s io o n ik o n s tan t , q= 5,5 g/cm3 — Maa tihedus, mis loetakse kons tandiks . Seega r = V 3 j i / £ )G ^ 8 4 min. 4 Pendel on harmooniline, kui tema korral ta a s t a v jõud F on võrdeline pendli hä lbega t a s a k a a lu a s e n d i s t л: (F——kx). Ha rmo o n i lise pendli võnkumise võr rande id tu ndva l lugejal pole va ja seda v a n a a jaki r ja vä lja otsida. Kerge on ju Kontrollida, et keha la n g e mist šah t -k a ev u s (joon. 44) ja rongi liikumist tunnelis kir je ldavad samad v õ r ran d id mis harilikku harmoonilis t pendlitki, muidugi kui j ä t t a a rv e s t ama t a õhutakis tus . J ä t am e luge ja enda hooleks selles ve enduda . ( 245
Viies peatükk
1 Elekt romagne tkahur id, mille loomisel mitmetes Lä äne sõjalise uurimise keskustes töötatakse, lubavad juba pra eg u a n d a erilistele mürskude le esimese kosmilise kiirusega võr re ldava kiiruse, s. t. mä rks a suurema kiiruse kui tavalised kahurid (vt. näiteks ajakirja: Phys ics Today, 1980, nr. 12, lk. 19; inglise keeles). 2 Sellest, mis on inimesele mõjuvad ülekoormused ja kuidas la he n d a tak s e suur te ülekoormuste probleem len n u n d u s e s ning kosmonautikas, on viimasel ajal ohtras ti kir juta tud. Tsite e rigem J. A. Ga ga r init: «Ülekoormused hakkas id kasvama . Tunds in, kuida s mingi ü le tama tu jõud surub mind üha tugevamini tooli va s tu. Ja ehkki tool oli p a ig u ta tu d nii, et minu kehale paiskuva hiigla suure raskuse mõju miinimumini v ä hendada , oli raske liigutada käsi ja j a l g u . . . Ülekoormused üha suurenes id . ..» Neile, kes küsimuse v a s tu rohkem huvi tunnevad, soovitame a r tiklit «Kiirendus ja ülekoormused. Nende mõju ja selle ületamine» ra ama tu s : Varvarov, N. A. P o p u la a rn e kosmonautika . — M.: Mašinostrojenije, 1981 (vene keeles).
Kuues peatükk
1 Mõndagi h uvi tava t selle lahe vee eba tava l is e l t su u re s t soolsuses t leiab lugeja ra ama tu s t : Paustovski, K. Ka ra -Boga z . — Kogutud teosed. — M.: Hu d o ž e s tv en n a ja Lite ratura, 1967, 1. k., lk. 401 (vene keeles). 2 Üks ikud laevatüübid, nä iteks Lääneme re basse inis u juvad Saksa laevad, v a ru s ta ta k s e kolme erineva laadjoonega , mis k a n ta k s e selgesti n ä h ta v a l t laeva keskosa pa rdale, nimelt: FW — teki kõrgus mag e d a s vees, S ja W — teki suvine ja talvine kõrgus merevees (vt. Dietrich, G., Kalle, К. Üldine mereõpetus: Si s s e ju h a tu s oke anogra af ias se . — L.: Gidrometeoizdat, 1961; vene keeles). 3 Rasket vett k a su ta tak s e laia lda se lt a a tomitehnika s , muu h ulga s tuuma re aktor ite s . Seda toodetakse töös tus likult su u r te s kogus te s t a v a lisest veest. Rääkides 17 raske vee erimist, peab J. I. P e re lman silma s H20 - tüüpi ühendeid, mis koosnevad vesiniku ja hapniku e r ineva te s t isotoopidest, nimelt tava l is e s t ve s inikus t H, deute er iumis t D, triitiumist T ja loodusliku hapniku isotoopidest ma s s ia rv u d e g a 16, 17 ja 18. Nende ühendite keemiline valem võib omad a kuju H20 , D20 , T20 , HDO, НТО või DTO ig aü h e g a kolmest hapniku isotoobist. Kõik need ühendid peale tava lise vee H20 Maal üleka a lus oleva hapniku kerge isotoobiga 160 ongi Pe re lmani jä rg i ra ske vee erimid, täpsemalt, erinevad vedelikud. Neid on 17. Hapniku tehisisotoopide, näiteks raske l90 või ke rgete 140 ja 150 lisamine su u re n d ab niigi pikka nimekirja vedelikest, mida on kombeks lugeda veeks. 4 Noorele lugejale meenub võib-olla a a tomijä ä lõ h k u ja «Arktika» hiljutine kuulus reis põhjapoolusele. See fakt illustreerib su u r e p ä r a selt tehnika progres s i 20. sa jandi l ja meie ma a jä ä lõ h k u ja te võimsust. 5 Moods a te a atomia llve ela evade kiirus on üle 50 sõlme. Need laevad võivad liikuda vee all kiirrongi kiirusega. Aa tomimootor iga v a ru s ta tu d allveelaev võima ldab inimesel läbida merede ja ooke a nide väheuur i tud sügavus i. Allveelaeva amme n d ama tu e n e rg iav a ru 246 lubab pinnale tõ u sma ta ka tta hiiglaslikke vahemaid. Nii näiteks sõitis Ameerika a atomia llve ela ev 1958. a. a javahemikus 22. juulis t kuni 5. a u g u s t in i vee all põhjapooluse lähedalt Beringi v ä in a s t Grööni merre. 6 Aa tomia llvee laevad ei sukeldu sü g a v ama le mõn e s ts a ja s t meetrist. 7 Hiljem loodi P r a n t su sma a l insener Wilmi ja I ta a lia s šveitsi teadlase P ic c a rd ’i projekti jä rg i erilised süvamere uurimise a p a r a a did — ba tüskaa f id. Nende täh t s a im erinevus ba tü s fä ä r id e s t on liikumisvõime: nad võivad suure s süg a v u s e s edasi ujuda, sellal kui batü s fä ä r id r ipuvad abitult trosside otsas. Algul laskus Piccard batüska a f i s rohkem kui 3 km sügavusele. Seejärel s a a v u ta s id p r a n t s lased Guillaume ja Wilrh sü g a v u s e 4050 m. 1959. a. novembris jõ u dis b a tü sk a a f 5670 km-ni, kuid seegi polnud piir. 1960. a. 9. j a a nuaril laskus Piccard 7300 m sügavusele, 23. ja a n u a r i l jõudis tema ba tüskaa f a g a Ch a l le n g ed süvikus 10,9 km-ni! 8 Töödes t u ppunud laevade tõstmisel ning avar iite inud a llveelaevade ja lennukite ots imis -pä ä s teope ra t s ioonide s t huvi ta tud lu g e ja tele soovitame ra ama tu t : Jurnev, A. P., Sakharov, B. D., Sõtin, A. V. Avariid vee all. — L.: Sudos trojenije, 1981 (vene keeles). Selles ra ama tu s leidub ka kõnesolevatele küsimustele p ü h enda tud ulatus lik k i r janduse loetelu. 9 Vedeliku vä ljavoolukiiruse leidmiseks pa is tab küllalt olevat, kui kor rutada vedeliku kiirus u = V 2 gh k ra ani ava pinda laga . Kuid na g u katseliselt võib ve enduda , pole asi hoopiski nii. Nimelt pole vedelikujoa eri osade kiirused vä ljumiskohal paralleelsed, vaid neil on voolu keskmesse su u n a tu d komponent. P a radoks i a n a lüüs i taks e ü k s ik a s ja likult ra ama tu s : Feynman, R., Leighton, R., Sands, M. Pidevate keskkondade füüsika. — M.: Mir. — (Feyn'mani füüsika loengud, VII k.), 1966, 40. ptk., § 3 (vene keeles). 10 Füüsiku, täpsemalt, v a akumtehniku se isukoha lt pa is tab selline väide va ie ldavana. Ilmselt liigeste vahel õhku siiski on ja selle rõhk on pe aaegu võrdne õhurõhuga. Kuid õhku on vähe, sest ka suletud ruumi maht on väike. Luude nihkumisel üksteise suhte s ne n d ev a h e line ruum võib suureneda ja seejuures tekib õhurõhu mõjul luusid kokkusuruv jõud. Seda n ä h tu s t on kerge demons tre er ida j a lg r a t t a - pumba abil. 11 Pindpinevus jõudus id arvesse ei võeta. 12 Joonisel 70 n ä ida tud katses muutub ke ta s te vahelise pilu m u u tumisel ülemisele kettale ja torule mõjuv jõud. Kui näiteks kinnitada avaga toru vedru abil mingi pinna kohale, puhuda seejärel torus se õhku ja mõõta tundliku andur i abil torule mõ juva t jõudu, võib sel moel kindlaks teha toru otsa ja pinna vahekauguse . Toru nihkumine piki mingit e tte an tu d kõve rat lubab mõõta pinna profiili. Sel p r in t siibil on ehita tud riis tad, millega sa ab v ä g a täpselt kindlaks teha v a lmi s ta tav a te detailide pinna kuju. 13 Neid v ä g a huvitava id ja tõepoolest keerulisi nähtus i kä s itle takse ra ama tu s : Kadomtsev, В. В., Rõdnik, V. I. Lained meie ümber. — М.: Znanije, 1981 (vene keeles). Soovitame lugejail tu tv u d a selle r a ama tu g a . 14 Pe ente s soonekestes on vere voolamine lamin a a rn e ja üleka alus on difusioonilised ülekandeprotse s s id. 15 Öhu temp e ra tu u r loetakse kons tantseks . 16 õ h u t iheduse v ä ä r tu s e d on e s ita tud suhte lis te s ühikutes (õhu n o rma a lt ih ed u s e suhtes) .
Seitsmes peatükk
1 Pe a le kõige muu on kõrgete v a b r ik u k o r s tn a te üles anne ka pa i sa ta he itga as id võimalikult kõrgele a tmos fä är i, et nad hiljem h a ju k sid suurele maa-alale. See vähendab mõ n in g a l mä ä r a l reostumisa s tet e ttevõtete lähedal, kuigi ei väldi seda. Kahjulike ainete a tmo s fä är i s a t tumi s t tuleb tõkes tada suitsu efektiivse f iltrimisega, n ä i teks tolmupüüdur i te abil. 2 Sellest, mis on kosmonautide k a a lutu köök, võib lugeda r a am a tust: Varvarov, N. A-. Po p u la a rn e kosmonautika . — M.: Mašinostrojenije, 1981, ptk. 5 (vene keeles). 3 Seda riis ta nime ta taks e ka termobarome etr iks . Mä rgime , et atmos fä är irõhule lähedase rõhu korral v a s tab puhta vee ke emistemperatuur i muutumine 0,1 °C võr ra õhurõhu muutus ele 2,5—3 mm Hg (ekvivalentne pa ikkonna kõrguse mu u tu s on 30 m). Moodsa termobaromeetr i ska a la on j a g a tu d kra adi sa jandikeks ehk v a s tav a te k s rõhuühikuteks mm Hg-des. Peale sk a a la g a termomeetr i kuulub riista ju urde keedunõu — me ta llan um puhta ve ega ja soojendiga . V a a t a ma ta lihtsale ehitusele on te rmobarome eter mu g a v k a su ta d a ja täpne riist, mis sobib ekspeditsioonide v a ru s tu s e hulka. 4 Atmos fä är irõhk Ma rs i pinnal on sama mis Ma a peal 30—35 km kõrgusel, s. t. alla 10 mm Hg, kuid a tmos fä ä r i koostis on erinev. 5 On va ja silmas pidada, et vee kohal oleva õhu rõhu jä r su l v ä h e nemisel eraldub sinna peale ve eauru ka vees la h u s tu n u d gaase. Mõningane analoogia on sel nähtavuse l sü s ih a p p e g a a s i mullikeste tekkimisega mineraa lveepudelis selle lahtikorkimise hetkel.
Kaheksas peatükk
1 Na g u vä idab Pla to n (5. saj. e. m. a.), pä r in e v a t nime tus «ma g net » Euripideselt, kes oma d ra ama d e s nime tas seda «Magne s ia kiviks». Magne ti i t ehk ma g n e t ra u ama a k (keemiline koostis 31% FeO ja 69% Fe203) kujutab e n da s t looduslikku ma g n e ed i tu d kivimit, mille tükid võivad mõnikord olla õige suured (mitu k i logrammi ) . Legende sõna «magne t» pä r itolus t ja palju muudki leiab lugeja ra ama tu s t : Kartsev, V. M. Magne ti kolm a a s ta tu h a n d e t . — М.: Atomizda t, 1978 (vene keeles). 2 Range l t võttes ei tohi v a ade lda üksikuid tera se tüki a atomeid, vaid domeene, v ä g a pa ljude s t a a tomite s t koosnevaid süs teeme, mida mõnikord võib palja s i lmagagi näha. Domeenis on a atomid or ienteer itud ühes suuna s , kuid mag n e e t ima ta tera se seme l tervikuna magne tmomenti pole, sest domeenid pa iknevad kaootiliselt. Alles tera se magneetimisel orienteerub osa domeene piki välise välja su u n d a ja s ä i litab selle asendi ka p ä r a s t magne e t imi se lõppu. 3 Erandiks on juht, mil hõõguva s meta llis voolab tugev vool. Siis tekib voolu magne tväli, mis võib v a s ta s t ikmõ ju s tu d a välise magne t - vä ljaga . 4 Enne revolutsiooni k a su ta s Ho b u r a u d te e d e ja Omnibus s ide Selts magne te id kaera p u h a s tami sek s rau d n a e lte s t , p ä ä s te s sel moel hob u seid ra skete s t t raumad e s t . On te ada veel terve hulk nii va n u kui ka suhteliselt moodsaid näiteid mag n e t i k a su tami s e s t ainete või esemete e raldamiseks ehk separeerimiseks, nä iteks r a u ama a g i r ikas tamisel. Ka a s a eg se te s füüs ika se admete s sor te er ivad mag n e t id ja elektromag-netid a atomeid ja ioone, sunnivad laetud osakesi liikuma kiirendi v a ak umk amb r i s r ingjooneliselt, tak i s ta v ad kuuma plasma jah tumis t jne. ^ > 5 ^ a *-s ?s on realiseeritud ning laborites k a su ta tak s e nn. diamagnetilist ripet, kus keha holjub vaba l t kindla kuju g a mitteühtlikus mag n e tv ä l ja s . G Ka t se te s t e le k t roma g n e tk a h u r ig a , mis su u d ab vä lja tuli s tada mürske esimese kosmilise kiirusega võr re ldava te kiirus tega, oli juba juttu (vt. m ä r k u s 1 lk. 246). 7 Ideed ma g n e t jõ u d u d e k a su tami se s t ra u d te e a s ja n d u s e s on meie päevil leidnud e d a s ia ren d amis t, mõn in g a d neist on realiseeritud praktikas. On isegi termin «rong m a g n e tp a d j a b . Tehnika e d u s ammud selles v a ld k o n n a s on seotud u ut tüüpi elektrimootorite, näiteks lineaarse sünkroonmootor i ja ülijuhtsolenoidide leiutamise ning ehitamisega. Nendes t probleemidest huvita tuile soovitame pöörduda tä iendava lt k i r janduse poole. Vt. näiteks ra ama tu t : Dmitrijenko, I. M. Ülijuhtivuse ma a ilmas . — Kiiev, Naukova dumka, 1981 (vene keeles). 8 Rahvusvahelise Geofüüsika Aa s ta (1957—58) p ro g rammi t ä i t misest võttis Nõukogude Liidu poolt osa k u u n a r «Zarja», millele magne tjõud ei mõju: kõigis laeva liidetes, mootor is ja a n k ru te s on raud ja te ra s a s e n d a tu d vase, pronksi, alumiiniumi ja teiste mittcmagnetiliste meta llidega . 9 On olemas suhte lise lt lihtne viis tu g ev a s ma g n e tv ä l ja s r ikutud kella demagneetimiseks. Mis te arvate, kuida s seda teha? 10 Esineb ka s a jandikke ja kümnendikke sekundeid kestvaid välke. On tähe lda tud mitmekordseid välke: mitmed (mõnikord kümned) välgud, mis jä rg n e v a d üksteisele esimese v ä lg u teki ta tud teed, nn. kanalit mööda; ni isugune mitmekordne vä lk kes tab vahel kuni 1,5 s. Sellest, millised on kõnealuse ülihuvitava loodusliku objekti füüs ika lised omadused ja kuidas te adlased u ur ivad välku, võib lugeda r a a matust: Uman, M. Välk. — M.: Mir, 1972 (vene keeles). 11 Selles p a ra g ra h v i s ki r je ldatakse katseid, mida esimesena tegi inglise füüsik lord Rayleigh. J. I. Pe re lman an n ab vedelikujoa käitumisest e lektrivä lja s liht sus ta tud pildi. Muu h u lg a s ei rä ä g i ta midagi sellest, et v ä lia tu g e v u s e edasisel kasvamisel, va s tupidi, p u ru neb ju g a kergemini tilgakes teks. Rayle igh’ katseid korda s 70 a a s ta t hiljem koos oma k a a s tö ö ta ja te g a nõukogude füüsik J. I. Frenkel, kes esitas ka teooria, mis seletab nende ka tsete tulemusi. Täps ema l t on see huvitav teooria toodud r a ama tu s : Geguzin, J. J. Tilk. — M.: Nauka, 1973 (vene keeles). 12 Tänapäeva töös tuse ttevõte te s lah e n d a ta k se s ta a tilise elektri probleemi sageli radioaktiivse te isotoopide abil. Lühikese vaba tee pikkusega laetud osakesi ki irgav radioaktiivne p r e p a ra a t se a takse üles hõõrduva te dielektriliste pindade, näiteks k a n g ru ru l l id e lähedale. Prepa ra adi kiirguse mõjul tekkiv õhu su u renenud e lektrijuhtivus takistab m ä rg a ta v a te e lekt ros ta a ti l is te la en g u te kogunemi s t hõõrduvatele pindadele. Sel moel likvideeritakse tuleoht.
Üheksas peatükk
1 Mitmekordse te fotode v a ad e ld a v a l saamisviisil on palju ühist iidse m ä n g u a s j a kaleidoskoobi tööpõhimõttega . Kaleidoskoobist r ä ä kis J. I. P e re lma n juba «Huvi tava füüsika» esimeses ra ama tu s . Lõbu- ' 249 said katseid va lguskii r te mitmekordse pe ege ldus ega leiab lugeja ra ama tu s t : Tolansky, S. Va lguse imelised omadused. — M.: Mir, 1969, 2. ptk. (vene keeles). Märgime, et peeglite suva lise n u rg a ja objekti erinevate a sendite korral peeglite suhte s polegi tekkivate k u ju tiste arvu nii lihtne kindlaks teha. Sellest on ju t tu ü le s ande s 5.15 ra ama tu s : Walker, J. Füüs ika line tulevärk. — M.: Mir, 1979 (vene keeles). 2 Tänapä eva l on selline k a su teg u r seadmetel, mis muu n d av a d pä ike se ene rgiat otse e lektrienergiaks , nimelt ränifotoelementidel, millest koos ta tud pa ta re id leiavad juba k a su tami s t nii Ma a peal kui kosmoses. Tõsi, selliste fotomuundite hind on seni suhteliselt kõrge. 3 P ra e g u ollakse seisukohal, et päikesekiirgus on tulevikus su u t e line pe a a egu täielikult ra h u ld ama inimkonna ene rg iav a jad u s e . S a mal ajal pole pä ikeseenergia ta rbimine seotud ümbr itseva keskkonna sa a s tami s e g a ja meie planeedi so o ju s ta s a k a a lu r ikkumisega. Seep ä r a s t omis ta taks egi su u r t täh t su s t programmidele, mis tegelevad pä ikeseenergia k a su tami s e g a energeetilistel eesmärkidel (heliotehnika ). Ka su ta d e s k a a s a egse id teadmis i füüsika, keemia ja elektrotehnika alalt, uusi tehnoloogiaid ja aineid, on viimastel a a s ta k ümnetel s a a v u ta tu d selles osas su u r t edu. Veel rohkem ootab aga tege mist. Kasulikku teavet neist töödes t ja heliotehnika ees seisvatest üle s anne te s t võib ammu tad a pop u la a r te a d u s l ik u s t r a ama tu s t : Brinkworth, В. J. Pä ikeseenergia inimkonna jaoks. — M.: Mir, 1976 (vene keeles). Päikeseenergia , samuti tuule-, ookeani- ja teiste allikate energia k a sutami se s t võib lugeda brošüür is t: Marotšek, V. /., Solovjov, S. P. Energe etika võõraslapsed. — M.: Znanije. — (Tehnika) 1981 (vene keeles). 4 Meie päevil su la ta tak s e pä ike se se adme tega peale väävli veel muudki: erilistes pä ike se ahjude s tõs tetakse temp e ra tu u r mitme tu h an d e kraadini, mis võima ldab toota mõninga id ülipuhta id ra sk sulavaid metalle. Seega võib täiesti põ h jen d a tu lt kinnitada , et pra egu areneb pä ikeseenergia ka sutami se uus suund — päikesemetallurgia. 5 On võimalik v a lmi s tad a «pe aa egu n ä h tama tu » seade, mis neelab vaid väikese osa v a lg u s tu n d l ik u le v a s tu v õ tja le (tehissilmale) langeva s t valgusvoos t. Põhimõtteliselt k a su ta tak s e niisuguse id s e a d meid la ser tehnika s võimsate va lg u sk imp u d e diagnos tika s . Kuid loomariigis on e rakordse lt tähtis juš t silma pi ir tundlikkus vähese v a l gu s tu se korral, s. t. siis, kui piltlikult öeldes võideldakse iga va lgus - kvandi eest, ja seal selline idee ei realiseeru. Se e p ä ra s t võibki veepinnal näha täiesti läbipa is tva id loomi, kellel on a g a mu s tad silmad (need neelavad v a lg u s t! ) . Küs imust, milline peab olema n ä h tama tu inimese silma mu rd umi sn ä i ta ja , v a ad e ld a k s e üle s ande s 5.2 r a am a tu s : Walker, J. Füüs ika l ine tulevärk. — M.: Mir, 1979 (vene keeles). 6 Loomariigis s a a v u ta ta k s e ma ske e r ing üldiselt kolmel erineval viisil, mida nime ta taks e v a s ta v a l t mimikriks (fooniga ühtesulamine voi teise looma jä l jen d amin e ) , mo o n u ta v a k s jooniseks või va r jevä r - vuseks. Elusolendite ma ske e rumi s t kä s itle takse ü ks ika s jalikult r a a ma tus : Tolansky, S. Optilised illusioonid. — M.: Mir, 1967 (vene keeles). 7 Siin on ju t tu n ä h ta v a s t va lgus e s t. Üldiselt vee n a g u teistegi ainete mu rd umi sn ä i ta ja oleneb lainepikkuses t (seda n ä h tu s t nime ta takse dispersiooniks ). Siit järe ldub, et piirnurk, mille kor ral algab 250 täielik pe egeldus , pole erinevate lainepikkus te korral ühe sugune , kuid vee ja õhu piirilt peegeldumisel muutub ta n ä h ta v a v a lg u s e korral vähem kui 1° ulatuses. 8 «Ka laoptika» oluliseks osaks oleks ka õpetus ka lade suure s t s ilma r ingis t vee peal, s. t. a v a r a s t nä g emi sv ä l ja s t õhus, mis k e rg e n dab kaladel ruumi jä lg imi s t veest väljas. Seda ka lade nägemise iseä rasus t pe avad meeles pidama õnge spor tla sed. 9 Üks ika s ja likuma l t me re sü g a v u s te v ä rvuse s t vt.: Suleikin, V. V. Lood mere füüs ikas t. — M.: Izd-vo AN SSSR, 1949, 8. lugu (vene keeles). 10 Üks ika s ja likuma l t a ru ta ta k s e selle ja teiste lähedas te küs imus te üle ra ama tu te s : Minnaert, M. Va lg u s ja vä rv looduses. — Tallinn: Valgus, 1976 (eesti keeles); Tolansky, S. Optilised illusioonid. — M.: Mir, 1967, lk. 78—95 (vene keeles). 11 Viimastel a a s ta te l on planeete ja nende ka a s la s i uu r i tu d ka planeetidevahelistelt a u toma a t ja ama d e l t . Need u u r in g u d ands id h u l ganisti huvitava t, nä ida te s muu h u lg a s ig a s u g u s te kanalite p u u d u mist Marsil. As ja s t huvita tuile võiks soovitada r a ama tu t : Bakulin, P. Kononovitš, /. V., Moroz, V. I. As tronoomia üldkursus . — M.: Nauka, 1974 (vene keeles). Teadlaste kä sutuse s on t än a p ä e v a l Kuu, Veenuse ja Marsi pinna detailfotod. J ä tk a ta k s e hiidplaneetide Jupiteri ja Sa turni, samuti nende k a a s la s te uurimist. Näiteks 1979. a. Ameerika a u toma a t ja a - malt «Voyager 1» s a a d u d informa ts ioon lubas kindlaks teha esimese Maa-välise tegevvulkaani olemasolu Jupiter i ka as la se l Iol. 1982. a. edas tas pehmelt Veenusel ma a n d u n u d Nõukogude a u tom a a t ja am Maale unikaa lsed fotod Veenuse p in n a s t ja teos ta s planeedi pinna analüüsi. See uur imi s suund (planeetide füüsika) areneb meie p ä e vil tormiliselt. Planeetide ja nende k a a s la s te v ah e tu s t uur imise s t kosmoseaparaatide abil r ä äg i ta k s e r a ama tu s : Kaufmann, W. J. Planeedid ja Kuu. Tõlge inglise keelest. — M.: Mir, 1982 (vene keeles). 12 Suur t osa mikroskoopias e tendab ka uurimisobjekti v a lg u s t a mise viis, mis võima ldab su u r e n d a d a ra sk e s t ie r is ta tav a te detailide kontras tsust. Üks ika s ja likuma l t võib tu tv u d a mikroskoobiga ja mikroskoopia mee toditega r a ama tu te s t : Rõdnik, V. I. Näha n ä h t am a tut. — M.: Ene rgoizda t , 1981; Suvorov, A. L. Mikroskoopia t e a d u ses ja tehnikas. — M.: Nauka, 1981 (mõlemad r a ama tu d on vene keeles). 13 Nägemi spe te te s t vt. Tolansky, S. Optilised illusioonid. M.: Mir, 1967 (vene keeles). Selles r a am a tu s va at leb au to r muidki lugejale vähe tuntud n ä gemi spe t te id peale nende, mida käsitleb J. I. Perelman. 14 Sellest, mida moe tegijad pe avad täidlas te le või saleda te le mä ä ra tud uute rõivamudelite vä lja töötami se l silmas pidama, on juttu se l le s s ama s Tolansky r a am a tu s (ptk. «Täidluse illusioon»). Autor a rvab optimistlikult, et optika võib «õnnetuid paksukesi» paljuski a id a ta (lk. 36). 15 Siin v a a d e ld a v a d näited kuuluvad illusioonide hulka, mis tekivad tähe lepanu kõikumisest: nn. Schröderi trepp (joon. 133), v õ n kuv kuup (joon. 134). Taolisi illusioone on v a ja a rv e s ta d a te a d u s töös (nä iteks foto teel s a a d u d informa ts iooni töötlemisel, pinnase reljeefi k u ju ta v a te s te reopa a r ide analüüs il jne.). 16 S. Tolansky r a am a tu s «Optilised illusioonid» a n a lüüs i taks e neid nägemispetteid üksika s jalikult: Müller i—Lyeri nooltepetet, lõikuvate 251 joonte illusiooni (Poggendor f f i illusioon). Küllalt deta ilselt kä s itle takse ka nende illusioonide toimemehhanismi. 17 Võte, mida J. I. P e re lman analüüs ib p a r a g r a h v i s ««Ajamikroskoop » tehnikas», sai a lgus eks praktika s k a su ta ta v a te le seadmetele stroboskoopidele, millega mä ä ra ta k s e mõnede kiiresti muu tu v a te protsesside sagedus t . Et v õnke sageduse kontrolli e lektronmeetodid on ühed kõige täp s emad füüsikalised mõõtmismneetodid, siis t a g a vad stroboskoobid mõõtmiste e rakordse l t suure täpsuse. 18 Esmakordselt mä ä ra t i põhimõtteliselt sama l meetodil 1920. a. hõbeda a a tomite v a akumi s se a u ru s tumi s e keskmine kiirus (Sterni ka tse) . 19 Insener Nipkow’ poolt 1884. a. leiutatud ke ta s t rakenda ti 20. saj. 2 0 . - 3 0 . a. nn. meha anilises televisioonis kujutise laotamiseks ja t a a s e sitamiseks. Nüüd k a su ta tak s e sel e e smä rgil e lektronkiirega süs te e me. Mä rgime , et k a a s a e g n e televiisor on mu g a v se ade stroboskoopilise efekti jälgimiseks. Sellest, kuida s niisuguse id katseid kor ra ldada , on ju t tu ra ama tu s : Walker, J. Füüs ika line tulevärk. — M.: Mir, 1979, lk. 138, 139 (vene keeles). 20 Vähese v a lg u s ta tu s e korral lakkab meie silm e r i s tama s t värvusi ja kaotab.- ka võime tab a d a esemete teravaid piirjooni. Seda nähtus t nime tatakse mõnikord öiseks lühinägelikkuseks. Sama l põhjusel on ha lva s ti v a lg u s ta tu d objekti korral v ä g a ra ske fokuseerida mikroskoopi.
Kümnes peatükk
1 Väide, et suvalise va lju s e g a heli levib õhus alati kiirusega 340 m/s, ei v a s ta ra n g e l t võtte s tegelikkusele: heli kiirus õhus v äg a v a ljude helide allikate, na g u plahva tus , püss ipauk, v ä lg u k a n a l jne., lähedal ületab vahel mitu korda tava lise heli kiiruse vä ä r tuse . Niisugus te l helidel on eri nimetus: lööklained õhus. Heliallikas t e emaldudes kahaneb heli (lööklaine) kiirus õige ru t tu n o rma a ls e ta s e meni. Heli kiirusele mõjub, tõsi küll, tühisel mä ä ra l , a tmos fä ä r i seisund: õhu niiskus, temp e ra tu u r ja mõned teised faktorid, ö h u temp e ratuur i tõusul Г võr ra suureneb heli kiirus p e a a eg u 0,6 m/s võrra. Vahel võib tempe ra tuur i muutumi se osa olla õige oluline, näiteks kiirlennunduses . Nii on heli kiirus 20 km-st kõrgemal, s. t. s t r a to s f ä ä ris, kus õh u temp e ra tu u r langeb kuni —60 °C, veidi suurem kui 1000 km/h, sellal kui merepinna tasemel õhutempe ra tuur il 15 °C levib heli kiirusega 1216 m/s. 2 Autor ei a rve s ta helivõnkumis te sumbumis t k a u g u s e g a , mis tege likult takis tab teid ve s tlemas t, sest toru teises o t s a s teid ei kuuldaks. Pe a le selle pole kõigis torudes heli kiirus s ama mis õhus. 3 Täps ema l t on õhu k a ja s t ju t tu ra ama tu s : Tyndall, J. Heli. Tõlge inglise keelest. — М.: Gos izdat, 1922 (vene keeles). Tõsi küll, see r a ama t on mu u tu n u d bibliograafiliseks ha rulduseks . Kui lugejal õnne s tub Tyndalli r a am a t hankida, tutvub ta huvi ta v a te v a a t lu s te ja ka ts e teg a õhuakus tika alal, mida tegi Tyndall ise ja mis omal ajal osutusid v ä g a olulisteks laevasõidu seisukohalt. 4 Moodsas tehnikas ja te aduse s k a s u t a t a v a ultraheli sageduse ülempiir on tublisti suurem. Ultraheli s a g e duspi irkond on pra egu tavaks j a g a d a kolmeks diapasooniks : ma d a la d s a g e d u s ed (1,5-104— — 105 Hz ) , keskmised (105— 107 Hz) ja kõrged (107— 109 Hz ) . Elastsus laineid s a g e d u s e g a 109-— 10 13 Hz nime ta tak s e hüperheliks. Igal 252 ma in i tu d piirkonnal on omad kiirgamise, v a s tu v õ tu ja levimise iseä ra sus ed. Ul t rah e li s ag e d u s te ülempiiri tekkimine on t ingi tud elastsu s la ine te füüsika lise s t omap ä ra s t. Nii näiteks mä ä ra ta k s e p i ir s age dus g a a s id e s tingimuse s t , et helilainete pikkus ja molekulide vaba tee pikkus pe avad olema ligikaudu võrdsed. Atmos fä är irõhul on see s a g e d u s umbes 109 Hz. Hüperheli korral v a s tab minima a lne laine pikkus a a tomitevahe lise le kauguse le tahke s kehas, see on ligi 1 0 - 10m, pi ir s ag e d u s tõuseb a g a 1012— 1013 Hz-ni. 5 Kva r t s ikr is ta llid on suhteliselt kallid ning väikese võimsusega ultraheliallikad ja neid k a su ta tak s e tava liselt laborites. Tehnikas on ka sutuse l sünteetilised tehisma te r ja lid, näiteks b a a r iumt i ta n a ad i keraamika . Pe a le piesoelektriliste muu n d u r ite k a su ta tak s e ultraheli tekitamiseks sage li vä iksemaid magne ts t r ikt s iooni li s i kiirgureid. 6 Ultrahe lide fektoskoopia meetodi e sitas 1928. a. nõukogude te a d lane S. J. Sokolov. P r a e g u k a su ta tak s e erilisi ul trahe l ivas tuvõtjaid, mis a s e n d av a d õli ja teevad mõõtmised lihlsamaks . Tööd heliväljade fokuseerimisel ja nende n ä h ta v a k s muutmisel, s amuti s igna alitöötlemise võimsate ma tema a t i li s te meetodite loomine kujutise ehitamiseks raali abil on k a a s a toonud terve uue ul trahelise adme te klassi, nn. heliviisorite ilmumise, mida r a k en d a ta k s e pra eg u erinevate s helinägemise süs teemides, näiteks meditsiinis ebaüht lus te kindlaks tegemiseks pehmetes kudedes. Sellest vt. lähemalt ra ama tu s : Ultraheli. Toim. Goljamina, I. P. — M.: Sove t ska ja ents iklopedija. — (Ma lenka ja ents iklopedija) 1979 (vene keeles). 7 Huvi tav on märkida, et ultraheli esineb ka looduses. Tuulemühina s ja merekohinas on sagedus i, mis v a s ta v a d ultrahelialale. Võime kiirata ja va s tu võtta ultraheli on paljudel elusolenditel: liblikatel, tsikaadidel jt. Nahkhiired k a su tav a d ultraheli lennul, s a ade s pe ege ldunud s igna alide kaudu te a d a teel oleva tes t takis tus te s t. Nahkhiir te peenike vile on omamoodi helilokaator, mis lubab hiirel v a b a l t or ientee ruda pimedas. Seal, kus on pa lju nahkhiiri, k a rd a v a d naised neid sageli t ak e rduva t juustes se. Tõepoolest, tihedalt juus tega '- ka etud pea on nagu «heliauk», millelt ultraheli ei peegeldu. Tahtes kinnises t ruumis t välja lenna ta, to rmab e ru ta tu d nahkhiir pähe, mida peab kuulmise jä rg i avaks. Helidest looduses ja looduslikest helilokaa tor ites t võib lugeda r a ama tu te s t : Bragg, W. Va lguse maailm. Heli maailm. Tõlge inglise keelest. Toim. Obreimov, I. V. — M.: Nauka, 1967; Literxetski, I. B. Bioonika. — M.: Prosveš tšenije, 1976. (Mõlemad r a a matud on venekeelsed.) 8 Tähtede kiirus te kohta vt. näiteks r a ama tu s t : Struve, О., Lynds, В., Pillans, E. Elemen ta a ra s t ro n o omia . Tõlge inglise keelest. Toim. Kaplan, S. A. — M.: Nauka, 1967; Kosmosefüüs ika. Toim. Pikeiner, S. B. — M.: Sove tska ja ents iklopedija. — (Ma la ja ents iklopedija) 1976 (mõlemad r a ama tu d on vene keeles). 9 Umbes s am a s u g u s t riista — puukeppi, millel on ot sa s k a u sike — k a su t a v a d kogenud meha anikud mä ä r ama k s pöörlevate mootorisõlmede ja teiste seadmete, näiteks k u u l la a g r i te rikkeid «kuulmise järgi».
Lahendus
Kui vaadata puhtalt mehaanika vaatevinklist, siis ei tohiks probleemi tekkida - vedeliku sifoonis paneb liikuma raskusjõud, mitte õhurõhk.
Omaette teema on see, et näiteks vesi vaakumis keeb ja nii tekkiv veeaur lõhub sifooni toimimise loogika ära - vedelikusammas ei püsi enam koos vaid vajub laiali.
Nii et vastus võiks olla "sõltub asjaoludest".
Lahendus
Kui gaas, mida soovime ümber valada, on õhust raskem, siis sifooni töötamise loogika jätkuvalt kehtib - pikemas voolikus on gaasi tung allapoole liikuda suurem (gaasi sammas on kõrgem) ja nii hakkab gaasisammas liikuma.
Aga seda tuleks reaalselt proovida - selline tegevus kindlasti ei ole nii lollikindel, kui vedeliku ümbervalamine. Süsinikdioksiid on ilmne valik.