Optika põhikursus
- Saateks
- Sissejuhatus
- 1 Kiirteoptika
- 2 Elektromagnetlaine
- 3 Optiline diapasoon
- Sissejuhatus
- 3.1 Elektromagnetlainete skaala
- 3.2 Elektromagnetlainete kiirus ja eksperiment
- 3.3 Monokromaatiline tasalaine ja valgusallikate spektrid ning lainefrondid
- 3.4 Polariseeritud valgus, valgusallika mudelÜlesandedPraktilised tööd
- 3.5 Radiomeetria
- 3.6 FotomeetriaÜlesandedPraktilised töödLisamaterjalid
- 3.7 Laineoptika versus soojuskiirgus
- Kokkuvõte
- 4 Peegeldumine ja murdumine
- Sissejuhatus
- 4.1 Normaallangemine, α = 0
- 4.2 Suvalises suunas leviva tasalaine lainefunktsioon
- 4.3 Peegeldumis- ja murdumisseadus
- 4.4 Fresneli valemid juhul, kui α≠0
- 4.5 Analüüs: N21>1→α>γÜlesandedPraktilised töödLisamaterjalid
- 4.6 Analüüs: N21<1→α<γÜlesandedPraktilised tööd
- 4.7 Pinnalaine
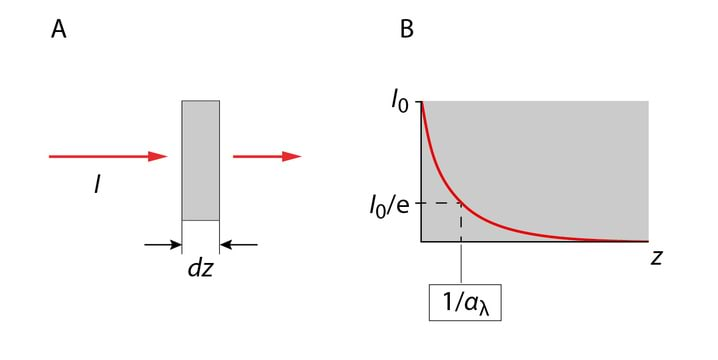
- 4.8 Valguse neeldumine
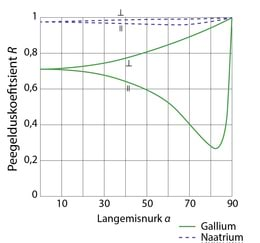
- 4.9 Fresneli võrrandid peegeldumisel kadudega keskkonnalt
- 5 Interferents
- 6 Difraktsioon
- 7 Valguse levikumehhanism keskkonnas
- 8 Valgus anisotroopses keskkonnas
- 9 Relativistlik optika
- 10 Mittelineaarne optika
- 11 Kvantoptika
- 12 Kirjandusallikad
Raamatukogudes on olemas lai valik inglise- ja venekeelseid hea tasemega optika õpikuid, kuid säilitamaks eesti keelt teaduskeelena, on ilmselt vajalikud ka füüsika baaskursuste eestikeelsed versioonid.
1979. aastal ilmus I.V. Saveljevi kolmeköitelise Füüsika üldkursuse optikat sisaldava kolmanda osa tõlge eesti keelde. Nimetatud õpiku sisu rahuldas täielikult tehniliste kõrgkoolide vajadused ja kattis ligikaudu 75% ulatuses ka tollajal kehtinud füüsika eriala programmi. Paraku, tänaseks on muutunud baasfüüsika õppeaja kestus ja programmid ning Saveljevi õpik ei kajasta ka olulisi uusi optika teadussaavutusi ja rakendusi.
Uuem, 2012. aasta Halliday baasfüüsika õpiku tõlge eesti keelde katab optikas vaid osaliselt probleemide ringi, mis vastab Euroopa füüsikahariduse standarditele.
Oluliseks lisafaktoriks, mis tingib uue õpiku olemasolu, on klassikalise loengupidamisviisi asendumine lektori-tudengi aruteluga; õpik võiks olla karkassiks, millel see arutelu baseerub.
Õpiku struktuur kujunes välja aastakümnete jooksul peetud loengute alusel ja on mõjutatud minu õpetajate ning kolleegide poolt. Viimati mainituist olen eriti tänulik Hans Korgele ja Koit Timpmannile.
Jaan Kalda esimeste peatükkide detailseid sisulised, vormistuslikud ja keelelised märkused olid kasulikud ka järgnevate peatükkide kujundamisel.
Nils Austa andis joonistele esinduslikuma ilme.
Nüüd siis jõuab tehtu põhihindajate - lektorite/tudengite – kätte, kes leiavad kindlasti rea vajakajäämisi.
Tagasisidet oodates,
Matti Laan
Veebruar 2020
Matti.Laan@ut.ee
Saateks parandatud ja täiendatud väljaandele
Tänu 2020. aasta kevadel lektoritelt/tudengitelt saadud tagasisidele ja Jaan Kalda poolt lõpuleviidud retsensioonile tehti õpikus mitmeid vormilisi, keelelisi ja ka sisulisi muudatusi. Katrin Laasi panuseks oli 7. peatüki retsenseerimine. Olen kõigile neile tänulik.
Minu eriline tänu kuulub toimetajale Kaido Reiveltile.
Matti Laan
Veebruar 2021
matti.laan @ut.ee
Füüsikaline optika tegeleb valgusega seonduvate protsessidega: valguse teke, levik ja vastasmõju ainega. Optika tähtsus ei piirdu vaid füüsikaga ja erinevate tehnoloogiliste lahendustega, valgus on põhiline ühendustee meie ja maailma vahel.
Tavaelus intuitiivselt mõistetavad sõnad omandavad füüsikas nii mõnigi kord teistsuguse tähenduse. Lisaks, mingi nähtuse ajalooliselt kord juba kasutuselevõetud nimetus ei pruugi vastata tänapäevasele arusaamale sellest nähtusest. Nii et – ettevaatust!
Optikas tuleb silmas pidada järgmist.
Valguskiir ei ole matemaatiline sirge. Rääkides valguskiirest tuleb arvestada, et
- Valguskiire ristlõige on alati lõplik, sest vastasel juhul oleks tema energiatihedus lõpmatu. Seega energeetiliste seoste leidmisel iseloomustame valguskiirt ka tema ristlõike pindalaga.
- Valguskiir annab energia leviku suuna
- Valguskiirest räägime ka siis, kui mängu tulevad valguse lainelised omadused nt rääkides mitmekiirelisest interferentsist peame silmas, et liituvad rohkem kui kaks lainet.
Valguse polarisatsioon ja aine polarisatsioon ei ole kokkulangevad mõisted. Valguse elektromagnetlaine mudelis iseloomustab polarisatsioon elektrivälja vektori geomeetrilist orientatsiooni. Aine polarisatsioon on aga seotud aine aatomite/molekulide dipool-momendiga, mis võib olla nii permanentne kui ka välise mõjutuse (sh valguse) poolt indutseeritud.
Tihtipeale iseloomustatakse ühte ja sama mõistet/nähtust erinevate nimetustega nt „paralleelne kiirtekimp“ ja „tasalaine“ iseloomustavad üht ja sama valguse levikuviisi.
Erinevate suuruste tähistamisel on püütud järgida traditsioonilist üldlevinud raamatute märgistust. Suures enamuses on tähistusteks vastava inglisekeelse sõna esitäht nt „“ – force, „“ – velocity, mõnikord on tagapõhjaks ka saksa, ladina või kreeka keel. Tabelis T 1.1 on esile tõstetud füüsikas kasutatavad kreeka tähed, nende tundmine kuulub füüsiku hariduse juurde.
Tabelis T1.2 on toodud suurustevahelist seost väljendavad matemaatilised märgid koos kommentaaridega.
Selles õpikus kasutame SI-s sätestatud ühikuid. Praktikas on kasutusel on ka nn süsteemivälised ühikud, optikas on neist tähtsaim pikkusühik ongström, Å=10−10m=0,1nm
Tabelis T1.3 on rahvusvaheliste lepetega kooskõlastatud erinevate ühikute eesliited.
Tabelis T 1.4 on tähtsamad konstandid tänaseks teadaoleva usaldusväärsete komakohtade arvuga.
Konstant | Tähis | Väärtus |
Valguse kiirus vaakumis | ||
Elementaarlaeng | ||
Plancki konstant | ||
Elektroni seisumass | ||
Prootoni seisumass | ||
Avogadro konstant | ||
Bohri raadius | ||
Boltzmanni konstant | ||
Stefan-Boltzmanni konstant | ||
Rydbergi konstant | ||
Elektronvolt | ||
Vaakumi dielektriline läbitavus | ||
Vaakumi magnetiline läbitavus |
Tihtipeale suudab õigesti mõistetud joonis anda rohkem teavet kui mitu pikka lauset.
Kujutava geomeetria jooniste puhul püütakse võimalikult hästi edastada objekti proportsioone ja tehnilised joonised on võimalikult detailsed, kuid füüsika joonised peavad eelkõige edastama arutlus- ja/või arvutuskäigu idee. Sel põhjusel ei pruugi mingi joonise detailide proportsioonid vastata tegelikkusele ja lisaks on joonisel kujutatud vaid antud probleemi lahendamiseks hädavajalikud detailid.
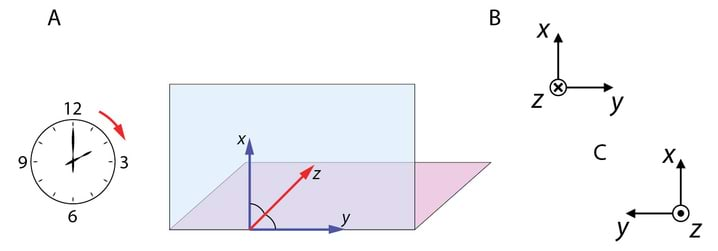
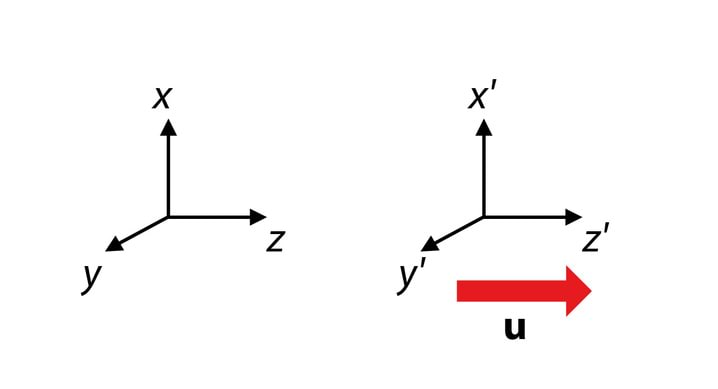
Ristkoordinaadistiku teljed valitakse nii, et nad moodustaksid parempoolse kolmiku: vaadates z-telje suunas, peab x-telje pööramine y-telje peale toimuma kellaosuti liikumissuunas, Jn 1.1.
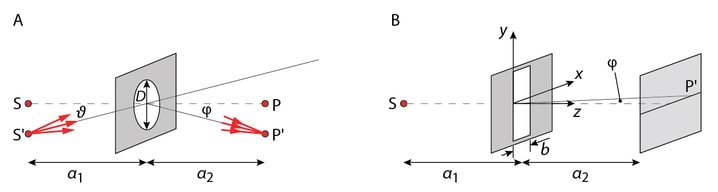
Enamikel juhtumitel on 3-mõõtmelised nähtused, Jn 1.2A, esitatud 2- mõõtmeliste lõigete, Jn 1.2.B, või projektsioonidena, seega horisontaalne joon sel joonisel on lahutuspinna lõikejoon langemistasandiga. Kui on võimalus mitmeti mõistmiseks, on joonisele lisatud ka koordinaattelgede orientatsioon. Joonistel kujutatakse valguse levikusuunda kiirena.
Harjumuspäraselt on nurkade mõõtühikuks kraad, kuid nii harmooniliste võnkumiste kui ka lainete hetkväärtusi määrava faasi puhul on füüsikas eelistatumaks ühikuks radiaan, T1.5.
Ligikaudsed arvutused baseeruvad funktsioonide rittaarendustel.
Kui , siis enamikel juhtudel saame arvutustes piisava täpsuse kasutades seoseid
1.
Näiteks kui , siis e0,1=1,1052 ja suhteline erinevus
2.
Kui , siis ja suhteline erinevus
Kui ning , siis ja suhteline erinevus
Kui nurgad on väikesed, siis võib trigonomeetriliste funktsioonide puhul lugeda, et
NB! Viimaste seoste puhul on nurk alati radiaanides.
Kas lähendusvalemite kasutamine on õigustatud, sõltub muidugi vajaminevast täpsusest.
Meie õpikus puudub ülevaade füüsika ajaloost ja seda mitmel põhjusel. Esiteks jõuab guugeldamisega kergesti mingi nähtuse ajaloolise tagapõhjani ja teiseks on olemas Ivar Piiri eestikeelne füüsika ajalugu ja seda nii paberkandjal kui ka e-õpikuna. Ja kolmandaks – kursuse ülesehitus ei järgi ajaloolist teed.
Füüsika, sh optika, areng on kõike muud kui rahumeelne samm-sammult kulgev protsess. 20. sajandi füüsika superstaarile Albert Einsteinile omistatakse ütlus „füüsika on ideede draama“ ja kohati on selle draama jälgimine võrreldav hea kriminaalromaaniga. Füüsika ideelised kokkupõrked ei ole ainult inimestevahelised, vaid nad on ka ühe indiviidi peas. Arusaadavamaks muutub see dramaatilisus siis, kui on tekkinud arusaamine probleemist endast – see on veel üks põhjus, miks loobusime ajaloolisest ülevaatest.
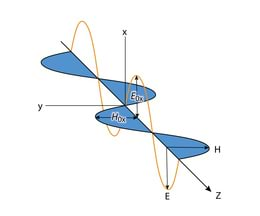
Valgusnähtused on seletatavad, eeldades, et mikromaailmas valitseb lainelis-korpuskulaarne dualism. Loomulikult on dualism vaid meie makromaailma kogemustel baseeruvates kujutlustes, Jn 1.5, loodus ei tea sellest midagi.
Valguse dualismi ilminguks on see, et osasid eksperimentaalseid tulemusi on võimalik kirjeldada valguse lainemudelitega, osasid aga on lihtsam seletada korpuskulaarmudeliga.
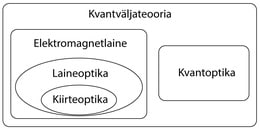
Valguse lainelisi omadusi kirjeldab kõige täielikumalt elektromagnetlaine mudel, kuid paljudel juhtudel annab tema lihtsustatud variantide rakendamine võrdväärse tulemuse. Laineoptika lähenduses jäävad kõrvale valguse elektromagnetilised omadused, säilib valguse laineline iseloom. Kiirteoptika (≡ geomeetrilise optika) kirjeldab nähtusi, mille puhul on vaja vaid energia levikusuunda.
Kvantoptika kirjeldab adekvaatselt valguse ja aine vastasmõju tuues sisse seda vastasmõju kirjeldavad fenomenoloogilised suurused. Kvantväljateooria ühendab laine- ja kvantoptika, Jn 1.6.
Meie optikakursuses on esiplaanil valguse lainemudel. Esmalt uurime elektromagnetlaine üldiseid omadusi ja seejärel siirdume optika spetsiifiliste probleemide lahendamisele. Seal kus võimalik, kasutame laineoptika lähendust. Kiirteoptika selle õpiku raamidesse ei mahu. Õpiku viimane peatükk on pühendatud kvantoptikale.
Toodud näiteülesannete põhieesmärgiks on anda ettekujutus erinevate suuruste arvväärtustest.
Lisainfo põhitekstile on nelja liiki linkides.
- Selgitavad kommentaarid (K).
- Viited õpiku eri osadele (vt ...)
- Matemaatilised abivalemid (M)
- Viited persoonidele (P).
Õpiku kirjutamisel on infot hangitud paljudest allikatest, kuid praegu on võimatu taastada, mis osa millisest allikast on võetud. Sel põhjusel on loobutud korrektsest viitamisest ja peamiste kasutatud raamatute loetelu on toodud õpiku lõpus.
Käesoleva kursuse konspekt tekstina kiirteoptika käsitlust ei sisalda, järgnevas anname vaid seda puudutava põhivara. Teadmised ja oskused omandame läbi praktikumide.
XVII sajandil hakkas kujunema eksperimentaalne meetod füüsikas st mingi väite tõesuse kriteeriumiks sai eksperiment. Selleks ajaks baseerus optika neljal tulemusel, mille kirjeldamisel kasutame tänapäeva terminoloogiat.
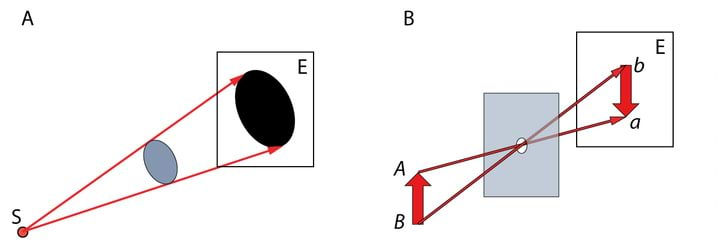
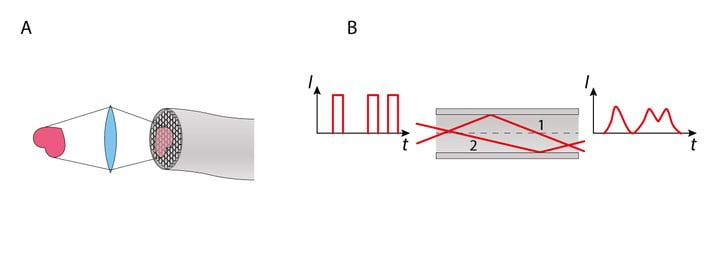
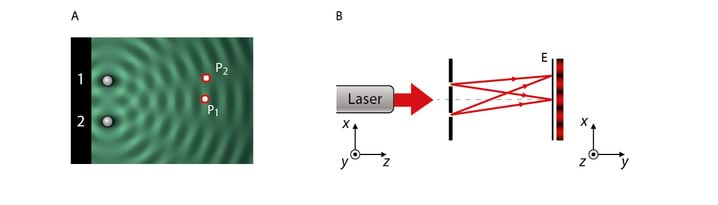
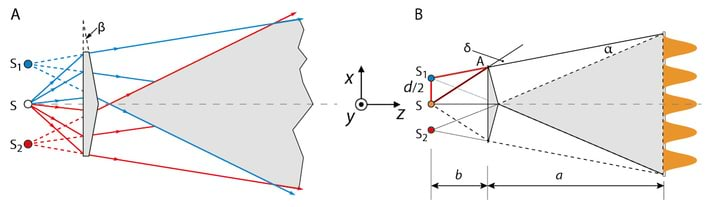
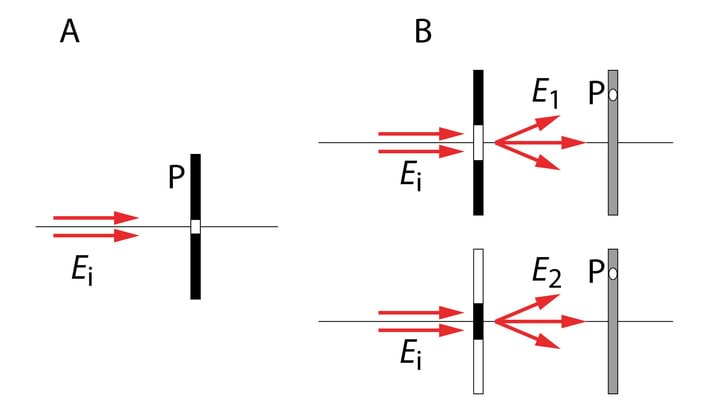
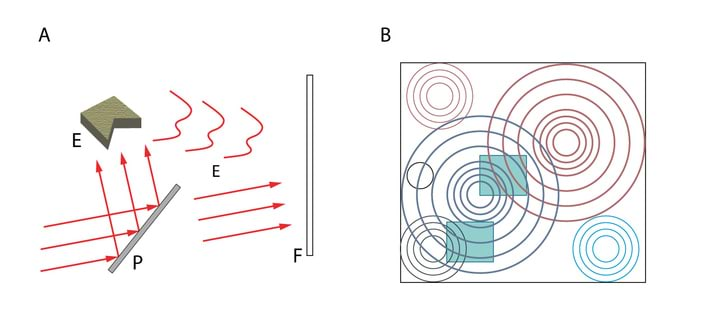
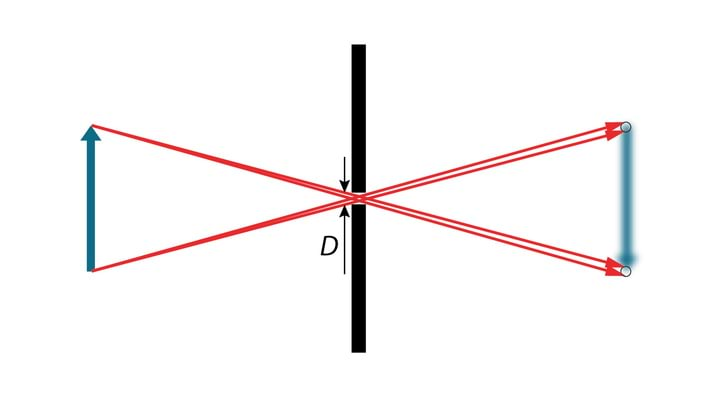
Valguse sirgjooneline levik Homogeenses keskkonnas levib valgus mööda sirgjoonelist teed. Selle väite tõestuseks on teravate servadega varju teke esemest, mis on ekraani ja väikeste mõõtmetega valgusallika vahel, Jn 1.3A.
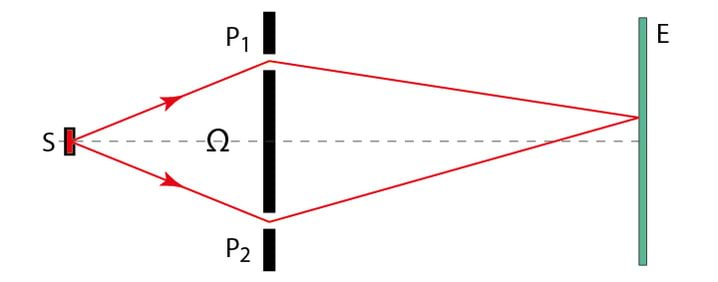
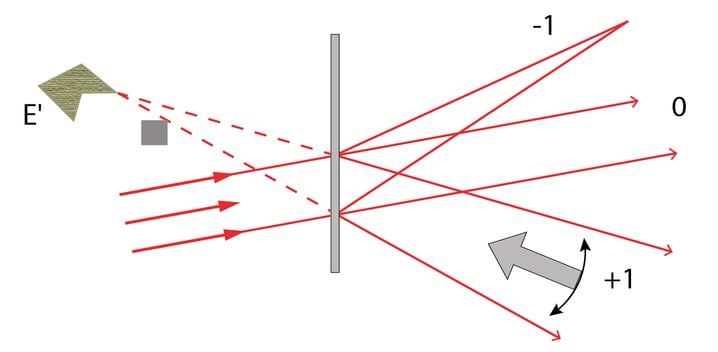
Teiseks valguse sirgjoonelise leviku näiteks on kujutise teke pimekambris (≡ camera obscura), 1.3B. Pimekambris on valguse teel tõke, milles on väike ava. Valguskiir, mis lähtub eseme AB mingist punktist ja läbib ava, tekitab ekraanil E selle punkti kujutise.
Valguse kiirtekimpude sõltumatus Mingi valguse kiirtekimbu levik keskkonnas on sõltumatu sellest, kas selles ruumipiirkonnas on teisi valguse kiirtekimpe. Sellest piirkonnast väljuv kiirtekimp ei ole mõjutatud teiste kiirtekimpude olemasolust.
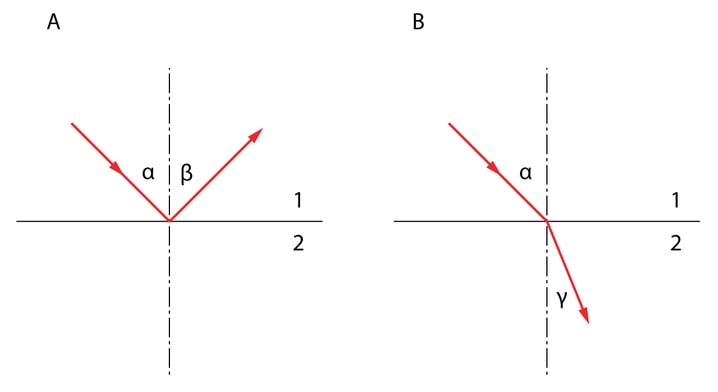
Peegeldumisseadus Olgu kahe keskkonna ja lahutuspinnaks tasapind, millele langeb kaldu valguskiir, mis osaliselt peegeldub tagasi esimesse keskkonda, Jn 1.4 A.
Langemisnurgaks nimetatakse nurka langemispunktist tõmmatud pinnanormaali ja langeva kiire vahel. Peegeldumisnurgaks nimetatakse nurka pinnanormaali ja peegelduva kiire vahel. Langemistasand on üheselt määratud langeva kiire ja pinnanormaaliga, ta on alati risti keskkondade lahutuspinnaga.
Peegeldumisseadus koosneb kahest osast
Murdumisseadus Valgus, langedes kahe keskkonna lahutuspiirile, murdub osaliselt teise keskkonda, 1.4B. Murdumisnurgaks nimetatakse nurka pinnanormaali ja murduva kiire vahel.
Murdumisseadus koosneb kahest osast
- Murduv kiir on langemistasandis
- Langemisnurga siinuse ja murdumisnurga siinuse suhe on konstantne, (Snelliuse seadus), kus on teise keskkonna suhteline murdumisnäitaja esimese suhtes
Kõigil loetletud seaduspärasustel on oma piiritletud kehtivuspiirkonnad, mille paneme paika edasises kursuse käigus.
Selles õpikus kasutame elektrivälja iseloomustamiseks kahte vektorit E ja D ning magnetvälja jaoks vektoreid B ja H K 2.1.
Elektromagnetismis jõutakse nelja Maxwelli võrrandini induktiivsel teel, lähtudes üksikjuhtudest ja neid järk-järgult üldistades. Läbime need teed kiirkorras.
Vastavalt Coulombi katsetele mõjub keskkonnas dielektrilise läbitavusega oleva kahe laengu ja vahel jõud, mis on võrdeline nende laengute korrutisega ja pöördvõrdeline nendevahelise kauguse ruuduga F∝qQεr2. Laengud on algebralised suurused ja samamärgiliste laengute puhul on tegemist tõukejõuga, erimärgilised laengud aga tõmbuvad. Võrdetegur jõu avaldises oleneb kasutatavast ühikute süsteemist, SI-s on võrdeteguriks . Vastavalt lähimõju printsiibile saab punktis asuvale (proovi)laengule mõjuda jõud vaid siis, kui jõu tekitaja on ka selles ruumipunktis. Praegusel juhtumil on jõu põhjustajaks laengu poolt tekitatud elektrostaatiline elektriväli
ja seega mõjub proovilaengule jõud F=qE. Elektrostaatilist välja iseloomustavad jõujooned algavad positiivsel laengul ja lõpevad negatiivsel laengul või lõpmatuses. Coulombi seaduse üldistuse järgmine aste on Gaussi teoreem, vastavalt millele elektrivälja nihkevektori D=εε0E voog läbi suletud pinna võrdub laengute algebralise summaga selle pinna sees.
Asendades diskreetsete laengute summa laengutihedusega ja minnes üle diferentsiaalkujule, saame
Selle seose paremal poolel on põhjus ja vasemal tagajärg: elektrostaatilise välja allikaks on laeng. Selline põhjuse-tagajärje vahekord kehtib ka järgnevate võrrandite v2.2-v2.4 puhul.
Kuna magnetlaenguid ei ole , siis
ja
Kui magnetvoog läbi pinna , mida ääristab juhtiv kontuur , muutub ajas, siis vastavalt Faraday elektromagnetilise induktsiooni seadusele indutseeritakse selles kontuuris elektromotoorjõud . Kuna elektromotoorjõud on kontuuri ulatuses laengu ümberpaigutamiseks tehtav töö ja dΦM=BdS, (B – magnetiline induktsioon) omandab seadus kuju
Vastavalt Maxwelli üldistusele pole kontuuri olemasolu vajalik – kui mingis ruumipiirkonnas magnetväli muutub, siis tekib seal elektriväli, mille tsirkulatsioon on nullist erinev. Selle seaduspära diferentsiaalkuju on
ehk sõnades: pööriselise elektrivälja allikaks on ajas muutuv magnetväli.
Seda fakti, et vooluga juhtme ümber tekib magnetväli, väljendab Ampere’i seadus. Kui keskkonna magnetiline läbitavus on ja magnetvälja tugevus
siis magnetvälja tugevuse tsirkulatsioon kontuuris võrdub juhtivusvoolude algebralise summaga läbi pinna , mida see kontuur ümbritseb
Juhul, kui piirduda vaid selle seosega, tekib vahelduvvoolu voolamisel läbi kondensaatori vastuolu: kuigi juhtivusvoolu kondensaatori plaatide vahel pole, eksisteerib ka seal magnetväli. Vastavalt Maxwellile on seal magnetvälja allikaks nihkevool tihedusega ja me saame täiendatud Ampere’i seaduse diferentsiaalkujul
(j –juhtivusvoolu tihedus), mis sätestab, et pööriselise magnetvälja allikaks on nii juhtivus- kui ka nihkevool.
Maxwelli neljast võrrandist koosnev süsteem, v 2.1 – v 2.4, on kasutu seni, kuni pole teada ainevõrrandid, mis seovad omavahel elektrinihke ja elektrivälja tugevuse vektorid, D=f(E), magnetvälja tugevuse ja magnetilise induktsiooni vektorid, H=f(B), ning voolutiheduse ja elektrivälja tugevuse vektorid, j=f(E).
Neid seostepaare iseloomustavad makroskoopilised karakteristikud, dielektriline läbitavus , magnetiline läbitavus ja juhtivus , on põhimõtteliselt leitavad, kui keskmistada kiirusega u liikuvale laengule elektri- ja magnetväljas mõjuv jõud
üle aine vabade ja seotud laengukandjate.
Sõltuvalt aine karakteristikutest , võib keskkond olla
Homogeenne või mittehomogeenne (nt sõltub koordinaatidest)
Isotroopne või anisotroopne (nt murdumisnäitaja on erinevates suundades erinev)
Lineaarne või mittelineaarne (nt valguse neeldumine sõltub tema intensiivsusest)
Statsionaarne või mittestatsionaarne (nt neeldumine sõltub valguse toime ajast)
Edaspidi on põhitähelepanu pööratud valgusnähtustele HILS keskkonnas, ka anisotroopiale on pühendatud üks peatükk.
Laine on mingis ruumipiirkonnas tekitatud häirituse levik ruumi.
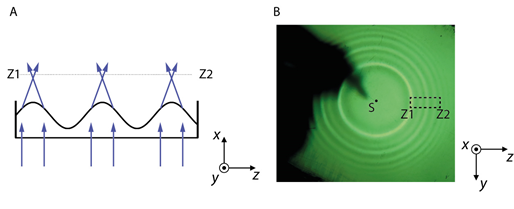
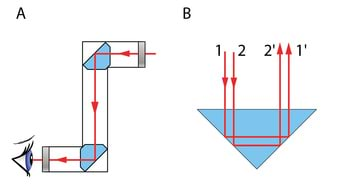
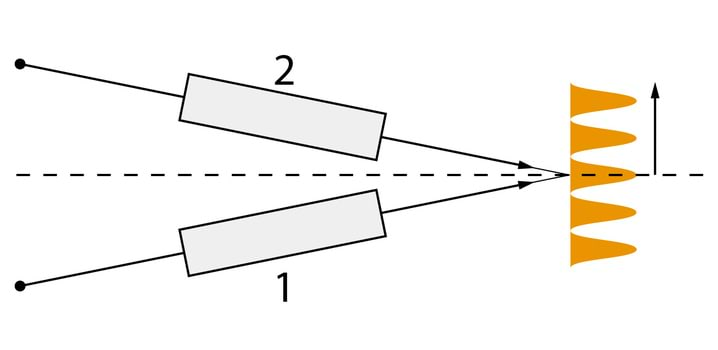
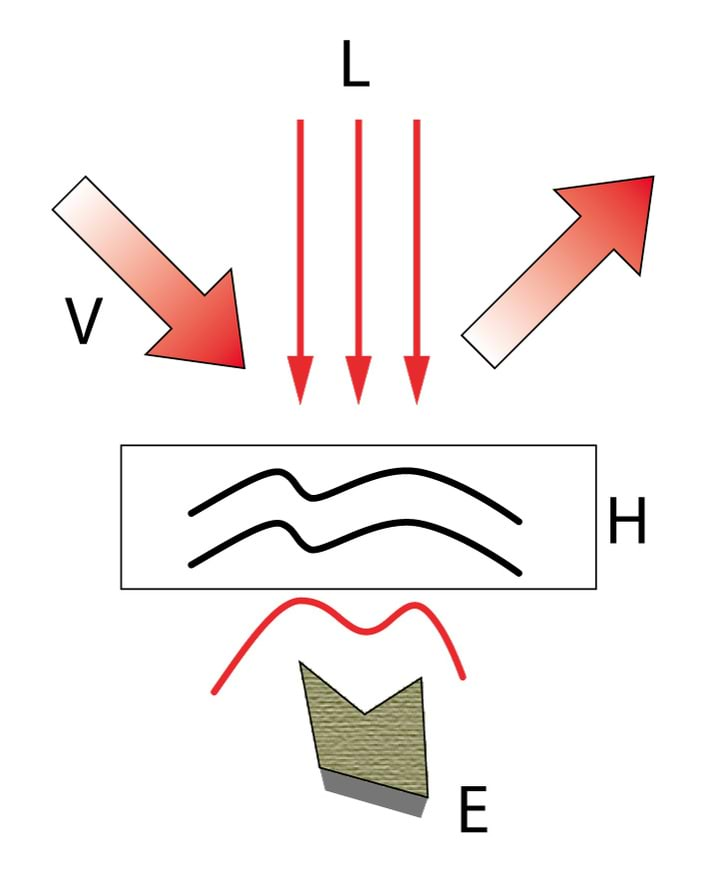
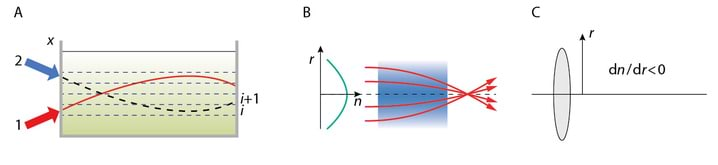
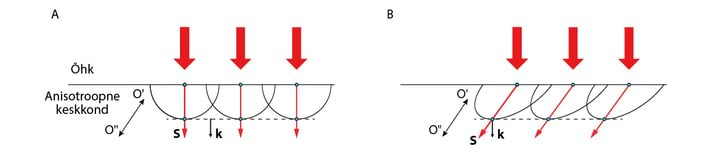
Loengudemonstratsioonides kasutatakse tihtipeale lainete visualiseerimiseks veevanni, Jn 2.1A. Kui lainevanni läbipaistvat põhja läbiv paralleelne kiirtekimp langeb lainelisele veepinnale, siis kumerpindadel murdumise tulemusena tekivad veepinna kohal heledamad ja tumedamad piirkonnad, mida on võimalik optilise süsteemi abil projekteerida ekraanile. Foto Jn 2.1B fikseerib veepinnal leviva lainepaketi, mille tekkepõhjuseks oli varasemal ajahetkel pipetist veepinnale langev tilk.
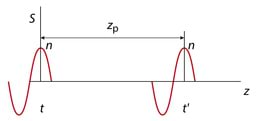
Kirjeldame nüüd ühe laineharja levikut lihtsaimal ühedimensionaalsel juhul.
Toimugu punktis sinusoidaalsed võnkumised s=s0sin(2πvt), Jn 2.2, ja momendil olgu tegemist laineharjaga, mille järjekorranumber on . Laine levikul korduvad need võnkumised teatud ajalise nihkega kaugemates ruumipunktides. Kui laineharjal kulub kaugusel zP olevasse ruumipunkti P levikuks aeg , siis võib kirjutada sP=s0sin(2πft′) kusjuures . Kui on laineharja numbriga levikukiirus (faasikiirus), saame
Alati, kui mingi suvalise funktsiooni argument (faas) on esitatav kujul (ehk kujul z/v−t, vt−z või z−vt), on meil tegemist lainega, mis levib z-telje positiivses suunas. Sellist argumenti omavat funktsiooni nimetatakse lainefunktsiooniks. Kui argumendis on aja- ja ruumimuutuja mõlemad positiivse (või mõlemad negatiivse) märgiga, levib laine ruumikoordinaadi kahanemise suunas („vasakule“).
Üldjuhtumil peab lainefunktsioon rahuldama lainevõrrandit, mis on teist järku osatuletistega diferentsiaalvõrrand
Olgu konkreetsuse mõttes tegemist sinusoidaalse lainega. Võtame funktsioonist teist järku osatuletise esmalt aja järgi
ja siis koordinaadi järgi
Asetades saadud tulemused võrrandisse (2.5), saame oodatud samasuse.
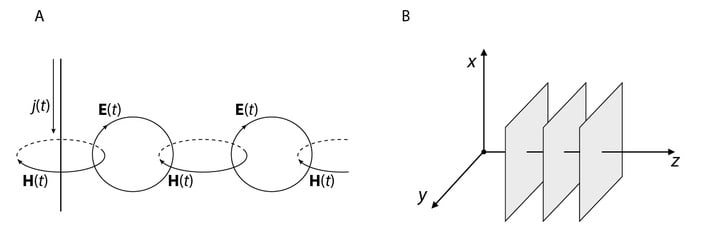
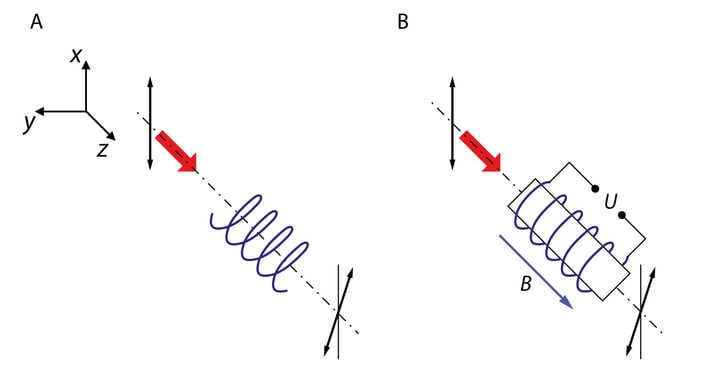
Näitame nüüd, et ühe järeldusena Maxwelli võrranditest peaks eksisteerima elektromagnetlaine. Algul lähtume üldistest kaalutlustest ja seejärel teeme sedasama matemaatika abil. Olgu meil juhe, milles on vool voolutihedusega j(t), Jn 2.3A. Vastavalt valemile v 2.4 tekitab vool juhtme ümber magnetvälja H(t). Kuna magnetväli muutub ajas, siis indutseeritakse v 2.3 järgi lähipiirkonnas elektriväli E(t) ja pöördudes jälle v 2.4 poole, näeme muutuva magnetvälja teket. Selline korduv, iseennast alalhoidev protsess ei vaja levikuks mingisugust spetsiifilist keskkonda.
Elektromagnetlaine eksistentsi matemaatiliseks tõestuseks eeldame, et meil on HILS keskkond ja on tegemist dielektrikuga, σ=0→j=0, ning ruumlaengud puuduvad, . Kirjutame nüüd valemid v 2.3 ja v 2.4 lahti komponentide kaupa
Lihtsustamaks uuritavaid võrrandeid, olgu meil tegemist juhuga, kus antud ajahetkel on tasandi kõigis punktides elektri- ja magnetvälja väärtused samad, Jn 2.3B. Järgmisel ajahetkel ja/või mingis teises tasandis omavad elektri- ja magnetväli teisi väärtusi. Seega kõigis süsteemi v 2.6 võrrandites on tuletised ∂∂x,∂∂y=0 ja seega
Saadud lihtsustunud võrrandid on piisavalt läbipaistvad, et teha mõningaid järeldusi. Esmalt, v 2.7 kolmas rida näitab, et z-telje sihilised E ja H komponendid ja ei osale välja levikus. Esimeses ja teises reas olevad võrrandipaarid aga osundavad, et põhjuslik seos on vaid teineteise suhtes risti olevatel E ja H komponentidel, ja , kuid ei ole põhjustatud muutustest ja vastupidi. Sama kehtib muidugi ka ja Hy vahekorra kohta. See leid lubab teha täiendava lihtsustuse – olgu elektriväli orienteeritud x – telje sihis ja kuna Ey=0, siis ka Hx=0. Seega eksisteerib vaid magnetvälja y-komponent ehk E⊥H. Järele jääb vaid kaks võrrandit
Diferentseerides neist ülemist võrrandit koordinaadi ja alumist – aja järgi , saame mõlemas võrrandis magnetvälja jaoks segatuletiste avaldised ja võrdsustades need, saame
Kui nüüd võtta v 2.8-s esimeses võrrandis tuletis aja järgi ja teises koordinaani järgi, saame magnetvälja jaoks võrrandiga v 2.9 identse tulemuse. Võrrelda saadud tulemust lainevõrrandi üldkujuga v 2.5, siis näeme , et eesmärk on saavutatud: elektromagnetväli levib z-telje suunas, kusjuures laine faasikiirus on
(K 2.5) Vaakumis, kus, , on elektromagnetlaine (EML) faasikiiruseks
mis langeb kokku eksperimendis mõõdetud valguse kiirusega vaakumis. Faasikiirus keskkonnas on
Võrrandid v 2.7 kirjeldavad lainet, mis levib z-telje positiivses suunas , kusjuures elektri- ja magnetvälja vektor on risti laine levikusuunaga, E⊥v, H⊥v. Põhjuslikus seoses olevad elektri- ja magnetvälja komponendid on risti ka omavahel, E⊥H. Erijuhtu, kus laine levikul E (seega ka H, kuna H⊥E) muutub vaid ühes fikseeritud tasandis, nimetatakse lineaarselt polariseeritud laineks. Elektrivälja E sihiga ja levikusuunaga määratud tasand on polarisatsioonitasand.
Pinda, millel asetsevad kõik laine samafaasi (nt laineharja ) punktid, nimetatakse lainefrondiks. Joonisel Jn2.3B on lainefrondiks tasapind, tegemist on tasalainega.
Lainet, mille hetkväärtus muutub siinus- või koosinusfunktsiooni järgi, nimetatakse harmooniliseks: funktsioonid
ja
kirjeldavad harmoonilist elektromagnetlainet. Sagedus (täisvõngete arv sekundis) on seotud perioodiga (ühe täisvõnke sooritamise aeg), f=1/T. Optikas kasutatakse enameelistatult ringsagedust, ω=2πf. Kui , on tegemist monokromaatilise lainega. Arvestades, et lainepikkus on vahemaa, mida laine läbib ühe perioodi jooksul, , teisendame lainefunktsiooni faasi
Tuues sisse lainearvu mõiste,
on faas kirjutatav kujul . Monokromaatilise elektromagnetlaine elektrivälja tugevuse lainefunktsiooni võib esitada kas siinusfunktsioonina või koosinusfunktsioonina
Mõlemad lainefunktsiooni trigonomeetrilised esitused oleksid samaväärsed, kui lisaksime neisse avaldistesse ka algfaasid. Magnetvälja lainefunktsioon on esitatav samuti kujul v2.13.
Faasikiirus on konstantse faasi, , edasikandumise kiirus. Kuna faasiavaldise diferentsiaal on , siis saame faasikiiruseks
Harmooniline laine on perioodiline nii ajas kui ka ruumis. Vastavalt seostele v2.12 näeme, et fikseeritud ruumipunktis, , muutub faas perioodiga ja fikseeritud ajahetkel on lainefunktsiooni ruumiliseks perioodiks lainepikkus .
Näide N 2.1
Lahendus
Arvutades leiame:
, m | , s | , m−1 | ||
Näeme, et võrgusagedusele vastab lainepikkus , kuid valguse lainepikkus on väiksem mikromeetrist, seega iseloomustab valgust suur lainearvu väärtus st antud ajahetkele vastav faas muutub ruumis võrra juba 300nm lõigul.
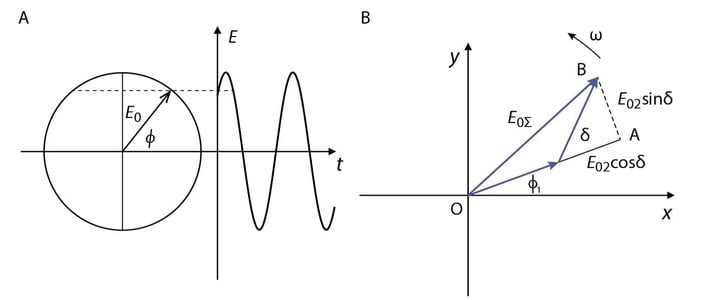
Harmoonilise laine
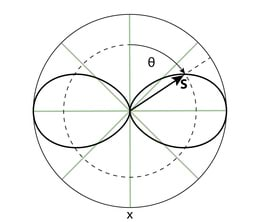
geomeetrilises esituses arvestatakse, et tema projektsioon vertikaalteljele, Jn 2.4A, langeb kokku nurkkiirusega vastupäeva pöörleva vektori, mille pikkus on , projektsiooniga. Hetkel on vektori ja x-telje vaheline nurk (algfaas). Näitena saab Jn 2.4B abil leida kahe sama sagedusega laine liitumisel tekkiva summaarse laine amplituudi ja faasi .
Kui lainete amplituudid on ja ning algfaasid ja , siis faasivahe kahe laine vahel on ja täisnurksest kolmnurgast saame
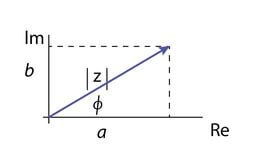
Teisenduste mõttes kõige efektiivsem laine esitusviis on kompleksesitus, Jn 2.5. Tasandil, mille horisontaalteljeks on kompleksarvu reaalosa ja vertikaalteljeks on imaginaarosa , on kompleksarv vektor, mille moodul on ja faasinurga saame seosest . Kuna ja on joonise täisnurkse kolmnurga kaatetid, siis
Eksponentfunktsiooni seob koosinus- ja siinusfunktsiooniga Euleri valem (vt M 2.2), seega
kusjuures , Im(z)=|z|sinϕ, ϕ=arctanIm(z)Re(z) ning .
Eksponentfunktsiooni tuletise ja integraali leidmine on väga lihtne. Kui f(x)=exp(ax), siis ja
Kuna , siis on lihtne leida kaks väga olulist seost
Kui me kasutame edaspidi mingi probleemi lahendamiseks lainefunktsiooni komplekskuju, tuleb lõpptulemus ikkagi esitada reaalkujul.
Keskkonnas murdumisnäitajaga z-telje positiivses suunas leviva harmoonilise laine lainefunktsiooni võib komplekskujul kirja panna mitmel erineval viisil, nt
Sellise kirjapaneku puhul me omistame füüsikalise tähenduse (tegelik väli antud punktis ja antud ajal) vaid avaldise reaalosale ja imaginaarosa on "ballastiks" kaasas.
Avaldises v 2.19 on on vastavalt amplituudi tavadefinitsioonile positiivne suurus. Kui nüüd tähistada kz=−δ, saame
ja lugedes amplituudiks lainefunktsiooni ajast sõltumatut osa
näeme, et sellise amplituudi mõiste üldistuse puhul on amplituud üldjuhul kompleksne. Erijuhul, kui , siis
st selle laine amplituud on negatiivne, . Füüsikaliselt tähendab see seda, et laine amplituudiga on vastasfaasis lainega, mille amplituud on .
Kasutades harmoonilise laine kompleksesitust on lihtne leida, kuidas on omavahel seotud ja hetkväärtused. Kuna mõlema välja faas on , siis seos v 2.8 omandab kuju
See tulemus sisaldab kaht olulist teabekildu vabas ruumis leviva laine ( kulgev laine) kohta: esiteks on elektromagnetlaines E ja H hetkväärtused üks-üheselt seotud ja teiseks, kui ja on reaalsed, siis elektri- ja magnetväli muutuvad faasis, Jn 2.5. Samasugust pilti näeksime, kui fikseeriksime ruumipunkti ja jälgiksime muutusi ajas.
Elektromagnetlaine levikul vaakumis on elektri- ja magnetväli võrdväärsed partnerid, ilma üheta poleks teist. Samas on aga laine elektri- ja magnetkomponendi mõju ainele kõvasti erinev. Näitamaks seda, leiame esmalt, kuidas on elektromagnetlaines seotud ja . Kuna B=μμ0H, siis v 2.21 saab kuju
ehk faasikiiruse vahendusel (vt v 2.10) ja vaakumis .
EMLi vastasmõju ainega on määratud jõuga
kus u on laengukandja kiirus, asendas suhtega E/c saame jõu mooduli maksimumväärtuse jaoks vaakumis
kus esimene liige nurksulgudes väljendab elektrivälja ja teine magnetvälja mõju laengukandjale . Seni kuni u/c≪1, on EML-i mõju ainele määratud elektriväljaga. See on põhjus, miks pöörame peatähelepanu elektriväljale.
Kuna ja on elektromagnetlaines omavahel üks-üheselt seotud, siis reeglina teeme teisendused vaid elektrivälja tugevusega , ka joonistel esitame eelistatult .
Näide N 2.2
Lahendus
Kontrollimaks lähenduse u/c≈0 õigustatust, hindame Bohri aatomi mudeli järgi ümber tuuma tiirleva elektroni kiirust . Kui on tegemist vesiniku aatomiga, siis elektroni kaugus tuumast on rH≈5×10−11m ja elektronile mõjub tuuma poolt jõud
mis põhjustab kesktõmbekiirenduse a=F/me. Kuna kiirendus avaldub elektroni joonkiiruse kaudu
siis
ehk elektroni kiirus orbiidil on rohkem kui kolm suurusjärku väiksem valguse kiirusest vaakumis.
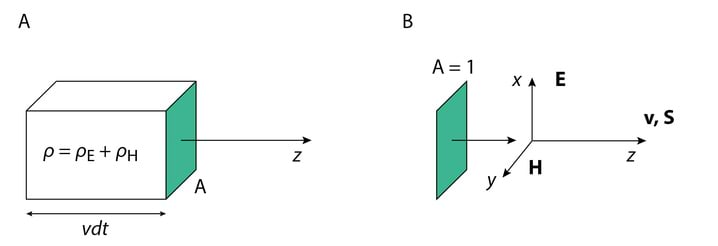
Olgu pinnatükk pindalaga risti z-teljega, mille suunas leviva tasalaine kiirus on . Leidmaks energiat, mis läbib aja jooksul pinnatükki, ehitame pinnatükile ristküliku, mille z-telje sihiliste külgede pikkused on . Ruumalas salvestunud energia on summa elektri- ja magnetvälja energiast.
Elektromagnetismi kursusest on teada, et elektrivälja ja magnetvälja energiatihedused on
ja
Kuna
siis elektromagnetlaine energiatihedus on
Ruumalas salvestatud energia on W=ρV=ρAvdt, Jn 2.7A.
Kiirgusvoo tihedus ( Poyntingi vektor) on ajaühikus laine levikusuunaga ristiolevat ühikulist pinda läbiv energia, tema moodul avaldub
ning
(K 2.11). Kuna elektrivälja tugevuse dimensioon on ja magnetvälja tugevuse dimensioon , saame kiirgusvoo tiheduse dimensiooniks definitsioonile vastava tulemuse
Voog omab suunda ja kuna meil on HILS keskkond, siis S ning v on samasuunalised ning risti nii elektri- kui ka magnetvälja tugevuse vektoritega (Jn 2.7B)
Kui meil on tegemist monokromaatilise tasalainega, siis
Optikas on tegemist kõrgete sagedustega ja Poyntingi vektori hetkväärtusi mõõta ei ole võimalik. Selle asemel iseloomustatakse elektromagnetlaine energeetilisi omadusi kiiritustihedusega , mis võrdub üle perioodi keskmistatud Poyntingi vektori väärtusega.
Kombineerides jällegi energiatiheduste ja faasikiiruse avaldisi, saame
Paljudel juhtumitel on meil vaja vaid võrrelda erinevaid kiirgusvoogusid, mitte aga leida kiiritustiheduse arvulisi väärtusi.Siis piisab teadmisest, et kiiritustihedus on võrdeline amplituudi ruuduga,
(K 2.13)
Näide N 2.3
Lahendus
Päikesevalguse kiiritustihedus atmosfääri ülapiiril ( solaarkonstant) integreerituna üle kõigi lainepikkuste on 1,36kWm−2. Kasutades valemit v 2.24, leiame sellele kiiritustihedusele vastava laine elektrivälja tugevuse amplituudväärtuse vaakumis
Võrdleme saadud väljatugevust väljatugevusega, mida tekitab vesiniku aatomi tuum Bohri raadiuse kaugusel
Näeme, et Päikese ELMi väli on väga nõrk võrreldes tuuma väljaga elektroni asukohas. Seega võib laine mõju vaadelda kui aatomi oleku väikest häiritust ning võib lugeda, et kiiritustiheduse poolt esilekutsutud muutused on võrdelised kiiritustiheduse endaga st meil on tegemist lineaarsete protsessidega. Laine-aine vastasmõju mittelineaarsed efektid on esitatud peatükis 10.
Magnetvälja amplituudväärtuse leiame v 2.21 abil
Õhus atmosfäärirõhul algavad ionisatsiooninähtused ( läbilöök) väljatugevusel 3×106Vm−1, seega päikesevalguse toimel õhu elektrijuhtivus ei muutu. Valgusele vastavatel sagedustel, vt pt. 3, on läbilöögiks vajalikke väljatugevusi võimalik saavutada laserkiirguse abil.
Genereerigu impulss-režiimis töötav laser nelinurkse kujuga impulsi, mille kestus on t=10ns ja energia W=1J. Kui laserkiirguse ristlõige on A=1cm−2, siis saame kiiritustiheduse väärtuseks
Rakendades nüüd valemit (*), saame väljatugevuseks
mis on piisav õhu ioniseerimiseks.
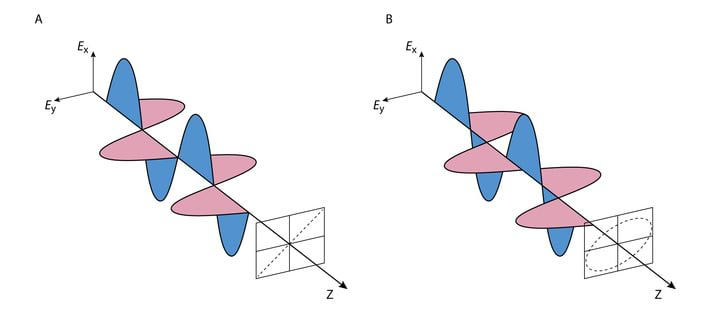
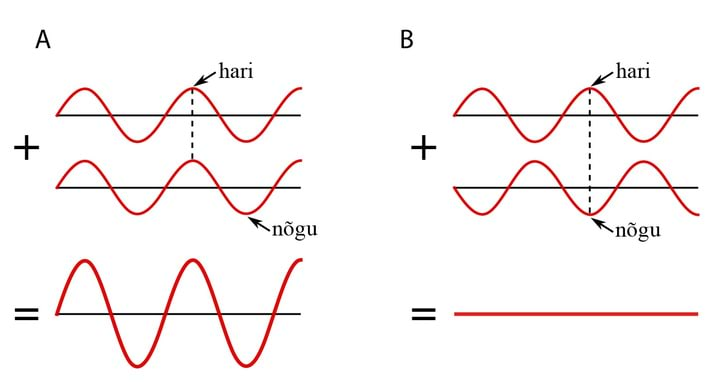
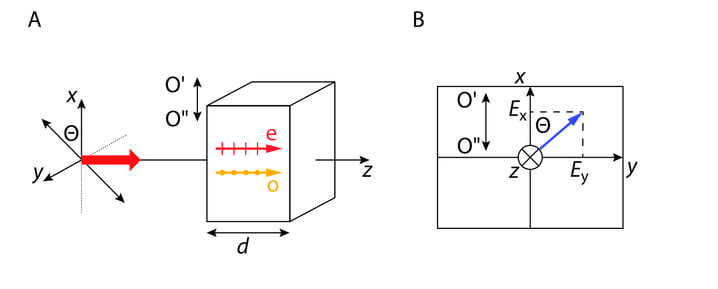
(K 2.14) Seni oli meil tegemist lihtsaima z-telje suunas leviva monokromaatilise lainega, kus . Selline vektor „joonistab“ tasandis perioodi jooksul sirglõigu pikkusega , siit ka nimetus „lineaarselt polariseeritud“. Laine jääb lineaarselt polariseerituks ka siis, kui , kuid faasivahe ja vahel on null, Jn 2.8A.
Kui ja vahel on konstantne (ajas muutumatu ) faasinihe , siis tasandis on elektrivälja x- ja y komponendid kujul:
st x-komponent on y-komponendist võrra faasis ees, Jn 2.8B. Nüüd muutub perioodi jooksul peale pikkuse ka tema siht. trajektoori leidmiseks tasandis z=const tuleb komponentide avaldistest elimineerida aeg, teisendame
Asendades avaldises (**) aega sisaldavad liikmed seostega (*), saame
Pärast vasaku ja parema poole ruutu võtmist ja liikmete ümbergrupeerimist saame teist järku kõvera võrrandi
Kuna ja muutumispiirkond on piiratud, on tasandis tegemist suletud kõveraga – ellipsiga, Jn 2.8B.
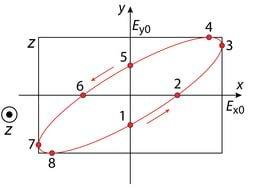
Elliptiliselt polariseeritud valguse detailsemaks uurimiseks koostame tabeli, lähtudes valemitest v 2.25.
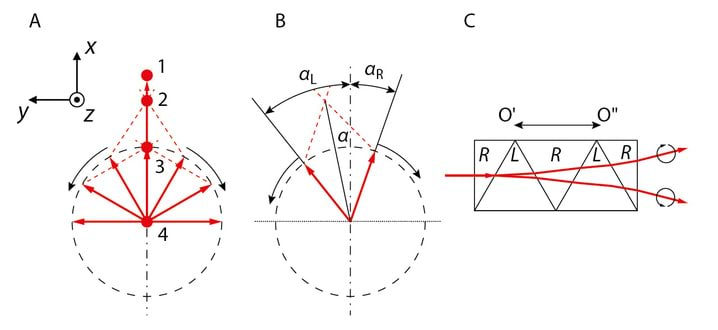
Olgu näitena ja seega ning . Vektori otspunkti trajektoori graafiliseks esitamiseks z-teljega ristiolevas tasandis joonistame ristküliku, mille külgede pikkused on võrdelised amplituudidega ja ning kanname joonisele tabeli alusel erinevatele ajahetkedele vastavad punktid, Jn 2.9. Kui vaatlejasuunas leviva laine E-vektor liigub vastupäeva nagu praegusel juhul, on tegemist vasakpoolselt elliptiliselt polariseeritud lainega. Kui on vastasmärgiline, siis muutub ka liikumissuund ja valgus on parempoolselt elliptiliselt polariseeritud.
Muutes faasivahet , muutub ellipsi pooltelgede orientatsioon ja nende suhe. Kui , siis v 2.26 omandab kuju
ehk
saame sirge võrrandi
st valgus on lineaarselt polariseeritud. Seega on lineaarne polarisatsioon elliptilise polarisatsiooni erijuht. Üldjuhul, kui () on valgus lineaarselt polariseeritud. Kui on null või paarisarv, muutub veerandites I ja III; kui on paaritu, toimub võnkumine II ja IV veerandis.
Kui faasivahe , saab v.2.26 kuju
st tegemist on ellipsiga, mille teljed ühtivad koordinaattelgedega. Kui lisaks sellele on võrdsed ka x- ja y-komponendi amplituudid, , siis vektor E liigub tasandis mööda ringjoont. Üldjuhtumil, kui faasivahe δ=(m+1/2)π () ja ristkomponentide amplituudid on võrdsed, , on valgus ringpolariseeritud. Nii nagu elliptiliselt polariseeritud valgus, on ka ringpolariseeritud valgus kas parem- või vasakpoolselt polariseeritud.
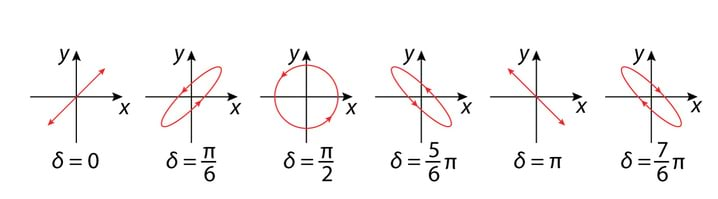
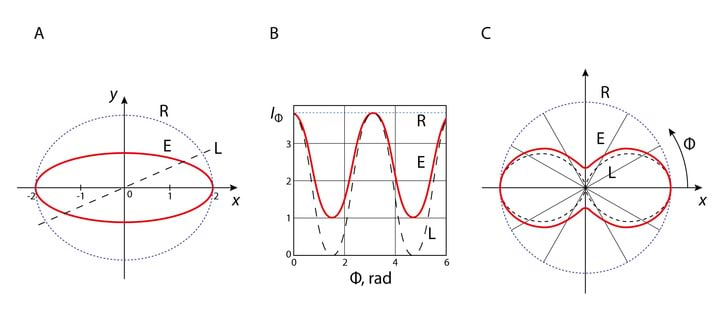
Joonisel 2.10 on kokkuvõte erinevatest polarisatsiooniliikidest.
Näide N 2.4
Lahendus
Kuna cosωt=sin(ωt+π/2), siis praegusel juhul on laine y-komponent x-komponendist faasis ees st üldjuhtumil kirjeldavad need komponendid parempoolselt elliptiliselt polariseeritud valgust, kusjuures ellipsi teljed on koordinaattelgede sihis. Kui , on tegemist parempoolse ringpolarisatsiooniga.
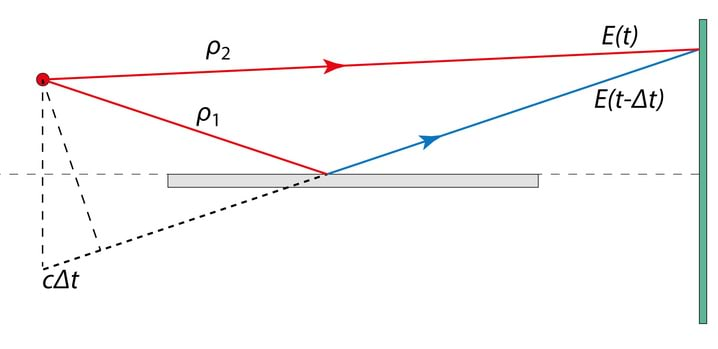
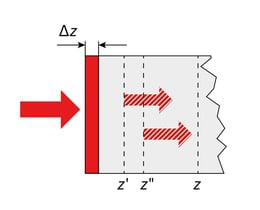
Vastavalt Maxwelli võrranditele on ajas muutuv juhtivusvool elektromagnetlaine allikaks, Jn 2.2. Kuna aga voolutiheduse definitsiooni järgi , siis elektromagnetlaine tekkeks peab laeng liikuma kiirendusega. Leiame nüüd seose vaakumis kiirendusega liikuva laengu ja tema poolt kaugusel tekitatud elektromagnetlaine vahel. Seose tuletamisel eeldame, et vaatluspunkt on liikuvast laengust väga kaugel. Lisaks olgu nii laengukandja kiirendus kui ka kiirus väikesed st relativistlikke efekte pole vaja arvestada. Kuna laine levikukiirus on lõplik, siis ja väärtused hetkel on määratud laengu kiirendusega varasemal ajahetkel, (t−r/c). Teiste sõnadega: laengu kiirendusega liikumise mõju kaugusel oleva väljale „hilineb“.
Kui laeng on paigal, siis tema välja iseloomustab radiaalsete jõujoonte parv mille tihedus kahaneb pöördvõrdeliselt kauguse ruuduga st eksisteerib vaid elektriväli
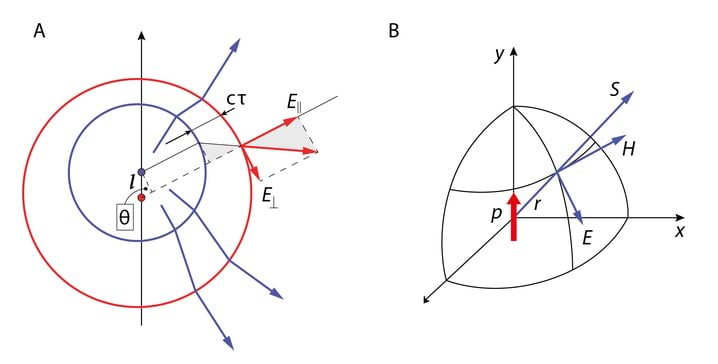
Liikugu nüüd algselt paigal olnud laeng aja jooksul kiirendusega ja seejärel olgu liikumine ühtlane kiirusega . Kui alghetkest on möödunud aeg , siis selle aja jooksul toimus laengukandja nihe võrra. Joonisel Jn 2.9A on laengu liikumisele vastav jõujoonte pilt. Kaugusele (K 2.16) vastav jõujoonte pilt on selline nagu oleks laeng algasendis ja kuna v≪c, siis kaugusele vastav jõujoonte pilt on selline nagu oleks laeng kaugusel .
Näeme, et suvalisele vaatesihile vastav jõujoonte paar on nihkes. Kuna kahe sfäärilise samafaasipinna vahel laenguid ei ole, siis vastavalt Gaussi teoreemile jõujooned ei katke ja seega laengu kiireneva liikumise tulemusena tekkis lisaks elektrivälja radiaalkomponendile ka ristkomponent .
Viirutatud kolmnurgad joonisel on sarnased , seega
kus on nurk laengu liikumissuuna ja vaatesuuna vahel. Ristkomponendi avaldises
teeme asendused ja ning esitades elektrivälja tugevuse ja kiirenduse koos nende argumentidega, saame
(K 2.18)
Näeme, et
- Elektrivälja ristkomponendi väärtus kaugusel ja hetkel on määratud laengu kiirendusega varasemal hetkel .
- Välja ristkomponent on pöördvõrdeline kaugusega, võrreldes paralleelkomponendiga kahaneb ta kauguse kasvades hulga aeglasemalt.
- Välja ristkomponent on mittehomogeenne, ta on maksimaalne sihis, mis on risti laengukandja liikumisega ja null laengukandja liikumissihis.
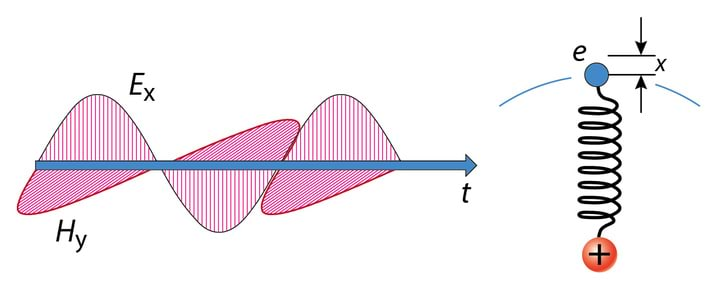
Üheks olulisemaks, kui mitte kõige tähtsamaks, elektromagnetlaine allikaks on võnkuv dipool, Jn 2.11B. Dipooli kiirgus kirjeldab nii raadiosaatjate kui ka aatomite kiirgust. Dipooli, mis koosneb kahest vastasmärgilisest laengust , iseloomustatakse dipoolmomendiga , kus on laengutevaheline kaugus. Dipooli staatiline väli kahaneb kaugusega kiiresti, .
Kui dipoolmoment muutub harmooniliselt, , siis tema teine tuletis on . Valemis v 2.27 võib korrutist tõlgendada kui dipoolmomendi teist tuletist aja järgi, ning tehes asenduse ¨p=qa, saame
Lähtudes valemist v 2.24, saame dipooli kiiritustiheduse jaotuse
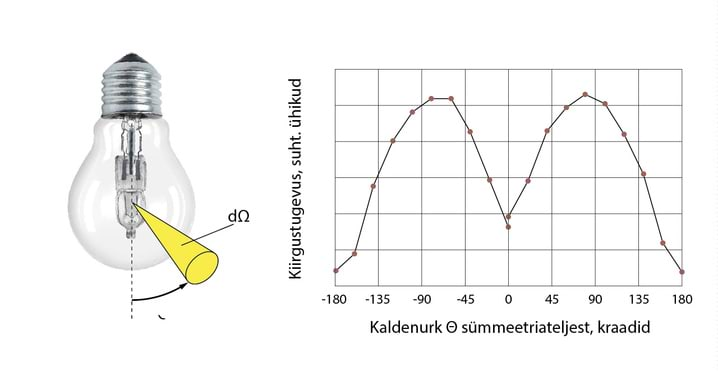
Kiiritustihedus sõltub väga tugevasti sagedusest, . Dipooli kiirgus lainefrondil, , sõltub nurgast : kiiritustihedus on maksimaalne sihis, mis on risti dipooli teljega ja oma telje sihis dipool ei kiirga, Jn 2.12.
(K 2.20)
Eelnevalt nägime, et monokromaatiline laine on Maxwelli võrrandi lahendiks ja teda on mugav kasutada matemaatilistes teisendustes. Nüüd vaatame, kuidas kasutada saadud tulemusi teiste lainete puhul, mille matemaatiline kirjeldamine on komplitseeritum.
Vastavalt Fourier’le võib mistahes perioodilise funktsiooni esitada summana konstandist ning erinevate kordajatega siinus- ja koosinusliikmetest
Kordaja leidmiseks korrutame avaldise mõlemat poolt teguriga ja seejärel integreerime nullist -ni, vasakul pool saame
Kuna
ja alati
siis saame paremal pool
Kordaja leidmiseks tuleb vasakut ja paremat poolt korrutada teguriga ning seejärel jälle integreerida. Nüüd saab välja kirjutada kordajate leidmise retsepti
Kui on tegemist paarisfunktsiooniga, siis on summas vaid koosinusliikmed, paaritu funktsiooni summas on vaid siinusliikmed. Kordajale vastab ja ei ole midagi muud kui keskväärtus lõigul
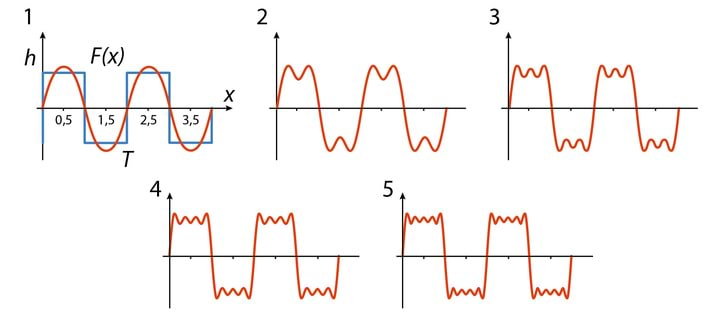
Hindamaks mitut liiget tuleks praktiliste ülesannete lahendamisel reas v.2.29 arvestada, leiame kordajad , täisnurksetest impulssidest koosnevale jadale , Jn 2.11.
Selle funktsiooni keskväärtus üle perioodi on null ja kuna on tegemist paaritu funktsiooniga, on summas vaid siinusliikmed. Lisaks sellele on nullist erinevad vaid paaritule -le vastavad liikmed ja me saame
Jn 2.13 esitatud graafikud demonstreerivad, kuidas liikmete lisamisel summa lähendab üha paremini funktsiooni .
Kasutades Euleri valemit,
saab Fourier' arenduse v 2.29 esitada eksponentfunktsioonide summana
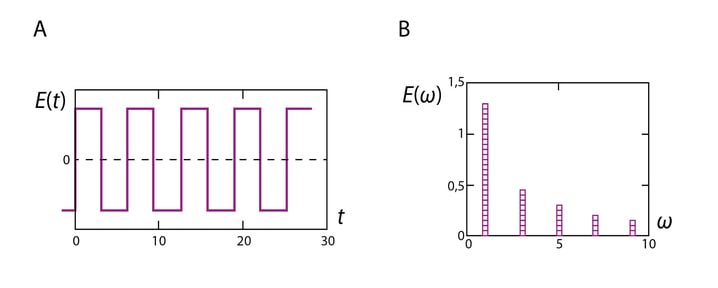
(K 2.21) Olgu nüüd tegemist ajalise sõltuvusega , Jn 2.14A, mida võib samuti esitada summana
Summa iga liige kujutab endast harmoonilist võnkumist, mille amplituud on
Joonisel 2.14B on funktsioonile vastavate monokromaatiliste komponentide amplituudide jaotus sageduse järgi – spekter.
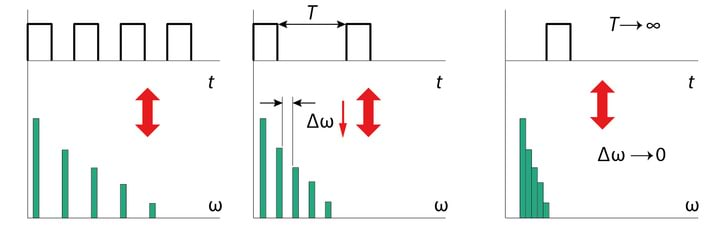
Näeme, et perioodilise funktsiooni spekter on diskreetne. Saab näidata, et mida suurem on korduva protsessi (nt impulsside jada) periood , seda väiksem on intervall monokromaatiliste komponentide vahel, Jn 2.13.
Piirjuhul, kui meil on tegemist üksikimpulsiga, on spekter pidev ning monokromaatiliste komponentide summeerimine asendub integreerimisega
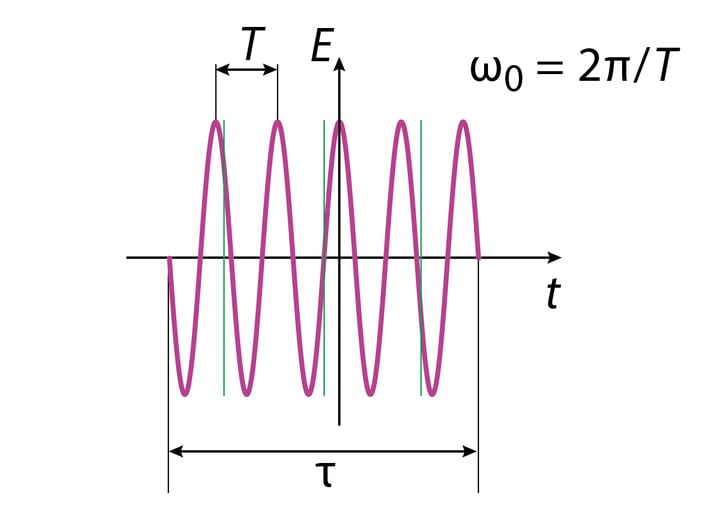
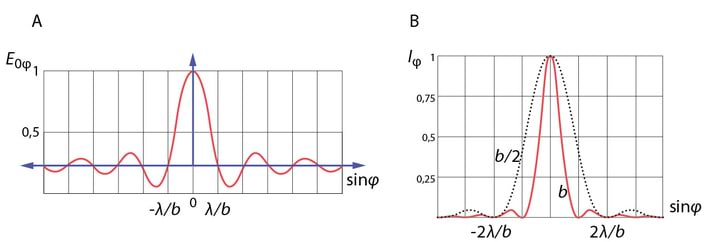
Kasutame nüüd saadud seoseid joonisel Jn 2.16 kujutatud siinuspaketi spektri leidmiseks.
Valides koordinaatide alguspunktiks siinuspaketi keskkoha, kirjeldab teda funktsioon
ja tema spektri leidmisel võib piirduda integreerimisega vahemikus
Kui tähistada , siis pärast integreerimist saame
Võrreldes saadud tulemust valemitega v2.18, näeme, et nurksulgudes on siinusfunktsiooni avaldis, seega spektrit iseloomustab sinc-funktsioon
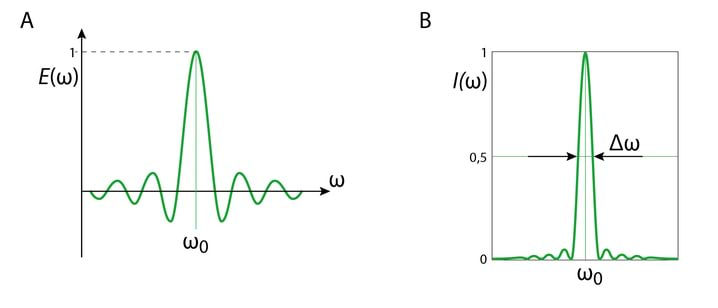
Kuna sinc-funktsioon mängib olulist rolli ka edaspidi, vaatame tema omadusi detailsemalt. Kohal on meil tegemist määramatusega ja funktsiooni väärtuse leidmiseks tuleb rakendada L’Hopitali reeglit
st kohal omab amplituud maksimaalset väärtust. Kuna null-kohtades peab , kuid , siis , kui Amplituud omab nii positiivseid kui ka negatiivseid väärtusi, Jn 2.15A, füüsikaliselt tähendab see, et kahes vastasmärgilises piirkonnas on monokromaatilised lained vastasfaasis.
Joonisel Jn 2.15B on kiiritustiheduse, , sõltuvus sagedusest – valdav osa siinuspaketi energiast on kontsentreeritud vahemikku . Spektri laiuseks loetakse riba , mis vastab kiiritustiheduse väärtustele , seega ja
(K 2.23) Näeme, et monokromaatilisele lainele, vastavas spektris on vaid üks sageduskomponent , sel ajal kui ühe nanosekundilisele siinuspaketile vastava spektri laius on .
Näide N 2.5
Lahendus
Kui lainepikkusel 800nm genereeriva femtosekund-laseri impulsi kestus on 10fs=10−14s, siis talle vastavad monokromaatilised komponendid on sagedusintervallis 1014Hz, mis katab ka suure osa nähtava valguse punasest piirkonnast, vt pt. 3. Laia spektraalriba tõttu tuleb selliste lühikeste impulsside levikul optilistes süsteemides arvestada dispersiooniga, vt pt 7.
Selle peatüki eesmärgiks on
- piiritleda uurimispiirkond
- leida vastavus Maxwelli võrranditest tuleneva ja reaalsuse vahel
- määratleda valguse lainemudeli kehtivuspiirid
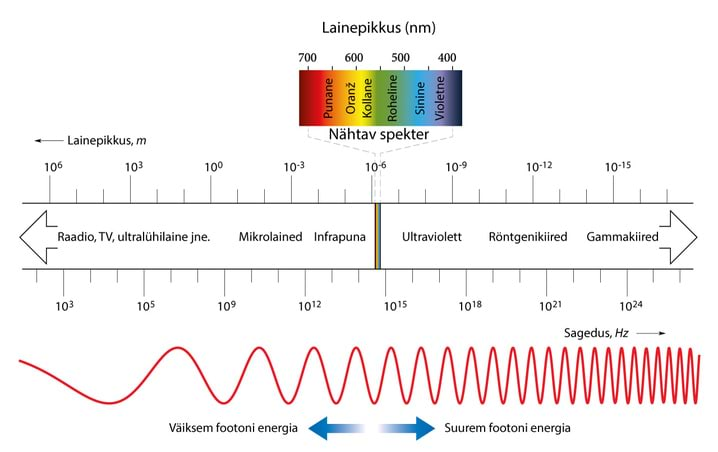
Elektromagnetlaineid on detekteeritud ja/või genereeritud sageduste (lainepikkuste) rohkem kui 20 suurusjärgu diapasoonis, Jn 3.1. Eelmises peatükis kirjeldatud elektromagnetlainete üldised omadused on sagedusest sõltumatud. Teisalt on aga lainete genereerimisviisid eri sagedustel väga erinevad ja ka lainete kasutusala on sagedusest sõltuv. Madalatel sagedustel, mille hulka kuulub ka võrgusagedus (lainepikkus ) tekitatakse laine vahelduvvoolu generaatoriga, sagedustel leiavad elektromagnetvälja lainelised omadused kasutamist sidepidamisel allveelaevadega. Raadiodiapasoonis, , genereeritakse elektromagnetlaineid elektroonikaseadmete vahendusel, kusjuures töösagedus on määratud L-C kontuuriga või tema modifikatsioonidega (resonaatorid). Raadiodiapasoon on omakorda jagatud kümnekonnaks alampiirkonnaks, sidepidamine on nihkunud järjest kõrgemate sageduste poole. Sagedusmodulatsiooniga (FM) raadiosaatjate kandevsagedus on , televisioonisaatjad töötavad vahemikus , positsioneerimissüsteem GPS - , Eesti mobiilifirmade sagedused on vahemikus 0,8−3GHz.
Sagedusvahemik - kannab infrapuna ( infravalgus) piirkonna nime, sellest piirkonnast lähtuvaid laineid tajume soojusena ja see kiirgus tekib peamiselt molekulisiseste pöörlemis- ja võnkeseisundite vahelistel üleminekutel. Sagedustel (lainepikkused ) põhjustab elektromagnetlaine inimese valgusaistingu, kusjuures erinevaid sagedusi tajub inimene eri värvustena. Summaarset sellest piirkonnast lähtuvat valgust nimetatakse valgeks valguseks. Piirkond on ultraviolettpiirkond (ultravalgus). Nii nähtavas kui ka ultravalguse piirkonnas tekib kiirgus aatomi väliskattes toimuvate elektron-üleminekute tulemusena. Röntgendiapasooni () kiirgus on fotoioniseeriv, ta tekib kas aatomi elektronkatete vaheliste üleminekute tulemusena (karakteristlik kiirgus) või kiirete elektronide pidurdumisel märklaual (pärsskiirgus). Kõrgeimat sagedust omab gammakiirgus, mis tekib tuumasiseste energeetiliste üleminekute tulemusena.
Optika vaatleb ühtsena elektromagnetlaineid sagedusvahemikus (lainepikkused ) ja seda järgmistel peamistel põhjustel
- Selles sagedusvahemikus tekib kiirgus aatomite/molekulide väliskattes toimuvate energeetiliste üleminekute tulemusena.
- Elektromagnetlaine lainepikkus on oluliselt suurem kui aatomi/molekuli mõõtmed ja võib eeldada, et antud ajahetkel on elektromagnetlaine elektrivälja tugevus aatomi/molekuli piires ühesugune. See tingimus lihtsustab laine-aine vastasmõju kirjeldamist.
- Elektromagnetlainete detekteerimismeetodid on samad, selles piirkonnas on kõige täpsemini mõõdetav suurus lainepikkus
Edaspidi tarvitame piirkonnas eksisteeriva elektromagnetlaine sünonüümina terminit valgus ning intervallis (lainepikkused ) on tegemist nähtava valgusega.
Maxwelli teooria annab valguse kiiruseks vaakumis
Valguse kiirust vaakumilähedastes tingimustes on mõõdetud korduvalt ja tänaseks on saavutatud fantastiline täpsus – mõõtemääramatus on m/s. Metroloogia loeb väärtust
täpseks ja nt pikkusühik on defineeritud valguse kiiruse järgi: üks meeter on vahemaa, mille valgus läbib sekundi jooksul.
Vastavalt Maxwellile on aines murdumisnäitajaga valguse faasikiirus , murdumisnäitaja aga on seotud dielektrilise ja magnetilise läbitavusega . Murdumisnäitaja on leitav murdumisseadusest mõõdetuna optilise diapasooni sagedustel, – kondensaatori mahtuvuse mõõtmisest ja – solenoidi induktiivsuse mõõtmisest suhteliselt madalatel sagedustel. Kui ei ole tegemist ferromagneetikutega, siis ja . Tabelis 3.1 on mõningate ainete dielektrilise läbitavuse ja murdumisnäitaja võrdlus. ja õhu puhul on vahekord ja vahel väga hea, ka puhul võib vastavust lugeda igati rahuldavaks, kuid vee puhul erinevad ja tohutult. Lainepikkusel on looduslike tahkismaterjalide murdumisnäitajad vahemikus 1,31 (jää) kuni 2,42 (teemant).
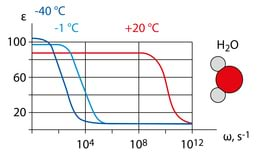
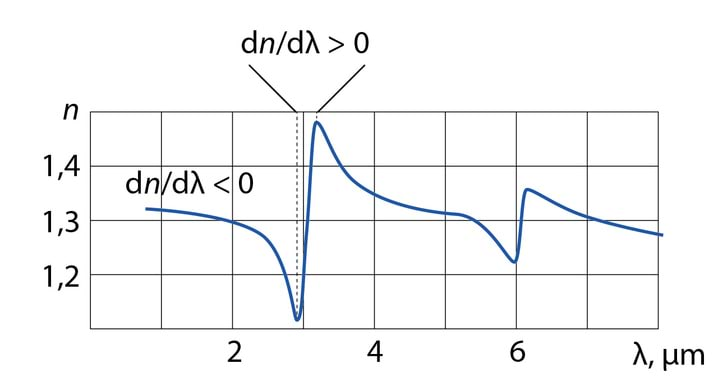
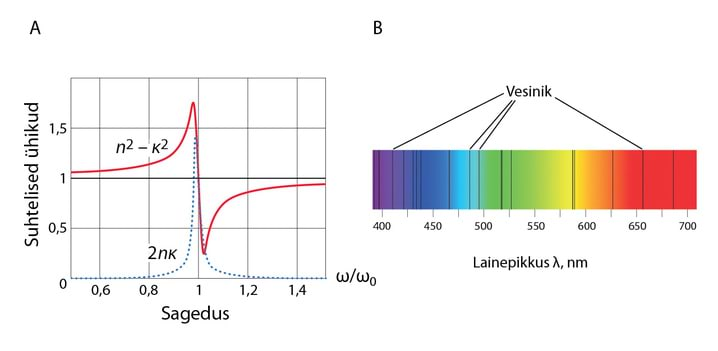
Lahknevus ja väärtuste vahel on paraku näiv, sest ja on mõõdetud väga erinevatel tingimustel. Mõõtes dielektrilise läbitavuse sõltuvust sagedusest, näeme kiiret kahanemist kõrgematel sagedustel, Jn 3.2.
Sõltuvus sagedusest on tingitud sellest, et on polaarne molekul ja kõrgematel sagedustel ei suuda ta pöörduda välise välja taktis. Arvestades väärtust optilises diapasoonis, saame, et seos kehtib. Teisalt annavad mõõtmised raadiosagedustel murdumisnäitaja väärtuseks .
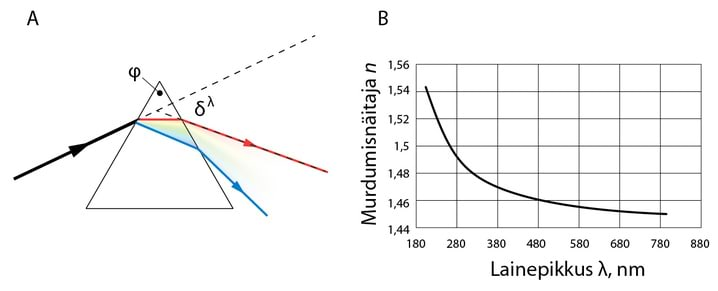
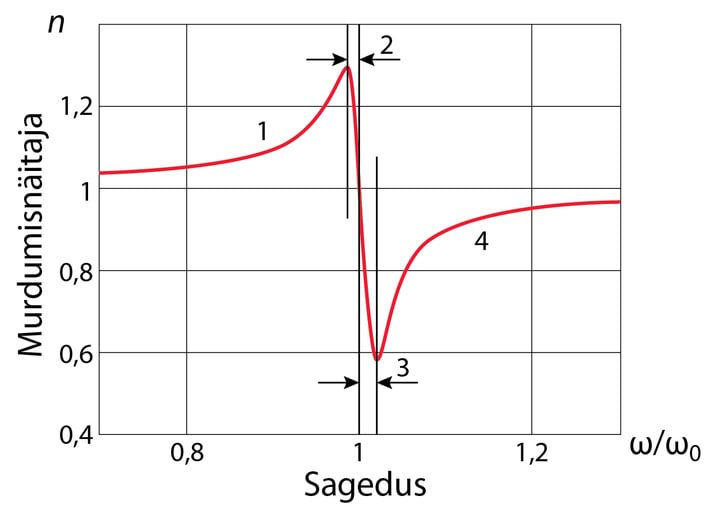
Murdumisnäitaja sõltuvus sagedusest (lainepikkusest), , on kergesti registreeritav ka suhteliselt kitsas nähtava valguse sagedusvahemikus. Näiteks flintklaasi murdumisnäitaja kollasele valgusele vastaval lainepikkusel on , kuid sinise valguse murdumisnäitaja on . Kuna faasikiirus , siis on ka faasikiirus funktsioon sagedusest (lainepikkusest).
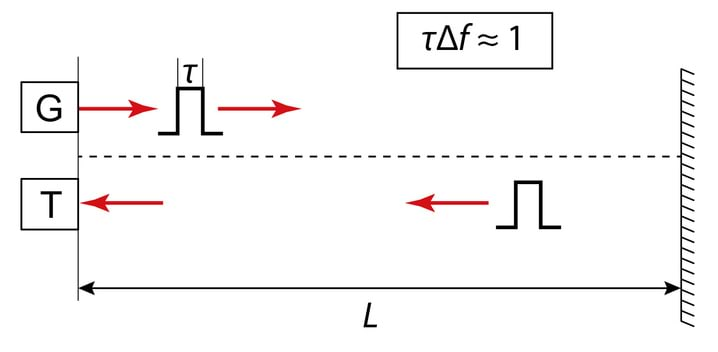
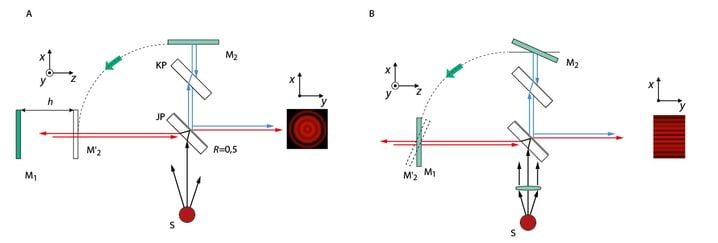
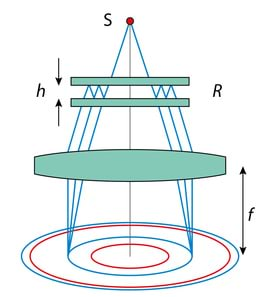
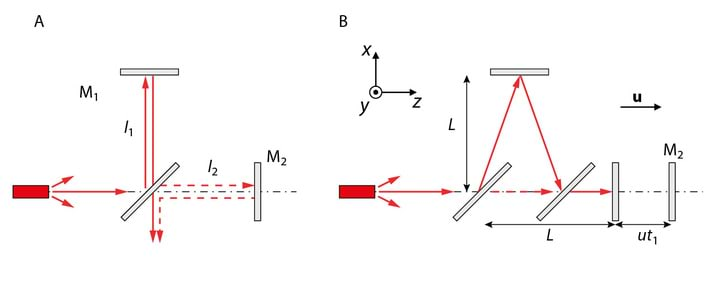
Joonisel Jn 3.3 on skeem valgusimpulsi kiiruse otseseks eksperimentaalseks mõõtmiseks. Generaator genereerib lühikese valgusimpulsi kestusega , mis levib kaugusel oleva peeglini. Mõõtes tajuriga levikuaja , saame valguse kiiruse , mis iseloomustab valgusenergia ülekannet.
Tihtipeale erineb väärtus märgatavalt faasikiirusest . Näiteks on väävelsüsinik , mille murdumisnäitaja on , kuid kiiruse otsesest mõõtmisest saame . Siit järeldub, et faasikiirus ei iseloomusta energia levikukiirust.
Tõepoolest, faasikiirus iseloomustab monokromaatilist lainet, kuid valgusimpulsile vastab spekter laiusega Δf=1/τ ehk . Iga komponent selles spektris omab erinevat sagedust , erinevat amplituudi ja erinevat lainearvu .
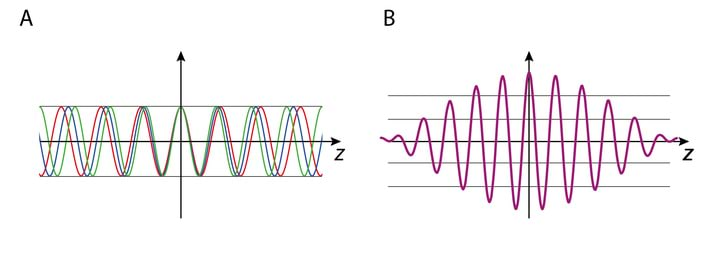
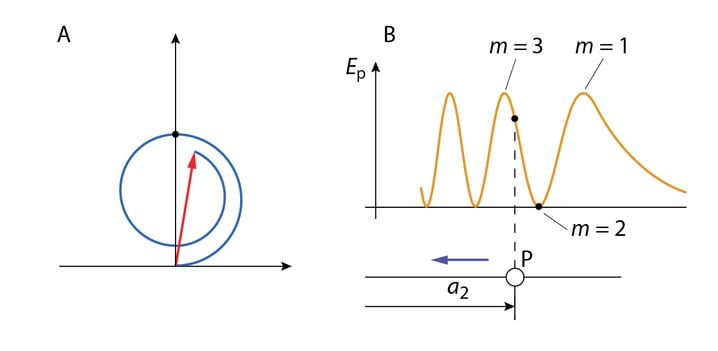
Valime valgusimpulsile vastavast spektrist välja kolm komponenti, joonisel Jn 3.4A langevad hetkel koordinaatide alguses nende kolme komponendi laineharjad kokku (st on faasis), mille tulemusena saame Joonisel Jn 3.4B kujutatud lainepaketi. Kuna komponentide kiirused on erinevad, siis hetkel ei ole punktis lained enam faasis. Kui nt pikemalainelised komponendid levivad lühemalainelistest komponentidest kiiremini, siis laineharjad kohtuvad uuesti mingis ruumipunktis , st toimub lainepaketi levik. Energia edasikandumise kiirust iseloomustab lainepaketi mähisjoone maksimumi levikukiirus, mis vastab olukorrale, kui kõik komponendid on faasis. Seega iseloomustab lainepaketi edasikandumist lainearvu ekstreemum.
Saame rühmakiiruse
Kuna ja , siis jõuame seoseni rühma- ja faasikiiruse vahel (Rayleigh valem)
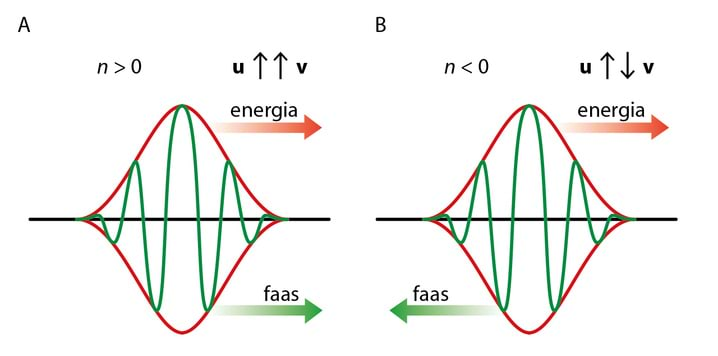
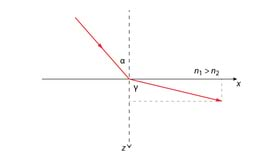
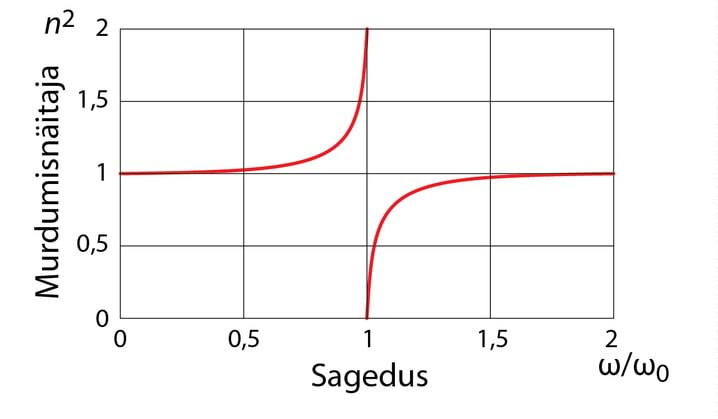
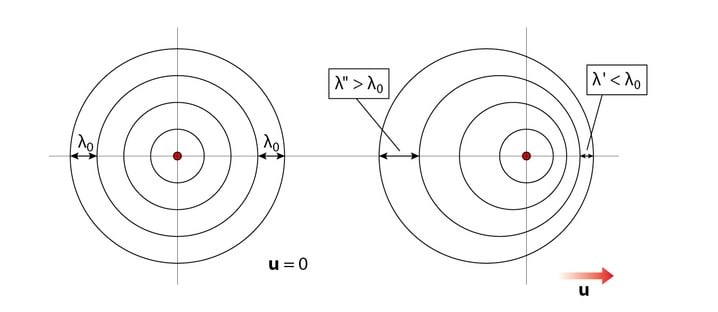
Rühma- ja faasikiiruse vahekord võib olla väga erinev. Isotroopses keskkonnas on u ja v samasihilised, kuid nende suund oleneb sellest, kas murdumisnäitaja on positiivne või negatiivne. Tavamaterjalide puhul ja , kuid Maxwelli võrrandid lubavad lahendit, mille puhul ja . Tänaseks on loodud nn metamaterjalid, mille murdumisnäitaja on negatiivne.. Sel juhul on rühma- ja faasikiirus vastassuunalised, Jn 3.5. Negatiivse murdumisnäitajaga aines on murduv ja langev kiir samal pool pinnanormaali.
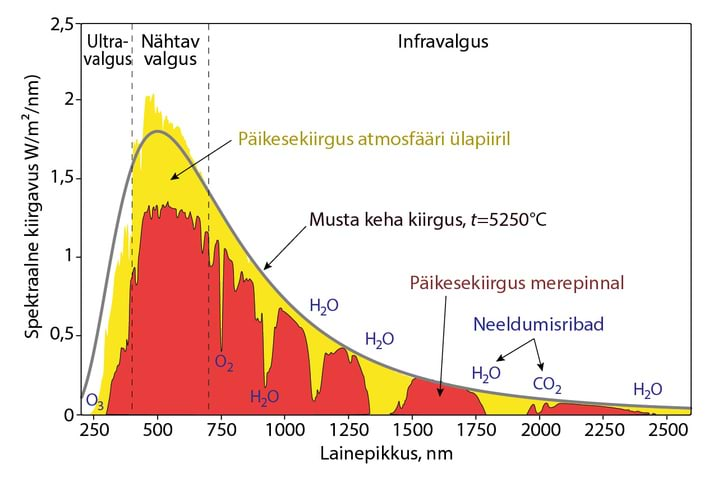
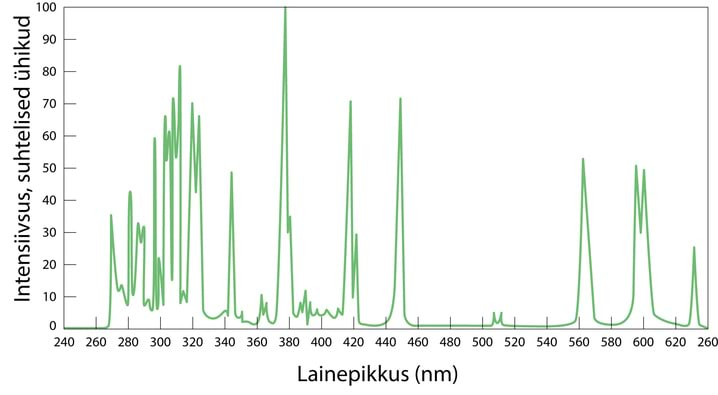
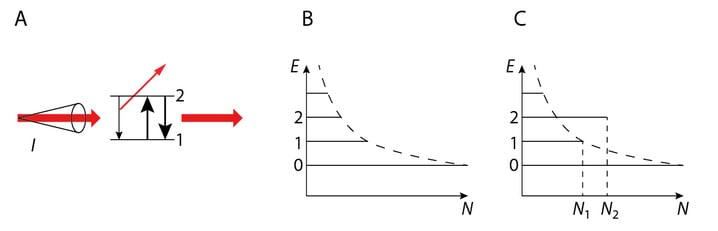
Selleks, et kehad kiirgaksid elektromagnetlaineid, on vaja energiat, mis kulub dipoolide võnkuma panemiseks (ergastamiseks). Lihtsaim viis ergastamiseks on soojusliikumise energia kasutamine. Alates temperatuurist >800K on soojusliikumise poolt tekitatud valgus registreeritav ka nähtavas piirkonnas. Sellise soojuskiirguri spektri näiteks on Päikese spekter, Jn 3.6A. Põhimõtteliselt on sellest spektrist võimalik välja filtreerida kitsad lainepikkuste intervallid , mida väiksem see intervall on, seda monokromaatilisem on sealt lähtuv valgus. Paraku pole see variant otstarbekas, sest kui , siis teeb seda ka selles intervallis kiiratav energia.
Oluliselt monokromaatilisemat valgust kiirgavad gaaslahendusplasmas ergastatud gaasi ja/või metalliauru aatomid, neil juhtudel on tegemist joonspektriga, Jn 3.6B. Kõige väiksem on kiiratavate lainepikkuste intervall laserite puhul.
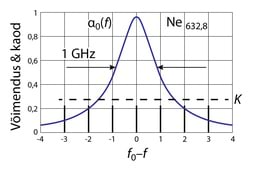
Tabelis 3.2 on joonspektrit omavate valgusallikate karakteersed spektrijooned, nende kiirgust võib teatud lähenduses vaadelda kui monokromaatilist lainet. Kui laine amplituud ajavahemiku ( – võnkeperiood) jooksul ei muutu ja Δf≪f, siis on meil tegemist kvaasimonokromaatilise lainega.
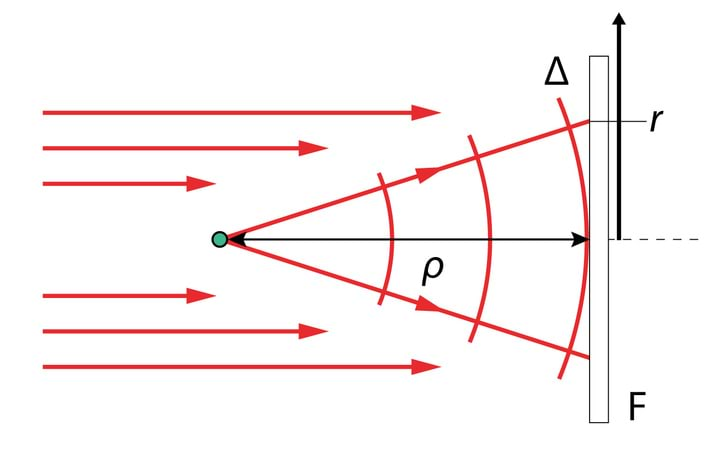
Tasalaine lähenduseks on osa punktallika lainefrondist juhul, kui me oleme allikast piisavalt kaugel.
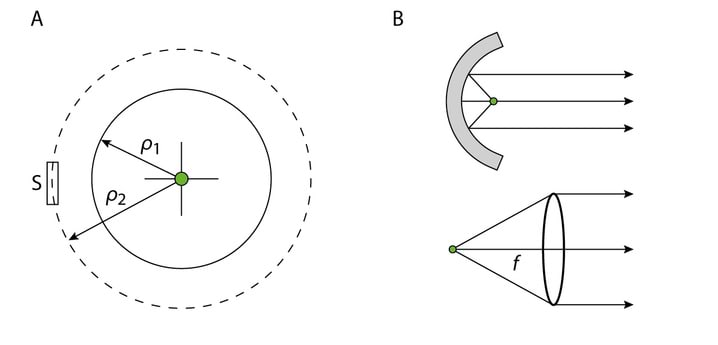
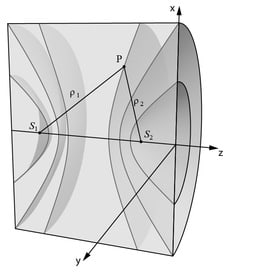
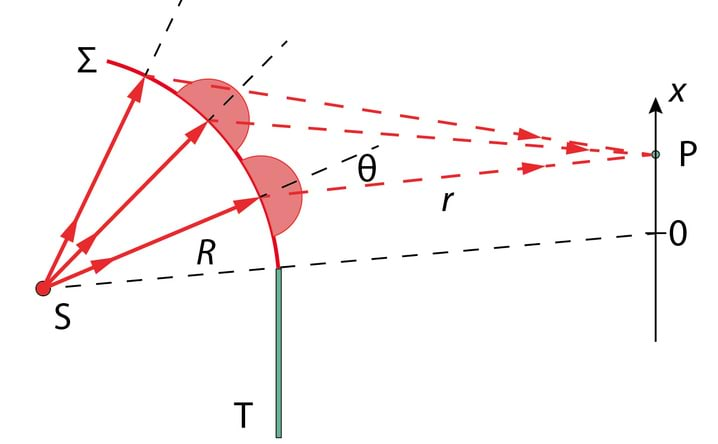
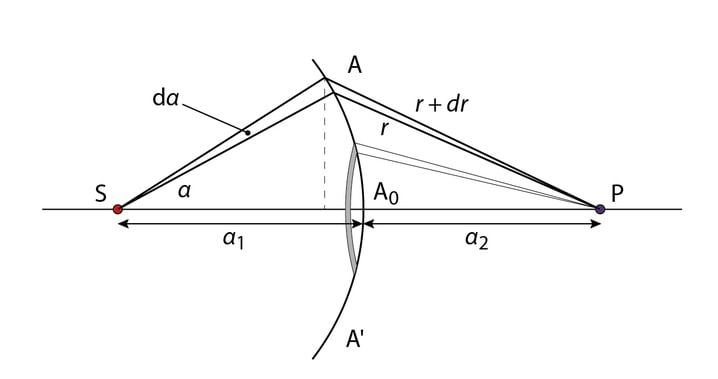
Leiame punktallikale vastava lainefunktsiooni. Ümbritseme punktallika kontsentriliste sfääridega, mille raadiused on ja , Joonis 3.7, ning vastavad kiiritustihedused on ja . Kui HILS keskkond on mitteneelav, siis ajaühikus mõlema sfääri pinda läbivad energiavood on võrdsed, see kehtib ka suvalise kauguse puhul
Kuna , siis ja sfäärilise laine lainefunktsioon on
(K 3.8)Heas lähenduses saadakse tasalaine kollimaatoritega, kus valgusallikas on läätse või nõguspeegli fokaaltasandis, Jn 3.7B. Väga heaks tasalaine lähenduseks on laserist lähtuv valgus, kuid ka tema puhul ei ole kiiritustiheduse jaotus levikusuunaga ristiolevas tasandis konstantne.
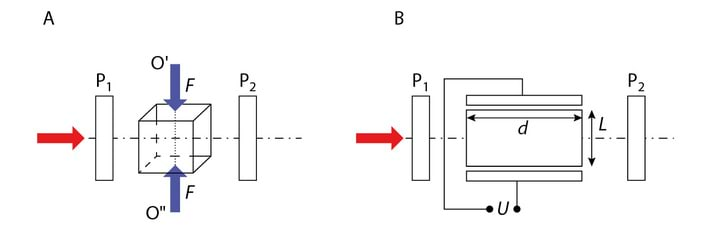
Üheks vahendiks, mille abil on võimalik saada lineaarselt polariseeritud valgust ja ka otsustada elektrimagnetlaine polarisatsiooni üle, on polaroid. Tema lihtsaimaks variandiks on paralleelsetest juhtivatest varrastest süsteem.
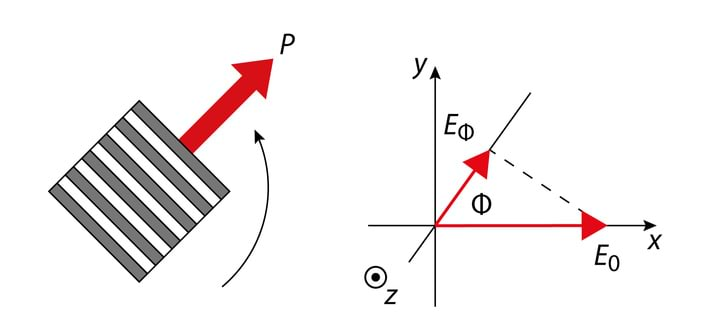
Joonisel Jn 3.8 langeb polaroidile z-telje suunas leviv ja horisontaaltasandis lineaarselt polariseeritud laine. Laine see komponent, mis on paralleelne varrastega, paneb sealolevad vabad elektronid võnkuma, elektronide energia aga transformeerub põrgetel kristallvõre sõlmedega soojuseks. Seega see lainekomponent neeldub. Varrastega ristiolevas sihis on elektronide võnkeamplituud väike ja neeldumine on tühine. Seda sihti nimetatakse polaroidi läbilaskesihiks .
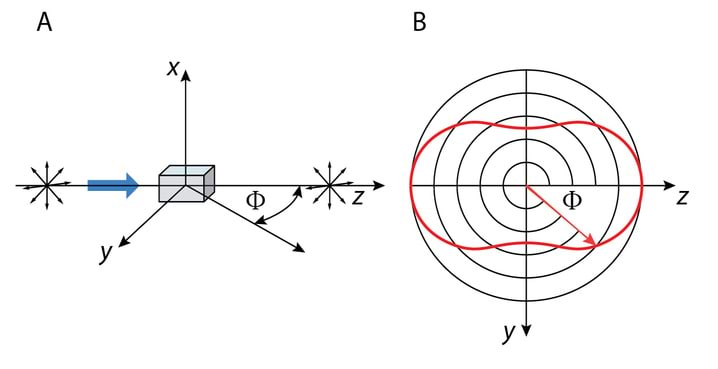
Moodustagu läbilaskesiht langeva valguse polarisatsioonitasandiga nurga . Kui langeva lineaarselt polariseeritud laine amplituud on , siis polaroidi läbib laine amplituudiga EΦ=E0cosΦ ja kuna kiiritustihedus on võrdeline amplituudi ruuduga, siis
saime Malus’i seaduse. Pöörates polaroidi ümber -telje, muutub IΦ vahemikus .
Sentimeeterlainete piirkonnas on sellist selektiivset, nurgast sõltuva läbilaskvusega seadet lihtne luua ja demonstreerida selle abil Malus’i seadust. Nähtava valguse piirkonna kilepolaroidides on juhtivate varraste funktsioonis pikad paralleelsed polümeermolekulid või ka klaasalusele kantud alumiiniumiribad, mille vahekaugus on lainepikkuse suurusjärgus.
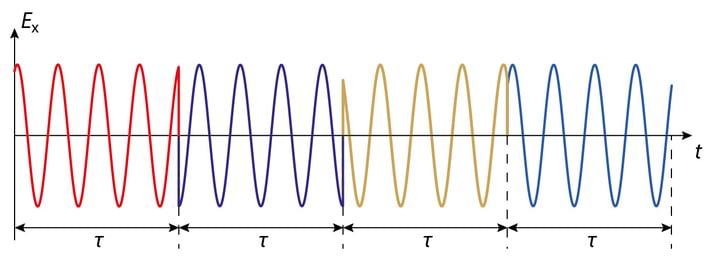
Paigutades tavalise valgusallika ja vaatlusekraani vahele polaroidi ning pöörates viimast, näeme, et valguse intensiivsus jääb sõltumatuks nurgast, . Saadud tulemuse mõistmine eeldab mõningast lisateavet valgusallikate omadustest. Vastavalt klassikalisele mudelile kiirgab mingil viisil ergastatud üksik isoleeritud dipool laine, mille amplituud kahaneb eksponentsiaalselt ajateguriga τ0, nähtavas piirkonnas on . Lihtsaimal juhul koosneb valgusallikas tohutust arvust omavahel põrkuvatest dipoolidest. Põrgetel kaotavad dipoolid oma energia ja tegelik kiirguse kestus on palju lühem ajast τ0, seetõttu on dipooli kiirgus lähendatav siinuspaketiga, vt Jn 2.4.
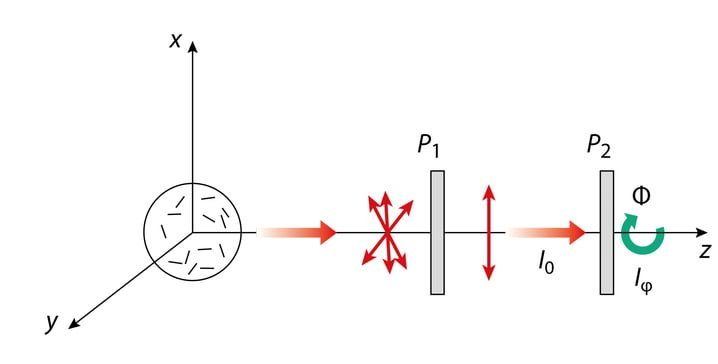
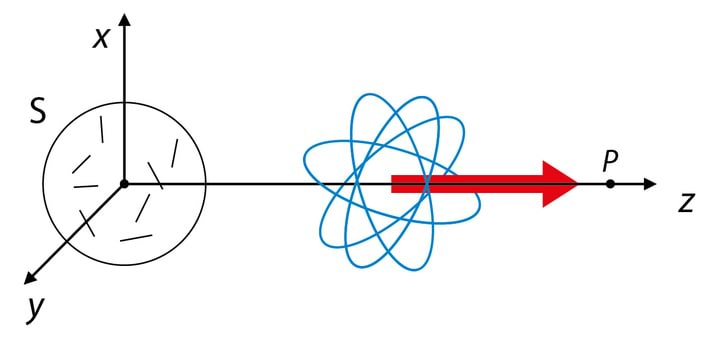
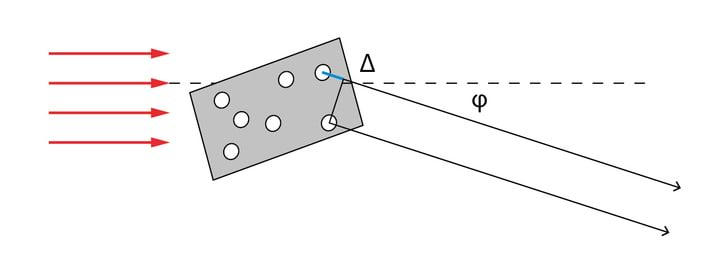
Dipoolide teljed on orienteeritud kaootiliselt, Jn 3.9. z-telje suunas kiirgavad vaid dipoolid, mis omavad kas x- või y-telje sihilist komponenti ja statistiliselt keskmiselt on nende telgede-sihiliste dipoolide arvud võrdsed.
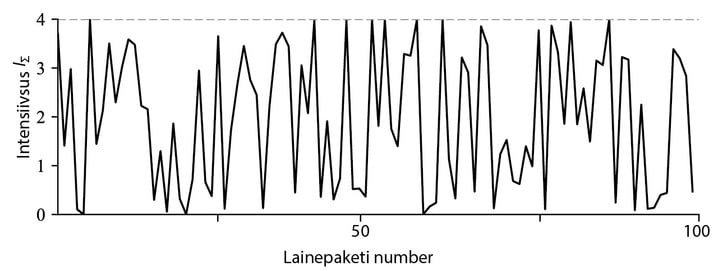
Kuna dipoolid hakkavad kiirgama suvalisel ajamomendil, siis on faasivahe valguse ja komponendi vahel juhuslik suurus ja me räägime loomulikust valgusest. Selle valgusallika mudeli paikapidavuses võib veenduda joonisel Jn 3.9 kujutatud katse abil. Loomuliku valguse tingmärgiks joonistel on kaheotsaliste ühepikkuste noolte kogum. Polaroid selekteerib välja langevast loomulikust valgusest ühes tasandis muutuva komponendi, st temast väljub lineaarselt polariseeritud valgus. Pöörates nüüd polaroidi , näeme, et valguse intensiivsus tema väljundis muutub vastavalt Malus’i seadusele, kusjuures on polaroidide läbilaskesihtide vaheline nurk.
Polaroid pole ainus vahend lineaarselt polariseeritud valguse saamiseks. Erinevaid polariseeritud valguse saamisviise vaatleme edaspidi.
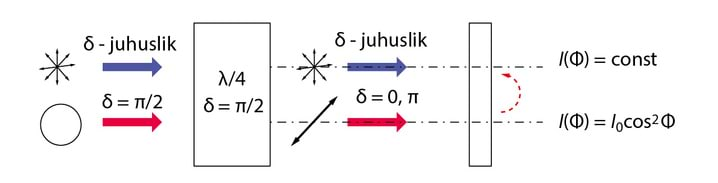
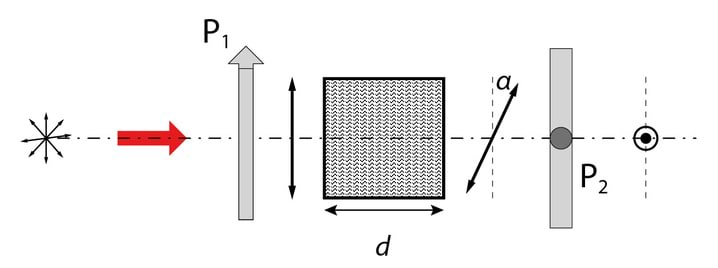
Polaroidi kasutamise näide valguse analüsaatorina on toodud joonisel Jn 3.10, kus polaroidile langeb erinevatel viisidel polariseeritud valgus.
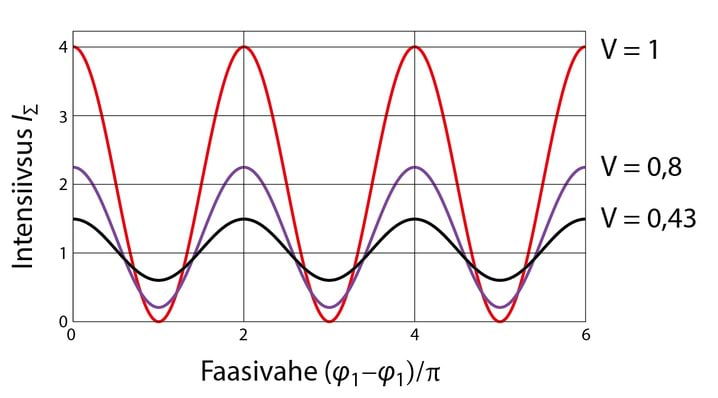
Koordinaatteljed on valitud kokkulangevatena ellipsi telgedega, seega faasinihe x- ja y-komponendi vahel on , vt 2.4. Lineaarselt ja elliptiliselt polariseeritud valguse puhul on amplituudide suhteks valitud . Ühe perioodi jooksul „joonistab“ elektriväli tasandis, mis on risti valguse levikusuunaga kas sirglõigu , ringjoone või ellipsi , Jn 3.10A. Kuna kiiritustihedus on võrdeline amplituudi ruuduga, saame z-teljega ristioleva polaroidi pööramisel joonistel Jn3.10B,C kujutatud sõltuvused . Märkigem, et kuna loomuliku ja ringpolariseeritud valguse sõltuvused on identsed, siis pole üksnes polaroidiga võimalik otsustada, kas meil on tegemist ringpolariseeritud või loomuliku valgusega.
Näide N 3.1
Lahendus
Polaroidi läbib vaid loomuliku valguse see komponent, mis on paralleelne polaroidi läbilaskesihiga ja seega väljundis on valguse intensiivsus I0/2. Kuna ja läbilaskesihtide vaheline nurk on , siis vastavalt Malusi seadusele v 3.4 on väljundis valguse intensiivsus I0/4 ja väljundis I0/8.
Radiomeetria tegeleb valguse erinevate energeetiliste karakteristikute mõõtmisega.
Seni oleme elektromagnetlainet (sh valgust) iseloomustanud kahe energeetilise karakteristikuga – kiirgusenergia tihedusega [ρ]=1[Jm−3] ja kiiritustihedusega
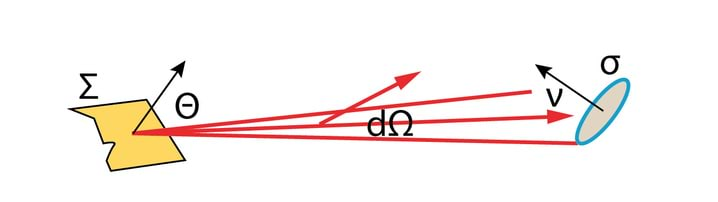
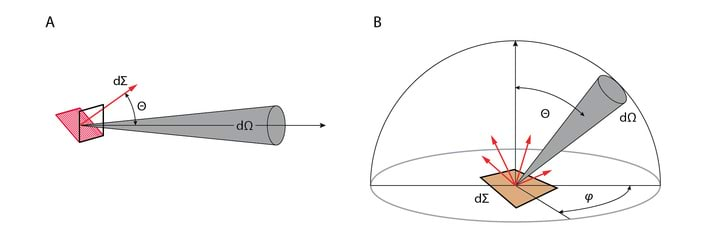
Vt 2.3. Kui meil oleks tegemist vaid monokromaatilise tasalainega, piisaks vaid neist suurustest. Tegelikkuses on hulk tegureid, mida tuleb arvestada kiirgusvoogude iseloomustamisel, Jn 3.11:
- valgusallika mõõtmed ja tajuri mõõtmed on lõplikud
- üldjuhul on allika ja tajuri vaheline kaugus lõplik, seepärast ei jõua tajurini tasalaine, vaid valgus on lahknenud teatud ruuminurga piires
- nii valgusallika kui ka tajuri pinnanormaalid moodustavad vaatesihiga nurgad ja .
Lisaks
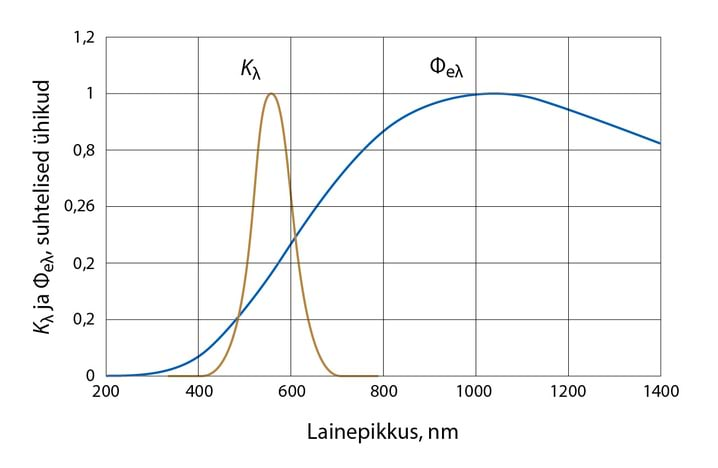
- valgusallika kiirgus sõltub lainepikkusest (sagedusest), Jn 3.12A
- tajuri tundlikkus (spektraalne koste) sõltub lainepikkusest (sagedusest), Jn 3.12B
- tajuril on lõplik ruumiline lahutusvõime
- tajur reageerib silmapilksele sisendsignaali muutusele lõpliku aja jooksul, seda ajalist kostet iseloomustatakse ajateguriga, mis võrdub ajaga, mille jooksul tajuri väljundsignaal kasvab korda.
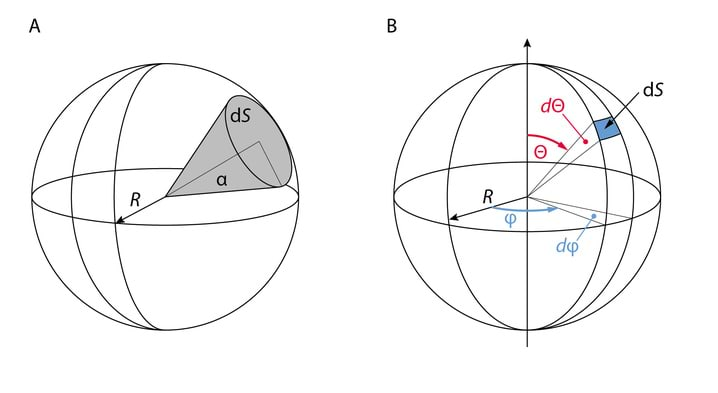
Defineerime esmalt ruuminurga. Ruuminurk on ruumi osa, mida piirab kooniline pind ja seda lõikav kate. Joonisel 3.13 A on sfäärilise katte juhtjoon ring, kuid üldjuhul võib juhtjoon olla suvaline, nt Joonisel 3.14B on juhtjooneks ristküliku küljed.
Kvantitatiivselt avaldub ruuminurk katte pindala ja raadiuse ruudu suhtena,
ja on seega dimensioonitu suurus. Ruuminurga ühikuks on sterradiaan (sr): on arvuliselt võrdne ühikulise pindalaga, mille koonus lõikab välja ühikulise raadiusega kera pinnast. Kuna kera pindala on , siis maksimaalne, kogu kera pinnale vastav ruuminurk on , poolsfäärile vastav ruuminurk on .
Kui ruuminurgad on väikesed, võib sfääri väikese pinnaosa asendada tasapinnaga ning selles lähenduses saame
Tihtipeale on radiomeetrias mugavam kasutada ristkoordinaatide asemel sfäärilisi, seepärast avaldame pinnatüki pindala sfäärilistes koordinaatides, Jn 3.12B. Pinnatüki külgede pikkused on ja ning ruuminurk avaldub
nurkade muutumispiirkonnad on , .
Kuna valguse mõõtmisega seonduv teadus- ja tehnikavaldkond on väga lai, on radiomeetrias kasutusel hulk erinevaid karakteristikuid, meie piirdume vaid kõige üldisematega.
Kuna valguse energiatihedus ruumis oleneb lainepikkusest (sagedusest) iseloomustatakse teda spektraalse kiirgusenergia tihedusega (või ρf). Nagu ikka jaotusfunktsioonide puhul, seisneb ka mõte selles, et korrutis annab ruumiühiku energia lainepikkuste intervallis . Funktsioonid ja ρf on üksüheselt seotult
kui on tegemist vaakumiga, siis f=c/λ ja
(K 3.12) seega
Valguse integraalseks kiirgusvooks (K 3.13) nimetatakse kõikides suundades ja kõikidel lainepikkustel ajaühikus kiiratavat energiat, mida mõõdetakse vattides. Spektraalse kiirgusvoo mõte on analoogiline spektraalse kiirgusenergia tiheduse omaga - annab kiirgusvoo, mida kiiratakse intervallis . SI-s on Φeλ dimensiooniks . Integreerides spektraalset kiirgusvoogu üle kõigi lainepikkuste, saame integraalse kiirgusvoo
Nii nagu kiirgusvoo puhul saab rääkida integraalsest ja spektraalsest kiirgusvoost, saab seda teha ka kõigi järgnevalt sissetoodavate suuruste puhul, kuid me ei hakka seda iga kord kordama.
Üldjuhul on valgusallika kiirgus sõltuv levikusuunast, Jn 3.14.
Punktallika antudsuunalist kiirgust iseloomustab kiirgustugevus , mis on defineeritud kui kiirgusvoog ühikulisse ruuminurka
Integreerides kiirgustugevust üle kogu ruuminurga saame kiirgusvoo,
Isotroopse kiirguse puhul saame
Juhtudel, kui tuleb arvestada valgusallika lõplikke mõõtmeid, on tähtis pinnatüki orientatsioon vaatesihi suhtes, Jn 3.15A. Pinnatüki projektsiooni vaatesihi risttasandile, , nimetatakse selle pinna nähtavaks pindalaks.
Kirkus , Jn 3.15B, on kiirgustugevus ühikuliselt nähtavalt pinnalt
Eksisteerivad pinnad, mille puhul võib lugeda, et nendelt lähtuva valguse kirkus on kõigis suundades ühesugune, . Kui kirkus on konstantne, siis fikseeritud kaugusel pinnatükist sõltub kiirgustugevus nurgast nagu
meil on tegemist Lamberti koosinuskiirguritega.
Kirkus annab kõige detailsemat informatsiooni kiirgurist lähtuva valguse ruumilisest jaotusest. Kui aga huvipakkuv on valgusallika pinnalt ruuminurka kiiratav summaarne valgus, siis iseloomustatakse seda kiirgavusega, mis on ühikuliselt pinnalt kõikides suundade ajaühikus kiiratav energia
Teisendame, kasutades seoseid v.3.6, v.3.8 ja v3.9
Kui meil on tegemist Lamberti kiirguriga, on seos kiirgavuse ja kirkuse abil väga lihtne: kuna Le=const, siis integreerides saame .
Kiirgust tajuri asukohas iseloomustatakse kiiritustihedusega, mis on defineeritud kui kiirgusvoog ühikulisele pinnale
Lähtudes joonisest Jn 3.16, seome kiiritustiheduse ja kiirgustugevuse . Kuna tajuri pinnanormaali ja vaatesihi vaheline nurk on , siis on ruuminurk ja kuna , siis
Näide N 3.2
Lahendus
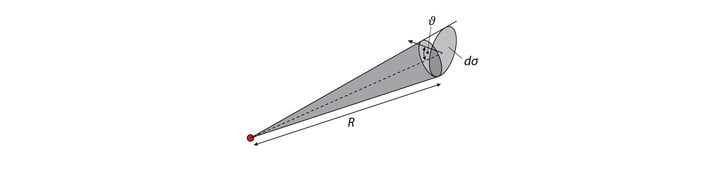
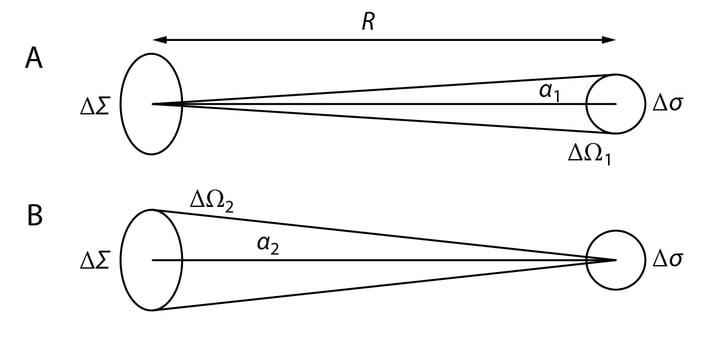
Loeme Päikese tasapinnaliseks kettaks, mille pindala on ΔΣ. Iga selle pinna punkt kiirgab vastuvõtjasse valguskoonuse, vastava ruuminurga suurus on ΔΩ1.
Valemi v 3.9 kaudu saame pinnalt ΔΣ vastuvõtjasse saadetava kiirgusvoo
Vasemal on meil ruuminurka ΔΩ1 kiirguri poolt saadetav kiirgusvoog ja paremal pool on nüüd vastuvõtjasse ruuminurgast ΔΩ2 saabuv kiirgusvoog. Kuna aga teisalt pinnale saabuv kiirgusvoog on seotud kiiritustihedusega, v 3.12, Φe=Eeδσ, siis saame LeΔσΔΩ2=EeΔσ e kirkus ja kiiritustihedus on seotud nagu
Kuna nurk α2=0,0045rad on väga väike, siis võime ruuminurga leidmiseks kasutada valemit v 3.6
ning saame Päikese kirkuse väärtuseks
Kuigi tänapäeval eksisteerib suur hulk valguse tajureid, mille koste on nullist erinev erinevates valguse spektri piirkondades, on meie jaoks tähtsaim meie silm, mille abil me saame valdava osa meid ümbritseva maailma infovoost.
Silma langev valgus kutsub esile silma võrkkestal olevates kepikestes (videvikunägemine) ja kolvikestes (päevanägemine ja värvusaisting) keemilised reaktsioonid, mis koostöös ajuga viivad valgusaistingu tekkele. Mingil fikseeritud lainepikkusel on valgusaistingu tugevus võrdeline logaritmiga valguse kiirgusvoo suurusest, tänu millele on võimalik adekvaatselt tajuda kiirgusvoo muutusi rohkem kui kümne suurusjärgu piires.
Kepikeste (koguarv ) spektraalne tundlikkus on vahemikus maksimumiga lainepikkusel , nende võime eristada valguse lähedasi lainepikkusi on väike.
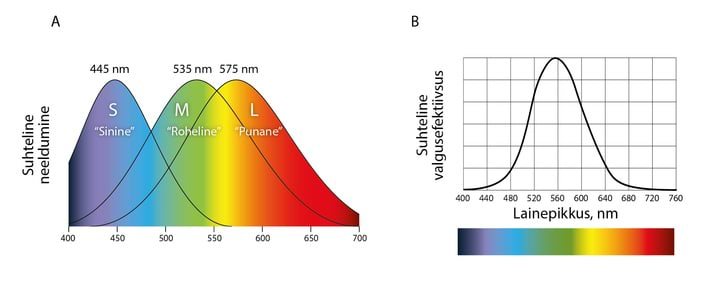
Kolvikesi (koguarv () on kolme tüüpi: S (ing k short), M (ing k medium) ja L (ing low), mille tundlikkuse maksimumid on vastavalt lainepikkustel („sinine"), („roheline") ja („punane"), Jn3.17A.
Erinevat tüüpi kolvikeste suhtarvud, L – , M – ja S – , määravad ära silma päevanägemise spektraalse tundlikkuse, Jn 3.17B. Ka spetsiaalselt treenimata silm suudab eristada värvitoone, millele vastab ca suurune lainepikkuste vahemik.
Erinevalt radiomeetriast, mis baseerub energeetilisel karakteristikutel, lähtub fotomeetria inimese silma spektraalse tundlikkuse kõverast, Jn3.17B. Fotomeetrias kasutatav suuruste süsteem on üles ehitatud SI põhiühiku – valgustugevuse – baasil.
Vastavalt tänapäevastele metroloogia kokkulepetele on valgustustugevuse ühik defineeritud kiirgustugevuse kaudu:
(K 3.16) Fotomeetria kasutab valgusallikate karakteriseerimiseks suurusi, mis on analoogilised radiomeetrias kasutatavatega, T3.1, kuid nad on defineeritud valgustugevuse kaudu. Nii nt on luumen valgusvoog, mille saadab valgusallikas valgustugevusega kandela ruuminurka (K 3.16). Isotroopse valgusallika valgusvoog on , st allikas valgustugevusega kiirgab valgusvoo luumenit. Lihtsalt mõõdetavaks suuruseks fotomeetrias on valgustatus, selleks kasutatavate luksmeetrite tundlikkuse kõver vastab inimese silmale, Jn3.17B. Nt kuupaisteta ööl on valgustatus ja otsesel päikesepaistel ; soovituslik valgustatus tööruumides on .
Teades nurka luksmeetri pinnanormaali ja vaatesihi vahel ning mõõtes mingis suunas kaugusel valgustatuse, saab fotomeetria põhivalemi
abil leida valgusallika valgustugevuse selles suunas.
| Valgustugevus J(cd) (luminous intensity) | ← | Kiirgustugevus J(W/sr) (radiant intensity) |
| Valgusvoog Φ(lm=1cd⋅sr) (luminous flux) | dΦ=JdΩ | Kiirgusvoog Φe(W) (radiant flux) |
| Heledus L(cd/m2) (luminance) | L=dJdΣcosθ | Kirkus Le(W/sr⋅m2) (radiance) |
| Valgsus M(lm/m2) (luminous exitance) | M=dΦdΣ | Kiirgavus Me(W/m2) (radiant exitance) |
| Valgustatus E(lx=1lm/m2) (illuminance) | E=dΦdσ E=JR2cosθ | Kiiritustihedus Ee(W/m2) (irradiance) |
Seos radiomeetriliste ja fotomeetriliste suuruste vahel on määratud valgusefektiivsusega
Valgusefektiivsuse väärtus on fikseeritud lainepikkusel 555 nm, , kõigi teiste lainepikkuste jaoks kasutatakse suhtelist valgusefektiivsust
väärtused mõningatel lainepikkustel on tabelis T3.4.
Suhtelist valguseefektiivsust kirjeldab piisava täpsusega sobitusvalem
kus on lainepikkus nanomeetrites.
Kui valgusallikast lähtub monokromaatiline valgus, siis on valgusvoog lihtsasti leitav , kuid kui allikas kiirgab lainepikkuste intervallis , saame valgusvoo integreerides
Kuigi valgusallikas võib kiirata väga laias lainepikkuste vahemikus , Jn 3.18, on integraalialune funktsioon nullist erinev vaid vahemikus , kus , Jn 3.18.
Näide N 3.3
Lahendus
Tabeli T 3.4 järgi vastavad lainepikkustele 480 ja 520nm suhtelise valgusefektiivsuse väärtused 0,139 ja 0,71. Kuna Φeλ=const ning joonise Jn 3.18 järgi võib lugeda, et on selles piirkonnas enam-vähem lineaarne funktsioon lainepikkusest, siis valemis v 3.15 oleva integraali arvutamine lihtsustub
ja valgusvoog on
(P 3.7) Selles alapunktis paneme paika laineoptika rakendatavuse piirid.
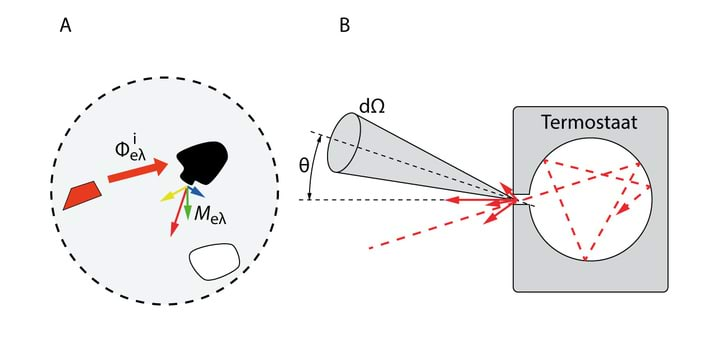
Nagu juba öeldud, vt 3.3, transformeeritakse osa keha soojusenergiast elektromagnetlaine energiaks. Vastavalt termodünaamikale saabub mingi aja möödudes paljudest osadest koosnevas isoleeritud süsteemis termodünaamiline tasakaal st kõik süsteemi osad on iseloomustatavad ühe ja sama makroparameetriga - temperatuuriga . Kujutagu meie isoleeritud süsteem õhutühja peegelseintega õõnsust, milles paiknevad erinevatest materjalidest osad, Jn 3.19A. Kuna on tegemist vaakumiga, siis ainsaks energiavahetuse viisiks süsteemi eri osade vahel on elektromagnetlained.
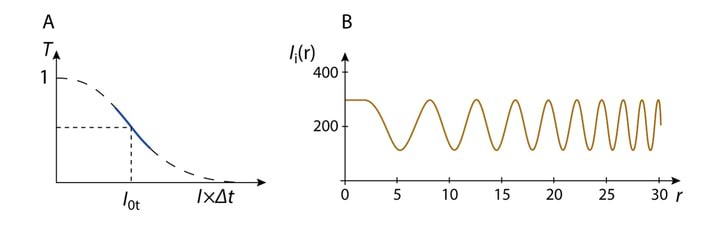
Termodünaamilise tasakaalu puhul kehtib detailse tasakaalu printsiip: iga elementaarprotsessi kiirus on võrdne vastassuunas kulgeva protsessi kiirusega. Vaadeldaval juhul on otseseks elementaarprotsessiks kiirgamine lainepikkuste intervallis {λ,λ+dλ} ja pöördprotsessiks neelamine samas intervallis. Kiirgamist iseloomustavaks suuruseks on spektraalne kiirgavus . Termodünaamilises tasakaalus on määratud temperatuuriga, mis võrdub õõnsuses olevate kehadega omaga.Neelamist iseloomustab spektraalne neelavus, mis on defineeritud neelduva kiirgusvoo ja langeva kiirgusvoo suhtena,
Mistahes õõnsusse kuuluva keha puhul peab ja suhe olema sõltumatu tema omadustest (materjal, kuju jms). Kui see nii ei oleks, siis võiks süsteemi mingi osa nt neelata rohkem kui kiirata ja ta temperatuur tõuseks, mille tulemuseks oleks temperatuuride vahe süsteemi eri osade vahel. Selline tulemus on aga termodünaamiliselt võimatu. Analoogilise arutelu tulemusena saame, et musta keha kiirgus on ühtlane kõigis suundades. Kokkuvõttes jõuame Kirchhoffi seaduseni, mis väidab, et süsteemi termodünaamilises tasakaalus on kiirgavuse ja neelavuse suhe kehadest sõltumatu universaalne funktsioon temperatuurist ja lainepikkusest
Funktsiooni on võimalik leida, mõõtes sellise keha kiirgavuse, mille neelavus . Sellist keha nimetatakse mustaks kehaks, must keha neelab kogu talle langeva valguse. Valemist 3.16 järgneb, et musta keha kiirgavus fikseeritud temperatuuril on suurem kui mistahes mittemusta soojuskiirguri kiirgavus samal temperatuuril.
Heaks musta keha mudeliks on väike avaus õõnsuses, Jn 3.19B. Õõnsusse sisenev valgus peegeldub korduvalt tema seintelt ja tõenäosus valguse väljumiseks on kaduvväike. Seega võib avaust vaadelda musta keha pinnatükina. Paigutades sellise õõnsuse termostaati, on võimalik mõõta musta keha spektraalset kiirgavust funktsioonina temperatuurist. Juba XIX sajandi lõpu eksperimenditehnika lubas mõõta musta keha spektreid piisava täpsusega.
Lähtudes nii eksperimenditulemuste analüüsist kui ka termodünaamilistest kaalutlustest leiti, et integraalne kiirgavus
on võrdeline temperatuuri neljanda astmega
kus võrdetegur
kannab Stefan-Boltzmanni konstandi nime.
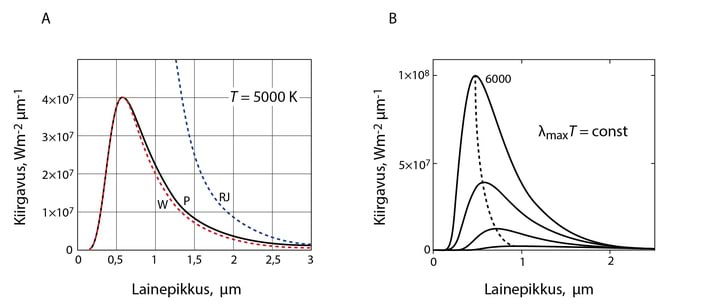
Jn 3.20A esitab eksperimentaalse spektraalse kiirgavuse võrdluse kolme erineva mudeliga.
W. Wien tuletas oma lähenduse eksperimendile, lähtudes termodünaamilistest kaalutlustest. Ta leidis, et
kus C1 ja on konstandid.
See seos kirjeldas täpselt musta keha kiirgust lühematel lainepikkustel, kuid pikematel lainepikkustel tulemused lahknesid. Wieni nihkeseadus, mis sidus kiirgavuse maksimumile vastava lainepikkuse temperatuuriga (Jn 3.20B), osutus täpseks
Range, klassikalise füüsika seisukohtadel baseeruv Rayleigh-Jeansi valem langes eksperimendi tulemustega kokku vaid pikematel lainepikkustel, kuid lühematel lainepikkustel lähenes kiirgavus lõpmatusele („ultravalguse katastroof“).
Leidmaks parimat vastavust eksperimendiga, tuli M. Planckil oletada, et musta keha kiirgus on kvantiseeritud, mingil sagedusel kiiratav energia avaldub vaid
kordsetena, kus
on Plancki konstant. Selle kiirguse kvandi tänapäevanimi on „footon“.
Näide N 3.4
Lahendus
Kuna ühe footoni energia on hν=hc/λ, siis footonite arv N1,2=Pλ1,2hc e ühel ja samal võimsusel kiiratavate footonite arv on võrdeline lainepikkusega. Lainepikkusel 248nm kiirgava laseri puhul on footonite arv sekundis
Teise laseri puhul on footonite arv 4,3 korda suurem.
Musta keha kiirgavust kirjeldab Plancki valem funktsioonina lainepikkusest ja sagedusest on
Tihtipeale on mõistlik esitada kiirgavus funktsioonina sagedusest. Nii nagu kiirgusenergia tiheduse puhul, vt 3.5, kehtib ka kiirgavuse puhul seos
ja seega
Tehes veel asenduse , saame musta keha kiirgavuse funktsioonina sagedusest
Plancki valem kirjeldab väga hästi musta keha kiirgust laias temperatuuride vahemikus, kaasa arvatud ka maailmaruumist lähtuva reliktkiirguse spektrit temperatuuril . Integreerides Plancki valemit üle lainepikkuste, jõuame Stefan-Boltzmanni valemini v 3.17 ja leides Plancki valemi ekstreemumi lainepikkuse järgi, saame Wieni nihkeseaduse v 3.19. Plancki valem taandub Wieni lähendusele, kui võib lugeda, et
Rayleigh-Jeansi lähendini jõuame, kui võib kirjutada
Kasutades fundamentaalkonstantide arvulisi väärtusi ja esitades lainepikkuse mikromeetrites ning temperatuuri kelvinites saame arvutusteks mugavama seose
Reaalsete soojuskiirgurite neelavus ja seetõttu on mingil fikseeritud temperatuuril nende kiirgavus alati väiksem kui mustal kehal. Selleks, et nad kiirgaksid musta kehaga ligilähedast võimsust, peab nende temperatuur olema kõrgem. Iseloomustamaks seda spektrit, tuuakse sisse värvustemperatuuri mõiste: see on sellise musta keha temperatuur, mille spekter (nähtavas piirkonnas seega ka värvus) on kõige lähedasem antud kiirguri spektrile. Paljudes optika rakendusvaldkondades (nt valgustustehnika puhul – külm ()) ja soe valgus () kasutatakse värvustemperatuuri mõistet ka allikate puhul, millel pole midagi pistmist soojuskiirgusega.
Näide N 3.5
Lahendus
a) Päikese pinna temperatuur on 5500K. Millega võrdub maksimaalsele kiirgavusele vastav lainepikkus?
Valemi v 3.19 järgi
See lainepikkus on üsna lähedane inimese silma tundlikkuse maksimumile, vt Jn 3.17B.
b) Maa kiirgavus on 240Wm−2. Milline peaks olema tasakaalulisele kiirgusele vastav temperatuur?
Valemi v 3.17 järgi
mis annab meile kiirgavuse maksimumile vastavaks lainepikkuseks λmax=11μm. Tegelikkuses on Maa keskmine temperatuur 14∘C. Erinevuse põhjus peitub valguse selektiivses neeldumises Maa atmosfääris: neeldumine on suurem pikematel lainepikkustel ja lisaks osa atmosfääri poolt neeldunud valgusest kiiratakse tagasi. Selle atmosfääri „kasvuhooneefekti“ tõttu puudub tasakaal Päikeselt saabuva energiavoo ja Maalt lahkuva energiavoo vahel.
c) Inimkeha kiirgusest tingitud energiakadude ligikaudseks hindamiseks võtame tema keha ligikaudseks pindalaks . Lugedes, et naha keskmine temperatuur on ja ümbritseva keskkonna temperatuuriks , saame leida maksimaalse summaarse võimsuskao
ning energiakadu ööpäevas on
inimese keskmiseks toidust saadavast energiaväärtuseks loetakse 2000kcal. Arvestades, et hinnangus tehtud väga ligikaudseid eeldusi (must keha, inimkeha pindala, riietuse ekraneeriva mõju mittearvestamine) võib saadud tulemust hinnata rahuldavaks.
Postuleeris valguse kiirgamise ja neeldumise kvantprotsessid, tuletas A. Einstein nende mehhanismide baasil valemi musta keha kiirgusenergia tiheduse ρνT jaoks, vt. 11.3. Saab näidata, et kiirgavuse ja kiirgusenergia tiheduse vahel kehtib seos
Nägime, et valgusallikate kiirgusmehhanismi kvantitatiivseks kirjeldamiseks valguse lainemudel ei tööta ja tuleb arvestada kiirguse kvantiseloomu. Järgmistes peatükkides aga näeme, et lainemudel on võimeline seletama väga laia nähtuste ringi.
Valgusnähtused ei ole kirjeldatavad ühe mudeliga, tegemist on mikromaailmale tüüpilisele korpuskulaar-lainelise dualismiga.
Kui valgus langeb kahe erineva murdumisnäitajaga keskkonna lahutuspinnale, siis osa valgusest tungib teise keskkonda, osa aga levib tagasi esimesse keskkonda. Leiame nende protsesside seaduspärasused järgmistel eeldustel
- Tegemist on HILS keskkondadega, mille murdumisnäitajad on ja , teise keskkonna suhteline murdumisnäitaja esimese keskkonna suhtes on
- Lahutuspinnale langeb tasalaine (paralleelne kiirtekimp)
- Keskkondade lahutuspinnaks on tasapind.
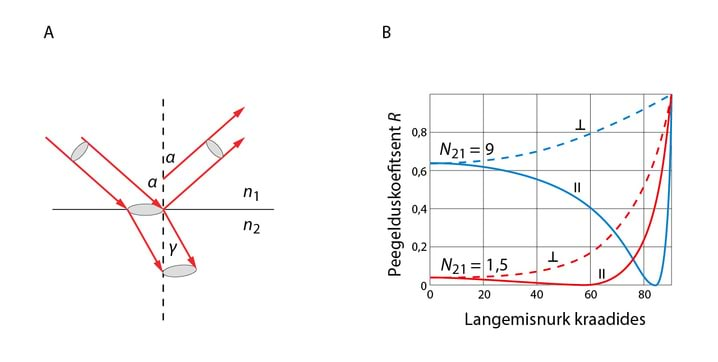
Lähtudes valguse elektromagnetlaine mudelist, tuletame nüüd lisaks peegeldumis- ja murdumisseadusele, vt 1.2.1, ka energeetilised seosed peegelduva ja murduva valguse jaoks. Nende Fresneli valemite tuletuskäik baseerub esimese ja teise keskkonna elektrivälja tugevuse E ja magnetvälja tugevuse H vektorite piki lahutuspinda suunatud komponentide ( tangensiaal-komponentide) hetkväärtuste võrdsusel
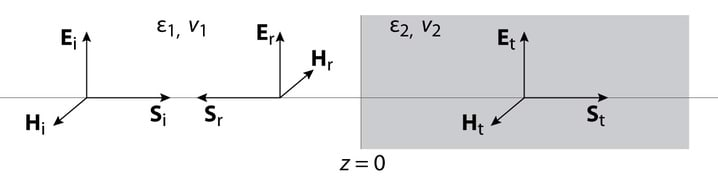
Vaatleme esmalt lihtsaimat juhtumit, kui valgus langeb keskkondade 1 ja 2 lahutuspinnale nurga all, Jn 4.1. Olgu keskkonnas 1 z-telje positiivses suunas leviv tasalaine Ei=Ei0exp[iω(t−z/v1)] (K 4.1) lineaarselt polariseeritud x-z tasandis. Lahutuspinnal valgus osaliselt peegeldub, osaliselt levib teise keskkonda. Algselt me ei tea, kas peegeldumisel sagedus muutub või mitte, seepärast esitame peegelduva laine kujul Er=Er0exp[iωr(t−z/v1)] ja keskkonda leviva laine kujul Et=Et0exp[iωt(t−z/v2)]. Samuti pole teada Er ja Et suund, kuid andes need ette, on üheselt määratud ka Hr ja Ht suund, sest S=E×H.
Vastavalt joonisele võib nüüd ja hetkväärtuse jaoks lahutuspinnal esitada tingimuse v 4.1 kujul
Et tingimus Ei0exp[iωt]+Er0exp[iωrt]=Et0exp[iωt] (K 4.3) peab olema täidetud mistahes ajahetkel, siis
st nii peegelduva kui ka teise keskkonda leviva valguse sagedus ei muutu ning
st tingimus v 4.1 kehtib ka amplituudväärtuste jaoks.
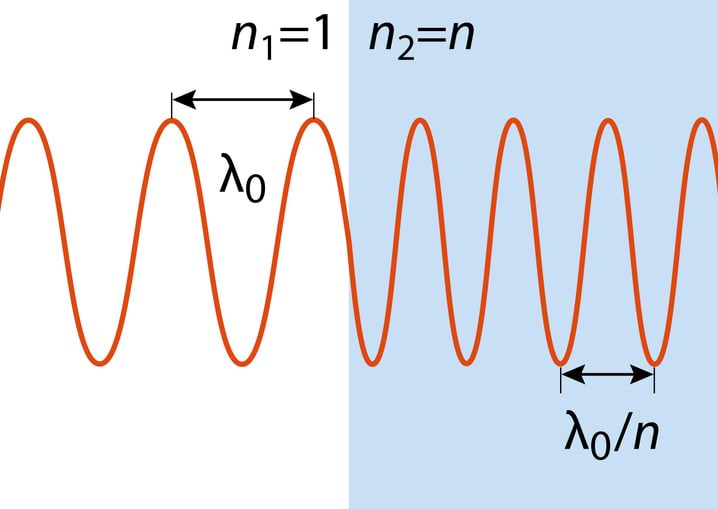
Kuna üleminekul ühest keskkonnast sagedus ei muutu ja
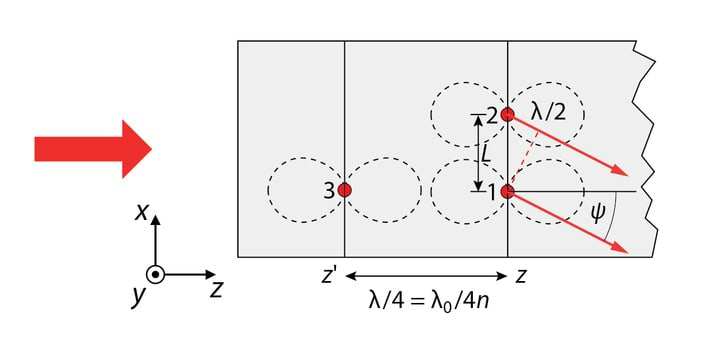
siis peab üleminekul ühest keskkonnast teise muutuma lainepikkus. Kui vaakumis on lainepikkus , siis keskkonnas murdumisnäitajaga on lainepikkus λn=λ0n, Jn 4.2.
Kuna elektromagnetlaines on elektri-ja magnetväli üks-üheselt seotud
vt. v 2.20, siis võib v 4.3-s asendada magnetvälja amplituudväärtused elektrivälja omadega ning me saame
kust on lihtne avaldada peegelduva ja läbiva laine amplituudid
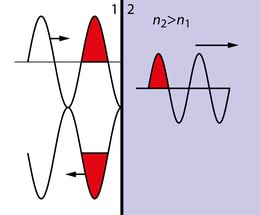
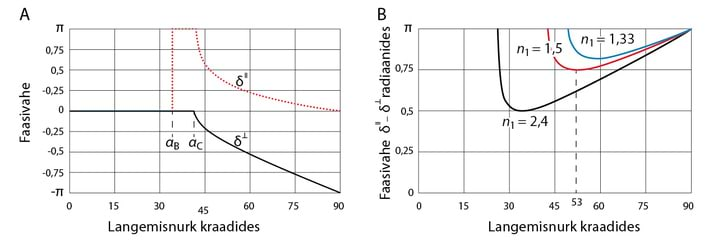
Näeme, et kui , nt valguse levikul õhust klaasi, siis on peegelduva laine amplituud negatiivne langeva laine amplituudi suhtes. Vastavalt v 2.20-le järeldub sellest, et peegeldumisel tekib faasihüpe , peegelduv ja langev laine on vastasfaasis, Jn 4.3.
Kuna harmoonilise laine levikul ulatuses muutub faas võrra, siis peegeldumisel suurema murdumisnäitajaga keskkonnal räägitakse poollaine „kaotusest“, vt 5.4. Kui aga , siis faasihüpe puudub, sellele olukorrale vastab Jn 4.1. Läbiv laine on alati faasis langevaga.
Valemid v 4.4 saime lähtudes sellest, et valgus on lineaarselt polariseeritud joonise tasandis, Jn 4.1. Sama tulemuseni jõuame, kui valime risti joonise tasandiga. Seega: normaallangemisel ja ei sõltu sellest, kuidas langev valgus on polariseeritud.
Kui valgus lahutuspinnal ei neeldu, siis vastavalt energia jäävusele on peegelduva ja läbiva kiirgusvoo summa võrdne lahutuspinnale langeva kiirgusvooga, .
Defineerides energeetilise peegelduskoefitsiendi kui peegelduva ja langeva kiirgusvoo suhte, ja energeetilise läbimiskoefitsiendi kui läbiva ja langeva kiirgusvoo suhte, , saame
mis on energia jäävuse seaduse üks erikujudest.
Avaldame nüüd peegeldumis- ja läbimiskoefitsiendid keskkondade murdumisnäitajate kaudu. Selleks arvestame seost kiirgusvoo kiiritustiheduse vahel, , kus on kiirtekimbu ristlõike pindala. Kuna ja , siis
Kasutades nüüd seoseid v 4.4, saame
Näide N 4.1
Lahendus
Eeldame, et kaod on põhjustatud vaid peegeldumisest ja langemisnurka võib lugeda väikeseks st peegelduskoefitsient on leitav valemiga v 4.7, läbimiskoefitsiendi leiame valemiga v 4.5.
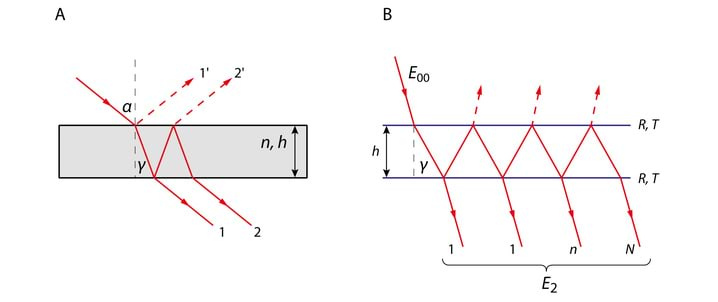
Pärast peegeldumist esimeselt pinnalt jõuab teise pinnani T=1−R osa langevast valgusest, kus
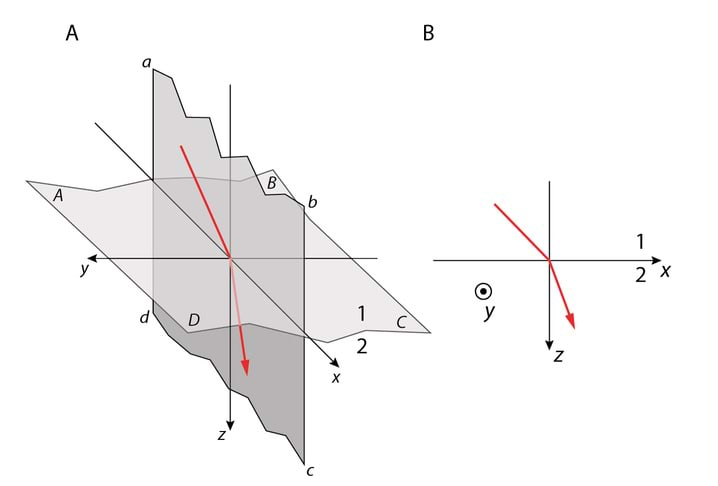
Seega teise pinnani jõuab 0,96 osa langevast valgusest. Pärast kuue peegeldava pinna läbimist on valguse intensiivsus (1−R)6×100=78% langeva valguse omast.
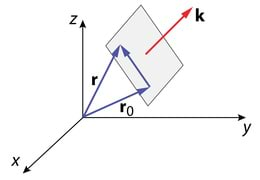
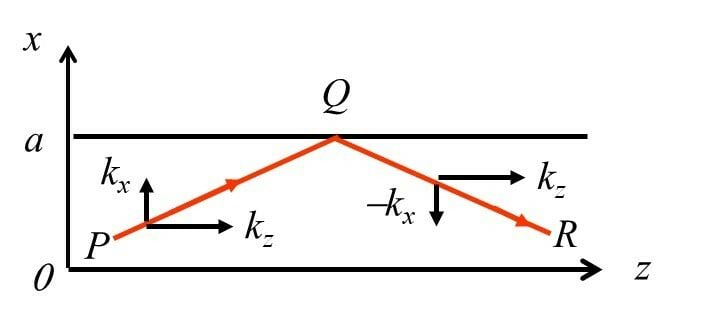
Seni kasutatud lainefunktsioon E=E0exp[i(ωt−kz)] kirjeldab ühedimensionaalset, z-telje positiivses suunas levivat tasalainet. Toome sisse lainefunktsiooni, mis kirjeldab suvalises suunas levivat tasalainet, Jn 4.4. Selleks defineerime lainevektori k, mille komponendid on , tema moodul |k|=√k2x+k2y+k2z langeb kokku lainearvuga ja ta on suunatud lainefrondi pinnanormaali sihis. HILS keskkonnas langeb k suund kokku Poyntingi vektoriga (valguskiirega).
Kuna lainefrondil olev vektor r−r0 ja lainevektor k on risti, siis skalaarkorrutis (r−r0)k=0, seega rk=const on tasalaine konstantse faasi tingimus üldjuhul ja suvalises suunas leviva tasalaine lainefunktsioon omandab kuju
Avaldades tingimuse rk=const lainefrondi mingi lainefrondi punkti koordinaatide ja lainevektori komponentide kaudu, saame
Tähistades nurgad lainevektori ja koordinaattelgede vahel
ning arvestades, et , omandab v 4.8 kuju
Kui valgus levib °z°-telje suunas, siis ja ning v 4.9 omandab eelnevast tuttava kuju.
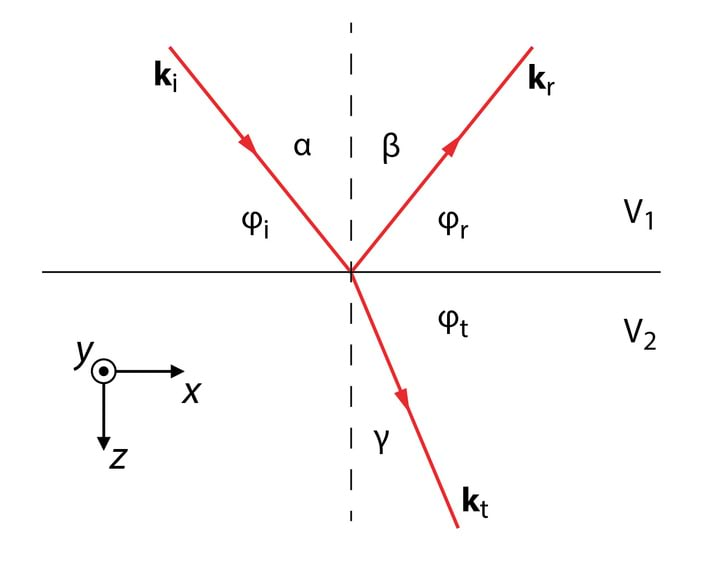
Tuletame peegeldumise ja murdumise seaduspärasused juhul, kui tasalaine langeb kahe keskkonna lahutuspinnale kaldu, . Jn 4.5 koordinaatteljestik on valitud nii, et tasand vastab langemistasandile ja lahutuspinnale vastab tasand . Lainevektorid kr ja kt ei pruugi olla joonise tasandis.
Kasutades v 4.9 lainefunktsiooni kuju, paneme kirja tangensiaalkomponentide võrdsuse elektrivälja tugevuse hetkväärtuste jaoks, . Arvestame, et langemistasandile vastab , kuid jätame alles võimaluse, et peegeldumisel ja murdumisel võib valguse sagedus muutuda
Kirjapandud seos peab kehtima mistahes ajahetkel kõigis lahutuspinna punktides.
- Selleks, et samasus kehtiks suvalisel ajahetkel koordinaatide alguspunktis, st siis, kui peale ka , peab sagedus peegeldumisel ja murdumisel jääma samaks, . Kuna sagedus ei muutu, siis taandub aeg samasuse avaldisest välja st samasus kehtib ka amplituudväärtuste jaoks.
- Selleks, et samasus kehtiks kõigis -telje punktides järgneb siit ehk kr ja kt (peegelduv ja murduv kiir) on langemistasandis.
- Selleks, et samasus kehtiks kõigis -telje punktides, peab
Siit võib teha kaks järeldust.
Esiteks, kuna
siis
ja vastavalt Jn 4.5-le saame, et peegeldumisnurk võrdub langemisnurgaga,
Teiseks, kuna
siis
Arvestades nüüd, et ja jõuame tulemuseni, et langemisnurga ja murdumisnurga siinuste suhe võrdub suhtelise murdumisnäitajaga, .
Kokkuvõtvalt: lähtudes vektorite E ja H tangentsiaalkomponentide võrdsusest kahe dielektriku lahutuspinnal saime peegeldumise ja murdumise jaoks tulemused, mis langevad kokku punktis 1.2.1. kirjeldatud empiiriliste seaduspärasustega. Toonitagem, et need tulemused on saadud HILS keskkonna ja monokromaatilise valguse jaoks.
Kui valgus langes keskkondade lahutuspinnale risti, olid peegelduva ja läbiva laine amplituudid sõltumatud polarisatsioonitasandi orientatsioonist. Näitame, et kaldu langemisel see enam nii ei ole.
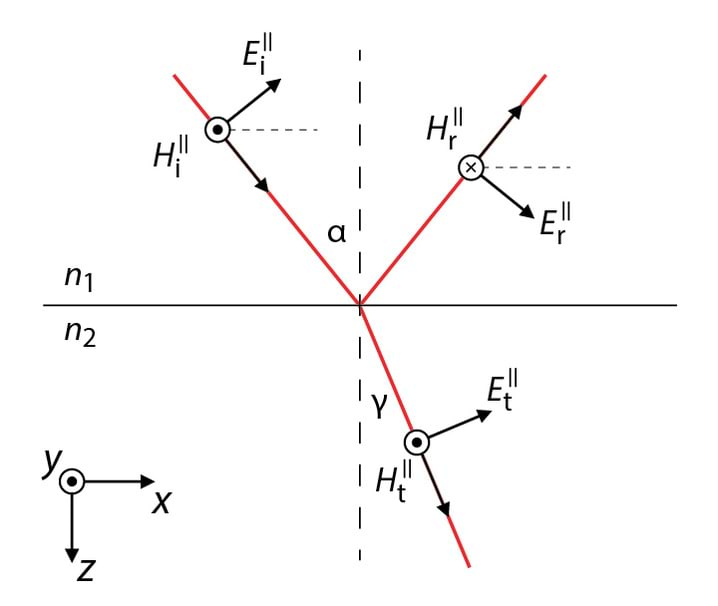
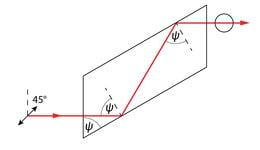
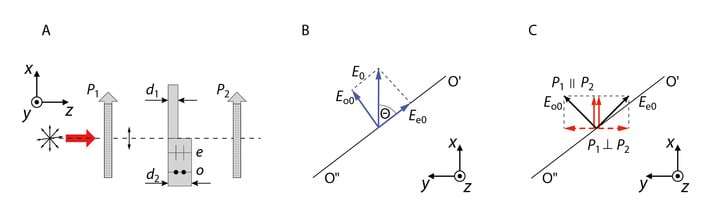
Selleks vaatleme kahte juhtu: esimesel on valgus lineaarselt polariseeritud langemistasandis (polarisatsioonitasandi asimuut ), tähis , ning teisel on polarisatsioonitasand risti langemistasandiga (), tähis (K 4.9). Kui on tegemist loomuliku („polariseerimata“) valgusega, siis on faasivahe kahe ristkomponendi vahel juhuslik suurus ja valguse amplituud avaldub
Kui valgus on lineaarselt polariseeritud langemistasandis, siis vastavalt Jn 4.6-le avalduvad amplituudide tangensiaalkomponentide võrdsused nagu
Arvestades viimases seoses elektri- ja magnetvälja omavahelist seotust, v 2.20, saame
Kombineerides valemeid v 4.10 ja v 4.11, saab elimineerida
ja avaldada peegelduva laine suhtelise amplituudi
Edasisel teisendamisel kasutame murdumisseadust
Saame
ja seejärel teisendusvalemeid trigonomeetriast
Jõuame tulemuseni
Peegelduva laine suhtelise amplituudi esitamine sellisel kujul võimaldab edasist lihtsat/läbipaistvat analüüsi.
Leidmaks teise keskkonda leviva valguse amplituudi, tuleb lähtuda uuesti tingimustest v 4.10, avaldada ning pärast teisendusi saame
Peegelduva valguse suhtelise amplituudi esitamiseks vaid langemisnurga kaudu teeme v 4.12-s asenduse ja lihtsad teisendused annavad seose
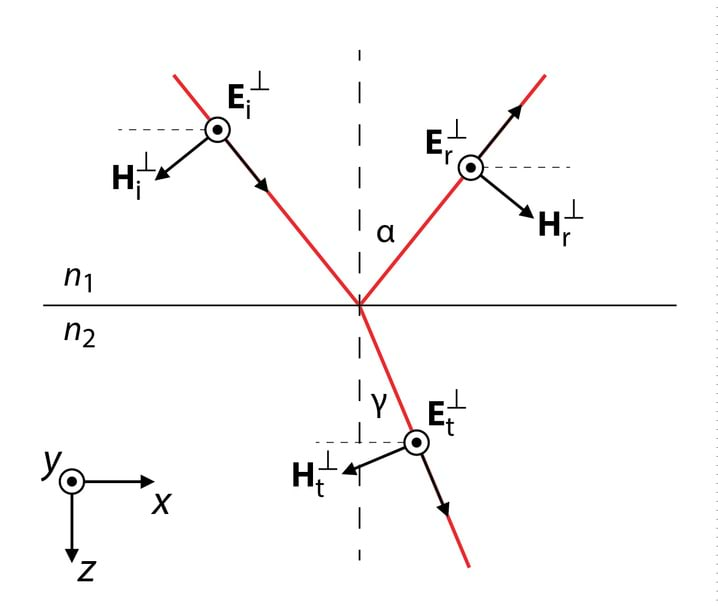
Kui valguse polarisatsioonitasand on risti langemistasandiga, Jn 4.7, saame järgmised ääretingimused
Nii nagu enne, arvestame, et ja elimineerides teisest tingimusest saame pärast teisendamist
Edasisel teisendamisel kasutame murdumisseadust
ja valemit trigonomeetriast ning tulemuseks on
Analoogiliselt on leitav ka teise keskkonda murduva valguse amplituud
Kui nüüd uuesti pöörduda v 4.16 poole ja elimineerida sealt , leiame peegelduva valguse suhtelise amplituudi sõltuvuse langemisnurgast ilmutatud kujul
(K 4.11) Alustame kahes erinevas tasandis polariseeritud valguse peegeldumist kirjeldavate valemite v 4.13 ja v 4.17
analüüsi väikestest nurkadest, mille puhul ning murdumisseaduse võib kirjutada kujul αγ=n2n1. Oodatult langeb tulemus
kokku normaallangemise tulemusega, vt 4.1.
Suurematel argumendi väärtustel erinevad tangens- ja siinusfunktsioon oluliselt, Jn 4.8, järelikult peegelduvad ka erinevalt polariseeritud lained erinevalt.
Kui langemis- ja murdumisnurga summa , siis nimetaja avaldises läheneb lõpmatusele, , ning seega sel tingimusel langemistasandis polariseeritud valgus ei peegeldu. Seda spetsiifilist nurka nimetatakse Brewsteri nurgaks, . Brewsteri nurga puhul omandab murdumisseadus kuju
st mõõtes Brewsteri nurga, on võimalik leida murdumisnäitaja .
Lisaks näeme, et kui , muudab tangensfunktsioon märki – kui väiksematel nurkadel oli langemistasandis polariseeritud peegelduv laine vastasfaasis langevaga, siis Brewsteri nurgast suurematel nurkadel faasihüpe kaob.
Peegeldumise puudumisele juhul, kui langemistasandis polariseeritud valgus langeb lahutuspinnale nurga all, on lihtne füüsikaline tagapõhi. Peegelduv laine tekib langeva valguse elektrivälja poolt teises keskkonnas ergastatud dipoolide kiirguse tulemusena. Kui nüüd , siis on dipoolide teljed sihis, mis vastab peegeldumisnurgale. Kuna aga dipool oma telje sihis ei kiirga, vt 2.5, siis peegelduv laine puudub. Kui langev valgus on polariseeritud risti langemistasandiga, toimub peegeldumine alati, sest dipoolide teljed on alati risti langemistasandiga.
Kuna siinusfunktsioon jääb vahemikus alati lõplikuks ega muuda märki, on risttasandis polariseeritud peegelduva valguse amplituud alati nullist erinev ning peegelduv laine on alati vastasfaasis langeva valgusega.
Suhtelise amplituudi ja peegelduva ja langeva laine faasivahe sõltuvus langemisnurgast on joonisel Jn 4.9.
Leidmaks energeetilisi peegelduskoefitsiente tuleb arvestada, et murdumisel teise keskkonda kiirtekimbu ristlõike pindala muutub, Jn 4.10A. Kui keskkondade lahutuspinnal on valguslaigu pindala A, siis langeva, peegelduva ja murduva valguse kiirgusvood on vastavalt , , .
Võrreldes normaalse langemise juhuga, v 4.6, jääb energeetilise peegelduskoefitsiendi avaldis muutumatuks
kuid läbimiskoefitsiendi avaldisse lisandub langemis- ja murdumisnurga koosinusi sisaldav tegur
Seega kaldu langemisel avalduvad peegelduskoefitsiendid nagu
Lihtsaim viis läbimiskoefitsiendi leidmiseks on seose kasutamine.
Peegelduskoefitsientide graafikud on joonisel Jn 4.10B. Näeme, et optilises diapasoonis peegeldub langemisnurkadel vähem kui pool langevast valgusest, kuid libiseval langemisel, α≈90∘, läheneb peegelduskoefitsient ühele. Lisaks sellele on laias langemisnurkade vahemikus, , loomuliku valguse, , langemisel lahutuspinnale peegelduva valguse ristkomponent rohkem kui kaks korda suurem kui paralleelkomponent. Viimast esiletoodud seika iseloomustavad läbi polaroidi pildistatud fotod, Jn 4.11.
Näide N 4.2
Lahendus
Peegeldumiskaod kahe keskkonna lahutuspiiril puuduvad, kui valgus on lineaarselt polariseeritud langemistasandis ja langemisnurk võrdub Brewsteri nurgaga, α=αB. Kuna need tingimused peavad olema täidetud murdumisel mõlemal prisma tahul, siis peab kiirtekäik prismas olema sümmeetriline murdva nurga nurgapoolitaja suhtes. Sellisel juhul saame kolmnurga 1 2 3 sisenurkade summa avaldisest
leida murdva nurga A=2γ.
Leiame Brewsteri nurga αB=atan(n) ja temale vastava murdumisnurga γ=asin(sinαBn) ning lõpptulemuseks saame A=63,7∘.
Kui langemisnurk α≠0∘,90∘, siis vastavalt Jn 4.10B-le ei jää langev loomulik valgus pärast peegeldumist enam loomulikuks, I⊥≠I∥. Sellist osaliselt polariseeritud valgust iseloomustatakse polarisatsiooniastmega
Loomuliku valguse polarisatsiooniaste ja all peegelduval valgusel , peegelduva valguse polarisatsiooniaste on alati positiivne. Peegeldumine Brewsteri nurgaga võrduval langemisnurgal on lihtsaim viis loomulikust valgusest lineaarselt polariseeritud valguse saamiseks, kuid paraku on sel viisil polariseeritud valguse intensiivsus langeva valguse intensiivsusest.
Ka läbiv valgus on osaliselt polariseeritud, polarisatsiooniastme hindamiseks leiame v 4.15 ja v 4.18 abil amplituudide suhte
ja seega st läbiva valguse polarisatsiooniaste on negatiivne. Kui valgus langeb αB all paljudest tasaparalleelsetest klaasplaatidest koosnevale paketile, Jn 4.12, siis igasse plaati sisenemisel ja väljumisel polarisatsiooniaste suureneb ja lõpptulemusena me saame langemistasandis lineaarselt polariseeritud valguse.
Näide N 4.3
Lahendus
Valemi v 4.20 järgi
ja murdumisseadusest γ=0,55(≡31,80∘). v 4.21 järgi leiame ja saame, et
Kuna T∥=1, saame läbiva valguse polarisatsiooniastmeks Δ=−9,44%.
(K 4.12) Levikul suurema murdumisnäitajaga keskkonnast väiksema murdumisnäitajaga keskkonda, nt klaasist õhku, on murdumisnurk suurem langemisnurgast. Seega eksisteerib mingi maksimaalne langemisnurk , mille puhul ja . Sellisel piirjuhul omandab murdumisseadus kuju
(K 4.14) Kui , siis rakendades Fresneli valemeid ja arvutamiseks, saame joonisel Jn 4.13 toodud sõltuvused. Kuna langemisnurga väärtustel murduv kiir puudub, siis me räägime täielikust peegeldumisest, mida iseloomustab täieliku peegeldumise piirnurk . Jooniselt Jn 4.13 näeme, et kui , on nii peegelduva valguse paralleel- kui ka ristkomponendi suhteline amplituud positiivne, st peegelduv valgus on faasis langeva lainega, kui aga , tekib langemistasandis polariseeritud valgusel faasihüpe .
Analüüsimaks nähtusi täieliku peegeldumise piirkonnas, pöördume valemite v 4.14 ja v 4.19 poole, kus suhtelised amplituudid on avaldatud vaid langemisnurga kaudu. Mõlema avaldise lugejas ja nimetajas on liikmed, kus ruutjuure all on , mis puhul saab negatiivseks. Kuna imaginaarühik , siis ja amplituudid omandavad kuju
Mõlemad suhtelised amplituudid avalduvad kompleks- ja kaaskompleksarvu suhtena, sellise suhte moodul võrdub aga alati ühega, mis näitab veelkord, et tegemist on täieliku peegeldumisega.
Lisaks näeme, et täieliku peegeldumise piirkonnas sõltub peegelduva ja langeva valguse vaheline faasivahe langemisnurgast .
Vastavalt valemitele v 2.16 võib v 4.25 lugejad ja nimetajad esitada kujul exp(iϕ)
ning langeva ja peegelduva valguse faasivahe δ=2ϕ sõltub langemisnurgast nagu
Peegelduva valguse faasivahe langeva valguse suhtes langemisnurkade vahemikus on esitatud joonisel Jn 4.14A. Kui , siis ja δ⊥=0 ning kui , siis ja , vahepealsetel väärtustel kahanevad faasivahed monotoonselt, kuid mingil fikseeritud langemisnurga väärtusel ei ole faasivahed võrdsed, δ∥≠δ⊥.
Suuname nüüd kahe keskkonna lahutuspinnale lineaarselt polariseeritud valguse, mille asimuut langemistasandi suhtes on , st langeva valguse paralleel- ja ristkomponent on võrdse amplituudiga. Täieliku peegeldumise piirkonnas on võrdsed ka peegelduva valguse komponentide moodulid, kuid nendevaheline faasivahe erineb nullist ja seega on peegelduv valgus üldjuhul elliptiliselt polariseeritud.
Joonisel Jn 4.14B on faasivahe sõltuvus langemisnurgast kolme erineva aine puhul. Kui või , siis on komponentide vaheline faasivahe , valgus on lineaarselt polariseeritud II ja IV veerandis, vt Jn 2.10. Teemanti puhul, Jn 4.14B, on maksimaalne faasivahe ning kuna , on peegelduv valgus ringpolariseeritud. Teemant on liialt eksootiline materjal valgusnähtuste uurimiseks, hulga lihtsam on saada ringpolariseeritud valgust Fresneli „rombiks“ kutsutava rööptahukaga, Jn 4.15.
Rööptahukasse sisenev ja väljuv valgus on tahkudega risti ja nurk on valitud nii, et täielikul peegeldumisel faasivahe paralleel- ja ristkomponendi vahel on , vt Jn 4.14B. Kuna täielikke peegeldusi on kaks, siis summaarne faasivahe komponentide vahel on . Kui lisaks veel lineaarselt polariseeritud langeva valguse asimuut on , siis väljub rööptahukast ringpolariseeritud valgus.
Täielikul peegeldumisel on meil tegemist ideaalse peegliga, , mis leiab kasutamist nii allveelaevade periskoopides kui ka kujutise ümberpööramiseks nt binoklites, Jn 4.16.
Olulisim täieliku peegelduse rakendus on aga energia ja info ülekanne kiudoptika (lainejuhi, fiibri) vahendusel. Lihtsaimal juhul on silindrilisel kiul kaks põhielementi: südamik murdumisnäitajaga ja ümbris murdumisnäitajaga , Jn 4.17. Kui südamiku ja ümbrise lahutuspinnal , siis st peegelduskaod puuduvad ja põhimõtteliselt võiks valgus levida piki kiudu kuitahes kaugele. Tegelikkuses panevad valguse levikukaugusele piiri mitmed teised kaod, millest mõningaid (neeldumine, hajumine) vaatleme edaspidi.
Piirnurk määrab ära maksimaalse nurga , mille all väliskeskkonnast murdumisnäitajaga fiibrisse sisenev valgus levib peegelduskadudeta. Vastavalt joonisele ehk . Kuna , siis fiibri numbriline apertuur NA on
Kui fiibri sisendis on õhk, siis võrdub numbriline apertuur siseneva kiirtekimbu poolnurga siinusega.
Kujutise edastamist kiude kimbu abil kasutatakse endoskoopias, Jn 4.18A. Selleks valgustatakse esmalt uuritavat objekti ja seejärel projekteeritakse sealt hajunud valgus kiudude kimbule, milles iga kiud kujutab endast pildielementi. Kimbu väljundis projekteeritakse objekti kujutis vastuvõtjale, mis muudab ta elektriliseks ja lõpptulemust jälgitakse kuvari ekraanil. Sellisel viisil eristatakse objekti elemente, mille vaheline kaugus on 10μm.
Kiudoptika kui sidevahendi puhul algselt elektriline signaal digitaliseeritakse, saadud impulsside jada abil moduleeritakse valgusallika (leed-lamp või pooljuhtlaser) kiirgus ja saadud valgusimpulsid suunatakse kiudu. Oma levikul kius algselt ristkülikukujuliste valgusimpulsside kuju deformeerub mitmel põhjusel. Üheks põhjuseks on see, et erinevate nurkade all siseneval valgusel kulub kiu läbimiseks erinev aeg, toimub impulsside ajaline „laialivalgumine“, mille tulemusena pole naaberimpulsid enam eristatavad, Jn 4.18B. Valguse trajektooride pikkuse erinevus pole kaugeltki ainus põhjus, mis määrab digitaliseeritud info edastamiskiiruse ja eksisteerivad erinevad võtted nende piiravate faktorite mõju vähendamiseks, vt. 5.8.
Võrreldes teiste info edastamisviisidega iseloomustab kiudoptikat
- Laiaribalisus, mis võimaldab üheaegselt edastada telefonikõnet või TV kanali signaali.
- Häirekindlus, kuna info edastamiseks kasutatav sagedus on mitmeid suurusjärke suurem kui elektromagnetiliste häireallikate oma; puudub ka vajadus kiudoptika elektriliseks isoleerimiseks
- Väikesed kaod, mis võimaldavad infot edastada suurtele kaugustele ilma vahevõimenduseta.
- Suhteline odavus.
- Edastatava info kaitstus.
Hetkel (2018.a.) on kiudoptika tipptulemuseks info saatmine kaugusele edastamiskiirusega .
Näide N 4.4
Lahendus
Kuna αcr=asin(ncnF)=69,6∘, siis levib 75∘ all langev kiir fiibris kadudeta. Vahemaa Lα, mida see kiir läbib kahe peegelduse vahel on
sel ajal kui piki telge leviv kiir läbib vahemaa
Kuna kokku toimub kius
peegeldust, siis saame levikuaegade erinevuseks vaadeldud kiirte vahel
Saadud ajaintervalli suur väärtus osundab, et selliste parameetritega kiud ei luba suurt info edastamiskiirust ja optiline side toimub ühemoodiliste, vt 5.8.1, kiude abil.
(K 4.18) Tulemus, et täielikul peegeldumisel langeva ja peegelduva valguse amplituudid on võrdsed, , näib vastu rääkivat tangensiaalkomponentide võrdsuse tingimusele , mille järgi peab valgus tungima ka teise keskkonda. Lahendamaks seda probleemi, paneme esmalt kirja murduva valguse lainefunktsiooni tavapärasest veidi erineval kujul.
Kui α>αcr, siis lähtudes joonisest Jn 4.19 esitame murduva laine komponentide kaudu
Saadud tulemust võib interpreteerida kui piki x-telge levivat tasalainet. Kirjeldamaks seda lainet juhul kui α>αcr, teeme asendused ja . Miinusmärk ruutjuure ees on valitud lähtudes füüsikalistest kaalutlustest – plussmärgi valik viiks tulemuseni, kus valguse amplituud teises keskkonnas kasvaks eksponentsiaalselt.
Teisendades
saame piki lahutuspinda leviva pinnalaine lainefunktsiooni
mille amplituud kahaneb teises keskkonnas eksponentsiaalselt. Kaugusel
lahutuspinnast on pinnalaine amplituud kahanenud korda. Seega täielikul peegeldumisel tungib valgus esmalt sügavuselt teise keskkonda ja seejärel pöördub tagasi esimesse keskkonda, Jn 4.20A.
Kui joonisel Jn 4.20B on kaugus kahe prisma diagonaaltahkude vahel siis levib osa valgust ka teise prismasse ja peegeldumine pole enam täielik. Selline häiritud täielik peegeldumine on kasutusel optilistes sidesüsteemides info jaotamisel erinevate fiibrite vahel, Jn 4.20C. Mikroskoopias lubab pinnalaine piiratud ruumiline ulatus elimineerida tema segava mõju valgustatavate objektide enda kiirgusele, Jn 4.20D.
Näide N 4.5
Lahendus
Olgu murdumisnäitajad n1=1,6 ning n2=1 ja valguse lainepikkus λ2=633nm ning langemisnurk on α=50∘. Kuna antud juhul αcr=asin(1n1)=38,8∘, siis α>αcr st peegeldumine on täielik. Valguse levikukauguse hindamiseks prismadevahelisse ruumi rakendame valemit v 4.27
st ligikaudu kümnendiku lainepikkuse sügavusel on valguse amplituud vähenenud korda ja seega prismadevaheline kaugus ei saa olla palju suurem sellest väärtusest.
Seni vaatlesime peegeldumist ja murdumist vaid kahe ideaalse, kadudeta, dielektriku lahutuspinnal ja nägime, et langemisnurkadel omab peegeldumiskoefitsient suhteliselt väikest suurust. Seepärast on dielektrikust peegli kasutamine väheefektiivne ja valdavas enamikus peeglitest kasutatakse peegeldumist metalli pinnalt. Metalle aga iseloomustab juhtivus, , mille tulemusena osa valguse energiast eraldub Joule’i soojusena. Selle tulemusena valguse levikul juhtivas keskkonnas kiirgusvoog muutub, mis peab ilmselt kajastuma ka Fresneli valemites.
Leiame esmalt kiirgusvoo muutumise seaduspära neelavas keskkonnas. Langegu kadudega HILS keskkonna kihile paksusega monokromaatiline tasalaine, mille kiiritustihedus on , Jn 4.21A.
Neeldumise tõttu väheneb kiiritustihedus suuruse võrra, mis on võrdeline kihi paksuse ja langeva valguse kiiritustihedusega, võrdetegur aga iseloomustab valguse neeldumist lainepikkusel mingis konkreetses aines
Leidmaks kiiritustihedust lõpliku paksuse kihis, eraldame muutujad
integreerime
ja võttes saadud tulemuse astmesse, saame
Selles valemis avaldub selgelt neeldumiskoefitsiendi füüsikaline mõte: on vahemaa, mille läbimisel kiiritustihedus väheneb korda, Jn 4.21B. (K 4.23)
Kui tuua sisse kompleksne murdumisnäitaja
(K 4.24) siis on neelavas keskkonnas leviv tasalaine kirjeldatav lainefunktsiooniga
mis oma kujult on identne kadudevabas keskkonnas leviva laine lainefunktsiooniga v 2.19.
Selle näitamiseks paigutame murdumisnäitaja v 4.29 avaldisse v 4.30 ja eraldades reaalosa ja imaginaarosa sisaldavad eksponendid, saame
kus on amplituud keskkonda sisenemisel.
Võrreldes nüüd laine amplituudi kiiritustiheduse avaldisega v 4.28 ja arvestades, et , võib kirjutada
st murdumisnäitaja imaginaarne osa iseloomustab valguse neeldumist.
Seega alati, kui murdumisnäitaja osutub kompleksseks, on meil tegemist valgust neelava keskkonnaga.
Kuna murdumisnäitaja on üheselt seotud dielektrilise läbitavusega, siis kompleksne murdumisnäitaja tähendab ka kompleksset dielektrilist läbitavust, .
Kompleksse dielektrilise läbitavuse kirjutame kujul
Kuna nüüd ei ole kordaja elektromagnetlaine elektri- ja magnetvälja hetkväärtusi siduvas avaldises, , enam reaalarv, siis neelavas keskkonnas on ja vahel faasivahe.
Kui juhtivust omavas HILS keskkonnas levib monokromaatiline laine, siis teisendades Maxwelli võrrandit v 2.4
saame imaginaarosa ~εIm seose juhtivusega
ja
Seosed aine optiliste ja elektriliste karakteristikute vahel, v 4.34, võimaldavad leida dielektrilise läbitavuse ja juhtivuse väärtused ka optilisele diapasoonile vastavatel sagedustel.
Kui , siis tehes valemites v 4.14 ja v 4.19 asenduse , saame
Näeme, et peegeldumisel juhtivalt keskkonnalt on alati langeva ja peegelduva laine amplituudide suhe kompleksne st nende vahel on langemisnurgast sõltuv faasivahe, kusjuures δ∥≠δ⊥. Kui nüüd juhtivale keskkonnale langeb lineaarselt polariseeritud valgus, mille asimuut , siis on peegelduv valgus elliptiliselt polariseeritud.
Murdumisnäitaja reaal- ja imaginaarosa leitakse eksperimentaalselt ellipsomeetrilisel meetodil. Selleks suunatakse peegeldavale pinnale lineaarselt polariseeritud valgus. Kui langeva valguse polarisatsioonitasandi asimuut on , siis on tema ja komponendid võrdse amplituudiga, kuid peegelduvad need komponendid erinevalt,
ja nende komponentide vahel on faasivahe . Nii amplituudide suhe kui ka faasivahe on leitavad peegelduva elliptiliselt polariseeritud valguse analüüsist ja kasutades seoseid v 4.35, on leitav ka .
Peegelduskoefitsiendi ja juhtivuse vahelist seost on lihtne analüüsida väikeste langemisnurkade puhul, . Selleks teeme valemis v 4.4 asendused ja n2=~n
Kuna
siis
Kui on tegemist dielektrikutega, , siis taandub v 4.36 seosele v 4.7 ja on väike. Mida suurem on neeldumine ja mida väiksem on , seda suurem on peegeldumiskoefitsient.
Näide N 4.6
Lahendus
Kui valguse lainepikkus on 633nm, siis saame v 4.31 rakendamisel
mis on oluliselt väiksem nähtava valguse lainepikkusest vaakumis. Lainepikkusel on naatriumi murdumisnäitajad n=0,04 ja κ=2,78 ning galliumil vastavalt n=1,32 ja κ=6,45. Arvutades v 4.36 järgi saame naatriumi peegelduskoefitsiendiks R=0,98 ja galliumil – R=0,88.
Joonisel Jn 4.22 on lõplikku juhtivust omavate materjalide peegelduskoefitsientide ja sõltuvused langemisnurgast. Erinevalt dielektrikust, ei ole nüüd langemistasandis lineaarselt polariseeritud ja Brewsteri nurga all langeva valguse peegelduskoefitsient null. Mida suurem on juhtivus, seda vähem sõltub peegelduskoefitsient langemisnurgast.
Kohtugu ruumis kaks harmoonilist lainet, mille amplituudid on võrdsed. Kui mingis ruumipunktis kohtuvad lained nii, et hetkel on selles punktis koos mõlema laine harjad (seega mõne aja pärast on sealsamas kohakuti lainete nõod jne), siis liitlaine amplituud on võrdne lainete ja amplituudide summaga, Jn 5.1A. Nende lainete faasivahe selles punktis on δ=2mπ (m=0,1,2…) ehk lained on faasis.
Kui aga mingis teises punktis kohtub hetkel ühe laine hari teise laine nõoga, Jn 5.1B, siis võrdub summaarne amplituud nulliga. Selles ruumipunktis on faasivahe lainete vahel δ=(2m+1)π ehk lained on vastasfaasis.
Sellist lainete liitumist, mille tulemusel toimub summaarse laine amplituudi ümberjaotumine ruumis, nimetatakse interferentsiks ja see on sõltumatu nii sellest, kas on tegemist piki- või ristilainetega kui ka sellest, milline on lainete tekkimise füüsikaline mehhanism.
Lihtsaim viis lainete liitumise visualiseerimiseks on lainevann, Jn 5.2, kus lained veepinnal tekitatakse kahe varda abil, mis võnguvad sünkroonselt, st nende võnkumiste algfaasid on samad. Selle pildi järgi on raske väita, et punktis on liitlaine amplituud maksimaalne, kuid selgelt on näha sihid, kus veepinna võnkumiste amplituud on null, nende sihtide punktides kohtuvad lained vastasfaasis.
Kui valgus on laine, siis peaks interferentsinähtused olema jälgitavad ka valguse puhul. Jn 5.2B kujutab katseskeemi, mis baseerub Youngi 1802.a. esmakatsel. Valgusallikateks on läbipaistmatus tõkkes olevad kaks y-teljega paralleelset pilu, millele meie juhul langeb laserist lähtuv tasalaine. Seetõttu võib pilusid vaadelda kui kaht sünkroonselt kiirgavat valgusallikat. Interferentsipilt tekib ekraanil , mis on risti joonise tasandiga. Ekraanil on näha perioodiline süsteem heledatest ja tumedatest ribadest, mis on paralleelsed tõkkes olevate piludega. Kohtades, kus lained on faasis, st δ=2mπ, tekib hele riba; ekraani kohtades, kus lained on vastasfaasis, st δ=(2m+1)π, on tumedad ribad.
Interferentsi kvantitatiivseks kirjeldamiseks lähtume väljade superpositsiooniprintsiibist. Kui ruumipiirkonnas kattuvad kaks lainet, siis summaarne väli mingis punktis on
Kuna kiiritustihedus on võrdeline Poyntingi vektori ajalise keskväärtusega I∝⟨E⟩2, siis leidmiseks võtame v 5.1 mõlemad pooled ruutu
Siit järeldub, et kahest allikast lähtuva laine summaarne intensiivsus võib erineda kummastki allikast lähtuva laine intensiivsuste summast, .
Summaarne kiiritustihedus oleneb interferentsiliikmest 2⟨E1E2⟩. Juhul, kui ⟨E1E2⟩=0, on . Skalaarkorrutis on alati null, kui lainete polarisatsioonitasandid on risti, E1⊥E2.
Selle peatüki raames käsitleme vaid juhte, kus vektoritel E1 ja E2 on alati olemas samasihiline komponent, st liituvate lainete hetkväärtuste skalaarkorrutis erineb nullist, E1E2≠0. Lugedes elektrivälja vektorid paralleelseteks puudub vajadus arvestada valgust kirjeldava elektromagnetlaine mudeli vektoriseloomu ja me piirdume laineoptika lähendusega, kus valgust iseloomustab skalaarne laine.
Nüüd sõltub lainete liitumise tulemusena tekkiv valguse intensiivsuse ümberjaotumine ruumis ( interferentsipilt) interferentsiliikme ajalisest keskväärtusest. Interferentsipilt on registreeritav siis, kui kogu vaatlusaja jooksul interferentsiliikme ajaline keskväärtus mingis ruumipunktis ei muutu. Kui suur on , sõltub suuresti interferentsipildi salvestamise vahenditest. Inimese silma kosteaeg on , seega peab interferentsipildi visuaalseks jälgimiseks interferentsiliige olema konstantne vähemalt . Kui , on meil tegemist statsionaarse interferentsipildiga.
Interferentsi põhimõisted toome sisse eeldusel, et meil on tegemist monokromaatiliste lainetega. Rangelt monokromaatilise laine kestus on lõpmatu ning tema sagedus , amplituud ja algfaas ei muutu ajas. Sellistel ideaalsetel tingimustel on interferentsipilt alati jälgitav. Kohtugu ruumipunktis , mille kohavektor on r, kaks monokromaatilist lainet
Teisendame kahte viimast liiget
(vt v 2.18) Saime, et interferentsiliige ja seega ka summaarne kiiritustihedus mingis punktis on üheselt määratud liituvate lainete faasivahega selles punktis
Kui faasivahe on
siis
Kui faasivahe on
siis
Kokkuvõtvalt: kiiritustihedus on maksimaalne, kui lained kohtuvad faasis ja minimaalne, kui lained kohtuvad vastasfaasis. Vahepealsetel väärtustel omab ka kiiritustihedus vahepealseid väärtusi.
Reaalsetes valgusallikates muutub faasivahe ajas ning interferentsiliige tuleb leida kui ajaline keskväärtus üle vaatlusaja
Kui nüüd vaatlusaja jooksul faasivahe muutub juhuslikult palju kordi, omandab koosinusfunktsioon nii positiivseid kui ka negatiivseid väärtusi, mille tulemusena interferentsiliige on null ning .
Saime tarviliku tingimuse interferentsipildi tekkeks: faasivahe liituvate lainete vahel peab olema muutumatu kogu vaatlusaja jooksul
Laineid, mille puhul see tingimus on täidetud, nimetatakse koherentseteks.
Kattugu ruumis koherentsed tasalained 1 ja 2, mille lainevektorite moodulid on võrdsed k1=k2=2π/λ ja vektorite vaheline nurk on α=∠(k1,k2). Joonisel Jn 5.3A on kujutatud pideva- ja kriipsjoonega nende lainete lainefrondid. Lainete 1 ja 2 lainefrontide lõikepunkte ühendavatel pindadel on faasivahe lainete vahel konstantne ja seega on neil pindadel ka intensiivsus konstantne, IΣ=const.
Leidmaks pindade IΣ=const ruumilist jaotust, avaldame faasivahe lainevektorite kaudu, vt v 5.3,
ja toome sisse vektori K=k2−k1 , Jn 5.3B. Nüüd näeme, et konstantsele faasivahele (ja seega ka konstantsele kiiritustihedusele) vastavad ruumis pinnad, mille puhul Kr=const. Vastavalt punktile 4.2 paiknevad need pinnad risti vektoriga K. Iga kord, kui faasivahe muutub võrra, omandab kiiritustihedus sama väärtuse. Seega vastab ruumis tingimusele tasapindade parv, kusjuures kahe pinna vaheline kaugus on leitav tingimusest . Võrdhaarsest kolmnurgast, Jn 5.3B, saame et
ning seega
Interferentsiriba laius ( kaugus kahe lähima sama kiiritustihedust omava pinna vahel) on üks peamisi interferentsipilti iseloomustavaid karakteristikuid, mida saab eksperimendis ka vahetult mõõta. Valdavas enamikus interferentsikatsetest on nurk interfereeruvate lainete lainevektorite vahel väike, st , ja riba laius avaldub
Riba laius on seda suurem, mida väiksem on liituvate lainete lainevektorite vaheline nurk.
Joonisel Jn 5.4 lähtuvad kahest sünkroonselt kiirgavast punktallikast ja sfäärilised lained. Nii nagu eelnevalt, vastavad kindlale kiiritustiheduse väärtusele pinnad, mille igas punktis on lainete vaheline faasivahe konstantne
Näeme, et konstantse faasivahe tingimus taandub konstantse käiguvahe tingimusele
Geomeetriast on teada, et tasapinnal vastavad tingimusele v5.12 hüperboolid, mille fookused on punktides ja ja ruumis – pöördhüperboloidide pinnad. Paigutades vaatlusekraani paralleelselt z-teljega, on seal nähtavad hüperboolide harude parv, kui aga ekraan on risti fookuseid läbiva z-teljega, tekib seal interferentsirõngaste süsteem.
Käiguvahe on konkreetse katsekorralduse puhul lihtsalt arvutatav ja tihtipeale ka otseselt mõõdetav. Seepärast on otstarbekas esitada interferentsipildi maksimumi ja miinimumi tingimused, v 5.6 ja v 5.7, ka käiguvahe kaudu.
Maksimumi tingimus käiguvahe kaudu
Miinimumi tingimus käiguvahe kaudu
Arvu nimetatakse interferentsijärguks ning see näitab, mitu lainepikkust mahub käiguvahesse.
Kokkuvõtvalt: kui käiguvahe on võrdne paarisarv poollainepikkusega, on meil tegemist interferentsi maksimumiga; kui käiguvahe on paaritu arv poollainepikkust, on tegemist interferentsimiinimumiga.
Rõhutagem, et interferentsi puhul on füüsikaliselt primaarne faasivahe, mitte käiguvahe. Üldjuhul võivad allikatest ja lähtuvad lained levida erineva murdumisnäitajaga keskkondades. Kui valgus levib keskkonnas murdumisnäitajaga n, siis avaldub tema lainepikkus nagu , kus on lainepikkus vaakumis. Lõigule pikkusega mahub keskkonnas, mille murdumisnäitaja on , ρ/λ0nlainepikkust. Selleks, et vältida iga kord lainepikkuse ümberarvutamist, kasutatakse optilise teepikkuse mõistet. Kui üks laine läbib keskkonnas murdumisnäitajaga teepikkuse ja teine laine läbib teepikkuse keskkonnas murdumisnäitajaga , siis optiline käiguvahe on n1ρ1−n1ρ2. Kui on lainepikkus vaakumis, siis omandavad maksimumi ja miinimumi tingimused v 5.13, v 5.14 kuju
st optilise käiguvahe kasutamisel interferentsipildi miinimumi/maksimumi tingimus ei erine tingimustest v 5.13, v 5.14.
Üldjuhul ei ole mingis ruumiosas kattuvad lained koherentsed ja interferentsipilti ei teki. Klassikalistes katsetes on katse/ekse meetodil välja selgitatud tingimused interferentsipildi tekkeks. Kõigis selles punktis kirjeldatud katsetes kasutatakse koherentsete laine saamiseks üht ja sama võtet: ühest reaalsest valgusallikast lähtuva laine lainefront jaotatakse algselt kaheks ja seejärel saadud lained liidetakse. Sellist võtet nimetatakse lainefrondi jagamise meetodiks.
Matemaatiliste seoste tuletamisel tehtud lihtsustused baseeruvad tõsiasjal, et interferentsikatsetes on reeglina nurk interfereeruvate lainete lainevektorite vahel väga väike. Selleks, et selgitada katse olemust, on joonistel õigetest ruumilistest proportsioonidest kõvasti kõrvale kaldutud.
Jn 5.5 on Youngi katse põhimõtteskeem. Meie juhul langeb läbipaistmatus tõkkes olevale kahele pilule laserist lähtuv tasalaine (paralleelne kiirtekimp).
Pilud on koherentsete lainete allikateks ja vastavalt geomeetrilise optika terminoloogiale on mõlemad valgusallikad tõelised. Piludest lähtuvad kiired kohtuvad ekraanil punktis, mille koordinaat on . Kuna piludevaheline kaugus , kaugus pilude ja ekraani vahel ja ekraanil tekkiva interferentsipildi riba laius , siis võime lugeda, et
Sellises lähenduses võime ekraanile jõudvaid laineid lugeda tasalaineteks. Interferentsiriba laiuse leidmiseks tuleb kiirtevaheline nurk siduda katsekorraldust iseloomustavate suurustega. Katseskeemi sümmeetriateljel olevas ekraanipunktis on kiirtevaheline käiguvahe null, seega on seal tegemist interferentsi maksimumiga. Tekkigu nüüd järgmine maksimum kaugusel . Tõmmates pilude tsentritest ristsirged ekraanini , moodustub kaks täisnurkset kolmnurka ja vastavalt Pythagorase teoreemile võib kirjutada
ja
Lahutades esimesest avaldisest teise, saame
Arvestades tingimusi v 5.16, võime kirjutada
ja seega
Kuna , siis nurk interfereeruvate kiirte vahel on ja Youngi katse ribalaius on
Leiame nüüd kiiritustiheduse jaotuse piki ekraani . Kui pilude läbilaskvused on ühesugused, siis ja v 5.5 omandab kuju
Pärast teisendusi saame
ning asendades
ja
jõuame tulemuseni, mis kirjeldab intensiivsuse jaotust ekraanil
Katseskeemi parameetritele vastav v 5.18 graafik on toodud joonisel Jn 5.6. Kriipsjoonega on samal joonisel toodud ka reaalses eksperimendis mõõdetud sõltuvus. Ribalaius langeb väga hästi kokku eksperimentaalse väärtusega, kuid ribade intensiivsus ei jää eksperimendis konstantseks. Selle lahknevuse tagamaa selgub järgmises peatükis.
Näide N 5.1
Lahendus
- Nullisele käiguvahele vastava riba nihkumine üles tähendab, et ülemise kiire optiline teepikkus suurenes st küvetis murdumisnäitaja kasvas st rõhk suurenes
- Vastavalt valemile v 5.15 (n2−n1)ρ=mλ0 ja
Kirjeldatud põhimõte leiab kasutamist Rayleigh interferomeetris gaaside ja vedelike murdumisnäitajate määramisel.
Joonisel Jn 5.7A on valgusallikaks pilu , mis on risti joonise tasandiga. Allikast lähtuv valgus jaotatakse kaheks interfereeruvaks laineks biprisma abil, mille murdvad tahud on ka risti joonise tasandiga. Prismad murravad valgust oma aluse poole ja selle tulemusena biprisma ülemisest ja alumisest poolest tulevad lained kattuvad. Nende kahe hajuva laine näivad allikad , saame, pikendades murduvaid kiiri kuni lõikumiseni.
Interferentsiriba laiuse, , leiame joonise Jn 5.7B abil. Interferentsikatses on biprisma murdvad nurgad väga väikesed, , seetõttu on väike ka kiire kaldenurk . Sellest tulenevalt võib lugeda, et näivate allikate vaheline kaugus on palju väiksem kui kaugus allika ja biprisma vahel ning kaugus biprisma ja ekraani vahel. Lisaks sellele võib kaldenurga arvutamisel siinusfunktsiooni asendada nurgaga radiaanides ( ) ja saab näidata, et kiire kaldenurk prismas avaldub kujul (K 5.9), kus on biprisma murdumisnäitaja.
Saadud seosest johtub, et kaldenurk on sõltumatu sellest, millise nurga all valgus langeb prismale. Leidmaks lainevektorite vahelist nurka , avaldame näivate allikate vahelise kauguse . Kuna nurk on väga väike, võib kolmnurga külje lugeda kokkulangevaks kaarega, mille tsenter on punktis ja mille raadius on . Seega saame . Kuna , siis
ja ribalaius on
Erinevalt Youngi katsest sõltub ribalaius kaugustest ja . Lisaks sellele sõltub tekkivate ribade arv kaugusest . Kuna riba laius sõltub lainepikkusest, siis valge valguse kasutamisel on eri lainepikkusega ribad on üksteise suhtes nihkes ja interferentsijärgu suurenemisel interferentsipildi kontrastsus väheneb.
Näide N 5.2
Lahendus
Teisendame riba laiuse avaldist v 5.19 ja arvestame, et b=−∞
Näeme, et praegusel juhul riba laius ei sõltu kaugustest , .
Kuna δ=β(n−1)=0,00058rad, siis maksimaalne kaugus on
Kuna kolmnurk 123 on võrdhaarne, siis maksimaalselt kattuvad lained 17m kaugusel biprismast ja selle piirkonna laius on 2cm, millele mahub Nmax=2⋅10−2/Δx≈40 riba.
Erinevalt Youngi ja Fresneli biprisma katsetest, on Lloydi peegli katsekorraldus asümmeetriline, Jn 5.8. Reaalne valgusallikas paikneb väikesel kaugusel peegli tasapinnast ja ekraanil tekib interferentsipilt otse langeva valguse ja peegelduva valguse liitumise tulemusena. Laine näiva allika asukoha saame peegelduva kiire pikendusel, seega on Lloydi katses ühe laine allikas tõeline ja teisel - näiv. Kuna , siis ja
Katses võib peegli asemel kasutada klaasplaati, siis kuna langemisnurk on , kus peegelduskoefitsient ,vt Jn 4.10B, ja seega on liituvate lainete intensiivsused võrdsed. Piki pinda libisevate kiirte puhul on geomeetriline käiguvahe .
Näide N 5.3
Lahendus
Vastus peitub joonises Jn 4.9B: risttasandis polariseeritud valguse puhul lisandub kiirtevahelisele geomeetrilisele käiguvahele alati faasihüppest tingitud liige , kui langemistasandis polariseeritud valgusel suurtel langemisnurkadel faasihüpe puudub. Seega muutes polarisatsioonitasandit vahetavad interferentsipildis maksimumid ja miinimumid oma kohad.
Eelmises punktis kirjeldasime katseid, mille puhul summaarne valguse intensiivsus mingis ruumipunktis ei võrdunud üksikallikate intensiivsusega selles punktis, ?. Teisalt aga tavatingimustes, nt kasutades kirjutuslaua valgustamiseks ühe valgusallika asemel kahte, saame, et mistahes punktis IΣ≠I1+I2. Interferentsipildi jälgitavuse kvantitatiivseks hindamiseks toome sisse nähtavuse funktsiooni
Kus Imax ja Imin on intensiivsused interferentsipildi miinimumi ja maksimumi asukohas.
Nähtavuse funktsioon võib omandada väärtusi ühest kuni nullini. Esimesel juhul on interferentsiribad maksimaalse kontrastsusega ja teisel juhul on valgus ekraanil ühtlaselt jaotunud. Joonisel Jn 5.9 on näitena toodud v 5.4 abil leitud interferentsipildid erinevatel suhetel ja ka neile vastavad nähtavuse funktsiooni väärtused.
Käesoleva punkti eesmärgiks on välja selgitada tingimused, mille puhul nähtavuse funktsioon .
Leidmaks tingimusi, mille puhul interferentsipilt on nähtav, pöördume punktis 3.4 mainitud mudeli poole, kus valgusallikat vaadeldakse kui dipoolide kogumikku. Selleks, et dipool kiirgaks, peab ta saama allikast mingi koguse energiat. Selline ergastatud isoleeritud dipool kiirgaks laine, mille amplituud kahaneb eksponentsiaalselt,
kus on „loomulik“ eluiga. Valgusallikad koosnevad aga väga suurest arvust dipoolidest. Näitena - gaasilises madalrõhu () keskkonnas on suurusjärguliselt aatomit, kui neist ka miljondik kiirgab, on ikkagi dipoolide arv kolossaalne. Aatomitevahelistes põrgetes kaotab dipool oma energia, mille tulemusena dipooli kiirgus katkeb. Kuna põrgetevaheline aeg on lühike, , siis võib lugeda, et põrgetevahelise aja jooksul kiirgab dipool muutumatu amplituudiga lainepaketi.
Dipoolide teljed on orienteeritud ruumis juhulikult. z-telje suunas kiirgavad vaid need dipoolid, mis omavad x– ja y-telje sihilisi komponente. Vastavalt mudelile on mingi lainepaketi ajal suunas kiirgavate x-telje sihiliste dipoolide arv ja kõigi dipoolide algfaas . Sama kehtib ka y-telje sihiliste dipoolide kohta, kusjuures ja valgusallikas kiirgab aja jooksul z-telje sihis elliptiliselt polariseeritud laine. Järgmise paketi ajal muutub nii kiirgavate dipoolide arv kui ka algfaasid , ning seega nii ellipsi telgede orientatsioon kui ka nende suhe muutuvad, Jn 5.10.
Sellisele mudelile vastava laine x-telje sihilise komponendi ajaline kulg on joonisel Jn 5.11. Tegelikkuses muidugi ei muutu algfaas hüppeliselt, kuna kõigi dipoolide kiirgus ei alga samaaegselt ja seetõttu on üleminek ühelt paketilt teisele sujuv.
Kui eeldada, et kõigil dipoolidel on sama sagedus ja nende amplituudid on võrdsed, kuid algfaasid muutuvad juhuslikult, siis summaarse laine jaoks vaatluspunktis võib kirjutada
Leidmaks intensiivsust,
avaldame summaarse laine amplituudi ruudu
Rühmitame nüüd summade korrutises liikmed nii, et esimene rühm sisaldaks korrutisi, milles faasid on samad ja teises rühmas on erinevate faasidega korrutised
Esimene liige loogelistes sulgudes on võrdne dipoolide koguarvuga , teise liikme puhul arvestame, et korrutis on juhulik suurus, mis omab väärtusi vahemikus (–1, 1). Kuna on väga suur, siis teine liige sulgudes võrdub suure täpsusega nulliga ja amplituudi ruut võrdub . Saame: juhuslikult muutuva algfaasiga dipooli kiirguse summaarne amplituud on võrdeline ruutjuurega dipoolide arvust
Vaatleme nüüd juhtu, kui Youngi katses, Jn 5.5, kumbagi pilu valgustatakse sõltumatutest valgusallikatest st nende poolt kiiratavate lainepakettide algfaaside vahe on juhuslik suurus. Siis on fikseeritud ekraani punktis faasivahe konstantne aja jooksul ja on leitav v 5.5 abil. Järgnevate siinuspakketide ajal omab faasivahe juba teisi väärtusi ja seega ka on erinev. Kui siis faasivahe juhuslikul muutumisel intervallis muutub kiiritustihedus vahemikus .
Joonisel Jn 5.12 on kujutatud muutumine mingis ekraanipunktis aja 100τ jooksul. Kui arvutada keskväärtus üle saja , saame konkreetse näite puhul väärtuseks ehk .
Kas me sõltumatute allikate puhul näeme interferentsipilti või mitte, sõltub mõõteaparatuuri ajalisest kostest, vt 3.5. Kui interferentsipildi registreerimisaeg , siis on nähtavus . Kui , siis .
Statsionaarsel juhul, st , on kahest sõltumatust allikast lähtuva laine interferentsipildi nähtavus .
Klassikalistes interferentsikatsetes, vt 5.3, saadakse statsionaarne interferentsipilt ühest allikast lähtuva valguse jagamisel kaheks laineks, mis läbivad erinevad teepikkused. Selle tulemusena kohtuvad vaatluspunktis kaks laineosa, mis väljuvad valgusallikast erinevatel ajamomentidel ja . Valemis v 5.2 tähendab see interferentsiliikme E1E2 asendamist korrutisega . Lloydi katses, Jn 5.13, kohtub otse ekraanile jõudva laine hetkväärtus peegelduva laine hetkväärtusega .
Selleks, et nähtavus , peavad ekraanil kohtuma ühe ja sama lainepaketi eri osad, sest vaid sel juhul on garanteeritud, et faasivahe kahe laine vahel jääb konstantseks. Interferentsipildi jälgimiseks peab kehtima võrratus
Seega määrab lainepaketi kestus ära maksimaalse võimaliku käiguvahe, koherentsuse teepikkuse , ja seetõttu nimetatakse suurust ka koherentsuse ajaks ja tingimust v 5.23 ajalise koherentsuse tingimuseks.
Tingimus v 5.23 määrab ära ka maksimaalse, veel registreeritava, interferentsiriba järgu
kui , siis ja kui , siis ja me näeme ribade asemel ühtlast fooni.
Kuna lainepaketi kestus on seotud valguse spektri laiusega
(vt v 2.32) ja
(vt v 3.5), siis
Asetame saadud avaldise seosesse v 5.24 ja avaldame maksimaalse interferentsijärgu
(K 5.10) kus on spektraalriba keskmine lainepikkus.
Registreeritavate interferentsiribade arv on seda suurem, mida monokromaatilisem on valgus.
Seni eeldasime, et valgusallikat võib lugeda punktallikaks, st kõik valgusallika eri punktidest vaatluspunkti jõudvad lained on samas faasis. Vaatame nüüd, mis muutub, kui allika mõõtmed on lõplikud. Lähtume jällegi Lloydi katseskeemist, Jn 5. 14.
Valgusallikas koosneb kahest sõltumatust punktallikast ja , nendevaheline kaugus on . ja on peegelduvate kiirte näivad allikad. Ekraanil tekib kaks teineteise suhtes nihutatud interferentsipilti. Olgu allikaid läbiva sirglõigu ning kiirte ja vahelised nurgad vastavalt ja . Analoogiliselt võib kirjutada ja . Arvestades katsekeemi reaalseid mõõtmeid, võib lugeda, et β′1≈β1 ja .
Nüüd võime kirjutada ja . Lahutades esimesest avaldisest teise ja rühmitades liikmed ümber, saame
Näeme, et esimeses sulgavaldises on käiguvahe lainete vahel, mis lähtuvad allikast ja teises - käiguvahe allika puhul. Nii et avaldise vasakul pool on käiguvahede vahe
Kui mingis ekraanipunktis , siis ja interferentsipildid langevad kokku ja . Kui aga , siis on kohakuti ühe interferentspildi maksimum ja teise miinimum ning . suurenedes muutub interferentsiribade kontrastsus perioodiliselt, Jn 5.15A ning vastavalt muutub ka nähtavus nulli ja ühe vahel, Jn 5.15B.
Tavaolukorras on tegemist mitte kahe diskreetse allikaga, vaid kiirgab kogu riba pikkusega . Leidmaks, kuidas sel juhul muutub funktsioonina käiguvahest , jagame mõtteliselt valgusallika suureks hulgaks mittekoherentseteks paarideks, mille vahekaugus on . Iga sellise paari puhul on , kui
ehk suurendamisel interferentsiribad kaovad esimest korda, kui
Edasisel suurendamisel ilmuvad ribad uuesti, kuid nende nähtavus on oluliselt väiksem, Jn 5.15B.
Kokkuleppeliselt loetakse interferentsipildi nähtavust heaks, kui
Kohandame nüüd tingimuse v 5.27 Youngi katseskeemi juhule, Jn 5.16.
Kuna katseskeem on sümmeetriline, siis seostest ja järeldub , et ning . Toome sisse nurga (apertuurnurk). Kuna , siis ja interferentsipildi heaks nähtavuseks peab olema täidetud tingimus
Seosel v 5.27 baseeruvad hinnangud näitavad, et interferentsipildi jälgimiseks klassikalistes interferentsikatsetes peavad valgusallika mõõtmed olema väikesed. Selle tulemusena on tavaallikate kasutamisel ja lainefrondi jagamise meetodil tekkivate interferentsipiltide intensiivsus nõrk ja interferentsiribad on palja silmaga halvasti jälgitavad. On aga võimalikud katsekorraldused, mis on vabad neist puudustest.
Pohli katse puhul, Jn 5.17, valgustab allikas , mille lineaarmõõde on , õhukest plaati paksusega ; koherentsed lained tekivad peegeldumisel plaadi ülemiselt ja alumiselt pinnalt. Koherentsete lainete allikate vaheline kaugus on . Plaadi kaugus vaatlusekraanist on palju suurem kui kaugus plaadist allikateni ja , .
Kirjeldatud skeemi kohaselt on tingimusele v 5.27 vastavad nurgad β1=∠SS′P, ja võib lugeda, et .
Kolmnurgast saame . Teisendame nüüd tingimust v 5.27 ja arvestame, et on väike
ja seega interferentsipildi heaks nähtavuseks peab valgusallika mõõde rahuldama tingimust
Kuna kolmnurga külg langeb heas lähenduses kokku punktist tõmmatud kaarega 2fsinβ, siis nurk interfereeruvate kiirte vahel on
ja saame lõpliku tulemuse nii valgusallika mõõtmete kui ka interferentsiriba laiuse jaoks
Seosest v 5.30 johtub, et allika maksimaalsed mõõtmed sõltuvad lineaarselt ekraani kaugusest , st antud korral on interferentsipilt nähtav vaid teatud ruumipiirkonnas – interferentsipilt on lokaliseeritud.
Näide N 5.5
Lahendus
Valemitest v 5.30 ja v 5.31 saame Pohli katse tulemused
Sellised parameetrid lubavad jälgida auditooriumis piisava intensiivsusega interferentsipilti ka ilma täiendavate optiliste vahendite kasutamiseta.
Valemiga v 5.17 saame Youngi katse ribalaiuseks
st jälgimaks interferentsiribasid auditooriumis, on vaja täiendavat optikat.
Rakendamaks kauguse b leidmiseks valemit v 5.28 loeme, et apertuurnurk on väike st
ja saame
mis on auditooriumi jaoks absurdselt suur vahemaa. Reaalne katse on korraldatav, kui valgusallika mõõtmed on ligikaudu kaks suurusjärku väiksemad.
Pohli katses kasutatud viis koherentsete lainete saamiseks erineb põhimõtteliselt eelnevalt teistes katsetes kirjeldatust, koherentsed lained tekivad kahe järjestikuse peegeldumise tulemusega – tegemist on amplituudi jagamise meetodiga. Joonisel Jn 5.18A on kujutatud amplituudi jagamise meetod juhul, kui valgus peegeldub lõpliku paksusega läbipaistvalt plaadilt ja seepärast tuleb arvestada valguse murdumist plaati sisenemisel ja väljumisel. Vastavalt tingimusele v 5.29 peab nurk interfereeruvate kiirte vahel olema seda väiksem, mida suuremad on valgusallika mõõtmed. Piirjuhtumil, kui , peab nurk interfereeruvate kiirte vahel lähenema nullile st piirjuhul on tegemist ühe kiire jagamisega kaheks.
Langegu valgus nurga all õhus olevale tasaparalleelsele plaadile, mille paksus on ja murdumisnäitaja , Jn 5.18B, ja olgu plaadi kahekordne optiline paksus väiksem kui koherentsuse teepikkus . Sel tingimusel on peegelduvad lained koherentsed ja iseloomustamaks tekkivat interferentsipilti, leiame nende lainete vahelise optilise käiguvahe.
Kiir 2 läbib plaadis murdumisnäitajaga vahemaa , kolmnurgast leiame, et
ja kiire 2 optiline teepikkus on
Kuna õhus on kiired ja paralleelsed, siis levib kiir õhus lõigu võrra pikema teepikkuse, mille leidmiseks lähtume kolmnurgast ja murdumisseadusest ja saame . Lõik on leitav kolmnurgast
ja kiirte 2 ja 1 optiline käiguvahe on
lisandus käiguvahe avaldisse, sest kiire 1 peegeldumisel suurema murdumisnäitajaga pinnalt toimub faasihüpe võrra, vt 4.1, millele vastab ruumis nihe võrra.
Lõpptulemuseks saame
Arvestades, et
saame avaldada käiguvahe ka langemisnurga kaudu
Üldjuhul sõltub käiguvahe nii paksusest kui ka langemisnurgast . Lihtsustamaks analüüsi, vaatleme kaht piirjuhtu.
Esmalt olgu tegemist tasaparalleelse plaadiga, . Nüüd sõltub käiguvahe vaid valguse langemisnurgast , tegemist on samakalde interferentsiga. Joonisel Jn 5.19 langeb hajuv kiirtekimp lõplike mõõtudega valgusallikast tasaparalleelsele klaasplaadile. Kuna käiguvahe sõltub vaid langemisnurgast , siis on ekraanil tekkiv interferentsipilt sümmeetriline valgusallikat läbiva plaadi TP ristsirge suhtes.
Nagu ikka interferentsi puhul, sõltub summaarne intensiivsus ekraani mingis punktis käiguvahest lainete ja vahel. Kui , on tegemist intensiivsuse maksimumiga, käiguvahe aga vastab miinimumile. Valemi v 5.33 järgi langemisnurga suurenemisel käiguvahe ja seega ka interferentsijärk väheneb; suurema diameetriga interferentsirõnga järk on väiksem. Interferentsijärk on maksimaalne, kui α=0 ja seega mmax=2hn/λ.
Näide N 5.6
Lahendus
Maksimaalne interferentsijärk vastab kahekordsele plaadi optilisele paksusele
Kuna samakalde interferentsi puhul langemisnurga suurenedes interferentsijärk väheneb, siis esimesele (sisemisele) rõngale vastav interferentsijärk on mmax−1=465. Nüüd saab v 5.33 kuju
Teisendades saame
Seega vastab esimesele heledale rõngale peegeldumisnurk α=arcsin0,098=0,098rad (=5,64∘).
Nii nagu Pohli katse puhul, vt v 5.30, sõltub ruumipiirkond, kus valgusallika lineaarmõõtest . Mida suurem on , seda kaugemal on piirkond, kus interferentsipilt on nähtav.
Kui interferentsipilt on nähtav vaid piiratud ruumiosas, siis räägitakse lokaliseeritud interferentsipildist.
Kui , siis suure valgusallika interferentsipilt on lokaliseeritud lõpmatuses, tema jälgimiseks tuleb kasutada lõpmatusse teravustatud optilist seadet. Punktallika interferentsipilt on aga lokaliseerimata, st ta on jälgitav mistahes ruumipiirkonnas.
Langegu nüüd lõplike mõõtmetega valgusallikalt lähtuvad paralleelsed kiired langemisnurga all muutuva paksusega plaadile. Nüüd on käiguvahe sõltuv vaid paksusest, , tegemist on samapaksusinterferentsiga. Jooniselt Jn 5.20 on näha, et kiired ja (või nende pikendused) lõikuvad vaid plaadi pinna lähedal, st vaid seal on ; samapaksusinterferents on lokaliseeritud pinna lähedal ja interferentsipildi jälgimiseks tuleb kasutada optikat, mis on teravustatud sellesse piirkonda.
Näide N 5.7
Lahendus
Kirjeldatud katsetingimustest järeldub, et tegemist on samapaksusinterferentsi ribadega, interferentsiribad on paralleelsed õhkkiilu murdva servaga.
Leiame esmalt õhkplaadi murdva nurga
järelikult
on väga väike, seega võib lugeda, et mõlemad peegelduvad lained levivad samas sihis. Kuna praegu on , siis v 5.32 järgi on kahe naabermaksimumi tingimuseks
ja
seega käiguvahe naaberribade vahel on zm+1−zm=λ2=273nm ning riba laius on
Samapaksusinterferentsi näiteks on Newtoni rõngad, mille katseskeem on Jn 5.21A.
Läätsest ja plaadist koosnevale telgsümmeetrilisele süsteemile ülalt langev paralleelne kiirtekimp on risti läätse ülemise pinnaga. Tavaliselt vaadeldakse interferentsipilti peegelduvas valguses. Valgus peegeldub osaliselt tagasi kolmelt pinnalt (kiired , , ). Läätse kõverusraadius on suur () ja seetõttu võib lugeda, et läätse kumerpinnal on langemisnurk ning seetõttu võib jätta arvestamata murdumisega sellel pinnal ning, st kõigilt pindadelt peegelduvad kiired on omavahel paralleelsed. Kui valgustamiseks kasutatakse tavalist valgusallikat (mitte laserit), siis ületab läätse keskkoha lähedal tema kahekordne optiline paksus koherentsuse teepikkuse ja laine ei ole koherentne lainetega ja ning teda pole vaja arvestada interferentsipildi tekkel. Läätse ja alusplaadi vahel on õhk murdumisnäitajaga . Loetletud tingimustel omandab optilise käiguvahe avaldis v 5.32 kuju
siin on lisamine tingitud faasihüppest , mis tekib peegeldumisel alusplaadi pinnalt. Õhukihi paksus ja seega ka sõltub kaugusest . Interferentsipilt, mis on lokaliseeritud õhkkiilu pinna lähedal, on sümmeetriline läätse ja alusplaadi puutepunkti suhtes, heledad rõngad tekivad, kui Δ12=mλ ja tumedad, kui Δ12=(m+1/2)λ. Lähtudes Pythagorase teoreemist , leiame avaldise tumeda rõnga raadius jaoks. Kuna R≫h, siis võib lugeda, et h2≈0 ja 2Rh=x2 ehk
Kombineerides seoseid v 5.34 ja v 5.35, leiame kaugused läätse ja alusplaadi puutepunktist, mille puhul on tegemist interferentsi miinimumiga
kus on interferentsijärk. Näeme, et samapaksusinterferentsi puhul suuremale interferentsijärgule vastab suurem rõnga raadius .
Joonisel Jn 5.21B on toodud intensiivsuse jaotus piki rõngaste raadiust. Kuna peegelduvas valguses , siis näeme kontrastseid ribasid, . Läätse ja alusplaadi puutepunkti lähedal kus , on käiguvahe , st lained ja on vastasfaasis ja kustutavad teineteist. Seetõttu on interferentsipildi keskosas tume laik. Tumeda laigu tekkimine on lihtne ja veenev eksperimentaalne kinnitus, et peegeldumisel suure murdumisnäitajaga pinnalt toimub faasihüpe võrra.
Newtoni rõngad on jälgitavad ka läbivas valguses. Kuna kiirel , Jn 5.21A, on kaks lisapeegeldust, siis ja interferentsirõngad on vähekontrastsed. Hoopis tähelepanuväärivam on aga teine nüanss: kuna peegeldub nüüd suurema murdumisnäitajaga pindadelt kaks korda, siis faasihüpped liituvad, , ja läätse kumera pinna ja alusplaadi kokkupuute lähedal on ning faasis, mille tulemusena on interferentsipildi keskel hele laik.
Muutumatu kontrastsusega interferentsirõngad on registreeritavad vaid valgustamisel monokromaatilise valgusega, Jn 5.21B. Vastavalt seosele v 5.25, mida laiem on valgustava valguse spekter , seda vähem rõngaid on võimalik jälgida. Kasutades valgustamiseks hõõglampi, on jälgitavad kuni interferentsirõngast.
Õhukeste kilede (linnusuled, liblikatiivad, õlilaik veelombil, seebimull) värvus on samuti määratud samapaksusinterferentsiga. Valges valguses võib lugeda, et ja kui kile murdumisnäitajaga paikneb õhus, siis tingimus lubab hinnata värvitooni järgi kile paksust, Jn 5.22.
Mingi detaili valmistamisel antakse ette tema mõõtmete lubatav kõrvalekalle (tolerants) etteantud suurustest. Optiliste süsteemide kvaliteeti hinnatakse võrdluses lainepikkusega, nt läätse pind ei tohi erineda sfäärilisest rohkem kui võrra või peegli pind peab olema tasapinnaline täpsusega . Lihtne meetod pinna kvaliteedi hindamiseks baseerub samapaksusinterferentsil (Jn 5.23).
Ruumiosa kõrge pinnakvaliteediga etalonpinna ja testobjekti pindade vahel moodustab õhkkiilu. Kui mõlemad õhkkiilu pinnad oleksid ideaalsed tasapinnad, siis paralleelse kiirtekimbu peegeldumisel kiilult tekiksid interferentsiribad, mis on paralleelsed kiilu servaga. Kuna kaks paralleelset naaberriba erinevad lainepikkuse võrra ja toodud joonisel on maksimaalne hälve mingist ribast , siis joonisel toodud testobjekti pinnakvaliteet on .
Kui valgus läbib õhus temaga ligikaudu risti olevat klaasplaati, mille murdumisnäitaja on , siis peegelduskaod ühelt pinnalt on , vt v 4.7. Kasutades selgendavaid katteid, on seda kadu võimalik vähendada.
Kui klaasplaadil on kate, mille murdumisnäitaja ja optiline paksus , Jn 5.24A, siis peegeldumisel katte mõlemalt pinnalt tekib faasihüpe , aga kuna optiline käiguvahe nende peegelduvate kiirte vahel on , millele vastab samuti faasi muutus võrra, siis need peegelduvad kiired nõrgendavad teineteist. Peegelduva summaarse laine täielik kustutamine on võimalik, kui lainete amplituudid on võrdsed,
ehk
Meie näite puhul peaks . Paraku selliseid materjale ei eksisteeri, vähimat murdumisnäitajat n=1,38 omab MgF2. Lisaks sellele tagasilöögile sõltub murdumisnäitaja lainepikkusest, seega on minimaalne peegelduskoefitsient saavutatav vaid ühe lainepikkuse lähedal. Ligilähedaselt ideaalne tulemus on saavutatav, kui kasutada mitmekattelist süsteemi, kus suure ja väikese murdumisnäitajaga paksusega katted paiknevad vaheldumisi.
Optilises diapasoonis on dielektrikute peegelduskoefitsiendid väikesed, vt pt 4. Märkimisväärne peegelduskoefitsiendi tõus on saavutatav , kui kanda alusplaadile murdumisnäitajaga kaks katet, kummagi optiline paksus on . Joonisel Jn 5. 24B omab ülemine kate suuremat murdumisnäitajat kui alumine. Peegeldumisega pindadelt ja kaasneb faasihüpe , kuid peegeldumisel pinnalt faashüpe puudub.
Arvestades faasimuutusi katete läbimisel saame, et kolm peegelduvat kiirt tugevdavad üksteist. Samadel põhjustel nagu selgendavate katete puhul, ei võimalda kahekatteline süsteem saavutada ideaaltulemust. Peegelduskoefitsiendi saavutamiseks tuleb kasutada suurt arvu kaksikkatteid.
Michelsoni interferomeetris, Jn 5.25, kasutatakse koherentsete lainete saamiseks amplituudi jagamise meetodit.
Valgusallikast langeb valgus nurga all olevale tasaparalleelsele jagamisplaadile , mille tagumisel pinnal (peegeldumiskoefitsient ) jaguneb ta kaheks teineteise suhtes risti levivaks laineks. Horisontaalsihis leviv laine peegeldub tagasi peeglilt , läbib uuesti plaadi ja suundub kiirguse vastuvõtjasse, kokku läbib see laine jagamisplaati kaks korda. Vertikaalsihis leviva laine teel on kompensatsiooniplaat , mille paksus ja murdumisnäitaja on samad, mis plaadil , kuid tal puudub peegeldav kate. Pärast peegeldumist peeglilt läbib vertikaalkiir plaadi teist kordaja ja pärast peegeldumist plaadilt levib ta vastuvõtja suunas. Kompensatsiooniplaadi lisamise mõte interferomeetri skeemi seisneb selles, et peeglite ja võrdsetel geomeetrilistel kaugustel jagamisplaadi peegeldavast pinnast on võrdsed ka vastavad optilised teepikkused.
Michelsoni interferomeetris tekkiva interferentsipildi karakteristikud on lihtsalt määratavad, kui asendada interferomeetri tegelik skeem optilise asendusskeemiga. Selleks pöörame mõtteliselt peeglit vastupäeva võrra, selle tulemusena paiknevad mõlemad interfereeruvad kiired ühes sihis ja peeglit asendab tema „kujutis“ M′2. Nüüd on näha, Jn 5. 25A, et tekib interferentspilt peegeldumiste tulemusena peeglite ja M′2 vahel olevalt tasaparalleelselt õhkplaadilt. Kuna interferomeetrile langes hajuv kiirtekimp, siis näeme me samakalde interferentsipilti, mis lõplike mõõtmetega valgusallika korral on lokaliseeritud lõpmatusse.
Kui aga pöörata peeglit ümber tema telje, tekib ja M′2 vahel õhkkiil. Suunates interferomeetrisse paralleelse kiirtekimbu, tekivad samapaksusinterferentsi ribad, mis on paralleelsed õhkkiilu murdva servaga, Jn 5.25B. Interferentsipilt on nüüd lokaliseeritud pinna lähedal
1881. aastal loodud interferomeeter ja selle modifikatsioonid on füüsikas mänginud väga suurt rolli.
Michelson-Morley katse interpretatsioon viis tänapäeva füüsika ühe põhipostulaadini (vt 9.1); Michelsoni interferomeetriga mõõdeti otseselt valguse koherentsuse teepikkus; Michelsoni interferomeeter viis täheinterferomeetria tekkeni (vt 6.6.2.), Michelsoni interferomeetril baseerub modernse Fourier' spektromeetri töö ja lõpetuseks - Michelsoni interferomeetriga detekteeriti 2016. aastal gravitatsioonilained, mis tekkisid kahe musta augu ühinemisel. Ühelt poolt oli gravitatsioonilainete detekteerimine kinnitus üldrelatiivsusteooriast järelduvale ja teisalt - eksperimenditehnika hiigelsaavutus. Prognoositav efekt oli väga väike ja selle usaldusväärseks registreerimiseks tuli maha suruda erinevate müraallikate (seismiline ja soojuslik müra, valguse ja jääkgaasi rõhk peeglitele, jne) mõju. Valesignaalide mõju vähendamiseks detekteeriti gravitatsioonilained samaaegselt kahe Michelsoni tüüpi interferomeetriga, mis olid teineteisest kaugusel, Jn 5.26.
Neis interferomeetrites oli peeglite kaugus jagamisplaadist , jääkrõhk süsteemis oli atmosfäärirõhust ja peeglite pinnakvaliteet oli . Detekteeritav signaal, Jn 5.26, vastas peeglitevahelisele nihkele ().
Näide N 5.8
Lahendus
Kohandame valemit v 5.32 Michelsoni interferomeetri juhule: õhkplaadi murdumisnäitaja ja murdumisnurk Kuna mõlemad lained peegelduvad suurema murdumisnäitajaga pindadelt, siis peegeldumise faasihüpped võrra kompenseeruvad vastastikku ja optiline käiguvahe on Δ=2h=9,5⋅10−2m. Vastavalt ülesande tingimustele võrdub see käiguvahe koherentsuse teepikkusega LC=cτ=λ2/Δλ, vt 5.4.2, ja
Seisulaine on interferentsi erijuht, kus liituvad lained levivad vastassuundades. Mehhaanikas on lihtne demonstreerida seisulaineid nt kummivooliku abil. Seisulained tekivad , kui ühest otsast seina külge kinnitatud elastse kummivooliku teist otsa perioodiliselt võngutada. Voolikus tekib paisude (neis kohtades on vooliku võnkeamplituud maksimaalne) ja sõlmede (vooliku võnkeamplituud on null) süsteem.
Vaatamata tekkemehhanismile, peavad seisulained eksisteerima kõigi laineliste protsesside puhul.
Leiame seosed, mis iseloomustavad elektromagnetilist seisulainet. Langegu langemisnurga all peeglile z-telje positiivses suunas leviv lineaarselt polariseeritud tasalaine, Jn 5.27A,
Ideaalselt peeglilt, (), peegelduva laine võib esitada kujul
kus ja on peegeldumisel tekkivad faasihüpped. Nüüd kohtuvad peeglist vasakul kaks koherentset lainet ja vastavalt superpositsiooniprintsiibile
ehk (M 5.2)
Siinusfunktsiooni ees olev avaldises puudub aeg, seega on tegemist summaarse laine amplituudiga, mis sõltub koordinaadist z. Olgu nüüd , siis ja , ja seega
Seostest v 5.37 näeme, et elektrivälja EΣ sõlmed tekivad kohtades jne ning magnetvälja HΣ sõlmed paiknevad kohtades z=λ/4,3λ/4,5λ/4 jne – magnetvälja sõlmed on elektrivälja sõlmede suhtes võrra nihkes, Jn 5.27B. Sama ruumiline nihe kehtib ka elektri- ja magnetvälja paisude kohta. Elektrivälja amplituudväärtus kohal on ja kohal – st võnkumised naabersõlmedes on vastasfaasis.
Mingis ruumipunktis on EΣ ja HΣ hetkväärtused võrra nihutatud, seega Poyntingi vektori ajaline keskväärtus
Teiste sõnadega - seisulaine puhul energia ülekannet ruumis ei toimu, perioodi jooksul toimub vaid ühe paisu piires elektrivälja energia pumpamine magnetvälja energiaks ja vastupidi (see protsess on analoogiline LC kontuuris toimuvaga).
Elektromagnetilise seisulaine paisukohti on lihtne registreerida sentimeeterlainete diapasoonis, kuid nähtava valguse piirkonnas () on seda raskem teha.
Seisulaine eksisteerimist nähtavas diapasoonis demonstreeris Wieneri katse (1890), mille skeem on joonisel Jn 5.28.
Seisulaine tekib peeglile langeva ja sealt peegelduva valguse liitumise tulemusena. Peegli kohal on plaat, mis on kaetud õhukese fotoemulsiooni kihiga. Peegel ja plaat moodustavad õhkkiilu, millele vastav nurk on väike. Valguse toimel emulsioonikiht tumeneb. Kuna valguse-aine vastasmõju on määratud elektriväljaga, vt 2.3, siis maksimaalne peab tumenemine olema kohtades, kus on elektrivälja paisukohad, Jn 5.27B. Kui δ≈1′, siis kahe naaberpaisu vaheline kaugus on ja sellele vastava lõigu pikkus
on kergesti mõõdetav.
Eelnevalt saime, vt 4.6, et lainejuhis, mille murdumisnäitaja nF on suurem kui ümbritseva keskkonna murdumisnäitaja nc, levib valgus kadudeta siis, kui langemisnurk on suurem/võrdne täieliku peegeldumise piirnurgast, . Lähtudes nüüd interferentsi-alastest teadmistest, täiendame seda pilti. Vaatleme lihtsaimat olukorda, kus lainejuht on tasapinnaline. Joonisel Jn 5.29 levib valgus vasakult paremale ja lainejuhi piirpindadeks on kaks lõpmatu suurt x-teljega ristiolevat tasandit, milledevaheline kaugus on .
Pinnale (ja ka pinnale ) langev ja sealt peegelduv laine on koherentsed ja esitades lainevektori k tema komponentide kaudu, Jn 5.29, võib kirjutada
Kui vahemiku 0<x<α murdumisnäitaja nF on suurem kui murdumisnäitaja nC väljaspool seda piirkonda ja lisaks α≥αcr, siis piirpinnal on tegemist täieliku peegeldumisega st summaarne laine ning saame
ja seega
Nüüd võib kirjutada
Teisendades saame
Saadud funktsioon kirjeldab z-telje suunas levivat tasalainet, mille amplituud lainefrondil sõltub koordinaadist x, st tegemist on mittehomogeense lainega. See laine peab rahuldama ka teist ääretingimust, pinnal peab samuti . Siit järeldub, et ja seega . Saame, et lainejuhis levivad vaid lained, mille lainevektori x-komponent omab diskreetseid väärtusi
väärtustele vastavaid laineid nimetatakse lainejuhi moodideks.
Tingimus v 5.39 on analoogiline tavalise seisulaine tingimusega: lainejuhis saavad levida z-telje suunas vaid need lained, mille puhul x-telje sihis on täisarv poollaine pikkusi, Jn 5.30.
Vähendades kaugust võib saavutada olukorra, kus tingimus v 5.39 on täidetud vaid ühe moodi jaoks. Kuna sellisesse ühemoodilisse lainejuhti sisenev valgusimpulss levib seal vaid ühele lainevektori väärtusele vastavat teed mööda, ei valgu impulss ajas laiali ja seepärast suureneb info edastamiskiirus.
View _exp_open not found
Näide N 5.9
Lahendus
Vastuste leidmiseks lähtume seosest v 5.39 ja arvestades, et kx=kcosα, avaldame moodi sõltuvuse langemisnurgast
Maksimaalsele moodi väärtusele vastab täieliku peegeldumise piirnurk
Seega võimalike moodide arv 50μm lainejuhis on
Lainejuht on ühemoodiline, kui mmax<2 ehk
Amplituudi jagamise meetodit kasutavates interferentsikatsetes, vt 5.5, saadi koherentsed lained klaasplaadi abil, mille pindade peegeldumiskoefitsient oli väike, . Interferentsipildi nähtavus oli hea vaid peegelduvas valguses, sest sel juhul on lainete ja intensiivsused ligikaudu võrdsed. Tegelikkuses lisandub lainetele ja veel hulk samas suunas levivaid laineid , kuid suhteliselt väikese intensiivsuse tõttu on nende mõju interferentsipildi karakteristikutele väike ja tavaliselt neid joonistel ei kujutata.
Plaati läbivas valguses on aga lainel 2 kaks lisapeegeldust ja seega ning interferentsiribade nähtavus on väike.
Olukord muutub, kui plaadi pinnad on hästi peegeldavad. Joonisel Jn 5.31B on kahe paralleelse klaasplaadi vahel õhk ja plaatide pinnad on kaetud suurt peegelduskoefitsienti omava dielektrilise kattega.
Nüüd eksisteerib nii „õhkplaati“ läbivas kui ka temalt peegelduvas valguses suur hulk võrreldava intensiivsusega koherentseid laineid. Võrreldes joonise Jn 5.31 ja osa, näeme, et geomeetriline käiguvahe kahe naaberlaine ja vahel on sama, mis kahekiirelise interferentsi puhul. Praegu vaadeldaval juhul seisneb optilise käiguvahe erinevus avaldisest v 5.32 selles, et nüüd on plaadi murdumisnäitaja võrdne ühega ja kuna naaberlaine mõlemad peegeldumised toimuvad suurema murdumisnäitajaga pinnalt, siis summaarne faasihüpe on , seega on optiline käiguvahe ja faasivahe ja laine vahel vastavalt
ja
Järgnevalt piirdume vaid õhkplaati läbiva valgusega, eesmärgiks on leida summaarne laine , Jn 5. 31B. Plaadi paksus on ja tema pindade energeetilised peegeldumiskoefitsient ja läbimiskoefitsient on ja , kusjuures . Langev laine, mille amplituud on , murdub õhkplaati nurga all ja jaguneb korduvate läbimiste ja peegelduste tulemusena osalaineteks, mille komplekssed amplituudid on erinevad. Leidmaks neid amplituude, arvestame, et igal läbimisel muutub amplituud korda ja igal peegeldumisel korda. Laine läbib plaadi pindasid kaks korda, seega on tema amplituud E00T. Laine läbib pindasid samuti kaks korda, kuid lisaks sellele ta peegeldub ka kaks korda. Arvestades faasimuutust võrra, saame laine amplituudiks ja analoogiliselt laine ja laine jaoks ja .
Läbiv laine on osalainete summa
Kui tähistada , näeme, et on tegemist geomeetrilise progressiooniga ja
Kuna , siis osalainete arvu suurenemisel, , ja äsjasaadud avaldis lihtsustub
Kasutame Euleri valemit ja eraldame nimetajas reaal- ja imaginaarosad
Kuna läbiva ja langeva laine intensiivsuste suhe on
Tehes lugejas asenduse , avades nimetajas sulud ja kasutades trigonomeetrilisi teisendusi ning võttes nimetajas sulgude ette, jõuame tulemuseni
Vaid peegelduskoefitsiendist sõltuvat kordajat
siinusfunktsiooni ees nimetatakse peensuseks (ingl k finesse). Nüüd on läbiva valguse intensiivsust kirjeldav avaldis kujul, mis on tuntud Airy funktsioonina
Kui peegelduskoefitsient , siis ka ja läbiva valguse intensiivsus on funktsioon vaid faasinihkest . Kuna
siis saame avaldisest v 5.40 tingimuse, mille puhul läbiva valguse intensiivsus on maksimaalne .
ehk
Sõnadega: läbiva valguse intensiivsus on maksimaalne sellistel murdumisnurga (ja seega ka vastava langemisnurga) väärtustel, mille puhul optiline käiguvahe kahe järjestikuse osalaine vahel on täisarv lainepikkusi. See maksimumide paiknemise tingimus ei erine samalaadsest tingimusest 2-kiirelise samakalde interferentsi puhul. Ka nüüd vastab suuremale interferentsijärgule väiksem murdumisnurk , seega interferentsijärk kasvab rõngaste tsentri suunas. Kui plaadile peegeldumiskoefitsiendiga langeb hajuv kiirtekimp, siis tekivad interferentsirõngad, mis on sarnased joonisel Jn 5.19 esitatutega.
Kui , on läbiva valguse intensiivsus minimaalne
ning faasivahele vastab intensiivsuse maksimaalne väärtus
Neist seostest on lihtne leida nähtavuse funktsiooni väärtust, mis sõltub ainuüksi peegelduskoefitsiendist
Peegeldumiskoefitsiendi suurenemisel kasvab monotoonselt ka nähtavuse funktsioon ja kui R≥0.9, siis , Jn 5.32A. Joonisel Jn 5.32B on Airy funktsioon erinevatel peegelduskoefitsientide väärtustel, kõik sõltuvused on normeeritud maksimumi järgi, . Juht vastab kahekiirelisele interferentsile läbivas valguses – interferentsribad on vähekontrastsed. -i kasvades kontsentreerub enamik läbivast valgusest piirkondadesse, kus δ≈2mπ ja teistel väärtustel läheneb läbiva valguse intensiivsus nullile.
Hajuva valguse langemisel plaadile tekkivate interferentsirõngaste asukoht sõltub lainepikkusest ja seda asjaolu kasutatakse liitvalguse lahutamiseks komponentideks. Fabry-Perot interferomeetri, Jn 5.33, töö baseerub mitmekiirelise interferentsi seaduspärasustel.
Langegu lõplike mõõtmetega valgusallikast interferomeetrile hajuv valgus, mis koosneb kahest monokromaatilisest lainest lainepikkustega ja . Kuna samakalde interferentsipilt on lokaliseeritud lõpmatusse, jälgitakse seda läätse fokaaltasandis. Vastavalt valemile v 5.41 võime nende lainepikkuste jaoks kirjutada
ja
st fikseeritud interferentsijärgu puhul paikneb suurema lainepikkusega interferentsirõngas seespool väiksema lainepikkusega rõngast.
Spektraalriista võimet eristada lähedasi lainepikkusi iseloomustatakse kahe põhisuurusega. Nurkdispersioon näitab, millise nurga all on võimalik lahku viia interferentsirõngad, mille lainepikkused erinevad võrra. Nurkdispersiooni leidmiseks diferentseerime avaldist v 5.41
ja saame
Näeme, et mida kõrgem on interferentsijärk , seda suurem on vahekaugus rõngaste vahel, mida iseloomustab lainepikkuste erinevus .
Nurkdispersioon ei ole ainus karakteristik, mis iseloomustab spektraalriista võimet eristada lähedasi lainepikkusi. Joonisel Jn 5.34 omab nurkdispersioon ja osas sama väärtust, kuid vaid osas on võimalik spektraalselt lahutada neid lainepikkusi. Kvantitatiivselt iseloomustatakse spektraalset lahutusvõimet suurusega , kus on kahe laine keskmine lainepikkus. Fabry-Perot interferomeetri lahutusvõime määrab peegelduskoefitsient .
Näide N 5.10
Lahendus
Olgu λ2=λ1+Δλ siis kattumise tingimus on mλ2=(m+1)λ1 ehk
st vaba spektraalne piirkond on seda kitsam, mida suurem on interferentsi järk .
v 5.41 seob interferentsijärgu m õhkplaadi paksusega . Kuna keskmiste rõngaste puhul cosγ≈1, siis 2h=mλ ja ning m+1 järk ei kattu, kui
Paljud lainefrondi muutused (nt peegeldumisel, murdumisel, levikul mittehomogeenses keskkonnas) on kirjeldatavad geomeetrilise optika lähenduses. Kui aga valguse teel oleva mingi, lainepikkusega võrreldes suure tõkke toimel toimub lainefrondi deformatsioon, mille põhjuseks ei ole geomeetrilise optika seaduspärasused, siis on tegemist difraktsiooniga.
Difraktsioon on kergesti demonstreeritav lainevanni katses. Joonisel Jn 6.1A langeb tasalaine tõkkele, millest möödumisel lainefront deformeerub - laine on nähtav ka tõkketaguses piirkonnas.
Valguse puhul tuleb difraktsiooni jälgimiseks vaateekraan paigutada risti valguse levikusuunaga. Kui valgus leviks sirgjooneliselt, näeksime ekraanil teravat varju, Jn 6.1B. Tegelikkuses aga terav varju piir puudub, tõkke serval, , on valguse intensiivsus sellest, mida ta omab servast kaugel. Selle joonise alusel võib anda difraktsiooni lihtsama määratluse: difraktsioon on valguse levik geomeetrilise varju piirkonda. Joonisel Jn 6.1.B toodud jaotus on lihtsalt jälgitav, kui valgustada pooltasandi serva monokromaatilise (nt laserist lähtuva) valgusega.
Põhimõtteliselt on intensiivsuse jaotus tõkke taga arvutatav lähtudes Maxwelli võrranditest ja ääretingimustest tõkke serval. Matemaatilise komplitseerituse tõttu on seda analüütiliselt tehtud vaid mõningatel erijuhtudel, nt lugedes tõkke materjali ülijuhtivaks.
Õnneks tagab difraktsiooni puhul piisavalt täpse tulemuse ka valguslaine skalaarne mudel, kus valgus on ristilaine hetkväärtusega . Valguse skalaarne mudel vajab valguse levikumehhanismi selgitamiseks abiprintsiipi, milleks on Huygens-Fresneli printsiip.
H-F printsiip kirjeldab, kuidas toimub valguslaine levik allikast suvalisse punkti . Vastavalt Huygensile on ajahetkele vastava lainefrondi iga punkt (fiktiivse) sfäärilise lainekese allikas ja hetkele t+δt vastavaks lainefrondiks on nende lainekeste mähispind. Huygensi konstruktsioon selgitab kvalitatiivselt valguse levikut paljudel juhtudel, sh ka anisotroopsetes keskkondades, vt pt 8, kuid ta ei võimalda leida valguse intensiivsust punktis . Fresneli järgi on lainekesed koherentsed, seega nad interfereeruvad ja valguse intensiivsus vaatluspunktis on määratud lainekeste faasivahega selles punktis. H-F printsiibil baseeruvad kvantitatiivsed tulemused kalduvad mõningal määral kõrvale elektromagnetlaine mudeli abil saadutest alles siis, kui ava mõõtmed <5λ.
Kokkuvõtvalt:
Toetudes joonisele Jn 6.2, leiame H-F printsiibile vastava matemaatilise seose, mille algselt koostas Fresnel.
Olgu punktallika ja vaatlusekraani vahel läbipaistmatu tõke . Sirge, mis läbib allikat ja tõkke serva, määrab ekraanil geomeetrilise varju piiri, .
Kui laine amplituud lainefrondil on
siis pinnaelement saadab punkti laine, mille amplituud on võrdeline suurusega
Vastavalt Fresnelile, pinnatükk ei kiirga igas suunas ühtemoodi, vastasel korral eksisteeriks ka allika poole leviv laine. Lainekese amplituudi sõltuvust nurgast lainefrondi pinnanormaali ja laine levikusuuna vahel arvestab kaldetegur , mis nurga kasvades kahaneb monotoonselt ühest nullini.
Summaarne laine punktis moodustub kõigist lainefrondist lähtuvate lainekeste summast
Hilisem, skalaarsest lainevõrrandist lähtuv ja matemaatiliselt hulga komplitseeritum, Kirchhoffi difraktsiooniteooria tõestas kirjeldatud valguse levikumehhanismi paikapidavust kõigil juhtudel, kui . Kirchhoff sai ka kaldeteguri analüütilise avaldise
Rakendame H-F printsiipi lihtsaimal juhul: levigu valgus vabas ruumis punktallikast punkti , Jn 6.3.
on sfääriline lainefront, millele kaugus allikast on . Lähtudes punktist , mis on lainefrondi lagipunktist kaugusel , joonistame lainefrondile ringjooned, mille raadiused erinevad võrra:
kus on punktid lainefrondi pinnal.
Lainefrondil moodustub rõngaste (Fresneli tsoonide) süsteem ja laine amplituud punktis on summa Fresneli tsoonidest lähtuvatest lainetest.
Vastavalt joonisele on rõnga ümbermõõt 2πa1sinα, tema paksus dαa1 ja pindala
Selleks, et esitada pindala otseselt mõõdetavate suuruste kaudu, kasutame kolmnurga külje avaldamiseks koosinusteoreemi
Diferentseerides saadud avaldist, saame
ning kuna teisalt
saame neist avaldistest avaldada korrutise dαsinα ja seega rõnga pindala on
Näeme, et saadud pindala avaldises puudub sõltuvus tsooni numbrist – kõik tsoonid on ühesuurused. Kui lisaks arvestada, et lainefrondil on ning naabertsoonide kaugused punktist erinevad vähe, rm≈rm+1, omandab v 6.1 kuju
e
Vastavalt tsoonide konstruktsioonile on kahest naabertsoonist, Jn 6.4A, lähtuvad lained vastasfaasis, krm+1−krm=π, ja seega summaarne kompleksne amplituud punktis avaldub nagu
Grupeerime avaldise parempoolse osa rühmadesse
Viimane liige selles jadas on kas , kui on paarisarv või , kui on paaritu arv. Suure tsoonide arvu puhul on -le vastav kaldetegur ja seepärast on panus tühine.
Kuna naabertsoonide amplituudide moodulite erinevus on väga väike, siis võib lugeda, et avaldised sulgudes võrduvad nulliga ja lõpptulemuseks saame
st esimese (tsentraalse) Fresneli tsooni poolt punkti saadetud laine amplituud on kaks korda suurem kui sinna kõigist N tsoonist saadetud summaarse laine amplituud. Kuna intensiivsus , siis punktis on esimesest tsoonist lähtuva valguse intensiivsus neli korda suurem kui kõigist tsoonidest lähtuva valguse intensiivsus.
Saadud tulemuste interpreteerimiseks kasutame laine amplituudi ja faasi vektoriaalset esitust, vt Jn 2.3. Jaotame esimese Fresneli tsooni võrdse pindalaga alamtsooniks, Jn 6.4B, seetõttu on alamtsoonide laineid iseloomustavate vektorite pikkus ühesugune. Kuna tsooni keskelt ja tsooni servast lähtuvate lainete vaheline faasinihe on , siis faasivahe kahest naaber-alamtsoonist väljuva laine vahel on . Joonise Jn 6.5A vektordiagrammil on esimene Fresneli tsoon jaotatud alamtsooniks, faasivahe esimesest ja teisest alamtsoonist lähtuva laine vahel on , . alamtsooni laine on vastasfaasis . alamtsooni lainega.
alamtsooni summaarset lainet iseloomustava vektori saame, kui ühendame esimese alamtsooni vektori alguse -nda vektori lõpuga. Summaarne amplituud saavutab maksimaalse väärtuse , kui on kaasatud kõik esimese tsooni alamtsooni. Lisades esimesest tsoonist lähtuvatele lainetele järk-järgult ka teise tsooni alamtsoonidest tulevad lained, summaarne laine kahaneb ja esimesest ja teisest tsoonist tulevate lainete summa E1+E2≫0. Järgmise, kolmanda tsooni lisamisel saavutab summa jälle lokaalse maksimumi, kuid E3<E1. Alati, kui on avatud paarisarv Fresneli tsooni, on intensiivsus punktis nullilähedane, ning paaritu arvu tsoonide puhul on intensiivsus maksimaalne. Jätkates summeerimist jõuame lõpptulemuseni EP=E1/2, v 6.5B. Jooniselt Jn 6.5A näeme, et vektori pikkus, mis iseloomustab kuue esimese alamtsooni summaarset lainet, on korda suurem kui kõiki Fresneli tsoone iseloomustava vektori pikkus.
Olgu valgusallika teel ümmargune ava diameetriga , Jn 6.6. Vaatluspunkt paikneb allikast lähtuval ava keskristsirgel, CBC′ on pilu servi läbiv lainefront ning kaar CAC′ vastab punktist konstrueeritud äärmisele Fresneli tsoonile . Meid huvitab, kuidas sõltub valguse intensiivsus diameetrist ja kaugustest ja .
Vastavalt Fresneli konstruktsioonile on rõngaste arv seotud käiguvahega , . Maksimaalne on käiguvahe ava keskpunktist ja servast lähtuvate lainete vahel, . Lähtudes Pythagorase teoreemist, avaldame kolnurgast SCO:
ja kolmnurgast CPO:
Lugedes, et , saame neist kahest seosest avaldada otsitava käiguvahe
Seega avas olev Fresneli tsoonide arv
sõltub nii diameetrist kui ka kaugustest ja . Analüüsime saadud avaldist eeldusel, et avale langeb tasalaine, , (K 6.2). Esmalt olgu sümmeetriatelje punkt fikseeritud kaugusel ja hakkame suurendama ava diameetrit . Vektordiagrammil, Jn 6.7A, vastab sellele summaarset lainet iseloomustava vektori liikumine mööda spiraali. Iga kord, kui avaldises v 6.7 saab võrdseks paaritu arvuga , on intensiivsus, , suur. Kui on paarisarv, on intensiivsus nullilähedane.
Fikseeritud ava diameetri puhul ja liikumisel piki sümmeetriatelge näeme analoogilist tsüklilist intensiivsuse muutumist, Jn 6.7B. Suurtel kaugustel, a2≈∞, mahub avasse vaid osa esimesest Fresneli tsoonist, . Kaugusel on maksimaalne ja kaugusel – minimaalne. Edasisel vähendamisel vahelduvad intensiivsuse maksimumid ja miinimumid üha kiiremini, sest .
Olgu nüüd punktallikast lähtuva valguse teel ümmargune läbipaistmatu tõke, Jn 6.8. Kui ei oleks difraktsiooni, tekiks ekraanil ühtlaselt tume kettakujuline vari. Lähtudes aga Fresneli tsooniteooriast, tähendab tõkke olemasolu seda, et seoses v 6.5 puuduvad esimest liiget
st geomeetrilise varju keskel peab tekkima hele Poissoni täpp.
Näide N 6.1
Lahendus
Ava diameeter D=2mm | Ava diameeter D=2cm | |
1. Fresneli tsoonide pindalad on ühesuurused, v 6.4, selle tuletamisel loeti, et
Arvutame: kui D=2cm ja a2=10cm, siis
ja
Näeme, et isegi sellise väga suure Fresneli tsoonide arvu puhul kehtib tehtud lähendus suure varuga ja kõigil ülejäänud tabelis toodud juhtudel on kehtivus veelgi parem.
2. Näitame, et kaugusest rm tingitud lainekese amplituudi muutus punktis on väike.
Olgu D=2cm ja a2=10cm. Äärmisele Fresneli tsoonile vastab kaugus
Suhteline kauguse muutus on
Suurematel väärtustel on suhteline kauguse muutus veel väiksem.
3. Olgu endiselt D=2cm ja a2=10cm. Hindamaks kaldeteguri K(θ) väärtust, vt v 6.2, leiame esmalt äärmisele Fresneli tsoonile vastava kaldenurga
Kaldetegur on
Seega, nii nagu kauguse rm mõju nii ka K(θ) efekt amplituudile on väike.
Fresneli naabertsoonidest lähtuvad lained on vastasfaasis, st nad kustutavad teineteist. Kui aga eemaldada valemis v 6.5 nt kõik paarituarvulised liikmed
siis on kõik punkti jõudvad lained faasis ja summaarne intensiivsus punktis kasvab oluliselt. Selle idee realiseerimiseks leiame esmalt valemi v 6.7 baasil -ndale Fresneli tsoonile vastava rõnga raadiuse
Arvutades selle valemi järgi tsoonide raadiused ja kattes nt kõik paaritud tsoonid läbipaistmatu kattega, saame plaadi, mida läbinud kõik lained on punktis faasis, Jn 6.9.
Teisendame nüüd valemit v 6.7 ja arvestades, et ja on algebralised suurused, saame
Kui nüüd lugeda, et
näeme, et oma kujult langeb v 6.9 kokku õhukese läätse valemiga: kui on teada esemepunkti S asukoht, saab leida ka tema kujutise asukoha, Jn 6.9A. See valemite kokkulangevus ei ole formaalne, sest ka läätse puhul on kõik läätse eri osasid läbivad lained kujutise punktis samas faasis.
Aga erinevalt läätsest, millel on üks eesmine ja üks tagumine fookus, on tsooniplaadil palju fookusi. Kui tsooniplaadile langeb tasalaine, , siis mingil kaugusel mahub tsooniplaadi tsentraalsesse läbipaistmatusse ossa Fresneli tsooni, järgmises läbipaistvas osas on neljas, viies ja kuues Fresneli tsoon jne. Seega sel kaugusel läbivad tsooniplaati lained
Kuna sulgavaldises olevad naaberlained (nt E5 ja E6 ning E11 ja E12) kustutavad teineteist, siis kõik kaugusel olevasse punkti jõudvad lained on faasis, st meil on tegemist uue fookusega, mille fookusekaugus on .
Nihkudes tsooniplaadile veel lähemale ja korrates ülaltoodud arutelu, saame järgmise fookuse jne, seega on tsooniplaadil palju fookusi fookusekaugustega
kus . Kuna fookusi on mitmeid, siis iseloomustab tsooniplaati ka kujutiste paljusus.
Tasalaine langemisel tsooniplaadile eksisteerivad ka hajunud valguses sihid, milles levivad lained on omavahel faasis, nende lainete pikenduste lõikepunkt on tsooniplaadi näiv fookus , Jn 6.9B. Ka näivaid fookusi on palju.
R. Wood asendas läbipaistmatud rõngad kiledega, mis muutsid faasi võrra, selle tulemusena olid kõigist tsoonidest punkti suunduvad lained faasis ja intensiivsus selles punktis kasvas oluliselt.
Tsooniplaat on väga ilus näide Fresneli difraktsiooniteooria paikapidavusest, kuid nähtava valguse diapasoonis jääb tema abil saadava kujutise kvaliteet alla sellele, mida võimaldavad läätsed. Lisaks sõltub tsooniplaadi fookusekaugus tugevasti lainepikkusest, (K 6.6). Samas on tsooniplaat ainuvõimalik viis kujutise saamiseks röntgendiapasoonis, kuna materjalid läätse valmistamiseks selles diapasoonis puuduvad. Tänapäeva mikrolitograafia areng lubab valmistada röntgendiapasoonis sobivaid tsooniplaate ja selle tulemusena saab tsooniplaadi kasutamisel läätsena eristada objekti detaile, mille vahekaugus on . Selline lahutusvõime, vt 6.5.2, ületab rohkem kui kümnekordselt nähtava valguse diapasoonis saavutatu.
Näide N 6.2
Lahendus
Esimese tsooni raadiuse leidmiseks kasutame valemit v 6.8
Kui läbipaistmatud on paaritunumbrilised rõngad, Jn 6.9, siis amplituud punktis on summa rõngast saabuvast valgusest
Loeme, et kaldeteguri muutus tsooni puhul on väike ja seega tsooniplaati läbinud valguse amplituud punktis on 10|E2|. Kuna tsooniplaadi puudumisel on amplituud |E2|/2, siis tsooniplaat põhjustab -kordse amplituudi kasvu e intensiivsuse kasv punktis on -kordne.
Näide N 6.3
Lahendus
Kuna 1eV=1,6⋅10−19J, siis lähtudes valemist v 3.20 leiame lainepikkuse
ja esimese rõnga raadius on
Eelnevalt saime informatsiooni difraktsioonist vaid tugevasti piiratud tingimustel: nii allikas kui ka vaatluspunkt paiknesid tõkkes oleva ümmarguse ava keskristsirgel. Üldjuhtumil, Jn 6.10A, ei ole allikas ja vaatluspunkt keskristsirgel ning ava kuju on suvaline. Sellisel juhul tuleb punkti saabuvate lainekeste vaheliste faasivahede leidmiseks arvestada peale ava mõõtmete ka nurki ja ning kaugusi ja .
Taandame ülesande kergemini interpreteeritavale juhule, Jn 6.10B. Olgu valguse teel olevas tõkkes ristküliku-kujuline ava (pilu), mille -telje-suunaline külg on mitu suurusjärku suurem kui x-telje sihiline laius . Kui nüüd pilule langeb tasalaine, , mille lainefront langeb kokku pilu tasandiga, muutub difraktsioonipilt vaid -telje sihis ja tema muutused sõltuvad pilu laiusest , kaugusest ja difraktsiooninurgast (nurk langeva laine ja punkti leviva laine lainevektorite ( kiirte) vahel).
Igast pilu tasandis oleva lainefrondi väikesest lõigust lähtub sfääriline laineke amplituudiga dE∝1rexp(ikr)dx, Jn 6.11.
Piirkonda, kus lainekese amplituud sõltub märkimisväärselt tegurist 1/r, nimetatakse lähivälja piirkonnaks, see piirkond jääb meie kursuses vaatlusest välja. Piirkonda, kus sõltuvus tegurist 1/r on nõrk, sest , nimetatakse kaugvälja piirkonnaks. Kaugvälja piirkond jaotatakse omakorda kaheks.
Seni, kuni pilu servadest lähtuvate lainekeste teepikkuste erinevus põhjustab veel -ga võrreldavaid faasimuutusi, on tegemist Fresneli difraktsiooniga ning difraktsioonipilt sõltub nii difraktsiooninurgast kui ka kaugusest , Jn 6.12. Joonisel toodud sõltuvused saadi lähtudes Kirchhoff-Fresneli integraalist v 6.1 eeldusel, et .
Fraunhoferi difraktsiooni piirkonnas on faasivahe . Faasivahe on tühine juhul, kui käiguvahe (r2−z) on lainepikkusega võrreldes väike. Lähtudes Pythagorase teoreemist
saame praktilise lõpmatuse tingimuse
st võib lugeda, et (K 6.8) ja difraktsioonipilt sõltub vaid nurgast .
Võrreldes Fresneli difraktsiooniga on Fraunhoferi difraktsiooni matemaatiline pool jõukohasem ja tulemused on kergemini interpreteeritavad. Lisaks sellele on Fraunhoferi difraktsioonil suur rakenduslik tähtsus.
Selleks, et realiseerida Fraunhoferi difraktsiooni tingimusi ka suhteliselt suuremõõtmeliste objektide juhul, suunatakse läätse või nõguspeegli abil saadud tasalaine objektile ja difraktsioonipilti jälgitakse teise läätse (peegli) fokaaltasandis.
Olgu meil tegemist joonisel Jn 6.10B kujutatud ühedimensionaalse juhuga ja pilu läbilaskvus olgu sõltumatu koordinaadist . Tasalaine amplituudiga langeb pilule nii, et lainefront langeb kokku pilu tasandiga. Leidmaks avaldist difrageerunud laine jaoks jaotame vastavalt H-F printsiibile lainefrondi elementideks , mis kiirgavad koherentseid sfäärilisi lainekesi amplituudiga dE, Jn 6.13.
Leiame laine, milles saadab pilu algusest kaugusel olev element nurgaga määratud suunas. Selle laine faas erineb koordinaatide alguses oleva elemendi faasist võrra, Δ=xsinφ on käiguvahe. Kuna lainekese amplituud on , siis saame
Kogu pilu saadab nurga all laine
ning pärast integreerimist saame
Kui tuua nurksulgude ette ning lisaks korrutada ja jagada avaldise nimetajat kahega, saame
Kui nüüd tähistada
ja meenutada, et
Saadud funktsiooni sõltuvus argumendist on tuttav juba varasemast, vt v 2.31: kui , omandab funktsioon maksimaalse väärtuse . Kuna funktsiooni nullkohtades , kuid , siis seosest v 6.11 saame -nda nullkoha jaoks tingimuse
kus (K 6.9).
Amplituudi sõltuvus difraktsiooninurga siinusest on joonisel Jn 6.14A. Sõltuvalt -st muudab amplituud märki, mis tähendab, et naaberpiirkondade lainete vahel on faasivahe .
Kuna kiiritustihedus
siis
Üle pilu läbinud valgusest on kontsentreerunud tsentraalse maksimumi piirkonda, . Esimese, teise ja kolmanda lisamaksimumi tippväärtused moodustavad ligikaudu , ja kiiritustiheduse väärtusest kohal (K 6.10).
Pilu läbiv summaarne valgusvoog ∫π2−π2Iφdφ muidugi kasvab koos pilu laiusega, kuid mida kitsam on pilu, seda laiem on tsentraalse maksimumi ulatus, Jn 6.14B. Kui , siis difraktsioonipildi esimene miinimum , st tsentraalne maksimum katab kogu vaatetasandi. Fikseeritud pilu laiusel paiknevad lühema lainepikkusega miinimumid tihedamini, tsentraalne maksimum on kitsam.
Näide N 6.4
Lahendus
Leiame esmalt 3. järku miinimumile vastava difraktsiooninurga
Lähtudes valemist v 6.13, avaldame pilu laiuse
Näide N 6.5
Lahendus
v 6.13 alusel leiame
ja
Juhuse tõttu on väärtus ligilähedane Cd helesinise joone lainepikkusega, λ=480nm.
Joonisel Jn 6.15 moodustab langeva laine lainefront pilu tasandiga nurga . Seetõttu tekib pilu servadest lähtuvate lainekeste vahel täiendav käiguvahe ±bsinθ.
Joonisel kujutatu järgi on difraktsiooninurgale vastav summaarne käiguvahe . Kui , on käiguvahe null, st tsentraalne maksimum tekib pilu keskristsirge suhtes nurga all. Miinimumide asukohad on aga leitavad tingimusest
Mitmetes rakendustes kasutatakse pilusid, mille läbilaskvus muutub sujuvalt
Sellele sõltuvusele vastav graafik on joonise Jn 6.16 osajoonisel. Saab näidata, et sel juhul avaldub intensiivsuse jaotus difraktsioonipildis nagu
kus endiselt
Nagu nähtub jooniselt Jn 6.16, on sujuva läbilaskvusega pilu tsentraalse maksimumi laius suurem ja lisamaksimumid pole märgatavad.
Seni eeldasime vaikimisi, et joonisel Jn 6.10B kujutatud pilu mõõtmed ei ole vertikaalsuunas piiratud ja seega y-telje sihis pole difraktsiooniga vaja arvestada. Kui aga mõlemas sihis on pilu mõõtmed lõplikud, siis ristkülikukujulise ava koherentsel valgustamisel tekib kaks teineteise juhtes risti paiknevat ühe pilu difraktsioonipilti, Jn 6.17.
Leidmaks ümmarguse ava, mille diameeter on , difraktsioonipilti, minnakse üle polaarkoordinaatidele ja lõpptulemuse saamiseks integreeritakse üle lainekeste, mis lähtuvad infinitesimaalse laiusega rõngastest. Lõpp-tulemus avaldub esimest järku Besseli funktsiooni kaudu
kus
Funktsiooni esimese nullkoha tingimus on
Joonisel Jn 6.18A on ümmarguse ava difraktsioonipildi ruumiline jaotus ja joonisel Jn 6.18B on ümmarguse ava ja pilu difraktsiooni võrdlus.
Nagu näha, on võrreldes piluga tsentraalne maksimum mõnevõrra laiem, kuid lisamaksimumide intensiivsus on oluliselt väiksem.
Paljude optiliste seadmete (teleskoop, mikroskoop, kaamera) detailid ja ka silmaava on ümmargused ning nende läbimisel valgus difrageerub vastavalt seosele v 6.18. Seega erinevalt geomeetrilisest optikast, kus esemeruumi punktile vastab punkt ka kujutise ruumis, vastab reaalsuses igale eseme punktile difraktsioonipilt.
Vastavalt Rayleigh kriteeriumile on kaks esemepunkti veel eristatavad, kui teise punkti difraktsioonipildi tsentraalne maksimum on esimese punkti difraktsioonimiinimumi asukohas ehk kaks esemepunkti on eristatavad, kui nendevaheline nurkkaugus rahuldab tingimust
Joonisel Jn 6.19A on kujutatud piirjuhule vastav summaarse intensiivsuse jaotus eeldusel, et mõlemate punktide intensiivsused on võrdsed.
Rayleigh kriteerium määrab ära lahutusvõime põhimõttelise piiri: kui optiliste detailide kvaliteet on hea ja lisaks on maha surutud kõik aberratsioonid, siis difraktsioon paneb paika piirlahutuse. Märgatavalt erinevate intensiivsuste puhul on punktide eristamine problemaatilisem, Jn 6.19B. Loomulikult on tänapäeva mõõtmistehnika ja andmetöötlusega võimalik eristada märksa lähedasemaid objekte, kuid Rayleigh kriteeriumi eeliseks on tema selge füüsikaline mõte.
Tingimusest järeldub, et registreeriva seadme diameetri suurendamisel kasvab ka lahutusvõime. Kui teleskoobi, Jn 6.20, põhipeegli diameeter on (K 6.12), siis lainepikkusel on ehk kaaresekundit. Võrdluseks: kui võtta inimese silmaava diameeteriks , siis samadel tingimustel saame kaaresekundit.
Kaugvälja mikroskoopias on suurim lahutusvõime kasv saavutatud tänu lühematele lainepikkustele: kui nähtavas piirkonnas on eristatavad objektid vahekaugusega , siis kasutades pehmet röntgenkiirgust on jõutud objektide eristamiseni, mille vahekauguse on .
Näide N 6.6
Lahendus
Pöörates ekraani nurga võrra, riba laius ekraanil muutub
Loeme, et ribade eristamiseks kehtib sama kriteerium, mis punktobjektide puhul ja arvestame, et nurkkaugus ribade vahel on väike
kus silmaava diameeter on D=3mm, teisalt aga
Seega 10m kaugusel interferentsipildi jälgimiseks peab riba laius olema
Ekraani kaldenurgaks saame
(P 6.5) Täiendtõketeks nimetatakse tõkkepaare (nt pilu ja traat, ümmargune ava ja ketas jms), milles ühe valgust läbilaskvad osad on asendatud teise läbipaistmatutega nii, et kui valguse teel on korraga mõlemad tõkked, siis valgus tõket ei läbi.
Kui on tegemist Fraunhoferi difraktsiooniga, siis tõkete puudumisel tekib ekraanil valguslaik vaid sümmeetriateljel, teljevälistes punktides valgus puudub, Jn 6.21A.
Tõkke olemasolul tuleb valguse amplituudi leidmiseks ekraani suvalises punktis integreerida üle kõikide lainekeste, mis lähtuvad tõkke läbipaistvatest osadest, v 6.1. Kuna meil on tegemist täiendekraanidega, siis peab ekraani kõigi punktide jaoks kehtima seos
Tõkete puudumisel on teljevälistes punktides , seega ja . Saadud tulemus kirjeldab Babinet printsiipi, mille järgi teljevälises piirkonnas on täiendekraanide difraktsioonipildid eristamatud. Kuigi v 6.20 kehtib alati, on teljevälised difraktsioonipildid eristamatud vaid Fraunhoferi difraktsiooni korral, sest ainult siis on .
Olgu valguse teel tõke, milles on suur arv ühesugust ava, Jn 6.22, mille valgustatus on koherentne.
Kui iga ava saadab suunas laine , mille amplituud on , siis summaarne laine on
Pärast ümberrühmitamist saame
Esimene summa, , kirjeldab ühe ava difraktsioonipilti, kuid on sellest korda intensiivsem.
Teine summa aga sõltub avade paiknemisest tõkkes. Ühe liikme arvuline väärtus selles summas,
oleneb faasivahest . Kui avad paiknevad tõkkes kaootiliselt, siis on käiguvahe naaberavade vahel juhuslik suurus ning faasivahe omab juhuslikke väärtusi vahemikus . Seega suure hulga avade puhul on liikme positiivne ja negatiivne osasumma võrdsed ja ta võib lugeda nulliks. Kaootiliselt paiknevate avade interferentsipildi sõltuvus difraktsiooninurgast on identne ühe ava sõltuvusega, kuid tema intensiivsus on korda suurem.
Kui on aga tegemist avade korrapärase paiknemisega, nii et , muutub interferentsipilt komplitseeritumaks.
Olgu tõkkes paralleelset pilu, kusjuures iga pilu laius on ja kaugus mingi pilu algusest naaberpilu alguseni ( periood) on , Jn 6.23.
Jaotame jällegi lainefrondi elementaarlainekeste allikateks. Kui langeva valguse lainefront langeb kokku tõkke tasandiga, siis on kõigi laineallikate algfaasid samad. Difraktsiooninurgaga määratud suunas on käiguvahe -da pilu algusest kaugusel lähtuva lainekese ja esimese pilu algusest lähtuva lainekese vahel
ja seega avaldub see laineke kujul
Kogu -da pilu poolt kiiratava laine saame integreerides üle selle pilu laiuse
ning rühmitades tegurid edasiseks analüüsiks sobival viisil, saame
Loogelistes sulgudes ei ole midagi muud, kui meile juba tuttav ühe pilu difraktsiooni, vt 6.5.1, amplituudjaotus , kus . Summa üle kõikide pilude annab meile suunas leviva kogulaine
Tähistades
näeme, et summa puhul on tegemist geomeetrilise progressiooniga
kus q=exp(−2iδ). Seega
(K 6.14) Meid huvitab intensiivsuse jaotus
Teisendame algul lugejat
ja kasutades abivalemeid jõuame tulemuseni
Talitades nimetajaga analoogiliselt, saame
Tegur kirjeldab ühe pilu difraktsiooni ja tema käitumine on meile teada. Tegur aga kirjeldab pilust koosmõjul tekkivaid lisaefekte ja tema sõltuvus difraktsiooninurgast vajab detailsemat uurimist.
L’Hospitali reegli rakendamine annab meile nüüd
st nendes spetsiifilistes suundades on valguse intensiivsus
nendes suundades on tegemist peamaksimumidega. Kuna , saame peamaksimumide tingimuse
V 6.22 omab selget füüsikalist mõtet: interferentsimaksimumid on suundades , mille puhul naaberpiludest lähtuvad lained on faasis e käiguvahe on täisarv lainepikkusi ja nendes suundades .
Funktsioonil on suur hulk nullkohti, mille puhul , kuid . Seega , kui
Iga kahe peamaksimumi (nt ja jne) vahel on suunda, mille puhul ja seega on kahe peamaksimumi vahel kõrvalmaksimumi.
Esimese nullkoha tingimusest, , saame, et , st peamaksimumi laius on pöördvõrdeline pilude koguarvuga . See peamaksimumi laiuse pöördvõrdeline sõltuvus pilude koguarvust kehtib mistahes peamaksimumi puhul
Funktsiooni graafik on joonisel Jn 6.24A, kahe peamaksimumi vahel on miinimumi ja kõrvalmaksimumi. Joonisel Jn 6.24B on ühe pilu difraktsioonipilt, millega on läbi moduleeritud pilu interferentsipildid joonistel Jn 6.24C, D
Toome välja mõned -pilu difraktsioonipildi üldistest seaduspärasustest:
- peamaksimumide asukoht ei sõltu pilude arvust;
- peamaksimumide intensiivsust kontrollib ühe pilu difraktsioon, mida suurem on suhe , seda rohkem peamaksimume mahub tsentraalse maksimumi raamesse;
- pilude koguarvu suurenemisel on -järku peamaksimumi intensiivsuse kasv , kõrvalmaksimumide intensiivsus sõltub aga nõrgalt pilude koguarvust;
- suuremale pilude arvule vastavad peamaksimumid on kitsamad, peamaksimumide laius ∝N−1.
Seni vaadeldud -pilu süsteemi läbilaskvus muutus hüppeliselt, olles iga pilu piires ja piludevahelisel alal. Kui tegemist on väikese perioodiga d∼1μm süsteemiga, on tema valmistamine kallis. Tänapäeval on hulga lihtsam valmistada nn sinusoidaalse läbilaskvusega süsteeme. Leidmaks sellisel juhul intensiivsuse jaotust , tuleb valemis v 6.21 asendada seosega v 6.17ning võtta , uue sõltuvuse graafik on joonisel Jn 6.25. Sealt näeme, et difraktsioonipildis on vaid kolm peamaksimumi, .
Interferentsi peatükis saadi Youngi katse kirjeldamisel tulemus, mis ei vastanud täielikult eksperimendile, vt Jn 5.6: nägime, et vastupidiselt oodatule interferentsiribade intensiivsus ei jäänud konstantseks. Interpreteerime nüüd Youngi katset kui kahe pilu difraktsiooni. Kuna , siis pilude koosmõju kirjeldav tegur on
(M 6.5) kus endiselt . Kuna , on difraktsioonipildis vaid peamaksimumid, Jn 6.26.
Joonisel on näha, et mida kitsamad on pilud, seda vähem muutub interferentsiribade intensiivsus. Piirjuhul taandub kahe pilu difraktsioonipilt interferentsipildile, st ribade intensiivsus ei muutu.
Peamaksimumide paiknemise tihedus aga oleneb piludevahelisest kaugusest. Tõepoolest, vastavalt jadale v 6.23 on kahe peamaksimumi vaheline nurkkaugus määratud tingimusega , kust saame
st maksimumid paiknevad seda tihedamini, mida suurem on piludevaheline kaugus (baaskaugus).
Vastavalt Rayleigh kriteeriumile, vt 6.5.2, on ühe ava puhul minimaalne objektidevaheline nurkkaugus määratud selle ava lineaarmõõtmega , Jn 6.27A
Kuna , siis kahe ava difraktsioonipildi registreerimisel on peamaksimumide vaheline nurkkaugus väiksem, kui Rayleigh kriteeriumiga määratud nurk.
Näitame, et kahe ava difraktsioonipildi registreerimine võimaldab eristada lähedasemaid objekte, kui see johtub Rayleigh kriteeriumist. Langegu valgus kahest mittekoherentsest allikast, mille nurkkaugus on , kahest avast koosnevale süsteemile, Jn 6.27B. Käiguvahe tõttu on mõlemast objektist tekkivad difraktsioonipildid nihutatud, kuid kui baaskaugus on väike, on difraktsiooniribad kontrastsed, , Jn 6.27C. Kui aga suurendada piludevahelist baaskaugust, siis ribade-vaheline nurkkaugus väheneb ja kui käiguvahe
ehk kaugusel on nähtavus , Jn 6.27D. Seega ribade kadumine annab meile minimaalse võimaliku objektide vahelise nurkkauguse, mis tõttu on oluliselt väiksem, kui see tuleneb Rayleigh kriteeriumist.
Enimkasutatud on kirjeldatud meetod astronoomias nii tähtedevahelise nurkkauguse kui ka tähtede diameetri mõõtmisel. Joonisel Jn 6.28A esitatud skeemi pakkus välja Michelson, nähtavas piirkonnas on maksimaalsed baaskaugused . Suurendades joonisel Jn 6.28A teleskoopide vahelist kaugust , nähtavus väheneb ja piirolukorras, näeme ühele teleskoobi difraktsioonipildile vastavat kujutist.
Vastavalt tingimusele
sõltub peamaksimumide asukoht lainepikkusest, st difraktsioonivõre võib kasutada liitvalguse lahutamiseks üksikuteks komponentideks (K 6.18).
Nii nagu Fabry-Perot interferomeetri puhul, vt 5.9.1, leiame difraktsioonivõre nurkdispersiooni
ja lahutusvõime
Selleks diferentseerime peamaksimumide tingimust, dcosφdφ=mdλ, saame
Kuna praktikas huvipakkuvate mõõteskeemide puhul , on seda suurem, mida kõrgem on difraktsioonijärk ja mida väiksem on võre periood . Saavutamaks mõõtmiseks piisavalt suuri nurki, on vaja vähendada perioodi (K 6.19). Sõltuvust difraktsioonijärgust demonstreerib joonis Jn 6.29A: kaks lähedast lainepikkust ja on selgelt eristatavad alates järgust .
Lahutusvõime leidmiseks rakendame Rayleigh kriteeriumi: -järku spektris on ja veel eristatavad, kui seosest
leitav peamaksimumi asukoht langeb kokku lainepikkuse difraktsioonipildi esimesele nullkohale vastava nurgaga , v 6.24,
Seega
ja
lahutusvõime on võrdeline nii spektri järguga kui ka pilude koguarvuga . Tõepoolest, joonis Jn 6.29B näitab, et pilude koguarvu suurenemisega kaasneb peamaksimumi kitsenemine ja seega on võimalik eristada lähedasemaid lainepikkusi.
Näide N 6.7
Lahendus
Koondame tabelisse edasiseks kasutamiseks vajaminevad suurused sobivas vormis; lainepikkusele ja peamaksimumile m=1 vastava difraktsiooninurga ja leiame v 6.27 abil minimaalse lainepikkuste vahe, mis oleks peamaksimumi järgu m=1 puhul veel eristatav
Lahutusvõime kasvab koos järguga , kuid iga võre puhul eksisteerib maksimaalne võimalik järk, mis on leitav peamaksimumi tingimusest. Kuna sinφ≤1, siis
m≤λ/d, kus on täisarv. Maksimaalne järk on tabeli 6. reas.
1 | Võre, joont/mm | |||
2 | Periood , m | |||
3 | ||||
4 | Difraktsiooninurk , rad | |||
5 | Minimaalne , m | |||
6 | Maksimaalne järk | |||
7 |
Tabelist näeme, et difraktsioonivõre karakteristikud ei piira vaadeldavate spektrijoonte lahutamist ja lahutusvõime on nüüd määratud pikslitevahelise kaugusega . Sellele suurusele vastav nurkkaugus on
Teisalt, kui m=1, siis saame peamaksimumide tingimusest lainepikkuste vahele λ2−λ1-vastava nurkkauguse
ehk
Tulemused on tabeli 7. reas.
δφ ja Δφ võrdlusest järeldub, et vaid võre 1200joont/ mm sobib püstitatud eesmärgi saavutamiseks ja antud juhul on lahutusvõimet piiravaks faktoriks laengukogumisseadme pikslite vaheline kaugus. Põhimõtteliselt võiks kasutada spektri registreerimiseks kõrgemaid spektrijärke, kuid praeguse lihtsa võre puhul muutub peamaksimumide intensiivsus μm−2.
Enamikel juhtudel on tänapäeva spektromeetrites kasutusel peegelvõred, mida lihtsustatult võib kujutada koosnevana paralleelsest peegliribast laiusega ja perioodiga , Jn 6.30A.
Kui naaberribadele langeb tasalaine nurga all, siis vastav käiguvahe on . Difraktsiooninurgaga määratud suunas lisandub käiguvahe Δ3,4=dsinφ. Kui mingitel väärtustel summaarne käiguvahe rahuldab tingimust , siis tekivad nendes suundades peamaksimumid. Joonisele Jn 6.30A vastaval juhul on peamaksimumi tingimuseks
mida võib (M 6.6) esitada ka kujul
Kui ("libisev langemine“), siis peegeldumisnurga lähedastel väärtustel on väike ja ning võib kirjutada
Libiseval langemisel asendub võrekonstant märksa väiksema suurusega , seetõttu suureneb nurkdispersioon ja saab võimalikuks difraktsioonivõrede kasutamine ka lühematel lainepikkustel, kus tavatingimustel on peamaksimumidele vastavad nurgad registreerimiseks liiga väikesed.
Spektraalanalüüsi vaatevinklist on lihtsate tasapinnaliste võrede puudujäägiks energia kontsentreerumine null-järku peamaksimumi, kus mingit valguse lahutamist spektriks ei toimu. Difraktsioonivõre lahutusvõime kasvab -i kasvades, kuid tihtipeale on kõrgemat järku peamaksimumide intensiivsus liiga väike nende usaldusväärseks registreerimiseks, Jn 6.29. Kasutades nn profileeritud võresid, on võimalik saavutada difrageerunud valguse kontsentreerumine sobivasse spektrijärku. Idee tasemel edastame selle joonise Jn 6.30B abil, kus difraktsioonivõrel on saehamba profiil. Ühe pilu difraktsiooni iseloomustav tegur valemis v 6.21 omab maksimumi tingimusega määratud suunas, vastav nurk on nüüd leitav pinnanormaali järgi. Teisalt on aga peamaksimumide asukoha määramisel lähtutud pinnanormaalist : muutes langemisnurka ja kaldenurka , võib ühe pilu tsentraalse maksimumi viia kokku -järku peamaksimumiga.
Näide N 6.8
Lahendus
Kirjeldatud tingimustel on difraktsioonivõre periood d=5⋅10−6m=5μm ja pilude koguarv N=3⋅104. Kui me tahame, et maksimaalne energia oleks koondunud järku , φ=φm, siis peegeldusseaduse põhjal on joonisel Jn 6.30B olevad nurgad on seotud nagu
ehk
ning peamaksimumide tingimus on
Vastavalt püstitatud eesmärgile θ=ε ( Littrowi paigutus) ja seega
Selleks, et difrageerunud valguse energia lainepikkusel 580nm oleks suurim järgus m=10, peab kaldenurk olema
Spektraalseks lahutuseks saame
ja minimaalne intervall kahe lähedase lainepikkuse vahel on
Littrowi paigutusega difraktsioonivõred leiavad kasutust mitmetes seadmetes valguse monokromaatilisuse suurendamiseks.
Tavaliselt saadakse fotograafias 3-mõõtmelise objekti 2-mõõtmeline kujutis läätsede süsteemi abil. Objekte, mis ise ei helendu, valgustatakse mingist välisest allikast ja lääts projekteerib objektilt hajunud valguse informatsiooni salvesti (tajuri) pinnale, Jn 6.31.
Objekti valgustamisel kiirgab iga tema väike piirkond (piksel ) sfäärilise hajuva laine (esemelaine)
mille 1:1 suurendusega lääts transformeerib koonduvaks laineks
Need lainefunktsioonid sisaldavad informatsiooni nii piksli poolt kiiratava laine intensiivsusest, kui ka piksli asukohast . Kui objekti valgustatakse mittekoherentse valgusega, siis muutub algfaas δi pikslist pikslisse juhuslikul viisil. Kuna hetkväärtust ja seega ka faasi pole optikas võimalik registreerida, siis informatsioon objekti ruumilisusest läheb tavafotograafias kaduma ja tajur salvestab vaid intensiivsusega võrdelised signaalid. Salvestus toimub kas fotokeemiliste (fotoplaat, film) või elektriliste (laengukogumisseadmed) protsesside tulemusena.
Lisamiinuseks tavafotograafias on piiratud sügavusteravus („teravusulatus“) – fikseeritud tajuri asendis saame ideaalse (st vaid difraktsiooniga piiratud) kujutise vaid objekti ühes tasandis olevatest punktidest. Nagu näha jooniselt Jn 6.31, tekib objekti teiste tasandite pikslitest hajumisrõngas. Sügavusteravuse all mõistetakse piire, mille raames kujutise punktide laialimääritus on veel aktsepteeritav.
Holograafia (P 6.6)on meetod esemelaine salvestamiseks ja taasesitamiseks. Saamaks infot objekti ruumilisusest, registreeritakse holograafias faasivahe kahe koherentse laine vahel. Liitugu fotoplaadil sfääriline esemelaine amplituudiga
ja tasalaine (tugilaine) amplituudiga , Jn 6.32.
Tekkiv interferentsipilt on telgsümmeetriline esemepunktist lähtuva fotoplaadi ristsirge suhtes. Leiame, kuidas sõltub lainetevaheline käiguvahe kaugusest . Vastavalt Pythagorase teoreemile ja lugedes, et , saame
Kuna interferentsimaksimumide tingimuseks on , siis -nda maksimumi asukohale vastab tingimus
Kui nüüd teisendada tsooniplaadi rõngaste jaotust kirjeldavat valemit v 6.8, võttes , siis näeme, et interferentsirõngad jaotuvad sama seaduspärasuse järgi nagu tsooniplaadi rõngad.
Esemelaine ja tugilaine koosmõjul muutub pikslit iseloomustav intensiivsus piki rõngaste raadiust nagu
kus
Üheks võimalikuks interferentsipildi salvestiks on fotoplaati kattev fotoemulsiooni kiht, mis sisaldab valgustundliku hõbebromiidi kristalle. Kristallid neelavad valgust ja selle tulemusena fotoplaat tumeneb, st tema läbilaskvus väheneb. Läbilaskvuse sõltuvus korrutisest , kus on kiiritustihedus ja – säriaeg, on mittelineaarne, Jn 6.33A. Vaid kõvera keskosas võib lugeda sõltuvust lineaarseks.
Tugilaine intensiivsus („tööpunkt“) valitakse nii, et interferentsipildi intensiivsuse jaotus jääks läbilaskvust iseloomustava kõvera lineaarsesse ossa. Sellisel juhul sõltub läbilaskvus valguse intensiivsusest nagu
kus on fotomaterjali iseloomustav suurus.
Kui nt , siis võib esimeses lähenduse avaldises v 6.30 liikme jätta arvestamata, saame
sellele sõltuvusele vastav graafik on joonisel Jn 6.33B.
Esemelaine taastamiseks suunatakse tugilaine hologrammile samas suunas nagu salvestamisel. Hologrammi läbiva laine Et×T(r) leiame, pannes seosesse v 6.31 avaldise v 6.30
Näeme, et läbiv laine omab kolme komponenti, Jn 6.34.
- Esimene neist on tasalaine, mis levib tugilainega samas suunas ja ei sisalda informatsiooni objekti kohta.
- Teine liige kirjeldab hajuvat sfäärilist lainet, mis on identne punktallikast lähtunud lainega, st see sisaldab informatsiooni nii punkti heleduse kui ka asukoha kohta.
- Kolmas laine on uus, teda ei olnud hologrammi registreerimisel. Kuna see sfääriline laine koondub hologrammist kaugusel , on meil tegemist esemepunkti tõelise kujutisega.
Niisiis, ühe esemepunkti hologramm kujutab endast interferentsirõngaste süsteemi ja valgustades hologrammi tugilainega, on võimalik taastada esemepunktist lähtuv laine. Eseme hologramm on summa suurest hulgast esemepunktide hologrammidest ja tema välisel vaatlusel ei näe me mingit sarnasust eseme tavakujutisega.
Kui registreerida hologramm joonisel Jn 6.32 kujutatud viisil, siis esemelaine taastamisel, Jn 6.34, kattub ta suure intensiivsusega tugilainega, mis komplitseerib esemelaine vaatlemist. Praktikas kasutatakse „teljevälist“ hologrammi salvestamist, mille üks variant on joonisel Jn 6.35A.
Valgusallikana kasutatakse laserit, mille koherentsuse teepikkus on suurem kui maksimaalne käiguvahe esemepunktidest lähtuvate lainete vahel. Peegel jagab talle langeva valguse kaheks. Läbiv laine on tugilaine, mis langeb fotoplaadile kaldu. Peegeldunud laine, hajudes esemelt , tekitab komplitseeritud lainefrondiga esemelaine. Fotoplaadil koherentsed esemelaine ja tugilaine interfereeruvad, Jn 6.35B. Kuna üksiku esemepunkti interferentsirõngad eksisteerivad kogu hologrammi ulatuses, siis võib öelda, et hologrammi iga väike osa (viirutatud piirkonnad joonisel Jn 6.35B) sisaldab informatsiooni kogu eseme kohta.
Eseme kujutise saamiseks suunatakse hologrammile tugilaine samasuguse nurga all nagu ta oli salvestamisel, Jn 6.36.
Peale tugilaine sihilise laine on läbivas valguses esemelained ja . Hajuv laine näib lähtuvat kujutisest , mis asetseb täpselt samal kohal, kus enne oli ese . See kujutis on ruumiline, st vaatleja vaatesihi muutmisel nihkuvad kaks eri kaugusel olevat eset teineteise suhtes (parallaks). Selle tulemusena saavad nt musta ruudu poolt algselt varju jäänud eseme osad teise vaatesihi all nähtavaks. Kui valgustada hologrammi väikest osa, siis laine tekitab ekraanil esemest tõelise kujutise nähtuna kindlas vaatesihis. Valgustades laserikiirega väikest osa hologrammi pinnast, tekib ekraanil eseme kujutis nähtuna mingis kindlas suunas. Liikudes laserikiirega piki pinda (skaneerimine), muutub ka vaatesuund, mille all me eset näeme.
Seni kirjeldatud hologrammid olid kahemõõtmelised, fotoemulsiooni paksus oli lainepikkusega võrreldes väike. Kui aga fotoemulsiooni kiht on paks, tekib seal laserist lainepikkusega lähtuva tugilaine ja esemelt hajunud laine liitumisel seisulainele omane paisude ja sõlmede süsteem, mille periood on , vt 5.8. Paisude asukohtades suureneb peale keemilist töötlust („ilmutamist“) peegelduskoefitsient ja moodustub ruumiline difraktsioonivõre, Jn 6.37. Esemelaine taastamine on nüüd võimalik ka valges valguses , sest hologrammis kujunenud struktuur käitub difraktsioonivõrena, mille peamaksimumid vastavad lainepikkusele .
Ühe laialt levinud väärarusaama järgi on difraktsioon jälgitav, kui valguse teel oleva ava (või tõkke) mõõtmed on võrreldavad lainepikkusega (∼1μm). Tegelikult on objekti valgustamisel kvaasimonokromaatilise valgusega difraktsioonipilt kergesti jälgitav ka siis, kui mõõtmed on rohkem kui sajakonna lainepikkuse suurused.
Seni eeldasime vaikimisi, et difraktsioonipildi tekkel on meil tegemist punktallikaga. Kui vaadelda lõplike mõõtmetega valgusallikat kui punktallikate kogumit, millest igaüks tekitab oma difraktsioonipildi, siis tekkinud difraktsioonipildid on üksteise suhtes nihutatud ja nt joonise Jn 6.12 pildi asemel saame struktuuritu sujuvalt kahanevate äärtega intensiivsuse jaotuse. Kui lisaks veel on tegemist valge valgusega, siis on difraktsiooniilmingud vähetajutavad ning üsna paljude optikanähtuste kirjeldamisel on ka kiirteoptika lähendus piisavalt hea.
Hindamaks piire, millest alates tuleb arvestada valguse lainelisi omadusi, lähtume Fresneli tsoonidest: mida vähem Fresneli tsoone mahub avasse, mille lineaarmõõde on , seda tugevamini avaldub kõrvalekaldumine geomeetrilisest optikast. Vastavalt valemile v 6.8 on ümmarguse ava diameetri ja seal olevate tsoonide arvu vahel seos
Hinnanguks olgu valgusallika ja vaatluspunkti kaugused avast võrdsed, a1=a2=ρ, siis on esimese Fresneli tsooni raadius
Jättes arvestamata teguri , võrdleme ava mõõdet esimese Fresneli tsooniga, defineerides difraktsiooni parameetri . Kui , pole difraktsiooni vaja arvestada, geomeetriline optika on hea lähendus valgusnähtuste kirjeldamiseks. Kui aga , tuleb arvestada difraktsiooniga. Rõhutagem, et on kombinatsioon kolmest suurusest. Fikseeritud korral avaldub difraktsioon seda selgemini, mida kaugemal me objektist oleme. Alati, kui võib lugeda, et , on kiirteoptika hea lähendus.
Laine- ja kiirteoptika kehtivuspiirkondade eristamise näiteks on kujutise tekkimine pimekambris (Camera obscura), Jn 6.38, kus eseme ja vaatlustasandi vahel olevas tõkkes on ümmargune ava diameetriga .
Kiirteoptika lähenduses tekib vaatlustasandis igast eseme punktist valguslaik ja me saame esemest ümberpööratud kujutise. Suure ava puhul lähedastele esemepunktidele vastavad kujutise laigud kattuvad ja kujutis on ebaterav. vähendamisel kujutise teravus algselt kasvab kuni difraktsiooni difraktsiooniparameeter saab võrreldavaks ühega ja esemepunktile vastav laik hakkab tänu difraktsioonile taas suurenema.
Kasutades kiirteoptika lähendust tuleb silmas pidada, et
- Laineoptika seisukohalt vastab kujutise punkt kohale, kus kõigist esemepunktist lähtuvate kiirte optilised teepikkused on võrdsed e kujutise asukoht vastab interferentsipildi maksimumile.
- Optilise süsteemi (nt läätse) abil eseme punktist saadud kujutisele vastab alati difraktsioonipilt, kusjuures energia on koondunud lõplike mõõtmetega tsentraalsese maksimumi.
Kui elektromagnetlaine levikumehhanism järeldub otseselt Maxwelli võrranditest, siis sarnaselt Huygens-Fresneli printsiibile laineoptikas vajab ka kiirteoptika valguse leviku selgitamiseks abiprintsiipi. Vastavalt Fermat printsiibile levib valgus mööda sellist teed, mille läbimiseks kulunud aeg on minimaalne (Jn 6.39A)
Joonis Jn 6.39B seob kiire ja laine levikumehhanismid. Sel joonisel levib valgus mittehomogeenses keskkonnas, .
Kui ajahetkel on lainefront teada, siis isotroopses keskkonnas lähtuvad igast lainefrondi punktist sfäärilised lainekesed, nende levikukaugus aja jooksul on määratud faasikiirusega selles ruumipiirkonnas. Ühendades samm-sammult lainekese lähtepunkti tema lainepinna ja uue lainefrondi puutepunktiga saame kiire trajektoori: reeglina on valguskiire trajektoor mittehomogeenses keskkonnas kõverjooneline.
Joonisel Jn 6.40A on kujutatud valguse levik keskkonnas, kus murdumisnäitaja muutub vaid x-telje sihis.
Jaotame mõtteliselt keskkonna õhukesteks x-teljega ristiolevateks kihtideks. Ühe kihi piires loeme murdumisnäitaja konstantseks, kahe kihi piiril valgus murdub. Kiire puhul on iga järgmise kihi murdumisnäitaja väiksem kui eelmisel, , seega . Kiir levib ülespoole niikaua, kui langemisnurk on väiksem täieliku peegelduse piirnurgast . Pärast täieliku peegeldumise piirnurga saavutamist hakkab kiir levima allapoole.
Levigu kiir keskkonnas, kus murdumisnäitaja gradient on vastasmärgiline, , kuna aga kiire algne levikusuund on ülalt alla, siis levib ta samuti kahaneva murdumisnäitajaga keskkonnas, (K 6.31). Kiudoptikas on kasutusel väikesegabariidilised silindrilise kujuga gradientläätsed, mille murdumisnäitaja muutub sujuvalt piki raadiust. Näiteks joonisel Jn 6.40B on kujutatud sellise läätsega paralleelse kiirtekimbu koondamist optilisse kiudu. Inimese silma läätse murdumisnäitaja, Jn 6.40C, on suurem optilise peatelje lähedases piirkonnas ja kahaneb monotoonselt serva suunas. Seetõttu murtakse silma tsentraalsesse ossa langevat valgust tugevamini ja väheneb sfäärilise aberratsiooni mõju kujutise kvaliteedile.
Kui valgus langeb vaakumist keskkonda murdumisnäitajaga , siis indutseeritakse seal dipoolide võnkumine. Nende dipoolide poolt kiiratavate koherentsete lainekeste mähisjoon on keskkonnas formeerunud sekundaarlaine lainefront. Nüüd liituvad keskkonnas kaks lainet: primaarlaine, mis levib kiirusega , ja polarisatsioonilaine, mis levib kiirusega . Algselt on need lained faasis, kuid erineva levikukiiruse tõttu tekib nende lainete vahel faasivahe, mille tulemusena primaarlaine nõrgeneb. Kaugusel lahutuspinnast on optiline käiguvahe nende lainete vahel ja faasivahe
kus on lainepikkus vaakumis. Lugedes, et primaarlaine on asendunud polarisatsioonilainega juhul, kui lained on vastasfaasis, , saame primaarlaine levikuulatuseks
Nähtava piirkonna lainepikkustel klaasis, , on levikuulatus ja õhus, , on levikuulatus .
Leiame nüüd, millised on suvalises vaatetasandis tasanditest ja lähtuvate ja kiirusega -telje suunas levivate tasalainete faasid, Jn 7.1. Kuna need lained genereeritakse erinevatel ajamomentidel, vastavalt t−z′n/c ja t−z′′n/c, ja nad levivad vaatetasandini erinevad vahemaad, vastavalt z−z′ ja z−z′′, siis nende faaside hetkväärtused tasandis on
ja
Näeme, et erinevatest tasanditest lähtuvad lained on vaatetasandis faasis.
Valguse levikumehhanismide detailsemaks kirjeldamiseks on vaja lähtuda aine ehitusest mikroskoopilisel tasemel. Meie lähenemine baseerub klassikalisel mehhaanikal, mis vaadeldavatel juhtudel annab kvalitatiivselt õige tulemuse.
Dispersioonil on optikas mitmeid eri tähendusi, seni oleme rääkinud spektraalsete seadmete (Fabry-Perot interferomeeter, vt 5.9.1; difraktsoonivõre, vt 6.6.3) nurkdispersioonist. Selles peatükis räägime aine dispersioonist, s o aine murdumisnäitaja sõltuvusest lainepikkusest (sagedusest), , (M) .
Murdumisel prismas lahutub erinevate lainepikkustega valgus spektriks, Jn 7.2A. Kui valguse langemisnurk on valitud nii, et kiire kaldenurk mingil lainepikkusel oleks minimaalne, δλ=δmin, siis on sellele lainepikkusele vastav murdumisnäitaja lihtsasti leitav (K 7.2).
kus on prisma murdev nurk. Kuna erinevatele lainepikkustele vastab erinev väärtus, siis muutub koos lainepikkusega ka murdumisnäitaja ja me saamegi aine dispersiooni iseloomustava sõltuvuse .
Joonisel Jn 7.2B on sel meetodil leitud dispersioonikõvera näide. Selle kõvera käik on tüüpiline spektraalpiirkonnale, kus ainet võib lugeda läbipaistvaks. Piirkonda, kus lainepikkuse kasvades murdumisnäitaja väheneb, , nimetatakse normaalse dispersiooni piirkonnaks.
Saadud dispersioonikõverat on võimalik lähendada erinevate empiiriliste valemitega. Cauchy valemi järgi on murdumisnäitaja kujul
kus , ja on sobitusparameetrid, mis leitakse võrdlusest eksperimendiga.
Kui registreerida murdumisnäitaja muutused laiemas lainepikkuste vahemikus, siis näeme, et dispersioonikõveral on mitmed nii negatiivset kui ka positiivset tõusu omavad piirkonnad, Jn 7.3. Piirkondasid, kus , nimetatakse anomaalse dispersiooni piirkondadeks.
Sõltuvuse n=f(ω) tuletamisel lähtume aatomi klassikalisest mudelist, kus tiirlevat elektroni massiga ja laenguga hoiab orbiidil massiivse, M≫me, tuuma elektrivälja poolt tekitatud kesktõmbejõud, Jn 7.4.
Eeldame, et valgus on vastasmõjus vaid ühe, aatomi väliskattes asuva „optilise“ elektroniga. Häirimata olukorras langeb üle elektroni tiirlemisperioodi keskmistatud negatiivse laengu laengukese kokku positiivse tuumaga. Valguse langemine aatomile põhjustab elektroni trajektoori häirituse, negatiivne laengukese nihkub lõigu võrra ja tulemuseks on dipoolmomendi indutseerimine.
Elektroni nihke leidmiseks lähtume Newtoni teisest seadusest
võrrandi paremal pool on summa kõigist -telje sihis mõjuvatest jõududest. Nihke dünaamika on määratud kolme jõuga.
- Valgus, mille sagedus on ja elektrivälja amplituud on , mõjub elektronile jõuga .
- Nii teised aatomi koosseisu kuuluvate elektronid kui ka naaberaatomid mõjuvad elektroni liikumisele pidurdavalt. Loeme, et see „hõõrdejõud“ on võrdeline elektroni kiirusega, .
- Kõrvalekalle tasakaaluasendist põhjustab nihkega vastassuunalise jõu , kus „jäikus“ on põhjustatud tuuma elektriväljas.
Saame teist järku diferentsiaalvõrrandi
mis oma kujult langeb kokku sundvõnkumisi sooritava vedrupendli liikumisvõrrandiga. Tähistades ja (K 7.4), jõuame võrrandini
Kuna tavavalguse elektrivälja tugevus on palju-palju väiksem kui tuuma väli elektroni asukohas, siis võib lugeda, et nihe muutub samuti harmooniliselt, . Paigutades selle proovilahendi võrrandisse v 7.4, jõuame pärast diferentseerimist elektroni nihke ja valguse elektrivälja tugevuse vahelise seoseni
Seega indutseeritakse valguse poolt aatomis dipoolmoment
Elektromagnetismist on teada, et aine makroskoopiline polarisatsioon on ruumiühiku dipoolmoment
kus on omavõnkesagedust omavate elektronide (ja ühe optilise elektroni eeldusel ka aatomite) kontsentratsioon.
Kuna
kus on dielektriline vastuvõtlikkus, siis
Näeme, et polarisatsioon muutub sama sagedusega nagu teda indutseeriva valguse elektriväli.
Arvestades dielektrilise läbitavuse ja dielektrilise vastuvõtlikkuse vahelist seost, , saame
Kuna on kompleksne, siis on seda ka murdumisnäitaja, vt 4.8
kus
kusjuures murdumisnäitaja reaalosa iseloomustab valguse levikukiirust ja imaginaarosa kadusid (neeldumist).
Tühine neeldumine tähendab seda, et sundvõnkumisi sooritava elektroni hõõrdumiskadusid pole valemis v 7.6 vaja arvestada, , seega on murdumisnäitaja reaalne
Kordaja dimensioon on , ruutjuur sellest kordajast on sageduse dimensiooniga ja seda suurust
nimetatakse plasma sageduseks.
Valemile v 7.7 vastav dispersioonikõver on joonisel Jn 7.5.
Nii valemist v 7.7 kui ka joonisest johtub, et valguse sagedusel on murdumisnäitaja väärtus määramatu ja seepärast ilmselt oletus tühistest kadudest piirkonnas ei kehti.
Väljaspool seda kahtlast piirkonda on aga võimalik teha dispersiooni kohta mõningaid järeldusi.
Esiteks näeme, et , st meil on tegemist normaalse dispersiooni piirkondadega. Lisaks on kaugemal resonantssagedusest murdumisnäitaja väärtus lähedane ühele. Võrdlemaks saadud dispersioonikõverat normaalse dispersiooni piirkonna jaoks saadud empiirilise valemiga v 7.3, teeme valemis v 7.7 mõningad lihtsustused. Kui on vähe erinev ühest, siis
ja v 7.7-st saame
Edasisel teisendamisel arvestame, et
Kuna , siis saime väliskujult valemiga v 7.3 kokkulangeva tulemuse ja kuna kordajad ja sisaldavad fundamentaalkonstante ja ainet iseloomustavaid suurusi, on võimalik nende valemite baasil arvutada murdumisnäitaja väärtused erinevatel sagedustel. Vaatamata sellele, et oli tegemist puhtalt klassikalise mudeliga, on sagedustel erinevus eksperimentaalsetest väärtustest vaid , mis kinnitab dispersioonimudeli põhiseisukohtade paikapidavust.
Näide N 7.1
Lahendus
Arvutusteks vajaminevad suurused , ja on hästi teada, kuid dipoolide kontsentratsiooni ja sageduse puhul piirdume vaid hinnanguga.
Suurusjärguliseks hinnanguks võrdugu dipoolide arv molekulide arvuga ruumiühikus. Ühes kilomoolis on Avogadro arv molekule, NA=6,02⋅1026kmol−1. Kuna lämmastiku molaarmass on , siis ühes kuupmeetris on ρ/28=2,5/28=0,045 kilomooli jagu molekule ja
Resonantssagedusele vastavaks lainepikkuseks võtame λ0=160nm.
Leiame
ja nexp väärtuste suurusjärguline kokkulangevus kinnitab mudeli realistlikust.
Kui ainele langeb röntgendiapasooni kuuluv laine, siis ω≫ω0 ja ning
röntgenkiirte murdumisnäitaja on ühest väiksem ja seepärast saab langemisel vaakumist ainele toimuda täielik peegeldumine, vt 4.6.
Plasmakeskkonnas on laengukandjad vabad, , ja tuues sisse plasmasageduse, v 7.8, saab v 7.7 kuju
Kui , siis mingeid piiranguid elektromagnetlaine levikuks plasmas ei ole, kuid madalamatel sagedustel on dielektriline läbitavus negatiivne ja murdumisnäitaja on imaginaarne, , st sagedustel laine plasmas levida ei saa. Rakendades selle juhu jaoks Fresneli valemeid, vt 4.6, saab näidata, et plasmalt peegeldumine on täielik.
Tegelikkuses ei koosne keskkond vaid üht omavõnkesagedust omavatest aatomitest, vaid aatomitel on palju omavõnkesagedusi. Kui on aatomite koguarv, siis aatomite mingi osa omavõnkesagedus on . Osakaalu nimetatakse ostsillaatori tugevuseks ja ta rahuldab normeerimistingimust . Arvestades ostsillaatorite paljusust, saame üldisema dispersiooniseose (K 7.9)
Elektromagnetlaine madalamasageduslikus spektri osas tuleb dispersiooni puhul arvestada ka laine ja ioonide vastasmõju, mis avaldub sagedustel ja ka vastasmõju dipoolmomenti omavate molekulidega, vt Jn 3.2.
Läbi aegade (P 7.2) emotsionaalselt kõige mõjuvamaks valguse dispersiooni ilminguks on vikerkaar.
Vikerkaar tekib valguse murdumise, peegeldumise ja dispersiooni tulemusena veepiiskades.
Monokromaatilisele valgusele vastav kiirtekäik sfäärilises veepiisas on joonisel Jn 7.6A (K 7.11).
Valgus, mis langeb veepiisale nurga all, murdub nurga all ja peegeldub osaliselt piisa tagumiselt pinnalt. Pärast teist murdumist veepiisas valgus väljub piisast. Jooniselt on näha, et valguse väljumisnurk piisast võrdub tema sisenemisnurgaga.
Nurk siseneva ja väljuva kiire vahel, kaldenurk , sõltub langemisnurgast.
Kui langemisnurk , siis on kaldenurk maksimaalne, . Kaldenurga ja langemisnurga vahelise seose leidmiseks üldjuhul kasutame kahte võrdset kolmnurka, millest üks on joonisel varjutatud.
Kuna mõlema kolmnurga sisenurkade summa avaldub nagu
siis
ja murdumisseaduse abil jõuame tulemuseni
Joonise Jn 7.6B on kujutatud kaldenurga sõltuvus langemisnurgast juhul, kui valgus langeb piisa ülemisele poolele. Näeme, et δ(α) muutub laias vahemikus, kusjuures väljuvate kiirte tihedus muutub sõltuvalt nurgast . Kõige tihedamalt paiknevad väljuvad kiired kaldemiinimumi piirkonnas, , kus langemisnurkade vahemikus paikneb väljuvaid kiiri rohkem kui korda tihedamalt kui nt nurgale vastavas piirkonnas ja seetõttu võib vikerkaare kirjeldamisel piirduda vaid kaldemiinimumi lähedaste kiirtega. Kaldemiinimumile vastavat kiirt nimetatakse vikerkaare kiireks. Kui murdumisnäitaja on (punakas valgus), siis vastab vikerkaare kiirele nurk .
Dispersiooni tõttu lahutub päikesevalgus kahel järjestikusel murdumisel värvilisteks komponentideks. Kuna on tegemist normaalse dispersiooniga dn/dλ<0, siis sinine valgus murdub rohkem kui punane, Jn 7.7A. Vaatlejani, Jn 7.7B, jõuab valgus, mis pärineb erinevatel kõrgustel paiknevatelt piiskadelt ja vaateväljas näeme värvilist kaart, mille tsenter paikneb Päikest ja vaatlejat ühendava sirge pikendusel, Jn 7.7C. Kõige üleval paikneb punane kaar ja kõige all violetne.
Seni kirjeldatu iseloomustab primaarset vikerkaart. Sekundaarne vikerkaar tekib, kui valgus siseneb tilga alaossa, Jn 7.7B. Sel juhul jõuab valgus vaatlejani pärast ühte täiendavat peegeldumist tilga sisepinnalt ja seepärast on tema intensiivsus on palju väiksem kui primaarsel vikerkaarel.
Eelnevalt nägime, Jn 7.5, et optilise elektroni kadude eiramine ei võimalda kirjeldada valguse ja aine vastasmõju omavõnkesageduse lähedastel sagedustel. Edasiseks analüüsiks eraldame dielektrilise läbitavuse, v 7.6, reaal- ja imaginaarosa
Kuna
ja
siis
Valemite v 7.13 graafikud on joonisel Jn 7.8A. Näeme, et erinevalt joonisest Jn 7.5 on nüüd dispersioonikõver pidev ja omavõnkesageduse lähedases piirkonnas on , st tegemist on anomaalse dispersiooni piirkonnaga. Kuna selles piirkonnas on murdumisnäitaja imaginaarosa suur, siis on see valguse neeldumise piirkond. Siit järeldub, et neeldumine on maksimaalne aatomite omavõnkesagedustel. Selle üheks eksperimentaalseks tõestuseks on nt Maa pinnal registreeritud Päikese neeldumisspekter, Jn 7.8B, kus pideva spektri foonil eksisteerivad tumedad neeldumisjooned ( Fraunhoferi jooned), mis asetsevad lainepikkustel, kus tekiksid sobivatel tingimustel (nt gaasikeskkonna kõrgem temperatuur) Päikese ja Maa atmosfääri kuuluvatele aatomite kiirgusjooned.
Vastavalt tänapäeva füüsika ühele põhipostulaadile on maksimaalseks võimalikuks energia ülekande kiiruseks valguse kiirus vaakumis. Valguse puhul iseloomustab energia ülekannet rühmakiirus, vt v 3.2
Võttes aluseks selle seose, hindame rühmakiirusi joonisel Jn 7.9 toodud neljas karakteristlikus piirkonnas.
- Normaalse dispersiooni piirkonnas 1 on faasikiirus ja kuna , siis .
- Anomaalse dispersiooni piirkonnas 2 on faasikiirus , kuid kuna , siis võib .
- Anomaalse dispersiooni piirkonnas 3 on faasikiirus ja , seega alati
- Normaalse dispersiooni piirkonnas 4 on faasikiirus , kuid kuna , siis vastuolu ei pruugi olla.
Näide N 7.2
Lahendus
Kasutades seost v 7. 10, jõuame faasikiiruse dispersiooniavaldiseni plasmas
Näeme, et laine levikut võimaldavatel sageduste, , on faasikiirus suurem kui valguse kiirus vaakumis.
Leiame plasmasageduse.
Kuna
siis
ehk faasikiirus ületab valguse kiirust vaakumis √1−2,7⋅10−17 korda.
Rühmakiiruse leidmiseks viime esmalt v 7.10 kujule
(*) teisalt aga
ehk
(**). (*) ja (**) vasakuid pooli diferentseerides saame
ja
Rühmakiirus plasmas on
väiksem valguse kiirusest vaakumis ja on seega vastavuses relatiivsusteooriga.
Anomaalse dispersiooni piirkondade tulemus, et rühmakiirus on suurem kui valguse kiirus vaakumis, osundab, et rühmakiiruse mõiste kasutamine neis piirkondades pole õigustatud. Tõepoolest, rühmakiiruse mõiste sissetoomisel eeldati, et lainepakett säilitab levikul oma kuju. Kuna aga piirkondades 2 ja 3 on lainepaketi monokromaatilistel komponentidel tugevasti sagedusest sõltuv neeldumine ja ka väärtus on suur, siis lainepaketi kuju deformeerub ning rühmakiiruse mõiste kaotab oma sisu.
Saab näidata, et vastuolu seisukohaga, mis postuleerib valguse levikukiiruse vaakumis kui maksimaalselt võimaliku energia levikukiiruse, puudub, kui kasutada lainepaketi leviku kirjeldamiseks signaalikiiruse mõistet.
Selle peatüki algosas vaatlesime vaid -telje suunas levivat valgust (vt Jn 7.1). Samas teame, et polarisatsioonilainet põhjustavad dipoolid kiirgavad kõigis suundades, vt p. 2.6. Kui dipoolile langev valgus on lineaarselt polariseeritud, siis hajunud valgus on ka lineaarselt polariseeritud ja tema intensiivsus kaugusel sõltub nii sagedusest (lainepikkusest) kui ka nurgast dipooli telje ja vaatesuuna vahel
Vaatleme nüüd lähemalt külgsuundades levivat valgust. Selleks rühmitame tasandis olevad dipoolid võrdse suurusega ruumaladesse , Jn 7.10.
Iga ruumala sisaldab suure arvu dipoole, , kuid selle ruumala lineaarmõõde on väiksem lainepikkusest . Sellistel tingimustel on valguse levik külgsuunas määratud ruumaladest lähtuvate koherentsete lainete liitumisega.
Igast ruumalast lähtuva laine intensiivsuse ruumiline jaotus langeb kokku üksiku dipooli kiirguse jaotusega. Olgu nurgaga määratud suunas ruumalade 1 ja 2 poolt saadetavate lainekeste intensiivsused vastavalt ja . Mistahes puhul saab ruumalale 1 leida sellisel kaugusel oleva paarilise 2, mille puhul on täidetud tingimus L=λ/2sinψ, st lained on vastasfaasis, Jn 7.14. Kui nüüd dipoolide arv ruumalades oleks võrdne, , siis summaarne intensiivsus oleks null, st ideaalselt homogeenses keskkonnas hajunud valgus puudub. Näitamaks, et ideaaljuhul valgus ei levi ka algsele suunale vastassuunas, valime tasandist kaugusel olevas tasandis ruumala 3. Sellest ruumalast ja ruumalast 1 tagasisuunas levivate lainekeste vaheline käiguvahe on ja lainekesed kustutavad teineteist. Koordinaatide alguse poole levivate lainekeste kustutamine pole täielik vaid siis, kui kaugus kahe keskkonna lahutuspinnast on väiksem kui . Nende lainekeste mähispind on keskkondade lahutuspinnalt peegelduva laine lainefront.
Tegelikkuses eksisteerivad keskkonnas alati mikroskoopilised ebaühtlused nagu dislokatsioonid kristallvõres; udu, suits jms gaasilises keskkonnas; osakesed emulsioonides. Loetletud põhjustel ei ole ruumaladest ja lähtuvate ning käiguvahet omavate lainete summaarne intensiivsus kunagi null.
Soojusliikumise fluktuatsioonide tõttu erineb ka ülipuhta keskkonna -ndas ruumalas dipoolide tihedus δNi võrra keskkonna tiheduse keskväärtusest. Loetletud põhjustel ei ole ruumaladest 1 ja 2 lähtuvate ning käiguvahet omavate lainete summaarne intensiivsus kunagi null, sel juhul on tegemist molekulaarse (≡ Rayleigh) hajumisega.
Kui langev valgus on loomulik, Jn 7.11A, siis hajumisnurgaga määratud suunas saadavad laine nii piki -telge kui ka piki -telge võnkuvad dipoolid. Tasandis ei sõltu -telje sihiliste dipoolide laine intensiivsus hajumisnurgast , sest vaatesuuna ja dipooli telje vaheline nurk on alati . -telje sihilistel dipoolidel aga nurk muutub ja kuna , siis sel puhul on intensiivsus võrdeline teguriga cos2ψ. Kuna loomuliku valguse puhul kahes risttasandis lainete vaheline faasivahe muutub juhuslikult, siis liituvad nende lainete intensiivsused, vt p. 5.1, ning tähistades otse leviva loomuliku valguse intensiivsuse mingil lainepikkusel -ga , saame hajunud valguse intensiivsuse sõltuvuse hajumisnurgast
Joonisel 7.11B on sellele valemile vastav graafik. Näeme, et hajunud valguse intensiivsuse jaotus on sümmeetriline -telje suhtes, seega toimub Rayleigh hajumine ühtmoodi nii valguse levikusuunas kui ka vastassuunas.
Hajutavat keskkonda otse läbiv valgus jääb loomulikuks, tema polarisatsiooniaste , vt v 4.22. Hajumisnurga kasvades polarisatsiooniaste kasvab ja kui , on valgus lineaarselt polariseeritud –tasandis, st polarisatsiooniaste .
Hajumise tõttu väheneb esialgses suunas leviva valguse intensiivsus ja saab näidata, et nii nagu neeldumisel, vt 4.8, toimub see eksponentsiaalselt, . Kuna vastavalt valemile v 7.14 on hajunud valguse intensiivsus , siis on ka hajumiskoefitsient .
Rayleigh hajumise väga tugev sõltuvus lainepikkusest seletab nii taeva sinise kui ka Päikese kollaka värvuse. Tõepoolest, mingi nurga all on hajumine nähtava valguse spektri sinises otsas, , rohkem kui kümme korda suurem kui spektri punases otsas, , ja sinise spektriosa hajumise tõttu omandab esialgselt valge päikesevalgus kollaka varjundi. Päikeseloojangul on valguse teel oleva õhukihi paksus suurem kui keskpäeval, valguse märgatav hajumine toimub nüüd laiemas spektriosas ja Päike muutub punakaks.
Valgusallika ja hajutava keskkonna vahele on paigutatud polaroid.
1.
Lahendus
Hajunud valguse intensiivsus muutub, sest muutub nurk hajutavas keskkonnas indutseeritud dipoolide telje ja y-telje vahel. Kui polaroidi läbilaskesiht on orienteeritud x-telje sihis, on dipoolide telg risti vaatesihiga ja seega on hajunud valguse intensiivsus maksimaalne. Kui aga dipoolide telg ühtib vaatajuv valgus on elliptiliselt esihiga, on valguse intensiivsus minimaalne. Seega polaroidi täispöörde jooksul on valguse intensiivsus kaks korda maksimaalne ja kaks korda minimaalne.
2.
Lahendus
Sõltuvana nurgast muutub ka hajunud valguse polarisatsioonitasand, sest x-komponent jääb muutumatuks, kuid y-komponent kahaneb ja kui ψ=π/2, eksisteerib vaid x-komponent. Kui langev valgus oleks ringpolariseeritud, siis hajunud valgus on elliptiliselt polariseeritud.
Vaadeldud molekulaarse hajumise juhul olid hajutava osakese, aatomi või molekuli lineaarmõõtmed palju väiksemad kui valguse lainepikkus. Teisel piirjuhul, kui valguse teel oleva tõkke mõõde on lainepikkusest suurem, kirjeldab valguse kõrvalekallet sirgjoonelisest levikust difraktsioonimudel. Vahepealsel juhul, kui hajutava objekti mõõde on lähedal lainepikkusele, kehtib hajumise puhul Mie hajumise mehhanism. Võrreldes molekulaarse hajumisega on Mie hajumisel kaks olulist erinevust. Esiteks, erinevalt joonisel Jn 7.15B toodud sõltuvusest levib valgus nüüd eelistatud -telje positiivses suunas. Teiseks on hajunud valguse sõltuvus lainepikkusest nõrk. Mie hajumise näiteks on valkjad pilved.
Kui meil on tegemist amorfsete ainetega või kuubiliste kristallidega, siis nende omadused on sõltumatud suunast, st keskkond on isotroopne. Olenevalt aine struktuurist võivad aga tema mehhaanilised, soojuslikud, elektrilised, optilised jm omadused olla erinevates suundades erinevad – selline keskkond on anisotroopne. Anisotroopia optikas avaldub valguse kiiruse sõltuvuses levikusuunast ja ka sellest, kuidas antud suunas leviv valgus on polariseeritud.
Toomaks sisse kristallide optikas vajaminevaid põhimõisted, alustame kaksikmurdumise kirjeldamisega.
Keskkonna anisotroopia ilmneb kõige selgemalt kaltsiidi () ühe kristallilise erivormi, islandi pao, puhul. Islandi pagu on dielektriline maak, mis on nähtava valguse piirkonnas läbipaistev, tema lõhestamisel tekkivad kristallid on paralleelsete vastastahkudega romboeedrid, Jn 8.1A.
Olgu -telg, piki mida levib väikese diameetriga paralleelne kiirtekimp, risti kristalli esitahuga, st langemisnurk . Kui langev valgus on loomulik, siis näeme kristalli väljundisse paigutatud ekraanil kahte valguslaiku. Pöörates kristalli ümber -telje näeme, et üks valguslaikudest jääb paigale, kuid teine laik liigub ümber esimese mööda ringjoont. Paigalejääv kiirtekimp käitub seega nii, nagu oleks tegemist isotroopse keskkonnaga ja teda nimetatakse tavaliseks kiireks ( -laine). Esialgsest levikuteest kõrvalekaldunud valguse puhul on tegemist ebatavalise kiirega ( -laine ).
Vaadates paberile tõmmatud kriipsu läbi islandi pao kristalli näeme selle kriipsu kahte kujutist, Jn 8.1B. Ühe kujutise siht langeb kokku paberil oleva kriipsuga, see kujutis on seega tekitatud -laine poolt, nihutatud kujutis aga vastab -lainele. Pöörates paberil lebavat kristalli, näeme, et kriipsu kujutiste vaheline kaugus muutub maksimaalsest väärtusest kuni kujutiste kokkulangemiseni.
Kui lihvida kristalli nii, et langemisnurgale vastav siht langeb kokku sirgega , mis ühendab ühte paari romboeedri nürinurkadest, Jn 8.1C, siis selles optilise telje sihis kaksikmurdumine puudub, , st valgus levib nii nagu isotroopses keskkonnas. Kaksikmurdumine puudub kõigi valguskiirte puhul, mis levivad paralleelselt optilise telje sihiga.
Mistahes optilist telge läbivat tasandit nimetatakse kristalli pea(lõike)tasandiks.
Kui mõõta joonisel 8.1A kujutatud kristalli murdumisnurga sõltuvust langemisnurgast , siis saame, et -laine puhul kehtib tavaline murdumisseadus sinαsinγ=no, kuid -laine murdumisnäitaja sõltub kristallis leviva kiire ja optilise telje vahelisest nurgast. Lainepikkusel λ=589nm on islandi pao tavalise kiire murdumisnäitaja , kuid ebatavalise kiire murdumisnäitaja muutub vahemikus .
Pöörates vaatlusekraani ja kristalli vahele paigutatud polaroidi , Jn 8.2, näeme ekraanil, et ühe valguslaigu heleduse kasvades teise oma kahaneb ja polaroidi pöördenurga teatud väärtusel üks laikudest ekraanil kaob ja teine, nt -laine, saavutab maksimaalse heleduse.
Edasisel polaroidi pööramisel võrra näeme, et nüüd puudub -lainele vastav valguslaik ja -laine laik on maksimaalse heledusega. Siit järeldub, et kaksikmurdumisel tekkinud - ja -laine on lineaarselt polariseeritud ja nende polarisatsioonitasandid on risti. -laine on polariseeritud kristallis leviva kiire ja optilise teljega määratud peatasandis ja -laine polarisatsioonitasand on risti selle tasandiga.
Kaksikmurdumise mehhanismi kvalitatiivseks selgitamiseks lähtume aatomite telgsümmeetrilisest paiknemisest islandi pao kristallvõres, Jn 8.3A.
Siit on näha, et elektriväljad, mis mõjuvad naaberaatomite poolt mingi aatomi väliskattes olevale optilisele elektronile, on üldiselt erinevates suundades erinevad. Telgsümmeetria tõttu võib aga lugeda, et viirutatud tasandites on elektriväli ja seega ka elektronile mõjuv jõud sõltumatu sihist. Nii nagu isotroopses keskkonnas, vt Jn 7.4, asendame kristallvõre mõju optilisele elektronile mehhaanilise mudeliga, Jn 8.3B, kus elektronile mõjuvat tasakaaluasendisse viivat jõudu iseloomustab vedru jäikus . Praegusel juhul on - ja -telje sihiliste vedrude jäikused võrdsed, kuid mingis teises kristallis võivad kõigi kolme koordinaattelje sihis paiknevad vedrud olla erineva jäikusega.
Kui nüüd valgus levib sihis, siis tema elektrivälja toimel hakkavad sundvõnkuma „vedrud“, mille jäikus on ja nende omavõnkesagedus on
Vastavalt valemile v 7.6 sõltub murdumisnäitaja ja seega ka valguse faasikiirus omavõnke- ja sundvõnkesageduse vahest
Kuna praegusel juhul on - ja -telje sihilised jäikused samad, siis on samad ka tasandites ja lineaarselt polariseeritud valguste levikukiirused. Teiste sõnadega – sihis levib valgus nii nagu isotroopses keskkonnas e on kristalli optiline telg.
Levigu nüüd valgus risti optilise teljega, nt piki -telge.
Olgu esmalt valgus lineaarselt polariseeritud tasandis , st polarisatsioonitasand on risti selle pealõiketasandiga, millel paikneb kristallis leviv kiir, Jn 8.3C. Nii nagu levikul piki optilist telge, on ka nüüd levikukiirus määratud omavõnkesagedusega . Seega ei sõltu risti peatasandiga polariseeritud valguse kiirus levikusuunast, tegemist on -lainega. Kuna faasikiirus , on konstantne kõigis suundades, on punktallikast lähtuva -laine samafaasipinnaks (≡ lainepind) sfäär.
Kui aga piki -telge levib laine, mis on lineaarselt polariseeritud pealõiketasandis, Jn 8.3D, siis iseloomustab kristalli ja optilise elektroni vastasmõju sagedus
ning levikukiirus on
Seega juhul, kui laine on lineaarselt polariseeritud pealõiketasandis, on optilise telje ja tema ristsihi suunas levivate lainete kiirused erinevad, mistahes muus sihis omab levikukiirus vahepealset, optilise telje ja levikusuuna vahelisest nurgast sõltuvat väärtust , tegemist on -lainega. Selle lainepinnaks on pöördellipsoid, mille sümmeetriateljeks on allikat läbiv optiline telg.
Eelmises punktis nägime islandi pao näitel, et levikul anisotroopses keskkonnas sõltus -laine faasikiirus levikusuunast. Kuna aga faasikiirus, murdumisnäitaja ja dielektriline läbitavus on üheselt seotud
siis pole dielektriline läbitavus skalaarne suurus, mis tähendab, et HILS keskkonnas kasutatav elektrinihke ja elektrivälja tugevuse vaheline lihtne seos, D=εε0E, (K 8.5) enam ei kehti. Nüüd sõltub nt elektrinihke vektori -komponent elektrivälja vektori kõigist kolmest komponendist
analoogilised seosed saame ka elektrinihke - ja -komponendi jaoks, kokkuvõtvalt võib esitada elektrinihke ja elektrivälja vektori komponentide vahelise sõltuvuse maatrikskujul
st anisotroopses keskkonnas on dielektriline läbitavus 9-komponendiline teist järku tensor. Näitame, et vaid osa neist komponentidest on sõltumatud.
Elektromagnetismi kursusest on teada, et HILS keskkonnas avaldub elektrivälja energiatihedus nagu
Kuna anisotroopses keskkonnas on dielektriline läbitavus tensor, siis omandab energiatihedus kuju
Midagi ei muutu, kui vahetame indeksid ringi, ,
Lahutame esimesest energiatiheduse avaldisest teise
See samasus kehtib vaid juhul, kui , st dielektrilise läbitavuse tensor on sümmeetriline. Koordinaattelgede valikuga saab sümmeetrilise tensori viia diagonaalkujule
Nii valitud koordinaattelgi nimetatakse dielektrilise läbitavuse peatelgedeks. Kuna üldjuhul , siis vektorid D ja E ei ole enam kollineaarsed, Jn 8.4.
Kasutades peatelgede sihiliste dielektriliste läbitavuste väärtusi, saab energiatiheduse avaldis v 8.1 kuju
ehk dielektrilise läbitavuse järgi
Toome sisse uued koordinaatteljed, mis oma suunalt langevad kokku teljestikuga , ,
ja arvestades, et saameSellele võrrandile vastavaks ruumiliseks kujundiks on ellipsoid, Jn 8.5A, mille piki , ja -telge suunatud pooltelgede pikkused on , ja nz, st selle ellipsoidi kuju ja suurus sõltub vaid murdumisnäitajaist.
Saadud murdumisnäitajate (≡ Fresneli) ellipsoidi abil saab leida suvalises suunas leviva kahe laine polarisatsioonitasandid ja ka vastavad murdumisnäitajad. Nende leidmiseks lõikame ellipsoidi tasandiga, mis on risti suunaga ja mis läbib koordinaatide alguspunkti, Jn 8.5B. Üldjuhtumil on lõikejooneks ellips, mille telgede ja suunaga on määratud levivate lainete polarisatsioonitasandid, ellipsi pooltelgede pikkused aga annavad nendele lainetele vastavad murdumisnäitajad.
Saadud murdumisnäitajate ( Fresneli) ellipsoidi abil saab leida mistahes suunas leviva kahe laine polarisatsioonitasandid ja ka vastavad murdumisnäitajad.
Näitena vaatleme esmalt juhtu, kui lainevektor k on peatelje suunaline ja võtame teadmiseks, et sõltumata keskkonnast on lainevektor ja elektrinihke vektor alati risti, , st nullist on erinevad vaid ja , vt 8.3. Kui valgus on lineaarselt polariseeritud vertikaaltasandis , iseloomustab keskkonna ja valguse vastasmõju murdumisnäitaja ja valguse faasikiirus on . Kui aga valgus on polariseeritud horisontaaltasandis , on keskkonna murdumisnäitaja ja valguse faasikiirus on . Geomeetriliselt pole ja midagi muud, kui sellise ellipsi pooltelgede väärtused, mis saadakse murdumisnäitajate ellipsoidi ning koordinaatide algust läbiva tasandi lõikumisel.
Olgu nüüd lainevektor suunatud peatelgede suhtes suvalises suunas , Jn 8.5B. Lõikame ellipsoidi -ga ristioleva tasandiga. Saab näidata, et ka nüüd on lõikejooneks oleva ellipsi poolteljed võrdsed suunda iseloomustavate murdumisnäitajatega ja seega saab leida ka vastavate lainete faasikiirused.
Teadmine, kuidas murdumisnäitajad sõltuvad -st, on vajalik mittelineaarses optikas, kus valguse sageduse kordistamisel kasutatakse anisotroopseid kristalle, vt 10.2 ja Jn 10.4.
Analüütilisest geomeetriast on teada, et ellipsoidi lõikamisel tasandiga eksisteerib kaks sihti, mille puhul ellipsoidi ja tasandi lõikejooneks on ringjoon. Seega neis sihtides leviva kahe laine murdumisnäitajad on võrdsed, st juhul, kui , on kristallil kaks optilist telge (≡ kaheteljeline kristall).
Kui aga ellipsoidi kaks pooltelge on võrdsed, nt , kõduneb ellipsoid pöördellipsoidiks, mille lõikumisel tasandiga on vaid üks ringikujuline lõige, tegemist on üheteljelise kristalliga. Muutes nüüd laine levikusihti Z′ näeme, et üks ellipsi pooltelgedest ei muutu, ta väärtus annab -laine murdumisnäitaja ; teise, -laine murdumisnäitaja väärtus aga sõltub nurgast optilise telje ja levikusihi vahel; vahe on maksimaalne, kui valgus levib risti optilise teljega. Üheteljelisi kristalle nimetatakse positiivseteks, kui () ja negatiivseteks, kui (). Tabelis T 8.1 on toodud mõningate kristallide murdumisnäitajad lainepikkusel .
| Aine | Murdumisnäitaja | |||
| Isotroopne | ||||
| Teemant | ||||
| Fluoriid | ||||
| Üheteljelised, positiivsed | Jää () | |||
| Kvarts () | ||||
| Tsirkoonium (ZrSiO2) | 1,923 | 1,968 | ||
| Rutiil | 2,616 | 2,903 | ||
| Üheteljelised, negatiivsed | Kaltsiit (CaCO3) | 1,6584 | 1,4864 | |
| Turmaliin | 1,669 | 1,638 | ||
| Naatriumnitraat | 1,5854 | 1,3369 | ||
| Be3Al2(SiO3) | 1,598 | 1,59 | ||
| n3 | ||||
| Kaheteljelised | CaSO4 | 1,520 | 1,523 | 1,530 |
| Vilgukivi | 1,552 | 1,582 | 1,588 | |
| Topaas | 1,619 | 1,620 | 1,627 |
Leidmaks valguse leviku seaduspärasusi anisotroopses keskkonnas, teisendame esmalt monokromaatilise tasalaine lainefunktsioonide avaldisi, tuues sisse lainevektori k suunalise ühikvektori k1=k/|k|, mille komponendid on
Analoogiliselt võib esitada magnetvälja
kusjuures E ja H on omavahel risti ja mõlemad vektorid on risti ka Poyntingi vektoriga S, so energia levikusuunaga
Asetame nüüd saadud lainefunktsioonid Maxwelli võrranditesse
ja avaldame esimese võrrandi -komponendi, vt 2.2,
ja peale diferentseerimist saame
Saadud avaldise sulgudes on vektorkorrutise k1×E -komponent, samalaadsed seosed saame ka y- ja z- komponendi jaoks, seega võib kirjutada
kust järeldub, et k1⊥H.
Korrates analoogilisi teisendusi rotH=∂D/∂t jaoks, jõuame tulemuseni
seega k1⊥D.
Rõhutagem, et v 8.5, v 8.6 ja v 8.7 on universaalse kehtivusega, st ei sõltu sellest, millise keskkonnaga on tegemist.
Rakendame nüüd saadud seoseid anisotroopse keskkonna juhule, kus elektrivälja tugevuse ja dielektrilise läbitavuse vektorid ei ole kollineaarsed, D∦E. Joonisel Jn 8.6 on ette antud vektorite E ja S paiknemine tasandis, seega paikneb vektor H tasandis ja on seejuures risti vektoriga E, v 8.5. Kuna nii lainevektor kui ka elektrinihke vektor on risti magnetväljaga, v 8.8 ja v 8.7, siis on nad samuti tasandis . Tulemuseks saame, et anisotroopses keskkonnas ei ole lainevektor ja energia levikusuunda iseloomustav Poytingi vektor samasihilised e Poytingi vektor ( kiir) ei ole risti lainefrondiga ( samafaasipinnaga). Kuna lainefrondi levikut iseloomustab faasikiirus ja energia levikut – rühmakiirus, vt 3.2, siis anisotroopses keskkonnas ei ole faasi- ja rühmakiirus samasihilised.
Siin punktis vaatleme vaid üheteljelisi kristalle, kus levib tavaline -laine, mille murdumisnäitaja on sõltumatu levikusihist ja ebatavaline -laine, mille murdumisnäitaja on erinevates sihtides erinev ja ühtib -laine murdumisnäitajaga vaid optilise telje sihis. Murdumise kirjeldamiseks on piisav tugineda vaid Huygensi printsiibil, mille järgi iga lainefrondi punkt on uue lainekese allikaks ja uus lainefront on nende lainekeste lainepindade mähispind ( samafaasipind).
Lähtudes Maxwelli võrranditest saab näidata, et Poytingi vektori ( kiire) suuna saame ühendades lainekese lähtepunkti ning lainepinna ja lainefrondi puutepunkti. See tulemus on üldine ja kehtib ka anisotroopses keskkonnas.
Langegu loomulik valgus anisotroopsele keskkonnale nurga all.
Murduva -laine levikumehhanism anisotroopses keskkonnas ei erine levikumehhanismist isotroopses keskkonnas, Jn 8.7A.
Keskkondade lahutuspinnalt lähtuva lainekese faasikiirus on sõltumatu suunast ja seepärast on lainepinnaks sfäär. Lainepindade mähispinnaks olev tasand on lainefrondiks. Poyntingi vektori suuna saame ühendades lainekese lähtepunkti ning lainepinna ja lainefrondi puutepunkti. Näeme, et -laine lainevektor ja Poyntingi vektor on kollineaarsed, k∥S, Jn 8.7A.
-lainekese lainepind on ellipsoid, mille üks telgedest on optilise telje O′O′′ sihiline, Jn 8.7B. Nagu jooniselt näha, Poyntingi vektori suund ei ühti nüüd enam lainevektori suunaga, k∦S.
Joonis Jn 8.8A annab selgituse islandi paoga tehtud eksperimendile, vt Jn 8.2. Kuna islandi pagu on negatiivne kristall, , siis ühtib -laine sfääriline lainepind -laine ellipsoidiga selle lühima telje sihis; mõlema laine lainefrondid on paralleelsed, kuid langemisnurgale vastav -laine murdumisnurk . -laine on lineaarselt polariseeritud pealõiketasandis, kus on ka murduv kiir ja -laine polarisatsioonitasand on temaga risti.
Kaldu langemisel, Jn 8.8B, ei ole lainefrontide tasandid enam paralleeled, sest . Lisaks, lähtudes Huygensi konstruktsioonist on lihtne näidata, et tavalise kiire jaoks murdumisseadus kehtib ja seega .
Üldjuhul ei pruugi optiline telg olla langemistasandis, siis pole ka -kiir enam langemistasandis.
Rakenduste mõttes tähtsal erijuhtumil on kristalli optiline telg paralleelne kristalli pinnaga. Kui , Jn 8.9, siis - ja -laine ruumilist lahknemist ei toimu, kuid erinev levikukiirus põhjustab nende lainete vahel täiendava faasivahe tekke.
Kristalle kasutatakse polariseeritud valguse saamiseks, valguse ühest polarisatsiooniliigist teise transformeerimiseks ja ka valguse polarisatsiooniseisundi analüüsiks.
Võrreldes teiste seadmetega, mille abil saadakse lineaarselt polariseeritud valgust, on anisotroopsetest kristallidest prismasüsteemid väiksema neeldumisega, nende abil saadava valguse polarisatsiooniaste on kõrge ja nad taluvad suuri kiiritustiheduse väärtusi.
Joonisel Jn 8.10A on kujutatud islandi paost Glani prisma(d). Mõlemad prisma omavahel paralleelsed optilised teljed on paralleelsed ka esimese prisma esitahuga ja kaldtahkude vahel on õhuvahe.
Kui loomulik valgus langeb risti esitahule, siis esimeses prismas levivate - ja -lainete murdumisnäitajate vahe on maksimaalne, kusjuures . Nurk on valitud nii, et -laine peegelduks täielikult, , -laine aga jätkaks levikut endises suunas. Kui lisaks sellele on -laine langemisnurk kaldtahule lähedane Brewsteri nurgale, , siis selle laine peegeldumiskaod on väikesed.
Wollastoni prismas, Jn 8.10B, on kahe islandi paost prisma kaldtahud optilises kontaktis. Prismade optilised teljed on paralleelsed esimese prisma esitahuga ja omavahel on optilised teljed risti. Murdumisel muutub esimese prisma -laine teises prismas -laineks ja kuna , siis see laine murtakse teise prisma aluse poole. Kuna esimese prisma -laine muutub teise prisma -laineks, murdub tema väiksema murdumisnäitajaga prismasse st laine levib allapoole. Kirjeldatud protsesside tulemusena väljub Wollastoni prismast kaks lahknevat lineaarselt polariseeritud lainet, mille polarisatsioonitasandid on omavahel risti.
Näide N 8.1
Lahendus
Langemisnurk prismade kaldtahule on (=0,52rad). Esimese prisma joonise tasandis lineaarselt polariseeritud e-laine murdub suurema murdumisnäitajaga keskkonda ja seepärast murdub ta teise prisma aluse poole (üles). Lähtudes murdumisseadusest leiame murdumisnurga
Vastavalt lisatud joonisele on ülespoole leviva kiire murdumisel õhku langemisnurk (θ−γ1) ja seega joonise tasandis lineaarselt polariseeritud laine väljumisnurk on
Korrates analoogilisi arvutusi allapoole leviva kiire jaoks, saame, et joonise risttasandis lineaarselt polariseeritud laine väljumisnurk on 8,5∘ ja summaarne kiirtevaheline nurk on ψ=14,1∘.
Faasinihkeplaat (≡ faasiplaat) on anisotroopsest materjalist tasaparalleelne plaat, mille optiline telg on paralleelne plaadi pindadega. Risti plaadile langev valgus jaotub kaheks risttasandites lineaarselt polariseeritud laineks, mis levivad samas suunas, kuid erineva kiirusega, Jn 8.9. Selle tulemusena tekib nende lainete vahel täiendav faasivahe. Kui plaadi paksus on , siis optiline käiguvahe on
ja faasivahe
Loomuliku valguse puhul on faasivahe ristkomponentide vahel juhuslik suurus. Kui juhuslikule suurusele lisada mingi konstantne arv, siis on tulemuseks jälle juhuslik arv, seega loomulik valgus jääb plaadi läbimisel loomulikuks. Kui aga faasiplaadile langeb lineaarselt polariseeritud valgus, Jn 8.11A, siis sõltuvalt plaadi paksusest ja nurgast optilise telje ning valguse polarisatsioonitasandi vahel võib väljundis saada mitmel erineval viisil polariseeritud valguse.
Olgu konkreetsuse mõttes lainetevaheline faasivahe plaadi väljundis (m+1/2)π, sellele vastav optiline optiline käiguvahe on
kus Selliseid plaate nimetatakse veerandlaineplaatideks (≡ plaat).
Kui nurk optilise telje ja polarisatsioonitasandi vahel on kas , , või , st langeva valguse polarisatsioonitasand on kas paralleelne või risti optilise teljega, siis väljub plaadist lineaarselt polariseeritud valgus. Kui aga , , , , Jn 8.11B, siis Ex0=Ey0 ja plaadist väljub ringpolariseeritud valgus, vt 2.5.
Kõigil teistel nurga väärtustel väljub - plaadist elliptiliselt polariseeritud valgus.
Peale uurimuslike eesmärkide vajatakse – plaati nt laserkiirgust kasutavates tehnoloogiates, kus on tähtis nurgast sõltumatu intensiivsuse jaotus.
Näide N 8.2
Lahendus
Nagu ikka faasiplaatide puhul, on optilised teljed risti plaatide külgedega. Üldjuhul levib plaadis nii - kui ka -laine. Kui teise plaadi optiline telg on risti esimese plaadi optilise teljega, siis esimesest plaadist väljuv -laine käitub teises plaadis -lainena ja esimese plaadi -laine on teises -laine. Summaarne optiline käiguvahe on
Kuna aga Δ=λ/4, siis
Plaatide paksuste vahe on 15μm.
Teiseks enamlevinud faasiplaadi tüübiks on – plaat, kus - ja -laine vahel tekib täiendav faasivahe võrra. Kui näiteks algselt horisontaaltasandis lineaarselt polariseeritud valgus langeb – plaadile ja , siis plaadist väljuv valgus on lineaarselt polariseeritud vertikaaltasandis.
Eelnevalt, vt Jn 3.10, nägime, et kasutades vaid polaroidi, on lihtne eristada lineaarselt polariseeritud valgust elliptiliselt polariseeritud või ringpolariseeritud valgusest. Selleks tuli paigutada polaroid risti valguse levikusuunaga ja registreerida valguse intensiivsuse sõltuvus polaroidi pöördenurgast . Samas aga pole võimalik vaid polaroidi kasutades eristada ringpolariseeritud valgust loomulikust valgusest, sest mõlemal juhul on intensiivsus sõltumatu nurgast . Eristamine osutub võimalikuks, kui kasutada – plaadist ja polaroidist koosnevat süsteemi, Jn 8.12.
Loomulik valgus jääb ka faasiplaadi läbimisel loomulikuks ja polaroidi pööramisel teda läbinud valguse intensiivsus ei muutu.
Ringpolariseeritud valguse puhul on faasinihe kahe suvalise risttasandis lineaarselt polariseeritud komponendi vahel , – plaadi läbimisel lisandub sellele veel faasinihe ning summaarne faasimuutus on kas või , st väljuv valgus on lineaarselt polariseeritud. Pöörates nüüd polaroidi, näeme, et intensiivsus muutub vastavalt Malusi seadusele ja kui , on intensiivsus null.
Kasutades vaid polaroidi ei ole võimalik ka vahet teha, kas valgus on elliptiliselt polariseeritud või on tegemist loomuliku ja lineaarselt polariseeritud valguse seguga, sest mõlemal juhul on sõltuvus sama. Kui meil oleks tegemist elliptiliselt polariseeritud valgusega, siis määraksid maksimumid ja miinimumid ellipsi telgede asukohad, millesihiliste komponentide faasivahe on , vt 2.5. Seega paigutades valguse teele – plaadi, mille optiline telg ühtib ühega ellipsi telgedest, saame lineaarselt polariseeritud valguse, milles võib veenduda polaroidi abil. Kui aga tegemist oleks lineaarselt polariseeritud ja loomuliku valguse seguga, siis polaroidi pööramisega pole võimalik saavutada olukorda, kus tema väljundis valguse intensiivsus oleks null.
Elliptiliselt polariseeritud valguse kvantitatiivseks analüüsiks on vaja teada uuritava valguse ristkomponentide vahelist faasivahet δi. Seda eesmärki täidavad kompensaatorid, mis täiendavad algset faasinihet δi nii, et väljundis oleks faasivaheks või . Joonis Jn 8.13 kujutab Babinet-Soleili kompensaatori põhielemendid, mis tavaliselt on valmistatud kristallilisest kvartsist, mille puhul , vt T 8.1.
Kompensaatori ülaosas on kaks väikese murdva nurgaga kiilu, millest ülemine on täppismehhanismi abil horisontaalsihis nihutatav. Kuna kiilude all paikneva tasaparalleelse plaadi optiline telg on risti kiilude optilise teljega, siis kiiludes leviv -laine muutub plaadis -laineks nii nagu ka -laine muutub -laineks. Kui mingil ülemise kiilu asendis on langeva valguse asukohas kiilude summaarne paksus ja kui plaadi paksus on , siis omandab langev valgus täiendava faasivahe
Sellisel nihke väärtusel, kus (), on kiile ja plaati läbinud valgus lineaarselt polariseeritud ja kui polaroidi läbilaskesiht on risti selle tasandiga, valgus seadet ei läbi. Nihutades ülemist kiilu muutub ka faasivahe ja kui on väljundis valguse intensiivsus uuesti null. Kasutades kaliibrimiskõverat δk=f(x) saab leida langevat valgust iseloomustava faasinihke δi.
Eelnevalt nägime, vt 5.1, et lainete ja liitumisel tekib interferentsipilt, kui nende lainete skalaarkorrutise ajaline keskväärtus on nullist erinev, ⟨E1E2⟩≠0. Selle tingimuse täitumiseks peab lainetevaheline faasivahe mingis ruumipunktis jääma muutumatuks kogu vaatlusaja jooksul ning vektorid E1 ja E2 ei tohi olla risti.
Joonisel Jn 8.14A on kujutatud katseskeem, mis lubab jälgida faasiplaadis tekkivate lainete interferentsi.
Faasiplaadile langeb polaroidi abil saadud x−z tasandis lineaarselt polariseeritud valgus, kusjuures polarisatsioonitasandi ja optilise telje vaheline nurk on . - ja -laine amplituudid ja on faasiplaadile langeva laine projektsioonid vastavalt optilisele teljele ja tema ristsihile, Jn 8.14B. Kuigi nii saadud lained on koherentsed, me faasiplaadi väljundis interferentsi ei näe, sest Eo⊥Ee.
Tekitamaks faasiplaadist väljunud koherentsetele lainetele samasihilisi komponente, lisatakse katseskeemi polaroid . Juhul, kui polaroidide läbilaskesihid on paralleelsed, , on - ja -laine projektsioonid ja sihile samamärgilised ja kui siis , Jn 8.14C. Kuna faasiplaadis paksusega tekib liituvate lainete vaheline faasivahe , siis vastavalt punktile 5.2 avaldub liitlaine amplituudi ruut nagu
ning (M 8.3)
Kui polaroidid on risti, , siis on projektsioonid sihile vastassuunalised, Jn 8.14C, st liituvate lainete vahel on täiendav faasivahe .
Seostest v 8.11, v 8.12 järeldub, et kui plaadi paksusega ja lainepikkusega määratud faasivahe on
siis
ja
Kui aga plaadi paksus on selline, et
siis
ja
Kui nüüd valgustada joonise Jn 8.14A faasiplaate valge valgusega, siis mingi paksuse jaoks on lainepikkusel täidetud tingimus
ja seega kui polaroidid on paralleelsed, on sellele lainepikkusele vastava värvuse intensiivsus maksimaalne. Mingil teisel lainepikkusel võib olla aga täidetud tingimus
st kui polaroidid on risti, on maksimaalne lainepikkusele vastav värvus. Seega pöörates vaid polaroidi , asendub üks värvus tema täiendvärvusega. Üldjuhul vastab igale faasiplaadi paksusele oma täiendvärvuste paar. Pildid joonisel Jn 8.15 tekivad, kui katseobjektiks on erinevate paksustega rööpküliku-kujulised faasiplaadid.
Mitmete vedelike ja amorfsete ainete puhul on tegemist statistilise isotroopiaga, st isotroopia on keskmistamise tulemus üle nende koosseisu kuuluvate koostisosade (molekulide, kristalliitide) kaootilise paiknemise. Kui mõjutada selliseid aineid mingi eelissuunalise mõjuga, siis võib tekkida mikroskoopiliste anisotroopsete osakeste eelisorientatsioon ja aine tervikuna muutub anisotroopseks.
Mehhaanilise deformatsiooni, nii surve kui ka venituse, tulemusena võib algselt amorfne aine, nt pleksiklaas (≡ polümetüülmetakrülaat), muutuda üheteljeliseks kristalliks. Joonisel Jn 8.16A on kahe ristiolevate läbilaskesihtidega polaroidi vahel amorfse aine tükk ja välise mõju puudumisel valgus süsteemi ei läbi.
Jõupaar muudab aatomite vahelist kaugust ja selle deformatsiooni tulemusena muutub aine üheteljeliseks anisotroopseks keskkonnaks, mida iseloomustavad murdumisnäitajad ja . Jõupaariga ristsuunas leviva laine ja komponendi vahelise faasivahe suurus on võrdeline deformeeriva mõju suurusega
kus on deformatsiooni poolt mõjutatud piirkonna ulatus.
Algselt lineaarselt polariseeritud valgus on nüüd elliptiliselt polariseeritud ja osa sellest valgusest läbib ka polaroidi . Kui polaroidide läbilaskesihtide ja optilise telje vahel on nurk ja faasivahe oleks , siis käituks deformeerunud ainetükk faasiplaadina ja kogu langenud valgus läbiks polaroidi , vt 8.5.2.
Kuna murdumisnäitajate vahe sõltub lainepikkusest, siis valge langeva valguse puhul aine mingile lokaalsele ruumiliselt ebaühtlasele deformatsioonile vastab väljundis värviline pilt.
Pärast välismõjude lakkamist ei pruugi algselt amorfse aine omadused täielikult taastuda. Selliste jääkdeformatsioonide olemasolu võib mõjutada nt objekti tugevust. Läbipaistva objekti paigutamine ristuvate polaroidide vahele võimaldab leida seal olevaid jääkdeformatsioone. Kui on aga tegemist läbipaistmatute ja/või suuremate objektidega, siis neis olevate deformatsioonide leidmiseks valmistatakse läbipaistvad maketid. Kirjeldatud meetodit nimetatakse fotoelastsuse meetodiks.
Kui statistiliselt isotroopsele läbipaistvale ainele mõjub staatiline elektriväli, võib see keskkond muutuda üheteljeliseks anisotroopseks kristalliks, mille optiline telg on paralleelne rakendatud elektriväljaga (≡ Kerri efekt). Kerri efekti puhul tekkiv murdumisnäitajate vahe on võrdeline elektrivälja tugevuse ruuduga
kus on Kerri konstant. Kerri efekt on detekteeritav nii aine gaasilises, vedelas kui ka tahkes faasis. Vedelike puhul on anisotroopia tekke põhjuseks anisotroopsete molekulide eelisorientatsiooni kujunemine välises elektriväljas, temperatuuri kasvades põhjustab molekulide soojusliikumine Kerri efekti nõrgenemise.
Kuna elektrivälja toimel anisotroopia tekib ja kaob jooksul, siis on nn Kerri raku, Jn 8.16B, abil võimalik formeerida lühikesi valgusimpulsse. Selleks on küvett ristiolevate läbilaskesihtidega polaroidide vahel täidetud nitrobenseeniga, mis omab suurimat Kerri konstanti . Kui tasaparalleelsete elektroodide vaheline kaugus on ja rakendatud pinge on , siis ning kasutades seost v 8.12, saame avaldise faasivahe jaoks
Kui |U|>0, siis Kerri rakku läbiv valgus on üldjuhul elliptiliselt polariseeritud. Erijuhul, kui polaroidide läbilaskesihtide ja elektrivälja vahel on nurk ning , on meil tegemist poollaine plaadiga, st küvetist väljuv valgus on polariseeritud läbilaskesihis. Praktikas otstarbekate ja suuruste puhul peab poollaine plaadi tingimusele vastav pinge Uλ/2 olema kõrge, kümnetes kilovoltides.
Teine elektrivälja-valguse vastasmõjul tekkiv efekt on Pockelsi efekt, mille puhul faasivahe on võrdeline elektroodidele rakendatud pingega. Erinevalt Kerri efektist, eksisteerib Pockelsi efekt vaid kindlat tüüpi kristallide puhul. Valguse modulatsiooniks kasutatavates rakkudes on võimalik elektrivälja rakendada nii valguse levikuga piki- kui ka ristisuunas, kusjuures plaadi loomiseks vajalik pinge on suurusjärk väiksem kui Kerri efekti puhul.
Analoogilised isotroopse keskkonna muundamised anisotroopseks on tehtavad ka magnetvälja abil.
(P 8.4) Optiliselt aktiivseteks aineteks nimetataks selliseid aineid, kus leviva lineaarselt polariseeritud valguse polarisatsioonitasand pöördub. Selles võib veenduda katseskeemi Jn 8.17 alusel, kus algselt loomulik valgus muudetakse polaroidiga lineaarselt polariseerituks. Teise polaroidi läbilaskesiht on risti sihiga, nii et aktiivkeskkonna puudumisel on valguse intensiivsus väljundis null.
Aktiivaine paigutamisel polaroidide vahele ilmub väljundisse valgus, mille intensiivsuse saab viia nulliks, kui pöörata polaroidi nurga võrra. See, et valgust saab pärast aktiivaine läbimist polaroidiga kustutada, näitab, et tõesti on tegemist polarisatsioonitasandi pöördumisega, mitte aga kaksikmurdumisega. Kui vaadata vastu valguse levikusuunale, siis osade aktiivainete puhul tuleb polaroidi pöörata kellaosuti liikumissuunas (≡ -pöörav aine) ja osade puhul vastu kellaosuti liikumissuunda (≡ -pöörav aine).
Aktiivaine pöördenurk on võrdeline valguse poolt läbitava kihi paksusega
kus võrdetegur on ainet iseloomustav eripöörang.
Aktiivained võivad olla nii kristallilised kui ka amorfsed.
Tüüpiline aktiivaine esindaja on kristalliline kvarts, millel on kaks erinevat kristallograafilist modifikatsiooni. Kuigi need struktuurid koosnevad samadest molekulidest, paiknevad need molekulid modifikatsioonides erinevalt, mille tulemusena on üks modifikatsioon -pöörav ja teine -pöörav. Sellest, et sulatatud kvarts polarisatsioonitasandit ei pööra, järeldub, et kvartsi optiline aktiivsus tuleneb tema kui terviku struktuurist. Kvartsi polarisatsioonitasandi pöördumist mõõdetakse juhul, kui valgus levib piki optilist telge, sest valguse levikul mingis teises sihis leiab aset ka kaksikmurdumine selle mõiste tavapärases mõttes. Nii nagu teiste aktiivainete, nii ka kvartsi eripöörang sõltub tugevasti lainepikkusest, , lainepikkusel on eripöörang (K 8.13).
Mitmed ained, nagu suhkur ja tärpentiin, on aktiivained nii vedelal kujul kui ka lahustes. Nende ainete molekulid on stereoisomeerid st molekulide atomaarne koostis ja aatomite seosed on samad, kuid ruumiline struktuur on selline, et see ei lange kokku oma peegelpildiga st puudub peegelsümmeetria. Optiline aktiivsus eksisteerib lahustes, kus domineerib üks stereoisomeer. Näitena mitteühilduva konfiguratsiooniga molekuli optilisest aktiivsusest on -pöörav D-glükoos, , ja -pööratav D-fruktoos . Meditsiinis- ja toiduainetetööstuses saab pöördenurga mõõtmise põhjal leida objekti suhkrusisalduse.
Näide N 8.3
Lahendus
Vastavalt ülesande tingimustele peab laine polarisatsioonitasand pöörduma aktiivkeskkonnas vähemalt kraadi võrra ja laine polarisatsioonitasand - vähemalt võrras, kus m=1,2,3,…. Üldjuhtumil peab kehtima
Elimineerime võrrandsüsteemist kordaja saame plaadi paksuseks
Polarisatsioonitasandi pööramise fenomenoloogilise seletuse andis Fresnel, oletades, et optiliselt aktiivses keskkonnas jaguneb lineaarselt polariseeritud valgus parem- ja vasakpoolselt ringpolariseeritud valguseks, mis levivad erinevate kiirustega. Tõepoolest, matemaatiliselt võib iga piki sirget toimuva võnkumise jaotada kaheks vastassuunaliseks ringliikumiseks. Joonisel Jn 8.18A on näidatud, kuidas piki -telge võrdse kiirusega, , leviva kahe ringliikumise summaks on tasandis polariseeritud laine.
Kui aga , siis levikul kauguseni on vasak- ja parempoolse polarisatsiooni pöördenurgad erinevad
kusjuures ja . Kuna mõlema laine puhul on ajast sõltuvus sama, siis faasivahe nende osalainete vahel puudub, st nende summa jääb alati lineaarselt polariseerituks.
Arvestades, et summaarset lainet iseloomustav vektor on võrdkülgse rööpküliku diagonaal, Jn 8.18B, saab leida polarisatsioonitasandi pöördenurga kaugusel
(M 8.4)
Kuna vahe on väga väike, on vasak- ja parempoolselt ringpolariseeritud lainete ruumiline eraldamine komplitseeritud. Fresnel kasutas kiirte lahknevuse suurendamiseks kvartsprismade jada, kus paremale- ja vasemalepööravad prismad paiknesid vaheldumisi, Jn 8.18C. Kuna , siis laine murdub teise prisma aluse poole, aga -laine murdub vastassuunas ja nii toimub ka kõigil teistel murdumistel. Lõpptulemusena oli kiirte lahknevus piisav leidmaks, et kiired on vastupidiselt ringpolariseeritud.
Optilise aktiivsuse nähtus on korrektselt kirjeldatav kvantmehaaniliselt, kuid kvalitatiivselt on ta seletatav ka lähtudes klassikalistest kaalutlustest. Järgnev interpretatsioon pärineb M. Bornilt.
Optiline aktiivsus on mõistetav, kui pidada silmas, et see nähtus esineb ainetes, mille komponendid (molekulid, kristalliidid jms) omavad asümmeetrilist struktuuri. Sellise aine näiteks on kristalliline kvarts, kus räni ja hapniku aatomid paiknevad spiraalselt ümber optilise telje. Kvartsi vasakule ja paremale pööravad struktuurid on teineteise peegelkujutised. Amorfsed aktiivained koosnevad kaootiliselt orienteeritud asümmeetrilistest molekulidest.
Üldine valguse levikumehhanism optilises aktiivaines ei erine mehhanismist isotroopses aines, mõlemal juhul indutseerib langev valgus aatomite/molekulide dipoolkiirguse. Näitena koosnegu aktiivaine parempoolset spiraalset struktuuri omavatest molekulidest. Olgu lihtsaimal juhul langev valgus lineaarselt polariseeritud tasandis ja spiraalne molekul on orienteeritud piki -telge, Jn 8.19A.
Kuna nüüd hakkab elektrivälja mõjul elektron liikuma piki spiraali, siis omandab ta liikumine ka -telje sihilise komponendi, st indutseeritud dipoolmomendi ja seega ka dipooli poolt kiiratava lainekese polarisatsioonitasand ei ühti langeva laine polarisatsioonitasandiga. See sekundaarlaine langeb omakorda järgmises aatomtasandites olevate molekulideni, kus kirjeldatud protsess kordub ja nii kasvab -i kasvades ka polarisatsioonitasandi pöördenurk.
Vasakpoolse spiraali kujulisi struktuurielemente omavad ained pööravad polarisatsioonitasandit vastassuunas.
Magnetvälja mõjul polarisatsioonitasandi pöördumine (≡ Faraday efekt) toimub ka ainetes, mis välismõjuta ei ole optiliselt aktiivsed. Kui diamagneetikust silinder on solenoidi homogeenses magnetväljas ja magnetiline induktsioon on , Jn 8.19B, siis polarisatsioonitasandi pöördenurk on
kus on silindri pikkus. Aineomadustega määratud Verdet constant ) väheneb kiiresti lainepikkuse kasvades.
Rangem magnetväljas toimuva polarisatsioonitasandi pöördumise mehhanismi kirjeldus baseerub kvantmehhaanikal, siin piirdume klassikalise kvalitatiivse kirjeldusega. Vastavalt joonisele Jn 8.18A on lineaarselt polariseeritud valgus superpositsioon kahest ringpolariseeritud lainest. Kummagi laine pöörlev -vektor põhjustab aatomis seotud elektroni tiirlemise ringorbiidil, mis omakorda tekitab tiirlemissuunaga määratud magnetvälja, parem- ja vasakpoolselt polariseeritud valguse magnetväljad on vastassuunalised. Tugevas, valguse levikusihilises magnetväljas mõjub elektronile lisaks tuuma poolt mõjuvale jõule samuti radiaalsuunas mõjuv jõud (M 8.5), mille tulemusena elektroni orbiidi raadius ja seega ka dipoolmoment muutub. Kuna parem- ja vasakpoolse valguse ringpolarisatsiooni magnetväljad olid vastassuunalised, siis on välises magnetväljas ka indutseeritud dipoolmomendid erinevad, mille tulemuseks on murdumisnäitajate, vt 7.1.2, ja seega ka levikukiiruste erinevus, .
Mõnedel materjalidel on Verdet konstant piisavalt suur selleks, et kasutada Faraday efekti nt valguse moduleerimiseks või magnetväljade mõõtmiseks.siis on suur ka pöördenurk ja Faraday efekt leiab kasutust mitmetes rakendustes, nt valguse moduleerimises, magnetväljade mõõtmisel jm.
Elektromagnetlaine eelsel perioodil toodi sisse laineoptika seaduspärasuste seletamiseks spetsiaalse keskkonna, eetri, mõiste. Valguse elektromagnetlaine mudeli puhul see eetri funktsioon kadus, sest elektromagnetlaine on iseennast alalhoidev protsess, vt Jn 2.2. Probleemid tekkisid aga Maxwelli võrrandite sobitamisel klassikalise Galilei teisendusega, mis seob sündmuste kirjeldamise erinevates koordinaatsüsteemides.
Kui meil on tegemist kahe koordinaatsüsteemiga ja , millest teine liigub piki z-telge esimese suhtes ühtlase kiirusega kiirusega , Jn 9.1, siis vastavalt Galileile saame mingi punkti koordinaatide ja aja vahelised seosed
ja kiiruste jaoks
Valem v 9.1 on kiiruste liitmise valem klassikalises mehaanikas. Lisaks toonitagem, et aeg on mõlemas koordinaatsüsteemis sama, ta on absoluutne.
Võttes koordinaatidest teise tuletise aja järgi, näeme, et Newtoni teine seadus näeb inertsiaalsetes koordinaatsüsteemides välja ühtemoodi
Teiste sõnadega, klassikalise mehaanika võrrandid on invariantsed Galilei teisenduse suhtes.
Maxwelli võrrandid aga ei ole invariantsed Galilei teisenduse suhtes ja nüüd jäi eetri ainsaks ülesandeks kindlustada Maxwelli võrrandite kehtivus üleminekul ühest inertsiaalsüsteemist teise. Lorentz oletas , et eeter on absoluutselt liikumatu ja tal puudub igasugune vastasmõju materiaalsete kehadega. Vastavalt sellele oletusele peaks kehade liikumine eetri suhtes kajastuma „eetri tuules“.
(P 9.3) Katse eetri tuule mõõtmisel baseerus eeldusel, et Maa kiirus eetri suhtes on sama, mis Maa kiirus tema orbiidil ümber Päikese, . Mõõtmisteks kasutati Michelsoni interferomeetrit, Jn 9.2A, kus tekkinud interferentsipildi järgi saab leida optilise käiguvahe .
Interferomeetri orientatsioon oli selline, et horisontaalse õla siht ühtis Maa kiiruse sihiga. Optilised teepikkused jagamisplaadist peegliteni olid võrdsed. Valguse levikuaegade leidmisel interferomeetris eeldame, et kehtib kiiruste liitmise valem v9.1. Koordinaatsüsteemis, kus valguse levikukiirus on ja mille suhtes interferomeeter liigub piki z-telge kiirusega , näeme joonisel Jn 9.2B kujutatud kiirtekäiku. Sel juhul saab valguse levikuaja jagamisplaadist peeglini leida seosest ja levikuaja tagasisuunas saame seosest ct2=L−ut2 ning kogu aeg horisontaalsihis edasi-tagasi levikuks on
(M 9.1) Teepikkus jagamisplaadist peeglini on , kust saame vastava levikuaja ning koguaeg vertikaalsihis edasi-tagasi levikuks on
(M 9.2) Seega on interfereeruvate kiirte levikuaegade erinevus
ja vastav optiline käiguvahe on
Interferomeetri pööramisel võrra vahetavad interferomeetri õlad oma kohad, optiline käiguvahe muutub võrra ja interferentsiribad nihkuvad riba võrra.
Michelsoni interferomeetri täiustamise tulemusena oli võimalik viia interferomeetri õla efektiivne pikkus meetrini ning seetõttu pidi eetri tuule olemasolul interferentsipilt nihkuma ligikaudu poole riba võrra. 1887. aasta eksperimenditingimustes oli mõõtemääramatus väiksem kui poolest ribalaiusest, kuid mingit ribade nihet ei leitud.
Michelson-Morley katse negatiivne tulemus viis A. Einsteini 1905. aastal erirelatiivsusteooria formuleerimiseni.
(K 9.2) Teooria baseerub kahel postulaadil
- Füüsikaseadused on samad kõigis inertsiaalsüsteemides, puudub eelistatud koordinaatsüsteem. Seega on võimalik detekteerida vaid ühe keha suhtelist liikumist teiste suhtes, ei eksisteeri absoluutset liikumist .
- Valguse kiirus vaakumis on sama kõigis koordinaatsüsteemides, valguse kiirus ei sõltu sellest, kas valgust kiirgav objekt liigub või liigub valguse tajur.
Saab näidata, et Galilei koordinaatide, aja ja kiiruse teisendused üleminekul ühest inertsiaalsest koordinaadistikust teise asenduvad nüüd Lorentzi teisendustega. Kui on z-telje suunaline koordinaadistiku liikumiskiirus suhtes, siis mingi punkti koordinaadid ja ajamomendid on seotud nagu
ja kiirused
(K 9.3) Kui kiirused on mitterelativistlikud, st , siis taanduvad teisendused klassikalisele juhule v 9.1. Lorentzi teisendused on vastavuses erirelatiivsusteooria postulaatidega. Rakendades kiiruste liitmisvalemit v 9.3 valguse kiiruse jaoks vaakumis, , saame
mis on vastavuses erirelatiivsusteooria teise postulaadiga ja selgitab ka Michelson –Morley katse negatiivset tulemust.
Kui aine liigub, siis peaks tema murdumisnäitaja ja seega ka valguse faasikiirus muutuma. Tõepoolest, kui valgus liigub vastassuunas aine liikumisele, kohtab ta oma teel ajaühikus rohkem aine molekule ja murdumisnäitaja peaks kasvama; kui aga aine ja valguse liikumissuunad ühtivad, peaks murdumisnäitaja vähenema.
Fizeau interferomeeter, Jn 9.3, võimaldab mõõta valguse kiirust vedelikus, mis liigub kiirusega .
Valgusallikast lähtuv valgus jaotatakse jagamisplaadi abil kaheks võrdse intensiivsusega kiireks, millest üks levib vedeliku liikumissuunas ja teine – vastassuunas. Jagamisplaadi ja peegli tasandite vahel on väike nurk ja seega näeme väljundis samapaksus interferentsiribasid. Kuna mõlemad kiired läbivad vedelikus samad teepikkused, siis vastassuunas levivate lainete vaheline faasivahe väljundis on tingitud vaid nende lainete erinevatest kiirustest. Kui muuta vedeliku liikumissuund vastupidiseks, toimub interferentsiribade nihe ja selle järgi on võimalik leida valguse faasikiirus keskkonnas, mille murdumisnäitaja on ja liikumiskiirus .
Liites kiirused ja klassikalise valemi v 9.1 järgi, on tulemus erinev eksperimendis saadust. Rakendades relativistlikku valemit v 9.3, omandab faasikiirus liikuvas keskkonnas kuju
Näeme, et erinevalt Michelson-Morley katsest, on relativistlik kiiruse korrektsioon võrdeline suhte esimese astmega ja on seega kergesti detekteeritav.
Kuna , võib kirjutada valguse jaoks, mis levib vedelikuvooga samas suunas
Kiiruse leidmine selle valemi järgi langeb hästi kokku eksperimentaalselt mõõdetud kiirusega.
Nurkkiirusega pöörlevas Sagnac’i interferomeetris, mille üks modifikatsioon on joonisel Jn 9.4A, on interferomeetri väljundis liituvate lainete vaheline faasivahe tingitud päri- ja vastupäeva levivate lainete erinevast levikuajast.
Pöörlev süsteem on mitteinertsiaalne ja rangel lähenemisel tuleks faasinihke leidmiseks lähtuda üldrelatiivsusteooriast. Kuna aga gravitatsioonivälja pole tuletuskäigus vaja arvestada, siis erirelatiivsusteooria annab üldrelatiivsusteooriaga identse lõpptulemuse ja võib piirduda lihtsama teooriaga.
Leidmaks faasinihet, lähtume rakenduslikult tähtsast interferomeetri skeemist, Jn 9.4B, kus interfereeruvad lained levivad mitmekeerulises optilises kius, mille murdumisnäitaja on .
Olgu ühe keeru raadius , siis tema pikkus on ja joonkiirus paigalseisvas ( laboratoorses) koordinaatsüsteemis on . Kasutades relativistlikku kiiruste liitmist v 9.4, saab leida päripäeva ja vastupäeva levivate lainete kiirused , . Olgu aeg, mille jooksul teeb päripäeva leviv valgus kius ühe täistiiru. Arvestades, et jagamisplaat nihkub selle aja jooksul vahemaa võrra, saame päripäeva leviva laine poolt läbitud summaarse vahemaa
Analoogiliselt arutledes saame, et vastupäeva leviv laine läbib vahemaa
Neist seostest saab leida levikuaegade erinevuse
Kui nüüd saadud seosesse paigutada v 9.4 järgi avaldatud kiirused ja , siis pärast algebralisi teisendusi jõuame tulemuseni
On märkimisväärne, et avaldises puudub sõltuvus murdumisnäitajast.
Kui interferomeetris ringleb valgus sagedusega , siis määrates interferentsipildi järgi faasinihke , saab leida süsteemi pöörlemiskiiruse . Vastavalt valemile v9.6 on pöörlemiskiirus määratav seda täpsemini, mida suurem on pikkus , tundlikkuse suurenemine saavutatakse optilise kiu keerdude arvu suurendamisega.
Faasinihke ja pöörlemiskiiruse vahelisel sõltuvusel baseerub optilise güroskoobi töö, mida kasutatakse navigatsioonis ja erinevate seadmete töö stabiliseerimisel.
Näide N 9.1
Lahendus
Maa pöörlemiskiirus on
seega minimaalne mõõdetav kiirus peaks olema
Güroskoobi ühe keeru pikkus on L=2πR=0,63m, rõnga kogupikkus on LΣ=nL. Kuna Φ=ωΔt, siis valemi v 9.6 abil leiame
nii et
Doppleri efekt on allika suhtes liikuva vaatleja poolt registreeritav laine sageduse/lainepikkuse muutus. Kui laine vajab oma levikuks keskkonda, nt häälelaine, siis võib Doppleri efekt olla põhjustatud nii vaatleja liikumisest, allika liikumisest ja ka keskkonna liikumisest. Valgus oma levikul vaakumis ei vaja aga spetsiifilist keskkonda ja seepärast on sageduse/lainepikkuse muutumine sõltuv vaid vaatleja ja allika omavahelisest suhtelisest liikumisest.
Olgu meil tegemist vaakumiga ja tuletame valguse lainepikkuse muutuse mitterelativistlikul juhul, st allika liikumiskiirus vaatleja suhtes on väike, .
Olgu vahemaa, mille valgus läbib aja jooksul, . Kui allikas ei liigu, Jn 9.5A, siis intervall sisaldab laineharja, ja seega
Liikugu nüüd allikas kiirusega vasakult paremale, Jn 9.5B. Uues intervallis on sama arv laineharju
kuid laineharjade vaheline kaugus ( lainepikkus) on nüüd teine
Leiame v9.7 ja v 9.8 vahe
Näeme, et kui valgusallikas liigub vaatleja poole, , siis registreeritav lainepikkus on lühem ( „sininihe“), allika eemaldumisel, , aga lainepikkus suureneb ( punanihe).
Relativistlikul juhul, , saaksime tulemuseks
mis väikestel kiirustel langeb kokku valemiga v 9.10.
Doppleri efektil on lai kasutusvaldkond. Astronoomias on võimalik Doppleri efektist põhjustatud tähtede spektrijoonte nihkest hinnata kiirusi, millega tähed kaugenevad/lähenevad, tähtede pöörlemiskiirusi jm. Maapealsete objektide kiiruse mõõtmiseks kasutatava radari töö baseerub samuti Doppleri efektil.
Näide N 9.2
Lahendus
Deuteeriumi aatomite energia SI-s on
ja aatomite kiirus on
Kuna kiirus on vaid valguse kiirusest , siis kasutame lainepikkuse hindamiseks lihtsamat valemit v 9.10
toimus kergesti registreeritav „sininihe“
Eelnevates peatükkides on vaikimisi eeldatud, et valguse elektrivälja tugevus on palju-palju väiksem kui aatomi tuuma elektrivälja tugevus optilise elektroni asukohas, . Sel juhul põhjustab valgus vaid elektroni aatomisisese liikumise väikese häirituse ning tuuma poolt mõjuv tasakaaluasendisse viiv jõud on kirjeldatav Hooke’i seadusega, , kus on hälve tasakaaluasendist.
Sel juhul on isotroopses keskkonnas aine polarisatsioon lineaarne funktsioon valguse elektrivälja tugevusest
kus on dielektriline vastuvõtlikkus. Seega on meil tegemist lineaarse optika lähendusega, mis kehtib suure varuga enamiku valgusallikate puhul, Jn 10.1A.
Laserid võimaldavad saavutada tuuma väljaga võrreldavaid (ja ka tunduvalt ületavaid) väljatugevusi, vt N 2.3. Hooke’i seadus kaotab nüüd oma kehtivuse, ja elektroni liikumisvõrrandi, vt v 7.4, koostamisel tuleb Hooke'i seaduse asemel kasutada rittaarendust
kus ja . Elektroni liikumisvõrrand on nüüd mittelineaarne ja lähtudes sellest võrrandist saab näidata, et mittelineaarne on ka aine polarisatsiooni ja valguse elektrivälja tugevuse E vaheline seos, Jn 10.1B Lihtsaimail juhul, kui nende vektorite suunad ühtivad ja keskkond on isotroopne, võib kirjutada
Siin on aine lineaarne vastuvõtlikkus ja on mittelineaarsed vastuvõtlikkused. Milline on nende koefitsientide osakaal valguse ja aine vastasmõju kirjeldamisel, sõltub valguse intensiivsusest ja aine ehitusest.
Järgnevalt piirdume juhuga, kus mittelineaarsetest koefitsientidest vaid . Kui sellisele keskkonnale langeb laine , siis peale lineaarse polarisatsiooni indutseeritakse seal ka mittelineaarne komponent
(M 10.1) Näeme, et valguse toimel indutseeritakse aines lisaks polarisatsioonile sagedusel ka polarisatsioon sagedusel ja ka ajast sõltumatu alaliskomponent.
Alaliskomponent on registreeritav potentsiaalide vahena kristalli tahkudel.
Põhisagedusest kõrgemate kordsete sageduste (º harmooniliste) ( – positiivne täisarv) indutseerimist nimetatakse sageduse kordistamiseks, erinevate võtetega on saavutatud maksimaalne sageduse kordsus .
Eelnevalt näitasime, vt v 7.2, et põhisagedusel jõuavad tasanditest ja kiiratavad sekundaarlained kaugemalolevasse vaatetasandisse samas faasis. Mittelineaarsel juhul indutseerib laine tasandites ja ka lained sagedusega . Näitame, et tasandisse jõudva laine faas sõltub nüüd lähtetasandist, Jn 10.2.
Tõepoolest, kui laine jõuab tasandisse ajahetkel , siis sellest tasandist lähtuva laine faas tasandis ( väljundis) on
Analoogilise avaldiseni jõuame ka tasandist z′′ lähtuva laine puhul
Dispersiooni, , tõttu tekib väljundis eri tasanditest lähtuvate lainete vahel faasivahe
Kui kahest naabertasandist lähtuvate lainete vahe on konstantne faasivahe, siis summaarne laine väljundis on leitav vektordiagrammi abil, Jn 10.2B. Väljundlaine kasvab seni, kuni äärmistest tasanditest ja lähtuvate lainete vaheline faasivahe saab võrdseks -ga. Tähistades , saame sellele piirjuhule vastavast tingimusest keskkonna kriitilise paksuse, millest alates väljuv hakkab nõrgenema
(M 10.2) Kui paksus saavutab väärtuse , siis laine puudub. Edasisel paksuse kasvatamisel saabuvad uued laine maksimumväärtused paksustel , kus
Joonisel Jn 10.3A on üks esimesi valguse sageduse kahekordistamise katseskeeme.
Valgus sagedusega suunatakse plaadile, kud indutseeritakse valgus sagedusega 2ω. Plaadi pööramisel muutub valguse teepikkus plaadis. Väljundvalguse teel on filter , mida läbib vaid valgus sagedusega . Kui teepikkus plaadis rahuldab tingimust v 10.4 või on tema paaritu arv kordne, on valguse intensiivsus sagedusel maksimaalne, Jn 10.3B.
Rakenduse seisukohast on oluline, et lained sagedustel ja leviksid keskkonnas ühesuguste faasikiirustega, . Faaside kooskõlastus ( sünkronisatsioon) on saavutatav anisotroopses keskkonnas. Olgu tegemist üheteljelise positiivse kristalliga, no≤ne, mille dispersioon on normaalne, .
Joonisel Jn 10.4A oleval kristalli pealõiketasandis lõikuvad murdumisnäitajatele ja vastavad lainepinnad neljas punktis, neis punktides on täidetud tingimus st vastavates suundades on faasid kooskõlastatud. Realiseerimaks faaside kooskõlastatust, on anisotroopse kristalli sisend- ja väljundtahk risti ühega sihtidest , Jn 10.4B.
Igapäevaeluga on mittelineaarsel optikal kokkupuude laserpointerite ( laserviip) vahendusel, kus laseri kiirgus lainepikkusele vastaval sagedusel kahekordistatakse ning pointerist väljub roheline valgus lainepikkusel vt Jn 11.14.
Kui mittelineaarsele keskkonnale suunata valgused sagedustega ja , võib peale sageduste ja ning alaliskomponendi tekitada ka summaarse sagedusega ja vahesagedusega valguse.
Eelnevalt nägime, vt 3.7, et sobitamaks musta keha kiirgusspektreid teoreetiliste kaalutlustega tuli oletada kiirguse kvantiseloomu. Vastavalt Plancki hüpoteesile kiiratakse valgust mitte pidevalt nagu see järelduks laineoptikast, vaid portsjonite kaupa. Valgusallika poolt kiiratav energia on elementaarkvandi ( footoni) energia täisarv-kordne, kus on valguse sagedus ja – Plancki konstant. Selgus, et Plancki oletus pole lihtsalt matemaatiline trikk eksperimenditulemuste interpreteerimiseks, vaid tegemist oli sammuga välja ja osakeste füüsikat ühendava universaalse mudeli poole, mida tänapäeval nimetatakse kvantväljateooriaks.
Foto(elektriline) efekt on nähtus, kus valgus kutsub esile elektronide ( fotoelektronide) emissiooni ainest. Fotoefekti esmane eksperimenditulemuste kirjeldus pärineb H. Hertzilt, P.Lenard näitas, et valguse toimel emiteeruvad elektronid ja eksperimentaalsete alusuuringute lõppfaasiks oli Plancki konstandi eksperimentaalne määramine R. Millikani poolt.
Joonisel Jn 11.1A on tüüpskeem fotoefekti uurimiseks.
Emitterist ja kollektorist koosnev elektroodide süsteem paikneb vaakumis. Emitteri ja kollektori vahelist pinge polaarsust ja suurust saab muuta. Valgus põhjustab erinevate kiirustega elektronide emissiooni emitterist ja vooluringis registreeritakse vool . Joonisel Jn 11.1B on konstantsel lainepikkusel ja kahel erineval valguse intensiivsusel registreeritud sõltuvus ( volt-amper tunnusjoon). Kui kollektori potentsiaal on emitteri suhtes positiivne, siis saavutab vool oma küllastusväärtuse juba väikestel väärtustel. Kui kollektori potentsiaal on emitteri suhtes negatiivne, tingivad voolu vaid need elektronid, mille kineetiline energia on suurem kui elektrivälja potentsiaalne energia . Kui pinge saavutab pidurduspotentsiaali väärtuse , vool lakkab. Sel juhul
Vastavalt valguse lainemudelile peaks
- maksimaalne kineetiline energia sõltuma valguse intensiivsusest – mida suurem on intensiivsus, seda suurema energia omandavad pinnalt lahkuvad elektronid
- valgus põhjustama fotovoolu suvalisel lainepikkusel (sagedusel)
Eksperiment aga näitas, et
- pidurdav potentsiaal, mis on võrdeline elektronide maksimaalse kineetilise energiaga, ei sõltu valguse intensiivsusest, Jn 11.1B
- eksisteerib piirsagedus , millest väiksematel sagedustel fotovool puudub
A. Einstein oma fotoefekti teoorias lähtus sellest, et valguslaine on kvantiseeritud st valgus on footonite voog ja fotoefekt on footoni ja elektroni vastasmõju tulemus, mille puhul kehtib energia jäävuse seadus
kus on väljumistöö ja Wk on emiteerunud elektroni kineetiline energia. Fotoefekti tekitamiseks vajalik minimaalne valguse sagedus on määratud tingimusega Φ=hf0, sel juhtumil kulub kogu footoni energia vaid elektroni viimiseks metalli pinnale. Seega seos kineetilise energia ja sageduse vahel saab kuju . Esitades nüüd energia funktsioonina sagedusest , saame lineaarse sõltuvuse, mille tõus on ja mille lõikepunkt y- teljega annab väljumistöö , Jn 11.1C.
Tabelis 11.1 on mõningate metallide väljumistööd elektronvoltides koos fotoefekti läveväärtusele ( fotoefekti punane piir) vastava sageduse ja lainepikkusega .
Kirjeldatud mehhanism vastab välisele fotoefektile lineaarse optika lähenduses. Kui aga valgusallika poolt ajaühikus kiiratavate footonite arv on piisavalt suur, siis võib realiseeruda mittelineaarne fotoefekt st ühe footoni energia on väiksem aine väljumistööst, , ja elektron emiteeritakse footoni koosmõjul, .
Seesmise fotoefekti puhul siirdub footoni toimel elektron pooljuhi või dielektriku valentstsoonist juhtivustsooni, juhtivus suureneb ja fotovool vooluringis suureneb.
Üksikuid footoneid on võimalik detekteerida fotokordistiga, mis koosneb valgustundlikust fotokatoodist ja vaakumis paiknevast pingestatud elektroodide (dinoodide) süsteemist, Jn 11.2. Dinoodid on valmistatud materjalidest, mille puhul võib elektronide toimel aset leida uue, sekundaarse, elektroni emissioon.
Erinevatest materjalidest fotokatoodid on valgustundlikud laias spektraalvahemikus . Footon lööb teatud tõenäosusega fotokatoodist välja elektroni, mis omandab elektriväljas energia, mille puhul saab võimalikuks esimesest dinoodist täiendava elektroni emissioon. Selline elektronide paljunemine toimub kõigi dinoodide puhul ja lõpptulemusena tekib anoodil ühe fotokatoodile langeva footoni kostena elektronist koosnev vooluimpulss, mida on kerge elektriliselt registreerida.
Võrreldes nüüd valguse interferentsi kirjeldamist laineoptika vahendusel ja fotoefekti kirjeldamiseks kasutatud valguse korpuskulaarset loomust, jõuame järelduseni, et valgusel on kahene loomus. Samasugune korpuskulaar-laineline dualism on omane kõigile mikromaailma osakestele ja seepärast on footonile kohaldatavad ka teised kvantmehhaanika põhiseosed.
Relativistlikul juhul avaldub seisumassi ja koguenergiat omava osakese impulss nagu
Kuna footoni seisumass on null, siis tema impulss on
Kui footon omab impulssi, siis peab valgus avaldama pinnale rõhku. Lähtudes valemist v.11.2, rõhu definitsioonist
ja kiiritustiheduse definitsioonist
saame, et valguse rõhk ideaalselt neelavale pinnale on
Kui valgus langeb ideaalsele peeglile, muutub footoni impulsi suund vastupidiseks ja vastavalt impulsi jäävusele on rõhk peeglile kaks korda suurem.
Vastavalt de Broglie'le ja kooskõlas elektronide difraktsiooni eksperimentidele on mikroosake iseloomustatav lainepikkusega
Siit saame footoni jaoks
Kuna aga f=c/λ, siis footoni energia on
mis langeb kokku Plancki energia-sageduse vahelise seosega.
Sarnaselt teiste mikroosakestega iseloomustab ka footonit spinn. Ühikutes ℏ=h/2π omab elektroni spinn poolarvulisi väärtusi , kuid footoni spinn on täisarvuline .
Footonite ja teiste mikromaailma osakeste ühtsus avaldub ka Heisenbergi määramatuse seose kaudu. Vastavalt valemile v 2.32 on lainepaketi kestuse ja sellele vastava spektri laiuse korrutis suurusjärguliselt üks
Korrutades selle avaldise vasakut ja paremat poolt Plancki konstandiga, saame
mis ütleb, et energia määramatuse ja aja määramatuse korrutis on suurusjärguliselt võrdne Plancki konstandiga.
Kuna vastavalt kvantmehaanikale on elektroni seoseeenergiad aatomis kvantiseeritud, on ka elektroni leidmise tõenäosus suurim kindlatel kaugustel tuumast ( orbiitidel).
Kui esiplaanil on seisunditevahelisel üleminekul toimuv energia neeldumine või vabanemine, võib aatomi kirjeldamisel piirduda energiadiagrammiga, Jn 11. 3. Horisontaalseid kriipse diagrammil nimetatakse energianivoodeks. Kriipsjoon diagrammil vastab ionisatsioonienergiale. Nagu ikka potentsiaalse energia puhul, on nullnivoo valik kokkuleppeline. Praegu valime nullnivooks energia seisundis 1 (≡põhiseisund). Energiadiagrammil kujutatud nool vastab üleminekule orbiidilt orbiidile . See üleminek võib aset leida põrke tulemusena või olla kiirguslik. Kiirguslikul üleminekul kiiratakse footon energiaga
Ka siis, kui aatomil puudub vastasmõju ümbritsevaga (≡ isoleeritud aatom), on tema viibimisaeg mingil energianivool (≡ loomulik eluiga) üldjuhul lõplik, möödudes siirdub aatom madalamale energianivoole. Vastavalt seosele v11.3 vastab aja määramatusele energia määramatus st energianivoo on lõpliku laiusega. Erandiks on vaid põhiseisund, mille eluiga on lõpmatu. Seega kiirguslikule üleminekule seisundist seisundisse ei vasta üks konkreetne sagedus f21, vaid aatom võib kiirata footoni sagedusintervallis Δf21, spektrijoon on lõpliku laiusega. Kui aatom ei ole isoleeritud, nt toimuvad põrked teiste aatomitega jpm, siis aatomi eluiga mingil energianivool on lühem loomulikust elueast ja spektrijoone laius on seetõttu suurem.
Soojuslikus liikumises osalevate aatomite erinevad kiirused põhjustavad lainepikkuse/sageduse erinevad nihked, vt 9.4, mis on täiendava nn Doppleri laienemise põhjuseks.
A. Einstein iseloomustas valguse ja aatomi vastasmõju kolme kvantprotsessiga.
Olgu meil tegemist lihtsaima aatomite kogumiga, kus igal aatomil on vaid kaks energianivood energiatega ja , aatomite kontsentratsioonid (≡ hõived, dimensioon ) neis seisundites on ja , Jn 11.4.
Kui aatomid on algselt seisundis , siis toimub ka ilma mingi välise mõjuta ise-eneslik (≡ spontaanne) kiirguslik üleminek seisundisse , mille tulemusena kiiratakse footonid energiaga hf21=E2−E1. Kiiratava footoni levikusuund on juhuslik kogu ruuminurga ulatuses. Sellise vabakiirguse (≡ spontaanse kiirguse) tulemusena seisundi 2 hõive väheneb, tema muutus ajaühikus (≡ kiirus, dimensioon m−3s−1) on võrdeline selle seisundi hõivega
Vabakiirgust iseloomustav koefitsient on määratud aatomi ehitusega. Eraldades muutujad ja integreerides saame
Näeme, et aja jooksul kahaneb seisundi hõive korda st selle seisundi kiirguslik eluiga on
Olgu nüüd aatomid välises (valgus)väljas, mille energiatihedus on ρf . Kui footonide arv ruumiühikus on Nf, siis
ja kuna vastavalt definitsioonile on kiiritustihedus If ajaühikus pinnaühikut läbiv energia, vt 2.4, siis saame
Kui nüüd footon sagedusega f21 langeb seisundis olevale aatomile, siis teatud tõenäosusega toimub kiirguslik üleminek ja uus footon, mis omab samuti sagedust f21, levib langeva footoniga samas suunas. Need footonid on eristamatud.
Sellise sundkiirguse (≡ stimuleeritud kiirguse) tulemusena aatomite hõive seisundis väheneb kiirusega
kusjuures on aatomi omadustega määratud sundkiirguse koefitsient.
Kui aga välises väljas olev aatom on seisundis , siis võib aatom siirduda sagedust f21 omava footoni toimel seisundisse st valgus neeldub. Neeldumise tõttu seisundi hõive väheneb ja seega seisundi hõive kasvab kiirusega
Nii nagu ja puhul, on ka määratud aatomi omadustega ja on sõltumatu välismõjudest.
Saadud tulemusi võib rakendada mitmetel spetsiifilistel juhtudel.
Termodünaamiliselt tasakaalulises süsteemis on nii aatomide kulgeva liikumise energia, siseenergia kui ka kiirgusenergia jaotused iseloomustatavad üheainsa parameetriga – temperatuuriga , vt 3.7. Lisaks kehtib detailse tasakaalu printsiip st otseste ja pöördprotsesside kiirused on võrdsed, mingi energianivoo hõive kahanemist kiirguse tõttu kompenseerib hõive suurenemine neeldumise tõttu. Teiste sõnadega, termodünaamilise tasakaalu olukorras seisundite hõive ei muutu.
Olgu meil endiselt tegu 2-nivooliste aatomite kogumiga, Jn 11.5.
Lähtudes valemitest v11.5, v 11.8 ja 11.9 võib kirjutada nivoo jaoks
ja avaldada siit kiirgustiheduse
Leidmaks hõivete suhet, kasutame teavet termodünaamikast, mille järgi termodünaamilise tasakaalu olukorras osakeste kontsentratsioon mingis olekus on määratud Boltzmanni jaotusega
kus on selle oleku energia ja on süsteemi temperatuur. Joonisel Jn 11.5B on kujutatud aatomi diskreetsete energianivoode ja neile nivoodele vastavate hõivete vaheline sõltuvus. tihedus välises väljas vastavalt Boltzmanni jaotusele
Lähtudes Boltzmanni jaotusest saame, et nivoode ja hõivete suhe on
Kiirgustihedus on nüüd kujul
Saadud tulemus peab kehtima mistahes temperatuuril. Kuna temperatuuri tõustes ρf kasvab piiramatult, ja, kuna , ja on temperatuurist sõltumatud, siis peab exp(hfkT)→1. Seega jõuame tulemuseni, et, ja me saame
Kui nüüd võrrelda saadud kiirgustiheduse ρf ja musta keha kiirgavuse valemit v 3.22, näeme, et vaba ja sundkiirguse koefitsientide suhe sõltub väga tugevasti sagedusest
Järgnevalt kirjeldame mõningaid mittetermilisi valguse tekitamise viise. Kuna nende puhul pole täidetud detailse tasakaalu printsiip so otseste ja pöördprotsesside võrdne kiirus, on meil tegemist termodünaamiliselt mittetasakaalulise kiirgusega, mis ei ole kirjeldatavad Plancki valemiga.
Langegu valgus kiiritustihedusega If 2-nivooliste aatomite kogumile, Jn 11.6A. Aatomite vabakiirguse koefitsient on ja algselt olgu .
Kui on täidetud tingimus , siis tõenäosusega footon neeldub, st aatom siirdub seisundisse . Aatomi eluiga selles seisundis, tema siirdumine seisundisse võib toimuda nii kiirguslike kui ka mittekiirguslike protsesside tulemusena. Kiirguslikul üleminekul kiirgab aatom aja möödudes juhuslikus suunas sama sagedusega footoni. Sellist kiirgusmehhanismi nimetatakse resonantskiirguseks. Kiiratud footon neelatakse naaberaatomi poolt, mis omakorda kiirgab sama sagedusega ning juhuslikus suunas leviva footoni jne. Mittekiirgusliku ülemineku näiteks on mitteelastne põrge naaberaatomiga, mille tulemusena seisundisse salvestatud energia transformeeritakse kulgeva liikumise energiaks ja esialgses suunas leviva valguse kiiritustihedus väheneb.
Olgu nüüd tegemist mitmenivooliste aatomite kogumiga, Jn 11.6B, kus aatomid ergastatakse (≡pumbatakse) nivoole footonite abil. Selle seisundi hõive väheneb nii kiirguslike ülemineminekute kui ka põrgetest põhjustatud üleminekute tulemusena. Nivoolt toimuvaid madalama sagedusega f<f21 kiirguslikke üleminekuid nimetatakse Stokesi üleminekuteks. On võimalik ka anti-Stokesi üleminek näiteks nivoole ja siis f<f21 . Kui ülemineku eluiga on suhteliselt lühike, nt , siis räägitakse fluorestsentskiirgusest, sekunditesse ja minutitesse ulatuvate eluigade puhul on tegemist luminesentsiga.
Joonise Jn 11.7 fotod demonstreerivad hajumise, ergastamise ja neeldumise sõltuvust fluorestseeruvale keskkonnale langeva valguse lainepikkusest , tekkinud pildid on seletatavad joonise Jn 11.6 baasil. Punane laserikiir ei ergasta, ei neeldu ega ka haju märgatavalt. Kuna hajunud valguse intensiivsus , siis lühema lainepikkusega rohelise laseri valgus hajub juba märgatavalt, kiir on nähtav ka külgsuunas, kuid märgatavat neeldumist ja ergastamist ei toimu. Sinise laseri valgus hajub tugevasti ja ergastab ka kristalli molekulid kõrgemale energianivoole, kus toimuvate üleminekute tulemusena kiiratakse pikemalaineline roheline valgus, mis on nähtav läbi kristalli külgseina.Nende protsesside tõttu laserikiire intensiivsus kahaneb oluliselt.
Sõltuvalt konkreetsest keskkonnast (dielektrik, pooljuht, gaasiline plasma) ergastatakse termodünaamiliselt mittetasakaaluline kiirgus kas välise valgusallika, elektrivoolu või elektriväljas kiirendatud elektronide vahendusel.
Pooljuhtseadmetes tekitatakse valgus reeglina elektrivoolu toimel. Leed - valgusti põhielemendiks on pooljuhi p-n siire. Pooljuhtidesse on manustatud lisandaineid ( dopeerimine) nii, et päripidise pinge rakendamisel on kohakuti n-piirkonnast lähtuvad elektronid ja p-piirkonnast tulevad augud, Jn 11.8A.
Elektronid ja augud rekombineeruvad ja kiiratakse footonid, mille energia on määratud keelutsooni laiusega. Leedi pinnal on kate, kus lühemalaineline rekombinatsioonkiirgus transformeerub osaliselt pikemalaineliseks kiirguseks, Jn 11.8B, mille spekter on heas vastavuses inimese silma tundlikkuse kõveraga.
Eelnevalt, vt 4.8, saime, et valguse intensiivsus sõltub eksponentsiaalselt läbitava ainekihi paksusest
neeldumiskoefitsiendi pöördväärtus on arvuliselt võrdne kihi paksusega, mille läbimisel intensiivsus kahaneb korda.
Lähtudes aatomi kiirguslikke üleminekuid kirjeldavatest seostest 11.5, 11.8 ja 11.8, leiame neeldumiskoefitsiendi sõltuvuse energianivoode hõivest.
Olgu kihis dz paiknevate 2-nivooliste aatomite hõived ja ning langev valgus kiiritustihedusega levib väikesesse ruuminurka dΩ, Jn 11.9A. Vabakiirguse panuse otsesuunas levivasse valgusse võib lugeda tühiseks, sest dΩ/4π≪1.
Neeldumisest põhjustatud kiiritustiheduse muutus on
ja kuna
siis
Analoogiliselt saame sundkiirgusest põhjustatud kiiritustiheduse muutuse
Arvestades, et , saame summaarse kiiritustiheduse muutuse
kust on lihtne jõuda neeldumiskoefitsiendi avaldiseni
(K 11.11) Näeme, et sõltuvalt hõivete vahest võib af olla nii positiivne kui ka negatiivne. Negatiivne af tähendab, et ainekihi läbimisel valguse intensiivsus kasvab. Tasakaalulises olukorras on nivood hõivatud vastavalt Boltzmanni jaotusele, Jn11.9B, st alati ja domineerib neeldumine. Valguse intensiivsus ainekihi läbimisel kasvab, kui tekitada mingil viisil pöördhõive st , Jn 11.9C.
Kiirgusel/neeldumisel vahe ja seega ka neeldumiskoefitsient, ei jää konstantseks, sest juba ühe footoni neelamisel kasvab ülemise seisundi hõive ühe võrra ja alumise seisundi hõive kahaneb ühe võrra. Konstantseks jääb vaid valguse/aine vastasmõjus osalevate aatomite koguarv . If suurenedes kahaneb hõivete vahe kuni küllastuse saabumiseni . Selle tingimuse täitumisel on keskkond läbipaistev, energia ei neeldu ja seega on ka edasine hõivete muutumine võimatu. Seega on pöördhõive saavutamine kahenivoolise skeemi abil võimatu ja kaasata tuleb rohkem nivoosid, näitena on joonisel Jn 11.10 kujutatud 4-nivooline skeem.
Esmalt ergastatakse tugeva pumpamise tulemusena aatomid nivoolt nivoole , kust toimub väga kiire üleminek nivoole . Selle nivoo eluiga on võrreldes nivoo elueaga suhteliselt pikk, mille tulemusena saavutatakse nende nivoode vahel pöördhõive.
Olgu silindrilise kujuga keskkonnas, mille kõrgus on palju suurem tema diameetrist, Jn 11.11A, tekitatud pöördhõive, .
Sellises aktiivkeskkonnas juhuslikult z-telje suunas leviv footon põhjustab sundkiirguse tõttu uue ning samas suunas leviva footoni tekke ja algab footonite laviinikujuline kasv, valguse intensiivsus kasvab nagu
Intensiivsuse kasvu võib lugeda eksponentsiaalseks vaid seni, kuni pöördhõive muutub vähe, . Tabelis 11.2 on toodud eksponentsiaalsele kasvule vastav nõrga signaali võimenduskoefitsient . Intensiivsuse suurenedes pöördhõive väheneb, seetõttu intensiivsus ei kasva enam eksponentsiaalselt ja lõpptulemusena jõuab intensiivsus küllastusväärtuseni, Jn 11.11B.
Leiame nüüd tingimuse kiiritustiheduse jaoks, mille puhul vabakiirguse mõju seisundi hõivele võib lugeda tühiseks st
kust teisendades, vt v 11.5, 11.7, 11.8, saame
Siit järeldub, et sundkiirguse domineerimiseks kõrgematel sagedustel on vaja hulga suuremaid kiiritustiheduse väärtusi nt nähtava sageduse piirkonnas on vajaminev kiiritustihedus ligikaudu suurusjärku suurem kui kiiritustihedus terahertsise sageduse piirkonnas.
Näide N 11.2
Lahendus
Põrgete tulemusena on molekulid neil energianivoodel jaotunud vastavalt Boltzmanni jaotusele, v 11.10, ja temperatuuril saame
Analoogiliselt arvutades saame
Kui madalamal temperatuuril võib lugeda molekulivaheliste põrgete mõju hõivele tühiseks, siis kõrgemal temperatuuril pöördhõive N2−N1 väheneb.
(K 11.12) Läbides aktiivkeskkonda, valguse intensiivsus suureneb, seega käitub keskkond võimsusvõimendina, mille võimendustegur on väljundintensiivsuse ja sisendintensiivsuse suhe, , Jn 11.12A.
Võimendus sõltub nii pöördhõive suurusest kui ka aktiivkeskkonna pikkusest . Elektroonikast on teada, et suunates osa võimendist väljuvast signaalist tagasi sisendisse muutub väljundsignaali suurus. Kui tagasisideahel on valitud nii, et sisendsignaal ja tagasiside signaal on faasis, toimub väljundsignaali kasv, tegemist on positiivse tagasisidega. Kui tagasiside tegur on valitud nii, et
eksisteerib signaal väljundis ka sisendsignaali puudumisel st tegemist on generaatoriga.
Tagasiside loomiseks optilise diapasooni generaatorites (≡ laserites) paigutatakse aktiivkeskkond peeglite vahele, Jn 11.11B. Generatsiooni tekke tingimus v11.16 omandab nüüd kuju
kus ja on peeglite peegelduskoefitsiendid. Mida väiksem on aktiivkeskkonna võimendus, seda suuremad peavad olema peegelduskoefitsiendid.
Generatsiooni lävele vastab olukord, mille puhul on tasakaal peeglitevahelises ruumis ( resonaatoris) tekkivate ja sealt kaduvate footonite vahel. Saabunud statsionaarne olukord tähendab seda, et valguse ühel edasi-tagasi levikul (≡ tsükkel) resonaatoris peab nii laine amplituud kui ka faas jääma muutumatuks. Amplituud jääb muutumatuks, kui võimendus võrdub kaoga . Faasi muutumatuse tingimuseks teepikkusel on
kus on peeglitevaheline kaugus ja m=1,2,.... Kui aktiivkeskkonna murdumisnäitaja on n≈1, siis teisendades jõuame tuttava seisulaine tingimuseni
ehk
kus on resonaatoris statsionaarselt eksisteerida võiva moodi number. Sagedusskaalas on kahe naabermoodi vaheline kaugus
mis sõltub vaid peeglitevahelisest kaugusest.
Kõikvõimalikest valemiga v 11.17 määratud moodidest pakuvad meile huvi vaid need, mis paiknevad laserkiirgusele vastava ülemineku raames. Ülejäänud moodid on tühjad, neis puuduvad footonid. Näitena on joonisel Jn 11.12 üks neoonile kuuluvatest spektrijoontest, punases He:Ne laseris tekitatakse sellele joonele vastavate seisundite vahel pöördhõive. Toodud näite puhul ületab võimendus kadusid kolme moodi puhul, laser võib genereerida kolmel eri sagedusel.
Moodidele vastavate generatsioonijoonte laius on määratud peeglite peegelduskoefitsientidega, sest resonaator kujutab endast Fabry-Perot interferomeetri, vt 5.9.1, modifikatsiooni, kus peegelpindade vahel paikneb aktiivkeskkond. Võrreldes tavaliste spektraallampidega on laserist väljuva valguse spektri laius kuni korda väiksem. Sellest, et laseri kiirgus on hulga monokromaatilisem, järgneb automaatselt ka tema suur ajaline koherentsus, vt 5.4.2, sest
ja ka maksimaalne interferentsijärk
on suur. Lisaks iseloomustab laserikiirt hea suunatus, laserikiire difraktsiooniga määratud lahknemisnurk, vt 6.5.2, on φ=1,22λD, kus on laseri kiirtekimbu minimaalne diameeter resonaatoris.
Näide N 11.3
Lahendus
Seisulaine tingimusest v 11.7 saame
ning v 11.8 järgi
Näeme, et peeglitevahelises ruumis võimalike moodide arv on väga suur, kuid antud tingimustel mahub laiuse spektrijoone piiridesse vaid üks mood, teised moodid on tühjad.
Lainepikkuste vahemik, milles laserkiirgus on tekitatud skeemi Jn 11.11 alusel, on kaugest infravalgusest, , kuni ultravalguseni, . Kasutades sageduse kordistamist jt võtteid, on jõutud pehme röntgenkiirguseni, .
Laserid töötavad pidevas ja välkerežiimis, femtosekund- laseri välke kestus on ligilähedane nähtava valguse ühe võnkeperioodiga.
Pidevas režiimis töötavate laserite võimsused ulatuvad kilovatini, välkelaserite hetkvõimsus läheneb petavatile.
| Laser, töökeskkond | Lainepikkus, | Pumpamine | Võimendustegur , m−1 | Resonaatori pikkus, m |
| Nd:YAG, kristall | 1064 | optiline | ||
| Erbium,fiiber | 1530−1560 | optiline | 1,35 | |
| , pooljuht | 405 | elektrivool | <5×10−4 | |
| He−Ne, plasma | elektronid | 0,15 | 0,25−1,5 | |
| , plasma | 10600 | elektronid | 0,9 | 0,3−2 |
Jn 11.14 kujutatud laseris, λ=1064nm, toimuvad protsessid vastavad joonisel Jn 11.10 toodud nivoode skeemile. Pöördhõive aktiivkeskkonnas tekitatakse vasakul paikneva pooljuhtlaseriga, λ=808nm. Aktiivkeskkond koos sagedust kahekordistava kristalliga paikneb dikromaatsete peeglite (ei ole joonisel kujutatud) vahel, millest vasakpoolne laseb läbi lainepikkust λ=808nm ja peegeldab lainepikkust λ=1064nm ning parempoolne peegeldab lainepikkust λ=1064nm ja on läbipaistev lainepikkusel λ=532nm. Filter neelab valguse lainepikkusel λ=1064nm. Üle poole laserviiba pikkusest moodustavad laseri toiteks kasutatavad patareid.
Valguse kahene loomus (≡ korpuskulaar-laineline dualism) seisneb selles, et interferentsi ja difraktsiooni puhul on seaduspärasused paremini kirjeldatavad klassikalise elektromagnetlaine mudeli abil, sel ajal kui vastasmõjus ainega käitub valgus nagu footonite voog. Laine- ja kvantoptika ühildamisel piirdume kvantväljateooria tulemuste kirjeldamisega.
Kvantteooria iseloomustab mikromaailma osakesi lainefunktsiooniga, mis annab tõenäosuse ühe osakese leidmiseks mingis kindlas seisundis.
Rakendame seda postulaati Youngi interferentsikatse tulemuste interpreteerimiseks. Kui footonite arv on suur , siis saame ekraanil laineoptikale vastava intensiivsuse jaotuse, vt Jn 5.6.
Joonisel 11.14 on valgusallikast lähtuv valgus nõrgendatud tasemini, mis lubab eristada ekraanil üksiku footoni tekitatud jälje.
Tõenäosus footoni leidmiseks mingis ekraani punktis on võrdeline klassikalise valguse intensiivsusega selles punktis. Joonisel on näha, kuidas footonite koguarvu suurenemisel hakkab intensiivsuse jaotus ekraanil järjest rohkem sarnanema klassikalisele intensiivsuse jaotusele. Samas aga ei tähenda see seda, et interferentsipilt kujuneb välja footonite vastasmõju tulemusena – igal individuaalsel footonil on laineomadused st kuigi footon on jagamatu, interfereerub ta vaid iseendaga.
Analoogiline interferentsipilt tekib ka massi omavate mikroosakeste puhul.
Esimese Moosese raamatu järgi oli maailma loomisel üks esimesi ettevõtmisi valguse loomine:
Ja Jumal ütles: „Saagu valgus!” Ja valgus sai.
Ja Inimene on üritanud aru saada, mis on valgus. Osa sellest arusaamisest on kirjas eespool.
- M. Born, E. Wolf, Principles of Optics, Pergamon Press
- S. E Frisch, A. V. Timoreva, Üldfüüsika kursus k 3 (vene k), Gos. Izd. tehniko-teoretitšeckoi literaturõ
- F. S. Grawford, Waves; Berkeley Physics Course, v 3, McGraw Hill Book Company
- D. Halliday, R. Resnick, J. Walker, Füüsika põhikursus: õpik kõrgkoolile k 2, Eesti Füüsika Selts
- A. Haav, Optika II, TRÜ rotaprint
- E. Hecht, A. Zajac, Optics, Addison-Wesley Publishing Company
- K. Krane, Modern Physics, John Wiley & Sons
- G. S. Landsberg, Optika (vene k), Nauka
- S. G. Lipson, H. Lipson, D. S. Tannhauser, Optical Physics, Cambridge University Press
- O. Mankin, Optika, TRÜ trükikoda
- A. N. Matvejev, Optika (vene k), Võsšaja škola
- J. R. Meyer-Arend, Introduction to Classical and Modern Optics, Prentice Hall International
- K. D. Möller, Optics, University Science Books
- R. E. I. Newton, Wave Physics, Hodder and Stoughton
- J. Orear, Physics v 2, Macmillan Publishing
- H. J. Pain, The Physics of Vibration and Waves, John Wiley & Sons
- F. L. Pedrotti, L. S, Pedrotti, Introduction to Optics, Prentice Hall International
- W. T. Silfvast, Laser Fundamentals, Cambridge University Press
- F. Zernike, J. E. Midwinter, Applied Nonlinear Optics, John Wiley & Sons
- A. M. Sarževski, Optika k 2 (vene k), Universitetskaja
- I. Saveljev, Füüsika üldkursus k 3, Valgus
- D. V. Sivuhhin, Üldfüüsika kursus, Optika (vene k), Nauka
- W. A. Shurkliff, Polarized light, Hravard University Press
- J. T. Verdeyen, Laser Electronics, Prentice Hall International