Katsed, mis lõid füüsika
Tõlkinud H Raudla
Retsenseerinud H. Käämbre
Kaane kujundanud T. Aru
Originaal:
H. Lipson
F. R. S. Professor of Physics University of Manchester Institute of Science and. Technology THE GREAT EXPERIMENTS IN PHYSICS
Oliver & Boyd Edinburgh 1968
12.11.2022 Raamat on sisestatud ja esmaselt üle kontrollitud.
Kirjutasin oma raamatu eksperimentaalfüüsika propageerimiseks. Teooria osa füüsikas on küll suur, kuid see toetub alati katsetele ega leia tunnustust enne katselist kontrollimist. Pole mingit alust paljude füüsikute veendumusel, et teooria on praktikast olulisem ja et uue teooria väljatöötamine on tähtsam kui otsustava katse korraldamine. Sageli on sellised katsed olemuselt nii lihtsad, et hilisematel uurijatel jääb tähele panemata kogu see leidlikkus ja vaev, mida on nõudnud nende väljamõtlemine. Selle raamatu kirjutamisel püüdsin ma veel kord rõhutada niisuguste katsete suurt tähtsust ja näidata, kuidas nad on mõjutanud nüüdisaegse füüsika kujunemist.
See raamat on lühike füüsika ajalugu eksperimentaatori pilgu läbi. Ma ei seadnud endale ülesandeks kirjeldada katseid detailselt, vaid selgitada, miks need katsed minu meelest sooritati, millist mõju nad avaldasid teistele füüsika aladele ja missugused olid neis osalenud teadlaste omavahelised suhted. Tuleb alati meeles pidada, et ka suured füüsikud olid ennekõike tavalised inimesed neile omaste kirgede ja eelarvamustega, mõnikord ebaloogilised ja mõnikord koguni ebameeldivad, kuid ma ei kõhelnud seda välja toomast kohas, kus see minu arvates mõjutas füüsika arengut.
Ilmselt olen nii eksperimente valides kui ka neid kirjeldades olnud üsna subjektiivne. Ma ei leia, et peaksin end seetõttu kellegi ees õigustama: kui oleksin püüdnud lähtuda puhtobjektiivse kõrvaltvaataja seisukohalt, oleks see tulnud raamatule kahjuks. Loodan, et lugeja mõistab, millistes kohtades olen andnud voli emotsioonidele ja rääkinud iseenda nimel. Pealegi, kuna olen tegevfüüsik, aga mitte füüsika ajaloolane, polnud mul võimalik täpselt viidata iga episoodi kirjeldamiseksnkasutatud allikaile. Püüdsin enamikul juhtudel kirjutada võimalikult originaalilähedaselt, kuid on ka palju mälu järgi esitatut, mis pärineb allikaist, mille taasleidmisega oli raskusi. Selle ja paljude teiste põhjuste tõttu ei tule käesolevat raamatut käsitada kui autoriteetset käsiraamatut. Viidete ja ääremärkuste puudumine peaks veenma lugejat lõplikult, et tegemist pole õpetliku traktaadiga.
H. Lipson
Liikumine on mateeria üks silmanähtavamaid omadusi. Inimene võib oma lihaste abil liigutada kehaosi ja liikuda ühest kohast teise, ta võib panna liikuma teisi kehi; ta oskab sõidukeid liikuma panna looduslikes kütustes peituva energiaga. Inimene teab, et kui jõupingutus katkeb, lõpeb ka liikumine. Mis on siis veel loomulikum kui oletada, et keha liigub vaid nii kaua, kui talle mõjub mingi jõud? Piisas selle mõtte väljaütlemisest hiidautoriteedi Aristotelese (384-322 e. m. a.) poolt, kui läbi sajandite võtsid öeldu hea usu peale omaks kõik mõtlejad.
Ent ometi on võimalik lihtsa arutluse teel veenduda selle kujutluse ekslikkuses. Horisondiga nurga all visatud keha trajektoor kõverdub. Miks? Aristotelese loogika järgi peaks keha saama liikumiseks impulsi, mis püsib mõni aeg muutumatuna, siis aga hakkab järk-järgult nõrgenema, mille tagajärjel tekib trajektoori kõverdunud osa. Lõpuks kaob impulss ja keha, kui Aristotelese väide on õige, kukub otse alla. Teine näide: Aristotelese järgi ei põrkaks vastu seina visatud keha tagasi. Selle peale ei mõelnud ilmselt keegi, aga kui mõtleski, oli targu vait.
Et murda kujunenud mõttebarjäärist läbi ja liikumisprobleemile uut moodi vaadata, oli vaja tõepoolest suurt mõistust. Esimese tõuke selle poole andis Galilei (1564—1642) tol tähelepanuväärsel 16. sajandil, mil tekkisid uued ideed paljudes inimtegevuse sfäärides. Galilei pooldas mõtet, et loogilisi järeldusi tuleb kontrollida katse abil. Millist naudingut võis ta tunda, kui tema katsed kinnitasid tema ideid ja inspireerisid uusi, ja kui rõhutud ning tujust ära võis ta olla, nähes, et tema poolt faktidest ja teooriatest püstitatud tubli ehitis pälvib vaid umbusku tema kaasaegseilt, kes oma tagakiusamisega tumestasid ta elu. Sellele vaatamata ei loobunud Galilei oma ideede kuulutamisest ja nende jäädvustamisest järeltulijate jaoks. Ta teadis, kui tähtsad need on. Ja kui õigus tal oli!
Galilei mõistis esimesena, et liikumine ise pole tähtis. Tõepoolest, inimene, kes asub igast küljest suletud ja ühtlaselt liikuvas kambris, ei saa aru, kas ta liigub või ei; inimene suudab tajuda vaid liikumise muutust - kiirendust. Galileile näis see nii enesestmõistetav, et ta seda kirja ei pannud. Ta ütles, et hõõrdumise puudumisel liigub keha mööda horisontaalpida jääva kiirusega, nagu oleks see kõige tavalisem seisukoht. Tegelikult tähendas öeldu otsustavat lahtiütlemist Aristotelese teooriast.
Huygens (1629—1695) arendas Galilei mõtet edasi, öeldes, et hõõrdumise puudumisel liigub keha mööda horisontaalpinda seni, kuni kohtab mingit takistust. Väide, et keha liigub jääva kiirusega, kuni talle ei mõju väline jõud, jäeti sõnastada Newtonile (1642—1727). Nüüd tunnemegi seda Newtoni esimese seadusena (Newtoni suur teene oli, et ta vermis füüsikaseadused lühidalt ja selgelt; on ju lühidus ja selgus õige mõtlemise head abilised). Niisiis, mõistes, et tähtsad on liikumise muutused, aga mitte ühtlane liikumine ise, oli Galilei teinud esimese suure sammu füüsikas. Jõudnud sellele järeldusele, hakkas ta uurima vabalt langeva keha kiirendust.
Kõigepealt pidi Galilei jõudma selgusele, mida mõista kiirenduse all, kas kiiruse muutust sõltuvalt ajast või läbitud tee pikkusest. Meil, kes me oleme harjunud esimese määratlusega, on raske mõista küsimuse niisuguse asetuse tähtsust, kuid Galileile oli see tõeline probleem. Ta arvas, et vabal langemisel liigub keha konstantse kiirendusega. Selle kontrollimiseks püüdis ta leida katseliselt seost läbitud tee pikkuse ja aja vahel, lähtudes mõlemast kiirenduse definitsioonist.
Teisest määratlusest suutis ta loobuda puhtloogilise arutluse teel. Kui keha kiirus on võrdeline läbitud tee pikkusega, peab kiirus mingi lõigu lõpul olema poole väiksem kui kaks korda pikema lõigu lõpul. Järelikult läbib keha kaks korda pikema tee sama ajaga kui lühema teelõigu, mis on aga ilmne absurdsus. (Nimelt ajas ta segamini lõpp- ja keskmise kiiruse mõiste.) Taolisi arutlusi mööda jõudis Galilei kiirenduse definitsioonini, mida meiegi nüüd kasutame. Oma „Dialoogides" pühendas ta palju tähelepanu just kiirendusele.
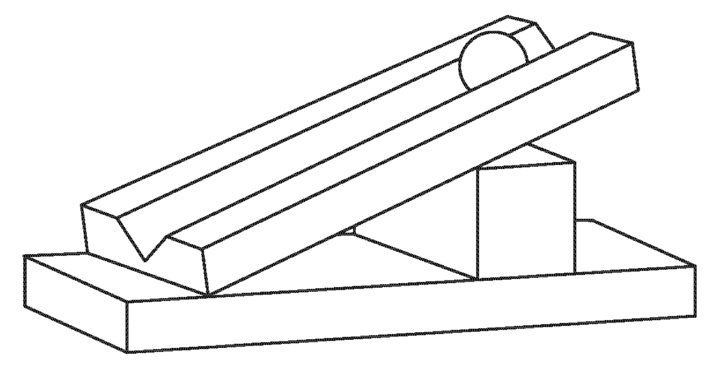
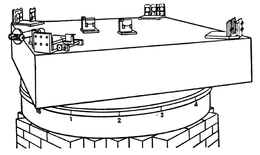
Galilei mõistis, et kehade vaba langemist uurides tekib tal raskusi aja mõõtmisega, ja ta otsustas muuta seda protsessi aeglasemaks, lastes kehal liikuda mööda kaldpinda. Ta teadis, et seejuures muutub vaid liikumise ulatus, ja nii korraldas ta järgmise katse. Ta lõikas kõvasse puusse renni, asetas selle kaldu, laskis pronkskeral paigalseisust mööda renni alla veereda (joonis 1) ja mõõtis eri lõikude läbimiseks kuluvaid aegu. Et kelli tol ajal veel ei olnud, siis kaalus Galilei vett, mis selle aja vältel suure anuma peenikesest torust välja voolas. See aeg oli üsna suure täpsusega võrdeline ruutjuurega läbitud tee pikkusest. Järelikult pidi kiirendus olema jääv. Tema ennustus oli leidnud kinnitust.
Kehade vaba langemise kiirendust mõõtes kontrollis Galilei kõigepealt Aristotelese väidet, et langeva keha kiirus on võrdeline tema kaaluga. Usutavasti tahtis Aristoteles sellega öelda, et kerge keha, näiteks puult lahti rebitud leht, langeb palju aeglasemalt kui kivi. Oma väite õigsust või ekslikkust näitavaid katseid ta kahtlemata ei sooritanud. Seetõttu oleks seda väidet võidud tõlgendada vaid kvantitatiivse seosena keha kaalu ja langemiskiiruse vahel. Aga kui suurmees on midagi öelnud, kas või muu seas, siis on lihtsurelikud nõus sellest rohkem välja lugema kui ütleja ise.
Galilei jõudis Aristotelese väite ebaõigsuseni järgmise arutluse teel. Vaatleme kaht eri raskusega keha ja oletame, et raskem keha langeb kiiremini kui kerge. Kuidas käituvad kehad siis, kui nad ühendada? Kergem keha peab raskemat aeglustama. Ent koos moodustavad nad veel raskema keha ja peaksid langema hoopis kiiremini. Ainsaks väljapääsuks sellest ummikust on oletus, et mõlemad kehad langevad ühesuguse kiirendusega.
Galilei korraldas katse. Ta võttis kaaluva suurtükikuuli ja kaaluva musketikuuli ning viskas nad kõrguselt alla. Mõlemad kehad jõudsid maapinnale üheaegselt. See kuulutas Aristotelese teooria lõppu. Legendi järgi olevat Galilei, kes oli suurema osa oma elust professoriks Pisas, kasutanud selleks eksperimendiks maailmakuulsat Pisa torni. Kahtlemata sobinuks see torn taoliseks eksperimendiks suurepäraselt, ent kusagil pole andmeid, et Galilei oleks seda tõepoolest kasutanud. Ta viitab kirjeldatud katsele oma „Dialoogides" õige mitu korda, kuid ei vaevu seda kuigi üksikasjaliselt kirjeldama, ehkki see oli võib olla tema katseist tähtsaim.
Galilei mõtteotsad võttis kokku Newton, kes sündis Galilei surmaaastal — 1642. Nagu me nägime, sõnastas Newton Galilei väite oma esimese liikumisseadusena. Seejärel andis ta sellele ka kvantitatiivse kuju — tohutu samm edasi! —, postuleerides, et kiirendus on võrdeline seda põhjustanud jõuga, kusjuures võrdeteguriks on keha mass.
Selle seaduse mõtte üle on palju vaieldud. Newton defineeris massi tiheduse ja ruumala korrutisena, kuigi tihedust saab defineerida üksnes massi kaudu. Aga äkki on mass defineerimatu nagu pikkus ja aegki? Mulle näib, et me võiksime pikkuse ja aja mõistet kasutades defineerida massi isegi siis, kui me ei teaks jõust midagi rohkemat kui seda, et jääva suurusega jõudu saab soovi korral tekitada üle ploki visatud nööri otsas rippuva vihi abil, kusjuures nööri teine ots on kinnitatud kerge vankri külge. Me võime mõõta, millise kiirendusega hakkab liikuma vanker, millel asub etteantud massiga keha. Mingi teine keha on niisama suure massiga siis, kui see jõud paneb ta liikuma niisama suure kiirendusega. Sel teel võime koguda mõned võrdse massiga kehad. Ühendanud omavahel erineva arvu niisuguseid kehi, võime veenduda, et jääva suurusega jõud põhjustab kiirenduse, mis on pöördvõrdeline massiga. Sellisel juhul võime leida tundmatu keha massi nii, et mõõdame kiirenduse, mille see jõud talle annab.
Kõigis neis katseis ei oletatud jõu suhtes midagi muud kui seda, et ta põhjustab kiirenduse. Et me nüüd teame massist kõike vajalikku, siis võime nööri otsas rippuvate vihtide arvu suurendades ja oletades, et jõud on võrdeline nende massiga, suurendada rakendatud jõudu. Nüüd võime veenduda selles, et etteantud massiga keha kiirendus on võrdeline talle mõjuva jõuga, ja leida tundmatu jõu kiirenduse järgi, mille ta annab teadaoleva massiga kehale. Need katsed annavad meile võimaluse kontrollida mõlemat liikumisseadust ja defineerida massi mõistet täiesti objektiivselt.
Neile mehaanika fundamentaalsetele alustele toetudes võime pöörduda eksperimendi juurde, mida peetakse füüsikas üheks suuremaks, kuid mis tegelikult ei olnudki eksperiment, sest polnud ette plaanitud ja eksperimentaator ise osales selles vaid vaatlejana. See oli õuna kukkumine Newtoni koduaias 1666. aastal.
See on tõestisündinud lugu, mida sageli kirjeldatakse liiga triviaalselt, et sellesse võiks uskuda. Neile, kes kujutlevad teadlasi üksnes tähtsate asjadega tegelevate tõsiste ja süngete inimestena, näib lugu lausa anekdootlik: üks maailma helgemaid päid peaks huvituma õuna langemisest? Võimatu! Need aga, kel on ettekujutust sellest, kuidas füüsikud töötavad, ei leia loos midagi uskumatut. Veel enam, neile on see heaks näiteks, kui palju võib järeldada nii tähtsusetust sündmusest.
Newton rääkis, et õuna kukkumist silmates küsis ta endalt: miks kukkus õun alla, aga mitte kõrvale või üles? Ta vastas, nagu vastanuks iga tolle aja haritud inimene: Maa gravitatsioonijõud sundis õuna langema Maa keskme poole. (Fakti, et kehad langevad Maa keskme poole, vaatlesid paljud kui tõestust, et Maa on universumi keskpunkt!) Siis küsis Newton endalt, kui kaugele selle jõu mõju ulatub. Mägede ja kõrgendike tippudeni ilmselt küll, aga kas ka kaugemale? Võib see ulatuda Kuuni? Teiste sõnadega, kas pole Kuu mitte nagu hiiglasuur õun, mida Maa kogu aeg tõmbab parajasti nii suure jõuga, mis takistab Kuud langemast mööda oma orbiidi puutujat kosmilisse ruumi?
Kujutlus gravitatsiooni mõjust läbi ruumi oli Newtoni hiigelpanus füüsikasse. Seda hüpoteesi oli võimalik ka kontrollida, kasutades teada olevaid andmeid — Kuu tiirlemisperioodi, Kuu kaugust Maast, Maa raadiust ja vaba langemise kiirendust . Kõik, mis Newtonil teha tuli, oli selgitada, kas Kuule mõjuv jõud on täpselt nii suur, et hoida teda ringorbiidil. Väiksema jõu korral jätaks Kuu Maaga hüvasti, suurema puhul läheneks spiraalselt Maale. Newton sooritas kiiresti arvutused, oletades, et gravitatsioonijõud väheneb pöördvõrdeliselt kauguse ruuduga, ja tegi kindlaks, et Kuu kiirendus on peaaegu selline, nagu on vaja, kõigest võrra väiksem.
Mõni teine tema asemel olnuks avastusest vapustatud ja püüdnuks seda reklaamida kõigi vahenditega. Ka Newtoni jaoks oli see tulemus kahtlemata huvitav, kuid ta oli pettunud selle ebatäpsuses. Alles aastat hiljem, kui talle said teatavaks täpsemad andmed ja arvutusviga vähenes kahe protsendini, avaldas ta oma avastuse.
Palju on kirjutatud Newtoni ebakindlusest. Ent kui ta oletaski, et gravitatsiooni kõrval eksisteerib ka mõni vähem oluline faktor, näiteks Descartes’i keerised, oli gravitatsioon tema jaoks siiski peamine. Vaevalt häiris teda see väike erinevus arvutatu ja tegeliku vahel, sest ta kasutas teadlikult oma arvutustes suuruste ligikaudseid väärtusi. Usutavam on, et pärast ülesande lahendamist oli ta endaga täiesti rahul. Ja kui temal vastus teada oli, siis mille üle ta veel muretsema pidi? Ka langeks see kokku tema käitumisega paljudel teistel juhtudel. Ta ei rutanud iialgi oma tulemuste avalikustamisega, enne kui miski teda selleks otseselt ei tõuganud.
Nii oli Newton 23-aastaselt teinud avastuse, mis oli kõigi aegade üks suuremaid: gravitatsioon on kogu universumis mõjuv universaalne jõud. Ülemaailmse gravitatsiooniseaduse rakendamine kogu Päikesesüsteemile võimaldas lõpuks teoreetiliselt põhjendada seadusi, mis Kepler oli suure vaevaga tuletanud Tycho Brahe astronoomilistest vaatlustest. Nõnda me näeme, kuidas suur mõistus võib vaid ülinõrgale pinnale toetudes rajada kõige kaugemale ulatuva tähendusega kontseptsioone.
Pöördume tagasi veel ühe Galilei katse juurde. See oli katse, mille käigus ta avastas pendli isokroonsuse. Võib näida, et oleks õigem vaadelda Galilei avastusi kronoloogilises järjekorras, ent see kahjustaks oluliselt meie raamatu eesmärki esitada füüsika arengut süsteemselt. Õpikutes on aine süsteemipärane esitus paratamatu, sest muidu poleks see õpilastele mõistetav, kuid neid ei tohi uskuma panna, et füüsika on ka loodud süsteemselt. Tavaliselt ilmuvad algul sügavad mõtted, mida viimistletakse tükk aega hiljem. Sageli, eriti füüsika koidikul, omandas mõni selline mõte lõpliku kuju alles pärast looja surma, nii et too ei saanudki näha oma ideede õitsengut. Näiteks ei näinud Galilei pikale eale vaatamata seda, kui kaunilt süstematiseeris Newton tema mehaanikateooriad. Galilei pendlikatse sarnanes paljuski Newtoni õunakatsega: näiliselt väheütlev sündmus, mida olid jälginud tuhanded, kuid mis ergutas kujutlusvõimet vaid ühel. Galilei ütles, et ta oli tuhandeid kordi jälginud lühtri kõikumist katedraalis. Kapriissed tõmbetuuled võisid panna lühtri võnkuma eri amplituudidega, kuid võngete periood, nagu talle näis, jäi alati samaks. Kuidas seda kontrollida? Ta vajas mingit ajamõõtjat, mida loomulikult polnud. Siis võttis ta appi pulsi, mis on üsna korrapärane kordusliikumine. (Sellisele mõttele võis tulla ainult füüsik.) Ja tal oli õigus: periood oli jääv.
Selles loos tuleb ühtaegu nähtavale mitu väljapaistva teadlase omadust. Esiteks, võime tunnetada, mis peitub igapäevaste nähtuste taga. Teiseks — see puudutab eelkõige füüsikut — omadust mõelda lakkamatult teadusprobleemide üle, seda ka kõige ebasobivamates oludes. (Galilei oli vaga mees ja oleks pidanud kirikus mõtlema hoopis kõrgematele asjadele. Kahtlemata pidi ta end õigustama ütlusega, et Jumal võib end ilmutada üleloomulikul viisil, kuid võib pakkuda universumi mõistmiseks ka maiseid, ent samal ajal hoopis peenemaid võimalusi.) Kolmandaks, teadlase leidlikkust mõõtevahendite otsingul.
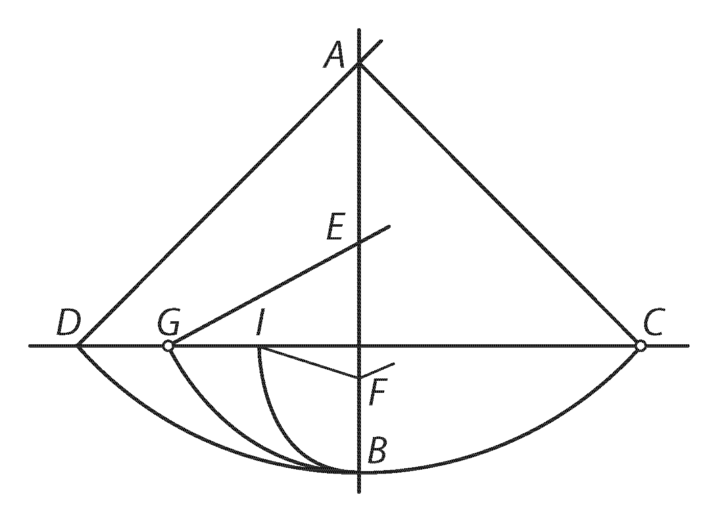
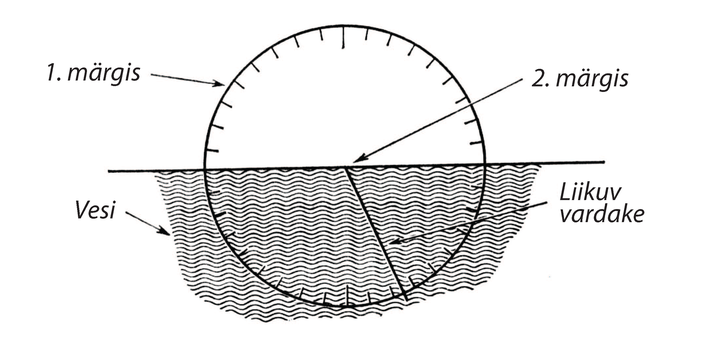
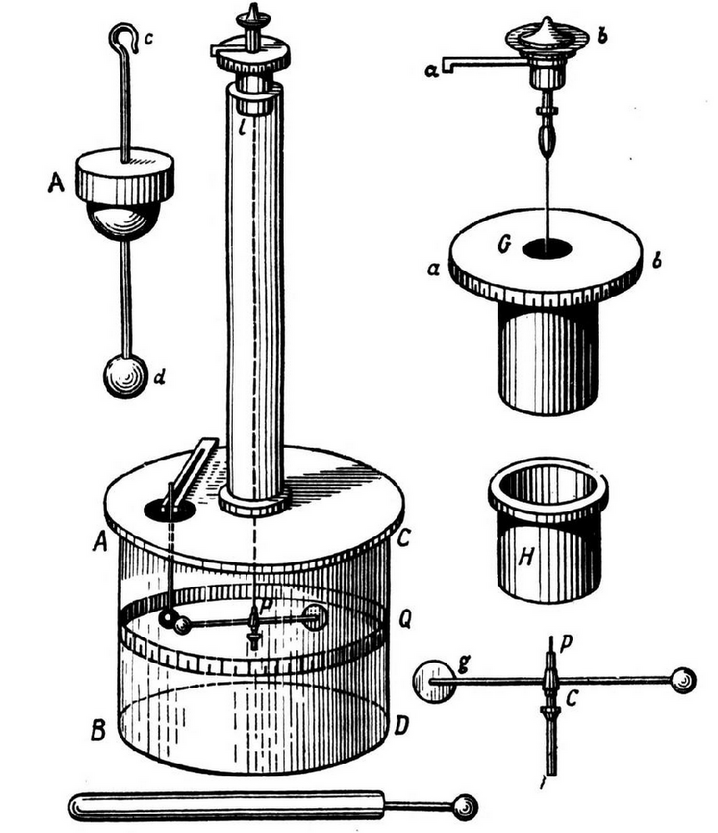
Galilei oli oma avastusega enam kui rahul. Hiljem on ta öelnud, et periood jäi muutumatuks pendli hälvetel kuni . (Galilei polnud nii piinlikult täpne teadlane kui Newton; näiteks väitis ta kategooriliselt, et kahest punktist kinnitatud homogeenne nöör võtab rippudes parabooli kuju, ehkki, nagu me nüüd teame, on see hoopis aheljoon.) Siiski võib Galilei-taolisele suurvaimule andestada, et ta laskis end vaimustusest kaasa viia. Tema ajamõõtmisvahend oli üsna puudulik, sest pulsi sagedus võis vabalt kasvada neil minuteil, mil talle näis, et ta mõte leiab kinnitust. Muide, tuhandendaks mõõtmiseks võis avastuse erutus ka juba vaibuda. Nüüd oli Galilei käsutuses objektiivne ajamõõtmisvahend ja ta võis oma katset laiendada. Ta leidis eri pikkustega pendlite perioodide suhte ja näitas, kasutades tinast ja korgist raskusi, et pendli periood ei sõltu massist, ehkki korgist raskusega pendli võnked sumbusid kiiremini. Ta märkas ka resonantsinähtust: pendli võnkeamplituud suureneb, kui sellele liikumise taktis puhuda. (Nagu me näeme 5. peatükis, kasutas ta seda asjaolu hiljem heli uurimisel.) Asetanud pendli teele nõela (joonis 2), jälgis Galilei lühendatud niidiga pendli liikumist ning järeldas, et raskus jõuab alati samale kõrgusele, kust alustas liikumist. Sellega rajas ta aluse meie kujutlusele potentsiaalsest ja kineetilisest energiast. Hämmastav, kuidas võis üksainus nähtus vallandada Galilei peas sellise mõttevoolu. Galilei avastus evis suurt praktilist tähtsust: seda rakendasid arstid haigete pulsi mõõtmisel ja see andis võimaluse luua mehhanism kellade käigu reguleerimiseks. Kuid mida põhjapanevat andis see tulemus füüsika jaoks? Sai võimalikuks senisest täpsemalt kontrollida vaba langemise kiirenduse konstantsust ning tekkis küsimus, millele pole tänini vastust.
See on küsimus massi olemusest. Newtoni seadustesse ilmub mass kahel teel: Newtoni teise seadusse kui võrdetegur jõu ja kiirenduse vahel (inertne mass) ja ülemaailmsesse gravitatsiooniseadusse kui konstant, mis määrab kahe massi vahelise tõmbejõu (raske mass). Pendlikatse näitas, et mõlemad massid on täpselt võrdsed. Newton mõistis selle tulemuse tähtsust ja jõudis Galilei katseid suurema täpsusega korrates samadele järeldustele. Miks on keha inertne ja raske mass võrdsed? Sellele küsimusele ei ole ikka veel vastust leitud.
Viimaseks sammuks Newtoni ülemaailmse gravitatsiooniseaduse vermimisel oli sellele kvantitatiivse kuju andmine. Teades planeetide masse ja nendevahelisi kaugusi, võime ligikaudselt hinnata gravitatsioonikonstandi väärtust. Ent isegi Maa massi on võimatu täpselt määrata, sest tema tihedus pole täpselt mõõdetav. Seepärast tuleb mõõta tõmbejõudu kehade vahel, mida saab kaaluda. See peaks olema väga väike. Tõepoolest, meie keha kaal pole kuigi suur, ehkki seda tekitab hiiglasuure massiga Maa. Kas võib siis loota kahe keha vahelise tõmbejõu mõõtmisele laboratooriumis? Seda, et gravitatsioonikonstanti saab laboratooriumis mõõta, teab nüüd iga füüsik. Õpikuis esitatakse Cavendishi (1731 —1810) sellekohase katse täielik kirjeldus, ent neis pööratakse vähe tähelepanu kaalutlustele, millest lähtudes ta valmistas oma katseseadme. Seepärast tasub püüda hinnata, millisel määral on katse teostatav, kujutledes, et teeme seda esmakordselt. Esiteks leiame mõõdetava jõu suurusjärgu. Selleks peame evima ettekujutust meie käsutuses olevatest suurustest, peame hindama,nagu füüsikud ütlevad, nende suurusjärku. Niisugused arvutused on etendanud füüsikas väga tähtsat osa ja kõik füüsikud peavad oskama neid kasutada.
Maa raadius on teada, see on ligikaudu (). Kera ruumala valemi järgi (see, et Maa pole täpselt sfäärilise kujuga, on suurusjärkudes arvutamisel tähtsusetu) on see . Mass on võrdne ruumala ja tiheduse korrutisega, kuid Maa keskmist tihedust me ei tea. Võib oletada, et see on vee tihedusest suurem, kuid vaevalt üle kümne korra, sest nii raskeid kivimeid on vähe. Oletame, et keskmine tihedus on . Sellisel juhul on Maa mass ligikaudu . Maa poolt kehale massiga mõjuv külgetõmbejõud, kui keha asub Maa keskpunktist kaugusel (s. t. Maa pinnal), on
kus on vaba langemise kiirendus Maa pinna lähedal. Seega siis
Et on teada ja ligikaudu võrdne , siis
Pidades silmas, et tulemus on saadud suurusjärguliselt, võime väärtuse võrdsustada -ga. See on väga väike suurus. Kaks kaugusel asuvat ühegrammise massiga keha tõmbuvad jõuga , mis on mõõtmiseks liiga väike. Kuidas seda suurendada? Võiksime võtta massiivsemad kehad, kuid siis tuleks suurendada nendevahelist kaugust. Pealegi oleks siis vaja palju massiivsemaid tugesid, mis raskendaksid väikese jõu täpset mõõtmist veelgi. Et välja selgitada, kas üldse on võimalik teha nii täpset katset, tuleb arvestada kõiki vastandlikke kaalutlusi.
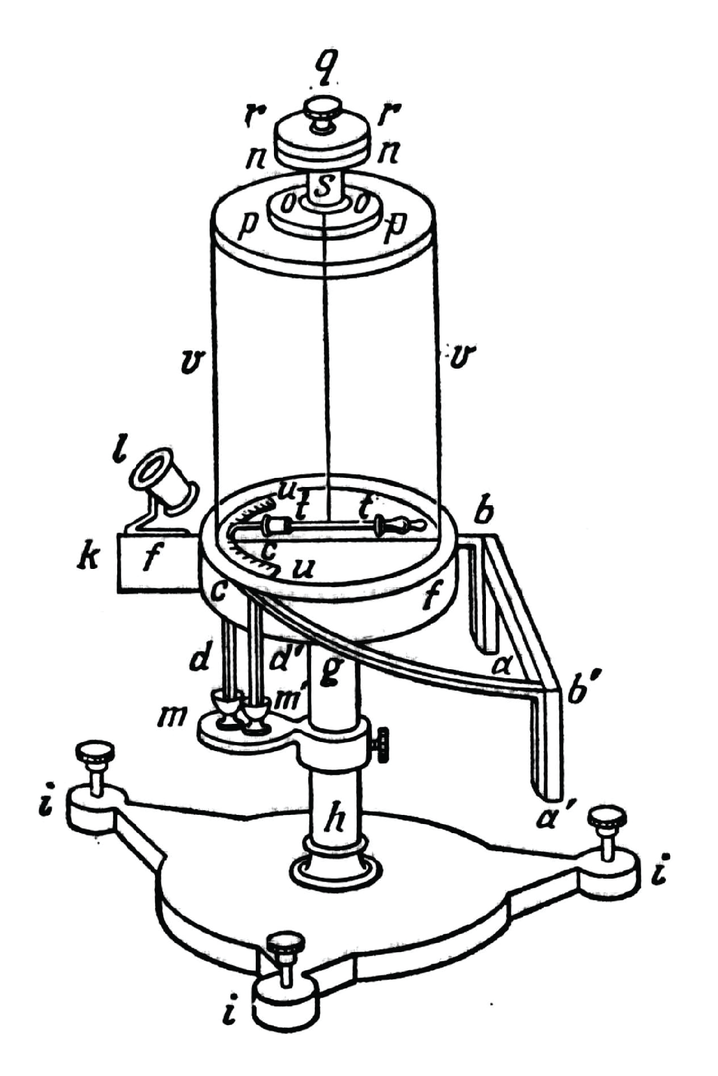
Cavendishi katse põhiidee seisnes selles, et mõõta jõudu, millega sfäärilise kujuga liikumatu keha tõmbab enda poole liikuvat keha. Kahe paari selliste kehade abil võib tekitada pöördemomendi ja seda siis pöördkaaludega mõõta. Pöördkaalud olid tollal tuntud seadmetest kõige tundlikumad. Neid oli väga edukalt kasutanud juba Coulomb (1736—1806) magnetiliste ja elektriliste jõudude mõõtmisel. Me võime lihtsustada oma ülesannet sellega, et võtame niisugused liikumatud ja liikuvad kehad, millel on eri mõõtmed. Nende valiku määravad täiesti eri kaalutlused.
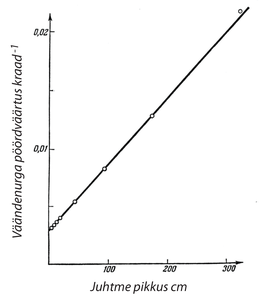
Vaatleme kõigepealt liikuvaid kehi. Need peavad olema kinnitatud peenikese vertikaaltraadi otsas rippuva pika horisontaalvarda otstesse. Kui liikuvate kehade mõõtmed on suured, peab traat olema tugev ja nõuab väändeks suuremat jõudu. Seega on parem teha nad väikesed: kao gravitatsioonijõus kompenseerib kuhjaga kaalu tundlikkuse tõus. Asi on selles, et külgetõmbejõud on võrdeline massiga, mis aga sõltub -st, kus on liikuva kera raadius. Väänduva traadi ristlõige peab olema võrdeline -ga, järelikult on traadi raadius võrdeline -ga. Ent väänduva traadi tundlikkus on pöördvõrdeline tema raadiuse neljanda astmega, s. o. võrdeline suurusega . Selline sõltuvus kompenseerib kuhjaga suurusega võrdelise jõukao väiksema raadiusega kera kasutamisel. Järelikult tuleb võtta kasutuskõlblikest traatidest peenim, sfäärilised kehad aga sellise massiga, et traat oleks katkemiseni pingul, kui need kehad ta külge kinnitatakse.
Ent kuidas on lugu liikumatute keradega? Mida suuremad need teha, seda kaugemale jäävad nad liikuvatest keradest. Kui nende raadius on , siis on mass võrdeline -ga ja kaugus liikuvatest keradest on ligikaudu . Järelikult on gravitatsioonijõud võrdeline suurusega . Seega tuleb liikumatud kerad teha võimalikult suured, kui suured aga just, see sõltub seadmestikust. Kõige mõistlikum on teha nad tinast, sest me vajame suure tihedusega materjali (tõsi küll, plaatina tihedus on kaks korda suurem, kuid tina on see-eest jälle odavam). 50kg kera, millega füüsiliselt tugev mees vabalt hakkama saab, on ligikaudu läbimõõduga. Katseseade oleks sellisel juhul täiesti mõistlike mõõtmetega. Kui võtta liikuvate kerade massiks , oleks gravitatsioonijõud ligikaudu , seega ikkagi veel erakordselt väike, kuid siiski juba mõõdetav suurus.
Arvatavasti juhindus ka Cavendish oma katseseadme konstrueerimisel analoogsetest kaalutlustest. Mulle näib, et neid tasub vaadelda üksikasjalikumalt, sest nad on suurepäraseks näiteks teadusliku eksperimendi kavandamisest. Meie kirjeldus polnud kaugeltki mitte täiuslik; arvatavasti oli ka liikuvate kerade kerge ja tugeva toe konstrueerimine seotud hoopis suuremate raskustega kui nende mõõtmete valik. Ent ma loodan, et katse kavandamisel ettetulevate probleemide tutvustamiseks juba toodud detailidest piisab.
Pole üldtuntud tõik, et seda katset ei mõelnud välja Cavendish, vaid reverend John Michell, kes ehitas seadme, kuid suri, jõudmata seda kasutada, misjärel seade läks üle Cavendishile. Cavendish täiustas seda nii palju, et lõi faktiliselt uue seadme. Sellega teostas ta oma kuulsa mõõtmise, mida kirjeldati 1798.a. ajakirjas Philosophical Transactions of the Royal Society.
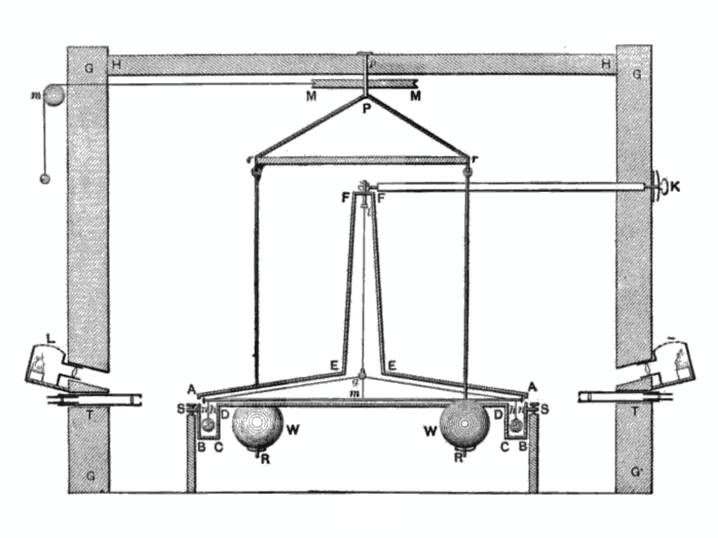
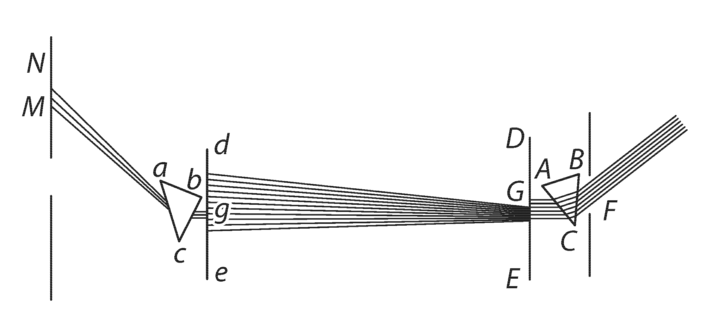
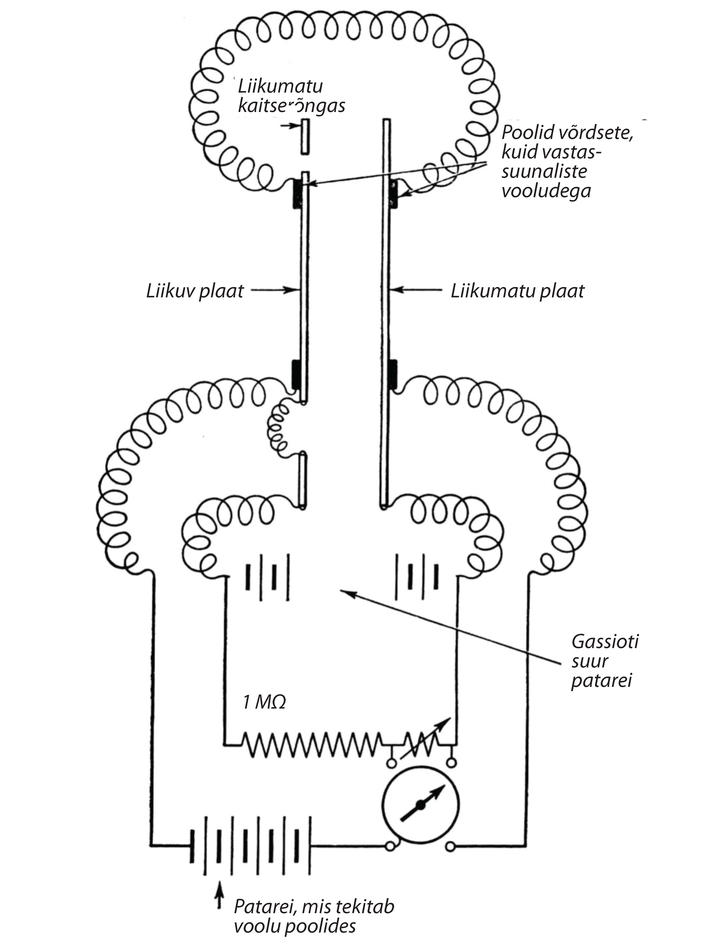
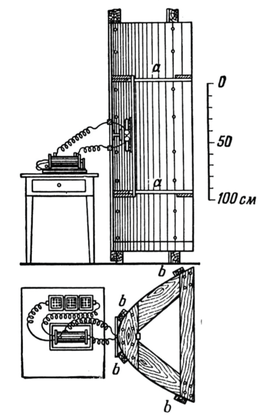
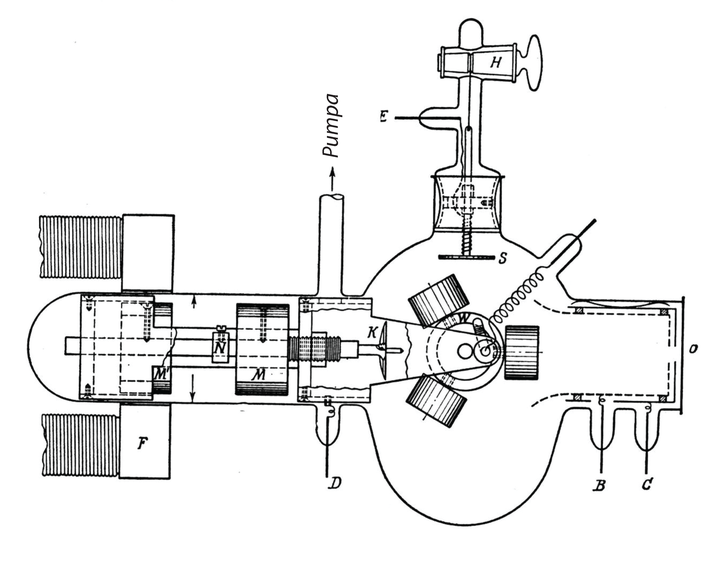
Cavendish mõistis, et raskeim probleem oli õhuvoolude mõju vältimine. Seepärast asetas ta oma seadme igast küljest suletud kambrisse (see on näidatud Cavendishi töödest pärit joonisel 3). Kerade hälbeid vaatles ta kambri seintesse asetatud pikksilmade abil ja niidi väände mooduli määras võnkumiste meetodil.
Katse oli märkimisväärselt hästi kavandatud. Hoolega oli püütud vältida süstemaatilisi vigu. Cavendishi tulemus ja sellest järelduv Maa tihedus () olid õiged 7%-lise täpsusega. See tulemus oli füüsika jaoks esmaklassilise tähtsusega, sest andis mõõdu planeetide ja Päikese massi määramiseks, mis oli esimene samm Päikesesüsteemi tundmaõppimisel.
Gravitatsioonikonstandi mõõtmine oli paljude tähelepanuväärsete saavutuste kulminatsioonipunktiks, ent nende lähtepunktiks olid, nagu nägime, märgatud tühiasjad, mille üle enamik inimesi ei mõelnudki, samal ajal kui suurvaimude Galilei ja Newtoni jaoks võrsusid neist hiiglasuure tähtsusega probleemid. Terveid teadlaste põlvkondi on ajanud segadusse üks Newtoni fraas: „Hüpoteese ma ei püstita." Mida ta sellega öelda tahtis?
Teadusfilosoofidele on Newtoni väide olnud suurima nördimuse allikaks. Loomulikult me püstitame hüpoteese ja kontrollime neid katse abil. Just nii füüsika edasi liigubki. Tuleb aga välja, et hüpoteese esitades peame tundma end süüdi olevat Newtoni ees. Ent ärgem hakakem seepärast Newtonile viltu vaatama. Ka tema võis ju vahel ebatäpselt väljenduda. Ilmselt tahtis ta rõhutada, et ei teinud mingeid oletusi gravitatsiooni olemuse kohta. Sellele vaatamata oli ta valmis laiendama oma gravitatsiooniteooriat kogu universumile. Aga see oli ju hüpotees, mille sarnast polnud veel keegi esitanud, ja ehkki seda pole võimalik kontrollida väljaspool Päikesesüsteemi, ei kahtle selle õigsuses keegi. Muuseas, Newtoni „Optika" viimased leheküljed on hüpoteese täis, ainult et neid nimetatakse seal küsimusteks. Näiteks: „Kas pole valguskiired helenduvate ainete poolt välja saadetud väga väikesed osakesed?"
Newton oskas püstitada hüpoteese niisama hästi kui iga teine teadlane.
Meie planeedil on gaasümbris, mis on meie jaoks erakordselt tähtis. Ilma selleta oleks elu võimatu, sest peaaegu kõik, mis on elus, vajab hapnikku - üht õhu peamist koostisosa. Atmosfäär kaitseb meid Päikese kahjulike kiirguste eest ja võimaldab veel ringelda looduses. Igaüks neist funktsioonidest väärib omaette uurimist, kuid käesolevas peatükis vaatleme vaid meid probleeme, mille uurimine on mõjutanud füüsika arengut.
Tänapäeva füüsikule näib atmosfääri uurimine täiesti loomulik, kuid eksperimentaalfüüsika koidikul muigasid nii mõnedki selle üle. Tookord näis, et Londoni Kuninglik Selts koosneb veidrikest, kellele ei tule pähe midagi muud kui hakata „õhku kaaluma". Seda pidas vist silmas ka Swift, kui ta kirjeldas oma Laputa filosoofe, kes püüdsid kurkidest päikesekiiri saada. Ma arvan, et ei ole inimtegevust, mida ei saaks rumalana näidata, ent igal oma ettevõtmisse uskujal peab jätkuma mehisust selle jätkamiseks, kui õela satiiri ja väljanaermise alla ta ka ei satuks.
Atmosfääri uurimisele nagu mitmele teiselegi füüsikaharule pani aluse Galilei. Vastupidiselt paljudele oma kaasaegsetele oletas ta, et õhk on üks mateeria vorme, mistõttu sel peab olema kaal. Ta nõustus Aristotelesega, kes oma veidras maneeris mõtetele kvantitatiivset väljendust andes arvas, et atmosfääri tihedus on ligikaudu kümnendik vee tihedusest. Ent Galilei otsustas õhu tihedust mõõta, mitte lihtsalt ära arvata.
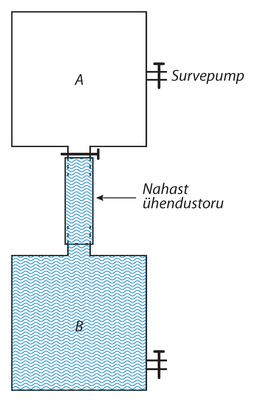
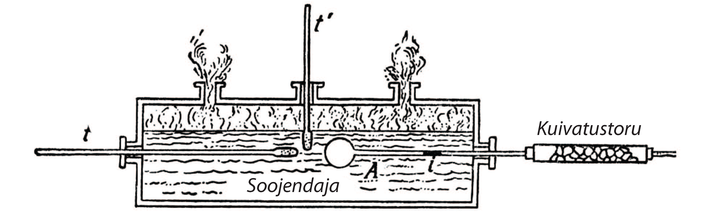
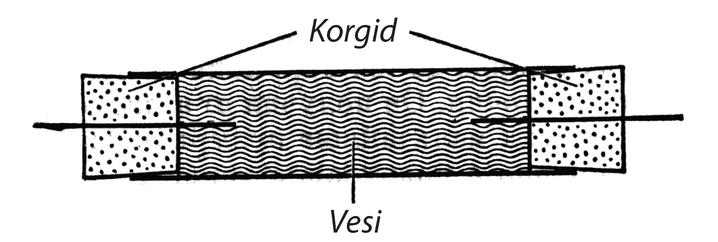
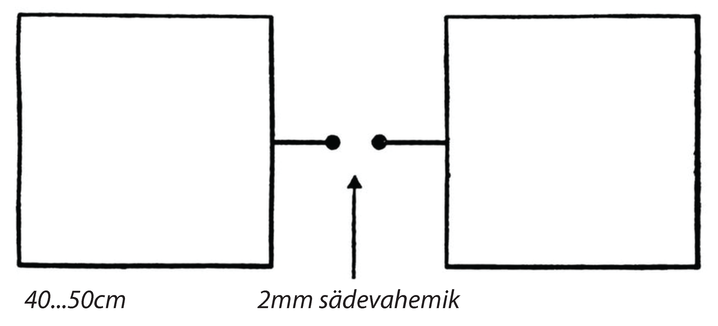
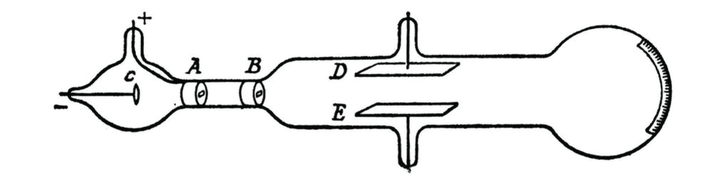
Oma primitiivset survepumpa kasutades suutis Galilei näidata, et nõu kaalub rohkem siis, kui selles oleva õhu rõhku suurendada. Tavalise õhu tiheduse mõõtmiseks mõtles ta välja hulga katseid, millest meie vaatleme lähemalt järgmist. Nõud ja (joonis 4) on ühendatud nahktoruga. Nõus on õhk suure rõhu all, nõus on vesi. Nõul on kraan, mille kaudu vesi võib välja voolata. Katse algul kaalutakse kokkusurutud õhku täis nõu . Siis ühendatakse nõu nõuga ja avatakse kraan. Lisarõhk surub osa vett -st välja, mis kogutakse kokku ja kaalutakse. Seejärel kaalutakse uuesti nõu .
Kirjeldatud katse annab küllaldaselt andmeid õhu erikaalu määramiseks. Nõust väljunud õhu kaal on meile teada selle nõu kahest kaalumisest; peale selle teame veel kaalu, mis on arvuliselt võrdne nõust väljunud õhu ruumalaga tavalisel rõhul. Galilei jõudis järeldusele, et õhu tihedus on vee tihedusest, mis langeb suurusjärgult kokku tegelikuga ().
Kui õhul on kaal, siis peab ta avaldama ka rõhku. Seda kinnitas üks tolle aja efektsemaid katseid — katse Magdeburgi poolkeradega aastal 1654.
Katse mõtles välja Otto von Guericke (1602—1686), kes oli rikas mees ja tegeles ka teadusega lõbu pärast. Ta valmistas kaks läbimõõduga metallist poolkera, mille servad olid nii hästi kokku sobitatud, et neid võis õhukindlalt kokku liita. Ta pumpas õhu kerast välja ja demonstreeris oma väärikatele külalistele, kelle hulgas oli ka imperaator Friedrich III, et poolkerade lahtirebimiseks läheb vaja kaht neljast hobusest koosnevat rakendit. Lahtirebimiseks vajalik kogujõud oli , seega tuli iga hobuse kohta ligikaudu . See on jõud, mida tavaline hobune suudab vabalt arendada.
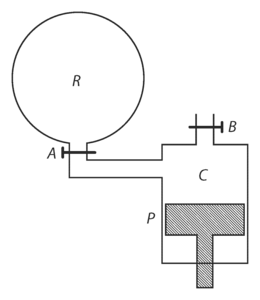
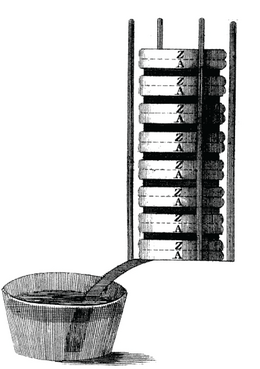
Guericke kasutatud pump oli väga lihtne. Selle tööpõhimõte on näidatud joonisel 5. Tühjakspumbatav nõu on ühendatud kraani abil silindriga , milles tihkelt liigub õlitatud nahaga kaetud kolb . Silindri ülemises osas on kraan . -st õhu väljapumpamisel suletakse kõigepealt kraan , avatakse kraan ja viiakse üles kolb ; siis suletakse , avatakse ning kolb lastakse alla. Nüüd läheb osa õhku nõust nõusse , järelikult rõhk nõus langeb. Siis suletakse jälle , avatakse , viiakse üles kolb ja kogu tsükkel kordub. Kuna kolb pandi liikuma hambulise lati ja hammasratta abil, siis võib arvata, et rõhu alandamine keras atmosfäärirõhuga võrreldes küllalt väikeseks oli kauakestev ja väsitav.
Umbes samal ajal olid teised teadlased ametis küll vähem efektsete, kuid see-eest teaberikkamate katsetega. Galileile oli igapäevasest elust teada veider fakt, et ükski imipump ei suuda tõsta vett kõrgemale kui 10m. Ta oletas, et see on seotud atmosfääri poolt avaldatava rõhuga või, kasutades tolleaegset kõnepruuki, „looduse tühjusekartuse mõõduga". Galilei õpilane Torricelli (1608—1647) otsustas seda kontrollida. Ta mõistis, et palju raskema vedeliku, näiteks elavhõbeda kasutamine võimaldaks seadme mõõtmeid tunduvalt vähendada. 1643. a. täitis teine Galilei õpilane Viviani meetripikkuse toru elavhõbedaga, pööras selle ümber elavhõbedaga täidetud vaagna kohal ja märkas oma rõõmuks, et elavhõbedasammas, langenud kõrgusele vaagnas oleva elavhõbeda vabast pinnast, seisab seal paigal. See oli esimene baromeeter.
Prantsuse teadlane Pascal (1623—1662) tuli järeldusele, et kõrguse muutudes peab baromeetriline rõhk muutuma. Ta tõusis koos baromeetriga kiriku kellatorni, kuid rõhu erinevust ei märganud. Siis tõusis ta veel kõrgemale, Puy de Dome’i tippu Auvergne’is, ja märkas, et elavhõbedasamba kõrgus oli mõne sentimeetri võrra väiksem kui Pariisis, mis asub merepinnaga praktiliselt ühel kõrgusel. Torricelli ise märkas, et eri päevadel on atmosfäärirõhk erinev ja taipas, et selle registreerimisel võib olla mingi tähendus. Nii pandi alus atmosfääri teaduslikule uurimisele.
Kuid mis on sellel kõigel ühist fundamentaalfüüsikaga? Baromeetrilise rõhu registreerimine evib suurt tähtsust ilma uurimise, mitte aga füüsika seisukohalt. Füüsikaseadused oleksid needsamad ka siis, kui atmosfääri ei olekski. Siiski tahan ma siin näidata, et atmosfääri uurimine viis väga tähtsa sammuni füüsikas — kvantitatiivse aatomiteooria rajamiseni.
Paljud inimesed pühendasid end ilmavaatlustele ja püüdsid leida vahendeid selle ennustamiseks ning võib-olla ka juhtimiseks. Üks nendest, John Dalton (1766 — 1844), pidas ilmavaatluspäevikuid oma elu viimaste päevadeni. Erinevalt teistest uurijatest püüdis ta mõista, mis kutsub esile neid atmosfäärirõhu muutusi, mida ta täheldas. Näiteks märkas ta, et temperatuurile avaldavad mõju ookeanid ja mandrid ja et rõhk on kõrge tavaliselt hea ilma korral, madal aga vihmase ilma puhul. Dalton arvas, et need nähtused on suuresti seotud veeauru liikumisega.
Aga mis on veeaur? Mõtet, et aine — nii gaasiline, vedel kui ka tahke — koosneb aatomitest, tunnistasid paljud tolle aja teadlased, kuid ilma vähegi tõsisema tõestuseta. Dalton võttis ette gaaside põhjaliku uurimise. Ta avastas seaduse, mis on nüüd tuntud Daltoni osarõhkude seadusena, ja uuris, kuidas gaaside lahustuvus vedelikes sõltub nende rõhust. Tema katsed polnud just päris täpsed, sest suurema osa neist tegi ta omatehtud .seadmetega, kuid nende katsete tähtsus oli tohutu. Esimesena jõudis ta tulemusteni, mida oli võimalik seletada aatomite abil, kuna enne teda olid teadlased vaid mõtisklenud nende olemasolu võimalikkuse üle.
Mille mõjul tärganud mõte kristalliseerus, pole täpselt teada. Dalton ise jutustas hiljem sellest eri inimestele erinevalt. Teaduses on vahel nii, et idee võib ilmuda mingil seletamatul viisil, nii et autor ei tea isegi, kuidas see sündis. Omajagu põhjust võis anda ka asjaolu, et Dalton uuris teiste gaaside hulgas süsivesinikke. Ta tegi seejuures kindlaks süsiniku- ja vesinikuhulga suhte gaaside eri komponentides ja jõudis järeldusele, et saadud tulemusi võib kõige paremini selgitada lähtudes oletusest, et gaasid koosnevad väikestest osakestest — molekulidest —, mis omakorda sisaldavad veel pisemaid osakesi, mida me nüüd nimetame aatomiteks. Dalton määras nende aatomite suhtelised massid. Uurinud samal viisil ka teisi ühendeid, nagu vett, süsinikdioksiidi ja ammoniaaki, lülitas ta oma aatomite nimekirja veel mõned, näiteks hapniku ja lämmastiku aatomid.
Nagu näeme tabelist 1, polnud Daltoni töö just eriti täpne, mõned tema keemilised valemid aga, näiteks vee jaoks, olid lausa valed. Kuid läbimurre tervikuna oli põhjapanev, sest lõpuks sai ka aatomiteooria kvantitatiivseks.
| Vesinik | 1,00 |
| Hapnik | 5,66 |
| Lämmastik | 4,00 |
| Süsinik | 4,50 |
| Vesi | 6,66 |
| Ammoniaak | 5,00 |
| Lämmastikoksiid | 9,66 |
| Naerugaas | 13,66 |
| Lämmastikhape | 15,32 |
| Väävel | 17,00 |
| Väävlishape | 22,66 |
| Väävelhape | 28,32 |
| Süsihape | 15,80 |
| Süsinikoksiid | 10,20 |
Daltoni aegadest peale on aatomihüpotees olnud aluseks kogu teadusele. Sellele toetudes loome oma kontseptsioone ja mõõdame aatomite omadusi niisuguse täpsusega, mida Dalton ei võinud aimatagi. Me „sorime" isegi aatomite sisemuses ja avastame nende koostisosade äraarvamatu keerukuse. Mõned Daltoni vaated olid ebaõiged. Näiteks mitte kõik, ühe ja sellesama elemendi aatomid pole täpselt ühesugused. Sellele vaatamata kuulub au ja kuulsus Daltonile kui inimesele, kes- esimesena mõistis, kuidas võib aatomikontseptsiooni, mida kaks tuhat aastat ei võetud tõsiselt, panna elama inimeste mõtteis ja. teha aluseks mõõtmistele, mis viivad teadust edasi.
On huvitav märkida, et kuigi Daltoni ideed arendati väljajhiba 19. sajandi algul ja sajandi lõpuks - neid tunnustasid peaaegu kõik, vaidlesid mõned teadlased nende vastu veel 20. sajandil. Ostwald 1904. a. ja Mach 1915. a. kaldusid arvama, et aatomid ei ole jälgitavad ega mõjuta aine vaadeldavaid omadusi, sest et nende mõõtmed on kõigest , nagu seda oli kindlaks teinud Thomson (hiljem lord Kelvin, 1824—1907), Aatomid, arvasid need teadlased, pole seega midagi muud kui mugav hüpotees. Kuidas küll võivad eksida isegi suured inimesed!
Oma näiva lihtsuse ja avaldumisvormide selguse kiuste jäi soojus füüsikutele mõistatuseks ka siis, kui seletuse olid saanud mitmed väliselt keerulisemadki nähtused. Veel 19. sajandi keskpaiku pidasid paljud teadlased soojust teatud liiki materiaalseks substantsiks, soojusvedelikuks, ja arvasid, et keha soojendamist põhjustab selle substantsi lisamine ainele. 1802. a. joonistas Dalton soojusatmosfääriga ümbritsetud aatomite skemaatilisi kujutisi. Idee oli küll primitiivne, kuid seda võis praktiliselt rakendada soojusliku tasakaalu võrrandite koostamisel. Carnot (1796—1832), kelle suurepärane traktaat „Tule liikumapanevast jõust" on jäänud tänini üheks füüsika nurgakiviks, uskus samuti soojusvedeliku olemasolu, ehkki ta hiljem oma vaateid revideeris.
Soojusvedelikule väga lähedane oli flogiston, mida arvati ainest erituvat põlemisel. Erinevalt Soojusvedelikust võidi flogistoni mõõta, kuid häda oli selles, et tema kaal tuli kord positiivne, kord negatiivne. Flogistoniteooria oli üsna vastuoluline ja eksisteeris edasi vaid tänu sellele, et keegi ei suutnud asemele pakkuda midagi paremat. Selles peatükis me vaatlemegi eksperimentaalse uurimise etappe, mida on oma arengus läbinud nüüdisaegne soojusteooria.
Esimese sammu tegi 18. sajandi lõpul Rumford (1753—1814). Ta lähtus jällegi kõige tavalisemast tähelepanekust, mida arvatavasti olid teinud paljud enne teda, kuid millele nad ei omistanud mingit tähtsust. Jutt on metallitüki soojenemisest, kui sellesse puuritakse auku, üheks Rumfordi tegevusalaks oli kahuritorude puurimine Müncheni sõjatöökojas. Ta märkas, et puurimisel metallitükk kuumeneb. Kust see soojus tuli? Soojusvedeliku allikad ilmselt puudusid.
Võis oletada, et puurimisel tekkivate väikeste puurmete seos soojusvedelikuga on nõrgem kui massiivsel metallitükil, kuhu auku puuritakse. Järelikult eraldub metalli puurimisel soojusvedelikku ja temperatuur tõuseb. Rumford kontrollis seda mõtet lihtsa katse abil. Nüri puuri kasutamisel tekib puurmeid vähem, mistõttu ka temperatuur peaks tõusma vähem, katse näitas aga vastupidist. Soojusvedelikuteooria abil ei olnud seda võimalik põhjendada.
Rumford meenutas varasemaid Boyle’i ja teiste teadlaste teooriaid, mille järgi soojus on seotud aineosakeste võnkumisega. Edasised katsed veensid teda, et soojust võib tekitada piiramatult. Lõpuks ütles ta välja julge väite: „Soojus on LIIKUMINE." (Rumfordi suurtähed.)
Seda väidet esitatakse sageli kui näidet Rumfordi suurest läbinägelikkusest. See võib nii olla, kuid ühtaegu annab tunnistust ka tema suurest ettevaatlikkusest. Soojus on liikumine, kuid milline? Kuidas seda saadakse? Kuidas muutub see liikumine keha jahtumisel? Taolisi küsimusi Rumford ei esitanud ega andnud neile ka vastust. Ent ta oli astunud suure sammu edasi: soojus on aine enda omadus, aga mitte midagi talle lisatavat.
Davy (1778—1829) sooritas Londonis katse täpsemini kontrollitud tingimustel. Ta asetas kaks jäätükki õhutühja nõusse ja hõõrus neid seal kellamehhanismi abil teineteise vastu. Jää osaliseks sulamiseks eraldus soojust, mida ei saadud võtta õhu soojavedelikust.
Nii oli esimene tähtis samm astutud: oli kindlaks tehtud, et soojus on kineetilise energia vorm. Järgmiseks oli vaja selgitada, kas soojuse ja mehaanilise energia vahel on mingi kvantitatiivne seos, aga enne seesuguste uurimiste juurde asumist oli vaja teada ainete soojuslikke omadusi, eriti seda, kuidas tõuseb soojuse saamisel eri ainete temperatuur. Seda omadust väljendatakse nõndanimetatud erisoojusega — soojushulgaga, mis on vajalik ühe massiühiku aine temperatuuri tõstmiseks ühe kraadi võrra.
Ilmselt oli vaja kokku leppida selle suhtes, mida mõista temperatuurikraadi all, sest aja jooksul oli kasutusele võetud mitmeid tem- peratuuriskaalasid. Et soojuse olemus oli veel tundmatu, siis said need skaalad olla ainult juhuslikud. Üldkasutataval skaalal peab olema kaks tähtsat omadust: ta peab olema defineeritud võimalikult täpselt ja olema hõlpsasti reprodutseeritav. Sel põhjusel olid mõnedki ettepanekud vastuvõetamatud, nagu 1720. a. esitatud Fahrenheiti idee kasutada temperatuuriskaala kahe fikseeritud punktina mingi segu külmumis- ja inimkeha temperatuuri. 1742. a. soovitas Celsius kasutada kinnispunktidena vee keemis- ja külmumistemperatuuri ning nimetas esimese nulliks ja teise . See skaala, tõsi küll, ümberpöördult, on nüüd teaduses üldkasutatav.* Varem kutsuti seda sajakraadiseks skaalaks, hiljem hakati aga nimetama Celsiuse skaalaks. Fahrenheiti skaalat kasutatakse endiselt paljudes teaduslikes uuringutes, kuid nüüd defineeritakse seda teisiti: vee külmumispunkt on ja keemispunkt .
*Raamatu ilmumisest möödunud aja jooksul on teaduses üldkasutatavaks temperatuuriskaalaks tunnistatud Kelvini skaala.
Kasutades täpseid temperatuuri- skaalasid, võisid teadlased maailma eri kohtades oma tulemusi võrrelda. Esimesena mõõtis ainete erisoojusi Black (1728—1799). Oma töödega ennetas ta nii Rumfordi kui ka Davyt, kuid esitas oma ideid peamiselt loengutel, mistõttu need avaldati täielikult alles pärast tema surma. Davy oli Rumfordist julgem ja ütles välja oletuse, et soojus on „ideaalne liikumine, tõenäoliselt keha moodustavate väikeste osakeste võnkumine". Ta oli andnud õige vastuse. Blacki meetodid olid kütkestavalt lihtsadja jõukohased igaühele, kes oskasid esitada õigeid küsimusi. Kui harva leidub selliseid inimesi! Black ja tema kaastöötaja Martine valasid ühesugustesse anumatesse võrdsed ruumalad vett ja elavhõbedat, asetasid need tulest võrdsetele kaugustele ning jälgisid nende temperatuuri tõusu. Kuna elavhõbeda mass oli 13,5 korda suurem, oli Black täiesti veendunud, et elavhõbeda temperatuur hakkab tõusma aeglasemalt. Võib kujutleda tema üllatust, kui ta nägi, et elavhõbeda temperatuur tõusis hoopis kaks korda kiiremini. Black avastas, et elavhõbeda eri- soojus on väike — ligikaudu või vee erisoojusest (tegelik väärtus ).
Leidub inimesi, kes arvavad, et teadlasel ei tohi olla mingeid eelarvamusi katse tulemuste suhtes; ta peab olema täiesti objektiivne. See on mõttetus. Tõeline teadlane kontrollib alati katse abil oodatavaid tulemusi. Ta tunneb naudingut, kui ta ootused täituvad, ja on pettunud, kui see nii ei ole; kui ta midagi ei oota, siis ei saa ta ka teada, mida tema katse tulemused tähendavad. Kõik teadmised on esialgu subjektiivsed; objektiivseteks saavad nad alles siis, kui teadlane paneb nad kirja nii, et neid võivad mõista ja kontrollida ka teised.
Erisoojuse mõõtmiseks pole tingimata vaja mõista soojuse olemust; piisab vaid soojuse ühiku määramisest. See ühik — kalor — tulenes nii loomulikult Celsiuse temperatuuriskaalast, et selle kasutuselevõtmisele pole antud kuigi tähtsat kohta teaduse ajaloos. Soojuse mõõtmine ise on aga erakordselt tähtis nii teadusele kui ka tehnikale. Silmas pidades Joule’i katset, millest varsti juttu tuleb, on siiski kaheldav, kas kalorit kaua teaduses ühikuna kasutatakse.
Blacki ja Martine’i katsed õhutasid paljusid teadlasi välja mõtlema veel täpsemaid meetodeid ning katsetama ikka uute ja uute ainetega. 1819. aastaks olid prantslased Petit (1791 — 1820) ja Dulong (1785—1838) kogunud piisavalt andmeid, et väita: keemiliste elementide erisoojused ei ole juhuslikud; need on seotud elementide aatommassidega.
Mõned vaatavad üleolevalt empiiriliste andmete kogumisele, mida Rutherford hiljem nimetas markide kogumiseks. Oma loomult sobib see töö neile, kel puudub loov mõistus, kuid kes suudavad omandada uurimismeetodid ja on piisavalt kannatlikud ja täpsed katsete korraldamisel. Teadusetegemise seisukohalt võib see ju näida teisejärguline, kuid teaduse arengut mõjutab siiski tublisti, öeldu kehtib ka Petit’ ja Dulongi töö kohta, milles nad seadsid enesele eesmärgiks mõõta kõigi neile kättesaadavate tahkete elementide erisoojus.
Nende meetod põhines ainete jahtumise mõõtmisel. Kui ainehulgad on asetatud ühesugustesse nõudesse ja seal kuumutatud, siis peaks nende järgnev soojuskadu sõltuma vaid kuumutatud aine ja ümbritseva keskkonna temperatuuri erinevusest. Seejärel, kõrvuta me võrrelda nende erisoojust. See meetod ei ole seotud Newtoni jahtumisseadusega, ühe tema vähem tuntud seadusega, sest kahe keha jahtumiskiirust võrreldakse ühest ja sellestsamast algtemperatuurist.
Katsete käigus avastasid Petit ja Dulong järgmise seaduspärasuse: mida raskem on element, seda väiksem on tema erisoojus. Selleks ajaks oli aatomi mõistel teadmiste süsteemis kindel koht ja välja töötatud Daltoni omadest palju täpsemad meetodid aatommassi mõõtmiseks. Et elemendi tihedus suureneb mõningal määral tema järjekorranumbri suurenedes, siis proovisid Dulong ja Petit korrutada erisoojust aatommassiga. Nad avastasid selle korrutise hämmastava konstantsuse, nagu näeme tagapool. Aatommassi ühikuks on võetud hapniku aatommass; kui kasutada selle nüüdisaegset väärtust , osutub aatomsoojusena tuntud korrutis võrdseks 6,0-ga.
Enne selle tulemuse tähtsuse vaatlemist analüüsime tabelis 2 toodud arve. Peale telluuri ja koobalti langeb enamiku keemiliste elementide erisoojus hästi kokku tänapäevaste väärtustega. Enamik aatommasse on samuti õiged, kuid jällegi peale telluuri ja koobalti. Miks nii?
Me võime vaid oletada, et Petit ja Dulong ei töötanudki telluuri ja koobaltiga, vaid hoopis teiste ainetega. Nad töötasid ajal, mil aatomiteooria oli alles lapseeas — vähem kui -aastane — ja mil ei teatudki veel täpselt, missugused ained on elemendid. Telluur oli avastatud 1782. a., aga temaga keemiliselt väga lähedane seleen 1817. a., seega kõigest kaks aastat enne Petit’ ja Dulongi eksperimenti. Kas on võimalik, et nad uurisid telluuri asemel seleeni? Tulemuste kokkulangevus tegelikuga oleks sel juhul märksa parem. Lugu koobaltiga on raskem seletada. Koobalti aatommass on ligikaudu ja on raske ette kujutada, missuguse metalliga võidi ta segi ajada. See jääbki mõistatuseks.
| Keemiline element | Erisoojus | Suhteline aatommass | Korrutis |
| Vismut | 0,0288 | 13.30 | 0,3830 |
| Plii | 0,0293 | 12,95 | 0,3794 |
| Kuld | 0,0298 | 12,43 | 0,3704 |
| Plaatina | 0,0314 | 11,16 | 0,3740 |
| Inglistina | 0,0514 | 7,35 | 0,3779 |
| Hõbe | 0,0557 | 6,75 | 0,3759 |
| Tsink | 0,0927 | 4,03 | 0,3736 |
| Telluur | 0,0912 | 4,03 | 0,3675 |
| Vask | 0,0949 | 3,957 | 0,3755 |
| Nikkel | 0,1035 | 3,69 | 0,3819 |
| Raud | 0,1100 | 3,392 | 0,3731 |
| Koobalt | 0,1498 | 2,46 | 0,3685 |
| Väävel | 0,1880 | 2,011 | 0,3780 |
Petit’ ja Dulongi katset on korratud palju täpsemate nüüdisaegsete kalorimeetriliste seadmetega ja on selgunud, et enamik keemilisi elemente allubki Petit’ ja Dulongi avastatud seaduspärasusele. Mida see aga tähendab? Paljudes õpikutes räägitakse sellest seaduspärasusest (üsnagi veidralt) kui mingist kurioosumist, mis aitab keemikutel määrata elementide aatommasse. Tegelikult on see palju rohkemat: esimene suurem üldistus tahke keha füüsikas ja ühe tähtsa füüsikaprintsiibi ilming. Lähemalt sellest aga hiljem, siis, kui jutustame Joule’i katsest määrata kvantitatiivset seost soojuse ja mehaanilise energia vahel.
Nüüd räägime veel ühest Blacki tähelepanuväärsest avastusest — varjatud soojusest. Black jõudis selleni, jälgides üht ammu tuntud ja õige tavalist nähtust — lume sulamist talve lõpul. Ta mõistis, kui tähtis on, et lumi sulab nii aeglaselt: sulaks kogu lumi kohe, kui õhutemperatuur on tõusnud jää sulamispunktini, tekiksid tohutud üleujutused. Black tuli mõttele, et lumi neelab sulades soojust, ilma et tema temperatuur seejuures muutuks. Teadlane nimetas selle soojuse varjatud soojuseks. Oma hüpoteesi kontrollimiseks asetas ta soojusallika lähedusse kaalult võrdse hulga vett ja jääd. Ilmnes, et vee temperatuur tõusis pidevalt, jää temperatuur aga sulamise ajal ei muutunud. Ta mõõtis jää sulamise ja vee aurustumise varjatud soojuse ning leidis, et mingi veehulga aurustamiseks kulub neli korda rohkem soojust kui sellesama veehulga temperatuuri tõstmiseks külmumispunktist keemispunktini. Nüüd me teame, et isegi see suur arv on tegelikust väiksem.
Toetudes erisoojuse ja varjatud soojuse mõistele, võime õpetuse soojushulkade mõõtmisest — kalorimeetria — muuta kvantitatiivseks ning püüda siduda Rumfordi ja Davy mõtteid Newtoni mehaanikaga. 1842. a. väitis Mayer teoreetilistele kaalutlustele toetudes, et soojuse ja mehaanilise energia vahel peab olema otsene kvantitatiivne seos. Seda tõestas katseliselt Joule (1818—1889), kes avaldas oma esimese töö sel teemal 1843. aastal.
Esmalt huvitus Joule alles leiutatud elektrimootoritest. Ta oli väga praktiliselt mõtlev inimene, kes püüdis luua igavest energiaallikat. Joule valmistas Volta patarei, pani selle abil käima omakonstrueeritud algelise elektrimootori ja nägi, et midagi pole võimalik saada eimillestki: tsink patareis korrodeerus ja patarei taastamine läks üsna kalliks. (Hiljem tõestas Joule omaenda rahulduseks, et hobuse toitmine on palju odavam kui patareides tsingi vahetamine, mistõttu elektrimootor ei tõrjuvat hobust kunagi välja.) See õhutas Joule’i uurima seost soojuse ja teiste energialiikide vahel ning ta otsustas välja selgitada, kas need pole ekvivalentsed.
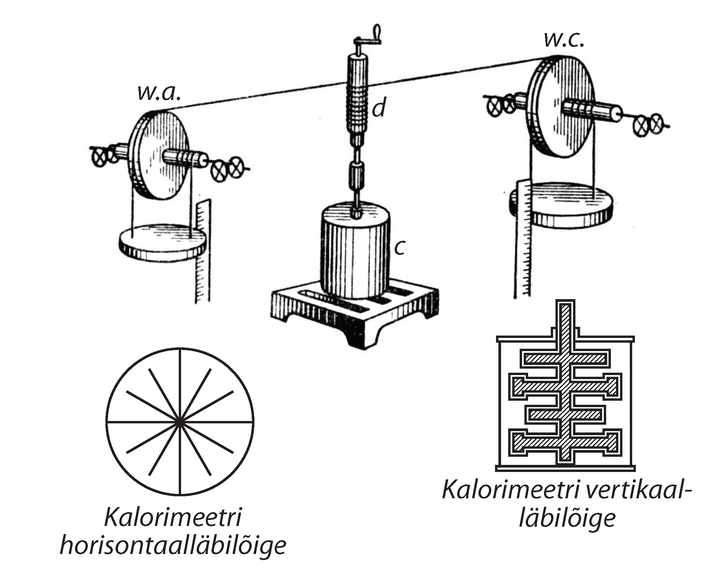
Joule pühendas nimetatud probleemile suurema osa oma elust. Esmalt oli vaja teha kindlaks, kas see ekvivalents eksisteerib, ja siis mõõta võimalikult täpselt nende võrdetegur (soojuse mehaaniline ekvivalent). Jämedalt (ligikaudu) võis ta hinnata selle väärtust juba Rumfordi katsete põhjal, kus oli üles tähendatud temperatuuri tõus teada oleva massiga metallitükil, mida puuriti hobuste jõul ringiaetava nüri puuriga. Et Rumford ei arvestanud soojuskadusid, pidi tulemus olema veidi suurem, kuid sel ei olnud tähtsust. Efekt oli üsna suur ja asi ei olnud ülipeentes mõõtmistes; olulisem oli temperatuuri täpne mõõtmine ja süstemaatiliste vigade vältimine. Joule’i kõige tuntum katse esines vee segamises pöörleva varda külge kinnitatud tiivikuga. See on kujutatud joonisel 6. Silinder on asetatud puust vardale (et vältida soojusjuhtivusest tingitud soojuskadusid), mille külge on omakorda kinnitatud mõned labad. Silindri paneb pöörlema kaaluvihtide tekitatud jõupaar. Vett segatakse vooderdatud labakujuliste vaheseintega kalorimeetris, kus labad pöörlevad kitsas pilus. Laskudes läbivad vihid teatud vahemaa ning me võime arvutada nende potentsiaalse energia kao. Tingimata tuleb arvestada ka kineetilist energiat, mille viht laskumise käigus omandab. Vee temperatuuri tõusu kalorimeetris jälgitakse kogu katse vältel, kusjuures arvestatakse ka jahtumisest tingitud parandust.
Et esimesel vihtide langemisel osutus temperatuuri tõus väikeseks, siis tuli seda korrata, ja Joule tegi lahtiühendatava silindri. Pärast -kordset vihtide allalaskmist tõusis vee temperatuur ligikaudu () võrra. Joule, kes kasutas üsna head termomeetrit, sai tulemuse, mis langeb nüüdisaegse väärtusega kokku -lise täpsusega. Ka tema teiste meetoditega saadud tulemused olid sellega heas kooskõlas. Energiaühik džaul on õigusega tema järgi nimetatud.
Nüüd mõistame paremini Petit’ ja Dulongi saadud tulemuse tähtsust: ühel ja selsamal temperatuuril on kõikide aatomite keskmine energia ühesuurune. See on ühe suurepärase üldise füüsikaprintsiibi erandjuhtum. Energia vabadusastmete järgi jaotumise printsiibi formuleeris esmakordselt Boltzmann (1844—1906) ja see kõlas nii: kui süsteemil on mitu vabadusastet, siis jaotub energia nende vahel võrdselt. Vabadusaste tähendab võimalust, mille abil süsteem võib kasutada oma mehaanilist energiat. Näiteks pika vedru otsa kinnitatud raskusel on mitu vabadusastet: ta võib võnkuda vasakule-paremale, ette-taha (nende võngete kombinatsioonid ei tähenda uusi vabadusastmeid) ning üles-alla. Boltzmanni printsiibi kohaselt langeb aja jooksul, mis ületab tunduvalt nende võngete perioode, igale võnkumise vabadusastmele keskmiselt võrdne hulk energiat.
Dulong ja Petit olid oma tulemustest vaimustatud ja arvasid, et kui mõõtmised oleksid veel täpsemad, tuleks aatommassi ja erisoojuse korrutis — aatomsoojus — täpselt konstantne. Nende pettumus olnuks suur, kui nad oleksid uurinud mõningaid elemente, näiteks süsinikku, mille erisoojus on väga väike, mistõttu ka nende aatomsoojus on tunduvalt väiksem, kui arvanuks Petit ja Dulong. Nüüd on teada, millest tekivad sellised erinevused. Boltzmanni seadus kehtib vaid juhul, kui energia on pidev. Kui väikesed energiahulgad ka poleks, nõuab see printsiip energia jaotumist mitme vabadusastme vahel. Kui aga energiagi koosneb jaotumatutest portsjonitest nagu aine aatomitest, siis Boltzmanni seadus alati ei kehti. Nii viivad ühe põlvkonna teadlaste avastatud lahknevused avastusteni teises põlvkonnas.
Blacki, Dulongi ja Petit’ tööd veensid füüsikuid, et soojus on kineetilise energia avaldumisvorme. Aatomid liiguvad pidevalt. Kas oleks mingi võimalus seda liikumist näha? Mikroskoobiga vaatamiseks on aatomid liiga väikesed. Ent lisame vedelikku mingeid vees hõljuvaid osakesi, mis on nähtavad. Energia võrdse jaotumise printsiip tagab, et neile kuuluva osa energiast nad saavad, ja kui nad on küllalt väikesed, võib nende liikumist mikroskoobis näha.
Püüame selgitada, millisel määral on seesugune eksperiment võimalik. Oletame, et osakesed on mõõtmetelt tuhat korda suuremad kui aatomid või molekulid. Siis on nende mass umbes 1010 korda suurem. Kui suure energia need osakesed saavad? Seda võime hinnata vaid, ligikaudselt, sest me ei tea ei aatomite masse ega energianivood, millest lähtudes hakkame mõõtma. Kuid temperatuuri muutusele vastab 1g ühikulise tihedusega aine kineetilise energia muutus ergi, mida võime pidada võrdseks 1010 ergiga. Thomsoni (lord Kelvini) hinnangu järgi on 1g aines ligi aatomit. Järelikult on iga aatomi energia 10−14 ergi. See on väga väike suurus, kuid osakesed, millele selline energia antakse, on samuti väikesed. Kui kiiresti liiguvad niisuguse energiaga osakesed? Galilei uurimised näitasid? kui paigaseisvae kehale mõjub jõud, mis nihutab keha teatud kaugusele, siis on nihkumise aeg võrdeline ruutjuurega sellest kaugusest. On võimalik tõestada, et teelõigu lõpul on ka kiirus võrdeline selle ruutjuurega. Kui defineerime tööd kui jõu ja teepikkuse korru- tist, aga energiat kui keha omadust, mille ta omandas temaga sooritatud töö tulemusena, peab energia olema võrdeline keha kiiruse ruuduga. Tõepoolest, massiga ja kiirusega liikuva keha energia on võrdne . Seega siis kui hõljuvate osakeste mass on ligikaudu 1010 korda suurem aatomi massist, s. o. , määratakse iga osakese kiirus avaldisega
mis on veidi suurem kui . Selline kiirus on loomulikult täiesti vaadeldav.
Taolist mõtterada mööda jõudis Einstein (1879—1955) 1905. a. järeldusele, et niisuguse nähtuse avastamist tasuks proovida. Ta ei teadnud, et see oli juba avastatud ja oma seletuse leidnud. 1827. a. jälgis botaanik Brown (1773— 1858) vees hõljuvate õietolmuosakeste korrapäratut liikumist. Browni osakesed olid eespool maiinitud osakestest palju suuremad: nende pikkus oli ja laius veidi väiksem. On hämmastav, et Brownil õnnestus seda liikumist vaadelda vaid ühe fookuskaugusega läätse abil. Algul mõtles Brown, et vaadeldav liikumine on mingi eluavaldus, kuid hiljem jälgis ta seda ka katses kuivatatud õietolmuga ja veel hiljem anorgaaniliste osakestega. Sellele Browni liikumisena tuntud nähtusele andis 1876. a. seletuse Ramsay (1852—1916).
Oleme jõudnud kaugele soojusvedeliku ja flogistoni aegadest ning leidnud, et soojus on mehaanilise energia avaldumisvorm ja et soojuse probleemid võib taandada mehaanika probleemideks. Ainus raskus on selles, et süsteemid, mida me uurime, sisaldavad nii palju osakesi, et nende detailne uurimine on võimatu; isegi kolme keha ülesanne ei ole veel korrektselt lahendatud. Ent kuna osakesi on nii hulganisti, võime ka statistikat kasutades saada täiesti täpseid tulemusi. Statistilise termodünaamika aine ei mahu aga meie eksperimentaalfüüsikale pühendatud raamatu raamesse. Siiski oli huvitav näidata, kuidas see füüsika valdkond arenes välja elava fantaasiaga eksperimentaatorite lihtsatest vaatlustest.
Peatükkides 2 ja 3 vaatlesime ühe gaasisegu - atmosfääri - omadusi ja seda, kuidas arenesid kujutlused soojuse olemusest. Selles peatükis ühendame need teemad ja saame esimese tähtsa üldistuse füüsikas - gaaside seadused.
Gaaside seadused väljenduvad nii lihtsalt ühesainsas võrrandis, et lihtsus lausa varjutab sellest johtuva tähtsuse. Võidakse arvata, et iga esimesel pilgul lihtsana näiv üldistus on triviaalne. See on vale. Üks füüsika eesmärke ongi otsida niisuguseid lihtsaid looduse üldisi seaduspärasusi. Need laiendavad meie teadmisi ja panevad aluse edasiseks arenguks. Gaaside seadused aitasid mõista gaasilise oleku olemust, määratleda täpsemalt, mis on temperatuur, ning paremini mõista aine tahket ja vedelat olekut, mis on palju komplitseeritumad kui gaasiline.
Esimese gaaside seaduse avaldas trükis Boyle (1627-1691) oma töös „Õhkvedrut puudutavad uued eksperimendid" (New Experiments Touching the Spring of the Air) 1660. a. Boyle oli üks esimesi Londoni Kuningliku Seltsi liikmeid ja hiilgav eksperimentaator. Räägiti, et ta tundis surma ees hirmu vaid sel põhjusel, et kartis sattuda maailma, kus pole vaja enam katsetada, sest kõik on juba teada. Boyle oli huvitatud Torricelli ja von Guericke töödest ning täiustas oluliselt viimase õhupumpa. Talle näis, et selle pumba tööprintsiibi mõistmiseks on vaja teada, kuidas sõltub õhuhulga ruumala selle rõhust, ja ta leiutas vajalike mõõtmiste tegemiseks mõned üsna lihtsad seadmed. Töö, milles ta uuris gaase kõrgemal ja madalamal rõhul kui atmosfäärirõhk, koosnes kahest osast.
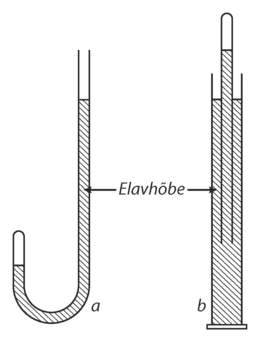
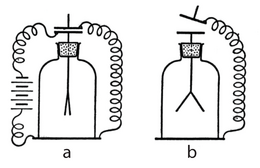
Esimene osa oli üsna lihtne. Boyle võttis väga pika kõvera klaastoru (joonis 7a) ja valas sinna elavhõbedat, nii et lühikesse harusse jääks suletuks ka veidi õhku. Ruumalamõõduks oli õhusamba pikkus. Elavhõbeda nivood olid mõlemas harus esialgu ühesugused. Boyle hakkas seejärel torusse elavhõbedat juurde valama, kuni õhu ruumala toru suletud osas vähenes kaks korda. Siis märkas ta oma suureks imestuseks, et erinevus mõlema elavhõbedanivoo vahel on ligikaudu võrdne baromeetrilise rõhuga. See viis ta mõttele, et sõltuvus gaasi rõhu ja ruumala vahel võiks olla pöördvõrdeline. Kontrolliks kordas Boyle katset, lisades elavhõbedat juurde väikeste portsjonitena. Saadud andmed kinnitasid tema oletust täielikult.
Boyle mõistis, et katse tuleb läbi viia ka atmosfäärirõhust väiksemate rõhkude korral, kuid selle jaoks läks vaja palju keerulisemat seadet. Ta asetas ligi 2m pikkuse toru jämedamasse elavhõbedaga täidetud torusse (joonis 7b).
Kuumutades ja jahutades sisemist toru, imes Boyle sinna elavhõbedat. Lõpuks jäi toru ülemisse ossa väike õhuga täidetud osa. Seejärel hakkas ta järk-järgult sisemist toru üles tõstma, nii et rõhk väheneks, ning mõõtis jälle rõhku ja ruumala. Sellisel teel suutis ta katta suure rõhkude diapasooni, palju suurema, kui seda õnnestub tänapäeva õpilastel Boyle’i seaduse kontrollimiseks ettenähtud õppevahendi abil. Tabelis 3a ja 3b on esitatud osa Boyle’i tulemustest.
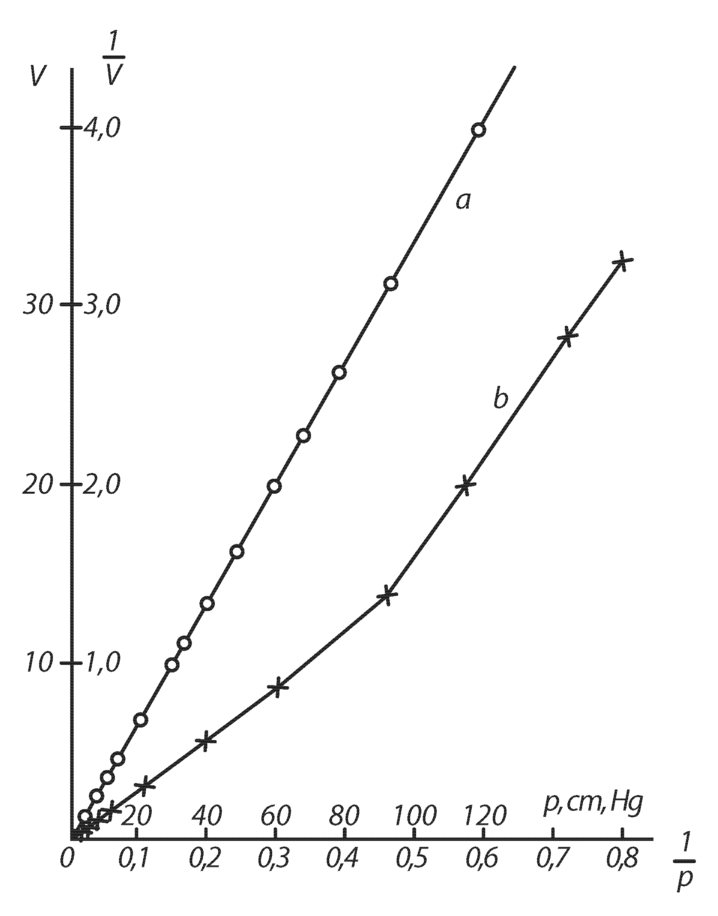
Õpetlik on siiski esitada Boyle’i tulemused graafiliselt, nagu seda praegu tehaksegi. Joonisel 8 on näidatud ruumalade pöördväärtuste sõltuvus rõhust (graafik ). Graafik on peaaegu ideaalne koordinaatide alguspunkti läbiv sirge. Aga kui kujutada graafikul ruumala sõltuvust rõhu pöördväärtustest? Nagu on näha graafikult , avastame koordinaatide alguspunkti juures (punkte on liiga palju, et neid kõiki joonestada) märgatavad hälbed lineaarsest sõltuvusest. Neid on lihtne seletada. Nad pole tingitud ruumala mõõtmise vigadest, mis peaksid olema suurimad väikeste ruumalade korral; vaevalt võis lubada -tollist viga atmosfäärirõhu mõõtmisel. Madalate rõhkude korral pole Boyle’i tulemused tõepoolest eriti head. tolli langeb halvasti kokku tegeliku väärtusega tolli. Kõikidel Boyle’i tulemustel madalate rõhkude juures esineb süstemaatiline viga, mille põhjust ei õnnestu tema poolt valitud ligikaudseid murde kasutades täpselt kindlaks teha.
Boyle’i seaduse avastas 1676.a. uuesti prantslane Mariotte (1620-1684), mistõttu Prantsusmaal nimetatakse seda seadust Mariotte’i seaduseks. Boyle’i prioriteedis ei kahtle arvatavasti keegi, kuid Mariotte mõistis nähtust sügavamini kui Boyle, kes pidas seda lihtsalt üheks õhu huvitavaks omaduseks.
Tundub igati loomulik, et järgmisena asuti mõõtma õhu paisumist soojendamisel. Seda oli võimalik teha alles siis, kui oli defineeritud temperatuuriskaala. Füüsikud ei jäänud ootama ideaalset temperatuuriskaalat. Nad alustasid töid ligikaudsete skaaladega, jälgides elavhõbeda paisumist klaastorus. Me teame, et see oli väga õnnestunud valik, tunduvalt parem sellest, kui elavhõbeda asemel oleks valitud näiteks vesi. Paistab, et esimesena sooritas rahuldavad mõõtmised Dalton aastal 1801. Eelmistel uurijatel olid mõõtmised ebaõnnestunud, sest nende uuritavad gaasid sisaldasid veeauru. Dalton uuris gaasidest hapnikku, lämmastikku, vesinikku ja süsihappegaasi. Ta kogus uuritavad gaasid, kuivatades neid hoolikalt, kinnijoodetud jaotustega torudesse, sulges torud elavhõbedatilgaga ja asetas soojendatavasse veenõusse.
Paistab, et esimesena sooritas rahuldavad mõõtmised Dalton aastal 1801. Eelmistel uurijatel olid mõõtmised ebaõnnestunud, sest nende uuritavad gaasid sisaldasid veeauru. Dalton uuris gaasidest hapnikku, lämmastikku, vesinikku ja süsihappegaasi. Ta kogus uuritavad gaasid, kuivatades neid hoolikalt, kinnijoodetud jaotustega torudesse, sulges torud elavhõbedatilgaga ja asetas soojendatavasse veenõusse.
| Ruumala suvalistes ühikutes | Rõhkude erinevus tollides elavhõbedasambast | Rõhk | Rõhk vastavalt Boyle'i oletustele |
| * | |||
| 14 | |||
* Boyle’il oli see väärtus 1662. a. ekslikult . Absurdsusele vaatamata trükitakse seda paljudes raamatutes tänini. Kuid kas see ongi kõige kestvam vea kordamine ajaloos?
Oma üllatuseks leidis Dalton, et kõik gaasid käitusid ühtemoodi. Ta sõnastas saadud tulemused väga ettevaatlikult: „Me ei näe üldiselt piisavat põhjust, mis segaks meil järeldumast, et kõik elastsed fluidumid* ühel ja selsamal rõhul paisuvad kuumutamisel võrdselt." Ent ta arvas, et temperatuuri tõustes gaaside paisumisvõime väheneb.
*St. gaasid. Fluidum on aine, mis võtab anuma kuju, milles ta on.
Gay-Lussac (1778-1850) vermis sama järelduse palju selgemalt ja kvantitatiivselt. Tema kasutatud seade on näidatud joonisel 9. Hoolikalt kuivatatud gaas asub balloonis , kuhu ta suletakse torus asuva elavhõbedatilga abil. Toru asetseb horisontaalselt, mistõttu rõhk paisumisel ei muutu. Temperatuuri mõõdetakse termomeetritega ja .
Gay-Lussac leidis gaasi ruumala eri temperatuuridel vee külmumispunktist keemispunktini, arvestades toru soojuspaisumisest tingitud parandust. Ta uuris läbi hulga gaase ja sai atmosfäärirhul järgmised paisumisteguri väärtused .
Keskmine väärtus on (), üksiktulemuste hälve suurusjärgus .
Gay-Lussac uuris samal meetodil ka eetriaure, kuid ei avastanud nende käitumises õhuga võrreldes märgatavaid erinevusi. Seejärel vermis ta tulemused järgmiselt.
- Kõik gaasid ja aurud paisuvad ühesugusel temperatuuritõusul võrdselt.
- Püsivate gaaside* ruumala suurenemine on jää sulamistemperatuuri ja vee keemistemperatuuri vahemikus võrdne -ga esialgsest ruumalast.
*Püsivate gaaside all mõeldi Gay-Lussaci ajal gaase, mida tollal ei õnnestunud veeldada.
**Sealhulgas ka meil.
Need seisukohad on Daltoni väidetest sedavõrd täpsemad, et keegi ei nimeta enam gaaside soojuspaisumise seadust tema nimega. Gay-Lussac nõudis temale omase õilsameelsusega, mida me teaduses kahjuks harva kohtame, et see seadus kannaks Charlesi (1746-1823) nime, kes oli saanud samad tulemused 1787. a., kuid ei olnud neid avaldanud. Seetõttu nimetatakse nüüd seda seadust Charlesi seaduseks, ehkki mõnedes maades on ta ikka veel tuntud Gay-Lussaci seadusena.**
Sellest seadusest järeldub üks väga tähtis mõiste - absoluutne null. Kui temperatuur langeb alla , siis gaasi ruumala vähenemine jätkub ja saab ideaalsel juhul mingil temperatuuril, sõltumata gaasi liigist, võrdseks nulliga, mistõttu sel temperatuuril on teatav fundamentaalne tähendus. Dalton mõistis seda ja nimetas selle temperatuuri absoluutseks külmanivooks. Mõningate põhjendamatute oletuste tõttu sai ta selle väärtuseks . Gay-Lussac tuletas tema enda avastatud seadusest märgatavalt kõrgema temperatuuri , mis on väga lähedane selle tegelikule väärtusele.
Absoluutse nulli mõiste on väga tähtis peaaegu kogu füüsika seisukohalt. Algul vaadeldi seda kui temperatuuri, mille korral keha kaotab kogu soojuse, või, kasutades molekulaarkineetilist teooriat, kui temperatuuri, mil kaob keha aatomite soojusliikumine. Muide, ükski gaas selle olekuni ei jõua, sest mingil temperatuuril nad veelduvad ega allu enam Charlesi seadusele. Sellele vaatamata võimaldab Charlesi seadus luua niisuguse teoreetilise temperatuuriskaala, mis ei sõltu ühegi aine omadustest. Seesugune skaala on vajalik kogu füüsika arenguks, sest varem või hiljem tulnuks nagunii seni kasutatavad juhuslikud skaalad, näiteks need, mis põhinevad paisumisel klaastorus, asendada millegi absoluutsemaga.
1851. a. soovitas lord Kelvin (William Thomson) termomeetrit, milles töötavaks kehaks on õhk normaalrõhul. Selle järgi oleks saanud kaliibrida teisi termomeetreid. Õhk on valitud vaid mugavust silmas pidades; tegelikult sobiks iga püsiv gaas, kuid loomulikult mitte tema veeldumispunkti lähedal. (Thomson läks veel kaugemale ja näitas, et Carnot’ „soojuse liikumapaneva jõu" teooria võimaldaks luua veelgi vastuvõetavama skaala, ent seda kui puhtteoreetilist küsimust me siin vaatlema ei hakka.) Kelvini auks tähistatakse temperatuuri, mida arvatakse absoluutsest nullist, tähega K. Absoluutse temperatuuriskaala ühikud on võrdsed Celsiuse skaala ühikutega.
Kirjeldatu näitab, missuguseid keerdkäike on tulvil füüsika areng. Gaaside omadusi uurides avastati mõned üllatavad seaduspärasused; mille detailsem uurimine võimaldas luua teooria seisukohalt vastuvõetavama temperatuuriskaala. Tänu sellele paranes mõõtmiste täpsus ja arenes termomeetria. Määrati elavhõbeda paisumisteguri sõltuvus temperatuurist (seda oli peetud konstantseks), millega õnnestus parandada paljusid varasemaid tulemusi.
Gaaside seadustest järeldub ühtteist tähtsamatki. Sellepärast nad üldse kehtivad. Vedelate ja tahkete kehade jaoks me niisuguseid seadusi ei tea. Kõik gaasid käituvad sarnaselt. See lihtne fakt näitab, et gaasid peavad millegi poolest vedelatest ja tahketest kehadest põhimõtteliselt erinema. Tahkete ja vedelate kehade omadused sõltuvad neid moodustavatest osakestest; kui aatomid ja molekulid erinevad, võivad suuresti erineda ka nendevahelised mõjud.
Gaasides on molekulidevahelised kaugused tavaliselt molekulide mõõtmetest palju suuremad ja ajavahemikud, mille vältel molekulid lähenevad sedavõrd, et võiksid üksteist mõjutada, suhteliselt tühised. Seega ei sõltu gaaside omadused molekulidevahelistest jõududest, mistõttu nad käituvadki nii sarnaselt. Ent kui rõhk ja temperatuur on kõrged, suurenevad molekulidevahelised vastasmõjud ja gaaside sarnasus kaob.
Kui gaasid erinevad üksteisest vaid molekulmasside poolest, võib nende tiheduse mõõtmine anda lisainformatsiooni. Nagu eespool nägime, oli esimene katse mõõta õhu tihedust üsnagi kohmakas, kuid 19. sajandiks oli seda õpitud tegema märkimisväärse täpsusega. Gay-Lussac töötas välja ka aurude tiheduse mõõtmise meetodid. Kõik saadud tulemused näitasid, et mingil temperatuuri ja rõhu väärtusel on gaasi tihedus võrdeline tema molekulmassiga.
Tabelis 4 on toodud selle illustreerimiseks mõned nüüdisaegsed tulemused. Tabeli andmed võivad tähendada vaid üht: kõik need gaasid sisaldavad ruumalaühikus võrdsel temperatuuril ja rõhul ühesuguse arvu molekule. See on üks tähtsamaid üldprintsiipe füüsikas, mille esimesena ütles välja Avogadro (1776-1856) aastal 1811. Dalton ja Lavoisier olid kindlaks teinud elementide vahekorra mõnes gaasilises ühendis ja Avogadro püüdis leida lihtsaid reegleid, mis seda seletaksid. Avogadro läbinägelikkus oli hämmastav. Dalton oli püstitanud oma aatomihüpoteesi alles mõne aja eest. Selle kujutlused molekulidest kui mõnede aatomite lihtsast grupeeringust olid teadusmaailmas alles vaidlusobjektiks. Avogadro hüpotees lükati tagasi ja selle tähtsust hakati mõistma alles pärast seda, kui Cannizzaro (1826—1910) oli selle 1854. a. taas ellu äratanud.
Sageli nimetatakse Avogadro väidet Avogadro hüpoteesiks. Hüpotees - see on oletus, mida ei saa vahetult kontrollida, kuid mis näib teada oleva põhjal õige. Avogadro väidet võib vaadelda kui hüpoteesi selles mõttes, et me tõepoolest ei suuda mingis ruumalaühikus olevaid molekule kokku arvata ega näidata, et see arv on kõikide gaaside jaoks võrdne. Kuid tabelis 4 toodud andmedki on selle hüpoteesi tõestusena veenvad. Seepärast võime praegusel ajal Avogadro väidet täie õigusega nimetada Avogadro seaduseks.
See on lihtsalt imetlusväärne seadus. Kas kellegi juhtiv käsi reguleerib gaasi molekulide arvu ruumalaühikus? Ei kehti ju Avogadro seadus mitte ainult elementide ja nende ühendite, vaid ka segude jaoks. Nii ei saa küsimust esitada. Õigem oleks teine mõttekäik: mingil temperatuuril tekitab võrdne arv gaasi molekule võrdsetes ruumalades võrdse rõhu. Aga seda võib ju vaadelda kui Boltzmanni tähtsa füüsikalise üldistuse, energia võrdse jaotumise printsiibi avaldumist.
Selle printsiibi järgi peab kõikide molekulide keskmine kineetiline energia ühel ja selsamal temperatuuril olema võrdne. Järelikult peavad raskemad molekulid liikuma aeglasemalt kui kerged ning nende kiirus muutub põrkel nõu seinaga vähem. Peale selle, et raskemad molekulid liiguvad aeglasemalt, siis põrkuvad nad anuma seintega harvemini. Kuid gaasi rõhk on molekulide poolt anuma seinale mõjuva jõu mõõt. Ehkki see jõud näib muutumatu, koosneb ta tegelikult erakordselt suurest arvust üliväikestest impulssidest.
Newtoni II seadus väidab, et jõud on võrdne massi ja kiirendil se korrutisega, teiste sõnadega, liikumishulga muutusega ajaühikus, liikumishulk on aga võrdne massi ja kiiruse korrutisega. Seega on siis rõhku tekitav keskmine liikumishulga muut võrdeline nii liikumishulga muudu kui ka kiirusega, s. t. on lõppkokkuvõttes võrdeline kineetilise energiaga. Aga see on Boltzmanni järgi kõigi molekulide jaoks ühesugune.
Nii me näeme, et gaaside seadused on peatükis 3 vaadeldud kineetilise teooria ilmingud. Kineetilise teooria abil saab uurida kõiki aine olekuid, ent ainult gaaside jaoks annab see eespool toodud põhjustel nii imeväärselt lihtsad seadused.
Kuid me pole avanud seda lihtsust lõpuni. Boyle’i ja Charlesi seadused võib ühendada kõikide gaaside jaoks ühisesse seadusse, gaaside olekuvõrrandisse
kus on Kelvini skaalas mõõdetud absoluutne temperatuur, ja aga vastavalt gaasi rõhk ja ruumala. See võrrand esitatakse füüsikaõpikuis tavaliselt nii primitiivselt ja ilma mõtet selgitamata, et räägib algajaile füüsikuile väga vähe. Muuseas, gaaside olekuvõrrand on imetlusväärne tulemus, millel ei ole analoogi üheski teises füüsikaharus.
Konstant võrrandi paremal poolel võib olla mõõdetud eri gaaside jaoks, kuid standardtingimustel; näiteks kui võtame ühe kilogrammi gaasi üheatmosfäärisel () rõhul ja temperatuuril , saame just sellele gaasile iseloomuliku konstandi väärtuse. Ent eri gaaside konstandid on üksteisega seotud, sest nagu me teame, on gaasimassi ruumala pöördvõrdeline tema molekulmassiga. Kui vaadelda mitte ühikulist, vaid molekulmassiga võrdelist massi, tuleb konstant olekuvõrrandis kõikide gaaside korral võrdne. Seepärast võtame standardmassiks gaasi massi grammides, mis on arvuliselt võrdne molekulmassiga, s. o. ühe gramm-molekuli (mooli) gaasiga. See tähendab ühtlasi, et standardruumalaks valitakse 22,4 liitrit. On kerge näha, et standardrõhu, -temperatuuri ja -ruumala korral sõltub see konstant nendest standardsuurustest, mitte aga mingitest valitud ainet iseloomustavatest suurustest. Sel juhul võime kirjutada olekuvõrrandi kujul
kus on ühesuguse väärtusega kõikide gaaside jaoks. See võrrand on füüsikas esimene suurepärane üldistus, mis väljendab terve aineklassi omadusi ühtede ja nendesamade põhisuuruste kaudu. Füüsika püüdlebki selle poole, et leida üldisi seadusi, mis ei sõltuks ühegi aine omadustest. Ei ole midagi imeks panna, et esimesena andsid sellise üldistuse olemuselt suhteliselt lihtsad gaasid.
Ma ei suutnud leida andmeid selle kohta, kes tõi esimesena valemisse gaasikonstandi . Tõenäoliselt tundus see nii enesestmõistetav, et keegi ei püüdnudki oma prioriteedist teatada. Kõik õpikud esitavad -i muu seas, nagu paratamatu järelduse Boyle'i ja Charlesi seadustest, mida see tõepoolest ka on. Tavaliselt on aga isegi silmanähtava asja märkamiseks vaja geeniust. Teaduse ajaloolased ei ole selle kasutuselevõtmist arvatavasti üles tähendanud: üheski raamatus, mida ma olen lugenud, ei ole omistatud gaaside seaduste tuletamisele piisavat tähelepanu.
Gaaside seadused on tegelikult aluseks termodünaamikale, mis pakub suurt praktilist ja teoreetilist huvi. Siinjuures tahaksin jutustada katseist, millele toetudes arenes see teadusharu: kuidas aastal 1840 mõõtis Regnault gaaside erisoojust, kuidas aastal 1869 vaatles Andrews hälbeid gaaside seadustest, kuidas aastal 1819 mõõtsid Clement ja Desormes gaaside erisoojuse suhteid.
Tahaksin rääkida ka uurimistest ülimadalate temperatuuride valdkonnas, kus aatomite liikumine praktiliselt puudub ja kus võib jälgida selliseid nähtusi nagu ülijuhtivus, kuid see kõik viiks liiga kaugele meie raamatu eesmärgist.
Teeme kokkuvõtte. Selles peatükis nägime, kuidas mõnede lihtsate katsete käigus ilmutasid gaasid omadusi, mida esimesed uurijad ei osanud oodatagi. Nende jaoks olid kõik gaasid lihtsalt „õhud", omadustelt niisama mitmekesised kui vedelikud või tahked kehadki. Nende leitud seadused panid aluse gaaside kineetilisele teooriale, mille järgi gaasid koosnevad lõpmata paljudest väikestest molekulidest, mis anumas korrapäratult liikudes põrkavad kokku selle seintega. Avogadro seadus väidab, et ühesugusel temperatuuril ja rõhul on kindlas ruumalas gaasis kindel arv molekule, millest järeldub tähtis füüsikaline konstant - Avogadro arv ehk molekulide arv ühes moolis.
Vahetuks mõõtmiseks on see arv muidugi liiga suur. Avogadro ajal ei saadud seda mõõta isegi kaudselt, sest ei osatud veel mõõta aatomite suurust. Nendest katsetest jutustame järgmistes peatükkides.
Ma ei tahtnud kirjutada selles raamatus helist. Heli on seotud eeskätt atmosfääriga ja ükski selle teema aspektidest ei ole nii põhjapanev, et sellele ei saaks läheneda mõnda teist teed mööda. Pealegi on akustika põhiprintsiibid üksikasjaliselt välja arendatud ja võivad vaevalt saada füüsikas täiesti uue tee lähtepunktiks. Ent samal ajal ma leidsin, et me kuuleme - aga kuulmine on tähtsuselt meie teine meel - tänu helidele ja heli aitaks illustreerida mõningaid tähtsamaid üldisi füüsikaprintsiipe; samuti kergendaks tutvus heliga valguse uurimist, sest esimesed mõtted valguse olemusest tuginesid sellele, mida teati helist. Lõpuks jõudsin järeldusele, et heli on seda väärt, et pühendada talle üks lühike peatükk.
Keelte ja õhusammaste võnkumise printsiibid on teadlastele selged, ent praktilised ülesanded, nagu kirikukella tooni või ruumi akustiliste omaduste määramine, on teoreetilise analüüsi jaoks liiga keerulised. Just sellepärast pakubki see teema ikka veel suurt praktilist huvi.
Mis on heli? Mis nimelt annab meile võimaluse kuulda üht või teist nähtust mingi kauguse tagant? Tava järgi tuleb küsimusele vastamiseks uurida meid huvitava nähtuse omadusi ja katsuda leida siis nende seletamiseks mingi ühendav skeem.
Esmalt peame selgitama, missugust keskkonda mööda kandub heli oma allikast meie kõrvani. Sellele küsimusele leiti vastus 18. sajandil õhupumba abil, mis, oli äsja leiutatud. Guericke asetas kellukese nõusse, mida oli võimalik õhust tühjaks pumbata, ja pani selle seal kellamehhanismi abil helisema. Selgus, et õhurõhu vähenedes heli nõrgenes.
Kas heli võib levida ka teistes keskkondades peale õhu? Von Guericke leidis sellele küsimusele vastuse suurepärase katse abil, mida võib vaevalt füüsikaliseks nimetada. Ta helistas kellukest iga kord, kui järves olevale kalale visati leiba. Hiljem helistas ta kellukest ka siis, kui leiba ei visatud, ja märkas, et kala tuli ikkagi kohale. (See katse meenutab hilisemaid Pavlovi katseid koerte tingitud reflekside uurimisel.) Mõned füüsikud keeldusid tunnistamast eksperimenti veenvaks, väites, et kala võis kellukese helistamist ka näha. Ent hiljem kinnitasid von Guericke katse tulemust tuukrid, kes kuulsid heli ka vee all.
Niisiis levib heli materiaalses keskkonnas. Aga kui kiiresti ta levib? Igaüks teab, et kui kaugel lüüakse palli või lõhutakse puid, nähakse toimingut enne, kui kuuldakse seda saatvat heli. Samuti on kõigile teada, et müristab alati hiljem, kui välku lööb. Järelikult peaks heli kiirus olema mõõdetav, kuid selleks on vaja suhteliselt keerulisi seadmeid.
Newton kahtlemata teadis heli kiirust õhus, sest ta oli hämmingus, kui tema poolt mõõdetu ei langenud arvutustega kokku. Ta oli siingi oma ajast ees. Tema arutluste järgi pidi heli kiirus olema võrdne kus on rõhk ja õhu tihedus.
Esimese arvestatava katse mõõta heli kiirust sooritasid aastal 1738 Prantsuse Akadeemia liikmed. See oli muuseas üks esimesi teadlasrühma ühiselt kavandatud ettevõtmisi, kuid kahjuks sõjalistel eesmärkidel.
Kahuritest, mis asusid üksteisest umbes kaugusel, tulistati poole tunni tagant. Iga kahuri juures oli vaatleja, kes märkis üles ajavahe sähvatuse ja lasu kuulmise vahel. Kaht rühma kahureid oli vaja õhu liikumisest tingitud vigade vältimiseks. Võrdsete ajavahemike järel tulistamine võimaldas arvatavasti valmistuda ette ajalugemiseks. Tõsi, pooletunnised ajavahed tunduvad liiga pikad, sest heli läbis valitud vahemaa ligikaudu kahe minutiga. Mõõdetud helikiirus osutus juures võrdseks . Et Newtoni teooria oli andnud , siis näis see küllaltki tõelähedane. (Newton arvas, et heli levib lokaalsete õhurõhumuutustena, mis panevad võnkuma kõrva trumminaha ja tekitavad sel moel kuulmisaistingu.) Ta piinles: teooria andis igati mõistliku ja tegelikule lähedase tulemuse, kuid erinevus arvutatu ja mõõdetu vahel ületas katsevea piirid siiski märgatavalt.
Selle mõistatuse lahendas Laplace (1749-1827). Ta mõistis, et rõhumuutused sõltuvad ka temperatuurist ning et nii kiirete rõhumuutuste korral kui need, mis toimuvad heli levimisel, Newtoni poolt kasutatud Boyle’i seadus ei kehti. Kui ei kehti Boyle’i seadus, peab kehtima mõni teine. Kuid milline? Vastuse sellele küsimusele andis õhu erisoojuse mõõtmine. Ohu erisoojus ei ole nii selgelt piiritletud mõiste kui tahkete kehade ja vedelike erisoojus, sest õhku võib soojendada jääval rõhul, lastes suureneda ruumalal, või jääval ruumalal, lastes suureneda rõhul. Esimesel juhul kulub energiat rohkem, sest gaas teeb ruumala suurendamiseks tööd. Nende erisoojuste suhet tähistatakse tähega . Laplace tõestas, et õige valem heli kiiruse arvutamiseks mingis gaasis on . Kui asetada sellesse väärtus õhu jaoks (ligikaudu ), siis Newtonit piinanud erinevus peaaegu kaob.
Asume nüüd detailsemalt vaatlema meid ümbritsevaid helisid. Kahuripaukudest rohkem oleme harjunud kuulama kõnet. Paljud meist tajuvad meelsasti rõhuerinevuste ühendite mõju, mis on tuntud muusikana. Mis teeb need helid ülalpool kirjeldatud laskudest erinevaks?
Kahtlemata arutleti selle üle juba ammu enne seda, kui hakati vaatlema asja formaalsemaid külgi. Eelajaloolistest aegadest on muusikahelid inimesi rahustanud ja erutanud ning juba varajased teadlased püüdsid jõuda nende saladuste jälile ammu enne seda, kui tõeliselt aru saadi, mis on muusika.
Põhimõtteliselt on muusikahelide saamiseks kaks võimalust, kui mitte arvestada mõningaid eripä- raseid instrumente nagu näiteks trumm ja triangel: puhkpillid, kus muusikalise heli tekitab õhusamba võnkumine, ja keelpillid, kus tooni tekitab pinguldatud keele võnkumine. Püüame nüüd mõista, miks nende pillide poolt kuuldavale toodud heli on kõrvale meeldivam kui harilik müra.
Üks esimesi heli uurijaid oli Pythagoras (580-500. a. e. m. a.). Pythagoras kasutas (tõenäoliselt tema enda leiutatud) monokordi, üle teravate nugade tõmmatud ja ühest otsast kinnitatud keelt, mille teise otsa võib keelele erineva pinge andmiseks kinnitada raskusi. Tol ajal teati juba üsna palju erinevate toonikombinatsioonide esile kutsutud aistingutest, ühed kombinatsioonid olid meeldivad, teised mitte. Pythagoras leidis, et eriti meeldivalt kõlavad ühesuguse pingega keeled, mille pikkused suhtuvad nagu 2:1; kaks sellist tooni erinevad teineteisest ühe oktaavi võrra. Puhkpillide korral saadakse sama toonide intervall, kui õhusammaste pikkuste suhe on samuti 2:1. Intervall, mida tuntakse kvandina, saadakse suhte korral. Seega näitas Pythagoras, et meeldivad helid on seotud täisarvudega. Kahjuks pole mingeid teateid selle kohta, et ta oleks püüdnud uurida asja sügavamalt, kui mitte arvestada mõningaid tema tehtud julgeid üldistusi.
Tänapäeval me teame, et muusikaheli olemus peitub tema perioodilisuses. Esimesena tuli sellele mõttele ilmselt Galilei seoses oma pendlikatsetega. Nagu eespool nägime, näitas Galilei, et pendli võnkeamplituud võib kasvada isegi väikese jõu mõjul (nagu nõrk tuulehoog), kui see toimib regulaarselt hetkedel, mil pendel läbib madalaimat punkti, pendli liikumise suunas. Teiste sõnadega, pendli võnkumine resoneerib perioodilise jõuga, kui selle sagedus ühtib pendli omavõnkesagedusega.
Neist kujutlusist lähtudes kinnitas Galilei klavikordi külgseinale eri pikkusega peened harjased ja märkas, et eri nootide kõlamisel võnkusid kaasa eri harjased. Sellest järeldas Galilei, õigemini pidas enesestmõistetavaks, et muusikalistel toonidel on oma võnkesagedused. Ta asetas suurde veega täidetud anumasse pokaali nii, et see oli servani vees, ja pani siis pokaali helisema. Veepind pokaali ümber hakkas virvendama (tahvel I).
Pokaali tekitatud heli ei olnud stabiilne ja muutus mõnikord oktaavi võrra kõrgemaks. Galilei märkas, et siis muutus ka pinnavirvendus kaks korda peenemaks. Kahjuks ta ei püüdnudki määrata võngete arvu sekundis, vaid märkis lihtsalt, et see oli mõõtmiseks liiga suur.
Galilei läks Pythagorasest kaugemale ka pinguldatud keele füüsikaliste omaduste ja helikõrguse vahelise seose uurimisel. Ent jällegi ei tea me täpselt, mida Galilei tegi, sest ta märkis üles ainult tulemused: ühesuguse pinge all olev poole lühem keel annab oktaavi võrra kõrgema tooni; kui suurendada keele pinget neli korda, tõuseb helikõrgus kahe oktaavi võrra. Helisagedus sõltub keele „mõõtme" ruutjuurest, mille all Galilei mõistis ühikulise pikkusega keele massi. Galilei väitis, et kuldniit heliseb kvindi võrra madalamalt kui samasugune vaskniit, sest kulla tihedus on vase tihedusest kaks korda suurem. Lõpetuseks võrdles ta tavalise keele ja samasuguse traadiga mähitud keele võnkumist. Mähitud keeli kasutatakse veel tänapäevalgi madalamate toonide tekitamiseks.
On hämmastav, et Galilei suutis selliste tulemusteni jõuda kvalitatiivsel teel, s. t. sagedusi mõõtmata. Ta väitis veendunult, et inimene tajub noodi kõrgusena kõrvale mõjuvate võngete sagedusi. Ta arutles ka harmoonia ja disharmoonia võimalike põhjuste üle. Harmoonia tekkivat siis, kui võnkesageduste vahel on lihtne seos. Ta kirjeldas järgmist eksperimenti.
Pendlitel, mille perioodid suhtusid nagu , lasti koos võnkuda. Pendliniitide võnkumist oli meeldiv vaadata. Kui pendlite perioodid ei oleks olnud lihtsal viisil seotud, oleksid niidid korrapäratult liikunud.
Galilei mõtteid arendasid edasi teised teadlased. 1701. a. pani Sauveur keele võnkumist vaadeldes aluse kujutlusele statsionaarseist olekuist ehk seisulaineist, nagu me neid praegu tunneme. Kohti, kus keelel nihe puudus, nimetas ta sõlmedeks, aga lühema lainepikkusega võnkeid kõige suurema lainepikkusega võngete harmoonilisteks (ka ülemtoonideks). 1862. a. pakkus Helmholtz (1821-1894) välja idee, mille järgi iga keerulist võnkumist võib vaadelda koosnevana põhivõngetest ja nende harmoonilistest. Sellisel juhul võib öelda, et pilli tämber sõltub ülemtoonidest. Seepärast kõlabki flöödil võetud noot teisiti kui sama noot viiulil. Kuigi nimetatud seisukoht on üldtunnustatud, ei ole see veel täielik lahendus. Oma osa on kindlasti ka meeleelundeil, mis näivad meile seda peenemate ja imepärasematena, mida enam me neist teada saame.
Kõige tähtsam, mida õpetus helist füüsikale andis, oli kahtlemata seisulainete mõiste. Hiljem näeme, et see mõiste on kasutatav paljude võnkesüsteemide uurimisel ning võimaldab lainemehaanika abiga tungida koguni aatomi saladustesse.
Inimese tähtsaim meel on nägemismeel. Seepärast on raske sõnades väljendada, kui tähtis on meie jaoks valgus ja tundub üsna loomulik, et juba ammu püüdsid mõtlejad mõista valguse olemust. Võib-olla sooritatigi esimesed mõõtmised füüsikas valguse omaduste uurimiseks. Igatahes on teada, et juba 3. saj. e. m. a. tundis Eukleides seadusi, mille järgi valgus peegeldub tasandilt, ja et 2. sajandil uuris Ptolemaios valguse murdumist.
Tõsiselt hakati valgust uurima alles 17. sajandil. Kõigepealt tuli leida vastus küsimusele, kuidas valgus levib. Esimese „katse" sooritas ilmselt Torricelli, kes märkas, et on võimalik vaadata läbi tema baromeetri ülaosas oleva tühiku, vaakuumi. Järelikult ei vaja valgus levimiseks mingit materiaalset keskkonda. See oli juba lausa müstika, sest heli, mis näis valgusega väga sarnane, teati levivat vaid läbi õhu või mõne muu materiaalse keskkonna. Alles 19. sajandi keskel mõisteti, miks on see nii.
Optika varasemat ajalugu jälgida pole kerge. Valguse omadusi uuris väga palju teadlasi, kuid midagi asjalikku õnnestus teada saada harva. Näiteks seadus, et valgus levib ühtlases keskkonnas sirgjooneliselt, oli üldtunnustatud enne, kui seda suudeti tõestada. (See tõestus on äärmiselt raske.) Veel enam, seda valguse omadust kasutati füüsikas hoopis mõiste „sirgjoonelisus" määratlemiseks. Fakt, et punktvalgusallikas annab terava varju, ei tähenda veel midagi; terava varju annaks ka kõveriti leviv valgus, kui vaid kõikide kiirte teed oleksid sarnased.
Esialgu nõustugem valguse sirgjoonelise levikuga ja vaadelgem, kuidas uuriti valguse teisi omadusi. 2. sajandi esimesel poolel sõnastas Ptolemaios valguse peegeldumise seadused peaaegu nii, nagu teame neid praegu. Tõsi küll, enamik tema teoseid on ajakeerises kaotsi läinud, mistõttu pole täpselt teada, kuidas ta oma tulemused sai. Ent tema valguse murdumise alane töö on säilinud. Sageli räägitakse, nagu oleks Ptolemaios avastanud murdumisseaduse mõõtmise abil, kui aga süveneda tema töösse, selgub, et selle seaduse avastamiseks ei olnud ta mõõtmised küllalt täpsed.
Ptolemaios uuris valguse murdumist vee ja õhu lahutuspinnal. Langemis- ja murdumisnurga mõõtis ta kraadijaotustega ketta abil, mille ta asetas poolenisti vette (joonis 10). Ta pani kettale kaks märki, ühe keskmesse, teise ketta servale, mis jäi veest välja, ja nihutas seejärel vees olevat sirget varrast nii, et see näis olevat märkidega ühel sirgel. Ptolemaios koondas saadud andmed tabelitesse ja rahuldus ilmselt murdumismõõturi leiutamisega, sest ta ei oletanud midagi seose kohta langemis- ja murdumisnurkade vahel.
Samal meetodil uuris ta valguse murdumist klaasis. Selleks valmistas ta klaasist poolsilindri. Sama poolsilindri abil uuris ta ka murdumist vee ja klaasi lahutuspinnal. Vaatleme tema tulemuste tabelit (tabel 5). Kas Ptolemaios võis nende andmete abil avastada murdumisseaduse? Nende andmete järgi arvutatud murdumisnäitajad () kõiguvad 1,25 ja vahel, s. o. erinevad üksteisest rohkem kui võinuks oodata; kuid ühelgi juhul peale viimase ei ületa nurga mõõtmise viga poolt kraadi.
Tabelit üksikasjalikumalt uurides avastame midagi kahtlast: vasakult paremale väheneb kõrvuti olevate murdumisnurkade vahe süstemaatiliselt võrra. See on ülimalt ebaloomulik. Tahtmatult tekib mõte, et Ptolemaios lihtsalt sobitas oma tulemused kujule, mis näis talle kõige mõistlikum. See kahtlus süveneb, kui leiame midagi samalaadset tema kõikidest tabelitest.
Et murdumisnurkade vahe kahaneb aritmeetilises progressioonis, siis peab langemisnurkade ja murdumisnurkade vahel olema lihtne ruutsuhe. Lugeja võib oma meelelahutuseks selle suhte leida. Tulemus, mille Ptolemaios oleks pidanud mõõtmisel saama, on loomulikult vale ega oma füüsikalist mõtet. Kas me ei avastanud siin esimese „sobitamise" näite teaduses? Loomulikult ei saa me Ptolemaioselt nõuda teaduslikku objektiivsust tänapäevase mõõdupuu järgi. Tal ei olnud toetuda kellegi eeltööle ja ega ta neid tulemusi kuigi tähtsaks pidanudki. Ta tegi selle katse rohkem lõbu pärast, nii et karmi kohut tema üle pidada ei maksa. Pigem tuleb meil endil ettevaatlikumad olla ja mitte uisapäisa otsustada, et kuna tal andmed juba kord olemas olid, siis tegi ta nendest ilmtingimata ka järeldused.
Ehkki tänapäeval peetakse murdumisseaduse avastajaks Snelliust (1580 või 1591-1626), on tõenäone, et teda ennetas Hariot (1560-1626). Hariot asetas klaasprisma lauale nii, et pind oli risti lauale tõmmatud joonega (joonis 11), ja palus oma sõbral nihutada nööpnõela , kuni see hakkas talle läbi prisma paistma suunas . Saadud andmeist võis ta arvutada valguskiire langemis- ja murdumisnurga. Korranud seda katset mitmesuguste prismadega, saigi ta tulemuse, mida me tänapäeval teame: suhe võrdub -ga.
Kirjeldatud meetod oli tülikas, sest nõudis iga langemisnurga jaoks uut prismat, kusjuures kõik prismad pidid olema ühesugusest klaasist. Ent see oli esimene meile teada olev seda laadi edukas katse, esimene nööpnõelakatseist, mis etendasid suurt osa optika õpetamisel, kuid mida nüüdisaja füüsikud on õppinud juba alavääristama. Veel enam, see oli eksperimentaalne töö, sest Snelliuse järeldus, mis pole kahjuks säilinud, oli arvatavasti teoreetiline. Descartes sidus aga murdumisseadust 1638. a. uuesti vermides selle Snelliuse nimega. Descartes vaatas katsetele ülalt alla ja temagi järeldas selle seaduse ilmselt teoreetiliselt. Võimalik, et ta lähtus samast kujutlusest millest hiljem Newtongi: murdumist põhjustab aine poolt valgusosakestele mõjuv tõmbejõud, mistõttu ainele lähenedes need kiirenevad. Kuid me peame järgima tavasid ja seostama murdumisseadust Snelliuse nimega.
Vaevalt hajus udu ühelt kohalt, kui kerkis teine probleem. Mõned kristallilised ained ei rahuldanud seda lihtsat murdumisseadust, vaid lahutasid valguskiired kaheks ja andsid kahekordse kujutise. Seda kaksikmurdumiseks nimetatud nähtust märkas esmakordselt Bartholinus (1625-1698) 1669. a. Bartholinus jälgis seda nähtust kaltsiumkarbonaadikristalli abil, mida nimetatakse ka islandi paoks. Islandi pagu peetakse tänini parimaks selle nähtuse demonstreerimise vahendiks.
Muide, oli võimalik, et mingitel põhjustel oli kristallil kaks murdumisnäitajat, nii et üks osa valgust murdus ühe, teine teise näitajaga. Ent mõõtmised näitasid, et üks murdumine ei allunud üldse Snelliuse seadusele: kui langemisnurk oli null, ei olnud murdumisnurk null, öeldakse, et selle kujutise tekitavad ebatavalised, ekstraordinaarsed kiired. Kiiri, mis rahuldavad Snelliuse seadust, nimetatakse tavalisteks ehk ordinaarseteks.
Meie ees on kenake probleem. Peame loobuma kujutlusest, et valgus käitub alati ühtmoodi, leidma, uue valguse murdumise mehhanismi ning andma valguse olemusele ka seletuse, mis ei oleks vastuolus vaadeldava nähtusega. Üsna pea asuti seda ülesannet lahendama. Aastaks 1690 oligi Huygens väljatöötanud oma valgusteooria.
Tuleb au anda Huygensile, et ta julges vastu vaielda Newtonile. See oli põhjus, miks tema tööd alati väärilist tunnustust ei leidnud. Oli ju füüsika tollal veel lapseeas: tema alused olid loodud kõigest, mõned aastakümned tagasi. Kuid Huygens oma erakordse mõistusega lõi juba tol ajal teooria, mis on suutnud vastu panna pikale ajaproovile ja muutunud tänaseks vaid esituslaadilt. (Meenutagem veel kord, et füüsika oli tollal veel lapseeas: selle alused olid rajatud kõigest mõned aastakümned tagasi.)
Teine probleem - miks kogu valgus ei käitu ühtmoodi - osutus tunduvalt kõvemaks pähkliks. See viis Newtoni ja Huygensi vahelise tuntud vaidluseni, kas valgus koosneb korpuskuleist või laineist. Nüüd on loomulikult kerge öelda, et eksis Newton (isegi Newton polnud eksimatu) ja õigus oli Huygensil.* Püüame jälgida, milliseid põhjendusi nad oma vaadete kasuks tõid. Newton eelistas korpuskuleid, sest valgus levib sirgjooneliselt: osakesed liiguvad sirgjooneliselt, kui neile ei mõju mingi jõud. Niisiis, siin on kõik korras. Aga kui valgus oleks helisarnane pikilainetus, oleks raske kujutleda, kuidas saaksid tema eri osad käituda erinevalt. Tõepoolest, Huygensi teooria kõige nõrgem osa oli just see, mis puudutas kaksikmurdumist, sest tema arvates oli valgus pikilainetus. Näis, et Huygens jättis selle küsimuse kõrvale lootuses, et teised optilised nähtused hiljem tunnistavad tema laineteooria kasuks.
*Õigus oli mõlemal. Need esialgu vastandlikena näivad seisukohad lepitas lainemehaanika, teooria, mille de Broglie lõi 1924. a. (vt. ptk. 12).
Newton võis see-eest seletada kaksikmurdumist korpuskulite abil mitmel viisil. Näiteks nii: valgus- osakesed on poolustega nagu magnetid ja kristallis sõltub nende murdumine sellest, kuidas need poolused kristalli suhtes paiknema juhtuvad. Newtoni sõnade kohaselt on „igal Valguskiirel kaks vastakuti asuvat külge, millel on Ebatavalist Murdumist Põhjustav Omadus, ja kaks vastakuti asuvat külge, millel see omadus puudub". Newtoni korpuskulid olid polariseeritud nagu magnetid. Muuseas, seda mõistet kasutati ka siis, kui Newtoni korpuskulaarteooria pikaks ajaks kõrvale jäeti. On imelik, et ei Newton ega Huygens tulnud mõttele, et valgus võiks olla hoopis ristlainetus.
Muide, on üks üsna lihtne nähtus, mida Newtoni hüpotees seletada ei suuda: valguse üheaegne peegeldumine ja murdumine klaasi pinnalt. Newton esitas selle kohta üsna uduseid mõtteid kergest peegeldumisest ja kergest murdumisest, sellest, et korpuskulite hulgast koosnev kiir võib teatud aja olla olekus, mil ta ennem peegeldub, kui murdub, ja siis jälle vastupidi jne. Interferentsinähtuse abil, mida me vaatleme hiljem, suutis Newton kergesti hinnata kaugust nende olekute vahel, mis punase valguse jaoks oli võrdne tolliga. See on , mis polegi nii kaugel poolest punase valguse lainepikkusest, nagu me nüüd teame.
Kummaline, difraktsiooni kui nähtust näis Newton täiesti ignoreerivat. Selle nähtuse avastas Grimaldi (1618-1663), kes arvatavasti püüdis korraldada katset piirtingimustel. Need on tingimused, mil tavalised nähtused enam ei toimu. Katsed piirtingimustel on füüsikutele tänuväärne tegevusväli, sest nende abil oh avastatud palju uut.
Käesoleval juhul oli probleem varju teravuses. On teada, et ruumiline valgusallikas annab laialivalguvate servadega varju, kuna väiksem valgusallikas annab teravamad varjud. Kui teravat varju on võimalik saada? Grimaldi leidis, et kui valgusallikana kasutada nõelasilma, valgub vari jälle laiali ja ilmuvad „paralleelsed triibud, mille kõrval on värviliste triipude read". Selle nähtuse avastas uuesti Hooke 1672. a.
Ka Newton huvitus difraktsioonist. Ta kordas katset ise. Kasutades eri suurusega avasid, sai ta palju mitmekülgsemaid tulemusi kui Grimaldi. Joonisel 12 on näidatud, milliseid efekte Newton otsast kitseneva pilu abil vaatles. Selgesti on näha varju laienemine pilu kitsama otsa juures.
Kuid siis veab Newton meid alt. Sooritanud suure hulga katseid ja mõõtnud, «kuidas Valguskiired painduvad Kehadest möödumisel», märgib ta äkki: „Kuid hiljem mind segati ja nüüd ei suuda ma mõelda nende asjade edasisele vaatlemisele." Ja ta jätabki difraktsiooni uurimise pooleli.
Kas ei ole kummaline, et difraktsiooninähtust uurides oletas Newton, et lained painduvad tõkete taha? Oli ju valguse sirgjooneline levik üks Newtoni argumente valguse laineteooria vastu, sest lained painduvad tõkete taha! Newtoni korpuskulaarteooria pidurdas optika arengut enam kui sajandi jooksul. See näitab, kui ohtlik on suurmeeste kultus isegi teaduses.
18. sajandi lõpul hakati valguse korpuskulaarteoorias kahtlema. Mõned teadlased leidsid, et Grimaldi vaadeldud nähtust oleks parem seletada laineteooria abil. Suurimaks neist teadlasist oli Fresnel (1788-1827). Ta elu jäi küll lühikeseks ja langes aega, mida vapustasid Napoleoni režiimi aegsed poliitilised rahutused, kuid ta nimi läks alatiseks füüsika ajalukku, sest ta töötas välja difraktsiooniteooria. Fresneli tuliseks pooldajaks sai Arago (1786-1853). Koos sooritasid nad katseid, millest ühed olid väga triviaalsed, teised seevastu omandasid suure tähtsuse, sest veensid isegi laineteooria vastaseid selle õigsuses. Algul õhutas neid katsetama Poisson (1781-1840), üks 19. saj. suuremaid prantsuse teadlasi.
Poisson jõudis järeldusele, et kui punktvalgusallikast kiirgunud valguskimbu teele risti kiire teljega asetada ümmargune ekraan, siis lained, kui valgus on lainetus, jõuavad ekraani servadeni ühes faasis. Varju keskmes nad liituvad ja annavad heleda täpi. See järeldus näis talle piisavalt absurdne, et lükata ümber kogu valguse laineteooria. Kuid Fresnel ja Arago olid jultunud. Nad tegid sellise katse ja avastasidki varju keskmes heleda täpi. Nii veendi ümber üks peamisi laineteooria vastaseid ja see teooria ise muutus üldtunnustatuks.
Loo moraal on: ei maksa loota ainult teooriale. Kui ilmsed teooria ennustused ka ei näiks, tuleb neid ikkagi katseliselt kontrollida. Kui katse kinnitab teooriat, on ta vastuvõetav ja tema järeleproovimiseks võib kavandada uusi katseid. Kuid niiviisi kontrollides võib ka selguda, et teooria on puudulik või ei kõlba kuhugi. Seetõttu peavad katse ja teooria minema alati käsikäes.
Valguse laineteooriat võib kontrollida ka interferentsi abil. Interferentsi- ja difraktsiooninähtusi võib teineteisest eristada, defineerides difraktsiooni kui ühe ja interferentsi kui mitme valguskimbu tekitatut.
Kõige tuntum ja ühtlasi ka kõige lihtsam interferentsikatse on Youngi katse. Young (1773-1829) mõistis, et ei saa loota eri valguskimpude interfereerumisele, ja korraldas seepärast 1807. a. järgmise katse. Ta torkas kardinasse terava nõelaga ava, millest päikesevalgus pääses pimedasse ruumi. Sel viisil saadud hajuva valguskoonuse jaotas ta millimeetrilaiuse pabeririba abil kaheks. Siis asetas ta poolitatud valguse teele ekraani ja avastas sellel sümmeetrilised triibud: keskel valge, äärtel värvilised. Triibud sarnanesid väga nendega, mida oli saanud oma difraktsioonikatses Fresnel. Kui Young nihutas pabeririba valguskoonuse ääre poole, triibud kadusid. Korduvad katsed kinnitasid, et see nähtus tekkis tõepoolest algse valguskimbu jaotamise tagajärjel.
Kirjeldatud katset võib teha ka palju lihtsamalt. Kui lõigata paberisse žiletiga kaks teineteisest poole millimeetri kaugusel asetsevat kitsast pilu ja vaadata neid silma ees hoides kauget valgusallikat, on näha täiesti selged interferentsitriibud.
Youngi katse lihtsus ja veenvus etendasid Fresneli laineteooria alaste tööde toetamisel suurt osa. Lihtsad katsed on alati palju veenvamad kui keerulised, sest mida rohkem on seadmeid, seda enam on ka võimalusi, et tekivad igasugused kõrvalefektid.
Youngi katse oli hea veel selle poolest, et seda võis ilma eriliste raskusteta muuta kvantitatiivseks. Ka Fresneli difraktsioonikatsest oli võimalik saada arvulisi tulemusi, kuid üksnes keerulise matemaatika abil. Youngi interferentsitriipe käsitlev teooria on seevastu väga lihtne. Selle abil võib valguse lainepikkust mõõta kuni -lise täpsusega.
Füüsika suurkatsed on harva midagi lõplikku ja iseseisvat. Tavaliselt viivad nad uute mõteteni, mille kontrollimiseks on vaja teha uusi katseid. Youngi katse on selle suurepärane näide. Ta õhutas Aragod ja Fresneli korraldama interferentsikatseid polariseeritud valgusega. Nende katsete alusel veenduti lõplikult, et valgus on ristlainetus. See mõte mõlkus peas paljudel tolle aja füüsikutel, puudus vaid katseline tõestus.
Arago ja Fresnel mõistsid: suudaksid nad näidata, et teineteise suhtes ristuvates suundades polariseeritud valguskimbud ei tekita interferentsitriipe, olekski tõestatud, et valgus on ristlainetus. Kõik, mis neil teha tuli, oli polariseerida Youngi seadme kahest pilust väljuvad valguskimbud ja vaadata, kas need interfereeruvad. Seda on kergem öelda kui teha. Arago ja Fresnel mõistsid hästi, kui tähtis on, et valguskimbud oleksid pärit ühest allikast, s. t. et nad oleksid koherentsed. Ühtlasi panid nad kahtluse alla oma esimesed katsed, kus nende polariseerimismeetod võis põhjustada mittekoherentsust.
1819. a. avaldatud töös kirjeldasid nad üksikasjaliselt kõiki nende korraldatud katseid ja panid kirja ka kahtlused tulemuste suhtes. On võib-olla kahetsusväärne, et tänapäeval sellist tööd avaldamiseks vastu ei võeta: toimetaja on sunnitud paluma autorit artiklit lühendada, nii et sellest jääb välja kõik peale töö lõppetapi, mis sisaldab vaid neid katseid, mis tõestavad otseselt autorite seisukohta. Loomulikult läheb nii suur osa tööst kaotsi. Kuid meilgi tuleb selles raamatus järgida sama põhimõtet.
Polariseerimiseks kasutasid Arago ja Fresnel kaksikmurdvast materjalist plaati. Kaheks valguskimbuks, mida läks vaja Youngi katses, olid tavaline ja ebatavaline kiir. Ent optiline teepikkus tuli kummagi jaoks erinev. Nende võrdsustamiseks panid nad ühe valguskimbu teele vajaliku paksusega klaasplaadi. Et Aragod ja Fresneli häiris selle katse „sõltuvus teoreetilistest kaalutlustest", siis korraldasid nad lõpuks järgmise eksperimendi.
Nad asetasid Youngi pilude ette homogeense kaksikmurdva seleniitplaadi (kipsi teisend ). Kumbki pilu andis nüüd kaks hajuvat kiirtekimpu: tavalise ja ebatavalise. Seetõttu võis oletada, et tekivad kolme liiki interferentsitriibud: ühe annavad kaks tavalist kimpu, teise kaks ebatavalist ning kolmanda tavaline ja ebatavaline. Kaks esimest pidid täpselt kattuma, sest nende asukoht sõltub üksnes piludevahelisest kaugusest, kolmas aga pidi sõltuma seleniitplaadi paksusest. Tegelikult, nagu oodatigi, mingit kolmandat triibukogumit ei tekkinud.
Ent eitav tulemus polnud veel küllalt veenev. Arago ja Fresnel lõikasid seleniitplaadi kaheks, asetasid need pilude ette ja pöörasid teineteisega risti. Nüüd jälgisid nad ainult ebatavalise ja tavalise kimbu liitumisel tekkinud triipe. Et kimpude vahel oli käiguvahe, siis moodustasid nad kaks teineteise suhtes nihutatud triibukogumit.
Arago ja Fresnel võisid neid katseid tehes rahuldust tunda. Need olid küll lihtsad, aga nõudsid üsna peeni manipulatsioone. Nad pöörasid üht seleniitplaati võrra ja nägid seejärel korraga kõiki triipe. Nad tõestasid, et teineteise suhtes ristuvates suundades polariseeritud kimbud ei interfereeru. Siit võis loogiliselt järeldada, et valgus on ristlainetus, valguse polariseerimine aga selle piiramine ühes tasandis. Ma olen veendunud, et ka Newtonile oleksid meeldinud need nii lihtsad ja ilmsed seletused enam kui tema enda segane kujutlus anisotroopsetest korpuskulitest.
Valgusel on teinegi silmapaistev omadus - värvus. Milline füüsikaline omadus lubab valgusel tekitada nii kauneid aistinguid? Õige lähedale selle küsimuse vastusele jõudis juba Newton 1666. a. oma prismakatsete abil, kuid kuni 1672. aastani ei avaldanud ta nende kohta midagi. Ta ei kiirustanud avaldamisega kunagi.
Newton oli võlutud tema ostetud prisma tekitatud spektrivärvidest ja korraldas sellega kodus lihtsaid katseid. Ka teised inimesed nägid taolisi spektreid, kuid keegi ei hakanud neid süsteemselt uurima. Selle asemel usuti, et prisma värvib mingil moel valgust, sest värvus olevat midagi, mida võib valgedusele lisada.
Newton laskis päikesevalguse pimedasse tuppa läbi väikese ava aknaluugis ja jälgis spektrit, mida prismat läbinud valgus ekraanil tekitas.
Teda pani imestama, et spektri pikkus oli laiusest ligi viis korda suurem. (Newton ilmselt lootis, et spekter on enam-vähem ümmargune.) Eespool ma juba selgitasin, kui tähtis on, et teadlane oskaks ennustada katsetulemusi. Seda kinnitab suurepäraselt Newtoni töö. Kuidas võib ülimalt lihtne vaatlus erutada suurimat inimmõistust! Ja ikkagi juhtub sageli nii, et kõige lihtsamad asjad, millele mõtlemist tavaline inimene peab lapsikuks ajaraiskamiseks, annavad tõuke geeniuse mõttelennule.
Siis tegi Newton katse, mida ta nimetas Experimentum Crusis'eks (otsustav katse). Ta tekitas prisma abil ekraanil spektri, kusjuures väike osa spektrist pääses läbi avade ja prismale abc. Niimoodi saadud valguskimp prismas abc enam spektriks ei lahutunud (joonis 13). Sellega oli ta näidanud, et spekter on valge valguse, aga mitte prisma omadus. Ta järeldas, et valge valgus koosneb paljudest värvidest, millel on erinevad murdumisnäitajad. Selle tõestamiseks koondas ta spektriks lahutatud hajuva valguskimbu uuesti läätse abil (joonis 14) ja sai valge värvuse.
Newton uskus, et valguse värvus on tingitud tema peegeldumis ja murdumisvõimest. Kui ta oleks neid veel seostanud lainepikkusega, oleks ta teadnud täit tõde. Newton kordas oma difraktsioonikatseid, kuid nüüd juba üksikute spektrivärvidega. Ta märkas, et triipude laius on punase valguse korral suurem kui violetse valguse puhul.
Sedakaudu jõudis Newton oletuseni (muide, ta ei saanud ju püstitada hüpoteese), et korpuskulid panevadisilma võrkkesta võnkuma, mis tekitab valgusaistingu, kusjuures kõige lühemad võnked tekitavad violetse valguse aistingu, aga kõige pikemad punase valguse aistingu. Kas oleks võimalik olla veel lähemal laineteooriale selleni siiski jõudmata!
Nii näeme, kuidas üksainuke vale oletus - valguslained on sarnased helilaineiga - viis Newtoni paljudele ebaõigetele, kuid tõele väga lähedastele mõtetele. Taolises olukorras on olnud enamik teadlasi. Et oma tulemusi kuidagi seletada ja otsa otsaga kokku viia, peavad nad tegema järjest eksootilisemaid oletusi. Selle peale võiks küsida, missugustes oletustes meie kõige kindlamad oleme. Vähemalt üks neist on kindlasti täiesti vale.
17. sajandil tuvastati, et valguse kiirus on lõplik. Tolle ajani ei oldud kindlad, et valguse kiirus on mõõdetav. Galilei oli püüdnud seda mõõta hästi kavandatud, kuid edutuks, jäänud katsega, millest võtsid osa tema ise ja ta teener, kes seisis temast teatud kaugusel, latern käes. Ent katse tulemustes polnud kooskõla ja Galilei oli sunnitud järeldama, et valguse kiirus on sel teel mõõtmiseks liiga suur. Nagu me nüüd teame, on inimese reaktsioon liiga aeglane ja valguse levimise aeg liiga lühike, et seda saanuks mõõta Galilei ajal.
Descartes’il ei olnud Galilei ettevaatlikkust. Ta väitis veendunult, et valguse kiirus on lõpmata suur.
Descartes’i „tõestus" tugines mõistlikule füüsikalisele meetodile. Ta soovitas kujutleda, mida me näeksime, kui valguse kiirus oleks väga väike, ja siis otsida, kas midagi taolist on võimalik tegelikkuses jälgida. Samas kasutas ta seda mõistlikku meetodit täiesti ebamõistlikult. Ta küsis, mida näeksime päikesevarjutuse ajal, kui valgus läbiks vahemaa Kuult Maale näiteks tunni ajaga. „Me ei näeks," ütles ta, „Kuu varju Maal, kui see asub Päikesega ühel sirgel, sest Kuu jõuaks selle tunni ajaga, mille jooksul tema vari meieni jõuab, läbida pika tee." See argument on ekslik kahel põhjusel. Esiteks, me saame Päikese asendit kindlaks teha vaid tänu sellele, et näeme teda, mistõttu meil ei ole mingit muud vahendit tema asukoha määramiseks kui tema kiiratud valgus. Nii et Päike, Kuu serv ja vari Maal näivad varjutuse hetkel ühel sirgel sõltumata sellest, missugune on valguse kiirus. Teiseks, ehkki Descartes kasutas tunduvalt pikemat baasi kui Galilei, polnud tal alust väita, et valguse kiirus on lõpmata suur, vaid ainult, et see on suurem teatud arvust. Niisugune arutlus oli aga Descartes’ile, kes vähimalgi määral polnud eksperimentaator, võõras.
Esimene arvestatav tõendus valguse kiiruse lõplikkuse kohta pärineb Rømerilt (1644-1710). 1675. a. märkas ta, et Jupiteri kuude varjutuste vaadeldavad alg- ja lõpphetked ei lange kokku arvutatutega. Juba Galilei avastas neli Jupiteri kaaslast (nüüd on teada veel ), mis liiguvad planeediga ühel tasandil ümber Päikese. Niisiis satuvad kõik kaaslased igal pöördel ümber Jupiteri selle hiiglaslikku varju; nii kaaslased kui ka planeet ise on nähtavad üksnes tänu sellele, et neilt peegeldub Päikese valgus.
Jupiteri kaaslaste varjutusajad ei ole püsivad: need kõiguvad sõltuvalt Maa ja Jupiteri asendist teineteise suhtes. Leiti, et kuue kuu jooksul varjutustevaheline intervall pikenes, järgmise kuue kuu jooksul aga lühenes. Erinevus oli märgatav (umbes ), varjutused aga toimusid selleks küllalt sageli, iga tunni järel, et tähele panna intervalli järkjärgulist muutumist.
Et Maa pöörlemine ei võinud nii kauge planeedi kaaslaste liikumist häirida, siis oletas Rømer, et põhjus on valguse kiiruse lõplikkuses. Kahe varjutuse vahelise aja jooksul läbib Maa umbkaudu miljonit kilomeetrit. sekundit, maksimaalne hälve keskmisest perioodist, on järelikult aeg, mis kulub valgusel selle vahemaa läbimiseks. Järelikult peab valguse kiirus olema veidi väiksem kui . Nii määrati esmakordselt suurus, mis on tänapäeval üks tähtsamaid konstante füüsikas.
| Nr | Kuu | Päev | h | Algus min | h | Lõpp min |
| 0 | Jaanuar | 9 | 7 | 48,0 | ||
| 10 | 27 | 0 | 32,3 | |||
| 20 | Veebruar | 13 | 17 | 17,5 | ||
| 30 | Märts | 2 | 12 | 22,0 | ||
| 40 | 20 | 5 | 9,1 | |||
| 50 | Aprill | 50 | 21 | 56,8 | ||
| 60 | 60 | 14 | 45,0 | |||
| 70 | Mai | 70 | 7 | 33,3 | ||
| 80 | 80 | 0 | 21,5 | |||
| 90 | Juuni | 16 | 17 | 9,4 | ||
| 100 | Juuli | 4 | 9 | 56,8 | ||
| 110 | 22 | 2 | 43,6 | |||
| Augustis ja septembris pole nähtav | ||||||
| 160 | Oktoober | 18 | 12 | 11,4 | ||
| 170 | November | 5 | 4 | 54,3 | ||
| 180 | 22 | 21 | 36,8 | |||
| 190 | Detsember | 10 | 14 | 18,9 | ||
| 200 | 28 | 7 | 1,1 | |||
Sel viisil esitatuna näib Rømeri töö üsna lihtsakesena. Ta oleks nagu möödaminnes märganud seda, mida võinuks tähele panna iga teinegi.
Tegelikult oli Rømeri töö ülimalt tähelepanuväärne, sest oli hulk vaatlusi takistavaid asjaolusid. Esiteks ei saa Jupiteri jälgida aasta ringi; vähemalt kaks kuud on ta selleks Päikesele liiga lähedal. Teiseks ei saa varjutusi jälgida päevavalges. Jupiteri kaaslane on küllalt suur, läbimõõdult võrdne heledus järsult, vaid suhteliselt aeglaselt. Sellepärast ei ole võimalik varjutuse alg- või lõpphetke kindlaks teha mõnesekundise täpsusega.
Et luua mingil määral kujutlust raskustest, mida Rømer kohtas oma töös, otsustasin panna sellesse raamatusse Jupiteri kaaslase lo ühe aasta (1956) varjutuste tabeli „Merealmanahhist".
Tabelis 6 esitatud andmed on loomulikult palju täpsemad kui need, mis olid kasutada Rømeril. Samuti on siin kirjas kõik varjutused, s. t. ka need, mis toimuvad päeval. Varjutuste alg- ja lõpphetked on antud täpsusega . Me näeme üksteisele järgnevate intervallide pidevat muutust, kuid erinevuste graafik vaadeldava ja arvutatava keskmise väärtuse vahel annab sama tulemuse, millest lähtudes Rømer saigi oma valguse kiiruse suuruse. Kui Rømeri käsutuses olnuksid nii täpsed andmed, oleks tema avastus vahest teisiti vastu võetud kui ainult usaldamatuse ja pilgetega.* Muuseas, Newton tunnistas oma „Optikat" kirjutades kõhklemata, et Rømer mõõtis valguse kiirust. Isegi kui Descartes’i arutlused oleksid paika pidanud, tulnuks tal tegelda mitte tundide, vaid sekunditega.
*Vaevalt küll. Romeri viga oli väiksem kui . Sellise reaktsiooni tekitas hoopis oletus, et valguse kiirus on lõplik.
Rømeri tulemuste kontrollimine maapealsetes oludes näis võimatu. Isegi kui valguse teepikkus oleks olnud mõni kilomeeter, tulnuks mõõta miljondiku sekundi suurusi ajavahemikke, kuid selline täpsus ei olnud 17. ja 18. sajandil võimalik. Järk-järgult, teaduse ja tehnika arenedes, sai võimatu võimalikuks. Esimestena mõõtsid maapealsetes oludes valguse kiirust Fizeau (1819-1896) ja Foucault (1819-1868) 1850. a. Nende katsed said võimalikuks tänu sellele, et olid loodud vastupidavad sulamid, millest valmistatud detailid pidasid vastu tohutule tsentrifugaaljõule.
Fizeau seadme põhiosaks oli pöörlev hammasratas, mis katkestas peene valgusvihu enne ja pärast selle peegeldumist kaugelt peeglilt. Foucault’ aparaadis kasutati selleks pöörlevat peeglit. Kui peegel pöördus märgatava nurga võrra aja jooksul, mis kulus valgusel kaugel asuva peeglini ja sealt tagasi jõudmiseks, oli täheldatav valgusallika kujutise nihkumine. Nende tulemused olid kooskõlas Rømeri arvutustulemustega. Fizeau seadmes pidi valguskiire teepikkus olema kilomeetreid, Foucault’ seadmes aga kõigest 20m. Seega oli viimane palju mugavam, Foucault võis mõõta valguse kiirust ka vees. Ta avastas, et see on väiksem kui õhus, mis tähistas valguse korpuskulaarteooria lõplikku lüüasaamist.**
**Laineteooria järgi peab valguse kiirus olema keskkonnas selle keskkonna murdumisnäitaja kordselt väiksem kui vaakuumis.
Seega olid siis valguse põhiomadused 1850. aastaks juba teada: valgus on väga lühikese lainepikkusega (suurusjärgus ) ristlainetus, mille levimiseks pole vaja mingit materiaalset keskkonda; tema liikumiskiirus on ligikaudu . Kuid me ei tea ikkagi veel, mis ta on. Lõplik vastus sellele anti hoopis teistes valdkondades tehtud mõõtmistega, millega seostub üks meeldejäävamaid episoode füüsika ajaloos. Me kirjeldame seda 9. peatükis. Füüsikuid on alati huvitanud ühe füüsikaharu mõju teisele. Seepärast tasub käesoleva peatüki lõpetuseks kirjeldada üht avastust, mis andis tugeva tõuke kogu füüsika arengule ja tõi samal ajal erakordset praktilist kasu. Jutt on joonspektrite avastamisest.
Me juba nägime, kuidas Newton uuris kuuma keha - Päikese - spektrit. Kõik kuumad tahked kehad annavad taolise pideva spektri. Samal ajal on teada, et mõned ained, kui neid leegis kuumutada, muudavad leegi värvi. Kui näiteks vasest jootkolbi gaasipõletil kuumutada, muutub põleti leek roheliseks.
Esimene teade diskreetse spektri vaatlemisest pärineb 1802. aastast ja kuulub Wollastonile (1766-1828). Ta nägi, kuidas päikesevalgus paistis läbi varbkardina, ja mõistis äkki, et kasutades valgusallikana pilu, võib saada palju selgema spektri, kui sai Newton oma ümmarguse ava abil. Ta oli esimene, kes märkas Päikese spektris musti jooni, mis nüüd kannavad Fraunhoferi nime.
Joonspektrid avastas tõenäoliselt Herschel (1792-1871) 1822.a. Ta viis leeki mõnede metallide sooli ja jälgis tekkinud spektreid prisma abil. Hiljem märkas Fraunhofer (1787-1826), et keedusoola kiiratud kollase spektri joone asend ühtib ühe tumeda joonega Päikese spektris.
Need sündmused panid füüsikas aluse uuele valdkonnale - spektroskoopiale. Mõõtmiste täpsus üha kasvas ja lõpuks loodi juba paljude elementide spektritest koosnevad atlased. Need osutusid hindamatuiks eri elementide identifitseerimisel tundmatu koostisega aineis ja said sel moel aluseks keemilise analüüsi uuele meetodile.
Nähtus ise jäi ülimalt salapäraseks. Miks kiirgavad aatomid kiirgust kindla lainepikkusega? Ilmselt kannab see teavet aatomite ehituse kohta. Ent enne, kui õnnestus lahendada joonspektrite saladus, möödus peaaegu sajand.
See on ainuke instrumentidele pühendatud peatükk käesolevas raamatus. Ehkki aparatuur on mänginud suurt osa ka teistes füüsikaharudes, pole minu arvates vaja pühendada eraldi tähelepanu näiteks kalorimeetriaseadmeile 3. peatükis või magnet- ja elektriaparatuurile 8. peatükis. Miks on siis optikariistad nii erilised?
Optikaseadmed ei ole ainult võimaldanud saada teavet valguse kohta; nad on andnud oma osa peaaegu kogu füüsika arengusse. Kindlasti on põhjuseks ka see, et enamiku teavet välismaailma kohta saame silmade abil. Optikariistade ja -meetodite kasutamine füüsikas on võimaldanud luua kujutlusi, mis poleks muidu ilmavalgust näinudki. Just nendel kaalutlustel võtsin ma sellesse raamatusse eripeatüki optikariistadest.
Esimesteks optikariistadeks olid kahtlemata läätsed ja prillid. Tänu prillidele ei pidanud inimesed kannatama enam oma kehva nägemise pärast. Kui palju tõeliselt tarku inimesi jäi iidsetel aegadel vääriliselt hindamata üksnes seetõttu, et neil oli halb nägemine! Õnneks on meie ajal elu selles suhtes paremini korraldatud.
Esimeseks tõeliseks optikainstrumendiks, s. o. seadmeks, mille abil inimesed võisid saavutada seda, mis neil varem ei õnnestunud, oli luup. See võimaldas näha paljale silmale nähtamatut. Hämmastav, kui palju inimesi, nende hulgas ka teadlasi, ei oska luupi õigesti kasutada: nad ei hoia seda mitte silma, vaid eseme lähedal. Kujutis on nii küll suurendatud, kuid hägune ja vaateväligi ahtake. Palju parem on hoida läätse võimalikult silma lähedal. Siis vaateväli ei ahene ja suurendatud kujutis on selge.
Esimesed luubid olid väiksesse avasse valatud puhta vee või mee tilgad.
Isegi 17. saj. algul, kui mikroskoop oli juba leiutatud, eelistasid paljud teadlased sellele üksikläätsi, arvates, et parem väiksem suurendus, kuid see-eest ka väiksem kujutise moonutus. Nagu nägime 3. peatükis, avastati ka Browni liikumine luubi abil ja seda enam kui a. pärast mikroskoobi leiutamist!
Teleskoop leiutati umbes samal ajal kui mikroskoop (1608). Hollandi optikameistri Lippershey õpipoiss, kes mängis jõudeolekull läätsedega, märkas, et kui kaks läätse panna ühele sirgele, võib läbi nende näha kauge eseme suurendatud kujutist. Tõsi, suurendus oli väike, kuid avastus tekitas elevust ja kuuldus sellest kandus üle kogu Euroopa. Avastusest kuulis, ka Galilei, kes koostas oma optikaalastele teadmistele tuginedes juba vaatluskõlbliku läätsedest koosneva seadme (joonis 15). See seade on tuntud Galilei pikksilmana, mille vaateväli on küll väike, kuid mille abil Galilei avas uued horisondid astronoomias. Tema avastustest on kirjutatud terveid raamatuid ja siin pole mõtet neid ümber jutustada, sest me huvitume ju eksperimentidest endist.
Siiski tuleb mainida, et Galilei kaasaegsed ei hinnanud uut optikariista vääriliselt. Tol ajal sooritati astronoomiavaatlusi väga pikkade läätsedeta vaatetorude abil ja nende kasutamise kohta oli olemas terve teadus. Vaadeldi spetsiaalselt selleks ehitatud hoonetes. Näiteks üks India pealinna Dehli vaatamisväärsusi on tänini säilinud 17. sajandi observatoorium. Meenutagem, et Kepler töötas planeetide liikumise seadused välja vaatluste alusel, mida Brache oli sooritanud ilma teleskoobita.
Seega siis ei võtnud astronoomid uut moodsat riista vastu avasüli. Nad said suurepäraseid tulemusi ka harilike ja neile mõistetavate instrumentidega. Miks oleks neid siis vaja asendada palju keerulisema riistaga, mis mõnikord annab halva teravuse ja on üsna ähmase tööprintsiibiga? Ja kas ei olnud vähemalt osa uue instrumendi abil nähtud detailidest ekslikud ning tekkinud seadmes endas?
Uus kutsub sageli esile vastupanu ja mõnikord ei olegi see halb. Nüüd, sajandite tagant on loomulikult kerge näha teleskoobi tohutuid potentsiaalseid võimalusi ja mõista, miks ei võimaldanud seda esimesed ebatäiuslikud teleskoobid. Ent kui palju on olnud viljatuid leiutisi, mis ei nihutanud tehnikat sammu võrragi edasi!
Kui leiutis on seda väärt, siis lööb ta igal juhul läbi, olgu vastuseis kui tugev tahes. Võib-olla saab ta tänu sellele veel paremgi kui esialgu kavandatu, kui vaid leiutajal jätkub meelekindlust oma vastastele vastu seista.
Ka teleskoopidega läks sedamoodi. Mõne aastakümne pärast oli kõigile selge, missugused eelised neil on, ja juba 1668. a. tegi Newton teleskoopides tähtsa täienduse, asendades läätse peegliga. Ta arvas, et oli leidnud ainsa lahenduse, kuidas vabaneda teleskoobi läätsedest tingitud värvimoonutustest - kromaatilisest aberratsioonist.
Et valguse peegeldumine ei sõltu tema värvusest, siis otsustas Newton, et sfääriline peegel on objektiivina parem kui lääts. Tal oli õigus. Ehkki tänapäeval osatakse teha ka värvimoonutustevabu läätsede kombinatsioone, põhineb kõikide suurte teleskoopide ehitus endiselt Newtoni ideel. Tema isiklik teleskoop on säilinud tänini ja on üks tuntumaid teadusriistu.
Mikroskoobi ajalugu nii hästi teada ei ole. Võimalik, et teleskoopi luues mõtles Galilei ühtlasi ka selle üle, kuidas suurendada lähedal asuvaid esemeid. Ta oli oma aja parim optikatundja ja on üsna tõenäone, et ta võis avastada ka mikroskoobi tööpõhimõtte. See näitab ülihästi põhiteadmiste tähtsust: teleskoop võidi leiutada küll juhuslikult, aga tema tööpõhimõtte mõistmine lubas sedasama ideed kasutada ka teiste seadmete loomiseks.
17. sajandi mikroskoopia esindajaist on tuntuim Hooke (1635-1703). Ta oli hiilgav eksperimentaator ja toetas Kuninglikku Seltsi selle algupäevil. Tollal oli selle seltsi ülesandeks arendada eksperimentaalteadusi. Hooke valmistas endale mikroskoobi ja sattus sellest niisugusesse vaimustusse, et kirjutas 1665. a. oma vaatlustest raamatu Micrographia. Ta illustreeris selle oma joonistega, millest üks on joonisel 16.
Tema mikroskoop on kujutatud joonisel 17. Toru pikkus oli umbes tolli () ja teravust oli võimalik reguleerida mikromeetrilise kruviga. Vaadeldav ese asetati nööpnõela otsa. Valgustamiseks kasutati tavaliselt päevavalgust. Joonisel on näha, kuidas see seade töötas kunstliku valgusega. Alates 17. sajandist on optikariistade ehitust, eriti aga läätsi täiustatud, mistõttu nüüdisaegsed mikroskoobid on tollastest võrratult paremad.
Eriti suure panuse klaasitootmise tehnoloogia ja läätsede lihvimise täiustamisse andsid saksa optikud, eeskätt Fraunhofer ja Abbe (1840-1905). Võib öelda, et optikatööstus võlgneb teooriale rohkem kui ükski teine tööstusharu. Siin ei olnud teooria üksnes praktika üldistaja, vaid ka juhendaja.
Paljude aastate kestel näis, et mikroskoope võib täiustada lõputult. Varasemaid saavutusi ekstrapoleerides usuti, et mikroskoobi lahutusvõimel puudub piir (s.t. temaga saab vaadelda kui tahes väikesi esemeid). Tagatipuks loodeti mikroskoobis näha aatomeidki. Mikroskoobi valmistajad püüdsid üksteist üle trumbata üha paremate instrumentidega ja soovitustega nende kasutamiseks.
Ent ekstrapoleerimine kätkeb alati ohtu. On üllatav, et just Abbe, üks tähtsamaid mikroskoobi täiustajaid, näitas, et mikroskoobi suurendusvõimel on piir, mis ei sõltu mitte mikroskoobi valmistajate hoolikusest, vaid sellest, et vaigus on lainetus: ükski mikroskoop, olgu tema võimsus milline tahes, ei suuda eristada detaile, mille mõõtmed on väiksemad kui pool valguse lainepikkusest. Mikroskoobimeistrid olid hingepõhjani solvunud. Mõned teatasid, et nende mikroskoobid võimaldavat eristada detaile ka allpool Abbe piiri, ja kuulutasid, et tema teooria on ekslik. Kuid nad ei arvestanud seda, et Abbe teooria mitte üksnes ei ennustanud ette eraldusvõime piire, vaid ütles veel, et iga mikroskoobis nähtav detail, mis on allpool seda piiri, on väär.
Abbe töö oli loomulikult teoreetiline, kuid avaldas optikale ja kogu füüsikale nii suurt mõju, et sellel tuleb lühidalt peatuda.
Abbe teooria järgi tekib kujutis mikroskoobis kahes järgus: algul hajutab ese valgust ja tekib diifraktsioonipilt; seejärel kogutakse difrageerunud valgus optilise seadme abil kokku ja tekib interferentsipilt, mis ongi eseme kujutis. Eseme valgustamise viisi, mis võib esimesel pilgul näida pisiasjana, peab Abbe teooria eriti tähtsaks: sellest sõltub kujutise tõepära.
Et mikroskoobi objektiivi satub ainult osa esemel hajunud valgusest, siis ei teki kujutiski tervest difraktsioonipildist ega ole seega eseme täpne koopia. Me võime seda mõttekäiku illustreerida, kõrvutades eseme difraktsioonipildi erineva suurusega osadest moodustatud kujutisi (tahvel III). Kujutis tuleb seda detailsem, mida suuremat osa difraktsioonipildist on selle moodustamiseks kasutatud, kuid selle detailsuse määrab triipude laius difraktsioonipildi äärtel. Muide, see ongi Abbe piir. 1905. a. kontrollis Porter Abbe teooriat. Ta moodustas kujutise difraktsioonipildi eri osadest ja näitas, et Abbe ennustused täitusid täpselt. Porter avaldas selle kohta ka artikli.
Mikroskoobimeistrite pettumuse kiuste tähistab Abbe teooria uut ajajärku füüsikas. Me teame nüüd, et kui tahame uurida mingit eset, peame kiirguse valima sõltuvalt uuritava eseme mõõtmetest. Täpsemalt kirjeldame seda järgmistes peatükkides.
Mis puutub mikroskoopi, siis näitas Abbe, et valgusmikroskoopidel on oma rakenduspiir, ja hoiatas seega läätsemeistreid viljatute katsete eest seda piiri ületada. Abbe teooriast järeldus, et kui tahetakse uurida väikesi detaile, tuleb leida selleks mõni teine tee. Näiteks aatomimaailma „detaile" uuritakse elektronide ja röntgenikiirte abil.
On tähtis mõista, et füüsikateooria toob endaga tihti kaasa lisakasu. Teoreetilist tõestust, et miski on võimatu, võidakse mitte uskuda: katseliselt pole seda kontrollitud. On ju inimlik, et igasugused piiramised tekitavad soovi neist mööda hiilida. Sageli saavutatakse nii edu ja võidakse avastada uued uurimismeetodid. On ju lõpuks alati olemas võimalus, et teooria on ekslik või piiratud.
Teleskoobi täiustamise lugu ei ole nii huvitav kui mikroskoobi oma. Viimati parandas teleskoobi konstruktsiooni oluliselt Newton. Sellest ajast on olnud eesmärgiks järjest suuremate ja täpsemalt lihvitud peeglite valmistamine. Tavaliselt nõutakse, et lihvimiskonarused oleksid kümme kuni viiskümmend korda väiksemad kui valguse lainepikkus. Ent isegi suurim nüüdisaegne teleskoop - USA -tolline (-meetrine) - ei erine põhimõtteliselt Newtoni -tollisest.*
*Tänapäeval on rekordteleskoobiks NSV Liidus ehitatud -meetrise peegliga teleskoop, ent ega seegi Newtoni omast põhimõtteliselt erine.
Teleskoopide üha laiem kasutamine viis Fraunhoferi mõttele kasutada neid teistel eesmärkidel. Teda huvitasid klaasi omadused, eriti aga klaasi dispersiooni** mõõtmine. Newtoni sellekohased mõõtmised olid ebatäpsed, sest ta kasutas valgusallikana ümmargust ava. Wollaston, kes tuli mõttele kasutada ümara ava asemel pilu, astus sellega suure sammu edasi. Fraunhofer läks veelgi kaugemale. Ta jõudis järeldusele, et kui pilu kujutis fokuseerida, suureneb mõõtmistäpsus hoopis enam. Muide, selleks piisaks täielikult ühest läätsest, kuid siis ei läbiks kogu üht värvi valgus dispergeerivat prismat ühes suunas. Seetõttu valmistas ta seadme, milles prisma asetatakse paralleelsete valguskiirte kimpu (joonis 18). See oli esimene spektromeeter.
**Kiirguse spektriks lahutamise võime.
Spektromeeter on füüsikas üks tähtsamaid instrumente, mis võimaldas täpsemalt uurida läätsi. See tegi omakorda võimalikuks täiuslikumate optikaseadmete valmistamise. Spektromeetriga uuriti spektri detaile. Tänu sellele võidi hakata uurima tähespektreid ja kindlaks tegema tähtede koostisse kuuluvaid elemente. See kõik andis tõuke astrofüüsika arenemisele.
Spektromeetreid täiustati tublisti seoses difraktsioonivõrede leiutamisega. Nagu tagapool selgus, tehti see leiutis juhuslikult, kuid vaid tark oskab hinnata vääriliselt talle osaks langenud juhust.
Fraunhofer nägi, et oma spektromeetri abil võib ta täiustada difraktsiooni uurimist. Eseme difraktsioonipilti paralleelsetes kiirtes - nüüd Fraunhoferi difraktsioonipildiks kutsutut - on lihtsam teoreetiliselt analüüsida kui Fresneli difraktsioonipilti, samuti on ta detailides usaldusväärsem. Pilu difraktsioonipilti võib tänapäeval jälgida iga tavalise spektromeetriga, kuid Fraunhoferi päevil oli see valgusallika vähese heleduse tõttu raske. Fraunhofer otsustas vea pärandada ja asetada ühe pilu asemel spektromeetri paralleelsete valguskiirte kimpu mitu pilu. Mugavuse tõttu tegi ta need üksteisest võrdsel kaugusel asetsevad. Oma imestuseks avastas Fraunhofer, et ühe difraktsioonipildi asemel oli tekkinud mitu. Ta oli valmistanud esimese difraktsioonivõre.
Fraunhofer mõistis kohe, kui tähtis oli tema leiutis, ja ta täiustas seda. Võrede valmistamiseks pingutas ta traati kahe paralleelse keerme vahel. See on tänini parim viis saada lihtsat õppeotstarbelist difraktsioonivõret. Ent täpse töö jaoks tuli pilude arvu suurendada. See oli vajalik spektrivärvide hälvitamiseks suurema nurga võrra. Lahutusvõime pilude arvust ei sõltu; see sõltub vaid võre pikkusest. Oli teadlasi, näiteks Rowland (1848-1901), kes pühendasid kogu oma töö difraktsioonivõrede valmistamiseks vajalike instrumentide täiustamisele ja valmistasid ülitäpseid võresid. Võib julgesti öelda, et difraktsioonivõrede abil tehtud mõõtmised on füüsikas suurima täpsusastmega - .
*Tänapäeval pole see ena*m piir. Mössbaueri efekt võimaldab täpsust .
Valguse spektriks lahutamisel on difraktsioonivõre igati parem kui prisma. Esiteks võib võrega, mille pilude vaheline kaugus on teada, määrata suvalise spektrijoone lainepikkuse valemist
kus on spektri järk ja spektrivärvi hälbe nurk võre normaalist. Muuseas, prismadel tuleb seos lainepikkuse ja sellele vastava hälbe vahel katseliselt kindlaks teha, kusjuures iga klaasisordi korral on see erinev. Teiseks, võre puhul sõltub palju tugevamini -st kui prisma puhul. Ja kolmandaks, kui kasutatakse peegelvõret, näiteks metallpeeglit, millele on kantud peenikesed kriipsud, võime mõõta isegi selliste lainete pikkusi, mis prismas täielikult neelduvad. Prisma ainus eelis on valguse suurem intensiivsus, sest spekter moodustub kogu teda läbinud valgusest, kuid isegi see eelis kaob, kui teha difraktsioonivõred erikujuliste piludega, mis koondavad suurema osa difrageerunud valgust ühte spektrijärku.
Hiljem näeme, millist tohutut mõju avaldas spektrite uurimine mateeria ehituse mõistmisele. Julgen isegi väita, et difraktsioonivõret tuleks pidada füüsikute üheks tähtsamaks leiutiseks. Ka mikroskoop on väga tähtis, kuid difraktsioonivõre võimaldab vaadata palju „sügavamale".
Ehkki Youngi katse etendas erakordselt tähtsat osa valguse laineteooria õigsuse tõestamisel, oli see liiga jäme heade arvtulemuste saamiseks. Kuid kokkupuutumine pikkustega suurusjärgus näitas uusi potentsiaalseid võimalusi. Kui õnnestuks suurendada interferentsitriipude teravust, siis suureneks ka mõõtetäpsus, ja kes teab, milliseid uusi nähtusi võiks siis vaadelda. Ribade teravus suureneks, kui valguslained üksteist vastastikku enam tugevdaksid. Selleks peab pilusid olema rohkem kui kaks. Just see ongi eespool kirjeldatud erikujuliste piludega difraktsioonivõre tööpõhimõte.
Ent on ka teine tee interfereeruvate lainete arvu suurendamiseks: kasutada mitmekordset peegeldust. Kui te olete toas, mille laes ripub lamp ja kahel vastasseinal on peeglid, võite peeglites näha lambi peegelduste pikka rida. Kui valmistame samal põhimõttel töötava, kuid tunduvalt väiksema seadme, võimegi väga lihtsalt saavutada üsna suure täpsuse.
Kõige tähtsama seda liiki seadme valmistasid Fabry (1867-1945) ja Perot (1863-1925). Nende seade koosnes kahest paralleelsest optiliselt tasasest plaadist, mille vahele oli jäetud mõne millimeetri laiune pilu. Plaatide pilupoolsed küljed olid hõbetatud, nii et nad peegeldasid neile langevast valgusest umbes (joonis 19). Mida suurem on peegeldusvõime, seda teravamad, kuid ühtlasi ka nõrgemad on interferentsiribad. Sajaprotsendilise peegeldusvõime korral oleksid nad nähtamatud.
Fabry-Perot’ etaloni abil, nagu seadist nüüd nimetatakse, saab vaadelda interferentsi üsna suurte järkudeni, kuid paljude spektrite kattumise tõttu ei õnnestu seadme suurt täpsust kasutada. Tulemused paranevad, kui kasutada seadet koos difraktsioonivõrega: eraldada difraktsioonivõre abil spektrist üks joon ja analüüsida seda Fabry-Perot’ etaloni abil üksipulgi. Nii võib avastada joone peenstruktuuri. Näiteks Fraunhoferi avastatud naatriumi -joon, mis näib enamikus difraktsioonivõredega spektromeetrites üksikuna, lahutub sel moel paljudeks peenteks triipudeks. Ent Fabry-Perot’ etaloni abil saadud triibuhulk osutub palju keerulisemaks kui üksikul joonel. Järelikult võib oletada, et jooni on kaks. Selle võimsa liitseadme teisi erakordselt tähtsaid rakendusi kirjeldame peatükis 10.
Ehkki suure lahutusvõimega spektromeetria põhineb suurel määral niinimetatud paljukiirelisel interferentsil ja Fabry-Perot’ etalon on vaid üks vahend niisuguse interferentsi saamiseks, on oma rakendused ka kahekiirelisel interferentsil: selle abil võib uurida pinna siledust palju täpsemini kui ükskõik millise mehaanilise vahendiga. Vaadeldes interferentsitriipe, mille tekitavad kaks pinda, millest üks on sile meid rahuldava täpsusega ja teise siledust kontrollime, võime sellel kergesti avastada pinnakonarusi suurusjärgus . Pindu, mille konarused on sellest väiksemad, nimetatakse optiliselt siledateks.
Neid kergesti sooritatavaid mõõtmisi, sisuliselt optiliste teepikkuste pisierinevuste mõõtmisi, oskasid füüsikud kohe vääriliselt hinnata. 19. sajandi jooksul leiutati nende asemel üsna täiuslikke seadmeid, mille abil oli näiteks võimalik mõõta õhu murdumisnäitajat või hinnata optiliste süsteemide osade sobitamise täpsust. Need seadmed nimetati interferomeetriteks ja neist ühe, Michelsoni interferomeetri abil tehti nii tähtis avastus, et seda tasub üksikasjalikult kirjeldada.
Michelsoni (1852-1931) võib täie õigusega nimetada optikageeniuseks. Juba üliõpilasena sooritas ta eksperimente, mis kurnasid nii tema juhendajate vaimseid kui ka rahalisi ressursse. Ta leiutas tähe- interferomeetri tähtede nurkläbi- mõõdu mõõtmiseks. Tema tähtsaim katse, mille ta sooritas koos oma kolleegi Morley’ga (1838-1925), oli katse mõõta Maa kiirust eetri suhtes.
Esimesel pilgul näis see lootusetu. Michelsoni interferomeetris peab valgus läbima ühe teepikkuse edasi-tagasi, mistõttu saab leida vaid tema keskmise kiiruse. Aga kõikidest optikaõpikuist on teada, et alla- ja seejärel ülesvoolu liikuva keha keskmine kiirus on peaaegu niisama suur kui sama teepikkuse edasi-tagasi-läbimisel vooluga risti. Need keskmised kiirused erinevad vaid teist järku lõpmata väikese suuruse* võrra, kus on voolu kiirus ja keha kiirus. Michelson—Morley katses on nn. kehaks valguslainete voog, aga vooluks Maast mööda liikuv eeter. Eetri kiirus võib vaevalt olla suurem kui tuhandik valguse kiirusest, sest Maa orbitaalkiirus on vaid 10−4 valguse kiirusest. Seega püüdsid Michelson ja Morley mõõta kiiruste erinevust suurusjärgus .
*Teist järku lõpmata väikeseks suuruseks nimetatakse lõpmata väikese suuruse ruutu, mis on palju väiksem suurusest endast. Näiteks 0,01 ruut on .
Vaatleme nende põhiseadet - Michelsoni interferomeetrit (joonis 20). Selles kasutatakse hõbetatud poolläbipaistvat peeglit, mis peegeldab niisama palju valgust, kui sellest läbi läheb. Seetõttu on võimalik jaotada üks valguskimp kaheks ja suunata need teineteisega risti, nii et nad peegelduvad kumbki eri peeglilt, kohtuvad uuesti poolläbilaskval peeglil ja interfereeruvad. Seejuures on võimalik nende kahe kimbu optilisi teepikkusi võrrelda: kui üks neist muutub poole lainepikkuse võrra, nihkub interferentsipilt ühe triibu võrra. Sel viisil mõõtsid Michelson ja Benoit 1894. a., mitu valguslainet mahtus täpselt määratud pikkusse. Nii seati lainepikkus täpsesse Vastavusse meetermõõdustikuga. (Nüüd kasutatakse seda meetodit meie pikkusühiku - meetri - pikkuse määramisel.)
Interferentsitriipude teket Michelsoni interferomeetris on sageli seletatud segaselt. Punktvalgusallika korral satub silma vaid ühes kindlas suunas leviv valgus. Sõltuvalt sellest, kas lained on faasis või mitte, võib näha muutuva intensiivsusega valgust, kuid mitte triipe. Kui aga valgusallikas on ruumiline, siseneb valgus silma eri suundadest, millest mõnes on valguse intensiivsus maksimaalne, mõnes minimaalne, ning triibud paistavadki. Teiste sõnadega, valgusallika kujutis paistab olevat kaetud triipudega.
Kui valguse kiirus sõltub suunast, siis peaksid triibud olema nihutatud võrreldes asendiga, mis vastab valguse kiiruse konstantsusele. Kuid sellist nihet polnud võimalik avastada, sest puudus etalon, millega võrrelda. Seetõttu oli Michelsoni ja Morley ülesanne ehitada pöörlev interferomeeter ja vaadelda, kuidas interferomeetri pööreldes interferentsitriibud nihkuvad. Kas nende instrument oli piisavalt tundlik? Ja kuidas saab ehitada piisavalt jäika, kuid ühtlasi pööratavat seadet? Nende probleemi võib võrrelda Cavendishi ees seisnuga.
Michelsoni ja Morley probleem oli järgmine. Nende seadme tundlikkus sõltus ilmselt selle mõõtmetest. Kui aga mõõtmeid suurendada, läheb raskemaks seadme pööramine. Michelson oli juba ehitanud interferomeetreid, milles valguse teepikkus oli meeter, kuid selle eksperimendi jaoks pidi see tema arvates olema ligi 10m. Näis olevat võimatu tasakaalustada 10m diameetriga massiivset, ketast interferentsikatsete jaoks. Seetõttu otsustasid Michelson ja Morley kasutada peeglite süsteemi, mis võimaldas suurendada valguskiire optilist teed seadme mõõtmeid suurendamata. Nad paigutasid kogu aparatuuri kiviplaadile, mille pindala oli umbes ja paksus (joonis 21) ning mis oli asetatud elavhõbedasse ujuma pandud puust alusele.
Igaüks, kes on mõõtnud interferomeetritega, oskab vääriliselt hinnata niisuguse seadme seadistamise ja sellega töötamise kunsti. Vaatlusteks pandi seade pidevalt pöörlema, sest kardeti, et ta võib seiskamisel deformeeruda, mille tagajärjel lugemiste täpsus väheneks. Triipude asendit jälgiti kuue pöörde kestel iga pöörde järel, kusjuures kiirus - üks pööre kuue minutiga - oli piisavalt madal selleks, et märgata valitud triibu asendit igast märgist möödumisel. Kahjuks oli kogu selle töö tulemus null.
Väikesed hälbed, mida märgati, olid Maa orbitaalliikumise kiirust arvestades oodatuist tunduvalt väiksemad. Muide, võis juhtuda, et just katse ajal oli Maa kiirus eetri suhtes null. Seetõttu korrati katset kolmekuiste intervallidega; liigub ju Maa oma orbiidil ümber Päikese kuue kuu pärast vastupidises suunas. Ja jälle ei täheldatud Maa liikumist.
Näis, et kõik oli pöördunud Michelsoni ja Morley vastu. Ei olnud usutav, et kogu universum, kaasa arvatud Päikesesüsteem, pöörlevad ümber tillukese Maa. Selle katse tulemusi püüdsid seletada tolle aja suurimad füüsikud, kes esitasid kõige erinevamaid mõtteid. Michelsoni kiituseks tuleb öelda, et tema tulemustes ei olnud kellelgi vaja kahelda. Michelson ja Morley olid algul segaduses, ent nad teadsid, et olid teinud oma töö põhjalikult, ja see rahustas neid mõnevõrra, õnneks elasid nad mõlemad ajani (a. 1905), mil Einstein (1879-1955) lõi relatiivsusteooria, mis andis täieliku seletuse nende katsetulemusele.
See lugu näitab, et tõeliselt tähtsa töö tegelikku väärtust on selle teostajad raske tunnetada, üksnes ajalugu võib välja selgitada tõe. See, mida peame ebaõnneks, võib osutuda hiilgavaks eduks.
Siiani oleme rääkinud nähtustest, mida meie meeleorganid vahetult tajuvad: liikumisest, soojusest, helist ja valgusest. Nagu nägime, kaasnes nende nähtuste uurimisega palju raskusi, kuid nende nähtuste olemasolus ei kahelnud keegi. Nüüd asume nähtuse juurde, mis ei ole vahetult tajutav. Näib, nagu oleks loodusel palju võtmeid oma saladuste juurde, ühed peidetud lausa nähtavale, teised väga sügavale. Katsetes jõuda nende saladusteni sünnivad uued füüsikaharud. Selle suurepäraseks näiteks on elekter ja magnetism. Mõlemad avastati juhuslikult. Algul ei paistnud neil midagi ühist olevat, kuid ajapikku nende uurimisteed põimusid ja tänapäevaks on nad omavahel nii seotud, et mitte üheski vähegi järjekindlas esituses ei saa neid vaadelda lahus. Neid võib vaadelda kui ühe nähtuse eri ilminguid, kuid mis ilmingud need on, seda ei saa seletada üksnes eelmistes peatükkides räägitu alusel.
Magnetism on tuntud vähemasti 5. sajandist e. m. a. Mõned kivid, mida leiti Türgis Magnesia (nüüd Manissa) linna ümbruses, orienteerusid nööri otsa riputatult alati ühes suunas. Kes selle omaduse avastas ja kuidas, ei tea keegi. Kas oli ta fetišite looja või ornamendimeister? Igatahes pidi ta olema terane inimene. Nagu ma eespool juba ütlesin, ei ole lihtne teha vahet tähtsa ja vähem tähtsa vahel; selleks on vaja suurt mõistust. Magnetmaagi - teenäitaja - avastamist tuleb hinnata kui suursaavutust, mis avas füüsikas uued ettenägematud arenemisteed.
Magnetismi uurimine arenes aeglaselt ja selles pole midagi imestamisväärset. Meremehed kasutasid magnetmaaki küll suunanäitajana, kuid nemad kirjutasid tema omadused millegi üleloomuliku arvele. Selle probleemi teaduslik uurimine arenes visalt, sest tolle aja teadlased suhtusid katsetesse põlglikult. 1269. a. avaldas Peregrini manuskripti oma avastuse kohta, kus ta kirjutas, et magnetil on kaks kohta, kus „magnetiline omadus" on eriti suur (nüüd nimetame neid poolusteks), ja et üks neist näitab põhja, teine lõunasse. Peregrini tegi kindlaks, et magnetite samanimelised poolused tõukuvad ja erinimelised tõmbuvad; kui magnetmaagi tükk teha pooleks, siis on kummalgi tükil samuti kaks poolust.
Lühidalt, ta oli avastanud magnetismi põhifaktid.
Inimene, kelle nimega tavaliselt seotakse magnetismi teadusliku uurimise algust, oli siiski Gilbert (1540-1603). Tema suur teene seisnes selles, et ta süstematiseeris äärmise objektiivsusega paljusid tuntud magnetilisi nähtusi, millest vähemalt osa sai ta teada Peregrini töödest. 1600. a. avaldas ta oma töö tulemused raamatuna De Magnete („Magnetist"). Tema kuulsaima eksperimendi eesmärk oli uurida Maa magnetismi. Ta valmistas magnetmaagist kera ja jälgis, kuidas see mõjub väikesele rauatükist kompassinõelale. Ta märkas, et nõel käitus nagu inklinaator (kompassinõel, mis pöörleb vabalt vertikaaltasandis) Maa läheduses (joonis 22). Ta järeldas, et Maa on hiiglamagnet. See on fakt, mida tunnistame meiegi, ehkki pole seda tänini täielikult mõistnud.
Gilbert ütles välja mõtte, et magnetmõju voolab magnetkehast välja igas suunas. Selle väitega ennetas ta nüüdisaegset kujutlust magnetväljast. Väli on füüsikas nii tähtis mõiste, et juba üksi selle pärast väärib Gilberti töö kõrget hinnangut.
Elektrinähtuste uurimine kulges veel aeglasemalt. Eks olnud omajagu põhjust ka selles, et neid ei osatud praktiliselt kasutada, ehkki merevaigu elektrilisi omadusi tunti kahtlemata varem, kui avastati magnetmaak.
Oletusi elektrinähtuste avastamise kohta ei olegi väga raske teha: näiteks võis mõni karjus märgata, kuidas villatükid kleepuvad merevaigust helmeste külge. Elektrinähtusi uurida on tunduvalt raskem, sest nad on väga lühiajalised.
Ka sellele valdkonnale puhus elu sisse Gilbert. Ta püüdis kindlaks teha, millised ained sarnanevad oma elektriliste omaduste poolest merevaiguga ja millised mitte. Viimased olid peamiselt metallid. Loomulikult ei osanud Gilbert aimatagi oma vaatluste tähtsust.
1660. a. valmistas von Guericke elektrimasina (joonis 23), mis koosnes raudvardal asuvast väävlikerast. Kera võis panna pöörlema, ja kui teda seejuures peopesaga puudutati, ta laadus. Seejuures võisid tekkida isegi väikesed sädemed. See oli esimene kord, kus katses täheldati sädemete teket. Von Guericke märkas, et kera tõmbas külge kergemaid esemeid, pärast kera puudutamist tõukusid need eemale ega tõmbunud uuesti enne, kuni olid puudutanud mõnda teist keha.
Meile on praegu need faktid arusaadavad, kuid tol ajal näisid nad saladuslikud. Magnetism ja elekter ilmutasid sarnaseid omadusi. Kas pole nad mitte ühe ja sellesama nähtuse eri ilmingud? Nad näivad tõepoolest väga sarnased, ent magnetism on seotud rauaga, elekter aga merevaiguga ja mõnede teiste materjalidega, mida Gilbert nimetas elektrikuteks. Ent magnetilised efektid on tunduvalt püsivamad kui elektrilised; magnetismi ei saa hävitada lihtsa kontakti teel teise kehaga.
Gilbert märkas veel üht üsna veidrat erinevust: elektrilised jõud mõjuvad sirget mööda, kuna magnetilised jõud on tavaliselt suunatud kaldu (joonis 22). Tänapäeval me teame, et viimane asjaolu on põhjustatud sellest, et magnetpoolused esinevad ainult paaridena, elektrilaengud aga võivad olla üksikud. Oli vaja geeniust, kes võtaks kokku kõik need mõtteotsad.
Kes see geenius oli, on raske täpselt öelda, kuid kindlasti möödus ligi sajand enne, kui ta ennast ilmutas. 1733. a. ütles Dufay välja mõtte, et elektrinähtusi saaks seletada, kui oletada, et elektrit on kaht liiki: klaasi (positiivne) elekter ja vaigu (negatiivne) elekter. Ta koostas nimistu, kus luges üles, kõik talle teada olevad ained, mis võimaldasid neid elektriliike saada. Eri liiki elektrid tõmbuvad ja üht liiki tõukuvad. Sellega oli alus pandud elektriõpetusele.
Edasised sündmused on tähelepanuväärsed teises suhtes: esmakordselt tõmbasid endale tähelepanu Ameerika teadlased. Põhja-Ameerikas asutati riik 1620. a. Vastse riigi kõik ressursid kulusid võitlusele olemasolu eest. Alles mõni põlvkond hiljem, kui riik oli kindlustunud, võisid ühendriiklased endale lubada tegelemist ka nende asjadega, millel polnud otsest praktilist tähtsust. Nad võisid pühendada oma vaba aega kunstile ja teadusele ning nende hulgast võrsus andekaid kunstnikke ja teadlasi.
Üks selliseid mehi oli B. Franklin (1706-1790). Ta tundis elektri vastu tõsiteaduslikku huvi ja näitas hiilgava eksperimendiga, et välk on elekter: ta laskis piksel lüüa tuulelohe märga nööri.
See oli hulljulge katse, mis oleks võinud maksta Franklinile elu. Vaevalt nõustuks keegi tänapäeval olema vabatahtlikult selline välgupüüdja. Kuid õnneliku juhuse tõttu Franklin viga ei saanud. Edaspidi tegeles ta küll vähem efektsete, kuid see-eest palju teaberikkamate katsetega.
Franklini tähelepanuväärne panus elektriõpetusse on see, et ta täiustas Dufay elektriteooriat. 1748. a. paiku ütles ta välja mõtte, et mõlemad elektriliigid on üheainsa elektriliigi liig või puue. „Kehad, mida hõõrutakse, tõmbavad hõõrumise hetkel enda poole elektrituld, järelikult võtavad nad seda hõõruvalt kehalt; samas on nad aga nõus saadud tuld ära andma igale kehale, millel seda vähem on." See on aluseks teooriale, mida nimetatakse elektrostaatikaks.
Suuresti abistas Franklinit selle teooria loomisel seade, mida nimetatakse Leydeni purgiks. Selle avastas - just nimelt avastas, mitte ei leiutanud - von Kleist 1745. а. Ta asetas naela rohuklaasi, kus oli veidike elavhõbedat, ja avastas, et see võib mahutada suure hulga elektrit. „Kui ma puudutasin elektriseeritud naela, sain löögi, millest mu käsi ja õlg võbelema hakkasid." Vapper mees!
Ehkki me peame elektrišokki ootuspäraseks, on tähelepanuväärne juba see, et inimkeha elektrivoolule sel moel reageerib. Elektrisignaalid juhivad meie elundite talitlust ja elektrilöök on sisuliselt keha mingi elektriskeemi ülekoormus. On imestusväärne, et organism talub sajatuhandekordset elektrilist ülekoormust, ilma et tekiksid püsivad kahjustused, tõsi küll, seda vaid ülilühikese aja vältel. Hiljem näeme, kuidas seos elektri ja elutalitluse vahel lubas luua uue füüsikaharu - õpetuse elektrivooludest.
Vaatleme edasi staatilist elektrit. Kuidas sõltuvad laengutevahelised tõmbe- ja tõukejõud laengute suurusest ja nendevahelisest kaugusest? Küsimuse teisele poolele leidis vastuse Coulomb (1736-1806), kelle nimi anti selle avastuse eest laenguühikule. Ma ei pea seda õigeks kahel põhjusel: esiteks, kulon on palju suurem kui laengud, millega töötasid Coulomb ja tema kaasaegsed; kahe kulani suuruse laengu vahel, mis asetsevad teineteisest meetri kaugusel, mõjub jõud, mis ulatub miljonitesse tonnidesse; teiseks, Coulomb’i ei huvitanud mitte sedavõrd elekter, kuivõrd katseseadmed. Ta oli leiutanud eriti tundliku seadme jõu mõõtmiseks - pöördkaalu - ja otsis sellele lihtsalt kasutamisvõimalusi.
Coulomb ei olnud selle seadme ainukasutaja. Umbes samal ajal mõõtis Cavendish pöördkaalu abil gravitatsioonikonstanti. Cavendishi huvi piirdus katsega, kuna Coulomb püüdis valmistada võimalikult väikese ja tundliku seadme. Ühes niisuguses seadmes kasutas ta siidniiti, mis pöördus jõu mõjul ühe kraadi võrra. Taoliste seadmete abil leidis Coulomb, et jõud kahe elektrilaengu või magnetpooluse vahel on pöörd võrdeline laengute- või poolustevahelise kauguse ruuduga.
Coulomb’i seaduse esimesest poolest - laengute vahel mõjuv jõud on võrdeline laengute suurusega - räägitakse õpikutes vähe. Seda peetakse enesestmõistetavaks, kuigi katseline teostus on äärmiselt raske, sest laengu suurust defineeritakse Coulomb’i seaduse kaudu. Ent me võime ülesannet lihtsustada, oletades, et kui puudutada laetud kera samasuguse, kuid laadimata keraga, jaguneb laeng nende vahel võrdselt. Võiksime sooritada Coulomb’i katse nii: mõõta kahe laetud kera vahel mõjuva jõu, siis muuta ühe kera laengu kaks korda väiksemaks ja mõõta uuesti kerade vahel mõjuva jõu. Kui need jõud suhtuvad nagu 2:1, on Coulomb’i seaduse esimene pool tõestatud, sest tulemus vabalt valitud suhte korral kehtib ka iga muu suhte korral. Muide, magnetismi korral on see meetod kõlbmatu, sest nii lihtsat magnetlaengute jagamise meetodit ei ole. Tuleb meeles pidada, et Coulomb’i seadus ei ole täiesti õige. Kui see täie rangusega kehtiks, puuduks vastasmõju laetud ja laadimata kehade vahel, aga just selle vastasmõju tõttu elekter avastatigi. Neid nn. polarisatsioonijõude me ei vaatle, sest see viiks meid käesoleva raamatu kohta liiga sügavale füüsikaprobleemidesse.
1774. a. pakkus Cavendish välja palju täpsema, kuigi mitte nii vahetu meetodi, mille abil kontrollida laengute vastasmõju sõltuvust kaugusest. See koosneb peamiselt tõestusest, et õõnsa laetud juhi sees elektriväli puudub vaid juhul, kui elektrivälja tugevus sõltub pöördvõrdeliselt kauguse ruudust. Selle seaduse kontrollimise täpsus sõltub ainult väljadetektori tundlikkusest. Praegu peetakse kauguse astmenäitajat Coulomb’i seaduses õigeks täpsusega ; see on täpsus, mis ületab kaugelt täpsuse, mida võimaldas Coulomb’i seade.
18. sajandi lõpuks olid magnetismi- ja elektrialased teadmised tunduvalt laialdasemad ja korrastatumad kui sajandi algul. Cavendish ja Gauss (1777-1855) allutasid elektri- ja magnetismiprobleemid teoreetilisele analüüsile, misjärel need muutusid iseseisvaks füüsikaharuks. Katseandmete tõlgendamiseks on alati vaja matemaatika abi. Sellega ei taha ma sugugi öelda, nagu oleks matemaatika füüsika asetäitja. Matemaatika on teadus omaette ja selle meetodeid füüsikalise maailma uurimisel kasutades peame kõigepealt mõistma vaadeldavate nähtuste füüsikalist sisu.
Kõige tähtsamast elektri kohta, elektri liikumisega seotud nähtustest, ei teatud tollal veel midagi. Nagu füüsikas tavaline, ei avastatud neidki otseselt, elektri liikumist jälgides. See poleks olnudki võimalik, sest hõõrdumise teel saadud laengud on selleks liiga väikesed. Aastal 1786 tegi anatoom Galvani ühe üpris ebatavalise avastuse. Tema katse sai eelkäijaks paljudele tähtsatele katsetele, mis sooritati esialgu kõik Itaalias, hiljem juba ka mujal, sealhulgas Inglismaal. Lõpuks muutsid need katsed elu kogu meie planeedil: neile tuginedes tekkis elektritööstus, mis on nüüdisaegsele tsivilisatsioonile vahest kõige iseloomulikum.
Kahjuks pole täpselt teada, kuidas Galvani oma avastuse tegi. Nähtavasti jutustas ta sellest eri inimestele erinevalt. Sellest on väga kahju, sest avastus oli äärmiselt ebatavaline ja kahtlemata oleks huvitav teada selle kõiki üksikasju. Ent kõikides nendes juttudes on neli ühist detaili: Galvani ise, tema naine, äsja amputeeritud konnajalg ja terasskalpell. Tol ajal ei olnud teadlased nii spetsialiseerunud kui tänapäeval ja Galvani laboratooriumis oli kõrvuti nii anatoomia- kui füüsikaseadmeid. Galvani sõnade järgi olevat tema naine märganud, et kui ta skalpelli otsaga konna jalga puudutas, hakkas see tõmblema. Ta seostas seda nähtust laetud Leydeni purgi lähedusega.
Efekt polnud järjekindel. Ilmselt oli mängus veel mõni tundmatu tegur. Pärast pikki otsinguid avastas Galvani, et kõik sõltub sellest, kuidas ta skalpelli käes hoiab: kui ta hoidis nuga selle terast või puutusid sõrmed vastu neete, hakkas konna jalg tõmblema, kui aga käsi puudutas vaid noa luust pead, siis mitte. Galvani oli hämmeldunud ja otsustas uurida, kas vaadeldavas efektis ei osale atmosfäärielekter.
Ta riputas maja ümbritseva raudvõre külge konnajalgu, kuid midagi ei juhtunud. Ootamisest väsinuna vajutas ta messingkonksule ja märkas mõnikord konna jalalihaste kokkutõmbumist. Efekt oli ikkagi juhuslik. Siis pöördus ta tagasi suletud ruumis tehtavate katsete juurde, kus katsetingimused on rohkem katsetaja kontrolli all. Ta asetas konnajalad raudplaadile, ja kui ta surus messingkonksu vastu plaati, tõmbusid jalalihased alati kokku. Järelikult peitus saladuse võti kahe metalli kontaktis. Teised metallid andsid samuti efekti, kuid isolaatorid, näiteks klaas, ei kutsunud esile mingit lihaste kokkutõmmet.
Milline ka polnud Galvani avastuse tõeline lugu, võis vaid geenius teha sellisest teabeuputusest järelduse, et elektrit tekitab lihtsalt kahe metalli kokkupuude.
Arvatavasti pöördus Galvani pärast seda avastust tagasi oma anatoomia juurde, sest füüsikaalastes teadusväljaannetes tema artikleid rohkem pole ilmunud. Kuid tema avastus vallandas pika sündmusteahela. Galvani kaasmaalane Volta (1745-1827) hakkas nähtust uurima ja vahetaski anatoomia füüsika vastu. Ta jõudis järeldusele, et vajalik on vaid kahe metalli kontakt nii, et nende metallide vahele jääb mingi vähejuhtiv aine, näiteks vedelik konna jalas. Sellest lähtudes valmistas ta esimese elektrielemendi, mis koosnes tsink- ja vaskplaatidest, mille vahel olid soolase vee või lahjendatud happega immutatud riidetükid. 1800. a. avaldas ta Volta sambaks nimetatava seadme kirjelduse. See oli üksikelementidest koosnev silindrikujuline sammas (joonis 25).
Volta valmistas veel teise seadme, mis sai nimeks la Couronne de lasses (tassipärg). Igasse soolalahusega tassi olid asetatud tsingi- ja hõberibad, ning kõik tassid olid omavahel juhtmega ühendatud. selliselt ühendatud elementi andsid märgatava elektrilöögi ja võimaldasid saada niisuguse soojushulga, millest piisas üsna jämeda juhtme sulatamiseks.
Elementide poolt arendatava elektrilise „rammu" tähistamiseks oli vaja mingit terminit. Seda „rammu" võis võrrelda veetasemete erinevuse poolt tekitatud rõhuga. Et kõrgemal tasemel oleval veel on kõrgem potentsiaal, siis võime seda elektrilist „jõudu" nimetada elektriliseks potentsiaaliks, et ta aga põhjustab voolu, siis elektromotoorjõuks. Volta auks nimetati elektrilise potentsiaali mõõtühikuks volt, aga pontentsiaalide vahet või pinget nimetatakse sageli voltaažiks.
Volta sambast saadava nn, fluidumi olemus kutsus ikka veel esile kahtlusi. Fakt, et see põhjustas löögi, ei tõestanud veel, et tegemist on elektriga. Oli vaja palju veenvamat tõestust. Selleks sobis katse elektroskoobiga, mille leiutas Benneti (1750-1799) 1787. a. Selle seadme tundlikuks osaks on ülalt kinnitatud kuldlehekesed, mis laadudes tõukuvad teineteisest eemale. Volta samba potentsiaalist lehtede kõrvalekallutamiseks ei piisa; suur soojushulk, mida eraldab Volta sammas, ei ole põhjustatud mitte kõrgest pingest, vaid voolu katkematust mõjust.
Kuid vahest on võimalik samba pinget tõsta?
Seda võib teha kondensaatori abil, mille üks plaat on ühendatud elektroskoobiga. Lülitame plaatide külge Volta samba (joonis 26a). Kui hakkame plaate teineteisest eemaldama, Volta samba enne lahti ühendanud, lähevad elektroskoobi lehekesed laiali (joonis 26b). Ma ei oska öelda, kes kirjeldatud katse esimesena sooritas, kuid igal juhul näitab see veenvalt, et mõlemat liiki elekter on tegelikult üks ja seesama. On võimalik, et esiotsa seda katset ei mõistetudki, sest ta on seotud märksa hiljem ilmunud kondensaatoriteooriaga. Kuldlehekestega elektroskoop näitab potentsiaalide vahet; mahtuvuse vähenemisel laengu potentsiaal suureneb ja osutub piisavaks lehekeste kõrvalekallutamiseks.
Volta sammas ja patarei olid suurepärased mänguasjad. Paljud tegid endale neid ja korraldasid paeluvaid katseid. Ent kas võisid nad kaasa aidata teaduse arenemisele? Üks vastus sellele küsimusele anti 1800. a., mil Nicholson ja Carlisle avastasid elektrolüüsi. Carlisle valmistas Volta samba 17 poolekroonisest mündist (siis tehti neid veel ehtsast hõbedast) ja 17 tsinkplaadist, mida eraldasid teineteisest soolveega immutatud pappkettakesed. Mingi pingekordisti abil õnnestus eksperimentaatoril kuldlehtedega elektroskoopi kasutades näidata, et samba hõbedane ots on laetud negatiivselt, tsinkots aga positiivselt.
Nicholson ja Carlisle veendusid selles, et Volta sammas ei mõju läbi selliste materjalide nagu klaas, kuid mõjuvad läbi metallide. Kindlama kontakti saamiseks panid nad juhet puudutavale plaadile veetilga ja märkasid väikesi gaasimullikesi, mis lõhnasid vesiniku järele. Seejärel tegid nad tõelise katse. Nad võtsid klaastoru, sulgesid selle mõlemast otsast korgiga ja torkasid läbi kummagi korgi traadi (joonis 27). Toru oli täidetud veega, juhtmed aga ühendati Volta samba vastupidiste otstega. Kui nad kasutasid messingplaati, oli hõbedaga ühendatud juhtme otsa juures näha gaasimullikeste pidev voog, teise juhtme otsa juures aga muutus vesi sogasemaks. Kui messing asendati plaatinaga, eraldus gaas mõlema otsa juures. Nicholson ja Carlisle järeldasid õigesti, et neil õnnestus lahutada vesi teda moodustavateks elementideks - vesinikuks ja hapnikuks.
On raske ülehinnata nii selle avastuse praktilist kui ka teoreetilist tähtsust. Siin meid küsimuse praktiline külg ei huvita, aga teoreetilist tähendust vaatleme 10. peatükis. Praegu märgime vaid, et elektrolüüs tõendas omakorda, et elektrostaatika ja galvanism on omavahel seotud; osutus ju võimalikuks lagundada vett elektrimasina laengu abil.
Selle katse tegi aastal 1801 Wollaston (1766-1828). Ta mõistis, et efekt on väike ja et gaasi võib selgelt näha vaid juhul, kui see eraldub teravikult. Seepärast võttis ta teritatud otsaga peene kuldtraadi, jootis selle klaasist kapillaartorusse ja käias toru otsa, kuni hakkas paistma kuldtraadi teravik. Tal õnnestus saada sellelt teravikult sädemeid ka vee all ning ta märkas, et üheaegselt sädemetega eraldusid teravikul ka gaasimullikesed. Nüüd polnud enam mingit kahtlust, et galvanism on elektri pidev voolamine - elektrivool.
Volta sammas köitis teadlasi aastaid. Üksteisega võisteldes valmistasid nad üha suuremaid ja paremaid patareisid, sulatades nende abil üha suuremaid metallitükke ja leiutades võimalusi elektrisignaalide kasutamiseks. Tagaplaanil oli tundmus, et elekter ja magnetism on omavahel kuidagi seotud. Kummaline, et selle seose avastamine laskis end oodata aastat. On see ju väga lihtne, seda otsiti ja kõik vahendid selle avastamiseks olid käepärast. Galvani tööga võrreldes lapsemäng, oli see avastus aeglane tulema. Võib-olla olid tolle aja teadlased liigselt haaratud uuest mänguasjast, mille oli nende jaoks välja mõelnud Volta?
Voolu ümbritseva magnetvälja avastas 1820. a. Ørsted (1777-1851). Räägitakse, et ta tegi selle avastuse loengu ajal, mil vaatles magnetismi, galvanismi ja elektri vahelist seost. Ta asetas kompassi juhtme lähedusse, mis kulges paralleelselt nõelaga. Kui juhet läbis vool, kaldus kompassinõel ida-lääne poole. See lihtne katse pani aluse uuele teadusharule - elektromagnetismile.
Ørstedi avastust kontrollisid kohe teised teadlased ning tegid seejuures tähtsaid leiutisi. Selsamal, 1820. a. leiutas Arago, lastes voolu läbi raudsüdamikule mähitud juhtme, elektromagneti. Ampere (1775-1836) tõestas teoreetiliselt ja kinnitas hiljem ka katseliselt, et paralleelsed voolud tõmbuvad. 1821. a. pani suurim eksperimendigeenius Faraday (1791-1867) magneti pidevalt pöörlema ümber vooluga juhi ja ehitas seega sisuliselt esimese elektrimootori. Ørstedi töö teine tähtis tulemus oli, et see andis objektiivse meetodi elektrimõõtmisteks. Kui mõned varasemad uurijad lootsid saadud elektrilöögi tugevuse hindamisele, siis nüüd võidi mõõta kompassinõela hälvet. See võimaldas hakata elektrinähtusi kvantitatiivselt uurima ja luua terviklik elektrinähtuste teooria - elektrodünaamika.
Kuidas sõltub vool kasutatavast patareist ja juhtmest, mida mööda ta kulgeb? Tänapäeval me teame, et vastuseks sellele küsimusele on Ohmi seadus. See seadus on nagu gaaside seadusedki nii lihtne, et vaadatakse mööda kõikidest raskustest, mis tuli selle leidmiseks ületada, ja unustatakse selle avastajat tabanud ebaõnn. Ohmi seadust ei ole kerge kontrollida ja seda kui silmanähtavat tõde võtta ei saa, seda enam, et paljude ainete korral see seadus ei kehtigi.
Milles siis peituvad need raskused? Kujutleme, et püüame kompassinõela abil mõõta voolu, mille tekitab juhis Volta sammas. Kas me ei saaks siis kontrollida, kuidas muutub vool, muutes elementide arvu Volta sambas? Seda tehes muudaksime kogu ahelat, sest lisatavad elemendid annaksid ka lisa- takistust. Seepärast peame leidma võimaluse pinge muutmiseks nii, et patarei jääks samaks. Pealegi soojendavad eri tugevusega voolud juhet erinevalt, mis võib samuti mõjutada voolu tugevust.
Ohm (1789-1854) ületas need raskused termoelektriliste nähtuste abil, mille oli aastal 1822 avastanud Seebeck (1770-1831). Seda nähtust on võimalik jälgida kahe metalli jootekoha kuumutamisel: tekib väike pinge, mis põhjustab voolu. Seebeck avastas selle, katsetades vismut- ja antimonplaatidega. Vooludetektoriks oli tal suure keerdude arvuga pool, mille sees oli väike magnet. Ta täheldas, et magnet hälbis vaid juhul, kui ta surus kätega plaate teineteise vastu. Varsti ta mõistis, et efekti põhjustab käte soojus. Siis soojendas ta plaate lambiga. Magnet hälbis nüüd hoopis enam. Ta ei saanud avastatud efektist täielikult aru ja nimetas selle magnetiliseks polarisatsiooniks.
Ohm mõistis, et termoelektriline efekt annab talle just soovitud elektromotoorjõu allika. Kui temperatuuride vahe on jääv, peab termoelement andma üsna stabiilse pinge, ja et vool on väike, siis ei tohiks juhtmed märgatavalt soojeneda. Neist kaalutlusist lähtudes valmistas Ohm seadme, mis on esimene elektrimõõtmisteks mõeldud seade (joonis 28). Selle ülemine silinder on vooludetektor — pöördkaal; ja on termoelemendid, kaks risti asetsevat vismutvarda külge joodetud vaskjuhet; ja on elavhõbedanõukesed, mille külge võis lülitada termoelemendid. Nõukestega ühendati juht, mille otsad puhastati iga kord enne elavhõbedasse panekut, sest Ohm mõistis, kui tähtis on materjalide puhtus. Jootekohta hoidis ta keevas vees, asetas vee ja jää segusse ning jälgis galvanomeetri hälvet. Ohmile omast tüüpilist saksa täpsust ja tähelepanelikkust võib vastandada peaaegu poisikeseliku entusiasmiga, millega töötas Faraday. Füüsikas on vaja mõlemat: entusiastid avastavad uusi valdkondi ja pedandid uurivad neid seejärel põhjalikult, et täpsete kvantitatiivsete andmete alusel luua range teooria.
Juhtidena kasutas Ohm kaheksat eri pikkusega vaskjuhet. Algul ei õnnestunud tal saada korratavaid tulemusi, kuid nädala pärast näis seade juba alistuvat ja ta sai iga juhi jaoks rea lugemeid. Need näidud (tabel 7) on riputusniidi väändenurgad. Ohm näitas, et kui valida sobivad konstandid ja , siis on pikkus ja väändenurk seotud järgmise võrrandiga:
Seda seost võib esitada ka graafiliselt funktsioonina (joonis 29).
Ohm kordas oma katset vaskjuhtmega ja leidis, et sama tulemuse saamiseks tuli vase jaoks valida teine väärtus, kuid jäi samaks. Ta kasutas termoelementide jootekohti temperatuuridel ja ( ja ) ning avastas, et magnetnõela hälve muutus see juures ligi kümme korda. Seega kui oletada, et seadme tekitatud pinge on võrdeline temperatuuriga - nagu me nüüd teame, on see ligikaudu nii -, siis on vool võrdeline pingega. Ohm näitas veel, et vool on pöördvõrdeline mingi juhtme pikkusest sõltuva suurusega. Ta nimetas selle takistuseks ja on alust oletada, et suurus on vooluringi ülejäänud osa takistus.
Järelikult näitas Ohm, et vool on võrdeline pingega ja pöördvõrdeline ahela kogutakistusega.
See oli hämmastavalt lihtne tulemus nii keerulise katse kohta või vähemalt näib see meile nii. Ohmi kaasaegsed, eriti tema kaasmaalased, mõtlesid teisiti. Võimalik, et neis tekitas kahtlust just tema seaduse lihtsus. Ohm põrkas raskustega kokku ka oma kutsealases karjääris, kõige rohkem rõhus teda aga see, et tema töid ei tunnustatud. Suurbritannia, eriti Londoni Kuningliku Seltsi auks tuleb öelda, et seal hinnati Ohmi tööd vääriliselt. Nüüd on ta üks neid suurmehi, kelle nime kohtame väikese tähega kirjutatuna: oom on elektritakistuse ühik.
Miks aga peetakse suurimaks eksperimentaatoriks Faraday’d? Oli ju ka teisi suuri teadlasi. Põhjus on selles, et teiste teadlaste - Coulomb’i, Galvani, Ørstedi, Arago, Ampere’i - tööd olid üksikud mäetipud, kuna Faraday püstitas omavahel seotud töödest terve mäeaheliku.
Faraday’l oli geniaalne võime probleemi uurima asudes kindlaks teha selle võtmepunktid. Isegi siis, kui näis, et ta lihtsalt kordas varem tehtut, nagu näiteks elektrolüüsikatsed, olid tema tööd teaduse jaoks fundamentaalse tähtsusega. Tal oli kuues meel, mille abil ta ühendas üksikfaktid ja lõi neist lõpetatud terviku. Faraday polnud teoreetik, kuid tema katsed innustasid teisi teadlasi looma kõige hiilgavamaid teooriaid selles valdkonnas.
Huvitavad olid Faraday suhted Ampere’iga. Faraday oli kõrgeima klassi eksperimentaator, Ampere aga väljapaistev teoreetik. Nad kirjutasid teineteisele oma töödest pikki kirju, kuid näis, et üks jäi teise töö suhtes külmaks. Neile piisas sellest, et nad said oma mõtted paberile panna; polnud vaja, et keegi neid hindaks. Näis, nagu oleksid mõlemad kirjutanud teisele arusaamatus keeles, ei, mitte inglise ega prantsuse keeles, vaid eksperimendi ja teooria keeles.
Mõlemad olid seadnud endale eesmärgiks leida seos magnetismi ja elektri vahel. Kui elekter tekitab magnetismi, miks siis ei peaks magnetism tekitama elektrit? Ampere andis varsti alla ja püüdis metafüüsiliste arutluste teel veenda Faraday’d toimima samuti. Ta kirjutas: „Te ühendasite sellega kaks olemuselt erinevat asja, kuna fundamentaalne mõju peab paratamatult tekkima vaid kahe ühesuguse olemusega entiteedi, näiteks kahe vooluelemendi vahel." Teda pimestas uhkus oma tulemusest, järeldusest, et paralleelsed voolud tõmbuvad, mistõttu teiselaadiliste seoste võimalikkust ta enam ei näinud.
Ent Faraday teadis, et on midagi leida, ja ta otsis seda üksteist aastat. Loomulikult oli tema otsingutes vaheaegu, sest tal oli teisigi muresid. Tema tööd raskendas materjalipuudus, näiteks ei olnud tal isoleeritud juhtmeid. Ka suur osa katseseadmeist tuli tal endal valmistada. Osa sellest polnud piisavalt tundlik, et reageerida otsitavatele nõrkadele efektidele. Oli juhuseid, mil ta katse oli kavandatud nii, et pidanuks olema edukas, kuid ta ise polnud küllalt nobe seda märkama. Ka teised tegid sama vea. 1825. a. sooritas Colladon (1802—1892) katse, mis oleks pidanud andma oodatud tulemuse*, kuid ta kartis, et võimas magnet, mida ta kasutas, võib mõjutada galvanomeetrit, ja ta viis galvanomeetri teise ruumi. Kui ta jõudis tagasi galvanomeetri juurde, oli selle osuti juba peatunud. Nii et mõnikord on liigne ettevaatus kurjast.
*Hetkeline galvanomeetri noole kõrvalekaldumine magneti väljavõtmisel poolist.
Faraday töödest on võimalik kirjutada palju, sest ta pidas väga täpset päevikut. Meie jutustame ainult eksperimendist, mida kroonis edu 1831. a., see on aastat pärast Ørstedi avastust. Faraday oli jõudnud järeldusele, et elektrilist efekti on kergem avastada siis, kui seda suurendada. Tollal oli juba üsna võimsaid elektromagneteid. Miks siis mitte kasutada neid ja püüda avastada elektrilisi efekte elektromagneti raudsüdamikul? Faraday valmistas 2cm laiuse ja 15cm läbimõõduga pehmest rauast rõnga ning mähkis kummalegi rõngapoolele suure hulga vaskjuhtmekeerde (joonis 30). Üks mähis oli suletud juhtmega, mis kulges üle kompassinõela. See asus piisavalt kaugel rõngast, et talle ei mõjuks rõngas tekkinud magnetism. Teise mähisesse lasti vool kümnest plaadipaarist koosnevast patareist.
Selline see seade oligi: lihtne ja vähetundliku galvanomeetriga. Faraday’l oli ka tundlikumaid galvanomeetreid. Võimalik, et ta lihtsalt ei uskunud sellest katsest enamat kui eelmistest ja valis seetõttu lihtsamad vahendid. Hiljem oleks ta võinud kasutada ka tundlikumaid seadmeid, kuid selgus, et seda polnud vajagi. Voolu sisselülitamisel ja katkestamisel kompassinõel võnkus. Faraday oli leidnud selle, mida otsis.
Tähelepanelikumal jälgimisel selgus, et voolu sisselülitamisel pöördus nõel ühele poole, katkestamisel aga teisele poole. Efekt oli üsna suur. Faraday ütles, et plaadipaarist koosneva patarei korral tegi kompassinõel või ringi. Tal õnnestus saada isegi väike säde. Faraday tegi kindlaks, et seda nähtust saab esile kutsuda ka tavalise magneti abil. Ta valmistas juhtmest spiraali, mille sisse pani pehmest rauast varda, võttis kaks pikkust sirgmagnetit ning moodustas magnetahela (joonis 31). Ka selle ahela sulgemisel ja avamisel kompassinõel hälbis.
Kõik need nähtused on väga lühiajalised. Tänapäeval me mõistame, miks see nii on, aga tollal sai just nähtuste lühiajalisus paljude katsete ebaõnnestumise põhjuseks.
Teated Faraday katseist hakkasid varsti levima, kuid enamasti moonutatuna. Ampere teatas, et tulemus olevat ilmselge ning tulenevat otseselt tema loodud elektrodünaamikast. Ta väitis koguni, et tema ja de la Rive olevat selle efekti avastanud juba 1822. a. Mingeid tõsiseid argumente ta ei esitanud ja tänapäeval ei kahtle enam keegi selles, et elektromagnetilise induktsiooni avastamise au kuulub Faraday’le.
Kui üldse keegi teine võiks pretendeerida sellele avastusele peale Faraday, siis on see ameeriklane Henry (1797-1878). Ta avastas elektromagnetilise induktsiooni Faraday’st sõltumatult, kuid ei olnud oma tulemustest teatanud ajaks, mil levis kuuldus Faraday avastusest. Ta avastas ka eneseinduktsiooni, nähtuse, et pooli läbiva voolu tekkimisel või katkemisel indutseeritakse poolis elektromotoorjõud.
Elektromagnetilisel induktsioonil on lai rakendusväli. Faraday seadme alusel loodi induktsioonipool: kui mähkida mõned keerud jämedat juhet pooli ühele ja palju keerde peent juhet pooli teisele poolele, tõuseb pinge märgatavalt. Koos seadmega, mis voolu katkestab, võimaldab induktsioonipool saada kõrgepingeimpulsse, mis annavad üsna tugeva sädemeseeria. Kui muuta esimeses mähises voolu suunda perioodiliselt, saadakse teises, sekundaarmähises samasugune, kuid teistsuguse pingega vahelduvvool. Sellel põhimõttel töötabki transformaator, mida kasutatakse meie elektrivarustussüsteemides ühesuguse pingega vahelduvvoolu muutmiseks teistsuguse pingega vahelduvvooluks. Ülekandmispinge peab olema kõrge, tarbimispinge madal. Pinge muundamise lihtsus ongi üks põhjusi, miks elektrienergia jaotussüsteemis kasutatakse just vahelduvvoolu.
Kuid meid huvitab praegu füüsika enda areng, aga mitte tema rakendused. Kas Galvani, Ørstedi ja Faraday avastused andsid võimaluse laiendada meie füüsikalisi ettekujutusi loodusest? Kahtlemata. Selle raamatu viimastes peatükkides näeme, kui tähtsad on tänapäeva füüsikas elektri- ja magnetisminähtused. Praegu meenutame aga veel kolme Faraday avastatud nähtust.
Kaks neist on väga sarnased - paramagnetism ja diamagnetism.* Eelmise sajandi 40. aastateks olid teadlased õppinud valmistama väga tugevaid elektromagneteid ja võistlesid üksteisega selles, kelle magnet suudab tõsta suuremat raskust. Faraday mõttemaailmale oli niisugune suhtumine võõras. Talle oli tugevaid magneteid vaja selleks, et otsida uusi nähtusi ja selgitada, kas ei saa uute, tugevamate magnetite abil avastada magnetilisi omadusi ka nendel ainetel, mida oli peetud mittemagnetiteks.
*Aga ainult väliselt. Olemuselt on nad täiesti erinevad.
See pole sugugi lihtne. Raud on nii tugev magneetik, et isegi tema tühine lisand võib täielikult muuta mis tahes aine magnetilisi omadusi. Seepärast pidi Faraday olema eriti nõudlik uuritavate materjalide puhtuse suhtes. Ta tegi kindlaks, et paljudel materjalidel on nõrgad magnetilised omadused. Kui ta riputas elektromagneti pooluste vahele pliiklaasist vardakese (pliiboriidilisandiga silikaatklaas), asetus see risti magnetväljaga, s. t. risti suunaga, mille võtaks raudvarras. Ta kontrollis hoolikalt, kas ei sõltu efekt äkki riputusniitide omadustest ega vardakese mõnest juhuslikust asendist magnetväljas. Selgus, et ei. Faraday mõistis, et oli avastanud uue magnetilise omaduse, mis sunnib ainet liikuma sinna, kus magnetväli on nõrgem. Ta nimetas selle diamagnetismiks. Ta leidis, et kõik ained evivad kaht liiki magnetilisi omadusi: nad käituvad kas sarnaselt pliiklaasiga - neid aineid nimetatakse diamagneetikuteks — või sarnaselt rauaga — need ained kannavad paramagneetikute nimetust. Ferromagnetism on paramagnetismi äärmuslik vorm.**
**Jällegi on need magnetismi eri liigid sarnased vaid väliselt. Füüsikaline sisu on kummalgi juhul erinev.
Kolmas avastus oli märksa ebatavalisem ja praegugi on raske öelda, kuidas Faraday selleni jõudis. 1845. a. avastas ta, et magnetväli võib pöörata valguse polarisatsioonitasandit!
Me nägime 6. peatükis, kuidas 19. sajandi algul tõestati, et valgus on ristlainetus, kuid noil aastail polnud kellelgi vähimatki ettekujutust sellest, mis nimelt võngub valguslainetes. Räägiti küll peenest fluidumist, mida hakati nimetama eetriks, ent nimetused ei lahenda probleeme ja me ei saa end kunagi petta illusiooniga, nagu piisaks mingi nähtuse mõistmiseks sellest, kui talle nime anname.
Faraday lähenemine oli palju sügavam. Teda huvitas, kas valguse ja mõne teise füüsikalise nähtuse vahel valitseb mingi seos. Kui prooviks õige magnetismiga?
View _exp_open not found
Faraday mõtles välja järgmise katse. Ta polariseeris Nicoli prisma abil valgusvihu, suunas selle oma suurima elektromagneti pooluste vahele ja kontrollis teise Nicoli prisma abil, kas magnetväli ei mõjuta valguse polarisatsiooniastet. Efekt puudus. Siis asetas ta magneti pooluste vahele pliiklaasi. Jällegi efekt puudus, kuid kas ta rakendas välja õigesti? Võib-olla peaks välja suund ühtima valguse levimise suunaga? Oli ilmne, et seda katset ei saa ta teha ühe elektromagnetiga, sest siis jääksid poolused valguse teele ette. Seetõttu kasutas ta kahte elektromagnetit (joonis 32). Seekord oli katse edukas. Valguse polarisatsiooniaste oli silmanähtavalt langenud.
See ei olnud veenev tulemus, kuid oli suunanäitaja. Faraday laenas veel tugevama elektromagneti ja proovis uuesti, seekord mitme klaasitükiga. Üks hästi lihvitud pindadega klaas andis „väga ilusa efekti". Kui teine Nicoli prisma voolu puudumisel valguse kustutas, siis voolu sisselülitamisel ilmus valgus uuesti ja Nicoli prisma pöörlemisel kustus taas. Faraday oli avastanud, et magnetväli pöörab valguse polarisatsioonitasandit.
See tulemus oli tähelepanuväärne, sest ei teatud ühtki põhjust, miks magnetismi ja valguse vahel peaks olema seos. Kuid nii see oli. Miks, sai mõistetavaks alles aastat hiljem, just enne Faraday surma, kui J. Clerk Maxwell avaldas valguse elektromagnetilise teooria.
Eelmistes peatükkides vaatlesime, mida võiks nimetada silmanähtavaks füüsikaks. Kasutades sõna „silmanähtav", ei mõelnud ma, et eespool kirjeldatud füüsikalisi nähtusi võiks jälgida igaüks. Tahtsin vaid vihjata sellele, et neid nähtusi võidi uurida suhteliselt väikese aja- ja rahakuluga. Nende nähtuste valdkonda - tavaline mehaanika, molekulaarfüüsika jt. - võib nimetada põhifüüsikaks. Kas see ongi kogu füüsika või tasuks otsida edasi?
See küsimus võiks olla käesoleva peatüki sümboolseks sissejuhatuseks, sest kiirguse uurimine nõudis ettevalmistust, milleks sai valguse uurimine. Tänapäeval me teame, et nähtav valgus moodustab kõigest tühise osa suurest elektromagnetlainete spektrist. Ent just tänu sellele, et teati selle väikese osa olemasolu, avastati ka teised elektromagnetkiirguse vormid, mille omadused näisid lausa ebatavalised ja mille uurimine viis füüsikat edasi. Nende kiirguste avastamine nõudis palju vaeva. Kõik edaspidised saavutused füüsikas tulid raskesti, ja mida kaugemale jõuti, seda suuremaid pingutusi nõudis edasiminek.
Esimese avastuse kiirguse valdkonnas tegi 1777. a. Scheele (1742-1786), kes uuris eri spektriosade mõju hõbekloriidile. See sool muudab päikesevalguse mõjul oma värvi valgest kuni purpurseni ja Scheele tahtis uurida, kas mõni spektriosa pole selles suhtes eriti mõjus. Ta leidis, et kõige suurem on spektri violetse osa mõju. Wollaston tõestas, et hõbekloriidi mõjutab tegelikult see spektriosa, mis asub violetsete kiirte taga.
1842. a. „fotografeeris" A. E. Becquerel (1820-1891) Päikese ultravioletset spektrit, mida võimaldas selle mõju hõbekloriidiga immutatud paberile, ja leidis spektris palju Fraunhoferi jooni. Valgus lahutati spektriks klaasprismade abil. Ent klaas, ehkki läbipaistev nähtava valguse jaoks, ei lase läbi ultraviolettkiirgust. Sellest raskusest saadi üle sel moel, et hakati kasutama peegel- difraktsioonivõresid. Tänaseks on ultravioletset kiirgust uuritud väga põhjalikult ning ta leiab mitmekesist kasutamist.
Mida võib aga öelda kiirguse kohta, mis jääb ultraviolettkiirgusest teisele poole nähtavat spektrit? Kas ka sellel on mingeid erilisi omadusi, tänu millele võiks teda avastada? Probleemi lahendas 1800. a. Herschel, kes oli huvitatud spektri eri osade soojendusvõimest. Ta suunas spektri eri osi tundliku termomeetri mustaks värvitud kuulikesele ja märkas, et soojusefekt on seda tugevam, mida punasem on valgus, ning tugevneb veelgi nähtava spektri punase osa taga: see oli infrapunakiirgus.
1840. a. tuli Herschel mõttele „fotografeerida" Päikese spektrit selle soojendusvõime järgi. Ta kattis pabeririba liimi ja lambitahmaga, et see neelaks hästi soojust, kastis siis piiritusse ja suunas sellele spektriks Jahutatud päikesevalguse. Seal, kus riba sai rohkem soojust, aurus piiritus kiiremini ja spektrit võis vaadelda erineva niiskusega ribadena. „Foto" ei olnud küll suurem asi, sest see polnud püsiv, ettevõtmine ise aga näitas suurepäraselt, kui suurt teravmeelsust võib ilmutada eksperimentaator, kui ta tõsiselt tahab mõnda katseülesannet lahendada. Sel viisil avastas Herschel infrapunaspektris veel teisigi Fraunhoferi jooni.
Teades, et Päikese spekter ulatub mõlemale poole nähtavat spektrit, võime kergesti kujutleda, et see ulatub veel kaugemalegi. Pole ju mingit põhjust arvata, et spektril oleksid piirid. Ent need omadused - nähtavus, soojendav toime ja keemiline aktiivsus - on omased vaid spektri mõnele osale ega anna mingeid lähtekohti ülejäänud spektri avastamiseks. Nagu füüsikas sageli juhtub, tuli lahendus hoopis teisest kandist.
Eelmise peatüki lõpus nägime, kuidas Faraday tõestas, et valguse ja magnetismi vahel on seos. See ja paljud teised katsed sundisid teda mõtisklema valguslainete olemuse üle. Faraday, kes oli,rohkem eksperimentaator, ei olnud harjunud kirjutama pikki teoreetilisi töid ega püüdnudki oma mõtteid paberile panna. Kord ta tegi seda siiski. Põhjus oli üsna ootamatu ja omapärane.
Ühele Kuningliku Instituudi traditsioonilisele reedeõhtusele seminarile, mida juhatas Faraday, oli kutsutud loengut pidama Wheatstone, seesama mees, kelle järgi sai nime Wheatstone’i sild. Need seminarid olid ja on ka praegu tähtsad sündmused, mistõttu Wheatstone pisut kartis. Kui saabus kätte aeg, mil loeng pidi algama, oli Wheatstone kadunud. Et Faraday’l olid Wheatstone’i märkmed, oli ta sunnitud pidama selle loengu ise. Ja nagu sageli juhtub võõraste märkmete kasutamisel, jäi loeng väga lühikeseks. Faraday otsustas aja täitmiseks rääkida oma mõtetest valguse olemuse kohta. Publik oli vaimustatud ja Faraday’d veendi kirjutama sellest artiklit ajakirjale Philosophical Magazine. Artikkel ilmus 1846. a. pealkirja all „Mõtisklusi kiirte võnkumisest".
Selles artiklis käsitles Faraday valgusvõngete olemust. Ta küsis, kas see pole seotud aatomitevaheliste jõududega, sest nii saaks vabaneda eetri mõistest. Edasi vaatles ta „kaht teineteisest kaugel olevat keha ja , mis teineteist mõjutavad ja on järelikult seotud jõujoontega ...; kui üks keha nihkub momentaanselt paremale või vasakule või kui mõju allikas viia hetkeks keha, sisse (mõlemat on raske realiseerida, kui ja on elektrilised ja magnetilised kehad), on meid huvitav resultantjõu muutumine ekvivalentne ristihäiritusega". Teiste sõnadega, Faraday esitas küsimuse, kas ei võiks lained levida mööda jõujooni nagu mööda pingul traati. (Jõujoonte mõiste, mille võttis kasutusele Faraday, on füüsikutele kasulik vahel praegugi.)
Faraday mõte innustas Maxwelli (1831-1879) uurima seda probleemi märksa sügavamalt. Maxwell oli suurepärane matemaatik ja suutis Faraday ideid tõlkida matemaatika keelde. 1864. a. ilmunud artiklis - see oli kolm aastat pärast Faraday surma - näitas Maxwell, et häiritus, mida pidas silmas Faraday, tekitab lõpliku kiirusega leviva laine. Laine kiirus sõltub konstantidest Coulomb’i elektrostaatiliste ja magnetiliste jõudude võrrandeis.
Aga mida nende konstantide all mõista? Paljudes õpikutes võrdsustatakse nad mõlemad ühega. Nii saame kaks ühikute süsteemi - elektrostaatilise ja elektromagnetilise süsteemi. Esimese annab kahe elektrilaengu vahelise jõu võrrand, teise kahe voolu vahelise jõu võrrand. Ent kuna voolud on lihtsalt liikuvad laengud, siis peavad mõlemad süsteemid olema omavahel seotud. Maxwell leidis selle seose 1868. a. katseliselt. Ta poinud mitte ainult tähelepanuväärne teoreetik, vaid ka suurepärane eksperimentaator.
Maxwelli meetod põhines kahe kõrge pinge all oleva plaadi vahelise tõmbejõu ning kahe pooli vahelise tõukejõu tasakaalustamisel (poolides kulgesid vastassuunalised voolud).
Tema seade on skitseeritud joonisel 33. Plaatidele anti potentsiaal „hr. Gassioti suurest - elemendilisest patareist". Pinget mõõdeti galvanomeetri ja muudetava takistusega sundi abil, kui vool läbis täpselt teada oleva takistusega šunti (umbes ). Läbi galvanomeetri teise pooli pääses vool tõukuvatesse poolidesse. Et registreerida vähimaidki tasakaalu häireid, asetati liikuv plaat ja liikuv pool pöördkaalude kangile. Katse ise oli järgmine. Plaatidevahelist kaugust muutes tasakaalustati pöördkaalud ja pärast seda nulliti galvanomeeter sundi abil. Täpsuse suurendamiseks oli vaja kõrvaldada Maa magnetvälja mõju. Selleks pandi liikuvale plaadile liikumatu kaitserõngas ja pöördkaalude kangi mõlemasse otsa asetati veel üks poolikomplekt.
Korraldati seeriat mõõtmisi. Plaatide vahekaugust muudeti vahemikus kuni . Keskmiseks tulemuseks saadi . Sama mõõtmise, ehkki teisel meetodil olid juba 1856. a. sooritanud Weber ja Kohlrausch, kuid nad ei viidanud selle teoreetilisele tähendusele. Nende tulemus oli . Et Foucault oli mõõtnud valguse kiiruseks , siis järeldas Maxwell, et tema teooria on kvantitatiivselt tõestatud.
Valguse olemuse mõistmine avas täiesti uued võimalused uute kiirgustüüpide leidmiseks. Kas ei saaks elektromagnetkiirgust tekitada vahetult, näiteks elektrilaengut või magnetit liigutades, nagu arvas Faraday? Seejuures peaksid võnked levima piki jõujooni. Pideva laine saamiseks tuleb selle allikas panna pidevalt võnkuma. Siin tekibki esimene raskus. Isegi kõige suurematel sagedustel, mida võime saada mehaaniliselt, kas või näiteks helihargi abil, on lainepikkus mõõtmiseks liiga suur. Kiirus on sageduse ja lainepikkuse korrutis, nii et kiirusel ja sagedusel 10000 võnget sekundis on lainepikkus .
Võnkeid tuli tekitada mingil muul moel. Idee selleks oli leidnud Henry 1842. а. Ta oli avastanud, et laetud kondensaator tühjeneb võnkudes. Loomulikult ei mõistnud Henry oma avastuse tähtsust ja esitas selle lihtsalt ühe punktina oma töös. (Muuseas, see töö sisaldas ka elektromagnetilise induktsiooni seaduse, mille Henry oli avastanud Faraday’st sõltumatult.)
Henry otsustas korrata mõningaid Savary katseid. Savary oli 1826. a. märganud, et kui Leydeni purk tühjeneb läbi spiraalmähise, siis selles asuvad terasnõelad magneetuvad. See kinnitas veelkord, et elektrivool on laengute liikumine. Kuid Savary imestuseks ei magneetunud kõik nõelad ühesuunaliselt. See oli üsna salapärane. Olnuks ju ootuspärane, et nõelad magneetuksid ühtmoodi sõltumata sellest, kas pooli läbib kondensaatori või patarei vool.
Henry katsed korrata Savary vaatlusi olid algul edutud. Kõik nõelad magneetusid ühes suunas. Mille poolest võis tema katse erineda Savary omast? Vahest oli. põhjus nõelte suuruses? Henry võttis tunduvalt väiksemad nõelad ja katse õnnestus kohe: nõelad magneetusid eri suundades.
Efekt oli seega täiesti ilmne, aga kuidas seda põhjendada? Lõpuks ta taipas, milles oli asi. Kondensaator ei tühjene nagu kann, millest vesi lihtsalt voolab välja, vaid rohkem nii, nagu peatub liikuma pandud kiik. Elekter voolab kondensaatorist välja küllaga, mille tagajärjel kondensaator laadub vastupidiselt ja tühjeneb seejärel uuesti, kuid voolu suund on esialgsega võrreldes vastupidine. Seejärel kõik kordub. Tühjenemine nõrgeneb järk-järgult, kuni vool lõpuks peatub.
Aga kuidas see aitab vaadeldud nähtust seletada? Esimene tühjenemisvool on kõige tugevam ja peaks nõelad magneetima ühesuunaliselt. Sellele järgnevad tühjenemisvoolud on juba nõrgemad ega suuda esimest magneetuvust kustutada. Seepärast magneetusidki kõik suured nõelad ühesuunaliselt. Kuid väikeste nõelte voolust tingitud magneetuvusel on piir. Selle piiri võib ületada nii esimese, teise, kolmanda kui ka veel mõne tühjenemistsükli poolt põhjustatud magneetuvus, kusjuures iga kord nõelad demagneeditakse ja magneeditakse seejärel teistpidi, kuni tühjenemisvool on sedavõrd nõrgenenud, et see nõelu enam demagneetida ei suuda. Niisugune oli Henry seletus, mis sai ühtlasi aluseks kondensaatori tühjenemise teooriale. See tulemus tekitas uusi mõtteid füüsikas ning avas uue ajastu sides.
Oli leitud viis panna elektrilaengud võnkuma nii kiiresti, et saadi registreerida nende tekitatud laineid, neid, mida olid ennustanud Faraday ja Maxwell. Kui sageli oli neid eksperimentide käigus tekitatud Leydeni purkide abil, ent polnud ei sobivat riista nende registreerimiseks ega meest, kes toimunut mõistnuks.
Esimesena hakkas selle asjaga tegelema Hertz (1857-1894). Igaüks, kes on kasutanud kõrgepingeseadmeid, teab, kui kergesti tekivad sädemed selle ligidal lähestikku asuvate metallesemele vahel, mis peaksid nagu olema võrdse potentsiaaliga. Seda nähtust oli märgatud ka enne Hertzi, kuid kahtlemata oli tema esimene, kes mõistis, kui tähtis see nähtus on. Ta uuris seda nii põhjalikult, et enam ei saanud keegi kahelda Maxwelli teooria õigsuses, mille suhtes oli olnud tõsiseid kahtlusi. Tollal arvati nimelt, et Maxwell on hiilgav noor teadlane, kelle tööd on küll matemaatiliselt väga peened, kuid füüsika jaoks tähtsusetud. Hertz nende mõtlejate kilda ei kuulunud, ehkki ka tema arvas, et mõistmiseks on Maxwelli teooria liiga keeruline. Ta tundis Henry töid, kuid arvas, et kondensaatori tühjenemisel tekkivad elektromagnetlained on avastamiseks liiga nõrgad. Sel teemal loengut ette valmistades avastas Hertz, et lähestikku asuvate juhtide vahel hüplevad sädemed on seda suuremad, mida väiksemat Leydeni purki katses kasutatakse. See sundis teda probleemi põhjalikumalt uurima. Miks mitte teha tõepoolest väike kondensaator, sest äkki on efekt siis veel tugevam? Hertz valmistas kahest 40cm servapikkusega ruudukujulisest tsinkplaadist vibraatori. See tekitas kergesti sädemeid lähestikku asuvate juhtide vahel.
Oma töö väärtust Hertz esiotsa ei mõistnud. Ta arvas, et kondensaatori tühjenemisel tekkinud häiritus on täpseks uurimiseks liiga turbulentne ja ebaregulaarne ning et ta oli tekitanud vaid elektrilist „müra". Oma uurimusi jätkas Hertz vaid seetõttu, et avastas elektrijuhi, millelt õnnestus eraldada sädemeid otstest, mitte keskelt. Ta oli avastanud elektrivõnkumiste võtmepunkti. Nüüd ta teadis, et tal on tegemist „selge ja korrapärase" nähtusega. Ta oli saanud puhta laine, aga mitte müra. Tema esimesed katsed nende lainetega polnud edukad; lainepikkus oli ning varsti ta mõistis, et registreeris oma seadmetega vaid hajunud kiirgust. Seepärast vähendas ta vibraatori mõõtmeid ja sai lainepikkuseks . Nüüd töötas seade suurepäraselt. Joonisel 35 on Hertzi skits sellest seadmest. Vibraator on paraboolse peegli fookuses. Vibraatori tekitatud kiirgust registreeris Hertz samasuguse seadme abil, jälgides selle sädevahemikus indutseeritavaid sädemeid.
1888. a. avaldas Hertz artikli, milles ta kirjeldas oma hiilgavaid tulemusi. Ta tõestas, et elektromagnetlained levivad sirgjooneliselt, tõkestades nende levi metallekraaniga. Isolaatorid, näiteks puu, lainete levile mõju ei avaldanud. Kui ta pööras peeglid teineteise suhtes risti, kadus sädelemine, mis tähendas, et lained on polariseeritud ja seega ristlained. Lainete peegeldumist demonstreeris Hertz suure tsinkpeegli abil, ehkki paraboolpeeglitega oli seda juba tõestatud. Tahkest bituumenist prisma abil näitas ta, et need lained murduvad; murdumisnäitajaks sai ta . Millist naudingut võis see töö talle pakkuda! Vaid vähestele on antud tunda rõõmu nii viljakast ja teabe rikkast katsest. Selle katsega rajas Hertz, aluse ka uuele tehnikaharule - raadiosidele.
Nii oli elektromagnetspekter laienenud lainepikkuses tuhandikelt millimeetritelt (valgus) meetrite ja kümnete meetriteni (raadiolained). Hiljem saadi nii pikema kui ka lühema lainepikkusega raadiolaineid ja täideti tühik spektris infrapunase kiirguse ja raadiolainete vahel. Ega pikkade infrapunalainete ja lühikeste raadiolainete vahel põhimõtteliselt erinevust olegi.
Ent see spektriosa, see mis jääb ultraviolettkiirguse taha? Siin ei tulnud avastused sugugi nii loogiliselt. Kõik algas uue kiirguse - röntgenikiirguse - avastamisega. See kiirgus oli nii ebatavaline, et jäi kauaks füüsikutele mõistatuseks. Möödus 17 aastat, enne kui suudeti kindlaks teha, et tegemist on elektromagnetkiirgusega, mille lainepikkus on ligi korda lühem valguse lainepikkusest.
Röntgenikiirguse avastamise kirjeldamiseks tuleb kõigepealt teha väike rännak möödanikku, aastasse 1675, mil Picard märkas, et pimedas ruumis kiirgab elavhõbedabaromeetri toru tipus olev Torricelli vaakuum valgussähvatusi. Muidugi jäi see nähtus täielikuks mõistatuseks nii Picard’ile kui ka neile, kes jälgisid seda hiljem. Alles siis, kui Faraday oli avastanud elektromagnetilise induktsiooni ja leiutanud induktsioonipooli, sai võimalikuks uurida asja süsteemsemalt. Seda tehti pikkade klaastorude abil, milles oli madala rõhu all õhk. Kui torudele rakendati kõrge pinge, tekkis neis ilus värviline helendus. Need gaaslahendustorudeks nimetatud seadmed on väga kaunid füüsikaseadmed, kaunid nii väliselt kui ka avastuste tõttu, mis nende abil on tehtud. Kes usub väidet, mida on nii sageli korratud, et 19. saj. füüsikud mõtlesid just selle nähtusega kokku puutudes, et füüsika lõpp on lähedal? Ainult vähesed lihtsameelsed.
Sellest kahtlemata ühest viljakamast füüsikakatsest järelduvaga tutvume põhjalikumalt järgmises peatükis. Siin räägime vaid ühest tähelepanekust: kui rõhku gaaslahendustorus vähendati, nõrgenes ka lahendus ja vahetult enne selle katkemist ümbritses lahendustoru roheline helendus. Mis oli siis juhtunud?
Tuleb meeles pidada, et 19. sajandi lõpul oli gaaslahendustoru kõige erutavam seade füüsikas ja et sellega katsetati enamikus maailma laboratooriumides. Kui mingit uut nähtust nii suure huviga uuritakse, jõutakse varem või hiljem tulemusteni. Ja aastal 1895 tegigi Röntgen (1845-1923) suurepärase avastuse. 1895 on aastaarv, mille peavad meelde jätma kõik, kes õpivad füüsikat. Siis algas see, mida meie nimetame nüüdisaegseks füüsikaks. Kuidas tulevased põlvkonnad seda ka ei nimetaks, on vaieldamatu, et sestpeale arenes füüsika edasi tohutu tempoga.
Röntgen eksperimenteeris gaaslahendustoruga ja märkas, et kui rõhku torus vähendati, hakkas selle läheduses asuv baariumi plaatinatsüaniid tugevasti helendama (fluorestseerima); tugevaim oli helendus just enne lahenduse katkemist, kui liiga kõrgeks muutunud vaakuum katkestas torus voolu. Ei tasu imestada, et katseseadme läheduses oli nimetatud ühendit. See on tuntud helendamise tõttu ultraviolettkiirtes ja seda leidus enamikus tollastes füüsikalaboratooriumides.
Röntgen arvas, et helenduse põhjustas torust väljuv ultraviolettkiirgus. Ta pani oletuse kontrollimiseks toru musta kartongkarpi. Tema imestuseks helendus ei vähenenud. See oli näha isegi siis, kui ekraan asus torust kahe meetri kaugusel. Röntgen mõistis kohe, et oli avastanud mingi uue kiirguse, mis suudab läbida aineid, mis on läbipaistmatud kõigile teistele kiirgustele, välja arvatud raadiolained.
Enamik teadlasi oleks tormanud sellisest avastusest kohe teatama, Röntgen aga arvas, et tema teade saab hoopis mõjuvam, kui ta lisab sellele andmeid avastatud kiirte olemuse kohta. Seepärast töötas ta kuus nädalat pingsalt ja kontrollis kõiki pähetulevaid oletusi. Ta tõestas, et kiired lähtusid torust, aga mitte mõnest teisest seadmeosast. Ta näitas, et enamik materjale on uue kiirguse jaoks läbipaistvad, kuid mõned neist on läbipaistvamad kui teised. lehekülje paksune raamat suutis selle kiirguse vaevu neelata, tina sisaldav klaas neelas seda rohkem kui tavaline klaas, luu tugevamini kui lihaskude, plaatina tugevamini kui hõbe ja vask. Lisaks baariumi plaatinatsüaniidile helendasid uute kiirte toimel ka paljud teised ained - mitmed klaasisordid, kaltsiit ja kivisool.
Röntgen mõistis, et kiired mõjuvad fotoemulsioonile, ning kasutas seda mõnede oma tulemuste illustreerimiseks. Ta ei suutnud tuvastada, et uutel kiirtel olnuks mingi soojuslik mõju silma võrkkestale, ehkki pani silma peaaegu vastu toru. See oli katse, mis peaks ajama hirmujudinad peale igaühele, kes teab midagi nende kiirte toimest eluskoele.
Röntgen ei märganud, et kiired oleksid murdunud alumiinium- ja kummiprismades. Nad ei hälbinud ei elektri- ega magnetväljas, et õnnestunud kindlaks teha ka nende interfereerumist. Ainus positiivne tulemus oli see, et kiirte mõjul kaotasid laetud kehad oma laengu, kuid selle avastas ta hiljem.
Niisiis ei selgitanud eksperimentidele kulutatud nädalad midagi. Ainus tuvastatud seaduspärasus oli, et rasked elemendid neelavad kiiri rohkem kui kerged. Seega käitusid uued kiired sootuks teisiti kui valgus, mis neeldub täielikult õhukeses alumiiniumikihis, kuid läbib kergesti mitmesentimeetrise pliiklaasi. Paistis, et see oli ka kõik. Uued kiired ei sarnanenud valgusega ega ka kiirtega gaaslahendustorus, mida magnet kergesti hälvitas. Röntgen avaldas oma töö tulemused ja nimetas kiired tagasihoidlikult -kiirteks.
See avastus ei vapustanud mitte ainult teadlasi, vaid kogu maailma. Röntgenikiiri kasutati juba nii meditsiinis kui ka tehnikas, kuid nende olemus jäi endiselt üheks tähtsamaks probleemiks füüsikas. Nagu kunagi oli vaieldud, kas valgus on lained või osakeste voog, vaieldi nüüd röntgenikiirte üle. Et kindlaks teha, kellel on õigus, korraldati palju katseid.
Röntgen oli tuvastanud, et -kiired hajuvad aines vähe, ehkki tal õnnestus mõõta nõrka kiirgust, mis oh hajunud üle . Aastal 1905 mõõtis Barkla (1877—1944) hajunud röntgenikiiri, kasutades nende omadust tühjaks laadida laetud kehi. Mõõtes aega, mille jooksul elektroskoop kaotas laengu, õnnestus tal kindlaks määrata kiirte intensiivsus. Oma hiilgavas eksperimendis uuris ta hajunud kiirgust nende teistkordse peegeldamise abil. Ta leidis, et võrra hajunud kiirgust ei õnnestu uuesti hajutada võrra (joonis 36). See kinnitas veenvalt, et röntgenikiired on ristlained.
Kui nii, siis kui suur on nende lainepikkus?
Oletades, et uue kiirguse lainepikkus on märksa väiksem valguse lainepikkusest, üritasid paljud teadlased teha difraktsioonikatseid, kuid need kõik ebaõnnestusid. Teistest enam suutsid Walter ja Pohl, kes püüdsid 1908. a. röntgenikiirtega korrata Newtoni omaaegset difraktsioonikatset (peatükk 6). Et neeldumine oleks suurem, katsid nad pilu servad kullaga. Kui pilu oli kitsaim (), täheldasid nad röntgenikiirte hajuvuse tunnuseid. Lainepikkus pidanuks siis olema suurusjärgus .
Korpuskulaarteooria pooldajad olid samuti aktiivsed. Näiteks W. H. Bragg (1862-1942) arvas end olevat tõestanud, et röntgenikiired on hoopis osakesed. Ta oli korranud Röntgeni vaatlusi ja veendunud kiirte võimes tühjaks laadida elektriseeritud kehi. Teati juba, et seda põhjustavad õhus tekkivad ioonid. Braggi arvates oli üksikutele gaasimolekulidele antav energia liiga suur, et selle võinuks anda pideva lainefrondi väike osa.
Sellele ilmsele vastuolude perioodile - Barkla ja Braggi tulemusi kooskõlastada oli võimatu - tegi 1912. a. ootamatult lõpu üksainus katse. Seda eksperimenti, mis korraldati tänu ideede ja inimeste õnnelikule kokkusattumisele, võib pidada üheks suuremaks saavutuseks füüsikas, millest tasub jutustada kui näitest selle kohta, et ta lendid suudavad üheskoos märksa enam kui eraldi.
Aspirant Ewald (sünd. 1888. a.) pöördus füüsikateoreetik Laue (1879-1960) poole palvega, et too selgitaks, kuidas mõista lainete dipoolvõre läbimise uut teooriat. Laue küsis Ewaldilt, miks see probleem teda huvitab. Ewald vastas, et üks selline võre on kristall. Laue oli üllatunud. Nähtavasti polnud ta tuttav juba mitu aastat tagasi välja töötatud kristalliteooriaga. (Joonis 37 illustreerib Haüy, 1743-1822, kujutlust, kuidas kristallid tekivad plokkidest.)
Ewaldi mõte intrigeeris Lauet. Ta teadis, et taoline korrapärane moodustis võib toimida difraktsioonivõrena, ja küsis seetõttu Ewaldilt, kui suur võiks olla kristalli elementaarrakk.
Ewald ei teadnud, kuid oletas, et see võib olla umbes valguse lainepikkusest. Ewaldile näis küsimus asjasse mittepuutuv, kuid ta ei võinud ju olla ebaviisakas inimese vastu, kelle poole oli pöördunud nõu saamiseks. Ta ei teadnud, et oli andnud Lauele suurepärase mõtte. See mõte oli järgmine. Et kontrollida, kas röntgenikiired on lained, tuleb teha difraktsioonikatse. Inimkätega tehtud difraktsioonivõre, näiteks Walteri ja Pohli oma, on selle jaoks liiga jäme. Looduslik difraktsioonivõre, kristall, on aga tunduvalt peenem kui ükskõik milline kunstlikult valmistatud difraktsioonivõre. Kas ei võiks röntgenikiired difrageeruda kristallides?
Laue polnud eksperimentaator ja vajas abi. Selleks pöördus ta Sommerfeldi (1868-1957) poole, kuid too ei toetanud Lauet, sest arvas, et soojusliikumine rikub tublisti kristalli korrapärast struktuuri. (Veel üks näide, kuidas eksib suur inimene.) Ta ei lubanud ka oma assistendil Friedrichil (1883-1968) kulutada aega sellisele mõttetule katsele, õnneks arvas Friedrich teisiti ja sooritas katse koos oma sõbra Knippingiga (1883-1935) salaja. Nad valisid vasksulfaadikristalli - neid oli enamikus laboratooriumides - ja panid seadme kokku.
Esimene ekspositsioon ei andnud mingit tulemust. Plaat asus toru ja röntgenikiirte allika ning kristalli vahel, sest arvati, et kristall peaks olema peegeldifraktsioonivõre. Teises katses nõudis Knipping, et fotoplaadid paigutataks kõikjale ümber kristalli, sest tuli ju arvestada igasugust võimalust.
Ühel plaadil - see asus kristalli taga röntgenikiirte kimbu teel - täheldatigi efekti. Nii avastati röntgenikiirte difraktsioon.
Sellega lõppes küll eksperimendi ajalugu, kuid ei lõppenud diskussioonid uute kiirte olemuse ümber. Saadi veel veenvamaid andmeid, ilusaid sümmeetrilisi pilte (tahvel V), kuid neid ei õnnestunud õigesti mõista. Korpuskulaarteooria pooldajad küsisid, kas ei või vaadeldavaid pilte tekitada hoopis korpuskulid, mis tungivad läbi kristallides olevate „tunnelite". Lõpuks jäid peale laineteooria pooldajad, sest selgus, et röntgenikiired hõlmavad sarnaselt valge valgusega terve lainepikkuste diapasooni. Nüüd klappis kõik ja katsetulemused ühtisid Laue ruumilise difraktsioonivõre teooriaga suurepäraselt. Jäi vaid üle leida võrekonstant. Seda vaatleme järgmises peatükis.
Oleme jõudnud kaugele sellest, millest lähtusime - nähtavast valgusest.
Nägime, kuidas laiendati spektri teadaoleva osa ulatust, nii et see hõlmas järgemööda ultraviolett- ja infrapunakiirguse, pikalainelise raadiokiirguse ja lühilainelise röntgenikiirguse. Need on vaid mõned näited, kuid neist peaks piisama näitamaks, kuidas füüsika laiendab end kõike uut omaks võttes ja edasi arendades.
Eelmistel lehekülgedel püüdsin anda pildi sellest, kuidas arenes füüsika. Oma algupäevil uuris ta kõige igapäevasemaid nähtusi, kuid jõudis üsna varsti kaugele välja igapäevase kogemuse piirest. Ühtlasi lõi füüsika oma arenemiseks tarvilikud instrumendid, mis tulid kasuks kogu inimkonnale. Just seda ei tohi füüsika ära unustada, et õigustada oma olemasolu.
Tänapäeval me teame aine ehitusest üsna palju. Nende teadmisteni jõudmiseks oli vaja instrumente. Füüsikud ei jäänud ootama, et need instrumendid neile kätte tuuakse. Nad on kärsitu rahvas, kes vajadust tunnetades loovad ise neile vajalikud vahendid. Mis puutub gaasidesse, siis töötasid juba Boyle ja tema kaasaegsed välja gaaside kineetilise teooria, mis sai 18. sajandi keskpaigaks üldtunnustatuks. Molekulidest ei teatud tollal veel midagi ja vahest polnud seda vajagi, sest gaasides on nad enamjagu aega üksteisest kaugel ja nendevaheline mõju praktiliselt puudub. Vedelikes, kus molekulid asuvad lähestikku, mõjutavad nad üksteist pidevalt ja nende omadusi tuleb arvestada. Millest alustada nende uurimist?
Seda võimaldab üks vedelike omadusi, mille poolest nad erinevad gaasidest: neil on vaba pind, üks esimesi, kes sellest nähtusest huvitus, oli Нооkе. Ta kirjutas oma tähelepanekuist raamatus Micrographia. Hooke avastas, et üksnes rõhu abil saab vett sundida voolama läbi väikese ava ja et sulatina tilgad on kerakujulised. Nendele nähtustele andsid seletuse Young 1804. a. ja Laplace 1806. aastal. Nad lähtusid mõistest, mida me nüüd nimetame pindpinevuseks. Vedeliku sees mõjutab igat molekuli kõigist suundadest ühesugune naabermolekulide tõmbejõud, kuid pinnal, millest väljaspool vedelikku ei ole, on igale molekulile mõjuv resultantjõud suunatud vedeliku sisse. Käesoleva raamatu kirjutamisel ei seadnud ma eesmärgiks tutvustada üksikasjaliselt teooriaid, seda enam, et pindpinevus on üldtuntud nähtus. Youngi ja Laplace’i teooriast ei ole aga sugugi lihtne järeldada, kuidas see nähtus avaldub. Vahest piisaks, kui öelda: nende teooriast järeldub, et vedelikul on pinnaenergia. Et püsivad süsteemid püüavad evida minimaalset energiat, siis püüab ka vedelik oma vaba pinna hoida võimalikult väikese. Seetõttu võtavad väikesed sulatinatilgad sfäärilise kuju, nagu seda märkas Hooke, aga suured vajuvad raskusjõu mõjul laperguseks. 1873. a. kirjeldas Plateau (1801-1883) teravmeelset meetodit, kuidas raskusjõu mõju kõrvaldada. Ta näitas, et vee ja piirituse segu, millel on samasugune tihedus kui oliiviõlil, võib selles moodustada suuri hõljuvaid sfäärilisi tilku. Selle katse nüüdisaegne variant on näidatud tahvlil II.
19. sajandi füüsikud mõtlesid pindpinevuse illustreerimiseks välja hulga ilusaid katseid, paljud praegusaja teadlased mõtlevad aga, et sellele on füüsikakursuses liiga palju tähelepanu pööratud, sest tänapäeval vääriks see nähtus vaid põgusat meenutust. Ma pole nendega nõus. Pindpinevuse tähtsus igapäevases elus ja tehnikas on nii suur, et ükski füüsik ei saa pidada oma haridust täielikuks, kui ta ei oska seda vajalikel juhtudel arvestada. Pealegi andis pindpinevus esimest korda võimaluse tutvuda molekulide maailmaga. Tõsi, see tutvumine oli küll väga põgus, kuid see-eest ei olnud vaja viimase aja füüsikale nii iseloomulikke keerulisi seadmeid ja teooriaid.
See võib näida üllatav, sest paljud nähtavasti arvavad, et aatomeid ja molekule saab uurida vaid mikromaailma sündmusi ükshaaval jälgides. Vaatame, kas see on nii. Oletame, et vedeliku sisemusse suunatud jõud mõjub ainult kaugusele , mis on ühes suurusjärgus molekuli mõõtmega. Kihi pindala on , paksus ja mass , kus on tihedus. Selle kihi aurustamiseks kulub soojushulk , kus on varjatud aurumise soojus. See soojushulk peab olema võrdne pindalaga seotud energiaga, s. t. , kus on pindpinevus.
Seega siis
või
Et näha, mida see tegelikkuses annab, võime asendada vee väärtused: , või . Niisiis
Saadud väärtus on liiga väike*, kuid arvestades varem tehtud jämedaid oletusi, pole selles midagi üllatavat.
*Tegelikust umbes korda väiksem.
Vahest on meie arutlus kasulikum hoopis sellest küljest, et ta näitab: pindpinevus pole vedelikel ebatavaline, vaid täiesti loomulik omadus. Kui ei oleks vedeliku sisemusse suunatud tõmbejõude, ei oleks ka vaba pinda ega varjatud aurumissoojust, teiste sõnadega, ei oleks mingit vahet vedela ja gaasilise oleku vahel. See vahe kaobki teatud rõhul ja temperatuuril, mida nimetatakse kriitiliseks ja mis on iga vedeliku jaoks erinevad. Aatomite ja molekulide olemasolu tunnistamine andis füüsikale 19. sajandi keskel kindla eesmärgi: olemasolevatele andmetele tuginedes saada võimalikult palju teada molekulidest ja aatomitest. Mis hoiab molekule koos? Äkki on aatomitelgi mingi siseehitus? Näis, et olemasolevad teadmised ei luba taolistele küsimustele vastata, kuid järk-järgult õnnestus teadlastel hankida hiiglasuur hulk informatsiooni, mille saamiseks näis esialgu puuduvat igasugune lootus. Osaliselt saadi informatsiooni tavaliste nähtuste vaatlemisel, osaliselt seetõttu, et võtmed uute teadmiste juurde olid peidetud teadmatusse just kättesaadavasse sügavusse. Üks võti oli elektrolüüs. Kui palju võis füüsikale anda elektrolüüsi uurimine, selgus alles Faraday töödest. Tema eksimatu vaist ütles talle alati, mida nimelt tuleb uurida.
Elektrolüüs paelus Färaday tähelepanu, sest ta aimas, et siin võib varjul olla veel mõni füüsika avastamata saladus. Elektrolüüsi võib üsna proosaliselt pidada vaid üheks keemilise füüsika haruks, mille tähtsus on rohkem praktiline kui fundamentaalne. Faraday nägi selles veel ühte märki, mis viitas seosele kahe väliselt kaugel asuva nähtuse vahel. Need olid elekter ja keemilised sidemed. Ta teadis, et siin peab peituma midagi sügavamat, ning seadis endale eesmärgiks teha kindlaks, mis see on.
Faraday kaasaegsed arendasid üsna veidraid elektrolüüsiteooriaid. Näiteks oletati, et vesi on keemiline element, aga vesinik ja hapnik selle ühendid, vastavalt positiivse ja negatiivse elektriga. Tekkinud segaduses püüdis esimesena korda luua Davy (1778-1829). 1806. a. korraldas ta katse kahte ahhaadist anumasse asetatud kaaliumsulfaadiga. Voolu toimel tekkis ühes nõus kaaliumkarbonaat, teises väävelhape. Mis võis veel veenvamalt tõestada elektri keemilist toimet?
Ent Davy arutlused selle nähtuse olemuse üle ei seletanud midagi. Nende peamine väärtus seisnes selles, et nad ergutasid Faraday mõtet. Faraday tegi Davy katse palju selgemaks, valmistades ainult ühe elektrolüüsielemendi (joonis 38). Keemilise lagunemise tegi ta kindlaks lakmus- ja kurkumpaberi värvumise järgi. Ehkki soola sisaldav želee ei puutunud elektroodidega kokku, oli värvumine märgatav üksnes elektroodide juures.
Saadud tulemustele toetudes visandas Faraday 1833. a. uue elektrolüüsiteooria põhijooned. Selle teooria järgi alluvad elektrolüüsile vedelikud, mis koosnevad kaht liiki osakestest (nüüd nimetame neid ioonideks), millele igast küljest mõjuvad naaberosakesed. Vaid elektroodide juures, kus osakesed ei ole täielikult ümbritsetud teistega, saavad neile mõjuda tasakaalustamata jõud. Kas ei tunne me selles ära nüüdisaegset elektrolüütide struktuuri teooriat?
Nagu kõik tõelised füüsikateooriad, nii näitas ka Faraday teooria, millises suunas tuleb edasi uurida. Esiteks tõestas Faraday, et dissotsieerunud molekulide hulk sõltub üksnes voolust ja mitte elektroodidest. Ta lülitas järjestikku mitu erineva suurusega elektroodi. Selgus, et kõigilt neilt eraldub ühepalju gaasi. Täpsus teda eriti ei häirinud - ükski Faraday töödest ei hiilanud oma täpsusega -, ja kui kahest torust ühes oli 1,9 ja teises 2,2 kuuptolli gaasi, luges ta need võrdseks. Et mõningane osa gaasi lendus piki ühendusjuhtmeid, siis asetas Faraday need torude ülemistesse osadesse, misjärel katsetulemused paranesid märgatavalt.
Seejärel asus ta mitmeid kuid kestva töö juurde, et kontrollida teiste ühenditega seaduspärasust, mis tema arvates pidi kehtima: elektrolüüsil eraldunud keemilise elemendi hulk on võrdeline selle elemendi hulgaga elektrolüüsis. Katsed gaasidega sooritas ta eelmises lõigus kirjeldatud viisil, kuna eraldunud tahkete ainete hulga määramiseks tegi ta kaalumise teel kindlaks, kui palju oli muutunud elektroodi mass elektrolüüsil. Näiteks katses kahe amalgaamitud tsinkplaadiga väävelhappes eraldus ühel elektroodil kuuptolli vesinikku, teisel elektroodil aga vähenes tsingi hulk 6,3 graani*. Arvestades vajalikke parandusi, sai ta ekvivalendi graanile veele. Sellest leidis ta järgmise võrdelisuse suhte:
(Meie päevil oleks tal liiga suure arvu tüvenumbrite kasutamise eest hinnet alandatud.) Arv langes tema arvates hästi kokku tsingi oletatava aatommassiga .
*graan - apteegikaaluühik.
Pidanud nõu teiste teadlastega, võttis Faraday kasutusele palju tänapäevalgi käibel olevaid mõisteid, nagu elektrolüüt, anioon, katioon jt. Ta pööras terminoloogiale suurt tähelepanu; näiteks meeldis talle tol ajal moodi läinud sõna scientist (teadlane), aga ei meeldinud physicist (füüsik) selle kolme üksteisele järgneva sisihääliku pärast.
1834. aasta alguseks oli Faraday põhjalikult välja töötanud elektrolüüsiteooria alused ja loonud uue teadusharu - elektrokeemia. Ent ka tema ei märganud kõike. Faraday seadustest johtub otseselt, et kõikide aatomite laengud on mingi laengu kordsed, mis tähendab, et elekter on nagu ainegi olemuselt atomistlik. Seda märkis 1881. a. Faraday auks peetud loengul Helmholtz (1821-1894). Faraday tööd nagu kõik füüsika suursaavutused avasid selle teaduse arenemiseks täiesti uued perspektiivid.
Ent see, mis järgnes, ei olnud eelneva loogiliseks järjeks. Avastati uus nähtus - gaaslahendus - ja seda uurides 1895. a. röntgenikiired. 1897. a. avastas J. J. Thomson elektroni. Füüsika ja kogu elu ei saanud enam kunagi olla niisugune nagu enne seda avastust. Mitte ühtki gaaslahendustorus vaadeldavat nähtust polnud võimalik selgitada tolle aja füüsikaliste ettekujutuste raames. Järelikult tuli neid ettekujutusi kas avardada või muuta. Suur osa füüsikuist kaldus lootma, et ummikust väljapääsemiseks piisab vaid mõistete avardamisest. Kaugemale nägevad teadlased arvatavasti mõistsid, et on vaja põhjalikke, võib-olla isegi revolutsioonilisi muutusi füüsikas, sest kõik avastatud efektid olid liiga ebatavalised.
Millest lähtuda, kui alustada mingi füüsikalise nähtuse uurimist? Üks võimalus on läbi proovida kõik uued mõõtmisviisid ja uurida, kas nii saadud tulemused ei vii mõne uue ideeni. (Sellel kohal tasub meenutada lord Rayleigh’ väidet, mida võib lühidalt väljendada sõnadega „füüsika - see on mõõtmine".) Teiseks võib katse korraldada võimalikult lihtsalt, et saada sealt kas või kvantitatiivseid andmeid.
Seekord kasutati mõlemat lähenemisviisi, kuid edukamaks osutus teine. Kui rõhku gaaslahendustorus vähendati sedavõrd, et helendavad ribad torus kadusid, võidi hakata detailselt uurima katoodkiirtega seotud pidevat kiirgust. Kõigepealt leiti, et need kiired hälbivad kergesti magnetväljas, kuna elektriväli neile peaaegu ei mõjunud. Kui nad langesid ainele, eraldus soojust. Nende trajektoor ei sõltunud anoodi asukohast. Katoodkiirte saamiseks oli vajalik teatud potentsiaalide vahe. Nad levisid sirgjooneliselt, mistõttu andsid teravaid varje.
Kõik need ilmingud jäid arusaamatuks. Osa neist rääkis nagu sellest, et katoodkiired on korpuskulid; nende hälbimise suund magnetväljas sobis kokku oletusega, et nad kannavad negatiivset laengut. Kuid miks ei kaldunud nad kõrvale elektriväljas?
Et katoodkiirtel on impulss, tegi kindlaks Crookes (1832-1919), kes pani nendega pöörlema kerge tasakaalus oleva tiiviku. 17. sajandil olid Newton ja Huygens omavahel vaielnud, kas valgus on osakesed või lained. Nüüd puhkes vaidlus taas, ent sedakorda vaieldi selle üle, kas katoodkiired on osakesed või lained. Hertzi hiilgavate avastuste mõju all olevad saksa teadlased pidasid neid laineiks. Kuid miks hälbivad nad siis magnetväljas? See on uus elektromagnetilise kiirguse liik, mis hälbib magnetväljas, vastasid nemad. Märksa kainemalt mõtlevad inglased arvasid, et katoodkiired
on siiski laetud osakesed. Kuid miks ei hälbi nad siis elektriväljas? Aga võib-olla ei olnud seda lihtsalt märgatud, sest katsed ei olnud piisavalt hoolikalt kavandatud? Just selles Thomson veenduski. Rõhul, millel katoodkiiri vaadeldakse, juhib õhk elektrit üsna hästi, ja nagu me teame, juhi sees elektrostaatilist välja ei teki. Seepärast kulgeb elektroodide vahel, kus toimub lahendus, küll vool, kuid elektrostaatilise välja tugevus on tähtsusetult väike.
See viis Thomsoni tema esimese tõeliselt eduka mõtteni: rõhku tuleb vähendada võimalikult palju, nii et katoodkiired oleksid vaevu nähtavad, ja proovida neid siis elektriväljas hälvitada. Katse õnnestus. Katoodkiired hälbisidki nagu negatiivselt laetud osakesed.
Lõpuks oli andmeid piisavalt Katoodkiired olid märkimisväärse impulsiga negatiivselt laetud osakesed. Nüüd, kui nii palju oli juba teada, võis Thomson mängu tuua ka kvantitatiivsed meetodid. Ei ole hea alustada kohe mõõtmisega, sest nähtust mõistmata võime mõõta valesid suurusi või võib mõõtmine ise osutuda nii keerukaks, et selle tulemustes pole võimalik orienteeruda.
Thomson teadis, mida teha. Ta konstrueeris seadme (joonis 39), milles katoodkiirte hälvet elektriväljas kompenseeris nende hälve magnetväljas. On teada, et jõud, millega elektriväli mõjub laengule, ei sõltu laengu kiirusest, aga jõud, millega mõjub magnetväli, sõltub, sest liikuv laeng käitub vooluna. Seevastu hälbe suurus sõltub kiirusest nii elektri- kui ka magnetväljas, sest mida kiiremini osake liigub, seda suuremat jõudu on vaja tema hälvitamiseks mingi nurga võrra (seejuures on nurgale vastavad kiirused elektri- ja magnetväljas erinevad).
Oma seadme abil sai Thomson kaks hämmastavat tulemust. Esiteks, osakeste kiirus on tohutu -umbkaudu kümnendik valguse kiirusest. Täpsem kiiruse väärtus polnud täiesti usaldatav, sest nagu me eespool nägime, ei olnud elektrivälja tugevus gaaslahendustorus täpselt mõõdetav. Ent polnud
mingit kahtlust selles, et osakesed liikusid kiirusega, mis ei mahtunud harjumuspärastesse kujutlustesse materiaalsete kehade liikumisest. Veel tähtsam oli, et massiühiku laeng, mida nüüd tähistatakse ja nimetatakse elektroni erilaenguks, osutus võrdseks 107 elektromagnetilise ühikuga grammi kohta.
Me juba rääkisime katsetulemuste ennustamise tähtsusest. Thomson oli selleks liiga tõsine teadlane, et mitte mõista saadud tulemuse ebatavalisust. Sada miljonit kulonit grammi kohta? Mitte ükski teine mateeria vorm ei evinud midagi seesugust. Vesinikioon elektrolüüsil evib , ja kui võtta arvesse seda, millise jõuga mõjuvad teineteisele kaks kulonisuurust laengut, on see ebanormaalselt suur. Aga siin on meil tegemist osakestega, mille elektrilaeng on veel tuhat korda suurem. Pole midagi imeks panna, et füüsikud rääkisid „aine neljandast olekust", mis võis olla elekter ise.
Thomson mõtles palju selle üle, mida tema tulemused võiksid tähendada. Üks kahest, kas ta avastas mingid uued tohutu laenguga aatomid või uued osakesed, mille mass on palju väiksem kui ühelgi teadaoleval aatomil. Kumma kasuks otsustada?
Vaatlusandmeid, millele toetuda, oli piisavalt, aga et neis orienteeruda ja osata hinnata nende tähtsust, oli vaja mõistust nagu Thomsonil.
1893. a. õnnestus Lenard’il (1862-1947) lasta katoodkiiri läbi väga õhukese alumiiniumakna õhku, kus nad mõne millimeetri kaugusel tekitasid ilusa helenduse. Mis oli sellel ühist vaadeldava probleemiga? Thomson teadis, et molekulide keskmine vabateepikkus (keskmine kaugus põrgete vahel) õhus atmosfäärirõhul oli ligi . Kui katoodkiired suudavad läbida 10000 korda pikema tee, peab ka nende vaba tee õhus olema palju pikem ning järelikult peavad osakesed olema erakordselt väikesed. Seepärast teadustas Thomson 1897. a., et ta peab katoodkiiri väga väikeste osakeste vooks, mis liiguvad valguse kiirusele lähedase kiirusega ja millel on Faraday ioonidega võrdne laeng, kuid mass, mis on korda väiksem kõige kergemast aatomist. Tõepoolest, mateeria uus vorm!
Kohe tekkis huvi, mitut liiki neid osakesi on. Sooritati katseid paljude gaasidega, kuid osakeste erilaengu väärtus tuli alati üks. Näis, et Thomsoni avastatud osake - Johnstone nimetas selle hiljem elektroniks - kuulub kõikide ainete koostisse. Eriti suure tähtsusega oli suhte leidmine: selle järgi õnnestus elektrone „ära tunda" ka siis, kui mõõtmine korraldati hoopis teistsugustes tingimustes. Hiljem selgus, et ka teistel osakestel on neile iseloomulik erilaeng.
Et elektroni täpselt kirjeldada, on peale tema erilaengu vaja leida veel eraldi tema laengu ja massi väärtus. See ülesanne on juba palju raskem, sest nõuab väga täpseid mõõtmisi väga väikeste suuruste valdkonnas. Suured teened selle ülesande lahendamisel on Millikanil (1868-1953), kelle sellekohane katse on üldtuntud. Vähem tuntud on tõik, et Millikani töö oli kulminatsiooniks arvukaile katseile, mida sooritasid C. T. R. Wilson (1869-1959), Townsend (1868-1957) ja J. J. Thomson.
Wilson huvitus pilvede tekkimisest. Ta teadis, et tilkade müriaadist koosnevate pilvede tekkeks on tarvilikud osakesed, millel tilgad kondenseeruvad. Miks ei võiks nendeks osakesteks olla äsja avastatud ioonid? Wilson ehitas kambri (joonis 40), kus võis gaasi adiabaatiliselt jahutades tekitada üleküllastunud auru, ning kasutas seda röntgenikiirte põhjustatud ionisatsiooni uurimiseks. Ta leidis, et kambris tekkinud udu oli hämmastavalt homogeenne, mis näitas, et kõik ioniseeritud osakesed on ühesuguste mõõtmetega.
Townsend ja Thomson kasutasid seda seadet elektroni uurimiseks. Nad proovisid mõõta udupilve moodustavate tilkade kogulaengut ja -massi. Kui õnnestunuks kindlaks määrata veel tilkade suurus, oleks ehk saanud leida ka ühe tilga laengu. Seejuures tuli oletada, et kõik tilgad on laetud ja kannavad ühte elektroni. See oli liiga ligikaudne oletus, et katse oleks saanud olla täpne. Kuid esimesed katsed on harva väga täpsed.
Et leida tilkade suurust, püüdsid Townsend ja Thomson mõõta monokromaatses valguses vaadeldavaid difraktsioonirõngaid, kuid tulemused olid samuti väga ebatäpsed. Siis tekkis neil mõte kasutada tilga suuruse määramiseks Stokes'i (1819-1903) teooriat, mis seob kera liikumise piirkiiruse mingis keskkonnas kera raadiuse ja keskkonna viskoossusega. Oli üsna julge samm rakendada seda teooriat nii väikestele kehadele.
Taoliste katsete abil leidis Townsend, et tilkade läbimõõt on tavaliselt ja et tema udupilv koosnes umbes 3⋅104 tilgast. Tilkade kogulaengu määras ta elektromeetriga. See osutus võrdseks kuloniga. Ühe tilga laeng oli seega ligikaudu kulonit. Tulemus oli erakordselt hea - umbes kaks kolmandikku õigest väärtusest. Selle kaudu leitud elektroni mass võrdus umbes tuhandikuga kõige kergema aatomi - vesiniku aatomi - massist, mis tõendas Thomsoni hüpoteesi õigsust.
Sellele tööle toetudes plaanis Millikan veel julgemat ettevõtmist - mõõta üksiktilkade laengud eraldi. Üksnes nii sai tema arvates loobuda jämedatest oletustest, mis on paratamatud, kui mõõdetakse korraga tervet udupilve. Hindame kõigepealt teda ees oodanud tehnilisi raskusi.
Kui suured olid jõud, mida tal tuli mõõta? Suurima tugevusega elektriväljas, kus õhus veel läbilööki ei teki ( volti meetri kohta), mõjub laengule kulonit jõud düüni. See on küll naeruväärselt väike, kuid rakendatud tilkadele, mille mass - umbkaudu - on samuti naeruväärselt väike. Nii et tilga liikumine selle jõu mõjul peaks olema jälgitav.
Seade, mida kasutas selles katses Millikan, on näidatud joonisel 41. Ta kasutas elektrivälja tugevusega . See tekitati läbimõõduga plaatide vahel, mida lahutasid optiliselt ühesuguse paksuseni (ligikaudu ) töödeldud klaasklotsikesed. Sellesse välja piserdas Millikan õlitilku. Et tilkade mass katse käigus aurumise tõttu ei muutuks, valiti madala aururõhuga õli. Millikan jälgis tilkade liikumist kahe horisontaalse okulaarniidiga mikroskoobi abil. Ta märkis üles aja, mille vältel tilk nende joonte vahe võrra vabalt langes, ja seejärel aja, mille vältel tilk sisse lülitatud elektrivälja toimel tõustes selle uuesti läbis. Ta omandas seadmega töötamisel erakordse osavuse ning väitis, et võib hoida ühte tilka vaateväljas viie või kuue tunni jooksul - suurepärane näide teadlase püsivusest.
Millikan leidis, et langemisaeg oli kõikidel tilkadel harukordselt püsiv, ja järeldas sellest, et tilga mass katse ajal ei muutunud. Seevastu aeg, mille vältel tilk üles liikus, tuli tihti erinev sõltuvalt laengust, mille tilk katse käigus sai. Tüüpiline Millikani saadud näitudeseeria on järgmine: ; ; ; ; ; ; ; ; ; ; ; sekundit. Mida me sellest võime järeldada?
Need ajad jagunevad viide gruppi: ; ; ; (kõige sagedasem väärtus) ja . Kui oletame, et vastavalt Stokesi valemile on kiirus, millega kera mingis keskkonnas liigub, talle mõjuva jõu mõõduks, tuleb võtta nende suuruste pöördväärtused. Saame
; ; ; ja . Need pöördväärtused ise midagi absoluutset ei anna, kuid nende vahed peaksid iseloomustama saadud või kaotatud laengu suurust. Kui arvutame need vahed, saame ; ; ja , seega tulemuse, mis annab tunnistust elektrilaengu atomistlikust olemusest.
Millikan väitis, et isegi tuhandeid katseid tehes ei saanud ta vahesid, mis oleksid ülaltoodust märgatavalt erinenud. See on üllatav: näib uskumatu, et minutise ajavahemiku jooksul katse tingimustes midagi ei muutunud. Võibolla need tilgad teadsid, et neid jälgitakse? Või muutus Millikan ise nii osavaks, et õppis katsetulemusi ette aimama ja jättis neist sobimatud mõõtmata?
Millikan jätkas katseid ja täiustas oma seadet. Lõpuks jõudis ta järeldusele, et elektroni laeng on . Nüüd võis ta leida ka teised aatomimaailma ühikud, nende seas Avogadro arvu, mis osutus võrdseks molekuliga moolis, ja elektroni massi, mis võrdus .
Seega oleme elektroni mõistatuse lahendanud. Aga kuidas on lugu aatomi nende osadega, mis pärast elektronide eraldumist järele jäävad? On ka neil meile midagi jutustada? Gaaslahendustorus peavad nad kahtlemata liikuma elektronidega vastupidises suunas, aga et nad on tunduvalt suuremad, siis põrkuvad nad liikumisel elektronidest tihemini. Seetõttu ei saa nad koguda nii suurt energiat ega põhjustada nii silmanähtavaid efekte. 1886. a. tegi Goldstein (1850-1931) kindlaks, et läbi gaaslahendustoru katoodi puuritud aukude võib jälgida nõrku osakeste vooge. Ehkki oli selge, et need osakesed on positiivselt laetud, näisid nad magnetväljas mitte hälbivat, kuni Wienil (1860-1930) õnnestus tekitada selleks piisavalt tugev väli.
Nende osakeste erilaengute mõõtmised andsid üpris segaseid tulemusi. Vesinikul tuli see samas suurusjärgus kui elektrolüüsil leitu, kuid teiste gaaside korral olid mõõtmistulemused väga ebaühtlased. Thomson otsustas, et selle segaduse tekitavad laetud osakeste omavahelised põrkumised, mille toimel nende laengud muutuvad. Seetõttu valmistas ta 1913. a. seadme, mis on näidatud joonisel 42. Seadmes tekitati elektri- ja magnetväli, mis olid paralleelsed. Seetõttu hälvitasid nad laetud osakest teineteisega risti olevates suundades. Et hoida rõhku võimalikult madalal, otsis Thomson võimalusi, mis hõlbustaksid gaaslahenduse tekkimist. Näiteks sobis selleks katoodi katmine kaltsiumikihiga.
Uue seadmega katsetades sai Thomson väga tähtsaid tulemusi. Ta teadis, et laetud osakese trajektoor tema seadmes on paraboolne, ja et selle pikkus sõltub osakese kiirusest. Vesinikul avastas ta kõigest kaks jälge. Ühe neist omistas ta ühekordselt laetud aatomile, teise ühekordselt laetud molekulile. See oli esimene arvestatav tõendus selle kohta, et vesinik on tõepoolest ühikelement. Enne oli vesinik perioodilisuse süsteemis asetatud esikohale üksnes seepärast, et temast kergemaid aatomeid ei teatud. Kui oleks leitud, et vesiniku aatomid võivad gaaslahendustorus kaotada kaks negatiivset laengut, oleks alati jäänud võimalus, et peab olema veel üks, temast kergem, ühe laenguga aatom. Kuid ühekordselt laetud vesinikuaatomile enam täiendavat laengut anda ei õnnestunud. Seetõttu pidi ta olema fundamentaalne ühik, mida hakati nimetame prootoniks. See-eest avastati katsetes heeliumiga kahekordselt laetud aatomid. Järelikult võidi heelium asetada perioodilisuse tabelis vesiniku järele.
Neooni (see on element aatommassiga veidi üle ) uurides täheldati ootamatult kahte jälge, millest üks vastas aatommassile ja teine . Thomson ja tema kolleeg Aston (1877-1945) olid hämmelduses. Võib-olla vastas suurem mass ühendile ? Või oli see veel üks element? Ent mis see aine ka poleks, peab ta omadustelt neoonist täiesti erinema. Seepärast püüdis Aston seda neoonist veeldamise teel eraldada, kuid gaas, mille ta sai, andis endiselt sama tulemuse. Thomson ja Aston olid sunnitud järeldama, et neooni aatomeid on kahte liiki - aatommassiga ja .
Tähendab Dalton eksis, arvates, et ühe elemendi aatomid on kõik ühesugused. Ainult massi poolest erinevad aatomid nimetati isotoopideks. Öeldakse, et neoon koosneb kahest isotoobist, millest ühe aatommass on ja teisel . Looduses esinevad nad vahekorras . Niiviisi seletati ära, miks neooni aatommass () on murdarv. Ka teiste elementide aatommassid, näiteks klooril , on samal põhjusel murdarvud. Nüüd asetus kõik oma kohale ja lahendati veel üks looduse kapriis.
Me ei vaatle siin üksikasjalikult Astoni tööd ega seda, kuidas ta oma massispektrograafiga mõõtis aatommasside väärtusi. Need kinnitasid täielikult Thomsoni oletusi, kuid tekitasid ühtlasi uusi küsimusi. Mille poolest erinevad üksteisest ühe elemendi isotoobid? Miks on nende keemilised omadused ühesugused? Vastame nendele küsimustele hiljem, kui oleme tutvunud radioaktiivsusega, mis aga on juba järgmise peatüki teema.
Kõik need avastused on tähelepanuväärsed, kuid nende sära ei tohi meid pimestada. Võib tõesti kiita inimmõistust ja -leidlikkust, et suudeti tungida aatomimaailma, kuid sellest teati siiski veel vähe. Mis ühendab aatomid meile igapäevases elus tuntud aineteks? Kas on lootust näha oma silmaga, kuidas paiknevad aatomid ainetes, näiteks metallitükis või keedusoolas?
Kui peame silmas nägemist nähtavas valguses, siis on vastus „ei". Miks? Abbe teooria järgi on nähtava valguse lainepikkus selleks liiga suur. Järelikult tuleb otsida väiksema lainepikkusega kiirgust. Võib-olla valida röntgenikiired? Nende lainepikkus on küll sobiv, aga kuidas neid kasutada? Nähtava valguse abil saame esemetest suurendatud kujutisi tänu valguse murdumisele klaasläätsedes, aga läätsi, mis murraksid röntgenikiirgust, meil ei ole. Võib-olla saab läbi ka läätsedeta?
Proovime vaadelda seda probleemi veidi teises valguses. Abbe teooria ütleb, et kujutis tekib objektist tänu sellel hajunud lainete interfereerumisele. Hajunud röntgenikiirgust on meil võimalik vaadelda, ent mida see annab! Laue püüdis vaadelda kristalle ruumilise difraktsioonivõrena. Et talle oli teadmata nii kasutatava kiirguse koostis kui ka aatomite paiknemine kristallides, siis käis saadud difraktsioonipiltide interpreteerimine talle üle jõu. Edu saavutas W. L. Bragg (1890-1971), kes läks märksa lihtsamat teed. Ta jäädvustas filmilindile kristallidel difrageerunud röntgenikiired. Filmile jäänud täppide kuju ja paiknemist analüüsides jõudis ta järeldusele, et kristallides oli toimunud midagi peegeldumisetaolist. Kuid röntgenikiired ei saa tavalisel viisil peegelduda. Siis tuli talle pähe erakordselt hea mõte: vaadelda kristalli koosnevana korrapäraselt paiknevatest tasanditest. Iga tasand võib küll hajutada väikese osa kiirgusest, kuid koguhajumine paljudelt tasanditelt kujuneb üsna suureks. Ent see kõik on mõeldav üksnes juhul, kui tasandeilt peegelduvad lained üksteist tugevdavad. Bragg leidis, et selleks peavad lained peegelduma nurkade all, mis rahuldavad võrrandit
Selles nn. Braggi võrrandis on täisarv, kiirguse lainepikkus ning kiirguse langemis- ja peegeldumisnurk. Võrrandit rahuldavaid väärtusi kutsutakse Braggi nurkadeks.
Mis need tasandid on? Vastus oli selge. Need on kristallivõres eri suundades mõtteliselt tõmmatud tasandid. Lihtsates kristallides võivad nad aatomite keskmeid läbida (joonis 43), kuid harilikult see nii ei ole, mingit teavet aatomite paiknemise kohta kristallivõres nad aga endas kindlasti kannavad. W. L. Bragg ja ta isa W. H. Bragg (1862-1942) otsustasid sellest mõttest lähtudes valmistada seadme, mille nad nimetasid ionisatsioonispektromeetriks. See oli spektromeeter, kus kollimaatorit asendas kitsaste pilude paar. Kristall oli kinnitatud pöörlevale alusele ja sellelt peegeldunud röntgenikiired registreeriti ionisatsioonikambris.
Selle seadme abil lahendasid Braggid esimese Lauet takistanud probleemi: tegid kindlaks röntgenitoru kiirguse koostise. Suhteliselt ühtlase pideva tausta, nn. valge kiirguse kõrval olid veel mõned kitsad spektrijooned, mis sõltusid anoodist. (Selle kiirguse olemasolu järeldas hajumiskatsetest juba Barkla ja neist tuleb juttu 12. peatükis.) Need andmed said Braggide edasise töö aluseks.
Otsustanud uurida kõigepealt lihtsaid kuubilise sümmeetriaga kristalle, valisid nad tavalise soola ja temaga isomorfse soola KCl. Tulemused on esitatud joonisel 44. Kõiki neist tulenevaid järeldusi ei ole võimalik siinkohal välja tuua, kuid on teavet, mida nad annavad juba esimesel pilgul. Esiteks, spektris on kaks joont, millest tugevamat nimetatakse ja nõrgemat . Teiseks kinnitavad nad Braggi seadust iga valitud tasandihulga jaoks, näiteks
KCl korral tasandite jaoks, mida tähistatakse () (üks, null, null). Kolmandaks näitavad nad, et peegeldustasanditevahelised kaugused tasandiseeriates (), () ja () suhtuvad nagu , mis kinnitab, et kristall on kuubilise sümmeetriaga.
Ent miks puudus esimest järku peegeldus KCl kristalli tasandeiit ()? Põhjus osutus lihtsaks: kaaliumil ja klooril on ligikaudu ühepalju elektrone. Saadud tulemused vastasid aatomite paigutusele, mis on näidatud joonisel 45. See oli esimene dešifreeritud kristallistruktuur ja dešifreerijaks oli W. L. Bragg 1913. a.
Arvatavasti pole liialdus öelda, et kristallistruktuuri dešifreerimine oli üks silmapaistvamaid saavutusi kogu teaduses, mis avas uued perspektiivid peaaegu kõigile loodusteadustele. Keemikud hakkasid aatomimaailmale lähenema uut moodi.
Näiteks selgus, et aatomid ei moodusta molekule (paljudel keemikutel oli seda raske mõista), vaid käituvad ioonidena. Mineraale võidi hakata klassifitseerima aatomite paigutuse järgi. Enamiku keemiliste elementide aatomite paigutus oli ilus ja lihtne. Kogu nüüdisaegne tahke keha füüsika tugineb teadmistele, mis on saadud röntgenikiirte difraktsiooni abil.
Kasu sai ka bioloogia: aastat pärast Braggi töid tehti kindlaks juba nii keerulise ühendi nagu hemoglobiini struktuur. Mida siis Bragg oli teinud? Mil moel vältis ta raskusi, mis näisid Abbe teooria järgi ületamatud? Ta lihtsalt oletas, et aatomid paiknevad teatud viisil ja kontrollis arvutustega, kas see annab samasuguse difraktsioonipildi kui uuritav kristall. Seda proovimiste ja vigade meetodit kasutati edukalt paljude aastate kestel, kuid nüüd võime minna märksa kaugemale: võime arvutamise teel saada pildi aatomite tegelikust paiknemisest ainetes ja seda palju täpsemalt, kui võimaldaksid optilised kujutised, sest kasutatakse hajutatud kiirguse palju laiemat diapasooni ning pealegi võivad pildid olla ruumilised. Põhimõtteliselt on need pildid niisama head kui mikroskoobi abil saadud, mistõttu võib öelda, et Braggid lõid uue füüsikaharu — röntgenmikroskoopia. Selle abil täideti kujutluses olev lõhe üksikaatomite ja aine vahel.
See peatükk on sisuliselt eelmise järg. Aine koosneb aatomitest, mistõttu aine omadused sõltuvad aatomite omadustest. Nagu me eespool nägime, andsid ainete keemiline afiinsus, elektroni avastamine ja elektrolüüsi uurimine juba 19. sajandi lõpul alust oletada, et ka aatomitel on siseehitus. Millise pika tee oli aatomiteooria läbinud Daltoni päevist alates! Oletati ju, et aatomid on looduse algosakesed ja et maailm koosneb kindlast arvust igavestest ja muutumatutest aatomitest.
Vahest kõige enam sundis endisi vaateid revideerima elektroni avastamine. Kõikides aatomites peab elektrone olema. Aga kus nad seal on? Selle üle võisid füüsikud vaid filosofeerida, toetudes teadmistele klassikalisest füüsikast. Lõpuks jooksid kõik need filosofeerimised kokku mudeli juures, mille pakkus välja J. J. Thomson (1856—1940). Selle järgi koosneb aatom positiivselt laetud ainest, millesse on pikitud elektrone, mis seal võibolla intensiivselt liiguvad. Nii meenutab aatom rosinapudingit. Ehkki Thomsoni mudelit ei saadud vahetult kontrollida, rääkisid selle kasuks kõikvõimalikud analoogiad.
Analoogiatesse tuleb suhtuda ettevaatlikult ja kunagi ei saa ükski neist olla tõestuseks, et mingit paremat võimalust aatomi ehituse kindlakstegemiseks ei teatud. Nagu juba palju kordi oli juhtunud, ei leitud väljapääsu mitte suunatud otsingute tulemusena, vaid tänu juhusele. Selleks oli radioaktiivsuse avastamine A. H. Becquereli (1852-1968) poolt. A. H. Becquereli isa - avastas ultraviolettkiirguse - ja vanaisa olid tuntud füüsikud, mistõttu võib öelda, et füüsika oli tal lausa veres. Ta sooritas oma suurtöö aastal 1896, s. o. aasta pärast röntgenikiirte avastamist ja aasta enne elektroni avastamist. Need kolm tähelepanuväärset sündmust muutsid kogu füüsikat.
Nähtavasti uuris Becquerel parajasti uraani ja kaaliumi kaksiksulfaadist lähtuvat kiirgust. Teda huvitas, miks osutusid soolaga ühes kastis olnud fotoplaadid veidi valgustatuks. Tasub märkida, et seda nähtust teati, mistõttu plaate hoiti soolast eemal. Becquerel oletas, et aine kiirgas päikesevalguse mõjul midagi röntgenikiirgusetaolist. Ta keeras fotoplaadi musta paberisse ja asetas selle koos soolatükiga päikese kätte. Pärast ilmutamist avastas ta valguse eest kindlalt kaitstud plaadil tumeda laigu. Ta kordas katset. Tulemus oli sama. Seejärel märkas Becquerel, et soola mõjul tekib tume laik fotoplaadil ka siis, kui päikesevalgus puudub, ja isegi täielikus pimeduses. Ta mõistis, et oli avastanud uue nähtuse, ja nimetas selle radioaktiivsuseks.
Becquerel uuris seda nähtust väga põhjalikult. Ta tõestas, et kõik uraaniühendid on radioaktiivsed, kusjuures nende aktiivsus on ligilähedaselt võrdeline neis leiduva uraanihulgaga. Uraaniühendite radioaktiivsus ei sõltunud temperatuurist vahemikus . Radioaktiivse kiirguse mõjul elektroskoop tühjenes, mis tähendas, et tal oli samasugune ioniseeriv toime kui röntgenikiirgusel. Mis ta siis on?
Nüüd on hädavajalik jutustada veel ühest füüsikute seas elevust tekitanud sündmusest, mis oli sisuliselt Becquereli tööde jätk. 1898. a. avastasid Pierre ja Marie Curie uue elemendi, mis ei erinenud uraanist palju, kuid oli ligi miljon korda radioaktiivsem. Selle elemendita olnuks paljud hilisemad tööd võimatud ja võib-olla ei mõistaks me tänini, mis on radioaktiivsus. Avastus on väärt, et sellest jutustada.
Pierre Curie (1859-1906) oli tol ajal juba tuntud teadlane, kes oli edukalt tegelnud paljude füüsika valdkondadega. Tema nimega on seotud mõiste „Curie punkt", mis tähistab temperatuuri, mille juures ferromagneetik kaotab oma ferromagnetilised omadused. Vastavastatud radioaktiivsuse vastu äratas temas huvi tema abikaasa Marie Curie (1867-1934). Nad otsustasid mõõta eri uraaniühendite radioaktiivsust.
Nende kasutatud seadme skeem on joonisel 46. See seade koosneb kahest 8cm läbimõõduga metallkettast ja , mis asuvad teineteisest kaugusel ja mille vahel tekitati ligi -voldine potentsiaalide vahe. Kiirgav aine kanti ühtlase kihina alumisele plaadile. Ahelasse lülitatud tundlik galvanomeeter näitas mõne aja möödudes küllastusvoolu suurusjärgus .
Metalliline uraan tekitas voolu , Joachimsthalist saadud uraanipigi aga peaaegu neli korda tugevama voolu - . Pierre ja Marie Curie oleksid võinud piirduda tulemuse fikseerimisega, sest see ei erinenud oodatust suurusjärgugi võrra, aga nad tahtsid teada, kas ka kunstlikult valmistatud uraanipigi on niisama radioaktiivne. Ei olnud: see andis vaid voolu. Looduslik aine osutus kümme korda aktiivsemaks.
Curie’d oletasid, et uraanipigi sisaldab mingit uraanist tunduvalt radioaktiivsemat ainet. Et seda leida, jaotasid nad maagi komponentideks ja mõõtsid nende radioaktiivsust. Kui nad hakkasid maaki töötlema meetodil, mis sarnanes baariumi eraldamisega, said nad fraktsiooni, mille kiirgus eraldamise jooksul järjest tugevnes. Lõpuks oli see nii tugev, et uurijail ei jäänud mingit kahtlust: nad on avastamas uut, erakordselt radioaktiivset elementi. Uurides saadud fraktsiooni optilist spektrit, nägid nad kolme kahvatut baariumijoont ja nende kõrval palju tugevamaid jooni, mis ei kuulunud ühelegi teada olevale elemendile. Nad nimetasid oma uue elemendi raadiumiks. Neil õnnestus saada raadiumi sisaldavaid preparaate, mis olid miljon korda radioaktiivsemad kui uraan.
Töö oli äärmiselt raske. Neil polnud laboratooriumi, kus sooritada aeganõudvaid ja keerulisi keemilisi analüüse. Nad olid tänulikud juba selle eest, kui said uraanipigi tükke tasuta. Tajudes, et nad on saavutamas midagi olulist, panid nad töösse kogu oma energia.
Puhta raadiumi soolad olid hämmastavate omadustega: sajandikud grammidki kutsusid esile sähvatusi mõne sentimeetri kaugusel oleval tsinksulfiidekraanil ja seda isegi siis, kui soola ja ekraani vahel asus paks pliikiht. Kogu tsiviliseeritud maailm oli Curie’de avastusest hämmastuses.
Uus nähtus lummas füüsikute meeli ja seda hakati uurima paljudes laboratooriumides. Erilist esiletõstmist nende uurijate seas väärib Rutherford (1871-1937). Noore mehena oli ta rohkem huvitunud rakendusfüüsikast ja otsinud võimalust hiljuti avastatud elektromagnetlainete kasutamiseks sides. Ka teda lummas radioaktiivsus. Asunud kord seda uurima, töötas ta selle kallal elu viimaste päevadeni.
Rutherfordil oli suure teadlase tähtsaim omadus: tunnetada vaistlikult kõiges uues olulisimat ja uurida seda. Uut nähtust uurima asudes võib kergesti eksida ja uppuda vähetähtsate detailide rägastikku, sest keegi ei tea, et need on väheolulised. Rutherfordil oli palju ühist Faraday’ga: nad mõlemad olid eeskätt eksperimentaatorid. Kuigi Rutherford oli üliõpilasena saanud väga head teadmised matemaatikast, kasutas ta neid hiljem vähe; vaid mõnedes tema töödes on matemaatikat ohtralt, seegi enamjagu elementaarmatemaatika. Faraday ja Rutherford erinesid teineteisest selle poolest, et esimene tõusis tippu, mis kõrgus kogu füüsika (ja suure osa keemia) kohal, kuna teine süvenes vaid ühte kitsasse füüsika valdkonda. Võib-olla olnuks Faraday’gi vaid ühe valdkonna eriteadlane, elanuks ta sajand hiljem. Rutherford hakkas uurima radioaktiivse kiirguse olemust. On see midagi röntgenikiirgusetaolist või hoopis erilaadsete kiirguste segu? Ei fotograafia, fluorestsents ega ionisatsioon võimaldanud eristada laineid osakestest, mistõttu Rutherford otsustas mõõta nende neeldumist ainetes ja hälbimist magnetväljas.
Tema tulemused on esitatud joonisel 47 oleval skeemil, mis on füüsikas üks tuntumaid, aga ka üks eksitavamaid. Esmakordselt avaldati see Marie Curie dissertatsioonis (1903. a.) ja sestpeale on see peaaegu kõigis füüsikaõpikuis. Skeemil on näidatud -, - ja -kiirte trajektoorid magnetväljas, mis on risti joonise tasandiga ja suunatud lugeja poole. Ent skeem on vaid lihtne illustratsioon: -kiired hälbivad tõesti kergesti, kuna -kiirte hälvet on väga raske kindlaks teha. Nagu edaspidi näeme, oli ainuüksi selle avastamine väga peen töö. Joonisel 47 toodud skeemile tuleb alati lisada, nagu tegi seda Rutherford oma raamatus „Radioaktiivsus", et -osakeste hälve on sellel tublisti liialdatud. Et -kiiri oli kerge magnetväljaga hälvitada, siis uuriti neid ka esimesena. Rutherford jõudis järeldusele, et -kiired käituvad täpselt nii nagu katoodkiired ja on tõenäoliselt elektronide voog. 1900. a. tegi Becquerel fotograafilisel meetodil kindlaks, et laengu ja massi suhe on -kiirtel ligikaudu sama mis elektronidel, aga kiirus umbes pool valguse kiirusest. Rutherford ei uskunud, et elektronid saavad selle kiiruse alles hetkel, mil nad aatomist välja paiskuvad. Usutavam näis, et nad liiguvad nii kiiresti juba aatomis.
Seejärel asuti uurima radioaktiivse kiirguse ülejäänud osa. Kas see üldse hälbibki magnetväljas? Rutherford otsustas uurida võimalikult peeni kiirgusvihke, mille saamiseks ta pidi kasutama väga kitsaid pilusid. See on üks katseid, mis oleks raadiumita olnud võimatu; näiteks uraani kiirgus on nii nõrk, et läbi väga kitsaste pilude seda peaaegu ei jõuagi. Ka katsetes raadiumiga olid omad ohud: raadiumist eraldub gaasi, mida nimetatakse radooniks või raadiumi emanatsiooniks ja mis on ise radioaktiivne. Seepärast oli tähtis, et seda ei satuks seadmeisse.
Kiired, mis jäid järele, kui -kiired olid magnetvälja abil eraldatud, põhjustasid samuti tugeva ionisatsiooni. Rutherford tegi kindlaks, et see oli korda tugevam kui ionisatsiooni mille põhjustasid -kiired. Ta mõõtis 1903. aastal nende kiirte hälbimist magnetväljas. Rutherfordi seadme skeem on näidatud joonisel 48. Et saada võimalikult suure intensiivsusega kiirgust, kasutas ta kollimaatoritena paralleelseid messingplaate. Plaatide kohale asetatud alumiiniumleht oli just nii paks, et laskis läbi kiirguse, kuid takistas raadiumi emanatsiooni pääsemist seadmesse. Kui magnetväli puudus, langes elektroskoobi potentsiaal kiirte mõjul volti minutis, pärast -gaussise magnetvälja rakendamist aga volti minutis. Niisiis olid kiired hälbinud. Üsna lihtne oli ka kindlaks teha, millises suunas nad hälbisid. Et nad kaldusid -kiirtega võrreldes vastupidises suunas kõrvale, siis pidid -kiired (nii hakati seda kiirgust nimetama) olema laetud positiivselt.
Niisiis oli avastatud kaht liiki kiirgus. On see kõik või leidub veel mõni senitundmatu kiirgus? Kui raadiumi kiirgus läbis ainekihi, mis täielikult neelas - ja -kiired, täheldati nõrka ionisatsiooni, umbes kümmet tuhandikku sellest, mille põhjustas -kiirgus. Aastal 1900 tõestas Villard, et selle nõrga ionisatsiooni põhjuseks on uus radioaktiivne kiirgus, mis nimetati -kiirguseks. Villard kasutas -kiirguse registreerimiseks fotoplaati ja kinnitas, et nende läbitungimisvõime on veel suurem kui röntgenikiirtel, mida tollal peeti kõige kalgimateks. Ei leitud aga vähimatki märki, et -kiired hälbiksid elektri- või magnetväljas.
Nüüd, kui kolme radioaktiivse kiirguse põhiomadused olid teada, võidi hakata analüüsima radioaktiivsete ainete kiirgusi. Näiteks leiti, et poloonium - väga radioaktiivne element, mille Curie’d avastasid raadiumi otsides - kiirgab ainult -kiiri: kui selle elemendi kiirguse teele asetati ekraan, mis neelab täielikult -kiirguse, ei täheldatud enam mingit ionisatsiooni. Leiti, et mitte alati ei olnud - ega -kiired ühesuguste omadustega; elementidel olid need erinevad. Ent -kiirgusega kaasnes alati -kiirgus.
Nagu nägime, taipasid radioaktiivsuse uurijad üsna ruttu, et -kiired on ülikiired elektronid. Aga mis olid -kiired? Erilaengu mõõtmisest oli vähe abi, sest suurt täpsust saavutada ei õnnestunud. Raadiumi -kiirguse jaoks oli see võimalikku mõõtetäpsust arvestades , s. t. ligikaudu pool vesiniku elektrokeemilisest ekvivalendist. Järelikult on -osakesed, olgu nende päritolu milline tahes, mõõtmetelt lähedased aatomitele. Kui nende laeng võrdub elektroni laenguga, peab nende mass olema kaks korda suurem kui vesinikuaatomi oma. Rutherford oletas, et -osakesed on kas vesiniku või heeliumi aatomid. 1908. aastaks oli ta peaaegu kindel, et need on heeliumi aatomid.
Ent kuidas veenduda selles lõplikult? Rutherford otsustas ette võtta otserünnaku: teha spektraalanalüüsi abil kindlaks, mis on -osakesed. See eksperiment näitab enam kui ükski teine, kui originaalseid lahendusi võis Rutherford probleemidele leida. Meile tundub spektraalanalüüsi kasutamine tuumafüüsikas tavaline, kuid Rutherfordi kaasaegseile, kes olid harjunud kasutama uurimiseks vaid fotograafiat ning mõjutamist elektri- ja magnetväljaga, võis see näida üsna ootamatu. See oli kahtlemata üks hiilgavamaid otsustavaid eksperimente füüsikas.
Rutherfordi mõte oli koguda piisavalt a-osakesi, tekitada neis elektrilahendus ja uurida siis tekkinud helendust spektromeetriga. Tõsi küll, selleks pidi ta olema kindel, et seadmesse ei .satu võõraid aatomeid. Rutherford ja tema kaastöötaja Royds valmistasid joonisel 49 näidatud seadme. Selle tähtsaim osa oli vilunud klaasipuhuja poolt meisterlikult valmistatud peenike klaastoru , milles oli puhastatud radoon, mis, nagu oli juba teada, kiirgab üksnes -osakesi. Mõne aja möödudes võib torus oleva gaasi pumbata lahendustorru ja seda seal uurida. Kui midagi ei avastata, võib suruda gaasi uuesti torru ja jätta ta sinna pikaks ajaks.
tunni möödudes sooritasid eksperimentaatorid esimese vaatluse, kuid ei märganud midagi. Järgmisel päeval nad kordasid katset ja nägid heeliumi spektri kõige heledama joone kohal nõrka kollast joont. Kuid ühest joonest tõestuseks ei piisanud. Nelja päeva pärast õnnestus jälgida heeliumi rohelist ja kollast joont ning kuue päeva möödudes oli nähtav kogu heeliumi spekter.
On kerge kujutleda, mida mehed tundsid. Eksperiment oli kavandatud hiilgavalt ja, nagu selgus, ei hoidnud teadlasi liiga kaua ärevas teadmatuses. Enam polnud kahtlust, et -osakesed on laetud heeliumiaatomid. Nende erilaengu väärtus lubas oletada, et nende laeng võrdub kahe elektroni laenguga. Teiste sõnadega, -osakesed on heeliumioonid. Rutherford tegi selle tulemuse teatavaks neli nädalat hiljem, kui talle anti kätte Nobeli preemia keemia alal.
Sellest alates said -osakesed Rutherfordi armsaimaks uurimisvahendiks. Nad olid talle nii lähedased, et ta pidas neid peaaegu elusateks. Nad olid massiivsed ja liikusid kiirusega, mis on võrdne umbes kümnendikuga valguse kiirusest, nii et võisid isegi purustada aatomeid, millega nad põrkusid. Selle kõige üleslugemine, mida Rutherford ja tema kaastöötajad -osakestega teha suutsid, viiks meid teemast liiga kaugele.
Lahendamist vajanud põhiküsimus seisnes järgmises: mis toimub radioaktiivsete elementide aatomites, et sealt eraldub elektrone, laetud heeliumiaatomeid või suure läbitungimisvõimega kiirgust, mis, nagu selgus, sarnanes röntgenikiirgusega. 1904. aastaks oli Rutherford jõudnud seisukohale, et radioaktiivsus tõestab aatomite lagunemist. Radioaktiivsed aatomid ei ole stabiilsed; mõnikord laguneb mingi aatom spontaanselt ja eraldub osa selle ainest - -osake. Ka uus aatom, mis seejuures tekib, ei pruugi olla stabiilne. Jälle kiiratakse aatomist välja osa selle ainest ja tekib uus aatom. Nii jätkub see, kuni tekib mitteradioaktiivne aatom, mis on stabiilne.
On üks katse -osakestega, millest lihtsalt peab siinkohal rääkima, sest see on üks tähtsamaid eksperimente füüsikas, Jutt on katsest, milles jälgiti -osakeste hajumist
aines. See võimaldas luua J. J. Thomsoni „rosinapudingist" kvalitatiivselt erineva kujutluse aatomist, mille järgi peaaegu kogu aatomi mass on koondunud tema keskmes asuvasse tillukesse tuuma.
Kõnesolev katse on huvitav juba selle poolest, et näib juhuste kokkusattumisena. Võib tunduda ülekohtune Rutherfordi suhtes, et tema, kes alati kavandas oma katsed suurima hoolega, tegi oma tähtsaima avastuse tänu juhusele, ehkki avastuse hiilgust see ei vähenda. Rutherfordil oli alati varuks tühiseid katsekesi uute õpilaste tarvis. Polnud viga, kui need kuhugi ei viinud, sest nende eesmärk oli treenida õpilasi katseseadmetega ümber käima.
Niisiis, 1909. aastal oli Marsdenile (sünd. 1889. a.), kes töötas Geigeri (1882-1945) juhendamisel, antud ülesanne uurida, kas -osakesed peegelduvad õhukeselt kuldlehelt. -osakeste jälgimiseks kasutati üht Rutherfordi lemmikmeetodit - tsinksulfiidekraani helendamist -kiirte toimel. Kui võtta nõrk kiirgusallikas, võib vaatleja, kelle silmad on pimedusega kohanenud, märgata väikese suurendusega mikroskoobi abil üksikuid valgussähvatusi. Iga sähvatus tähendaks ühe -osakese sattumist ekraanile. Nii võidi jälgida aatomimaailma üksiksündmusi. Rutherfordile kahtlemata meeldis, et tema õpilased seda nähtust jälgisid ja rakendasid. Ta ise oli absoluutselt veendunud, et õhukest kuldlehte läbivad massiivsed -osakesed hälbivad oma teelt üsna vähe. Enamik osi läbis lehe tõepoolest vaid veidi kõrvale kaldudes, kuid mõned osakesed, ligikaudu üks -st, nagu märkis Marsden, kaldusid kõrvale rohkem kui võrra. Marsden ei julgenud sellest kohe Rutherfordile rääkida ja kontrollis hoolikalt, kas tema katsetes pole vigu. Rutherford ei suutnud seda uskuda ja hüüdis, et see on kõige ebatõepärasem asi, millest ta on kuulnud. Kuid ebatõepärasesse tuli siiski uskuda. 1911. aastal jõudis Rutherford veendumusele, et -osakeste hajumist õhukeses kuldlehes saab selgitada üksnes siis, kui oletada, et osakesed mööduvad väga lähedalt teistest positiivselt laetud osakestest, mis on aatomitest palju väiksemad. Kulla aatomil peab olema väike positiivselt laetud tuum, mida ümbritsevad elektronid. See oli uue füüsikaharu - tuumafüüsika - sünd.
Rutherfordi mõte polnud 1911. aastal mitte päris uus. Juba enne 1906. aastat oli Johnstone Stoney selle välja pakkunud kui ühe võimaliku seletuse aatomi ehituse kohta, kuid ilmselt jäi see tähele panemata või unustati, sest see oli mitte millelegi toetuv hüpotees. Seevastu Rutherfordi tulemuse vastu vaielda ei saadud.
Järgmiseks sammuks oli leida, millest koosneb aatomituum. Raadiumi tuum oli võimeline lagunema ja kiirgama heeliumi tuumi, mille mass võrdus nelja prootoni omaga, ent see ei tähendanud veel, et raadiumi tuumas oleks heeliumi tuum. Nad võivad olla vaid püsivad rühmad, mis kergesti moodustuvad. Samuti ei tähendanud -osakeste kiirgumine, et neid peaks olema aatomituumades. Kuid ikkagi püsis aastaid kujutlus, et aatomid koosnevad tuumadest, kus on tihedalt koos elektrone ja prootoneid, ning tuuma ümber tiirlevatest elektronidest ja et see kõik püsib koos mingil imelisel moel. Et aatom saaks olla elektriliselt neutraalne, peab elektrone ja prootoneid olema ühepalju.
See kujutlus muutus alles siis, kui Chadwick (1891-1974) avastas uue elementaarosakese — neutroni. Uus osake avastati berülliumi pommitamisel -osakestega - veel üks eksperiment Rutherfordi moodi. Tekkinud läbivat kiirgust peeti esmalt -kiirguseks, sest see ei põhjustanud ionisatsiooni ega hälbinud elektri- ja magnetväljas. Ent Chadwick mõistis, et kiirguse energia ei sobi selle vaatega kokku, ja tõestas, et avastatud läbiv kiirgus peab olema prootonitega massilt võrdsete, kuid laenguta osakeste voog. Berüllium ja heelium ühinesid süsinikuks ja selles protsessis kiirati neutroneid.
Oma hoogsas jutustuses libisesime mööda mitmetest nende aastate füüsika suursaavutustest: 1919. aastal kunstlik radioaktiivsus, 1930. aastal osakeste kiirendamine ning aastal 1931 tsüklotron. Selleks ajaks teati juba, et aatomituuma võib vaadelda koosnevana neutronitest ja prootonitest, kusjuures kaks neutronit ja kaks prootonit moodustavad eriti püsiva rühmituse, mida kiiratakse -osakestena; -osakeste kiirgumine oli tõlgendatav kui neutronite muundumine prootoniteks. Kas need kujutlused vastavad rohkem tegelikkusele kui kujutlus tuumasisestest ja -välistest elektronidest, ei tea keegi.
Sellest ajast peale hakkas tuumafüüsika jõudsasti arenema. 1939. a. saadi esimesed katseandmed selle kohta, et tuum võib jaguneda ka kaheks ligikaudu võrdseks osaks, kusjuures vabaneb palju energiat. See protsess nimetati tuuma lõhustumiseks. 1942. a. said teadlased tuumade lõhustumise oma kontrolli alla, mis andis inimkonnale uue energiaallika, kuid ka aatomipommi. 1952. a. teostati tuumasüntees - kahe tuuma ühinemine, misjuures vabanes palju rohkem energiat kui tuuma lõhustumisel. See võimaldas luua võimsama relva - vesinikupommi. Mis puutub tuumasünteesi juhtimisse, siis ei tea praegu keegi, kas see on võimalik, küll aga teatakse, et see võimaldaks saada energiat peaaegu piiramatul hulgal ja et tänapäeval on inimkond selle hüve kasutamisest veel kaugel.
Niisiis võimaldas lihtne vaatlus, mille sooritas Becquerel aastal 1896, füüsikal seitsmekümne aastaga läbi käia pika tee. Avanes võimalus vaadata aatomi sisse. Purunes suur hulk Daltoni kujutlusi aatomist, kuid tema keemiateooriad jäid peaaegu täiesti puutumata. Inimkond sai uued, lausa ammendamatud energiaallikad ja ühtlasi võimaluse hävitada täielikult elu meie planeedil.
Selles peatükis püüan ühendada mitmed eraldi vaadeldud teemad. Asjaolude sunnil pean kasutama äärmist lihtsustamist, sest mõningaid küsimusi ei saa argikujutluste raames üldse seletada. Nii olen ma sunnitud kasutama mudeleid, mida enamik füüsikateoreetikuid peaks täiesti ebarahuldavaiks. õigustan end sellega, et need mudelid on näitlikud - pole tähtis, kas nad on ekslikud või mitte -, ja aitasid füüsikal jõuda nüüdisaegsele tasemele. Kõigil, kes õpivad füüsikat, on kasulik teada, kuidas füüsika arenes. See võib olla tähtsamgi kui nüüdisaegsete seisukohtade ülipõhjalik uurimine, sest nagunii need muutuvad.
On lihtsalt hämmastav, kui kaugele arenes füüsika puhtklassikalistele kujutlustele toetudes. Meie aju on ehitatud kohanema selle maailmaga, mida tajume oma meeleorganitega. Ei ole aga mingit põhjust oletada, et meid ümbritsevas tavalises maailmas kasutatavad seadused kehtivad ka aatomimaailmas. Ent me oleme võimelised tegema tohutuid ekstrapolatsioone ja leidma oma tulemustele veel mingi tähenduse. Selle suurepäraseks näiteks on aatomituuma (mõõtmed suurusjärgus ) avastamine Rutherfordi poolt, kes tugines seadusele, mida rakendatakse planeetide liikumise uurimisel.
Seda tüüpi ekstrapolatsioone ei saa jätkata lõputult, kusagil peab klassikaliste seisukohtade rakendatavus lõppema. Tõepoolest, me teame kõige tavalisemaid nähtusi, mida klassikaline füüsika seletada ei suuda. 19. sajandil jäeti need vaatlemata lootuses, et äkki nad seletavad end ajapikku ise. Seda ei ole nad teinud.
Üks seletamatutest nähtustest on keha värvuse muutumine kuumutamisel. Keha, mille temperatuur on kõrgem ümbritseva keskkonna temperatuurist, hakkab kiirgama rohkem energiat, kui ta seda saab, ja me tunneme, et keha on soe. Temperatuuril umbes hakkab keha punaselt hõõguma. Kui temperatuur veelgi tõuseb, siis kiiratav spektririba laieneb ja temperatuuril hakkab keha hõõguma valkjalt. Miks on see nii?
Rayleigh (1842-1919) oli üks füüsikutest, kes mõistis, kui tähtis on selle ülesande lahendamine. Ta väitis, et kui süsteemi energia jaguneks võrdselt kõigi võimalike võnkumiste vahel, langeks lühematele lainetele palju suurem energia kui pikkadele, sest neid on palju rohkem, nagu seda võib näha ka analoogiast seisulainetega pingul keelel.
Esimesena mõõtsid energia jaotumist kuumutatud tahkete kehade kiirgusspektrites Lummer (1860-1925) ja Pringsheim (1859-1917) 1893. a. Absoluutsete tulemuste saamiseks oli vaja kasutada absoluutselt musta keha, s. o. keha, mis neelab kogu talle langeva kiirguse. Üsna hästi sobis selleks väikese avaga õõnes keha. Kui seda keha kuumutada, on avast väljuv kiirgus sarnane absoluutselt musta keha kiirgusega. See kiirgus lahutati sulapaost (fluoriidist) prismaga spektriks ja mõõdeti bolomeetriga — seadmega, mille töö põhineb plaatina takistuse sõltuvusel temperatuurist. Tundliku Wheatstone’i silla abil oli võimalik mõõta väga väikesi takistuse muutusi, mistõttu oli jälgitav temperatuuri kõikumine.
Tulemused on esitatud joonisel 50. Nagu näeme, on kiirguse intensiivsus teatud lainepikkuse kohal maksimaalne, temperatuuri tõustes aga nihkub see lühema lainepikkuse poole. Keha hõõgub punaselt temperatuuril, mil tema kiirguse lühilaineline piir jõuab spektri punasesse osasse. Kõrgematel temperatuuridel haarab kiirgus üha suurema osa nätavast spektrist
ja jõuab temperatuuri tõustes spektri ultraviolettosani. Kiirguse intensiivsuse tõus lainepikkuse lühenedes - graafikul joonte parempoolsed harud - oli heas kooskõlas Rayleigh’ ja Jeansi (1877-1946) teooriaga, kuna intensiivuse vähenemine lühematel lainepikkustel erines sellest märgatavalt.
See oli probleem teoreetikutele.
Teine probleem kerkis üles seoses aatomisoojuste mõõtmisega. Nagu eespool nägime, lootsid Dulong ja Petit, et tulevikus kinnitavad täpsed mõõtmised, et kõikide elementide aatomisoojused on võrdsed. See näis järelduvat ka teooriast. Ent hilisemad mõõtmised näitasid hoopis, et mõnel elemendil, näiteks süsiniku teisendil teemandil, on erisoojus väga väike.
Teadlased on väga pettunud, saades uusi andmeid, mis lükkavad allesloodud teooriad ümber. Käesoleval juhul oli lohutuseks fakt, et temperatuuri tõustes teemandi erisoojus kasvab ja ühtib kõrgel temperatuuril teoreetilisega. Täpselt samuti käitusid ka kõik teised elemendid, mille erisoojus ei langenud kokku teooria poolt ennustatuga. Kuid see nihutas vaid probleemi teisele tasandile. Miks sõltus erisoojus temperatuurist? Seegi oli küsimus, millele klassikaline füüsika ei suutnud vastata.
Kolmandaks probleemiks oli valguse kummaline mõju mõnele materjalile.
Juba 1839. a. märkas A. C. Becquerel (1788-1878) - radioaktiivsuse avastaja A. H. Becquereli vanaisa -, et ühe tema galvaanielemendi elektromotoorjõud muutus, kui selle ühele elektroodile langes valgus. 1873. a. oli Willoughby Smith häiritud ühe elektriahela vastuolulisest käitumisest. Ta avastas lõpuks, et see on seotud ilmaga: kui päike paistis, muutus ahelasse lülitatud seleenitüki takistus. 1887. a. märkas Hertz, kes uuris allesavastatud elektromagnetlainete levimist, et indutseeritav säde tekkis kergemini siis, kui sädevahemik polnud indutseeriva sädeme eest millegagi varjatud.
See oli veel üks Hertzi hiilgav avastus. Märgata nii tühiselt väikest efekti, mida võinuks selgitada ka teisiti, nõudis tõelist teadlase vaistu. Et teha kindlaks, kas see pole mitte tingitud valgusest, asetas Hertz sädevahemiku vahele läbipaistmatu ekraani ja veendus, et indutseeritud säde oli tunduvalt nõrgem. Ta proovis klaasiga. Tulemus oli sama. Hertz oli segaduses. Siis ta mõistis, et klaas laseb läbi ainult nähtavat valgust. Kui ta kasutas ekraanina ultraviolettkiiri läbilaskvat kvartsi, jäi indutseeritud säde muutumatuks. Järelikult põhjustas selle nähtuse indutseerivast sädemest lähtuv ultraviolettkiirgus. Tänapäeval saab seda efekti demonstreerida palju ilmekamalt, kui suunata ultraviolettkiired otse sädevahemikku.
Muide, ükski nendest nähtustest ei tekitanud klassikalisele füüsikale tõsiseid raskusi. Nad polnud ebatavalisemad kui näiteks Faraday avastus, et valguse polarisatsioonitasand magnetväljas pöördub. Võis loota, et neile leitakse seletus klassikalise füüsika raames.
Järgmine efekt oli märksa salapärasem. Aastal 1888 avastas Hallwachs (1859-1922), et ultraviolettkiired laadisid tühjaks negatiivselt laetud elektroskoobi, kuna positiivselt laetuga ei juhtunud midagi. Millest niisugune erinevus? Põhjus seisneb selles: elektronide ülekülluse korral suudab ultraviolettkiirgus anda neile piisava energia elektroodidest väljumiseks, kuid ei suuda midagi teha siis, kui elektrone on puudu. See nn. fotoefekt muutus mõistetavamaks alles pärast elektroni avastamist. Probleemi hakati lahendama. 1899. a. kinnitas Thomson, et ultraviolettkiirguse mõjul kiirguvad osakesed on tõepoolest elektronid. Ta tegi kindlaks magnetvälja tugevuse, mille korral kiirguvad osakesed ei suutnud enam jõuda positiivse potentsiaaliga plaadini, mis asus vaakuumis teada oleval kaugusel osakeste allikast. Ta määras osakeste erilaenguks . See oli sama mis elektronidelgi. Thomson märkas, et vastu ootusi ei kahanenud vool vaakuumtorus nullini momentaanselt, ning pakkus ühe võimaliku selgitusena, et elektronid kiiratakse välja nullist erineva kiirusega.
1900. a. sai Lenard sama tulemuse veidi teisiti ning kontrollis, kas elektronid ikka kiiratakse nullist erineva kiirusega. Kui emiteerivate elektronide kiirus nullist erineb, võivad nad teise elektroodini jõuda isegi juhul, kui see on negatiivselt laetud. Emiteerivate elektronide kiirust võiks seega määrata voolu nulliks muutva pinge järgi. Lenard avastas hämmastava fakti: emiteerivate elektronide kiirus ei sõltu valguse intensiivsusest. Intensiivsuse suurendamisel kiirgus küll rohkem elektrone, kuid nende väljalendamiskiirus jäi samaks.
Kiirus sõltus valguse lainepikkusest, olles seda suurem, mida lühem on lainepikkus. Klassikaline füüsika oli selle probleemi ees jõuetu.
Neljas probleem oli, et gaaslahendusel olid joonspektrid, mida me eespool vaatlesime kui kasulikku tähelepanekut. Klassikaline füüsika ei andnud võtit selle nähtuse tõlgendamiseks. Ilmselt pidi aatomites midagi võnkuma ja usutavasti olid need elektronid. Samuti ei osatud seletada Balmeri (1825-1898) poolt 1885. a. tehtud tähelepanekut, et lihtne valem
seob omavahel osa jooni vesiniku spektris. Selles valemis on spektrijoone sagedus (kiirus/lainepikkus), täisarv ja konstant, mis on tänaseks teada seitsmekohalise täpsusega. Ka teised teadlased leidsid Balmeri seeriaga sarnaseid seeriaid, mille intensiivseimad jooned asuvad spektri nähtavas osas.
Need olid, tähtsamad lahendamist ootavad füüsikaprobleemid 19. sajandi lõpul ja esimene neist - musta keha kiirgus - lahendatigi esimesena. Lahendust ei mõistetud kohe ega nii selgelt, et oleks vastuvaidlematult usutud selle õigsusse.
Planck (1858-1947) mõistis, et lühilainelise kiirguse intensiivsuse langemise uurimiseks tuleb leida mingi põhjus energia vähendamiseks. Kuidas toimib valitsus, kui ta püüab vähendada kulutusi mingisugusteks teenusteks? Ta paneb peale maksud, mistõttu teenused lähevad kallimaks. See ei tähenda suurema hulga raha kulutamist, sest kõrgemat hinda on võimelised maksma vähesed inimesed. Nii ütles Planck 1900. a. välja oletuse, et võib-olla jaguneb kiirgusenergia väikesteks portsjoniteks (kvantideks), mille suurus on võrdeline sagedusega . Võrdeteguri - nüüd nimetatakse seda Plancki konstandiks - tähistas Planck -ga. Planck näitas, et tema teooria põhjendaks suurepäraselt Lummeri ja Pringsheimi tulemusi.
Arvatavasti pole ühtki teooriat arendatud nii vastumeelselt. Planck pakkus selle välja vaid kui probleemi empiirilise lahenduse, mille lootis ajapikku asendatavat paremaga. Uus teooria ei meeldinud õieti kellelegi, sest näis liiga veider. Ja see jäetigi kõrvale, kuid mitte kauaks. 1905. a. taaselustas kvantteooria Einstein, kes seletas selle abil Lenard’i fotoefektikatse tulemusi. Oletame, et elektron vabaneb ja väljub metallist ühe Plancki kvandi mõjul. Elektroni energia sõltub üksnes kvandi energiast. See oligi seletus Lenard’i üllatanud tulemusele, et emiteerivate elektronide energia ei sõltu valguse intensiivsusest. Mida suurem on intensiivsus, seda rohkem kvante ja elektrone vabaneb. Nüüd oli asi selge vähemalt kvantitatiivselt. Enamik teadlasi võttis Einsteini teooria kohe vastu, mis tähendas, et koos sellega tunnistati ka kvantteooriat. Korraga oli astutud kaks tähtsat sammu.
Ent Einsteini teooriat oli vaja täpsemalt kontrollida. Senised katsetulemused polnud head selleks, et olla veenvad. Pinnaefektide uurimine on üldse raske, sest ka tühine mustus pinnal võib põhjustada väga suuri mõõtevigu. Seepärast otsustas Millikan 1916. a. suunata oma jõupingutused tõeliselt usaldusväärsete tulemuste saamisele. Ta valmistas seadme (joonis 51), milles sai valguse suunata mitmele vaakuumis asuvale pinnale, mida oli võimalik puhastada sealsamas vaakuumis. Tema töö põhines Lenard’i meetodil: tuli mõõta pinge, mille korral emiteerunud elektronid ei jõua enam vastas asuvale elektroodile.
Kasutades erineva lainepikkusega kiirgusi, näitas ta, et kvandi energia on täpselt võrdne elektroni kineetilise energia ja veel mingi suuruse summaga. See oli oletatavasti energia, mis kulus elektronil metalli pinnast väljumiseks.
Seega lahendas Plancki kvant- teooria kaks ülaltoodud probleemi. 1912. a. näitas Debye (1884-1966) kaudsel teel, et kvantteooria abil võib seletada mõnede ainete anomaalseid erisoojusi. Debye vaatles tahket keha kui pidevat keskkonda, mis võib võnkuda sarnaselt pingul keelega, kuid kolmes mõõtmes. Lühematel lainetel oli sagedus suurem ning energia jaotus lainete vahel kvantteooria nõuetele vastavalt. Debye teooria järgi sõltub ainete erisoojus nii temperatuurist kui ka aatomitevahelistest jõududest. Nüüd selgus, miks mõnedel ainetel oli anomaalne erisoojus. Polnud siis ime, et teemandil, kõige tugevamal teada oleval ainel, milles aatomitevahelised jõud on kõige tugevamad, on see anomaalia kõige suurem.
Kõige raskem oli lahendada joonspektrite probleemi, kuid ka see vandus kvantteooriale alla; tuli vaid püstitada veel üks argikujutlustele risti vastu käiv oletus. Vesiniku aatom koosneb tuumast ja selle ümber tiirlevast elektronist. Kui elektron liiguks mööda ringorbiiti samade seaduste järgi kui planeedid - külgetõmbejõud on analoogselt gravitatsioonijõuga pöördvõrdeline elektroni ja tuuma vahelise kaugusega -, peaks ta liikuma mingi kindla sagedusega. Kuid pole põhjust, mis sunniks teda sagedust säilitama: tiirlev elektron kiirgab energiat ja peab tuumale järk-järgult lähenema, kuni lõpuks kukub selle sisse. Kuid vesiniku aatomid ei käitu sugugi nii; nad on püsivad kui tahes pika aja kestel ja kiirgavad samal ajal muutumatutel sagedustel.
1913. a. pöördus Bohr (1885-1962) abi saamiseks kvantteooria poole. Ta ütles, et kuna elektron ei saa kiirata osa kvandist, siis ta normaalolekus ei kiirga üldse, vaid asub nn. kindla energiaga statsionaarses olekus. Kui elektroni mingil moel ergutada ja sundida teda üle minema suurema energiaga olekusse, võib ta, kiiranud kvandi, naasta madalama energiaga olekusse. Lihtsate ja tõenäoste oletuste abil suutis Bohr näidata, et kiiratavad kvandid vastavad täpselt võrrandist tulenevatele lainepikkustele. See järeldus oli nii tähelepanuväärne, et leidis kohe tunnustust, ehkki Rutherford avaldas mõningaid kahtlusi teooria suhtes, mis nii palju erines tema enda „mehhanistlikest ideedest".
Tänapäevaks on Bohri teooria oma tähtsuse siiski kaotanud. See näib küll olevat tõenäone, kuid kaugeltki mitte veenev. Selle abil ei ole võimalik seletada ülejäänud aatomite käitumist. Mõned õppejõud väidavad isegi, et Bohri teooriat kui eksitavat ja puudulikku pole vaja üliõpilastele õpetada. Tegelikult oleks Bohri teooria õppeprogrammist väljajätmine viga, sest sellega võeti mikroosakeste füüsikas kasutusele kujutlus statsionaarsetest olekutest. Bohri idee on füüsika jaoks nii teedrajava tähtsusega, et oleks väga kahju, kui üliõpilased ei teaks midagi selle dramaatilisest ilmumisest ja mõtleksid, et see sündis lihtsalt teoreetikute loogiliste manipulatsioonide tulemusena. Füüsika ei koosne aga mitte ainult õigete vastuste loetelust.
Joonspektreid pidanuks olema kõikides elektromagnetkiirgustes. Varsti avastatigi need veel spektri infrapunases ja ultravioletses osas. Meie lihtsa ainekäsitluse jaoks on tähtsam, et igal ainel on joonspekter ka röntgenikiirguses. Seda nimetatakse karakteristlikuks kiirguseks. Barkla avastas karakteristliku kiirguse hajunud röntgenikiiri uurides 1908. a., seega varem kui röntgenikiirte difraktsiooni. On tähelepanuväärne, et ta suutis sellise fundamentaalse avastuse teha nii algelisel moel.
Barkla täheldas seost materjali paksuse ja seda läbinud röntgenikiirte kimbu intensiivsuse vahel. Kui kiirgus oleks olnud homogeenne, oleks selle intensiivsus pidanud vähenema proportsionaalselt ainekihi paksenemisega ja intensiivsuse logaritmi sõltuvust ainekihi paksusest oleks esitanud graafikul sirge (joon a joonisel 52). Kui kiirgus oleks olnud mittehomogeenne, pidanuksid kiirguse rohkem neelduvad komponendid järk-järgult välja filtreeruma, neelamis-tunnusjoon oleks muutunud ja graafik ei oleks olnud enam sirge (joon b joonisel 52).
Sellisel lihtsal teel uurisid Barkla ja Sadler 1908. a. eri elementide poolt hajutatud röntgenikiiri. Kõigepealt leidsid nad neeldumis-tunnusjoone röntgenitorust väljuva kiirguse jaoks, asetades selle teele paksustest alumiiniumlehtedest paki, mille paksust järk-järgult suurendati. Kiirgus oli mittehomogeenne. Kui uuriti eri elementides hajunud kiirgust, saadi kuni väävlini sarnased tunnusjooned. See näitas, et hajunud kiirgus oli samasuguse olemusega, kuigi märksa väiksema intensiivsusega. Elementidel kroomist tsingini avastati graafikutel sirgestumise tendents (graafik c joonisel 52), mis vihjas mingi domineeriva komponendi olemasolule. Graafikute sirge osa kalle oli elemenditi erinev, vähim tsingil ja suurim kroomil. Seepärast järeldati, et igas elemendis hajunud kiirgus sisaldab selle elemendi jaoks iseloomulikku komponenti. Nad nimetasid selle -kiirguseks. Röntgenitoru erinevaid ergutuspingeid kasutades avastasid nad, et samadel elementidel on ka vähem läbitungivad karakteristlikud kiirgused. Nad nimetasid need -kiirguseks.
Nagu me nüüd teame, avastas W. H. Bragg need kiirgused röntgenikiirte difraktsioonikatsetes uuesti. Kahjuks ei kasutanud Barkla uusi meetodeid ja tema järgnev avastus, -kiirgusest palju kalgim J-kiirgus, ei leidnudki kinnitust. Füüsikas ei ole haruldane, et vanemad teadlased ei võta omaks uusi, täiuslikumaid uurimisvahendeid.
Braggi avastust kasutas Moseley (1887-1915), kes fotografeeris eri elementide poolt kiiratud difraktsioonipilte. Ta tõestas (tahvel IV), et keemiliste elementide karakteristlikud röntgenispektrid muutuvad süsteemselt nende järjekorranumbri kasvades. Seda kasutades parandas ta elementide järjekorda Mendelejevi perioodilisussüsteemis. Ta näitas väga täpselt, et raud, koobalt ja nikkel paiknevad just selles, aga mitte nende aatommasside poolt antud järjekorras (; ; ).
Moseley töö oli hiilgav. Ajal, mil kangelasteoks peeti isegi hariliku röntgenitoru tegemist, valmistas ta toru pöördanoodiga, nii et katoodkiirte teele oli võimalik seada anoodi eri osi. Ta jätkas katseid, ehkki Rutherford keelitas teda ühinema oma radioaktiivsust uuriva rühmaga, sest teised uurijad olevat röntgenikiirte valdkonnas, palju kompetentsemad kui Manchesteri koolkond. Moseley langes Esimeses maailmasõjas just ajal mil oli juba antud käsk tema demobiliseerimiseks. Füüsika oli kaotanud suure eksperimentaatori. Tema tööd avasid aatomi järjekorranumbri füüsikalise mõtte. Enne peeti neid vaid arvudeks, mis määravad elementide järjekorda perioodilisuse süsteemis.
Nagu nägime, laiendasid füüsikasündmused aastail 1895-1913 füüsika uurimisvaldkonda ning põhjustasid muutuse, mida võiks nimetada isegi teadusrevolutsiooniks. Alates 1913. aastast, kui mitte arvestada Esimesest maailmasõjast tingitud lünka, ilmus uusi ideid sellisel hulgal, et on võimatu neid kõiki siin isegi lühidalt kokku võtta.
Kuid ühest neist lausa peab rääkima, sest nii suur on selle teoreetiline ja praktiline tähtsus.
Jutt on lainemehaanikast, mille võttis aastal 1924 kasutusele L. de Broglie (sünd. 1892). Tema idee lähtus füüsikalise sümmeetria printsiibist: kui põhjustab -s mingi efekti, siis tingib -s sellesama või mõne teise efekti. Just seda liiki kaalutlused veensid kunagi Faraday’d, et magnetism peab tekitama elektrit. De Broglie argumentatsioon seisnes järgmises: kui Plancki teooria näitas, et lainetel on teatud mõttes korpuskulaarsed omadused, siis miks ei võiks osakestel olla lainete omadusi? Ta püstitas isegi konkreetse oletuse: keha impulsiga käitub kui laine pikkusega , kus on Plancki konstant.
Selle absurdsena näiva ettepaneku võtsid teadlased tõsiselt vastu ning mõne aasta jooksul sooritati kaks katset, mis näitasid, et elektronid võivad tõepoolest difrageeruda.
Esimene neist katseist - selle korraldasid Davisson (1881-1958) ja Germer (1896-1971) - oli teatud mõttes juhuslik, kuid teine, mille sooritas J. J. Thomsoni poeg G. P. Thomson (1892-1977), tehti spetsiaalselt de Broglie teooria kontrollimiseks.
Davisson uuris elektronide hajumist nikli pinnal ja sattus segadusse, sest mõõtmistulemuste seas olid ootamatud maksimumid. Mingil põhjusel pääses seadmesse niiskust ja nikkel oksüdeerus. Davisson püüdis oksiidi eemaldada, kuumutades niklit vaakuumis, ja kui ta katset kordas, oli hajumispilt märgatavalt muutunud. Maksimumid olid näha palju selgemini. Nikkel oli muutunud, paljude üliväikeste kristallide asemele olid ilmunud mõned suured! Kui Davisson kuulis Inglismaal toimunud konverentsil de Broglie ideest, seostas ta oma tulemusi kohe uue teooriaga. Järgmistes katsetes mõõtsid Davisson ja Germer elektronide hajumist nikli monokristallil, kasutades üksnes kiirendavat pinget. 1928. aastaks saavutasid nad täieliku kooskõla de Broglie teooriaga.
Thomsoni katsed olid märksa vahetumad. Ta asetas pingega kiirendatud elektronide teele õhukese kuldlehe. Seda läbinud elektronid tekitasid fotoplaadil pildi, mis oli üsna sarnane röntgenikiirte difraktsioonipildiga. Ka tema saavutas aastal 1928 oma katsetulemuste ja de Broglie teooria vahel täieliku kooskõla.
Ei ole teada, kuidas saab osake käituda nagu laine, ja seetõttu tundub, et de Broglie mõte pole veel nüüdki, aastat hiljem füüsikaga täielikult ühinenud.* Arvatavasti ei ole võimalik registreerida üheaegselt aine korpuskulaarseid ja lainelisi omadusi. Kuid teoreetikutest füüsikud olid õnnelikud ka füüsikalise pildita ja lõid teooria - lainemehaanika, mille abil lahendatakse edukalt füüsika- ja keemiaprobleeme. Näiteks asendas see Bohri vesinikuaatomi teooria. Lainemehaanika üksikasjalisem esitus viiks meid käesoleva raamatu eesmärkidest kaugele.
*Nüüdisfüüsikul on sellega vist siiski raske soostuda.
Kolmest praktilisest tulemusest peab siiski rääkima. Et osakesed, nagu elektronid ja neutronid, difrageeruvad, siis võiksid nad aine ehituse kohta anda samasugust informatsiooni nagu röntgenikiired. Kui elektrone kiirendav pinge on 50kV, on elektronide lainepikkus märksa väiksem kui röntgenikiirtel. Elektronid ei tungi sügavale materjalide sisse ja seetõttu on nende difraktsiooni väga edukalt rakendatud tahkete kehade pindade uurimisel. Neutroneid on raskem kasutada, sest intensiivse neutronikimbu tekitamiseks on vaja tuumareaktorit. Ent tulemused, mis saadi neutronite difraktsiooni uurimisel, osutusid lausa revolutsioonilisteks selle kõrval, mida oli andnud elektronide difraktsiooni uurimine. Neutronid käituvad nagu väikesed magnetid ja mõjuvad seetõttu vastastikku vaid aatomi nende osadega, millest on tingitud aine paramagnetilised omadused; paljude aatomite korral mõjuvad nad vastastikku üksnes tuumaga. Magnetilist vastastikust mõju uurides saadi otsene kinnitus mõttele, mille Neel (sünd. 1904. a.) oli esitanud 1932. a.: lisaks ferromagnetismile, paramagnetismile ja diamagnetismile on olemas veel mõned magnetismiliigid. Kuid Neeli tööde üksikasjalisem kirjeldus ja jutustus sellest, kuidas neutronite difraktsioon tema seisukohti kinnitab, ei mahu minu raamatusse.
Kolmas lainemehaanika rakendus on veel tähtsam. Nimelt loodi lainemehaanikale toetudes uus instrument - elektronmikroskoop. Et elektronid on võimelised murduma - nende trajektoor kõverdub nii elektri- kui ka magnetväljas -, siis on võimalik väljadele sobivat kuju andes valmistada elektronläätsi. Et elektronide lainepikkust saab kergesti vähendada alla , siis võib elektronmikroskoobi lahutusvõime olla väiksem aatomite mõõtmetest. Sellise ettepaneku tegi 1926. a. Busch. Ideest haarasid kinni paljud teadlased, kuid kõigil tekkis suuri tehnilisi raskusi stabiilsete pingete ja sobiva kujuga väljade saamisel. Kolmekümnendate aastate lõpuks olid olemas elektronmikroskoobid, millel oli niisama suur lahutusvõime kui optilistel mikroskoopidel. Tänapäeval on elektronmikroskoopide lahutusvõime suurusjärgus .
Elektronmikroskoobil on suuri puudusi: preparaadid peavad olema väga õhukesed, et elektronid suudaksid neid läbida, ja nende omadused ei tohi vaakumis muutuda. Neile raskustele vaatamata on elektronmikroskoobid andnud teadusele väga palju. Esmakordselt oli võimalik „näha" kristallides molekule (tahvel VI) suurepärases kooskõlas varasemate uurijate loodud kujutlustega kristallide moodustumisest. Võib julgelt öelda, et bioloogias põhjustas elektronmikroskoop revolutsiooni.
Sellega pean ma peatüki lõpetama. Ausalt öeldes olen rahul, et sain seda teha kirjeldades, kuidas edukate katsete najal luuakse uued teooriad, mis omakorda viivad teadlaste mõtted uute, teaduse edendamiseks tarvilike seadmete loomisele. Kui kaua võiks see kesta?
Kordan küsimust, mis lõpetas eelmise peatüki: kas füüsika arenemine jätkub või kas keegi selles üldse kahtleb? Kui aus olla, siis näiteks mina kahtlen küll. Iga füüsik teab, et ekstrapoleerimine on ohtlik asi, millega ei tohi liialdada.
Loomulikult on füüsikal liikumapanevat jõudu, kuid kas tal on ühtlasi nii palju seesmist energiat, et ületada arenemisel paratamatult tekkivad takistused? Füüsikud tegutsevad kahes suunas: uurivad uusi mõistatuslikke nähtusi ja süvendavad olemasolevaid teadmisi. Esimene suund pakub vähe lootusi: pole meil ju teada midagi, mis oleks niisama saladuslik kui gaaslahendus möödunud sajandil. Teisest võimalusest rääkides tuleb nimetada kolme valdkonda.
Kõigepealt gravitatsioon ja elektromagnetism. Enamik füüsikuid tunnetab kahtlemata, nagu tunnetas
omal ajal Faraday’gi, et nendel nähtustel peab olema midagi ühist, kuid siiani pole seda leitud.
Teiseks, tuuma koos hoidvate jõudude olemus. Milline jõud hoiab positiivselt laetud osakesi koos ruumiosas, mille läbimõõt on ? Elektrostaatiliste jõudude toimel peaksid nad otsekohe laiali lendama. Ent aatomituumad teatavasti on stabiilsed.
Ja lõpuks elu ise. Kuidas suudavad meie keha moodustavad aatomid anda meile liikumis-, paljunemis- ja mõtlemisvõime? Sellele küsimusele ei ole lihtne vastata ega ole ka õige seda füüsikaprobleemiks taandada. On väidetud, et „elu on suurte molekulide iseloomulik omadus", teisiti öeldes, kui me mõistame, mil moel kasvavad polümeeride molekulid, oleme lahendanud ka elu saladuse.
Paljud teadlased arvavad, et selle hüpoteesiga on raske nõustuda. Meie keha aatomite kooslus on nii imepäraselt otstarbekas normaalseks funktsioneerimiseks ja oma rikutud korrapära taastamiseks, et on raske loobuda mõttest, nagu olnuks sellel kavandaja, nimetatagu seda kas või Jumalaks. Aga nime andmisega pole ju ühtki probleemi lahendatud. Minu arvamus on, et eksisteerib midagi teadusele senitundmatut, mida võib-olla ei olegi võimalik avastada.
Selle kinnitamiseks pöördugem tagasi magnetismi juurde. Oletame, et ferromagneetikuid ei oleks olnud. Kas oleks siis avastatud magnetismi teised vormid? Nende avastamiseks on vaja eelkõige tugevat magnetvälja, mille loomiseks vajame rauda, s. o. ferromagneetikut. Me oleksime võinud luua vastuoludeta pildi perioodilisussüsteemist ka magnetismist midagi teadmata, kuid sellele lõpetatud kuju andmiseks tulnuks ikkagi postuleerida mingi tundmatu nähtuse olemasolu.
Nii võib juhtuda, et läheneme füüsika lõpule. Gravitatsiooni ja elektromagnetismi vahelise seose leidmine võib olla meie jaoks liiga raske, tuumajõudude olemuse mõistmine liiga kallis (niigi on eksperimendid selles valdkonnas enamiku maade jaoks ülearu kulukad), aga elu mõistatuse lahendamiseks võib vaja minna teadmisi, mida meil ei ole.
Siiski, füüsikale veel tegevust jätkub. Näiteks on väga vähe teada atmosfääri funktsioneerimisest, sellest, kuidas kujuneb ilm ja kuidas sünnib äike. Taoliste probleemide lahendamiseks vajatakse endiselt andekaid inimesi. On võimalik, et füüsika on oma arenemises kõrgpunkti juba läbinud ja teadusliku tegevuse raskuspunkt nihkub mingi teise distsipliini, näiteks bioloogia valdkonda, kus füüsika osa on küll tähtis, kuid siiski juba alluv.
Võib-olla pole mul üldse õigus. Mind abistasid suuresti raamatud, mis olid kirjutatud selliste teadlaste nagu Lodge’i, Hertzi ja J. J. Thomsoni poolt üle aasta tagasi. Aga kas pöördub keegi aasta pärast minu raamatu poole, et teada saada, mis probleemid erutasid meid? Saavad nad vaid naerda mu liig naiivsete mõtete üle või on nad minu oletustest hämmastunud? Ma ei saa seda kunagi teada.