Miks on otsene välgutabamus harilikult surmav? Kas äikese ajal tuleks puu alla varju ronida või lagedal väljal seista? Kas mõistlikum on rahulikult seista, kükitada või joosta? Miks inimestel juuksed püsti tõusevad, kas see on ohu märk? Miks on äikesetormi ajal lehmad, hobused ja lambad tavaliselt suuremas ohus kui inimesed?

On palju lugusid sellest, kuidas kuulus USA teadlane ja riigimees Benjamin Franklin lennutas läheneva äikesetormi ajal tuulelohet, et näidata selle loodusnähtuse elektrilisi omadusi. Miks välk teda ei tapnud?

Kas äikesepilve saaks põhimõtteliselt ka kompassiga leida?

Välk kusagil	Franklin oma katset tegemas. Arvatakse, et päris nii see asi tal siiski ei käinud.

Tänapäeval ümbritsevad meid kõikjal esemed ja nähtused, mille iseloomustamisel kasutame sõna elekter. See sõna on jõudnud meieni kreeka keelest. Nii nimetasid vanad kreeklased kuldse läikega metallisulamit ja ka sellega väliselt sarnast ainet – merevaiku (kr - elektron). Nad märkasid, et villase riidega hõõrutud merevaigutükk suudab kergeid ainekübemeid enda külge tõmmata. Ajapikku hakati kõiki selliseid loodusnähtusi nimetama merevaigu-sarnasteks ehk elektrilisteks.

Kreeka päritoluga on ka sõna magnet. Magnesia kivina (kr - Magnetis lithos) tunti vanas Kreekas kivimit, mis oli suuteline raudesemeid enda külge tõmbama. Elektrilise ja magnetilise tõmbejõu sarnasusest lähtuvalt oli vana- ja keskajal kombeks arvata, et need jõud põhimõtteliselt ei erinegi. Alles uusaegsetes esimestes teaduslikes käsitlustes hakati elektri- ja magnetnähtusi selgelt omavahel eristama. 19. sajandi keskel avastati, et elektrilistel ja magnetilistel jõududel on siiski ühine allikas. Elektri- ja magnetnähtused on looduses toimiva üldise elektromagnetilise vastastikmõju avaldumisvormid. Jõud, millega me oma igapäevases elutegevuses vältimatult kokku puutume, on valdavalt elektromagnetilise päritoluga. Nendeks on näiteks elastsusjõud, hõõrdejõud ja ka elusorganismide lihasjõud. Elektrijõud hoiavad koos lihtaine aatomeid. Vedeliku või gaasi molekulideks, tahkisteks ja keerulisteks orgaanilisteks ühenditeks liidab aatomeid keemiline side, mis on samuti tingitud elektromagnetilisest vastastikmõjust.

Elektromagnetjõudude kaks tähtsaimat tehnilist rakendust on elektroenergeetika ning elektriline side- ja infotehnika. Elektroenergeetika hõlmab kogu inimtegevust elektrienergia tootmisel, ülekandel ja kasutamisel. Elektrijaamades muudetakse elektrienergiaks mingi osa kütuse põlemisel vabanevast soojusest, voolava vee kineetilisest energiast või koguni aatomituumade seoseenergiast. Neid jaamu nimetatakse seetõttu vastavalt soojus-, hüdro- ja tuumaelektrijaamadeks. Päikesepatarei muundab elektrienergiaks valguskiirguse energiat. Taskulambipatareis, autoakus ja teistes keemilistes vooluallikates saadakse elektrienergiat keemilisel reaktsioonil vabaneva energia arvelt.

Tarvitis leiab aset vastupidine protsess. Elektrienergia muundub mehaaniliseks energiaks (elektrimootoris), valguskiirguse energiaks (elektrilambis), soojuseks (kütteseadmes) või mingiks muuks energia liigiks. Elektrienergia on mugav vahelüli loodusest ammutatava ja inimtegevuses kasutatava energia vahel. Seda soodustab asjaolu, et elektrienergiat saab üle kanda juhtmete abil. Pole vaja mingeid rihmu, võlle ega hammasrattaid.

Elektrienergia suurima puudusena võiks nimetada raskusi suurte energiakoguste salvestamisel.	Tulevikus saame oma ekraanid pärast tööd kokku rullida?

Elektrienergia suurima puudusena võiks nimetada raskusi suurte energiakoguste salvestamisel. Elektrilise energia tootmine ja tarbimine peavad toimuma samaaegselt.

Elektroenergeetikast veelgi kiiremini areneb tänapäeval elektromagnetiline infotehnika. See hõlmab andmete, kõne, muusika või muu sellise esitamist ja ülekandmist elektromagnetilise signaalina. Samas on ka tegemist info elektrilise, magnetilise või optilise salvestamise ning töötlemisega. Elektriliste infotöötlus- ja sidesüsteemide kiiretoimelisuse aluseks on elektromagnetilise vastastikmõju suur levimiskiirus – kuni 3·10⁸ m/s.

Käesolev õpik käsitleb elektromagnetilise vastastikmõju seaduspärasusi, mille tundmine aitab meil mõista väga paljude loodusnähtuste tekkimist. Nendel seaduspärasustel põhineb ka elektriliste ja optiliste seadmete töö, mida me oma igapäevases elus pidevalt kasutame. Seega on vastavad teadmised nii tunnetusliku kui ka rakendusliku väärtusega.

W. Gilberti uurimuse tiitelleht.	W. Gilbert näitab elektri­katseid kuninganna Elisabeth I õukonnas.

Elektromagnetismi teadusliku uurimise algatajaks peetakse Inglise arsti ja füüsikut William Gilbertit. Aastal 1600 ilmus trükist tema töö De magnete..., mille täieliku pealkirja võib eesti keelde tõlkida kujul: Magnetist, magnetilistest kehadest ja suurest magnetist – Maast. Gilbertist oli juttu juba põhikooli Elektriõpetuses. Seal mainiti ka Benjamin Franklinit, kes lõi esimese tervikliku elektrinähtuste teooria, esimest bioelektromagnetismi uurijat Luigi Galvanit ning esimese vooluallika loojat Alessandro Voltat. Põgusalt oli juttu Ohmi seaduse avastajast Georg Simon Ohmist ning voolu magnetvälja esmauurijast Hans Christian Örstedist.

Käesolevas kursuses on aga aukohal elektrostaatika põhiseaduse formuleerija Charles Coulomb, magnetostaatika põhiseaduse formuleerija André Marie Ampère, elektromagnetilise induktsiooni avastaja Michael Faraday ning kõiki elektromagnetnähtusi kirjeldava ühtse teooria looja James Clerk Maxwell. Eestimaalt pärit mehena pälvib meie erilist tähelepanu ka Emil Lenz, induktsioonivoolu suunda määrava reegli formuleerija.

Valgusnähtuste teaduslik käsitlus sai alguse 17. sajandil, kui I. Newton püstitas hüpoteesi valgusest kui silmale nähtamatute osakeste voost, mis levivad ühtlases keskkonnas sirgjooneliselt. Neid osakesi nimetas ta korpuskuliteks, mida võib pidada nüüdisaegsete kvantide eelkäijateks.

Isaac Newton (1642-1727)	Christiaan Huygens (14. aprill1629 – 8. juuli 1695)

Mõned aastad pärast Newtonit püstitas C. Huygens teise hüpoteesi, mille kohaselt valgus levib lainetena. Ta arvas, et valguslaine levimiseks on vajalik mingi eriline keskkond, mis täidab kogu universumi. Seda ainet nimetati eetriks. Tänapäeval on teada, et mingit erilist, valguse levimiseks vajalikku keskkonda ei eksisteeri ja valgus levib ka tühjuses.

Aastal 1802 tegi T. Young katseid, mis näitasid, et kitsast avast läbi minnes kaldub valgus oma esialgsest levimissuunast kõrvale, valguse teel oleva tõkke taha. Kuna veelained levivad ka tõkete, näiteks kivide taha, siis Youngi katse tõestas, et valgusel on laineline olemus.

Järgmise olulise sammu valguse laineteoorias tegi J. C. Maxwell, kes 1865.a. tõestas teoreetiliselt, et on olemas elektromagnetlained, mis levivad ka tühjuses ja seda kiirusega 3·10⁸ m/s. See tulemus langes küllalt hästi kokku tolleks ajaks määratud valguse kiirusega. Sellest järeldas Maxwell, et valgus on elektromagnetlaine.

Nüüdisaegsele valguse kvantteooriale pani aluse 1900.a. M. Planck, kes võttis kasutusele valgusosakesed ehk kvandid. Muidu ei suutnud ta teoreetiliselt seletada tahkete kehade kiirgusspektreid. Planck pidas kvante vaid teooriat lihtsustavateks abivahenditeks.

A. Einstein näitas 1905.a., et kvandid on reaalselt olemas, sest ta seletas nende abil ära fotoefekti katsed, mida laineteooria ei suutnud seletada.

Sellest alates on selge, et valgusnähtusi pole võimalik kirjeldada ainult lainete või ainult osakeste abil. On nähtusi, mida saab seletada lainete abil ja teisi nähtusi saab seletada kvantide abil. On ka selliseid nähtusi, mida saab seletada nii lainete kui kvantide abil. Tutvume nendega põgusalt ka käesoleva kursuse raames.

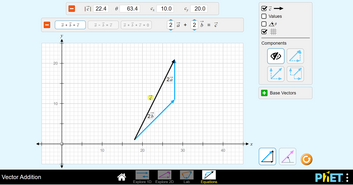
Me alustame elektromagnetismi õppimist tutvumisest staatilise ehk ajas muutumatu elektrivälja ning magnetväljaga. Saame teada, mida on nende kahe välja kirjeldustes ühist ja mida erinevat. Tutvume kummagi välja põhiseadusega (Coulomb’i  ja Ampère'i seadused) ning peamiste neid välju iseloomustavate vektorsuurustega, milleks on elektrivälja tugevus E ja magnetinduktsioon B. Kursuse teises osas vaatleme elektri- ja magnetvälja muutumist ajas. Elektromag­netilise induktsiooni nähtuse uurimisel selgub meile, et elektri­väli ja magnetväli on ühtse elektro­magnetvälja kaks piirjuhtu. Tutvume ka välja energiat salvestavate seadmetega, milleks elektrivälja korral on kondensaator ja magnetvälja puhul induktiivpool. Kursuse kolmandas osas uurime elektromagnetvälja levikut elektromagnetlainetena. Vaatleme valguse tekkimisel ja kadumisel ilmnevaid valguse osakese-omadusi ning valguse levimisel avalduvaid laineomadusi. Õpime kirjeldama vastavaid optilisi nähtusi: inter­ferentsi, difraktsiooni ja polarisatsiooni. Kursuse neljandas osas vaatleme valguse ja aine vastastikmõju. Põhiteemadeks on geomeetriline ehk kiirteoptika, valguse levimiskiiruse erinev muutumine eri ainetes ja valguse tekkeprotsessid. Käsitleme valguse kahte peamist tekkemehhanismi: soojuskiirgust ja luminestsentsi.

Lihtsaim elektrinähtus, mida me kõik kindlasti kogenud oleme, seisneb kehade elektriseerumises nende vastastikusel hõõrdumisel. Elektriseerunud kehade vahel mõjub jõud. Näiteks liibub kuivale nahale kunstkiust valmistatud särk. Pärast pestud ja kuivade juuste kammimist tõmbuvad juuksed kammi külge. Elektriseerunud kehade kohta öeldakse ka, et nad on laadunud või omandanud elektrilaengu.

Elektrilaeng ehk edaspidi lihtsalt laeng (tähis q või Q) on mingit keha iseloomustav füüsikaline suurus. Laeng näitab, kui tugevasti keha osaleb elektromagnetilises vastastikmõjus. Laengu olemasolu kehal saab kindlaks teha vaid elektri- ja magnetjõudude põhjal.

Sõna laeng kasutatakse õige mitmes tähenduses. Esiteks nimetatakse laenguks keha omadust osaleda elektromagnetilises vastastikmõjus. Rääkides elementaarosakese laengust, peame silmas selle osakese omadust osaleda elektri- ja magnetnähtustes. Sõna laeng teine tähendus on nimetatud omadust kirjeldav füüsikaline suurus. Kõneldes laengu suurusest, rõhutame laengu mõõtmise võimalikkust. Laengu kui suuruse mõõtmine on aga tegelikult kehade võrdlemine nende laengu kui omaduse põhjal. Peale selle mõistetakse füüsikas laengu all ka niisuguste osakeste kogumit, millel on olemas laeng kui omadus. Näiteks räägitakse ruumi mingis osas paiknevast laengust või siis laengu liikumisest. Neid väljendeid tuleb aga käsitleda lühenditena. Tegelikult on jutt ikkagi laengut omavate osakeste paiknemisest või liikumisest.

Juba 9. klassi Elektriõpetusest teame, et looduses on kahte liiki laenguid. Neid on kokkuleppeliselt hakatud nimetama positiivseteks ja negatiivseteks. Selline nimetusviis võimaldab laengu liiki väljendada märgiga arvväärtuse ees (+ või –).

Meile mehaanika kursusest tuttav gravitatsioonijõud on ainult tõmbejõud. Samas tuntakse ka vaid ühte liiki “gravitatsioonilaengut”, mida on kombeks nimetada massiks. Elektrijõud võivad aga olla nii tõmbe- kui tõukejõud. Seega peab ka laenguid olema kahte liiki. Laengu arvväärtus määrab jõu suuruse, märk aga suuna. Samanimeliselt laetud kehade vahel mõjub tõukejõud, erinimeliste laengute korral aga tõmbejõud.

Elektrit mittejuhtiva niidi otsas rippuvat kerget metall­fooliumist keha nimetatakse sageli elektripendliks. Ka meie toimime edaspidi nii.

Füüsikalise looduskäsitluse aluste (FLA) kursuses õpitud atomistliku printsiibi põhjal teame, et ainel on olemas osakesed, mis pole jagatavad veel väiksemateks osakesteks. Kuna laeng on osakese omadus, siis ei tohiks ka laeng olla kuitahes väike.

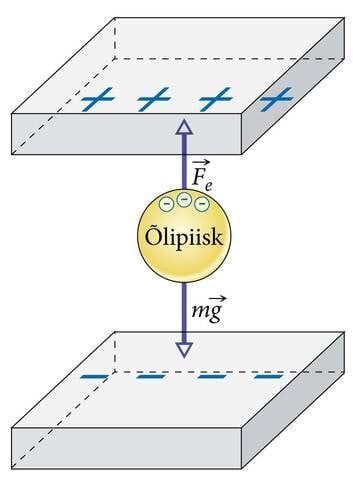
J.1.3 Robert Andrews Millikani katse on oma olemuselt ühtaegu lihtne ja geniaalne - väga väikeste laengute mõõtmiseks on väga raske leida piisavalt tundlikku mõõteriista. Aga elementaarlaengutele mõjuvat elektrijõudu oli võimalik võrrelda õlipiiskadele mõjuva raskusjõuga.	Robert Andrews Millikani katse on oma olemuselt ühtaegu lihtne ja geniaalne - väga väikeste laengute mõõtmiseks on väga raske leida piisavalt tundlikku mõõteriista. Aga elementaarlaengutele mõjuvat elektrijõudu oli võimalik võrrelda õlipiiskadele mõjuva raskusjõuga.

Laengu jagatavuse küsimust asus 20. sajandi algul uurima ameerika füüsik Robert Andrews Millikan. Ta vaatles mikroskoobi abil tillukesi laetud õlipiisku, millele mõjus vertikaalselt üles suunatud elektrijõud. Kui see jõud tasakaalustas piisa raskusjõu, jäi piisk mikroskoobi vaateväljas seisma.

Olles mõõtnud piisa ruumala ning teades õli tihedust, suutis Millikan määrata piisa massi ja raskusjõu, järelikult ka elektrijõu. Selle põhjal leidis Millikan piisa laengu. Ta märkas peagi, et kõik tema katsetulemused olid mingi kindla laengu väärtuse täisarv-kordsed.

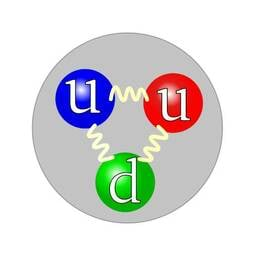
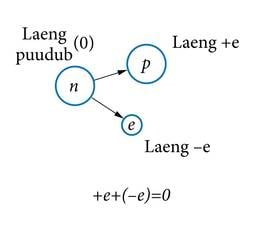
Vähimat katseliselt tuvastatavat laengu väärtust on hakatud nimetama elementaarlaenguks (e). 20. sajandil tehti kindlaks, et kõigi ainete aatomid koosnevad prootonitest, neutronitest ja elektronidest. Prootonid ja neutronid moodustavad aatomi tuuma, mille ümber liiguvad elektronid. Prootonil on laeng +e, elektronil –e, neutronil laeng puudub. Seega on iga keha laengu suurus nende osakeste laengute summa.

Keemiast teame, et aatomi tuum käitub keemilistes reaktsioonides stabiilse tervikuna. Aatomi kuuluvus kindlale elemendile on määratud prootonite arvuga tuumas. Neutraalses aatomis on elektrone ja prootoneid ühepalju. Elektronide lisandumisel aatomisse moodustub negatiivne ioon ja elektronide lahkumisel positiivne ioon. See võimaldab mõista kehade elektriseerumist hõõrdumisel. Sõltuvalt vastavate ainete aatomite ehitusest võivad väliskihi elektronid ehk valentselektronid ühelt kehalt teisele üle minna. Keha, mis saab elektrone juurde, laadub negatiivselt. Seevastu keha, millelt elektronid ära rebiti, laadub positiivselt, sest tema aatomi­tuumade positiivne laeng on osaliselt tasakaalustamata. Elementaarlaenguga osakeselt ei saa tema laengut ära võtta nii nagu elektriseerimisel rebitakse kehalt lahti elektrone. Laeng on osakesele sama kindlalt omane suurus nagu mass. Kui näiteks elektronil ei oleks laengut –e, siis ta polekski enam elektron. Negatiivse elementaarlaengu olemasolu on üks tunnustest, mis määrab elektroniks nimetatava osakese. Elementaarlaengu jagamatuses avaldub atomistlik printsiip.

Mehaanikast teame, et impulss ja energia on suletud süsteemis jäävad suurused. Elektrinähtuste uurimisel selgub, et ka elektrilaeng on jääv. Laeng ei teki ega kao. Kehade süsteemi kogulaeng saab muutuda vaid laetud osakeste sisenemisel süsteemi või väljumisel sellest. Kui laetud osakeste niisugust liikumist ei toimu, nimetatakse süsteemi elektriliselt isoleerituks. Tegemist on tüüpilise suletud süsteemiga. Selle mõistega tutvusime juba Füüsikalise looduskäsitluse aluste kursuses.

Laengu jäävuse seadust pole kuigi lihtne rangelt tõestada. Vastavas katses peaks ju mõõtemääramatus olema väiksem elementaarlaengust. Paljud erinevad elektrinähtused on aga seletatavad vaid lähtudes laengu jäävusest. Seetõttu usuti laengu jäävuse seaduse kehtivusse juba ammu enne elektronide ja prootonite avastamist.

Selgeid viiteid laengu jäävuse seadusele leiame keemiast. Tervikuna neutraalne keedusoola (NaCl) kristall dissotsieerub lahustumisel vees positiivseteks naatriumi ja negatiivseteks kloori ioonideks (Na⁺ ja Cl_–), mida tekib ühepalju.

Laengu jäävuse seadus sai füüsikas lõpliku kinnituse alles osakeste vahel toimuvate muundumisreaktsioonide uuri­misel. Selgus, et laetud osakeste teke või kadumine nendes reaktsioonides on võimalik vaid paarikaupa. Uue positiivse osakese tekkimisel ilmub ka negatiivne osake. Nii näiteks tekivad vaba neutroni lagunemisel üheaegselt positiivne prooton ja negatiivne elektron (J.1.4). Neutron ongi siin see elektriliselt isoleeritud süsteem, millest oli juttu eespool.

Laengu jäävus väljendab maailma üldist keskmist elektrilist neutraalsust. Kujutlegem hetkeks, mis juhtuks, kui kõigis kehades oleksid ühte liiki laenguga osakesed ülekaalus. Sel juhul mõjuksid ju kõigi kehade vahel elektrilised tõukejõud. Seda me aga looduses ei näe. Meid ümbritsevad kehad on tavaliselt neutraalsed. Positiivse ja negatiivse laenguga osakesi on neis ühepalju. Kui üks keha saab positiivse laengu, siis laadub mingi teine keha negatiivselt. Kehade laengute summa jääb muutumatuks. Aga see ju ongi laengu jäävus.

Niisiis kehtib laengu jäävuse seadus: elektriliselt isoleeritud süsteemi kogulaeng on jääv suurus.

Hõõrdeelektrit uurides märkame kohe, et ained erinevad oma elektrijuhtivuse poolest. Kui näiteks kuivad juuksed kammi külge tõmbuma hakkavad, siis võime sellest jagu saada kammi niisutades. Seega on kraanivesi elektrit juhtiv aine. Läbi tema lahkuvad laetud osakesed kammilt. Puhas (destilleeritud) vesi aga ei juhi elektrit. Samuti ei õnnestu meil tavaliselt hõõrumise teel laadida märgi esemeid ja metallkehi, sest tasakaalustamata laeng lahkub neilt. Laenguga osakesed liiguvad läbi eseme ja seejärel läbi meie käte.

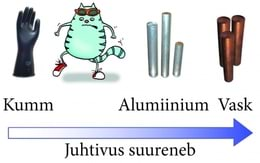
Inimkeha juhib elektrit suhteliselt hästi. Metalleset ei õnnestu hõõrumise teel elektriseerida just seetõttu, et nii ese kui ka seda hoidev käsi juhivad elektrit. Olles tõmmanud kätte kummikinda, võime elektriseerida ka metalleset. Kummi elektrit ei juhi ning laeng püsib esemel.

Põhikooli Elektriõpetusest teame, et metall ja kraanivesi sisaldavad arvukalt liikumisvõimelisi laetud osakesi ehk vabu laengukandjaid. Sõnaga vaba tähistame seejuures laetud osakese võimet liikuda elektrijõudude toimel kogu vaadeldava keha või ainekoguse piires. Nagu kõik aineosakesed, nii osalevad ka laengukandjad kaootilises soojusliikumises. Kui aga neile mõjub kindla suunaga elektrijõud, hakkavad nad täiendavalt liikuma ka selle jõu mõjul.

Vabade laengukandjate sisalduse järgi jagunevad ained kolme rühma: juhid, dielektrikud (ehk mittejuhid või ka isolaatorid) ja pooljuhid.

Juhid on ained, milles vabade laengukandjate arv on väga suur. See ei erine oluliselt aatomite (või molekulide) üldarvust. Tüüpilised juhid on metallid, kuna valentselektronid pole neis seotud ühegi kindla aatomiga ja on järelikult vabadeks laengukandjateks. Elektrit juhtivates vedelikes (näiteks kraanivees) täidavad vabade laengukandjate osa keemiliste lisandite ioonid.

Dielektrikud ehk mittejuhid sisaldavad väga vähe vabu laengukandjaid ning seetõttu on neis tekkiv elektrivool reeglina väga nõrk. Vabade laengukandjate puudumine gaasilises või vedelas dielektrikus on enamasti põhjustatud sellest, et dielektriku aatom või molekul on elektriliselt neutraalne süsteem. Elektrijõud ei suuda laetud osakesi sellest süsteemist välja rebida. Tahke dielektrik võib küll koosneda erimärgiliselt laetud ioonidest, aga elektrijõud ei suuda neid liikuma panna.

Pooljuhid on saanud oma nime vahepealse elektrijuhtivuse järgi juhtide ja dielektrikute kui kahe äärmuse vahel. Laengukandjad ei ole pooljuhtides küll alati vabad, kuid neid saab suhteliselt kergesti vabadeks muuta. Seetõttu on pooljuhtidele iseloomulik vabade laengukandjate arvu tugev sõltuvus temperatuurist, pealelangevast valgusest, lisandite sisaldusest põhiaines jne. Pooljuhi elektrijuhtivus on nende tingimuste muutmise teel reguleeritav. See pooljuhtide väärtuslik omadus leiab laialdast kasutamist nüüdisaegses elektroonikas.

Kindlaid piire ainete kolme rühma vahel pole. Näiteks on metallis vabade laengukandjate arv aatomite üldarvust tavaliselt suurem, sest aatomil võib olla väliskihis mitu elektroni, mis saavad muutuda vabadeks laengukandjateks. Ainet loetakse aga juhiks veel ka siis, kui mitme tuhande aatomi või molekuli kohta tuleb vaid üks vaba laengukandja. Nii on see näiteks kraanivee korral. Pooljuhtides on vabade laengukandjate arv aatomite arvust väiksem ligikaudu miljon korda, dielektrikutes aga reeglina üle miljardi korra.

Veel tuleb märkida, et sõna juht kasutatakse nii elektrit juhtiva aine kui ka sellest ainest valmistatud keha tähistamiseks.

Laengukandjate suunatud liikumist nimetatakse elektrivooluks.

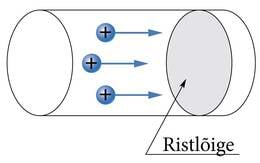
Voolu tekkimiseks on vajalik nii vabade laengukandjate olemasolu kui ka nende liikumist põhjustav jõud. Elektrivoolu iseloomustavaks suuruseks on voolutugevus I. Voolutugevus näitab, kui suur laeng läbib ajaühikus juhi ristlõiget

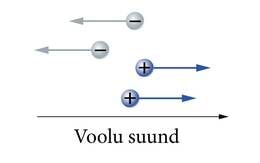
Ristlõike all mõistetakse seejuures voolu suunaga ristuva lõike pinda (J.1.5). Voolu suunaks on kokkuleppeliselt valitud positiivsete laengukandjate liikumise suund. Negatiivsed laengukandjad (näiteks elektronid metallis) liiguvad seega voolu kokkuleppelisele suunale vastupidises suunas (J.1.6).

On oluline mõista, et pole üldse tähtis, kumma märgiga laengukandjad reaalselt aines liiguvad. Nii positiivsete laengukandjate liikumine paremale kui negatiivsete liikumine vasakule joonisel 1.6 tähendab üht ja sedasama voolu suunda. Liikuvate laengukandjate märgi määramine on võimalik vaid keerulisemates katsetes. Tavalise vooluringi korral me laengukandjate märki teada ei saagi, aga see asjaolu ei sega vooluringide uurimist.

Voolutugevuse ühikuks on üks amper (1 A). Amper on SI elektriline põhiühik. See tähendab, et kõik teised elektriliste suuruste mõõtühikud tuletatakse tema abil. Amper defineeritakse vooluga juhtmete magnetilise vastastikmõju kaudu (p.1.4.2). Voolutugevuse I leidmiseks peame juhi ristlõiget läbiva laengu q jagama selleks kuluva ajaga t (valem 1.1 ). Laeng ise on seega esitatav voolutugevuse ja aja korrutisena

Viimase seose põhjal on defineeritud elektrilaengu SI-ühik üks kulon (1 C). Kui voolutugevus juhis on üks amper, siis läbib ühe sekundi jooksul juhi ristlõiget laeng suurusega üks kulon. Järelikult

Elementaarlaengu väärtus on 1,6021892·10^-19 kulonit. Prak­ti­listes arvutustes piisab reeglina täpsusest

Üks kulon on väga suur laeng. Kammi või klaaspulka elektriseerides anname talle laengu, mille suurusjärk on üks nanokulon kuni üks mikrokulon (1 μC = 10^-6 C). Ta­be­lis 1.1 on toodud mõned iseloomulikud voolutugevused.

Maksimaalset laengut, mille vooluallikas suudab vooluringist läbi viia, nimetatakse sageli vooluallika mahutavuseks (mitte mahtuvuseks!) ja teda mõõdetakse amper-tundides. Kui voolutugevus juhis on üks amper, siis läbib ühe tunni jooksul juhi ristlõiget laeng üks amper-tund (1 A·h).

Kuna ühes tunnis on 3600 sekundit, siis 1 A·h = 1 A·3600 s = 3600 C.

Elektrijõude asus 1784. aastal mõõtma Charles de Coulomb. Mõõteseadmena kasutas ta väändkaalu ehk torsioonkaalu. Väändkaalu töö aluseks on mõõdetava jõu võrdlemine peenikese traadi väändel tekkiva elastsusjõuga.Coulomb’i poolt kasutatud väändkaalu korral (J.1.7) rippus traadi (1) küljes horisontaalne mittejuhtiv varras (2), mille ühes otsas paiknes uuritav metallkuulike (3), teises otsas aga kuulikest tasakaalustav raskus (4). Vardaga ristuva jõu rakendumisel kuulikesele pöördus varras seni, kuni traadi väände elastsusjõud tasakaalustas kuulikesele mõjuva jõu. Coulomb tegi kindlaks, et nurk j, mille võrra varras joonisel punktiiriga kujutatud tasakaaluasendist välja pöördus, oli võrdeline jõuga. See võimaldas pöördenurga kaudu jõudu mõõta. Oma katsete korraldamisel lähtus Coulomb eeldusest, et varda küljes paikneva, algselt neutraalse kuulikese (3) puudutamisel teise täpselt samasuguse, kuid laetud kuulikesega (5) jaotub laeng kahe kuulikese vahel võrdselt.

Coulomb'i väändkaalu ehk torsioonkaalu põhimõtteskeem.	Coulomb'i katse, nii nagu seda kunagi tehti.

Coulomb mõõtis kuulikeste vahel mõjuva jõu F ja suurendas kuulikeste vahekaugust kaks korda. Selle tulemusena vähenes jõud neli korda. Nüüd suurendas Coulomb kuulikeste vahekauguse esialgsega võrreldes kolmekordseks ja veendus selles, et jõud oli üheksa korda esialgsest väiksem. Seega vahekaugusel r mõjus laetud kuulikeste vahel jõud F, vahekaugusel 2r jõud F/4, vahekaugusel 3r jõud F/9 jne. Tulemus oli esitatav ka kujul

Nii võis Coulomb teha järelduse, et laetud kehade vahekauguse ruudu ja elektrijõu korrutis on konstantne, teiste sõnadega: laetud kehade vahel mõjuv elektrijõud on pöördvõrdeline kehade vahekauguse ruuduga

Selleks et uurida kuulikeste muutumatu vahekauguse korral jõu sõltuvust laengu suurusest, juhtis Coulomb ühelt vaadeldavalt kuulikeselt laengu ära ning viis kuulikesed uuesti kokkupuutesse. Kui esialgu oli mõlemal kuulikesel laeng q, siis nüüd jäi mõlemale kuulikesele laeng q/2. Kuulikeste vahel mõjuv jõud aga oli sama vahekauguse korral esialgsest neli korda väiksem, seega F/4. Sellise protseduuri kordamisel jäi kuulikestele laeng q/4, jõud aga kahanes väärtuseni F/16. Coulomb mõistis, et kui laeng kahaneb mingi arv kordi, siis jõud kahaneb see arv ruudus kordi. Teisiti öeldes: jõu ja laengu ruudu jagatis on konstantne

Coulomb järeldas, et jõud on võrdeline laengu ruuduga

Teatavasti on mingi arvu ruudu leidmine korrutamise erijuht. Selle põhjal võis Coulomb nüüd väita, et erinevalt laetud kehade vahel mõjuv jõud on võrdeline laengute korrutisega.

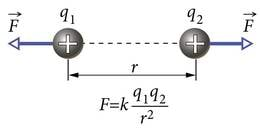
Coulomb jõudis gravitatsiooniseadusega väga sarnase tulemuseni: kahe laetud keha vahel mõjuv elektrijõud $F_e$ on võrdeline kummagi keha laenguga ja pöördvõrdeline kehade vahekauguse ruuduga

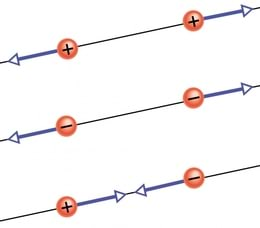
kus $k$ on võrdetegur. See jõud mõjub laetud kehi ühendava sirge sihis ning sõltub ainest, milles laetud kehad asuvad. Jõud on suurim vaakumis, aga peaaegu niisama suur on ta ka õhus. Jõud on samanimeliste laengute jaoks tõukejõud ja erinimeliste laengute korral tõmbejõud. Jõu mõjumise siht on kehade asukohtadega määratud. Järelikult on jõul kui vektoril vaid kaks võimalikku suunda. Jõu suunda antud sihil võib kirjeldada jõu arvväärtuse ees paikneva märgiga (+ või – ). See omakorda on leitav laengute märkide põhjal. Niisiis tähistab $F_e$ valemis 1.3 ja ka edaspidi jõuvektori pikkust, mis võib olla nii positiivne kui ka negatiivne.

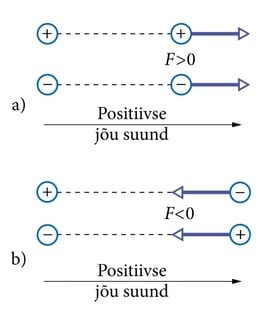
Me vaatleme ühele laetud kehale mõjuvat jõudu positiivsena, kui see on suunatud teisest kehast eemale. Negatiivseks loeme jõudu aga siis, kui see on suunatud teise keha poole. Samanimeliste laengute korrutis on valemis 1.3 alati positiivne. Seega mõjub samanimeliselt laetud kehade vahel positiivne jõud ehk tõukejõud. Erinimeliste laengute korrutis on negatiivne ning kehade vahel mõjub negatiivne jõud ehk tõmbejõud (J.1.8). Sellise kokkuleppega vabaneme vajadusest kasutada jõudu sisaldavates valemites vektorkuju.

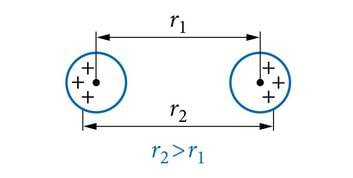
Kõigi Coulomb’i katsete kirjeldustes nimetasime vahekauguseks kuulikeste tsentrite vahelist kaugust. Kui kuulikeste läbimõõt on tühiselt väike võrreldes kuulikeste vahekaugusega, pole selle asjaolu rõhutamine eriti tähtis. Kui aga kuulikeste läbimõõt on vahekaugusele lähedane, siis tuleb vahekauguse mõistet täpsustada. Omavahelise tõukumise tõttu asetuvad samamärgilist laengut kandvad osakesed kummagi kuulikese sellesse ossa, mis jääb teisest kuulikesest võimalikult kaugele (J.1.9). Selle tagajärjel on laengutevaheline kaugus kuulikeste tsentrite vahekaugusest suurem.

J.1.9 Kehade tsentrite vahekauguse r1 ja laengute vahekauguse r2 erinevus.	J.1.10 Punktlaengu mõiste selgitus.

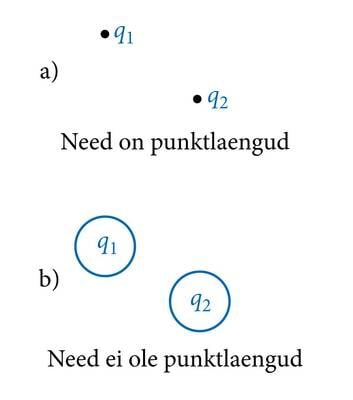
Kuulikeste vahel mõjuv jõud on aga Coulomb’i seaduse põhjal väiksem sellest jõust, millega mõjutaksid teineteist kuulikeste tsentrites paiknevad laengud. Sõna laeng tähendab siin mõistagi laetud osakeste kogumit. Coulomb’i seadus on lühidalt ja täpselt sõnastatav vaid niisuguste laetud kehade jaoks, mille mõõtmed on tühised võrreldes kehade vahekaugusega. Selliseid laetud kehi nimetatakse punktlaenguteks (J.1.10). Punktlaeng mängib elektriõpetuses sama rolli, mis punktmass Mehaanika kursuses. Mistahes keha võib käsitleda punktlaenguna juhul, kui laengu jaotumise keha osade vahel tohib antud ülesandes arvestamata jätta. Keha laengut vaadeldakse siis koondununa ühte punkti. Mingi keha võib ühes ülesandes esineda punktlaenguna, teises aga mitte. Näiteks on laetud veepiisake äikesepilve ja Maa vahel vaadeldav punktlaenguna. Piisa pinna lähedal asuva üksiku iooni jaoks aga laetud veepiisk kindlasti punktlaeng ei ole.

Avaldades valemist 1.3 võrdeteguri $k$, saame

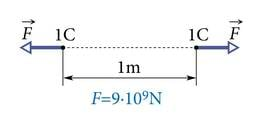
Tegur $k$ võrdub arvuliselt jõuga, mis mõjub vaakumis kahe teineteisest 1 m kaugusel paikneva punktlaengu 1 C vahel (J.1.11). Katsetest on kindlaks tehtud, et see jõud oleks 9·10⁹ N ehk niisuguse keha raskusjõud, mille mass on peaaegu miljon tonni. Nii koletule jõule ei suuda vastu panna ükski terastross ega mingi muu ühenduslüli. On ju raske rongi mass “ainult” mõni tuhat tonni ja suure laeva mass ulatub mõnekümne tuhande tonnini. Järelikult on üks kulon väga suur laeng.

Võrdetegur $k$ Coulomb’i seaduses on seega vaakumi korral esitatav kujul

Näide 1.2.

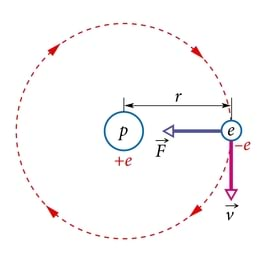
Leiame Coulomb’i seaduse kohaselt elektrijõu $F_e$, millega ringjoonelisel orbiidil liikuv elektron ja ringjoone tsentris paiknev prooton mõjutavad teineteist vesiniku aatomi planetaarses mudelis (vt joonist). Osakeste vahekauguseks loeme vesiniku aatomi raadiuse, mis Bohri mudeli kohaselt on $5,3\cdot {10}^{11}\text{m}$.

Lahendus

Leiame Coulomb’i seaduse kohaselt elektrijõu $F_e$, millega ringjoonelisel orbiidil liikuv elektron ja ringjoone tsentris paiknev prooton mõjutavad teineteist vesiniku aatomi planetaarses mudelis (vt joonist). Osakeste vahekauguseks loeme vesiniku aatomi raadiuse, mis Bohri mudeli kohaselt on $5,3\cdot {10}^{-11}\text{m}$.

Andmed

$r=5,3\cdot {10}^{-11}\text{m}$
$q_1=e=1,6\cdot {10}^{-19}\text{C}$

$q_2=-e{F}_e=?$

Arvutused:

Teame, et

$F_e=k\frac{q_1{q}_2}{r^2}$

kus

$k=9\cdot {10}^9\frac{\text{N}\cdot {\text{m}}^2}{{\text{C}}^2}$

Seega

$F_e=-k\frac{e^2}{r^2}$

(miinusmärk näitab, et tegemist on tõmbejõuga). Järelikult

$F_e=-9\cdot {10}^9\frac{\text{N}\cdot {\text{m}}^2}{{\text{C}}^2}\frac{(1,6\cdot {10}^{-19}\text{C})}{(5,3\cdot {10}^{-11}\text{m})}\approx -8,2\cdot {10}^{-8}\text{N}$

Vastus: Elektroni ja prootoni vahel mõjub elektriline tõmbejõud $-8,2\cdot {10}^{-8}\text{N}$. Nende osakeste vahel mõjuv gravitatsioonijõud on samas vaid $-3,7\cdot {10}^{-47}\text{N}$. Seega on elektrijõud vesiniku aatomis gravitatsioonijõust suurem üle $2\cdot {10}^{39}$ korra.

Juba 9. klassi Elektriõpetuses oli juttu sellest, et vooluga juhet ümbritseb magnetväli. Elektrivool on aga laengukandjate suunatud liikumine. Seega tekib laengukandjate suunatud liikumise tulemusena magnetväli.

Magnetväljaks nimetatakse laetud osakeste liikumisel tekkivat jõuvälja. Paigalseisev laeng (laetud keha) kutsub esile elektrivälja, liikuv laeng (elektrivool) aga täiendavalt ka magnetvälja. Seega on magnetvälja olemasolu mingi vaatleja jaoks niisama suhteline kui liikumine ise.

Samas pole magnetnähtuste tekkimiseks sugugi alati vaja elektrivoolu. Esmase kogemuse magnetismiga on igaüks meist saanud mitte voolu vaid just püsimagneti magnetvälja kaudu.

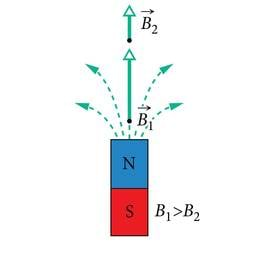
Püsimagnet on olemuslikult magnetvälja omav keha. Selle magnetvälja tekitavad osakesed, millest püsimagnet koosneb. Nii elektron, prooton kui ka neutron tekitavad juba üksnes oma olemasoluga magnetvälja. Seejuures määrab püsimagneti omadused eelkõige elektronide olemuslik magnetväli.

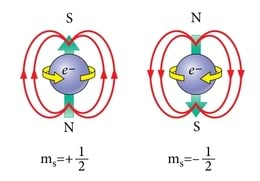
Aineosakese omamagnetväli on seotud osakese sisemise liikumise ehk spinniga. Nimetus tuleneb spinni tõlgendamisest aineosakese pöörlemisena ümber oma telje (ingl.k. to spin - pöörlema). Seda pöörlemist ei saa peatada. Võib vaid muuta pöörlemistelje asendit ruumis. Spinniga kaasneb alati kindel magnetväli, mis on suunatud piki pöörlemistelge. Spinn on osakest sama kindlalt iseloomustav suurus nagu laeng või mass. Seetõttu käsitletakse spinni omalaadse "pöörlemislaenguna". Spinnil puudub lihtne klassikaline mudel, mis kirjeldaks kõiki katsetulemusi. Seetõttu oleme sunnitud leppima üpris ebakonkreetse määratlusega "sisemine liikumine".

Püsimagneti juures võib tinglikult eristada kahte piirkonda, mille mõttelisi keskmeid nimetatakse põhjapooluseks ja lõunapooluseks (tähised vastavalt N ja S). Tähistusviis tuleneb väikese pöördumisvõimelise püsimagneti ehk magnetnõela käitumisest Maa magnetväljas. Nimelt on magnetnõelal kalduvus orienteeruda ehk asetuda ligikaudu piki geograafilist põhja-lõuna suunda.

Orienteerunud magnetnõela seda otsa, mis näitab geograafilist põhjasuunda, on hakatud nimetama magnetnõela või püsimagneti põhjapooluseks ja magnetnõela geograafiliselt lõunapoolset otsa lõunapooluseks.

Magnetnõela kindlaviisiline asetumine magnetväljas määrab magnetvälja kirjeldava vektoriaalse suuruse ehk B-vektori suuna. B-vektorist tuleb lähemalt juttu punktis 1.5.2.

Juba 13. sajandil tehti kindlaks, et ühe püsimagneti põhjapoolus ja teise lõunapoolus tõmbuvad, sama liiki poolused aga tõukuvad. See tulemus oli pöördelise tähtsusega, kuna tavakogemuse kohaselt püsimagnet vaid tõmbab raudesemeid enda poole.

Raudesemete tõmbumist püsimagneti mistahes pooluse suunas põhjustab rauatüki ajutine muutumine magnetiks. Seejuures tekitab püsimagneti üks poolus just rauatüki endapoolses küljes vastupidise magnetpooluse ja kutsub niimoodi esile tõmbejõu. Nähtust, mille korral magnetvälja paigutamise tulemusena hakkab aine ka ise tekitama magnetvälja, nimetatakse aine magneetumiseks.

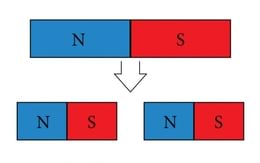
Magnetpooluste uurimisel avastati veel, et püsimagneti poolitamise tulemuseks ei ole mitte kaks lahutatud magnetpoolust, vaid kaks uut püsimagnetit, millel on kummalgi oma põhjapoolus ja oma lõunapoolus (J.1.13). See näitab selgesti pooluste tinglikkust. Järelikult on sarnasus kahe märgiga elektrilaengute ja kahte liiki magnetpooluste vahel vaid näiline. Erimärgilisi elektrilaenguid on ju võimalik ruumis lahku viia, magnetpoolustega seda aga teha ei saa.

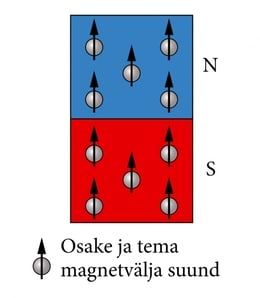
Arvestades, et püsimagneti väli on põhjustatud osakeste omamagnetväljadest, on niisugune tulemus aga kergesti mõistetav. Koosnevad ju kõik püsimagneti piirkonnad ühtedest ja samadest osakestest. Järelikult ei saagi püsimagneti osade vahel põhimõttelist erinevust olla. Magnetpooluste eristamisega kirjeldatakse vaid püsimagneti poolt tekitatava magnetvälja suunda (J.1.14).

Pärast seda, kui Coulomb oli 1785. aastal avastanud elektrijõu pöördvõrdelise sõltuvuse laetud kehade vahekauguse ruudust, asus ta korraldama samalaadseid katseid püsimagnetitega. Coulomb jõudis järeldusele, et ka magnetpooluste vahel mõjuv jõud on pöördvõrdeline poolustevahelise kauguse ruuduga. Niisiis on jõu sõltuvus vastastikmõjus olevate kehade vahelisest kaugusest ühesugune nii elektrijõu kui magnetjõu korral.

Mitte kõik ained ei käitu magnetväljas ühtmoodi. Pildil näeme ülaltvaates konna, kes hõljub konnast allpool oleva vertikaalse solenoidi voolu poolt tekitatud magnetväljas.	Lihtsalt huvitav fakt: vedelal hapnikul on magnetilised omadused. Täpsemalt, vedel hapnik on paramagneetiline. Mis muuhulgas tähendab seda, et vedel hapnik jääb magneti külge.

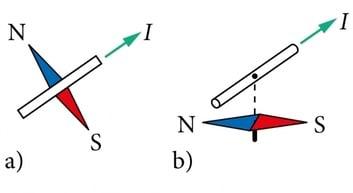
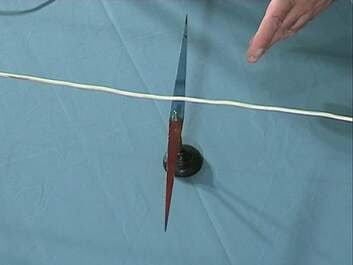
Elektrivoolu magnetvälja uurimise alguseks võib pidada aastat 1820, mil oma töö põhitulemuse avaldas Taani füüsik Hans Christian Oersted. Nimelt avastas Oersted, et juhet läbiv elektrivool avaldab magnetnõelale orienteerivat mõju. Magnetnõel pöördub juhtmega ristuvasse asendisse. Orienteerunud magnetnõel ei ole aga risti mitte ainult juhtme endaga, vaid ka tasandiga, mille määravad juhe ning magnetnõela keskme kinnituspunkt (J.1.15).

J.1.15 Oersted’i katse: a) vaade ülalt, b) vaade poolküljelt.	Oersted’i katse demo.

See oli tõeliselt üllatav tulemus. Kõik 19. sajandi alguseks tuntud jõud olid ju suunatud piki teineteist mõjutavate kehade keskmeid ühendavat sirget. Seetõttu arvati, et vooluga juhe võiks magnetnõela ühte poolust tõmmata ja teist tõugata. Nagu näeme, on magnetnõelale mõjuvad jõud hoopis risti juhet ja magnetnõela ühendava sirglõiguga.

Oerstedi katse vallandas elektrivoolu magnetvälja uurimisel tõelise laviini. Juba samal 1820. aastal avastasid prantslased Jean-Baptiste Biot [bioo] ja Felix Savart [savaar], et vooluga juhtme mingi lõigu poolt magnetnõela mingile kindlale poolusele mõjuv ja magnetnõela pöörav jõud on võrdeline vaadeldava juhtmelõigu pikkusega ning voolutugevusega juhtmes (J.1.16).

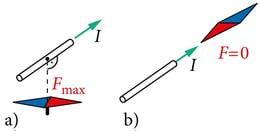
Samas osutus see jõud pöördvõrdeliseks juhtmelõigu ning magnetnõela vahelise kauguse ruuduga, nii nagu Coulomb’i seaduse kohaselt kahe punktlaengu vahel mõjuv jõud. Biot ja Savart leidsid ka, et magnetjõud on tugevaim juhul, kui magnetnõel paikneb vaadeldava juhtmelõigu keskristsirgel. Kui aga magnetnõel asetseb juhtmelõigu pikendusel (juhtmega samal sirgel), siis muutub nõelale mõjuv jõud nulliks (J.1.17). Biot ja Savart mõõtsid magnetjõudu, lastes magnetnõelal võnkuda oma tasakaaluasendi ümber. Mida kiirem (suurema sagedusega) see võnkumine on, seda tugevam on tasakaaluasendi poole suunatud magnetjõud. Täpsemalt öeldes on magnetjõud võrdeline magnetnõela võnkesageduse ruuduga.

Lähtudes teadmisest, et elektrivool on suuteline mõjutama püsimagnetit, on loomulik küsida, kas ka kaks vooluga juhet teineteist magnetjõuga mõjutavad. Veel samal 1820. aastal näitas André Marie Ampère, et see on tõesti nii. Ampère tuli esimesena mõttele, et magnetvälja tekitab laengukandjate liikumine. Enne teda püüti voolu magnetvälja taandada püsimagneti väljale. Nimelt arvati, et voolu tekitamine juhtmes muudab juhtme mingil viisil püsimagnetiks. Ampère aga esitas julgelt vastupidise hüpoteesi: just püsimagneti väli on põhjustatud tema sees kulgevatest ringvooludest. Hiljem selgus, et Ampère’il oli selles ka üksjagu õigus. Mõnede ainete magnetilised omadused on tõesti määratud neis moodustunud vooluringide magnetväljaga.

Ampère uuris kõigepealt kahe juhtme vastastikmõju juhtmete muutumatu pikkuse ja vahekauguse korral ning avastas järgmised seaduspärasused:

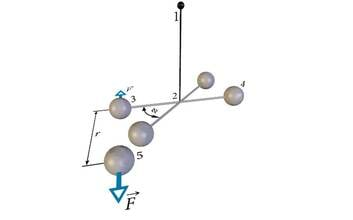
1. Kui kaks juhtmelõiku paiknevad erinevates tasandites, kuid risti nende keskpunkte ühendava lõiguga, kusjuures paiknemistasandi määravad kummagi juhtme jaoks juhe ise ja ühenduslõik, siis juhtmelõikude vahel mõjuv jõud sõltub nurgast nende vahel. Paralleelsete juhtmete korral on jõud maksimaalne. Ristuvate juhtmete keskmete vahel jõudu ei mõju.
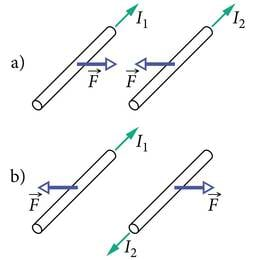
2. Kui paralleelsetes juhtmetes kulgevad samasuunalised voolud, siis mõjub juhtmete vahel tõmbejõud. Vastassuunaliste voolude korral mõjub tõukejõud (J.1.18).
3. Jõud on alati risti juhtmelõiguga, millele ta mõjub.

Erisuunaliste vooludega juhtmed tõukuvad, demokatse.	Samasuunaliste vooludega juhtmed tõmbuvad, demokatse.

Seega on voolude vastastikmõju mingis mõttes vastupidine laengute vastastikmõjule. Teatavasti mõjub samanimeliste laengute vahel tõukejõud, samasuunaliste voolude vahel aga tõmbejõud. Vastandmärgilised laengud tõmbuvad teineteise poole, vastandlike suundadega voolud aga tõukuvad teineteisest eemale. Järgnevalt asus Ampère välja selgitama paralleelsete sirgjuhtmete vastastikmõju sõltuvust nende pikkusest ja vahekaugusest. Ta tegi kindlaks, et juhtmete vahel mõjuv magnetjõud $F_m$ on võrdeline voolutugevustega $I_1$ ja $I_2$ kummaski juhtmes ning vaadeldava juhtmeosa pikkusega $l$. Samas osutus see jõud pöördvõrdeliseks juhtmete vahekaugusega $r$. Katsete tulemused võis Ampère kokku võtta valemisse

milles sisalduv konstant $K$ sõltub üldjuhul ainest, kus juhtmed asuvad.

Ampère’i seaduse (valem 1.7 ) kaudu on määratud voolutugevuse ühik amper (1 A).

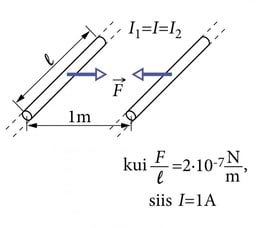
Kui kahe paralleelse, lõpmata pika ja lõpmata peenikese sirgjuhtme vahel, mille vahekaugus on üks meeter ja milles voolab ühesuguse tugevusega vool, mõjub vaakumis juhtmete pikkuse iga meetri kohta jõud 2·10^–7 njuutonit, siis on voolutugevus juhtmetes üks amper (J.1.19). Valemis 4.1 sisalduva konstandi $K$ väärtus on vaakumi korral seega 2·10^–7 N/A².

Lõpmata pikki ja peenikesi juhtmeid tegelikkuses mõistagi olemas ei ole. Seetõttu loetakse ampri etalonkatse teostatuks seda paremini, mida suurem on juhtmete vahekaugus võrreldes nende läbimõõduga ning mida pikemad on omakorda juhtmed võrreldes nende vahekaugusega. Amper on SI elektriliseks põhiühikuks. Selle kaudu tuletatakse kõigi teiste elektriliste suuruste mõõtühikud. Samas on ampri definitsioon niivõrd pikk, et lõppu välja jõudes kipub algus juba meelest minema. Seepärast ei tasuks seda mitte luuletuse kombel pähe õppida, vaid püüda silme ees hoida joonist 1.19.

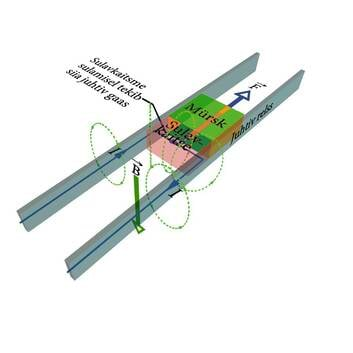
Relsskahur selles tekitatud vooluga i. See vool põhjustab sulavkaitsme kiire aurustumise. Vool tekitab relsside vahel magnetvälja B ja see magnetväli rakendab jõudu F juhtivale gaasile, mis on osa voolu kulgemisteest. Gaas lükkab mürsku piki relsse ja lennutab selle minema.	Relsskahuri mürsk lendab ... miks on sellel taga "tulesaba", ehkki midagi selle mürsu juures ei põle?

Aine ja tema olekute kirjeldamiseks kasutatakse mitmesuguseid füüsikalisi suurusi, millest mõned on meile ka juba põhikoolist tuttavad. Välja võib samuti kirjeldada mingi suuruse abil. Kuna välja olemasolu tuleb esile jõu kaudu, siis on mõistlik elektri- ja magnetvälja iseloomustada jõuga, mis mõjub selles väljas mingile kindlale kehale.

Jõud $F_{\text{12}}$, millega ühe punktlaengu $q_1$ poolt tekitatav elektriväli mõjutab teist punktlaengut $q_2$, sõltub Coulomb’i seaduse (valemi 1.3 )

kohaselt mõlema laengu suurusest. Seega ei sobi jõud kirjeldama elektrivälja, mida tekitab esimene punktlaeng $q_1$. Elektrivälja iseloomustava suuruse väärtused ei tohi ju sõltuda vahendist (proovikehast laenguga $q_2$), mida me kasutame välja olemasolu tuvastamiseks. Kui me jagame proovikehale mõjuva jõu $F_{\text{12}}$ selle keha laenguga $q_2$, siis saame suuruse, mis tõepoolest ei sõltu enam laengust $q_2$. See ongi esimese keha poolt tekitatava elektrivälja tugevus $E_{\text{1}}$

Elektrivälja tugevus näitab, kui suur jõud mõjub selles väljas ühikulise positiivse laenguga kehale. Väljatugevus on vektoriaalne (suunda omav) suurus. Seetõttu võib väljatugevust lühidalt nimetada ka E-vektoriks. Edaspidi teeme nii eelkõige siis, kui soovime rõhutada väljatugevuse vektoriaalsust. Kui aga jutt on E-vektori pikkusest (moodulist), siis ütleme lihtsalt väljatugevus $E$. Topeltindeksiga jõu tähises $F_{\text{12}}$ rõhutame, et tegemist on jõuga, mis mõjub esimese keha poolt teisele kehale.

E-vektori kokkuleppelise suuna määrab elektrivälja tugevuse definitsioonis sisalduv sõna positiivne. Kuna kahe positiivselt laetud keha vahel mõjub tõukejõud, siis on positiivse laenguga keha poolt tekitatud elektrivälja tugevus vektorina suunatud sellest kehast eemale. Me võiksime valemis 1.10 kasutada vektorimärke, sest proovikeha laengu $q_2$ positiivsuse tõttu on jõud $F_{\text{12}}$ ja väljatugevus $E_{\text{1}}$ vektoritena samasuunalised. Negatiivse laenguga keha mõjutab positiivset proovilaengut $q_2$ tõmbejõuga, mistõttu vastav elektrivälja tugevus on vektorina suunatud negatiivse laenguga keha poole.

Üldiselt tuleb vektoriaalsete suuruste tähiseid käesoleva õpiku valemites siiski mõista kui vastavate vektorite pikkusi. Pikkuse negatiivsus tähendab aga seda, et vektor on suunatud vastupidiselt kokkuleppelisele positiivsele suunale. Näiteks on jõud $F_{\text{12}}$ ja väljatugevus $E_{\text{1}}$ negatiivse laenguga väljatekitaja korral valemis 1.10 mõlemad negatiivsed. Valemite lihtsuse nimel hoidume vektorimärkide kasutamisest.

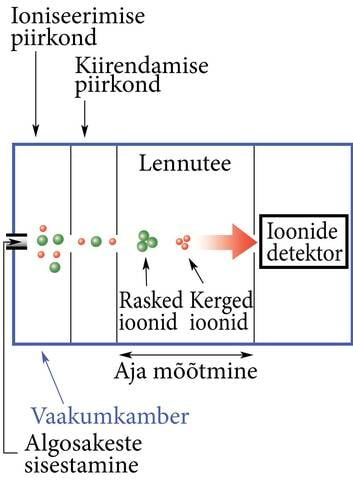
Osakeste lennuaega mõõtvate mass-spektromeetrite töö põhineb elektrivälja mõjul laenguga kehale. Siin erineva massiga, aga ühesuguse laenguga ioonid läbivad homogeense elektrivälja (vt punkt 1.6.2) piirkonna ja saavad seal tänu oma erinevatele massidele erineva kiirenduse. Osakeste lennuaegasid mõõtes saab siis teada, missuguse massiga ioone uuritavas gaasis leidub.	Ka õhus tekkivad sädemed annavad märku tugeva elektrivälja olemasolust

Valemi 1.10  põhjal on elektrivälja tugevuse ühikuks üks njuuton kuloni kohta ($1\text{N}/\text{C}$). Üks njuuton kuloni kohta on sellise elektrivälja tugevus, milles punktlaengule suurusega $1\text{C}$ mõjub jõud $1\text{N}$. Praktikas see esitus eriti kasutamist ei leia. Rohkem on levinud sama mõõtühiku teine esitusviis - üks volt meetri kohta ($1\text{V}/\text{m}$). Sellega tutvume lähemalt punktis 1.6.

Elektrivälja tugevuse kohta toodud mõned näited tabelis 1.2.

Edaspidi tuleb meil korduvalt väljatugevuse $E$ kaudu leida kehale laenguga $q$ selles väljas mõjuvat elektrijõudu  $F$. Valemi 1.10  põhjal

jõud on laengu ja väljatugevuse korrutis. Indekseid me enam ei kasuta, sest valemis 1.11  sisalduv väljatugevus $E$ ei pruugi enam olla põhjustatud konkreetsest punktlaengust ega üldse mingist ühest kindlast kehast. See on enamasti paljude eri väljade tugevuste summa.

Eespool veendusime selles, et laeng täidab Coulomb’i seaduses sama rolli mida mass gravitatsiooniseaduses. Võrdlemist jätkates võiksime küsida, milline Mehaanika kursusest tuntud suurus vastab elektrivälja tugevusele $E$. Pole kuigi raske märgata, et selleks suuruseks on raskuskiirendus $g$. Raskuskiirendus näitab, kui suur raskusjõud $mg$ mõjub ühikulise massiga kehale. Analoogiliselt näitab elektrivälja tugevus meile, kui suur elektrijõud $qE$ mõjub selles väljas ühikulise laenguga kehale.

Kui uurime katseliselt vooluga juhtme käitumist mitte ainult teise juhtme magnetväljas (p.1.4.2) vaid suvalise päritoluga väljas, siis võime järeldada, et juhtmelõigule mõjuv magnetjõud $F_m$ on alati võrdeline juhet läbiva voolu tugevusega $I$, juhtmelõigu pikkusega $l$ ja siinusega nurgast $\alpha$ voolu suuna ning magnetvälja suuna vahel (J.1.20)

kus $B$ on võrdetegur. Meenutagem siinkohal, et magnetvälja suuna määrab selles väljas orienteerunud magnetnõel. Peagi veendume, et seos 1.12 on Ampère’i poolt tuletatud valemi 1.7 üldistus, mis arvestab ka magnetvälja suunda ja ei eelda enam magnetvälja tekitajana vooluga juhet. Seetõttu nimetatakse valemit 1.12 sageli Ampère’i seaduseks, ehkki Ampère ise kasutas kuju 1.7 .

J.1.20. Ampère’i seaduses esinevate suuruste graafiline interpretatsioon ja jõu suuna määramine vasaku käe reegli abil.	Millises suunas mõjub vooluga juhtmele püsimagneti magnetväljas jõud? Demokatse.

Jõu suuna määramiseks Ampère’i seaduses võib kasutada vasaku käe reeglit. See väidab, et kui vasaku käe väljasirutatud sõrmed osutavad voolu suunda ja magnetväli on suunatud peopessa, siis väljasirutatud pöial näitab juhtmelõigule mõjuva jõu suunda (J.1.20). Vooluga juhtmele mõjuv magnetjõud on suunatud alati risti nii voolu kui ka magnetvälja suunaga. Nüüd märkame, et meil on mõtet avaldada valemist 1.12  võrdetegur $B$, tehes seda juhul, kui magnetväli on voolu suunaga risti ($\alpha =\pi /2$ ja $\sin \alpha =1$). Me saame, et

suurus $B$ näitab uuritavas magnetväljas mingile kindlale kehale (vooluga juhtmele) mõjuvat jõudu. Seega on ta sobiv kasutamiseks magnetvälja iseloomustava suurusena. Suurust $B$ on hakatud nimetama magnetinduktsiooniks.

Magnetinduktsioon $B$ näitab magnetjõudu $F_m$ , mis mõjub ühikulise vooluga ja ühikulise pikkusega juhtmelõigule selle juhtmega ristuvas magnetväljas.

Magnetinduktsioon on vektoriaalne suurus ja tema suunda näitab magnetväljas orienteerunud magnetnõela põhjapoolus  (J.1.20).

Kuna magnetinduktsiooni üldlevinud tähiseks on $B$, siis võib teda lühidalt nimetada ka B-vektoriks. Pole raske märgata, et B-vektor on analoogiline elektrivälja kirjeldava E-vektoriga. Mõlemad on defineeritud jõu kaudu, mis mõjub proovikehale. Erinevus on vaid selles, et E-vektori suund ühtib laetud proovikehale mõjuva jõu mõjumise sihiga, B-vektor on aga proovijuhtmele mõjuva jõu suunaga risti. Viimane asjaolu muudab täiesti võimatuks vektorimärkide kasutamise valemites 1.12 ja 1.13 . Allpool (p.1.5.4) saab ka selgemaks, miks B-vektori pikkuse defineerimisel kasutatakse vooluga juhet, suuna määramisel aga püsimagnetit.

Nikola Tesla (1856 – 1943)	Nikola Tesla imetlusväärsed leiutised tegid ta maailmakuulsaks. Sellel pildil on ta istumas oma laboris Colorado Springsis.

Magnetinduktsiooni SI-ühikut nimetatakse horvaadi päritoluga Ameerika elektrotehniku ja leiutaja Nikola Tesla (1856 – 1943) järgi teslaks. Kui juhtmele, mille pikkus on üks meeter ja milles kulgeb vool tugevusega üks amper, mõjub selle juhtmega ristuva magnetvälja poolt jõud üks njuuton, siis on välja magnetinduktsioon üks tesla (1 T) (J.1.21).

Seega valemi 1.13  kohaselt

Üks tesla on väga suur magnetinduktsioon. Seetõttu mõõdetakse Maal esinevate magnetväljade induktsioone tavaliselt milli- ja mikroteslades. Keskmise suurusega püsimagneti pinna lähedal on magnetinduktsioon mõnikümmend milliteslat. Tabelis 1.3 on toodud veel mõned näited magnetinduktsiooni väärtuste kohta.

Coulomb’i seaduse 1.3 ja valemi 1.10 abil saame punktlaengu $q_1$ elektrostaatilise välja tugevuse esitada kujul

Seega on punktlaengu $q_1$ väljatugevus võrdeline selle laengu suurusega ning pöördvõrdeline laengu ja uuritava punkti vahekauguse $r$ ruuduga.

Teades Oerstedi katse kirjelduse (p.1.4.2) põhjal seda, kuidas on suunatud sirgvoolu magnetväli, võime nüüd omavahel seostada Ampère’i seaduse kaks kuju (1.7 ja 1.12) ning ühtlasi avaldada vooluga sirgjuhtme poolt tekitatava magnetinduktsiooni. Kahe paralleelse juhtme korral on ühe juhtme magnetväli teise juhtmega risti (J.1.22).

Seega nurk $\alpha$  on täisnurk ja $\sin \alpha =1$. Vas­tavalt avaldub esimese juhtme poolt teisele mõjuv jõud kujul

kus $B_1$ on esimese juhtme magnetinduktsioon teise juhtme asukohas ja $I_2$ on voolutugevus teises juhtmes. Kuna jõud avaldub samas ka valemiga 1.7

siis saame

Vooluga sirgjuhtme poolt tekitatav magnetinduktsioon on võrdeline voolutugevusega juhtmes ning pöördvõrdeline kaugusega juhtmest. Valemi 1.15 juures tuleb arvestada, et $l$ on selle juhtmelõigu pikkus, millele vaadeldav jõud mõjub. Vaikimisi eeldatakse magnetinduktsiooni $B_1$ tekitava (joonisel vasakpoolse) juhtme lõpmatut pikkust.

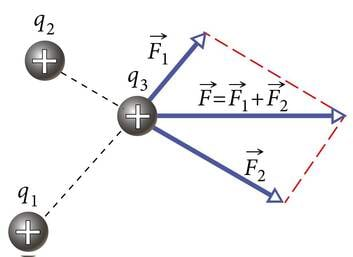
Nii elektri- kui magnetväljas kehtib superpositsiooniprintsiip ehk liitumise põhimõte. Selle printsiibi kohaselt võrdub elektrivälja korral laetud kehade süsteemi väljatugevus üksikutest kehadest põhjustatud väljatugevuste vektoriaalse summaga. Magnetväljas võrdub väljatekitajate (püsimagnetite või vooluga juhtmete) süsteemi magnetinduktsioon üksikutest väljatekitajatest põhjustatud magnetinduktsioonide vektoriaalse summaga. Veel lihtsamalt öeldes: nii E-vektoreid kui B-vektoreid tuleb vektoriaalselt liita.

Kolme laengu vahel mõjuvate elektrijõudude vektoriaalne liitmine.	Simulatsioon vektorite liitmise harjutamiseks.

Superpositsiooniprintsiip tuleneb otseselt välja omadusest mitte segada teist välja ehk siis Füüsikalise looduskäsitluse aluste kursuses vaadeldud tõrjutusprintsiibist. Täpsemalt tuleneb see küll tõrjutusprintsiibi mittekehtivusest väljade korral. Kui mingile kehale mõjub korraga mitu välja, siis liituvad vektoriaalselt nendest väljadest tingitud jõud. Piltlikult öeldes: väljad ei lähe omavahel konflikti. Nad jagavad omavahel ära võimaluse vaadeldavat keha jõuga mõjutada. Lõpptulemuses kajastub aga loomulikult rohkem selle välja mõju, mis ise on tugevam. Konkreetselt uurime superpositsiooniprintsiibi rakendamist punktis 1.6.

Elektri- ja magnetvälja kirjeldused tunduvad esmapilgul üksjagu erinevat. E-vektori suund ühtib laetud proovikehale mõjuva jõu mõjumise sihiga, B-vektor on aga proovijuhtmele mõjuva jõu suunaga risti. Punktlaengu elektrivälja tugevus (E-vektori pikkus) on pöördvõrdeline vahekauguse $r$ ruuduga välja tekitava punktlaengu ja uuritava väljapunkti vahel (valem 1.14). Lõpmata pika sirgjuhtme magnetinduktsioon (B-vektori pikkus) on aga pöördvõrdeline selle kaugusega esimeses astmes (valem 1.15). Need erinevused tulenevad looduse objektiivsest omadusest. Magnetväljal lihtsalt on kaks erinevat tekitajat: laetud osakeste suunatud liikumine (elektrivool) ja osakeste omamagnetväli, mis põhjustab püsimagneti välja. Kui magnetvälja kirjeldav suurus $B$ oleks defineeritud lähtuvalt vaid ühest välja tekitajast, siis oleks teise tekitajaga seotud nähtuste kirjeldamine ääretult raske. Seetõttu on tänapäeval B-vektori pikkus määratud vooluga juhtme, suund aga püsimagneti (magnetnõela) abil.

Magnetvälja algne kirjeldus ehitati üles sarnasusele punktlaengute ja magnetpooluste käitumise vahel. Magnetismi tehnilised rakendused aga osutusid üha rohkem seotuks elektrivooluga, mistõttu elektriliseks põhiühikuks valiti amper ja B-vektori pikkus defineeriti süsteemis SI vooluga juhtmele mõjuva jõu kaudu. See tingis magnetvälja silindrilise sümmeetria: kõigis vooluga juhtmest (kui silindri teljest) ühesugusel kaugusel paiknevates punktides on sama magnetinduktsioon. Seevastu punktlaengu elektrivälja sümmeetria on sfääriline: kõigis punktlaengust (kui sfääri tsentrist) ühesugusel kaugusel asuvates punktides on sama elektrivälja tugevus. Sfääri pindala ($4\pi r^2$) on võrdeline raadiuse ruuduga, silindri külgpindala ($2\pi rl$) on aga võrdeline raadiusega esimeses astmes.

Homogeenset välja ning elektri- ja magnetvälja jõujooni uurime lähemalt allpool (p.1.6). Olgu veel märgitud, et suur kõlaline erinevus välja jõu kaudu kirjeldavate vektorsuuruste nimetustes (elektrivälja tugevus E ja magnetinduktsioon B) tuleneb samuti asjaolust, et magnetvälja algne kirjeldus ehitati üles sarnasusele punktlaengute ja magnetpooluste käitumise vahel. Magnetvälja tugevuseks nimetatakse suurust, mis on elektrivälja tugevuse analoogiks magnetpooluste-põhises magnetvälja käsitluses. Kuna see käsitlus ei ole kooskõlas tänapäeval domineeriva ühikusüsteemiga SI, siis me seda lähemalt ei vaatle.

Elektri- ja magnetväli pole meie meeleorganitega vahetult tajutavad. Välja olemasolu avaldub vaid tema mõjus aine osakestele. Samas võib aga korraldada katseid, milles väikesed ainekübemed moodustavad E- või B-vektoriga paralleelseid jooni. Neid jooni on hakatud nimetama vastava vektori joonteks või vastava välja jõujoonteks. Jõujooned võimaldavad meil tekitada vahetult nähtavaid välja mudeleid. Teisisõnu – nad võimaldavad elektri- või magnetvälja visualiseerida. Ei tohi unustada, et jõujooni looduses tegelikult pole. Nad on vaid inimeste poolt välja mõeldud abivahend välja kirjeldamisel. Magnetvälja jõujoontest oli juttu juba põhikooli Elektriõpetuses, kuna nende katseline uurimine on tehniliselt hulga lihtsam. Meie aga alustame elektrivälja jõujoontest.

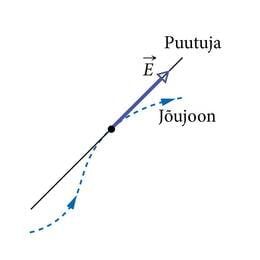
Elektrivälja jõujoon on mõtteline joon, mille igas punktis on E-vektor suunatud piki selle joone puutujat. E-vektori suund määrab ka jõujoone suuna, mida markeeritakse noolekesega jõujoonel (J.1.23). Jõujoone üldlevinud tähiseks joonistel ongi noolekesega katkendjoon, mille läheduses paikneb viide konkreetse välja vektorile (täht E või B). Seal, kus väli on tugevam, paiknevad jõujooned tihedamalt. See võimaldab võrrelda väljatugevusi ruumi eri osades.

J.1.24 Positiivse punktlaengu E-vektor on suunatud laengust eemale.	Negatiivse punktlaengu E-vektor on suunatud laengu poole.

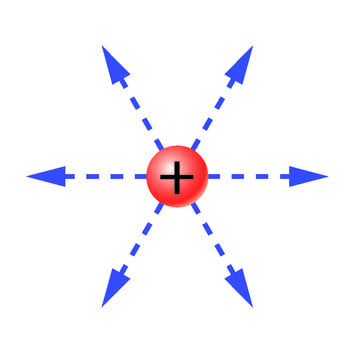
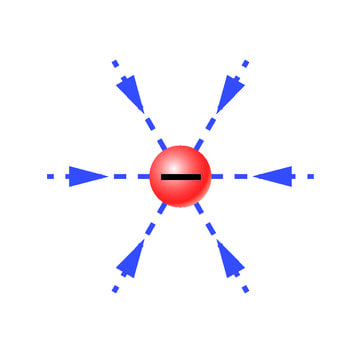
Kui punktlaengu läheduses ei leidu teisi laetud kehi, siis täidab seda ruumi vaid punktlaengu enda elektriväli. Positiivse punktlaengu E-vektor on suunatud laengust eemale ja negatiivse punktlaengu E-vektor laengu poole (J.1.24). Niisiis väljuvad positiivse punktlaengu elektrivälja jõujooned laengu asukohast nagu päikesekiired. Negatiivse punktlaengu välja jõujooned aga tulevad laengu asukohta kokku.

Sageli väidetakse, et positiivselt laetud keha elektrivälja jõujooned lähevad kehalt lõpmatusse ning negatiivse laenguga keha välja jõujooned tulevad lõpmatusest. Päris nii see siiski ei ole. Laengu jäävuse seaduse (p.1.2.4) põhjal teame, et kui on olemas positiivne, siis peab kuskil olema ka negatiivne laeng. Positiivse laenguga kehalt väljuvad elektrivälja jõujooned kulgevad kindlasti mingitele negatiivsetele laengutele. Kui negatiivse laenguga kehad on väga kaugel, siis nende olemasolu positiivselt laetud keha läheduses tunda ei ole ning punktlaengu elektrivälja jõujoonte pilt on tsentraalsümmeetriline.

J.1.25 Summaarse elektrivälja leidmine kahest ühesuurusest kuid erinimelisest punktlaengust koosnevas süsteemis.	J.1.26. Mannaterad asetsevad elektriväljas piki jõujooni ridadesse. Demokatse.

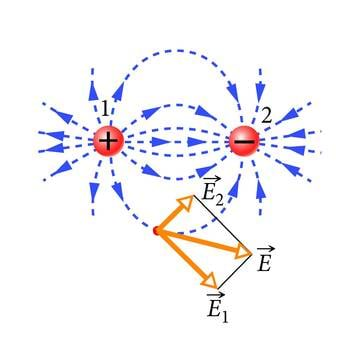
Kahe või enama punktlaengu või muu laetud keha piisavalt väikese vahekauguse korral liituvad superpositsiooniprintsiibi kohaselt nende kehade poolt tekitatud elektriväljade E-vektorid. Summaarse elektrivälja ehk resultantvälja E-vektori leidmise näitena vaatleme kahest ühesuurusest, kuid erinimelisest punktlaengust koosnevat süsteemi (J.1.25). Positiivse punktlaengu väljatugevus $E_1$ on joonisel negatiivse laengu väljatugevusest $E_2$ suurem seetõttu, et vaadeldav punkt paikneb laengule $+q$ lähemal kui laengule $-q$. Liites analoogiliselt E-vektoreid teistes punktides, saame resultantvälja jõujoonte täieliku pildi. Näiteid erinevate kehade ja nende süsteemide elektrivälja jõujoonte konstrueerimisest võib leida veebiõpikust.

Neid elektrivälja jõujoonte pilte saab ka katseliselt kontrollida, kasutades tahke aine kübemeid, mis paiknevad vedelas dielektrikus. Suurepäraselt sobivad selleks mannaterad õlis. Mannaterad asetuvad elektriväljas piki jõujooni ridadesse. 

Veelgi lihtsam võimalus erinevaid situatsioone läbi mängida on arvutisimulatsioonid.

Eemaldumisel punktlaengust väheneb punktlaengu väljatugevus valemi 1.14 kohaselt niisamuti nagu kooskõlas Mehaanika kursuses õpituga väheneb raskuskiirendus eemal­dumisel Maast. Maapinnal asetsevad kehad on aga kõik ligikaudu ühesugusel kaugusel Maa keskpunktist. Seetõttu võib raskuskiirenduse väärtust Maa pinnal lugeda konstantseks. Jättes Maa pinna kõveruse arvestamata, võime lugeda muutumatuks ka raskuskiirenduse suuna. Raskusjõu välja nimetatakse sel juhul homogeenseks (kr homogenes - ühtlane, ühesugune).

J.1.27 Elektriväli kahe ühesuuruse ja erimärgiliselt laetud tasase plaadi vahel.	J.1.28 Mannaterad näitavad elektrivälja plaatkondensaatoris. Demokatse.

Ka elektriväli võib olla homogeenne. Homogeense välja E-vektor on kogu vaadeldavas ruumis ühesuguse pikkuse ja suunaga ning välja jõujooned on omavahel paralleelsed sirged, mille vahekaugus ei muutu.

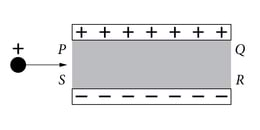
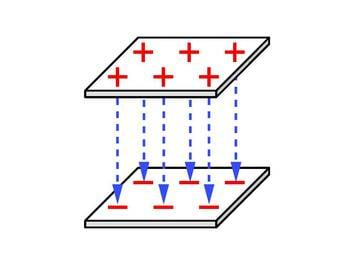
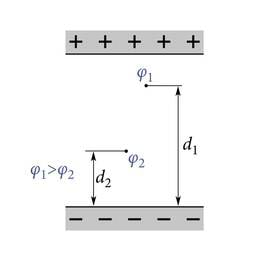
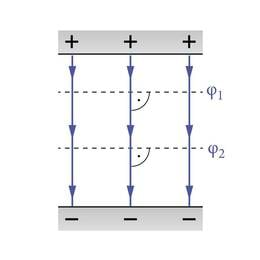
Elektriväli on homogeenne näiteks kahe paralleelse ühtlaselt laetud tasase plaadi vahel, mille pinnaühikul paiknevad suuruselt võrdsed ja vastandmärgilised laengud, plaatide vahekaugus on tühiselt väike võrreldes plaatide joonmõõtmetega ja uuritav piirkond asub piisavalt kaugel plaadi äärest (ääre mõju ei avaldu, J.1.27). Selline elektriväli tekib plaatkondensaatoris, millega tutvume lähemalt allpool (p.2.6.3). Katseline elektrivälja jõujoonte pilt kondensaatoris on joonisel 1.28 (selle saamist kirjeldav video on leitav veebiõpikust). Plaatkondensaatoris tekkivat elektrivälja tasub detailsemalt uurida põhjusel, et kondensaator on üks tähtsamatest elektrostaatika rakendustest.

Mannateradest moodustuvate ridade omavaheline paralleelsus ja ridade keskeltläbi konstantne vahekaugus näitavad, et elektriväli kahe ühtlaselt laetud plaadi vahel on homogeenne. Samas näeme ka, et väljaspool plaatidevahelist ruumi mannaterade reastumist ei toimu. Seega puudub seal elektriväli. Kui ühe plaadi mingil pinnaosal paikneva positiivse laengu jaoks asetseb sama suur negatiivne laeng vahetus läheduses naaberplaadi sama suurel pinnaosal, siis moodustavad need kaks laengut tervikuna neutraalse süsteemi, mis süsteemist väljapoole ulatuvat elektrivälja ei tekita. Piltlikult öeldes: iga pluss on juba “oma” miinuse leidnud ja “lisa otsida” pole enam vaja. “Miinuse otsimist” ehk positiivse laengu ülehulka süsteemis väljendaks selles näites süsteemist väljapoole suunduv jõujoon, mida me aga katses ei tuvasta.

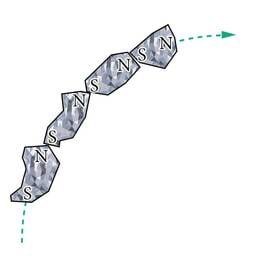
Analoogiliselt elektrivälja jõujoontega kasutatakse ka magnetvälja kirjeldamiseks jõujooni. Magnetvälja jõujoon on mõtteline joon, mille igas punktis on B-vektor suunatud piki selle joone puutujat (analoogiliselt joonisega 1.23). Jõujoonel on ka suund, mis ühtib B-vektori suunaga antud punktis ja mida järelikult näitab orienteerunud magnetnõela põhjapoolus. Seega on võimalik magnetvälja jõujoonte kuju uurida piisavalt suure hulga magnetnõelte abil. Veel paremini saab jõujoonte paigutust nähtavaks muuta rauapuruga. Rauapuru kübemed käituvad magnetväljas nagu väikesed magnetnõelad. Nad pöörduvad oma pikima mõõtmega magnetvälja suunas, üritades püsimagnetite kombel moodustada ahelaid, milles ühe tükikese põhjapoolus on tõmbunud vastu teise lõunapoolust (J.1.29). Sellised ahelad kujutavadki magnetvälja jõujooni.

Ka magnetvälja korral võimaldavad jõujooned võrdlevalt hinnata väljavektori pikkust ruumi eri piirkondades. Seal, kus jõujooned paiknevad tihedamalt, näiteks püsimagneti ühe pooluse läheduses (J.1.30), on magnetinduktsioon suurem ja proovikehale mõjuvad tugevamad magnetjõud.

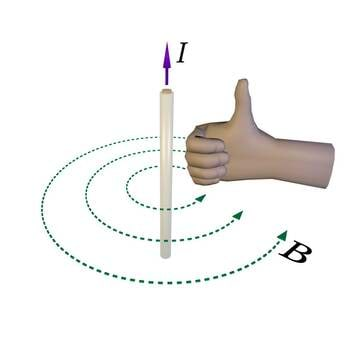
Korraldades Oerstedi katse (p.1.4.2) vertikaalse sirgjuhtme abil, millest ühesugusel kaugusel horisontaalsel alusplaadil paikneb suur hulk magnetnõelu, võime veenduda selles, et magnetvälja jõujooned ümbritsevad vooluga juhet kontsentriliste ringjoontena. Välja suuna määramiseks jõujoonel kasutatakse mitmeid mnemotehnilisi võtteid, millest levinuimaks on tänapäeval parema käe rusikareegel (J.1.31). See väidab, et kui rusikasse tõmmatud parema käe väljasirutatud pöial näitab voolu suunda, siis neli kõverdatud sõrme näitavad selle voolu magnetvälja suunda.

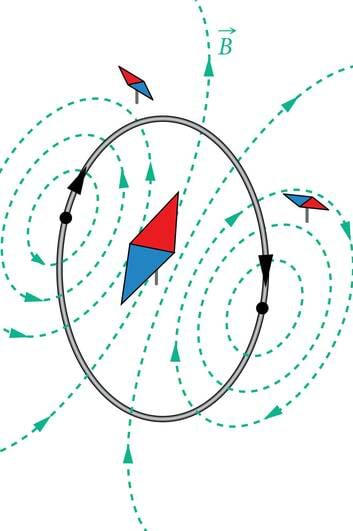
Ka magnetinduktsiooni kohta kehtib superpositsiooniprintsiip ehk liitumise põhimõte. Selle järgi on kehade süsteemi poolt tekitatud magnetvälja B-vektor võrdne üksikute kehade B-vektorite summaga. Ehk teisiti: erinevate kehade poolt mingis punktis tekitatud magnetväljade B-vektoreid tuleb resultantvälja B-vektori saamiseks liita. Seda põhimõtet illustreerib hästi ringvoolu magnetvälja jõujoonte määramine (J.1.32).

J.1.31. Parema käe rusikareegel sirgjuhtme magnetvälja suuna määramiseks.	J.1.32 Vooluga ringjuhtme magnetvälja jõujooned.

Parema käe rusikareeglit rakendades veendume selles, et vooluga ringjuhtme kõik osad tekitavad ringi keskpunktis piki ringjuhtme telge suunatud magnetvälju. Ringjuhtme teljel on resultantväli just ringvoolu keskpunktis kõige tugevam, sest keskpunkt on kõigile ringjuhtme osadele lähim telje punkt ning just keskpunktis on kõigi ringjuhtme osade magnetväljad omavahel paralleelsed. Näeme, et ringvoolu magnetvälja jõujooned ei ole ise küll rangelt ringjoonelised, kuid nad on siiski kinnised kõverad.

Ringvoolu magnetvälja suuna määramiseks võib samuti kasutada parema käe rusikareeglit, mis nüüd kõlab järgmiselt: kui rusikasse tõmmatud parema käe neli kõverdatud sõrme näitavad ringvoolu suunda mingis juhtmekeerus, siis väljasirutatud pöial näitab selle voolu magnetvälja suunda juhtmekeeru teljel. Seega tuleb üleminekul sirgvoolu magnetvälja juurest ringvoolu magnetvälja käsitlemisele parema käe rusikareeglis sõnad vool ja magnetväli omavahel ära vahetada. Ringjuhtme magnetvälja jõujoonte katseline pilt on leitav veebiõpikust.

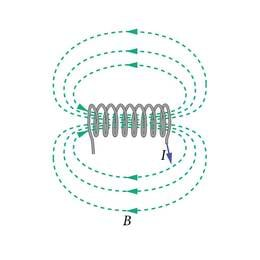
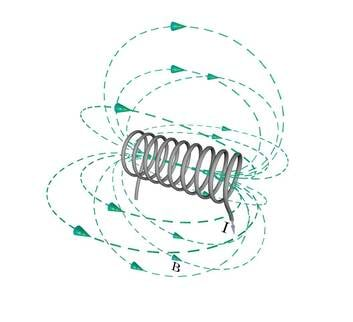
Kõrvutiasetsevatest keerdudest koosneva juhtmepooli ehk solenoidi korral liituvad solenoidi teljel paljude ringvoolude samasuunalised magnetväljad. Seetõttu on resultantväli solenoidi sees väga tugev (J.1.33). Vooluga solenoidi magnetvälja jõujoonte katseline pilt on joonisel 1.34.

Rauapuru kübemed moodustavad vooluga solenoidi sees solenoidi teljega paralleelseid ja ühtlase tihedusega ridu. Seega on magnetväli vooluga solenoidi sees homogeenne. Jõujoonte hajumine solenoidi otste juures näitab, et seal magnetväli mõnevõrra nõrgeneb. Samas puudub magnetväli väljaspool solenoidi (solenoidi kõrval) pea täiesti, sest mitte mingit rauapuru reastumist me seal ei tähelda. Olukord on analoogiline elektrivälja puudumisega väljaspool plaatkondensaatorit (p.1.6.2).

Solenoidi magnetvälja 3D mudel.	J.1.34 Solenoidi magnetväli. Demokatse.

Mõistagi sõltub magnetvälja suund solenoidis voolu suunast ja on määratav parema käe rusikareegli abil, analoogiliselt ringjuhtme välja juhuga. Vooluga solenoidis tekkivat homogeenset magnetvälja tasub detailsemalt uurida põhjusel, et solenoid on üks tähtsamatest magnetismi rakendustest. Me puutume sellega veel korduvalt kokku käesoleva õpiku 2. osas.

Näeme, et püsimagneti magnetvälja jõujooned kulgevad ka väljaspool magnetit pooluselt poolusele. Läbides ka magnetit ennast, moodustavad nad ikkagi kinnisi kontuure, niisamuti nagu voolujuhtmete puhul. Seega ei ole olemas punkte, kus magnetvälja jõujooned algaksid või lõpeksid.

Välja, mille jõujooned on kinnised (alguse ja lõputa), nimetatakse solenoidaalseks väljaks ehk pöörisväljaks. Seega magnetväli on pöörisväli.

Elektrivälja võib iseloomustada mitte ainult jõuga, mis temas mõjub ühikulise laenguga kehale, vaid ka tööga, mida see jõud võib ära teha. Juba põhikoolis õpitud suuruseks, mis kirjeldab elektrivälja töö kaudu, on pinge. Üldiselt tähendab sõna pinge alati seda, et kohe võib midagi juhtuda. Mõelgem siinkohal väljenditele pingeline olukord või suhted on pingestunud. Seal, kus on tegu elektrilise pingega, võib meie teele juba jääda silt: Kõrgepinge, elukardetav! Mis siis ikkagi on pinge?

Mehaanika kursusest teame, et tööks nimetatakse jõu ja selle mõjumise suunal sooritatud nihke korrutist. Kui keha sooritab jõu $F$ mõjul nihke $s$, siis töö avaldub kujul

kus $\alpha$ on nurk jõu ja nihke suundade vahel.

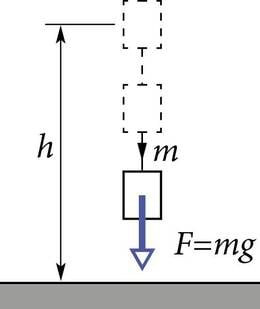
Asume uurima tööd, mida teeb kahe erinimeliselt laetud metallplaadi vahel esinev homogeenne elektriväli punktlaengu $q$ nihutamisel. Seejuures lähtume sarnasusest Maa raskusvälja ja homogeense elektrivälja vahel. Vaatleme müürilt kõrgusega $h$ alla pudenevat kivi massiga $m$. Kivi kukub raskusväljas vaba langemise kiirendusega $g$, sest talle mõjub raskusjõud $mg$ (J.1.35).

Kivi langeb raskusjõu suunas. Järelikult töö valemis (1.18 ) $\alpha =0$ ja $\cos \alpha =1$. Maapinnale jõudmise hetkeks on kivi sooritanud nihke s ning raskusväli on seega teinud töö, mis on jõu $mg$ ja sooritatud nihke $s$ (või kõrguse $h$) korrutis $A=mgh$ .

Kivi võib lohistada või veeretada ka mööda horisontaalset maapinda. Raskusvälja tööd see aga ei mõjuta, sest jõud ei tee tööd liikumisel jõuga ristuvas sihis (valemis 1.18 $\alpha =\pi /2$ ja $\cos \alpha =0$).

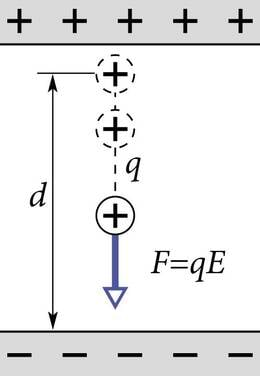
Laengut q omava keha liikumine homogeenses elektriväljas toimub samal viisil (J.1.36). Kehale mõjub elektrijõud $F$ , mis on valemi (1.11 ) kohaselt esitatav laengu ja väljatugevuse korrutisena $qE$. Kui keha on sooritanud selle jõu suunalise nihke s (või läbinud pikkuse $d$) siis elektriväli on teinud töö $A$, mis on jõu ja läbitud tee pikkuse korrutis: $A=qEd$.

Laetud keha võib samuti liikuda elektrijõuga ristuvas suunas. Elektrivälja tööd see aga ei mõjuta. Ei raskusväljas ega elektriväljas ei sõltu töö liikumistee ehk trajektoori kujust. Ta sõltub ainult jõujoone sihis läbitud pikkusest (vastavalt $h$ või $d$).

Välja, milles töö ei sõltu liikumistee kujust, nimetatakse potentsiaalseks väljaks, kuna tema kirjeldamisel võib kasutada potentsiaalse energia ja potentsiaali mõisteid. Potentsiaalne energia on tingitud keha vastastikmõjust teiste kehadega välja vahendusel. Kui keha asend võimaldab väljal teha keha nihutades tööd, siis on kehal potentsiaalne energia (ld potentis - suuteline, võimeline). Välja jõudude mõjul liikuva keha potentsiaalne energia kahaneb, sest töö varu kulutatakse ära.

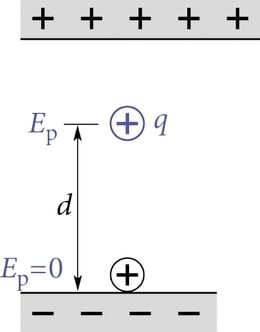
Potentsiaalse energia nulltasemeks on loomulik valida keha niisugune asend, millest keha antud ülesande tingimustes enam välja jõudude mõjul edasi liikuda ei saa. Toodud näites on selleks negatiivselt laetud plaadi asukoht (J.1.37).

Raskusjõu väljas aga on potentsiaalse energia loomulikuks nulltasemeks maapind. Sealt ei ole enam võimalik edasi kukkuda ja raskusjõud rohkem tööd teha ei saa.

Kui kogu potentsiaalne energia liikumisel ära kulutatakse, siis on tema algväärtus võrdne välja poolt tehtud tööga. Raskusväljas kehtib seega Mehaanikast hästi tuntud valem $E_p=mgh$. Punktlaengu $q$ potentsiaalne energia homogeen­ses elektriväljas avaldub vastavalt kujul

kus $d$ on punktlaengu kaugus energia nulltasemest või pikkus, mille laetud keha saab nulltasemeni liikudes läbida. Kuna indeksita $E$ tähistab elektrifüüsikas alati väljatugevust, siis hakkame edaspidi energia tähistamiseks kasutama E-tähte koos energia liigile viitava indeksiga (siin näiteks kujul $E_p$). Väljatugevuse tähisena toimiva E-tähe juures kasutame indekseid vaid erandjuhtudel, mil väljatugevuse ja energia segiajamine on välistatud.

Nagu näeme, sisaldab energia valem nii raskus- kui elektriväljas kõigepealt vaadeldavat keha iseloomustavat suurust ($m$ või $q$), seejärel välja tugevuse kirjeldajat ($g$ või $E$) ning lõpuks vaadeldava punkti kaugust energia nulltasemest ($h$ või $d$).

Nüüd jääb üle vaid küsida, mis on sel kõigel pistmist kodus kasutatava elektrienergiaga. Kui kummaline see ka ei tundu, on seos siiski olemas. Elektriseadmetes liiguvad laengukandjad elektrivälja jõudude mõjul. Laengukandjad liiguvad sealt, kus nende potentsiaalne energia on suur, sellisesse piirkonda, kus energia on väiksem. Seejuures teeb elektriväli meile vajalikku tööd.

Me jõudsime äsja järeldusele, et laetud keha liikumisel elektriväljas tehtav töö võib olla üks ja seesama liikumisel mööda täiesti erinevaid teid. Järelikult pole olulised ka E-vektori pikkuse ja suuna muutused liikumise käigus. Näiteks ei sõltu elektrilambi põlemine üldse lambi hõõgniidi kujust ja E-vektori suuna muutumisest piki hõõgniiti. Oluline on vaid energia, mis vabaneb laengukandjate läbiminekul hõõgniidist. Seetõttu on elektrivälja iseloomustamiseks võetud kasutusele veel üks suurus - välja potentsiaal.

Väljatugevus E näitab teatavasti ühikulise positiivse laenguga kehale vaadeldavas punktis mõjuvat jõudu. Potentsiaal $\phi$ aga näitab, kui suur on selles punktis ühikulise positiivse laenguga keha potentsiaalne energia. Elektrivälja mingi punkti potentsiaali leidmiseks tuleb jagada sellesse punkti paigutatud laengu potentsiaalne energia $E_p$ laengu suurusega $q$

Seejuures tähistab sõna laeng mõistagi laetud keha või laetud osakeste kogumit.

Potentsiaal on skalaarne ehk suunata suurus, nii nagu rõhk või temperatuur.

Paigutades potentsiaali definitsioonivalemisse (1.21) energia avaldise $E_p=qEd$ (valem 1.19), saame homogeense välja potentsiaali (J.1.38) avaldada kujul

Kehade tegelik liikumine ei sõltu kuigivõrd potentsiaali nulltaseme asukohast. Seetõttu võib potentsiaali nulltaseme valida lähtuvalt konkreetse ülesande tingimustest. Reeglina valitakse selleks punkt, millest laetud keha elektrivälja mõjul enam edasi liikuda ei saa. Elektrotehnikas loetakse tavaliselt nulliks Maa potentsiaal või siis elektriseadme maandatud metallkorpuse potentsiaal.

Ühesugust potentsiaali omavate elektrivälja punktide hulka nimetatakse ekvipotentsiaalpinnaks.

Homogeenses elektriväljas kahe erimärgiliselt laetud plaadi vahel (J.1.39) on ekvipotentsiaalpindadeks plaatidega paralleelsed tasandid. Potentsiaal muutub kõige kiiremini liikumisel piki elektrivälja jõujoont. Liikumisel jõujoonega ristuvas suunas jääb potentsiaal konstantseks.

Ekvipotentsiaalpinnad on alati jõujoontega risti. Jõujooned ja ekvipotentsiaalpinnad on kaks eri vahendit elektrivälja kirjeldamiseks. Nad on nagu kaks erinevat keelt, mis annavad edasi üht ja sama mõtet.

See pilv on tõenäoliselt laetud ning pinge pilve ja maa vahel on väga suur. On oodata äikest.	Joonisel näha olev naine on positiivselt laetud üle tema pea kulgenud äikesepilve tõttu.

Keha liikumine potentsiaalse välja kahe punkti vahel ei sõltu punktide potentsiaalide absoluutsest suurusest. Ta sõltub vaid nende punktide potentsiaalide vahest. Nii näiteks voolab jõgi ühtemoodi aeglaselt tasasel kõrgustikualal (platool) ja merelähedasel madalal tasandikul. Voolu kiirust ei määra mitte absoluutne kõrgus (merepinnast), vaid jõe vaadeldava lõigu otspunktide kõrguste vahe. Analoogiliselt on ka laengukandjate liikumise kiirus elektriväljas määratud potentsiaalide vahega.

Elektrivälja kahe punkti potentsiaalide vahet nimetatakse elektriliseks pingeks $U$. Potentsiaali definitsiooni (valemi 1.21) kohaselt võib pinge avaldada kujul

$E_{\text{p1}}$ ja $E_{\text{p2}}$ on seejuures laengut $q$ omava keha potentsiaalse energia väärtused elektrivälja kahes punktis. Nende väärtuste vahe võrdub tööga, mida teeb väli selle keha nihutamisel ühest punktist teise. Järelikult

kahe punkti vaheline pinge näitab, kui suurt tööd teeb elektriväli ühikulise positiivse laenguga keha viimisel ühest punktist teise. Laetud keha liikumisel piki jõujoont on keha nihe võrdne teekonna algus- ja lõpp-punkti vahekaugusega d ning tehtav töö avaldub kujul $A=qEd$. Järelikult valemi 1.24 põhjal

Siit tuleneb praktiline eeskiri elektrivälja tugevuse leidmiseks. Nimelt saame elektrivälja tugevuse, jagades kahe punkti vahelise pinge $U$ nende punktide vahekaugusega $d$, mis on mõõdetud piki välja mõjumise suunda. Seega

Valem 1.26 on täiesti täpne homogeenses elektriväljas. Mittehomogeenses väljas annab ta keskmise väljatugevuse vaadeldavas piirkonnas.

Valemiga 1.24 on määratud potentsiaali ja pinge ühik volt (1 V). Elektrivälja kahe punkti vahel on pinge üks volt, kui laengu 1 C viimisel ühest punktist teise tehakse töö 1 J. Seega

Samast seosest tuleneb töö ja energia ühik elektronvolt (1 eV). Kuna valemi 1.24 põhjal $A=qU$ , siis üks elektronvolt on töö, mida teeb elektriväli elementaarlaengut omava osakese (elektroni) viimisel ühest punktist teise, kui pinge nende punktide vahel on üks volt.

Üks elektronvolt on järelikult sama arv kordi väiksem ühest džaulist kui mitu korda elementaarlaeng on väiksem ühest kulonist. Elektronvolt on sobivaks töö ja energia ühikuks mikromaailma protsesside kirjeldamisel, millega tutvume gümnaasiumi füüsikakursuse lõpus.

Valemi 1.26 abil on saadud elektrivälja tugevuse SI-ühik volt meetri kohta (1 V/m). See on identne valemist (1.10 ) tuleneva ühikuga 1 N/C, sest

Üks volt meetri kohta on sellise elektrivälja tugevus, milles potentsiaal muutub liikumisel piki välja suunda igal meetril ühe voldi võrra.

Pinge ja potentsiaali teema lõpetuseks meenutagem Füüsikalise looduskäsitluse aluste kursust, milles tutvusime töö kui protsessi kirjeldava suuruse ja potentsiaalse energia kui süsteemi olekut (seisundit) kirjeldava suurusega. Pole raske märgata, et Elektromagnetismis kirjeldab protsessi pinge, olukorda elektrivälja mingis punktis aga potentsiaal. Protsess viib süsteemi ühest olekust teise, mistõttu töö on kahe potentsiaalse energia vahe ning pinge kahe potentsiaali vahe. Samas võib potentsiaale vaadelda kui pingeid mingi ühise kokkuleppelise nulltaseme suhtes.

Elektrivälja tugevus juhtiva keha pinna lähedal sõltub pinna kujust. Teraviku ümbruses saavutab väljatugevus väga suure väärtuse, sest teravik käitub punktlaenguna, millele lähenemisel väljatugevus kiiresti suureneb. Elektrivälja tugevnemisega teravike läheduses võib kaasneda laengu äravool teravikelt, sest õhk teraviku ümber muutub elektrit juhtivaks. Vastavalt püütakse kõrgepingeseadmetes vältida teravaid nurki ja väljaulatuvaid osi. Ka välgueelne elektriväli õhus on kõige tugevam maast lähtuva teraviku läheduses. Seetõttu on hoonetele parimaks kaitseks piksevarras. Välgulöök tabab suure tõenäosusega eelkõige piksevarrast, aga mitte hoonet.

Burj Khalifa Dubais, Araabia Ühendemiraatides on maailma kõrgeim ehitis. Ilmselt on see ka alus maailma kõige atraktiivsemale piksevardale.	Mida rohkem on üks jalg välgutabamuse asukohale lähemal kui teine, seda suurem pinge nende vahel tekib.

Kui välk lööb maasse, siis on maapinna potentsiaal välgust tabatud kohas hetkeks oluliselt erinev Maa üldisest potentsiaalist. Selle tagajärjel muutub potentsiaal piki maapinda lähenemisel välgust tabatud kohale. Mida rohkem on inimese üks jalg välgutabamuse asukohale lähemal kui teine, seda suurem potentsiaalide erinevus (pinge) tekib tema kahe jala vahel. Niisugust pinget nimetatakse sammupingeks. Sammupinge võib esineda ka elektrijuhtmestiku rikke tagajärjel. Igatahes on elektriohu korral soovitav liikuda võimalikult lühikeste sammudega, et vältida suure sammupinge tekkimist.

Äikese ajal pole soovitav ujuda või sõita paadiga. Välisantenni kasutamise korral ei maksa äikese ajal vaadata telerit. Tasub hoiduda ahju kütmisest, kuna suitsusammas sisaldab harilikust õhust oluliselt rohkem laetud osakesi. Seetõttu võib välk tema kaudu majja sisse lüüa.

Ei ole üldse kindel, et Benjamin Franklin oma lohekatset ka tegelikult tegi. Jah, ta kirjeldas sellist katset oma 1750 a. artiklis, aga ta andis endale ka aru ohtudest, mis sellise katse tegijat ähvardavad. Nii hästi ei läinud Peterburis töötanud Saksa päritolu teadlasel Georg Wilhelm Richmann’il, kes välgutabamuse saanud lohe tekitatud plahvatuses surma sai. Igal juhul sai 18. sajandi lõpul kinnitust hüpotees, et välk on elektriline nähtus ja majad said endale Franklini leiutatud väga kasuliku seadeldise - piksevarda.