Energia

Eessõna
1 Alalisvool
2 Elektrivool keskkondades
3 Vahelduvvool
4 Molekulide soojusliikumine
5 Termodünaamika (soojusenergia)
Lisad ja täiendused
Raudvara
1. Raudvara

Eessõna

Impressum

Autor Madis Reemann

Retsenseerinud Jaan Paaver, Uku Pütsepp
Toimetanud Kaido Reivelt
Keeletoimetaja Piret Põldver
Korrektuuri lugenud Lauri Kaldamäe
Joonised teinud Nils Austa
Pildid joonistanud Urmas Nemvalts

Õpiku lugejale

Käesolev õpik käsitleb energiat, mille liikidest on inimese jaoks olulisemad soojus- ja elektrienergia. Energia tarbimise kasv on lahutamatult seotud tsivilisatsiooni arenguga ja uute ressursside kasutuselevõtt pole üksnes tehnoloogiline, vaid globaalne probleem.
Õpiku põhitekst koosneb 25st õppetükist. Energiakursuse omandamist peaksid soodustama õpiku teises pooles õppetükkide kaupa toodud täiendused: lisamaterjal, ajalooline taust, pisut keerukamad probleemid ja kokkuvõte. Raudvara ja indeks on e-õpikus veel arenduses, paberõpikus asuvad nad õpiku lõpus lk 98–104. Raamatus on antud ka viiteid teistele õpikutele, kusjuures FLA – „Füüsikalise looduskäsitluse alused”, M – „Mehaanika”, EM – „Elektromagnetism” ja MM – „Mikro- ja megamaailma füüsika”.

Õpikust paberversioon saate endale hankida raamatupoest või otse kirjastusest Maurus.

Energilist õppimist!

Versioonid ja parandused

Tehtud

28.01.2022 Väiksemad parandused läbi terve õpiku, K.Reivelt

31.01.2022 Kõik valemid ja tähised latexisse pandud, Stiina

Planeeritud

Läbivalt valemite ja tekstisisese matemaatika konverteerimine latex formaati.

Sissejuhatus

Valgus-, soojus-, toiduainete, tuule- ja voolava vee energia on pärit Päikeselt. Energia jõuab Maa atmosfääri välispiirini elektromagnetkiirgusena, mille võimsus ruutmeetri kohta on umbes $1400 k W$ . Atmosfäär laseb läbi nähtavat valgust ning soojuskiirgust. See energia käivitab fotosünteesi ja hoovused, paneb liikuma õhu, põhjustades tuule ning aurustades vett, mis kondenseerub kõrgemates kohtades, tekitades vee loodusliku ringkäigu. Päikeselt tulnud energia arvel on toimunud väga pika aja jooksul fossiilsete kütuste tekkimine maakoores. Päritolult on eriline tuumaenergia, sest arvatakse, et näiteks uraan on tekkinud umbes $6, 6$ miljardi aasta eest supernoovas. Fossiilseid kütuseid ja tuumaenergiat loetakse taastumatuks energialiigiks.

Organismi eksistentsiks on vajalik nii aine- kui ka energiavahetus väliskeskkonnaga. Inimese päevane energiatarve toidus on viimase $100000$ aasta jooksul olnud oluliste muutusteta ligi $10 M J$ ( $2400 k c a l$ ). Küll aga on ühiskonna arenguga väga palju kasvanud üldine energiatarve, eeskätt seoses uute energialiikide kasutuselevõtuga. Tule tegemine soojendamiseks ja toidu valmistamiseks suurendas energiavajadust üle kahe korra. Paikseks jäänud põllumees ja käsitööline tarbis juba $50 M J$ energiat päevas. Edasi võeti kasutusele veoloomad, purjelaevad, tuulikud ja vesiveskid. Olulise muutuse energiatarbes andis aurumasina ja elektrienergia kasutuselevõtt. Inimesed hakkasid rohkem reisima ja soovisid koduses majapidamises suuremaid mugavusi. 20. sajandi esimesel poolel oli majanduslikult arenenud riikides energiakulu inimese kohta päevas jõudnud üle $300 M J$ . Tänapäevase tehnika- ja infoühiskonna liige tarbib keskmiselt $1000 M J$ ööpäevas, millest maailma keskmine on umbes viis korda väiksem.

Termin energiaallikas pole füüsikalises mõttes täpne, sest tegelikult ei toimu energia tekitamist, vaid üks energialiik muutub teiseks. Päikeses toimub
näiteks tuumaenergia muundumine soojusenergiaks. Põhilised inimese kasutatavad energialiigid on soojus- ja elektrienergia. Soojusenergiat kasutatakse ruumide kütmiseks ja vee soojendamiseks. Üle $80 %$ elektrienergiast saadakse soojus- ja tuumaelektrijaamades, kus vahelduvvoolugeneraatori paneb käima auruturbiin. Tööstuses ja viimasel ajal ka transpordis eelistatakse elektrienergiat, mida saab suhteliselt hea kasuteguriga muundada jõumasinates mehaaniliseks tööks ja mis ei saasta oluliselt ümbritsevat keskkonda. Inimeste energiatarve pole ajalises plaanis ühtlane ning see tekitab energia salvestamise vajaduse. Naftat, kivisütt ja põlevkivi võib koguda tagavaraks, kuid elektrienergia salvestamine suures koguses on keeruline ja kallis. Soojusenergia salvesta mine mitte eriti kõrgel temperatuuril pole kasulik, kuna sellise energia muundamine mehaaniliseks tööks oleks väikse kasuteguriga.

Energia tarbimises on valitsenud kogu aeg ebavõrdsus. Väga palju inimesi piirdub ka kaasajal eluks vajaliku miinimumiga. Samuti on ressursid piiratud ja jaotunud riigiti väga erinevalt. Need vastuolud on põhjustanud energiakriise ja riikidevahelisi konflikte. Maailma rahvastiku kasv ja nõudmiste suurenemine pingestab ka tulevikus energiaprobleemide lahendamist. Tehniliste küsimuste kõrval on kõige raskem muuta inimese mõtteviisi ja panna teda vähem ja säästlikumalt tarbima. Mõiste energia tänapäevases mõttes toodi füüsikasse 19. sajandi keskel. Energia jäävuse seadus on kirja pandud ka esimeses eestikeelses füüsikaõpikus 1855. aastal:

Alalisvool

Elektrivoolu tekkemehhanism

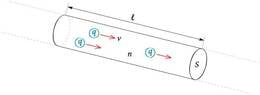
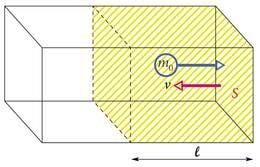
Elektrivooluks nimetatakse laengukandjate suunatud liikumist. Elektrivoolu iseloomustavaks suuruseks on voolutugevus, mis näitab, kui suur elektrilaeng läbib juhtme ristlõiget ajaühikus. Voolutugevuse SI -ühik on $1$ amper ( $1 A$ ). Juhi ristlõiget läbib sel juhul $1$ sekundi jooksul laeng $1$ kulon. Voolu suunaks on kokku lepitud positiivsete laengute suunatud liikumise suund. Joonisel 1.1. on kujutatud ühte vooluringi lõiku pikkusega $l$ , milles liiguvad elektrivälja sihis ühesugused osakesed laenguga $q$ keskmise kiirusega $v$ .

Olgu vabade laetud osakeste arv juhtme ruumalaühikus ehk kontsentratsioon $n$ ja aja $t$ jooksul jõuavad kõik osakesed läbida juhtmelõigu parempoolse otsa pindalaga $S$ . Laetud osakeste arv

N = n V = n S l

milles

l = v t

ja juhtme ristlõiget läbinud kogulaeng

q N = q n S v t

Voolutugevuse leidmiseks tuleb kogulaeng jagada ajaga, seega

(1.1.)

I = q n S v

Saadud valemist on näha, millised suurused määravad voolutugevuse juhis. Kolm nendest, $q$ , $n$ ja $v$ , on mikroosakesi iseloomustavad suurused. Metallide puhul on laengukandjateks tuuma mõjupiirkonnast vabanenud juhtivuselektronid, mis liiguvad positiivsete laengukandjate liikumise vastassuunas ning nendel on elementaarlaeng $q = - e = - 1, 60 \cdot 10^{- 19} C$ . Vabade elektronide kontsentratsioon $n$ välistingimustest oluliselt ei sõltu, küll aga elektronide triivimise kiirus v metalli kristallvõre aatomite vahel. Vabade elektronide puhul tuleb eristada kahte arvväärtuse poolest oluliselt erinevat kiirust, kaootilise soojusliikumise kiirus ja elektrivälja poolt tekitatud triivikiirus. Esimene nendest on palju suurem, aga kaootilisuse tõttu triivliikumisse mingit panust ei anna. Elektrivoolu tugevuse määrab elektrivälja poolt tekitatud aeglane triivikiirus. Kui $1 m m$ diameetriga vaskjuhtmes triivivad elektronid kiirusega $0, 1 m m / s$ , on voolutugevus umbes $1 A$ . Elektronide kaootilise liikumise kiirus on toatemperatuuril ligi miljard korda suurem.

Võib jääda mulje, et taskulambi sisselülitamisel võtaks süttimine kaua aega, kuni elektronid patareist lambini triivivad. Nii see ei ole, sest vabu elektrone on kogu vooluringi ulatuses ning elektriväli levib väga kiiresti, valguse kiirusega.

Küsimused

Mille poolest erinevad vabade elektronide soojusliikumise ja suunatud liikumise kiirused?

Miks elektronide soojusliikumise suur kiirus voolutugevust ei mõjuta?

Kokkuvõte

Elektrivool on laengukandjate suunatud liikumine. Voolu suunaks loetakse kokkuleppeliselt positiivsete laengute liikumise suunda. Voolutugevus on arvuliselt võrdne juhi ristlõiget ajaühikus läbinud laenguga

I = \frac{q}{t}

Voolutugevuse ühik üks amper on SI põhiühik ja ta on defineeritud vooluga juhtide vastastikmõju kaudu. 1 A voolutugevuse korral läbib juhi ristlõiget 1 s jooksul laeng 1 C.

Ülesanded

Kuuldeaparaadi vooluallikas mahutab

430 m A h

. Kui suure tugevusega voolu tarbitakse keskmiselt, kui vooluallikas peab vastu kolm kuud?

LED-valgustit läbib vool tugevusega

15 m A

ja tootja lubab tema tööeaks

25000

tundi. Kui suur elektrilaeng läbib valgustit selle aja jooksul?

Vasest juhtmes ristlõikepindalaga

1, 5 \times 10^{- 6} m^{2}

vabade elektronide kontsentratsioon

8, 4 \times 10^{28} m^{- 3}

ja kiirus

0, 37 \times 10^{- 3} m / s

. Arvuta voolutugevus juhtmes.

On kaks samasugust juhet, üks vasest, teine alumiiniumist. Voolutugevus neis on sama, aga vabade elektronide kontsentratsioon on alumiiniumist juhtmes

1, 4

korda väiksem. Kas alumiiniumist juhtmes on elektronide triivkiirus suurem või väiksem? Mitu korda?

Lisamaterjalid Lisaülesanded

Ohmi seadus

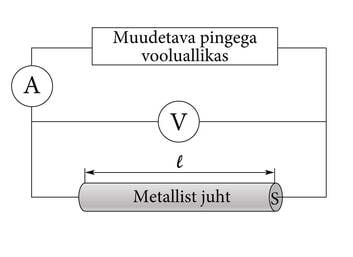
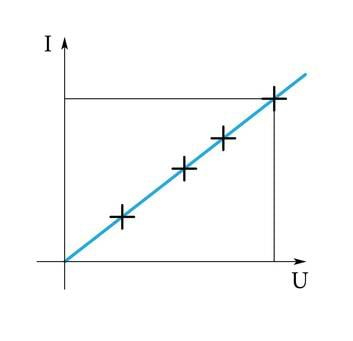
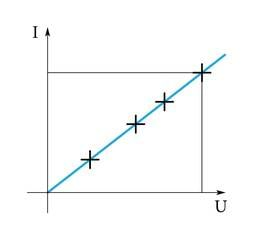
Kui mõõta metallist juhti läbiva voolutugevuse sõltuvust tema otstele rakendatud pingest (joonis 1.2. a), siis on näha, et voolutugevus juhis on võrdeline pingega juhi otstel (joonis 1.2. b).


Joonis 1.2. a	Joonis 1.2. b

Seega on antud juhi jaoks pinge ja voolutugevuse suhe sama ning seda suhet, takistust $R$ , võib kasutada metallist keha iseloomustamiseks voolu takistamise seisukohalt. Seos ongi valemi kujul esitatud Ohmi seadus.

(1.2.)

I = \frac{U}{R}

Kui sama kehaga korrata katset kõrgemal temperatuuril, jääb sõltuvus võrdeliseks, kuid graafiku tõus on väiksem. Temperatuuri tõus suurendab metallist keha takistust. Saksa füüsiku Georg Simon Ohmi poolt korraldatud katsed näitasid, et metalli takistus sõltub juhi pikkusest, ristlõikepindalast ja materjalist, ning hilisemate mõõtmistega leiti seos, kus $ρ$ on materjali eritakistus, mis määratakse katseliselt.

(1.3.)

R = \frac{ρ l}{S}

Võrdeline sõltuvus pinge ja voolutugevuse vahel pole üldkehtiv. Näiteks ioone sisaldavas lahuses, pooljuhis ja elektrivoolu juhtivas gaasis on sõltuvus keerulisem.

Eritakistuse järgi võib aineid ja materjale jaotada juhtideks, isolaatoriteks ja pooljuhtideks. Juhtidel on eritakistus suhteliselt väike ja isolaatoritel (dielektrikutel) suur. Pooljuhtide eritakistus on vahepealne, kusjuures see sõltub olulisel määral temperatuurist, valgustatusest ja lisanditest.

Küsimused

Mõõteriistu saab ühendada vooluringi erinevalt, näiteks jadamisi või rööbiti tarbijaga. Kuidas tuleks ühendada tarbija suhtes ampermeeter ja voltmeeter?

Missuguse takistusega peaks olema ideaalne amper- ja voltmeeter?

Juhtivus

G

on takistuse pöördväärtus. Missugune näeks välja Ohmi seaduse valem juhtivuse kaudu?

Kokkuvõte

Voolutugevus juhis on võrdeline pingega juhi otstel

I = \frac{U}{R}

Võrdeteguri pöördväärtust nimetatakse takistuseks ja selle ühikuks on Ω (oom). Takistuse tõttu esineb elektrivoolu soojuslik toime.

Takistus on võrdeline juhi eritakistuse ja pikkusega ning pöördvõrdeline juhi ristlõikepindalaga

R = \frac{ρ l}{S}

Võrdetegurit ρ nimetatakse aine eritakistuseks, mis näitab ühikulise pikkuse ja ristlõikega juhi takistust.

Juhi takistus oleneb temperatuurist kujul

R = R_{0} (1 + α t)

Ülesanded

Juhi otstele rakendati pinge

6 V

ja siis läbis seda vool

1, 5 A

. Kui suur vool läbis sama juhti, kui talle rakendati pinge

2 V

Vooluallikaga Varta AA rakendati tarbijale takistusega

0, 2 k Ω

pinge

1, 5 V

. Arvuta voolutugevus tarbijas amprites ja milliamprites.

Metalljuhtme takistus on

0, 2

oomi. Kui suur on

6

korda pikema ja

6

korda väiksema ristlõikepindalaga samast materjalist juhtme takistus?

Arvuta reostaadi takistus, kui reostaat kujutab endast

20 m

pikkust,

0, 4 m m^{2}

ristlõikepindalaga konstantaanist takistustraati eritakistusega

0, 49 Ω \cdot m m^{2} / m

Lisamaterjalid Lisaülesanded

Elektrimõõtmised

Elektrimõõteriistu võib jaotada osutmõõteriistadeks ja numbrilisteks mõõteriistadeks. Vastavad sünonüümid on analoog- ja digitaalmõõteriist.


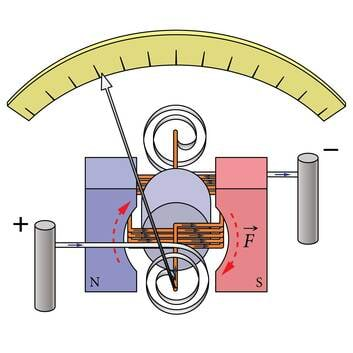
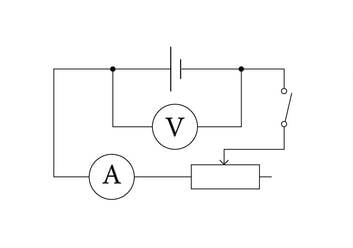
Joonis 1.3. a Osutmõõteriist	Joonis 1.3. b Osutmõõteriista tööpõhimõte

Vooluga raamile mõjub magnetväljas jõud ja voolutugevust saab mõõta magnetväljas vooluga raamile mõjuva jõu kaudu (joonis 1.3.). Raami vastaskülgedele mõjuvad jõud pööravad seda päripäeva. Raami külge pannakse osuti ja jõu tasakaalustamiseks spiraalvedrud.

Osuti kaldenurga järgi saab määrata voolutugevuse. Kui laseme voolu läbi takistuse, saame määrata ka pinget, mis on võrdeline voolutugevusega. Digitaalses mõõteriistas muudetakse pinge muunduriga kahendkoodiks ja see omakorda ekraanil numbriliseks näiduks (joonis 1.4.).


Joonis 1.4. a Digitaalmõõteriista põhimõtteline skeem	Joonis 1.4. b Multimeeter

Elektriliste suuruste mõõtmisel esinevad erineva päritoluga vead FLA. Elektrimõõtmistel on tegemist B-tüüpi mõõtemääramatusega, mis saadakse mõõteriista tootja poolt antud mõõteriista täpsuse hinnangust. Ebatäpsust iseloomustatakse absoluutse ja relatiivse piirveaga. Üleskirjutus katse protokollis $I = (1, 26 \pm 0, 05) A$ tähendab seda, et voolutugevuse mõõdetud väärtus on $1, 26 A$ , absoluutne piirviga $Δ I = 0, 05 A$ ja voolutugevuse tegelik väärtus asub vahemikus $1, 21 A$ kuni $1, 31 A$ . Relatiivne piirviga on absoluutse piirvea ja mõõtetulemuse suhe, mis antud juhul on umbes $4 %$ ning iseloomustab ka mõõtmise täpsust.

Osutmõõteriistale on kirjutatud täpsusklass (joonis 1.3. a). See on arv, mis näitab mõõteriista suhtelist piirviga protsentides maksimaalse näidu korral. Täpsusklassid võivad olla $4$ ; $2, 5$ ; $2, 0$ ; $1, 5$ ; $1$ ; $0, 5$ ; $0, 2$ ; $0, 1$ ; $0, 05$ ja $0, 02$ . Mida väiksem arv, seda täpsem mõõteriist. Kui laboratoorses töös kasutataval amper- meetril on täpsusklass $2, 5$ ja mõõtepiirkond $2 A$ , siis ampermeetri mõõtemääramatus (absoluutne piirviga) $Δ I = \pm 0, 05 A$ . Numbrilise mõõteriista passis on esitatud mõõtemääramatus näiteks kujul $\pm 0, 5 % \pm 2 D$ . See tähendab, et piirviga on $0, 5 %$ näidust pluss näidu viimase numbri $2$ ühikut.

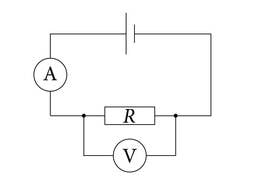
Elektrimõõtmistel tuleb arvestada, et mõõteriistad on samuti elektrivoolu tarbijad (tarvitid). Mõõteriistade ühendamisel vooluringi peaks riistade põhjustatud muutused olema võimalikult väiksed. Voolutugevust mõõdetakse ampermeetriga, mis ühendatakse tarvitiga jadamisi. Ampermeetril endal on samuti takistus ja see muudab voolutugevust vooluringis. Selleks, et muutus oleks väike, peaks ampermeetri takistus olema tarviti omast oluliselt väiksem. Voltmeeter seevastu ühendatakse rööbiti ja tema takistus peaks olema võimalikult suur.

Elektrimõõtmisi kasutatakse ka mitteelektriliste suuruste kaudseks mõõtmiseks. Selleks tuleb mõõdetav suurus muuta pingeks või vooluks. Termopaar koosneb kahest erinevast metallist vardast, mille ühed otsad on kokku joodetud. Kui jootekohta kuumutada, tekib vabade otste vahel pinge, mille väärtus oleneb jootekoha temperatuurist. Teades pinge ja temperatuuri seost, saame määrata temperatuuri kaudselt pinge mõõtmise abil. Lisaks toodud näitele on palju füüsikalisi nähtusi, kus mehaaniline, soojuslik või kiirguse energia muudetakse elektrienergiaks.

Elektrimõõtmiste eeliseks on asjaolu, et mõõtetulemusi on hea üle kanda, salvestada, töödelda ja kasutada protsesside automaatseks juhtimiseks.

Vigade arvutamise ja katsetulemuste esitamise näide

Mõõdame osutmõõteriistaga, mille mõõtepiirkond on $250 V$ ja täpsusklass $2, 5$ , võrgupinget ja saame tulemuseks $232 V$ . Arvutame absoluutse piirvea $Δ U = 250 \cdot 2, 5 / 100 = 6, 25 V$ . Mõõdetud pinge viimaseks numbriks on ühelised. Ka vea ümardame ühelisteks, aga alati ülespoole $Δ U = 6, 25 V \approx 7 V$ . Seega võrgupinge on $U = (232 \pm 7) V$ .

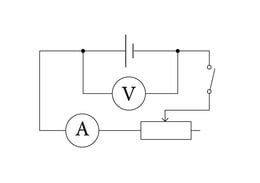
Kaudse mõõtmise korral võib viga arvutada erinevate meetoditega. Vaatame ülem- ja alamtõkke meetodit, mida kutsutakse ka halvima võimaluse meetodiks. Oletame, et määrame järgneval joonisel toodud vooluringiga takisti takistust pinge ja voolutugevuse kaudu. Mõõtes voltmeetriga pinge takisti otstel ja ampermeetriga voolutugevuse, saame Ohmi seadusest arvutada takistuse valemiga

R = \frac{U}{I}

Kui tahame hinnata takistuse mõõtemääramatust, siis tuleb arvestada mõlema mõõteriista viga. Lahendame ülesande konkreetse näite põhjal.

Voltmeeter mõõtepiirkonnaga $6 V$ ja täpsusklassiga $4$ näitas pinget $4, 3 V$ ning ampermeeter mõõtepiirkonnaga $2, 5 A$ ja täpsusklassiga $2, 5$ näitas voolutugevust $2, 25 A$ . Arvutades voltmeetri ja ampermeetri absoluutse piirvead, saame $Δ U = 0, 24 V$ ja $Δ I = 0, 0625 A$ . Suurima takistuse väärtuse ehk ülemtõkke saame siis, kui pinge on kõige suurem ja voolutugevus kõige väiksem.

R_{¨ u} = \frac{U_{¨ u}}{I_{¨ u}} = \frac{4, 3 + 0, 24}{2, 25 - 0, 0625} = 2, 075 Ω

Vähima takistuse ehk alamtõkke saame siis, kui pinge on vähim ja voolutugevus suurim.

R_{a} = \frac{U_{a}}{I_{a}} = \frac{4, 3 - 0, 24}{2, 25 + 0, 0625} = 1, 756 Ω

Takistuseks oleks mõistlik võtta nende aritmeetiline keskmine $R = 1, 916 Ω$ ja absoluutseks piirveaks pool nende erinevusest.

Δ R = \frac{R_{¨ u} - U_{a}}{2} = 0, 160 Ω

Absoluutne piirviga ümardatakse ülespoole ühe tüvenumbrini ( $0, 160 \approx 0, 2$ ). Määratud suuruse väärtus ümardatakse nii, et viga parandab selle viimast numbrit. Lõpuks kirjutame takistuse koos absoluutse piirveaga $R = (1, 9 \pm 0, 2) Ω$ .

Takistuse arvutamiseks tuleb pinge jagada voolutugevusega. Saab näidata, et jagatise ja korrutise relatiivne piirviga avaldub suuruste relatiivsete piirvigade summaga.

\frac{Δ R}{R} = \frac{Δ U}{U} + \frac{Δ I}{I}

Kui asetada ülaltoodud andmed valemisse, avaldada takistuse absoluutne piirviga ja esitada takistus koos veaga parajasti ümardatult, saab veenduda, et erinevus halvima võimaluse meetodiga saadud tulemusest on tühine.

Küsimused

Kas osutmõõteriista absoluutne viga sõltub näidust?

Miks soovitatakse valida mõõtepiirkond, milles näit on võimalikult suur?

Kokkuvõte

Elektrimõõteriista täpsusklass on relatiivne piirviga protsentides mõõteriista maksimaalse näidu korral.

Numbrilise mõõteriista korral on mõõtemääramatuse arvutamise valem toodud riista passis.

Ülesanded

Voltmeetri täpsusklass on

4

ja mõõtepiirkond

6 V

. Arvutage voltmeetri absoluutne piirviga. Kui suur on relatiivne piirviga

3 V

näidu korral?

Digitaalne voltmeeter näitab pinget

403 V

. Mõõtepiirkond on

1000 V

ja mõõteriista passis seisab kirjas, et selle mõõtepiirkonna määramatus on

\pm 0, 8 % \pm 2 D

. Esitage pinge koos absoluutse piirveaga.

Lisamaterjalid Lisaülesanded

Takistuse sõltuvus temperatuurist

Temperatuuri tõustes väheneb metallis vabade elektronide triivikiirus, kuna intensiivistub kristallvõre aatomite võnkumine. See takistabki elektronide liikuvust ja metalli takistus kasvab. Katsed näitavad, et metalli takistuse sõltuvus temperatuurist on ligikaudu lineaarne (joonis 1.5. a).

Selle sõltuvuse võib kirja panna valemiga, kus $R_{0}$ on takistus $0^{\circ} C$ juures, $a$ ( $^{\circ} C^{- 1}$ või $K^{- 1}$ ) takistuse temperatuuritegur ja $t$ temperatuur Celsiuse kraadides.

(1.4.)

R = R_{0} (1 + α t)

Takistuse temperatuuritegur on puhastel metallidel suurusjärgus $10^{- 3}^{\circ} C^{- 1}$ , näiteks volframil $0, 0045^{\circ} C^{- 1}$ .

Lülitades toas põlema algul toatemperatuuril oleva hõõglambi, tõuseb volframist hõõgniidi temperatuur kiiresti rohkem kui kaks tuhat kraadi ja hõõgniidi takistus ligi kümme korda. Hõõglamp kipubki läbi põlema sisselülitamisel, mil tema takistus on veel väike ja lambis eralduv võimsus umbes $10$ korda suurem kui stabiliseerunud tööolukorras. Elektrilistes küttekehades kasutatakse tavaliselt sulameid, mille takistuse temperatuuritegur on väike. Näiteks nikeliinil on see umbes $10^{- 4}^{\circ} C^{- 1}$ ja elektripliidi takistus on külmalt ja kuumutatult praktiliselt ühesugune. On aineid, mille takistuse temperatuuritegur on negatiivne, st takistus temperatuuri tõustes väheneb. Elektrolüütide, grafiidi ja pooljuhtide takistus väheneb mittelineaarselt.

Teades keha takistuse sõltuvust temperatuurist, saame seda keha kasutada näiteks takistustermomeetri andurina: vooluallikaga ühendatud anduri temperatuuri muutus põhjustab takistuse ja voolutugevuse muudu. Voolu muutust on aga mugav mõõta, salvestada, töödelda ning protsesside automatiseeritud juhtimisel rakendada.

20. sajandi alguses avastati nähtus, kus metalli takistus muutus väga madalal temperatuuril hüppeliselt nulliks. Tahke elavhõbedaga toimus see temperatuuril $- 269^{\circ} C$ (joonis 1.5. b). Sellises olukorras voolu soojuslik toime kaob ja kord liikuma pandud vool ei lakkagi. Hiljem avastati ülijuhtivus veel paljudel ainetel ja ka kõrgematel temperatuuridel. Kui saaksime ülijuhtivuse tekitada looduses esinevatel temperatuuridel, saaksime elektrienergia edastamisel esinevaid soojuslikke kadusid vältida. On valmistatud aineid, milles ülijuhtivusele üleminek toimub kõrgemal temperatuuril, näiteks $H g B a C u O - 138^{\circ} C$ juures.


Joonis 1.5. b

Ülijuhtivus

Elavhõbeda ülijuhtivuse avastas 1911. aastal hollandi füüsik Heike Kamerlingh- Onnes. Hiljem tehti takistuse kadumine kindlaks ka teistes ainetes. 1986. aastal avastasid saksa füüsik Johannes Georg Bednorz ja šveitsi füüsik Karl Alexander Müller rühma aineid, mille ülijuhtivus tuli esile juba vedelas lämmastikus. Ülijuhtivuse uurimise eest on saadud mitmeid Nobeli füüsikapreemiaid.

Ülesanded

Kui hõõglamp põleb, on tema takistus

810 Ω

ja volframist hõõgniidi temperatuur

2400^{\circ} C

. Arvutage lambi takistus toatemperatuuril

20^{\circ} C

juures, kui volframi takistuse temperatuuritegur on

4, 5 \times 10^{- 3}^{\circ} C^{- 1}

.Mitu korda muutub jahtunud lambi takistus sisselülitamisel? Mitu korda muutub lambi võimsus?

Kui hõõglamp põleb, on tema takistus

810 Ω

ja volframist hõõgniidi temperatuur

2400^{\circ} C

. Arvutage lambi takistus

0^{\circ} C

juures, kui volframi takistuse temperatuuritegur on

4, 5 \times 10^{- 3}^{\circ} C^{- 1}

Kokkuvõte

Pooljuhtide, elektrolüütide ja gaaside takistus temperatuuri kasvuga väheneb.

Juhi takistus oleneb temperatuurist kujul

R = R_{0} (1 + α t)

Ülijuhtivus on nähtus, kus ained madalal temperatuuril ei oma elektrilist takistust.

Küsimused

Elektrivoolul võib esineda soojuslik, magnetiline ja keemiline toime. Missugune nendest esineb alati?

Elektrivoolu tööd saab arvutada valemiga

A = I U t

. Kirjutage valem elektrivoolu võimsuse arvutamiseks ja andke valemis olevate füüsikaliste suuruste nimetused.

Kirjutage vooluga juhis eralduva soojushulga valem voolutugevuse, takistuse ja aja järgi.

Lisamaterjalid Lisaülesanded

Elektromotoorjõud. Ohmi seadus kogu vooluringi kohta

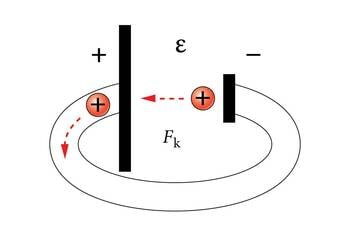
Vooluring koosneb vooluallikast, tarbijatest ja ühendusjuhtmetest. Et tekiks püsiv vool, peab vooluring olema suletud. Kui positiivne laeng on jõudnud vooluallika plussklemmilt läbi vooluringi miinusklemmile, peab voolu säilitamiseks mingi kõrvaljõud $F_{k}$ (joonis 1.6. a) elektriväljale vastu töötades selle laengu uuesti plussklemmile viima.


Joonis 1.6. a	Joonis 1.6. b

Selle kõrvaljõu töö arvelt saabki vooluringis eralduda soojushulk. Kõrvaljõud teevad tööd vooluallikas, kus toimub mingi teise energialiigi (mehaanilise, keemilise vms) muutmine elektrienergiaks positiivsete ja negatiivsete laengute lahutamise teel. Vooluallika elektromotoorjõud on võrdne kõrvaliste jõudude tööga ühikulise laengu ümberpaigutamisel kogu suletud vooluringi ulatuses.

(1.5.)

E = \frac{A_{k}}{q}

Elektromotoorjõu ühik on sarnaselt pinge ühikuga volt, sest

\frac{1 J}{1 C} = 1 V

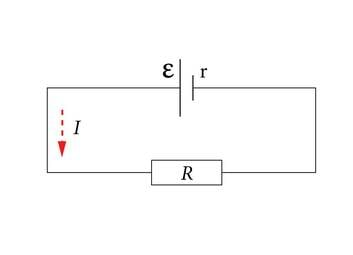
Kõrvaljõudude töö muutub vooluringis soojushulgaks, mis eraldub nii voolu- ringi välisosas kui ka vooluallikas (joonis 1.6. b). $A_{k} = ε q = ε I t = I^{2} R t + I^{2} r t$ , kus $R$ on vooluringi välisosa takistus ja $r$ vooluallika sisetakistus. Avaldades viimasest võrdusest voolutugevuse, saame:

(1.6.)

I = \frac{E}{(R + r)}

Saadud seos väljendab Ohmi seadust kogu suletud vooluringi kohta. Voolutugevus suletud vooluringis on võrdne vooluallika elektromotoorjõu ja vooluringi kogutakistuse suhtega.

Vooluringi kogutakistus koosneb vooluallika sisetakistusest $r$ ja vooluringi välisosa takistusest $R$ . Üldjuhul tuleb viimase hulka arvestada ka ühendusjuhtmete takistus.

Vooluallika elektromotoorjõudu ja sisetakistust võib vaadelda kui vooluallikat iseloomustavaid suurusi, mis lühikese aja jooksul ei muutu. Kui aga keemiline vooluallikas vananeb, väheneb pisut tema elektromotoorjõud ja suureneb oluliselt sisetakistus.

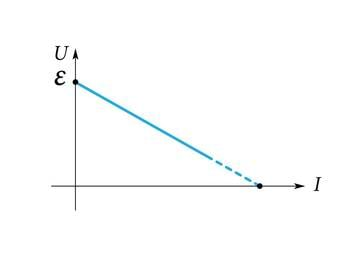
Avaldades valemist 1.6. elektromotoorjõu, saame $ε = I R + I r$ , milles suurus $I R = U$ on vooluallika klemmipinge $U = ε - I r$ . Viimasest valemist on näha, et elektromotoorjõud on vooluallika maksimaalne klemmipinge ja voolu kasvades vooluallika klemmipinge väheneb. Joonisel 1.7. a on klemmipinge mõõtmise vooluringi skeem ja katsetulemuste graafik 1.7. b.


Joonis 1.7. a	Joonis 1.7. b

Kui vooluringi välisosa takistus muutub nulliks, tekib lühis. Lühisvoolu tugevus on määratud vooluallika elektromotoorjõu ja sisetakistuse suhtega

I_{l} = \frac{E}{r}

Küsimused

Nii pinge kui ka elektromotoorjõud defineeritakse töö ja laengu suhtega. Missuguste jõudude tööd need on ja mille poolest nad erinevad?

Miks voolutugevuse kasvades vooluallika klemmpinge väheneb?

Mida tähendab lühis? Mida võib lühis esile kutsuda koduses majapidamises?

Kokkuvõte

Voolutugevus suletud vooluringis on võrdeline vooluallika elektromotoorjõuga ja pöördvõrdeline vooluringi välisosa ja vooluallika sisetakistuse summaga

I = \frac{E}{(R + r)}

Vooluallika elektromotoorjõud on arvuliselt võrdne kõrvaljõudude tööga ühikulise laengu ümberpaigutamisel kogu suletud vooluringi ulatuses

E = \frac{A_{k}}{q}

Ülesanded

Keemilise vooluallika elektromotoorjõud on

1, 5 V

. Kui suure töö teevad kõrvaljõud

1 C

laengu viimisel läbi kogu vooluringi?

Keemilise vooluallika elektromotoorjõud on

1, 5 V

. Kui suur laeng läbib vooluallikat kogu töötamise aja jooksul, kui temasse salvestatud energiast saame kasutada

2700 J

Keemilise vooluallika elektromotoorjõud on

1, 5 V

. Kui pikk on vooluallika tööiga voolutugevusel

0, 25 A

, kui temasse salvestatud energiast saame kasutada

2700 J

Kui joonisel 1.7. olev vooluring on avatud, näitab voltmeeter

3, 1 V

. Vooluringi sulgemisel on mõõteriistade näidud

2, 8 V

0, 5 A

. Määrake vooluallika elektromotoorjõud, vooluringi välisosa takistus ja vooluallika sisetakistus.

Arvutage voolutugevus vooluallikas, kui vooluringis tekib lühis. Vooluallika elektromotoorjõud on

3, 1 V

, vooluringi välisosa takistus on

5, 6 Ω

ja vooluallika sisetakistus

0, 6 Ω

Lisamaterjalid Lisaülesanded

Elektrivool keskkondades

Elektrivool vedelikes

Keemiliselt puhas vesi on dielektrik (isolaator). Ohutustehnika juhib tähelepanu ohtudele elektriseadmete kasutamisel vesistes ja niisketes kohtades. Hoiatus on õigustatud, kuna vesi, lahustades aineid, tekitab ioone. Juba väike lahustatava aine kogus ( $10^{- 8} %$ ) muudab puhta vee elektrijuhiks. Elektrolüüt on aine, milles laengukandjateks on ioonid.

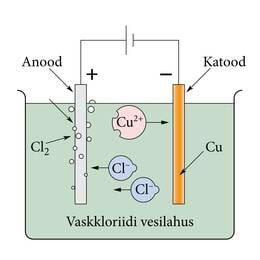
Kui näiteks vaskkloriidi lahustada vees, siis veemolekulide toimel laguneb sool ioonideks $C u C l_{2} = C u^{2 +} + 2 C l^{-}$ . Sellist protsessi nimetatakse elektrolüütiliseks dissotsiatsiooniks ja tekkinud lahus on elektrolüüt. Paneme lahusesse elektroodid, näiteks söepulgad. Katoodiks nimetatud elektrood on ühendatud vooluallika miinusklemmiga ja anood plussklemmiga (joonis 1.8.).

Vooluallika tekitatud elektriväli paneb ioonid lahuses triivima elektroodide poole. Positiivselt laetud vase ioonid liiguvad katoodile, saavad puuduvad elektronid ja vask sadestub katoodile. Negatiivselt laetud kloori ioonid liiguvad anoodile, annavad seal ära liigse elektroni ja eralduvad gaasilise kloorina. Selliseid elektrivoolu toimel kulgevaid redoksreaktsioone nimetatakse elektrolüüsiks. Elektrivool elektrolüütides on ioonide suunatud liikumine. Vooluga elektrolüütides kaasneb ainete eraldumine elektroodidel. Esimesena võeti elektrolüüs kasutusele esemete katmisel kulla- või hõbedakihiga. Elektrolüüsi seaduse avastas Michael Faraday. Elektrolüüsil eraldunud aine mass on võrdeline elektrolüüti läbinud laenguga, kus võrdetegurit nimetatakse aine elektrokeemiliseks ekvivalendiks.

(1.7.)

m = k q

Katsest saadud vase elektrokeemiline ekvivalent on $0, 33 m g / C$ . See tähendab, et eelnevalt kirjeldatud katses eraldub iga elektrolüüti läbinud $1 C$ laengu kohta katoodile $0, 33 m g$ vaske.

Ka metallimaagi või soola sulatamisel tekivad ioonid ja seda asjaolu saab kasutada näiteks alumiiniumi elektrolüütiliseks tootmiseks boksiidist või naatriumi saamiseks keedusoolast. Alati ei ole elektrolüüsil toimuvad protsessid nii lihtsad kui eespool kirjeldatud. Sõltuvalt metalli aktiivsusest ja elektroodide materjalist võivad eralduda erinevad ained. Näiteks sulatatud $N a C l$ elektrolüüsil eralduvad naatrium ja kloor, kuid $N a C l$ vesilahuse elektrolüüsil eralduvad hoopis vesinik ja kloor.

Küsimused

Vooluallikaga on jadamisi ühendatud elektrolüüsivannid, millest ühes eraldub nikkel ja teises tsink. Teatava aja jooksul eraldus

300 m g

niklit. Kui palju eraldus sama aja jooksu tsinki? Elektrokeemiline ekvivalent on niklil

0, 30 m g / C

ja tsingil

0, 34 m g / C

Soolhappe (

H C l

) elektrolüüsis eraldus katoodil

1 g

vesinikku. Mitu grammi eraldus anoodil kloori? Vesiniku aatommass on

1

amü ja klooril

35, 5

amü.

Kokkuvõte

Elektrolüütideks on ained, milles vabadeks laengukandjateks on ioonid.

Elektrolüüs on protsess, milles alalisvool põhjustab redoksreaktsiooni.

Elektrolüüsi käigus elektroodile eraldunud aine mass on võrdeline elektrolüüti läbinud laenguga.

m = k q

Võrdetegurit $k$ nimetatakse aine elektrokeemiliseks ekvivalendiks. See määratakse katseliselt ja on arvuliselt võrdne aine massiga, mis eraldub elektrolüüti läbinud ühikulise laengu korral.

Ülesanded

Elektrolüüsis eraldus

0, 5

grammi hõbedat. Arvutage elektrolüüti läbinud laeng, kui hõbeda elektrokeemiline ekvivalent on

1, 118 \times 10^{- 6} k g / C

. Arvutage hõbetamise aeg, kui voolutugevus oli

0, 2 A

Kui palju vesinikku ja hapnikku tekib

3, 6 k g

vee elektrolüüsil? Vesiniku ja hapniku aatommassid on vastavalt

1

16

aatommassiühikut.

Lisamaterjalid Lisaülesanded

Elektrivool gaasis

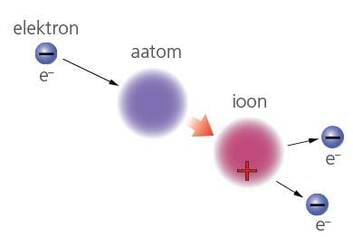
Kõrgepingeliine ei kaeta isoleeriva kihiga, sest õhk on tavaoludes isolaator. Ent kui isoleerimata juhtmed piisavalt lähestikku viia, tekib nende vahel elektriline läbilöök. Püüame uurida, millistel tingimustel elektrivool gaasis tekib. Anname hõõrdumisega elektriseeritud eboniitpulgaga elektroskoobile laengu. Laengu saavad ka elektroskoobiga ühendatud metallist plaadid – katood ja anood. Näeme, et laeng võib püsida küllaltki kaua. Viies plaatide vahele leegi, märkame laengu kahanemist (joonis 1.9. a), aga leegi eemaldamisel laengu kahanemine jälle seiskub.


Joonis 1.9. a	Joonis 1.9. b

Õhus vabad laengukandjad praktiliselt puuduvad. Kuid leegilt saadud energia arvelt toimub elektronide vabanemine õhus olevatest neutraalsetest gaasi molekulidest. Tekivad vabad elektronid ja positiivselt laetud ioonid. Seda nähtust nimetatakse ionisatsiooniks. Plaatidevaheline elektriväli paneb elektronid ja ioonid vastassuunaliselt liikuma ning vähendab laengut ja osuti hälvet. Leegi kustutamisel hakkavad elektronid ja positiivsed ioonid plaatide vahel uuesti neutraalseteks molekulideks ühinema – rekombinatsioon – ja gaas muutub jällegi isolaatoriks.

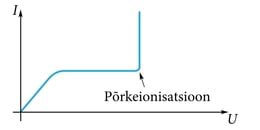
Neutraalse molekuli võib ioniseerida ka sellega põrkav elektriväljas piisavalt suure kineetilise energiani kiirendatud elektron (joonis 1.9. b). Nähtust nimetatakse põrkeionisatsiooniks ja selle tekkimiseks peab elektroni energia olema vähemalt võrdne elektroni väljumistööga gaasi molekulist.

E_{k} = \frac{m_{e} v^{2}}{2} \geq A

Joonis 1.10. Gaasi pinge-voolu tunnusjoon

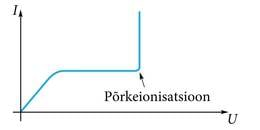
Joonisel 1.10. on esitatud voolutugevuse sõltuvus pingest gaasis. Graafiku algus on sarnane metalliga, kuid teatavast pingest alates voolutugevus enam ei kasva. Seda voolu nimetatakse küllastusvooluks $I_{k}$ ja põhjuseks on asjaolu, et kõik ajaühikus tekkinud vabad laengukandjad jõuavad elektroodidele. Pinge edasisel suurenemisel tekib põrkeionisatsioon ja voolutugevus kasvab järsult.

Elektroni energiat saab suurendada elektrivälja tugevdamise või gaasi hõrendamisega. Hõrendamine suurendab elektroni vaba tee pikkust ja aega järgmise põrkeni. Sellisel juhul saab elektron koguda põrkeionisatsiooniks vajalikku energiat.

Elektrivoolu gaasis nimetatakse gaaslahenduseks, mis jaotatakse sõltuvaks ja sõltumatuks lahenduseks. Eeltoodud katses sõltus lahendus leegist, kõrvalisest ioniseerivast energiaallikast. Ionisatsiooni tekitajaks võib olla ka valgus ja radioaktiivne kiirgus. Üks viis mõõta radioaktiivset kiirgust on loendada kiirguse poolt gaasis põhjustatud vooluimpulsse. Pärast põrkeionisatsiooni on tegemist juba sõltumatu gaaslahendusega, sest vabad laengukandjad tekitatakse elektriväljas saadud energia arvelt.

Küsimused

Miks tekib sõltumatu gaaslahendus hõrendatud gaasis madalamal pingel?

Miks vaakum tavatingimustes elektrit ei juhi, ehkki vaakumit võib vaadelda kui tugevasti hõrendatud gaasi?

Kokkuvõte

Tavatingimustes on gaasid halvad elektrijuhid. Elektrivoolu juhib ainult ioniseeritud gaas.

Põrkeionisatsiooniks nimetatakse nähtust, kus elektriväljas kiirendatud elektron põrkudes gaasi aatomiga lööb sellest välja elektrone.

Sõltumatu gaaslahendus tekib pärast põrkeionisatsiooni algust ja kestab edasi ka välise ionisaatori eemaldamisel.

Elektrivoolu gaasis nimetatakse gaaslahenduseks.

Ülesanded

Metallplaatide vahel on elektrivälja tugevus

2850 V / m

ja plaatide vaheline kaugus on

10 c m

. Arvutage pinge plaatide vahel. Kui suure töö teeb elektriväli elektroni viimisel ühelt plaadilt teisele?

Üks elektronvolt (

e V

) on energia, mille saab elektron läbides elektriväljas punktid, millevaheline pinge on üks volt. Teisenda elektronvolt SI-energiaühikuks džaul. Kui kiiresti liigub elektron, mille kineetiline energia on

1 e V

Lisamaterjalid Lisaülesanded

Pooljuhtide elektrijuhtivus

Pooljuhid on kaasaegse elektroonika kõige olulisemaks lähtematerjaliks. Neist valmistatakse transistore, dioode ja teisi pooljuhtseadeldisi.

Kõige olulisem pooljuhi omadus on eritakistus, mis sõltub tugevalt lisanditest ning on kergesti mõjutatav väliste energiaallikatega. Kõrgem temperatuur, valgustatus ja lisandid parandavad oluliselt pooljuhi juhtivusomadusi.

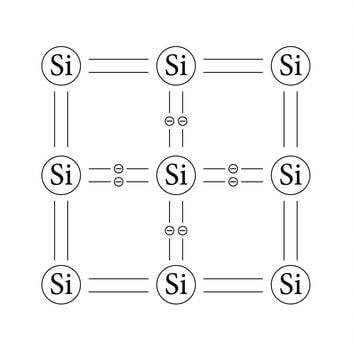
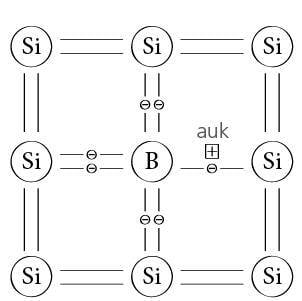
Olulisteks pooljuhtmaterjalideks on räni ja germaanium, mis paiknevad elementide perioodilisuse süsteemis 14. ehk IV A rühmas. Nende aatomite väliskihis on $4$ elektroni ja nad on omavahel seotud kovalentsete sidemetega (joonis 1.11. a).


Joonis 1.11. a Pooljuhtide elektrijuhtivus	Joonis 1.11. b pooljuhtide elektrijuhtivus

Madalatel temperatuuridel on sidemed tugevad ja pooljuht käitub isolaatorina. Kõrgemal temperatuuril räni aatomiga nõrgalt seotud elektronid vabanevad. Struktuurist lahkunud elektronide asemele jäävad nn augud (joonis 1.11. b), mida võime vaadelda positiivsete laengutena. Pooljuhti on tekkinud elektron-auk paarid.

Rakendades pooljuhile elektrivälja, hakkavad vabanenud elektronid liikuma. Positiivse laenguga auk tõmbab enda kohale kõrvalaatomi elektroni, tekitades omakorda kõrvalaatomis augu. Elektrivool pooljuhis on vabade elektronide ja aukude suunatud liikumine. Sellist puhaste pooljuhtide juhtivust, kus vastassuunas liigub sama hulk elektrone ja auke, nimetatakse omajuhtivuseks. Nähtust rakendatakse termo- või fototakistis, mida omakorda saab kasutada temperatuuri ja valgustatuse elektrilisel registreerimisel.

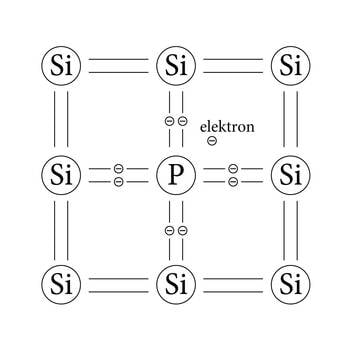
Viies pooljuhti sobivaid lisandiaatomeid, saab tekitada lisandjuhtivuse. Kui neljavalentsele ränile lisada pisut viievalentset lisandit, näiteks fosforit (joonis 1.12. a), siis jääb räniaatomitest ümbritsetud fosforil üks elektron üle, sest talle ei leidu struktuuris kindlat kohta.


Joonis 1.12. a pooljuhtide elektrijuhtivus	Joonis 1.12. b Pooljuhtide elektrijuhtivus

Iga lisandiaatomi kohta jääb vabaks üks elektron, mis hakkab elektrivälja rakendamisel pooljuhis triivima. Sellises pooljuhis on põhilisteks laengukandjateks elektronid ja vastavat juhtivust nimetatakse laengukandjate negatiivse laengu tõttu n-juhtivuseks. Sünonüümideks on ka elektronjuhtivus ja doonorjuhtivus.

Lisades neljavalentsele põhiainele kolmevalentset lisandit (joonis 1.12. b), näiteks ränile boori, jääb räniaatomil booriga üks side moodustamata ja tekib auk. Vastavat juhtivust nimetatakse p-juhtivuseks, millel on veel samatähenduslikeks terminiteks auk- ja aktseptorjuhtivus.

Koos lisandjuhtivusega kaasneb alati ka omajuhtivus, mida püütakse üldjuhul võimalikult vähendada. Enamuslaengukandjateks on n-juhtivuse korral elektronid ja p-juhtivuse korral augud. Pooljuhtide elektrijuhtivus on seotud oluliselt ainete kristallstruktuuriga ja seetõttu algab pooljuhtseadiste tehnoloogia eriti puhaste ainete saamisest.

Küsimused

Omajuhtivuse korral on vabadeks laengukandjateks elektronid ja augud. Kumma arv on suurem?

Kokkuvõte

Pooljuhid on ained, mille eritakistus on metallide ja dielektrikute vahepealne ning mille juhtivus sõltub oluliselt temperatuurist, valgustatusest ja lisanditest.

Sõltuvalt sellest, kas lisandi valents on suurem või väiksem kui põhiainel, saadakse vastavalt elektron- ja aukjuhtivus. Elektrivool pooljuhtides on elektronide ja aukude suunatud liikumine.

Ülesanded

Kui palju vabu elektrone tekib pooljuhis juurde, kui ränile lisada

1

mikrogramm fosforit? Fosfori molaarmass on

31 g / m o l

ja Avogrado arv

N_{A} = 6, 02 \times 10^{23} m o l^{- 1}

Lisamaterjalid Lisaülesanded

p-n siire. Pooljuhtdiood

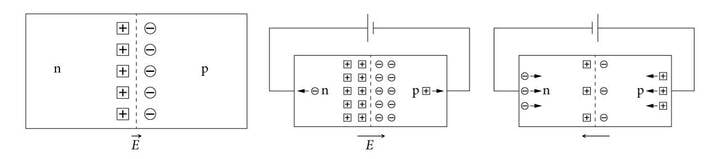
Kui tekitada pooljuhis kaks erineva juhtivusega osa, siis p- ja n-juhtivusega osade üleminekupiirkonda nimetatakse p-n siirdeks. Selline olukord saavutatakse erinevate lisandite sisseviimisega pooljuhtkristalli (dopeerimine ehk legeerimine). Siirdel hakkab toimuma laengukandjate vahetus. Doonorlisandiga n-osas on hulk elektrone, millel puudub kristallvõres sobiv koht. Need kohad on olemas aga kõrvalolevas p-osas. Elektronid hakkavad soojusliikumisest põhjustatud difusiooni toimel liikuma p-osas olevatele vabadele kohtadele, mille tulemusel enne neutraalne p-osa saab negatiivse laengu ja n-osa, kaotades elektrone, samasuguse positiivse laengu (joonis 1.13. a). Laengukandjate difusioon toimub ainult siirdes, sest seda hakkab takistama tekkiv elektriväli $\to E$ . See elektriväli soodustaks vähemuslaengukandjate liikumist läbi siirde, st elektronide liikumist p-osast n-ossa ja aukude liikumist n-osast p-ossa. Piirkihis puuduvad voolu tekkimiseks vajalikud laengukandjad ja olukorda võime vaadelda kui takistava kihi tekkimist erineva juhtivusega osade piiril.

Kui ühendada pooljuhi p-osaga vooluallika miinusklemm ja n-osaga plussklemm, siis siirde elektriväli tugevneb veelgi (joonis 1.13. b). Enamuslaengukandjad ei saa siiret üldse läbida. Väike hulk vähemuslaengukandjaid saab siiret läbida, põhjustades nõrga nn vastuvoolu. Pingestades p-n siirde päripidiselt (joonis 1.13. c), muudetakse elektrivälja suund siirdes eelnevaga võrreldes vastupidiseks, mis soodustab enamuslaengukandjate liikumist läbi siirde. Tekkinud pärivool on vastuvoolust oluliselt tugevam.


Joonis 1.14.

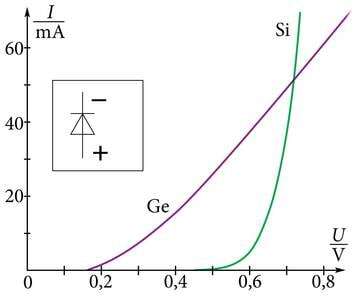
Joonisel 1.14. on graafik, mis näitab p-n siiret läbiva voolutugevuse sõltuvust pingest (pinge-voolu tunnusjoon). Eelpoolkirjeldatud p-n siiret rakendatakse pooljuhtdioodis. Pooljuhtdiood töötab ventiilina, mis laseb elektrivoolu läbi praktiliselt ainult ühes suunas.

Küsimused

Missugused võiksid olla pooljuhtseadiste puudused?

Kokkuvõte

Pooljuhtdioodis on p-n siire, mille põhiomaduseks on juhtida elektrivoolu ühes suunas.

Transistor on pooljuhtseadis, mille abil saab tekitada, lülitada, võimendada ja muundada elektrisignaali (voolu).

Ülesanded

Arvuta ränidioodi takistus joonise 1.14. põhjal pingetel

0, 6 V

0, 7 V

Lisamaterjalid Lisaülesanded

Elektrist valgus ja valgusest elekter

p-n siirdel on peale pooljuhtdioodi mitmeid muid rakendusi. Siirde päripidisel pingestamisel võib eralduda valgus (valgusdiood) ja vastupidi, siirde valgustamisel võib tekkida elektromotoorjõud (fotorakk).

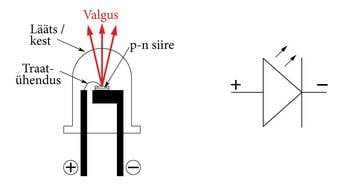
Hõõglambis muutub väga väikene osa, umbes $4 %$ elektrienergiast valguseks. Paremaid tulemusi, umbes $15 %$ , võib saavutada säästulambiga. Viimasel ajal saab poest osta ka LED-valgusteid, mille tehnilised näitajad on veel paremad. Valgusdiood – LED, lühend sõnast light emitting diode – on pooljuhtseadis, mis muudab elektrienergia optiliseks kiirguseks (infravalgus, nähtav valgus või ultravalgus). Valgusdioodis nagu tavaliseski dioodis on p-n siire. Traditsioonilises pooljuhtdioodis on pärivoolu korral energia eraldumist siirdes püütud minimeerida. Seevastu valgusdioodis muudetakse p-n siirdel elektronide ja aukude rekombineerumisel eralduv energia vahetult valguseks. Päripinge rakendamisel läbivad siiret enamuslaengukandjad. Ained püütakse valida selliselt, et toimuks võimalikult paljude elektronide ja aukude rekombinatsioon ning et selle protsessi käigus kiirguks just vajaliku värvusega valgus. Konstruktsioon peab tagama, et siirdel tekkinud kiirgus pääseks välja. Valgusdioodid võivad kiirata erinevat värvi või ka valget valgust. Nende eeliseks on väikesed mõõtmed, põrutuskindlus, pikk eluiga (tuhat korda pikem kui hõõglampidel), kiire süttimine ja vastupidavus sisse-välja lülitamistele. Puuduseks on kõrge hind ja kõrgete temperatuuride mittetalumine.


Joonis 1.15 a,b LEDi ehitus ja skeemitähis.	Joonis 1.15 c LED-lamp

Vastupidine protsess toimub fotorakus, kus siirdele langev valgus eraldab erimärgilised laengud, tekitades elektromotoorjõu. Seda nähtust kasutatakse valgusenergia muutmiseks elektriks. Kui fotorakud ühendada suuremaks süsteemiks, saame näiteks päikesepatarei või digikaamera pildisensori – CCD (charge-coupled device). Kui kaamerale on kirjutatud $10 M p x$ , siis tähendab see, et sensoril on $10$ miljonit imepisikest kujutist salvestavat fotorakku.


Joonis 1.16 b Päikesepatarei.	Joonis 1.16 c Fotoraku skeemitähis.

Inimene saab olulise osa informatsioonist valgusest nägemisaistingu abil. Selle info salvestamiseks saame kasutada ka digikaamerat, kus CCD muudab kujutise elektrisignaaliks ja salvestab selle mälus. Vajadusel saame salvestise uuesti taastada kujutisena näiteks LEDide abil. Nobeli 2009. aasta füüsikapreemia antigi CCD ja optilise kaabli arendamise eest.

Päikeselt saabub Maale hiiglaslik kiirgusenergia hulk, õhkkonna ülakihtides umbes $1400 J / s$ iga ruutmeetri kohta. Kui me suudaksime selle muuta elektrienergiaks, kaoksid inimkonna energiaprobleemid. Päikesepatareide efektiivsuse kasv võib muuta nende kasutamise Eestis majanduslikult efektiivseks.

Küsimused

Loetle säästulambi puudusi võrreldes teiste valgusallikatega.

Missugused on LED-lampide eelised võrreldes teiste valgusallikatega?

Kokkuvõte

LEDis muutub elektrivoolu energia p-n siirdel erimärgiliste laengute
rekombinatsioonil vahetult valguseks.

Fotorakus esineb valgusdioodiga vastupidine protsess, kus p-n siirdele langev valgus eraldab erineva märgiga laengukandjad, tekitades elektromotoorjõu.

Ülesanded

Valgusallikat iseloomustatakse valgusviljakusega, mis on kiiratud valgusvoo ja tarbitud võimsuse suhe. Valgusvoog arvestab ka inimsilma nägemisaistingu omapära. SI-s on tema ühikuks luumenit vati kohta (

l m / W

). Arvuta hõõglambi, säästulambi ja LED-lambi valgusviljakused piltide põhjal.

Tõraveres oli 2012. aasta juunis ühele ruutmeetrile langeva päikesekiirguse energia

605 M J

. Kui palju oleks saanud selles kuus maksimaalselt elektrienergiat päikesepaneeliga, mille pindala on

20 m^{2}

ja kasutegur

15 %

? Kui palju tuleks selle energia eest maksta, ostes seda võrgust hinnaga

0, 14 € / k W h

Lisamaterjalid Lisaülesanded

Vahelduvvool

Vahelduvvoolu genereerimine

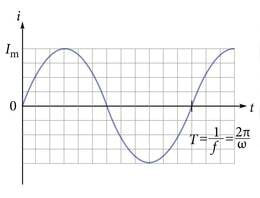
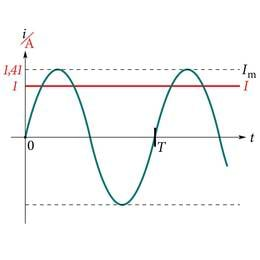
Vahelduvvool on elektrivool, mille tugevus ja suund perioodiliselt muutuvad. Energiasüsteemides kasutatakse sinusoidaalset voolu (joonis 1.17.), mida väljendab voolutugevuse ajas muutumise võrrand, kus i on voolutugevuse hetkväärtus, $I_{m}$ voolutugevuse maksimaalne väärtus ja $ω$ ringsagedus (võngete arv $2 π$ sekundis).

(1.8.)

i = I_{m} sin (ω t)

Tegemist on elektromagnetilise harmoonilise sundvõnkumisega, sest sinusoidaalselt muutuv vool tekib perioodiliselt muutuva elektromotoorjõu mõjul.

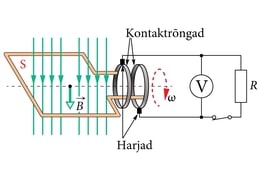
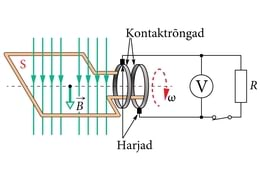
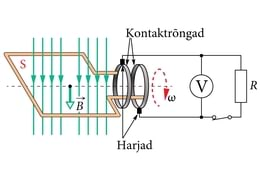
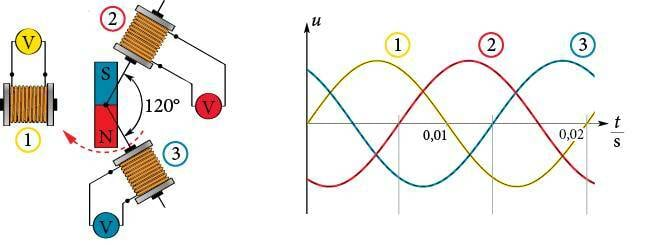
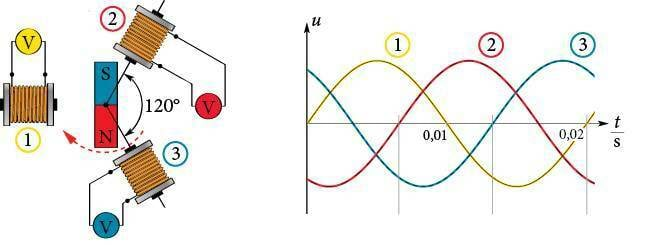
Vahelduvvoolu toodetakse vahelduvvoolugeneraatoriga, mille töö põhineb elektromagnetilise induktsiooni nähtusel. Kui asetada juhtivast materjalist kontuur (juhtmekeerd) pindalaga $S$ magnetvälja magnetinduktsiooniga $B$ , siis läbib kontuuri magnetvoog

Φ = B S cos β

EM. Nurk $α$ kirjeldab kontuuri asendit magnetvälja jõujoonte suhtes. Magnetvoo muutumisel indutseeritakse kontuuris elektromotoorjõud, mille suurus sõltub magnetvoo muutumise kiirusest

E = - \frac{Δ Φ}{Δ t}

Tehniliselt lihtsaim viis magnetvoogu muuta on panna kontuur magnetväljas pöörlema. Joonisel 1.18. a kujutatud asendis on kontuuri läbiv magnetvoog maksimaalne, sest $α = 0$ ja $cos α = 1$ . Magnetvoog muutub harmooniliselt ja kõige kiiremini siis, kui kontuur on teinud veerand pööret. Sellel hetkel on ka indutseeritud elektromotoorjõud maksimaalne. Kui kontuur pöörleb nurkkiirusega

ω = \frac{α}{t}

siis tekib temas samuti harmooniliselt muutuv elektromotoorjõud

(1.9.)

E = E_{m} sin (ω t)


Joonis 1.18. a) Vahelduvvoolu generaatori tööpõhimõte.	Joonis 1.18. b) Pinge graafik

Elektromotoorjõu maksimaalne väärtus εm sõltub võrdeliselt magnetinduktsioonist, pindalast ja nurkkiirusest. Elektromotoorjõud on magnetvoo suhtes veerand perioodi nihkes nagu siinuse ja koosinuse graafikud.

Kui pöörleva kontuuri otsad ühendada tarbijaga, läbib teda vahelduvvool. Voolu tugevus on Ohmi seaduse järgi (valem 1.6.) määratud elektromotoorjõu ja vooluringi kogutakistuse suhtega

i = \frac{E}{(R + r)} = \frac{E_{m} sin (ω t)}{(R + r)}

Voolu maksimaalväärtuse ja pinge maksimumi valemid on analoogsed alalisvoolu vastavate seostega.

(1.10.)

I_{m} = \frac{E_{m}}{(R + r)}

(1.11.)

U_{m} = I_{m} R

Vooluallika sisetakistuseks r võime lugeda antud juhul generaatori pöörleva mähise takistust.

Euroopa vahelduvvooluvõrkudes kasutatakse sagedust $f = 50 H z$ , seega $ω = 314 r a d / s$ .

Küsimused

Määrake joonise 1.18. a põhjal raamis tekkiva induktsioonivoolu suund. Tooge esile lahenduse kõik etapid.

Hetkel, kui vahelduvvoolu generaatori pöörlevat mähist läbiv magnetvoog on maksimaalne, mähises induktsiooni elektromotoorjõud puudub, kui aga magnetvoog puudub, siis on elektromotoorjõud maksimaalne. Miks see nii on?

Miks on vahelduvvoolu generaatori mähises tavaliselt palju juhtmekeerde?

Kokkuvõte

Vahelduvvool on elektrivool, mille suund ja tugevus ajas perioodiliselt
muutub.

Vahelduvvoolu tekitamine põhineb elektromagnetilise induktsiooni nähtusel. Näiteks tekib magnetväljas pöörlevas juhtmekeerus sinusoidaalselt muutuv elektromotoorjõud. Põhiline osa elektrienergiast toodetakse vahelduvvoolugeneraatoritega, mille kä

Ülesanded

Vahelduvvoolu võrgus on sagedus

50 H z

. Arvutage vahelduvvoolu ringsagedus ja periood.

Kui suur magnetvoog läbib kontuuri joonisel 1.18. a? Kui suur on magnetvoog läbi kontuuri, kui see sooritab veerand pööret, pool pööret, täispöörde?

Määrake joonise põhjal raami läbiva magnetvoo muutumise kiirus. Raam sooritab veerand pööret. Kas selles asendis magnetvoo muutumise kiirus on suurem või väiksem?

Lisamaterjalid Lisaülesanded

Voolutugevuse, pinge ja võimsuse efektiivväärtused

Kui paigalolevat juhti läbib vool, eraldub temas elektrivoolu tööga võrdne soojushulk

Q = A = I U t = I^{2} R t

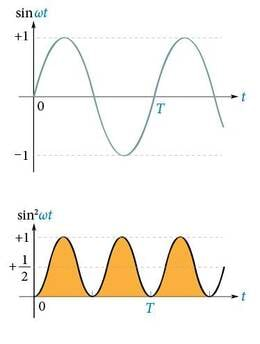
Valem kehtib alalisvoolu korral, kuid vahelduvvoolu tugevus ajas muutub. Seetõttu tuleb vahelduvvoolu puhul valemisse panna voolutugevuse ruudu keskmine väärtus. Trigonomeetriliste teisendustega saab näidata, et siinuse absoluutväärtuse keskmine ühe perioodi jooksul on $1 / \sqrt{2}$ .

Kui üheoomist takistit läbib alalisvool tugevusega $1 A$ , eraldub takistis $1$ sekundi jooksul $1$ džaul energiat. Kui sama takistit läbib sama aja jooksul vahelduvvool maksimaalväärtusega

I_{m} = \sqrt{2} A \approx 1, 41 A

eraldub ka sama hulk energiat (joonis 1.19.). Vahelduvvoolu tugevuse efektiivväärtuseks nimetatakse sellist alalisvoolu tugevust, mille korral eraldub vahelduvvooluringis võrdse aja jooksul sama suur soojushulk kui alalisvoolu korral.

(1.12.)

I = \frac{I_{m}}{\sqrt{2}}

Vahelduvvoolu pinge muutub ajas samuti siinuseliselt ja pinge efektiivväärtus on

(1.13.)

U = \frac{U_{m}}{\sqrt{2}}

Koduse pistikupesa klemmidel peaks olema pinge $230 V$ . Siin on tegemist pinge efektiivväärtusega. Teataval hetkel on vastava siinuseliselt muutuva pinge maksimaalväärtus $\sqrt{2}$ korda suurem, st $U_{m} \approx 325 V$ . Takistil eraldunud võimsuse saame arvutada valemiga

(1.14.)

P = I U = \frac{I_{m} U_{m}}{2}

Alalisvoolu korral kehtisid Ohmi seadused vooluringi osa ja kogu suletud vooluringi kohta vastavalt

I = \frac{U}{R}

I = \frac{E}{(R + r)}

Seosed kehtivad ka vahelduvvoolu hetkväärtuste jaoks, sest väga väikese ajavahemiku jooksul pinge ja voolutugevus ei jõua oluliselt muutuda. Hetkväärtusi tähistame väikeste tähtedega. Voolutugevuse hetkväärtus on

i = \frac{u}{R}

Kui voolutugevuse maksimum saabub samal ajal pingemaksimumiga, saame voolutugevuse maksimumi

I_{m} = \frac{U_{m}}{R} = I \sqrt{2} = \frac{U \sqrt{2}}{R}

millest voolutugevuse efektiivväärtuse jaoks saame

I = \frac{U}{R}

Efektiivväärtused on kasutusele võetud seetõttu, et nende abil saame vahelduvvoolu arvutustes kasutada alalisvoolu valemeid.

Vahelduvvoolu ampermeeter ja voltmeeter näitavad meile samuti efektiivväärtusi. Oluline tingmärk mõõteriista skaalal on vooluliik. Vahelduvvoolu tähiseks on $\sim$ ja alalisvoolul $-$ .

Kui vahelduvvooluringis on induktiivpool, siis pinge kasvades voolutugevuse kasv eneseinduktsiooni (EM lk 69) tõttu hilineb. Voolutugevuse maksimum jääb pingemaksimumist maha ja vooluringis eralduvat võimsust ei saa valemi 1.14. abil enam arvutada. Aga kui vahelduvvooluahelas on kondensaator, siis voolutugevuse maksimum saabub pingemaksimumist varem ja voolutugevus ei võngu samuti sünkroonselt pingega.

Küsimused

Vahelduvvoolu graafikuks on sinusoid, mille keskmine väärtus ajas on

0

. Kuidas on siis üldse võimalik soojusenergia eraldumine elektripliidis?

Vahelduvvoolu ja alalisvoolu generaatoritel on mõlemal nimipinge

115 V

. Kumma generaatoriga ühendamiseks peaks juhtmete isolatsioonikiht olema paksem? Miks?

Kokkuvõte

Vahelduvvoolu tugevuse efektiivväärtus on selline alalisvoolu tugevus, mille korral juhis eraldub samasugune võimsus kui vahelduvvoolu korral.

Pinge ja voolutugevuse maksimaalväärtuste ning efektiivväärtuste vahel on järgmised seosed:

U = \frac{U_{m}}{\sqrt{2}}

I = \frac{I_{m}}{\sqrt{2}}

Vahelduvvoolu mõõteriistad näitavad mõõtmisel efektiivväärtusi.

Ülesanded

Mõõtes vahelduvvoolu voltmeetriga seinakontaktis pinget, saime näiduks

241 V

. Arvutage pinge maksimaalväärtus. Missuguse vähima ajavahemiku jooksul saabub pingemaksimum ja -miinimum? Võrgupinge sagedus on

50 H z

Pinge

241 V

mõõdeti voltmeetriga, mille mõõtepiirkond oli

250 V

ja täpsusklass

2, 5

. Arvutage mõõtmise absoluutne ja suhteline piirviga.

Lisamaterjalid Lisaülesanded

Trafo. Elektrienergia ülekanne

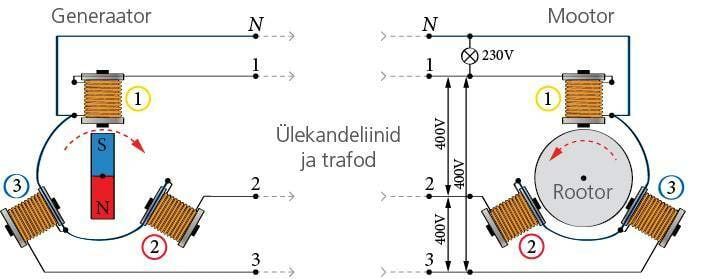
Elektrienergiat on mugav kasutada, aga keeruline suurel hulgal salvestada. Seetõttu tarnitakse elektrienergia jaotusvõrgu vahendusel elektrijaamast otse lõpptarbijani. Ent mida pikemad on liinid, seda suuremad on ka kaod. Ülekandmisel suurtele kaugustele ja paljudele tarbijatele esineb ebasoodsaid asjaolusid. Koos pikkusega kasvab juhtme takistus ja soojuslikud energiakaod ning väheneb pinge. Tarbijad ühendatakse rööbiti, mis suurendab voolutugevust generaatoris ja vähendab tarbimise kasvamisel klemmipinget. 19. sajandi lõpukümnendil jõuti järeldusele, et oleks parem kasutada vahelduvvoolu ja tõsta selle pinge enne ülekannet võimalikult kõrgele. Pinge tõstmiseks oli äsja leiutatud transformaator ehk trafo.

Juhis eralduv soojushulk on võrdeline voolutugevuse ruuduga ( $Q = I^{2} R t$ ). Vähendades voolutugevust ülekandeliinides $2$ korda, vähenevad soojuskaod $4$ korda. Kui aga tahame edastada eelnevaga võrdset võimsust $P = U I$ , peame pinget tõstma $2$ korda.

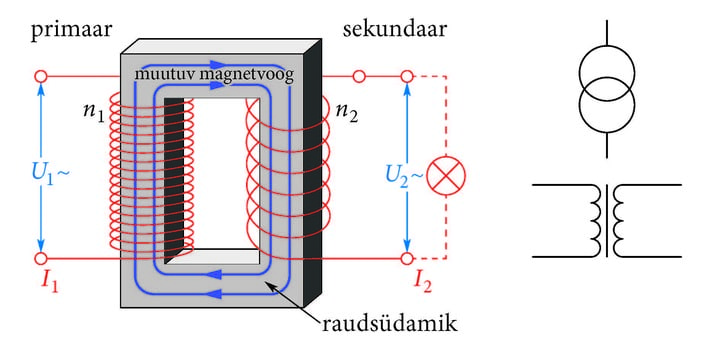
Trafo on elektromagnetilise induktsiooni nähtusel põhinev seadis vahelduvpinge muutmiseks. Trafo koosneb vähemalt kahest erineva keerdude arvuga $n_{1}$ ja $n_{2}$ raudsüdamikule keritud mähisest (joonis 1.20. a). Vooluallikaga ühendatud mähist nimetatakse primaarmähiseks ja tarbijaga ühendatud mähist sekundaarmähiseks.

Joonis 1.20. a - lülitus vooluallika ja tarbijaga (hõõglamp), b - skeemitähised

Primaarmähist läbiv vahelduvvool tekitab muutuva magnetvälja, mida mähise sees olev raudsüdamik annab edasi sekundaarmähisesse. Muutuv magnetväli tekitab sekundaarmähises muutuva elektromotoorjõu. Kui sekundaarmähisega ühendada tarbija, läbib teda muudetud pingega vahelduvvool.

Magnetvoo muut on mõlemas mähises ligikaudu võrdne. Seega mähiste pinged on võrdelised keerdude arvuga ja ligikaudu pöördvõrdelised voolutugevustega.

(1.15.)

\frac{U_{1}}{U_{2}} = \frac{n_{1}}{n_{2}} \approx \frac{I_{2}}{I_{1}}

Kui vahetada vooluallika ja tarbija kohad, saame pinget vähendava trafo (joonis 1.20. a) asemel pinget tõstva trafo.

Generaatori pinge ei ole ülekande jaoks piisav ja seetõttu tõstetakse elektrijaamas trafoga pinge vajalikule tasemele (näiteks $330 k V$ ). See rakendatakse kõrgepinge ülekandeliinidele. Lähenedes tarbijatele, vähendatakse alajaamades järk-järgult pinget, kuni pistikupessa jõudva $230 V$ -ni. Elektrijaamad ei tegutse eraldi, vaid on ühendatud ühtsesse võrku teiste Eestis asuvate jaamadega ja ka Venemaa ning Lätiga. Soomega saame vahetada elektrienergiat kõrgepingelise alalisvooluna kahe merekaabli kaudu.

Trafos puuduvad liikuvad osad, energiakaod mähistes ja südamikus on püütud viia minimaalseks. Võimsate trafode kasutegur

η = \frac{P_{1}}{P_{2}}

küünib kuni $99 %$ -ni.

Küsimused

Miks peab pinget madaldava trafo sekundaarmähis olema jämedamast traadist?

Miks ei ole otstarbekas elektrijaama trafoga pinget tõsta ükskõik kui kõrgele?

Kokkuvõte

Trafo on elektriseadis vahelduvpinge muutmiseks ja see töötab elektromagnetilise induksiooni nähtusel.

Ühe ja sama trafoga on võimalik vahelduvpinget nii tõsta kui ka langetada.

Ülesanded

Transformaatori primaarmähises on

2300

keerdu. Mitu keerdu peaks olema sekundaarmähises, et muuta tavaline võrgupinge

10

-voldiseks? Tavaline võrgupinge on

230 V

Mitu korda muudab (suurendab/vähendab) vahelduvpinget joonisel 1.20. a kujutatud trafo?

Joonisel 1.20. a kujutatud trafo primaarmähise vool on

1 A

. Kui suur vool on sekundaarmähises, kui trafo kasutegur on

70 %

Lisamaterjalid Lisaülesanded

Elektrimootor. Elektriohutusest

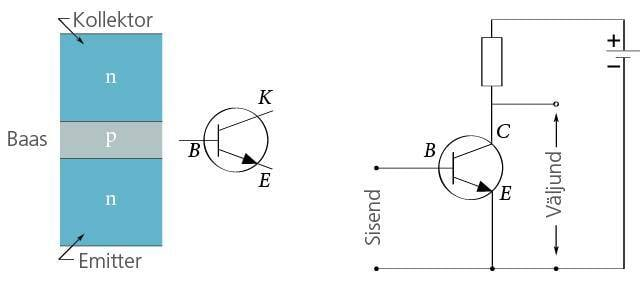
Elektrimootor muudab elektrienergia mehaaniliseks tööks. Elektrimootori töö põhineb voolu ja magneti ning kahe voolu vahelise vastastikmõju kasutamisel.

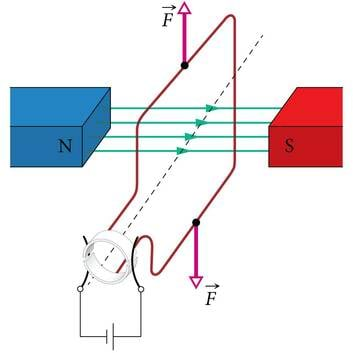
Paigutame magneti pooluste vahele juhtivast materjalist raami (mähise), mis saab pöörelda ja millest saab elektrivoolu läbi juhtida (joonis 1.21. a). Paigalolev osa staator ja pöörlev osa rootor on elektriliselt ühendatud kommutaatori abil. Kommutaator koosneb paigalolevatest harjadest, mis on surutud vastu poolrõngakujulisi lamelle. Harjad on ühendatud vooluallikaga ja lamellid rootorimähisega.

Vooluga juhile mõjub magnetväljas jõud (EM lk 29). Jõu suunda saab määrata nn vasaku käe reegliga. Raami vastaskülgedele mõjuvad jõud on vastassuunalised. Tekkinud jõudude paar pöörab raami veerand pööret päripäeva. Selles asendis (joonis 1.21 b) jõud raami enam ei pööra, kuid inertsi tõttu pöörleb lamellidega ühendatud raam edasi ja muudab voolu suuna raamis vastupidiseks. Raamile hakkab uuesti mõjuma teda päripäeva pöörav jõudude paar, st raam jääbki pöörlema.


Joonis 1.21. a	Joonis 1.21. b

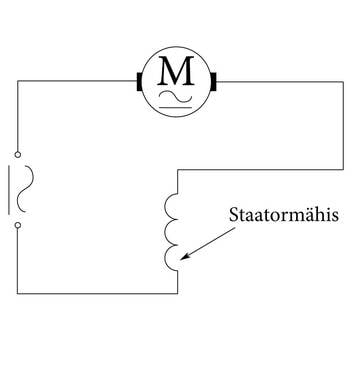
Eeltoodud põhimõttel töötab nii alalisvoolumootor kui ka nn universaalmootor (joonis 1.22. a), milles pöörleva rootorimähisega jadamisi on ühendatud magnetvälja tekitav paigalseisev staatorimähis. Kui rakendame mootorile vahelduvpinge (joonis 1.22. b), siis muutub voolu suund mõlemas mähises ja rootori pöörlemissuund jääb samaks.


Joonis 1.22. a) Universaalmootor	Joonis 1.22. b) Lülitusskeem

Universaalmootor on kasutatav nii alalisvoolu kui ka vahelduvvoolu korral. See pole küll kõige parema kasuteguriga, kuid pöörlemiskiiruse reguleeritavuse ja odavuse tõttu leiab sageli rakendust kodumasinates ja elektrilistes käsitööriistades. Tööstuses kasutatakse rohkem vahelduvvoolu asünkroonmootoreid (vt lisandused lk 82).

Elektrikahjustusteks on kõige sagedamini tulekahjud, elektrilöögid ning pingekõikumistest ja voolukatkestustest põhjustatud arvutite jm rikked. Tulekahjud tekivad tavaliselt juhtmete halbade kontaktide, küttekehade järelevalve puudumise ja vanade elektrisüsteemide ülekoormamise tõttu. Elektrilöögi saanud inimese kahjustusteks on põletus, gaasi tekkimine veres, südame seiskumine või lämbumine lihaste krambi tagajärjel. Inimese närvisüsteemi ja lihaste talitus põhineb elektrisignaalidel, mille elektrilöök võib rivist välja viia, seetõttu ongi inimese jaoks ohtlikum vahelduvvool. Voolutugevus $100 m A$ on juba surmavalt ohtlik.

Elektrist tulenevate õnnetuste levinumad põhjused on elektriliste majapidamisriistade isolatsiooni rikkiminek, elektri kasutamine niisketes ruumides, tormide tõttu ülekandeliinide mahalangemine, välgulöök, töötamine elektriliinide vahetus läheduses ja tähelepanematus.

Küsimused

Miks ei koosne rootorimähis tavaliselt ühest, vaid paljudest juhtmekeerdudest?

Mootoris tekitatakse magnetväli tavaliselt raudsüdamikule keritud mähisega. Miks?

Kokkuvõte

Elektrimootor muudab elektrienergia mehaaniliseks tööks. Elektrimootoris kasutatakse voolu ja magnetvälja vastastikmõju.

Ülesanded

Elektrimootori rootoriks on ruudukujuline raam küljepikkusega

1 d m

. Arvutage raami ühele küljele mõjuv maksimaalne jõud, kui voolutugevus raamis on

2 A

ja staator tekitab magnetvälja

0, 1 T

Tehke joonisega 1.21. a analoogne joonis, kui raam on teinud pool pööret. Määrake raamile mõjuvate jõudude suunad ja tähistage need joonisel.

Lisamaterjalid Lisaülesanded

Molekulide soojusliikumine

Temperatuur

Tihti kasutatakse vestluses sõnu soe ja külm. Kumb on soojem, kas soe talv või külm suvi? Ütlus „kraanivesi on kuum” tähendab, et vesi on soojem kui seda katsuv käsi. Täpsemate väidete korral kasutatakse mõistet temperatuur, mille määramiseks on juba väga ammu valmistatud mõõteriistu – mitmesuguseid termomeetreid. Termomeeter mõõdab soojuspaisumist, termoelektromotoorjõu tekkimist, infrapunakiirgust või muud temperatuurist sõltuvat suurust. Arusaam temperatuuri olemusest tekkis aga hiljem, 19. sajandil koos teadmiste avardumisega ainete siseehitusest.


Joonis 1.23.

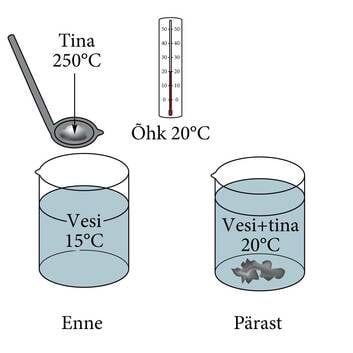
Oletame, et õnnevalamisel kallasime külma vette teatava koguse sulatina (joonis 1.23.). Vee temperatuur tõusis kiiresti ja sai võrdseks toatemperatuuriga ning edasi mingeid muutusi enam ei toimunud. Kuum keha (tina) andis teatud hulga soojust külmale kehale (veele). Tina temperatuur alanes ja vee temperatuur tõusis seni, kuni nende temperatuurid võrdsustusid. Kuna nende ühine temperatuur osutus võrdseks toatemperatuuriga, siis edasisi muutusi ei toimunud ja süsteem jäi tasakaalu. Soojus läheb iseenesest üle soojemalt kehalt külmemale, kuni nende temperatuurid võrdsustuvad. Selline olek vastab soojuslikule tasakaalule. Keha temperatuur iseloomustab soojusliku tasakaalu olekut. Tal on ühesugune väärtus soojuslikus tasakaalus oleva süsteemi kõikides osades.

Temperatuur oleneb keha koostisosakeste energiast – siseenergiast.

Euroopas kasutatakse temperatuuri mõõtmisel ühikuna Celsiuse kraadi. Temperatuurile $0^{\circ} C$ vastab jää sulamine ja $100^{\circ} C$ -le vee keemine normaalrõhul.


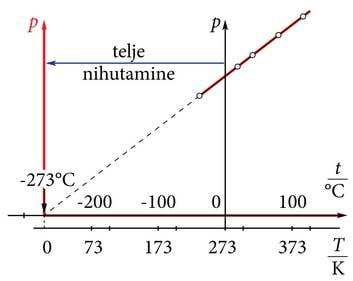
Joonis 1.24. a) Piirtemperatuur - absoluutne null	Joonis 1.24. b) Celciuse ja Kelvini võrdlus

17. ja 18. sajandi vahetusel uuris prantsuse füüsik Guillaume Amonton gaasi rõhu sõltuvust temperatuurist jääval ruumalal (joonis 1.24. a). Ta leidis, et temperatuuri vähenedes kahanes rõhk lineaarselt. Mingil temperatuuril, $- 273, 15^{\circ} C$ , peaks gaasi rõhk muutuma nulliks. Seda temperatuuri alumist piiri nimetatakse absoluutseks nulliks. Inglise füüsik lord Kelvin võttis kasutusele nn absoluutse temperatuuriskaala FLA. Selle skaala nullpunktiks on absoluutne null ja ühik $1 K$ (üks kelvin) on võrdne Celsiuse skaala ühikuga. Temperatuur $T$ Kelvini skaalas on alati positiivne ja Celsiuse temperatuurist $273$ võrra suurem.

(1.16)

T = t + 273

Rõhu telje nihutamisel absoluutsesse nulli saame lineaarsest sõltuvusest võrdelise. Jääval ruumalal on gaasi rõhk võrdeline absoluutse temperatuuriga.

Küsimused

Missugune on kõige madalam ja kõige kõrgem temperatuur?

Missugustel füüsikalistel nähtustel lisaks eelpool nimetatutele võiks põhineda termomeetri töö?

Kokkuvõte

Soojus levib iseenesest soojemalt kehalt külmemale, kuni temperatuurid võrdsustuvad.

Soojusliku tasakaalu korral on temperatuur keha kõikides osades ühesugune.

On olemas kõige madalam piirtemperatuur absoluutne null, millest keha temperatuur on alati suurem.

Rahvusvahelise mõõtühikute süsteemi temperatuuri põhiühik on $1 K$ (kelvin). Kelvini absoluutses temperatuuriskaalas on temperatuurid umbes $273$ võrra suuremad võrreldes Celsiuse skaalaga $T = t + 273$ .

Ülesanded

Teisenda toatemperatuur

20^{\circ} C

ja kehatemperatuur

36^{\circ} C

kelviniteks.

Termotuumareaktsioon toimub temperatuuril

10^{8} K

. Mitu kraadi Celsiust see on?

Lisamaterjalid Lisaülesanded

Ideaalne gaas

Reaalset looduses esineva gaasi lihtsamaks uurimiseks ja mõistmiseks kasutatakse ideaalse gaasi mudelit. Ideaalse gaasi puhul ei arvestata molekulide mõõtmeid ja nendevahelist vastastikmõju. Selle tingimuse ligikaudseks täitmiseks peaks gaas olema piisavalt hõre ja mitte liiga madalal temperatuuril. Ideaalseks gaasiks võib näiteks lugeda kuiva õhku tavalisel temperatuuril ja rõhul.

Olgu suletud anumas (joonis 1.25.) ideaalne gaas, mille molekulid liiguvad kaootiliselt ja põrkuvad elastselt anuma seintega. Mõtteliselt eraldatud osas ruumalaga $V$ on $N$ molekuli igaüks massiga $m_{0}$ . Anuma seinale pindalaga $S$ lähenevate molekulide keskmine kiirus on $v$ .

Proovime hinnata molekulide põrgetest tulenevat anuma seinale avaldatavat rõhku. Seinaga jõuavad aja $t$ jooksul põrkuda pooled molekulidest, mis ei asu kaugemal kui

I = v t = \frac{V}{S}

Mehaanikast on teada (M), et impulsi muut elastsel põrkel on $2 m_{0} v$ . Kehale mõjuv jõud (M) on võrdne impulsi muutumise kiirusega.

F = \frac{Δ p}{t}

ja ühe molekuli poolt seinale avaldatav jõud on

\frac{2 m_{0} v^{2}}{t}

Kogu seinale mõjuva jõu saame, korrutades selle põrgete arvuga $N / 2$ . Seinale avaldatav jõud

F = \frac{N}{2} \frac{2 m_{0} v}{t} = \frac{N m_{0} v^{2} S}{V}

Arvestades, et molekulide kontsentratsioon

n = \frac{N}{V}

saame rõhuks

p = \frac{F}{S} = n m_{0} v^{2}

Arutluses eeldasime, nagu liiguksid molekulid ühes sihis. Tegelikult pole kaootilise liikumise korral ükski suund eelistatud ja täpsema tuletuskäigu korral saame:

(1.17.)

p = \frac{1}{3} n m_{0} v^{2}

Valem annab ideaalse gaasi rõhu sõltuvuse mikroparameetritest: kontsentratsioonist, molekuli massist ja kiirusest. Rõhk kui makroparameeter on mõõdetav näiteks baromeetri või manomeetriga.

Kui võtame kasutusele mõiste molekulide keskmine kineetiline energia

¯ E = \frac{m_{0} v^{2}}{2}

saame:

(1.18.)

p = \frac{2}{3} n ¯ E

Ideaalse gaasi rõhk on võrdeline molekulide kaootilise liikumise keskmise kineetilise energiaga.

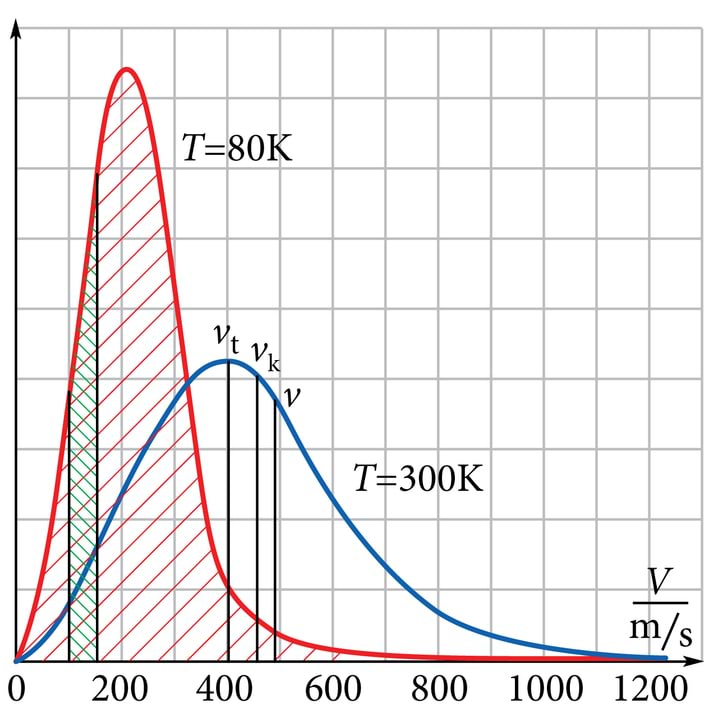
Eelmises õppetükis saime teada, et gaasi rõhk oli ka võrdeline absoluutse temperatuuriga. Kokkuvõtvalt saab järeldada, et ideaalse gaasi molekulide keskmine kineetiline energia on võrdeline gaasi absoluutse temperatuuriga:

(1.19.)

¯ E = \frac{3}{2} k T

kus suurust $k = 1, 38 \cdot 10^{- 23} J / K$ nimetatakse Boltzmanni konstandiks.

Valemis 4.17 esinev suurus $v^{2}$ on molekulide kiiruste ruutude keskmine väärtus. Ruutjuur sellest on ruutkeskmine kiirus:

(1.20.)

¯ v = \sqrt{v^{2}}

Küsimused

Loetlege mikroparameetreid, mis määravad gaasi rõhu.

Klassi õhus esineb nii lämmastiku kui ka hapniku molekule. Missuguse aine molekulid liiguvad kiiremini? Põhjendage.

Kokkuvõte

Ideaalne gaas on selline gaas, mille molekulide mõõtmeid pole vaja arvestada ja mille molekulide vastastikmõju on tühine.

Gaasi rõhk on tingitud kaootiliselt liikuvate molekulide põrgetest vastu anuma seina. Rõhk sõltub molekulide kontsentratsioonist, massist ja kiirusest

p = \frac{1}{3} n m_{0} v^{2}

Molekulide keskmine kineetiline energia on võrdeline absoluutse temperatuuriga

¯ E = \frac{3}{2} k T

Ülesanded

Gaasi temperatuur muutus

20^{\circ} C

kuni temperatuurini

200^{\circ} C

. Mitu korda muutus temperatuur Celsiuse ja Kelvini skaala põhjal? Mitu korda suurenes rõhk ja gaasimolekulide keskmine kineetiline energia?

Balloonis on hapnik normaaltingimustel (

0^{\circ} C

10^{5} P a

). Arvuta molekulide keskmine kineetiline energia, ühe molekuli mass, kiiruste ruutude keskmine väärtus ja ruutkeskmine kiirus.

Lisamaterjalid Lisaülesanded

Ideaalse gaasi olekuvõrrand

Gaasiga toimuvate protsesside käigus võivad muutuda selle rõhk, ruumala ja temperatuur – olekuparameetrid. Näitame, et ideaalse gaasi olekuparameetrid on omavahel seotud nn ideaalse gaasi olekuvõrrandiga.

Valemitest 1.17, 1.18 ja 1.19 saame rõhu jaoks:

\begin{matrix} p = \frac{1}{3} n m_{0} v^{2} = \frac{2}{3} n ¯ E = = n k T = \frac{N}{V} k T \end{matrix}

Molekulide arvu saame avaldada ainehulga ja Avogadro arvu järgi:

N = \frac{m}{M} N_{A}

kus $m$ on gaasi mass ja $M$ molaarmass. Asendades ja avaldades, saame rõhu ja ruumala korrutiseks:

p V = \frac{m}{M} N_{A} k T

Suurust $R = N_{A} k = 8, 31 J / (m o l \cdot K)$ nimetatakse gaasikonstandiks ja seega:

(1.21.)

p V = \frac{m}{M} R T

Ideaalse gaasi rõhu ja ruumala korrutis on võrdeline tema absoluutse temperatuuriga. Kui me vaatleme antud gaasikogust kahes erinevas olekus, saame olekuvõrrandi teise kuju:

(1.22.)

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}

Antud gaasikoguse rõhu ja ruumala korrutis jagatud absoluutse temperatuuriga on jääv suurus. Viimase valemi kontrolliks on vaja määrata gaasi ruumala, mõõta manomeetriga rõhk ning termomeetriga temperatuur (joonis 1.26.). Valemi 1.21. kontrollimiseks peab määrama gaasi massi ja teadma molaarmassi (piisab ka ainehulgast).


Joonis. 1.26. Katseseade gaasi seaduste uurimiseks.	Kass ja kamin

Gaaside omadused sõltuvad temperatuurist ja õhurõhust. Seetõttu on võetud kasutusele mõiste normaaltingimused: temperatuur $0^{\circ} C \approx 273 K$ ja rõhk $760 m m H g \approx 1, 01 \cdot 10^{5} P a$ . Ühe mooli gaasi ruumala normaaltingimustel on $22, 4$ liitrit.

Küsimused

Kahes sama suures anumas on ideaalne gaas samal temperatuuril. Ühes on

32 g

hapnikku ja teises

28 g

lämmastikku. Kumma gaasi rõhk on suurem?

Selgel suvepäeval unustati murule kaks ühesugust tühja plastpudelit. Hilisõhtuks oli üks neist tõmbunud kortsu, teine oli aga endise kujuga. Põhjendage nähtust, kasutades olekuparameetreid.

Kokkuvõte

Ideaalse gaasi olekuvõrrand ühendab omavahel makroskoopilised olekuparameetrid rõhu, ruumala ja absoluutse temperatuuri. Ideaalse gaasi rõhu ja ruumala korrutis on võrdeline tema absoluutse temperatuuriga

p V = \frac{m}{M} R T

kus $m$ on gaasi mass, $M$ molaarmass ja $R = 8, 31 J / m o l \cdot K$ gaasikonstant.

Antud ideaalse gaasikoguse rõhu ja ruumala korrutis jagatud absoluutse temperatuuriga on jääv suurus

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}} = c o n s t

Ülesanded

Balloonis ruumalaga

200

liitrit on

0, 4 k g

argooni temperatuuril

295 K

. Arvutage argooni rõhk, kui tema molaarmass on

0, 04 k g / m o l

Kindla hulga ideaalse gaasi olekuparameetrid muutusid. Rõhk vähenes kaks korda ja absoluutne temperatuur suurenes kaks korda. Mitu korda muutus gaasi ruumala? Kas see suurenes või vähenes?

Lisamaterjalid Lisaülesanded

Isoprotsessid

Isoprotsessi käigus ei muutu üks olekuparameetritest ja vastav parameeter taandub gaasi olekuvõrrandist välja.

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}}

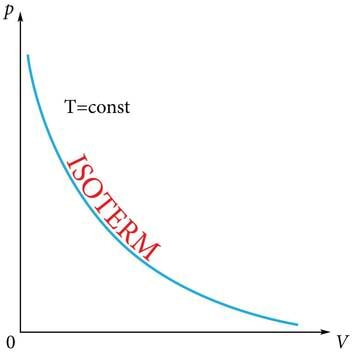
Isotermilise protsessi käigus ei muutu temperatuur. Saame ideaalse gaasi jaoks võrrandi:

p_{1} V_{1} = p_{2} V_{2}

millest järgnev valem annab pöördvõrdelise sõltuvuse rõhu ja ruumala vahel (joonis 1.27. a).

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}


1.27a Isoterm	1.27b Isobaar

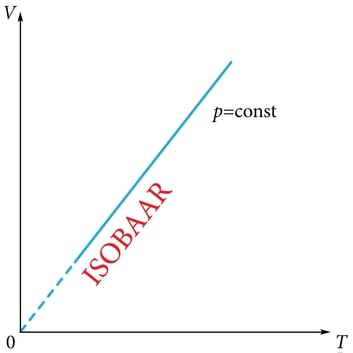
Isobaarilise protsessi käigus ei muutu rõhk. Saame gaasi jaoks võrrandi:

\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}

millest järgnev valem väljendab ruumala võrdelist sõltuvust absoluutsest temperatuurist (joonis 1.27. b).

\frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}}

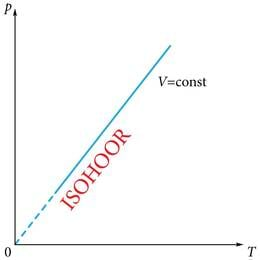
Isohoorilise protsessi käigus ei muutu ruumala. Saame võrrandi:

\frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}}

millest järgnev valem väljendab ideaalse gaasi rõhu võrdelist sõltuvust absoluutsest temperatuurist (joonis 1.27. c).

\frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}}

Isoprotsessidest koosnev ringprotsess

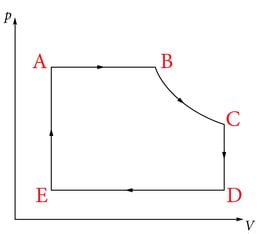
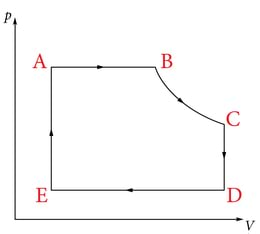
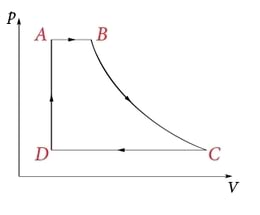
Joonisel on kujutatud erinevatest isoprotsessidest koosnev lõpuks samasse olekusse tagasi jõudev ringprotsess $p V$ -teljestikus. $A B$ on isobaariline paisumine, $B C$ isotermiline paisumine, $D E$ isobaariline kokkusurumine ning isohooriline protsess $E A$ lõpetab ringprotsessi ühe tsükli.

Küsimused

Tooge näide protsessist, milles gaasi rõhk ja temperatuur muutuvad, aga ruumala ei muutu.

Gaasi võib kokku suruda aeglaselt või kiiresti. Kuidas peaks seda tegema, et protsess oleks isotermiline? Põhjendage.

Kokkuvõte

Isoprotsessi käigus ei muutu keha üks olekuparameetritest.

Isotermilise protsessi käigus ei muutu temperatuur ja ideaalse gaasi rõhk on pöördvõrdeline ruumalaga:

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}

Isobaarilise protsessi käigus ei muutu rõhk ja ideaalse gaasi ruumala on võrdeline absoluutse temperatuuriga:

\frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}}

Isohoorilise protsessi käigus ei muutu ruumala ja ideaalse gaasi rõhk on võrdeline absoluutse temperatuuriga:

\frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}}

Ülesanded

Isotermilises protsessis suureneb ideaalse gaasi ruumala

2

korda. Mitu korda suureneb või väheneb gaasi rõhk?

Suletud silindris on hõre gaas ning hõõrdevabalt liikuv kolb. Mitu korda suureneb silindris oleva gaasi ruumala, kui temperatuur muutub miinus kahekümnelt pluss kahekümnele kraadile Celsiusele?

Lisamaterjalid Lisaülesanded

Siseenergia ja selle muutumise viisid

Kõik ained koosnevad osakestest, mis liiguvad kaootiliselt ja mõjutavad üksteist. Järelikult omavad kehade koostisosad nii kineetilist kui ka potentsiaalset energiat. Keha siseenergiaks nimetatakse tema kõikide koostisosakeste kineetiliste ja potentsiaalsete energiate summat. Seda energiat vaadeldakse kehaga seotud taustsüsteemi suhtes.

Vastastikmõju potentsiaalset energiat on raske arvutada. Seepärast toome näite ideaalsest gaasist, mis koosneb ühesugustest üksikuna esinevatest aatomitest, ehk üheaatomilisest ideaalsest gaasist. Ideaalse gaasi molekulid ei mõjuta üksteist (potentsiaalne energia on $0$ ) ja sellise gaasi siseenergia on kõikide molekulide kineetiliste energiate summa. Siseenergia leidmiseks tuleb molekuli keskmine kineetiline energia korrutada molekulide (antud juhul aatomite) arvuga.

U = N ¯ E = \frac{m}{M} N_{A} \frac{3}{2} k T = \frac{3}{2} \frac{m}{M} R T

Üheaatomilise ideaalse gaasi siseenergia on võrdeline absoluutse temperatuuriga. Kui ideaalse gaasi molekulis on rohkem aatomeid, siis võrdelisus absoluutse temperatuuriga jääb kehtima, aga võrdetegur on erinev. Näiteks kaheaatomilise gaasi korral on see $3 / 2$ asemel $5 / 2$ . Siseenergia on suurem seetõttu, et kaheaatomilise gaasi puhul lisanduvad võnkumise ja pöörlemise energiad.

Siseenergia sõltub ainult keha või kehade süsteemi siseolekust. Siseenergia hõlmab kõigi süsteemi osakeste, näiteks molekulide, aatomite, ioonide ja vabade elektronide liikumise, kineetilise ning vastastikmõju potentsiaalse energia, samuti nende sisestruktuuriga seoses oleva elektronkatte, tuuma jne energia. Rakenduste korral on oluline siseenergia muut, seetõttu jäetakse tavaliselt arvestamata need komponendid, mis uuritavas protsessis ei muutu. Soojusliku tasakaalu olekus on siseenergial kindel väärtus, siseenergia on olekufunktsioon. Siseenergia seob omavahel makro- ja mikrosuurused ning soojusõpetuse mehaanikaga.

Kui keha on soojusvahetuses teiste kehadega soojusjuhtivuse, konvektsiooni ja soojuskiirguse kaudu, nimetatakse saadud või ära antud siseenergiat soojushulgaks.

Soojushulk on siseenergia hulk, mille keha saab või annab ära soojusülekandel.

Jalgrattakummi pumpamisel kokkusurutud õhk ja pump soojenevad. Kuum gaas teeb mootoris paisudes tööd siseenergia vähenemise arvelt ja jahtub. Keha siseenergia muutmiseks on kaks võimalust – soojushulga saamine või äraandmine ja mehaaniline töö. Järgnevatel fotodel on raudlati temperatuuri ja siseenergia suurendamine soojushulga saamisega koldes ning lati töötlemisel ketaslõikuriga.


Metall hõõgub punaselt	Ketassaag lõikab

Küsimused

Miks reaalse gaasi siseenergia sõltub peale temperatuuri ka ruumalast?

Kas prootonite ja neutronite vastastikmõju energia aatomituumas on ka siseenergia?

Kokkuvõte

Keha siseenergia on tema kõikide koostisosakeste kineetiliste ja potentsiaalsete energiate summa.

Ideaalse gaasi siseenergia on võrdeline tema absoluutse temperatuuriga.

Soojushulk on siseenergia, mille keha saab või annab ära soojusvahetuses teiste kehadega.

Ülesanded

Arvutage

80 g

argooni siseenergia temperatuuril

127^{\circ} C

. Argooni massiarv on

40

Hermeetiliselt suletud kilekotis tõusis õhu temperatuur päikse käes

10^{\circ} C

-lt kuni

30^{\circ} C

-ni. Mitu korda suurenes/vähenes õhu siseenergia?

Lisamaterjalid Lisaülesanded

Termodünaamika (soojusenergia)

Gaasi töö. Soojushulk

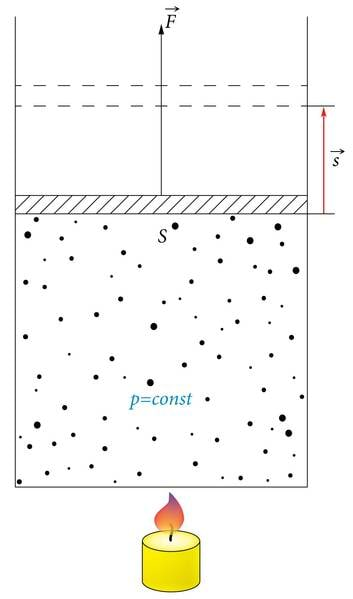
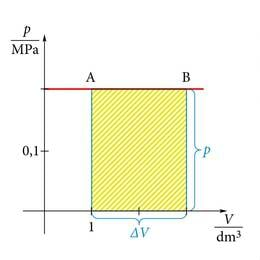
Joonisel 1.28a on pealt lahtine gaasi täis silinder, milles saab hõõrdevabalt liikuda kolb. Kui gaasi piirituslambiga kuumutada, siis gaas paisub ja lükkab kolbi ülespoole. Kolvile mõjuv jõud teeb tööd

A = F s = p S s = p Δ V

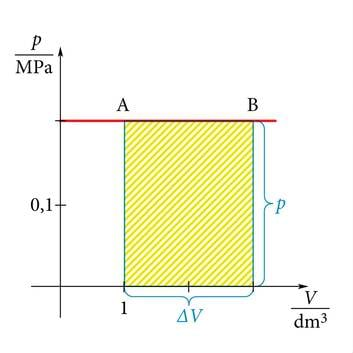
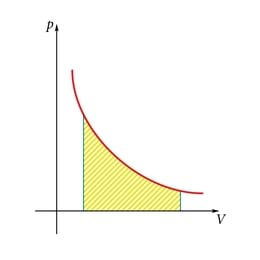
milles $Δ V$ on ruumala muut. Isobaarilise protsessi korral on gaasi töö

(1.23.)

A = p Δ V


1.28a	1.28b

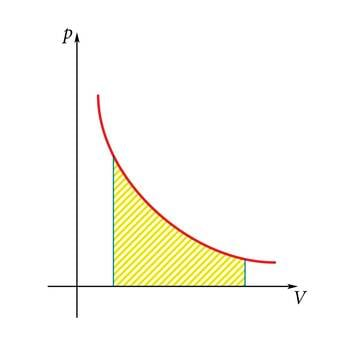
Joonisel 1.28. b on selle protsessi graafik $p V$ -teljestikus. Graafikult on näha, et $p Δ V$ on ühtlasi arvuliselt võrdne graafiku ja ruumala telje vahelise ristküliku pindalaga. Sama kehtib ka teiste protsesside, näiteks isotermilise korral (joonis 1.28. c).


1.28c

Mehaanilist tööd tehakse alati mingi teise energia arvel. Joonisel 1.28. a on selleks piirituse põlemisel eraldunud soojushulk. Kui gaasil lastakse paisuda, aga mingit energiat juurde ei anta, toimub protsess gaasi siseenergia vähenemise arvel ja gaasi temperatuur väheneb. Toodud näidete põhjal järeldub, et nii töö kui ka soojushulk muudavad keha siseenergiat.

Kütuse põlemise, gaasi kondenseerumise, vedeliku tahkumise ja keha jahtumisega kaasneb soojushulga eraldumine. Need soojushulgad on võrdelised keha massiga. Keha jahtumisel eraldunud soojushulk on lisaks võrdeline temperatuuri muuduga. Vt alljärgnevaid valemeid.

Põlemine

Q = r m

kus $r$ – kütuse kütteväärtus

Aurustumine ja kondenseerumine

Q = L m

kus $L$ – aurustumissoojus

Sulamine ja tahkumine

Q = λ m

kus $α$ – sulamissoojus

Temperatuuri muutus

Q = c m Δ t^{\circ} = c m (t_{2}^{\circ} - t_{1}^{\circ})

kus $c$ – erisoojus

Küsimused

Millistel tingimustel teeb gaas tööd?

Missuguse isoprotsessi korral tööd ei tehta?

Kokkuvõte

Isobaarilises protsessis on gaasi töö

A = p Δ V

Gaas teeb tööd siis, kui tema ruumala muutub.

Ülesanded

Gaasi ruumala vähenes normaalrõhul (

101 k P a

) ühe liitri võrra. Arvutage gaasi töö.

Arvutage gaasi töö joonisel 1.28. b protsessis

A B

Lisamaterjalid Lisaülesanded

Termodünaamika seadused

18. sajandi teisest poolel alanud tööstuslik pööre soodustas uute jõumasinate konstrueerimist ja nende tehniliste näitajate parandamist. Vesi- ja tuuleveskitele lisandusid aurumasinad, mille kasutegur oli esialgu väike, ühe protsendi lähedal. 19. sajandi esimesel poolel uurisid paljud teadlased tule nn liikumapanevat jõudu. Uurimuste käigus tekkis ja täpsustus füüsikaline suurus energia, mis osutus looduslike protsesside kirjeldamisel väga üldiseks. Selgusid mehaaniliste ja soojuslike protsesside seosed ja erinevused. Uuriti, kuidas saab muuta mehaanilist ja elektrienergiat soojuseks ning vastupidi. Sajandi keskel jõuti üldistatud arusaamani energia jäävusest ja muundumisest – sõnastati termodünaamika 1. seadus.

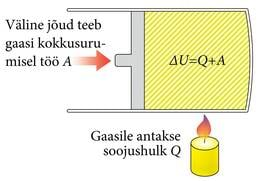
Keha siseenergia muut on võrdne kehale antud soojushulga ja väliste jõudude poolt tehtud töö summaga

(1.24.)

Δ U = Q + A

Kõik seaduse valemis esinevad suurused võivad olla nii positiivsed kui ka negatiivsed. Joonisel 1.29. on kujutatud olukord, kus silindris olevale gaasile antakse soojushulk ja samal ajal suruvad välised jõud gaasi kokku.

Tavaliselt loetakse saadud soojushulka positiivseks ja äraantud soojushulka negatiivseks. Töö on negatiivne siis, kui keha ise teeb tööd oma siseenergia kahanemise arvel. Joonisel on nii soojushulk kui ka väliste jõudude töö positiivsed.

Protsessi, mille korral ei toimu soojusvahetust väliskeskkonnaga, nimetatakse adiabaatiliseks protsessiks. Selles protsessis $Q = 0$ ja keha siseenergia muutub üksnes mehaanilise töö tõttu. Isohoorilise protsessi korral ei tehta tööd, $A = 0$ , ja keha siseenergia muut on võrdne saadud või ära antud soojushulgaga. Mehaanikast on teada, et hõõrde- ja takistusjõudude esinemisel keha mehaaniline koguenergia väheneb, muutudes teiseks energialiigiks – siseenergiaks M. Augustikuise meteoorivoolu juures on näha, kuidas suure kiiruse, takistusjõu ja temperatuuritõusu tõttu meteoor Maa atmosfääris süttib ja aurustub.

Paljude katsete põhjal on sõnastatud ka üldine energia jäävuse seadus. Suletud süsteemi koguenergia on jääv. Energia liik pole oluline, oluline on vaid see, et ei toimu energiavoolu süsteemist välja või sisse FLA M. Samuti võib toimuda süsteemi sees ühe energialiigi muutumine teiseks.

Temperatuuri peatükis 4.1 on kirjas, et soojus läheb iseenesest soojemalt kehalt külmemale, kuni soojusliku tasakaalu saabumiseni. Äsja sõnastatud termodünaamika esimene seadus ei keela ka vastupidise protsessi toimumist, aga millegipärast vette visatud sulatina iseenesest uuesti soojaks ei lähe. Iseeneslikud (spontaansed) soojuslikud protsessid toimuvad soojusliku tasakaalu suunas. Termodünaamika 2. seadus väidab, et soojus ei saa minna iseeneslikult külmemalt kehalt soojemale. Külmkapis ja soojapumbas toimub küll soojuse ülekanne külmemalt kehalt soojemale, kuid see ei toimu spontaanselt, vaid välisjõudude töö tulemusel.

Täpsustusi termodünaamika esimese seaduse kohta

Esimese seaduse valemist

Δ U = Q + A

saame mitmed erijuhud:

Isohoorilises protsessis $A = 0$ $Δ U = Q$ , siseenergia muutub ainult soojusvahetusega.
Adiabaatiline protsessis $Q = 0$ $Δ U = A$ , siseenergia muutub ainult tehtud töö tõttu.
Isotermilises protsessis $Δ U = 0$ $Q = - A$ , siseenergia ei muutu.
Isobaarilises protsessis $p = c o n s t$ $Δ U = Q - p Δ V$ .

Küsimused

Kas valemis 1.24. (

Δ U = Q + A

) võivad olla

Q

A

Δ U

negatiivsed?

Kas on võimalik, et gaas sai soojushulga, aga tema temperatuur alanes?

Kokkuvõte

Keha siseenergia muut on võrdne kehale antud soojushulga ja väliste jõudude poolt tehtud töö summaga.

Δ U = Q + A

Adiabaatilises protsessis ei toimu keha või kehade süsteemi soojusvahetust väliskeskkonnaga.

Soojus ei saa iseeneslikult üle minna külmemalt kehalt soojemale.

Iseeneslikud (spontaansed) protsessid viivad keha soojusliku tasakaalu olekusse.

Suletud süsteemi koguenergia on jääv.

Ülesanded

Gaas annab ära soojushulga

5 k J

ja välised jõud teevad gaasi kokkusurumisel tööd

12 k J

. Arvutage siseenergia muut.

Gaasile antakse soojushulk

130 k J

ja gaas paisub samal ajal jääval rõhul

1, 0 \cdot 10^{5} P a

2

liitri võrra. Arvutage gaasi paisumistöö ja siseenergia muut. Kas gaasi temperatuur tõusis või langes?

Lisamaterjalid Lisaülesanded

Entroopia

Olgu meil anum ruumalaga $V$ . Jaotame selle mõttes $n$ võrdseks osaks. Kui anumas on üks molekul, siis on selles ruumalaosas

V_{n} = \frac{V}{n}

molekuli leidmise tõenäosus

w_{1} = \frac{1}{n}

Kui anumas on $2$ molekuli, siis on nende üheaegse leidmise tõenäosus samas osas

w_{2} = w_{1} w_{1} = {(\frac{1}{n})}^{2}

Kui anumas on $N$ molekuli, on nende kõigi leidmise tõenäosus samas

w_{n} = {(\frac{1}{n})}^{N} = {(\frac{V_{n}}{V})}^{N}

Oletame, et esimeses olekus (joonis 1.30. a) on kõik gaasi molekulid koondunud anuma vasakusse ossa, mille ruumala on $V_{I}$ , ja teises olekus on kõik molekulid anuma osas $V_{I I}$ (joonis 1.30. b). Leiame nende olekute tõenäosuste suhte:

w = \frac{w_{I I}}{w_{I}} = \frac{{(\frac{V_{I I}}{V})}^{N}}{{(\frac{V_{I}}{V})}^{N}} = {(\frac{V_{I I}}{V_{I}})}^{N}


1.30a Molekulid anuma osas V₁	1.30b Molekulid anuma osas V₂

Kui anumas on $10$ molekuli ja ruumalad $V_{I I}$ ja $V_{I}$ suhtuvad nagu $1 / 2 : 1 / 3 = 3 / 2$ , on tõenäosuste suhe $(3 / 2)^{10} \approx 58$ , st teise oleku tõenäosus on esimese omast u $58$ korda suurem. Kui molekule oleks $100$ , siis teise oleku tõenäosus oleks esimese omast u $4 \cdot 10^{17}$ korda suurem ja $500$ molekuli korral oleks teine olek ligikaudu $1, 1 \cdot 10^{88}$ korda tõenäosem. Siit võib järeldada, et suure arvu molekulide puhul on kõige suurema tõenäosusega olek selline, kus osakesed on jaotunud ühtlaselt kogu anuma ulatuses. Sellele vastab soojusliku tasakaalu olek. Iseeneslikud protsessid viivad süsteemi suurima tõenäosusega olekusse.

Ideaalne gaas saab temperatuuril $T$ soojushulga $Δ Q$ . Saadud soojushulga ja absoluutse temperatuuri suhet nimetatakse entroopia muuduks:

(1.25.)

Δ S = \frac{Δ Q}{T}

Entroopia ja tema muudu ühikuks SI-s on $J / K$ . Sama ühik on ka Boltzmanni konstandil. Saab näidata, et entroopia muutu võib arvutada ka tõenäosuste suhte põhjal valemist

(1.26.)

Δ S = k l n w

kus $k$ on Boltzmanni konstant ja $ln w$ naturaallogaritm tõenäosuste suhtest.

Soojuslikke protsesse jaotatakse pööratavateks ja pöördumatuteks. Pööratav protsess koosneb üksteisele järgnevatest tasakaaluolekutest ja entroopia muut nendes on $0$ . Protsessidele, milles entroopia kasvab, vastavad pöördumatud muutused süsteemis, mis vähendavad süsteemi võimet teha tööd, sest osa energiast on pöördumatult muundunud soojuseks. Suletud süsteemis ei saa entroopia kahaneda.

(1.27.)

Δ S = \frac{Δ Q}{T} \geq 0

Viimane lause ja võrratus on oma sisult termodünaamika 2. seadus, mis väljendab teiste sõnadega asjaolu, et soojus saab iseenesest (spontaanselt) levida ainult kõrgema temperatuuriga kehalt madalama temperatuuriga kehale.

Küsimused

Tooge näide protsessi kohta, milles entroopia kahaneb.

Suletud süsteemis on soojusliku tasakaalu olek. Kui kaua see kestab?

Kokkuvõte

Kehade süsteemi entroopia muut on võrdne süsteemi poolt saadud soojushulga ja absoluutse temperatuuri suhtega:

Δ S = \frac{Δ Q}{T}

Iseeneslikud protsessid viivad süsteemi kõige suurema tõenäosusega soojuslikku tasakaalu.

Suletud süsteemis, kus ei toimu aine ega energiavahetust väliskeskkonnaga, ei saa entroopia kahaneda.

Ülesanded

Gaas sai temperatuuril

27^{\circ} C

soojushulga

15000 J

. Arvutage entroopia muut.

Kumb olekutest joonisel 1.30. oleks tõenäosem ja mitu korda, kui anumas oleks

20

kaootiliselt liikuvat molekuli?

V_{I} = 1 / 3 V

V_{I I} = 1 / 2 V

Lisamaterjalid Lisaülesanded

Soojusmasin

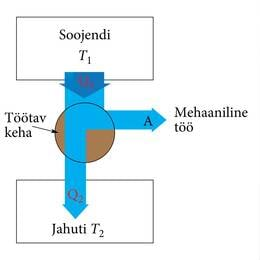
Soojusmasin muundab soojushulga mehaaniliseks tööks. Ajalooliselt oli esimeseks soojusmasinaks aurumasin, mida kasutati alates 17. sajandi lõpust kaevandusest vee väljapumpamiseks ja õhutamiseks. 19. sajandi algul oli aurumasin piisavalt väike, et kasutada teda jõumasinana transpordis, auruvedurites ja aurulaevades. Hiljem leiutati sisepõlemismootorid, auruturbiinid, reaktiivmootorid jne. Soojusmasinal on alati kolm põhilist osa: soojendi, töötav keha ja jahuti (joonis 1.31. a).

Töötavale kehale, milleks on tavaliselt gaas, antakse soojendist soojushulk $Q_{1}$ . Gaas teeb paisudes mehaanilist tööd $A$ . Pideva töö tegemiseks peab töötava keha olek taastuma teatava aja – tsükli – jooksul, milleks tuleb soojendist saadud soojushulgast anda osa $Q_{2}$ jahutile. Jahutiks on üldjuhul ümbritsev keskkond. Tsükli lõpus on gaas jälle algolekus ja siseenergia muut $0$ . Termodünaamika esimese seaduse kohaselt on mehaaniline töö gaasi paisumisel $A = Q_{1} - Q_{2}$ . Soojusmasina kasutegur $η$ on mehaanilise töö ja soojendist saadud energia suhe, mida väljendatakse tihti protsentides.

(1.28.)

η = \frac{A}{Q_{1}} = \frac{Q_{1} - Q_{2}}{Q_{1}}

Prantsuse teadlane Carnot näitas 19. sajandi alguses, et nn ideaalse soojusmasina kasutegur on

(1.29.)

η = \frac{T_{1} - T_{2}}{T_{1}}

kus $T_{1}$ ja $T_{2}$ on vastavalt soojendi ja jahuti absoluutsed temperatuurid.

Valem 1.29. näitab, et ülekantavast soojushulgast saab seda rohkem mehaanilist tööd, mida suurem on temperatuuride vahe soojusülekandel.

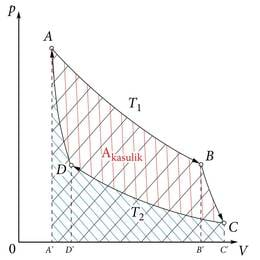
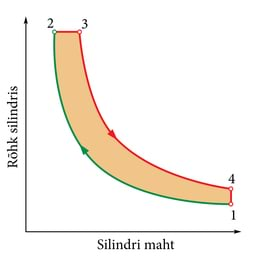
Ideaalse soojusmasina tsükkel koosneb kahest isotermilisest ja kahest adiabaatilisest protsessist (joonis 1.31. b).Ideaalse soojusmasina kasutegur on suurim antud temperatuurivahemikus töötavate masinate hulgas.

Gaas teeb paisudes tööd, mis on arvuliselt võrdne kujundi $A B C C^{'} A^{'}$ pindalaga. Osa sellest tööst tuleb aga kulutada gaasi kokkusurumiseks protsessis $C D A$ . Selleks vajalik töö on arvuliselt võrdne sinisega viirutatud kujundi $C D A A^{'} C^{'}$ pindalaga. Kasuliku töö hulk on võrdne punasega viirutatud osa $A B C D$ pindalaga.

Soojusmasinate tegelik kasutegur ei ole suur, sest soojendi temperatuur on piiratud materjali sulamistemperatuuriga ja jahuti temperatuur ümbritseva keskkonna omaga.

Soojusmasinateks loetakse ka vastassuunalise tsükliga töötavaid masinaid (külmuti, soojuspump), mis tööd tehes liigutavad soojust külmemalt kehalt soojemale. Mõiste kasutegur omandab nende juures teise tähenduse.

Kasutades soojusmasina mõistet, võime anda termodünaamika 2. seadusele uue sõnastuse. Ei ole võimalik ehitada soojusmasinat, mis muudab soojuse täielikult tööks.

Küsimused

Miks ei saa soojusmasina kasutegur olla üle

100 %

Missugused asjaolud piiravad soojusmasina kasuteguri tõstmist?

Kokkuvõte

Soojusmasin muudab soojusenergia mehaaniliseks tööks.

Soojusmasina kasutegur on saadud mehaanilise töö ja kulutatud soojusenergia suhe (tavaliselt protsentides):

η = \frac{A}{Q_{1}} (100 %)

Ideaalse soojusmasina kasutegur on määratud soojendi ja jahuti absoluutsete temperatuuridega:

η = \frac{T_{1} - T_{2}}{T_{1}}

Ülesanded

Töötav keha saab soojendilt soojushulga

9 M J

ja ja annab jahutile soojushulga

6 M J

. Arvutage kasulik töö ja soojusmasina kasutegur.

Kui suur maksimaalne kasutegur võib olla soojusmasinal, mille soojendi temperatuur on

1000^{\circ} C

ja jahutil

80^{\circ} C

Lisamaterjalid Lisaülesanded

Sisepõlemismootor

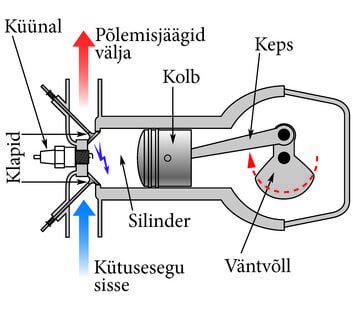
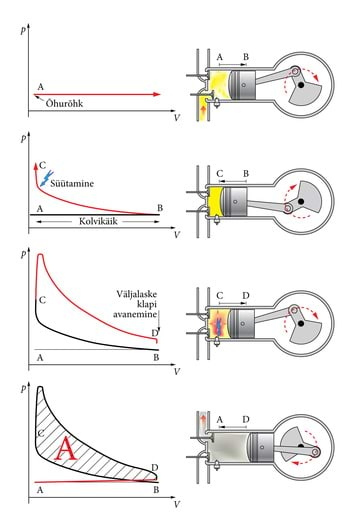
Enamikul sõiduautodel ning väiksematel veoautodel on $4$ -taktiline bensiinimootor. Selle mootori põhimõtted töötati välja juba poolteist sajandit tagasi ning need on suuresti samad ka tänapäeval. Bensiinimootori töö (joonis 1.32.) põhineb silindris elektrisädemega süüdatud küttesegu (bensiini ja õhu segu) paisumisel. Paisuv gaas paneb kolvi silindris liikuma ja see muudetakse kepsu abil väntvõlli pöörlevaks liikumiseks. Mootori jõuülekanne paneb rattad pöörlema ja auto kulgevalt liikuma.


1.32 Sisepõlemismootori ehitus	1.33 4-taktiline sisepõlemismootor

Gaasiline küttesegu, mis silindri sees põleb ja paisub, valmistatakse eelnevalt ette (näiteks karburaatoris). Joonisel 1.33. on toodud silindris oleva gaasi rõhu sõltuvus ruumalast ja mootori kolvi asendid nelja erineva takti jooksul.

Sisselasketakt $A B$ : sisselaskeklapp avatakse, kolb liigub paremale ning bensiini ja õhu segu imetakse silindrisse.
Survetakt $B C$ : klapid on suletud, kolb liigub vasakule ning kütusesegu surutakse kokku ja pannakse plahvatama elektrisädeme toimel.
Töötakt $C D$ : kolb surutakse paisuva gaasi poolt paremale ja kolviga ühendatud keps sunnib väntvõlli pöörlema.
Väljalasketakt $D A$ : väljalaskeklapp avaneb, kolb liigub vasakule ja põlemisjäägid surutakse silindrist välja.

Üks tsükkel on sellega läbi ja edasi protsess kordub. Mehaanilist tööd teeb mootor ainult töötakti jooksul ja osa sellest kulub esimese, teise ja neljanda takti sooritamiseks. Töötakti ajal tehtud ja ülejäänud taktide sooritamiseks kulutatud töö vahe ongi mootori kasulik töö. $p V$ -graafikult näeme, et kasulik töö on arvuliselt võrdne tsükli kinnise viirutatud osa pindalaga. Mootori kasutegur oleks suur, kui gaasi paisumine toimuks kõrgel, aga kokkusurumine madalal temperatuuril. Seda tüüpi mootorite kasutegur on umbes $30 %$ . Auto puhul läheb kasulikuks tööks (hõõrdejõudude ületamiseks) ainult $15 %$ .

Kuidas töötab diiselmootor

Selleks, et bensiinimootori kasutegur oleks kõrge, peaks küttesegu enne süütamist tugevasti kokku suruma. Sellel kokkusurumisel on aga piir, sest kiiresti kokkusurutud õhu ja bensiini segu kuumeneb ja võib enneaegselt süttida. Diiselmootoris on seda välditud ning silindrisse tõmmatakse ja surutakse kokku vaid õhk (joonisel protsess $1 - 2$ ). Alles siis hakatakse silindrisse pihustama diiselkütust, mis kuumas õhus süttib ( $2$ ) ja teeb paisudes tööd ( $2 - 3 - 4$ ). Sellises mootoris on kütuse põlemine ühtlasem (kütus ei sütti plahvatusega) ja kasutegur on kõrgema rõhu tõttu parem. Joonisel on toodud diiselmootori tsükkel $p V$ -teljestikus.

Küsimused

Mille poolest erineb sisepõlemismootor elektrimootorist?

Missuguseid kütuseid võiks kasutada sisepõlemismootoris?

Kokkuvõte

Sisepõlemismootor on soojusmasin, kus gaasilise või vedela kütuse põlemine toimub põlemiskambris (silindris).

Sisepõlemismootori tsükkel koosneb neljast või kahest taktist.

Ülesanded

Mitu pööret teeb neljataktilise mootori võll ühe tsükli jooksul?

Mitu tsüklit teeb neljataktilise mootori väntvõll ühes sekundis pöörlemiskiirusel

3000 p / m i n

Lisamaterjalid Lisaülesanded

Auruturbiin ja külmik

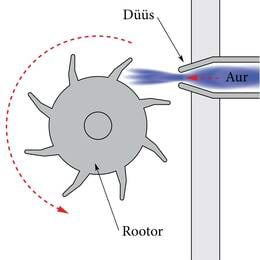
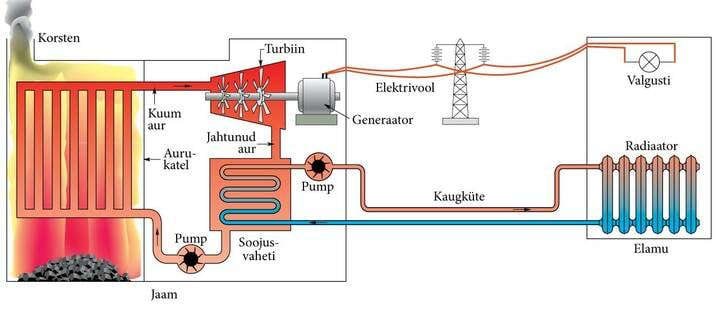
Põhiline osa maailma elektrienergiast toodetakse soojus- ja tuumaelektrijaamades. Nendes toodab elektrit auruturbiin, mille paneb enamasti käima vee soojendamisest saadud kõrge rõhuga aur. Vett soojendatakse fossiilsete kütuste põletamisega või tuumareaktsioonides eraldunud soojusega. Kiire veeauru juga suunatakse turbiini labadele (joonis 1.34.) ja turbiin hakkab pöörlema. Auruturbiin muudab kuuma auru potentsiaalse energia paisumise töö kaudu pöörleva turbiini kineetiliseks energiaks.

Turbiinis paisunud ja jahtunud auru võidakse kasutada mitmeti. Üks võimalustest on aur veekogust pumbatava veega kondenseerida ja juhtida uuesti aurukatlasse. Kondensaatori (jahuti) temperatuur peab parema kasuteguri saavutamiseks olema võimalikult madal. Seetõttu on vaja $1 k g$ auru kondenseerimiseks kuni $100 k g$ jahutusvett (umbes $150$ liitrit $1 k W h$ elektrienergia kohta). Väljast võetava jahutusvee temperatuur tõuseb kondensaatoris ainult paarikümne kraadi võrra. Selle madalatemperatuurilise, st madalakvaliteedilise energiaga ei ole tavaliselt midagi peale hakata. Kondenseerimisega läheb kaduma umbes $55 %$ energiast ja kasutegur on ligikaudu $40 %$ . Teine võimalus on kasutada täielikult või osaliselt läbitöötatud auru hoonete kütmiseks, sooja vee saamiseks ja tehaste tehnoloogilistes protsessides. Nn koostootmisjaamad (joonis 1.35.) annavad nii elektri- kui ka soojusenergiat ja nende kasutegur ulatub $60 %$ -ni. Luunja ja Väo koostootmisjaamade elektriline võimsus on umbes $25 M W$ ja soojuslik võimsus $50 M W$ .

Tuumaelektrijaam erineb soojuselektrijaamast selle poolest, et kuum aur saadakse tuumareaktoris toimuvate tuumareaktsioonide arvelt FLA MMF. Tuumajaamas rakendatakse oluliselt karmimaid ohutustehnika meetmeid.

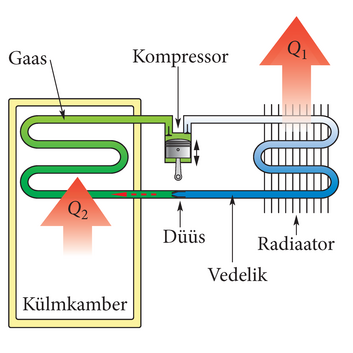
Külmik on soojusmasin, mis võtab mingilt kehalt soojushulga ja annab selle teisele, kõrgema temperatuuriga kehale. Termodünaamika 2. seaduse kohaselt ei toimu selline protsess iseeneslikult, vaid väliste jõudude töö arvelt. Külmiku tsükkel kulgeb seega vastupidiselt sisepõlemismootori ja turbiini omaga.


1.36 Külmiku tööpõhimõte

Kompressor surub gaasi vedelikuks kokku (joonis 1.36.). Vedelik pressitakse läbi väikese ava – düüsi.. Vedelik aurustub, tekkinud gaas paisub ja võtab jahutatavalt kehalt külmakambris soojushulga $Q_{2}$ . Edasi surutakse gaas uuesti kompressoriga kokku, et selle temperatuur ületaks ümbritseva keskkonna temperatuuri. Soojenemine toimub väljaspool kambrit asuvas radiaatoris, kust soojushulk $Q_{1}$ läheb toaõhku.

Küsimused

Miks on Narva veehoidla veetemperatuur kõrgem kui teistes lähedal asuvates veekogudes?

Missugustes elektrijaamades töötab auruturbiin, kuid ei kasutata fossiilset või tuumakütust?

Külmkapis võetakse toiduainetelt ära soojushulk

Q_{2}

ja antakse radiaatori kaudu toaõhule soojushulk

Q_{1}

. Kumb on suurem ja miks?

Kokkuvõte

Auruturbiin on soojusmasin, mis muudab kuuma kokkusurutud auru potentsiaalse energia turbiini rootori pöörlemise energiaks.

Põhiline osa elektrienergiast saadakse jaamadest, kus fossiilse kütuse põlemisel või tuumareaktsioonidel vabanenud soojusenergia muundatakse auruturbiini ja vahelduvvoolugeneraatori vahendusel elektrienergiaks.

Külmik on soojusmasin, mis tehtud töö tulemusel viib soojushulga külmemalt kehalt soojemale.

Ülesanded

Mitu

k W h

elektrienergiat toodaks a) aastas ja b) kuus Väo koostootmisjaam, kui ta töötaks pidevalt installeeritud elektrilisel võimsusel

25 M W

Mootorite ja turbiinide päripidi kulgeva ringprotsessiga soojusmasinaid iseloomustatakse kasuteguriga. Mille sarnasega võiks iseloomustada külmutit?

Lisamaterjalid Lisaülesanded

Lisad ja täiendused

Lisa 1.1. Elektrivoolu tekkemehhanism

Valem

I = q n S v

seob omavahel mikro- ja makromaailma iseloomustavaid füüsikalisi suurusi. Oletades, et iga metalli aatomi kohta vabaneb üks elektron, saame hinnata vabade elektronide kontsentratsiooni

n = \frac{N}{V} = \frac{m N_{A}}{M V} = \frac{ρ N_{A}}{M}

kus lugejas esinevad aine tihedus ja Avogadro arv ning nimetajas molaarmass. Näiteks hõbeda jaoks saaksime:

\begin{matrix} n = \frac{10500 \frac{k g}{m^{3}}}{0, 108 \frac{k g}{m o l}} 6, 02 \cdot 10^{23} \frac{1}{m o l} \approx 5, 9 \cdot 10^{28} \frac{1}{m^{3}} \end{matrix}

Mõõtes katses hõbedast juhi ristlõikepindala ja teda läbiva voolu tugevuse, saaksime määrata ka elektronide triivliikumise kiiruse.

Elektrivoolu uurimise ajaloost

Elektrivoolu uurimine sai võimalikus pärast itaalia füüsiku Alessandro Giuseppe Antonio Anastasio Volta poolt 1799. aastal konstrueeritud vooluallikat (Volta sammas). Taani füüsiku Hans Christian Oerstedi avastus elektrivoolu ja magneti vastastikmõjust viis peagi voolutugevuse mõõteriista leiutamiseni. Klassikalise elektronteooria rajas 20. sajandi algul hollandi füüsik Hendrik Antoon Lorentz. See käsitleb vabade elektronide liikumist nagu gaasimolekulide kaootilist soojusliikumist. Elektronid püüavad liikuda elektrivälja sihis, kuid põrked kristallvõre aatomitega takistavad seda. Antud teooria seletab hästi Ohmi seadust ja elektrivoolu soojuslikku toimet, kuid ei seleta takistuse sõltuvust temperatuurist.

Probleem

Temperatuuri tõustes metalljuhet läbiva voolu tugevus väheneb, ehkki vabade elektronide kontsentratsioon praktiliselt ei muutu. Mis muutub metallis, et voolutugevus väheneb?

Kokkuvõte

I = \frac{q}{t}

Voolutugevuse ühik üks amper on SI põhiühik ja ta on defineeritud vooluga juhtide vastastikmõju kaudu. $1 A$ voolutugevuse korral läbib juhi ristlõiget $1 s$ jooksul laeng $1 C$ .

Lisa 1.2. Ohmi seadus

Takistite värvikoodid

Elektriskeemides kasutatakse sageli väikeste mõõtmetega takisteid, mille peale ei saa tema arvulist takistust kanda. Seetõttu kasutatakse takistite värvikoodi.

Juhtide takistuse uurimise ajaloost

Pärast Oerstedi katset voolu mõjust magnetnõelale hakati konstrueerima riistu elektrivoolu mõõtmiseks, mis põhinesid voolu ja magneti vastastikmõjul. Neid hakati itaalia teadlase Luigi Galvani järgi kutsuma galvanomeetriteks. Tänapäeval nimetatakse voolutugevuse mõõtmise riistu tavaliselt (prantsuse füüsiku André-Marie Ampère’i järgi) ampermeetriteks. Sõna galvanomeeter kasutatakse põhiliselt suure tundlikkusega mõõteriista eristamiseks.

Millegipärast ei huvitanud teadlasi esialgu elektrijuhis toimuv, ning seda peeti voolu kasutamise kõrval vähemtähtsaks. Seetõttu ei tuntud alguses huvi ka Georg Simon Ohmi uurimistööde vastu. Ohm tegi katseid erineva pikkuse ja läbimõõdu ning erinevast materjalist juhtmetega, st uuris voolutugevuse sõltuvust juhtmete takistusest. 1827. aastal avaldas ta oma põhiteose „Matemaatiliselt töödeldud galvaaniline ahel”, milles sisaldus kogu suletud vooluringi teooria. Muide, hiljem võttis ta kasutusele tunduvalt stabiilsema pingega Tallinnast pärit Thomas Johann Seebecki konstrueeritud termoelektrilise patarei. Ohmi tööde vastu hakati huvi tundma alles siis, kui tekkisid probleemid elektritelegraafi rakendamisel.

Probleem

Katses tuleb määrata takistit läbiva voolutugevuse sõltuvus pingest. Meil on kasutada keemiline vooluelement AA, voltmeeter, ampermeeter, takisti, reostaat ja ühendusjuhtmed. Joonistage vastava vooluringi skeem.

Graafik näitab metallist juhti läbiva voolu tugevuse sõltuvust selle otstele rakendatud pingest. Skitseerige analoogne sõltuvus pooljuhi jaoks, mille takistus pinge kasvades järjest väheneb.

Kokkuvõte

Voolutugevus juhis on võrdeline pingega juhi otstel

I = \frac{U}{R}

Võrdeteguri pöördväärtust nimetatakse takistuseks ja selle ühikuks on

Ω

(oom). Takistuse tõttu esineb elektrivoolu soojuslik toime.

Takistus on võrdeline juhi eritakistuse ja pikkusega ning pöördvõrdeline juhi ristlõikepindalaga

R = \frac{ρ l}{S}

Võrdetegurit

ρ

nimetatakse aine eritakistuseks, mis näitab ühikulise pikkuse ja ristlõikega juhi takistust.

Juhi takistus oleneb temperatuurist.

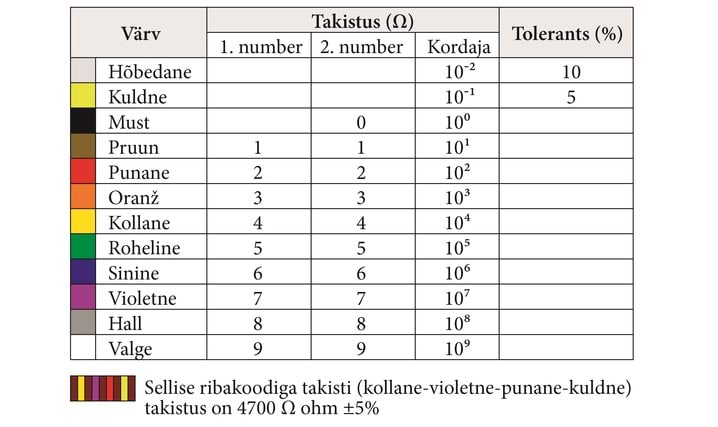
[£[1131]£]

Lisa 1.3 Elektrimõõtmised

Vigade arvutamise ja katsetulemuste esitamise näide

R = \frac{U}{I}

Kui tahame hinnata takistuse mõõtemääramatust, siis tuleb arvestada mõlema mõõteriista viga. Lahendame ülesande konkreetse näite põhjal.

R_{¨ u} = \frac{U_{¨ u}}{I_{¨ u}} = \frac{4, 3 + 0, 24}{2, 25 - 0, 0625} = 2, 075 Ω

Vähima takistuse ehk alamtõkke saame siis, kui pinge on vähim ja voolutugevus suurim.

R_{a} = \frac{U_{a}}{I_{a}} = \frac{4, 3 - 0, 24}{2, 25 + 0, 0625} = 1, 756 Ω

Takistuseks oleks mõistlik võtta nende aritmeetiline keskmine $R = 1, 916 Ω$ ja absoluutseks piirveaks pool nende erinevusest.

Δ R = \frac{R_{¨ u} - U_{a}}{2} = 0, 160 Ω

Takistuse arvutamiseks tuleb pinge jagada voolutugevusega. Saab näidata, et jagatise ja korrutise relatiivne piirviga avaldub suuruste relatiivsete piirvigade summaga.

\frac{Δ R}{R} = \frac{Δ U}{U} + \frac{Δ I}{I}

Elektrimõõtmiste ajaloost

Esimeseks elektrimõõteriistaks võib lugeda inglise teadlase William Gilberti 1600. aasta paiku loodud elektroskoopi. Elektroskoobiga saab mõõta laengut, elektrivälja tugevust, pinget ja isegi radioaktiivset kiirgust. Aastal 1820 leiutas saksa teadlane Johann Salomo Christoph Schweigger mõõteriista voolutugevuse määramiseks. Riista tööpõhimõtteks oli magnetnõela kõrvalekaldumine pooli sees, kui poolist lasta läbi uuritav vool.

Kokkuvõte

Elektrimõõteriista täpsusklass on relatiivne piirviga protsentides mõõteriista maksimaalse näidu korral.

Numbrilise mõõteriista korral on mõõtemääramatuse arvutamise valem toodud mõõteriista passis.

Lisa 1.4. Takistuse sõltuvus temperatuurist

Ülijuhtiv magnet

Ülijuhtiva mähisega elektromagneteid kasutatakse tugeva magnetvälja tekitamiseks muu hulgas magnetresonantstomograafis (MRT) organismi sisekuvamisel ja mikroosakeste kiirendites. Elektromagnetilise levitatsiooni (EM lk 79) jaoks on vajalik samuti ülijuhtivus.

Ajaloost

Probleem

Arvestades lambi hõõgniidi takistuse kasvu temperatuuri tõustes, skitseerige lampi läbiva voolutugevuse pingest sõltuvuse graafik.

Takistuse temperatuuritegur näitab takistuse suhtelist muutu ühikulise temperatuurimuudu kohta. Teisendage valemit 1.4., et antud väide tuleks esile.

Kokkuvõte

Metalli takistus kasvab temperatuuri tõustes lineaarselt

R = R_{0} (1 + α t)

Pooljuhtide, elektrolüütide ja gaaside takistus temperatuuri kasvuga väheneb.

Ülijuhtivus on nähtus, kus ained madalal temperatuuril ei oma elektrilist takistust.

Lisa 1.5. Elektromotoorjõud. Ohmi seadus kogu vooluringi kohta

Vooluallikatest

Vooluallikaid võib liigitada, lähtudes nendes toimuvatest erinevatest energeetilistest muutustest. Keemilises vooluallikas saadakse elektrienergiat elektrokeemiliste reaktsioonide arvel. Elektrienergiaks võib muuta samuti mehaanilist energiat, soojust ja valgust.

Patarei koosneb mitmetest vooluallikatest, mis on tavaliselt ühendatud suurema elektromotoorjõu saavutamiseks jadamisi (suurema voolutugevuse jaoks ka rööbiti). Näiteks $9$ -voldine patarei 6F22 (Krona) koosneb kuuest jadamisi ühendatud $1, 5 V$ elemendist.

Akumulaator ehk aku on korduvkasutusega keemiline vooluallikas. Tühja akut laadides muudetakse elektrienergia uuesti keemiliseks energiaks. Akusid kasutatakse küttesegu süütamiseks autode bensiinimootorites. Üha sagedamini esineb linnapildis elektrijalgrattaid ja elektriautosid. Energiaallikaks on aku sülearvutites, digikaamerates, katkematu toite allikates (UPS, ingl Uninterruptible Power Supply).

Elektrienergiat on suurtes kogustes raske talletada ning selleks vajatakse suuri ja kalleid seadmeid. Põhiline elektrienergia kogus saadakse siiski, kasutades elektromagnetilise induktsiooni nähtust, kus magnetvoo muutumine ajas põhjustab elektromotoorjõu tekke (elektrivoolu generaator). Selleks on vajalik elektrijaamade ja jaotusvõrgu pidev töö.

Keemiline vooluallikas

Keemilise vooluallika põhiosadeks on negatiivne ja positiivne elektrood ning elektrolüüt. Elektroodide pinnal on elektrokeemiliselt aktiivsed ained, metallid või nende ühendid. Elektrolüüdiks on hapete, aluste ja soolade lahused või ioonvedelik.

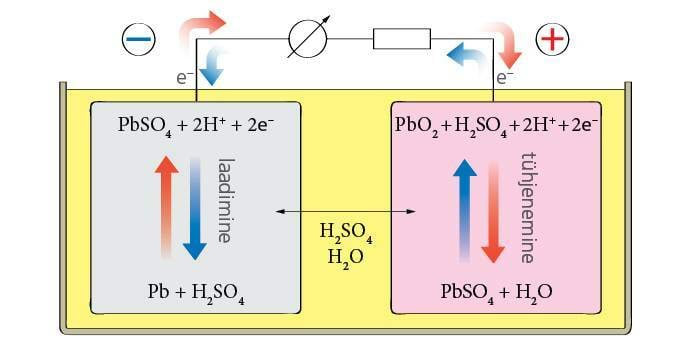
Elektrokeemilised protsessid põhinevad redoksreaktsioonidel. Vooluallika negatiivsel elektroodil toimub elektrolüüdiga reageerides metalli oksüdeerumine ja elektronide loovutamine. Kui ühendada vooluallika klemmidega tarbija, siis elektronid hakkavad suunatult miinusklemmilt läbi tarbija pluss- klemmile liikuma, kus nad redutseeritakse. Näitena olgu toodud plii- ehk happeakus toimuv reaktsioon.

Laetud akus on ühel elektroodil peaaegu puhas plii ja teisel pliioksiid ning nende vahel väävelhappe ( $33, 6 %$ vol) vesilahus (vt järgnev joonis). Tühjas akus seevastu on elektroodidel plii(II)sulfaat ja nende vahel vesi.

Peale happeakude on veel kasutusel mitmesugused leelisakud ja suhteliselt hiljuti leiutatud liitiumakud. Uuemaks tehniliseks rakenduseks on päikese- paneelid, kus kiirgusenergia muudetakse ventiilfotoefektiga vahetult elektrienergiaks, kuid paneelide hind on laialdaseks kasutuselevõtuks veel liiga kõrge.

Keemiliste vooluallikate põhilisteks näitajateks on elektromotoorjõud, nimipinge, sisetakistus, nimilaeng ehk mahutavus ( $A h$ ), energiatihedus ( $W h / k g$ ), laadimise kasutegur ja säilivus (alles on $90 %$ nimilaengust).

Ajaloost

Juba antiikmaailmas tunti hõõrdeelektrit. Hiljem avastati püroelekter ja piesoelekter. Konstrueeriti elektrofoormasin, mis eraldas erinimelised laengud mehaanilise energia arvel. Kõikide selliste vooluallikate puudus oli ebaühtlane pinge ja väike elektrilaeng. See ei võimaldanud elektrivoolu iseloomustavaid suurusi täpselt mõõta ning mitmed seaduspärasused jäidki märkamata. Olukord paranes, kui Volta leiutas nn Volta samba, mis võimaldas stabiilset pinget hoida suhteliselt pika aja jooksul. 1858. aastal leiutas prantslane Gaston Planté korduvalt kasutatava pliiaku, ning taolisi kasutatakse siiani. 20. sajandi alguses võeti kasutusele leelisaku ja 1991. aastal liitiumaku.

Kui tööstus vajas üha rohkem energiat ja seda ka jõumasinast kaugel, osutus kõige sobivamaks elektrienergia. 1831. aastal avastas Faraday elektromagnetilise induktsiooni nähtuse ja juba 19. sajandi lõpul realiseeriti elektrienergia tootmise ja ülekandmise tänapäevani kehtivad üldpõhimõtted.

Probleem

Miks võib elektromotoorjõudu vaadelda nagu vooluallika maksimaalset klemmipinget?

Kas vooluringi välisosal eralduv võimsus võib olla sama suur erinevatel voolutugevustel? Põhjenda.

Kokkuvõte

Vooluallika elektromotoorjõud on arvuliselt võrdne kõrvaljõudude tööga ühikulise laengu ümberpaigutamisel kogu suletud vooluringi ulatuses

E = \frac{A_{k}}{q}

Voolutugevus suletud vooluringis on võrdeline vooluallika elektromotoorjõuga ja pöördvõrdeline vooluringi välisosa ja vooluallika sisetakistuse summaga

I = \frac{E}{(R + r)}

Lisa 2.1. Elektrivool vedelikes

Alumiiniumi tootmine

Elektrolüüsi oluliseks rakenduseks on alumiiniumi tootmine. Alumiiniumi kasutusvõimalused on avarad ja maakoores leidub seda palju, kuid ebaühtlaselt. Paraku esineb ta erinevate ühenditena ja puhta alumiiniumi saamise kõige sobivam meetod on elektrolüütiline. Elektrienergia vajadus on seejuures suur ja tehased ehitatakse elektrijaamade lähedusse. Näiteks osutub kasulikuks isegi alumiiniumimaagi transportimine Austraaliast Islandile, kus on suur taastuva elektrienergia ressurss.

Naatriumhüdroksiidi tootmine

$N a O H$ on keemiatööstuses väga oluline aine, mida saadakse näiteks keedusoola lahuse elektrolüüsil, milles eralduvad vesinik ja kloor ning naatriumhüdroksiid jääb lahusesse.

Kütuseelement

Vee elektrolüüsil võib saada vesinikku ja hapnikku. Sellest vesinik on kõrgekvaliteediline kütus, mis ühinedes hapnikuga nn kütuseelemendis muundab keemilise energia vahetult elektrienergiaks. Erinevalt tavakütustest on vesiniku põlemisproduktiks ainult vesi. Kütuseelemendid võeti kasutusele 1960ndatel kosmose- ja sõjatehnikas. Nende massiline kasutamine on seni veel piiratud liiga kuluka vesiniku tootmise ja säilitamise tõttu. Vesiniku tootmiseks oleks mõistlik kasutada päikese ja tuule energiat.

Ajaloost: elektrivool vedelikes

Elektrokeemik Wilhelm Ostwald on ainus Eestis õppinud ja õpetanud nobelist. Tema mälestustahvel asub TÜ Toomemäe-poolsel seinal.

1785. aastal sai hollandi füüsik Martin van Marum elektrostaatilist generaatorit kasutades tina, tsinki ja antimoni. 1800. aastal lagundasid William Nickolson ja sir Anthony Carlisle Volta vooluallikat kasutades vee vesinikuks ja hapnikuks. 1833. aastal sõnastas Faraday elektrolüüsi seaduse. Temalt pärinevad terminid elektrood, elektrolüüt, elektrolüüs, ioon, anood, katood jm. Elektrolüüsi abil on avastatud paljud keemilised elemendid, muu hulgas $K$ , $N a$ , $B a$ , $M g$ , $G a$ ja $F$ . Aastal 1886 lõid Paul Louis Toussaint Héroult ja Charles Martin Hall alumiiniumi tootmise elektrolüütilise meetodi, mida kasutatakse tänapäevani. Väga oluliseks tootmisharuks kujunes galvaanika, milles kaetakse näiteks terase pind roostetamisvastase tsingi, nikli või kroomi õhukese kihiga. Moritz Hermann Jakobi, kes oli ka Tartu ülikooli professor, leiutas galvanoplastika (esemest täpse jäljendi tegemine elektrolüüsi abil).

Elektrolüüsi on kasutatud ka mitmete oluliste füüsikakonstantide määramiseks ja ühikute defineerimiseks. Samuti on olnud elektrolüüs pikka aega füüsikat ning keemiat siduv probleem. Elektrokeemik Wilhelm Ostwald on ainus Eestis õppinud ja õpetanud nobelist (tema mälestustahvel (vt eelnev foto) asub TÜ Toomemäe-poolsel seinal).

Probleem

Vee elektrolüüsil tekivad gaasiline vesinik ja hapnik. Kuidas suhtuvad gaaside massid ja ruumalad? Andke selgitus.

Elektrolüüsi kasutegur on

90 %

ja pinge

5 V

. Kui palju energiat kilovatt-tundides kulub

1 k g

alumiiniumi saamiseks, kui alumiiniumi elektrokeemiline ekvivalent on

0, 093 m g / C

? Kui palju see maksab, kui

1 k W h

elektrienergia hind on

0, 15

eurot?

Aine elektrokeemiline ekvivalent on võrdeline aine molaarmassiga

μ

ja pöördvõrdeline valentsiga

z

kus Faraday arv

F = 96500 C / m o l

on elementaarlaengu ja Avogadro arvu korrutis.

k = 1 / F \cdot μ / z

Tuletage see valem, lähtudes asjaolust, et ühe iooni jõudmisel elektroodile on elektrolüüti läbinud laeng

z \cdot e

ja elektroodi mass suurenenud ühe aatomi massi võrra.

Kokkuvõte

Elektrolüütideks on ained, milles vabadeks laengukandjateks on ioonid.

Elektrolüüs on protsess, milles alalisvool põhjustab redoksreaktsiooni.

Elektrolüüsi käigus elektroodile eraldunud aine mass on võrdeline elektrolüüti läbinud laenguga.

m = k q

Võrdetegurit $k$ nimetatakse aine elektrokeemiliseks ekvivalendiks. See määratakse katseliselt ja on arvuliselt võrdne aine massiga, mis eraldub elektrolüüti läbinud ühikulise laengu korral.

Lisa 2.2. Elektrivool gaasis

Sõltumatu lahenduse liikideks on huum-, kaar-, säde- ja koroonalahendus, millest kaks esimest toimuvad suhteliselt väiksel elektrivälja tugevusel. Lahendusega kaasneb tihti helenduva ioniseeritud gaasi – plasma – teke. Huumlahendust kasutatakse luminofoorlampides (EM lk 133), mille üheks liigiks on kompaktne säästulamp (kõrvaloleval pildil).


Erinevad ise tehtud gaaslahenduslambid, selgitustega. Tegemist on huumlahendusega, st lahendus tekib hõredas gaasis ja madalal pingel.	Kaarleeki kohtame kõige sagedamini keevitustöödel.

Elektrikeevitusel kasutatakse kaarlahendust, kus plasma temperatuur on piisavalt kõrge metalli sulatamiseks. Välk on võimas looduslik sädelahendus, mille kahjuliku mõju vältimiseks kasutatakse teravatipulist kõrgele tõstetud maandatud elektrijuhti – piksevarrast. Koroonalahendus võib avalduda Püha Elmo tuledena teravike läheduses, tugeva elektrivälja korral, näiteks äikese ajal.


Kõrgepingeliinide kontaktide avamine. Tekib suure voolu ja suure pingega sädelahendus.	Sellised võivad olla koroonalahendused.

Ajaloost: elektrivool gaasides

Hõõrdeelektri juures täheldati tihti ka sädemete teket. 18. sajandil olid olemas juba vahendid küllalt suurte elektrilaengute tekitamiseks (induktsioonigeneraator ja Leideni purk). Jõuti veendumuseni, et hõõrdeelekter ja välk on ühesuguse olemusega. Palju elektrikatseid tegi Ameerika teadlane Benjamin Franklin, kes leiutas selle käigus ka piksevarda. Tema välgu uurimine sai tuntuks ning katseid korrati ja modifitseeriti. Äikese püüdmise katses sai 1753. aastal välgulöögist surma Eesti aladelt pärit baltisakslasest Peterburi akadeemik Georg Wilhelm Richmann. Elektrikeevitust kaarleegiga kasutas 1881. aastast vene leidur Nikolai Benardos. Ajaloost on teada, et Hugo Treffneri gümnaasiumi poisid tarvitasid õpetaja innustusel kaar- lampi kooli liuvälja valgustamiseks Emajõel 20. sajandi alguses.

Probleem

Joonisel kujutatud gaasis on voolutugevus veerand küllastusvoolust. Mitu protsenti vabadest elektronidest ja ioonidest sellel voolutugevusel rekombineerub?

Kas Ohmi seadust kujul

I = U / R

võib kasutada ka gaasi puhul?

Kokkuvõte

Tavatingimustes on gaasid halvad elektrijuhid. Elektrivoolu juhib ainult ioniseeritud gaas.

Põrkeionisatsiooniks nimetatakse nähtust, kus elektriväljas kiirendatud elektron põrkudes gaasi aatomiga lööb sellest välja elektrone.

Sõltumatu gaaslahendus tekib pärast põrkeionisatsiooni algust ja kestab edasi ka välise ionisaatori eemaldamisel.

Elektrivoolu gaasis nimetatakse gaaslahenduseks.

Lisa 2.3. Termistor ja fototakisti

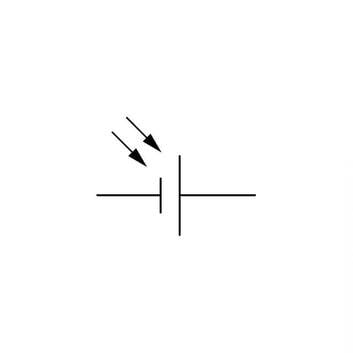
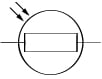
Termistor on pooljuhtseadis, mille takistus sõltub oluliselt temperatuurist. Takistuse temperatuuritegur võib olla nii negatiivne kui ka positiivne. Termistori kasutatakse temperatuuri andurina ja ülekoormuse piiramiseks elektrisüsteemides.


Termistorid	Termistori tingmärk skeemil

Fototakisti takistus väheneb valguse toimel. Olenevalt materjalist võib ta reageerida ka ultra- või infravalgusele. Fototakistit saab kasutada andurina kiirguse mõõtmisel ja valguse automaatlülitustes.


Fototakisti	Fototakisti skeemitähis

Ajaloost: pooljuhid

Pooljuhi omadustega hõbesulfiidi kirjeldas juba aastal 1833 Faraday. 1874. aastal avastas Karl Ferdinand Braun metalli ja loodusliku kristalli kontaktil ühesuunalise juhtivuse. Sellised pooljuht-kristall-detektorid võeti kasutusele 20. sajandi algul raadiotehnikas. Saavutuste eest nn traadita sides sai Braun 1909. aastal Nobeli auhinna. 1920ndate lõpust alates kasutati tööstuses vahelduvvoolu alaldamiseks kuproks- ja seleenventiile. Kuni 1940. aastani kasutati peamiselt polükristalseid pooljuhte, kuid sajandi keskel hakati tegelema germaaniumi ja räniga, millest valmistati esimesed pooljuhtdioodid. 1958. aastal loodi Tallinna pooljuhttakistite yehas, mis hakkas valmistama NSV Liidu sõjatööstusele soojustundlikke fototakisteid. Koos vastava optikaga kasutati neid rakettide suunamiseks lendava lennuki soojale mootorile.

Probleem

Miks pooljuhi valgustamisel võib tema takistus väheneda?

Miks kõrgetel temperatuuridel muutub lisandjuhtivus väheoluliseks?

Kokkuvõte

Pooljuhid on ained, mille eritakistus on metallide ja dielektrikute vahepealne ning mille juhtivus sõltub oluliselt temperatuurist, valgustatusest ja lisanditest.

Sõltuvalt sellest, kas lisandi valents on suurem või väiksem kui põhiainel, saadakse vastavalt elektron- ja aukjuhtivus.

Elektrivool pooljuhtides on elektronide ja aukude suunatud liikumine.

Lisa 2.4. p-n siire, pooljuhtdioodid

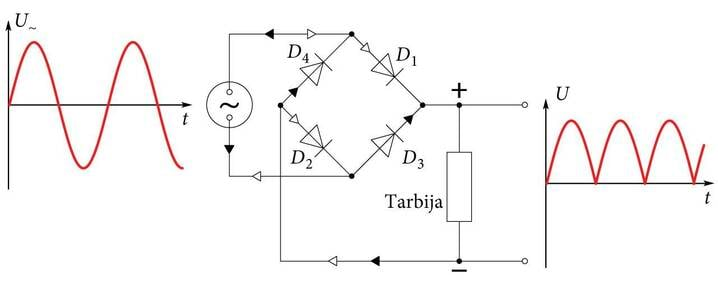
Alaldi

Elektrivõrgus on vahelduvvool, mille suurus ja suund perioodiliselt muutuvad. Paljud elektriseadmed või nende komponendid vajavad alalisvoolu. Seetõttu tuleb vahelduvvoolu alaldada, st muuta alalisvooluks. Vastavas seadises, alaldis, kasutatakse pooljuhtdioode vastavalt järgnevale skeemile.

Joonise vasakul pool on alaldile rakendatud vahelduvpinge $U_{\sim}$ . Alaldi koosneb neljast pooljuhtdioodist. Olenemata voolu suunast sisendis, läbib tarbijaks olevat takistit ühesuunaline vool. Pulseeriva pinge saab vajadusel pooli ja kondensaatoriga muuta alalispingeks.

Transistor

Transistor on pooljuhtseadis, mille abil saab elektrisignaali võimendada, lülitada, tekitada ja muundada. Transistor koosneb kolmest eri juhtivusega piirkonnast, millest keskmine on baas ning äärmised emitter ja kollektor (all vasakpoolne joonis). Seega on transistoris kaks p-n siiret.

Kui emitteriks on n-juhtivusega pooljuht, siis transistori tüübiks on npn. Vaatame sellist transistorit ühise emitteriga lülituses (eelnev parempoolne joonis), mis on sobiv elektrisignaalide võimendamiseks. Emitteri piirkonnas on tunduvalt rohkem lisandiaatomeid, antud juhul ka vabu elektrone. Esimest siiret läbib elektronide pärivool. Baas on õhuke ja temas jõuab rekombineeruda väga väike arv elektronidest. Peamine osa suundub läbi teise siirde kollektorisse. Baasivoolu väikene muutus põhjustab kollektorvoolu suuri muutusi, millel põhinebki transistori võimendusefekt. Elektroonikas kasutatakse erinevat tüüpi transistore ja ühendusviise.

Kõrgsagedusvõnkumise generaator

Madalsagedusliku vahelduvvoolu tekitamiseks paneb turbiin generaatori pöörlema. Kõrgemate sageduste jaoks ei saa kasutada mehaanilist meetodit, vaid poolist ja kondensaatorist koosnevat võnkeringi, kus võnguvad väikese massi ja inertsiga elektronid. Võnkeringis toimuva elektromagnetvõnkumise perioodi valemist on näha, et kõrgsagedusvõnkumise saamiseks peavad võnkeringi induktiivsus ja mahtuvus olema väikesed.

T = 2 π \sqrt{L C}

Selleks, et võnkumised ei sumbuks, peab võnkeringi õigel ajal energiat lisama. Seda saab teha nn tagasiside kaudu. Järgneval joonisel on kujutatud kõrg- sagedusvõnkumise generaatori põhimõtteskeem, kus võnkeringi pool $L$ indutseerib teises tema lähedal asuvas poolis induktsioonivoolu. See vool on ka transistori avav baasivool, mille tulemusel saab võnkering vooluallikast õigel ajal energiat juurde. Antud juhul on tegemist induktiivse tagasisidega.

Kondensaatori klemmidelt saame sumbumatu elektromagnetvõnkumise, mille sagedus sõltub pooli induktiivsusest ja kondensaatori mahtuvusest. Selline generaator on oluline raadiosides elektromagnetlainete tekitamisel.

Ajaloost: pooljuhtdiood

Esimesed pooljuhtdioodid võeti kasutusele 20. sajandi algul raadiovastuvõtjas detektorina. Oluliseks murranguks elektroonikas kujunes sama sajandi keskpaigas leiutatud kolme elektroodiga pooljuhtseadis transistor, mille eest sai John Bardeen 1956. aastal Nobeli füüsikapreemia. Järgmine oluline muutus oli paljude pooljuhtseadiste, takistite, kondensaatorite jm tihe integreerimine ühisele õhukesele räniplaadile. Nii saadi kiip ehk integraallülitus, kus ühel ruutmillimeetril võib paikneda mitu miljonit transistori. Kiipide kasutamine tavalistes elektroonikaseadmetes (arvuti, mobiiltelefon jms) sai võimalikuks nende tootmise madala hinna, vastupidavuse, vähese energiatarbimise ja signaalide ülikiire vahetamise tõttu. Esimese teadaoleva kiibi valmistas 1958. aastal Ameerika elektroonikainsener Jack St. Clair Kilby, kes sai selle eest 2000. aastal Nobeli füüsikapreemia.

Probleem

Mida võiks öelda tõkkekihi paksuse kohta pooljuhtdioodis päri- ja vastupinge korral?

Mille arvel toimub transistoris elektrisignaali võimendamine?

Kokkuvõte

Pooljuhtdioodis on p-n siire, mille põhiomaduseks on juhtida elektrivoolu ühes suunas.

Transistor on pooljuhtseadis, mille abil saab tekitada, lülitada, võimendada ja muundada elektrisignaali (voolu).

Lisa 2.5. Elektrist valgus ja valgusest elekter

Digikaameras kasutatakse fotoraku omadust muuta valguskiirgus elektrienergiaks. Kaameras tekitatakse objektiiviga kujutis fotorakkude ridadest ja veergudest moodustatud pildisensorile. Fotorakul tekkiv laeng on võrdeline pealelangeva valguse energiaga. CCD-pildisensoris nihutatakse laengupakette samm-sammult pildielemente mööda iga rea lõppu ja sealt võimendi ja muunduri kaudu töötlemiseks pildiprotsessorisse. Fotorakud reageerivad üksnes kujutise intensiivsusele. Värvilise kujutise saamine põhineb RGB-värvimudelil: kolme värvusega – punane (R red), roheline (G green), sinine (B blue) – kiirguste eri annustes liitmisel on võimalik saada kõik värvused. Seega peavad sensori väljundisse jõudma nende kolme põhivärvuse infot esitavad signaalid. Objektiivist saabuvast valgusest põhivärvuste eraldamiseks võib kasutada fotorakkude ette asetatud filtreid. Inimsilm tajub kõige paremini rohelist valgust, seepärast on pooltel elementidel rohelised filtrid, teistel vaheldumisi punased ja sinised. Niisuguse filtriga sensorit nimetatakse Bayeri sensoriks. Iga pildielemendi kohta registreerib pildiprotsessor üheaegselt kolme põhivärvuse väärtused: üheks värvuseks on piksli filtri värvus, kahe ülejäänud värvuse väärtused arvutab protsessor, hinnates infot naaberpikslite rühma kohta. Selliselt salvestatud pildi eeliseks võrreldes traditsioonilise fotoga on lihtne pilditöötlus ja väike ruuminõudlus.

Päikesepatarei ehk päikesepaneel koosneb samuti suurest hulgast fotorakkudest, mis on ühendatud omavahel patareiks. Pooljuhtmaterjalina kasutatakse peamiselt räni. Selliste paneelide kasutegur on $15 - 20 %$ . Päikeseenergiast elektri tootmisega tegeldakse kõige intensiivsemalt Euroopas, USAs, Indias ja Hiinas. Kalifornia osariigis asuva suurima päikesepaneelidel töötava elektrijaama võimsus ületas 2014. aasta juunis $500 M W$ . Eestis Võrumaal Kurenurme külas valmis 2013. aastal $100 k W$ võimsusega suunatavate paneelidega elektrijaam, kuid lahkarvamuste tõttu võrguettevõttega pole see elektrivõrguga veel ühendatud. Eesti oludes on novembrist kuni märtsini päikesekiirguse intensiivsus nõrk, kuid päikesepatareide kasuteguri paranedes ja hinna alanedes võib osutuda elektrienergia tootmine kirjeldatud moel kasulikuks ka meil. Päikeseenergia on kõige puhtam energia. Saastamine toimub siiski päikesepaneelide ja muu elektrijaama jaoks vajaliku materjali tootmisel. Ka vanade paneelide taaskasutus on võimalik.

Ajaloost: valgustid

Kui inimene võttis kasutusele tule, sobis see nii valgustamiseks, toidu valmistamiseks kui ka kiskjate peletamiseks. Hiljem võeti kasutusele küünlad, õli-, petrooleumi- ja gaasilambid. Elektri abil valgustamine algas kaarlambiga. Hiljem lisandusid söest ja metallist hõõgniitidega lambid. Hõõgniit peab taluma kõrget temperatuuri, sest nähtava valguse tekitamiseks peab tõusma niidi temperatuur üle $500^{\circ}$ . Päikesevalgusele vastab temperatuur $5800^{\circ} C$ . Hõõglampide niidid valmistatakse tavaliselt kõrge sulamistemperatuuriga volframist. Hõõglampide kasutegur on mõni protsent ja seepärast võeti ajapikku tarvitusele paremad luminofoorlambid, hiljem kompaktluminofoorlambid ehk säästulambid. Praegu toimub LED-lampide intensiivne arendamine, mille tõttu on paranenud tehnilised näitajad ja vähenenud hind.

Ajaloost: fotograafia

Juba antiikajal tunti camera obscurat, mille abil sai pimeda ruumi seinale väikse ava abil tekitada väljaspool kambrit asuvast esemest kujutise. Prantsuse leiutaja J. N. Niépce ühendas camera obscura valgustundliku paberiga ja tal õnnestus 1816. aastal jäädvustada esimene foto. Hiljem asetati avasse lääts ja katsetuste põhjal leiti kõige sobivamaks fotomaterjaliks hõbedaühendid. 19. sajandi viimasel veerandil töötati välja nn klassikaline tehnoloogia, mida kasutatakse siiani. Pildistamisel tekitatakse valgustundlikule materjalile varjatud kujutis, mis pärast keemilist töötlemist – ilmutamist – muutub nähtavaks fotonegatiiviks. Negatiiv kinnistatakse keemiliselt. Pärast negatiivi läbivalgustamist – kopeerimist – ja teistkordset ilmutamist saame tegelikkusele vastava positiivi. Selline protsess on küllaltki töömahukas, eriti siis, kui on tegemist värvifotoga.

Aastal 1975 leiutas Steven Sasson esimese digikaamera, kus kasutas Willard Serling Boyle’i ja George Elwood Smith’i 1969. aastal leiutatud CCD sensorit. Täielik läbimurre tuli 21. sajandi alguses, sest digikaamera hind pole enam kuigi kõrge ja pildistamine ja pilditöötlus arvutis ei nõua erilist ettevalmistust. Esimene kaameratelefon tuli turule Jaapanis aastal 2000. Boyle ja Smith said 2009. aastal CCD sensori leiutamise eest Nobeli füüsikapreemia.

Ajaloost: päikesepatarei

1954. aastal valmistati Ameerika Ühendriikides esimene pooljuhtpäikesepatarei kosmoselaeva jaoks. Selle hinnaks arvutati $286$ dollarit võimsusühiku vati kohta ja kasuteguriks $4 %$ . Esimesed võrku energiat andvad päikeseelektrijaamad ehitati USAs 1980ndatel. 20. sajandi lõpus odavnesid päikesepaneelid sedavõrd, et jaamade rajamine muutus majanduslikult otstarbekaks. Aastal 2006 valmis Saksamaal Pockingis suurem päikeseelektrijaam võimsusega $10 M W$ .

Ajaloost: valgusdiood

Esimese, punast valgust kiirgava valgusdioodikonstrueeris Nick Holonyak aastal 1962. Selle valgus oli nõrk ja punaseid LEDe kasutati indikaatoritena mõõteriistade tabloodes. Rohkem kui kümme aastat hiljem leiutati kollast valgust kiirgavad dioodid. Alles 1990ndatel jõudis Shuji Nakamura (Nobeli auhind 2014) sinise LEDi valmistamiseni. Erinevad värvused olid vajalikud valget päevavalgust kiirgavate valgusdioodide saamiseks. Viimastel aastatel on valge valgusega dioode kasutatud autolaternates, taskulampides, jalgratastel, valgusfoorides ja ekraanides. Esimesena rakendati LED-tänavavalgustuse süsteemi Hollandis Ede linnas 2006. aastal. Aastal 2013 otsustas Tartu minna täielikult üle LED-tänavavalgustitele. Säästlike valgustite kasutuselevõtt on oluline, kuna maailmas kulub $19 %$ elektrienergiast valgustusele.

Probleem

Mida oleks vaja arvestada erinevate valgustite majandusliku tasuvuse võrdlemisel?

Miks on LEDi kasutegur hõõglambi omast parem?

Punane ja roheline valgusdiood kiirgavad sama võimsusega valgust. Kas nende valgusviljakused on võrdsed? Põhjendage.

Missugused on digifotograafia eelised võrreldes varasemate tehnoloogiatega?

Kas päikesepaneelid on Eestis majanduslikult säästlikud?

Kokkuvõte

LEDis muutub elektrivoolu energia p-n siirdel erimärgiliste laengute
rekombinatsioonil vahetult valguseks.

Fotorakus esineb valgusdioodiga vastupidine protsess, kus p-n siirdele langev valgus eraldab erineva märgiga laengukandjad, tekitades elektromotoorjõu.

Lisa 3.1. Vahelduvvoolu genereerimine

Miks vahelduvvool?

Elektrienergiat toodetakse eelkõige vahelduvvooluna seetõttu, et vahelduv- voolu pinget on lihtne trafoga muundada. Lisaks on tüüpilise vooluvõrgu trafo kasutegur $98 - 99 %$ . Pinge tõstmise abil saame vähendada soojuslikke energiakadusid ülekandeliinides. Pikad elektriliinid vähendavad takistuse tõttu tarbijani jõudnud vahelduvpinget. Jämedamate juhtmete kasutamine vähendab küll takistust, aga suurendab materjali kulukust. Enne tarbimist saab vähenenud pinget trafo abil vajaliku väärtuseni tõsta. Elektromagnetilise induktsiooni nähtust saab kasutada ka kõrgepinge tekitamiseks madala- pingelisest alalisvoolust. Katkestades mehaaniliselt või elektrooniliselt väga kiiresti alalisvooluringi, võime indutseerida kõrge pinge. Nii toimub see auto süütepoolis ja fotoaparaadi välklambis.

Ajaloost: vahelduvvoolu genereerimine

Esimesed kommertselektrivõrgud ehitati aastal 1882 Londonis ning New Yorgis Ameerika leiduri ja ärimehe Thomas Alva Edisoni juhtimisel. Need olid alalisvooluvõrgud, mida kasutati eelkõige valgustuse jaoks. Kui neid võrke laiendati, selgus, et pinge kõigub ja juhtmetes on suured energiakaod. Algul polnud vahelduvvoolu jaoks sobilikku mootorit ja elektrienergia arvestit. 1880ndatel tehti mitu vahelduvvoolu jaoks kasulikku leiutist. Nendeks olid transformaator, mitmefaasiline mootor ja vahelduvvoolu energia arvesti. Edison pooldas alalisvoolu kasutuselevõttu, aga leidur ja suurtööstur George Westinghouse ning serbia päritolu füüsik Nikola Tesla pidasid vahelduvvoolu perspektiivikamaks. Majanduslike huvide tõttu algas nn voolude sõda, milles vastased alati kõige viisakamalt ei käitunud. Edison püüdis rahvale näidata vahelduvvoolu erilist ohtlikust, tuues intriigi sisse esimesed mitte kõige õnnestunumad hukkamised elektritoolil. Mihhail Dolivo-Dobrovolski, kes töötas Saksamaal firmas AEG peakonstruktorina, leiutas 1891. aastal kolmefaasilise vahelduvvoolu, mis võimaldas konstrueerida suhteliselt lihtsa ehitusega kolmefaasilise vahelduvvoolumootori. Sellega algas vahelduvvoolu võidukäik.

Probleem

Tavalises vahelduvvoolugeneraatoris tekitab elektromotoorjõu pöörlev liikumine. Milliseid võimalusi on veel vahelduvvoolu tekitamiseks magnetvoo muutmisega?

Kokkuvõte

Vahelduvvool on elektrivool, mille suund ja tugevus ajas perioodiliselt
muutub.

Vahelduvvoolu tekitamine põhineb elektromagnetilise induktsiooni nähtusel. Näiteks tekib magnetväljas pöörlevas juhtmekeerus sinusoidaalselt muutuv elektromotoorjõud.

Põhiline osa elektrienergiast toodetakse vahelduvvoolugeneraatoritega, mille käitavad enamikul juhtudel auruturbiinid.

Lisa 3.2. Voolutugevuse, pinge ja võimsuse efektiivväärtused

Tõestame trigonomeetrilisi seoseid kasutades vahelduvvoolu efektiivväärtuse valemi

I = \frac{I_{m}}{\sqrt{2}}

Seosest kahekordse nurga kohta on teada, et

{sin}^{2} α = \frac{1}{2} (1 - cos (2 α))

Takistil $R$ eralduv hetkvõimsus

P = I u = i^{2} R = i_{m}^{2} R {sin}^{2} ω t = \frac{I_{m}^{2} R}{2} (1 - cos (2 ω t))

Kui tahame saada takistil eralduvat ajas keskmist võimsust, siis on valemist näha, et ajast sõltub ainult liige $cos (2 ω t)$ , mille keskmine väärtus sinusoidil on $0$ .

Keskmine võimsus on seega

P = \frac{I_{m}^{2} R}{2}

milles

\frac{I_{m}^{2}}{2}

peab olema voolutugevuse ruudu keskmine väärtus. Ruutjuurt voolutugevuse ruudu keskväärtusest nimetatakse vahelduvvoolu tugevuse efektiivväärtuseks, mis ongi valem 1.12.

I = \sqrt{\frac{I_{m}^{2}}{2}} = \frac{I_{m}}{\sqrt{2}}

Kui vaadata järgnevat joonist, kus ülemise graafiku siinuse keskmine väärtus ühe perioodi jooksul on $0$ , aga alumise siinuse ruudu keskmine väärtus perioodi jooksul $\frac{1}{2}$ , on ka piltlikult arusaadav voolutugevuse efektiivväärtuse ja maksimaalväärtuse vaheline seos.

Probleem

Õppetükis 1.3.2. öeldi, et kui vahelduvvooluringis on kondensaator, siis voolutugevuse maksimum saabub pingemaksimumist varem. Seletage nähtust, kasutades kondensaatori ja vahelduvvoolu omadusi.

Kokkuvõte

Vahelduvvoolu tugevuse efektiivväärtus on selline alalisvoolu tugevus, mille korral juhis eraldub samasugune võimsus kui vahelduvvoolu korral.

Pinge ja voolutugevuse maksimaalväärtuste ning efektiivväärtuste vahel on järgmised seosed:

U = \frac{U_{m}}{\sqrt{2}}

I = \frac{I_{m}}{\sqrt{2}}

Vahelduvvoolu mõõteriistad näitavad mõõtmisel efektiivväärtusi.

Lisa 3.3. Trafo. Elektrienergia ülekanne

Trafod ja muundurid

Trafosid kasutatakse väga erinevates elektriahelates. Lisaks pingejaotusvõrkudele ka raadiotes, arvutites, elektriautodes jm. Seoses pooljuhttehnoloogia arenguga võetakse trafode asemel üha enam kasutusele transistorlülitustel põhinevad nn impulssmuundureid. Need on trafodest oluliselt väiksemate mõõtmete ja massiga, hõlpsamini reguleeritavad ning väikeste võimsuste juures ka odavamad. Impulssmuunduri põhikomponentideks on transistor, induktiivpool ning diood. Pooli induktiivsuse ning transistori sisse- välja-lülitamise valikuga võib muunduri väljundist saada mistahes sageduse ja pingega väljundvoolu.

Väiksemates elektrijaamades (tuulikud ja päikesepaneelid) kasutatakse juba praegu süsteemi, kus tuulikute muutuva sagedusega vahelduvvool või paneelidelt saadav muutliku pingega alalisvool muudetakse sobiva sageduse ja pingega vahelduvvooluks. See võimaldab väiketootjal ülejääva energia müüa üldisesse elektrivõrku.

Suure võimsusega vahelduvvoolu ülekandeliinide pikkus ei ületa 1000 km, sest energiakaod läheksid muidu liiga suureks. Suure võimsuse ja vahemaa korral kasutatakse kõrgepingelist alalisvooluliini HVDC (high-voltage direct current). Liini alguses muudetakse muunduriga vahelduvvool alalisvooluks ja lõpus uuesti vahelduvvooluks. HVDC korral on energiakaod niipalju väiksemad, et õigustavad kallite muundurite ja kaablite kasutamist. Sellise süsteemi abil saab ühendada ka erinevate parameetritega regionaalseid vahelduvvooluvõrke, võimaldades kiiresti reageerida tarbimisvajaduse muutusele. 2013. aastal oli kõige pikem $2375 k m$ Rio Madeira HVDC Brasiilias, milles ülekantav võimsus on kuni $7100 M W$ .

Ajaloost: vahelduvvooluvõrkude areng

Aastal 1881 ehitasid Lucien Gaulard ja John Dixon Gibbs Londonis esimese trafo. Aasta hiljem said ungarlased Karoly Zipernowsky, Miksa Deri, Otto Titusz Blathy trafole patendi, mille järgi hakati neid ka tootma. Westinghouse importis Euroopast erinevaid trafosid ja aastal 1886 ehitati Massachusettsis vahelduvvoolu liini, milles $500$ -voldine generaatoripinge tõsteti trafoga $3000$ voldini ja tarbijani jõudes langetati $100$ voldini. Saksa insener Oskar von Miller ehitas 1891. aasta Frankfurti rahvusvahelise elektrotehnikanäituse jaoks $175 k m$ pikkuse kolmefaasilise ülekandeliini, mille alguses oli $55$ -voldine kolmefaasiline vahelduvvoolugeneraator. Generaatori pinge tõsteti kolmefaasilise trafoga $15000$ voldini. Näitusel põles $1000$ lampi ja kolmefaasilise mootoriga ühendatud pump tekitas kunstliku kose. Pärast näitust hakati kogu maailmas eelistatult ehitama vahelduvvoolu elektrivõrke, mis on kasutusel ka praegu. Huvitav on märkida, et viimane alalisvoolu võrk New Yorgis lõpetas tegevuse alles 2007. aastal ning Kalifornia osariigis ja mujal on praegugi alalisvoolu „saarekesi”.

Ajaloost: elektrienergeetika Eestis

Elektrienergia kasutuselevõtt Eestis toimus samal ajal kui mujal arenenud riikides, 19. sajandi viimastel kümnenditel. Aastal 1882 seati Narva Kreenholmis ja Tallinna Wiegandi tehases ruumide valgustamiseks üles generaatorid. Tootmise tarbeks alustasid 1893. aastal Kunda tsemenditehases tööd kaks generaatorit koguvõimsusega $200 k W$ . Kõik eelpoolnimetatud jaamad töötasid auru jõul ja andsid alalisvoolu. Esimene vahelduvvoolugeneraator võimsusega $450 k W$ paigutati aastal 1899 Tallinna Dvigateli tehasesse. Müügiks hakati elektrit tootma Pärnus, kus 1907. aastal alustas tööd $100 k W$ võimsusega elektrijaam. Elektriga valgustati tänavaid ja puhkeasutusi.

Esimese $15 k V$ ülekandeliini projekteeris ja ehitas diplomeeritud insener Kotri Hangelaid (Gottfried Hacker). See kulges Aru turbarabas asuvast elektrijaamast Rakvereni ja valmis 1918. aastal. Kõrgepingeliinide ehitamine ja elektri tootmine hoogustusid pärast 1923. aastat, kui hakkasid voolu andma Ellamaa ( $1400 k W$ ) ja Ulila ( $1000 k W$ ) turbaküttel jaamad. Aastal 1924 oli generaatorite koguvõimsus Eestis $24 M W$ . 1940. aastal toodeti elaniku kohta $181 k W h$ elektrienergiat. 1950ndate lõpuks oli Eesti jaamade elektriline koguvõimsus $103 M W$ . 1959. aastal valmis Narvas põlevkiviküttel Balti Soojuselektrijaam, mis saavutas täisvõimsuse $1435 M W$ 1966. aastal. Aastal 1973 läks käiku Eesti Elektrijaam võimsusega $1610 M W$ . Energiat toodeti rohkem kui Eestis tarbiti ning 1960. aastal ehitati kõrgepingeliinid Leningradi ja Riiga. 1962. aastal formeerus lõplikult ringliin Narva-Tartu- Viljandi-Pärnu-Tallinn-Narva, mis tagas stabiilsema varustamise elektriga. 1960ndate alguses jõudis elekter massiliselt ka maakodudesse. Aastatel 2006 ja 2014 lasti käiku kaks merekaablit Estlink Eesti ja Soome vahel, mis võimaldavad elektrienergia mõlemasuunalist liikumist. Nendes kasutatakse elektrienergia kõrgepingelise alalisvooluna edastamise süsteemi sest merekaabli vahelduvvoolu kaod oleksid eriti suured. Nimetatud kaablid on suurendanud Eesti energia- julgeolekut.

Probleem

Miks on trafo mähised vasest ja südamik rauast?

Kuidas toimub autos küttesegu süütamiseks vajaliku kõrge pinge saamine akust pingega

12 V

Kokkuvõte

Trafo on elektriseadis vahelduvpinge muutmiseks ja see töötab elektromagnetilise induksiooni nähtusel.

Ühe ja sama trafoga on võimalik vahelduvpinget nii tõsta kui ka langetada.

Lisa 3.4. Elektrimootor. Elektriohutusest

Elektriohutusest

Järgnevalt olgu toodud mõned lihtsad, aga olulised ohutustehnika reeglid: 1) pistiku väljatõmbamisel hoidke pistikust, ärge sikutage juhtmest; 2) ärge kasutage elektriseadmeid vannis ja duši all; 3) ärge lähenege maha kukkunud liinijuhtmele, vaid eemalduge sellest lühikeste sammudega vähemalt $20 m$ kaugusele; 4) teavitage elektririketest telefonil 1343; 5) voolu alla sattunud inimese lahtirebimisel kasutage isoleerivast materjalist eset ja lülitage elekter esimesel võimalusel välja; 6) kutsuge kiirabi telefonil 112.

Juba $50 m A$ vool, mis läbib organismi, võib osutuda eluohtlikuks. Õues tööd tehes on pistikupesale otstarbekas monteerida lekkevoolukaitse nimivooluga $30 m A$ . Elektritarvitite metallist korpus peaks olema maandatud. Kasutage tooteid, millel on Euroopa Liidu kvaliteedimärge CE.

Kolmefaasiline vool

Kui vahelduvvoolugeneraatoris paiknevad kolm mähist üksteise suhtes $1 / 3$ pöörde võrra nihutatult, saame kolmefaasilise generaatori. Pinge maksimumid saabuvad mähistes järgemööda kolmandikperioodi võrra nihutatult (alljärgnev joonis).

Mähiste algused ühendatakse kokku ja sealt saab alguse neutraal- ehk nulljuhe. Iga mähise lõpp ühendatakse erineva faasijuhtmega (järgneva joonise vasakpoolne osa). Selline neljajuhtmeline liin veetakse elektrijaamast tarbijani. Nulljuhe maandatakse – ühendatakse maaga. Kolmes faasijuhtmes kulgevate voolude maksimaalväärtused saabuvad kordamööda $1 / 3$ perioodilise hilinemisega ja seetõttu on kahe faasijuhtme vaheline pinge $\sqrt{3}$ korda suurem kui pinge nulljuhtme ja mistahes faasijuhtme vahel (vastavalt $400 V$ ja $230 V$ ). Selline süsteem võimaldab kolm korda suuremat võimsust, kuid sisaldab kõrgema pinge tõttu suuremat riski.

Asünkroonmootor

Kui paigutame staatorile mähised, mis asuvad üksteise suhtes $1 / 3$ pöörde võrra nihutatult, ja ühendame mähiste ühed otsad igaüks erineva faasijuhtmega ning teised otsad nulljuhtmega, saame staatoris nn pöörleva magnetvälja.

Voolutugevuse maksimumid liiguvad kolmandikperioodi kaupa ühelt mähiselt järgnevale. Kui staatori sisse paigutada pöörlemisteljega rauatükk (rootor), hakkab pöörlev magnetväli seda kaasa vedama, st paneb rootori pöörlema. Kuna rootori pöörlemine toimub magnetvälja pöörlemise suhtes viivitusega, nimetatakse seadet asünkroonmootoriks ehk mittesünkroonseks mootoriks. Kolmefaasilist vahelduvvoolu rakendatakse just seetõttu, et see võimaldab kasutada lihtsa ehitusega ja odavat asünkroonmootorit.

Ajaloost: elektrimootorid

Pärast Oerstedi katset voolu toimest magnetile leiutati mitmeid algelisi elektrimootoreid, näiteks Faraday varras, Barlow’ ratas, Jedliki magnetvälguga isepöörleja jms. Esimese praktikas kasutatava mootori konstrueeris Potsdamis aastal 1834 Moritz Hermann von Jacobi, kes oli mõnda aega ka Tartu ülikooli tsiviilarhitektuuri professor. 1938. aastal varustas ta paadi umbes $220 W$ elektrimootoriga, mis arendas Peterburis Neeva jõe $7, 5 k m$ lõigul kiirust $2, 5 k m / h$ . Võimsamate mootorite ehitamist takistas esialgu vastavate vooluallikate puudumine. Anyos Istvan Jedlik’i, Hippolyte Pixii, Sören Hjorth’i leiutised ja eeltöö võimaldasid 1866. aastal saada saksa leiutajal ja ettevõtjal Werner von Siemensil patent generaatorile, nn dünamomasinale. Seda aega võib lugedaelektrotehnika ja elektroenergeetika kiire arengu alguseks.

Probleem

Miks on trafo mähised vasest ja südamik rauast?

Kuidas toimub autos küttesegu süütamiseks vajaliku kõrge pinge saamine akust pingega

12 V

Kokkuvõte

Elektrimootor muudab elektrienergia mehaaniliseks tööks. Elektrimootoris kasutatakse voolu ja magnetvälja vastastikmõju.

Lisa 4.1. Temperatuur

Tuulekülm

Liikuv õhk jahutab nahka intensiivsemalt kui paigalolev.

Tuule kiirusel kuni $2 m / s$ pole veel erinevust tunda, aga tuulekiiruse kasvades tugevneb külmatunne olulisel määral.

	Tegelik temperatuur ( $^{\circ} C$ )
$v$ ( $m / s$ )	30	20	10	0	-10	-20	-30
$v$ ( $m / s$ )	Ekvivalentne temperatuur ( $^{\circ} C$ )
2	30	20	10	0	-10	-20	-30
5	29	17	5	-7	-19	-31	-43
10	29	15	1	-13	-27	-40	-54
15	29	14	-1	-16	-30	-45	-60
20	28	13	-2	-17	-32	-48	-63

Ajaloost: temperatuur

Temperatuuri saab kõige lihtsamal viisil hinnata soojusaistingu põhjal. Pistes küünarnuki vette, saame aru, kas vee temperatuur on imiku vannitamiseks sobiv. Enne 17. sajandit kasutati ilma skaalata mõõteriista termoskoopi, mida võib pidada termomeetri eelkäijaks. Viimast täiustades jõudis Daniel Gabriel Fahrenheit 1709. aastal eelkäijatest täpsema mõõteriista, piiritustermomeetrini, mille töö põhines piirituse küllalt suurel ja ühtlasel soojuspaisumisel. Fahrenheit valis skaala nullpunktiks lume ja ammooniumkloriidi segu madalaimatemperatuuri ( $- 17, 8^{\circ} C$ ). Teiseks lähtepunktiks valis ta inimese normaalse kehatemperatuuri $96^{\circ} F$ ( $36, 6^{\circ} C$ ).

Selles skaalas sulab jää $32^{\circ} F$ juures ja vesi keeb temperatuuril $212^{\circ} F$ . Hiljem asendas Fahrenheit termomeetris piirituse elavhõbedaga. Selliseid mõõteriistu hakkas ta valmistama ja müüma. Tänapäeval kasutatakse Fahrenheiti skaalat Ameerika Ühendriikides.

Rootsi teadlane Anders Celsius valmistas aastal 1742 piiritustermomeetri, mille fikseeritud punktideks olid jää sulamine $100^{\circ} C$ ja vee keemine $0^{\circ} C$ juures. Skaala pöörati paar aastat hiljem ümber praegusele kujule. Külmemates piirkondades tuleb õhutemperatuuri mõõtmiseks kasutada piiritustermomeetrit, sest elavhõbe tahkub $- 39^{\circ} C$ juures, aga piiritus alles temperatuuril $- 117^{\circ} C$ . William Thomsoni (aastast 1892 lord Kelvin) 1848. aastal esitatud temperatuuriskaala algab temperatuuri alumisest piirist – absoluutsest nullist – ja ühik $K$ (kelvin) on võrdne Celsiuse kraadiga. Temperatuuri mõõtmiseks võib lisaks eelpoolnimetatud soojuspaisumisele kasutada ka püromeetrilist ja termoelektrilist meetodit. Esimene põhineb asjaolul, et helenduva keha värvus sõltub temperatuurist. Seda meetodit on eriti sobiv kasutada kõrgetel temperatuuridel ja kaugete või ligipääsmatute objektide temperatuuri mõõtmiseks. Teine meetod põhineb Seebecki avastatud termoelektrilisel efektil, kus kahe metalli kontakti kuumutamisel tekib temperatuurist sõltuv elektromotoorjõud. Selle meetodi eelis seisneb temperatuuri vahetus muutmises elektriliseks signaaliks, mis võimaldab andmete automaatset kogumist ja töötlemist. On olemas ka termomeetreid, mille töö põhineb pooljuhi või metalli takistuse sõltuvusel temperatuurist.

Probleem

Põhjendage, miks toatemperatuur

20^{\circ} C \neq 20 K

, aga

4200 J / (k g \cdot^{\circ} C) = 4200 J / (k g \cdot K)

Võrrelge erinevaid temperatuuri mõõtmise meetodeid. Tooge esile nende head ja halvad küljed.

Kokkuvõte

Soojus levib iseenesest soojemalt kehalt külmemale, kuni temperatuurid võrdsustuvad.

Soojusliku tasakaalu korral on temperatuur keha kõikides osades ühesugune.

On olemas kõige madalam piirtemperatuur absoluutne null, millest keha temperatuur on alati suurem.

Lisa 4.2. Ideaalne gaas

Gaasi molekulide kiiruste jaotus

Gaasi molekulid liiguvad kaootiliselt erineva kiirusega. Järgnevalt on graafiliselt kujutatud sama gaasi molekulide kiiruste jaotust kahel erineval temperatuuril. Kiiruste jaotust madalal temperatuuril $80 K$ näitab punane joon ja punasega viirutatud osa pindala mõõdab molekulide koguarvu. Rohelisega viirutatud pindala mõõdab kiiruste vahemikus $100 - 150 m / s$ liikuvate molekulide arvu. Pindalade suhe näitab, mitmendik osa molekulidest liigub kiirusega $100 - 150 m / s$ .

Sinisele kõverale on märgitud tõenäoseim kiirus $v_{t}$ , keskmine kiirus $v_{k}$ ja ruutkeskmine kiirus $v$ . Mõlema kõvera alla jääva kujundi pindala on võrdne, aga madalamal temperatuuril on kiiruste vahemik väiksem.

Ajaloost: gaaside omaduste uurimine

Gaaside omaduste uurimist soosis vajadus ehitada paremaid aurumasinaid. Täpsemate mõõteriistade valmistamine võimaldas ka selgemalt eristada gaaside omadusi erinevates olekutes. Selgus, et suhteliselt kõrge temperatuuriga hõrendatud gaaside omadused on praktiliselt sõltumatud gaasi ainest. Võeti kasutusele ideaalse gaasi mudel, mille teooriat rakendades saadi alus aurumasinate efektiivsuse tõstmiseks. Keemia edusammud alates 18. sajandi lõpust soodustasid atomismi arengut. Just gaaside uurimine John Daltoni, Lorenzo Romano Amedeo Carlo Avogadro, Joseph Louis Gay-Lussac’i jt poolt lõi kujutluse keemilisest elemendist ja aine molekulaarsest ehitusest. Paraku jäi atomistlik maailmapilt soojuse ja aineosakeste liikumise seostamisel veel tahaplaanile.

Saksa füüsikud August Karl Krönig ja Rudolf Julius Emanuel Clausius avaldasid 19. sajandi keskel artiklid gaaside kineetilisest teooriast. Peagi andis Johann Josef Loschmidt küllaltki täpse hinnangu molekulide mõõtmetele ja kontsentratsioonile. Šoti füüsikateoreetik James Clerk Maxwell avaldas aastal 1859 seaduse, mis näitab molekulide jaotumist kiiruse järgi. Austria füüsik Ludvig Boltzmann lõi statistilise füüsika meetodeid rakendades tervikliku gaaside kineetilise teooria, mille avaldas raamatuna 1872. aastal. Maxwelli jaotuse ja sellega ka Boltzmanni teooria kehtivust kontrollis katseliselt alles 1920. aastal Otto Stern, kes sai 1943. aastal selle eest Nobeli füüsikaauhinna.

Probleem

Analüüsides valemeid 1.17. kuni 1.19. leidke, millises matemaatilises sõltuvuses on ideaalse gaasi rõhk ja tema absoluutne temperatuur.

Toaõhus on süsinikdioksiidi tavaliselt rohkem kui välisõhus. Kumb õhk on omaduste poolest lähemal ideaalsele gaasile talvel? Põhjendage.

Määrake kiiruste jaotuse graafikult, kui suur osa gaasimolekulidest liigub temperatuuril

300 K

kiiruste intervallis

300 - 400 m / s

Kokkuvõte

Ideaalne gaas on selline gaas, mille molekulide mõõtmeid pole vaja arvestada ja mille molekulide vastastikmõju on tühine.

Gaasi rõhk on tingitud kaootiliselt liikuvate molekulide põrgetest vastu anuma seina. Rõhk sõltub molekulide kontsentratsioonist, massist ja kiirusest

p = \frac{1}{3} n m_{0} v^{2}

Molekulide keskmine kineetiline energia on võrdeline absoluutse temperatuuriga

¯ E = \frac{3}{2} k T

Lisa 4.3. Ideaalse gaasi olekuvõrrand

Küttekolle ja gaasi olekuvõrrand

Ahju lõõrid on selleks, et juhtida põlemisel tekkivad gaasid koldest korstnasse. Samal ajal talletavad lõõride seinad soojust ja soojendavad tuba ka pärast kütmise lõpetamist. Põlemiseks on vajalik hapnik ja sellepärast peab koldest korstna suunas gaasi rõhk vähenema. See tekitab tõmbe, mis imeb toast põlemiseks vajalikku õhku juurde, paneb kuumad põlemisel tekkinud gaasid lõõrides liikuma ja juhib põlemisgaasid korstna kaudu välja. Tõmbe tekitamiseks tuleb arvestada gaasi olekuvõrrandit. Lõõride ristlõige võib väheneda vastavalt temperatuuri langusele, aga alati peab olema tõmmet tekitav rõhkude vahe.

Reaalsed gaasid

Ideaalse gaasi mudel ei arvesta molekulide mõõtmeid ja vastastikmõju. Teda võiks justkui lõpmatult kokku suruda. Tegelikkuses on teatav kriitiline temperatuur, millest allpool muutub gaas kokkusurumisel vedelikuks (MM lk 15). Transportida suurematele kaugustele on mõistlik oluliselt tihedamaks vedelikuks muudetud, veeldatud gaasi. Perspektiivseks on osutunud gaasitorustikust sõltumatu veeldatud maagaas LNG (Liquefied Natural Gas).

Ajaloost: ideaalse gaasi olekuvõrrand

Esimese seose gaaside olekuparameetrite, rõhu ja ruumala vahel jääval temperatuuril avastas iiri teadlane Robert Boyle 1662. aastal. Prantsuse teadlane Guillaume Amontons tegi aastal 1702 kindlaks seose gaasi rõhu ja temperatuuri vahel. Prantslane Jaques Alexandre César Charles avastas aastal 1787 seaduse isohoorilise protsessi kohta ja kaasmaalane Joseph Louis Gay-Lussac publitseeris 19. sajandi alguses isohoorilise ja isobaarilise protsessi seaduspärasused. Absoluutse nulli idee pakkus välja 1779. aastal šveitslane Johann Heinrich Lambert. Amedeo Avogadro väitis 1811. aastal, et sama ruumala, temperatuuri ja rõhuga gaasid sisaldavad sama arvu osakesi, ning prantsuse teadlane Benoit Paul Émile Clapeyron ühendas 1834. aastal varem teada saadud tulemused üheks gaaside seaduseks. Siinjuures peab mainima, et teatmeteostes valitseb gaasi uurimise ajaloos teatav segadus, sest erinevates kultuuripiirkondades seostatakse teadlasi ja avastusi erinevalt.

Probleem

Kuidas saaks valemite abil tõestada, et sõltumata gaasi ainest on tema ühe mooli ruumala normaaltingimustel

22, 4

liitrit?

Mõõdeti gaasi temperatuur, ruumala ja rõhk kahes erinevas olekus. Kuidas saab näidata, et tegemist on ideaalse gaasiga?

Kokkuvõte

Ideaalse gaasi olekuvõrrand ühendab omavahel makroskoopilised olekuparameetrid: rõhu, ruumala ja absoluutse temperatuuri. Ideaalse gaasi rõhu ja ruumala korrutis on võrdeline tema absoluutse temperatuuriga

p V = \frac{m}{M} R T

kus $m$ on gaasi mass, $M$ molaarmass ja $R = 8, 31 J / m o l \cdot K$ gaasikonstant.

Antud ideaalse gaasikoguse rõhu ja ruumala korrutis jagatud absoluutse temperatuuriga on jääv suurus

\frac{p_{1} V_{1}}{T_{1}} = \frac{p_{2} V_{2}}{T_{2}} = c o n s t

Lisa 4.4. Isoprotsessid

Isoprotsessidest koosnev ringprotsess

Probleem

Määrake ringprotsessi graafikult ligikaudu, mitu korda on punktides

A

C

D

absoluutne temperatuur suurem kui punktis

B

Kokkuvõte

Isoprotsessi käigus ei muutu keha üks olekuparameetritest.

Isotermilise protsessi käigus ei muutu temperatuur ja ideaalse gaasi rõhk on pöördvõrdeline ruumalaga:

\frac{p_{1}}{p_{2}} = \frac{V_{2}}{V_{1}}

Isobaarilise protsessi käigus ei muutu rõhk ja ideaalse gaasi ruumala on võrdeline absoluutse temperatuuriga:

\frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}}

Isohoorilise protsessi käigus ei muutu ruumala ja ideaalse gaasi rõhk on võrdeline absoluutse temperatuuriga:

\frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}}

Lisa 4.5. Siseenergia ja selle muutumisviisid

Tule kasutamisest

Inimese eellane Homo erectus oli tulekasutaja juba pool miljonit aastat tagasi. Tuli andis sooja, sellega sai liha küpsetada ja kiskjaid peletada. Arvatakse, et hirmu võitmine tule suhtes andis inimesele eelisarengu. Umbes $10000$ aastat tagasi hakati valmistama keraamilisi nõusid toidu keetmiseks ja hoidmiseks. Keedetud toitu, eriti taimset, omastab organism paremini kui toorest.

Tavaliselt saadi tuld välgu või vulkaanipurske tekitatud tulekahjust, mida püüti lõkkeasemel või koldes säilitada. Hiljem õpiti hõõrumisega tuld süütama.

Kasutades füüsika terminoloogiat, võiks öelda, et ürginimene kasutas soojusülekande erinevaid liike (soojuskiirgus, soojusjuhtivus, konvektsioon) ja mehaanilist tööd keha siseenergia suurendamiseks.

Tule tekitamine hõõrdumist kasutades pole lihtne. Tänapäeval on proovimise käigus saadud ainult mõned tulemuslikud võtted, näiteks terava pulga kiirel pööramisel vastavas süvendis. Alljärgneval vasakpoolsel pildil on kujutatud katse nn ellujäämislaagris ürginimese moodi tuld süüdata. Oskuse teha tööd keha siseenergia arvelt õppis inimene oluliselt hiljem. Esimesed sellised masinad, algelised aurumasinad, ehitati 17. sajandi lõpus ja 18. sajandi alguses.

Parempoolsel pildil on vana gravüür, millel kujutatud Thomas Newcomeni poolt Inglismaal 1712. aastal ehitatud aurujõul töötav kaevandusest vee eemaldamise pump.

Ajaloost: soojus

Soojuse olemuse kohta oli juba antiikajal kaks erinevat seisukohta: soojus kui kaaluta vedelik ja soojus kui aineosakeste siseliikumine. Pikapeale kaldus kaalukauss atomistliku lähenemisviisi kasuks. Siseenergia mõiste võttis aastal 1851 kasutusele William Thomson. See võimaldas omavahel siduda makroskoopilised ja mikroskoopilised suurused ningkaks füüsika olulist osa: soojusõpetuse ja mehaanika.

Probleem

Ühe mooli üheaatomilise ideaalse gaasi siseenergia on

U = 3 ∕ 2 R T

. Kas ühe mooli ideaalse gaasi, mille molekulid koosnevad kahest aatomist, siseenergia on võrdne, suurem või väiksem? Põhjendage.

Pärast ahju kütmist tõusis toaõhu temperatuur, aga siseenergia jäi praktiliselt samaks. Miks on see nii?

Kokkuvõte

Keha siseenergia on tema kõikide koostisosakeste kineetiliste ja potentsiaalsete energiate summa.

Ideaalse gaasi siseenergia on võrdeline tema absoluutse temperatuuriga.

Soojushulk on siseenergia, mille keha saab või annab ära soojusvahetuses teiste kehadega.

Lisa 5.1. Gaasi töö ja soojushulk

Kalorimeeter

Soojushulkade võrdlemiseks kasutatakse kalorimeetrit, mida võib vaadelda kui termost, mille soojusvahetus väliskeskkonnaga on püütud viia miinimumini. Välispind on hele vähendamaks soojuse kadu kiirguse teel. Sisemise ja välimise anuma vahe on konvektsiooni vähendamiseks täidetud soojusisolatsiooniga (nt vahtpolüstürool). Kalorimeetril on peal kaas, mis vähendab vedeliku aurustumist. Kaanes on avad termomeetri ja katsekehade jaoks. Kalorimeetriga saab määrata vedelike ja tahkiste erisoojust.


Kalorimeetri välimus	Kalorimeetri sisemus

Soojusülekande liigid

Tahkised, vedelikud ja gaasid vahetavad energiat erinevalt. Seetõttu eristatakse kolme soojusülekande liiki: soojusjuhtivus, konvektsioon ja soojuskiirgus. Soojuse levimine paigalolevas gaasis ja vedelikus seletub molekulide kaootiliste põrgetega, mille tagajärjel soojusliikumise energia kandub kõrgema temperatuuriga piirkonnast madalama suunas. Kristallilistes kehades määrab energia ülekande kiiruse nii kristallvõre aatomite seotus kui ka vabade elektronide liikumine.

Kui toas on soojem kui õues, siis läheb läbi seina soojushulk $Q$ , mis on võrdeline temperatuuride vahega toas ja õues $Δ T$ , seina pindala $S$ ja ajaga $t$ ning pöördvõrdeline seina paksusega $d$ .

Q = λ \frac{Δ T S t}{d}

Võrdetegur $λ$ iseloomustab seina materjali ja seda nimetatakse soojusjuhtivusteguriks. Selle ühikuks SI-s on

\frac{J m}{K m^{2} S} = \frac{W}{K m}

Soojusjuhtivustegur näitab, kui suur soojushulk läbib ühe kraadi temperatuuride vahe korral üheruutmeetrise pindala ja ühe meetri paksust seina ühes sekundis. Paekivi soojusjuhtivustegur on $1, 2 W / (K \cdot m)$ . See tähendab, et paekivist ühe meetri paksuse müüri igast ruutmeetrist läheb ühes sekundis läbi $1, 2$ džauli energiat, kui müüri pindade temperatuuride vahe on üks kraad. Seisva õhu soojusjuhtivustegur samades ühikutes on $0, 025$ , st soojusjuhtivus on $48$ korda väiksem. Soojustusmaterjalides püütaksegi tekitada olukord, et neis oleks soojuse liikumise suunas võimalikult paks kiht liikumatut õhku (nt vahud, villad).

Gaaside ja vedelike puhul on vaja arvestada ka konvektsiooni. Üldjuhul gaasid ja vedelikud soojenedes paisuvad ning nende tihedus väheneb. Tekivad tõusvad voolud, mis kõrgemal jahtudes uuesti alla liiguvad. Ringlevad õhuvoolud ühtlustavad keskkonna temperatuuri ja konvektsiooni tõttu ringlev õhk juhib oluliselt paremini soojust kui seisev. Konvektsiooninähtused mängivad olulist rolli atmosfääri ja maailmamere energiavahetuses.

Kõik kehad kiirgavad olenevalt temperatuurist ja pinna omadustest soojust. Soojuskiirgus ei vaja levimiseks keskkonda ning levib ka vaakumis. Rohkem kiirgavad kõrge temperatuuriga ja tumedad kehad. Elu maakeral on võimalik tänu Päikese soojuskiirgusele.

Ajaloost: soojushulk

Termin soojushulk pärineb ajast, mil soojust käsitleti kui kaalutut vedelikku, mis soojusülekande käigus valgub ühest kehast teise. Samast ajast pärineb ka termin soojusmahtuvus, mis viitab kehale kui anumale, mis mahutab teatava koguse sellist vedelikku. Hiljem selgus, et soojusülekandel pole oluline aine-, vaid energiaülekanne, kuid mitmed ajaloolised terminid on muutmata jäänud.

Probleem

Joonisel on gaasi isotermiline paisumine. Kas gaas saab väljastpoolt energiat juurde?

Kokkuvõte

Gaas teeb tööd siis, kui tema ruumala muutub.

Isobaarilises protsessis on gaasi töö

A = p Δ V

Lisa 5.2. Termodünaamika seadused

Täpsustusi termodünaamika esimese seaduse kohta

Esimese seaduse valemist

Δ U = Q + A

saame mitmed erijuhud:

Isohoorilises protsessis $A = 0$ $Δ U = Q$ , siseenergia muutub ainult soojusvahetusega.
Adiabaatiline protsessis $Q = 0$ $Δ U = A$ , siseenergia muutub ainult tehtud töö tõttu.
Isotermilises protsessis $Δ U = 0$ $Q = - A$ , siseenergia ei muutu.
Isobaarilises protsessis $p = c o n s t$ $Δ U = Q - p Δ V$ .

Ajaloost: termodünaamika seadused

Nicolas Léonard Sadi Carnot märkmetes seisab: „Soojus – see pole muud kui liikumapanev jõud, täpsemalt oma vormi muutev liikumine. See on keha osakeste liikumine. Kõikjal, kus kaob liikuma panev jõud, tekib soojus, mille hulk on võrdeline kulunud liikumapaneva jõuga. Vastupidi, soojuse kadumisega kaasneb liikumapaneva jõu tekkimine.” Kui arvestada, et liikumapaneva jõu all mõeldi siis kineetilist energiat, on tegemist termodünaamika esimese seadusega. Kahjuks jäid Carnot’ tööd vajaliku tähelepanuta.

Soojuse olemuse küsimuses sai otsusutavaks energia jäävuse ja muundumise seaduse avastamine 19. sajandi keskel. Selles osalesid noored mitte-füüsikutest uurijad Julius Robert von Meyer, inglise õllevabrikant James Prescott Joule ja saksa füsioloog Hermann Ludwig Ferdinand von Helmholtz. Joule avaldas aastal 1841 uurimuse elektrivoolu soojuseks muutmise kohta. Hiljem uuris ta ülestõstetud keha raskusjõu töö muutumist soojuseks ja määras katseliselt nn soojuse mehaanilise ekvivalendi ( $4, 16 J / c a l$ ). Helmholtz tõestas, et gravitatsioonijõu mõju all oleva kehade süsteemi potentsiaalse ja kineetilise energia summa on jääv. Termodünaamika 2. seadusesse andsid panuse Sadi Carno, Clapeyron, lord Kelvin, Boltzmann jt. Termodünaamika tehnilistele rakendustele pööras põhilist tähelepanu šotlane William John Macquorn Rankin. Temalt pärinevad terminid energia, potentsiaalne energia, adiabaatiline ja isotermiline protsess.

Ostwald uskus energia ülimuslikkusesse ja võttis selle oma maailmapildi aluseks. Ta lõi nn energetismi filosoofilise kontseptsiooni, mille pooldajad püüdsid ületada materialismi ja idealismi vastuolusid, pidasid oluliseks vahetuid aistinguid ja kogemust ning suhtusid eitavalt atomismi.

Probleem

Kas protsessides

A B

B C

C D

D E

gaas saab või annab ära soojust?

Miks on gaaside erisoojused jääval ruumalal ja rõhul erinevad? Kumb on suurem?

Kokkuvõte

Keha siseenergia muut on võrdne kehale antud soojushulga ja väliste jõudude poolt tehtud töö summaga.

Δ U = Q + A

Adiabaatilises protsessis ei toimu keha või kehade süsteemi soojusvahetust väliskeskkonnaga.

Soojus ei saa iseeneslikult üle minna külmemalt kehalt soojemale.

Iseeneslikud (spontaansed) protsessid viivad keha soojusliku tasakaalu olekusse.

Suletud süsteemi koguenergia on jääv.

Lisa 5.3. Entroopia

Entroopia kasv

Võtame naturaallogaritmi tõenäosuste suhtest

w = \frac{w_{I I}}{w_{I}} = \frac{{(\frac{V_{I I}}{V})}^{N}}{{(\frac{V_{I}}{V})}^{N}} = {(\frac{V_{I I}}{V_{I}})}^{N}

Naturaallogaritmiks ( ${log}_{e} w = ln w = a$ ) nimetatakse arvu, millega arvu $e \approx 2, 71828$ astendades saame logaritmitava ( $e^{a} = w$ ).

l n w = N l n \frac{V_{I I}}{V_{I}} = \frac{m}{M} N_{A} l n \frac{V_{I I}}{V_{I}} = \frac{m}{M} \frac{R}{k} l n \frac{V_{I I}}{V_{I}}

kus $N$ on osakeste arv, $N_{A}$ Avogadro arv, $m$ gaasi mass, $μ$ molaarmass, $R$ on gaasikonstant ja $k$ Boltzmanni konstant.

Suurust

Δ S = k l n w

nimetatakse entroopia muuduks protsessis I – II.

Δ S \frac{m}{M} R l n \frac{V_{I I}}{V_{I}}

Kuna $V_{I I} > V_{I}$ , siis $Δ S > 0$ ja protsessis I – II entroopia kasvab.

Kui ideaalne gaas paisub isotermiliselt temperatuuril $T$ ja saab seejuures soojushulga $Δ Q$ , siis jagatis $Δ Q / T$ osutub samuti entroopia muuduks:

Δ S = \frac{Δ Q}{T}

Järnev valem on üks võimalustest väljendada termodünaamika 2. seadust:

Δ S = l n w \frac{Δ Q}{T} \geq 0

Ajaloost: entroopia

Entroopia mõiste võttis aastal 1865 kasutusele Rudolf Clausius, et kirjeldada kvantitatiivselt termodünaamika 2. seadust. 1872. aastal andis Boltzmann entroopiale statistilise tõlgenduse, ühendades oleku tõenäosuse süsteemi entroopiaga. Max Planck andis aastal 1906 entroopia muudu arvutamiseks valemi $Δ S = k ln w$ .

Probleem

Klassis on suur arv õpilasi. Poisse ja tüdrukuid on enam-vähem ühepalju. Vaatame kahte olukorda. Esimeses on kõik vaba liikumise tõttu jaotunud ühtlaselt kogu klassi peale, aga teisel juhul on poisid ja tüdrukud kogunenud klassi erinevatesse nurkadesse. Kummas olukorras on entroopia suurem? Kumb olukord sisaldab rohkem informatsiooni?

Kokkuvõte

Kehade süsteemi entroopia muut on võrdne süsteemi poolt saadud soojushulga ja absoluutse temperatuuri suhtega:

Δ S = \frac{Δ Q}{T}

Iseeneslikud protsessid viivad süsteemi kõige suurema tõenäosusega soojuslikku tasakaalu.

Suletud süsteemis, kus ei toimu aine ega energiavahetust väliskeskkonnaga, ei saa entroopia kahaneda.

Lisa 5.4. Soojusmasin

Soojusmasinate liigid

Enamkasutatavad soojusmasinad on auruturbiin ja sisepõlemismootor. Auruturbiinid annavad põhilise osa maailma elektrienergiast ja sisepõlemismootorid on enamlevinud maa- ja veepealses transpordis. Soojusmasinateks on samuti reaktiivlennukite turbiinid ja rakettmootorid. Mehaanilise töö saamine soojusmasina vahendusel on kahjuks väikese kasuteguriga protsess, mida piiravad nii põhimõttelised kui ka tehnilised probleemid. Näiteks olgu Ida-Virumaal maa sees teatud kogus põlevkivi, mis sisaldab $100$ ühikut energiat. Kui kaevandame, transpordime ja põletame selle soojuselektrijaamas, saame ainult umbes $15$ ühikut elektrienergiat.

Koduses majapidamises kasutatakse külmikut, mis on samuti soojusmasin, kuid selle tsükkel $p V$ -teljestikus käib vastupäeva. Pööratud tsükliga töötab ka soojuspump. Nende soojusmasinate ülesandeks ei ole teha mehaanilist tööd, vaid tööd tehes viia soojushulk külmemalt kehalt soojemale.

Ajalugu: soojusmasin

Madalal rõhul töötavaid soojusmasinaid ehitati juba 17. sajandi lõpus ja neid kasutati eelkõige kaevandustes. Aurumasinad olid esialgu väga massiivsed ja kulutasid palju kütust. Areneva tööstuse tõttu oli nõudlus efektiivsemate masinate järele suur ja selle rahuldamiseks oli vaja probleemide teaduslikku uurimist. Sadi Carnot avaldas 1824. aastal raamatu soojusmasinate kohta („Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance” – Arutlused tule liikumapanevast jõust ja masinatest, mis seda jõudu arendavad), mis jäi esialgu tähelepanuta. Kümme aastat hiljem andis Clapeyron sellele kaasajastatud matemaatilise kuju. Aurumasinat võib pidada 19. sajandi sümboliks. Selle vahetasid järgmisel sajandil välja auruturbiin ja sisepõlemismootor, mis on energeetikas ja transpordis ka tänapäeval väga olulised. Lokomotiivid olid 20. sajandi esimesel poolel Eesti põllumajanduses oluliseks jõuallikaks (rehepeksumasinad, saekaatrid). Auruvedurite ajastu Eestis lõppes 1950ndatel.

Probleem

Miks on soojusmasinas vajalik soojendi ja jahuti temperatuuri suur erinevus?

Kui suur on Päikese kui soojusmasina kasutegur?

Kokkuvõte

Soojusmasin muudab soojusenergia mehaaniliseks tööks.

Soojusmasina kasutegur on saadud mehaanilise töö ja kulutatud soojusenergia suhe (tavaliselt protsentides):

η = \frac{A}{Q_{1}} (100 %)

Ideaalse soojusmasina kasutegur on määratud soojendi ja jahuti absoluutsete temperatuuridega:

η = \frac{T_{1} - T_{2}}{T_{1}}

Lisa 5.5. Sisepõlemismootor

Kuidas töötab diiselmootor

Ajaloost: sisepõlemismootor

Neljataktilise sisepõlemismootori patenteeris 1860. aastal saksa leidur Christian Reithmann. Nicolaus August Otto asutas aastal 1864 esimese mootoritehase ja aastal 1876 ehitas $4$ -taktilise gaasil või piiritusel töötava mootori. Aastatel 1885–1886 ehitas ja patenteeris Carl Benz kolmerattalise auto, millel olid kõik tänapäevase auto põhiosad: neljataktiline mootor, väntvõll, elektrisüüde ja vesijahutus. Kütuseks oli toorbensiin – ligroiin, mida sai tol ajal osta apteegist. Henry Fordi konveiertootmisest alates on neljataktilise töötsükliga bensiinimootoriga autod siiani massilises kasutuses. Kõrvaloleval pildil on maailma esimene autode reklaamprospekt.

Probleem

Missuguseid füüsikakursuses käsitletud termodünaamilisi protsesse on leida bensiini- ja diiselmootori töötsüklite graafikutelt?

Millised konstruktsioonilised ja muud iseärasused võiksid määrata mootori võimsuse?

Kokkuvõte

Sisepõlemismootor on soojusmasin, kus gaasilise või vedela kütuse põlemine toimub põlemiskambris (silindris).

Sisepõlemismootori tsükkel koosneb neljast või kahest taktist.

Lisa 5.6. Auruturbiin ja külmik

Kütuseta soojuselektrijaamad

Maal on piirkondi, kus pilves ilma esineb harva, ja kohti, kus maapinnale pressitakse tulist vett. Neid nähtusi on inimene õppinud kasutama elektrienergia tootmiseks. Päikese-soojuselektrijaamades kogutakse kiirguse energia peeglitega ühele kehale, mille temperatuur tõuseb nii kõrgele, et sellega saab panna tööle soojuselektrijaama. Päikese energia on kõrgetemperatuuriline ja nn puhas energia, sest selle tootmisega ei kaasne saastet. 2014. aastal läks USA-s käiku Ivanpahi päikese-SEJ võimsusega $392 M W$ , kus kiirguse koondamiseks on $300000$ $6, 3 m^{2}$ peeglit ja korduvkasutuses olevat vett kondenseeritakse õhuga.

Geotermilistes elektrijaamades kasutatakse maa seest tulevat tulist vett ja auru auruturbiinide käitamiseks. Näiteks Islandil on tuntud turismiobjekt Sinine Laguun, mille vett soojendab lähedal asuva elektrijaama auru kondenseerimine.

* EER Energy efficiency ratio **COP coefficient of performance

Külmikust ja soojuspumbast

Külmiku puhul räägitakse külmategurist

E E R = \frac{Q_{2}}{A} = \frac{Q_{2}}{Q_{1} - Q_{2}} *

mis näitab, kui palju on külmemalt kehalt äravõetud soojushulk suurem tehtud mehaanilisest tööst.

Kui kasutada külmikut nii, et radiaator asub toas ja külmemaks kehaks on mingi väga suur energiareservuaar (veekogu, maa sisemus, põhjavesi, jahe välisõhk), siis saame tööd tehes võtta soojushulga külmemalt reservuaarilt ja anda see radiaatori vahendusel toaõhule. Sellist seadet nimetatakse soojuspumbaks ja tema tsükkel on sama mis külmikul. Piltlik ettekujutus võiks olla selline. Asetame aknaavasse ukseta külmiku nii, et radiaator asuks toas ja külmuti sisemusse pääseks välisõhk.

Soojuspumba kasulikkust näitab soojategur

C O P = \frac{Q_{1}}{A} = \frac{Q}{Q_{1} - Q_{2}} * *

Maasoojuspumba soojategur võib olla umbes $5$ . See tähendab, et kulutades soojapumba tööks $1 k W h$ elektrienergiat, saame toale anda soojushulga $5 k W h$ , millest $4 k W h$ tuleb maa seest. Sellise soojuspumbaga kulutame kütmiseks $5$ korda vähem elektrienergiat kui tavalise elektriradiaatoriga.

Terminid külmategur ja soojategur on autori keelend, sest nii kodumaises kui ka välismaises kirjanduses valitseb veel teatav segadus ja ebajärjekindlus.

Ajaloost: auruturbiin

Esimeseks auruturbiiniks võib lugeda 1. sajandil Vanas Kreekas konstrueeritud auru reaktiivjõul pöörlevat nn Heroni kera (M lk 78). Auruturbiinide kasutamine algas koos elektrijaamade käikulaskmisega. 1883. aastal ehitas rootsi insener ja tööstur Carl Gustaf de Laval turbiini, mille töörattale suunati düüsidest suure kiirusega aur. Aastal 1892 ehitas iiri päritolu inglise insener Charles Algernon Parsons esimese kondensatsiooniturbiini, mille paigutas paar aastat hiljem laevale Turbinia ning millega saavutati enneolematu sõidukiirus $34, 5$ sõlme (umbes $64 k m / h$ ). Uut tüüpi erineva otstarbega turbiine leiutasid Auguste Camille Edmond Rateau ja Charles Gordon Curtis. 1910. aastaks olid soojuselektrijaamades aurumasinad asendatud auruturbiinidega. Auruturbiinlaev Turbina

Probleem

Kasutades soojusmasinat iseloomustavaid suurusi

Q_{1}

A

Q_{2}

η

, leidke kasuteguri seosed külma- ja soojateguriga.

Kokkuvõte

Auruturbiin on soojusmasin, mis muudab kuuma kokkusurutud auru potentsiaalse energia turbiini rootori pöörlemise energiaks.

Külmik on soojusmasin, mis tehtud töö tulemusel viib soojushulga külmemalt kehalt soojemale.

Raudvara

I = \frac{q}{t}

Voolutugevuse ühik üks amper on SI põhiühik ja ta on defineeritud vooluga juhtide vastastikmõju kaudu. $1 A$ voolutugevuse korral läbib juhi ristlõiget $1 s$ jooksul laeng $1 C$ .

Voolutugevus juhis on võrdeline pingega juhi otstel

I = \frac{U}{R}

Võrdeteguri pöördväärtust nimetatakse takistuseks ja selle ühikuks on

Ω

(oom). Takistuse tõttu esineb elektrivoolu soojuslik toime.

Takistus on võrdeline juhi eritakistuse ja pikkusega ning pöördvõrdeline juhi ristlõikepindalaga

R = \frac{ρ l}{S}

Võrdetegurit

ρ

nimetatakse aine eritakistuseks, mis näitab ühikulise pikkuse ja ristlõikega juhi takistust.

Juhi takistus oleneb temperatuurist.

[£[1131]£]

Elektrimõõteriista täpsusklass on relatiivne piirviga protsentides mõõteriista maksimaalse näidu korral.

Numbrilise mõõteriista korral on mõõtemääramatuse arvutamise valem toodud mõõteriista passis.

Metalli takistus kasvab temperatuuri tõustes lineaarselt

R = R_{0} (1 + α t)

Pooljuhtide, elektrolüütide ja gaaside takistus temperatuuri kasvuga väheneb.

Ülijuhtivus on nähtus, kus ained madalal temperatuuril ei oma elektrilist takistust.

Vooluallika elektromotoorjõud on arvuliselt võrdne kõrvaljõudude tööga ühikulise laengu ümberpaigutamisel kogu suletud vooluringi ulatuses

E = \frac{A_{k}}{q}

Voolutugevus suletud vooluringis on võrdeline vooluallika elektromotoorjõuga ja pöördvõrdeline vooluringi välisosa ja vooluallika sisetakistuse summaga

I = \frac{E}{(R + r)}

Elektrolüütideks on ained, milles vabadeks laengukandjateks on ioonid.

Elektrolüüs on protsess, milles alalisvool põhjustab redoksreaktsiooni.

Elektrolüüsi käigus elektroodile eraldunud aine mass on võrdeline elektrolüüti läbinud laenguga.

m = k q