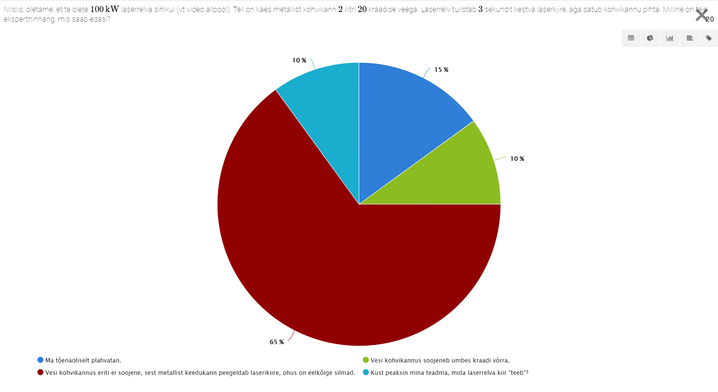
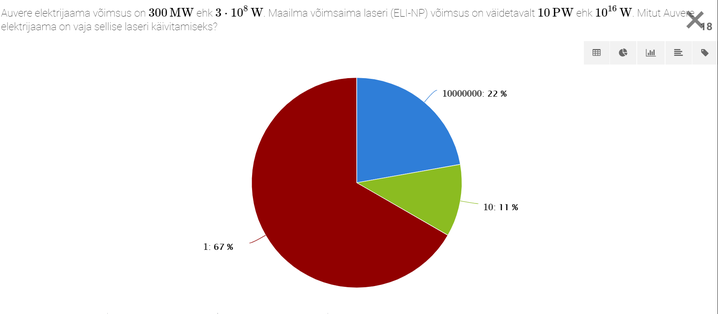
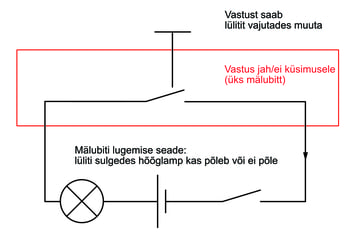
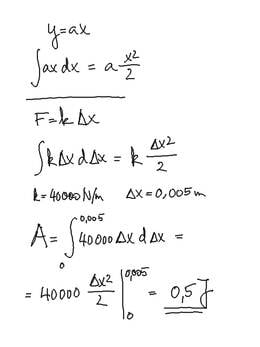Füüsika õpetaja raamat
- Sissejuhatus
- 1 Hea kogemus
- 2 Lugemist
- 3 Seminarid, muidu kokkusaamised
- 4 Nädalakiri Mesilane esimene hooaeg
- 4.1 Nädalakiri Mesilane 1/1
- 4.2 Nädalakiri Mesilane 1/2
- 4.3 Nädalakiri Mesilane 1/3
- 4.4 Nädalakiri Mesilane 1/4
- 4.5 Nädalakiri Mesilane 1/5
- 4.6 Nädalakiri Mesilane 1/6
- 4.7 Nädalakiri Mesilane 1/7: Pöördosmoos
- 4.8 Nädalakiri Mesilane 1/8: Helendavad teed
- 4.9 Nädalakiri Mesilane 1/9: Tapvad katsed
- 4.10 Nädalakiri Mesilane 1/10: Kole ilm
- 4.11 Nädalakiri Mesilane 1/11:
- 5 Nädalakiri Mesilane
- 5.1 Nädalakiri Mesilane 2/1: Kogemus
- 5.2 Nädalakiri Mesilane 2/2: Kogemus
- 5.3 Nädalakiri Mesilane 2/3: Kogemus
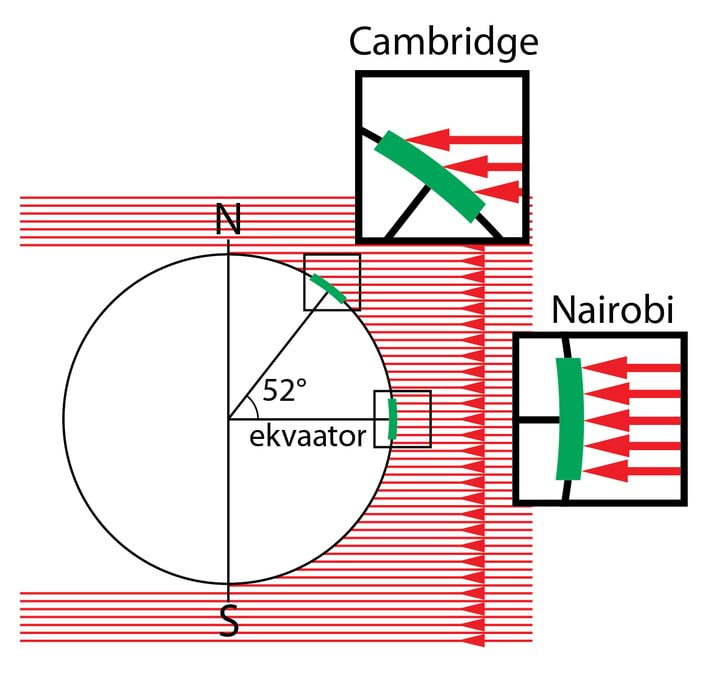
- 5.4 Nädalakiri Mesilane 2/4: Päike, varjud, vetikad
- 5.5 Nädalakiri Mesilane 2/5: Kosmiline, tehisnina
- 5.6 Nädalakiri Mesilane 2/6: kahtlane ja rämpsteadus
- 5.7 Nädalakiri Mesilane 2/7: Ujub või upub?
- 5.8 Nädalakiri Mesilane 2/8: Kogemus
- 5.9 Nädalakiri Mesilane 2/9: Pilv pudelis, tappev CO2
- 5.10 Nädalakiri Mesilane 2/10: Kristallid
- 5.11 Nädalakiri Mesilane 2/11: Mullid
- 5.12 Nädalakiri Mesilane 2/12: Elekter liigub
- 5.13 Nädalakiri Mesilane 2/13: Osakesed liiguvad
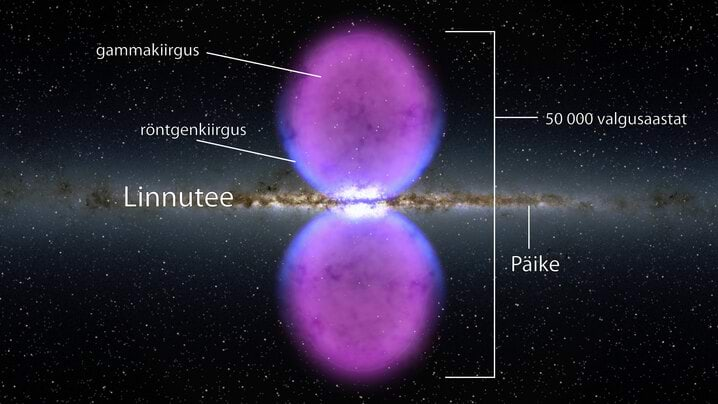
- 5.14 Nädalakiri Mesilane 2/14: Gammakiirgus
- 5.15 Nädalakiri Mesilane 2/15: Uurimistöö
- 6 Nädalakiri Mesilane III
- 6.1 Nädalakiri Mesilane 3/1: Tume aine või tumeaine?
- 6.2 Nädalakiri Mesilane 3/2: Kuidas näha Kuu sisse?
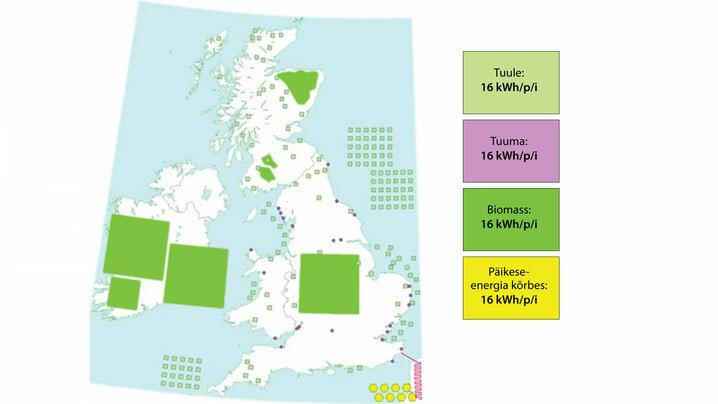
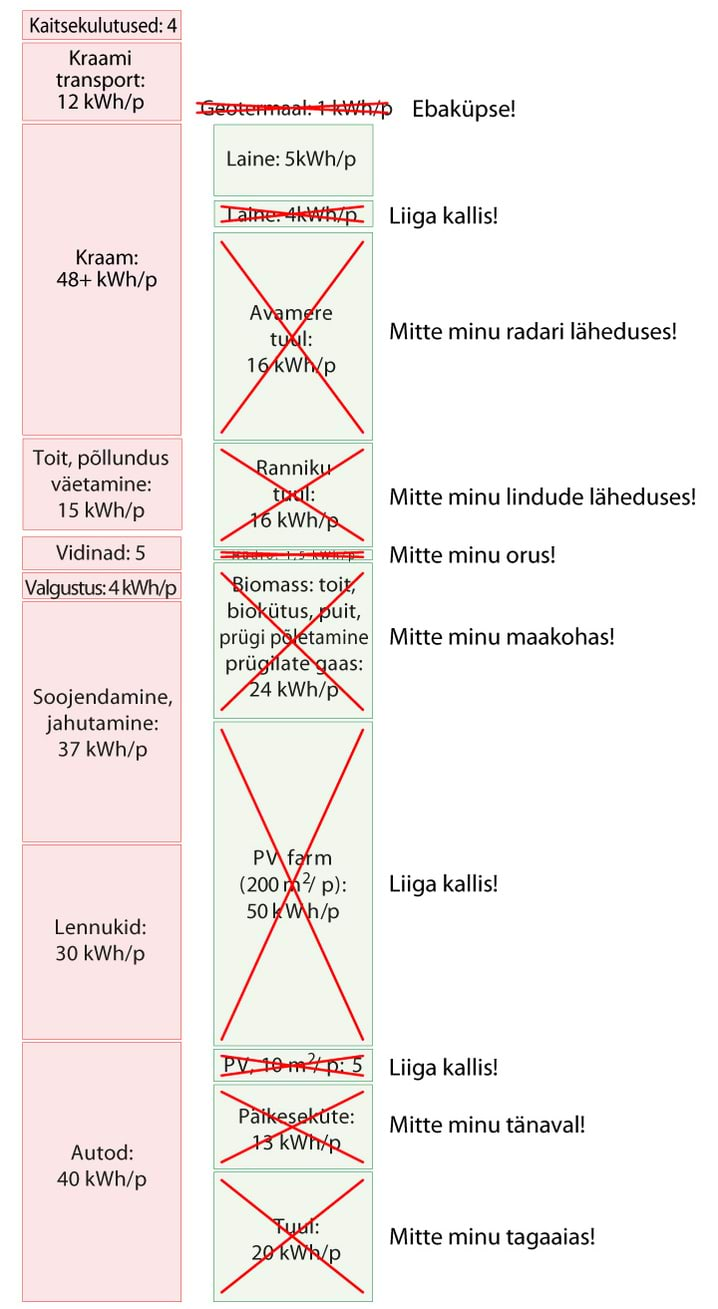
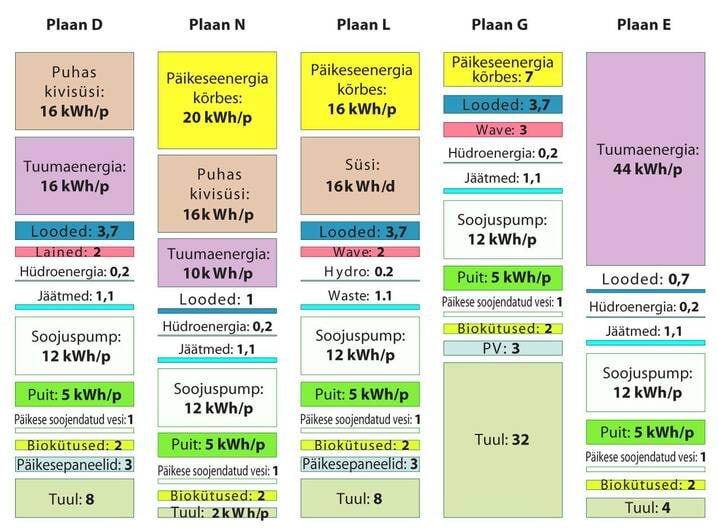
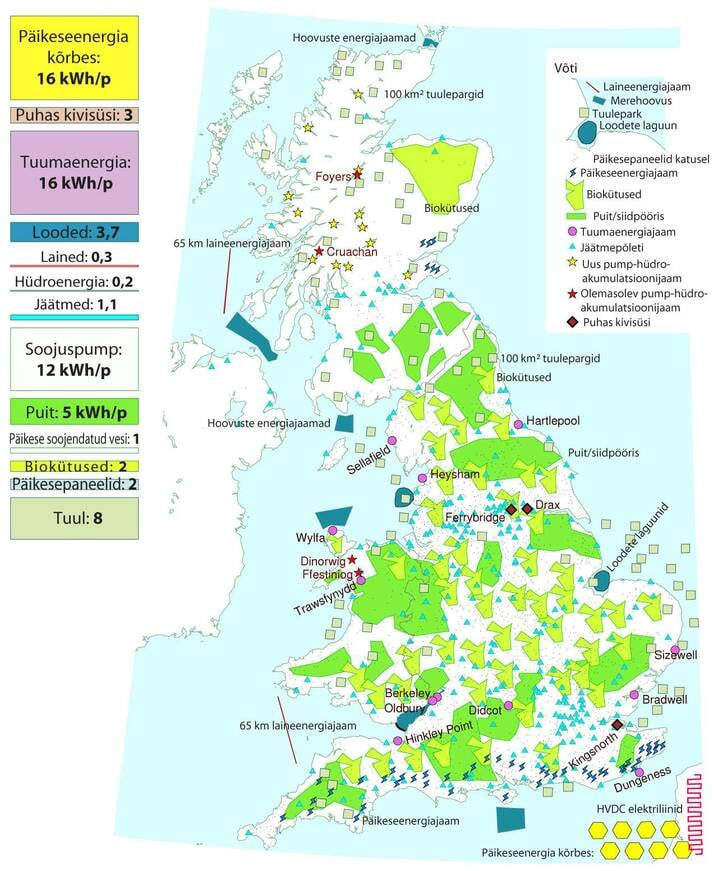
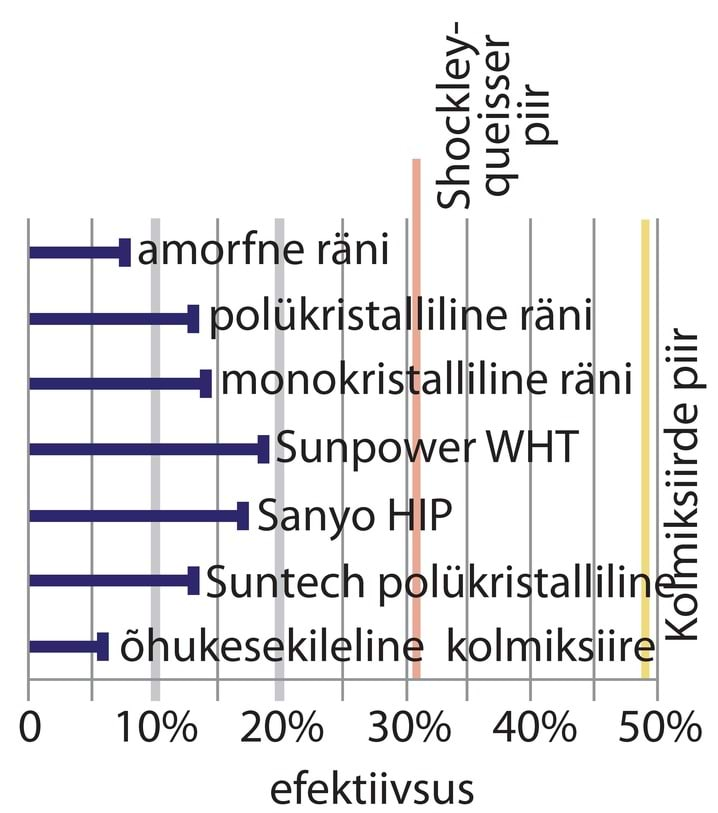
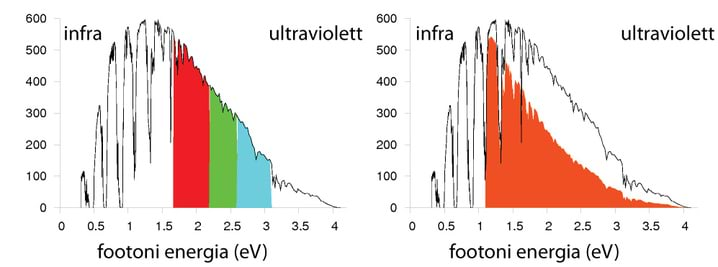
- 6.3 Nädalakiri Mesilane 3/3: Taastuvenergia
- 6.4 Nädalakiri Mesilane 3/4: Kuidas näha molekuli?
- 6.5 Nädalakiri Mesilane 3/5: Astronoomia ja laserid?
- 6.6 Nädalakiri Mesilane 3/6: Lainetab!
- 6.7 Nädalakiri Mesilane 3/7: Must keha kiirgab
- 6.8 Nädalakiri Mesilane 3/8: Hyperloop
- 6.9 Nädalakiri Mesilane 3/9: Kes on näinud aatomit?
- 6.10 Nädalakiri Mesilane 3/10: Külm
- 6.11 Nädalakiri Mesilane 3/11: Pöörleb
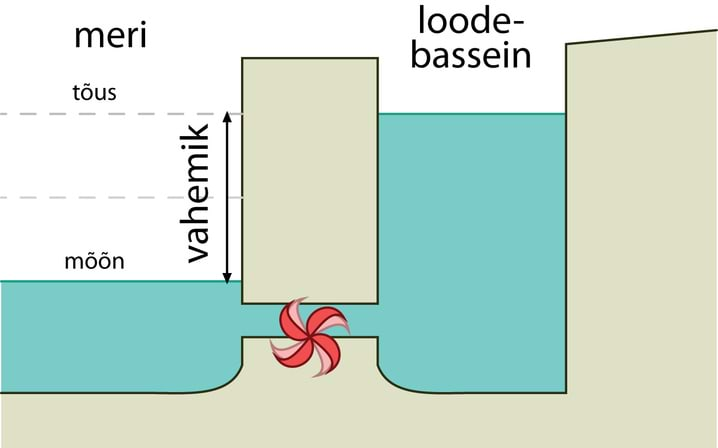
- 6.12 Nädalakiri Mesilane 3/12: Rahutu vesi
- 6.13 Nädalakiri Mesilane 3/13: Valguse päev
- 7 Nädalakiri Mesilane IV
- 7.1 Nädalakiri Mesilane 4/0
- 7.2 Mesilane 4/1
- 7.3 Mesilane 4/2
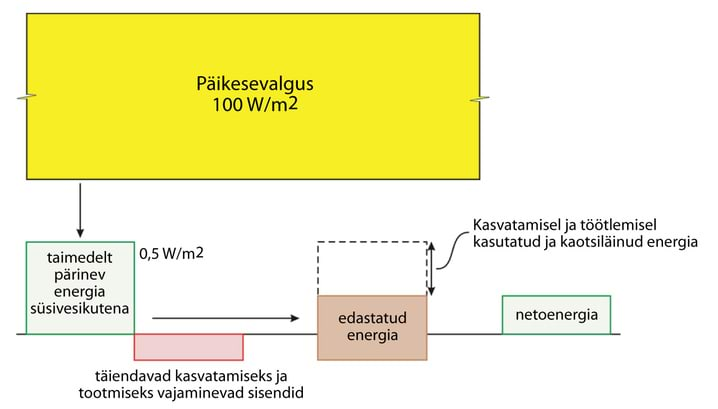
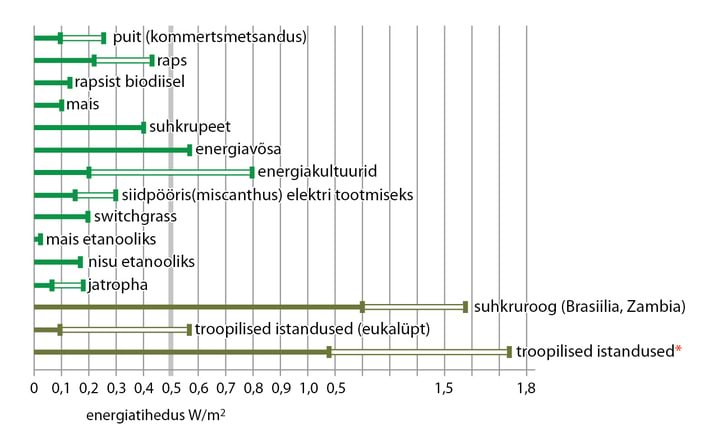
- 7.4 Nädalakiri Mesilane 4/3: Energia
- 7.5 Nädalakiri Mesilane 4/4: Pendlid
- 7.6 Nädalakiri Mesilane 4/5: Väljakutsed
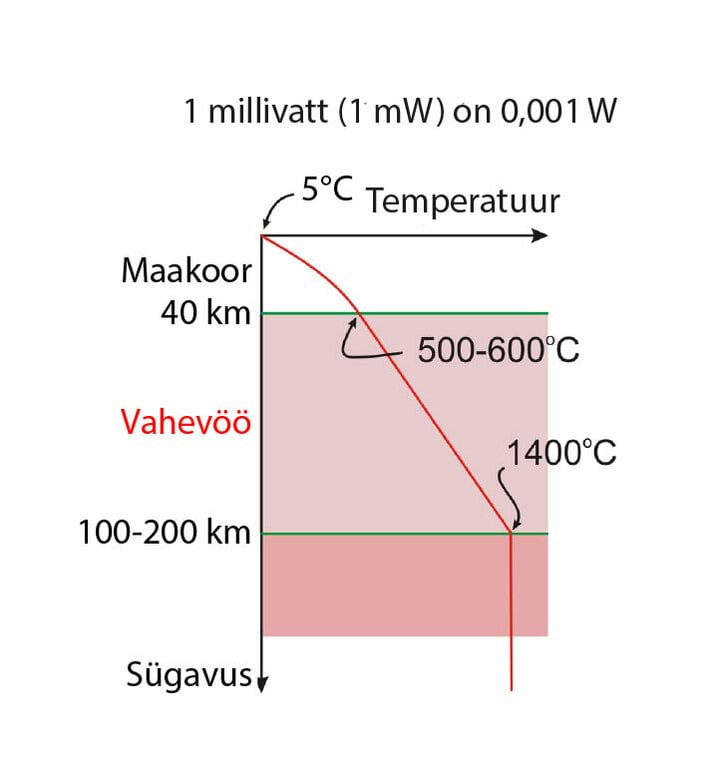
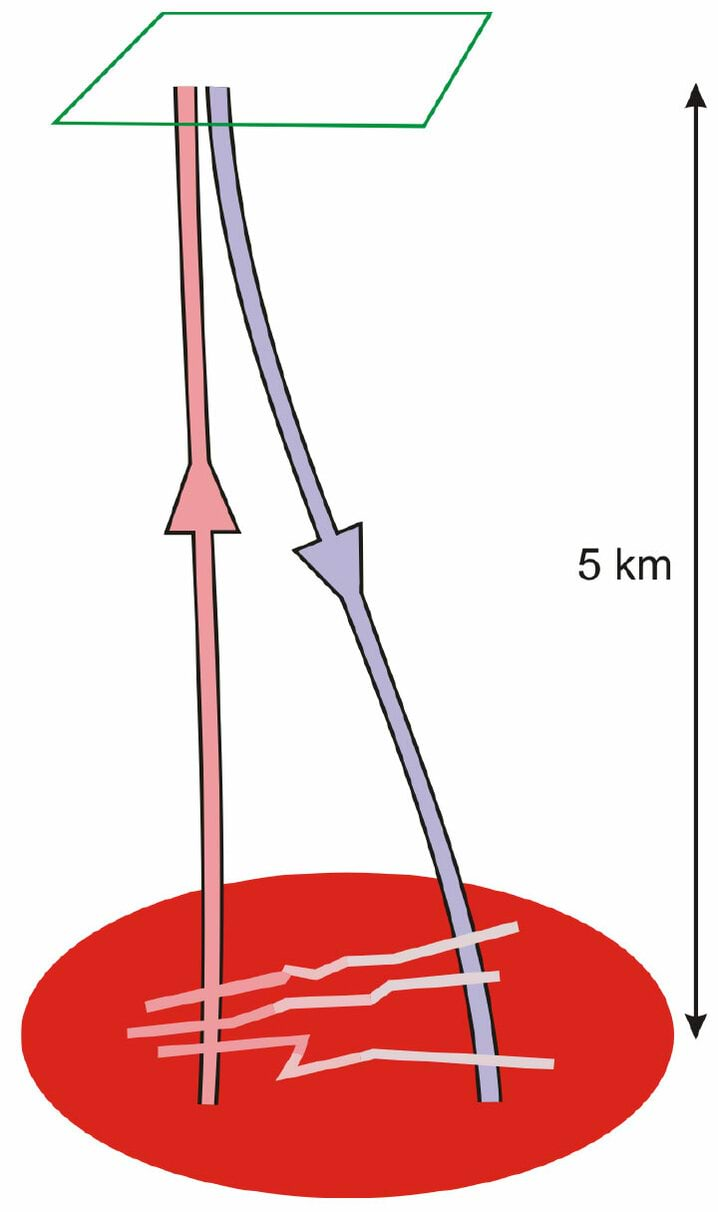
- 7.7 Nädalakiri Mesilane 4/6: Geotermiline
- 7.8 Nädalakiri Mesilane 4/7: Musta auk
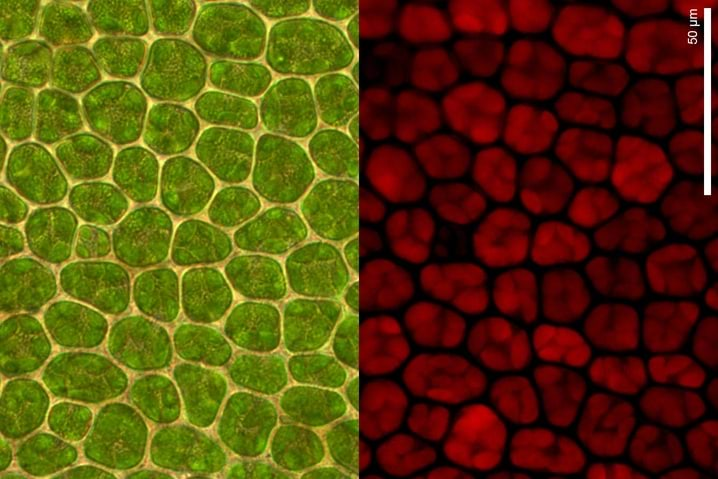
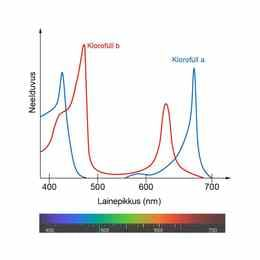
- 7.9 Nädalakiri Mesilane 4/8: Fotosüntees
- 7.10 Nädalakiri Mesilane 4/9: Marsile
- 7.11 Nädalakiri Mesilane 4/10: Orbiidid ja trajektoorid
- 7.12 Nädalakiri Mesilane 4/11: Koos?
- 7.13 Nädalakiri Mesilane 4/11: Nagu saunas?
- 7.14 Nädalakiri Mesilane 4/13: Mehaaniline koguenergia
- 8 Nädalakiri Mesilane V
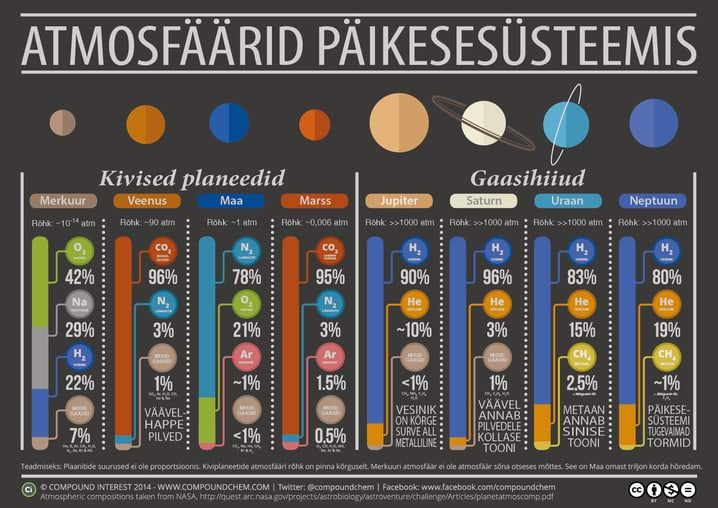
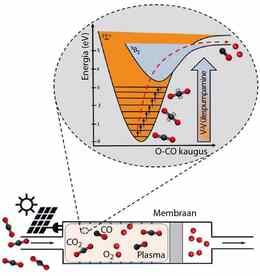
- 8.1 Nädalakiri Mesilane 5/1: Süsiniku püüdmine atmosfäärist
- 8.2 Nädalakiri Mesilane 5/2: Astronoomia õpik
- 8.3 Nädalakiri Mesilane 5/3: Elus valgusõpetus
- 8.4 Nädalakiri Mesilane 5/4: Sügiskool?
- 8.5 Nädalakiri Mesilane 5/5: LennukidAllikad, millele me tuginesime
- 8.6 Nädalakiri Mesilane 5/6: Kukub ... kuhu?
- 8.7 Nädalakiri Mesilane 5/7: Liblikas läbi nõelasilma
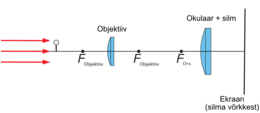
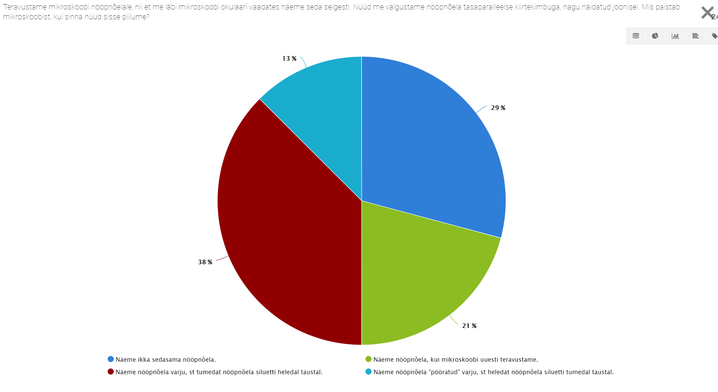
- 8.8 Nädalakiri Mesilane 5/8 : Jälle see mikroskoop
- 8.9 Nädalakiri Mesilane 5/9: Valgus kui laine
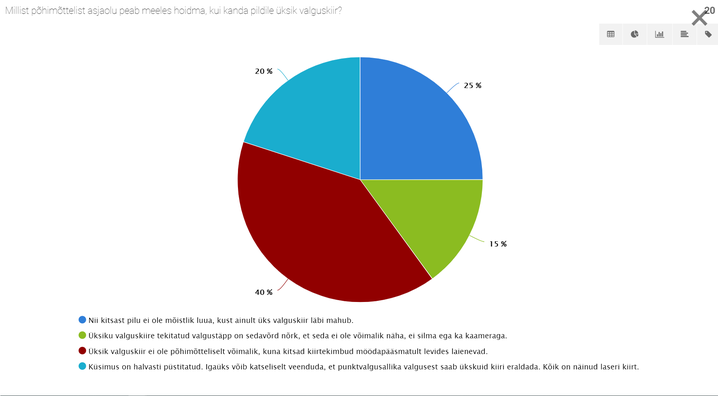
- 8.10 Nädalakiri Mesilane 5/10: Kuidas joonistada laserit?
- 8.11 Nädalakiri Mesilane 5/11: Testida või mitte testida
- 8.12 Nädalakiri Mesilane 5/12: Kiire või aeglane ja ajalik
- 8.13 Nädalakiri Mesilane 5/13: Hoiame sooja
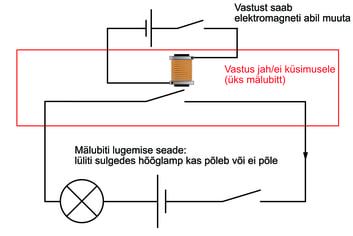
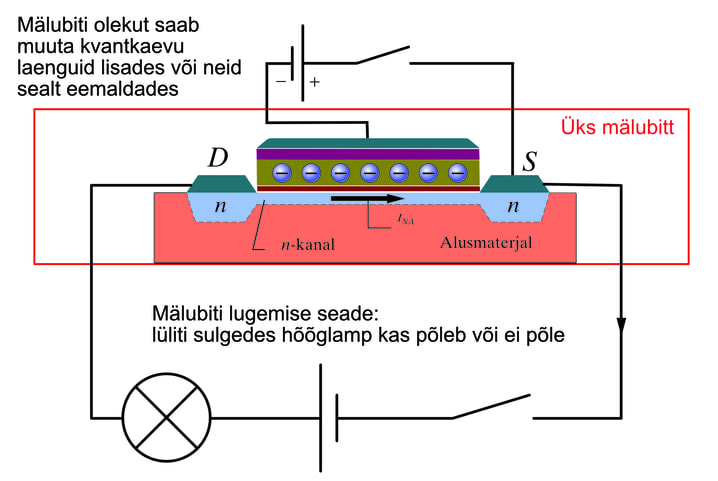
- 8.14 Nädalakiri Mesilane 5/14 : Mis on ja kuidas töötab välkmälu?
- 9 Nädalakiri Mesilane VI
- 9.1 Nädalakiri Mesilane 6/1: Kust tuleb energia?
- 9.2 Nädalakiri Mesilane 6/2: Programm "Lae end"
- 9.3 Nädalakiri Mesilane 6/3: Auru rõhk ja Armstrongi piir
- 9.4 Nädalakiri Mesilane 6/4: 2022/2023
- 9.5 Nädalakiri Mesilane 6/5: Kütus süsinikdioksiidist?
- 9.6 Nädalakiri Mesilane 6/6: Füüsika sisseastumiseksam
- 10 Nädalakiri Mesilane VII
- 11 Nädalakiri Mesilane VIII
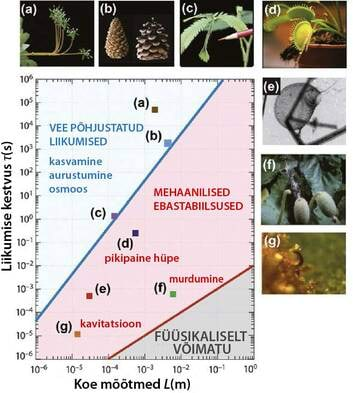
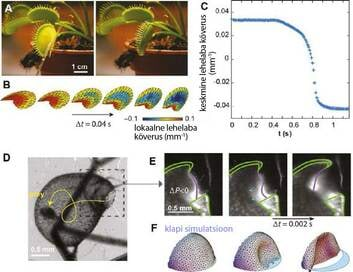
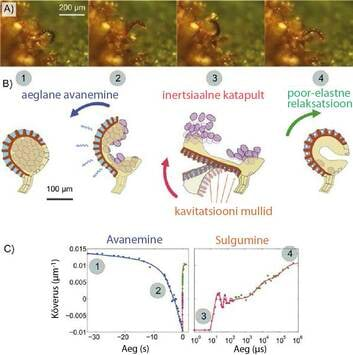
See e-õpik sisaldab põhiliselt materjale, mis on moel või teisel avaldatud nädalakirjas Mesilane.
27.11.2017 seisuga kärpisime selle sisu e-õpikut ennast puudutavate videote võrra. Eelkõige sellepärast, et varasemalt katsetatud formaat ei tundunud piisavalt hea ja ülevaatlik, osalt sellepärast, et e-õpikus on nüüd loodetavasti paremaid võimalusi videote kogude esitamiseks, lõpuks ka sellepärast, et need videod käivad e-õpiku eelmiste versioonide kohta. Ära me ei kustuta midagi, allpool on nupp, mida huvi korral saab vajutada.
Algodoo võib alla laadida aadressilt www.algodoo.com See on tasuta kasutamiseks.
Alustamiseks vajalikud teadmised
Esimese juhendi eesmärgiks on Algodooga tutvumine. Alustuseks õpime, kuidas Algodoos luua tegevuskoht ehk stseen (scene). Kui sellega oleme hakkama saanud, siis õpime tundma erinevaid tööriistu, mida Algodoo pakub. Lõpuks vaatame, kuidas kasutada maagilisena mõjuvat visandamise tööriista (sketch tool).
1. Seadistamine
Esiteks tuleks avalehelt käivitada seadistamise juhend (setup), et kohandada seadeid vastavalt oma vajadustele. Veelgi suurema seadete valiku võib leida Algodoo ülemisest menüüribast, seadete (settings) nupu alt.
2. Juhiste avamine
Avage Algodoosse sisseehitatud juhised, klikkides Algodoo avalehel olevale juhiste (tutorial) nupule või ülemises menüüribas olevale küsimärgile (?).
3. Juhis “Crash course” – kiirkursus
Avage kiirkursuse juhis (tutorial). Selles kursuses loote, Algodoo funktsioone järgi proovides, esimese stseeni.
4. Juhis “Tools” – tööriistad
Kui kiirkursus on läbitud, võtke ette järgmine, tööriistu tutvustav juhis. Selle juhise abi õpite Algodoo erinevaid tööriistu paremini tundma. Lugege läbi ka tööriistade kohta leiduv lisainfo, et õppida tundma erinevaid seadistusi ning kasulikke võtteid.
5. Juhis “Sketch tool” – visandamise tööriist
Viimane algteadmisi õpetav juhis. Visandamise tööriist on univeraalne vahend, mis aitab selgeks õppida ka paljude teiste tööriistade kasutamise. Erinevaid äratuntavaid žeste kasutades, saab visandamise tööriista abil kokku hoida aega, mis kuluks tööriistade vahetamisele.
Näiteid:
Kaheksanda klassi tiheduse ülesannete hulgast:
Kui palju kaalub üks tellis?
[Kaalu ja massi küsimus? Massi määratakse kaalumisega. Kuidas määratakse kaalu?]
Tegu on sellist tüüpi ülesandega, kus mingeid arvandmeid antud ei ole. [Õppekava soosib sedasorti ülesannete kasutamist. Oskus leida ja hinnata infot, probleem jms.] Asume siis kõigepealt andmeid koguma. Rõhu ülesannete hulgas (Erna ja Venda Paju, Füüsika ülesannete kogu põhikoolile) on tellise mõõtudeks antud 250X120X65mm. Tegemist on nn vene fassaaditellisega. Sama suured on ka paljud siinkandis toodetud korstna ja ahjutellised. Kuulus suur valge silikaattellis on paksem, 88mm. Vanemad ahjud ja korstnad on tihti laotud tellistest mõõtudega 240X120X60mm ja sellist mõõtu on ka praegu saada. Üldse on telliste mõõte läbi ajaloo väga palju, aga jääme esimesena nimetatud, meil väga levinud mõõdu juurde.
[Kui võimalik, võiks siin minna päris tellise (parem mitmete telliste) mõõtmisele. Paar tellist võiks füüsikaklassis õppevahendina alati kohal olla. Neist võib abi olla rõhu teemas, (ülesannet vt nimetatud kogust) soojusõpetuses, kapillaartõusu saab näidata jms. Kaheksandas klassis leidub alati mõni hakkaja õpilane, kes on valmis homseks tellise kooli tooma. Kui koolis juhtub olema tellissein, saab sealt hulga telliseid ära mõõta. Mõnel väiksemal seinajupil ei paista tellise ots välja, aga näiteks postilt või hoone nurgalt saab kõik mõõdud kätte. Ja palju mõõte, saab statistikat teha.]
Savitellise tiheduseks annavad tootjad ja teatmikud 1800 kuni 2400kg/m3, keskmiselt 2100kg/m3. Nüüd on andmed koos ja lahendus tuleb selline:
a = 250mm = 0,25m
b = 120mm = 0,12m
c = 65mm = 0,065m
ρtellis = 2100kg/m3
[Kordsete ühikute kasutamise traditsioonist. Tehnikas on väga tavaline, et mõõdud antakse millimeetrites. Võib-olla välditakse nii komakohtade kasutamist, kuigi alati see mõistlik ei tundu. Siin läheme kohe üle põhiühikutele, sest lõppvastust ootame kilogrammides. Muidugi võib tellise ruumala arvutada kuupmillimeetrites ja teisendada järgmise arvutuse eel. Või koguni viia tihedus ühikule mg/mm3. Nii tuleb vastus milligrammides. Hea füüsikatava (svv) vaataks sellele ilmselt viltu.]
Vtellis – ?
mtellis – ?
Vtellis= 0,25·0,12·0,065 = 0,002m3
mtellis= 2100·0,002 = 4,2kg
[Kuigi praktiline oli arvutada ruumala kuupmeetrites, on siin hea koht meenutada ruumalaühikute teisendamist ja võib-olla on isegi huvitav teada, et tellis on tavalisest piima- või mahlapakist kaks korda suurem. 0,002m3=2dm3=2000cm3=2·106mm3]
Näide igapäevaelust
Kolm meest seisavad ilusal suveõhtul ümber sõiduauto haagise. Tarvis on ära viia keldrist välja tassitud vanad, aga üsna korralikud ahjutellised. Käru põhi on juba kaetud ühes kihis lapiti laotud tellistega. Kas paneks teise kihi veel peale või sõidaks pigem kaks korda?
Sel moel sõnastatult on see Fermi ülesanne. Tuleb arvutada nendest andmetest, mis meil on, mida me suudame kohapeal meenutada või ära arvata. OK, muidugi võib minna tuppa mõõdulinti otsima ja surfata internetist tellisetootjate andmeid massi või tiheduse kohta. Telefonid kõigil taskus.
Läheb aga nii, et üks mees teab oma auto pärakäru põhja mõõtu (120X240cm). Teine meenutab, et tellise tihedus on vist 1800kg/m3. Kolmas ütleb, et tellise paksus on tavaliselt kuus sentimeetrit. Seega on juba koormas olevate kivide koguruumala 1,2m·2,4m·0,06m=0,17m3 ja mass 0,17·1800=300kg. Seda ei tundu kuigi palju olevat, ametlikult on kandevõime 560kg. Laotud kiht telliseid ei ole ka päris tihe, väikesed õhuvahed on vahel. Teiselt poolt teeb ettevaatlikuks, et kivid on niiskest keldrist toodud ja tunduvad käega katsudes üsna märjad. Võib-olla on tihedus hoopis 2000kg/m3. Jääb nii, et kuna viia pole kaugele ja aega on, sõidetakse kaks korda.
[Miks ei ole tellised kõik ühte mõõtu? Miks ei ole isegi samast vormist ja läbi sama ahju tulnud tellised kõik täpselt ühte mõõtu?]
Lisaküsimusi
Teatud sorti tellistel on augud sees, neid nimetatakse kärgtellisteks. Aukude võrra on kivis vähem materjali, odavam on nii tellis ise kui ka selle transport. Soojapidavus ei kannata, küll aga tugevus. [Soojusest, sh õhuvahede mõjust materjalide soojusjuhtivusele tuleb juttu 9. klassis, siis on hea kärgtellist meenutada.] Mõnikord pole tugevus probleem, kui müürid on madalad ja ei pea kandma rakseid lagesid või ülemisi korruseid. Kui tavalisse savitellisesse on enne põletamist tehtud augud 20% kivi mahust, kui suur on siis saadud kärgtellise tihedus? [Keskmine tihedus. Tellise materjali tihedus sellest ei muutu, kui me sinna augu sisse teeme. Tellise kui keha keskmine tihedus muutub, sest kehana jääb ruumala samaks, aga massi on nüüd vähem. Ujuvuse teemas tuleb keskmine tihedus uuesti jutuks. Miks laevad ujuvad? Miks on vahtplast nii väikese tihedusega? Täpsemalt kui väike see tihedus siis ikkagi on? Mida tähendab, raud on raske, puu on kerge? Jne.]
Suuri silikaattelliseid müüakse 300 kaupa pakendis ja see kaalub kokku 1,56 t. Kui suur on silikaattellise tihedus? [Selleski ülesandes on andmeid puudu, aga kes kogu eelneva läbi luges, leiab puuduva kergesti siitsamast tekstist.]
Õpilased esitavad füüsikatunnis keerulisi küismusi. Teinekord on raske aru saada, millest jutt või on teema küsijale nii võõras, et terminid ja ühikud lähevad sassi. Kas ja kuidas vastata vigasele küsimusele?
Küsimus, mis haakub üheksanda klassi soojushulga arvutamise teemaga.
Kui palju kulub energiat 100 liitri vee temperatuuri tõstmiseks 40-ne kraadini. Kui mitu kw/h selleks kulub, ehk palju see on eurodes?
[See ei tundu olevat füüsika ülesanne. Pigem on tegemist internetifoorumi tüüpi küsimusega, enne küsi, siis mõtle. Ja küsimus on vigane.
Vigase ülesande võib vahele jätta, aga võib ka püüda parandada ja ikkagi ära lahendada. Mõnikord võib sellest isegi õppida. On olemas ka meelega vigaste ülesannete tüüp, kus lõpuks küsitakse, mis oli valesti.]
Parandame kõigepealt andmetes esinevad vead ja leiame küsitavad kohad.
A) Võimalik, et on mõeldud vee soojendamist 40 kraadi võrra (Δt°=40°C). Kui on mõeldud siiski 40 kraadini, siis on vaja teada, kui külm vesi algul oli. Külma kraanivee temperatuur on umbes 8°C, st tuleb soojendada 32 kraadi võrra
(Δt°=t°alg-t°lõpp=32°C).
B) Ei ole olemas ühikut kw/h. Töö ja energia süsteemiväline, laialt kasutatav ja praktiline ühik on kW·h (kilovatt-tund). W nagu James Watt (1736-1819), šoti leiutaja ja mehaanikainsener, aurumasinate täiustaja. 1kW·h=3,6MJ.
C) Lõppküsimus on rahaline, aga pole vähimatki vihjet, millise kütusega ja mis seadmes peaksime vett soojendama. Paratamatult tuleb kinni maksta soojuskaod, mille kohta pole ka midagi teada.
[kW/h ei ole siiski päris mõttetu ühik. Võimsus on ajaühikus tehtud töö ehk kulutatud energia. (N=ΔE/t). Võib öelda, et võimsus on energia tarbimise (muundamise) kiirus. Muutuva võimsuse korral on lihtne ette kujutada võimsuse muutumise kiirust (X=ΔN/t=ΔE/t2). See on energia kulutamise kiirendus, SI ühikuga W/s=J/s2.
Hüdroelektrijaam saavutab 1MW võimuse 15 minutiga. Kui suur on jaama käivitamise kiirus?
Analüüsige ühikut üks kilovatt-tund aastas. Mille ühik see on? Kui palju see on SI ühikutes ja SI põhiühikutes?]
mvesi=100kg
cvesi=4200J/kg·C°
Δt°=32°C
---------------
Q – ?
[Massi võib tiheduse kaudu arvutada või loota, et see on kõigile teada. Kindlasti ei tohi kirjutada 100l võrdub 100kg. Tabelist leitud erisoojusele võib panna võrdväärse ühiku J/kg·K. Võimalik, et Δt°=40°C, oleneb vigase küsimuse tõlgendusest.]
Q=cmΔt°
---------------
Q=4200·100·32=13440000J=13,4MJ=3,7kW·h
Mis see maksab? Aga kuidas ja millega kütame?
Tõenäoliselt on küsimus esitatud elektribolieri kohta. Elektrienergia hind on tänapäeval rohkem ühiskonna- ja majandusõpetuse tunni kui füüsika teema. Üht-teist sõltub olukorrast turul, lepingutesse pandud otsustest, asukohast, ööst ja päevast, maksudest. Üsna ebamäärase keskmisena võib kirja panna tariifi 12 senti kW·h eest (elektrienergia koos võrgutasu ja kõigi maksude ning tasudega). Sel juhul kulub 45 senti.
Kütuste põletamisega vee soojendamisel lähevad arvesse kütuse kütteväärtus (k), põletamise ja soojushulga veele ülekandmise kasutegurid.
Mõnede tuntud kütuste umbkaudne kulu eelpool arvutatud soojushulga saamiseks:
Veeldatud segugaas (propaan-butaan, balloonigaas) k=46MJ/kg – 290g – 66 senti.
Halupuud k=1300kW·h/rm=13MJ/kg – 1kg – 15 senti.
Puitpelletid k=18MJ/kg – 740g – 14 senti.
[Põlemisest, kütteseadmete konstruktsioonist ja kasuteguritest kirjutatakse pakse raamatuid ja kaitstakse teaduskraade. Teema on huvitav ja kasulik, head pesupäeva!]
Henn Voolaid soovitab:
Kumb kasvab kiiremini: kas loode emaihus või juba sündinud inimene? Mitu korda kasvukiirused erinevad?
Ülesanne kuulub jälle nende hulka, kus mingeid andmeid antud pole. Hullem veel, natukesest järelemõtlemisest tekib rida probleeme küsimuse enda kohata. Ettevalmistuseta klassis (või ükskõik millises seltskonnas) võib alustuseks kerkida küsimus, kas see on füüsika ülesanne või kas see on üldse mingi ülesanne? Kindlasti on sellist ülesannet vaja ise lahendada, kui „õige” lahenduskäik ja vastus ära näidata on see kasuta ja igav. Seepärast siin lahendust ei olegi.
Selle ülesande juures on tore, et aeg-ajalt peab otsustama. Üks otsus, mille poole tasuks õpilasi suunata on keskendumine inimese pikkuse kasvule. Arutlused massi ja ümbermõõdu kasvamise kiiruste teemal on huvitavad, aga on raske lisanduvate küsimuste rägastikust mõistliku aja jooksul välja jõuda ja mingigi tulemus saada. Kui jõuab leida andmeid soolise või rassilise erinevuse kohta, siis võib sellest kujuneda jätkuküsimus. Vähemalt esialgu tuleks tegelda julge keskmistamisega.
Kui õpilased lahendamisega eriti paigast ei nihku või takerduvad vaidlustesse pisiasjade ja kõrvalteemade ümber, võib anda mõne vihje, aga parem oleks seegi sõnastada suunava küsimusena. (Näiteks: Kui vana on täiskasvanud inimene? Kui pikk on täiskasvanud inimene? Loode alustab kasvu nullpikkusest, aga sündinud inimene? Ilmselgelt ei ole siin tegu liikumiskiirusega, st kui kiiresti (mitu meetrit sekundis) loode ühest kohast teise liigub, kas ei oleks mõistlik mõelda ühikute peale?).
Ülesande autor soovitab jätta õpilased pärast küsimuse esitamist mõneks ajaks üldse üksipäini, et poleks võimalik õnnetu näoga õpetaja poole vaadata ja abi või vähemalt pisikest vihjet oodata. Tuleb ise harutama hakata. Harutada on nii lühikese küsimuse kohta päris palju.
Füüsika teemadest ja märksõnadest haakub see küsimus mitmetega: tavaelu ja füüsika seos; lõiming bioloogiaga (kasvamine); info leidmine ja hindamine; kiiruse mõiste ja ühikud; mõõtemääramatuse hindamise võimalus; huvi tekitamine füüsika ja ülesannete vastu ning kindlasti veel midagi.
Üks vana hea füüsika ülesanne, mille sarnaseid esineb paljudes kogudes.
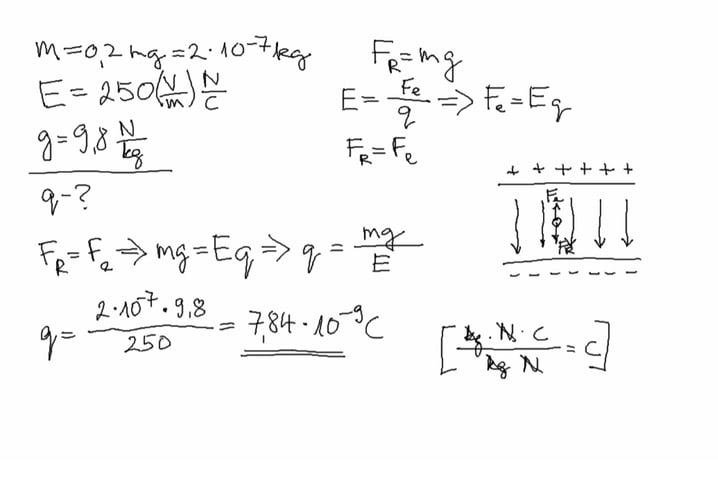
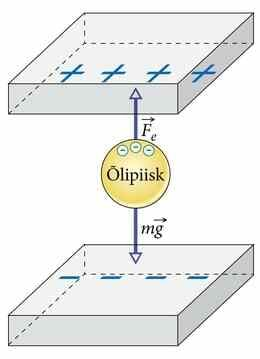
0,2-milligrammise massiga õlipiisk on tasakaalus homogeenses elektriväljas, mille jõujooned on suunatud ülalt alla. Väljatugevus on 250V/m. Milline laeng on õlipiisal? Erna ja Venda Paju Füüsika ülesannete kogu gümnaasiumile. [Ül 14.21 vastus 7,8·10-9C]
Lisaküsimused
Laeng on negatiivne. Aga kuidas me teame, et laeng on negatiivne?
Mitu liigset elektroni annavad piisale sellise laengu?
Oletame, et õlipiisa laeng muutub ühe elektroni laengu võrra. Kui palju peab elektrivälja tugevust muutma tasakaalu taastamiseks?
Teaduse ajaoost
See ülesanne viitab ilmselgelt Robert A Millikani ja Harvey Fletcheri 1909. aasta kuulsale elektroni laenugu määramise eksperimendile.
Jälgides paljusid väga väikeseid ja väikese laenguga piisku elektriväljas hõljumas, ilmneb, et nende laengud on mingi väga väikese laengu täisarvkordsed. See siis ongi elementaarlaeng, ühe elektroni laeng. Elektroni avastaja J.J. Thomson näitas juba 1897. aastal, et vesiniku aatomi ja elektroni masside suhe on umbes 1840. Elektron on on väga väike ja ka tema laeng peab olema väike, aga kas see on alati sama laeng, polnud Millikani katse ajal veel sugugi üheselt selge. Elektrodünaamika sai hästi hakkama käsitledes laengut pidevana, elementaarportsjoniteks jagamata. Seega oli elementaarlaengu määramine omas ajas oluline.
Katse ise osutus siiski keerulisemaks, kui eelpool lahendatud ülesanne. Õli pihustati metallplaatide vahelisse ruumi ja tilgad elektriseeriti rötgenikiirtega. Valiti mikroskoobi vaateväljas sobiv tilgake ja hoiti seda elektrivälja sisse-välja lülitades keskel, kuni teistsuguse kaalu ja laenguga piisad olid vaateväljast lahkunud. Seejärel lasti valitud piisal langeda ilma elektriväljata ruumis püsiva kiirusega. Püsiva kiirusega langemisel on takistusjõud võrdne kaaluga. Teades õhu dünaamilist viskoossust ja kasutades Stokesi seadust, saab arvutada piisa raadiuse ning edasi kaalu, mis arvestab nii raskusjõudu kui ka õhu üleslükkejõudu. Kui nüüd reguleerida elektrivälja tugevus nii, et piisk jääb paigale, saab võrdsustada kaalu ja elektrijõu. Praktisemaks osutus siiski kasutada tugevamat elektrivälja ja lasta katse teises pooles tilgal tõusta püsiva kiirusega.
Millikan sai elektroni laenguks tänapäevasesse ühikusüsteemi arvutatuna 1,5924(17)·10−19C, mis erineb tänapäeval aktsepteerivast vähem kui 1%. Palju pahandust tekitas see, et Millikani antud statistiline mõõtemääramatus oli väga väike. Sellest kasvas aastakümneid hiljem tuntud näide, milline psühholoogiline lõks varitseb teadlasi nende töös.
Richard Feynman pidas 1974. aastal Caltech'i lõpetajatele kõne, mis hiljem sai tema raamatu „Te kindlasti naljatate, mr Feynman” lõpupeatükiks „Lennukikummardajate teadus”:
„Me oleme kogemustestst palju õppinud saamaks hakkama mõnede enesepetmise vormidega. Üks näide: Millikan mõõtis langevate õlitilkade katses elektroni laengu ja sai, nagu me nüüd teame, mitte päris õige tulemuse. See tuli veidi väiksem tegelikust, sest kasutatud õhu viskoossuse väärtus ei olnud õige.
Huvitav on jälgida elektroni laengu määramise ajalugu pärast Millikani. Kui kanda mõõtmistulemused graafikule aja funktsioonina, selgub, et üks on veidike Millikani omast suurem ja järgmine eelmisest napilt suurem ja järgmine jälle suurem, kuni nad lõpuks jõuavad kõrgema väärtuseni. Miks nad kohe ei avastanud, et tegelikult on õige arv suurem? Teadlased häbenevad seda lugu, sest ilmselt tehti nii: kui saadi Millikani tulemusega võrreldes liiga suur arv, arvati, et miski peab olema valesti ja hakati oma katse juures vigu otsima; kui erinevus oli väike, siis ei kontrollitud nii hoolega. Nii kõrvaldatigi suured lahknevused. Praegu me tunneme neid trikke ja seda sorti haigust enam ei põe.”
[Feynman on optimistlik ja enesekindel, nagu alati. Vaevalt võib olla kindel, et teadlased on nüüd enesepettuse haigusest vabad. Kogemustest muidugi õpitakse, aga samas jäävad inimlikud omadused, nagu eduelamuse soov ja karjääriiha ikka alles ja nimetatud haigus võtab uusi, kavalamaid vorme. Feynmani kõne sõnum (üks sõnumitest) tuleb paar lõiku hiljem, kui ta toob välja teadusliku aususe põhiprintsiibi. Seejuures ei räägi ta igapäevaelulisest aususest, jättes inimestevahelise luiskamise ja pettuse nende enda sisetunde ja usu küsimuseks.
„Esimene põhimõte on, mitte petta iseennast. Ennast ongi kõige kergem petta, nii et sellega peab olema väga hoolas. Kui te ennast ei lollita, on juba kerge teisi teadlasi mitte petta. Peate lihtsalt olema aus tavatähenduses.”]
Millikani viga tuli ilmselt mitmest pisikesest efektist, mida ei osatud täpselt arvestada: õhu viskoossus ja üleslükkejõud, Maa elektriväli jms. Hiljem on katset päris palju korratud ja tuleb välja, et lihtsa praktilise tööna on see tore, aga väga täpseks minnes osutub üsna kalliks ja töömahukas.
Optimistlikult väike mõõtemääramatus tuli, nagu nüüd paistab, sellest, et mõõtmistulemuste hulgast valiti välja „paremad”. Laboripäevikutest on leitud mitmeid märkusi, mis seda kinnitavad. Kõigi tulemuste kasutamine poleks küll muutnud keskmist, aga oleks andnud laiema statistlise määramatuse. Kõigele vaatamata oli tegu suure saavutusega, sest elektroni laengu elementaarsus sai veenvalt tõestatud. On teada, et mitmed teadlased ja insenerid, kes varem kõhklesid, lasid end Millikani katsest veenda. Nobeli preemia sai Robert Millikan 1923. aastal. See, et Millikan ja tema doktorant Harvey Fletcher tegid kokkuleppe, millega elektroni laengu määramise au jäi puhtalt Millikani teeneks, püsis saladuses kuni Fletcheri surmani 1981.
Tänapäeval ei määrata elementaarlaengut enam ühe paljukorratud eksperimendiga vaid CODATA meetodil. CODATA 2014 (avaldatud 25. juunil 2015) elektroni laeng on 1,6021766208(98)·10-19C.
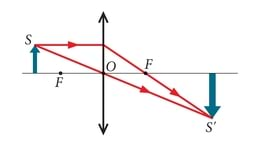
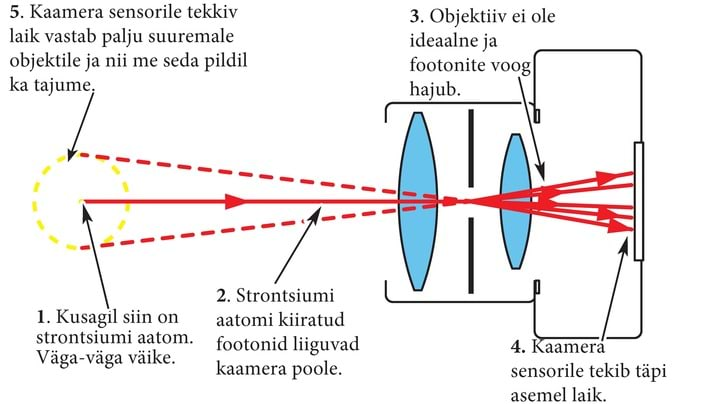
Koondava läätsega on lihtne kaugetest esemetest ekraanile kujutist saada. Mis juhtub, kui kujutise saamiseks on kasutada ainult pool läätse? Kas tõesti tuleb siis ka pool kujutist? Kumb pool?
Üks esimesi kujutiste teema jooniseid, näitab kiirte käiku tõelise kujutise tekitamisel koondava läätsega. Sellelt jooniselt võib jääda mulje, et kujutise loovad need kiired, mis läbivad läätse ülemist poolt. Sellel joonisel on puudu iseloomulik kiir, mis läbib algul esemele (S) lähema fookuse ja pöörab siis optilise peateljega paralleelseks, jõudes samasse punkti (S') kuhu ülemised kiired. Tegelikult töötab kujutise loomisel kogu lääts, ükski koht ei ole eelistatud.
Seda on lihtne järgi proovida. Võtke lääts ja tehke mõnest valgusallikast paberilehele kujutis. Valgel ajal saab hea kujutise päevapoolsest aknast vastasseinale. Nüüd katke pool läätse kinni. Kujutisega ei juhtu peaaegu midagi. Kui veel rohkem kinni katta, muutub kujutise eredus. See on loogiline, valgust tuleb vabaks jäänud osast vähem kui kogu läätsest. Samas kujutis ei moondu ega muutu poolikuks.
Fotoaparaadiga seda proovida ei saa. Blaa-blaa, mis ei saa?
Fotoaparaadis kaetakse ka enamasti osa läätsest (objektiivist) kinni. Tõsi, läätse ei kaeta mitte küljelt vaid diafragama abil servadest, vähendades objektiivi ava läbimõõtu. Seega jääb kujutise loomisel tööle objektiivi keskmine osa.
Ava vähendamisest on kasu siis, kui valgust on liiga palju. Näiteks päikeselisel päeval pildistades saab sensor liiga palju valgust, pilt tuleb eredamalt valgustatud kohtades täiesti valge ja detailideta. Fotograafid ütlevad, et kõrbes ära. Sellisel juhul tuleb ava väiksemaks reguleerida, et vähem valgust kaamerasse pääseks.
Avaga saab reguleerida ka teravussügavust (sügavusteravust, teravusulatust, DOF-i).
Mõnikord ei õnnestu väikse valgusallika (S) kujutist sensorile teravustada, sest teravustada on vaja mingitele olulisematele esemetele sellest lähemal või kaugemal. Õige kujutise koht on siis näiteks sensori taga ja saadud pilt on udune, laiali määritud (a). Ava vähendamine sunnib kogu valguse kaamerasse „pugema” läätse keskosast (b). Nii on sensorini jõudvad kiired rohkem koos ja kuigi pilt ei ole päris terav, on see kindlasti palju parem. Võib juhtuda, et kaugemalt vaadates (näitusel näiteks) pole udusust mägatagi.
Lisaülesanne
Säti akanalauale mingi ese, näiteks potilill. Vaata, et taustale jääksid mõned kergestimärgatavate detailidega esemed, mis poleks ka liiga kaugel. Õues seisev auto või naabermaja korsten sobivad hästi. Roheline põõsas ja kauge-kauge kirikutorn ei sobi. Lülita fotoaparaat ava käsitsi seadmise režiimi või veel parem, lülita kogu automaatika välja. Teravusta (või lase autofookusel teravustada) lillepotile ja tee mõned pildid erinevate avadega. Võrdle pilte.
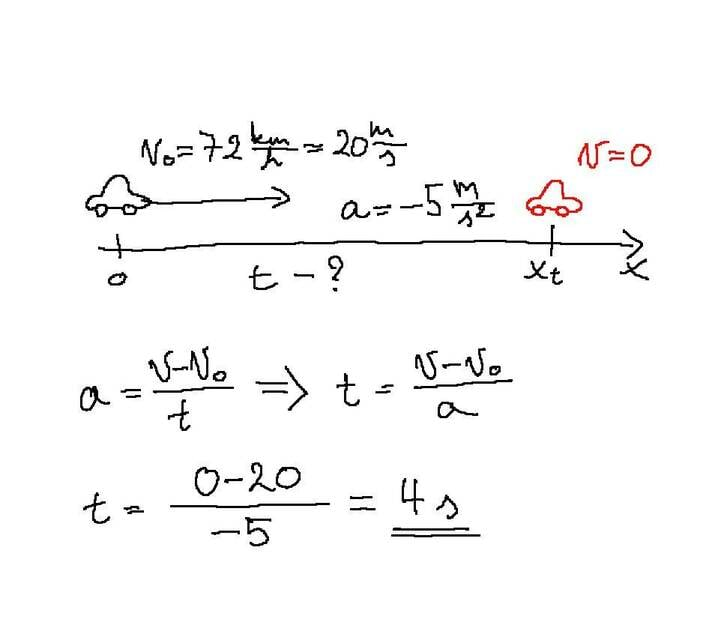
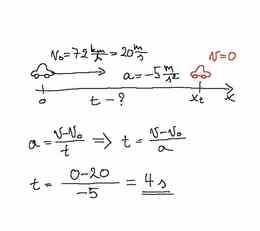
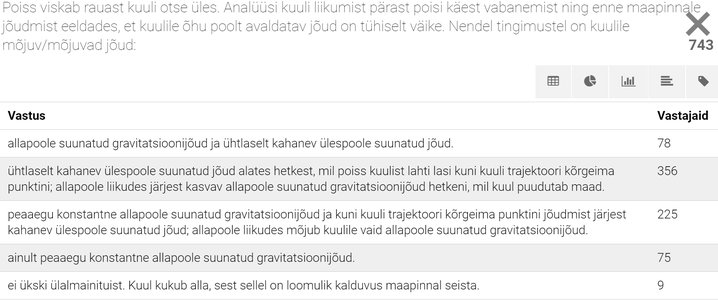
Millise ajavahemiku jooksul võib peatada kiirusega 72km/h sõitva auto, kui maksimaalse pidurdamise korral on kiirendus -5m/s2?
Rehkendus:
Pidurdusaeg arvutatakse siin kiirenduse definitsioonvalemist. Saame teada, et pidurdamine selliselt, mitte väga suurelt kiiruselt seismajäämiseni võtab väga palju aega. Neli sekundit on liikluses päratult pikk aeg. Tegemist on tavapärase kinemaatikaülesandega, mis sel kujul on siiski üsna igav ja isegi veidi eksitav. Asja saab parandada lisaküsimustega:
A) Kui kaua võtab juhil aega pidurdamise alustamine, reageerimine pidurdamise põhjusele ja füüsiline liigutus piduripedaalini jõudmiseks ja vajutuse alusatamine? Teiste sõnadega, kui pikk on juhi reaktsiooniaeg?
B) Kui palju liigub auto edasi enne pidurduse algust?
C) Kui pikk on pidurdusmaa, st kui palju liigub auto edasi sel ajal, kui kiirendus -5m/s2 juba toimub?
D) Kui pikk on kogu pidurdusmaa (koos reaktsiooniajal liigutuga) alustades kiirustelt 36km/h ja 108km/h?
E) Milline on algkiiruse ja pidurdusmaa vaheline sõltuvus? Esitage see seos graafiliselt.
[Koos lisaküsimustega on sellest lihtsast, valemi järgi arvutamise harjutusest saanud liiklusohutuse probleemülesanne. Võib probleemile veelgi tuld alla panna ja küsida, kui pikk on just sinu reaktsiooniaeg? Kuidas seda mõõta ja millest see sõltub? Kuidas muutub pidurdustee, kui pidurdajaks pole juht, vaid auto ise ehk liiklev robot. Samuti oleks oluline välja uurida, mida tähendab ja kuidas tundub pidurdamine ülesandes antud kiirendusega. Kas äkilisemalt ei saaks pidurdada?]
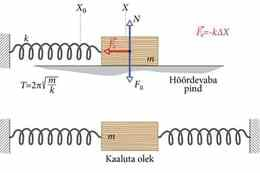
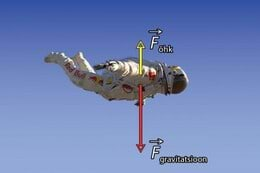
Kaalumine kaalutuses – tundub kui oksüümoron. Tegelikult on küsimus asjalik, sest kaalumisega määratakse massi. Kaalu määramine kaaluta olekus on päris eraldi teema, seejuures päris huvitav ja arutlusväärne teema.
Maapinnal viibides kipume me massi määrama kaalutava keha ja Maa vahelise gravitatsioonilise vastastikmõju kaudu, aga tegelikult saab massi määramiseks kasutada ka inertsiga seotud nähtusi.
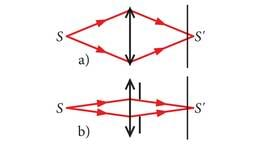
Vedru otsa riputatud raskus jääb üles-alla võnkuma, kui ta alustuseks veidi tasakaaluasendist välja viia. Üles-alla võnkumine võib viia mõttele, et vedrupendlil on miskit pistmist gravitatsiooniga, aga perioodi valemis on ainult pendlikeha mass ja vedru jäikus. Ei mingit gravitatsiooni. Nii võibki pendli võnkuma panna ka küliliasendis (a) või kaaluta olekus (b).
Niisiis vedrupendli võnkumise periood sõltub pendli massist. Ja seda teadmist võib kasutada ka massi mõõtmiseks, nagu näitab alljärgnev video:
Ülesanne
Meenutage mehaanika kurusest veel kolme nähtust, kus mass ilmutab enda inertsi kaudu. Kas need nähtused kõlbavad massi määramiseks kaaluta olekus?
Kosmosejaamas
Kaalutus on üldtuntud teemaks kerkinud alles viimase poolsajandi kestnud kosmoseajastuga. Mida teha, kui kosmoselennul on vaja mingeid kehi (näiteks toitu või inimesi) kaaluda? Gravitatsioonilise võimaluse nullib ära kosmoselaeva liikumise iseloom. Orbitaalne liikumine on olemuselt vaba langemine ja kõik kehad (sh toit, inimesed ja kaalud) langevad ühtviisi. Seega ei ole võimalik midagi kaaludele tõsta või vedrukaalu konksu otsa riputada. Jääb üle kasutada kehade inertsust ja arvutada Newtoni II seaduse järgi.
Kosmosejaamas on tegelikult väga palju asju, mis tuleb kaaluda. Täpsemalt, kõik peab olema kaalutud ja arvestatud ning peaaegu kõik kaalutakse enne starti. Mõned asjad küll muutuvad ja nende massid püütakse enamasti arvutada. Näiteks tühjad toidupakendid, kasutatud riided jms loetakse prügiks ja ka nende mass on vajalik üldises massibilansis arvesse võtta. Selliste asjade kohta on välja töötatud arvutuseeskirjad ja loodud sobiv tarkvara. Mõni üksik probleem siiski jääb.
Rahvusvahelise kosmosejaama (ISS) meeskonda kaalutakse kaaluta olekus. Kuna organismil on pikaajalise kaaluta oleku talumisel suuri probleeme, siis meditsiiniline kontroll (sh kaalumine) on sage ja põhjalik.
Kehamassi mõõtmiseks on kasutusel kaaluta olekus kaalumise seade (KOKS) ehk Space Linear Acceleration Mass Measurement Device (SLAMMD). Kaalutav inimene sätib end kindlalt mõõtmisasendisse. Jalad põimitakse ümber ühe toe, lõug või pea toetatakse teisele. Kõht surutakse tugevasti vastu keskmist tuge. Mõõtmise käivitamisel vabastab elektromagnet lühikese aja pärast kaks vedru, mis tõmbavad kaalutavat inimest muutumatu jõuga 23,3N. Kiirenevat liikumist jälgitakse optilise kaugusmõõtjaga ja arvutisse salvestuvad aja ning läbitud teepikkuse toorandmed. Massi arvutamine toimub sülearvutis KOKSi jaoks väljatöötatud takrvara abil. Aparaadi töö ei ole väga lihtne. KOKS ei saa eraldi inimest kiirendada, vaid peab liikuma panema ka seadme enda. Ühelt poolt tõmbab ta kosmonauti koos kõigi tugedega, mis teda fikseerivad. Teiselt poolt hakkab vastu liikuma kogu ülejäänud seade. Kuigi jaama sees püütakse liikuvate osadega seadmeid mitte jäigalt kinni kruvida, liigub veidi vastu kogu ISS. Meeskonna liikmeid võivad olla ka erineva kasvu ja massijaotusega, seetõttu peab KOKSi kinnitusi veidi reguleerima ja tarkvarainsenerid pidid kõiki erisusi Maal st kaaluga olekus arvesse võtma.
Lisaülesanded
Niitpendel (l=40cm) ja vedrupendel (k=20N/m) on sama võnkeperioodiga. Kui suur on pendlikeha mass? Millised oleksid nende pendlite võnkeperioodid Marsil?
Määra füüsikaklassist leitavate vahenditega mutri mass, ilma teda gravitatsioonilises mõttes kaalumata?
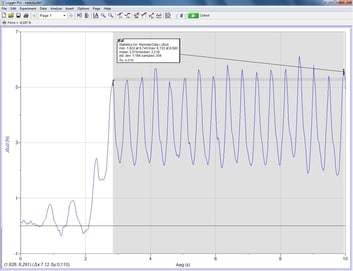
Võimalusi on kindlasti mitu. Valime ringliikumise ja Newtoni teise seaduse. Teibime joonlaua külge jõuanduri (mõõtepiirkond 10N) ja ühendame selle andmekoguriga. Vältimaks juhtmete keerdumist (ja hilisemat tüütut harutamist) teibime ka andmekoguri ja juhtmed joonlaua külge. Kinnitame mutri jõuanduri konksu külge ja mõõdame kauguse joonlaua otsas olevast august. Paneme andmesalvestuse käima ja keerutame kogu seadet võimalikult ühtlaselt umbes 10 sekundit.
Andmekoguri salvestiselt on näha, et 16 enam-vähem ühtlast ringi võtsid aega 7,12 sekundit. Jõud on muutuv, sest seadme alumises asendis liitub tsentrifugaaljõule raskusjõud, üleval seesama lahutub. Kaaluta olekus seda erinevust ei oleks. Andmekoguri statistika järgi on keskmine jõud valitud mõõteperioodis 3,578N. Arvutus näitab, et mutri mass on 36g.
Lisaküsimus
Muidugi ei ole füüsika klassis keeruline mutter päris tavapäraselt ära kaaluda või näiteks sellesama jõuanduri otsa riputada. Newtoni II seadusest arvutatud mass osutub pisut suuremaks kui gravitatsiooniliselt mõõdetu. Mis võib olla see erinevuse põhjus?
Suur Internet ütleb, et geostatsioonaarse orbiidi kõrgus on 35786 kilomeetrit.
Geostatsionaarsel orbiidil olev Maa kaaslane (satelliit) teeb täisringi ühe päevaga. Kuna ka maapind teeb ringi ühe päevaga, siis on geostatsionaarne satelliit maapinna suhtes paigal. Ainuke täiesti satsionaarne ringorbiit on otse Maa ekvaatori kohal. See on väga mugav side- ja meteosatelliitide jaoks, vastuvõtuantennid ei pea neid taevast otsima ja jälitama. Geostatsionaarsele orbiidile on suunatud ka kõik satelliitelevisooni ja -raadiot vastu võtvad antennid, nn taevakanalite taldrikud.
Kui internet parasjagu ei vasta, võib geostatsionaarse orbiidi ise välja arvutada. Tõsi, siis on vaja raamatutest otsida või järgi küsida gravitatsioonikonstant (G) ja Maa mass (M), täpsemalt nende korrutis (μ). See korrutis, mida taevamehaanikas tuntakse ühtse gravitatsioonilise parameetrina, on tänu väga pikaajalistele vaatlustele Päikesesüsteemi planeetide kohta teada isegi täpsemalt kui massid ja gravitatsioonikonstant. (μMaa=398600,442km3s−2; μMarss=42828km3s−2; μKuu=4902,8km3s−2; μPäike=132712440020km3s−2)
Kui suur on geostatsionaarse satellidi kiirus?
v =ωr ≈3,07km/s
Maapealse vaatleja suhtes on kiirus siiski null, selles ju nimetet orbiidi mõte ongi.
Mitu satelliiti mahub geostatsionaarsele orbiidile?
Geostatsionaarse satelliidi idee ilmus esmalt 1928. aastal Herman Potočniku raamatus „Kosmosereisi probleem – rakettmootor”. 1945. aastal ilmus briti kirjaniku Arthur C. Clarke'i ennustuslik artikkel „Maaväline side – kas rakettjaamad võivad katta raadiosidega kogu Maa?” Artikkel räägib kolmest geostatsionaarsest sidejaamast, mis annavad levi kogu maa- ja veepinnale. Esimene satelliit saadeti statsionaarsele orbiidile 20 aastat hiljem. Kolme sidejaamaga siiski ei piirdutud. Tänapäeval on sel ainsal ringil juba ruumipuudus.
Hea kokkulepe orbiidi jagamiseks oleks – kraadi kohta üks. Paraku ei ole kõik kohad päris võrdsed. Tihedalt asustatud alade kohal asuvad satelliidid on väärtuslikumad, kui näiteks see, mis vaatab Vaikset ookeani. Samuti on probleeme satelliitide püsimisega. Mitmete mõjude tõttu (olulisemad neist on Kuu ja Päikese gravitatsiooniline mõju ning Maa lapikus) kalduvad orbiidid ekvaatori tasandist välja. Sellised satelliidid näivad Maalt vaadates kõikuvat statsionaarse orbiidi lähedal. Kuna nad jõuavad ööpäeva jooksul taevavõlvil samasse kohta tagasi, siis nimetakse neid geosünkroonseteks. Paigalt nihkumine võib toimuda ka mööda orbiiti, sest Maa ekvaator ei ole täpselt ringikujuline ja statsionaarsel orbiidil on stabiilsemaid kohti. Enamasti on need häired seotud vanemate seadmetega, mille liikumise korrigeerimiseks mõeldud kütus on otsas, aga sideseadmed veel töötavad. Ühesõnaga, päris head korda orbiidil ei ole. Erinevatel andmetel on geostatsionaarsel (või sellele lähedasel) orbiidil 410 kuni 415 satelliiti, mõned neist koguni umbes kümnendikkraadise vahega.
Lisaküsimused?
Kui 415 geostatsionaarset satelliiti jagaksid orbiiti vennaliku kokkuleppe järgi võrdselt, kui kaugel nad siis oleksid üksteisest?
Kui kõrgel Marsi pinna kohal on areostatsionaarne orbiit? Kas oleks mõtet sellele orbiidile satelliite paigutada?
Kas võiks arvutada statsionaarse orbiidi kõrguse ümber Kuu tiirlevale satelliidile?
Ringkiirendi 27 km pikkuses kiirekanalis sunnib kiirusega 299 792 455,3 m/s liikuvad prootonid ringe tegema kallutusmagnetite magnetväli. Kui suur on kiirekanalis tekitatava magnetvälja magnetinduktsioon?
Magnetväljas kallutab prootonit ringile Lorentzi jõud (FL). Selle võib arvutada ka kesktõmbekiirenduse ja Newtoni II seaduse järgi (FC).
[Need jõud võtame võrdseks – mitte sellepärast, et need oleks võrdsed jõud, vaid sellepärast, et see ongi sama jõud. Arvestades, et magnetväljas toimuvat peab vaatama väga ruumiliselt, on joonisest kindlasti palju abi.]
Tuleb arvestada, et nii suurel kiirusel käituvad osakesed relativistlikult. Kuigi seda ei peeta tänapäeval sisuliselt õigeks, on võimalik arvutada nagu kasvaks prootoni mass kiirenemisel (mpr – prootoni mass täiskiirusel, m0-pr – prootoni seisumass, γ – Lorentzi kordaja).
Lisaülesanne
Arvutus on siiski tublisti lihtsustatud. Kuidas kiirendid tegelikult töötavad ja mis kiirekanalis peale ringile kallutamise veel toimub?
LHC kallutusmagnetid võivad ametlikel andmetel tekitada magnetvälja kuni 8,3 T.
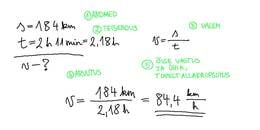
Kui suur on keskmine kiirus, kui sõita Tartust Tallinna 2 tunni ja 11 minutiga?
Tavaline füüsika ülesanne, arvatavasti üks esimesi, mida kiiruse teemat käsitledes võib lahendada. Kiiruse teema on õpilastele tuttav matemaatika ja loodusõpetuse tundidest, midagi keerulist siin ei ole. Pigem võiks keskenduda füüsika ülesannete lahendamise heale tavale.
[Kui pikk on tee Tartust Tallinna? Aastakümneid on teatud ja ka paljud teedeatlased ütlevad, et see tee on 186 kilomeetrit pikk. Aga linnad ei ole punktid, kuhu siis tuleks alustuseks mõõdulindi ots maha panna ja kuhu tõmmata finišijoon? Briti impeeriumi hiilgeaegadest pärineb väga laialt levinud ja kaua kestnud traditsioon mõõta linnade vahelist kaugust ühest peapostkontori eesukse trepist teiseni. Paraku on ajad muutunud ja postkontorid, mida nüüd nimetatakse postisorteerimise keskusteks, pole enam auväärsed hooned linna keskväljakul, vaid tihti poolrobootilised tehased linnaäärsetel tühermaadel. Aga see postkontorite vaheline tee Tartust Tallinna on tõepoolest praegugi 186 km 2021. aastal juba 183 km ja paistab lühenevat.
Kui mõõta kaugus bussijaamade vahel või kõhutunde järgi linnade keskelt (Raekoja plats – Viru väljak), on kaugus 184 km. kõigest 180 km. Eks ole viimasel ajal teeremontidega kurve laugemaks tõmmatud ja asulatest sõidetakse üha rohkem mööda.]
Lisaülesanne
Arvutus eeldaks justkui ühtlase kiirusega sõitmist. Tegelikult ei saa maanteedel kuigi pikalt ühtlase kiirusega sõita ja vastuseks on hoopis keskmine kiirus.
Oletame, et poole teest saab sõita keskmiselt 80km/h. Siis läheb pimedaks ja hakkab sadama märga lund. Teine pool teest tuleb sõita keskmiselt 70km/h. Kui palju on siis keskmine kiirus kogu teel?
Tundub, et kiiruste keskmine ja keskmine kiirus ei erine kuigi palju. Tasub siis üldse juukskarva lõhki ajada? Vaatame ühte vähemelulist näidet, et saada aimu kuidas erinevad mõisted pool teed ja pool aega.
Tähtis saadetis on vaja viia Tallinnast Tartusse. Pool teed kannab seda Ülemiste Vanake, liikudes kiirusega 4km/h. Siis võtab üle Tartu Vaim, kes kihutab teise poole püssikulli kiirusel 600m/s=2160km/h. Kui suur on saadetise keskmine kiirus kogu teel?
Võttes nüüd kiiruste keskmise (vale arvutus), saame 1082km/h. Ilmselgelt pole sel tulemusel mingit füüsikalist sisu. Arvutades eraldi esimese ja teise teekonna poole ajad, saame, et vanakesel kulub 23 tundi, aga vaimul umbes 2,5 minutit. Kokku on tähtis saadetis teel 23,043h ja keskmiseks kiiruseks tuleb ~8km/h (7,99km/h, kui täpsust taga ajada).
Lõpetuseks. Tartust Tallinna on vaja saata üks signaal. Poole teest läbib see valgusvälgatusena mööda optilist kiudu. Seal teeb suur põrgumasin nii kõva paugu, et see kostab Tallinna ära. Kui suur on signaali keskmine liikumiskiirus ja kaua aega kulub kohalejõudmiseni?
Lisame siis veel sama arvutuse teistpidi. Vana autoloks roomab ülesmäge 1 miili keskmise kiirusega 15 mph. Jõudnud üles, sõidab ta 1 miili allamäge ja jaksab nüüd muidugi liikuda kiiremini. Kui suure kiirusega peaks ta laskuva teepoole läbima, et keskmine kogu teel tuleks 30 mph.
Selle ülesande saatis psühholoog Max Wertheimer 1934. aastal Albert Einsteinile. Arvatavasti oleks võinud Einstein ülesandesse peidetud väikese triki kohe ära tabada, aga nii ei läinud. Väidetavalt tuli ahnii-efekt alles siis, kui ta oli vastuse korralikult välja arvutanud. Asi seegi.
461. Alumiiniumkalorimeetrisse massiga 0,030 kg, milles oli petrooleum temperatuuril 20°C, lasti 100°C-ni kuumutatud 0,60 kg massiga inglistinast silinder. Kui palju petrooleumi oli kalorimeetris, kui lõpptemperatuuriks jäi 29,5°C ja soojuskadu oli 15%? [Füüsika ülesannete ja küsimuste kogu tehnikumidele, Tallinn „Valgus 1985” Vastus 0,43 kg]
[Päris huvitav viis petrooleumi koguse mõõtmiseks. Muidugi, kui ei ole mingit võimalust petrooleumi ruumala ega massi määramiseks, aga teadaoleva massiga inglistinast silinder, kalorimeeter ja keev vesi on käepärast... Miks mitte?]
mAl=0,030kg
mSn=0,60kg
t°Al;Pet=20°C
t°Sn=100°C
t°lõpp=28,5°C
cAl=9,2·102J/kg·K
cSn=2,5·102J/kg·K
cPet=2,14·103J/kg·K
mPet – ?
[Ülesanne on lahendatav mitmel moel. Võib alustada soojusbilansi võrrandist. Inglistina jahtub ja annab kalorimeetrisse soojushulga QSn, millest tuleb maha arvata 15% soojuskadu, st tegelkult soojendab kalorimeetrit soojushulk 0,85QSn. Kalorimeeter ja petrooleum saavad soojushulgad QAl ja QPet, millest nad soojenevad. Antud soojushulk on võrdne saadud soojushulkade summaga, 0,85QSn=QAl+QPet. Edasi tuleb appi soojenemise ja jahtumise üldvalem Q=cm(t2-t1) ja natuke matemaatikat. Võib-olla on siiski sisulisem ja huvitavam arvutada järjest kõik soojushulgad välja ja anda igale arvutusele selge tähendus. Kindlasti on vaja enne ülesande lahendamist päris kalorimeetrit näha ja soovitavalt ka katsuda. Pärast lahendamist on õige aeg kalorimeetrit praktiliselt kasutada.]
Temperatuuride muutused. Kalorimeeri alumiiniumist anum ja sellesse valatud petrooleum soojenevad temperatuurilt 20°C temperatuurile 29,5°C. Tina jahtub temperatuurilt 100°C temperatuurile 29,5°C.
Δt°Al;Pet=9,5°C
Δt°Sn=70,5°C
Tina annab jahtumisel ära soojushulga:
QSn=cSnmSnΔt°Sn=250·0,6·70,5=10575J
Sellest läheb kaduma 15%, seega on kalorimeetri soojendamisel kasulik soojushulk:
QSn(kasulik)=0,85·QSn=0,85·10575=8989J
Alumiinumnõu soojendamiseks kulub soojushulk:
QAl= cAlmAlΔt°Al;Pet=920 0,03·9,5=262J
Petroolelumi soojendamiseks jääb:
QPet=QSn(kasulik) – QAl=8989 – 262=8727J
Petrooleumi mass, mis selle soojuhulga (QPet) saamisel soojeneb 9,5 kraadi võrra:
QPet= cPetmPetΔt°Al;Pet
mPet=QPet / (cAl·Δt°Al;Pet)=8727 / (2140·9,5)=0,43kg
[Selle üldiselt üsna tüütu ja ebapraktilise ülesande lahendamine loob siiski võimaluse minna edasi kalorimeetri praktilise töö juurde. Metallsilindri algtemperatuur (100°C) annab veel ühe vihje. Silinder võetakse keevast veest ja tõstetakse kiiresti kalorimeetrisse. Selle asemel, et määrata kalorimeetrisse valatud petroolemumi massi, võiks koolitunnis määrata erinevate vedelike (toiduõli, soolvesi, kange suhkrulahus, lambiõli, glütseriin, mootori jahutusvedelik, auto klaasipesuvedelik (talvine ja suvine), erinevad süütevedelikud) erisoojusi. NB! Mõned igapäevaelus kasutatavad vedelikud on mürgised või tuleohtlikud. Kuum ja külm vesi ei pruugi vaatamise järgi erinevad olla, küll aga katsumise järgi. Ohutuse peatükk on eksperimendi plaanis kohustuslik.]
Lisaküsimused
Kui suur on kalorimeetris olnud petrooleumi ruumala ja kui palju see soojenemise tõttu muutub?
Kas kalorimeeter on mõõteriist? [Vana hea altvedamise küsimus põhikooli lõpueksamilt!]
Milleks kõlbab kasutada kalorimeetriline pomm ehk pommkalorimeeter?
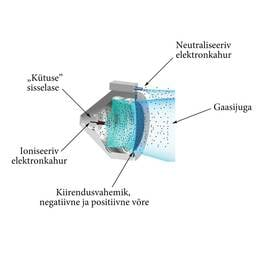
Raketiteadus näeb üldiselt ette kosmoselaevade kiirendamise põlemisel saadud gaasijoaga. Põlemisgaaside juga paiskub düüsidest välja ja impulsi jäävuse seaduse järgi kiirendab kogu ülejäänud rakett vastassuunas. Ioonmootor kiirendab kosmosetehnikat sarnaselt, aga kiire gaasjuga tekitatakse seal elektri või magnetjõuga (Coulomb'i või Lorentzi jõuga).
Ioonmootori eeliseks on väga kiire gaasijuga (20-50 m/s), aga sellest saadav jõud on siiski väike. Nii sobibki ioonmootor kosmosereisideks, kus peab kütust pikal teel kokku hoidma, aga on aega kiirust koguda. Päris mõistlik on kasutada ioonmootoreid satelliitidel, kus on vaja aeg-ajalt teha pisikesi liigutusi asendi või suuna hoidmiseks.
Ioonmootorite rekordit hoiab kosmosesond „Dawn”, mis suutis koguda kiiruseks üle 10 km/s. Mootori veojõud oli vaid 90mN ja kogu seadme mass algselt 1240kg. Nii võib kiirenduseks Newtoni teisest seadusest arvutada:
F=ma ⇒ a = F/m = 0,09N/1240kg = 7,3·10-5 m/s2 =
0,95 km/h2
Ioonmootorite kiirusrekordi (v=10000m/s) saavutamiseks sellise kiirendusega kuluks (v0=0):
a= v-v0/t ⇒ t= v/a =10000/0,000073 = 1,37·108 s =
4 aastat ja 4 kuud
Raketiteadus ei ole siiski nii lihtne. Tuleb arvestada, et ioonmootoriga ei saa startida maapinnalt ja kui saaks, siis maapinna kiirus ei ole kosmilises taustsüsteemis null.
Ioonmootor kasutab „kütust” (milleks tihti on ksenoon) ja muutub nii ise kergemaks. Sellega muutub ka kiirendus, nagu see käib ka tavapäraste põlemisrakettide korral. „Dawn” startis Maa orbiidilt 17. detsembril 2007 pärast ioonmootori katsetamist ja kasutas vaid 72 kg ksenooni kiiruse suurendamiseks 1,81 km/s võrra. Pärast täiendavat kiirendamist Marsi gravitatsiooniväljas suundus „Dawn” uurima asteroide. Mitmete häirete kiuste uuris sond Vestat ja jõudis Cerese orbiidile 6. märtsil 2015. „Dawni” päikesepaneelide pindala on tervelt 36,4 m2, sest elektrit on vaja ioonide kiirendamiseks ja asteroidide vöösse lennates jääb Päike üha kaugemale.
Ei ole! Legend, et Suur Hiina müür on ainus inimkätega tehtud asi, mis palja silmaga Kuult näha, pärineb koguni 18. sajandist. Omajagu hoogu andis sellele loole Marsi kanalite „uurimine” 19. sajandil. Väidet on üha sagedamini korratud kahekümnendal sajandil (nii enne kui ka pärast kosmoseajastu algust) ning omistatud mitmetele kosmonautidele, astronautidele ja taikonautidele. Apollo kuulendude astronaudid on sellekohasele küsimusele mitmel korral vastama pidanud ja tõesti, Suurt Hiina müüri pole Kuu pealt näha. Ometi elab legend popkultuuris visalt edasi.
Kas Suur Hiina müür on näha kosmosejaamast või mõnelt madalamalt Maa orbiidilt?
Tõenäolielt ei näe seda ka kosmosejaamast, aga väga heades tingimustes võib väga hea nägemisega inimene selle siiski ära näha mõnel madalamal orbitaallennul, kui ta täpselt teab, kust otsida. Inimesed on loonud asju, mis on kosmosest tõesti näha: veekogud, linnad (eriti öösel), kasvuhooned (eriti sobivalt langevas päikesevalguses), lagedaks raiutud alad suurtes metsades jms. Kogu jutt on muidugi palja silmaga vaatamisest, kui teleskoobid mängu võtta, tuleb kogu küsimus algusest peale uuesti läbi mõelda.
Üldiselt on teada, et inimene näeb esemeid, mille nurkmõõde on üle 1 kaareminuti (1´=1/60º=60´´). Kuna see nn eraldusvõime on individuaalne, igal inimesel erinev, tuleks ise järgi proovida.
Joonista paberile kaks ringi, läbimõõtudega 1mm ja 5mm ja tõmba ka mõned paralleeljooned vahekaugusega 1 ja 5 mm. Riputa paber seinale, vaata ja kõnni kaugemale. Väiksem ring muutub täpiks umbes 2-3 meetri kaugusel, suurem on näha veel 7-10 meetri pealt. Kui kaks joont paistavad ühena ja ringid sulavad täpiks lähemalt vaadates, tasub sellest silmaarstile rääkida. Kui näed ringe kaugemalt, tasub rõõmustada oma terava nägemise üle ja see on asi, mida peab hoidma.
Inimese silma on tihti võrreldud kaameraga. Üks laialt levinud keskmise inimsilma eraldusvõimet kirjeldav suurus on 576 megapikslit. See on arvutatud nägemisrakkude suuruse ja vaatevälja laiuse järgi ja tundub fotoaparaatidega võrreldes väga palju. Tegelikult ei ole megapikslid selle loo lõpp. Nii kaameras kui silmas oleneb hea pildi saamine veel paljudest muudest oludest. Kõigepealt muidugi valgus, värv ja kontrast, aga samavõrra ka optika (objektiivi või silmaläätse) kvaliteet ja puhtus.
Kurb tõsiasi on, et kui fotonäitusel on segamini pildid, mille trükkimisel on resolutsiooniks valitud 150dpi ja 300dpi, siis valdav enamus vahet ei märka. 150dpi (dots per inch) tähendab, et trükimasin teeb ühe tolli (2,54cm) kohta 150 täpikest. Ühe täpi läbimõõt tuleb 0,17mm. 300dpi korral on iga punkti mõõt 0,085mm. Lugemiskauguselt (40cm) on 150dpi üksikpunkti nurkläbimõõt 1´28´´, 300dpi korral 43´´. Kui eralduspiiriks on 1´, peaks vahe olema märgatav. Uuringud näitavad, et üksikpunktide nägemisest olulisem on teravus, st eri värvi (või kontrastsete) pindade serval ei tohiks olla vahepealse värvi või heledusega üleminekupunkte. Siis tundub pilt hea. Digiajastul on seda lihtne järgi aidata ja uduseid pilte tagantjärgi „teravustada”.
Me ütleme „ma näen seda”, mitte siis kui võrkkestal tekib kujutis, vaid siis kui aju on kahe silma signaalid läbi töötanud. Mälu ja kujundite äratundmine on väga oluline. Lisaks sellele ei pildista me oma nägemises üksikkaadreid, vaid mõtleme pideva signaalivoo kokku üheks pildiks. Seepärast ongi parem näha liikuvaid esemeid, vaadata ise liikudes, pead keerates ja silmi pööritades. Silma valgustundlikud rakud ei ole võrkkestas ühtlaselt jaotund. Suure osa värvilisest pildist teeb silma keskosa. Aga väga olulist (ja siiani vaieldavat) lisa annab perifeerne nägemine. Silmanurgast piilumine on tervikpildi saamiseks väga vajalik, aga seda ei saa alati usaldada. Tuleb välja, et kogu nägemise teema kipub veereva lumepallina paisuma, kogudes enda külge üha uusi küsimusi.
Valgustundlikud rakud on kepikesed ja kolvikesed. Naistel on võrkkestas rohkem kolvikesi, mis koostöös kepikestega näitavad värve. Meestel on rohkem kepikesi, mis aitavad näha hämaras ja teevad värvilist pilti kontrastsemaks. Suur Hiina müür ei erine värvide poolest kuigi palju ümbritsevast maastikust, aga võib olla sobiva valgustatuse korral üsna kontrastne omaenda varjuga. Paistab, et meeskosmonautidel on väike eelis müüri otsimisel.
Lisaülesanne. Arvuta välja kui kaugelt peaks olema näha lauatennise palli (d=4cm) ja jalgpalli (d=22cm). Pane pallid looduses arvutatud kaugustele ja kutsu sõbrad vaatama. Nüüd too mõlemad pallid täpselt kaks korda lähemale ja vaadake uuesti. Mida märkate?
Kui kaugelt tasub pallimängu üldse vaadata? Kas suurima staadioni tribüüni ülemiselt realt on jalgpall üldse nähtav?
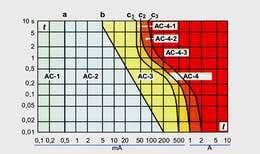
Miks on elektiliini postide hoiatussiltidele kirjutatud „ETTEVAATUST! – KÕRGEPINGE”? On ju teada, et hoopis suur voolutugevus võib inimesi tappa. Küsib Paul G. Hewitt õpikus Conceptual Physics.
Ohmi seadus seob kolm olulist vooluringi iseloomustavat füüsikalist suurust: pinge, voolutugevus ja takistus. Oht, mille tõttu peab ette vaatama, on selles, et mida kõrgem on pinge, seda tugevam on vool, kui takistus ei muutu. Võib ka öelda, et kui on tekkinud tugev vool, siis järelikult pidi olema selle põhjuseks kõrge pinge või väike takistus. Küll aga ei tohiks arvata, et tugev vool võib põhjustada kõrget pinget. See kõik on õige, aga küsima peab, kas takistus on muutumatu?
Inimese takistuses on määrav osa nahal, sest pindmised surnud naharakud moodustavad päris hea isolaatori kihi (eritakistus, ρ = 1,5 – 2 MΩ·cm). Siseorganite, lihaste ja vere takistus on sellega võrreldes väike (ρ = 100 – 800 Ω·cm). Seega võib öelda, et elektrilöögi korral päästab meid naha suur takistus ja kasuks tuleb, kui nahk on terve ning kuiv. Aga kõik inimesed ei ole ühtviisi paksu nahaga ja ka ühel inimesel ei ole naha takistus kõigis kehapiirkondades sama. Kui inimene „satub voolu alla”, siis keha või kehaosa takistus, mida vool läbib, sõltub tingimustest, kehapiirkonnast ja isiku eripärast ja võib olla vaid umbes 600Ω, aga võib olla ka ligi 100kΩ.
Kui arvutada Ohmi seaduse järgi voolutugevus, siis koduse elektrivõrgu pinge (U=230V) korral on see:
Suurim võimalik: Imax=U/Rmin=230V/ 600Ω=0,38A=380mA
Vähim võimalik: Imin=U/Rmax=230V/ 100000Ω=0,0023A=2,3mA
Vaadates diagrammi, mis näitab erinevate voolutugevuste mõju inimesele, paistab, et suurim võimalik voolutugevus lõpeb tõenäoliselt surmaga, kui see kestab üle poole sekundi. Vähim võimalik voolutugevus on küll tuntav (st valus või ebamugav), aga püsivat kahju tervisele ei tohiks tekitada. Tehku meid siiski ettevaatlikuks see, et inimesed on surnud ka puhtalt elektrilöögi saamise ehmatusest. Samas andku meile lootust, et vähemalt ühel korral on eluga pääsenud inimene, kes sai elektrilöögi 340kV ülekandeliinist.
Enamus inimesi suudab vähemalt pool sekundit ilma suurema kahjuta kannatada voolutugevust 20mA. Kui arvestada inimese takistuseks umbes 6000Ω, oles lubatav pinge:
U=IR=0,02A·6000Ω=120V
Umbes sellist pinget koduses vooluvõrgus paljudes riikides pakutaksegi.
Kõrgepinge eest hoiatamine on igati asjalik veel ühel põhjusel. Pingel üle 500V võib inimese nahas tekkida läbilöök, nagu see võib juhtuda tegelikult kõigis isolaatorites. Läbilöögi korral muutub isolaatori (algselt väga suur) takistus korraks väga palju väiksemaks, millega kaasneb voolutugevuse äkiline kasv. Kahjuks põhjustab läbilöök nahas põletusega sarnase elektrikahjustuse. Kahjustatud naha takistus jääbki oluliselt väikemaks kui tervel ja tugev vool pääseb siseelundeid kahjustama.
Kõrgepinge hoiatusest tasub välja teha, sest kui jätate alajaama ukse avamata või posti otsa ronimata, ei saa teie kehas kuidagi tekkida ohtliku tugevusega voolu. Vooluga juhe ei ole ohtlik, ei karga kellelegi kallale, kes teda ise torkima ei lähe.
Miks peab koolis õppima siinuseid ja neid teisi asju, kui neid elus vaja ei ole?
[Tuntud küsimus, mis kerkib tihti esile, kui kellelgi on vaja veel kord tõestada, kui elukauge ja kasutu on koolis õpetatav teadus. Ja kui valesti seda kõike tundides tehakse. Ja kuivõrd on õpetajad ning ainekavad ajast maha jäänud. Ja kui ainekeskene on meie kool, selle asemel, et olla õppijakeskne. Ja need teised asjad.]
Siinused ei ole tegelikult kasutud. Kolm näidet:
1. Maamõõtjad, arhitektid ja projekteerijad lasevad tänapäeval suurema osa arvutustest teha arvutitel ja ei pruugi tõesti teada, kuidas seal kolmnurksed või rombikujulised pinnad paika pannakse ja välja arvutatakse. Tarkvarainsener ja programmeerija, kes arvuti neid arvutusi tegema õpetab, peab seda ometi teadma ja siinuseid tundma. Peale selle on olemas üsna suur ja löögivalmis seltskond disainereid ning meistreid, kes näiteks teevad üksiktellimuste järgi mööblit ja õmblevad rõivaid. Nemad arvutavad kapiriiulite kuju ja konstrueerivad lõikeid ikka trigonomeetria ja Pythagorase teoreemi järgi. Kuidas siis teisiti?
2. Kui pikk on päev detsembri lõpus?
Pööripäeva paiku, kõige pimedamal ajal jääb neli päeva lühemaks kui 6 tundi ja 22 minutit. Vanarahvas ütles selle kohta, et Päike püsib kolm päeva pesas. Kas pole see mitte siinusfunktsiooni omadus, et maksimumi (ja tegelikult ka miinimumi) juures muutub ta väga aeglaselt, peaaegu seisabki paigal?
|
Kuupäev |
18.12. |
19.12. |
20.12. |
21.12. |
22.12. |
23.12. |
24.12. |
25.12. |
|
Päeva pikkus |
6:22:49 |
6:22:17 |
6:21:55 |
6:21:43 |
6:21:40 |
6:21:47 |
6:22:04 |
6:22:31 |
|
Muutus |
-40s |
-31s |
-22s |
-12s |
-3s |
+7s |
+16s |
+26s |
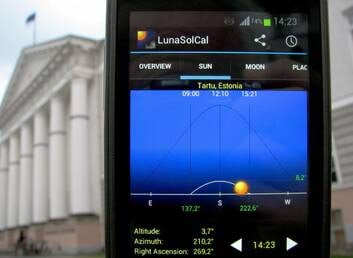
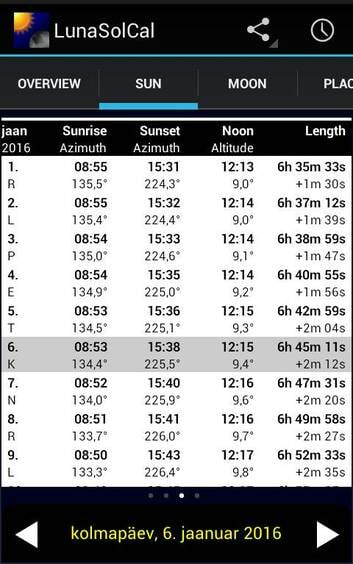
| Toomapäev Tartus. Päike on vaid 3,7 kraadi üle horisondi ja pilvine päev pole päris valgeks läinudki. Telefon näitab kalendris heleda joonega Päikese näiva teekonna madalat kaart. Tumeda joonega märgitakse suvise pööripäeva valgusolusid. See näeb ju päris sinusoidi moodi välja? | Programmi LunaSolCal ekraanivaade: tabel |
Kui lapsed jaanuari teisel nädalal jälle kooli lähevad, on päev juba umbes pool tundi pikem ja kogub pikkust üle kahe minuti iga pöördega. Rahvakalender lubab küll päeva pikenemist kukesammu võrra alles Tõnisepäevaks 17. jaanuaril. Kevadisel võrdpäevsusel, kui ka loodus pööraselt edasi tõttab, on päevane muutus 5 minutit. See püsib nii umbes kaks ja pool nädalat, siis hakkab tasapisi hoogu maha võtma.
3. Last but not least. Kes koolis koosinusvaba elu järgi õhkamise asemel trigonomeetria ära õpib, saab hiljem oma kooliealised lapsed kerge vaeva sellest samast teemast üle aidata. Valguse võit pimeduse üle!
Lisaküsimus
30° nurga siinus on ½ (pool). Millest pool? Miks pool?
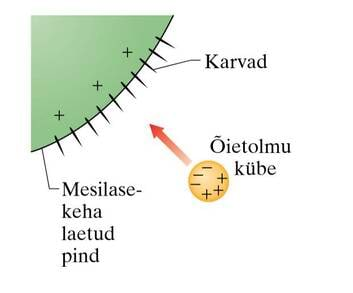
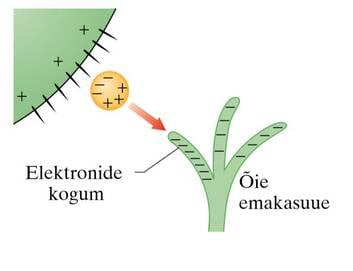
Kui suure gravitatsioonijõuga mõjutavad teineteist kaks 45-kilogrammise massiga pliikuuli, mille masskeskmed paiknevad teineteisest 20 cm kaugusel? Võrdle seda jõudu raskusjõuga, mis mõjub ühele kuulile. Erna Paju, Venda Paju, Füüsika ülesannete kogu gümnaasiumile, ül 4.5.
Miks on oluline, et need kuulid on just pliist?
Kui kuulid oleks mõnest väiksema tihedusega ainest ja seepärast ruumalalt suuremad, ei saaks neid teineteisele nii lähedale paigutada. Muidugi võib ülesande suurema kauguse peale ümber teha. Jõud on nii ehk naa väga väike, sest gravitatsiooniline vastastikmõju on nõrk. Võib-olla on pliikuulidel teaduse ajaloos oluline koht?
1783. aasta paiku planeeris inglise loodusfilosoof, nagu tol ajal teadlasi nimetati, John Michell maakera kaalumise katse. Valmistati suur väändkaal (torsioondünamomeeter), millega loodeti mõõta imepisikest pliikuulide vahelist gravitatsioonilist tõmbumist. Kasutati nelja, mitte väga suurt kuuli. Kaks massiivset kera olid 30cm läbimõõduga (158kg), kaks pisemat 5,1cm (730g). Michell suri enne katse toimumist ja seade jäi Henry Cavendishi kätte. Tema täiustas aparatuuri ja kuigi põhimõte pärineb Michellilt, tuntakse mõõtmist nüüd Cavendishi eksperimendina. Seda nimetatakse ka gravitatsioonikonstandi määramiseks, kuigi omal ajal oli küsimuseks ikkagi Maa tihedus.
Mõõtmine ei olnud lihtne. Jõud on väga väike (umbes võrdne suuremale liivaterale mõjuva raskusjõuga) ja igasugused kõrvalmõjud võivad tulemuse rikkuda. Temperatuuri muutuste ja õhu liikumise vähendamiseks paigutas Cavendish kogu seadme kinnisesse ruumi ja eraldi hoonesse. Liikumisi vaatles ta läbi seina paigaldatud teleskoopidega.
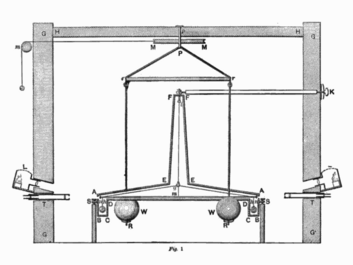
| Cavendishi seadme makett. Mõõtkava paneb paika taburett pildi vasakus servas. | Aparatuur koosneb kahest põhiosast. Pliikuulid ripuvad paariti pikkade (1,8m) kangide otstel. Suuremad kuulid ühel, väiksemad teisel. Väiksemate kuulide riputamiseks kasutatud traat töötab väändvedruna, mille jäikus määratakse päripäeva-vastupäeva võnkumise perioodi, kangi pikkuse ja massi järgi. Cavendishi seadmes oli periood umbes 20 minutit. Seejärel tuuakse kaugjuhtimisega lähedale suuremad kuulid ja väikesed kuulid tõmbuvad gravitatsiooniliselt nende poole, pöörates oma kangi teatud nurga võrra. Seadme väiksemate kuulidega pöörduv osa ei jäänud paigale, vaid võnkus lõputult edasi-tagasi ja varda otste kõrvalekalle tuli mõõta liikumise pealt. |
Cavendish oli väga kinnise iseloomu ja veidrate käitumismaneeridega mees. Häbelikkusest jättis ta mitmeid oma töid avaldamata. Neist on hiljem leitud üht-teist, mille teised teadlased pidid hiljem uuesti avastama. Maa tiheduse katse kokkuvõte ilmus siiski 1798. aastal Kuningliku Ühingu ajakirjas „Philosophical Transactions”. Kuigi Cavendishil jäi sisse väike arvutusviga, ei muutnud see lõpptulemust kuigi palju. Maa keskmiseks tiheduseks saadi tänapäevastesse ühikutesse pandult umbes 5,4g/cm3. See on üllatavalt suur tihedus, sest pea kõik, mida me maapinnalt leiame (vesi, kivid, puud, loomad) on väiksema tihedusega. Tõsi, võib leida ka mõned terakesed suurema tihedusega aineid, näiteks kulda, aga seda on ilmselgelt liiga vähe. Maakera tuumas peab olema midagi väga rasket.
Põhjendatud küsimus. Igapäevakogemus ütleb meile, et kõik asjad, mis maapinna kohal lahti pääsevad, kukuvad alla ehk maha. Samas planeedisüsteemid püsivad ja kaaslased tiirutavad miljoneid aastaid ümber planeetide. Tõesti, miks?
Võib öelda, et Kuu siiski kukub alla, aga kuna tal on ka kukkumisega ristsuunaline hoog sees, siis ta kukub mööda. Igal järgneval ajahetkel kukub Kuu jälle Maast mööda ja neist pisikukkumistest kujuneb orbiit. Maapinna lähedal liiguvad kõik heidetud, visatud, tulistatud, lahti lastud jne kehad trajektooril, mille üheks komponendiks on Maa masskeskme poole suunatud kiirenev liikumine raskuskiirendusega (g=9,8m/s2). Ka Kuu trajektooris on Maa poole suunatud kiiredus, kui suur see on?
Kuu kiirenduse võib arvutada ringliikumise kinemaatikast, aga võib ka tuletada gravitatsiooniseaduse loogikast (pöördruudu seadusest).
Proovime järele.
Andmed
Kuu keskmine kaugus maast (orbiidi pikem pooltelg) on: rKuu=384400km=3,844⋅108m.
Kuu periood (üks kuu): T=27,32d=2360400s.
Raskuskiirendus (gravitatsioonivälja tugevus): g=9,8m/s2.
Maa raadius (õuna kaugus Maa keskmest): r˜oun=6371km=6,371⋅106m.
Esiteks ringliikumise kinemaatika:
Kuu kiirendus (allakukkumine) on 0,0027m/s2–––––––––––––
Teiseks gravitatsiooniseaduse loogika:
St teadmine, et gravitatsioonijõus kahe objekti vahel sõltub nende kauguse ruudu pöördväärtusest. Kuu ja õuna kaugus Maa keskpunktist suhtuvad nagu:
Järelikult on raskuskiirendus Kuu asukohas 60,3 ruudus korda väiksem:
Tulemus on sama, mis annab meile julgust nimetada gravitatsiooniseadust ülemaailmseks. Newtoni Ülemaailmne Gravitatsiooniseadus, kõlab uhkelt.
Orelivile annab puhumisel kindla kõrgusega tooni. Kui vile täita õhu asemel metaaniga, on toon kõrgem. Millise järelduse võib siit teha heli levimiskiiruse kohta maagaasis? (Erna ja Venda Paju ülesannete kogust)
Lihte ülesanne, kui lisaküsimusi mitte esitada. Lainepikkuse ja sageduse korrutis on laine kiirus (v=λ·f). Lainepikkuse määrab vile pikkus, see on paigas, ei sõltu orelisse õhu asemel puhutava gaasi omadustest. Toon (sagedus) on kõrgem, st ka kiirus peab olema suurem. Katsed kinnitavad, et heli kiirus (20°C) on õhus 343 m/s, metaanis 446 m/s.
Selles lihtsas (ja õiges) vastuses on üks lause, mis võiks tekitada lisaküsimusi. Kuidas vile pikkus lainepikkuse ära määrab? Tegemist ei ole selle helilainega, mis heli vilest meie kõrvadeni (või mõõteriistadeni) toob. Kui täita vile metaani või mõne muu gaasiga, siis väljaspool vilet on ikka õhk. Kui ka kogu orel on metaanis, arvatavasti kuulaja kõrvas on ikka õhk.
Vilistamiseks on mitmeid võimalusi:
- Vilesse puhutava õhuvoolu suund muutub kiiresti. Enamasti on vahetuvaks suunaks sisse-välja, st õhuvool jagatakse vile aval kaheks ja keeriste tekkimine sunnib suurema osa õhuvoolust minema kord vile sisse, siis jälle välja, sisse, välja jne. Nii töötavad paljud spordikohtunike ja politseinike viled, oreliviled, plokkflööt, paju- ja roopill.
- Õhuvool suunatakse üle suletud toru või anuma ava. Pudelisse puhumine, paaniflööt, mõned spordiviled.
- Õhuvoolu kiire katkestamine või takistamine. Sireenid.
- Mitme õhuvoolu kohtumine. Peruu vilistavad pudelid, tuule vilin traatidel ja puuokstel.
- Õhu läbivool kahest järjestikusest avast. Piiksuvad ja viiksuvad kummist mänguasjad, teekannu vile.
- Mitmesugused kombineeritud õhu suuna muutmised ja avade läbimised. Huulte ja näppudega vilistamine.
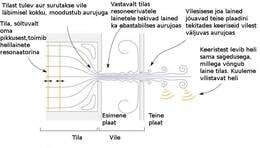
19. sajandi lõpupoole hakkasid leiutajad nuputama, kuidas vältida tulele pandud ja unustatud teekannu tühjaks keemist. Lihtne, odav ja töökindel lahendus sündis umbes 1915. aasta paiku ja just sellest ajast on võetud ridamisi patente erinevatele vilistavatele teekannudele. Tuntuim teekannuvile koosneb kahest üksteise taha paigutatud auguga plaadist. Terve sajandi jooksul ei osatud välja mõelda, kuidas selline lihtne seade vilistab või miks ta üldse vilistab. 2013. aastal avaldasid Cambridge'i ülikooli teadlased Ross Henrywood ja Anurag Agarwal ajakirjas „Physics of Fluids” artikli „The aeroacoustics of a steam kettle”. Vilistav kann on andnud artiklile pealkirja, aga teaduslik tulemus on muidugi palju laiemalt rakendatav.
Orelivile alumises otsas asuv vile (umbes nagu spordikohtuniku viles) või keel (umbes nagu suupillis) tekitab heli, mis levib resonaatorisse. Resonaatoriks on orelivile metallist (plii ja tina sulamist) või puidust toru, see mille võiks põhimõtteliselt õhu asemel täita metaani või mõne muu gaasiga. Torus olevas gaasis tekib seisulaine, mille võnkumine levib saali. Koos ülemtoonide, toruseintes tekkivate seisulainete ning teiste vilede ja kogu oreli konstruktsiooni kaasahelisemisega tekib see orelivile heli, mille iseloomuliku tämbri me eksimatult ära tunneme. Veidi üllatav on see, et küsimus on esitatud just selle vilet täitvas õhus või metaanis leviva seisulaine kiiruse kohta. Seisulaine justkui seisab, kuidas ta siis levib?
Seisulaine tekib ikkagi laine levimisest. Täpsemalt, seisulaine tekib piki vilet leviva laine interfereerumisest sama lainega, kui see vile otsast vastasuunas tagasi tuleb. Seda on lihtne ette kujutada, kui toru ots on kinni. Jah, orelites on ka kinnise otsaga vilesid. Heli on pikilaine, st keskkond (näiteks õhu molekulid) võngub samas sihis laine levikuga. Osakeste liikumise mõttes on suletud toru otsas seisulaine sõlm (osakesed liiguvad vähe). Rõhu muutuste järgi vaadates on selles kohas seisulaine pais (rõhk muutub palju).
Good, so far... Miks on lahtises vileotsas seisulaine pais?
Lahtises toruotsas on osakeste liikumise järgi seisulaine pais, osakesed liiguvad palju. Rõhu muutuste järgi on samas sõlm, rõhk muutub vähe. Orelivilesse puhutakse alumisest otsast õhku (käesoleval erandjuhtumil metaani) juude. Lahtise otsaga viles liigub lisaks pikilainele ka kogu õhk mööda toru edasi, hoides seal pidevalt väikest ülerõhku. Ülemisest otsast väljumisel saab osa õhku paisuda ka külgsuunas ja seepärast tervikuna õhu vool torust väljumisel pidurdub. Toru otsa kohal tekib nn näivtakistus, ehk akustiline impedants. Lahtise otsaga vile akustiline pikkus sõltub ka toru jämedusest ja on veidi suurem, kui tegelik pikkus, sest väljuva õhu paisumine võtab veidi ruumi. Veelgi täpsemaks minnes tuleks arvestada ka vilesse puhutava gaasi omadusi. Suurema viskoossusega gaas pidurdub veidi enam toru seinte lähedal ja muudab ka natuke helienergia väliskeskkonnas laiali levimist.
Miks vile toon on kergemas gaasis kõrgem? Miks heeliumi hinganud inimene räägib veidra Piilupardi häälega?
Igale liikumisele, sh gaasi molekulidele, kõlbavad rakendada Newtoni seadused, niisamuti termodünaamika printsiibid. Heliallikas tekitab gaasis lokaalse tihenduse, surub veidi gaasi kokku. Kokkusurutud gaas paisub kõrvalolevasse veidi madalama rõhuga alasse, sest nii postuleerib termodünaamika teine printsiip. Kui gaasi molekulid on kergemad, on neid lihtsam kiirendada ja nad jõuavad rutem tasakaaluseisundisse ehk olukorda, kus rõhud kogu gaasis on võrdsustunud. Muidugi ei saa molekulid vastavalt inertsiseadusele kohe pidama, sõidavad eesolevatele selga. Sellega tekib uus tihendus ja sinna, kust molekulid läbi kihutasid jääb kerge hõrendus. Pikilaine on ühe lainepikkuse võrra edasi levinud ja kergemate molekulidega põrgatades on see käinud kiiremini. Kui üks samm teha kiiremini, mahub samme sekundisse rohkem ehk sagedus on suurem, toon on kõrgem.
Metaan on tuleohtlik. Vaevalt, et orelite omanikud ja orelimängijad rõõmustavad, kui viledesse õhu asemel põlevaid gaase puhutakse. Heelium ei ole hingatav. Kopsude täitmine erinevate gaasidega ei pruugi olla hingamine. Õhu hingamisel on meie eluspüsimise ja hea tervise tagamisel tähtis koht. Heaküll, tegite selle nalja üks kord ära ja aitab. Terve õhtu heeliumipiiksumisega seltskonda lõbustada pole sugugi ohutu.
Lisaküsimused
70 cm pikkune tšello keel annab heli põhitooniks 220 Hz. Kui suur on laine kiirus? Milline laine see on? Kus see laine levib?
Kuidas saab heli kiirust määrata?
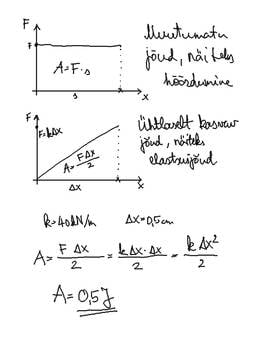
373. Kui palju tööd peab tegema, et venitada vedru, mille jäikus on 40 kN/m, 0,5 cm võrra?
Andrei Rõmkevitš, Füüsika ülesannete kogu VIII-XI klassile. Tallinn „Valgus”1988
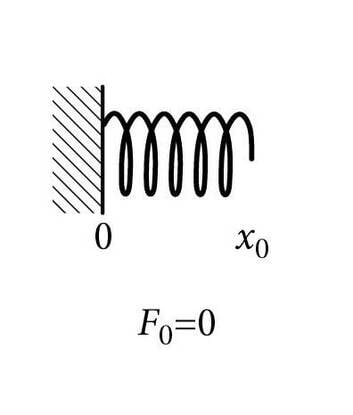
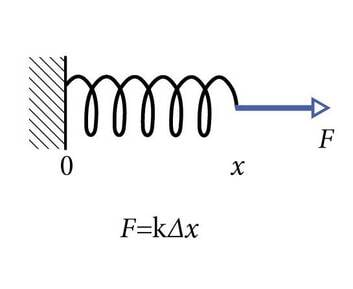
[Aegumatu klassika! Kõigepealt peame eeldama, et küsimus on esitatud nn ideaalvedru ehk Hooke'i vedru kohta. Väga paljud (kuigi mitte kõik) vedrud käituvad mõistliku deformeerimise korral vastavalt Hooke'i seadusele: Fe=-k Δx. Siit saab edasi minna mudelite paratamatu piiratuse ja üle kriitilise piiri deformeerimise teemaga.
Võtame teadmiseks, et vedru venitav jõud ja elastsusjõud, millega vedru deformeerimisele vastab, on samasihilised, kuigi vastassuunalised. Sellega saab illustreerida Newtoni III seaduse jõudude paari, täpsemalt seda, et kõik jõud, mis on võrdsed ja vastasuunalised, ei ole seda mitte Newtoni III seaduse mõttes.
Jõu ja deformatsiooni samasihilisus tähendab aga seda, et mehaanilise töö valem A=F s cos α, lihtsustub A=F s, sest tingimusel α=0 on cos α=1 ja α=180° on cos α=-1. Mis selle miinusega peale hakata?]
I Keskmine jõud
Jõud, mille me saame ülesande andmetest arvutada, ei sobi pikemalt mõtlemata lihtsustatud mehaanilise töö valemisse panna. Venitamisel pole esimese millimeetrise (ülesande väga jäiga vedru korral pigem mikromeetrise) deformatsiooni tekitamiseks peaaegu üldse jõudu vaja. Kui vedru on juba venitatud (või kokku surutud), läheb iga järgmise millimeetri jaoks vaja üha suuremat jõudu. On hea, et see nii käib, meenutagem kasvõi terve sajandi heaolu ja edukust sümboliseerinud vedruvankrit ja vedrumadratsit.
Muutuv jõud on tähtis ja huvitav teema. Näiteks raketiteaduses on raskusjõud muutuv. Jõud, mille vastu rakettmootorid töötavad, väheneb Maast kaugenemisel vastavalt pöördruudu seadusele. Õhutakistus, mille ületamisele transpordivahendid kulutavad lõviosa kütusest, suureneb kiiruse kasvuga ja ruutvõrdelisus tuleb teatud tingimustel jälle mängu. Ideaalvedru juhtumil kasvab jõud ühtlaselt, mis võimaldab lihtsalt välja arvutada keskmise jõu ja see sobib töö valemisse.
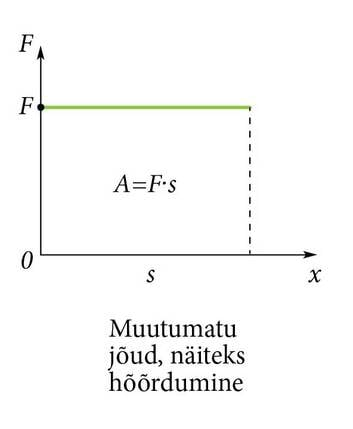
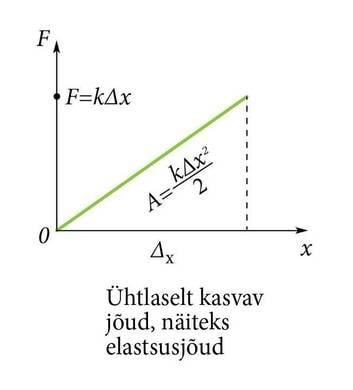
II Töö graafikul
Graafilise esitusviisi korral on lihtne märgata, et ühtlase jõu korral jääb graafiku alla ristkülik, mille üks külg on jõud, teine teepikkus. Ristküliku pindala on töö. Kui graafikualune pindala ei ole jõu muutumise tõttu ristkülik, vaid näiteks kolmnurk, on pindala ikkagi töö. Kolmnurga pindala valemist tuleb murrujoone alla jälle seesama kaks, mis eelmises arvutuses tuli keskmistamisest. Asja ilu on tegelikult selles, et nimetet pindala on alati töö. Keerukalt muutuva jõu korral ei pruugi olla võimalust pindala lihtsa valemiga arvutada, aga see polegi oluline. Kõlbab ükskõik milline pindala leidmise viis ja töö saab ikkagi mõõdetud.
III Üldisemalt
Kui õnnestub muutuvat jõudu matemaatiliselt (valemiga, funktsiooniga) kirjeldada, võib pindaladega jahmerdamisest loobuda ja tehtava töö (muudetava energia) leida integreerimisega. Vedru venitamiseks tehtav töö on nii lihtne nähtus, et tegelikult pole vaja matemaatilist kahurväge välja veeretada. Samas, just lihtsuse pärast kõlbab see meetodi tutvustamiseks päris hästi. Hooke'i vedrus tekkiv elastsusjõud on deformatsiooni lineaarfunktsioon. Töö on selle integraal nullist poole sentimeetrini.
Lisaülesanded
Arvatavasti on pea igaüks kunagi vedru üle kriitilise piiri venitanud, näiteks pastakavedru. Teatud (st vedru ise teab seda) deformatsioonist alates lõpetab Hooke'i seadus toimimise ja vedru venib pikemaks, aga venitamiseks vajalik jõud enam ei kasva.
1) Valmista ise pehmest traadist vedru ja määra selle deformatsiooni kriitiline piir. Kui palju tööd tegid vedru venitamisel kuni kriitilise piirini? Kui palju tööd tegid pärast kriitlise piiri ületamist?
2) Hooke'i vedru salvestab deformeerimisel tehtud töö ja võib pärast ise tööd teha (üleskeeratavad kellad ja mänguasjad). Mis juhtub, kui üle kriitilise piiri venitatud vedru pingest vabastada? Kui palju selline rikutud vedru on energiat salvestanud?
Gaasiseadmete kasutamise reeglites on öeldud, et gaas antakse põletiteni rõhu all 100–200 mm veesammast. Kuidas seda väljendust mõista?
Vladimir Zolotov, Füüsika ülesannete kogu VI–VIII klassile „Eesti Raamat” Tallinn 1965
Rõhk on oma segaste ühikute poolest maailmakuulus füüsikaline suurus. Igal võimalikul ja võimatul tehnika- või teadusalal on omad ühikud. Riigiti kasutatakse erinevaid ühikuid ja mitmed vananenud ühikud on endiselt siin-seal kasutuses.
Rõhu SI ühik on paskal (Pa) ehk njuuton ruutmeetri kohta (N/m2) ehk kg·m-1·s-2. Kuna üks paskal on päris väike rõhk, on laialt kasutuses kPa ja MPa. Tehnikas on arvatavasti tuntuim ühik atmosfäär (atm), mis on võrdne normaal- ehk standardrõhuga, 101325 Pa, st tavalise õhurõhuga. Sünoptikud on püüdnud paskalitele või hektopaskalitele üle minna, aga enamasti ikka pöördunud tagasi ajaloolise õhurõhu ühiku juurde, millimeeter elavhõbedasammast ehk torr (mmHg). 760 mmHg on 101,3 kPa ehk jällegi umbes keskmine õhurõhk. Sellega võiks piirduda.
Kahjuks sellega ei ole sugugi piirdutudud. Lugematutes normides, juhendites, mõõteriistadel, kirjanduses jne tulevad ette: baar (bar), tehniline atmosfäär (at) ehk jõukilogramm ruutsentimeetri kohta (kgf/cm2 või kp/cm2), psi ehk jõunael ruuttolli kohta (lbf/in2), barad (Ba) ehk düün ruutsentimeetri kohata, kip ruutjala kohta (1000 lbf/ft2), tonn ruutjala kohta (võib olla pikk või lühike) ja kindlast veel üht-teist.
Aga on olemas ka hüdrotehnikute ja torustikuinseneride lemmikühik. Rõhku nimetatakse tihti surveks ja mõõdetakse meetrites. Täpsemalt tähendab see veesamba kõrgust, meetrit veesammast (mH2O). Mõnelpool on vana traditsiooni järgides ühikuks in WC (inch of water column) või in Aq. Ühik on temperatuuritundlik, seepärast enamasti standardiseeritud temperatuurile 4°C või 39°F.
Veesamba rõhu võib väga lihtsalt ükskõik millistesse ühikutesse ümber arvutada. Google otsingusõnad „pressure unit conversion” või mõni vingem taskuarvuti äpp telefonis. Võib-olla veelgi lihtsam on näiteks 150 mm kõrguse veesamba rõhk välja arvutada.
Last but not least. Põletisse saadetava gaasi rõhu korral käib jutt muidugi ülerõhust, st rõhk põletidüüsi taga on umbes 1000–2000 Pa ehk 100–200 mmH20 atmosfäärirõhust suurem. Mõnel võõral maal võib ülerõhk olla isegi 4–8 "WC.
Kuidas gaasi lubatud rõhu all põletitesse antakse? Torustikes või balloonides on rõhk palju kõrgem kui põletamiseks, läbipuhumiseks, hingamiseks vms vajalik. Püsiva madala rõhu hoidmiseks on välja mõeldud erakordselt lihtne ja töökindel mehaaniline seade, reduktor (vähendaja). Kodused reduktorid on tavaliselt halli või pruuni värvi karbikud torustikus või gaasiballooni kraani juures. Pärisreduktoril on kaks manomeetrit. Üks näitab kõrget, veel vähendamata rõhku sageli megapaskalites või atmosfäärides. Teine manomeeter näitab vähendatud rõhku ja sellel võib olla mitmesuguseid skaalasid. Enamasti on seal rõhk sobivates ühikutes, aga kindla seadme juures võib olla ka näiteks gaasi kulu (l/min, ft3/h).
Lisaküsimus
Pump võib anda survet kuni kaheksa meetrit. Kuidas seda mõista?
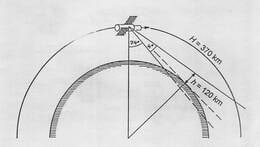
Esimesena pildistas robot. Robootika tänapäevase taseme kõrguselt vaadates on seda automaatkaamerat natuke liiga pidulik robotiks nimetada, aga tõsi on, et inimene seda pilti ei teinud. Rakettidega kosmose vallutamise idee oli 20. sajandi alguseks piisavalt läbi töötatud, et rakettmootorite katsetamisega algust teha. Fotoaparaat ning fotograafiline protsess olid seks ajaks ka sobival kujul olemas ja arenesid kiiresti. Kahjuks oli maailmal muid probleeme lahendada. Raketid loodi alles teise suure sõja ajal ja sugugi mitte kosmoselendude tarvis. Sõjast üle jäänud V-2 raketid kulusid siiski ära kosmoseprogrammide arendamiseks. 24. oktoobril 1946 lasti White Sands'i polügoonilt New Mexicos üles Saksamaalt rekvireeritud rakett, millele oli paigaldatud ümberehitatud filmikaamera. Rakett tõusis 65 miili (105 km) kõrgusele ja kaamera pildistas maapinda automaatselt iga 2 sekundi järel. Raketi allakukkumisel kaamera purunes, aga tugevdatud kestas film viga ei saanud. Eelmine, õhupallilt tehtud pildistamise kõrgusrekord (1935. a – 22 km) oli sellega ületatud peaaegu viis korda. Sündmust peeti siiski pigem fotograafia kui kosmosevallutuse saavutuseks. Paari aastaga ületati ka 100 miili kõrguselt pildistamise piir ja monteeriti juba kokku suuremaid panoraame.
Kui kaugel on kosmos?
Atmosfäär jääb maapinnast kaugenedes üha hõredamaks, kindlat piiri ei ole. See on inimestele hästi teada kõrgeltele mägedele ronimisest ja oli enne kosmoseajastut uuritud õhupallilendudega. Kuhu siis tõmmata kosmilise ruumi piir? Võiks kokku leppida näiteks 100 km peale. See on päris hea pakkumine ja mitte ainult kahe nulli pärast. Umbes sellel kõrgusel asub Kármáni piir, arvutatud selle järgi, et lennuk, mis nii hõredas õhus üritaks aerodünaamilist tõstejõudu hoida, peaks lendama esimese kosmilise kiirusega. Üldiselt on kõik tehiskaaslased sellest piirist palju kõrgemal. Näiteks ISS asub 400 km kaugusel maapinnast, ESTCube-1 tiirutab umbes 650 km kõrgusel.
Esimesed kosmose piirilt tehtud fotod andsid aimu, et maapinna ja atmosfääri vaatlemine ülalt võib abiks olla kartograafiale ja meteoroloogiale. Selleks, et päriselt Maad seirata, jäi hüpetest kosmose piirile ilmselgelt väheks. Oli vaja päriselt orbiidile jõuda. Esimesed satelliitidelt saadud fotod ei olnud kuigi head, aga asi paranes kiiresti. Ja varsti jõudsid orbiidile inimesed. Kas mõni neist oli ka fotograaf?
Sputnik-1, esimene päriselt orbiidile saadetud tehiskaaslane, saatis maale raadiosignaale, aga ei võtnud midagi vastu, ei mõõtnud ega pildistanud. Ometi osutus piiksude vastuvõtt Maal huvitavaks ja kasulikuks. Väidetavalt kerkis globaalse positsioneerimise idee just sellest, et signaalide väga täpsel jälgimisel sai võimalikuks Sputniku trajektoor välja arvutada. Sellest on ainult üks samm selleni, et teadaoleva trajektooriga satelliitidelt tuleva signaali järgi määrata oma asukoht maapinnal. GPS ongi tänapäeval lausa laiatarbekaup.
Miks Juri Gagarin ei pildistanud Maad? Tundub tõesti uskumatu. Ei või olla, et ta lihtsalt ei tulnud selle peale ja kogu lennuprogrammis polnud kedagi, kes selle lihtsa mõtte oleks välja käinud. Võib-olla aitab fotode puudumist seletada kaks mõtet:
- Tänapäevane arusaam pildistamisest on üsnagi erinev sellest, mis toimus pool sajandit tagasi Nõukogude Liidu rangelt salastatud kosmoseprogrammi raames. Gagarin oli nõukogude armee ohvitser, vaevalt oleks talle vastuvõetav kõige ja kõigi valimatu pildistamise idee. Tehti ikkagi ainult seda, mida programm ette nägi. Meie võime mõelda: Selfi Maaga ja kohe Insatasse üles, kuidas saab sellise võimaluse maha magada? Gagarin poleks sellest lausest arugi saanud.
- Nagu aastaid hiljem välja tuli, oli suure saladuskatte all toimunud esimese inimese orbiidile viimise programmi planeeritud pettus. Kuna Gagarini kosmosekapsel ei olnud projekteeritud pehmeks maandumiseks, pidi kosmonaut maapinnale jõudma eraldi langevarjuga, aga seda tõsiasja taheti varjata. Ei olnud ka päris täpselt teada, kus maandumine aset leiab, kas kosmonaut ja kapsel satuvad lähestikku ning kas lend üldse õnnestub. Arvatavasti ei ole sellistes oludes fotoaparaat kõige parem kaaslane.
Lennu ajal tehtud fotode puudumine on muidugi andnud hoogu vandenõuteooriatele, kuni selleni, et Gagarin üldse kosmoses ei käinudki. Samas on sarnaseid jutte põhjustand ka see, et Apollo kuulendudelt on pilte väga palju, justkui liiga palju. Võta siis kinni.
| Kuulsaks on saanud esimese täisorbitaalse lennu teinud NASA astronaudi John Glenni fotod kosmosest. Ta kasutas tavalist 35mm filmiga fotoaparaati. Fotod ilmusid hiljem populaarses raamatus „Exploring Space With a Camera”. | Madalatelt orbiitidelt ei ole võimalik Maad korraga kaadrisse saada. See on sama lootusetu, kui üritada selfi tegemist ninaotsast poole sentimeetri kauguselt. Pilt Maast kui helesinisest pallist (Blue Marble) ilmus 1972. aastal, see on pildistatud umbes 45000 km kauguselt. Pilt on saanud väga kuulsaks ja hiljem palju kordi üle pidistatud mitmetelt satelliitidelt. |
Seitsmekümnendate alguseks oli juba päris selge, et Maa jälgimine kosmoset on väga praktiline ja kasulik tegevus. Kartograafia ja meteoroloogia huvidega ühinesid kiiresti põllumajandus, geoloogia, vulkanooloogia, metsandus, linnaplaneerimine, luure, haridus jpm. Algatati mitmed spetsiaalsed seiresatelliitide programmid, näiteks Landsat ja Meteosat.
1136. 1) Magnetvoog sirgmagnetis ja hoburauakujulises magnetis (kooli tüüpi) on 4,0·10-5 ja 5,0·10-5 Wb. Määrake mõlema magneti magnetvälja induktsioon. Puuduvad andmed leidke mõõtmisega. V. Demkovitš, Füüsika küsimuste ja ülesannete kogu keskkoolile - „Valgus” Tallinn 1969
A) Sirgmagnetid
Sväike=8,5X2,2mm=18,7mm2=0,0000187m2
Ssuur=20,4X10,5mm=214,2mm2=0,0002142m2
Φ=4,0·10-5Wb
B-?
B=Φ/S
Bväike=4,0·10-5Wb / 0,0000187m2 = 2,1T
Bsuur=4,0·10-5Wb / 0,0002142m2 = 0,19T
Vastus: Arvutada võib muidugi kõike, aga ei ole võimalik, et need magnetid tõesti nii vinged on.
B) Kodune ülesanne Otsige kooli tüüpi hoburaudmagnet üles, mõõtke see ära ja arvutage magnetinduktsioon välja. Kas tundub usutav?
2) Määrata nelinurkset tasapinda, mille küljepikkused on 30 cm ja 50 cm, läbiv magnetvoog. Magnetiline induktsioon pinna kõigis punktides on 2,0 T. Magnetilise induktsiooni vektor moodustab pinnanormaaliga järgmised nurgad. 1) 0°, 2) 45°, 3) 90°. 0,3; 0,21 ja 0 Wb.
a=30cm=0,3m
b=50cm=0,5m
S=ab=0,15m2
B=2,0T
β=0 kuni 360°
Φ=BS cosβ
1969. aastal see vaevalt võimalik oli, aga praegu võib teise küsimuse vastamiseks arvuti appi võtta. Siis pole ka põhjust piirduda kolme nurgaga ja võib pinnanormaaliga B-vektrorile terve ringi peale teha.
Oodatult on tulemuseks koosinuskõver. Teatud nurkade korral on magnetvoog negatiivne. Kas oskame nende miinusmärkide füüsikalist sisu seletada?
Filmides juhtub vahest, et liikuvate sõidukite rattad pöörlevad tagurpidi või seisavad paigal. Tegelikult pöörlevad rattad ikka õigetpidi, aga miks see siis filmis valesti paistab?
Liikuvad pildid (kino, videoprojektsioon, arvutiekraan jms) petavad meie silmi ja veel enam aju kiire pildivahetusega. Kino loob liikumise illusiooni vilgutades ekraanile 24 kaadrit sekundis ja kaadrivahetuse ajal on ekraan hoopis pime. 24 fps (frames per second – kaadrit sekundis) ei ole tänapäeval enam päris täpselt kõigi liikuvate piltide korral õige, aga kuna see kino kuldajastust pärinev standard on üsna levinud praegugi, siis jääme selle juurde. Inimese silmad ja aju ei jõua nii kiirele vilkumisele reageerida ja nii sulavad järjestikused kaadrid meie jaoks kokku üheks liikuvaks pildiks. Eks ole ju kino tegelikult üks suur pettus, mitte ainult tehnilises, vaid enamgi veel psühholoogilises mõttes.
Viie kodaraga ratas on pärast pöördumist 72° võrra jälle samas asendis. Tegelikult on ratas samas asendis iga täispöörde järel, aga kui kodarad on piisavalt sarnased, siis näib ratas olevat samas asendis iga viiendikpöörde järel. Filmimisel tehakse 24 pilti sekundis ja kui ratas pöördub 1/24 sekundi jooksul just 72°, siis satub ta igasse järgmisesse kaadrisse justkui samas asendis. Filmi esitamisel on kõigis järgnevates kaadrites samasugune ratas ja see paistab olevat paigal, kuigi tegevus, mis ümberringi käib, on muutuv. Kui ratas jõuab enne järgmise kaadri võtet pöörduda natuke rohkem, näeb see ekraanil välja aeglase edaspidi pöörlemisena. Kui aga pööre ei jõua 72 kraadini, siis tekib näiv tagurpidi pöörlemine.
Kui kiiresti peaks auto sõitma, et filmile jääda näivalt seisvate ratastega? Sõltub ratastest, võtame arvutada viie kodaraga ratta, mille läbimõõt on 50 cm.
d = 0,5 m
C = πd = 1,57 m
l = C/5 = 0,31 m (auto sõidab edasi viiendiku ratta ümbermõõdust, kui ratas pöördub 72°)
t = 1/24 s (aeg järgmise kaadrini)
––––––––––––––
v = l/t = 7,4 m/s =27 km/h
Kiirus võib olla ka selle täisarvkordne, sest näiteks 144° pööre annab jälle sarnase kodarate asendi.
Lisaülesanded
1. 19. sajandi lõpul, kui filmimine tehniliselt võimalikuks sai ja populaarseks muutus, olid suurlinnade tänavaid täitvate hobusõidukite esimesed rattad väiksemad kui tagumised. Selle väga populaarse coupé esirataste läbimõõt on 33", tagumistel 44".
Kui suure kiirusega peaks sõitma, et esiratas paistaks filmil seisvat paigal. (Kaadrisageduseks võiks olla 24 fps, kuigi tol ajal ei tehtud sellest kuigi suurt numbrit.) Kuidas näib siis pöörlevat tagaratas?
2. Miks olid ja on praegugi paljude vankrite ja tõldade esirattad väiksemad kui tagumised? Muidugi, Jänku-onu vastab: „Kui sa õige hoolega vaatad, siis vankri tagumised rattad käivad kiiremini ringi kui esimesed ja kui tagumine ratas jõuab esimesele järele, siis kukub nende vahelt kuldraha maha.” Kas selle, kasumlikkusele rõhuva vastuse kõrval on teada ka mõni tehniline põhjendus? Autodel on ju ühesuurused rattad, aga näiteks traktoritel jälle erinevad.
Kui suur on kogutakistus, kui skeemil näidatud viisil on ühendatud kolm takistit? R1=10Ω, R2=10Ω, R3=4Ω.
[Hea ülesanne, võtab kokku mitemeid põhikooli elektriteemasid. Takistuse mõiste, tähis, ühik. Vooluring ja selle osa. Takistid ja ühendusviisid. Kogutakistus. Lihtne on sellele vastata, kui kõik on enne läbi harjutatud. Tihti on seesama küsimus eraldi või pikema arvutusülesande osana põhikooli lõpueksamis ja gümnaasiumi vastuvõtutestides. Äraarvamise või välistamisega siin hakkama ei saa ja seepärast väga paljud kahjuks punkti ei teeni.]
Lisaülesanded.
1) Ülesannet on lihtne keeruliseks ajada. Joonis jääb samaks, muudame takistusi, jätame ära valikvastused ja küsime kogutaksitust:
A) R1=20Ω, R2=10Ω, R3=4Ω.
B) R1=20Ω, R2=20Ω, R3=4Ω.
C) R1=20Ω, R2=20Ω, R3=20Ω.
D) R1=10Ω, R2=20Ω, R3=4Ω.
E) R1=200Ω, R2=10Ω, R3=4Ω.
F) R1=200kΩ, R2=10Ω, R3=4Ω.
G) R1=0,01Ω, R2=10Ω, R3=4Ω.
H) R1=10Ω, R2=10Ω, R3=400kΩ.
2) Lisame vooluallika ja arvutame pinged kõigil takistitel.
3) 4) jne Lisame andmetesse vooluallika sisetakistuse. Asendame ühe takisti juhtmepooli või kondensaatoriga. Vooluallikas võib anda vahelduvpinget. Jne.
On olemas organisme (näiteks klaasiksääse vastne jt), keda vees nende läbipaistvuse tõttu pole näha. Miks paistavad nende silmad mustade punktidena?
Enn Pärtel, Füüsika VIII kalssile, Valguse peegeldumine ja murdumine, probleem nr 9.
Tegelikult ei ole klaasiksääse vastsed päris nähtamatud. Nende keha on tõesti üsna suures osas läbipaistev, st valgus peegeldub ja neeldub vähe ja ka murdumisnäitaja on neil elukeskkonnale lähedane. Heas valguses ja ühtlasel taustal on vastsete veidi pruunika tooniga keha siiski päris hästi jälgitav ja jääb ka pildile. Veekogudes, taimede vahel ja mudase põhja kohal, õnnestub neil päris hästi peitust mängida ja vähemalt osa neist jäävad märkamatuks kaladele, kes sääsevastseid hea meelega söövad. Silmad on mustad selleks, et valguse kantavat infot vastu võtta. Kui valgus silmast täielikult läbi läheks, ei jääks sellest ka mingit jälge, valgustundlikus rakus ei toimuks mingit keemilist muutust ja nägemisaistingut ei tekiks.
| Läbipaistvaid asju on teinekord tõesti raske märgata ja eriti hästi saab neid peita sobiva murdumisnäitajaga keskkonda. Klaasi murdumisnäitaja erineb oluliselt õhu murdumisnäitajast, sestap on läbipaistvad klaasid õhus hästi nähtavad ... | ... aga näiteks klaasist asi ei ole peaaegu üldse nähtav toiduõlis või soolvees. Tähelepanelik vaataja leiab õlisse peidetud klaasi siiski pildilt üles, sest murdumisnäitajad päris võrdsed ei ole ja klaasi põhja alla on õli valamisel pidama jäänud mõned õhumullid. |
Lisaküsimus
Klaasiksääse vastse kehas on peale silmade veel kaks hästi nähtavat neerukujulist organit, mis võivad olenevalt valgusoludest paista tumedad või hõbedased. Neid väga pisikesi õhukotte kasutab vastne horisontaalse asendi hoidmiseks ja vees üles-alla liikumiseks. Mustad silmad on seletatavad, aga miks ei saa õhukotid olla läbipaistvad?
Kui keegi tõesti soovib olla nähtamatu, tuleb kõne alla mitu erinevat trikki.
Võib proovida olla läbipaistev, nagu klaasiksääse vastne. Kui olla piisavalt väike, on lootust, et sind keegi ei näe ja kui isegi näeb, ei pane tähele või ei tee välja.
Keerukam on olla nähtamatu, kui oled suur ja ei paista läbi. Võib proovida maskeerumist, peegeldada samu värve ja mustreid, mis ümbrus ja taust. Hästi oskavad seda sõjaväelased, kes riietuvad lapilistesse vormidesse, mille põhitoonid sobivad maastikuga ja riputavad enda ja oma tehnika külge kohapealt korjatud oksi või heina. See ei ole küll päris nähtamatuks muutumine, pigem on tegu vaataja nägemismälu ärapetmisega. Nähtamatuse asemel võiks siis pigem öelda märkamatuks jäämine. Kahjuks tuleb seejuures asukohta vahetades alati arvestada ümbermaskeerimise vajadusega.
Muidugi, võib ka kasutada infotehnoloogia abi:
| Richard Hammond sõitis Top Geari erisaates „50 aastat Bondi autosid”, Ford Transiti kaubikuga, mis oli „nähtamatuks” muudetud külgedele ja taha paigutatud ekraanidega, kuhu kuvati vastaskülje kaamerast võetud pilt. Saateformaadile omaselt sai palju nalja ja võis jääda mulje, et katse kukkus läbi. Tehnika vajaks muidugi arendamist, aga saatelõigus on üsna mitmes kohas näha, et auto tõepoolest maskeerub ehmatavalt hästi. Eriti hästi tuli nähtamatus välja tagantvaates. | Tanki külge kinnitatakse paneelid, mis saavad kiiresti oma temperatuuri muuta. Nii et tanki saab teha sellise temperatuuriga nagu on taust ning soojusele reageerivatele mistahes relvadele muutub asi enam-vähem nähtamatuks. |
Rohkem pärisnähtamatuse moodi oleks, kui saaks oma keha või riietuse värve vastavalt olukorrale muuta. Kehavärvi muutjatest on tuntuimad mõned kala- ka kameeleoniliigid. Kameeleonid küll kasutavad vahest oma erilist oskust peitumiseks, aga samavõrra või rohkemgi suhtlevad nad värvivahetusega omavahel. Kunstliku kameeleoninaha väljatöötamisega tegeldakse. Praegu veel värvi muutvat maskeerimisriietust poest osata ei saa, aga arengud on lootustandvad.
Põhimõtteliselt on ka võimalik seljatagant tulev valgus teelt kõrvele kallutada ja vaataja poole liikuvad kiired jälle kokku viia. K.Tarkpea ja H.Voolaiu elektromagnetismi õpik räägib sellest niimoodi:
Alustuseks on ehk paslik mainida, et ei ole hea mõte saada päriselt nähtamatuks, nagu mõnes raamatus või filmis seda kujutatud on. Miks? Lihtne – kui keegi on nähtamatu, siis on nähtamatud ka tema silmad, st tema silmaläätsed ei murra valgust ning tema võrkkest ei neela valgust. Järeldus on ilmne – nähtamat inimene on ühtlasi pime. See arvatavasti nullib kõik eelised, mis nähtamatuks olemine muidu anda võiks.
Vaadake joonist 4.35 ning proovige vastata küsimusele, mida näeb vaatleja, kui ta vaatab suunaga vasakult paremale punase valgusallika poole? Õige vastus on, et sedasama üksikut valgusallikat. Sest silm ei saa kuidagi aru, kas valguskiir on vahepeal mõne käänu sisse teinud, kui tema lõpp-suund teekonna lõpus on samasugune, kui alguses - kui suund on sama, siis koonduvad nad ikkagi punktiks, mis on valgusallika kujutiseks silma võrkkestal. Kui tõdeme, et igasugust objekti võib vaadelda kui punktvalgusallikate kogumit ja kui sfääriline objekt käitub niimoodi suvalisest suunast temale langevate valguskiirtega, siis ongi küsimus „kuidas saada nähtamatuks“ põhimõtteliselt vastatud – suur sfääriline objekt silma ja valgusallika vahel on nähtamatu.
Aga panna valguskiirt sellist käänakut tegema? Jah, see on keeruline koht. Sest valguskiired ei muuda niisama heast peast oma suunda. Ning te võite kontrollida - optiliselt hõredamast keskkonnast (õhk) optiliselt tihedamasse keskkonda (sfäär) liikudes murduvad nad “teistpidi”.
Edasises arutluses peaksime eristama kahte olukorda. Ühel juhul asetseb vaatleja objektist nii kaugel, et nägemise stereoefekt ning võimalikud erinevated rakursid (liigutad pead ühele ja teisel poole) ei mängi erilist rolli. Teisel juhul on objekt vaatlejale lähedal.
Kaugel asetseva objekti “nähtamatuks” tegemiseks võime objekti ette paigutada seda varjava ekraani, millele kuvatakse pilt, mis on vaatlejat poolt vaadates objekti taga (J.4.36). Nii et objekti poole vaadates näeme seda, mis on objekti taga (ja mis tegelikult ongi ju nähtamatuse definitsioon). Aga vaatleja peab siis olema ühes kindlas punktis ning kui objekt liigub, siis peab muutuma ka ekraani asukoht ja pilt sellel … põhimõtteliselt on see nagu suure pildi taha varjumine.
Nähtamatuks tegeva sfäärilise kookoni valmistamiseks (J.4.35) peaksime kasutama eriliste omadustega materjale – metamaterjale - mis on parajasti “kuum teema” teadusajakirjanduses. Selgub nimelt, et metamaterjalide murdumisnäitaja on negatiivne ning joonisel J.4.35 kujutatud olukord on põhimõtteliselt võimalik.
| Eksperimentaalselt demonstreeriti nähtamatuks tegeva mantli võimalikkust esmakordselt 2006.aastal Duke’i Ülikoolis. Kui vasakul pildil liigub keralaine vabalt, siis paremal pildil on tema teele asetatud silindriline takistus. Näeme, et pärast sellist takistust moodustuvad uuesti keralaine lainefrondid. Eksperiment on tehtud infravalgusega. | J.4.37 Sellised näevad välja metamaterjalid. |
Miks on negatiivne murdumisnäitaja eriline nähtus?
Aga eranditult kõigi “normaalsete” materjalide murdumisnäitaja on positiivne. Ja metamaterjalid ei ole materjalid selle sõna tavalises mõistes, pigem on tegemist ülitiheda kärgstruktuuriga (J.4.37). Ja tõelise nähtamatuks tegeva mantlini on teadlastel veel väga pikk tee minna.
Jõud 3,2·10-4N mõjutab laetud kondensaatoris pisikest, 1,6·10-10C laenguga vedelikutilka. Kui suur on elektrivälja tugevus?
Lihtne küsimus, nn ühe valemi ülesanne.
E=F/q=3,2·10-4N/1,6·10-10C=2·106V/m
Keerukam on vastata lisaküsimustele, mis peavad paratamatult kerkima:
1) Miks küsitakse just sellise laengu ja jõu kohta? Hea küsimus! Võib-olla selle pärast, et just praegu koguvad miljardid tinditilgad (umbes antud laenguga) elektriväljas (umbes arvutatud tugevusega) kiirust või muudavad liikumsisuunda (umbes nimetatud jõu toimel). Nii loovad meile pilte ja dokumente tindiprinterid.
2) Kust ilmub välja elektrivälja tugevuse ühik, volti meetri kohta (V/m)? Väga hea küsimus! Tõesti, kui vaadata arvutust, siis sealt tuleb välja ühik njuutonit kuloni kohta (N/C). Samas on igaühele, kes umbeski teab mismoodi elektrivälja tekitatakse, mis ühik on volt ja kuidas elektriväli laetud osakeste või laenguga kehade liigutamisel töötab, selge, et V/m kohta on hea ühik. Ja ikkagi peab olema võimalik need erinevad ühikud ka pliiatsiga paberil sehkendades üksteiseks teisendada. Võib-olla oleks veel parem mõlemad üle viia SI põhiühikutele. Dimensioonavaldis peab tulema sama, ükskõik kummast otsast (V/m või N/C) alustada. Tasub proovida, sest see õpetab mehaanika ja elektromagnetismi vahel seoseid nägema.
3) Kas kaks miljonit volti meetri kohta on suur väljatugevus? Raske öelda. Kui meile oleks antud näiteks pikkus, siis igapäevasest kogemusest julgeks kohe arvata, et sentimeeter on lühike, meeter on pikk. Kilomeeter on veel pikem, millimeeter on veel lühem. Kuigi see on teatud määral suhteline, siis pikkust (ka aega, massi, isegi ruumala ja pindala) on võimalik subjektiivselt hinnata, kui jääda mikromeetrist üles- ja valgusaastast allapoole. Väljatugevus... Tõesti raske ette kujutada, aga võiks hinnata teada-tuntud pingete kaudu.
Kui sülearvuti aku pinge on näiteks umbes 20V, siis saaks sellega tekitada kondensaatoris, mille plaatide vahe on 1m, elektrivälja tugevuse 20V/m. Muidugi ei ole sellisel kondensaatoril mingit mõtet. Kondensaatori plaatide vahe peab olema väike, näiteks 1mm. Siis on väljatugevus 20kV/m.
4) Kuidas tindiprinter tilkadest pildi teeb? OK, see on hea küsimus, aga elu on alati keerulisem kui füüsika ülesanne.
Võimalik, et sinu mitte-just-väga-odav tindiprinter liigutab prindipead lehe kohal ja tekitab termiliselt või piesoelektriliselt just sobivatel hetkedel tinditilga. Tilkade läbimõõt on tavaliselt alla 100 mikromeetri ja et vähegi vastuvõetava ajaga pilt valmis saada, tuleb tekitada vähemalt 3000 tilka sekundis. Parem oleks üle 6000 sekundis igast avast ja trükipeas võiks olla näiteks 400 ava.
Võimalik, et sinu oh-see polegi-nii-kallis tindiprinter liigutab prindipead paberi kohal ja tekitab pideva tinditilkade joa. Osa neist tilkadest on laetud. Laadimata tilgad paberini ei jõua ja lähevad kõik taaskasutusse. Laetud tilgad suunatakse elektrivälja abil teelt kõrvale just sellel hetkel ja just selles koguses, mis on vajalik pildi loomiseks. Ülejäänud laetud tilgad lähevad samuti taaskasutusse.
5) Miks on tindiprinterid odavamad kui laserprinterid? See ei ole füüsikatunni küsimus. Asi on ärimudelis. Tindiprintereid müüakse odavalt, aga nende pidamine, varustamine tindikassettidega ja teinekord isegi sobiva paberiga, on sellevõrra kallim. Täpsemat seletust tasuks küsida majandusõpetuse tunnis.
Mõõda ära, kui suur on paberi ja pliiatsitera vaheline hõõrdetegur?
Katsekehad: paber ja pliiats. Mõõteriistad: joonlaud.
Ülesanne füüsikaolümpiaadi eksperimentide hulgast.
Võiks alustada dünamomeetriga pliiatsit mööda paberit vedades, aga mõõteriistade nimekiri seda võimalust ei anna. Proovime jõudu komponentideks jagada.
Pane paber siledale kõvale alusele ja pliiats sellele püsti. Vajuta tera kergelt vastu paberit. Jõud (F), millega pliitas mõjutab paberit, tekitab toereaktsiooni (N). Need kaks jõudu on vastasuunalised, võrdsed ja mõjuvad mõlemad piki pliiatsit. Jõudude resultant on null, pliiats ja paber püsivad vatavalt Newtoni esimesele seadusele paigal (või liiguvad ühtlaselt ja sirgjooneliselt). Tasub märkida, et tegu pole Newtoni kolmanda seaduse jõudude paariga. Kolmanda seaduse jõud peavad mõjuma erinevatele kehadele ja peavad olema sama liiki. Nüüd katse juurde.
Kalluta pliiatsit aeglaselt kõrvale nii kaugele kui võimalik. Sel hetkel, kui pliiats näpu alt minema lipsab, on pliiatsile mõjuva jõu üks komponent (Fp – piki paberit) võrdne hõõrdejõuga (Fh). Teine komponent on nagu ikka toereaktsioon (N). Mõõda pliiatsi asend sel hetkel. Mõõta võib nii pliiatsi otsa kõrguse kui ka selle projektsiooni paberile. Pliiatsi pikkus võib ka vajalik olla.
Katsest on näha, et jõuvektorite kolmnurk on sarnane pliiatsist, paberist ja joonlauast moodustuva kolmnurgaga. Hõõrdetegur on jõudude suhe, mille saab arvutada sarnasest kolmnurgast.
Pane tähele, et tegemist on seisuhõõrdega. Kui pliiats juba libisema hakkab, väheneb hõõrdetegur veidi. Just seepärast on pliiatsi sõrme alt ära libisemine üsna äkiline. Katse tuleb hästi välja siledal ja kõval pinnal. Näiteks puidust laud osutub liiga pehmeks, katsetulemused hajuvad palju ja sõltuvad sellest, milline on katsepunktis puidu süü ja libisemise suund.
Lisaküsimused
Kui katseseade on juba kord üles seatud, on üsna odav ka teisi hõõrdetegureid mõõta. Kõigepealt vaata, kas pliiatsi teises otsas juhtub olema kustukumm. Otsi veel erinevad kirjutusvahendeid ja muid pulki. Proovi teistsugust paberit, näiteks liivapaberit.
Kas hõõrdetegurit saab sel moel määrata ka kaaluta olekus? Aga kiirendavas rongis?
Millisel füüsikalisel nähtusel põhineb käteräti kasutamine?
Oodatav vastus, mida mõnikord nimetatakse ka õigeks vastuseks, on – kapillaarsus. Pole sugugi halb vastus, kuigi sama hästi võiks öelda – märgamine, adhesioon, molekulaarjõud või elektromagnetiline vastastikmõju. Siiski on üsna vaimuvaene arvata, et käterätiga kuivatatakse käsi ja mitte midagi muud teha ei saa ega tohi.
Lisaküsimus, mis lõpuks osutub põhiküsimuseks
Leidke igapäevaelust käteräti kasutusviise, mis ei põhine kapillaarsusel või kus kapillaarsus ei ole kõige tähtsam. Millised nähtused neis näidetes mängu tulevad?
Jaan Paaver: Täna meenutasime just tööl Hennu takistuseta langeva vihmapiisa ülesannet. Me oleme seda tunnis proovinud. Tulemused on vastakad ja tundub, et suures klassis kipub selline mitmeharuline ja palju küsimusi kergitav ülesanne jääma väikese hulga huviliste arutleda. Teistele peab siis tegevust leidma ja nad tunnevad end ikka veidi halvasti.
Svetlana Ganina: Jah, see ongi selle nö "terve klassiga arutamise" efekt, kaasa tulevad kas kõige aktiivsemad, nutikamad või need, kellele just see teema korda läheb. Soovitada võiks seda, et enne ülesande tutvustust palub õpetaja moodustada klassis paarid-kolmikud, just väiksed rühmad. Ja las õpilased valivad seltskonna ise. Siis anda ülesanne ja las nad püüavad arutada. Selleks ajaks võib isegi klassist välja minna, et nende arutelud oleksid julgemad. Siis nt 5-7 min pärast tuleb õpetaja tagasi ja nt annab vihje. Pärast seda las nad püüavad/pusivad veel mõda aega. Pärast seda võib anda sõna rühmale, kes arvab, et sai hakkama. Kui te pole vastusega rahul, siis läheb sõna järgmistele. Kui keegi ei oska, siis õpetaja selgitab. Ja kui nad ise juba mugavas seltskonnas pusisid, siis kindlasti kuulavad tähelepanelikumalt mis see "õige" lahendus on. Esimene kord ei pruugi välja tulla, teine kord on nad juba osavamad ja kolmas/neljas hakkavad ise selliseid ülesandeid paluma :)
Tuntud katse teadusteatritest. Võtame suurema suuga pudeli, viskame sellesse (ettevaatlikult) põleva paberi ning asetame siis pudeli suule veega täidetud õhupalli. Õhupall imetakse pudelisse. Miks?
Selge on see, et õhupall läheb pudelisse siis, kui õhupallile ülalt ja alt mõjuv rõhk on erinevad (neid asju õppisime mehaanika kursuses). Et õhurõhk katse käigus ei muutu, siis saab rõhu erinevuse põhjuseks olla vaid rõhu vähenemine pudelis.
Tihti seletatakse seda katset nii, et pudelis olev õhk paberi põlemisel tekkiva soojuseneriga toel soojeneb ja paisub, pärast paberi kustumist jälle jahtub ja tõmbub kokku. Kuna muna katab terve pudeli suu nii, et õhk pudelist välja pääseb, aga välisõhk pudelisse ei pääse, siis rõhk pudelis väheneb ja muna "imetakse" pudelisse. See on füüsikaline seletus.
Vahel ka räägitakse et küünal "kulutab põledes kogu hapniku ära" ja alarõhk tekib just sellest. Põlemine on keemiline protsess.
Milline seletus on õige?
Teeme kontrollkatse. Paneme põleva küünla veeanumasse püsti ning asetame kummuli selle peale pudeli. Põleva paberi rolli täidab nüüd küünal ja õhupalli rolli anumas olev vesi.
Kui õhupalli pudelisse minek oleks põhjustatud õhu soojenemisest ja jahtumisest, siis peaks vesi sellises katses pudelisse tõusma pärast küünla kustumist. Hapniku "ära põlemise" teooria ennustab, et vesi tõuseb pudelisse nii kaua, kui küünal põleb, pärast seda tõus lõpeb.
Katses näeme, et vedeliku tase tõuseb ka siis, kui küünal põleb ning taseme tõus jätkub pärast küünla kustumist. Sellist tulemust ei ennustanud kumbki teooria.
Võtame appi keemia. Põlemine on keemiline protsess ja keemia annab selle teooria arendamiseks tööriistad. Eeldame, et küünlas põleb parafiin. Siis saame kirjutada
C31 H64 + 47O2 → 31CO2 + 32H2O
Seega tekivad küünla põlemisel süsinikdioksiid ja veeaur. Aga kui suur on reaktsioonisaaduste ruumala? Keemiast teame, et ühe mooli ükskõik millise gaasi ruumala standardtingimustel on alati ühesugune. Parafiini põlemisel reageerib 47 mooli gaasi ja tekib 63 mooli gaasi, nii et gaasi ruumala reaktsioonis hoopis suureneb.
Paberiga on samamoodi. Siis põleb tselluloos:
C6H10O5 + 3O2 → 6CO2 + 5H20
või mittetäielikul põlemisel
2C6H10O5 + 5O2 → 5CO + CO2 + 5H20
Gaasilise aine moolide arv kasvab, järelikult põlemisel gaasi ruumala hoopis kasvab?
Kui teise katse videot tähelepanelikult uurida, siis võib märgata, et pudeli siseküljele tekivad veepiisad. Reaktsioonis eraldunud veeaur kondenseerub pudeli seinale, mistõttu põlemise käigus gaasi normaaltingimustele vastav ruumala väheneb ja veetase pudelis tõuseb.
Pärast küünla kustumist gaas jahtub ja see on põhjus, miks veetase pudelis tõuseb ka mõnda aega pärast küünla kustumist.
On ka teada, et süsinikdioksiid lahustub üsna hästi vees ja osa gaasi võib niimoodi kaotsi minna. Aga see on pigem väiksem efekt.
Seega on vee kondenseerumine ning gaasi kokkutõmbumine jahtumisel kaks peamist põhjust, miks õhupall pudelisse läheb. Lisaks füüsikale tuleb appi võtta ka keemia.
Vahel räägitakse, et peegel vahetab ära parema ja vasaku külje Tõepoolest, peeglit vaadates näib, nagu tõstaks peegelpilt vasakut kätt, kui ise peegli ees tõstad paremat kätt. Veidi asja üle järele mõeldes saab selgeks, et kujutisel peeglis on ära vahetatud esimene-tagumine, mitte aga parem-vasak pool. Selles veendumiseks tasub kasvõi tähele panna, et kõik, mis on inimesest vasakul, on ka peegelpildis inimesest vasakul, samas peegli suunas või sellest eemale liikudes teeb kujutis peeglis täpselt vastupidi.
Segadus tekib sellest, et oma peegelpilti mõtestades me pöörame ennast mõtteliselt ümber vertikaaltelje, st vahetame ära nii parema-vasaku külje kui ka esimese ja tagumise poole, seda paneb meid tegema reaalse maailma kogemus teiste inimestega suhtlemisel.
See, mida inimene tajub peegelpildis oma parema käena, on tegelikult vasaku käe kujutis. Peegel ei tee paremast vasakut ja vastupidi. Selle mõistmiseks pöörake ennast niimoodi paremale, et vasak käsi jääb peegli lähedale. Te saate aru, et eespool mainitud mõtteline pööre paremast vasakuks ei oma enam mingit loogilist sisu.
Sai selgemaks?
Mida hapnikurikkam atmosfäär, seda kiirem põlemine. Hapnikuvaeses keskkonnas ei ole põlemine võimalik.
Viitame siin mõnele eksperimendile, mis on rohkem või vähem käepärased ja mis õpetavad meile hapniku ja põlemisega seotud looduse seaduseid.
| Väikses kinnises ruumis ei saa põlemine kuigi kaua kesta - põlemiseks tarvilik vaba hapnik saab lihtsalt otsa. | Küünla põlemine mikrogravitatsioonis. Põlemiseks vajalik keskkond on justkui olemas, aga puudub gravitatsiooni põhjustatud konvektsioon, leek jääb iseenda tekitatud CO2-rikkasse keskkonda ja kustub. |
Hapniku pealevoolu on võimalik suurendada, kui suunata põlemise koldesse hapnikurikka õhu voog. Puhast hapnikku on võimalik gaasilisel kujul saada firmadest nagu AGA üsna odavalt.
Kõige intensiivsem hapniku pealevool tekib siis, kui kasutada vedelat hapnikku.
Kuidas saada hapnik vedelaks?
Põhimõte on lihtne. Kuna hapniku veeldumise temperatuur on kõrgem, kui lämmastikul, aga vedel lämmastik on üsna vabalt kättesaadav, siis tuleb tekitada olukord, kus hapnik gaasina viiakse võimalikult efektiivselt vedela lämmastiku temperatuurile. Kõrvalolevas videos näidatud nipp on selleks ülimalt sobiv.
Vedelas hapnikus põlevad asjad väga intensiivselt, nagu on näha alljärgnevates videotes.
Kui teil on juba olemas vedel hapnik, siis võite teha kõrvalepõike materjalimaailma. Nimelt on hapnik paramagneetiline ja seda on võimalik magnetiga mõjutada. Nagu näidatakse alljärgnevates videotes.
Soovitame sirvida e-õpiku repositioorimus olevaid katseid (vt nupp "Katsed e-õpiku repositooriumis" selle alajaotuse lõpus).
Tee ära
Uuri videot. Selgita katset füüsikaliselt. Soovi korral ehita seade, ent ära kasuta selleks katsekomplekti CD-ümbrist.
Komplekt koosneb erinevatest magnetalusel läätsede mudelitest ja peeglitest, prismast, ristkülikust, poolringidest, lainejuhist ning magnetalusel optiliste süsteemide skeemidest. Eraldi tuleb hankida laserkiirte kimp.
Komplekti on lihtne kasutada, kui klassis on olemas metalltahvel. Komplekti on võimalik anda ka õpilastele isiklikuks kasutamiseks või rühmatööks. Teha saab praktiliselt kogu õppekavas nõutud kiirteoptika, nagu loodetavasti näha ka järgnevas videos:
Ainus puudus mis komplektiga tutvudes välja tuli on see, et optiliste süsteemide pildid, mis magnetitega tahvlile käivad, ei ole alati päris tahvli vastas ning tekkivate väikeste ebatasasuste taha kipub laserikiir "kinni jääma" ja katkema, seda on ka videos näha.
Demokomplekt sai meie käest hindeks "5-", kus miinus tuleb just nende ebatasasuste pärast. Aga kindlasti julgeme soovitada. Ka hinna-kvaliteedi suhe on meie hinnangul hea.
Väga heaks hindame ka laserkiirte kimbu tekitaja.
Huvi korral saab komplekti hankimise kohta uurida total.ee-st.
Valguse interferents on üks neid teemasid, kust veenvaid eksperimente on väga raske korraldada. Soovitame katsekomplekti, mis on tõepoolest hea interferentsinähtuste demonstreerimiseks.
Üldvaade ja sissejuhatav video:
Valik katseid mida komplektiga teha saab:
Arvame, et komplekt on hea ja mõnus kasutada - kõik neil piltidel näidatud eksperimendid on võimalik püsti panna sekunditega.
Komponentide kvaliteet on üldiselt hea. Veidi jätab soovida difraktsiooni uurimiseks mõeldud maskide komplekt.
Edasimüüja Eestis: total.ee
Tutvustame siin meie esimest käed-külge katsekomplekti, millega saab läbi uurida kogu põhikooli 8.klassi valgusõpetuse. Idee järgi on need katsekomplektid kasutamiseks 1-3 õpilasele, tööd viiakse läbi frontaalselt. Iga katsekomplekti hind on ca 15 EUR.
Alljärgnevad näited katsete kohta, mis selle katsekomplektiga teha saab, on valgusõpetuse esimesest osast, kus räägime valgusallikatest, valguse sirgjoonelisest levimisest, peegeldumisest ja murdumisest, samuti värvustest. Aga me jõuame välja mikroskoobi, teleskoobi ja virtuaalreaalsuseni.
Katsekomplekti e-materjalid (nagu ka komplekt ise) ei ole veel valmis, seda on kindlasti ka nende lehitsemisel näha. Arendus käib ja me loodame teiega kohtuda koolitustel, et tagasiside põhjal tulemus parem saaks.
Niisiis, valik valgusõpetuse katseid.
Indrek Peil, Saaremaa Ühisgümnaasium
Käesolev artikkel uurimis- ja loovtöödest koolis üldse ja nende kasutamisest füüsikaõppe toetamisel põhineb suures osas Saaremaa Ühisgümnaasiumi (SÜG) õpetajate kogemustel. Nimelt on selles koolis juba aastakümneid aktiivselt uurimistöid juhendatud ning 2001. aastast alates peavad kõik gümnasistid vähemalt ühe uurimistöö koostama ja kaitsma. SÜG-i õpilasteadurid on edukalt esinenud nii vabariiklikel kui ka rahvusvahelistel konverentsidel ja konkurssidel. Peale selle korraldatakse ka ise iga-aastast õpilaskonverentsi Saaremaa Miniteaduspäevad.
Suurem osa artiklist käsitleb põhjalikumalt uurimistööde kui keerulisema loovtöö vormiga seonduvat. Siin-seal peatutakse lähemalt ka põhikooli loovtööde spetsiifikal.
Riiklikus õppekavas on sätestatud, et põhikooli lõpetamise ühe tingimusena peab õpilane kolmandas kooliastmes (7.–9. kl) koostama ja kaitsma loovtöö ning gümnaasiumi lõpetamise tingimuseks on õpilasuurimuse või praktilise töö koostamine ja kaitsmine. Millal ja kuidas seda tehakse, on jäetud kooli otsustada ja oma õppekavas kindlaks määrata. Koolile on siin antud üsna vabad käed. Ka aktiivsel õpetajal on vabad käed ja seega lausa kohustus avanenud võimalusi ära kasutada.
Ameerika psühholoogi Benjamin J. Bloomi järgi on õppe-kasvatustöö tunnetuslike eesmärkide kõrgemateks kategooriateks analüüs ja süntees. Traditsiooniliste õppemeetoditega on nende eesmärkideni jõudmine raske. Küll aga saab õpilaste vastavat suutlikkust arendada loova ja uurimusliku tegevuse kaudu. Füüsika uurib kõike seda, mis on reaalselt olemas. Tegemist on ühtaegu nii empiirilise kui ka eksaktse teadusega, mille uurimismeetoditeks on vaatlus, katse ja andmetöötlus. Seepärast sobib loov- või uurimistöö just füüsikas eriti hästi õppetööd mitmekesistama. Füüsiku taustaga õpetajad on võimelised õpilasi juhendama mitte ainult füüsikaga seotud, vaid pea mistahes teemal. Füüsika uurib ju kogu reaalset maailma ja kõike selles toimuvat.
Uurimis- ja loovtööle esitatavad põhinõuded
Sõltumata teemast ja vormist peab uurimistöö täitma kindlaid nõudeid. Esimene nõue on see, et töö peab sisaldama uurija oma panust. Ei piisa vaid kirjandusallikatest leitud mõtete oma sõnadega ümberkirjutamisest. Nii saadakse pelgalt referaat. Tulemus peab kasutatud algmaterjaliga võrreldes sisaldama midagi kvalitatiivselt uut. Omapoolse panuse loomiseks on palju teid: vaatlused, katsete käigus tehtavad mõõtmised, küsitlused, intervjuud, õppevahendi koostamine, millegi valmisehitamine, kirjandusallikatest leitud materjali süstematiseerimine ning üldistamine jne. Omapoolne panus on vältimatu ka mistahes muud liiki loovtöös (projekt, muusikateos või kunstitöö). Loovuse käigus luuakse uudseid ideid, esemeid, kunstiteoseid jmt. Loovuse tulemus on kindlasti uudne ehk olemasolevast erinev ja samas ka asjakohane, tõhus (loomisel peab olema mõistlik eesmärk). Hea tunnus loovuse olemasolu kinnituseks on see, et loodut saab näidata.
Teiseks peab igal uurimistööl olema selgelt sõnastatud uurimiseesmärk. Kõik algab mingist lahendamist ootavast probleemist. Probleem võib olla mis iganes, näiteks: pole head õppevahendit, tahaks endise õpetaja kohta rohkem teada või klassiruum tundub olevat pime ja jahe. Probleemi lahendamiseks püstitatakse hüpoteesid või sõnastatakse uurimisküsimused. Kvantitatiivses (arvude abil kirjeldavas) uurimuses on eesmärgiks teaduslikult põhjendatud oletuste ehk hüpoteeside kinnitamine või ümberlükkamine. Kvalitatiivses (lugude kaudu kirjeldavas) töös otsitakse uurimise teel vastust uurimisküsimusele. Hüpotees(id) või uurimisküsimus(ed) tuleb uurimistöösse kindlasti sisse kirjutada. Mitteuurimuslikes loovtöödes ei saa enamasti hüpoteese või uurimisküsimusi välja tuua, kuid töö eesmärk tuleb ka nendes sõnastada.
Kolmandaks peab uurimistöö ülesehitus vastama kindlale struktuurile, mida on kirjeldatud kooli kehtestatud juhendis. Tavaliselt nõutakse juhendites uurimistöö vormistamist väitekirjana, milles on kohustuslikud kuus osa: tiitelleht, sisukord, teemat, uurimiseesmärke ja meetodeid tutvustav sissejuhatus, soovitatavalt kolmeks mahult võrdseks osaks jagatud sisuline osa, kus esitatakse ülevaade teemakohasest kirjandusest, oma uurimistegevuse kirjeldus ja saadud tulemused koos analüüsiga, kokkuvõte saadud tulemuste ja järeldustega ning kasutatud allikate loetelu. Vajaduse korral võib töösse panna ka lühendite loetelu ja lisad. Mitteuurimuslike loovtööde puhul pole selline väitekirjaline vormistus otstarbekas. Siin võib töö kirjaliku kokkuvõtte vormistada artiklina, kus pealkirja ja autori nime all on toodud lühike sisukokkuvõte ning järgnevad pealkirjastatud lõigud teematutvustuse ja eesmärkidega, metoodika ja tegevuse kirjeldusega ning tulemuste esitamise ja analüüsiga. Kõige lõppu paigutatakse viidatud allikate nimekiri.
Neljandaks on nii uurimis- kui ka loovtöödes kõikidele kasutatud allikmaterjalidele viitamise nõue. Teksti sees tuleb viidata nii raamatutele, artiklitele, internetilehekülgedele kui ka arhiivimaterjalidele, telesaadetele, teatrikavadele, isiklikele fotokogudele ja autori poolt intervjueeritutele. Õpilane peab harjuma intellektuaalset omandit väärtustama ja mõistma, et viitamata jätmise korral on tegu plagiaadi ehk vargusega. Noorte seas on laialt levinud väärarusaam, et kui raamatust leitud mõtted on oma sõnadega ümber kirjutatud, siis polegi viidata vaja. Siin aitab lihtne võrdlus: kas varastatud auto ülevärvimisel saab auto värvija omaks? Allikatele viitamine on kohustuslik mistahes liiki tööde korral!
Uurimistöö referatiivne osa
Uurimistöö sisulisest osast umbes kolmandik peab olema ülevaade teemakohasest kirjandusest – ülevaade sellest, mida teised on samas valdkonnas teinud. Kirjanduse refereerimine õpetab allikaid otsima ja analüüsima, annab ideid, aitab teemat täpsustada ja sobivaid uurimismeetodeid leida ning väldib nn jalgratta leiutamist ehk teiste poolt juba tehtu tarbetut kordamist.
Refereeritu peab olema kindlasti teemaga seotud. Kui teemaks on näiteks jalgratta kasutamine õpilaste sõiduks kooli ja koolist koju, siis ei anta ülevaadet mitte jalgratta leiutamise ajaloost, vaid jalgrattasõiduks sobivatest teedest, jalgrattahoidlatest ja ‑lukkudest, õpilaste liiklus- ja keskkonnateadlikkusest ning õpilastele sobivatest rattamarkidest. Kui tegu pole just ajaloouurimusega, tuleks teemaga seonduvaid ajaloolisi ülevaateid vältida.
Uurimistöö vormistus
Uurimis- ja loovtööde vormistus peab vastama koolis kehtestatud juhendile. Erandiks on tööd, mis on plaanitud esitada olümpiaadidele või konkurssidele, kus vormistusnõuded võivad kooli omadest erineda. Pole mõtet sundida õpilast oma tööd mitmes variandis vormistama.
Töös kasutatav keel peab olema ladus ja korrektne. Probleemid tekivad enamasti erinevatest kirjandusallikatest leitud info sidumisel õpilase oma tekstiga. Seepärast tuleb info sõnasõnalisele tsiteerimisele eelistada oma sõnadega ümberkirjutamist. Vältida tuleb kirja- ja keelevigu. Teadustöö keel ei luba slängi ja minavormi kasutamist. Põhikooli loovtöödes võiks minavorm siiski lubatud olla.
Nii uurimis- kui ka loovtöös on soovitatav esitada illustreerivat materjali: pilte, tabeleid, graafikuid jne. Kindlasti on omal kohal tööprotsessi ja/või olulisemaid tulemusi kirjeldavad fotod, miks mitte ka selfie’d! Nende tegemist peab juhendaja soovitama kohe tööprotsessi alguses, kuna tagantjärele pole see tihti enam võimalik. Illustratsioonide hulk olgu optimaalne ja nende sisu asjakohane. Töösse pole mõtet kuhjata kümneid diagramme, kui tulemused saab paari lausega kokku võtta. Vältida tuleks sektor- või tulpdiagramme, mis väljendavad näiteks vaid küsitletute jagunemist poisteks ja tüdrukuteks.
Füüsika omandamist toetavad uurimisvaldkonnad
Füüsikateemaline uurimistöö ei pea sugugi olema hästi sisustatud laboris tehtud klassikalisel eksperimendil põhinev uurimus. Tööd võivad olla vägagi erinevad ja täppisteaduslikust füüsikast esmapilgul kaugel. Teadusliku tunnetusprotsessi olemust, töö koostamist ja vormistamist õpetavad nad sellegipoolest kõik suurepäraselt.
Kindlasti peaks füüsikaõpetaja välja pakkuma ja juhendama eksperimentaalseid uurimistöid, kus õpilane teeb katseid ja sooritab mõõtmisi. Siin saab hästi ära kasutada erinevaid andmehõiveseadmega ühendatud andureid. Mõõtmiste juures ei tohi muidugi unustada mõõtmistäpsuse hindamist. Uurida saab õpi- ja elukeskkonda, võrrelda valgusallikaid, määrata kehade erinevaid omadusi, leida sõltuvusi, otsida energiasäästu võimalusi jmt.
Neile, kellele meeldib meisterdamine, sobivad praktilise väljundiga tööd. Ehitatakse näiteks tuulegeneraator, akvaariumi termoregulaator või elektrikitarr ning uuritakse selle toimimist, restaureeritakse kummut või tuunitakse automootorit. Eelnevalt otsitakse ja töötatakse läbi muidugi ka teemakohast kirjandust. Õpilasele tuleb selgitada, et praktiline töö ei tähenda vaid pelgalt asja valmisehitamist. Praktiline töö = teoreetiline taustauuring + millegi valmistegemine + hinnang valminule. Just praktilise väljundiga tööd sobivad suurepäraselt põhikooli loovtöödeks.
Õpetaja jaoks on tarbimisväärtusega füüsikaõpetuse metoodikat käsitlevad tööd. Ka need on enamasti praktilise väljundiga. Õpilased saavad eri allikatest kokku otsida füüsikaülesandeid, neid siis läbi lahendada ja koondada ülesannete koguks. Võib ehitada mudeleid ja demonstratsioonivahendeid, filmida nähtusi selgitavaid videoklippe, koostada füüsikateemalisi arvutiesitlusi, foto- ja lingikogusid ning interaktiivseid õpilehekülgi. Suureks abiks õpetajale on laboratoorsete tööde juhendi koostamine koos vajalike vahendite valmistamisega. Lõpuks saab kokku panna isegi temaatilise füüsikaõhtu kava või teadusteatri etenduse ning selle ka ise läbi viia. Ka metoodiliste materjalide koostamisel tuleb teemakohast kirjandust läbi töötada ning väärtust annab juurde valminud materjali katsetamine õppetöös.
Neile, kellele täppisteadused vähem sobivad, saab välja pakkuda ka humanitaarsemaid teemasid. Siin on tihti tegemist kvalitatiivsete töödega, mille käigus otsitakse lugu ehk narratiivi. Näiteks võib koostada koduloouurimusi erinevate füüsikarakenduste (elekter, telefon, raudtee, veevärk, digi-TV jne) kasutuselevõtust oma kodukandis. Kindlasti on ajalooline väärtus isiku-uurimustel legendaarsetest õpetajatest ning oma koolist või kodumaakonnast pärit füüsikutest ja inseneridest. Füüsikaga saab siduda isegi keele- ja kirjandusuuringuid. Võib uurida suuruste ja ühikute tähiste ning füüsikaterminite keelelist päritolu või analüüsida füüsikanähtuste ja ‑probleemide kajastamist luules ja ilukirjanduses. Kuigi sellised humanitaarse suunitlusega tööd on füüsikateadusest kaugel, panevad nad siiski õpilase mõnesse füüsikateemasse põhjalikumalt süvenema ja toetavad sellega loodusteadusliku maailmapildi kujunemist.
Õpilasele sobiva uurimisteema leidmine
Teemavalik on väga tähtis. Teema olgu õpilasele huvipakkuv ja samas jõukohane. See ei tohi olla liiga lai, kuid peab siiski võimaldama täita kõik uurimistööle seatud nõuded. Näiteks teemad „Elekter” ja „Füüsikaülesannete kogu” on liiga mahukad ja laialivalguvad. Palju paremini sobib „Katsevahend pendlite resonantsi demonstreerimiseks”. Pole vaja karta, et töö ei tule piisavalt teaduslik. Õpilasuurimuse eesmärk pole ju suured avastused, mis teadust edasi viivad, vaid teaduse tegemise õppimine. Omaaegne Tartu Descartes’i Lütseumi õpetaja Tanel Lepsoo on öelnud, et teadustöö kogemuste omandamiseks ei pea esimesel korral midagi ääretult keerukat ja üliteaduslikku tegema. Tähtis on lihtsalt kõik selle erinevad etapid läbi mängida.
Hea teema on selline, mis võimaldab maksimumi, st annab võimaluse teha kõike, mida juhendis nõutakse. Teema peab võimaldama sõnastada hüpoteesi või uurimisküsimuse ja sellest tuleneva uurimusliku eesmärgi, leida teemakohast allikmaterjali, valida sobiva meetodi ja seda põhjendada, oma uuringu iseseisvalt läbi viia ning tulemusi teistele arusaadavalt interpreteerida ja vormistada.
Hea uurimisteema on uudne ja päevakajaline. Originaalne uurimistöö sisaldab seniuurituga võrreldes midagi uut ja esmakordset, õpilane saab töösse lisada oma panuse. Seejuures ei pea vältima juba varem käsitletud teemasid. Varasemate tööde kordamine annab hea võimaluse võrdlusteks ning ajaliste trendide väljaselgitamiseks. Päevakajaliste ehk aktuaalsete, tänapäeval huvipakkuvate teemade leidmiseks tasub jälgida ajakirjandust.
Teema olgu õpilasele jõukohane. Kirjandus ja töövahendid peavad olema kättesaadavad. Uurimuse läbiviimine (katseriistad, transport jms) ei tohi olla kallis. Alusteooria, uurimismeetodid ja andmetöötlus peavad olema õpilasele arusaadavad. Tegevuste füüsiline ja ajaline maht ei tohi olla suur.
Meelepärase ja jõukohase teema otsimist võiks õpilane alustada iseendast. Mis teda eriti huvitab, millega ta vabal ajal tegeleb? Sageli on uurimistööd kerge seostada hobiga. Teiseks tasub läbi mõelda oma võimalused info hankimiseks või katsete tegemiseks. Äkki on sugulaste või sõprade hulgas inimesi, kellel on elukutse või harrastuse tõttu rohkesti huvipakkuvat teavet või töökoda seadmetega, kus eksperimenteerida saaks. Kolmandaks võib õpilane siduda uurimistöö oma tulevikuplaanidega. Kui näiteks on soov õppimist jätkata filmitegemise alal, tuleb sisseastumisel kasuks, kui on ette näidata omatehtud videoklippe või animatsioone. Miks siis mitte koostada uurimistööna videoklippe ja animatsioone sisaldav õppevahend.
Sageli on õpilased leidlikud ning pakuvad põneva ja väga hea teema ise välja. Siis jääb juhendajal vaid üle vajaduse korral soovitada teemat konkretiseerida või sobivamalt ümber sõnastada. Ülejäänutele peab teema leidmisel abiks olema kool. Soovitatav on luua teemapank ehk suur hulk teemasid, mida õpetajad välja pakuvad. Iga teema juures peaks olema õpetajate nimed, kes on nõus juhendajaks hakkama. Kindlasti on abiks ka varasemate uurimistööde nimekiri. See, et keegi on teemat juba varem uurinud, ei vähenda töö õpetuslikku eesmärki, vaid pigem suurendab. Lisandub nüüd ju võimalus oma tulemusi varasematega võrrelda. Kui oma koolil on varasemaid töid vähe, võib neid otsida ka teiste koolide kodulehtedelt. Teemapank ja varasemate tööde nimekiri tuleb teha kõigile õpilastele kergesti kättesaadavaks ja nende olemasolule tuleb aeg-ajalt tähelepanu juhtida.
On õpilasi, kes ennast alahinnates ei julge oma valitud teemaga välja tulla või kardavad õpetajat endale juhendajaks paluda. Selliste olukordade avastamiseks tuleb teemade registreerimise protsessi hoolikalt jälgida ning vajaduse korral õpilastele individuaalselt läheneda. Individuaalselt on soovitatav läheneda ka siis, kui õpetajal on hea teema ja ta teab õpilast, kellele see sobiks. Õpetajapoolne enda juhendajaks pakkumine on õpilase jaoks tunnustus ja võetakse tänuga vastu.
Juhendaja osa uurimistöö valmimise protsessis
Juhendaja peab töö valdkonda tundma ja suhtuma juhendamisse tõsiselt, mitte pealiskaudselt. Ta peab tundma oma suurt vastutust. Juhendaja ja õpilase vahel peab toimuma koostöö. Juhendaja roll on selle juures õpetav, abistav, meeldetuletav ja innustav. Ei tohi ootama jääda õpilase initsiatiivi, seda eriti põhikoolis.
Juhendaja peab võimaldama õpilasel olla juhendatava rollis ja laskma õpilasel ise otsustada. Otsustamisega kaasneb õpilase oma vastutus. Näiteks uurimismeetodi väljapakkumise asemel tuleks lasta õpilasel endal paari meetodi hulgast sobiv valida.
Juhendaja ei tohi midagi õpilase eest ära teha, vaid peab vajalike tegevuste juurde suunama. Näiteks pole vaja hakata üles lugema vormistusnõudeid, selle asemel tuleb lihtsalt juhendile viidata. Õpetaja ei otsi vajalikke kirjandusallikaid ise üles, vaid näitab, kuidas raamatukogude andmebaasidest ja internetist neid otsida saab. Loomulikult pole siiski välistatud, et juhendaja ka oma raamaturiiulist midagi välja toob.
Tööprotsessi alguses peab juhendaja kindlasti abiks olema teema täpsustamisel ja ajakava paikapanemisel. Et tegevused lõppu ei kuhjuks, peab algusest peale selge olema, millal otsitakse kirjandust ja seda läbi töötatakse, millal tehakse katseid ning muid andmeid kogutakse ja töödeldakse, millal valmib esialgne mustand. Samuti lepitakse kokku lähemate uute kohtumiste kuupäevad, mida õpetaja vajaduse korral meelde tuletab. Teine lõpptulemust määrav oluline töö, millel juhendaja pilku peal hoiab, on uurimistöö sisulise kava (ülesehituse) koostamine.
Pärast kava koostamist ja selle täitmise algust jälgib juhendaja töö edenemist, annab nõu ning aitab surnud punkte ületada. Kindlasti tuleb juhendajal töö vormistuslik külg enne komisjonile esitamist põhjalikult üle vaadata. Eraldi tähelepanu nõudev teema, kus juhendaja saab õpilasele toeks olla, on kaitsmise ettevalmistamine.
Õpilaste innustamisel uurimis- ja loovtöid tegema tuleks välisele motivatsioonile eelistada sisemist. Kohustuse teadvustamise asemel võiks olla soov tegutseda. Liikumapanevaks jõuks peaks sunni ja hirmu asemel olema huvi ja rõõm. Siin on palju abi tunnustamisest. Tunnustamine ei tähenda mitte igale liigutusele järgnevat kiitust või autasu. Teinekord piisab ka vaid märkamisest või imestuse väljendamisest (nt „Hoiad jootekolbi käes õigesti.”, „Ma ei teadnudki, et sa nii hästi puutööd mõistad!”).
Õpilast saab innustada ja tunnustada valmivale uurimistööle lisaväljundeid pakkudes. Korraldada võib oma kooli konkursi või suunata töö erinevatele võistlustele ja konverentsidele.
Näiteid füüsikaga seotud uurimis- ja loovtöödest
Füüsikateemaliste uurimisteemade leidmise lihtsustamiseks on allpool esitatud valik Saaremaa Ühisgümnaasiumis viimase 20 aasta kestel koostatud ja kaitstud töödest. Nagu näha, on teemaspekter lai – koduloouurimustest ja küsitluste läbiviimisest kuni erinevate seadmete ehitamise ja katsetamiseni välja. Kindlasti tekib neid teemasid vaadates hulgaliselt uusi ideid. Kui uusi ideid kohe ei leia, võib ka varasemaid töid korrata. Füüsikalise tunnetuse seisukohalt on neil õpetuslik väärtus ikka alles.
Kvalitatiivsed tööd
- Füüsikaõpetaja Endel Kurgpõllu elust ja tööst
- Füüsikaliste terminite ja tähiste keeleline päritolu
- Kõnekeeles kasutatavad ajaühikud
- Elekter Saaremaal (koduloouurimus elektri kasutuselevõtu ajaloost)
- Lubja tootmine Lümandas
- Tuumaenergeetika kasutuselevõtu perspektiivid Eestis (kirjanduse analüüs, teadlaste intervjueerimine, arvamusküsitluse läbiviimine)
- Energia säästlik kasutamine SÜG-i 11. klasside õpilaste kodudes
- Õpilaste arvamused UFO-dest
- Õhk meie ümber (füüsikaõhtu kava koostamine ja läbiviimine)
Metoodikaalased tööd
- Füüsikaolümpiaadide maakonnavoorud läbi aegade (olümpiaadiülesannete analüüs)
- SÜG-i füüsika riigieksamite tulemused läbi aegade
- Füüsika õppevahend (arvutiesitlus koos omafilmitud videoklippidega)
- Mehaaniliste liikumiste liigitamine ja kirjeldamine (õppevahend)
- Õppefilm õhurõhu kohta
- Lorentzi jõu laboritöö (katsekomplekti ja tööjuhendi koostamine)
- Caius Plinius Secunduse maailmakäsitlus (ülevaate andmine ja võrdlus kaasaegsega)
Praktilise väljundiga tööd
- Kodune biodiisli valmistamine ja katsetamine
- Kinkuri (kingalusikas + helkur) valmistamine ja katsetamine
- Päike-õhk küttepaneeli ehitamine ja selle kasutamine Saaremaa talves
- Tuulegeneraator oma majapidamisse (generaatori ehitamine ja töölerakendamine)
- Tesla trafo (trafo ehitamine ja katsetamine)
- Elektrikitarri modifitseerimine ja selle väärtus järelturul
- LED-tabloo ehitamine ja katsetamine
- Ventilaatoriga nokamüts kuuma ilma jaoks
- Ruuporkõlar LABhorn (ehitamine ja parameetrite mõõtmine)
- Sõiduauto Lada 1600 cm3 mootori toitesüsteemi modifitseerimine
Vaatlustel ja katsetel põhinevad tööd
- Valgusallikad Saaremaa kodudes (küsitlus õpilaste hulgas ning erinevate lampide eksperimentaalne võrdlus)
- Küünal kui valgusallikas (erinevate küünalde eksperimentaalne võrdlemine)
- Patareide vastupidavuse testimine
- Autotranspordi mõju atmosfäärile (õhutahma mõõtmine erineva liiklusega paikades)
- Klassiruumi 220 õhutemperatuuri vastavus tervisekaitsenõuetele
- Õhu keemiline koostis SÜG-i klassiruumis 320
- Toalillede mõju klassiruumi õhukvaliteedile
- Valgustid ja energiasääst Saaremaa Ühisgümnaasiumis
- Kruusakattega teede mõju elukeskkonnale ja turismile (õhu tolmusisalduse määramine ja elanike küsitlus)
- SÜG-i koolitoidu toiteväärtuse analüüs
- Saarlaste mõõtmetest
- Globaalse soojenemise (võimalike üleujutuste) mõjust Kuressaare kinnisvarahindadele
- Elektriautod ja nende tasuvusaeg võrdluses sisepõlemismootoriga autodega
- Erinevate tõrvasegude vastupidavus katusekimmidel
- Äikesevaatlused Muhus 2006. aastal
- Eesti õhutemperatuuride erinevused nov. 2010 – veebr. 2011 (ilmajaama andmete põhjal)
Kõik ei mahu õpikute kaante vahele. Aga kui tund jääb õpiku kaante vahele, siis on hea võimalus alt minna - ka koolifüüsika võiks servapidi igapäevaellu või tänasesse teadusesse puutuda.
Alljärgnev lugemismaterjali valimisel on olnud kaks peamist kriteeriumi - peab olema põnev ja vähemasti kaude mõistetav õppekavas (ja õpikus) antud õppesisust lähtudes. Et oleks hea tunnis vahelepõigeteks kasutada.
Franco Bagnoli
Carl Barksi klassikalises koomiksis „Suur rahasalv Seisaku mäel“ [1] täidab Onu Robert, järgides Piilupart Donaldi nõuannet, oma rahasalve veega, et seda Penipoiste eest kaitsta. Kahjuks juhtub see olema üks Pardilinna külmemaid öid. Vesi jäätub ja lõhub varasalve kolme meetri paksused seinad. Selle tulemusel pääseb valla hiiglaslik rahaga täidetud jääkamakas, mis libiseb mäest alla otse Penipoiste hoovi.
Jäätuva vee paisumine on kõigile teada-tuntud fakt. Just see nähtus põhjustab sügavkülma jäetud õllepudelitega tihti palju pahandust. Aga miks vesi niimoodi käitub? Ja mis veel keerulisem, kuidas seda nähtust lihtsalt ja arusaadavalt selgitada?
Kõigepealt tuleb meeles pidada, et temperatuur on seotud molekulide kineetilise energiaga. Molekulid aga eelistavad püsida miinimumenergia seisundis. Kui võtta aluseks lihtne palli mudel, siis on aatomid miinimumenergia seisundis paigutunud kompaktsemalt kui rohkem energiat nõudvas (korrapäratus) struktuuris. See seaduspärasus ei kehti vee puhul.
Veemolekulid meenutavad kujult Miki Hiire pead (vt joonis 1), kellel on kõrvadeks kaks vesinikuaatomit. Et vee kristalli struktuur on olemuselt kolmemõõtmeline, on seda keeruline joonistada. Siinkohal on hea kasutada Mercedes-Benzi mudelit [2].
Selles mudelis kujutatakse veemolekule kuulsa Mercedes-Benzi sümbolina (vt joonis 2) ning miinimumenergia seisund saavutatakse kahe teraviku ühinemisel (suunamata vesinikside). Mercedes-Benzi molekule on üsna lihtne papist valmistada, et inimesed saaks nendega nähtuse läbi mängida.
Selle mudeli abil on kerge selgitada miinimumenergia seisundiga kaasnevat tühimikku jää struktuuris (vt joonis 3, parempoolne osa) ja põhjendada jää väiksemat tihedust veega võrreldes. Samuti võib selle abil näitlikustada taasjäätumise nähtust (jää sulab rõhu all ja jäätub uuesti, kui rõhku vähendada). Püsiva jää struktuuri saamiseks tuleb kõigepealt vähendada veemolekulide kineetilist energiat. Seejärel tuleb ületada van der Waalsi jõust tulenva seose ja vesiniksideme energeetiline erinevus, st soojus peab eralduma. Makrokäsitluses nimetatakse esimest vee soojusmahtuvuseks (vee erisoojus: c = 4,187 kJ/kg·K) ja teist jää sulamissoojuseks (λ = 334 kJ/kg). Kui tahta veel jää temperatuuri alandada, tuleb eraldada energiakogus, mis vastab jää erisoojusele (2,108 kJ/kg·K).
Carl Barksi koomiksis ütleb Onu Robert korduvalt, et tema rahasalve maht on kolm kuupaakrit, mis ilmselgelt ei vasta tõele, sest aaker on pindala ühik. Kui oletada, et kuubi iga külg on aakri suurune (umbes 4000 m2), on serv umbes 60 m ja maht V ligikaudu 200 000 m3. Mul ei õnnestunud leida andmeid korrapäratult pakitud müntide kohta (paistab, et selles valdkonnas on uuritud ainult kerasid ja M&Mi komme [3]), seega tegin ma ise 174 kümnesendise mündiga väikse katse. Pakkimistiheduse tulemus oli umbes 0,55, mis on palju väiksem kui keradel (0,64), kuid näha on piiratud ruumala mõju1. Seega on vee koguhulk m = 0,45·2·105·103 = 9·107 kg. Oletades, et algul on rahasalv (ja selles olev vesi) temperatuuril t = 10°C, tuleb 0°C temperatuuriga jää saamiseks eraldada soojushulk m·(c·t+k) = 3,4·1013 J. Arvestamata jääb müntide soojusmahtuvus (vasel või messingil vaid 0,4 kJ/kg·K) ja seinte soojusmahtuvus (umbes 0,8 kJ/kg·K). Kui jäätumine toimub näiteks 5 tunni jooksul, on jahutusvõimsus umbes 2 GW! Vee külmutamine pole tõepoolest kerge ülesanne. Seetõttu pannaksegi viljapuude lähedusse veetünnid, et neid külma eest kaitsta. Lõpetame nuputamisülesandega: milline on veetemperatuur merepõhjas?2
Viited
[1] http://coa.inducks.org/story.php?c=W+WDC+135-02 (1951). Internetis kättesaadav leheküljel http://it.paperpedia.wikia.com/wiki/File:-Big_bin_on_killmotor_hill.pdf
[2] K.A.T. Silverstein, A.D.J. Haymet, K.A. Dill, J. Am. Chem. Soc. 120, 3166 (1998).
[3] A. Donev, I. Cisse, D. Sachs, E.A. Varano, F.H. Stillinger, R. Connelly, S. Torquato, P.M. Chaikin, Science 303, 990 (2004).
1Selle abil saame välja arvutada, kui rikas on Onu Robert. Ühedollarilise mündi maht on umbes 1,1 cm3 ja pakkimistiheduse 0,55 juures võtab see enda alla ligikaudu 2 cm3. Jagades V selle arvuga, saame tulemuseks umbes 1011 dollarit, sada tuhat miljonit ehk sada miljardit.
2Analüüsime seda olukorda kõigepealt magevee tingimustes (sügava järve puhul). Meie mudeli järgi on vee tihedus suurim temperatuuril veidi üle nulli (reaalsel puhtal veel on see umbes 4°C). Madalamal temperatuuril tekivad vees tihti jääsarnased struktuurid, kus on rohkelt vesiniksidemeid. Need muudavad tiheduse väiksemaks, jää tiheduse suunas. Kõrgema temperatuuri korral domineerivad van der Waalsi jõud ja vesi käitub rohkem tavavedeliku moodi. Soolasisaldus veidi muudab olukorda, tahkumistemperatuur on seal madalam ja vee maksimumtihedus samuti väiksem. Seega on ookeanipõhjas veetemperatuur umbes 3°C.
Artikkel on originaalis saadaval aadressil http://www.europhysicsnews.org või http://dx.doi.org/10.1051/epn/2015301
Sung Chang, tõlgitud ajakirjast Physics Today
Vesinik on kõige lihtsam ja kõige levinum keemiline element universumis. Aga vastupidiselt sellele näilisele lihtsusele on vesiniku omadused tihti ettearvamatud. Siin võtame ette ühe näite: erinevalt kõigist perioodilisustabelis vesiniku all olevatest leelismetallidest jääb vesinik isegi tahkes olekus mittejuhiks kuni kõige madalamate temperatuurideni välja.
Eugene Wigner ja Hillard Huntington ennustasid juba 1935.aastal, et vesinik võib piisavalt kõrgel rõhul vabaneda oma molekulaarsetest sidemetest ja muutuda atomaarseks metalliks. Algas võidujooks vesiniku isolaator-metall faasisiirde avastamiseks, aga see kujunes pigem maratoniks kui sprindiks.
Kõrgrõhu eksperimentide on kurikuulsad oma keerukuse pärast. Vesinikuga tehtavad eksperimendid veel eriti. Kui tavaliselt kasutatakse staatilistes kõrgrõhueksperimentides teemantalasiga kõrgrõhurakkude, siis vesinikuga tehtavates eksperimentides on nende kasutamine raskendatud, kuna vesinik tungib teemantisse ning tekitab seal pragusid. Löök-kokkusurumist kasutavates dünaamilistes eksperimentides saavutatakse küll kõrgemaid rõhkusid, aga need soojendavad uuritava aine kõrgete temperatuurideni ja saavutatavad on vaid teatud rõhu ja temperatuuri väärtused, kusjuures need sõltuvad süsteemi algolekust. Seni on eksperimentaatorid suutnud vesinikule avaldada staatilistes eksperimentides 320 GPa ja dünaamilistes eksperimentides 500GPa rõhku. Aga metallilist vesinikku ei ole suudetud saada.
Nüüd on Marcus Knudson ja Mike Sesjarlais Sandia riiklikust laboratooriumist (Sandia National Laboratory) ja nende kolleegid Sandia ja Rostocki Ülikoolidest avaldanud tulemused, mille kohaselt nad on jälginud seda raskesti tabatavat üleminekut. Töörühm saavutas üle 300GPa rõhu temperatuuridel 1000 – 2000 K kasutades selleks Sandia Z masinat. Nende mõõtmised näitasid, et vedela deuteeriumi üleminek mittejuhtivast juhtivasse, st metallilisse olekusse toimub umbes 300GPa juures.
Kohutav surve
Maailma võimsaimat elektromagnetiliste impulsside generaatorit, Z masinat (vt pilti), tuntakse eelkõige fusiooni (termotuumareaktsiooni) ja relvatööstusega seotud uuringute kaudu. Deuteeriumi metallilisse olekusse pressimiseks vabastasid uurijad Sandia Rahvusliku Laboratooriumi z masina 2160 kondensaatori energia ning vormisid sellest sobiliku 1 mikrosekund kestva impulsi. Sellesse impulssi mahtus tervelt 2MJ energiat. Masina jõukaablid, on uputatud destilleeritud vette, mis täidab masinas isolaatori rolli. Pildil on näha kaarlahendused, mis tekivad masina kohale hetkel, kui laeng vabastatakse.
Uurijad on näinud märke metallilise vesiniku olemasolust ka varem. 1996. aastal tulistasid Samuel Weir, Arthur Mitchell ja William Nellis gaasikahuriga metallkettaid vedela vesiniku ja deuteeriumi märklaudade pihta ja saavutasid kuni 180Gpa rõhke. Üle 140 GPa küündivate rõhkude juures mõõtsid nad märklaudades vedelale metallile iseloomulikku elektrilise takistuse käitumist.
Aga need vaatlused toimusid kuni 3000K ulatuvatel temperaturidel. Samas on teoreetikute hinnangul mittejuht-metall faasisiirde kriitiline punkt umbes 2000K juures. Sellepärast arvatakse, et nendes eksperimentides oli enamus vesinikust endiselt molekulaarses, st mittejuhtivas olekus ja metallilisus oli pigem kõrvalefekt. Sandia-Rostocki töörühm tahtis esile kutsuda faasisiirde kriitilises punktis. „Eksperimendi suurim väljakutse oli saavutada kõrged rõhud ilma, et temperatuur liiga kõrgeks läheks“, seletas Knudson.
Uurijate arvutused näitasid, et kui nad tekitavad Z masinaga täpselt õige ajalise kujuga impulsi, saavad nad ühekorraga kasutada kaht tavapärast kokkusurumise meetodit – lööki ja rõhu järk-järgulist tõstmist (dünaamilist ja staatilist rõhku) . Impulsi esimene osa lennutab alumiiniumplaadi vastu alumiiniumist valmistatud krüorakku, milles on 150 mikromeetri paksune kiht 22K jahutatud vedelat deuteeriumi. 2- 3.5 km/s kiirusel toimuvad kokkupõrked tõstavad deuteeriumi temperatuuri 800 kuni 1400K, rõhk on sealjuures 20-50Kpa. Impulsi teine osa surub deuteeriumi kasvava elektromagnetilise rõhu toimel kokku juba rahulikumas tempos, nii et deuteeriumi temperatuur jääb alla 2000K isegi kui rõhk kasvab üle 300GPa.
Töörühm tegi oma katseid deuteeriumi, mitte vesinikuga. Selle põhjuseks oli asjaolu, et deuteerium on suurema tihedusega ja seega on eksperimendi parameetrite paika timmimine kergem ülesanne. Nüüd, kui deuteeriumiga on katsed edukalt läbi viidud on, võtavad nad ette ka vesiniku.
Täismahus artiklit loe ajakirjast Physics Today
Maa magnetväli muutub järk-järgult ja seetõttu muutub ka põhjasuund, mida kompass näitab. Mitmel põhjusel tahavad uurijad teada, milline oli magnetiline põhjasuund mingil ajahetkel minevikus. Ajaloolisi kompassinäitude ülestähendusi leitakse aga harva. Teadlased said hoopis abi iidsetest saviseintega põletusahjudest, milles põletati keraamikat, ja väga vanadest maalidest, näiteks seinamaalidest Bibliotheca Apostolica Vaticanas, Vatikani raamatukogu pühitsetud eeskojas. Kuidas saab põletusahi või seinamaal magnetilist põhjasuunda näidata?
Vastus Iidsete põletusahjude seintes ja põrandas leiduv savi sisaldab raudoksiide magnetiiti ja hematiiti. Üldiselt koosnevad need terakestest, milles on domeenid – piirkonnad, milles aine magnetväli on ühesugune. Magnetiidi teras on palju mikroskoopilisi domeene; hematiidi tera koosneb ühest domeenist, mis võib olla kuni millimeetri suurune.
Savi kuumutamisel mitmesaja kraadini Celsiuse järgi (põletusahju kasutamisel) muutuvad domeenid mõlemat tüüpi terades. Magnetiidis domeenide piirid liiguvad: domeenid, mis on Maa magnetvälja suunas, kasvavad, samal ajal kui teised kahanevad. Hematiidi domeenid pöörduvad ja joondavad ennast paremini Maa magnetvälja järgi. Mõlema protsessi puhul on savis tulemuseks magnetväli, mis on joondatud Maa magnetvälja järgi. Põletusahju jahtumisel pärast kasutamist jääb domeenide paigutus muutumatuks ning seega ka magnetväli savis. Seda nimetatakse termiliseks jääkmagnetismiks.
Arheoloog, kes soovib kindlaks teha Maa magnetvälja suunda ajal, mil põletusahi viimati kuumenes ja jahtus, märgib ära väikese osa põrandast, mõõdab hoolikalt selle asendi horisontaalpinna ja geograafilise põhjasuuna (põhjapooluse) suhtes ning eemaldab siis selle põranda osa. Järgmisena saab arheoloog määrata magnetvälja suuna eemaldatud tükis ning seega ka põletusahjus. Niimoodi selgub Maa magnetvälja suund ajal, mil põletusahju viimati kasutati. Kui ahju vanus õnnestub määrata radioaktiivse süsiniku või mõne muu meetodi abil, siis saab selgeks ka see, millal Maa magnetväljal selline suund oli.
Paljud vanad seinamaalid sisaldavad hematiiti. Kunstis kasutatavad värvained on suspensioonid, mis koosnevad vedelikus hõljuvatest erinevatest tahketest ainetest. Värvaine kandmisel seinale pöörleb iga hematiiditerake seni, kuni see joondub Maa magnetvälja järgi. Värvi kuivamisel lukustuvad terad paika ja salvestavad seega maalimise ajal kehtinud Maa magnetvälja suuna.
Teadlased saavad Maa magnetvälja suuna seinamaali tegemise hetkel määrata hematiiditerakeste suuna järgi värvis. Maalile kleebitakse lühike jupp kleeplinti, selle kleeplindi asukoht horisontaaltasandi ja magnetilise põhjasuuna suhtes märgitakse täpselt üles. Kleeplindi eemaldamisel jääb sellele õhuke värvikiht. Laboris pannakse kleeplint seadmesse, mis määrab ära hematiiditerade suuna värvikihis.
Gregory P. Thiel
Kuna Maa elanikkond kasvab ja magevesi muutub üha hinnalisemaks ressursiks, otsivad teadlased ja insenerid võimalusi, kuidas suurendada merevee magestamise tõhusust ja vähendada selle maksumust.
Greg Thiel kaitses eelmisel kuul Cambridge’is Massachusettsi Tehnikaülikoolis järeldoktorantuuris olles edukalt oma doktoritööd masinaehituses.
On uskumatu, et miljardil inimesel – ühel seitsmendikul kogu maailma rahvastikust – puudub juurdepääs puhtale joogiveele. Igal aastal surevad miljonid lapsed saastunud veest põhjustatud haigustesse, mida oleks võimalik vältida. Ning kliimamuutuste, rahvastiku juurdekasvu ja üha suurema kalorsusega toitumise koosmõju ähvardab kurnata meie kõige olulisema, eluks vajaliku ressursi suhteliselt ahtaks nireks.
Kuigi eeltoodu iseloomustab inimkonda varitsevate murede ulatuslikkust ja kiireloomulisust, on ülemaailmse veepuuduse kogupilt hoopis nüansirikkam – magevee nappust mõjutavad nii kohalikud majandused, kliima, ajalugu, inimasustuse muster kui ka ühiskonna areng. Vihmarikas, kuid halva kanalisatsiooniga piirkond ei nõua samasugust taristut kui maalilisel, aga põuasel rannikul asuv suur inimasustus. Kuna kohalikud probleemid on väga spetsiifilised, tuleb lahendused neile leida kohapeal.
Ülemaailmset imerohtu ei ole olemas. Kuid leidub rohtu, mis aitab paljudel juhtudel – see on magestamistehnoloogia. Peaaegu kõiki veega segunenud lisandeid eemaldada suutev magestamine on lahendus, mis suudab vett mitte ainult puhastada, vaid ka suurendada Maa hüdroloogilises ringluses oleva magevee kogust. Nende asjade saavutamine on oluline, sest mõningate hinnangute kohaselt võib maailma elanikkond kasutada 2025. aastal 70% planeedi taastuvast mageveest.
Pöördosmoos
| (a) Barcelona merevee magestusjaam Hispaanias, avatud 2009. aastal. | (b) Kui soolane vesi (roheline) ja magevesi (sinine) on eraldatud poolläbilaskva membraaniga, mis laseb läbi ainult magevett, liigub vesi magevee ruumist soolase vee ruumi, mida nimetatakse osmoosiks (vasakul). Kui soolase vee ruumi rõhk P jõuab niinimetatud osmootse rõhuni π (keskel), siis süsteem saavutab tasakaalu. Kui soolase vee ruumile rakendada rõhku P > π (paremal), siis magevesi surutakse soolase vee ruumist välja, mida nimetatakse pöördosmoosiga magestamiseks. |
Kõige säravam lahendus on pöördosmoos (RO). Esimest korda 1950ndate lõpus esitletud pöördosmoos moodustab praegu 65% magestamiseks paigaldatud võimsustest ja üle 50% viimastel aastatel ehitatud uutest võimsustest. (Joonise paneelil a on Barcelona pöördosmoosi jaam Hispaanias.) Protsess on põhimõtteliselt lihtne: soolane voolus surutakse rõhu all – merevee süsteemides tavaliselt 60…70 baari – läbi membraani, mis laseb läbi veemolekulid, kuid tõkestab lahustunud soolasid. Niikaua, kuni soolase vooluse hüdrauliline rõhk ületab osmootset rõhku (selgitatakse joonise paneelil b), läheb magevesi läbi membraani ja jätab soola maha. Me ei saa veel täielikult aru tõkestamise ja läbilaskmise mehhanismidest, kuid üldtunnustatud teooria, niinimetatud vakants-difusioon, postuleerib, et soolase poole vesi lahustub membraani materjalis ja hajub puhtale poolele palju kiiremini kui sool.
Parimal juhul peaks pöördosmoosi süsteem tarbima vähe energiat ja raha ning tõkestama palju soola. Väiksem energiatarve on üldiselt seotud madalama keskmise töörõhuga; väiksemad kulud tähendavad üldiselt membraani, millel on odavam pinnaühik või mille võib teha väiksema, sest selle veeläbilaskvus on suurem; ning parem soolatõkestus on üldiselt seotud väiksema soolaläbilaskvusega. Kulusid võiks vähendada ka parem ummistumiskindlus, mida on võimalik saavutada täiustatud membraanide või merevee parema eeltöötlusega, aga ka muude uuendustega, nagu paremate merevee sissevõtusüsteemidega ja kontsentreeritud soola kõrvaldamisega. Selles lühitutvustuses keskendume rõhule ja läbilaskvusele.
Energia- ja kapitalikulud
Soolavesi ja magevesi segunevad iseeneslikult. Seetõttu on termodünaamika seaduste kohaselt vaja nende eraldamiseks, st magestamiseks vaid veidi energiat. Tavalise mereveesüsteemi puhul, mis toodab ühest kilogrammist mereveest 1/2 kg magevett, on see umbes 1 kWh (kilovatt-tund elektrienergiat) kuupmeetri magevee kohta, mis on ligikaudu sama palju energiat, kui palju on vaja akna kliimaseadme ühetunniseks käitamiseks kuumal suvepäeval. Uued suured merevee pöördosmoosijaamad tarbivad enamasti ligikaudu 3…4 kWh/m³; võrreldes parimate suurte aurustamisega magestussüsteemidega, mis vajavad kuumutamiseks ligikaudu 20 kWh/m³. Tuleb arvesse võtta, et moodsate pöördosmoosijaamade puhul ei saa eeldada energiakulu olulist vähendamist – tase on juba üsna hea.
Sellele vaatamata on täiustamine võimalik. Selleks, et puhast vett soolasest voolusest eraldada, peab toiterõhk ületama selle osmootset rõhku. Soolase vooluse kontsentratsiooni suurenemisel selle osmootne rõhk tõuseb. Seega peab süsteemi kõrgeim rõhk ületama kõrgeimat osmootset rõhku – s.o kontsentreeritud soolase vooluse rõhku – piisavalt palju, et saada mõistlik veevool.
Pöördosmoosi protsess ei pea töötama alati selle kõige kõrgema rõhuga. Astmelises süsteemis tõstetakse rakendatavat rõhku olenevalt osmootse rõhu tõusust. Suur osa puhastusest toimub suhteliselt madalal rõhul, mis vähendab üldist energiatarvet. Puuduseks on sama koguse magevee tootmiseks vajalike täiendavate pumpade ja membraanide lisakulu. Ühte uuendust, mis pakub ilma lisakuludeta astmelisele süsteemile sarnast tulemust, nimetatakse suletud pöördosmoosiks, kus soolane voolus ringleb ja rõhk tõuseb kontsentreerumise käigus aeglaselt.
USA tööstustarbijate keskmine elektritariif oli 2014. aastal ligikaudu 7 senti/kWh, seega kulutavad suured pöördosmoosijaamad 3…4 kWh/m³ tootlikkuse korral 21…28 senti/m³. Sellise jaama käituse kogukulu on vahemikus 60…80 senti/m³, mis on ligikaudu pool tüüpilisest elamu veetariifist.
Suure osa kogukulu ja energiakulu vahest moodustab membraanide enda maksumus. Teadlased arendavad jätkuvalt selliseid membraane, mis lasevad vett paremini läbi ja hoiavad sooli paremini kinni. Edu korral võiksid väiksemad membraanid toota kompaktsemates süsteemides sama koguse vett odavamalt, kui seda toodavad praegused magestussüsteemid.
Tseoliite (teatud liiki mineraalid) ja mitmesuguseid tehismaterjale, näiteks süsiniknanotorusid ja nanopoorset grafeeni, kasutades on võimalik valmistada uut tüüpi üliläbilaskvaid membraane, millel on palju suurem veeläbilaskvuse võime kui tavalistel õhukesekilelistel komposiitmaterjalidel.
Paljudel juhtudel on eesmärk timmida nanomeetrist väiksemate pooride suurust, et luua molekulaarsõel. Ideed toetab intuitiivne füüsika: ioonid on lahuses ümbritsetud solvaatkihiga, veemolekulide keraga, mis orienteeruvad iooni ümber vee polaarsuse tõttu. See ümbritsev veekera teeb solvateerunud iooni üksikust 0,3 nm veemolekulist ligikaudu kaks korda suuremaks. Sel juhul peaksid õige suurusega poorid vee läbi laskma, kuid tõkestama suuremaid, solvateerunud ioone. Kuid tegelikkuses tuginevad üliläbilaskvad membraanid soovitud separeerimise saavutamisel pigem enamate tegurite kombinatsioonile kui lahustunud ainete suurusepõhisele tõkestamisele: need hõlmavad laengupõhist tõkestamist, teatavate lahustunud aineid funktsionaalsete rühmade omavahelist keemilist toimet ja soola läbipääsu takistavaid geomeetrilisi tõkkeid.
Ehituslikud kompromissid
Paljude üliläbilaskvate membraanide oluline puudus on selles, et nagu tavalised membraanid, ei tõkesta need täielikult soola läbipääsu. Eelkõige seetõttu, et üliläbilaskvad materjalid lasevad veel soolast palju lihtsamini läbi pääseda, hakkab soolakiht ladestuma vee väljapressimise käigus membraani pinnale. See ladestumine või polarisatsiooni kontsentratsioon soodustab soola imendumist läbi membraani. Mida suurema tootlusega vett soolasest voolusest eraldatakse, seda suurem on soola kontsentratsioon membraani pinnal ja seda suurem on soola läbiimbumine. Teiselt poolt tähendab suurem veevool vähemat aega teatud magevee koguse tootmiseks ja seega vähemat aega soola läbiimbumiseks. Seega on üliläbilaskvate membraanide suur veevool seotud kompromissidega: lõppkokkuvõttes määrab soolade tõkestuse pöördosmoosi süsteemi ehituse ja membraani soolaläbilaskvuse kombinatsioon.
Üks membraani materjal, mis võib näidata erakordset veeläbilaskvust ja soolatõkestust, on nanopoorne grafeen. Nagu on näidatud joonise paneelil c, on molekulaardünaamika simulatsioonid ennustanud, et nanopoorse grafeeni membraanid võivad saavutada tavalistest õhukesekihilistest komposiitmembraanidest kolm suurusjärku parema veeläbilaskvuse. Tegelikud membraanid ei pruugi saavutada nii suurt veeläbilaskvust või see võib olla piiratud polarisatsiooni kontsentratsiooniga. Kuid isegi praeguste moodsate membraanide veeläbilaskvuse kolmekordistamine võiks vähendada membraanide maksumust ligi 50%.
Energiatarbe jõulise vähendamisega kuni termodünaamilise piirini ja moodsate membraanidega, mis võivad puhastada vett tavalistest membraanidest mitu korda kiiremini, astub magestamise tehnoloogia kõige tõhusamate tööstustehnoloogiate hulka. Kuna praegused teadusuuringud täiustavad veelgi võimalusi vähendada energiatarvet ja kulusid, aitab magestamine üha enam üle saada kohalikust ja üleilmsest veenappusest.
Lisaallikad
- M. Elimelech, W. A. Phillip, „The future of seawater desalination: Energy, technology, and the environment”, Science 333, 712 (2011).
- M. M. Pendergast, E. M. V. Hoek, „A review of water treatment membrane nanotechnologies”, Energy Environ. Sci. 4, 1946 (2011).
- T. Humplik et al., „Nanostructured materials for water desalination”, Nanotechnology 22, 292001 (2011). ■
Viide:
Physics Today 68(6), 66 (2015); doi: 10.1063/PT.3.2828
Vaadake internetis aadressil http://dx.doi.org/10.1063/PT.3.2828
Vaadake sisukorda aadressil http://scitation.aip.org/content/aip/magazine/physicstoday/68/6?ver=pdfcov
Väljaandja: AIP Publishing
1981. aasta 17. juulil oli äsja avatud Hyatt Regency hotell Kansas Citys täidetud inimestega, kes nautisid elavas esituses 1940ndate parimaid palasid ning tantsisid nende saatel. Paljud seisid platvormidel, mis rippusid nagu sillad laia aatriumi kohal. Äkki kukkusid kaks platvormi kokku ja sadasid kaela all olnud lõbutsejatele. Surma sai 114 inimest ning vigastada rohkem kui 200.
Miks konstruktsioon kokku varises? Kindlasti mõjutas seda rahvamassi kaal, kuid kas platvormide ehituses oli ka põhimõttelisi vigu? Pärast mõnepäevast uurimist avaldati Kansas City ajalehes teade, et algset konstruktsiooni oli ehituse käigus muudetud. Esialgu oli ette nähtud, et kõigi kolme platvormi ühe poole otsad kinnituvad ühele laest rippuvale metallvardale. Platvormide raskust pidid kandma vardasse puuritud seib ja mutter (joonis 1-17a).
Platvormide ehitamise eest vastutav isik avastas aga, et sellist konstruktsiooni on praktiliselt võimatu ehitada ning asendas ühe pika varda kahe alusest välja ulatuva vardaga (joonis 1-17b). Kuidas võis selline lihtne ja mõistlik muudatus viia sellise reedeõhtuse katastroofini?
Vastus Vaatleme, kuidas jaotus raskus kõrgeima platvormi otstel. Algselt pidi konstruktsiooni ja inimeste raskus toetuma varda külge keeratud mutrile. Aga uue, kahe mutriga variandi puhul? Allapoole suunduva varda otsas olnud mutter pidi kandma kahe alumise platvormi raskust. Ülespoole suunduva varda mutril lasus aga kõigi kolme platvormi raskus. Kui rahvast kogunes juurde, purustas nende summaarne kogumass mõne mutri ja süsteem variseski kokku. Väike muutus, kuid traagiline tulemus.
Mõningates piirkondades, kus külmikud väga levinud ei ole, valmistatakse jääd järgmisel viisil: mingisugune lame nõu täidetakse veega, isoleeritakse maapinnast ja jäetakse ööseks välja. Loomulikult külmub vesi, kui temperatuur väljas langeb alla külmumispunkti. Samas, selgetel öödel võib vesi külmuda isegi siis, kui välistemperatuur jääb üle vee külmumispunkti. Mis põhjustab sellistel õhtutel vee jäätumise?
Vastus Selgetel õhtutel võib taevast vaadelda kui ühtlast pinda, mille temperatuur on alla vee külmumispunkti. Öö jooksul toimub taevast moodustava pinna ja vee vahel soojusvahetus infrapunakiirguse näol. Vesi, mis on algul soojem kui jäätumistemperatuur, kiirgab rohkem soojust ära kui taevast juurde saab ning jahtub. Kui õhutemperatuur vee ümber ei ole liiga palju üle külmumispunkti, võib vesi kaotada piisavalt soojust, et jäätuda. Veeanum peab aga olema maast isoleeritud, vastasel juhul juhib maapind vette soojust juurde ning takistab jäätumist.
Kui päike loojub selge horisondi taha, võib olla näha teravat rohelist helki täpselt siis, kui päikeseketta ülemine serv silmapiiri taha vajub. Tegu ei ole järelkujutisega silma võrkkestal, sest seda on ka pildistatud ning päikesetõusul täheldatud. Suurtel laiuskraadidel võib seda helki näha ka pikema aja jooksul, isegi kuni 30 minutit, kui päike liigub koidikul pärast pikka talveööd piki horisonti. Et nähtust jälgida, on vaja selget ja teravat silmapiiri, nagu see on näiteks ookeani kohal.
Palju harvem võib näha punast helki, kui päike, mis on madalal taevas, piilub pilve alt välja. (Rohelise ja punase helgi otsingul tasub otse päikese poole vaatamisel ettevaatlik olla: valgus võib võrkkesta kahjustada, ilma et oleks tunda valu. Kõrge päikese poole ei tohi vaadata üle sekundi ning mitte kunagi ei tohi seda teha binokli või teleskoobiga. Kui päike loojub, nõrgendab valguse hajumine kiirgust selle pikale teele jäävatelt arvukatelt molekulidelt, mistõttu vaatlemine on mõnevõrra ohutum.)
Mis põhjustab rohelist ja punast helki?
Vastus Rohelise helgi tekkimisega on seotud mitu tegurit. Peamine neist on valguse jagunemine värvusteks, kui selle trajektoor Maa atmosfääri läbimisel kõverdub. Traditsiooniline põhjendus on järgmine: kui päike on madalal, sõltub selle näiv asukoht värvusest. Kõige madalamal on punase valguse tekitatud kujutis ning järjest kõrgemal on kollase, rohelise ja sinise valguse tekitatud kujutised. Kui päike loojub, on näha vaid ühte summaarset kujutist. Hetkel, mil päikeseketta ülemine äär vajub horisondi taha, elimineeritakse aga spektri punane ja kollane osa ning alles jääb vaid roheline ja sinine osa. Sinine kujutis on valguse hajumise tõttu teel läbi atmosfääri tajumiseks liiga tuhm. Seetõttu on viivuks nähtav viimane kujutis roheline – roheline järelhelk.
Selles traditsioonilises argumendis on aga konks. Päikeseloojangut vaadates lakkavad töötamast need silma valgustundlikud pigmendid, mis näevad rohelist. Kui viimane valgus, mida päikeselt näha on, on peamiselt kollane, siis mainitud häire tõttu tundub see roheline. Kui pöörduda äkiliselt loojuva päikese poole, paistab viimane valgus kollasena, nagu see on ka tegelikult ja fotodel. Selline füsioloogiline ümberlülitus ei esine päikesetõusul, sest valgustundlikke pigmente ei valgustata üle.
Kui viimane seletus on täielik, siis miks ei ole rohelist helki võimalik näha alati, kui päike loojub selgel horisondil, ning kuidas on võimalik rohelist helki pildistada? Haruldust põhjustab lisategur. Helki võivad tugevdada atmosfäärikihid, milles temperatuur muutub. Kihistumine võib mõnikord eraldada päikese kujutise ülemise osa ja seda suurendada. Kui suurendatud ülemine serv muutub roheliseks, siis on parim võimalus rohelise helgi silmamiseks. Sellisel juhul on roheline helk päriselt olemas ja seda saab pildistada.
Erakordselt haruldane punane helk ilmneb siis, kui päike ilmub pilve tagant välja, nii et on näha üksnes selle punast kujutist. Teised värvused on veidi liiga kõrgel, et pilve tagant välja paista. Haruldust põhjustab ilmselt asjaolu, et päike peab olema küllalt madalal, kuid siiski kauge pilvemassiivi tagant nähtav.
Patarei ning kondensaatori tugevaim ühine nimetaja on võime muundada nendesse talletatud potentsiaalne energia elektrienergiaks, ehk panna vooluahel tööle. Ent energia salvestamise viis on neil hoopis erinev. Kui patareis talletub energia elektrokeemiliselt, siis kondensaatoris salvestub energia elektrivälja. Ometi on neil mõistetel mikromaailmas ühisosa, sest ka keemilised reaktsioonid toimuvad elektrivälja vahendusel, ent tegelikkuses pole see enamatel juhtudel määrav.
Teiseks erinevad patarei ning kondensaator energiatiheduse poolest. Võtame keskmise AA-suurusega leelispatarei. Selle mahtuvus on tavaliselt vahemikus 1800-2600 mAh, klemmpinge 1,5 V ning kaalub ligikaudu 23 g. Otsime internetist juhusliku vastava massiga elektrolüütkondensaatori: see laadub maksimaalselt pingeni 25 V, on mahtuvusega 1000 µF ning kaalub 25 g.
Nüüd tuleb teha ka tavaelus praktiline ühikute teisendamine:
mAh ehk milliampertundi kasutatakse patareide mahtuvuse kirjeldamisel sageli. Teisendame selle ühikuks, mida on hõlbus kondensaatori võrdluses kasutada: 1 A·h = 3600 s·A = 3600 s·C/s = 3600 C. Ehk meie valitud AA patarei, mille keskmine mahtuvus on 2200 mAh, mahutab 7920 C (kulonit) laengut. See on tegelikult väga suur laeng - varsti selgub, miks. Et patarei kaalub 23 g, saame selle energiatiheduseks 7920 C / 23 g = 344,3 C/g.
Kondensaatorisse talletatud laengu saab arvutada sõbralikust valemist
kus Q on laeng kulonites, C on kondensaatori mahtuvus faradites ning V on kondensaatori plaatide vaheline pinge voltides.
Leiame valitud kondensaatori maksimaalse laengu: Q=1000·10-6 F · 25 V = 0,025 C! Erinevus on kolmesaja tuhande kordne. Selle kondensaatori energiatihedus on seega 0,025 C / 25 g = 1 mC / g.
Selgub, et samas kaalukategoorias mahub harilikku AA patareisse kondensaatorist tuhat korda rohkem elektrienergiat!
Nüüd jõuame kolmanda väga olulise erinevuseni: olgugi, et patareisse mahub väga palju kuloneid laengut, suudab kondensaator enda laengust (elektrivälja potentsiaalsest energiast) palju kiiremini vabaneda. Mida rohkem energiat ajaühikus välja anda, seda võimsam kaadervärk on.
Selle tõdemuse muljetavaldav tegelikkus kajastub pildil, millel lendab parasjagu õhku arbuus. Arbuusi lühistati kondensaator (suur plokk pildi paremas pooles), mis andis hetkeliselt välja 9000 J pingel 9000 V. Teisendame selle ümber kuloniteks: C=J/V, ehk kõrvitsvilja vallandati laeng 1 C. Hämmastav, aga tõsi, 7000 korda vähem energiat kui ühes väikses AA patareis kokku.
Praegune maapealne kiirusrekord püstitati 1997. aastal Nevadas Black Rocki kõrbes reaktiivmootoriga autoga Thrust SSC. Auto kiirus oli ühes suunas 1222 kilomeetrit tunnis, vastassuunas aga 1233 kilomeetrit tunnis. Mõlemad kiirused ületasid helikiiruse (1207 kilomeetrit tunnis) ning pealtvaatajad võisid tunda selle tagajärjel tekkinud mööda kõrbe levinud lööklaineid. Kiirusrekordi püstitamine oli väga ohtlik mitmel põhjusel. Näiteks oli oht, et esiosa alla tekkinud õhusurve tõstab auto nina õhku ja auto lendab tahapoole uppi (samal ajal helist kiiremini liikudes!). Varjatum oht oli seotud auto rehvidega. Kas suudad selle välja mõelda?
Vastus Ülehelikiirusel liikuva auto rattad sooritasid kõrbepinnal 6800 pööret minutis, mis tekitas ratta pöiale mõjuva 35 000g suuruse tsentripetaalkiirenduse (35 000-kordne raskuskiirendus). Kuigi rattad olid valatud alumiiniumist, tõi kiirendus need rebenemise piirile. Ei olnud teada, kuidas rattad seda kõrbepinnal kihutades taluvad. Isegi väikesest objektist üle sõitmise tagajärjel oleks ratas tükkideks lennanud ja auto ennast puruks sõitnud. Kuna seda kõrbeosa oli kasutatud suurtükkide harjutuslaskmisteks, pidi meeskond osaliselt pinnasesse mattunud mürsukestade ja muu sarnase eemaldamiseks kogu raja enne sõitu tähelepanelikult läbi käima.
Suurte kiiruste saavutamiseks on vaja suurt jõudu.
Autode arenguga on alatasa käinud kaasas soov sõita kiiremini. 20. sajandi alguse võistlusautod jääksid aga tänapäeval linnaliikluselegi jalgu. Nüüd hoiab ratastel sõiduki maismaa kiirusrekordit kahe reaktiivmootoriga rakettauto ThrustSSC, mis ületas 1997. aasta 15. oktoobril helibarjääri ja saavutas kiiruse 1227,9 km/h.
Olgu stardijoonel auto, lennuk, jalgratas või rakett, on nende kõigi finišisse jõudmise suurimaks vaenlaseks õhutakistus. See leitakse avaldisest:
- FD - takistusjõud
- ρ - õhu tihedus
- v - auto kiirus
- CD - auto kujust sõltuv ühikuta takistustegur
- A - auto ristläbilõikepindala
Et jõu avaldises on kõik suurused peale kiiruse konstandid, võib need võrdluse eesmärgil koondada ühe muutuja alla ja öelda, et õhu takistus on võrdeline kiiruse ruuduga.
Eesti linnades kehtib kiiruspiirang 50 km/h. Võrreldes seda ThrustSSC rekordkiirusega 1227,9 km/h selgub, et ülehelikiirusel liikuv auto peab tänaval sõitvast autost ületama kuussada korda suurema õhutakistuse - vägev! Ent veelgi vägevam on tõsiasi, et selle takistuse ületamiseks vajalik võimsus sõltub kiiruse kuubist:
Ehk ThrustSSC on linnaautost ligikaudu viisteist tuhat korda võimsam!
Näib, et raskuste ületamine on inimeste üks põhilisi ülesandeid, olgu autospordis või argielus. Õnneks ei ole igal hommikul 07:15 ärkamisel ja koolitükkide tegemisel õhutakistust vaja arvestada.
2000. aasta augustis korraldas Venemaa Põhjalaevastik Barentsi meres õppuseid, mille käigus uppus saladuslikult tuumaallveelaev Kursk. Kui teade laeva uppumisest levis, taipasid põhjapoolkera seismoloogid, et nad olid Kurski uppumispäeval registreerinud kummalisi Barentsi merest lähtunud seismilisi laineid. Nende andmete analüüsist selgus allveelaeva tõenäoline uppumispõhjus ja – mis veelgi üllatavam – õnnestus kindlaks teha ka see, kui sügaval allveelaev paikneb. Kuidas on võimalik väga kaugelt tehtud mõõtmistega selgitada välja laeva paiknemise sügavus?
Vastus Seismilised lained on lained, mis liiguvad kas läbi maakera sisemuse või mööda maakoort. Üldiselt ehitatakse seismoloogiajaamu selleks, et registreerida maavärinate tekitatud seismilisi laineid. Neis suudetakse aga registreerida ka laineid, mis on tingitud maapinna lähedal vabanevast suurest energiahulgast, näiteks plahvatusest. Kui seismilised lained mööduvad jaamast, panevad nad salvestuspliiatsi võnkuma ning see joonistab paberile graafiku. Graafikul, mida seostatakse Kurski hukkumisega, võis esmalt näha väikese amplituudiga lainete seeriat, 134 sekundit hiljem järgnesid palju suurema amplituudiga võnkumised.
Analüütikud tegid järelduse, et esimesed lained tekitas laeval toimunud plahvatus, ilmselt põhjustas selle torpeedo, mille väljatulistamine ebaõnnestus. See plahvatus purustas tõenäoliselt Kurski kere, tekitas tulekahju ja uputas allveelaeva. Tugevamad seismilised lained tekkisid pärast aluse uppumist ning neid põhjustas tulekahju tõttu süttinud mitme (arvatavasti viie) võimsa raketi üheaegne plahvatus. Need tugevad lained jõudsid jaama impulsside jadadena, ühe plahvatuse tekitatud impulsside vahe oli umbes 0,11 sekundit.
Selle ajavahe järgi said analüütikud arvutada allveelaeva asukoha sügavuse. Tugevam plahvatus toimus sellal, kui Kursk oli juba merepõhja vajunud. Laev saatis laineimpulsi merepõhja poole ja läbi vee ülespoole. Läbi vee levinud impulss „põrkus” korduvalt merepinna ja -põhja vahel. Iga kord, kui laine vastu põhja põrkas, levis ta osaliselt ka maakoorde. Maakoores levinud laineid registreerisidki seismoloogiajaamad. 0,11-sekundiline viivitus oli aeg, mis kulus impulsil merepõhjast veepinnani ja uuesti alla jõudmiseks. Selle abil said analüütikud arvutada laeva uppumiskoha hinnanguliseks sügavuseks 80 meetrit. Tegelikult leiti laev hiljem 115 meetri sügavuselt – see on arvutatud sügavusega küllalt hästi kooskõlas.
Seismoloogid on registreerinud ka teisi suuri plahvatusi, näiteks veoautopommi plahvatuse Keenia pealinnas Nairobis 1998. aastal, mil rünnati USA saatkonda. Samuti registreeriti 1989. aastal kosmosesüstiku Columbia Los Angelesest ülelennul (akustiline) lööklaine. Süstik naasis edukalt õhujõudude baasi Edwardsis. Seismoloogidele ei jäänud märkamata ka 11. septembril 2001. aastal toimunud kaaperdatud lennukite kokkupõrge Maailma Kaubanduskeskusega ja sellele järgnenud tornide kokkuvarisemine.
Franco Bagnoli
astronoomiaosakond ning keerulise dünaamika uurimiskeskus,
Firenze ülikool, Itaalia, franco.bagnoli@unifi.it, DOI: 10.1051/epn/2015205
„Titanicu” filmis ütleb Jack Dawson (Leonardo DiCaprio) Rose DeWitt Bukaterile (Kate Winslet), kui ahter hakkab vajuma, et naine oleks valmis ujuma, sest uppuv laevakere tõmbaks nad meresügavikku. Kas see tõmbefenomen tekib ka päriselt? Ja kui, siis miks?
Tõmme tekib kindlasti. Oma mälestustes [1] kirjeldab Tameichi Hara uppuvast laevast välja hüppamise kogemust ja tekkinud imikeerist. Niisuguse nähtuse olemasolust on juttu ka ühes „Müüdimurdjate” osas [2], kus see efekti ei toimi, ent seal kasutati väikest paati.
Internetist võib leida üldiselt kolme liiki seletusi. Esimese kohaselt pääseb laevas olnud õhk uppumise ajal välja ja vähendab vee tihedust. Teine seletus on see, et laeva tühjadesse ruumidesse sisenev vesi tõmbab inimesed endaga kaasa. Kolmas on seotud viskoosse tõmbeefektiga, mis tekitab vedelikku läbiva keha taha keerise. See on sama efekt, mis keerutab kabrioletiga sõites pikki juuksed vastu nägu. Seda on lihtne ette kujutada, kui puhute käe taga seisva küünla poole (st, muudate taustsüsteemi) või liigutate kätt vees, kus on hõljuvat puru.
Efekt sõltub ka liikuva eseme kiirusest, vähemalt väikeste kiiruste puhul.
Vastavalt Archimedese seadusele on olemas siiski nähtavam efekt, mida üldiselt eiratakse (seotud kuidagimoodi nn tühjusesse imemise efektiga). Kui keegi soovib seda n-ö etendusena esitada, soovitan osta sissejuhatuseks Tubtanicu [3]. Vaja on ka „jäämäge” (mida kasutatakse sissejuhatuses ja viimases ülesandes), läbipaistvat silindrikujulist anumat ja paksu põhjaga (stabiilsuse ja suurema veeväljasurve pärast) klaasi, mille diameeter on umbes pool silindri omast.
Täitke silinder poolenisti veega ja laske klaasil (meie Titanicul) veepinnal ujuda. Märkige veetase markeriga silindrile ja paluge, et publik valiks ühe kolmest võimalikust vastusest küsimusele „Kui ma lasen klaasil uppuda, siis milline on veetase pärast meie Titanicu põhjavajumist?” (vt joonist). Kas veetase on a) kõrgem kui praegu, b) sama või c) madalam?
Üllataval kombel valivad enamik inimesi minu katses vastuse a, aga katse näitab, et „merepind” on pärast laevahukku madalam (efekt on paremini näha siis, kui klaasi poolt välja tõrjutava vee hulk on suur ja kui silinder on kitsas).
Selgitus eeldab Archimedese seaduse kiiret meenutamist: vedelikus asetsevale kehale mõjuv üleslükkejõud on võrdne selle keha poolt väljatõrjutud vedeliku kaaluga. Üleslükkejõud on võrdne klaasi kaaluga. Kuid kuna klaasi tihedus on suurem, tõrjub see välja rohkem vett, kui tema enda mass on, mis on mõistagi võimalik tänu õhuga täidetud osale. Pärast põhja vajumist tõrjub klaas välja ainult oma ruumalaga võrdse hulga vett ning veetase alaneb. Uppuva laeva puhul tähendab see, et laev kipub ookeani justkui auku kaevama ning ümbritsev vesi täidab selle augu kohe. Kõnealune efekt, nagu ka tõmbeefekt, sõltub uppumise kiirusest, mistõttu on nende kahe vahel raske vahet teha.
Pärast katset võib klaasi eemaldada ja panna silindrisse „jäämäe”, märkida uuesti ära veetaseme ja küsida kõigepealt, mis juhtub veetasemega pärast jää sulamist? Kuna vastuse saamiseks tuleb veidi oodata, on otstarbekas teha see katse etenduse alguses, koguda kokku vastused ja naasta selle teema juurde lõpus.
Ja nüüd viimane ülesanne: asetage golfipall veeklaasi, kuhu lisage nii palju soola, et pall napilt ujuks. Mis juhtub palliga, kui klaasi lisada mõnd kergemat vedelikku (õli või vedelseepi) [4]? Kas pall a) tõuseb, b) jääb samale kõrgusele või c) upub?
Viited
[1] Tameichi Hara, Japanese Destroyer Captain, Ballantine Books, New York & Toronto, 1961. ISBN 0-345-27894-1.
[2] http://www.discovery.com/tv-shows/mythbusters/videos/sinking-titanic-minimyth.htm.
[3] http://www.amazon.co.uk/Paladone-PP0258-Tubtanic-Bath-Plug/dp/B003Y3Q1GW.
[4] Ülesanne on võetud Veritasiumist
https://www.youtube.com/watch?v=C_covjcIcZ4
Mis juhtuks, kui näiteks tennisepall lendaks üle võrgu kiirusega 90% valguse kiirusest?
Makrokehi ei ole võimalik sellise kiirusega liikuma panna, küll aga saab kiirendada osakesi. Prootonite kiirus LHC kiirekanalis on 0,999999991c, st valguse kiirusest jääb puudu umbes 3m/s. Kosmilistes kiirtes esineb veelgi kiiremaid osakesi.
Küsimus nii suure kiirusega liikuvast hüpoteetilisest pallist on vastatud Randall Munroe raamatus „Mis oleks kui..? Tõsised teaduslikud vastused absurdsetele hüpoteetilistele küsimustele” („What If?: Serious Scientific Answers to Absurd Hypothetical Questions”). [1] Ameeriklasena võtab autor näiteks loomulikult pesapalli, aga sel kiirusel ei ole erinevus mistahes palliga juhtuvast märkimist väärt.
--------------
Vastab ja joonistab Randall Munroe:
Jätame kõrvale küsimuse, kuidas me saaks pesapalli nii kiiresti liikuma. Eeldame, et tegu on muidu normaalse sööduga, ainult hetkel, kui söötja laseb palli lahti, kiirendab see võluväel kiiruseni 0,9c. Pärast seda hetke kehtib jälle tavaline füüsika.
Mis juhtub? Tuleb välja, et juhtub „päris palju asju” ja see ei lõpe hästi lööjale (ja söötjale samuti mitte) [2]. Istusin füüsika raamatute taha, Nolan Ryani kujuke laual [3], vaatasin hunniku tuumakatsetuste salvestisi ja püüdsin ses kõiges selgusele jõuda. Järgnev on mu parim hinnang selle kohta, mis toimuks nanosekund-nanosekundilt.
Pall liigub nii kiiresti, et kõik muu on praktiliselt paigal. Isegi õhu molekulid seisavad ühel kohal. Õhu molekulid vibreerivad edasi-tagasi kiirusega mõnisada miili tunnis, aga pall liigub nende hulgas kiirusega 600 miljonit miili tunnis. See tähendab, et sel ajal kui pall on mängus, seisavad molekulid lihtsalt tardunult paigal.
Aerodünaamika siin ei rakendu. Tavaliselt voolab õhk ümber kõige, mis õhus liigub, kuid selle palli ees olevatel molekulidel pole aega, et lasta end eest ära trügida. Pall kihutab neile otsa sellise jõuga, et õhu molekulide aatomid tungivad palli pinna aatomitesse. Igast põrkest lahvatab gammakiirgus ja hajuvad osakesed.*
Gammakiirgus ja tuumade killud moodustavad paisuva mulli, mille keskmeks on söödumägi. Algab õhu molekulide lõhkumine ja elektronid kooritakse tuumadelt maha. Õhk staadionil muutub paisuvaks hõõguva plasma mulliks. Mulli välispiir jõuab lööjani peaaegu valguse kiirusega, ainult veidi enne palli.
Palli esiküljel toimuv tuumareaktsioon surub palli tagasi ja aeglustab seda. See on nagu saba ees lendav töötava mootoriga rakett. Kahjuks liigub palli nii kiiresti, et isegi termotuumaplahvatuse kohutav jõud suudab teda vaevu pidurdada. Siiski hakkab see lagundama palli pinnakihti, kihutades laiali pisikesi tükikesi. Need purud liiguvad nii kiiresti, et põrkudes õhu molekulidega käivitavad teise ja kolmanda ringi fusiooni.
Umbes 70 nanosekundiga jõuab pall kodupesale. Lööja isegi ei näe, et söötja on palli teele saatnud, sest infot kandev valgus jõuab kohale peaaegu samal ajal kui pall. Põrkumine õhuga on palli peaaegu täielikult läbi söönud. Nüüd liigub see püssikuuli kujulise paisuva plasmapilvena õhku rammides (põhiliselt süsinik, hapnik, vesinik ja lämmastik) ja käivitades veel täiendavalt fusioonireaktsioone. Lööjat tabab esmalt röntgenkiirguse front, mõni nanosekund hiljem saab ta löögi tuumareaktsioonide saaduste pilvelt.
Kui see jõuab kodupesani, liigub pilve keskpunkt ikka veel valguse kiirusega võrreldava kiirusega. See tabab kurikat, aga lööja, pesa ja püüdja kantakse kaasa läbi väljakupiirde, seejuures nad kõik lagunevad laiali. Röntgenikiirguse ja kuuma plasma ala laieneb ja kerkib, haarates endasse väljakupiirded, mõlemad võistkonnad, tribüünid ja kogu naabruse. Kõik see juhtub esimese mikrosekundiga.
Oletame, et vaatate seda linnalähedase künka tipust. Esimese asjana näete pimestavat valgust, tublisti eredamat kui Päike. Valgus tuhmub mõne sekundiga, kui kasvav tulekera kerkib seenekujuliseks pilveks. Siis saabub suure lärmiga lööklaine, kiskudes puid juurtega maast ja purustades hooneid.
Umbes miili ulatuses on kõik maatasa ja tuletorm ujutab üle ümbritseva linna. Palliväljaku asemel on suur kraater, mille keskpaik jääb mõnisada jalga endisest väljakupiirdest väljapoole.
MLB reegel 6.08(b) soovitab, et sellises olukorras loetaks lööja sööduga pihtasaanuks ja ta saab minna takistuseta esimesele pesale.
* Pärast selle artikli ilmumist võttis minuga ühendust MIT-i füüsik Hans Rinderknecht ja ütles, et nad on oma labori arvutitel seda stsenaariumi simuleerinud. Ta leidis, et palli lennu algul liigub suuremjagu õhu molekule liiga kiiresti, et fusiooni tekitada. Need lähevad pallist otse läbi kuumutades seda aeglasemalt ja ühtlasemalt kui mu algne artikkel kirjeldas.
[1] Autor rõhutab oma raamatus, et ta ei ole teadlane vaid koomiksijoonistaja. Aga ta on huviline ja võtab veidratele küsimustele vastamist tõsiselt, samas rõõmuga ja loominguliselt. Ta peab kodulehte: http://xkcd.com/.
[2] Pesapalli reeglid võib leida Eesti Pesapalli ja Softpalli Liidu kodulehelt: http://www.baseball.ee/et/content/reeglid. Selle vastuse mõistmiseks on hea teada, et söötja viskab pesapalliväljaku keskelt (söödumäelt) palli 18,4m kaugusel kodupesal seisva lööja poole, kes püüab palli kurikaga väljakule tagasi lüüa. Lööjast tahapoole jääb püüdja, väljakupiire, kohtunikud, võistkonnad. Ülejäänud reeglid on mängu seisukohalt olulised, selle küsimuse jaoks mitte.
[3] Nolan Ryan (sündinud 1947) on tuntud pesapallimängja, kelle nimel on mitmeid saavutusi. Ta on kuulus selle poolest, et söötis pika karjääri jooksul regulaarselt kiirusega üle 100mph (161km/h).
Mis on süsinikkiud? Lihtne vastus – süsinikust kiud.
See on muidugi mingi piirini õige, aga ei ole piisav ja jätab mitu küsimust vastamata. Kas tõesti ainult süsinik? Milline on süsinikkiu struktuur mikrotasandil? Millest süsinikkiudu tehakse? Milles on süsinikkiud kõigi teiste kiudude hulgas eriline ja mis põhjustab tema imematerjali kuulsuse?
Süsinikkiuks (carbon fibre) nimetatakse nii kiudu ennast kui ka sellest valmistatud lõnga ja kangast, mille kõige laiemalt tuntud kasutusala on plastiku armeerimine, kuigi armeerida saab ka keraamikat ja veel ühte-teist. Terminoloogiliselt ranget vahet tehes tuleks seda komposiitmaterjali nimetada süsinikkiuga armeeritud plastikuks. Peaaegu alati nimetatase seda samuti süsinikkiuks. (Näiteks: süsinikkiust jalgratas on tegelikult jalgratas, mille mõned osad on tehtud süsinikkiuga armeeritud plastikust.) Klaasplastik ehk klaaskiuga armeeritud plastik on selle vanem ja odavam vend. Klaaskiud on lihtne asi, sest klaasi saab pehmeks kuumutada ja peenikeseks niidiks tõmmata. Süsinikuga on asi keerulisem.
Kuigi süsinikkiu saamiseks on erinevaid tehnoloogiais, on kõige levinum, et algul tehakse polüakrüülnitriilist kunstkiud. Võimalik (mõne erisorti süsinikkiu saamiseks isegi vajalik) on alustada pigist või tselluloosi kiududest. Kõigepealt saadud kiudu stabiliseeritakse. Tehniliselt tähendab see mitmekordset immutamist, pesemist, venitamist, keetmist, rullimist, gaasidega läbipuhumist jms. Keemiliselt muutub pikk süsivesinikust ahel tsükliliseks. Pikad molekulid koosnevad nüüd kuusnurkadest. See näeb juba veidi sedamoodi välja, nagu grafeeni üks riba, aga ei ole seda mitte. Kuusnurkades ei ole mitte kuus süsinikuaatomit, üks nurk on endiselt lämmastik. Stabliseerimisel muutub kiud ka peenemaks ja tihedamaks, ei sisalda enam poorides kuigi palju õhku ning pikad polümeerimolekulid on suures osas paigutunud piki kiudu.
Päris süsinikkiu saab grafiidistamisega, võiks ka grafeenistamiseks nimetada. Eelpolümeerist kuumutatakse välja kõik peale süsiniku. Natuke süsinikku läheb ka kaduma, aga olulisem on see, et algul vesinik ja hiljem ka lämmastik kaovad. Moodustuvad pikad ja kitsad grafeeni ribad. Ainult ribade servades on veidi lämmastiku aatomeid. Süsinikku laias laastus üle 95%. Mõnes mõttes on see nagu pikk grafiidi kristall, aga erinevus on siiski oluline. Grafiidis on samasugused kärjestruktuuriga tükikesed väikesed ja omavahel suhteliselt nõrkade molekulaarjõudega seotud. Seepärast on grafiit pehme ja pudenev. Kius on ribad pikad ja põimunud nagu nende eelmaterjaliks olnud polümeeris ja seepärast ongi kiud nii tugev.
Viimase etapi temperatuur ulatub 1300 kraadini, mõnes tehnoloogias isegi 3000 kraadini. Juhtub, et seda nimetatakse kiu põletamiseks, mis on vale. Tegelikult hoitakse hapnik sellest etapist hoolega eemal, muidu põleks kiud kohe ära. Nii palju kui kiud enne õhku sisaldab, seevõrd on seal ka põlemist. Üldiselt on tegu ikka polümeriseerumisega.
Kaubandusliku süsinikkiu saamiseks järgneb veel hulk tehnoloogiat. Kiudu puhutakse gaasidega läbi, kaetakse immutades või elektriliselt mitmesuguste ainetega, kedratakse, kootakse, põimitakse. Üks probleem on see, et kui kiud (enamasti kangas) läheb plastiku armeerimiseks, peab ta vaikudega hästi nakkuma. Selleks tehakse erinevatele sortidele sobivate vaikudega eelimmutamine. Samuti on oluline, et kiud omavahel veidi kleepuksid, et saaks nad niidiks kokku kerida. Muidu on neid keeruline poolidele ja maha kerida ning kangaks kududa.
Üks süsiniku mikrostruktuur, mida hästi teatakse, on süsiniknanotoru. Kui seda torustruktuuri pildilt vaadata, paistab ta pikk peenike asi ja tekib kiusatus sedagi süsinikkiuks pidada. Nanotoru on siiski nii struktuurilt kui ka omadustelt täiesti teine asi. Tõsi küll, mõnel harval juhul lisatakse kiududele natuke nanotorusid, et saada veel erilisemate omadustega materjale.
Ajalooliselt peetakse esimeseks süsinikkiuks Thomas Edisoni süsiniidiga hõõglambi katsetusi 1879. aastal. Tänapäevase süsinikkiuga on sel väga vähe ühist, mida näitab ka pikk tühik ajaloos. Kaasaegse tehnoloogia alguse võib märkida aastasse 1958, kui poolsünteetilisest tselluloosi kiust saadi esimesed, kõigest 20 kuni 50% süsinikusisaldusega süsinikkiud. Vastav tootmisharu ja rahvusvaheline süsinikkiu turg kujunesid välja 1970. aasta paiku.
Süsinikplastik on tänapäeval hästituntud materjal. Sellest tehakse võidusõiduautosid, mootor- ja jalgrattaid, lennukeid ja satelliite. Päris igapäevast kasutust piirab veel veidi hind, aga ajad muutuvad. Kas aga lihtsalt puhtal süsinikkiul on ka mõni rakendusvõimalus?
Üksikut kiudu saab kasutada mikroelektroodina biokeemiliste signaalide analüüsil. Tuhandetest süsinikkiududest korraga tehakse lennukite maandusharjad. Need on nii pikkuse kui ka läbimõõdu poolest joogikõrre mõõtu süsinikkiu pundid. Kinnitatud on harjad lennuki tiibade ja saba taha umbes ühemeetriste vahedega. Maandusharjad kaitsevad lennukikeret hõõrdeelektri (õhumolekulid vastu lennukikeret) ja äikesetabamuse kahjuliku mõju eest.
Toime seisneb selles, et teravike lähedusse tekib erakordselt mittehomogeenne elektriväli, mille tugevus varieerub suures ulatuses. Tekib koroonalahendus ja selle käigus elektrilaeng eraldub keskkonda. Võiks öelda, et hõõrdumisel kere laadub ja koroonalahenduse käigus tühjeneb. Mida tugevam on elektrivälja gradient, seda efektiivsemalt maandamisprotsess toimib. Välgutabamuse ajal harjakesed sulavad üles ja mehaanikutel tuleb need välja vahetada, nagu ka needid, mis on viga saanud.
Ross C. McPhedran ja Andrew R. Parker
Elusolendite efektseid värvusi tekitavad sageli keerukad nanostruktuurid, nn fotoonilised kristallid. Nende hulgas on selliseid, mille peale teadlased muidu ei oleks mõelnudki.
Kogu oma ajaloo jooksul on teadus ammutanud inspiratsiooni loodusest. Aga tänaseks päevaks on teaduse, sh optika arsenalis rikkalik varamu ideid, meetodeid ja tehnoloogiaid ning loodsnähtustest otsitakse inspiratsiooni üha vähem.
Kuid teaduse arenedes oleme saanud oma käsutusse ka uusi tööriistu, mille abil saame uurida looduse peenemaid struktuure ja avastada senitundmatuid asju. Optiline biomimeetika on valdkond, kus püütakse uurida elussüsteemide struktuure, et mõista, kuidas tekivad optilised efektid, mida looduses kohata võib ja võib-olla leida meie jaoks uudseid, evolutsiooni käigus tekkinud optilisi süsteeme ja struktuure, mida võiks tehnoloogias rakendada.
Selles artiklis tutvustame mõningaid näiteid looduse optilistest süsteemidest, mille abil me võime õppida kasutama iidseid lahendusi uutes rakendustes. Me usume, et kõikidel valgusega tegelevatel teadlastel on põhjust optilisest biomimeetikast huvituda - see annab meile teadmise sellest, kuidas füüsika elussüsteemides "töötab" ja arvatavasti on meil looduselt ka üht-teist õppida. Näiteks kui teadlased keskenduvad tihti materjali ühele parameetrile või omaduselele, näiteks äärmusliku murdumisnäitaja saamisele, siis bioloogiline maailm teiselt poolt pakub näiteid lahendustest, kus kogu lõpptulemuse saavutamiseks tarvilik omaduste gamma on saavutatud väga väheste vahenditega.
Looduse värvid
Bioloogilised süsteemid saavad oma värvid kahel viisil. Esiteks keemiliselt, kui elusorganisme katvad värvipigmendid neelavad ühtesid valguse lainepikkuseid ja peegeldavad teisi. Selliselt saadud värvide palett on efektne ja rikkalik. Kui pigmendid aja jooksul lagunevad ning organismil tuleb kulutada energiat nende asendamiseks. Ja soovitud värviefekti saamiseks sobivad pigmendid ei pruugi olla üldsegi saadaval.
Teine mehhanism - struktuurne (keha struktuurist tulenev) värvumine - kasutab füüsikat. Seal tekivad värvid ruumilistes nanostruktuurides interferentsi, difraktsiooni või hajumise tagajärjel. Selliselt tekkinud värvid on juba oma olemuselt püsivad, kestes niikaua, kuni struktuur säilub. Vaadates muuseumis säilitatavat liblikakogu, saab kohe eristada ikka veel eredaid struktuurseid värvusi tuhmunud pigmendivärvustest.
Üks paljudes looduslikes fotoonilistes struktuurides leiduv materjal on kitiin. Seda sisaldub paljude putukate välisskeletis, koorikloomade koorikus, seente rakumembraanis ja mujal. Nähtaval lainepikkusel on selle murdumisnäitaja nc = 1,53…1,56, mis pakub õhule (murdumisnäitaja ligi 1) või veele (murdumisnäitaja 1,33) vaid nõrka kontrasti. Kuid sellele vaatamata suudavad kitiinstruktuurid esile kutsuda tugevaid värvusefekte, mis sageli ilmnevad sillerduse või värvuse muutumisena sõltuvana suunast.
Kihilised süsteemid
Lihtsa näitena vaadelgem õhukihtidega eraldatud õhukeste kitiinkilede pakki. Üksikut õhukest kitiinkilet iseloomustab suur läbipaistvus ja väike peegelduvus kogu nähtava spektri ulatuses, nagu on näidatud joonisel 1a.
Seevastu struktuuril, kus 10 kitiinikihti on eraldatud 9 õhukihiga sõltub peegelduvus lainepikkusest ning punastel lainepikkustel täheldame tugevat maksimumi, nagu on näidatud joonisel 1b.
10-kihilist süsteem võib vaadelda kui õhukeste kilede pakki – või tänapäevastes terminites, kui ühemõõtmelist footonkristalli. Fotoonika vaatenurgast määrab kitiinikihtide arv fotooniliste keelutsoonide arvu, mis ilmnevad spektris kui läbipaistvuse miinimumid või peegelduvuse maksimumid. Pinna normaali suunas langeva valguse jaoks on peegelduvus ja läbilaskvus polarisatsioonist sõltumatud. Muude nurkade all langevas valguse jaoks sõltub peegelduvus tugevalt polarisatsioonist; Kui valgus langeb Brewsteri nurga all, tan-1nc, on peegeldunud valgus täielikult polariseeritud, nagu näidatud joonisel 1c.
Keerukamaid efekte võib saavutada, kui muuta kihtide struktuure. Näiteks kitiinikiht, mis sisaldab massiivi pikkasid rööpseid silindrilisi õhupoore, võib käituda, nagu oleks sellel anisotroopne murdumisnäitaja, millel on piki poore üks väärtus ja risti poore teine. Peegelduvus võib siis olla polarisatsioonist sõltuv isegi normaali suunas langeva valguse jaoks. Tugevamaid polarisatsiooniefekte on võimalik saavutada õhupooridega, mis on kihi pindade suhtes kaldu Bioloogilistes süsteemides esinevad kõik need variandid. Ja mitte ainult need.
Näiteks on kihilisi struktuure leitud mõnedel kaladel, kes ujuvad mere või järve veepinna lähedal. Neil on sageli läikivad kõhualused ja tuhmid seljad, et vähendada võimalust, et röövloomad märkavad neid alt ja ülevalt. Tänu täielikule sisepeegeldusele paistab veepind altpoolt nagu läikiv peegel. Ülevalt vaadates paistab sügav vesi halli ja tuhmina. Nende efektide imiteerimisega saab kala sulanduda oma keskkonda – huvitav vihje stealth-tehnoloogiale, mille nn vaipvarjamise (carpet cloaking) tehnika kavandasid John Pendry ja kolleegid (vt Martin Wegeneri ja Stefan Lindeni artiklit 2010. aasta oktoobri Physics Today's lk-l 32). Ühe sellise kala kõhualuste peeglilaadsete soomuste elektron-mikroskoopiline analüüs näitas, et need koosnevad guaniinikristallide juhuslike vahedega kihtidest.
Võrreldes joonisel 1b kujutatud korrapäraste vahekaugustega kihtide spektriga alandab juhuslik vahekaugus peegelduvuse maksimumi ja teeb kõrgendatud peegelduvuse piirkonna laiemaks.
Troopilisel süvakirveslaste sugukonda kuuluval kalal (hatchetfish), kes elab 200 kuni 1000 m sügavusel, kus päikesevalgus paistab sinine, on lisaks peeglilaadsetele struktuuridele tema hõbedastel külgedel, veel ka "sisseehitatud" valgusjuhtide süsteem. Spetsiaalne valgust tootev organ saadab sinise valguse valgusjuhtidesse, mis suunavad selle ühte paljudest väljumispunktidest kala alaosas. Kala kohandab toodetava valguse tugevust sõltuvalt seljale langeva päikesevalguse tugevusest ja saavutab selle, et ükski tema all ujuv röövkala ei näe enam ülal olevat siluetti – kala lihtsalt kaob pildilt! Sellist kaitsevärvi strateegiat kopeeriti II maailmasõja ajal UK ja USA sõjalennukitel. Kui lennukid olid kuulmiseks veel liiga kaugel, süüdati nende esiserva paigaldatud tuled, et teha neid silmapiiri taustal nähtamatuks. See kavalus oli just toimima saadud, kui leiutati radar.
Võred ja footonkristallid
Mitmekihilised materjalid on perioodilised pinna normaali suunas. Teine võimalus struktuursete värvuste saavutamiseks on perioodilised struktuurid normaaliga ristuvates suundades. Kui perioodilisus esineb vaid ühes suunas räägime me difraktsioonivõredest ning võime kasutame mõistet 2D-footonkristallid (vt artiklit „Quick Study”, Peter Vukusic, Tänapäeva Füüsika, oktoober 2006, lk 82).
Kui difraktsioonvõre samm on d ja valgus lainepikkusega λ langeb võrele nurga θi all, siis võrelt difrageerub valgus nurkade sinθm = sinθi + mλ/d all. On võimalik ka arvutada, kui palju energiat difrageerub m-ndasse järku1. Selgub, et energia jagunemine järkude vahel sõltub tugevalt polarisatsioonist ja võib muutuda kiiresti koos lainepikkuse või langemisnurgaga, eriti kui järgu difraktsiooninurk on 90° lähedal.
Difraktsioonvõrede kuhja võib vaadelda kui 2D-footonkristalli ja valguse levikut sellises struktuuris võib kirjeldada sarnase tsoonidiagrammiga nagu me oleme harjunud kasutama elektronide jaoks pooljuhtides. Kui võre elementide murdumisnäitaja on piisavalt suur, siis võib selline võrede "pakk" peatada mingis lainepikkuste vahemikus kogu valguse, sõltumata selle levimise suunast. Nimetame seda vahemikku täielikuks keelutsooniks. Kuigi elussüsteemidel nii kõrge murdumisnäitajaga struktuure ei ole, võivad seal siiski tekkida osalised keelutsoonid ning seeläbi suurepärased värviefektid.
Esimesed inimese loodud difraktsioonivõred võred pärinevad USA astronoomi David Rittenhouse2 töödest 1780. aastatel ja footonkristalle tutvustati Eli Yablonovitchi ja Sajeev Johni3 1987. aasta töödes. Loodus on kasutanud selliseid struktuure elusolendites rohkem kui 500 miljonit aastat. Näiteks Kanadas Briti Columbias 508 miljoni aasta vanuses Burgessi põlevkivis leitud erakordselt hästi säilinud näidised pakuvad meile ammu väljasurnud loomade, aga ka mõnede nende tänapäevaste sugulaste struktuursete värvide näiteid. Kui meil on õnne, siis saame jälgida optiliste struktuuride arengut üha suurema keerukuse ja parema efektiivsuse suunas mööda loomade evolutsioonipuu harusid.
| Joonis 2a Merihiir (Aphrodita aculeata) (a) kannab oma keha alumisel serval sillerdavat vilti ja seljal sillerdavaid astlaid. | Joonis 2b Ühe merihiire astla pilt elektronmikroskoobis näitab 88 kihist koosnevat tihedalt pakitud 510 nm läbimõõduga mikrotorude massiivi. Nii mikrotorude suur hulk kui ka nende korrapärane asetus on olulised astelde värvuse kujunemisel. (Mugandatud R.C. McPhedran et al., Aust. J. Chem. 54, 241, 2001.) |
Vaatame nüüd, kuidas toimib toreda nimega tagasihoidlik mereolevus merihiir ehk Aphrodita aculeata; see on harjasuss, kes elab merepõhjas mõne kuni mõne tuhande meetri sügavusel. Nagu näha jooniselt 2a, on ta tavaliselt tuhmi värvusega, et sobituda liivase või mudase merepõhjaga.
Aga tema keha alumises servas on pikad kauni sillerdusega karvad ja looma ülemisi servi kaunistavad jämedad, kuid samaväärselt värvilised astlad. Eeldatavasti peavad sillerdavad väljapaistvad astlad hoiatama röövloomi, et olend ei ole eriti hea söök.
Sillerdus oli kaluritele teada sajandeid tagasi ja Carl von Linne, kes klassifitseeris liigid 1758. aastal, märkis seda samuti. See on imekspandav, et loom võib saavutada sellise kontrastsusega sädeleva värvuse talle kättesaadavatest materjalidest: tema harjased on kitiinist ja ta elab vees. Joonisel 2b on elektronmikroskoobi kuva astalast, mis peegeldab ligi 100% sellele langevast punasest valgusest - selgub, et astel on õõnes toru, mille seinad on augustatud hämmastavalt korrapärase massiivi tihedalt pakitud mikrotorudega.
Astla struktuuri võib vaadata interferentsifiltrite komplektina, millest igaüks lisab üldisele optilisele efektile veidi peegelduvust. Tugeva värvusefekti saavutamiseks peab astlal olema suur hulk kihte, mille vahekaugused on peaaegu täiesti ühesugused.
Kui vaadelda astelt footonkristallina, siis peab see struktuursete värviefektide saavutamisel tuginema pigem osalistele kui täielikele keelutsoonidele. Tulemus on kohane merihiire eesmärkidele: astlad tekitavad kitsas lainevahemikus tugeva peegelduvuse, mis muutub koos valguse langemisnurgaga ja annab olendile iseloomuliku sillerduse.
Sama mehhanismi kasutatakse mikrostruktuursetes optilistes kiududes, mille töötasid 1990. aastatel välja Philip Russell ja tema kolleegid Bathi Ülikoolist. Kiud piiravad valguse läbipääsu kasutades korduvaid tagasipeegeldusi. Üks märkimisväärne edusamm, mille tegid võimalikuks mikrostruktuursed kiud, oli eriti laia spektriga superkontiinum, mida tunnustati 2005. aasta Nobeli füüsikapreemiaga (vt artiklit 2005. aasta detsembri Physics Today's lk-l 19 ning John Dudley ja Goery Genty artiklit 2013. aasta juuli Physics Todays lk-l 29).
Muud peegeldajad
Punased jooned oleksid järsemad ja lühemad, sinised jooned ei muutuks
Elusolendites leiduvad optilised süsteemid sisaldavad sageli segu perioodilistest ja kaheliperioodilisusest elementidest. Näiteks joonisel 3 visandatud struktuur näitab elementide kombinatsioone, mida erinevates variatsioonides esineb paljude liblikate soomustel. Aluskihi kaheliperioodiline akende massiiv võib toimida peegeldina, kombineerituna keemiliste pigmentidega võib see neelata peaaegu kogu langeva valguse. Vahetult selle peal asuv võrestruktuur toimib lainepikkus-selektiivse peegeldina, mille omadused võivad sõltuda polarisatsioonist. Põikvõrel jõulupuuokstena paiknevad ribad on nagu õhukeste kihtide pakid. Erineval viisil paigutatuna tekitavad need kolm elementi liblikatel erinevaid struktuurseid sillerdavaid efekte.
Liblikate soomustel on leitud ka muid optilisi elemente: nanoharjadega mikroribid, nõgusad mitmekihilised lohud, juhuslikult augustatud nanokihid ja „häälestatud” difraktsioonivõred, mis tähendab, et need koondavad suurema osa peegeldunud valgusest ühte difraktsioonijärku. Enamiku neist avastas 1970. ja 1980. aastatel John Huxley Londoni Loodusmuuseumis, kuhu ta jättis teistele õppimiseks ja avaldamiseks elektronmikrograafide aardelaeka.4 Mikrograafidega avastati struktuursed mustvalged soomused, topeltpeegeldusega mikrosüvendid, fluorestsentsi toetavad struktuurid ja igasugused muud kooslused, mida tänapäeval katsetatakse kasutamiseks kaubanduslikel toodetel. Praeguste prototüüpide uurimistööde põnevad tulemused avalikustatakse aasta või kahe jooksul.
Vääriskivil opaalil esineb lihtne, kuid oluline kolmekordne perioodiline struktuur, mille värvus tuleneb ligikaudu 500 nm läbimõõduga ränidioksiidi tihedalt pakitud sfääridest, mis paiknevad kuusnurksetes või tahktsentreeritud kuupvõredes. Struktuuri kasutatakse footonkristallide disainimisel, sageli vastupidisel kujul, kus väikese murdumisnäitja sfäärilised lisandid on paigutatud suure murdumisnäitajaga materjalile.
Opaali struktuur on avastatud õielõikajate perekonna Metapocyrtus soomustes. Joonisel 4a näidatud mikrostruktuuri 3D-perioodilisuse ja -isotroopsuse tulemuseks on soomuse värvitoonid (joonis 4b), mis paistavad kõigist vaatamissuundadest samasugused, osaliselt meie silma üldistusvõime tõttu. Kummalisel kombel kasutab joonisel 4c toodud sarnase ilmega õielõikaja ümberpööratud opaalstruktuuri.
Paljudel linnuliikidel on struktuursete värvustega suled. Koolibri sulgede kidad sisaldavad üliõhukesi vahelduva poorsusega kihte, mis tekitavad sillerdavaid efekte. Neid struktuure on jäljendatud, kasutades vesilahustel põhinevaid kihistustehnikaid. Sinised struktuursed suled, nagu näiteks joonisel 5 toodud Cotinga suled, sisaldavad tihedate vahedega õhutaskuid, millelt valguskiired koosmõjus peegelduvad.
Praegu on arendamisel värvid, mis moodustavad pärast kuivamist sarnased vorme.
Paljude mardikate väliskestad sisaldavad struktuurilt kiraalseid kilesid, mis toodavad ring- või elliptiliselt polariseerivate omadustega sillerdavaid efekte. Nende struktuurid on jäljendatud titaani eriotstarbelistes kattekihtides. Mimeetilisi näidiseid katsetakse mudelmardikal, kuni saavutatakse peegelduvuse täpne taasesitamine olenevalt nurgast. Seejärel saab titaani mimeetikat nanotehniliselt häälestada, et saada resonantseid lainepikkusi laias vahemikus.
Mittepeegeldavad pinnad
Seni on meie tähelepanu keskmes olnud valguse peegeldumisel tekkivad struktuursed värvused. Aga mõned putukad kasutavad ka mittepeegeldavaid (selgendatud) pindasid, kas oma silmades, et aidata neil hämaras näha, või oma tiibadel, et vähendada pinna helkimist, mis võiks püüda kiskja tähelepanu. Selgendatud pindasid esineb kõikide koide ja liblikate silmade sarvkestades ja surulaste läbipaistvates tiibades. Need koosnevad ligikaudu 240 nm sammuga kuusnurksesse massiivi paigutatud ümaratipulistest sõlmedest. Sõlme profiil tekitab sujuva murdumisnäitaja muutuse üleminekul õhust kitiini. Kui puuduvad järskud murduminäitaja muutusted väheneb pindade tagasipeegeldumine 10 korda.
| Joonis 6a Mittepeegeldavad, st selgendava kattega pinnad on aidanud putukatel näha miljoneid aastaid. Selline, 240-nanomeetriste ümardatud osakeste massiiv, katab liblika- ja koisilmade sarvkestasid. | Joonis 6b Läbi plastlehe pildistatud universumi kujutist Lehe keskele on kantud selgendava kattena toimiv nanostruktuur, mis on võetud merevaigus säilinud kärbse sarvkestalt. |
Joonisel 6a näidatud nn koi-silma struktuur taastoodeti esmakordselt oma õiges mõõtkavas kolme litograafiliselt toodetud võre 120° ristamisel. Tootmises kasutati seda esimest korda Skandinaavias klaasakende selgendava kattena. Tänapäeval saab koi-silma struktuuri teha äärmise täpsusega, kasutades elektronkiirega aurustamist. Seda kasutatakse tootmises tahkel plastil ja läätsedel.
Teistsugune peegeldusvastane struktuur, 250 nm sammuga siinuselise võre, avastati merevaigus säilinud 45 miljoni aasta vanuse kärbse sarvkestas. Selline struktuur on eriti kasulik, kui valgus langeb ühe tasapinna ulatuses teatud nurkade vahemikus võre soontega täisnurga all. Seda on rakendatud päikesepaneelide pindadel, et suurendada energia püüdmist kuni 10%. Selle peegeldust vähendava võime tutvustust on näidatud joonisel 6b.
Rakukultuur
Mõnikord on looduses esinevad optilised nanostruktuurid oma väikeste mõõtmetega nii keerulise ehitusega, et praegusi meetodeid kasutades ei saa me neid lihtsalt kopeerida. Mõnikord on see küll põhimõtteliselt võimalik kuid sedavõrd kulukas ja keeruline, et tööstuslik tootmine ei tasuks end kunagi ära.
Teine võimalus oleks teha selliseid struktuure samamoodi, nagu seda teevad loomad või taimed – kasvatedes neid elusrakkudest. Rakukultuuri edukus sõltub nii liigist kui ka rakutüübist. Kui näiteks putukarakke võib kasvatada toatemperatuuril, siis imetajate rakkude jaoks on vajalik inkubaator. Rakukultuur ei ole lihtne meetod – tuleb leida õige sööde, millel rakud kasvavad.
Praegu keskenduvad tööd selles valdkonnas liblikate soomustele. Soomuseid moodustavad rakud on tuvastatud ja neid kogutakse krüüslilt. Seejärel üksikud rakud eraldatakse, hoitakse kultuuris elus ja pannakse kasvuhormoonide lisamise teel soomuseid tootma. Üks meist (Parker) ja Helen Townley on hiljuti kasvatatud sinise Morpho liblika soomused, mille omadused on identsed looduslike soomuste optiliste ja struktuursete omadustega.5 Kahjuks kasutavad liblikarakud oma sisemised struktuurid ära juba ühe soomuse tegemise ajal. Samas õielõikaja rakud, vastupidi, ei kasuta, nii et potentsiaalselt võiks luua kultiveeritud õielõikaja rakke, et teha opaalseid struktuure, kuni neid toidetakse ja elus hoitakse.
Ülesanne on tunduvalt lihtsam, kui sillerdav organism on ise üks rakk, nagu näiteks ränivetikas. Ränivetikad on ainuraksed fotosünteesivad mikroorganismid. Nende üle 100 000 liigist on enamik 20…200 μm suurused, kuid mõned võivad olla kuni 2 mm pikkused. Nende rakuseinad, mida nimetatakse ränipantseriks (frustule), on valmistatud räniga immutatud pektiinist. Ränipantseris on poorid ja pilud, sageli väga keerulise struktuuriga, mis annavad raku sisemusele pääsu väliskeskkonda. Kuigi ränipantserite optiliste omaduste bioloogiline otstarve on teadmata, võivad need mõjutada fotosünteesi jaoks valguse kogumist. Ränivetikatest inspireeritud footonseadmeid saab teha ränist, kasutades sügava fotokeemilise söövituse tehnikat. Kuid ränivetikate enda rakendamine oleks kasulik vahetult 3D-seadmete ehitamiseks. Ränivetikate eelis on arvu eksponentsiaalne suurenemine: iga isend võib tekitada 100 miljonit järeltulijat kuus. Ja erinevalt enamikust tootmisprotsessidest saavutavad ränivetikad mõõdukates füsioloogilistes tingimustes suure keerukuse ja hierarhilise struktuuri.
Kasutades rakukultuuri tehnikat koos geenitehnoloogiaga või ilma selleta, võivad teadlased luua mõningaid looduse valgusvoo vormimise tehnikaid ja teha need suures ulatuses kättesaadavaks. Siis võiksime saada erinevaid nutikaid materjale sellistele rakendustele nagu püsivad värviekraanid, mis ei allu fotopleegituse toimele, väikse peegelduvusega katted päikesepatareide tõhustamiseks, uued stealth-tehnoloogiad, mis kasutavad visuaalset pettust, mitte lairibanähtamatust, lainepikkusest sõltuvad polarisaatorid ja paljud teised – kõik inspireeritud looduse kooli õppetundidest.6
See artikkel on pühendatud meie kolleegide ja sõprade Nicolae Nicorovici ja Jean-Pol Vigneron mälestusele.
Viited
- M. C. Hutley, Diffraction Gratings, Academic Press (1982); E. Popov, ed., Gratings: Theory and Numeric Applications, 2nd ed., Fresnel Institute (2014).
- M. Born, E. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed., Cambridge U. Press (1999).
- J. D. Joannopoulos et al., Photonic Crystals: Molding the Flow of Light, 2nd ed., Princeton U. Press (2008).
- A. L. Ingram, A. R. Parker, Philos. Trans. R. Soc. B 363, 2465 (2008).
- A. R. Parker, H. E. Townley, Bioinspir. Biomim. Nanobiomater. 4, 68 (2015).
- For further reading, see M. Large, ed., Optical Biomimetics: Materials and Applications, Woodhead (2012); A. Parker, In the Blink of an Eye, Perseus (2003); S. Berthier, Iridescences: The Physical Colors of Insects, C. Lafait, trans., Springer (2007); O. Karthaus, ed., Biomimetics in Photonics, CRC Press/Taylor & Francis (2012).
Ross McPhedran on Austraalia Sydney Ülikooli füüsika professor ja optiliste süsteemide ülikõrge laineala seadmete keskuses uurimisjuht.
Andrew Parker on Londoni Loodusajaloo Muuseumi bioteaduste osakonna teadusjuht.
Viide: Physics Today 68(6), 32 (2015); doi: 10.1063/PT.3.2816
Vaadake internetis aadressil http://dx.doi.org/10.1063/PT.3.2816
Vaadake sisukorda aadressil http://scitation.aip.org/content/aip/magazine/physicstoday/68/6?ver=pdfcov
Väljaandja: AIP Publishing
Oleme harjunud ütlema, et difraktsiooni tõttu ei saa optilise mikroskoobi lahutusvõime olla parem umbes poolest mikromeetrist. Ja nii on see ka kõige kaasaegsema tehnoloogia kontekstis: läätse või läätsede süsteemi abil ei ole võimalik tekitada fokaaltäppi, kus enamus energiat oleks koondunud väiksemasse piirkonda. Meeldetuletus sellest, kuidas määratakse nn Rayleigh’ kriteerium:
| Ümmarguse ava difraktsioonipilt. Kettakujulist tsentraalset maksimumi ümbritsevad rõngakujulised kõrvalmaksimumid. Selleks, et neid palju nõrgemaid kõrvalmaksimume esile tuua, on foto ülevalgustatud. | Ülal on kahe punkti kujutised, mis on saadud koondava läätsega. All on kujutiste intensiivsuste jaotused. Juhul (a) on punktidevaheline nurkkaugus punktide lahutamiseks liiga väike; juhul (b) on punktid vaevalt eristatavad; juhul (c) on punktid selgelt eristatavad. Rayleigh’ kriteerium on täidetud juhul (b), kui ühe difraktsioonipildi tsentraalne maksimum langeb kokku teise difraktsioonipildi esimese miinimumiga. |
Kokkuvõtlikult: punktvalgusallika kujutis lõpliku apertuuriga (läbimõõduga) optilises süsteemis on kujult samasugune, kui ümmarguse ava difraktsioonipilt. Kahe punktvalgusallika kujutised on veel eristatavad kui kaks sellist kõrvalmaksimumidega kujutist on eristatavad.
Superlahutusvõimega fluorestsentsmikroskoopia väljatöötamise eest said 2014.a. Nobeli keemia preemia Stefan W. Hell ja W.E. Moerner. Vaadake järgnevaid pilte:
| Ülemises paremas nurgas on tavalise konfokaalse mikroskoobiga saadud kujutis, alumises vasemas nurgas superlahutusega kujutis. Skaala on alumises vasemas nurgas. Superlahutuse paremus tavapärase mikroskoopia ees on ilmne. Siit ka nimi nanoskoopia. | Fluorestsentsmikroskoobi pilt hiire ajust lõigatud preparaadis. Iga närvirakk toodab erinevas proportsioonis eri värvi fluorestseeruvaid proteiine ja nii on kogu närvivõrgustik hästi jälgitav. |
Kuidas seda tehakse?
Seda on päris raske paari lausega seletada. Proovime siiski:
- Kõigepealt, sellises mikroskoobis ei vaatle me objektilt hajunud valgust vaid objekti poolt kiiratud valgust, fluorestsentsi. Teiseks, sellised mikroskoobid on skaneerivad, st korraga vaadeldakse vaid üht punkti ja pilt kogutakse kokku objekti seadmes skaneerides.
- Objekti molekule ergastava laseri fokaaltäpi ümber tekitatakse sõõrikukujuline valgusväli, nn tühjendav kiir, mis seal objekti molekulid teistele energiatasemetele viib. Teistelt energiatasemetelt lähtuv fluorestsents annab ka teist värvi fluorestsentsi ning seda on võimalik valgusfiltritega kustutada.
- Lõpptulemusena saame registreerida fluorestsentsi, mis lähtub väga väikesest objekti piirkonnast.
Ei saa bioloogid ilma füüsikata ...
Väga ilusad pildid!
Allikad:
http://dx.doi.org/10.1051/epn/2015502
https://en.wikipedia.org/wiki/STED_microscopy
Vaatle oma pea varju hommikukastesel rohul. Seda võib ümbritseda hele valgus, mis kannab nime aupaiste (joonis 6-15a). Sarnast heledat ala võib oma varju ümbritsemas näha ka mitmel muul pinnal: kuival rohul või muul taimestikul, madalal veeväljal, mis on lainesäbruga kaetud, ning paljudel kuivadel karedatel pindadel. Heledat triipu võib näha ka liikuva auto varjul, kui see ulatub rohuplatsile.
Otsi lennukiga lendamise ajal aupaistet maapinnalt lennuki varjupunktist (punktist, mis jääb täpselt päikese vastu). Sellal, kui vari liigub üle rohu, puude, palja maapinna, tänavate ja pilvede, aupaiste ilmub ja kaob. Maapinna lähedal vaadates võib helenduses näha äkilisi sähvatusi. Maapinnast palju kõrgemal olles võib mõnikord näha tumedat joont, mis aupaistest välja ulatub. Mis tekitab aupaistet, heledaid sähvatusi ja tumedat joont?
Kui teatud taimi, mis on kastega kaetud, valgustatakse taskulambi või stroboskoobiga, siis hakkavad valgusallikat hoidva inimese jaoks taimed helendama. Teised inimesed küljelt seda helendust aga ei näe. Kuidas selline helendus tekib ja miks kõik taimed niimoodi ei helenda?
Just siis, kui on täiskuu, saavutavad kõik valgustatud alad Kuu pinnal oma heleduse maksimumi. Mistahes ala Kuu pinnal võib olla 25% heledam kui päev enne või pärast täiskuud. Mis põhjustab Kuu pinnalt hajunud päikesevalguse intensiivsuse äkilise suurenemise? (Enne astronautide Kuule saatmist muretses NASA, et see pinnaselt tagasi hajunud valgus võib astronaute Kuul pimestada, kui nende kiivritel ei ole spetsiaalseid kaitseklaase.)
Kui spordiväljaku muru teatud viisil niita, paistab muru nagu malelaud, kus on heledad ja tumedad ruudud. Mis põhjustab sellist erinevust heleduses? Kas vanas ütluses, et rohi on kaugemal rohelisem, leidub teaduslikku tõtt?
Vastus Vaatleme esmalt kuiva muru. Kui vaadelda piirkonda, mis jääb ümber varju, võib näha ainult rohuliblesid. Varje, mida need heidavad, pole näha, sest need jäävad rohuliblede taha. Niisiis on piirkond hele, sest silma jõuab ainult sellelt peegeldunud päikesevalgus. Kui vaadata heledast piirkonnast kaugemale, on juba näha ka rohuliblede varjud ja summaarne heledus kahaneb. Kontrastina on piirkond pea varju ümber hele.
Karedal pinnal võivad aupaistet tekitada väikesed lohukesed, mis on ligikaudu täisnurkse kolmnurga kujulised. Sellised piirkonnad peegeldavad valgust allika poole tagasi ja osa peegeldunud kiirgusest jõuab vaatlejani. Teised vormid ja materjalid võivad veel lisaks valgust tagasi saata, seda eriti siis, kui pind on poorne ja selles on „tunnelid”. Kui vaadata varju oma pea ümber, võib näha valgust, mis on tagasi hajunud nende tunnelite sisepindadelt, kuid rohkem külje pool neid näha ei ole.
Kastesel rohul võib valgus kastepiiska siseneda, selle tagapinnalt ja rohuliblelt peegelduda ning siis piisast enam-vähem päikese suunas väljuda. Rohi ümber pea varju paistab hele, sest näha on osa peegeldunud valgusest. Kui vaadelda rohkem küljele jäävat muru, ei jõua kastelt peegeldunud valgus silma ja rohi ei ole seal nii hele.
Kerakujuline tilk fookustab valguse väikeseks täpiks veidi maad enda taga. Naasev valgus on kõige heledam siis, kui rohulible asub täpselt fookuses, kuid tavaliselt paikneb piisk otse lible peal. Teatud tüüpi lehed on kaetud väikeste karvakestega, mis hoiavad piiska mõnevõrra kõrgemal, ning sellised lehed tekitavad väga heleda aupaiste.
Kui lamp valgustab veepiisku taimestikul, siis saadetakse osa valgusest aupaistena umbes lambi suunas tagasi. Naasnud valgus on palju heledam siis, kui piisad on peaaegu kerakujulised. Teatud taimede vahajastel lehtedel moodustab vesi kerakujulisi piisku. Kui sellist taime tabab välklambi sähvatus, tundub see võrreldes teiste taimedega kiirgavat.
Heledaid sähvatusi aupaistes põhjustavad tavaliselt peegeldid, mis on harilikult klaas- või plastkuulid, mis suunavad valgust allika poole tagasi. Sellised pisikesed peegeldid võivad olla näiteks liiklusmärkide värvis, et saata esitulede valgust juhi poole tagasi. Niimoodi on märke pimedas hästi näha. Kui lennuki vari möödub sellisest märgist, jõuab vaatlejani osa valgusest, mille märk saadab enam-vähem päikese suunas. Tume joon, mis mõnikord aupaistet saadab, on tingitud kondensatsioonitriibust, mille lennuk taevasse jätab.
Kui lennuk on küllalt madalal, et selle varju näha, siis võib olla näha ka hele riba varju ümber. Riba võib olla tingitud valgusest, mille taimestikul olevad veepiisad saadavad enam-vähem päikese suunas (seega aupaiste), kuid need piisad võivad ka õhus hõljuda. Siiski võib sellist riba näha ka siis, kui veepiisku pole (näiteks kuiva ja viljatu maapinna kohal). Samuti võib heledat riba näha mõne teise lennuki varju ümber. Viimast nähtust ei saa kindlasti põhjustada veepiisad. Sellisel juhul on hele riba tajude tekitatud illusioon. Kui tume piirkond (näiteks lennuki vari) on vaateväljas heleda ala kõrval, siis tekitab nägemissüsteem kahe piirkonna lahutuspinnale heleda riba (tuntud Machi ribana).
Päikesevalgus võib Kuu pinnalt hajuda peaaegu igas suunas. Siiski on hajunud valgus kõige heledam Päikese suunas, sest valguskiired saavad üksteist selles suunas tugevdada. Kaks kiirt, mis on teineteisest veidi eraldatud, võivad läbida Kuu pinnases sama tee, kuid vastassuundades. Pinnasest väljumisel liiguvad kiired tagasi Päikese poole (joonis 6-15b). Lained neis kahes kiires on enam-vähem samas faasis ja tugevdavad niimoodi teineteist; nende kombineerumisel tekib hele valgus. Täiskuu ajal jääme me sellesse heledasse Päikese suunas hajunud valgusesse ja nii paistab Kuu meile eriti hele. Teistel öödel väljuvad valguskiired pinnasest suvaliselt ning üldiselt ei võimenda üksteist. Seetõttu pole Kuu nii hele.
Mõned samblad võivad samuti valgust Päikese poole niimoodi tagasi saata, et valguslained üksteist võimendavad. Seda heledat valgust võib näha siis, kui vaatleja varju tipp langeb suhteliselt kaugele samblale. Rohkem on seda märgatud samblarohketest piirkondadest tehtud aerofotodel.
Malelaua muster niidetud murul tekib asendist, millesse niiduk jätab rohulibled. Mõnes kohas paiknevad libled nii, et peegeldavad valgust vaatleja poole, samal ajal teistes kohtades need seda ei tee ja näha on hoopis nende varjud.
Muru võib kaugelt tunduda rohelisem, sest kui vaadata muru peale kaldu, ei paista selle all olev pruun muld, seda näeb paremini, kui vaadata ülevalt alla. (Kindlasti peitub siin ka võrdpilt elu ja suhete kohta, kuid sellega võib juba lugeja ise edasi tegeleda.)
Pika järelhelendusega on pulbrilised ained, nagu Eu ja Dy dopeeringuga strontsium aluminaat. Esimesest videost näeb, mismoodi see on, kui sellist materjali laseriga valgustatakse. Järelhelendus kestab mitmeid minuteid. Materjal, muide on eBay's vabalt müügil, kui keegi tahab kodus asja järele proovida.
Alumistel videotel on kaks visiooni sellest, kuidas võiks maailm olla, kui materjaliteadus ja tehnoloogia mõttele järele jõuavad.
Grand Prix’ võistlusel lauget kurvi läbivat autot hoiab teel hõõrdejõud. Kui aga auto liigub liiga kiiresti, osutub hõõrdumine ebapiisavaks ja auto libiseb kurvist välja. Vanasti pidid autod kurve võtma üsna aeglaselt. Uued võidusõiduautod on aga konstrueeritud nii, et nad piltlikult väljendudes surutakse rajale, andes nii rehvidele hea pidamise. Tegelikkuses on see alla vajutamine, mida nimetatakse ka negatiivseks tõsteks, nii tugev, et mõned juhid hooplevad, et suudavad oma autot juhtida ka n-ö pea alaspidi piki lage. Mis põhjustab negatiivset tõstet ja kas võidusõiduautot saab tõesti juhtida rattad ülespoole, nagu seda tehti ulmelise sedaaniga esimeses „Mehed mustas” filmis?
Negatiivne tõste sõltub sellest, kas auto on ainsana rajal, näiteks kiiruskatsel, kuid kogenud juht teab, et negatiivne tõste võib võidusõidu jooksul kaduda. Mis seda kadumist põhjustab?
Vastus Umbes 70% negatiivsest tõstest põhjustab spoiler (neid võib olla ka rohkem kui üks), mis mööduvat õhku ülespoole suunab. Ülejäänud negatiivset tõstet nimetatakse pinnaefektiks ja see on seotud õhuvooluga auto all. Mida kiiremini auto liigub, seda suuremad mõlemad negatiivse tõste osad on. Grand Prix’ võistlustele tüüpilistel suurtel sõidukiirustel on negatiivne tõste suurem kui autole mõjuv gravitatsioon ehk raskuskiirendus. Kui auto sõidaks tavaliselt rajalt laele (seejuures aeglustamata), siis sellises olukorras ületaks suurem negatiivne tõste alla kiskuva gravitatsiooni jõu. Nii et autoga tõesti saab sõita rattad ülespoole, nagu filmis „Mehed mustas”.
Pinnaefekti põhjustab kokkusurutud õhuvool auto all. Kui õhk on pressitud väiksesse läbikäiguruumi auto all, siis õhu kiirus suureneb rõhu arvelt. Niisiis on auto all madalam õhurõhk kui auto peal ja seesama rõhuvahe surubki autot vastu rada. Võidusõidul võib juht vähendada auto õhutakistust, sõites tihedalt eelmise võistleja järel, seda tuntakse tuules sõitmisena. Ent ees liikuv auto rikub jälitava auto all oleva ühtlase õhuvoolu, kõrvaldades nii sellele mõjuva pinnaefekti. Kui taga sõitev juht ei arvesta seda kadumist ja vajalikul moel ei aeglusta, võib auto kurvist välja libiseda.
Chaparral 2J oli üks esimesi võistlusautosid, mis kasutas pinnaefekti ära. Sel oli taga kaks tiivikut, et imeda õhku masina alt ära, samal ajal kui vastu teed hoidev silindriline ääris külgedel takistas sealt õhu juurdevoolu. Madal rõhk auto all hoidis seda kiiretes kurvides rajal ja tiivikutest põhjustatud väljavool minimeeris tavapärast keeriste tekkimist auto taga, vähendades nii õhutakistust. Selle tulemusena oli auto sirgetel märgatavalt kiirem ja kurvides võitmatu. See oli tegelikult nii hea, et sai võistlustel osalemise keelu (mitte headuse, vaid liikuvate aerodünaamiliste osade tõttu).
1989. aasta filmi „Fat Man and Little Boy” üks kõige haaravamaid stseene ei ole Trinity katse meisterlik kujutamine. See on hoopis stseen, kus väljamõeldud füüsik Michael Merriman keerab vussi kriitilisuse katse ja saab selle käigus surmavalt kiiritada. Merrimani tegelaskujus on ühendatud kaks tõelist füüsikut, kelle surm tegi neist teistlaadi sõjaohvrid.
Kriitilisuse uuringud Los Alamose riiklikus laboratooriumis olid äärmiselt ohtlikud radioaktiivsete ainete tõttu, mida nende käigus käsitseti. Robert R. Wilson meenutas omaenese nappi surmast pääsemist, kui ta abistas kriitiliste agregaatide rühma kuuluvat füüsikut määramisel, millal saavutatakse kriitilisus, kui laduda järjest virna rikastatud uraanhüdriidi kuubikuid. Rühm ei kasutanud tavalisi keerukaid ohutusseadiseid, mida sel ajal tsüklotronide juures tarvitati. Selle asemel oli neil lihtne sisseseade, mis hõlmas puust lauda, ühte neutroniloendurit kriitilisuse jälgimiseks ja mitut rikastatud uraanhüdriidi kuubikut.
Wilson jälgis, kuidas füüsik hakkab uraanikuubikuid virna laduma, ja märkas siis ehmatusega, et neutroniloendur ei tööta, sest toitepingeallikas on läbi põlenud. Kui loendur jälle sisse lülitati, süttis selle märgutuli kohe. „Veel paar kuubikut ja virn oleks kriitilisuse ületanud ning võinud väga hästi surmavaks muutuda,” meenutas Wilson.
Raevunult kaebas Wilson selle kohta Oppenheimerile endale. Et ta pidi aga Trinityst järgmisel päeval lahkuma, lasi ta vahejuhtumil vaibuda. Wilson uskus, et kui ta oleks kohale jäänud ja asjaga edasi tegelenud, oleks ta võinud päästa kahe inimese elu. „See vahejuhtum vaevab siiani mu südametunnistust.” Need kaks inimest olid Harry K. Daghlian noorem ja Louis Slotin, kes mõlemad surid akuutse radiatsioonimürgituse tagajärjel pärast õnnetusjuhtumeid, mis leidsid aset kriitilisusega seotud katsete käigus sama plutooniumsüdamikuga, mida nimetati deemonsüdamikuks.
Daghlian oli Armeenia päritolu Ameerika füüsik, kes liitus kriitiliste agregaatide rühmaga juba 1944. aastal, kui oli alles ülikoolilõpetaja. 21. augustil 1945 ehitas ta neutronipeegeldit, ümbritsedes plutooniumist südamikku hoolikalt volframkarbiidist klotsidega, et saada parem kiirgusvarje. Ta pillas ühe klotsi kogemata keskkohta ja käivitas kriitilise reaktsiooni. Reaktsiooni peatamiseks lammutas Daghlian reaktori kangelaslikult käsitsi, aga talle endale läks see kalliks maksma. Selle tagajärjel sai ta nii suure kiirgusdoosi, et suri 25 päeva pärast õnnetust.
Füüsilise seisundi halvenemine oli õudustäratav ja Daghlian lubas selle järeltulevate põlvede tarbeks täielikult dokumenteerida. Tema paremale käele tekkisid villid, küüned muutusid siniseks ja nahk hakkas punetama sedamööda, kuidas mõlemad käed ja alakeha üles paistetasid. Punetus laienes ja nahk hakkas kihtidena maha kooruma; meest vaevasid kõhukrambid ja kõhulahtisus. Viimaks halastavasse koomasse vajudes oli ta kurtunud, olles kaotanud suurema osa nahka kõhult ja rindkere alaosalt. Surmatunnistuses märgiti surma põhjuseks rängad põletushaavad ülajäsemetel ja kehal.
Kanadas sündinud Slotin pani kokku südamiku Trinity katseks ja oli ühtlasi asjatundja sellise täbara katse sooritamisel, mida nimetati „lohe sabast sikutamiseks”. Selles asetati kaks berülliumist poolkera ümber südamiku ning hakati neid lähemale ja kaugemale liigutama. Samal ajal jälgiti neutronite paljunemise kiirust südamikus, viies reaktori päris kriitilisuse piirile. Kui kaks berülliumpoolkera isegi hetkeks sulguksid, muutuks mass kriitiliseks ja vallandaks ioniseeriva kiirguse valangu.
Slotin oli veidi hulljulge endine amatöörpoksija, kes eelistas teksapükse ja kauboisaapaid ning rääkis lugusid oma õhutõrjelaskuri päevist Hispaania kodusõja ajal, ehkki hiljem väitis tema vend, et Slotin olevat olnud vaid jalgsirännakul läbi Hispaania ja polevat sõjas kuidagi osalenud. Ta tõi veidi sellest suhtumisest kaasa ka oma uurimistöösse, hoolimata sellest, et oli olnud Daghliani lõpu tunnistajaks. Katset tehes eelistas ta ikka eemaldada poolkerasid lahus hoidvad vahetükid ja eraldada need kõigest tavalise kruvikeeraja teraga. Kohkunud Enrico Fermi ütles Slotinile, et kui too jätkab ohutuskorra eiramist, on ta aasta pärast surnud.
Kahjuks oli Fermil õigus. 21. mail 1946. aastal libises kruvikeeraja, mille abil Slotin kuue pealtvaataja juuresolekul poolkerasid lahus hoidis, ning need puutusid kokku. Südamik muutus sinise valgussähvatuse ja ulatusliku neutronkiirguse laine saatel superkriitiliseks. Slotin varjas kolleege plahvatuse eest oma kehaga nii palju kui võimalik, lükates samal ajal kaks poolkera kiiresti teineteisest eemale, et ahelreaktsioon seisma panna. Keegi kokkukogunenud meestest ei kandnud oma dosimeetrimärki, nii et andmed nende võimaliku kiirgusdoosi kohta on erinevad. Ent Slotini jaoks oli see surmav.
Slotin ütles, et tundis suus kohe haput maitset ja vasakus käes (millega ta poolkerad lahku lükkas) põletustunnet. Ta hakkas oksendama, kui teda haiglasse viidi, ja tema seisund halvenes kiiresti: ta kannatas ränka kõhulahtisust, käed paistetasid üles, tekkis hulgaliselt ville ja gangreen.
Üheksa päeva pärast õnnetust suri Slotin „keha talitluse täieliku ülesütlemise” tõttu. Iroonilisel kombel oli ta sõjajärgsetes aatomikatsetustes pettunud ja saatusliku katse üks eesmärke oli asendaja väljaõpetamine, et Slotin saaks jätkata Chicago ülikoolis oma sõjaeelseid uuringuid biofüüsika ja radiobioloogia vallas. Seda võimalust ta ei saanudki.
Reaktsioonina tema surmale lõpetati Los Alamoses kõik praktilised katsed kriitiliste agregaatidega ja hakati operaatorite kaitseks kasutama kaugjuhitavaid seadeldisi. Mis puutub tapjast „deemonsüdamikku”, siis kasutati seda Bikini atollil ühes esimestest sõjajärgsetest aatomipommidest kõigest viis nädalat pärast Slotini surma. Katse õnnestus mingite tõrgeteta.
Lisalugemist
- Miller, Richard L. Under the Cloud: The Decades of Nuclear Testing. Woodlands, Texas: Two Sixty Press, 1991.
- Rhodes, Richard. The Making of the Atomic Bomb. New York: Simon & Schuster, 1987.
- A Review of Criticality Accidents, 26. september 1967, Los Alamose Riiklik Laboratoorium.http://library.lanl.gov/cgi-bin/getfile?00314607.pdf
Erinevate võistlussarjade võidusõitjad püüavad teineteise ees edu saavutada tuules sõitmisega, mille puhul jälitav auto sõidab peaaegu täpselt eesliikuva auto taga, tekitades seeläbi silmanähtavalt ohtliku olukorra. Millise eelise see siis annab?
Vastus Olenemata aerodünaamilisest konstruktsioonist, mõjub võidusõiduautole siiski küllalt suur õhutakistus. Üks selle põhjustest on rõhkude erinevus auto esi- ja tagaosa vahel. Esiosas tekitab õhuga kokkupõrge kõrge rõhu. Tagaosas laguneb õhuvool keeristeks, milles õhurõhk on vähenenud. Selline õhurõhkude erinevus auto ees- ja tagaosa vahel aeglustab sõidukit, nõudes sama kiiruse säilitamiseks suuremat võimsust.
Kui jälitav auto võtab end juhtiva auto järele, saavad mõlemad sellest kasu. Jälitav auto lõhestab juhtiva auto taga tekkivat keeriste kogumit, nii et viimasel on väiksem eest-taha rõhkude erinevus. Jälitava auto esiosale mõjub väiksem õhusurve ja ka temal on väiksem rõhkude vahe suunas eest taha.
Jälitava auto juht võib eesliikujast möödumiseks kasutada nn lingumöödumist: ta tõmbab veidi tagasi, lastes juhtiva auto taha tekkida keeristel. Madala rõhuga keerised samal ajal aeglustavad esimest autot ja tõmbavad jälitavat autot edasi. Täpselt ajastades saab jälitava auto juht kiirendada keeriste alasse ja siis lipsata juhtivast autost külje pealt mööda.
Teadaolevalt oli Junior Johnson esimene, kes 1960. aasta NASCAR-sarja rallil Daytona 500 selliseid aerodünaamilisi lahendusi kasutas. Ta võitis ralli, kuigi tema auto hinnati võrreldes teiste võistelnud autodega aeglasemaks.
Tuules liikumist kasutatakse ka muudel spordialadel, seda eriti jalgrattavõidusõidus. Seda harrastavad ka loomad, näiteks siis, kui emapart juhib oma poegi üle tiigi. Pardid muidugimõista ei liigu nii kiiresti, et peaksid aerodünaamika pärast muretsema, kuid pardipojad saavad kasu lõigata rahulikust veest, mis teed juhatava ema järele jääb.
Laserrelva põhiidee on ju tegelikult iidvana – legend räägib, et juba Archimedes kasutas nõgusa peegliga koondatud päikeseenergiat, et vaenlase laevastikku hävitada. Mida üks laserrelvgi muud teha saab, kui koondada väga intensiivne valgus sihtmärgile, üritades seda sel teel kahjustada. Neil päevil tuli teade, et Boeing on võitnud 29,5 miljonit dollarit maksva lepingu laserrelva laserikiire stabiliseerimise süsteemi täiustamiseks.
Huvitav on lugeda andmeid laserkiire võimsuse kohta. Räägitakse 10 ja 30 kW lasersüsteemidest ning eesmärgist jõuda 150kW-ni. Kas seda on vähe või palju?
Esmalt kinnitame, et vatt on ikka vatt, sõltumata sellest, kas jutt käib laserikiirest või näiteks küttespiraalist. Poest saab endale osta 2-3 kilovatise küttekeha, kolme sellisega ilmselt sõjalaeva vastu võitlusesse ei lähe … Või siiski? Sest 1kW laseritega lõigatakse metalli, äkki saab laeva kere sisse augu lõigata?
Eks siit tulebki mängu vajadus laseri kiirt väga täpselt ja stabiilselt sihtida – ehkki laeva või tanki 10 kilovatiga üles ei sulata, on see võimsus hästi fokusseerituna suuteline nii mõndagi korda saatma. Aga kuidas hoida kõikuval laeval paikneva laseri kiir mitme kilomeetri kaugusel oleval liikuval sihtmärgil, nii et selle täpp sentimeetritki ei nihkuks? Sellega hakataksegi 29,5 miljoni dollari eest tegelema.
Kui Archimedese juurde tagasi tulla, siis Eestis on päikesepaistelisel päeval ühele ruutmeetrile langev päikese energia veidi rohkem kui pool kilovatti, 10 kilovatti saab järelikult 15-20 ruutmeetriselt pinnalt. 4 korda 4 meetrine nõguspeegel ei tundugi nii võimatu ise valmis ehitada? Sellise peegli fookuses on tõepoolest võimalik tuli otsa saada kõigele, mis vähegi põleb, aga metalli seal ei lõika, kuna peegeldunud valgust ei ole kuidagi võimalik millimeetriseks täpiks fokusseerida ning mida kaugemale peeglist, seda suuremaks see fokaaltäpp muutub. Rääkimata vajadusest igale uuele kaugusele fokuseerimiseks peegli kõverusraadiust muuta. Nii et laser on igal juhul parem.
On avaldatud ka video sellest, kuidas olemasolevat süsteemi on katsetatud. Tõepoolest – sihtmärgid on üsna väiksed. Aga see-eest ei kulu üldse laskemoona. Elektrit laeva generaatorist ikka saab.
Allikas: http://optics.org/news/6/2/26
Laserkuule me arvatavasti oleme näinud ulmefilmides. Aga mis on tegelikkus?
Hiljuti levis internetis Poola füüsikute T.Fok, Y.Stepanenko ja W.Wegrzynski tehtud veidi sürreaalne video sellest, kuidas ülivõimsa laseri tekitatud valgusimpulss (“valguskuuli”) "lendab" mööda koridori. Videost on näha, et tõepoolest, midagi helendavat liigub piki koridori. Aga siin on nii mõndagi seletamist.
Esiteks, kui tavaliselt näeme väikestel osakestel (näiteks tolm või veeaur) hajunud valgust, siis käesoleval juhul on laserkiir sedavõrd võimas, et see ioniseerib õhu aatomid ja valgus tekib elektronide ja positiivsete ioonide rekombineerumisel. Poolel teel vastasseinani on maha asetatud õhuniisuti, hele sähvatus tekib valguse veepilvest läbiminekul.
Teiseks, igasuguse valguskuuli levimise kiiruseks on ikkagi valguse kiirus ehk ca 300000km/s. Videos on kasutatud laseriga sünkroniseeritud ülikiiret kaamerat, mis valib pildistamise hetki nii, et igasse järgmisesse kaadrisse satuks sobivas kohas olev valgusimpulss (laserist tuli neid välja sagedusega kümme tükki sekundis). Ehk siis iga selle video kaader näitab erinevat valgusimpulssi. Vaatajale jääb mulje aeglasest liikumisest.
Pange tähele, et kasutatud kaamera parameetritest annab aimu videos näha oleva impulsi (valguskuuli) pikkus. 30cm läbimiseks kulub valgusel nanosekundit, selles suurusjärgus peab olema ka kasutatud kaamera ajaline lahutus. See on tõepoolest väga vinge kaamera – nanosekundeid mahub sekundisse miljard tükki! Muide, selline ülilühike säriaeg seletab ka mustvalge pildi – lühike säriaeg tähendab vähe valgust ja suure valgustundlikkusega kaamerad salvestavad üldjuhul mustvalge pildi.
Kui võimas on võimas?
2018.a. saab valmis Extreme Light Infrastructure (ELI) nime kandev taristu Tšehhis, Ungaris ja Rumeenias, kuhu koondatakse tipptasemel laserid teadusuuringute läbiviimiseks. Käesoleval aastal anti teada, et Kalifornias asuvas Lawrence Livermore riiklikus laboratooriumis on kokku pandud üks neljast laserist, mis annab “esimese valguse” ELI kiirekanalite (ELI beamlines) kompleksi suure väljundvõimsusega laserikiirde. Milline see laser on?
Suured laserisüsteemid ei ole sellised, nagu neid igapäevakogemusest ette kujutame. Pigem näeme tervet lauda täitvat seadet, kust paistavad peeglid ja võred – see ongi kõnealune laser. Laseri nimi on GigaShot-HE. Ta suudab anda nanosekundilisi impulsse, milles sisaldub energia , genereeritava valguse lainepikkus on . Aga selle laserikiirega ei tehta eksperimente. Tulevases kompleksis suunatakse see järgmisesse, Titaan-safiir (Ti:sapphire) laserisse. Ka see on suurte laserisüsteemide korral tavapärane – need koosnevad üldjuhul mitmest astmest, kus esimene aste genereerib “esimese valguse”, kõik järgnevad võimendavad seda või muudavad mõnel teisel moel.
Prahasse ehitatava ELI kiirekanali lõppväljundiks on laserimpulsside jada, kus iga impulss on femtosekundit pikk ja sisaldab sealjuures energiat. Impulsside genereerimise sagedus on .
Proovime selle nüüd konteksti panna
džaul on energia, mis tuleb kulutada massi viimiseks ca kõrgusele maapinnast. Ühes genereeritavas laserimpulsis on järelikult piisavalt energiat, et viia 3m kõrgusele. Ei ole eriti muljetäratav? Aga arvestage ka, et seda tehakse femtosekundi jooksul, kui me jagame tehtud töö selleks kulunud ajaga saame võimsuseks vatti, ehk petavati. Seda on palju rohkem, kui kõigi Eesti elektrijaamade koguvõimsus.
Et asi jälle maa peale tagasi tuua peaksime arvutama ka keskmise võimsuse, näiteks ühe sekundi jooksul. See on korda energiat jagada ühega, ehk . Suurte arvude maagia.
Sõnaga, võimsad laserid on petavatt-laserid. Aga ka sellistega ei saa midagi otsesõnu "õhku lasta".
Allikas: http://optics.org/news/6/3/3
Raudteel kasutatavad tsisternid on väga vastupidavad ja tavaoludes vigastab neid vaid suurel kiirusel toimuv kokkupõrge. Siiski võib neid purustada ka olukorras, kus ignoreeritakse teatavaid füüsika põhitõdesid. Siin on üks eluline näide. Tsisterni sisemust pesti ühel pärastlõunal kuuma auruga. Kuna töö jäi vahetuse lõppemise tõttu pooleli, otsustas meeskond tsisterni ööseks sulgeda. Järgmisel hommikul nägid nad, et miski oli tsisterni tema ülitugevatest terasseintest hoolimata puruks litsunud. Vaatepilt oli selline, nagu oleks tsistern peale astunud madalama klassi ulmefilmi koletis. Mis raudteetsisterni tegelikult purustas?
Vastus Puhastamise käigus täitus tsisterni sisemus kuuma veemolekulidest koosneva auruga. Vahetuse lõppemisel sulges meeskond kõik tsisterni kraanid ja jättis kuuma auru sinna sisse. Tol hetkel oli mahutis oleva gaasi rõhk võrdne atmosfäärirõhuga, sest puhastamise ajal olid kraanid avatud. Kui tsistern öösel jahtuma hakkas, jahtus ka aur ja suur osa sellest kondenseerus, mistõttu temperatuur alanes ja gaasi molekulide arv vähenes, kuid ei vähenenud gaasi ruumala. Selle tulemusena langes gaasi rõhk. Mingil hetkel öösel langes gaasi rõhk tsisternis nii madalale, et ümbritsev atmosfäärirõhk muljus tsisterni seinad sisse ja purustas selle. Puhastusmeeskond oleks saanud õnnetust vältida, kui oleks jätnud kraanid ööseks lahti. Sel juhul oleks õhk tsisterni sisse pääsenud ja rõhud oleksid sees ja väljas jäänud samaks.
Sel kevadel avaldati artikkel, mis väidab, et esimest korda on mõõdetud vahetult eksoplaneedilt peegeldunud valguse spektrit. Selle uudise tõukel võtame eksoplaneetide teema uuesti kõneks.
Eksoplaneet on planeet, mis ei tiirle ümber Päikese, vaid mõne teise tähe, tähe jäänuki või pruuni kääbuse. Arvatavasti on kõik neist vähemalt midagi kuulnud. Või siis näinud kunstnike joonistatud pilte sellest, kuidas nende meelest eksoplaneedid välja näeksid, kui me neid näeksime. Aga me ei näe.
Eksoplaneetide avastamiseks kasutatakse alljärgnevaid meetodeid:
- Dünaamiline – tähe radiaalkiiruse perioodilised muutused. Kui midagi piisavalt massiivset tiirleb ümber tähe, siis Newtoni seaduste kohaselt peab liikuma ka täht ise;
- Tähe spektri Doppleri nihked – ümber tähe tiirlev planeet nihutab gravitatsioonilise vastastikmõju tõttu veidi selle kiirguse spektrit;
- Fotomeetriline – perioodilised tähevarjutused. Sellel meetodil on NASA satelliit Kepler on leidnud 1019 planeeti, üle 3100 kandidaadi ootab oma planeedi staatuse kinnitamise järge. Vt ka ajakirja The Physics Teacher asjakohast artiklit;
- Gravitatsiooniliste mikroläätsede heleduse variatsioonide uurimine;
- Otsekujutised.
Tänaste hinnangute kohaselt leidub meie Galaktikas iga tähe kohta keskmiselt 1 kuni 1,6 planeeti. Tähti on rohkem kui 1011, nii et kandidaate eluks sobiliku planeedi otsimisel on rohkem kui piisavalt. Samas jääb populaarsetes teadusuudistest tihti tagaplaanile, kui keeruline on selliseid planeete tippteleskoopide andmetest üles leida ja kui kaugel on see protsess piltidest ja kujutlustest, mille üks esindaja on ka käesolevas postituses (vt esimene pilt) ning mille kohta on kombeks öelda “nägema”.
Planeedid reeglina ise valgust ei kiirga, vaid peegeldavad (ja hajutavad) oma ematähe valgust. Väikest planeeti tähe läheduses on selles peegeldunud valguses väga raske otsepildile saada. Kasutatakse spetsiaalseid seadmeid, mis tähe valguse ära blokeerivad (nagu koronograaf Päikese krooni uurimiseks). Esimene planeet mida otseselt nähti oli Fomalhaut b. Tänaseks päevaks on mõned näited peale Fomalhaut b veel juurde tulnud, aga enamik eksoplaneete on avastatud ikka Doppleri efekti kaudu või varjutustest, mida nad tähe eest läbi minnes tekitavad.
Nüüd on siis avaldatud tulemus, kus esimest korda on õnnestunud eraldada planeedilt peegeldunud valgus tähe 51 Peg spektris. Küll üsna detekteerimise piiril, aga siiski statistiliselt usaldusväärselt. Selle järgi on täpsustatud planeedi massi ja orbiidi kallet. Autorid on ŕahul, et selline meetod töötab juba 3,6-meetrise teleskoobi vaatluste puhul ja loodavad, et tulevaste suuremate teleskoopide ja nende külge riputatavate riistade abil saab juba tõsisemalt detekteerida eksoplaneetide spektreid ja sealt teha järeldusi nende atmosfääride kohta.
2015.a. füüsikapäevadel pidas Laurits Leedjärv (Tartu Observatoorium) loengu teemal “Päikesevarjutusest tähevarjutuseni ehk 20 aastat eksoplaneete.” ning rääkis kõigist neist meetoditest. Ettekanne jäi videosse ning on siis järelvaadatav. Soovitame see pool tundi võtta ja ettekanne ära kuulata, saate endale nö pildi ette ja taustateadmised selleteemalistest teadusuudiste mõistmiseks ja hindamiseks.
1862.–1865. aastani toimunud Ameerika Ühendriikide kodusõjas sõltusid nii Konföderatsiooni kui ka Uniooni vägede ülemad suuresti helist, mille abil tehti kindlaks, millal lahingud hakkasid ning kus neid peeti. Mitmetel juhtudel jagas väeülem oma väed kaheks, et vaenlasi kahelt poolt rünnata, kuid ainus viis rünnakut juhtida, oli lasta ühel grupil teisele grupile rünnaku signaal anda. Et kaks gruppi võisid üksteisest paari kilomeetri kaugusel asuda, siis paistis see plaan mõistlik, kuid nurjus siiski mõnikord otsustavate lahingute ajal.
Sarnast imelikku efekti märkasid 1862. aasta juunis Konföderatsiooni sõjaminister ning üks tema alamohvitser, kui nad jälgisid Gaines Milli lahingut umbes kahe kilomeetri kauguselt mäetipult. Orus toimuvas lahingus oli vähemalt 50 000 meest ja 100 kahurit ning see tekitas kohutavat müra ja pidi võitlevaid mehi ilmselt kurdistama. Siiski ei kuulnud kaks vaatlejat kahe tunni jooksul mingeid lahinguhelisid. Kuidas võis selline lahing kõigest paari kilomeetri kaugusel kuulmatu olla?
Vastus On kolm peamist põhjust, miks sellist valju lahingut isegi paari kilomeetri kauguselt kuulda pole. 1) Teel asuv tihe mets võis heli summutada, sest neelas helilained. 2) Maapinna lähedal tekkinud helilained võisid liikuda mööda trajektoori, mis paindus horisontaalse liikumise asemel hoopiski ülespoole. 3) Helilaine trajektoor võis kaarduda, kui temperatuur või tuulekiirus kõrgusega muutusid.
Kolmandal põhjusel, mille korral temperatuur kõrgusega alanes, võisid ülespoole suunatud nurga all liikunud helilained hakata liikuma hoopis mööda järsemaid trajektoore ning need ei jõudnudki mitu kilomeetrit eemal olnud vaatlejateni (joonis 3-3a). Üldiselt suureneb kõrgusega ka tuulekiirus. Sellises tavapärases olukorras ning kui heli saadetakse välja tuulega samas suunas, kipub see üldiselt otse maapinnale langema ning on seega kuuldav (joonis 3-3b). Kui heli saadetakse välja aga tuulele vastupidises suunas, kipub see liikuma mööda sellist trajektoori, mis paindub ülespoole ega ole seega ka kuuldav.
Mõningates Ameerika Ühendriikide kodusõja lahingutes asus komandör lahingust ülestuult olukorras, kus tuul kõrgusega märgatavalt kasvas. Öeldakse, et komandör oli akustilises varjupiirkonnas. Veelgi imelikumad olid olukorrad, kus temperatuuriefekt suunas helilained üles, kuid tuule mõju suunas need uuesti alla maapinna poole, mistõttu need jõudsid maapinnale alles lahingust väga kaugel. Seega kuulsid lahingut kaugel asuvad sõdurid, kuid mitte need, kes asusid sellele võrdlemisi lähedal.
Mis te ütleksite, kui mullid vedelikus hakkaksi ühtäkki valgust kiirgama? Frenzel ja Schultes nägid sellist valgust 1934.a. Kölni Ülikoolis sonareid katsetades. Tõsi küll, lisaks veele on vaja ka võimsat ultraheliallikat. Aga valgust kiirgavad mullid on tõepoolest olemas ja nähtust on hakatud nimetama sonoluminestsentsiks.
Nagu paljude teistegi nähtuste korral on sonoluminestsentsi seletuses olemas lihtne ja keeruline pool.
Lihtne on seletada seda, kust tuleb energia ja miks protsess käivitub.
On mitu nö kodus tehtavat katset, mis demonstreerivad hävitavat jõudu, millega vedelikud või gaasid mingil põhjusel tekkinud vaakumit täidavad. Näiteks võiks tuua nn vaakumkahuri ja selle, kuidas klaaspudelil põhi alt lendab, kui seda tugevalt lüüa.
Neis kahes katses oli alarõhuga ruumala enam-vähem silindriline. Kui alarõhuga ruumala on sfäär, siis selle tulemusena lööklaine energia kontsentreerub palju väiksemasse ruumipiirkonda. Akustilise laine fokusseerimine tähendab palju suuremat rõhku fookuspunktis. Kiire rõhu kasv tähendab omakorda suuri temperatuure. Teatud tingimustel võib temperatuur mullis tõusta kuni 10000K.
Sellega teemasse puutuv lihtne füüsika ka lõpeb. Tegelikult on sonoluminestsents äärmiselt keeruline nähtus ning seda on ka äärmiselt keeruline uurida. Mõelge ise - tegemist on protsessiga, mis kestab vaid murdosa mikrosekundist ja toimub imepisikeses, ca 1 mikromeetrise läbimõõduga ruumipiirkonnas.
BBC on teinud sonoluminestsentsist videoloo, mille jätame siinkohal "mängima". Ja võtame asja kokku nentides, et vahel on lihtsatest nähtustest kaasaegse teaduse keeruliste probleemideni vaid üks samm.
Allikas: wikipedia
Google’i prillid on liitreaalsusega prillid, mille abil reaalsele keskkonnale lisatakse virtuaalne – reaalsust rikastatakse andurite abil saadud infoga nii, et inimene näeb rohkem kui tegelikus maailmas olemas on. Kuidas tekitavad need prillid silma ette sellise virtuaalse infoekraani?
Prillide sangades on projektor. Sangadest ulatub välja klaasist kuup. Kuubi sees on näha kile, mis on valgusele „poolläbilaskev“, st osa valgust pääseb sealt läbi, osa peegeldub. Klaaskuubi ots on kaetud alumiiniumikihiga ja peegeldab sellele langenud valguse kuupi tagasi (vt pilti).
Poolläbilaskva kile või ka lihtsalt klaasplaadiga saab tekitada näiva kujutise reaalsete objektide „peale“ või kõrvale. Selles veendumiseks vaadake õhtul hämaras läbi akna õue. Lisaks õues olevate objektide kujutistele näete aknaklaasile tekkiva peegelduse kaudu kindlasti ka toas toimuvat. Just samamoodi „riputataksegi“ läbi prillide vaatava silma ette lisaks reaalsele pildile ka projektorist tulev infoekraan.
Mida neil piltidel tähele panna?
Me võime piirduda sellise lihtsa seletusega, kuid lähemalt vaadeldes tekib küsimusi juurde. Näiteks peab klaaskuubi peegeldav ots olema sfääriline, st moodustama seestpoolt vaadatuna nõguspeegli – kui suur peaks aga olema selle kõverusraadius ja fookuskaugus? Kui kaugele silmas peaks tekkima infoekraani näiv kujutis, et ekraani vaadates end mugavalt tunda? Kuidas on neis prillides välditud kujutise moonutusi? Google’i prillide mudeli saab üsna lihtsate vahenditega ise teha, seega on nende küsimuste uurimiseks olemas hea võimalus.
Lõpuks üks realistlikum skeem, kus peal palju lisakomponente, aga mille põhiline idee on seesama.
Maa füüsikute käes
John Baez, PhysicsWorld 31.07.2009
Teadlased on hakanud tasapisi mõistma kui oluline on tegelikult see roll, mida kokkupõrked teiste taevakehadega, meteoriidipommitused ja muud katastroofid meie planeedi arengus mänginud on. Järgnevas artiklis heidabki John Baez pilgu meie kahvatusinise täpi vägivaldsesse minevikku.
Inimtegevusest tingitud kliimamuutused, mis võivad meid tulevikus ees oodata, on paljud murelikuks teinud – kliimaprobleem puudutab ju meid kõiki. Lisahirmu tekitab ka asjaolu, et kliimamuutuste toimemehhanisme ei ole niisama lihtne mõista. Maa käitumist on äärmiselt raske täpselt prognoosida ning arvutitest üksi jääb siinkohal väheks: just seepärast peaksidki tulevased kliimamudelid lähtuma eelkõige põhjalikest füüsikaalastest teadmistest ning Maa ajaloo ja selle praeguse käitumise mõistmisest.
Õnneks oleme me viimase aastakümne jooksul Maa ajaloo kohta nii mõndagi uut teada saanud. Ajaloo hämarusse on hakanud paistma esimesed päiksekiired ning paistab, et me pole ainsad, kes on pidanud raskeid aegu üle elama. Maad on aegade jooksul tabanud nii mõnedki hirmsad katastroofid. Et jutt liiga pikaks ei veniks, peatume siin pikemalt vaid neljal sellisel sündmusel, milleks on 4,55 miljardit aastat tagasi toimunud hiiglaslik kokkupõrge (big splat), 4 miljardi aasta eest aset leidnud hiline äge meteoriidipommitus (late heavy bombardment), hapnikukatastroof (oxygen catastrophe), mis toimus umbes 2,5 miljardit aastat tagasi ning 850 miljoni aasta tagune Jää-Maa periood (Snowball Earth). Nende sündmuste üksikasjad – nagu ka see, kas nad üldse kunagi aset leidsid või mitte – on aga vaieldavad. Sellele vaatamata leidub nende kohta mitmeid üldtunnustatud teooriaid, mille kontrollimiseks on abi saadud just füüsikavallast.
Kuu sünd
Päike tekkis ilmselt gaasist ning tolmust koosneva pilve gravitatsioonilise kollapsi tagajärjel. Esimesed tähtede tekkimist kujutavad mudelid võtsid aluseks sfäärilise sümmeetria, kuid sellise lähenemise puhul on selgelt tegemist liigse lihtsustamisega, mille lõksu ka teiste valdkondade teadlased tihtipeale langevad. Siin mängib olulist rolli ka impulsimoment. Kui selline pilv omaenda raskusjõu mõjul kokku langeb, peaks moodustuma pöörlev akretsiooniketas.
Kui selle ketta keskosa muutus sedavõrd tihedaks, et selle rõhk suutis keskpunkti üleval hoida, tekkiski meie Päike. Päikese esimene eluetapp prototähena kestis vaid 100 000 aastat; selleks ajaks oli sealne temperatuur tõusnud juba nii kõrgeks, et Päikesest eralduv kuum gaas ei lasknud tal enam ümbritsevat ainet enda poole tõmmata. Sellest hetkest sai Päikesest T Tauri tüüpi täht ning kuna tema ainsaks energiaallikaks oli nüüd gravitatsioonienergia, muutus ta tasapisi üha väiksemaks ja väiksemaks. Umbes 100 miljoni aasta pärast käivitus tuumasüntees, mille algmaterjaliks oli Päikeses tuumas olev vesinik, ning Päikesest sai tavaline peajada täht.
Osa noore Päikese ümber tiirlevast kosmilisest tolmust kuumenes ja sulas ning mõned neist sulanud piisakestest tahenesid hiljem kondruliteks – millimeetri suurusteks keradeks, mis koosnevad lihtsatest mineraalidest nagu pürokseen ja oliviin, mille peamisteks koostisosadeks on naatrium, kaltsium, magneesium, alumiinium, raud, räni ja hapnik. Needsamad kondrulid on ka ühtede kõige primitiivsemate Päikesesüsteemis ringi rändavate objektide – kivimeteoriitide hulka liigitatavate kondriitide – peamiseks koostisosaks.
Edasi hakkas Päikese ümber tiirlev kosmiline tolm moodustama ainekogumeid, mida kutsutakse algmeteoroidideks ehk planetesimaalideks. Omavahel põrkudes ja ühinedes muutusid nad üha suuremaks ja suuremaks kuni tekkisid meilegi tuntud ja teatud asteroidid ning planeedid. Osad planetesimaalid sulasid ning selle tagajärjel vajusid raskemad metallid tuuma, jättes kergemad ained meteoroidi pinnale. Teised põrkasid aga omavahel kokku ja purunesid, moodustades kondriite ja teisi meteoriite, nagu raudmeteoriidid või kivimeteoriitide hulka kuuluvad akondriidid.
Radiomeetria abil meteoriite uurides on teadlased suutnud kindlaks teha ka üllatavalt täpse ajavahemiku – 4,56 ja 4,55 miljardit aastat tagasi – mil kõik need sündmused aset leidsid. Selles sündmustekeerises tekkis ka meie koduplaneet Maa ning siit algab ka meie lugu.
Maa ajalugu jaotatakse nelja eooni: Hadaikum, Arhaikum ehk Ürgeoon, Proterosoikum ehk Agueoon ja Fanerosoikum. Veel hiljuti oli vanim geograafiaõpikutes kirjas olev ajastu Kambrium, kui mitte arvestada üsna ebamäärase määratlusega Eelkambriumit. Kambrium algas aga vaid 540 miljoni aasta eest. See tähistab käimasoleva eooni – Fanerosoikumi – algust. Eesti keelde panduna oleks Fanerosoikumi sõnasõnaliseks vasteks "nähtava elu ajastu" – see on aeg, kus maailma valitsemise haarasid enda kätte hulkraksed organismid, kelle kivistisi veel tänagi rohkelt leida võib. Selles artiklis kaevume me aga veelgi sügavamale: Fanerosoikum saab olema meie teekonna lõpp-punktiks.
Nüüd aga tagasi Hadaikumisse, mis on saanud oma nime vanakreeka allilma jumala Hadese järgi. Nagu nimestki oletada võib, valitses Maal tol ajal põrgulik kuumus. Selles oli süüdi 4,53 miljardi aasta tagune sündmus, mille tagajärjel sai Maa endale Kuu. Millest Kuu siis tekkis? Hetkel arvatakse, et kõige adekvaatsema vastuse sellele küsimusele annab hiiglasliku kokkupõrke teooria.
Teooria põhineb oletusel, et ühel Maa orbiidil asuvatest Lagrange’i punktidest tekkis veel teinegi planeet. Nimelt tõestas Joseph Louis Lagrange 1772. aastal, et kui planeet tiirleb ümber Päikese ringjoonelisel orbiidil, siis samal kaugusel Päikesest tiirleb ka teine, temast märksa kergem taevakeha, kuid seda vaid siis, kui kõnealune taevakeha asub planeedist 60° ees- või tagapool. Jupiteri Lagrange’i punktide läheduses võib leida tiirlemas tõepoolest üsna mitmeid asteroide ning neid on näha ka Marsi ja Neptuuni Lagrange’i punktides. Maa vastavates punktides asteroide märgatud ei ole, kuid hiiglasliku kokkupõrke teooria kohaselt on ühes neist planeet kunagi siiski olnud. Kui selle mass oli kasvanud aga umbes Marsi massi suuruseks, ei suutnud ta enam oma orbiidil püsida ning liikus järk-järgult Maale lähemale, kuni viimaks sellega kokku põrkas. Just selline võiski olla meie Kuu sünnilugu.
See teooria kõlab küll uskumatult, kuid selle kasuks räägib hunnik tõendusmaterjale, mis on ilmekalt kokku võetud teaduskirjaniku Dana Mackenzie hiljuti ilmunud raamatus "The Big Splat, Or How Our Moon Came to Be". Näiteks on teada, et loodeline hõõrdumine sunnib Kuud tasapisi Maast eemalduma ning hetkel on eemaldumise kiiruseks umbes 3,8 cm aastas. Endisaegsed tõusud ja mõõnad on talletatud vanades settekivimetes, mis annavad tõestust sellest, et juba vähemalt Eelkambriumist alates on meie kuud järk-järgult pikemaks muutunud. Nende andmete põhjal võime oletada, et Hadaikumis oli Kuu Maale üsna lähedal. Kas tsentrifugaaljõud võis selle Maa küljest eemale paisata; või tekkis Kuu juba algselt Maa lähedal; või püüdis selle kinni hoopis Maa gravitatsiooniväli? Ühtegi neist teooriatest ei saa lõplikult maha kanda, kuid hiiglasliku kokkupõrke teooria sobib meie käsutuses olevate andmetega kõige paremini kokku. Sellesse teooriasse suhtutakse nii tõsiselt, et oletatav Maad tabanud planeet on endale isegi nime saanud: seda kutsutakse Theiaks. Vanakreeka mütoloogia kohaselt oli Theia naistitaan, kes tõi ilmale Kuu.
2004. aastal avaldas USAs Boulderi linnas asuva Southwest Research Institute’i haru juures töötav astrofüüsik Robin Canup oma arvutisimulatsioonid hiiglaslikust kokkupõrkest. Et meie Kuu sarnane kuu saaks tekkida – ja mitte selline, mis oleks liiga rauarikas või väike või muul viisil vale – tuli kõigepealt "luua" õiged tingimused. Canup leidis, et tõenäoliselt pidanuks Theia olema pisut raskem kui Mars, moodustades umbes 10% – 15% Maa massist. Samuti oleks pidanud see alguses maa poole liikuma üsna aeglaselt ning tabama Maad vaid riivates.
Selle tulemuseks oli üks äraütlemata halb päev Maa ajaloos. Theia põrkas Maaga kokku ning lõi sellest välja suure tüki, mille tagajärjel paiskus maailmaruumi purustatud, sulanud ja aurustunud kivimeid. Tunni aja möödudes oli juba pool Maa pinnast tulikuum ning kivisodist koosnev juga oli venitanud ennast juba pea nelja maa raadiuse kaugusele kosmosesse. Kolme kuni viie tunni pärast prantsatasid Theia rauast tuum ja suurem osa kivisodist tagasi Maale. Kogu maakoor ning pindmine osa vahevööst sulasid üles. Selleks hetkeks oli neljandik Theiast juba aurustunud.
Ainest, mis polnud päeva möödudes Maale tagasi langenud, moodustus selle ümber tiirlev kivisodist rõngas. Tekkinud rõngas ei olnud aga stabiilne ning juba sajandi jooksul grupeerus kiviklibu ümber, moodustades meie Kuu. Theia rauast tuum oli selle aja peale juba Maa keskmesse vajanud.
Diskussioon hiiglasliku kokkupõrke teooria õigsuse üle kestab aga edasi. Osalt on selle põhjuseks kindlasti tõsiasi, et otseseid tõendeid on säilinud äärmiselt vähe: näiteks vanimad Maalt leitud kivimid tekkisid alles pea pool miljardit aastat hiljem.
Hiline äge meteoriidipommitus
Arhaikumi ehk Ürgeooni alguseks loetakse vanimate tänini säilinud kivimite teket umbes 4 miljardit aastat tagasi. Basalt, nagu ka paljud teised tardkivimid, pidi aga tekkima juba varem. Tegelikult võisid ka ookeanid kujunema hakata juba 4,2 miljardit aastat tagasi, kuid nii varajasest ajast ei ole säilinud ühtegi asitõendit. Selle üheks võimalikuks põhjuseks võib olla Arhaikumi algusaegade rahutu iseloom.
Ka pärast Kuu tekkimist tabasid Maad mitmed sarnased katastroofid. Selle asemel, et nende sagedus aga järk-järgult langeks, võis see 3,8 kuni 4 miljardit aastat tagasi toimunud hilise ägeda meteoriidipommituse ajal hoopis järsult tõusta. Kuu vanimad ja suurimad kraatrid pärinevad just sellest perioodist ning loogiliselt võttes oleks pidanud ka Maa oma osa saama – siin oleks aga ilmastik ning geoloogilised protsessid kõik nii vanad jäljed tänaseks niikuinii hävitanud. Seetõttu tulebki meil tõestusmaterjali just Kuu pinnalt otsida.
Hilise ägeda meteoriidipommituse ajal tabas Kuud ligi 1700 meteoori, mis jätsid selle pinnale üle 100-meetrise läbimõõduga kraatrid. Maale võis sellise suurusega meteoore langeda 10 korda enam ning lisaks ilmselt mõned palju suuremadki. Et mõista säärase turmtule tagajärgi, on seda hea võrrelda 65 miljonit aastat tagasi Kriidiajastu lõpul Maad tabanud meteooriga, mis võis olla ka dinosauruste väljasuremise põhjuseks ning mille jäetud kraater oli 180-kilomeetrise läbimõõduga. Hilise ägeda meteoriidipommituse ajal võisid sellise suurusega meteoorid olla Maal lausa igapäevased külalised.
Miks oli aga see periood Maa ajaloos siis ometi nii vägivaldne? Ühe teooria kohaselt sattusid Jupiter ja Saturn sel ajal positsioonidele, kus Jupiter suutis teha oma orbiidil sama ajaga kaks ringi kui Saturn ühe ning see häiris Päikese ümber tiirlevate asteroidide ning jääst koosnevate objektide tavapärast tasakaalu. 2005. aastal avaldas planeetide uurimisele pühendunud füüsikute rahvusvaheline töörühm, kuhu kuulus ka Southwest Research Institute’i juures töötav Hal Levison – üks neist, kes propageerisid Pluuto nimetamist kääbusplaneediks – artikli, mis käsitles huvitavamaid meie päikesesüsteemi kohta loodud arvutisimulatsioone (Nature 435 466). Neis oli pandud meie neli hiidplaneeti tiirlema ringjoone-kujulistele orbiitidele, mis asusid üksteisele palju lähemal kui praegu. Algmeteoroidide mõjul hakkasid Saturn, Uraan ja Neptuun tasapisi päikesest eemalduma. Kui Saturn oli jõudnud punkti, kus iga tema tiiru kohta tegi Jupiter ümber Päikese kaks, muutus kogu Päikesesüsteemi välimine osa järsku ebastabiilseks. Neptuuni ja Uraani orbiidid muutusid ebakorrapärasemaks ning viskasid oma orbiitidelt eemale palju algmeteoriite. Mõned neist paiskusid ka Päikesesüsteemi sisemise osa poole – see seletaks ka hilist ägedat meteoriidipommitust.
Hapnikukatastroof
Arvatakse, et juba enne hilist ägedat meteoriidipommitust suutis Maa pind maakoore tekkimiseks piisavalt jahtuda. Vulkaanilised protsessid paiskasid siin õhku tohututes kogustes veeauru, süsihappegaasi ja ammoniaaki, millest moodustus Maa teine atmosfäär (peamiselt vesinikust ja heeliumist koosnenud esimene atmosfäär oli selleks ajaks juba kosmosesse kadunud). Teise atmosfääri peamisteks koostisosadeks olid süsihappegaas ja veeaur, veidi leidus selles ka lämmastikku. Hapnikku sisaldas teine atmosfäär aga ilmselt äärmiselt vähe. Arvatavasti oli Maa teises atmosfääris umbes 100 korda rohkem gaase kui meie praeguses kolmandas atmosfääris.
Maa jahtudes moodustusid ookeanid. Kokkupõrkel mõne suure meteooriga võisid nad küll täielikult aurustuda, kuid tekkisid peagi uuesti. Suur osa atmosfääris leiduvast süsihappegaasist lahustus merevees ning sadestus hiljem karbonaatidena. Sellega algas uus faas mineraalide arenguloos ehk mineraalide evolutsioonis, nagu Washingtoni Geofüüsika Laboratooriumi juures asuvas Carnegie Institution’is töötav Robert Hazen ja tema kolleegid seda kutsuda armastavad. Loomulikult ei ole sel midagi pistmist Darwini evolutsiooniteooriaga, jutt käib vaid mineraalide "sortimendi" järk-järgulisest laienemisest Maa ajaloo käigus. 2008. aastal tegi Hazeni juhitud geoloogidest koosnev uurimisrühm oma arvutuste põhjal kindlaks, et Hadaikumis võis Maal leiduda umbes 350 liiki mineraale, kuid mida vanemaks sai Maa, seda rohkem tekkis ka uusi mineraale. Tänu ookeanide ning laamtektoonika tekkimise oli neid Ürgeooni lõpuks juba 1500.
Esimene samm laamtektoonika arengus oli kraatonite teke – need on iidsed maakoore osad, kus Maa koor ja vahevöö on omavahel kindlalt ühendatud ning millest paljud ka praeguse ajani säilinud on. Näiteks Ühendkuningriigis asuvad Walesi kagupoolne ning Inglismaa läänepoolne osa osaliselt Kesk-Inglismaa kraatonil. Kuigi enamik kraatone saavutas oma lõpliku kuju alles 2,7 miljardit aastat tagasi, hakkasid paljud neist kujunema juba ammu enne seda. Kraatonid koosnevad põhiliselt graniidist või muudest sarnastest tardkivimitest, mis on oma ehituselt tunduvalt keerukamad kui basalt. Graniit võib tekkida mitmel eri viisil, üks neist on näiteks settekivimite sulamine. Päris esimesed graniidi tüüpi kivimid olid ilmselt lihtsama ülesehitusega.
Laamtektoonika sai alguse juba 3 miljardit aastat tagasi, kui kraatonid hakkasid tasapisi liituma ning moodustama suuremaid üksuseid, millest koosneb ka meie praegune maakoor. Laamade liikumise käigus toimub pidev maakoore ümbertöötlemine ehk subduktsioon, mille käigus ookeanilised laamad libisevad mandriliste laamade alla ning sukelduvad vahevöösse. Laamtektoonikaga kaasneb ka veealune vulkaaniline aktiivsus, mis viib tihti kuumaveeallikate tekkeni ookeanide põhjas.
Võimalik, et just needsamad allikad mängisid olulist rolli ka Ürgeooni kõige olulisema sündmuse – elu tekkimise – juures. Kuna noorel Maal puudus vaba hapnik, pidid esimesed organismid olema anaeroobsed. Ka tänapäeval leidub veel mõningaid organisme, kes hapnikku taluda ei suuda: nendeks on vanimad meile teada olevad mikroobid, kelle hulka kuuluvad ka need, kes ülalmainitud kuumaveeallikates elutsevad. 3,6 miljardit aastat tagasi panid anaeroobsed organismid aluse aktiivsele väävliringele ning sulfaatide ladestumisele. Nende elutegevuse tulemusena jõudis atmosfääri ühe rohkem ja rohkem metaani.
Mingist hetkest alates hakkasid mõned mikroobid miskipärast fotosünteesima ning hapnikku atmosfääri paiskama. Tõenäoliselt omandasid ka esimesed taimed oma fotosünteesivõime just selliste bakteritega sümbioosis elades – on ju taimedes olevatel kloroplastidel praegugi veel oma DNA.
Pole täpselt teada, millal fotosüntees algas – erinevaid arvamusi kõrvutades saame tema oletatavaks algusajaks 3,5 kuni 2,6 miljardit aastat tagasi. Umbes sel ajal hakkas moodustuma raudkvartsiit – vöödilise tekstuuriga moondekivim, kus õhukesed raudoksiidi kihid vahelduvad vähese rauasisaldusega kivimi kihtidega. Raudkvartsiidi tekkele võisid panna aluse esimesed fotosünteesivad organismid, kelle toodetud hapnik reageerisid merevees leiduva rauaga. Seda, miks kivimi rauarikkad kihid vahelduvad väiksema rauasisaldusega kihtidega, ei oska aga keegi seletada.
Läks kaua aega, enne kui fotosüntees Maa atmosfäärile olulist mõju avaldama hakkas – kui see lõpuks umbes 2,5 miljardit aastat tagasi aga juhtus, oli tulemuseks järjekordne katastroof Maa ajaloos. Kuna gaasilises olekus hapnik on äärmiselt reaktsioonivõimeline ning suurem osa esimestest elusorganismidest ei suutnud seda taluda, kutsutakse seda perioodi ka hapnikukatastroofiks. Õnneks leidis evolutsioon pääsetee ning nüüd vajab enamik elusolendeid oma elutegevuseks just hapnikku.
Hapnikukatastroof tähistab Ürgeooni lõppu ning Agueooni algust. Järgmisel aastamiljardil laius Maal nn vaheookean, kus oli küll kordades rohkem hapnikku kui kunagi varem, kuid siiski veel palju vähem kui praegu.
Jää-Maa
850 miljonit aastat tagasi algas järjekordne katastroof: järgneva 200 miljoni aasta jooksul tabas Maad mitu pidurdumatu jäätumise perioodi, mil terve Maa (või vähemalt suurem osa sest) oli kaetud paksu jääkilbiga. Kuna päikesevalgus peegeldub jäält tagasi maailmaruumi ning temperatuur langeb seetõttu veelgi, pole just raske mõista, kuidas selline lumepalliefekt töötab. Praegu käimasolev lumepalliefekt on täpselt vastupidine – jää sulamise tõttu muutub Maa pind tumedamaks ning seetõttu ka soojemaks. Palju keerulisem on leida vastusi aga küsimustele, miks selline ebastabiilsus tihemini äärmuslikke temperatuure ei põhjusta, miks Jää-Maa just siis aset leidis ning miks Maa igavesti jääplaneediks ei jäänud.
Viimasele küsimusele on meil olemas ka võimalik vastus. On nimelt teada, et jääkate aeglustab kivimite murenemist. Murenemise käigus muudetakse süsihappegaas mitmesugusteks karbonaatseteks mineraalideks ning seetõttu on see üks põhilistest pikaajalistest protsessides, mis kasutab ära atmosfääris sisalduvat süsihappegaasi. Vulkaanid, mis suurtes kogustes süsihappegaasi õhku paiskavad, tegutsevad aga edasi ka jääga kaetud maailmas. Nii jääbki süsihappegaas atmosfääri ning põhjustab lõpuks kasvuhooneefekti, mille tagajärjel temperatuur uuesti tõusma hakkab. Kui jää sulab, suureneb ka murenemine ning süsihappegaasi kontsentratsioon atmosfääris langeb. Need protsessid ei juhtu aga üleöö. Arvatakse, et kuumimal hetkel võis süsihappegaasi sisaldus atmosfääris olla isegi kuni 13% – umbes 350 korda rohkem kui praegu.
Jäätumistsüklite lõpuks oli atmosfääri hapnikusisaldus tõusnud 2%-lt 15%-le (praegu on see 21%). See võib olla ka põhjuseks, miks esimesed hulkraksed hapnikku hingavad organismid just sel perioodil tekkisid. Teise teooria kohaselt pani selline "külmutus-kuumutus" protsess elu Maal tõsiselt proovile ning tekitas sellega eeldused kiireks evolutsiooniks. Reaalsuses võivad aga õigeks osutuda ka mõlemad teooriad. (Täpsemalt võib selle kohta lugeda Gabrielle Walkeri raamatust "Snowball Earth")
Hulkraksete organismide teke tähistab Agueooni lõppu ning käimasoleva eooni, Fanerosoikumi algust. Sellega lõppeb ka meie lugu – Maa ajalugu läheb aga edasi.
Me elame Fanerosoikumi eoonil, täpsemalt Kainosoikumis ehk Uusaegkonnas. Holotseen on lõppenud ning alanud on Antropotseen, mida iseloomustab inimtegevuse tugev mõju Maa ökosüsteemidele ja kliimale. Looduskeskkonda hävitades on inimesed käivitanud liikide massilise väljasuremise, mida võiks vast võrrelda isegi 65 miljoni aasta taguse katastroofiga Kriidiajastu lõpul. Meie tõttu suureneb tublisti ka süsihappegaasi sisaldus atmosfääris. Kui temperatuur Maal tõuseb veel vaid 1 kraadi võrra, saab see olema viimase 1,35 miljoni aasta kõrgeim – sama kõrge oli see viimati enne käimasoleva külmhooneperioodi algust. Mis meist edasi saab, ei tea keegi.
Maa ajaloo uurimine annab meile õigete oletuste tegemiseks aga paremad eeldused. Me ei saa teha katseid, mis testiksid Maa reaktsiooni erinevatele kasvuhoonegaaside kogustele. Arvutisimulatsioonid on seetõttu hädavajalikud ning tõestused Jää-Maast ning muudest sündmustest Maa ajaloos aitavad meil nende mudelite paikapidavust ka paremini kontrollida. Samuti võib minevikus aset leidnud massiliste väljasuremiste ning Maa järgneva taastumisprotsessi uurimine aidata ennustada meie planeedi tulevast bioloogilist mitmekesisust.
Waco, Texas, 15. September, 1896: Willian Crush Missourist, Kansasest ja Texase Raudteekompanii mõtlesid välja lollikindla idee kuidas rahvast kokku meelitada ja etendusega raha teenida. Kuuekilomeetrise raudteejupi kumbagi otsa paigutas Crush vananenud veduri, üks värviti roheliseks, teine punaseks. Asja mõte oli lasta veduritel täiskiirusel teineteisega kokku põrgata. Kokkupõrke tulemusena lõhkesid vedurite katlad ning toimus plahvatus, mis oli võrdne 50 kg dünamiidi õhkamisega. Kolm inimest sai surma, hulgi vigastada. Sellest hoolimata korraldati taolisi üritusi veel aastakümneid. Inimloomus on kummaline.
1895. aastal ei osanud Ameerika Missouri ja Kansase osariigi raudteeametnik William George Crush midagi peale hakata kahe vananenud auruveduriga. Et tol ajal olid raudteeõnnetused ühed meedias enamkajastatud sündmused ja kahe raske kiiresti liikuva asja laubiti kokkpõrge on tavaliselt vaatemänguline tekkis Crushil äriidee. Ta otsustas vanad vedurid meelega kokku põrgatada.
Crush sai ürituse korraldamiseks ametliku loa ning alustas tühermaale uue linna ehitamist. 500 töölist ehitasid spetsiaalse sirge 6,4 km pikkuse lõigu raudteed, mis ühendus otsapidi üleriigilisse raudteevõrku. Asukohale kerkis ka restoran, mitmed kõnepuldid ja üks VIP tribüün, kaks telegraafijaama, kaks-ühes restoran ja tsirkuseareen, mitmeid meelelahutusasutusi. Et pealtvaatajate saabumine oleks võimalikult mugav, ehitati ka vaksal ja 640 m pikk perroon. Ajutise linna nimeks sai irooniliselt "Crush" ehk "Põrge" või "Kärts", kuidas võtta.
Suursündmuse päevaks, 1896. aasta 15. septembriks, oli asukohta saabunud enam kui 40000 huvilist, kes olid kõik eelnevalt lunastanud ainsa linna toonud transpordi - rongi - 2 dollarit maksnud pileti. Inflatsiooni arvestades on see tänapäeval võrdne ligikaudu 55 dollariga. Enne põrget peeti poliitkõnesid, laata ja piknike. Kell 17:00 anti teineteise pihta sihitud ereroheliseks värvitud Old No. 999 ja erepunasele Old No. 1001 vedurile start. Vedurijuhid lasid katelde ventiilid lahti, ootasid, kuni rattad olid teinud neli täispööret ning hüppasid siis hukule määratud liikuritelt maha. Kokkupõrkekohani jõudes oli mõlema veduri kiirus ligikaudu 72 km/h. Kusjuures mõlema veduri taha ühendati vanu rongirattaid täis lastitud veovagun.
Politsei nägi vaeva, et inimesi ohutus kauguses hoida. Pealtvaatajad ei osanud midagi karta, sest härra Crush kinnitas, et vedurite katlad ei plahvata. Ta oli vastava tehnilise kinnituse saanud vagunid tootnud tehaste inseneridelt. Siiski, rongid lendasid kokkupõrkes õhku ning vähemalt kaks pealtvaatajat sai surma, mitmed vigastada. Üks ürituse ametlikke fotograafe, Jarvis Deane kaotas silma lennanud uitpoldist nägemise. Sellest hoolimata roniti õnnetuse jäänuste otsa ühispiltidele ning suveniirijahile. Rahvast üle jäänud romud veeti kohale saadetud uute veduritega minema. Õhtuks oli "Crush" linn kaardilt kadunud.
Kui võimas selline kokkupõrge olla võis? Internetiallikate järgi kaalus kumbki vedur ning selle haagis kokku ligikaudu 35 tonni (vedur eraldi 11 tonni). Vedurite kiirus on teada. Jääb üle panna arvud kineetilise energia avaldisse. Teame, et
kus Ek - kineetiline energia, m - (veduri ja vaguni) mass ja v - (veduri) kiirus
Vagunid sõitsid teineteisele otsa sirgjoones, seega liitus kokkupõrkesse mõlemi kineetiline energia, ehk kokku 181,44·106 J! Ent see pole kõik. Plahvatasid ka vedurite katlad. Termodünaamikast on teada, et anumasse rõhustatud jääval temperatuuril gaasi energia avaldub kujul:
kus
- pB - gaasi rõhk
- vB - anuma ruumala
- pA - välisrõhk
Auruvedurite katlad töötasid tol ajal keskmiselt rõhul 1,38 - 1,72 MPa. Välis- ehk normaalrõhk on 101325 Pa. Vedurite katlas võis olla hinnanguliselt kolm kuupmeetrit auru. Pannes arvud valemisse, saame kateldesse talletatud energiaks 25,36·106 J. Energia on jääv suurus, see ei saa kaduda ega tekkida, ainult muunduda ja visata Old No. 999 ja Old No. 1001 vedurite esiotsad õhku ja paisata metalli sadade meetrite kaugusele. Kokkupõrge oli samaväärne 50 kg dünamiidi õhkamisega.
William George Crush lasti veel samal päeval töölt lahti, ent järgmisel päeval tunnistati ta õigeks ning võeti jälle tööle. Surmadest ja vigastustest, üleüldisest plahvatuse riskiastmest hoolimata korraldati sarnaseid kokkupõrkeid veel aastakümneid. Öeldakse, et raha ei haise. Nüüd oleks see mõeldamatu. Inimese elu väärtus on tõusnud ja raha haiseb rohkem. Või siiski?
Mesilased aitavad taimedel tolmelda. Nad koguvad õietolmu ühelt õielt ja kannavad selle teisele. Protsess ei ole juhuslik, mesilased ei hõõru ennast kogemata õietolmu vastu. Tegelikult hüppavad õietolmu terakesed esimesel õiel mesilasele ja teisel õiel mesilasest eemale. Miks õietolm niimoodi hüppab?
Vastus Tarust lahkudes saab mesilane läbi õhu lennates tavaliselt positiivse laengu. Elektriliselt neutraalse tolmuka lähedale lenneldes (joonis 5-6a) tekitab mesilase elektriväli mõnedes õietolmu terades indutseeritud laengu. Need terakesed on elektriliselt neutraalsed, kuid mesilase elektriväli jagab neis laengut ümber: mõned elektronid liiguvad mesilasepoolsele küljele, et olla positiivselt laetud putukale võimalikult lähedal. Niimoodi jääb tera kaugemale küljele positiivne laeng. Tera on endiselt elektriliselt neutraalne, kuid selle ühel küljel on negatiivne ja teisel positiivne laeng.
Negatiivset poolt tõmmatakse mesilase poole, positiivset tõugatakse temast eemale. Negatiivselt laetud pool on mesilasele lähemal ja tõmbejõud võidab. Terake hüppab läbi õhu mesilasele. (Täpsemalt maandub see mesilase karvakestele. Kui see puudutaks mesilase laetud keha, kaotaks ta elektrone. Tera jääks üleni positiivselt laetuks, see surutaks mesilasest eemale ega jõuaks kunagi teisele õiele.)
Õietolm jõuab teisele õiele siis, kui mesilane läheneb lille emakale, mis on maaga elektriliselt ühendatud. Mesilase elektriväli tõmbab emakas elektrone võimalikult putuka lähedale. Emaka ülemine osa saab negatiivse laengu (joonis 5-6b). Õietolmu terakest tõmmatakse endiselt mesilase poole, kuid veel tugevamini tõmmatakse seda emaka ülaosasse kogunenud laengu poole. Niisiis hüppab terake mesilaselt emakale ja lill saab tolmeldud.
Puäntillistlikud maalid, näiteks Georges Seurat’ „Pühapäeva pärastlõuna Grande-Jatte’i saarel”, on maalitud mitte pintslitõmbeid, vaid tohutut hulka värvilisi punkte kasutades. Kui seista maalile lähedal, on punktid nähtavad, kuid eemalt vaadates sulavad need kokku ja pole eristatavad. Veelgi enam, iga maaliosa värvus võib eemale liikudes muutuda, mis ongi puäntillistliku maali punktidest koosnemise mõte. Mis sellist värvimuutust põhjustab?
Vastus Kui valgus liigub läbi vikerkesta, toimub selle difraktsioon, see tähendab, et valgus valgub laiali ja moodustab interferentsimustri. Kui vaatame punktvalgusallikasse, tekib difraktsiooni tulemusena võrkkestale ringikujuline kujutis. Kui vaatame kaht kõrvuti asetsevat valgusallikat, moodustab neist kumbki oma ringkujulise kujutise, ent kui need on väga lähestikku, siis kujutised kattuvad ja me eristame ainult üht, ühendkujutist. Sellise kattumise tekkimine paneb piiri meie võimele eristada kaht erinevas punktis paiknevat valgusallikat.
Kaks kõrvuti asetsevat puäntillistliku maali värvipunkti toimivad nagu kaks valgusallikat. Oletame, et punktid on erinevat värvi. Kui me seisame vahetult maali ees, on punktid meile piisavalt lähedal, et võrkkestale tekiks kaks erinevat kujutist, ja seega näeme punkte tõelistes värvides. Kui liikuda maalist eemale, tekib punktidest silmas kattunud kujutis ja me ei eralda enam üksikuid punkte. Ajust teadvusesse jõudev punkti värv ei pruugi enam olla kummagi üksiku punkti värv ega isegi nende lihtsustatud keskmine – aju võib sünteesida täiesti uue värvitooni. Oletame näiteks, et fuksiin (sinise ja punase segu) värvi punkt on kollase punkti kõrval. Nende kahe punkti kombinatsiooni tajume roosana. Nõnda kasutab puäntillistlik kunstnik oma teose loomisel ära meie nägemissüsteemi.
Traditsiooniline õlimaal on enamasti tumedamates toonides kui puäntillistlik, sest esimese värvid tekivad värvikihtide segust lõuendil. Valgus peab värvikihi läbima, peegelduma ja taas värvikihi läbima, enne kui vaatajani jõuab. Mida enam on värvikihis pigmenti, seda tumedamana maal paistab. Kuna puäntillistliku maali värvidest moodustub pilt ajus, mitte lõuendil, ei tumene valgus nii palju.
Mitmevärvilistele pindadele, näiteks mosaiikidele, kootud riidele, värvitrükile ja värvilistele ekraanidele annavad nende värvi paljud väikesed eri värvi punktid. Traditsioonilise värviteooria kohaselt on kõikvõimalike erinevate värvitoonide loomiseks vaja kolme põhivärvi (punast, sinist ja rohelist). Seega on värvilises ekraanis neid kolme värvi punkte sisaldavad read. Iga soovitud värv moodustatakse eri värvi punktide heleduse muutmisega.
California ja Nevada kuivanud järvede põhjas vedelevate kivide taga on tihti pikad vaod, mis algavad kivi juurest ja võivad ulatuda kümneid meetreid üle kõvaks kuivanud kõrbepinnase. Kivid ise kaaluvad kuni 300 kilo. Mis neid jälgi tekitab? Kas kivid üritavad Las Vegase kasiinodesse murda? Või käib mõni veidrik neid lükkamas? Igal juhul peab jälgede tekitamine keeruline olema, sest hõõrdumine kivide ja kõrbepinna vahel on suur.
Vastus Jälgede tekkimist on üritanud seletada paljud teooriad. Üks neist põhineb harvaesineval vihmavee külmumisel. Õhukeses jääkihis kinni olevad kivid liiguvad edasi tuuleiilide toel ning kraabivad kõrbepinda, selleks peab aga tuul olema piisavalt tugev, et kive ja jääkihti liigutada.
Teine teooria pakkus välja, et jäljed tekivad, kui tuul liigutab kive mõne kõrbepiirkonna jaoks haruldase vihmahoo ajal. Kuna vesi toimib määrdeainena, saab tormituul kivi edasi libistada või rullida ning kivi jätab jälje. Hõõrdejõud on vähim siis, kui vesi tekitab endiselt tahkele pinnasele õhukese mudakihi. Tuuleiil võib siis kivi liikuma panna ning kui see juba liigub, ei ole enam vaja nii suurt jõudu rakendada.
Hiljutises uurimuses on see küsimus lõpuks lahendati. Selgus,et kivide liikumiseks kuivanud järvepõhjal on vaja üsna konkreetseid olusid. Kõigepealt peab järvepõhjale sadama veekiht, mis on piisavalt paks, et vesi külma käes põhjani ära ei külmuks, aga samas piisavalt õhuke, et kivid ei oleks tervenisti vee all. Kui öösel temperatuur langeb, siis tekib veepinnale jääkiht. See kiht peab olema piisavalt õhuke, et see saaks vabalt liikuda, aga samas ka piisavalt paks, et koos püsida. Seejärel päikesepaistelisel hommikul jää hakkab sulama ning murdub tükkideks. Järve keskel olnud jää sulab esimesena ja tekkinud vesi voolab kallaste poole. Jääplaate võib liigutada ka kerge tuul, sest neil on väga suur pindala ja seega on tuulel neile suur mõju. Jääplaadid võivad olla kuni 100 m läbimõõduga, seega on nad olenemata väikesest paksusest ka üsna massiivsed. Kui sellise veevoolude ja tuule mõjul liikuva suure jääplaadi teele jääb ette kivi, siis see lükatakse kaasa. Libisemist lihtsustab mudane järvepõhi, kus on hõõrdumine väiksem kui kuival pinnal. Liikuvad kivid jätavad mudasesse järvepõhja vaod, mida on võimalik hiljem näha.
Kivide liikumist sellisel moel on ka otseselt jälgitud. Jääplaadid lükkavad kive kaasa väga aeglaselt, umbes kiirusega paar meetrit minutis.
Kummarduv lind (joonis 4-8) on populaarne mänguasi nii koolitunnis kui ka mujal. Et lind koogutama panna, tuleb selle pea märjaks teha. Seejärel vajub lind aeglaselt ettepoole, kuni pöördub järsku peaaegu horisontaalsesse asendisse. Ühe või kahe kõikumise järel jääb lind paigale. Kui asetada linnu ette klaas veega, kuhu see saab nokka kasta, siis kordub liikumine lõputult. Mis paneb linnu niimoodi liikuma? Kas peale pea märjakstegemise on ka teisi võimalusi panna lind kummarduma? Sellisel juhul saaks linnu kummarduma panna ka suure õhuniiskuse juures, mis tavaolukorras hakkaks linnu kummardumist takistama.
Vastus Linnu keha (alumine osa) on osaliselt täidetud kergesti aurustuva vedelikuga, tavaliselt metüleenkloriidiga. Avatud osa linnu peas ja kehas sisaldab sama kemikaali auru. Linnu pea ja nokk on kaetud vildiga. Kael koosneb torust, mis ulatub peast kehasse. Kusagile kaela külge kinnitub telg, mis laseb linnu peal ja kehal jalgade suhtes vabalt liikuda.
Pärast pea piserdamist veega hakkab vesi ümbritsevasse õhku aurustuma. Et vee oleku muutus vedelast gaasilisse vajab soojusenergiat, jahutab aurumine vilti, pead ja auru pea sees. (Vildi peale puhumine hoogustab kuivamist.) Kui pea sees oleva auru temperatuur langeb, langeb ka tema rõhk. Et aurutasku linnu kehas pole otse peas oleva auruga ühendatud (ühendava toru ots on vedelikku sukeldunud), säilib seal kõrgem rõhk. Kahe osa vahel olev aururõhkude erinevus surub osa vedelikku läbi toru. Vedeliku liikumine muudab linnu peaosa raskemaks ja see hakkab ümber jalgade juurde kinnituva telje pöörduma. Alguses on pöördumine aeglane, seejärel pöördub lind äkitselt peaaegu horisontaalsesse asendisse. Siis põrkub see kas veeklaasi servalt nõksu tagasi või piirab liikumist jalgade asend.
Sel hetkel, kui lind on enam-vähem horisontaalasendis, tõuseb toru alumine ots vedelikust välja ja hetke jooksul ühenduvad kaks aurutaskut ning nende rõhud võrdsustuvad. Ülespoole liikumise ajal võimaldab ühendustoru kalle voolata vedelikul peast tagasi kehasse, mille tulemusena taastub algne kaalujaotus ja lind pöörab end püstiasendisse tagasi. Kui lind kummardudes oma noka vette kastab, imendub vildi sisse täiendavat vett ja kogu protsess kordub.
Linnu kummardama panemiseks ilma selle pead veega kastmata on mitu võimalust. Nii võib pead katvat vilti niisutada alkoholiga, mis aurustub isegi suure õhuniiskuse juures. (Näiteks sobib väga hästi kange viski, kuid see võib pead katva vildi ka ära rikkuda.) Võib ka linnu ereda päikesevalguse kätte asetada, varjates tema pead ja kaela päikese eest, kuid jättes keha varjamata. Kui lisaks veel linnu keha mustaks värvida, hakkab ta hullumeelse kiirusega liikuma.
Joel Plawsky koos kolleegidega Rensselaer’i Polytehnilisest Instituudist New York’is on leidnud, et mõned vedelike voolamisega seotud protsessid ei kulge kosmoses, st mikrogravitatsiooni tingimustes üldsegi nii, nagu maapealsele kogemusele tuginedes arvata võiks. Et vedelike voolamine kapillaarides on väga oluline kosmoseaparaatide seadmete jahutussüsteemides, siis omab see uurimus väga praktilist tähendust. Meie saame ühe näite põhjal teada, miks on justkui lihtsaid asju vaja kosmoses üle kontrollida.
Kõige parem masin on lihtne masin. Eelistatavalt ilma ühegi liikuva osata – selline ei lähe rikki ja ei vaja pidevat hooldust. Üks selliseid seadmeid on nn soojustoru (ingl heat pipe). Kõrvaloleval pildil te tunnete soojustorud arvatavasti lihtsalt ära – need on need vaskselt läikivad torud, mis hoiavad radiaatorit arvuti emaplaadi küljes. Aga need ei ole lihtsalt vasktorud, kaugel sellest.
Soojustorude töö põhineb vedelike aurustamisel ja kondenseerumisel – toru “soojas otsas”, st jahutatava seadmega kokkupuutes olevas otsas vedelik aurustatakse, aurustatud gaas liigub soojustoru külma otsa, kondenseerub seal ning liigub siis tagasi soojustoru külma otsa.
Aga see ei ole veel kõik. Et jahutusvedelik õigel, st jahutatava seadme töötemperatuuril aurustuks, selleks tekitatakse soojustorus alarõhk. Alarõhul teatavasti vedelike keemistemperatuurid langevad. Soojatorudes on tihti ka kapillaarsed struktuurid, mis juhivad kondenseerunud vedeliku selle sooja otsa.
Sellised soojustorud on väga töökindlad ning sellistena kosmoseaparaatides laialdaselt kasutusel.
Nüüd tagasi Joel Plawsky ja tema kolleegide tulemuste juurde. Nende uurimuses selgus, kõrgel temperatuuril sõltub soojustoru võime soojust ära kanda ka gravitatsioonijõust – kui gravitatsiooniväljas kipub soojustoru soe ots ära kuivama (vedelik aurustub kõrgetel temperatuuridel liiga kiiresti), siis mikrogravitatsioonis seal ujutab. Miks?
Põhjuseks arvatakse olevat meile köögist hästi tuttav nn Marangoni efekt, kus pesuvahendi tilk paneb veepinnal puru ja rasvaplekid liikuma. Täpsemalt, leiti, et see efekt töötab mikrogravitatsioonis teistpidi.
Sest kui vedelike pindpinevustegur on kõrgematel temperatuuridel väiksem ja madalamatel temperatuuridel suurem, siis peaks . pindpinevusjõud jahutavat vedelikku soojustoru külma otsa poole tõmbama. Ometi näitasid katsed vastupidist efekti.
Kes see oligi, kes ütles, et lihtsus on ülim keerukus?
Allikad:
http://physics.aps.org/synopsis-for/10.1103/PhysRevLett.114.146105
http://en.wikipedia.org/wiki/Heat_pipe
Vana-Egiptuse kolossaalsete monumentide ehitajad võisid lisada kõrbeliivadele vett, et suurte kelkude vedamist kergemaks teha. Selline on rahvusvahelise füüsikute töögrupi järeldus, milleni jõuti erinevat tüüpi liivades oleva vee koguse ning hõõrdumise vahelist seost uurides. Uurimusest selgus, et Egiptuse kõrbetes leiduv liivatüüp muutub veega niisutamisel eriti livedaks – fakt, mis võis püramiidide ehitamiseks kasutatud suurte kivimürakate liigutamise kergemaks muuta.
Uurimuse viisid läbi Saksamaal asuva Saarlandi Ülikooli teadlane Christian Wagner ja kolleegid koostöös teadlastega Hollandist, Iraanist ja Prantsusmaalt. Oma idee said nad iidselt (ca 1800 eKr) Egiptuse seinamaalingult, millel kujutatakse kelguga liival transporditavat suurt skulptuuri. Maaling sisaldab detaili, mis on egüptolooge juba kaua painanud: kelgu ees seisev töötaja paistab liivale vett valavat, samas kui teised töölised vajaminevat veekogust täiendavad.
Rituaal või määre?
Kuigi mitmed ajaloolased usuvad veevalamise mingit sorti rituaali olevat, mõtisklesid Wagner ja kolleegid selle üle, kas vee liivale valamisel võis olla ka praktiline mõõde – vähendada liiva ja kelgu vahelist hõõrdumist. Seda mõtet inspireeris ka Wagneri ja tema kolleegi Jorge Fiscina poolt 2007. aastal sooritatud uurimus, milles leiti, et vaid väike kogus vett käitub määrdena, mis vähendab läbi toru surutava liiva hõõrdumist. (vt. “Wet sand flows better than dry“).
Oma uue teooria proovilepanekuks mõõtsid Wagner, Fiscina ja kolleegid erinevatel liivatüüpidel libisevale kelgule mõjuvat takistust. Katses kasutatud kelk suurusega 11 x 7,5 cm oli valmistatud PVCst ning omas lihvitud servi, sarnanedes nii Vana-Egiptuses kasutatud kelkudele. Kelgule asetati raske koorem, mistõttu avaldas kelk liivale allapoole suunatud jõudu suurusega 250 kg/m2, olles võrreldav täiskoormaga Egiptuse kelguga. Kelgu vedamiseks kasutati eksperimendis tõmbetugevuse mõõtmiseks mõeldud seadet, mis mõõtis kelgu liigutamiseks vajaminevat jõudu. See võimaldas teadlastel arvutada dünaamilise hõõrdeteguri. Kuigi teadlased leidsid, et vee kasutamine tõepoolest vähendas hõõrdumist, polnud see seetõttu, et vesi võimaldas liival vabamalt liikuda. Tegu oli hoopiski vastupidise efektiga.
Betooni-sarnane pind
Teadlased mõistsid kiiresti, et kelgu ette kuhjuval liival oli suur osakaal kelgule mõjuvale hõõrdumisele. Kui liiv on kuiv või veidi niiske, liiguvad liivaterad üksteisest mööda ning kuhjuvad kergesti, mistõttu on kelgu liigutamine raske. Liivale vee lisamisel kipuvad liivaterad aga üksteise külge kleepuma ning moodustavad lõpuks tahkema betooni-sarnase pinna, millel kelgu liigutamine on palju lihtsam kui kuival liival. Seda teradevahelist kleepumist täheldas Wagner ka oma 2007. aasta uurimuses, kus see takistas liiva voolamist.
Ühe konkreetse testitud liivatüübi puhul oli dünaamiline hõõrdetegur 5% veekoguse juures peaaegu poole väiksem. Antud liiv on sarnane Egiptuse kõrbetes leiduva liivatüübiga, viidates faktile, et liiva märgamine oleks iidsetele monumendiehitajatele suureks kasuks olnud. Katse tulemused näitavad ka seda, et püramiidiehitajatel vedas – Egiptuse liiv on polüdispersiivne ehk sisaldab erinev suurusega liivaterasid. Kui Wagner ja kolleegid kasutasid ühtlase suurusega liivatüüpe, oli kahanes hõõrdetegur vähem kui Egiptuse tüüpi liiva puhul. Antud nähtust võib põhjustada see, et erinevat tüüpi liivaterad võimaldavad liival rohkem kokku pakkuda kui olukord, kus liivaterad on ühtlase suurusega.
Suurem kogus vett pole kasulik
Töörühma teiseks oluliseks leiuks on fakt, et kui veekogus liivas on suurem kui 5%, hõõrdumine suureneb. Mõnel juhul oli 10% vee koguse juures hõõrdumine liival isegi suurem kui kuiva liiva puhul. Wagneri sõnul on selle põhjus ebaselge, sest kelgu ees ei tekkinud liivakuhjasid. Ta pakkus aga, et märjem liiv on pehmem kui betooni-sarnane liiv, mistõttu kipub kelk liiva sisse vajuma. ,,Võib-olla on see sarnane erinevusega, mida näeme betoonil ja kummist pinnasel libisemise vahel,“ lausus Wagner. ,,Igal juhul tuleb seda edasistes katsetes uurida.“
Rutgersi Ülikooli teadlane Troy Shinbrot nimetas eksperimenti paeluvaks, kuid leidis ka, et hõõrdumise ja liiva tahkuse vaheliste seoste mõistmiseks tuleb sooritada edasisi uurimusi. Kui rääkida aga praktilistest rakendustest peale püramiidide ehitamise, pakkus Shinbrot ka välja, et antud uurimus võib meil aidata mõista niiskuse mõju teraliste ainete töötlemisele nii ravimitööstuses kui ka tööstussegudes.
Allikas: “Did slippery sand help Egyptians build the pyramids?“
Koolis me räägime valguslainetest rohkem kui helilainetest. Teame, et valgust saab fokusseerida, tekivad kujutised, esineb difraktsioon ja interferents, näiteks pilul ja aval. Ja optilistel mikroskoopidel on olemas maksimaalne võimalik lahutusvõime. Ja et on olemas laserid. Jne.
Hea uudis on see, et need teadmised on rakendatavad ka akustikas, st helilainete kirjeldamisel ja uurimisel. Difraktsioon ja interferents niikuinii, sellest on põgusalt ka mehaanika kursuse juttu. Tegelikult ka fokusseerimine - tuleb meelde paraboolpeegel. Lihtsa akustilise läätse saab süsinikdioksiidiga täidetud õhupallist.
Ja audiolaser?
MIT teadlased on leiutanud ja tootmisesse suunanud seadme, mida nimetatakse Audio Spotlight. See on peaaegu nagu laser, võimaldades helilaineid saada väga suunatult ja väga kaugele. Allpool on kaks videot. Esimene neist on populaarne, sisaldab omajagu ümmargust ja ebatäpset juttu. Teine on väljavõte ühest füüsika loengust, kus asja selgitatakse.
Lühidalt:
- Seade genereerib ultrahelisignaali, mis on moduleeritud helisignaaliga, mida me tahame edasi anda;
- Ultrahelisignaal levib juba loomu poolest sarnase kõlari läbimõõdu juures palju kaugemale (analoogia valguslainetega, nende difraktsiooniga avalt);
- Moduleeritud ultraheli teatud punktis mittelineaarses protsessis interakteerub keskkonnaga, st õhuga, sealjuures tekib kuuldav helisignaal.
Ühesõnaga, asi on tegelikult päris keeruline. Aga väga ilus!
Allikas: https://en.wikipedia.org/wiki/Sound_from_ultrasound
T.Gasser töörühma poolt 2015. a. augustis ajakirjas Nature Communications Pariisi avaldatud uurimus näitab, et Pariisi kliimakokkulepete täitmiseks tuleb lisaks kasuvhoonegaaside emissiooni vähendamisele arendada ka tehnoloogiaid, mis atmosfäärist kasvuhoonegaase eemaldavad.
12.detsembril 2015 võtsid maailma 195 riigi esindajad vastu ajaloolise kokkuleppe globaalse soojenemise peatamiseks. Kokkuleppe,eesmärk on tagada, et maakera keskmine temperatuur ei tõuseks sel sajandil rohkem kui 2 kraadi Celsiuse järgi võrrelduna tööstusrevolutsiooni eelse ajaga.
Lepe [1] näeb ette kasvuhoonegaaside emissiooni piiramist "nii kiiresti kui võimalik". Konkreetseid numbreid leppes ei nimetata.
Selge see, et riikidele nõudmiste esitamine ongi ülimalt keeruline. Aga kas me teame, mis on vaja teha selleks, et kliima soojenemine peatuks?
Kliima modelleerimine on väga keeruline. Mudelis peaks olema arvesse võetud nii Maa kui süsteemi keerukus kui ka inimfaktor.
Kõige sagedamini jõuab poliitikute ja avalikkuseni tulemused, mille saamiseks on kasutatud midagi, mida nimetatakse integreeritud hindamismudeliteks (IAM, integrated assessment model) [2]. See süsteem püüab arvestada ka inimtegevusse puutuvat, nagu erinevate tehnoloogiate kasutamine, majanduses ja ühiskondades toimuv ning paneb need ühte mudelisse looduslike protsessidega [2]. Mõte on selles, et niimoodi peaks olema võimalik anda poliitikutele soovitusi tegevuste planeerimiseks.
T.Gasseri füüsikutest koosnev töörühm modelleeris Maad kui süsteemi (ESM, earth system model) [3]. "Inimfaktor" on toodud sisse ühe parameetrina, milleks on emissiooni vähendamise "põrand", ehk nivoo, millest allapoole ei ole inimkond võimeline oma kasvuhoonegaaside emissiooni vähendama. See on uudne lähenemine, mis on ühtaegu arusaadav nii arusaadav kui ka praktilist väljundit andev. Lisaks sellele on arvutuste tulemusel konkreetsed veahinnangu, mis IAM meetodite puhul puuduvad (!).
Uuringu järeldused võib lühidalt kokku võtta alljärgnevalt:
Arvutuse näitavad, et Pariisi kliimakokkulepete täitmiseks tuleb lisaks kasuvhoonegaaside emissiooni vähendamisele arendada ka tehnoloogiaid, mis atmosfäärist kasvuhoonegaase eemaldavad. Hinnanguliselt on vaja atmosfäärist eemaldada heal juhul 0,5-3Gt süsinikku, kehvemate stsenaariumide käivitumise korral 7-11Gt süsinikku aastas, kusjuures ladustada on vaja vastavalt 50-250Gt või 1000-1600Gt süsinikku. Hea ja halva stsenaariumi erinevus on just inimfaktor, ehk maksimaalne võimalik emissiooni vähendamine. Järeldus: süsinikku siduvate tehnoloogiate arendamine on vajalik.
Selliste tehnoloogiate arendamisega ka tegeletakse. Näiteks Klaus Lackner Arizona Riiklikust Ülikoolist tutvustas 2014.a. sünteetilist materjali, mis seob süsinikdioksiidi tuhat korda efektiivsemalt kui puud. Lackner’i töörühm on loonud membraani, mida läbinud õhust seotakse 10 – 50% süsinikdioksiidist. Membraani töötavaks komponendiks on vaik, täpsemalt ioonvahetusvaik – vaigu positiivsed ioonid seovad süsinikdioksiidi maksimaalselt üks süsinikdioksiidi molekul iga positiivse laengu kohta. See protsess on niiskusetundlik selliselt, et vaik absorbeerib süsinikdioksiidi kuivas õhus ja vabastavad selle niiskes õhus. Materjal on juba kättesaadav, kuna seda kasutatakse vee puhastamisel ja pehmendamisel. Nii et põhimõtteliselt on võimalik hakata atmosfääri süsinikdioksiidist “puhastama”.
Rehkendused näitavad, et efekti saavutamiseks on seda vaja sada miljonit konteineritäit.
Kokkuvõtlikult võib öelda, Pariisi kliimalepe kõlab küll hästi, aga põguski pilk lepete teaduslikku telgitagusesse võtab hingetuks. Nii et tavakodanike jaoks on see puhtalt usu küsimus - kes usub poliitikuid, kes tööstureid, kes teadlaseid, kes aktiviste.
Allikad:
[1] http://www.nytimes.com/interactive/2015/12/12/science/document-final-cop21-draft.html?_r=0
[2] https://en.wikipedia.org/wiki/Integrated_assessment_modelling
[3] http://www.nature.com/ncomms/2015/150803/ncomms8958/full/ncomms8958.html
Umbes 50. laiuskraadi kandis võib näha kummituslikke hõbesiniseid pilvi, mis ilmuvad tükk aega pärast päikeseloojangut, seda eriti suvisel ajal Briti saartel ja Skandinaavia maades. Miks tekivad need helkivad ööpilved? Miks on neid näha ainult mõnda aega pärast loojangut ja miks jätavad need mõnikord lainetaolise mulje? Miks märgati neid esimest korda alles 1885. aastal ja miks on pärast seda pilvede heledus suurenenud ja vaatlemiste arv üldiselt kasvanud?
Vastus Need pilved tekivad väga kõrgel (umbes 80 kilomeetrit) atmosfääri osas, mida kutsutakse mesosfääriks. Seetõttu kutsutakse neid tihti mesosfääri pilvedeks. Sellisel kõrgusel valgustab neid päike ka veel siis, kui vaatleja on olnud juba umbes tunni pimeduses. Tõenäoliselt koosnevad need pilved väikestest jäätükkidest, mille on tekitanud komeedi-, meteoriidi- või (harvem) vulkaanipurske tolm. Sellised pilved on liiga õhukesed, et neid näha päeval või ka loojangu ajal. Nende lainelist välimust põhjustavad ilmselt tiheduslained (lainetaolised õhurõhu ja temperatuuri varieerumised), mis läbi pilvede liiguvad.
Esimest korda märgati helkivaid pilvi 1885. aastal ilmselt Jaava lähedal paikneva Krakatau vulkaani purske tõttu. See tohutu plahvatus paiskas nii tolmu kui ka vett väga kõrgele. Umbes 80 kilomeetri kõrgusel kondenseerus vesi vulkaanilisele tolmule (võib-olla ka komeedi- ja meteoriiditolmule), tekitades väikeseid (väiksemad kui mikromeeter) osakesi. Nii tekkis esimene vaadeldav helkiv ööpilv. 1885. aastast on pilvi on üha rohkem ja heledamaid, sest tööstus, riisipõllud, prügilad ja loomakarjad toodavad järjest suuremas koguses metaani. Metaan jõuab atmosfääri ülemistesse kihtidesse, muundub ning põhjustab veemolekulide ja jäätükkide koguse suurenemist. Need jäätükid tekitavadki helkivaid ööpilvi.
Mõnikord võib laevamastide ja teiste teravate objektide tipus näha elektrisädemeid. Mis neid põhjustab? Neid sädemeid nimetatakse püha Elmo tuledeks või koroonalahenduseks. Mis põhjustab väga haruldast öist helendust Andide kaugetel tippudel?
Vastus Püha Elmo tulesid põhjustab elektriline läbilöök õhus, mis toimub elektrit juhtivast materjalist teravate esemete, näiteks laevamastide, antennide ja lennuki tiibade lähedal. Kui elektriväli õhus on tavalisest tugevam, võib see olla eriti tugev just elektrit juhtiva eseme tipus, sest objektis liikuvad laengud kogunevad sinna. Kui elektrivälja tugevus teraviku juures ületab kriitilise väärtuse, võib väli elektronid õhu molekulidest ära tõmmata ja neid kiirendada. Kiirendatud elektronid põrkuvad õhu molekulidega ja ergastavad neid ning panevad ka need kiiremini liikuma. Kui hiljem ergastus kaob, tekib nähtav valgus. Molekulide liikumise kiirenemine tähendab õhutemperatuuri tõusu, mille tagajärjel võib tekkida praksuv heli, mida mõnikord elektrilahenduse ajal kuulda võib. Püha Elmo tulesid ei peeta ohtlikuks.
Andide kuma pole siiani suudetud seletada ja seda märgatakse väga harva. Ilmselt ei saa seda põhjustada püha Elmo tuled, sest vaatleja peaks nii väikesemõõtmelise elektrilahenduse nägemiseks palju lähemal olema. Tõenäolisem on, et tegu on suuremamõõtmeliste lahendustega, mis on tingitud laengut kandvast liikuvast lumest.
| USA kosmoseagentuuri NASA programm Landsat on maailma vanim kaugseiremissioon. Kust saab alla laadida LANDSAT'i andmeid ja kuidas neid andmeid töödelda? | Meris on mõeldud eelkõige veekogude seireks, kuid on sobiv ka atmosfääri ja taimestiku uurimiseks. Tutvume Merise andmetega lähemalt Beamis, mis on vabavaraline programm eelkõige optiliste satelliidipiltide töötlemiseks. |
Hirmsasti tahaks teada, eksole. Ja asi ei ole ainult uudishimus - selline teadmine on oluline ka närvihaiguste mõistmiseks, diagnoosiks ja raviks.
Kindlasti olete te teadusest populaarselt rääkivates väljaannetes kohanud pilte, kus on näidatud aju aktiivseid piirkondi ja räägitud, mida see tähendada võiks. Kuidas seda enda jaoks mõtestada, kui lähtuda koolihariduses räägitavast, st üldisest füüsikalisest maailmapildist.?
Nagu ikka, kogu loo ära rääkimine on võimatu. Aga anname siin mõned märksõnad ja juhtmõtted, mis riiklike õppekavade konteksti sobivad. Ehk aitavad need infos veidi paremini orienteeruda.
Ütleme alustuseks ära, et neuronites tekivad tõepoolest elektrivoolu impulsid ja see on seesama laetud osakeste (käesoleval juhul ioonide) suunatud liikumine, millest me füüsika või loodusõpetuse tunnis räägime. Seega peab meie ajus olema ka elektriväli, mis neid voolusid tekitab. Ja kui on elektrivool, siis on alati ka magnetväli (ka seda me füüsikas õpime). Küsimus on vaid nende signaalide mõõtmises, sest need on väga nõrgad.
Detekteeritava signaali saamiseks peab vähemalt 50 000 neuronit sünkroniseeritult oma signaali välja saatma. Siit ka piirangud: signaali on võimalik mõõta vaid piirkondadest, kus on võimalik lähestikku paiknevate neuronite sünkroniseeritud töö. Samuti ei ole leitud moodust, kuidas võtta vastu signaale, mis tulevad sügavamalt kui otse ajukoorest.
Meetodit, mis mõõdab aju magnetvälja nimetatakse magnetoentsefalograafiaks, elektrivälju mõõdab elektroentsefalograafia (EEG).
Halliday "Füüsika põhikursus" ütleb asja kohta alljärgnevalt. Tekstis viidatav valem 29-1 on Biot-Savart'i seaduse diferentsiaalkuju
Teadlased, meedikud ja psühholoogid tahaksid mõista, kuidas funktsioneerib inimaju. Üheks nende töömeetodiks on magnetoentsefalograafia (MEG) - protseduur, milles jälgitakse inimaju magnetvälja ajal, mil inimene sooritab teatud tegevusi, nagu näiteks sõnade lugemine. See tegevus aktiveerib teatud piirkonna ajus, näiteks lugemisega seotud piirkonna, ja põhjustab nõrku elektriimpulsse, mis saadetakse edasi mööda juhtivaid kanaleid ajurakkude vahel. Nagu igasugune vool, nii tekitavad ka ajuvoolu impulsid magnetvälja.
MEG-aparatuuriga avastatud magnetvälja tekitavad arvatavasti elektriimpulsid, mis kulgevad piki kurdusid (lõhesid) aju pinnal (joonis 29-7). Püüame kasutada valemit 29-1, et hinnata sellise magnetvälja suurust punktis P, mis asub kaugusel r = 2 cm vooluimpulsist. Olgu impulsi teekond aju pinnale puutujaks, nii et nurk θ valemis 29-1 on 90°. Tüüpilise vooluimpulsi korral ajus vool i = 10μA ja impulsi teepikkus on umbes 1 mm. Eeldame, et see teepikkus on küllalt lühike selleks, et asendada see 1 mm pikkuse diferentsiaaliga ds valemis 29-1. Siis annab valem 29-1 meile
See on väga väike magnetväli, rohkem kui miljon korda nõrgem kui Maa magnetväli aju asukohas. Seega ei piisa aju magnetvälja avastamiseks sellest, et lihtsalt hoida kompassi oma aju lähedal ja loota, et ajutegevus suudab pöörata kompassi magnetnõela. Kompassi asemel on vaja ülimalt tundlikku instrumenti, milleks on ülijuhtiv kvantinterferentsseade (SQUID) ja mis on võimeline mõõtma magnetvälju suurusega vähem kui 1 pT; isegi siis tuleb võtta tarvitusele kõikvõimalikud abinõud, et kõrvaldada mõõtmispaiga lähedalt muutuvat magnetvälja tekitavad lisaallikad.
MEG ja EEG ei ole loomulikult ainsad meetodi inimese sisemaailma uurimiseks. Aga kõigi teiste tööpõhimõttest arusaamiseks on vaja rääkida kvantmehaanika keeles ja see on ühe teise loo teema.
Siiski, tsiteerime siin üht lugu J.Walkeri raamatust "Lendav füüsikatsirkus".
Magnetresonantstomograafia (MRT; ingl magnetic resonance imaging) on meetod, mille abil saadakse pilt objekti (inimese, looma, fossiili ja muu) sisemusest. Meetodit nimetati algselt tuuma magnetresonantsiks (nuclear magnetic resonance), kuid teadaolevalt muudeti nimi MRT-ks siis, kui Ohio osariigis asuv Clevelandi haigla sattus avalikkuse surve alla pärast seda, kui oli teada andnud, et planeeritakse tuumaseadet. (Avalikkus ei saanud ilmselt aru, et sõna „tuum” viitab aatomi kesksetele osakestele.)
MRT kasutab keha läbistamiseks ja mõnede tuumade prootonite pööramiseks kindla sagedusega elektromagnetlaineid (neid nimetatakse raadiolaineteks). Need prootonid on esialgu suunatud tugeva magnetvälja järgi ning pärast seda, kui elektromagnetlained neid pööravad, saavad need oma algse asendi kiiresti tagasi. Jälgitakse esialgse asendi taastumist ja väga keerulised arvutiprogrammid muudavad saadud tulemused pildiks, mis kujutab ainet, milles prootonid on. Protsess on täiesti ohutu, sest magnetväli ja raadiolained ei tee mingit kahju. Tõepoolest, raadiolained, mida kiirgavad raadiojaamad, sideantennid ja isegi sidesatelliidid, läbivad inimest pidevalt.
Miks saavad hoolimata protseduuri ohutusest väga harvadel juhtudel mõned patsiendid põletada? Miks on mõned tätoveeringutega patsiendid tundnud kehamaalingute piirkonnas torkimist ja sikutamist? Miks on mõned neist kõvasti põletada saanud? Miks pole see protsess lubatud või soovitatav patsientidele, kellel on metallist implantaate (näiteks silmas, silmalaul, hammastel, samuti ei soovitata seda nendele, kel on teatud tüüpi rinnatoed või südameklapi osad)? Miks ei soovitata seda protseduuri tihti ka neile, kes on töötanud keevitajana või metallitöödel?
Vastus Enne kui ohtu hakati teadvustama, said mõned patsiendid põletada, kui neid puudutasid uuringute teostamisel kasutatavad elektrijuhid. Ükskord kinnitati narkoosi all oleva patsiendi sõrme külge seade, mis mõõdab hapnikusisaldust veres. See ainuke ühendus patsiendi ja jälgimisaparatuuri vahel (mis asus väljaspool MRT-seadmeid) ei kujutanud endast mingit ohtu. Sõrme külge kinnitatud juhe puudutas aga juhtumisi patsiendi käsivart. Juhtmeosa sõrme ja käsivarre vahel ning käsi nende kahe punkti vahel toimis suletud vooluringina. Raadiolainete sisselülitamisel tekitas muutuv magnetväli selles ahelas kiiresti voolu. Suur elektritakistus naha ja juhtme kokkupuutekohas põhjustas seal tugevat kuumenemist ja põletust. Et patsient oli narkoosi all, siis ei märgatud vigastust enne, kui ta MRT-seadmest välja võeti.
Teine oht patsienti põletada tekib siis, kui tema külge on kinnitatud pikk elektrijuht, mis toimib raadiolainete jaoks vastuvõtuantennina. Piki juhti tekib märkimisväärne elektriväli ja selle otsas on väli nii tugev, et tekitab sädemeid, mis patsienti põletavad.
Mõned mustad ja sinakasmustad värvained, mida kasutatakse tätoveerimisel ning silmalaineris, sisaldavad ferromagnetilist ainet (magnetiidinimelist raudoksiidi). Kui patsienti, kelle kehal on sellist pigmenti, liigutatakse MRT-seadmes magnetvälja sisse või sellest välja või kui magnetvälja tugevus muutub, siis muudab ferromagnetiline materjal oma paigutust. See sarnaneb paljuski sellega, kuidas kompassinõel magnetvälja või sellest eemale liikudes suunda muudab. Mõned patsiendid tunnevad seda torkimise ja sikutamisena nahal. Nendel üksikutel juhtudel, kui nahk on saanud põletada, on moodustanud tätoveeringu ferromagnetiline pigment kinnise (või peaaegu kinnise) ahela. Ilmselt suudavad raadiolained sellises ahelas tekitada voolu, mis on piisavalt tugev, et nahka kuumutada ja põletada.
Metallimplantaadid raskendavad MRT kasutamist, sest need moonutavad kujutist. Implantaadid, milles on ferromagnetilist materjali, võivad patsiendi magnetvälja viimisel ja sealt eemaldamisel pöörduda nagu kompassinõel. Tihti polegi seda liikumist märgata, kuid südameklapi või kehas oleva terasest kuuli pööramine võib olla ohtlik. Silmas olevate implantaatide või keevitusel ja metallitöödel sinna sattunud prahi liikumine võib samuti ohtlik olla. Minevikus olid mõnede kunstrindade detailid ferromagnetilisest materjalist ja need kippusid indutseeritud voolude tõttu kuumenema. Tänapäeval aga MRT-spetsialistid teavad ohte ja oskavad anda suuniseid, mis tagavad patsiendi ohutuse.
Allikad:
https://en.wikipedia.org/wiki/Neuroimaging
https://en.wikipedia.org/wiki/Magnetoencephalography
https://en.wikipedia.org/wiki/Electroencephalography
Halliday, Resnick, Walker "Füüsika põhikursus"
Walker, "Lendav füüsikatsirkus"
Teadmine, et vooluga juhtmele mõjub magnetväljas jõud võib isegi elukauge tunduda. Aga see juhtub vaid siis, kui seletada asja põhiprintsiibina, st ilma konteksti ja näideteta. Vaatame nüüd mõnd näidet, kuidas seda mõju katsetes demonstreerida:
| Terve pesakond erineva kuju ja "olekuga" homopolaarseid mootoreid, mis kõik ometigi töötavad ühel ja sellelsamal põhimõttel. Milline see põhimõte on? | Helivõimendist tulev vahelduvvool lastakse läbi paberile kleebitud juhtiva pleki riba või traadi. Ei juhtu midagi, ei peagi juhtuma. Aga kui lähendame sellisele ribale või traadile magneti, muutub heli ühtäkki kuuldavaks. Miks? |
Niisiis, vooluga juhtmele mõjub magnetväljas jõud. Alati. Küsimus on vaid jõu suunas ja suuruses. Jõu suuna teada saamiseks on aja teada, milline on magnetväli juhtme asukohas, st millisedd on selle magnetvälja jõujooned. Jõu suuna määramiseks saab kasutada vasaku käe reeglit:
Kui võtame nüüd teadmiseks, et voolu tekkimiseks ei pea meil tingimata juhet olema, laetud osakesed saavad liikuda ka gaasis või vaakumis, siis saame näiteks selgitada, miks liiguvad Euroopa Tuumauuringute Keskuses prootonid mööda ringjoont - loomulikult tekitatakse nende ümber õige suuna ja õige tugevusega magnetväli.
Tuleb küll tähele panna, et üksikutele laetud osakestele magnetväljas mõjuvat jõudu nimetatakse Lorentzi jõuks, aga sisuliselt on tegemist sellesama jõuga, mis ka juhtmejupile mõjub.
Konnasid (ja teisi väikseid loomi) saab solenoidi (rullikeeratud vooluga juhtme) abil magnetväljas hõljuma panna. Kuid konn ei ole ju magnetiline, muidu lendaks ta köögis hüpates iga kord külmkapi metallukse külge. Piisavalt tugevas väljas saaks ka inimest hõljutada ja inimene ei lenda kohe kindlasti vastu külmiku ust. Kuidas on võimalik bioloogilisi objekte hõljutada?
Vastus Mõned konnad on nüüdseks saanud kuulsaks, sest neid on solenoidiga magnetväljas hõljutatud. (Konnadele ei valmista see mingit ebamugavast, tunne on sama kui hõljuda vees, mis on konnadele väga meeltmööda.) Solenoid paigutati vertikaalselt ja konn pandi selle ülemise otsa lähedale, kust magnetväli solenoidist väljub. Kuigi konn ei ole tavaliselt magnetiline, ilmnevad tal magnetvälja asetades magnetilised omadused. Öeldakse, et konnad (nagu ka inimesed ja paljud materjalid) on diamagnetilised. Sellises aines mõjutab magnetväli elektrone ja aine muutub magnetiliseks. Konna asetamisel solenoidi otsa juurde, kust jõujooned laiali hargnevad, tõukab magnetväli teda ülespoole. Konn tõuseb kõrgusele, millel ülespoole suunatud jõud tasakaalustab gravitatsioonilise tõmbe, ja jääb sinna hõljuma.
Väike magnet, mis konna asemele pannakse, on ebastabiilne ega jää hõljuma. Konn erineb magnetist selle poolest, et tema magnetilised omadused sõltuvad talle mõjuvast solenoidi tekitatud magnetväljast. Näiteks konna eemaldumisel piirkonda, kus magnetväli on nõrgem, nõrgenevad ka tema magnetilised omadused. Väikese magneti puhul need aga ei muutuks.
Magneti saab panna hõljuma, kui see pöörleb ja pretsesseerib nagu vurr. Levitroni nime all müüdav lõbus mänguasi põhineb järgneval ideel: kiiresti pöörlev magnetvurr hõljub mõne sentimeetri kõrgusel keraamilise magnetplaadi kohal. Õhutakistus aga aeglustab pöörlemist ja lõpuks on see liiga aeglane, et vurri stabiilsena hoida, ning viimaks kukub vurr maha.
Kes diamagnetismi kohta veidi rohkem teada tahab, see võiks järgmise asjana heita pilgu Halliday õpiku vastavale alajaotusele ... eksole, läheb kohe palju keerulisemaks:
Selles kursuses ei saa me käsitleda diamagnetismi kvantfüüsika seisukohast, kuid võime siiski anda klassikalise seletuse mudeli baasil, mis on näidatud joonistel 32-11 ja 32-12. Esmalt eeldame, et diamagnetilise aine aatomis võib iga elektron tiirelda ainult kellaosuti liikumise suunas nagu joonisel 32-12d või sellele vastupidi nagu joonisel 32-12b. Kuna magnetism puudub, kui aine pole asetatud välisesse magnetvälja , siis võime eeldada, et aatomis puudub summaarne magnetiline dipoolmoment. Sellest järeldub, et enne aine asetamist välisesse magnetvälja tiirleb mõlemas suunas võrdne arv elektrone, mille tulemusena on aatomi ülespoole suunatud summaarne magnetiline dipoolmoment võrdne aatomi allapoole suunatud summaarse magnetilise dipoolmomendiga.
Vaatleme nüüd ebaühtlast magnetvälja joonisel 32-12a, milles on suunatud ülespoole, kuid on hõrenev (magnetvälja jõujooned eemalduvad üksteisest). Sellise olukorra saavutamiseks võime suurendada voolu läbi elektromagneti või liigutada pulkmagneti põhjapoolust lähemale elektroni trajektoori alla. Kuna magnetvälja suurus muutub nullist kuni lõpliku maksimaalse püsiväärtuseni, siis indutseeritakse kellaosuti liikumise suunaline elektriväli elektroni orbiidi ümber vastavalt Faraday ja Lenzi seadustele. Vaatleme, kuidas indutseeritud elektriväli mõjutab tiirlevaid elektrone joonistel 32-12b ja d.
Joonisel 32-12b kiirendab kellaosuti liikumise suunaline elektriväli kellaosuti liikumisele vastassuunas liikuvat elektroni. Kui magnetväli kasvab oma maksimaalse väärtuseni, kasvab ka elektroni kiirus oma maksimaalse väärtuseni. See tähendab seda, et ka vastav vool i ja voolust i tingitud allapoole suunatud magnetiline dipoolmoment kasvavad.
Joonisel 32-12d pidurdab kellaosuti liikumise suunaline elektriväli kellaosuti liikumise suunas liikuvat elektroni. Seega antud juhul kahanevad nii elektroni kiirus, sellega kaasnev vool kui ka voolust tingitud ülespoole suunatud magnetiline dipoolmoment . Kui tekitame magnetvälja , siis anname aatomile summaarse magnetilise dipoolmomendi, mis on suunaga allapoole. Sama juhtuks ka siis, kui magnetväli oleks ühtlane.
Ka magnetvälja ebaühtlus mõjub aatomile. Kuna vool joonisel 32-12b suureneb, siis ülespoole suunatud magnetjõud joonisel 32-12c suureneb koos voolusilmusele mõjuva ülespoole suunatud resultantjõuga. Kuna vool joonisel 32-12d väheneb, siis allapoole suunatud magnetjõud joonisel 32-12e väheneb samuti ning seda teeb ka voolusilmusele mõjuv allapoole suunatud resultantjõud. Seega lülitades sisse ebaühtlase magnetvälja , tekitame me aatomile mõjuva resultantjõu. Täpsemalt: see jõud on suunatud eemale suurema magnetväljaga piirkonnast.
Oleme oma arutlustes kasutanud elektronide fiktiivseid orbiite (voolusilmuseid), kuid lõpptulemuseks oleme saanud just selle, mis tõepoolest juhtub diamagnetilise ainega: kui rakendame sellele ainele magnetvälja nagu joonisel 32-12, siis tekib aines allapoole suunatud magnetiline dipoolmoment ja ainele mõjub ülespoole suunatud jõud. Kui väline magnetväli eemaldada, siis nii dipoolmoment kui ka jõud kaovad. Seejuures ei pea väline magnetväli olema suunatud nii, nagu näidatud joonisel 32-12. Analoogilised argumendid kehtivad ka teistsuguste suundade korral. Üldiselt:
Konn joonisel 32-13 on diamagnetiline (nagu ka mistahes muu loom). Kui konn asetati hajuvasse magnetvälja vertikaalse solenoidi ülemise otsa lähedal, kus solenoidi läbiva voolu põhjustatud magnetväli ülespoole pidevalt väheneb, siis konna iga aatomit tõugati ülespoole eemale suuremast magnetväljast. Konn liikus ülespoole ikka väiksema ja väiksema magnetvälja piirkonda seni, kuni ülespoole suunatud magnetjõud tasakaalustati konnale mõjuva gravitatsioonijõuga ning siis jäi konn õhku rippuma. Kui ehitaksime solenoidi, mis on suur küllalt, siis saaksime ka inimese tänu tema diamagnetismile õhus hõljuma panna.
KONTROLLKÜSIMUS 5
Kui väike tüdruk, kes istub tekil, võtab kätte kõik neli teki nurka ning tõstab neid kogu jõuga, siis kas ta tõuseb õhku? Muidugi mitte. Kuid kuidas siis õnnestub Mehhiko hüplevatel ubadel (Mehhikos kasvava piimalille Sebastiana pavoniana seemned) õhku hüpata?
Vastus Oa sees on pisike liblikaröövik, kes esmalt tõukab end üles oa põhjalt ning põrkab siis vastu selle ülemist osa, liigutades uba ülespoole. Liikumist põhjustav väline jõud (jõud väljaspool rööviku-oa süsteemi) on ülespoole suunatud jõud hetkel, kui see hüppama hakkab.
Yoël Forterre1, Philippe Marmottant2, Catherine Quilliet2 ja Xavier Noblin3 – DOI: 10.1051/epn/2016104
Taimed liiguvad mitte ainult tuule mõjul või kasvades. Kuigi neil ei ole lihaseid, on mõnedel taimedel välja arenenud mehhanismid, mille abil nad saavad teha hämmastavalt kiireid liigutusi (kiirused ulatuvad kuni 10 m/s) ja kiirendusi (tuhandeid g-sid), mis on võrreldavad loomade liigutuste kiirusega ja isegi ületavad neid.
Neid kiireid liikumisi vajavad taimed elutähtsate funktsioonide täitmiseks, nagu seda on paljunemine (mõnede orhideede õietolmu katapulteerumine, seemnete plahvatuslik väljutamine), kaitse kahjurite vastu (häbeliku mimoosil (Mimosa pudica) kokkuvoltimine) ja toitumine (loomtoiduliste taimede püünised). Millised on taimede selliseid kiireid liikumisi tekitavad füüsikalised mehhanismid. Artikli aluseks on hiljutised uuringud, mis on läbi viidud füüsika ja bioloogia piirimail.
Vee põhjustatud liikumised: siserõhk, osmoos ja aurumine
Esimese asjana paneme tähele, et erinevalt loomarakkudest on taimerakud ümbritsetud peamiselt tselluloosist koosnevate jäikade rakukestadega [1]. See takistab taimerakkudes, kokkutõmbumisvõimeliste valkude kasutamist nagu see toimub loomade lihasrakkudes. See-eest võimaldavad taimerakkude jäigad seinad hoida väga kõrget vee siserõhku, mis on tüüpiliselt 4-8 baari ja erilistes rakkudes isegil kuni 40 baari. Veel võib taimedes olla ka negatiivne rõhk (alarõhk), mille põhjustab kohesioonijõud vee molekulide vahel. Sellise rõhu puhul tõmbuvad raku seinad sissepoole, sealjuures takistab puittaimede täielikult välja arenenud rakukest struktuuri kahjustumist isegi kõrgeimate alarõhkude korral (~ 100 baari).
Füüsikaliset on sellised kõrged hüdrostaatilise rõhu absoluutvärtused põhjustatud osmoosist ja aurustumisest [2,3]. Vee liikumine, voog taime ja seda ümbritseva keskkonna vahel kutsub esile taimede rakkude paisumise või kokkutõmbumise. See põhjustab siserõhu, mis omakorda põhjustab silmaga nähtavaid mehaanilisi liigutusi. Mõned sellised liigutused on põhjustatud pöördumatust rakukestade deformatsioonist, nagu näiteks kasvamine ja valguse poole suunatud või gravitatsiooni järgi orienteeritud liikumine (Joonis 1a). Mõnedel teistel juhtudel on tegemist pööratavate liikumistega, nagu näiteks häbeliku mimoosi tundlike lehtede osmootiliselt indutseeritud kokkuvoltimine (Joonis 1c), või männikäbide avanemine/sulgumine vastavalt õhuniiskusele (Joonis 1b).
| Joonis 1 Taimede liigutuste füüsikaline klassifikatsioon liigutuste kestuse τ ja tüüpilise liigutustesse haaratud koe suuruse L järgi (artikli [4] järgi). Piirjoon τ = τp (sinine joon) annab poor- elastse aja (st kiireima liigutuse, mis on võimalik ainult vee transportimisel), ja on arvutatud kasutades diffusiooni koefitsienti D ~ 10-8 m²/s, mis on keskmine väärtus vee liikumisel taimede kudedes. Piirjoon τ = τi (punane joon) annab inertsiaalse aja, st kiireima võimaliku liikumise, kui rakenduvad inerts ja elastsus, ja on arvutatud kasutades tiheduse väärtust ρ = 1000 kg/m3 ja Youngi moodulit E = 10 MPa. (a) Kasvu vastus gravitatsioonile (geotropism). (b) Männi käbisoomuste liikumine vastavalt õhuniiskuse muutustele. (c) Häbeliku mimoosi lehtede osmoosist põhjustatud kokkuvoltimine. (d) Loomtoiduline taim kärbsepüünis. (e) Loomtoiduline taim vesihernes (Utricularia) perekonnast (f) Pritskurgi (Ecballium elaterium) seemnete väljapaiskumine (g) Sõnajala eosla katapuldi-laadne liikumine. | Niimoodi toimub häbeliku mimoosi lehtede kiire kokkuvoltimine. |
Vee põhjustatud liigutuste kiiruse füüsikalised piirid: poor-elastne ajaskaala
Ainult vee põhjustatud liigutuste kiirus on piiratud vee voolamise kiirusega kudedes. [4]. Poorses ja elastses keskkonnas, nagu seda on taime kude, on voolamine difusiivne protsess, mis toimub karakteristliku aja τp=L/D jooksul, kus L on vee liikumise ulatus ja D on efektiivne difusiooni koefitsient. Seda aega τp, nimetatakse „poor-elastseks ajaks“ (poroelastic time), ja joonisel 1 on seda võrreldud taimeriigis toimuvate liigutuste kestustega τ ja liigutusse haaratud koe suurusega L. Tõepoolest, liikumised mis on põhjustatud kasvamisest (Joonis. 1a) või õhuniiskuse muutumisega (Joonis 1b) paiknevad sellel graafikul ülevalpool piirjoont τ = τp ja see on kooskõlas nende puhtalt „hüdraulilise“ iseloomuga. Ka häbeliku mimoosi lehe kiire kokkuvoltimine kuulub sellese rühma - ehkki liigutuse on väga kiire (tüüpiliselt 1 s) on väiksed ka liikumisse haaratud koe mõõtmed.
Taimede liigutuste kiirenemine: elastsus ja mehaaniline ebastabiilsus
Kui taimed kasutaksid liigutustes vaid vee transporti, ei saaks nende liikumised olla kiiremad, kui seda määrab poor-elastne aeg. Samas joonis 1 näitab, et paljud taimed siiski suudavad seda hüdrodünaamilist piiri ületada. Sellised liigutused kasutavad mehaanilisi ebastabiilsusi, st varasemalt salvestatud energia kiiret vabastamist. Taimede juures saab eristada kaht tüüpi ebastabiilsusi: (i) pikipaindest põhjustatud ebastabiilsused, ja (ii) tahke aine või vedeliku purse seemnete või pooride väljapaiskumine. Vaatleme neid kaht mehhanismi lähemalt.
| Joonis 2 Pikipaine ebastabiilsus kärbsepüünises (a-c) ja vesihernes (d-f). (A) kärbsepüünis on avatud (pilt vasakul) ja suletud (pilt paremal). (B) Sulguva lehelaba kuju 3D mudel (eksperimendi andmed, ?t on aeg kahe järjestikuse pildi vahel). (C) Ruumiliselt keskmistatud lehelaba kumeruse sõltuvus ajast. Püünis sulgus ajahetkel t = 0. (D) Vesihernes püünis ja väikeste vähiliste trajektoor, mis imeti püünisesse pärast sulguri avanemist. (E) Sulguri kuju muutumine avanemisel, nähtuna fluorestsents-mikroskoobis. (F) Sulguri avanemise arvutisimulatsioon. (joonised A-C on artikli [5] järgi; joonised D-F on artikli [7] järgi) | Kärbsepüünis oskab oma lehelabadest moodustunud püünist väga kiiresti kokku tõmmata. |
Pikipaine ebastabiilsus: kärbsepüünis and vesihernes
Kärbsepüünis koosneb kahest alusele kinnitunud lehelabast (Joonis. 2A). Iga lehelaba sisemine külg sisaldab tundlikke karvakesi, mis tekitavad elektrilise signaali, kui neid puudutatakse. Püünis sulgub mõne sekundi kümnendiku jooksul, nii et selline liigutus ei saa olla põhjustatud vaid vee liikumisest (Joonis 1). Hiljutised uurimused on näidanud, et sulgumise kiirust suurendav mehhanism on ebastabiilne pikipaine – lehed käituvad sarnaselt, kui plõksuga ümber randme keerduv helkur-käevõru [5,6]. Taime kaks lehelaba on avatud asendis kõverdunud väljapoole ja suletud asendis sissepoole (Joonis 2B,C). Enne sulgumist lehelabad „püüavad“ kõverduda sissepoole. Aga kuna oma kumera geomeetrilise kuju tõttu ei ole see võimalik, siis akumuleerub püünise labadesse elastsusjõu energia. Kui elastsusjõud muutub piisavalt suureks, toimub lehelaba liigutus ühest olekust teise ning püünis sulgub kiiresti.
Uurimused on näidanud, et samasugust mehhanismi liigutab vesiherne imemispüünist [7]. Iga selle veetaime püünis on elastne, suletud, põiekujuline leht, kus rõhk aeglaselt väheneb (Joonis 2d). Püünis on hermeetiline tänu painduvale sulgurile, millel paiknevad ka mõned pikad tundlikud karvakesed. Algasendis on põie uks justkui kuppel, mis on kumerdunud väljapoole ning mis sellisena paneb rõhu vähenemisele vastu sarnaselt gooti stiilis kiriku kuplitega. Kui selle kupli tugevusvaru ammendub, kas siis elektrisignaali mõjul või lihtsalt mõne nõrga koha tõttu, pöördub kuppel teisipidi ja avaneb kiiresti (Joonis 2E,F). Kuna püünises on alarõhk imetakse sinna väga kiiresti (vaid ühe millisekundi jooksul) vett. Kiirendus selles protsessis on kuni 600g-d, ja väiksed putukad ei suuda vastu sellist voolu ujuda, sattudes püünisesse. (Joonis 2D).
Kavitatsiooniline ebastabiilsus: eoste väljapaiskumine
Kiireid liigutusi on vaja ka seemnete, õietolmu ja eoste väljaheitmiseks. Pritskurk (Joonis 1f) on oma seemnete väljaheitmise meetodi pärast hästi tuntud, aga kõige elegantsemat mehhamisi oma eoste väljaheitmiseks kasutab tõenäoliselt sõnajalg (Joonis 3A). Enamustel sõnajala liikidel on eosed sfäärilistes kapslites (eosla), mida ümbritsed kaarekujuline, paljusid veega täidetud rakke sisaldav riba (??) (Joonis 3B). Vee aurumine neist rakkudest tekitab negatiivse rõhu, mis tõmbab raku seinu sissepoole. Kuna raku seinad on ringi välisosas õhemad, saab ring painduda eosla suunas. Nii tekib eosla väljapoole paindumine kuni hetkeni, kui rakkudesse tekivad kavitatsioonimullid (negatiivne rõhk ca 100 baari), mis vabastavad kiiresti kogunenud elastsusjõu energia, eosla sulgub ja heidad selle käigus eosed välja nagu katapuldist.
| Joonis 3 (A) Sõnajala eosla avanemine ja sulgumine (konkreetne eosla on oma esoed juba välja heitnud). (B) Heite mehhanismi neli etappi, mis vastavad neljale fotole piltidel (A). (C) Eosla keskmise kõveruse sõltuvus ajast, aeglane avanemine (sinine joon) ja kiire sulgumine (punane joon). Logaritmiline skaala aitab märgata kiireid ostsillatsioone sulgumise esimeses etapis ja aeglast poor-elastset sulgumist teises etapis (joonised on artikli [8] järgi). | Sõnajala eoste avanemine ja sulgumine, mille käigus heidetakse eosed välja nagu katapuldist. |
Kirjeldatud mehhanismi on ligikaudselt teatud juba üle saja aasta, aga paljud sellega seotud küsimused on saanud vastused alles hiljuti. Näiteks: kuidas suudab sõnajalg oma eosed nii efektiivselt välja heita ilma, et oleks ühtki liikumist järsult katkestavat takistust või stopperit? Keskaegsetes katapultides kasutati stopperit katapuldi heitja poolel teel peatamiseks, et projektiil lendaks minema enne selle suunamist allapoole. Hiljutised uuringu ülikiirete kaameratega on sellele küsimusele vastuse andnud [8]. Protsessis on kaks faasi, mis toimuvad väga erinevate kiirustega (Joonis 3C). Esimene faas toimub kohe pärast kavitatsiooni ja selle käigus ring osaliselt sulgub mõnekümne mikrosekundi jooksul (see n tõenäoliselt kiireim liigutus, mis taimedel esineb). See inertsiaalne faas on nii kiire, et vesi rõnga poorsetes seintes ei jõus ümber paikneda. Selle tõttu vee rõhk järsult tõuseb ja rõnga sulgumise peatub poolel teel, võimaldades ühtlasi eoste katapulteerimise kiirustega rohkem kui 10 m/s. Teises faasis vee rõhk aeglaselt väheneb ja eosla sulgub täielikult mõnesaja millisekundi jooksul. See on hämmastav, kuidas selline väike, veest ja mõnest rakust koosnev süsteem suudab täita kõiki katapuldi olulisi funktsioone, alustades katapuldi vinnastamisest (vee kohesioon ja aurumine) ja vabastamisest (kavitatsioon) ning lõpetades rakkude seinte poor-elastsetest omadustest põhjustatud äkilise pidurdamisega.
Taimed on hüdraulilised süsteemid ja enamik nende liigutustest on lihtsalt osmoosi ja aurumise põhjustatud vee liikumise tulemus. Selliste liigutuste kiirus on seega piiratud vee difusiooni kiirusega taimede kudedes. Selles artiklis me näitasime, kuidas taimed kasutavad mehaanilisi ebastabiilsusi selleks, et kiiresti vabastada pikema aja jooksul salvestatud energia nii, et tekkivate liikumiste kiirus ületab oluliselt poor-elastse piiri. Selliste liigutuste kiirus on piiratud massi kiirendamiseks kuluva ajaga [4], mis määratakse elastsuslainete levimise kiirusega kehas, τi = L/c, kus L on keha suurus ning c=(E/ρ)1/2 on elastsuslainete levimise kiirus kehas ja E on Youngi moodul ning ρ on keha tihedus. Ei ole leitud ühtki taime, mille liigutuse ületaksid seda piiri (Joonis 1).
Kiired taimed ei ole ainult looduse imed. Koos biomimeetika arenguga on nad lootustandev inspiratsiooniallikas tehislike mikrosüsteemide loomiseks, olgu nendeks siis mikro-vedelik täiturid [10], kiiresti toimivad pinnad [11] või hüppavad robotid [12].
Viited:
[1] L. Taiz and E. Zeiger, Plant Physiology, Sunderland MA, Sinauer Assoc. 3rd ed. (2002).
[2] J. Dumais and Y. Forterre, Annu. Rev. Fluid Mech. 44, 453 (2012).
[3] Y. Forterre, J. Exp. Bot. 64, 4745 (2013).
[4] J. M. Skotheim and L. Mahadevan, Science 308, 1308 (2005).
[5] Y. Forterre et al, Nature 433, 421 (2005).
[6] S. Poppinga and M. Joyeux, Phys. Rev. E 84, 041928 (2011).
[7] O. Vincent et al. Proceedings of the Royal Society B 278, 2909 (2011).
[8] X. Noblin et al, Science 335, 1322 (2012)
[9] Llorens C et al., J. R. Soc. Interface 13: 20150930 (2016)
[10] D. Kim and D. J. Beebe, Lab Chip 7, 193 (2007)
[11] D. P. Holmes and A. J. Crosby, Adv. Mater. 19, 3589 (2007).
[12] H. Lee et al, Soft Matter 6, 4342 (2010)
1 Aix-Marseille Universite´ – CNRS UMR 7343, IUSTI – 13453 Marseille Cedex 13, France
2 Universit´e Grenoble Alpes – CNRS UMR 5588, LiPhy – 38402 Saint-Martin-d’H`eres, France
3 Laboratoire de Physique de la Mati`ere Condens´ee – Universit´e Nice Sophia Antipolis CNRS UMR 7336 – 06108 Nice Cedex 2
Kui satute järgmisel korral propelleritega lennukiga sõitma, siis lõbustage ennast ja kaasreisijaid sellega, et pildistate või filmite oma nutitelefoniga lennuki propellerit. Sest tulemus arvatavasti üllatab – pildile võib jääda just selline täiesti mittesümmeetriline objekt. Võib isegi tekkida kartus, kas lennukiga on kõik korras.
Sellise kõvera pildi põhjuseks ei ole siiski mitte katkine propeller vaid mobiiltelefoni kaamera.
Teame, et lääts (objektiiv) tekitab kaamera sensorile optilise kujutise. Kallites peegelkaamerates on sensori ees katik, mis laseb sensorile valgust vaid lühikeseks viivuks, misjärel saadetakse pildi andmed kaamera mällu. Mobiiltelefonides kasutatavate CMOS tüüpi sensorite ees sellist katikut ei ole, sensor on kogu aeg valgustatud. Mällu edastatakse pilt sensori pikslite ridade kaupa ning edastamisele läheb see, mida iga selline rida parajasti “näeb”. Nii et kogu pilt pannakse kokku erinevatel ajahetkedel pildistatud ridadest. Selge see, et kiiresti pöörlev propeller jõuab ühe sellise tsükli jooksul end pöörata, sellest ka moonutused.
Siit tuleb üks õpetlik efekti selgitav animatsioon ja video, mismoodi see lennukist läbi kaamera vaadates välja paistab.
Nüüd peaks olema lihtne aru saada ka sellistest piltidest:
Veel paar pilti:
Sondijaam on seade, mis võimaldab sondidega (teravate nõeltega) mõõta väga väikeste objektide induktiivsust, mahtuvust, takistust, voolutugevus, pinget, nende parameetrite omavahelist sõltuvust ning nende sõltuvust ajast, sagedusest ja temperatuurist
Seadme mark on EPS150 TRIAX ja see on Tartu Ülikooli füüsika instituudi kiletehnoloogia labori kasutuses.
Sõna "holograafia" ja "hologramm" kasutatakse tänapäeval ka siis, kui jutt käib näivkujutise tekkimisest mingis optilises skeemis, mida on võimalik silmaga vaadelda, aga ei ole võimalik käega katsuda. See ei ole alati niimoodi olnud ning holograafiast rääkides peaks alati mõtlema, millest õigupoolest jutt käib.
Soovitame ära vaadata video Litiholo komplekti kasutamisest, sealt saab "päris" hologramme.
Ja viitame vastavat osa Tarkpea/Voolaiu Elektromagnetismi õpikust:
Holograafia leiutas 1947. aastal Ungari päritolu füüsik Dennis Gabor, kes sai selle eest 1971. aastal Nobeli füüsikapreemia. Hologrammile nime andes lähtus D. Gabor kreeka keelest, kus "holos" tähendab täielik ja "gramma" – üleskirjutus. Seega tähendab "hologramm" täielikku üleskirjutust.
Mis aga on hologramm ja kuidas teda tehakse? Hologramm on holograafilisel meetodil saadud kolmemõõtmeline ehk ruumiline kujutis. Holograafia on esemete ruumilise kujutise fotograafiline jäädvustamine. Selle tulemusena saadakse esemest ruumiline pilt, mida nimetatakse hologrammiks ja mis põhimõtteliselt erineb nii tavalisest fotost kui ka 3D-kinos esitatavast ruumilisest elamusest.
Fotol jäädvustatakse esemete tasapinnaline, mitteruumiline kujutis. Tähtis on tähele panna, et fotografeerimisel me salvestame valguse E-vektori ruudu keskväärtuse, aga kogu info valguslainete faasi kohta läheb paratamatult kaduma. Fotot vaadates tekib küll mingi ruumilisuse mulje, sest harilikult on fotol meile tuttavad asjad ja neid me oskame omale ette kujutada. Ruumilisuse muljet aitavad tekitada perspektiiv, samuti varjud fotol. Põhiline erinevus foto ja hologrammi vahel seisneb selles, et fotol pole võimalik näha mingi eseme taga olevat teist eset, aga hologrammil on. Selleks tuleb ainult pead liigutada, et vaadata hologrammi teisest suunast.
3D-filmis ruumilise elamuse tekkimise põhimõtet tutvustame punktis 3.4.2 .
Vaatame lähemalt hologrammi valmistamist fotograafilisel meetodil ehk holografeerimist. Mingi eseme holografeerimiseks kasutatakse kahe koherentse kiirtekimbu interferentsi. Nende kimpude saamiseks kasutatakse kõigepealt kaht kumerläätse, mille abil muudetakse kitsas laserikiir laiaks paralleelsete lainete kimbuks. Üks osa sellest kimbust, nn tugikimp, suunatakse peegliga enne holografeeritava esemeni jõudmist fotoplaadile või -filmile (J.3.24)
Teine osa suunatakse sinna pärast holografeeritavalt esemelt peegeldumist. See on esemekimp.
Tugikimbus olevad lained jõuavad kõik fotoplaadini samas faasis, sest tegemist on tasalainega (paralleelne kimp). Esemekimp ei ole aga enam tasalaine – esemelt peegeldudes sisaldab selle lainefront kogu informatsiooni eseme väliskujust. Fotoplaadil kimbud kohtuvad ja interfereeruvad, sest laserivalgus on koherentne. Tulemuseks on keerulise kujuga interferentspilt, milles kajastub eseme ruumiline kujutis. Selgub, et sellises interferentsipildis on olemas ka info valguse E-vektori faasi kohta.
See pilt salvestatakse fotograafiliselt ja hologramm ongi valmis.
Hologrammi vaatamiseks kasutatakse ainult tugikimpu, st laiaks muudetud laserikiirte kimpu. See kimp suunatakse hologrammile, kus toimub valguse difraktsioon. Et hologrammis on salvestatud ka informatsioon valguse ajalise käitumise kohta, siis tekib täpselt samasugune lainekimp, nagu oli esemekimp. Kui seda kimpu vaadata, siis näeme esemega sarnast kujutist (J.3.25). Tekkinud kujutis on ruumiline.
Hologrammil on fotoga võrreldes mitmeid erinevaid omadusi:
- lihtne on koopiate tegemine, sest pole erinevust positiivi ja negatiivi vahel;
- purunemisel säilib igal tükil tervikpilt, sest valmistamisel pole kasutatud koondavat optikat ja kõik hologrammi osad sisaldavad infot kõigi originaali osade kohta;
- ühele fotoplaadile saab jäädvustada palju hologramme, piisab, kui näiteks iga kord enne holografeerimist fotoplaati pisut pöörata;
- kujutise suurust saab muuta, kui muuta vaatamisel kasutatava laseri lainepikkust: mida suurem lainepikkus, seda suurem kujutis.
| Hologramm hiirest. Seda hologrammi on pildistatud kahest suunast. Nagu näeme, erinevatest suundadest paistab pilt erinev, ruumiline info on hologrammi salvestatud. | Holograafia on väga võimas meetod ka teistsugustes kehade ruumilist kuju uurivates ülesannetes. Sellel pildil on näeme interferentsimustris kohti, kus kitarr rohkem võngub. |
Oleme seni rääkinud objektide ruumilise kuju üleskirjutamisest, aga valguslainete abil saab teha veel palju rohkem. Nii on interferentsinähtuse abil võimalik üles kirjutadada ka esemete liikumist, st põhimõtteliselt on võimalik hologrammi salvestada liikuvat ruumilist pilti sisaldav film. Selliste teemadega tegeleb nn. aegruumiline ehk 4D holograafia. Aegruumilise holograafia võimalikkuse tõestasid 1983. aastal Eesti TA Füüsika Instituudi (tänane TÜ Füüsika Instituut) teadlased akadeemik Peeter Saari juhtimisel.
Aga kui see kõik nii hea ja võimas on, miks me siis endiselt kasutame fotograafiat ja 2D videosid, selle asemel, et salvestada elu kogu oma täiuses? Põhjused on ühtaegu tehnilised ja põhimõttelised. Näiteks on üsna lihtne aru saada, et esemete ruumilise kuju üleskirjutamine tähendab rohkem informatsiooni ning holografeerimisel tuleb see ka kusagile üles kirjutada ja see tähendab suurema pikslite arvuga salvestus- ja esitlusseadmete kasutamist. Kui suure lahutusega fotoaparaatide tegemine ei ole täna põhimõtteliselt probleem, siis kättesaamatuks jääb holografeerimiseks tarvilik piksli suurus - ca poole mikromeetrilise serva pikkusega piksleid ei ole täna võimalik valmistada. Nii et ainus võimalus on kasutada vanamoodsaid fotoplaate. Vist isegi põhimõttelisem probleem on see, et igapäevaste olukordade holografeerimiseks on vaja kasutada üsnagi spetsiifilist laserivalgust.
Viimastel aastatel on aga tekkinud tehnika arengus uued suunad, mis annavad lootust, et vahepeal unustusehõlma vajunud tõeliselt ruumilise kino idee uuesti ellu ärkab. Nimelt on võimalik hologramme ka arvutada, kui on teada holografeeritavate objektide täpne kuju. 3D-animatsioonides on see info olemas, ainsaks põhimõtteliseks probleemiks jääb videoprojektorite lahutusvõime, mis peaks olema tuhandeid kordi suurem.
Aga kuidas jääb reaalse elu holografeerimisega? Ka siin võib läbimurre tulla tänu järjest kasvavale arvutusvõimsusele - põhimõtteliselt on võimalik esemete täpne kuju välja arvutada, kui on olemas piisav hulk erinevatest rakurssidest tehtud fotosid. Tulevik näitab, kas ja millises suunas see seni realiseerumata võimalus edasi areneb.
| Hologramm ühest optika õppevahendite komplektist. Annab aimu, mis moodi sellised hologrammid reaalselt välja näevad ja kuidas neid vaadatakse - ülemises vasakus nurgas on laser, millest väljub hajuv kiirtekimp ja satub hologrammile. Võrdle joonisega 3.25. | Hologrammi valmistamise komplekti LitiHalo Kit tutvustav video. Vaata, kas tunned seal ära protsessi etapoid, mis ülalpool tekstis juba räägitud. |
Kui keegi tõesti soovib olla nähtamatu, tuleb kõne alla mitu erinevat trikki.
Võib proovida olla läbipaistev, nagu klaasiksääse vastne. Kui olla piisavalt väike, on lootust, et sind keegi ei näe ja kui isegi näeb, ei pane tähele või ei tee välja.
Keerukam on olla nähtamatu, kui oled suur ja ei paista läbi. Võib proovida maskeerumist, peegeldada samu värve ja mustreid, mis ümbrus ja taust. Hästi oskavad seda sõjaväelased, kes riietuvad lapilistesse vormidesse, mille põhitoonid sobivad maastikuga ja riputavad enda ja oma tehnika külge kohapealt korjatud oksi või heina. See ei ole küll päris nähtamatuks muutumine, pigem on tegu vaataja nägemismälu ärapetmisega. Nähtamatuse asemel võiks siin öelda pigem märkamatuks jäämine. Kahjuks tuleb seejuures asukohta vahetades alati arvestada ümbermaskeerimise vajadusega.
Muidugi, võib ka kasutada infotehnoloogia abi:
| Richard Hammond sõitis Top Geari erisaates „50 aastat Bondi autosid”, Ford Transiti kaubikuga, mis oli „nähtamatuks” muudetud külgedele ja taha paigutatud ekraanidega, kuhu kuvati vastaskülje kaamerast võetud pilt. Saateformaadile omaselt sai palju nalja ja võis jääda mulje, et katse kukkus läbi. Tehnika vajaks muidugi arendamist, aga saatelõigus on üsna mitmes kohas näha, et auto tõepoolest maskeerub ehmatavalt hästi. Eriti hästi tuli nähtamatus välja tagantvaates. | Tangi külge kinnitatakse paneelid, mis saavad kiiresti oma temperatuuri muuta. Nii et tangi saab teha sellise temperatuuriga nagu on taust ning soojusele reageerivatele mistahes relvadele muutub asi enam-vähem nähtamatuks. |
Enamus füüsikat õppinud inimesi teab, et sfääriline klaaskera fokusseerib valgust samamood, kui seda teeb lääts või plussidega prilliklaas.
Päris hiljuti ilmus artikkel, milles näidatakse, et sfäärilise kujuga üherakne tsüanobakter toimib kui lääts, fokusseerides talle langeva valguse oma tagumisele küljele, valguse poolt vaadatuna. Enamgi veel, need bakterid oskavad nii ka valguse poole liikuda.
Füüsikaliselt on asi selge - sfääri kujuga läätse fookuskaugus on sedavõrd väike, et valgus koondub päris sfääri pinnale, kusjuures fookustäpi asend annab ka teada, kustpoolt valgus paistab. Nii on end lihtne valguse poole pöörata ja sinna liikuda.
(a) Tsüanobakterite perekonda kuuluv Synechocystis üherakuline bakter erinevatest suundadest valgustatuna. Kõige parempoolsem pilt on ühe bakteri suurendus. Valge skaala pikkus on 5 mikromeetrit (b) Synechocystis bakterite uurimise skeem fotolitograafilisel meetodil (mõõdeti lähivälja) (c) Sellise jälje jättis uuritav rakk valgustundlikule pinnale (b) kujutatud eksperimendis (d) Valguslainete levimine Synechocystis bakteris. Valguse lainepikkus on selles simulatsioonis 365 nanomeetrit, valgus langeb bakterile ülevalt. Paneme tähele fookuspunkti bakteri tagumisel seinal. Synechocystis bakterite liikumine valguse suunas. LED valgusallikas, mille poole bakterid liiguvad on pildi alumises osas. Ekraani keskosas paistev punane täpp on sinna tekitatud laseriga. Pange tähele heledaid fokaaltäppe bakteritel.
Vahva on see, et teadlased jõudsid niisuguse avastuseni üsna juhuslikult, kui nad hakkasid uurima tsüanobakterite käitumist erinevatest suundadest paistvas valguses - heledad valgustäpid hakkasid mikroskoobis silma.
Kes otsib, see leiab.
Kes tahab täpsemalt teada, avab alljärgnevad lingid.
Allikad:
https://elifesciences.org/content/5/e12620v1
http://physicsworld.com/cws/article/news/2016/mar/15/bacteria-act-as-tiny-lenses-to-move-towards-light
Priit Ennet pani 2008.aastal kokku sellise teadusuudise:
Teadlased on vähemalt nelikümmend aastat tõsiselt vaielnud, kas linnud näevad magnetvälja lausa sõna otseses mõttes või mitte. Seni ei ole keegi tõestanud, et see niiöelda keemiliselt võimalik oleks. Aga nüüd on saadud häid asitõendeid, mis kinnitavad, et rändlinnud suudavad ehk tõepoolest Maakera magnetvälja suunda lihtsalt silmaga vaadata. Klaus Schulten Ameerika Ühendriikide Illinois' Ülikoolist tuli nelja aastakümne eest välja hüpoteesiga, et rändlindudel on kas silmas või ajus molekulid, mis reageerivad magnetväljale. Probleem on olnud selles, et keegi ei ole suutnud leida nii tundlikku kemikaali, mida Maa nõrk geomagnetiline väli võiks piisavalt mõjutada.
Inglismaal Oxfordi Ülikoolis on Peter Hore ja ta kolleegid nüüd just niisuguse aine leidnud.
Krüptokroomid on valgustundlikud valgud, mida leidub nii loomade kui ka taimede sees ning mis arvatakse olevat seotud niinimetatud bioloogilise kellaga. Mõned aastad tagasi avastati, et neid aineid leidub ka aed-põõsalinnu silma võrkkesta närvirakkudes.
Laboris ei ole krüptokroome seni valmistada õnnestunud ja ka muidu on neid raske kätte saada, kuid Hore'i juhitud rühm on nüüd näidanud, et üks ligikaudu samasuguse struktuuriga molekul on tõepoolest nõrga magnetvälja suhtes tundlik. Väga tõenäoliselt on samasugune tundlikkus siis ka võrkkestaneuronite krüptokroomidel ja see annaks juba keemilise aluse väita, et rändlinnud tõepoolest ehk näevadki magnetvälja. [1]
Heameel on tõdeda, et teadlased on oma töös vahepeal edenenud, mõndagi on selgemaks saanud. Värsked tulemused Oxfordi ja Oldenburgi ülikoolide teadlastelt (füüsikutelt) pakuvad esimest korda välja matemaatilist mudelit sellele lindude silmas töötavale kompassile [2][3].
Sedapuhku on vaatluse all sebravindi silmas toimuv. Jätkuvalt käib jutt krüptokroomides toimuvatest valguse põhjustatud keemilistest reaktsioonidest. Selliste reaktsioonide tundlikkus magnetväljale oli teada ka varasemast, aga seni ei oldud suudetud mõista, kuidas saab Maa magnetvälja suunda mõõta 5 kraadise täpsusega, nagu linnud seda teadaolevalt suudavad.
| Sebravint | Mis toimub sebravindi silmas? Puhas kvantmehaanika! Joonisel (A) on uuritav molekul, joonisel (B) on graafik mis näitab, kuidas teatud keemilise reaktsiooni saaduse hulk sõltub tehtud arvutustes magnetvälja suunast - kui koherentsusaeg on 100 mikromeetri pikkune tekib sellesse graafikusse terav miinimum. Ülejäänud joonised illustreerivad seda tulemust ruumiliselt, täpsema seletuse võib leida algallikast. |
Sisult on kogu arutelu kvantmehaaniline. Selgus, et kui arvestada krüptokroomide koostises olevate aatomide tuumade ja elektronide spinnidega ning eeldada, et keemilistes reaktsioonides elektronide üleminekul tekkiv spinnide vaheline koherentsus kestab kauem, kuni sada mikrosekundit, siis tekkis süsteemi tundlikkuse kõverale "nõel", st selle suunatundlikkus magnetväljas kasvas hüppeliselt.
Kõik see on päris keeruline. Sest loodus ongi keeruline, kui tahta sellest lõpuni, st molekulaarsel tasemel aru saada. Aga ainult niimoodi on võimalik looduselt füüsikat, keemiat ja materjaliteadust õppida.
Küllap saame endale kunagi osta suunatundlikud kontaktläätsed.
Allikas:
[1] http://www.horisont.ee/node/495
[2] http://www.pnas.org/content/early/2016/03/30/1600341113.full
[3] http://physicsworld.com/cws/article/news/2016/apr/07/birds-measure-magnetic-fields-using-long-lived-quantum-coherence
Superkondensaator vs kondensaator vs patarei:
Selle valdkonna asjatundjana kirjutab Tavo Romann 26.04 Novaatoris [1] niimoodi:
"Superkondensaator on lihtne elektrienergia salvestamise seade, mis koosneb kahest suure eripinnaga süsinikelektroodist, need on eraldatud poorse membraaniga ja kastetud ioonjuhtiva elektrolüüdi lahusesse. Superkondensaatoril on kõrgem kasutegur, pikem eluiga ja suurem võimsus kui akudel, ent väiksem energiatihedus massiühiku kohta.
Suur võimsus tähendab, et superkondensaatori laadimine võtab kümme sekundit, seda akude tunni vastu. Väiksem energiatihedus tähendab, et kui liitium-ioon akuga sõidab elektriauto 160 kilomeetrit, siis superkondensaatoriga ainult 12 kilomeetrit.
Seega akut superkondensaator enamasti ei asenda, aga mõningaid rakendusi leidub näiteks elektriliste tõstukite näol või pidurdusenergia salvestamisel elektrirongides. Kõige suurem turul oleva klassikalise superkondensaatori energiatihedus on praegu kümme Wh/kg, mida toodab Tartust võrsunud ettevõte Skeleton Technologies. Siiski on üsna reaalne lähitulevikus uute grafeeni ja ioonsete vedelike tehnoloogiate kasutamisel kahekordistada superkondensaatorite energiatihedust."
Tänaseks ongi teada antud, et uudsetes grafeenil põhinevates superkondensaatorites on saavutatud energiatiheduseks 131 Wh/kg ja see on peaaegu neli korda rohkem, kui oli eelnev rekord [2]. Li-ioon akude vastav näitaja on 200 Wh/kg. Siinkohal on ka paslik mainida, et hinnanguliselt on fossiilkütustel töötavate autode võistlemiseks tarvis saavutada 1000Wh/kg [2].
Siiski, uurimistöö superkondensaatorite parendamiseks käib väga suure hooga (vt kasvõi füüsikaportaali kokku kogutud uudiste voogu). Küllap tulevad ka läbimurded ja elektriauto aku saabki 15 sekundiga laetud.
Lisaküsimus: Milline peab olema voolutugevus selleks, et 15 sekundiga ära laadida 100 kg kaaluv 1000Wh/kg energiatihedusega superkondensaator?
Allikad:
[1] novaator.err.ee
[2] http://spectrum.ieee.org/nanoclast/semiconductors/materials/supercapacitors-take-huge-leap-in-performance
Faasidiagrammid ehk olekudiagrammid on tõelised tarkuse allikad, kui asi puudutab ainete käitumist erinevatel temperatuuridel ja rõhkudel. Tahke või vedel? Vedel või gaasiline? Plahvatab või ei plahvata?
Kaks kõige tavalisemat ebatavalist näidet on kuiv jää (tahke süsinikdioksiid) ja vedel lämmastik.
Kuiva jääd nimetatakse kuivaks sellepärast, et see ei sula vaid sublimeerub, muutub otse tahkest faasist gaasiliseks. Faasidiagrammi uurides peaks olema üsna selge, et kõrgematel rõhkudel peaks olema võimalik ka vedel faas:
Mis muud, kui proovime järele. Jälgime sealjuures loomulikult ohutust - katses kasutatud anum on päris paksude seintega, tavaline pudel võib samades tingimustes kergesti lõhkeda! Vedel faas ilmub tõepoolest. Faasidiagrammilt võib ka ennustada, et kui vedela lämmastiku temperatuur hakkab tõusma, st kui kuiva jää tükid viimseni vedelaks muutuvad, tõuseb rõhk veelgi. Nii et see katse kindlasti ei ole ohutu!
Vedela lämmastikuga saame läbi teha sarnase arutluskäigu.
Faasidiagrammilt selgub, et madalatel rõhkudel ei ole lämmastikul vedelat faasi, nii et õhutühjas ruumis peab vedel lämmastik "otsustama" - ta muutub kas tahkeks või gaasiliseks. Alternatiiviks on langetada temperatuuri normaalrõhul. Rõhu langetamine on lihtsam, proovime selle järele.
Vaakumpump, mida sellistes katsetes kasutada peab olema piisavalt võimas, et pidevalt aurustuvat lämmastikku vaakumkuplist eemaldada. Katse tulemust näete kõrvalolevas videos.
Järgmisena võib ette võtta süsiniku faasidiagrammi, et otsida sealt teemantite tegemise võimalusi. Selle kohta räägib loo Jaan Paaveri Mikro- ja megamaailma õpik. Vaata järele!
Yaakov Vilenchik, Emanuel Peled ja David Andelman, PhysicsWorld
Vesiniku kasutamine autokütusena võib näida hetkel veel küll üsna kauge tulevikuna, kuid kliimamuutustega võitlemise ajastul on see siiski täiesti realistlikuks alternatiiviks bensiinile ja diislikütusele.
2008. aasta suvel lakke tõusnud naftahinnad sundisid pea igat maalast oma rahakotti kergendama. Kõige rängema hoobi said sõidukijuhid, sest bensiini hind tanklates oli kõrgem kui kunagi varem, kuid suurenenud transpordikulud hakkasid peagi kajastuma ka toidukaupade hinnas ning selle tõusu eest ei suutnud pageda enam ükski tarbija.
Tolle ajaga võrreldes on hinnad tänaseks tublisti langenud – osaliselt võime selle eest tänada ülemaailmset majanduslangust, mille tõttu on vähenenud ka energianõudlus. Sellegi poolest ei takista miski naftabarreli hinda jälle uutesse kõrgustesse tõusmast. Kuigi naftatootjad ei väsi meile kinnitamast, et naftavarude tuleviku pärast pole mõtet muretseda, võib ülemaailmne tootmine juba enne käimasoleva sajandi keskpaika uude haripunkti jõuda ning sel juhul ei suuda pakkumine enam nõudlust rahuldada ja hinnad tõusevad jälle lakke.
Kõikuvate naftahindade nõiaringist pääsemiseks tuleb meil leida alternatiive praegustele bensiini- ja diiselmootoritele. Alternatiivsete võimaluste nimekiri pole küll pikk, kuid seal on siiski paar ideed, mida tasuks tõsiselt kaaluda – nendeks on elektriautode jõuallikana kasutatavad laaditavad akud ja kütuseelemendid. Kuna töötamisel ei eraldu neist kasvuhoonegaase, võiksid nad anda suure panuse ka kliimamuutustega võitlemisse, sest rahvusvahelise mootorsõidukitootjate organisatsiooni OICA andmetel on autotranspordi osa kogu maailma süsihappegaasi emissioonist hetkel tervelt 16%.
Laaditaval akul on mitmeid eelisi – tal on kõrge kasutegur, kulub aeglaselt ning töötab suhteliselt vaikselt ja puhtalt. Viimaste aastate jooksul on tublisti arenenud ka liitiumtehnoloogial põhinevad akud, mis on nüüd kergemad, väiksemad ning vastupidavamad kui kunagi varem. Neid hakati hiljuti testima ka hübriidautodes nagu Toyota Prius, kus akut kasutatakse koos väikese ja ökonoomse, konstantsel kiirusel töötava sisepõlemismootoriga. Pidurdamisel aku laeb ning see aitab vähendada nii kütusekulu (2/5 võrra) kui ka emiteeritavate kasvuhoonegaaside hulka. Väikestest hübriidelektriautodes kasutatavatest akudest ei piisa aga tõelise ökoloogilise revolutsiooni vallandamiseks – selleks läheks vaja juba selliseid elektriautosid, kus laetavad akud oleks ainsaks jõuallikaks.
| General Motors on tootnud Chevrolet Equinoxil põhineva kütuseelemendil töötavat sõiduriista, mille tippkiirus on 160 km/h ning mis kiirendab nullist sajani 12 sekundiga. | 440 kütuseelementi annavad võimsuseks 93kW. Süsteemis on ka akud. Mootori maksimaalseks võimsuseks on 94kW, keskmiseks pidevaks võimsuseks 73kW (320Nm). Vesiniku mahutid on 700atm rõhu all, sisaldades 4,2kg vesinikku. Seda jätkub 320 km jaoks. |
Ainult elektri jõul töötavad autod on küll juba praegu olemas, kuid neil on veel mitmeid puudusi: kuna akud on rasked ning ei suuda kuigi palju energiat talletada, jätkub neil jõudu vaid umbes 250 km pikkuse vahemaa läbimiseks; akud töötavad vaid äärmiselt kitsas temperatuurivahemikus; kui aku saab tühjaks, on auto täiesti kasutuskõlbmatu; laadimine võtab mitu tundi ning aku pidev kasutamine ja laadimine vähendab selle jõudlust. Peale selle on probleeme ka ohutusega, sest lühised ning kõrged temperatuurid võivad tekitada elektroodide ja elektrolüüdi vahel reaktsiooni, mis muudab aku kasutuskõlbmatuks. Lisaks on elektriautod ka äärmiselt kallid. Nendele probleemidele vaatamata mängivad nii hübriidajami kui akudega töötavad elektriautod tulevikus kindlasti olulist rolli meie naftatarbimise vähendamises.
Eelneva info valguses tundub kütuseelement olevat auto jaoks igati mõistlikum lahendus – selle tugevad küljed on suuresti samad mis akudel, kuid puuduste nimekiri on märkimisväärselt lühem. Erinevalt akust ei talletata kütuseelemendi keemilist energiat mitte selle sees, vaid eraldi mahutis (näiteks autosse sisse ehitatud vesinikupaagis), kust seda siis pideva ühtlase survega kütuseelementi suunatakse. See on aga määrava tähtsusega, sest just tänu välisele kütusemahutile suudab kütuseelementi kasutav auto läbida korraga pikema vahemaa kui tema akutoitel rivaal ning lisaks on vesinikupaagi täitmine pea sama lihtne kui bensiini tankimine.
Kütuseelemendiga autod on oma akutoitega sugulastest ka tunduvalt kergemad. Näiteks saab ühe 130 kg kaaluva 300 liitrise paagiga, kuhu mahub 6 kg vesinikku, sõita maha umbkaudu 500 km. Liitiumioonakuga masinal läheks sama vahemaa läbimiseks vaja 800 kg kaaluvat 650 liitrise mahuga akut. Kütuseelemendid on akudest etemad ka oma tööks vajaliku temperatuurivahemiku poolest ning nad suudavad toota energiat, mille võimsus ulatub vattidest megavattideni – see võimaldab neid kasutada ka transpordist sootuks erinevates valdkondades. Vaatamata kõigile neile eelistele, on kütuseelementidel aga ka omad puudused, millest allpool täpsemalt juttu tuleb ning seetõttu pole ka sugugi kindel, milline neist kahest tehnoloogiast tulevikust domineerima hakkab.
|
Lühiülevaade: kütuseelemendid
|
Kütuseelemendi arendamisel on suurimaks väljakutseks materjalide ja meetodite leidmine, mis muudaksid jõuallika efektiivsemaks ja majanduslikult tasuvamaks ning annaks talle seega võimaluse võistelda bensiini- ja diiselmootoritega. Hetkel töötavad selle eesmärgi saavutamise nimel mitmed maailma juhtivad autotootjad ning General Motors, Toyota, Mercedes Benz, Fiat ja mitmed teisedki on tulnud välja ka oma ideeautodega. General Motors on astunud veel ühe sammukese edasi ning tootnud umbkaudu 100 kütuseelemendil töötavat Chevrolet Equinoxi, mis on kokku läbinud juba üle 1,5 miljoni kilomeetri. Ettevõtmise eesmärgiks on analüüsida auto käitumist ning saada tagasisidet juhtidelt ja kaasreisijatelt. Järgmise kümne aasta jooksul loodavad nad turule lasta mõni tuhat sellist sõiduriista.
Roheline elektrienergia
Kütuseelemendid erinevad üksteisest küll disaini, materjalide, tööks vajaliku temperatuurivahemiku ja väljundvõimsuse poolest, kuid tööpõhimõte on neil kõigil üks. Protsess algab anoodil, kus vesiniku molekul lõhutakse kaheks vesinikiooniks ning kaheks elektroniks. Elektriväli ja kahe elektroodi vahelised kontsentratsioonigradiendid suunavad tekkinud vesinikioonid (prootonid) edasi katoodile. Teel läbivad nad negatiivse laenguga prootonjuhtmembraani (vt joonis). Kuna membraan laseb läbi vaid prootoneid, siis anoodil vesiniku molekulidest eraldatud elektronid seda läbida ei suuda. Laengute eraldumine tekitab kahe elektroodi vahel pinge, mis vastabki elemendi väljundpingele. Selle maksimumväärtus on küll vaid 1,23 volti, kuid elemente omavahel ühendades (kokku võib neid olla isegi mõnisada) on võimalik toota ka märkimisväärselt kõrgemat pinget.
| Pulbitsev elu kütuseelemendi sees. | Kütuseelement toodab energiat keemilise reaktsiooniga, kus osalevad hapnik, vesinikioonid ja elektronid. Anoodil tekkinud vesinikioonid suunatakse läbi membraani katoodile. Membraane tehakse enamasti Nafioni-nimelisest polümeerist, millel on teflonist „karkass“, kuhu kinnituvad negatiivse laenguga vääveltrioksiidi rühmad. Anoodil tekkinud elektronid ei suuda membraani läbida ning suunatakse seetõttu katoodile läbi välise vooluringi. Vt ka https://et.wikipedia.org/wiki/Kütuseelement |
Kui kütuseelemendi kahe elektroodi vahele on loodud väline vooluring, liiguvad membraani poolt „hüljatud“ elektronid seda mööda anoodilt katoodile, kus tekib keemilise reaktsiooni käigus vesi. Reaktsioonis osalevad nii õhuhapniku molekulid, mis on eelnevalt hapniku aatomiteks lõhutud, läbi membraani läinud vesinikioonid kui ka välist vooluringi pidi saabunud elektronid. Kuna vee molekulide keemiline energia on väiksem kui vesiniku ja hapniku molekulide energiad kokku, jääb energiat üle ning see suudab elektriga varustada mistahes elektriseadet, mis elektroodide vahelisse välisesse vooluringi ühendada.
Siin tuleb ilmsiks ka sarnasus elektriakuga. Nad mõlemad muundavad keemilist energiat elektrienergiaks, kuid kütuseelemendis ei hoita keemilise energia varusid mitte jõuallika sees, vaid juhitakse sinna eraldi vesinikumahutist. Ka kasutatakse kütuseelementides katalüsaatorit, sest reaktsiooni toimumise kiirus süsielektroodidel oleks muidu piisava koguse elektri tootmiseks liiga aeglane. On kulutatud palju aega ja vaeva, et töötada välja katalüsaatoreid, mis kataks elektroodid, tõstaksid oksüdatsiooni ja reduktsiooni kiirust ning võimendaksid sellega välisesse vooluringi jõudvat elektrivoolu.
Kasutegurite kõrvutamine
Kütuseelementide kasutegur on äärmiselt kõrge – tavaliselt muundavad nad vesinikus ja hapnikus talletunud keemilisest energiast elektrienergiaks 50–70%. Elektrimootor ei suuda aga kogu seda elektrienergiat mehaaniliseks energiaks muundada. Selle protsessi käigus läheb raisku umbes 10% kütuseelementidelt saadud energiast. Autode puhul kulutavad lisaenergiat ka õhutakistus ja rehvide hõõrdumine. Kütuseelemente kasutava auto üldine kasutegur on seega umbkaudu 35–40% (paagist rattani), mis on märkimisväärselt kõrgem kui keskmise sisepõlemismootori 15% kasutegur (silmas tuleb pidada siin ka seda, et viimase tehnoloogia täiustamiseks on olnud märksa rohkem aega).
Kütuseelemendid ei ole sisepõlemismootoritest paremad aga mitte üksnes praktilisest vaatenurgast, vaid on võimelised saavutama ka märksa kõrgemaid teoreetilisi kasutegureid. Sisepõlemismootori (aga ka aurumootori) kõrgeima võimaliku kasuteguri määrab kindlaks termodünaamika teine seadus, mille kohaselt saab suletud süsteemi entroopia kas kasvada või samaks jääda, kuid mitte kunagi väheneda. Sisepõlemismootorid muundavad kütuses leiduva keemilise energia soojuseks, mis on oma olemuselt „entroopne“ energia. Seejärel muundatakse soojus mehaaniliseks tööks, mis on märksa „vaoshoitum“ energialiik ning entroopia mootoris kahaneb. Kuna teine seadus ei luba entroopial aga väheneda, soojendab ülejäänud energia ümbritsevat keskkonda, suurendades selle entroopiat. Töö käigus läheb sisepõlemismootori põlemiskamber aga nii kuumaks, et seda on vaja jahutada ning nii läheb raisku veel hulganisti väärtuslikku soojusenergiat. Lisaks sellele kaob soojusenergiat ka kuumade heitgaaside näol.
Kütuselemendi puhul, kus keemiline energia muundatakse elektrienergiaks aeglaselt ja rahulikult, on teoreetiline kasutegur aga 100%. Põhjuseks on see, et kütuseelemendid pole soojusmootorid ning aeglaste elektrokeemiliste ja oksüdatsiooniprotsesside käigus eraldub vähe soojust. Madalal töövõimsusel võivad praegused kütteelemendid jõuda 100% väga lähedale, kuid väljundvõimsuse tõstmisel suureneb ka eralduva soojuse hulk ning kasutegur langeb drastiliselt.
Kütuseelemendi ja sisepõlemismootoriga sõidukite kasutegurite ausaks võrdlemiseks tuleb võtta arvesse ka vastavate kütuste – bensiini, diislikütuse, vesiniku – tootmisega seotud kasutegurid. See ei ole aga niisama lihtne, sest vesinikku saab toota väga mitmel eri viisil ning kõigil neil on erinevad kasutegurid ja kõrvalsaadused.
Taustsüsteemid
Kütuseelemendid vajavad küll veel täiustamist, kuid sellele vaatamata tundub olevat tegu äärmiselt hea ja kõrge kasuteguriga energiaallikaga – on ju selle ainsaks kõrvalsaaduseks vaid vesi ning ka elemendi kütusena kasutatavat vesinikku leidub Maal küllaga. Kütuseelementidel on aga ka omad puudused. Näiteks tuleb gaasilises olekus vesinik kõigepealt toota, konteinerisse kokku suruda ja ladustada ning kuigi kõik need etapid on üsna kõrge kasuteguriga, eraldub nende protsesside käigus ka omajagu kasvuhoonegaase. Probleemiks on ka see, et kuigi vesinikku on Maal palju – oma rohkuse poolest on ta elementidest kolmandal kohal – moodustab kütuseelementide tööks vajalik gaasiline vesinik õhust vaid ühe miljondiku.
Õnneks on vesiniku tööstuslik tootmine üsna levinud. Naftatöötlemistehastes tarvitatakse seda naftast väävli eemaldamiseks ning süsivesinike lõhkumiseks. Lisaks sellele kasutatakse vesinikku ka ammoniaagi ja muude kemikaalide tootmisel. Vesiniku tootmismaht on sedavõrd suur, et selle valmistamine moodustab 2% kogu maailma energiatarbimisest – kui seda kasutataks vaid autokütusena, moodustaks see tervelt 1/5 vajaminevast kütusekogusest.
Enamasti toodetakse vesinikku naftast ja maagaasist. Kuigi õhusaaste seisukohast võttes pole need just parimad lahendused, toetub lähituleviku vesinikumajandus arvatavasti siiski just nendele toorainetele. See tooks kaasa vesiniku laialdasema kasutamise ning võimaldaks minna tasapisi üle ka „puhtama ja rohelisema“ vesiniku tootmisele. Vesiniku tootmisel tekib kõrvalsaadusena küll ka süsihappegaas, kuid hea uudis asja juures on, et selle emissiooni saab palju kergemini kontrolli alla hoida kui sisepõlemismootori tekitatavaid kasvuhoonegaase.
Vesiniku tootmiseks on aga ka alternatiivseid meetodeid. Üks neist on näiteks biomassi soojendamine hapniku ja veeauru keskkonnas. Kuigi ka see protsess tekitab kasvuhoonegaase, tarbisid toorainena kasutatavad taimed oma elu jooksul fotosünteesi käigus rohkesti süsihappegaasi. Tähelepanu tasub pöörata ka sellele, et kasutatavad taimed eraldaksid kasvuhoonegaase ka siis, kui nad loodusesse mädanema ja lagunema jätta. Teise keskkonnasäästliku lähenemise puhul kasutatakse päikese-, tuule- ja tuumaenergiat, mille jõul käivitatakse elektrolüüs ning lõhutakse vee molekule. See tehnoloogia on aga alles lapsekingades ning tootmiskulud hetkel veel äärmiselt kõrged.
Kütuseelemendi kahjuks räägib ka asjaolu, et kuna gaasilises olekus vesinik on lenduv ning äärmiselt tuleohtlik, on sellega keeruline ümber käia. Olukorra teeb veelgi ohtlikumaks see, et vesiniku põlemisel tekkiv leek on peaaegu nähtamatu ning gaasi põlemiseks vajalik kontsentratisoonivahemik õhus väga lai. Neile probleemidele vaatamata transpordivad ja ladustavad vesinikku mitmed tööstusettevõtted ning seda ilma õnnetusjuhtumiteta – samu ettevaatusabinõusid saaks kasutada ka kütuseelementide vesinikupaakidega tegelemise puhul. Mis puudutab aga kütuseelementi ennast, siis on seal sees oleva gaasi hulk niivõrd väike, et seda ei peeta eriti ohtlikuks.
Suureks puuduseks on ka see, et vesiniku transportimine on keeruline ja kallis. Enne ühest kohast teise sõidutamist viiakse vesinik tavaliselt kas 700-atmosfäärilise rõhu alla, või veeldatakse, külmutades seda 20 K-ni (-253°C). Mõlemad meetodid kulutavad palju energiat ning nõuavad lisaks ka mahuteid, mis suudaks taluda kas äärmuslikult kõrget rõhku või säilitada väga madalat temperatuuri – see on ka üks põhjuseid, miks vesinik on kallim kui bensiin või diislikütus. Seetõttu on mõistlik toota gaasilist vesinikku seal, kus seda parasjagu vajatakse ning valida selleks just selline tehnoloogia, mis sobib kõige paremini kohalike oludega. Näiteks võiks isoleeritud või päikeseküllastes piirkondades toota vesinikku vee molekulide lõhkumise teel ning kasutada selleks päikeseenergiat.
Üleminekuperiood
Et sõidukiomanikud oma vanad autod kütuseelemendil töötavate vastu ümber vahetaks, tuleks tõsta oluliselt ka nende kasutegurit ja eluiga. Elemendis kasutatavas membraanis on nanoskoopilised veekanalid, mida vesiniku ioonid oma teekonnal läbivad, kuid kuna ioonid haaravad endaga vahel kaasa ka mõned vee molekulid, võivad kanalid pikapeale „kuivale jääda“ ning kütuseelemendi kasutegur langeb. Selle parandamiseks võib muuta kas elektroodidevahelist rõhku, mis surub vee membraani tagasi, või lisada kütusele veeauru, mis imendub membraani ning ei lase veekanalitel ära kuivada. Ka katalüsaatorit annaks tublisti täiustada. Neid tehakse enamasti 3–5 nm suurustest plaatina osakestest – väga haruldasest ja kallist metallist. Kui õnnestuks tõsta katalüsaatorite kasutegurit, vähendaks see vajamineva plaatina hulka ning seega ka tootmiskulusid.
Põhiline takistus kütuseelementide leviku teel on aga majanduslik, mitte tehniline. Vesinik on fossiilkütustest kallim ning kütuseelementide tegemine sisepõlemismootorite valmistamisest umbes 5 korda kulukam. Praegu ongi peamiseks väljakutseks just kuluvahe vähendamine, kuid see nõuaks kütuseelementidel töötavate autode masstootmist ning hetkel ei tundu see just eriti realistliku võimalusena. Et avalikkuse huvi vesinikul sõitvate autode vastu suureneks, oleks vaja rohkem vastavaid tanklaid, kuid ükski ettevõte pole nõus investeerima infrastruktuuri enne, kui ollakse täiesti kindlad, et see tulevikus neile ka kasumit tootma hakkab.
Kuna kütuseelemendiga sõidukid ei saa oma tanklatest eriti kaugele sõita, kasutatakse neid täna peamiselt kohaliku transpordivahendina. Maailmas on hetkel vaid umbes sada vesinikutanklat, millest enamik asub suurlinnades, tööstuspiirkondades ning katsekeskustes. Oma väiksele arvule vaatamata on sellised tanklad siiski väärtuslikud, sest just seal saab olemasolevaid tehnoloogiaid kõige paremini proovile panna ning see viib meid vesinikupõhisele majandusele jällegi sammukese lähemale.
Kui naftahinnad lähiaastatel uuesti lakke tõuseksid, suurendaks see märgatavalt elektriautode läbimüüki. Kuna nõudlus vesiniku järele kasvaks, siis tootmiskulud väheneksid ning uue põlvkonna autode ülalpidamine muutuks taskukohasemaks. Kui vesiniku hind energiaühiku kohta oleks kaks korda bensiini ja diislikütuse omast kõrgem – mis on lähiajal täiesti reaalne – kompenseeriks kütuseelemendi suurem kasutegur vesiniku hinna. See annaks meile kõigile võimaluse nautida autosõitu ilma, et peaksime emiteeritavate kasvuhoonegaaside pärast süümepiinu tundma. Loodetavasti täitub see unistus juba lähiaastatel.
| Kütuseelemendid pisielektroonikale? |
|
Viimase kümne aasta jooksul on mobiiltelefonide, sülearvutite ja teiste kaasaskantavate elektrooniliste seadmete läbimüük hüppeliselt kasvanud. Kuna nõudmised toiteallikatele on järsult kasvanud, on nähtud palju vaeva ka laaditavate liitium- ja nikkelakude täiustamisega. See tehnoloogia peab aga kurja vaeva nägema, et uue põlvkonna seadmetega sammu pidada, sest need nõuavad üha kergemaid, võimsamaid ja suurema mahutavusega energiaallikaid – ikka selleks, et mobiiltelefoni ei peaks nii tihti laadima, kuigi see võtab rohkem voolu kui vanemad mudelid. Kuigi on võimalik, et kütuseelemendid ühel heal päeval akud välja vahetavad, on vesinikkütuste kasutamine mikroelektroonika puhul tõeline väljakutse. Rõhu all oleva gaasilise vesinikuga ümberkäimine on keeruline ja kallis ning selliste seadmete puhul tuleb vesinikumahuti väljatöötamisel arvesse võtta ka seda, et kütuseelement peab olema kerge. Lisaks on rõhu alla oleva vesiniku ohutu kasutamine kaasaskantavates seadmetes kordi keerulisem kui sõidukites, kus on vesiniku kasutamisega kaasnevate riskide maandamiseks mõeldud kontrollsüsteemide paigaldamiseks palju rohkem ruumi. Viimase probleemi on mitmed kaasaskantavate kütuseelementide tootjad lahendanud – kuigi see vähendab kasutegurit, kasutavad nad vesiniku asemel vedelat alkoholi (peamiselt metanooli, aga ka etüleenglükooli). Kahte sellist tehnikaimet on näha ka juuresolevatel piltidel. Ülemine neist on ühe selle artikli autori (Emanuel Peledi) loodud kütuseelement, kust jagub väikesele sülearvutile voolu kuueks tunniks. Alumisel pildil oleva vidina töötasid välja Fujitsu teadlased. See mahutab 18cm3 metanooli, millest piisab kolme liitiumaku laadimiseks. Sedalaadi kaasaskantavates seadmetes kasutatavatesse energiaallikatesse on investeerinud ka teised ettevõtted, nagu Toshiba, Motorola, Samsung ja NEC. Seda silmas pidades, võivad meie sülearvutid ja mobiiltelefonid juba õige pea alkoküttele üle minna. |
Franco Bagnoli, Firenze ülikool, Itaalia
Talviti puistame tänavatele soola, et jää ära sulaks. Teadusteatris võib seda sulamist näidates olla üsna kindel, et küsimusele, kas temperatuur seejuures tõusis või langes, vastatakse, et tõusis. Aga ei! Temperatuur langeb isegi nii palju, et sellega võib etenduse lõpetuseks jäätist valmistada [1].
Selle nähtusega võib ka endale viga teha [2] (kui keegi ei usu, paluge neil jääkuubikut koos soolaga peos hoida). Selge see, et vaatajate tähelepanu saab lihtsalt köita, valmistades mõne minutiga jäätist, ainult tavalist köögikraami kasutades (st ilma vedela lämmastikuta). Ometi ei ole nähtust kuigi kerge seletada, sest siin ei saa kaalutlustes toetuda ainuüksi energiale.
Tõepoolest, veemolekulid ja keedusoola ioonid (naatrium- ja kloriidioonid) eelistavad energeetilisest vaatepunktist lähtudes püsida eraldi ja seda nad teevadki, kui temperatuur on alla -21°C1.
Jooniselt 1 on näha, et kloriid- ja naatriumioonid (laenguga), sobituvad hästi polaarsete veemolekulide vahele, aga löövad seejuures segi nii jää kui ka soola korrastatud struktuuri. Nagu sulamisel, nii ka siin on segu stabiilne kõrgel temperatuuril ja eraldi kristallid on stabiilsed madalal temperatuuril, alla -21°C.
Niisiis, miks temperatuur langeb, kui sool seguneb jääga? Tagasi eelmise väite juurde. Kaootilised struktuurid on stabiilsed kõrgetel temperatuuridel, korrastatud struktuurid madalatel temperatuuridel. Teine variant on selgelt energeetiliselt eelistatud, aga esimene? Siin peame juurde tooma entroopia kontseptsiooni. Entroopia (S) on võimalike paigutuste arv (logaritm sellest arvust).
Vaadates ühemõõtmelist molekulide paigutuse mudelit (joonis 2) võib märgata, et võimalike paigutuste arv, mis annavad korrastatud ja kaootlise struktuuri, on erinev. Kahte tüüpi paigutuse suure energeetilise erinevuse korral on eelistatud struktuuriks korrastatus koos juhuslike ja kohalike fluktuatsioonidega (temperatuuril üle absoluutse nulli ja klassikalise füüsika raames). Kui aga energiate vahe ei ole väga suur, juhtub fluktuatsioone palju sagedamini. Kui korrastatus on rikutud, on selle taastamine keeruline, sest kaootlisi seisundeid on nii palju ja nad pole energeetiliselt kättesaamatud. Samas on aga ainult üks korrastatud seisund.
Võtame nüüd appi vabaenergia kontseptsiooni G=U-TS, kus U on energia ja T on temperatuur. Süsteemi stabiilsus on määratud G miinimumiga. Valemist on näha, et temperatuur annab võidu energiale kui ta on madal, aga entroopiale (millel on miinusmärk) kui on kõrge.
Kui soola lisada jääle temperatuuril üle -21°C, püüavad molekulid saavutada stabiilset paigutust segunemisega. See aga vajab energiat jää vesiniksidemete lõhkumiseks ja soola lahustamiseks. Jää sulamissoojus on 6,01 kJ/mol ja naatriumkloriidi lahustamiseks kulub 3,87 kJ/mol.
Ja nüüd küsimus neile, kes kasutavad Rahvusvahelist Mõõtühikute Süsteemi (SI). Miks on Fahrenheiti skaala nii veider ja miks selle nullpunkt on (umbes) -18°C?
Viited:
[1] Steve Spangler, The Spangler Effect – Homemade Ice Cream,
https: //www.youtube.com/watch?v=Y5XzhcDq5Bw.
[2] Salt and ice challenge,
http://en.wikipedia.org/wiki/Salt_and_ice_challenge.
[3] Fahrenheiti skaala, https://et.wikipedia.org/wiki/Fahrenheiti_skaala
1 Seepärast on kasutu soola jäätunud tänavatele puistata, kui temperatuur on madalam.
2 Daniel Gabriel Fahrenheiti (1686–1736) eluajal oli jäävee ja soola segu madalaim temperatuur, mida sai kerge vaevaga, ilma laboriseadmeid kasutmata saavutada. Selleks kasutati võrdseid jää ja keedusoola koguseid ning segu temperatuur määras Fahrenheiti skaala nullpunkti. 100 kraadi vastas (umbes) kehatemperatuurile [3]. Sellise skaala eeliseks on, et negatiivseid temperatuure ei lähe igapäevaelus kunagi tarvis ja et tänapäevasel, täpsustatud skaalal on vee keemise ning külmumise punktide vahe 180 kraadi, mis vähendab komakohtade kasutamist temperatuuri mõõtmisel.
Vana tava võimaldab päevadel, kui koolimaja ruumid on hõivatud eksamite, võistluste vms tegevusega, korraldada koolitööd õuesõppe või õppekäikudena. Uuema aja võimalusena korraldatakse neil päevadel töö hoopis internetis nn e-õppepäevadena. Mõte on hea, sest annab õpilastele võimaluse kogeda neid igapäevaelu tahke, mis tundideks jagatud koolipäevade pikas jadas hästi välja ei tule. Tavaliselt e-päevadel tunniplaani ei järgita ja keskendutakse pigem ühele-kahele pikemale teemale. Tehakse rühmatöid, rõhutatakse lõiminguid. Mõned näiteid:
-
Keeleõpetus lõimub füüsikaga. Loeme saksa, vene, aga kndlasti ka baltisaksa teadlaste töid (kui keeleoskus ei luba, siis elulugusid) saksa või vene keeles (palun mitte inglise keeles) ja koostame neist magnetismi tundide jaoks lühikesed ettekanded.
-
Töötame läbi e-õpiku peatüki „Ringliikumise dünaamika” ja lahendame mõned pesumasina ja vasaraheite kohta käivad ülesanded, mille lahenduskäike järgmisel päeval klassis kaitseme. Kui laheduse juures on nõutud kirjalik seletus, mis peab klassikaaslastele arusaadav olema, siis on tegu emakeele ja füüsika lõiminguga.
-
Matemaatika tund nõuab funktsioonde esitamist graafikuna. Koostame lisaks mõned lihtsad ülesanded, mis küsivad füüsikalistesse nähtustesse peidetud funktsioone.
Mõistlik on mõelda ka nende õpilaste peale, kellel parasjagu ei ole võimalust töötada internetis või kelle kodused arvutid ja nutisedmed otsustaval hetkel tõrguvad. Kogemus ütleb, et neid on väga vähe, enamasti pole ühtegi.
HTG-s võtsid õpilased viimatisel e-õppe päeval ette töölehe funktsioonidest, st uurisid füüsika ja matemaatika kokkupuutepunkte.
Funktsioonid füüsikas
- Ühtlaselt kiireneval (sh ka aeglustuval) liikumisel on läbitud tee pikkus (s) aja (t) funktsioon. Vaata valemit.
Joonista selle funktsiooni graafik ajavahemikule 0 kuni 12 sekundit. Algkiirus v0= 10m/s; kiirendus
a= -2m/s2. Mis funktsioon see on?
- Magnetvälja võivad elektronid lennata väljajoonte suhtes erinevate nurkade all. Vaata valemit.
Elektroni sirgelt teelt kõrvele kallutav Lorentzi jõud (FL) on välja sisenemise nurga (α) funktsioon, joonista selle gaafik nurkadele 0° kuni 90°.
Elektroni laeng e=1,6·10-19C; elektronide liikumiskiirus v=2000m/s; välja magnetinduktsioon B=0,5T.
- Üks hästituntud looduslik protsess. Leia selle graafik e-õpikust. Mis funktsioon see on?
Kasuta õpikuid. Otsing töötab, sisukord on olemas.
Graafikuid võib teha tabelarvutusega (xy-graafik, scatter) või mõne sobiva matemaatikavahendiga. Huvi või vajaduse korral võib graafiku ka paberile joonistada, pildistada või skännida. Viimases hädas võib isegi paberi järgmisel päeval kooli kaasa võtta.
Kopeeri graafikud tekstifaili. Jälgi piltide tekstifaili lisamise head tava ja uurimistööde vormistamise juhendit.
Lubatud failiformaadid - .doc, .docx, .odt, .pdf.
--------------------------
Näidisülesanne. Kuidas ideaalse gaasi rõhu sõltuvust temperatuurist tabelarvutuse abil graafiliselt kujutada?
Kuidas sõltub 1 mooli ideaalse gaasi rõhk 10 liitrise ruumalaga balloonis temperatuurist? Mis funktsioon seda kirjeldab?
John Baez on matemaatika professor Kalifornia Ülikoolis, kes on saanud tuntuks oma töödega kvantgravitatsiooni alal. Laiemale avalikkusele on tuntud paljude populaarteaduslike kirjutiste autorina. Alljärgnev on test pärineb tema kodulehelt.
- Algseis: -5 punkti
- 1 punkt iga väite eest, mis suurema osa teadlaste arvates paika ei pea.
- 2 punkti iga väite eest, mis on täiesti sisutu.
- 3 punkti iga väite eest, mis on ebaloogiline.
- 5 punkti iga sellise väite eest, millele jäädakse kindlaks isegi siis, kui seda ise tublisti korrigeeritakse.
- 5 punkti mõttelise eksperimendi kasutamise eest, mille tulemused on vastuolus mõne laialdast tunnustust saavutanud päris eksperimendi omadega.
- 5 punkti iga sõna eest, mis on kirjutatud ainult suurtähtedega (välja arvatud siis, kui suurtähtede põhjustajaks on vigane klaviatuur).
- 5 punkti iga korra eest kui mainitakse "Einstieni", "Hawkinsit" või "Feynmanni".
- 10 punkti iga korra eest kui väidetakse (ilma piisava tõendusmaterjalita), et kvantmehhaanika on juba oma olemuselt eksitav.
- 10 punkti kui mainitakse, et omatakse kooliharidust (justkui tõestaks see terve mõistuse olemasolu).
- 10 punkti selle eest, kui teooria tutvustamist alustatakse sellest kui kaua antud teooria kallal vaeva nähti. (10 lisapunkti saab kui rõhutatakse, et töötati üksi.)
- 10 punkti selle eest, kui teooria saadetakse kellelegi, keda isiklikult ei tunta ning palutakse tal sellest mitte kellelegi teisele rääkida selgitades oma kartust, et keegi võiks sealt ideid varastada.
- 10 punkti kui lubatakse anda rahaline preemia igaühele, kes suudab teooriat tõestada või selles vigu leiab.
- 10 punkti iga uue termini leiutamise ja kasutamise eest, mida kuskil korrektselt ei defineerita.
- 10 punkti iga väite eest stiilis "Ma ei ole matemaatikas eriti hea, aga mu teooria on põhimõtteliselt õige, nii et ma vajan veel ainult kedagi, kes oskaks seda valemite abil väljendada".
- 10 punkti selle eest, kui väidetakse, et mõni hetkel laialdaselt tunnustatud teooria on „ainult teooria“ (nagu see väide peaks teooriat kõigutama).
- 10 punkti selle eest, kui väidetakse, et mõni hetkel laialdaselt tunnustatud teooria prognoosib küll nähtusi õigesti, kuid ei seleta „miks“ need esinevad või ei suuda välja pakkuda vastavat „mehhanismi“.
- 10 punkti iga korra eest, kui võrreldakse ennast Einsteiniga või väidetakse (ilma piisava tõendusmaterjalita), et eri- ja üldrelatiivsusteooria on juba oma olemuselt eksitavad.
- 10 punkti selle eest, kui „teadlane“ väidab, et tema töö on „paradigma muutuse“ esirinnas.
- 20 punkti mulle meilimise ja halva teadlase näitaja kallal vingumise eest. (Näiteks öeldes, et see „rõhub originaalselt mõtlejaid“ või väites, et ma kirjutasin „Einstein“ 8. punktis valesti.)
- 20 punkti selle eest, kui „teadlane“ vihjab, et talle tuleks oma töö eest Nobeli preemia anda.
- 20 punkti iga korra eest, kui võrreldakse ennast Newtoniga või väidetakse (ilma piisava tõendusmaterjalita), et klassikaline mehhaanika on juba oma olemuselt eksitav.
- 20 punkti iga korra eest, kui ulmekirjanduslikke teoseid või müüte käsitletakse faktidena.
- 20 punkti selle eest, kui üritatakse kaitsta oma teooriat tuues (väljamõeldud või tegelikke) näiteid sellest, kuidas teised „teadlase“ eelmiseid teooriaid on naeruvääristanud.
- 20 punkti selle eest, kui „teadlane“ mõnele teooriale või valemile oma nime annab. (Näiteks kui ta räägib „Evansi väljavalemist“ ning ta nimi juhtub täiesti juhuslikult Evans olema.)
- 20 punkti selle eest, kui kiidetakse oma teooriat taevani, kuid ei seletata kordagi, milles see tegelikult seisneb.
- 20 punkti iga korra eest, kui kasutatakse väljendit „kitsarinnaline reaktsionäär“.
- 20 punkti iga korra eest, kui kasutatakse väljendit „isehakanud vanade tavade kaitsja“.
- 30 punkti selle eest, kui väidetakse, et mõni kuulsus on salaja kahelnud teoorias, mida „teadlane“ ise avalikult toetanud on. (Näiteks: nagu võib välja lugeda tema ülikooli esimese aasta füüsikaraamatutest, kahtles Feymani tugevalt erirelatiivsusteooria õigsuses.)
- 30 punkti selle eest, kui avaldatakse arvamust nagu oleks Einstein oma viimastel eluaastatel jõudnud ideedele, mida „teadlane“ nüüd propageerib, väga lähedale.
- 30 punkti selle eest, kui „teadlane“ väidab (ilma piisava tõendusmaterjalita), et tema teooriad arendas välja mõni Maa-väline tsivilisatsioon.
- 30 punkti väite eest, et töö valmimine venis pikale kuna „teadlane“ viibis hullumajas või kuna psühhiaater üritas panna teda oma teooriast loobuma.
- 40 punkti selle eest, kui „teadlane“ võrdleb neid, kes tema ideedega vaielda julgevad, natside, rünnakrühmlaste või pruunsärklastega.
- 40 punkti väite eest, et „valitsevad teadusringkonnad“ sepitsevad „teadlase“ vastu „vandenõud“, et tema teooriad kunagi õiglast tunnustust ei saavutaks vms.
- 40 punkti iga korra eest, kui võrreldakse ennast Galileoga väites, et nüüdisaegne inkvisitsioon on su juhtumi tõsiselt käsile võtnud jne.
- 40 punkti väite eest, et kui „teadlase“ teooriat ükskord lõpuks hinnata osatakse, hakatakse tänapäeva teadussesse suhtuma kui häbiplekki teaduse ajaloos. (30 lisapunkti kui „teadlane“ maalib kujutluspilte näitlikest kohtuprotsessidest, kus teadlased, kes autori tööd seni pilganud on, peavad kõik oma sõnad tagasi võtma.)
- 50 punkti selle eest, kui „teadlane“ väidab, et tema teooria on pöördelise tähtsusega, kuid ei prognoosi midagi, mida oleks võimalik katseliselt kontrollida.
2003. aastal tuli välja ameerika-briti kirjaniku Bill Brysoni aimekirjanduse bestseller „A Short History of Nearly Everything”, eesti keeles 2007 „Kõiksuse lühiajalugu” Henn Käämbre tõlkes. Raamat on tõepoolest huvitav. Käsitlemist leidavad pea kõik teaduse lood, kosmoloogiast, osakestefüüsikast, geoloogiast, paleontoloogiast, geneetikast... Autori kirjutamisstiil on isikupärane ja teaduslikus mõttes mitte alati väga korrektne, millele tõlkija ja konsultandid juhivad tähelepanu järelsõnas ning joonealustes märkustes. Eessõnas räägib Bryson mõtlemapaneva loo lapsepõlvekogemusest õpikuga. Kui hästi me suudame aimata, mis on õppijakeskne haridus sealtpoolt vaadates?
"Minu enda lähtekohaks, uskuge või mitte, oli ühe mu enda neljanda või viienda klassi õpiku illustratsioon. See oli tavaline 1950ndate aastate õpik: nätsutatud, näotu, eemaletõukavalt kõhukas, kuid üsna selle alguses oli illustratsioon, mis mind paelus. Skeemil oli lõikepilt Maast, nii nagu ta paistaks, kui keegi võtaks hiigelnoa ja eemaldaks hiidkerast neljandiku.
Raske uskuda, et ma polnud säärast illustratsiooni varem näinud. Aga vist mitte, sest mäletan selgesti, kuivõrd lummatud ma olin. Ausalt öeldes , esialgse lumma tekitas mu peas sündinud kujutlus kusagil Ameerika lauskmaadel kihutavatest pahaaimamatuist autosõitjaist, kes tormavad järsku alla 4000 miili kõrgusest järsakust, mis laiub Põjanaba ja Kesk-Ameerika vahel. Järk-järgult hakkas mu tähelepanu paeluma joonise teaduslik süvasisu, kujutlus, et Maa koosneb üksikutest kihtidest, tema keskmes on aga Päikesena hõõgvel rauast ja niklist koosnev kera. Meenub seegi, et ise täis imetlust, mõistatasin: „Kuidas nad seda ometi teavad?”
Ma ei kahelnud hetkekski, et skeem on õige. Siiamaani kaldun usaldama teadlaste arvamusi nõndasama kui ma usaldan kirurge, torulukkseppi ning kõiki teisi salatarkuste valdajaid. Ometi pole ma kunagi taibanud, kuidas inimmõistus suudab kirjeldada nende asjade väljanägemist, mis asuvad meie all tuhandete miilide sügavuses, hoomata seda, mida inimsilm pole eales näinud ja milleni ei küüni mingi röntgen. Minu jaoks oli see selge ime. Ja selliseks on minu suhtumine teadusesse jäänudki.
Põnevil võtsin tol äratundmise õhul raamatu endaga kaasa avasin enne õhtusööki alustasin esimesest leheküljest. Seepeale kompas ema mu laupa ja küsis, ega ma järsku haige ei ole.
Ja mis tuli välja? Tuli välja, et raamat polnud üldsegi põnev ega õpetlik. Eelkõige ei vastanud see ainsalegi küsimusele, mida too joonis uudishimulikus peas äratas. Kuidas saab Päike olla meie planeedi tuumikuks? Ja kui see on tõesti nii, miks siis pole maapind meie jalge all tuline? Ning miks ei sula Maa sisemuses üles kõik ülejäänu? Või sulabki? Ja kui meie planeedi tuumik on nii tuline, peaks see ometi kõrvetama maakoorde päratu augu, millest üksjagu Maad sisse vajub. Ja kuidas seda ometi teada saadakse?
Kuid kummalisel kombel ei pööranud autor säärastele pisiasjadele üldse tähelepanu. Ta vaikis kõigest peale antiklinaalide, sünklinaalide, asksiaalhälvete ja muu taolise. Näis, et ta tahtis põnevat ainet salastada, tehes selle hallilt hoomamatuks. Aastate kestel hakkasin arvama, et see pole üksnes minu isiklik mulje. Õpikute autorid näisid olevat sõlminud isekeskis üldise salanõu rangelt hoiduda käsitlustest, mis võisid äratada kahvatutki huvi, põnevusest rääkimata."
Bill Bryson
A Short History of Nearly Everything
Pakume kõigile meile vastamiseks kolme küsimust:
- Kuidas õppisid koolis füüsikat?
- Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
- Kas koolifüüsikas on midagi, mille peab pähe õppima?
Allpool on vastused, mis juba meieni jõudnud.
Kuidas õppisid koolis füüsikat?
Sellest on muidugi terve igavik möödas ja ei mäleta, et ma oleks koolis füüsikat nii väga õppinud. Mul oli kooliajal kolm füüsika õpetajat, kes õpetasid kindlasti tublilt ja hoolsalt, aga eriti palju mälestusi mul füüsikaklassist pole. Olid tavalised koolitunnid ja üldse on selles eas inimesel iseendaga palju rohkem muret kui miski teadusega. Keskkooli füüsikaõpetaja suutis küll kuidagi salmisi ära näidata, et füüsikas (kenas naksakas valemis, lahedas eksperimendis, omamoodi lahendatud ülesandes) on tubli annus elegantsi, millesse võib armuda. Päriselt tõmbas mind loodus (tõmbab praegugi) ja vaimustas keemia. Meil pidid olema vene keelest tõlgitud füüsika õpikud. Olen neid nüüd huvi pärast vaadanud, aga ei tule tuttavad ette. Samas on meeles näiteks Landau ja Kitaigorodski „Füüsika kõigile” ja Asimovi „Vaade kõrgelt”. Head raamatud, tasus lugeda.
Tõeliselt kahju on astronoomiast. Astronoomia oli keskkoolis eraldi õppeaine, lõpuklassis üks tund nädalas. See lendas nii mööda, et mul pole vähimatki mälestust jäänud. Kuigi oli ju teada-tuntud kosmosevaimustuse aeg. Läks mitu aastakümmet, kui jäin täiesti juhuslikult loojuvat Kuud vaatama ja taipasin, et ma ei tea sellest mitte midagi.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Üks lugu on küll meenutada. Esimesel õpetaja-aastal oli üks kaheksanda klassi poiss, kellel oli nii palju isiklikke, sotsiaalseid ja perekondlikke probleeme, et ta koolitööga kohe sugugi hakkama ei saanud. Igaveseks saladuseks jäänud põhjustel ilmus see poiss teise veerandi lõpus järeltööd tegema. Olukord oli täiesti lootusetu, sest ta oli üldse väga vähe kohal käinud ja polnud algusest peale vähimatki huvi ilmutanud. Ei mul ega temal polnud aimugi, mida ta saaks järgi teha. Aga ta paistis rahumeelne ja võib-olla isegi motiveeritud. Ja siis me lahendasime temaga koos füüsika ülesannet ja ma näitasin, kuidas seda tehakse. Valemeid, tähistusi ja ühikuid. Ühel hetkel taipas ta, et kui on näiteks teada valem v=s/t, siis võib sellest järeldada, et s=vt ja saab arvutada ka mingit teist asja. Avastus oli nii vapustav, et tal jäi suu lahti ja silma läksid suureks kui supitaldrikud. Ta võttis oma suure üllatuse kokku, öeldes sedasi vaikselt omaette: „Assakurat!”
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Vaevalt, et midagi peab lausa pähe õppima, aga mõni valem või konstant võiks pikas koolitundide jadas meelde jääda küll. Ma olen seda meelt, et kõik võiksid õppida lugema ja veidi arvutama. Hea oleks osata mõnd võõrkeelt, teada midagi ühiskonna ja looduse toimimisest. Kõik muu, nagu tänapäeval öeldakse – sõltub. Matemaatika ja füüsika seoste, ühikute ja suuruste süsteemi, keemiliste elementide sümbolite, ainete valemite ning nimetuste jms teadmine ja tundmine teeb muidugi loodusteaduse ja inseneriala inimeste elu väga palju lihtsamaks nii koolis kui ka tööl. Praktiliselt on see möödapääsmatu. Kes kalduvad rohkem teiste elualade poole, neil omad teemad, mida nad unepealt teavad.
Kunagi ma ütlesin mõtlematult lõbusas seltskondlikus vestluses, et haritud inimene teab peast vee tihedust. Tekkis piinlik vaikus. Olen seda hiljem hästi paljude käest küsinud. Ma üles ei kirjutanud ja seega statistikat ei ole. Tunde järgi ütlen, et neid, kes ilma vihjeteta kohe peast vee tiheduse koos ühikuga ära ütlevad on alla poole. Kaheksandikke, kellele ma olen tiheduse teemat õpetanud, on kindlasti üle viiesaja. Võiks ju loota, et neile õnnestus see oluline teadmine külge harjutada, aga parem ma ei taha teada.
Kuidas õppisid koolis füüsikat?
Põhikoolis õpetas meil füüsikat Enn Sakk. Kord oli majas, tehti katseid ja praktikume. Oli selline isikupärane ja võimas kuju. Keskkoolis tuli asendusõpetaja, kes klassiga hakkama ei saanud, seega seal ka ei õpitud midagi.
Õnneks või kahjuks veetsin ma ise suurema osa keskkoolist spordilaagrites.
Mõte füüsikat õppima minna tuli tõepoolest ei-tea-kust. Aga kui ta juba tuli, siis veetsin omajagu tunde füüsika käsiraamatu seltsis ... kuidagi sain eksamid tehtud ... nii ta läks.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Minu füüsikast rääkimise kogemus on käinud koos Teadusbussiga, selle nimel etendusi andes ... või kuidas iganes neid 45 minutit kestvaid etteasteid siis ka nimetada. Ja kõige toredam mis siis juhtuda saab on äratundmine, et publik hingab kaasa, et kaasa mõtlevad ka need, kes alguses olid omaette või üleolevad.
Koolis ma ühtki tundi andnud ei ole. Aga arvatavasti ei jää õpetaja amet mul järele proovimata. Kui see aeg kord kätte jõuab, siis ma vähemasti tean, mille poole püüelda.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Mina olen sellest parteist, kes fännab teadmist ja mäletamist. Sest ma teisest otsast juba olen üks nendest, kelle püsimälu on internetti kolinud. Nii saab elada küll, aga see ei ole päris see.
Need kes peavad asju pähe õppima (tuupima) jätku see parem tegemata ja kasutagu e-õpikut. Aga ma kõigile soovitan treenida oma mälu, hoida seda vormis. Ja kui sellega hakkama on saadud, siis võib ju kusagile selle soppi ka koolifüüsika paigutada ...
Kuidas õppisid koolis füüsikat?
Gümnaasiumis õpetas mulle füüsikat Märt Kask ja õpe käis suhteliselt klassikaliselt ehk loengu vormis. Teooriaosale järgnes ülesannete lahendamine. Õpetajal oli süsteem, et iga õpilane pidi vähemalt korra perioodis, kas kohepealt või tahvli ees mõne ülesande lahendama ja seda ka hinnati. Kui teadsid, et sinu nimi hakkas lähenema, siis ikka kodus vaatasid teooria igaks juhuks üle. Kooli ajal ei tundnud ma füüsika vastu väga suurt huvi ja lisakirjandust ja materjale juurde ei otsinud.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Mulle endale meeldib kõige rohkem õpetada geomeetrilist optikat. Sealsete jooniste tegemine ja nende seletamine on tore ning meeldib ka õpilastele. Samuti haakub teema hästi fotograafiaga, mille vastu on õpilastel enamasti päris suur huvi.
Samas üheks raskemaks teemaks on elektromagnetiline induktsioon. Ka igapäevaelus tuleb nö füüsikaga kokku puutuda kõige rohkem majapidamiselektri juures.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Tuimalt pähe õppida ei ole vaja midagi, vaja on ikka arusaamist. Samas mõned seosed võiksid ka pärast kooli lõppu meelde jääda, näiteks Newtoni II või Ohmi seadus. Samuti peaks teadma ka mõne konstandi väärtust.
Kuidas õppisid koolis füüsikat?
Oma kooliajast mäletan kahte õpetajat, kes mulle füüsikat õpetasid. Kõigepealt meenuvad tunnid õpetajaga, kelle tundides pidi vist ainult arvutusülesandeid lahendama. Vaevalt see muidugi päris nii oli, aga muud ma neist tundidest paraku ei mäleta. Kuna arusaamist ega ka julgust küsida, kuidas see lahendamine õigupoolet käima peaks, ei olnud, siis olid need tunnid päris hirmsad. Seejärel, peale õpetaja vahetumist, said füüsikatundidest tunnid, kus sai tegeleda sellega, millega oli parasjagu tegeleda vaja ja see ei pruukinud olla otseselt füüsikaga seotud. Ühegi konkreetse teema õppimist (katseid, näiteid) ei suuda kahjuks kuidagi meenutada. On vaid kaks vastandlikku kogemust ja mälestust, mis ei suutnud kuidagi panna uskuma, et füüsika võiks olla põnev õppeaine, täis igapäevaelust tuttavaid näiteid ja seoseid. Sellise arusaamiseni jõudsin oma ülikooliõpingute ajal tänu tõeliselt inspireerivatele õppejõududele ja siinkohal ei saa ma nimetamata jätta õppejõude Henn Voolaid ja Enn Pärtel. Nende loengutes ja praktikumides käies, nende igapäevaelust tuttavaid näiteid kuulates ja ise asju läbi katsetades, jõudsin endalegi üllatuseks arusaamiseni, et füüsika polegi hirmus, vaid on hoopis päriselt põnev!
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud.
Füüsikat olen õpetanud kokku viis aastat, 8. ja 9. klassis. Käsitletavate teemade peale mõeldes on kõige enam õpilastel arusaamatust ja küsimusi tekitanud aatomifüüsika ning optikast kujutiste tekke teema. Väga on meeldinud alati inertsuse teema õppimine, mis peale igapäevaeluliste näidete toomist omandab õpilaste jaoks palju selgema ja täpsema arusaamise.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Ma pean päheõppimisest ja peast teadmisest olulisemaks oskust asju vajalikul hetkel õigest kohast leida ja leitud informatsiooni kriitiliselt hinnata. Siiski päris ilma peast teadmata ka ei saa, mitu sentimeetrit on ühes meetris võiks ka ilma järele kontrollimata või -vaatamata teada. Samuti SI ühikuid. Selle üle aga, kas nende asjade teadmine on just eluliselt tähtis, võib pikemalt arutleda. Mis puudutab valemite peast teadmist, siis usun, et lihtsamad põhikoolis kasutatavad valemid (nt kiirus) jäävad meelde õppimise ja pideva kasutamise käigus. Olulisem teadmisest, et kiiruse põhiühik on meeter sekundis, on siiski arusaamine, millist informatsiooni antud ühik endas peidab. Et ei tekiks olukorda, kus küsimusele, kui kaugele jõuab keha, mis liigub kiirusega 5 m/s ühe sekundi jooksul, vastuse leidmine tundub olevat keeruline ülesanne…
Kuidas õppisid koolis füüsikat?
Koolis hakkasin ma füüsikat õppima juba kuuendas klassis ja tollest ajast ei mäleta ma suurt rõõmu ega hirmu – lihtsalt oli üks paljudest tundidest, mis oli vaja nö läbida. Füüsikat õpetas mulle tol ajal klassijuhataja ja kuna ta ise oli väga hea ja armas inimene, oli kuidagi häbi ja andestamatu tunniks mitte valmistuda. Seega õppisin tubli õpilasena pigem pähe ilma, et oleksin asju endale selgeks teinud. Mul tuli hästi välja ülesannete lahendamine, sest füüsikaliste suuruste nimetused, tähistused ja mõõtühikud olid peas ja valemid loomulikult ka. Iga ülesande lahendamist võtsin nagu mõistatuse lahendamist, ehk püüdsin alguses teksti kodeerida sümboliteks, vastavalt sümbolitele leida vastav valem ja siis jõudsingi õige vastuseni. Suutsin ehk jätta õpetajale asjatundja muljet, sest tihti kutsuti mind ka tahvli ette ülesandeid lahendama. Samas pelgasin ma igasuguste katsete ja laboratoorsete katsete tegemist, sest tõesti ei saanud mitte millestki aru ja mine tea, mis nende vidinatega juhtuda võib. Selle eest meeldis mu pinginaabritest klassivennale just katsetada ja proovida ja niimoodi moodustasime hea tandemi – tema eksperimenteeris, mina selle eest oskasin asju ilusti kirja panna. Kooliajast jäid füüsikatundidest meelde ainult üksikud kas põnevad või huvitavad asjad. Üks nendest on kondensaator, mille pidime ise lahti võtma ja uurima, kuidas see tehtud on ja mida kõik koostisosad tähendavad (see oli iseenesest mõistetav, et igal õpilasel on kondensaator olemas :)).
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kui olin asunud tööle füüsika õpetajana väikeses maakonnakoolis, siis esimese asjana alustasin suure puhastusega füüsika laboratooriumis, kus olid kaks suurt kappi igasuguseid asju täis: standardsed laboritööde komplektid, pakkimata salapärased karbid, juhtmed, mõõteriistad ja ka üksikud imelikud vidinad. Oli suur väljakutse selles segaduses süsteemi leida, aga appi tulid uudishimulikud külapoisid. Panime kõik asjad põrandale ja nad käisid pärast tunde nö igiliikurit leiutamas ja leiutasidki palju põnevat! Näiteks panid manuaali alusel hüdraulilise pressi kokku, mis töötas päris korralikult. Siis mingil imelikul kombel oli jõudnud pisikesse maakonnakooli füüsika laborisse väga korralik hõljukrongi mudel, kui sai ka see kokku pandud, töötas see imehästi. Me ei saanudki aru, et see oli õppimine, aga nägin, kuidas õpilastel silmad särasid ja nad tahtsid just ise katsetada ja proovida. Kuna kuuldused imeasjadest levivad külas ülikiiresti, hakkasid labori vastu huvi tundma ka nooremad õpilased. Sellest kasvas välja iga-aastane kevadine füüsika näitus füüsika kabinetis, mida korraldasid üheksanda klassi õpilased. Nad seisid uhkelt oma eksponaadi juures ja andsid vastavad seletused publikule. Tore oli näha, kuidas noored õed-vennad vaatasid neile alt üles ja küsisid – millal ka mina saan seda põnevat füüsikat õppida?
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Ma siiski pooldan sellist arusaama, et kõike saab õppida kas läbi praktika või probleemülesannete kaudu. Kui on loodud hea ja sõbralik õhkkond klassis, lahendamiseks on pakutud huvitavad ja kaasahaaravad probleemid, saab seoseid luua, siis teooriat on lihtsam vastu võtta ja vajalikud teadmised jäävad meelde nö iseenesest ning selleks pole vaja eraldi pingutada. Ma tõesti arvan, et just füüsikas polegi vaja asju pähe õppida - võib näiteks korraldada katse impulsi jäävuse seaduse kohta, paluda, et õpilased ise sõnastavad selle, mis nad nägid ja panevad oma mõtted valemi kujul kirja. Massi ja kiiruse tähiseid nad arvatavasti mäletavad, impulssi tähise võivad nad ise välja mõelda ja pärast võrrelda teadusmaailmas kokkulepitud tähisega. Kui uus teadmine on seotud äsja saadud kogemusega, siis kinnistub see paremini.
Kuidas õppisid koolis füüsikat?
Kui klassijuhataja meile 8. klassi alguses uut tunniplaani ette luges (siis ei olnud veel eKooli), ütles ta: „See füüsika on päris keeruline“ ja „nüüd hakkab teil kahtesid-kolmesid tulema, sest praktiliselt keegi ei saa füüsikast aru“. Esimest kontrolltööd kirjutama asudes otsustasin, et vaatan, kas oskan lahendada vähemalt nii palju ülesandeid, et saaks kolme kätte nagu õpetaja meilt ootas. Oskasin. Tegin kõik ära ja sain viie!
Käisin saksa keele eriklassis ja sain füüsikat, keemiat ja mõningaid muid aineid õppida paralleelselt eesti ja saksa keeles, kusjuures saksa keeles õpetasid päris sakslased. Eesti ja saksa tundides tehti veidi erinevaid asju, sest õpe toimus erinevate riikide õpikute järgi. Saksa füüsikas, kus oli korraga pool klassi, oli rohkem eksperimente, rühmatöid ja esitlusi, eesti füüsikas, kus oli korraga terve klass, rohkem teooriat ja referaate. Arvan, et õpetajad kooskõlastasid oma tegevusi, et saaksime parima suure ja väikese rühma tundidest.
Kuna füüsika ja teised loodusained mulle meeldisid, tegelesin nendega hea meelega põhjalikumalt, näiteks lugesin raamatuid ja tegin oma tarbeks märkmeid. Nüüd õpin füüsikat ülikoolis.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Alates 2010. aastast olen seotud füüsika põhikooli õpikojaga http://fyysika.ee/opikojad/. Selle programmi raames käime koolides tegemas seda, mille jaoks sageli tundides aega ja vahendeid ei ole – katseid. Õpikojas on väike rühm ja vahendeid piisavalt palju, et kõik lapsed ise käed külge panna saaksid. Põhikooli õpikoja materjal on 8. ja 9. klassi õppekavast, seega saab hiljem meie katseid oma tundides või olümpiaadiks ette valmistamisel kasutada.
Veel olen õpetanud loodusteaduste õpetajatele optikat ja esinenud Teadusbussiga.
Mulle meeldib näha heureka-hetki, kus inimesed enda jaoks uutest asjadest järsku aru saama hakkavad või mõtlevad välja, kuidas üht või teist probleemi lahendada.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Füüsika on nagu võõrkeel – kirjutamiseks ja lugemiseks ei piisa tähestiku omandamisest, tuleb tunda ka kõne ja kirja omavahelisi seoseid, teada kas kirjutatakse vasakult paremale, paremalt vasakule või kuidagi muud moodi, osata õiges kohas suurtähti kasutada jms.
Koolilõpetaja võiks mäletada loodusainetest piisavalt, et eristada MMSi soolveest, valgusaastat tavalisest aastast ja pseudoteadust päristeadusest. Kõike ei saa peast teada, kahtlaste faktide kontrollimine pole häbiasi.
Kuidas õppisid koolis füüsikat?
Minu õpetaja Kohtla-Järve I Keskkoolis oli Lehho Jõumees. Teda me kartsime ja tunnis oli range kord. Õpetaja tegi palju näitkatseid ja vihikusse sai kirja põhjalik ning süsteemne konspekt - seda eeskuju järgin õpetajana siiamaani. Kooli ajal olid mul pigem humanitaarsed huvid, millele füüsikaõpetaja Jõumees hoogu juurde andis - soovitas raamatuid, suunas džassi kuulama ja toetas meie kamba käike Ermitaaži. Sügavam huvi füüsika vastu kujunes välja alles ülikoolis ja ise füüsikat õpetades, aga ka siis sain abi oma füüsikaõpetajalt. Tänud talle selle eest!
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Alati on põnev alustada 8. klassis optikaga. Näen õpilaste hämmastunud nägusid, kui nende teadvusesse jõuab küsimus, et mis või milline on see asi, mida me näeme või arvame nägevat. Üheksandikele on põnevust pakkunud välja arvutamine, kui palju vabaneb kooliesise lombi jäätumisel energiat või kas mahlajäätis annab või võtab meilt energiat. 11. klassis elektromagnetismi katse magneti, mähise ja mikroampermeetriga on pakkunud sageli ahaa-ohoo momenti. Nimetatud teema ongi õpilastele vahest raskemini mõistetav osa koolifüüsikas. Toredat õpetamise ja õppimise rõõmu on mul jagunud igasse nädalasse ja see rõõm ei ole aastatega kahanenud.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Pähe õppimisel pähe õppimise enda pärast pole mingit mõtet. Minu kogemus näitab, et tõhusam on pähe kulumine. Järjepidev töö valemite, seaduspärasustega ja nähtuste kirjeldamisega ning nende omavaheline seostamine soodustavad meelde jätmist. Olulisem, kui valemi peast teadminine, on oskus valemit mõista, ehk kuidas füüsikalised suurused omavahel seotud on. Kumb on kasulikum teadmine, kas I võrdub U jagatud R-ga või see,et elektrivoolu toime on tugevam, kui kasutada suurema pingega patareisid ja vasest juhtmeid, mis on korralikult tarvitiga ühendatud?
Aga kindlasti ma ei jäta kordamast õpilastele, et oluliste valemite, seoste ja seaduste peast teadmine aitab õppimisele kaasa, eriti kui on soov reaalainetega sügavuti tegeleda, ning boonusena treenib ka mälu ;-)
Kuidas õppisid koolis füüsikat?
Koolis olid füüsika tunnid igavad, kõik ootasid, kunas küsimine läbi saab, et siis sai hakata oma asjadega tegelema. Mina mängisin tavaliselt pinginaabriga kaarte, vähemalt abituuriumis. Ma ei saa öelda, et füüsika mind ei huvitanud. Aga seda õpetati väga elukaugelt, jäi mulje, et füüsikat on vaja ainult füüsikale endale. Tehti küll kaunis palju katseid, aga nende seletus jäi reeglina arusaamatuks. Näiteks on mul siiani meeles, kuidas seletati polaroidi tööpõhimõtet: Kui valguslaine tuleb vastu polaroidi, mille läbilasketasand on risti valguslaine võnketasandiga, siis laine trummeldab vastu polaroidi ja sellest läbi ei saa. Kui aga läbilasketasand ja võnketasand on paralleelsed, siis valgus läbib polaroidi. See trummeldamise jutt jäi täiesti segaseks, aga paraku hästi meelde. Peamiselt pidi valemeid peast teadma. Need jäid mulle hästi meelde ja seepärast polnud ka ülesannete lahendamine raske, sest need olid sisuliselt matemaatika ülesanded, kus tuli valemisse ainult õiged arvud panna. Aga kui lugesin raamatuid nagu J. Perelmani „Huvitav füüsika“, siis oli kõik selge ja väga põnev. Püüdsin ka ise katseid teha. Mäletan, et raamatus „Noor elektrik“ soovitati elektrilaengute vastastikmõju uurida leedripuust kuulikeste abil. Meil õues kasvas leedripuu. Lõikasin sealt ühe parajalt jämeda oksa ja hakkasin sellest kuule välja lõikuma. See ei õnnestunud kuidagi, ainult lõikasin noaga näppu. Jäidki elektrostaatika katsed tegemata. Sellised raamatud tekitasid tõsise huvi füüsika ja looduse ning tehnika seoste vastu. Ja see huvi pole kuhugi kadunud. Paraku jätkus füüsika elukauge õpetamine ka ülikoolis. Ikka tuli välja, et füüsikat on vaja peamiselt selleks, et järgmistest kursustest aru saada. Teooria kinnitamiseks näidati palju katseid ja neid seletati paremini kui koolis, aga seos loodusega piirdus ikka ainult mõne näitega, mis tõestas, et ka looduses kehtivad füüsika seadused. Ja seda, miks kehtib looduses näiteks energia jäävuse seadus, ma ülikoolis teda ei saanud. Üks mu tark kursusevend teadis, et see on järeldus aja homogeensusest. Aga miks on aeg homogeenne, ei teadnud ka tema. Olin kindel, et füüsikat saab ka arusaadavalt õpetada ja oma elu teise poole olengi pühendanud sellele, et füüsikat õppijaile huvitavaks teha.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kõige toredamad on alati need asjad, mille õpetamine sulle endale rõõmu pakub. Ja rõõmu pakub see, kui õppur hakkab füüsika vastu huvi tundma. Selleks on algul vaja jõuda Ohhoo – efektini. See tekib siis, kui õppur näeb midagi ootamatut, midagi, mis on üllatav. Edasi tuleb jõuda Ahhaa-efektini, mis tekib siis, kui õppur saab aru, mida ta just oli näinud. Selliseid efekte saab tekitada ka väga lihtsate vahenditega. Näiteks mõned aastad tagasi, kui uurisin oma tudengeilt (tulevased loodusainete õpetajad) milline oli kursuse kõige meeldejäävam katse, siis tunnistati selleks katse plastiliinitükiga, mis vette panduna uppus, aga laevukeseks vormituna jäi vee peale ujuma. Archimedese seaduse esitlust sellisel kujul polnud nad koolis paraku näinud. Tore on ka see, et olen õpetamise käigus saanud omale küllalt palju noori kolleege, kellega kohtumine teeb ikka tuju heaks. Mõned oma kunagised õpilased olen suutnud meelitada ka tulevasi füüsika õpetajaid õpetama.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Oleneb, mida ja kuidas pähe õppida. Kindlasti pole vaja midagi papagoi moodi pähe õppida, ilma aru saamata, mis mul peas on. Aga põhitõed tuleb meelde jätta selliselt, et vajadusel poleks vaja pikemalt arutleda. Ei ole ju mõeldav , et korvpalli või malet mängides hakkad alles mänguolukorras mõtlema, mitu sammu võid teha palli käes hoides või kuidas ratsu käib. Miks peaks füüsikas teisiti olema? Kuid see kehtib ainult neile, kes tunnevad huvi füüsika vastu. Teisi pole mõtet piinata mingite valemite, seaduste, konstantide ja muu sellisega. Neile tuleks teadvustada looduse üldised toimimise printsiibid ja kogu lugu. (12.10.2015).
Kuidas õppisid koolis füüsikat?
Tundides seletati teooriat ning lahendati ka ülesandeid. Töödes pidi kindlasti teadma mõistete seletusi ning seaduseid. Ei piisanud sellest, et olid asjast aru saanud, vaid pidi olema täpne mõiste/seaduse sõnastus. Seetõttu sain ka tööde eest enamasti kaks hinnet – “2” ja “5”. 2 teooria eest, kuna ma ei teadnud mõistete/seaduste sõnastusi peast ning 5 selle eest, oskasin mõisteid/valemeid kasutada ülesannete lahendamisek. Vabal ajal sai aegajalt lahendatud nii keemia, füüsika kui matemaatika ülesandeid – lihtsalt huvist ning igavusest. Samuti sai ise tehtud igasugu katseid – katsetamine oli lahe.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Probleeme on enamasti elektriteemade mõistmisega. Samuti on probleeme nende teemadega, mis nõuavad kujutlusvõimet – nagu näiteks suhteline liikumine. Liikumisest maal saavad õpilased ilusti aru, aga kui vaadelta liikumist veel, siis paljude jaoks on taustsüsteemi valik keeruline – ei saada aru, kuidas saab vee seisma panna ning vaadelda liikumist seisva vee suhtes. Enamasti saab kõige paremini teemasid seletada katsete läbi. Kui reaalselt saab asja vaadata, siis jääb ka paremini meelde. Ainult abstraktsed teemad tekitavad segadust.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Mõistete ja seaduste sõnastusi minu arvates ei pea peast teadma – oliuline on neid mõista ning osata neid kasutada mingite probleemide/ülesannete lahendamisel. Valemite koha pealt niipalju, et mõningaid lihtsamaid valemeid, mida meil kõigil võib elus vaja minna võiks ikka peast teada nagu näiteks, kiiruse ja tiheduse valemid. Ühikuid võiks ikka teada – millisele füüsikalisele suurusele mingi ühik vastab. Näiteks võiks ikka teada, mida tähendab pirnide peal 6W, 230V.
(10.10.2015)
Kuidas õppisid koolis füüsikat?
Kuigi koolis algasid minu füüsikatunnid kuuendas klassis, siis juba viiendas klassis oli mul selge, et tahan ülikooli füüsikat õppima minna. Põhjus oli selles, et tähistaevas pakkus huvi ja sain teada, et astronoomiat õpetatakse füüsikaosakonnas. Tähistaeva tundmaõppimine toimus suuresti iseseisvalt raamatutest abi saanuna. Koolitundidest kahjuks eriti midagi meeles pole. Meenub, et millalgi nooremates klassides tuli kodutööna katseliselt leida mingi papist kujundi massikese ja sellega oli tükk tegemist. Väljaspool kooli lennutasin suveti raketti (mõni võib-olla mäletab – vesi sees ja pumbaga suruõhku lisaks). Kosmoseajastu algus 1960ndatel aastatel hoidis huvi üleval. Veel on meeles, et kontrolltööde ajal istus õpetaja oma toolil ja jälgis meie peegeldusi klassiakendelt, et sulisid vahele võtta. Sisseastumiseksamiteks lahendasin ise üpris palju ülesandeid. Olingi suuresti omaette tegutseja. Kui saaksin uuesti alustada, läheksin ikka füüsikat õppima. Ah-jaa, mitu aastat tegime pinginaabriga keemiakatseid. Meil oli klaasist laborinõusid (pinginaabri vanemad olid meedikud ja nad hankisid kuidagi neid meile) ja sel ajal sai apteegist mitmesuguseid kemikaale osta ja tellida. Põhiliselt sellised katsed, mis poistele huvi pakuvad – suits, pauk ja tulevärk. Pinginaabrist saigi keemik.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Raskemad teemad on loomulikult need, mille mõistmiseks on vaja abstraktset mõtlemist, head kujutlusvõimet ja ka häid teadmisi. Tihti ei aita ka demonstratsioonkatsed õpilasel asjast paremini aru saada. Seega paljutki elektri- ja magnetisminähtuste käsitlemisel.
1994.a aprillis, kui käisin Rootsis Göteborgi ülikooli pedagoogika osakonna korraldatud rahvusvahelisel seminaril „Teaching or learning?“ , pakuti mulle kohtumist seal töötanud eestlase Aadu Otiga, kes näitas mulle oma katsevahendeid ja tutvustas üht katset, mille ta vist ise välja mõtles. Ta suunas fotovälklambi valgusvälgatuse statiivi küljes rippuva trummitaldriku poole ja pani selle niimoodi helisema. Kodus hankisin endale ka vastavad vahendid ja olen seda katset näidanud kõigil aastatel. Aadu Ott ütles, et nii saab näidata, et footonitel on mass, aga akadeemik Peeter Saari kahtles, kas see ikka on nii, vast on helisema hakkamise põhjus muus. Aga efektne on see küll!
Küsitud on selle pika aja jooksul igasuguseid küsimusi, aga midagi erilist ei meenu. Heameel on siis, kui õpilane julgeb tulla küsima ja kui ta siis lõpuks ütleb, et sai aru.
Mul on heameel, et sattusin kooli, kus oli ees vanem koloriitne mees. Ta õpetas mind palju ja meil koolis on enamus veneaegseid katsevahendeid siiani käigus. Kuigi õpingute järel polnud mul mingit tahtmist õpetajaks saada, juhtus see siiski tänu kolleegidele oma koolis ja paljude teiste koolide õpetajatega suhtlemisele, aga kindlasti ka õpilaste heatahtlikkusele.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Mina olen seda meelt, et teadma peab palju, muidu pole võimalik ei mõtelda, olulist ebaolulisest eristada ega ka vajalikku täiendavat teavet otsida-leida. Termodünaamika II printsiipi õpime-õpetame, aga et see kehtib kõigis valdkondades (ka õppimisel, õpetamisel ja asjadest arusaamisel), seda me ei kipu arvestama. Nii peaks füüsikaõpetajaks õppija tundma lisaks füüsikale ja matemaatikale ka psühholoogiat, õpetamistehnikaid, igasuguseid käsitöövõtteid ja –riistu, filosoofiat ja nii lõputult. Kahjuks. Kui õpetaja teab ise vähe, on suur kiusatus õpilaselt ka enamust, mida ta õpetab, tagasi küsida. Siis jääbki tunne, et seda ja seda ja seda ka veel peab pähe õppima. Õpetaja näitab oma eeskujuga, mida ja kui palju peaks peast teadma.
Kuidas õppisid koolis füüsikat?
Kooliajal olid füüsika tunnid päris erinevad. Põhikoolis oli meil väga konkreetse ülesehitusega tund. Õpetaja dikteeris mõisted ja valemid, kirjutasime need vihikusse, lahendasime tunni teises pooles valemite kohta ülesanded ja kõik. Keskkoolis käis kolme aasta jooksul meie klassist läbi neli füüsika õpetajat. Esimene neist oli süsteemitu lähenemisega, kelle tundides me enamasti lobisesime niisama maailma asjadest. Küll aga oli ta ainus õpetaja, kellega me mingit eksperimendi taolist asja tegime – terve keskkooli vältel mängisime ühe korra vedela lämmastikuga. Edasi oli meil õpetaja, kes enamuse oma ajast veetis Šnelli tiigi pargipingil odavat alkoholi juues. Tundides teda eriti tihti ei kohanud. Kolmas õpetaja oli süstemaatilisema lähenemisega, kes proovis asju selgitada ja lasi meil mõned ülesanded lahendada. Tema sõnul pidid meist kõigist saama kraavikaevajad või müüad, seega tahtmiseni midagi tema tunnis õppida, me ei jõudnudki.
Keskkooli ajal osalesin tihti keemia olümpiaadidel ning olin ka kooli esindusvõistkonnas Riia-Vilnius-Tallinn võistlusel. Ikka juhtus, et keemia ja füüsika mõnes ülesandes kohtusid, seega nägin ise vaeva, et mõned asjad endale selgeks teha. Selleks kasutasin mõnd vanemat füüsika õpikut kodusest riiulist. Rohkema jaoks huvi aga ei jätkunud.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Oma sõpradelt ja tuttavatelt saan kõige rohkem küsimusi elektromagnetlainete teemal: kuidas töötab mobiil, mikrolaineahi, kas röntgen on ikka kahjulik, kas mikrolaineahi tekitab mu toidus vähki soodustavaid osakesi jne. Uues seltskonnas end tutvustades tuleb ikka teemaks, millega keegi tegeleb. See tavaliselt jätkub sellega, et ma selgitan, miks on taevas sinine, aga päikeseloojangul punane, kumb kukub kiiremini, paber või raamat jne. Viimasel koosviibimisel tekkis arutelu lihtsatest peotrikkidest. Käepäraste vahenditega näitasin kuidas küünla leegi kuju muuta, küünalt kaugelt uuesti põlema panna, piimaga pilte joonistada jms.
Proovin klassiruumis asjadele läheneda rohkem praktilisest vaatenurgast. Tunni häälestuseks on enamasti mingi lihtne näitlik katse või posu küsimusi, miks mingi asi just nii on. Selle tulemusega õpilastel väga palju küsimusi ei teki. Suurim väljakutse siiani on olnud minu jaoks kuidas õpilastele selgitada elektrimootori tööpõhimõtet ning mis jõud reaalselt sunnib rootorit pöörlema. Võttes aga appi magneti, patarei ja vasktraadi, saime ka sellest raskusest üle, enam-vähem.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Ma olen ise väga väga halb asjade pähe õppija. Kolme aastaga on mõned tüüpdefinitsioonid lihtsalt pähe kulunud, kuid enamasti ma tahan leida mingi sellise sõnastuse, millest õpilane aru saaks. Lisaks on minu jaoks oluline, et ta suudaks oma sõnadega asja sisu edasi anda. Ka valemite puhul leian, et mõned asjad lihtsalt kuluvad pähe, kui neid järjepidevalt kasutada. Ainus, mille puhul ma järeleandmisi ei tee on ühikud ja ühikute teisendamine. Eriti nõuan igapäevaselt kasutusel olevate ühikute teisendusi.
Väga tore on olla füüsika ja keemia õpetaja ja õpilastega põnevatel teemadel diskuteerida.
Kuidas õppisid koolis füüsikat?
Olen pärit Võru linnast. Õppisin Võru Kreutzwaldi Gümnaasiumis. Põhikooli ja gümnaasiumi peale oli mul kokku kolm füüsikaõpetajat – Imre Oolberg, Ott Ojaveer, Aarne Lillemaa. Nemad olid kindlasti targemad kui mina, suur aukartus oli nende ees, neil oli kindlasti ka suurem kogemus. Nemad olid see põlvkond, kes oskasid valemite kaasabil ainesse süveneda ja häid tulemusi nii olümpiaadidel kui ka riigieksamitel saavutada. Imetlesin oma õpetajaid, nii teadsingi, et tahan ülikooli minna füüsikat õppima. Mäletan tänaseni kuidas õpetaja Aarne Lillemaa õpetas: „cos α võrdub KOOS sinuga olev kaatet jagatud hüpotenuusiga ja sin α võrdub SINU vastas olev kaatet jagatud hüpotenuusiga“.
Kodus, koolivabal ajal meeldis mulle vaadata, mis on „karul kõhus“. Võtsin lahti kõik mänguasjad, raadiod, kellad, elektroonika jne. ikka selleks, et vaadata, mis seal sees on. Hiljem, gümnaasiumis käies, suutsin mõned lõhutud asjad ka kokku panna ja isegi terveks teha, nii tõidki sõbrad tuttavad oma seadmed remontimiseks minu kätte – mängukonsoolid, telerid, raadiod – kõik parandasin ära.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Eks kindlasti alateadlikult annan edasi neid õpetussõnu, mis minu õpetajad minuga jaganud on. Olen natuke selline nagu minu õpetajad mulle meelde on jäänud.
Ühtteist on ka juurde tulnud. Näiteks üks põnevamaid väljakutseid on iga-aastane doominoefekti ülesanne, mis seob omavahel Newtoni seadused, impulsi ja impulsi jäävuse seaduse ja esmased videomontaaži oskused. Alguses lubasin efekti üles seada klassis, aga kui ruum seadis piirangud ja prügi ei mahtunud prügikonteinerisse, siis palusin doominoefekti üles seada kodus ja seda filmida. Nüüdseks on mul videoklippe juba sadades, kokku ca 20 GB eest. Ise olen seadnud ka mõned tingimused, näiteks peaks efekti pikkus olema minimaalselt 20 sekundit (kusjuures sekkumisel ja kaasaaitamisel lahutan 5 sekundit lõpptulemusest maha), efekt peab olema korratav ja video lõpus peab nähtavale ilmuma rühm ja rühma liikmete nimed.
Vahvad on ka iga-aastased välipraktikad. Teeme looduses mõõtmisi – rakendame tunnis omandatud looduse keskel. Koostan neile mapid, kus on ülesanded. Siis nad moodustavad väikesed grupid ja toimetavad mitu päeva. Teevad töid nagu keha ning ainete tiheduse ja koostise analüüsimine, mulla niiskuse ja temperatuuri määramine pikema aja jooksul, suvalise tundmatu veekogu sügavuse määramine. Oleme mõne järve ääres ja proovime erinevate vahenditega, ilma et peaksime järve peale minema, selle sügavust määrata. Siis veel puude kõrguse ja vanuse määramine, päikese läbimõõdu määramine, vaatleme päikest ja öötaevast jne. Kokkuvõttes: teeme vaatlusi, mõõtmisi; Leiutame: ehitame ise vaatlus-, abiseadmeid.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Olen päri, et õpilased, kes on kindlad oma otsuses, et ei asu ülikoolis reaalained õppima, pean silmas humanitaarklasside õpilasi, siis nemad kindlasti ei peaks valemeid pähe õppima. Tänapäeval on tunnis nii palju võimalusi aine põnevamaks muutmiseks, aine tuleb õpilasele lähemale tuua.
Reaalsuunaga klassis tuleks valemeid teada ja osata neid kasutada ehk teisisõnu tuleb osata füüsikat väljendada matemaatiliste lahenduste ilu kaudu. Kui lahendame mõne eriti raske ülesande ära, siis on hea tunne nii õpilastel kui õpetajal. Selleks, et rääkida võõrkeelt, peab teadma sõnavara.
Kuidas õppisid koolis füüsikat?
Mõistlik on alustada ausalt sellest, et ega kooliajal füüsika mind kõige rohkem ei paelunudki. Rohkem võlus matemaatika, selle korrektsus ja alati „õiged ja ilusad“ vastused. See oligi ehk midagi, mis tekitas minu sees konflikti – füüsikas mõõtmistulemused erinesid üksteisest olulisel määral. Juhtus, et erinevused mõõtmistulemuste vahel tulid suuremad kui tulemuse väärtus ise (eks oli siin peidus ka raasike oskamatust J), seetõttu ei leidnud üles ka seoseid teooria ja praktiliste tulemuste vahel ja selle taha kadus füüsika ilusam pool. Selle ilusa poole aitas tegelikult minu jaoks üles leida, seda küll juba siis ülikoolis õppides, Henn Voolaid. Aitäh!
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Päris raske küsimus. Keeruline vastata. Tahaks pugeda väikese õpetamiskogemuse taha, aga ka sealt peaks siiski üht-teist toredat leidma, kuid loodan, et suuremad toredad hetked on veel ees. Ise loodan, et kõik õpetatav on tore, aga meenutus iseenda kooliaega toob maa peale tagasi J. Eks ma kaldun pigem arvama, et huvitavam pool füüsikast peitub praktilistes töödes, mis ühtlasi loob parema taju teooria ja tegelikkuse vahel. Eriti juhul, kui saadud tulemused kinnitavad üldtuntud teooriaid. Hoopis teiseks teevad olemise tunnid looduses ning sealt leitav füüsika. Minu enda viimase aja suuremaks huviks on saanud atmosfäärifüüsika ning sellega kaasnev ja tekkinud on esimesed mõtted, kuidas siduda seda koolitundidesse. Sest eks kõige toredam on jagada asju, mis ka endale suurt huvi pakuvad.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Võrdlemisi intrigeeriv küsimus ning tean ja tunnen inimesi, kes esindavad nii üht kui teist poolt ning eks nii sel ühel kui teisel poolel on oma tõde ja õigus. Ja kuhugi nende vahele seguneb ka minu arvamus. Füüsikaga seonduvast ei mäletagi, et ma ise kunagi oleksin õppinud midagi pähe. Küll tuleb seda meelde teistest ainetest, näiteks ajalugu ja keeled. Pean ka tunnistama, et päheõppimises ma eriti tugev pole. Pigem on olnud tundide kaupa mingisuguste materjalide taga istumist ja nendega tõtt vahtimist, lehekülgede edasi-tagasi keeramist, seoste otsimist, märkmete tegemist, ise samal ajal püüdes üles ehitada süsteemi, millest aru saan. Ja eks selle tegevuse käigus jääb ikka üht-teist meelde ka. Ka valemeid pole ma pidanud kunagi pähe õppima, need on kulunud sinna ülesannete lahendamise käigus. See kõik ei anna aga ühest vastust ülal esitatud küsimusele ja mina arvan, et sellist polegi olemas. Eks see sõltub ikka inimesest ning sellest, millised õpiviisid kellegi peal kõige paremini töötavad.
Kuidas õppisid koolis füüsikat?
Minul algas füüsika õppimine 6. klassis ja toimus väga omapäraselt. Üks noor mees, tõenäoliselt üliõpilane, andis mõned tunnid. Pärast esimest tundi anti läbi lugeda pool raamatut ja järgmisel tunnil oli selle kohta kontrolltöö. Sama kordus ka teise poole raamatu jaoks ja sellega kuuenda klassi õppetöö umbes piirduski. Seitsmendas ja kaheksandas klassis oli küll õpetaja olemas, kuid tema kulutas põhilise aja meie kasvatamisele. Minu pinginaaber veenis mind temaga koos astuma Tartu 1. Keskkooli (praegu Hugo Treffneri Gümnaasium) füüsika eriklassi. Füüsika õpetajaks oli kooli direktor ja palju tunde jäi ära või toimus iseseisev töö. Kõige rohkem on meeles füüsika praktikumid, mis toimusid Tartu Riikliku Ülikooli laboratooriumites. Keskkooli lõpueksami tegin ka füüsikas ja sain isegi viie. Minu isa oli füüsik ja vanem õde õppis ülikoolis füüsikat. Elasime linna lähedal Füüsika ja Astronoomia Instituudi aktinomeetriajaama juures. Seal töötasid atmosfäärifüüsikud ja oli ilmajaama vaatlusväljak ning me käisime tihti koos vaatlejatega andmeid kogumas. Kõrval asus viiekümnendate lõpus ehitatud satelliitide jälgimise paviljon, kus asusid postamentidel suhteliselt võimsad piirivalve binoklid. Lükkasime salamahti paviljoni katused pealt ja vaatasime binoklitega nii taevast kui ka maapealseid objekte. Lõpuks said sellest teada ka ametimehed, kuid nad lasid meid lapsi seal edasi tegutseda. Kuskil viiendas-kuuendas klassis ehitasin isa abiga seebikarbi sisse transistorraadio.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Sugulased, sõbrad ja tuttavad esitavad mulle väga laia diapasooniga küsimusi füüsika ja selle rakenduste kohta. Tundub, et tavakodaniku teadmised on kõige napimad kvantfüüsikas. Tundub, et koolis pole sellele piisavat tähtsust omistatud. Samas kosmoloogilised teemad huvitavad praktiliselt kõiki. Kui ma korraldan oma kodus linnast väljas planeetide ja tähevaatlusi on huvilisi palju. Peale oma õpilaste tulevad ka nende sõbrad. Füüsika õppimisel on vaieldamatult kõige raskemaks teemaks elektromagnetism ja selle sees eriti elektromagnetilise induktsiooni nähtus.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Valemeid tuleb füüsikas kindlasti õpetada, kuid need võib ka õpilastele ette anda. Eesti haridussüsteemis on siiski tavaks, et paljusid asju peab teadma peast. See ei käi ainult füüsika kohta. Kui olin füüsika riigieksami komisjoni liige otsustasime, et alati küsitakse Newtoni teist seadust kui näidet edasiminekust Aristotelese füüsikast.
Kuidas õppisid koolis füüsikat?
Füüsika õppimisest kuni kaheksanda klassini mäletan seda, et tuleb ikka asju reaalse mõistusega võtta. Seda toonitas mu esimene füüsikaõpetaja. Keskkooli füüsikaõpetaja jutust on meelde jäänud see, et antimaailmast ei tasu naist võtta - esimene suudlus ja oleme mõlemad energiaks haihtunud. Hea näide, siiamaani on meeles. Tallinna Pedagooiline Instituut (nüüdne Tallinna Ülikool) võlus mind eelkõige tööõpetusega, aga suurepärased õppejõud sütitasid minus nii füüsika , astronoomia, matemaatika kui ka psühholoogiahuvi. Vello Kornel, Hannes Tammet, Tamara Sõrmus, Peep Kalv – isiksused, kes vanemat füüsikutepõlvkonda kindlasti kõnetavad.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kõige rohkem tavaelus on ilmselt pöördutud minu poole elektriga seotud küsimustes. Ka tähistaevast olen tutvustanud. Olen olnud ka ühes kohtuasjas konsultant, see puudutas purunenud toote ekspertiisiandmete tõlgendamist. Kuna koolitundides olen käsitlenud liikluse ja tehniliste spordialade füüsikalisi aspekte, siis on ka sealt tulnud küsimusi auto juhitavuse ja oda lendamise kohta.
Mulle meeldib füüsika õpetamisel lähtuda sellest, et kerge on seletada seda, mida näed. Aga inimesel on võime teha nähtavaks asju ka kujutlemise läbi, seepärast on tähtis osata kujutleda nähtusi, mida seletad. Kujutlusvõimel on tohutu tähtsus asjadest arusaamisel. Ja kui kujutluspilt ei hakka tööle, siis teeme asjad näitlikult selgeks. Tuleb meelde lugu gümnaasiumiklassist kellele ei mahtunud kuidagi pähe aatomi kvantmehhaanilised seaduspärasused. Egas midagi, läksime saali, jagasime rollid ja mängisime aatomi kvantmudeli läbi nagu rahvatantsu etenduse. Keskel olid prootonid ja neutronid koos ja ümber nende suures ringis tiirles laineline elektron. Ja kui laineline elektron tahtis tuumale lähemale tulla, pidid osad ringis olijad lahkuma (nagu footon aatomist). Juurdetulemisel aga laienes ring iseenesest. Uskumatu, aga see oli paljude jaoks parim ja õpetlikum füüsikatund kogu kooliaja vältel.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Kas valemid pähe? Kas seadused pähe? Kui midagi muud ei ole võtta, kui loogika ei tööta, aitab päheõpitud seadus, seda õigesti rakendades, tulemuseni jõuda. Valemeid kontrollin pärast teema läbimist. Kui on sisuliselt tööd tehtud ja piisavalt oma peaga ülesandeid lahendatud on valemid pähe kulunud. Hea kontroll hindamaks tegeliku õpilase töö mahtu. Füüsika koolivalemid on nii lihtsad, et neid saab igal ajal reaalse olukorra analüüsimisega välja tuletada. Olen proovinud põhikooli õpilastega, tuleb välja küll, seepärast tasub vaeva näha ja selline arutlemisoskus omandada. Eelkõige peab aga oskama õiget valemit valida ja teadma , mida antud täht selle valemi kontekstis tähendab. Kui võimsuse valemis t tähendab temperatuuri, on ikka mõtlemine väga mööda. Vajalike valemite meeldejätmiseks on ka mõnusad naljad omal kohal: „Nuiaga pähe kui võimsuse valemit ei tea“ (N=UI), kõlab elektriõpetuses. „OOO - mega, täna on sööklas kaks pihvi“, on mu õnestunumaid lööklauseid ringliikumise ja laineteooria ühe valemi (ω=2πf) meeldejätmiseks. Ka aastate pärast mäletatakse.
Kuidas õppisid koolis füüsikat?
Alustasin füüsika õppimist mehaanikast ja leian siiani, et see on õigem kui praegune, mil alustatakse optikast. Optika võib tunduda küll „põnevam“, aga mehaanika on ikkagi kuidagi paremini tajutav. Õppisin Ida-Virumaal Oru koolis (praegu seal enam kooli ei ole), aga siis moodustasime piisavalt suure nutikate õpilaste koosluse. Füüsikaõpetaja oli väga nõudlik, ütleksin isegi, et kohati liigagi. Mäletan, et olin jätnud Ohmi seaduse rakendamise ülesandes voolutugevuse arvutamisel vastuse teisendamata milliampritesse ja sain nelja. Sellest hoolimata olen talle väga tänulik. Ma ei ütleks, et huvitusin füüsikast. Mulle meeldis õppida ja ükski aine raskusi ei valmistanud, aga pigem olin huvitatud ajaloost. Keskkoolis tegin valiku füüsika kasuks ja seda just tänu oma füüsika õpetajale.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Tihti võib kohata õpilasi, kelle suhtumine füüsikasse on juba blokeeritud, sest talle on (tavaliselt) vanemate poolt sisendatud, et juba mina ei saanud füüsikast aru; füüsika see on väga raske jne. Sellisel juhul kulub palju energiat õpilase sellisest arusaamast „vabastamiseks“. Just see hetk kui õpilane tajub, et ta saab füüsikast aru, peaks olema iga füüsikaõpetaja unistuseks.
Õpetamine on õpilase ja õpetaja vastastikuse rikastamise protsess. Minu egot ei riiva karvavõrdki kui õpilane on mõnes küsimuses targem kui mina. Seega ei ole ma teinud kunagi numbrit kui õpilane on mõnes füüsika teemas targem kui mina. Kui õpetaja hakkab põdema oma autoriteedi pärast, siis ei tule õpetamisest midagi välja. Tuleb olla sina ise – oma positiivsete omadustega ja samuti veidrustega.
Õpetan füüsikat suurima mõnuga ja kui õpilasedki seda mõistavad, siis on kõik kordaläinud.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Füüsika on tegelikult imelihtne, tuleb ainult ära tunnetada süsteem. Mõneti sarnaneb füüsika õppimine ja ka õpetamine muusikale. See küsimus viib muidugi kohe paljuräägitud valemite peast teadmise juurde. Leian, et õpilased valemeid peast teadma ei pea. Õpilasele, kes on füüsikast sügavamalt huvitatud (käivad olümpiaadidel, planeerivad oma edasised õpingud siduda füüsikaga jne.) jäävad need iseenesest pähe. Kes on huvitatud headest õpitulemustest nendel on valemilehtedest kasu. Kes on tulnud lihtsalt aega veetma, sellel ei ole ka valemilehtedest mingit kasu.
Samas on väga paljudel õpilastel tekkinud valemitest nagu mingi dogma. Nad saavad valemilehelt mingi valemi ja proovivad seda kohe rakendada suvalise situatsiooni lahendamiseks. Püüan luua õpilastes arusaamist, et oma mõttekäike tuleb argumenteerida ja põhjendada (kasvõi valemitele toetudes). Oskuslikus valemilehtede kasutamisest on tegelikult väga palju abi. Seaduste sõnastamiseks tuleb näiteks valem lihtsalt panna sobivasse keelevormi. Rõhutan alati, et füüsika õppimisel tuleb lähtuda sellest, et aju ei ole prügikast ja seda tuleb kasutada ratsionaalselt.
Kuidas õppisid koolis füüsikat?
Füüsika õpe algas 8.klassis. Õpe oli meil üsna üksluine, kuna vahendeid koolil ei olnud ja seega praktilised tööd piirdusid elektriringi kokkupanekuga. Õpetaja pani rõhku teooriast põhimõtteliselt aru saamisele ja ülesannete lahendamisele.
Füüsika ei olnud küll koolis kõige põnevam tund, kuid pani huvitavatele probleemidele mõtlema. Huvi füüsika vastu kasvas gümnaasiumis. Eks siis sain vanemaks ja oskasin ümbritsevat rohkem mõtestada.
Loodus üldiselt on mind aga alati huvitanud, selle pisiku sain kodust. Bioloogist ema, kes õpetas Suislepa kohalikus põhikoolis kõiki loodusaineid peale füüsika, oskas alati loodusest rääkida ja küsimustele vastata. Mida rohkem looduse kohta teada sain seda põnevam see tundus. Vanusega kasvas arusaam, et kõik looduse seaduspärasused taanduvad füüsikale.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kõige raskemini mõistetavad tunduvad elektromagnetismi teemad. Selle teemaga seoses on ka tunnis endal taipamist ja avastamist koos õpilastega. Aga pean tõdema, et „õpetan ja õpetan ja lõpuks saan ise ka aru“ momente on tulnud paljude teemade juures.
Ümbritsevate inimetega vesteldes tõstatub palju küsimusi. Kosmose teema on olnud alati intrigeeriv. Eriti suurt arutelu tekitav on olnud Universumi lõputuse ja lõpu küsimus.
Üldiselt paljud võõrad noored inimesed ehmatavad ära, kui öelda, mis ametit ma pean, kui aga esimesest ehmatusest on üle saadud siis tullakse lagedale väga laia valiku küsimustega. Küsitud on nii linnu lendamise kohta kui selle kohta, et millal Päike Maa „alla neelab“, nii et tegelikult on teemadering lai, mis inimesi huvitab.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Valemite õppimisest niipalju, et need valemid, mis on õppekava järgselt kohustuslikud peast teada on täiesti piisav. Kui on olemas mõistmine nende sisust, tuleb nende valemite teadmine juba ilma suurema pingutuseta. Nende korrektne rakendamine on aga juba iseasi…
Kuidas õppisid koolis füüsikat?
Füüsikat õppisin kõige rohkem põhikoolis. Õpetajaks oli kooli direktor, kes õpetas väga matemaatikakeskselt. Lahendasime ülesandeid, mingeid katseid tegime ka. Kuna mulle meeldis matemaatikas ülesandeid lahendada, siis füüsikas polnud ka mingit probleemi. Andmed kirja ja valemid ka ja kombineerisin. Sisulist arutelu, miks ja kuidas ja mispärast, ma ei mäleta. Keskkooli esimeses klassis oli õpetaja, kel olid väga head konspektid, kuid tundides tegeles ise muude asjadega. Keegi õpilastest luges tema konspekti ette ja teised kirjutasid. Vahel siiski rääkis ise ka. Ülesandeid tegime temaga päris palju. Järgmisel aastal oli õpetajaks noor mees, kes ei julgenud klassi poole eriti vaadatagi. Ma olin korralik õpilane ja kui kästi midagi lugeda, siis läbi lugesin ikka, erilist huvi küll ei olnud. Kolmandal aastal oli jälle uus õpetaja, tema püüdis meid siis ikka õpetada ja asju selgeks teha. Keskkooli osast ei mäleta ma ühtegi katset.
Vanema vennaga arutasime vahel kuidas ja miks looduses asjad nii käivad. Temaga uurisime ka, kuidas miski töötab. Näiteks, mis on mänguautode sees jne. Ükskord lammutasin ära ühe isa lüliti, et näha, mis seal sees on. See oli ilus karp musta ja punase nupuga. Kahjuks ei osanud pärast kokku panna ja sain isa käest riielda, et ära lammutasin.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kõige raskem teema tundub elektromagnetism ja üldse elektriga seonduv praktiline tegevus.
Kõige toredam on näha, kui õpilased mõtlevad kaasa ja küsivad ning arutavad. Vahel jõuame nii ka hoopis teiste teemade juurde, aga kui huvitab, siis ka seletame ja räägime. Tore on ka see, kui õpilane on kodus midagi uurinud või kuulnud ja siis tahab täpsemalt teada, kuidas asi käib.
Aastakäikude õpilased on väga erinevad. Ühel aastal ei saadud aru, miks valguse kiirus on erinevates keskkondades erinev. Mängisime siis läbi, nii et igaüks oli kas keskkonna osake või valguse osake. Peale seda liikumist oli kõigil asi selge. Järgmisel aastal tegin sama järgmise klassiga, mille peale pärast üks õpilane küsis: „Õpetaja, kas te arvate, et me nii lollid oleme, et nii titekalt peab seletama?”
Kuna kõikide teemade juures püüan panna õpilasi mõtlema ja tooma näiteid elust enesest, ütles kord üks õpilane vahetunnis teisele – füüsika on raske, seal peab mõtlema!
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Mina olen seda meelt, et põhimõisteid, tähistusi ja ühikuid peab teadma, muidu ei saa hiljem aru, millest üldse jutt käib. Põhimõisteid võib seletada ka oma sõnadega nii, et on näha, kas õpilane on asjast õigesti aru saanud. Põhikoolis ei luba ka valemite lehte, gümnaasiumis küll. Gümnaasiumis peavad ka peast teadma, mida mingi täht tähendab ja mille kohta valem üldse käib. Teisendada peavad oskama, aga kui ka mõni eesliide meelest ära läheb, siis võib vaadata ka. Need kuluvad nagunii pähe. Ja kui piisavalt tähistusi ja ühikuid kasutada, jäävad need ka isegi pähe. Kui mõnele tõesti ei jää, siis tuleb ära õppida. Oluline on maailma asjadest aru saamine ja nende omavaheline seostamine.
Kuidas õppisid koolis füüsikat?
Minu kooliaja füüsika oli väga eklektiline. Õppisin füüsikat kahes koolis – Kohtla-Järve 1. Keskkoolis ja Rapla Keskkoolis – kokku kuus aastat (VI – XI klass) seitsme erineva õpetaja käe all. Iga õpetaja oli eriline, lausa omaette isiksus, kellest eredamalt on meelde jäänud Lehho Jõumees Kohtla-Järve koolist ja Hans Makus Rapla koolist.
Kuna tegelesin koolis kõige muuga, võiksin lausa öelda, et käisin koolis kõige muu kõrvalt, siis polnud mul eriti aega kooliasjadega tegelemiseks. Üks inimtüüp vist kohe on selline, kes pingutab tulemuse saamiseks nii vähe kui võimalik ja ometigi tuli kõik kuidagi iseenesest kätte.
Füüsika õpetajaks saamisega oli aga nii, et üheksandas (keskkooli esimeses) klassis küsis mult naabritädi, et kelleks Enn ka suureks kasvades (olin siis 183 cm pikk ja umbes 110 kg raske) saada tahab. Tulistasin puusalt, et õpetajaks. Mõni päev hiljem mõtlesin, et miks ka mitte. Kuna reaalained olid apoliitilised ning füüsika tundus elulähedasem kui matemaatika ja lihtsam kui keemia, siis nii see valik kujuneski.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Füüsikaga (ilmselt kõigi teiste ainetegagi) on nii, et mida rohkem sama asja teistele seletada, seda paremini sellest ise aru saad. Küsitakse igasugu asju. Mõni on raadiost kuulunud mõnda fakti ja küsib selle kohta. Teine jälle kuskilt portaalist miskit kummalist lugenud. Viimasel ajal on mul kiusatus võidelda/vaielda portaalist telegram.ee „teaduslike“ artiklite jagajatega. Paraku olen jõudnud tõdemusele, et kui inimene tahab midagi uskuda, siis ta seda lihtsalt usubki ega lase faktidel oma usku kõigutada.
Peeglisse vaadates tuleb tunnistada, et küllap on meil, füüsikaõpetajatel, selles oluline osa. Kui me võtaks rohkem aega, et õpilastel tekiks võimaluski faktide ja ainete vaheliste seoste loomiseks, siis poleks hiljem tarvis võidelda lapiku Maa teooria absurdiks või absoluutkiirusest kiiremini liikuvate rakettide ehituslike iseärasuste võimatuks tunnistamisega.
Silma võtab (positiivselt) märjaks aga see, kui sama asja viienda nurga all selgitades hüüatab muidu tagumises pingis sind tuhmi pilguga vaadanud õpilane, et „Aaa, sain aru – nii lihtne see ongi!“
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Minu arvates võiks koolifüüsikas olla tõesti paar kolm printsiipi, mida peast teada. Absoluutkiiruse printsiip, massi ja energia ekvivalentsuse printsiip, energia miinimumi printsiip … võib-olla mõni veel. Ise kordan oma õpilastele, et kui neil on gümnaasiumi lõpuks meeles, et absoluutkiirus on ligikaudu 300 tuh. km/s, teavad Newtoni kolme seadust ning Ohmi seadust, siis pole nad kolme gümnaasiumi-aastat tühja lasknud.
Kõik definitsioonvalemid (ja seda mitte ainult füüsikas vaid ka matemaatikas) võiksid aga õpilastel olla (koos tähiste ja ühikutega) vabalt kätte saadavad. Hindan faktiteadmistest palju kõrgemalt seda, et õpilane suudab ära tunda, millise probleemiga on tegu, leida selle probleemi lahendamiseks sobiva(d) valemi(d) ning nende abil probleemi lahendada.
Kindlasti ei poolda füüsikast „jutustava“ õppeaine tegemist. Füüsika kasutab objektide ja protsesside kirjeldamisel matemaatika keelt ning seetõttu on arvutusülesannete lahendamine praktiliste tööde tegemise kõrval füüsika lahutamatu osa. Olgu pigem „läbi võetavaid“ teemasid poole vähem, kuid nendele kuluv aeg poole pikem – nii saaksid õpilased midagigi jäädavat endaga kaasa võtta. Praegu ratsutame enamuse materjalist lihtsalt läbi ja siis imestame, miks usuvad inimesed, et Maa on lapik või muid sarnaseid jaburusi.
Kuidas õppisid koolis füüsikat?
Mina õppisin nii põhikoolis kui ka gümnaasiumis Jõgeval, Jõgeva Gümnaasiumis. 8.klassis oli õpetajaks Laine Kaasik, kelle õpetusest on spektri värvused eluks ajaks meeles, ning 9.-12.klassis oli mu õpetajaks Vello Mägi, kellega nüüd kolleegidena kogemusi jagame.
Koolis õppides oli füüsika alati aine, mida ma ei õppinud pähe, sest üsna õpingute alguses tekkis arusaam, et kõik õpitav on pärit meid ümbritsevast maailmast. Seetõttu peab saama loogiliselt meelde jätta ja tuletada õpitavat. Ja parim viis õppimiseks oli ikka teistele seletada, sest siis tuli ju ise materjal läbi mõelda ja iga seletusega hakkas ka ise üha paremini aru saama, millest on jutt. Seetõttu koduseid õppimisi füüsika jaoks oli vähe, vaid kui kirjalikke töid oli vaja teha, muidu vahetundides seletades klassikaaslastele õpitavat materjali.
Mäletan siiani gümnaasiumi lõpuaktust, kus õp Mägi võttis sõna ja ütles, alati oli huvitav lugeda minu ja mu klassivenna töid, sest sealt võis midagi põnevat leida. Ja nii oli, sest kui päris täpselt tol hetkel õpiku teksti ei mäletanud, siis tuli loogika alusel kohapeal teooriaid ja füüsikat luua – õnnestumine – oli häid ja oli paremaid päevi.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Meenub paari aasta tagune tund 12.klassiga. Enne jõuluvaheaega oli räägitud radioaktiivsusest ja kiirgusdoosidest rääkides saime teada, et banaan on radioaktiivne puuvili. Kevadel, üks viimastest tundidest, tuli õpilastel esitleda oma füüsikalist maailmapilti. Ja üks tütarlaps tuli banaaniga, millele olid peale kirjutatud valemid. Lugu: „Kuidas spikerdada? Kuna banaan on radioaktiivne, siis selle asetamisel lauale õpetaja ehk väldib seda pinki ning jalutab kaugemalt mööda. Ja siis ma saangi valemeid vaadata. J“
Üldiselt on toredad kõik need hetked, kui näen, et õpilastel tekkivat sädet silmas või kui neil tekivad küsimused teemal, millest räägime. Tahavad teada, kas see või teine asi toimibki nii, sest kehtib just käsitletav füüsika. Ja kõige parem õppimine ongi ikkagi vahvate ja särasilmsete noortega koostöös.
Samuti on tore arutada, miks on seelikuga talvel soojem kui vaid teksapükstega? Või kui arvutatakse Kuu tiirlemisperioodi, siis tulemuse õigsuse hindamine, kas 27 päeva sobib? Ja kellele need jõud ikka mõjuvad, kas kelgutajale nõlval või õhule 2 m kõrval?
Üks vahva seik oli mõni suvi tagasi rongiga Jõgevalt Tallinna sõites, kui sattusin istuma vastamisi noormehega, kellega tuli juttu autode ümberehitamisest ja nende sõiduomadustest. Ning pärast mõningat mõttevahetusi jäi vastasistuja järsku mõtlikuks ja küsis: „Sa oled naine. Miks sa nii palju autodest tead?“. Aga kuna juttu oli füüsikal põhinevatel nähtustel (soojuspaisumine, tuuletakistus jne), siis oli see kõik lihtsalt loogiline.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Kindlasti on enne igat kontrolltööd õpilastel tunne, et asju tuleb pähe õppida ja seda ka tehakse. Kuid see ei ole edasiviiv meetod. Jah, mõni asi tuleb mõnikord pähe õppida, sest kui üks asi on peas, hakkab meie tark aju seda seedima ning järgmiste analoogiliste tulemuste saamine on juba märksa lihtsam.
Olen aga ise seisukohal ja püüan õpetada ning anda õpilastele edasi oskust näha/tajuda õpitava teema loogikat, aru saada, miks need asjad nii on. Seostatult maksimaalselt palju igapäevaste nähtustega meie ümbert, sest just nii saame aru. Ja kui ka humanitaarklassi õpilasel läheb nägu pärast pikka pusimist rõõmsaks ja ta teavitab „Ma sain aru!“, siis elu tõestabki, et loogika on füüsikas väga oluline komponent. Valemite pähe õppimine vähetõenäoliselt (humanitaarklasside) füüsikaga seonduvat edasiõppima minejatelt ma ei nõua. Sest kes neid vajab, see peab neid nagunii meelde tuletama ja tänapäeval on infot meie ümber nii palju. Väga tähtis on oskus osata etteantud materjali kasutada. Sest isegi kui valem on peas, siis selle rakendamise oskus ei kaasne valemi teadmisega. Pähe õppimise oskust ei soovi ma kontrollida, vaid ikka ju temaatika tundmist, maailma toimimisest arusaamist.
Kuidas õppisid koolis füüsikat?
Laisalt – tegemist oli ju üsna loogilise ja minu tolle-aja teadmistega kooskõlas oleva ainega ning siis sai tunnis lulli lüüa. Kui anekdoodid mida pinginaabritega rääkida otsa said, siis lahendasime ka mõne tüdruku ülesanded ära. Otseloomulikult jagas õps peagi välja, et me igavleme ning püüdis minust ja veel mõnest olümpiaadimaterjali hakata kasvatama, kuid ma ei allunud provokatsioonile – eelistasin tüdrukute aitamist. Pinginaaber seevastu käis isegi teises linnas! edasijõudnute voorus. Gümnaasiumi osas olid ka mõned teemad, mis oli sisuliselt nii huvitavad, et lugesin isegi omal algatusel mõne raamatu läbi. Kuigi jah, tuleb pattu tunnistada, et astronoomia kursusest õnnestus mul viilida. Ja nagu Murphy seadustele kohane viis saatus mind õppima füüsikat ülikoolis ja elama Tõraverre (Observatooriumi teadusküla), kus keegi ütle sulle tere ka mitte, kui sa teleskoobi tööpõhimõtet ei tea. Nüüdseks olen siis täheteaduse algtõed omandanud elu sunnil.
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Kõige huvitavam on õpetada noori ja süüdimatuid müügimehi/naisi. Kui teile järgmine kord pakutakse tolmuimeja esitlust, kodu õhukvaliteedi kontrolli või kvantripatsit – kutsuge nad julgelt endale külla ning te ei kahetse. Iga teine/kolmas esitlus eksib omal vahval moel energia jäävuse, termodünaamika või kõige elementaarsema loogika vastu – ning toredad on need suured müügiinimese silmad kui ta lõpuks sinu seletamise peale aru saab, kuidas tolmuimeja päriselt töötab.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Jah, on! Täpselt nii, nagu remondi tegemiseks peavad kruvikeeraja ja haamer „käe sees“ olema, peavad ka lihtsam matemaatika ja tähiste süsteem peas olema. Kui mina alustasin õpetamist, siis olin kohe aasta alguses vastik ära ja lasin pähe õppida eesliidete tabelid ning tähis-nimetus seosed. Lisaks tegime vana hea „avalda täht võrrandist“ puust ja punaseks. Ülejäänud aasta sai tegeleda jutustava ainega ning klass püsis enamasti pardal, kui ma mõne valemi tahvlile kritseldasin. Vähe sellest, ma suutsin selle sõgeda laste piinamise metoodika ka maha müüa Avitale, kelle vähemalt kahes õpikus on toodud tuupimise osa kohe algusesse kokku. Kõige parem asja juures on see, et ma ise vihkan pähe tuupimist.
Kuidas õppisid koolis füüsikat?
Põhikoolis oli klassis 11 õpilast. (Tali 8-klassiline kool Pärnumaal) Viilida eriti ei saanud ja kuna füüsika meeldis, siis väga ei olnud tarvidust viilida ka. Õpetajaks oli tegelikult matemaatika õpetaja, aga ka füüsikat õpetas ta päris hästi. Keskkooli lõpetasin Nõos. Õpetajaks oli Valdo Väinaste. Sel ajal oli ka tavalises koolis küllaltki heal tasemel füüsikaõpe. Nõos sai natuke rohkem ülesandeid lahendatud. Olid ka praktikumid. Osalesin päris usinalt olümpiaadidel. Põhikoolis ka vabariiklikul. Tunnid olid peamiselt loengu vormis õpetaja suutis aine üpris hästi ära seletada. Igatahes mulle meeldisid. Meelde on jäänud, et kontrolltööd olid päris pikad ja ega eriti lahenduste kontrollimiseks aega ei jäänud. Kooliväliselt väga rohkem füüsikaga ei tegelenud. Ega maal elades selleks suurt aega jäänutki. Ega mul keskkoolis ei olnudki sellist sihti, et füüsikaga pikemalt seotuks jään. Füüsikuks aitas saada sõda Afganistanis (see on eraldi lugu).
Mis on kõige toredamad füüsikaga seotud asjad, mida oled ise teistele õpetanud?
Tegelikult on kõige raskem minul õpetamise mõttes mehaanika. Siis on õpilastel veel kõik võõras. Tegelikult saab kõike õpetada. Selleks on vaja ainult piisavalt aega ja oskust õpetada. (Vastav matemaatika peab ka muidugi selge olema.)
Küsitakse igasuguseid asju. Küsivad enamasti õpilased. Aga olen aidanud ka teisi. Hea mälestus on bio-geo õpetajatega käidud Saksamaa ekskursioonist, kus tuli põhjalikult seletada tõusude ja mõõnade tekkimist. Kuna olen tegelenud lennundusega, siis olen ka selles vallas päris palju selgitusi andnud. Viimane kord oli seotud füüsikaõpetajate CERN-is käiguga. Sattusime istuma lennukitiiva taha ja siis oli hea seletada mis on mis ja milleks.
Üks asi millega on hea inimesi testida on Newtoni seadused. Kui vähemalt ühe suudab ära seletada, siis võib täiskasvanud inimesega füüsikast rääkida. Kui ei suuda, siis tegelikult vahet ei ole, mida räägid.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Kindlasti. Kujutage ette liiklust kui liikluseeskirjad ei oleks peas. Sõidud saaksid tehtud aga…..? Või vestlust inglise keeles, kus mõlemad vestlejad piiluvad kogu aeg sõnaraamatusse... Millegipärast arvatakse, et füüsikas saab kõike järele vaadata. Nii see ei ole. Tegelikult on ka füüsika keel mille mõistmiseks peavad „tähed“ ja „sõnad“ peas olema. Kindlasti peaks peas olema valemid ja põhimõisted. Näiteks kaal, kiirendus. Loomulikult mitte sõnasõnalt, aga piisavalt täpselt. Tegelikult on nii, et kui lahendada piisavalt ülesandeid , siis valemid kuluvad iseenesest pähe.
Hiljuti oli mul 12. klassis kontrolltööks ettevalmistamise tund. Mina midagi suurt ei teinud. Seletasin natuke raskemaid kohti. Sain rahulikult õpilasi jälgida. Õpilased lahendasid iseseisvalt või siis teiste abiga ülesandeid. Vestlus toimus füüsikavõõrale täiesti arusaamatus keeles. Kasutati tähiseid, jne. Hea tunne oli. Tundsin, et minu töö ei ole asjatu olnud. Minu meelest see ongi see, millest algab füüsikaline maailmapilt. See et võib-olla need mõisted jne varsti ununevad ei olegi tegelikult tähtis. Midagi jääb ikka alles ja see mis alles jääb ongi füüsika. Selleni jõudmiseks tuleb paar aastat vaeva näha.
Kuidas õppisid koolis füüsikat?
Koolipõlves oli mul kolm füüsikaõpetajat. Põhikoolis tegime palju praktilisi töid, mis mulle meeldisid kõige enam. Vahel jäi puudu täielikust arusaamisest, aga arvutusülesannete lahendamisega tulin päris hästi toime. Gümnaasiumis püüdsin ma alati kõigest aru saada, ja see võimaldas, vaatamata suurele koormusele, õppida küllaltki edukalt. Juba gümnaasiumis võtsin osa olümpiaadidest. Füüsika polnud küll minu lemmikaine, kuna rohkem meeldisid mulle matemaatika ja keemia. Kuid tänu õpetajatele minu huvi füüsika vastu kasvas, lugesin erialast kirjandust, mis oli seotud katsetega, ise huvitusin tehnikast. Gümnaasiumis ei olnud piisavalt laboratoorseid töid, mis oleksid näitlikult kinnitanud teooriat. Ajapikku saabus mõistmine ümbritseva maailma teadmiste vajalikkusest ja neist seadustest, mis valitsevad looduses. Juba koolis avastasid klassikaaslased minus oskuse seletada materjali. Maha kirjutada ma ei lasknud, aga selgitama olin alati valmis.
Mis on kõige toredam füüsikaga seotust, mida oled ise teistele õpetanud?
Väga raske on öelda, milline füüsikateema on mõistmiseks kõige raskem. See sõltub klassist, õpilaste huvist antud teema vastu. Kuid sagedamini kutsub esile raskusi mehaanika ja elektrodünaamika. Kõige sagedamini pärivad õpilased saadud teadmiste praktilise rakendamise kohta. Vahel kutsuvad need küsimused esile tormilise arutelu klassis. Nad esitavad ise küsimusi ja ise püüavad neile läbivõetud materjali kasutades vastata. Mina esinen ainult partneri ja abilise rollis. Eriti meeldib mulle laste reaktsioon, kui nad ise kas või väikesi avastusi teevad. Nimelt see jääb neile meelde eluks ajaks. Just see teeb neile füüsika huvitavaks.
Kas koolifüüsikas on midagi, mille peab pähe õppima?
Ma arvan, et koolifüüsika peab rajama vundamendi selle mõistmiseks. Seaduste ja seaduspärasuste mõistmine, seosed suuruste vahel praktiliste tööde abil ja probleemsete ülesannete lahendamine on minu arvates põhilisteks momentideks füüsika õppimisel koolis. Valemitest pole tolku, kui sa ei tea, mis nende taga seisab. Kui sa ise leiad tee mõne valemi juurde, siis on see esimene samm mõistmise poole. Sellise õppimise protsessis jäävad põhivalemid ja füüsikalised suurused automaatselt pähe. Peamine on osata neid valemeid rakendada eri liiki ülesannete lahendamisel. Üks tähtsamatest ülesannetest on näidata meetodeid, mille abil võib nähtusi kirjeldada, samuti oskus leida tee nende mudeli juurde või rakendada valmis mudelit.
Laserite leiutamisloos on küllaga põnevust ja dramatismi. Järgneva kirjatüki autor on Henn Käämbre ning see on omal ajal ilmunud õpiku Aatom, molekul, kristall õpetajaraamatus.
Kui Charles Townes 1939. aastal lõpetas PhD kraadiga Kalifornia Tehnoloogiainstituudi (Caltechi), sai ta tööle firma Bell Telephone uurimislaborisse. Seal sai ta esialgu üsna mitmesuguseid ülesandeid. Kuid peagi tuli peale sõda, ka Belli laborilt nõuti maa sõjavõimsusele kaasaaitamist. Huvikeskmes oli sõdalaste raadiosilm – radar. Raadiolokaatorite täiustamisega tuli Townes'ilgi tegelema hakata. Tellijad nõudsid üha lühemal lainepikkusel töötavaid lokaatoreid: mida lühemad lained, seda suurem lahutusvõime (nagu mikroskoobi puhulgi). Townes oli tegev sentimeeter-laine radari loomisel. Radar sai valmis, kuid ei võtnud vedu: vee (udu, sademete, pilvede) neeldumine oli ses lainealas liiga tugev ja kustutas signaali. Kuid radaritöödest saadud ohtrad mikrolainekogemused innustasid Townesi neid kasutama aine süvastruktuuri uurimiseks raadiospektroskoopia meetoditega.
1948 avanes Townes'il võimalus siirduda tööle Columbia ülikooli. Rõõmuga võtab ta pakutud professorikoha vastu, sest "… Columbia oli enam huvitatud füüsikast, neist asjust, mis mindki huvitasid. Pealegi meeldis mulle elu ülikoolis palju enam [kui tööstuslaboris], olen ikka sinna kippunud."
Järgmisel, 1949. aastal saabub Columbiasse äsja Toronto ülikoolis promoveerunud Schawlow. Kuna temagi on huvitunud mikrolaine-spektromeetriast, satub ta Townes'i rühma. Sõlmub nende pikaajaline koostöö ja koguni sugulussidemed: Schawlow'st saab peagi Townes'i õemees. 1955 ilmub nende ühine raamat Mikrolaine-spektroskoopia. Townes meenutab Einsteini poolt juba 1916. aastal osundatud stimuleeritud kiirguse olemasolu ja murrab pead, kuidas seda rakendada molekulide uurimiseks. Siit algaski tee maseriteni ja hiljem laseriteni. Ta teab, et lühemate mikrolainete vastastikmõju molekulidega on tugevam, seega on nad paremad tööriistad spektroskopisti käes. Kuid kuidas neid tekitada? Vajalikud õõsresonaatorid olnuks valmistamiseks liiga pisikesed.
Townes tuleb mõttele kasutada kiirguritena molekule endid. Kuid talle näivad ületamatuna mõned printsipiaalsed takistused. Hiljem on ta jutustanud, et õnnelik idee tuli talle ühe nõupidamise eeli hommikul Washingtonis pargipingil istudes. Naasnud Columbiasse, paneb ta oma doktorandile James P.Gordonile ette üritada ehitada mikrolainegeneraator stimuleeritud kiirgusel. "Ma loodan, et see hakkab tööle, kuid kindel ma ei ole," sõnab Townes ülesannet andes. Hiljem värbab Townes veel appi L.Zeigeri. Tööaineks valitakse Townes'ile mitmete omaduste poolest hästi tuttav ammoniaagi (NH3) aur. Selekteerides mittehomogeenses magnetväljas välja ergastatud ammoniaagimolekulid, suunatakse need resonaatorisse, kus pannakse stimuleeritult kiirgama. Teades, et võistlejaid pole, keegi teine midagi taolist teha ei kavatse, töötatakse suhteliselt aeglaselt ja süstemaatiliselt, "doktorandi tempos".
1953 võisid nad demonstreerida töötavat lämmastikmaserit. Stimuleeritud kiirgus oli rakkesse pandud. Umbes samal ajal said ammoniaakmaseri tööle ka Bassov ja Prohhorov Moskvas. Kuid kõik mõistsid, et see pole kaugeltki piir. Võimalik on stimuleeritud kiirgus tööle panna ka infrapuna ja nähtavas spektripiirkonnas.
Schawlow oli vahepeal siirdunud firma Bell laboritesse. Nad hakkavad jälle tihedamini kohtuma Townes'iga, kui viimane võtab 1956 vastu professoritöö kõrval ka Belli labori konsultandikoha. Vestlustes selgub, et mõlemad mõtlevad pingsalt võimaluste üle kvantgeneraatorite loomiseks spektri optilises piirkonnas ja otsustavad jõupingutused ühendada. Tublisti teeb muret vajaliku üliminiatuurse resonaatori probleem. Schawlow leiab lahenduse: õõsresonaatori asemel tuleb kasutada avatud resonaatorit, ära jättes kõik teised seinad peale kahe vastastikuse, mille vahel siis tekivad võimendatava/genereeritava kiirguse seisulained. Teisisõnu – jutt on laseri peeglipaarist. Samalaadne ja enamvähem samaaegne mõte tuleb ka A.Prohhorovil Venemaal.
Nõndaviisi valmib 1958 Schawlowi ja Townesi ühisartikkel laseri teoreetilistest ja tehnilistest alustest, mis ilmub Physical Review detsembrinumbris. Sellest hetkest arvestatakse tihti laseri vanust, kuigi töötavat laserit "rauas", tegelikkuses ei olnud veel olemas. Ühtlasi annavad nad sisse patenditaotluse, mis kahe aasta pärast, 1960 rahuldatakse. Samal aaastal, 16. mail saab Th. Maiman esimesi välkeid maailma esimeseslt, rubiinlaserilt. Kuid siinkohal oleks kohane anda sõna sündmuste vahetule osalisele, Dr. Ammon Yariv'ile Caltechist.
1998 korraldas USA firma Lucent vastuvõtu laseri 40nda sünnipäeva puhul, tähistamaks Schawlow' ja Townes'i artikli ilmumise ümmargust tähtpäeva. Kohal olid ka Schawlow ja Townes ise. Dr Amnon Yariv Kalifornia Tehnoloogiainstituudist jagas seal oma mälestusi.
"1960ndal aastal ma liitusin väikese uurimisrühmaga Belli laboris. Schawlow' ja Townes'i artikkel oli ilmunud juba kaks aastat tagasi, ja kogu maailmas käis äge rebimine: kes saab valmis esimeses laseri.
Belli juures mässas sellega kolm-neli rühma: Derrick Scoville, C.G.Garrett, Ali Javan ja veel mõned. Igaüks rühkis edasi omamoodi. Kes saab esimeseks? Mis seal salata, me vedasime kihlagi.
Suvel läksin naise ja äsjasündinud beebiga puhkusele San Diegosse. Saime nädalakese seal olla, kui helistas mu boss Jim Gordon: "Kuule, üks kutt Hughesi laborist Malibus ütleb, et ta on teinud laseri. Kas sa võiksid võtta firma kulul päevakese ja kihutada Malibusse? Vaata, mis seal's päris on." Öeldud, tehtud.
Tegin siis selle kolmetunnise otsa ära ja otsisin Ted Maimani välja. Ta näitas mulle oma esimesi tulemusi, ise ilmselt kõvasti närvis. Aimasin, et ega ta endas päris kindel olnud. Aga kui te kuulutate, et olete teinud maailma esimese laseri, eks ta ajab närvi küll. Ja talle oli nii kangesti julgustust vaja.
Noh mulle tundus, et tal oli tõepoolest laser käes ja seda ma talle ka ütlesin. Siis helistasin Jim Gordonile tagasi ja ütlesin: "Jim, mulle paistab, et me oleme võidujooksu kaotanud."
Kuid ega me kaotusega leppida tahtnud. See on nii Belli rahva moodi. Seletasime: "See on vaid impulsseade. Mis see ka ära ei ole." Kuid eks te tea, kui palju impulsslasereid sest ajast peale on tehtud ja tööle pandud.
Oma kvantelektroonika tudengitele jutustan ma alati sellest õppetunnist: meie töötasime laseri loomiseks, kõvasti, meil oli taga tugev tehniline abiteenistus, aga meil oli mõttes ainult pidevalt kiirgav alalislaser. Ja meil ei tulnud kordagi pähe üritada teha impulsslaserit, mis on muidugi palju lihtsam.
Aga Ted Maiman, töötades Hughesi laboris üksipäini, tegelikult vastu oma šefi tahtmist, oskas leida teise, edukama lähenemise. Niisiis meil oli, mida temalt õppida.
Need olid väga erutavad päevad, sest peaaegu kõik, mis me tegime, oli tollal uus ja pikemata trükis avaldatav".
Maimani erutus saab eriti mõistetavaks, kui arvestada, et tollal oli tal ainsaks tõestuseks, et laseri genereerimislävi oli ületataud, spektri kiirgusjoone järsk kitsenemine. Mõistnuks ta ereda valguslaigu laserist lihtsalt seinal suunata, olnuks see palju näitlikum ja kindlam argument.
Jääb vaid lisada, et 10. detsembril 1964 ulatas Rootsi kuningas aastakümnetega välja kujunenud rituaali kohaselt Bassovile, Prohhorovile ja Townes'ile Nobeli preemia kuldmedalid ja sertifikaadid. Preemia formulatsioonis on öeldud, et see anti "teedrajavate tööde eest kvantelektroonikas, mis viisid maseri/laseri põhimõttel rajanevate generaatorite ja võimendite loomisele". 17 aastat hiljem, 1981 sai Nobeli ka Schawlow, "teenete eest laserspektroskoopia arendamisel". "Lõpuks tasuti ammune võlg", ütles seepeale Townes.
Laseri lugu jääks aga ülekohtuselt poolikuks, kui me ei mainiks veel üht Ameerika leidurit, Gordon Gouldi (s. 17.07.1920). Columbia ülikooli assistendina puutub Gould kokku Townesiga ja suure leiundusfännina hakkab samuti juurdlema laseri loomisvõimaluste üle. Ööl vastu 10. novembrit 1957, otsekui äkilise ilmutuse ajel, leiab Gould lahtise resonaatoriga laseri printsiibi, visandab tema konstruktsiooni ja näeb ette rea tema rakendusvõimalusi tööstuses. Ta notariseerib sedamaid oma märkmed, kuid ekslikult arvates, et patenteerimiseks peab tal olema töötav laseri prototüüp, esitab avalduse alles 1959. Muidugi hilja: Schawlow' ja Townes'i artikkel on juba ilmunud ja patenditaotluski sees. Järgneb raudsete närvidega Gouldi ja tema toetajate 30-aastane patendisõda, milles on ajuti helgemaid hetki, kuid enamasti musta lootusetust. Siiski, 1985-86 saab ta lõpuks rea patente laseri teistel leiutajatel kahe silma vahele jäänud aspektide peale ja on nüüd rikas mees: teiste patendid on juba aegunud, tema honorarid alles jooksevad. Selge, et Gouldi taotlused äratasid nii laseritööstureis kui ka teistes leidureis raevu ja laseriloo tavakäsitlustes teda ei mainita. (Lähemalt vt H.Käämbre, Kolmekümneaastane patendisõda, Luup nr 13(122), 21.07.2000, lk 22-23.)
Laseri leiutamislugu on suurepärane näide alusuuringute praktilistest viljadest. Mitte keegi ei planeerinud ja kavandanud "projekti" (nagu nüüd igast asjast kombeks öelda) nimega "Ülivalgusallikas laser". Schawlow meenutab: "Oletasime, et tal võiks olla mõnesuguseid rakendusi sidepidamises ja teadustöös, kuid muid rakendusi ei tulnud meil pähegi. Kui neid olnukski, oleks nad meid vaid kammitsenud ja loonud tarbetut pinget."
Ja Townes lisab: "Milline uurimisplaneerija, kavandades ereda valgusallika loomist, oleks alustanud molekulide mikrolaineuurimisega? Või milline tööstur, otsides uusi lõike- ja keevitusriistu, või arst, soovides uut kirurgiainstrumenti, oleks õhutanud uurima mikrolainespektroskoopiat? Kogu kvantelektroonika on tõeliselt krestomaatiline näide sellest, kuidas kõige laiema rakendusväljaga tehnoloogia kasvab ootamatult ja ettekavatsematult välja alusuuringutest."
Suurte ja pöördeliste, kogu teaduse paradigmat pea peale pööravate avastustega pole tihti kerge harjuda isegi suurtel meestel. Ch.Townes kirjeldab om kohtumist Bohriga 1954. aastal Kopenhaagenis. Bohr päris temalt, millega ta tegeleb. Townes kirjeldas talle maserit ja selle ülimalt ainusageduslikku kiirgust. "Aga see pole ju võimalik!" hüüatas Bohr. Townes püüdis teda veenda, kuid toetudes Heisenbergi ebatäpsuse relatsioonile, jäi Bohr kindlaks, et kui molekulid lipsavad maseris läbi resonaatori suure kiirusega, peavad nende kiirgusjooned olema laiad. Kui Townes ajas ikkagi oma, Bohr taandus: "Nojah, võibolla teil on tõesti õigus." Kuid Townes'ile jäi ikkagi mulje, et see oli vaid Bohri tavaline viisakus, veenda teda ei õnnestunud. Väga sarnane jutuajamine oli Townes'il mingil banketil ühega kompuutrite isadest, ungari matemaatiku John von Neumanniga. Üksnes selle vahega, et mõne aja pärast loovis Neumann Townes'i juurde tagasi ja sõnas: "Jah, teil on ikkagi õigus." Tema ümberveendumisest andis kõige kindlamat tunnistust see, et tema järelejäänud paberite hulgas leidus kirjakontsept Edward Tellerile, kus ta arutleb võimaluse üle luua infrapunalaserit pooljuhtidel, mida tugevasti pommitatakse neutronitega.
Ääremärkmeid ühe vana vaidluse kohta.
Ülo Lepik
Koos Eesti iseseisvumisega 1918.a. toimus koolides ja ülikoolis üleminek eesti õppekeelele. Suureks probleemiks oli siin eestikeelse teadusterminoloogia puudumine. Paljud õppejõud lõid omi termineid, mis tänapäeval tunduvad üsna kummalistena, nagu näiteks “ärakargamise vägi” (elastsusjõud J.Vilip), “sissekukkumise vinkel” (langemisnurk, J.Vilip), “kolmnurga nukid ja joonejupid” (J.Sarv), “valgusel on seitse värvi ja iga värv on ise karva” (J.Vilip). Vajadus teadustermiloogia korrastamiseks oli ilmne ja sellele pöörati 1920-ndatel aastatel ka suurt tähelepanu.
Üheks vaidlusobjektiks oli küsimus , kuidas tõlkida eesti keelde saksakeelset terminit “Kraft” – kas tung või jõud. Kui ma tõstatan selle küsimuse, siis pole minu eesmärgiks midagi tagasi pöörata, vaid tutvustada ja kommenteerida mõningaid seiku selles vaidluses. Alljärgnevad andmed põhinevad olulises osas jutuajamistele dots. J. Langiga, kes osales selles diskussioonis ab ovo.
Juhan Langu andmetel toimus 1920-ndate aastate alguses Eesti füüsikaõpetajate kongress (täpse toimumisaja olen kahjuks unustanud), kus põhjalikult kaaluti mõistete “tung” ja “jõud” sobivust. Kongress asus seisukohane, et ainulubatav termin on “tung”. Peamiseks argumendiks oli siin, et eesti keeles on terminil “jõud” võimsuse tähendus (näit. elujõud, jõujaam, hobujõud, elektromotoorne jõud jne.) . Mitmetes keeltes on eristamiseks eriterminid : saksa keeles “Kraft” ja “Stärke”, inglise keeles “force” ja “power”. Erinevad terminid puuduvad vaid prantsuse ja vene keeles (“sila” tähendab nii “jõudu” kui ka “tungi”). Miks me peaksime oma keelt vaesestama jättes ära paralleeltermini!
Termin “tung” oli Eestis ainuvalitsejaks kuni 1941.aastani ja tõenäoliselt ka Saksa okupatsiooni perioodil 1941-44. Alates 1945.aastast, mil hakkas kehtima Vene võim, toimus üleminek vene koolides kasutavatele füüsikaõpikutele. Et vene keelest eriharidusega tõlkijaid ei jätkunud, siis see töö anti sageli juhuslikele inimestele, kes polnud eriti kursis füüsika terminoloogiaga. Nad tõlkisid vene keele termini “sila” eesti keelde “jõuna “. Nii see levis koolidesse ja võeti mõne aja möödudes kasutusele ka Tallinna Polütehnilises Instituudis. Tartu ülikool jäi “tungi” juurde kuni 1970.aastani. Märgime veel, et füüsika õpetajate kongressi otsust 1920-ndatest aastatest pole kunagi ära muudetud.
Järgnev seik on pärit dots. Langilt. 1960-ndatel aastatel (täpset aeg ei mäleta), kutsuti Tallinnas prof. A.Humala juhtimisel kokku nõupidamine tungi ja jõu küsimuses. Tartu esindajana kutsuti sinna J.Lang ,kes pidi esitama oma argumendid “tungi” kaitseks. Lang valmistus ettekandeks põhjalikult ette. Pärast ettekannet aga mingit diskussiooni ei tekkinud, ka ei lükatud J.Langi väiteid ümber. Ainus sõnavõtt olevat olnud prof. Humalalt, kes olevat öelnud, et tungi ei tohi kasutada juba sellepärast, et vanarahval on ütlus:”Kui tunned tungi tulevat , siis jookse metsa poole!” Et nõupidamisel olid peale Langi kõik teised “jõumehed”, siis oli otsus ettearvatav.
Kolimise, remondi või mööbli nihutamisega tuleb mõnikord kapi alt või põrandaliistu tagant välja paberitükk, mis võib äratada armsaid mälestusi aastakümnete tagant.
Paberi teisel küljel on kirjas kontrolltöö tulemused, seal on ka kuupäev, 6. mai 1974. Tore on märgata, et kuigi elu on palju muutunud, on siiski üht-teist jäänud kestma ka uuel sajandil.
Nimesid nimetamata (isikuandmete kaitse seadus), kontrolltöö tulemused on keskmised. Suurepäraseid (5+) töid ei olnud või koonerdas õpetaja nii ilusate hinnetega. Kuus õpilast pidid ilmselt lootma järeltööle. Kas nad seda tegid, sellest ajalugu esialgu vaikib ja võib-olla see nii jääbki. Kahtedele plusse-miinuseid ei pandud ja ühega kedagi ei hinnatud. Kaks õpilast puudusid ja ühele tuli teha märkus kontrolltööde vihiku unustamise pärast, aga hinne oli tal sellele vaatamata neli.
Sander Muhu, tuletõrjeajoloo uurija, PM23.12.2015
50 aastat tagasi puhkes tulekahju Tartu ülikooli peahoones. Hävinud aulast on üsna palju kuuldud. Kuid seni ei ole räägitud sellest, kes ja kuidas tulekahju avastas ja mida nägid kohale kutsutud tuletõrjujad. Sündmuse kohta levib tänaseni palju linnalegende, mis paraku ei vasta tõele, kirjutab tuletõrjeajaloo uurija Sander Muhu.
Esmaspäev, 20.detsember 1965. aastal möödus Tartu ülikooli peahoones tavapäraselt. Õhtul kell 19.30 algas aulas moskvalanna Isabella Petrosjani (26) viiulikontsert, mida oli nautima tulnud umbes 40 inimest. Viiulihelide sekka kostus saali kõrvalruumis toimuva kooriproovi lauluhääli. Enne kella kaheksat hakkas ootamatult esimese korruse lõpus üks keskkütte radiaator lekkima. Kütjad üritasid veevoolu peatada, kuid tulutult. Ei jäänud muud üle, kui süsteemist vesi välja lasta.
Kella 22.00 ajal tuli tööle peahoone valvur Helmi (56). Umbes 23.30 saabus santehnik katkist radiaatorit üle vaatama, parandamine otsustati ette võtta hoopis hommikul ja läks peagi koju ära. Nii jäid peale keskööd majja vaid valvur ja katlakütja. Valvur istus oma putkas, mis asus peauksest sisenedes kohe paremal pool ja õmbles. Katlakütja Felix (48) oli keldris katlaruumis ja luges öösel raamatut.
Kell 3.45 helises äratuskell ühes Kalevi tänava korteris. Pereema Erna (40) oli novembrist asunud tööle ülikooli keeltemaja (Ülikooli tn 18a) kütjana. Tema ülesandeks oli hoolitseda selle eest, et ruumid oleksid kella kaheksaks köetud. Nii pidi ta kütmist alustama juba enne koitu, 3-4 ajal. Varajasest tõusmisest ei pääsenud ka pojad Enn (18) ja Allar (14). Nemad aitasid emal puid kanda. Umbes paarikümne minuti pärast astusid nad härmas tänavale ja ees ootas 1,1 kilomeetri pikkune jalutuskäik peahooneni.
Linn oli udune ja külm. Keemiahoone (Jakobi tn 2) nurga juurde jõudes oli tunda õhus nõrka suitsu lõhna. Jõudnud peahoone ette, käskis Erna poegadel minna keeltemajja ja astus ise sammaste vahelt ukseni ning andis kella.
Mõni minut enne uksekella oli valvurit ehmatanud tugev mürtsatus. Helmi oli toolilt püsti tõusnud ja läinud koridori uudistama – suur kell näitas seinal 3.45. Nüüd avas ta ukse ja Erna sisenes valgustatud vestibüüli. Ka sees oli tunda suitsu lõhna ja seepeale küsis ta valvurilt, et mis neil lahti on. Valvur kehitas vaid õlgu ja ütles, et tema küll siin mingit lõhna ei tunne. Siis hakkas Erna kirjutama oma nime tööletuleku registreerimise raamatusse. Selgus, et ta oli sel hommikul esimeseks tulijaks. Saabumisaja märkimiseks vaatas ta koridori seinal asuvat suurt kella. See näitas endiselt 3.45. See ei saanud ometi õige olla - peale neljat oli ta ju kodunt väljunud, kell pidi olema seisma jäänud! Valvur aga vaidles vastu, et kell ei ole seisma jäänud. Erna mõtles, et äkki oli siis noorem poeg hoopis kodus kella valeks keeranud ja nii ongi ta varem kohale jõudnud. Raamatusse märkis ta tööletuleku aja peahoone kella järgi.
Suurt kella vaadates oli ta märganud suitsu ja juhtis valvuri tähelepanu sellele: «Ei tea, kas see on minu silmadest, kuid sinakas suitsuvine on koridoris». Valvur vastas selle peale, et keskküttest ajavat suitsu sisse. Erna astus majast välja ja valvur järgnes talle. Mõlemad seisatasid maja ees ja vaatasid ülespoole. Nüüd oli näha, et ka katuse paremal pool asuvalt küljelt tuli kõvasti suitsu. Valvurile ütles ta, et «eest korstnast suits ei tule, vaid tuleb tagantpoolt». Suitsu tuli hooti, see pani Erna omaette mõtlema, et jätab täna need ahjud kütmata, mis tuulise ilmaga suitsu sisse ajavad. Kahtlustada ta midagi ei osanud ja seadis sammud keeltemajja ahjusid kütma.
Valvur läks sisse tagasi. Nüüd tundis ka tema peahoones suitsulõhna ja läks alla kütteruumi uurima, kas see äkki sealt ei tule. Kell oli siis umbes 4.30. Katlakütja Felix (48) tuli koos valvuriga üles vestibüüli ja märkas samuti kerget suitsuvinet ning tundis puupõlemise lõhna. Nad läksid peauksest välja ja nägid, kuidas keskkütte korstna juurest ajas suitsu mööda katuse äärt alla. Katlakütja arvas, et suits tuleb keemiahoonest. Nüüd läksid nad läbi maja hoovipoolse ukseni, valvur keeras selle lukust lahti ning nad astusid hoovi. Õpperaamatukogu (endine ülikooli kirik) kohalt vaadates oli aga juba näha, kuidas teise korruse vasakult kolmandast aknast ehk dotsent Miti tööruumist paistis tugev punane tulekuma. Kuma paistis poole aknani ja jäi mulje, nagu põleks ruumi sisemine sein. Teistes akendes kuma ega suitsu näha ei olnud.
Mõlemad jooksid sisse, et tuletõrjesse helistada. Valvur valis telefonil 01, kuid ei saanud ühendust. Seejärel valis ta haldusprorektori abi Osvald Mägi (43) numbri ja teatas, et ülikool põleb. Osvald uuris, kas tuletõrje on välja kutsutud ja kas haldusprorektorile on helistatud. Valvur seletas, kuidas ta on helistanud tuletõrjesse, kuid pole tuletõrjet kätte saanud. «Käskisin tal uuesti helistada». Osvald riietus kähku ja asus pooljoostes ülikooli poole teele.
Väljakutse
Kell 4.37 helises Tartu tuletõrje maleva dispetšeri laual telefon ning naisterahva närviline hääl teatas, et ülikooli peahoones on suits ruumides. Põlemise asukohta ta öelda ei teadnud kuid palus kiiresti välja sõita. Ülikooli peahoone kuulus objektide hulka, millele tulekahju teate korral antakse kohe kõrgendatud väljakutse. Dispetšer hakkas tegutsema vastavalt juhenditele. Andis alarmsignaali linna kutselise tuletõrje vahtkonnale, helistas kahele vabatahtlikule komandole, tuletõrje juhtkonnale, miilitsasse ja julgeoleku komitee korrapidajale.
Tartu kutselises tuletõrjekomandos (asus peahoonest u 900 m kaugusel) Kalevi tänaval kostus pikk sireen (tähendas väljakutse nr.2). Mehed riietusid kiiresti ja minuti pärast avanesid garaažiuksed ja kaks tuletõrjeautot 12-liikmelise meeskonnaga sõitsid välja.
Umbes 4.42 jõudsid autod peahoone ette. Ülikooli esiküljel põlemist näha ei olnud, kõik aknad olid pimedad, vaid katuse kohal oli näha suitsu ja õhus oli tunda suitsu lõhna. Vahtkonna ülem, jaokomandörid ja kaks tõrjujat läksid majja sisse. Alumisel korrusel kohtasid nad «üht kohkunud vanaeidekest», kes juhatas nad teisele korrusele ühe ukse taha, kus sees pidi tuli olema. Uksed olid aga lukus ja ülevaadet põlengu ulatusest ei saadud. Siis kostus alt hüüe: «Õuest on tuli näha!»
Mehed jooksid kiiresti välja ja nägid, kuidas kahest teise korruse aknast käisid tuleleegid välja.
Vahtkonna ülem andis korralduse esimesel masinal sõita maja teisele küljele hoovi ning teisel masinal asuda veevõtukohale ehk hüdrandile. Sidelane andis raadio teel dispetšerile korralduse saata välja kõik jõud (väljakutse nr.3), st appi tulid veel neli vabatahtliku komandot, raudtee ja sõjaväelennuvälja tuletõrje kokku seitsme autoga.
Meenutab Tartu õlletehase vabatahtliku komando ülem Ferdinand Taškin (62): «Õlletehases asub üks tuletõrjemasin, mis on komplekteeritud tehase vabatahtlike tuletõrjujatega. Kord on selline, et vajaduse korral antakse tehase väravavalvesse telefoni teel teade tulekahjust, siis antakse sireeniga häire. 21.detsembri hommikul kuulsin häiresignaali kella 4.45 ajal. Jooksin kiiresti Õlletehasesse. Kohale tulid veel kolm meest, kellega sõitsime peahoone juurde. Kahjutule kohalt lahkusin kell 14 ajal, siis sõitsime tehasesse ja saatsime uue vahetuse.»
Mööda redelit anti veejoad teise korruse akendesse. Kohale saabunud vabatahtlikud juhatati voolikuliiniga füüsika-matemaatika teaduskonna dekanaadi ukse taha «Vastu paiskus tihedat suitsu, mis tungis silma ja kurku, pöördusin kohe köhides tagasi, märgates siiski lahtist tuld järgmise ruumi ukseavast» kirjeldas nähtud haldusprorektori abi Osvald Mägi, kes parasjagu oli tuletõrjujad põlevasse ruumi saatnud. Tuli oli lae läbi põletanud ja pikad leegid tungisid välja juba kolmanda korruse akendest ning ulatusid räästani. Mööda keerdtreppi üritati pääseda pööningule, kuid see oli tuld täis.
Tulemöllu peatamine oli Tartu tuletõrjele tõeliseks katsumuseks. Leegid võimutsesid kolmel korrusel, nendest jagusaamiseks nappis jõudu – puudus redelauto kõrgustes töötamiseks, puudusid hingamisaparaadid, ei olnud piisavalt voolikuid, kustutusvett napis, sest veevõtukohad asusid hoonest kaugel, ka tuletõrjujaid oli vähe. Piimaautod tulid vett vedama.
Umbes poole kuue ajal langes sisse aula lagi koos katusega. Sellega küll põlemisala suurenes, kuid andis kustutajatele parema ligipääsu tulele. Paakautosid tuletõrjel ei olnud, nii ei jäänud muud üle kui paluda piimakombinaadist appi veeveoks tsisternautosid.
Evakueerimine
Olukorda kirjeldab eesti keele kateedri juhataja prof Arnold Kask: «Jõudsin ülikooli umbes kella 6 paiku või veidi peale seda. Et elektrit ei olnud, siis olid alumised ruumid pimedad. Ainult valvuril oli koridoris küünal. Tormasin kohe alumisel korrusel olevatesse kateedri ruumidesse: vastu tuli siit vingu ja auru, laest ja korstnat pidi jooksis ruumi ülevalt sooja vett.
Inimesi peale tuletõrjujate oli peahoones vähe: koridoris olid rektor Feodor Klement, prorektor Viktor Simm, ohutustehnika ala õppejõud Valdek Ritslaid ja veel paar inimest. Lootsin, et Ritslaiult saan juhiseid murdekogude ja aparatuuri evakueerimise kohta, kuid tal nähtavasti ei olnud selget ülevaadet olukorrast. Püüdsin selgitada, kas on võimalik väärtuslikumaid kogusid õuel asuvasse raamatukoguhoonesse viia, kuid kõik uksed olid kinni. Õnneks sain õuel olevalt tuletõrjejuhilt näpunäiteid varade päästmise kohta. Nimelt avaldas ta kindlat lootust, et tuletõrje suudab ülikooli peahoone tiibu kaitsta ja et varade väljaviimiseks tulest haaratud hoone keskosast on kõige parem neid vedada rektoripoolsesse tiibhoonesse.
Vahepeal jõudis ka professor Ariste kohale, ja et tal enam korda ei läinud pääseda meie kateedrite 3. korrusel olevasse ruumi, mis oli tuld täis, siis hakkasime alumisel korrusel olevatest ruumidest oma materjale süles vedama koridori teise otsa, klassikalise muinasteaduse muuseumi ukse taha. Esialgu oli vedajaid vähe, kuid peagi tuli rohkesti üliõpilasi appi ja siis läks materjalide väljavedamine juba kiiresti.
Kõige suuremaks raskuseks algul oli küünalde puudumine. Et kateedri ruumides üle kinga ulatus sooja vett, põrandal oli ja laest vahetpidamata vett kaela langes, see ei takistanud tööd. Peagi saime klassikalise muinasteaduse muuseumi ruumi uksed lahti ja hakkasime oma materjale sinna vedama, kuna teaduskonna raamatukogu materjalid keldrisse suunasime. Üliõpilastest moodustati ahelikke ja teaduskonna raamatukogugi läks korda tule- ja veeohust päästa.»
Tulekahju saadi kontrolli alla kell 8.40 ja likvideeriti päeval kella kaheks, kuid järelkustutustööd kestsid veel järgmise päeva õhtul kella kuueni. Ühtekokku olid põlengut kustutamas 22 tuletõrjeautot ligi 100 tõrjujaga.
21.detsembri öösel puhkenud tulekahjus sai tugevasti kannatada peahoone keskosa. Täielikult hävines pööning, katus, aula ja sellega külgnenud teise ja kolmanda korruse ruumid: füüsika-matemaatikateaduskonna dekaani kabinet, üldfüüsika kateedri üldpraktikumi ruumid, eksperimentaalfüüsika praktikumi ruumid, eesti keele kateedri ja soome-ugri kateedri ruumid ning seminari raamatukogu, riigi ja õiguse ajaloo kateedri, tsiviilõiguse ja –protsessi kateedri ning riigi- ja haldusõiguse kateedri ruumid. Hävinesid ka nendes ruumides olnud teaduse ja kultuuriväärtused ning sisseseaded. Peahoone põrandapinnast hävitas tuli umbes 900 ruutmeetrit, lisaks said vee- ja suitsukahjustusi umbes 2500 ruutmeetrit.
Tulekahju põhjus
Tulekahjuekspertiisi käigus tehti kindlaks, et tuli sai alguse teisel korrusel asunud üldfüüsika kateedri ilma akendeta ruumi põrandaaluses kaablikanalis tekkinud sädelusest. Tulekahju oli alguse saanud mitu tundi enne selle avastamist - juba südaööd paiku. Esialgu, kui hapniku juurdepääs oli väike, arenes tulekahju aeglaselt. Valvurit umbes kella 4.20 paiku ehmatanud mürtsatus ei olnud mingi plahvatus, vaid selleks hetkeks oli praktikumi ruumi lagi tulest sedavõrd kahjustatud, et kolmandalt korruselt kukkus alla ahi. Peahoones puudus tuletõrjesignalisatsioon, valvuril ei olnud kohustust teha hoones ringkäiku, seetõttu tulekahju avastati alles siis, kui see oli paisunud väga suureks.
Tulekahju oleks võinud olemata olla...
Kolm päeva varem oli praktikumi kõrval asuvas dekaani ruumis tunda põlemise lõhna. Kohale kutsutud haldustöötajad käisid ruumid läbi, kuid mindagi kahtlast ei tuvastanud. Süttimisprotsess kulges põranda all aeglaselt ja ilmselt tol korral see õhupuuduse tõttu kustus. Kui siis oleks suudetud põranda all toimuvale jälile jõuda, oleks see tulemöll ära hoitud.
Artikli kirjutamisel on kasutatud riigiarhiivi ja Eesti Tuletõrjemuuseumi materjale.
H.Treimann
See pole mäng. Teaduslik uurimistöö õppeprotsessi lahutamatuks osaks.
Artikkel ilmus ajalehes Rahva Hääl 11.juunil 1963.
Allikas: http://www.to.ee/to50/instrumendid_ja_eksperimendid_.htm
Esimesest Tõraveres valmistatud kosmose-teleradiomeetrist SFM-4 oli juttu peatükis 2.2.2. Seitsmekümnendate aastate algul arendati tolleaegses Eesti Teaduste Akadeemia Astrofüüsika ja Atmosfäärifüüsika Instituudis (Charles Villmann, Olev Avaste, Uno Veismann, Kalju Eerme) välja kosmiline teleradiomeeter “Mikron”, millega sai mõõta kosmoselaeva pardalt kaugete objektide (atmosfäärikihid, helkivad ööpilved, maapind, Kuu) heledust lähedases infrapunases spektrilõigus (neli spektririba lainepikkuste vahemikus 1 - 3 μm). Et sel ajal Eestis puudusid veel kogemused kosmose-aparaadiehituse alal, siis konstruktoritöö ja valmistamine jäid kahele Venemaa suurfirmale: optikaploki tegi valmis LOMO Peterburis ja elektroonikaploki pani kokku “Kometa” Moskvas. Esimene neist firmadest oli tuntud juba tsaariajast ja kõigi Tõravere teleskoopide valmistaja, teises oli varasematel aastatel välja arendatud NLiidu ülisalajane õhukaitsesüsteem Berkut.
ikron kujutas endast nelja 50-mm läbimõõduga objektiiviga varustatud teleradiomeetrit, mille vaatenurk oli umbes 20 kaareminutit. Kokku kaalus aparatuur umbes 20 kg. Mõõdetavale objektile suunamist ja/või skaneerimist sai toimetada vaid kogu kosmoseaparaati pöörates. Edasi seati eesmärgiks atmosfääri heledusprofiilide massiline ülesvõtmine laiemas spektraalpiirkonnas, milleks 1978-1984 arendati välja ja valmistati seeria teleradiomeetreid FAZA (Olev Avaste teadusprogramm, Uno Veismanni aparatuurikontseptsioon). Ka sellel instrumendil oli neli objektiivi, kuid läbimõõduga 100 mm ja kiirguse jaotamisega kaheks iga objektiivi taga . Nii osutus võimalikuks korraga mõõta 8 lainepikkusel, mis olid määratud valgusfiltritega vahemikus 0,3 – 2,8 μm. Optikaplokil oli skaneerimisajam, millega vaatesuunda sai üles-alla kõigutada 4o30´ võrra. Ka selle teleradiomeetri optikaploki konstrueeris ja valmistas LOMO, elektroonikaploki arendustöö ja valmistamine toimusid TA SKB Tartu filiaalis (Eik Mölder, Rein Kull, Avo Hilpus). Signaalide võimendites rakendati Mart Mini (Tallinna Tehnikaülikool) originaalset sünkroondetekteerimise skeemilahendust.
Teadusaparatuur anti üle tootmiskoondisele Energia, mida hüüti ka Koroljovi firmaks. Viimased katsetused toimusid Bajkongõri kosmodroomil, mida salastamise huvides nimetati siis lihtsalt polügooniks. Lähimaks asustatud punktiks oli tegelikult Sõrdarja jõe ääres Tjuratam ning kasahhide Bajkongõr paiknes hoopis 370 km kaugusel. Katsetajatel Leo Märtinil, Rein Kolgil, Margus Sisaskil ja Priit Vürstil tuli palju taluda Venemaa asutustes valitsevat bürokraatiat, lahendada alatasa tekkivaid tehnosüsteemide kooskõlastamise probleeme ning üle elada olmeraskusi. Lendudele eelnevat kosmonautide väljaõpet ja instrueerimist viisid Tähelinnas läbi Charles Villmann ja Kalju Eerme.
Tolleaegses Astrofüüsika ja Atmosfäärifüüsika Instituudis tegeles kosmoseeksperimentide ettevalmistamise ja tehnilise tagamisega 1975-1985 enam kui paarkümmend inimest Charles Villmanni ja Uno Veismanni juhtimisel, moodustati elektroonikalaboratoorium (Leo Märtin, Kalev Toots, Gunnar Raadi, Rein Rätsep), sõlmiti miljonitesse rubladesse ulatuvaid lepinguid. Omaette probleemiks, millest arenes terve tegevusvaldkond, oli aparatuuri kalibreerimine. Gradueerimiseks möödapääsmatute etalonkiirgurite osas oli NLiidu seisund halb, puudus ka nende kasutamise metoodika teleradiomeetrite jaoks. Nii tuli välja arendada optilise radiomeetria etalonbaas ja läbi viia vastavad uuringud. Viimastest moodustus seda suunda juhtinud Teofilus Tõnnissoni dissertatsioon ning kujunes välja optilise radiomeetria laboratoorium. Antud valdkonnas tehtud jõupingutused leidsid tunnustamist Moskva juhtivas metroloogiainstituudis VNIIOFI ning seda külastanud USA metroloogiainstituudi NIST esindajad Robert Saunders ja Klaus Mielenz tegid visiidi ka Tõraveresse. Sõjalennuvälja tõttu nn. kinnise linna staatuses seisnud Tartus oli see sündmus peaaegu ime.
Teatavasti olid eelmise sajandi teisel poolel NLiidu kosmoseorganisatsioonid koondunud kahe keskuse ümber: Koroljovi (järglaste) firma ja Tšelomei firma. Kuuekümnendatel aastatel tuldi orbitaaljaamade loomise juurde mõlemas firmas. Vladimir Tšelomei alustas varem ja nimetas oma jaama sõjalis-luureotstarbeliseks orbitaaljaamaks Almaz (vene k. teemant), mõne aasta pärast hakkas samalaadse projekti DOS (dolgovremennaja orbitalnaja stantsija) kallal tööle ka Koroljovi firma, mida siis juhtis juba Vassili Mišin. Viimane seadis aga esiplaanile Kuu-ekspeditsioonide ettevalmistamise ja kuna Tšelomeilgi olid tekkinud muud huvid, siis takerdus projekteerimine korduvalt. Töö koordineerimiseks moodustati asutustevaheline komisjon, kuhu kuulusid ka eestlane Arvid Pallo Koroljovi firmast ja tema noorem vend Vladimir Pallo Tšelomei juurest. Mõlemad firmad viisid projektid lõpule ja ehitasid hulga jaamu valmis, valitsuse otsusega anti aga kõigile edukalt startinud orbitaaljaamadele nimeks Saljut. Nõukogude Liidu kosmonautika ametlikus ajaloos on fikseeritud seitse seda tüüpi orbitaaljaama, ent oli veel ebaõnnestunud starte ja mõned jaamad jäid kasutamata; nii ei olegi selge, mitu jaama firmad üldse valmistasid (niipalju on teada, et üle 20). Kõigi orbitaaljaamade orbiidile toimetamiseks kasutati kanderaketti Proton.
Esimene avalikkusele teatatud orbitaaljaam startis Bajkongõrist 19. aprillil 1971. Jaama mass oli 18,9 tonni, välisläbimõõt 13,1 meetrit, teadusaparatuuri mass 1,5 tonni. Tõraverest oli jaamas instrument SFM-4. Esimesel jaama juurde saadetud kosmoselaeva meeskonnal ei õnnestunud põkkumine ja ei saadud jaama siseneda, järgmine meeskond viibis jaamas 22 päeva, kuid hukkus naasmisel. Peale 175 päevast lendu orbitaaljaam hävitati. Järgmise orbitaaljaama start ebaõnnestus kandurraketi teise astme rikke tõttu ja sellest avalikkust ei teavitatud. Kolmas orbitaaljaam jõudis orbiidile ja talle anti nimeks Saljut 2, kuid 13 päeva pärast oli ta kaotanud hermeetilisuse ning hävitati. See oli sõjaväe programme täitma pidanud ja luureaparatuuri kandnud jaam (Almaz), millel Tõravere instrumente ei olnud.
11. mail 1973 startinud järgmise jaama üle kaotati orbiidil kontroll ja ta hävitati mõne päeva pärast kui Kosmos-557, avalikkust orbitaaljaamast teavitamata. Esimeseks üsna õnnestunud lennuks võib pidada viiendana startinud orbitaaljaama Saljut 3 (Almaz) lendu, mis kestis 212 päeva. Tõravere aparatuuri paigutati vaid DOS-orbitaaljaamadele, sest mittesalajased teadusinstrumendid ei sobinud kokku Almazide sõjaväeaparatuuriga.
Väga hästi õnnestus 26. detsembril 1974 startinud “Saljut 4” lend. Jaam jäi orbiidile 769 päevaks ja teda külastasid kaks meeskonda, esimene viibis jaamas kuu aega, teine kaks kuud. Sellest jaamast tegid mõlemad meeskonnad (Aleksei Gubarev, Georgi Gretško, Pjotr Klimuk, Vitali Sevastjanov) edukalt vaatlusi “Mikroniga”. Teise meeskonnana pidanuksid algselt jaama lendama kosmonaudid Vassili Lazarev ja Oleg Makarov, kuid kandurraketiga toimunud avariis katapulteeris päästesüsteem kabiini kosmonautidega ja nad laskusid langevarju kasutades kuhugi Altai kraisse. “Saljut 5” kuulus jälle Almazide klassi ja pidi täitma sõjaväe vaatlusprogramme.
DOS-tüüpi orbitaaljaamade konstruktsiooni täiustati, nende mass ulatus kahekümne tonnini ja päikesepatareidelt saadav võimsus kahe kilovatini, lisati mootor manööverdamiseks ja teine põkkumisadapter. 1977. aastal startinud Saljut 6 jäi orbiidile peaaegu viieks aastaks ja selles käis 16 meeskonda. Saadi häid tulemusi ka Eesti aparatuuriga.
1982. aastal startinud Saljut 7 osutus veel pikaealisemaks, jäädes orbiidile 8 aastaks 10 kuuks ja võttes vastu 10 külastusmeeskonda. Jaamakompleks koostati orbiidil moodulitest. Algusest peale kuulusid jaama teadusvarustusse Mikron ja RUF, lisamooduliga Kosmos-1686 viidi sinna veel FAZA.
Eesti teadusaparatuur NL orbitaaljaamadel
1 | Saljut(1) (DOS) | 1971 | SFM4 | Ei saanud kasutada* |
2 | Saljut (Almaz) | 1972 | Mikron | Hävis raketi avariis |
3 | Saljut 2 (Almaz) | 1973 | - | Mittehermeetiline |
4 | Kosmos-557 (DOS) | 1973 | SFM-4 | Kadus kontroll, hävitati |
5 | Saljut 3 (Almaz) | 1974-1975 | - | |
6 | Saljut 4 (DOS) | 1974-1977 | Mikron SFM-4UF | Saadi vaatlustulemusd |
7 | Saljut 5 (Almaz) | 1976-1977 | - | |
8 | Saljut 6 (DOS) | 1977-1982 | Mikron SFM-4UF | Saadi vaatlustulemused |
9 | Saljut 7 (DOS) | 1982-1991 | Mikron, Faza RUF | Saadi vaatlustulemused |
10 | Mir | 1987-2001 | FAZA | Saadi vaatlustulemused |
"Vaatlusinstrument SFM-4 paiknes koos mitme muu teadusaparaadiga orbitaaljaama ühe külje õõnsuses, mida üleslaskmise ajal kattis kaitsekaas. Kaane eemaldamiseks määratud püropadrunid ei toiminud orbiidil ja SFM-4 jäigi varjatuks, tema olemasolu ei avalikustatud üldse.
Järgmisest NLiidu orbitaaljaamast Mir kujunes kompleks, mis lisaks baasmoodulile hõlmas viit täiendmoodulit. Tõravere FAZA viidi jaama täiendmooduliga Kvant 2. USA kosmosesüstikud põkkusid jaamaga üheksal korral. Jaama töö lõpetati 23. märtsil 2001, sest ta oli küllalt amortiseerunud ja nõudis orbiidil pidamiseks umbes 250 miljonit dollarit aastas.
Atmosfääri uurimisel oli teleradiomeetri vaatekiir suunatud horisondile ja üles-alla kõigutamise (skaneerimise) teel registreeriti atmosfääri vertikaalseid heledusprofiile, mille põhjal hiljem lahendati atmosfäärioptika pöördülesannet. Maa atmosfääri hajuskiirguse mõõtmine skaneeriva teleradiomeetriga – kosmiline kaugsondeerimine ehk kaugseire – annab väärtuslikku teavet atmosfääri füüsikalis-keemilise koostise kohta.
Nii on kosmosest kaugsondeerimise abil võimalik määrata veeauru, osooni, aerosooli ja nn. väikeste gaaskomponentide (siia kuuluvad ka inimtekkelised saasteained atmosfääris) kontsentratsiooni kõrguste vahemikus 5-50 km. Nende komponentide muutlikkus ajas on üsna suur (10-100 korda), mistõttu keskmiste kontsentratsioonide teadmisest ei piisa atmosfääri seisundi hindamiseks. Olev Avaste, Gennadi Vainikko ja Rein Rõõm koostasid metoodika, mis võimaldas Maa hajuskiirguse mõõtmistest arvutada aerosooli ekstinktsioonitegurit ja mitmel lainepikkusel toimetatud mõõtmiste korral hinnata ka aerosooli keemilist koostist ning kontsentratsiooni. Analoogilise meetodi esitas Juri Knjazihhin veeauru kontsentratsiooni leidmiseks.
Eelpool kirjeldatud metoodikat kasutati orbitaaljaamadelt Saljut 4, Saljut 6, ja Saljut 7 tehtud kiirgusmõõtmiste interpreteerimisel. Saadi aerosooli ekstinktsiooniteguri vertikaalprofiilid mitme geograafilise piirkonna jaoks, hinnati veeauru kontsentratsiooni atmosfääri ülakihtides (Kalju Eerme). Eriti produktiivseks osutus orbitaaljaamas Saljut 7 lennanud FAZA, millega saadi enam kui 10000 atmosfääri heleduslõiget. Teadusprogrammi püstitajate (O.Avaste, G.Vainikko, R.Rõõm) juhendamisel formeerus andmetöötluse grupp (K.Eerme, Sirje Keevallik, Rutt Koppel jt.), kes olemasolevate võimaluste piires rakendas tolleaegseid elektronarvuteid.
Märkimisväärne osa vaatlustest toimus ka jaama orbiidi nadiiri suunas. Teine orbiidile viidud FAZA oligi mõeldud maapinna optiliste omaduste määramiseks koos samaaegse mitmevärvi-pildistusega. See oli teatud sissejuhatuseks andmebaasi moodustamisel atmosfääri ja maapinna spektraalheleduste kohta mitmesugustes geograafilistes piirkondades, arvesse võttes ka spektraalheleduste päevaseid ja sesoonseid muutusi (K. Eerme). Selles liinis korraldati veel 1991.a. koostöö-eksperiment Austromir koos Austria teadlastega, mis seisnes Austria maapinna fotode radiomeetrilises sidumises FAZA mõõtmistega.
Kosmosest toimetatud atmosfääriuuringute teaduslikest tulemustest avaldati 1977-1989 viis artiklite kogumikku vene keeles (inglisekeelsete resümeedega) ning hulk üksikartikleid rahvusvahelistes väljaannetes, viimane neist veel 1996. aastal. Neli teadlast Tõraverest ja neli kosmonauti pälvisid 1977 Eesti riikliku teaduspreemia.
NLiidu kosmosefirmadega saavutatud kontaktid ja kosmosest eksperimentide läbiviimise kogemused tõid meie juurde helkivate ööpilvede uurija, Aberdeeni ülikooli professori Michael Gadsdeni, kes esitas oma ööpilvede vaatlusprogrammi ja aparatuurikontseptsiooni. Meie vahendatud läbirääkimised Energija esindajatega kulgesid edukalt ning sõlmiti kokkulepe projekti NOCLO (Noctilucent Clouds) elluviimiseks 1990-1992 kogumaksumusega umbes 800 000 dollarit. Eesmärgiks oli seatud helkivate ööpilvede uurimine kosmosest subarktilistel geograafilistel laiustel. Moodustati rahvusvaheline töörühm, saadi nõusolek Koroljovi firmast, kuid töö katkes Aberdeeni ülikoolist sõltuvalt.
Füüsikaklasside riiuleilt võib leida vanu raamatuid. Kellelgi on olnud kahju neid vanapaberiks saata. Mõnest võib leida toredaid näiteid või ülesandeid, mis veidi kaasajastatud sõnastuses kõlbavad kasutada väga hästi. Newtoni seadused on ju ikka alles. Pole ka tähtsuseta, et need õpikud või ülesannete kogud võivad meenutada tänastele õpetajatele nende oma koolipäevi. Harvem tuleb ette selliseid õpikuid, mis enam otseselt midagi meelde ei tuleta. Õpetajad, kes nende järgi õpetasid, on lahkunud. Võib-olla on veel alles mõni õpilane, kes neist õppis? Võimalik, aga eks ole ajad olnud meie inimestele üsna keerukad ja rasked.
E. Klikson – J. Lang, Füüsika gümnaasiumi I ja II klassile – Tartu Eesti Kirjastus 1943. Eessõnas seletavad autorid, et õpik on võrreldes 1938. aasta õppekavades mõelduga muudetud lihtsamaks, näitlikumaks, ja konkreetsemaks. Peatükke on lühendatud või lihtsustatud matemaatilise elemendi redutseerimise ja rakendusliku elemendi suurendamise suunas. Põhjuseks on uus kava, mille kohaselt langeb kogu füüsikaõpetus gümnaasiumis varasemale ajale.
Kliksoni ja Langi õpik on lihtne ja mahult üsna tagasihoidlik, st õhuke. 220 leheküljele mahuvad teemad: mõõtmisi ja mõõduühikuid, mehhaanika põhimõisteid, vedelikud ja gaasid, soojus, hääl, valgus, magnetism, elekter. Küllap vastas see nn uuele kavale, mille järgi Saksamaa okupeeritud ida-aladel õpetus pidi käima.
Mehaanika osa kõige pikem peatükk on „Tung ja töö” (kaasaegses terminoloogias: „Jõud ja mehaanilline töö”). Newtoni seadusi ei nimetata. Käsitlus algab Galilei inertsiseadusega ja läheb kiiresti edasi jõu mõõtmise (dünamomeetri) ja mehaanilise töö juurde. Ära on trükitud lühike Galilei elulugu. Newton ei ole õpikust päris välja jäänud. Tema veelgi lühem elulugu on paigutatud raamatu tagumisse ossa, valguse peatüki juurde.
Kuigi Newtoni seadusi otsesõnu ei esitata, on nende rakendamise harjutuseks antud väga tore küsimustik, mis kõlbab tänapäevalgi õpilastele esitada. Meie igapäevased tegemised ja kõnelemise viis on vahepeal veidi muutunud ja seepärast kulub mõne küsimuse juurde ära väike kommentaar.
Inerts, küsimused harjutamiseks
1) Seo tükk niiti näiteks tooli külge ja vea pikkamisi. Tool nihkub edasi. Äkitselt tõmmates katkeb niit. Mispärast?
2) Kui raudteerongid kiirel sõidul kokku põrkavad, purunevad vagunid. Mispärast? [1]
3) Miks pole alati võimalik rongi piduriga enne õnnetust peatada?
4) Millest on tingitud maavärisemise hävitav (purustav) mõju?
5) Pane pabeririba laual seisva veeklaasi või mõne teise väiksema asja alla ja tõmba äkki ära. Mida paned tähele ja kuidas seda seletada? Tõmba pikkamööda – mida märkad siis?
6) Kui sõiduk äkki liikuma hakkab, langevad reisijad tahapoole. Äkilisel seismajäämisel toimub vastupidine nähtus. Mispärast?
7) Mispärast tuleb tolm kloppimisel või raputamisel riietest välja?
8) Kui veega täidetud klaasi äkki liikuma või seisma panna, läheb vett üle ääre. Mispärast ja kuhu poole?
9) Me teame, et Maa pöörleb oma telje ümber läänest itta. Mispärast langeme meie maapinnalt üles hüpates samale kohale tagasi, aga mitte üleshüppamiskohast lääne poole? [2]
10) Kuhu poole tuleb liikuvalt sõidukilt maha hüpata, et mitte maha kukkuda? [3]
11) Mispärast koputatakse varre pihta, kirvest või luuda varre otsa pannes?
12) Mispärast ei saa raudteerongi järsku seisma ega liikuma panna?
13) Kastega on kergem niita kui kuivaga. Kuidas seda seletada? [4]
14) Mispärast õunad puu raputamisel maha langevad? [5]
15) Miks roomad sagedasti katkevad, kui hobune äkitselt tõmbab? [6]
16) Tagaajamisel on kasulik suuna äkilise muutmisega end kaitseda. Mispärast?
[1] Kui rongid kokku sõidavad, purunevad vedurid. Ilmselt on küsitud, miks kiirel sõidul kokku põrkumise korral purunevad KA vagunid. Aeglasemal sõidul vagunid ei pruugi viga saada ja veduritest kaugemad (sõidusuunas tagumised) vagunid saavad alati vähem viga. Mispärast?
[2] Kui inimene ei hüppa mitte otse üles, vaid ida poole, siis lükkab ta hüppel maapinda lääne poole, vastu Maa pöördumise suunale. On hästi teada, et kui näiteks kinnitamata paadist kaldale hüpata, liigub paat kaldast eemale. Kui hulgakesi hüpata, võiks sedaviisi Maa pöörlemist aeglustada? 1943. aastal oleks see küsimus toonud füüsikatundi matemaatilist (mitte rakenduslikku) elementi. Tänapäeval on Google otsingusõnad „world jump day”.
[3] Küsimuses kasutatakse sõna „maha” kahes tähenduses. Sõidukilt maha hüppamine võib tähendada sõnasõnaliselt maapinnale ehk maha hüppamist, aga võib ka tähendada mingile teisele aluspinnale (näiteks rongist perroonile) hüppamist. Teine asi on see, et pärast maha hüppamist, tuleb tegelda sellega, et püsti jääda, mitte pikali maha kukkuda või kukumisel võimalikult vähe haiget saada.
Sõidukitest välja (või maha) hüppamine on keelatud ja tegelikult päris paljudel juhtudel ka peaaegu võimatu. Raske on ette kujutada, kuidas näiteks praegu Eesti raudteedel liikuvast rongist saab sõidu ajal maha hüpata, ilma üleriigilist skandaali põhjustamata.
[4] On üldiselt teada, et kastest või vihmamärga muru on pea võimatu niita. Kogu niidetud materjal kleepub niiduki kere siseküljele, ummistab väljaviskeava, takistab tera pöörlemist ja koormab ülearu mootorit. On huvitav märkida, et tegelikult on ligi pool tänastest gümnasistidest vähemalt kord elus ka vikatiga niitnud, lihtsalt raske on kohe selle peale tulla, et 1943. aastal ei muretsetud nii väga igalaupäevase õuemuru silumise pärast.
[5] Kaks ühes. Üks küsimus on see, miks õunad MAHA kukuvad. See suunab meid pigem gravitatsiooniseaduse poole. Teine on see, miks õunad puu RAPUTAMISEL kukuvad. Siit paisatab inertsiseadus. Õunad kukuvad lõpuks maha ka ilma raputamiseta. Mispärast?
[6] Loogarakend on nutikas insenerilahendus, mis aitas omal ajal hobuste jõudu ja osavust optimaalselt ära kasutada. Tehniline progress enne soojusmasinaid ja elektrimootoreid toetus üsnagi palju veoloomadele. Kui ei ole just erilist huvi hoburakendite ajaloo või hobuste vastu, võib selle, mitte just kõige lihtsama küsimuse ka vahele jätta.
| Vana aja teadusmehed ei tundnud inertsiseadust. Alles kuulus itaalia teadusmees Galileo Galilei (1564–1642) esimesena avastas selle kõigi kehade üldise omaduse. Galilei oli matemaatika-, füüsika- ja täheteaduseprofessoriks Pisa ja Padova ülikoolis. Peale inertsiseaduse tegi Galilei terve rea teisi tähtsaid avastusi loodusteaduse alalt: avastas kehade vaba langemise seadused, pendli võnkumise seadused, tungide rööpküliku seaduse jne. Ka ehitas Galilei pikksilma, millega esimesena vaatles Päikest ja tegi kindlaks, et Päikese pinnal on tumedad laigud. Galilei pooldas ka avalikult Koperniku õpetust Maa liikumisest ümber Päikese. Selle eest pandi ta vangi ja sunniti vägivaldselt koguni lahti ütlema oma õpetusest. Kuulus Torricelli oli Galilei õpilane ja jätkas Galilei tööd. | Isaac Newton (sünd. 1643. a., surn. 1727. a.), inglise kuulsaim füüsik, avaldas teedrajava tähtsusega töid füüsika, astronoomia ja matemaatika alal. Esitas mehaanika põhilaused, gravitatsiooniseaduse, avastas valguse lahutamise jne. |
1906. aastal asutati Eesti Noorsoo Kasvatuse Seltsi I järgu Tütarlaste Kool, mida tänapäeval, mitmete nimemuutuste järel, tunneme Miina Härma Gümnaasiumina. Õppekeeleks sai eesti keel, eksamid tuli siiski õiendada vene keeles. Sel ajal ei olnud Eesti- ja Liivimaal (ega ka Venemaal, Euroopas ja terves Maailmas) kuigi palju neid, kes oleksid uskunud, et eesti keeles on võimalik gümnaasiumi tasemel õpetada, teadusest rääkida ja kirjutada. Üks, kes sellesse uskus, oli füüsika ja matemaatika õpetaja Jaan Sarv. Töötades 1909. aastast tütarlastekooli õpetajana, korraldas ta lahtisi tunde, näitamaks, et eesti keel on täiesti kõlblik loodusteadustest rääkimiseks. Ühele klassile andis ta avaliku tunni Vanemuises, et kõik skeptikud saaksid kuulama tulla ja veenduda, matemaatika õpetamisel ei tule sõnadest puudu. Tunni teemaks olevat olnud – viltu väli. Samal ajal kirjutas ta kaks füüsika õpikut – Füüsika õpetus ja Elekter. 1918. aastal kutsus tuntud haridustegelane Peeter Põld oma sõbra ja mõttekaaslase Jaan Sarve Eesti ülikooli rajamise tööle. Probleem, täpsemalt üks probleemidest, oli sama, mis gümnaasiumi asutamisel. Paljud saksa ja vene keeles õpetavad professorid ei uskunud, et eesti keelest võib saada teaduskeel.
„Füüsika õpetus” on üle 100 aasta vana, terminoloogia ja keelekasutus on aja jooksul veidi muutunud, aga teemade käsitlus on üllatavalt kaasaegne. Muu hulgas esitab autor näidisküsimusi, tänapäevases kõnepruugis püstitab probleeme, millega varemõpitut seostab ja kokku võtab. Ka klassikaline hõõrdevaba kaldpinna ülesanne leiab siin kasutamist vektori komponentideks jagamise seletamisel.
Olgu üks keha A pärissiledal viltupinnal MN (joon. 38). Olgu see pind maa peal seisva päriskindla keha pind. Kuidas mõjub raskuse tung selle keha peale?
Jaan Sarv, Füsika õpetus – Tallinnas, 1910. Näidisülesanne peatükist „Raskus”.
PDF: http://www.digar.ee/arhiiv/nlib-digar:101608
Tähendame noole c-qa seda otse allapoole sihitud liikumise hulka, mida raskuse tung igal sekundil kehale A anda püüab. Lahutame selle liikumise hulga mõttes kaheks, nii et üks pinnale MN parallelne ja teine temale perpendikularne on. Siis tähendab nool a parallelset ja nool b perpendikularset liikumise hulka. Liikumise hulk b ei saa ilmuda, sest pind MN takistab teda. Liikumise hulk a ilmub igal sekundil ja jääb täielikult kehale A, sest pärissiledal pinnal ei ole hõõrumist. Keha A saab siis igal sekundil ühepalju kiirust juurde, nagu vabalt langev keha. Aga see juurdetulev kiirus on 9,81 m/s-st nii mitu korda vähem, kui mitu korda nool a noolest с lühem on. Kui siht МО vertikalne on ja siht NO temaga õige nurga sünnitab, siis nimetatakse kaugust MO viltupinna kõrguseks, kaugust NO tema aluseks ja kaugust MN tema pikkuseks. Joonistuselt selgub, et kolmnurk MNO nooltekolmnurgaga sarnane on.
Selle põhjal võib lühendatult ütelda: raskuse kiirestus viltupinnal on nii mitu korda vähem raskuse kiirestusest vabas ruumis,kui mitu korda viltupinna kõrgus tema pikkusest vähem on. Olgu näituseks MО=30 m ja MN= 60 m. Olgu sellele viltupinnale üks keha pandud, ilma et teda kudagi oleks lükatud. See keha hakkab pinda mööda alla libisema ja saab igal sekundil 9,81/3 m/s ehk ligi 5 m/s kiirust juurde. Kolme sekundi päralt on siis selle keha kiirus 3·5=15 m/s.
Libisemist viltupinnal näeme jõgedes, kus vesi jõe põhja mööda libiseb või vee ülemised kihid alumiste kihtide üle libisevad. Hariliku langemise ja libisemise kohta ei ole kõik rehkenduse otsused mitte täieste õiged, sest harilikult takistab õhk visatud kivi või suurtüki kuuli liikumist ja iga hariliku pinna peal kaotavad libisevad kehad hõõrumise mõjul oma liikumist. Aga mida vähem õhu takistus ja mida siledam libisemise pind on, seda vähem läheb harilik kehade liikumine väljarehkendatud liikumisest lahku.
Sügisseminar toimus 17.-18. novembril Voore Puhkekeskuses, korraldajateks EFS füüsikaõpetajate osakond ja TÜ koolifüüsika keskus. Seminari tegemist toetab HTM.
Pakkusime pisut üldhuvitavat, palju praktiliselt kasulikku ja ohtralt suhtlemisvõimalusi.
Ettekandjate ja töötubade läbiviijate lahkel loal jagame siin ka Voorel kasutatud materjale.
Sügisseminar toimus 15.-16. novembril Voore Puhkekeskuses, korraldajateks EFS füüsikaõpetajate osakond ja TÜ koolifüüsika keskus. Seminari tegemist toetas HTM.
Oli kolm läbivat teemat: tark tehnoloogia, energia ja õppimine.
Matemaatika-, loodusteaduste- ja tehnoloogiaalane pädevus
matemaatika-, loodusteaduste- ja tehnoloogiaalane pädevus – suutlikkus kasutada matemaatikale ja loodusteadustele omast keelt, sümboleid, meetodeid ja mudeleid, lahendades erinevaid ülesandeid kõigis elu- ja tegevusvaldkondades; mõista loodusteaduste ja tehnoloogia tähtsust ning mõju igapäevaelule, loodusele ja ühiskonnale; mõista teaduse ja tehnoloogiaga seotud piiranguid ja riske; teha tõenduspõhiseid otsuseid erinevates eluvaldkondades; kasutada uusi tehnoloogiaid loovalt ja uuendusmeelselt;
Miks kogunesime?
Me sõltume fossiilkütustest ja see ei ole jätkusuutlik.
Esiteks saavad kergesti kättesaadavad fossiilkütused ühel päeval otsa, seega peame lõpuks energiat saama kusagilt mujalt.
Teiseks on fossiilkütuste põletamisel kliimale mõõdetav ja väga tõenäoliselt ohtlik mõju. Ohtliku kliimamuutuse vältimine ajendab meid viivitamata oma fossiilkütuste tarbimises muudatust tegema.
Kolmandaks, isegi kui me ei hooli kliimamuutusest, võiksime me siiski hoolida tarnekindlusest.
Kuidas vabaneda fossiilkütuste sõltuvusest?
Üks ilmne võimalus on taastuvenergia allikate kasutuselevõtt.
Täna on ühiskonnas energeetika teemadel raske arendada laiapõhjalist diskussiooni, sest puudub kooliharidusele tuginev teaduspõhine, üldarusaadav raamistik. Miks on vesinikumajandus kasulikum kui näiteks biomassi kasvatamine? Kui palju energiat on võimalik saada tuuleparkidest? Kui palju me kulutame energiat transpordile, kui palju küttele? Kas telefoni laadija seinast välja tõmbamine tasub vaeva?
Koolitusseminari eesmärk tervikuna on otsida raamistikku, mis võimaldaks koolis õpilastega teaduspõhiselt ja argumenteeritult Eesti energiavarustuse tuleviku üle arutleda.
Kõigepealt pisut energiast.
Vt järgnet joonist. Kas on võimalik ainult koolifüüsikat kasutades öelda, kui kaugele on võimalik sellise masinaga kivi visata? Täpsed rehkendused on väga väga keerulised, aga energia kontseptsiooni kasutamine lubab paika panna selle, kus on selle masina põhimõtteline piir, lihtsalt, kui saad aru, mida vaadata.
Meie käsitluse algallikas
Sustainable energy without hot air
David JC MacKay raamatu "Taastuvenergiast ilma udujututa" koduleht.Selle kümneleheküljeline kokkuvõte:
Laseme autoril endal rääkida.
Videos kasutatud andmed ja joonised:
| Võimsus maismaa või veepinna pindala kohta | |
| Tuul | 2,5W/m2 |
| Tuul merel | |
| Tõusud ja mõõnad | |
| Vee voolamine tõusudel ja mõõnadel | 6W/m2 |
| Päikesepaneelid | 5−20W/m2 |
| Taimed | |
| Vihmavesi (mägistes piirkondades) | |
| Hüdroelekter | |
| Geotermiline soojus | 0,017W/m2 |
| Päikeseahjud | 0,1W/m2 |
| Ookeani soojus | 5W/m2 |
| Päikeseenergia koondamine (kõrbetes) | 15−20W/m2 |
Maailmapanga andmetel oli Eesti kogu energiatarbimine 2015.aastal 132 kWh/p/i
Näidatud on primaarenergia tarbimist, st arvesse ei ole võetud nende muundamist teisteks lõppkasutusse minevateks kütusteks, mis võrdub kohalik toodang pluss börsitehingud miinus eksport ja kütusekulu rahvusvahelises transpordis lennukites ja laevades.Näidisülesanne
Maailmapank annab oma statistika ühikutes "õli ekvivalenti inimese kohta" (oil equivalent per capita). Kui palju on 4173kg õli ekvivalenti inimese kohta (2015. aasta) kilovattundides aastas inimese kohta?
Lahendus
Selliste probleemide puhul tasub pöörduda veebis leiduvate kalkulaatorite poole, mis ütlevad, et 4173kg õli ekvivalenti inimese kohta on 48532kWh inimese kohta. Kes võtab täpsemalt uurida, see saab teada, et õli ekvivalendi väärtus on 41868kJ/kg (viide, eurostat).
See on hinnang aasta kohta. Jagame 365ga, saame 132kWh/p/i.
Kogu energiatarbimise võimsus
Lahendus
Võtame rahvaarvuks Eestis miljonit inimest. Siis kokku tarbitakse aastas energiat
Kilovatttund on energia ühikuna üsna keeruline kasutada. Teeme seda siin nii, saame esmalt lahti eesliitest "kilo"
ja jagame siis tulemuse tundide arvuga aastas (8760), saame
kus eesliide G tähendab giga- ja GW on gigavatt ehk 109=1000000000W.
Kogu energiatarbimine (132kWh/p/i) tähendab seega keskmist võimsust 7,14GW.
Elektrienergia tootmine eestis - 2018. aastal 26 kWh/i/p, 2019. aastal 16 kWh/i/p
Elektrienergia tootmine, kuu. Statistikaameti andmed.Näidisülesanne
Lahendus
Statistikaamet annab 2018. aasta elektrienergia tootmise kohta arvu 12327GWh ja 2019. aasta kohta 7529GWh.
See teeb vastavalt 12327000000kWh ja 7529000000kWh - gigavatt-tund on kilovatt-tunnist suurem miljon korda. Inimese kohta vastavalt
ja
Ühes päevas vastavalt
ja
See on 2019. aastal ligikaudu 12% kogu Eesti energiatarbimisest.
Tuuleenergia tootmine Eestis 2019.a. - 1,44 kWh/p/i
Elektrienergia tootmine, import, eksport ja müük (kuud). Statistikaameti andmed, tabel KE21.Näidisülesanne
Lahendus
Statistikaamet annab 2019. aasta tuuleenergia tootmise kohta arvu 688GWh.
See teeb vastavalt 688000000kWh - gigavatt-tund on kilovatt-tunnist suurem miljon korda.
Inimese kohta
Ühes päevas
Niisiis, hakkame joonistama punaseid tarbimise tulpasid, kus on toodud välja mõne energiat kulutava tegevuse energiakulu; ja rohelisi taastuvenergia tulpasid, kus on kokku liidetud potentsiaalsed taastuvenergia allikad.
Kust tulevad andmed Eesti kohta?
Näited: Tootmine
Looded
Näited: Tarbimine
Ääremärkused
Carbon neutrality
Carbon neutrality, or having a net zero carbon footprint, refers to achieving net zero carbon dioxide emissions by balancing carbon emissions with carbon removal (often through carbon offsetting) or simply eliminating carbon emissions altogether (the transition to a "post-carbon economy"). It is used in the context of carbon dioxide-releasing processes associated with transportation, energy production, agriculture and industrial processes. Carbon-neutral status can be achieved in two ways:
- Balancing carbon dioxide emissions with carbon removal beyond natural processes, often through carbon offsetting, or the process of removing or sequestering carbon dioxide from the atmosphere to make up for emissions elsewhere.Some carbon-neutral fuels work in much the same way by being made from carbon dioxide themselves, either through natural or man-made processes, despite producing carbon emissions as well. Much more extreme forms of carbon dioxide removal may also be used.
- Simply eliminating carbon emissions altogether (the concept of the "post-carbon economy") through the use of renewable energy that does not produce carbon emissions at all (such as wind and solar power) and making changes to industrial and agricultural processes to eliminate carbon production.[dubious – discuss] Carbon projects and emissions trading are often used to reduce carbon emissions, and carbon dioxide can even sometimes be prevented from entering the atmosphere entirely (such as by carbon scrubbing).
Teie mõtted
Väärtus on ka selles, kui mingi osa meist toimetab ühes taustsüsteemis, st ühtede katsevahenditega. See annab võimaluse vahetada kogemusi.
Kogemuste vahetamise aluseks võiks olla ka muud õppematerjalid?
Teemad
- Praktilised tööd
- IKT ja IT, kodu-, kaug- ja klassitöö
- Arusaamise mõõtmine
- Repositoorium või ePortfoolio
Iga teema kohta küsime
- Millist probleemi me õigupoolest lahendame
Tegevused
- Teeme läbi
- Arutame
- Tagasisidestame
Eesmärk
- Defineerida ideaalne, aga siiski realistlik, Eesti oludele vastav lahendusmudel.
- Instrumentaariumiga harjumise aeg peab olema võimalikult lühike, sest see ei ole põhikoolis eesmärk. Eksole, see ei olegi nii triviaalne - enamik katsevahendid on teaduses kasutatavate tööriistade kõhnemad koopiad.
Esimene
Julge pealehakkamine on vähemalt pool võitu!
Igapäevatöö kõrvalt iseenda harimine on peaaegu kõige keerulisem asi maailmas. Ega asjata öelda, et mida Juku ei õpi, seda Juhan ei tea.
Oleme ka ise õppija rollis - sellist kursuse formaati ei ole varem proovitud ning iseenda välja antud vekslite lunastamine ei lähe meil kindlasti lihtsalt.
Me loodame, et need nädalakirja aitavad teid teha oma füüsikatunde huvitavamaks ja sisukamaks.
Jõudu meile!
Alustuseks
Tehke õpilastele kiirküsitlus: Kõik kirjutavad kolm sõna, mis seostuvad sõnaga "kaal", aega on 30 sekundit. Pastakad lauale ja käetõstmisega kokkuvõte. Kes kirjutas kilo, gramm või kilogramm? Kes kirjutas köök või midagi toiduainetega seostuvat? Kes kirjutas Mati? Mis on keha kaal, kaalumine ja kaalud?
Füüsika e-õpik: esimesed sammud
Füüsika e-õpik ei ole asi iseeneses vaid tööriist õpiku andmebaasi sisestatud materjalide mugavaks ja uue aja lisavõimalusi pakkuvaks kasutamiseks. Materjale on meil kogunenud üksjagu - avaldatud või valmimas on kõik füüsika kursused (nii põhikool kui ka gümnaasium), ca 400 praktiliste tööde juhendit, kolme kogu jagu ülesandeid, suur hulk põnevaid lisamaterjale.
Tasub järele proovida: kui seni oleme kasutanud füüsika videote leidmiseks veebilehte www.fyysika.ee/opik, siis uue e-õpiku repositoorium pakub palju mugavamaid tööriistu selliste õppematerjalide otsimiseks, teemade, õpikute ja tüüpide järgi selekteerimiseks ning õpimappideks kokku panemiseks.
Esimesel korral on meil kaks ülesannet:
- Me palume teha omale õpikusse kasutajanimi (kes ei ole seda veel teinud).
- Õpime, kuidas saab e-õpikus videotest, piltidest, simulatsioonidest, valemitest ja ülesannetest endale õpimappi kokku panna.
NB Repositooriumi kasutamiseks peaksite end e-õpikusse sisse logima. Algodoo illustratsioon
Universaalne füüsika arvutisimulatsioon Algodoo
Algodoo on programm, millega saab mehaanika ja optika süsteemide toimimist arvutil näitlikustada. See on mänguline, lihtsalt kasutatav, praktiliselt piiramatute võimalustega ning väga hea põhjus, miks kooli puutetundlik ekraan hankida. Selles kursuses me tegeleme Algodoo-ga õige mitu nädat, õppides selle võimalusi kasutama.
Esimesel nädalal palume
- programm omale arvutisse installeerida ning
- vaadata ära üks programmi võimalusi tutvustav video.
Algodoo saab alla laadida aadressilt www.algodoo.com. See on tasuta kasutamiseks.
Maagiline katseklaas
Füüsika tund kisub igavaks kätte? Õhurõhu vägeva jõu demonstreerimiseks on palju nippe. Aga üks hästi unustatud vana võte on ka see, kuidas vanasti kuppe pandi. Selline teeklaasi iseenda otsaette kinnitamine kindlasti elavdaks tundi. Koduse ülesandena harjutame, kuidas selline katse õnnestuks siduda suvalise parajasti jutuks oleva teemaga. Sest see side ei pea olema pelgalt füüsikaline.
Kas ja millised ohud selle katse tegemisega kaasnevad?
- Proovi, kas leiad selle katse e-õpikust üles ja oskad selle omale lemmikuks märkida?
Füüsika võlu
Robert March'i raamat on nüüd kõigile e-õpikuna kättesaadav aadressil õpik.füüsika.ee. See on kõike muud, kui füüsika saamise loo kuiv üleskirjutus, soovitame! Ja mitte ainult õpetajale - selle raamatu osasid saab anda lisalugemiseks õpilastele, kes mõne asja vastu sügavamat huvi tunnevad või kes tahavad füüsikas näha ka inimest. Autor ei eelda lugejalt mingeid eelteadmisi. Raamatu lugemiseks peab küll õpikute keskkonda sisse logima.
Füüsika ajalugu
Füüsika ajalugu Ivar Piiri rohkete faktidega kirjatud raamat on nüüd kõigile ka e-õpikuna kättesaadav aadressil õpik.füüsika.ee. Selle allika poole on alati mõtet pöörduda, kui on vaja mõni teadlase nimi või sündmuste ahel konteksti panna.
Teine
Teine tuleb alati raskemalt, kui esimene!
Jõudu meile!
Alustuseks
Selle tunni lõpus, kus te ütlesite õpilastele, mis on füüsika, andke igaühele kaks väikest paberitükki ja paluge kirjutada kummalegi üks loodusseadus. Täpsemalt, igaüks kirjutab kaks sõna või sõnapaari (mitte lauseid, paberid on ju pisikesed) sellest, mida nemad ise loodusseadusteks peavad. Sorteerige, analüüsige ja andke tagasisidet järgmises tunnis. See võib osutuda väga harivaks, annab klassi kohta olulist infot ja aitab õppetööd planeerida.
E-õpiku repositooriumis: eksperimendid õhuga
Lihtsad, samas efektsed ja kättesaadavate vahenditega tehtavad eksperimendid on teadagi kulda väärt materjal. Sel korral pakume tutvumiseks Tik L. Liem'i raamatust "Invitation to Science Inquiry" pärinevaid katseid, mida saab kasutada õhu uurimiseks.
Vaata ka järele, kuidas saab e-õpiku repositooriumist erinevatele teemadele vastavaid erinevat tüüpi õppematerjale.
Kiirtutvus Algodoo'ga
Sel korral teeme läbi kiirkursuse (Tutorial), mis tutvustab Algodoo peamiste funktsioonide kasutamist. Ei ole keeruline, ei võta kaua, on väga kasulik!
Kiirkursus on programmis sees, seal juhendatakse teie tegevusi sammhaaval. Kuidas täpselt, seda näitab alljärgnev video. NB Juslikult on videos jäänud esimene samm - küsimärgile vajutamine ülemises menüüs - serva varju. Videot vaatama ... Algodoo saab alla laadida aadressilt www.algodoo.com. See on tasuta kasutamiseks.
Mis on Lendav füüsikatsirkus?
Veel selle aastanumbri sees ilmutame eestikeelse tõlke Jearl Walkeri raamatust Lendav füüsikatsirkus ("Flying Circus of Physics"). Pakume siin ja edaspidi näiteid selles raamatus sisalduvast.
Ülesanne
Räägivad
Füüsika, keemia ja bioloogia õpikojad alustavad uut hooaega
Õpikojad on jõudnud oma kuuenda hooajani ja lähevad muudkui edasi. Mahud on endised - nii füüsika gümnaasiumi, füüsika põhikooli, keemia kui ka bioloogia õpikodade rühmad avatakse 12-15 koolis üle Eesti.
Uuel aastal toimuvad õpikojad nendes koolides.
Kolmas
Hakkab asisemaks minema.
Ei ole veel hilja asjal sarvist haarata!
Eksperimendid õhuga: miks muna läheb pudelisse?
Algodoo tööriistad
Sel korral teeme läbi kiirkursuse Algodoo kõigi funktsioonide kasutamisest. Jällegi, ei ole keeruline, ei võta kaua, on väga kasulik!
Teine variant on muidugi ise kõike avastada. Aga me võime kinnitada - avastamisrõõm ei saa sellest programmist otsa, kui esimesed sammud "karkudega" selgeks õppida.
Vaata ka üht praktilist näidet - kuidas teha Algodoos "atmosfääri", mis näeb projektoriekraanil täiesti adekvaatne välja. (Lubame, et meie videod saavad endale varsti ka heli.)
Algodoo saab alla laadida aadressilt www.algodoo.com. See on tasuta kasutamiseks.
Toimus Reaal- ja loodushariduse konverents
Neil päevil toimus Tallinna Reaalkoolis Reaal- ja loodushariduse konverents. Siinkirjutaja jaoks oli konverentsi kõige väärtuslikumaks osaks paneeldiskussioon, kus osalesid Volli Kalm (TÜ), Tiit Land (TLÜ), Erkki Truve (TTÜ), Katrin Soika (GAG), Kersti Veskimets (Reaalkool) ja moderaatorina Martin Saar (Reaalkool). Paneelis osalejad tõdesid, et just õpetajate sotsiaalne staatus võib olla see, mis mõjutab noorte andekate inimeste valikuid, samas ei saa ülikoolid selle muutmiseks palju rohkem teha, kui rääkida.
Saime teada, et TÜ ja TLÜ näevad kõvasti vaeva selleks, et õpetaja kutse omandamine ülikoolides oleks võimalikult paindlik. Rõhutati ka ainealaste teadmiste olulisust õpetajahariduse juures. Diskussioonis oli vähe loosunglikkust ja mõttestampe, osalejad ilmselgelt valdasid teemat ja just nimelt see muutis diskussiooni jälgimise nauditavaks (loodetavasti muutub ka selle videosalvestus varsti kättesaadavaks).
Siiski, konkreetsest plaanidest jäi ainsana lauale töö õppekavade atraktiivsemaks ja paindlikumaks muutmise nimel. Konverentsi kogumikus oli iga lehekülje servale trükitud “Palju toredaid mõtteid …”. Katastroofiline olukord füüsika õpetajate järelkasvuga annab sellele sloganile kurb-irooniline alatooni. Loodame siiski, et uus aasta toob siin uusi tuuli.
Uue nädala märksõnad
Teadlaste Öö, Algodoo, konverents/seminar e-õpikutest ja digiõppevarast.
Neljas
Katsed magnetitega, ühe elektrostaatika ülesande kommentaar, isetehtud matemaatiline pendel, uudised, lugemist ... ja kodune ülesanne.
Ei ole veel hilja asjal sarvist haarata!
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
1. Provokatsioonid
- Tahvlil esitatavasse meelega vea tegemine. See näitab, kuivõrd tudengid jälgivad tahvlil tehtavat. Näiteks mööda kaldpinda keha ülesvedamiseks tehtava töö arvutamisel „läheb segamini” siinus ja koosinus. Tulemuseks saame paradoksi, et mida madalam on kaldpind, seda rohkem tuleb koorma vedamisel tööd teha.
- Katse, mis „ei tule välja”. Näiteks Newtoni kolmanda seaduse demonstreerimisel ei tule dünamomeetrite näidud võrdsed, sest nullnäidud pole paigas.
- Trikk-katsed. Näiteks liniku kiire ja aeglane tõmbamine vaasi alt.
- Kihlveod. Näiteks Kes soovib kihla vedada, et kumerläätse saab panna valgust hajutama?
Lõik pärineb Svetlana Ganina ja Henn Voolaiu artiklist "Kas füüsika õpe kõrgkoolis peab olema huvitav?"
Algodoo: ehitame matemaatilise pendli ja uurime/demonstreerime selle omadusi
Matemaatilise pendli uurimiseks on loodud suur hulk arvutisimulatsioone. Kui seda nüüd Algogoo abil uurima hakkame siis mitte sellepärast, et teisi võimalusi ei oleks. Pigem on see hea näide, kuidas seda väga universaalset programmi ühe konkreetse süsteemi uurimiseks rakendada.
Esimeses videos ehitame matemaatilise pendli valmis. Teises videos uurime matemaatilise pendli omadusi. Algodoo saab alla laadida aadressilt www.algodoo.com. See on tasuta kasutamiseks.
e-õpiku LEGO: Füüsika õpetaja raamat
Nüüd on ta nähtaval kujul olemas, teiste e-õpikute hulgas. Sisuks see, millest siiamaani Mesilastes räägitud. Edaspidi lisandub see, mis juurde tuleb.
NB Õpiku nägemiseks ja lugemisesk peab õpikukeskkonda sisse logima,
Tekstid ja pildid selles e-õpikus on teile tuttavad. Kes on proovinud, on need tükid eraldiseisvatena ka e-õpiku repositooriumist üles leidnud. Nii et see õpik on ühtlasi näide sellest, kuidas e-õpiku keskkonnas saab õppematerjale olemasolevatest õppematerjalidest "kokku laduda". Edaspidi juba täpsemalt.
Varisevad platvormid
Toimus e-õpikuid käsitleva projekti LEARNMIX lõpukonverents
Ilmselgelt on e-õpikute teemal joonistatud sektordiagrammide hulk viimasel ajal eksponentsiaalselt kasvanud. Riik on asjal tugevamalt sarvist võtnud, loob eKoolikotti, kirjastused arendavad oma veebiplatvorme, lisaks sellele kirev seltskond omaalgatuslikku tegevust. Rääkimata laias maailmas toimuvatest arengutest.
Konverentsi materjale sirvides saab kõigest sellest aimu.
Tallinna Ülikool on selle protsessis HTM, HITSA jt asutuste koostööpartner ja nõustaja Eestis. LEARNMIX oli TLÜ Haridustehnoloogia keskuse ja Digitehnoloogiate instituudi digiõpikute rakendusuuring, mis tegeles e-õpikute mõtestamise ja ümbermõtestamisega.
Terje Väljataga slaididelt saab aimu projekti tulemusena tekkinud ideestikust.
Mart Laanpere slaididel on visandatud pakutavad tehnilised lahendused. Selle Mesilase päises ja siin pisipildina on projekti loodud visioon digiõppevara pilvest.
Füüsika e-õpik oli kohal ja lahkus mõtlikus meeleolus.
Ühelt poolt me nõustume kõigi heade soovide ja kavatsustega mis sellel ja sarnastel konverentsidel välja on toodud, need on aluseks ka meie endi tegevusele. Aga me oleme ka näinud, missugune probleemide padrik tuleb vastu, kui neid soove ja kavatsusi realiseerima hakata ja kuidas sealt läbimurdmine seab hoopis teistsugused ääretingimused, kui lihtsalt head soovid.
Konverentsi slaididel füüsika e-õpikut ei mainita. Kas me uitame vales metsas?
Ilmub uus füüsika 8.klassi õpik
Kuulutame ette, et selline õpik on tõepoolest ilmumas, oktoobris. Autoriks on Erkki Tempel on Tartu Miina Härma Gümnaasiumi füüsika ja keemia õpetaja.
Õpik on jagatud kaheks osaks: valgusõpetus ja mehaanika. Materjali jaotus vastab kehtivale õppekavale – valgusõpetuse osa algab valgusallikate ja valguse levimise käsitlusest ning lõpeb optiliste riistade kirjeldustega, mehaanika osa defineerib esmalt liikumise mõiste ning lõpetab võnkumiste ja lainete uurimisega. Iga teema juures on näiteid ja lugusid loodusest ja tehnikast.
Puudutatakse ka kõige uuemaid tehnoloogiaid ja võimalusel antakse viiteid parajasti teaduses toimuvale. Õpik sisaldab erineva tasemega küsimusi, ülesandeid ja teemasid iseseisvaks uurimiseks, samuti soovitusi praktiliste tööde läbiviimiseks.
Õpikuga käib kaasas e-õpik aadressil õpik.füüsika.ee, mis pakub ohtralt lisamaterjale. Lisaks sellele võimaldab e-õpiku õpikeskkond efektiivselt tunde ette valmistada, pakkudes lisaks õpiku materjalile ka tehnilisi vahendeid interaktiivsete tundide läbiviimiseks, testide ja koduste tööde koostamiseks ning nende õpilastele mobiiltelefonidesse esitamiseks.
Viies
Katsed staatikas ja dünaamikas. Ühe optikaülesande kommentaar ja optika Algodoos. Mitu lugemist.
Teadus, see ei ole imelihtne. Teadus on põnev.
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
Eksperimendid, tasakaalukad ja jõurikkad
Jätkame Tik K. Liem'i raamatu tutvustamist. Sel korral siis mehaanika katsed. Uurime tasakaalu, masskeskme liikumist natuke ka voolamist. On ka mõned inimkatsed, mis kindlasti klassis elevust tekitavad.
Jah, neid töid on ka sel korral päris arvukalt. Aga vaadake esimese hooga kasvõi lihtsalt pilte ... et kui tekib vajadus tundi elavdada, siis tuleks meelde.
Algodoo: optika
Videos näidatud tegevuste tulemusena tekkiva faili saate alla laadida siit:
Lae fail alla ...
Eelmisel korral me demonstreerisime matemaatilise pendli loomist ja uurimist Algodoos. Aga unustasime jagada seda faili, mis videos näidatud sammude tulemusena tekkis. Saadame seekord.
Lae fail alla ...
Algodoo saab alla laadida aadressilt www.algodoo.com. See on tasuta kasutamiseks.
Maa magnetiline poolus liigub
Füüsikaõpetajate sügisseminar 2015 Voore Puhkekeskuses
Kutsume teid osa võtma 6.-7. novembril Voore Puhkekeskuses toimuvast füüsikaõpetajate sügisseminarist. Pakume näpuotsaga huvitavaid akadeemilisi loenguid ja rohkesti igapäevatöös kasulikku. Loomulikult ka võimalust kolleegidega suhelda.
Alustame oma päeva reedel, 06.11 kell 10.30, lõpetame laupäeval lõunasöögiga.
Seminaril on osavõtutasu 15EUR, millest on vabastatud kõik üle mere tulijad.
Tartust Voorele sõiduks tellime bussi.
Kuues
Mehaanika katsed. Algatus katsevahendite tutvustamiseks. Loodus, valgus, värvid, fotoonika. Mitu lugemist.
Koolivaheaeg ei ole enam kaugel ....
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
Kirjandusteosed
Mida on meil õppida kosmoseteadusest?
Jätkame Tik K. Liem'i raamatu tutvustamist.
Katsetasime ühe optika demokomplektiga
Katsevahenditega on alati keeruline - isegi kui kataloogis mõne justkui õige asja üles leiad on väga raske öelda, milline on selle hinna kvaliteedi suhe ... või kas sellega üldse midagi mõistlikku teha annab.
Käesolevaga algatame rubriigi, kus võtame ette mõne kaubandusvõrgus saadaoleva vahendi või komplekti ning näitame videos, mida sellega teha saab. Videod teeme ühes jutis, st me ei lõika sealt midagi välja, kõik on "nagu päris".
Esimesel korral siis optika demokomplekt, mis sai meie käest hindeks "5", st julgeme soovitada.
Füüsikaõpetajate sügisseminar 2015 Voore Puhkekeskuses
Kutsume teid osa võtma 6.-7. novembril Voore Puhkekeskuses toimuvast füüsikaõpetajate sügisseminarist. Pakume näpuotsaga huvitavaid akadeemilisi loenguid ja rohkesti igapäevatöös kasulikku. Loomulikult ka võimalust kolleegidega suhelda.
Alustame oma päeva reedel, 06.11 kell 10.30, lõpetame laupäeval lõunasöögiga.
Seminaril on osavõtutasu 15EUR, millest on vabastatud kõik üle mere tulijad.
Tartust Voorele sõiduks tellime bussi.
Tähtaeg registreerumiseks on 19.oktoober.
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
Viimase minuti kirjalikud küsimused
Lõik pärineb Svetlana Ganina ja Henn Voolaiu artiklist "Kas füüsika õpe kõrgkoolis peab olema huvitav?"
Mida on meil õppida kosmoseteadusest?
Jätkame Tik K. Liem'i raamatu tutvustamist.
Kui eelmisel korral nägite esimest kümmet selle teema praktilist tööd, siis täna seda linki vajutades on neid seal kakskümmend.
Kuidas leida Mesilase materjale e-õpikutes
Huvitavad ja põhimõtteliselt kasulikud asjad on head, aga ka sellistest tekib ajapikku hunnik ... näiteks sobib kasvõi seesama Mesilaste sari - midagi justkui oli, aga kus täpselt ...
e-õpiku rusikareegel ütleb, et sinna pandud materjalid peavad end näitama oma kodus (Mesilase puhul siis füüsika õpetaja raamatus) pluss kõigis kohtades, kus üks või teine materjal konteksti sobitub.
Uuel nädalal on koolivaheaeg. Ka Meslane võtab korraks aja maha.
Mesilane, see on (tähestikulises järjekorras):
Allar Nirk, Henn Voolaid Jaan Paaver, Kadri Veende, Kaido Reivelt, Kristel Uiboupin, Nils Austa, Svetlana Ganina.
Seekord palume teil anda Mesilasele tagasisidet.
Tagasiside küsimustikule vastama!
Meile võib kirjutada ka e-maili aadressile opik@fyysika.ee.
Soovitusi, kuidas on võimalik õppijaid füüsikatunnis aktiveerida
Konkursid
Konkursid Mingi seadme tööpõhimõtte seletamine. Näiteks esitada uksesilma optiline skeem. Kirjeldus sellest, mis juhtuks, kui midagi muutuks füüsikalises maailmas. Näiteks kirjeldada, mis juhtuks, kui elektroni laeng muutuks kümme korda suuremaks või väiksemaks? või Mis juhtuks, kui Maa pöörlemine lakkaks? Mis juhtuks, kui Päike ära kustuks?
Lõik pärineb Svetlana Ganina ja Henn Voolaiu artiklist "Kas füüsika õpe kõrgkoolis peab olema huvitav?"
Kuidas mõjub soojus?
Soojusõpetuses kasutatavaid praktilisi töid ja demokatseid on üldiselt keerukam leida, kui näiteks mehaanika või optika omi. Siit tuleb üks jagu ideid Tik L. Liemi raamatust.
E-õpik - nüüd viis korda kiirema ja värskendatud simulatsioonidega
Kolm head uudist:
- Füüsika e-õpik avaneb nüüd vähemasti viis korda kiiremini
- Uuendasime ära kõik oma seni tehtud 3D mudelid
- Phet simulatsioone tehakse tasapisi ümber html5 formaati, mis töötab kõigis seadmetes (samas kui Java ja flash mobiilsetel seadmetel reeglina ei avane). Uuendasime simulatsioonide andmebaasi viisil, kus need kolm varianti oleks selgelt eristuvad.
Kuna meil on jagu uusi lugejaid, siis: Füüsika e-õpik on kõigile vabalt kättesaadav õppekeskkond, kus on ohtralt õppematerjale ning tööriistad nende kasutamiseks Õpikut sammhaaval arendatakse ning selle arenduse tulemustest antakse siin nädalakirjas teada.
Varem ilmunud juhised Varem ilmunud juhised ja ka Mesilases ilmunud materjalid on Füüsika õpetaja raamatus kättesaadaval. Mõnusaks kasutamiseks peaks endale kasutajanime tegema.
Füüsika ei paku mudeleid ühiskonna kirjeldamiseks?
Otse elust - kaos, siis väike rühm, kes käib koos. Edasi ühinevad kaasajooksjad, jäävad mõned vaprad iseteadvad ...
Aupaiste Aupaiste ja kuu heledus
Just siis, kui on täiskuu, saavutavad kõik valgustatud alad Kuu pinnal oma heleduse maksimumi. Mistahes ala Kuu pinnal võib olla 25% heledam kui päev enne või pärast täiskuud. Mis põhjustab Kuu pinnalt hajunud päikesevalguse intensiivsuse äkilise suurenemise? Kuidas on see nähtus seotud lennuki "aupaistega" maaipinnal või pilvedel? Selgub, et meid ümbritsevad looduslikud helkurid.
Kuidas valgust salvestada?
Valguse kogumiseks kasutatakse kõige sagedamini päikesepatareisid, mis teevad valgusest elektri, elektrienergia salvestatakse ning ilma pimenedes tehakse uuesti valguseks.
Aga mis oleks, kui tee ise salvestaks ja siis kiirgaks valgust? Sest me teame ju luminofooridest, mis justnimelt seda teevadki.
Viimastel aastatel on selles vallas toimunud huvitavad arengud - täna on juba olemas suhteliselt odavad materjalid, mis helendavad minuteid pärast ergastava valguse kadumist. Oletame, et me jõuaksime materjalideni, mis töötavad niimoodi tunde?
Asjakohane on ka meelde tuletada, põhiteadmised luminofooridest. Materjalimaailm on siin heaks abimeheks.
Õpetajad räägivad
Oleks huvitav teada, kuidas õpetajad ise õppisid ja kuidas neil õpetamine hästi läheb. Küsime nende käest. Sel korral on kõnetoolis MHG füüsika õpetaja ja füüsika õpetajate eestvedaja Riina Murulaid Lugema ...
Tartu ülikoolis sai valmis ja läks kooskõlastusringile uus õppekava nimega Loodus- ja reaalainete õpetamine põhikoolis. Füüsika õpetajate jaoks tähendab see paindlike, loodetavasti sisuliste ja vajalike täiendkoolituskursuste avanemist - kursused ehitatakse üles nii, et õpetajad saaksid praktilisi teadmisi ja tõhusaid näpunäiteid füüsika kursuste õpetamiseks.
Täpsemalt tuleb asjast juttu juba 6.-7. novembril, Voore sügisseminaril. See on juba pooleteise nädala pärast.
Koolivaheajal te andsite meile tagasisidet, Mesilase kohta. Tagasiside oli valdavalt positiivne ja see annab meile julgust asjaga edasi minna. Loodame siiralt, et te leiate neist nädalakirjadest ainest, mis aitab füüsikat õhinaga õpetada.
Oleme jätkuvalt kontaktsed aadressil opik@fyysika.ee, igasugustes küsimustes.
Deemonsüdamik
Voorel mängime!
Sel korral siis eriti praktiliselt - eksperimendisessioonidesse on kogunemas 15 katsekomplekti, mida 3-5 liikmelised rühmad saavad uurima hakata. Küllap kajastame Voorel toimunut ja räägitut ka tulevastes Mesilastes.
Kohtume juba ülehomme, 6.-7. novembril, Voore sügisseminaril.
Sellised me oleme
Füüsika õpetajate sügisseminaril, 6.-7. novembril 2015.a. Voore Puhkekeskuses.TÜ koolifüüsika keskus ja EFS kutsusid sel kevadel õpilasi üles esitama oma uurimistöösid õpilaste füüsikaalaste uurimistööde konkursile. Laekus kaheksa tööd. Tööd on hinnatud, ette kantud ja autasustatud.
Lugema...
Töid koos žürii kommentaaridega saab uurida e-õpiku repositooriumis.
Tartu Tamme Gümnaasiumi füüsika õpetaja Tanel Liira ajab asja nimega Nutisensor. Selle programmilises dokumendis seisab:
Meie eesmärk on Vernieri ja PASCO jt. digiandmekogujad asendada lahendustega , mis võimaldaks õpilastel laboratoorseid töid analüüsida mugavalt oma tuttavas seadmes – mobiiltelefonis. Hoolitseme nii riistvara kui ka tarkvara eest.
Anname ka siitkaudu teada, et Nutisensor on osalemas Ajujahil ja läbinud seal esimese sõela.
Tooteni on veel pikk tee minna, aga julge pealehakkamine on Tanelil igatahes olemas. Toetame!
On nüüd lõpuks ilmunud. Nii paberil kui e-õpikuna.
Töövihiku ja metoodiliste materjalidega tegeleme. Ka 9. klassi materjalid on töös.
Loodame, et jumalapäike siis veel paistab, kui kogu see 2006.a. alanud füüsika õppematerjalide projekt enam-vähem komplektse ja töötava kuju saab.
Lisamaterjalid e-õpikus
Õpikute lisamaterjale saab sirvida e-õpiku repositooriumis. Õpikute seest viib reposse parempoolsel pildil punasega rõhutatud ikoon. St me oleme asju veidi ümber korraldanud - kuna
Energiast räägitakse kõigis loodusainetes. Aga näiteks bioloogia ja füüsika saavad koolikursuses harva kokku. Nii võib energia käsitlus jääda liiga ainepõhiseks, füüsikas pakutavaid mudeleid ei osata kasutada bioloogias, keemias või geograafias, samuti ei jõua geograafias või keemias käsitletavad näited füüsika (aga ka näiteks matemaatika) tundi elavdama.
Mesilane leidis internetist USA-s tegutseva mittetulundusühingu The Concorde Consortium. See on päris muljetavaldav, mille kallal nad töötavad ja millega on juba hakkama saanud, mitmeski mõttes ägedam kui Phet. Tegime tutvust, hakkame tõlkima, ehk õnnestub ka koostööd teha.
Allpool on näiteks otselink kasvuhooneefekti seletavale simulatsioonile, laiema ülevaate saab e-õpiku repositooriumist. Edaspidi tutvustame lähemalt.
Pool sajandit pärast seda, kui hakati otsima elu mujalt universumist, on tulemuseks endiselt pea ümmargune null. Paul Daviese arvates tuleks need otsingud taaskäivitada, kuid seekord ei peaks uurima mitte ainult raadiosignaale, vaid kõiki füüsikalisi ja astronoomilisi anomaaliaid.
Paljud meist on ehk juba sattunud rakendusele nimega Earth Nullschool. Kui ei, siis kindlasti soovitame. Rakendus näitab reaalajas kõikvõimalikke atmosfääri ja maailmamerd iseloomustavaid parameetreid väga vingelt animeerituna. Tuulte tugevus ja suund, temperatuur, õhuniiskus, sademed, õhusaaste, CO2, hoovused, jne. Rakendus kasutab mitmete Ameerika ilmateenistuste andmeid.
Kliki pildile. Ja ära piirdu vaid vaikimisi seadetega. Alumises vasakus nurgas on sõna earth, millele vajutades avaneb menüü kõikvõimalike valikutega.
Suurepärane animeeritud ilmamudel. Saab vaadata õhumasside liikumis Maa erinevates projektsioonides ja erineva taustainfoga.Andi Hektor arutleb 2013.aastal ajakirjas Sirp ilmunud loos Higgsi bosoni avastamisega seonduva üle. Kõrge (aga kiiduväärselt ladusalt seletatud) füüsika kõrval on loos ka tuntav inimlik mõõde.
Makerspace on füüsiline ruum, kus on võimalik kohata omasuguseid hakkajaid-tegijaid inimesi ning ühiselt projekte-ideid reaalsuseks muuta. SPARK Makerlab hakkab pakkuma võimalust ehitada peaaegu kõike, mida hing ihaldab.
MESILANE usub!
Kalle Olli räägib planktonist. Kirjatükk pärineb ajakirjas Sirp. Oleme koos autoriga lisanud hulga pildimaterjali. Aeg hakata suviseks sinivetikate hooajaks taustateadmisi koguma.
Kaasaskantavad nutiseadmed võiks sisaldada õhu saastegaaside ja peenosakeste sensoreid. Miks see nii ei ole? Kas on lootust, et tulevikus saab nii olema? TÜ füüsika instituudi vanemteadur Raivo Jaaniso räägib ajakirja Horisont 6/2016 kaaneloos oma uurimistööst.
Ninaga nutiseadmed
On ilmselge, et astroloogia kuulub pseudoteaduste alla ja püüdlused teadusliku meetodi abil tõestada päikesemärgi mõju inimese eluõnnele on juba ette määratud läbikukkumisele. Sellest hoolimata kinnitavad väga paljud tublid ja arukad inimesed horoskoopidest rääkides, et „midagi seal ikkagi on“. Horoskoobid näivad sageli kõnelevat tõtt, hoolimata põhjusliku seose absurdsusest. Miks see nii on?
Puhkpüss on sihitud lakke riputatud raskusele. Raskus lastakse laest lahti täpselt lasu hetkel. Kui kõvasti peaks puhuma, et puhkpüssi kuul raskusele pihta saaks? Selgub, et vahet ei ole.
Niisiis, füüsikaõpetajad korraldavad koos füüsikutega füüsikapäevi, kus sees ka füüsikaõpetajate päev.
Toimuvad Tartus, TÜ füüsikumis 24.-25. märtsil.
Tutvuge füüsikapäevade kavaga. Tulla tahtmise tunnet saab väljendada registreerumisvormis.
NB Laupäeval pakume ka korraliku lõunasöögi.
Kuidas küünal põleb, see tähendab, kuidas see oma põletusainet tarbib? Miks on küünlaleegi valgus peamiselt kollane ja miks on leegi äärtes tavaliselt sinised alad? Miks on küünlatahi ja leegi kollase osa vahel tume koonus? Miks mõned küünlad suitsevad, teiste leek aga võbeleb?
Kiidame tegijaid ja korraldajaid, eesotsas Tiit Sepaga!
Ülesanded jäid järele ja on nüüd taaskasutatavad - neist saab nüüd sealsamas e-õpikute keskkonnas kokku panna oma viktoriini või kontrolltöö.
Üks veider number: hetkel on seal e-õpikus kokku 4259 küsimust või ülesannet.
Pulsar 2017
Kui seista mäetipu lähedal sellal, kui päike on madalal, paistab mäe vari kolmnurkne. Selle kolmnurga tipp ulatub vaatlejast eemale. Miks tekitavad kõik mäed enam-vähem ühesuguse varju?
1986. aasta augustis tappis mürgine gaasipilv Kamerunis asuvas Nyose järve orus 1700 inimest ja lugematul arvul loomi. Uurijad, kes jõudsid kohale mitu päeva hiljem, teatasid, et süüdlane oli järv ise, mitte mingit liiki mürgine vulkaaniline gaas. Kuidas sai järv eraldada mürgist gaasi?
Šokolaadi tegemiseks ei ole palju komponente vaja - kakaojahu, kakaovõi, emulgaator (kondenspiim või letsitiin) ja suhkur. Aga šokolaaditegu nässu ajada ei ole üldse keeruline. Kööki me teadust tavaliselt kaasa ei võta? Nojah, meile vaid tundub nii.
Šokolaaditeadus
Kodune jäätisemasin koosneb kesksest metallanumast, mida ümbritsevad soola ja purustatud jää kihid. Mida sellise masina kasutamisel tähele panna?
Vaskvitriol ehk vask(II) sulfaat annab ilusaid siniseid kristalle. Ise kasvatasime sellised mõned aastad tagasi Teaduslaagris. Sealne kogemus on kokku võetud järgneval paaril slaidil.
Füüsika on see, kui üks printsiip võimaldab aru saada paljudest nähtustest ning lubab ka ise uusi katseid välja mõelda.
Pärast seda, kui patarei on elektripirni põlema pannud, tasub läbi käia (näiteks) Oomipoest ja küsida mähisetraati (so lakiga kaetud vasktraati). Allpool on mõned ideed, mida sellega peale hakata.
Browni liikumine vääriks omaette lugu. Tuleb välja, et Browni liikumise jälgimine oli esimene katse, mille kaudu oli võimalik tõestada aatomite ja molekulide olemasolu (vt näiteks seda artiklit). Ja Browni liikumisele andis füüsikalise selgituse Albert Einstein, see on ühtlasi tema enim tsiteeritud artikkel üldse. Ja Robert Brown ei olnud üldse esimene, kes Browni liikumist jälgis.
Teeme siinkohal vaid esimese sammu ja vaatame seda katset. Videojuhis allpool. Soovitame soojalt ise järele proovida!
On kuri kahtlus, et Browni osakeste Browni liikumine aetakse tihti segi aatomite ja molekulide soojusliikumisega. Browni osakeste läbimõõt on mõned mikromeetrid ja nad koosnevad paljudes aatomitest või molekulidest. Ja liiguvad nad sellepärast, et aatomid ja molekulid pommitavad neid erinevatelt külgedelt erineva intensiivsusega.
Alljärgnevalt pakume kolme simulatsiooni, mis lubavad näitlikustada aatomite ja molekulide soojusliikumist gaasides, vedelikes ja tahkistes. (Jah, concord.org simulatsioonide tõlkimine on jätkuvalt plaanis).
Pindadel, mida valgustab hele päikesevalgus, võib näha teralist mustrit (täpikestest koosnevat mustrit), mis koosneb heledatest ja tumedatest punktidest. Tihti võivad sellel mustril olla eredad värvid.
Alljärgnevas loos ei saa mööda ka Browni liikumisest.
Suvi on tulemas, otsival silmal on, mida otsida.
Lugu pärineb 1998.a. aastast, aga räägib ka täna asjakohase loo gammakiirguse sähvatuste avastamisest ja nende uurimisest. Selge see, et sellel sajandil on gammakiirgust mõõtvaid satelliite juurde tulnud (ja ka läinud), kõige ägedamat neist mainitakse ka allpool. Muide, loo pealkiri ei ole kunstiline liialdus.
Allpool on pilt, mille sarnaseid te arvatavasti varemgi näinud olete. See konkreetne pärineb Fermi gammakiirguse kosmoseteleskoobist (vt pilt paremal) ning videos on näha, kuidas Fermi mullid ilmuvad pärast mitmeastmelist andmetöötlust. Alumisest pildist aru saamiseks võrrelge seda ülemisega!
Natuke Linnutee keskpunktist eemal on täht, mida tuntakse nime all S2 ja mis liigub mööda elliptilist orbiiti perioodiga 17 aastat. Selge see, et täht ei saa niimoodi liikuda, kui läheduses ei oleks mõnd massiivset objekti. Kuna näha ei ole seal midagi, siis arvatakse, et tegemist on musta auguga - objektiga, mille gravitatsiooniväli on nii tugev, et sellest eemale ei pääse isegi valgus.
Gammakiirgusega kodus eksperimente teha ei ole võimalik. Sestap soovitame tegevust, mis meelitab uksest välja astuma. Mõõdame ära, kui suur see meie täht ikkagi on.
TÜ loodus- ja täppisteaduste valdkond ja TÜ Teaduskool korraldavad õpilaste loodus- ja täppisteaduslikke teemasid käsitlevate loov- ja uurimistööde konkursi.
Oma loov- ja uurimistöid on oodatud esitama üldharidus- ja kutsekoolide õpilased.
Kõigi osalenud õpilaste vahel loosime välja iPad mini Tööde hindamisel väärtustame:
- Töö uurimuslikkust,
- Originaalsust, analüüsi- ja üldistusoskust;
- Teksti korrektsust ja arusaadavust;
- Kasutatud kirjanduse ja veebimaterjalide valiku otstarbekust ja viitamise korrektsust.
Vähemalt pool töö mahust peab olema autoritekst. Töö võib olla kirjutatud eesti, vene või inglise keeles. Töid võib esitada nii individuaalselt kui ka kollektiivselt. Tööd tuleb üles laadida elektroonselt (soovitavalt pdf) 15. juuniks e-õpikusse aadressil: http://opik.fyysika.ee/index.php/poll/view/code/uurimus2017.
Konkursi käiguga hoidke end kursis FB lehel: https://www.facebook.com/uurimisryhm/
Kontakt: kaido.reivelt@ut.ee
1976-1977. aastal kaardistas ameeriklaste kosmosesond "Viking" Marsi pinda. Aparaat lähetas Maale hulgaliselt unikaalseid fotosid, mille seas oli ka pilt, mis pani hiljem aluse omalaadsele "kosmilise folkloori" lainele.
Küsisime neil päevil õpetajatelt veebipõhiste õppematerjalide keskkondade kohta. Saime teada, et füüsika õpetajad otsivad kõige sagedamini simulatsioone. Allpool mõned, mida te ehk seni leidnud ei olnud. Sobivad 9. klassis soojusõpetuse õpetamiseks ja on sees ka 9.klassi õpikusse mis varsti ilmavalgust näeb. (Jah, eestikeelsed tõlked on jätkuvalt tulemas.)
Päikesesüsteemis liigub Merkuur oma orbiidil ca 10 korda aeglasemalt kui Pluuto. Kui Vera Rubin ja tema kaastöötaja Kent Ford mõõtsid Arizonas Kitt Peaki Rahvusobservatooriumis kaugete galaktikate orbitaalkiirusi, olid nende nende tulemused üllatavad – tähtede orbitaalkiirus galaktika nähtaval välisäärel on peaaegu niisama suur kui galaktika keskmele lähedastel tähtedel. Tumeaine sünniloost arusaamiseks ei ole vaja mingit tavakodanikule kättesaamatut tähefüüsikat, lihtne pöördliikumise dünaamika.
Galaktikad on kaugel. Ja kuna nende pöörlemise periood on väga pikk (Linnuteel näiteks üle 200 miljoni aastat), siis näivad nad üsna paigal seisvat. Kuidas me teame, et nad siiski pöörlevad?
Pöörlevad galaktikad kiirgavad valgust. Pöörleva galaktika valguses spektrijooned Doppleri efekti tõttu laienevad ja see tõestab, et galaktikad pöörlevad. Kui galaktikad vilistaksid ... proovime sarnase eksperimendi läbi viia helilainetega. Füüsika on sarnane, aga eksperimendi metoodika palju maalähedasem.
Teades pöörleva objekti kiirust, pöörlemise raadiust ja jõudu, mis seda objekti orbiidil hoiab, saab hinnata objekti massi. Ja selliseid mõõtmiseid saab füüsika tunnis korraldada. Gümnaasiumi mehaanika kursus lubab selliseid katseid ka läbi rehkendada. Tumeaine on see, kui katse tulemus teooriaga kokku ei lähe.
Kuidas teha katseid tumeainega?
Nöör pistetakse läbi toru ja kinnitatakse selle mõlemasse otsa raskus. Kui nüüd haarata torust ja ühte neist raskustest keerutada, siis nöör püsib torus paigal vaid juhul, kui teise massi tekitatud raskusjõud ja kes
Uppsalas 27. novembril 1701 sündinud rootsi füüsik, astronoom ja geodeet Anders Celsius on üks mitmest sama perekonnanimega Uppsala ülikooli professorist, kes kõik olid omavahel sugulased. Ehkki Celsiuse nime teab iga koolijuts, on tema elukäik ja uurimistöö tuttavad vähestele. Samas on vähemasti üks koht kooliõpikutes, kus Celsiust veel mainida võiks.
Maavärin tekib, kui Maa sisemuse kivimitesse kogunenud pinge ühtäkki vabaneb, pannes laamad või magma liikuma. Füüsiku mättalt vaadates on maavärin laine levimine maakoores ja tuumas.
Lainete levimist me oleme koolis õppinud. Me teame, kuidas murdub valguskiir liikumisel optiliselt hõredamast keskkonnast optiliselt tihedamasse, oleme ka näinud valguskiiri, mis kõverduvad, kui nad liiguvad ühtlaselt muutuva murdumisnäitajaga keskkonnas. Mehaaniliste lainetega, nagu maavärinas tekivad, kehtivad kvalitatiivselt sarnased lainete levimise seadused, selles veendumiseks uurige järgnevat joonist. Pange tähele, kuidas näiteks tekib varju piirkond ja kuidas see piirkond on määratud Maa sisemise struktuuriga.
Pilt on loomulikult palju detailirohkem, kui siin paari lausega edasi anda saab. Aga on justkui ilmselge, et maavärinad ei peaks jääma vaid geograafia tundi ja lainete levimise seadused vaid füüsika tundi.
Ja Maa sisemise struktuuri uurimiseks tuleb mõõta selle võnkumisi.
Ka Kuu uurimisel ei ole võimalik selle sisse sügavat auku puurida ja näha, "mis seal sees on". Tuleb uurida seismiliste lainete levimist. Aga Kuu pind ei värise kuigi tihti, sagedamini tekivad seismilised lained, kui erinevad objektid Kuu pinda rammivad.
Maailma üks paremini säilinud meteoriidikraatreid asub Eestis, Saaremaal Kaali külas. Kraatri põhjustanud meteoriidi kineetiline energia oli pea sama, mis Hiroshimale heidetud aatompommi plahvatuses.
Me oleme kõrvalolevaga analoogilisi pilte näinud paljudes õpikutes, kus on vaja seletada, miks on ekvaatoril soojem ja talvel külmem. Aga peaksime ka lisama, et kuna kogu taastuvenergia jõuab meieni päikesekiirgusena, siis energia jäävuse seaduse kohaselt ei ole võimalik ühelt ruutmeetrilt maapinnalt saada rohkem taastuvenergiat, kui see, mis Päike meile annab. Kasutame me siis päikesepaneele, kasvatame biomassi või püüame tuult.
Söör David John Cameron MacKay (1967 - 2016) oli Briti füüsik ja matemaatik, kes on rahvusvaheliselt tuntud raamatu "Sustainable energy - without the hot air" (Taastuvenergiast ilma udujututa, withouthotair.com) autorina. See on väga märkimisväärne raamat - muidu udune ja laialivalguv jutt taastuvenergia kasutamisest ja kasulikkusest on tõlgitud kergesti mõistetavate arvude keelde. Pakume ja soovitame soojalt eestikeelsena lugemiseks selle raamatu kokkuvõtet.
Niisiis, taastuvenergia ilma udujututa. Mida see reaalselt tähendaks, kui tahaksime kogu Suurbritannia energiavajaduse rahuldada taastvuenergia allikatest? Jah, see on võimalik. Aga taastuvenergiarajatised peavad olema hiigelsuured, sest kõik taastuvenergiaallikad on väga hajusad.
Allpool joonis uurimiseks. Täpsemalt juba viidatud eestikeelses kokkuvõttes. Veel täpsemalt raamatus endas, mis on meie meelest suurepärane abimaterjal ainetundides tulevikuenergeetika väljakutsete käsitlemisel. Plaanime ka raamatu tõlkimisega jätkata ning hakata selle osasid e-õpikute asjakohastes alajaotustes lisamaterjalina pakkuma.
Ka Eestis on taastuvenergiatele üleminek tihti jutuks. Võtaks õige ette ja prooviks sarnaseid arutlusi ka Eesti konteksti üle tuua? See ei ole ülejõu käiv ülesanne ja võiks muuta arutelud näiteks põlevkivienergeetika vajalikkusest või tuuleenergia võimalustest palju sisulisemaks. Sest hästi rakendatud füüsika on halastamatu, aga õiglane.
Kuidas seda tehakse?
Kui äge on kõige ägedam mikroskoop, mille saab teha mobiiltelefonist?
Kui valguslaine on kui merelaine, mille lainepikkus on pool meetrit, siis aatom selle laine ees oleks kui otsapidi vette pistetud traadijupp läbimõõduga 0,5mm (päriselus vastavalt u 500 nm ja u 1Å ). Kui kaugele ulatuks selle traadi vari?
Kui ei ole varju, siis ei ole ka infot, mida vaatleja saaks lainemustrist välja lugeda. Tankeriga on lihtsam (vt pilti).
Molekulid on valgusega vaatamiseks liiga väiksed. Või on valguse lainepikkus liiga suur, kuidas võtta ...
Elektroni kujutatakse kooliõpikutes tihti kui kuulikest, millele on miinusmärk küljele joonistatud. Aga elektron võib ka käituda kui laine (üks mikromaailma veidrustest, millest räägib 11.klassi füüsika). Ja kui ta seda teeb, siis saame rakendada kogu seda tarkust, mida me oleme valgust uurides õppinud. Lihtsalt valgusallika asemel on elektronkahur ning elektronlaineid koondavad läätsed ei ole tehtud klaasist, selle asemel tekitatakse elektrivoolu abil sobiva kuju ja tugevusega magnetväli.
Trikk on selles, et elektronlainete lainepikkus on kuni 100000 korda väiksem, kui valguslainetel.
2017.a. Nobeli auhind keemias omistati Jacques Dubochet'le, Joachim Frankile ja Richard Hendersonile "kõrglahutusega krüo-elektronmikroskoopia arendamise eest biomolekulide struktuuri määramiseks". Kõik laureaadid on hariduselt füüsikud.
Aga võib minna kaugemale. Optika komponentide tootjad pakuvad sfäärilisi läätsi, nn kuulläätsi. Kui paigutada 1mm kuullääts mobiiltelefoni objektiivi ette, siis väidetavalt on võimalik saada suurendus 350x. Üks selline kuullääts maksab 22 dollarit. Väga suurepärane väljakutse mõneks uurimistööks ...
Valgus levib sirgjooneliselt vaid juhul, kui keskkond tema teel on ühtlane, st selle murdumisnäitaja ei muutu. Temperatuuri erinevused ja õhu liikumine kallutavad valgust selle sirgjoonelisest levimisest kõrvale.
Proovige järele: kui suunata laseri kiir läbi põlevast küünlast kerkiva kuuma õhujoa hakkab laseri täpp seinal värisema.
Samamoodi hakkab värisema tähe kujutis teleskoobi sensoril, sest atmosfäär on turbulentne ja ebaühtlase temperatuurijaotusega.
Kui tähe kujutis teleskoobi sensoril liigub, siis see tähendab, et kujutise moodustavate kiirte suund muutub. Kui me teaksime, kust poolt täht parajasti paistab, siis saaksime teleskoobi peegli asendit või kuju niimoodi muuta, et tähe kujutis sensoril paigale jääks. Umbes samamoodi, kui auto tahavaatepeegli asendit reguleerime, kui erineva pikkusega juhid rooli istuvad.
Aga kuidas me reguleerime auto tahavaatepeeglit? Meil on orientiiriks auto tahavaateakna serv. Teleskoobi peegli kuju muutmist saab juhtida jälgides tähtede kujutisi - reguleerida tuleb nii, et need paigal püsiksid. Arvutid saavad sellega hakkama. Kui vaadeldavas piirkonnas ühtki piisavalt heledat tähte ei ole, siis tekitatakse laseriga "kunstlik täht".
Lugu on veel üks aste põnevam. Atmosfääris on 80-105 km kõrgusel ca 5 km paksune ioniseeritud naatriumi kiht. Laserite lainepikkus valitakse nii, et see selles kihis neelduks. Sest kui juba neeldub, siis ka kiirgab ja ongi nagu täht! Vt ka videot ja selgitust allpool.
Minge pimedas välja, vaadake, et ühtki lennukit teist parajasti üle ei lenda ning suunake laser taevasse. Tulemus võib teid üllatada - laseri kiir levib, levib ja siis justkui katkeb järsult.
Tegelikult ei katke. Aga kui see jõuab välja atmosfääri piirkihist (planetaarsest piirkihist), siis satub selle teele palju vähem valgust hajutavaid osakesi (aerosooli). Ja kui valgus ei haju, siis me seda ka ei näe.
Laineenergia on lainetes. Aga kui palju seda energiat on? Kas lainete energia on piisav selleks et mõne saareriigi energiavajadus ära katta? Näiteks Suurbritannia?
Pakume lugemiseks järgmist lõiku David JC MacKay raamatust "Taastuvenergiast ilma udujututa".
Waco, Texas, 15. September, 1896: Willian Crush Missourist, Kansasest ja Texase Raudteekompanii mõtlesid välja lollikindla idee kuidas rahvast kokku meelitada ja etendusega raha teenida. Kuuekilomeetrise raudteejupi kumbagi otsa paigutas Crush vananenud veduri, üks värviti roheliseks, teine punaseks. Asja mõte oli lasta veduritel täiskiirusel teineteisega kokku põrgata.
Teadusteatris saab teha katset, kus vedel lämmastik suletakse plastikpudelisse, mis siis kiirest kasvava rõhu mõjul lõhkeb, nii et käib vägev kõmakas.
Selge see, et niisugune katse on ohtlik. Aga kui ohtlik? Kui arutleks selle üle füüsikuna?
Tahaksime ka näidata, et lihtsad "paugutamise" katsed on võimalik koolifüüsikasse puutuv sisuga täita, nii et asjast ka sisulist kasu oleks.
Kes kardab AA patareid? Eriti mitte keegi? Aga võtaks seda niipidi, et ühes keskmises sellises patareis on peidus üle 10000J energiat. Teoreetiliselt saab selle energiaga 100kg kaaluva mehemüraka h = E/mg = 10m kõrgusele tõsta ... või visata, kui energia peaks eriti kiiresti vabanema. Näiteks käsirelvade kuulide kineetiline energia on üle 5000J vaid äärmuslikel juhtudel.
Ja nüüd lubatud mõtteharjutus: Võistlusdistantsi pikkus on kolm meetrit. Ehita auto, mille energiaallikaks on üks AA patarei ja mis läbiks selle distantsi võimalikult kiiresti. Auto võib sisselülitatud olekus stardiks valmistuda kuni pool tundi.
Aineosakesed (aatomid ja molekulid) on pidevas soojusliikumises. Teame ka, et kehad kaotavad ja saavad energiat soojuskiirguse kaudu. Aga tasub ka teada, et soojuskiirguse allikaks on soojusliikumises olevate aineosakeste põrked. Mis ehk veelgi olulisem - kuna kõigi kehade soojuskiirgusel on ühine algpõhjus, siis on selle kiirguse spekter ühesugune sõltumata ainest või keha kujust.
Kuidas töötab infrapunatermomeeter ja termokaamera? Kuidas ja mida mõõdab infrapunatermomeeter? Jah, nuppu on vajutada lihtne, samuti lugemit võtta. Aga selline mittekontaktne mõõtmine pakub kindlasti üllatusi. Loodetavasti lubab siit avanev selgitus kõige suurematest karidest mööda loovida.
Vasakul pildil termomeetri vaateväljas taevas, paremal ka tükike pilve. Mõõtetulemus erineb neil kahel juhul oluliselt. Mida me mõõdame?
Soojuskiirgus on väga oluline ... kosmoses. Sest vaakumis muid mehhanisme soojusvahetuseks ei ole. Termoses püsivad asjad nii soojad kui ka külmad, kosmoses siis ei tohiks külm olla? Või ikkagi on ja külmume hetkega purikaks? Proovime arutleda.
Muide, Hyperloop on avatud tehnoloogiaga projekt - kõik saavad kaasa mõelda. Ja Elon Muski esmane artikkel peaks olema arusaadav kõigile, kes koolis füüsikat õppinud.
Arusaamine tähendab võimet ja võimalust kaasa mõelda. Ka kaasa rääkida. Ka koolitunnis.
Tõepoolest! Sest ka üsna tavalise väljanägemisega rongid sõidavad kuni 600km/h.
Torusse, sest Elon Musk tahaks kiiremini - ülehelikiirusega. Ja torust saab osa õhku välja pumbata.
Jätame muu mehaanika seekord rahule, räägime õhust. Ja teistmoodi elektrimootoritest.
Suurte kiiruste saavutamiseks on vaja suurt jõudu. Ratastel sõiduki maismaa kiirusrekord on kahe reaktiivmootoriga rakettauto ThrustSSC käes. Teeme mõned hinnangud - kui palju õhk sellist liikumist takistab?
Kuidas teha katseliselt kindlaks, et hõredas õhus kulub kiirelt edasi liikumiseks vähem energiat? Lihtne! Tuleb hüpata kõrgelt (näiteks 40 km kõrguselt) alla ja registreerida üheaegselt oma kiirust ja õhu tihedust.
Väga kiiresti liikumiseks ei ole rattad enam väga sobivad - tsentrifugaaljõud tahab neid puruks rebida ja stabiilsus ei ole kõige parem. Hea oleks, kui vagun üldse millegi vastu ei puutuks. Hyperloopi "rattad" näevad välja sellised:
Jalase ja aluspinna vahel on õhkpadi. Õhkpadja tekkimiseks vajalik õhk tuleb kapsli ninas paiknevast kompressorist. Ei midagi põhimõtteliselt uut: Hyperloopi vaguneid hoiab vastu toru pinda puutumast sama põhimõte, mis hoiab tuntud CD plaadi hõljukit vastu lauda puutumast.
Lineaarne selles mõttes, et tõmbab/tõukab otsejoones, mitte ei pane pöörlema, nagu ehk harjunud oleme. Kuidas sellised mootorid töötavad? Ehk siis missugune jõud tõukab õhkpadjal hõljuvat Hyperloopi kapslit torus edasi?
Olgu siinkohal vahemärkusena öeldud-reklaamitud. Omal ajal on paljusid innustanud Jakov Perelmani raamat nimega Huvitav füüsika. Ja see on hea raamat ka tänaste standardite järele. Sest kui paljud meist oskavad rääkida loodusteadusest läbi lugude? Eestikeelse väljaande teine köide on olemas ka e-õpikuna.
Muinasjutuline tee
Sama pilt veidi suuremalt. Tõepoolest, pildi keskel tumedal taustal kahe nõelataolise elektroodi vahel on kahvatu heledam täpp. Ehkki see näeb välja kui tolmutera, on see märk millestki palju-palju väiksemast: kusagil seal on ioonlõksustatud valgust kiirgav üksik strontsiumi aatom. Loomulikult õhutühjas ruumis. Delfi Forte väidab, et "See helesinine täpike ongi strontsiumiaatom".
Aatomid on väiksed. Väga väiksed. Aatomi läbimõõt on umbes 0,25 nanomeetrit (miljardikku meetrit). Ühe verelible sisse mahub vabalt miljardeid aatomeid. Kui aatomeid on võimalik pildistada, siis punane verelible peaks olema eriti lihtne saak. Tõesti? Mäletate, hiljuti rääkisime 2017.a. Nobeli keemia auhinnast mis anti "kõrglahutusega krüo-elektronmikroskoopia arendamise eest biomolekulide struktuuri määramiseks". Asjata anti?
Mida siis tegelikult tehti? David Nadlinger kasutas tavalist digikaamerat. Muidugi, tal oli kasutada ka Oxfordi lõksustatud ioonidel põhinevate kvantarvutuste labori (Oxford's Ion Trap Quantum Computing lab) seadmed ja just selliste seadmete puudumine ei lase meil sarnaseid fotosid teha. Aga, pildistamine ise käib ju tuttava, koolis õpitud põhimõtte järgi?
Nagu ikka, pilt läheb selgemaks, kui veidi süüvida. Loe järgnevat joonist sellel olevate tekstide numbrite järjekorras.
Kõnealuse strontsiumi aatomi kiiratud valgus peab ikkagi olema päris ere, et see suudaks tavakaamera sensori mitu pikslit piisava koguse valgusega (footonitega) täita. Kui palju valgust suudab kiirata üks aatom? Aatom kiirgab, kui selle mõni elektron läheb kõrgema energiaga olekust madalama energiaga olekusse. Aga kõigepealt peab aatom piisaval hulgal energiat neelama, et kõrgema energiaga olekusse saada.
Selliste üleminekute käigus kiirgub tavaliselt üks footon, footonite arvu mingis ajaühikus määrab see, kui kaua viibib elektron ühes või teises olekus enne, kui uuesti neelab või kiirgab footoni. Need viivitused ei ole tavaliselt pikemad, kui mõni nanosekund. Nii et jõuab kiirata päris palju.
Tähed on tähistaevast tehtud piltidel tihti umbes sellised, nagu allpool näha. Kas punktide suurus pildil peegeldab kuidagi tähtede tegelikku suurust või kaugust?
Kõik tähed on tähistaevas tegelikult palju väiksemad, kui nad silmale või kaamerale paistavad. Isegi teleskoopidele on tähed valdavalt ilma mõõtmeteta punktid, erandiks vaid kõige lähemad ja suuremad tähed kõige võimsamates teleskoopides.
Tähe kujutise suurus pildil midagi tähe suuruse (või kuju) kohta, ainult selle heleduse, salvestava seadme ja atmosfääri selle hetke turbulentsuse kohta.
Hoopis see on kõnealuse eksperimendi põnev osa! Sest lõksustatud ioonidel töötavad näiteks maailma kõige täpsemad nn valguskellad. Ioone hoiab paigal elektriväli. Aga see ei ole niisama lihtne - saab näidata, et ükski paigalseisvate laengute kombinatsioon ei anna olukorda, kus ioon jääb nö hõljuma. Kuidas siis saab?
Kuidas lõksustada iooni?
Meeldetuletuse ühest varasemast Mesilasest.
Kui väga puhast vett jahutada, siis võib juhtuda, et vee molekulid "kleepuvad" üksteise külge samamoodi korrastamata kujul, nagu nad on vedelas vees. See ei ole energeetiliselt kasulik, aga see on võimalik. Sellist vett nimetame alajahutatud veeks ja sellise (täitsa vedela vee) temperatuur võib olla palju madalam, kui null kraadi. Põnevaks läheb siis, kui sellist vett raputada.
Külmuv ja alajahutatud vesi
Kes ei viitsi lugeda, see vaatab ära järgneva video.
Hoorattale hoogu andes salvestame sinna energiat. Selle energiaga saaks tööd teha ... aga kui palju? Tänased taastuvenergial töötavad autod saavad oma energia akudest. Kuidas paistab selles võrdluses välja hooratas? Selgub, hooratas on põhimõtteliselt suurema energiatihedusega salvesti, kui Tesla Roadsteri akupatarei.
Hooratas kui energia salvestaja
Falklandi saarte lahing ja Pariisi kahur
Inimesed on aegade algusest olnud suured leiutajad. Alles suhteliselt hiljuti hakati oma teadmisi teaduseks vormima.
Bolad
Tuletame alustuseks meelde, mida me teame lainetest. Arvatavasti seda, et on piki ja ristlained. Näiteks helilaine on pikilaine, elektromagnetlaine jälle ristlaine. Ja näiteks maavärinate korral esinevad nii piki- kui ka ristilained. Aga mis on merelaine, st laine, mis levib veepinnal?
Aga on olemas ka teistmoodi lained. Tõusulained võivad teatud jõeosast üles levides oluliselt vee sügavust suurendada. Severni jõel Inglismaal võib mööda jõge üles liikuv laine olla teatud juhtudel piisavalt kõrge, et sellel mitu kilomeetrit lainelauaga sõita.
Kes eelnevat teksti lugesid, need panid ehk tähele sõna soliton. Sellise laine matemaatiline tagapõhi on tõsiselt keeruline, kuid laine ise on lihtne - näeme veepinnal levivat üksikut lainet. Solitoni energia ei haju, nii et ta levib väga kaugele. Ja soliton tõesti viib vett endaga kaasa. Solitonide avastamise kohta räägitakse ka üht lugu.
Tagasi meie pilvede juurde. Kahe erineva temperatuuriga ja üksteise suhtes liikuva õhukihi piirpind võib lainetada ja see lainetus on nagu soliton. Kui füüsik tahab täpsemalt teada, siis ta vaatab esmalt eelmise loo juures olevat kommentaari solitonide matemaatilise esituse keerukuse kohta, geograafile ja keskkonnafüüsikule pakuks ehk huvi Münchenis asuva Ludwig Maximiliani ülikooli teadlaste teemaleht. Allpool on üks pilt ja üks katse video, mis ehk asja kodusemaks teevad.
See on meil veel rääkimata. Vahel on nii, et maapinnast palju kõrgemal asuv õhukiht on soojem kui selle all asuv õhukiht – olukord, mida tuntakse inversiooni nime all. Meie pilvede tekkimiseks on see vajalik. Aga mitte ainult.
16. mai 2018 on kuulutatud rahvusvaheliseks valguse päevaks. Sel puhul kutsume teaduse- ja tulevikuhuvilisi Tartu Ülikooli Füüsikumi (aadressil W.Ostwaldi tn.1, Tartus).
Räägime, seletame, katsetame, arutleme, näitame, tutvustame, anname aru.
Arvame, et enda jaoks huvitavat leiavad nii põhikooli kui ka gümnaasiumi õpilased ja õpetajad.
Teemad leiavad paari lausega tutvustamist allpool. Erinevalt tavapärasest Mesilasest ei leia te sealt teemade arendusi. Peate ise kohale tulema ...
Kes tuleb, see võiks end kirja panna:
13.-14. augustil toimus Lepanina Hotellis füüsikaõpetajate suvekool. Kohale tuli 96 õpetajat, loenguid, töötubasid, arutelu ja suminat jätkus kaheks päevaks. Jagati välja ka mitmeid veksleid. Kõige sellega saab tutvuda (ja end jooksvalt kursis hoida) taasavatud füüsika õpetajate võrgustiku kodulehel:
- Suvekooli kava ja pildigalerii.
- Välja jagatud vekslid.
Oleme vorgustik@fyysika.ee
Käib hoogne (teadus)huvihariduse edendamine. Formaalharidus vaatab natuke kurva näoga pealt. Samas on neil kahel kokkupuutepunkt olemas, miks mitte see üles otsida, et seda siis igapäevases koolitöös rakendada? Sel aastal me Teaduslaagris piloteerisime tegevusi, millel võiks olla sellist potentsiaali. Juuresoleval pildil sobitatakse kokku füüsikat ja robootikat, teiste teemade kohta saad aimu allpool viidatud lehelt. Täpsemalt võtame need Mesilases ette siis, kui juhendmaterjalid päriselt valmis saavad.
Füüsika e-õpik on elus ja areneb. Mesilase materjalid tulevad otse sealt, e-õpikusse tekib Mesilase arhiiv ja e-õpiku repositooriumi otsing annab välja ka Mesilase materjalid. Ja neid materjale, samuti kui erinevate õpikute alapeatükke, on hea jagada ja vistutada (st teistesse e-keskkondadesse istutada). Lingid saab selle noolekujulise ikooni alt. Vaata näiteks Mesilase arhiivi.
SPARK Makerlab tänab kõiki õpetajaid, kes gravitatsiooniauto meisterdamisel osalesid! Nagu töötoas mainitud, oleme arendamas EduLabi nime all loodusteaduste ja tehnika huvitegevuse täispaketti. Meie eesmärgiks on viia praktiline õpe noorteni ning lihtsustada märgatavalt inseneeriateemaliste huviringide ja laagrite käivitamist. Kes soovib paketti tasuta saada, arendudes kaasa lüüa või muidu lisainfot saada, võtke ühendust tarvo@makerlab.ee, uurige www.edulab.ee lehte või vaadake meie videokokkuvõtet.
Kui vedel lämmastik suletakse plastikpudelisse, mis siis kiiresti kasvava rõhu mõjul see lõhkeb. Kui ohtlik selline katse on? Koolifüüsika on piisavalt võimas, et sellel teemal arutleda ja praktilisi järeldusi teha. Kus on energia? Kui palju seda on? Kuidas see vabaneb ja tööd teeb?
Katsel on ka teine moraal: ka muidu pigem teadusteatrite repertuaari kuuluvad katsed saavad olla sisukad, kui neid sellisena esitatakse.
Ütleme, et:
Järeldus 1: ka väga väike energia võib anda suure võimsuse , kui see kantakse üle väga lühikese aja jooksul. Ja lühikese aja jooksul üle kantud suur energia võib anda tohutu võimsuse.
Järeldus 2: väga suur energia võib anda väikese võimsuse, kui see kantakse üle väga pika aja jooksul. Ja pika aja jooksul vabanev üsna suur energia võib meile jääda märkamatuks.
Näited
Mitu raskuskiirendust?
Kõigepealt valgusest:
Kaasaegne ettekujutus valgusest
Nüüd siis asjast:
Aatomites on elektronid kindlail energiatasemeil, mis püsivalt omased igale aatomiliigile (elemendile). Aatomid saavad kiirata vaid valgust, mille footonite energia vastab olemasolevate energiatasemete vahele.
Samamoodi saavad aatomid valguse energiat vastu võtta üksnes kindlate portsjonite kaupa - neelatavate footonite energiad peavad vastama aatomi energiatasemete vahedele.
Kõlab kuivalt, aga nende lihtsate tõdede omaks võtmine avab tee terve müriaadi nähtuste mõistmiseks.
Need kaks tõdemust on lahti seletatud paljudes füüsika õpikutes. Viitame siin Henn Käämbre käsitlust:
Kuna reaalsetes materjalides on aatomid tihedasti koos, mõjutavad nad üksteist tugevasti. Elektronkatte sisekihtide elektronide energiatasemed jäävad kristallis peaaegu muutumata, kuid väliselektronide tasemed paisutab aatomite elektriline vastastikmõju laiadeks, mitme elektronvoldi laiusteks energiavöötmeteks e. energiatsoonideks. Ka selliste tsoonide vahel on keelutsoonid, kuhu elektronid mingil juhul sattuda ei saa. Nii et jällegi - materjalid saavad neelata ja kiirata vaid teatud energiatega footoneid.
Näited
Taastuvenergia on hea. Põlevkivi põletamine halb. Kõik teavad seda. Aga mida see tähendaks, kui tahaksime näiteks asendada Eesti Elektrijaamad päikesepaneelidega? Kui palju peaks neid paneele olema? Kui palju võtaksid nad ruumi? Selle ja sarnaste küsimustega tegelemiseks annab füüsika tööriistad. Need hinnangud peavad vett ja võivad teid üllatada.
Päikeselt saabuva päikesekiirguse energia soojendab Maad ja see on hea - muidu ei oleks elu siin võimalik. Ka kasvuhooneefekt on hea - ilma selleta soojeneks vaid atmosfääri ülemine osa, termosfäär. Tõepoolest, kui mõelda atmosfäärist kui valgusfiltrist, siis kõik mis neelduma peab, neeldub ära atmosfääri ülakihtides Mis ei neeldu ja jõuab maapinnani, võiks ju peegeldudes ka atmosfäärist välja pääseda? Kuidas ikkagi juhtub nii, et soojeneb ka atmosfääri alumine kiht?
Füüsika ja bioloogia liiga tihti ühe jutu sisse ära ei mahu - misiganes bioloogiline süsteem on vähegi täpsema füüsikalise mudeli abil kirjeldamiseks liiga keeruline. Energia kontseptsioon on siiski universaalne ja bioenergeetika on ühtviisi mõistetav nii füüsikule kui ka bioloogile. Kuidas lugeda kokku toiduenergia džaulid? Kuidas fotosünteesis päikeseenergia džaulidest toiduenergia džaulid saavad?
Mobiiltelefonis on sensorid, mida on võimalik looduse uurimisel kasutada. Selles miniuurimuses ehitame mobiiltelefonist pendli ja mõõdame kiirendust selle võnkumisel. Tulemused lubavad meil kontrollida mehaanilise energia jäävuse seaduse paikapidavust.
Mobiiltelefoniga mehaanilise energia jäävuse uurimine pendli võnkumisel
Study of the conservation of mechanical energy in the motion of a pendulum using a smartphone
Theodoros Pierratos and Hariton M Polatoglou
A common method that scientists use to validate a theory is to utilize known principles and laws to produce results on specific settings, which can be assessed using the appropriate experimental methods and apparatuses. Smartphones have various sensors built-in and could be used for measuring and logging data in physics experiments. In this work, we propose the use of smartphones for students to study a simple pendulum's conservation of mechanical energy. It is well known that common smartphones do not have a velocity sensor, which could make the verification of the conservation of mechanical energy a simpler task. To overcome this, one can use an accelerometer to measure the centripetal acceleration on the mass and from that, deduce the maximum velocity. In this study, we show that this can be achieved with reasonable uncertainty, using a mobile device. Thus, we developed an experiment which corroborates with the conservation of mechanical energy and can be performed in the classroom.
XLIX Eesti füüsikapäevad ja XXXXI füüsikaõpetajate päevad toimuvad 26.-27. aprillil Tallinnas, Eesti Teaduste Akadeemia hoones ja Tartus, TÜ Füüsikumis.
Koos seekordsete füüsikapäevadega tähistame Eesti Füüsika Seltsi asutamise 30. aastapäeva.
Reede, 26. aprill on füüsikaõpetajate päev, mis toimub Tartus, TÜ Füüsikumis. Lisaks õpetamist puudutavatele ettekannetele ja töötubadele võtame aruteludes ette kaks teemat: kavandatavad õppekava muudatused ja füüsikaolümpiaadide olevik ja tulevik.
Laupäeval, 27. aprillil räägime Tallinnas, Eesti Teaduste Akadeemia hoones teadusest. Muuhulgas võtame aruteludes ette Eesti füüsikateaduse ja füüsikahariduse tänase olukorra ja tulevikuperspektiivid.
Täpsem info ja registreerumine: http://www.fyysika.ee/vorgustik/?page_id=1544
Pendel stabiliseerib
Füüsika ja igapäevaelu paralleele on põnev otsida ja leida. Füüsikaõpetajate päevade roll on tugevdada kogukonda ja tasakaalustada füüsikaõpetajate ja füüsikast pidavate inimeste kogukonda, protsesse ühiskonnas üleüldiselt. Täpselt nagu pendel, kui see õigesti häälestada.
On valmis saanud kogumik, kuhu on koondatud 200 gümnaasiumi ülesannet Eesti füüsikaolümpiaadi piirkonnavoorudest, lõppvoorudest ja lahtistest võistlustest. Igale ülesandele on juurde kirjutatud paarilauseline vihje ja ka lahendus.
Hea öökapiraamat! Saadaval ka elektrooniliselt.
200 Eesti füüsikaolümpiaadide ülesannet aastatest 2012-2018
Siia on koondatud 200 gümnaasiumi ülesannet Eesti füüsikaolümpiaadi piirkonnavoorudest, lõppvoorudest ja lahtistest võistlustest. Igale ülesandele on juurde kirjutatud paarilauseline vihje. Juhul kui õpilane jääb ülesannet lahendades toppama, on tal võimalik vihjet lugeda ning teisele katsele minna.
Ülesanded on jaotatud teemade kaupa ning teemasiseselt raskuse järgi. Raskustaset tähistatakse kuni viie tärniga. Ülesannete lihtsamaks otsimiseks on ülesannete numbrite ette pandud “Ü”, vihjete ette “V” ja lahenduste ette “L”. Näiteks ülesande 133 teksti number on kujul Ü133. Iga ülesande juures on kirjas ka selle autor ning olümpiaadi vooru lühinimetus, lisaks lühendid P 1, G 1 jne, kus tähed tähistavad põhikooli- ja gümnaasiumiastet. Näiteks G 9 viitab gümnaasiumiastme 9. ülesandele.
Mugavamaks navigeerimiseks lingib veebiversioonis iga ülesande number tekstist vihjeteni, vihjetest lahendusteni ja lahendustest tekstini.
Kogumiku koostamise käigus eemaldati erinevatel põhjustel 4 ülesannet, mis asendati 2011. aasta füüsika lahtise võistluse ülesannetega.
Järgmine veebipõhine füüsikaviktoriin "Spekter" toimub 9. mail 2019 ajavahemikus kl 8:00 kuni 20:00. Viktoriin on mõeldud 8.-12. klasside õpilastele, aga ka nooremate klasside õpilased on oodatud viktoriinist osa võtma. Viktoriin toimub paralleelselt eesti ja vene keeles.
Info Teaduskooli kodulehel
Kui juba hakkasime väljakutseid pakkuvatest asjadest rääkima ... Oleme kunagi siin Mesilases akustilisest levitatsioonist rääkinud, õigupoolest viidanud sellise nähtuse olemasolule. Ilma süvenemata. Nüüd oleme penoplastist kuulikesi heli abil hõljumas hoidva seadme ise valmis ehitanud. Kes tahab täpsemalt teada, see loeb. Kes tahab tulemust vaadata, see klikib videole allpool. Füüsikaõpetajate päevade minimessil saab seda seadet ka oma käega katsuda.
Akustilise läätse (st helilaineid fokusseeriva läätse) ehitamine süsinikdioksiidiga täidetud õhupallist oli meile ideena juba ette sattunud. Proovisime, ei töötanud eriti hästi. Selles videos töötab. Pani mõtlema, et kui uuemal ajal ultraheli generaator koos vastuvõtjaga maksab paar eurot komplekt, siis äkki saaks leiutada katsekomplekti, kus kõik need katsed saaks A4 paberi suurusel alal ära korraldada? katsed ära teha. Vaja proovida. Kõik huvilised ja kaasamõtlejad on teretulnud.
Mõned üldised printsiibid, mis lihtsustavad järgneva mõistmist. Aga võib ka otse järgmise alajaotuse juurde minna.
Energia ja võimsus
Energia ja entroopia
Erinevate energialiikide võrdlemisest
Nüüd siis lõpuks lubatud avastamisrõõm - geotermilise energia kättesaamist takistab see, et soojusenergia liigub ainetes teatud lõpliku kiirusega. Ja see toob kogu teema otsejoones 9.klassi füüsikasse, kus räägitaks muuhulgas ka soojusjuhtivusest. Sest entroopia mõistest annab mööda vingerdada. Eriti tore mõtteharjutus on soojuse kaevandamine. Esimese hooga ei õnnestunud välja mõelda ühtki lihtsalt läbi viidavat praktilist tööd, mis asja olemuse kokku võtaks. Aga küllap ka see tuleb.
Asi ei ole ju ainult füüsikas, mida tuleb reaalse eluga siduda. Veel tähtsamgi on see, et füüsika annab võimaluse taastuvenergeetikast rääkides esitada numbritel ja hinnangutel põhinevaid argumente. Ja hinnata teiste esitatud argumente. Eriti hariv võiks olla koos õpilastega Eestile taastuvenergia allikatel põhineva energiaplaani kokku panemine. Aga sellest edaspidi.
Mida meelde tuletada enne asja kallale asumist.
Kui valguskiir möödub massiivsest kehast, siis see selle trajektoor paindub
Selles loengus annab TÜ Tartu Observatooriumi vanemteadur Peeter Tenjes vajalikud taustateadmised mustast august M87* tehtud pildi mõistmiseks. Saame ka teada, miks on selle Mesilase päises musta auku just sellisena kujutatud. Ka seda, kuidas tekkisid universumisse kuld ja teised rasked elemendid - siin on meie arusaamine universumi evolutsioonist tublisti muutunud.
Pakume siin lugemiseks Piret Kuuse kirjutatud kokkuvõtet, mis ilmus 2008. aastal ajakirjas Horisont. Mustade aukude uurimise ajalooline perspektiiv saab siin täpsemalt läbi räägitud. Mainimist leiab Tartu Ülikooli panus. Samuti võimalus raadiuteleskoopide abil musti auke detekteerida ... nagu seda nüüd tehtud ongi.
| Kui massiivsed objektid painutavad ruumi, levib ka valgus kõverat teed pidi. Gravitatsiooniläätse efekti saab simuleerida spetsiaalse kujuga läätsedega. Neid läätsesid saab ... veiniklaaside alustest ise meisterdada. | Selles videos on veiniklaasi alusest tehtud lääts tähistaeva kujutisel. Efekt on üsna sarnane sellele, mida võib näha teleskoopides gravitatsiooniläätse efektis. |
Kuidas meie Linnutee galaktika tekkis? Kuidas mustad augud kasvavad? Milline on meie Päikesesüsteemi päritolu? Kas on olemas teisi eluks sobivaid maailmu? Need on mõned küsimustest, millega Euroopa Kosmoseagentuuri teadusmissioonid praegu tegelevad.Hetkel planeerime tulevikumissioone ning Euroopa Kosmoseagentuuri teadusdirektor Günther Hasigner kutsub Teid oma seisukohti jagama.
Selle lühikese veebipõhise küsitluse kaudu tahaksime kuulda, milliseid teaduse suuri küsimusi peaksid adresseerima tulevased kosmosemissioonid 2050. aastani.
Küsitlusele vastama
Sissejuhatuseks üks aimeloeng. Laurits Puust on teinud teadust valgusega. Ja üritanud oma tulemusi ka igapäevaelus tööle panna. Nii et on igati paslik see 2019. aasta füüskaõpetajate päevade loeng siin ära vaadata. Saate teada, milliste valgusallikate jaoks ei ole elektrit vaja, kuidas näha inimese sisse, kuidas inimese sees valgusega vähirakke hävitada, kuidas sealjuures temperatuuri mõõta. Muud ka.
Fotosüntees
Fotosüntees, nagu me seda 7. klassis õpime, on see, kui taimed kasutavad valgust veest ja süsihappegaasist glükoosi tootmiseks. Lisaks eraldub reaktsiooni käigus hapnik:
süsihappegaas + vesi + energia → glükoos + hapnik
Kui taim kasutab valgust fotosünteesis, siis füüsika keeles öeldakse, et taim neelab osa valgusallika tekitatud liitvalgusest. Millise osa täpselt, seda ütleb neeldusmisspekter. Kõige efektiivsem valgusallikas fotosünteesi käivitamiseks on see, mille valgus neeldub taimes täielikult.
Rakust eraldatud klorofüll kiirgab punast valgust (luminestseerub). Taime leht ei tee seda mitte. Miks? Peaks olema nii, et kui valgustada pikalt pimedas olnud rohelist lehte, siis hakkab see punaselt luminestseeruma, kuni fotosünteesi reaktsioonitsentrid uuesti ergastuvad ja käivituvad fotokeemilised protsessid (Kautsky effekt). Ehk siis luminestsents kaob ära, kui neeldunud valguse energiat hakatakse kasutama suhkrute tootmiseks.
Katse: võtke sinine laser, minge mõne "magava" taime juurde ja valgustage seda laseriga. Kas hakkab punaselt luminestseeruma?
Füüsika ei peaks ette kujutama, et ta saab tema mudelid kirjeldavad meid ümbritsevat elurikkust täpselt. Aga me võime ja peame üritama, kus see iganes võimalik. Taimede valgustamise energeetika kindlasti pakub sellise võimaluse.
Luunjas kasutatakse naatriumlampe. Kõrvutame kaht tüüpi naatriumlampide spektreid klorofülli neeldumisspektritega ja teeme oma järeldused.
Marsile reisimist ei saa alustada suvalisel ajal. Ka lahkuda ei saa sealt siis, kui tahtmine peale tuleb. Tuleb oodata, kuni Maa ja Marss asetsevad üksteise suhtes sobivalt.
Kas me suudame oma koolitarkust appi võttes analüüsida Marsile jõudmise, seal maandumise ja ellu jäämise ning sealt tagasi sõitmise olulisemaid väljakutseid? Või on see kõik raketiteadus?
Energia, energia jäävuse seadus Üldine energia jäävuse seadus. Mehaanilise energia jäävuse seadus. Keemiline side, sidemeenergia. Elektrivool gaasides
Tegelikult läheb tarvis ka arusaamist mikromaailma toimimisest, nimelt sellest, et seal energiat neelatakse ja kiiratakse kindlate portsjonite, so kvantide kaupa. Sellest räägima gümnaasiumis, mikro- ja megamaailma kursuses. Aga mitte kohe alguses.
Marsi atmosfäär on parajasti nii hõre, et ainult sellest kosmoselaeva pidurdamiseks ei piisa, peab kasutama ka rakettmootoreid. Samas on see parajasti nii tihe, et ilma kuumakilbita kuidagi läbi ei saa. Mis ongi põhjus, et Marsile laskumine on tehniliselt palju keerulisem ettevõtmine, kui maandumine või kuundumine.
Marsi atmosfääris leiduvat süsinikdioksiidi saab kasutada kohaliku toorainena hapniku tootmiseks. Sellise protsessi aluseks võib olla süsinikdioksiidi keemiliste sidemete lõhkumine, nii et tekiks süsinikmonooksiid ja hapnik. Füüsika teeb keemiat.
Marsil hapniku tootmisel saame ka CO-d, mis koos hapnikuga võib olla ka raketikütuseks. Mis veelgi põnevam - niimoodi saaksime CO2 neutraalse kütusetsükli. Ja see kõlbaks kasutada ka Maal, kui CO2 lõhkumiseks kasutada taastuvenergiat?
CO2-neutral fuels
Mimicking the biogeochemical cycle of System Earth, synthetic hydrocarbon fuels are produced from recycled CO2 and H2O powered by renewable energy. Recapturing CO2 after use closes the carbon cycle, rendering the fuel cycle CO2 neutral. Non-equilibrium molecular CO2 vibrations are key to high energy efficiency. Adelbert Goede ja Richard van de Sanden, EPN 47/3
Õpilased peavad ehitama pudelist ja olemasolevatest materjalidest raketisüsteemi, mille külge kinnitatud toores muna jääb ka pärast raketi lendu ja maandumist terveks ja millega startiv muna lend kestab võimalikult kaua. Katsetasime sel kolmapäeval Tõrvas. Tüdrukud tegid poistele ära ...tegid ära ka ühele robotiehitajast tudengile.
Põhjendatud küsimus. Igapäevakogemus ütleb meile, et kõik asjad, mis maapinna kohal lahti pääsevad, kukuvad alla ehk maha. Samas planeedisüsteemid püsivad ja kaaslased tiirutavad miljoneid aastaid ümber planeetide. Tõesti, miks?
Tarvilik koolitarkus:
Jah, kukub. Kukkumise kiirenduse võib arvutada ringliikumise kinemaatikast, aga võib ka tuletada gravitatsiooniseaduse loogikast (pöördruudu seadusest). Tulemus on sama.
Kuu allumist Maal avastatud gravitatsiooniseadusele võib võtta ka kui tõestust sellele, et Kuud hoiab ümber Maa tiirlemas sama jõud, mis paneb õuna alla kukkuma. Mõelge hetkeks ... äge, eksole?
Kui kiiresti peab siis satelliit liikuma, et ta jääkski Maast mööda kukkuma? Vastamiseks piisab ringliikumise kinemaatikast ja gravitatsiooniseadusest.
Algodoo: orbitaalliikumine
Selle simulatsiooni algseisuks on ühesuguste kiirustega kehad erinevatel kõrgustel maapinnast. Kui simulatsioon käivitada, siis saab vaadata, milised trajektoorid need kehad valivad. Lihtne on ka muuta kehade algkiiruseid või näiteks uurida nende kiiruste muutumist ajas. Simulatsioonis on olemas ka ümber Maa tiirlev Kuu.
Miks on kosmoseturistide orbiidile viimine ca 100 korda kallim, kui kosmoseturistide kosmosesse, st vähemalt saja kilomeetri kõrgusele viimine? Võrdleme energiaid.
Allpool näete graafikut kosmoselaev Voyager 2 kiirusest, kui see Maalt alustades läbi päikesesüsteemi lendas. Ei ole üldse igav reis, eksole? Selle graafiku seletamine on päris hea harjutus oma füüsikalise mõtlemise edendamiseks.
Kuidas planeedid kosmoselaeva kiirendavad
Algodoo: Lingutamine
Selle Algodoo simulatsiooni algseisuks on olukord, kus kergem objekt (kosmoselaev) hakkab mööduma raskest kehast (planeet). Nii kerge kui ka raske objekt liiguvad ja nende liikumiste suunad on risti. Kehade vahel mõjub gravitatsioonijõud, nii et jälgida saab gravitatsioonilist lingutamist.
Kutsume teid osa võtma füüsikaõpetajate sügisseminarist, mis toimub 15.-16. novembril Voore Puhkekeskuses.
Kolm teemat: tark tehnoloogia, energia ja õppimine. Lisaks mõndagi praktiliselt kasulikku ja ohtralt suhtlemisvõimalusi.
Veidi pikemalt saab lugeda ja ennast seminarile ka kirja panna seminari kodulehel. Registreeruda tuleb 15. oktoobriks.
Kui katseks vajalikud vahendid ei maksa palju, aga kõik nad tuleb hankida erinevatest kohtadest, kusjuures ei ole üldse selge, milline variant töötab, siis moodustab suurema osa kulust aeg, mis kulub komplektide kokku otsimisele. Ühe sellise komplekti ja tuhande sellise komplekti hankimine võtab umbes sama palju vaeva. Järelikult on mõistlik osta ühiselt.
Kui on vaja tellida väikeseeria tootmine (vt allpool demoläätsed), siis üldiselt tähendab suurem tellimus odavamat tükihinda.
Julgeme välja pakkuda järgnevaid 8. klassi valgusõpetuse katsekomplekte.
Oleme kaheksanda klassi valgusõpetuse materjali katvad katsevahendid jaganud kolmeks komplektiks.
Katsevahenditega peavad kaasas käima ka õppematerjalid ja metoodika. Selliste materjalide koostamine käib. Need antakse välja töövihikuna ja e-töövihikuna.
Jah, töö käib ka 8.klassi mehaanika katsevahendite komplekti kallal.
Plaanis on ka koolitused. Esimene selleteemaline läbimäng leiab aset Voorel, sügisseminaril.
Oma andmed ja mõtted võiksid kirja panna need, kes asja vastu ühel või teisel viisil huvi tunnevad.
Füüsikaseadus on nagu hea raamat või film - seda uuesti lugedes leiad ikka kihte, mis esmasel või teisesel tutvusel silma ei hakanud. Või ei tulnud lihtsalt pähe õigeid küsimusi küsida.
Meie seekordne staar on graafik, mis kirjeldab küllastunud veeauru tiheduse temperatuurist sõltuvust. Mikro- ja megamaailma õpikus antakse see graafik sellisena:
Jah, aga mis kasu sellisest graafikust õigupoolest tõuseb. Eraldi võetuna võib-olla ei tõusegi. Aga lisame komplekti teadmise, et aurustumiseks kulub energiat, nii et kui kehalt aurustub vett, siis ta jahtub. Ja selle, et aurustumise intensiivsus on seda suurem, mida väiksem on õhuniiskus.
Ja aurustumisest põhjustatud jahtumine on meile eluliselt tähtis - niimoodi kaitseme end ülekuumenemise eest. See toob meid tagasi saunafüüsika juurde.
Kes ei mäleta, mis imeloom on psühromeeter, see läheb lugema:
Inimesed pole loodud elama 90 kraadise temperatuuriga keskkonnas,aga just see ongi keskmise soome sauna temperatuur. Kuidas me siis vastu peame nii ränkades oludes? Me ju oleme seda kõike koolis õppinud. Aga võib-olla ei osanud siis kõik konteksti panna, nii et ...
Kuidas saunas ellu jääda
Eelmise loo toel peaksime nüüd oskama ka selgitada, miks kipub talvel suhteline õhuniiskus siseruumides langema. Umbes nagu saunas, ainult et ... kes soovib, võib oma sõnastuse ka e-õpikusse kirja panna, Mesilasel oleks huvitav lugeda.
Hügroskoopilistel materjalidel (näiteks puidul) on võime siduda vett ja seda ümbritseva keskkonna suhtelise õhuniiskuse langedes jälle vabastada. Kondenseerumine ja aurustumine, kas sellega kaasnevad ka temperatuuri muutused? Uuri järgnevat joonist, kus peal saunas leili viskamisel mõõdetud graafikud.
The principles of sauna physics
The interaction of the wood surface and indoor climate has been of increasing interest the last decade. The fluctuating air humidity reacts with the wood surface to seek equilibrium moisture content. This reaction is crucial when experiencing a sauna. The instant heat contribution of the latent heat from the released damp when pouring water on the oven gives the intense perceptible sauna experience. This paper shows a set of measurements and calculations conducted in a Norwegian sauna. One sauna event includes in three parts. The heating of the sauna, increasing the temperature and drying out the wood. Then when visiting the sauna is, with the changes between warm and cold, like taking a cold bath in between being heated in the sauna. Usually also this heating includes pouring water on the oven. The physics around this moistening of the sauna is of special interest in this paper. Finally, the visitors leave the sauna and it cools down.
The focus in this paper is on the increase of temperature when pouring water on the oven in the sauna. Different moisture protocols are ran with varying amounts of moistening. The protocols follow real sauna experiences. Surface temperature is carefully measured and recalculated. The key role of the wood surface sorption, providing this latent heat phenomenon, is presented in the results. The sensible heat increase is not due to the change of humidity, as often stated. The heat conductivity is actually higher in dry air compared to moist air. The damp transport energy from the sauna oven through high enthalpy in the air. The damp is absorbed in the dried wood surface and consequently emits latent heat energy back to the room. That is, the surfaces becomes substantial heating panels. The heat release due to wood surface sorption is an extreme employment of the potential of the latent heat. The authors believe that this effect may be significant also in other cases, with smaller water potentials. This is elaborated in the paper.
K. Nore*, D. Kraniotis, C. Brückner, Energy Procedia 78 (2015) 1907 – 1912
Märja termomeetri temperatuur on tavaliselt kuiva termomeetri temperatuurist madalam. Ka saunas. Kui märja termomeetri temperatuur tõuseb 35 kraadist kõrgemale ei saa inimene oma keha temperatuuri hoidmisega enam hakkama. Arvate, et Euroopas on liiga palav? Mujal on jõutud juba inimkeha ülekuumenemise piirini.
Suvi linnas võib olla lämmatav, seda eelkõige kuuma asfaldi ja umbset õhku puhuvate konditsioneeride tõttu. Siiski on õigete pindmaterjalide ja taimestikuga võimalik keskkonda jahutada, tehes elu ka odavamaks ja rohelisemaks. Siin viidatud loos ei mainita mõistet evapotranspiratsiooni, aga just see on asja juurikas: puu lehtedes kasutatakse metabolismis ära vaid väike osa veest, ülejäänud aurustub ja jahutab puu lehti.
Mehaanilise koguenergia jäävuse seadus on üks ilusamaid ja tähtsamaid põhikooli füüsikas. Reaalsetes katsetes on seda paraku keeruline kontrollida. Alati ei ole ka varnast võtta elulisi näiteid, mis selle tähtsust rõhutaksid. Sestap pakume uurimiseks ühe katse ja lugemiseks hüdroelektrienergia loo.
Pendli mehaaniline koguenergia on jääv, see on õpikus kirjas. Kas seda saab katseliselt kontrollida? Saab, aga pendli maksimaalse kiiruse mõõtmine nõuab andmekoguja ja fotovärava kasutamist. Paljudes koolides on olemas vähemasti üks andmekoguja koos sensoritega. Proovige ise järele ja näidake õpilastele ka, demokatsena.
Pendli maksimaalse potentsiaalse energia ja maksimaalse kineetilise energia võrdlus
Hüdroelektri tootmiseks on vaja kõrgusi ja vihma. Hinnakem vihma koguenergiat selle langemisel meretasemeni. Rakendagem seda arutlust ka Eestile.
Taastuvenergia tootmine paratamatult kõigub. Pumpelektrijaamad pumpavad odava elektri perioodil vett madalamal asuvast järvest ülalpool asuvasse järve ning toodavad turbiinide abil (just nagu tavalised hüdroelektrijaamad) elektrit ajal, mil see on kallim.
Nojah, avapildil kujutatud masina nimi on trebuchet ja sellise vinnastamisel salvestatud energia, mis masina ideaalse toimimise korral visatava kivi kineetiliseks energiaks muundatakse, on vana hea m korda g korda h. Igasugused muud detailid saavad seda ülekantavat energiat vähendada, aga suuremaks ei saa seda ühegi tehnoloogiaga.
Uuringud näitavad, et Pariisi kliimakokkulepete täitmiseks tulnuks lisaks emissiooni vähendamisele eraldada atmosfäärist hinnanguliselt 0,5−3Gt või 7−11Gt süsinikku aastas (sõltuvalt sellest, kas me suudame emissiooni vähendada), kusjuures ladustada on vaja vastavalt 50−250Gt või 1000−1600Gt süsinikku.
Üks gigatonn süsinikku on miljard tonni. Gigatonne on raske ette kujutada – et see mõistlikku skaalasse tuua, kujutagem ette ühe tonni süsiniku põletamist (ligikaudu sellise hulga põletad sa oma maja kütmiseks igal aastal). Nüüd kujutagem ette, et kõik planeedi elanikud põletavad aastas sama palju süsinikku: see teeb 7GtC aastas, sest meie planeedil on miljardit inimest.
Võib ka mõelda, et 1Gt süsinikku oleks ühe jalgpalliväljaku suuruse põhja pindalaga kõrgune risttahukas.
mõistmine
Eurooplase aastase tonni suuruse saasteprobleemiga võitlemiseks tuleks viiendikul Eesti territooriumist kasvatada metsa, ja leida ka koht, kuhu see 7,5 tonni ( kuupmeetrit) puitu inimese kohta hiljem maha matta (mitte põletada!).
Heameel on teatada, et füüsika e-õpikute keskkonnas on nüüd kõigile lugemiseks Peeter Tenjese astronoomia õpik. Teemadest on kaetud kõik, mis tarvilik kaasaegse ettekujutuse saamiseks Päikese, päikesesüsteemi, galaktikate ja universumi tekkimisest, arengust, olevikust ja tulevikust. Aga mitte ainult. Vähemalt sama põnev on teada saada, kust me seda kõike teame. Lugema!
Oleksime ka väga tänulikud, kui vastaksite pärast õpikuga tutvumist neljale küsimusele selles tagasisidevormis.
Siin on järjestatult 53 katsevideot, mis mu kokku pandud põhikooli valgusõpetuse katsekomplektidega teha annab. Variante oleks palju rohkem, aga see on üks võimalik valik. Kõik järjest läbi vaadata teeb pisut rohkem kui tund. Ja see on reaalne aeg, st mingeid keerulisi kohti või ootamisi vahelt ära lõigatud ei ole. Katsekomplektide kohta vaata https://praktiline.fyysika.ee/, sealt on võimalik neid ka osta.
Metoodilised materjalid tulevad ka lõpuks, 8. klassi töövihikuna. Selle tooriku toorikut võib otsida füüsika e-õpikute keskkonnast (on vaja sisse logida).
Mis on kaasahaarav füüsikatund? Kas selline asi on üleüldse võimalik ilma, et füüsika kaasahaaravusele ohvriks toome? Kas selline asi on võimalik e-õppes? Kuidas teha haridusuuendust füüsikahariduses?
Tule EFS loodus- ja täppisteaduste sügiskooli, mudime koos füüsikahariduse tulevikku!
Alustame sellest, et kaardistame mõned küsimuste puntrad, mis vajaksid korrastamist või värsket pilku. Edasises töös lähtume ideedest ja lahendustest, mis on esimese kohtumise reaalsusega üle elanud. Omamoodi post-häckaton - proovime defineerida nende protüüpide versiooni 2.0.
See võiks olla ka hea viis mõne uue, lootustandva idee sünniks.
Teemad: praktilised tööd, aktiivõppe meetodid, kaug- ja e-õppe lahendused.
Oodatav tulemus: Kirjeldame ära maailma parima Eesti oludesse sobiva kontakt- ja e-õpet toetava katse- ja IT-vahendite süsteemi, mis järgneva aasta jooksul ka realiseeritakse.
Keda ootame osalema?
Tulla võivad kõik, kes tahaksid füüsikahariduse arengusse aktiivselt panustada - õpetajad, tudengid, õpilased, kõigi elualade esindajad. Oldagu lihtsalt valmis kaasa töötama.
Sügiskool toimub 30.-31. oktoobril Voore Puhkekeskuses. Algus reedel, 30.10 kell 18.00. Lõpetame laupäeval, 31.10 hiljemalt kell 16.00.
Registreerimisvorm (registreeruda tuleks hiljemalt 19.oktoobriks)
Lennukid püsivad õhus (üleval), sest paiskavad õhku alla. Kui lennuk surub õhku alla, surub õhk lennukit üles (sest Newtoni kolmas seadus ütleb seda). Lennuk ei söösta alla, kui see ülespoole suunatud jõud, mida kutsutakse tõstejõuks, tasakaalustab allapoole suunatud raskusjõu.
Lendamine erineb mööda teed sõitmisest eelkõige selle poolest, et ligikaudu pool energiast kulub õhus püsimisele.
Mõned rehkendused
Väljakutse
Stardiplatvormilt stardib mänguauto ning sõidab mingi algkiirusega üle laua serva. Vaja on asetada laua kõrvale tops selliselt, et auto sinna sisse kukuks. Topsi diameeter olgu võimalikult väike. Kasutada on vaid üks katse, st auto peaks kukkuma topsi juba esimesel katsel.
Kogemus
- Kasutame viskekeha liikumise seaduseid, impulsi jäävuse seadust ja energia jäävuse seadust praktilise ülesande lahendamisel.
- Näeme, kuidas oma tulemuste mõõtemääramatuste hindamine võib olla vägagi oluline, lausa eluliselt oluline.
Õpilased sisenevad sellistesse õpiradadesse läbi eVastuse, kasutage koodi "mesilane56", süsteem nõuab sisse logimist.
Arvame, et kui veel veidi pusida, siis saab sama idee realiseerida ka 10EUR katsekomplektidega. Hoiame sidet!
Tee ära
Sul on kasutada mustast paberist mask, millesse on lõigatud liblikakujulised avad, LED-lamp, auguga must paber, valge ekraan ja CD ümbris. Tee nii, et ekraanile tekiks paberisse lõigatud liblikate kujutis.
Me näeme objekti või kujutisena kohti, kus valguskiired koonduvad. Kõige sagedamini on selliseks kohaks matt pind või hajutav materjal, millel valgus hajub - niimoodi käituvad kõik meid ümbritsevad objektid, va peeglid. Kui valgus peegeldub, siis me näeme kujutisena valguskiirte või nende pikenduste lõikumise kohta, kus tekib tõeline või näivkujutis.
Kommenteerime järgmisel nädalal.
Tee ära
Mikroskoop ei ole miskit ... raketiteadus ... või keemia, näita see õpilastele ette, nii et nad mõistvalt noogutaksid.
Mikroskoobis on kaks läätse. Esimese läätse (objektiiv) tekitatud kujutist vaadatakse teise läätsega (okulaari ja silma moodustatud liitlääts). Kahe läätse vahele tekkiv kujutis on päriselt olemas, seda on võimalik vaadata ekraanil. Läbi teise läätse selle vahekujutise vaatamine on samaväärne päris objekti vaatamisele.
Kommenteerime küsimust järgmisel nädalal.
Esitasime sellise küsimuse:
Õigeks tuleb lugeda vastust, mis lubab varjul olla ruudukujuline või ümmargune või midagi vahepealset. Ehk siis suurte valgusallikate valguses tekkiva varju kuju ei ole igal pool ühesugune.
Tegemist on väga ammusest ajast tuntud probleemiga, mille üle juurdles juba Aristoteles. Pärast seda veel 2000 aastat, mis nägi suurt hulka alternatiivseid seletusi.
Olukorda hästi seletava mudelini jõudis lõpuks Kepler. Võti arusaamiseni on meie tänane koolitarkus - suurte valgusallikate korral tuleb iga selle punkti vaadelda kui punktvalgusallikat (vt joonised allpool).
Pikemalt saab selle kohta lugeda allpool viidatud artiklis.
| Aristotelese "optiline mõistatus". Ümmarguse valgusallika tekitatud valguslaik ruudukujulise avaga maski taga on maskile lähedal ruudukujuline, aga kaugemal ümmargune. | Kepleri mõtteline eksperiment.Kepler kasutas oma mõttelises eksperimendis augu asemel takistust. Joonisel näeme, kuidas ruudukujulise valgusallika valgus langeb ümmargusele takistusele. Kui vaadelda iga valgusallika punkti punktvalgusallikana moodustub nii üksteisega kattuvate ümmarguste varjude kogum, mis tervikuna on ruudukujuline. Kui liikuda sellises olukorras valgusallikaga maskist kaugemale, siis ümmargused varjud nihkuvad varju keskosale lähemale ja suurenevad, nii et lõpuks moodustub üks suur ümmargune vari. |
Christos Dedes,Konstantinos Ravanis, History of Science and Conceptual Change: The Formation of Shadows by Extended Light Sources
Sci & Educ (2009) 18:1135–1151
This study investigates the eVectiveness of a teaching conXict procedure whose purpose was the transformation of the representations of 12–16-year-old pupils in Greece concerning light emission and shadow formation by extended light sources.
Tee ära
Mõtle üks valgustatud olukord ja kirjelda selles valgust kiirtega. Tõlgi see pilt valguslainete keelde.
Valgus on ikka valgus. Mõnikord käitub see viisil, kus seda on hea kirjeldada kiirtena. Mõnikord on seda parem kirjeldada lainena. Mõnikord seda lausa peab kirjeldama lainena. Aga mis ka ei oleks, kui me kirjeldatavat situatsiooni reaalselt vaatame, näeb see ikka ühtmoodi välja.
Valguskiired ja valguslained
Esitasime küsimuse:
Seekordse kommentaari esitame videona.
Tee ära
Pane laser põhikooli valgusõpetuse konteksti ja demonstreeri, et see ei ole lihtsalt kast või toru, millest tuleb üks valguskiir välja.
Laserikiir ei ole valguskiir, nagu me neid geomeetrilises optikas joonistame. Sest laserikiir on päriselt olemas, aga geomeetrilise optika valguskiir on lihtsalt üks noolega joon tahvlil, mis näitab valguse levimise suunda ja mille abil me sõnastame mõningaid üldiseid seaduspärasusi valguse (sh laserikiire) käitumises.
Esitasime küsimuse:
Kommentaar selle kohta on meie selle nädala laseri joonistamise teema videos. Vastused kujunesid selliselt:
Keegi ei alusta füüsika õpinguid puhta lehena. Meil on kaasas terve seljatäis kogemust, mida me oleme hulk aastaid edukalt otsuste vastu võtmisel kasutanud.
Füüsika võib igapäevakogemuse seisukohalt olla täiesti jabur ja ebaloogiline. Selgub, et nii tundub õpilastele üle maailma üsna ühtmoodi. Nii on välja töötatud terve hulk nn mõistelisi teste, mis näitavad, mil määral rakendavad õpilased situatsioonide analüüsimisel "talupojatarkust", mil määral füüsikaseaduseid.
Mõistelised testid
Mõistelisteks testideks nimetatakse spetsiifiliste füüsikateemade mõistmistaseme hindamiseks mõeldud ning teaduslikult välja töötatud kontrollmeetodit. Tänu nendele testidele saate vastata sellistele küsimustele nagu „Milline on minu õpilaste tase võrreldes teiste omavanustega?“ või „Kuidas mõjutas minu õpetamismeetodite muutmine minu õpilaste tulemusi?“
Eesti keelde on tõlgitud või tõlkimisel testid mehaanikast, optikast, soojusõpetusest ja elektromagnetismist. Huvi korral kirjutage e-maili aadressil kaido@fyysika.ee.
Esitasime küsimuse:
Teistmoodi vastuseid välja mõeldes saime ilmselt piisavalt hästi "koolifüüsika närvile" pihta, nii et enamik ei pidanud ülesandes kirjeldatud olukorda eriti tõsiseks või siis pidas eelkõige silmade terveks jäämise pärast muretsevat vastusevarianti kõige vähem absurdseks.
See tundub hea ülesanne, et kinnitada õpilaste usku füüsikasse, kui universaalsesse tööriista erinevate olukordade analüüsimisel. Sest tõepoolest, kui on kolme sekundi jooksul, siis üle ei ole energiat kusagilt võtta ning me teame, kui palju kulub energiat vee soojendamiseks või aurustamiseks. Tuleb muidugi silmas pidada ja sobivas kohas rõhutada, et reaalne elu on hulga nüansseeritum. Õnneks konkreetselt laserrelvaga kokkupuuteid meil igapäevaelus ei ole, nii ei saa ka keegi hakata sellega kohvi keetma ... nagu väidetavalt I maailmasõjas teatud tüüpi kuulipildujatega tehti, kasutades selle jahutusvee süsteemi.
Vastused kujunesid selliselt:
Eesti Füüsika Selts on teaduslaagreid korraldanud alates 2008.a. aastast. Arvame, et edukalt. Nüüd siis 14. kord (kui arvestada, et eelmisel aastal ära jäänud laager oli kolmeteistkümnes).
TÜ Teaduslaager 2021 toimub 10.-15. august Türi Ühisgümnaasiumis. Sel korral on laager suunatud 7.-9. klassi noortele. Teemad on traditsioonilised - tükk keemiat, füüsikat, bioloogiat ja materjaliteadust. Tegijateks TÜ üliõpilased ja magistrandid, sekka Teaduslaagri taustaga loodusainete õpetajaid. Selge see, et laagrist ei puudu ka muud vahvad seltskondlikud tegevused.
Kogu vajaliku info leiab teaduslaagri kodulehelt. Ootame huvilisi registreerimisvormi
Õpikojad on koolis toimuv tunniplaani sobituv või eraldiseisev laboritundide programm, kus 7.-12. klasside õpilased saavad teha füüsika-, keemia- ja bioloogiakatseid. Õpikojad aitavad rikastada õppekava ja tugevdada kooli võimekust reaal- ja loodusteadustes.
Kutsume koole üles oma huvi näitama. Taotluseid FKB õpikodade programmis osalemiseks saab esitada 15. juunini.
Loe lähemalt: https://www.teaduskool.ut.ee/et/oppetoo/opikojad
Esitasime küsimuse
Terve mõistus ütleb, et ei ole võimalik lähenemine, kus jagame vajamineva võimsuse ( petavatti) ühe elektrijaama võimsusega ( megavatti) ja ütlemegi, et vaja on vähemalt miljonit elektrijaama. Nii ongi - petavatt laserid ei kiirga valgust pidevalt vaid lühikeste impulssidena, ühe impulsi kestvus on kuni , impulsi energia on ja igas sekundis genereeritakse üks niisugune impulss (vt https://www.eli-np.ro). Keskmine võimsus on seega .
Võib ka näiteks arvutada, kui suurt võimsust arendab kaaluv ja 2m/s liikuv haamer, kui sellega lüüa vastu üsna jäika pinda, nii et selle kiirus väheneb ühtlaselt nullini teepikkuse jooksul. Aga kui jäik pind oleks selline, et kiirus peaks vähenema nullini jooksul? Arvutades saab selgeks, et liigne jäikus ei ole hea taktika ka eluta looduses.
Vastused kujunesid selliselt:
Pakume ka lugemiseks lugu laserkuulidest, mis on Mesilasest korra juba läbi käinud.
Objektide võime soojuskiirgust neelata ja kiirata sõltub väga olulisel määral nende materjalist ja pinna viimistlusest. On nii, et kui materjal kiirgab hästi soojuskiirgust siis see ka neelab hästi soojuskiirgust.
Kui palju energiat?
Lahendus
Mesilaste moodustatud kera pindala on
Teame ka, et
ja
Soojuskiirgusena kaotab keha energiat võimsusega (ajaühikus kiiratav energiahulk), mis on keha poolt neelatud võimsuse ja kiiratud võimsuse vahe. See võimsus sõltub objekti pindalast ja selle pinnatemperatuurist kelvinites ja on antud seosega
kus on Stefani-Boltzmanni konstant ja on kera pinna kiirgustegur.
Arvutades saame
Järelikult peab iga mesilane minuti jooksul tootma
Erinevate materjalide kiirgustegurid
Esitasime küsimuse
Vastused kujunesid selliselt:
Kujutame ette kahe klemmiga karpi. Klemmidele pinge rakendades kas tekib või ei teki elektrivool. Niimoodi saab meeles hoida vastuse parajasti ühele jah/ei küsimusele.
| Mälubiti sees võib lüliti olla avatud või suletud. Kui see on suletud, siis välimise lüliti sulgedes tekib vooluringis vool, hõõglamp süttib ja me saame teada, et vastus on "jah". Kui hõõglamp ei sütti, siis on vastus "ei". | Enne transistori leiutamist kasutati elektriskeemides lülititena releesid, kus lüliteid avasid ja sulgesid elektromagnetid. |
Välkmälus kasutatavates mälubittides muudetakse elektritakistust elektrivälja abil. Elektrivälja tekitavad laengud lõksustatakse kvantkaevu nii, et nende sealt välja pääsemine on võimatu.
Esitatud küsimus koos lahendusega allpool. Selge see, et niisuguseid valemeid me koolis ei kasuta. On ehk siiski hea teada, et kiirguslikud soojuskaod on väikesed, võrreldes soojusülekande ja konvektsiooniga (keemistemperatuurile lähenevatel temperatuuridel on need rohkem kui vatti).
Lahendus
Oletame, et tops on täidetud pilgeni veega. Et vee ja alumiinumi kiirgustegurid erinevad oluliselt (vastavalt 0,96 ja 0,03), siis peame nende pindade soojuskiirguse võimsust eraldi hindama.
Alumiinumi pindalaks saame:
Vee pindalaks saame
Soojukiirguse võimsust arvutame valemist
Alumiiniumi ja vee korral annab see vastavalt
ja
Jahtumise kiiruse arvutamiseks kasutame valemit
Kokku jahtub vesi võimsusega
Teades jahtumise võimsust saame minutiga tekkiva temperatuuri muutuse jaoks valemi
Vee massiks on meil
Nii saame jahtumisel tekkiva temperatuurierinevuse jaoks
Alljärgnevat sõnumit te olete arvatavasti juba näinud. Võib-olla olete te juba ka kellegi esitanud. Aga saadame ikkagi uuesti. Sest on ju tore, et ettevõtjad/ettevõtted on lisaks muretsemisele hakanud ka reaalselt panustama. Sellesse, et füüsika õpetajad ja füüsika õpetamine Eestis parema tuule tiibadesse saaksid. Ühtlasi lubame, et hakkame selle kanali kaudu jagama kõike seda, mis vahepeal füüsika õpetamisega seoses kogetud ja õpitud. Niisiis
Hea koolipere!
Kutsume kõiki märkama särtsakat füüsikat õpetavat õpetajat ning esitama ta programmi „Lae end“ osalejaks.
Ettevõtted ABB, Eesti Energia, Fermi Energia, LHV, Metrosert ja Nordecon koos Eesti mõjukate haridusentusiastidega Eesti Füüsika Seltsist, Praktikalist, Videoõpsist lõid programmi „Lae end“, et tuua kokku Eesti koolide säravamad arenemishuviga õpetajad, haridusmaastiku uuendajate ja füüsikaõpetajate kogukonna esindajad. Programmi nimi viitab õpetajale kui energiaallikale, kes annab noortele positiivse teadmiste laengu.
Kui ka sinu koolis on inspireeriv ja arengusooviga füüsikat õpetav õpetaja, siis anna meile temast märku programmi veebilehel.
Oma kandidaadi esitamisega saad anda panuse, et just sinu kooli õpetaja saaks märgatud, tunnustatud ja kelle kaasabil valmiksid uued inspireerivad ning põnevad õppematerjalid ja videod. Neid saab hakata kasutama mitte vaid sinu kool, vaid erinevate põhikoolide õppurid üle terve Eesti.
Programmi kandideerima ootame õpetajaid, kes suudavad juba täna oma õpilasi üllatada ja inspireerida, kuid kelles peegeldub soov saada oma töös veel paremaks. Osalemiseks peab kandidaadil olema kolmanda isiku soovitus ning tutvustusvideo.
„Lae end“ võimaldab kaasa lüüa inspireeriva õppesisu loomisel põhikooli füüsikatundideks ja populariseerida füüsika eriala ning mainet. Kõik programmi valitud õpetajad saavad:
- tasuta osaleda Eesti Füüsika Seltsi koolitussarjas;
- tasuta Praktikali välja töötatud õppekogumid 8. ja 9. klassi tarbeks (vähemalt ühe teema jagu õppekomplekte kõikidele lastele mõlemas vanuseastmes);
- rahalise preemia, mis on võrdne õpetaja ühe kuu keskmise palgaga;
- kaasa lüüa õppesisu loomisel.
Ühendame jõud ja viime parima õppekogemuse kättesaadavaks kõigile füüsikat õpetavatele pedagoogidele üle Eesti!
Märkame, kiidame, areneme!
„Lae end“ programmi ellukutsujad:
Ettevõtted ABB, Eesti Energia, Fermi Energia, LHV, Metrosert ja Nordecon
Eksperdid Eesti Füüsika Seltsist, Praktikalist ja Videoõpsist
Loe programmist täpsemalt: laeend.ee/fyysika
Eesti Füüsika Seltsi füüsikaõpetajate osakond, kodusemalt nimetatud ka füüsikaõpetajate võrgustikuks, on Eestis füüsikaõpetajaid ühendav aineliit. Lisaks igapäevasele suhtlusele füüsikaõpetajate meililistis hoiame end kursis Eestis haridusmaastikul toimuvaga ja reageerime, kui vaja. Igal aastal korraldame ka ühe suurema kokku saamise. Sel aastal siis füüsikaõpetajate suvekool.
Aeg-ajalt sähvatab ka seesama nädalakiri, Mesilane. Nende uuema aja arhiivi leiad e-õpikust.
Ja muidugi ka selle suve täht, programm LAE END.
Ühendust saab meiega meiliaadressil fo@fyysika.ee.
Füüsikaõpetajate suvekool 2022
Füüsikaõpetajate suvekool toimub 8.-9. augustil Setomaa Turismitalus. Veel on võimalik end kirja panna. Täpsemalt vaata füüsikaõpetajate võrgustiku kodulehelt.Haridusteaduste ja "puhta" füüsika vahele jääb üsna hall ala, mida võiks nimetada füüsika didaktikaks või üldistatud kogemusel põhinevaks õpetuseks sellest, kuidas füüsikat õppida ja õpetada. Hall sellepärast, et üldiselt diskussioonides need kaks poolt, haridusteadus ja füüsika, kipuvad üksteist kaevikutest põrnitsema.
Üsna levinud on arusaam, et füüsikatunde saab kaasahaaravamaks muuta läbi katsete või praktiliste tegevuste. Sestap lähtume oma tegevuses just sellest hüpoteesist, üritades luua käepäraseid, kättesaadavaid ja tõenduspõhiselt õpet efektiivsemaks muutvaid katsevahendeid ja katsetel põhinevaid õppemetoodikaid.
Meiega saab kaasa mõelda ja tegutseda.
- Kaasa saab mõelda, kui ühinete FB grupiga, mille nimi on "Füüsika katsevahendid".
- Tartu Ülikoolis oleme TÜ koolifüüsika keskuses ja TÜ teaduskoolis.
- Praktikas katsetame oma ideid üldhariduskoolidele suunatud/pakutavates füüsika õpikodades.
- Elus karastunud ideed muudab tooteks startup ettevõte Praktikal.
Füüsika keemia ja bioloogia õpikojad
Õpikojad on koolis toimuv tunniplaani sobituv või eraldiseisev laboritundide programm, kus 7.-12. klasside õpilased saavad teha füüsika-, keemia- või bioloogiakatseid.Praktikal
Pakub inspireeriv käed-külge terviklahendus koolidele, mis teeb õppimise ja õpetamise põnevaksE-õpikute üks kiiduväärsemaid omadusi on arvatavasti see, et nad ei kao ära ega lähe katki. E-õpikute keskkond opik.fyysika.ee on elus ja üsna stabiilne.
Uuest aastast ootame uusi materjale ja uusi sõpru. Mainime ka koostööd Videoõps'iga selle füüsika videote stsenaariumide loomisel.
Uus elektromagnetismi õpik
Õpiku autoriks on Riina Murulaid. See link viib veebiversiooni juurde. Trükiversioon on saadaval kirjastusest Maurus.Tasub ehk mainimist, et TÜ teaduskooli vahendusel on Jaan Tallinn toetamas õppematerjalide loomist, mis aitaksid õpetajaid ja õpilasi olümpiaadiks valmistuda. Tööd peaksid saama tehtud käesoleva aasta lõpuks.
Tahaksime ka enne projekti lõppu saada füüsikaõpetajate tagasisidet, kas mõeldud õppematerjalide formaat on piisavalt hea. Aga selleni on veel veidi minna.
Eesti Füüsika Selts on teaduse populariseerimist korraldanud juba pikka aega, alates 2005. aastast. Muidugi, tegijad vahetuvad. Aga värskus ja julge pealehakkamine ... on justkui püsiväärtus, mis neid tegevusi iseloomustab. Kõik on teretulnud huvi tundma, külla kutsuma ja kaasa lööma.
Teaduslaager 2022
TÜ Teaduslaager 2022 toimub Toila Gümnaasiumis 18.07.-23.07.2022. Osa ootame võtma 6.-9. klassi lõpetanud õpilasi.Teadusbuss
Oleme TÜ keemia, materjaliteaduse ja füüsika tudengid. Teeme teadusteatrit. Kutsu meid külla!Eesti Füüsika Seltsil on osakond, mille nimi on Füüsikaüliõpilaste Selts ehk FÜS.
FÜS ühendab ja esindab Eesti Vabariigis füüsikat ja sellega seonduvaid erialasid õppivaid tudengeid. FÜSi eesmärkideks on füüsikaõppe parandamine, harivate ürituste korraldamine, füüsika ja loodusteadusliku õppe populariseerimine ning tudengite, õppejõudude ja teadlaskonna vahelise sidususe suurendamine. FÜS loodi 2012. aasta kevadel.
FÜS hoiab elus EFS täppisteaduste sügiskoolide traditsiooni. Sel suvel tuleb ka suvekool, FÜS'i 10 juubeli tähistamiseks.
5. juulil 2022. aastal toimus Tartu Ülikoolis üle hulga aja sisseastumiseksam füüsikas, küll mitte füüsika vaid meditsiinivaldkonna üliõpilastele. Eksami koostasid Kaido Reivelt ja Kalev Tarkpea. Retsenseerida aitasid eksamit mitmed tublid füüsikaõpetajad.
Pakume siin võimalust eksami ülesannetega tutvuda. Reaalselt toimus eksam paberil, kus eksamineeritavad märkisid vastuste lehele nende meelest sobivaid vastusevariante.
Kõik ülesanded olid esitatud valikvastustega küsimustena. Nende kaalud olid erinevad, kas 1, 1,5 või 2 punkti. Maksimaalne võimalik tulemus oli 50 punkti. Eksamil oli võimalik kasutada valemilehte, millega saab samuti tutvuda alljärgeva lingi kaudu.
Eksam koosnes füüsika ja keemia osast. Eksami sooritamiseks oli aega 4 tundi.
View _exp_test not found
Kes on huvi tundnud, see on juba arvatavast järele proovinud. Aga jagame siin üht Sixty Symbols kanali videot, mis asja hetkeseisu üsna hästi kokku võtab, mis füüsikat puudutab. Ehkki, jah, täna olla selles süsteemis juba ka matemaatika moodul olemas.
Igal juhul näib, et lõputu jada ulmekirjandust on tuleviku ennustamisel "puusse pannud". Sest tehisintellekti on kujutatud kui midagi ürgtarka, mis keerulistele küsimustele õigeid vastuseid välja ... mõtleb. Nüüd näib, et inimese saab ära petta ka ilma mõtlemiseta - võta piisavalt suur tekstide korpus ning arvuti on suuteline selle põhjal tuletama vastuseid kõikvõimalikele küsimustele.
Või mis see mõtlemine üleüldse on? Või kas meie endi aju üleüldse käitubki oluliselt teistmoodi?
Ja siit tulevad kaks lubatud e-raamatut. Usume, et mõlemast võiks loodusainete õpetajatele kasu tõusta.
Tuuma füüsika
Raamatu on kokku pannud autorite kollektiiv, kes on seotud TTÜ, TÜ ja Fermi Energiaga. Selles antakse ülevaade kõigest tuumaelektrijaamade planeerimise, ehitamise ja käitamisega seonduvast.Katsed, mis lõid füüsika
Füüsika on eksperimentaalne teadus, st igasugune teooria peab moel või teisel katses kinnitust leidma. Füüsikast huvituv lugeja leiab siit kompaktsel kujul info katsetest ... mis lõid füüsika. Ja see on olnud põnev teekond ... mõjub sama silmiavavalt, kui puhta teooria kõrvale mõne reaalse katse tegemine.Mesilane 8/0
View _exp_open not found
View _exp_open not found
View _exp_open not found
View _exp_open not found
Mis on liiva patarei?
Soomes paiknev firma pakub uudset võimalust keskkonnasõbralikuks energia salvestamiseks.View _exp_open not found
Õppekava materjalide veeb, 9. klassi füüsika
Haridus- ja Teadusministeeriumi hallatav leht, kust leiab soovituslikud juhised 2023. aasta märtsis kehtima hakanud ajakohastatud riiklike õppekavade rakendamiseks.Tuukrikellasid kasutati Euroopas esmakordselt 1600. aastatel suurtükkide, metallide ja muude väärtuslike materjalide otsimiseks madalatest lahtedest ja järvedest. Tuukrikellad valmistati puidust tünnidest, metallist kateldest ja muudest anumatest, mis olid õhuruumi säilitamiseks ümber pööratud ning millele lisati nii palju raskust, et need vajuksid põhja.
1690. aastal konstrueeris Edmund Halley – Halley komeedi avastanud inglise teadlane – joonisel kujutatud tuukrikella. Halley tuukrikella eripära ja geniaalsus seisnes selles, et seda sai õhuga varustada väiksemate õhuga täidetud alt lahtiste tünnidega, mida laevadelt üles-alla tõsteti ning nahast voolikute abil tuukrikellaga ühendati. Kuna sellised tünnid lasti tuukrikellast pisut sügavamale, voolas õhk neist tuukrikella, tünnid ise täitusid veega. Edasi tõmmati tünnid jälle pinnale ja lasti siis õhuga täiedetuna merepõhja tagasi. Tuukrikella katuseks oli aken, kust pääses valgus kella sisse. Tuukrikellas oli ka ventiil kasutatud õhu välja laskmiseks.
Joonisel on kujutatud tuukrikell. See on ligikaudu silindri kujuga, mille diameeter on 2 meetrit ning kõrgus 2,5 meetrit. Oletame, et tuukrikella mass on 100 kg.
Tuukrikell on altpoolt avatud, tagurpidi pööratud tünn, mis ka vee all on täidetud õhuga. Tuukrikellale mõjub ka arvestatav üleslükkejõud, nii et selle põhjas hoidmiseks kinnitatakse selle külge rauast raskus.
| A | Kui suur on sellisele tuukrikellale mõjuv üleslükkejõud? | N | |
| B | Kui suurt jõudu on minimaalselt vaja, et sellist tuukrikella veekogu põhjas hoida? | N | |
| C | Kui suur on tuukrikellale mõjuv raskusjõud? | N | |
| D | Tuukrikellale mõjuv raskusjõud on suunatud | ||
| E | Kui suurt allapoole suunatud lisajõudu lisaks raskusjõule on vaja tuukrikellale rakendada, et seda veekogu põhjas hoida? | N | |
| F | Milline peab olema keha mass, et sellele mõjuks sellise suurusega raskusjõud? | ||
| G | Milline on sellise massiga keha ruumala, kui eeldame, et keha on valmistatud rauast? Raua tihedus | ||
| H | Kui suur on sellisele kehale mõjuv üleslükkejõud? | N | |
| I | Kui suur on sellise raskuse kaal vees? | N | |
| J | Kui suurt allapoole suunatud lisajõudu peaksime rakendama, et tuukrikell ikkagi veekogu põhja jääks? | N | |
| K | Kas olukorra parandaks see, kui valmistaksime sellise ühe kuupmeetrise raskuse mitte rauast vaid pliist? Plii tihedus on | ||